Techniques for measuring astronomical distances generally come in two variates, absolute and relative.
|
|
|
- Reynard Newman
- 5 years ago
- Views:
Transcription
1 Chapter 6 Distances 6.1 Preliminaries Techniques for measuring astronomical distances generally come in two variates, absolute and relative. Absolute distance measurements involve objects possibly unique with known intrinsic properties; their observed properties depend on distance D: Known candles have luminosity L. Assuming L is radiated isotropically, the flux received is F = L/4!D 2. Known rulers have size S. In the small-angle limit, the apparent angular size at distance D is " = S/D radians. Relative distance measurements involve sets of objects with standardized properties; intercomparison of observed properties then yields distance ratios: Standard candles are sources which all have the same luminnosity; if F 1 and F 2 are the observed fluxes from standard candles at distances D 1 and D 2, then D 1 /D 2 = F 2 /F 1. Standard rulers are objects which all have the same size; if " 1 and " 2 are the observed angular diameters of standard rulers at distances D 1 and D 2, then D 1 /D 2 = " 2 /" 1. Our knowledge of astronomical distances is built on a interconnected web of absolute and relative distance measurements. Relative measurements are used to build a scale model of the universe with correct proportions. Absolute measurements are used to determine the scale factor needed to express this model in physical units. In principle a single chain of relative measurements could fix the proportions of the model, and single absolute measurement could determine the scale. In practice, however, multiple absolute and relative distance measurements are used to guard against errors, insure consistency, and estimate uncertainties. This entire web of measurements is known as the cosmic distance ladder. 41
2 42 CHAPTER 6. DISTANCES 6.2 Distances to Stars Geometric methods Distances to stars near the Sun can be determined by trigonometric parallax. This uses the radius of the Earth s orbit, 1AU = m, as a known ruler. Let 2p be the maximum shift in the apparent position of a nearby star as the Earth orbits the Sun (equivalently, 2p is the angular diameter of the Earth s orbit as seen from the star). Then the star s distance is D = 1AU/p if p is expressed in radians, or D = AU(1 /p) if p is expressed in seconds of arc. The quantity AU = 1 pc is known as a parsec. Ground-based astrometric techniques can measure p with errors of order 0.01, yielding distances good to ±20% at 20pc. The Hipparcos satellite obtained parallaxes for 10 4 fairly bright stars with errors of only 0.001, extending the scope of trigonometric parallax measurements to 200pc. To extend ground-based parallax measurements to greater distances requires the use of a baseline larger than the Earth s orbit. One option is to use the Sun s motion of 4AU/yr with respect to the standard of rest defined by stars in our neighborhood; for example, over an interval of 50yr this yields a baseline of 200 AU, so the resulting secular parallax is 100 times the trigonometric parallax. The catch is that other stars also move with respect to the standard of rest, so there s no way to determine how much of an individual star s proper motion represents secular parallax. However, proper motions of an ensemble of stars distributed over the entire sky will be partly correlated due to the Sun s motion, and a analysis can determine the distance of stars in the ensemble. A related technique, known as statistical parallax, assumes that the radial velocities of an ensemble of stars are representative of their motions in three dimensions and uses proper motions to estimate distances; the details are complex, but the basic idea is simply that if some set of stars have similar random velocities with respect to the standard of rest, their average proper motions will be inversely proportional to their distances. A final geometrical technique, of considerable historical importance, is the moving cluster method. In the simplest terms, consider a star cluster of fixed physical diameter which is receding at a known velocity v cl. Let " 1 and " 2 be the cluster s angular diameters at times t 1 and t 2. The distances to the cluster at these times have a ratio of D 2 /D 1 = " 1 /" 2 and a difference of D 2 D 1 = v(t 2 t 1 ). Knowing the ratio and difference of the distances yields the distance at either time. This technique was used to estimate the distance to the Hyades cluster, with results of D Hyades (45 ± 2)pc and (48 ± 1) pc in two different determinations. (In contrast, Hipparcos obtained a distance to the center of the Hyades of D Hyades (46.3 ± 0.3)pc.) Photometric methods To extend distance measurements beyond the maximum range of geometric methods we exploit the uniform photometric properties of stars. One powerful uniformity is provided by main sequence stars, which exhibit a well-defined relationship between luminosity and surface temperature. The relative distances of two star clusters can be estimated by comparing their color-magnitude diagrams; neglecting dust obscuration, the cluster whose main sequence appears # m magnitudes fainter is # m times further away. In practice, dust influences the observed colors and magnitudes, and
3 6.3. DISTANCES TO GALAXIES 43 its effects must be independently determined, for example by use of reddening-free indicies (BM98, Ch ), before reliable results can be obtained. Further uncertainties arise if the clusters compared have different metallicities or ages. Nonetheless, the technique of main sequence fitting, calibrated by absolute estimates of the distance to the Hyades, is important in constructing the distance ladder. Pulsating variable stars were used to demonstrate for the first time the existence of galaxies beyond the Milky Way, and figure prominently in the most recent determinations of the Hubble constant. Such stars are valuable for distance measurements because they obey period-luminosity (PL) relations. The calibration of these relations is a critical problem; variable stars of a given period P may have a small range of luminosities, but unless the typical luminosities of these stars can somehow be determined by other means, they can only be used for relative distance estimates. (Classical) Cepheid variables are massive stars which become unstable after becoming red giants. They are intrinsically bright (M V 3) and can thus be detected to distances of many Mpc. A few Cepheid variables are close enough for Hipparcos to obtain reliable distances, but these are insufficient to define an accurate PL relation. The LMC contains many Cepheids, and the uncertainty in the LMC s distance is presently the dominant source of uncertainty in the Cepheid PL relation. RR Lyrae variables are old metal-poor horizontal branch stars. They are less luminous than Cepheids (M V 0.6), and thus too faint to detect beyond the Local Group. RR Lyrae stars are found in globular clusters and elsewhere in the bulge and halo of the Milky Way; some are also found among old, metal-poor disk stars. Mira variables are AGB stars relatively low-mass stars which have evolved ot the point where they are burning helium in a shell around an inert carbon/oxygen core. They have large amplitudes and periods longer than 100day. In the K band they exhibit a well-defined period-luminosity relationship (Feast et al. 1989). Independent estimates of distances to variable stars are needed to calibrate PL relationships. In addition to trigonometric parallaxes, statistical parallaxes, and main-sequence fitting (for variables in star clusters), the absolute distance to a pulsating variable star can be estimated by the Baade- Wesselink method. This technique employs high-resolution spectroscopy to measure the variation of a star s radial velocity as it expands and contracts. The time integral of the velocity gives the absolute change in the star s radius from minimum to maximum, R max R min ; meanwhile, the variation in observed flux together with the Stefan-Boltzmann law gives the ratio of the star s radii, R max /R min. These quantities can be combined with surface temperature data to determine the star s radius and hence its absolute luminosity. Observations of eclipsing spectroscopic binary stars can provide relatively clean absolute distance measurements. The main idea is to determine the star s orbital velocities from the periodic shifts in their spectral lines; with the observed durations of eclipses, it s possible to solve for the stars radii. Knowledge of radii and surface temperatures then yield absolute luminosities. 6.3 Distances to Galaxies Galaxies close enough to be resolved into individual stars are often good candidates for distance determinations using the photometric methods outlined above. For more distant galaxies, a variety
4 44 CHAPTER 6. DISTANCES of relative methods exist; these are calibrated by comparison with nearby galaxies Luminosity functions Populations of various objects in galaxies globular clusters, planetary nebulae, and stars have luminosity functions which are relatively independent of local conditions. When a large sample of these objects can be observed, their apparent brightnesses may be analyzed to obtain an estimate for the distance of their parent galaxy: Globular cluster luminosity functions are Gaussian in M: $ GC (M) % exp [ (M M GC ) 2 ] 2& 2 GC (6.1) In the Milky Way, M GC 7.4±0.1 in the V band, and globulars in other galaxies appear to be drawn from the same luminosity function. In practice, the census of globular clusters in a galaxy must be complete well below the peak of the luminosity function to obtain a reliable distance. Planetary nebulae luminosity functions cut off sharply at the bright end: M cut PN 4.6±0.1 in M31 (assuming a distance of 740kpc). Surface-brightness fluctuations in early-type galaxies depend on the stellar luminosity function. Suppose we observe two galaxies at distances D 1 < D 2 with the same surface brightness. The average number of stars per resolution element N scales as the square of the distance, so N 2 /N 1 = (D 2 /D 1 ) 2. The actual number of stars per resolution element exhibits N fluctuations about the average value N, creating a slightly mottled appearance. For either galaxy the variance in the flux is & F N/N = 1/ N, so the more distant galaxy appears smoother than its nearby counterpart: & F,2 /& F,1 = D 1 /D 2. This method is most reliable in the IR where variations in the intrinsic luminosity function from galaxy to galaxy are not so significant. The tip of the red giant branch has a well-defined maximum brightness. A star s path up the red giant branch (RGB) ends when helium ignites in its core, and for RGB stars with ages over 2Gyr this event occurs at a specific bolometric luminosity. In the I band, this corresponds to absolute magnitude M TRGB = [Fe/H]+ 0.14[Fe/H] 2, (6.2) where the dependence on metallicity [Fe/H] is largely due to line-blanketing in stellar atmospheres (Bellazzini et al. 2004) Kinematic indicators Photometric and kinematic properties of galaxies are often related; since kinematic parameters are distance-independent, these relations can be calibrated to determine distances. The Tully-Fisher relation (Tully & Fisher 1977) connects the rotation velocity of a spiral galaxy to its absolute luminosity. This relationship is conveniently expressed in terms of
5 6.3. DISTANCES TO GALAXIES 45 the width W of a galaxy s integrated velocity profile; after correcting for inclination and the contribution of random velocities, the galaxy s I-band absolute magnitude is (Pierce & Tully 1992). M I = 8.72(logW 2.50) ± 0.10 (6.3) The Faber-Jackson relation (Faber & Jackson 1976) connects the central velocity dispersion of an elliptical galaxy to its total luminosity; see (4.14). In practice, the intrinsic scatter in this relationship is rather large, so it s of limited use in determining distances. The fundamental plane of elliptical galaxies introduces a third parameter correlated with the scatter in the Faber-Jackson relation. For example, (4.15) expresses the effective radius R e in terms of the central velocity dispersion & and the surface brightness at the effective radius I e ; both & and I e are distance-independent, so this relationship may be used to calculate R e. A slight variant is the D n & relation; the diameter D n within which the mean surface brightness is 20.75mag/ in B is empirically ( ) & 1.33 D n = 2.05kpc. (6.4) 100 km/s The calibration of these indicators requires reasonably large samples of suitable galaxies with independently determined distances. For the Tully-Fisher relation, Cepheid variables are often used to obtain the necessary distances. Cepheids are not found in elliptical galaxies, so the calibration of the D n & relation rests on a more heterogeneous set of distance determinations. However, elliptical galaxies occur in clusters, and the distance to a cluster can be determined more precisely by averaging estimated distances to individual cluster members Supernovae Type Ia Supernovae (Sn Ia) are thought to occur when mass accretion causes a white dwarf star to exceed the Chandrasekhar limit of 1.4M. As such, they are basically standard bombs with properties such as peak absolute magnitude M peak very nearly independent of local conditions. In practice things are more complex; M peak is correlated with the rate of decline in a manner which must be empirically calibrated. Moreover, dust extinction must be determined by simultaneous observations at several wavelengths. Nonetheless, SN Ia are so bright that they are visible to redshifts z > 1, and distances determined in this way are crucial for cosmological studies, including recent evidence that the expansion of the universe is accelerating.
The cosmic distance scale
 The cosmic distance scale Distance information is often crucial to understand the physics of astrophysical objects. This requires knowing the basic properties of such an object, like its size, its environment,
The cosmic distance scale Distance information is often crucial to understand the physics of astrophysical objects. This requires knowing the basic properties of such an object, like its size, its environment,
Practice Problem!! Assuming a uniform protogalactic (H and He only) cloud with a virial temperature of 10 6 K and a density of 0.
 Practice Problem Assuming a uniform protogalactic (H and He only) cloud with a virial temperature of 10 6 K and a density of 0.05 cm -3 (a) estimate the minimum mass that could collapse, (b) what is the
Practice Problem Assuming a uniform protogalactic (H and He only) cloud with a virial temperature of 10 6 K and a density of 0.05 cm -3 (a) estimate the minimum mass that could collapse, (b) what is the
The Cosmological Distance Ladder. It's not perfect, but it works!
 The Cosmological Distance Ladder It's not perfect, but it works! First, we must know how big the Earth is. Next, we must determine the scale of the solar system. Copernicus (1543) correctly determined
The Cosmological Distance Ladder It's not perfect, but it works! First, we must know how big the Earth is. Next, we must determine the scale of the solar system. Copernicus (1543) correctly determined
The Extragalactic Distance Scale
 One of the important relations in Astronomy. It lets us Measure the distance to distance objects. Each rung on the ladder is calibrated using lower-rung calibrations. Distance Objects Technique 1-100 AU
One of the important relations in Astronomy. It lets us Measure the distance to distance objects. Each rung on the ladder is calibrated using lower-rung calibrations. Distance Objects Technique 1-100 AU
Page # Astronomical Distances. Lecture 2. Astronomical Distances. Cosmic Distance Ladder. Distance Methods. Size of Earth
 Size of Astronomical istances ecture 2 Astronomical istances istance to the Moon (1 sec) istance to the Sun (8 min) istance to other stars (years) istance to centre of our Galaxy ( 30,000 yr to centre)
Size of Astronomical istances ecture 2 Astronomical istances istance to the Moon (1 sec) istance to the Sun (8 min) istance to other stars (years) istance to centre of our Galaxy ( 30,000 yr to centre)
AST-1002 Section 0459 Review for Final Exam Please do not forget about doing the evaluation!
 AST-1002 Section 0459 Review for Final Exam Please do not forget about doing the evaluation! Bring pencil #2 with eraser No use of calculator or any electronic device during the exam We provide the scantrons
AST-1002 Section 0459 Review for Final Exam Please do not forget about doing the evaluation! Bring pencil #2 with eraser No use of calculator or any electronic device during the exam We provide the scantrons
The Extragalactic Distance Scale
 One of the important relations in Astronomy. It lets us Measure the distance to distance objects. Each rung on the ladder is calibrated using lower-rung calibrations. Distance Objects Technique 1-100 AU
One of the important relations in Astronomy. It lets us Measure the distance to distance objects. Each rung on the ladder is calibrated using lower-rung calibrations. Distance Objects Technique 1-100 AU
The Next 2-3 Weeks. Important to read through Chapter 17 (Relativity) before I start lecturing on it.
 The Next 2-3 Weeks [27.1] The Extragalactic Distance Scale. [27.2] The Expansion of the Universe. [29.1] Newtonian Cosmology [29.2] The Cosmic Microwave Background [17] General Relativity & Black Holes
The Next 2-3 Weeks [27.1] The Extragalactic Distance Scale. [27.2] The Expansion of the Universe. [29.1] Newtonian Cosmology [29.2] The Cosmic Microwave Background [17] General Relativity & Black Holes
Lecture 25: The Cosmic Distance Scale Sections 25-1, 26-4 and Box 26-1
 Lecture 25: The Cosmic Distance Scale Sections 25-1, 26-4 and Box 26-1 Key Ideas The Distance Problem Geometric Distances Trigonometric Parallaxes Luminosity Distances Standard Candles Spectroscopic Parallaxes
Lecture 25: The Cosmic Distance Scale Sections 25-1, 26-4 and Box 26-1 Key Ideas The Distance Problem Geometric Distances Trigonometric Parallaxes Luminosity Distances Standard Candles Spectroscopic Parallaxes
Determining distance. L 4π f. d = d = R θ. Standard candle. Standard ruler
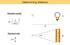 Determining distance Standard candle d = L 4π f 1 2 d L Standard ruler d = R θ θ R Determining distance: Parallax RULER tanπ = R d π R d π R = 1AU = 1.5 10 13 cm Define new distance unit: parsec (parallax-second)
Determining distance Standard candle d = L 4π f 1 2 d L Standard ruler d = R θ θ R Determining distance: Parallax RULER tanπ = R d π R d π R = 1AU = 1.5 10 13 cm Define new distance unit: parsec (parallax-second)
MEASURING DISTANCES IN ASTRONOMY
 Basic Principles: MEASURING DISTANCES IN ASTRONOMY Geometric methods Standard candles Standard rulers [the last two methods relate quantities that are independent of distance to quantities that depend
Basic Principles: MEASURING DISTANCES IN ASTRONOMY Geometric methods Standard candles Standard rulers [the last two methods relate quantities that are independent of distance to quantities that depend
Lecture 32: The Expanding Universe Readings: Sections 26-5 and 28-2
 Lecture 32: The Expanding Universe Readings: Sections 26-5 and 28-2 Key Ideas Measuring the Distances to Galaxies and Determining the Scale of the Universe Distance Methods: Trigonometric Parallaxes Spectroscopic
Lecture 32: The Expanding Universe Readings: Sections 26-5 and 28-2 Key Ideas Measuring the Distances to Galaxies and Determining the Scale of the Universe Distance Methods: Trigonometric Parallaxes Spectroscopic
Outline. Go over AGN problem, again, should be rotating BH Go over problem 6.6 Olber's paradox Distances Parallax Distance ladder Direct checks
 Outline Go over AGN problem, again, should be rotating BH Go over problem 6.6 Olber's paradox Distances Parallax Distance ladder Direct checks Why is the night sky dark? (Olber s Paradox 1826) Or what
Outline Go over AGN problem, again, should be rotating BH Go over problem 6.6 Olber's paradox Distances Parallax Distance ladder Direct checks Why is the night sky dark? (Olber s Paradox 1826) Or what
Relativity and Astrophysics Lecture 15 Terry Herter. RR Lyrae Variables Cepheids Variables Period-Luminosity Relation. A Stellar Properties 2
 Stellar Properties Relativity and Astrophysics Lecture 15 Terry Herter Outline Spectroscopic Parallax Masses of Stars Periodic Variable Stars RR Lyrae Variables Cepheids Variables Period-Luminosity Relation
Stellar Properties Relativity and Astrophysics Lecture 15 Terry Herter Outline Spectroscopic Parallax Masses of Stars Periodic Variable Stars RR Lyrae Variables Cepheids Variables Period-Luminosity Relation
Survey of Astrophysics A110
 Goals: Galaxies To determine the types and distributions of galaxies? How do we measure the mass of galaxies and what comprises this mass? How do we measure distances to galaxies and what does this tell
Goals: Galaxies To determine the types and distributions of galaxies? How do we measure the mass of galaxies and what comprises this mass? How do we measure distances to galaxies and what does this tell
Exam 4 Review EXAM COVERS LECTURES 22-29
 Exam 4 Review EXAM COVERS LECTURES 22-29 Theoretically is there a center of the universe? Is there an edge? Do we know where Earth is on this? There is no center to the Universe, What kind of light we
Exam 4 Review EXAM COVERS LECTURES 22-29 Theoretically is there a center of the universe? Is there an edge? Do we know where Earth is on this? There is no center to the Universe, What kind of light we
Set 5: Expansion of the Universe
 Set 5: Expansion of the Universe Cosmology Study of the origin, contents and evolution of the universe as a whole Expansion rate and history Space-time geometry Energy density composition Origin of structure
Set 5: Expansion of the Universe Cosmology Study of the origin, contents and evolution of the universe as a whole Expansion rate and history Space-time geometry Energy density composition Origin of structure
Hubble s Law. Tully-Fisher relation. The redshift. λ λ0. Are there other ways to estimate distances? Yes.
 Distances to galaxies Cepheids used by Hubble, 1924 to show that spiral nebulae like M31 were further from the Sun than any part of the Milky Way, therefore galaxies in their own right. Review of Cepheids
Distances to galaxies Cepheids used by Hubble, 1924 to show that spiral nebulae like M31 were further from the Sun than any part of the Milky Way, therefore galaxies in their own right. Review of Cepheids
Astronomy from 4 Perspectives Bi-national Heraeus Sumer School Series for Teacher Students and Teachers
 Astronomy from 4 Perspectives Bi-national Heraeus Sumer School Series for Teacher Students and Teachers I. Cosmology Prof. Dr. Andreas Just Zentrum für Astronomie Heidelberg University Cosmic Distances
Astronomy from 4 Perspectives Bi-national Heraeus Sumer School Series for Teacher Students and Teachers I. Cosmology Prof. Dr. Andreas Just Zentrum für Astronomie Heidelberg University Cosmic Distances
Galaxies. The majority of known galaxies fall into one of three major classes: spirals (78 %), ellipticals (18 %) and irregulars (4 %).
 Galaxies Collection of stars, gas and dust bound together by their common gravitational pull. Galaxies range from 10,000 to 200,000 light-years in size. 1781 Charles Messier 1923 Edwin Hubble The distribution
Galaxies Collection of stars, gas and dust bound together by their common gravitational pull. Galaxies range from 10,000 to 200,000 light-years in size. 1781 Charles Messier 1923 Edwin Hubble The distribution
4.1 The Scale of the Universe: Basis of the Cosmological Distance Scale
 4.1 The Scale of the Universe: Basis of the Cosmological Distance Scale 1 The Scale of the Universe The Hubble length, D H = c/h 0, and the Hubble time, t H = 1/H 0 give the approximate spatial and temporal
4.1 The Scale of the Universe: Basis of the Cosmological Distance Scale 1 The Scale of the Universe The Hubble length, D H = c/h 0, and the Hubble time, t H = 1/H 0 give the approximate spatial and temporal
24.1 Hubble s Galaxy Classification
 Chapter 24 Galaxies Units of Chapter 24 24.1 Hubble s Galaxy Classification 24.2 The Distribution of Galaxies in Space 24.3 Hubble s Law 24.4 XXActive Galactic Nuclei XXRelativistic Redshifts and Look-Back
Chapter 24 Galaxies Units of Chapter 24 24.1 Hubble s Galaxy Classification 24.2 The Distribution of Galaxies in Space 24.3 Hubble s Law 24.4 XXActive Galactic Nuclei XXRelativistic Redshifts and Look-Back
The Milky Way Galaxy (ch. 23)
 The Milky Way Galaxy (ch. 23) [Exceptions: We won t discuss sec. 23.7 (Galactic Center) much in class, but read it there will probably be a question or a few on it. In following lecture outline, numbers
The Milky Way Galaxy (ch. 23) [Exceptions: We won t discuss sec. 23.7 (Galactic Center) much in class, but read it there will probably be a question or a few on it. In following lecture outline, numbers
AST1100 Lecture Notes
 AST1100 Lecture Notes 11 12 The cosmic distance ladder How do we measure the distance to distant objects in the universe? There are several methods available, most of which suffer from large uncertainties.
AST1100 Lecture Notes 11 12 The cosmic distance ladder How do we measure the distance to distant objects in the universe? There are several methods available, most of which suffer from large uncertainties.
The Milky Way, Hubble Law, the expansion of the Universe and Dark Matter Chapter 14 and 15 The Milky Way Galaxy and the two Magellanic Clouds.
 The Milky Way, Hubble Law, the expansion of the Universe and Dark Matter Chapter 14 and 15 The Milky Way Galaxy and the two Magellanic Clouds. Image taken from the European Southern Observatory in Chile
The Milky Way, Hubble Law, the expansion of the Universe and Dark Matter Chapter 14 and 15 The Milky Way Galaxy and the two Magellanic Clouds. Image taken from the European Southern Observatory in Chile
The Cosmic Distance Ladder
 The Cosmic Distance Ladder (Mário Santos) What is it? A way to calculate distances to objects very far away based on the measured distances to nearby objects: 1. Start with the distance to the Sun (1 AU)
The Cosmic Distance Ladder (Mário Santos) What is it? A way to calculate distances to objects very far away based on the measured distances to nearby objects: 1. Start with the distance to the Sun (1 AU)
Week 1 Introduction: GR, Distances, Surveys
 Astronomy 233 Spring 2011 Physical Cosmology Week 1 Introduction: GR, Distances, Surveys Joel Primack University of California, Santa Cruz Modern Cosmology A series of major discoveries has laid a lasting
Astronomy 233 Spring 2011 Physical Cosmology Week 1 Introduction: GR, Distances, Surveys Joel Primack University of California, Santa Cruz Modern Cosmology A series of major discoveries has laid a lasting
Exam # 3 Tue 12/06/2011 Astronomy 100/190Y Exploring the Universe Fall 11 Instructor: Daniela Calzetti
 Exam # 3 Tue 12/06/2011 Astronomy 100/190Y Exploring the Universe Fall 11 Instructor: Daniela Calzetti INSTRUCTIONS: Please, use the `bubble sheet and a pencil # 2 to answer the exam questions, by marking
Exam # 3 Tue 12/06/2011 Astronomy 100/190Y Exploring the Universe Fall 11 Instructor: Daniela Calzetti INSTRUCTIONS: Please, use the `bubble sheet and a pencil # 2 to answer the exam questions, by marking
Building the cosmic distance scale: from Hipparcos to Gaia
 The Fundamental Distance Scale: state of the art and the Gaia perspectives 3-6 May 2011 Building the cosmic distance scale: from Hipparcos to Gaia Catherine TURON and Xavier LURI 1 ESA / ESO-H. Heyer Fundamental
The Fundamental Distance Scale: state of the art and the Gaia perspectives 3-6 May 2011 Building the cosmic distance scale: from Hipparcos to Gaia Catherine TURON and Xavier LURI 1 ESA / ESO-H. Heyer Fundamental
AST1100 Lecture Notes
 AST1100 Lecture Notes 11-12 The cosmic distance ladder How do we measure the distance to distant objects in the universe? There are several methods available, most of which suffer from large uncertainties.
AST1100 Lecture Notes 11-12 The cosmic distance ladder How do we measure the distance to distant objects in the universe? There are several methods available, most of which suffer from large uncertainties.
Chapter 8: Simple Stellar Populations
 Chapter 8: Simple Stellar Populations Simple Stellar Population consists of stars born at the same time and having the same initial element composition. Stars of different masses follow different evolutionary
Chapter 8: Simple Stellar Populations Simple Stellar Population consists of stars born at the same time and having the same initial element composition. Stars of different masses follow different evolutionary
Chapter 14 The Milky Way Galaxy
 Chapter 14 The Milky Way Galaxy Spiral Galaxy M81 - similar to our Milky Way Galaxy Our Parent Galaxy A galaxy is a giant collection of stellar and interstellar matter held together by gravity Billions
Chapter 14 The Milky Way Galaxy Spiral Galaxy M81 - similar to our Milky Way Galaxy Our Parent Galaxy A galaxy is a giant collection of stellar and interstellar matter held together by gravity Billions
Galaxies. With a touch of cosmology
 Galaxies With a touch of cosmology Types of Galaxies Spiral Elliptical Irregular Spiral Galaxies Spiral Galaxies Disk component where the spiral arms are Interstellar medium Star formation Spheroidal
Galaxies With a touch of cosmology Types of Galaxies Spiral Elliptical Irregular Spiral Galaxies Spiral Galaxies Disk component where the spiral arms are Interstellar medium Star formation Spheroidal
Simple Stellar Populations
 Stellar Objects: Simple Stellar Populations 1 Simple Stellar Populations 1 Theoretical isochrones Update date: December 14, 2010 Simple Stellar Population consists of stars born at the same time and having
Stellar Objects: Simple Stellar Populations 1 Simple Stellar Populations 1 Theoretical isochrones Update date: December 14, 2010 Simple Stellar Population consists of stars born at the same time and having
AST2000 Lecture Notes
 AST2000 Lecture Notes Part 3A The cosmic distance ladder Questions to ponder before the lecture 1. How do we know that the distance to our closest star is 4 light years? 2. How do we know that our galaxy
AST2000 Lecture Notes Part 3A The cosmic distance ladder Questions to ponder before the lecture 1. How do we know that the distance to our closest star is 4 light years? 2. How do we know that our galaxy
Chapter 8: The Family of Stars
 Chapter 8: The Family of Stars Motivation We already know how to determine a star s surface temperature chemical composition surface density In this chapter, we will learn how we can determine its distance
Chapter 8: The Family of Stars Motivation We already know how to determine a star s surface temperature chemical composition surface density In this chapter, we will learn how we can determine its distance
Lecture Outlines. Chapter 23. Astronomy Today 8th Edition Chaisson/McMillan Pearson Education, Inc.
 Lecture Outlines Chapter 23 Astronomy Today 8th Edition Chaisson/McMillan Chapter 23 The Milky Way Galaxy Units of Chapter 23 23.1 Our Parent Galaxy 23.2 Measuring the Milky Way Discovery 23-1 Early Computers
Lecture Outlines Chapter 23 Astronomy Today 8th Edition Chaisson/McMillan Chapter 23 The Milky Way Galaxy Units of Chapter 23 23.1 Our Parent Galaxy 23.2 Measuring the Milky Way Discovery 23-1 Early Computers
The Great Debate: The Size of the Universe (1920)
 The Great Debate: The Size of the Universe (1920) Heber Curtis Our Galaxy is rather small, with Sun near the center. 30,000 LY diameter. Universe composed of many separate galaxies Spiral nebulae = island
The Great Debate: The Size of the Universe (1920) Heber Curtis Our Galaxy is rather small, with Sun near the center. 30,000 LY diameter. Universe composed of many separate galaxies Spiral nebulae = island
Galaxy formation and evolution. Astro 850
 Galaxy formation and evolution Astro 850 Introduction What are galaxies? Systems containing many galaxies, e.g. 10 11 stars in the Milky Way. But galaxies have different properties. Properties of individual
Galaxy formation and evolution Astro 850 Introduction What are galaxies? Systems containing many galaxies, e.g. 10 11 stars in the Milky Way. But galaxies have different properties. Properties of individual
80 2 Observational Cosmology L and the mean energy
 80 2 Observational Cosmology fluctuations, short-wavelength modes have amplitudes that are suppressed because these modes oscillated as acoustic waves during the radiation epoch whereas the amplitude of
80 2 Observational Cosmology fluctuations, short-wavelength modes have amplitudes that are suppressed because these modes oscillated as acoustic waves during the radiation epoch whereas the amplitude of
XII. The distance scale. h"p://sgoodwin.staff.shef.ac.uk/phy111.html
 XII. The distance scale h"p://sgoodwin.staff.shef.ac.uk/phy111.html 0. How far away are galaxies? We discussed galaxies without thinking about how we know the distances to these galaxies. Only in the past
XII. The distance scale h"p://sgoodwin.staff.shef.ac.uk/phy111.html 0. How far away are galaxies? We discussed galaxies without thinking about how we know the distances to these galaxies. Only in the past
Lecture 14: Other Galaxies A2020 Prof. Tom Megeath. The Milky Way in the Infrared 3/17/10. NGC 7331: the Milky Way s Twins. Spiral Galaxy bulge halo
 Lecture 14: Other Galaxies A2020 Prof. Tom Megeath Our Galaxy: Side View We see our galaxy edge-on Primary features: Disk: young and old stars where we live. Bulge: older stars Halo: oldest stars, globular
Lecture 14: Other Galaxies A2020 Prof. Tom Megeath Our Galaxy: Side View We see our galaxy edge-on Primary features: Disk: young and old stars where we live. Bulge: older stars Halo: oldest stars, globular
Distance Measuring Techniques and The Milky Way Galaxy
 Distance Measuring Techniques and The Milky Way Galaxy Measuring distances to stars is one of the biggest challenges in Astronomy. If we had some standard candle, some star with a known luminosity, then
Distance Measuring Techniques and The Milky Way Galaxy Measuring distances to stars is one of the biggest challenges in Astronomy. If we had some standard candle, some star with a known luminosity, then
Chapter 23 The Milky Way Galaxy Pearson Education, Inc.
 Chapter 23 The Milky Way Galaxy The Milky Way is our own galaxy viewed from the inside. It is a vast collection of more than 200 billion stars, planets, nebulae, clusters, dust and gas. Our own sun and
Chapter 23 The Milky Way Galaxy The Milky Way is our own galaxy viewed from the inside. It is a vast collection of more than 200 billion stars, planets, nebulae, clusters, dust and gas. Our own sun and
ASTR Look over Chapter 15. Good things to Know. Triangulation
 ASTR 1020 Look over Chapter 15 Good things to Know Triangulation Parallax Parsecs Absolute Visual Magnitude Distance Modulus Luminosity Balmer Lines Spectral Classes Hertzsprung-Russell (HR) diagram Main
ASTR 1020 Look over Chapter 15 Good things to Know Triangulation Parallax Parsecs Absolute Visual Magnitude Distance Modulus Luminosity Balmer Lines Spectral Classes Hertzsprung-Russell (HR) diagram Main
Learning Objectives. distances to objects in our Galaxy and to other galaxies? apparent magnitude key to measuring distances?
 The Distance Ladder Learning Objectives! What is the distance ladder? How do we measure distances to objects in our Galaxy and to other galaxies?! How are the concepts of absolute magnitude and apparent
The Distance Ladder Learning Objectives! What is the distance ladder? How do we measure distances to objects in our Galaxy and to other galaxies?! How are the concepts of absolute magnitude and apparent
2. OBSERVATIONAL COSMOLOGY
 2. OBSERVATIONAL COSMOLOGY 1. OBSERVATIONAL PARAMETERS i. Introduction History of modern observational Cosmology ii. Cosmological Parameters The search for 2 (or more) numbers Hubble Parameter Deceleration
2. OBSERVATIONAL COSMOLOGY 1. OBSERVATIONAL PARAMETERS i. Introduction History of modern observational Cosmology ii. Cosmological Parameters The search for 2 (or more) numbers Hubble Parameter Deceleration
6. Star Colors and the Hertzsprung-Russell Diagram
 In addition to its brightness, light in general is characterized by its color. 6. Star Colors and the Hertzsprung-Russell Diagram http://apod.nasa.gov/apod/ Depending on the temperature of the matter at
In addition to its brightness, light in general is characterized by its color. 6. Star Colors and the Hertzsprung-Russell Diagram http://apod.nasa.gov/apod/ Depending on the temperature of the matter at
ASTR 1040: Stars & Galaxies
 ASTR 1040: Stars & Galaxies Our wide world (universe) of Galaxies Expanding universe: Hubble s discovery #2 Challenge of measuring s in universe review methods used Subtle concept of Lookback time Active
ASTR 1040: Stars & Galaxies Our wide world (universe) of Galaxies Expanding universe: Hubble s discovery #2 Challenge of measuring s in universe review methods used Subtle concept of Lookback time Active
Structure of the Milky Way. Structure of the Milky Way. The Milky Way
 Key Concepts: Lecture 29: Our first steps into the Galaxy Exploration of the Galaxy: first attempts to measure its structure (Herschel, Shapley). Structure of the Milky Way Initially, star counting was
Key Concepts: Lecture 29: Our first steps into the Galaxy Exploration of the Galaxy: first attempts to measure its structure (Herschel, Shapley). Structure of the Milky Way Initially, star counting was
Recent Researches concerning Semi-Regular Variables
 Recent Researches concerning Semi-Regular Variables I.S. Glass (SAAO) ASSA Symposium, Durban 2008 Distances in the Universe - the distance ladder a summary Trig parallaxes only direct method Variable stars
Recent Researches concerning Semi-Regular Variables I.S. Glass (SAAO) ASSA Symposium, Durban 2008 Distances in the Universe - the distance ladder a summary Trig parallaxes only direct method Variable stars
Science Olympiad Astronomy C Division Event National Exam
 Science Olympiad Astronomy C Division Event National Exam University of Central Florida May 17, 2014 Team Number: Team Name: Instructions: 1) Please turn in all materials at the end of the event. 2) Do
Science Olympiad Astronomy C Division Event National Exam University of Central Florida May 17, 2014 Team Number: Team Name: Instructions: 1) Please turn in all materials at the end of the event. 2) Do
The Cosmic Distance Ladder. Hubble s Law and the Expansion of the Universe!
 The Cosmic Distance Ladder Hubble s Law and the Expansion of the Universe! Last time: looked at Cepheid Variable stars as standard candles. Massive, off-main sequence stars: at a certain stage between
The Cosmic Distance Ladder Hubble s Law and the Expansion of the Universe! Last time: looked at Cepheid Variable stars as standard candles. Massive, off-main sequence stars: at a certain stage between
Lecture 9. Basics Measuring distances Parallax Cepheid variables Type Ia Super Novae. Gravitational lensing Sunyaev-Zeldovich effect
 Lecture 9 H 0 from the Hubble diagram Basics Measuring distances Parallax Cepheid variables Type Ia Super Novae H 0 from other methods Gravitational lensing Sunyaev-Zeldovich effect H 0 from the Hubble
Lecture 9 H 0 from the Hubble diagram Basics Measuring distances Parallax Cepheid variables Type Ia Super Novae H 0 from other methods Gravitational lensing Sunyaev-Zeldovich effect H 0 from the Hubble
ASTR 1120 General Astronomy: Stars & Galaxies
 ASTR 1120 General Astronomy: Stars & Galaxies!NNOUNCEMENTS HOMEWORK #6 DUE TODAY, by 5pm HOMEWORK #7 DUE Nov. 10, by 5pm Dark matter halo for galaxies Dark matter extends beyond visible part of the galaxy
ASTR 1120 General Astronomy: Stars & Galaxies!NNOUNCEMENTS HOMEWORK #6 DUE TODAY, by 5pm HOMEWORK #7 DUE Nov. 10, by 5pm Dark matter halo for galaxies Dark matter extends beyond visible part of the galaxy
OPTION E, ASTROPHYSICS TEST REVIEW
 IB PHYSICS Name: DEVIL PHYSICS Period: Date: BADDEST CLASS ON CAMPUS OPTION E, ASTROPHYSICS TEST REVIEW S1. This question is about the nature of certain stars on the Hertzsprung-Russell diagram and determining
IB PHYSICS Name: DEVIL PHYSICS Period: Date: BADDEST CLASS ON CAMPUS OPTION E, ASTROPHYSICS TEST REVIEW S1. This question is about the nature of certain stars on the Hertzsprung-Russell diagram and determining
MIT Invitational, Jan Astronomy C. 2. You may separate the pages, but do not forget to put your team number at the top of all answer pages.
 MIT Invitational, Jan 2019 Astronomy C Competitors: School name: Team number: INSTRUCTIONS 1. Please turn in all materials at the end of the event. 2. You may separate the pages, but do not forget to put
MIT Invitational, Jan 2019 Astronomy C Competitors: School name: Team number: INSTRUCTIONS 1. Please turn in all materials at the end of the event. 2. You may separate the pages, but do not forget to put
The Stars. Background & History The Celestial Sphere: Fixed Stars and the Luminaries
 The Stars Background & History The Celestial Sphere: Fixed Stars and the Luminaries The Appearance of Stars on the Sky Brightness and Brightness Variations Atmospheric Effects: Twinkling Variable Stars
The Stars Background & History The Celestial Sphere: Fixed Stars and the Luminaries The Appearance of Stars on the Sky Brightness and Brightness Variations Atmospheric Effects: Twinkling Variable Stars
6. Star Colors and the Hertzsprung-Russell Diagram
 What we can learn about stars from their light: II Color In addition to its brightness, light in general is characterized by its color (actually its wavelength) 6. Star Colors and the Hertzsprung-Russell
What we can learn about stars from their light: II Color In addition to its brightness, light in general is characterized by its color (actually its wavelength) 6. Star Colors and the Hertzsprung-Russell
The Family of Stars. Chapter 13. Triangulation. Trigonometric Parallax. Calculating Distance Using Parallax. Calculating Distance Using Parallax
 The Family of Stars Chapter 13 Measuring the Properties of Stars 1 Those tiny glints of light in the night sky are in reality huge, dazzling balls of gas, many of which are vastly larger and brighter than
The Family of Stars Chapter 13 Measuring the Properties of Stars 1 Those tiny glints of light in the night sky are in reality huge, dazzling balls of gas, many of which are vastly larger and brighter than
ASTR 1120 General Astronomy: Stars & Galaxies
 ASTR 1120 General Astronomy: Stars & Galaxies!NNOUNCEMENTS HOMEWORK #6 DUE TODAY, by 5pm HOMEWORK #7 DUE Nov. 10, by 5pm Dark matter halo for galaxies REVIEW Dark matter extends beyond visible part of
ASTR 1120 General Astronomy: Stars & Galaxies!NNOUNCEMENTS HOMEWORK #6 DUE TODAY, by 5pm HOMEWORK #7 DUE Nov. 10, by 5pm Dark matter halo for galaxies REVIEW Dark matter extends beyond visible part of
OPTION E, ASTROPHYSICS TEST REVIEW
 IB PHYSICS Name: DEVIL PHYSICS Period: Date: # Marks: XX Raw Score: IB Curve: BADDEST CLASS ON CAMPUS OPTION E, ASTROPHYSICS TEST REVIEW S1. This question is about the nature of certain stars on the Hertzsprung-Russell
IB PHYSICS Name: DEVIL PHYSICS Period: Date: # Marks: XX Raw Score: IB Curve: BADDEST CLASS ON CAMPUS OPTION E, ASTROPHYSICS TEST REVIEW S1. This question is about the nature of certain stars on the Hertzsprung-Russell
The Milky Way. Mass of the Galaxy, Part 2. Mass of the Galaxy, Part 1. Phys1403 Stars and Galaxies Instructor: Dr. Goderya
 Foundations Chapter of Astronomy 15 13e Our Milky Way Seeds Phys1403 Stars and Galaxies Instructor: Dr. Goderya Selected Topics in Chapter 15 A view our Milky Way? The Size of our Milky Way The Mass of
Foundations Chapter of Astronomy 15 13e Our Milky Way Seeds Phys1403 Stars and Galaxies Instructor: Dr. Goderya Selected Topics in Chapter 15 A view our Milky Way? The Size of our Milky Way The Mass of
Spatial distribution of stars in the Milky Way
 Spatial distribution of stars in the Milky Way What kinds of stars are present in the Solar neighborhood, and in what numbers? How are they distributed spatially? How do we know? How can we measure this?
Spatial distribution of stars in the Milky Way What kinds of stars are present in the Solar neighborhood, and in what numbers? How are they distributed spatially? How do we know? How can we measure this?
This Week in Astronomy
 Homework #8 Due Wednesday, April 18, 11:59PM Covers Chapters 15 and 16 Estimated time to complete: 40 minutes Read chapters, review notes before starting This Week in Astronomy Credit: NASA/JPL-Caltech
Homework #8 Due Wednesday, April 18, 11:59PM Covers Chapters 15 and 16 Estimated time to complete: 40 minutes Read chapters, review notes before starting This Week in Astronomy Credit: NASA/JPL-Caltech
Astronomical Distance Determination
 Distance ladder: Determine distances, d 1, for a nearby set of objects using technique 1, but then Astronomical Distance Determination http://apod.nasa.gov/apod/ Find new brighter objects at distances
Distance ladder: Determine distances, d 1, for a nearby set of objects using technique 1, but then Astronomical Distance Determination http://apod.nasa.gov/apod/ Find new brighter objects at distances
Astronomy A BEGINNER S GUIDE TO THE UNIVERSE EIGHTH EDITION
 Astronomy A BEGINNER S GUIDE TO THE UNIVERSE EIGHTH EDITION CHAPTER 14 The Milky Way Galaxy Lecture Presentation 14.0 the Milky Way galaxy How do we know the Milky Way exists? We can see it even though
Astronomy A BEGINNER S GUIDE TO THE UNIVERSE EIGHTH EDITION CHAPTER 14 The Milky Way Galaxy Lecture Presentation 14.0 the Milky Way galaxy How do we know the Milky Way exists? We can see it even though
Classical Methods for Determining Stellar Masses, Temperatures, and Radii
 Classical Methods for Determining Stellar Masses, Temperatures, and Radii Willie Torres Harvard-Smithsonian Center for Astrophysics 2010 Sagan Exoplanet Summer Workshop 1 Outline Basic properties of stars
Classical Methods for Determining Stellar Masses, Temperatures, and Radii Willie Torres Harvard-Smithsonian Center for Astrophysics 2010 Sagan Exoplanet Summer Workshop 1 Outline Basic properties of stars
Galaxies and the expansion of the Universe
 Review of Chapters 14, 15, 16 Galaxies and the expansion of the Universe 5/4/2009 Habbal Astro 110-01 Review Lecture 36 1 Recap: Learning from Light How does light tell us what things are made of? Every
Review of Chapters 14, 15, 16 Galaxies and the expansion of the Universe 5/4/2009 Habbal Astro 110-01 Review Lecture 36 1 Recap: Learning from Light How does light tell us what things are made of? Every
Luminosity Functions of Planetary Nebulae & Globular Clusters. By Azmain Nisak ASTR 8400
 Luminosity Functions of Planetary Nebulae & Globular Clusters By Azmain Nisak ASTR 8400 Calculating Distance! m = apparent magnitude! M = absolute magnitude! r = distance in pc GLOBULAR CLUSTERS AS DISTANCE
Luminosity Functions of Planetary Nebulae & Globular Clusters By Azmain Nisak ASTR 8400 Calculating Distance! m = apparent magnitude! M = absolute magnitude! r = distance in pc GLOBULAR CLUSTERS AS DISTANCE
University of Naples Federico II, Academic Year Istituzioni di Astrofisica, read by prof. Massimo Capaccioli. Lecture 16
 University of Naples Federico II, Academic Year 2011-2012 Istituzioni di Astrofisica, read by prof. Massimo Capaccioli Lecture 16 Stellar populations Walter Baade (1893-1960) Learning outcomes The student
University of Naples Federico II, Academic Year 2011-2012 Istituzioni di Astrofisica, read by prof. Massimo Capaccioli Lecture 16 Stellar populations Walter Baade (1893-1960) Learning outcomes The student
AS1001: Galaxies and Cosmology
 AS1001: Galaxies and Cosmology Keith Horne kdh1@st-and.ac.uk http://www-star.st-and.ac.uk/~kdh1/eg/eg.html Text: Kutner Astronomy:A Physical Perspective Chapters 17-21 Cosmology Today Blah Title Current
AS1001: Galaxies and Cosmology Keith Horne kdh1@st-and.ac.uk http://www-star.st-and.ac.uk/~kdh1/eg/eg.html Text: Kutner Astronomy:A Physical Perspective Chapters 17-21 Cosmology Today Blah Title Current
6. Star Colors and the Hertzsprung-Russell Diagram
 6. Star Colors and the Hertzsprung-Russell Diagram http://apod.nasa.gov/apod/ Supernovae Type Ia in M82 January 22, 2014 Still rising may go to m = 8 (or 10?) What we can learn about stars from their light:
6. Star Colors and the Hertzsprung-Russell Diagram http://apod.nasa.gov/apod/ Supernovae Type Ia in M82 January 22, 2014 Still rising may go to m = 8 (or 10?) What we can learn about stars from their light:
6. Star Colors and the Hertzsprung-Russell Diagram.
 6. Star Colors and the Hertzsprung-Russell Diagram http://apod.nasa.gov/apod/ Supernovae Type Ia in M82 January 22, 2014 Still rising may go to m = 8 (or 10?) What we can learn about stars from their light:
6. Star Colors and the Hertzsprung-Russell Diagram http://apod.nasa.gov/apod/ Supernovae Type Ia in M82 January 22, 2014 Still rising may go to m = 8 (or 10?) What we can learn about stars from their light:
The Milky Way. Finding the Center. Milky Way Composite Photo. Finding the Center. Milky Way : A band of and a. Milky Way
 The Milky Way Milky Way : A band of and a The band of light we see is really 100 billion stars Milky Way probably looks like Andromeda. Milky Way Composite Photo Milky Way Before the 1920 s, astronomers
The Milky Way Milky Way : A band of and a The band of light we see is really 100 billion stars Milky Way probably looks like Andromeda. Milky Way Composite Photo Milky Way Before the 1920 s, astronomers
HNRS 227 Lecture 18 October 2007 Chapter 12. Stars, Galaxies and the Universe presented by Dr. Geller
 HNRS 227 Lecture 18 October 2007 Chapter 12 Stars, Galaxies and the Universe presented by Dr. Geller Recall from Chapters 1-11 Units of length, mass, density, time, and metric system The Scientific Method
HNRS 227 Lecture 18 October 2007 Chapter 12 Stars, Galaxies and the Universe presented by Dr. Geller Recall from Chapters 1-11 Units of length, mass, density, time, and metric system The Scientific Method
Science Olympiad Astronomy C Division Event Golden Gate Invitational February 11, 2017
 Science Olympiad Astronomy C Division Event Golden Gate Invitational February 11, 2017 Team Name: Team Number: Directions: ~Answer all questions on the answer sheet provided. ~Please do NOT access the
Science Olympiad Astronomy C Division Event Golden Gate Invitational February 11, 2017 Team Name: Team Number: Directions: ~Answer all questions on the answer sheet provided. ~Please do NOT access the
Chapter 10 Measuring the Stars
 Chapter 10 Measuring the Stars Some of the topics included in this chapter Stellar parallax Distance to the stars Stellar motion Luminosity and apparent brightness of stars The magnitude scale Stellar
Chapter 10 Measuring the Stars Some of the topics included in this chapter Stellar parallax Distance to the stars Stellar motion Luminosity and apparent brightness of stars The magnitude scale Stellar
Chapter 7: From theory to observations
 Chapter 7: From theory to observations Given the stellar mass and chemical composition of a ZAMS, the stellar modeling can, in principle, predict the evolution of the stellar bolometric luminosity, effective
Chapter 7: From theory to observations Given the stellar mass and chemical composition of a ZAMS, the stellar modeling can, in principle, predict the evolution of the stellar bolometric luminosity, effective
Star systems like our Milky Way. Galaxies
 Galaxies Star systems like our Milky Way Galaxies Contain a few thousand to tens of billions of stars,as well as varying amounts of gas and dust Large variety of shapes and sizes Gas and Dust in
Galaxies Star systems like our Milky Way Galaxies Contain a few thousand to tens of billions of stars,as well as varying amounts of gas and dust Large variety of shapes and sizes Gas and Dust in
Measuring the Hubble Constant through Cepheid Distances
 Measuring the Hubble Constant through Cepheid Distances Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant Freedman, Madore, Gibson, et al., Astrophysical Journal
Measuring the Hubble Constant through Cepheid Distances Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant Freedman, Madore, Gibson, et al., Astrophysical Journal
Science Olympiad Astronomy C Division Event. National Cathedral School Invitational Washington, DC December 3 rd, 2016
 Science Olympiad Astronomy C Division Event National Cathedral School Invitational Washington, DC December 3 rd, 2016 Name: Start Time: Directions: 1) Please turn in all materials at the end of the event.
Science Olympiad Astronomy C Division Event National Cathedral School Invitational Washington, DC December 3 rd, 2016 Name: Start Time: Directions: 1) Please turn in all materials at the end of the event.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Earth, Atmospheric, and Planetary Sciences Department. Final Exam
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Earth, Atmospheric, and Planetary Sciences Department Physics 8.282J EAPS 12.402J May 20, 2005 Final Exam Name Last First (please print) 1. Do any
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Earth, Atmospheric, and Planetary Sciences Department Physics 8.282J EAPS 12.402J May 20, 2005 Final Exam Name Last First (please print) 1. Do any
Ch. 25 In-Class Notes: Beyond Our Solar System
 Ch. 25 In-Class Notes: Beyond Our Solar System ES2a. The solar system is located in an outer edge of the disc-shaped Milky Way galaxy, which spans 100,000 light years. ES2b. Galaxies are made of billions
Ch. 25 In-Class Notes: Beyond Our Solar System ES2a. The solar system is located in an outer edge of the disc-shaped Milky Way galaxy, which spans 100,000 light years. ES2b. Galaxies are made of billions
Lecture Outlines. Chapter 24. Astronomy Today 8th Edition Chaisson/McMillan Pearson Education, Inc.
 Lecture Outlines Chapter 24 Astronomy Today 8th Edition Chaisson/McMillan Chapter 24 Galaxies Units of Chapter 24 24.1 Hubble s Galaxy Classification 24.2 The Distribution of Galaxies in Space 24.3 Hubble
Lecture Outlines Chapter 24 Astronomy Today 8th Edition Chaisson/McMillan Chapter 24 Galaxies Units of Chapter 24 24.1 Hubble s Galaxy Classification 24.2 The Distribution of Galaxies in Space 24.3 Hubble
Hubble sequence galaxy classification scheme, originally based on appearance, but correlates with other properties as well.
 Normal Galaxies (Ch. 24) Here we will cover topics in Ch. 24 up to 24.4, but then skip 24.4, 24.5. The sections we are skipping are all about processes that occur in the centers of galaxies, so I d like
Normal Galaxies (Ch. 24) Here we will cover topics in Ch. 24 up to 24.4, but then skip 24.4, 24.5. The sections we are skipping are all about processes that occur in the centers of galaxies, so I d like
Structure of Our Galaxy The Milkyway. More background Stars and Gas in our Galaxy
 Structure of Our Galaxy The Milkyway More background Stars and Gas in our Galaxy "What good are Mercator's North Poles and Equators Tropics, Zones, and Meridian Lines?" So the Bellman would cry, and the
Structure of Our Galaxy The Milkyway More background Stars and Gas in our Galaxy "What good are Mercator's North Poles and Equators Tropics, Zones, and Meridian Lines?" So the Bellman would cry, and the
AST 101 INTRODUCTION TO ASTRONOMY SPRING MIDTERM EXAM 2 TEST VERSION 1 ANSWERS
 AST 101 INTRODUCTION TO ASTRONOMY SPRING 2008 - MIDTERM EXAM 2 TEST VERSION 1 ANSWERS Multiple Choice. In the blanks provided before each question write the letter for the phrase that best answers the
AST 101 INTRODUCTION TO ASTRONOMY SPRING 2008 - MIDTERM EXAM 2 TEST VERSION 1 ANSWERS Multiple Choice. In the blanks provided before each question write the letter for the phrase that best answers the
Lecture 16 The Measuring the Stars 3/26/2018
 Lecture 16 The Measuring the Stars 3/26/2018 Test 2 Results D C B A Questions that I thought were unfair: 13, 18, 25, 76, 77, 80 Curved from 85 to 79 Measuring stars How far away are they? How bright are
Lecture 16 The Measuring the Stars 3/26/2018 Test 2 Results D C B A Questions that I thought were unfair: 13, 18, 25, 76, 77, 80 Curved from 85 to 79 Measuring stars How far away are they? How bright are
The Hubble Constant. Measuring the Scale of the Universe. The Scale of the Universe. In this lecture:
 Ay 127, Spring 2013 Extragalactic Distance Scale In this lecture: S. G. Djorgovski Hubble constant: its definition and history The extragalactic distance ladder The HST Key Project and the more modern
Ay 127, Spring 2013 Extragalactic Distance Scale In this lecture: S. G. Djorgovski Hubble constant: its definition and history The extragalactic distance ladder The HST Key Project and the more modern
MSci Astrophysics 210PHY412
 MSci Astrophysics 210PHY412 Stellar structure and evolution Dr. Stephen Smartt (Room S039) Department of Physics and Astronomy S.Smartt@qub.ac.uk Online resources - QoL and http://star.pst.qub.ac.uk/~sjs/teaching.html
MSci Astrophysics 210PHY412 Stellar structure and evolution Dr. Stephen Smartt (Room S039) Department of Physics and Astronomy S.Smartt@qub.ac.uk Online resources - QoL and http://star.pst.qub.ac.uk/~sjs/teaching.html
Einführung in die Astronomie II
 Einführung in die Astronomie II Teil 12 Peter Hauschildt yeti@hs.uni-hamburg.de Hamburger Sternwarte Gojenbergsweg 112 21029 Hamburg 13. September 2017 1 / 77 Overview part 12 The Galaxy Historical Overview
Einführung in die Astronomie II Teil 12 Peter Hauschildt yeti@hs.uni-hamburg.de Hamburger Sternwarte Gojenbergsweg 112 21029 Hamburg 13. September 2017 1 / 77 Overview part 12 The Galaxy Historical Overview
Chapter 20 Galaxies And the Foundation of Modern Cosmology. Agenda. Lunar Eclipse. Saturn. Lunar Eclipse
 Chapter 20 Galaxies And the Foundation of Modern Cosmology Agenda Lunar Eclipse Gallery Saturn Pic/Movie Jim Carrey on Quantum Physics Gravitational Lensing Picture Ch. 20 Galaxies Crab Lab Lunar Eclipse
Chapter 20 Galaxies And the Foundation of Modern Cosmology Agenda Lunar Eclipse Gallery Saturn Pic/Movie Jim Carrey on Quantum Physics Gravitational Lensing Picture Ch. 20 Galaxies Crab Lab Lunar Eclipse
Scale height and Luminosity
 The Milky Way I suggest to consult the excellent lectures held at Saas-Fee by Gilmore, King and van der Kruit in the Book The Milky Way as a Galaxy edited by Buser & King and published by the University
The Milky Way I suggest to consult the excellent lectures held at Saas-Fee by Gilmore, King and van der Kruit in the Book The Milky Way as a Galaxy edited by Buser & King and published by the University
Cosmic Distance Determinations
 Cosmic Distance Determinations Radar (works for inner solar system) Parallax D(pc) = 1 p(arcsec) GAIA satellite (2013) 20 micro-arcsec resolution! Thus D < 10 kpc Beyond Parallax: Standard Candles Use
Cosmic Distance Determinations Radar (works for inner solar system) Parallax D(pc) = 1 p(arcsec) GAIA satellite (2013) 20 micro-arcsec resolution! Thus D < 10 kpc Beyond Parallax: Standard Candles Use
Measuring the Properties of Stars (ch. 17) [Material in smaller font on this page will not be present on the exam]
![Measuring the Properties of Stars (ch. 17) [Material in smaller font on this page will not be present on the exam] Measuring the Properties of Stars (ch. 17) [Material in smaller font on this page will not be present on the exam]](/thumbs/85/91935248.jpg) Measuring the Properties of Stars (ch. 17) [Material in smaller font on this page will not be present on the exam] Although we can be certain that other stars are as complex as the Sun, we will try to
Measuring the Properties of Stars (ch. 17) [Material in smaller font on this page will not be present on the exam] Although we can be certain that other stars are as complex as the Sun, we will try to
ASTRONOMY II Spring 1995 FINAL EXAM. Monday May 8th 2:00pm
 ASTRONOMY II - 79202 Spring 1995 FINAL EXAM Monday May 8th 2:00pm Name: You have three hours to complete this exam. I suggest you read through the entire exam before you spend too much time on any one
ASTRONOMY II - 79202 Spring 1995 FINAL EXAM Monday May 8th 2:00pm Name: You have three hours to complete this exam. I suggest you read through the entire exam before you spend too much time on any one
Astronomy Stars, Galaxies and Cosmology Exam 3. Please PRINT full name
 Astronomy 132 - Stars, Galaxies and Cosmology Exam 3 Please PRINT full name Also, please sign the honor code: I have neither given nor have I received help on this exam The following exam is intended to
Astronomy 132 - Stars, Galaxies and Cosmology Exam 3 Please PRINT full name Also, please sign the honor code: I have neither given nor have I received help on this exam The following exam is intended to
CALCULATING DISTANCES. Cepheids and RR Lyrae India Jackson-Henry
 CALCULATING DISTANCES Cepheids and RR Lyrae India Jackson-Henry What are Cepheids and RR Lyrae Stars As stars evolve, their atmospheres become unstable and the star becomes intrinsically variable. Two
CALCULATING DISTANCES Cepheids and RR Lyrae India Jackson-Henry What are Cepheids and RR Lyrae Stars As stars evolve, their atmospheres become unstable and the star becomes intrinsically variable. Two
29:50 Stars, Galaxies, and the Universe Final Exam December 13, 2010 Form A
 29:50 Stars, Galaxies, and the Universe Final Exam December 13, 2010 Form A There are 40 questions. Read each question and all of the choices before choosing. Budget your time. No whining. Walk with Ursus!
29:50 Stars, Galaxies, and the Universe Final Exam December 13, 2010 Form A There are 40 questions. Read each question and all of the choices before choosing. Budget your time. No whining. Walk with Ursus!
