10/16/ Detecting Planets Around Other Stars. Chapter 10: Other Planetary Systems The New Science of Distant Worlds
|
|
|
- Lizbeth Bell
- 5 years ago
- Views:
Transcription
1 10/16/17 Lecture Outline 10.1 Detecting Planets Around Other Stars Chapter 10: Other Planetary Systems The New Science of Distant Worlds Our goals for learning: How do we detect planets around other stars? How do we detect planets around other stars? Why are extrasolar planets difficult to detect? A Sun-like star is about a billion times brighter than the light reflected from its planets. Planets are close to their stars, relative to the distance from us to the star. This is like being in San Francisco and trying to see a pinhead 15 meters from a grapefruit in Washington, D.C. Planet Detection Planet Detection Direct: pictures or spectra of the planets themselves (very few to date) Indirect: measurements of stellar properties revealing the effects of orbiting planets (almost all extrasolar planet discoveries) 1) Gravitational Tugs 2) Transits Direct: pictures or spectra of the planets themselves (images taken with the Large Binocular Telescope) 1
2 Gravitational Tugs Gravitational Tugs The Sun and Jupiter orbit around their common center of mass. The Sun therefore wobbles around that center of mass with same period as Jupiter. The Sun's motion around the solar system's center of mass depends on tugs from all the planets. Astronomers around other stars that measured this motion could determine the masses and orbits of all the planets. Astrometric Technique Doppler Technique We can detect planets by measuring the change in a star's position on sky. However, these tiny motions are very difficult to measure (~ arcsecond). Measuring a star's Doppler shift can tell us its motion toward and away from us. Current techniques can measure motions as small as 1 m/s (walking speed!). First Extrasolar Planet Transits and Eclipses Doppler shifts of the star 51 Pegasi indirectly revealed a planet with 4-day orbital period. This short period means that the planet has a small orbital distance. This was the first extrasolar planet to be discovered around a Sun-like star (1995). A transit is when a planet crosses in front of a star. This reduces the star's apparent brightness and tells us planet's radius. Sometimes an eclipse the planet passing behind the star, can also be detected 2
3 Kepler Kepler NASA's Kepler mission searched for transits from It was designed to measure the 0.008% decline in brightness when an Earth-mass planet eclipses a Sun-like star. NASA's Kepler mission stopped taking data in Other Planet-Hunting Strategies Gravitational Lensing: Mass bends light in a special way when a star with planets passes in front of another star. Features in Dust Disks: Gaps, waves, or ripples in disks of dusty gas around stars can indicate presence of planets The Nature of Planets Around Other Stars Our goals for learning: What properties of extrasolar planets can we measure? How do extrasolar planets compare with planets in our solar system? What properties of extrasolar planets can we measure? Measurable Properties Orbital period, distance, and shape Planet mass, size, and density Atmospheric properties 3
4 Planet Mass and Orbit Tilt Thought Question We cannot measure an exact mass for a planet without knowing the tilt of its orbit, because Doppler shift tells us only the velocity toward or away from us. Doppler data give us lower limits on masses. Suppose you found a star with the same mass as the Sun moving back and forth within a period of 16 months. What could you conclude? A. It has a planet orbiting at less than 1 AU. B. It has a planet orbiting at greater than 1 AU. C. It has a planet orbiting at exactly 1 AU. D. It has a planet, but we do not have enough information to know its orbital distance. Thought Question The Kepler 11 system Suppose you found a star with the same mass as the Sun moving back and forth with a period of 16 months. What could you conclude? A. It has a planet orbiting at less than 1 AU. B. It has a planet orbiting at greater than 1 AU. C. It has a planet orbiting at exactly 1 AU. D. It has a planet, but we do not have enough information to know its orbital distance. The periods and sizes of Kepler 11's 6 known planets can be determined using transit data. Orbits and masses of extrasolar planets from Kepler Calculating density Using mass, which is determined using the Doppler technique, and size, which is determined using the transit technique, density can be calculated. 4
5 How do extrasolar planets compare with planets in our solar system? Orbits of Extrasolar Planets Most of the detected planets have orbits smaller than Jupiter's. Planets at greater distances are harder to detect with the current techniques. Orbits of some extrasolar planets are much more elongated (have a greater eccentricity) than those in our solar system. Orbits and sizes of extrasolar planets from Kepler Orbits and sizes of extrasolar planets from Kepler Masses and sizes of extrasolar planets Results from Kepler indicate that planets are common, and small planets greatly outnumber large planets! 5
6 Surprising Characteristics Planets show huge diversity in size and density. Some extrasolar planets have highly elliptical orbits. Planets show huge diversity in size and density. Some massive planets, called hot Jupiters, orbit very close to their stars. Surprising Characteristics 10.3 The Formation of Other Planetary Systems Our goals for learning: Do we need to modify our theory of solar system formation? Are planetary systems like ours common? Some extrasolar planets have highly elliptical orbits. Do we need to modify our theory of solar system formation? Revisiting the Nebular Theory The nebular theory predicts that massive Jupiter-like planets should not form inside the frost line (at << 5 AU). The discovery of hot Jupiters has forced reexamination of nebular theory. Planetary migration or gravitational encounters may explain hot Jupiters. 6
7 Planetary Migration Gravitational Encounters and Resonances A young planet's motion can create waves in a planet-forming disk. Models show that matter in these waves can tug on a planet, causing its orbit to migrate inward. Close gravitational encounters between two massive planets can eject one planet while flinging the other into a highly elliptical orbit. Multiple close encounters with smaller planetesimals can also cause inward migration. Resonances may also contribute. Planetary Types Thought Question There seem to be a much greater variety of planet types than we find in our solar system. This includes gas giants with very different densities and water worlds. What happens in a gravitational encounter that allows a planet's orbit to move inward? A. It transfers energy and angular momentum to another object. B. The gravity of the other object forces the planet to move inward. C. It gains mass from the other object, causing its gravitational pull to become stronger. Thought Question Modifying the Nebular Theory What happens in a gravitational encounter that allows a planet's orbit to move inward? A. It transfers energy and angular momentum to another object. B. The gravity of the other object forces the planet to move inward. C. It gains mass from the other object, causing its gravitational pull to become stronger. Observations of extrasolar planets have shown that the nebular theory was incomplete. Effects like planetary migration and gravitational encounters might be more important than previously thought. 7
8 Are planetary systems like ours common? Are planetary systems like ours common? 8
Chapter 13 Other Planetary Systems. Why is it so difficult to detect planets around other stars? Brightness Difference
 Chapter 13 Other Planetary Systems The New Science of Distant Worlds 13.1 Detecting Extrasolar Planets Our goals for learning:! Why is it so difficult to detect planets around other stars?! How do we detect
Chapter 13 Other Planetary Systems The New Science of Distant Worlds 13.1 Detecting Extrasolar Planets Our goals for learning:! Why is it so difficult to detect planets around other stars?! How do we detect
Chapter 13 Other Planetary Systems. The New Science of Distant Worlds
 Chapter 13 Other Planetary Systems The New Science of Distant Worlds 13.1 Detecting Extrasolar Planets Our goals for learning Why is it so difficult to detect planets around other stars? How do we detect
Chapter 13 Other Planetary Systems The New Science of Distant Worlds 13.1 Detecting Extrasolar Planets Our goals for learning Why is it so difficult to detect planets around other stars? How do we detect
Chapter 13 Lecture. The Cosmic Perspective. Seventh Edition. Other Planetary Systems: The New Science of Distant Worlds Pearson Education, Inc.
 Chapter 13 Lecture The Cosmic Perspective Seventh Edition Other Planetary Systems: The New Science of Distant Worlds 13.1 Detecting Planets Around Other Stars Our goals for learning: Why is it so challenging
Chapter 13 Lecture The Cosmic Perspective Seventh Edition Other Planetary Systems: The New Science of Distant Worlds 13.1 Detecting Planets Around Other Stars Our goals for learning: Why is it so challenging
Chapter 13 Lecture. The Cosmic Perspective Seventh Edition. Other Planetary Systems: The New Science of Distant Worlds Pearson Education, Inc.
 Chapter 13 Lecture The Cosmic Perspective Seventh Edition Other Planetary Systems: The New Science of Distant Worlds 13.1 Detecting Planets Around Other Stars Our goals for learning: Why is it so challenging
Chapter 13 Lecture The Cosmic Perspective Seventh Edition Other Planetary Systems: The New Science of Distant Worlds 13.1 Detecting Planets Around Other Stars Our goals for learning: Why is it so challenging
Chapter 13 Lecture. The Cosmic Perspective Seventh Edition. Other Planetary Systems: The New Science of Distant Worlds Pearson Education, Inc.
 Chapter 13 Lecture The Cosmic Perspective Seventh Edition Other Planetary Systems: The New Science of Distant Worlds 13.1 Detecting Planets Around Other Stars Our goals for learning: Why is it so challenging
Chapter 13 Lecture The Cosmic Perspective Seventh Edition Other Planetary Systems: The New Science of Distant Worlds 13.1 Detecting Planets Around Other Stars Our goals for learning: Why is it so challenging
Chapter 13 Other Planetary Systems. Why is it so difficult to detect planets around other stars? Size Difference. Brightness Difference
 Chapter 13 Other Planetary Systems Why is it so difficult to detect planets around other stars? Size Difference Planets are small compared to interstellar distances 10 billion to 1 scale Sun is size of
Chapter 13 Other Planetary Systems Why is it so difficult to detect planets around other stars? Size Difference Planets are small compared to interstellar distances 10 billion to 1 scale Sun is size of
» How vast those Orbs must be, and how inconsiderable this Earth, the Theatre upon which all our mighty Designs, all our Navigations, and all our
 » How vast those Orbs must be, and how inconsiderable this Earth, the Theatre upon which all our mighty Designs, all our Navigations, and all our Wars are transacted, is when compared to them. A very fit
» How vast those Orbs must be, and how inconsiderable this Earth, the Theatre upon which all our mighty Designs, all our Navigations, and all our Wars are transacted, is when compared to them. A very fit
2010 Pearson Education, Inc.
 Thought Question Suppose you found a star with the same mass as the Sun moving back and forth with a period of 16 months. What could you conclude? A. It has a planet orbiting at less than 1 AU. B. It has
Thought Question Suppose you found a star with the same mass as the Sun moving back and forth with a period of 16 months. What could you conclude? A. It has a planet orbiting at less than 1 AU. B. It has
Doppler Technique Measuring a star's Doppler shift can tell us its motion toward and away from us.
 Doppler Technique Measuring a star's Doppler shift can tell us its motion toward and away from us. Current techniques can measure motions as small as 1 m/s (walking speed!). Sun motion due to: Jupiter:
Doppler Technique Measuring a star's Doppler shift can tell us its motion toward and away from us. Current techniques can measure motions as small as 1 m/s (walking speed!). Sun motion due to: Jupiter:
Extrasolar Planets. Properties Pearson Education Inc., publishing as Pearson Addison-Wesley
 Extrasolar Planets Properties 2007 Pearson Education Inc., publishing as Pearson Addison-Wesley Finding extrasolar planets is hard quick recap Planet Detection Direct: pictures or spectra of the planets
Extrasolar Planets Properties 2007 Pearson Education Inc., publishing as Pearson Addison-Wesley Finding extrasolar planets is hard quick recap Planet Detection Direct: pictures or spectra of the planets
Other Solar Systems. Week 15 (Chapter 13): Other Planetary Systems
 Week 15 (Chapter 13): Other Planetary Systems Nov. 30 Please pickup your grade sheet at front. We ll discuss at end of class. Other Solar Systems First one (51 Pegasi) discovered in 1995 Currently 268
Week 15 (Chapter 13): Other Planetary Systems Nov. 30 Please pickup your grade sheet at front. We ll discuss at end of class. Other Solar Systems First one (51 Pegasi) discovered in 1995 Currently 268
Planet Detection. AST 105 Intro Astronomy The Solar System
 Review AST 105 Intro Astronomy The Solar System MIDTERM III this THURSDAY 04/8 covering LECT. 17 through We ve talked about the Terrestrial Planets and the Jovian Planets - What about planets around other
Review AST 105 Intro Astronomy The Solar System MIDTERM III this THURSDAY 04/8 covering LECT. 17 through We ve talked about the Terrestrial Planets and the Jovian Planets - What about planets around other
12.3 Pluto: Lone Dog No More
 12.3 Pluto: Lone Dog No More Our goals for learning: How big can a comet be? What are the large objects of the Kuiper belt like? Are Pluto and Eris planets? How big can a comet be? Pluto s Orbit Pluto
12.3 Pluto: Lone Dog No More Our goals for learning: How big can a comet be? What are the large objects of the Kuiper belt like? Are Pluto and Eris planets? How big can a comet be? Pluto s Orbit Pluto
Other Planetary Systems (Chapter 13) Extrasolar Planets. Is our solar system the only collection of planets in the universe?
 Other Planetary Systems (Chapter 13) Extrasolar Planets Is our solar system the only collection of planets in the universe? Based on Chapter 13 No subsequent chapters depend on the material in this lecture
Other Planetary Systems (Chapter 13) Extrasolar Planets Is our solar system the only collection of planets in the universe? Based on Chapter 13 No subsequent chapters depend on the material in this lecture
[25] Exoplanet Characterization (11/30/17)
![[25] Exoplanet Characterization (11/30/17) [25] Exoplanet Characterization (11/30/17)](/thumbs/86/94788164.jpg) 1 [25] Exoplanet Characterization (11/30/17) Upcoming Items APOD 12/2/16 1. Read chapters 24.1-24.3 for Tuesday 2. We will have a final exam review in the last discussion section (Friday, Dec 8) and also
1 [25] Exoplanet Characterization (11/30/17) Upcoming Items APOD 12/2/16 1. Read chapters 24.1-24.3 for Tuesday 2. We will have a final exam review in the last discussion section (Friday, Dec 8) and also
Extrasolar Planets. Today. Dwarf Planets. Extrasolar Planets. Next week. Review Tuesday. Exam Thursday. also, Homework 6 Due
 Extrasolar Planets Today Dwarf Planets Extrasolar Planets Next week Review Tuesday Exam Thursday also, Homework 6 Due will count best 5 of 6 homeworks 2007 Pearson Education Inc., publishing as Pearson
Extrasolar Planets Today Dwarf Planets Extrasolar Planets Next week Review Tuesday Exam Thursday also, Homework 6 Due will count best 5 of 6 homeworks 2007 Pearson Education Inc., publishing as Pearson
Lecture 12: Extrasolar planets. Astronomy 111 Monday October 9, 2017
 Lecture 12: Extrasolar planets Astronomy 111 Monday October 9, 2017 Reminders Star party Thursday night! Homework #6 due Monday The search for extrasolar planets The nature of life on earth and the quest
Lecture 12: Extrasolar planets Astronomy 111 Monday October 9, 2017 Reminders Star party Thursday night! Homework #6 due Monday The search for extrasolar planets The nature of life on earth and the quest
Extrasolar planets. Lecture 23, 4/22/14
 Extrasolar planets Lecture 23, 4/22/14 Extrasolar planets Extrasolar planets: planets around other stars Also called exoplanets 1783 exoplanets discovered as of 4/21/14 Orbitting 1105 different stars Number
Extrasolar planets Lecture 23, 4/22/14 Extrasolar planets Extrasolar planets: planets around other stars Also called exoplanets 1783 exoplanets discovered as of 4/21/14 Orbitting 1105 different stars Number
Why is it hard to detect planets around other stars?
 Extrasolar planets Why is it hard to detect planets around other stars? Planets are small and low in mass Planets are faint The angular separation between planets and their stars is tiny Why is it hard
Extrasolar planets Why is it hard to detect planets around other stars? Planets are small and low in mass Planets are faint The angular separation between planets and their stars is tiny Why is it hard
Detecting Extra Solar Planets
 Detecting Extra Solar Planets The Extrasolar Planet Count Currently, 288 stars have been discovered to have planets. Some of these have more than one, so a total of 380 planets have been discovered as
Detecting Extra Solar Planets The Extrasolar Planet Count Currently, 288 stars have been discovered to have planets. Some of these have more than one, so a total of 380 planets have been discovered as
Lecture #15: Plan. Telescopes (cont d) Effects of Earth s Atmosphere Extrasolar planets = Exoplanets
 Lecture #15: Plan Telescopes (cont d) Effects of Earth s Atmosphere Extrasolar planets = Exoplanets Resolving Power (review) The bigger the size of the telescope, the better it is at discerning fine details
Lecture #15: Plan Telescopes (cont d) Effects of Earth s Atmosphere Extrasolar planets = Exoplanets Resolving Power (review) The bigger the size of the telescope, the better it is at discerning fine details
What Have We Found? 1978 planets in 1488 systems as of 11/15/15 (http://exoplanet.eu/ ) 1642 planets candidates (http://exoplanets.
 Exoplanets. II What Have We Found? 1978 planets in 1488 systems as of 11/15/15 (http://exoplanet.eu/ ) 1642 planets + 3787 candidates (http://exoplanets.org) Detected by radial velocity/astrometry: 621
Exoplanets. II What Have We Found? 1978 planets in 1488 systems as of 11/15/15 (http://exoplanet.eu/ ) 1642 planets + 3787 candidates (http://exoplanets.org) Detected by radial velocity/astrometry: 621
Planets are plentiful
 Extra-Solar Planets Planets are plentiful The first planet orbiting another Sun-like star was discovered in 1995. We now know of 209 (Feb 07). Including several stars with more than one planet - true planetary
Extra-Solar Planets Planets are plentiful The first planet orbiting another Sun-like star was discovered in 1995. We now know of 209 (Feb 07). Including several stars with more than one planet - true planetary
13 - EXTRASOLAR PLANETS
 NSCI 314 LIFE IN THE COSMOS 13 - EXTRASOLAR PLANETS Dr. Karen Kolehmainen Department of Physics, CSUSB http://physics.csusb.edu/~karen/ EXTRASOLAR PLANETS? DO PLANETS ORBIT AROUND OTHER STARS? WE WOULD
NSCI 314 LIFE IN THE COSMOS 13 - EXTRASOLAR PLANETS Dr. Karen Kolehmainen Department of Physics, CSUSB http://physics.csusb.edu/~karen/ EXTRASOLAR PLANETS? DO PLANETS ORBIT AROUND OTHER STARS? WE WOULD
Key Ideas: The Search for New Planets. Scientific Questions. Are we alone in the Universe? Direct Imaging. Searches for Extrasolar Planets
 The Search for New Planets Key Ideas: Search for planets around other stars. Successful Search Techniques: Astrometric Wobble Doppler Wobble major discovery method Planetary Transits planets we can study
The Search for New Planets Key Ideas: Search for planets around other stars. Successful Search Techniques: Astrometric Wobble Doppler Wobble major discovery method Planetary Transits planets we can study
The Problem. Until 1995, we only knew of one Solar System - our own
 Extrasolar Planets Until 1995, we only knew of one Solar System - our own The Problem We had suspected for hundreds of years, and had confirmed as long ago as the 1800s that the stars were extremely distant
Extrasolar Planets Until 1995, we only knew of one Solar System - our own The Problem We had suspected for hundreds of years, and had confirmed as long ago as the 1800s that the stars were extremely distant
9. Formation of the Solar System
 9. Formation of the Solar System The evolution of the world may be compared to a display of fireworks that has just ended: some few red wisps, ashes, and smoke. Standing on a cool cinder, we see the slow
9. Formation of the Solar System The evolution of the world may be compared to a display of fireworks that has just ended: some few red wisps, ashes, and smoke. Standing on a cool cinder, we see the slow
Planets & Life. Planets & Life PHYS 214. Please start all class related s with 214: 214: Dept of Physics (308A)
 Planets & Life Planets & Life PHYS 214 Dr Rob Thacker Dept of Physics (308A) thacker@astro.queensu.ca Please start all class related emails with 214: 214: Today s s lecture Assignment 1 marked will hand
Planets & Life Planets & Life PHYS 214 Dr Rob Thacker Dept of Physics (308A) thacker@astro.queensu.ca Please start all class related emails with 214: 214: Today s s lecture Assignment 1 marked will hand
Lecture #15: Plan. Telescopes (cont d) Effects of Earth s Atmosphere Extrasolar planets = Exoplanets
 Lecture #15: Plan Telescopes (cont d) Effects of Earth s Atmosphere Extrasolar planets = Exoplanets Collecting Area Light bucket : the bigger the area of the telescope s mirror or lens, the more photons
Lecture #15: Plan Telescopes (cont d) Effects of Earth s Atmosphere Extrasolar planets = Exoplanets Collecting Area Light bucket : the bigger the area of the telescope s mirror or lens, the more photons
18 An Eclipsing Extrasolar Planet
 Name: Date: 18 An Eclipsing Extrasolar Planet 18.1 Introduction One of the more recent new fields in astronomy is the search for (and discovery of) planets orbiting around stars other than our Sun, or
Name: Date: 18 An Eclipsing Extrasolar Planet 18.1 Introduction One of the more recent new fields in astronomy is the search for (and discovery of) planets orbiting around stars other than our Sun, or
The Main Point(s) Lecture #36: Planets Around Other Stars. Extrasolar Planets! Reading: Chapter 13. Theory Observations
 Lecture #36: Planets Around Other Stars Extrasolar Planets! Theory Observations Detection methods Results to date... Implications for "Habitable Zones" Reading: Chapter 13 Astro 102/104 1 The Main Point(s)
Lecture #36: Planets Around Other Stars Extrasolar Planets! Theory Observations Detection methods Results to date... Implications for "Habitable Zones" Reading: Chapter 13 Astro 102/104 1 The Main Point(s)
Chapter 15 The Formation of Planetary Systems
 Chapter 15 The Formation of Planetary Systems Units of Chapter 15 15.1 Modeling Planet Formation 15.2 Formation of the Solar System 15.3 Terrestrial and Jovian Planets 15.4 Interplanetary Debris 15.5 Solar
Chapter 15 The Formation of Planetary Systems Units of Chapter 15 15.1 Modeling Planet Formation 15.2 Formation of the Solar System 15.3 Terrestrial and Jovian Planets 15.4 Interplanetary Debris 15.5 Solar
Searching for Other Worlds
 Searching for Other Worlds Lecture 32 1 In-Class Question What is the Greenhouse effect? a) Optical light from the Sun is reflected into space while infrared light passes through the atmosphere and heats
Searching for Other Worlds Lecture 32 1 In-Class Question What is the Greenhouse effect? a) Optical light from the Sun is reflected into space while infrared light passes through the atmosphere and heats
Class 15 Formation of the Solar System
 Class 16 Extra-solar planets The radial-velocity technique for finding extrasolar planets Other techniques for finding extrasolar planets Class 15 Formation of the Solar System What does a successful model
Class 16 Extra-solar planets The radial-velocity technique for finding extrasolar planets Other techniques for finding extrasolar planets Class 15 Formation of the Solar System What does a successful model
The formation & evolution of solar systems
 The formation & evolution of solar systems Content expectations Birth of the Solar System What did the material that eventually became the Sun and planets look like originally? Interstellar clouds like
The formation & evolution of solar systems Content expectations Birth of the Solar System What did the material that eventually became the Sun and planets look like originally? Interstellar clouds like
Lecture Outlines. Chapter 15. Astronomy Today 8th Edition Chaisson/McMillan Pearson Education, Inc.
 Lecture Outlines Chapter 15 Astronomy Today 8th Edition Chaisson/McMillan Chapter 15 Exoplanets Units of Chapter 15 15.1 Modeling Planet Formation 15.2 Solar System Regularities and Irregularities 15.3
Lecture Outlines Chapter 15 Astronomy Today 8th Edition Chaisson/McMillan Chapter 15 Exoplanets Units of Chapter 15 15.1 Modeling Planet Formation 15.2 Solar System Regularities and Irregularities 15.3
Lecture 20: Planet formation II. Clues from Exoplanets
 Lecture 20: Planet formation II. Clues from Exoplanets 1 Outline Definition of a planet Properties of exoplanets Formation models for exoplanets gravitational instability model core accretion scenario
Lecture 20: Planet formation II. Clues from Exoplanets 1 Outline Definition of a planet Properties of exoplanets Formation models for exoplanets gravitational instability model core accretion scenario
Credit: NASA/Kepler Mission/Dana Berry. Exoplanets
 Credit: NASA/Kepler Mission/Dana Berry Exoplanets Outline What is an exoplanet? Why are they interesting? How can we find them? Exolife?? The future... Jon Thaler Exoplanets 2 What is an Exoplanet? Most
Credit: NASA/Kepler Mission/Dana Berry Exoplanets Outline What is an exoplanet? Why are they interesting? How can we find them? Exolife?? The future... Jon Thaler Exoplanets 2 What is an Exoplanet? Most
RING DISCOVERED AROUND DWARF PLANET
 RING DISCOVERED AROUND DWARF PLANET Haumea, a dwarf planet in the Kuiper Belt was just found to have a ring. Why? Hint: what causes the Jovian planet rings? Artist's conception, not a real photo RING DISCOVERED
RING DISCOVERED AROUND DWARF PLANET Haumea, a dwarf planet in the Kuiper Belt was just found to have a ring. Why? Hint: what causes the Jovian planet rings? Artist's conception, not a real photo RING DISCOVERED
Lecture Outlines. Chapter 15. Astronomy Today 7th Edition Chaisson/McMillan Pearson Education, Inc.
 Lecture Outlines Chapter 15 Astronomy Today 7th Edition Chaisson/McMillan Chapter 15 The Formation of Planetary Systems Units of Chapter 15 15.1 Modeling Planet Formation 15.2 Terrestrial and Jovian Planets
Lecture Outlines Chapter 15 Astronomy Today 7th Edition Chaisson/McMillan Chapter 15 The Formation of Planetary Systems Units of Chapter 15 15.1 Modeling Planet Formation 15.2 Terrestrial and Jovian Planets
Transiting Hot Jupiters near the Galactic Center
 National Aeronautics and Space Administration Transiting Hot Jupiters near the Galactic Center Kailash C. Sahu Taken from: Hubble 2006 Science Year in Review The full contents of this book include more
National Aeronautics and Space Administration Transiting Hot Jupiters near the Galactic Center Kailash C. Sahu Taken from: Hubble 2006 Science Year in Review The full contents of this book include more
Planets: Name Distance from Sun Satellites Year Day Mercury 0.4AU yr 60 days Venus yr 243 days* Earth 1 1 yr 1 day Mars 1.
 The Solar System (Ch. 6 in text) We will skip from Ch. 6 to Ch. 15, only a survey of the solar system, the discovery of extrasolar planets (in more detail than the textbook), and the formation of planetary
The Solar System (Ch. 6 in text) We will skip from Ch. 6 to Ch. 15, only a survey of the solar system, the discovery of extrasolar planets (in more detail than the textbook), and the formation of planetary
The Hertzprung-Russell Diagram. The Hertzprung-Russell Diagram. Question
 Key Concepts: Lecture 21: Measuring the properties of stars (cont.) The Hertzsprung-Russell (HR) Diagram (L versus T) The Hertzprung-Russell Diagram The Stefan-Boltzmann Law: flux emitted by a black body
Key Concepts: Lecture 21: Measuring the properties of stars (cont.) The Hertzsprung-Russell (HR) Diagram (L versus T) The Hertzprung-Russell Diagram The Stefan-Boltzmann Law: flux emitted by a black body
Which of the following correctly describes the meaning of albedo?
 Which of the following correctly describes the meaning of albedo? A) The lower the albedo, the more light the surface reflects, and the less it absorbs. B) The higher the albedo, the more light the surface
Which of the following correctly describes the meaning of albedo? A) The lower the albedo, the more light the surface reflects, and the less it absorbs. B) The higher the albedo, the more light the surface
Chapter 19 Origin of the Solar System
 Foundations of Astronomy 13e Seeds Phys1411 Introductory Astronomy Instructor: Dr. Goderya Foundations of Astronomy 13e Seeds Chapter 19 Origin of the Solar System Topics for this Class I. Survey of Solar
Foundations of Astronomy 13e Seeds Phys1411 Introductory Astronomy Instructor: Dr. Goderya Foundations of Astronomy 13e Seeds Chapter 19 Origin of the Solar System Topics for this Class I. Survey of Solar
What is it like? When did it form? How did it form. The Solar System. Fall, 2005 Astronomy 110 1
 What is it like? When did it form? How did it form The Solar System Fall, 2005 Astronomy 110 1 Fall, 2005 Astronomy 110 2 The planets all orbit the sun in the same direction. The Sun spins in the same
What is it like? When did it form? How did it form The Solar System Fall, 2005 Astronomy 110 1 Fall, 2005 Astronomy 110 2 The planets all orbit the sun in the same direction. The Sun spins in the same
Formation of the Solar System
 Formation of the Solar System What theory best explains the features of our solar system? The nebular theory states that our solar system formed from the gravitational collapse of a giant interstellar
Formation of the Solar System What theory best explains the features of our solar system? The nebular theory states that our solar system formed from the gravitational collapse of a giant interstellar
Young Solar-like Systems
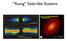 Young Solar-like Systems FIG.2. Panels(a),(b),and(c)show 2.9,1.3,and 0.87 mm ALMA continuum images of other panels, as well as an inset with an enlarged view of the inner 300 mas centered on the (f) show
Young Solar-like Systems FIG.2. Panels(a),(b),and(c)show 2.9,1.3,and 0.87 mm ALMA continuum images of other panels, as well as an inset with an enlarged view of the inner 300 mas centered on the (f) show
Observations of Extrasolar Planets
 Observations of Extrasolar Planets Hamilton 2005 Shay Zucker Observations of Extrasolar Planets Spectroscopic detection of exoplanets Emerging properties of the sample Transiting planets Future prospects
Observations of Extrasolar Planets Hamilton 2005 Shay Zucker Observations of Extrasolar Planets Spectroscopic detection of exoplanets Emerging properties of the sample Transiting planets Future prospects
Can We See Them?! Planet Detection! Planet is Much Fainter than Star!
 Can We See Them?! Planet Detection! Estimating f p! Not easily! Best cases were reported in late 2008! Will see these later! Problem is separating planet light from star light! Star is 10 9 times brighter
Can We See Them?! Planet Detection! Estimating f p! Not easily! Best cases were reported in late 2008! Will see these later! Problem is separating planet light from star light! Star is 10 9 times brighter
Planet Detection. Estimating f p
 Planet Detection Estimating f p Can We See Them? Not yet, but there are plans 3 recent claims, but planets very far from star, so some doubts Problem is separating planet light from star light Star is
Planet Detection Estimating f p Can We See Them? Not yet, but there are plans 3 recent claims, but planets very far from star, so some doubts Problem is separating planet light from star light Star is
Astronomy. physics.wm.edu/~hancock/171/ A. Dayle Hancock. Small 239. Office hours: MTWR 10-11am
 Astronomy A. Dayle Hancock adhancock@wm.edu Small 239 Office hours: MTWR 10-11am Planetology II Key characteristics Chemical elements and planet size Radioactive dating Solar system formation Solar nebula
Astronomy A. Dayle Hancock adhancock@wm.edu Small 239 Office hours: MTWR 10-11am Planetology II Key characteristics Chemical elements and planet size Radioactive dating Solar system formation Solar nebula
Data from: The Extrasolar Planet Encyclopaedia.
 Data from: The Extrasolar Planet Encyclopaedia http://exoplanet.eu/ 2009->10 Status of Exoplanet Searches Direct Detection: 5->9 planets detected Sensitive to large planets in large orbits around faint
Data from: The Extrasolar Planet Encyclopaedia http://exoplanet.eu/ 2009->10 Status of Exoplanet Searches Direct Detection: 5->9 planets detected Sensitive to large planets in large orbits around faint
Solar System Formation
 Solar System Formation Solar System Formation Question: How did our solar system and other planetary systems form? Comparative planetology has helped us understand Compare the differences and similarities
Solar System Formation Solar System Formation Question: How did our solar system and other planetary systems form? Comparative planetology has helped us understand Compare the differences and similarities
PLANETARY FORMATION THEORY EXPLORING EXOPLANETS
 PLANETARY FORMATION THEORY EXPLORING EXOPLANETS This is what we call planets around OTHER stars! PLANETARY FORMATION THEORY EXPLORING EXOPLANETS This is only as of June 2012. We ve found at least double
PLANETARY FORMATION THEORY EXPLORING EXOPLANETS This is what we call planets around OTHER stars! PLANETARY FORMATION THEORY EXPLORING EXOPLANETS This is only as of June 2012. We ve found at least double
Solar System Formation
 Solar System Formation Solar System Formation Question: How did our solar system and other planetary systems form? Comparative planetology has helped us understand Compare the differences and similarities
Solar System Formation Solar System Formation Question: How did our solar system and other planetary systems form? Comparative planetology has helped us understand Compare the differences and similarities
Exoplanets detection and properties
 Researching Physics Higher Researching Physics Contents Advice to students Page 3 Page 4 Page 5 Overview of the unit and activities Organising your work and carrying out the activities Assessment issues
Researching Physics Higher Researching Physics Contents Advice to students Page 3 Page 4 Page 5 Overview of the unit and activities Organising your work and carrying out the activities Assessment issues
Planet Detection! Estimating f p!
 Planet Detection! Estimating f p! Can We See Them?! Not easily! Best cases were reported in late 2008! Will see these later! Problem is separating planet light from star light! Star is 10 9 times brighter
Planet Detection! Estimating f p! Can We See Them?! Not easily! Best cases were reported in late 2008! Will see these later! Problem is separating planet light from star light! Star is 10 9 times brighter
Lab #5. Searching for Extrasolar Planets
 Lab #5 Searching for Extrasolar Planets Introduction Since the beginning of recorded history, humans have wondered whether we are alone in the Universe. Recently, Astronomers have begun to make significant
Lab #5 Searching for Extrasolar Planets Introduction Since the beginning of recorded history, humans have wondered whether we are alone in the Universe. Recently, Astronomers have begun to make significant
Solar System Formation
 Solar System Formation Solar System Formation Question: How did our solar system and other planetary systems form? Comparative planetology has helped us understand Compare the differences and similarities
Solar System Formation Solar System Formation Question: How did our solar system and other planetary systems form? Comparative planetology has helped us understand Compare the differences and similarities
Activities: The transit method, exploring distant solar systems, the chemistry of life.
 Kendall Planetarium Extreme Planets Planetarium Show Teacher s Guide PROGRAM OUTLINE Description: Extreme Planets immerses audiences in the cutting-edge science of finding planets orbit around stars other
Kendall Planetarium Extreme Planets Planetarium Show Teacher s Guide PROGRAM OUTLINE Description: Extreme Planets immerses audiences in the cutting-edge science of finding planets orbit around stars other
Name Period Date Earth and Space Science. Solar System Review
 Name Period Date Earth and Space Science Solar System Review 1. is the spinning a planetary object on its axis. 2. is the backward motion of planets. 3. The is a unit less number between 0 and 1 that describes
Name Period Date Earth and Space Science Solar System Review 1. is the spinning a planetary object on its axis. 2. is the backward motion of planets. 3. The is a unit less number between 0 and 1 that describes
II Planet Finding.
 II Planet Finding http://sgoodwin.staff.shef.ac.uk/phy229.html 1.0 Introduction There are a lot of slides in this lecture. Much of this should be familiar from PHY104 (Introduction to Astrophysics) and
II Planet Finding http://sgoodwin.staff.shef.ac.uk/phy229.html 1.0 Introduction There are a lot of slides in this lecture. Much of this should be familiar from PHY104 (Introduction to Astrophysics) and
Extrasolar Planets = Exoplanets III.
 Extrasolar Planets = Exoplanets III http://www.astro.keele.ac.uk/~rdj/planets/images/taugruishydra2.jpg Outline Gravitational microlensing Direct detection Exoplanet atmospheres Detecting planets by microlensing:
Extrasolar Planets = Exoplanets III http://www.astro.keele.ac.uk/~rdj/planets/images/taugruishydra2.jpg Outline Gravitational microlensing Direct detection Exoplanet atmospheres Detecting planets by microlensing:
The Kepler Mission: 20% of all Stars in the Milky Way Have Earth like Planets!
 The Kepler Mission: 20% of all Stars in the Milky Way Have Earth like Planets! Kepler Spacecraft Can we believe this result? What techniques and data were used to derive this important result? 1 How to
The Kepler Mission: 20% of all Stars in the Milky Way Have Earth like Planets! Kepler Spacecraft Can we believe this result? What techniques and data were used to derive this important result? 1 How to
Searching for planets around other stars. Searching for planets around other stars. Searching for other planetary systems this is a hard problem!
 Reading: Chap. 21, Sect.21.4-21.6 Final Exam: Tuesday, December 12; 4:30-6:30PM Homework 10: Due in recitation Dec. 1,4 1 Brief review of last time: Formation of Planetary Systems Observational Clues:
Reading: Chap. 21, Sect.21.4-21.6 Final Exam: Tuesday, December 12; 4:30-6:30PM Homework 10: Due in recitation Dec. 1,4 1 Brief review of last time: Formation of Planetary Systems Observational Clues:
Observations of extrasolar planets
 Observations of extrasolar planets 1 Mercury 2 Venus radar image from Magellan (vertical scale exaggerated 10 X) 3 Mars 4 Jupiter 5 Saturn 6 Saturn 7 Uranus and Neptune 8 we need to look out about 10 parsecs
Observations of extrasolar planets 1 Mercury 2 Venus radar image from Magellan (vertical scale exaggerated 10 X) 3 Mars 4 Jupiter 5 Saturn 6 Saturn 7 Uranus and Neptune 8 we need to look out about 10 parsecs
Activity 2 MODELING LAB
 Activity 2 MODELING LAB PURPOSE. This activity sets up the rest of the ExoLab investigation, and is intended to help your students predict what the signal of an alien world might look like. They use the
Activity 2 MODELING LAB PURPOSE. This activity sets up the rest of the ExoLab investigation, and is intended to help your students predict what the signal of an alien world might look like. They use the
Who was here? How can you tell? This is called indirect evidence!
 1 Who was here? How can you tell? This is called indirect evidence! 2 How does a planetary system form? The one we can study in the most detail is our solar system. If we want to know whether the solar
1 Who was here? How can you tell? This is called indirect evidence! 2 How does a planetary system form? The one we can study in the most detail is our solar system. If we want to know whether the solar
Planets and Brown Dwarfs
 Extra Solar Planets Extra Solar Planets We have estimated there may be 10 20 billion stars in Milky Way with Earth like planets, hospitable for life. But what evidence do we have that such planets even
Extra Solar Planets Extra Solar Planets We have estimated there may be 10 20 billion stars in Milky Way with Earth like planets, hospitable for life. But what evidence do we have that such planets even
Chapter 15: The Origin of the Solar System
 Chapter 15: The Origin of the Solar System The Solar Nebula Hypothesis Basis of modern theory of planet formation: Planets form at the same time from the same cloud as the star. Planet formation sites
Chapter 15: The Origin of the Solar System The Solar Nebula Hypothesis Basis of modern theory of planet formation: Planets form at the same time from the same cloud as the star. Planet formation sites
Astronomy 101 Lab: Hunt for Alien Worlds
 Name: Astronomy 101 Lab: Hunt for Alien Worlds Be prepared to make calculations in today s lab. Laptops will also be used for part of the lab, but you aren t required to bring your own. Pre-Lab Assignment:
Name: Astronomy 101 Lab: Hunt for Alien Worlds Be prepared to make calculations in today s lab. Laptops will also be used for part of the lab, but you aren t required to bring your own. Pre-Lab Assignment:
Habitability Outside the Solar System. A discussion of Bennett & Shostak Chapter 11 HNRS 228 Dr. H. Geller
 Habitability Outside the Solar System A discussion of Bennett & Shostak Chapter 11 HNRS 228 Dr. H. Geller 1 Chapter Overview Distant Suns (11.1) Life cycle of stars and their habitability zones Extrasolar
Habitability Outside the Solar System A discussion of Bennett & Shostak Chapter 11 HNRS 228 Dr. H. Geller 1 Chapter Overview Distant Suns (11.1) Life cycle of stars and their habitability zones Extrasolar
Chapter 19 The Origin of the Solar System
 Chapter 19 The Origin of the Solar System Early Hypotheses catastrophic hypotheses, e.g., passing star hypothesis: Star passing closely to the the sun tore material out of the sun, from which planets could
Chapter 19 The Origin of the Solar System Early Hypotheses catastrophic hypotheses, e.g., passing star hypothesis: Star passing closely to the the sun tore material out of the sun, from which planets could
Extrasolar Planets. Methods of detection Characterization Theoretical ideas Future prospects
 Extrasolar Planets Methods of detection Characterization Theoretical ideas Future prospects Methods of detection Methods of detection Methods of detection Pulsar timing Planetary motion around pulsar
Extrasolar Planets Methods of detection Characterization Theoretical ideas Future prospects Methods of detection Methods of detection Methods of detection Pulsar timing Planetary motion around pulsar
Agenda. International Space Station (ISS) International Space Station (ISS) Can we see light from first stars? 9. Formation of the Solar System
 9. Formation of the Solar System The evolution of the world may be compared to a display of fireworks that has just ended: some few red wisps, ashes, and smoke. Standing on a cool cinder, we see the slow
9. Formation of the Solar System The evolution of the world may be compared to a display of fireworks that has just ended: some few red wisps, ashes, and smoke. Standing on a cool cinder, we see the slow
Importance of the study of extrasolar planets. Exoplanets Introduction. Importance of the study of extrasolar planets
 Importance of the study of extrasolar planets Exoplanets Introduction Planets and Astrobiology (2017-2018) G. Vladilo Technological and scientific spin-offs Exoplanet observations are driving huge technological
Importance of the study of extrasolar planets Exoplanets Introduction Planets and Astrobiology (2017-2018) G. Vladilo Technological and scientific spin-offs Exoplanet observations are driving huge technological
EXOPLANET DISCOVERY. Daniel Steigerwald
 EXOPLANET DISCOVERY Daniel Steigerwald WHAT IS AN EXOPLANET? An exoplanet is a planet outside of our solar system Extrastellar Rogue 1853 Planets 1162 planetary systems 473 Multiple planetary systems HISTORY
EXOPLANET DISCOVERY Daniel Steigerwald WHAT IS AN EXOPLANET? An exoplanet is a planet outside of our solar system Extrastellar Rogue 1853 Planets 1162 planetary systems 473 Multiple planetary systems HISTORY
Active Galaxies and Galactic Structure Lecture 22 April 18th
 Active Galaxies and Galactic Structure Lecture 22 April 18th FINAL Wednesday 5/9/2018 6-8 pm 100 questions, with ~20-30% based on material covered since test 3. Do not miss the final! Extra Credit: Thursday
Active Galaxies and Galactic Structure Lecture 22 April 18th FINAL Wednesday 5/9/2018 6-8 pm 100 questions, with ~20-30% based on material covered since test 3. Do not miss the final! Extra Credit: Thursday
Earth 110 Exploration of the Solar System Assignment 6: Exoplanets Due in class Tuesday, March 3, 2015
 Name: Section: Earth 110 Exploration of the Solar System Assignment 6: Exoplanets Due in class Tuesday, March 3, 2015 Up until the mid 1990 s, we did not know if planets existed around other stars. Advancements
Name: Section: Earth 110 Exploration of the Solar System Assignment 6: Exoplanets Due in class Tuesday, March 3, 2015 Up until the mid 1990 s, we did not know if planets existed around other stars. Advancements
Galaxies and Star Systems
 Chapter 5 Section 5.1 Galaxies and Star Systems Galaxies Terms: Galaxy Spiral Galaxy Elliptical Galaxy Irregular Galaxy Milky Way Galaxy Quasar Black Hole Types of Galaxies A galaxy is a huge group of
Chapter 5 Section 5.1 Galaxies and Star Systems Galaxies Terms: Galaxy Spiral Galaxy Elliptical Galaxy Irregular Galaxy Milky Way Galaxy Quasar Black Hole Types of Galaxies A galaxy is a huge group of
Planets Around Other Stars Extrasolar Planet Detection Methods. February, 2006
 Planets Around Other Stars Extrasolar Planet Detection Methods February, 2006 Distribution of this File Extrasolar_planet_detection.ppt This Powerpoint presentation was put together for the purpose of
Planets Around Other Stars Extrasolar Planet Detection Methods February, 2006 Distribution of this File Extrasolar_planet_detection.ppt This Powerpoint presentation was put together for the purpose of
Star Systems and Galaxies
 Star Systems and Galaxies Why Does the Milky Way Look Hazy? 1. Using a pencil, carefully poke at least 20 holes close together in a sheet of white paper. 2. Tape the paper to a chalkboard or dark-colored
Star Systems and Galaxies Why Does the Milky Way Look Hazy? 1. Using a pencil, carefully poke at least 20 holes close together in a sheet of white paper. 2. Tape the paper to a chalkboard or dark-colored
Sombrero Galaxy. The Sombrero Galaxy is located on the southern edge of the rich Virgo cluster of galaxies.
 Sombrero Galaxy The Sombrero Galaxy is located on the southern edge of the rich Virgo cluster of galaxies. Sombrero Galaxy This galaxy is 28 million light-years away. For comparison, it takes sunlight
Sombrero Galaxy The Sombrero Galaxy is located on the southern edge of the rich Virgo cluster of galaxies. Sombrero Galaxy This galaxy is 28 million light-years away. For comparison, it takes sunlight
Why Should We Expect to Find Other Planets? Planetary system formation is a natural by-product of star formation
 1 Why Should We Expect to Find Other Planets? Planetary system formation is a natural by-product of star formation 2 Why Should We Expect to Find Other Planets? Observations show young stars are surrounded
1 Why Should We Expect to Find Other Planets? Planetary system formation is a natural by-product of star formation 2 Why Should We Expect to Find Other Planets? Observations show young stars are surrounded
Other planetary systems
 Exoplanets are faint! Other planetary systems Planets are seen only by reflected light at optical wavelengths At the distance of another star the faint light of a planet is lost in the glare of the star
Exoplanets are faint! Other planetary systems Planets are seen only by reflected light at optical wavelengths At the distance of another star the faint light of a planet is lost in the glare of the star
MS-ESS1-1 Earth's Place in the Universe
 MS-ESS1-1 Earth's Place in the Universe Students who demonstrate understanding can: MS-ESS1-1. Develop and use a model of the Earth-sun-moon system to describe the cyclic patterns of lunar phases, eclipses
MS-ESS1-1 Earth's Place in the Universe Students who demonstrate understanding can: MS-ESS1-1. Develop and use a model of the Earth-sun-moon system to describe the cyclic patterns of lunar phases, eclipses
Searching for Other Worlds: The Methods
 Searching for Other Worlds: The Methods John Bally 1 1 Center for Astrophysics and Space Astronomy Department of Astrophysical and Planetary Sciences University of Colorado, Boulder The Search Extra-Solar
Searching for Other Worlds: The Methods John Bally 1 1 Center for Astrophysics and Space Astronomy Department of Astrophysical and Planetary Sciences University of Colorado, Boulder The Search Extra-Solar
Exoplanets. Saturday Physics for Everyone. Jon Thaler October 27, Credit: NASA/Kepler Mission/Dana Berry
 Exoplanets Saturday Physics for Everyone Jon Thaler October 27, 2012 Credit: NASA/Kepler Mission/Dana Berry Outline What is an exoplanet? Why are they intereskng? How can we find them? Exolife?? The future...
Exoplanets Saturday Physics for Everyone Jon Thaler October 27, 2012 Credit: NASA/Kepler Mission/Dana Berry Outline What is an exoplanet? Why are they intereskng? How can we find them? Exolife?? The future...
ASTRO Fall 2012 LAB #6: Extrasolar Planets
 ASTRO 1050 - Fall 2012 LAB #6: Extrasolar Planets ABSTRACT This is an exciting time in astronomy. Over the past two decades we have begun to indirectly detect planets that orbit stars other than our sun.
ASTRO 1050 - Fall 2012 LAB #6: Extrasolar Planets ABSTRACT This is an exciting time in astronomy. Over the past two decades we have begun to indirectly detect planets that orbit stars other than our sun.
ASTRO 1050 Extrasolar Planets
 ASTRO 1050 Extrasolar Planets ABSTRACT This is an exciting time in astronomy. Over the past two decades we have begun to indirectly detect planets that orbit stars other than our Sun. Methods of detection
ASTRO 1050 Extrasolar Planets ABSTRACT This is an exciting time in astronomy. Over the past two decades we have begun to indirectly detect planets that orbit stars other than our Sun. Methods of detection
Astro 1010 Planetary Astronomy Sample Questions for Exam 3
 Astro 1010 Planetary Astronomy Sample Questions for Exam 3 Chapter 6 1. Which of the following statements is false? a) Refraction is the bending of light when it passes from one medium to another. b) Mirrors
Astro 1010 Planetary Astronomy Sample Questions for Exam 3 Chapter 6 1. Which of the following statements is false? a) Refraction is the bending of light when it passes from one medium to another. b) Mirrors
Extrasolar Planet Detection Methods. Tom Koonce September, 2005
 Extrasolar Planet Detection Methods Tom Koonce September, 2005 Planets Around Other Stars? How is it possible to see something so small, so far away? If everything is aligned perfectly, we can see the
Extrasolar Planet Detection Methods Tom Koonce September, 2005 Planets Around Other Stars? How is it possible to see something so small, so far away? If everything is aligned perfectly, we can see the
Chapter 23: Dark Matter, Dark Energy & Future of the Universe. Galactic rotation curves
 Chapter 23: Dark Matter, Dark Energy & Future of the Universe Galactic rotation curves Orbital speed as a function of distance from the center: rotation_of_spiral_galaxy.htm Use Kepler s Third Law to get
Chapter 23: Dark Matter, Dark Energy & Future of the Universe Galactic rotation curves Orbital speed as a function of distance from the center: rotation_of_spiral_galaxy.htm Use Kepler s Third Law to get
Is there life outside of Earth? Activity 2: Moving Stars and Their Planets
 Is there life outside of Earth? Activity 2: Moving Stars and Their Planets Overview In this activity, students are introduced to the wobble-method (officially known as the radial velocity method) of detecting
Is there life outside of Earth? Activity 2: Moving Stars and Their Planets Overview In this activity, students are introduced to the wobble-method (officially known as the radial velocity method) of detecting
Finding exoplanets (planets orbi2ng other stars)
 Finding exoplanets (planets orbi2ng other stars) Why is this hard? Well, take the Earth and the Sun? The Sun is bright, Earth is faint; Earth doesn t weigh much 1/300,000 th of Sun. As seen from nearest
Finding exoplanets (planets orbi2ng other stars) Why is this hard? Well, take the Earth and the Sun? The Sun is bright, Earth is faint; Earth doesn t weigh much 1/300,000 th of Sun. As seen from nearest
Astronomy 210 Midterm #2
 Astronomy 210 Midterm #2 This Class (Lecture 27): Birth of the Solar System II Next Class: Exam!!!! 2 nd Hour Exam on Friday!!! Review Session on Thursday 12-1:30 in room 236 Solar Observing starts on
Astronomy 210 Midterm #2 This Class (Lecture 27): Birth of the Solar System II Next Class: Exam!!!! 2 nd Hour Exam on Friday!!! Review Session on Thursday 12-1:30 in room 236 Solar Observing starts on
Earth Space Systems. Semester 1 Exam. Astronomy Vocabulary
 Earth Space Systems Semester 1 Exam Astronomy Vocabulary Astronomical Unit- Aurora- Big Bang- Black Hole- 1AU is the average distance between the Earth and the Sun (93 million miles). This unit of measurement
Earth Space Systems Semester 1 Exam Astronomy Vocabulary Astronomical Unit- Aurora- Big Bang- Black Hole- 1AU is the average distance between the Earth and the Sun (93 million miles). This unit of measurement
The evolution of a Solar-like system. Young Solar-like Systems. Searching for Extrasolar Planets: Motivation
 Young Solar-like Systems The evolution of a Solar-like system FIG.2. Panels(a),(b),and(c)show2.9,1.3,and0.87mmALMAcontinuum images of HL Tau. Panel (d) shows the 1.3 mm psf for the same FOV as the other
Young Solar-like Systems The evolution of a Solar-like system FIG.2. Panels(a),(b),and(c)show2.9,1.3,and0.87mmALMAcontinuum images of HL Tau. Panel (d) shows the 1.3 mm psf for the same FOV as the other
AST2000 Lecture Notes
 AST2000 Lecture Notes Part 1C Extrasolar planets Questions to ponder before the lecture 1. Why is it only during recent years that we have started to detect planets orbiting stars outside our solar system?
AST2000 Lecture Notes Part 1C Extrasolar planets Questions to ponder before the lecture 1. Why is it only during recent years that we have started to detect planets orbiting stars outside our solar system?
