arxiv:math/ v2 [math.nt] 6 May 2001
|
|
|
- Ursula Bradley
- 5 years ago
- Views:
Transcription
1 A Elemetary Problem Equivalet to the Riema Hypothesis Jeffrey C. Lagarias (May 5, 200 versio) arxiv:math/000877v2 [math.nt] 6 May 200 ABSTRACT. The problem is: Let H =, that with equality oly for =. j= j d H + exp(h )log(h ), d AMS Subject Classificatio (2000): Primary M26, Secodary A25 Keywords: Riema hypothesis, colossally abudat umbers. Itroductio We cosider the followig problem. Problem E. Let H = j= with equality oly for =. j. Show that, for each, be the -th harmoic umber. Show, for each d H + exp(h )log(h ), (.) d The fuctio σ() = d d is the sum of divisors fuctio, so for example σ(6) = 2. The umber H is called the -th harmoic umber by Kuth, Graham ad Patashik [9, Sect. 6.3], who detail various properties of harmoic umbers. The E i Problem E might stad for either easy or elemetary. Perhaps H for hard would be a better letter to use, sice our object is to show the followig equivalece. Theorem. Problem E is equivalet to the Riema hypothesis. The Riema hypothesis, stated by Riema [7] i 859, cocers the complex zeros of the Riema zeta fuctio. The Riema zeta fuctio ζ(s) is defied by the Dirichlet series ζ(s) = s, = which coverges for R(s) >, ad it has a aalytic cotiuatio to the complex plae with oe sigularity, a simple pole with residue at s =. The Riema hypothesis states that the oreal zeros of the Riema zeta fuctio ζ(s) all lie o the lie R(s) = 2. Oe reaso for the great iterest i the Riema hypothesis, regarded by may as the most importat usolved problem
2 i pure mathematics, is its coectio with the distributio of prime umbers, described below. More sigificatly, the Riema hypothesis is a special case of questios cocerig geeralizatios of the zeta fuctio (L-fuctios) ad their coectios with problems i umber theory, algebraic geometry, topology, represetatio theory ad perhaps eve physics, see Berry ad Keatig [3], Katz ad Sarak [8] ad Murty[]. The coectio of the Riema hypothesis with prime umbers was the origial questio studied by Riema [7]. Let π(x) cout the umber of primes p with < p x. C. F. Gauss oted empirically that π(x) is well approximated by the logarithmic itegral which itself satisfies Li(x) = x 2 dt log t, Li(x) = x log x + O( x (log x) 2). The Riema hypothesis is equivalet to the assertio that for each ǫ > 0 there is a positive costat C ǫ such that π(x) Li(x) C ǫ x /2+ǫ for all x 2, see Edwards [5, p. 90]. The force of the Riema hypothesis lies i the small size of the error term. The strogest form kow of the Prime Number Theorem with error term asserts that π(x) Li(x) C x exp( C 2 (log x) 3/5 ǫ ), for ay positive ǫ, for certai positive costats C ad C 2 depedig o ǫ; this result is due to Viogradov ad Korobov i 958. Problem E ecodes a modificatio of a criterio of Guy Robi [8] for the Riema hypothesis. Robi s criterio states that the Riema hypothesis is true if ad oly if σ() < e γ log log for all 504, (.2) where γ is Euler s costat. This criterio is related to the desity of primes, as explaied i 2. Our aim was to obtai a problem statemet as elemetary as possible, cotaiig o udefied costats. However the hard work uderlyig the equivalece resides i the results of Robi stated i 3, where we give a proof of Theorem.. Before comig to the proof, i the ext sectio we describe how the Riema hypothesis is related to the sum of divisors fuctio. The coectio traces back to Ramauja s work o highly composite umbers, ad ivolves several results of Erdős with coauthors. 2. Colossally Abudat Numbers The Riema hypothesis is ecoded i the criterio of Theorem. i terms of the very thi set of values of σ() that are large. The sum of divisors fuctio is give by σ() = ( + p + p p a ) = ( + p pa), (2.) p a where the product is take over all primes p dividig ad the otatio p a, meas p a divides but p a+ does ot divide. Most values of σ() are o the order of C. The average size of σ() was essetially foud by Dirichlet i 849, ad is give by the followig result of Bachma, cf. Hardy ad Wright [7, Theorem 324]. p a 2
3 Theorem 2. (Bachma) The average order of σ() is π2 6. More precisely, as. j= σ(j) = π O( log ) The maximal order of σ() is somewhat larger, ad was determied by Growall i 93, see Hardy ad Wright [7, Theorem 323, Sect. 8.3 ad 22.9]. Theorem 2.2 (Growall) The asymptotic maximal size of σ() satisfies where γ is Euler s costat. lim sup σ() log log = eγ, This result ca be deduced from Mertes theorem, which asserts that ( p ) eγ log x. p x as x. A much more refied versio of the asymptotic upper boud, due to Robi [8, Theorem 2], asserts (ucoditioally) that for all 3, I 3 we will show that σ() < e γ log log log log. (2.2) H + exp(h )log(h ) e γ log log + 7 log, the right side of which is oly slightly smaller tha that of (2.2). Comparig this boud with (2.2) shows that the iequality (.), if ever false, caot be false by very much. The study of extremal values of fuctios of the divisors of is a brach of umber theory with a log history. Let d() cout the umber of divisors of (icludig ad itself). Highly composite umbers are those positive itegers such that d() > d(k) for k. Superior highly composite umbers are those positive itegers for which there is a positive expoet ǫ such that d() ǫ d(k) k ǫ for all k >, so that they maximize d() over all ; these form a subset of the highly composite umbers. The ǫ study of these umbers was iitiated by Ramauja. Oe ca formulate similar extrema for the sum of divisors fuctio. Superabudat umbers are those positive itegers such that σ() > σ(k) k for k. 3
4 σ() Factorizatio of Table : Colossally abudat umbers up to 0 8. Colossally abudat umbers are those umbers for which there is a positive expoet ǫ such that σ() σ(k) +ǫ k +ǫ for all k >. so that attais the maximum value of σ(k) k +ǫ over all k. The set of colossally abudat umbers is ifiite. They form a subset of the superabudat umbers, a fact which ca be deduced from the defiitio. Table gives the colossally abudat umbers up to 0 8, as give i []. Robi showed that if the Riema hypothesis is false, there will ecessarily exist a couterexample to the iequality (.2) which is a colossally abudat umber, cf. [8, Propositio of Sectio 3]; the same property ca be established for couterexamples to (.). (There could potetially exist other couterexamples as well.) Superabudat ad colossally abudat umbers were studied i detail by Alaoglu ad Erdős [] i 944. As evideced i the table, colossally abudat umbers cosist of a product of all the small primes up to some boud, with expoets which are oicreasig as the prime icreases. The values of these expoets have a characteristic smooth shape which ca be almost completely described (see (2.3) below). I fact these classes of umbers had bee studied earlier, by Ramauja, i his 95 work o highly composite umbers [4]. The otes i Ramajua s Collected Papers report: The Lodo Mathematical Society was i some fiacial difficulty at the time, ad Ramauja suppressed part of what he had writte i order to save expese. [4, p. 339]. Oly the first 52 of 75 sectios were prited. The mauscript of the upublished part was evetually rediscovered amog the papers of G. N. Watso, i Ramauja s Lost Notebook (see Adrews [2] Alaoglu ad Erdős [] use a slightly stroger defiitio of colossally abudat umber; they impose the additioal requiremet that σ() > σ(k) must hold for k <. With their defiitio the colossally abudat umbers are +ǫ k +ǫ exactly those give by (2.3) below. 4
5 ad Ramauja [5, pp ]) ad fially published i 997, i [6]. I it superabudat ad colossally abudat umbers are cosidered i Sectio 59, as special cases of the cocepts of geeralised highly composite umbers ad superior geeralised highly composite umbers, for the parameter value s =. Ramauja derived upper ad lower bouds for the maximal order of geeralised highly composite umbers i Sectio 7, assumig the Riema hypothesis. (The Riema hypothesis was assumed from Sectio 40 oward i his paper.) His bouds imply, assumig the Riema hypothesis, that (.2) holds for all sufficietly large. The results of Alaoglu ad Erdős i their 944 paper are ucoditioal, ad maily cocered the expoets of primes occurrig i highly composite ad superabudat umbers. I cosiderig the expoets of primes appearig i colossally abudat umbers, they raised the followig questio, which is still usolved. Cojecture. (Alaoglu ad Erdős) If p ad q are both primes, is it true that p x ad q x are both ratioal oly if x is a iteger? This cojecture would follow as a cosequece 2 of the four expoetials cojecture i trascedetal umber theory, which asserts that if a,a 2 form a pair of complex umbers, liearly idepedet over the ratioals Q, ad b,b 2 is aother such pair, also liearly idepedet over the ratioals, the at least oe of the four expoetials {e a ib j : i,j = or 2} is trascedetal, see Lag [0, pp. 8-]. Alaoglu ad Erdős [, Theorem 0] showed that for geeric values of ǫ there is exactly oe maximizig iteger, ad the expoet a p (ǫ) of each prime p i it is a p (ǫ) = log(p+ǫ ) log(p ǫ ) ; (2.3) log p furthermore for all ǫ > 0 this value of is maximizig. However for a discrete set of ǫ there will be more tha oe maximizig iteger. Erdős ad Nicolas [6, p. 70] later showed that for a give value of ǫ there will be exactly oe, two or four itegers that attai the maximum value of σ(k). If k +ǫ the cojecture of Alaoglu ad Erdős above has a positive aswer, the o values of ǫ will have four extremal itegers. This would imply that the ratio of two cosecutive colossally abudat umbers, the larger divided by the smaller, will always be a prime, ad that every colossally abudat umber has a factorizatio (2.3) for some oempty ope iterval of geeric values of ǫ. Now we ca explai the relevace of the Riema hypothesis to the extremal size of σ(). Colossally abudat umbers are products of all the small primes raised to powers that are a smoothly decreasig fuctio of their size. Fluctuatios i the distributio of primes will be reflected i fluctuatios i the growth rate of σ() take over the set of colossally abudat umbers. Recall that the Riema hypothesis is equivalet to the assertio that for each ǫ > 0, π(x) Li(x) < x /2+ǫ holds for all sufficietly large x. It is also kow that if the Riema hypothesis is false, the there will exist a specific positive costat δ such that the oe-sided iequality π(x) > Li(x) + x /2+δ is true for a ifiite set of values with x. Heuristically, if we choose a value of x where such a excess of primes over Li(x) occurs, ad the take a product of all primes up to this boud, choosig 2 For o-ratioal x cosider a = log p, a 2 = log q, b = ad b 2 = x i the four expoetials cojecture. For o-iteger ratioal x a direct argumet is used. 5
6 appropriate expoets, oe may hope to costruct umbers with σ() exceedig e γ log log by a small amout. If the Riema hypothesis holds, there is a smaller upper boud for excess of the umber of primes above Li(x), ad from this oe ca deduce a slighly better upper boud for σ(). The aalysis of Robi [8] gives a quatitative versio of this, as formulated i Propositios 3. ad 3.2 below. Oe ca prove ucoditioally that the iequality (.) holds for early all itegers. Eve if the Riema hypothesis is false, the set of exceptios to the iequality (.) will form a very sparse set. Furthermore, if there exists ay couterexample to (.), the value of will be very large. 3. Proofs The proof of Theorem. is based o the followig two results of Robi [8]. Propositio 3. (Robi) If the Riema hypothesis is true, the for each 504, d e γ log log, (3.) where γ is Euler s costat. d Proof. This is Theorem of Robi [8]. Propositio 3.2 (Robi) If the Riema hypothesis is false, the there exist costats 0 < β < 2 ad C > 0 such that d e γ C log log log log + (log ) β (3.2) holds for ifiitely may. d Proof. This appears i Propositio of Sectio 4 of Robi [8]. The costat β ca be chose to take ay value b < β < 2, where b = R(ρ) for some zero ρ of ζ(s) with R(ρ) > 2, ad C > 0 must be chose sufficietly small, depedig o ρ. The proof uses ideas from a result of Nicolas [2], [3, Propositio 3], which itself uses a method of Ladau. We prove two prelimiary lemmas. Lemma 3. For 3, exp(h )log(h ) e γ log log. (3.3) Proof. Lettig t deote the iteger part of t ad {t} the fractioal part of t, we have t t 2 dt = r t dt t 2 = ( r ) = H. r= Thus H = + t {t} t 2 dt = log + {t} dt. (3.4) t2 6
7 From this we obtai H = log + γ + where we have set {t} γ := t 2 dt. This is Euler s costat γ = , sice lettig yields which is its usual defiitio. Now (3.5) gives which o expoetiatig yields γ = lim (H log ), H > log + γ, {t} dt, (3.5) t2 exp(h ) e γ. (3.6) Fially H log so log(h ) log log > 0 for 3. Combiig this with (3.6) yields (3.3). Lemma 3.2 For 20, Proof. The formula (3.4) implies, for 3, H + exp(h )log(h ) e γ log log + 7 log. (3.7) log H log(log + ) log log + log( + ). (3.8) Next, (3.5) yields Sice we obtai from (3.9) that ( exp(h ) = exp log + γ + ( e γ exp ( = e γ exp dt t 2 exp(x) + 2x for 0 x, ) ( exp(h ) e γ + 2 ) ) {t} t 2 dt ). (3.9). (3.0) Combiig this boud with (3.8) yields exp(h )log(h ) e γ e γ log log + log( + ) + 2eγ (log log + ) e r log log + 6 log for 0. Usig H log + ad log log + for 20 yields (3.7). 7
8 Proof of Theorem. Suppose the Riema hypothesis is true. The Propositio 3. ad Lemma 3. together give, for 504, d e γ log log < H + exp(h )log H. d For 5040 oe verifies (.) directly by computer, the oly case of equality beig =. Suppose (.) holds for all. We argue by cotradictio, ad suppose that the Riema hypothesis is false. The Propositio 3.2 applies. However its lower boud, valid for ifiitely may, cotradicts the upper boud of Lemma 3.2 for sufficietly large. We coclude that the Riema hypothesis must be true. Ackowledgemets. I thak Michel Balazard for brigig Robi s criterio to my attetio, ad J.-L. Nicolas for refereces, particularly cocerig Ramauja, Eric Rais for checkig (.) for 5040 o the computer, ad Jim Reeds for correctios. I thak the reviewers for simplificatios of the proofs of Lemmas 3. ad 3.2. Refereces [] L. Alaoglu ad P. Erdős, O Highly Composite ad Similar Numbers, Tras. Amer. Math. Soc. 56 (944), [2] G. E. Adrews, A Itroductio to Ramauja s Lost Notebook, Amer. Math. Mothly 86 (979), [3] M. V. Berry ad J. P. Keatig, The Riema zeros ad eigevalue asymptotics, SIAM Review 4 (999), [4] M. Davis, Hilbert s Teth Problem: Aspects of a egative solutio, i: Mathematical Developmets arisig from Hilbert Problems, Proc. Symp. Pure Math. No. XXVIII, America Math. Society: Providece 976, pp [5] H. E. Edwards, Riema s Zeta Fuctio, Academic Press: New York 974. [6] P. Erdős ad J.-L. Nicolas, Répartitio des ombres superabodats, Bull. Math. Soc. Frace 03 (975), [7] G. H. Hardy ad E. M. Wright, A Itroductio to the Theory of Numbers. Fifth Editio. Oxford Uiv. Press: Oxford 979. [8] N. Katz ad P. Sarak, Zeros of zeta fuctios ad symmetry, Bull. Amer. Math. Soc. 36 (999), 26. [9] D. Kuth, R. L. Graham ad O. Patashik, Cocrete Mathematics (Secod Editio), Addiso- Wesley: Readig, MA 994. [0] S. Lag, Trascedetal Number Theory, Addiso-Wesley: Readig, Mass [] M. R. Murty, A motivated itroductio to the Laglads program, i: Advaces i Number Theory, Oxford U. Press: New York 993, pp
9 [2] J. L. Nicolas, Petites valeurs de la foctio d Euler et hypothèse de Riema, Semiar o umber theory, Paris (Parius 98/982), Birkhäuser, Bosto 983, pp [3] J. L. Nicolas, Petites valeurs de la foctio d Euler, J. Number Theory 7 (983), [4] S. Ramauja, Highly composite umbers, Proc. Lodo Math. Soc. 4 (95), (Also, S. Ramauja, Collected Papers,, Chelsea 962, pp , otes pp ) [5] S. Ramauja, The Lost otebook ad other upublished papers. With a itroductio by George E. Adrews, Narosa: New Delhi ad Spriger-Verlag: Berli-New York 988. [6] S. Ramauja, Highly composite umbers. Aotated ad with a foreword by J.-L. Nicholas ad G. Robi, Ramauja J. (997), [7] G. F. B. Riema, Ueber die Azahl der Primzahle uter eier gegebee Grösse, Moatsber. Akad. Berli (859), (Also i: G. F. B. Riema, Gesammelte Mathematische Werke (Ed. H. Weber), Dover reprit 953.) [Eglish traslatio i: Edwards (974), pp ] [8] G. Robi, Grades valeurs de la foctio somme des diviseurs et hypothèse de Riema, J. Math. Pures Appl. 63 (984), AT&T Labs Research, Florham Park, NJ , USA address: jcl@research.att.com 9
RIEMANN HYPOTHESIS PROOF
 RIEMANN HYPOTHESIS PROOF IDRISS OLIVIER BADO October, 08 Abstract The mai cotributio of this paper is to achieve the proof of Riema hypothesis. The key idea is based o ew formulatio of the problem ζ(s)
RIEMANN HYPOTHESIS PROOF IDRISS OLIVIER BADO October, 08 Abstract The mai cotributio of this paper is to achieve the proof of Riema hypothesis. The key idea is based o ew formulatio of the problem ζ(s)
arxiv: v1 [math.nt] 5 Jan 2017 IBRAHIM M. ALABDULMOHSIN
![arxiv: v1 [math.nt] 5 Jan 2017 IBRAHIM M. ALABDULMOHSIN arxiv: v1 [math.nt] 5 Jan 2017 IBRAHIM M. ALABDULMOHSIN](/thumbs/89/98516099.jpg) FRACTIONAL PARTS AND THEIR RELATIONS TO THE VALUES OF THE RIEMANN ZETA FUNCTION arxiv:70.04883v [math.nt 5 Ja 07 IBRAHIM M. ALABDULMOHSIN Kig Abdullah Uiversity of Sciece ad Techology (KAUST, Computer,
FRACTIONAL PARTS AND THEIR RELATIONS TO THE VALUES OF THE RIEMANN ZETA FUNCTION arxiv:70.04883v [math.nt 5 Ja 07 IBRAHIM M. ALABDULMOHSIN Kig Abdullah Uiversity of Sciece ad Techology (KAUST, Computer,
Dr. Clemens Kroll. Abstract
 Riema s Hypothesis ad Stieltjes Cojecture Riema s Hypothesis ad Stieltjes Cojecture Dr. Clemes Kroll Abstract It is show that Riema s hypothesis is true by showig that a equivalet statemet is true. Eve
Riema s Hypothesis ad Stieltjes Cojecture Riema s Hypothesis ad Stieltjes Cojecture Dr. Clemes Kroll Abstract It is show that Riema s hypothesis is true by showig that a equivalet statemet is true. Eve
MATH 6101 Fall Problems. Problems 11/9/2008. Series and a Famous Unsolved Problem (2-1)(2 + 1) ( 4) 12-Nov-2008 MATH
 /9/008 MATH 60 Fall 008 Series ad a Famous Usolved Problem = = + + + + ( - )( + ) 3 3 5 5 7 7 9 -Nov-008 MATH 60 ( 4) = + 5 48 -Nov-008 MATH 60 3 /9/008 ( )! = + -Nov-008 MATH 60 4 3 4 5 + + + + + + +
/9/008 MATH 60 Fall 008 Series ad a Famous Usolved Problem = = + + + + ( - )( + ) 3 3 5 5 7 7 9 -Nov-008 MATH 60 ( 4) = + 5 48 -Nov-008 MATH 60 3 /9/008 ( )! = + -Nov-008 MATH 60 4 3 4 5 + + + + + + +
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
(I.D) THE PRIME NUMBER THEOREM
 (I.D) THE PRIME NUMBER THEOREM So far, i our discussio of the distributio of the primes, we have ot directly addressed the questio of how their desity i the atural umbers chages as oe keeps coutig. But
(I.D) THE PRIME NUMBER THEOREM So far, i our discussio of the distributio of the primes, we have ot directly addressed the questio of how their desity i the atural umbers chages as oe keeps coutig. But
MATH 6101 Fall 2008 Series and a Famous Unsolved Problem
 MATH 60 Fall 2008 Series ad a Famous Usolved Problem Problems = + + + + = (2- )(2+ ) 3 3 5 5 7 7 9 2-Nov-2008 MATH 60 2 Problems ( 4) = + 25 48 2-Nov-2008 MATH 60 3 Problems ( )! = + 2-Nov-2008 MATH 60
MATH 60 Fall 2008 Series ad a Famous Usolved Problem Problems = + + + + = (2- )(2+ ) 3 3 5 5 7 7 9 2-Nov-2008 MATH 60 2 Problems ( 4) = + 25 48 2-Nov-2008 MATH 60 3 Problems ( )! = + 2-Nov-2008 MATH 60
Math 2784 (or 2794W) University of Connecticut
 ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
and each factor on the right is clearly greater than 1. which is a contradiction, so n must be prime.
 MATH 324 Summer 200 Elemetary Number Theory Solutios to Assigmet 2 Due: Wedesday July 2, 200 Questio [p 74 #6] Show that o iteger of the form 3 + is a prime, other tha 2 = 3 + Solutio: If 3 + is a prime,
MATH 324 Summer 200 Elemetary Number Theory Solutios to Assigmet 2 Due: Wedesday July 2, 200 Questio [p 74 #6] Show that o iteger of the form 3 + is a prime, other tha 2 = 3 + Solutio: If 3 + is a prime,
Two Topics in Number Theory: Sum of Divisors of the Factorial and a Formula for Primes
 Iteratioal Mathematical Forum, Vol. 2, 207, o. 9, 929-935 HIKARI Ltd, www.m-hiari.com https://doi.org/0.2988/imf.207.7088 Two Topics i Number Theory: Sum of Divisors of the Factorial ad a Formula for Primes
Iteratioal Mathematical Forum, Vol. 2, 207, o. 9, 929-935 HIKARI Ltd, www.m-hiari.com https://doi.org/0.2988/imf.207.7088 Two Topics i Number Theory: Sum of Divisors of the Factorial ad a Formula for Primes
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Asymptotic Formulae for the n-th Perfect Power
 3 47 6 3 Joural of Iteger Sequeces, Vol. 5 0, Article.5.5 Asymptotic Formulae for the -th Perfect Power Rafael Jakimczuk Divisió Matemática Uiversidad Nacioal de Lujá Bueos Aires Argetia jakimczu@mail.ulu.edu.ar
3 47 6 3 Joural of Iteger Sequeces, Vol. 5 0, Article.5.5 Asymptotic Formulae for the -th Perfect Power Rafael Jakimczuk Divisió Matemática Uiversidad Nacioal de Lujá Bueos Aires Argetia jakimczu@mail.ulu.edu.ar
The log-behavior of n p(n) and n p(n)/n
 Ramauja J. 44 017, 81-99 The log-behavior of p ad p/ William Y.C. Che 1 ad Ke Y. Zheg 1 Ceter for Applied Mathematics Tiaji Uiversity Tiaji 0007, P. R. Chia Ceter for Combiatorics, LPMC Nakai Uivercity
Ramauja J. 44 017, 81-99 The log-behavior of p ad p/ William Y.C. Che 1 ad Ke Y. Zheg 1 Ceter for Applied Mathematics Tiaji Uiversity Tiaji 0007, P. R. Chia Ceter for Combiatorics, LPMC Nakai Uivercity
(I.C) THE DISTRIBUTION OF PRIMES
 I.C) THE DISTRIBUTION OF PRIMES I the last sectio we showed via a Euclid-ispired, algebraic argumet that there are ifiitely may primes of the form p = 4 i.e. 4 + 3). I fact, this is true for primes of
I.C) THE DISTRIBUTION OF PRIMES I the last sectio we showed via a Euclid-ispired, algebraic argumet that there are ifiitely may primes of the form p = 4 i.e. 4 + 3). I fact, this is true for primes of
Sequences of Definite Integrals, Factorials and Double Factorials
 47 6 Joural of Iteger Sequeces, Vol. 8 (5), Article 5.4.6 Sequeces of Defiite Itegrals, Factorials ad Double Factorials Thierry Daa-Picard Departmet of Applied Mathematics Jerusalem College of Techology
47 6 Joural of Iteger Sequeces, Vol. 8 (5), Article 5.4.6 Sequeces of Defiite Itegrals, Factorials ad Double Factorials Thierry Daa-Picard Departmet of Applied Mathematics Jerusalem College of Techology
Harmonic Number Identities Via Euler s Transform
 1 2 3 47 6 23 11 Joural of Iteger Sequeces, Vol. 12 2009), Article 09.6.1 Harmoic Number Idetities Via Euler s Trasform Khristo N. Boyadzhiev Departmet of Mathematics Ohio Norther Uiversity Ada, Ohio 45810
1 2 3 47 6 23 11 Joural of Iteger Sequeces, Vol. 12 2009), Article 09.6.1 Harmoic Number Idetities Via Euler s Trasform Khristo N. Boyadzhiev Departmet of Mathematics Ohio Norther Uiversity Ada, Ohio 45810
ON THE LEHMER CONSTANT OF FINITE CYCLIC GROUPS
 ON THE LEHMER CONSTANT OF FINITE CYCLIC GROUPS NORBERT KAIBLINGER Abstract. Results of Lid o Lehmer s problem iclude the value of the Lehmer costat of the fiite cyclic group Z/Z, for 5 ad all odd. By complemetary
ON THE LEHMER CONSTANT OF FINITE CYCLIC GROUPS NORBERT KAIBLINGER Abstract. Results of Lid o Lehmer s problem iclude the value of the Lehmer costat of the fiite cyclic group Z/Z, for 5 ad all odd. By complemetary
Sequences and Limits
 Chapter Sequeces ad Limits Let { a } be a sequece of real or complex umbers A ecessary ad sufficiet coditio for the sequece to coverge is that for ay ɛ > 0 there exists a iteger N > 0 such that a p a q
Chapter Sequeces ad Limits Let { a } be a sequece of real or complex umbers A ecessary ad sufficiet coditio for the sequece to coverge is that for ay ɛ > 0 there exists a iteger N > 0 such that a p a q
Solutions to Tutorial 5 (Week 6)
 The Uiversity of Sydey School of Mathematics ad Statistics Solutios to Tutorial 5 (Wee 6 MATH2962: Real ad Complex Aalysis (Advaced Semester, 207 Web Page: http://www.maths.usyd.edu.au/u/ug/im/math2962/
The Uiversity of Sydey School of Mathematics ad Statistics Solutios to Tutorial 5 (Wee 6 MATH2962: Real ad Complex Aalysis (Advaced Semester, 207 Web Page: http://www.maths.usyd.edu.au/u/ug/im/math2962/
Math 140A Elementary Analysis Homework Questions 3-1
 Math 0A Elemetary Aalysis Homework Questios -.9 Limits Theorems for Sequeces Suppose that lim x =, lim y = 7 ad that all y are o-zero. Detarime the followig limits: (a) lim(x + y ) (b) lim y x y Let s
Math 0A Elemetary Aalysis Homework Questios -.9 Limits Theorems for Sequeces Suppose that lim x =, lim y = 7 ad that all y are o-zero. Detarime the followig limits: (a) lim(x + y ) (b) lim y x y Let s
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MATH 324 Summer 2006 Elementary Number Theory Solutions to Assignment 2 Due: Thursday July 27, 2006
 MATH 34 Summer 006 Elemetary Number Theory Solutios to Assigmet Due: Thursday July 7, 006 Departmet of Mathematical ad Statistical Scieces Uiversity of Alberta Questio [p 74 #6] Show that o iteger of the
MATH 34 Summer 006 Elemetary Number Theory Solutios to Assigmet Due: Thursday July 7, 006 Departmet of Mathematical ad Statistical Scieces Uiversity of Alberta Questio [p 74 #6] Show that o iteger of the
On the Equivalence of Ramanujan s Partition Identities and a Connection with the Rogers Ramanujan Continued Fraction
 JOURNAL OF MATHEMATICAL ANALYSIS AND APPLICATIONS 98, 0 996 ARTICLE NO. 007 O the Equivalece of Ramauja s Partitio Idetities ad a Coectio with the RogersRamauja Cotiued Fractio Heg Huat Cha Departmet of
JOURNAL OF MATHEMATICAL ANALYSIS AND APPLICATIONS 98, 0 996 ARTICLE NO. 007 O the Equivalece of Ramauja s Partitio Idetities ad a Coectio with the RogersRamauja Cotiued Fractio Heg Huat Cha Departmet of
Abstract. Keywords: conjecture; divisor function; divisor summatory function; prime numbers; Dirichlet's divisor problem
 A ew cojecture o the divisor summatory fuctio offerig a much higher predictio accuracy tha Dirichlet's divisor problem approach * Wiki-like trasdiscipliary article (Ope developmet iterval: 28 -?) - workig
A ew cojecture o the divisor summatory fuctio offerig a much higher predictio accuracy tha Dirichlet's divisor problem approach * Wiki-like trasdiscipliary article (Ope developmet iterval: 28 -?) - workig
Math 104: Homework 2 solutions
 Math 04: Homework solutios. A (0, ): Sice this is a ope iterval, the miimum is udefied, ad sice the set is ot bouded above, the maximum is also udefied. if A 0 ad sup A. B { m + : m, N}: This set does
Math 04: Homework solutios. A (0, ): Sice this is a ope iterval, the miimum is udefied, ad sice the set is ot bouded above, the maximum is also udefied. if A 0 ad sup A. B { m + : m, N}: This set does
Bertrand s Postulate
 Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
The Boolean Ring of Intervals
 MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
Dirichlet s Theorem on Arithmetic Progressions
 Dirichlet s Theorem o Arithmetic Progressios Athoy Várilly Harvard Uiversity, Cambridge, MA 0238 Itroductio Dirichlet s theorem o arithmetic progressios is a gem of umber theory. A great part of its beauty
Dirichlet s Theorem o Arithmetic Progressios Athoy Várilly Harvard Uiversity, Cambridge, MA 0238 Itroductio Dirichlet s theorem o arithmetic progressios is a gem of umber theory. A great part of its beauty
IRRATIONALITY MEASURES, IRRATIONALITY BASES, AND A THEOREM OF JARNÍK 1. INTRODUCTION
 IRRATIONALITY MEASURES IRRATIONALITY BASES AND A THEOREM OF JARNÍK JONATHAN SONDOW ABSTRACT. We recall that the irratioality expoet µα ( ) of a irratioal umber α is defied usig the irratioality measure
IRRATIONALITY MEASURES IRRATIONALITY BASES AND A THEOREM OF JARNÍK JONATHAN SONDOW ABSTRACT. We recall that the irratioality expoet µα ( ) of a irratioal umber α is defied usig the irratioality measure
Definition 4.2. (a) A sequence {x n } in a Banach space X is a basis for X if. unique scalars a n (x) such that x = n. a n (x) x n. (4.
 4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
Prime Number Theorem Steven Finch. April 27, 2007
 Prime Number Theorem Steve Fich April 7, 007 Let π(x) = P p x, the umber of primes p ot exceedig x. GaussadLegedre cojectured a asymptotic expressio for π(x). Defie the Möbius mu fuctio μ() = if =, ( )
Prime Number Theorem Steve Fich April 7, 007 Let π(x) = P p x, the umber of primes p ot exceedig x. GaussadLegedre cojectured a asymptotic expressio for π(x). Defie the Möbius mu fuctio μ() = if =, ( )
Short and fuzzy derivations of five remarkable formulas for primes
 SHORT AND FUZZY DERIVATIONS Short ad fuzzy derivatios of five remarkable formulas for primes THOMAS J. OSLER. Itroductio The prime umbers have fasciated us for over 600 years. Their mysterious behaviour
SHORT AND FUZZY DERIVATIONS Short ad fuzzy derivatios of five remarkable formulas for primes THOMAS J. OSLER. Itroductio The prime umbers have fasciated us for over 600 years. Their mysterious behaviour
On a Smarandache problem concerning the prime gaps
 O a Smaradache problem cocerig the prime gaps Felice Russo Via A. Ifate 7 6705 Avezzao (Aq) Italy felice.russo@katamail.com Abstract I this paper, a problem posed i [] by Smaradache cocerig the prime gaps
O a Smaradache problem cocerig the prime gaps Felice Russo Via A. Ifate 7 6705 Avezzao (Aq) Italy felice.russo@katamail.com Abstract I this paper, a problem posed i [] by Smaradache cocerig the prime gaps
An application of the Hooley Huxley contour
 ACTA ARITHMETICA LXV. 993) A applicatio of the Hooley Huxley cotour by R. Balasubramaia Madras), A. Ivić Beograd) ad K. Ramachadra Bombay) To the memory of Professor Helmut Hasse 898 979). Itroductio ad
ACTA ARITHMETICA LXV. 993) A applicatio of the Hooley Huxley cotour by R. Balasubramaia Madras), A. Ivić Beograd) ad K. Ramachadra Bombay) To the memory of Professor Helmut Hasse 898 979). Itroductio ad
Beurling Integers: Part 2
 Beurlig Itegers: Part 2 Isomorphisms Devi Platt July 11, 2015 1 Prime Factorizatio Sequeces I the last article we itroduced the Beurlig geeralized itegers, which ca be represeted as a sequece of real umbers
Beurlig Itegers: Part 2 Isomorphisms Devi Platt July 11, 2015 1 Prime Factorizatio Sequeces I the last article we itroduced the Beurlig geeralized itegers, which ca be represeted as a sequece of real umbers
A PROOF OF THE TWIN PRIME CONJECTURE AND OTHER POSSIBLE APPLICATIONS
 A PROOF OF THE TWI PRIME COJECTURE AD OTHER POSSIBLE APPLICATIOS by PAUL S. BRUCKMA 38 Frot Street, #3 aaimo, BC V9R B8 (Caada) e-mail : pbruckma@hotmail.com ABSTRACT : A elemetary proof of the Twi Prime
A PROOF OF THE TWI PRIME COJECTURE AD OTHER POSSIBLE APPLICATIOS by PAUL S. BRUCKMA 38 Frot Street, #3 aaimo, BC V9R B8 (Caada) e-mail : pbruckma@hotmail.com ABSTRACT : A elemetary proof of the Twi Prime
MDIV. Multiple divisor functions
 MDIV. Multiple divisor fuctios The fuctios τ k For k, defie τ k ( to be the umber of (ordered factorisatios of ito k factors, i other words, the umber of ordered k-tuples (j, j 2,..., j k with j j 2...
MDIV. Multiple divisor fuctios The fuctios τ k For k, defie τ k ( to be the umber of (ordered factorisatios of ito k factors, i other words, the umber of ordered k-tuples (j, j 2,..., j k with j j 2...
Proc. Amer. Math. Soc. 139(2011), no. 5, BINOMIAL COEFFICIENTS AND THE RING OF p-adic INTEGERS
 Proc. Amer. Math. Soc. 139(2011, o. 5, 1569 1577. BINOMIAL COEFFICIENTS AND THE RING OF p-adic INTEGERS Zhi-Wei Su* ad Wei Zhag Departmet of Mathematics, Naig Uiversity Naig 210093, People s Republic of
Proc. Amer. Math. Soc. 139(2011, o. 5, 1569 1577. BINOMIAL COEFFICIENTS AND THE RING OF p-adic INTEGERS Zhi-Wei Su* ad Wei Zhag Departmet of Mathematics, Naig Uiversity Naig 210093, People s Republic of
Math 140A Elementary Analysis Homework Questions 1
 Math 14A Elemetary Aalysis Homewor Questios 1 1 Itroductio 1.1 The Set N of Natural Numbers 1 Prove that 1 2 2 2 2 1 ( 1(2 1 for all atural umbers. 2 Prove that 3 11 (8 5 4 2 for all N. 4 (a Guess a formula
Math 14A Elemetary Aalysis Homewor Questios 1 1 Itroductio 1.1 The Set N of Natural Numbers 1 Prove that 1 2 2 2 2 1 ( 1(2 1 for all atural umbers. 2 Prove that 3 11 (8 5 4 2 for all N. 4 (a Guess a formula
A Simplified Binet Formula for k-generalized Fibonacci Numbers
 A Simplified Biet Formula for k-geeralized Fiboacci Numbers Gregory P. B. Dresde Departmet of Mathematics Washigto ad Lee Uiversity Lexigto, VA 440 dresdeg@wlu.edu Zhaohui Du Shaghai, Chia zhao.hui.du@gmail.com
A Simplified Biet Formula for k-geeralized Fiboacci Numbers Gregory P. B. Dresde Departmet of Mathematics Washigto ad Lee Uiversity Lexigto, VA 440 dresdeg@wlu.edu Zhaohui Du Shaghai, Chia zhao.hui.du@gmail.com
Sequences and Series of Functions
 Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Solutions to Math 347 Practice Problems for the final
 Solutios to Math 347 Practice Problems for the fial 1) True or False: a) There exist itegers x,y such that 50x + 76y = 6. True: the gcd of 50 ad 76 is, ad 6 is a multiple of. b) The ifiimum of a set is
Solutios to Math 347 Practice Problems for the fial 1) True or False: a) There exist itegers x,y such that 50x + 76y = 6. True: the gcd of 50 ad 76 is, ad 6 is a multiple of. b) The ifiimum of a set is
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS
 THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
Ramanujan s Famous Partition Congruences
 Ope Sciece Joural of Mathematics ad Applicatio 6; 4(): - http://wwwopescieceoliecom/joural/osjma ISSN:8-494 (Prit); ISSN:8-494 (Olie) Ramauja s Famous Partitio Cogrueces Md Fazlee Hossai, Nil Rata Bhattacharjee,
Ope Sciece Joural of Mathematics ad Applicatio 6; 4(): - http://wwwopescieceoliecom/joural/osjma ISSN:8-494 (Prit); ISSN:8-494 (Olie) Ramauja s Famous Partitio Cogrueces Md Fazlee Hossai, Nil Rata Bhattacharjee,
THE ZETA FUNCTION AND THE RIEMANN HYPOTHESIS. Contents 1. History 1
 THE ZETA FUNCTION AND THE RIEMANN HYPOTHESIS VIKTOR MOROS Abstract. The zeta fuctio has bee studied for ceturies but mathematicias are still learig about it. I this paper, I will discuss some of the zeta
THE ZETA FUNCTION AND THE RIEMANN HYPOTHESIS VIKTOR MOROS Abstract. The zeta fuctio has bee studied for ceturies but mathematicias are still learig about it. I this paper, I will discuss some of the zeta
The Nicolas and Robin inequalities with sums of two squares
 Moatsh Math (2009) 157:303 322 DOI 10.1007/s00605-008-0022-x The Nicolas ad Robi iequalities with sums of two squares William D. Baks Derrick N. Hart Pieter Moree C. Wesley Nevas Received: 12 October 2007
Moatsh Math (2009) 157:303 322 DOI 10.1007/s00605-008-0022-x The Nicolas ad Robi iequalities with sums of two squares William D. Baks Derrick N. Hart Pieter Moree C. Wesley Nevas Received: 12 October 2007
If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero?
![If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero? If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero?](/thumbs/89/99848926.jpg) 2 Lebesgue Measure I Chapter 1 we defied the cocept of a set of measure zero, ad we have observed that every coutable set is of measure zero. Here are some atural questios: If a subset E of R cotais a
2 Lebesgue Measure I Chapter 1 we defied the cocept of a set of measure zero, ad we have observed that every coutable set is of measure zero. Here are some atural questios: If a subset E of R cotais a
The value of Banach limits on a certain sequence of all rational numbers in the interval (0,1) Bao Qi Feng
 The value of Baach limits o a certai sequece of all ratioal umbers i the iterval 0, Bao Qi Feg Departmet of Mathematical Scieces, Ket State Uiversity, Tuscarawas, 330 Uiversity Dr. NE, New Philadelphia,
The value of Baach limits o a certai sequece of all ratioal umbers i the iterval 0, Bao Qi Feg Departmet of Mathematical Scieces, Ket State Uiversity, Tuscarawas, 330 Uiversity Dr. NE, New Philadelphia,
ON MEAN ERGODIC CONVERGENCE IN THE CALKIN ALGEBRAS
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Pages 000 000 S 0002-9939(XX0000-0 ON MEAN ERGODIC CONVERGENCE IN THE CALKIN ALGEBRAS MARCH T. BOEDIHARDJO AND WILLIAM B. JOHNSON 2
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Pages 000 000 S 0002-9939(XX0000-0 ON MEAN ERGODIC CONVERGENCE IN THE CALKIN ALGEBRAS MARCH T. BOEDIHARDJO AND WILLIAM B. JOHNSON 2
COMPUTING THE EULER S CONSTANT: A HISTORICAL OVERVIEW OF ALGORITHMS AND RESULTS
 COMPUTING THE EULER S CONSTANT: A HISTORICAL OVERVIEW OF ALGORITHMS AND RESULTS GONÇALO MORAIS Abstract. We preted to give a broad overview of the algorithms used to compute the Euler s costat. Four type
COMPUTING THE EULER S CONSTANT: A HISTORICAL OVERVIEW OF ALGORITHMS AND RESULTS GONÇALO MORAIS Abstract. We preted to give a broad overview of the algorithms used to compute the Euler s costat. Four type
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
SOME PROPERTIES OF THE SEQUENCE OF PRIME NUMBERS
 Applicable Aalysis ad Discrete Mathematics available olie at http://pefmath.etf.bg.ac.yu Appl. Aal. Discrete Math. 2 (2008), 27 22. doi:0.2298/aadm080227c SOME PROPERTIES OF THE SEQUENCE OF PRIME NUMBERS
Applicable Aalysis ad Discrete Mathematics available olie at http://pefmath.etf.bg.ac.yu Appl. Aal. Discrete Math. 2 (2008), 27 22. doi:0.2298/aadm080227c SOME PROPERTIES OF THE SEQUENCE OF PRIME NUMBERS
CSE 1400 Applied Discrete Mathematics Number Theory and Proofs
 CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
Boundaries and the James theorem
 Boudaries ad the James theorem L. Vesely 1. Itroductio The followig theorem is importat ad well kow. All spaces cosidered here are real ormed or Baach spaces. Give a ormed space X, we deote by B X ad S
Boudaries ad the James theorem L. Vesely 1. Itroductio The followig theorem is importat ad well kow. All spaces cosidered here are real ormed or Baach spaces. Give a ormed space X, we deote by B X ad S
The Arakawa-Kaneko Zeta Function
 The Arakawa-Kaeko Zeta Fuctio Marc-Atoie Coppo ad Berard Cadelpergher Nice Sophia Atipolis Uiversity Laboratoire Jea Alexadre Dieudoé Parc Valrose F-0608 Nice Cedex 2 FRANCE Marc-Atoie.COPPO@uice.fr Berard.CANDELPERGHER@uice.fr
The Arakawa-Kaeko Zeta Fuctio Marc-Atoie Coppo ad Berard Cadelpergher Nice Sophia Atipolis Uiversity Laboratoire Jea Alexadre Dieudoé Parc Valrose F-0608 Nice Cedex 2 FRANCE Marc-Atoie.COPPO@uice.fr Berard.CANDELPERGHER@uice.fr
Classroom. We investigate and further explore the problem of dividing x = n + m (m, n are coprime) sheep in
 Classroom I this sectio of Resoace, we ivite readers to pose questios likely to be raised i a classroom situatio. We may suggest strategies for dealig with them, or ivite resposes, or both. Classroom is
Classroom I this sectio of Resoace, we ivite readers to pose questios likely to be raised i a classroom situatio. We may suggest strategies for dealig with them, or ivite resposes, or both. Classroom is
Read carefully the instructions on the answer book and make sure that the particulars required are entered on each answer book.
 THE UNIVERSITY OF WARWICK FIRST YEAR EXAMINATION: Jauary 2009 Aalysis I Time Allowed:.5 hours Read carefully the istructios o the aswer book ad make sure that the particulars required are etered o each
THE UNIVERSITY OF WARWICK FIRST YEAR EXAMINATION: Jauary 2009 Aalysis I Time Allowed:.5 hours Read carefully the istructios o the aswer book ad make sure that the particulars required are etered o each
M17 MAT25-21 HOMEWORK 5 SOLUTIONS
 M17 MAT5-1 HOMEWORK 5 SOLUTIONS 1. To Had I Cauchy Codesatio Test. Exercise 1: Applicatio of the Cauchy Codesatio Test Use the Cauchy Codesatio Test to prove that 1 diverges. Solutio 1. Give the series
M17 MAT5-1 HOMEWORK 5 SOLUTIONS 1. To Had I Cauchy Codesatio Test. Exercise 1: Applicatio of the Cauchy Codesatio Test Use the Cauchy Codesatio Test to prove that 1 diverges. Solutio 1. Give the series
MORE ON CAUCHY CONDITIONS
 Volume 9, 1984 Pages 31 36 http://topology.aubur.edu/tp/ MORE ON CAUCHY CONDITIONS by S. W. Davis Topology Proceedigs Web: http://topology.aubur.edu/tp/ Mail: Topology Proceedigs Departmet of Mathematics
Volume 9, 1984 Pages 31 36 http://topology.aubur.edu/tp/ MORE ON CAUCHY CONDITIONS by S. W. Davis Topology Proceedigs Web: http://topology.aubur.edu/tp/ Mail: Topology Proceedigs Departmet of Mathematics
Interesting Series Associated with Central Binomial Coefficients, Catalan Numbers and Harmonic Numbers
 3 47 6 3 Joural of Iteger Sequeces Vol. 9 06 Article 6.. Iterestig Series Associated with Cetral Biomial Coefficiets Catala Numbers ad Harmoic Numbers Hogwei Che Departmet of Mathematics Christopher Newport
3 47 6 3 Joural of Iteger Sequeces Vol. 9 06 Article 6.. Iterestig Series Associated with Cetral Biomial Coefficiets Catala Numbers ad Harmoic Numbers Hogwei Che Departmet of Mathematics Christopher Newport
Fourier Analysis, Stein and Shakarchi Chapter 8 Dirichlet s Theorem
 Fourier Aalysis, Stei ad Shakarchi Chapter 8 Dirichlet s Theorem 208.05.05 Abstract Durig the course Aalysis II i NTU 208 Sprig, this solutio file is latexed by the teachig assistat Yug-Hsiag Huag with
Fourier Aalysis, Stei ad Shakarchi Chapter 8 Dirichlet s Theorem 208.05.05 Abstract Durig the course Aalysis II i NTU 208 Sprig, this solutio file is latexed by the teachig assistat Yug-Hsiag Huag with
a 3, a 4, ... are the terms of the sequence. The number a n is the nth term of the sequence, and the entire sequence is denoted by a n
 60_090.qxd //0 : PM Page 59 59 CHAPTER 9 Ifiite Series Sectio 9. EXPLORATION Fidig Patters Describe a patter for each of the followig sequeces. The use your descriptio to write a formula for the th term
60_090.qxd //0 : PM Page 59 59 CHAPTER 9 Ifiite Series Sectio 9. EXPLORATION Fidig Patters Describe a patter for each of the followig sequeces. The use your descriptio to write a formula for the th term
The Riemann Zeta Function
 Physics 6A Witer 6 The Riema Zeta Fuctio I this ote, I will sketch some of the mai properties of the Riema zeta fuctio, ζ(x). For x >, we defie ζ(x) =, x >. () x = For x, this sum diverges. However, we
Physics 6A Witer 6 The Riema Zeta Fuctio I this ote, I will sketch some of the mai properties of the Riema zeta fuctio, ζ(x). For x >, we defie ζ(x) =, x >. () x = For x, this sum diverges. However, we
Solutions for Math 411 Assignment #8 1
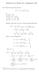 Solutios for Math Assigmet #8 A8. Fid the Lauret series of f() 3 2 + i (a) { < }; (b) { < < }; (c) { < 2 < 3}; (d) {0 < + < 2}. Solutio. We write f() as a sum of partial fractios: f() 3 2 + ( ) 2 ( + )
Solutios for Math Assigmet #8 A8. Fid the Lauret series of f() 3 2 + i (a) { < }; (b) { < < }; (c) { < 2 < 3}; (d) {0 < + < 2}. Solutio. We write f() as a sum of partial fractios: f() 3 2 + ( ) 2 ( + )
University of Colorado Denver Dept. Math. & Stat. Sciences Applied Analysis Preliminary Exam 13 January 2012, 10:00 am 2:00 pm. Good luck!
 Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
Fall 2013 MTH431/531 Real analysis Section Notes
 Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Notes on Snell Envelops and Examples
 Notes o Sell Evelops ad Examples Example (Secretary Problem): Coside a pool of N cadidates whose qualificatios are represeted by ukow umbers {a > a 2 > > a N } from best to last. They are iterviewed sequetially
Notes o Sell Evelops ad Examples Example (Secretary Problem): Coside a pool of N cadidates whose qualificatios are represeted by ukow umbers {a > a 2 > > a N } from best to last. They are iterviewed sequetially
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Sequences, Series, and All That
 Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Solutions to Tutorial 3 (Week 4)
 The Uiversity of Sydey School of Mathematics ad Statistics Solutios to Tutorial Week 4 MATH2962: Real ad Complex Aalysis Advaced Semester 1, 2017 Web Page: http://www.maths.usyd.edu.au/u/ug/im/math2962/
The Uiversity of Sydey School of Mathematics ad Statistics Solutios to Tutorial Week 4 MATH2962: Real ad Complex Aalysis Advaced Semester 1, 2017 Web Page: http://www.maths.usyd.edu.au/u/ug/im/math2962/
Analytic Continuation
 Aalytic Cotiuatio The stadard example of this is give by Example Let h (z) = 1 + z + z 2 + z 3 +... kow to coverge oly for z < 1. I fact h (z) = 1/ (1 z) for such z. Yet H (z) = 1/ (1 z) is defied for
Aalytic Cotiuatio The stadard example of this is give by Example Let h (z) = 1 + z + z 2 + z 3 +... kow to coverge oly for z < 1. I fact h (z) = 1/ (1 z) for such z. Yet H (z) = 1/ (1 z) is defied for
RELATING THE RIEMANN HYPOTHESIS AND THE PRIMES BETWEEN TWO CUBES
 RELATING THE RIEMANN HYPOTHESIS AND THE PRIMES BETWEEN TWO CUBES COPIL, Vlad Faculty of Mathematics-Iformatics, Spiru Haret Uiversity, vcopilmi@spiruharetro Abstract I this paper we make a evaluatio for
RELATING THE RIEMANN HYPOTHESIS AND THE PRIMES BETWEEN TWO CUBES COPIL, Vlad Faculty of Mathematics-Iformatics, Spiru Haret Uiversity, vcopilmi@spiruharetro Abstract I this paper we make a evaluatio for
Chapter 2 Elementary Prime Number Theory for
 Chapter 2 Elemetary Prime Number Theory for 207-8 [5 lectures] I keepig with the elemetary theme of the title I will attempt to keep away from complex variables. Recall that i Chapter we proved the ifiitude
Chapter 2 Elemetary Prime Number Theory for 207-8 [5 lectures] I keepig with the elemetary theme of the title I will attempt to keep away from complex variables. Recall that i Chapter we proved the ifiitude
Stochastic Matrices in a Finite Field
 Stochastic Matrices i a Fiite Field Abstract: I this project we will explore the properties of stochastic matrices i both the real ad the fiite fields. We first explore what properties 2 2 stochastic matrices
Stochastic Matrices i a Fiite Field Abstract: I this project we will explore the properties of stochastic matrices i both the real ad the fiite fields. We first explore what properties 2 2 stochastic matrices
On the Inverse of a Certain Matrix Involving Binomial Coefficients
 It. J. Cotemp. Math. Scieces, Vol. 3, 008, o. 3, 5-56 O the Iverse of a Certai Matrix Ivolvig Biomial Coefficiets Yoshiari Iaba Kitakuwada Seior High School Keihokushimoyuge, Ukyo-ku, Kyoto, 60-0534, Japa
It. J. Cotemp. Math. Scieces, Vol. 3, 008, o. 3, 5-56 O the Iverse of a Certai Matrix Ivolvig Biomial Coefficiets Yoshiari Iaba Kitakuwada Seior High School Keihokushimoyuge, Ukyo-ku, Kyoto, 60-0534, Japa
Physics 116A Solutions to Homework Set #1 Winter Boas, problem Use equation 1.8 to find a fraction describing
 Physics 6A Solutios to Homework Set # Witer 0. Boas, problem. 8 Use equatio.8 to fid a fractio describig 0.694444444... Start with the formula S = a, ad otice that we ca remove ay umber of r fiite decimals
Physics 6A Solutios to Homework Set # Witer 0. Boas, problem. 8 Use equatio.8 to fid a fractio describig 0.694444444... Start with the formula S = a, ad otice that we ca remove ay umber of r fiite decimals
Math 299 Supplement: Real Analysis Nov 2013
 Math 299 Supplemet: Real Aalysis Nov 203 Algebra Axioms. I Real Aalysis, we work withi the axiomatic system of real umbers: the set R alog with the additio ad multiplicatio operatios +,, ad the iequality
Math 299 Supplemet: Real Aalysis Nov 203 Algebra Axioms. I Real Aalysis, we work withi the axiomatic system of real umbers: the set R alog with the additio ad multiplicatio operatios +,, ad the iequality
On the behavior at infinity of an integrable function
 O the behavior at ifiity of a itegrable fuctio Emmauel Lesige To cite this versio: Emmauel Lesige. O the behavior at ifiity of a itegrable fuctio. The America Mathematical Mothly, 200, 7 (2), pp.75-8.
O the behavior at ifiity of a itegrable fuctio Emmauel Lesige To cite this versio: Emmauel Lesige. O the behavior at ifiity of a itegrable fuctio. The America Mathematical Mothly, 200, 7 (2), pp.75-8.
sin(n) + 2 cos(2n) n 3/2 3 sin(n) 2cos(2n) n 3/2 a n =
 60. Ratio ad root tests 60.1. Absolutely coverget series. Defiitio 13. (Absolute covergece) A series a is called absolutely coverget if the series of absolute values a is coverget. The absolute covergece
60. Ratio ad root tests 60.1. Absolutely coverget series. Defiitio 13. (Absolute covergece) A series a is called absolutely coverget if the series of absolute values a is coverget. The absolute covergece
AMS Mathematics Subject Classification : 40A05, 40A99, 42A10. Key words and phrases : Harmonic series, Fourier series. 1.
 J. Appl. Math. & Computig Vol. x 00y), No. z, pp. A RECURSION FOR ALERNAING HARMONIC SERIES ÁRPÁD BÉNYI Abstract. We preset a coveiet recursive formula for the sums of alteratig harmoic series of odd order.
J. Appl. Math. & Computig Vol. x 00y), No. z, pp. A RECURSION FOR ALERNAING HARMONIC SERIES ÁRPÁD BÉNYI Abstract. We preset a coveiet recursive formula for the sums of alteratig harmoic series of odd order.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 19 11/17/2008 LAWS OF LARGE NUMBERS II THE STRONG LAW OF LARGE NUMBERS
 MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
TRIGONOMETRIC POLYNOMIALS WITH MANY REAL ZEROS AND A LITTLEWOOD-TYPE PROBLEM. Peter Borwein and Tamás Erdélyi. 1. Introduction
 TRIGONOMETRIC POLYNOMIALS WITH MANY REAL ZEROS AND A LITTLEWOOD-TYPE PROBLEM Peter Borwei ad Tamás Erdélyi Abstract. We examie the size of a real trigoometric polyomial of degree at most havig at least
TRIGONOMETRIC POLYNOMIALS WITH MANY REAL ZEROS AND A LITTLEWOOD-TYPE PROBLEM Peter Borwei ad Tamás Erdélyi Abstract. We examie the size of a real trigoometric polyomial of degree at most havig at least
EXTREMAL ORDERS OF COMPOSITIONS OF CERTAIN ARITHMETICAL FUNCTIONS. Abstract
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 (2008), #A34 EXTREMAL ORDERS OF COMPOSITIONS OF CERTAIN ARITHMETICAL FUNCTIONS József Sádor Babeş-Bolyai Uiversity, Departmet of Mathematics
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 (2008), #A34 EXTREMAL ORDERS OF COMPOSITIONS OF CERTAIN ARITHMETICAL FUNCTIONS József Sádor Babeş-Bolyai Uiversity, Departmet of Mathematics
A NOTE ON BOUNDARY BLOW-UP PROBLEM OF u = u p
 A NOTE ON BOUNDARY BLOW-UP PROBLEM OF u = u p SEICK KIM Abstract. Assume that Ω is a bouded domai i R with 2. We study positive solutios to the problem, u = u p i Ω, u(x) as x Ω, where p > 1. Such solutios
A NOTE ON BOUNDARY BLOW-UP PROBLEM OF u = u p SEICK KIM Abstract. Assume that Ω is a bouded domai i R with 2. We study positive solutios to the problem, u = u p i Ω, u(x) as x Ω, where p > 1. Such solutios
Proof of Fermat s Last Theorem by Algebra Identities and Linear Algebra
 Proof of Fermat s Last Theorem by Algebra Idetities ad Liear Algebra Javad Babaee Ragai Youg Researchers ad Elite Club, Qaemshahr Brach, Islamic Azad Uiversity, Qaemshahr, Ira Departmet of Civil Egieerig,
Proof of Fermat s Last Theorem by Algebra Idetities ad Liear Algebra Javad Babaee Ragai Youg Researchers ad Elite Club, Qaemshahr Brach, Islamic Azad Uiversity, Qaemshahr, Ira Departmet of Civil Egieerig,
Large holes in quasi-random graphs
 Large holes i quasi-radom graphs Joaa Polcy Departmet of Discrete Mathematics Adam Mickiewicz Uiversity Pozań, Polad joaska@amuedupl Submitted: Nov 23, 2006; Accepted: Apr 10, 2008; Published: Apr 18,
Large holes i quasi-radom graphs Joaa Polcy Departmet of Discrete Mathematics Adam Mickiewicz Uiversity Pozań, Polad joaska@amuedupl Submitted: Nov 23, 2006; Accepted: Apr 10, 2008; Published: Apr 18,
Lecture 10: Mathematical Preliminaries
 Lecture : Mathematical Prelimiaries Obective: Reviewig mathematical cocepts ad tools that are frequetly used i the aalysis of algorithms. Lecture # Slide # I this
Lecture : Mathematical Prelimiaries Obective: Reviewig mathematical cocepts ad tools that are frequetly used i the aalysis of algorithms. Lecture # Slide # I this
BIRKHOFF ERGODIC THEOREM
 BIRKHOFF ERGODIC THEOREM Abstract. We will give a proof of the poitwise ergodic theorem, which was first proved by Birkhoff. May improvemets have bee made sice Birkhoff s orgial proof. The versio we give
BIRKHOFF ERGODIC THEOREM Abstract. We will give a proof of the poitwise ergodic theorem, which was first proved by Birkhoff. May improvemets have bee made sice Birkhoff s orgial proof. The versio we give
2.4.2 A Theorem About Absolutely Convergent Series
 0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
Some p-adic congruences for p q -Catalan numbers
 Some p-adic cogrueces for p q -Catala umbers Floria Luca Istituto de Matemáticas Uiversidad Nacioal Autóoma de México C.P. 58089, Morelia, Michoacá, México fluca@matmor.uam.mx Paul Thomas Youg Departmet
Some p-adic cogrueces for p q -Catala umbers Floria Luca Istituto de Matemáticas Uiversidad Nacioal Autóoma de México C.P. 58089, Morelia, Michoacá, México fluca@matmor.uam.mx Paul Thomas Youg Departmet
Lecture 6 Simple alternatives and the Neyman-Pearson lemma
 STATS 00: Itroductio to Statistical Iferece Autum 06 Lecture 6 Simple alteratives ad the Neyma-Pearso lemma Last lecture, we discussed a umber of ways to costruct test statistics for testig a simple ull
STATS 00: Itroductio to Statistical Iferece Autum 06 Lecture 6 Simple alteratives ad the Neyma-Pearso lemma Last lecture, we discussed a umber of ways to costruct test statistics for testig a simple ull
WHEN IS THE (CO)SINE OF A RATIONAL ANGLE EQUAL TO A RATIONAL NUMBER? 1. My Motivation Some Sort of an Introduction
 WHEN IS THE (CO)SINE OF A RATIONAL ANGLE EQUAL TO A RATIONAL NUMBER? JÖRG JAHNEL 1. My Motivatio Some Sort of a Itroductio Last term I taught Topological Groups at the Göttige Georg August Uiversity. This
WHEN IS THE (CO)SINE OF A RATIONAL ANGLE EQUAL TO A RATIONAL NUMBER? JÖRG JAHNEL 1. My Motivatio Some Sort of a Itroductio Last term I taught Topological Groups at the Göttige Georg August Uiversity. This
A LIMITED ARITHMETIC ON SIMPLE CONTINUED FRACTIONS - II 1. INTRODUCTION
 A LIMITED ARITHMETIC ON SIMPLE CONTINUED FRACTIONS - II C. T. LONG J. H. JORDAN* Washigto State Uiversity, Pullma, Washigto 1. INTRODUCTION I the first paper [2 ] i this series, we developed certai properties
A LIMITED ARITHMETIC ON SIMPLE CONTINUED FRACTIONS - II C. T. LONG J. H. JORDAN* Washigto State Uiversity, Pullma, Washigto 1. INTRODUCTION I the first paper [2 ] i this series, we developed certai properties
A REMARK ON A PROBLEM OF KLEE
 C O L L O Q U I U M M A T H E M A T I C U M VOL. 71 1996 NO. 1 A REMARK ON A PROBLEM OF KLEE BY N. J. K A L T O N (COLUMBIA, MISSOURI) AND N. T. P E C K (URBANA, ILLINOIS) This paper treats a property
C O L L O Q U I U M M A T H E M A T I C U M VOL. 71 1996 NO. 1 A REMARK ON A PROBLEM OF KLEE BY N. J. K A L T O N (COLUMBIA, MISSOURI) AND N. T. P E C K (URBANA, ILLINOIS) This paper treats a property
MAS111 Convergence and Continuity
 MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
Solutions to Problem Sheet 1
 Solutios to Problem Sheet ) Use Theorem. to rove that loglog for all real 3. This is a versio of Theorem. with the iteger N relaced by the real. Hit Give 3 let N = [], the largest iteger. The, imortatly,
Solutios to Problem Sheet ) Use Theorem. to rove that loglog for all real 3. This is a versio of Theorem. with the iteger N relaced by the real. Hit Give 3 let N = [], the largest iteger. The, imortatly,
The Positivity of a Sequence of Numbers and the Riemann Hypothesis
 joural of umber theory 65, 325333 (997) article o. NT97237 The Positivity of a Sequece of Numbers ad the Riema Hypothesis Xia-Ji Li The Uiversity of Texas at Austi, Austi, Texas 7872 Commuicated by A.
joural of umber theory 65, 325333 (997) article o. NT97237 The Positivity of a Sequece of Numbers ad the Riema Hypothesis Xia-Ji Li The Uiversity of Texas at Austi, Austi, Texas 7872 Commuicated by A.
