8.1 Arc Length. What is the length of a curve? How can we approximate it? We could do it following the pattern we ve used before
|
|
|
- Brook Fletcher
- 5 years ago
- Views:
Transcription
1 .1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments get smaller (and the number of segments gets larger,) t seems reasonable that the approxmaton wll get closer to the actual length. But how long s each segment? P "#$ P " = (x " x "#$ ) + + (y " y "#$ ) + = ( x) + + ( y) + By the Mean Value Theorem, we know that, for every nterval, there exsts some x * such that f(x ) f(x -1 ) = f (x * ) (x x -1 ) or y = f (x * ) x so
2 P -1 P = ( x) + + ( y " ) + = ( x) + + [f 2 x " x] + = 1 + [f 2 x " ] + x So L = 1 + [f 2 x ] + dx Ex: Fnd the length of y 2 = x 3 between the ponts (1, 1) and (4, ). hat does the graph look lke? y = x 3/2 :; :< = = + x1/2 so :; :< + = >? x so L =? $ 1 + >? x dx
3 Sometmes, nstead of smply measurng a partcular arc, we want to set up an arc length functon that wll gve us a formula for the length n general. Ex 4: Fnd the arc length functon for the curve y = x 2 1/ lnx, wth P 0 (1,1) as the startng pont. Fnd f (x)= Then fnd 1 + [f (x)] 2 = So 1 + [f 2 x ] + = hch means that the arc length, s(x), s gven by < $ 1 + [f 2 x ] + = hat s the arc length along the curve from (1, 1) to (2, f(2))?
4 .2 Area of a Surface of Revoluton hat s a surface? Lateral surface of a crcular cylnder: Lateral surface area of a cylnder: A = 2πrh Lateral surface of a cone: Lateral surface are of a cone: A = πrl (from an earler result)
5 Surfaces of Revoluton If the surface s more complcated than a cone or a cylnder, how can we calculate ts surface area? Frst, mage the surface created when you revolve a curve around the x-axs: Then, magne breakng the curve down nto smaller peces, whch are revolved around the x-axs to make bands. hat s the area of ths band? The trck s to look at that band as beng smply a pece of a rght, crcular cone. On page 546, Stewart explans why the surface area of ths band s
6 A = 2πrl where l s the slant length (or wdth) of the band. So the surface has area S = S = S = 2πrl dx 2πf(x)(arc length) dx 2πf(x) 1 + [f 2 x ] + dx Ex: The arc of the parabola y = x 2 from (1, 1) to (2, 4) s rotated about the y-axs. Fnd the area of the resultng surface. The book gves 2 solutons one n x and one n y. e ll go through the frst one. S = 2πx ds + $ S = 2πx 1 + :; :< + dx y = x 2 :; :< = 2x
7 S = + 2πx 1 + 4x + dx $ e can use a u substtuton to evaluate the ntegral: u = du = (Look at Page 54 for the other verson of the soluton.)
8 .3 Applcatons Physcs and Teeter-totters Queston: If you have an adult and a chld who want to play on a teeter-totter, how should they st f the adult s much heaver than the chld? In fact, Archmedes dscovered that the teeter-totter wll balance f m 1 d 1 = m 2 d 2 (Law of the Lever) where d 1 and d 2 are measured from the center of the teeter-totter (more generally called the fulcrum): Each of the products m d s a measure of how much each person s pushng down on the end of ther sde of the teeter-totter. Ths s called the torque, whch s one type of moment. Because the force s beng appled to the end of a lever connected to a sngle pont, the torque s a rotatonal force.
9 If, nstead of a lne, we have a thn plate of any gven shape, then we can talk about the center of mass as beng the pont where the plate wll balance horzontally, as shown: e can also consder the center of mass for our teeter-totter example t would le at the fulcrum of the teeter-totter. Le the teeter-totter along the x-axs, where m 1 les at x 1 and m 2 les at x 2, and label the center of mass as x. Then d 1 = x - x 1 and d 2 = x 2 - x e know: m 1 d 1 = m 2 d 2 so then also m 1 (x - x 1 ) = m 2 (x 2 - x) and then m 1 x + m 2 x = m 1 x 1 + m 2 x 2 whch means that x = M NO N P M Q O Q M N P M Q
10 If you have a system wth n masses at dfferent ponts along the x-axs, you can extend ths result further: x = T SUN R S < S T SUN R S = T SUN R S < S R where m = "X$ m " s the total mass of the system and M = "X$ m " x " s the moment of the system about the orgn whch makes the equaton above nto mx = M Smlarly, we can extend these results to masses arranged on the plane to get M y = "X$ m " x " the moment of the system about the y-axs and M x = "X$ m " y " the moment of the system about the x-axs wth the correspondng equatons x = Y Z and y = Y [ R R
11 Ex: Fnd the moments and center of mass of the system of objects that have masses 3, 4, and at the ponts (-1, 1), (2, -1), and (3, 2), respectvely. e need to fnd M y and M x M y = "X$ m " x " = 3(-1) + 4(2) + (3) = 2 M x = "X$ m " y " and then we need to fnd x and y m = "X$ m " = so x = Y Z R = y = Y [ R = So, now that we have a formula for the center of mass of a lne segment, can we extend ths to fnd the center of mass for the thn plate of a gven shape (whch s also known as the centrod of the regon R)? To make t easer, assume the plate has a unform densty, p. (Hand wavng) As before, we ll break the regon down nto rectangles that are f(x \ ) by x, where the centrod of the th rectangle s gven by (x \, $ + f(x \)), where x \ s the mdpont of the subnterval n the x drecton.
12 The mass of each rectangle s then m = p f(x \ ) x (Densty * Area) and the moment of the th subnterval about the y-axs s gven by p f(x \ ) x * x \, whch means that the moment of the regon as a whole about the y-axs s: M y = lm b "X$ p x \ f(x \ ) x = p x f x dx Smlarly, we can fnd M x, whch s gven by M x = lm p $ "X$ f(x b + \) + x = p $ f x + dx + Fnally, we can calculate x and y: x = Y Z = f h < g < :< R h f g < :< = h < g < :< h g < :< = $ j x f x dx y = Y [ R = f hn Q g < Q :< h f g < :< = hn Q g < Q :< h = $ g < :< j $ f x + dx +
13 Ex #6: Fnd the centrod of the regon bounded by the lne y = x and the parabola y = x 2. Step 1: Fnd the area of the regon A = (x x + ) dx Step 2: Calculate x and y x = $ j x f x g(x) dx y = $ j $ + f x + g x + dx
Module 14: THE INTEGRAL Exploring Calculus
 Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
ACTM State Calculus Competition Saturday April 30, 2011
 ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
PES 1120 Spring 2014, Spendier Lecture 6/Page 1
 PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
MEASUREMENT OF MOMENT OF INERTIA
 1. measurement MESUREMENT OF MOMENT OF INERTI The am of ths measurement s to determne the moment of nerta of the rotor of an electrc motor. 1. General relatons Rotatng moton and moment of nerta Let us
1. measurement MESUREMENT OF MOMENT OF INERTI The am of ths measurement s to determne the moment of nerta of the rotor of an electrc motor. 1. General relatons Rotatng moton and moment of nerta Let us
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
Rotational Dynamics. Physics 1425 Lecture 19. Michael Fowler, UVa
 Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Lecture 3: Probability Distributions
 Lecture 3: Probablty Dstrbutons Random Varables Let us begn by defnng a sample space as a set of outcomes from an experment. We denote ths by S. A random varable s a functon whch maps outcomes nto the
Lecture 3: Probablty Dstrbutons Random Varables Let us begn by defnng a sample space as a set of outcomes from an experment. We denote ths by S. A random varable s a functon whch maps outcomes nto the
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
Chapter Twelve. Integration. We now turn our attention to the idea of an integral in dimensions higher than one. Consider a real-valued function f : D
 Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
One Dimension Again. Chapter Fourteen
 hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
20. Mon, Oct. 13 What we have done so far corresponds roughly to Chapters 2 & 3 of Lee. Now we turn to Chapter 4. The first idea is connectedness.
 20. Mon, Oct. 13 What we have done so far corresponds roughly to Chapters 2 & 3 of Lee. Now we turn to Chapter 4. The frst dea s connectedness. Essentally, we want to say that a space cannot be decomposed
20. Mon, Oct. 13 What we have done so far corresponds roughly to Chapters 2 & 3 of Lee. Now we turn to Chapter 4. The frst dea s connectedness. Essentally, we want to say that a space cannot be decomposed
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
7.2 Volume. A cross section is the shape we get when cutting straight through an object.
 7. Volume Let s revew the volume of smple sold, cylnder frst. Cylnder s volume=se re heght. As llustrted n Fgure (). Fgure ( nd (c) re specl cylnders. Fgure () s rght crculr cylnder. Fgure (c) s ox. A
7. Volume Let s revew the volume of smple sold, cylnder frst. Cylnder s volume=se re heght. As llustrted n Fgure (). Fgure ( nd (c) re specl cylnders. Fgure () s rght crculr cylnder. Fgure (c) s ox. A
Singular Value Decomposition: Theory and Applications
 Sngular Value Decomposton: Theory and Applcatons Danel Khashab Sprng 2015 Last Update: March 2, 2015 1 Introducton A = UDV where columns of U and V are orthonormal and matrx D s dagonal wth postve real
Sngular Value Decomposton: Theory and Applcatons Danel Khashab Sprng 2015 Last Update: March 2, 2015 1 Introducton A = UDV where columns of U and V are orthonormal and matrx D s dagonal wth postve real
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Chapter 11: Angular Momentum
 Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
Physics 207: Lecture 20. Today s Agenda Homework for Monday
 Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Electricity and Magnetism - Physics 121 Lecture 10 - Sources of Magnetic Fields (Currents) Y&F Chapter 28, Sec. 1-7
 Electrcty and Magnetsm - Physcs 11 Lecture 10 - Sources of Magnetc Felds (Currents) Y&F Chapter 8, Sec. 1-7 Magnetc felds are due to currents The Bot-Savart Law Calculatng feld at the centers of current
Electrcty and Magnetsm - Physcs 11 Lecture 10 - Sources of Magnetc Felds (Currents) Y&F Chapter 8, Sec. 1-7 Magnetc felds are due to currents The Bot-Savart Law Calculatng feld at the centers of current
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Complex Numbers Alpha, Round 1 Test #123
 Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
CONDUCTORS AND INSULATORS
 CONDUCTORS AND INSULATORS We defne a conductor as a materal n whch charges are free to move over macroscopc dstances.e., they can leave ther nucle and move around the materal. An nsulator s anythng else.
CONDUCTORS AND INSULATORS We defne a conductor as a materal n whch charges are free to move over macroscopc dstances.e., they can leave ther nucle and move around the materal. An nsulator s anythng else.
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Unit 5: Quadratic Equations & Functions
 Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Part C Dynamics and Statics of Rigid Body. Chapter 5 Rotation of a Rigid Body About a Fixed Axis
 Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
π e ax2 dx = x 2 e ax2 dx or x 3 e ax2 dx = 1 x 4 e ax2 dx = 3 π 8a 5/2 (a) We are considering the Maxwell velocity distribution function: 2πτ/m
 Homework Solutons Problem In solvng ths problem, we wll need to calculate some moments of the Gaussan dstrbuton. The brute-force method s to ntegrate by parts but there s a nce trck. The followng ntegrals
Homework Solutons Problem In solvng ths problem, we wll need to calculate some moments of the Gaussan dstrbuton. The brute-force method s to ntegrate by parts but there s a nce trck. The followng ntegrals
b ), which stands for uniform distribution on the interval a x< b. = 0 elsewhere
 Fall Analyss of Epermental Measurements B. Esensten/rev. S. Errede Some mportant probablty dstrbutons: Unform Bnomal Posson Gaussan/ormal The Unform dstrbuton s often called U( a, b ), hch stands for unform
Fall Analyss of Epermental Measurements B. Esensten/rev. S. Errede Some mportant probablty dstrbutons: Unform Bnomal Posson Gaussan/ormal The Unform dstrbuton s often called U( a, b ), hch stands for unform
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Review of Taylor Series. Read Section 1.2
 Revew of Taylor Seres Read Secton 1.2 1 Power Seres A power seres about c s an nfnte seres of the form k = 0 k a ( x c) = a + a ( x c) + a ( x c) + a ( x c) k 2 3 0 1 2 3 + In many cases, c = 0, and the
Revew of Taylor Seres Read Secton 1.2 1 Power Seres A power seres about c s an nfnte seres of the form k = 0 k a ( x c) = a + a ( x c) + a ( x c) + a ( x c) k 2 3 0 1 2 3 + In many cases, c = 0, and the
THE SUMMATION NOTATION Ʃ
 Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
Workshop: Approximating energies and wave functions Quantum aspects of physical chemistry
 Workshop: Approxmatng energes and wave functons Quantum aspects of physcal chemstry http://quantum.bu.edu/pltl/6/6.pdf Last updated Thursday, November 7, 25 7:9:5-5: Copyrght 25 Dan Dll (dan@bu.edu) Department
Workshop: Approxmatng energes and wave functons Quantum aspects of physcal chemstry http://quantum.bu.edu/pltl/6/6.pdf Last updated Thursday, November 7, 25 7:9:5-5: Copyrght 25 Dan Dll (dan@bu.edu) Department
Conservation of Angular Momentum = "Spin"
 Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
kq r 2 2kQ 2kQ (A) (B) (C) (D)
 PHYS 1202W MULTIPL CHOIC QUSTIONS QUIZ #1 Answer the followng multple choce questons on the bubble sheet. Choose the best answer, 5 pts each. MC1 An uncharged metal sphere wll (A) be repelled by a charged
PHYS 1202W MULTIPL CHOIC QUSTIONS QUIZ #1 Answer the followng multple choce questons on the bubble sheet. Choose the best answer, 5 pts each. MC1 An uncharged metal sphere wll (A) be repelled by a charged
Why? Chemistry Crunch #4.1 : Name: KEY Phase Changes. Success Criteria: Prerequisites: Vocabulary:
 Chemstry Crunch #4.1 : Name: KEY Phase Changes Why? Most substances wll eventually go through a phase change when heated or cooled (sometmes they chemcally react nstead). Molecules of a substance are held
Chemstry Crunch #4.1 : Name: KEY Phase Changes Why? Most substances wll eventually go through a phase change when heated or cooled (sometmes they chemcally react nstead). Molecules of a substance are held
CHAPTER 14 GENERAL PERTURBATION THEORY
 CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
Lecture 10: May 6, 2013
 TTIC/CMSC 31150 Mathematcal Toolkt Sprng 013 Madhur Tulsan Lecture 10: May 6, 013 Scrbe: Wenje Luo In today s lecture, we manly talked about random walk on graphs and ntroduce the concept of graph expander,
TTIC/CMSC 31150 Mathematcal Toolkt Sprng 013 Madhur Tulsan Lecture 10: May 6, 013 Scrbe: Wenje Luo In today s lecture, we manly talked about random walk on graphs and ntroduce the concept of graph expander,
NUMERICAL DIFFERENTIATION
 NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
What would be a reasonable choice of the quantization step Δ?
 CE 108 HOMEWORK 4 EXERCISE 1. Suppose you are samplng the output of a sensor at 10 KHz and quantze t wth a unform quantzer at 10 ts per sample. Assume that the margnal pdf of the sgnal s Gaussan wth mean
CE 108 HOMEWORK 4 EXERCISE 1. Suppose you are samplng the output of a sensor at 10 KHz and quantze t wth a unform quantzer at 10 ts per sample. Assume that the margnal pdf of the sgnal s Gaussan wth mean
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
PHYS 705: Classical Mechanics. Newtonian Mechanics
 1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
Linear Momentum. Center of Mass.
 Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
Modelli Clamfim Equazioni differenziali 7 ottobre 2013
 CLAMFIM Bologna Modell 1 @ Clamfm Equazon dfferenzal 7 ottobre 2013 professor Danele Rtell danele.rtell@unbo.t 1/18? Ordnary Dfferental Equatons A dfferental equaton s an equaton that defnes a relatonshp
CLAMFIM Bologna Modell 1 @ Clamfm Equazon dfferenzal 7 ottobre 2013 professor Danele Rtell danele.rtell@unbo.t 1/18? Ordnary Dfferental Equatons A dfferental equaton s an equaton that defnes a relatonshp
Mathematics Intersection of Lines
 a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
Statistics Chapter 4
 Statstcs Chapter 4 "There are three knds of les: les, damned les, and statstcs." Benjamn Dsrael, 1895 (Brtsh statesman) Gaussan Dstrbuton, 4-1 If a measurement s repeated many tmes a statstcal treatment
Statstcs Chapter 4 "There are three knds of les: les, damned les, and statstcs." Benjamn Dsrael, 1895 (Brtsh statesman) Gaussan Dstrbuton, 4-1 If a measurement s repeated many tmes a statstcal treatment
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Comparative Studies of Law of Conservation of Energy. and Law Clusters of Conservation of Generalized Energy
 Comparatve Studes of Law of Conservaton of Energy and Law Clusters of Conservaton of Generalzed Energy No.3 of Comparatve Physcs Seres Papers Fu Yuhua (CNOOC Research Insttute, E-mal:fuyh1945@sna.com)
Comparatve Studes of Law of Conservaton of Energy and Law Clusters of Conservaton of Generalzed Energy No.3 of Comparatve Physcs Seres Papers Fu Yuhua (CNOOC Research Insttute, E-mal:fuyh1945@sna.com)
ANSWERS. Problem 1. and the moment generating function (mgf) by. defined for any real t. Use this to show that E( U) var( U)
 Econ 413 Exam 13 H ANSWERS Settet er nndelt 9 deloppgaver, A,B,C, som alle anbefales å telle lkt for å gøre det ltt lettere å stå. Svar er gtt . Unfortunately, there s a prntng error n the hnt of
Econ 413 Exam 13 H ANSWERS Settet er nndelt 9 deloppgaver, A,B,C, som alle anbefales å telle lkt for å gøre det ltt lettere å stå. Svar er gtt . Unfortunately, there s a prntng error n the hnt of
Problem Do any of the following determine homomorphisms from GL n (C) to GL n (C)?
 Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
MAGNETISM MAGNETIC DIPOLES
 MAGNETISM We now turn to magnetsm. Ths has actually been used for longer than electrcty. People were usng compasses to sal around the Medterranean Sea several hundred years BC. However t was not understood
MAGNETISM We now turn to magnetsm. Ths has actually been used for longer than electrcty. People were usng compasses to sal around the Medterranean Sea several hundred years BC. However t was not understood
Integrals and Invariants of Euler-Lagrange Equations
 Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
(2mn, m 2 n 2, m 2 + n 2 )
 MATH 16T Homewk Solutons 1. Recall that a natural number n N s a perfect square f n = m f some m N. a) Let n = p α even f = 1,,..., k. be the prme factzaton of some n. Prove that n s a perfect square f
MATH 16T Homewk Solutons 1. Recall that a natural number n N s a perfect square f n = m f some m N. a) Let n = p α even f = 1,,..., k. be the prme factzaton of some n. Prove that n s a perfect square f
Lecture 6/7 (February 10/12, 2014) DIRAC EQUATION. The non-relativistic Schrödinger equation was obtained by noting that the Hamiltonian 2
 P470 Lecture 6/7 (February 10/1, 014) DIRAC EQUATION The non-relatvstc Schrödnger equaton was obtaned by notng that the Hamltonan H = P (1) m can be transformed nto an operator form wth the substtutons
P470 Lecture 6/7 (February 10/1, 014) DIRAC EQUATION The non-relatvstc Schrödnger equaton was obtaned by notng that the Hamltonan H = P (1) m can be transformed nto an operator form wth the substtutons
2 Finite difference basics
 Numersche Methoden 1, WS 11/12 B.J.P. Kaus 2 Fnte dfference bascs Consder the one- The bascs of the fnte dfference method are best understood wth an example. dmensonal transent heat conducton equaton T
Numersche Methoden 1, WS 11/12 B.J.P. Kaus 2 Fnte dfference bascs Consder the one- The bascs of the fnte dfference method are best understood wth an example. dmensonal transent heat conducton equaton T
Module 2. Random Processes. Version 2 ECE IIT, Kharagpur
 Module Random Processes Lesson 6 Functons of Random Varables After readng ths lesson, ou wll learn about cdf of functon of a random varable. Formula for determnng the pdf of a random varable. Let, X be
Module Random Processes Lesson 6 Functons of Random Varables After readng ths lesson, ou wll learn about cdf of functon of a random varable. Formula for determnng the pdf of a random varable. Let, X be
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Solutions to Homework 7, Mathematics 1. 1 x. (arccos x) (arccos x) 1
 Solutons to Homework 7, Mathematcs 1 Problem 1: a Prove that arccos 1 1 for 1, 1. b* Startng from the defnton of the dervatve, prove that arccos + 1, arccos 1. Hnt: For arccos arccos π + 1, the defnton
Solutons to Homework 7, Mathematcs 1 Problem 1: a Prove that arccos 1 1 for 1, 1. b* Startng from the defnton of the dervatve, prove that arccos + 1, arccos 1. Hnt: For arccos arccos π + 1, the defnton
Important Dates: Post Test: Dec during recitations. If you have taken the post test, don t come to recitation!
 Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Spring 2002 Lecture #13
 44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
Physics 240: Worksheet 30 Name:
 (1) One mole of an deal monatomc gas doubles ts temperature and doubles ts volume. What s the change n entropy of the gas? () 1 kg of ce at 0 0 C melts to become water at 0 0 C. What s the change n entropy
(1) One mole of an deal monatomc gas doubles ts temperature and doubles ts volume. What s the change n entropy of the gas? () 1 kg of ce at 0 0 C melts to become water at 0 0 C. What s the change n entropy
Physics 4B. Question and 3 tie (clockwise), then 2 and 5 tie (zero), then 4 and 6 tie (counterclockwise) B i. ( T / s) = 1.74 V.
 Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
Lecture Notes on Linear Regression
 Lecture Notes on Lnear Regresson Feng L fl@sdueducn Shandong Unversty, Chna Lnear Regresson Problem In regresson problem, we am at predct a contnuous target value gven an nput feature vector We assume
Lecture Notes on Lnear Regresson Feng L fl@sdueducn Shandong Unversty, Chna Lnear Regresson Problem In regresson problem, we am at predct a contnuous target value gven an nput feature vector We assume
International Mathematical Olympiad. Preliminary Selection Contest 2012 Hong Kong. Outline of Solutions
 Internatonal Mathematcal Olympad Prelmnary Selecton ontest Hong Kong Outlne of Solutons nswers: 7 4 7 4 6 5 9 6 99 7 6 6 9 5544 49 5 7 4 6765 5 6 6 7 6 944 9 Solutons: Snce n s a two-dgt number, we have
Internatonal Mathematcal Olympad Prelmnary Selecton ontest Hong Kong Outlne of Solutons nswers: 7 4 7 4 6 5 9 6 99 7 6 6 9 5544 49 5 7 4 6765 5 6 6 7 6 944 9 Solutons: Snce n s a two-dgt number, we have
Math 702 Midterm Exam Solutions
 Math 702 Mdterm xam Solutons The terms measurable, measure, ntegrable, and almost everywhere (a.e.) n a ucldean space always refer to Lebesgue measure m. Problem. [6 pts] In each case, prove the statement
Math 702 Mdterm xam Solutons The terms measurable, measure, ntegrable, and almost everywhere (a.e.) n a ucldean space always refer to Lebesgue measure m. Problem. [6 pts] In each case, prove the statement
Physics 4B. A positive value is obtained, so the current is counterclockwise around the circuit.
 Physcs 4B Solutons to Chapter 7 HW Chapter 7: Questons:, 8, 0 Problems:,,, 45, 48,,, 7, 9 Queston 7- (a) no (b) yes (c) all te Queston 7-8 0 μc Queston 7-0, c;, a;, d; 4, b Problem 7- (a) Let be the current
Physcs 4B Solutons to Chapter 7 HW Chapter 7: Questons:, 8, 0 Problems:,,, 45, 48,,, 7, 9 Queston 7- (a) no (b) yes (c) all te Queston 7-8 0 μc Queston 7-0, c;, a;, d; 4, b Problem 7- (a) Let be the current
Problem Set 9 Solutions
 Desgn and Analyss of Algorthms May 4, 2015 Massachusetts Insttute of Technology 6.046J/18.410J Profs. Erk Demane, Srn Devadas, and Nancy Lynch Problem Set 9 Solutons Problem Set 9 Solutons Ths problem
Desgn and Analyss of Algorthms May 4, 2015 Massachusetts Insttute of Technology 6.046J/18.410J Profs. Erk Demane, Srn Devadas, and Nancy Lynch Problem Set 9 Solutons Problem Set 9 Solutons Ths problem
Statistical Inference. 2.3 Summary Statistics Measures of Center and Spread. parameters ( population characteristics )
 Ismor Fscher, 8//008 Stat 54 / -8.3 Summary Statstcs Measures of Center and Spread Dstrbuton of dscrete contnuous POPULATION Random Varable, numercal True center =??? True spread =???? parameters ( populaton
Ismor Fscher, 8//008 Stat 54 / -8.3 Summary Statstcs Measures of Center and Spread Dstrbuton of dscrete contnuous POPULATION Random Varable, numercal True center =??? True spread =???? parameters ( populaton
C/CS/Phy191 Problem Set 3 Solutions Out: Oct 1, 2008., where ( 00. ), so the overall state of the system is ) ( ( ( ( 00 ± 11 ), Φ ± = 1
 C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD
 COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD Ákos Jósef Lengyel, István Ecsed Assstant Lecturer, Professor of Mechancs, Insttute of Appled Mechancs, Unversty of Mskolc, Mskolc-Egyetemváros,
COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD Ákos Jósef Lengyel, István Ecsed Assstant Lecturer, Professor of Mechancs, Insttute of Appled Mechancs, Unversty of Mskolc, Mskolc-Egyetemváros,
Scattering by a perfectly conducting infinite cylinder
 Scatterng by a perfectly conductng nfnte cylnder Reeber that ths s the full soluton everywhere. We are actually nterested n the scatterng n the far feld lt. We agan use the asyptotc relatonshp exp exp
Scatterng by a perfectly conductng nfnte cylnder Reeber that ths s the full soluton everywhere. We are actually nterested n the scatterng n the far feld lt. We agan use the asyptotc relatonshp exp exp
A particle in a state of uniform motion remain in that state of motion unless acted upon by external force.
 The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
CSCE 790S Background Results
 CSCE 790S Background Results Stephen A. Fenner September 8, 011 Abstract These results are background to the course CSCE 790S/CSCE 790B, Quantum Computaton and Informaton (Sprng 007 and Fall 011). Each
CSCE 790S Background Results Stephen A. Fenner September 8, 011 Abstract These results are background to the course CSCE 790S/CSCE 790B, Quantum Computaton and Informaton (Sprng 007 and Fall 011). Each
10.34 Fall 2015 Metropolis Monte Carlo Algorithm
 10.34 Fall 2015 Metropols Monte Carlo Algorthm The Metropols Monte Carlo method s very useful for calculatng manydmensonal ntegraton. For e.g. n statstcal mechancs n order to calculate the prospertes of
10.34 Fall 2015 Metropols Monte Carlo Algorthm The Metropols Monte Carlo method s very useful for calculatng manydmensonal ntegraton. For e.g. n statstcal mechancs n order to calculate the prospertes of
Economics 101. Lecture 4 - Equilibrium and Efficiency
 Economcs 0 Lecture 4 - Equlbrum and Effcency Intro As dscussed n the prevous lecture, we wll now move from an envronment where we looed at consumers mang decsons n solaton to analyzng economes full of
Economcs 0 Lecture 4 - Equlbrum and Effcency Intro As dscussed n the prevous lecture, we wll now move from an envronment where we looed at consumers mang decsons n solaton to analyzng economes full of
DECOUPLING THEORY HW2
 8.8 DECOUPLIG THEORY HW2 DOGHAO WAG DATE:OCT. 3 207 Problem We shall start by reformulatng the problem. Denote by δ S n the delta functon that s evenly dstrbuted at the n ) dmensonal unt sphere. As a temporal
8.8 DECOUPLIG THEORY HW2 DOGHAO WAG DATE:OCT. 3 207 Problem We shall start by reformulatng the problem. Denote by δ S n the delta functon that s evenly dstrbuted at the n ) dmensonal unt sphere. As a temporal
Errors for Linear Systems
 Errors for Lnear Systems When we solve a lnear system Ax b we often do not know A and b exactly, but have only approxmatons  and ˆb avalable. Then the best thng we can do s to solve ˆx ˆb exactly whch
Errors for Lnear Systems When we solve a lnear system Ax b we often do not know A and b exactly, but have only approxmatons  and ˆb avalable. Then the best thng we can do s to solve ˆx ˆb exactly whch
On the Multicriteria Integer Network Flow Problem
 BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 5, No 2 Sofa 2005 On the Multcrtera Integer Network Flow Problem Vassl Vasslev, Marana Nkolova, Maryana Vassleva Insttute of
BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 5, No 2 Sofa 2005 On the Multcrtera Integer Network Flow Problem Vassl Vasslev, Marana Nkolova, Maryana Vassleva Insttute of
Chapter 4: Root Finding
 Chapter 4: Root Fndng Startng values Closed nterval methods (roots are search wthn an nterval o Bsecton Open methods (no nterval o Fxed Pont o Newton-Raphson o Secant Method Repeated roots Zeros of Hgher-Dmensonal
Chapter 4: Root Fndng Startng values Closed nterval methods (roots are search wthn an nterval o Bsecton Open methods (no nterval o Fxed Pont o Newton-Raphson o Secant Method Repeated roots Zeros of Hgher-Dmensonal
10. Canonical Transformations Michael Fowler
 10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
Section 8.1 Exercises
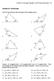 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
A be a probability space. A random vector
 Statstcs 1: Probablty Theory II 8 1 JOINT AND MARGINAL DISTRIBUTIONS In Probablty Theory I we formulate the concept of a (real) random varable and descrbe the probablstc behavor of ths random varable by
Statstcs 1: Probablty Theory II 8 1 JOINT AND MARGINAL DISTRIBUTIONS In Probablty Theory I we formulate the concept of a (real) random varable and descrbe the probablstc behavor of ths random varable by
Some modelling aspects for the Matlab implementation of MMA
 Some modellng aspects for the Matlab mplementaton of MMA Krster Svanberg krlle@math.kth.se Optmzaton and Systems Theory Department of Mathematcs KTH, SE 10044 Stockholm September 2004 1. Consdered optmzaton
Some modellng aspects for the Matlab mplementaton of MMA Krster Svanberg krlle@math.kth.se Optmzaton and Systems Theory Department of Mathematcs KTH, SE 10044 Stockholm September 2004 1. Consdered optmzaton
Module 9. Lecture 6. Duality in Assignment Problems
 Module 9 1 Lecture 6 Dualty n Assgnment Problems In ths lecture we attempt to answer few other mportant questons posed n earler lecture for (AP) and see how some of them can be explaned through the concept
Module 9 1 Lecture 6 Dualty n Assgnment Problems In ths lecture we attempt to answer few other mportant questons posed n earler lecture for (AP) and see how some of them can be explaned through the concept
Chapter 9. The Dot Product (Scalar Product) The Dot Product use (Scalar Product) The Dot Product (Scalar Product) The Cross Product.
 The Dot Product (Scalar Product) Chapter 9 Statcs and Torque The dot product of two vectors can be constructed by takng the component of one vector n the drecton of the other and multplyng t tmes the magntude
The Dot Product (Scalar Product) Chapter 9 Statcs and Torque The dot product of two vectors can be constructed by takng the component of one vector n the drecton of the other and multplyng t tmes the magntude
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
Analytical Chemistry Calibration Curve Handout
 I. Quck-and Drty Excel Tutoral Analytcal Chemstry Calbraton Curve Handout For those of you wth lttle experence wth Excel, I ve provded some key technques that should help you use the program both for problem
I. Quck-and Drty Excel Tutoral Analytcal Chemstry Calbraton Curve Handout For those of you wth lttle experence wth Excel, I ve provded some key technques that should help you use the program both for problem
JEE ADVANCE : 2015 P1 PHASE TEST 4 ( )
 I I T / P M T A C A D E M Y IN D IA JEE ADVANCE : 5 P PHASE TEST (.8.7) ANSWER KEY PHYSICS CHEMISTRY MATHEMATICS Q.No. Answer Key Q.No. Answer Key Q.No. Answer Key. () () (). () () (). (9) () (). () ()
I I T / P M T A C A D E M Y IN D IA JEE ADVANCE : 5 P PHASE TEST (.8.7) ANSWER KEY PHYSICS CHEMISTRY MATHEMATICS Q.No. Answer Key Q.No. Answer Key Q.No. Answer Key. () () (). () () (). (9) () (). () ()
Salmon: Lectures on partial differential equations. Consider the general linear, second-order PDE in the form. ,x 2
 Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
PHYS 1101 Practice problem set 12, Chapter 32: 21, 22, 24, 57, 61, 83 Chapter 33: 7, 12, 32, 38, 44, 49, 76
 PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
ALGEBRA MID-TERM. 1 Suppose I is a principal ideal of the integral domain R. Prove that the R-module I R I has no non-zero torsion elements.
 ALGEBRA MID-TERM CLAY SHONKWILER 1 Suppose I s a prncpal deal of the ntegral doman R. Prove that the R-module I R I has no non-zero torson elements. Proof. Note, frst, that f I R I has no non-zero torson
ALGEBRA MID-TERM CLAY SHONKWILER 1 Suppose I s a prncpal deal of the ntegral doman R. Prove that the R-module I R I has no non-zero torson elements. Proof. Note, frst, that f I R I has no non-zero torson
NP-Completeness : Proofs
 NP-Completeness : Proofs Proof Methods A method to show a decson problem Π NP-complete s as follows. (1) Show Π NP. (2) Choose an NP-complete problem Π. (3) Show Π Π. A method to show an optmzaton problem
NP-Completeness : Proofs Proof Methods A method to show a decson problem Π NP-complete s as follows. (1) Show Π NP. (2) Choose an NP-complete problem Π. (3) Show Π Π. A method to show an optmzaton problem
CHAPTER 10 ROTATIONAL MOTION
 CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
DUE: WEDS FEB 21ST 2018
 HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
