Automata theory and its applications
|
|
|
- Charlene Watson
- 5 years ago
- Views:
Transcription
1 Automata theory and its applications Lecture 12-14: Automata over ranked finite trees Zhilin Wu State Key Laboratory of Computer Science, Institute of Software, Chinese Academy of Sciences January 16, 2013 Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
2 Ranked and unranked alphabets Ranked alphabet: A finite set pσ, arityq with arity : Σ Ñ N. Every node labeled by σ have aritypσq children Motivation: Terms, e.g. p5, p3, 4qq A tree domain D: A subset of N satisfying D is prefix-closed, P D, it holds x P P D, xj P D for every j : 0 j i. A tree t over a ranked alphabet pσ, arityq is a tupe pd, Lq where D is a tree domain, L : D Ñ Σ P D, the number of children of x is arityplpxqq. Let T Σ denote the set of ranked trees over the alphabet Σ. Unranked alphabet: A finite set Σ Every node labeled by σ can have an arbitrary number of children Motivation: XML documents Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
3 Outline 1 Bottom-up versus top-down 2 Determinization and closure properties 3 Pumping lemma 4 Regular tree grammars 5 Relationship with CFL 6 Regular tree expressions 7 Equivalence with MSO 8 Minimization of tree automata 9 Decision problems 10 Tree-walking automata Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
4 Bottom-up finite tree automata (BUTA) A BUTA A is a tuple pq, Σ, δ, F q, where δ includes the tuples of the following form pq 1,..., q k, a, qq s.t. k aritypaq. In particular, if aritypaq 0, then δ includes the tuples pa, qq. Runs of BUTA: Let t pd, Lq be a tree and A pq, Σ, δ, q 0, F q be a BUTA, a run of A over t is a tree r A,t pd, L 1 q, where L 1 : D Ñ Q P D with children x 1,..., x k, pqpx 1 q,..., qpx k q, a, qpxqq P δ. A run r A,t pd, L 1 q is accepting if L 1 pεq P F. Deterministic BUTA (DBUTA): for every pq 1,..., q k, a, qq, pq 1,..., q k, a, q 1 q P δ, it holds q q 1. Example: Boolean expressions that evaluate to true. A ptq 0, q 1 u, t^, _, 0, 1u, δ, tq 1 uq where δ is defined as follows, p0, q 0 q, p1, q 1 q P δ, pq 0, q 0, _, q 0 q, pq 1, q 0, _, q 1 q, pq 0, q 1, _, q 1 q, pq 1, q 1, _, q 1 q P δ, pq 0, q 0, ^, q 0 q, pq 1, q 0, ^, q 0 q, pq 0, q 1, ^, q 0 q, pq 1, q 1, ^, q 1 q P δ. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
5 Top-down finite tree automata (TDTA) A TDTA A is a tuple pq, Σ, δ, Iq, where δ includes the tuples of the following form pq, a, q 1,..., q k q s.t. k aritypaq. In particular, if aritypaq 0, then δ includes the tuples pq, aq. Runs of TDTA: Similar to those of BUTA. A run pd, L 1 q is accepting if L 1 pεq P I. Deterministic TDTA (DTDTA): I is a singleton, for every pq, a, q 1,..., q k q, pq, a, q1, 1..., qk 1 q P δ, it holds q 1 q1, 1..., q k qk 1. Proposition. BUTA TDTA. pq 1,..., q k, a, qq ðñ pq, a, q 1,..., q k q Regular languages over ranked trees: Tree languages defined by BUTAs. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
6 Outline 1 Bottom-up versus top-down 2 Determinization and closure properties 3 Pumping lemma 4 Regular tree grammars 5 Relationship with CFL 6 Regular tree expressions 7 Equivalence with MSO 8 Minimization of tree automata 9 Decision problems 10 Tree-walking automata Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
7 BUTA DBUTA Let A pq, Σ, δ, F q be BUTA. Construct an equivalent DBUTA A 1 pq 1, Σ, δ 1, F 1 q. Idea: Extension of subset construction. Q 1 2 Q, ps 1,..., S k, a, Sq P δ 1, where S tq Dq 1,..., q k.pq 1,..., q k, a, qq P i P S i u, F 1 ts S X F Hu. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
8 TDTA DTDTA Proposition. Let A pq, Σ, δ, q 0, F q be a DTDTA. Suppose t apt 1,..., t k q, t 1 apt 1 1,..., t 1 kq P LpAq, then t 2 apt 2 1,..., t 2 k q P LpAq, t2 i t i or t 2 i t1 i. Proof. Let x (resp. x 1 ) be the root of t (resp. t 1 ), x 1,..., x k (resp. x 1 1,..., x 1 k ) be the children of x (resp. x 1 ). A is deterministic and the run r A,t, r A,t 1 are accepting ñ r A,t pxq r A,t 1px 1 q q 0 P I, r A,t 1px i q r A,t 1px 1 i q. Thus, r A,t 2, a composition of r A,t Dptiq s or r A,t 1 Dpt 1 i q s, is also accepting. q 0 a q 1 t 1... t k q k q t... 1 t 1 q k k q 0 a... Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
9 TDTA DTDTA Proposition. Let A pq, Σ, δ, q 0, F q be a DTDTA. Suppose t apt 1,..., t k q, t 1 apt 1 1,..., t 1 kq P LpAq, then t 2 apt 2 1,..., t 2 k q P LpAq, t2 i t i or t 2 i t1 i. Corollary. TDTA DTDTA. Proof. Let L: The Boolean expressions that evaluate to true. Claim. L cannot be defined by DTDTA. To the contrary, suppose that L is recognized by a DTDTA. Then _p0, 1q, _p1, 0q P L implies that _p0, 0q P L, a contradiction. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
10 Closure properties Theorem. Regular tree languages are closed under union, intersection and complementation. Union: Suppose A 1 pq 1, Σ, δ 1, F 1 q and A 2 pq 2, Σ, δ 2, F 2 q. Then A pq 1 Y Q 2, Σ, δ 1 Y δ 2, F 1 Y F 2 q defines LpA 1 q Y LpA 2 q. Intersection: Suppose A 1 pq 1, Σ, δ 1, F 1 q and A 2 pq 2, Σ, δ 2, F 2 q. Then A pq 1 Q 2, Σ, δ, F 1 F 2 q defines LpA 1 q X LpA 2 q, where ppq 1, q 1 1q,..., pq k, q 1 k q, a, pq, q1 qq P δ iff pq 1,..., q k, a, qq P δ 1 and pq 1 1,..., q 1 k, a, q1 q P δ 2. Complementation: Let L T Σ be defined by a DBUTA A pq, Σ, δ, F q. Then pq, Σ, δ, QzF q defines T Σ zl. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
11 Closure properties Proposition. Regular tree languages are closed under letter projection (θ : Σ Ñ Σ 1 ). Proof. Let L T Σ be defined by a BUTA A pq, Σ, δ, F q. Then A 1 pq, Σ 1, δ 1, F q s.t. pq 1,..., q k, a 1, qq P δ 1 iff Da P Σ.pq 1,..., q k, a, qq P δ and θpaq a 1. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
12 Outline 1 Bottom-up versus top-down 2 Determinization and closure properties 3 Pumping lemma 4 Regular tree grammars 5 Relationship with CFL 6 Regular tree expressions 7 Equivalence with MSO 8 Minimization of tree automata 9 Decision problems 10 Tree-walking automata Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
13 Pumping lemma Contexts over Σ: A ranked tree over the alphabet Σ Y t u s.t. the arity of is zero. Let C Σ,n denote the set of all contexts over Σ with n occurrences of. By convention, C Σ,0 T Σ. We also use C Σ to denote C Σ,1. Let C P C Σ,n and C 1 P C k1,..., C n P C kn. Then CrC 1,..., C n s is the context obtained from C by replacing the i-th (from left to right) occurrence of with C i for every i : 1 i n. C... C 1... C k Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
14 Pumping lemma Pumping lemma. Let L T Σ be a regular tree language. Then there exists k P N s.t. if the depth of a tree t P L is k (the root is of depth 0), then DC, C 1 P C Σ and t 1 P T Σ s.t. t CrC 1 rt 1 ss and for all n P N, CrC 1n rt 1 ss P L. Proof. Let L defined by a BUTA A pq, Σ, δ, F q and k Q. q C C q t... Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
15 Pumping lemma Pumping lemma. Let L T Σ be a regular tree language. Then there exists k P N s.t. if the depth of a tree t P L is k (the root is of depth 0), then DC, C 1 P C Σ and t 1 P T Σ s.t. t CrC 1 rt 1 ss and for all n P N, CrC 1n rt 1 ss P L. Proof. Let L defined by a BUTA A pq, Σ, δ, F q and k Q. Application of pumping lemma: The tree language fpg i paq, g i paqq i P N ( is not regular. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
16 Outline 1 Bottom-up versus top-down 2 Determinization and closure properties 3 Pumping lemma 4 Regular tree grammars 5 Relationship with CFL 6 Regular tree expressions 7 Equivalence with MSO 8 Minimization of tree automata 9 Decision problems 10 Tree-walking automata Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
17 Regular tree grammar (RTG) A regular tree grammar: G pn, Σ, S, Rq, where N nonterminals, Σ: terminals, S P N : Start symbol, R contains rules of the form A Ñ α, where α P T ΣYN Symbols in N has arity zero. Derivation relation s Ñ G t: DC P C ΣYN, A P N, and A Ñ α P R s.t. s CrAs, t Crαs. The language generated by G (denoted LpGq): LpGq tt P T Σ S Ñ G tu. Example: S Ñ ^ps, Sq, S Ñ _ps, Sq, S Ñ 0, S Ñ 1. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
18 BUTA RTG RTG ñ Reduced RTG Reachable nonterminals (RpGq): N P N is reachable from S iff Dt P T ΣYN, S Ñ G t and N occurs in t. Productive nonterminals (P pgq): N P N is productive iff Dt P T Σ s.t. N Ñ G t. Reduced regular tree grammars: A RTG whose nonterminals are all reachable and productive. Computation of RpGq (resp. P pgq): Computation of a fixpoint. R 0 pgq tsu (resp. P 0 pgq tn P N Dα P T Σ. N Ñ αu), R i 1 pgq R i pgq Y tn P N DN 1 P R i pgq. N 1 Ñ α, N occurs in αu (resp. P i 1 pgq P i pgq Y N P N Dα P T ΣYPipGq. N Ñ α ( ). Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
19 BUTA RTG Reduced RTG ñ Normalized RTG Normalized RTG: Reduced RTG whose rules are of the form A Ñ apa 1,..., A k q or A Ñ a (where a P Σ, A 1,..., A k P N ). Repeat the following rule until a normalized RTG is obtained: Select a rule A Ñ α not of the desired form, let α apα 1,..., α k q, introduce new nonterminals A 1,..., A k, replace A Ñ α by A Ñ apa 1,..., A k q, A 1 Ñ α 1,..., A k Ñ α k. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
20 BUTA RTG Reduced RTG ñ Normalized RTG Normalized RTG: Reduced RTG whose rules are of the form A Ñ apa 1,..., A k q or A Ñ a (where a P Σ, A 1,..., A k P N ). Repeat the following rule until a normalized RTG is obtained: Select a rule A Ñ α not of the desired form, let α apα 1,..., α k q, introduce new nonterminals A 1,..., A k, replace A Ñ α by A Ñ apa 1,..., A k q, A 1 Ñ α 1,..., A k Ñ α k. Normalized RTG ñ TDTA TDTA ñ RTG Idea: Nonterminals as states, A Ñ apa 1,..., A k q ñ pa, a, A 1,..., A k q P δ, A Ñ a ñ pa, aq P δ. Idea: States as nonterminals, pq, a, q 1,..., q k q P δ ñ q Ñ apq 1,..., q k q. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
21 Outline 1 Bottom-up versus top-down 2 Determinization and closure properties 3 Pumping lemma 4 Regular tree grammars 5 Relationship with CFL 6 Regular tree expressions 7 Equivalence with MSO 8 Minimization of tree automata 9 Decision problems 10 Tree-walking automata Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
22 Yield operator Compute a word from a tree by concatenating the leaves of the tree from the left to the right. Yieldpaq a if a P Σ and aritypaq 0, Yieldpapt 1,..., t n qq Yieldpt 1 q... Yieldpt n q. E E id ( E ) id + id Yieldptq pid idq id. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
23 Ranked derivation trees of CFG Let G pn, Σ, S, Rq be a CFG. For each A P N s.t. there is a rule A Ñ α P R with α k, introduce a new nonterminal pa, kq. A ranked derivation tree is obtained from a derivation tree as follows: For every node x labeled by A with k-children, replace A by pa, kq. Let DT R pgq denote the set of ranked derivation trees of words in LpGq. E : id E E E (E, 3) E peq (E, 3) (E, 1) ( (E, 3) ) id (E, 1) + (E, 1) id id Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
24 CFL and Regular tree languages Theorem. The following fact hold. 1 For each CFG G, DT R pgq is a regular tree language. 2 For each regular tree language L T Σ, YieldpLq is a CFL. 3 There exists a regular tree language which is not the set of derivation trees of any CFG. Proof. 1. CFG G pn, Σ, P, Sq ñ RTG G 1 pn, Σ 1, S, Rq Σ 1 Σ Y tεu Y tpa, pq DA Ñ α s.t. α pu. R: A Ñ a 1... a p ñ A Ñ pa, pqpa 1,..., a p q, A Ñ ε ñ A Ñ pa, 0qpεq. 2. Let L generated by a normalized RTG G pn, Σ, S, Rq. Then the CFG pn, Σ, P, Sq generates YieldpLq, where P : A Ñ apa 1,..., A k q ñ A Ñ A 1... A k. 3. The regular tree language L tfpgpaq, gpbqqu is not the derivation tree of any CFG. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
25 Outline 1 Bottom-up versus top-down 2 Determinization and closure properties 3 Pumping lemma 4 Regular tree grammars 5 Relationship with CFL 6 Regular tree expressions 7 Equivalence with MSO 8 Minimization of tree automata 9 Decision problems 10 Tree-walking automata Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
26 Syntax of regular tree expressions Regular expressions: Regular tree expressions: r : a r 1 Y r 2 r 1 r 2 r 1 How to define concatenation and star operator over ranked trees? Main idea: Use a finite set of ports P t 1,..., k u to denote the positions of trees where concatenations happen Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
27 Syntax of regular tree expressions Regular expressions: Regular tree expressions: r : a r 1 Y r 2 r 1 r 2 r 1 How to define concatenation and star operator over ranked trees? Main idea: Use a finite set of ports P t 1,..., k u to denote the positions of trees where concatenations happen Regular tree expressions over Σ and P (denoted by RegpΣ, Pq): where r : a fpr 1,..., r n q r 1 Y r 2 r 1 i r 2 pr 1 q, i, a P Σ Y P such that aritypaq 0 (where ports in P have arity 0), f P Σ such that aritypfq n, i : 1 i k and i P P. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
28 Semantics of regular tree expressions r : a fpr 1,..., r n q r 1 Y r 2 r 1 i r 2 pr 1 q, i a tau, fpr 1,..., r n q tfps 1,..., s n q s 1 P r 1,..., s n P r n u, r 1 Y r 2 r 1 Y r 2, r 1 i r 2 r 1 i r 2, pr 1 q, i r 1, i. Suppose L, L 1 T ΣYP, then L i L 1 tr i Ð L 1 s, where tr i Ð L 1 s is defined as follows: Suppose i occurs n times in t, then tr i Ð L 1 s is the set of trees obtained from t by choosing n trees s 1,..., s n P L 1 and replacing the j-th (left-to-right) occurrence of i by s j. Let L T ΣYP, then tpl L 0, i t i u, and L n 1, i L i L n, i. In addition, let L, i L n, i. npn Example: pfp 1, 0qq, Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
29 BUTA Regular tree expressions From regular tree expressions to BUTA By induction on the structure of regular tree expressions, show that for every regular tree expression r, r is a regular tree language. Proposition. If L and L 1 are regular tree languages, then L i L 1 and L, i are also regular tree languages. L i L 1 : Suppose A pq, Σ Y P, δ, F q and A 1 pq 1, Σ Y P, δ 1, F 1 q are two BUTAs defining L and L 1 such that Q X Q 1 H. Then L i L 1 is defined by B pq 2, Σ Y P, δ 2, F 2 q, where Q 2 Q Y Q 1, F 2 F, δ 2 δ Y δ 1 Y tpq 1 1,..., q 1 n, σ, qq p i, qq P δ, Dq 1 P F 1.pq 1 1,..., q 1 n, σ, q 1 q P δ 1 u. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
30 BUTA Regular tree expressions From regular tree expressions to BUTA By induction on the structure of regular tree expressions, show that for every regular tree expression r, r is a regular tree language. Proposition. If L and L 1 are regular tree languages, then L i L 1 and L, i are also regular tree languages. L, i : Suppose A pq, Σ Y P, δ, F q is a BUTA defining L such that if p i, qq P δ, then there are no transitions pq 1,..., q n, σ, qq with σ P Σ. The BUTA A 1 pq, Σ Y P, δ 1, F 1 q defines L, i, where δ 1 δ Y tpq 1,..., q n, σ, qq p i, qq P δ, Dq 1 P F. pq 1,..., q n, σ, q 1 q P δu, F 1 tq p i, qq P δu. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
31 BUTA Regular tree expressions From BUTA to regular tree expressions Let A pq, Σ, δ, F q be a BUTA such that Q tq 1,..., q n u. The goal: Define a regular tree expression r A over Σ and Q for LpAq. The idea: Notation T pi, j, Kq s.t. 1 i n, 0 j n, and K Q. The set of trees t pd, Lq satisfying that D a run of A over t, say r A,t, s.t. r A,t pεq q i, for every leaf x in t, Lpxq P K or Lpxq a P Σ s.t. aritypaq 0, and for all the non-leaf nodes x ε in t, r A,t pxq P tq 1,..., q j u. LpAq T pi, n, Hq. q i PF Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
32 BUTA Regular tree expressions From BUTA to regular tree expressions Let A pq, Σ, δ, F q be a BUTA such that Q tq 1,..., q n u. The goal: Define a regular tree expression r A over Σ and Q for LpAq. The idea: Notation T pi, j, Kq s.t. 1 i n, 0 j n, and K Q. Induction on j. j 0: T pi, 0, Kq is the set of trees q i P K, or σ P Σ s.t. aritypσq 0 and pσ, q i q P δ, or trees σpθ 1,..., θ k q s.t. j 0: aritypσq : 1 j k, θ j P K or θ j P Σ s.t. aritypθ j q 0, there are q 1 1,..., q 1 k P Q : 1 j k, either q1 j θ j or pθ j, q 1 j q P δ, and pq 1 1,..., q 1 k, σ, q iq P δ. T pi, j, Kq T pi, j 1, Kq Y T pi, j 1, K Y tq juq qj T pj, j 1, K Y tq juq,q j qj T pj, j 1, Kq. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
33 From BUTA to regular tree expressions: An example Example: Boolean expressions that evaluate to true. BUTA A ptq 1, q 2 u, t^, _, 0, 1u, δ, tq 2 uq, where δ is defined as follows, p0, q 1 q, pq 1, q 1, _, q 1 q, pq 1, q 1, ^, q 1 q, pq 2, q 1, ^, q 1 q, pq 1, q 2, ^, q 1 q P δ, p1, q 2 q, pq 2, q 1, _, q 2 q, pq 1, q 2, _, q 2 q, pq 2, q 2, _, q 2 q, pq 2, q 2, ^, q 2 q P δ. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
34 From BUTA to regular tree expressions: An example Example: Boolean expressions that evaluate to true. BUTA A ptq 1, q 2 u, t^, _, 0, 1u, δ, tq 2 uq, where δ is defined as follows, p0, q 1 q, pq 1, q 1, _, q 1 q, pq 1, q 1, ^, q 1 q, pq 2, q 1, ^, q 1 q, pq 1, q 2, ^, q 1 q P δ, p1, q 2 q, pq 2, q 1, _, q 2 q, pq 1, q 2, _, q 2 q, pq 2, q 2, _, q 2 q, pq 2, q 2, ^, q 2 q P δ. Then T p2, 2, Hq T p2, 1, Hq Y T p2, 1, 2q q2 T p2, 1, 2q,q 2 q2 T p2, 1, Hq. T p2, 1, Hq T p2, 0, Hq Y T p2, 0, 1q q1 T p1, 0, 1q,q 1 q1 T p1, 0, Hq. T p2, 1, 2q T p2, 0, 2q Y T p2, 0, 1q q1 T p1, 0, t1, 2uq,q 1 q1 T p1, 0, 2q. T p2, 0, Hq 1 Y _p0, 1q Y _p1, 0q Y _p1, 1q Y ^p1, 1q, T p1, 0, Hq 0 Y _p0, 0q Y ^p0, 0q Y ^p1, 0q Y ^p0, 1q, T p2, 0, 1q T p2, 0, Hq Y _p1, q 1q Y _pq 1, 1q, T p1, 0, 1q T p2, 0, 2q T p1, 0, Hq Y _pq 1, 0q Y _p0, q 1q Y _pq 1, q 1q Y ^ p0, q 1q Y ^pq 1, 0q Y ^pq 1, 1q Y ^p1, q 1q Y ^pq 1, q 1q, T p2, 0, Hq Y _p0, q 2q Y _pq 2, 0q Y _ pq 2, q 2q Y ^pq 2, 1q Y ^p1, q 2q Y ^pq 2, q 2q, T p1, 0, 2q T p1, 0, Hq Y ^p0, q 2q Y ^pq 2, 0q, T p1, 0, t1, 2uq T p1, 0, 1q Y T p1, 0, 2q Y ^pq 1, q 2q Y ^pq 2, q 1q. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
35 Outline 1 Bottom-up versus top-down 2 Determinization and closure properties 3 Pumping lemma 4 Regular tree grammars 5 Relationship with CFL 6 Regular tree expressions 7 Equivalence with MSO 8 Minimization of tree automata 9 Decision problems 10 Tree-walking automata Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
36 MSO over ranked trees Let Σ be a ranked alphabet and k maxtaritypσq σ P Σu. Syntax of MSOrpP σ q σpσ, psuc i q 1 i k s ϕ : P σ pxq x y suc i px, yq x y Xpxq ϕ 1 _ϕ 2 ϕ 1 Dxϕ 1 DXϕ 1 Semantics Let t P T Σ, then t pd, Lq can be seen as a relational structure pd, pp σ q σpσ, psuc i q 1 i k, q s.t. P σ tx P D Lpxq σu, suc i tpx, xpi 1qq x, xpi 1q P Du and is the transitive closure of suc i. i Then MSO formulas are interpreted over t P T Σ in a natural way. Example: There is a path of even length in the tree DX 1 X 2 pdxpϕ ε pxq ^ X 1 pxqq ^ ϕ path px 1, X 2 q ^ ϕ even px 1, X 2 qq, where ϕ path 1pxq _ X 2pxqq ^ px 1pyq _ X 2pyqq Ñ px y _ x y _ y xqq, ϕ even : rpxq ^ ϕ leaf pxqq Ñ _ isuc ipx, yq ^ X 3 rpyqq ^ Dxpϕ leaf pxq ^ X 2pxqq ϕ εpxq y _ x yq, ϕ leaf pxq : Dypx yq. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40,
37 MSO BUTA From MSO to BUTA: Normal form for MSOrpP σ q σpσ, psuc i q 1 i k s formulas: ϕ : X P σ X Y SingpXq suc i px, Y q ϕ 1 _ ϕ 2 ϕ 1 DXϕ 1 Induction on the structure of MSO formulas, utilizing the closure of BUTAs under projection and Boolean operations. From BUTA to MSO: Let A pq, Σ, δ, F q be a BUTA such that Q tq 1,..., q n u. Then where ϕ init : ϕ trans : ϕ : Dq 1... q n pϕ init ^ ϕ trans ^ ϕ acc q, aritypσq0 pq 1,...,q r,σq ϕ acc Dxpϕ ε pxq ^ š leaf pxq ^ P σ pxqq Ñ š pσ,qqpδ qpxqq, ppσ pxq ^ ^i suc š i px, y i q ^ ^i q i py i 1... y r Ñ qpxq, qpf pq 1,...,q r,σ,qqpδ Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
38 Outline 1 Bottom-up versus top-down 2 Determinization and closure properties 3 Pumping lemma 4 Regular tree grammars 5 Relationship with CFL 6 Regular tree expressions 7 Equivalence with MSO 8 Minimization of tree automata 9 Decision problems 10 Tree-walking automata Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
39 Myhill-Nerode theorem for tree languages Let L T Σ. Define a congruence L on T Σ as follows: t L t 1 iff for all contexts C, Crts P L ô Crt 1 s P L. Proposition. L is a congruence, that is, if t L t 1, then for all contexts C, Crts L Crt 1 s. Proof. For all contexts C 1, if C 1 rcrtss P L, then rc 1 rcssrts P L. From the fact that t L t 1, we have rc 1 rcssrt 1 s P L, that is, C 1 rcrtss P L. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
40 Myhill-Nerode theorem for tree languages Let L T Σ. Define a congruence L on T Σ as follows: t L t 1 iff for all contexts C, Crts P L ô Crt 1 s P L. Theorem. Let L T Σ. Then L is regular iff L is of finite index. Proof. Only if direction: Suppose L is recognized by a deterministic BUTA A pq, Σ, δ, F q. Define A as follows: t A t 1 iff r A,t pεq r A,t 1pεq. Evidently, A is of finite index, since Q is finite. It remains to show A L. If t A t 1, then r A,t pεq r A,t 1pεq. context C, r A,Crts pεq r A,Crt 1 s pεq. Thus, for every context C, Crts P L iff Crt 1 s P L, we have t L t 1. If direction: Suppose L is of finite index. Define A L pq L, Σ, δ L, F L q as follows. Q L is the set of equivalence classes of L, F L trts t P Lu, for every σ P Σ s.t. aritypσq k and rt 1 s,..., rt k s P Q, prt 1 s,..., rt k s, σ, rσpt 1,..., t k qsq P δ L. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
41 Myhill-Nerode theorem for tree languages Let L T Σ. Define a congruence L on T Σ as follows: t L t 1 iff for all contexts C, Crts P L ô Crt 1 s P L. Theorem. Let L T Σ. Then L is regular iff L is of finite index. Corollary. For every regular tree language L T Σ, there is a unique deterministic BUTA of the minimum size defining L. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
42 Minimization of deterministic tree automata Let A pq, Σ, δ, F q be a deterministic BUTA defining L. Compute inductively an equivalence relation A over Q as follows, until i A i 1 A. q 0 A q1 iff q P F ô q 1 P F, q i 1 A q1 iff q i A q1 and for every σ P Σ s.t. aritypσq k, q 1,..., q j 1, q j 1,..., q k P Q, δpq 1,..., q j 1, q, q j 1,..., q k, σq i A δpq 1,..., q j 1, q 1, q j 1,..., q k, σq. t 1 P T Σ, t L t 1 iff r A,t pεq A r A,t 1pεq. Lemma. The following two facts hold. 1 For every t, t 1 P T Σ and context C, r A,t pεq A r A,t 1pεq implies r A,Crts pεq A r A,Crt 1 s pεq. 2 t L t 1 implies r A,t pεq A r A,t 1pεq. Proof. 1. Induction on the depth of in C. 2. By an induction on i, prove that t L t 1 implies r A,t pεq i A r A,t 1pεq. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
43 Outline 1 Bottom-up versus top-down 2 Determinization and closure properties 3 Pumping lemma 4 Regular tree grammars 5 Relationship with CFL 6 Regular tree expressions 7 Equivalence with MSO 8 Minimization of tree automata 9 Decision problems 10 Tree-walking automata Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
44 Membership and emptiness Membership problem: Given t P T Σ and a BUTA A pq, Σ, δ, F q, is t P LpAq? Nonemptiness problem: Given a BUTA A pq, Σ, δ, F q, is LpAq H? Theorem. The membership and nonemptiness problem can be solved in polynomial time. Proof. Membership: A bottom-up computation of the reachable states pr x q xpt. Let t pd, Lq P T Σ and A pq, Σ, δ, F q be a BUTA. for every leaf x of t, R x tq plpxq, qq P δu, for every non-leaf node x labeled by Lpxq σ of arity k, R x tq Dq 1 P R x0,..., q k P R xpk 1q. pq 1,..., q k, σ, qq P δu. t P LpAq iff R ε X F H Nonemptiness: Bottom-up computation of the set of reachable states R. R 0 tq pσ, qq P δu, R i 1 R i Y tq Dσ P Σ, Dq 1,..., q k P R i. pq 1,..., q k, σ, qq P δu. LpAq H iff R X F H Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
45 Language inclusion Language inclusion: Given two BUTAs A 1 pq 1, Σ, δ 1, F 1 q and A 2 pq 2, Σ, δ 2, F 2 q, is LpA 1 q LpA 2 q? Universality: Given a BUTA A pq, Σ, δ, F q, is LpAq T Σ? Theorem. The language inclusion and universality problem are EXPTIME-complete. Proof. Upper bound: Construct a BUTA A 1 2 defining the complement of LpA 2 q, decide whether LpA 1 q X LpA 1 2q H. Lower bound (Universality): Reduction from polynomial space alternating Turing machines. Use a BUTA to describe the unsuccessful computations. C ε C 0 C 1 i C 00 C01 C10 C i Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
46 Outline 1 Bottom-up versus top-down 2 Determinization and closure properties 3 Pumping lemma 4 Regular tree grammars 5 Relationship with CFL 6 Regular tree expressions 7 Equivalence with MSO 8 Minimization of tree automata 9 Decision problems 10 Tree-walking automata Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
47 Definition We restrict our attention to binary trees. Let T ypes tr, 0, 1u tl, iu. Let t pd, Lq be a binary tree and x P D, then the type of x (denoted by typepxq), is an element of T ypes s.t. the first component of typepxq: r: the root, 0: the left-child, 1: the right-child, the second component of typepxq: l: a leaf, i: an internal node. A tree walking automaton (TWA) A is a tuple pq, Σ, I, F, δq, where Q: the set of states, I : the set of initial states, F : the set of accepting states, δ Q T ypes Σ tò, 0, 1u Q s.t. for every pq, pb, lq, σ, act, q 1 q P δ, we have act Ò. A deterministic TWA is a TWA A pq, Σ, I, F, δq such that I is a τ, σq P Q T ypes Σ, δpq, τ, σq is a singleton. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
48 Definition: continued Let A be a TWA and t be a binary tree. A configuration of A over t is a pair pq, xq s.t. q P Q and x is a node in t. An initial configuration is a configuration pq, εq with q P I. A run of A over t is a sequence pq 0, x 0 qpq 1, x 1 q... pq n, x n q such that pq 0, x 0q is an initial : 0 j n, Dact s.t. pq j, typepx jq, Lpx jq, act, q j 1q P δ, and if act Ò and typepx j q P tp0, lq, p0, iqu, then x j x j 1 0, if act Ò and typepx j q P tp1, lq, p1, iqu, then x j x j 1 1, if act 0 and typepx j q P tr, 0, 1u tiu, then x j 1 x j 0, if act 1 and typepx j q P tr, 0, 1u tiu, then x j 1 x j 1. A run pq 0, x 0 qpq 1, x 1 q... pq n, x n q is accepting iff q n P F. A tree t is accepted by A if there is an accepting run of A over t. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
49 TWA: Example Depth-first search of trees Three states tq, q left, q right u pq, pb, iq, a, 0, qq P δ, where b r, 0, 1, pq, xq s.t. x is not a leaf ñ goes to the left child of x and the state is changed to q. pq, p0, lq, a, Ò, q left q P δ (resp. pq, p1, lq, a, Ò, q right q P δ), pq, xq s.t. x is a leaf and the left (resp. right) child of its parent ñ goes to the parent of x and the state is changed to q left (resp. q right ). Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
50 TWA: Example Depth-first search of trees Three states tq, q left, q right u pq, pb, iq, a, 0, qq P δ, where b r, 0, 1, pq, xq s.t. x is not a leaf ñ goes to the left child of x and the state is changed to q. pq, p0, lq, a, Ò, q left q P δ (resp. pq, p1, lq, a, Ò, q right q P δ), pq, xq s.t. x is a leaf and the left (resp. right) child of its parent ñ goes to the parent of x and the state is changed to q left (resp. q right ). pq left, pb, iq, a, 1, qq P δ, pq left, xq s.t. x is a not a leaf ñ goes to the right child of x and the state is changed to q. pq right, p0, lq, a, Ò, q left q, pq right, p0, iq, a, Ò, q left q P δ, pq right, xq s.t. x is the left child of its parent ñ goes to the parent of x and the state is changed to q left. pq right, p1, lq, a, Ò, q right q, pq right, p1, iq, a, Ò, q right q P δ, pq right, xq s.t. x is the right child of its parent ñ goes to the parent of x and the state is changed to q right. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
51 TWA BUTA Theorem. From every TWA, an equivalent BUTA can be constructed. Let A pq, Σ, I, F, δq be a TWA. W.l.o.g. assume that for every tree t, every accepting run of A over t stops at the root of t. The idea: For each non-leaf node x in t pd, Lq, define Rpxq Q Q as follows. pp, qq P Rpxq iff D a partial run of A over t, say pq 1, x 1 q... pq n, x n q, s.t. x 1 x, q 1 : 1 i n, x i P t x, x n is the parent of x, q n q, and pq n 1, typepxq, Lpxq, q n, Òq P δ. Observation. Rpxq only depends on t x. p R(x) x0 p q q x q p x1 Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
52 TWA BUTA Theorem. From every TWA, an equivalent BUTA can be constructed. Let A pq, Σ, I, F, δq be a TWA. W.l.o.g. assume that for every tree t, every accepting run of A over t stops at the root of t. For every leaf node x, Rpxq tpp, qq pp, typepxq, Lpxq, q, Òq P δu. For every non-leaf node x, Rpxq is computed from Rpx0q, Rpx1q as follows. If there exist p 1,..., p k, q 1,..., q k 1 P Q, b 1,..., b k P t0, 1u : 1 i k. pq i, typepxq, Lpxq, p i, b i q P δ, pp i, q i 1 q P Rpxb i q, p q 1, pq k 1, typepxq, Lpxq, q, Òq P δ, then pp, qq P Rpxq. There is an accepting run of A over t iff Rpεq X pi F q H. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
53 TWA BUTA Let Σ ta, b, cu such that aritypaq aritypcq 0 and aritypbq 1. Theorem. The language K T Σ defined in the following cannot be defined by TWAs. Let t P T Σ and x be a non-leaf node in t. Then x is balanced if both t x0 and t x1 contain a leaf labeled by a. Define K T Σ as follows: t P K iff for every leaf x labeled by a in t, there are an even number of balanced proper ancestors of x. Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
54 Proof. Emptiness of TWA Theorem. The emptiness of TWAs is EXPTIME-complete. Upper bound: Translation to BUTAs. Lower bound: Reduction from Polynomial space alternating Turing machines. Encode the successful computations of PSPACE ATMs by binary trees and check the consistency of adjacent configurations using TWAs. C ε i C 0 C 1 i C 00 C01 C10 C Zhilin Wu (SKLCS) Automata over ranked finite trees January 16, / 40
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
DM17. Beregnelighed. Jacob Aae Mikkelsen
 DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
Büchi Automata and their closure properties. - Ajith S and Ankit Kumar
 Büchi Automata and their closure properties - Ajith S and Ankit Kumar Motivation Conventional programs accept input, compute, output result, then terminate Reactive program : not expected to terminate
Büchi Automata and their closure properties - Ajith S and Ankit Kumar Motivation Conventional programs accept input, compute, output result, then terminate Reactive program : not expected to terminate
Further discussion of Turing machines
 Further discussion of Turing machines In this lecture we will discuss various aspects of decidable and Turing-recognizable languages that were not mentioned in previous lectures. In particular, we will
Further discussion of Turing machines In this lecture we will discuss various aspects of decidable and Turing-recognizable languages that were not mentioned in previous lectures. In particular, we will
CPSC 421: Tutorial #1
 CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
Logic and Automata I. Wolfgang Thomas. EATCS School, Telc, July 2014
 Logic and Automata I EATCS School, Telc, July 2014 The Plan We present automata theory as a tool to make logic effective. Four parts: 1. Some history 2. Automata on infinite words First step: MSO-logic
Logic and Automata I EATCS School, Telc, July 2014 The Plan We present automata theory as a tool to make logic effective. Four parts: 1. Some history 2. Automata on infinite words First step: MSO-logic
An Introduction to Description Logic VIII Inherent intractability of terminological reasoning
 An Introduction to Description Logic VIII Inherent intractability of terminological reasoning Marco Cerami Palacký University in Olomouc Department of Computer Science Olomouc, Czech Republic Olomouc,
An Introduction to Description Logic VIII Inherent intractability of terminological reasoning Marco Cerami Palacký University in Olomouc Department of Computer Science Olomouc, Czech Republic Olomouc,
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Context-Free Languages (Pre Lecture)
 Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Finite Automata and Regular languages
 Finite Automata and Regular languages Huan Long Shanghai Jiao Tong University Acknowledgements Part of the slides comes from a similar course in Fudan University given by Prof. Yijia Chen. http://basics.sjtu.edu.cn/
Finite Automata and Regular languages Huan Long Shanghai Jiao Tong University Acknowledgements Part of the slides comes from a similar course in Fudan University given by Prof. Yijia Chen. http://basics.sjtu.edu.cn/
Automata Theory. Lecture on Discussion Course of CS120. Runzhe SJTU ACM CLASS
 Automata Theory Lecture on Discussion Course of CS2 This Lecture is about Mathematical Models of Computation. Why Should I Care? - Ways of thinking. - Theory can drive practice. - Don t be an Instrumentalist.
Automata Theory Lecture on Discussion Course of CS2 This Lecture is about Mathematical Models of Computation. Why Should I Care? - Ways of thinking. - Theory can drive practice. - Don t be an Instrumentalist.
Great Theoretical Ideas in Computer Science. Lecture 4: Deterministic Finite Automaton (DFA), Part 2
 5-25 Great Theoretical Ideas in Computer Science Lecture 4: Deterministic Finite Automaton (DFA), Part 2 January 26th, 27 Formal definition: DFA A deterministic finite automaton (DFA) M =(Q,,,q,F) M is
5-25 Great Theoretical Ideas in Computer Science Lecture 4: Deterministic Finite Automaton (DFA), Part 2 January 26th, 27 Formal definition: DFA A deterministic finite automaton (DFA) M =(Q,,,q,F) M is
Theory of Computation (II) Yijia Chen Fudan University
 Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
Computational Models - Lecture 3
 Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
CS 154, Lecture 2: Finite Automata, Closure Properties Nondeterminism,
 CS 54, Lecture 2: Finite Automata, Closure Properties Nondeterminism, Why so Many Models? Streaming Algorithms 0 42 Deterministic Finite Automata Anatomy of Deterministic Finite Automata transition: for
CS 54, Lecture 2: Finite Automata, Closure Properties Nondeterminism, Why so Many Models? Streaming Algorithms 0 42 Deterministic Finite Automata Anatomy of Deterministic Finite Automata transition: for
Theory of Computation
 Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Lecture 17: Language Recognition
 Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Introduction to the Theory of Computation. Automata 1VO + 1PS. Lecturer: Dr. Ana Sokolova.
 Introduction to the Theory of Computation Automata 1VO + 1PS Lecturer: Dr. Ana Sokolova http://cs.uni-salzburg.at/~anas/ Setup and Dates Lectures Tuesday 10:45 pm - 12:15 pm Instructions Tuesday 12:30
Introduction to the Theory of Computation Automata 1VO + 1PS Lecturer: Dr. Ana Sokolova http://cs.uni-salzburg.at/~anas/ Setup and Dates Lectures Tuesday 10:45 pm - 12:15 pm Instructions Tuesday 12:30
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 5-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY NON-DETERMINISM and REGULAR OPERATIONS THURSDAY JAN 6 UNION THEOREM The union of two regular languages is also a regular language Regular Languages Are
5-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY NON-DETERMINISM and REGULAR OPERATIONS THURSDAY JAN 6 UNION THEOREM The union of two regular languages is also a regular language Regular Languages Are
Simplifying XML Schema:
 Simplifying XML Schema: Single-type approximations of regular tree languages Wenbo Lian National Engineering Research Center of Fundemental Software, Institute of Software, Chinese Academy of Sciences
Simplifying XML Schema: Single-type approximations of regular tree languages Wenbo Lian National Engineering Research Center of Fundemental Software, Institute of Software, Chinese Academy of Sciences
Introduction to Automata
 Introduction to Automata Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr 1 /
Introduction to Automata Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr 1 /
Theory of Computation 4 Non-Deterministic Finite Automata
 Theory of Computation 4 Non-Deterministic Finite Automata Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Theory of Computation
Theory of Computation 4 Non-Deterministic Finite Automata Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Theory of Computation
6.1 The Pumping Lemma for CFLs 6.2 Intersections and Complements of CFLs
 CSC4510/6510 AUTOMATA 6.1 The Pumping Lemma for CFLs 6.2 Intersections and Complements of CFLs The Pumping Lemma for Context Free Languages One way to prove AnBn is not regular is to use the pumping lemma
CSC4510/6510 AUTOMATA 6.1 The Pumping Lemma for CFLs 6.2 Intersections and Complements of CFLs The Pumping Lemma for Context Free Languages One way to prove AnBn is not regular is to use the pumping lemma
CS 455/555: Finite automata
 CS 455/555: Finite automata Stefan D. Bruda Winter 2019 AUTOMATA (FINITE OR NOT) Generally any automaton Has a finite-state control Scans the input one symbol at a time Takes an action based on the currently
CS 455/555: Finite automata Stefan D. Bruda Winter 2019 AUTOMATA (FINITE OR NOT) Generally any automaton Has a finite-state control Scans the input one symbol at a time Takes an action based on the currently
Introduction to the Theory of Computation. Automata 1VO + 1PS. Lecturer: Dr. Ana Sokolova.
 Introduction to the Theory of Computation Automata 1VO + 1PS Lecturer: Dr. Ana Sokolova http://cs.uni-salzburg.at/~anas/ Setup and Dates Lectures and Instructions 23.10. 3.11. 17.11. 24.11. 1.12. 11.12.
Introduction to the Theory of Computation Automata 1VO + 1PS Lecturer: Dr. Ana Sokolova http://cs.uni-salzburg.at/~anas/ Setup and Dates Lectures and Instructions 23.10. 3.11. 17.11. 24.11. 1.12. 11.12.
Functions on languages:
 MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
Chapter 3. Regular grammars
 Chapter 3 Regular grammars 59 3.1 Introduction Other view of the concept of language: not the formalization of the notion of effective procedure, but set of words satisfying a given set of rules Origin
Chapter 3 Regular grammars 59 3.1 Introduction Other view of the concept of language: not the formalization of the notion of effective procedure, but set of words satisfying a given set of rules Origin
The View Over The Horizon
 The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
Büchi Automata and Their Determinization
 Büchi Automata and Their Determinization Edinburgh, October 215 Plan of the Day 1. Büchi automata and their determinization 2. Infinite games 3. Rabin s Tree Theorem 4. Decidability of monadic theories
Büchi Automata and Their Determinization Edinburgh, October 215 Plan of the Day 1. Büchi automata and their determinization 2. Infinite games 3. Rabin s Tree Theorem 4. Decidability of monadic theories
Introduction to computability Tutorial 7
 Introduction to computability Tutorial 7 Context free languages and Turing machines November 6 th 2014 Context-free languages 1. Show that the following languages are not context-free: a) L ta i b j a
Introduction to computability Tutorial 7 Context free languages and Turing machines November 6 th 2014 Context-free languages 1. Show that the following languages are not context-free: a) L ta i b j a
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata. We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata.
 Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
What we have done so far
 What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
Properties of Context-Free Languages
 Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Uses of finite automata
 Chapter 2 :Finite Automata 2.1 Finite Automata Automata are computational devices to solve language recognition problems. Language recognition problem is to determine whether a word belongs to a language.
Chapter 2 :Finite Automata 2.1 Finite Automata Automata are computational devices to solve language recognition problems. Language recognition problem is to determine whether a word belongs to a language.
Non-context-Free Languages. CS215, Lecture 5 c
 Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Unranked Tree Automata with Sibling Equalities and Disequalities
 Unranked Tree Automata with Sibling Equalities and Disequalities Wong Karianto Christof Löding Lehrstuhl für Informatik 7, RWTH Aachen, Germany 34th International Colloquium, ICALP 2007 Xu Gao (NFS) Unranked
Unranked Tree Automata with Sibling Equalities and Disequalities Wong Karianto Christof Löding Lehrstuhl für Informatik 7, RWTH Aachen, Germany 34th International Colloquium, ICALP 2007 Xu Gao (NFS) Unranked
Context-Free Grammars (and Languages) Lecture 7
 Context-Free Grammars (and Languages) Lecture 7 1 Today Beyond regular expressions: Context-Free Grammars (CFGs) What is a CFG? What is the language associated with a CFG? Creating CFGs. Reasoning about
Context-Free Grammars (and Languages) Lecture 7 1 Today Beyond regular expressions: Context-Free Grammars (CFGs) What is a CFG? What is the language associated with a CFG? Creating CFGs. Reasoning about
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Equivalence of DFAs and NFAs
 CS 172: Computability and Complexity Equivalence of DFAs and NFAs It s a tie! DFA NFA Sanjit A. Seshia EECS, UC Berkeley Acknowledgments: L.von Ahn, L. Blum, M. Blum What we ll do today Prove that DFAs
CS 172: Computability and Complexity Equivalence of DFAs and NFAs It s a tie! DFA NFA Sanjit A. Seshia EECS, UC Berkeley Acknowledgments: L.von Ahn, L. Blum, M. Blum What we ll do today Prove that DFAs
Closure Properties of Regular Languages. Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism
 Closure Properties of Regular Languages Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism Closure Properties Recall a closure property is a statement
Closure Properties of Regular Languages Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism Closure Properties Recall a closure property is a statement
Formal Languages, Automata and Compilers
 Formal Languages, Automata and Compilers Lecure 4 2017-18 LFAC (2017-18) Lecture 4 1 / 31 Curs 4 1 Grammars of type 3 and finite automata 2 Closure properties for type 3 languages 3 Regular Expressions
Formal Languages, Automata and Compilers Lecure 4 2017-18 LFAC (2017-18) Lecture 4 1 / 31 Curs 4 1 Grammars of type 3 and finite automata 2 Closure properties for type 3 languages 3 Regular Expressions
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner. Tel Aviv University. November 21, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner. Tel Aviv University. November 21, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Finite Automata and Regular Languages (part III)
 Finite Automata and Regular Languages (part III) Prof. Dan A. Simovici UMB 1 / 1 Outline 2 / 1 Nondeterministic finite automata can be further generalized by allowing transitions between states without
Finite Automata and Regular Languages (part III) Prof. Dan A. Simovici UMB 1 / 1 Outline 2 / 1 Nondeterministic finite automata can be further generalized by allowing transitions between states without
Automata extended to nominal sets
 Bachelor thesis Computer Science Radboud University Automata extended to nominal sets Author: Joep Veldhoven s4456556 First supervisor/assessor: Jurriaan Rot jrot@cs.ru.nl Second and third supervisor:
Bachelor thesis Computer Science Radboud University Automata extended to nominal sets Author: Joep Veldhoven s4456556 First supervisor/assessor: Jurriaan Rot jrot@cs.ru.nl Second and third supervisor:
CS 154. Finite Automata, Nondeterminism, Regular Expressions
 CS 54 Finite Automata, Nondeterminism, Regular Expressions Read string left to right The DFA accepts a string if the process ends in a double circle A DFA is a 5-tuple M = (Q, Σ, δ, q, F) Q is the set
CS 54 Finite Automata, Nondeterminism, Regular Expressions Read string left to right The DFA accepts a string if the process ends in a double circle A DFA is a 5-tuple M = (Q, Σ, δ, q, F) Q is the set
Finite Universes. L is a fixed-length language if it has length n for some
 Finite Universes Finite Universes When the universe is finite (e.g., the interval 0, 2 1 ), all objects can be encoded by words of the same length. A language L has length n 0 if L =, or every word of
Finite Universes Finite Universes When the universe is finite (e.g., the interval 0, 2 1 ), all objects can be encoded by words of the same length. A language L has length n 0 if L =, or every word of
NPDA, CFG equivalence
 NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
Definition of Büchi Automata
 Büchi Automata Definition of Büchi Automata Let Σ = {a,b,...} be a finite alphabet. By Σ ω we denote the set of all infinite words over Σ. A non-deterministic Büchi automaton (NBA) over Σ is a tuple A
Büchi Automata Definition of Büchi Automata Let Σ = {a,b,...} be a finite alphabet. By Σ ω we denote the set of all infinite words over Σ. A non-deterministic Büchi automaton (NBA) over Σ is a tuple A
What is this course about?
 What is this course about? Examining the power of an abstract machine What can this box of tricks do? What is this course about? Examining the power of an abstract machine Domains of discourse: automata
What is this course about? Examining the power of an abstract machine What can this box of tricks do? What is this course about? Examining the power of an abstract machine Domains of discourse: automata
SYLLABUS. Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 3 : REGULAR EXPRESSIONS AND LANGUAGES
 Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
Complexity of Model Checking Recursion Schemes for Fragments of the Modal Mu-Calculus
 Complexity of Model Checking Recursion Schemes for Fragments of the Modal Mu-Calculus Naoki Kobayashi 1 C.-H. Luke Ong 2 1 Tohoku University 2 University of Oxford Abstract. Ong has shown that the modal
Complexity of Model Checking Recursion Schemes for Fragments of the Modal Mu-Calculus Naoki Kobayashi 1 C.-H. Luke Ong 2 1 Tohoku University 2 University of Oxford Abstract. Ong has shown that the modal
Properties of Context-Free Languages. Closure Properties Decision Properties
 Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
Simplifying XML Schema: Single-Type Approximations of Regular Tree Languages
 Simplifying XML Schema: Single-Type Approximations of Regular Tree Languages Wouter Gelade c, Tomasz Idziaszek a, Wim Martens b,,1, Frank Neven c, Jan Paredaens d a University of Warsaw, Warsaw, Poland
Simplifying XML Schema: Single-Type Approximations of Regular Tree Languages Wouter Gelade c, Tomasz Idziaszek a, Wim Martens b,,1, Frank Neven c, Jan Paredaens d a University of Warsaw, Warsaw, Poland
CS 154 Introduction to Automata and Complexity Theory
 CS 154 Introduction to Automata and Complexity Theory cs154.stanford.edu 1 INSTRUCTORS & TAs Ryan Williams Cody Murray Lera Nikolaenko Sunny Rajan 2 Textbook 3 Homework / Problem Sets Homework will be
CS 154 Introduction to Automata and Complexity Theory cs154.stanford.edu 1 INSTRUCTORS & TAs Ryan Williams Cody Murray Lera Nikolaenko Sunny Rajan 2 Textbook 3 Homework / Problem Sets Homework will be
CS256/Spring 2008 Lecture #11 Zohar Manna. Beyond Temporal Logics
 CS256/Spring 2008 Lecture #11 Zohar Manna Beyond Temporal Logics Temporal logic expresses properties of infinite sequences of states, but there are interesting properties that cannot be expressed, e.g.,
CS256/Spring 2008 Lecture #11 Zohar Manna Beyond Temporal Logics Temporal logic expresses properties of infinite sequences of states, but there are interesting properties that cannot be expressed, e.g.,
Timed pushdown automata and branching vector addition systems
 Timed pushdown automata and branching vector addition systems Lorenzo Clemente, Sławomir Lasota, Ranko Lazić :, and Filip Mazowiecki : Faculty of Mathematics, Informatics and Mechanics, University of Warsaw,
Timed pushdown automata and branching vector addition systems Lorenzo Clemente, Sławomir Lasota, Ranko Lazić :, and Filip Mazowiecki : Faculty of Mathematics, Informatics and Mechanics, University of Warsaw,
Before We Start. The Pumping Lemma. Languages. Context Free Languages. Plan for today. Now our picture looks like. Any questions?
 Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Obtaining the syntactic monoid via duality
 Radboud University Nijmegen MLNL Groningen May 19th, 2011 Formal languages An alphabet is a non-empty finite set of symbols. If Σ is an alphabet, then Σ denotes the set of all words over Σ. The set Σ forms
Radboud University Nijmegen MLNL Groningen May 19th, 2011 Formal languages An alphabet is a non-empty finite set of symbols. If Σ is an alphabet, then Σ denotes the set of all words over Σ. The set Σ forms
This lecture covers Chapter 7 of HMU: Properties of CFLs
 This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
Automata & languages. A primer on the Theory of Computation. Laurent Vanbever. ETH Zürich (D-ITET) October,
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Part 3 out of 5. Automata & languages. A primer on the Theory of Computation. Last week, we learned about closure and equivalence of regular languages
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
Parikh s theorem. Håkan Lindqvist
 Parikh s theorem Håkan Lindqvist Abstract This chapter will discuss Parikh s theorem and provide a proof for it. The proof is done by induction over a set of derivation trees, and using the Parikh mappings
Parikh s theorem Håkan Lindqvist Abstract This chapter will discuss Parikh s theorem and provide a proof for it. The proof is done by induction over a set of derivation trees, and using the Parikh mappings
CSE 105 THEORY OF COMPUTATION. Spring 2018 review class
 CSE 105 THEORY OF COMPUTATION Spring 2018 review class Today's learning goals Summarize key concepts, ideas, themes from CSE 105. Approach your final exam studying with confidence. Identify areas to focus
CSE 105 THEORY OF COMPUTATION Spring 2018 review class Today's learning goals Summarize key concepts, ideas, themes from CSE 105. Approach your final exam studying with confidence. Identify areas to focus
1 More finite deterministic automata
 CS 125 Section #6 Finite automata October 18, 2016 1 More finite deterministic automata Exercise. Consider the following game with two players: Repeatedly flip a coin. On heads, player 1 gets a point.
CS 125 Section #6 Finite automata October 18, 2016 1 More finite deterministic automata Exercise. Consider the following game with two players: Repeatedly flip a coin. On heads, player 1 gets a point.
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL) Objectives Introduce Pumping Lemma for CFL Apply Pumping Lemma to show that some languages are non-cfl Pumping Lemma
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL) Objectives Introduce Pumping Lemma for CFL Apply Pumping Lemma to show that some languages are non-cfl Pumping Lemma
CS 154, Lecture 3: DFA NFA, Regular Expressions
 CS 154, Lecture 3: DFA NFA, Regular Expressions Homework 1 is coming out Deterministic Finite Automata Computation with finite memory Non-Deterministic Finite Automata Computation with finite memory and
CS 154, Lecture 3: DFA NFA, Regular Expressions Homework 1 is coming out Deterministic Finite Automata Computation with finite memory Non-Deterministic Finite Automata Computation with finite memory and
Automata and Languages
 Automata and Languages Prof. Mohamed Hamada Software Engineering Lab. The University of Aizu Japan Nondeterministic Finite Automata with empty moves (-NFA) Definition A nondeterministic finite automaton
Automata and Languages Prof. Mohamed Hamada Software Engineering Lab. The University of Aizu Japan Nondeterministic Finite Automata with empty moves (-NFA) Definition A nondeterministic finite automaton
Valence automata as a generalization of automata with storage
 Valence automata as a generalization of automata with storage Georg Zetzsche Technische Universität Kaiserslautern D-CON 2013 Georg Zetzsche (TU KL) Valence automata D-CON 2013 1 / 23 Example (Pushdown
Valence automata as a generalization of automata with storage Georg Zetzsche Technische Universität Kaiserslautern D-CON 2013 Georg Zetzsche (TU KL) Valence automata D-CON 2013 1 / 23 Example (Pushdown
Complexity Theory VU , SS The Polynomial Hierarchy. Reinhard Pichler
 Complexity Theory Complexity Theory VU 181.142, SS 2018 6. The Polynomial Hierarchy Reinhard Pichler Institut für Informationssysteme Arbeitsbereich DBAI Technische Universität Wien 15 May, 2018 Reinhard
Complexity Theory Complexity Theory VU 181.142, SS 2018 6. The Polynomial Hierarchy Reinhard Pichler Institut für Informationssysteme Arbeitsbereich DBAI Technische Universität Wien 15 May, 2018 Reinhard
Introduction to the Theory of Computing
 Introduction to the Theory of Computing Lecture notes for CS 360 John Watrous School of Computer Science and Institute for Quantum Computing University of Waterloo June 27, 2017 This work is licensed under
Introduction to the Theory of Computing Lecture notes for CS 360 John Watrous School of Computer Science and Institute for Quantum Computing University of Waterloo June 27, 2017 This work is licensed under
Outline. Complexity Theory EXACT TSP. The Class DP. Definition. Problem EXACT TSP. Complexity of EXACT TSP. Proposition VU 181.
 Complexity Theory Complexity Theory Outline Complexity Theory VU 181.142, SS 2018 6. The Polynomial Hierarchy Reinhard Pichler Institut für Informationssysteme Arbeitsbereich DBAI Technische Universität
Complexity Theory Complexity Theory Outline Complexity Theory VU 181.142, SS 2018 6. The Polynomial Hierarchy Reinhard Pichler Institut für Informationssysteme Arbeitsbereich DBAI Technische Universität
Theory of Computation
 Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
3515ICT: Theory of Computation. Regular languages
 3515ICT: Theory of Computation Regular languages Notation and concepts concerning alphabets, strings and languages, and identification of languages with problems (H, 1.5). Regular expressions (H, 3.1,
3515ICT: Theory of Computation Regular languages Notation and concepts concerning alphabets, strings and languages, and identification of languages with problems (H, 1.5). Regular expressions (H, 3.1,
UNIT-II. NONDETERMINISTIC FINITE AUTOMATA WITH ε TRANSITIONS: SIGNIFICANCE. Use of ε-transitions. s t a r t. ε r. e g u l a r
 Syllabus R9 Regulation UNIT-II NONDETERMINISTIC FINITE AUTOMATA WITH ε TRANSITIONS: In the automata theory, a nondeterministic finite automaton (NFA) or nondeterministic finite state machine is a finite
Syllabus R9 Regulation UNIT-II NONDETERMINISTIC FINITE AUTOMATA WITH ε TRANSITIONS: In the automata theory, a nondeterministic finite automaton (NFA) or nondeterministic finite state machine is a finite
Final exam study sheet for CS3719 Turing machines and decidability.
 Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Lecture 24: Randomized Complexity, Course Summary
 6.045 Lecture 24: Randomized Complexity, Course Summary 1 1/4 1/16 1/4 1/4 1/32 1/16 1/32 Probabilistic TMs 1/16 A probabilistic TM M is a nondeterministic TM where: Each nondeterministic step is called
6.045 Lecture 24: Randomized Complexity, Course Summary 1 1/4 1/16 1/4 1/4 1/32 1/16 1/32 Probabilistic TMs 1/16 A probabilistic TM M is a nondeterministic TM where: Each nondeterministic step is called
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Classes and conversions
 Classes and conversions Regular expressions Syntax: r = ε a r r r + r r Semantics: The language L r of a regular expression r is inductively defined as follows: L =, L ε = {ε}, L a = a L r r = L r L r
Classes and conversions Regular expressions Syntax: r = ε a r r r + r r Semantics: The language L r of a regular expression r is inductively defined as follows: L =, L ε = {ε}, L a = a L r r = L r L r
Nondeterministic Finite Automata
 Nondeterministic Finite Automata Not A DFA Does not have exactly one transition from every state on every symbol: Two transitions from q 0 on a No transition from q 1 (on either a or b) Though not a DFA,
Nondeterministic Finite Automata Not A DFA Does not have exactly one transition from every state on every symbol: Two transitions from q 0 on a No transition from q 1 (on either a or b) Though not a DFA,
Warshall s algorithm
 Regular Expressions [1] Warshall s algorithm See Floyd-Warshall algorithm on Wikipedia The Floyd-Warshall algorithm is a graph analysis algorithm for finding shortest paths in a weigthed, directed graph
Regular Expressions [1] Warshall s algorithm See Floyd-Warshall algorithm on Wikipedia The Floyd-Warshall algorithm is a graph analysis algorithm for finding shortest paths in a weigthed, directed graph
Finite State Automata
 Trento 2005 p. 1/4 Finite State Automata Automata: Theory and Practice Paritosh K. Pandya (TIFR, Mumbai, India) Unversity of Trento 10-24 May 2005 Trento 2005 p. 2/4 Finite Word Langauges Alphabet Σ is
Trento 2005 p. 1/4 Finite State Automata Automata: Theory and Practice Paritosh K. Pandya (TIFR, Mumbai, India) Unversity of Trento 10-24 May 2005 Trento 2005 p. 2/4 Finite Word Langauges Alphabet Σ is
Automata, Logic and Games: Theory and Application
 Automata, Logic and Games: Theory and Application 1. Büchi Automata and S1S Luke Ong University of Oxford TACL Summer School University of Salerno, 14-19 June 2015 Luke Ong Büchi Automata & S1S 14-19 June
Automata, Logic and Games: Theory and Application 1. Büchi Automata and S1S Luke Ong University of Oxford TACL Summer School University of Salerno, 14-19 June 2015 Luke Ong Büchi Automata & S1S 14-19 June
Section 1 (closed-book) Total points 30
 CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
Tree languages defined in first-order logic with one quantifier alternation
 Tree languages defined in first-order logic with one quantifier alternation Miko laj Bojańczyk, Luc Segoufin Warsaw University, INRIA - LSV March 9, 2010 Abstract We study tree languages that can be defined
Tree languages defined in first-order logic with one quantifier alternation Miko laj Bojańczyk, Luc Segoufin Warsaw University, INRIA - LSV March 9, 2010 Abstract We study tree languages that can be defined
Advanced Automata Theory 2 Finite Automata
 Advanced Automata Theory 2 Finite Automata Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Advanced Automata Theory 2 Finite
Advanced Automata Theory 2 Finite Automata Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Advanced Automata Theory 2 Finite
Parameterized Regular Expressions and Their Languages
 Parameterized Regular Expressions and Their Languages Pablo Barceló a, Juan Reutter b, Leonid Libkin b a Department of Computer Science, University of Chile b School of Informatics, University of Edinburgh
Parameterized Regular Expressions and Their Languages Pablo Barceló a, Juan Reutter b, Leonid Libkin b a Department of Computer Science, University of Chile b School of Informatics, University of Edinburgh
60-354, Theory of Computation Fall Asish Mukhopadhyay School of Computer Science University of Windsor
 60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
Automata theory. An algorithmic approach. Lecture Notes. Javier Esparza
 Automata theory An algorithmic approach Lecture Notes Javier Esparza July 2 22 2 Chapter 9 Automata and Logic A regular expression can be seen as a set of instructions ( a recipe ) for generating the words
Automata theory An algorithmic approach Lecture Notes Javier Esparza July 2 22 2 Chapter 9 Automata and Logic A regular expression can be seen as a set of instructions ( a recipe ) for generating the words
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Today's learning goals Summarize key concepts, ideas, themes from CSE 105. Approach your final exam studying with
CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Today's learning goals Summarize key concepts, ideas, themes from CSE 105. Approach your final exam studying with
arxiv: v1 [cs.fl] 19 Mar 2015
![arxiv: v1 [cs.fl] 19 Mar 2015 arxiv: v1 [cs.fl] 19 Mar 2015](/thumbs/92/110021537.jpg) Regular realizability problems and regular languages A. Rubtsov arxiv:1503.05879v1 [cs.fl] 19 Mar 2015 1 Moscow Institute of Physics and Technology 2 National Research University Higher School of Economics
Regular realizability problems and regular languages A. Rubtsov arxiv:1503.05879v1 [cs.fl] 19 Mar 2015 1 Moscow Institute of Physics and Technology 2 National Research University Higher School of Economics
PUSHDOWN AUTOMATA (PDA)
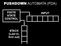 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
Chapter Five: Nondeterministic Finite Automata
 Chapter Five: Nondeterministic Finite Automata From DFA to NFA A DFA has exactly one transition from every state on every symbol in the alphabet. By relaxing this requirement we get a related but more
Chapter Five: Nondeterministic Finite Automata From DFA to NFA A DFA has exactly one transition from every state on every symbol in the alphabet. By relaxing this requirement we get a related but more
