The Capacity Region of 2-Receiver Multiple-Input Broadcast Packet Erasure Channels with Channel Output Feedback
|
|
|
- Kelly Greene
- 5 years ago
- Views:
Transcription
1 IEEE TRANSACTIONS ON INFORMATION THEORY, ONLINE PREPRINT The Capacity Region of 2-Receiver Multiple-Input Broadcast Packet Erasure Channels with Channel Output Feedack Chih-Chun Wang, Memer, IEEE, Jaemin Han, Student Memer, IEEE Astract This work studies the capacity of the 2-receiver multiple-input roadcast packet erasure channels PECs with channel output feedack, which is in contrast with the singleinput setting of the existing works. Motivated y the immense success of linear network coding LNC in theory and in practice, this work first focuses on LNC schemes and characterizes the LNC feedack capacity region of 2-receiver multiple-input roadcast PECs. A new linear-space-ased approach is proposed, which unifies the prolems of finding a capacity outer ound and devising the achievaility scheme into a single linear programming LP prolem. Specifically, an LP solver is used to exhaustively search for the LNC schemes with the est possile throughput, the result of which is thus guaranteed to attain the LNC feedack capacity. It is then proven y pure algeraic arguments that the LNC capacity region matches a simple capacity region outer ound, which proves that the derived LNC capacity region is indeed the true capacity. A yproduct of the aove results is a complete LNC capacity region characterization for 2-receiver partially Markovian and partially controllale roadcast PECs. Index Terms Broadcast capacity; roadcast channels; channel output feedack; linear network coding; multiple-input/multipleoutput MIMO channels; packet erasure channels. I. INTRODUCTION It is well known that channel output feedack can potentially enlarge the capacity region of roadcast channels [2], [13]. Recently the feedack capacity region of K-receiver roadcast packet erasure channels PECs has een fully characterized for K 3 [6], [15]. For the case of K > 3, the full feedack roadcast capacity region has een characterized for the setting of perfectly symmetric channels and for the setting of one-sidedly-fair capacity with spatially independent erasure events, respectively [6], [15]. Numerically tight capacity inner and outer ounds have also een proposed in [15], which can e computed efficiently y linear programming LP solvers for aritrary K and aritrary channel characteristics. Specifically, a 1-to-K PEC takes an input symol also known as a packet W from some large finite field GFq and each destination d k out of K destinations receives either the input This work was supported in parts y NSF Grants CCF and CNS Part of this paper was presented in the IEEE International Symposium on Information Theory, C.-C. Wang and J. Han are with the School of Electrical and Computer Engineering, Purdue University, West Lafayette, IN, USA; {chihw,han83}@purdue.edu Manuscript received in May 2012; revised in May Copyright c 2014 IEEE. Personal use of this material is permitted. However, permission to use this material for any other purposes must e otained from the IEEE y sending a request to pus-permissions@ieee.org. packet Z k = W or an erasure Z k =, depending on whether the packet W has successfully arrived at d k. The single-input roadcast PEC model in [6], [15] captures closely the network coding capacity for the downlink transmission from a single access point to multiple clients with one antenna and simple modulation schemes [9]. On the other hand, such a single-input roadcast PEC model does not take into account several commonly used modern communication schemes. For example, 2 antennas may e used at oth the source s and the destinations d k, which corresponds to a multiple-input roadcast PEC [4] that takes W [1], W [2] GFq 2 as input, and each d k may receive one of the four possile outcomes W [1],,, W [2], W [1], W [2], and, depending on whether the packet W [m] sent y antenna m, m = 1, 2, is decodale or not. Even when only a single antenna is used, source s may use Orthogonal Frequency Division Multiple Access OFDMA, which, in each time slot, can send out multiple streams of packets over different su-carriers. Each su-carrier may experience different random erasure events. Each d k constantly scans all sucarriers and records any overheard packets. The multiple su-carriers in OFDMA can again e modeled as a multiple-input roadcast PEC. This works considers the multiple-input roadcast PEC with 2 receivers and channel output feedack. That is, in each time slot t, the source s sends M symols W [1], W [2],, W [M]. Depending on the channel realization, each destination d i, i = 1, 2, may hear a random set of W [ ] symols. At the end of time t, each d i reports ack to s which suset of symols it has received in the current time slot through the use of ACK or NACK. The setting of interest generalizes the existing work [4] y further considering the throughput enefits of channel output feedack. Motivated y the immense success of linear network coding LNC [11], this work first focuses on LNC schemes and characterizes the full LNC feedack capacity region R1, R2. A new framework is proposed that unifies the prolems of finding an LNC capacity outer ound and designing the corresponding ound-achieving solution into a single linear-programming LP prolem. Namely, we first drastically simplify the LNC design choices in a lossless way y leveraging upon the underlying linear space structures. Then we use an LP solver to search exhaustively over all possile LNC design choices and find the LNC solution that achieves the highest throughput. The exhaustiveness guarantees that the resulting LNC scheme is throughput optimal among all LNC solutions and thus achieves the LNC capacity.
2 IEEE TRANSACTIONS ON INFORMATION THEORY, ONLINE PREPRINT Remark 1: Such a constructive optimality proof has een widely used in the networking community ut not in the information theory community. For example, in the networking society, the optimal multi-path routing throughput is found y simply searching over all possile routing decisions that oey the flow-conservation law, which is in contrast with the traditional information-theoretic approach that first finds a cut and an achievaility scheme and later proves that the achievale throughput meet the cut value. This exhaustivesearch-ased approach was previously not possile since there are too many LNC design choices. With a new framework that leverages upon the underlying linear space structure of LNC, we can greatly reduce the numer of design choices and are thus ale to design provaly optimal LNC schemes without the need of finding any cut condition! Remark 2: This work considers the so-called inter-flow NC prolem with two coexisting traffic flows. When there is only one flow in the network, termed the intra-flow NC prolem, [3] proves that channel output feedack does not increase the endto-end capacity of any aritrary erasure networks, and random linear network coding [8] achieves the capacity. After characterizing the LNC capacity region of 2-receiver multi-input roadcast PECs, we will prove y some pure algeraic arguments that the LNC capacity region matches a simple capacity region outer ound. The results thus prove that the newly derived LNC capacity region is indeed the capacity. The rest of this paper is organized as follows. Section II introduces the prolem formulation. Section III discusses several existing results. The main results of this work are the full LNC feedack capacity characterization and the equivalence etween the LNC capacity region and the true capacity, which are presented in Section IV. Section V contains the proof for the case of M = 1 input, which illustrates several key concepts of this work. Section VI generalizes the proof for the case of aritrary M inputs. Section VII discusses in details a concrete multi-input roadcast PEC example and some further implications of the capacity results, including the LNC feedack capacity of the partially Markovian and partially controllale roadcast PECs. Section VIII concludes this work. II. PROBLEM FORMULATION Given a finite field GFq, the M-input 2-receiver roadcast PEC is defined as follows. For any time slot, source s sends M symols W = W [1], W [2],, W [M] GFq M and each d i receives a random suset rx i {1, 2,, M} of the symols for i = 1, 2. Each of the M input symols W [m] takes values in GFq. The randomness of an M- input 2-receiver roadcast PEC can e descried y the joint W [ ] reception proaility p rx1,rx 2 such that rx 1,rx 2 p rx1,rx 2 = 1. For example, when M = 3, p {1,2},{2,3} is the proaility that d 1 receives Z 1 = W [1], W [2], and d 2 receives Z 2 =, W [2], W [3]. We consider only stationary and memoryless channels, i.e., {p rx1,rx 2 } remains constant over time and the reception events for any distinct time slots t 1, t 2, are independent. For any given joint proaility distriution p rx1,rx 2, two independence conditions can e defined as follows. Definition 1: An M-input 2-receiver roadcast PEC is cross-input independent if for any m m, the two 2-dimensional random vectors 1 {m rx1 }, 1 {m rx2 } and 1 { m rx1}, 1 { m rx2} are independent where 1 { } is the indicator function. Definition 2: An M-input 2-receiver roadcast PEC is cross-receiver independent 1 if the two random sets rx 1 and rx 2 are independently distriuted. Throughout this work we focus mostly only on M-input 2-receiver roadcast PECs that are cross-input independent ut may or may not e cross-receiver independent. For comparison, the M, 2 erasure roadcast channel defined in [4] is equivalent to the M-input 2-receiver model that is oth cross-input and cross-receiver independent. to denote the marginal reception proailities for the m-th symol W [m] where each it a i indicates whether d i receives W [m] or not for i = 1, 2. For example, y definition We use a 1 a 2 10 = rx 1,rx 2 s.t. m rx 1,m/ rx 2 p rx1,rx 2 is the proaility that the m-th input symol W [m] is successfully received y d 1 ut not y d 2. Consider the following communication prolem. For any rate vector R 1, R 2, within n time slots source s would like to send two independent packet streams X i = X i,1, X i,2,, X i,nri GFq nri to destination d i for i = 1, 2, respectively. At the end of each time slot, each d i reports ack to s which suset of symols it has received the rx i value through the use of ACK or NACK. This channel output feedack setting was not considered in the existing work [4]. If we use the input argument t, t = 1, 2,, n, to distinguish the n channel usages, a network code can e descried y n encoding functions: for all t = 1,, n, Wt = f t X 1, X 2, [rx 1, rx 2 ] t and two decoding functions: for all i = 1, 2, ˆX i = g i [Zi ] n 1, {f t,, [rx 1, rx 2 ] t 1 1 : t = 1,, n}, 2 where [Z i ] n 1 denotes what d i has received from time 1 to n, and [rx 1, rx 2 ] t 1 1 denotes the channel output information from time 1 to t 1. In 2 we assume that each d i knows 2 how the coded symols are generated the functions f t,, [rx 1, rx 2 ] t 1 1 ut does not know the actual information symols X 1 and X 2 used to generate Wt. A network code is linear if the encoders f t are linear with respect to X 1 and X 2, i.e., when 1 can e written as Wt = X C t, 1 Cross-receiver independence is also termed spatial independence in [15]. 2 In general, d i always knows f t,,, the overall communication scheme that is agreed upon efore transmission. But d i does not know f t,, [rx 1, rx 2 ] t 1 1 since it depends on the random channel realization of the other destination d j. As a result, a more realistic definition of the decoder should e ˆX i = g i [Z i ] n 1. 3
3 IEEE TRANSACTIONS ON INFORMATION THEORY, ONLINE PREPRINT where C t is an nr 1 + nr 2 M matrix in GFq and X = X 1, X 2 is an nr 1 + R 2 -dimensional row vector consisting of all information symols. The choice of C t depends on [rx 1, rx 2 ] t 1 1 ut not on X. In practice [1], the coding coefficients C t are often emedded in the header of the packets so that upon the successful reception of a packet W [m] t, the corresponding coding coefficients used to generate W [m] t are known to the receiver. Hence a decoder of the form of 2 can e used. Definition 3: Given a finite field GFq, a rate vector R 1, R 2 is achievale if for any ϵ > 0 there exists a network code of length n such that Pro ˆX i X i < ϵ for all i = 1, 2. The capacity region is defined as the closure of all R 1, R 2 that are achievale. Definition 4: A rate vector R 1, R 2 is LNC-achievale if it can e achieved y a linear network code. The LNC capacity region is the closure of all LNC-achievale R 1, R 2. Note that the unit of the aove capacity definition is packets per time slot. It can e converted to the traditional unit its per time slot y multiplying a factor of log 2 q since each packet can carry log 2 q its of information. Throughout this paper, we use exclusively packets per time slot as the unit. III. DISCUSSION OF THE EXISTING RESULTS A. A Pair of Simple Inner and Outer Bounds A simple inner ound on the aove capacity prolem can e derived y performing LNC over the M individual single-input roadcast PECs one for each of the M inputs separately. Therefore, we have the following lemma: Lemma 1: For any fixed GFq, a rate vector R 1, R 2 is LNC-achievale if there exist 2M non-negative variales R [m] 1 and R [m] 2, for all m = 1,, M, such that the following conditions are satisfied. i = 1, 2, R [m] i = R i 4 m = 1,, M, R [m] p[m] 11 R [m] p[m] 01 +p[m] 11 R [m] p[m] 01 +p[m] 11 + R[m] p[m] 11 < 1 < 1. 5 Proof: 4 follows from summing up the per-input LNC rates and 5 follows from the feedack capacity region results for 1-input 2-receiver roadcast PECs [7]. Following similar steps as in [7] we can derive the following capacity outer ound. Lemma 2: For any fixed GFq, consider any M-input 2- receiver roadcast PEC that is cross-input independent. A rate vector R 1, R 2 is achievale only if there exist 4M However, the capacity difference etween the stronger 2 and the weaker 3 decoders is negligile when a sufficient large GFq is used. The reason is that in addition to the allotted n time slots, s can simply use a few extra time slots to roadcast the inary channel status [rx 1, rx 2 ] n 1 to oth destinations so that a more powerful decoder in 2 can e used. The overhead of using extra time slots to convey the inary receptions status [rx 1, rx 2 ] n 1 to {d 1, d 2 } diminishes to zero when a sufficiently large GFq is used. As a result, the capacity gap is negligile for large q. In this work we focus exclusively on decoders of the form of 2. Also see [1] and our discussion of the practical LNC implementation. non-negative variales R [m,k] i for all i, k {1, 2} and m {1,, M} such that the following conditions are satisfied. i, k {1, 2}, and for all m {1,, M}, R [m,1] p[m] 11 R [m,2] p[m] 01 + p[m] 11 R [m,k] i = R i 6 R [m,1] p[m] 01 + p[m] 11 + R[m,2] p[m] Proof: The proof simply comines the capacity outer ound construction in [13] and the zero-feedack capacity results in [4]. Specifically, we first construct a new M-input 2-receiver roadcast PEC from the original roadcast PEC in the following way. Namely, we allow d 1 to oserve oth Z 1 and Z 2, the latter of which is what d 2 receives in each time slot. Since d 1 can oserve additional information Z 2, the feedack capacity of the new roadcast PEC is an outer ound of the feedack capacity of the original PEC. Further, for the new roadcast PEC, d 2 is a physically degraded receiver when compared to d 1. By [5], channel output feedack does not improve the performance of a physically degraded roadcast channel. As a result, the feedack capacity of the new roadcast PEC equals to the feedack-free capacity of the new roadcast PEC. By the capacity expression 3 in [4], the feedack-free capacity of the new roadcast PEC is descried y 6 with k = 2 and y 8, which, y our aforementioned reasoning, serves as an outer ound for the feedack capacity of the original roadcast PEC. If we swap the roles of d 1 and d 2 and repeat the same argument, we can show that 6 with k = 1 and 7 must also e an outer ound for the feedack capacity of the original roadcast PEC. The proof of this lemma is completed y taking the intersection of the two outer ounds. B. An Improved Inner Bound The capacity inner ound in Lemma 1 turns out e e suoptimal due to the fact that it performs network coding separately for each of the M su-channels. To tighten the inner ound, one can follow the ideas of [7], [10] and devise a simple LNC scheme that encodes jointly over all M suchannels and achieves the following improved inner ound. Lemma 3: For any fixed GFq, a rate vector R 1, R 2 is LNC-achievale if there exist 2M non-negative variales R [m] 1 and R [m] 2, for all m = 1,, M, such that the following 3 The newly constructed roadcast PEC is cross-input independent ut crossreceiver dependent. Although the results in [4] were stated for the setting of cross-input and cross-receiver independence, we can use Sato s argument [14] to relax the condition of cross-receiver independence.
4 IEEE TRANSACTIONS ON INFORMATION THEORY, ONLINE PREPRINT conditions are satisfied: i = 1, 2, R [m] i = R i 9 m = 1,, M, R 1 + R 2 + R[m] 2 R [m] 1 + R [m] p[m] 10 + p[m] p[m] p[m] 01 + p[m] 11 R[m] p[m] p[m] 01 + p[m] 11 < < < p[m] p[m] The main idea ehind Lemma 3 is to first divide the information packets among the M inputs, see 9, and send the packets uncodedly until each one is received y at least one of d 1 and d 2, see 10. Then collect all the newly created network coding opportunities [7], [10], [12], redistriute the coding opportunities among all M inputs, and use the remaining time slots of each of the M su-channels to send linear cominations of the packets that have not arrived at their intended destinations. The proof of Lemma 3 and detailed discussion are relegated to Appendix A. One can also verify from the proof that the inner ound in Lemma 3 always contains the inner ound in Lemma 1. C. An Illustrative Example Both the inner ounds in Lemmas 1 and 3 are suoptimal in the following sense. For some special choices of the parameters a 1 a 2, the two inner ounds in Lemmas 1 and 3 coincide with the outer ound in Lemma 2. However, for some a 1 a 2 values even the improved inner ound in Lemma 3 is strictly contained in the outer ound in Lemma 2. Take the following 2-input, 2-receiver MIMO roadcast PEC for example. Suppose the joint reception proaility {p rx1,rx 2 } are p [1] 00 = 0, p[1] 01 = 0.125, p[1] 10 = 0, p[1] 11 = 0.875; p [2] 00 = 0.04, p[2] 01 = 0.16, p[2] 10 = 0.16, p[2] 11 = 0.64, 13 and the channel is cross-input independent. This is asically a setting of cross-input and cross-receiver independence with the m-th-input-to-d i su-channel having success proaility 0.875, 1, 0.8, and 0.8 for m, i = 1, 1, 1, 2, 2, 1, and 2, 2, respectively. We plot in Fig. 1 the inner and outer ounds in Lemmas 1 and 2 for this example. As can e seen, there is a non-zero gap. Further, one can verify that for these particular a 1a 2 values, the rate vector R 1, R 2 = 0.875, 0.96, a point within the outer ound in Lemma 2, is strictly outside the closure of the improved inner ound in Lemma 3. To close the gap etween the inner and outer ounds, we need to either design a more powerful achievaility scheme or R LNC capacity Per input LNC inner ound R 1 Fig. 1. The LNC capacity computed y Proposition 1 versus the per-input LNC inner ound in Lemma 1. The LNC capacity also coincides with the capacity outer ound in Lemma 2. further sharpen the outer ounding arguments. Both are nontrivial tasks since i for aritrary M, there is an exponentially large numer of ways of designing a coding scheme and we can no longer rely on the ad-hoc design methodology as used in Lemma 3; ii We do not have many analytical tools for feedack capacity analysis other than the existing approach discussed in Lemma 2. In this work, we circumvent the aove difficulties y first focusing on LNC. We characterize the LNC capacity region for cross-input independent M-input 2-receiver roadcast PECs. As will e seen shortly after, this work derives a new systematic, constructive LNC capacity proof that does not rely on the ad-hoc design nor on the outer ounding arguments in the existing results. After characterizing the LNC capacity, we use some pure algeraic arguments to prove that the LNC capacity region is identical to the outer ound in Lemma 2. Therefore, the LNC capacity region is the true capacity of the M-input 2-receiver roadcast PECs. IV. MAIN RESULTS Consider a finite index set FTs of 18 elements: FTs = {0, 1, 2, 3, 7, 9, 11, 15, 18, 19, 23, 27, 31, 47, 63, 87, 95, 127}. 14 It will e clear in Section V why we consider such an index set. Let = {0, 1} 7 denote a 7-it string. We can also view as a ase-2 expression with the leftmost it eing the most significant it MSB. We append zeros in the prefix to make the length always 7. For example, the statement = 9 is equivalent to = and the statement FTs and 7 = 0 is equivalent to {0, 2, 18}. The main results of this work can now e stated as follows. Proposition 1: For any fixed GFq, consider any crossinput independent M-input 2-receiver roadcast PEC. A rate vector R 1, R 2 is in the LNC capacity region if and only if there exist 18M non-negative variales for all FTs and m = 1,, M, and 7 non-negative variales y 1 to y 7 such that jointly they satisfy the following 4 groups of linear conditions:
5 IEEE TRANSACTIONS ON INFORMATION THEORY, ONLINE PREPRINT Group 1, termed the time-sharing conditions, has M equalities: m = 1,, M, FTs Group 2, termed the rank-conversion conditions, has 7 equalities: y 1 = 10 + p[m] y 2 = y 3 = R 1 + y 4 = R 2 + y 5 = y 6 = R 1 + y 7 = R 2 + FTs and 1=0 FTs and 2=0 FTs and 3 =0 FTs and 4 =0 FTs and 5 =0 FTs and 6=0 FTs and 7 = p[m] p[m] p[m] p[m] 01 + p[m] p[m] 01 + p[m] p[m] 01 + p[m] Group 3, termed the rank-comparison conditions, has 7 inequalities: y 3 y 6, y 4 y 7 23 y 6 R 1 + R 2, y 7 R 1 + R 2 24 y 5 + y 3 y 6 y 1 25 y 5 + y 4 y 7 y 2 26 y 6 + y 7 R 1 + R 2 y Group 4, termed the decodaility conditions, has 2 equalities: y 3 = y 1 and y 4 = y Oviously, the LNC capacity region in Proposition 1 is an inner ound of the true capacity region. A stronger result can then e proven as follows. Proposition 2: For any fixed GFq, the LNC capacity region in Proposition 1 matches the outer ound in Lemma 2. Therefore, the Shannon capacity region can e descried either y the LP prolem in Lemma 2 that contains 4M variales and 4 + 2M inequalities, or y the LP prolem in Proposition 1 that contains 18M + 7 variales and M + 16 inequalities. The proof of Proposition 1 is relegated to Sections V and VI. The proof of Proposition 2 is y some pure algeraic arguments, which are provided in Appendix B. A yproduct of : m, a 1, a 2 {0, 1}} while CH 1 is cross-input independent ut CH 2 is not. Any R 1, R 2 that is achievale resp. LNC achievale for CH 1 is also achievale resp. LNC achievale for CH 2. This lemma can e proven y interleaving several CH 1 - ased constituent codes over the time axis and the M-symols, and then apply the interleaved super code to CH 2. A detailed proof is provided in Appendix C. the proof of Proposition 2 is the following lemma that sheds further insights to the LP prolem in Proposition 1. Lemma 4: For any given R 1, R 2 value, if the corresponding LP prolem in Proposition 1 is feasile, then there exist 18M and 7 y i variales satisfying simultaneously 15 to 28 and the following additional property: 0 only if {0, 9, 18, 27, 31, 63, 95}. The proof of Lemma 4 is provided in Appendix B. Algeraically, the aove lemma implies that we can, without loss of generality, reduce the numer of variales from 18M to 7M when solving the LP prolem in Proposition 1. The physical meaning of Lemma 4 will e discussed in Section VI-D. Proposition 1 characterizes the capacity of cross-input independent roadcast PECs, and it can also e used as an inner ound for cross-input dependent roadcast PECs through the following lemma. Lemma 5: For any fixed GFq, consider two M-input 2- receiver roadcast PECs CH 1 and CH 2 that have the same perinput marginal reception proailities { a 1 a 2 V. PROOF OF PROPOSITION 1 FOR M = 1 We first provide the proof of Proposition 1 for the case of M = 1, which can e viewed as an alternative proof for the existing M = 1 achievaility results in [7]. The concepts and terminology used in the proof of M = 1 case will e useful when proving the general case of M 2 in Section VI. A. Basic Definitions Consider the case of M = 1. That is, for each time slot, s sends one symol W t = X c T t where c t is an nr 1 + R 2 -dimensional row coding vector consisting of the coding coefficients and c T t is the transpose of c t. When M = 1 the receiving set rx i of d i can take values as either rx i = or rx i = {1} where the former indicates that d i received an erasure while the latter indicates that d i received the first and also the only transmitted symol W t. For each d i, we define the knowledge space S i t in the end of time t y S i t = span{c τ : τ t s.t. 1 rx i at time τ}. 29 That is, S i t is the linear span of the vectors of those packets that have successfully arrived at d i. By convention, we define the linear span of an empty vector set to e a linear su-space containing only the all-zero vector 0. Namely, span = {0}. For example, S i 0 = {0} y this definition. One can easily see that in the end of time t, d i is ale to compute the value of X v T for all v S i t y linearly comining Z i τ for all τ t.
6 IEEE TRANSACTIONS ON INFORMATION THEORY, ONLINE PREPRINT For j = 1 to nr 1 + R 2, let δ j denote an nr 1 + R 2 - dimensional elementary delta row vector with its j-th coordinate eing one and all the other coordinates eing zero. Define Ω = span{δ j : j = 1,, nr 1 + R 2 } as the overall message space and define Ω 1 = span{δj : j = 1,, nr 1 } and Ω 2 = span{δj : j = nr 1 + 1,, nr 1 + R 2 } as the individual message spaces for d 1 and d 2, respectively. Both S i t and Ω i are linear suspaces of Ω for i = 1, 2. Sometimes we also call Ω the overall coding vector space since any interflow coding vector c t must e in Ω. For any two linear suspaces A, B Ω, define A B = span{v : v A B} as the linear sum space of A and B. From the discussion in the eginning of this susection, d i can decode the desired X i,1,, X i,nri symols if and only if in the end of time n we have Ω i S i n, or equivalently B. Break Down The Design Choices S i n Ω i = S i n. 30 We now demonstrate how to use the knowledge spaces to reak down the design choices of LNC. In the eginning of time t or equivalently in the end of time t 1, there are q nr 1+R 2 different ways of designing the coding vector c t Ω. To simplify the design choices, we consider the following 7 linear suspaces: A 1 = S1 ; A 2 = S2 ; 31 A 3 = S1 Ω 1 ; A 4 = S2 Ω 2 ; A 5 = S1 S 2 ; 32 A 6 = S1 S 2 Ω 1 ; A 7 = S1 S 2 Ω 2, 33 for which we use S 1 and S 2 as shorthand for S 1 t 1 and S 2 t 1, the knowledge spaces in the end of time t 1. In the susequent discussion, we often drop the input argument t 1 when the time instant of interest is clear in the context. We can now partition the overall coding vector space Ω into 2 7 = 128 disjoint susets depending on whether c t is in A k or not, for k = 1,, 7. Each suset is termed a coding type and can e indexed y a 7-it string = where each k indicates whether c t A k or not. For example, type contains the coding vectors that are in A 3 A 5 A 6 A 7, ut not in any of A 1, A 2, and A 4. Those coding vectors are now denoted y TYPE 23 = TYPE = A 3 A 5 A 6 A 7 \A 1 A 2 A 4 34 = A 3 A 5 \A 1 A 4 35 where 35 follows from the fact that y 31 to 33 we have A 5 A 6 A 7 and A 2 A 4. Note that some of the 128 coding types are always empty, which are termed the infeasile types. For example, type is infeasile since there cannot e any v Ω that is in A 1 = S 1 ut not in A 3 = S 1 Ω 1 A 1. Overall, there are only 18 Feasile Types FTs and the list of them is the FTs defined in 14. This new framework allows us to focus on the types of the coding choices without worrying aout designing the exact values of the individual coordinates of c t Ω. Specifically, we will focus on the following design prolem: From which one of the 18 FTs should we choose c t in order to maximize the throughput? We will also analyze the performance of any given scheme y quantifying how frequently a coding vector c t of type- is sent. C. The Only If Analysis of Proposition 1 For The Case of M = 1 Fix any given linear network code such that d i can decode all X i,1 to X i,nri in the end of time n for all i = 1, 2 with close-to-one proaility. Since the 18 disjoint FTs fully cover 4 Ω, for each time t we can always lael the coding choice c t of the given LNC scheme as one of the 18 FTs. Define x [1] = 1 n E { n t=1 1 {c t TYPE }} as the normalized expected numer of c t of type. Since the total numer of time slots is n, 15 holds for the case of M = 1 y the time-sharing argument. In the following, we will estalish additional linear equalities/inequalities that govern the values of x. Consider the linear spaces A k, k = 1 to 7, in the eginning of time 1 and in the end of time n, and denote them y A k 0 and A k n, respectively. Consider A 6 = S 1 S 2 Ω 1 for example. By 29 and 33 we have RankA 6 0 = RankΩ 1 = nr 1. We then note that when source s sends a c t TYPE for some with 6 eing 0, then that c t is not in A 6 = S 1 S 2 Ω 1. Therefore, whenever one of d 1 and d 2 receives W t = X c T t successfully, the rank of A 6 will increase y one. We thus have RankA n w. 6=0 t=1 1 { c t TYPE, and } one of {d 1, d 2 } receives it = RankA 6 n 36 Define y k = 1 n E {RankA kn} as the normalized expected rank of A k n. Taking the normalized expectation of 36, counting only the FTs, and y the linearity of expectation and the stationarity and memorylessness of the channel, we have proven 21 for M = 1. By similar rank-conversion arguments, we can also prove 16 to 22 for M = 1. Detailed derivation of 16 to 22 is relegated to Appendix D. In the following, we will derive the rank comparison inequalities in Group 3. By 31 to 33, in the end of time n we must have A 3 A 6, A 4 A 7, A 6 Ω, and A 7 Ω. 37 Considering the normalized expected ranks of the aove inequalities in the end of time n, we have proven 23 and 24. Before continuing, we present the following self-explanatory lemma. Lemma 6: For any two linear spaces B 1 and B 2, we have RankB 1 B 2 +RankB 1 B 2 = RankB 1 +RankB 2. We then consider the following inequality: RankS 1 S 2 + RankS 1 Ω 1 RankS 1 S 2 Ω 1 = RankS 1 S 2 S 1 Ω 1 38 RankS The actual set of vectors in a type, e.g., 34, evolves over time since the A k definitions in 31 to 33 depend on the knowledge spaces S 1 and S 2 in the end of time t 1. However, the 18 FTs always cover Ω for any t value.
7 IEEE TRANSACTIONS ON INFORMATION THEORY, ONLINE PREPRINT where 38 follows from Lemma 6, and 39 follows from simple set operations. By taking the normalized expectation of 39 in the end of time n, we have proven 25. Similarly, we can derive the following inequalities: RankS 1 S 2 + RankS 2 Ω 2 RankS 1 S 2 Ω 2 RankS 2 40 RankS 1 S 2 Ω 1 + RankS 1 S 2 Ω 2 RankΩ RankS 1 S 2, 41 and use them to prove 26 and 27, respectively. Finally, y definition we have 0 RankS i n Ω i RankS i n RankS i n Ω i RankΩ = n R 1 + R 2. By the decodaility condition 30, ProRankS i n Ω i RankS i n < ϵ. We thus have 0 E{RankS i n Ω i } E{RankS i n} ϵ n R 1 + R 2. Taking the normalized expectation and y 31 and 32, we have 0 y 3 y 1 ϵ R 1 + R 2 and 0 y 4 y 2 ϵ R 1 + R The aove construction shows that given any ϵ > 0, we can use the corresponding LNC scheme to compute the x [1] and y k values that satisfy and 42. Since the aove construction holds for aritrarily small ϵ > 0, it is guaranteed that the feasile region of the linear inequalities 15 to 28 is non-empty. The aove discussion thus proves that for the case of M = 1, if R 1, R 2 is LNC-achievale, there exist x [1] and y 1 to y 7 values satisfying Proposition 1. D. The If Analysis of Proposition 1 For the Case of M = 1 Part I: A Polytope-Based View For the achievaility proofs in this section, we temporarily assume that the underlying GFq satisfies q 3. In Section VI-C, we will relax this assumption and allow for the case of GF2. A critical difference etween Lemma 2 and the outer ounding part of Proposition 1 is that the latter is a constructive approach while the former is implicitly a cut condition. As will e demonstrated, any {x [1] : FTs} and y 1 to y 7 satisfying Proposition 1 can e directly translated to a rate- R 1, R 2 LNC scheme. On the other hand, it is not clear how the auxiliary variales R [m,k] i in Lemma 2 could guide the LNC design. We first introduce some notation efore elaorating the main ideas of the new achievaility scheme. Consider M = 1 and any rate vector R 1, R 2 that is in the interior 5 of the capacity region in Proposition 1. Denote the companying variale values in Proposition 1 y {ẍ [1] : FTs} and 5 Being in the interior of the capacity region means that oth R 1 and R 2 are strictly positive and there exists a small δ > 0 such that rate R 1 +δ, R 2 +δ is also in the capacity region. ÿ 1 to ÿ 7 such that jointly these variale values and R 1, R 2 satisfy 15 to 28. Note that the difference etween ẍ [1] and x [1] is that the former is a constant scalar value corresponding to the R 1, R 2 of interest while the latter is a variale of a linear programming prolem. For simplicity, oftentimes we use the notation {ẍ [1] : } that implicitly assumes that must e in FTs. Our main idea is as follows. For any t, in the eginning of time t source s first uses the previous reception status [rx 1, rx 2 ] t 1 1 to determine the suspaces A 1 to A 7. Then we simply let s choose the c t from 6 one of the 18 FTs as discussed in Section V-B. To etter descrie the operations, we define random processes X [1] t, FTs, as follows: FTs, X [1] t = 1 n t 1 {cτ TYPE } 43 τ=1 eing the cumulative frequency 7 of using type- coding choices until time t. We then have the following critical oservation: If we can choose the coding type used at time t for all t = 1,, n in a way that ensures that in the end of time n, the cumulative frequencies n = ẍ[1] for all FTs, then the outer ound analysis in Section V-C guarantees that the resulting LNC scheme achieves rate R 1, R 2 with close-to-one proaility. X [1] The reason is as follows. If we can attain the desired frequency {ẍ [1] : } with proaility one, then the proof of the rank-conversion equalities in Section V-C ensures that for this particular scheme, for any k = 1,, 7, the normalized expected rank of A k n is the same as the ÿ k value corresponding to the target frequency {ẍ [1] : }. Therefore, in the end of time n, we will have E{RankA 1 n} = E{RankA 3 n}. Note that y definition we always have RankA 1 n RankA 3 n. This thus implies RankA 1 n = RankA 3 n with proaility one and d 1 can decode its desired messages. By symmetry, so does d 2. Note that in practice, we may not e ale to attain the target frequency {ẍ [1] : } with proaility one. However, as long as the {X [1] n : } can e made sufficiently close to {ẍ [1] : }, then we can achieve 1 ϵ fraction of the target rate pair R 1, R 2 with proaility 1 ϵ for aritrary ϵ > 0 y the continuous nature of the LP prolem and y the law of large numers. As can e seen from this argument, the decodaility condition the Group 4 equalities in Proposition 1 is now converted to a new goal of attaining the target relative frequency {ẍ [1] : }. 6 If there are more than one vector in a FT of interest, then s chooses aritrarily one of them. 7 The cumulative frequency up to time t is often defined with 1 as the t normalization factor. However, in 43 we use 1 as the normalization factor n instead. The enefit of using 1 as the normalization factor is that we can n concentrate on the increments over time without worrying aout the timedependent normalization factor 1 t. Also, for comparison, X [1] t is the cumulative frequency until time t while X i,1 to X i,nri are the message symols.
8 IEEE TRANSACTIONS ON INFORMATION THEORY, ONLINE PREPRINT Before proceeding, we first descrie the polytope of the cumulative frequency, which, for the case of M = 1, is a polytope in the 18-dimensional Euclidean space. We now specify how to construct this polytope. Fix R 1, R 2. We first notice that among the four groups of conditions, Group 2 the rank conversion conditions are equalities that convert {x [1] : } to {y 1,, y 7 }. As a result, we can sustitute all the y variales in Group 3 y the equalities of Group 2. In the end, Groups 1 and 3 ecome linear inequalities governing the 18 non-negative variales {x [1] : }. We now define Γ, the polytope of the cumulative frequency, as the polytope 8 in the first quadrant of the 18-dimensional Euclidean space governed y the inequalities of Groups 1 and 3. We then note that in the sense of the first-order analysis, for any time t the empirical cumulative frequency {X [1] t : } must e inside the polytope Γ since X[1] t = t n 1 and the rank-comparison inequalities are derived y the relationships among the linear suspaces A 1 to A 7 and thus hold for any time instant t. Also note that y the definition in 43, we have X [1] 0 = 0 for all FTs. As a result, from this polytope interpretation the new goal ecomes to make sure that as time t increases, the cumulative frequency {X [1] t : } until time t has a trajectory within the polytope Γ that starts from the origin and ends in the 18-dimensional point ẍ = {ẍ [1] : }. Since there are infinitely many ways of designing a trajectory {X [1] t : } in Γ with the start point eing the origin and the end point eing ẍ, there are infinitely many ways of designing an LNC scheme achieving rates R 1, R 2. We propose to use the following tunneling approach, which is named after the fact that its goal is to create a tunnel in the polytope Γ. More specifically, the tunneling approach takes the most straightforward approach, which ensures that the trajectory {X [1] t : } follows a straight tunnel connecting the origin and the end point ẍ. Note that in general the trajectory cannot e a straight line connecting 0 and ẍ. The reason is that for every time t, we can only choose one of the 18 different coding types. Therefore, the trajectory can only zigzag along the 18 orthogonal axes and cannot follow a straight line connecting the origin and ẍ. As will e formalized in the later discussion, the tunneling approach first defines a tunnel with strictly positive volume and then allows the trajectory to zigzag within the tunnel and finally reach the end point ẍ. We conclude this susection y discussing some properties of the 18-dimensional polytope. Lemma 7: The aove 18-dimensional polytope, denoted y Γ, satisfies the following properties: Property 1: Both the point ẍ and the origin elong to Γ. Property 2: If R 1, R 2 is in the interior of the capacity region in Proposition 1 and the 2-receiver roadcast PEC is not physically degraded, then the interior of Γ is non-empty. The proof of Lemma 7 is relegated to Appendix E. 8 One can see that Γ depends on the given target rates R 1, R 2, which are assumed to e constant in our discussion. E. The If Analysis of Proposition 1 For the Case of M = 1 Part II: The Tunneling Approach We now define the tunnel in a given polytope. Definition 5: Consider two points x start and x end in a polytope Γ such that each coordinate of x end is strictly larger than each coordinate of x start. The line connecting x start and x end contains all the convex cominations of the terminal points x start and x end. For any δ > 0, a size-δ tunnel T connecting x start and x end is the maximum closed set of points satisfying the following conditions: i x T implies that x satisfies the coordinate-wise inequality x start x x end ; and ii x T implies that there exists a point y in the line connecting x start and x end such that the Euclidean distance d x, y δ. The intuition ehind the aove definition is straightforward. Condition ii allows each tunnel to have a positive volume; and Condition i ensures that a tunnel is confined etween the two terminal points x start and x end. Definition 6: A tunnel T of a polytope Γ is proper if T is contained in the interior of Γ. As discussed in Section V-D, the goal is to design an LNC scheme with the trajectory of {X [1] t : } confined in a proper tunnel T connecting 0 and ẍ. Unfortunately, such a proper tunnel T does not exist in general. As a result, we slightly revise our approach in the following way: For any ϵ > 0 we find a pair of starting and ending nodes x start and x end in the interior of Γ that satisfy x start < x end in a coordinate-wise sense; 44 d 0, x start < ϵ and d x end, ẍ < ϵ. 45 We can then divide the trajectory construction into 3 phases: Phase 1: The first mile from 0 to x start ; Phase 2: From x start to x end along a proper tunnel T; and Phase 3: The last mile from x end to ẍ. For the following discussion, we assume that the 2-receiver roadcast PEC is not physically degraded. The physicallydegraded setting can e viewed as a degenerate case and the corresponding achievaility scheme can e derived in a similar way. Property 2 of Lemma 7 ensures that we can always 9 find in the interior of Γ the starting and ending node pair x start and x end that satisfy 44 and 45. Since oth x start and x end are in the interior of Γ, there is a proper tunnel T connecting x start and x end. Since 45 is satisfied, it is intuitive that the amount of time necessary for executing Phases 1 and 3 is roughly Oϵn time slots. The time duration of executing Phases 1 and 3 is thus negligile 10 when we use a sufficiently small 9 Lemma 7 ensures that 0 and ẍ are in the oundary of the polytope Γ. Lemma 7 also ensures that the interior of Γ is not empty. Therefore, we can always find an x start in the interior that is aritrarily close to 0 and find another x end in the interior that is aritrarily close to the final destination ẍ, which satisfy the distance requirement 45. Moreover, since x end is in the interior of Γ, all its coordinates are strictly positive. Since x start only needs to e chosen aritrarily close to 0, we can thus choose x start to also satisfy More explicitly, in Appendix F we have shown that the amount of time to execute Phase 1 is Oϵn time slots and the information-loss for skipping Phase 3 is also Oϵn packets when compared to the nr 1 and nr 2 information symols. As a result, the throughput loss from the normalized rate region s perspective can e made aritrarily small when choosing a sufficiently small ϵ in 45.
9 IEEE TRANSACTIONS ON INFORMATION THEORY, ONLINE PREPRINT ϵ and a sufficiently large n. In the following, we thus only explain how to implement Phase 2 while relegating the detailed implementation of Phases 1 and 3 to Appendix F. We first descrie how to implement Phase 2: From x start to x end along a proper tunnel T. This phase can e divided into finitely many su-phases. For the eginning of each suphase, say time t, if the cumulative frequency {X [1] t : } is not the same as the end point x end, then y the definition of the tunnel T, there must exist at least one FTs and a sufficiently small δ > 0 such that the 18-dimension point {X [1] t : } {X [1] t + δ } is still inside the tunnel T. Choose aritrarily one such and fix it. Then choose the largest possile δ such that {X [1] t : } {X [1] t + δ } is still inside the tunnel T. After selecting the and δ values, we will keep sending coding vectors of type- for the current su-phase, and this su-phase will last for n δ time slots. After the current suphase ends, i.e., in the end of time t = t + nδ, we will restart the process and choose a new set of and δ ased on {X [1] t : }. Repeat this process until the cumulative frequency ecomes x end. One can easily see that this iterative construction ends after finitely 11 many su-phases. Moreover, since x end is in the interior of Γ, it implies that x end satisfies 15 with strict inequality. By the definition of X [1] t in 43, when {X [1] t : } = x end, we must have t < n. That is, Phase 2 will finish within the time udget n. To prove the correctness of the aove implementation, we need to show that for each su-phase the chosen coding type TYPE must remain non-empty for the allocated time duration of nδ time slots with close-to-one proaility so that with close-to-one proaility we can choose a coding vector from TYPE for every time slot of the su-phase of interest. Instead of proving a particular TYPE eing non-empty, we prove the following stronger statement instead: Consider any fixed GFq with q 3. If the cumulative frequency {X [1] t : } is within the proper tunnel T in time t, then with close-to-one proaility TYPE for all FTs. This implies that we can freely choose from the 18 FTs at any time t as long as we let {X [1] t : } stay within the proper tunnel T. Such a fact/oservation is the uilding foundation of the tunneling approach. Again we rely on the law of large numers and the firstorder expectation-ased analysis to prove the aove central statement. For any {X [1] t : } T in time t, since T is a proper tunnel, it must satisfy 15 and with strict inequality. Since 15 is satisfied with strict inequality, we have not used up the total time udget of n time slots and we can still choose a coding vector for the current time slot. Since 23 to 27 are satisfied with strict inequality in the eginning of the current time slot t, y the rank conversion arguments in Section V-C, the set/rank inequalities in for time t are strict inequalities with close-to-one proaility. What remains to e proven is that when The numer of su-phases depends only on the size of the tunnel T and does not depend on n, the lock length of the network code. This oservation is critical when applying the arguments of the law of large numers. Also see the discussion in Appendix A-C. TABLE I THE CODING TYPES AND THE ASSOCIATED RANK COMPARISON CONDITIONS THAT GUARANTEE NON-EMPTINESS. TYPE 0 A 6 Ω, A 7 Ω; TYPE 1 A 6 Ω, A 4 A 7 ; TYPE 2 A 7 Ω, A 3 A 6 ; TYPE 3 strict 41, A 3 A 6, TYPE 7 A 3 A 6, A 4 A 7 ; A 4 A 7 ; TYPE 9 A 6 Ω; TYPE 11 strict 41, A 3 A 6 ; TYPE 15 strict 40, A 3 A 6 ; TYPE 18 A 7 Ω; TYPE 19 strict 41, A 4 A 7 ; TYPE 23 strict 39, A 4 A 7 ; TYPE 27 strict 41; TYPE 31 strict 39 and 40; TYPE 47 A 3 A 6 ; TYPE 63 strict 39; TYPE 87 A 4 A 7 ; TYPE 95 strict 40; TYPE 127 is always non-empty. For coding type 3, we further assume the underlying GFq satisfies q 3. are strict inequalities, TYPE for all FTs. We first prove the case in which = 23. Note that TYPE 23 is defined in 35 and whether TYPE 23 holds can e decided y comparing the sizes of A 3 A 5 and A 3 A 5 A 1 A 4. Also note that A 3 A 5 = q RankA 3 A 5 and q maxranka3 A5 A1,RankA3 A5 A4 46 = max A 3 A 5 A 1, A 3 A 5 A 4 A 3 A 5 A 1 A 4 47 A 3 A 5 A 1 + A 3 A 5 A = q RankA3 A5 A1 + q RankA3 A5 A4 1, 49 where 47 follows from simple set operations and 48 follows from that the origin 0 is always in the intersection of two suspaces A 3 A 5 A 1 and A 3 A 5 A 4. Since q 2, we thus have TYPE 23 if and only if RankA 3 A 5 > maxranka 3 A 5 A 1, RankA 3 A 5 A In Appendix G we have proven that and RankA 3 A 5 RankA 3 A 5 A 1 = RankS 1 Ω 1 + RankS 1 S 2 RankS 1 S 2 Ω 1 RankS 1 51 RankA 3 A 5 RankA 3 A 5 A 4 = RankS 1 S 2 Ω 2 RankS 2 Ω 2 = RankA 7 RankA 4. The aove analysis shows that when oth 39 and A 4 A 7 are strict inequalities, TYPE 23 and choosing a c t from TYPE 23 is possile. By similar arguments, it can e proven that i Each FT is associated with a suset of inequalities of 37 41; and ii A FT is non-empty if and only if the inequalities in the corresponding suset are all strict. Tale I summarizes the mapping from the FT of interest eing non-empty to the corresponding suset of inequalities eing strict. The detailed derivation of Tale I is relegated to Appendix G. Therefore, when all 7 inequalities in are strict, all 18 TYPE are non-empty. As a result, we have proven that if the cumulative frequency {x [1] t : } is within the proper
10 IEEE TRANSACTIONS ON INFORMATION THEORY, ONLINE PREPRINT tunnel T, then with close-to-one proaility TYPE for all FTs. The If analysis of Proposition 1 is complete. VI. PROOF OF PROPOSITION 1 FOR ARBITRARY M The proof for the case of M = 1 can e readily generalized for the case of aritrary M. A. The Only If Analysis of Proposition 1 For The Case of Aritrary M We follow the knowledge-space-ased approach as in the case of M = 1. Specifically, recall that the nr 1 + nr 2 M coding matrix C t for time t can e descried as C t = [c T t,1, c T t,2,, c T t,m ] where the nr 1 + R 2 -dimensional row vector c t,m descries the coding vector used to generate the m-th input W [m] at time t for all m {1,, M}. For any i {1, 2}, t {1,, n}, and m {1,, M}, we now define the knowledge space S i t.m y S i t.m = span{c τ,h : τ and h such that either i τ < t and h rx i at time τ; or ii τ = t, h m, and h rx i at time t}. 52 That is, S i t.m is the linear span of the vectors of those packets that have successfully arrived at d i either efore time instant t or at time instant t ut only counting the vectors from the first m input packets W [1] t to W [m] t. In the roadest sense, it is equivalent to splitting each time index t into M su time instants denoted y t.1 to t.m and assuming that each of the M inputs W [1] t to W [M] t is sent sequentially at the split time instant t.m, m = 1 to M. In the eginning of any split time instant t.m, we define A 1 to A 7 in the same way as in 31 to 33 ased on the knowledge spaces S 1 t.m 1 and S 2 t.m 1 in the end of the split time instant t.m 1. We can also define 18 feasile coding types TYPE in the same way as descried in Section V-B. Fix any given linear network code such that d i can decode all X i,1 to X i,nri in the end of time n for all i = 1, 2 with close-to-one proaility. Since the 18 disjoint FTs fully cover Ω, for each split time instant t.m we can always lael the coding choice c t,m of the given LNC scheme as one of the 18 FTs. Define } { = 1 n n E t=1 1 {ct,m TYPE in the eginning of time t.m} as the normalized expected numer of c t,m of type where TYPE is evaluated in the eginning of the split time instant t.m. Since the total numer of time slots is n, the aove construction of must satisfy 15 for the case of aritrary M values. We now estalish the rank conversion inequalities 16 to 22. Consider the linear spaces A k, k = 1 to 7, in the eginning of the split time instant 1.1 and in the end of the split time instant time n.m, and denote them y A k 0 and A k n.m, respectively. Consider A 6 = S 1 S 2 Ω 1 for example. By 52 and the same reasoning as in Section V-C, we have RankA w. 6 =0 n 1 c t,m TYPE in the t=1 eginning of time t.m; and one of {d 1, d 2} receives it = RankA 6 n.m. 53 Define y k = 1 n E {RankA kn.m} as the normalized expected rank of A k n.m. Taking the normalized expectation of 53, counting only the FTs, noting that the channel is cross-input independent, and y the linearity of expectation and the stationarity and memorylessness of the channel, we have proven that 21 must hold for aritrary M values. By similar rank-conversion arguments, we can also prove 16 to 22 for aritrary M values. Note that the argument for the rank comparison inequalities and the decodaility equalities in Section V-C does not depend on the value of M. Therefore the rank comparison inequalities and the decodaility equalities still hold. The Only If direction of Proposition 1 has thus een proven for aritrary M values. B. The If Analysis of Proposition 1 For the Case of Aritrary M Benefiting from the constructive nature of our approach, we can easily prove the following statement y the same arguments as used in Sections V-D and V-E. Suppose that the source node s designs the coding vectors c t,m sequentially in the order of t, m = 1, 1, 1, 2,, 1, M, 2, 1,, 2, M, 3, 1,, n, M. Also suppose when s designs c t,m, there is a genie informing s the reception status of all c t, m for all t, m efore t, m. Then we can achieve any R 1, R 2 that is in the interior of Proposition 1. That is, we simply need to use the tunneling approach to achieve the desired long-term relative frequency {ẍ [m] :, m} in the same way as descried in Sections V-D and V-E. However, the aove statement alone is not sufficient to prove the If direction of Proposition 1 due to the fact that there exists no such genie. More specifically, each destination d i can only report its reception status rx i after the time instant t rather than reporting its reception after every split time instant t.m. As a result, in the eginning of time t, source s needs to design the coding vectors c t,m for all m {1,, M} simultaneously, and cannot design c t,m sequentially since the latter requires the information of the knowledge spaces S i t.m 1 for every split time instant t.m. In the following, we argue that even without the help from the genie, source s can still achieve the outer ound estalished in Section VI-A. The main difference etween a genie-aided solution and a practical solution is the following. For any t {1,, n} and m {1,, M}, when designing the coding vector c t,m for the m-th input at time t, a genie-aided solution has
Common Information of Random Linear Network Coding Over A 1-Hop Broadcast Packet Erasure Channel
 Wang, ISIT 2011 p. 1/15 Common Information of Random Linear Network Coding Over A 1-Hop Broadcast Packet Erasure Channel Chih-Chun Wang, Jaemin Han Center of Wireless Systems and Applications (CWSA) School
Wang, ISIT 2011 p. 1/15 Common Information of Random Linear Network Coding Over A 1-Hop Broadcast Packet Erasure Channel Chih-Chun Wang, Jaemin Han Center of Wireless Systems and Applications (CWSA) School
Content Delivery in Erasure Broadcast. Channels with Cache and Feedback
 Content Delivery in Erasure Broadcast Channels with Cache and Feedack Asma Ghorel, Mari Koayashi, and Sheng Yang LSS, CentraleSupélec Gif-sur-Yvette, France arxiv:602.04630v [cs.t] 5 Fe 206 {asma.ghorel,
Content Delivery in Erasure Broadcast Channels with Cache and Feedack Asma Ghorel, Mari Koayashi, and Sheng Yang LSS, CentraleSupélec Gif-sur-Yvette, France arxiv:602.04630v [cs.t] 5 Fe 206 {asma.ghorel,
On the Capacity of Wireless 1-Hop Intersession Network Coding A Broadcast Packet Erasure Channel Approach
 1 On the Capacity of Wireless 1-Hop Intersession Networ Coding A Broadcast Pacet Erasure Channel Approach Chih-Chun Wang, Member, IEEE Abstract Motivated by practical wireless networ protocols, this paper
1 On the Capacity of Wireless 1-Hop Intersession Networ Coding A Broadcast Pacet Erasure Channel Approach Chih-Chun Wang, Member, IEEE Abstract Motivated by practical wireless networ protocols, this paper
Structuring Unreliable Radio Networks
 Structuring Unreliale Radio Networks Keren Censor-Hillel Seth Gilert Faian Kuhn Nancy Lynch Calvin Newport March 29, 2011 Astract In this paper we study the prolem of uilding a connected dominating set
Structuring Unreliale Radio Networks Keren Censor-Hillel Seth Gilert Faian Kuhn Nancy Lynch Calvin Newport March 29, 2011 Astract In this paper we study the prolem of uilding a connected dominating set
On queueing in coded networks queue size follows degrees of freedom
 On queueing in coded networks queue size follows degrees of freedom Jay Kumar Sundararajan, Devavrat Shah, Muriel Médard Laboratory for Information and Decision Systems, Massachusetts Institute of Technology,
On queueing in coded networks queue size follows degrees of freedom Jay Kumar Sundararajan, Devavrat Shah, Muriel Médard Laboratory for Information and Decision Systems, Massachusetts Institute of Technology,
Capacity of 1-to-K Broadcast Packet Erasure Channels with Channel Output Feedback
 Capacity of 1-to-K Broadcast Packet Erasure Channels with Channel Output Feedback Chih-Chun Wang Center of Wireless Systems and Applications (CWSA School of Electrical and Computer Engineering, Purdue
Capacity of 1-to-K Broadcast Packet Erasure Channels with Channel Output Feedback Chih-Chun Wang Center of Wireless Systems and Applications (CWSA School of Electrical and Computer Engineering, Purdue
Depth versus Breadth in Convolutional Polar Codes
 Depth versus Breadth in Convolutional Polar Codes Maxime Tremlay, Benjamin Bourassa and David Poulin,2 Département de physique & Institut quantique, Université de Sherrooke, Sherrooke, Quéec, Canada JK
Depth versus Breadth in Convolutional Polar Codes Maxime Tremlay, Benjamin Bourassa and David Poulin,2 Département de physique & Institut quantique, Université de Sherrooke, Sherrooke, Quéec, Canada JK
Inter-Session Network Coding Schemes for 1-to-2 Downlink Access-Point Networks with Sequential Hard Deadline Constraints
 Inter-Session Network Coding Schemes for -to- Downlink Access-Point Networks with Sequential Hard Deadline Constraints Xiaohang Li, Chih-Chun Wang, and Xiaojun Lin Center for Wireless Systems and Applications,
Inter-Session Network Coding Schemes for -to- Downlink Access-Point Networks with Sequential Hard Deadline Constraints Xiaohang Li, Chih-Chun Wang, and Xiaojun Lin Center for Wireless Systems and Applications,
On the Expected Rate of Slowly Fading Channels with Quantized Side Information
 On the Expected Rate of Slowly Fading Channels with Quantized Side Information Thanh Tùng Kim and Mikael Skoglund 2005-10-30 IR S3 KT 0515 c 2005 IEEE. Personal use of this material is permitted. However,
On the Expected Rate of Slowly Fading Channels with Quantized Side Information Thanh Tùng Kim and Mikael Skoglund 2005-10-30 IR S3 KT 0515 c 2005 IEEE. Personal use of this material is permitted. However,
Expansion formula using properties of dot product (analogous to FOIL in algebra): u v 2 u v u v u u 2u v v v u 2 2u v v 2
 Least squares: Mathematical theory Below we provide the "vector space" formulation, and solution, of the least squares prolem. While not strictly necessary until we ring in the machinery of matrix algera,
Least squares: Mathematical theory Below we provide the "vector space" formulation, and solution, of the least squares prolem. While not strictly necessary until we ring in the machinery of matrix algera,
Representation theory of SU(2), density operators, purification Michael Walter, University of Amsterdam
 Symmetry and Quantum Information Feruary 6, 018 Representation theory of S(), density operators, purification Lecture 7 Michael Walter, niversity of Amsterdam Last week, we learned the asic concepts of
Symmetry and Quantum Information Feruary 6, 018 Representation theory of S(), density operators, purification Lecture 7 Michael Walter, niversity of Amsterdam Last week, we learned the asic concepts of
Capacity Region of the Permutation Channel
 Capacity Region of the Permutation Channel John MacLaren Walsh and Steven Weber Abstract We discuss the capacity region of a degraded broadcast channel (DBC) formed from a channel that randomly permutes
Capacity Region of the Permutation Channel John MacLaren Walsh and Steven Weber Abstract We discuss the capacity region of a degraded broadcast channel (DBC) formed from a channel that randomly permutes
Merging and splitting endowments in object assignment problems
 Merging and splitting endowments in oject assignment prolems Nanyang Bu, Siwei Chen, and William Thomson April 26, 2012 1 Introduction We consider a group of agents, each endowed with a set of indivisile
Merging and splitting endowments in oject assignment prolems Nanyang Bu, Siwei Chen, and William Thomson April 26, 2012 1 Introduction We consider a group of agents, each endowed with a set of indivisile
On Gaussian MIMO Broadcast Channels with Common and Private Messages
 On Gaussian MIMO Broadcast Channels with Common and Private Messages Ersen Ekrem Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland, College Park, MD 20742 ersen@umd.edu
On Gaussian MIMO Broadcast Channels with Common and Private Messages Ersen Ekrem Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland, College Park, MD 20742 ersen@umd.edu
Online Supplementary Appendix B
 Online Supplementary Appendix B Uniqueness of the Solution of Lemma and the Properties of λ ( K) We prove the uniqueness y the following steps: () (A8) uniquely determines q as a function of λ () (A) uniquely
Online Supplementary Appendix B Uniqueness of the Solution of Lemma and the Properties of λ ( K) We prove the uniqueness y the following steps: () (A8) uniquely determines q as a function of λ () (A) uniquely
Lecture 12: Grover s Algorithm
 CPSC 519/619: Quantum Computation John Watrous, University of Calgary Lecture 12: Grover s Algorithm March 7, 2006 We have completed our study of Shor s factoring algorithm. The asic technique ehind Shor
CPSC 519/619: Quantum Computation John Watrous, University of Calgary Lecture 12: Grover s Algorithm March 7, 2006 We have completed our study of Shor s factoring algorithm. The asic technique ehind Shor
SVETLANA KATOK AND ILIE UGARCOVICI (Communicated by Jens Marklof)
 JOURNAL OF MODERN DYNAMICS VOLUME 4, NO. 4, 010, 637 691 doi: 10.3934/jmd.010.4.637 STRUCTURE OF ATTRACTORS FOR (a, )-CONTINUED FRACTION TRANSFORMATIONS SVETLANA KATOK AND ILIE UGARCOVICI (Communicated
JOURNAL OF MODERN DYNAMICS VOLUME 4, NO. 4, 010, 637 691 doi: 10.3934/jmd.010.4.637 STRUCTURE OF ATTRACTORS FOR (a, )-CONTINUED FRACTION TRANSFORMATIONS SVETLANA KATOK AND ILIE UGARCOVICI (Communicated
Solving Systems of Linear Equations Symbolically
 " Solving Systems of Linear Equations Symolically Every day of the year, thousands of airline flights crisscross the United States to connect large and small cities. Each flight follows a plan filed with
" Solving Systems of Linear Equations Symolically Every day of the year, thousands of airline flights crisscross the United States to connect large and small cities. Each flight follows a plan filed with
IN this paper, we show that the scalar Gaussian multiple-access
 768 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 50, NO. 5, MAY 2004 On the Duality of Gaussian Multiple-Access and Broadcast Channels Nihar Jindal, Student Member, IEEE, Sriram Vishwanath, and Andrea
768 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 50, NO. 5, MAY 2004 On the Duality of Gaussian Multiple-Access and Broadcast Channels Nihar Jindal, Student Member, IEEE, Sriram Vishwanath, and Andrea
Upper Bounds for Stern s Diatomic Sequence and Related Sequences
 Upper Bounds for Stern s Diatomic Sequence and Related Sequences Colin Defant Department of Mathematics University of Florida, U.S.A. cdefant@ufl.edu Sumitted: Jun 18, 01; Accepted: Oct, 016; Pulished:
Upper Bounds for Stern s Diatomic Sequence and Related Sequences Colin Defant Department of Mathematics University of Florida, U.S.A. cdefant@ufl.edu Sumitted: Jun 18, 01; Accepted: Oct, 016; Pulished:
Load Balancing Congestion Games and their Asymptotic Behavior
 Load Balancing Congestion Games and their Asymptotic Behavior Eitan Altman, Corinne Touati Inria CRS, LIG, Univ. Grenole Alpes, LIG, F-38000 Grenole, France Email: {eitan.altman, corinne.touati}@inria.fr
Load Balancing Congestion Games and their Asymptotic Behavior Eitan Altman, Corinne Touati Inria CRS, LIG, Univ. Grenole Alpes, LIG, F-38000 Grenole, France Email: {eitan.altman, corinne.touati}@inria.fr
Continuous-Model Communication Complexity with Application in Distributed Resource Allocation in Wireless Ad hoc Networks
 Continuous-Model Communication Complexity with Application in Distributed Resource Allocation in Wireless Ad hoc Networks Husheng Li 1 and Huaiyu Dai 2 1 Department of Electrical Engineering and Computer
Continuous-Model Communication Complexity with Application in Distributed Resource Allocation in Wireless Ad hoc Networks Husheng Li 1 and Huaiyu Dai 2 1 Department of Electrical Engineering and Computer
Lecture 6 January 15, 2014
 Advanced Graph Algorithms Jan-Apr 2014 Lecture 6 January 15, 2014 Lecturer: Saket Sourah Scrie: Prafullkumar P Tale 1 Overview In the last lecture we defined simple tree decomposition and stated that for
Advanced Graph Algorithms Jan-Apr 2014 Lecture 6 January 15, 2014 Lecturer: Saket Sourah Scrie: Prafullkumar P Tale 1 Overview In the last lecture we defined simple tree decomposition and stated that for
Lecture 4 Noisy Channel Coding
 Lecture 4 Noisy Channel Coding I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw October 9, 2015 1 / 56 I-Hsiang Wang IT Lecture 4 The Channel Coding Problem
Lecture 4 Noisy Channel Coding I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw October 9, 2015 1 / 56 I-Hsiang Wang IT Lecture 4 The Channel Coding Problem
IN this paper we study a discrete optimization problem. Constrained Shortest Link-Disjoint Paths Selection: A Network Programming Based Approach
 Constrained Shortest Link-Disjoint Paths Selection: A Network Programming Based Approach Ying Xiao, Student Memer, IEEE, Krishnaiyan Thulasiraman, Fellow, IEEE, and Guoliang Xue, Senior Memer, IEEE Astract
Constrained Shortest Link-Disjoint Paths Selection: A Network Programming Based Approach Ying Xiao, Student Memer, IEEE, Krishnaiyan Thulasiraman, Fellow, IEEE, and Guoliang Xue, Senior Memer, IEEE Astract
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 52, NO. 2, FEBRUARY Uplink Downlink Duality Via Minimax Duality. Wei Yu, Member, IEEE (1) (2)
 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 52, NO. 2, FEBRUARY 2006 361 Uplink Downlink Duality Via Minimax Duality Wei Yu, Member, IEEE Abstract The sum capacity of a Gaussian vector broadcast channel
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 52, NO. 2, FEBRUARY 2006 361 Uplink Downlink Duality Via Minimax Duality Wei Yu, Member, IEEE Abstract The sum capacity of a Gaussian vector broadcast channel
CHAPTER 5. Linear Operators, Span, Linear Independence, Basis Sets, and Dimension
 A SERIES OF CLASS NOTES TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS LINEAR CLASS NOTES: A COLLECTION OF HANDOUTS FOR REVIEW AND PREVIEW OF LINEAR THEORY
A SERIES OF CLASS NOTES TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS LINEAR CLASS NOTES: A COLLECTION OF HANDOUTS FOR REVIEW AND PREVIEW OF LINEAR THEORY
NEW generation devices, e.g., Wireless Sensor Networks. Battery-Powered Devices in WPCNs. arxiv: v2 [cs.it] 28 Jan 2016
![NEW generation devices, e.g., Wireless Sensor Networks. Battery-Powered Devices in WPCNs. arxiv: v2 [cs.it] 28 Jan 2016 NEW generation devices, e.g., Wireless Sensor Networks. Battery-Powered Devices in WPCNs. arxiv: v2 [cs.it] 28 Jan 2016](/thumbs/75/72863493.jpg) 1 Battery-Powered Devices in WPCNs Alessandro Biason, Student Memer, IEEE, and Michele Zorzi, Fellow, IEEE arxiv:161.6847v2 [cs.it] 28 Jan 216 Astract Wireless powered communication networks are ecoming
1 Battery-Powered Devices in WPCNs Alessandro Biason, Student Memer, IEEE, and Michele Zorzi, Fellow, IEEE arxiv:161.6847v2 [cs.it] 28 Jan 216 Astract Wireless powered communication networks are ecoming
TIGHT BOUNDS FOR THE FIRST ORDER MARCUM Q-FUNCTION
 TIGHT BOUNDS FOR THE FIRST ORDER MARCUM Q-FUNCTION Jiangping Wang and Dapeng Wu Department of Electrical and Computer Engineering University of Florida, Gainesville, FL 3611 Correspondence author: Prof.
TIGHT BOUNDS FOR THE FIRST ORDER MARCUM Q-FUNCTION Jiangping Wang and Dapeng Wu Department of Electrical and Computer Engineering University of Florida, Gainesville, FL 3611 Correspondence author: Prof.
Performance Bounds for Bi-Directional Coded Cooperation Protocols
 1 Performance Bounds for Bi-Directional Coded Cooperation Protocols Sang Joon Kim, Patrick Mitran, and Vahid Tarokh arxiv:cs/0703017v4 [cs.it] 5 Jun 2008 Astract In coded i-directional cooperation, two
1 Performance Bounds for Bi-Directional Coded Cooperation Protocols Sang Joon Kim, Patrick Mitran, and Vahid Tarokh arxiv:cs/0703017v4 [cs.it] 5 Jun 2008 Astract In coded i-directional cooperation, two
Optimal Routing in Chord
 Optimal Routing in Chord Prasanna Ganesan Gurmeet Singh Manku Astract We propose optimal routing algorithms for Chord [1], a popular topology for routing in peer-to-peer networks. Chord is an undirected
Optimal Routing in Chord Prasanna Ganesan Gurmeet Singh Manku Astract We propose optimal routing algorithms for Chord [1], a popular topology for routing in peer-to-peer networks. Chord is an undirected
A vector version of Witsenhausen s counterexample: Towards convergence of control, communication and computation
 A vector version of Witsenhausen s counterexample: Towards convergence of control, communication and computation Pulkit Grover and Anant Sahai Wireless Foundations, Department of EECS University of California
A vector version of Witsenhausen s counterexample: Towards convergence of control, communication and computation Pulkit Grover and Anant Sahai Wireless Foundations, Department of EECS University of California
Information in Aloha Networks
 Achieving Proportional Fairness using Local Information in Aloha Networks Koushik Kar, Saswati Sarkar, Leandros Tassiulas Abstract We address the problem of attaining proportionally fair rates using Aloha
Achieving Proportional Fairness using Local Information in Aloha Networks Koushik Kar, Saswati Sarkar, Leandros Tassiulas Abstract We address the problem of attaining proportionally fair rates using Aloha
#A50 INTEGERS 14 (2014) ON RATS SEQUENCES IN GENERAL BASES
 #A50 INTEGERS 14 (014) ON RATS SEQUENCES IN GENERAL BASES Johann Thiel Dept. of Mathematics, New York City College of Technology, Brooklyn, New York jthiel@citytech.cuny.edu Received: 6/11/13, Revised:
#A50 INTEGERS 14 (014) ON RATS SEQUENCES IN GENERAL BASES Johann Thiel Dept. of Mathematics, New York City College of Technology, Brooklyn, New York jthiel@citytech.cuny.edu Received: 6/11/13, Revised:
K User Interference Channel with Backhaul
 1 K User Interference Channel with Backhaul Cooperation: DoF vs. Backhaul Load Trade Off Borna Kananian,, Mohammad A. Maddah-Ali,, Babak H. Khalaj, Department of Electrical Engineering, Sharif University
1 K User Interference Channel with Backhaul Cooperation: DoF vs. Backhaul Load Trade Off Borna Kananian,, Mohammad A. Maddah-Ali,, Babak H. Khalaj, Department of Electrical Engineering, Sharif University
Interactive Interference Alignment
 Interactive Interference Alignment Quan Geng, Sreeram annan, and Pramod Viswanath Coordinated Science Laboratory and Dept. of ECE University of Illinois, Urbana-Champaign, IL 61801 Email: {geng5, kannan1,
Interactive Interference Alignment Quan Geng, Sreeram annan, and Pramod Viswanath Coordinated Science Laboratory and Dept. of ECE University of Illinois, Urbana-Champaign, IL 61801 Email: {geng5, kannan1,
arxiv: v1 [cs.fl] 24 Nov 2017
![arxiv: v1 [cs.fl] 24 Nov 2017 arxiv: v1 [cs.fl] 24 Nov 2017](/thumbs/72/67148428.jpg) (Biased) Majority Rule Cellular Automata Bernd Gärtner and Ahad N. Zehmakan Department of Computer Science, ETH Zurich arxiv:1711.1090v1 [cs.fl] 4 Nov 017 Astract Consider a graph G = (V, E) and a random
(Biased) Majority Rule Cellular Automata Bernd Gärtner and Ahad N. Zehmakan Department of Computer Science, ETH Zurich arxiv:1711.1090v1 [cs.fl] 4 Nov 017 Astract Consider a graph G = (V, E) and a random
820 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 2, FEBRUARY Stefano Rini, Daniela Tuninetti, and Natasha Devroye
 820 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 2, FEBRUARY 2012 Inner and Outer Bounds for the Gaussian Cognitive Interference Channel and New Capacity Results Stefano Rini, Daniela Tuninetti,
820 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 2, FEBRUARY 2012 Inner and Outer Bounds for the Gaussian Cognitive Interference Channel and New Capacity Results Stefano Rini, Daniela Tuninetti,
Capacity of a Two-way Function Multicast Channel
 Capacity of a Two-way Function Multicast Channel 1 Seiyun Shin, Student Member, IEEE and Changho Suh, Member, IEEE Abstract We explore the role of interaction for the problem of reliable computation over
Capacity of a Two-way Function Multicast Channel 1 Seiyun Shin, Student Member, IEEE and Changho Suh, Member, IEEE Abstract We explore the role of interaction for the problem of reliable computation over
Error Exponent Region for Gaussian Broadcast Channels
 Error Exponent Region for Gaussian Broadcast Channels Lihua Weng, S. Sandeep Pradhan, and Achilleas Anastasopoulos Electrical Engineering and Computer Science Dept. University of Michigan, Ann Arbor, MI
Error Exponent Region for Gaussian Broadcast Channels Lihua Weng, S. Sandeep Pradhan, and Achilleas Anastasopoulos Electrical Engineering and Computer Science Dept. University of Michigan, Ann Arbor, MI
Approximately achieving the feedback interference channel capacity with point-to-point codes
 Approximately achieving the feedback interference channel capacity with point-to-point codes Joyson Sebastian*, Can Karakus*, Suhas Diggavi* Abstract Superposition codes with rate-splitting have been used
Approximately achieving the feedback interference channel capacity with point-to-point codes Joyson Sebastian*, Can Karakus*, Suhas Diggavi* Abstract Superposition codes with rate-splitting have been used
On Common Information and the Encoding of Sources that are Not Successively Refinable
 On Common Information and the Encoding of Sources that are Not Successively Refinable Kumar Viswanatha, Emrah Akyol, Tejaswi Nanjundaswamy and Kenneth Rose ECE Department, University of California - Santa
On Common Information and the Encoding of Sources that are Not Successively Refinable Kumar Viswanatha, Emrah Akyol, Tejaswi Nanjundaswamy and Kenneth Rose ECE Department, University of California - Santa
1 Hoeffding s Inequality
 Proailistic Method: Hoeffding s Inequality and Differential Privacy Lecturer: Huert Chan Date: 27 May 22 Hoeffding s Inequality. Approximate Counting y Random Sampling Suppose there is a ag containing
Proailistic Method: Hoeffding s Inequality and Differential Privacy Lecturer: Huert Chan Date: 27 May 22 Hoeffding s Inequality. Approximate Counting y Random Sampling Suppose there is a ag containing
Ahmed Nazeem and Spyros Reveliotis
 Designing compact and maximally permissive deadlock avoidance policies for complex resource allocation systems through classification theory: the non-linear case Ahmed Nazeem and Spyros Reveliotis Astract
Designing compact and maximally permissive deadlock avoidance policies for complex resource allocation systems through classification theory: the non-linear case Ahmed Nazeem and Spyros Reveliotis Astract
Superposition Encoding and Partial Decoding Is Optimal for a Class of Z-interference Channels
 Superposition Encoding and Partial Decoding Is Optimal for a Class of Z-interference Channels Nan Liu and Andrea Goldsmith Department of Electrical Engineering Stanford University, Stanford CA 94305 Email:
Superposition Encoding and Partial Decoding Is Optimal for a Class of Z-interference Channels Nan Liu and Andrea Goldsmith Department of Electrical Engineering Stanford University, Stanford CA 94305 Email:
Example: Bipolar NRZ (non-return-to-zero) signaling
 Baseand Data Transmission Data are sent without using a carrier signal Example: Bipolar NRZ (non-return-to-zero signaling is represented y is represented y T A -A T : it duration is represented y BT. Passand
Baseand Data Transmission Data are sent without using a carrier signal Example: Bipolar NRZ (non-return-to-zero signaling is represented y is represented y T A -A T : it duration is represented y BT. Passand
Local network coding on packet erasure channels -- From Shannon capacity to stability region
 Purdue University Purdue e-pubs Open Access Dissertations Theses and Dissertations Spring 2015 Local network coding on packet erasure channels -- From Shannon capacity to stability region Wei-Chung Wang
Purdue University Purdue e-pubs Open Access Dissertations Theses and Dissertations Spring 2015 Local network coding on packet erasure channels -- From Shannon capacity to stability region Wei-Chung Wang
Compactness vs Collusion Resistance in Functional Encryption
 Compactness vs Collusion Resistance in Functional Encryption Baiyu Li Daniele Micciancio April 10, 2017 Astract We present two general constructions that can e used to comine any two functional encryption
Compactness vs Collusion Resistance in Functional Encryption Baiyu Li Daniele Micciancio April 10, 2017 Astract We present two general constructions that can e used to comine any two functional encryption
LOW-density parity-check (LDPC) codes were invented
 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL 54, NO 1, JANUARY 2008 51 Extremal Problems of Information Combining Yibo Jiang, Alexei Ashikhmin, Member, IEEE, Ralf Koetter, Senior Member, IEEE, and Andrew
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL 54, NO 1, JANUARY 2008 51 Extremal Problems of Information Combining Yibo Jiang, Alexei Ashikhmin, Member, IEEE, Ralf Koetter, Senior Member, IEEE, and Andrew
Efficient Compression of Monotone and m-modal Distributions
 Efficient Compression of Monotone and m-modal Distriutions Jayadev Acharya, Ashkan Jafarpour, Alon Orlitsky, and Ananda Theertha Suresh ECE Department, UCSD {jacharya, ashkan, alon, asuresh}@ucsd.edu Astract
Efficient Compression of Monotone and m-modal Distriutions Jayadev Acharya, Ashkan Jafarpour, Alon Orlitsky, and Ananda Theertha Suresh ECE Department, UCSD {jacharya, ashkan, alon, asuresh}@ucsd.edu Astract
Upper Bounds on the Capacity of Binary Intermittent Communication
 Upper Bounds on the Capacity of Binary Intermittent Communication Mostafa Khoshnevisan and J. Nicholas Laneman Department of Electrical Engineering University of Notre Dame Notre Dame, Indiana 46556 Email:{mhoshne,
Upper Bounds on the Capacity of Binary Intermittent Communication Mostafa Khoshnevisan and J. Nicholas Laneman Department of Electrical Engineering University of Notre Dame Notre Dame, Indiana 46556 Email:{mhoshne,
CS 4120 Lecture 3 Automating lexical analysis 29 August 2011 Lecturer: Andrew Myers. 1 DFAs
 CS 42 Lecture 3 Automating lexical analysis 29 August 2 Lecturer: Andrew Myers A lexer generator converts a lexical specification consisting of a list of regular expressions and corresponding actions into
CS 42 Lecture 3 Automating lexical analysis 29 August 2 Lecturer: Andrew Myers A lexer generator converts a lexical specification consisting of a list of regular expressions and corresponding actions into
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 57, NO. 11, NOVEMBER On the Performance of Sparse Recovery
 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 57, NO. 11, NOVEMBER 2011 7255 On the Performance of Sparse Recovery Via `p-minimization (0 p 1) Meng Wang, Student Member, IEEE, Weiyu Xu, and Ao Tang, Senior
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 57, NO. 11, NOVEMBER 2011 7255 On the Performance of Sparse Recovery Via `p-minimization (0 p 1) Meng Wang, Student Member, IEEE, Weiyu Xu, and Ao Tang, Senior
A POMDP Framework for Cognitive MAC Based on Primary Feedback Exploitation
 A POMDP Framework for Cognitive MAC Based on Primary Feedback Exploitation Karim G. Seddik and Amr A. El-Sherif 2 Electronics and Communications Engineering Department, American University in Cairo, New
A POMDP Framework for Cognitive MAC Based on Primary Feedback Exploitation Karim G. Seddik and Amr A. El-Sherif 2 Electronics and Communications Engineering Department, American University in Cairo, New
On Scalable Coding in the Presence of Decoder Side Information
 On Scalable Coding in the Presence of Decoder Side Information Emrah Akyol, Urbashi Mitra Dep. of Electrical Eng. USC, CA, US Email: {eakyol, ubli}@usc.edu Ertem Tuncel Dep. of Electrical Eng. UC Riverside,
On Scalable Coding in the Presence of Decoder Side Information Emrah Akyol, Urbashi Mitra Dep. of Electrical Eng. USC, CA, US Email: {eakyol, ubli}@usc.edu Ertem Tuncel Dep. of Electrical Eng. UC Riverside,
The Capacity Region of the Gaussian Cognitive Radio Channels at High SNR
 The Capacity Region of the Gaussian Cognitive Radio Channels at High SNR 1 Stefano Rini, Daniela Tuninetti and Natasha Devroye srini2, danielat, devroye @ece.uic.edu University of Illinois at Chicago Abstract
The Capacity Region of the Gaussian Cognitive Radio Channels at High SNR 1 Stefano Rini, Daniela Tuninetti and Natasha Devroye srini2, danielat, devroye @ece.uic.edu University of Illinois at Chicago Abstract
A Polynomial-Time Algorithm for Pliable Index Coding
 1 A Polynomial-Time Algorithm for Pliable Index Coding Linqi Song and Christina Fragouli arxiv:1610.06845v [cs.it] 9 Aug 017 Abstract In pliable index coding, we consider a server with m messages and n
1 A Polynomial-Time Algorithm for Pliable Index Coding Linqi Song and Christina Fragouli arxiv:1610.06845v [cs.it] 9 Aug 017 Abstract In pliable index coding, we consider a server with m messages and n
Approximation Metrics for Discrete and Continuous Systems
 University of Pennsylvania ScholarlyCommons Departmental Papers (CIS) Department of Computer & Information Science May 2007 Approximation Metrics for Discrete Continuous Systems Antoine Girard University
University of Pennsylvania ScholarlyCommons Departmental Papers (CIS) Department of Computer & Information Science May 2007 Approximation Metrics for Discrete Continuous Systems Antoine Girard University
1Number ONLINE PAGE PROOFS. systems: real and complex. 1.1 Kick off with CAS
 1Numer systems: real and complex 1.1 Kick off with CAS 1. Review of set notation 1.3 Properties of surds 1. The set of complex numers 1.5 Multiplication and division of complex numers 1.6 Representing
1Numer systems: real and complex 1.1 Kick off with CAS 1. Review of set notation 1.3 Properties of surds 1. The set of complex numers 1.5 Multiplication and division of complex numers 1.6 Representing
Minimizing a convex separable exponential function subject to linear equality constraint and bounded variables
 Minimizing a convex separale exponential function suect to linear equality constraint and ounded variales Stefan M. Stefanov Department of Mathematics Neofit Rilski South-Western University 2700 Blagoevgrad
Minimizing a convex separale exponential function suect to linear equality constraint and ounded variales Stefan M. Stefanov Department of Mathematics Neofit Rilski South-Western University 2700 Blagoevgrad
Chapter 4. Data Transmission and Channel Capacity. Po-Ning Chen, Professor. Department of Communications Engineering. National Chiao Tung University
 Chapter 4 Data Transmission and Channel Capacity Po-Ning Chen, Professor Department of Communications Engineering National Chiao Tung University Hsin Chu, Taiwan 30050, R.O.C. Principle of Data Transmission
Chapter 4 Data Transmission and Channel Capacity Po-Ning Chen, Professor Department of Communications Engineering National Chiao Tung University Hsin Chu, Taiwan 30050, R.O.C. Principle of Data Transmission
Linear Codes, Target Function Classes, and Network Computing Capacity
 Linear Codes, Target Function Classes, and Network Computing Capacity Rathinakumar Appuswamy, Massimo Franceschetti, Nikhil Karamchandani, and Kenneth Zeger IEEE Transactions on Information Theory Submitted:
Linear Codes, Target Function Classes, and Network Computing Capacity Rathinakumar Appuswamy, Massimo Franceschetti, Nikhil Karamchandani, and Kenneth Zeger IEEE Transactions on Information Theory Submitted:
Luis Manuel Santana Gallego 100 Investigation and simulation of the clock skew in modern integrated circuits. Clock Skew Model
 Luis Manuel Santana Gallego 100 Appendix 3 Clock Skew Model Xiaohong Jiang and Susumu Horiguchi [JIA-01] 1. Introduction The evolution of VLSI chips toward larger die sizes and faster clock speeds makes
Luis Manuel Santana Gallego 100 Appendix 3 Clock Skew Model Xiaohong Jiang and Susumu Horiguchi [JIA-01] 1. Introduction The evolution of VLSI chips toward larger die sizes and faster clock speeds makes
Binary Dirty MAC with Common State Information
 Binary Dirty MAC with Common State Information Anatoly Khina Email: anatolyk@eng.tau.ac.il Tal Philosof Email: talp@eng.tau.ac.il Ram Zamir Email: zamir@eng.tau.ac.il Uri Erez Email: uri@eng.tau.ac.il
Binary Dirty MAC with Common State Information Anatoly Khina Email: anatolyk@eng.tau.ac.il Tal Philosof Email: talp@eng.tau.ac.il Ram Zamir Email: zamir@eng.tau.ac.il Uri Erez Email: uri@eng.tau.ac.il
A Sufficient Condition for Optimality of Digital versus Analog Relaying in a Sensor Network
 A Sufficient Condition for Optimality of Digital versus Analog Relaying in a Sensor Network Chandrashekhar Thejaswi PS Douglas Cochran and Junshan Zhang Department of Electrical Engineering Arizona State
A Sufficient Condition for Optimality of Digital versus Analog Relaying in a Sensor Network Chandrashekhar Thejaswi PS Douglas Cochran and Junshan Zhang Department of Electrical Engineering Arizona State
Joint Energy and SINR Coverage in Spatially Clustered RF-powered IoT Network
 Joint Energy and SINR Coverage in Spatially Clustered RF-powered IoT Network Mohamed A. Ad-Elmagid, Mustafa A. Kishk, and Harpreet S. Dhillon arxiv:84.9689v [cs.it 25 Apr 28 Astract Owing to the uiquitous
Joint Energy and SINR Coverage in Spatially Clustered RF-powered IoT Network Mohamed A. Ad-Elmagid, Mustafa A. Kishk, and Harpreet S. Dhillon arxiv:84.9689v [cs.it 25 Apr 28 Astract Owing to the uiquitous
1 Systems of Differential Equations
 March, 20 7- Systems of Differential Equations Let U e an open suset of R n, I e an open interval in R and : I R n R n e a function from I R n to R n The equation ẋ = ft, x is called a first order ordinary
March, 20 7- Systems of Differential Equations Let U e an open suset of R n, I e an open interval in R and : I R n R n e a function from I R n to R n The equation ẋ = ft, x is called a first order ordinary
Interference Channels with Source Cooperation
 Interference Channels with Source Cooperation arxiv:95.319v1 [cs.it] 19 May 29 Vinod Prabhakaran and Pramod Viswanath Coordinated Science Laboratory University of Illinois, Urbana-Champaign Urbana, IL
Interference Channels with Source Cooperation arxiv:95.319v1 [cs.it] 19 May 29 Vinod Prabhakaran and Pramod Viswanath Coordinated Science Laboratory University of Illinois, Urbana-Champaign Urbana, IL
Performance Analysis for Transmission of Correlated Sources over Non-Orthogonal MARCs
 1 Performance Analysis for Transmission of Correlated Sources over Non-Orthogonal MARCs Jiguang He, Iqal Hussain, Valtteri Tervo, Markku Juntti, Tad Matsumoto Centre for Wireless Communications, FI-914,
1 Performance Analysis for Transmission of Correlated Sources over Non-Orthogonal MARCs Jiguang He, Iqal Hussain, Valtteri Tervo, Markku Juntti, Tad Matsumoto Centre for Wireless Communications, FI-914,
On the Capacity of MISO Channels with One-Bit ADCs and DACs
 1 On the Capacity of MISO Channels with One-Bit ADCs and DACs Yunseo Nam Heedong Do Yo-Se Jeon and Namyoon Lee Astract arxiv:1811.5637v1 [cs.it] 1 Nov 18 A one-it wireless transceiver is a promising communication
1 On the Capacity of MISO Channels with One-Bit ADCs and DACs Yunseo Nam Heedong Do Yo-Se Jeon and Namyoon Lee Astract arxiv:1811.5637v1 [cs.it] 1 Nov 18 A one-it wireless transceiver is a promising communication
Point-Based Value Iteration for Constrained POMDPs
 Point-Based Value Iteration for Constrained POMDPs Dongho Kim Jaesong Lee Kee-Eung Kim Department of Computer Science Pascal Poupart School of Computer Science IJCAI-2011 2011. 7. 22. Motivation goals
Point-Based Value Iteration for Constrained POMDPs Dongho Kim Jaesong Lee Kee-Eung Kim Department of Computer Science Pascal Poupart School of Computer Science IJCAI-2011 2011. 7. 22. Motivation goals
IN this paper, we consider the capacity of sticky channels, a
 72 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 54, NO. 1, JANUARY 2008 Capacity Bounds for Sticky Channels Michael Mitzenmacher, Member, IEEE Abstract The capacity of sticky channels, a subclass of insertion
72 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 54, NO. 1, JANUARY 2008 Capacity Bounds for Sticky Channels Michael Mitzenmacher, Member, IEEE Abstract The capacity of sticky channels, a subclass of insertion
Characterization of the Burst Aggregation Process in Optical Burst Switching.
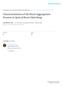 See discussions, stats, and author profiles for this pulication at: http://www.researchgate.net/pulication/221198381 Characterization of the Burst Aggregation Process in Optical Burst Switching. CONFERENCE
See discussions, stats, and author profiles for this pulication at: http://www.researchgate.net/pulication/221198381 Characterization of the Burst Aggregation Process in Optical Burst Switching. CONFERENCE
Finding Complex Solutions of Quadratic Equations
 y - y - - - x x Locker LESSON.3 Finding Complex Solutions of Quadratic Equations Texas Math Standards The student is expected to: A..F Solve quadratic and square root equations. Mathematical Processes
y - y - - - x x Locker LESSON.3 Finding Complex Solutions of Quadratic Equations Texas Math Standards The student is expected to: A..F Solve quadratic and square root equations. Mathematical Processes
A matroid associated with a phylogenetic tree
 Discrete Mathematics and Theoretical Computer Science DMTCS vol. 16:, 014, 41 56 A matroid associated with a phylogenetic tree Andreas W.M. Dress 1 Katharina T. Huer Mike Steel 3 1 CAS-MPG Partner Institute
Discrete Mathematics and Theoretical Computer Science DMTCS vol. 16:, 014, 41 56 A matroid associated with a phylogenetic tree Andreas W.M. Dress 1 Katharina T. Huer Mike Steel 3 1 CAS-MPG Partner Institute
Mathematics Background
 UNIT OVERVIEW GOALS AND STANDARDS MATHEMATICS BACKGROUND UNIT INTRODUCTION Patterns of Change and Relationships The introduction to this Unit points out to students that throughout their study of Connected
UNIT OVERVIEW GOALS AND STANDARDS MATHEMATICS BACKGROUND UNIT INTRODUCTION Patterns of Change and Relationships The introduction to this Unit points out to students that throughout their study of Connected
Design Variable Concepts 19 Mar 09 Lab 7 Lecture Notes
 Design Variale Concepts 19 Mar 09 La 7 Lecture Notes Nomenclature W total weight (= W wing + W fuse + W pay ) reference area (wing area) wing aspect ratio c r root wing chord c t tip wing chord λ taper
Design Variale Concepts 19 Mar 09 La 7 Lecture Notes Nomenclature W total weight (= W wing + W fuse + W pay ) reference area (wing area) wing aspect ratio c r root wing chord c t tip wing chord λ taper
Optimal Power Allocation for Parallel Gaussian Broadcast Channels with Independent and Common Information
 SUBMIED O IEEE INERNAIONAL SYMPOSIUM ON INFORMAION HEORY, DE. 23 1 Optimal Power Allocation for Parallel Gaussian Broadcast hannels with Independent and ommon Information Nihar Jindal and Andrea Goldsmith
SUBMIED O IEEE INERNAIONAL SYMPOSIUM ON INFORMAION HEORY, DE. 23 1 Optimal Power Allocation for Parallel Gaussian Broadcast hannels with Independent and ommon Information Nihar Jindal and Andrea Goldsmith
Feasibility Conditions for Interference Alignment
 Feasibility Conditions for Interference Alignment Cenk M. Yetis Istanbul Technical University Informatics Inst. Maslak, Istanbul, TURKEY Email: cenkmyetis@yahoo.com Tiangao Gou, Syed A. Jafar University
Feasibility Conditions for Interference Alignment Cenk M. Yetis Istanbul Technical University Informatics Inst. Maslak, Istanbul, TURKEY Email: cenkmyetis@yahoo.com Tiangao Gou, Syed A. Jafar University
Long non-crossing configurations in the plane
 Long non-crossing configurations in the plane Adrian Dumitrescu Csaa D. Tóth July 4, 00 Astract We revisit some maximization prolems for geometric networks design under the non-crossing constraint, first
Long non-crossing configurations in the plane Adrian Dumitrescu Csaa D. Tóth July 4, 00 Astract We revisit some maximization prolems for geometric networks design under the non-crossing constraint, first
ERASMUS UNIVERSITY ROTTERDAM Information concerning the Entrance examination Mathematics level 2 for International Business Administration (IBA)
 ERASMUS UNIVERSITY ROTTERDAM Information concerning the Entrance examination Mathematics level 2 for International Business Administration (IBA) General information Availale time: 2.5 hours (150 minutes).
ERASMUS UNIVERSITY ROTTERDAM Information concerning the Entrance examination Mathematics level 2 for International Business Administration (IBA) General information Availale time: 2.5 hours (150 minutes).
Generalized Reed-Solomon Codes
 Chapter 5 Generalized Reed-Solomon Codes In 1960, I.S. Reed and G. Solomon introduced a family of error-correcting codes that are douly lessed. The codes and their generalizations are useful in practice,
Chapter 5 Generalized Reed-Solomon Codes In 1960, I.S. Reed and G. Solomon introduced a family of error-correcting codes that are douly lessed. The codes and their generalizations are useful in practice,
On BCJR State Metric Quantization for Turbo Equalization
 On BCJR State Metric Quantization for Turo Equalization Brian M. Kurkoski, Kazuhiko Yamaguchi and Kingo Koayashi Dept. of Information and Computer Engineering University of Electro-Communications Chofu,
On BCJR State Metric Quantization for Turo Equalization Brian M. Kurkoski, Kazuhiko Yamaguchi and Kingo Koayashi Dept. of Information and Computer Engineering University of Electro-Communications Chofu,
II. THE TWO-WAY TWO-RELAY CHANNEL
 An Achievable Rate Region for the Two-Way Two-Relay Channel Jonathan Ponniah Liang-Liang Xie Department of Electrical Computer Engineering, University of Waterloo, Canada Abstract We propose an achievable
An Achievable Rate Region for the Two-Way Two-Relay Channel Jonathan Ponniah Liang-Liang Xie Department of Electrical Computer Engineering, University of Waterloo, Canada Abstract We propose an achievable
ECE Information theory Final (Fall 2008)
 ECE 776 - Information theory Final (Fall 2008) Q.1. (1 point) Consider the following bursty transmission scheme for a Gaussian channel with noise power N and average power constraint P (i.e., 1/n X n i=1
ECE 776 - Information theory Final (Fall 2008) Q.1. (1 point) Consider the following bursty transmission scheme for a Gaussian channel with noise power N and average power constraint P (i.e., 1/n X n i=1
1 Caveats of Parallel Algorithms
 CME 323: Distriuted Algorithms and Optimization, Spring 2015 http://stanford.edu/ reza/dao. Instructor: Reza Zadeh, Matroid and Stanford. Lecture 1, 9/26/2015. Scried y Suhas Suresha, Pin Pin, Andreas
CME 323: Distriuted Algorithms and Optimization, Spring 2015 http://stanford.edu/ reza/dao. Instructor: Reza Zadeh, Matroid and Stanford. Lecture 1, 9/26/2015. Scried y Suhas Suresha, Pin Pin, Andreas
On the complexity of maximizing the minimum Shannon capacity in wireless networks by joint channel assignment and power allocation
 On the complexity of maximizing the minimum Shannon capacity in wireless networks by joint channel assignment and power allocation Mikael Fallgren Royal Institute of Technology December, 2009 Abstract
On the complexity of maximizing the minimum Shannon capacity in wireless networks by joint channel assignment and power allocation Mikael Fallgren Royal Institute of Technology December, 2009 Abstract
Power Control for Discrete-Input Block-Fading Channels. K. D. Nguyen, A. Guillén i Fàbregas and L. K. Rasmussen
 Power Control for Discrete-Input Block-Fading Channels K. D. Nguyen, A. Guillén i Fàregas and L. K. Rasmussen CUED / F-INFENG / TR 582 August 2007 Power Control for Discrete-Input Block-Fading Channels
Power Control for Discrete-Input Block-Fading Channels K. D. Nguyen, A. Guillén i Fàregas and L. K. Rasmussen CUED / F-INFENG / TR 582 August 2007 Power Control for Discrete-Input Block-Fading Channels
RADAR Oxford Brookes University Research Archive and Digital Asset Repository (RADAR)
 RADAR Oxford Brookes University Research Archive and Digital Asset Repository (RADAR) Cuzzolin, F Alternative formulations of the theory of evidence ased on asic plausiility and commonality assignments.
RADAR Oxford Brookes University Research Archive and Digital Asset Repository (RADAR) Cuzzolin, F Alternative formulations of the theory of evidence ased on asic plausiility and commonality assignments.
Random Access: An Information-Theoretic Perspective
 Random Access: An Information-Theoretic Perspective Paolo Minero, Massimo Franceschetti, and David N. C. Tse Abstract This paper considers a random access system where each sender can be in two modes of
Random Access: An Information-Theoretic Perspective Paolo Minero, Massimo Franceschetti, and David N. C. Tse Abstract This paper considers a random access system where each sender can be in two modes of
Genetic Algorithms applied to Problems of Forbidden Configurations
 Genetic Algorithms applied to Prolems of Foridden Configurations R.P. Anstee Miguel Raggi Department of Mathematics University of British Columia Vancouver, B.C. Canada V6T Z2 anstee@math.uc.ca mraggi@gmail.com
Genetic Algorithms applied to Prolems of Foridden Configurations R.P. Anstee Miguel Raggi Department of Mathematics University of British Columia Vancouver, B.C. Canada V6T Z2 anstee@math.uc.ca mraggi@gmail.com
Amobile satellite communication system, like Motorola s
 I TRANSACTIONS ON INFORMATION THORY, VOL. 45, NO. 4, MAY 1999 1111 Distributed Source Coding for Satellite Communications Raymond W. Yeung, Senior Member, I, Zhen Zhang, Senior Member, I Abstract Inspired
I TRANSACTIONS ON INFORMATION THORY, VOL. 45, NO. 4, MAY 1999 1111 Distributed Source Coding for Satellite Communications Raymond W. Yeung, Senior Member, I, Zhen Zhang, Senior Member, I Abstract Inspired
Alphabet Size Reduction for Secure Network Coding: A Graph Theoretic Approach
 ALPHABET SIZE REDUCTION FOR SECURE NETWORK CODING: A GRAPH THEORETIC APPROACH 1 Alphabet Size Reduction for Secure Network Coding: A Graph Theoretic Approach Xuan Guang, Member, IEEE, and Raymond W. Yeung,
ALPHABET SIZE REDUCTION FOR SECURE NETWORK CODING: A GRAPH THEORETIC APPROACH 1 Alphabet Size Reduction for Secure Network Coding: A Graph Theoretic Approach Xuan Guang, Member, IEEE, and Raymond W. Yeung,
ON THE COMPARISON OF BOUNDARY AND INTERIOR SUPPORT POINTS OF A RESPONSE SURFACE UNDER OPTIMALITY CRITERIA. Cross River State, Nigeria
 ON THE COMPARISON OF BOUNDARY AND INTERIOR SUPPORT POINTS OF A RESPONSE SURFACE UNDER OPTIMALITY CRITERIA Thomas Adidaume Uge and Stephen Seastian Akpan, Department Of Mathematics/Statistics And Computer
ON THE COMPARISON OF BOUNDARY AND INTERIOR SUPPORT POINTS OF A RESPONSE SURFACE UNDER OPTIMALITY CRITERIA Thomas Adidaume Uge and Stephen Seastian Akpan, Department Of Mathematics/Statistics And Computer
Branching Bisimilarity with Explicit Divergence
 Branching Bisimilarity with Explicit Divergence Ro van Glaeek National ICT Australia, Sydney, Australia School of Computer Science and Engineering, University of New South Wales, Sydney, Australia Bas
Branching Bisimilarity with Explicit Divergence Ro van Glaeek National ICT Australia, Sydney, Australia School of Computer Science and Engineering, University of New South Wales, Sydney, Australia Bas
Codes in the Damerau Distance for Deletion and Adjacent Transposition Correction
 1 Codes in the Damerau Distance for Deletion and Adjacent Transposition Correction Ryan Garys, Eitan Yaakoi, and Olgica Milenkovic ECE Department, University of Illinois, Urana-Champaign Technion University
1 Codes in the Damerau Distance for Deletion and Adjacent Transposition Correction Ryan Garys, Eitan Yaakoi, and Olgica Milenkovic ECE Department, University of Illinois, Urana-Champaign Technion University
TRANSMISSION STRATEGIES FOR SINGLE-DESTINATION WIRELESS NETWORKS
 The 20 Military Communications Conference - Track - Waveforms and Signal Processing TRANSMISSION STRATEGIES FOR SINGLE-DESTINATION WIRELESS NETWORKS Gam D. Nguyen, Jeffrey E. Wieselthier 2, Sastry Kompella,
The 20 Military Communications Conference - Track - Waveforms and Signal Processing TRANSMISSION STRATEGIES FOR SINGLE-DESTINATION WIRELESS NETWORKS Gam D. Nguyen, Jeffrey E. Wieselthier 2, Sastry Kompella,
A Unified Continuous Greedy Algorithm for Submodular Maximization
 A Unified Continuous Greedy Algorithm for Sumodular Maximization Moran Feldman Technion Joseph (Seffi) Naor Technion Roy Schwartz Technion Astract The study of cominatorial prolems with a sumodular ojective
A Unified Continuous Greedy Algorithm for Sumodular Maximization Moran Feldman Technion Joseph (Seffi) Naor Technion Roy Schwartz Technion Astract The study of cominatorial prolems with a sumodular ojective
Capacity of the Discrete Memoryless Energy Harvesting Channel with Side Information
 204 IEEE International Symposium on Information Theory Capacity of the Discrete Memoryless Energy Harvesting Channel with Side Information Omur Ozel, Kaya Tutuncuoglu 2, Sennur Ulukus, and Aylin Yener
204 IEEE International Symposium on Information Theory Capacity of the Discrete Memoryless Energy Harvesting Channel with Side Information Omur Ozel, Kaya Tutuncuoglu 2, Sennur Ulukus, and Aylin Yener
Rollout Policies for Dynamic Solutions to the Multi-Vehicle Routing Problem with Stochastic Demand and Duration Limits
 Rollout Policies for Dynamic Solutions to the Multi-Vehicle Routing Prolem with Stochastic Demand and Duration Limits Justin C. Goodson Jeffrey W. Ohlmann Barrett W. Thomas Octoer 2, 2012 Astract We develop
Rollout Policies for Dynamic Solutions to the Multi-Vehicle Routing Prolem with Stochastic Demand and Duration Limits Justin C. Goodson Jeffrey W. Ohlmann Barrett W. Thomas Octoer 2, 2012 Astract We develop
