Review for Mastery. Integer Exponents. Zero Exponents Negative Exponents Negative Exponents in the Denominator. Definition.
|
|
|
- Douglas Burke
- 5 years ago
- Views:
Transcription
1 LESSON 6- Review for Mastery Integer Exponents Remember that means 8. The base is, the exponent is positive. Exponents can also be 0 or negative. Zero Exponents Negative Exponents Negative Exponents in the Denominator Definition For any nonzero number x, x 0. For any nonzero number x and any integer n, x n n x. For any nonzero number x and any integer n, n x x n. Examples and 0 n are undefined. Simplify. Simplify x y z 0. x y z 0 6 Write without negative exponents. Write in expanded form. x z y 0 x () y x y Write without negative exponents. z 0. Fill in the blanks to simplify each expression y a x b x y a b 9xy x y
2 LESSON 6- Review for Mastery Integer Exponents continued Evaluate a b for a and b. a b ( )( ) Substitute. 6 Write without negative exponents. When evaluating, it is important to determine whether the negative is raised to the power. Evaluate x for x 0. Evaluate ( x) for x 0. The negative is not raised to the power. The negative is raised to the power. x ( x) 0 Substitute. ( 0) Substitute. 0 Write in expanded form Write without negative exponents ( 0) ( 0) ( 0) 00 Write without negative exponents Write in expanded form. Evaluate each expression for the given value(s) of the variable(s). 0. x y 0 for x and y. a b for a and b. z for z and y. a b for a and b y. n m for m 6 and n. ( u) v 6 for u and v
3 6. Review for Mastery Rational Exponents To simplify a number raised to the power of, write the nth root of the number. n Simplify Think: What number, when taken as a factor times, is equal to 6? , so 6 6. When an expression contains two or more expressions with fractional exponents, evaluate the expressions with the exponents first, then add or subtract. Simplify Simplify each expression
4 6. Review for Mastery Rational Exponents continued A fractional exponent may have a numerator other than. To simplify a number raised to the power of m, write the nth root of the number raised to the mth power. n Simplify. 6 To find, think: what number, when taken as a factor times, equals?, so Simplify To find 6, think: what number, when taken as a factor 6 times, equals 6? 6 6 6, so 6. Simplify each expression
5 6. Review for Mastery Polynomials A monomial is a number, a variable, or a product of numbers and variables with wholenumber exponents. A polynomial is a monomial or a sum or difference of monomials. The degree of the monomial is the sum of the exponents in the monomial. Find the degree of 8x y. Find the degree of a 6 b. 8x y The exponents are and. a 6 b The exponents are 6 and. The degree of the monomial The degree of the monomial is. is 6 7. The degree of the polynomial is the degree of the term with the greatest degree. Find the degree of x y 9x. Find the degree of ab 9a. x y 9{ x { ab 9 { a 7 Degree of the polynomial is 7. The standard form of a polynomial is written with the terms in order from the greatest degree to the least degree. The coefficient of the first term is the leading coefficient. Write x 6x x in standard form. { x 6 { x { 0 x 6x x { x The leading coefficient is. Find the degree of each term. Write the terms in order of degree. Degree of the polynomial is. Find the degree of each monomial.. 7m n. 6xyz. x y Find the degree of each polynomial.. x x y. x y y 7 6. x xy y Write each polynomial in standard form. Then give the leading coefficient. 7. x x 6x 8. x x x 9. 8x 7x
6 6. Review for Mastery Polynomials continued Polynomials have special names based on their degree and the number of terms they have. Degree 0 6 or more Name Constant Linear Quadratic Cubic Quartic Quintic 6th degree Name Monomial Binomial Trinomial Polynomial Classify 7x x according to its degree and number of terms. 7x x is a quartic trinomial. Polynomials can be evaluated. A ball is thrown straight up in the air from a height of feet at a speed of 6 feet per second. The height of the ball in feet is given by 6t 6t where t is the time in seconds. How high is the ball after seconds? Evaluate for t. 6t 6t 6() 6() 6() 6() After seconds, the ball is 70 feet high. Terms or more Degree: Terms: Substitute for t. Follow the order of operations to simplify. Classify each polynomial according to its degree and number of terms. 0. 7x x. b b b. A ball is thrown straight up in the air from a height of 6 feet at a speed of 80 feet per second. The height of the ball in feet is given by 6t 80t 6 where t is the time in seconds. What is the height of the ball after seconds?
7 6. Review for Mastery Adding and Subtracting Polynomials You can add or subtract polynomials by combining like terms. The following are like terms: The following are not like terms: Add x x x 6x. x x x 6x x x x 6x 8x 0x Identify like terms. Rearrange terms so that like terms are together. Add (y 7y ) (y y 8). (y 7y ) (y y 8 ) Identify like terms. (y y ) ( 7y y ) ( 8 ) Rearrange terms so that like terms are together. 9y 8y 0 Determine whether the following are like terms. Explain.. x and x. y and 7y. z and x Add.. y y 7y y. 8m m m 6. x 0x 8x 7. (6x x) (x 6x) 8. (m 0m ) (8m ) 9. (6x x) (x x x 9) 0. (y 6y ) (y 8y y )
8 6. Review for Mastery Adding and Subtracting Polynomials continued To subtract polynomials you must remember to add the opposite. Find the opposite of (m m ). (m m ) (m m ) m m Subtract (x x 7) (x ). (x x 7) (x ) Write the opposite of the polynomial. Write the opposite of each term in the polynomial. (x x 7) ( x ) Rewrite subtraction as addition of the opposite. (x x 7) ( x ) Identify like terms. (x x ) x 7 Rearrange terms so that like terms are together. x x 7 Subtract (6y y 7) (y y ). (6y y 7) (y y ) (6y y 7) ( y y ) Rewrite subtraction as addition of the opposite. (6y y 7 ) ( y y ) Identify like terms. (6y y ) ( y y ) ( 7 ) Rearrange terms so that like terms are together. y y Find the opposite of each polynomial.. x 7x. x x 8. x x 7x Subtract.. (9x x) (x). (6t ) ( t ) 6. (x x ) (x 6) 7. (t t) (t t 6) 8. (c 8c c ) (c c )
9 6. Review for Mastery Multiplying Polynomials To multiply monomials, multiply the constants, then multiply variables with the same base. Multiply (a b) (ab ). (a b) (ab ) ( ) (a a) (b b ) Rearrange so that the constants and the variables with the same bases are together. a b To multiply a polynomial by a monomial, distribute the monomial to each term in the polynomial. Multiply x(x + x + 7). x(x x 7) (x)x (x)x (x)7 x 6x x Distribute.. ( x y ) (xy). (xyz) ( x yz). (x) (x y ) Fill in the blanks below. Then finish multiplying.. (x ). x(x 8) 6. x(x 6x ) x x + 8 x 6x 7. (x 9) 8. x(x 8) 9. x (x x ) 0. ( x ). (a b) (ab). y( y 7y )
10 6. Review for Mastery Multiplying Polynomials continued Use the Distributive Property to multiply binomials and polynomials. Multiply (x ) (x 7). (x ) (x 7) x(x 7) (x 7) (x)x (x)7 ()x ()7 x 7x x x x Multiply (x ) (x x ). (x ) (x x ) x(x x ) (x x ) Distribute. Distribute again. (x)x (x)x (x) ()x ()x () x x x x x 0 x 8x 9x 0 Distribute. Distribute again. Fill in the blanks below. Then finish multiplying.. (x ) (x ). (x ) (x 8). (x ) (x 6) (x ) (x ) (x 8) (x 8) (x 6) (x 6) 6. (x ) (x ) 7. (x 7) (x 7) 8. (x ) (x ) Fill in the blanks below. Then finish multiplying. 9. (x ) (x x 8) 0. (x ) (6x x ) (x x 8) (x x 8) (6x x ) (6x x )
11 6.6 Review for Mastery Special Products of Binomials A perfect-square trinomial is a trinomial that is the result of squaring a binomial. (a b) a ab b (a b) a ab b Multiply (x ). Multiply (x ). (x ) a: x (x ) a: x b: b: x (x)() Middle term is added. 6x (x)() Middle term is subtracted. x 8x 6 Square a. Square a. 6x x 9 Square b. Add product of, a, and b. Square b. Subtract product of, a, and b. State whether each product will result in a perfect-square trinomial.. (x ) (x ). (x ) (x ). (x 6) (x 6) Fill in the blanks. Then write the perfect-square trinomial.. (x 7). (x ) 6. (x 0) Square a: Square a: Square a: (a)(b): (a)(b): (a)(b): Square b: Square b: Square b: 7. (x 8) 8. (x ) 9. (7x )
12 6.6 Review for Mastery Special Products of Binomials continued When you multiply certain types of binomials, the middle term will be zero. Multiply (a b) (a b). (a b) (a b) a(a b) b(a b) a ab ab b a b Distribute. This type of special product is called a difference of squares. Multiply (x ) (x ). (a b) (a b) a b Square a. Subtract. Multiply (7 8x) (7 8x). (x ) (x ) a: x (7 8x) (7 8x) a: 7 b: b: 8x (x) () (7) (8x) Square b. x 6 9 6x State whether the products will form a difference of squares or a perfect-square trinomial. 0. (x 0) (x 0). (y 6) (y 6). (z ) (z ) Fill in the blanks. Then write the difference of squares. (a 7) (a 7). ( m) ( m). (x ) (x ) Square a: Square a: Square a: Square b: Square b: Square b: 6. (x 8) (x 8) 7. (0 x) (0 x) 8. (x y) (x y)
5.3. Polynomials and Polynomial Functions
 5.3 Polynomials and Polynomial Functions Polynomial Vocabulary Term a number or a product of a number and variables raised to powers Coefficient numerical factor of a term Constant term which is only a
5.3 Polynomials and Polynomial Functions Polynomial Vocabulary Term a number or a product of a number and variables raised to powers Coefficient numerical factor of a term Constant term which is only a
Something that can have different values at different times. A variable is usually represented by a letter in algebraic expressions.
 Lesson Objectives: Students will be able to define, recognize and use the following terms in the context of polynomials: o Constant o Variable o Monomial o Binomial o Trinomial o Polynomial o Numerical
Lesson Objectives: Students will be able to define, recognize and use the following terms in the context of polynomials: o Constant o Variable o Monomial o Binomial o Trinomial o Polynomial o Numerical
Topic 7: Polynomials. Introduction to Polynomials. Table of Contents. Vocab. Degree of a Polynomial. Vocab. A. 11x 7 + 3x 3
 Topic 7: Polynomials Table of Contents 1. Introduction to Polynomials. Adding & Subtracting Polynomials 3. Multiplying Polynomials 4. Special Products of Binomials 5. Factoring Polynomials 6. Factoring
Topic 7: Polynomials Table of Contents 1. Introduction to Polynomials. Adding & Subtracting Polynomials 3. Multiplying Polynomials 4. Special Products of Binomials 5. Factoring Polynomials 6. Factoring
I CAN classify polynomials by degree and by the number of terms.
 13-1 Polynomials I CAN classify polynomials by degree and by the number of terms. 13-1 Polynomials Insert Lesson Title Here Vocabulary monomial polynomial binomial trinomial degree of a polynomial 13-1
13-1 Polynomials I CAN classify polynomials by degree and by the number of terms. 13-1 Polynomials Insert Lesson Title Here Vocabulary monomial polynomial binomial trinomial degree of a polynomial 13-1
Algebra I Polynomials
 Slide 1 / 217 Slide 2 / 217 Algebra I Polynomials 2014-04-24 www.njctl.org Slide 3 / 217 Table of Contents Definitions of Monomials, Polynomials and Degrees Adding and Subtracting Polynomials Multiplying
Slide 1 / 217 Slide 2 / 217 Algebra I Polynomials 2014-04-24 www.njctl.org Slide 3 / 217 Table of Contents Definitions of Monomials, Polynomials and Degrees Adding and Subtracting Polynomials Multiplying
Never leave a NEGATIVE EXPONENT or a ZERO EXPONENT in an answer in simplest form!!!!!
 1 ICM Unit 0 Algebra Rules Lesson 1 Rules of Exponents RULE EXAMPLE EXPLANANTION a m a n = a m+n A) x x 6 = B) x 4 y 8 x 3 yz = When multiplying with like bases, keep the base and add the exponents. a
1 ICM Unit 0 Algebra Rules Lesson 1 Rules of Exponents RULE EXAMPLE EXPLANANTION a m a n = a m+n A) x x 6 = B) x 4 y 8 x 3 yz = When multiplying with like bases, keep the base and add the exponents. a
Ready To Go On? Skills Intervention 7-1 Integer Exponents
 7A Evaluating Expressions with Zero and Negative Exponents Zero Exponent: Any nonzero number raised to the zero power is. 4 0 Ready To Go On? Skills Intervention 7-1 Integer Exponents Negative Exponent:
7A Evaluating Expressions with Zero and Negative Exponents Zero Exponent: Any nonzero number raised to the zero power is. 4 0 Ready To Go On? Skills Intervention 7-1 Integer Exponents Negative Exponent:
Algebra I. Polynomials.
 1 Algebra I Polynomials 2015 11 02 www.njctl.org 2 Table of Contents Definitions of Monomials, Polynomials and Degrees Adding and Subtracting Polynomials Multiplying a Polynomial by a Monomial Multiplying
1 Algebra I Polynomials 2015 11 02 www.njctl.org 2 Table of Contents Definitions of Monomials, Polynomials and Degrees Adding and Subtracting Polynomials Multiplying a Polynomial by a Monomial Multiplying
Chapter 5: Exponents and Polynomials
 Chapter 5: Exponents and Polynomials 5.1 Multiplication with Exponents and Scientific Notation 5.2 Division with Exponents 5.3 Operations with Monomials 5.4 Addition and Subtraction of Polynomials 5.5
Chapter 5: Exponents and Polynomials 5.1 Multiplication with Exponents and Scientific Notation 5.2 Division with Exponents 5.3 Operations with Monomials 5.4 Addition and Subtraction of Polynomials 5.5
POLYNOMIAL EXPRESSIONS PART 1
 POLYNOMIAL EXPRESSIONS PART 1 A polynomial is an expression that is a sum of one or more terms. Each term consists of one or more variables multiplied by a coefficient. Coefficients can be negative, so
POLYNOMIAL EXPRESSIONS PART 1 A polynomial is an expression that is a sum of one or more terms. Each term consists of one or more variables multiplied by a coefficient. Coefficients can be negative, so
Day 131 Practice. What Can You Do With Polynomials?
 Polynomials Monomial - a Number, a Variable or a PRODUCT of a number and a variable. Monomials cannot have radicals with variables inside, quotients of variables or variables with negative exponents. Degree
Polynomials Monomial - a Number, a Variable or a PRODUCT of a number and a variable. Monomials cannot have radicals with variables inside, quotients of variables or variables with negative exponents. Degree
MathB65 Ch 4 IV, V, VI.notebook. October 31, 2017
 Part 4: Polynomials I. Exponents & Their Properties II. Negative Exponents III. Scientific Notation IV. Polynomials V. Addition & Subtraction of Polynomials VI. Multiplication of Polynomials VII. Greatest
Part 4: Polynomials I. Exponents & Their Properties II. Negative Exponents III. Scientific Notation IV. Polynomials V. Addition & Subtraction of Polynomials VI. Multiplication of Polynomials VII. Greatest
Polynomial comes from poly- (meaning "many") and -nomial (in this case meaning "term")... so it says "many terms
 Polynomials Polynomial comes from poly- (meaning "many") and -nomial (in this case meaning "term")... so it says "many terms Polynomials A polynomial looks like this: Term A number, a variable, or the
Polynomials Polynomial comes from poly- (meaning "many") and -nomial (in this case meaning "term")... so it says "many terms Polynomials A polynomial looks like this: Term A number, a variable, or the
Math 101 Study Session Spring 2016 Test 4 Chapter 10, Chapter 11 Chapter 12 Section 1, and Chapter 12 Section 2
 Math 101 Study Session Spring 2016 Test 4 Chapter 10, Chapter 11 Chapter 12 Section 1, and Chapter 12 Section 2 April 11, 2016 Chapter 10 Section 1: Addition and Subtraction of Polynomials A monomial is
Math 101 Study Session Spring 2016 Test 4 Chapter 10, Chapter 11 Chapter 12 Section 1, and Chapter 12 Section 2 April 11, 2016 Chapter 10 Section 1: Addition and Subtraction of Polynomials A monomial is
A polynomial is an algebraic expression that has many terms connected by only the operations of +, -, and of variables.
 A polynomial is an algebraic expression that has many terms connected by only the operations of +, -, and of variables. 2x + 5 5 x 7x +19 5x 2-7x + 19 x 2 1 x + 2 2x 3 y 4 z x + 2 2x The terms are the
A polynomial is an algebraic expression that has many terms connected by only the operations of +, -, and of variables. 2x + 5 5 x 7x +19 5x 2-7x + 19 x 2 1 x + 2 2x 3 y 4 z x + 2 2x The terms are the
27 Wyner Math 2 Spring 2019
 27 Wyner Math 2 Spring 2019 CHAPTER SIX: POLYNOMIALS Review January 25 Test February 8 Thorough understanding and fluency of the concepts and methods in this chapter is a cornerstone to success in the
27 Wyner Math 2 Spring 2019 CHAPTER SIX: POLYNOMIALS Review January 25 Test February 8 Thorough understanding and fluency of the concepts and methods in this chapter is a cornerstone to success in the
Section September 6, If n = 3, 4, 5,..., the polynomial is called a cubic, quartic, quintic, etc.
 Section 2.1-2.2 September 6, 2017 1 Polynomials Definition. A polynomial is an expression of the form a n x n + a n 1 x n 1 + + a 1 x + a 0 where each a 0, a 1,, a n are real numbers, a n 0, and n is a
Section 2.1-2.2 September 6, 2017 1 Polynomials Definition. A polynomial is an expression of the form a n x n + a n 1 x n 1 + + a 1 x + a 0 where each a 0, a 1,, a n are real numbers, a n 0, and n is a
A monomial is measured by its degree To find its degree, we add up the exponents of all the variables of the monomial.
 UNIT 6 POLYNOMIALS Polynomial (Definition) A monomial or a sum of monomials. A monomial is measured by its degree To find its degree, we add up the exponents of all the variables of the monomial. Ex. 2
UNIT 6 POLYNOMIALS Polynomial (Definition) A monomial or a sum of monomials. A monomial is measured by its degree To find its degree, we add up the exponents of all the variables of the monomial. Ex. 2
Polynomials 370 UNIT 10 WORKING WITH POLYNOMIALS. The railcars are linked together.
 UNIT 10 Working with Polynomials The railcars are linked together. 370 UNIT 10 WORKING WITH POLYNOMIALS Just as a train is built from linking railcars together, a polynomial is built by bringing terms
UNIT 10 Working with Polynomials The railcars are linked together. 370 UNIT 10 WORKING WITH POLYNOMIALS Just as a train is built from linking railcars together, a polynomial is built by bringing terms
MathB65 Ch 4 VII, VIII, IX.notebook. November 06, 2017
 Chapter 4: Polynomials I. Exponents & Their Properties II. Negative Exponents III. Scientific Notation IV. Polynomials V. Addition & Subtraction of Polynomials VI. Multiplication of Polynomials VII. Greatest
Chapter 4: Polynomials I. Exponents & Their Properties II. Negative Exponents III. Scientific Notation IV. Polynomials V. Addition & Subtraction of Polynomials VI. Multiplication of Polynomials VII. Greatest
Algebra I Unit Report Summary
 Algebra I Unit Report Summary No. Objective Code NCTM Standards Objective Title Real Numbers and Variables Unit - ( Ascend Default unit) 1. A01_01_01 H-A-B.1 Word Phrases As Algebraic Expressions 2. A01_01_02
Algebra I Unit Report Summary No. Objective Code NCTM Standards Objective Title Real Numbers and Variables Unit - ( Ascend Default unit) 1. A01_01_01 H-A-B.1 Word Phrases As Algebraic Expressions 2. A01_01_02
Multiplication of Polynomials
 Summary 391 Chapter 5 SUMMARY Section 5.1 A polynomial in x is defined by a finite sum of terms of the form ax n, where a is a real number and n is a whole number. a is the coefficient of the term. n is
Summary 391 Chapter 5 SUMMARY Section 5.1 A polynomial in x is defined by a finite sum of terms of the form ax n, where a is a real number and n is a whole number. a is the coefficient of the term. n is
Controlling the Population
 Lesson.1 Skills Practice Name Date Controlling the Population Adding and Subtracting Polynomials Vocabulary Match each definition with its corresponding term. 1. polynomial a. a polynomial with only 1
Lesson.1 Skills Practice Name Date Controlling the Population Adding and Subtracting Polynomials Vocabulary Match each definition with its corresponding term. 1. polynomial a. a polynomial with only 1
Unit 13: Polynomials and Exponents
 Section 13.1: Polynomials Section 13.2: Operations on Polynomials Section 13.3: Properties of Exponents Section 13.4: Multiplication of Polynomials Section 13.5: Applications from Geometry Section 13.6:
Section 13.1: Polynomials Section 13.2: Operations on Polynomials Section 13.3: Properties of Exponents Section 13.4: Multiplication of Polynomials Section 13.5: Applications from Geometry Section 13.6:
Algebra 1: Hutschenreuter Chapter 10 Notes Adding and Subtracting Polynomials
 Algebra 1: Hutschenreuter Chapter 10 Notes Name 10.1 Adding and Subtracting Polynomials Polynomial- an expression where terms are being either added and/or subtracted together Ex: 6x 4 + 3x 3 + 5x 2 +
Algebra 1: Hutschenreuter Chapter 10 Notes Name 10.1 Adding and Subtracting Polynomials Polynomial- an expression where terms are being either added and/or subtracted together Ex: 6x 4 + 3x 3 + 5x 2 +
Solving Multi-Step Equations
 1. Clear parentheses using the distributive property. 2. Combine like terms within each side of the equal sign. Solving Multi-Step Equations 3. Add/subtract terms to both sides of the equation to get the
1. Clear parentheses using the distributive property. 2. Combine like terms within each side of the equal sign. Solving Multi-Step Equations 3. Add/subtract terms to both sides of the equation to get the
Math 1 Variable Manipulation Part 6 Polynomials
 Name: Math 1 Variable Manipulation Part 6 Polynomials Date: 1 VOCABULARY Constant: A term that does not have a variable is called a constant. Example: the number 5 is a constant because it does not have
Name: Math 1 Variable Manipulation Part 6 Polynomials Date: 1 VOCABULARY Constant: A term that does not have a variable is called a constant. Example: the number 5 is a constant because it does not have
Sections 7.2, 7.3, 4.1
 Sections 7., 7.3, 4.1 Section 7. Multiplying, Dividing and Simplifying Radicals This section will discuss the rules for multiplying, dividing and simplifying radicals. Product Rule for multiplying radicals
Sections 7., 7.3, 4.1 Section 7. Multiplying, Dividing and Simplifying Radicals This section will discuss the rules for multiplying, dividing and simplifying radicals. Product Rule for multiplying radicals
A field trips costs $800 for the charter bus plus $10 per student for x students. The cost per student is represented by: 10x x
 LEARNING STRATEGIES: Activate Prior Knowledge, Shared Reading, Think/Pair/Share, Note Taking, Group Presentation, Interactive Word Wall A field trips costs $800 for the charter bus plus $10 per student
LEARNING STRATEGIES: Activate Prior Knowledge, Shared Reading, Think/Pair/Share, Note Taking, Group Presentation, Interactive Word Wall A field trips costs $800 for the charter bus plus $10 per student
LESSON 9.1 ROOTS AND RADICALS
 LESSON 9.1 ROOTS AND RADICALS LESSON 9.1 ROOTS AND RADICALS 67 OVERVIEW Here s what you ll learn in this lesson: Square Roots and Cube Roots a. Definition of square root and cube root b. Radicand, radical
LESSON 9.1 ROOTS AND RADICALS LESSON 9.1 ROOTS AND RADICALS 67 OVERVIEW Here s what you ll learn in this lesson: Square Roots and Cube Roots a. Definition of square root and cube root b. Radicand, radical
Polynomials and Polynomial Equations
 Polynomials and Polynomial Equations A Polynomial is any expression that has constants, variables and exponents, and can be combined using addition, subtraction, multiplication and division, but: no division
Polynomials and Polynomial Equations A Polynomial is any expression that has constants, variables and exponents, and can be combined using addition, subtraction, multiplication and division, but: no division
Algebra 1. Math Review Packet. Equations, Inequalities, Linear Functions, Linear Systems, Exponents, Polynomials, Factoring, Quadratics, Radicals
 Algebra 1 Math Review Packet Equations, Inequalities, Linear Functions, Linear Systems, Exponents, Polynomials, Factoring, Quadratics, Radicals 2017 Math in the Middle 1. Clear parentheses using the distributive
Algebra 1 Math Review Packet Equations, Inequalities, Linear Functions, Linear Systems, Exponents, Polynomials, Factoring, Quadratics, Radicals 2017 Math in the Middle 1. Clear parentheses using the distributive
Lesson 3 Algebraic expression: - the result obtained by applying operations (+, -,, ) to a collection of numbers and/or variables o
 Lesson 3 Algebraic expression: - the result obtained by applying operations (+, -,, ) to a collection of numbers and/or variables o o ( 1)(9) 3 ( 1) 3 9 1 Evaluate the second expression at the left, if
Lesson 3 Algebraic expression: - the result obtained by applying operations (+, -,, ) to a collection of numbers and/or variables o o ( 1)(9) 3 ( 1) 3 9 1 Evaluate the second expression at the left, if
Algebra I. Slide 1 / 216. Slide 2 / 216. Slide 3 / 216. Polynomials
 Slide 1 / 216 Slide 2 / 216 lgebra I Polynomials 2015-11-02 www.njctl.org Table of ontents efinitions of Monomials, Polynomials and egrees dding and Subtracting Polynomials Multiplying a Polynomial by
Slide 1 / 216 Slide 2 / 216 lgebra I Polynomials 2015-11-02 www.njctl.org Table of ontents efinitions of Monomials, Polynomials and egrees dding and Subtracting Polynomials Multiplying a Polynomial by
mn 3 17x 2 81y 4 z Algebra I Definitions of Monomials, Polynomials and Degrees 32,457 Slide 1 / 216 Slide 2 / 216 Slide 3 / 216 Slide 4 / 216
 Slide 1 / 216 Slide 2 / 216 lgebra I Polynomials 2015-11-02 www.njctl.org Slide 3 / 216 Table of ontents efinitions of Monomials, Polynomials and egrees dding and Subtracting Polynomials Multiplying a
Slide 1 / 216 Slide 2 / 216 lgebra I Polynomials 2015-11-02 www.njctl.org Slide 3 / 216 Table of ontents efinitions of Monomials, Polynomials and egrees dding and Subtracting Polynomials Multiplying a
Alg 1B Chapter 7 Final Exam Review
 Name: Class: Date: ID: A Alg B Chapter 7 Final Exam Review Please answer all questions and show your work. Simplify ( 2) 4. 2. Simplify ( 4) 4. 3. Simplify 5 2. 4. Simplify 9x0 y 3 z 8. 5. Simplify 7w0
Name: Class: Date: ID: A Alg B Chapter 7 Final Exam Review Please answer all questions and show your work. Simplify ( 2) 4. 2. Simplify ( 4) 4. 3. Simplify 5 2. 4. Simplify 9x0 y 3 z 8. 5. Simplify 7w0
Adding and Subtracting Polynomials Add and Subtract Polynomials by doing the following: Combine like terms
 POLYNOMIALS AND POLYNOMIAL OPERATIONS STUDY GUIDE Polynomials Polynomials are classified by two different categories: by the number of terms, and the degree of the leading exponent. Number Classification
POLYNOMIALS AND POLYNOMIAL OPERATIONS STUDY GUIDE Polynomials Polynomials are classified by two different categories: by the number of terms, and the degree of the leading exponent. Number Classification
5.2. Adding and Subtracting Polynomials. Objectives. Know the basic definitions for polynomials. Add and subtract polynomials.
 Chapter 5 Section 2 5.2 Adding and Subtracting Polynomials Objectives 1 2 Know the basic definitions for polynomials. Add and subtract polynomials. Objective 1 Know the basic definitions for polynomials.
Chapter 5 Section 2 5.2 Adding and Subtracting Polynomials Objectives 1 2 Know the basic definitions for polynomials. Add and subtract polynomials. Objective 1 Know the basic definitions for polynomials.
Algebra I. Book 2. Powered by...
 Algebra I Book 2 Powered by... ALGEBRA I Units 4-7 by The Algebra I Development Team ALGEBRA I UNIT 4 POWERS AND POLYNOMIALS......... 1 4.0 Review................ 2 4.1 Properties of Exponents..........
Algebra I Book 2 Powered by... ALGEBRA I Units 4-7 by The Algebra I Development Team ALGEBRA I UNIT 4 POWERS AND POLYNOMIALS......... 1 4.0 Review................ 2 4.1 Properties of Exponents..........
When you square a binomial, you can apply the FOIL method to find the product. You can also apply the following rules as a short cut.
 Squaring a Binomial When you square a binomial, you can apply the FOIL method to find the product. You can also apply the following rules as a short cut. Solve. (x 3) 2 Step 1 Square the first term. Rules
Squaring a Binomial When you square a binomial, you can apply the FOIL method to find the product. You can also apply the following rules as a short cut. Solve. (x 3) 2 Step 1 Square the first term. Rules
Sections 7.1, 7.2: Sums, differences, products of polynomials CHAPTER 7: POLYNOMIALS
 Sections 7.1, 7.2: Sums, differences, products of polynomials CHAPTER 7: POLYNOMIALS Quiz results Average 73%: high h score 100% Problems: Keeping track of negative signs x = + = + Function notation f(x)
Sections 7.1, 7.2: Sums, differences, products of polynomials CHAPTER 7: POLYNOMIALS Quiz results Average 73%: high h score 100% Problems: Keeping track of negative signs x = + = + Function notation f(x)
LESSON 7.2 FACTORING POLYNOMIALS II
 LESSON 7.2 FACTORING POLYNOMIALS II LESSON 7.2 FACTORING POLYNOMIALS II 305 OVERVIEW Here s what you ll learn in this lesson: Trinomials I a. Factoring trinomials of the form x 2 + bx + c; x 2 + bxy +
LESSON 7.2 FACTORING POLYNOMIALS II LESSON 7.2 FACTORING POLYNOMIALS II 305 OVERVIEW Here s what you ll learn in this lesson: Trinomials I a. Factoring trinomials of the form x 2 + bx + c; x 2 + bxy +
5.1 Monomials. Algebra 2
 . Monomials Algebra Goal : A..: Add, subtract, multiply, and simplify polynomials and rational expressions (e.g., multiply (x ) ( x + ); simplify 9x x. x Goal : Write numbers in scientific notation. Scientific
. Monomials Algebra Goal : A..: Add, subtract, multiply, and simplify polynomials and rational expressions (e.g., multiply (x ) ( x + ); simplify 9x x. x Goal : Write numbers in scientific notation. Scientific
Answer Key. Solve each equation x - 9 = (n + 2) = b - 6 = -3b + 48
 Solve each equation. 1. -3x - 9 = -27 2. 25 + 2(n + 2) = 30 3. -9b - 6 = -3b + 48 x = 6 n = 1 / 2 b = -9 4. 5 - (m - 4) = 2m + 3(m - 1) 5. -24-10k = -8(k + 4) - 2k 6. f - (-19) = 11f + 23-20f m = 2 no
Solve each equation. 1. -3x - 9 = -27 2. 25 + 2(n + 2) = 30 3. -9b - 6 = -3b + 48 x = 6 n = 1 / 2 b = -9 4. 5 - (m - 4) = 2m + 3(m - 1) 5. -24-10k = -8(k + 4) - 2k 6. f - (-19) = 11f + 23-20f m = 2 no
LESSON 6.2 POLYNOMIAL OPERATIONS I
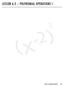 LESSON 6. POLYNOMIAL OPERATIONS I LESSON 6. POLYNOMIALS OPERATIONS I 63 OVERVIEW Here's what you'll learn in this lesson: Adding and Subtracting a. Definition of polynomial, term, and coefficient b. Evaluating
LESSON 6. POLYNOMIAL OPERATIONS I LESSON 6. POLYNOMIALS OPERATIONS I 63 OVERVIEW Here's what you'll learn in this lesson: Adding and Subtracting a. Definition of polynomial, term, and coefficient b. Evaluating
Functions: Polynomial, Rational, Exponential
 Functions: Polynomial, Rational, Exponential MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Spring 2014 Objectives In this lesson we will learn to: identify polynomial expressions,
Functions: Polynomial, Rational, Exponential MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Spring 2014 Objectives In this lesson we will learn to: identify polynomial expressions,
Unit 2: Polynomials Guided Notes
 Unit 2: Polynomials Guided Notes Name Period **If found, please return to Mrs. Brandley s room, M 8.** Self Assessment The following are the concepts you should know by the end of Unit 1. Periodically
Unit 2: Polynomials Guided Notes Name Period **If found, please return to Mrs. Brandley s room, M 8.** Self Assessment The following are the concepts you should know by the end of Unit 1. Periodically
Unit 7: Factoring Quadratic Polynomials
 Unit 7: Factoring Quadratic Polynomials A polynomial is represented by: where the coefficients are real numbers and the exponents are nonnegative integers. Side Note: Examples of real numbers: Examples
Unit 7: Factoring Quadratic Polynomials A polynomial is represented by: where the coefficients are real numbers and the exponents are nonnegative integers. Side Note: Examples of real numbers: Examples
UNIT 2 FACTORING. M2 Ch 11 all
 UNIT 2 FACTORING M2 Ch 11 all 2.1 Polynomials Objective I will be able to put polynomials in standard form and identify their degree and type. I will be able to add and subtract polynomials. Vocabulary
UNIT 2 FACTORING M2 Ch 11 all 2.1 Polynomials Objective I will be able to put polynomials in standard form and identify their degree and type. I will be able to add and subtract polynomials. Vocabulary
Variables and Expressions
 Variables and Expressions A variable is a letter that represents a value that can change. A constant is a value that does not change. A numerical expression contains only constants and operations. An algebraic
Variables and Expressions A variable is a letter that represents a value that can change. A constant is a value that does not change. A numerical expression contains only constants and operations. An algebraic
Module 11 Lesson 3. Polynomial Functions Quiz. Some questions are doubled up if a pool wants to be set up to randomize the questions.
 Module 11 Lesson 3 Polynomial Functions Quiz Some questions are doubled up if a pool wants to be set up to randomize the questions. Question 1: Short answer/fill in the blank Find the limit graphically:
Module 11 Lesson 3 Polynomial Functions Quiz Some questions are doubled up if a pool wants to be set up to randomize the questions. Question 1: Short answer/fill in the blank Find the limit graphically:
review To find the coefficient of all the terms in 15ab + 60bc 17ca: Coefficient of ab = 15 Coefficient of bc = 60 Coefficient of ca = -17
 1. Revision Recall basic terms of algebraic expressions like Variable, Constant, Term, Coefficient, Polynomial etc. The coefficients of the terms in 4x 2 5xy + 6y 2 are Coefficient of 4x 2 is 4 Coefficient
1. Revision Recall basic terms of algebraic expressions like Variable, Constant, Term, Coefficient, Polynomial etc. The coefficients of the terms in 4x 2 5xy + 6y 2 are Coefficient of 4x 2 is 4 Coefficient
Name: Chapter 7: Exponents and Polynomials
 Name: Chapter 7: Exponents and Polynomials 7-1: Integer Exponents Objectives: Evaluate expressions containing zero and integer exponents. Simplify expressions containing zero and integer exponents. You
Name: Chapter 7: Exponents and Polynomials 7-1: Integer Exponents Objectives: Evaluate expressions containing zero and integer exponents. Simplify expressions containing zero and integer exponents. You
Maintaining Mathematical Proficiency
 Chapter 7 Maintaining Mathematical Proficiency Simplify the expression. 1. 5x 6 + 3x. 3t + 7 3t 4 3. 8s 4 + 4s 6 5s 4. 9m + 3 + m 3 + 5m 5. 4 3p 7 3p 4 1 z 1 + 4 6. ( ) 7. 6( x + ) 4 8. 3( h + 4) 3( h
Chapter 7 Maintaining Mathematical Proficiency Simplify the expression. 1. 5x 6 + 3x. 3t + 7 3t 4 3. 8s 4 + 4s 6 5s 4. 9m + 3 + m 3 + 5m 5. 4 3p 7 3p 4 1 z 1 + 4 6. ( ) 7. 6( x + ) 4 8. 3( h + 4) 3( h
Beginning Algebra MAT0024C. Professor Sikora. Professor M. J. Sikora ~ Valencia Community College
 Beginning Algebra Professor Sikora MAT002C POLYNOMIALS 6.1 Positive Integer Exponents x n = x x x x x [n of these x factors] base exponent Numerical: Ex: - = where as Ex: (-) = Ex: - = and Ex: (-) = Rule:
Beginning Algebra Professor Sikora MAT002C POLYNOMIALS 6.1 Positive Integer Exponents x n = x x x x x [n of these x factors] base exponent Numerical: Ex: - = where as Ex: (-) = Ex: - = and Ex: (-) = Rule:
Assignment #1 MAT121 Summer 2015 NAME:
 Assignment #1 MAT11 Summer 015 NAME: Directions: Do ALL of your work on THIS handout in the space provided! Circle your final answer! On problems that your teacher would show work on be sure that you also
Assignment #1 MAT11 Summer 015 NAME: Directions: Do ALL of your work on THIS handout in the space provided! Circle your final answer! On problems that your teacher would show work on be sure that you also
Rising 8th Grade Math. Algebra 1 Summer Review Packet
 Rising 8th Grade Math Algebra 1 Summer Review Packet 1. Clear parentheses using the distributive property. 2. Combine like terms within each side of the equal sign. Solving Multi-Step Equations 3. Add/subtract
Rising 8th Grade Math Algebra 1 Summer Review Packet 1. Clear parentheses using the distributive property. 2. Combine like terms within each side of the equal sign. Solving Multi-Step Equations 3. Add/subtract
Unit 2: Polynomials Guided Notes
 Unit 2: Polynomials Guided Notes Name Period **If found, please return to Mrs. Brandley s room, M 8.** Self Assessment The following are the concepts you should know by the end of Unit 1. Periodically
Unit 2: Polynomials Guided Notes Name Period **If found, please return to Mrs. Brandley s room, M 8.** Self Assessment The following are the concepts you should know by the end of Unit 1. Periodically
Lesson 2: Introduction to Variables
 Lesson 2: Introduction to Variables Topics and Objectives: Evaluating Algebraic Expressions Some Vocabulary o Variable o Term o Coefficient o Constant o Factor Like Terms o Identifying Like Terms o Combining
Lesson 2: Introduction to Variables Topics and Objectives: Evaluating Algebraic Expressions Some Vocabulary o Variable o Term o Coefficient o Constant o Factor Like Terms o Identifying Like Terms o Combining
LT1: Adding and Subtracting Polynomials. *When subtracting polynomials, distribute the negative to the second parentheses. Then combine like terms.
 LT1: Adding and Subtracting Polynomials *When adding polynomials, simply combine like terms. *When subtracting polynomials, distribute the negative to the second parentheses. Then combine like terms. 1.
LT1: Adding and Subtracting Polynomials *When adding polynomials, simply combine like terms. *When subtracting polynomials, distribute the negative to the second parentheses. Then combine like terms. 1.
2-2: Evaluate and Graph Polynomial Functions
 2-2: Evaluate and Graph Polynomial Functions What is a polynomial? -A monomial or sum of monomials with whole number exponents. Degree of a polynomial: - The highest exponent of the polynomial How do we
2-2: Evaluate and Graph Polynomial Functions What is a polynomial? -A monomial or sum of monomials with whole number exponents. Degree of a polynomial: - The highest exponent of the polynomial How do we
TABLE OF CONTENTS. Introduction to Finish Line Indiana Math 10. UNIT 1: Number Sense, Expressions, and Computation. Real Numbers
 TABLE OF CONTENTS Introduction to Finish Line Indiana Math 10 UNIT 1: Number Sense, Expressions, and Computation LESSON 1 8.NS.1, 8.NS.2, A1.RNE.1, A1.RNE.2 LESSON 2 8.NS.3, 8.NS.4 LESSON 3 A1.RNE.3 LESSON
TABLE OF CONTENTS Introduction to Finish Line Indiana Math 10 UNIT 1: Number Sense, Expressions, and Computation LESSON 1 8.NS.1, 8.NS.2, A1.RNE.1, A1.RNE.2 LESSON 2 8.NS.3, 8.NS.4 LESSON 3 A1.RNE.3 LESSON
5.2 Polynomial Operations
 5.2 Polynomial Operations At times we ll need to perform operations with polynomials. At this level we ll just be adding, subtracting, or multiplying polynomials. Dividing polynomials will happen in future
5.2 Polynomial Operations At times we ll need to perform operations with polynomials. At this level we ll just be adding, subtracting, or multiplying polynomials. Dividing polynomials will happen in future
Algebra Final Exam Review Packet
 Algebra 1 00 Final Eam Review Packet UNIT 1 EXPONENTS / RADICALS Eponents Degree of a monomial: Add the degrees of all the in the monomial together. o Eample - Find the degree of 5 7 yz Degree of a polynomial:
Algebra 1 00 Final Eam Review Packet UNIT 1 EXPONENTS / RADICALS Eponents Degree of a monomial: Add the degrees of all the in the monomial together. o Eample - Find the degree of 5 7 yz Degree of a polynomial:
Math 2 Variable Manipulation Part 3 Polynomials A
 Math 2 Variable Manipulation Part 3 Polynomials A 1 MATH 1 REVIEW: VOCABULARY Constant: A term that does not have a variable is called a constant. Example: the number 5 is a constant because it does not
Math 2 Variable Manipulation Part 3 Polynomials A 1 MATH 1 REVIEW: VOCABULARY Constant: A term that does not have a variable is called a constant. Example: the number 5 is a constant because it does not
Polynomials. Eve Rawley, (EveR) Anne Gloag, (AnneG) Andrew Gloag, (AndrewG)
 Polynomials Eve Rawley, (EveR) Anne Gloag, (AnneG) Andrew Gloag, (AndrewG) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book,
Polynomials Eve Rawley, (EveR) Anne Gloag, (AnneG) Andrew Gloag, (AndrewG) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book,
ALGEBRA 2 Summer Review Assignments Graphing
 ALGEBRA 2 Summer Review Assignments Graphing To be prepared for algebra two, and all subsequent math courses, you need to be able to accurately and efficiently find the slope of any line, be able to write
ALGEBRA 2 Summer Review Assignments Graphing To be prepared for algebra two, and all subsequent math courses, you need to be able to accurately and efficiently find the slope of any line, be able to write
20A. Build. Build and add. Build a rectangle and find the area (product). l e s s o n p r a c t i c e 1. X X X 2 + 6X X
 l e s s o n p r a c t i c e 0A Build.. X X. X 6X 8 3. X 8 Build and add. 4. X 6X 3 3X 7X 9 5. X 8 X 6X 7 6. X 0X 7 X 8X 9 Build a rectangle and find the area (product). 7. (X )(X ) = 8. (X 4)(X 3) = 9.
l e s s o n p r a c t i c e 0A Build.. X X. X 6X 8 3. X 8 Build and add. 4. X 6X 3 3X 7X 9 5. X 8 X 6X 7 6. X 0X 7 X 8X 9 Build a rectangle and find the area (product). 7. (X )(X ) = 8. (X 4)(X 3) = 9.
6-3 Polynomials. Warm Up Lesson Presentation Lesson Quiz. Holt McDougal Algebra 1
 6-3 Polynomials Warm Up Lesson Presentation Lesson Quiz Algebra 1 Objectives Classify polynomials and write polynomials in standard form. Evaluate polynomial expressions. A polynomial is a monomial or
6-3 Polynomials Warm Up Lesson Presentation Lesson Quiz Algebra 1 Objectives Classify polynomials and write polynomials in standard form. Evaluate polynomial expressions. A polynomial is a monomial or
What is a constant? A Constant is a number representing a quantity or value that does not change.
 Worksheet -: Algebraic Expressions What is a constant? A Constant is a number representing a quantity or value that does not change. What is a variable? A variable is a letter or symbol representing a
Worksheet -: Algebraic Expressions What is a constant? A Constant is a number representing a quantity or value that does not change. What is a variable? A variable is a letter or symbol representing a
Chapter Six. Polynomials. Properties of Exponents Algebraic Expressions Addition, Subtraction, and Multiplication Factoring Solving by Factoring
 Chapter Six Polynomials Properties of Exponents Algebraic Expressions Addition, Subtraction, and Multiplication Factoring Solving by Factoring Properties of Exponents The properties below form the basis
Chapter Six Polynomials Properties of Exponents Algebraic Expressions Addition, Subtraction, and Multiplication Factoring Solving by Factoring Properties of Exponents The properties below form the basis
Summer Prep Packet for students entering Algebra 2
 Summer Prep Packet for students entering Algebra The following skills and concepts included in this packet are vital for your success in Algebra. The Mt. Hebron Math Department encourages all students
Summer Prep Packet for students entering Algebra The following skills and concepts included in this packet are vital for your success in Algebra. The Mt. Hebron Math Department encourages all students
Answers to Sample Exam Problems
 Math Answers to Sample Exam Problems () Find the absolute value, reciprocal, opposite of a if a = 9; a = ; Absolute value: 9 = 9; = ; Reciprocal: 9 ; ; Opposite: 9; () Commutative law; Associative law;
Math Answers to Sample Exam Problems () Find the absolute value, reciprocal, opposite of a if a = 9; a = ; Absolute value: 9 = 9; = ; Reciprocal: 9 ; ; Opposite: 9; () Commutative law; Associative law;
= (Type exponential notation with positive exponents)
 1. Subtract. Simplify by collecting like radical terms if possible. 2 2 = (Simplify your answer) 2. Add. Simplify if possible. = (Simplify your answer) 3. Divide and simplify. = (Type exponential notation
1. Subtract. Simplify by collecting like radical terms if possible. 2 2 = (Simplify your answer) 2. Add. Simplify if possible. = (Simplify your answer) 3. Divide and simplify. = (Type exponential notation
Answers of the MATH97 Practice Test Form A
 Answers of the MATH97 Practice Test Form A A1) Answer B Section 1.2: concepts of solution of the equations. Pick the pair which satisfies the equation 4x+y=10. x= 1 and y=6 A2) Answer A Section 1.3: select
Answers of the MATH97 Practice Test Form A A1) Answer B Section 1.2: concepts of solution of the equations. Pick the pair which satisfies the equation 4x+y=10. x= 1 and y=6 A2) Answer A Section 1.3: select
Lesson 3: Polynomials and Exponents, Part 1
 Lesson 2: Introduction to Variables Assessment Lesson 3: Polynomials and Exponents, Part 1 When working with algebraic expressions, variables raised to a power play a major role. In this lesson, we look
Lesson 2: Introduction to Variables Assessment Lesson 3: Polynomials and Exponents, Part 1 When working with algebraic expressions, variables raised to a power play a major role. In this lesson, we look
Study Guide for Math 095
 Study Guide for Math 095 David G. Radcliffe November 7, 1994 1 The Real Number System Writing a fraction in lowest terms. 1. Find the largest number that will divide into both the numerator and the denominator.
Study Guide for Math 095 David G. Radcliffe November 7, 1994 1 The Real Number System Writing a fraction in lowest terms. 1. Find the largest number that will divide into both the numerator and the denominator.
7-6 Adding and Subtracting Polynomials
 Example 1: Adding and Subtracting Monomials Add or Subtract.. A. 12p 3 + 11p 2 + 8p 3 12p 3 + 11p 2 + 8p 3 12p 3 + 8p 3 + 11p 2 20p 3 + 11p 2 B. 5x 2 6 3x + 8 5x 2 6 3x + 8 5x 2 3x + 8 6 5x 2 3x + 2 Rearrange
Example 1: Adding and Subtracting Monomials Add or Subtract.. A. 12p 3 + 11p 2 + 8p 3 12p 3 + 11p 2 + 8p 3 12p 3 + 8p 3 + 11p 2 20p 3 + 11p 2 B. 5x 2 6 3x + 8 5x 2 6 3x + 8 5x 2 3x + 8 6 5x 2 3x + 2 Rearrange
Section 5.1 Polynomial Functions and Models
 Term: A term is an expression that involves only multiplication and/or division with constants and/or variables. A term is separated by + or Polynomial: A polynomial is a single term or the sum of two
Term: A term is an expression that involves only multiplication and/or division with constants and/or variables. A term is separated by + or Polynomial: A polynomial is a single term or the sum of two
Quick-and-Easy Factoring. of lower degree; several processes are available to fi nd factors.
 Lesson 11-3 Quick-and-Easy Factoring BIG IDEA Some polynomials can be factored into polynomials of lower degree; several processes are available to fi nd factors. Vocabulary factoring a polynomial factored
Lesson 11-3 Quick-and-Easy Factoring BIG IDEA Some polynomials can be factored into polynomials of lower degree; several processes are available to fi nd factors. Vocabulary factoring a polynomial factored
NAME DATE PERIOD. Power and Radical Functions. New Vocabulary Fill in the blank with the correct term. positive integer.
 2-1 Power and Radical Functions What You ll Learn Scan Lesson 2-1. Predict two things that you expect to learn based on the headings and Key Concept box. 1. 2. Lesson 2-1 Active Vocabulary extraneous solution
2-1 Power and Radical Functions What You ll Learn Scan Lesson 2-1. Predict two things that you expect to learn based on the headings and Key Concept box. 1. 2. Lesson 2-1 Active Vocabulary extraneous solution
Solving Quadratic Equations
 Solving Quadratic Equations MATH 101 College Algebra J. Robert Buchanan Department of Mathematics Summer 2012 Objectives In this lesson we will learn to: solve quadratic equations by factoring, solve quadratic
Solving Quadratic Equations MATH 101 College Algebra J. Robert Buchanan Department of Mathematics Summer 2012 Objectives In this lesson we will learn to: solve quadratic equations by factoring, solve quadratic
MATH98 Intermediate Algebra Practice Test Form A
 MATH98 Intermediate Algebra Practice Test Form A MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the equation. 1) (y - 4) - (y + ) = 3y 1) A)
MATH98 Intermediate Algebra Practice Test Form A MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the equation. 1) (y - 4) - (y + ) = 3y 1) A)
TEKS: 2A.10F. Terms. Functions Equations Inequalities Linear Domain Factor
 POLYNOMIALS UNIT TEKS: A.10F Terms: Functions Equations Inequalities Linear Domain Factor Polynomials Monomial, Like Terms, binomials, leading coefficient, degree of polynomial, standard form, terms, Parent
POLYNOMIALS UNIT TEKS: A.10F Terms: Functions Equations Inequalities Linear Domain Factor Polynomials Monomial, Like Terms, binomials, leading coefficient, degree of polynomial, standard form, terms, Parent
Teacher's Page. Mar 20 8:26 AM
 Teacher's Page Unit 4.1 in two parts: Part 1: Polynomials and Part 2: Quadratics Benchmarks: A.SSE.3 Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity
Teacher's Page Unit 4.1 in two parts: Part 1: Polynomials and Part 2: Quadratics Benchmarks: A.SSE.3 Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity
We will work with two important rules for radicals. We will write them for square roots but they work for any root (cube root, fourth root, etc.).
 College algebra We will review simplifying radicals, exponents and their rules, multiplying polynomials, factoring polynomials, greatest common denominators, and solving rational equations. Pre-requisite
College algebra We will review simplifying radicals, exponents and their rules, multiplying polynomials, factoring polynomials, greatest common denominators, and solving rational equations. Pre-requisite
Order of Operations Practice: 1) =
 Order of Operations Practice: 1) 24-12 3 + 6 = a) 6 b) 42 c) -6 d) 192 2) 36 + 3 3 (1/9) - 8 (12) = a) 130 b) 171 c) 183 d) 4,764 1 3) Evaluate: 12 2-4 2 ( - ½ ) + 2 (-3) 2 = 4) Evaluate 3y 2 + 8x =, when
Order of Operations Practice: 1) 24-12 3 + 6 = a) 6 b) 42 c) -6 d) 192 2) 36 + 3 3 (1/9) - 8 (12) = a) 130 b) 171 c) 183 d) 4,764 1 3) Evaluate: 12 2-4 2 ( - ½ ) + 2 (-3) 2 = 4) Evaluate 3y 2 + 8x =, when
6.1 Using Properties of Exponents 1. Use properties of exponents to evaluate and simplify expressions involving powers. Product of Powers Property
 6.1 Using Properties of Exponents Objectives 1. Use properties of exponents to evaluate and simplify expressions involving powers. 2. Use exponents and scientific notation to solve real life problems.
6.1 Using Properties of Exponents Objectives 1. Use properties of exponents to evaluate and simplify expressions involving powers. 2. Use exponents and scientific notation to solve real life problems.
Algebra. Practice Pack
 Algebra Practice Pack WALCH PUBLISHING Table of Contents Unit 1: Algebra Basics Practice 1 What Are Negative and Positive Numbers?... 1 Practice 2 Larger and Smaller Numbers................ 2 Practice
Algebra Practice Pack WALCH PUBLISHING Table of Contents Unit 1: Algebra Basics Practice 1 What Are Negative and Positive Numbers?... 1 Practice 2 Larger and Smaller Numbers................ 2 Practice
Common Core Standards Addressed in this Resource
 Common Core Standards Addressed in this Resource.EE.3 - Apply the properties of operations to generate equivalent expressions. Activity page: 4 7.RP.3 - Use proportional relationships to solve multistep
Common Core Standards Addressed in this Resource.EE.3 - Apply the properties of operations to generate equivalent expressions. Activity page: 4 7.RP.3 - Use proportional relationships to solve multistep
Solving Linear Equations
 Solving Linear Equations Golden Rule of Algebra: Do unto one side of the equal sign as you will do to the other Whatever you do on one side of the equal sign, you MUST do the same exact thing on the other
Solving Linear Equations Golden Rule of Algebra: Do unto one side of the equal sign as you will do to the other Whatever you do on one side of the equal sign, you MUST do the same exact thing on the other
NAME DATE PERIOD. A negative exponent is the result of repeated division. Extending the pattern below shows that 4 1 = 1 4 or 1. Example: 6 4 = 1 6 4
 Lesson 4.1 Reteach Powers and Exponents A number that is expressed using an exponent is called a power. The base is the number that is multiplied. The exponent tells how many times the base is used as
Lesson 4.1 Reteach Powers and Exponents A number that is expressed using an exponent is called a power. The base is the number that is multiplied. The exponent tells how many times the base is used as
8.5 Addition and Subtraction of Polynomials
 8.5. Addition and Subtraction of Polynomials www.ck12.org 8.5 Addition and Subtraction of Polynomials Learning Objectives Write a polynomial expression in standard form. Classify polynomial expression
8.5. Addition and Subtraction of Polynomials www.ck12.org 8.5 Addition and Subtraction of Polynomials Learning Objectives Write a polynomial expression in standard form. Classify polynomial expression
Algebraic Expressions
 Algebraic Expressions 1. Expressions are formed from variables and constants. 2. Terms are added to form expressions. Terms themselves are formed as product of factors. 3. Expressions that contain exactly
Algebraic Expressions 1. Expressions are formed from variables and constants. 2. Terms are added to form expressions. Terms themselves are formed as product of factors. 3. Expressions that contain exactly
IES Parque Lineal - 2º ESO
 UNIT5. ALGEBRA Contenido 1. Algebraic expressions.... 1 Worksheet: algebraic expressions.... 2 2. Monomials.... 3 Worksheet: monomials.... 5 3. Polynomials... 6 Worksheet: polynomials... 9 4. Factorising....
UNIT5. ALGEBRA Contenido 1. Algebraic expressions.... 1 Worksheet: algebraic expressions.... 2 2. Monomials.... 3 Worksheet: monomials.... 5 3. Polynomials... 6 Worksheet: polynomials... 9 4. Factorising....
Extending the Number System
 Analytical Geometry Extending the Number System Extending the Number System Remember how you learned numbers? You probably started counting objects in your house as a toddler. You learned to count to ten
Analytical Geometry Extending the Number System Extending the Number System Remember how you learned numbers? You probably started counting objects in your house as a toddler. You learned to count to ten
NAME DATE PERIOD. Operations with Polynomials. Review Vocabulary Evaluate each expression. (Lesson 1-1) 3a 2 b 4, given a = 3, b = 2
 5-1 Operations with Polynomials What You ll Learn Skim the lesson. Predict two things that you expect to learn based on the headings and the Key Concept box. 1. Active Vocabulary 2. Review Vocabulary Evaluate
5-1 Operations with Polynomials What You ll Learn Skim the lesson. Predict two things that you expect to learn based on the headings and the Key Concept box. 1. Active Vocabulary 2. Review Vocabulary Evaluate
The number part of a term with a variable part. Terms that have the same variable parts. Constant terms are also like terms.
 Algebra Notes Section 9.1: Add and Subtract Polynomials Objective(s): To be able to add and subtract polynomials. Recall: Coefficient (p. 97): Term of a polynomial (p. 97): Like Terms (p. 97): The number
Algebra Notes Section 9.1: Add and Subtract Polynomials Objective(s): To be able to add and subtract polynomials. Recall: Coefficient (p. 97): Term of a polynomial (p. 97): Like Terms (p. 97): The number
Chapter 6. Polynomials
 Chapter 6 Polynomials How to Play the Stock Market 6.1 Monomials: Multiplication and Division 6.2 Polynomials 6.3 Addition and Subtraction of Polynomials 6.4 Multiplication of Polynomials Chapter Review
Chapter 6 Polynomials How to Play the Stock Market 6.1 Monomials: Multiplication and Division 6.2 Polynomials 6.3 Addition and Subtraction of Polynomials 6.4 Multiplication of Polynomials Chapter Review
MATH 190 KHAN ACADEMY VIDEOS
 MATH 10 KHAN ACADEMY VIDEOS MATTHEW AUTH 11 Order of operations 1 The Real Numbers (11) Example 11 Worked example: Order of operations (PEMDAS) 7 2 + (7 + 3 (5 2)) 4 2 12 Rational + Irrational Example
MATH 10 KHAN ACADEMY VIDEOS MATTHEW AUTH 11 Order of operations 1 The Real Numbers (11) Example 11 Worked example: Order of operations (PEMDAS) 7 2 + (7 + 3 (5 2)) 4 2 12 Rational + Irrational Example
