Curves I: Curvature and Torsion. Table of contents
|
|
|
- Albert Howard
- 5 years ago
- Views:
Transcription
1 Math 48 Fall 07 Curves I: Curvature and Torsion Disclaimer. As we have a textbook, this lecture note is for guidance and sulement only. It should not be relied on when rearing for exams. In this lecture we study how a curve curves. We will show that the curving of a general curve can be characterized by two numbers, the curvature and the torsion. The required textbook sections are:.,.. The examles in this note are mostly dierent from examles in the textbook. Please read the textbook carefully and try your hands on the exercises. During this lease don't hesitate to contact me if you have any questions. Table of contents Curves I: Curvature and Torsion Curvature Curvature for arc length arametrized curves Alternative characterization of the curvature (otional) Examles Torsion The osculating lane Denition of torsion Examles Curvature and torsion in general arametrization Formulas
2 Dierential Geometry of Curves & Surfaces. Curvature Curvature measures how quickly a curve turns, or more recisely how quickly the unit tangent vector turns... Curvature for arc length arametrized curves Consider a curve (s): (; ) 7! R. Then the unit tangent vector of (s) is given by T (s) := _(s). Consequently, how quickly T (s) turns can be characterized by the number which call the curvature of the curve. (s) := T_(s) = k(s)k () As k_(s)k =, we have (s)?_(s). This leads to the following denition. Definition. Let (s) be a curve arametrized by arc length. Then its curvature is dened as (s) := k(s)k. We further denote by N(s) the unit vector (s)/k(s)k and call it the normal vector at s. We also denote the unit tangent vector _(s) by T (s). Formulas for curves in arc length arametrization. Curvature. Tangent and Normal vectors. (s 0 ) = k(s 0 )k: () T (s 0 ) = _(s 0 ); N(s 0 ) = (s 0) k(s 0 )k : ().. Alternative characterization of the curvature (otional) Consider a curve (s): (; ) 7! R. Let = (s 0 ) for some s 0 (; ). We try to understand how quickly (s) turns aways from the tangent line at x(s 0 ). The equation for the tangent line is (s 0 ) + t _(s 0 ). The distance from a oint (s) to the tangent line is := k((s) (s 0 )) _(s 0 )k (4) Note that here we have used the fact that _(s 0 ) is a unit vector. Now recall Taylor exansion: (s) (s 0 ) = _(s 0 ) (s s 0 ) + (s 0) (s s 0 ) + R(s; s 0 ) (5) where lim s!s0 kr(s; s 0 )k (s s 0 ) = 0. Substituting (5) into (4), we see that = (s s 0) ((s 0 ) _(s 0 )) + R(s; s 0 ) _(s 0 ) (6)
3 Math 48 Fall 07 and consequently lim s!0 (s s 0 ) / = k(s 0) _(s 0 )k (7) Exercise. Prove (7). Thus we see that the quantity k(s 0 ) _(s 0 )k=(s 0 ) measures how the curve curves at the oint (s 0 ). Exercise. Prove that k(s 0 ) _(s 0 )k = k(s 0 )k = (s 0 ). Exercise. (7) can be derived slightly dierently as follows. i. Find T such that (s) [(s 0 ) + T _(s 0 )]?_(s 0 ). ii. Then = k(s) [(s 0 ) + T _(s 0 )]k. iii. Calculate the limit lim.. Examles (s s 0) /. Examle. For the unit circle, the curvature is constantly. For a circle with radius R, the curvature is constantly /R. sin t. We Examle. (Shifrin06) Let (t) = calculate cos t + sin t; cos t; cos t Tangent vector: _(t) = sin t + cos t; sin t; sin t cos t k_(t)k = so we are already in arc length arametrization. We have k(t)k =. So the curvature of this curve is constantly. Examle 4. (Shifrin06) Let (t) = e t ; e t ; t. We calculate Tangent vector: and therefore k_(t)k = e t + e t. Solve we obtain S(t) = e t e t. Solve t as a function of s: _(t) = e t ; e t ; (8) (9) S 0 (t) = e t + e t (0) e t = s + s + 4 : ()
4 Dierential Geometry of Curves & Surfaces Thus (s) is given by s + s + 4 s ; + 4 s!! s + s ; + 4 ln : () We calculate _(s) = + s s ; s + 4 s + 4 ; s + 4! : () To make sure our calculation is correct, we check k_(s)k = : (4) Finally we calculate (s) = 8 (s + 4) / ; 8 (s + 4) / ; s (s + 4) / (5) which gives (s) = k(s)k = s + 64 s : (6) + 4. Torsion Torsion measures how quickly a curve twists... The osculating lane Motivation. Consider a oint on a sace curve. We have seen that to measure how quickly it curves, we should measure the rate of change for the unit tangent vector. Similarly, to measure how quickly it twists, we should measure the change rate of the tangent lane. The osculating lane. Let (s) be a sace curve. Its osculating lane at (s 0 ) is the lane assing (s 0 ) that is sanned by the unit tangent vector T (s 0 ) := _(s 0 ) and the unit normal vector N(s 0 ) := (s 0) k(s 0 )k. We see that the osculating lane contains the tangent line. The unit normal vector of the osculating lane is then given by B(s) := T (s) N(s) (7) which we call the unit binormal vector of the curve (s). Exercise 4. Prove that T (s) = N(s) B(s), N(s) = B(s) T (s). Among all the lanes containing the tangent line, the osculating lane is the one that ts the curve best. See Exercise 5 below. 4
5 Math 48 Fall 07.. Denition of torsion How quickly the osculating lane turns is clearly characterized by how quickly the unit binormal vector turns. We calculate B _ (s) = T _ (s) N(s) + T (s) N _ (s) = T (s) N _ (s): (8) Now notice that kn(s)k = =) N_ (s) N(s) = 0. As T (s) N(s) = 0 too, we see that B_ (s) k N(s). Consequently there is a scalar function (s) such that B_ (s) = (s) N(s): (9) We call (s) the torsion of the curve (s). Formula for (s). We calculate N _ (s) = d (s) dt (s) Thus = (s) (s) _(s) (s): (0) (s) (s) = T (s) N_ (s) N(s) T (s) (s) = (s) _(s) (s) = N(s) (s) = Formula for torsion (arc length arametrization). _(s) T (s) (s) (s) N(s) (_(s) (s)) (s) : () (s) (s) = (_(s) (s)) (s) (s) () Remark 5. Alternative denition of torsion. Distance to osculating lane. We easily see that = k((s) (s 0 )) B(s 0 )k () Exercise 5. Prove that, among all lanes assing (s 0 ), the osculating lane is the only one satisfying = 0: (4) (s s 0 ) lim s!s 0 Taylor exansion of x(s) x(s 0 ) to order three: (s) (s 0 ) = _(s 0 ) (s s 0 ) + (s 0) kr(s; s where lim 0 )k s!s0 = 0. (s s 0 ). There is no articular reason for the negative sign. (s s 0 ) + (s 0) 6 (s s 0 ) + R(s; s 0 ) (5) 5
6 Dierential Geometry of Curves & Surfaces Substituting (5) into () we see that.. Examles lim s!s 0 (s s 0 ) /6 = j (s 0) B(s 0 )j: (6) Exercise 6. Show that j (s 0 ) B(s 0 )j = (_(s) (s)) (s) (s) : (7) Comare to (). Discuss ossible reasons for the dierence. Do you think () is a more reasonable denition for torsion? Why? Examle 6. We calculate the torsion of the curve (t) = cos t + sin t; cos t; cos t sin t. Note that we have seen there that t is already the arc length arameter. _(t) = sin t + cos t; sin t; sin t cos t ; (8) (t) = cos t sin t; cos t; cos t + sin t = x(t): (9) Thus clearly (_(t) (t)) (t) = 0 =) (t) = 0: (0). Curvature and torsion in general arametrization.. Formulas The key idea is that ; ; T ; N ; B should be indeendent of arametrization. In other words, if (t) and (s) are two arametrizations of the same curve, and = (t 0 ) = (s 0 ), then we must have (t 0 ) = (s 0 ); (t 0 ) = (s 0 ), and so on. We will try to obtain the formulas intuitively here. For rigorous derivation, lease see. of the textbook. In the following let (t) be a curve not necessarily in arc length arametrization. T is the unit tangent vector. So we must have T (t) = _(t) k_(t)k : () B. Since N clearly lies in the lane sanned by _ and, B k _. Consequently we must have _(t) (t) B(t) = k_(t) (t)k : () N. We have (_(t) (t)) _(t) N(t) = B(t) T (t) = k_(t) (t)k k_(t)k : () 6
7 Math 48 Fall 07. We have = dt ds N = k_(t)k T_ N which gives (t) [(_(t) (t)) _(t)] k_(t) (t)k (t) = = : (4) k_(t)k k_(t) (t)k k_(t)k. We have = db N which gives ds = (_(t) (t)) [(_(t) (t)) _(t)] k_(t)k k_(t) (t)k (_(t) (t)) (t) = k_(t) (t)k (_(t) (t)) (t) = : (5) k_(t) (t)k Exercise 7. In the above we have used the vector identity (u v) w = (v w) u + (u w) v (6) for u; v; w R. Prove this identity and identify where it is used. Warning DG of Curves: Formulas for general arametrization = = k_ k k_k : (7) (_ ) k_ k : (8) T = _ k_ k ; (9) B = _ k_ k ; (40) N = B T : (4) In exams, the formulas (7) and (8) will be rovided, but (840) will not be rovided. 7
Lecture 8: The First Fundamental Form Table of contents
 Math 38 Fall 2016 Lecture 8: The First Fundamental Form Disclaimer. As we have a textbook, this lecture note is for guidance and sulement only. It should not be relied on when rearing for exams. In this
Math 38 Fall 2016 Lecture 8: The First Fundamental Form Disclaimer. As we have a textbook, this lecture note is for guidance and sulement only. It should not be relied on when rearing for exams. In this
Lectures 12: The Second Fundamental Form. Table of contents
 ectures 1: The Second Fundamental Form Disclaimer. As we have a textbook, this lecture note is for guidance sulement only. It should not be relied on when rearing for exams. In this lecture we introduce
ectures 1: The Second Fundamental Form Disclaimer. As we have a textbook, this lecture note is for guidance sulement only. It should not be relied on when rearing for exams. In this lecture we introduce
Lectures 15: Parallel Transport. Table of contents
 Lectures 15: Parallel Transport Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams. In this lecture we study the
Lectures 15: Parallel Transport Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams. In this lecture we study the
Section Arclength and Curvature. (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes.
 Section 10.3 Arclength and Curvature (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes. MATH 127 (Section 10.3) Arclength and Curvature The University
Section 10.3 Arclength and Curvature (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes. MATH 127 (Section 10.3) Arclength and Curvature The University
Lectures 18: Gauss's Remarkable Theorem II. Table of contents
 Math 348 Fall 27 Lectures 8: Gauss's Remarkable Theorem II Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams.
Math 348 Fall 27 Lectures 8: Gauss's Remarkable Theorem II Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams.
13.3 Arc Length and Curvature
 13 Vector Functions 13.3 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. We have defined the length of a plane curve with parametric equations x = f(t),
13 Vector Functions 13.3 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. We have defined the length of a plane curve with parametric equations x = f(t),
jf 00 (x)j ds (x) = [1 + (f 0 (x)) 2 ] 3=2 (t) = jjr0 (t) r 00 (t)jj jjr 0 (t)jj 3
![jf 00 (x)j ds (x) = [1 + (f 0 (x)) 2 ] 3=2 (t) = jjr0 (t) r 00 (t)jj jjr 0 (t)jj 3 jf 00 (x)j ds (x) = [1 + (f 0 (x)) 2 ] 3=2 (t) = jjr0 (t) r 00 (t)jj jjr 0 (t)jj 3](/thumbs/78/77303345.jpg) M73Q Multivariable Calculus Fall 7 Review Problems for Exam The formulas in the box will be rovided on the exam. (s) dt jf (x)j ds (x) [ + (f (x)) ] 3 (t) jjt (t)jj jjr (t)jj (t) jjr (t) r (t)jj jjr (t)jj
M73Q Multivariable Calculus Fall 7 Review Problems for Exam The formulas in the box will be rovided on the exam. (s) dt jf (x)j ds (x) [ + (f (x)) ] 3 (t) jjt (t)jj jjr (t)jj (t) jjr (t) r (t)jj jjr (t)jj
MTH234 Chapter 15 - Multiple Integrals Michigan State University
 MTH24 Chater 15 - Multile Integrals Michigan State University 6 Surface Area Just as arc length is an alication of a single integral, surface area is an alication of double integrals. In 15.6 we comute
MTH24 Chater 15 - Multile Integrals Michigan State University 6 Surface Area Just as arc length is an alication of a single integral, surface area is an alication of double integrals. In 15.6 we comute
MA 351 Fall 2007 Exam #1 Review Solutions 1
 MA 35 Fall 27 Exam # Review Solutions THERE MAY BE TYPOS in these solutions. Please let me know if you find any.. Consider the two surfaces ρ 3 csc θ in spherical coordinates and r 3 in cylindrical coordinates.
MA 35 Fall 27 Exam # Review Solutions THERE MAY BE TYPOS in these solutions. Please let me know if you find any.. Consider the two surfaces ρ 3 csc θ in spherical coordinates and r 3 in cylindrical coordinates.
Tangent and Normal Vector - (11.5)
 Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out bythe vector-valued function r!!t # f!t, g!t, h!t $. The vector T!!t r! % r! %!t!t is the unit tangent vector
Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out bythe vector-valued function r!!t # f!t, g!t, h!t $. The vector T!!t r! % r! %!t!t is the unit tangent vector
Week 3: Differential Geometry of Curves
 Week 3: Differential Geometry of Curves Introduction We now know how to differentiate and integrate along curves. This week we explore some of the geometrical properties of curves that can be addressed
Week 3: Differential Geometry of Curves Introduction We now know how to differentiate and integrate along curves. This week we explore some of the geometrical properties of curves that can be addressed
Tangent and Normal Vector - (11.5)
 Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out by the vector-valued function rt vector T t r r t t is the unit tangent vector to the curve C. Now define N
Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out by the vector-valued function rt vector T t r r t t is the unit tangent vector to the curve C. Now define N
1 Vectors and 3-Dimensional Geometry
 Calculus III (part ): Vectors and 3-Dimensional Geometry (by Evan Dummit, 07, v..55) Contents Vectors and 3-Dimensional Geometry. Functions of Several Variables and 3-Space..................................
Calculus III (part ): Vectors and 3-Dimensional Geometry (by Evan Dummit, 07, v..55) Contents Vectors and 3-Dimensional Geometry. Functions of Several Variables and 3-Space..................................
There is a function, the arc length function s(t) defined by s(t) = It follows that r(t) = p ( s(t) )
 MATH 20550 Acceleration, Curvature and Related Topics Fall 2016 The goal of these notes is to show how to compute curvature and torsion from a more or less arbitrary parametrization of a curve. We will
MATH 20550 Acceleration, Curvature and Related Topics Fall 2016 The goal of these notes is to show how to compute curvature and torsion from a more or less arbitrary parametrization of a curve. We will
Exercises for Multivariable Differential Calculus XM521
 This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017
 Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017 This week we want to talk about curvature and osculating circles. You might notice that these notes contain a lot of the same theory or proofs
Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017 This week we want to talk about curvature and osculating circles. You might notice that these notes contain a lot of the same theory or proofs
THE FUNDAMENTAL THEOREM OF SPACE CURVES
 THE FUNDAMENTAL THEOREM OF SPACE CURVES JOSHUA CRUZ Abstract. In this paper, we show that curves in R 3 can be uniquely generated by their curvature and torsion. By finding conditions that guarantee the
THE FUNDAMENTAL THEOREM OF SPACE CURVES JOSHUA CRUZ Abstract. In this paper, we show that curves in R 3 can be uniquely generated by their curvature and torsion. By finding conditions that guarantee the
3 = arccos. A a and b are parallel, B a and b are perpendicular, C a and b are normalized, or D this is always true.
 Math 210-101 Test #1 Sept. 16 th, 2016 Name: Answer Key Be sure to show your work! 1. (20 points) Vector Basics: Let v = 1, 2,, w = 1, 2, 2, and u = 2, 1, 1. (a) Find the area of a parallelogram spanned
Math 210-101 Test #1 Sept. 16 th, 2016 Name: Answer Key Be sure to show your work! 1. (20 points) Vector Basics: Let v = 1, 2,, w = 1, 2, 2, and u = 2, 1, 1. (a) Find the area of a parallelogram spanned
Math 317 M1A, October 8th, 2010 page 1 of 7 Name:
 Math 317 M1A, October 8th, 2010 page 1 of 7 Name: Problem 1 (5 parts, 30 points): Consider the curve r(t) = 3 sin(t 2 ), 4t 2 + 7, 3 cos(t 2 ), 0 t < a) (5 points) Find the arclength function s(t) giving
Math 317 M1A, October 8th, 2010 page 1 of 7 Name: Problem 1 (5 parts, 30 points): Consider the curve r(t) = 3 sin(t 2 ), 4t 2 + 7, 3 cos(t 2 ), 0 t < a) (5 points) Find the arclength function s(t) giving
Tangent and Normal Vectors
 Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
Lecture 2: Review of Prerequisites. Table of contents
 Math 348 Fall 217 Lecture 2: Review of Prerequisites Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams. In this
Math 348 Fall 217 Lecture 2: Review of Prerequisites Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams. In this
OHSx XM521 Multivariable Differential Calculus: Homework Solutions 14.1
 OHSx XM5 Multivariable Differential Calculus: Homework Solutions 4. (8) Describe the graph of the equation. r = i + tj + (t )k. Solution: Let y(t) = t, so that z(t) = t = y. In the yz-plane, this is just
OHSx XM5 Multivariable Differential Calculus: Homework Solutions 4. (8) Describe the graph of the equation. r = i + tj + (t )k. Solution: Let y(t) = t, so that z(t) = t = y. In the yz-plane, this is just
Solutions to Assignment #02 MATH u v p 59. p 72. h 3; 1; 2i h4; 2; 5i p 14. p 45. = cos 1 2 p!
 Solutions to Assignment #0 MATH 41 Kawai/Arangno/Vecharynski Section 1. (I) Comlete Exercises #1cd on. 810. searation to TWO decimal laces. So do NOT leave the nal answer as cos 1 (something) : (c) The
Solutions to Assignment #0 MATH 41 Kawai/Arangno/Vecharynski Section 1. (I) Comlete Exercises #1cd on. 810. searation to TWO decimal laces. So do NOT leave the nal answer as cos 1 (something) : (c) The
Contents. 1. Introduction
 FUNDAMENTAL THEOREM OF THE LOCAL THEORY OF CURVES KAIXIN WANG Abstract. In this expository paper, we present the fundamental theorem of the local theory of curves along with a detailed proof. We first
FUNDAMENTAL THEOREM OF THE LOCAL THEORY OF CURVES KAIXIN WANG Abstract. In this expository paper, we present the fundamental theorem of the local theory of curves along with a detailed proof. We first
GEOMETRY HW (t, 0, e 1/t2 ), t > 0 1/t2, 0), t < 0. (0, 0, 0), t = 0
 GEOMETRY HW CLAY SHONKWILER Consider the map.5.0 t, 0, e /t ), t > 0 αt) = t, e /t, 0), t < 0 0, 0, 0), t = 0 a) Prove that α is a differentiable curve. Proof. If we denote αt) = xt), yt), zt0), then it
GEOMETRY HW CLAY SHONKWILER Consider the map.5.0 t, 0, e /t ), t > 0 αt) = t, e /t, 0), t < 0 0, 0, 0), t = 0 a) Prove that α is a differentiable curve. Proof. If we denote αt) = xt), yt), zt0), then it
The Frenet Serret formulas
 The Frenet Serret formulas Attila Máté Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet Serret frame of a space curve 1 2 The Frenet Serret formulas
The Frenet Serret formulas Attila Máté Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet Serret frame of a space curve 1 2 The Frenet Serret formulas
HOMEWORK 2 SOLUTIONS
 HOMEWORK SOLUTIONS MA11: ADVANCED CALCULUS, HILARY 17 (1) Find parametric equations for the tangent line of the graph of r(t) = (t, t + 1, /t) when t = 1. Solution: A point on this line is r(1) = (1,,
HOMEWORK SOLUTIONS MA11: ADVANCED CALCULUS, HILARY 17 (1) Find parametric equations for the tangent line of the graph of r(t) = (t, t + 1, /t) when t = 1. Solution: A point on this line is r(1) = (1,,
Series Handout A. 1. Determine which of the following sums are geometric. If the sum is geometric, express the sum in closed form.
 Series Handout A. Determine which of the following sums are geometric. If the sum is geometric, exress the sum in closed form. 70 a) k= ( k ) b) 50 k= ( k )2 c) 60 k= ( k )k d) 60 k= (.0)k/3 2. Find the
Series Handout A. Determine which of the following sums are geometric. If the sum is geometric, exress the sum in closed form. 70 a) k= ( k ) b) 50 k= ( k )2 c) 60 k= ( k )k d) 60 k= (.0)k/3 2. Find the
CHAPTER 3: TANGENT SPACE
 CHAPTER 3: TANGENT SPACE DAVID GLICKENSTEIN 1. Tangent sace We shall de ne the tangent sace in several ways. We rst try gluing them together. We know vectors in a Euclidean sace require a baseoint x 2
CHAPTER 3: TANGENT SPACE DAVID GLICKENSTEIN 1. Tangent sace We shall de ne the tangent sace in several ways. We rst try gluing them together. We know vectors in a Euclidean sace require a baseoint x 2
Motion in Space Parametric Equations of a Curve
 Motion in Space Parametric Equations of a Curve A curve, C, inr 3 can be described by parametric equations of the form x x t y y t z z t. Any curve can be parameterized in many different ways. For example,
Motion in Space Parametric Equations of a Curve A curve, C, inr 3 can be described by parametric equations of the form x x t y y t z z t. Any curve can be parameterized in many different ways. For example,
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algo
 Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Arc Length and Curvature
 Arc Length and Curvature. Last time, we saw that r(t) = cos t, sin t, t parameteried the pictured curve. (a) Find the arc length of the curve between (, 0, 0) and (, 0, π). (b) Find the unit tangent vector
Arc Length and Curvature. Last time, we saw that r(t) = cos t, sin t, t parameteried the pictured curve. (a) Find the arc length of the curve between (, 0, 0) and (, 0, π). (b) Find the unit tangent vector
Vector-valued functions
 Vector-valued functions MATH 243 2018 Victoria University of Wellington Wellington, New Zealand For a complimentary reading, this set of slides corresponds roughly to Chapter of the same title from Anton,
Vector-valued functions MATH 243 2018 Victoria University of Wellington Wellington, New Zealand For a complimentary reading, this set of slides corresponds roughly to Chapter of the same title from Anton,
Taylor and Maclaurin Series
 Taylor and Maclaurin Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Background We have seen that some power series converge. When they do, we can think of them as
Taylor and Maclaurin Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Background We have seen that some power series converge. When they do, we can think of them as
Math 1270 Honors ODE I Fall, 2008 Class notes # 14. x 0 = F (x; y) y 0 = G (x; y) u 0 = au + bv = cu + dv
 Math 1270 Honors ODE I Fall, 2008 Class notes # 1 We have learned how to study nonlinear systems x 0 = F (x; y) y 0 = G (x; y) (1) by linearizing around equilibrium points. If (x 0 ; y 0 ) is an equilibrium
Math 1270 Honors ODE I Fall, 2008 Class notes # 1 We have learned how to study nonlinear systems x 0 = F (x; y) y 0 = G (x; y) (1) by linearizing around equilibrium points. If (x 0 ; y 0 ) is an equilibrium
Joseph B. Keller and Ravi Vakil. ( x p + y p ) 1/p = 1. (1) by x, when y is replaced by y, and when x and y are interchanged.
 =3 π, the value of π in l Joseh B. Keller and Ravi Vakil The two-dimensional sace l is the set of oints in the lane, with the distance between two oints x, y) and x, y ) defined by x x + y y ) 1/, 1. The
=3 π, the value of π in l Joseh B. Keller and Ravi Vakil The two-dimensional sace l is the set of oints in the lane, with the distance between two oints x, y) and x, y ) defined by x x + y y ) 1/, 1. The
APPM 2350 Section Exam points Wednesday September 26, 6:00pm 7:30pm, 2018
 APPM 2350 Section Exam 1 140 points Wednesday September 26, 6:00pm 7:30pm, 2018 ON THE FRONT OF YOUR BLUEBOOK write: (1) your name, (2) your student ID number, (3) lecture section/time (4) your instructor
APPM 2350 Section Exam 1 140 points Wednesday September 26, 6:00pm 7:30pm, 2018 ON THE FRONT OF YOUR BLUEBOOK write: (1) your name, (2) your student ID number, (3) lecture section/time (4) your instructor
Mo, 12/03: Review Tu, 12/04: 9:40-10:30, AEB 340, study session
 Math 2210-1 Notes of 12/03/2018 Math 2210-1 Fall 2018 Review Remaining Events Fr, 11/30: Starting Review. No study session today. Mo, 12/03: Review Tu, 12/04: 9:40-10:30, AEB 340, study session We, 12/05:
Math 2210-1 Notes of 12/03/2018 Math 2210-1 Fall 2018 Review Remaining Events Fr, 11/30: Starting Review. No study session today. Mo, 12/03: Review Tu, 12/04: 9:40-10:30, AEB 340, study session We, 12/05:
Exercise: concepts from chapter 3
 Reading:, Ch 3 1) The natural representation of a curve, c = c(s), satisfies the condition dc/ds = 1, where s is the natural parameter for the curve. a) Describe in words and a sketch what this condition
Reading:, Ch 3 1) The natural representation of a curve, c = c(s), satisfies the condition dc/ds = 1, where s is the natural parameter for the curve. a) Describe in words and a sketch what this condition
 - - - - - - - - - - - - - - - - - - DISCLAIMER - - - - - - - - - - - - - - - - - - General Information: This midterm is a sample midterm. This means: The sample midterm contains problems that are of similar,
- - - - - - - - - - - - - - - - - - DISCLAIMER - - - - - - - - - - - - - - - - - - General Information: This midterm is a sample midterm. This means: The sample midterm contains problems that are of similar,
8.7 Associated and Non-associated Flow Rules
 8.7 Associated and Non-associated Flow Rules Recall the Levy-Mises flow rule, Eqn. 8.4., d ds (8.7.) The lastic multilier can be determined from the hardening rule. Given the hardening rule one can more
8.7 Associated and Non-associated Flow Rules Recall the Levy-Mises flow rule, Eqn. 8.4., d ds (8.7.) The lastic multilier can be determined from the hardening rule. Given the hardening rule one can more
Chapter Four. Derivatives. in the interior of a set S of real numbers means there is an interval centered at t 0
 Chapter Four Derivatives 4 Derivatives Suppose f is a vector function and t 0 is a point in the interior of the domain of f ( t 0 in the interior of a set S of real numbers means there is an interval centered
Chapter Four Derivatives 4 Derivatives Suppose f is a vector function and t 0 is a point in the interior of the domain of f ( t 0 in the interior of a set S of real numbers means there is an interval centered
MAT 272 Test 1 Review. 1. Let P = (1,1) and Q = (2,3). Find the unit vector u that has the same
 11.1 Vectors in the Plane 1. Let P = (1,1) and Q = (2,3). Find the unit vector u that has the same direction as. QP a. u =< 1, 2 > b. u =< 1 5, 2 5 > c. u =< 1, 2 > d. u =< 1 5, 2 5 > 2. If u has magnitude
11.1 Vectors in the Plane 1. Let P = (1,1) and Q = (2,3). Find the unit vector u that has the same direction as. QP a. u =< 1, 2 > b. u =< 1 5, 2 5 > c. u =< 1, 2 > d. u =< 1 5, 2 5 > 2. If u has magnitude
Lecture D4 - Intrinsic Coordinates
 J. Peraire 16.07 Dynamics Fall 2004 Version 1.1 Lecture D4 - Intrinsic Coordinates In lecture D2 we introduced the position, velocity and acceleration vectors and referred them to a fixed cartesian coordinate
J. Peraire 16.07 Dynamics Fall 2004 Version 1.1 Lecture D4 - Intrinsic Coordinates In lecture D2 we introduced the position, velocity and acceleration vectors and referred them to a fixed cartesian coordinate
II. Unit Speed Curves
 The Geometry of Curves, Part I Rob Donnelly From Murray State University s Calculus III, Fall 2001 note: This material supplements Sections 13.3 and 13.4 of the text Calculus with Early Transcendentals,
The Geometry of Curves, Part I Rob Donnelly From Murray State University s Calculus III, Fall 2001 note: This material supplements Sections 13.3 and 13.4 of the text Calculus with Early Transcendentals,
Multi Variable Calculus
 Multi Variable Calculus Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 3, 03 Functions from R n to R m So far we have looked at functions that map one number to another
Multi Variable Calculus Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 3, 03 Functions from R n to R m So far we have looked at functions that map one number to another
Curves from the inside
 MATH 2401 - Harrell Curves from the inside Lecture 5 Copyright 2008 by Evans M. Harrell II. Who in the cast of characters might show up on the test? Curves r(t), velocity v(t). Tangent and normal lines.
MATH 2401 - Harrell Curves from the inside Lecture 5 Copyright 2008 by Evans M. Harrell II. Who in the cast of characters might show up on the test? Curves r(t), velocity v(t). Tangent and normal lines.
e 2 = e 1 = e 3 = v 1 (v 2 v 3 ) = det(v 1, v 2, v 3 ).
 3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
1. (4 % each, total 20 %) Answer each of the following. (No need to show your work for this problem). 3 n. n!? n=1
 NAME: EXAM 4 - Math 56 SOlutions Instruction: Circle your answers and show all your work CLEARLY Partial credit will be given only when you present what belongs to part of a correct solution (4 % each,
NAME: EXAM 4 - Math 56 SOlutions Instruction: Circle your answers and show all your work CLEARLY Partial credit will be given only when you present what belongs to part of a correct solution (4 % each,
Review of Power Series
 Review of Power Series MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Introduction In addition to the techniques we have studied so far, we may use power
Review of Power Series MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Introduction In addition to the techniques we have studied so far, we may use power
MA3D9. Geometry of curves and surfaces. T (s) = κ(s)n(s),
 MA3D9. Geometry of 2. Planar curves. Let : I R 2 be a curve parameterised by arc-length. Given s I, let T(s) = (s) be the unit tangent. Let N(s) be the unit normal obtained by rotating T(s) through π/2
MA3D9. Geometry of 2. Planar curves. Let : I R 2 be a curve parameterised by arc-length. Given s I, let T(s) = (s) be the unit tangent. Let N(s) be the unit normal obtained by rotating T(s) through π/2
Math 3c Solutions: Exam 2 Fall 2017
 Math 3c Solutions: Exam Fall 07. 0 points) The graph of a smooth vector-valued function is shown below except that your irresponsible teacher forgot to include the orientation!) Several points are indicated
Math 3c Solutions: Exam Fall 07. 0 points) The graph of a smooth vector-valued function is shown below except that your irresponsible teacher forgot to include the orientation!) Several points are indicated
Multiple Choice. 1.(6 pts) Find symmetric equations of the line L passing through the point (2, 5, 1) and perpendicular to the plane x + 3y z = 9.
 Multiple Choice.(6 pts) Find smmetric equations of the line L passing through the point (, 5, ) and perpendicular to the plane x + 3 z = 9. (a) x = + 5 3 = z (c) (x ) + 3( 3) (z ) = 9 (d) (e) x = 3 5 =
Multiple Choice.(6 pts) Find smmetric equations of the line L passing through the point (, 5, ) and perpendicular to the plane x + 3 z = 9. (a) x = + 5 3 = z (c) (x ) + 3( 3) (z ) = 9 (d) (e) x = 3 5 =
10.3 Parametric Equations. 1 Math 1432 Dr. Almus
 Math 1432 DAY 39 Dr. Melahat Almus almus@math.uh.edu OFFICE HOURS (212 PGH) MW12-1:30pm, F:12-1pm. If you email me, please mention the course (1432) in the subject line. Check your CASA account for Quiz
Math 1432 DAY 39 Dr. Melahat Almus almus@math.uh.edu OFFICE HOURS (212 PGH) MW12-1:30pm, F:12-1pm. If you email me, please mention the course (1432) in the subject line. Check your CASA account for Quiz
No calculators, books, notebooks or any other written materials are allowed. Question Points Score Total: 40
 Be sure this exam has 6 ages including the cover The University of British Columbia MATH 317, Section 11, Instructor Tai-Peng Tsai Midterm Exam 1 October 16 Family Name Student Number Given Name Signature
Be sure this exam has 6 ages including the cover The University of British Columbia MATH 317, Section 11, Instructor Tai-Peng Tsai Midterm Exam 1 October 16 Family Name Student Number Given Name Signature
12.3 Curvature, torsion and the TNB frame
 1.3 Curvature, torsion and the TNB frame Acknowledgments: Material from a Georgia Tech worksheet by Jim Herod, School of Mathematics, herod@math.gatech.edu, is incorporated into the section on curvature,
1.3 Curvature, torsion and the TNB frame Acknowledgments: Material from a Georgia Tech worksheet by Jim Herod, School of Mathematics, herod@math.gatech.edu, is incorporated into the section on curvature,
Examiner: D. Burbulla. Aids permitted: Formula Sheet, and Casio FX-991 or Sharp EL-520 calculator.
 University of Toronto Faculty of Applied Science and Engineering Solutions to Final Examination, June 216 Duration: 2 and 1/2 hrs First Year - CHE, CIV, CPE, ELE, ENG, IND, LME, MEC, MMS MAT187H1F - Calculus
University of Toronto Faculty of Applied Science and Engineering Solutions to Final Examination, June 216 Duration: 2 and 1/2 hrs First Year - CHE, CIV, CPE, ELE, ENG, IND, LME, MEC, MMS MAT187H1F - Calculus
MA304 Differential Geometry
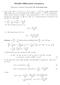 MA34 Differential Geometr Homework solutions, Spring 8, 3% of the final mark Let I R, where I = (a, b) or I = [a, b] Let α : I R 3 be a regular parameterised differentiable curve (not necessaril b arc
MA34 Differential Geometr Homework solutions, Spring 8, 3% of the final mark Let I R, where I = (a, b) or I = [a, b] Let α : I R 3 be a regular parameterised differentiable curve (not necessaril b arc
 - - - - - - - - - - - - - - - - - - DISCLAIMER - - - - - - - - - - - - - - - - - - General Information: This is a midterm from a previous semester. This means: This midterm contains problems that are of
- - - - - - - - - - - - - - - - - - DISCLAIMER - - - - - - - - - - - - - - - - - - General Information: This is a midterm from a previous semester. This means: This midterm contains problems that are of
Examiner: D. Burbulla. Aids permitted: Formula Sheet, and Casio FX-991 or Sharp EL-520 calculator.
 University of Toronto Faculty of Applied Science and Engineering Solutions to Final Examination, June 017 Duration: and 1/ hrs First Year - CHE, CIV, CPE, ELE, ENG, IND, LME, MEC, MMS MAT187H1F - Calculus
University of Toronto Faculty of Applied Science and Engineering Solutions to Final Examination, June 017 Duration: and 1/ hrs First Year - CHE, CIV, CPE, ELE, ENG, IND, LME, MEC, MMS MAT187H1F - Calculus
= =5 (0:4) 4 10 = = = = = 2:005 32:4 2: :
 MATH LEC SECOND EXAM THU NOV 0 PROBLEM Part (a) ( 5 oints ) Aroximate 5 :4 using a suitable dierential. Show your work carrying at least 6 decimal digits. A mere calculator answer will receive zero credit.
MATH LEC SECOND EXAM THU NOV 0 PROBLEM Part (a) ( 5 oints ) Aroximate 5 :4 using a suitable dierential. Show your work carrying at least 6 decimal digits. A mere calculator answer will receive zero credit.
MATH Final Review
 MATH 1592 - Final Review 1 Chapter 7 1.1 Main Topics 1. Integration techniques: Fitting integrands to basic rules on page 485. Integration by parts, Theorem 7.1 on page 488. Guidelines for trigonometric
MATH 1592 - Final Review 1 Chapter 7 1.1 Main Topics 1. Integration techniques: Fitting integrands to basic rules on page 485. Integration by parts, Theorem 7.1 on page 488. Guidelines for trigonometric
Math 116 Final Exam December 17, 2010
 Math 116 Final Exam December 17, 2010 Name: Instructor: Section: 1. Do not open this exam until you are told to do so. 2. This exam has 11 pages including this cover. There are 9 problems. Note that the
Math 116 Final Exam December 17, 2010 Name: Instructor: Section: 1. Do not open this exam until you are told to do so. 2. This exam has 11 pages including this cover. There are 9 problems. Note that the
Topic 2-2: Derivatives of Vector Functions. Textbook: Section 13.2, 13.4
 Topic 2-2: Derivatives of Vector Functions Textbook: Section 13.2, 13.4 Warm-Up: Parametrization of Circles Each of the following vector functions describe the position of an object traveling around the
Topic 2-2: Derivatives of Vector Functions Textbook: Section 13.2, 13.4 Warm-Up: Parametrization of Circles Each of the following vector functions describe the position of an object traveling around the
8. THE FARY-MILNOR THEOREM
 Math 501 - Differential Geometry Herman Gluck Tuesday April 17, 2012 8. THE FARY-MILNOR THEOREM The curvature of a smooth curve in 3-space is 0 by definition, and its integral w.r.t. arc length, (s) ds,
Math 501 - Differential Geometry Herman Gluck Tuesday April 17, 2012 8. THE FARY-MILNOR THEOREM The curvature of a smooth curve in 3-space is 0 by definition, and its integral w.r.t. arc length, (s) ds,
MATH 1372, SECTION 33, MIDTERM 3 REVIEW ANSWERS
 MATH 1372, SECTION 33, MIDTERM 3 REVIEW ANSWERS 1. We have one theorem whose conclusion says an alternating series converges. We have another theorem whose conclusion says an alternating series diverges.
MATH 1372, SECTION 33, MIDTERM 3 REVIEW ANSWERS 1. We have one theorem whose conclusion says an alternating series converges. We have another theorem whose conclusion says an alternating series diverges.
Notes on uniform convergence
 Notes on uniform convergence Erik Wahlén erik.wahlen@math.lu.se January 17, 2012 1 Numerical sequences We begin by recalling some properties of numerical sequences. By a numerical sequence we simply mean
Notes on uniform convergence Erik Wahlén erik.wahlen@math.lu.se January 17, 2012 1 Numerical sequences We begin by recalling some properties of numerical sequences. By a numerical sequence we simply mean
MATH 162. FINAL EXAM ANSWERS December 17, 2006
 MATH 6 FINAL EXAM ANSWERS December 7, 6 Part A. ( points) Find the volume of the solid obtained by rotating about the y-axis the region under the curve y x, for / x. Using the shell method, the radius
MATH 6 FINAL EXAM ANSWERS December 7, 6 Part A. ( points) Find the volume of the solid obtained by rotating about the y-axis the region under the curve y x, for / x. Using the shell method, the radius
= ( 2) = p 5.
 MATH 0 Exam (Version ) Solutions Setember, 00 S. F. Ellermeyer Name Instructions. Your work on this exam will be raded accordin to two criteria: mathematical correctness clarity of resentation. In other
MATH 0 Exam (Version ) Solutions Setember, 00 S. F. Ellermeyer Name Instructions. Your work on this exam will be raded accordin to two criteria: mathematical correctness clarity of resentation. In other
Final exam (practice) UCLA: Math 31B, Spring 2017
 Instructor: Noah White Date: Final exam (practice) UCLA: Math 31B, Spring 2017 This exam has 8 questions, for a total of 80 points. Please print your working and answers neatly. Write your solutions in
Instructor: Noah White Date: Final exam (practice) UCLA: Math 31B, Spring 2017 This exam has 8 questions, for a total of 80 points. Please print your working and answers neatly. Write your solutions in
MATH 12 CLASS 5 NOTES, SEP
 MATH 12 CLASS 5 NOTES, SEP 30 2011 Contents 1. Vector-valued functions 1 2. Differentiating and integrating vector-valued functions 3 3. Velocity and Acceleration 4 Over the past two weeks we have developed
MATH 12 CLASS 5 NOTES, SEP 30 2011 Contents 1. Vector-valued functions 1 2. Differentiating and integrating vector-valued functions 3 3. Velocity and Acceleration 4 Over the past two weeks we have developed
CSC165H, Mathematical expression and reasoning for computer science week 12
 CSC165H, Mathematical exression and reasoning for comuter science week 1 nd December 005 Gary Baumgartner and Danny Hea hea@cs.toronto.edu SF4306A 416-978-5899 htt//www.cs.toronto.edu/~hea/165/s005/index.shtml
CSC165H, Mathematical exression and reasoning for comuter science week 1 nd December 005 Gary Baumgartner and Danny Hea hea@cs.toronto.edu SF4306A 416-978-5899 htt//www.cs.toronto.edu/~hea/165/s005/index.shtml
MATH 32A: MIDTERM 2 REVIEW. sin 2 u du z(t) = sin 2 t + cos 2 2
 MATH 3A: MIDTERM REVIEW JOE HUGHES 1. Curvature 1. Consider the curve r(t) = x(t), y(t), z(t), where x(t) = t Find the curvature κ(t). 0 cos(u) sin(u) du y(t) = Solution: The formula for curvature is t
MATH 3A: MIDTERM REVIEW JOE HUGHES 1. Curvature 1. Consider the curve r(t) = x(t), y(t), z(t), where x(t) = t Find the curvature κ(t). 0 cos(u) sin(u) du y(t) = Solution: The formula for curvature is t
1 The pendulum equation
 Math 270 Honors ODE I Fall, 2008 Class notes # 5 A longer than usual homework assignment is at the end. The pendulum equation We now come to a particularly important example, the equation for an oscillating
Math 270 Honors ODE I Fall, 2008 Class notes # 5 A longer than usual homework assignment is at the end. The pendulum equation We now come to a particularly important example, the equation for an oscillating
APPM 2350, Summer 2018: Exam 1 June 15, 2018
 APPM 2350, Summer 2018: Exam 1 June 15, 2018 Instructions: Please show all of your work and make your methods and reasoning clear. Answers out of the blue with no supporting work will receive no credit
APPM 2350, Summer 2018: Exam 1 June 15, 2018 Instructions: Please show all of your work and make your methods and reasoning clear. Answers out of the blue with no supporting work will receive no credit
g(t) = f(x 1 (t),..., x n (t)).
 Reading: [Simon] p. 313-333, 833-836. 0.1 The Chain Rule Partial derivatives describe how a function changes in directions parallel to the coordinate axes. Now we shall demonstrate how the partial derivatives
Reading: [Simon] p. 313-333, 833-836. 0.1 The Chain Rule Partial derivatives describe how a function changes in directions parallel to the coordinate axes. Now we shall demonstrate how the partial derivatives
Geometry of Cylindrical Curves over Plane Curves
 Applied Mathematical Sciences, Vol 9, 015, no 113, 5637-5649 HIKARI Ltd, wwwm-hikaricom http://dxdoiorg/101988/ams01556456 Geometry of Cylindrical Curves over Plane Curves Georgi Hristov Georgiev, Radostina
Applied Mathematical Sciences, Vol 9, 015, no 113, 5637-5649 HIKARI Ltd, wwwm-hikaricom http://dxdoiorg/101988/ams01556456 Geometry of Cylindrical Curves over Plane Curves Georgi Hristov Georgiev, Radostina
Geometric Modelling Summer 2016
 Geometric Modelling Summer 2016 Exercises Benjamin Karer M.Sc. http://gfx.uni-kl.de/~gm Benjamin Karer M.Sc. Geometric Modelling Summer 2016 1 Dierential Geometry Benjamin Karer M.Sc. Geometric Modelling
Geometric Modelling Summer 2016 Exercises Benjamin Karer M.Sc. http://gfx.uni-kl.de/~gm Benjamin Karer M.Sc. Geometric Modelling Summer 2016 1 Dierential Geometry Benjamin Karer M.Sc. Geometric Modelling
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 2013
 SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
AP Calculus Testbank (Chapter 10) (Mr. Surowski)
 AP Calculus Testbank (Chater 1) (Mr. Surowski) Part I. Multile-Choice Questions 1. The grah in the xy-lane reresented by x = 3 sin t and y = cost is (A) a circle (B) an ellise (C) a hyerbola (D) a arabola
AP Calculus Testbank (Chater 1) (Mr. Surowski) Part I. Multile-Choice Questions 1. The grah in the xy-lane reresented by x = 3 sin t and y = cost is (A) a circle (B) an ellise (C) a hyerbola (D) a arabola
Geometry and Motion Selected answers to Sections A and C Dwight Barkley 2016
 MA34 Geometry and Motion Selected answers to Sections A and C Dwight Barkley 26 Example Sheet d n+ = d n cot θ n r θ n r = Θθ n i. 2. 3. 4. Possible answers include: and with opposite orientation: 5..
MA34 Geometry and Motion Selected answers to Sections A and C Dwight Barkley 26 Example Sheet d n+ = d n cot θ n r θ n r = Θθ n i. 2. 3. 4. Possible answers include: and with opposite orientation: 5..
MTH 277 Test 4 review sheet Chapter , 14.7, 14.8 Chalmeta
 MTH 77 Test 4 review sheet Chapter 13.1-13.4, 14.7, 14.8 Chalmeta Multiple Choice 1. Let r(t) = 3 sin t i + 3 cos t j + αt k. What value of α gives an arc length of 5 from t = 0 to t = 1? (a) 6 (b) 5 (c)
MTH 77 Test 4 review sheet Chapter 13.1-13.4, 14.7, 14.8 Chalmeta Multiple Choice 1. Let r(t) = 3 sin t i + 3 cos t j + αt k. What value of α gives an arc length of 5 from t = 0 to t = 1? (a) 6 (b) 5 (c)
Curves. Contents. 1 Introduction 3
 Curves Danilo Magistrali and M. Eugenia Rosado María Departamento de Matemática Aplicada Escuela Técnica Superior de Arquitectura, UPM Avda. Juan de Herrera 4, 8040-Madrid, Spain e-mail: danilo.magistrali@upm.es
Curves Danilo Magistrali and M. Eugenia Rosado María Departamento de Matemática Aplicada Escuela Técnica Superior de Arquitectura, UPM Avda. Juan de Herrera 4, 8040-Madrid, Spain e-mail: danilo.magistrali@upm.es
Math 116 Second Midterm March 23, 2010
 Math 6 Second Midterm March 23, 2 Name: EXAM SOLUTIONS Instructor: Section:. Do not open this exam until you are told to do so. 2. This exam has pages including this cover. There are 9 problems. Note that
Math 6 Second Midterm March 23, 2 Name: EXAM SOLUTIONS Instructor: Section:. Do not open this exam until you are told to do so. 2. This exam has pages including this cover. There are 9 problems. Note that
Vectors, dot product, and cross product
 MTH 201 Multivariable calculus and differential equations Practice problems Vectors, dot product, and cross product 1. Find the component form and length of vector P Q with the following initial point
MTH 201 Multivariable calculus and differential equations Practice problems Vectors, dot product, and cross product 1. Find the component form and length of vector P Q with the following initial point
Curves - A lengthy story
 MATH 2401 - Harrell Curves - A lengthy story Lecture 4 Copyright 2007 by Evans M. Harrell II. Reminder What a lonely archive! Who in the cast of characters might show up on the test? Curves r(t), velocity
MATH 2401 - Harrell Curves - A lengthy story Lecture 4 Copyright 2007 by Evans M. Harrell II. Reminder What a lonely archive! Who in the cast of characters might show up on the test? Curves r(t), velocity
MATH 829: Introduction to Data Mining and Analysis Consistency of Linear Regression
 1/9 MATH 829: Introduction to Data Mining and Analysis Consistency of Linear Regression Dominique Guillot Deartments of Mathematical Sciences University of Delaware February 15, 2016 Distribution of regression
1/9 MATH 829: Introduction to Data Mining and Analysis Consistency of Linear Regression Dominique Guillot Deartments of Mathematical Sciences University of Delaware February 15, 2016 Distribution of regression
Surfaces of Revolution with Constant Mean Curvature H = c in Hyperbolic 3-Space H 3 ( c 2 )
 Surfaces of Revolution with Constant Mean Curvature H = c in Hyerbolic 3-Sace H 3 ( c 2 Kinsey-Ann Zarske Deartment of Mathematics, University of Southern Mississii, Hattiesburg, MS 39406, USA E-mail:
Surfaces of Revolution with Constant Mean Curvature H = c in Hyerbolic 3-Sace H 3 ( c 2 Kinsey-Ann Zarske Deartment of Mathematics, University of Southern Mississii, Hattiesburg, MS 39406, USA E-mail:
Lecture 6: Isometry. Table of contents
 Mth 348 Fll 017 Lecture 6: Isometry Disclimer. As we hve textook, this lecture note is for guidnce nd sulement only. It should not e relied on when rering for exms. In this lecture we nish the reliminry
Mth 348 Fll 017 Lecture 6: Isometry Disclimer. As we hve textook, this lecture note is for guidnce nd sulement only. It should not e relied on when rering for exms. In this lecture we nish the reliminry
MATH 332: Vector Analysis Summer 2005 Homework
 MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
The Method of Laplace Transforms.
 The Method of Laplace Transforms. James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University May 25, 217 Outline 1 The Laplace Transform 2 Inverting
The Method of Laplace Transforms. James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University May 25, 217 Outline 1 The Laplace Transform 2 Inverting
16.2. Infinite Series. Introduction. Prerequisites. Learning Outcomes
 Infinite Series 6.2 Introduction We extend the concet of a finite series, met in Section 6., to the situation in which the number of terms increase without bound. We define what is meant by an infinite
Infinite Series 6.2 Introduction We extend the concet of a finite series, met in Section 6., to the situation in which the number of terms increase without bound. We define what is meant by an infinite
Math 273 (51) - Final
 Name: Id #: Math 273 (5) - Final Autumn Quarter 26 Thursday, December 8, 26-6: to 8: Instructions: Prob. Points Score possible 25 2 25 3 25 TOTAL 75 Read each problem carefully. Write legibly. Show all
Name: Id #: Math 273 (5) - Final Autumn Quarter 26 Thursday, December 8, 26-6: to 8: Instructions: Prob. Points Score possible 25 2 25 3 25 TOTAL 75 Read each problem carefully. Write legibly. Show all
3 More applications of derivatives
 3 More alications of derivatives 3.1 Eact & ineact differentials in thermodynamics So far we have been discussing total or eact differentials ( ( u u du = d + dy, (1 but we could imagine a more general
3 More alications of derivatives 3.1 Eact & ineact differentials in thermodynamics So far we have been discussing total or eact differentials ( ( u u du = d + dy, (1 but we could imagine a more general
Math 230 Mock Final Exam Detailed Solution
 Name: Math 30 Mock Final Exam Detailed Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and
Name: Math 30 Mock Final Exam Detailed Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and
Math 116 Second Midterm March 20, 2013
 Math 6 Second Mierm March, 3 Name: EXAM SOLUTIONS Instructor: Section:. Do not open this exam until you are told to do so.. This exam has 3 pages including this cover. There are 8 problems. Note that the
Math 6 Second Mierm March, 3 Name: EXAM SOLUTIONS Instructor: Section:. Do not open this exam until you are told to do so.. This exam has 3 pages including this cover. There are 8 problems. Note that the
 Otimal exercise boundary for an American ut otion Rachel A. Kuske Deartment of Mathematics University of Minnesota-Minneaolis Minneaolis, MN 55455 e-mail: rachel@math.umn.edu Joseh B. Keller Deartments
Otimal exercise boundary for an American ut otion Rachel A. Kuske Deartment of Mathematics University of Minnesota-Minneaolis Minneaolis, MN 55455 e-mail: rachel@math.umn.edu Joseh B. Keller Deartments
Chapter 14: Vector Calculus
 Chapter 14: Vector Calculus Introduction to Vector Functions Section 14.1 Limits, Continuity, Vector Derivatives a. Limit of a Vector Function b. Limit Rules c. Component By Component Limits d. Continuity
Chapter 14: Vector Calculus Introduction to Vector Functions Section 14.1 Limits, Continuity, Vector Derivatives a. Limit of a Vector Function b. Limit Rules c. Component By Component Limits d. Continuity
Our goal is to solve a general constant coecient linear second order. this way but that will not always happen). Once we have y 1, it will always
 October 5 Relevant reading: Section 2.1, 2.2, 2.3 and 2.4 Our goal is to solve a general constant coecient linear second order ODE a d2 y dt + bdy + cy = g (t) 2 dt where a, b, c are constants and a 0.
October 5 Relevant reading: Section 2.1, 2.2, 2.3 and 2.4 Our goal is to solve a general constant coecient linear second order ODE a d2 y dt + bdy + cy = g (t) 2 dt where a, b, c are constants and a 0.
The common oscillating lawn sprinkler has a hollow curved sprinkler arm, with a
 Design of an Oscillating Sprinkler Bart Braden Northern Kentucky University Highland Heights, KY 41076 Mathematics Magazine, January 1985, Volume 58, Number 1, pp. 9 38. The common oscillating lawn sprinkler
Design of an Oscillating Sprinkler Bart Braden Northern Kentucky University Highland Heights, KY 41076 Mathematics Magazine, January 1985, Volume 58, Number 1, pp. 9 38. The common oscillating lawn sprinkler
