Lecture 4 February 5
|
|
|
- Ann Kelley
- 5 years ago
- Views:
Transcription
1 Math 239: Discrete Mathematics for the Life Sciences Spring 2008 Lecture 4 February 5 Lecturer: Lior Pachter Scribe/ Editor: Michaeel Kazi/ Cynthia Vinzant 4.1 Introduction to Gröbner Bases In this lecture we provide a brief introduction to Gröbner bases. Our presentation is based on the introductory article [1] and lecture [2]. Gröbner Bases can be viewed as generalizations of Gaussian elimination, the Euclidean algorithm, and the simplex algorithm for linear programming. To find a Gröbner Basis for a finitely generated ideal of polynomials, we ll use Buchberger s Algorithm, whose input is a set of generators and whose output is a Gröbner Basis for the ideal they generate. Input: F = {f 1, f 2,..., f n }, polynomials in several variables Output: G = {g 1, g 2,..., g m }, a Gröbner basis The actual algorithm appears in a later section. Example. Gaussian elimination. Consider the following system of equations: 2x + 3y + 4z = 5 3x + 4y + 5z = 2. We seek a simpler description of the solution set: x = z 14 y = 11 2z. So using our algorithm or Gaussian elimination (which are the same in this linear case), F = {2x + 3y + 4z 5, 3x + 4y + 5z 2} G = {x z + 14, y + 2z 11}. Here we have solved for x and y in terms of z. We could have also solved for x and z in terms of y. In computing our Gröbner Basis G, the difference between these is our choice of term order, (a total ordering of monomials), which we will discuss later. In our example, we used an ordering with x > y > z, whereas solving for x and z in terms of y would correspond to using an ordering with x > z > y. 4-1
2 Example. Euclidean algorithm for computing the GCD of two polynomials in one variable. If we were to look for the greatest common divisor of two polynomials, f 1 and f 2, f 1 = x 4 12x x 3 78x + 40 f 2 = x 5 5x 4 + 5x 3 + 5x 2 6x, Gaussian elimination would give us gcd(f 1, f 2 ) = x 2 3x + 2. With respect to our Gröbner basis algorithm we have input F = {f 1, f 2 } = {x 4 12x x 2 78x + 40, x 5 5x 4 + 5x 3 + 5x 2 6x} and output G = {x 2 3x + 2}. Example. Integer Programming Suppose we wanted to minimize the linear function P +N +D+Q subject to the constraint P, N, D, Q Z 0 and P + 5N + 10D + 25Q = 117. (This problem refers to making change in US currency with the fewest number of coins.) Our optimal solution would be (P, N, D, Q) = (2, 1, 1, 4). We can solve this problem using Gröbner bases as follows. Replace the values of each coin with polynomials: F = {p 5 n, p 10 d, p 25 q}. So one nickel is five pennies, etc. Then our algorithm outputs G = {p 5 n, n 2 d, d 2 n q, d 3 nq}, which indicates the moves you may perform to reach an optimal solution. For example, we start with 117 pennies and replace every 5 pennies by a nickel, every two nickels with a dime, and so forth, leading to a solution with the fewest number of coins. Notice this is not true of the relations we started out with, since you might have to increase your number of coins (trading in two dimes and a nickel for twenty-five pennies) before reducing them again (trading in those twenty-five pennies for a quarter). 4.2 Background Information Let F be a set of polynomials in k[x 1,..., x n ] = k[x], where k is some field. The ideal generated by F is the set < F >= {p 1 f p r f r : f i F and p i k[x]}. 4-2
3 Theorem 4.1. (Hilbert s Basis Theorem) Every ideal of k[x 1,..., x n ] is finitely generated. Proof. Homework. (Hint: Noetherian rings have the ascending chain property.) Looking back at our three examples, we see that the ideals generated by our input and our output, < F > and < G >, are equal Term Order Definition 4.2. A term order on the set of variables x 1,..., x n is a total order < on the set of monomials x a a = x 1 a2 a 1 x 2 x n n satisfying 1. If x a, x b, and x c are monomials, then x a < x b = x c x a < x c x b, and 2. 1 < x a, a 0. For example, for k[x], there is only one order: 1 < x < x 2 <... < x n <... For k[x 1, x 2 ], there are many possibilities, such as Degree lexicographic: 1 < x 1 < x 2 < x 2 1 < x 1 x 2 < x 2 2 < x 3 1 <... Pure lexicographic: 1 < x 1 < x 2 1 < x 3 1 <... < x 2 < x 1 x 2 < x 2 1x 2 <... Once we establish a term order we can speak of the initial ideal of an ideal I k[x]. Definition 4.3. Every f k[x] has an initial monomial in < (f), the largest monomial with a nonzero coefficient. Given an ideal I in k[x] we have in < (I) := {in < (f) : f I} =< in < (f) : f I >. Definition 4.4. A finite subset G of an ideal I is a Gröbner basis with respect to < if in < (< G >) =< in < (g) : g G >= in < (I). Notice that Gröbner bases are not unique. You can put any element of I into G that isn t already in it, and you will still have a Gröbner basis. For uniqueness we need... Definition 4.5. A reduced Gröbner basis for an ideal I is a Gröbner basis G satisfying 1. For each g G the coefficient of in < (g) is The set of {in < (g) : g G} minimally generates in < (I). 3. No trailing (non-initial) terms of any g G lie in in < (I). Theorem 4.6. The reduced Gröbner basis is unique. Every Gröbner basis can be turned into a reduced Gröbner basis through autoreduction. 4-3
4 4.3 Buchberger s Algorithm Is G a Gröbner basis? To test whether or not G is a Gröbner basis, we need to check that in < (G) generates in < (I), that is check whether or not any elements of I have initials terms that are not divisible by an element of in < (G). For any g, g G, the S-polynomial of g and g is as follows: S g,g = m g mg, where m, m are the monomials of smallest degree that cancel out the leading terms of g and g. Example. F = {x 2 + 3x 4, x 3 5x + 4} Form the S-polynomial of the first two polynomials: S = x(x 2 + 3x 4) 1(x 3 5x + 4) = 3x 2 + x 4. Definition 4.7. Let I k[x] be an ideal with term order <. A monomial x a is standard if it is not in the ideal in < (I). Example. in < (I) =< x 3 1, x 4 2, x 5 3 > The standard monomials are x a 1x b 2x c 3 where a < 3, b < 4, c < 5. Example. in < (I) =< x 3 1, x 4 2, x 1 x 4 3 > In this case, the number of standard monomials is infinite because x n 3 is standard for every n. In general, the set of standard monomials is a Q-vector space basis for the quotient Q[x]/I. Therefore every polynomial modulo I can be expressed as a linear combination of standard monomials. This expression is called its normal form. Definition 4.8. The normal form of a polynomial f Q[x] with respect to I is the polynomial f mod I expressed in terms of standard monomials. Theorem 4.9. G is a Gröbner basis iff the normal form of S g,g is 0 for all g, g G. 4-4
5 4.3.2 The Algorithm Using S-polynomials to check whether G is a Gröbner basis motivates Buchberger s algorithm for constructing one. Input: A set of polynomials, F. 1. Check if F is a Gröbner basis. That is, check if the normal form of S g,g is zero for all g, g F. 2. If yes, then perform autoreduction and output the reduced Gröbner basis. 3. If not, then let F new = F old {p} where p is the nonzero normal form of some S g,g. 4. Repeat from Step 1. Theorem Buchberger s algorithm terminates. Proof. If p be a nonzero normal form of some S g,g. Each time we add some p to our collection F we (strictly) increase the size of the ideal generated by F s initial ideals. So: < in < (F old ) >=< in < (f 1 ),..., in < (f d ) > < in < (f 1 ),..., in < (f d ), in < (p) >=< in < (F new ) > This gives us an ascending chain of ideals, which must become stationary because k[x] is Noetherian. Thus eventually we will not be able to find such a p and the algorithm will terminate. This algorithm has immense applications, for example in finding solutions to systems of polynomial equations, which is useful in finding equilibria of dynamical systems. 4.4 Varieties and Parametrizations Definition If F is a set of polynomials then the variety defined by F is V (F ) = {z = (z 1,..., z n ) C n : f i (z) = 0 f i F } Note that V (F ) = V (< F >), so we might as well talk only about the variety of an ideal. Definition Let I(S) = {f(x 1,..., x n ) C[x 1,..., x n ] : f(a 1,..., a n ) = 0 (a 1,..., a n ) S}. We call I(S) the vanishing ideal of S. For our purposes, we are interested in a particular type of S, which you may think about as a statistical model. 4-5
6 Definition S is a polynomial parametrization if it takes the form with parameters g 1,..., g n C[t 1,..., t s ]. S = { (g 1 (a),... g n (a)) : a C s }, Theorem If S is a polynomial parametrization and I(S) =< f 1,..., f M V (f 1,..., f M ) and S differ by a set of dimension less than dim(s). >, then 4-6
7 Bibliography [1] B. Sturmfels What is a Gröbner basis? Notices of the American Mathematical Society, 52 (2005) [2] B. Sturmfels Gröbner bases MSRI lectures, available from 7
Polynomials, Ideals, and Gröbner Bases
 Polynomials, Ideals, and Gröbner Bases Notes by Bernd Sturmfels for the lecture on April 10, 2018, in the IMPRS Ringvorlesung Introduction to Nonlinear Algebra We fix a field K. Some examples of fields
Polynomials, Ideals, and Gröbner Bases Notes by Bernd Sturmfels for the lecture on April 10, 2018, in the IMPRS Ringvorlesung Introduction to Nonlinear Algebra We fix a field K. Some examples of fields
GRÖBNER BASES AND POLYNOMIAL EQUATIONS. 1. Introduction and preliminaries on Gróbner bases
 GRÖBNER BASES AND POLYNOMIAL EQUATIONS J. K. VERMA 1. Introduction and preliminaries on Gróbner bases Let S = k[x 1, x 2,..., x n ] denote a polynomial ring over a field k where x 1, x 2,..., x n are indeterminates.
GRÖBNER BASES AND POLYNOMIAL EQUATIONS J. K. VERMA 1. Introduction and preliminaries on Gróbner bases Let S = k[x 1, x 2,..., x n ] denote a polynomial ring over a field k where x 1, x 2,..., x n are indeterminates.
Lecture 15: Algebraic Geometry II
 6.859/15.083 Integer Programming and Combinatorial Optimization Fall 009 Today... Ideals in k[x] Properties of Gröbner bases Buchberger s algorithm Elimination theory The Weak Nullstellensatz 0/1-Integer
6.859/15.083 Integer Programming and Combinatorial Optimization Fall 009 Today... Ideals in k[x] Properties of Gröbner bases Buchberger s algorithm Elimination theory The Weak Nullstellensatz 0/1-Integer
Notes 6: Polynomials in One Variable
 Notes 6: Polynomials in One Variable Definition. Let f(x) = b 0 x n + b x n + + b n be a polynomial of degree n, so b 0 0. The leading term of f is LT (f) = b 0 x n. We begin by analyzing the long division
Notes 6: Polynomials in One Variable Definition. Let f(x) = b 0 x n + b x n + + b n be a polynomial of degree n, so b 0 0. The leading term of f is LT (f) = b 0 x n. We begin by analyzing the long division
POLYNOMIAL DIVISION AND GRÖBNER BASES. Samira Zeada
 THE TEACHING OF MATHEMATICS 2013, Vol. XVI, 1, pp. 22 28 POLYNOMIAL DIVISION AND GRÖBNER BASES Samira Zeada Abstract. Division in the ring of multivariate polynomials is usually not a part of the standard
THE TEACHING OF MATHEMATICS 2013, Vol. XVI, 1, pp. 22 28 POLYNOMIAL DIVISION AND GRÖBNER BASES Samira Zeada Abstract. Division in the ring of multivariate polynomials is usually not a part of the standard
5 The existence of Gröbner basis
 5 The existence of Gröbner basis We use Buchberger s criterion from the previous section to give an algorithm that constructs a Gröbner basis of an ideal from any given set of generators Hilbert s Basis
5 The existence of Gröbner basis We use Buchberger s criterion from the previous section to give an algorithm that constructs a Gröbner basis of an ideal from any given set of generators Hilbert s Basis
MATH 497A: INTRODUCTION TO APPLIED ALGEBRAIC GEOMETRY
 MATH 497A: INTRODUCTION TO APPLIED ALGEBRAIC GEOMETRY These are notes from the Penn State 2015 MASS course Introduction to Applied Algebraic Geometry. This class is taught by Jason Morton and the notes
MATH 497A: INTRODUCTION TO APPLIED ALGEBRAIC GEOMETRY These are notes from the Penn State 2015 MASS course Introduction to Applied Algebraic Geometry. This class is taught by Jason Morton and the notes
The Euclidean Algorithm and Multiplicative Inverses
 1 The Euclidean Algorithm and Multiplicative Inverses Lecture notes for Access 2009 The Euclidean Algorithm is a set of instructions for finding the greatest common divisor of any two positive integers.
1 The Euclidean Algorithm and Multiplicative Inverses Lecture notes for Access 2009 The Euclidean Algorithm is a set of instructions for finding the greatest common divisor of any two positive integers.
Lecture 7: Polynomial rings
 Lecture 7: Polynomial rings Rajat Mittal IIT Kanpur You have seen polynomials many a times till now. The purpose of this lecture is to give a formal treatment to constructing polynomials and the rules
Lecture 7: Polynomial rings Rajat Mittal IIT Kanpur You have seen polynomials many a times till now. The purpose of this lecture is to give a formal treatment to constructing polynomials and the rules
Chapter 14: Divisibility and factorization
 Chapter 14: Divisibility and factorization Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Summer I 2014 M. Macauley (Clemson) Chapter
Chapter 14: Divisibility and factorization Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Summer I 2014 M. Macauley (Clemson) Chapter
Groebner Bases and Applications
 Groebner Bases and Applications Robert Hines December 16, 2014 1 Groebner Bases In this section we define Groebner Bases and discuss some of their basic properties, following the exposition in chapter
Groebner Bases and Applications Robert Hines December 16, 2014 1 Groebner Bases In this section we define Groebner Bases and discuss some of their basic properties, following the exposition in chapter
Lecture Notes Math 371: Algebra (Fall 2006) by Nathanael Leedom Ackerman
 Lecture Notes Math 371: Algebra (Fall 2006) by Nathanael Leedom Ackerman October 17, 2006 TALK SLOWLY AND WRITE NEATLY!! 1 0.1 Factorization 0.1.1 Factorization of Integers and Polynomials Now we are going
Lecture Notes Math 371: Algebra (Fall 2006) by Nathanael Leedom Ackerman October 17, 2006 TALK SLOWLY AND WRITE NEATLY!! 1 0.1 Factorization 0.1.1 Factorization of Integers and Polynomials Now we are going
Intermediate Math Circles February 29, 2012 Linear Diophantine Equations I
 Intermediate Math Circles February 29, 2012 Linear Diophantine Equations I Diophantine equations are equations intended to be solved in the integers. We re going to focus on Linear Diophantine Equations.
Intermediate Math Circles February 29, 2012 Linear Diophantine Equations I Diophantine equations are equations intended to be solved in the integers. We re going to focus on Linear Diophantine Equations.
Lecture 2: Gröbner Basis and SAGBI Basis
 Lecture 2: Gröbner Basis and SAGBI Basis Mohammed Tessema Suppose we have a graph. Suppose we color the graph s vertices with 3 colors so that if the vertices are adjacent they are not the same colors.
Lecture 2: Gröbner Basis and SAGBI Basis Mohammed Tessema Suppose we have a graph. Suppose we color the graph s vertices with 3 colors so that if the vertices are adjacent they are not the same colors.
Coding Theory ( Mathematical Background I)
 N.L.Manev, Lectures on Coding Theory (Maths I) p. 1/18 Coding Theory ( Mathematical Background I) Lector: Nikolai L. Manev Institute of Mathematics and Informatics, Sofia, Bulgaria N.L.Manev, Lectures
N.L.Manev, Lectures on Coding Theory (Maths I) p. 1/18 Coding Theory ( Mathematical Background I) Lector: Nikolai L. Manev Institute of Mathematics and Informatics, Sofia, Bulgaria N.L.Manev, Lectures
Linear Algebra III Lecture 11
 Linear Algebra III Lecture 11 Xi Chen 1 1 University of Alberta February 13, 2015 Outline Minimal Polynomial 1 Minimal Polynomial Minimal Polynomial The minimal polynomial f (x) of a square matrix A is
Linear Algebra III Lecture 11 Xi Chen 1 1 University of Alberta February 13, 2015 Outline Minimal Polynomial 1 Minimal Polynomial Minimal Polynomial The minimal polynomial f (x) of a square matrix A is
Discrete Math, Second Problem Set (June 24)
 Discrete Math, Second Problem Set (June 24) REU 2003 Instructor: Laszlo Babai Scribe: D Jeremy Copeland 1 Number Theory Remark 11 For an arithmetic progression, a 0, a 1 = a 0 +d, a 2 = a 0 +2d, to have
Discrete Math, Second Problem Set (June 24) REU 2003 Instructor: Laszlo Babai Scribe: D Jeremy Copeland 1 Number Theory Remark 11 For an arithmetic progression, a 0, a 1 = a 0 +d, a 2 = a 0 +2d, to have
Groebner Bases, Toric Ideals and Integer Programming: An Application to Economics. Tan Tran Junior Major-Economics& Mathematics
 Groebner Bases, Toric Ideals and Integer Programming: An Application to Economics Tan Tran Junior Major-Economics& Mathematics History Groebner bases were developed by Buchberger in 1965, who later named
Groebner Bases, Toric Ideals and Integer Programming: An Application to Economics Tan Tran Junior Major-Economics& Mathematics History Groebner bases were developed by Buchberger in 1965, who later named
ABSTRACT. Department of Mathematics. interesting results. A graph on n vertices is represented by a polynomial in n
 ABSTRACT Title of Thesis: GRÖBNER BASES WITH APPLICATIONS IN GRAPH THEORY Degree candidate: Angela M. Hennessy Degree and year: Master of Arts, 2006 Thesis directed by: Professor Lawrence C. Washington
ABSTRACT Title of Thesis: GRÖBNER BASES WITH APPLICATIONS IN GRAPH THEORY Degree candidate: Angela M. Hennessy Degree and year: Master of Arts, 2006 Thesis directed by: Professor Lawrence C. Washington
Honors Algebra 4, MATH 371 Winter 2010 Assignment 3 Due Friday, February 5 at 08:35
 Honors Algebra 4, MATH 371 Winter 2010 Assignment 3 Due Friday, February 5 at 08:35 1. Let R 0 be a commutative ring with 1 and let S R be the subset of nonzero elements which are not zero divisors. (a)
Honors Algebra 4, MATH 371 Winter 2010 Assignment 3 Due Friday, February 5 at 08:35 1. Let R 0 be a commutative ring with 1 and let S R be the subset of nonzero elements which are not zero divisors. (a)
Chapter 3 Basic Number Theory
 Chapter 3 Basic Number Theory What is Number Theory? Well... What is Number Theory? Well... Number Theory The study of the natural numbers (Z + ), especially the relationship between different sorts of
Chapter 3 Basic Number Theory What is Number Theory? Well... What is Number Theory? Well... Number Theory The study of the natural numbers (Z + ), especially the relationship between different sorts of
Mathematical Foundations of Cryptography
 Mathematical Foundations of Cryptography Cryptography is based on mathematics In this chapter we study finite fields, the basis of the Advanced Encryption Standard (AES) and elliptical curve cryptography
Mathematical Foundations of Cryptography Cryptography is based on mathematics In this chapter we study finite fields, the basis of the Advanced Encryption Standard (AES) and elliptical curve cryptography
Announcements. CompSci 102 Discrete Math for Computer Science. Chap. 3.1 Algorithms. Specifying Algorithms
 CompSci 102 Discrete Math for Computer Science Announcements Read for next time Chap. 3.1-3.3 Homework 3 due Tuesday We ll finish Chapter 2 first today February 7, 2012 Prof. Rodger Chap. 3.1 Algorithms
CompSci 102 Discrete Math for Computer Science Announcements Read for next time Chap. 3.1-3.3 Homework 3 due Tuesday We ll finish Chapter 2 first today February 7, 2012 Prof. Rodger Chap. 3.1 Algorithms
Math 4370 Exam 1. Handed out March 9th 2010 Due March 18th 2010
 Math 4370 Exam 1 Handed out March 9th 2010 Due March 18th 2010 Problem 1. Recall from problem 1.4.6.e in the book, that a generating set {f 1,..., f s } of I is minimal if I is not the ideal generated
Math 4370 Exam 1 Handed out March 9th 2010 Due March 18th 2010 Problem 1. Recall from problem 1.4.6.e in the book, that a generating set {f 1,..., f s } of I is minimal if I is not the ideal generated
g(x) = 1 1 x = 1 + x + x2 + x 3 + is not a polynomial, since it doesn t have finite degree. g(x) is an example of a power series.
 6 Polynomial Rings We introduce a class of rings called the polynomial rings, describing computation, factorization and divisibility in such rings For the case where the coefficients come from an integral
6 Polynomial Rings We introduce a class of rings called the polynomial rings, describing computation, factorization and divisibility in such rings For the case where the coefficients come from an integral
1 Implicit Differentiation
 MATH 1010E University Mathematics Lecture Notes (week 5) Martin Li 1 Implicit Differentiation Sometimes a function is defined implicitly by an equation of the form f(x, y) = 0, which we think of as a relationship
MATH 1010E University Mathematics Lecture Notes (week 5) Martin Li 1 Implicit Differentiation Sometimes a function is defined implicitly by an equation of the form f(x, y) = 0, which we think of as a relationship
Intro to Rings, Fields, Polynomials: Hardware Modeling by Modulo Arithmetic
 Intro to Rings, Fields, Polynomials: Hardware Modeling by Modulo Arithmetic Priyank Kalla Associate Professor Electrical and Computer Engineering, University of Utah kalla@ece.utah.edu http://www.ece.utah.edu/~kalla
Intro to Rings, Fields, Polynomials: Hardware Modeling by Modulo Arithmetic Priyank Kalla Associate Professor Electrical and Computer Engineering, University of Utah kalla@ece.utah.edu http://www.ece.utah.edu/~kalla
8 Appendix: Polynomial Rings
 8 Appendix: Polynomial Rings Throughout we suppose, unless otherwise specified, that R is a commutative ring. 8.1 (Largely) a reminder about polynomials A polynomial in the indeterminate X with coefficients
8 Appendix: Polynomial Rings Throughout we suppose, unless otherwise specified, that R is a commutative ring. 8.1 (Largely) a reminder about polynomials A polynomial in the indeterminate X with coefficients
4 Hilbert s Basis Theorem and Gröbner basis
 4 Hilbert s Basis Theorem and Gröbner basis We define Gröbner bases of ideals in multivariate polynomial rings and see how they work in tandem with the division algorithm. We look again at the standard
4 Hilbert s Basis Theorem and Gröbner basis We define Gröbner bases of ideals in multivariate polynomial rings and see how they work in tandem with the division algorithm. We look again at the standard
Intermediate Math Circles February 26, 2014 Diophantine Equations I
 Intermediate Math Circles February 26, 2014 Diophantine Equations I 1. An introduction to Diophantine equations A Diophantine equation is a polynomial equation that is intended to be solved over the integers.
Intermediate Math Circles February 26, 2014 Diophantine Equations I 1. An introduction to Diophantine equations A Diophantine equation is a polynomial equation that is intended to be solved over the integers.
Example: This theorem is the easiest way to test an ideal (or an element) is prime. Z[x] (x)
![Example: This theorem is the easiest way to test an ideal (or an element) is prime. Z[x] (x) Example: This theorem is the easiest way to test an ideal (or an element) is prime. Z[x] (x)](/thumbs/96/126601816.jpg) Math 4010/5530 Factorization Theory January 2016 Let R be an integral domain. Recall that s, t R are called associates if they differ by a unit (i.e. there is some c R such that s = ct). Let R be a commutative
Math 4010/5530 Factorization Theory January 2016 Let R be an integral domain. Recall that s, t R are called associates if they differ by a unit (i.e. there is some c R such that s = ct). Let R be a commutative
Gröbner Bases. eliminating the leading term Buchberger s criterion and algorithm. construct wavelet filters
 Gröbner Bases 1 S-polynomials eliminating the leading term Buchberger s criterion and algorithm 2 Wavelet Design construct wavelet filters 3 Proof of the Buchberger Criterion two lemmas proof of the Buchberger
Gröbner Bases 1 S-polynomials eliminating the leading term Buchberger s criterion and algorithm 2 Wavelet Design construct wavelet filters 3 Proof of the Buchberger Criterion two lemmas proof of the Buchberger
Lecture 7.5: Euclidean domains and algebraic integers
 Lecture 7.5: Euclidean domains and algebraic integers Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Modern Algebra M. Macauley
Lecture 7.5: Euclidean domains and algebraic integers Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Modern Algebra M. Macauley
Name: Solutions Final Exam
 Instructions. Answer each of the questions on your own paper. Be sure to show your work so that partial credit can be adequately assessed. Put your name on each page of your paper. 1. [10 Points] All of
Instructions. Answer each of the questions on your own paper. Be sure to show your work so that partial credit can be adequately assessed. Put your name on each page of your paper. 1. [10 Points] All of
Math 615: Lecture of January 10, 2007
 Math 615: Lecture of January 10, 2007 The definition of lexicographic order is quite simple, but the totally ordered set that one gets is not even if there are only two variables one has 1 < x 2 < x 2
Math 615: Lecture of January 10, 2007 The definition of lexicographic order is quite simple, but the totally ordered set that one gets is not even if there are only two variables one has 1 < x 2 < x 2
Algorithms for Algebraic Geometry
 Chapter 2 Algorithms for Algebraic Geometry Outline: 1. Gröbner basics. 39 47 9 2. Algorithmic applications of Gröbner bases. 48 56 9 3. Resultants and Bézout s Theorem. 57 69 13 4. Solving equations with
Chapter 2 Algorithms for Algebraic Geometry Outline: 1. Gröbner basics. 39 47 9 2. Algorithmic applications of Gröbner bases. 48 56 9 3. Resultants and Bézout s Theorem. 57 69 13 4. Solving equations with
Abstract Algebra for Polynomial Operations. Maya Mohsin Ahmed
 Abstract Algebra for Polynomial Operations Maya Mohsin Ahmed c Maya Mohsin Ahmed 2009 ALL RIGHTS RESERVED To my students As we express our gratitude, we must never forget that the highest appreciation
Abstract Algebra for Polynomial Operations Maya Mohsin Ahmed c Maya Mohsin Ahmed 2009 ALL RIGHTS RESERVED To my students As we express our gratitude, we must never forget that the highest appreciation
M3P23, M4P23, M5P23: COMPUTATIONAL ALGEBRA & GEOMETRY REVISION SOLUTIONS
 M3P23, M4P23, M5P23: COMPUTATIONAL ALGEBRA & GEOMETRY REVISION SOLUTIONS (1) (a) Fix a monomial order. A finite subset G = {g 1,..., g m } of an ideal I k[x 1,..., x n ] is called a Gröbner basis if (LT(g
M3P23, M4P23, M5P23: COMPUTATIONAL ALGEBRA & GEOMETRY REVISION SOLUTIONS (1) (a) Fix a monomial order. A finite subset G = {g 1,..., g m } of an ideal I k[x 1,..., x n ] is called a Gröbner basis if (LT(g
Lecture Notes Math 371: Algebra (Fall 2006) by Nathanael Leedom Ackerman
 Lecture Notes Math 371: Algebra (Fall 2006) by Nathanael Leedom Ackerman October 17, 2006 TALK SLOWLY AND WRITE NEATLY!! 1 0.1 Integral Domains and Fraction Fields 0.1.1 Theorems Now what we are going
Lecture Notes Math 371: Algebra (Fall 2006) by Nathanael Leedom Ackerman October 17, 2006 TALK SLOWLY AND WRITE NEATLY!! 1 0.1 Integral Domains and Fraction Fields 0.1.1 Theorems Now what we are going
Divisibility. Def: a divides b (denoted a b) if there exists an integer x such that b = ax. If a divides b we say that a is a divisor of b.
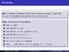 Divisibility Def: a divides b (denoted a b) if there exists an integer x such that b ax. If a divides b we say that a is a divisor of b. Thm: (Properties of Divisibility) 1 a b a bc 2 a b and b c a c 3
Divisibility Def: a divides b (denoted a b) if there exists an integer x such that b ax. If a divides b we say that a is a divisor of b. Thm: (Properties of Divisibility) 1 a b a bc 2 a b and b c a c 3
Math 203A - Solution Set 1
 Math 203A - Solution Set 1 Problem 1. Show that the Zariski topology on A 2 is not the product of the Zariski topologies on A 1 A 1. Answer: Clearly, the diagonal Z = {(x, y) : x y = 0} A 2 is closed in
Math 203A - Solution Set 1 Problem 1. Show that the Zariski topology on A 2 is not the product of the Zariski topologies on A 1 A 1. Answer: Clearly, the diagonal Z = {(x, y) : x y = 0} A 2 is closed in
4 Powers of an Element; Cyclic Groups
 4 Powers of an Element; Cyclic Groups Notation When considering an abstract group (G, ), we will often simplify notation as follows x y will be expressed as xy (x y) z will be expressed as xyz x (y z)
4 Powers of an Element; Cyclic Groups Notation When considering an abstract group (G, ), we will often simplify notation as follows x y will be expressed as xy (x y) z will be expressed as xyz x (y z)
1. Factorization Divisibility in Z.
 8 J. E. CREMONA 1.1. Divisibility in Z. 1. Factorization Definition 1.1.1. Let a, b Z. Then we say that a divides b and write a b if b = ac for some c Z: a b c Z : b = ac. Alternatively, we may say that
8 J. E. CREMONA 1.1. Divisibility in Z. 1. Factorization Definition 1.1.1. Let a, b Z. Then we say that a divides b and write a b if b = ac for some c Z: a b c Z : b = ac. Alternatively, we may say that
Lecture 2. The Euclidean Algorithm and Numbers in Other Bases
 Lecture 2. The Euclidean Algorithm and Numbers in Other Bases At the end of Lecture 1, we gave formulas for the greatest common divisor GCD (a, b), and the least common multiple LCM (a, b) of two integers
Lecture 2. The Euclidean Algorithm and Numbers in Other Bases At the end of Lecture 1, we gave formulas for the greatest common divisor GCD (a, b), and the least common multiple LCM (a, b) of two integers
Toric Ideals, an Introduction
 The 20th National School on Algebra: DISCRETE INVARIANTS IN COMMUTATIVE ALGEBRA AND IN ALGEBRAIC GEOMETRY Mangalia, Romania, September 2-8, 2012 Hara Charalambous Department of Mathematics Aristotle University
The 20th National School on Algebra: DISCRETE INVARIANTS IN COMMUTATIVE ALGEBRA AND IN ALGEBRAIC GEOMETRY Mangalia, Romania, September 2-8, 2012 Hara Charalambous Department of Mathematics Aristotle University
COMMUTATIVE RINGS. Definition 3: A domain is a commutative ring R that satisfies the cancellation law for multiplication:
 COMMUTATIVE RINGS Definition 1: A commutative ring R is a set with two operations, addition and multiplication, such that: (i) R is an abelian group under addition; (ii) ab = ba for all a, b R (commutative
COMMUTATIVE RINGS Definition 1: A commutative ring R is a set with two operations, addition and multiplication, such that: (i) R is an abelian group under addition; (ii) ab = ba for all a, b R (commutative
Solution Sheet (i) q = 5, r = 15 (ii) q = 58, r = 15 (iii) q = 3, r = 7 (iv) q = 6, r = (i) gcd (97, 157) = 1 = ,
 Solution Sheet 2 1. (i) q = 5, r = 15 (ii) q = 58, r = 15 (iii) q = 3, r = 7 (iv) q = 6, r = 3. 2. (i) gcd (97, 157) = 1 = 34 97 21 157, (ii) gcd (527, 697) = 17 = 4 527 3 697, (iii) gcd (2323, 1679) =
Solution Sheet 2 1. (i) q = 5, r = 15 (ii) q = 58, r = 15 (iii) q = 3, r = 7 (iv) q = 6, r = 3. 2. (i) gcd (97, 157) = 1 = 34 97 21 157, (ii) gcd (527, 697) = 17 = 4 527 3 697, (iii) gcd (2323, 1679) =
x 3 2x = (x 2) (x 2 2x + 1) + (x 2) x 2 2x + 1 = (x 4) (x + 2) + 9 (x + 2) = ( 1 9 x ) (9) + 0
 1. (a) i. State and prove Wilson's Theorem. ii. Show that, if p is a prime number congruent to 1 modulo 4, then there exists a solution to the congruence x 2 1 mod p. (b) i. Let p(x), q(x) be polynomials
1. (a) i. State and prove Wilson's Theorem. ii. Show that, if p is a prime number congruent to 1 modulo 4, then there exists a solution to the congruence x 2 1 mod p. (b) i. Let p(x), q(x) be polynomials
Computational methods in the study of symplectic quotients
 Computational methods in the study of symplectic quotients Hans-Christian Herbig, UFRJ and Christopher Seaton, Rhodes College Instituto de Matemática Aplicado, Universidade Federal do Rio de Janeiro January
Computational methods in the study of symplectic quotients Hans-Christian Herbig, UFRJ and Christopher Seaton, Rhodes College Instituto de Matemática Aplicado, Universidade Federal do Rio de Janeiro January
Math 0310 Final Exam Review
 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the linear equation and check the solution. 1) 13(x - 52) = 26 1) A) {26} B) {52} C) {50} D)
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the linear equation and check the solution. 1) 13(x - 52) = 26 1) A) {26} B) {52} C) {50} D)
Factorization in Polynomial Rings
 Factorization in Polynomial Rings Throughout these notes, F denotes a field. 1 Long division with remainder We begin with some basic definitions. Definition 1.1. Let f, g F [x]. We say that f divides g,
Factorization in Polynomial Rings Throughout these notes, F denotes a field. 1 Long division with remainder We begin with some basic definitions. Definition 1.1. Let f, g F [x]. We say that f divides g,
On the minimal free resolution of a monomial ideal.
 On the minimal free resolution of a monomial ideal. Caitlin M c Auley August 2012 Abstract Given a monomial ideal I in the polynomial ring S = k[x 1,..., x n ] over a field k, we construct a minimal free
On the minimal free resolution of a monomial ideal. Caitlin M c Auley August 2012 Abstract Given a monomial ideal I in the polynomial ring S = k[x 1,..., x n ] over a field k, we construct a minimal free
Number Theory Math 420 Silverman Exam #1 February 27, 2018
 Name: Number Theory Math 420 Silverman Exam #1 February 27, 2018 INSTRUCTIONS Read Carefully Time: 50 minutes There are 5 problems. Write your name neatly at the top of this page. Write your final answer
Name: Number Theory Math 420 Silverman Exam #1 February 27, 2018 INSTRUCTIONS Read Carefully Time: 50 minutes There are 5 problems. Write your name neatly at the top of this page. Write your final answer
Lecture 7.4: Divisibility and factorization
 Lecture 7.4: Divisibility and factorization Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Modern Algebra M. Macauley (Clemson)
Lecture 7.4: Divisibility and factorization Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Modern Algebra M. Macauley (Clemson)
WORKSHEET MATH 215, FALL 15, WHYTE. We begin our course with the natural numbers:
 WORKSHEET MATH 215, FALL 15, WHYTE We begin our course with the natural numbers: N = {1, 2, 3,...} which are a subset of the integers: Z = {..., 2, 1, 0, 1, 2, 3,... } We will assume familiarity with their
WORKSHEET MATH 215, FALL 15, WHYTE We begin our course with the natural numbers: N = {1, 2, 3,...} which are a subset of the integers: Z = {..., 2, 1, 0, 1, 2, 3,... } We will assume familiarity with their
Summer Project. August 10, 2001
 Summer Project Bhavana Nancherla David Drescher August 10, 2001 Over the summer we embarked on a brief introduction to various concepts in algebraic geometry. We used the text Ideals, Varieties, and Algorithms,
Summer Project Bhavana Nancherla David Drescher August 10, 2001 Over the summer we embarked on a brief introduction to various concepts in algebraic geometry. We used the text Ideals, Varieties, and Algorithms,
Ch 7 Summary - POLYNOMIAL FUNCTIONS
 Ch 7 Summary - POLYNOMIAL FUNCTIONS 1. An open-top box is to be made by cutting congruent squares of side length x from the corners of a 8.5- by 11-inch sheet of cardboard and bending up the sides. a)
Ch 7 Summary - POLYNOMIAL FUNCTIONS 1. An open-top box is to be made by cutting congruent squares of side length x from the corners of a 8.5- by 11-inch sheet of cardboard and bending up the sides. a)
Homework #2 solutions Due: June 15, 2012
 All of the following exercises are based on the material in the handout on integers found on the class website. 1. Find d = gcd(475, 385) and express it as a linear combination of 475 and 385. That is
All of the following exercises are based on the material in the handout on integers found on the class website. 1. Find d = gcd(475, 385) and express it as a linear combination of 475 and 385. That is
2 Lecture 2: Logical statements and proof by contradiction Lecture 10: More on Permutations, Group Homomorphisms 31
 Contents 1 Lecture 1: Introduction 2 2 Lecture 2: Logical statements and proof by contradiction 7 3 Lecture 3: Induction and Well-Ordering Principle 11 4 Lecture 4: Definition of a Group and examples 15
Contents 1 Lecture 1: Introduction 2 2 Lecture 2: Logical statements and proof by contradiction 7 3 Lecture 3: Induction and Well-Ordering Principle 11 4 Lecture 4: Definition of a Group and examples 15
Definitions. Notations. Injective, Surjective and Bijective. Divides. Cartesian Product. Relations. Equivalence Relations
 Page 1 Definitions Tuesday, May 8, 2018 12:23 AM Notations " " means "equals, by definition" the set of all real numbers the set of integers Denote a function from a set to a set by Denote the image of
Page 1 Definitions Tuesday, May 8, 2018 12:23 AM Notations " " means "equals, by definition" the set of all real numbers the set of integers Denote a function from a set to a set by Denote the image of
THE REGULAR ELEMENT PROPERTY
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 126, Number 7, July 1998, Pages 2123 2129 S 0002-9939(98)04257-9 THE REGULAR ELEMENT PROPERTY FRED RICHMAN (Communicated by Wolmer V. Vasconcelos)
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 126, Number 7, July 1998, Pages 2123 2129 S 0002-9939(98)04257-9 THE REGULAR ELEMENT PROPERTY FRED RICHMAN (Communicated by Wolmer V. Vasconcelos)
PREMUR Seminar Week 2 Discussions - Polynomial Division, Gröbner Bases, First Applications
 PREMUR 2007 - Seminar Week 2 Discussions - Polynomial Division, Gröbner Bases, First Applications Day 1: Monomial Orders In class today, we introduced the definition of a monomial order in the polyomial
PREMUR 2007 - Seminar Week 2 Discussions - Polynomial Division, Gröbner Bases, First Applications Day 1: Monomial Orders In class today, we introduced the definition of a monomial order in the polyomial
Practice problems for first midterm, Spring 98
 Practice problems for first midterm, Spring 98 midterm to be held Wednesday, February 25, 1998, in class Dave Bayer, Modern Algebra All rings are assumed to be commutative with identity, as in our text.
Practice problems for first midterm, Spring 98 midterm to be held Wednesday, February 25, 1998, in class Dave Bayer, Modern Algebra All rings are assumed to be commutative with identity, as in our text.
Part IX. Factorization
 IX.45. Unique Factorization Domains 1 Part IX. Factorization Section IX.45. Unique Factorization Domains Note. In this section we return to integral domains and concern ourselves with factoring (with respect
IX.45. Unique Factorization Domains 1 Part IX. Factorization Section IX.45. Unique Factorization Domains Note. In this section we return to integral domains and concern ourselves with factoring (with respect
Finite Fields. Mike Reiter
 1 Finite Fields Mike Reiter reiter@cs.unc.edu Based on Chapter 4 of: W. Stallings. Cryptography and Network Security, Principles and Practices. 3 rd Edition, 2003. Groups 2 A group G, is a set G of elements
1 Finite Fields Mike Reiter reiter@cs.unc.edu Based on Chapter 4 of: W. Stallings. Cryptography and Network Security, Principles and Practices. 3 rd Edition, 2003. Groups 2 A group G, is a set G of elements
Elementary Properties of the Integers
 Elementary Properties of the Integers 1 1. Basis Representation Theorem (Thm 1-3) 2. Euclid s Division Lemma (Thm 2-1) 3. Greatest Common Divisor 4. Properties of Prime Numbers 5. Fundamental Theorem of
Elementary Properties of the Integers 1 1. Basis Representation Theorem (Thm 1-3) 2. Euclid s Division Lemma (Thm 2-1) 3. Greatest Common Divisor 4. Properties of Prime Numbers 5. Fundamental Theorem of
Math 611 Homework 6. Paul Hacking. November 19, All rings are assumed to be commutative with 1.
 Math 611 Homework 6 Paul Hacking November 19, 2015 All rings are assumed to be commutative with 1. (1) Let R be a integral domain. We say an element 0 a R is irreducible if a is not a unit and there does
Math 611 Homework 6 Paul Hacking November 19, 2015 All rings are assumed to be commutative with 1. (1) Let R be a integral domain. We say an element 0 a R is irreducible if a is not a unit and there does
Math 210B. Artin Rees and completions
 Math 210B. Artin Rees and completions 1. Definitions and an example Let A be a ring, I an ideal, and M an A-module. In class we defined the I-adic completion of M to be M = lim M/I n M. We will soon show
Math 210B. Artin Rees and completions 1. Definitions and an example Let A be a ring, I an ideal, and M an A-module. In class we defined the I-adic completion of M to be M = lim M/I n M. We will soon show
Section 19 Integral domains
 Section 19 Integral domains Instructor: Yifan Yang Spring 2007 Observation and motivation There are rings in which ab = 0 implies a = 0 or b = 0 For examples, Z, Q, R, C, and Z[x] are all such rings There
Section 19 Integral domains Instructor: Yifan Yang Spring 2007 Observation and motivation There are rings in which ab = 0 implies a = 0 or b = 0 For examples, Z, Q, R, C, and Z[x] are all such rings There
Handout - Algebra Review
 Algebraic Geometry Instructor: Mohamed Omar Handout - Algebra Review Sept 9 Math 176 Today will be a thorough review of the algebra prerequisites we will need throughout this course. Get through as much
Algebraic Geometry Instructor: Mohamed Omar Handout - Algebra Review Sept 9 Math 176 Today will be a thorough review of the algebra prerequisites we will need throughout this course. Get through as much
Selected Math 553 Homework Solutions
 Selected Math 553 Homework Solutions HW6, 1. Let α and β be rational numbers, with α 1/2, and let m > 0 be an integer such that α 2 mβ 2 = 1 δ where 0 δ < 1. Set ǫ:= 1 if α 0 and 1 if α < 0. Show that
Selected Math 553 Homework Solutions HW6, 1. Let α and β be rational numbers, with α 1/2, and let m > 0 be an integer such that α 2 mβ 2 = 1 δ where 0 δ < 1. Set ǫ:= 1 if α 0 and 1 if α < 0. Show that
Algebraic Varieties. Chapter Algebraic Varieties
 Chapter 12 Algebraic Varieties 12.1 Algebraic Varieties Let K be a field, n 1 a natural number, and let f 1,..., f m K[X 1,..., X n ] be polynomials with coefficients in K. Then V = {(a 1,..., a n ) :
Chapter 12 Algebraic Varieties 12.1 Algebraic Varieties Let K be a field, n 1 a natural number, and let f 1,..., f m K[X 1,..., X n ] be polynomials with coefficients in K. Then V = {(a 1,..., a n ) :
WORKSHEET ON NUMBERS, MATH 215 FALL. We start our study of numbers with the integers: N = {1, 2, 3,...}
 WORKSHEET ON NUMBERS, MATH 215 FALL 18(WHYTE) We start our study of numbers with the integers: Z = {..., 2, 1, 0, 1, 2, 3,... } and their subset of natural numbers: N = {1, 2, 3,...} For now we will not
WORKSHEET ON NUMBERS, MATH 215 FALL 18(WHYTE) We start our study of numbers with the integers: Z = {..., 2, 1, 0, 1, 2, 3,... } and their subset of natural numbers: N = {1, 2, 3,...} For now we will not
4 Number Theory and Cryptography
 4 Number Theory and Cryptography 4.1 Divisibility and Modular Arithmetic This section introduces the basics of number theory number theory is the part of mathematics involving integers and their properties.
4 Number Theory and Cryptography 4.1 Divisibility and Modular Arithmetic This section introduces the basics of number theory number theory is the part of mathematics involving integers and their properties.
Polynomial interpolation over finite fields and applications to list decoding of Reed-Solomon codes
 Polynomial interpolation over finite fields and applications to list decoding of Reed-Solomon codes Roberta Barbi December 17, 2015 Roberta Barbi List decoding December 17, 2015 1 / 13 Codes Let F q be
Polynomial interpolation over finite fields and applications to list decoding of Reed-Solomon codes Roberta Barbi December 17, 2015 Roberta Barbi List decoding December 17, 2015 1 / 13 Codes Let F q be
1 Lecture # 1: Gröbner bases.
 Gröbner Bases: a Tutorial Mike Stillman These notes are based on lectures given in Berkeley at M.S.R.I. in August 1998. They are meant to be an elementary introduction to the very useful notion of a Gröbner
Gröbner Bases: a Tutorial Mike Stillman These notes are based on lectures given in Berkeley at M.S.R.I. in August 1998. They are meant to be an elementary introduction to the very useful notion of a Gröbner
Homework 6 Solution. Math 113 Summer 2016.
 Homework 6 Solution. Math 113 Summer 2016. 1. For each of the following ideals, say whether they are prime, maximal (hence also prime), or neither (a) (x 4 + 2x 2 + 1) C[x] (b) (x 5 + 24x 3 54x 2 + 6x
Homework 6 Solution. Math 113 Summer 2016. 1. For each of the following ideals, say whether they are prime, maximal (hence also prime), or neither (a) (x 4 + 2x 2 + 1) C[x] (b) (x 5 + 24x 3 54x 2 + 6x
Non-commutative reduction rings
 Revista Colombiana de Matemáticas Volumen 33 (1999), páginas 27 49 Non-commutative reduction rings Klaus Madlener Birgit Reinert 1 Universität Kaiserslautern, Germany Abstract. Reduction relations are
Revista Colombiana de Matemáticas Volumen 33 (1999), páginas 27 49 Non-commutative reduction rings Klaus Madlener Birgit Reinert 1 Universität Kaiserslautern, Germany Abstract. Reduction relations are
CHAPTER 10: POLYNOMIALS (DRAFT)
 CHAPTER 10: POLYNOMIALS (DRAFT) LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN The material in this chapter is fairly informal. Unlike earlier chapters, no attempt is made to rigorously
CHAPTER 10: POLYNOMIALS (DRAFT) LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN The material in this chapter is fairly informal. Unlike earlier chapters, no attempt is made to rigorously
Section III.6. Factorization in Polynomial Rings
 III.6. Factorization in Polynomial Rings 1 Section III.6. Factorization in Polynomial Rings Note. We push several of the results in Section III.3 (such as divisibility, irreducibility, and unique factorization)
III.6. Factorization in Polynomial Rings 1 Section III.6. Factorization in Polynomial Rings Note. We push several of the results in Section III.3 (such as divisibility, irreducibility, and unique factorization)
D-MATH Algebra I HS18 Prof. Rahul Pandharipande. Solution 6. Unique Factorization Domains
 D-MATH Algebra I HS18 Prof. Rahul Pandharipande Solution 6 Unique Factorization Domains 1. Let R be a UFD. Let that a, b R be coprime elements (that is, gcd(a, b) R ) and c R. Suppose that a c and b c.
D-MATH Algebra I HS18 Prof. Rahul Pandharipande Solution 6 Unique Factorization Domains 1. Let R be a UFD. Let that a, b R be coprime elements (that is, gcd(a, b) R ) and c R. Suppose that a c and b c.
, a 1. , a 2. ,..., a n
 CHAPTER Points to Remember :. Let x be a variable, n be a positive integer and a 0, a, a,..., a n be constants. Then n f ( x) a x a x... a x a, is called a polynomial in variable x. n n n 0 POLNOMIALS.
CHAPTER Points to Remember :. Let x be a variable, n be a positive integer and a 0, a, a,..., a n be constants. Then n f ( x) a x a x... a x a, is called a polynomial in variable x. n n n 0 POLNOMIALS.
Polynomial Rings. i=0
 Polynomial Rings 4-15-2018 If R is a ring, the ring of polynomials in x with coefficients in R is denoted R[x]. It consists of all formal sums a i x i. Here a i = 0 for all but finitely many values of
Polynomial Rings 4-15-2018 If R is a ring, the ring of polynomials in x with coefficients in R is denoted R[x]. It consists of all formal sums a i x i. Here a i = 0 for all but finitely many values of
Math 547, Exam 2 Information.
 Math 547, Exam 2 Information. 3/19/10, LC 303B, 10:10-11:00. Exam 2 will be based on: Homework and textbook sections covered by lectures 2/3-3/5. (see http://www.math.sc.edu/ boylan/sccourses/547sp10/547.html)
Math 547, Exam 2 Information. 3/19/10, LC 303B, 10:10-11:00. Exam 2 will be based on: Homework and textbook sections covered by lectures 2/3-3/5. (see http://www.math.sc.edu/ boylan/sccourses/547sp10/547.html)
CS280, Spring 2004: Prelim Solutions
 CS280, Spring 2004: Prelim Solutions 1. [3 points] What is the transitive closure of the relation {(1, 2), (2, 3), (3, 1), (3, 4)}? Solution: It is {(1, 2), (2, 3), (3, 1), (3, 4), (1, 1), (2, 2), (3,
CS280, Spring 2004: Prelim Solutions 1. [3 points] What is the transitive closure of the relation {(1, 2), (2, 3), (3, 1), (3, 4)}? Solution: It is {(1, 2), (2, 3), (3, 1), (3, 4), (1, 1), (2, 2), (3,
PROBLEM SET 1 SOLUTIONS 1287 = , 403 = , 78 = 13 6.
 Math 7 Spring 06 PROBLEM SET SOLUTIONS. (a) ( pts) Use the Euclidean algorithm to find gcd(87, 0). Solution. The Euclidean algorithm is performed as follows: 87 = 0 + 78, 0 = 78 +, 78 = 6. Hence we have
Math 7 Spring 06 PROBLEM SET SOLUTIONS. (a) ( pts) Use the Euclidean algorithm to find gcd(87, 0). Solution. The Euclidean algorithm is performed as follows: 87 = 0 + 78, 0 = 78 +, 78 = 6. Hence we have
ALGEBRAIC GEOMETRY COURSE NOTES, LECTURE 2: HILBERT S NULLSTELLENSATZ.
 ALGEBRAIC GEOMETRY COURSE NOTES, LECTURE 2: HILBERT S NULLSTELLENSATZ. ANDREW SALCH 1. Hilbert s Nullstellensatz. The last lecture left off with the claim that, if J k[x 1,..., x n ] is an ideal, then
ALGEBRAIC GEOMETRY COURSE NOTES, LECTURE 2: HILBERT S NULLSTELLENSATZ. ANDREW SALCH 1. Hilbert s Nullstellensatz. The last lecture left off with the claim that, if J k[x 1,..., x n ] is an ideal, then
MATH 361: NUMBER THEORY TENTH LECTURE
 MATH 361: NUMBER THEORY TENTH LECTURE The subject of this lecture is finite fields. 1. Root Fields Let k be any field, and let f(x) k[x] be irreducible and have positive degree. We want to construct a
MATH 361: NUMBER THEORY TENTH LECTURE The subject of this lecture is finite fields. 1. Root Fields Let k be any field, and let f(x) k[x] be irreducible and have positive degree. We want to construct a
3 The fundamentals: Algorithms, the integers, and matrices
 3 The fundamentals: Algorithms, the integers, and matrices 3.4 The integers and division This section introduces the basics of number theory number theory is the part of mathematics involving integers
3 The fundamentals: Algorithms, the integers, and matrices 3.4 The integers and division This section introduces the basics of number theory number theory is the part of mathematics involving integers
1. Algebra 1.5. Polynomial Rings
 1. ALGEBRA 19 1. Algebra 1.5. Polynomial Rings Lemma 1.5.1 Let R and S be rings with identity element. If R > 1 and S > 1, then R S contains zero divisors. Proof. The two elements (1, 0) and (0, 1) are
1. ALGEBRA 19 1. Algebra 1.5. Polynomial Rings Lemma 1.5.1 Let R and S be rings with identity element. If R > 1 and S > 1, then R S contains zero divisors. Proof. The two elements (1, 0) and (0, 1) are
Algebraic structures I
 MTH5100 Assignment 1-10 Algebraic structures I For handing in on various dates January March 2011 1 FUNCTIONS. Say which of the following rules successfully define functions, giving reasons. For each one
MTH5100 Assignment 1-10 Algebraic structures I For handing in on various dates January March 2011 1 FUNCTIONS. Say which of the following rules successfully define functions, giving reasons. For each one
ABSTRACT. HEWITT, CHRISTINA M. Real Roots of Polynomials with Real Coefficients. (Under the direction of Dr. Michael Singer).
 ABSTRACT HEWITT, CHRISTINA M. Real Roots of Polynomials with Real Coefficients. (Under the direction of Dr. Michael Singer). Polynomial equations are used throughout mathematics. When solving polynomials
ABSTRACT HEWITT, CHRISTINA M. Real Roots of Polynomials with Real Coefficients. (Under the direction of Dr. Michael Singer). Polynomial equations are used throughout mathematics. When solving polynomials
Math 312/ AMS 351 (Fall 17) Sample Questions for Final
 Math 312/ AMS 351 (Fall 17) Sample Questions for Final 1. Solve the system of equations 2x 1 mod 3 x 2 mod 7 x 7 mod 8 First note that the inverse of 2 is 2 mod 3. Thus, the first equation becomes (multiply
Math 312/ AMS 351 (Fall 17) Sample Questions for Final 1. Solve the system of equations 2x 1 mod 3 x 2 mod 7 x 7 mod 8 First note that the inverse of 2 is 2 mod 3. Thus, the first equation becomes (multiply
ADVANCED TOPICS IN ALGEBRAIC GEOMETRY
 ADVANCED TOPICS IN ALGEBRAIC GEOMETRY DAVID WHITE Outline of talk: My goal is to introduce a few more advanced topics in algebraic geometry but not to go into too much detail. This will be a survey of
ADVANCED TOPICS IN ALGEBRAIC GEOMETRY DAVID WHITE Outline of talk: My goal is to introduce a few more advanced topics in algebraic geometry but not to go into too much detail. This will be a survey of
MATH 115, SUMMER 2012 LECTURE 4 THURSDAY, JUNE 21ST
 MATH 115, SUMMER 2012 LECTURE 4 THURSDAY, JUNE 21ST JAMES MCIVOR Today we enter Chapter 2, which is the heart of this subject. Before starting, recall that last time we saw the integers have unique factorization
MATH 115, SUMMER 2012 LECTURE 4 THURSDAY, JUNE 21ST JAMES MCIVOR Today we enter Chapter 2, which is the heart of this subject. Before starting, recall that last time we saw the integers have unique factorization
Reversely Well-Ordered Valuations on Polynomial Rings in Two Variables
 Reversely Well-Ordered Valuations on Polynomial Rings in Two Variables Edward Mosteig Loyola Marymount University Los Angeles, California, USA Workshop on Valuations on Rational Function Fields Department
Reversely Well-Ordered Valuations on Polynomial Rings in Two Variables Edward Mosteig Loyola Marymount University Los Angeles, California, USA Workshop on Valuations on Rational Function Fields Department
Counting Zeros over Finite Fields with Gröbner Bases
 Counting Zeros over Finite Fields with Gröbner Bases Sicun Gao May 17, 2009 Contents 1 Introduction 2 2 Finite Fields, Nullstellensatz and Gröbner Bases 5 2.1 Ideals, Varieties and Finite Fields........................
Counting Zeros over Finite Fields with Gröbner Bases Sicun Gao May 17, 2009 Contents 1 Introduction 2 2 Finite Fields, Nullstellensatz and Gröbner Bases 5 2.1 Ideals, Varieties and Finite Fields........................
Math.3336: Discrete Mathematics. Primes and Greatest Common Divisors
 Math.3336: Discrete Mathematics Primes and Greatest Common Divisors Instructor: Dr. Blerina Xhabli Department of Mathematics, University of Houston https://www.math.uh.edu/ blerina Email: blerina@math.uh.edu
Math.3336: Discrete Mathematics Primes and Greatest Common Divisors Instructor: Dr. Blerina Xhabli Department of Mathematics, University of Houston https://www.math.uh.edu/ blerina Email: blerina@math.uh.edu
Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers Solutions
 Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers Solutions Warm-up Problems 1. What is a prime number? Give an example of an even prime number and an odd prime number. A prime number
Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers Solutions Warm-up Problems 1. What is a prime number? Give an example of an even prime number and an odd prime number. A prime number
Answers of the MATH97 Practice Test Form A
 Answers of the MATH97 Practice Test Form A A1) Answer B Section 1.2: concepts of solution of the equations. Pick the pair which satisfies the equation 4x+y=10. x= 1 and y=6 A2) Answer A Section 1.3: select
Answers of the MATH97 Practice Test Form A A1) Answer B Section 1.2: concepts of solution of the equations. Pick the pair which satisfies the equation 4x+y=10. x= 1 and y=6 A2) Answer A Section 1.3: select
