Bounded error flowpipe computation of parameterized linear systems

Transcription

1 Boundd rror flowpip compuaion of paramrizd linar sysms Raan Lal IMDEA Sofwar Insiu, Madrid, Spain Pavihra Prabhakar IMDEA Sofwar Insiu, Madrid, Spain ABSTRACT W considr problm of compuing a boundd rror approximaion of soluion ovr a boundd im [0, T ], of a paramrizd linar sysm, ẋ() = Ax(), whr A is consraind by a compac polyhdron Ω. Our mhod consiss of sampling im domain [0, T ] as wll as paramr spac Ω consrucing a coninuous picwis bilinar funcion which inrpolas soluion of paramrizd sysm a s sampl poins. Mor prcisly, givn an ɛ > 0, w compu a sampling inrval δ > 0, such ha picwis bilinar funcion obaind from sampl poins is wihin ɛ of original rajcory. W prsn xprimnal rsuls which suggs ha our mhod is scalabl. Cagoris Subjc Dscripors D.2.4 Sofwar/Program Vrificaion [Formal mhods]: Gnral Trms Algorihms, Vrificaion, Exprimnaion Kywords Formal modling vrificaion, absracions, boundd rror approximaions, paramrizd linar dynamical sysms 1. INTRODUCTION Hybrid sysms ar sysms which xhibi mixd discrconinuous bhaviors aris naurally in modlling mbddd sysms which consis of sofwar, a discr sysm, inracing wih a coninuous physical sysm. In his papr, w invsiga a fundamnal problm in safy vrificaion of hybrid sysms, namly, compuaion of rachabl s of a coninuous dynamical sysm. Rachabl s compuaion is a primiiv rquird in boh absracion basd safy analysis [3, 2, 8] symbolic sa-spac xploraion basd fixpoin compuaion [12, 6]. Givn a coninuous dynamical sysm, w ar inrsd in compuing s of all poins rachd by is soluions saring from a givn s of iniial sas wihin a givn im inrval. In paricular, on is inrsd in a rprsnaion of rachabl s, for which opraions such as inrscion mpinss chcking can b fficinly prformd. Evn for linar dynamical sysm ẋ() = Ax(), whr drivaiv of xcuion a any im dpnds linarly on sa a ha im, soluion is an xponnial funcion x() = A x(0), which can no, for insanc, b rprsnd in firs ordr ory of rals wih addiion muliplicaion. I nds xponniaion in ory, for which dcidabiliy of saisfiabiliy is unknown. Hnc, rsarch focus has shifd owards compuaion of igh ovrapproximaions of rachabl ss. On s of chniqus for compuing ovrapproximaion of rachabl ss is basd on flowpip compuaion. Hr, soluion of dynamical sysm is valuad a crain sampl ims, which is n usd o compu an nvlop flowpip around soluion. This has bn xnsivly invsigad, spcially for linar dynamical sysms [20, 15, 12, 25], svral daa srucurs for rprsning ovrapproxima ss hav bn proposd, including zonoops, polyops, llipsoids suppor funcions. Ths chniqus hav bn xndd o non-linar sysms using Taylor modls [6]. Anor class of chniqus for compuing rach ss is basd on hybridizaion [27, 4, 9], whr sa-spac is pariiond ino a fini numbr of rgions coninuous dynamics in ach of rgions is approximad by a simplr dynamics. For insanc, in [27], a hybridizaion chniqu which approximas non-linar dynamics by rcangular dynamics is prsnd. Finally, dduciv approachs for compuing invarians by solving for cofficins of mplas hav bn invsigad [26, 30]. In his papr, w considr problm of compuing rachabl s of a paramrizd linar sysm, ha is, ẋ() = Ax(), whr A Ω is a squar marix Ω is a compac polyhdral s. Hr, marix A is no fixd, bu aks valus from a s Ω, which can b inrprd as a s of prurbaions o which sysm nds o b robus. This is an inrsing class of sysms, which ar usful, for insanc, in modling dynamics of wo dimnsional robo moion which is paramrizd by angular vlociy. This is usd in [23] o capur dynamics of an aircraf, is givn by following paramrizd linar sysm, whr x = (x 1, x 2) is posiion of aircraf in

2 wo dimnsional plan, d = (d 1, d 2) is vlociy. ẋ 1 x 1 ẋ 2 d 1 = x ω d ω 0 d 2 d 2 Hr, ω is angular vlociy, which is a paramr ha changs dpnding on mod of airplan. In paricular, som complicad compuaion is usd o s is valu during a mod chang. Hnc, valu of ω is no known a priori, howvr, a bound on is valu can b infrrd. Our broad chniqu for approximaing soluion of paramrizd linar sysm is as follows. L Φ(x 0, A, ) b soluion of ẋ() = Ax(), whr x X 0 is a s of iniial sas, A Ω is a s of prurbaion marics, [0, T ] is im inrval. W sampl boh paramr spac Ω im domain [0, T ] using a sampl inrval δ. W compu soluion Φ(x 0, A, ) of diffrnial quaion a s sampl poins (A, ), consruc a picwis coninuous funcion approximaing Φ by inrpolaing a sampl valus. Th approxima funcion ˆΦ is a picwis bilinar funcion which is picwis linar in im marix paramrs A, approximas Φ o wihin δ. Hnc, safy vrificaion of paramrizd linar sysms can b rducd o problm of solving bilinar consrains. This class of consrains has bn xnsivly sudid in conx of bilinar marix inqualiis (BMIs) [13, 16] givn imporanc of his class in solving conrol ory problms, r ar svral ools [18] which hav bn dvlopd for sam. Th main highlighs of papr ar: 1. A mhod for compuing boundd rror approximaions of rachabl s for paramrizd linar sysms. 2. Our mhod consrucs a funcion which approximas soluions of paramrizd linar sysm, hnc, conains mor informaion han ha providd by an ovrapproxima rach s. 3. In paricular, approxima picwis bilinar funcion conains informaion abou rlaion bwn im sa of sysm, which is crucial for composiional vrificaion. 4. Th algorihm for consrucion of boundd rror approximaion is fficin as illusrad by xprimnal rsuls, approxima funcion is fficinly analysabl. Rlad work. Th problm of rachabl s compuaion of linar dynamical sysms wih uncrain inpus ẋ = Ax+ Bu, whr inpu u U blongs o a compac s, has bn invsigad in svral works [15, 17, 5]. Howvr, paprs invsigaing paramrizd linar dynamical sysms whr A blongs o a prurbaion s Ω is limid. For insanc, [1] invsigas a slighly mor gnral class of sysms whr marix A() is im varying. In conras, w assum ha onc a marix is chosn, i is fixd. Howvr, r ar fundamnal diffrncs in approachs of [1] ours. Whil w prsn an algorihm which sampls paramr spac, consrucs a picwis bilinar funcion approximaing soluions, mhod in [1] approximas ransiion rlaion by a zonoop using inrval arihmic [31, 29]. In anor dircion, our mhod xplicily aims o consruc an approximaion for a givn rror bound. Though rror bounds can b obaind for rachabl s compuaion of or mhods, i is no sraighforward o compu an approximaion for a givn bound on rror, implmnaions of sam do no xis. For insanc, in [1], o find an approximaion wihin an rror bound of ɛ, on would nd o iraiv ovr diffrn dgrs of polynomials o runca Taylor xpansion unil rror sima providd dcrass o wihin ɛ. Robus conrol [11] is a branch of conrol ory ha dals wih conrol dsign in prsnc of uncrainy. Whil robus conrol dals wih sabiliy prformanc, our mhod sudis safy propris. drach [19] is anor rachabiliy analysis ool ha ncods xcuions of soluion as a formula in a ory wih ordinary diffrnial quaions chcks for saisfiabiliy using ool dral [14]. Howvr, o bs of our knowldg, i dos no addrss paramrizd dynamical sysms. In his papr, w compar our work wih ha of [1] which considrs paramrizd linar sysms. Though or algorihms basd on flowpip consrucion [7, 12, 24] hybridizaion [4] can possibly b xndd o paramrizd sysms, w ar no awar of sam. Organizaion of papr. This papr is organizd as follows. Scion 2 dfins som basic noaions usd in rs of x. Scion 3 formulas boundd rror rach s compuaion problm for paramrizd linar sysm. Scion 4 prsns sampling basd algorihm for compuing approxima funcion sas is corrcnss; daild proof is movd o Scion 8. Scion 5 discusss xprimnal rsuls comparison wih or ools. Scion 6 xplains safy vrificaion wih bilinar approximaion. In Scion 7, w prsn conclusion fuur work. 2. PRELIMINARIES Numbrs funcions. L R, R 0 Z dno s of ral numbrs, non-ngaiv ral numbrs ingrs, rspcivly. L [n] dno s {1,..., n}. Givn a funcion F : A B A A, F (A ) rprsns s {F (a) a A }. Euclidan Spac Norms. W us R n o dno n-dimnsional Euclidan spac. Givn x R n, (x) i dnos projcion of x on i-h componn ha is, if x = (x 1, x 2,..., x n) n (x) i = x i. In his papr, w us infiniy norms on vcors. Givn x R n, l x = max { (x) 1, (x) 2,..., (x) n }

3 dno infiniy norm, whr x i dnos absolu valu of x i. Givn x R n ɛ > 0, w us B ɛ(x) o dno an ɛ-ball around x, ha is, B ɛ(x) = {x x x ɛ}. Givn a s of vcors, w also dfin an opraion which dfins poinwis absolu maximum. Givn X R n X = {x 1, x 2,..., x m}, for 1 i n, (X) i = { (x 1) i, (x 2) i,..., (x m) i } M(X) = (max (X) 1,..., max (X) n ). Givn wo ss X 1, X 2 R n, l d H(X 1, X 2) dno Hausdorff disanc bwn wo ss i is dfind as: d H(X 1, X 2) = max( sup inf x y, sup inf x y ). y X 2 y X 1 x X 1 x X 2 Finally, w dfin grid poins of Y wih prcision γ o b vrics of grid lmns wih prcision γ which hav a non-mpy inrscion wih Y. GP(Y, γ) = Vr(Z). Z Grid(Y,γ) 3. REACHABLE SET COMPUTATION PROB- LEM In his scion, w dfin approxima rachabl s compuaion problm. L us considr a paramrizd linar dynamical sysm of form ẋ() = Ax(), x(0) X 0 R n, A Ω, [0, T ] (1) whr X 0 Ω R n2 ar compac polyhdral ss, A is an n n dimnsional marix [0, T ] is im domain of inrs. Marics Norms. L us us M[i, j] o rprsn lmn of marix M R n n corrsponding o i-h row j-h column. W us I o dno idniy marix J o dno uni marix (a marix wih all 1 nris). W dfin Hadamard produc on marics. Givn M, M R n n, M M R n n such ha (M M )[i, j] = M[i, j]m [i, j]. W will us M o dno inducd infiniy norm of M, ha is, M = sup { Mx x R n, x = 1}. Th inducd infiniy norm of a marix can b compud using following propry: n M = max M[i, j]. 1 i m j=1 Polyhdral ss. W us Vr(P ) o dno vrics of a compac polyhdral s. Grids. W will nd an opraion which grids a givn s basd on a sampling priod γ. L GE(γ, d) dno s of all rcangular ss obaind by gridding spac R d wih prcision γ; w assum ha gridding sars a origin. GE(γ, d) = {Z Z = Π i [d] [k iγ, (k i + 1)γ], k i Z}. W rfr o lmns of GE(γ, d) as grid lmns. Evry grid lmn can b spcifid using wo vcors of appropria dimnsion. Givn Z = Π i [d] [k iγ, (k i + 1)γ], w us Z Z o rprsn minimum maximum poins in lmn, namly, Z = (k 1γ,..., k d γ), Z = ((k 1 + 1)γ,..., (k d + 1)γ). Givn a s Y R d γ > 0, w us Grid(Y, γ) o b s of all grid lmns wih prcision γ which hav a non-mpy inrscion wih Y. Grid(Y, γ) = {Z Z GE(γ, d), Z = Z Y, Z }. Dfiniion 1. Th sa of Sysm 1 saring from an iniial sa x(0) X 0 for a marix A Ω a im is givn by sa ransiion funcion i is dfind as: Φ(x(0), A, ) = A x(0) Nx, w dfin s of sas rachabl using a soluion of dynamical sysm. Dfiniion 2. L X 0, Ω b as in Sysm 1. L F : X 0 Ω [0, T ] R n. Th rachabl s of F is givn by Rach F (X 0, Ω, [0, T ]) = { F (x(0), A, ) x(0) X0, A Ω, [0, T ] } (2) W wan o compu an ovr-approximaion of rachabl s Rach Φ(X 0, Ω, [0, T ]). Morovr, w wan o nsur ha ovr-approximaion is no oo consrvaiv. Furr, ovr-approxima s should b rprsnd using a formalism in which Boolan opraions (inrscion, union, c.) mpinss chcking can b compuaionally prformd. Problm 1. Compu a s ha Rach Φ(X 0, Ω, [0, T ]) Rach Φ(X 0, Ω, [0, T ]) such Rach Φ(X 0, Ω, [0, T ]), d H( Rach Φ(X 0, Ω, [0, T ]), Rach Φ(X 0, Ω, [0, T ])) ɛ. Our broad approach is o consruc a picwis bilinar funcion Φ ɛ/2 which is wihin ɛ/2 of Φ, xp is rach s by an ɛ/2. Proposiion 1. L Φ ɛ b such ha for all x(0) X 0, A Ω [0, T ], Φ ɛ(x(0), A, ) Φ(x(0), A, ) ɛ. (3) Thn, Rach Φ(X 0, Ω, [0, T ]) B ɛ(rach Φɛ (X 0, Ω, [0, T ])), d H(Rach Φ(X 0, Ω, [0, T ]), B ɛ(rach Φɛ (X 0, Ω, [0, T ]))) 2ɛ

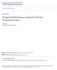
4 Paramrizdlinar linarsysms sysms Paramrizd Hnc, by choosing Main ida: Main ida: \ Rach Φ (X0, Ω, [0, T ]) (x0(x,!,0,)!, ) = B /2 (RachΦ /2 (X0, Ω, [0, T ])), Sampl spac s. In Sampl boh paramr spac w boh obain an paramr ovr-approximaion of rachabl squl, w focus on compuaion of approximaim domain! im domain! ion funcion Φ. d linar sysms!! TION ForFor! In his scion, w prsn an algorihm which aks as inpu a bound on rror compus funcion φ which saisfis inqualiy in 3. This is givn in Algorihm 2. ha i suffics singl iniial sa for![! 2Firs, [!!1w,!show 2,[21(x,o02fix,],!,a ) 2 ] of φ [ ], 1, compuaion 2 ]. 1 Thn, w prsn a sampling basd algorihm o compu picwis affin approximaion of!! φ saring from a singl 1 poin Figur 1: Illusraion of sampling!!, = ) = x0 x0 0, ) (x0(x,!, ˆ (xˆ0(x ) = + (1 ) ) }+}+ 0,!,,!, ) = [ [{ { + (1 Rducion o a singl iniial poin! ! } ] x 0 +approximaion (1 ) ) (1o(1compu ) { )boundd { +rror (1 }func] x0 W show how ion φ saisfying inqualiy 3 for a compac polyhdral s ns!1, assuming 2 2 w know = how!o boundd rror ap1 compu 0= whr whr =X =!!!2 saring s. No ha funcion for a1 singlon 2 proxima X0 is s of convx combinaions of is P vrics, ha is, X0 = {α1 v αk vk i, αi [0, 1], i αi = 1}, whr Figur 1: Illusraion of sampling vi s ar is vrics. Consruc a picwis bilinar funcion ERROR Consruc bilinar funcion 4.a picwis ALGORITHM FOR BOUNDED inrpolaing valus afunction sampl poins APPROXIMATE COMPUTAinrpolaing valus a sampl poins! !2 1!1!1 2 1!2!2! ! Figur 2: Approximaion Figur 2: Approxima funcion consrucion (x0,!, ) = x0 Main chnical challng: Main chnical challng:,, v } b Proposiion 2. L V = {v vrics Rducion o a singl Compuaion 4.2 Compuaion offf of4.1 compac polyhdral s Xoiniial. an For ipoin [k],max{ lmax{ F :, TT} T }of 1 2 Finding corrsponding 4.2, T Finding corrsponding o an }+ T show compu boundd rror approximaion func 4 T ΩW [0, T ] how Ro b such ha Now, w focus on compuaion of a funcion F which ) n 2 2 ion k i saisfying inqualiy 3 for a compac polyhdral s kfi (A, ) )k A Ω, [0, Trror ]. i, A,how know wφ(v o,compu boundd ap} ] x0x0, assuming!p 1 proxima s. No ha For any x funcion X0 givnfor by ax singlon = i αi vsaring i, dfin: X0 is s of convx combinaions of is vrics, ha is, X P! ) = X0 = { 1 v1 +.φ..(x, + 1], = 1}, whr A,k 2v k 8i, iα2 i F[0, i2(a, ). i i 1 vi s ar is vrics. i Thn, φ saisfis inqualiy 3. max{ Proposiion 2. L V0 = {v1,, vk } b vrics of wcompac polyhdral sox0approxima. For i 2 [k], l Fi : Nx, show ha i suffics a funcion [0,isTindpndn ]! Rn b such hainiial sa. L us dfin a which of as follows:t funcion kf Fi (A,, ) T (vi,}a, )k, T 8A 2, 2 [0, T ]. 4 F(A, ) = A, A (4) P Ω, [0, T ] For any x 2 X0 givn by x = i i vi, dfin: "18 X n n ) = i F:i (A, (x,aa, Problm 2. Find funcion F Ω ).[0, T ] R, such ha for all A Ω, [0, Ti], Thn, saisfiskfinqualiy 3. (A, ) F (A, )k. Proposiion Lixsuffics Lapproxima a funcion Nx, w show 3. ha 0 X0. o which is indpndn of iniial sa. L us dfin a kf (A, ) F (A, )k /kx0 k, A Ω, [0, T ] funcion F as follows: Thn, F (A, ) = A, 8A 2, 2 [0, T ] (4) kφ (x0, A, ) Φ(x0, A, )k, A Ω, [0, T ]. Proposiion 3. L x0 2 X0. L For a fixd x0, abov proposiion says ha i suffics o kf (A, )F o F (A, )k /kxφ. 8A 2, 2 w [0, T ] approxima approxima squl, solv 0 k, In Problm 2. Thn, k (x0, A, ) (x0, A, )k, 8A 2, 2 [0, T ]. For a fixd x0, abov proposiion says ha i suffics o approxima F o approxima. In squl, w solv Now, w focus on compuaion of a funcion F which 4 solvs Problm Problm 2.2. Our Our broad broad approach approach isis oo sampl sampl solvs "18 "18 domainofoff, F,namly, namly,ω [0, [0,TT],], compu compuaapicwis picwis domain bilinarfuncion funcionwhich whichinrpolas inrpolas valus valusofofffaas s bilinar sampl poins. Th sampl poins corrspond o vrics sampl poins. Th sampl poins corrspond o vrics rcangular rcangularss ss inin gridding griddingofof domain. domain.this This ofof illusradininfigur Figur1 1. PP: In Figur 1, w considr isisillusrad Figur 2. on dimnsion paramr spac! im horizon. W sampl1 paramr spacpoins im as shown in Figur shows sampl for horizon a on dimnsional Figur 1. Nx w sampl original soluion (x(0),!, ) sysm wih on paramr ω. A bilinar funcion is cona all sampld iniialinpoin Th srucd for ach poin of for clls as fixd illusrad Figurx(0). 2. Hr, of bilinar shown acompuaion sampl inrval [ω1, ω2 ]approximaion for paramr is spac inafigur sampl2. im inrval [1, 2 ] is considrd. Th valus of soluion of dynamical sysm a sampl poins (ω1, 1 ), (ω1, 2 ), PP: In Figur 2, w considr sampld inrval [!1,!2 ] (ω 2, 1 ) (ω2, 2 ) ar compud; s valus ar givn by ω1 1paramr ω2 1 im inrval spac ]. W compu 1, 2for for x(0), ω1 2 x(0), x(0) ω2 2[ x(0) a givn ini bilinar approximaion for sampldb inrval. L us ial sa x(0). Th approxima funcion Φ(x(0), ω, ) can considr fixd iniial poin x(0) soluion poins b!1inrprd as composiion of wo sps. Th firs 1,!1 2,!2 1,!2 2 of considrd sampld inrval. For sp consiss of consrucing a linar inrpolaion of valany! 2 [!,!2 ], 2 [1, 2 ], w compu bilinar apus along 1 paramr axis, ha is, poins ω1 1 x(0), proximaion ω2 1 ω1 2 ω1 2 x(0), x(0), x(0). Th scond sp con siss of inrpolaing valus on linar inrpolaions!!2 1 b (x(0),!, ) = ( 1 1s along im axis. Tha is, for any+ω(1 [ω1,)ω2 ], )+ [1, 2 ], b bilinar approximaion Φ(x(0), ω, ) is givn by ω1 1 ω2 1!1 2 ω1!22 2 (1 )( )+(1 α)(β + (1 ) +(1 β) ) x(0),ω2 2 )]x(0), [α(β +(1 β) whr saisfy ) = α + (1 α)2 )! ω 2=asβω 1 + whrα = β shown 1 + (1 2 1! =!1 + (1 (1in Figur β)ω2. 2. Formally, picwis bilinar funcion associad wih F Nx, w dfin picwis bilinar funcion associad corrsponding o a sampl inrval wih γ, dnod pwa(f, γ), is wih F by sampling domain prcision, dnod pwa(f, ). For Z 2 Grid(, ), [T1, T2 ] 2 Grid([0, T ], ), any [[A]] 2 Z 2 [T1, T2 ], pwa(f, )(A, ) = ( F (A1, T1 ) + (U ) F (A2, T1 )))

5 as dfind blow. Dfiniion 3. For Z Grid(Ω, γ), [T 1, T 2] Grid([0, T ], γ), any [[A]] Z [T 1, T 2], pwa(f, γ)(a, ) = α(β F(A 1, T 1) + (J β) F(A 2, T 1))) +(1 α)(β F(A 1, T 2) + (J β) F(A 2, T 2)), whr α β ar such ha = αt 1 + (1 α)t 2, A = β A 1 + (J β) A Algorihm 1: Approxfun(v, Z, [T 1, T 2], ɛ): Algorihm for compuing approximaion F ɛ for Z [T 1, T 2] Inpu: vrx poin v, a grid lmn Z, a im inrval [T 1, T 2], rror olranc ɛ > 0 Oupu: Approxima funcion Φ ɛ saisfying Inqualiy 3 bgin L α b T 2 T 1 T 2 A 1 := Z, A 2 := Z Th main challng is o compu sampling inrval γ basd on rror olranc ɛ such ha rror bwn pwa(f, γ) F is wihin ɛ. This is givn by nx orm. Thorm 1. L Ω T b as dfind by Sysm 1. Givn ɛ > 0, l γ > 0 saisfy max{γ M(Ω) γ M(Ω), γt γt ɛ } 4. M(Ω) T Thn, pwa(f, γ)(a, ) F(A, ) ɛ, A Ω, [0, T ]. Th broad ida is o compu a γ such ha funcion F in a γ-ball dos no vary by mor han ɛ. Such a γ xiss, sinc, F is a coninuous funcion. Th daild proof is givn in Scion 8. Th compl procdur for compuing Φ ɛ is dividd ino wo algorihms. For a fixd iniial poin v, a fixd grid lmn Z Grid(Ω, γ), a fixd im inrval [T 1, T 2] Grid([0, T ], γ), Algorihm 1 compus F ɛ, which nsurs ha Φ ɛ is wihin ɛ of Φ along soluion saring from v. Lins 2 4 compu xprssions for α β wih variabls ω, rspcivly. Lin 5 valuas funcion F a grid poins of Z. Lin 6 consrucs a formula rprsning approxima funcion for iniial poin v. No ha f Z,[T 1,T 2 ] is linar in boh variabls ω. Hnc F ɛ is rprsnd as a picwis bilinar funcion. Algorihm 2 compus Φ ɛ approximaion of Φ for all x in X 0 ovr im domain [0, T ] paramr spac Ω. Lin 3 compus rror olranc for approximaing F givn an rror olranc ɛ for approximaing Φ. Lins 4 5 provid condiions for choosing grid siz γ such ha pwa(f, γ)(a, ) approximas F by ɛ. Lins 6 7 corrspond o compuing grid lmns of Ω [0, T ], rspcivly. Lins 10 calls Algorihm 1 o compu bilinar funcion F ɛ. 4.3 Exampl W illusra our algorihm on aircraf dynamics from [23] givn in Scion 1, ẋ() = A(ω)x(), ω [0, 1] (5) whr A(ω) rprsns paramrizd marix in diffrnial quaion. L us ak x 0 = (1, 1, 1, 1) as a singl iniial poin, im horizon T = 1, rror olranc ɛ = nd L β[i, j] b ω i,j A 2 [i,j] A 1 [i,j] A 2 [i,j] C 1 := A 1T 1, C 2 := A 2T 1, C 3 := A 1T 2, C 4 := A 2T 2 Consruc an xprssion f Z,[T 1,T 2 ] (, ω) as (α((β C 1) + ((J β) C 2)) +(1 α)((β C 3) + ((J β) C 4))) Formula rprsning φ ɛ(v, A, ), givn by ϕ v (, ω, y), is [(T 1 T 2 A 1[i, j] ω i,j A 2[i, j]) = y = f Z,[T 1,T 2 ] (, ω)v] W g γ = 1 by solving inqualiy of Algorihm 2, Lin 5. This givs us singlon s S Ω = Grid(Ω, γ). Th grid lmn Z S Ω is rprsnd by 4 marics, A 1 = , A2 = , A 3 = , A4 = Hr, Z = A 1, Z = A 2. W consruc approxima funcion in rms of variabls, ω. For vry cll in grid of Ω [0, T ], r is a bilinar approxima funcion. Blow, w show approxima funcion pwa(f, γ)(a(ω), ) for grid Z im inrval [0, 1]. Firs, w compu xprssions for α β. α is such ha = αt 1 + (1 α)t 2 = α.0 + (1 α)1. Hnc, α = 1, 1 α = Similarly, β is such ha A = β A 1 + (J β) A 2. No ha only paramr, ω of A appars in posiions (3, 4) (4, 3) (all or valus in A 1 A 2 ar sam). Hnc, ω = β[3, 4]( 1) + (1 β[3, 4]).0 ω = β[4, 3].0 + (1 β[4, 3]).1. Thrfor, β[3, 4] = ω, β[4, 3] = 1 ω.

6 Algorihm 2: Algorihm for compuing approximaion F ɛ for Ω [0, T ] Inpu: A s of sas X 0, a s of marics Ω, im horizon T, rror olranc ɛ > 0 Oupu: Approxima funcion Φ ɛ saisfying Inqualiy 3 bgin forall v Vr(X 0) do ɛ := ɛ v Choos γ such ha, max{γ M(Ω) γ M(Ω), γt γt } S Ω := Grid(Ω, γ) S T := Grid([0, T ], γ) forall Z S Ω do forall [T 1, T 2] S T do Approxfun(v, Z, [T 1, T 2], ɛ) ɛ 4 M(Ω) T Formula rprsning φ ɛ(x, A, ), givn by ϕ(x,, ω, y), is α [ (x = i α iv i) = (y = i α iy i i ϕ v i (, ω, y i))] algorihm aks as inpu s of marics Ω (a rcangular s), rror olranc ɛ, im horizon T, iniial s of sas X 0 (spcifid using is vrics) oupus an SMT formula ncoding picwis bilinar funcion approximaing soluion Φ. 5.1 Aircraf dynamics xprimn Firs, w xprimnd on paramrizd linar dynamical sysm of aircraf dynamics in Equaion 5. In abls, w rpor n, m, T, ɛ, δ, R, which corrspond o dimnsion of marix, numbr of paramrs (0 m n 2 ), im horizon, rror olranc, sampl inrval siz, oal run im (sconds) rquird o oupu SMT formula, rspcivly. In xprimns, w valua run im sampl siz by varying im horizon T, rror olranc ɛ inrval for paramr ω. Th rsuls of xprimns ar rpord in Tabl 1. Rows T ɛ ω δ R (sc.) 1 2 1E-01 [0, 3] 3.69E E E-01 [0.5,2.5] 1.03E E E-01 [1, 2] 2.6E E E+01 [0.5, 2.5] 1.02E E E+01 [0.5, 2.5] 3.36E E E+01 [0.5, 2.5] 4.70E E E-01 [1, 2] 7.50E E E-02 [1, 2] 2.18E E E-03 [1, 2] 3.17E E nd Th approxima funcion pwa(f, γ)(a(ω), ) is, (1 ) ω ω (1 ) ω ω ω ω ω ω EXPERIMENTAL RESULTS W hav implmnd our boundd rror approximaion algorihm in Algorihm 2 in Pyhon 2.7 in ool BEAVER [21]. W rpor xprimnal valuaion of Algorihm 2, which was prformd wih Ubunu OS, Inl R Pnium(R) CPU B GHz 2 Procssor, 2GB RAM. Our Tabl 1: Aircraf dynamics xampl for n = 4, m = 1 wih varying ω, T, ɛ In Tabl 1, rows 1 3 vary inrval for paramr ω, rows 4 6 vary im horizon T, rows 7 9 vary rror olranc ɛ. Th dcras in sampl inrval siz δ incras in run im R is almos linar wih rspc o incras in inrval siz of paramr ω. Th dcras in sampl inrval siz δ incras in run im R is slighly spr wih incras in im horizon T, bcaus δ is uppr boundd by O( T ) (s Scion 5.4 ). Th dcras in δ incras in R wih rspc o dcras in ɛ is rasonably slow as wll. No ha w dcras ɛ by an ordr of magniud obain similar dcras/incras in δ R. Th xprimnal rsuls ar in accordanc wih bounds givn in Thorm Rom xprimns Nx, w xprimnd wih romly gnrad paramrizd linar dynamical sysms. W chos s Ω by choosing wo rom marics: nominal marix S whos nris ar in inrval [ 1, 1] prurbaion marix P wih lmns in inrval [0, 1]. For P, w romly chos m posiions for which prurbaion was non-zro. W rpad his xprimn 10 ims for ach variaions in im horizon T, rror olranc ɛ, dimnsion of sysm marix n, numbr of paramr m. In Tabl 2, w rpor dimnsion of sysm marix n, numbr of paramr m, im horizon T, rror olranc ɛ, (avrag) numbr of sampl poins K. avg, max min rprsns avrag running im, maximum im minimum im of 10 rom xprimns rspcivly. W firs

7 vary im horizon T (rows 1-4), n vary ɛ (rows 5-8), followd by dimnsion n (rows 9-12) numbr of paramrs m (rows 13-16). Rows n m T ɛ K max min avg E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E+01 Tabl 2: Rom marics: varying T, ɛ, n, m W obsrv a similar dpndnc of im horizon T ɛ on running im as bfor. Th variaion among max, min, avg in ach row occur du o rom marics. In addiion, w no ha numbr of paramrs affcs running im mor sharply han dimnsion islf, sinc, numbr of sampl poins grows xponnially wih numbr of paramrs. 5.3 Exprimnal comparison Nx, w compar Algorihm 2 wih algorihm in [1] which approximas ransiion rlaion corrsponding o a s of marics Ω by a zonoop using inrval arihmic. Whil r is an implmnaion of algorihm which rpors rror in rach s in on sp, i dos no ak rror olranc as inpu. Hnc, in our xprimnal comparison, w ran som romly gnrad xampls on algorihm in [1], usd rror bound obaind on xampls as rror olranc for inpu o our ool. Th xprimnal rsuls ar rpord in Tabl 3, whos columns n, m, ɛ, T R ar as bfor column ˆR rpors run-im of algorihm [1]. Rows n m ɛ T R R E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E-01 Tabl 3: Comparison bwn R R W obsrv ha our algorihm consisnly prforms br han algorihm in [1] in rms of compuaion im. W bliv rason is ha our algorihm is fin und for boundd rror approximaion compuaion, whras, ha is no ncssarily goal of [1]. On or h, igh bounds ar crucial, sinc, y dica qualiy of ovr-approximaion of rach s. Also, no ha wo approachs ar diffrn in rprsnaion of oupu rach s w rprsn i using a picwis bilinar funcion, whras algorihm in [1] oupus a s of zonoops. I would b inrsing o compar ffcs of s rprsnaions in conx of safy vrificaion. W lav his for fuur work. 5.4 Dpndncy of γ on T L us ak fixd compac paramr spac Ω rror bound ɛ 0. W considr following inqualiis from Lmma 1, Lmma 2 rspcivly, γt γt ɛ M(Ω) T (6) γ M(Ω) γ M(Ω) ɛ M(Ω) T (7) whr γ, T R 0. L us assum ha maximum valu of γ is γ 0, which saisfis Inqualiy 6 for any givn T 0. γt γt = γt (1 + γt 1! This implis, + (γt )2 2! (γ 0T ) 2 γ 0T γ 0T +... ) = (γt ) 2 γt γt W will show asympoic rlaion bwn γ 0 T. Hnc w assum ha T is larg nough saisfis M(Ω) T 1 T 1. For any M(Ω) T 1, following inqualiy holds, From Inqualiy 6, 8, 9, (8) M(Ω) T M(Ω) T (9) (γ 0T ) 2 ɛ M(Ω) T = γ0 2 ɛ M(Ω) T M(Ω) = γ 0 ɛ ɛ M(Ω) T T = γ 0 = O( T ) Similarly, i can b shown ha γ 0 = O( T ) holds for Inqualiy SAFETY VERIFICATION WITH BILIN- EAR APPROXIMATION In his scion, w discuss applicaion of approxima funcion compuaion for safy vrificaion. 6.1 Bilinar consrain solving Th approxima funcion is ncodd as a conjuncion of bilinar funcions, on corrsponding o ach cll. For safy vrificaion of paramrizd linar dynamical sysms, w nd solv bilinar consrains. This problm can b ncodd as a bilinar marix inqualiy fasibiliy problm (BMIFP) which is known o b NP-hard[13] [16]. Howvr, his is a vry rlvan problm ha ariss in conrol ory hnc, has bn invsigad xnsivly, svral spcific ools hav bn dvlopd o addrss his class of problms, for insanc, PENOPT [18]. In gnral, for hybrid sysms, ncoding for safy vrificaion may conain disjuncions as wll. In ha cas, on can us ools

8 such as Z3 [10] which can hl non-linar arihmic ovr rals. Though complxiy of solving bilinar consrain ovr ral domain is L log L log log L(md) O(n) [28], whr L is numbr of bis ndd o rprsn cofficins in snnc whos valu is o b drmind, m is numbr of polynomials in snnc, d is ir oal dgr n is numbr of variabl, our xprimns 5 wih Z3 for solving bilinar consrains showd ha i can b fficinly prformd. 6.2 Composiional Vrificaion W ncod funcion Φ ɛ(x, A, ) as a formula ϕ(x,, ω, y), whr x y ar n-upls of variabls ω consiss of n 2 variabls. Mor prcisly, if Φ ɛ(x, A, ) = y, n formula ϕ(x,, ω, y) wih x,, ω, y subsiud by x, A,, y rspcivly will b ru. Th rachabl s can b xprssd by a formula wih fr variabl Rach(z) as: x,, ω, y : x X 0, [0, T ], ω Ω, ϕ(x,, ω, y), z y ɛ. Sinc, w ovr-approxima funcion Φ insad of dircly approximaing rachabl s, w can asily prform composiional analysis. For insanc, suppos ha givn wo dynamical sysms whos soluions ar givn by Φ 1 Φ 2, w nd o compu if r xiss a im a which sas of soluions ar wihin d (a propry ofn rquird in collision avoidanc proocols). W can asily xprss his as ϕ 1 (x 1,, ω 1, y 1) ϕ 2 (x 2,, ω 2, y 2) y 1 y 2 d + ɛ, whr ϕ 1 ϕ 2 ar formulas for ɛ approximaions of Φ 1 Φ 2, rspcivly. If formula dos no hold, n w know ha sas from wo sysm ar nvr wihin disanc d. This can b vrifid, for insanc, by using an SMT solvr. Th sam analysis would no hav bn possibl if w jus had Rach(z) for wo sysms insad. 6.3 Applicaion o aircraf collision avoidanc proocol W apply our approximaion algorihm for vrificaion of aircraf collision avoidanc proocol. Th proocol consiss of four mods, namly, fr, nry, circ, xi. Th dynamics a ach mod is idnical is givn by paramrizd linar dynamical sysm Equaion 1. Th angular vlociy omga is paramr which is assignd a valu a bginning of ach mod. Th safy rquirmn of proocol is o mainain a minimum disanc bwn aircraf a all ims. W brifly skch sps in safy vrificaion of aircraf collision avoidanc proocol. Dails can b found in [22]. Firs, w approxima soluion of dynamics a ach mod wihin ɛ > 0. In addiion, w also approxima guard condiion bwn mods. Now, w prform composiion of approximaion soluions of all sas wih approximad guard condiions such ha approximaion soluion of any sa is wihin ɛ > 0 from original soluion. Nx, w prform composiional vrificaion of collision avoidanc proocol as dscribd in Subscion CONCLUSION In his papr, w prsnd an algorihm for compuing boundd rror approximaions of flow funcion rachabl s of a paramrizd linar sysm. Our algorihm consrucs a picwis bilinar approximaion of flow funcion, which capurs rlaion bwn im spac. This is paricularly hlpful in composiional analysis whr r is an implici synchronizaion of im. In fuur, w will conduc cas sudis for hybrid sysm modls wih paramrizd linar sysms as coninuous dynamics. 8. PROOFS W nd crain propris of marics. L M, M R n n x R n. P0 M + M M + M. P1 Mx M x. P2 MM M M. P3 M M. P4 If 0 M[i, j] 1 for all i, j, n M M M. P5 M+M M M M M. P6 X M(X). Proof of Proposiion 1. (Par A) If x Rach Φ(X 0, Ω, [0, T ]), n x = Φ(x(0), A, ) for som x(0) X 0, A Ω [0, T ]. Thn y = Φ ɛ(x(0), A, ) is such ha x y ɛ y Rach Φɛ (X 0, Ω, [0, T ]). Thrfor, (Par B) To show ha x B ɛ(rach Φɛ (X 0, Ω, [0, T ])). d H(Rach Φ(X 0, Ω, [0, T ]), B ɛ(rach Φɛ (X 0, Ω, [0, T ]))) 2ɛ, w nd o show ha Rach Φ(X 0, Ω, [0, T ]) B 2ɛ(B ɛ(rach Φɛ (X 0, Ω, [0, T ]))) B ɛ(rach Φɛ (X 0, Ω, [0, T ])) B 2ɛ(Rach Φ(X 0, Ω, ξ)u[0, T ]). Th firs par follows from Par A. For scond par, suppos ha x B ɛ(rach Φɛ (X 0, Ω, [0, T ])). Thn r xiss y Rach Φɛ (X 0, Ω, [0, T ]) such ha x y ɛ. Also, r xiss z Rach Φ(X 0, Ω, [0, T ]) such ha y z ɛ. Thrfor, x B 2ɛ(Rach Φ(X 0, Ω, [0, T ])). Proof of Proposiion 2. For any x X 0 givn by x = i αivi, Φ ɛ(x, A, ) Φ(x, A, ) = i α if i(a, ) Φ(x, A, ). No ha Φ(x, A, ) = A x = A ( i αivi) = i αia v i. Thrfor, Φ ɛ(x, A, ) Φ(x, A, ) = i Φ ɛ(x, A, ) Φ(x, A, ) i α i(f i(a, ) φ(v i, A, )) α iɛ = ɛ.

9 8.1 Proof of Thorm 1 Bfor proving Thorm 1, w nd o prov following lmmas. Lmma 1. L Ω T b as dfind by Sysm 1. Givn ɛ > 0, l γ > 0 saisfy γt γt ɛ. M(Ω) T For any A 1, A 2 Ω such ha A 1 A 2 γ, for any [0, T ], F(A 1, ) F(A 2, ) ɛ. Proof. L us ak A 1, A 2 Ω such ha A 1 A 2 γ. F(A 1, ) F(A 2, ) = A 1 A 2. L = A 1 A 2. Thn, from Propry P5, F(A 1, ) F(A 2, ) = A 2+ A 2 A 2. Sinc, 0 T, γ = A 1 A 2 γ, A 2 M(Ω) (from Propry P6), w hav ha F(A 1, ) F(A 2, ) γt M(Ω) γt ɛ. Th las inqualiy follows from hyposis. Lmma 2. L Ω T b as dfind by Sysm 1. Givn ɛ > 0, l γ > 0 saisfy γ M(Ω) γ M(Ω) ɛ. M(Ω) T For any 1, 2 [0, T ] such ha 1 2 γ, for any A Ω, F(A, 1) F(A, 2) ɛ. Proof. L us ak 1, 2 [0, T ] such ha 1 2 γ. Assum w.l.o.g 1 2. F(A, 1) F(A, 2) = ( A 1 A 2 ). L γ = 1 2. Thn, from Propry P5, w hav, F(A, 1) F(A, 2) = A 2+Aγ A 2 Aγ A 2 Aγ. Furr, from Propry P 3 on Aγ Aγ, w obain F(A, 1) F(A, 2) A γ A 2 A γ. Sinc A M(Ω) (from Propry P6) 0 T, w hav F(A, 1) F(A, 2) M(Ω) γ M(Ω) T M(Ω) γ ɛ. Th las inqualiy follows from hyposis. Lmma 3. L Ω T b as dfind by Sysm 1. Givn ɛ > 0, l γ > 0 saisfy max{γ M(Ω) γ M(Ω), γt γt ɛ }. M(Ω) T For any A 1, A 2 Ω, 1, 2 [0, T ] such ha A 1 A 2 γ, 1 2 γ, F(A 1, 1) F(A 2, 2) 2ɛ. Proof. L us ak A 1, A 2 Ω, 1, 2 [0, T ] such ha A 1 A 2 γ 1 2 γ. F(A 1, 1) F(A 2, 2) = ( A 1 1 A 2 ) = A 1 1 A A 1 2 A 2 2 F(A 1, 1) F(A 2, 2) A 1 1 A A 1 2 A 2 2 From hyposis, γ M(Ω) γ M(Ω) ɛ, which M(Ω) T saisfis hyposis of Lmma 2. Thrfor, A 1 1 A 1 2 ɛ. Similarly, from Lmma 1, w hav A 1 2 A 2 2 ɛ. Hnc, F(A 1, 1) F(A 2, 2) 2ɛ Proof of Thorm 1. L A Ω, [0, T ]. Thr is a grid lmn Z Grid(Ω, γ) [T 1, T 2] Grid([0, T ], γ) such ha [[A]] Z [T 1, T 2]. L A 1 =]]Z[[ A 2 =]]Z[[. Now, w can wri in rms of T 1, T 2 marix A in rms of A 1 A 2 as = αt 1 + (1 α)t 2, A = β A 1 + (J β) A 2, for som 0 α 1, 0 β[i, j] 1. Thn, pwa(f, γ)(a, ) F(A, ) = α((β A 1 1 )+ ((J β) A 2 1 )) + (1 α)((β A 1 2 ) + ((J β) A 2 2 )) (αβ + α(j β) + (1 α)β + (1 α)(j β)) F(A, ) = α(β ( A 1 1 A )) + α((j β) ( A 2 1 A )) +(1 α)(β ( A 1 2 A )) + (1 α)((j β) ( A 2 2 A )) α (β ( A 1 1 A )) +α ((J β) ( A 2 1 A )) +(1 α) (β ( A 1 2 A )) + (1 α) ((J β) ( A 2 2 A )) Sinc 0 β[i, j] 1, from Propry P4, w can ignor β in abov xprssion. Thrfor abov xprssion is uppr boundd by α ( A 1 1 A ) + α ( A 2 1 A ) +(1 α) ( A 1 2 A ) + (1 α) ( A 2 2 A ) Sinc A 1 A, A 2 A, 1, 2 γ, from Lmma 3, w hav: pwa(f, γ)(a, ) F(A, ) α(ɛ/2) + α(ɛ/2) + (1 α)(ɛ/2) + (1 α)(ɛ/2) ɛ 9. REFERENCES [1] Mahias Alhoff, Bruc H. Krogh, Olaf Sursbrg. Analyzing rachabiliy of linar dynamic sysms wih paramric uncrainis. Modling, Dsign, Simulaion of Sysms wih Uncrainis Mamaical Enginring, pags 69 94, 2011.

10 [2] Rajv Alur, Thao Dang, Franjo Ivancic. Counr-xampl guidd prdica absracion of hybrid sysms. In Tools Algorihms for Consrucion Analysis of Sysms, pags , [3] Rajv Alur, Thao Dang, Franjo Ivancic. Prdica absracion for rachabiliy analysis of hybrid sysms. ACM Transacions on Embddd Compuing Sysms, 5(1): , [4] Eugn Asarin, Thao Dang, Anoin Girard. Hybridizaion mhods for analysis of nonlinar sysms. ACTA INFORMATICA, [5] Eugn Asarin, Thao Dang, Odd Malr, Olivir Bournz. Approxima rachabiliy analysis of picwis-linar dynamical sysms. In Hybrid Sysms: Compuaion Conrol, pags 20 31, [6] Xin Chn, Erika Abraham, Sriram Sankaranarayanan. Taylor modl flowpip consrucion for non-linar hybrid sysms. In Procdings of IEEE Ral-Tim Sysms Symposium, [7] Xin Chn, Erika Abraham, Sriram Sankaranarayanan. Flow*: An analyzr for non-linar hybrid sysms. In Procdings of Inrnaional Confrnc on Compur Aidd Vrificaion, [8] Edmund M. Clark, Ansgar Fhnkr, Zhi Han, Bruc H. Krogh, Joël Ouaknin, Olaf Sursbrg, Michal Thobald. Absracion counrxampl-guidd rfinmn in modl chcking of hybrid sysms. In. J. Found. Compu. Sci., 14(4): , [9] T. Dang, O. Malr, R. Tsylir. Accura hybridizaion of nonlinar sysms. In Hybrid Sysms: Compuaion Conrol, pags 11 20, [10] Lonardo Mndonça d Moura Nikolaj Bjørnr. Z3: an fficin SMT solvr. In Tools Algorihms for Consrucion Analysis of Sysms, pags , [11] Gir E. Dullrud Frno G. Paganini. A cours in robus conrol ory : a convx approach. Txs in applid mamaics. Springr, Nw York, [12] Goran Frhs, Colas L Gurnic, Alxr Donzé, Sco Coon, Rajarshi Ray, Olivir Lbll, Rodolfo Ripado, Anoin Girard, Thao Dang, Odd Malr. Spacx: Scalabl vrificaion of hybrid sysms. In Procdings of Inrnaional Confrnc on Compur Aidd Vrificaion, [13] Miuhiro Fukuda Masakazu Kojima. Branch--cu algorihms for bilinar marix inqualiy ignvalu problm. Compuaional Opimizaion Applicaions, [14] Sicun Gao, Soonho Kong, Edmund M. Clark. dral: An SMT solvr for nonlinar oris ovr rals. In Auomad Dducion - CADE-24-24h Inrnaional Confrnc on Auomad Dducion, Lak Placid, NY, USA, Jun 9-14, Procdings, pags , [15] A. Girard. Rachabiliy of uncrain linar sysms using zonoops. In Hybrid Sysms: Compuaion Conrol, pags , [16] Ka-Choon Goh, Michal G. Safonov, Gorg P. Papavassilopoulos. Global opimizaion for biaffin marix inqualiy problm. Journal of Global Opimizaion, [17] Colas L Gurnic Anoin Girard. Rachabiliy analysis of hybrid sysms using suppor funcions. In Procdings of Inrnaional Confrnc on Compur Aidd Vrificaion, pags , [18] Michal Kocvara Michal Singl. Pnnon: Sofwar for linar nonlinar marix inqualiis. Inrnaional Sris in Opraions Rsarch Managmn Scinc, [19] Soonho Kong, Sicun Gao, Wi Chn, Edmund M. Clark. drach: δ-rachabiliy analysis for hybrid sysms. In Tools Algorihms for Consrucion Analysis of Sysms, pags , [20] A.B. Kurzhanski P. Varaiya. Ellipsoidal chniqus for rachabiliy analysis. In Hybrid Sysms: Compuaion Conrol, pags , [21] Raan Lal Pavihra Prabhakar. Bavr ool for boundd rror approxima vrificaion. hp://sofwar.imda.org/projcs/bavr/bavr.hml. [22] Raan Lal Pavihra Prabhakar. Composiional analysis of fligh collision avoidanc manuvrs using boundd rror approximaions. hp://sofwar.imda.org/projcs/bavr/publicaion.hml. [23] André Plazr Edmund M. Clark. Formal vrificaion of curvd fligh collision avoidanc manuvrs: A cas sudy. In Formal Mhods, [24] Pavihra Prabhakar Mahsh Viswanahan. A dynamic algorihm for approxima flow compuaions. In Hybrid Sysms: Compuaion Conrol, pags , [25] Pavihra Prabhakar Mahsh Viswanahan. A dynamic algorihm for approxima flow compuaions. In Hybrid Sysms: Compuaion Conrol, pags , [26] Sphn Prajna Ali Jadbabai. Safy vrificaion of hybrid sysms using barrir crificas. In Hybrid Sysms: Compuaion Conrol, [27] Anuj Puri, Vivk S. Borkar, Pravin Varaiya. Epsilon-approximaion of diffrnial inclusions. In Hybrid Sysms III: Vrificaion Conrol, Procdings of DIMACS/SYCON Workshop, Ocobr 22-25, 1995, Rugrs Univrsiy, Nw Brunswick, NJ, USA, pags , [28] Jams Rngar. On compuaional complxiy gomry of firs-ordr ory of rals, par III: quanifir liminaion. J. Symb. Compu., 13(3): , [29] S.M. Rump. INTLAB - INTrval LABoraory. In Tibor Csnds, dior, Dvlopmns in Rliabl Compuing, pags Kluwr Acadmic Publishrs, Dordrch, [30] Sriram Sankaranarayanan, Hnny Sipma, Zohar Manna. Consrucing invarians for hybrid sysms. In Hybrid Sysms: Compuaion Conrol, [31] J. Zmk. B4m: A Fr Inrval Arihmic Toolbox for Malab Basd on BIAS. Brich ds Forschungsschwrpunks Informaions- und Kommunikaionschnik