EE4.07 Coding Theory
|
|
|
- June King
- 5 years ago
- Views:
Transcription
1 EE4.07 Coding Theory W. Dai Imperial College London (IC) 2017 W. Dai (IC) EE4.07 Coding Theory 2017 page 0-1
2 Syllabus Instructor: Dr. Wei Dai Lectures: Monday 16:00-17:00, 509B (Wks 2-11, 09/10/ /12/2017) Wednesday 11:00-12:00 (Wks 2-11, 11/10/ /12/2017) 407B, Wk 3, 18/10/ A, Wks 2,4-11?? Wednesday 11:00-13:00?? Assessment: Exam (75%) and coursework (25%) Textbook: No textbook is required. You can rely on lecture notes. References: Introduction to coding theory Ron M. Roth Coding Theory: a First Course, S. Lin and C. Xing Codes: An Introduction to Information Communication and Cryptography, N. L. Biggs W. Dai (IC) EE4.07 Coding Theory Syllabus 2017 page 0-1
3 Contents 1. Mathematical foundations: finite fields 2. Cryptography Password management: store, exchange, and share Public key cryptography Digital signature 3. Error correcting codes Linear block codes Hamming codes Reed-Solomon codes and decoding 4. Modern codes Brief introduction to information theory Low-density parity check (LDPC) codes Polar codes W. Dai (IC) EE4.07 Coding Theory Syllabus 2017 page 0-2
4 Section 1 Finite Fields Basic facts Euclidean algorithm Unique factorisation theorem Finite fields: definition and construction Finite fields: general properties Primitive elements Polynomial factorisation and minimal polynomials For basic number theory, the best reference is Wikipedia. For contents relevant to finite fields, refer to Lin&Xing s book, Chapter 3. W. Dai (IC) EE4.07 Coding Theory Finite Fields 2017 page 1-1
5 Two Facts for Coding Theory Euclidean geometry: all theorems are derived from a small number of axioms. This course: mostly relies on two facts. A polynomial of degree n has at most n roots. Every positive integer n > 1 can be uniquely represented as a product of prime numbers. (will be proved.) W. Dai (IC) EE4.07 Coding Theory Finite Fields 2017 page 1-2
6 Greatest Common Divisor (GCD) How to find the gcd for 0 < b < a? gcd (5, 13) = 1. (Easy!) gcd (20, 36) = 4. (OK) But gcd (654, 2406) =? W. Dai (IC) EE4.07 Coding Theory Finite Fields Euclidean algorithm 2017 page 1-3
7 The Euclidean Algorithm Lemma 1.1 (Euclidean Algorithm) Let a, b Z +. Without loss of generality (WLOG), assume a > b. To find the greatest common divisor of a and b, a = q 1 b +r 1 b = q 2 r 1 +r 2 r 1 = q 3 r 2 +r 3... r n 2 = q n r n 1 +r n r n 1 = q n+1 r n Then d := gcd (a, b) = r n. W. Dai (IC) EE4.07 Coding Theory Finite Fields Euclidean algorithm 2017 page 1-4
8 The Euclidean Algorithm: An Example Example 1.2 gcd (654, 2406) =?: gcd (654, 2406) = = = = = = = 3 6 W. Dai (IC) EE4.07 Coding Theory Finite Fields Euclidean algorithm 2017 page 1-5
9 The Euclidean Algorithm: Theory Theorem 1.3 For 0 < b < a, define r = a mod b 0. Then gcd (a, b) = gcd (b, r). Proof: Let a = bq + r where 1 r < b. Let d 1 = gcd (a, b) and d 2 = gcd (b, r). Want to show d 1 = d 2. } d 1 a and d 1 b d 1 (a bq) d 1 r d d 2 = gcd (b, r) 1 d 2. } d 2 b and d 2 r d 2 (bq + r) d 2 a d d 1 = gcd (a, b) 2 d 1. Therefore, d 1 = d 2. Corollary 1.4 (Validation of Euclidean Alg.) In the Euclidean algorithm, gcd (a, b) = gcd (b, r 1 ) = = gcd (r n 1, r n ) = r n. W. Dai (IC) EE4.07 Coding Theory Finite Fields Euclidean algorithm 2017 page 1-6
10 Bézout s Identity Lemma 1.5 (Bézout s Identity or Bézout s Lemma) Given positive integers a and b, let d = gcd (a, b). Then d can be written as an integer linear combination of a and b, i.e., x, y Z s.t. d = gcd (a, b) = xa + yb. Proof: r n = q n r n 1 + r n 2 = q n ( q n 1 r n 2 + r n 3 ) + r n 2 = (1 + q n q n 1 ) r n 2 q n r n 3 = = xa + yb. Example 1.6 (gcd (13, 5) = 1) Euclidean Alg. 13 = = = = 2 1 Bézout s Identity 1 = 3 2 = 3 (5 3) = = 2 (13 2 5) 5 = W. Dai (IC) EE4.07 Coding Theory Finite Fields Euclidean algorithm 2017 page 1-7
11 GCD of Polynomials The GCD of two polynomials is a polynomial, of the highest degree, that divides both original polynomials. In this course, the convention is that the leading coefficient is 1. Example 1.7 gcd ( x 2 1, 2x 2 ) = { x 1, 2x 2, 1 2 x 1 2, 106 x 10 6}. By convention, gcd ( x 2 1, 2x 2 ) = x 1. W. Dai (IC) EE4.07 Coding Theory Finite Fields Euclidean algorithm 2017 page 1-8
12 Euclidean Algorithm for Polynomials Extend the Euclidean algorithm to polynomials. Example 1.8 Let a (x) = x 4 + x 2 + x + 1 and b (x) = x 2 + x. Find gcd (a (x), b (x)). Note that x 4 + x 2 + x + 1 = ( x 2 x + 2 ) ( x 2 + x ) + ( x + 1) x 2 + x = ( x 2) ( x + 1) + 2 x + 1 = ( 1 2 x + 1 2) 2. One has 2 = ( x 2 + x ) + (x + 2) ( x + 1) = b (x) + (x + 2) ( a (x) ( x 2 x + 2 ) b (x) ) = (x + 2) a (x) + ( x 3 x 2 3 ) b (x). As a result, 1 = gcd (a (x), b (x)) = 1 2 (x + 2) a (x) 1 ( 2 x 3 + x ) b (x). W. Dai (IC) EE4.07 Coding Theory Finite Fields Euclidean algorithm 2017 page 1-9
13 All Start from About 330 B.C. In Book VII of Elements, Euclid proved the following three results: Euclid s lemma: If a prime number p divides a product ab, then p divides at least one of the two numbers a and b. Fundamental theorem of arithmetic: Every natural number is either prime or else can be expressed as a product of primes in a way that is unique apart from the order in which they are written. There are infinitely many primes. W. Dai (IC) EE4.07 Coding Theory Finite Fields Unique factorisation Theorem 2017 page 1-10
14 Fundamental Theorem of Arithmetic Theorem 1.9 (Unique Factorisation Theorem) Any n Z +, n > 1, can be uniquely represented as a product of prime powers: n = p α 1 1 pα 2 2 pα k k = k i=1 pα i i Example 1.10 (Applications) If we know the factorisation of a and b, Greatest common divisor: gcd(a, b) = 2 min(a 2,b 2 ) 3 min(a 3,b 3 ) 5 min(a 5,b 5 ) 7 min(a 7,b 7) = p min(ap i,bp i ) i, Least common multiple: lcm(a, b) = 2 max(a 2,b 2 ) 3 max(a 3,b 3 ) 5 max(a 5,b 5 ) 7 max(a 7,b 7) = p max(ap i,bp i ) i. W. Dai (IC) EE4.07 Coding Theory Finite Fields Unique factorisation Theorem 2017 page 1-11
15 Some Examples Example = = = = = = gcd (4, 6) = = 2. lcm (4, 6) = = 12. gcd (4, 9) = = 1. lcm (4, 9) = = 36. gcd (654, 2406) = 6. lcm (654, 2406) = W. Dai (IC) EE4.07 Coding Theory Finite Fields Unique factorisation Theorem 2017 page 1-12
16 Proof of Unique Factorisation Theorem Existence: By induction. Assume it is true for all numbers less than n. If n is prime, n is the product of one prime n. Otherwise, a, b where n = a b and 1 < a b < n. By the induction hypothesis, a = p 1 p 2 p n and b = q 1 q 2 q m are products of primes. Then n = p 1 p 2 p n q 1 q 2 q m is the product of primes. Uniqueness: will need the Euclid s lemma. W. Dai (IC) EE4.07 Coding Theory Finite Fields Unique factorisation Theorem 2017 page 1-13
17 Euclid s Lemma Lemma 1.12 (Euclid s Lemma) Let p be a prime number. If p ab, then p a or p b (or both). Or equivalently, If p a and p b, then p ab. If p a and p ab, then p b. Proof of the last statement: Since p a, gcd (p, a) = 1. By Bézout s Identity, x, y Z s.t. xp + ya = 1. Multiply both sides by b, xpb + yab = b. Since p xpb and p ab (by assumption), it holds that p xpb + yab. Hence p b. W. Dai (IC) EE4.07 Coding Theory Finite Fields Unique factorisation Theorem 2017 page 1-14
18 Proof of Unique Factorisation Theorem (Uniqueness) Assume that n > 1 is the product of primes in two different ways: n = p 1 p 2 p m, and n = q 1 q 2 q n. We shall show m = n and that the q j are a rearrangement of the p i. WLOG, assume m n. By Euclid s lemma, p 1 must divide one of the q j. Relabel the q j if necessary, say that p 1 q 1. But q 1 is prime. Hence p 1 = q 1 so that n p 1 = p 2 p m = q 2 q n. Repeat the process, we eventually arrive at n p 1 p m = 1 = q m+1 q n. From this, it is clear that m = n and every q j is a p i. W. Dai (IC) EE4.07 Coding Theory Finite Fields Unique factorisation Theorem 2017 page 1-15
19 Gauss s Clock Arithmetic In 1801 when Gauss was 24, he wrote a book Disquisitiones Arithmeticae, one of the most influential mathematics books ever. One of the topics is finite arithmetic. Modulus of arithmetic: Count hours as 0, 1, 2,, 11. Then where stands for congruence. Similarly, (mod 12), (mod 12), (mod 12), (mod 12). It is clear that 1/5 5 (mod 12) and 7/5 11 (mod 12). However, 5/6 (mod 12) is not defined. W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-16
20 Fields: Definition Definition 1.13 (Field) A field F is a nonempty set of elements with two operations, called addition (+) and multiplication ( ). F is closed under + and, i.e., a + b and a b are in F. Commutative: a + b = b + a Associative: a + (b + c) = (a + b) + c Distributive a (b + c) = ab + ac Exists two distinct identity 0 and 1 (additive and multiplicative identities, respectively) a + 0 = a, a F a 1 = a and a 0 = 0, a F Additive inverse: a F, ( a) F, s.t. a + ( a) = 0. Multiplicative inverse: a F\ {0}, a 1 F, s.t. a a 1 = 1. Example: R, Q, Z 7 are fields, Z is not. W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-17
21 Integer Ring Definition 1.14 (Modulo) The modulo operator finds the remainder of one number divided by another. Examples: 5 mod 4 = 1, 14 mod 4 = 2. Definition 1.15 (Integer Ring) Z m = {0,, m 1}: a nonempty set of elements. + operator: + mod m operator: mod m. Example of m = 4: Z m = {0, 1, 2, 3} = 2 (mod 4); = 1 (mod 4). 3 3 = 1 (mod 4); 2 2 = 4 = 0 (mod 4). W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-18
22 Examples: Integer Rings Versus Fields Z 3 is a field. 0 = 0, 1 = 2, 2 = = 1, 2 1 = 2. Z 4 is not a field. 0 = 0, 1 = 3, 2 = 2, 3 = = 1, 2 1, 3 1 = 3. W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-19
23 When a Multiplicative Inverse Exists Lemma 1.16 (Existence of the multiplicative inverse) Let a, n Z + with a < n. The multiplicative inverse a 1 (mod n) exists iff gcd (a, n) = 1. Proof: 1. If gcd (a, n) = 1, by Bézout s identity x, y s.t. 1 = xn + ya ya (mod n). Hence y is a If a 1 (mod n) exists, want to show that gcd (a, n) = 1. Suppose not, i.e., d = gcd (a, n) > 1. By assumption that a 1 exists, x = a 1 and y s.t. 1 = xa mod n = xa yn. As d a and d n, it follows d (xa yn), i.e. d 1. This contradicts with d > 1. W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-20
24 Finite Fields of Integers Theorem 1.17 Z m is a field if and only if m is a prime. (Hence notation F p.) Proof of the if part: m be a prime Z m is a field. a Z m \ {0}, since m is a prime, one has gcd (a, m) = 1. By Lemma 1.16, a 1 exists. Proof of the only if part: Z m is a field m is a prime. Suppose m is not a prime. 1 < a, b < m s.t. a b = m. Since a = gcd (a, m) 1, by Lemma 1.16, a 1 does not exist. W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-21
25 An Alternative Proof Recall: Z m is a field if and only if m is a prime. (Hence notation F p.) Lemma 1.18 Let a, b F p. Then ab = 0 implies a = 0 or b = 0. Proof: Suppose that a 0. Then 0 = a 1 0 = a 1 (a b) = b. Alternative proof of the only if part: Suppose m is not a prime. 1 < a, b < m s.t. a b = m = 0 (mod m). But from Lemma 1.18, either a or b is zero mod m. Contradict with 1 < a, b < m. W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-22
26 Polynomials Polynomials over a field F p : f (x) = d i=0 a ix i, a i F p. Degree: highest degree of its terms: deg (f) = d if a d 0. Monic polynomials: a d = 1. Polynomial division: a (x) = q (x) b (x) + r (x) where 0 deg (r (x)) < deg (b (x)). Example: Let a (x) = x 3 + x + 1 F 2 [x] and b (x) = x 2 + x F 2 [x]. Then a (x) = (x + 1) b (x) + 1. f (x) F [x] is irreducible if f (x) = g (x) h (x), g, h F [x], implies either g or h is a constant (similar to prime numbers). W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-23
27 Finite Fields: Polynomials { F p [x]= g (x) = d i=0 a ix i : a i F p }. F p [x] /f (x): F p [x] with mod f (x) algebra. It contains all the polynomials with degree less than deg (f). Example: f (x) = x 2 + x F 2 [x]. F 2 [x] /f (x) = {0, 1, x, x + 1}. x (x + 1) = x 2 + x 0 mod f (x). Theorem 1.19 F p [x] /f (x) is a field iff f (x) is irreducible over F p. Proof: Same idea as before. W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-24
28 Some Comments Examples of Irreducible polynomials and those that are not x R [x] is irreducible. x F 2 [x] is not irreducible (reducible). x F 3 [x] is irreducible. x F 5 [x] is not irreducible. A systematic way to write the elements in a polynomial ring F p [x] /f (x) where d = deg (f (x)). α d x d + α d 1 x d α 1 x + α 0, where α i F p. It contains p d many distinct polynomials. Size of the finite field F q F q contains numbers: q = p. F q contains polynomials: q = p d where d = deg (f). W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-25
29 Example Fields Containing Polynomials Some irreducible polynomials over F 2 x, x + 1, x 2 + x + 1, x 3 + x + 1, x 3 + x 2 + 1, x 4 + x + 1, Each of these polynomial generates a finite field. Example 1.20 F 2 [x] /x 3 + x + 1 F 2 [x] /x 3 + x x x x x 2 x 2 x 2 x 3 x + 1 x x 4 x 2 + x x 2 + x + 1 x 5 x 2 + x + 1 x + 1 x 6 x x 2 + x W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-26
30 Another Example Example 1.21 (An Example of F 16 ) F 2 [x] /x 4 + x + 1 F 2 [x] /x 4 + x x 7 x 3 + x x 8 x x x x 9 x 3 + x x 2 x 2 x 10 x 2 + x + 1 x 3 x 3 x 11 x 3 + x 2 + x x 4 x + 1 x 12 x 3 + x 2 + x + 1 x 5 x 2 + x x 13 x 3 + x x 6 x 3 + x 2 x 14 x W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-27
31 Useful Exercise Example 1.22 (An Exercise) 1. Understand Examples 1.20 and For the field F 2 [x] /x 4 + x + 1 in Example 1.21, compute: ( x 3 + x 2) ( x 3 + x ) =? ( x 3 + x 2) 1 =? (Use Euclidean algorithm) Answer: x + 1. ( x 3 + x ) 1 =? (Use Euclidean algorithm) Answer: x 3 + x. Answer: x 2. W. Dai (IC) EE4.07 Coding Theory Finite Fields Definition 2017 page 1-28
32 Finite Fields: General Properties? Previously, we saw two ways to construct finite fields. F p : p many integers. F p [x] /f (x): p deg(f) many polynomials. What can we say about the size of a finite field F in general? W. Dai (IC) EE4.07 Coding Theory Finite Fields Size 2017 page 1-29
33 Characteristic: Definition Let F be an arbitrary field. By definition, a multiplicative identity, denoted by 1. Consider a sequence in F q : 1, 1 + 1, Since F q = q <, we will see repetitions. That is, t Z + s.t. 1 } + {{ + 1 } = t 1 = 0. t times Remark: To compute = t 1, we have used the algebra defined for this field F. Definition 1.23 The smallest t s.t. t 1 = 0 is called characteristic of F. W. Dai (IC) EE4.07 Coding Theory Finite Fields Size 2017 page 1-30
34 Characteristic: Property Lemma 1.24 The characteristic t is always a prime. Proof: Otherwise, t 1 = ab 1 = 0. 1st equation uses normal algebra for integers. 2nd equation uses the algebra for the finite field. This implies a = 0 or b = 0 (by Lemma 1.18). Contradict with that t is the smallest. W. Dai (IC) EE4.07 Coding Theory Finite Fields Size 2017 page 1-31
35 Finite Fields: Size Theorem 1.25 All finite fields are of the size p m. Proof: For any given finite field F q, let p be its characteristic. Choose a nonzero element from F q, say b 1. Choose another nonzero element from F q, say b 2, such that b 2 and b 1 are linearly independent, i.e., λ 1 b 1 + λ 2 b 2 = 0, λ 1, λ 2 F p λ 1 = λ 2 = 0. Consider a maximal set B = {b 1,, b m } F which are linearly independent over F p. Define the linear span of B span (B) = {λ 1 b λ m b m : λ i F p }. W. Dai (IC) EE4.07 Coding Theory Finite Fields Size 2017 page 1-32
36 Finite Fields: Size and Dimension Proof continued: 1. Then span (B) = p m F q. ( ) ( ) If λ (1) 1,, λ(1) m λ (2) 1,, λ(2) m, then λ (1) i b i λ (2) i b i. Suppose not, i.e., λ (1) i b i = λ (2) i b i. Then ( ) λ (1) i λ (2) i b i = 0 which, by linear independence of b i s, implies that ( λ (1) i = λ (2) i. ) This contradicts the assumption that λ (1) 1,, λ(1) m ( ) λ (2) 1,, λ(2) m. 2. It also holds that span (B) = F q : Otherwise b m+1 linearly independent of B. This contradicts with the definition of the maximal independent set B. Hence, for any finite field F q, q = p m. B is a basis of F q. m is the dimension of F q. W. Dai (IC) EE4.07 Coding Theory Finite Fields Size 2017 page 1-33
37 Primitive Elements a F, consider the sequence a, a 2, a 3,. Since F q = q is finite, we will see repetitions. That is, t s.t. a t = 1. Definition 1.26 The order of a F (ord (a)) is the smallest t s.t. a t = 1. An element of order q 1 is called a primitive element of F q. Example 1.27 Consider the field F 2 [x] /x 4 + x + 1 in Example It can be verified that ord (x) = ord ( x 2) = ord ( x 4) = 15. Hence x, x 2, and x 4 are primitive elements (Primitive element is not unique). It can also be verified that ord ( x 3) = 5. Hence x 3 is not a primitive element. W. Dai (IC) EE4.07 Coding Theory Finite Fields Primitive Elements 2017 page 1-34
38 Represent a Field by a Primitive Element Let α be a primitive element. Since α 0 = 1, α,, α q 2 are distinct, F = { 0, 1, α,, α q 2}. Standard notation: F = F\ {0} = { α 0,, α q 2}. Why primitive elements? Recall Example 1.22 Calculate multiplication: ( x 3 + x 2) ( x 3 + x ) =? α6 α 13 = α 19 = α 15+4 = α 4 = x + 1. Find inverse: ( x 3 + x 2) 1 ( =?; x 3 + x ) 1 =? Note that α q 1 = 1 = α 0. The multiplicative inverse of α a = α q 1 a. α 6 = α 15 6 = α 9 = x 3 + x; α 13 = x 2. W. Dai (IC) EE4.07 Coding Theory Finite Fields Primitive Elements 2017 page 1-35
39 Existence of Primitive Elements Theorem 1.28 Every finite field F q contains a primitive element. To prove this theorem, we need several lemmas. After presenting and proving these lemmas, we shall prove the theorem. W. Dai (IC) EE4.07 Coding Theory Finite Fields Primitive Elements 2017 page 1-36
40 Lemma 1: Fermat s Little Theorem Theorem 1.29 (Fermat s Little Theorem) For every β F q, we have β q 1 = 1. Or equivalently, β F q, it holds that β q = β. History (from Wikipedia): Pierre de Fermat first stated the theorem in a letter dated October 18, 1640, to his friend and confidant Frénicle de Bessy. Fermat did not prove his assertion, only stating:, the proof of which I would send to you, if I were not afraid to be too long. Euler provided the first published proof in 1736, but Leibniz had given virtually the same proof in an unpublished manuscript from sometime before (The same proof technique will be used to prove Euler s Theorem.) W. Dai (IC) EE4.07 Coding Theory Finite Fields Primitive Elements 2017 page 1-37
41 Proof of Fermat s Little Theorem Proof: For any β F q, define βf q = {ββ 1,, ββ q 1 }. ββ i 0 βf q F q. Otherwise β i = β 1 ββ i = β 1 0 = 0. A contradiction. ββ i ββ j for i j. βf q = q 1. Otherwise β i = β 1 (ββ i) = β 1 (ββ j) = β j. A contradiction. Hence, F q = βf q. Therefore, γ F q γ = γ βf q γ. That is, β 1 β 2 β q 1 = (ββ 1 ) (ββ 2 ) (ββ q 1 ) = β q 1 (β 1 β 2 β q 1 ). We conclude β q 1 = 1. W. Dai (IC) EE4.07 Coding Theory Finite Fields Primitive Elements 2017 page 1-38
42 Examples Related to Fermat s Little Theorem Example 1.30 Let F = F 5. Find F and β F for all β F. F = 1 F = {1, 2, 3, 4} 2 F = {2, 4, 1, 3} 3 F = {3, 1, 4, 2} 4 F = {4, 3, 2, 1} Example 1.31 Let F = F 2 [x] / ( x 2 + x + 1 ). Find F and β F for all β F. F = 1 F = {1, x, x + 1} x F = {x, x + 1, 1} (x + 1) F = {x + 1, 1, x} W. Dai (IC) EE4.07 Coding Theory Finite Fields Primitive Elements 2017 page 1-39
43 Existence of Primitive Elements: Lemma 2 Lemma 1.32 For any β F, if β t = 1 for some t Z +, then ord (β) t. Proof: Let a = ord (β) & t = ka + b where 0 < b < a. Then β t = β b = 1. Contradict with that a is the smallest number that β a = 1. Corollary 1.33 β F q = F q \ {0}, it holds that ord (β) q 1. Proof: This is proved by Fermat s little theorem (Theorem 1.29) and Lemma W. Dai (IC) EE4.07 Coding Theory Finite Fields Primitive Elements 2017 page 1-40
44 Existence of Primitive Elements: Lemma 3 Lemma 1.34 Suppose that ord (β 1 ) = r 1, ord (β 2 ) = r 2, and gcd (r 1, r 2 ) = 1. Let r = ord (β 1 β 2 ). Then r = r 1 r 2. Proof: 1. Since (β 1 β 2 ) r 1r 2 = 1, it holds r r 1 r 2 by Lemma r 1 r 2 r: 1 = (β 1 β 2 ) rr 1 = (β r 1 1 )r β rr 1 2 = β rr 1 2. Then r 2 rr 1. Then r 2 r. Similarly, r 1 r. Hence lcm (r 1, r 2 ) r or equivalently r 1 r 2 r. 3. That r r 1 r 2 and r 1 r 2 r implies r = r 1 r 2. W. Dai (IC) EE4.07 Coding Theory Finite Fields Primitive Elements 2017 page 1-41
45 An Example Related to Lemmas 2 & 3 Consider F = F 7. F = {1, 2, 3, 4, 5, 6} ord (1) = 1 ord (2) = 3 ord (3) = 6 ord (4) = 3 ord (5) = 6 ord (6) = 2 You may check the above results with Corollary Note that ord (2) = 3 and ord (6) = 2. Fact 1.34 implies that ord (2 6) = 3 2 = 6 = ord (5). W. Dai (IC) EE4.07 Coding Theory Finite Fields Primitive Elements 2017 page 1-42
46 Existence of Primitive Elements: the Proof (1) Proof of Theorem 1.28 (the existence): Let F q = {α 1,, α q 1 } and r i = ord (α i ). Define m := lcm (r 1,, r q 1 ). Based on the unique factorisation theorem (Theorem 1.9), m can be written as m = p k 1 1 pk l l. Let r 1 = p k(1) 1 1 p k(1) l Then r q 1. l, = p k(q 1) 1 1 p k(q 1) l ( k i = max k (1) i Hence, α i F q s.t. p k 1 1 ord (α i): l.,, k (q 1) i Let β 1 = α ord(α i)/p k 1 1 i, then ord (β 1 ) = p k 1 Similarly, find β 2,, β l. 1. ). W. Dai (IC) EE4.07 Coding Theory Finite Fields Primitive Elements 2017 page 1-43
47 Existence of Primitive Elements: the Proof (2) Let β = β 1 β l. Clearly, ord (β) = m (Lemma 1.34). ord (β i ) s are co-prime. Hence, m (q 1) (Corollary 1.33) or m q 1. On the other hand, by the definition of m, all q 1 elements in F q are roots of x m 1. Therefore m q 1. It then can be concluded that m = q 1 and β is a primitive element. W. Dai (IC) EE4.07 Coding Theory Finite Fields Primitive Elements 2017 page 1-44
48 Uniqueness of Finite Fields Definition 1.35 Two fields F and G are isomorphic if there exists a one-to-one mapping ϕ : F G that satisfies ϕ (ab) = ϕ (a) ϕ (b), ϕ (a + b) = ϕ (a) + ϕ (b). Theorem 1.36 The finite field F q is unique up to isomorphism. Proof is not required. Example: F 2 [x] / ( x 3 + x + 1 ) and F 2 [x] / ( x 3 + x ) are isomorphic. W. Dai (IC) EE4.07 Coding Theory Finite Fields Uniqueness 2017 page 1-45
49 Example ϕ : F 2 [x] / ( x 3 + x ) F 2 [y] / ( y 3 + y + 1 ) x ϕ (x) = y + 1 ϕ : F 2 [x] / ( x 3 + x ) F 2 [y] = y 3 + y x y + 1 x 2 y x y 2 x 2 + x + 1 y 2 + y + 1 x + 1 y x 2 + x y 2 + y Verify ϕ (ab) = ϕ (a) ϕ (b): ϕ ( x 2 (x + 1) ) = ϕ ( x 3 + x 2) = ϕ ( x x 2) = ϕ (1) = 1. ϕ ( x 2) ϕ (x + 1) = ( y ) y = y 3 + y = y y = 1. W. Dai (IC) EE4.07 Coding Theory Finite Fields Uniqueness 2017 page 1-46
50 Polynomial Factorisation Problem: factorise the polynomial x qm 1 1 in F q [x]. Be careful about the concept of irreducible polynomial : Have to specify the field we are considering. Example 1.37 Consider a polynomial M (x) = x M (x) is irreducible w.r.t. R. 2. M (x) is reducible w.r.t. C: M (x) = (x + j) (x j). Consider a polynomial M (x) = x 2 + x M (x) is irreducible w.r.t. F M (x) is reducible w.r.t. F 4 = F 2 [y] /y 2 + y + 1 F4 = {0, 1, y, y + 1}. M (x) = (x y) (x (y + 1)) = x 2 (y + y + 1) x + y (y + 1). W. Dai (IC) EE4.07 Coding Theory Finite Fields Polynomial Factorisation 2017 page 1-47
51 An Example of Factorisation Factorise x 3 1 R [x]: Consider the easier problem: factorise x 3 1 in C [x]. Group terms of conjugate roots x3 1 = (x 1) ( x e j2π/3) ( x e j4π/3) = (x 1) ( x 2 + x + 1 ). To factorise the polynomial x qm 1 1 in F q [x], we use the same strategy: Factorise x qm 1 1 in F q m [x]. Let α be a primitive element of Fq m: x qm 1 1 = q m 2 i=0 Group appropriate terms together: ( x α i ) (Irreducible polynomials in F q m [x]). x qm 1 1 = s k=1 M (k) (x) (Irreducible polynomials in F q [x]). W. Dai (IC) EE4.07 Coding Theory Finite Fields Polynomial Factorisation 2017 page 1-48
52 A Preview of the Final Result Example 1.38 Want to factorise x 3 1 F 2 [x]. Let α be a primitive element of F 4 = F 2 [y] /y 2 + y + 1. That is, F 4 = { 1, α, α 2} = {1, y, y + 1}. x 3 1 = (x 1) (x α) ( x α 2) = (x 1) (x y) (x (y + 1)) = (x 1) ( x 2 + x + 1 ). Both x 1 and x 2 + x + 1 are irreducible polynomial in F 2 [x]. We have obtained the factorisation of x 3 1 in F 2 [x]. W. Dai (IC) EE4.07 Coding Theory Finite Fields Polynomial Factorisation 2017 page 1-49
53 Construction of Minimal Polynomials Definition 1.39 (Cyclotomic Coset) The cyclotomic coset of q modulo n = q m 1 containing i is C i := { i q j mod n : j = 0, 1, 2, } Z n Example 1.40 Cyclotomic cosets of 2 mod 15 ( = ) are C 0 = {0}, C 1 = {1, 2, 4, 8}, C 3 = {3, 6, 12, 9}, C 5 = {5, 10}, C 7 = {7, 14, 13, 11}. Definition 1.41 (Minimal Polynomial) Let α be a primitive element of F q m. The minimal polynomial of α i in F q [x] is M (i) (x) = j C i ( x α j ), where C i is the cyclotomic coset of q modulo q m 1 containing i. W. Dai (IC) EE4.07 Coding Theory Finite Fields Polynomial Factorisation 2017 page 1-50
54 Towards Factorisation Want to show: M (i) (x) F q [x]. M (i) (x) is irreducible. x qm 1 1 = s k=1 M (k) (x) Lemma 1.42 Every F q m contains a sub-field F q. For any β F q m, β F q iff β q = β. Proof: : If β F q, by Fermat s little theorem (Theorem 1.29) β q = β. : The polynomial x q x has at most q distinct roots in F q m. As all elements in F q are roots of x q x and F q = q, it holds F q = {all roots of x q x in F q m}. W. Dai (IC) EE4.07 Coding Theory Finite Fields Polynomial Factorisation 2017 page 1-51
55 A Useful Lemma Lemma 1.43 Let p be the characteristic of F q. It holds that (x + y) p = x p + y p. Proof: (x + y) p = p ( p i=0 i) x i y p i. Clearly ( ( p 0) = p p) = 1. For any 1 i p 1, ( ) p i = p! i!(p i)! = p(p 1) (p i+1) i! Z +. Note that gcd (i!, p) = 1 but ( p i) Z +. By Euclid s Lemma (Theorem 1.12), i! (p 1) (p i + 1) and ( p i) = p s for some s Z +. By the definition of the characteristic, ( p i) = 0, 1 i p 1. Corollary 1.44 On the field F q m, (x + y) q = x q + y q. W. Dai (IC) EE4.07 Coding Theory Finite Fields Polynomial Factorisation 2017 page 1-52
56 Properties of Cyclotomic Cosets Lemma 1.45 Let C i be the cyclotomic coset of q modulo q m 1 containing i. Define qc i := {qj mod q m 1 : j C i }. Then qc i = C i. Proof: Note that i q m = i mod q m 1. It is clear that C i = { i q j mod q m 1 : j = 0, 1,, m 1 } = { i q j mod q m 1 : j = 1, 2,, m } = qc i. Corollary 1.46 Let α be a primitive element of F q m. Then M (i) (x) = j C i ( x α j ) = j C i ( x α jq ). Proof: j C i ( x α jq ) = l qc i ( x α l ) = j C i ( x α j ). W. Dai (IC) EE4.07 Coding Theory Finite Fields Polynomial Factorisation 2017 page 1-53
57 M (i) (x) F q [x] Let r = C i. Write M (i) (x) = l a lx l = j C i ( x α j ) (a) = l ( j 1,,j r l αj1 α j r l ) x l, where (a) comes from the expansion of ( j C i x α j ). At the same time, M (i) (x) = ( j C i x α j ) (a) = ( j C i x α jq ) = ( ) l j 1,,j αj 1q r l α j r lq x l (b) = l ( j 1,,j r l αj1 α j r l) q x l = l aq l xl, where (a) comes from Corollary 1.46, (b) comes from Corollary Hence, a l = a q l, which implies a l F q and M (i) (x) F q [x]. W. Dai (IC) EE4.07 Coding Theory Finite Fields Polynomial Factorisation 2017 page 1-54
58 M (i) (x) is Irreducible Step 1: For all f (x) F q [x] s.t. f ( α i) = 0, it holds that M (i) (x) f (x). Write f (x) = f 0 + f 1 x + + f n x n. For any j C i, l s.t. j = iq l mod q m 1. f ( α j) ( = f α iql) = f 0 + f 1 α iql + + f n α iql n = f ql 0 + f ql 1 αiql + + f ql n α iql n = ( f 0 + f 1 α i + + f n α in) q l = f ( α i) q l = 0. That is, α j is also a root of f. Hence, M (i) (x) f (x). Step 2: M (i) (x) is irreducible in F q [x]. Suppose not. Then M (i) (x) = g (x) h (x) for nontrivial g (x) and h (x). α i is a root of M (i) (x) α i is a root of one of g (x) and h (x). W.l.o.g., α i is a root of g (x). Then M (i) (x) g (x) which is impossible. Hence M (i) (x) is irreducible. W. Dai (IC) EE4.07 Coding Theory Finite Fields Polynomial Factorisation 2017 page 1-55
59 Representatives of Cyclotomic Cosets Definition 1.47 Consider the cyclotomic cosets of q mod n. A subset {i 1,, i j } Z n is a complete set of representatives of cyclotomic cosets if C i1 Cij = Z n. Example 1.48 Cyclotomic cosets of 2 mod 15 are C 0 = {0}, C 1 = {1, 2, 4, 8}, C 3 = {3, 6, 12, 9}, C 5 = {5, 10}, C 7 = {7, 14, 13, 11}. The complete set of representatives is {0, 1, 3, 5, 7}. W. Dai (IC) EE4.07 Coding Theory Finite Fields Polynomial Factorisation 2017 page 1-56
60 Factorisation Theorem 1.49 Let α be a primitive element of F q m. Let {i 1,, i s } be a complete set of representatives of cyclotomic cosets of q modulo q m 1. Then x qm 1 1 = q m 2 ( i=0 x α i ) = s k=1 M (ik) (x). Proof: The first equality: The degrees are the same. The coefficients before x qm 1 are the same. The roots are also the same. The second equality: holds from the definitions of M (i k) (x) and the complete set of representatives. W. Dai (IC) EE4.07 Coding Theory Finite Fields Polynomial Factorisation 2017 page 1-57
61 Section 2 Cryptography Introduction Password management: store, exchange, and secret share The public key cryptography The RSA cryptosystem The ElGamal cryptosystem Digital signature The contents are heavily based on Biggs book, Chapters 13 & 14. W. Dai (IC) EE4.07 Coding Theory Cryptography 2017 page 2-1
62 Cryptography Definition 2.1 (Cryptography) A framework of cryptography includes a set of plaintext messages M, a set of ciphertext messages C, and a set of keys K. For each k K, there is an encryption function E k : M C and the corresponding decryption function D l : C M such that D l (E k (m)) = m, for all m M. W. Dai (IC) EE4.07 Coding Theory Cryptography Introduction 2017 page 2-2
63 Cryptography: An Example One of the oldest cryptographic systems is said to have been used by Julius Caesar over two thousand years ago. Let A be the English alphabet set. Let K = {1, 2,, 25}. For a given key k K, replace each letter by the one that is k places later. For example, if k = 5, then the message SEE YOU TOMORROW becomes XJJ DTZ YTRTWWTB For the Caesar system, a simple attack is exhaustive search as there are only 25 keys. A natural extension is to use any permutation of 26 letters, yielding 26! keys. Exhaustive search is impossible. However, in this case another method, called frequency analysis, is a much more effective attack. It uses the observation that the frequencies of the English letters are fairly constant over a wide range of texts. W. Dai (IC) EE4.07 Coding Theory Cryptography Introduction 2017 page 2-3
64 Another Example: Hill s Cryptography System Consider a 29-symbol alphabet including 26 English letters, the space, comma, and full stop. It is mapped to F 29. Given a stream of symbols, split it into blocks of size n so that each block can be written as m F n 29. A key K Fn n 29 is an invertible matrix. The encryption function is given by and the decryption function is c = Km, m = K 1 c. W. Dai (IC) EE4.07 Coding Theory Cryptography Introduction 2017 page 2-4
65 Diagram of Cryptography Systems Adapted from Popular cryptography systems are built on large prime numbers. Symmetric cryptography: encryption key k = decryption key l. Asymmetric cryptography: k l. W. Dai (IC) EE4.07 Coding Theory Cryptography Introduction 2017 page 2-5
66 Existence of Large Prime Numbers Theorem: There exist infinitely many prime numbers. Proof: 1. Suppose that there exist only finitely many prime numbers. 2. List all these prime numbers, p 1, p 2,, p N. 3. Let x = p 1 p 2 p N Claim: x is a prime number. Proved by the Unique Factorisation Theorem 1.9 as gcd (p i, x) = This contradicts the assumption that the list of p 1, p 2,, p N contains all the prime numbers. W. Dai (IC) EE4.07 Coding Theory Cryptography Prime Numbers 2017 page 2-6
67 Large Prime Numbers A list of large prime numbers ( Prime When Prime When Prime When Large prime numbers matter: To check whether a 64bit number is a prime or not by brute force, how long will it take? Assume a computer can evaluate 1G (10 9 ) basic operations per second /( ) 585 years! Nowadays, a prime number between 512b and 1024b is often used. Any brute force method is impractical! W. Dai (IC) EE4.07 Coding Theory Cryptography Prime Numbers 2017 page 2-7
68 How to Store Passwords on a Server? A set of users wish to log in securely to a server. Each user choose a password. The passwords are stored in a file Should not be saved in the raw format. Easy to check whether a password is valid. Very difficult to extract the passwords from the file. Solution: use the discrete logarithmic function. W. Dai (IC) EE4.07 Coding Theory Cryptography Store Passwords 2017 page 2-8
69 The Discrete Logarithm Normal exponential function: x y = b x, Normal logarithmic function: y x = log b y. It can be solved by Taylor expansion efficiently. Definition 2.2 (Discrete logarithm problem (DLP)) Let p be a prime number and b F p be a primitive element. For any given y F p, find the x F p such that y = b x (mod p). It is well-defined if and only if b is primitive. W. Dai (IC) EE4.07 Coding Theory Cryptography Store Passwords 2017 page 2-9
70 Computation Complexity Discrete exponential function: computational complexity O (log (p)) Example: =? (mod 811) Note that 211 = One has = (mod 811). It can be achieved by computing 3 2 = 3 3 (mod 811), 3 4 = (mod 811),, 3 2k = 3 2k 1 3 2k 1 (mod 811). Discrete logarithmic function: computational complexity O (p). It is usually solved by brute force search. No sufficiently efficient algorithm in general. W. Dai (IC) EE4.07 Coding Theory Cryptography Store Passwords 2017 page 2-10
71 Examples Let p = 811 and b = 3. The output of discrete logarithmic function looks random: log 3 2 = 717; log 3 3 = 1; log 3 4 = 624; log 3 5 = 494;. 7 Normal Logarithmic Function: b=3 800 Discrete Logarithmic Function: p=811, b= y=log(x) y=dlog(x) (mod p) x x W. Dai (IC) EE4.07 Coding Theory Cryptography Store Passwords 2017 page 2-11
72 Store Passwords on a Server: A Solution The administrator chooses a prime p and a primitive element b. The values of p and b are also kept on the server. The user i chooses a password. This is converted into a number x i F p. Let y i = b x i (mod p) and the pair (i, y i ) is stored. W. Dai (IC) EE4.07 Coding Theory Cryptography Store Passwords 2017 page 2-12
73 Cryptography for Information Exchange In the previous scheme: Decoding is difficult for everyone. In the information exchange scenario, for example, Alice sends some message to Bob. Alice s information to Bob should be encrypted. Bob would like to be able to decrypt the message easily. The traditional choice: Symmetric cryptography The encryption and decryption keys are the same, i.e., k = l. The keys are known to both Alice and Bob for encryption and decryption respectively. Disadvantages: A secure channel is needed for key exchange. Disasters may happen if the key is leaked. W. Dai (IC) EE4.07 Coding Theory Cryptography Encryption Key Exchange 2017 page 2-13
74 Symmetric Key Cryptography From The key is to keep the key safe. W. Dai (IC) EE4.07 Coding Theory Cryptography Encryption Key Exchange 2017 page 2-14
75 Key Exchange Problem: Alice and Bob want to share a secret key but their information exchange could be observed by their adversary Eve. How is it possible for Alice and Bob to share a key without making it known to Eve? Solution: Diffie-Hellman key exchange. Wikipedia: The scheme was first published by Whitfield Diffie and Martin Hellman in 1976, although it had been separately invented a few years earlier within GCHQ, the British signals intelligence agency, by James H. Ellis, Clifford Cocks and Malcolm J. Williamson but was kept classified. W. Dai (IC) EE4.07 Coding Theory Cryptography Encryption Key Exchange 2017 page 2-15
76 Diffie-Hellman Key Exchange 1. Alice and Bob agree on a large prime p and an integer g mod p. The values of p and g are publicly known. 2. Alice picks a secret integer a that she does not reveal to anyone, and Bob picks an integer b that he keeps secret. They compute A = g a mod p, and B = g b mod p, respectively. They next exchange these computed values. Note that Eve sees the values of A and B. 3. Alice and Bob uses their secret integers to compute A = B a mod p, and B = A b mod p, respectively. Note that A = B = g ab is the shared secret key for information exchange. W. Dai (IC) EE4.07 Coding Theory Cryptography Encryption Key Exchange 2017 page 2-16
77 Secret Share: Motivation Secrecy-reliability tradeoff in storing an encryption key Maximum secrecy: keep a single copy of the key in one location What if it gets lost. Reliability: store multiple copies at different locations What if a copy falls into the wrong hand. Secret Sharing: (k, n) threshold scheme. Store the secret S into n pieces of encrypted words S 1,, S n such that Knowledge of any K or more S i pieces makes S easily computable. Knowledge of any k 1 or fewer S i pieces leaves S undetermined. W. Dai (IC) EE4.07 Coding Theory Cryptography Secret Share 2017 page 2-17
78 Shamir s Secret Sharing Idea of Adi Shamir s threshold scheme: k points to define a polynomial of degree k 1. 2 points are sufficient to define a line, 3 points are sufficient to define a parabola, 4 points to define a cubic curve and so forth. A (k, n) threshold scheme to share our secret S: 1. Let p be a prime number. Let n < p and S < p. 2. Randomly choose k 1 positive integers a 1,, a k 1. Set a 0 = S. 3. Set f (x) = a 0 + a 1 x + a 2 x a k 1 x k Evaluate f (x) at n points to obtain (t i, f (t i )), t i F p and i = 1,, n. Claim: given any k such pairs (t i, f (t i )), we can find the coefficients of the polynomial and therefore a 0. W. Dai (IC) EE4.07 Coding Theory Cryptography Secret Share 2017 page 2-18
79 Finding the Polynomial Coefficients Polynomial coefficients can be found via Solving the linear system: f (t i1 ) f (t i2 ). f (t ik ) = 1 t i1 t k 1 i 1 1 t i2 t k 1 i t ik t k 1 i k a 0 a 1. a k 1. Or polynomial interpolation: f (x) = k f ( ) x t il t ij. x ij x il j=1 l j W. Dai (IC) EE4.07 Coding Theory Cryptography Secret Share 2017 page 2-19
80 Cryptography for Information Exchange (2) A modern solution: Public key algorithms (Asymmetric Cryptography) Encryption key k l decryption key. The encryption key is public while the decryption key is kept secret. From W. Dai (IC) EE4.07 Coding Theory Cryptography Public Key Cryptography 2017 page 2-20
81 Comparison Comparisons of asymmetric cryptography over the symmetric one. Advantages: No secret channel is necessary for the key exchange. Less key-management problems. Only 2n keys are needed for n entities to communicate securely with one another (each entity maintains a private key and a public key). In a system based on symmetric ciphers, you would need ( n 2) = n (n 1) /2 secret keys (each pair of entities agrees on a key). More robust to brute-force attack in which all possible keys are attempted. Can provide digital signatures. Disadvantages: Much slower. The computational complexity of asymmetric cryptography is much larger. In practice, these two schemes are rarely used exclusively. For example, your browser encrypts a symmetric key using the server s public key. W. Dai (IC) EE4.07 Coding Theory Cryptography Public Key Cryptography 2017 page 2-21
82 The ElGamal Cryptography Key generation: Choose a prime p and a primitive element b F p. Private key: choose an integer a N. Public key: a = b a F p. Encryption: Alice transmits her public key a to Bob and keeps the private key a secret. Bob randomly choose t N and encrypt the message m to ( b t, ma t) Decryption: Alice can recover m via m = ma t ( b t) a = ma t a t mod p. Advantage: The random number t generates a random encryption function. W. Dai (IC) EE4.07 Coding Theory Cryptography Public Key Cryptography 2017 page 2-22
83 RSA Cryptography RSA public key cryptography: Published in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman at MIT. Key generation: Choose primes p 1 p 2. Let n = p 1 p 2 and t = (p 1 1) (p 2 1). Public key: (n, e) where 1 < e < t and gcd (e, t) = 1. Private key: d where 1 < d < t and d e mod t = 1. Find d by the Euclidean algorithm. Encryption: Bob sends his public key (n, e) to Alice and keeps the private key d secret. Alice encrypts the message m to c via c = m e mod n. Decryption: Bob can recover m from c via m = c d mod n W. Dai (IC) EE4.07 Coding Theory Cryptography Public Key Cryptography 2017 page 2-23
84 An Example Bob chooses p 1 = 47 and p 2 = 59. n = = t = = e = 157 is a valid public key as gcd (e, 2668) = 1. Use Euclidean algorithm, d = 17. To send a message m = 5, Alice computes the ciphertext c = m e = = 1044 (mod 2773). Bob deciphers the ciphertext via ˆm = c d = = 5 (mod 2773), which is the correct message. W. Dai (IC) EE4.07 Coding Theory Cryptography Public Key Cryptography 2017 page 2-24
85 Theory Behind RSA Recall Fermat s Little Theorem (Thm 1.29): a F p, a p 1 = 1 mod p Theorem 2.3 (Euler s Theorem) Let p 1 p 2 be two prime numbers. Define n := p 1 p 2 and t := (p 1 1) (p 2 1). Then a Z +, a kt+1 = a mod n, k 0 The correctness of RSA: (m e ) d = m ed = m qt+1 = m qt m = m mod n. W. Dai (IC) EE4.07 Coding Theory Cryptography Public Key Cryptography 2017 page 2-25
86 Proof of Euler s Theorem: A Lemma With a slight abuse of notation, define x = y mod p if x y = 0 mod p. Lemma 2.4 For any two positive integers x and y, if x = y mod p 1 and x = y mod p 2, then x = y mod p 1 p 2. Proof: Since x = y mod p 1 and x = y mod p 2, it is clear that x y = k 1 p 1 = k 2 p 2 for some integers k 1 and k 2. By Euclid s Lemma (Lemma 1.12), p 2 (p 1 k 1 ) and gcd (p 2, p 1 ) = 1 imply that p 2 k 1, or equivalently k 1 = k 3 p 2 for some integer k 3. Hence, x y = (k 3 p 2 ) p 1 and x y mod p 1 p 2. W. Dai (IC) EE4.07 Coding Theory Cryptography Public Key Cryptography 2017 page 2-26
87 Proof of Euler s Theorem Fix an a {1, 2,, p 1 p 2 1}. We first show that a de = a mod p 1. If p 1 a, then it is clear that a de = a + ( a de 1 ) a = a mod p 1. If p 1 a, then by Fermat s Little Theorem (Thm 1.29) a p mod p 1 and therefore a de a k(p 1 1)(p 2 1)+1 a mod p 1. Similarly a de = a mod p 2. Hence a de = a mod p 1 p 2. Euler s Theorem is therefore proved. W. Dai (IC) EE4.07 Coding Theory Cryptography Public Key Cryptography 2017 page 2-27
88 Attack Decryption is hard without the private key. Decryption is the inverse function of encryption. Uniquely defined as m = c d. Find d from public available information? d = e 1 mod t (t = (p 1 1) (p 2 1)). Without knowing the factorization n = p 1 p 2, it is difficult to find t and hence d. W. Dai (IC) EE4.07 Coding Theory Cryptography Public Key Cryptography 2017 page 2-28
89 Digital Signature: The General Principle Problem: Alice wishes to send a message m to Bob. Bob would like to verify that the message comes from Alice. In physical world, Alice sign the letter. In digital world, any fixed signature can be easily copied. General principle: Alice sends (m, y = s (m)), y = s (m) is the message dependent signature. The signature function s should kept secret. Bob checks whether m = s 1 (y). He doesn t know the signature function s. W. Dai (IC) EE4.07 Coding Theory Cryptography Digital Signature 2017 page 2-29
90 RSA Signature Scheme Let p 1 p 2, n = p 1 p 2, and t = (p 1 1) (p 2 1). Public key: (n, e) where 1 < e < t & gcd (e, t) = 1. Private key: 1 < d < t s.t. d e = 1 mod t. Sign the message: Alice computes y = s (m) = m d mod n and sends (m, y). Read the signature: If the message comes from Alice, then y e = ( m d) e = m kt+1 = m mod n. W. Dai (IC) EE4.07 Coding Theory Cryptography Digital Signature 2017 page 2-30
91 Extend ElGamal Cryptography to ElGamal Signature? RSA based schemes: In cryptography, we have D l (E k (m)). In digital signature, we have E k (D l (m)). This works as (m e ) d = ( m d) e. This principle cannot be directly applied to ElGamal scheme. W. Dai (IC) EE4.07 Coding Theory Cryptography Digital Signature 2017 page 2-31
92 ElGamal Signature Scheme Notation: x F p, let x {1, p 1} be the integer to represent x F p. Choose a prime p and a primitive element b F p. Choose a private key a N. Set the public key a = b a F p. Random choose 1 t p 1 such that gcd (t, p 1) = 1. Set u s.t. t u = 1 mod p 1. The signature function s t : M ( F p, N ) is defined by s t (m) = (i, j), where i = b t, j = u ( m a i ). The algebra in computing j is w.r.t. normal integers. That is, the multiplication and subtraction are not w.r.t. F p. (i, j) is a valid signature for the message m if a i i j = b a i b tu( m a i ) = b m in F p. W. Dai (IC) EE4.07 Coding Theory Cryptography Digital Signature 2017 page 2-32
93 Summary Factorize a product of two large prime numbers RSA public key cryptography RSA signature scheme Discrete logarithm problem Polynomial Store passwords Diffie-Hellman key exchange ElGamal public key cryptography ElGamal signature scheme Secret share W. Dai (IC) EE4.07 Coding Theory Cryptography Summary 2017 page 2-33
Lecture 5: Arithmetic Modulo m, Primes and Greatest Common Divisors Lecturer: Lale Özkahya
 BBM 205 Discrete Mathematics Hacettepe University http://web.cs.hacettepe.edu.tr/ bbm205 Lecture 5: Arithmetic Modulo m, Primes and Greatest Common Divisors Lecturer: Lale Özkahya Resources: Kenneth Rosen,
BBM 205 Discrete Mathematics Hacettepe University http://web.cs.hacettepe.edu.tr/ bbm205 Lecture 5: Arithmetic Modulo m, Primes and Greatest Common Divisors Lecturer: Lale Özkahya Resources: Kenneth Rosen,
Definition: For a positive integer n, if 0<a<n and gcd(a,n)=1, a is relatively prime to n. Ahmet Burak Can Hacettepe University
 Number Theory, Public Key Cryptography, RSA Ahmet Burak Can Hacettepe University abc@hacettepe.edu.tr The Euler Phi Function For a positive integer n, if 0
Number Theory, Public Key Cryptography, RSA Ahmet Burak Can Hacettepe University abc@hacettepe.edu.tr The Euler Phi Function For a positive integer n, if 0
Lemma 1.2. (1) If p is prime, then ϕ(p) = p 1. (2) If p q are two primes, then ϕ(pq) = (p 1)(q 1).
 1 Background 1.1 The group of units MAT 3343, APPLIED ALGEBRA, FALL 2003 Handout 3: The RSA Cryptosystem Peter Selinger Let (R, +, ) be a ring. Then R forms an abelian group under addition. R does not
1 Background 1.1 The group of units MAT 3343, APPLIED ALGEBRA, FALL 2003 Handout 3: The RSA Cryptosystem Peter Selinger Let (R, +, ) be a ring. Then R forms an abelian group under addition. R does not
Discrete mathematics I - Number theory
 Discrete mathematics I - Number theory Emil Vatai (based on hungarian slides by László Mérai) 1 January 31, 2018 1 Financed from the financial support ELTE won from the Higher Education
Discrete mathematics I - Number theory Emil Vatai (based on hungarian slides by László Mérai) 1 January 31, 2018 1 Financed from the financial support ELTE won from the Higher Education
CRYPTOGRAPHY AND NUMBER THEORY
 CRYPTOGRAPHY AND NUMBER THEORY XINYU SHI Abstract. In this paper, we will discuss a few examples of cryptographic systems, categorized into two different types: symmetric and asymmetric cryptography. We
CRYPTOGRAPHY AND NUMBER THEORY XINYU SHI Abstract. In this paper, we will discuss a few examples of cryptographic systems, categorized into two different types: symmetric and asymmetric cryptography. We
Review. CS311H: Discrete Mathematics. Number Theory. Computing GCDs. Insight Behind Euclid s Algorithm. Using this Theorem. Euclidian Algorithm
 Review CS311H: Discrete Mathematics Number Theory Instructor: Işıl Dillig What does it mean for two ints a, b to be congruent mod m? What is the Division theorem? If a b and a c, does it mean b c? What
Review CS311H: Discrete Mathematics Number Theory Instructor: Işıl Dillig What does it mean for two ints a, b to be congruent mod m? What is the Division theorem? If a b and a c, does it mean b c? What
RSA. Ramki Thurimella
 RSA Ramki Thurimella Public-Key Cryptography Symmetric cryptography: same key is used for encryption and decryption. Asymmetric cryptography: different keys used for encryption and decryption. Public-Key
RSA Ramki Thurimella Public-Key Cryptography Symmetric cryptography: same key is used for encryption and decryption. Asymmetric cryptography: different keys used for encryption and decryption. Public-Key
Lecture 1: Introduction to Public key cryptography
 Lecture 1: Introduction to Public key cryptography Thomas Johansson T. Johansson (Lund University) 1 / 44 Key distribution Symmetric key cryptography: Alice and Bob share a common secret key. Some means
Lecture 1: Introduction to Public key cryptography Thomas Johansson T. Johansson (Lund University) 1 / 44 Key distribution Symmetric key cryptography: Alice and Bob share a common secret key. Some means
Public Key 9/17/2018. Symmetric Cryptography Review. Symmetric Cryptography: Shortcomings (1) Symmetric Cryptography: Analogy
 Symmetric Cryptography Review Alice Bob Public Key x e K (x) y d K (y) x K K Instructor: Dr. Wei (Lisa) Li Department of Computer Science, GSU Two properties of symmetric (secret-key) crypto-systems: The
Symmetric Cryptography Review Alice Bob Public Key x e K (x) y d K (y) x K K Instructor: Dr. Wei (Lisa) Li Department of Computer Science, GSU Two properties of symmetric (secret-key) crypto-systems: The
Discrete Mathematics GCD, LCM, RSA Algorithm
 Discrete Mathematics GCD, LCM, RSA Algorithm Abdul Hameed http://informationtechnology.pk/pucit abdul.hameed@pucit.edu.pk Lecture 16 Greatest Common Divisor 2 Greatest common divisor The greatest common
Discrete Mathematics GCD, LCM, RSA Algorithm Abdul Hameed http://informationtechnology.pk/pucit abdul.hameed@pucit.edu.pk Lecture 16 Greatest Common Divisor 2 Greatest common divisor The greatest common
Public Key Algorithms
 Public Key Algorithms Raj Jain Washington University in Saint Louis Saint Louis, MO 63130 Jain@cse.wustl.edu Audio/Video recordings of this lecture are available at: http://www.cse.wustl.edu/~jain/cse571-09/
Public Key Algorithms Raj Jain Washington University in Saint Louis Saint Louis, MO 63130 Jain@cse.wustl.edu Audio/Video recordings of this lecture are available at: http://www.cse.wustl.edu/~jain/cse571-09/
Week 7 An Application to Cryptography
 SECTION 9. EULER S GENERALIZATION OF FERMAT S THEOREM 55 Week 7 An Application to Cryptography Cryptography the study of the design and analysis of mathematical techniques that ensure secure communications
SECTION 9. EULER S GENERALIZATION OF FERMAT S THEOREM 55 Week 7 An Application to Cryptography Cryptography the study of the design and analysis of mathematical techniques that ensure secure communications
CPSC 467b: Cryptography and Computer Security
 CPSC 467b: Cryptography and Computer Security Michael J. Fischer Lecture 11 February 21, 2013 CPSC 467b, Lecture 11 1/27 Discrete Logarithm Diffie-Hellman Key Exchange ElGamal Key Agreement Primitive Roots
CPSC 467b: Cryptography and Computer Security Michael J. Fischer Lecture 11 February 21, 2013 CPSC 467b, Lecture 11 1/27 Discrete Logarithm Diffie-Hellman Key Exchange ElGamal Key Agreement Primitive Roots
CIS 551 / TCOM 401 Computer and Network Security
 CIS 551 / TCOM 401 Computer and Network Security Spring 2008 Lecture 15 3/20/08 CIS/TCOM 551 1 Announcements Project 3 available on the web. Get the handout in class today. Project 3 is due April 4th It
CIS 551 / TCOM 401 Computer and Network Security Spring 2008 Lecture 15 3/20/08 CIS/TCOM 551 1 Announcements Project 3 available on the web. Get the handout in class today. Project 3 is due April 4th It
Cryptography IV: Asymmetric Ciphers
 Cryptography IV: Asymmetric Ciphers Computer Security Lecture 7 David Aspinall School of Informatics University of Edinburgh 31st January 2011 Outline Background RSA Diffie-Hellman ElGamal Summary Outline
Cryptography IV: Asymmetric Ciphers Computer Security Lecture 7 David Aspinall School of Informatics University of Edinburgh 31st January 2011 Outline Background RSA Diffie-Hellman ElGamal Summary Outline
Cryptography. P. Danziger. Transmit...Bob...
 10.4 Cryptography P. Danziger 1 Cipher Schemes A cryptographic scheme is an example of a code. The special requirement is that the encoded message be difficult to retrieve without some special piece of
10.4 Cryptography P. Danziger 1 Cipher Schemes A cryptographic scheme is an example of a code. The special requirement is that the encoded message be difficult to retrieve without some special piece of
INTEGERS. In this section we aim to show the following: Goal. Every natural number can be written uniquely as a product of primes.
 INTEGERS PETER MAYR (MATH 2001, CU BOULDER) In this section we aim to show the following: Goal. Every natural number can be written uniquely as a product of primes. 1. Divisibility Definition. Let a, b
INTEGERS PETER MAYR (MATH 2001, CU BOULDER) In this section we aim to show the following: Goal. Every natural number can be written uniquely as a product of primes. 1. Divisibility Definition. Let a, b
Number theory (Chapter 4)
 EECS 203 Spring 2016 Lecture 12 Page 1 of 8 Number theory (Chapter 4) Review Compute 6 11 mod 13 in an efficient way What is the prime factorization of 100? 138? What is gcd(100, 138)? What is lcm(100,138)?
EECS 203 Spring 2016 Lecture 12 Page 1 of 8 Number theory (Chapter 4) Review Compute 6 11 mod 13 in an efficient way What is the prime factorization of 100? 138? What is gcd(100, 138)? What is lcm(100,138)?
LECTURE 5: APPLICATIONS TO CRYPTOGRAPHY AND COMPUTATIONS
 LECTURE 5: APPLICATIONS TO CRYPTOGRAPHY AND COMPUTATIONS Modular arithmetics that we have discussed in the previous lectures is very useful in Cryptography and Computer Science. Here we discuss several
LECTURE 5: APPLICATIONS TO CRYPTOGRAPHY AND COMPUTATIONS Modular arithmetics that we have discussed in the previous lectures is very useful in Cryptography and Computer Science. Here we discuss several
Lecture Notes, Week 6
 YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467b: Cryptography and Computer Security Week 6 (rev. 3) Professor M. J. Fischer February 15 & 17, 2005 1 RSA Security Lecture Notes, Week 6 Several
YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467b: Cryptography and Computer Security Week 6 (rev. 3) Professor M. J. Fischer February 15 & 17, 2005 1 RSA Security Lecture Notes, Week 6 Several
Public Key Cryptography
 Public Key Cryptography Spotlight on Science J. Robert Buchanan Department of Mathematics 2011 What is Cryptography? cryptography: study of methods for sending messages in a form that only be understood
Public Key Cryptography Spotlight on Science J. Robert Buchanan Department of Mathematics 2011 What is Cryptography? cryptography: study of methods for sending messages in a form that only be understood
Number Theory & Modern Cryptography
 Number Theory & Modern Cryptography Week 12 Stallings: Ch 4, 8, 9, 10 CNT-4403: 2.April.2015 1 Introduction Increasing importance in cryptography Public Key Crypto and Signatures Concern operations on
Number Theory & Modern Cryptography Week 12 Stallings: Ch 4, 8, 9, 10 CNT-4403: 2.April.2015 1 Introduction Increasing importance in cryptography Public Key Crypto and Signatures Concern operations on
Ma/CS 6a Class 3: The RSA Algorithm
 Ma/CS 6a Class 3: The RSA Algorithm By Adam Sheffer Reminder: Putnam Competition Signup ends Wednesday 10/08. Signup sheets available in all Sloan classrooms, Math office, or contact Kathy Carreon, kcarreon@caltech.edu.
Ma/CS 6a Class 3: The RSA Algorithm By Adam Sheffer Reminder: Putnam Competition Signup ends Wednesday 10/08. Signup sheets available in all Sloan classrooms, Math office, or contact Kathy Carreon, kcarreon@caltech.edu.
8.1 Principles of Public-Key Cryptosystems
 Public-key cryptography is a radical departure from all that has gone before. Right up to modern times all cryptographic systems have been based on the elementary tools of substitution and permutation.
Public-key cryptography is a radical departure from all that has gone before. Right up to modern times all cryptographic systems have been based on the elementary tools of substitution and permutation.
Chapter 8 Public-key Cryptography and Digital Signatures
 Chapter 8 Public-key Cryptography and Digital Signatures v 1. Introduction to Public-key Cryptography 2. Example of Public-key Algorithm: Diffie- Hellman Key Exchange Scheme 3. RSA Encryption and Digital
Chapter 8 Public-key Cryptography and Digital Signatures v 1. Introduction to Public-key Cryptography 2. Example of Public-key Algorithm: Diffie- Hellman Key Exchange Scheme 3. RSA Encryption and Digital
OWO Lecture: Modular Arithmetic with Algorithmic Applications
 OWO Lecture: Modular Arithmetic with Algorithmic Applications Martin Otto Winter Term 2008/09 Contents 1 Basic ingredients 1 2 Modular arithmetic 2 2.1 Going in circles.......................... 2 2.2
OWO Lecture: Modular Arithmetic with Algorithmic Applications Martin Otto Winter Term 2008/09 Contents 1 Basic ingredients 1 2 Modular arithmetic 2 2.1 Going in circles.......................... 2 2.2
10 Public Key Cryptography : RSA
 10 Public Key Cryptography : RSA 10.1 Introduction The idea behind a public-key system is that it might be possible to find a cryptosystem where it is computationally infeasible to determine d K even if
10 Public Key Cryptography : RSA 10.1 Introduction The idea behind a public-key system is that it might be possible to find a cryptosystem where it is computationally infeasible to determine d K even if
ICS141: Discrete Mathematics for Computer Science I
 ICS141: Discrete Mathematics for Computer Science I Dept. Information & Computer Sci., Jan Stelovsky based on slides by Dr. Baek and Dr. Still Originals by Dr. M. P. Frank and Dr. J.L. Gross Provided by
ICS141: Discrete Mathematics for Computer Science I Dept. Information & Computer Sci., Jan Stelovsky based on slides by Dr. Baek and Dr. Still Originals by Dr. M. P. Frank and Dr. J.L. Gross Provided by
10 Modular Arithmetic and Cryptography
 10 Modular Arithmetic and Cryptography 10.1 Encryption and Decryption Encryption is used to send messages secretly. The sender has a message or plaintext. Encryption by the sender takes the plaintext and
10 Modular Arithmetic and Cryptography 10.1 Encryption and Decryption Encryption is used to send messages secretly. The sender has a message or plaintext. Encryption by the sender takes the plaintext and
MATH 158 FINAL EXAM 20 DECEMBER 2016
 MATH 158 FINAL EXAM 20 DECEMBER 2016 Name : The exam is double-sided. Make sure to read both sides of each page. The time limit is three hours. No calculators are permitted. You are permitted one page
MATH 158 FINAL EXAM 20 DECEMBER 2016 Name : The exam is double-sided. Make sure to read both sides of each page. The time limit is three hours. No calculators are permitted. You are permitted one page
Introduction to Modern Cryptography. Benny Chor
 Introduction to Modern Cryptography Benny Chor RSA Public Key Encryption Factoring Algorithms Lecture 7 Tel-Aviv University Revised March 1st, 2008 Reminder: The Prime Number Theorem Let π(x) denote the
Introduction to Modern Cryptography Benny Chor RSA Public Key Encryption Factoring Algorithms Lecture 7 Tel-Aviv University Revised March 1st, 2008 Reminder: The Prime Number Theorem Let π(x) denote the
Encryption: The RSA Public Key Cipher
 Encryption: The RSA Public Key Cipher Michael Brockway March 5, 2018 Overview Transport-layer security employs an asymmetric public cryptosystem to allow two parties (usually a client application and a
Encryption: The RSA Public Key Cipher Michael Brockway March 5, 2018 Overview Transport-layer security employs an asymmetric public cryptosystem to allow two parties (usually a client application and a
Topics in Cryptography. Lecture 5: Basic Number Theory
 Topics in Cryptography Lecture 5: Basic Number Theory Benny Pinkas page 1 1 Classical symmetric ciphers Alice and Bob share a private key k. System is secure as long as k is secret. Major problem: generating
Topics in Cryptography Lecture 5: Basic Number Theory Benny Pinkas page 1 1 Classical symmetric ciphers Alice and Bob share a private key k. System is secure as long as k is secret. Major problem: generating
Public-Key Cryptosystems CHAPTER 4
 Public-Key Cryptosystems CHAPTER 4 Introduction How to distribute the cryptographic keys? Naïve Solution Naïve Solution Give every user P i a separate random key K ij to communicate with every P j. Disadvantage:
Public-Key Cryptosystems CHAPTER 4 Introduction How to distribute the cryptographic keys? Naïve Solution Naïve Solution Give every user P i a separate random key K ij to communicate with every P j. Disadvantage:
Mathematical Foundations of Public-Key Cryptography
 Mathematical Foundations of Public-Key Cryptography Adam C. Champion and Dong Xuan CSE 4471: Information Security Material based on (Stallings, 2006) and (Paar and Pelzl, 2010) Outline Review: Basic Mathematical
Mathematical Foundations of Public-Key Cryptography Adam C. Champion and Dong Xuan CSE 4471: Information Security Material based on (Stallings, 2006) and (Paar and Pelzl, 2010) Outline Review: Basic Mathematical
RSA RSA public key cryptosystem
 RSA 1 RSA As we have seen, the security of most cipher systems rests on the users keeping secret a special key, for anyone possessing the key can encrypt and/or decrypt the messages sent between them.
RSA 1 RSA As we have seen, the security of most cipher systems rests on the users keeping secret a special key, for anyone possessing the key can encrypt and/or decrypt the messages sent between them.
Mathematics of Cryptography
 UNIT - III Mathematics of Cryptography Part III: Primes and Related Congruence Equations 1 Objectives To introduce prime numbers and their applications in cryptography. To discuss some primality test algorithms
UNIT - III Mathematics of Cryptography Part III: Primes and Related Congruence Equations 1 Objectives To introduce prime numbers and their applications in cryptography. To discuss some primality test algorithms
Slides by Kent Seamons and Tim van der Horst Last Updated: Oct 1, 2013
 RSA Slides by Kent Seamons and Tim van der Horst Last Updated: Oct 1, 2013 Recap Recap Number theory o What is a prime number? o What is prime factorization? o What is a GCD? o What does relatively prime
RSA Slides by Kent Seamons and Tim van der Horst Last Updated: Oct 1, 2013 Recap Recap Number theory o What is a prime number? o What is prime factorization? o What is a GCD? o What does relatively prime
CPSC 467b: Cryptography and Computer Security
 CPSC 467b: Cryptography and Computer Security Instructor: Michael Fischer Lecture by Ewa Syta Lecture 13 March 3, 2013 CPSC 467b, Lecture 13 1/52 Elliptic Curves Basics Elliptic Curve Cryptography CPSC
CPSC 467b: Cryptography and Computer Security Instructor: Michael Fischer Lecture by Ewa Syta Lecture 13 March 3, 2013 CPSC 467b, Lecture 13 1/52 Elliptic Curves Basics Elliptic Curve Cryptography CPSC
CPE 776:DATA SECURITY & CRYPTOGRAPHY. Some Number Theory and Classical Crypto Systems
 CPE 776:DATA SECURITY & CRYPTOGRAPHY Some Number Theory and Classical Crypto Systems Dr. Lo ai Tawalbeh Computer Engineering Department Jordan University of Science and Technology Jordan Some Number Theory
CPE 776:DATA SECURITY & CRYPTOGRAPHY Some Number Theory and Classical Crypto Systems Dr. Lo ai Tawalbeh Computer Engineering Department Jordan University of Science and Technology Jordan Some Number Theory
Course 2BA1: Trinity 2006 Section 9: Introduction to Number Theory and Cryptography
 Course 2BA1: Trinity 2006 Section 9: Introduction to Number Theory and Cryptography David R. Wilkins Copyright c David R. Wilkins 2006 Contents 9 Introduction to Number Theory and Cryptography 1 9.1 Subgroups
Course 2BA1: Trinity 2006 Section 9: Introduction to Number Theory and Cryptography David R. Wilkins Copyright c David R. Wilkins 2006 Contents 9 Introduction to Number Theory and Cryptography 1 9.1 Subgroups
Security Issues in Cloud Computing Modern Cryptography II Asymmetric Cryptography
 Security Issues in Cloud Computing Modern Cryptography II Asymmetric Cryptography Peter Schwabe October 21 and 28, 2011 So far we assumed that Alice and Bob both have some key, which nobody else has. How
Security Issues in Cloud Computing Modern Cryptography II Asymmetric Cryptography Peter Schwabe October 21 and 28, 2011 So far we assumed that Alice and Bob both have some key, which nobody else has. How
Cryptography. pieces from work by Gordon Royle
 Cryptography pieces from work by Gordon Royle The set-up Cryptography is the mathematics of devising secure communication systems, whereas cryptanalysis is the mathematics of breaking such systems. We
Cryptography pieces from work by Gordon Royle The set-up Cryptography is the mathematics of devising secure communication systems, whereas cryptanalysis is the mathematics of breaking such systems. We
The RSA cryptosystem and primality tests
 Mathematics, KTH Bengt Ek November 2015 Supplementary material for SF2736, Discrete mathematics: The RSA cryptosystem and primality tests Secret codes (i.e. codes used to make messages unreadable to outsiders
Mathematics, KTH Bengt Ek November 2015 Supplementary material for SF2736, Discrete mathematics: The RSA cryptosystem and primality tests Secret codes (i.e. codes used to make messages unreadable to outsiders
Integers and Division
 Integers and Division Notations Z: set of integers N : set of natural numbers R: set of real numbers Z + : set of positive integers Some elements of number theory are needed in: Data structures, Random
Integers and Division Notations Z: set of integers N : set of natural numbers R: set of real numbers Z + : set of positive integers Some elements of number theory are needed in: Data structures, Random
Introduction to Cryptography. Lecture 8
 Introduction to Cryptography Lecture 8 Benny Pinkas page 1 1 Groups we will use Multiplication modulo a prime number p (G, ) = ({1,2,,p-1}, ) E.g., Z 7* = ( {1,2,3,4,5,6}, ) Z p * Z N * Multiplication
Introduction to Cryptography Lecture 8 Benny Pinkas page 1 1 Groups we will use Multiplication modulo a prime number p (G, ) = ({1,2,,p-1}, ) E.g., Z 7* = ( {1,2,3,4,5,6}, ) Z p * Z N * Multiplication
Public-key Cryptography and elliptic curves
 Public-key Cryptography and elliptic curves Dan Nichols University of Massachusetts Amherst nichols@math.umass.edu WINRS Research Symposium Brown University March 4, 2017 Cryptography basics Cryptography
Public-key Cryptography and elliptic curves Dan Nichols University of Massachusetts Amherst nichols@math.umass.edu WINRS Research Symposium Brown University March 4, 2017 Cryptography basics Cryptography
Cryptography and RSA. Group (1854, Cayley) Upcoming Interview? Outline. Commutative or Abelian Groups
 Great Theoretical Ideas in CS V. Adamchik CS 15-251 Upcoming Interview? Lecture 24 Carnegie Mellon University Cryptography and RSA How the World's Smartest Company Selects the Most Creative Thinkers Groups
Great Theoretical Ideas in CS V. Adamchik CS 15-251 Upcoming Interview? Lecture 24 Carnegie Mellon University Cryptography and RSA How the World's Smartest Company Selects the Most Creative Thinkers Groups
Introduction to Cybersecurity Cryptography (Part 5)
 Introduction to Cybersecurity Cryptography (Part 5) Prof. Dr. Michael Backes 13.01.2017 February 17 th Special Lecture! 45 Minutes Your Choice 1. Automotive Security 2. Smartphone Security 3. Side Channel
Introduction to Cybersecurity Cryptography (Part 5) Prof. Dr. Michael Backes 13.01.2017 February 17 th Special Lecture! 45 Minutes Your Choice 1. Automotive Security 2. Smartphone Security 3. Side Channel
Math.3336: Discrete Mathematics. Mathematical Induction
 Math.3336: Discrete Mathematics Mathematical Induction Instructor: Dr. Blerina Xhabli Department of Mathematics, University of Houston https://www.math.uh.edu/ blerina Email: blerina@math.uh.edu Fall 2018
Math.3336: Discrete Mathematics Mathematical Induction Instructor: Dr. Blerina Xhabli Department of Mathematics, University of Houston https://www.math.uh.edu/ blerina Email: blerina@math.uh.edu Fall 2018
Public-key Cryptography and elliptic curves
 Public-key Cryptography and elliptic curves Dan Nichols nichols@math.umass.edu University of Massachusetts Oct. 14, 2015 Cryptography basics Cryptography is the study of secure communications. Here are
Public-key Cryptography and elliptic curves Dan Nichols nichols@math.umass.edu University of Massachusetts Oct. 14, 2015 Cryptography basics Cryptography is the study of secure communications. Here are
during transmission safeguard information Cryptography: used to CRYPTOGRAPHY BACKGROUND OF THE MATHEMATICAL
 THE MATHEMATICAL BACKGROUND OF CRYPTOGRAPHY Cryptography: used to safeguard information during transmission (e.g., credit card number for internet shopping) as opposed to Coding Theory: used to transmit
THE MATHEMATICAL BACKGROUND OF CRYPTOGRAPHY Cryptography: used to safeguard information during transmission (e.g., credit card number for internet shopping) as opposed to Coding Theory: used to transmit
Final Exam Math 105: Topics in Mathematics Cryptology, the Science of Secret Writing Rhodes College Tuesday, 30 April :30 11:00 a.m.
 Final Exam Math 10: Topics in Mathematics Cryptology, the Science of Secret Writing Rhodes College Tuesday, 0 April 2002 :0 11:00 a.m. Instructions: Please be as neat as possible (use a pencil), and show
Final Exam Math 10: Topics in Mathematics Cryptology, the Science of Secret Writing Rhodes College Tuesday, 0 April 2002 :0 11:00 a.m. Instructions: Please be as neat as possible (use a pencil), and show
Eindhoven University of Technology MASTER. Kleptography cryptography with backdoors. Antheunisse, M. Award date: 2015
 Eindhoven University of Technology MASTER Kleptography cryptography with backdoors Antheunisse, M. Award date: 2015 Disclaimer This document contains a student thesis (bachelor's or master's), as authored
Eindhoven University of Technology MASTER Kleptography cryptography with backdoors Antheunisse, M. Award date: 2015 Disclaimer This document contains a student thesis (bachelor's or master's), as authored
Introduction to Cybersecurity Cryptography (Part 4)
 Introduction to Cybersecurity Cryptography (Part 4) Review of Last Lecture Blockciphers Review of DES Attacks on Blockciphers Advanced Encryption Standard (AES) Modes of Operation MACs and Hashes Message
Introduction to Cybersecurity Cryptography (Part 4) Review of Last Lecture Blockciphers Review of DES Attacks on Blockciphers Advanced Encryption Standard (AES) Modes of Operation MACs and Hashes Message
Chapter 4 Asymmetric Cryptography
 Chapter 4 Asymmetric Cryptography Introduction Encryption: RSA Key Exchange: Diffie-Hellman [NetSec/SysSec], WS 2008/2009 4.1 Asymmetric Cryptography General idea: Use two different keys -K and +K for
Chapter 4 Asymmetric Cryptography Introduction Encryption: RSA Key Exchange: Diffie-Hellman [NetSec/SysSec], WS 2008/2009 4.1 Asymmetric Cryptography General idea: Use two different keys -K and +K for
Asymmetric Cryptography
 Asymmetric Cryptography Chapter 4 Asymmetric Cryptography Introduction Encryption: RSA Key Exchange: Diffie-Hellman General idea: Use two different keys -K and +K for encryption and decryption Given a
Asymmetric Cryptography Chapter 4 Asymmetric Cryptography Introduction Encryption: RSA Key Exchange: Diffie-Hellman General idea: Use two different keys -K and +K for encryption and decryption Given a
Number Theory: Applications. Number Theory Applications. Hash Functions II. Hash Functions III. Pseudorandom Numbers
 Number Theory: Applications Number Theory Applications Computer Science & Engineering 235: Discrete Mathematics Christopher M. Bourke cbourke@cse.unl.edu Results from Number Theory have many applications
Number Theory: Applications Number Theory Applications Computer Science & Engineering 235: Discrete Mathematics Christopher M. Bourke cbourke@cse.unl.edu Results from Number Theory have many applications
Ti Secured communications
 Ti5318800 Secured communications Pekka Jäppinen September 20, 2007 Pekka Jäppinen, Lappeenranta University of Technology: September 20, 2007 Relies on use of two keys: Public and private Sometimes called
Ti5318800 Secured communications Pekka Jäppinen September 20, 2007 Pekka Jäppinen, Lappeenranta University of Technology: September 20, 2007 Relies on use of two keys: Public and private Sometimes called
Public Key Encryption
 Public Key Encryption KG October 17, 2017 Contents 1 Introduction 1 2 Public Key Encryption 2 3 Schemes Based on Diffie-Hellman 3 3.1 ElGamal.................................... 5 4 RSA 7 4.1 Preliminaries.................................
Public Key Encryption KG October 17, 2017 Contents 1 Introduction 1 2 Public Key Encryption 2 3 Schemes Based on Diffie-Hellman 3 3.1 ElGamal.................................... 5 4 RSA 7 4.1 Preliminaries.................................
Notes. Number Theory: Applications. Notes. Number Theory: Applications. Notes. Hash Functions I
 Number Theory: Applications Slides by Christopher M. Bourke Instructor: Berthe Y. Choueiry Fall 2007 Computer Science & Engineering 235 Introduction to Discrete Mathematics Sections 3.4 3.7 of Rosen cse235@cse.unl.edu
Number Theory: Applications Slides by Christopher M. Bourke Instructor: Berthe Y. Choueiry Fall 2007 Computer Science & Engineering 235 Introduction to Discrete Mathematics Sections 3.4 3.7 of Rosen cse235@cse.unl.edu
NUMBER THEORY AND CODES. Álvaro Pelayo WUSTL
 NUMBER THEORY AND CODES Álvaro Pelayo WUSTL Talk Goal To develop codes of the sort can tell the world how to put messages in code (public key cryptography) only you can decode them Structure of Talk Part
NUMBER THEORY AND CODES Álvaro Pelayo WUSTL Talk Goal To develop codes of the sort can tell the world how to put messages in code (public key cryptography) only you can decode them Structure of Talk Part
Simple Math: Cryptography
 1 Introduction Simple Math: Cryptography This section develops some mathematics before getting to the application. The mathematics that I use involves simple facts from number theory. Number theory is
1 Introduction Simple Math: Cryptography This section develops some mathematics before getting to the application. The mathematics that I use involves simple facts from number theory. Number theory is
Course MA2C02, Hilary Term 2013 Section 9: Introduction to Number Theory and Cryptography
 Course MA2C02, Hilary Term 2013 Section 9: Introduction to Number Theory and Cryptography David R. Wilkins Copyright c David R. Wilkins 2000 2013 Contents 9 Introduction to Number Theory 63 9.1 Subgroups
Course MA2C02, Hilary Term 2013 Section 9: Introduction to Number Theory and Cryptography David R. Wilkins Copyright c David R. Wilkins 2000 2013 Contents 9 Introduction to Number Theory 63 9.1 Subgroups
MATHEMATICS EXTENDED ESSAY
 MATHEMATICS EXTENDED ESSAY How does the RSA algorithm function and why is it used in modern communication? Candidate Name: Murtuza Kainan Candidate Session Number: 003077006 Word Count: 3908 1 P a g e
MATHEMATICS EXTENDED ESSAY How does the RSA algorithm function and why is it used in modern communication? Candidate Name: Murtuza Kainan Candidate Session Number: 003077006 Word Count: 3908 1 P a g e
Addition. Ch1 - Algorithms with numbers. Multiplication. al-khwārizmī. al-khwārizmī. Division 53+35=88. Cost? (n number of bits) 13x11=143. Cost?
 Ch - Algorithms with numbers Addition Basic arithmetic Addition ultiplication Division odular arithmetic factoring is hard Primality testing 53+35=88 Cost? (n number of bits) O(n) ultiplication al-khwārizmī
Ch - Algorithms with numbers Addition Basic arithmetic Addition ultiplication Division odular arithmetic factoring is hard Primality testing 53+35=88 Cost? (n number of bits) O(n) ultiplication al-khwārizmī
Introduction to Cybersecurity Cryptography (Part 4)
 Introduction to Cybersecurity Cryptography (Part 4) Review of Last Lecture Blockciphers Review of DES Attacks on Blockciphers Advanced Encryption Standard (AES) Modes of Operation MACs and Hashes Message
Introduction to Cybersecurity Cryptography (Part 4) Review of Last Lecture Blockciphers Review of DES Attacks on Blockciphers Advanced Encryption Standard (AES) Modes of Operation MACs and Hashes Message
CRYPTOGRAPHY AND LARGE PRIMES *
 CRYPTOGRAPHY AND LARGE PRIMES * B. Hartley University of Manchester, England, and National University of Singapore The word "cryptography" derives from Greek and means "secret writing". Since ancient times,
CRYPTOGRAPHY AND LARGE PRIMES * B. Hartley University of Manchester, England, and National University of Singapore The word "cryptography" derives from Greek and means "secret writing". Since ancient times,
Univ.-Prof. Dr. rer. nat. Rudolf Mathar. Written Examination. Cryptography. Tuesday, August 29, 2017, 01:30 p.m.
 Cryptography Univ.-Prof. Dr. rer. nat. Rudolf Mathar 1 2 3 4 15 15 15 15 60 Written Examination Cryptography Tuesday, August 29, 2017, 01:30 p.m. Name: Matr.-No.: Field of study: Please pay attention to
Cryptography Univ.-Prof. Dr. rer. nat. Rudolf Mathar 1 2 3 4 15 15 15 15 60 Written Examination Cryptography Tuesday, August 29, 2017, 01:30 p.m. Name: Matr.-No.: Field of study: Please pay attention to
CS March 17, 2009
 Discrete Mathematics CS 2610 March 17, 2009 Number Theory Elementary number theory, concerned with numbers, usually integers and their properties or rational numbers mainly divisibility among integers
Discrete Mathematics CS 2610 March 17, 2009 Number Theory Elementary number theory, concerned with numbers, usually integers and their properties or rational numbers mainly divisibility among integers
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer 1 Lecture 13 October 16, 2017 (notes revised 10/23/17) 1 Derived from lecture notes by Ewa Syta. CPSC 467, Lecture 13 1/57 Elliptic Curves
CPSC 467: Cryptography and Computer Security Michael J. Fischer 1 Lecture 13 October 16, 2017 (notes revised 10/23/17) 1 Derived from lecture notes by Ewa Syta. CPSC 467, Lecture 13 1/57 Elliptic Curves
Public-Key Encryption: ElGamal, RSA, Rabin
 Public-Key Encryption: ElGamal, RSA, Rabin Introduction to Modern Cryptography Benny Applebaum Tel-Aviv University Fall Semester, 2011 12 Public-Key Encryption Syntax Encryption algorithm: E. Decryption
Public-Key Encryption: ElGamal, RSA, Rabin Introduction to Modern Cryptography Benny Applebaum Tel-Aviv University Fall Semester, 2011 12 Public-Key Encryption Syntax Encryption algorithm: E. Decryption
NUMBER THEORY FOR CRYPTOGRAPHY
 1 CHAPTER 4. NUMBER THEORY FOR CRYPTOGRAPHY 1 INSTITÚID TEICNEOLAÍOCHTA CHEATHARLACH INSTITUTE OF TECHNOLOGY CARLOW NUMBER THEORY FOR CRYPTOGRAPHY Contents 1 Number Theory for Cryptography 2 1.1 Linear
1 CHAPTER 4. NUMBER THEORY FOR CRYPTOGRAPHY 1 INSTITÚID TEICNEOLAÍOCHTA CHEATHARLACH INSTITUTE OF TECHNOLOGY CARLOW NUMBER THEORY FOR CRYPTOGRAPHY Contents 1 Number Theory for Cryptography 2 1.1 Linear
Notes 10: Public-key cryptography
 MTH6115 Cryptography Notes 10: Public-key cryptography In this section we look at two other schemes that have been proposed for publickey ciphers. The first is interesting because it was the earliest such
MTH6115 Cryptography Notes 10: Public-key cryptography In this section we look at two other schemes that have been proposed for publickey ciphers. The first is interesting because it was the earliest such
Great Theoretical Ideas in Computer Science
 15-251 Great Theoretical Ideas in Computer Science Lecture 22: Cryptography November 12th, 2015 What is cryptography about? Adversary Eavesdropper I will cut your throat I will cut your throat What is
15-251 Great Theoretical Ideas in Computer Science Lecture 22: Cryptography November 12th, 2015 What is cryptography about? Adversary Eavesdropper I will cut your throat I will cut your throat What is
Math 299 Supplement: Modular Arithmetic Nov 8, 2013
 Math 299 Supplement: Modular Arithmetic Nov 8, 2013 Numbers modulo n. We have previously seen examples of clock arithmetic, an algebraic system with only finitely many numbers. In this lecture, we make
Math 299 Supplement: Modular Arithmetic Nov 8, 2013 Numbers modulo n. We have previously seen examples of clock arithmetic, an algebraic system with only finitely many numbers. In this lecture, we make
1 Recommended Reading 1. 2 Public Key/Private Key Cryptography Overview RSA Algorithm... 2
 Contents 1 Recommended Reading 1 2 Public Key/Private Key Cryptography 1 2.1 Overview............................................. 1 2.2 RSA Algorithm.......................................... 2 3 A Number
Contents 1 Recommended Reading 1 2 Public Key/Private Key Cryptography 1 2.1 Overview............................................. 1 2.2 RSA Algorithm.......................................... 2 3 A Number
1 Number Theory Basics
 ECS 289M (Franklin), Winter 2010, Crypto Review 1 Number Theory Basics This section has some basic facts about number theory, mostly taken (or adapted) from Dan Boneh s number theory fact sheets for his
ECS 289M (Franklin), Winter 2010, Crypto Review 1 Number Theory Basics This section has some basic facts about number theory, mostly taken (or adapted) from Dan Boneh s number theory fact sheets for his
dit-upm RSA Cybersecurity Cryptography
 -upm Cybersecurity Cryptography José A. Mañas < http://www.dit.upm.es/~pepe/> Information Technology Department Universidad Politécnica de Madrid 4 october 2018 public key (asymmetric) public key secret
-upm Cybersecurity Cryptography José A. Mañas < http://www.dit.upm.es/~pepe/> Information Technology Department Universidad Politécnica de Madrid 4 october 2018 public key (asymmetric) public key secret
Theme : Cryptography. Instructor : Prof. C Pandu Rangan. Speaker : Arun Moorthy CS
 1 C Theme : Cryptography Instructor : Prof. C Pandu Rangan Speaker : Arun Moorthy 93115 CS 2 RSA Cryptosystem Outline of the Talk! Introduction to RSA! Working of the RSA system and associated terminology!
1 C Theme : Cryptography Instructor : Prof. C Pandu Rangan Speaker : Arun Moorthy 93115 CS 2 RSA Cryptosystem Outline of the Talk! Introduction to RSA! Working of the RSA system and associated terminology!
2. Cryptography 2.5. ElGamal cryptosystems and Discrete logarithms
 CRYPTOGRAPHY 19 Cryptography 5 ElGamal cryptosystems and Discrete logarithms Definition Let G be a cyclic group of order n and let α be a generator of G For each A G there exists an uniue 0 a n 1 such
CRYPTOGRAPHY 19 Cryptography 5 ElGamal cryptosystems and Discrete logarithms Definition Let G be a cyclic group of order n and let α be a generator of G For each A G there exists an uniue 0 a n 1 such
CS483 Design and Analysis of Algorithms
 CS483 Design and Analysis of Algorithms Lectures 2-3 Algorithms with Numbers Instructor: Fei Li lifei@cs.gmu.edu with subject: CS483 Office hours: STII, Room 443, Friday 4:00pm - 6:00pm or by appointments
CS483 Design and Analysis of Algorithms Lectures 2-3 Algorithms with Numbers Instructor: Fei Li lifei@cs.gmu.edu with subject: CS483 Office hours: STII, Room 443, Friday 4:00pm - 6:00pm or by appointments
AN ALGEBRAIC PROOF OF RSA ENCRYPTION AND DECRYPTION
 AN ALGEBRAIC PROOF OF RSA ENCRYPTION AND DECRYPTION Recall that RSA works as follows. A wants B to communicate with A, but without E understanding the transmitted message. To do so: A broadcasts RSA method,
AN ALGEBRAIC PROOF OF RSA ENCRYPTION AND DECRYPTION Recall that RSA works as follows. A wants B to communicate with A, but without E understanding the transmitted message. To do so: A broadcasts RSA method,
8 Elliptic Curve Cryptography
 8 Elliptic Curve Cryptography 8.1 Elliptic Curves over a Finite Field For the purposes of cryptography, we want to consider an elliptic curve defined over a finite field F p = Z/pZ for p a prime. Given
8 Elliptic Curve Cryptography 8.1 Elliptic Curves over a Finite Field For the purposes of cryptography, we want to consider an elliptic curve defined over a finite field F p = Z/pZ for p a prime. Given
ECE596C: Handout #11
 ECE596C: Handout #11 Public Key Cryptosystems Electrical and Computer Engineering, University of Arizona, Loukas Lazos Abstract In this lecture we introduce necessary mathematical background for studying
ECE596C: Handout #11 Public Key Cryptosystems Electrical and Computer Engineering, University of Arizona, Loukas Lazos Abstract In this lecture we introduce necessary mathematical background for studying
Introduction to Public-Key Cryptosystems:
 Introduction to Public-Key Cryptosystems: Technical Underpinnings: RSA and Primality Testing Modes of Encryption for RSA Digital Signatures for RSA 1 RSA Block Encryption / Decryption and Signing Each
Introduction to Public-Key Cryptosystems: Technical Underpinnings: RSA and Primality Testing Modes of Encryption for RSA Digital Signatures for RSA 1 RSA Block Encryption / Decryption and Signing Each
Candidates must show on each answer book the type of calculator used. Only calculators permitted under UEA Regulations may be used.
 UNIVERSITY OF EAST ANGLIA School of Mathematics May/June UG Examination 2010 2011 CRYPTOGRAPHY Time allowed: 2 hours Attempt THREE questions. Candidates must show on each answer book the type of calculator
UNIVERSITY OF EAST ANGLIA School of Mathematics May/June UG Examination 2010 2011 CRYPTOGRAPHY Time allowed: 2 hours Attempt THREE questions. Candidates must show on each answer book the type of calculator
Elliptic curves: Theory and Applications. Day 4: The discrete logarithm problem.
 Elliptic curves: Theory and Applications. Day 4: The discrete logarithm problem. Elisa Lorenzo García Université de Rennes 1 14-09-2017 Elisa Lorenzo García (Rennes 1) Elliptic Curves 4 14-09-2017 1 /
Elliptic curves: Theory and Applications. Day 4: The discrete logarithm problem. Elisa Lorenzo García Université de Rennes 1 14-09-2017 Elisa Lorenzo García (Rennes 1) Elliptic Curves 4 14-09-2017 1 /
THE RSA ENCRYPTION SCHEME
 THE RSA ENCRYPTION SCHEME Contents 1. The RSA Encryption Scheme 2 1.1. Advantages over traditional coding methods 3 1.2. Proof of the decoding procedure 4 1.3. Security of the RSA Scheme 4 1.4. Finding
THE RSA ENCRYPTION SCHEME Contents 1. The RSA Encryption Scheme 2 1.1. Advantages over traditional coding methods 3 1.2. Proof of the decoding procedure 4 1.3. Security of the RSA Scheme 4 1.4. Finding
1. multiplication is commutative and associative;
 Chapter 4 The Arithmetic of Z In this chapter, we start by introducing the concept of congruences; these are used in our proof (going back to Gauss 1 ) that every integer has a unique prime factorization.
Chapter 4 The Arithmetic of Z In this chapter, we start by introducing the concept of congruences; these are used in our proof (going back to Gauss 1 ) that every integer has a unique prime factorization.
b = 10 a, is the logarithm of b to the base 10. Changing the base to e we obtain natural logarithms, so a = ln b means that b = e a.
 INTRODUCTION TO CRYPTOGRAPHY 5. Discrete Logarithms Recall the classical logarithm for real numbers: If we write b = 10 a, then a = log 10 b is the logarithm of b to the base 10. Changing the base to e
INTRODUCTION TO CRYPTOGRAPHY 5. Discrete Logarithms Recall the classical logarithm for real numbers: If we write b = 10 a, then a = log 10 b is the logarithm of b to the base 10. Changing the base to e
9 Knapsack Cryptography
 9 Knapsack Cryptography In the past four weeks, we ve discussed public-key encryption systems that depend on various problems that we believe to be hard: prime factorization, the discrete logarithm, and
9 Knapsack Cryptography In the past four weeks, we ve discussed public-key encryption systems that depend on various problems that we believe to be hard: prime factorization, the discrete logarithm, and
MODULAR ARITHMETIC KEITH CONRAD
 MODULAR ARITHMETIC KEITH CONRAD. Introduction We will define the notion of congruent integers (with respect to a modulus) and develop some basic ideas of modular arithmetic. Applications of modular arithmetic
MODULAR ARITHMETIC KEITH CONRAD. Introduction We will define the notion of congruent integers (with respect to a modulus) and develop some basic ideas of modular arithmetic. Applications of modular arithmetic
CODING AND CRYPTOLOGY III CRYPTOLOGY EXERCISES. The questions with a * are extension questions, and will not be included in the assignment.
 CODING AND CRYPTOLOGY III CRYPTOLOGY EXERCISES A selection of the following questions will be chosen by the lecturer to form the Cryptology Assignment. The Cryptology Assignment is due by 5pm Sunday 1
CODING AND CRYPTOLOGY III CRYPTOLOGY EXERCISES A selection of the following questions will be chosen by the lecturer to form the Cryptology Assignment. The Cryptology Assignment is due by 5pm Sunday 1
Ma/CS 6a Class 1. Course Details
 Ma/CS 6a Class 1 By Adam Sheffer Course Details Adam Sheffer. adamsh@caltech.edu 1:00 Monday, Wednesday, and Friday. http://www.math.caltech.edu/~2014-15/1term/ma006a/ 1 Course Structure No exam! Grade
Ma/CS 6a Class 1 By Adam Sheffer Course Details Adam Sheffer. adamsh@caltech.edu 1:00 Monday, Wednesday, and Friday. http://www.math.caltech.edu/~2014-15/1term/ma006a/ 1 Course Structure No exam! Grade
arxiv: v3 [cs.cr] 15 Jun 2017
![arxiv: v3 [cs.cr] 15 Jun 2017 arxiv: v3 [cs.cr] 15 Jun 2017](/thumbs/95/126251828.jpg) Use of Signed Permutations in Cryptography arxiv:1612.05605v3 [cs.cr] 15 Jun 2017 Iharantsoa Vero RAHARINIRINA ihvero@yahoo.fr Department of Mathematics and computer science, Faculty of Sciences, BP 906
Use of Signed Permutations in Cryptography arxiv:1612.05605v3 [cs.cr] 15 Jun 2017 Iharantsoa Vero RAHARINIRINA ihvero@yahoo.fr Department of Mathematics and computer science, Faculty of Sciences, BP 906
download instant at
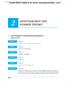 2 CRYPTOGRAPHY AND NUMBER THEORY 2.1 CRYPTOGRAPHY AND MODULAR ARITHMETIC Pages 54 to 56 Problem 1 Problem 2 Problem 3 Problem 4 14 mod 9 = 5; 1 mod 9 = 8; 11 mod 9 = 7. KHUH LV D PHVVDJH. EBOB FP X JBPPXDB.
2 CRYPTOGRAPHY AND NUMBER THEORY 2.1 CRYPTOGRAPHY AND MODULAR ARITHMETIC Pages 54 to 56 Problem 1 Problem 2 Problem 3 Problem 4 14 mod 9 = 5; 1 mod 9 = 8; 11 mod 9 = 7. KHUH LV D PHVVDJH. EBOB FP X JBPPXDB.
A Few Facts from Number Theory and the RSA Cryptosystem OVERVIEW. RSA Producing Big Primes. Table of Contents. Overview Basic Facts of Number Theory
 A Few Facts from Number Theory and the RSA Cryptosystem Larry Susanka Mathematics Department Bellevue College September 25, 2018 Table of Contents Overview Basic Facts of Number Theory The Idea of Public
A Few Facts from Number Theory and the RSA Cryptosystem Larry Susanka Mathematics Department Bellevue College September 25, 2018 Table of Contents Overview Basic Facts of Number Theory The Idea of Public
L7. Diffie-Hellman (Key Exchange) Protocol. Rocky K. C. Chang, 5 March 2015
 L7. Diffie-Hellman (Key Exchange) Protocol Rocky K. C. Chang, 5 March 2015 1 Outline The basic foundation: multiplicative group modulo prime The basic Diffie-Hellman (DH) protocol The discrete logarithm
L7. Diffie-Hellman (Key Exchange) Protocol Rocky K. C. Chang, 5 March 2015 1 Outline The basic foundation: multiplicative group modulo prime The basic Diffie-Hellman (DH) protocol The discrete logarithm
Number theory. Myrto Arapinis School of Informatics University of Edinburgh. October 9, /29
 Number theory Myrto Arapinis School of Informatics University of Edinburgh October 9, 2014 1/29 Division Definition If a and b are integers with a 6= 0, then a divides b if there exists an integer c such
Number theory Myrto Arapinis School of Informatics University of Edinburgh October 9, 2014 1/29 Division Definition If a and b are integers with a 6= 0, then a divides b if there exists an integer c such
