Series Expansion with Wavelets. Advanced Signal Processing Reinisch Bernhard Teichtmeister Georg
|
|
|
- Lee Davidson
- 5 years ago
- Views:
Transcription
1 Series Expasio wih Waveles Advaced Sigal Processig - 7 Reiisch Berhard Teicheiser Georg
2 Iroducio Series expasio Fourier Series: Eiher periodic or badliied sigals Tiedoai: No frequecy iforaio Fourierdoai: No ie iforaio Is here soehig bewee? ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio /6
3 Coes Basics of sigal represeaio Waveles Haar wavele Muliresoluio aalysis Cosrucio of he Sic - Wavele Waveles derived fro ieraed filer baks Haar case, Sic case, geeral cosrucio Wavele series ad is properies Pracical oulook iage processig ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 3/6
4 Recap of Series expasio Sigals are pois i a Vecorspace Tie-Doai: Basis fucios are ifiie shor ipulses Sigals ca be projeced oo oher basis fucios f ϕ u, k k f u ϕ u, k f u ϕ * ϕ u f u du k k ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 4/6
5 Possible Basis Fucios Fourierseries periodic Fourierrasfor badliied STFT f x[ ] Ifiie se of Fourier Trasfors Piecewise Fourier Series Waveles k π π π F[ k] e X e jω jπk/ T e jω dω ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 5/6
6 Shor Tie Fourier Trasfor Widow Sigal Copue he Fourier Trasfor Shif widow ad repea Specrogra, Periodogra ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 6/6
7 Tie ad Frequecy Resoluio Widow has Eergydisribuio i boh: Frequecy σ ω ad Tie σ. Uceraiy priciple: σ ω σ Opialiy is oly reached by Gaussia widow ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 7/6
8 STFT T/F-Resoluio Cosa over Tie ad Frequecy ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 8/6
9 Piecewise Fourierseries Fourier Series wih o-overlappig recagular widows i ie ad periodic expasio Why? Overlappig widows are reduda iforaio Good Tie Resoluio Represeaio of arbirary fucios Bad Frequecy Resoluio Errors a boudaries ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 9/6
10 Desired Feaures of Basis Fucios Siple characerizaio Localizaio Properies i Tie ad Frequecy Ivariace uder cerai operaios Soohess properies Moe properies ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio /6
11 Haar - Expasio Siples Wavele Expasio Scaled ad shifed Waveles: φ φ, Scale Tieshif / ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio /6
12 Dyadic Tilig Resoluio depeds o Frequecy ow φ / φ, ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio /6
13 Orhooral Basis for L? Two waveles o he sae Scale have o coo suppor Shorer wavele always averages o zero Shifig so ha jup aches, is o possible ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 3/6
14 Proof: Defiiios Cosider fucios which are cosa o [, ] ad have fiie suppor o [, ] Ca approxiae L arbirarily well We call i f ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 4/6
15 5/6 ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio Proof: Scalig fucio The scalig fucio Approxiaig he piecewise cosa fucio < oherwise, ϕ, N N f f N f f ϕ
16 Proof: Illusraio ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 6/6
17 Proof: Keysep Exaiaio of wo adjace Iervals Now [ [, ad, f ca be expressed as f ϕ, f, ϕ For,, his eas [,3 ad [3,4 f ϕ, f3 ϕ,3 ϕ, 3ϕ,3 ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 7/6
18 8/6 ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio Proof: Average ad Differece The fucio ca also be expressed as he average ad he differece over wo iervals f, f f ϕ, f f φ
19 9/6 ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio Proof: Coefficies Wih We ge f f d f f f,,,, d f f f φ ϕ ϕ ϕ
20 /6 ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio Proof: Fializaio Applyig all he higs we ca wrie Repeaig he Average/Differece schee for higher scales leads o / /, / /, N N N N d f d f f φ ϕ M M d d f f ε φ φ,,
21 Proof: Illusraio ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio /6
22 Muliresoluio Successive approxiaio Coarse approxiaio added deails Coarse ad deail subspace are orhogoal Leads o self-siilar Waveles i Scale Useful for applicaios ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio /6
23 Axioaic Defiiio Sequece of ebedded closed subspaces K V V V V V K Upward Copleeess U V Z L R Dowward Copleeess I V Z {} ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 3/6
24 Axioaic Defiiio Scale Ivariace f V f V Shif Ivariace f V f V Z Exisace of a orhooral Basis No-orhogoal Basis ca be orhogoalized ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 4/6
25 Orhogoal Coplees V is a subspace of V - We defie W he orhogoal subse of V i V - V V W V is he space of he scalig fucios W he space of he waveles By repeaig we ge L R Z W M ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 5/6
26 Cosrucig he Sic Wavele Now he scalig fucios will be he space of badliied fucios V is badliied bewee [-π, π], V - bewee [-π, π] W he fucios badliied o [-π, -π] cobied wih [π, π] V V W ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 6/6
27 Scalig fucio The scalig fucio is give by siπ ϕ π ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 7/6
28 8/6 ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio Represeaio of φ V belogs o V - φ ca be represeed by basis fucios of V - Wihou proof, ] [ ; ] [ ] [ g g g ϕ ϕ ϕ ϕ Z g g g ] [ ] [ ] [ ϕ φ
29 Cosrucio Kerel g is give by g [ ] G e jω si π / π / e jω Ad fially he wavele π ω oherwise π si π / φ cos3π / π / ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 9/6
30 Sic Wavele: Illusraio ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 3/6
31 Ieraed filer baks Uil ow we cosruced waveles by scalig ad shifig of orhooral fucio failies Based o uliresoluio aalysis Differe approach by filer baks Ieraio leads o a wavele Key proberies regulariy degree of regulariy ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 3/6
32 Haar case Low- ad Highpass g, ; g, Ierae he filer bak o he lowpass chael Mulirae sigal processig resuls ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 3/6
33 Haar case size-8 discree Haar rasfor Nuber of coefficies growh expoeially Coiuous ie fucio Legh bouded, piecewise cosa ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 33/6
34 Sic case Ipulse resposes low ad highpass filer g si π / [ ] ; g[ ] π / g [ ] Fourier rasfor Now cosider he ieraed filer bak Upsaplig filer ipulse Eulae he Haar cosrucio wih g [], g [] Ad defie a scalig fucio ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 34/6
35 35/6 ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio Sic case For furher aalysis: ipora par is i he brackes This produc is i π periodic -> i he ed i s oly a perfec lowpass sic scalig fucio / i / / / i / / si : rewrie ca we M : shor... : where / / si of rasfor Fourier Φ Φ i i j i k k j j j j j i i i j j i i i i i i i e M e G e G e G e G e G e e G ω ω ω ω ω ω ω ω ϕ ω ω ω ω ω ω ω ω
36 Sic case 3 Cubersoe way Bu we have gaied a ore geeral cosrucio The key is he ifiie produc Does his produc coverge ad o wha Coverge o wha kid of scalig fucio ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 36/6
37 Ieraed filer baks co. Geeral cosrucio Two chael orhogoal filer bak g [], g [] are low- ad highpass filer Ierae o he brach of he lowpass filer ad process his o ifiiy Express he wo filers afer i-seps Mulirae coclusios Filerig wih G i z followed by upsaplig by is equivale o upsaplig by followed by filerig wih G i z ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 37/6
38 Ieraed filer baks co. Discree ie ieraed filers cobied wih he coiuous ie fucios Noralizaio ad rescalig Graphical fucio piecewise cosa halvig he iervall ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 38/6
39 Ieraed filer baks co. 3 Fourier doai ac as above I he ieraio schee we are ieresig i covergece This will lead us o regulariy discussio ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 39/6
40 Regulariy The exisece of he lii are criical codiios Liis exis if g [] are regular Regular filer leads hrough ieraio o a scalig fucio wih soe degree of soohess regulariy Bu o oly covergece is sufficie we eed also L covergece o build orhooral bases A lo of sufficie codiios, differe approaches ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 4/6
41 Wavele series ad properies Eueraio of soe geeral properies of basis fucios f, Z F[, ] Wavele F[, ] ψ ψ,,, f ψ,, f d Lieariy, Shif, Dyadic saplig ad ie frequecy ilig, Scalig, Localizaio, decay properies ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 4/6
42 Lieariy suppose operaor T T[f] F[,] ψ he for ay a,b R T[ a f,, f b g ] at f bt g The wavele series is liear. The proof follows fro he lieariy of he ier produc ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 4/6
43 43/6 ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio Shif For Fourier rasfor pair: f, Fω f-au, e -jωau Fω Now for he wavele series [ ] [ ] [ ] k F k f Z k k Z d f F d f F < ',,, or,, ' ' / ', ' τ τ τ ψ τ ψ
44 Scalig For Fourier rasfor F F pair: f, Fω fa, /a*fω/a ' ' [, ] ψ f a [ ] /, / a ψ f a f k k, k Z k, F [ k, ] d a d ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 44/6
45 Dyadic saplig ad ie frequecy ilig I is ipora o locae he basis fucios i he ie-frequecy plae saplig i ie, a scale, wih period ψ ψ,, The frequecy is he iverse of scale, we fid if he wavele is ceered aroud ω he: Ψ, ω is ceered aroud ω / This leads o dyadic saplig of ie frequecy plae ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 45/6
46 Dyadic saplig The dos idicae he ceer of he waveles The scale axis is logarihic ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 46/6
47 Tie localizaio Suppose we are ieresed i he sigal aroud Which values of F[,] carry iforaio abou sigal f a > f Suppose wavele ψ is suppored o he ierval [-, ] Ψ, is suppored o [-, ] Ψ, is suppored o [-, ] ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 47/6
48 Tie localizaio A scale, wavele coefficies wih idex saisfy - ca be rewrie - ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 48/6
49 Frequecy localizaio Suppose ow i localizaio, bu ow i frequecy doai ψ, F[, ] / ψ he Fourier rasfor is / Ψ ω F[, ] e ψ, π j ω f / F d j ω ω Ψ ω e dω ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 49/6
50 Frequecy localizaio Suppose ha he wavele vaishes i he Fourier doai ouside he regio [ω i,ω ax ] A specific scale, he suppor of Ψ, ω will be [ω i /,ω ax / ] Therefore, a frequecy copoe ω iclueces a scale ωi ω ω rewrie log ω ω i ax ASP 7 Teicheiser G. Reiisch B. log ω ω ax Wavele cosrucio 5/6
51 Decay properies Fourier series ca be used o characerize he regulariy of a sigal decay of he rasfro coefficies Global regulariy The wavele rasfor ca be used i a siiliar way Local regulariy ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 5/6
52 Mulidiesioal waveles A way o build ulidiesioal waveles is o use esor producs of heir oe diesioal couerpars This will lead o differe oher waveles Scale chages are ow represeed i arices offers diagoal scalig bu is also ore resriced ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 5/6
53 Pracical aspecs Waveles i alab Iages Iage copressio Edge deecio De-oisig ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 53/6
54 Malab Malab wavele oolbox Coad lie Help wavele Gui ool waveeu D waveles aalysis D waveles aalysis De-oisig Iage Fusio Copressio ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 54/6
55 Exaple D wavele rasfor Discree/coiuous wavele rasfor coefs cws, SCALES, wae ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 55/6
56 Copressio Wavele calculaio Fid sall coefficies ad discard he Sore oly reaiig coefficies Lossy copressio Good copressio wih a fas covergece speed of he wavele ad good decay of he coefficies ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 56/6
57 Copressio ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 57/6
58 Edge deecio origial decoposiio approxiaio is se o zero recosrucio ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 58/6
59 Refereces [] Waveles ad Subbad Codig, Mari Veerli, Jelea Kovacevic, ISBN [] Waveles prakische Aspeke, Markus Graber, VO6 [3] AK Copuergrafik Bildverarbeiug ud Musererkeug WS 6/7 ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 59/6
60 Series Expasio wih Waveles Thak you for you aeio! Advaced Sigal Processig 7 Teicheiser Georg Reiisch Berhard ASP 7 Teicheiser G. Reiisch B. Wavele cosrucio 6/6
Series Expansion with Wavelets
 Series Expasio wih Waveles Advaced Sigal Processig 7 Berhard Reiisch Georg Teicheiser SERIES EXPANSION WITH WAVELETS... ADVANCED SIGNAL PROCESSING 7... INTRODUCTION... SIGNAL REPRESENTATION.... TIME DOMAIN
Series Expasio wih Waveles Advaced Sigal Processig 7 Berhard Reiisch Georg Teicheiser SERIES EXPANSION WITH WAVELETS... ADVANCED SIGNAL PROCESSING 7... INTRODUCTION... SIGNAL REPRESENTATION.... TIME DOMAIN
Ideal Amplifier/Attenuator. Memoryless. where k is some real constant. Integrator. System with memory
 Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
BE.430 Tutorial: Linear Operator Theory and Eigenfunction Expansion
 BE.43 Tuorial: Liear Operaor Theory ad Eigefucio Expasio (adaped fro Douglas Lauffeburger) 9//4 Moivaig proble I class, we ecouered parial differeial equaios describig rasie syses wih cheical diffusio.
BE.43 Tuorial: Liear Operaor Theory ad Eigefucio Expasio (adaped fro Douglas Lauffeburger) 9//4 Moivaig proble I class, we ecouered parial differeial equaios describig rasie syses wih cheical diffusio.
EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D. S. Palimkar
 Ieraioal Joural of Scieific ad Research Publicaios, Volue 2, Issue 7, July 22 ISSN 225-353 EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D S Palikar Depare of Maheaics, Vasarao Naik College, Naded
Ieraioal Joural of Scieific ad Research Publicaios, Volue 2, Issue 7, July 22 ISSN 225-353 EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D S Palikar Depare of Maheaics, Vasarao Naik College, Naded
Lecture 15 First Properties of the Brownian Motion
 Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
Principles of Communications Lecture 1: Signals and Systems. Chih-Wei Liu 劉志尉 National Chiao Tung University
 Priciples of Commuicaios Lecure : Sigals ad Sysems Chih-Wei Liu 劉志尉 Naioal Chiao ug Uiversiy cwliu@wis.ee.cu.edu.w Oulies Sigal Models & Classificaios Sigal Space & Orhogoal Basis Fourier Series &rasform
Priciples of Commuicaios Lecure : Sigals ad Sysems Chih-Wei Liu 劉志尉 Naioal Chiao ug Uiversiy cwliu@wis.ee.cu.edu.w Oulies Sigal Models & Classificaios Sigal Space & Orhogoal Basis Fourier Series &rasform
Notes 03 largely plagiarized by %khc
 1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
In this section we will study periodic signals in terms of their frequency f t is said to be periodic if (4.1)
 Fourier Series Iroducio I his secio we will sudy periodic sigals i ers o heir requecy is said o be periodic i coe Reid ha a sigal ( ) ( ) ( ) () or every, where is a uber Fro his deiiio i ollows ha ( )
Fourier Series Iroducio I his secio we will sudy periodic sigals i ers o heir requecy is said o be periodic i coe Reid ha a sigal ( ) ( ) ( ) () or every, where is a uber Fro his deiiio i ollows ha ( )
12 Getting Started With Fourier Analysis
 Commuicaios Egieerig MSc - Prelimiary Readig Geig Sared Wih Fourier Aalysis Fourier aalysis is cocered wih he represeaio of sigals i erms of he sums of sie, cosie or complex oscillaio waveforms. We ll
Commuicaios Egieerig MSc - Prelimiary Readig Geig Sared Wih Fourier Aalysis Fourier aalysis is cocered wih he represeaio of sigals i erms of he sums of sie, cosie or complex oscillaio waveforms. We ll
Manipulations involving the signal amplitude (dependent variable).
 Oulie Maipulaio of discree ime sigals: Maipulaios ivolvig he idepede variable : Shifed i ime Operaios. Foldig, reflecio or ime reversal. Time Scalig. Maipulaios ivolvig he sigal ampliude (depede variable).
Oulie Maipulaio of discree ime sigals: Maipulaios ivolvig he idepede variable : Shifed i ime Operaios. Foldig, reflecio or ime reversal. Time Scalig. Maipulaios ivolvig he sigal ampliude (depede variable).
The Eigen Function of Linear Systems
 1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
Energy Density / Energy Flux / Total Energy in 1D. Key Mathematics: density, flux, and the continuity equation.
 ecure Phys 375 Eergy Desiy / Eergy Flu / oal Eergy i D Overview ad Moivaio: Fro your sudy of waves i iroducory physics you should be aware ha waves ca raspor eergy fro oe place o aoher cosider he geeraio
ecure Phys 375 Eergy Desiy / Eergy Flu / oal Eergy i D Overview ad Moivaio: Fro your sudy of waves i iroducory physics you should be aware ha waves ca raspor eergy fro oe place o aoher cosider he geeraio
Section 8 Convolution and Deconvolution
 APPLICATIONS IN SIGNAL PROCESSING Secio 8 Covoluio ad Decovoluio This docume illusraes several echiques for carryig ou covoluio ad decovoluio i Mahcad. There are several operaors available for hese fucios:
APPLICATIONS IN SIGNAL PROCESSING Secio 8 Covoluio ad Decovoluio This docume illusraes several echiques for carryig ou covoluio ad decovoluio i Mahcad. There are several operaors available for hese fucios:
A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY
 U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
Sampling Example. ( ) δ ( f 1) (1/2)cos(12πt), T 0 = 1
 Samplig Example Le x = cos( 4π)cos( π). The fudameal frequecy of cos 4π fudameal frequecy of cos π is Hz. The ( f ) = ( / ) δ ( f 7) + δ ( f + 7) / δ ( f ) + δ ( f + ). ( f ) = ( / 4) δ ( f 8) + δ ( f
Samplig Example Le x = cos( 4π)cos( π). The fudameal frequecy of cos 4π fudameal frequecy of cos π is Hz. The ( f ) = ( / ) δ ( f 7) + δ ( f + 7) / δ ( f ) + δ ( f + ). ( f ) = ( / 4) δ ( f 8) + δ ( f
N! AND THE GAMMA FUNCTION
 N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
λiv Av = 0 or ( λi Av ) = 0. In order for a vector v to be an eigenvector, it must be in the kernel of λi
 Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Comparison between Fourier and Corrected Fourier Series Methods
 Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
EGR 544 Communication Theory
 EGR 544 Commuicaio heory 7. Represeaio of Digially Modulaed Sigals II Z. Aliyazicioglu Elecrical ad Compuer Egieerig Deparme Cal Poly Pomoa Represeaio of Digial Modulaio wih Memory Liear Digial Modulaio
EGR 544 Commuicaio heory 7. Represeaio of Digially Modulaed Sigals II Z. Aliyazicioglu Elecrical ad Compuer Egieerig Deparme Cal Poly Pomoa Represeaio of Digial Modulaio wih Memory Liear Digial Modulaio
1 Notes on Little s Law (l = λw)
 Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
LIMITS OF FUNCTIONS (I)
 LIMITS OF FUNCTIO (I ELEMENTARY FUNCTIO: (Elemeary fucios are NOT piecewise fucios Cosa Fucios: f(x k, where k R Polyomials: f(x a + a x + a x + a x + + a x, where a, a,..., a R Raioal Fucios: f(x P (x,
LIMITS OF FUNCTIO (I ELEMENTARY FUNCTIO: (Elemeary fucios are NOT piecewise fucios Cosa Fucios: f(x k, where k R Polyomials: f(x a + a x + a x + a x + + a x, where a, a,..., a R Raioal Fucios: f(x P (x,
Clock Skew and Signal Representation
 Clock Skew ad Sigal Represeaio Ch. 7 IBM Power 4 Chip 0/7/004 08 frequecy domai Program Iroducio ad moivaio Sequeial circuis, clock imig, Basic ools for frequecy domai aalysis Fourier series sigal represeaio
Clock Skew ad Sigal Represeaio Ch. 7 IBM Power 4 Chip 0/7/004 08 frequecy domai Program Iroducio ad moivaio Sequeial circuis, clock imig, Basic ools for frequecy domai aalysis Fourier series sigal represeaio
Moment Generating Function
 1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS
 BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
Review Exercises for Chapter 9
 0_090R.qd //0 : PM Page 88 88 CHAPTER 9 Ifiie Series I Eercises ad, wrie a epressio for he h erm of he sequece..,., 5, 0,,,, 0,... 7,... I Eercises, mach he sequece wih is graph. [The graphs are labeled
0_090R.qd //0 : PM Page 88 88 CHAPTER 9 Ifiie Series I Eercises ad, wrie a epressio for he h erm of he sequece..,., 5, 0,,,, 0,... 7,... I Eercises, mach he sequece wih is graph. [The graphs are labeled
Paper Introduction. ~ Modelling the Uncertainty in Recovering Articulation from Acoustics ~ Korin Richmond, Simon King, and Paul Taylor.
 Paper Iroducio ~ Modellig he Uceraiy i Recoverig Ariculaio fro Acousics ~ Kori Richod, Sio Kig, ad Paul Taylor Tooi Toda Noveber 6, 2003 Proble Addressed i This Paper Modellig he acousic-o-ariculaory appig
Paper Iroducio ~ Modellig he Uceraiy i Recoverig Ariculaio fro Acousics ~ Kori Richod, Sio Kig, ad Paul Taylor Tooi Toda Noveber 6, 2003 Proble Addressed i This Paper Modellig he acousic-o-ariculaory appig
b : the two eigenvectors of the Grover iteration Quantum counting algorithm
 .5.3. Quau couig algorih How quickly ca we deerie he uber of arge saes i Grover s algorih, i.e. arked saes, r, o a N= daa base search proble, if r is o kow i advace. Classical search ~ ( N ) Quau search
.5.3. Quau couig algorih How quickly ca we deerie he uber of arge saes i Grover s algorih, i.e. arked saes, r, o a N= daa base search proble, if r is o kow i advace. Classical search ~ ( N ) Quau search
STK4080/9080 Survival and event history analysis
 STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
Discrete-Time Signals and Systems. Introduction to Digital Signal Processing. Independent Variable. What is a Signal? What is a System?
 Discree-Time Sigals ad Sysems Iroducio o Digial Sigal Processig Professor Deepa Kudur Uiversiy of Toroo Referece: Secios. -.4 of Joh G. Proakis ad Dimiris G. Maolakis, Digial Sigal Processig: Priciples,
Discree-Time Sigals ad Sysems Iroducio o Digial Sigal Processig Professor Deepa Kudur Uiversiy of Toroo Referece: Secios. -.4 of Joh G. Proakis ad Dimiris G. Maolakis, Digial Sigal Processig: Priciples,
Lecture 15: Three-tank Mixing and Lead Poisoning
 Lecure 15: Three-ak Miig ad Lead Poisoig Eigevalues ad eigevecors will be used o fid he soluio of a sysem for ukow fucios ha saisfy differeial equaios The ukow fucios will be wrie as a 1 colum vecor [
Lecure 15: Three-ak Miig ad Lead Poisoig Eigevalues ad eigevecors will be used o fid he soluio of a sysem for ukow fucios ha saisfy differeial equaios The ukow fucios will be wrie as a 1 colum vecor [
Research Article A Generalized Nonlinear Sum-Difference Inequality of Product Form
 Joural of Applied Mahemaics Volume 03, Aricle ID 47585, 7 pages hp://dx.doi.org/0.55/03/47585 Research Aricle A Geeralized Noliear Sum-Differece Iequaliy of Produc Form YogZhou Qi ad Wu-Sheg Wag School
Joural of Applied Mahemaics Volume 03, Aricle ID 47585, 7 pages hp://dx.doi.org/0.55/03/47585 Research Aricle A Geeralized Noliear Sum-Differece Iequaliy of Produc Form YogZhou Qi ad Wu-Sheg Wag School
Using Linnik's Identity to Approximate the Prime Counting Function with the Logarithmic Integral
 Usig Lii's Ideiy o Approimae he Prime Couig Fucio wih he Logarihmic Iegral Naha McKezie /26/2 aha@icecreambreafas.com Summary:This paper will show ha summig Lii's ideiy from 2 o ad arragig erms i a cerai
Usig Lii's Ideiy o Approimae he Prime Couig Fucio wih he Logarihmic Iegral Naha McKezie /26/2 aha@icecreambreafas.com Summary:This paper will show ha summig Lii's ideiy from 2 o ad arragig erms i a cerai
The analysis of the method on the one variable function s limit Ke Wu
 Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
2D DSP Basics: Systems Stability, 2D Sampling
 - Digital Iage Processig ad Copressio D DSP Basics: Systes Stability D Saplig Stability ty Syste is stable if a bouded iput always results i a bouded output BIBO For LSI syste a sufficiet coditio for stability:
- Digital Iage Processig ad Copressio D DSP Basics: Systes Stability D Saplig Stability ty Syste is stable if a bouded iput always results i a bouded output BIBO For LSI syste a sufficiet coditio for stability:
Big O Notation for Time Complexity of Algorithms
 BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
SUMMATION OF INFINITE SERIES REVISITED
 SUMMATION OF INFINITE SERIES REVISITED I several aricles over he las decade o his web page we have show how o sum cerai iiie series icludig he geomeric series. We wa here o eed his discussio o he geeral
SUMMATION OF INFINITE SERIES REVISITED I several aricles over he las decade o his web page we have show how o sum cerai iiie series icludig he geomeric series. We wa here o eed his discussio o he geeral
King Fahd University of Petroleum & Minerals Computer Engineering g Dept
 Kig Fahd Uiversiy of Peroleum & Mierals Compuer Egieerig g Dep COE 4 Daa ad Compuer Commuicaios erm Dr. shraf S. Hasa Mahmoud Rm -4 Ex. 74 Email: ashraf@kfupm.edu.sa 9/8/ Dr. shraf S. Hasa Mahmoud Lecure
Kig Fahd Uiversiy of Peroleum & Mierals Compuer Egieerig g Dep COE 4 Daa ad Compuer Commuicaios erm Dr. shraf S. Hasa Mahmoud Rm -4 Ex. 74 Email: ashraf@kfupm.edu.sa 9/8/ Dr. shraf S. Hasa Mahmoud Lecure
Actuarial Society of India
 Acuarial Sociey of Idia EXAMINAIONS Jue 5 C4 (3) Models oal Marks - 5 Idicaive Soluio Q. (i) a) Le U deoe he process described by 3 ad V deoe he process described by 4. he 5 e 5 PU [ ] PV [ ] ( e ).538!
Acuarial Sociey of Idia EXAMINAIONS Jue 5 C4 (3) Models oal Marks - 5 Idicaive Soluio Q. (i) a) Le U deoe he process described by 3 ad V deoe he process described by 4. he 5 e 5 PU [ ] PV [ ] ( e ).538!
K3 p K2 p Kp 0 p 2 p 3 p
 Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
Math 6710, Fall 2016 Final Exam Solutions
 Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)
![th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x) th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)](/thumbs/80/81319353.jpg) 1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
Linear Time Invariant Systems
 1 Liear Time Ivaria Sysems Oulie We will show ha he oupu equals he covoluio bewee he ipu ad he ui impulse respose: sysem for a discree-ime, for a coiuous-ime sysdem, y x h y x h 2 Discree Time LTI Sysems
1 Liear Time Ivaria Sysems Oulie We will show ha he oupu equals he covoluio bewee he ipu ad he ui impulse respose: sysem for a discree-ime, for a coiuous-ime sysdem, y x h y x h 2 Discree Time LTI Sysems
Update. Continuous-Time Frequency Analysis. Frequency Analysis. Frequency Synthesis. prism. white light. spectrum. Coverage:
 Updae Coiuous-Time requecy alysis Professor Deepa Kudur Uiversiy of Toroo Coverage: Before Readig Wee: 41 Wih Ema: 42, 43, 44, 51 Today ad Wed: Brief Rev of 41, 42, 43, 44, 51 ad Secios 52, 54, 55 Joh
Updae Coiuous-Time requecy alysis Professor Deepa Kudur Uiversiy of Toroo Coverage: Before Readig Wee: 41 Wih Ema: 42, 43, 44, 51 Today ad Wed: Brief Rev of 41, 42, 43, 44, 51 ad Secios 52, 54, 55 Joh
MITPress NewMath.cls LAT E X Book Style Size: 7x9 September 27, :04am. Contents
 Coes 1 Temporal filers 1 1.1 Modelig sequeces 1 1.2 Temporal filers 3 1.2.1 Temporal Gaussia 5 1.2.2 Temporal derivaives 6 1.2.3 Spaioemporal Gabor filers 8 1.3 Velociy-ued filers 9 Bibliography 13 1
Coes 1 Temporal filers 1 1.1 Modelig sequeces 1 1.2 Temporal filers 3 1.2.1 Temporal Gaussia 5 1.2.2 Temporal derivaives 6 1.2.3 Spaioemporal Gabor filers 8 1.3 Velociy-ued filers 9 Bibliography 13 1
Wavelet Transform Theory. Prof. Mark Fowler Department of Electrical Engineering State University of New York at Binghamton
 Wavelet Trasfor Theory Prof. Mark Fowler Departet of Electrical Egieerig State Uiversity of New York at Bighato What is a Wavelet Trasfor? Decopositio of a sigal ito costituet parts Note that there are
Wavelet Trasfor Theory Prof. Mark Fowler Departet of Electrical Egieerig State Uiversity of New York at Bighato What is a Wavelet Trasfor? Decopositio of a sigal ito costituet parts Note that there are
FIXED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE
 Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
Calculus Limits. Limit of a function.. 1. One-Sided Limits...1. Infinite limits 2. Vertical Asymptotes...3. Calculating Limits Using the Limit Laws.
 Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
INVESTMENT PROJECT EFFICIENCY EVALUATION
 368 Miljeko Crjac Domiika Crjac INVESTMENT PROJECT EFFICIENCY EVALUATION Miljeko Crjac Professor Faculy of Ecoomics Drsc Domiika Crjac Faculy of Elecrical Egieerig Osijek Summary Fiacial efficiecy of ivesme
368 Miljeko Crjac Domiika Crjac INVESTMENT PROJECT EFFICIENCY EVALUATION Miljeko Crjac Professor Faculy of Ecoomics Drsc Domiika Crjac Faculy of Elecrical Egieerig Osijek Summary Fiacial efficiecy of ivesme
Fresnel Dragging Explained
 Fresel Draggig Explaied 07/05/008 Decla Traill Decla@espace.e.au The Fresel Draggig Coefficie required o explai he resul of he Fizeau experime ca be easily explaied by usig he priciples of Eergy Field
Fresel Draggig Explaied 07/05/008 Decla Traill Decla@espace.e.au The Fresel Draggig Coefficie required o explai he resul of he Fizeau experime ca be easily explaied by usig he priciples of Eergy Field
6.003 Homework #5 Solutions
 6. Homework #5 Soluios Problems. DT covoluio Le y represe he DT sigal ha resuls whe f is covolved wih g, i.e., y[] = (f g)[] which is someimes wrie as y[] = f[] g[]. Deermie closed-form expressios for
6. Homework #5 Soluios Problems. DT covoluio Le y represe he DT sigal ha resuls whe f is covolved wih g, i.e., y[] = (f g)[] which is someimes wrie as y[] = f[] g[]. Deermie closed-form expressios for
10.3 Autocorrelation Function of Ergodic RP 10.4 Power Spectral Density of Ergodic RP 10.5 Normal RP (Gaussian RP)
 ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
ODEs II, Supplement to Lectures 6 & 7: The Jordan Normal Form: Solving Autonomous, Homogeneous Linear Systems. April 2, 2003
 ODEs II, Suppleme o Lecures 6 & 7: The Jorda Normal Form: Solvig Auoomous, Homogeeous Liear Sysems April 2, 23 I his oe, we describe he Jorda ormal form of a marix ad use i o solve a geeral homogeeous
ODEs II, Suppleme o Lecures 6 & 7: The Jorda Normal Form: Solvig Auoomous, Homogeeous Liear Sysems April 2, 23 I his oe, we describe he Jorda ormal form of a marix ad use i o solve a geeral homogeeous
Extremal graph theory II: K t and K t,t
 Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
UNIT 6 Signals and Systems
 UNIT 6 ONE MARK MCQ 6. dy dy The differeial equaio y x( ) d d + describes a sysem wih a ipu x () ad a oupu y. () The sysem, which is iiially relaxed, is excied by a ui sep ipu. The oupu y^h ca be represeed
UNIT 6 ONE MARK MCQ 6. dy dy The differeial equaio y x( ) d d + describes a sysem wih a ipu x () ad a oupu y. () The sysem, which is iiially relaxed, is excied by a ui sep ipu. The oupu y^h ca be represeed
TAKA KUSANO. laculty of Science Hrosh tlnlersty 1982) (n-l) + + Pn(t)x 0, (n-l) + + Pn(t)Y f(t,y), XR R are continuous functions.
 Iera. J. Mah. & Mah. Si. Vol. 6 No. 3 (1983) 559-566 559 ASYMPTOTIC RELATIOHIPS BETWEEN TWO HIGHER ORDER ORDINARY DIFFERENTIAL EQUATIONS TAKA KUSANO laculy of Sciece Hrosh llersy 1982) ABSTRACT. Some asympoic
Iera. J. Mah. & Mah. Si. Vol. 6 No. 3 (1983) 559-566 559 ASYMPTOTIC RELATIOHIPS BETWEEN TWO HIGHER ORDER ORDINARY DIFFERENTIAL EQUATIONS TAKA KUSANO laculy of Sciece Hrosh llersy 1982) ABSTRACT. Some asympoic
1. Solve by the method of undetermined coefficients and by the method of variation of parameters. (4)
 7 Differeial equaios Review Solve by he mehod of udeermied coefficies ad by he mehod of variaio of parameers (4) y y = si Soluio; we firs solve he homogeeous equaio (4) y y = 4 The correspodig characerisic
7 Differeial equaios Review Solve by he mehod of udeermied coefficies ad by he mehod of variaio of parameers (4) y y = si Soluio; we firs solve he homogeeous equaio (4) y y = 4 The correspodig characerisic
B. Maddah INDE 504 Simulation 09/02/17
 B. Maddah INDE 54 Simulaio 9/2/7 Queueig Primer Wha is a queueig sysem? A queueig sysem cosiss of servers (resources) ha provide service o cusomers (eiies). A Cusomer requesig service will sar service
B. Maddah INDE 54 Simulaio 9/2/7 Queueig Primer Wha is a queueig sysem? A queueig sysem cosiss of servers (resources) ha provide service o cusomers (eiies). A Cusomer requesig service will sar service
David Randall. ( )e ikx. k = u x,t. u( x,t)e ikx dx L. x L /2. Recall that the proof of (1) and (2) involves use of the orthogonality condition.
 ! Revised April 21, 2010 1:27 P! 1 Fourier Series David Radall Assume ha u( x,) is real ad iegrable If he domai is periodic, wih period L, we ca express u( x,) exacly by a Fourier series expasio: ( ) =
! Revised April 21, 2010 1:27 P! 1 Fourier Series David Radall Assume ha u( x,) is real ad iegrable If he domai is periodic, wih period L, we ca express u( x,) exacly by a Fourier series expasio: ( ) =
6/10/2014. Definition. Time series Data. Time series Graph. Components of time series. Time series Seasonal. Time series Trend
 6//4 Defiiio Time series Daa A ime series Measures he same pheomeo a equal iervals of ime Time series Graph Compoes of ime series 5 5 5-5 7 Q 7 Q 7 Q 3 7 Q 4 8 Q 8 Q 8 Q 3 8 Q 4 9 Q 9 Q 9 Q 3 9 Q 4 Q Q
6//4 Defiiio Time series Daa A ime series Measures he same pheomeo a equal iervals of ime Time series Graph Compoes of ime series 5 5 5-5 7 Q 7 Q 7 Q 3 7 Q 4 8 Q 8 Q 8 Q 3 8 Q 4 9 Q 9 Q 9 Q 3 9 Q 4 Q Q
Stochastic Processes Adopted From p Chapter 9 Probability, Random Variables and Stochastic Processes, 4th Edition A. Papoulis and S.
 Sochasic Processes Adoped From p Chaper 9 Probabiliy, adom Variables ad Sochasic Processes, 4h Ediio A. Papoulis ad S. Pillai 9. Sochasic Processes Iroducio Le deoe he radom oucome of a experime. To every
Sochasic Processes Adoped From p Chaper 9 Probabiliy, adom Variables ad Sochasic Processes, 4h Ediio A. Papoulis ad S. Pillai 9. Sochasic Processes Iroducio Le deoe he radom oucome of a experime. To every
Math 2414 Homework Set 7 Solutions 10 Points
 Mah Homework Se 7 Soluios 0 Pois #. ( ps) Firs verify ha we ca use he iegral es. The erms are clearly posiive (he epoeial is always posiive ad + is posiive if >, which i is i his case). For decreasig we
Mah Homework Se 7 Soluios 0 Pois #. ( ps) Firs verify ha we ca use he iegral es. The erms are clearly posiive (he epoeial is always posiive ad + is posiive if >, which i is i his case). For decreasig we
CLOSED FORM EVALUATION OF RESTRICTED SUMS CONTAINING SQUARES OF FIBONOMIAL COEFFICIENTS
 PB Sci Bull, Series A, Vol 78, Iss 4, 2016 ISSN 1223-7027 CLOSED FORM EVALATION OF RESTRICTED SMS CONTAINING SQARES OF FIBONOMIAL COEFFICIENTS Emrah Kılıc 1, Helmu Prodiger 2 We give a sysemaic approach
PB Sci Bull, Series A, Vol 78, Iss 4, 2016 ISSN 1223-7027 CLOSED FORM EVALATION OF RESTRICTED SMS CONTAINING SQARES OF FIBONOMIAL COEFFICIENTS Emrah Kılıc 1, Helmu Prodiger 2 We give a sysemaic approach
A Two-Level Quantum Analysis of ERP Data for Mock-Interrogation Trials. Michael Schillaci Jennifer Vendemia Robert Buzan Eric Green
 A Two-Level Quaum Aalysis of ERP Daa for Mock-Ierrogaio Trials Michael Schillaci Jeifer Vedemia Rober Buza Eric Gree Oulie Experimeal Paradigm 4 Low Workload; Sigle Sessio; 39 8 High Workload; Muliple
A Two-Level Quaum Aalysis of ERP Daa for Mock-Ierrogaio Trials Michael Schillaci Jeifer Vedemia Rober Buza Eric Gree Oulie Experimeal Paradigm 4 Low Workload; Sigle Sessio; 39 8 High Workload; Muliple
A note on deviation inequalities on {0, 1} n. by Julio Bernués*
 A oe o deviaio iequaliies o {0, 1}. by Julio Berués* Deparameo de Maemáicas. Faculad de Ciecias Uiversidad de Zaragoza 50009-Zaragoza (Spai) I. Iroducio. Le f: (Ω, Σ, ) IR be a radom variable. Roughly
A oe o deviaio iequaliies o {0, 1}. by Julio Berués* Deparameo de Maemáicas. Faculad de Ciecias Uiversidad de Zaragoza 50009-Zaragoza (Spai) I. Iroducio. Le f: (Ω, Σ, ) IR be a radom variable. Roughly
14.02 Principles of Macroeconomics Fall 2005
 14.02 Priciples of Macroecoomics Fall 2005 Quiz 2 Tuesday, November 8, 2005 7:30 PM 9 PM Please, aswer he followig quesios. Wrie your aswers direcly o he quiz. You ca achieve a oal of 100 pois. There are
14.02 Priciples of Macroecoomics Fall 2005 Quiz 2 Tuesday, November 8, 2005 7:30 PM 9 PM Please, aswer he followig quesios. Wrie your aswers direcly o he quiz. You ca achieve a oal of 100 pois. There are
Optimum design of complementary transient experiments for estimating thermal properties
 Opiu desig of copleeary rasie experies for esiaig heral properies Jaes V. Beck*, Filippo de Moe, Doald E. Aos *Depare of Mechaical Egieerig, Michiga Sae Uiversiy, USA Depare of Idusrial ad Iforaio Egieerig
Opiu desig of copleeary rasie experies for esiaig heral properies Jaes V. Beck*, Filippo de Moe, Doald E. Aos *Depare of Mechaical Egieerig, Michiga Sae Uiversiy, USA Depare of Idusrial ad Iforaio Egieerig
6.003: Signals and Systems
 6.003: Sigals ad Sysems Lecure 8 March 2, 2010 6.003: Sigals ad Sysems Mid-erm Examiaio #1 Tomorrow, Wedesday, March 3, 7:30-9:30pm. No reciaios omorrow. Coverage: Represeaios of CT ad DT Sysems Lecures
6.003: Sigals ad Sysems Lecure 8 March 2, 2010 6.003: Sigals ad Sysems Mid-erm Examiaio #1 Tomorrow, Wedesday, March 3, 7:30-9:30pm. No reciaios omorrow. Coverage: Represeaios of CT ad DT Sysems Lecures
Sampling. AD Conversion (Additional Material) Sampling: Band limited signal. Sampling. Sampling function (sampling comb) III(x) Shah.
 AD Coversio (Addiioal Maerial Samplig Samplig Properies of real ADCs wo Sep Flash ADC Pipelie ADC Iegraig ADCs: Sigle Slope, Dual Slope DA Coverer Samplig fucio (samplig comb III(x Shah III III ( x = δ
AD Coversio (Addiioal Maerial Samplig Samplig Properies of real ADCs wo Sep Flash ADC Pipelie ADC Iegraig ADCs: Sigle Slope, Dual Slope DA Coverer Samplig fucio (samplig comb III(x Shah III III ( x = δ
ECE-314 Fall 2012 Review Questions
 ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
Spectral Simulation of Turbulence. and Tracking of Small Particles
 Specra Siuaio of Turbuece ad Trackig of Sa Parices Hoogeeous Turbuece Saisica ie average properies RMS veociy fucuaios dissipaio rae are idepede of posiio. Hoogeeous urbuece ca be odeed wih radoy sirred
Specra Siuaio of Turbuece ad Trackig of Sa Parices Hoogeeous Turbuece Saisica ie average properies RMS veociy fucuaios dissipaio rae are idepede of posiio. Hoogeeous urbuece ca be odeed wih radoy sirred
2D DSP Basics: 2D Systems
 - Digital Image Processig ad Compressio D DSP Basics: D Systems D Systems T[ ] y = T [ ] Liearity Additivity: If T y = T [ ] The + T y = y + y Homogeeity: If The T y = T [ ] a T y = ay = at [ ] Liearity
- Digital Image Processig ad Compressio D DSP Basics: D Systems D Systems T[ ] y = T [ ] Liearity Additivity: If T y = T [ ] The + T y = y + y Homogeeity: If The T y = T [ ] a T y = ay = at [ ] Liearity
Integrality Gap for the Knapsack Problem
 Proof, beiefs, ad agorihms hrough he es of sum-of-squares 1 Iegraiy Gap for he Kapsack Probem Noe: These oes are si somewha rough. Suppose we have iems of ui size ad we wa o pack as may as possibe i a
Proof, beiefs, ad agorihms hrough he es of sum-of-squares 1 Iegraiy Gap for he Kapsack Probem Noe: These oes are si somewha rough. Suppose we have iems of ui size ad we wa o pack as may as possibe i a
ECE 350 Matlab-Based Project #3
 ECE 350 Malab-Based Projec #3 Due Dae: Nov. 26, 2008 Read he aached Malab uorial ad read he help files abou fucio i, subs, sem, bar, sum, aa2. he wrie a sigle Malab M file o complee he followig ask for
ECE 350 Malab-Based Projec #3 Due Dae: Nov. 26, 2008 Read he aached Malab uorial ad read he help files abou fucio i, subs, sem, bar, sum, aa2. he wrie a sigle Malab M file o complee he followig ask for
After the completion of this section the student
 Real Fucios REAL FUNCTIONS Afer he copleio of his secio he sude - should recall he defiiio of he asic algeraic ad rascedeal fucios - should e ale o deerie he ai properies of he fucios ad graph he fucios.
Real Fucios REAL FUNCTIONS Afer he copleio of his secio he sude - should recall he defiiio of he asic algeraic ad rascedeal fucios - should e ale o deerie he ai properies of he fucios ad graph he fucios.
Online Supplement to Reactive Tabu Search in a Team-Learning Problem
 Olie Suppleme o Reacive abu Search i a eam-learig Problem Yueli She School of Ieraioal Busiess Admiisraio, Shaghai Uiversiy of Fiace ad Ecoomics, Shaghai 00433, People s Republic of Chia, she.yueli@mail.shufe.edu.c
Olie Suppleme o Reacive abu Search i a eam-learig Problem Yueli She School of Ieraioal Busiess Admiisraio, Shaghai Uiversiy of Fiace ad Ecoomics, Shaghai 00433, People s Republic of Chia, she.yueli@mail.shufe.edu.c
C(p, ) 13 N. Nuclear reactions generate energy create new isotopes and elements. Notation for stellar rates: p 12
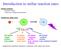 Iroducio o sellar reacio raes Nuclear reacios geerae eergy creae ew isoopes ad elemes Noaio for sellar raes: p C 3 N C(p,) 3 N The heavier arge ucleus (Lab: arge) he ligher icomig projecile (Lab: beam)
Iroducio o sellar reacio raes Nuclear reacios geerae eergy creae ew isoopes ad elemes Noaio for sellar raes: p C 3 N C(p,) 3 N The heavier arge ucleus (Lab: arge) he ligher icomig projecile (Lab: beam)
Available online at J. Math. Comput. Sci. 4 (2014), No. 4, ISSN:
 Available olie a hp://sci.org J. Mah. Compu. Sci. 4 (2014), No. 4, 716-727 ISSN: 1927-5307 ON ITERATIVE TECHNIQUES FOR NUMERICAL SOLUTIONS OF LINEAR AND NONLINEAR DIFFERENTIAL EQUATIONS S.O. EDEKI *, A.A.
Available olie a hp://sci.org J. Mah. Compu. Sci. 4 (2014), No. 4, 716-727 ISSN: 1927-5307 ON ITERATIVE TECHNIQUES FOR NUMERICAL SOLUTIONS OF LINEAR AND NONLINEAR DIFFERENTIAL EQUATIONS S.O. EDEKI *, A.A.
Math-303 Chapter 7 Linear systems of ODE November 16, Chapter 7. Systems of 1 st Order Linear Differential Equations.
 Mah-33 Chaper 7 Liear sysems of ODE November 6, 7 Chaper 7 Sysems of s Order Liear Differeial Equaios saddle poi λ >, λ < Mah-33 Chaper 7 Liear sysems of ODE November 6, 7 Mah-33 Chaper 7 Liear sysems
Mah-33 Chaper 7 Liear sysems of ODE November 6, 7 Chaper 7 Sysems of s Order Liear Differeial Equaios saddle poi λ >, λ < Mah-33 Chaper 7 Liear sysems of ODE November 6, 7 Mah-33 Chaper 7 Liear sysems
6.003: Signal Processing Lecture 2a September 11, 2018
 6003: Sigal Processig Buildig Block Sigals represeig a sigal as a sum of simpler sigals represeig a sample as a sum of samples from simpler sigals Remiders From Las Time Piloig a ew versio of 6003 focused
6003: Sigal Processig Buildig Block Sigals represeig a sigal as a sum of simpler sigals represeig a sample as a sum of samples from simpler sigals Remiders From Las Time Piloig a ew versio of 6003 focused
Some Properties of Semi-E-Convex Function and Semi-E-Convex Programming*
 The Eighh Ieraioal Symposium o Operaios esearch ad Is Applicaios (ISOA 9) Zhagjiajie Chia Sepember 2 22 29 Copyrigh 29 OSC & APOC pp 33 39 Some Properies of Semi-E-Covex Fucio ad Semi-E-Covex Programmig*
The Eighh Ieraioal Symposium o Operaios esearch ad Is Applicaios (ISOA 9) Zhagjiajie Chia Sepember 2 22 29 Copyrigh 29 OSC & APOC pp 33 39 Some Properies of Semi-E-Covex Fucio ad Semi-E-Covex Programmig*
Fourier transform. Continuous-time Fourier transform (CTFT) ω ω
 Fourier rasform Coiuous-ime Fourier rasform (CTFT P. Deoe ( he Fourier rasform of he sigal x(. Deermie he followig values, wihou compuig (. a (0 b ( d c ( si d ( d d e iverse Fourier rasform for Re { (
Fourier rasform Coiuous-ime Fourier rasform (CTFT P. Deoe ( he Fourier rasform of he sigal x(. Deermie he followig values, wihou compuig (. a (0 b ( d c ( si d ( d d e iverse Fourier rasform for Re { (
Hadamard matrices from the Multiplication Table of the Finite Fields
 adamard marice from he Muliplicaio Table of he Fiie Field 신민호 송홍엽 노종선 * Iroducio adamard mari biary m-equece New Corucio Coe Theorem. Corucio wih caoical bai Theorem. Corucio wih ay bai Remark adamard
adamard marice from he Muliplicaio Table of he Fiie Field 신민호 송홍엽 노종선 * Iroducio adamard mari biary m-equece New Corucio Coe Theorem. Corucio wih caoical bai Theorem. Corucio wih ay bai Remark adamard
Calculus BC 2015 Scoring Guidelines
 AP Calculus BC 5 Scorig Guidelies 5 The College Board. College Board, Advaced Placeme Program, AP, AP Ceral, ad he acor logo are regisered rademarks of he College Board. AP Ceral is he official olie home
AP Calculus BC 5 Scorig Guidelies 5 The College Board. College Board, Advaced Placeme Program, AP, AP Ceral, ad he acor logo are regisered rademarks of he College Board. AP Ceral is he official olie home
E will be denoted by n
 JASEM ISSN 9-8362 All rigs reserved Full-ex Available Olie a p:// wwwbiolieorgbr/ja J Appl Sci Eviro Mg 25 Vol 9 3) 3-36 Corollabiliy ad Null Corollabiliy of Liear Syses * DAVIES, I; 2 JACKREECE, P Depare
JASEM ISSN 9-8362 All rigs reserved Full-ex Available Olie a p:// wwwbiolieorgbr/ja J Appl Sci Eviro Mg 25 Vol 9 3) 3-36 Corollabiliy ad Null Corollabiliy of Liear Syses * DAVIES, I; 2 JACKREECE, P Depare
CS623: Introduction to Computing with Neural Nets (lecture-10) Pushpak Bhattacharyya Computer Science and Engineering Department IIT Bombay
 CS6: Iroducio o Compuig ih Neural Nes lecure- Pushpak Bhaacharyya Compuer Sciece ad Egieerig Deparme IIT Bombay Tilig Algorihm repea A kid of divide ad coquer sraegy Give he classes i he daa, ru he percepro
CS6: Iroducio o Compuig ih Neural Nes lecure- Pushpak Bhaacharyya Compuer Sciece ad Egieerig Deparme IIT Bombay Tilig Algorihm repea A kid of divide ad coquer sraegy Give he classes i he daa, ru he percepro
Applying the Moment Generating Functions to the Study of Probability Distributions
 3 Iformaica Ecoomică, r (4)/007 Applyi he Mome Geerai Fucios o he Sudy of Probabiliy Disribuios Silvia SPĂTARU Academy of Ecoomic Sudies, Buchares I his paper, we describe a ool o aid i provi heorems abou
3 Iformaica Ecoomică, r (4)/007 Applyi he Mome Geerai Fucios o he Sudy of Probabiliy Disribuios Silvia SPĂTARU Academy of Ecoomic Sudies, Buchares I his paper, we describe a ool o aid i provi heorems abou
INTEGER INTERVAL VALUE OF NEWTON DIVIDED DIFFERENCE AND FORWARD AND BACKWARD INTERPOLATION FORMULA
 Volume 8 No. 8, 45-54 ISSN: 34-3395 (o-lie versio) url: hp://www.ijpam.eu ijpam.eu INTEGER INTERVAL VALUE OF NEWTON DIVIDED DIFFERENCE AND FORWARD AND BACKWARD INTERPOLATION FORMULA A.Arul dass M.Dhaapal
Volume 8 No. 8, 45-54 ISSN: 34-3395 (o-lie versio) url: hp://www.ijpam.eu ijpam.eu INTEGER INTERVAL VALUE OF NEWTON DIVIDED DIFFERENCE AND FORWARD AND BACKWARD INTERPOLATION FORMULA A.Arul dass M.Dhaapal
CS 450: COMPUTER GRAPHICS INTRODUCTION TO MATRICES SPRING 2016 DR. MICHAEL J. REALE
 CS 45: COPUTER GRAPHICS INTRODUCTION TO ATRICES SPRING 26 DR. ICHAEL J. REALE hp://www.papeleparee.e c.br/wallpapers/coigoari_2283_2824.jpg ENTER THE ATRIX ari = (p X q) 2D arra of ubers (scalars) p =
CS 45: COPUTER GRAPHICS INTRODUCTION TO ATRICES SPRING 26 DR. ICHAEL J. REALE hp://www.papeleparee.e c.br/wallpapers/coigoari_2283_2824.jpg ENTER THE ATRIX ari = (p X q) 2D arra of ubers (scalars) p =
Clock Skew and Signal Representation. Program. Timing Engineering
 lock Skew ad Sigal epreseaio h. 7 IBM Power 4 hip Iroducio ad moivaio Sequeial circuis, clock imig, Basic ools for frequecy domai aalysis Fourier series sigal represeaio Periodic sigals ca be represeed
lock Skew ad Sigal epreseaio h. 7 IBM Power 4 hip Iroducio ad moivaio Sequeial circuis, clock imig, Basic ools for frequecy domai aalysis Fourier series sigal represeaio Periodic sigals ca be represeed
ES 330 Electronics II Homework 03 (Fall 2017 Due Wednesday, September 20, 2017)
 Pae1 Nae Soluios ES 330 Elecroics II Hoework 03 (Fall 017 ue Wedesday, Sepeber 0, 017 Proble 1 You are ive a NMOS aplifier wih drai load resisor R = 0 k. The volae (R appeari across resisor R = 1.5 vols
Pae1 Nae Soluios ES 330 Elecroics II Hoework 03 (Fall 017 ue Wedesday, Sepeber 0, 017 Proble 1 You are ive a NMOS aplifier wih drai load resisor R = 0 k. The volae (R appeari across resisor R = 1.5 vols
Lecture 9: Polynomial Approximations
 CS 70: Complexiy Theory /6/009 Lecure 9: Polyomial Approximaios Isrucor: Dieer va Melkebeek Scribe: Phil Rydzewski & Piramaayagam Arumuga Naiar Las ime, we proved ha o cosa deph circui ca evaluae he pariy
CS 70: Complexiy Theory /6/009 Lecure 9: Polyomial Approximaios Isrucor: Dieer va Melkebeek Scribe: Phil Rydzewski & Piramaayagam Arumuga Naiar Las ime, we proved ha o cosa deph circui ca evaluae he pariy
Pure Math 30: Explained!
 ure Mah : Explaied! www.puremah.com 6 Logarihms Lesso ar Basic Expoeial Applicaios Expoeial Growh & Decay: Siuaios followig his ype of chage ca be modeled usig he formula: (b) A = Fuure Amou A o = iial
ure Mah : Explaied! www.puremah.com 6 Logarihms Lesso ar Basic Expoeial Applicaios Expoeial Growh & Decay: Siuaios followig his ype of chage ca be modeled usig he formula: (b) A = Fuure Amou A o = iial
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 4 9/16/2013. Applications of the large deviation technique
 MASSACHUSETTS ISTITUTE OF TECHOLOGY 6.265/5.070J Fall 203 Lecure 4 9/6/203 Applicaios of he large deviaio echique Coe.. Isurace problem 2. Queueig problem 3. Buffer overflow probabiliy Safey capial for
MASSACHUSETTS ISTITUTE OF TECHOLOGY 6.265/5.070J Fall 203 Lecure 4 9/6/203 Applicaios of he large deviaio echique Coe.. Isurace problem 2. Queueig problem 3. Buffer overflow probabiliy Safey capial for
MATH 507a ASSIGNMENT 4 SOLUTIONS FALL 2018 Prof. Alexander. g (x) dx = g(b) g(0) = g(b),
 MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
Dynamic h-index: the Hirsch index in function of time
 Dyamic h-idex: he Hirsch idex i fucio of ime by L. Egghe Uiversiei Hassel (UHassel), Campus Diepebeek, Agoralaa, B-3590 Diepebeek, Belgium ad Uiversiei Awerpe (UA), Campus Drie Eike, Uiversieisplei, B-260
Dyamic h-idex: he Hirsch idex i fucio of ime by L. Egghe Uiversiei Hassel (UHassel), Campus Diepebeek, Agoralaa, B-3590 Diepebeek, Belgium ad Uiversiei Awerpe (UA), Campus Drie Eike, Uiversieisplei, B-260
6.003: Signals and Systems Lecture 20 April 22, 2010
 6.003: Sigals ad Sysems Lecure 0 April, 00 6.003: Sigals ad Sysems Relaios amog Fourier Represeaios Mid-erm Examiaio #3 Wedesday, April 8, 7:30-9:30pm. No reciaios o he day of he exam. Coverage: Lecures
6.003: Sigals ad Sysems Lecure 0 April, 00 6.003: Sigals ad Sysems Relaios amog Fourier Represeaios Mid-erm Examiaio #3 Wedesday, April 8, 7:30-9:30pm. No reciaios o he day of he exam. Coverage: Lecures
A Note on Random k-sat for Moderately Growing k
 A Noe o Radom k-sat for Moderaely Growig k Ju Liu LMIB ad School of Mahemaics ad Sysems Sciece, Beihag Uiversiy, Beijig, 100191, P.R. Chia juliu@smss.buaa.edu.c Zogsheg Gao LMIB ad School of Mahemaics
A Noe o Radom k-sat for Moderaely Growig k Ju Liu LMIB ad School of Mahemaics ad Sysems Sciece, Beihag Uiversiy, Beijig, 100191, P.R. Chia juliu@smss.buaa.edu.c Zogsheg Gao LMIB ad School of Mahemaics
The Central Limit Theorem
 The Ceral Limi Theorem The ceral i heorem is oe of he mos impora heorems i probabiliy heory. While here a variey of forms of he ceral i heorem, he mos geeral form saes ha give a sufficiely large umber,
The Ceral Limi Theorem The ceral i heorem is oe of he mos impora heorems i probabiliy heory. While here a variey of forms of he ceral i heorem, he mos geeral form saes ha give a sufficiely large umber,
Bernstein Direct Method for Solving. Variational Problems
 Ieraioal Maheaical Foru, 5,, o. 48, 35-37 Bersei Direc Mehod for Solvig Variaioal Probles Sadeep Dixi*, Viee K. Sigh**, Ai K. Sigh*, O P. Sigh* *Depare of Applied Maheaics, Isiue of echology, Baaras Hidu
Ieraioal Maheaical Foru, 5,, o. 48, 35-37 Bersei Direc Mehod for Solvig Variaioal Probles Sadeep Dixi*, Viee K. Sigh**, Ai K. Sigh*, O P. Sigh* *Depare of Applied Maheaics, Isiue of echology, Baaras Hidu
Solutions to Problems 3, Level 4
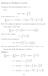 Soluios o Problems 3, Level 4 23 Improve he resul of Quesio 3 whe l. i Use log log o prove ha for real >, log ( {}log + 2 d log+ P ( + P ( d 2. Here P ( is defied i Quesio, ad parial iegraio has bee used.
Soluios o Problems 3, Level 4 23 Improve he resul of Quesio 3 whe l. i Use log log o prove ha for real >, log ( {}log + 2 d log+ P ( + P ( d 2. Here P ( is defied i Quesio, ad parial iegraio has bee used.
