Causality. but that does not mean it is local in time, for = 1. Let us write ɛ(ω) = ɛ 0 [1 + χ e (ω)] in terms of the electric susceptibility.
|
|
|
- Clement Gilbert
- 5 years ago
- Views:
Transcription
1 We have seen that the issue of how ɛ, µ n depend on ω raises questions about causality: Can signals travel faster than c, or even backwards in time? It is very often useful to assume that polarization is linear local in space, the polarizability is not time dependent, meaning D( x, ω) = ɛ(ω) E( x, ω), but that does not mean it is local in time, for D( x, t) = = = 1 2π 1 2π 1 2π dω D( x, ω)e iωt dω e iωt ɛ(ω) E( x, ω) dω e iωt ɛ(ω) dt E( x, t )e iωt Let us write ɛ(ω) = ɛ [1 + χ e (ω)] in terms of the electric susceptibility.
2 G(t t ) Let G(τ) be the fourier transform of χ e (ω), G(τ) = 1 2π dω e iωτ χ e (ω). Then we have the relation between D E given by { } D( x, t) = ɛ E( x, t) + dτ G(τ) E( x, t τ). Thus we see that D( x, t) depends linearly on the function E( x, t ) of time t, but not on the single value E( x, t). That is, the dependence is non-local in time. Of course if ɛ(ω) were constant, G(τ) δ(τ) we would have the local D( x, t) = ɛ E( x, t), but that is not the case generally. As D( x, t) E( x, t) are both real, D ( x, ω) = D( x, ω) similarly for E, so for real ω, ɛ (ω) = ɛ( ω). This means G(τ) is real (for real τ).
3 That the polarization at time t might depend on the electric field at some earlier time t is not surprising, but shouldn t it be blind to fields at later times? That is, shouldn t we insist G(τ) = for τ < )? Let s consider our oscillator strength model, with χ e (ω) = ω 2 P ω 2 ω2 iγω (or a sum of such contributions with different ω s γ s). Then G(τ) = ω2 P 2π = ω2 P 4πν e iωτ dω ω 2 ω2 iγω ( dω where ν = ω 2 γ2 /4. e iωτ ω + ν + iγ/2 e iωτ ). ω ν + iγ/2
4 Evaluating G(τ) for oscillators The integrals can be easily done by closing the contours in the complex plane. The integral dω e iωτ ω ± ν + iγ/2 can be done by closing the contour with a large semicircle in the upper or lower half plane, whichever gives zero contribution because of the exponential. For negative τ, e iωτ = e τ Imω, so the contribution of the green infinite-radius semicircle in the upper half plane vanishes, as the integr is analytic in the enclosed region, the integral is zero. Thus we do have G(τ) = for τ <.
5 For τ >, the contour is closed in the lower half plane, the integral is given by 2πi times the sum of the residues, which are e ±iν τ γτ/2. So the two terms for positive τ fill in the result: G(τ) = ω 2 P sin(ν τ) Θ(τ). ν Typical values for the lifetime of states, hence the line-widths of the photons emitted, give γ i from 1 7 /s to 1 9 /s, so the effective τ s are of the order of nanoseconds. While the response of D to E is not instantaneous, it is quick.
6 Model-independent ɛ s We will now find constraints on possible forms of ɛ(ω) without assumptions on the model of molecular behavior. We have seen that reality of the fields in the time domain requires ɛ (ω) = ɛ( ω) for real ω. We have only defined used ɛ(ω) for real ω, but if we would like to continue ɛ as a complex valued analytic function, we need to extend the constraint to ɛ (ω ) = ɛ( ω), χ e(ω ) = χ e ( ω). We will also insist that G(τ) is finite real for positive τ zero for negative τ. We might expect G τ which is true for dielectrics, but DC currents correspond to singular polarizability for DC conditions, with ɛ iσ/ω, as we saw in for zero-mode oscillators. This will come from G τ σ/ɛ. In any case, we will assume G does not blow up at infinity.
7 For large ω, χ e is determined by G(τ) near τ =. Indeed, if G(t) = t n d n G n! dt n, n χ e (ω) = 1 d n G n! dt n t n e iωt n = d n G dt n ( iω) (n+1) = i G() n ω G () ω Note G() = by continuity from negative τ s, so the leading term is 1/ω 2. With G thus well-behaved, χ e (ω) = G(τ)e iωτ dτ is a well defined integral for all ω with Im ω, except for the possible pole at ω =. Thus χ e (ω) is an analytic function in the upper half plane.
8 Therefore, by Cauchy s theorem, for z in the upper half plane, χ e (z) = 1 χ e (ω ) 2πi C ω z dω with C the contour consisting of the black real axis the green semicircle, going over under z if it lies on the real axis. Because χ e (ω) goes to zero at infinity, we can discard the green semicircle. If z = ω + iδ, with δ > χ e (z) = 1 2πi dω χ e (ω ) ω ω iδ. We are interested in z approaching the real axis from above, δ, so we may use ( ) 1 1 ω ω iδ = P ω + iπδ(ω ω), ω where the principal part P means P dω 1 ω ω f(ω ) := lim ɛ ( ω ɛ ) dω + ω+ɛ ω ω f(ω ).
9 The δ(ω ω) term just cancels half the left h side, so doubling it, for real ω, we have χ e (ω) = 1 iπ P = 1 iπ P = 1 iπ P dω χ e(ω ) ω ω ( dω χe (ω ) ω ω χ e( ω ) ω + ω ) ( dω χe (ω ) ω ω χ e(ω ) ω + ω Taking real imaginary parts separately, Re χ e (ω) = 1 ( 1 π P dω Im χ e (ω ) ω ω + 1 ) ω + ω = 1 π P dω Im χ e (ω 2ω ) ω 2 ω 2 Im χ e (ω) = 1 ( 1 π P dω Re χ e (ω ) ω ω 1 ) ω + ω = 1 π P dω Re χ e (ω 2ω ) ω 2 ω 2 )
10 Maxwell s Equations in Linear Media Recall the basis equations: H D t E + B t D = 1 ɛ ρ Gauss for D B = Gauss for B = µ J Ampère (+Max) = Faraday plus the Lorentz force: F = q( E + v B) the constitutive relations (in frequency space) D = ɛe, B = µ H.
11 Interface between conductor non-conductor Consider the interface between a dielectric an good conductor c. Conductor c: if perfect, no E. Surface charge Σ eddy currents can prevent fields from penetrating, so no H inside conductor. Γ Across the interface: n ξ Faraday on loop Γ E continuous conductor Gauss on pillbox S B continuous c S Thus just outside the conductor E =, B =.
12 Good (not perfect) conductor For good (not perfect) conductor, take J = σ E with large conductivity σ. Assume time-dependence e iωt Let ξ be distance inside conductor. H varies rapidly with ξ. H c = J + D t σ E, E c = B t = iωµ ch c Rapid variation with depth ξ dominates, = ˆn ξ, E c = 1 J σ = 1 σ ˆn H c ξ, Hc = i ˆn E c ωµ c ξ
13 E c = 1 J σ = 1 σ ˆn H c ξ, Hc = i ˆn E c ωµ c ξ so ˆn H c = ˆn H c = ( i ˆn ˆn E c ωµ c ξ ( [ = i σωµ c ˆn = ˆn ) i 2 ( σωµ c ξ 2 ˆn H ) c. ]) ˆn 2 Hc ξ 2 Simple DEQ, exponential solution, with δ = H c = H e ξ/δ e iξ/δ, 2 µ c ωσ, H is tangential field outside surface of conductor.
14 E inside conductor at boundary From H c = H e ξ/δ e iξ/δ, E c = 1 σ ˆn H c ξ = µ c ω 2σ (1 i)ˆn H e ξ/δ e iξ/δ, which means, by continuity, that just outside the conductor µ c ω E = 2σ (1 i)ˆn H.
Joel A. Shapiro January 21, 2010
 Joel A. shapiro@physics.rutgers.edu January 21, 20 rmation Instructor: Joel Serin 325 5-5500 X 3886, shapiro@physics Book: Jackson: Classical Electrodynamics (3rd Ed.) Web home page: www.physics.rutgers.edu/grad/504
Joel A. shapiro@physics.rutgers.edu January 21, 20 rmation Instructor: Joel Serin 325 5-5500 X 3886, shapiro@physics Book: Jackson: Classical Electrodynamics (3rd Ed.) Web home page: www.physics.rutgers.edu/grad/504
3 Constitutive Relations: Macroscopic Properties of Matter
 EECS 53 Lecture 3 c Kamal Sarabandi Fall 21 All rights reserved 3 Constitutive Relations: Macroscopic Properties of Matter As shown previously, out of the four Maxwell s equations only the Faraday s and
EECS 53 Lecture 3 c Kamal Sarabandi Fall 21 All rights reserved 3 Constitutive Relations: Macroscopic Properties of Matter As shown previously, out of the four Maxwell s equations only the Faraday s and
Chapter 11: Dielectric Properties of Materials
 Chapter 11: Dielectric Properties of Materials Lindhardt January 30, 2017 Contents 1 Classical Dielectric Response of Materials 2 1.1 Conditions on ɛ............................. 4 1.2 Kramer s Kronig
Chapter 11: Dielectric Properties of Materials Lindhardt January 30, 2017 Contents 1 Classical Dielectric Response of Materials 2 1.1 Conditions on ɛ............................. 4 1.2 Kramer s Kronig
For the magnetic field B called magnetic induction (unfortunately) M called magnetization is the induced field H called magnetic field H =
 To review, in our original presentation of Maxwell s equations, ρ all J all represented all charges, both free bound. Upon separating them, free from bound, we have (dropping quadripole terms): For the
To review, in our original presentation of Maxwell s equations, ρ all J all represented all charges, both free bound. Upon separating them, free from bound, we have (dropping quadripole terms): For the
Fourier transforms, Generalised functions and Greens functions
 Fourier transforms, Generalised functions and Greens functions T. Johnson 2015-01-23 Electromagnetic Processes In Dispersive Media, Lecture 2 - T. Johnson 1 Motivation A big part of this course concerns
Fourier transforms, Generalised functions and Greens functions T. Johnson 2015-01-23 Electromagnetic Processes In Dispersive Media, Lecture 2 - T. Johnson 1 Motivation A big part of this course concerns
Macroscopic dielectric theory
 Macroscopic dielectric theory Maxwellʼs equations E = 1 c E =4πρ B t B = 4π c J + 1 c B = E t In a medium it is convenient to explicitly introduce induced charges and currents E = 1 B c t D =4πρ H = 4π
Macroscopic dielectric theory Maxwellʼs equations E = 1 c E =4πρ B t B = 4π c J + 1 c B = E t In a medium it is convenient to explicitly introduce induced charges and currents E = 1 B c t D =4πρ H = 4π
Wave Phenomena Physics 15c. Lecture 11 Dispersion
 Wave Phenomena Physics 15c Lecture 11 Dispersion What We Did Last Time Defined Fourier transform f (t) = F(ω)e iωt dω F(ω) = 1 2π f(t) and F(w) represent a function in time and frequency domains Analyzed
Wave Phenomena Physics 15c Lecture 11 Dispersion What We Did Last Time Defined Fourier transform f (t) = F(ω)e iωt dω F(ω) = 1 2π f(t) and F(w) represent a function in time and frequency domains Analyzed
Time dependent perturbation theory 1 D. E. Soper 2 University of Oregon 11 May 2012
 Time dependent perturbation theory D. E. Soper University of Oregon May 0 offer here some background for Chapter 5 of J. J. Sakurai, Modern Quantum Mechanics. The problem Let the hamiltonian for a system
Time dependent perturbation theory D. E. Soper University of Oregon May 0 offer here some background for Chapter 5 of J. J. Sakurai, Modern Quantum Mechanics. The problem Let the hamiltonian for a system
1 Fundamentals of laser energy absorption
 1 Fundamentals of laser energy absorption 1.1 Classical electromagnetic-theory concepts 1.1.1 Electric and magnetic properties of materials Electric and magnetic fields can exert forces directly on atoms
1 Fundamentals of laser energy absorption 1.1 Classical electromagnetic-theory concepts 1.1.1 Electric and magnetic properties of materials Electric and magnetic fields can exert forces directly on atoms
LINEAR RESPONSE THEORY
 MIT Department of Chemistry 5.74, Spring 5: Introductory Quantum Mechanics II Instructor: Professor Andrei Tokmakoff p. 8 LINEAR RESPONSE THEORY We have statistically described the time-dependent behavior
MIT Department of Chemistry 5.74, Spring 5: Introductory Quantum Mechanics II Instructor: Professor Andrei Tokmakoff p. 8 LINEAR RESPONSE THEORY We have statistically described the time-dependent behavior
Introduction to electromagnetic theory
 Chapter 1 Introduction to electromagnetic theory 1.1 Introduction Electromagnetism is a fundamental physical phenomena that is basic to many areas science and technology. This phenomenon is due to the
Chapter 1 Introduction to electromagnetic theory 1.1 Introduction Electromagnetism is a fundamental physical phenomena that is basic to many areas science and technology. This phenomenon is due to the
Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Electro Dynamic
 Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Name Electro Dynamic Instructions: Use SI units. Short answers! No derivations here, just state your responses clearly. 1. (2) Write an
Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Name Electro Dynamic Instructions: Use SI units. Short answers! No derivations here, just state your responses clearly. 1. (2) Write an
Electromagnetic Wave Propagation Lecture 2: Time harmonic dependence, constitutive relations
 Electromagnetic Wave Propagation Lecture 2: Time harmonic dependence, constitutive relations Daniel Sjöberg Department of Electrical and Information Technology September 2, 2010 Outline 1 Harmonic time
Electromagnetic Wave Propagation Lecture 2: Time harmonic dependence, constitutive relations Daniel Sjöberg Department of Electrical and Information Technology September 2, 2010 Outline 1 Harmonic time
Drude theory & linear response
 DRAFT: run through L A TEX on 9 May 16 at 13:51 Drude theory & linear response 1 Static conductivity According to classical mechanics, the motion of a free electron in a constant E field obeys the Newton
DRAFT: run through L A TEX on 9 May 16 at 13:51 Drude theory & linear response 1 Static conductivity According to classical mechanics, the motion of a free electron in a constant E field obeys the Newton
Fiber Optics. Equivalently θ < θ max = cos 1 (n 0 /n 1 ). This is geometrical optics. Needs λ a. Two kinds of fibers:
 Waves can be guided not only by conductors, but by dielectrics. Fiber optics cable of silica has nr varying with radius. Simplest: core radius a with n = n 1, surrounded radius b with n = n 0 < n 1. Total
Waves can be guided not only by conductors, but by dielectrics. Fiber optics cable of silica has nr varying with radius. Simplest: core radius a with n = n 1, surrounded radius b with n = n 0 < n 1. Total
Problem 1. Arfken
 All Arfken problems are reproduced at the end of this assignment Problem 1. Arfken 11.2.11. Problem 2. (a) Do Arfken 11.3.3 (b) The integral Integrals 4 3i 3+4i (x 2 iy 2 ) dz (1) is not defined without
All Arfken problems are reproduced at the end of this assignment Problem 1. Arfken 11.2.11. Problem 2. (a) Do Arfken 11.3.3 (b) The integral Integrals 4 3i 3+4i (x 2 iy 2 ) dz (1) is not defined without
13 Definite integrals
 3 Definite integrals Read: Boas h. 4. 3. Laurent series: Def.: Laurent series (LS). If f() is analytic in a region R, then converges in R, with a n = πi f() = a n ( ) n + n= n= f() ; b ( ) n+ n = πi b
3 Definite integrals Read: Boas h. 4. 3. Laurent series: Def.: Laurent series (LS). If f() is analytic in a region R, then converges in R, with a n = πi f() = a n ( ) n + n= n= f() ; b ( ) n+ n = πi b
PHOTON PROPAGATOR (A REVIEW) The inhomogeneous wave equation for the four-dimensional vector
 PHOTON PROPAGATOR A REVIEW I. THE VECTOR POTENTIAL The inhomogeneous wave equation for the four-dimensional vector potential A µ = A 0 = Φ, A, A 2, A 3 is 2 A µ x x 0 2 2 A µ x = J µ x where Φ is the scalar
PHOTON PROPAGATOR A REVIEW I. THE VECTOR POTENTIAL The inhomogeneous wave equation for the four-dimensional vector potential A µ = A 0 = Φ, A, A 2, A 3 is 2 A µ x x 0 2 2 A µ x = J µ x where Φ is the scalar
e iωt dt and explained why δ(ω) = 0 for ω 0 but δ(0) =. A crucial property of the delta function, however, is that
 Phys 531 Fourier Transforms In this handout, I will go through the derivations of some of the results I gave in class (Lecture 14, 1/11). I won t reintroduce the concepts though, so you ll want to refer
Phys 531 Fourier Transforms In this handout, I will go through the derivations of some of the results I gave in class (Lecture 14, 1/11). I won t reintroduce the concepts though, so you ll want to refer
Electromagnetic Wave Propagation Lecture 2: Time harmonic dependence, constitutive relations
 Electromagnetic Wave Propagation Lecture 2: Time harmonic dependence, constitutive relations Daniel Sjöberg Department of Electrical and Information Technology September 2015 Outline 1 Harmonic time dependence
Electromagnetic Wave Propagation Lecture 2: Time harmonic dependence, constitutive relations Daniel Sjöberg Department of Electrical and Information Technology September 2015 Outline 1 Harmonic time dependence
Theorie der Kondensierten Materie II SS Scattering in 2D: the logarithm and the renormalization group
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theorie der Kondensierten Materie II SS 2017 PD Dr. B. Narozhny Blatt 2 M. Sc. M. Bard Lösungsvorschlag 1. Scattering
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theorie der Kondensierten Materie II SS 2017 PD Dr. B. Narozhny Blatt 2 M. Sc. M. Bard Lösungsvorschlag 1. Scattering
Summary of Beam Optics
 Summary of Beam Optics Gaussian beams, waves with limited spatial extension perpendicular to propagation direction, Gaussian beam is solution of paraxial Helmholtz equation, Gaussian beam has parabolic
Summary of Beam Optics Gaussian beams, waves with limited spatial extension perpendicular to propagation direction, Gaussian beam is solution of paraxial Helmholtz equation, Gaussian beam has parabolic
Green s functions for planarly layered media
 Green s functions for planarly layered media Massachusetts Institute of Technology 6.635 lecture notes Introduction: Green s functions The Green s functions is the solution of the wave equation for a point
Green s functions for planarly layered media Massachusetts Institute of Technology 6.635 lecture notes Introduction: Green s functions The Green s functions is the solution of the wave equation for a point
PSI Lectures on Complex Analysis
 PSI Lectures on Complex Analysis Tibra Ali August 14, 14 Lecture 4 1 Evaluating integrals using the residue theorem ecall the residue theorem. If f (z) has singularities at z 1, z,..., z k which are enclosed
PSI Lectures on Complex Analysis Tibra Ali August 14, 14 Lecture 4 1 Evaluating integrals using the residue theorem ecall the residue theorem. If f (z) has singularities at z 1, z,..., z k which are enclosed
Electromagnetism. Christopher R Prior. ASTeC Intense Beams Group Rutherford Appleton Laboratory
 lectromagnetism Christopher R Prior Fellow and Tutor in Mathematics Trinity College, Oxford ASTeC Intense Beams Group Rutherford Appleton Laboratory Contents Review of Maxwell s equations and Lorentz Force
lectromagnetism Christopher R Prior Fellow and Tutor in Mathematics Trinity College, Oxford ASTeC Intense Beams Group Rutherford Appleton Laboratory Contents Review of Maxwell s equations and Lorentz Force
Lecture notes for ELECTRODYNAMICS.
 Lecture notes for 640-343 ELECTRODYNAMICS. 1 Summary of Electrostatics 1.1 Coulomb s Law Force between two point charges F 12 = 1 4πɛ 0 Q 1 Q 2ˆr 12 r 1 r 2 2 (1.1.1) 1.2 Electric Field For a charge distribution:
Lecture notes for 640-343 ELECTRODYNAMICS. 1 Summary of Electrostatics 1.1 Coulomb s Law Force between two point charges F 12 = 1 4πɛ 0 Q 1 Q 2ˆr 12 r 1 r 2 2 (1.1.1) 1.2 Electric Field For a charge distribution:
Inductance. thevectorpotentialforthemagneticfield, B 1. ] d l 2. 4π I 1. φ 12 M 12 I 1. 1 Definition of Inductance. r 12
![Inductance. thevectorpotentialforthemagneticfield, B 1. ] d l 2. 4π I 1. φ 12 M 12 I 1. 1 Definition of Inductance. r 12 Inductance. thevectorpotentialforthemagneticfield, B 1. ] d l 2. 4π I 1. φ 12 M 12 I 1. 1 Definition of Inductance. r 12](/thumbs/72/67161747.jpg) Inductance 1 Definition of Inductance When electric potentials are placed on a system of conductors, charges move to cancel the electric field parallel to the conducting surfaces of the conductors. We
Inductance 1 Definition of Inductance When electric potentials are placed on a system of conductors, charges move to cancel the electric field parallel to the conducting surfaces of the conductors. We
Characterization of Left-Handed Materials
 Characterization of Left-Handed Materials Massachusetts Institute of Technology 6.635 lecture notes 1 Introduction 1. How are they realized? 2. Why the denomination Left-Handed? 3. What are their properties?
Characterization of Left-Handed Materials Massachusetts Institute of Technology 6.635 lecture notes 1 Introduction 1. How are they realized? 2. Why the denomination Left-Handed? 3. What are their properties?
Inductance - Lecture 3
 Inductance - Lecture 3 1 Further Discussion of Faraday s Law In Lecture 2 Faraday s law was developed using the Lorentz force on a charge within a moving, conducting loop with the magnetic field is at
Inductance - Lecture 3 1 Further Discussion of Faraday s Law In Lecture 2 Faraday s law was developed using the Lorentz force on a charge within a moving, conducting loop with the magnetic field is at
Landau-Fermi liquid theory
 Landau- 1 Chennai Mathematical Institute April 25, 2011 1 Final year project under Prof. K. Narayan, CMI Interacting fermion system I Basic properties of metals (heat capacity, susceptibility,...) were
Landau- 1 Chennai Mathematical Institute April 25, 2011 1 Final year project under Prof. K. Narayan, CMI Interacting fermion system I Basic properties of metals (heat capacity, susceptibility,...) were
e iωt dt and explained why δ(ω) = 0 for ω 0 but δ(0) =. A crucial property of the delta function, however, is that
 Phys 53 Fourier Transforms In this handout, I will go through the derivations of some of the results I gave in class (Lecture 4, /). I won t reintroduce the concepts though, so if you haven t seen the
Phys 53 Fourier Transforms In this handout, I will go through the derivations of some of the results I gave in class (Lecture 4, /). I won t reintroduce the concepts though, so if you haven t seen the
Optical Solitons. Lisa Larrimore Physics 116
 Lisa Larrimore Physics 116 Optical Solitons An optical soliton is a pulse that travels without distortion due to dispersion or other effects. They are a nonlinear phenomenon caused by self-phase modulation
Lisa Larrimore Physics 116 Optical Solitons An optical soliton is a pulse that travels without distortion due to dispersion or other effects. They are a nonlinear phenomenon caused by self-phase modulation
Electromagnetically Induced Flows in Water
 Electromagnetically Induced Flows in Water Michiel de Reus 8 maart 213 () Electromagnetically Induced Flows 1 / 56 Outline 1 Introduction 2 Maxwell equations Complex Maxwell equations 3 Gaussian sources
Electromagnetically Induced Flows in Water Michiel de Reus 8 maart 213 () Electromagnetically Induced Flows 1 / 56 Outline 1 Introduction 2 Maxwell equations Complex Maxwell equations 3 Gaussian sources
Landau-Fermi liquid theory
 Landau-Fermi liquid theory Shreyas Patankar Chennai Mathematical Institute Abstract We study the basic properties of Landau s theory of a system of interacting fermions (a Fermi liquid). The main feature
Landau-Fermi liquid theory Shreyas Patankar Chennai Mathematical Institute Abstract We study the basic properties of Landau s theory of a system of interacting fermions (a Fermi liquid). The main feature
Overview in Images. S. Lin et al, Nature, vol. 394, p , (1998) T.Thio et al., Optics Letters 26, (2001).
 Overview in Images 5 nm K.S. Min et al. PhD Thesis K.V. Vahala et al, Phys. Rev. Lett, 85, p.74 (000) J. D. Joannopoulos, et al, Nature, vol.386, p.143-9 (1997) T.Thio et al., Optics Letters 6, 197-1974
Overview in Images 5 nm K.S. Min et al. PhD Thesis K.V. Vahala et al, Phys. Rev. Lett, 85, p.74 (000) J. D. Joannopoulos, et al, Nature, vol.386, p.143-9 (1997) T.Thio et al., Optics Letters 6, 197-1974
Electrodynamics Exam Solutions
 Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Evaluation of integrals
 Evaluation of certain contour integrals: Type I Type I: Integrals of the form 2π F (cos θ, sin θ) dθ If we take z = e iθ, then cos θ = 1 (z + 1 ), sin θ = 1 (z 1 dz ) and dθ = 2 z 2i z iz. Substituting
Evaluation of certain contour integrals: Type I Type I: Integrals of the form 2π F (cos θ, sin θ) dθ If we take z = e iθ, then cos θ = 1 (z + 1 ), sin θ = 1 (z 1 dz ) and dθ = 2 z 2i z iz. Substituting
Electromagnetic Waves
 Physics 8 Electromagnetic Waves Overview. The most remarkable conclusion of Maxwell s work on electromagnetism in the 860 s was that waves could exist in the fields themselves, traveling with the speed
Physics 8 Electromagnetic Waves Overview. The most remarkable conclusion of Maxwell s work on electromagnetism in the 860 s was that waves could exist in the fields themselves, traveling with the speed
(z + n) 2. n=0. 2 (z + 2) (z + n). 2 We d like to compute this as an integral. To this end, we d like a function with residues
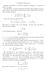 8. Stirling Formula Stirling s Formula is a classical formula to compute n! accurately when n is large. We will derive a version of Stirling s formula using complex analysis and residues. Recall the formula
8. Stirling Formula Stirling s Formula is a classical formula to compute n! accurately when n is large. We will derive a version of Stirling s formula using complex analysis and residues. Recall the formula
221B Lecture Notes on Resonances in Classical Mechanics
 1B Lecture Notes on Resonances in Classical Mechanics 1 Harmonic Oscillators Harmonic oscillators appear in many different contexts in classical mechanics. Examples include: spring, pendulum (with a small
1B Lecture Notes on Resonances in Classical Mechanics 1 Harmonic Oscillators Harmonic oscillators appear in many different contexts in classical mechanics. Examples include: spring, pendulum (with a small
10. KRAMERS-KRONIG RELATIONS AND SUM RULES
 1. KRAMERS-KRONIG RELATIONS AND SUM RULES The Kramers-Kronig relation 99,1 is a consequence of our experience that observable effects are causal, i. e., that the cause precedes the effect. This notion
1. KRAMERS-KRONIG RELATIONS AND SUM RULES The Kramers-Kronig relation 99,1 is a consequence of our experience that observable effects are causal, i. e., that the cause precedes the effect. This notion
PHYS 3900 Homework Set #03
 PHYS 3900 Homework Set #03 Part = HWP 3.0 3.04. Due: Mon. Feb. 2, 208, 4:00pm Part 2 = HWP 3.05, 3.06. Due: Mon. Feb. 9, 208, 4:00pm All textbook problems assigned, unless otherwise stated, are from the
PHYS 3900 Homework Set #03 Part = HWP 3.0 3.04. Due: Mon. Feb. 2, 208, 4:00pm Part 2 = HWP 3.05, 3.06. Due: Mon. Feb. 9, 208, 4:00pm All textbook problems assigned, unless otherwise stated, are from the
Problem Set #4: 4.1,4.7,4.9 (Due Monday, March 25th)
 Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
Waveguides and Cavities
 Waveguides and Cavities John William Strutt also known as Lord Rayleigh (1842-1919) September 17, 2001 Contents 1 Reflection and Transmission at a Conducting Wall 2 1.1 Boundary Conditions...........................
Waveguides and Cavities John William Strutt also known as Lord Rayleigh (1842-1919) September 17, 2001 Contents 1 Reflection and Transmission at a Conducting Wall 2 1.1 Boundary Conditions...........................
Phys460.nb Back to our example. on the same quantum state. i.e., if we have initial condition (5.241) ψ(t = 0) = χ n (t = 0)
 Phys46.nb 89 on the same quantum state. i.e., if we have initial condition ψ(t ) χ n (t ) (5.41) then at later time ψ(t) e i ϕ(t) χ n (t) (5.4) This phase ϕ contains two parts ϕ(t) - E n(t) t + ϕ B (t)
Phys46.nb 89 on the same quantum state. i.e., if we have initial condition ψ(t ) χ n (t ) (5.41) then at later time ψ(t) e i ϕ(t) χ n (t) (5.4) This phase ϕ contains two parts ϕ(t) - E n(t) t + ϕ B (t)
Guided waves - Lecture 11
 Guided waves - Lecture 11 1 Wave equations in a rectangular wave guide Suppose EM waves are contained within the cavity of a long conducting pipe. To simplify the geometry, consider a pipe of rectangular
Guided waves - Lecture 11 1 Wave equations in a rectangular wave guide Suppose EM waves are contained within the cavity of a long conducting pipe. To simplify the geometry, consider a pipe of rectangular
Maxwell s Equations. In the previous chapters we saw the four fundamental equations governging electrostatics and magnetostatics. They are.
 Maxwell s Equations Introduction In the previous chapters we saw the four fundamental equations governging electrostatics and magnetostatics. They are D = ρ () E = 0 (2) B = 0 (3) H = J (4) In the integral
Maxwell s Equations Introduction In the previous chapters we saw the four fundamental equations governging electrostatics and magnetostatics. They are D = ρ () E = 0 (2) B = 0 (3) H = J (4) In the integral
Joel A. Shapiro January 20, 2011
 Joel A. shapiro@physics.rutgers.edu January 20, 2011 Course Information Instructor: Joel Serin 325 5-5500 X 3886, shapiro@physics Book: Jackson: Classical Electrodynamics (3rd Ed.) Web home page: www.physics.rutgers.edu/grad/504
Joel A. shapiro@physics.rutgers.edu January 20, 2011 Course Information Instructor: Joel Serin 325 5-5500 X 3886, shapiro@physics Book: Jackson: Classical Electrodynamics (3rd Ed.) Web home page: www.physics.rutgers.edu/grad/504
Part IB. Further Analysis. Year
 Year 2004 2003 2002 2001 10 2004 2/I/4E Let τ be the topology on N consisting of the empty set and all sets X N such that N \ X is finite. Let σ be the usual topology on R, and let ρ be the topology on
Year 2004 2003 2002 2001 10 2004 2/I/4E Let τ be the topology on N consisting of the empty set and all sets X N such that N \ X is finite. Let σ be the usual topology on R, and let ρ be the topology on
So far we have derived two electrostatic equations E = 0 (6.2) B = 0 (6.3) which are to be modified due to Faraday s observation,
 Chapter 6 Maxwell Equations 6.1 Maxwell equations So far we have derived two electrostatic equations and two magnetostatics equations E = ρ ɛ 0 (6.1) E = 0 (6.2) B = 0 (6.3) B = µ 0 J (6.4) which are to
Chapter 6 Maxwell Equations 6.1 Maxwell equations So far we have derived two electrostatic equations and two magnetostatics equations E = ρ ɛ 0 (6.1) E = 0 (6.2) B = 0 (6.3) B = µ 0 J (6.4) which are to
KINGS COLLEGE OF ENGINEERING DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING QUESTION BANK
 KINGS COLLEGE OF ENGINEERING DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING QUESTION BANK SUB.NAME : ELECTROMAGNETIC FIELDS SUBJECT CODE : EC 2253 YEAR / SEMESTER : II / IV UNIT- I - STATIC ELECTRIC
KINGS COLLEGE OF ENGINEERING DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING QUESTION BANK SUB.NAME : ELECTROMAGNETIC FIELDS SUBJECT CODE : EC 2253 YEAR / SEMESTER : II / IV UNIT- I - STATIC ELECTRIC
Set 5: Classical E&M and Plasma Processes
 Set 5: Classical E&M and Plasma Processes Maxwell Equations Classical E&M defined by the Maxwell Equations (fields sourced by matter) and the Lorentz force (matter moved by fields) In cgs (gaussian) units
Set 5: Classical E&M and Plasma Processes Maxwell Equations Classical E&M defined by the Maxwell Equations (fields sourced by matter) and the Lorentz force (matter moved by fields) In cgs (gaussian) units
Reflection/Refraction
 Reflection/Refraction Page Reflection/Refraction Boundary Conditions Interfaces between different media imposed special boundary conditions on Maxwell s equations. It is important to understand what restrictions
Reflection/Refraction Page Reflection/Refraction Boundary Conditions Interfaces between different media imposed special boundary conditions on Maxwell s equations. It is important to understand what restrictions
Chapter 1 Mathematical Foundations
 Computational Electromagnetics; Chapter 1 1 Chapter 1 Mathematical Foundations 1.1 Maxwell s Equations Electromagnetic phenomena can be described by the electric field E, the electric induction D, the
Computational Electromagnetics; Chapter 1 1 Chapter 1 Mathematical Foundations 1.1 Maxwell s Equations Electromagnetic phenomena can be described by the electric field E, the electric induction D, the
MAT389 Fall 2016, Problem Set 11
 MAT389 Fall 216, Problem Set 11 Improper integrals 11.1 In each of the following cases, establish the convergence of the given integral and calculate its value. i) x 2 x 2 + 1) 2 ii) x x 2 + 1)x 2 + 2x
MAT389 Fall 216, Problem Set 11 Improper integrals 11.1 In each of the following cases, establish the convergence of the given integral and calculate its value. i) x 2 x 2 + 1) 2 ii) x x 2 + 1)x 2 + 2x
9 The conservation theorems: Lecture 23
 9 The conservation theorems: Lecture 23 9.1 Energy Conservation (a) For energy to be conserved we expect that the total energy density (energy per volume ) u tot to obey a conservation law t u tot + i
9 The conservation theorems: Lecture 23 9.1 Energy Conservation (a) For energy to be conserved we expect that the total energy density (energy per volume ) u tot to obey a conservation law t u tot + i
22 Phasor form of Maxwell s equations and damped waves in conducting media
 22 Phasor form of Maxwell s equations and damped waves in conducting media When the fields and the sources in Maxwell s equations are all monochromatic functions of time expressed in terms of their phasors,
22 Phasor form of Maxwell s equations and damped waves in conducting media When the fields and the sources in Maxwell s equations are all monochromatic functions of time expressed in terms of their phasors,
Functions of a Complex Variable (S1) Lecture 11. VII. Integral Transforms. Integral transforms from application of complex calculus
 Functions of a Complex Variable (S1) Lecture 11 VII. Integral Transforms An introduction to Fourier and Laplace transformations Integral transforms from application of complex calculus Properties of Fourier
Functions of a Complex Variable (S1) Lecture 11 VII. Integral Transforms An introduction to Fourier and Laplace transformations Integral transforms from application of complex calculus Properties of Fourier
Lecture 15 Perfect Conductors, Boundary Conditions, Method of Images
 Lecture 15 Perfect Conductors, Boundary Conditions, Method of Images Sections: 5.4, 5.5 Homework: See homework file Perfect Conductors 1 metals such as Cu, Ag, Al are closely approximated by the concept
Lecture 15 Perfect Conductors, Boundary Conditions, Method of Images Sections: 5.4, 5.5 Homework: See homework file Perfect Conductors 1 metals such as Cu, Ag, Al are closely approximated by the concept
Magnetic Force on a Moving Charge
 Magnetic Force on a Moving Charge Electric charges moving in a magnetic field experience a force due to the magnetic field. Given a charge Q moving with velocity u in a magnetic flux density B, the vector
Magnetic Force on a Moving Charge Electric charges moving in a magnetic field experience a force due to the magnetic field. Given a charge Q moving with velocity u in a magnetic flux density B, the vector
Microscopic-Macroscopic connection. Silvana Botti
 relating experiment and theory European Theoretical Spectroscopy Facility (ETSF) CNRS - Laboratoire des Solides Irradiés Ecole Polytechnique, Palaiseau - France Temporary Address: Centre for Computational
relating experiment and theory European Theoretical Spectroscopy Facility (ETSF) CNRS - Laboratoire des Solides Irradiés Ecole Polytechnique, Palaiseau - France Temporary Address: Centre for Computational
Kramers-Kronig relations and the properties of conductivity and permittivity in heterogeneous media
 Kramers-Kronig relations and the properties of conductivity and permittivity in heterogeneous media arxiv:181.461v1 [cond-mat.dis-nn] 1 Jan 218 Abstract Claude Bédard et Alain Destexhe UNIC, CNRS, Gif
Kramers-Kronig relations and the properties of conductivity and permittivity in heterogeneous media arxiv:181.461v1 [cond-mat.dis-nn] 1 Jan 218 Abstract Claude Bédard et Alain Destexhe UNIC, CNRS, Gif
Pulse shape dependence in the dynamically assisted Sauter-Schwinger effect
 Pulse shape dependence in the dynamically assisted Sauter-Schwinger effect Joachim Sicking, Nikodem Szpak, Ralf Schützhold Fakultät für Physik, Universität Duisburg-Essen 20 March 2014, DPG Tagung Berlin
Pulse shape dependence in the dynamically assisted Sauter-Schwinger effect Joachim Sicking, Nikodem Szpak, Ralf Schützhold Fakultät für Physik, Universität Duisburg-Essen 20 March 2014, DPG Tagung Berlin
Green s Tensors for the Electromagnetic Field in Cylindrical Coordinates
 Chapter 25 Green s Tensors for the Electromagnetic Field in Cylindrical Coordinates The solutions of the vector Helmholtz equation in three dimensions can be expressed by a complete set of vector fields
Chapter 25 Green s Tensors for the Electromagnetic Field in Cylindrical Coordinates The solutions of the vector Helmholtz equation in three dimensions can be expressed by a complete set of vector fields
The RC Circuit: An Approach with Fourier Transforms
 The RC Circuit: An Approach with Fourier Transforms In this article we shall mathematically analyse the Resistor- Capacitor RC) circuit with the help of Fourier transforms FT). This very general technique
The RC Circuit: An Approach with Fourier Transforms In this article we shall mathematically analyse the Resistor- Capacitor RC) circuit with the help of Fourier transforms FT). This very general technique
Electromagnetic Wave Propagation Lecture 1: Maxwell s equations
 Electromagnetic Wave Propagation Lecture 1: Maxwell s equations Daniel Sjöberg Department of Electrical and Information Technology September 3, 2013 Outline 1 Maxwell s equations 2 Vector analysis 3 Boundary
Electromagnetic Wave Propagation Lecture 1: Maxwell s equations Daniel Sjöberg Department of Electrical and Information Technology September 3, 2013 Outline 1 Maxwell s equations 2 Vector analysis 3 Boundary
EECS 117 Lecture 19: Faraday s Law and Maxwell s Eq.
 University of California, Berkeley EECS 117 Lecture 19 p. 1/2 EECS 117 Lecture 19: Faraday s Law and Maxwell s Eq. Prof. Niknejad University of California, Berkeley University of California, Berkeley EECS
University of California, Berkeley EECS 117 Lecture 19 p. 1/2 EECS 117 Lecture 19: Faraday s Law and Maxwell s Eq. Prof. Niknejad University of California, Berkeley University of California, Berkeley EECS
THE KRAMERS-KRONIG RELATIONS FOR LIGHT MOVING BACKWARDS IN TIME. Evangelos Chaliasos. 365 Thebes Street. GR Aegaleo.
 THE KRAMERS-KRONI RELATIONS FOR LIHT MOVIN BACKWARDS IN TIME Evangelos Chaliasos 365 Thebes Street R-12241 Aegaleo Athens, reece Abstract The recent discovery of light moving backwards in time, when it
THE KRAMERS-KRONI RELATIONS FOR LIHT MOVIN BACKWARDS IN TIME Evangelos Chaliasos 365 Thebes Street R-12241 Aegaleo Athens, reece Abstract The recent discovery of light moving backwards in time, when it
Indiana University Physics P331: Theory of Electromagnetism Review Problems #3
 Indiana University Physics P331: Theory of Electromagnetism Review Problems #3 Note: The final exam (Friday 1/14 8:00-10:00 AM will be comprehensive, covering lecture and homework material pertaining to
Indiana University Physics P331: Theory of Electromagnetism Review Problems #3 Note: The final exam (Friday 1/14 8:00-10:00 AM will be comprehensive, covering lecture and homework material pertaining to
Supplementary Information for Experimental signature of programmable quantum annealing
 Supplementary Information for Experimental signature of programmable quantum annealing Supplementary Figures 8 7 6 Ti/exp(step T =.5 Ti/step Temperature 5 4 3 2 1 0 0 100 200 300 400 500 Annealing step
Supplementary Information for Experimental signature of programmable quantum annealing Supplementary Figures 8 7 6 Ti/exp(step T =.5 Ti/step Temperature 5 4 3 2 1 0 0 100 200 300 400 500 Annealing step
Mathematical Tripos, Part IB : Electromagnetism
 Mathematical Tripos, Part IB : Electromagnetism Proof of the result G = m B Refer to Sec. 3.7, Force and couples, and supply the proof that the couple exerted by a uniform magnetic field B on a plane current
Mathematical Tripos, Part IB : Electromagnetism Proof of the result G = m B Refer to Sec. 3.7, Force and couples, and supply the proof that the couple exerted by a uniform magnetic field B on a plane current
Finite Temperature Field Theory
 Finite Temperature Field Theory Dietrich Bödeker, Universität Bielefeld 1. Thermodynamics (better: thermo-statics) (a) Imaginary time formalism (b) free energy: scalar particles, resummation i. pedestrian
Finite Temperature Field Theory Dietrich Bödeker, Universität Bielefeld 1. Thermodynamics (better: thermo-statics) (a) Imaginary time formalism (b) free energy: scalar particles, resummation i. pedestrian
Dielectric wave guides, resonance, and cavities
 Dielectric wave guides, resonance, and cavities 1 Dielectric wave guides Instead of a cavity constructed of conducting walls, a guide can be constructed of dielectric material. In analogy to a conducting
Dielectric wave guides, resonance, and cavities 1 Dielectric wave guides Instead of a cavity constructed of conducting walls, a guide can be constructed of dielectric material. In analogy to a conducting
Progress on the Method of Mached Expansions in Schwarzschild
 Progress on the Method of Mached Expansions in Schwarzschild Marc Casals (University College Dublin, Perimeter Institute, University of Guelph) In collaboration with A.Ottewill Capra 14 - Southampton,
Progress on the Method of Mached Expansions in Schwarzschild Marc Casals (University College Dublin, Perimeter Institute, University of Guelph) In collaboration with A.Ottewill Capra 14 - Southampton,
Special Relativity and Electromagnetism
 1/32 Special Relativity and Electromagnetism Jonathan Gratus Cockcroft Postgraduate Lecture Series October 2016 Introduction 10:30 11:40 14:00? Monday SR EM Tuesday SR EM Seminar Four lectures is clearly
1/32 Special Relativity and Electromagnetism Jonathan Gratus Cockcroft Postgraduate Lecture Series October 2016 Introduction 10:30 11:40 14:00? Monday SR EM Tuesday SR EM Seminar Four lectures is clearly
12. Nonlinear optics I
 1. Nonlinear optics I What are nonlinear-optical effects and why do they occur? Maxwell's equations in a medium Nonlinear-optical media Second-harmonic generation Conservation laws for photons ("Phasematching")
1. Nonlinear optics I What are nonlinear-optical effects and why do they occur? Maxwell's equations in a medium Nonlinear-optical media Second-harmonic generation Conservation laws for photons ("Phasematching")
Relevant Electrostatics and Magnetostatics (Old and New)
 Unit 1 Relevant Electrostatics and Magnetostatics (Old and New) The whole of classical electrodynamics is encompassed by a set of coupled partial differential equations (at least in one form) bearing the
Unit 1 Relevant Electrostatics and Magnetostatics (Old and New) The whole of classical electrodynamics is encompassed by a set of coupled partial differential equations (at least in one form) bearing the
Quantum Light-Matter Interactions
 Quantum Light-Matter Interactions QIC 895: Theory of Quantum Optics David Layden June 8, 2015 Outline Background Review Jaynes-Cummings Model Vacuum Rabi Oscillations, Collapse & Revival Spontaneous Emission
Quantum Light-Matter Interactions QIC 895: Theory of Quantum Optics David Layden June 8, 2015 Outline Background Review Jaynes-Cummings Model Vacuum Rabi Oscillations, Collapse & Revival Spontaneous Emission
Derivation of the General Propagation Equation
 Derivation of the General Propagation Equation Phys 477/577: Ultrafast and Nonlinear Optics, F. Ö. Ilday, Bilkent University February 25, 26 1 1 Derivation of the Wave Equation from Maxwell s Equations
Derivation of the General Propagation Equation Phys 477/577: Ultrafast and Nonlinear Optics, F. Ö. Ilday, Bilkent University February 25, 26 1 1 Derivation of the Wave Equation from Maxwell s Equations
5 Electromagnetic Waves
 5 Electromagnetic Waves 5.1 General Form for Electromagnetic Waves. In free space, Maxwell s equations are: E ρ ɛ 0 (5.1.1) E + B 0 (5.1.) B 0 (5.1.3) B µ 0 ɛ 0 E µ 0 J (5.1.4) In section 4.3 we derived
5 Electromagnetic Waves 5.1 General Form for Electromagnetic Waves. In free space, Maxwell s equations are: E ρ ɛ 0 (5.1.1) E + B 0 (5.1.) B 0 (5.1.3) B µ 0 ɛ 0 E µ 0 J (5.1.4) In section 4.3 we derived
E E D E=0 2 E 2 E (3.1)
 Chapter 3 Constitutive Relations Maxwell s equations define the fields that are generated by currents and charges. However, they do not describe how these currents and charges are generated. Thus, to find
Chapter 3 Constitutive Relations Maxwell s equations define the fields that are generated by currents and charges. However, they do not describe how these currents and charges are generated. Thus, to find
RF cavities (Lecture 25)
 RF cavities (Lecture 25 February 2, 2016 319/441 Lecture outline A good conductor has a property to guide and trap electromagnetic field in a confined region. In this lecture we will consider an example
RF cavities (Lecture 25 February 2, 2016 319/441 Lecture outline A good conductor has a property to guide and trap electromagnetic field in a confined region. In this lecture we will consider an example
r r 1 r r 1 2 = q 1 p = qd and it points from the negative charge to the positive charge.
 MP204, Important Equations page 1 Below is a list of important equations that we meet in our study of Electromagnetism in the MP204 module. For your exam, you are expected to understand all of these, and
MP204, Important Equations page 1 Below is a list of important equations that we meet in our study of Electromagnetism in the MP204 module. For your exam, you are expected to understand all of these, and
1 Fundamentals. 1.1 Overview. 1.2 Units: Physics 704 Spring 2018
 Physics 704 Spring 2018 1 Fundamentals 1.1 Overview The objective of this course is: to determine and fields in various physical systems and the forces and/or torques resulting from them. The domain of
Physics 704 Spring 2018 1 Fundamentals 1.1 Overview The objective of this course is: to determine and fields in various physical systems and the forces and/or torques resulting from them. The domain of
Physics 505 Fall 2005 Homework Assignment #7 Solutions
 Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
Physics GRE: Electromagnetism. G. J. Loges 1. University of Rochester Dept. of Physics & Astronomy. xkcd.com/567/
 Physics GRE: Electromagnetism G. J. Loges University of Rochester Dept. of Physics & stronomy xkcd.com/567/ c Gregory Loges, 206 Contents Electrostatics 2 Magnetostatics 2 3 Method of Images 3 4 Lorentz
Physics GRE: Electromagnetism G. J. Loges University of Rochester Dept. of Physics & stronomy xkcd.com/567/ c Gregory Loges, 206 Contents Electrostatics 2 Magnetostatics 2 3 Method of Images 3 4 Lorentz
Electromagnetic Relaxation Time Distribution Inverse Problems in the Time-domain
 Electromagnetic Relaxation Time Distribution Inverse Problems in the Time-domain Prof Nathan L Gibson Department of Mathematics Joint Math Meeting Jan 9, 2011 Prof Gibson (OSU) Inverse Problems for Distributions
Electromagnetic Relaxation Time Distribution Inverse Problems in the Time-domain Prof Nathan L Gibson Department of Mathematics Joint Math Meeting Jan 9, 2011 Prof Gibson (OSU) Inverse Problems for Distributions
Electromagnetic Wave Propagation Lecture 1: Maxwell s equations
 Electromagnetic Wave Propagation Lecture 1: Maxwell s equations Daniel Sjöberg Department of Electrical and Information Technology September 2, 2014 Outline 1 Maxwell s equations 2 Vector analysis 3 Boundary
Electromagnetic Wave Propagation Lecture 1: Maxwell s equations Daniel Sjöberg Department of Electrical and Information Technology September 2, 2014 Outline 1 Maxwell s equations 2 Vector analysis 3 Boundary
Chapter 7. Time-Varying Fields and Maxwell s Equations
 Chapter 7. Time-arying Fields and Maxwell s Equations Electrostatic & Time arying Fields Electrostatic fields E, D B, H =J D H 1 E B In the electrostatic model, electric field and magnetic fields are not
Chapter 7. Time-arying Fields and Maxwell s Equations Electrostatic & Time arying Fields Electrostatic fields E, D B, H =J D H 1 E B In the electrostatic model, electric field and magnetic fields are not
Suggested Homework Solutions
 Suggested Homework Solutions Chapter Fourteen Section #9: Real and Imaginary parts of /z: z = x + iy = x + iy x iy ( ) x iy = x #9: Real and Imaginary parts of ln z: + i ( y ) ln z = ln(re iθ ) = ln r
Suggested Homework Solutions Chapter Fourteen Section #9: Real and Imaginary parts of /z: z = x + iy = x + iy x iy ( ) x iy = x #9: Real and Imaginary parts of ln z: + i ( y ) ln z = ln(re iθ ) = ln r
Electric fields in matter
 Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
Lecture 3. E α (ω) exp( iωt) dω = F 1 [E α ](t), (1 )
, (1 ) Lecture 3. E α (ω) exp( iωt) dω = F 1 [E α ](t), (1 )](/thumbs/88/116554615.jpg) Nonlinear Optics 5A551 (200) Lecture notes Lecture Susceptibility tensors in the frequency domain The susceptibility tensors in the frequency domain arise when the electric field E α (t) of the light is
Nonlinear Optics 5A551 (200) Lecture notes Lecture Susceptibility tensors in the frequency domain The susceptibility tensors in the frequency domain arise when the electric field E α (t) of the light is
Power Loss. dp loss = 1 = 1. Method 2, Ohmic heating, power lost per unit volume. Agrees with method 1. c = 2 loss per unit area is dp loss da
 How much power is dissipated (per unit area?). 2 ways: 1) Flow of energy into conductor: Energy flow given by S = E H, for real fields E H. so 1 S ( ) = 1 2 Re E H, dp loss /da = ˆn S, so dp loss = 1 µc
How much power is dissipated (per unit area?). 2 ways: 1) Flow of energy into conductor: Energy flow given by S = E H, for real fields E H. so 1 S ( ) = 1 2 Re E H, dp loss /da = ˆn S, so dp loss = 1 µc
3. Greens functions. H = H 0 + V t. V t = ˆBF t. e βh. ρ 0 ρ t. 3.1 Introduction
 3. Greens functions 3.1 Introduction Greens functions appear naturally as response functions, i.e. as answers to the function how a quantum mechanical system responds to an external perturbation, like
3. Greens functions 3.1 Introduction Greens functions appear naturally as response functions, i.e. as answers to the function how a quantum mechanical system responds to an external perturbation, like
Chapter 2: Complex numbers
 Chapter 2: Complex numbers Complex numbers are commonplace in physics and engineering. In particular, complex numbers enable us to simplify equations and/or more easily find solutions to equations. We
Chapter 2: Complex numbers Complex numbers are commonplace in physics and engineering. In particular, complex numbers enable us to simplify equations and/or more easily find solutions to equations. We
EECS 117. Lecture 17: Magnetic Forces/Torque, Faraday s Law. Prof. Niknejad. University of California, Berkeley
 University of California, Berkeley EECS 117 Lecture 17 p. 1/? EECS 117 Lecture 17: Magnetic Forces/Torque, Faraday s Law Prof. Niknejad University of California, Berkeley University of California, Berkeley
University of California, Berkeley EECS 117 Lecture 17 p. 1/? EECS 117 Lecture 17: Magnetic Forces/Torque, Faraday s Law Prof. Niknejad University of California, Berkeley University of California, Berkeley
H ( E) E ( H) = H B t
 Chapter 5 Energy and Momentum The equations established so far describe the behavior of electric and magnetic fields. They are a direct consequence of Maxwell s equations and the properties of matter.
Chapter 5 Energy and Momentum The equations established so far describe the behavior of electric and magnetic fields. They are a direct consequence of Maxwell s equations and the properties of matter.
Electromagnetic Field Theory Chapter 9: Time-varying EM Fields
 Electromagnetic Field Theory Chapter 9: Time-varying EM Fields Faraday s law of induction We have learned that a constant current induces magnetic field and a constant charge (or a voltage) makes an electric
Electromagnetic Field Theory Chapter 9: Time-varying EM Fields Faraday s law of induction We have learned that a constant current induces magnetic field and a constant charge (or a voltage) makes an electric
Chapter 7. Time-Varying Fields and Maxwell s Equation
 Chapter 7. Time-Varying Fields and Maxwell s Equation Electrostatic & Time Varying Fields Electrostatic fields E, D B, H =J D H 1 E B In the electrostatic model, electric field and magnetic fields are
Chapter 7. Time-Varying Fields and Maxwell s Equation Electrostatic & Time Varying Fields Electrostatic fields E, D B, H =J D H 1 E B In the electrostatic model, electric field and magnetic fields are
Boundary value problems
 1 Introduction Boundary value problems Lecture 5 We have found that the electric potential is a solution of the partial differential equation; 2 V = ρ/ǫ 0 The above is Poisson s equation where ρ is the
1 Introduction Boundary value problems Lecture 5 We have found that the electric potential is a solution of the partial differential equation; 2 V = ρ/ǫ 0 The above is Poisson s equation where ρ is the
