Combinatorially Thinking
|
|
|
- Merryl Thomas
- 5 years ago
- Views:
Transcription
1 Combiatorially Thiig SIMUW 2008: July 4 25 Jeifer J Qui jjqui@uwashigtoedu Philosophy We wat to costruct our mathematical uderstadig To this ed, our goal is to situate our problems i cocrete coutig cotexts Most mathematicias appreciate clever combiatorial proofs But faced with a idetity, how ca you create oe? This course will provide you with some useful combiatorial iterpretatios, lots of examples, ad the challege of fidig your ow combiatorial proofs Throughout the ext two wees, your matra should be to eep it simple
2 Cotets Basic Tools 3 Some Combiatorial Iterpretatios 3 2 Coutig Techique : As a Questio ad Aswer Two Ways 6 3 Coutig Techique 2: Descriptio-Ivolutio-Exceptio (DIE) 7 2 Biomial Idetities 8 2 Worig Together 8 22 O Your Ow 9 23 What s the Parity of? 0 3 Fiboacci Idetities 3 3 Tilig with Squares ad Domioes 3 32 Worig Together 4 33 O Your Ow 5 34 Combiatorial Proof of Biet s Formula 6 4 Geeralizatios Lucas, Giboacci, ad Liear Recurreces 8 4 Tilig i Circles, Tilig with Weights 8 42 Worig Together 9 43 O Your Ow 9 44 Biet Revisited 20 5 Cotiued Fractios 2 5 Itroductios ad Exploratios 2 52 O Your Ow Primes of form 4m Alteratig Sums 24 6 Worig Together O Your Ow Exted ad Geeralize by Playig with Parameters 26 7 Determiats 27 7 The Big Formula Worig Together O Your Ow Vadermode Determiat 30 2
3 Basic Tools Some Combiatorial Iterpretatios First, we eed combiatorial iterpretatios for the objects occurrig i our idetities While there are may possible iterpretatios, oly oe is preseted for each mathematical object tryig, of course, to eep it simple I have icluded at least oe method to compute each object for completeess though we will rarely rely o computatio! factorial Combiatorial: The ways to arrage umbers, 2, 3,, i a lie Computatioal:! ( ) ( 2) 2 ( ) biomial coefficiet, choose Combiatorial: The ways to select a subset cotaiig elemets from the set [] {, 2, 3,, }! Computatioal:!( )! (( )) multichoose Combiatorial: The ways to cast votes for elemets from the set [] {, 2, 3,, } Computatioal: () + [ ] (usiged) Stirlig umber of the first id Combiatorial: The ways to arrage people aroud idetical (oempty) circular tables [ ] { [ ] 0 Computatioal: Recursively ad ( )! For 2, [ ] [ ] + ( + ) [ ] 3
4 { } Stirlig umber of the secod id Combiatorial: The ways to distribute people ito idetical (oempty) rooms { } { { } 0 Computatioal: Recursively ad For 2, { } f the th Fiboacci umber { } + { } Combiatorial: The ways to tile a board usig squares ad 2 domioes Computatioal: f 0, f, ad for 2 f f + f 2 or f φ φ where φ WARNING: You might be used to the Fiboacci umbers defied i the more traditioal way F 0 0, F, ad for 2 F F + F 2 L the th Lucas umber Combiatorial: The ways to tile a circular board usig squares ad 2 domioes Computatioal: L 0 2, L, ad for 2 L L + L 2 G the th Giboacci umber or L φ + φ Combiatorial: The ways to tile a board usig squares ad 2 domioes where the first tile is distiguished There are G choices for a leadig square ad G 0 choices for a leadig domio Computatioal: G 0 ad G are give ad for 2 G G + G 2 or G αφ + β φ where α (G + G 0 /φ)/ 5 ad β (φg 0 G )/ 5 4
5 D the th Deragemet umber Combiatorial: The ways to arrage, 2,, i a lie so that o umber lies i its atural positio ( Computatioal: D!! + 2! 3! + + ) ( )! C the th Catala umber Combiatorial: The umber of lattice paths from (0, 0) to (, ) usig right ad up edges ad stayig below the lie y x Computatioal: C 2 + [a 0,a,,a ] the fiite cotiued fractio a 0 + a + a a p q Combiatorial: Numerator: The ways to tile a + board usig squares ad domioes where cell i ca cotai half a domio or as may as a i squares, 0 i Deomiator: The ways to tile a board usig squares ad domioes where cell i ca cotai half a domio or as may as a i squares, i Computatioal: Attac with algebra to ratioalize the complex fractio det(a) the determiat of the matrix A {a ij } Combiatorial: The siged sum of oitersectig -routes i a directed graph with origis, destiatios, ad a ij directed paths from origi i to destiatio j Computatioal: det(a) sig(σ)a σ() a 2σ(2) a σ() σ S Example: det
6 2 Coutig Techique : As a Questio ad Aswer Two Ways We will use oe of two techiques to cout a idetity The first poses a questio ad the aswers it i two differet ways Oe aswer is the left side of the idetity; the other aswer is the right side Sice both aswers solve the same coutig questio, they must be equal Idetity For,!! Questio: The umber of ways to arrage, 2, 3,, except for Aswer : Aswer 2: Idetity 2 For, 0, () + Questio: How may ways ca we allocate votes to cadidates? Aswer : Aswer 2: 6
7 3 Coutig Techique 2: Descriptio-Ivolutio-Exceptio (DIE) The secod techique is to create two sets, cout their sizes, ad fid a correspodece betwee them The correspodece could be oe-to-oe, may-to-oe, almost oe-to-oe, or almost may-to-oe Idetity 3 For, 0, () + Descriptio: Set : Set 2: Ivolutio: Exceptio: Idetity 4 For 0, ) 0( ) ( 0 Descriptio: Set : Set 2: Ivolutio: Exceptio: What happes is we chage the upper idex of the summatio to somethig smaller tha? larger tha? 7
8 2 Biomial Idetities 2 Worig Together Let s use these techiques to prove some idetities Idetity 5 For 0!!( )! Idetity 6 The Biomial Theorem For 0, (x + y) x y x y + x 2 y x 0 y Idetity 7 For
9 22 O Your Ow Idetity 8 For 0, (except 0), + The techique above ca be modified to prove: Idetity 9 For 0, 0, (except 0), Idetity 0 For, Idetity For, [ ] { } [ ] + ( ) { } + () () + [ { } ] (( )) Idetity 2 For, 0 2 Idetity 3 For, 2 0 Idetity 4 For q 0, q q 2 q ( q ) Idetity 5 For m, 0, m m j j j Idetity 6 For j 0, m ( m j )( m j ) + + Idetity 7 For oegative itegers, 2,,, let N i i 2 The i + i<j ( i 2 ) j i 4 N 2 9
10 23 What s the Parity of? Pascal s Triagle Serpisi-lie Triagle Theorem For 0, the umber of odd itegers i the th row of Pascal s triagle is equal to 2 b where b the umber of s i the biary expasio of Questio How may odd umbers occur i the 76 th row of Pascal s triagle? LemmaThe parity of will be the same as the parity of the umber of palidromic sequeces with oes ad zeros Descriptio Biary sequeces with oes ad zeros Ivolutio Exceptio As: 76 (0000) 2 Eight odd umbers 0
11 Cout palidromic sequeces with oes ad zeros eve odd eve eve odd eve odd odd Cosequece If is eve ad is odd, the ( ) is eve, otherwise, has the same parity as /2 /2 where we roud /2 ad /2 dow to the earest iteger, if ecessary Examples Compute the parity: Thi ( biary! ) (0000)2 (0000)2 (0000)2 (000) 2 (00000) 2 (00000) 2
12 Oly way to have a odd umber is if the s i the biary represetatio of are directly below s i biary represetatio of It tells us exactly which umbers produce odd biomial coefficiets: biary represetatio Extesio There a similar procedure to determie the remaider of whe divided by ay prime p? Lucas Theorem For ay prime p, we ca determie the remaider of whe divided by p from the base p expasios of ad If b t p t + b t b t + + b p + b 0 c t p t + c t b t + + c p + c 0 the ad bt bt c t c t b b0 c c 0 have the same remaider whe divided by p Example Calculate the remaider of 97 whe divided by 5 35 As: ( 97 35) ( 3 )( 4 2)( 2 0) 3 mod 5 2
1. n! = n. tion. For example, (n+1)! working with factorials. = (n+1) n (n 1) 2 1
 Biomial Coefficiets ad Permutatios Mii-lecture The followig pages discuss a few special iteger coutig fuctios You may have see some of these before i a basic probability class or elsewhere, but perhaps
Biomial Coefficiets ad Permutatios Mii-lecture The followig pages discuss a few special iteger coutig fuctios You may have see some of these before i a basic probability class or elsewhere, but perhaps
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
MT5821 Advanced Combinatorics
 MT5821 Advaced Combiatorics 1 Coutig subsets I this sectio, we cout the subsets of a -elemet set. The coutig umbers are the biomial coefficiets, familiar objects but there are some ew thigs to say about
MT5821 Advaced Combiatorics 1 Coutig subsets I this sectio, we cout the subsets of a -elemet set. The coutig umbers are the biomial coefficiets, familiar objects but there are some ew thigs to say about
CSE 191, Class Note 05: Counting Methods Computer Sci & Eng Dept SUNY Buffalo
 Coutig Methods CSE 191, Class Note 05: Coutig Methods Computer Sci & Eg Dept SUNY Buffalo c Xi He (Uiversity at Buffalo CSE 191 Discrete Structures 1 / 48 Need for Coutig The problem of coutig the umber
Coutig Methods CSE 191, Class Note 05: Coutig Methods Computer Sci & Eg Dept SUNY Buffalo c Xi He (Uiversity at Buffalo CSE 191 Discrete Structures 1 / 48 Need for Coutig The problem of coutig the umber
Properties and Tests of Zeros of Polynomial Functions
 Properties ad Tests of Zeros of Polyomial Fuctios The Remaider ad Factor Theorems: Sythetic divisio ca be used to fid the values of polyomials i a sometimes easier way tha substitutio. This is show by
Properties ad Tests of Zeros of Polyomial Fuctios The Remaider ad Factor Theorems: Sythetic divisio ca be used to fid the values of polyomials i a sometimes easier way tha substitutio. This is show by
Section 5.1 The Basics of Counting
 1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
Zeros of Polynomials
 Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Combinatorics and Newton s theorem
 INTRODUCTION TO MATHEMATICAL REASONING Key Ideas Worksheet 5 Combiatorics ad Newto s theorem This week we are goig to explore Newto s biomial expasio theorem. This is a very useful tool i aalysis, but
INTRODUCTION TO MATHEMATICAL REASONING Key Ideas Worksheet 5 Combiatorics ad Newto s theorem This week we are goig to explore Newto s biomial expasio theorem. This is a very useful tool i aalysis, but
Math 475, Problem Set #12: Answers
 Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
Chapter 7 COMBINATIONS AND PERMUTATIONS. where we have the specific formula for the binomial coefficients:
 Chapter 7 COMBINATIONS AND PERMUTATIONS We have see i the previous chapter that (a + b) ca be writte as 0 a % a & b%þ% a & b %þ% b where we have the specific formula for the biomial coefficiets: '!!(&)!
Chapter 7 COMBINATIONS AND PERMUTATIONS We have see i the previous chapter that (a + b) ca be writte as 0 a % a & b%þ% a & b %þ% b where we have the specific formula for the biomial coefficiets: '!!(&)!
0 1 sum= sum= sum= sum= sum= sum= sum=64
 Biomial Coefficiets I how may ways ca we choose elemets from a elemet set? There are choices for the first elemet, - for the secod,..., dow to - + for the th, yieldig *(-)*...*(-+). So there are 4*3=2
Biomial Coefficiets I how may ways ca we choose elemets from a elemet set? There are choices for the first elemet, - for the secod,..., dow to - + for the th, yieldig *(-)*...*(-+). So there are 4*3=2
Lecture Overview. 2 Permutations and Combinations. n(n 1) (n (k 1)) = n(n 1) (n k + 1) =
 COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
A NOTE ON PASCAL S MATRIX. Gi-Sang Cheon, Jin-Soo Kim and Haeng-Won Yoon
 J Korea Soc Math Educ Ser B: Pure Appl Math 6(1999), o 2 121 127 A NOTE ON PASCAL S MATRIX Gi-Sag Cheo, Ji-Soo Kim ad Haeg-Wo Yoo Abstract We ca get the Pascal s matrix of order by takig the first rows
J Korea Soc Math Educ Ser B: Pure Appl Math 6(1999), o 2 121 127 A NOTE ON PASCAL S MATRIX Gi-Sag Cheo, Ji-Soo Kim ad Haeg-Wo Yoo Abstract We ca get the Pascal s matrix of order by takig the first rows
Books Recommended for Further Reading
 Books Recommeded for Further Readig by 8.5..8 o 0//8. For persoal use oly.. K. P. Bogart, Itroductory Combiatorics rd ed., S. I. Harcourt Brace College Publishers, 998.. R. A. Brualdi, Itroductory Combiatorics
Books Recommeded for Further Readig by 8.5..8 o 0//8. For persoal use oly.. K. P. Bogart, Itroductory Combiatorics rd ed., S. I. Harcourt Brace College Publishers, 998.. R. A. Brualdi, Itroductory Combiatorics
Injections, Surjections, and the Pigeonhole Principle
 Ijectios, Surjectios, ad the Pigeohole Priciple 1 (10 poits Here we will come up with a sloppy boud o the umber of parethesisestigs (a (5 poits Describe a ijectio from the set of possible ways to est pairs
Ijectios, Surjectios, ad the Pigeohole Priciple 1 (10 poits Here we will come up with a sloppy boud o the umber of parethesisestigs (a (5 poits Describe a ijectio from the set of possible ways to est pairs
In number theory we will generally be working with integers, though occasionally fractions and irrationals will come into play.
 Number Theory Math 5840 otes. Sectio 1: Axioms. I umber theory we will geerally be workig with itegers, though occasioally fractios ad irratioals will come ito play. Notatio: Z deotes the set of all itegers
Number Theory Math 5840 otes. Sectio 1: Axioms. I umber theory we will geerally be workig with itegers, though occasioally fractios ad irratioals will come ito play. Notatio: Z deotes the set of all itegers
CALCULATION OF FIBONACCI VECTORS
 CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
Complex Numbers Solutions
 Complex Numbers Solutios Joseph Zoller February 7, 06 Solutios. (009 AIME I Problem ) There is a complex umber with imagiary part 64 ad a positive iteger such that Fid. [Solutio: 697] 4i + + 4i. 4i 4i
Complex Numbers Solutios Joseph Zoller February 7, 06 Solutios. (009 AIME I Problem ) There is a complex umber with imagiary part 64 ad a positive iteger such that Fid. [Solutio: 697] 4i + + 4i. 4i 4i
arxiv: v1 [math.nt] 10 Dec 2014
![arxiv: v1 [math.nt] 10 Dec 2014 arxiv: v1 [math.nt] 10 Dec 2014](/thumbs/82/85433827.jpg) A DIGITAL BINOMIAL THEOREM HIEU D. NGUYEN arxiv:42.38v [math.nt] 0 Dec 204 Abstract. We preset a triagle of coectios betwee the Sierpisi triagle, the sum-of-digits fuctio, ad the Biomial Theorem via a
A DIGITAL BINOMIAL THEOREM HIEU D. NGUYEN arxiv:42.38v [math.nt] 0 Dec 204 Abstract. We preset a triagle of coectios betwee the Sierpisi triagle, the sum-of-digits fuctio, ad the Biomial Theorem via a
The Pascal Fibonacci numbers
 Notes o Number Theory ad Discrete Mathematics Vol. 19, 013, No. 3, 5 11 The Pascal Fiboacci umbers J. V. Leyedekkers 1 ad A. G. Shao 1 Faculty of Sciece, The Uiversity of Sydey NSW 00, Australia Faculty
Notes o Number Theory ad Discrete Mathematics Vol. 19, 013, No. 3, 5 11 The Pascal Fiboacci umbers J. V. Leyedekkers 1 ad A. G. Shao 1 Faculty of Sciece, The Uiversity of Sydey NSW 00, Australia Faculty
Lecture 10: Mathematical Preliminaries
 Lecture : Mathematical Prelimiaries Obective: Reviewig mathematical cocepts ad tools that are frequetly used i the aalysis of algorithms. Lecture # Slide # I this
Lecture : Mathematical Prelimiaries Obective: Reviewig mathematical cocepts ad tools that are frequetly used i the aalysis of algorithms. Lecture # Slide # I this
arxiv: v1 [math.co] 23 Mar 2016
![arxiv: v1 [math.co] 23 Mar 2016 arxiv: v1 [math.co] 23 Mar 2016](/thumbs/92/108877827.jpg) The umber of direct-sum decompositios of a fiite vector space arxiv:603.0769v [math.co] 23 Mar 206 David Ellerma Uiversity of Califoria at Riverside August 3, 208 Abstract The theory of q-aalogs develops
The umber of direct-sum decompositios of a fiite vector space arxiv:603.0769v [math.co] 23 Mar 206 David Ellerma Uiversity of Califoria at Riverside August 3, 208 Abstract The theory of q-aalogs develops
A Combinatorial Proof of a Theorem of Katsuura
 Mathematical Assoc. of America College Mathematics Joural 45:1 Jue 2, 2014 2:34 p.m. TSWLatexiaTemp 000017.tex A Combiatorial Proof of a Theorem of Katsuura Bria K. Miceli Bria Miceli (bmiceli@triity.edu)
Mathematical Assoc. of America College Mathematics Joural 45:1 Jue 2, 2014 2:34 p.m. TSWLatexiaTemp 000017.tex A Combiatorial Proof of a Theorem of Katsuura Bria K. Miceli Bria Miceli (bmiceli@triity.edu)
1 Summary: Binary and Logic
 1 Summary: Biary ad Logic Biary Usiged Represetatio : each 1-bit is a power of two, the right-most is for 2 0 : 0110101 2 = 2 5 + 2 4 + 2 2 + 2 0 = 32 + 16 + 4 + 1 = 53 10 Usiged Rage o bits is [0...2
1 Summary: Biary ad Logic Biary Usiged Represetatio : each 1-bit is a power of two, the right-most is for 2 0 : 0110101 2 = 2 5 + 2 4 + 2 2 + 2 0 = 32 + 16 + 4 + 1 = 53 10 Usiged Rage o bits is [0...2
3.2 Properties of Division 3.3 Zeros of Polynomials 3.4 Complex and Rational Zeros of Polynomials
 Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
CSE 1400 Applied Discrete Mathematics Number Theory and Proofs
 CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
Lecture 4 The Simple Random Walk
 Lecture 4: The Simple Radom Walk 1 of 9 Course: M36K Itro to Stochastic Processes Term: Fall 014 Istructor: Gorda Zitkovic Lecture 4 The Simple Radom Walk We have defied ad costructed a radom walk {X }
Lecture 4: The Simple Radom Walk 1 of 9 Course: M36K Itro to Stochastic Processes Term: Fall 014 Istructor: Gorda Zitkovic Lecture 4 The Simple Radom Walk We have defied ad costructed a radom walk {X }
(ii) Two-permutations of {a, b, c}. Answer. (B) P (3, 3) = 3! (C) 3! = 6, and there are 6 items in (A). ... Answer.
 SOLUTIONS Homewor 5 Due /6/19 Exercise. (a Cosider the set {a, b, c}. For each of the followig, (A list the objects described, (B give a formula that tells you how may you should have listed, ad (C verify
SOLUTIONS Homewor 5 Due /6/19 Exercise. (a Cosider the set {a, b, c}. For each of the followig, (A list the objects described, (B give a formula that tells you how may you should have listed, ad (C verify
ENGI Series Page 6-01
 ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
Course : Algebraic Combinatorics
 Course 8.32: Algebraic Combiatorics Lecture Notes # Addedum by Gregg Musier February 4th - 6th, 2009 Recurrece Relatios ad Geeratig Fuctios Give a ifiite sequece of umbers, a geeratig fuctio is a compact
Course 8.32: Algebraic Combiatorics Lecture Notes # Addedum by Gregg Musier February 4th - 6th, 2009 Recurrece Relatios ad Geeratig Fuctios Give a ifiite sequece of umbers, a geeratig fuctio is a compact
CIS Spring 2018 (instructor Val Tannen)
 CIS 160 - Sprig 2018 (istructor Val Tae) Lecture 5 Thursday, Jauary 25 COUNTING We cotiue studyig how to use combiatios ad what are their properties. Example 5.1 How may 8-letter strigs ca be costructed
CIS 160 - Sprig 2018 (istructor Val Tae) Lecture 5 Thursday, Jauary 25 COUNTING We cotiue studyig how to use combiatios ad what are their properties. Example 5.1 How may 8-letter strigs ca be costructed
Solutions to Final Exam
 Solutios to Fial Exam 1. Three married couples are seated together at the couter at Moty s Blue Plate Dier, occupyig six cosecutive seats. How may arragemets are there with o wife sittig ext to her ow
Solutios to Fial Exam 1. Three married couples are seated together at the couter at Moty s Blue Plate Dier, occupyig six cosecutive seats. How may arragemets are there with o wife sittig ext to her ow
x c the remainder is Pc ().
 Algebra, Polyomial ad Ratioal Fuctios Page 1 K.Paulk Notes Chapter 3, Sectio 3.1 to 3.4 Summary Sectio Theorem Notes 3.1 Zeros of a Fuctio Set the fuctio to zero ad solve for x. The fuctio is zero at these
Algebra, Polyomial ad Ratioal Fuctios Page 1 K.Paulk Notes Chapter 3, Sectio 3.1 to 3.4 Summary Sectio Theorem Notes 3.1 Zeros of a Fuctio Set the fuctio to zero ad solve for x. The fuctio is zero at these
MT5821 Advanced Combinatorics
 MT5821 Advaced Combiatorics 9 Set partitios ad permutatios It could be said that the mai objects of iterest i combiatorics are subsets, partitios ad permutatios of a fiite set. We have spet some time coutig
MT5821 Advaced Combiatorics 9 Set partitios ad permutatios It could be said that the mai objects of iterest i combiatorics are subsets, partitios ad permutatios of a fiite set. We have spet some time coutig
Problem 4: Evaluate ( k ) by negating (actually un-negating) its upper index. Binomial coefficient
 Problem 4: Evaluate by egatig actually u-egatig its upper idex We ow that Biomial coefficiet r { where r is a real umber, is a iteger The above defiitio ca be recast i terms of factorials i the commo case
Problem 4: Evaluate by egatig actually u-egatig its upper idex We ow that Biomial coefficiet r { where r is a real umber, is a iteger The above defiitio ca be recast i terms of factorials i the commo case
David Vella, Skidmore College.
 David Vella, Skidmore College dvella@skidmore.edu Geeratig Fuctios ad Expoetial Geeratig Fuctios Give a sequece {a } we ca associate to it two fuctios determied by power series: Its (ordiary) geeratig
David Vella, Skidmore College dvella@skidmore.edu Geeratig Fuctios ad Expoetial Geeratig Fuctios Give a sequece {a } we ca associate to it two fuctios determied by power series: Its (ordiary) geeratig
Homework 3. = k 1. Let S be a set of n elements, and let a, b, c be distinct elements of S. The number of k-subsets of S is
 Homewor 3 Chapter 5 pp53: 3 40 45 Chapter 6 p85: 4 6 4 30 Use combiatorial reasoig to prove the idetity 3 3 Proof Let S be a set of elemets ad let a b c be distict elemets of S The umber of -subsets of
Homewor 3 Chapter 5 pp53: 3 40 45 Chapter 6 p85: 4 6 4 30 Use combiatorial reasoig to prove the idetity 3 3 Proof Let S be a set of elemets ad let a b c be distict elemets of S The umber of -subsets of
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Intermediate Math Circles November 4, 2009 Counting II
 Uiversity of Waterloo Faculty of Mathematics Cetre for Educatio i Mathematics ad Computig Itermediate Math Circles November 4, 009 Coutig II Last time, after lookig at the product rule ad sum rule, we
Uiversity of Waterloo Faculty of Mathematics Cetre for Educatio i Mathematics ad Computig Itermediate Math Circles November 4, 009 Coutig II Last time, after lookig at the product rule ad sum rule, we
Permutations, Combinations, and the Binomial Theorem
 Permutatios, ombiatios, ad the Biomial Theorem Sectio Permutatios outig methods are used to determie the umber of members of a specific set as well as outcomes of a evet. There are may differet ways to
Permutatios, ombiatios, ad the Biomial Theorem Sectio Permutatios outig methods are used to determie the umber of members of a specific set as well as outcomes of a evet. There are may differet ways to
On Divisibility concerning Binomial Coefficients
 A talk give at the Natioal Chiao Tug Uiversity (Hsichu, Taiwa; August 5, 2010 O Divisibility cocerig Biomial Coefficiets Zhi-Wei Su Najig Uiversity Najig 210093, P. R. Chia zwsu@ju.edu.c http://math.ju.edu.c/
A talk give at the Natioal Chiao Tug Uiversity (Hsichu, Taiwa; August 5, 2010 O Divisibility cocerig Biomial Coefficiets Zhi-Wei Su Najig Uiversity Najig 210093, P. R. Chia zwsu@ju.edu.c http://math.ju.edu.c/
Topic 5: Basics of Probability
 Topic 5: Jue 1, 2011 1 Itroductio Mathematical structures lie Euclidea geometry or algebraic fields are defied by a set of axioms. Mathematical reality is the developed through the itroductio of cocepts
Topic 5: Jue 1, 2011 1 Itroductio Mathematical structures lie Euclidea geometry or algebraic fields are defied by a set of axioms. Mathematical reality is the developed through the itroductio of cocepts
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
Lecture 3: Catalan Numbers
 CCS Discrete Math I Professor: Padraic Bartlett Lecture 3: Catala Numbers Week 3 UCSB 2014 I this week, we start studyig specific examples of commoly-occurrig sequeces of umbers (as opposed to the more
CCS Discrete Math I Professor: Padraic Bartlett Lecture 3: Catala Numbers Week 3 UCSB 2014 I this week, we start studyig specific examples of commoly-occurrig sequeces of umbers (as opposed to the more
Math 4707 Spring 2018 (Darij Grinberg): homework set 4 page 1
 Math 4707 Sprig 2018 Darij Griberg): homewor set 4 page 1 Math 4707 Sprig 2018 Darij Griberg): homewor set 4 due date: Wedesday 11 April 2018 at the begiig of class, or before that by email or moodle Please
Math 4707 Sprig 2018 Darij Griberg): homewor set 4 page 1 Math 4707 Sprig 2018 Darij Griberg): homewor set 4 due date: Wedesday 11 April 2018 at the begiig of class, or before that by email or moodle Please
Introduction To Discrete Mathematics
 Itroductio To Discrete Mathematics Review If you put + pigeos i pigeoholes the at least oe hole would have more tha oe pigeo. If (r + objects are put ito boxes, the at least oe of the boxes cotais r or
Itroductio To Discrete Mathematics Review If you put + pigeos i pigeoholes the at least oe hole would have more tha oe pigeo. If (r + objects are put ito boxes, the at least oe of the boxes cotais r or
Bertrand s Postulate
 Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS. Mircea Merca
 Idia J Pure Appl Math 45): 75-89 February 204 c Idia Natioal Sciece Academy A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS Mircea Merca Departmet of Mathematics Uiversity
Idia J Pure Appl Math 45): 75-89 February 204 c Idia Natioal Sciece Academy A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS Mircea Merca Departmet of Mathematics Uiversity
( ) GENERATING FUNCTIONS
 GENERATING FUNCTIONS Solve a ifiite umber of related problems i oe swoop. *Code the problems, maipulate the code, the decode the aswer! Really a algebraic cocept but ca be eteded to aalytic basis for iterestig
GENERATING FUNCTIONS Solve a ifiite umber of related problems i oe swoop. *Code the problems, maipulate the code, the decode the aswer! Really a algebraic cocept but ca be eteded to aalytic basis for iterestig
subcaptionfont+=small,labelformat=parens,labelsep=space,skip=6pt,list=0,hypcap=0 subcaption ALGEBRAIC COMBINATORICS LECTURE 8 TUESDAY, 2/16/2016
 subcaptiofot+=small,labelformat=pares,labelsep=space,skip=6pt,list=0,hypcap=0 subcaptio ALGEBRAIC COMBINATORICS LECTURE 8 TUESDAY, /6/06. Self-cojugate Partitios Recall that, give a partitio λ, we may
subcaptiofot+=small,labelformat=pares,labelsep=space,skip=6pt,list=0,hypcap=0 subcaptio ALGEBRAIC COMBINATORICS LECTURE 8 TUESDAY, /6/06. Self-cojugate Partitios Recall that, give a partitio λ, we may
MAT 271 Project: Partial Fractions for certain rational functions
 MAT 7 Project: Partial Fractios for certai ratioal fuctios Prerequisite kowledge: partial fractios from MAT 7, a very good commad of factorig ad complex umbers from Precalculus. To complete this project,
MAT 7 Project: Partial Fractios for certai ratioal fuctios Prerequisite kowledge: partial fractios from MAT 7, a very good commad of factorig ad complex umbers from Precalculus. To complete this project,
UNIVERSITY OF NORTHERN COLORADO MATHEMATICS CONTEST. First Round For all Colorado Students Grades 7-12 November 3, 2007
 UNIVERSITY OF NORTHERN COLORADO MATHEMATICS CONTEST First Roud For all Colorado Studets Grades 7- November, 7 The positive itegers are,,, 4, 5, 6, 7, 8, 9,,,,. The Pythagorea Theorem says that a + b =
UNIVERSITY OF NORTHERN COLORADO MATHEMATICS CONTEST First Roud For all Colorado Studets Grades 7- November, 7 The positive itegers are,,, 4, 5, 6, 7, 8, 9,,,,. The Pythagorea Theorem says that a + b =
Let us consider the following problem to warm up towards a more general statement.
 Lecture 4: Sequeces with repetitios, distributig idetical objects amog distict parties, the biomial theorem, ad some properties of biomial coefficiets Refereces: Relevat parts of chapter 15 of the Math
Lecture 4: Sequeces with repetitios, distributig idetical objects amog distict parties, the biomial theorem, ad some properties of biomial coefficiets Refereces: Relevat parts of chapter 15 of the Math
Basic Combinatorics. Math 40210, Section 01 Spring Homework 7 due Monday, March 26
 Basic Combiatorics Math 40210, Sectio 01 Sprig 2012 Homewor 7 due Moday, March 26 Geeral iformatio: I ecourage you to tal with your colleagues about homewor problems, but your fial write-up must be your
Basic Combiatorics Math 40210, Sectio 01 Sprig 2012 Homewor 7 due Moday, March 26 Geeral iformatio: I ecourage you to tal with your colleagues about homewor problems, but your fial write-up must be your
Lecture 6 April 10. We now give two identities which are useful for simplifying sums of binomial coefficients.
 Lecture 6 April 0 As aother applicatio of the biomial theorem we have the followig. For 0. 0 I other words startig with the secod row ad goig dow if we sum alog the rows alteratig sig as we go the result
Lecture 6 April 0 As aother applicatio of the biomial theorem we have the followig. For 0. 0 I other words startig with the secod row ad goig dow if we sum alog the rows alteratig sig as we go the result
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
P. Z. Chinn Department of Mathematics, Humboldt State University, Arcata, CA
 RISES, LEVELS, DROPS AND + SIGNS IN COMPOSITIONS: EXTENSIONS OF A PAPER BY ALLADI AND HOGGATT S. Heubach Departmet of Mathematics, Califoria State Uiversity Los Ageles 55 State Uiversity Drive, Los Ageles,
RISES, LEVELS, DROPS AND + SIGNS IN COMPOSITIONS: EXTENSIONS OF A PAPER BY ALLADI AND HOGGATT S. Heubach Departmet of Mathematics, Califoria State Uiversity Los Ageles 55 State Uiversity Drive, Los Ageles,
Applied Mathematics Letters. On the properties of Lucas numbers with binomial coefficients
 Applied Mathematics Letters 3 (1 68 7 Cotets lists available at ScieceDirect Applied Mathematics Letters joural homepage: wwwelseviercom/locate/aml O the properties of Lucas umbers with biomial coefficiets
Applied Mathematics Letters 3 (1 68 7 Cotets lists available at ScieceDirect Applied Mathematics Letters joural homepage: wwwelseviercom/locate/aml O the properties of Lucas umbers with biomial coefficiets
The Random Walk For Dummies
 The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
Generating Functions
 Geeratig Fuctios Geeratig Fuctios are a powerful tool i combiatorics Wilf describes them, quite appropriately, as a clotheslie o which we hag up a sequece of umber for display What does he mea by that?
Geeratig Fuctios Geeratig Fuctios are a powerful tool i combiatorics Wilf describes them, quite appropriately, as a clotheslie o which we hag up a sequece of umber for display What does he mea by that?
Carleton College, Winter 2017 Math 121, Practice Final Prof. Jones. Note: the exam will have a section of true-false questions, like the one below.
 Carleto College, Witer 207 Math 2, Practice Fial Prof. Joes Note: the exam will have a sectio of true-false questios, like the oe below.. True or False. Briefly explai your aswer. A icorrectly justified
Carleto College, Witer 207 Math 2, Practice Fial Prof. Joes Note: the exam will have a sectio of true-false questios, like the oe below.. True or False. Briefly explai your aswer. A icorrectly justified
2.1. The Algebraic and Order Properties of R Definition. A binary operation on a set F is a function B : F F! F.
 CHAPTER 2 The Real Numbers 2.. The Algebraic ad Order Properties of R Defiitio. A biary operatio o a set F is a fuctio B : F F! F. For the biary operatios of + ad, we replace B(a, b) by a + b ad a b, respectively.
CHAPTER 2 The Real Numbers 2.. The Algebraic ad Order Properties of R Defiitio. A biary operatio o a set F is a fuctio B : F F! F. For the biary operatios of + ad, we replace B(a, b) by a + b ad a b, respectively.
1 Last time: similar and diagonalizable matrices
 Last time: similar ad diagoalizable matrices Let be a positive iteger Suppose A is a matrix, v R, ad λ R Recall that v a eigevector for A with eigevalue λ if v ad Av λv, or equivaletly if v is a ozero
Last time: similar ad diagoalizable matrices Let be a positive iteger Suppose A is a matrix, v R, ad λ R Recall that v a eigevector for A with eigevalue λ if v ad Av λv, or equivaletly if v is a ozero
Complex Analysis Spring 2001 Homework I Solution
 Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Theorem: Let A n n. In this case that A does reduce to I, we search for A 1 as the solution matrix X to the matrix equation A X = I i.e.
 Theorem: Let A be a square matrix The A has a iverse matrix if ad oly if its reduced row echelo form is the idetity I this case the algorithm illustrated o the previous page will always yield the iverse
Theorem: Let A be a square matrix The A has a iverse matrix if ad oly if its reduced row echelo form is the idetity I this case the algorithm illustrated o the previous page will always yield the iverse
and each factor on the right is clearly greater than 1. which is a contradiction, so n must be prime.
 MATH 324 Summer 200 Elemetary Number Theory Solutios to Assigmet 2 Due: Wedesday July 2, 200 Questio [p 74 #6] Show that o iteger of the form 3 + is a prime, other tha 2 = 3 + Solutio: If 3 + is a prime,
MATH 324 Summer 200 Elemetary Number Theory Solutios to Assigmet 2 Due: Wedesday July 2, 200 Questio [p 74 #6] Show that o iteger of the form 3 + is a prime, other tha 2 = 3 + Solutio: If 3 + is a prime,
RADICAL EXPRESSION. If a and x are real numbers and n is a positive integer, then x is an. n th root theorems: Example 1 Simplify
 Example 1 Simplify 1.2A Radical Operatios a) 4 2 b) 16 1 2 c) 16 d) 2 e) 8 1 f) 8 What is the relatioship betwee a, b, c? What is the relatioship betwee d, e, f? If x = a, the x = = th root theorems: RADICAL
Example 1 Simplify 1.2A Radical Operatios a) 4 2 b) 16 1 2 c) 16 d) 2 e) 8 1 f) 8 What is the relatioship betwee a, b, c? What is the relatioship betwee d, e, f? If x = a, the x = = th root theorems: RADICAL
Essential Question How can you recognize an arithmetic sequence from its graph?
 . Aalyzig Arithmetic Sequeces ad Series COMMON CORE Learig Stadards HSF-IF.A.3 HSF-BF.A. HSF-LE.A. Essetial Questio How ca you recogize a arithmetic sequece from its graph? I a arithmetic sequece, the
. Aalyzig Arithmetic Sequeces ad Series COMMON CORE Learig Stadards HSF-IF.A.3 HSF-BF.A. HSF-LE.A. Essetial Questio How ca you recogize a arithmetic sequece from its graph? I a arithmetic sequece, the
P1 Chapter 8 :: Binomial Expansion
 P Chapter 8 :: Biomial Expasio jfrost@tiffi.kigsto.sch.uk www.drfrostmaths.com @DrFrostMaths Last modified: 6 th August 7 Use of DrFrostMaths for practice Register for free at: www.drfrostmaths.com/homework
P Chapter 8 :: Biomial Expasio jfrost@tiffi.kigsto.sch.uk www.drfrostmaths.com @DrFrostMaths Last modified: 6 th August 7 Use of DrFrostMaths for practice Register for free at: www.drfrostmaths.com/homework
Chapter 6. Advanced Counting Techniques
 Chapter 6 Advaced Coutig Techiques 6.: Recurrece Relatios Defiitio: A recurrece relatio for the sequece {a } is a equatio expressig a i terms of oe or more of the previous terms of the sequece: a,a2,a3,,a
Chapter 6 Advaced Coutig Techiques 6.: Recurrece Relatios Defiitio: A recurrece relatio for the sequece {a } is a equatio expressig a i terms of oe or more of the previous terms of the sequece: a,a2,a3,,a
Recursive Algorithms. Recurrences. Recursive Algorithms Analysis
 Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
[ 47 ] then T ( m ) is true for all n a. 2. The greatest integer function : [ ] is defined by selling [ x]
![[ 47 ] then T ( m ) is true for all n a. 2. The greatest integer function : [ ] is defined by selling [ x] [ 47 ] then T ( m ) is true for all n a. 2. The greatest integer function : [ ] is defined by selling [ x]](/thumbs/80/81982179.jpg) [ 47 ] Number System 1. Itroductio Pricile : Let { T ( ) : N} be a set of statemets, oe for each atural umber. If (i), T ( a ) is true for some a N ad (ii) T ( k ) is true imlies T ( k 1) is true for all
[ 47 ] Number System 1. Itroductio Pricile : Let { T ( ) : N} be a set of statemets, oe for each atural umber. If (i), T ( a ) is true for some a N ad (ii) T ( k ) is true imlies T ( k 1) is true for all
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Generating Functions II
 Geeratig Fuctios II Misha Lavrov ARML Practice 5/4/2014 Warm-up problems 1. Solve the recursio a +1 = 2a, a 0 = 1 by usig commo sese. 2. Solve the recursio b +1 = 2b + 1, b 0 = 1 by usig commo sese ad
Geeratig Fuctios II Misha Lavrov ARML Practice 5/4/2014 Warm-up problems 1. Solve the recursio a +1 = 2a, a 0 = 1 by usig commo sese. 2. Solve the recursio b +1 = 2b + 1, b 0 = 1 by usig commo sese ad
ENGI Series Page 5-01
 ENGI 344 5 Series Page 5-01 5. Series Cotets: 5.01 Sequeces; geeral term, limits, covergece 5.0 Series; summatio otatio, covergece, divergece test 5.03 Series; telescopig series, geometric series, p-series
ENGI 344 5 Series Page 5-01 5. Series Cotets: 5.01 Sequeces; geeral term, limits, covergece 5.0 Series; summatio otatio, covergece, divergece test 5.03 Series; telescopig series, geometric series, p-series
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES
 SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
SECTION 1.5 : SUMMATION NOTATION + WORK WITH SEQUENCES Read Sectio 1.5 (pages 5 9) Overview I Sectio 1.5 we lear to work with summatio otatio ad formulas. We will also itroduce a brief overview of sequeces,
PUTNAM TRAINING PROBABILITY
 PUTNAM TRAINING PROBABILITY (Last udated: December, 207) Remark. This is a list of exercises o robability. Miguel A. Lerma Exercises. Prove that the umber of subsets of {, 2,..., } with odd cardiality
PUTNAM TRAINING PROBABILITY (Last udated: December, 207) Remark. This is a list of exercises o robability. Miguel A. Lerma Exercises. Prove that the umber of subsets of {, 2,..., } with odd cardiality
Math 120 Answers for Homework 23
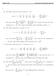 Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Modern Algebra 1 Section 1 Assignment 1. Solution: We have to show that if you knock down any one domino, then it knocks down the one behind it.
 Moder Algebra 1 Sectio 1 Assigmet 1 JOHN PERRY Eercise 1 (pg 11 Warm-up c) Suppose we have a ifiite row of domioes, set up o ed What sort of iductio argumet would covice us that ocig dow the first domio
Moder Algebra 1 Sectio 1 Assigmet 1 JOHN PERRY Eercise 1 (pg 11 Warm-up c) Suppose we have a ifiite row of domioes, set up o ed What sort of iductio argumet would covice us that ocig dow the first domio
Summary: Congruences. j=1. 1 Here we use the Mathematica syntax for the function. In Maple worksheets, the function
 Summary: Cogrueces j whe divided by, ad determiig the additive order of a iteger mod. As described i the Prelab sectio, cogrueces ca be thought of i terms of coutig with rows, ad for some questios this
Summary: Cogrueces j whe divided by, ad determiig the additive order of a iteger mod. As described i the Prelab sectio, cogrueces ca be thought of i terms of coutig with rows, ad for some questios this
REVIEW FOR CHAPTER 1
 REVIEW FOR CHAPTER 1 A short summary: I this chapter you helped develop some basic coutig priciples. I particular, the uses of ordered pairs (The Product Priciple), fuctios, ad set partitios (The Sum Priciple)
REVIEW FOR CHAPTER 1 A short summary: I this chapter you helped develop some basic coutig priciples. I particular, the uses of ordered pairs (The Product Priciple), fuctios, ad set partitios (The Sum Priciple)
Basic Counting. Periklis A. Papakonstantinou. York University
 Basic Coutig Periklis A. Papakostatiou York Uiversity We survey elemetary coutig priciples ad related combiatorial argumets. This documet serves oly as a remider ad by o ways does it go i depth or is it
Basic Coutig Periklis A. Papakostatiou York Uiversity We survey elemetary coutig priciples ad related combiatorial argumets. This documet serves oly as a remider ad by o ways does it go i depth or is it
1 Counting and Stirling Numbers
 1 Coutig ad Stirlig Numbers Natural Numbers: We let N {0, 1, 2,...} deote the set of atural umbers. []: For N we let [] {1, 2,..., }. Sym: For a set X we let Sym(X) deote the set of bijectios from X to
1 Coutig ad Stirlig Numbers Natural Numbers: We let N {0, 1, 2,...} deote the set of atural umbers. []: For N we let [] {1, 2,..., }. Sym: For a set X we let Sym(X) deote the set of bijectios from X to
Math 2784 (or 2794W) University of Connecticut
 ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
WORKING WITH NUMBERS
 1 WORKING WITH NUMBERS WHAT YOU NEED TO KNOW The defiitio of the differet umber sets: is the set of atural umbers {0, 1,, 3, }. is the set of itegers {, 3,, 1, 0, 1,, 3, }; + is the set of positive itegers;
1 WORKING WITH NUMBERS WHAT YOU NEED TO KNOW The defiitio of the differet umber sets: is the set of atural umbers {0, 1,, 3, }. is the set of itegers {, 3,, 1, 0, 1,, 3, }; + is the set of positive itegers;
Sequences of Definite Integrals, Factorials and Double Factorials
 47 6 Joural of Iteger Sequeces, Vol. 8 (5), Article 5.4.6 Sequeces of Defiite Itegrals, Factorials ad Double Factorials Thierry Daa-Picard Departmet of Applied Mathematics Jerusalem College of Techology
47 6 Joural of Iteger Sequeces, Vol. 8 (5), Article 5.4.6 Sequeces of Defiite Itegrals, Factorials ad Double Factorials Thierry Daa-Picard Departmet of Applied Mathematics Jerusalem College of Techology
Week 5-6: The Binomial Coefficients
 Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
Worksheet on Generating Functions
 Worksheet o Geeratig Fuctios October 26, 205 This worksheet is adapted from otes/exercises by Nat Thiem. Derivatives of Geeratig Fuctios. If the sequece a 0, a, a 2,... has ordiary geeratig fuctio A(x,
Worksheet o Geeratig Fuctios October 26, 205 This worksheet is adapted from otes/exercises by Nat Thiem. Derivatives of Geeratig Fuctios. If the sequece a 0, a, a 2,... has ordiary geeratig fuctio A(x,
Math 2112 Solutions Assignment 5
 Math 2112 Solutios Assigmet 5 5.1.1 Idicate which of the followig relatioships are true ad which are false: a. Z Q b. R Q c. Q Z d. Z Z Z e. Q R Q f. Q Z Q g. Z R Z h. Z Q Z a. True. Every positive iteger
Math 2112 Solutios Assigmet 5 5.1.1 Idicate which of the followig relatioships are true ad which are false: a. Z Q b. R Q c. Q Z d. Z Z Z e. Q R Q f. Q Z Q g. Z R Z h. Z Q Z a. True. Every positive iteger
CALCULATING FIBONACCI VECTORS
 THE GENERALIZED BINET FORMULA FOR CALCULATING FIBONACCI VECTORS Stuart D Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithacaedu ad Dai Novak Departmet
THE GENERALIZED BINET FORMULA FOR CALCULATING FIBONACCI VECTORS Stuart D Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithacaedu ad Dai Novak Departmet
2.4 - Sequences and Series
 2.4 - Sequeces ad Series Sequeces A sequece is a ordered list of elemets. Defiitio 1 A sequece is a fuctio from a subset of the set of itegers (usually either the set 80, 1, 2, 3,... < or the set 81, 2,
2.4 - Sequeces ad Series Sequeces A sequece is a ordered list of elemets. Defiitio 1 A sequece is a fuctio from a subset of the set of itegers (usually either the set 80, 1, 2, 3,... < or the set 81, 2,
Series with Central Binomial Coefficients, Catalan Numbers, and Harmonic Numbers
 3 47 6 3 Joural of Iteger Sequeces, Vol. 5 (0), Article..7 Series with Cetral Biomial Coefficiets, Catala Numbers, ad Harmoic Numbers Khristo N. Boyadzhiev Departmet of Mathematics ad Statistics Ohio Norther
3 47 6 3 Joural of Iteger Sequeces, Vol. 5 (0), Article..7 Series with Cetral Biomial Coefficiets, Catala Numbers, ad Harmoic Numbers Khristo N. Boyadzhiev Departmet of Mathematics ad Statistics Ohio Norther
Pascal s Labeling and Path Counting. October 4, Construct Pascal s labeling of lattice points of Euclidean plane.
 Pascal s Labelig ad Path Coutig Ko-Wei Lih Istitute of Mathematics Academia Siica Naag, Taipei 5, Taiwa E-mail: mawlih@siica.edu.tw Daphe Der-Fe Liu Departmet of Mathematics Califoria State Uiversity,
Pascal s Labelig ad Path Coutig Ko-Wei Lih Istitute of Mathematics Academia Siica Naag, Taipei 5, Taiwa E-mail: mawlih@siica.edu.tw Daphe Der-Fe Liu Departmet of Mathematics Califoria State Uiversity,
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
GENERATING FUNCTIONS AND RANDOM WALKS
 GENERATING FUNCTIONS AND RANDOM WALKS SIMON RUBINSTEIN-SALZEDO 1 A illustrative example Before we start studyig geeratig fuctios properly, let us look a example of their use Cosider the umbers a, defied
GENERATING FUNCTIONS AND RANDOM WALKS SIMON RUBINSTEIN-SALZEDO 1 A illustrative example Before we start studyig geeratig fuctios properly, let us look a example of their use Cosider the umbers a, defied
6.003 Homework #3 Solutions
 6.00 Homework # Solutios Problems. Complex umbers a. Evaluate the real ad imagiary parts of j j. π/ Real part = Imagiary part = 0 e Euler s formula says that j = e jπ/, so jπ/ j π/ j j = e = e. Thus the
6.00 Homework # Solutios Problems. Complex umbers a. Evaluate the real ad imagiary parts of j j. π/ Real part = Imagiary part = 0 e Euler s formula says that j = e jπ/, so jπ/ j π/ j j = e = e. Thus the
P.3 Polynomials and Special products
 Precalc Fall 2016 Sectios P.3, 1.2, 1.3, P.4, 1.4, P.2 (radicals/ratioal expoets), 1.5, 1.6, 1.7, 1.8, 1.1, 2.1, 2.2 I Polyomial defiitio (p. 28) a x + a x +... + a x + a x 1 1 0 1 1 0 a x + a x +... +
Precalc Fall 2016 Sectios P.3, 1.2, 1.3, P.4, 1.4, P.2 (radicals/ratioal expoets), 1.5, 1.6, 1.7, 1.8, 1.1, 2.1, 2.2 I Polyomial defiitio (p. 28) a x + a x +... + a x + a x 1 1 0 1 1 0 a x + a x +... +
MATH 324 Summer 2006 Elementary Number Theory Solutions to Assignment 2 Due: Thursday July 27, 2006
 MATH 34 Summer 006 Elemetary Number Theory Solutios to Assigmet Due: Thursday July 7, 006 Departmet of Mathematical ad Statistical Scieces Uiversity of Alberta Questio [p 74 #6] Show that o iteger of the
MATH 34 Summer 006 Elemetary Number Theory Solutios to Assigmet Due: Thursday July 7, 006 Departmet of Mathematical ad Statistical Scieces Uiversity of Alberta Questio [p 74 #6] Show that o iteger of the
k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c 1. Introduction
 Acta Math. Uiv. Comeiaae Vol. LXXXVI, 2 (2017), pp. 279 286 279 k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c N. IRMAK ad M. ALP Abstract. The k-geeralized Fiboacci sequece { F (k)
Acta Math. Uiv. Comeiaae Vol. LXXXVI, 2 (2017), pp. 279 286 279 k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c N. IRMAK ad M. ALP Abstract. The k-geeralized Fiboacci sequece { F (k)
