Geometric Predicates P r og r a m s need t o t es t r ela t ive p os it ions of p oint s b a s ed on t heir coor d ina t es. S im p le exa m p les ( i
|
|
|
- Bryce Austin
- 5 years ago
- Views:
Transcription
1 Automatic Generation of SS tag ed Geometric PP red icates Aleksandar Nanevski, G u y B lello c h and R o b ert H arp er PSCICO project h ttp: / / w w w. cs. cm u. ed u / ~ ps ci co
2 Geometric Predicates P r og r a m s need t o t es t r ela t ive p os it ions of p oint s b a s ed on t heir coor d ina t es. S im p le exa m p les ( in 2 D) : Orientation test (in convex hull) does C lie left/right/on the line AB? C B A I nc irc l e test (in Dela una y t r ia ng ula t ion) does D lie in/ou t/on the c irc le ABC? A D B C 2
3 Geometric Predicates (cont d) O r i e n t a t i o n ( A, B, C ) = W e o n l y c o n s i d e r t h e sign o f a n e x p r e s s i o n i n v o l v i n g +, - a n d 3
4 Convex Hull Miscomputed U s i n g O r i e n t a t i o n P r e d i c a t e i n e x a c t a r i t h m e t i c B U s i n g O r i e n t a t i o n P r e d i c a t e i n f l o a t i n g -p o i n t a r i t h m e t i c B C D C D E E A A!! F l o a t i n g p o i n t a r i t h m e t i c e r r s i n c o n s i s t e n t l y!! 4
5 Floating-p p oint Filte rr ss G e t correct sign (-1, 0 o r 1 ) o f a n e x a c t e x p r e s s i o n E u s i n g f l o a t i n g -p o i n t! filters out the ea sy c a ses let F = E (X) in floating point if F > e r r or b ou nd th en 1 els e if F > er r o r b o u nd th en 1 els e inc r e as e pr e c is ion a nd r ep ea t o r s w itc h to ex a c t a r ith m etic I f th e c o r r ec t r es u lt is 0, m u s t g o to ex a c t p h a s e 5
6 Current Methods I n t e r v a l a r i t h m e t i c ( R. E. M o o r e, U. K u l i s c h ) +l i t t l e m o d i f i c a t i o n t o t h e s o u r c e p r o g r a m -d o e s n o t p e r f o r m w e l l i n l o w d e g r e e s S i n g l e -p h a s e f i l t e r s ( F o r t u n e & V a n W y k, L E D A ) +c o m p i l e r a v a i l a b l e -s u r p a s s e d b y m u l t i -p h a s e f i l t e r s 6
7 Current Methods (cont d) M u l t i -p h a s e f i l t e r s ( J. S h e w c h u k ) f o u r p h a s e s o f i n c r e a s i n g p r e c i s i o n +r e -u s e o f r e s u l t s f r o m e a r l i e r p h a s e s +b e t w e e n % s l o w e r t h a n f p i m p l e m e n t a t i o n -r e q u i r e s e s t i m a t i n g r o u n d i n g e r r o r s -i n v o l v e d a n d h a r d t o i m p l e m e n t : S h e w c h u k s I n s p h e r e C i m p l e m e n t a t i o n > l i n e s o f c o d e -o n l y e x i s t i n g a r e 2 D a n d 3 D O r i e n t a t i o n a n d I n s p h e r e p r e d i c a t e s, b u t w e n e e d m o r e 7
8 Functional p r og r am COMPILER num e r ical analy s is S tag e d g e om p r e d icate e tr ic 8
9 Contributions S o u r c e l a n g u a g e e x p r e s s i o n i n v o l v i n g +, -, a r i t h m e t i c t o b e p e r c e i v e d a s e x a c t n e s t e d a n o n y m o u s f u n c t i o n s ( s t a g i n g ) C o m p i l e r t o M L ( o r C ) m u l t i -p h a s e t a r g e t c o d e e r r o r b o u n d s e s t i m a t e d a u t o m a t i c a l l y f o r m a l l y s p e c i f i e d ( s o, c a n a r g u e c o r r e c t n e s s ) 9
10 Staging T o t e s t a s e t o f p o i n t s f o r p o s i t i o n w i t h r e s p e c t t o l i n e A C : -c o m p u t e a s m u c h a s p o s s i b l e k n o w i n g o n l y A a n d C -r e t u r n t h e r e m a i n i n g w o r k a s f u n c t i o n -a p p l y t h i s f u n c t i o n t o e a c h o f t h e p o i n t s A C 10
11 Overview I n t r o d u c t i o n A r b i t r a r y p r e c i s i o n a r i t h m c o m p u t i n g i n p h a s e s S t a g e c o m p i l a t i o n P e r f o r m a n c e C o n c l u s i o n s a n d F u t u r e W e t i c a n d o r k 11
12 Notation O p e r a t i o n s : EE xx aa cc tt + - FF ll oo aa tt ii nn g g pp oo ii nn tt ª P r e c i s i o n p = # b i t s i n m M a c h i n e E p s i l o n a n t i s s a - i f o p e r a t i o n r e s u l t i s 1. 0, t h e n t h e r o u n d i n g e r r o r i s s m a l l e r t h a n - 12
13 Error recovery Theorem. (Knuth) If x = a b, t h e r o u n d i n g e r r o r o f x c a n b e r e c o v e r e d b y fl o a t i n g -p o i n t o p e r a t i o n s. If i s t h e r o u n d i n g e r r o r, a n d c = x ª a t h e n S o e x a c t l y. 13
14 How to Increase Precision? K n u t h s t h e o r e m : P a i r ( x, ) t w i c e t h e p r e c i s i o n. ( D. P r i e s t ) S o r t e d l i s t o f f p -n u m b e r s a r b i t r a r y p r e c i s i o n. E x p a n s i o n = l i s t o f m a g n i t u d e d e c r e a s i n g n o n - o v e r l a p p i n g f l o a t s
15 Phases and re-u u se ( J. S h e w c h u k ) A r bi t r a r y p r e c i s i o n a r i t h m e t i c p h a s e s c a n r e u s e t h e r e s u l t s o f t h e i r p r e d e c e s s o r s. E x a m p l e : L e t a 1 b 1 = x a n d a 2 b 2 = x E x p a n d E a s 15
16 Phases and re-u u se (( cc oo nt d) S t r a t e g y f o r f i n d i n g t h e sign o f E v a l u a t e E i n p h a s e s, i n c r e a s i n g p r e c i s i o n o n d e m a n d. E x a m p l e : floating point phase ex ac t phase 16
17 Reusing results A x1 x 1 x 2 x 2 17
18 Reusing results A B x1 x 1 x 2 x 2 18
19 Reusing results C A B x1 x 1 x 2 x 2 2x 1 1 2x
20 Reusing results D C A B x1 x 1 x 2 x 2 2x 1 1 2x
21 Overview I n t r o d u c t i o n A r b i t r a r y p r e c i s i o n a r i t h m c o m p u t i n g i n p h a s e s S t a g e c o m p i l a t i o n P e r f o r m a n c e C o n c l u s i o n a n d F u t u r e W e t i c a n d o r k 21
22 Source Language B a s i c a r i t h m e t i c o p e r a t i o n s : +, -,, u n a r y -, s q A s s i g n m e n t s : v a l x = s o m e e x p r e s s i o n N e s t e d a n o n y m o u s f u n c t i o n s E x a m p l e : I m p l i c i t s i g n t e s t a t t h e l a s t a s s i g n m e n t. 22
23 Stage compilation E v e r y s t a g e c o m p i l e d i n t o : -f l o a t i n g -p o i n t c o d e ( p h a s e A ) -c o d e f o r e s t i m a t i n g t h e r o u n d i n g e r r o r L a t e r p h a s e s ( B, C a n d D ) s u s p e n d e d u n t i l e x p l i c i t l y e x e c u t e d 23
24 Stage 1 H e l p e r c o d e : - -m o d u l e s f o r a r b i t r a r y p r e c i s i o n a r i t h m e t i c C o m p i l e r o u t p u t : A C B D 24
25 Stage 2 A C B D 25
26 Overview I n t r o d u c t i o n A r b i t r a r y p r e c i s i o n a r i t h m c o m p u t i n g i n p h a s e s S t a g e c o m p i l a t i o n P e r f o r m a n c e C o n c l u s i o n a n d F u t u r e W e t i c a n d o r k 26
27 Performance E x p e r i m e n t s t o m a t c h S h e w c h u k s h a n d -g e n e r a t e d p r e d i c a t e s T a r g e t l a n g u a g e C N o s t a g i n g! OO rr ii ee nn tt 22 DD OO rr ii ee nn tt 33 DD II nn CC ii rr cc ll ee II nn SS pp hh ee rr ee UU nn ii ff oo rr m m RR aa nn dd oo m m PP oo ii nn t t DD ii ss tt rr ii bb uu tt ii oo nn S h e w c h u k s v e r s i o n m s m s m s m s A u t o m a t i c a l l y g e n e r a t e d v e r s i o n m s m s m s m s S l o w d o w n
28 Performance (cont d) uu nn ii ff oo rr m m rr aa nn dd oo mm tt ii ll tt ee d d gg rr ii dd 2D De ll aa uu nn aa y y TT rr ii aa nn gg uu ll aa tt ii oo nn S h e w c h u k s v e r s i o n m s m s A u t o m a t i c a l l y g e n e r a t e d v e r s i o n m s m s S l o w d o w n cc oo -c c ii rr cc uu ll aa rr m s m s B e t w e e n 1 a n d 2. 4 t i m e s s l o w e r t h a n h a n d -g e n e r a t e d c o d e P o s s i b i l i t y f o r i m p r o v e m e n t w i t h a b e t t e r t r a n s l a t i o n t o C 28
29 Future Work E x t e n d t h e l a n g u a g e : -m u l t i p l i c a t i o n b y 2 n d o e s n t i n t r o d u c e e r r o r s. -s u m m a t i o n o f m o r e t h a n 2 e l e m e n t s c a n b e d o n e q u i c k e r. E v a l u a t e t h e e f f e c t s o f s t a g i n g. A l l o w b e t t e r c o n t r o l o v e r t h e F P a r i t h m e t i c i n S M L. -p r o c e s s o r f l a g s -p r e c i s i o n o f i n t e r n a l F P r e g i s t e r s D e s i g n a l a n g u a g e t h a t c a n c o m p i l e a n d run t h e p r e d i c a t e s -r u n -t i m e c o d e g e n e r a t i o n a n d m e t a -p r o g r a m m i n g -a p p l i c a t i o n : r o b u s t s o l i d m o d e l e r 29
30 Conclusions Automated conversion o f e x a c t p r e d i c a t e s i n t o f l o a t i n g p o i n t c o d e : p r e s e r v e s c o r r e c t n e s s o f c o m c o m p i l e -t i m e e r r o r a n a l y s i s n e s t e d a n o n y m o u s f u n c t i o n s ( s t a g i n g ) p e r f o r m c o d e p u t a t i o n d e s p i t e r o u n d i n g a n c e o f g e n e r a t e d p r e d i c a t e s c l o s e t o h a n d -g e n e r a t e d F ormal sp ecif ication o f t h e c o m p i l e r. M ore control n e e d e d o v e r f l o a t i n g p o i n t i n S M L. -p r o c e s s o r f l a g s -p r e c i s i o n o f i n t e r n a l F P r e g i s t e r s C omp il er c a n b e f o u n d a t h t t p : / / w w w.c s.c m u.e d u / ~ p s c i c o 30
31 Operations on Expansions (arbitrary precision arithmetic) Example: Adding two expansions E = e1 e3 e5 F = e e 2 4 Merge Lists e e 1 2 e e e H = h h h h4 h
32 Source Language B a s i c a r i t h m e t i c o p e r a t i o n s : +, -,, s q, u n a r y A s s i g n m e n t s : v a l x = s o m e e x p r e s s i o n N e s t e d a n o n y m o u s f u n c t i o n s ( s t a g i n g ) 32
33 Compiling a Program C A D B 33
34 Compiling a Program (cont d) A reused 34
35 Here goes example for OO ri en tt 22 D D ii n n SS MM L L or CC Nothing! They are just often mistaken for real numbers. type pnt=real*real f u n o ri ent( A : pnt, B : pnt, C : pnt) = let v al ( a1, a2 ) = A v al ( b 1, b 2 ) = B v al ( c 1, c 2 ) = C v al d = ( c 1 -a1 ) *( c 2 -b 2 ) - ( c 2 -a2 ) *( c 1 -b 1 ) i n i f d > 0 th en L ef t els e i f d < 0 th en R i g h t els e O n end 35
36 What s Wrong With Floating PP oint NN uu mm bb ee rs? Floats are unevenly distributed on the real axis, thus introduc ing rounding errors in the c om p utation. 36
37 What s Wrong? (cont d) Example: Assume precision of 2 decimal digits. Denote th e operation of ( rounded) addition on floats. F lo at s ar e a subset b u t N O T a subty p e o f r at i o n als an d r eals. 37
38 + - Types of Numbers Real numbers Usually assumed when dev elo p i ng o r p r o v i ng alg o r i t hms B asi c o p er at i o ns no t c o mp ut ab le + - Rat i o nal numbers C lo sed under b asi c o p er at i o ns S lo w F lo at i ng -p o i nt numbers F ast N o t c lo sed under b asi c ar i t hmet i c o p er at i o ns ( r o undi ng er r o r s) D o no t sat i sf y usual laws li k e asso c i at i v i t y, di st r i b ut i v i t y 38
39 Phase A Compilation J u d g m e n t. S e l e c t e d r u l e s 39
40 Phase B Compilation J u d g m e n t. S e l e c t e d r u l e s 40
41 Operations on Expansions Example: Adding a double to an expansion. e1 e2 e3 e4 sum sum sum sum roundoff roundoff roundoff roundoff b h 1 h 2 h 3 h 4 h 5 41
42 Overlapping and Machine ε p b i t s p b i t s a n d x d o n o t o v e r l a p 2 -p x. I n I E E E d o u b l e p r e c i s i o n, p=
43 Phases of Increasing Precision let R = F (X) in floating point if ab s (R) > estimated error bound th en s ign(r) els e inc rease p rec ision and r epeat or s w itc h to ex ac t ar ith m etic floating point phase inter m ed iate phases ex ac t phase F initel y many intermediate p h ases! 43
44 Arithmetic R ational nu m + e x a c t - s l o w b e r s Floating-p oint nu m b e r s - i n e x a c t + f a s t 44
45 Non-ov ov ee rr ll aa pp pp ii ng T h e r o u n d e d s u m x a n d i t s r o u n d i n g e r r o r d o n o t o v e r l a p M a t h e m a t i c a l l y, 45
46 m Expansions and Compiler Exact e xp r e s s i o n F c om p i l a t i on filters out the ea sy c a ses let R = F (X) in floating point if R > error bound th en 1 els e if R > er r or b ou nd th en 1 els e i nc rea s e p rec i s i on and r epeat or s w itc h to ex ac t ar ith m etic U s e ex pans ions for or e pr ec is e c om pu tations 46
47 Phases and Compiler Exact e xp r e s s i o n F let R = F (X) in floating point if R > error bound th en 1 els e if R > er r or b ou nd th en 1 els e R2 = ph as e B if ab s (R2 ) > er r or b ou nd th en s ign(r2 ) els e R3 = ph as e C if ab s (R3 ) > er r or b ou nd th en s ign(r3 ) els e c om p i l a t i on R4 = ph as e D ; (* ex ac t ph as e * ) s ign (R4 ) 47
48 Bounding the Rounding Error F l o a t i n g -p o i n t o p e r a t i o n s a r e c o r r e c t l y r o u n d e d. C o n s e q u e n c e : f o r a n y o p e r a t i o n 2 { +, -, } N o t i c e : ε i s s t a t i c p a r t o f t h e e r r o r w h i l e x y i s d y n a m i c. 48
49 Bounding Error of Composite Ex pressions I f X 1 = x 1 δ 1 p 1 a n d X 2 = x 2 δ 2 p 2 t h e n 49
50 Error Bounds and CC om pp ii ll at ii on S t a t i c e r r o r b o u n d -O b t a i n e d E X A C T L Y i n c o m p i l e -t i m e. -R o u n d e d a n d t h e n e m i t t e d i n t o t h e t a r g e t p r o g r a m a s a f l o a t i n g -p o i n t c o n s t a n t. D y n a m i c e r r o r b o u n d -C o d e m u s t b e g e n e r a t e d f o r i t s c o m p u t a t i o n a n d e m i t t e d i n t o t h e t a r g e t p r o g r a m. 50
51 Error Bounds and Compilation (( cc ont d) compilation Exact e xp r e s s i o n F let R = F (X) in floating point d y nam ic _ er r or = D (X) er r or = s tatic _ er r or * d y nam ic _ er r or if R > er r or th en 1 els e if R > er r or th en 1 els e j u m p to ph as es B, C and D 51
52 Compilation example S o u r c e e x p r e s s i o n c ( a + b ) 2 T a r g e t S t a n d a r d M L p r o g r a m : 52
53 Source Language B a s i c a r i t h m e t i c o p e r a t i o n s : +, -,, s q, u n a r y - A s s i g n m e n t s : v a l x = s o m e e x p r e s s i o n N e s t e d a n o n y m o u s f u n c t i o n s 53
54 Staging (cont d) 54
55 Overview I n t r o d u c t i o n A r b i t r a r y p r e c i s i o n a r i t h m c o m p u t i n g i n p h a s e s M u l t i -s t a g e f i l t e r s P e r f o r m a n c e C o n c l u s i o n a n d F u t u r e W e t i c a n d o r k 55
Agenda Rationale for ETG S eek ing I d eas ETG fram ew ork and res u lts 2
Internal Innovation @ C is c o 2 0 0 6 C i s c o S y s t e m s, I n c. A l l r i g h t s r e s e r v e d. C i s c o C o n f i d e n t i a l 1 Agenda Rationale for ETG S eek ing I d eas ETG fram ew ork
P a g e 5 1 of R e p o r t P B 4 / 0 9
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
A L A BA M A L A W R E V IE W
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
P a g e 3 6 of R e p o r t P B 4 / 0 9
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
T h e C S E T I P r o j e c t
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
Table of C on t en t s Global Campus 21 in N umbe r s R e g ional Capac it y D e v e lopme nt in E-L e ar ning Structure a n d C o m p o n en ts R ea
G Blended L ea r ni ng P r o g r a m R eg i o na l C a p a c i t y D ev elo p m ent i n E -L ea r ni ng H R K C r o s s o r d e r u c a t i o n a n d v e l o p m e n t C o p e r a t i o n 3 0 6 0 7 0 5
Fragment Processor. Textures
Cg: A system for programming graph ic s hh ard ww are in a C-l ik e ll angu age U n i v e r s i t y o f T e x a s a t A u s t i n S t e v e n G v N V I D I A K u A y N V I D I A a n d S t a n f o r d U
6 Lowercase Letter a Number Puzzles
1 2 3 4 5 6 7 8 9 10 10 20 30 40 50 60 70 80 90 100 6 Lowercase Letter a Nuber Puzzles 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1 10 20 30 40 50 60 70 80 90 100 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1
COMPILATION OF AUTOMATA FROM MORPHOLOGICAL TWO-LEVEL RULES
Kimmo Koskenniemi Re se ar ch Unit for Co mp ut at io na l Li ng ui st ic s University of Helsinki, Hallituskatu 11 SF-00100 Helsinki, Finland COMPILATION OF AUTOMATA FROM MORPHOLOGICAL TWO-LEVEL RULES
THIS PAGE DECLASSIFIED IAW EO IRIS u blic Record. Key I fo mation. Ma n: AIR MATERIEL COMM ND. Adm ni trative Mar ings.
T H S PA G E D E CLA SSFED AW E O 2958 RS u blc Recod Key fo maon Ma n AR MATEREL COMM ND D cumen Type Call N u b e 03 V 7 Rcvd Rel 98 / 0 ndexe D 38 Eneed Dae RS l umbe 0 0 4 2 3 5 6 C D QC d Dac A cesson
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
Dangote Flour Mills Plc
SUMMARY OF OFFER Opening Date 6 th September 27 Closing Date 27 th September 27 Shares on Offer 1.25bn Ord. Shares of 5k each Offer Price Offer Size Market Cap (Post Offer) Minimum Offer N15. per share
" = Y(#,$) % R(r) = 1 4& % " = Y(#,$) % R(r) = Recitation Problems: Week 4. a. 5 B, b. 6. , Ne Mg + 15 P 2+ c. 23 V,
Recitation Problems: Week 4 1. Which of the following combinations of quantum numbers are allowed for an electron in a one-electron atom: n l m l m s 2 2 1! 3 1 0 -! 5 1 2! 4-1 0! 3 2 1 0 2 0 0 -! 7 2-2!
1. The graph of a function f is given above. Answer the question: a. Find the value(s) of x where f is not differentiable. Ans: x = 4, x = 3, x = 2,
1. The graph of a function f is given above. Answer the question: a. Find the value(s) of x where f is not differentiable. x = 4, x = 3, x = 2, x = 1, x = 1, x = 2, x = 3, x = 4, x = 5 b. Find the value(s)
I N A C O M P L E X W O R L D
IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
Beechwood Music Department Staff
Beechwood Music Department Staff MRS SARAH KERSHAW - HEAD OF MUSIC S a ra h K e rs h a w t r a i n e d a t t h e R oy a l We ls h C o l le g e of M u s i c a n d D ra m a w h e re s h e ob t a i n e d
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
database marketing Database Marketing Defined Loyalty as Competitive Advantage DBM is Incremental in Nature DBM is a complete framework for Marketing
Database Marketing Defined database marketing DBM is a complete framework for Marketing Research, Segmentation, Contact, Measurement any activity which creates and exploits a direct relationship between
Executive Committee and Officers ( )
Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
Lesson Ten. What role does energy play in chemical reactions? Grade 8. Science. 90 minutes ENGLISH LANGUAGE ARTS
Lesson Ten What role does energy play in chemical reactions? Science Asking Questions, Developing Models, Investigating, Analyzing Data and Obtaining, Evaluating, and Communicating Information ENGLISH
Bellman-F o r d s A lg o r i t h m The id ea: There is a shortest p ath f rom s to any other verte that d oes not contain a non-negative cy cle ( can
W Bellman Ford Algorithm This is an algorithm that solves the single source shortest p ath p rob lem ( sssp ( f ind s the d istances and shortest p aths f rom a source to all other nod es f or the case
F l a s h-b a s e d S S D s i n E n t e r p r i s e F l a s h-b a s e d S S D s ( S o-s ltiad t e D r i v e s ) a r e b e c o m i n g a n a t t r a c
L i f e t i m e M a n a g e m e n t o f F l a-b s ah s e d S S D s U s i n g R e c o v e r-a y w a r e D y n a m i c T h r o t t l i n g S u n g j i n L e, e T a e j i n K i m, K y u n g h o, Kainmd J
shhgs@wgqqh.com chinapub 2002 7 Bruc Eckl 1000 7 Bruc Eckl 1000 Th gnsis of th computr rvolution was in a machin. Th gnsis of our programming languags thus tnds to look lik that Bruc machin. 10 7 www.wgqqh.com/shhgs/tij.html
c. What is the average rate of change of f on the interval [, ]? Answer: d. What is a local minimum value of f? Answer: 5 e. On what interval(s) is f
![c. What is the average rate of change of f on the interval [, ]? Answer: d. What is a local minimum value of f? Answer: 5 e. On what interval(s) is f](/thumbs/87/95703678.jpg "c. What is the average rate of change of f on the interval [, ]? Answer: d. What is a local minimum value of f? Answer: 5 e. On what interval(s) is f")
Essential Skills Chapter f ( x + h) f ( x ). Simplifying the difference quotient Section. h f ( x + h) f ( x ) Example: For f ( x) = 4x 4 x, find and simplify completely. h Answer: 4 8x 4 h. Finding the
Gen ova/ Pavi a/ Ro ma Ti m i ng Count er st at Sep t. 2004
Ti m i ng Count er st at us @ Sep t. 2004 1 Ti m i n g Cou n t er act i vi t i es Ti m i n g r esol u t i on : 100 p s FWHM h ave b een ach i eved. PM s ch ar act er ised i n t h e COBRA m ag n et f or
THIS PAGE DECLASSIFIED IAW E
THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
I zm ir I nstiute of Technology CS Lecture Notes are based on the CS 101 notes at the University of I llinois at Urbana-Cham paign
I zm ir I nstiute of Technology CS - 1 0 2 Lecture 1 Lecture Notes are based on the CS 101 notes at the University of I llinois at Urbana-Cham paign I zm ir I nstiute of Technology W hat w ill I learn
Welcome to the Public Meeting Red Bluff Road from Kirby Boulevard to State Highway 146 Harris County, Texas CSJ No.: December 15, 2016
Welcome to the Public Meeting Red Bluff Road from Kirby Boulevard to State Highway 146 Harris County, Texas CSJ No.: 0912-72-340 December 15, 2016 No formal presentation will be made. Seabrook Intermediate
Worksheets for GCSE Mathematics. Quadratics. mr-mathematics.com Maths Resources for Teachers. Algebra
Worksheets for GCSE Mathematics Quadratics mr-mathematics.com Maths Resources for Teachers Algebra Quadratics Worksheets Contents Differentiated Independent Learning Worksheets Solving x + bx + c by factorisation
Alles Taylor & Duke, LLC Bob Wright, PE RECORD DRAWINGS. CPOW Mini-Ed Conf er ence Mar ch 27, 2015
RECORD DRAWINGS CPOW Mini-Ed Conf er ence Mar ch 27, 2015 NOMENCLATURE: Record Draw ings?????? What Hap p ened t o As- Built s?? PURPOSE: Fur n ish a Reco r d o f Co m p o n en t s Allo w Locat io n o
Model answers for the 2012 Electricity Revision booklet:
Model answers for the 0 Electricity Revision booklet: SAMPLE ASSESSMENT SCHEDULE Physics 973 (.6): Demonstrate understanding of electricity and electromagnetism Assessment Criteria Achievement Achievement
ARC 202L. Not e s : I n s t r u c t o r s : D e J a r n e t t, L i n, O r t e n b e r g, P a n g, P r i t c h a r d - S c h m i t z b e r g e r
ARC 202L C A L I F O R N I A S T A T E P O L Y T E C H N I C U N I V E R S I T Y D E P A R T M E N T O F A R C H I T E C T U R E A R C 2 0 2 L - A R C H I T E C T U R A L S T U D I O W I N T E R Q U A
Regular Semigroups with Inverse Transversals
International Mathematical Forum, Vol. 7, 2012, no. 31, 1547-1552 Regular Semigroups with Inverse Transversals Junwei Shi Zhenji Tian School of Sciences Lanzhou University of Technology Lanzhou, Gansu,
Cataraqui Source Protection Area Stream Gauge Locations
Cqu u P m Gu s Ts Ez K Ts u s sp E s ms P Ps s m m C Y u u I s Ts x C C u R 4 N p Ds Qu H Em us ms p G Cqu C, s Ks F I s s Gqu u Gqu s N D U ( I T Gqu C s C, 5 Rs p, Rs 15, 7 N m s m Gus - Ps P f P 1,
Building Harmony and Success
Belmont High School Quantum Building Harmony and Success October 2016 We acknowledge the traditional custodians of this land and pay our respects to elders past and present Phone: (02) 49450600 Fax: (02)
What are S M U s? SMU = Software Maintenance Upgrade Software patch del iv ery u nit wh ich once ins tal l ed and activ ated prov ides a point-fix for
SMU 101 2 0 0 7 C i s c o S y s t e m s, I n c. A l l r i g h t s r e s e r v e d. 1 What are S M U s? SMU = Software Maintenance Upgrade Software patch del iv ery u nit wh ich once ins tal l ed and activ
Instruction Sheet COOL SERIES DUCT COOL LISTED H NK O. PR D C FE - Re ove r fro e c sed rea. I Page 1 Rev A
Instruction Sheet COOL SERIES DUCT COOL C UL R US LISTED H NK O you or urc s g t e D C t oroug y e ore s g / as e OL P ea e rea g product PR D C FE RES - Re ove r fro e c sed rea t m a o se e x o duct
M M 3. F orc e th e insid e netw ork or p rivate netw ork traffic th rough th e G RE tunnel using i p r ou t e c ommand, fol l ow ed b y th e internal
C i s c o P r o f i l e C o n t a c t s & F e e d b a c k H e l p C isc o S M B S up p ort A ssistant Pass Routing Information over IPsec VPN Tunnel between two ASA/PIX H ome > W ork W ith M y S ec urity
e-hm REPAIR PARTS REPAIR PARTS ReHM R3
e-hm REPAIR PARTS REPAIR PARTS ReHM R3 TABLE OF CONTENTS Rating Plate..........................................................................................2 A li ati n ene t an n t......................................................................3
Classification of Components
Classification of Components Classification of SMD LEDs TLM.31../TLM.32../TLM.33../ + 3... series, Mini LEDs TLM.21... / TLM.23.. / TLM.2.. and 63 LEDs TLM.11../TLM1.. Light Intensity / Color Devices are
Terms of Use. Copyright Embark on the Journey
Terms of Use All rights reserved. No part of this packet may be reproduced, stored in a retrieval system, or transmitted in any form by any means - electronic, mechanical, photo-copies, recording, or otherwise
How do regular expressions work? CMSC 330: Organization of Programming Languages
How do regular expressions work? CMSC 330: Organization of Programming Languages Regular Expressions and Finite Automata What we ve learned What regular expressions are What they can express, and cannot
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
Lesson seven What is a chemical reaction? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading Informational Text,
A A A A A A A A A A A A. a a a a a a a a a a a a a a a. Apples taste amazingly good.
Victorian Handwriting Sheet Aa A A A A A A A A A A A A Aa Aa Aa Aa Aa Aa Aa a a a a a a a a a a a a a a a Apples taste amazingly good. Apples taste amazingly good. Now make up a sentence of your own using
Engine Control <2TR-FE> I
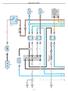Engine Control (AT) (AT) (I) 0A EFI A A/F HEATER A IN AM I R C I R ST I Ignition S R R R EA 0A AM R C 0A EFI N. R A EFI Relay A 0 A A 0 A A A/F HEATER Relay A C/PN Relay F Fuel Suction Pump and
CDS 101/110: Lecture 6.2 Transfer Functions
CDS 11/11: Lecture 6.2 Transfer Functions November 2, 216 Goals: Continued study of Transfer functions Review Laplace Transform Block Diagram Algebra Bode Plot Intro Reading: Åström and Murray, Feedback
A/P Warrants. June 15, To Approve. To Ratify. Authorize the City Manager to approve such expenditures as are legally due and
T. 7 TY LS ALATS A/P rrnts June 5, 5 Pges: To Approve - 5 89, 54.3 A/P rrnts 6/ 5/ 5 Subtotl $ 89, 54. 3 To Rtify Pges: 6-, 34. 98 Advnce rrnts 5/ 6/ 5-4 3, 659. 94 Advnce rrnts 6/ / 5 4, 7. 69 June Retirees
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A. Ήχος Πα. to os se e e na aș te e e slă ă ă vi i i i i
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
Patterns of soiling in the Old Library Trinity College Dublin. Allyson Smith, Robbie Goodhue, Susie Bioletti
Patterns of soiling in the Old Library Trinity College Dublin Allyson Smith, Robbie Goodhue, Susie Bioletti Trinity College aerial view Old Library E N S W Old Library main (south) elevation Gallery Fagel
Software Process Models there are many process model s in th e li t e ra t u re, s om e a r e prescriptions and some are descriptions you need to mode
Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
Using the Rational Root Theorem to Find Real and Imaginary Roots Real roots can be one of two types: ra...-\; 0 or - l (- - ONLl --
Using the Rational Root Theorem to Find Real and Imaginary Roots Real roots can be one of two types: ra...-\; 0 or - l (- - ONLl -- Consider the function h(x) =IJ\ 4-8x 3-12x 2 + 24x {?\whose graph is
Classwork. Example 1 S.35
Classwork Example 1 In the picture below, we have a triangle AAAAAA that has been dilated from center OO by a scale factor of rr = 1. It is noted 2 by AA BB CC. We also have triangle AA BB CC, which is
Journal of Integer Sequences, Vol. 5 (2002), Article
1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 5 (2002), Article 02.2.7 ON SHANKS ALGORITHM FOR COMPUTING THE CONTINUED FRACTION OF log b a TERENCE JACKSON 1 AND KEITH MATTHEWS 2 1 Department of Mathematics
Fr anchi s ee appl i cat i on for m
Other Fr anchi s ee appl i cat i on for m Kindly fill in all the applicable information in the spaces provided and submit to us before the stipulated deadline. The information you provide will be held
Building Validation Suites with Eclipse for M odel-based G eneration Tools
Building Validation Suites with Eclipse for M odel-based G eneration Tools 24.6.2010 D r. O scar Slotosch Validas A G C ontent M o d el-b ased D evelo p m en t (o f Em b ed d ed Syst em s) ISO 26262 Valid
CPU. 60%/yr. Moore s Law. Processor-Memory Performance Gap: (grows 50% / year) DRAM. 7%/yr. DRAM
ecture 1 3 C a ch e B a s i cs a n d C a ch e P erf o rm a n ce Computer Engineering 585 F a l l 2 0 0 2 What Is emory ierarchy typical memory hierarchy today "! '& % ere we focus on 1/2/3 caches and main
Results as of 30 September 2018
rt Results as of 30 September 2018 F r e e t r a n s l a t ion f r o m t h e o r ig ina l in S p a n is h. I n t h e e v e n t o f d i s c r e p a n c y, t h e Sp a n i s h - la n g u a g e v e r s ion
I n t e r n a t i o n a l E l e c t r o n i c J o u r n a l o f E l e m e n t a r y E.7 d u, c ai ts is ou n e, 1 V3 1o-2 l6, I n t h i s a r t
I n t e r n a t i o n a l E l e c t r o n i c J o ue rlne am l e not fa r y E d u c a t i o n, 2 0 1 4, 1 37-2 ( 16 ). H o w R e a d i n g V o l u m e A f f e c t s b o t h R e a d i n g F l u e n c y
English 1 Name:
English 1 Name: 2A 2014-2015 English 1 Name: 2B 2014-2015 Alphabet Aa (ei) Bb (bi) Cc (si) Dd (di) Ee (i) Ff (ef) Gg (lli) Hh (eich) Ii (ai) Jj (llei) Kk (quei) Ll (el) Mm (em) Nn (en) Oo (Ou) Pp (pi)
This Specification is subject to change without notice
ProductS p e ci f i ca ti on BE31597E-0 1 a l p e f i n F T C D e M l a m e : E 3 1 5 9 7 E 1 l i m i n a p e f i i n a l p e f i ProductF un cti on S ci ca ti on 31.5 i ch C ol ort -L M odul ode N B -0
General Strong Polarization
General Strong Polarization Madhu Sudan Harvard University Joint work with Jaroslaw Blasiok (Harvard), Venkatesan Gurswami (CMU), Preetum Nakkiran (Harvard) and Atri Rudra (Buffalo) December 4, 2017 IAS:
I.U L ~ 32 ~ 2.2 IIII ~~~~ Lg O ~ 2 ~ I I ~~ I.8 101P 25 IIII ~ ~
r - AD A062 775 WVERSTY OF SOW RN CALFORNA LOS ANGELES DEPT 0 ETC FG 5F2 A*AAL NTERM SC ENTFC REPORT (U) SEP 78 R S BUCY AFOSR 76 3100 UNCLASSFED AFosR TR m 5 ;9 N t L U L L 11 11 28 25 32 22 Lg O 2 8
Magic Letterland. Welcome agic. the. Letterland!
Mi Leernd Weme i Leernd! e 5 Mi Leernd / 2. ire nd wrie e eers. s e z e u m mpuer 3. Jin e ds nd ur e piure. 18 17 19 20 21 22 23 24 16 11 25 26 14 15 13 10 12 6 9 1 8 2 3 30 7 4 29 5 28 27 2. ire nd wrie
M Line Card Redundancy with Y-Cab l es Seamless Line Card Failover Solu t ion f or Line Card H ardw or Sof t w are Failu res are Leverages hardware Y-
Line Card Redundancy with Y-Cab l es Technical Overview 1 M Line Card Redundancy with Y-Cab l es Seamless Line Card Failover Solu t ion f or Line Card H ardw or Sof t w are Failu res are Leverages hardware
HMX 4681 Kratos. Apollo N CD 5, IP,
PUXP 2791 PUXP 2782 Ares PUXP 2618 onus PUXP 2719.7) C 1 HMX 4681 Kratos Apollo N Gladiator PUXP 2724 Magic Lantern Magic Wand HMX 468 4 P 'n < A: g. -P ' k...) 4,235 3,63 'LA.4= 2,94 2,178 U.) '-." (...)
INST T N DLS. - Ext t t. Carefully read these instructions before first use. Code: Date: / /201 Rev.:.0
INST T N - Ext t t Carefully read these instructions before first use. DLS GB Code: Date: / /201 Rev.:.0 DLS IMPORTANT SAFETY INSTRUCTIONS This manual contains important safety information, which must
FOR SALE T H S T E., P R I N C E AL BER T SK
FOR SALE 1 50 1 1 5 T H S T E., P R I N C E AL BER T SK CHECK OUT THIS PROPERTY ON YOUTUBE: LIVINGSKY CONDOS TOUR W W W. LIV IN G S K YC O N D O S. C A Th e re is ou tstan d in g val ue in these 52 re
The distribution of characters, bi- and trigrams in the Uppsala 70 million words Swedish newspaper corpus
Uppsala University Department of Linguistics The distribution of characters, bi- and trigrams in the Uppsala 70 million words Swedish newspaper corpus Bengt Dahlqvist Abstract The paper describes some
Vero Beach Elks Lodge # th Street Vero Beach, FL /
1350-26th Street Vero Beach, FL 32960 772/562-8450 Annual Harry-Anna Saturday, February 13, 2016 Featuring our Popular Roast Beef Dinner Potatoes, Corn-on-the-Cob, Salad & Dessert by Chef Vic Cocktails:
Lecture No. 1 Introduction to Method of Weighted Residuals. Solve the differential equation L (u) = p(x) in V where L is a differential operator
Lecture No. 1 Introduction to Method of Weighted Residuals Solve the differential equation L (u) = p(x) in V where L is a differential operator with boundary conditions S(u) = g(x) on Γ where S is a differential
Lesson 7: Linear Transformations Applied to Cubes
Classwork Opening Exercise Consider the following matrices: AA = 1 2 0 2, BB = 2, and CC = 2 2 4 0 0 2 2 a. Compute the following determinants. i. det(aa) ii. det(bb) iii. det(cc) b. Sketch the image of
7.3 The Jacobi and Gauss-Seidel Iterative Methods
7.3 The Jacobi and Gauss-Seidel Iterative Methods 1 The Jacobi Method Two assumptions made on Jacobi Method: 1.The system given by aa 11 xx 1 + aa 12 xx 2 + aa 1nn xx nn = bb 1 aa 21 xx 1 + aa 22 xx 2
J A D A V PUR U N IV ERS IT Y K O LK AT A Fa cu lty of En gi n eer in g & T e ch no lo gy N O T I C E
J A D A V PUR U N IV ERS IT Y K O LK AT A 7 0 00 3 2 Fa cu lty of En gi n eer in g T e ch no lo gy N O T I C E D at e: D ec em b er 1 4, 2 0 18 As dir ec t ed V ic e -C h anc el l or t h e n ext m e et
Secondary 3H Unit = 1 = 7. Lesson 3.3 Worksheet. Simplify: Lesson 3.6 Worksheet
Secondary H Unit Lesson Worksheet Simplify: mm + 2 mm 2 4 mm+6 mm + 2 mm 2 mm 20 mm+4 5 2 9+20 2 0+25 4 +2 2 + 2 8 2 6 5. 2 yy 2 + yy 6. +2 + 5 2 2 2 0 Lesson 6 Worksheet List all asymptotes, holes and
Quantitative Screening of 46 Illicit Drugs in Urine using Exactive Ultrahigh Resolution and Accurate Mass system
Quantitative Screening of 46 Illicit Drugs in Urine using Exactive Ultrahigh Resolution and Accurate Mass system Kevin Mchale Thermo Fisher Scientific, San Jose CA Presentation Overview Anabolic androgenic
STANDARDIZATION OF BLENDED NECTAR USING BANANA PSEUDOSTEM SAP AND MANGO PULP SANTOSH VIJAYBHAI PATEL
STANDARDIZATION OF BLENDED NECTAR USING BANANA PSEUDOSTEM SAP AND MANGO PULP BY SANTOSH VIJAYBHAI PATEL B.Sc. (Hons.) Horticulture DEPARTMENT OF POST HARVEST TECHNOLOGY ASPEE COLLEGE OF HORTICULTURE AND
Big Bang Planck Era. This theory: cosmological model of the universe that is best supported by several aspects of scientific evidence and observation
Big Bang Planck Era Source: http://www.crystalinks.com/bigbang.html Source: http://www.odec.ca/index.htm This theory: cosmological model of the universe that is best supported by several aspects of scientific
Definition: A sequence is a function from a subset of the integers (usually either the set
Math 3336 Section 2.4 Sequences and Summations Sequences Geometric Progression Arithmetic Progression Recurrence Relation Fibonacci Sequence Summations Definition: A sequence is a function from a subset
TSOKOS READING ACTIVITY Section 7-2: The Greenhouse Effect and Global Warming (8 points)
IB PHYSICS Name: Period: Date: DEVIL PHYSICS BADDEST CLASS ON CAMPUS TSOKOS READING ACTIVITY Section 7-2: The Greenhouse Effect and Global Warming (8 points) 1. IB Assessment Statements for Topic 8.5.
o C *$ go ! b», S AT? g (i * ^ fc fa fa U - S 8 += C fl o.2h 2 fl 'fl O ' 0> fl l-h cvo *, &! 5 a o3 a; O g 02 QJ 01 fls g! r«'-fl O fl s- ccco
> p >>>> ft^. 2 Tble f Generl rdnes. t^-t - +«0 -P k*ph? -- i t t i S i-h l -H i-h -d. *- e Stf H2 t s - ^ d - 'Ct? "fi p= + V t r & ^ C d Si d n. M. s - W ^ m» H ft ^.2. S'Sll-pl e Cl h /~v S s, -P s'l
Chapter 22 : Electric potential
Chapter 22 : Electric potential What is electric potential? How does it relate to potential energy? How does it relate to electric field? Some simple applications What does it mean when it says 1.5 Volts
CS311 Computational Structures Regular Languages and Regular Expressions. Lecture 4. Andrew P. Black Andrew Tolmach
CS311 Computational Structures Regular Languages and Regular Expressions Lecture 4 Andrew P. Black Andrew Tolmach 1 Expressions Weʼre used to using expressions to describe mathematical objects Example:
Support Vector Machines. CSE 4309 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington
Support Vector Machines CSE 4309 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1 A Linearly Separable Problem Consider the binary classification
Ash Wednesday. First Introit thing. * Dómi- nos. di- di- nos, tú- ré- spi- Ps. ne. Dó- mi- Sál- vum. intra-vé-runt. Gló- ri-
sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
tc., ,if. l/ ft 6 & L 8. livteya.halaf6e feoreox es Pp I +41 Sc C Qn 4-er 70-y Cc, inoor f,?cr LA I }or 1.er
vksivirginiaunivemq HEALTH AND SAFEIN 1-1 Pp I +41 Sc C Qn 4-er Dec,e,v,i,er 3, x1013 o 0-0 )-9'-1 70-y Cc, inoor f,?cr LA I }or 1.er 1. COrx k.--laics 2. 2 3. -----,54doc A vf N\ 89-CP._ ( where y ou
i;\-'i frz q > R>? >tr E*+ [S I z> N g> F 'x sa :r> >,9 T F >= = = I Y E H H>tr iir- g-i I * s I!,i --' - = a trx - H tnz rqx o >.F g< s Ire tr () -s
5 C /? >9 T > ; '. ; J ' ' J. \ ;\' \.> ). L; c\ u ( (J ) \ 1 ) : C ) (... >\ > 9 e!) T C). '1!\ /_ \ '\ ' > 9 C > 9.' \( T Z > 9 > 5 P + 9 9 ) :> : + (. \ z : ) z cf C : u 9 ( :!z! Z c (! $ f 1 :.1 f.
MATH 1080: Calculus of One Variable II Fall 2018 Textbook: Single Variable Calculus: Early Transcendentals, 7e, by James Stewart.
MATH 1080: Calculus of One Variable II Fall 2018 Textbook: Single Variable Calculus: Early Transcendentals, 7e, by James Stewart Unit 2 Skill Set Important: Students should expect test questions that require
Provider Satisfaction
Prider Satisfaction Prider Satisfaction [1] NOTE: if you nd to navigate away from this page, please click the "Save Draft" page at the bottom (visible to ONLY logged in users). Otherwise, your rpons will
NVLAP Proficiency Test Round 14 Results. Rolf Bergman CORM 16 May 2016
NVLAP Proficiency Test Round 14 Results Rolf Bergman CORM 16 May 2016 Outline PT 14 Structure Lamp Types Lab Participation Format for results PT 14 Analysis Average values of labs Average values of lamps
Homework 3/ Solutions
MTH 310-3 Abstract Algebra I and Number Theory S17 Homework 3/ Solutions Exercise 1. Prove the following Theorem: Theorem Let R and S be rings. Define an addition and multiplication on R S by for all r,
Please read carefully. Good luck & Go Gators!!!
Page 1/12 Exam 1 May the Schwartz be with you! Instructions: Turn off all cell phones and other noise making devices and put away all electronics Show all work on the front of the test papers Box each
ECE4270 Fundamentals of DSP Lecture 20. Fixed-Point Arithmetic in FIR and IIR Filters (part I) Overview of Lecture. Overflow. FIR Digital Filter
ECE4270 Fundamentals of DSP Lecture 20 Fixed-Point Arithmetic in FIR and IIR Filters (part I) School of ECE Center for Signal and Information Processing Georgia Institute of Technology Overview of Lecture
Systems of Linear Equations
Systems of Linear Equations As stated in Section G, Definition., a linear equation in two variables is an equation of the form AAAA + BBBB = CC, where AA and BB are not both zero. Such an equation has
The Ind ian Mynah b ird is no t fro m Vanuat u. It w as b ro ug ht here fro m overseas and is now causing lo t s o f p ro b lem s.
The Ind ian Mynah b ird is no t fro m Vanuat u. It w as b ro ug ht here fro m overseas and is now causing lo t s o f p ro b lem s. Mynah b ird s p ush out nat ive b ird s, com p et ing for food and p laces
I/O7 I/O6 GND I/O5 I/O4. Pin Con fig u ra tion Pin Con fig u ra tion
2M x 8 HIGH SPEED LOW POWER ASYRONOUS CMOS STATIC RAM Ex tended Tem per a ture TTS2MWV8 FEATURES High Speed access times 25, 35ns High-perfromace, low power CMOS process Multiple center power and ground
TECHNICAL NOTE AUTOMATIC GENERATION OF POINT SPRING SUPPORTS BASED ON DEFINED SOIL PROFILES AND COLUMN-FOOTING PROPERTIES
COMPUTERS AND STRUCTURES, INC., FEBRUARY 2016 TECHNICAL NOTE AUTOMATIC GENERATION OF POINT SPRING SUPPORTS BASED ON DEFINED SOIL PROFILES AND COLUMN-FOOTING PROPERTIES Introduction This technical note
Gary Callicoat Available All Day! Blue Plate Specials Monday: Gary s 3-Way Tuesday: Taco Salad Beef Stroganoff Wednesday: Spaghetti n Meatballs
Wc f fs fy c c js. W f k xcs f vs f s sff s G Hsy Bck fs y f cf s s s y k. Ec vy y v y Rsy Bck I s y s ks s! Gy Cc Dy! A Av s c P B s c Txs s fs c 3-Wy s s y c s G s My: c c.89 s 10 c c v s s s f f s ss
Tausend Und Eine Nacht
Connecticut College Digital Commons @ Connecticut College Historic Sheet Music Collection Greer Music Library 87 Tausend Und Eine Nacht Johann Strauss Follow this and additional works at: https:digitalcommonsconncolledusheetmusic