I = I = I for this case of symmetry about the x axis, we find from
|
|
|
- Tobias Dalton
- 5 years ago
- Views:
Transcription
1 8-5. THE MOTON OF A TOP n his secion, we shll consider he moion of n xilly symmeric body, sch s op, which hs fixed poin on is xis of symmery nd is ced pon by niform force field. The op ws chosen becse i is relively simple exmple of body whose forced moion is mrkedly ffeced by gyroscopic momens ssocied wih he spin bo is xis of symmery. The resls, however, hve pplicion in he nlysis of oher sysems, sch s gyroscopes nd spinning projeciles. Generl Eqions. Consider he roionl moion of he op shown in Fig is ssmed o spin wiho fricion sch h he poin O on he xis of symmery is fixed. The only exernl momen bo O is h de o he consn grviionl force mg cing hrogh is cener of mss C. Le s nlyze he moion of he op by sing Lgrnge's eqions nd choosing he Elerin ngles s coordines. We noe h his is n exmple of forced moion; hence H is no fixed in spce. So le s se he originl Eler ngle definiion of Sec. 7- in which he vecor is ssmed o poin vericlly downwrd in he direcion of he grviionl force. f we choose he fixed poin O s he reference poin, he ol kineic energy my be wrien in erms of he Eler ngle res. Noing h nd yy zz for his cse of symmery bo he x xis, we find from Eq. (8-87) h T ( & φ & sin ) (& & cos ) (8-4) where he momens, of ineri re ken bo principl xes O. Assming horizonl reference level hrogh O, he grviionl poenil energy is V mgl sin (8-4) where l is he disnce of he mss cener from. he fixed poin. Now we cn wrie he Lgrngin fncion: xx L T V (& φ& sin ) (& & cos ) mgl sin (8-4) The generlized momen re of he sme form s we obined in Eq. (8-) for he nforced cse. We see h
2 p p p L Ω sin & cos & L & & L Ω & φ (8-43) where we recll h he ol spin Ω is given by Ω & φ & sin. The sndrd form of Lgrnge's eqion, nmely, d d L L q& i q i is now pplied ogeher wih Eq. (8-43) o obin from which we see h boh dp dp d d φ, (8-44) p nd p φ re consn. Hence we find h Ω is consn for his cse where here is no pplied momen bo he symmery xis. Also, he precession re & cn be obined from Eq. (8-43) wih he following resl: p Ω sin &. (8-45) cos Now le s se he principle of conservion of energy o obin n inegrl of he eqion of moion. From Eqs. (8-4) nd (8-4), we see h he ol energy is E T V Ω (& & cos ) mgl sin (8-46) where we recll h Ω & φ & sin is consn. follows h he ol energy mins he kineic energy ssocied wih he ol spin Ω is lso consn. Clling his qniy E', we cn wrie E' E Ω (& & cos ) mgl sin. (8-47) Sbsiing for & from Eq. (8-45) nd solving for &, we obin & Ω sin E' p mgl sin cos. (8-48) Noe h is he only vrible on he righ-hnd side of his eqion. Ths we see from Eqs. (8-45) nd (8-48) h he precession re & nd he nion re & cn be wrien s fncions of lone for ny given cse.
3 n order o simplify he semen of Eq. (8-48), le s mke he sbsiion from which i follows h sin, (8-49) & & cos. (8-5) Also, le s define he consn prmeers, b, c, nd e s follows: p, Ω b, Now mliply Eq. (8-48) by The resling eqion is f we se he noion mgl c, hen we cn wrie Eq. (8-5) in he form 3 E' e. (8-5) cos nd mke he foregoing sbsiions. & ( )( e c) ( b). (8-5) f ( ) ( )( e c) ( b), (8-53) & f (). (8-54) Now le s consider he fncion f () in greer deil. Figre 8-4 shows plo of f () verss for ypicl cse. We cn ssme h he prmeer c is posiive since we cn lwys consider he disnce l from he sppor poin o he cener of mss o be posiive. Frhermore, we see from Eq. (8-53) h he cbic erm predomines for lrge bsole mgnides of. Hence we find h f () ms be negive for lrge negive vles of nd ms be posiive for lrge posiive vles of. Now f () is coninos fncion of so i ms be zero for les one rel vle of. Th f () is clly zero for hree rel vles of will now be shown. is eviden h & is zero or posiive for ll physiclly relizble siions, so f () ms be zero or posiive some poin in he inervl which is he rnge in which ms lie in he cl cse. B if we se ± in Eq. (8-53) we find h f () is zero or negive hese wo poins since ( b) ms be zero or posiive. Therefore here re wo roos in he inervl nd he hird roo 3 ms lie in he rnge 3. Smmrizing, we cn wrie. Looking gin Eq. (8-48) or (8-5), we find h he moion in sops only when or. is ppren, hen, h ms oscille beween hese vles nd will ndergo corresponding oscillion. To nlyze he moion of in ime, le s wrie Eq. (8-54) in he form Now we define 3 & f ) c( )( )( ). (8-55) ( 3
4 nd we see h w, k, p c( 3 ), (8-56) 3 & w&. (8-57) ( )( ) Mking hese sbsiions, we cn wrie Eq. (8-55) he following form: w& p ( w )( k w ). (8-58) f we mesre he ime from he insn when is is minimm vle nd, we find h w dw p F(sin w, k). (8-59) ( w )( k w ) where we recognize he inegrl s n ellipic inegrl of he firs kind. Conversely, we cn solve for w, obining w sn p, (8-6) where, we recll, he ellipic fncion, sn, ws inrodced previosly in Sec Now we se he definiion of w in Eq. (8-56) o solve for ( ) sn p. (8-6) Becse he sn fncion is sqred, he period of he nion in is js hlf he period of w. Ths he period of or is K( k) 4K( k) T, (8-6) p c( 3 ) where K(k) is he complee ellipic inegrl of he firs kind. Referring o Eqs. (8-45) nd (8-5), we see h he precession re & cn be expressed s fncion of s follows: b &. (8-63) Hving solved for s fncion of ime, we cn lso obin & s fncion of ime. Also, from he definiion of he ol spin Ω given in Eq. (8-), we see h & φ Ω &, (8-64) where Ω is consn. Hence & φ is known fncion of ime. Noe h boh & nd & φ hve he sme period s. Ph of he Symmery Axis. Le s consider he ph of poin P loced on he xis of symmery ni disnce from he fixed poin O. Tking horizonl reference hrogh O, we find h 4 sin represens he heigh of P. The vles nd which & is zero correspond o posiions of
5 minimm nd mximm heigh nd re known s rning poins. f we represen he moion of he symmery xis by he ph of P on he srfce of ni sphere, we find h P will remin beween wo horizonl "lide" circles given by nd, corresponding o he exreme vles of. The ph of P in ny given cse cn be clssified s one of hree generl ypes. n order o simplify his clssificion, le s define p. (8-65) b p φ From Eq. (8-63) we see h & when (excep if ±, in which cse & is indeermine). Hence he moion of he symmery xis he insn when is sch h he ph of P is ngen o vericl circle of "longide." () Le s consider firs he cse where >. n oher words, lies oside he possible rnge of, nd herefore he precessionl re & does no eql zero ny ime dring he moion. This cse is shown in Fig. 8-5(), where he rrows indice he direcion of he velociy of P for posiive Ω. (b) Nex consider he cse in which < <. As shown in Fig. 8-5(b), we see h & is zero wice dring ech nion cycle, nd, for >, i clly reverses is sign compred o he verge vle of &. n generl, for cerin op wih given ol spin Ω, he ph rced by P is dependen pon he iniil vles of, &, nd &. cn be seen, for exmple, h he formion of loops s in Fig. 8-5(b) cn be ccomplished by giving he xis of symmery n iniil precession re which is opposie in direcion o is verge vle. Cspidl Moion. (c) The cse in which is known s cspidl moion nd is illsred in Fig. 8-5(c). Noe h nd -& re boh zero when, resling in csp which poins pwrd. This ype of moion 5
6 will occr, for exmple, if he xis of spinning op is relesed wih zero iniil velociy. The xis begins o fll vericlly, csing gyroscopic ineril momens which resl in combinion of nion nd precession sch h he xis is moionless csp reglr inervls. ncidenlly, we see from energy considerions h he xis cn be sionry only when P is is highes poin, corresponding o. n oher words, he poenil energy ms be mximm when he kineic energy is minimm. To find he limis of he nion for cspidl moion, le s se & or f () eql o zero. Consider he following wo cses: () & becse & ; () & becse cos. Cse : when &. Using he definiion of given in Eq. (8-65), we see from Eq. (8-5) h e c, (8-66) since & he csp. We cn hen wrie n expression for f () in he form f ( ) c( )( ) b ( ). (8-67) We hve lredy shown h one limi of he nionl moion occrs. Dividing o his roo, we obin or ( c ) b ( ), λ (λ ), (8-68) where λ is posiive consn given by Ω b λ. (8-69) c 4 mgl Solving for he roos of Eq. (8-68) nd inclding he one fond previosly, we cn smmrize he roos of f ( ) for his cse s follows: 3 λ λ λ λ λ λ, (8-7) where we ke he posiive sqre roo. For <, n evlion of Eq. (8-7) will show h 6 3 regrdless of he vle of λ nd in greemen wih or erlier resls. The limis of he moion in or re fond by evling from Eq. (8-66), λ from Eq. (8-69), nd hen sing Eq. (8-7) o obin. Noe gin h l 3 hs no physicl mening. Cse : & when. Consider firs h. This cse ±
7 pplies when he symmery xis psses hrogh he pper vericl posiion wih non-zero nglr velociy. We see from Eq. (8-65) h b (8-7) nd, since & > his momen, we noe from Eqs. (8-48) nd (8-5) h So we cn express f () in he form e> c. (8-7) f ( ) ( )( e c) b ( ) (8-73) nd solve for he rning poins. Dividing o he known fco (-) corresponding o, here remins ( )( e c) b ( ), which cn be wrien in he form b e b e. (8-74) c c One of he roos of his eqion corresponds o rning poin. The oher roo 3 is greer hn nd hs no physicl mening. A similr procedre cn be followed for he cse where &. n his insnce, he symmery xis psses hrogh he boom poin on he ni sphere wih non-zero velociy. We see from Eq. (8-65) h Also, since & >, we see h So we cn wrie b. (8-75) e c>. (8-76) f ( ) ( )( e c) b ( ). (8-77) Dividing o he known fcor ( ) corresponding o he roo, we obin b e b e. (8-78) c c The roos of his eqion re he pper rning poin nd he nonphysicl roo 3 which gin is lrger hn niy. Sbiliy of Moion ner he Vericl. An exmple of op moion of priclr ineres occrs if he xis poins vericlly pwrd when & is zero. This flls nder Cse of cspidl moion, nd in his insnce. From Eq. (8-7), we see h he roos re, (λ ),, (8-79), 3 where ( λ ) is designed s or 3 ccording s λ. is less hn or 7
8 greer hn. Now le s consider he moion for he following vles of λ : () λ <, (b) λ nd (c) λ >. () Cse : λ < or Ω < 4 mgl / 8. For his cse he csp occrs posiion of nsble eqilibrim. This cn be seen from Fig. 8-6 by noing h smll disrbnce his posiion will cse nionl moion dring which decreses nil he minimm vle corresponding o λ is reched; wherepon reversl of his moion rerns he xis o he vericl. The doble roo is illsred by he fc h he slope f '( ) is zero his poin, s my be seen from Eq. (8-67). is ineresing o noe h he period of nion cycle is infinie. To show his, we refer o Eq. (8-56) nd we find h he modls k ; hence he complee ellipic inegrl K(k) is infinie. follows from Eq. (8-6) h he period is lso infinie. (b) Cse : λ or Ω 4 mgl /. Here Here is he borderline cse in which here is nerl sbiliy he vericl. All hree roos re eql o niy nd hs here is n inflecion poin of f (). (c) Cse 3: λ > or Ω > 4 mgl /. The spin is sfficienly lrge in his cse h he vericl posiion is sble, h is, n infiniesiml disrbnce will no cse finie deviion of he symmery xis from he vericl. Agin we find h f '(), b in his cse he hird roo (λ). 3 > A op which is spinning s in Cse 3 is known s sleeping op. This nme rises becse smooh, xilly symmeric op wih is xis vericl nd λ > migh pper firs glnce o be no moving ll, nd hence "sleeping." n n cl cse here re smll fricionl momens which slowly decrese he spin nil λ becomes less hn niy. A his poin wobble or nion ppers nd grdlly increses nil he body of he op his he horizonl srfce. ncidenlly, he biliy of n cl op wih lrge spin o righ iself nd rech he sleeping condiion is de o he cion of fricionl
9 forces on is ronded poin. These forces hve been omied in his nlysis. Nion Freqency nd Amplide for he Cse of Lrge Spin. Now le s se Eq. (8-7), which ws obined in he nlysis of cspidl moion, o find he pproxime mplide nd freqency of he nionl moion of fs op, h is, one for which λ >>. We cn wrie he expression for in he form λ λ, λ λ or, sing he binomil expnsion nd neglecing erms of order higher hn / λ, we obin λ λ ( ). (8-8) λ λ λ λ The mplide of he nion is mgl ( ) ( λ Ω ). (8-8) Noe h he nion mplide vries inversely wih he sqre of he ol spin re Ω. becomes zero for, h is, for vericl op, he spin being mch lrger hn h reqired for sbiliy. We see from Eq. (8-7), hen, h he roos nd hve smll seprion; b he hird roo 3 is pproximed by nd hs is widely sepred from he ohers. 3 λ, (8-8) To find he nion freqency of fs op, le s refer o Eq. (8-6) which gve he generl solion for in erms of ellipic fncions. However, becse 3 is widely sepred from nd, we see from Eq. (8-56) h he modls k is very smll; hence we cn pproxime he ellipic fncion sn p by he rigonomeric fncion sin p. Ths we obin ( ) sin p, (8-83) where he ime is mesred from he momen when. Using Eq. (8-8) nd rigonomeric ideniies, we cn rewrie his resl in he form: mgl ( )( cos p ). (8-84) Ω From Eqs. (8-5), (8-56), (8-69), nd (8-8), we' see h he circlr freqency of he nion is Ω p c( 3 ) cλ. (8-85) An expression for he precession re & cn now be obined, for we 9
10 noe from Eqs. (8-63) nd (8-65) h b &. Sbsiing for b nd ( ) from Eqs. (8-5) nd (8-84), we obin B we see from Eq. (8-84) h or ( mgl & ( cos p). (8-86) Ω ) where we neglec erms of order of fs op h he precession re is ( mgl ) ( cos p) Ω ( cos p), (8-87) λ / λ or higher. So we obin for his cse mgl & ( cos p) ; (8-88) Ω he pproximion being vlid even for cspidl moion ner he vericl, so long s λ >>. Precession wih No Nion. Precession wih no nion is indiced by hving, h is, by he presence of doble roo of f () poin oher hn ±. The condiions for doble roo re h f () nd f '( ) be zero for he sme vle of, s shown in Fig Ths, sing Eq. (8-53) we cn wrie Also, f ( ) ( )( e c) ( b). (8-89) f '( ) ( e c) c( ) b( b). (8-9) From Eqs. (8-89) nd (8-9), we hve ( b) c( ) b( b) e c,
11 from which we obin he following qdric eqion in ( b) : ( b) b( )( b) c( ). (8-9) Solving for ( b), we obin b b± b c. (8-9) B we recll from Eq. (8-63) h so we find h he precession re is or, in erms of, b & ( ) & cos, (8-93) b c & ±, (8-94) b b csin & ±. (8-95) sin b is ineresing o noe h wo sedy precession res re possible, provided h he vles of nd b Ω / re sch h he sqre roo in Eq. (8-95) is rel. This ls reqiremen is similr o reqiring sfficien spin for sbiliy in vericl op. Ths we see h he condiion on he ol spin Ω in order h sedy precession be possible given vle of is h Consider now he cse in which 4 mgl Ω > sin. (8-96) Ω >> 4 mgl sin / ; h is, he spin is lrge enogh so h he second erm in he sqre roo of Eq. (8-95) is smll compred o niy. Then we cn pproxime (8-95) by b csin & ±, sin b from which we obin he following possible res of niform precession: ( & ) ( & ) c mgl b Ω. (8-97) b Ω sin sin Noe h he slow precession re (& ) is independen of. This is he precession re which is slly observed in fs op or gyroscope nd is lso eql o he men vle of & fond in Eq. (8-88). On he oher hnd, he fs precession re (& ) is independen of he ccelerion of grviy nd, in fc, is idenicl wih he free precession re obined previosly in Eq. (8-4).
12 Exmple 8-7. A op wih ol spin Ω nd velociy v is sliding on smooh horizonl floor wih is symmery xis vericl (Fig. 8-8). Sddenly,, he poin srikes crck O nd is prevened from moving frher lhogh he nglr moion is nhindered. f is he ngle beween he xis of symmery nd he floor, find. The nglr velociy & ( ) js fer he verex is sopped. b. The liner implse exered on he op. c. min in he ensing moion, ssming h Ω v / l g / l nd (/ 4) ml / 5, where he momens of ineri re ken bo xes hrogh he verex. Or pproch will be o noe h he nglr momenm bo he verex O is conserved dring he iniil insn becse he recion forces of he floor pss hrogh his poin. Hence he nglr implse pplied is zero. Eqing expressions for he horizonl componen of nglr momenm before nd fer he impc, we obin H mvl & ( ), (8-98) h where his componen is direced ino he pge. Ths we find h & mvl (). (8-99) The liner implse is fond by clcling he chnge in he liner momenm dring impc. Noing h we obin v ( ) & ()l, ~ ml F mv( ) mv mv( ), (8-) where he implse is posiive when direced o he righ. n order o clcle he minimm vle of, we noe firs h & sin. Therefore we hve he cspidl moion which ws described previosly nder Cse on pge 47. Evling he consn
13 prmeers b, c, nd e from Eq. (8-5), we hve Ω g b 4 l mgl 8g c 5l E' mvl e mgl 56g 5l. (8-) The rning poin is fond by sbsiing hese vles ino Eq. (8-74) wih he resl: The roos of his eqion re nd 3, he hird roo of f ( ) being. We obin Ths we find h sin (.958) min Exmple 8-8. A niform circlr disk of mss m, rdis, rolls on horizonl srfce in sch mnner h is plne is inclined wih he vericl consn ngle nd is cener of mss describes circlr ph of rdis R - Fig. 8-9(). Solve for he precession re &. Firs Mehod: Alhogh he disk is n xilly symmeric body sbjec o grviionl momens, he geomery nd he consrins re differen from hose enconered in he nlysis of op. So le s sr gin wih he bsic roionl eqion M H &, where we shll choose he fixed poin O s reference. Le s se Elerin ngles o describe he orienion of he disk. The precession re & cn be obined in erms of he ol spin Ω by 3
14 eqing wo expressions for he rnslionl velociy of he cener of mss. from which we hve v R& Ω, & Ω. (8-) R cn be seen h & ms be consn. A chnging & wold imply chnging kineic energy. B, since is consn nd no slipping occrs, here re no working forces cing on he disk; hence, by he principle of work nd kineic -energy, & cnno chnge. From Eq. (8-), we see h Ω is lso consn. Consider now he xil nd rnsverse componens of he nglr momenm bo he cener of mss. From Eqs. (8-6) nd (8-), we cn wrie H H Ω ( R / ) &. & cos To find he ol nglr momenm bo O, we ms dd he nglr momenm de o he rnslionl velociy of he cener of mss bo O. Tking horizonl nd vericl componens of his porion, we obin H H mr & mr& cos As he disk rvels in is circlr ph, he sysem of for componen vecors roes wih nglr velociy &, s shown in Fig. 8-9(b). Ths we see h he ol nglr momenm vecor H is of consn mgnide b precesses bo vericl xis he sme re s he disk. Now we cn evle H & by noing h H & & H (8-3) for his cse in which he mgnide H is consn. We find h H & & H H cos H sin ) e (8-4) ( h or, sbsiing he preceding expressions for where H h, H nd H, we obin H & R & cos mr sin e, (8-5) e is ni vecor direced o of he pge. The pplied momen bo O is independen of where we noe h F h nd is given by M mg sine, (8-6) F v mg since he mss cener hs no vericl moion. Eqing he expressions on he righ hnd sides of Eqs. (8-5) nd (8-6), we obin 4
15 or R & cos mr sin mgsin, mg n &. (8-7) R mr sin F or hin niform disk, we recll h m, m. 4 Sbsiing hese vles ino Eq. (8-7), we obin 4g n &. (8-8) 6R sin Second Mehod: Now le s consider his problem from he Lgrngin viewpoin. Using Eq. (8-98) for he roionl kineic energy nd dding he rnslionl kineic energy, we obin he ol kineic energy T m( R & & ) (& φ& sin ) (& & cos ). (8-9) n order o se sndrd form of Lgrnge's eqion, he coordines ms be independen. B we sw in Eq. (8-) h he condiion of rolling imposes he consrin h Ω & R φ& sin &, So he coordines,, φ re no independen s hey snd. f, however, we wrie he consrin eqion in he form & R' sin φ & sin &, (8-) nd sbsie ino he kineic energy expression of Eq. (8-9), we obin he resl T m ( R' sin ) & ( ' & & cos ), (8-) where we hve le ' m nd R R' sin, (8-) in ccordnce wih Fig. 8-9(). Now φ hs been elimined s generlized coordine nd he remining coordines nd re independen in he kinemic sense. Also, we hve inrodced new consn, R, becse R is no longer consn if is considered o be vrible. cn be seen h he sysem is conservive nd he poenil energy is 5
16 6 given by mg cos V. (8-3) The generlized forces re sin mg V M V M. (8-4) Le s se Lgrnge's eqion in he form of Eq. (6-73), nmely, i i i Q q T q T d d &. Firs we obin he generlized momen: & & & & T p R m T p ' cos ) sin ' (. (8-5) Also, we evle he following erms: cos sin ) sin ' ( & R m T T. (8-6) From Eqs. (8-4), (8-5), nd (8-6), we cn now wrie he eqion in he form d dp, (8-7) indicing h p is consn. For his priclr cse in which is consn, i follows from Eq. (8-5) h he precession re & is consn. n similr fshion we find h he eqion is sin cos sin ) sin ' ( ' mg R m & & &. (8-8) Seing & & nd solving for &, we obin sin n R mr mg & in greemen wih or erlier resl.
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
1. Find a basis for the row space of each of the following matrices. Your basis should consist of rows of the original matrix.
 Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
15/03/1439. Lecture 4: Linear Time Invariant (LTI) systems
 Lecre 4: Liner Time Invrin LTI sysems 2. Liner sysems, Convolion 3 lecres: Implse response, inp signls s coninm of implses. Convolion, discree-ime nd coninos-ime. LTI sysems nd convolion Specific objecives
Lecre 4: Liner Time Invrin LTI sysems 2. Liner sysems, Convolion 3 lecres: Implse response, inp signls s coninm of implses. Convolion, discree-ime nd coninos-ime. LTI sysems nd convolion Specific objecives
2D Motion WS. A horizontally launched projectile s initial vertical velocity is zero. Solve the following problems with this information.
 Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Available online at Pelagia Research Library. Advances in Applied Science Research, 2011, 2 (3):
 Avilble online www.pelgireserchlibrry.com Pelgi Reserch Librry Advnces in Applied Science Reserch 0 (): 5-65 ISSN: 0976-860 CODEN (USA): AASRFC A Mhemicl Model of For Species Syn-Ecosymbiosis Comprising
Avilble online www.pelgireserchlibrry.com Pelgi Reserch Librry Advnces in Applied Science Reserch 0 (): 5-65 ISSN: 0976-860 CODEN (USA): AASRFC A Mhemicl Model of For Species Syn-Ecosymbiosis Comprising
( ) 2 a b ab. To do this, we are to use the Ricci identity (which we use to evaluate the RHS) and the properties of the Lie derivative.
 Exercise [9.6] This exercise sks s o show h he ccelerion of n (infiniesiml volme mesre V long he worlline he volme s cener e o he effecs of spceime crvre is given by: D V = R V ( b b To o his, we re o
Exercise [9.6] This exercise sks s o show h he ccelerion of n (infiniesiml volme mesre V long he worlline he volme s cener e o he effecs of spceime crvre is given by: D V = R V ( b b To o his, we re o
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
 PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
Version 001 test-1 swinney (57010) 1. is constant at m/s.
 Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
Physic 231 Lecture 4. Mi it ftd l t. Main points of today s lecture: Example: addition of velocities Trajectories of objects in 2 = =
 Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Motion in a Straight Line
 Moion in Srigh Line. Preei reched he mero sion nd found h he esclor ws no working. She wlked up he sionry esclor in ime. On oher dys, if she remins sionry on he moing esclor, hen he esclor kes her up in
Moion in Srigh Line. Preei reched he mero sion nd found h he esclor ws no working. She wlked up he sionry esclor in ime. On oher dys, if she remins sionry on he moing esclor, hen he esclor kes her up in
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Physics 101 Lecture 4 Motion in 2D and 3D
 Phsics 11 Lecure 4 Moion in D nd 3D Dr. Ali ÖVGÜN EMU Phsics Deprmen www.ogun.com Vecor nd is componens The componens re he legs of he righ ringle whose hpoenuse is A A A A A n ( θ ) A Acos( θ) A A A nd
Phsics 11 Lecure 4 Moion in D nd 3D Dr. Ali ÖVGÜN EMU Phsics Deprmen www.ogun.com Vecor nd is componens The componens re he legs of he righ ringle whose hpoenuse is A A A A A n ( θ ) A Acos( θ) A A A nd
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
(b) 10 yr. (b) 13 m. 1.6 m s, m s m s (c) 13.1 s. 32. (a) 20.0 s (b) No, the minimum distance to stop = 1.00 km. 1.
 Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Forms of Energy. Mass = Energy. Page 1. SPH4U: Introduction to Work. Work & Energy. Particle Physics:
 SPH4U: Inroducion o ork ork & Energy ork & Energy Discussion Definiion Do Produc ork of consn force ork/kineic energy heore ork of uliple consn forces Coens One of he os iporn conceps in physics Alernive
SPH4U: Inroducion o ork ork & Energy ork & Energy Discussion Definiion Do Produc ork of consn force ork/kineic energy heore ork of uliple consn forces Coens One of he os iporn conceps in physics Alernive
1. Consider a PSA initially at rest in the beginning of the left-hand end of a long ISS corridor. Assume xo = 0 on the left end of the ISS corridor.
 In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
3 Motion with constant acceleration: Linear and projectile motion
 3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
 Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
Phys 110. Answers to even numbered problems on Midterm Map
 Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
RESPONSE UNDER A GENERAL PERIODIC FORCE. When the external force F(t) is periodic with periodτ = 2π
 RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
An object moving with speed v around a point at distance r, has an angular velocity. m/s m
 Roion The mosphere roes wih he erh n moions wihin he mosphere clerly follow cure phs (cyclones, nicyclones, hurricnes, ornoes ec.) We nee o epress roion quniiely. For soli objec or ny mss h oes no isor
Roion The mosphere roes wih he erh n moions wihin he mosphere clerly follow cure phs (cyclones, nicyclones, hurricnes, ornoes ec.) We nee o epress roion quniiely. For soli objec or ny mss h oes no isor
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
T-Match: Matching Techniques For Driving Yagi-Uda Antennas: T-Match. 2a s. Z in. (Sections 9.5 & 9.7 of Balanis)
 3/0/018 _mch.doc Pge 1 of 6 T-Mch: Mching Techniques For Driving Ygi-Ud Anenns: T-Mch (Secions 9.5 & 9.7 of Blnis) l s l / l / in The T-Mch is shun-mching echnique h cn be used o feed he driven elemen
3/0/018 _mch.doc Pge 1 of 6 T-Mch: Mching Techniques For Driving Ygi-Ud Anenns: T-Mch (Secions 9.5 & 9.7 of Blnis) l s l / l / in The T-Mch is shun-mching echnique h cn be used o feed he driven elemen
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
ME 141. Engineering Mechanics
 ME 141 Engineeing Mechnics Lecue 13: Kinemics of igid bodies hmd Shhedi Shkil Lecue, ep. of Mechnicl Engg, UET E-mil: sshkil@me.bue.c.bd, shkil6791@gmil.com Websie: eche.bue.c.bd/sshkil Couesy: Veco Mechnics
ME 141 Engineeing Mechnics Lecue 13: Kinemics of igid bodies hmd Shhedi Shkil Lecue, ep. of Mechnicl Engg, UET E-mil: sshkil@me.bue.c.bd, shkil6791@gmil.com Websie: eche.bue.c.bd/sshkil Couesy: Veco Mechnics
4.2 Continuous-Time Systems and Processes Problem Definition Let the state variable representation of a linear system be
 4 COVARIANCE ROAGAION 41 Inrodcion Now ha we have compleed or review of linear sysems and random processes, we wan o eamine he performance of linear sysems ecied by random processes he sandard approach
4 COVARIANCE ROAGAION 41 Inrodcion Now ha we have compleed or review of linear sysems and random processes, we wan o eamine he performance of linear sysems ecied by random processes he sandard approach
An Integral Two Space-Variables Condition for Parabolic Equations
 Jornl of Mhemics nd Sisics 8 (): 85-9, ISSN 549-3644 Science Pblicions An Inegrl Two Spce-Vribles Condiion for Prbolic Eqions Mrhone, A.L. nd F. Lkhl Deprmen of Mhemics, Lborory Eqions Differenielles,
Jornl of Mhemics nd Sisics 8 (): 85-9, ISSN 549-3644 Science Pblicions An Inegrl Two Spce-Vribles Condiion for Prbolic Eqions Mrhone, A.L. nd F. Lkhl Deprmen of Mhemics, Lborory Eqions Differenielles,
Flow Networks Alon Efrat Slides courtesy of Charles Leiserson with small changes by Carola Wenk. Flow networks. Flow networks CS 445
 CS 445 Flow Nework lon Efr Slide corey of Chrle Leieron wih mll chnge by Crol Wenk Flow nework Definiion. flow nework i direced grph G = (V, E) wih wo diingihed erice: orce nd ink. Ech edge (, ) E h nonnegie
CS 445 Flow Nework lon Efr Slide corey of Chrle Leieron wih mll chnge by Crol Wenk Flow nework Definiion. flow nework i direced grph G = (V, E) wih wo diingihed erice: orce nd ink. Ech edge (, ) E h nonnegie
The order of reaction is defined as the number of atoms or molecules whose concentration change during the chemical reaction.
 www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
2IV10/2IV60 Computer Graphics
 I0/I60 omper Grphics Eminion April 6 0 4:00 7:00 This eminion consis of for qesions wih in ol 6 sqesion. Ech sqesion weighs eqll. In ll cses: EXPLAIN YOUR ANSWER. Use skeches where needed o clrif or nswer.
I0/I60 omper Grphics Eminion April 6 0 4:00 7:00 This eminion consis of for qesions wih in ol 6 sqesion. Ech sqesion weighs eqll. In ll cses: EXPLAIN YOUR ANSWER. Use skeches where needed o clrif or nswer.
UNIT # 01 (PART II) JEE-Physics KINEMATICS EXERCISE I. 2h g. 8. t 1 = (4 1)i ˆ (2 2) ˆj (3 3)kˆ 1. ˆv = 2 2h g. t 2 = 2 3h g
 J-Physics UNI # (PR II) KINMICS XRCIS I ( )i ˆ ( ) ˆj ( )kˆ i. ˆ ˆ ˆ j i ˆ ˆ j ˆ 6i ˆ 8ˆj 8. h h h C h h.. elociy m/s h D. ˆ i i cos6ˆi sin 6ˆj f ˆ i ˆj i ˆ ˆj i ˆ ˆj i ˆ ˆj f i ˆj ˆj m/s. For,, nd d d
J-Physics UNI # (PR II) KINMICS XRCIS I ( )i ˆ ( ) ˆj ( )kˆ i. ˆ ˆ ˆ j i ˆ ˆ j ˆ 6i ˆ 8ˆj 8. h h h C h h.. elociy m/s h D. ˆ i i cos6ˆi sin 6ˆj f ˆ i ˆj i ˆ ˆj i ˆ ˆj i ˆ ˆj f i ˆj ˆj m/s. For,, nd d d
Think of the Relationship Between Time and Space Again
 Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
A MATHEMATICAL MODEL OF FOUR SPECIES SYN-ECOSYMBIOSIS COMPRISING OF PREY-PREDATION, MUTUALISM AND COMMENSALISMS-I (FULLY WASHED OUT STATE)
 VOL. 6, NO. 4, APRIL 0 ISSN 89-6608 ARPN Jornl of Engineering nd Applied Sciences 006-0 Asin Reserch Pblishing Nework (ARPN). All righs reserved. www.rpnjornls.com A MATHEMATICAL MODEL OF FOUR SPECIES
VOL. 6, NO. 4, APRIL 0 ISSN 89-6608 ARPN Jornl of Engineering nd Applied Sciences 006-0 Asin Reserch Pblishing Nework (ARPN). All righs reserved. www.rpnjornls.com A MATHEMATICAL MODEL OF FOUR SPECIES
MASS, STIFFNESS, AND DAMPING MATRICES FROM MEASURED MODAL PARAMETERS
 IS 74 Inernionl Insrmenion-omion Conference & Exhibi Ocober, 974 MSS, STIFFNESS, ND DMPING MTRICES FROM MESURED MODL PRMETERS Ron Poer nd Mr Richrdson Digil Signl nlysis HEWLETT-PCKRD COMPNY Sn Clr, Cliforni
IS 74 Inernionl Insrmenion-omion Conference & Exhibi Ocober, 974 MSS, STIFFNESS, ND DMPING MTRICES FROM MESURED MODL PRMETERS Ron Poer nd Mr Richrdson Digil Signl nlysis HEWLETT-PCKRD COMPNY Sn Clr, Cliforni
Sph3u Practice Unit Test: Kinematics (Solutions) LoRusso
 Sph3u Prcice Uni Te: Kinemic (Soluion) LoRuo Nme: Tuey, Ocober 3, 07 Ku: /45 pp: /0 T&I: / Com: Thi i copy of uni e from 008. Thi will be imilr o he uni e you will be wriing nex Mony. you cn ee here re
Sph3u Prcice Uni Te: Kinemic (Soluion) LoRuo Nme: Tuey, Ocober 3, 07 Ku: /45 pp: /0 T&I: / Com: Thi i copy of uni e from 008. Thi will be imilr o he uni e you will be wriing nex Mony. you cn ee here re
PARABOLA. moves such that PM. = e (constant > 0) (eccentricity) then locus of P is called a conic. or conic section.
 wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
EXERCISE - 01 CHECK YOUR GRASP
 UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
4 3 a b (C) (a 2b) (D) (2a 3b)
 * A balloon is moving verically pwards wih a velociy of 9 m/s. A sone is dropped from i and i reaches he grond in 10 sec. The heigh of he balloon when he sone was dropped is (ake g = 9.8 ms - ) (a) 100
* A balloon is moving verically pwards wih a velociy of 9 m/s. A sone is dropped from i and i reaches he grond in 10 sec. The heigh of he balloon when he sone was dropped is (ake g = 9.8 ms - ) (a) 100
M r. d 2. R t a M. Structural Mechanics Section. Exam CT5141 Theory of Elasticity Friday 31 October 2003, 9:00 12:00 hours. Problem 1 (3 points)
 Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
Physics Worksheet Lesson 4: Linear Motion Section: Name:
 Physics Workshee Lesson 4: Liner Moion Secion: Nme: 1. Relie Moion:. All moion is. b. is n rbirry coorine sysem wih reference o which he posiion or moion of somehing is escribe or physicl lws re formule.
Physics Workshee Lesson 4: Liner Moion Secion: Nme: 1. Relie Moion:. All moion is. b. is n rbirry coorine sysem wih reference o which he posiion or moion of somehing is escribe or physicl lws re formule.
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
Probability, Estimators, and Stationarity
 Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Srednicki Chapter 20
 Srednicki Chaper QFT Problems & Solions. George Ocober 4, Srednicki.. Verify eqaion.7. Using eqaion.7,., and he fac ha m = in his limi, or ask is o evalae his inegral:! x x x dx dx dx x sx + x + x + x
Srednicki Chaper QFT Problems & Solions. George Ocober 4, Srednicki.. Verify eqaion.7. Using eqaion.7,., and he fac ha m = in his limi, or ask is o evalae his inegral:! x x x dx dx dx x sx + x + x + x
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
CHAPTER 11 PARAMETRIC EQUATIONS AND POLAR COORDINATES
 CHAPTER PARAMETRIC EQUATIONS AND POLAR COORDINATES. PARAMETRIZATIONS OF PLANE CURVES., 9, _ _ Ê.,, Ê or, Ÿ. 5, 7, _ _.,, Ÿ Ÿ Ê Ê 5 Ê ( 5) Ê ˆ Ê 6 Ê ( 5) 7 Ê Ê, Ÿ Ÿ $ 5. cos, sin, Ÿ Ÿ 6. cos ( ), sin (
CHAPTER PARAMETRIC EQUATIONS AND POLAR COORDINATES. PARAMETRIZATIONS OF PLANE CURVES., 9, _ _ Ê.,, Ê or, Ÿ. 5, 7, _ _.,, Ÿ Ÿ Ê Ê 5 Ê ( 5) Ê ˆ Ê 6 Ê ( 5) 7 Ê Ê, Ÿ Ÿ $ 5. cos, sin, Ÿ Ÿ 6. cos ( ), sin (
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
1. VELOCITY AND ACCELERATION
 1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
Lecture 3: 1-D Kinematics. This Week s Announcements: Class Webpage: visit regularly
 Lecure 3: 1-D Kinemics This Week s Announcemens: Clss Webpge: hp://kesrel.nm.edu/~dmeier/phys121/phys121.hml isi regulrly Our TA is Lorrine Bowmn Week 2 Reding: Chper 2 - Gincoli Week 2 Assignmens: Due:
Lecure 3: 1-D Kinemics This Week s Announcemens: Clss Webpge: hp://kesrel.nm.edu/~dmeier/phys121/phys121.hml isi regulrly Our TA is Lorrine Bowmn Week 2 Reding: Chper 2 - Gincoli Week 2 Assignmens: Due:
3D Transformations. Computer Graphics COMP 770 (236) Spring Instructor: Brandon Lloyd 1/26/07 1
 D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
Name: Per: L o s A l t o s H i g h S c h o o l. Physics Unit 1 Workbook. 1D Kinematics. Mr. Randall Room 705
 Nme: Per: L o s A l o s H i g h S c h o o l Physics Uni 1 Workbook 1D Kinemics Mr. Rndll Room 705 Adm.Rndll@ml.ne www.laphysics.com Uni 1 - Objecies Te: Physics 6 h Ediion Cunel & Johnson The objecies
Nme: Per: L o s A l o s H i g h S c h o o l Physics Uni 1 Workbook 1D Kinemics Mr. Rndll Room 705 Adm.Rndll@ml.ne www.laphysics.com Uni 1 - Objecies Te: Physics 6 h Ediion Cunel & Johnson The objecies
CHAPTER 2 KINEMATICS IN ONE DIMENSION ANSWERS TO FOCUS ON CONCEPTS QUESTIONS
 Physics h Ediion Cunell Johnson Young Sdler Soluions Mnul Soluions Mnul, Answer keys, Insrucor's Resource Mnul for ll chpers re included. Compleed downlod links: hps://esbnkre.com/downlod/physics-h-ediion-soluions-mnulcunell-johnson-young-sdler/
Physics h Ediion Cunell Johnson Young Sdler Soluions Mnul Soluions Mnul, Answer keys, Insrucor's Resource Mnul for ll chpers re included. Compleed downlod links: hps://esbnkre.com/downlod/physics-h-ediion-soluions-mnulcunell-johnson-young-sdler/
t s (half of the total time in the air) d?
 .. In Cl or Homework Eercie. An Olmpic long jumper i cpble of jumping 8.0 m. Auming hi horizonl peed i 9.0 m/ he lee he ground, how long w he in he ir nd how high did he go? horizonl? 8.0m 9.0 m / 8.0
.. In Cl or Homework Eercie. An Olmpic long jumper i cpble of jumping 8.0 m. Auming hi horizonl peed i 9.0 m/ he lee he ground, how long w he in he ir nd how high did he go? horizonl? 8.0m 9.0 m / 8.0
ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER 2
 ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER Seion Eerise -: Coninuiy of he uiliy funion Le λ ( ) be he monooni uiliy funion defined in he proof of eisene of uiliy funion If his funion is oninuous y hen
ANSWERS TO EVEN NUMBERED EXERCISES IN CHAPTER Seion Eerise -: Coninuiy of he uiliy funion Le λ ( ) be he monooni uiliy funion defined in he proof of eisene of uiliy funion If his funion is oninuous y hen
A new model for limit order book dynamics
 Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
Suggested Practice Problems (set #2) for the Physics Placement Test
 Deparmen of Physics College of Ars and Sciences American Universiy of Sharjah (AUS) Fall 014 Suggesed Pracice Problems (se #) for he Physics Placemen Tes This documen conains 5 suggesed problems ha are
Deparmen of Physics College of Ars and Sciences American Universiy of Sharjah (AUS) Fall 014 Suggesed Pracice Problems (se #) for he Physics Placemen Tes This documen conains 5 suggesed problems ha are
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
R. I. Badran Solid State Physics
 I Bdrn Solid Stte Physics Crystl vibrtions nd the clssicl theory: The ssmption will be mde to consider tht the men eqilibrim position of ech ion is t Brvis lttice site The ions oscillte bot this men position
I Bdrn Solid Stte Physics Crystl vibrtions nd the clssicl theory: The ssmption will be mde to consider tht the men eqilibrim position of ech ion is t Brvis lttice site The ions oscillte bot this men position
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
Physics 180A Fall 2008 Test points. Provide the best answer to the following questions and problems. Watch your sig figs.
 Physics 180A Fall 2008 Tes 1-120 poins Name Provide he bes answer o he following quesions and problems. Wach your sig figs. 1) The number of meaningful digis in a number is called he number of. When numbers
Physics 180A Fall 2008 Tes 1-120 poins Name Provide he bes answer o he following quesions and problems. Wach your sig figs. 1) The number of meaningful digis in a number is called he number of. When numbers
Physics 221 Fall 2008 Homework #2 Solutions Ch. 2 Due Tues, Sept 9, 2008
 Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
The Finite Element Method for the Analysis of Non-Linear and Dynamic Systems
 Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
CBSE 2014 ANNUAL EXAMINATION ALL INDIA
 CBSE ANNUAL EXAMINATION ALL INDIA SET Wih Complee Eplnions M Mrks : SECTION A Q If R = {(, y) : + y = 8} is relion on N, wrie he rnge of R Sol Since + y = 8 h implies, y = (8 ) R = {(, ), (, ), (6, )}
CBSE ANNUAL EXAMINATION ALL INDIA SET Wih Complee Eplnions M Mrks : SECTION A Q If R = {(, y) : + y = 8} is relion on N, wrie he rnge of R Sol Since + y = 8 h implies, y = (8 ) R = {(, ), (, ), (6, )}
Scalar Conservation Laws
 MATH-459 Nmerical Mehods for Conservaion Laws by Prof. Jan S. Heshaven Solion se : Scalar Conservaion Laws Eercise. The inegral form of he scalar conservaion law + f ) = is given in Eq. below. ˆ 2, 2 )
MATH-459 Nmerical Mehods for Conservaion Laws by Prof. Jan S. Heshaven Solion se : Scalar Conservaion Laws Eercise. The inegral form of he scalar conservaion law + f ) = is given in Eq. below. ˆ 2, 2 )
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
Motion on a Curve and Curvature
 Moion on Cue nd Cuue his uni is bsed on Secions 9. & 9.3, Chpe 9. All ssigned edings nd execises e fom he exbook Objecies: Mke cein h you cn define, nd use in conex, he ems, conceps nd fomuls lised below:
Moion on Cue nd Cuue his uni is bsed on Secions 9. & 9.3, Chpe 9. All ssigned edings nd execises e fom he exbook Objecies: Mke cein h you cn define, nd use in conex, he ems, conceps nd fomuls lised below:
2.1 Position. 2.2 Rest and Motion.
 Moion In ne Dimenion. Poiion. ny objec i ied poin nd hree oberer from hree differen plce re looking for me objec, hen ll hree oberer will he differen oberion bo he poiion of poin nd no one will be wrong.
Moion In ne Dimenion. Poiion. ny objec i ied poin nd hree oberer from hree differen plce re looking for me objec, hen ll hree oberer will he differen oberion bo he poiion of poin nd no one will be wrong.
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
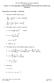 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
2001 November 15 Exam III Physics 191
 1 November 15 Eam III Physics 191 Physical Consans: Earh s free-fall acceleraion = g = 9.8 m/s 2 Circle he leer of he single bes answer. quesion is worh 1 poin Each 3. Four differen objecs wih masses:
1 November 15 Eam III Physics 191 Physical Consans: Earh s free-fall acceleraion = g = 9.8 m/s 2 Circle he leer of he single bes answer. quesion is worh 1 poin Each 3. Four differen objecs wih masses:
Tax Audit and Vertical Externalities
 T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
Collision Detection and Bouncing
 Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
Chapter 2 PROBLEM SOLUTIONS
 Chper PROBLEM SOLUTIONS. We ssume h you re pproximely m ll nd h he nere impulse rels uniform speed. The elpsed ime is hen Δ x m Δ = m s s. s.3 Disnces reled beween pirs of ciies re ( ) Δx = Δ = 8. km h.5
Chper PROBLEM SOLUTIONS. We ssume h you re pproximely m ll nd h he nere impulse rels uniform speed. The elpsed ime is hen Δ x m Δ = m s s. s.3 Disnces reled beween pirs of ciies re ( ) Δx = Δ = 8. km h.5
Module 3: The Damped Oscillator-II Lecture 3: The Damped Oscillator-II
 Module 3: The Damped Oscillaor-II Lecure 3: The Damped Oscillaor-II 3. Over-damped Oscillaions. This refers o he siuaion where β > ω (3.) The wo roos are and α = β + α 2 = β β 2 ω 2 = (3.2) β 2 ω 2 = 2
Module 3: The Damped Oscillaor-II Lecure 3: The Damped Oscillaor-II 3. Over-damped Oscillaions. This refers o he siuaion where β > ω (3.) The wo roos are and α = β + α 2 = β β 2 ω 2 = (3.2) β 2 ω 2 = 2
graph of unit step function t
 .5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
.5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
Week 1 Lecture 2 Problems 2, 5. What if something oscillates with no obvious spring? What is ω? (problem set problem)
 Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Location is relative. Coordinate Systems. Which of the following can be described with vectors??
 Locion is relive Coordine Sysems The posiion o hing is sed relive o noher hing (rel or virul) review o he physicl sis h governs mhemicl represenions Reerence oec mus e deined Disnce mus e nown Direcion
Locion is relive Coordine Sysems The posiion o hing is sed relive o noher hing (rel or virul) review o he physicl sis h governs mhemicl represenions Reerence oec mus e deined Disnce mus e nown Direcion
