11. Introduction to Liouville s Theorem Michael Fowler
|
|
|
- Grant Butler
- 5 years ago
- Views:
Transcription
1 11 Introducton to Louvlle s Theorem Mchael Fowler Paths n Smple Phase Spaces: the SHO and Fallng Bodes Let s frst thnk further about paths n phase space For example the smple harmonc oscllator wth Hamltonan H = p /2 m+ mω q /2 descrbes crcles n phase space parameterzed wth the varables ( pm q) ω (A more usual notaton s to wrte the potental term as Queston: are these crcles the only possble paths for the oscllator to follow? kq ) Answer: yes: any other path would ntersect a crcle and at that pont wth both poston and velocty defned there s only one path forward (and back) n tme possble so the ntersecton can t happen Here s an example from Taylor of paths n phase space: four dentcal fallng bodes are released smultaneously see fgure x measures dstance vertcally down Two are released wth zero momentum from the orgn O and from a pont x 0 meters down the other two are released wth ntal momenta p 0 agan from the ponts O x 0 (Note the dfference n ntal slope) O Four phase space trajectores for fallng objects Check: convnce yourself that all these paths are parts of parabolas centered on the x -axs (Just as the smple harmonc oscllator phase space s flled wth crcular paths ths one s flled wth parabolas) Bodes released wth the same ntal velocty at the same tme wll keep the same vertcal dstance apart those released wth dfferent ntal veloctes wll keep the same velocty dfference snce all accelerate at g Therefore the area of the parallelogram formed by the four phase space ponts at a later tme wll have the same area as the ntal square Exercse: convnce yourself that all the ponts of an ntal vertcal sde of the square all stay n lne as tme goes on even though the lne does not stay vertcal The four sdes of the square deform wth tme to the four sdes of the parallelogram pont by pont Ths means that f we have a fallng stone correspondng ntally to a pont nsde the square t wll go to a pont nsde the parallelogram because f somehow ts path reached the boundary we would have two
2 2 paths n phase space ntersectng and a partcle at one pont n phase space has a unquely defned future path (and past) Followng Many Systems: a Gas n Phase Space We ve looked at four paths n phase space correspondng to four fallng bodes all begnnng at t = 0 but wth dfferent ntal co-ordnates n ( px ) Suppose now we have many fallng bodes so that at t = 0 a regon of phase space can be magned as flled wth a gas of ponts each representng one p x = 1 N fallng body ntally at The argument above about the phase space path of a pont wthn the square at t = 0 stayng nsde the square as tme goes on and the square dstorts to a parallelogram must also be true for any dynamcal system and any closed volume n phase space snce t depends on phase space paths never ntersectng: that s f at t = 0 some closed surface n phase space contans a number of ponts of the gas those same ponts reman nsde the surface as t develops n tme -- none ext or enter For the number of ponts N suffcently large the phase space tme development looks lke the flow of a flud Louvlle s Theorem: Local Gas Densty Is Constant along a Phase Space Path The fallng bodes phase space square has one more lesson for us: vsualze now a unformly dense gas of ponts nsde the ntal square Not only does the gas stay wthn the dstortng square the area t covers n phase space remans constant as dscussed above so the local gas densty stays constant as the gas flows through phase space Louvlle s theorem s that ths constancy of local densty s true for general dynamcal systems Landau s Proof Usng the Jacoban Landau gves a very elegant proof of elemental volume nvarance under a general canoncal transformaton provng the Jacoban multplcatve factor s always unty by clever use of the generatng functon of the canoncal transformaton Jacobans have wde applcablty n dfferent areas of physcs so ths s a good tme to revew ther basc propertes whch we do below as a prelmnary to gvng the proof It must be admtted that there are smpler ways of dervng Louvlle s theorem drectly from Hamlton s equatons the reader may prefer to skp the Jacoban proof at frst readng Jacoban for Tme Evoluton As we ve establshed tme development s equvalent to a canoncal coordnate transformaton ( p q) ( p q ) ( PQ ) t t t+ τ t+ τ
3 Snce we already know that the number of ponts nsde a closed volume s constant n tme Louvlle s theorem s proved f we can show that the volume enclosed by the closed surface s constant that s wth V denotng the volume V evolves to become we must prove V dq dq dp dp dq dq dp dp 1 s 1 s = 1 s 1 s? V If you re famlar wth Jacobans you know that (by defnton) dq dq dp dp = Ddq dq dp dp 1 s 1 s 1 s 1 s where the Jacoban ( Q1 Qs P1 Ps) ( q q p p ) D = 1 s 1 s Louvlle s theorem s therefore proved f we can establsh that D = 1 If you re not famlar wth Jacobans or need remndng read the next secton! Jacobans 101 You can skp ths secton f you're already famlar wth Jacobans Suppose we are ntegratng a functon over some regon of ordnary three-dmensonal space V ( ) I = f x x x dx dx dx but we want to change varables of ntegraton to a dfferent set of coordnates ( 1 2 ) example ( r θφ ) The new coordnates are of course functons of the orgnal ones ( ) q q q such as for q1 x1 x2 x etc and we assume that n the regon of ntegraton they are smooth well-behaved functons We can t smply re-express f n terms of the new varables and replace the volume dfferental dx1dx2dx by dq1dq2dq that gves the wrong answer n a plane you can t replace dxdy wth drdθ you have to use rdrdθ That extra factor r s called the Jacoban t s clear that n the plane a small element wth sdes of fxed lengths( δ r δθ ) s bgger the further t s from the orgn not all δ rδθ elements are equal so to speak Our task s to construct the Jacoban for a general change of coordnates We need to thnk carefully about the volumes n the three-dmensonal space represented by dx1dx2dx and by dq1dq2dq Of course the x s are just ordnary perpendcular Cartesan axes so the volume s just the product of the three sdes of the lttle box dx1dx2dx Imagne ths lttle box ts corner closest x x x and ts furthest pont at the other end of the body dagonal at to the orgn at ( ) ( x dx x dx x dx ) Let s take these two ponts n the q coordnates to be at ( ) q q q and
4 4 ( q dq q dq q dq ) In vsualzng ths bear n mnd that the q axes need not be perpendcular to each other (but they cannot all le n a plane that would not be well-behaved) For the x coordnate ntegraton we magne fllng the space wth lttle cubcal boxes For the q ntegraton we have a system of space fllng nfntesmal paralleleppeds n general pontng dfferent ways n dfferent regons (thnk ( r θ ) ) What we need to fnd s the volume of the ncremental parallelepped wth sdes we ll wrte as vectors n x -coordnates dq 1 dq 2 dq These three ncremental vectors are along the correspondng q coordnate axes and the three added together are x + dx x + dx x + dx q + dq q + dq q + dq the dsplacement from ( x x x ) to Hence n components q1 q1 q 1 dq1 = dx1 dx2 dx x1 x2 x Now the volume of the parallelepped wth sdes the three vectors from the orgn abc s a b c (recall b c s the area of the parallelogram then the dot product sngles out the component of a perpendcular to the plane of bc ) So the volume correspondng to the ncrements dq1 dq2 dq n q space s q1 q1 q1 x1 x2 x q q q dq dq dq = dx dx dx = Ddx dx dx x1 x2 x q q q x x x wrtng D (Landau s notaton) for the determnant whch s n fact the Jacoban often denoted by J The standard notaton for ths determnantal Jacoban s D = ( q1 q2 q) ( x x x ) So the approprate replacement for the three dmensonal ncremental volume element represented n the ntegral by dq1dq2dq s
5 5 dq dq dq ( q1 q2 q) ( x x x ) dx dx dx The nverse D = ( x x x ) ( q q q ) 1 ths s easly establshed usng the chan rule for dfferentaton Exercse: check ths! Thus the change of varables n an ntegral s accomplshed by rewrtng the ntegrand n the new varables and replacng ( x1 x2 x) ( q q q ) I = f x x x dx dx dx = f q q q dq dq dq V V The argument n hgher dmensons s just the same: on gong to dmenson n + 1 the hypervolume element s equal to that of the n dmensonal element multpled by the component of the new vector perpendcular to the n dmensonal element The determnantal form does ths automatcally snce a determnant wth two dentcal rows s zero so n addng a new vector only the component perpendcular to all the earler vectors contrbutes We ve seen that the chan rule for dfferentaton gves the nverse as just the Jacoban wth numerator and denomnator reversed t also readly yelds and ths extends trvally to n dmensons x x x q q q x x x = q q q r r r r r r It s also evdent form the determnantal form of the Jacoban that x x x x x = q q x q q dentcal varables n numerator and denomnator can be canceled Agan ths extends easly to n dmensons Jacoban proof of Louvlle s Theorem After ths rather long detour nto Jacoban theory recall we are tryng to establsh that the volume of a regon n phase space s unaffected by a canoncal transformaton we need to prove that dq dq dp dp = dq dq dp dp 1 s 1 s 1 s 1 s
6 6 and that means we need to show that the Jacoban ( Q1 Qs P1 Ps) ( q q p p ) D = = 1 1 s 1 Usng the theorems above about the nverse of a Jacoban and the chan rule product s Q1 Qs P1 Ps q1 qs p1 ps D = / q q P P q q P P 1 s 1 s 1 s 1 s Now nvokng the rule that f the same varables appear n both numerator and denomnator they can be cancelled D ( s) ( ) ( s) ( ) Q Q p p / 1 1 = q1 qs P constant 1 P P= s q= constant Up to ths pont the equatons are vald for any nonsngular transformaton but to prove the numerator and denomnator are equal n ths expresson requres that the equaton be canoncal that s be gven by a generatng functon as explaned earler Recall now the propertes of the generatng functon ( qpt ) Φ ( ) ( ) dφ q P t = d F + PQ = p dq + Q dp + H H dt from whch p = Φ qpt / q Q= Φ qpt / P H = H+ Φ qpt / t In the expresson for the Jacoban D the kelement of the numerator s Q / q k In terms of the generatng functon Φ ( qp ) ths element s / P 2 Φ qk Exactly the same procedure for the denomnator gves the kelement to be P p =Φ q P 2 / k / k In other words the two determnants are the same (rows and columns are swtched but that doesn t affect the value of a determnant) Ths means D = 1 and Louvlle s theorem s proved Smpler Proof of Louvlle s Theorem Landau s proof gven above s extremely elegant: snce phase space paths cannot ntersect pont nsde a volume stay nsde no matter how the volume contorts and snce tme development s a canoncal transformaton the total volume gven by ntegratng over volume elements dqdp stays the same snce t s an ntegral over the correspondng volume elements dqdp and we ve just shown that dqdp = dqdp
7 7 Here we ll take a slghtly dfferent pont of vew: we ll look at a small square n phase space and track how ts edges are movng to prove ts volume sn t changng (We ll stck to one dmenson but the generalzaton s straghtforward) The ponts here represent a gas of many systems n the two dmensonal ( qp ) phase space and wth a small square area q p tagged by havng all the systems on ts boundary represented by dots of a dfferent color What s the ncremental change n area of ths ntally square pece of phase space n tme dt? Begn wth the top edge: the partcles are all movng wth veloctes ( qp ) but of course the only change n area comes from the p term that s the outward movement of the boundary so the area change n dt from the movement of ths boundary wll be p qdt Meanwhle there wll be a smlar term from the bottom edge and the net contrbuton top plus bottom edges wll depend on the change n p from bottom to top that s a net area change from p / p p qdt movement of these edges Addng n the other two edges (the sdes) wth an exactly smlar argument the total area change s ( / / ) p p +q q p qdt But from Hamlton s equatons p =H / q q = H / p so and therefore = = 2 2 p/ p H/ pq q/ q H/ pq p / p+q / q= 0 establshng that the total ncremental area change as the square dstorts s zero The concluson s that the flow of the gas of systems n phase space s lke an ncompressble flud but wth one mportant qualfcaton: the densty may vary wth poston! It just doesn t vary along a dynamcal path Energy Gradent and Phase Space Velocty For a tme-ndependent Hamltonan the path n phase space ( qp ) s a constant energy lne and we can thnk of the whole phase space as delneated by many such lnes exactly analogous to contour lnes jonng ponts at the same level on a map of uneven terran energy correspondng to heght above sea level The gradent at any pont the vector pontng exactly uphll and therefore perpendcular to the constant energy path s H = H / q H / p
8 8 here H = E The velocty of a system s pont movng through phase space s v = q p = H / p H / q Ths vector s perpendcular to the gradent vector as t must be of course snce the system moves along a constant energy path But nterestngly t has the same magntude as the gradent vector! What s the sgnfcance of that? Imagne a small square sandwched between two phase space paths close together n energy and suppose the dstance between the two paths s decreasng so the square s gettng squeezed at a rate equal to the rate of change of the energy gradent But at the same tme t must be gettng stretched along the drecton of the path an amount equal to the rate of change of phase space velocty along the path and they are equal So ths s just Louvlle agan ts area doesn t change
10. Canonical Transformations Michael Fowler
 10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Physics 207: Lecture 20. Today s Agenda Homework for Monday
 Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
6. Hamilton s Equations
 6. Hamlton s Equatons Mchael Fowler A Dynamcal System s Path n Confguraton Sace and n State Sace The story so far: For a mechancal system wth n degrees of freedom, the satal confguraton at some nstant
6. Hamlton s Equatons Mchael Fowler A Dynamcal System s Path n Confguraton Sace and n State Sace The story so far: For a mechancal system wth n degrees of freedom, the satal confguraton at some nstant
Poisson brackets and canonical transformations
 rof O B Wrght Mechancs Notes osson brackets and canoncal transformatons osson Brackets Consder an arbtrary functon f f ( qp t) df f f f q p q p t But q p p where ( qp ) pq q df f f f p q q p t In order
rof O B Wrght Mechancs Notes osson brackets and canoncal transformatons osson Brackets Consder an arbtrary functon f f ( qp t) df f f f q p q p t But q p p where ( qp ) pq q df f f f p q q p t In order
PHYS 705: Classical Mechanics. Calculus of Variations II
 1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
Mathematical Preparations
 1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
PHYS 705: Classical Mechanics. Canonical Transformation II
 1 PHYS 705: Classcal Mechancs Canoncal Transformaton II Example: Harmonc Oscllator f ( x) x m 0 x U( x) x mx x LT U m Defne or L p p mx x x m mx x H px L px p m p x m m H p 1 x m p m 1 m H x p m x m m
1 PHYS 705: Classcal Mechancs Canoncal Transformaton II Example: Harmonc Oscllator f ( x) x m 0 x U( x) x mx x LT U m Defne or L p p mx x x m mx x H px L px p m p x m m H p 1 x m p m 1 m H x p m x m m
Linear Momentum. Center of Mass.
 Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
CHAPTER 14 GENERAL PERTURBATION THEORY
 CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
Chapter Twelve. Integration. We now turn our attention to the idea of an integral in dimensions higher than one. Consider a real-valued function f : D
 Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
The Feynman path integral
 The Feynman path ntegral Aprl 3, 205 Hesenberg and Schrödnger pctures The Schrödnger wave functon places the tme dependence of a physcal system n the state, ψ, t, where the state s a vector n Hlbert space
The Feynman path ntegral Aprl 3, 205 Hesenberg and Schrödnger pctures The Schrödnger wave functon places the tme dependence of a physcal system n the state, ψ, t, where the state s a vector n Hlbert space
Canonical transformations
 Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
THE VIBRATIONS OF MOLECULES II THE CARBON DIOXIDE MOLECULE Student Instructions
 THE VIBRATIONS OF MOLECULES II THE CARBON DIOXIDE MOLECULE Student Instructons by George Hardgrove Chemstry Department St. Olaf College Northfeld, MN 55057 hardgrov@lars.acc.stolaf.edu Copyrght George
THE VIBRATIONS OF MOLECULES II THE CARBON DIOXIDE MOLECULE Student Instructons by George Hardgrove Chemstry Department St. Olaf College Northfeld, MN 55057 hardgrov@lars.acc.stolaf.edu Copyrght George
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
Mechanics Physics 151
 Mechancs Physcs 151 Lecture 3 Lagrange s Equatons (Goldsten Chapter 1) Hamlton s Prncple (Chapter 2) What We Dd Last Tme! Dscussed mult-partcle systems! Internal and external forces! Laws of acton and
Mechancs Physcs 151 Lecture 3 Lagrange s Equatons (Goldsten Chapter 1) Hamlton s Prncple (Chapter 2) What We Dd Last Tme! Dscussed mult-partcle systems! Internal and external forces! Laws of acton and
A particle in a state of uniform motion remain in that state of motion unless acted upon by external force.
 The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
How Differential Equations Arise. Newton s Second Law of Motion
 page 1 CHAPTER 1 Frst-Order Dfferental Equatons Among all of the mathematcal dscplnes the theory of dfferental equatons s the most mportant. It furnshes the explanaton of all those elementary manfestatons
page 1 CHAPTER 1 Frst-Order Dfferental Equatons Among all of the mathematcal dscplnes the theory of dfferental equatons s the most mportant. It furnshes the explanaton of all those elementary manfestatons
PHYS 705: Classical Mechanics. Hamilton-Jacobi Equation
 1 PHYS 705: Classcal Mechancs Hamlton-Jacob Equaton Hamlton-Jacob Equaton There s also a very elegant relaton between the Hamltonan Formulaton of Mechancs and Quantum Mechancs. To do that, we need to derve
1 PHYS 705: Classcal Mechancs Hamlton-Jacob Equaton Hamlton-Jacob Equaton There s also a very elegant relaton between the Hamltonan Formulaton of Mechancs and Quantum Mechancs. To do that, we need to derve
χ x B E (c) Figure 2.1.1: (a) a material particle in a body, (b) a place in space, (c) a configuration of the body
 Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Celestial Mechanics. Basic Orbits. Why circles? Tycho Brahe. PHY celestial-mechanics - J. Hedberg
 PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
From Biot-Savart Law to Divergence of B (1)
 From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
Physics 53. Rotational Motion 3. Sir, I have found you an argument, but I am not obliged to find you an understanding.
 Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Mechanics Physics 151
 Mechancs Physcs 151 Lecture 22 Canoncal Transformatons (Chater 9) What We Dd Last Tme Drect Condtons Q j Q j = = j P, Q, P j, P Q, P Necessary and suffcent P j P j for Canoncal Transf. = = j Q, Q, P j
Mechancs Physcs 151 Lecture 22 Canoncal Transformatons (Chater 9) What We Dd Last Tme Drect Condtons Q j Q j = = j P, Q, P j, P Q, P Necessary and suffcent P j P j for Canoncal Transf. = = j Q, Q, P j
Mechanics Physics 151
 Mechancs hyscs 151 Lecture Canoncal Transformatons (Chater 9) What We Dd Last Tme Drect Condtons Q j Q j = = j, Q, j, Q, Necessary and suffcent j j for Canoncal Transf. = = j Q, Q, j Q, Q, Infntesmal CT
Mechancs hyscs 151 Lecture Canoncal Transformatons (Chater 9) What We Dd Last Tme Drect Condtons Q j Q j = = j, Q, j, Q, Necessary and suffcent j j for Canoncal Transf. = = j Q, Q, j Q, Q, Infntesmal CT
Lecture 20: Noether s Theorem
 Lecture 20: Noether s Theorem In our revew of Newtonan Mechancs, we were remnded that some quanttes (energy, lnear momentum, and angular momentum) are conserved That s, they are constant f no external
Lecture 20: Noether s Theorem In our revew of Newtonan Mechancs, we were remnded that some quanttes (energy, lnear momentum, and angular momentum) are conserved That s, they are constant f no external
Mechanics Physics 151
 Mechancs Physcs 5 Lecture 0 Canoncal Transformatons (Chapter 9) What We Dd Last Tme Hamlton s Prncple n the Hamltonan formalsm Dervaton was smple δi δ p H(, p, t) = 0 Adonal end-pont constrants δ t ( )
Mechancs Physcs 5 Lecture 0 Canoncal Transformatons (Chapter 9) What We Dd Last Tme Hamlton s Prncple n the Hamltonan formalsm Dervaton was smple δi δ p H(, p, t) = 0 Adonal end-pont constrants δ t ( )
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
coordinates. Then, the position vectors are described by
 Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Spin. Introduction. Michael Fowler 11/26/06
 Spn Mchael Fowler /6/6 Introducton The Stern Gerlach experment for the smplest possble atom, hydrogen n ts ground state, demonstrated unambguously that the component of the magnetc moment of the atom along
Spn Mchael Fowler /6/6 Introducton The Stern Gerlach experment for the smplest possble atom, hydrogen n ts ground state, demonstrated unambguously that the component of the magnetc moment of the atom along
Kinematics of Fluids. Lecture 16. (Refer the text book CONTINUUM MECHANICS by GEORGE E. MASE, Schaum s Outlines) 17/02/2017
 17/0/017 Lecture 16 (Refer the text boo CONTINUUM MECHANICS by GEORGE E. MASE, Schaum s Outlnes) Knematcs of Fluds Last class, we started dscussng about the nematcs of fluds. Recall the Lagrangan and Euleran
17/0/017 Lecture 16 (Refer the text boo CONTINUUM MECHANICS by GEORGE E. MASE, Schaum s Outlnes) Knematcs of Fluds Last class, we started dscussng about the nematcs of fluds. Recall the Lagrangan and Euleran
4. Laws of Dynamics: Hamilton s Principle and Noether's Theorem
 4. Laws of Dynamcs: Hamlton s Prncple and Noether's Theorem Mchael Fowler Introducton: Galleo and Newton In the dscusson of calculus of varatons, we antcpated some basc dynamcs, usng the potental energy
4. Laws of Dynamcs: Hamlton s Prncple and Noether's Theorem Mchael Fowler Introducton: Galleo and Newton In the dscusson of calculus of varatons, we antcpated some basc dynamcs, usng the potental energy
PES 1120 Spring 2014, Spendier Lecture 6/Page 1
 PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
PHYS 1101 Practice problem set 12, Chapter 32: 21, 22, 24, 57, 61, 83 Chapter 33: 7, 12, 32, 38, 44, 49, 76
 PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
Snce h( q^; q) = hq ~ and h( p^ ; p) = hp, one can wrte ~ h hq hp = hq ~hp ~ (7) the uncertanty relaton for an arbtrary state. The states that mnmze t
 8.5: Many-body phenomena n condensed matter and atomc physcs Last moded: September, 003 Lecture. Squeezed States In ths lecture we shall contnue the dscusson of coherent states, focusng on ther propertes
8.5: Many-body phenomena n condensed matter and atomc physcs Last moded: September, 003 Lecture. Squeezed States In ths lecture we shall contnue the dscusson of coherent states, focusng on ther propertes
PHYS 705: Classical Mechanics. Newtonian Mechanics
 1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
Physics 106a, Caltech 11 October, Lecture 4: Constraints, Virtual Work, etc. Constraints
 Physcs 106a, Caltech 11 October, 2018 Lecture 4: Constrants, Vrtual Work, etc. Many, f not all, dynamcal problems we want to solve are constraned: not all of the possble 3 coordnates for M partcles (or
Physcs 106a, Caltech 11 October, 2018 Lecture 4: Constrants, Vrtual Work, etc. Many, f not all, dynamcal problems we want to solve are constraned: not all of the possble 3 coordnates for M partcles (or
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Module 14: THE INTEGRAL Exploring Calculus
 Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
Physics 607 Exam 1. ( ) = 1, Γ( z +1) = zγ( z) x n e x2 dx = 1. e x2
 Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
8.6 The Complex Number System
 8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Affine transformations and convexity
 Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
Lagrange Multipliers. A Somewhat Silly Example. Monday, 25 September 2013
 Lagrange Multplers Monday, 5 September 013 Sometmes t s convenent to use redundant coordnates, and to effect the varaton of the acton consstent wth the constrants va the method of Lagrange undetermned
Lagrange Multplers Monday, 5 September 013 Sometmes t s convenent to use redundant coordnates, and to effect the varaton of the acton consstent wth the constrants va the method of Lagrange undetermned
Open Systems: Chemical Potential and Partial Molar Quantities Chemical Potential
 Open Systems: Chemcal Potental and Partal Molar Quanttes Chemcal Potental For closed systems, we have derved the followng relatonshps: du = TdS pdv dh = TdS + Vdp da = SdT pdv dg = VdP SdT For open systems,
Open Systems: Chemcal Potental and Partal Molar Quanttes Chemcal Potental For closed systems, we have derved the followng relatonshps: du = TdS pdv dh = TdS + Vdp da = SdT pdv dg = VdP SdT For open systems,
Module 3: Element Properties Lecture 1: Natural Coordinates
 Module 3: Element Propertes Lecture : Natural Coordnates Natural coordnate system s bascally a local coordnate system whch allows the specfcaton of a pont wthn the element by a set of dmensonless numbers
Module 3: Element Propertes Lecture : Natural Coordnates Natural coordnate system s bascally a local coordnate system whch allows the specfcaton of a pont wthn the element by a set of dmensonless numbers
Open string operator quantization
 Open strng operator quantzaton Requred readng: Zwebach -4 Suggested readng: Polchnsk 3 Green, Schwarz, & Wtten 3 upto eq 33 The lght-cone strng as a feld theory: Today we wll dscuss the quantzaton of an
Open strng operator quantzaton Requred readng: Zwebach -4 Suggested readng: Polchnsk 3 Green, Schwarz, & Wtten 3 upto eq 33 The lght-cone strng as a feld theory: Today we wll dscuss the quantzaton of an
10.34 Fall 2015 Metropolis Monte Carlo Algorithm
 10.34 Fall 2015 Metropols Monte Carlo Algorthm The Metropols Monte Carlo method s very useful for calculatng manydmensonal ntegraton. For e.g. n statstcal mechancs n order to calculate the prospertes of
10.34 Fall 2015 Metropols Monte Carlo Algorthm The Metropols Monte Carlo method s very useful for calculatng manydmensonal ntegraton. For e.g. n statstcal mechancs n order to calculate the prospertes of
Physics 114 Exam 3 Spring Name:
 Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
DECOUPLING THEORY HW2
 8.8 DECOUPLIG THEORY HW2 DOGHAO WAG DATE:OCT. 3 207 Problem We shall start by reformulatng the problem. Denote by δ S n the delta functon that s evenly dstrbuted at the n ) dmensonal unt sphere. As a temporal
8.8 DECOUPLIG THEORY HW2 DOGHAO WAG DATE:OCT. 3 207 Problem We shall start by reformulatng the problem. Denote by δ S n the delta functon that s evenly dstrbuted at the n ) dmensonal unt sphere. As a temporal
Quantum Mechanics I Problem set No.1
 Quantum Mechancs I Problem set No.1 Septembe0, 2017 1 The Least Acton Prncple The acton reads S = d t L(q, q) (1) accordng to the least (extremal) acton prncple, the varaton of acton s zero 0 = δs = t
Quantum Mechancs I Problem set No.1 Septembe0, 2017 1 The Least Acton Prncple The acton reads S = d t L(q, q) (1) accordng to the least (extremal) acton prncple, the varaton of acton s zero 0 = δs = t
π e ax2 dx = x 2 e ax2 dx or x 3 e ax2 dx = 1 x 4 e ax2 dx = 3 π 8a 5/2 (a) We are considering the Maxwell velocity distribution function: 2πτ/m
 Homework Solutons Problem In solvng ths problem, we wll need to calculate some moments of the Gaussan dstrbuton. The brute-force method s to ntegrate by parts but there s a nce trck. The followng ntegrals
Homework Solutons Problem In solvng ths problem, we wll need to calculate some moments of the Gaussan dstrbuton. The brute-force method s to ntegrate by parts but there s a nce trck. The followng ntegrals
11. Dynamics in Rotating Frames of Reference
 Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
The classical spin-rotation coupling
 LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space
NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
MTH 263 Practice Test #1 Spring 1999
 Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
MA 323 Geometric Modelling Course Notes: Day 13 Bezier Curves & Bernstein Polynomials
 MA 323 Geometrc Modellng Course Notes: Day 13 Bezer Curves & Bernsten Polynomals Davd L. Fnn Over the past few days, we have looked at de Casteljau s algorthm for generatng a polynomal curve, and we have
MA 323 Geometrc Modellng Course Notes: Day 13 Bezer Curves & Bernsten Polynomals Davd L. Fnn Over the past few days, we have looked at de Casteljau s algorthm for generatng a polynomal curve, and we have
1 GSW Iterative Techniques for y = Ax
 1 for y = A I m gong to cheat here. here are a lot of teratve technques that can be used to solve the general case of a set of smultaneous equatons (wrtten n the matr form as y = A), but ths chapter sn
1 for y = A I m gong to cheat here. here are a lot of teratve technques that can be used to solve the general case of a set of smultaneous equatons (wrtten n the matr form as y = A), but ths chapter sn
Physics 207: Lecture 27. Announcements
 Physcs 07: ecture 7 Announcements ake-up labs are ths week Fnal hwk assgned ths week, fnal quz next week Revew sesson on Thursday ay 9, :30 4:00pm, Here Today s Agenda Statcs recap Beam & Strngs» What
Physcs 07: ecture 7 Announcements ake-up labs are ths week Fnal hwk assgned ths week, fnal quz next week Revew sesson on Thursday ay 9, :30 4:00pm, Here Today s Agenda Statcs recap Beam & Strngs» What
Integrals and Invariants of Euler-Lagrange Equations
 Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
Iterative General Dynamic Model for Serial-Link Manipulators
 EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
= z 20 z n. (k 20) + 4 z k = 4
 Problem Set #7 solutons 7.2.. (a Fnd the coeffcent of z k n (z + z 5 + z 6 + z 7 + 5, k 20. We use the known seres expanson ( n+l ( z l l z n below: (z + z 5 + z 6 + z 7 + 5 (z 5 ( + z + z 2 + z + 5 5
Problem Set #7 solutons 7.2.. (a Fnd the coeffcent of z k n (z + z 5 + z 6 + z 7 + 5, k 20. We use the known seres expanson ( n+l ( z l l z n below: (z + z 5 + z 6 + z 7 + 5 (z 5 ( + z + z 2 + z + 5 5
CSci 6974 and ECSE 6966 Math. Tech. for Vision, Graphics and Robotics Lecture 21, April 17, 2006 Estimating A Plane Homography
 CSc 6974 and ECSE 6966 Math. Tech. for Vson, Graphcs and Robotcs Lecture 21, Aprl 17, 2006 Estmatng A Plane Homography Overvew We contnue wth a dscusson of the major ssues, usng estmaton of plane projectve
CSc 6974 and ECSE 6966 Math. Tech. for Vson, Graphcs and Robotcs Lecture 21, Aprl 17, 2006 Estmatng A Plane Homography Overvew We contnue wth a dscusson of the major ssues, usng estmaton of plane projectve
Module 1 : The equation of continuity. Lecture 1: Equation of Continuity
 1 Module 1 : The equaton of contnuty Lecture 1: Equaton of Contnuty 2 Advanced Heat and Mass Transfer: Modules 1. THE EQUATION OF CONTINUITY : Lectures 1-6 () () () (v) (v) Overall Mass Balance Momentum
1 Module 1 : The equaton of contnuty Lecture 1: Equaton of Contnuty 2 Advanced Heat and Mass Transfer: Modules 1. THE EQUATION OF CONTINUITY : Lectures 1-6 () () () (v) (v) Overall Mass Balance Momentum
Module 9. Lecture 6. Duality in Assignment Problems
 Module 9 1 Lecture 6 Dualty n Assgnment Problems In ths lecture we attempt to answer few other mportant questons posed n earler lecture for (AP) and see how some of them can be explaned through the concept
Module 9 1 Lecture 6 Dualty n Assgnment Problems In ths lecture we attempt to answer few other mportant questons posed n earler lecture for (AP) and see how some of them can be explaned through the concept
One Dimension Again. Chapter Fourteen
 hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
Lecture Note 3. Eshelby s Inclusion II
 ME340B Elastcty of Mcroscopc Structures Stanford Unversty Wnter 004 Lecture Note 3. Eshelby s Incluson II Chrs Wenberger and We Ca c All rghts reserved January 6, 004 Contents 1 Incluson energy n an nfnte
ME340B Elastcty of Mcroscopc Structures Stanford Unversty Wnter 004 Lecture Note 3. Eshelby s Incluson II Chrs Wenberger and We Ca c All rghts reserved January 6, 004 Contents 1 Incluson energy n an nfnte
Physics 114 Exam 2 Fall 2014 Solutions. Name:
 Physcs 114 Exam Fall 014 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse ndcated,
Physcs 114 Exam Fall 014 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse ndcated,
AP Physics 1 & 2 Summer Assignment
 AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
Indeterminate pin-jointed frames (trusses)
 Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
8.1 Arc Length. What is the length of a curve? How can we approximate it? We could do it following the pattern we ve used before
 .1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
.1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
Physics 4B. Question and 3 tie (clockwise), then 2 and 5 tie (zero), then 4 and 6 tie (counterclockwise) B i. ( T / s) = 1.74 V.
 Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
MAGNETISM MAGNETIC DIPOLES
 MAGNETISM We now turn to magnetsm. Ths has actually been used for longer than electrcty. People were usng compasses to sal around the Medterranean Sea several hundred years BC. However t was not understood
MAGNETISM We now turn to magnetsm. Ths has actually been used for longer than electrcty. People were usng compasses to sal around the Medterranean Sea several hundred years BC. However t was not understood
Rotational Dynamics. Physics 1425 Lecture 19. Michael Fowler, UVa
 Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
THEOREMS OF QUANTUM MECHANICS
 THEOREMS OF QUANTUM MECHANICS In order to develop methods to treat many-electron systems (atoms & molecules), many of the theorems of quantum mechancs are useful. Useful Notaton The matrx element A mn
THEOREMS OF QUANTUM MECHANICS In order to develop methods to treat many-electron systems (atoms & molecules), many of the theorems of quantum mechancs are useful. Useful Notaton The matrx element A mn
Module 2. Random Processes. Version 2 ECE IIT, Kharagpur
 Module Random Processes Lesson 6 Functons of Random Varables After readng ths lesson, ou wll learn about cdf of functon of a random varable. Formula for determnng the pdf of a random varable. Let, X be
Module Random Processes Lesson 6 Functons of Random Varables After readng ths lesson, ou wll learn about cdf of functon of a random varable. Formula for determnng the pdf of a random varable. Let, X be
Electricity and Magnetism - Physics 121 Lecture 10 - Sources of Magnetic Fields (Currents) Y&F Chapter 28, Sec. 1-7
 Electrcty and Magnetsm - Physcs 11 Lecture 10 - Sources of Magnetc Felds (Currents) Y&F Chapter 8, Sec. 1-7 Magnetc felds are due to currents The Bot-Savart Law Calculatng feld at the centers of current
Electrcty and Magnetsm - Physcs 11 Lecture 10 - Sources of Magnetc Felds (Currents) Y&F Chapter 8, Sec. 1-7 Magnetc felds are due to currents The Bot-Savart Law Calculatng feld at the centers of current
Section 8.1 Exercises
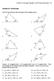 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Calculus of Variations Basics
 Chapter 1 Calculus of Varatons Bascs 1.1 Varaton of a General Functonal In ths chapter, we derve the general formula for the varaton of a functonal of the form J [y 1,y 2,,y n ] F x,y 1,y 2,,y n,y 1,y
Chapter 1 Calculus of Varatons Bascs 1.1 Varaton of a General Functonal In ths chapter, we derve the general formula for the varaton of a functonal of the form J [y 1,y 2,,y n ] F x,y 1,y 2,,y n,y 1,y
ENGN 40 Dynamics and Vibrations Homework # 7 Due: Friday, April 15
 NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
