LIMITS AND DERIVATIVES
|
|
|
- Gerald Lee
- 5 years ago
- Views:
Transcription
1 Capter LIMITS AND DERIVATIVES. Overview.. Limits of a fuctio Let f be a fuctio defied i a domai wic we take to be a iterval, say, I. We sall study te cocept of it of f at a poit a i I. We say f ( ) is te epected value of f at a give te values of f ear to te a left of a. Tis value is called te left ad it of f at a. We say f ( ) + is te epected value of f at a give te values of f ear to te a rigt of a. Tis value is called te rigt ad it of f at a. If te rigt ad left ad its coicide, we call te commo value as te it of f at a ad deote it by f ( ). a Some properties of its Let f ad g be two fuctios suc tat bot f ( ) ad g( ) eist. Te a (i) [ f ( ) + g( )] f( ) + g( ) a a a (ii) [ f ( ) g( )] f( ) g( ) (iii) a a a For every real umber α ( α f )( ) α f( ) a a (iv) [ f ( ) g( )] [ f( ) g( )] a a a f( ) f ( ) a a g ( ) g ( ), provided g () 0 a a
2 6 EXEMPLAR PROBLEMS MATHEMATICS Limits of polyomials ad ratioal fuctios If f is a polyomial fuctio, te f ( ) eists ad is give by f ( ) f( a) a a A Importat it A importat it wic is very useful ad used i te sequel is give below: a a a a Remark Te above epressio remais valid for ay ratioal umber provided a is positive. Limits of trigoometric fuctios To evaluate te its of trigoometric fuctios, we sall make use of te followig its wic are give below: (i) si 0 (ii) cos (iii) si Derivatives Suppose f is a real valued fuctio, te f ( + ) f( ) f ()... () 0 is called te derivative of f at, provided te it o te R.H.S. of () eists. Algebra of derivative of fuctios Sice te very defiitio of derivatives ivolve its i a rater direct fasio, we epect te rules of derivatives to follow closely tat of its as give below: Let f ad g be two fuctios suc tat teir derivatives are defied i a commo domai. Te : (i) Derivative of te sum of two fuctio is te sum of te derivatives of te fuctios. (ii) d d d d + f ( ) + g( ) d d [ f ( ) g( ) ] Derivative of te differece of two fuctios is te differece of te derivatives of te fuctios. d d d d f ( ) g( ) d d [ f ( ) g( ) ]
3 LIMITS AND DERIVATIVES 7 (iii) (iv) Derivative of te product of two fuctios is give by te followig product rule. d d d d f ( ) g( ) + f( ) g( ) d d [ f ( ) g( ) ] Tis is referred to as Leibitz Rule for te product of two fuctios. Derivative of quotiet of two fuctios is give by te followig quotiet rule (werever te deomiator is o-zero). d f( ) d g( ) d d f ( ) g( ) f( ) g( ) d d ( ) g ( ). Solved Eamples Sort Aswer Type ( ) Eample Evaluate + Solutio We ave ( ) + ( ) ( )( ( ) ( ) ( )( ) 5+ 6 ( )( ) ( )( ) ( )( ) [ 0] ( )
4 8 EXEMPLAR PROBLEMS MATHEMATICS Eample Evaluate 0 + Solutio Put y + so tat we 0, y. Te 0 + y y y () Eample Fid te positive iteger so tat Solutio We ave 08. () Terefore, () 08 (7) () Comparig, we get Eample Evaluate (sec ta ) Solutio Put y. Te y 0 as. Terefore (sec ta ) [sec( y) ta ( y)] y 0 (cosec y cot y) y 0 cosy y y 0 si y si cosy y 0 si y
5 LIMITS AND DERIVATIVES 9 y si y 0 y y si cos y cosy sice, si y y si y si cos y ta y 0 0 Eample 5 Evaluate Solutio (i) We ave si ( + ) si( ) 0 si ( + ) si( ) 0 ( + + ) ( + + ) cos si 0 cos si 0 si cos si cos as 0 0 Eample 6 Fid te derivative of f () a + b, were a ad b are o-zero costats, by first priciple. Solutio By defiitio, f () 0 f ( + ) f( ) a( + ) + b ( a+ b) 0 0 Eample 7 Fid te derivative of f() a + b + c, were a, b ad c are oe-zero costat, by first priciple. Solutio By defiitio, b b f () 0 f ( + ) f( )
6 0 EXEMPLAR PROBLEMS MATHEMATICS a( + ) + b( + ) + c a b c 0 b + a + a 0 0 a + a + b b + a Eample 8 Fid te derivative of f (), by first priciple. Solutio By defiitio, f () 0 f ( + ) f( ) ( + ) ( + ) 0 0 ( + ( + )) Eample 9 Fid te derivative of f() by first priciple. Solutio By defiitio, f () 0 f ( + ) f( ) ( ). Eample 0 Fid te derivative of f () si, by first priciple. Solutio By defiitio, f () 0 f ( + ) f( )
7 LIMITS AND DERIVATIVES si ( + ) si 0 + cos si 0 si ( + ) cos 0 0 cos. cos Eample Fid te derivative of f (), were is positive iteger, by first priciple. Solutio By defiitio, f () f ( + ) f( ) ( + ) Usig Biomial teorem, we ave ( + ) C 0 + C C ( + ) Tus, f () 0 Eample Fid te derivative of +. Solutio Let y + Differetiatig bot sides wit respect to, we get ( ] 0. dy d d d ( ) + ( ) d d + 0
8 EXEMPLAR PROBLEMS MATHEMATICS Terefore, 8 + d ( + ) 8 d +. Eample Fid te derivative of cos. Solutio Let y cos Differetiatig bot sides wit respect to, we get dy d d ( cos ) d Log Aswer Type d d (cos ) + cos ( ) d d ( si) + cos () cos si Eample Evaluate Solutio Note tat si + si si si + 6 si + si ( si ) (si + ) si si + ( si ) (si ) Terefore, si + si + (si )(si+ ) (si )(si ) 6 si si 6 si + si 6 + si 6 si 6 (as si 0)
9 LIMITS AND DERIVATIVES Eample 5 Evaluate Solutio We ave ta si 0 si ta si 0 si si cos si 0 cos cos si 0 si 0 cos si cos. Eample 6 Evaluate a+ a a+ Solutio We ave a+ a a+ a+ a+ + a a+ a+ + a a+ a ( a+ )( a+ + ) ( a ) ( a+ + ) ( a+ + )( a+ )( a+ + ) a ( a ) a+ + ( a+ + )( a+ )
10 EXEMPLAR PROBLEMS MATHEMATICS a a. 9 Eample 7 Evaluate cos a cosb 0 cos c ( a+ b) ( a b) si si Solutio We ave 0 si c ( a+ b) ( a b) si si 0 c si ( a+ b) ( a b) c si si c 0 ( a+ b) ( a b) c si a+ b a b a+ b a b c a b c Eample 8 Evaluate ( a+ ) si( a+ ) a sia 0 Solutio We ave ( a + ) si( a+ ) a sia 0 ( a + + a)[siacos+ cosasi ] a sia 0 a si a(cos ) a cosasi [ + + ( + a)(siacos+ cosasi )] 0
11 LIMITS AND DERIVATIVES 5 a si a( si ) a cos asi ( a) si ( a ) a si a 0 + a cos a () + a si a a cos a + a si a. Eample 9 Fid te derivative of f () ta (a + b), by first priciple. f ( + ) f( ) Solutio We ave f () 0 ( ) ta a( + ) + b ta ( a+ b) 0 0 si ( a + a + b) si ( a + b) cos ( a + a + b) cos ( a + b) si ( a + a + b) cos ( a + b) si ( a + b) cos ( a + a + b) 0 cos ( a+ b) cos ( a+ a+ b) asi ( a) 0 a cos ( a+ b) cos ( a+ a+ b) a si a 0 cos ( a + b) cos ( a + a + b) a 0 a [as 0 a 0] a cos ( a + b) a sec (a + b). Eample 0 Fid te derivative of f ( ) si, by first priciple. Solutio By defiitio, f () 0 f ( + ) f( )
12 6 EXEMPLAR PROBLEMS MATHEMATICS 0 0 si ( + ) si ( si ( + ) si ) ( si ( + ) + si ) ( si ( + ) + si ) si ( + ) si 0 ( si ( + ) + si ) + cos si 0 si( + ) + si ( ) cos si cot si Eample Fid te derivative of cos. + si Solutio Let y cos + si Differetiatig bot sides wit respects to, we get dy d d cos d + si d d ( + si ) (cos ) cos ( + si ) d d ( + si ) ( + si ) ( si ) cos (cos ) ( + si )
13 LIMITS AND DERIVATIVES 7 si si cos ( + si ) ( + si ) ( + si ) + si Objective Type Questios Coose te correct aswer out of te four optios give agaist eac Eample to 8 (M.C.Q.). Eample si 0 ( + cos ) is equal to (A) 0 (B) Solutio (B) is te correct aswer, we ave (C) (D) si 0 ( + cos ) si cos 0 cos ta 0 Eample si is equal to cos (A) 0 (B) (C) (D) does ot eit Solutio (A) is te correct aswer, sice si cos si y y cos y takig y 0
14 8 EXEMPLAR PROBLEMS MATHEMATICS cosy y 0 si y y si y 0 y y si cos y ta y 0 0 Eample 0 is equal to (A) (B) (C) 0 (D) does ot eists Solutio (D) is te correct aswer, sice R.H.S + 0 ad L.H.S 0 Eample 5 [ ], were [.] is greatest iteger fuctio, is equal to (A) (B) (C) 0 (D) does ot eists Solutio (D) is te correct aswer, sice R.H.S [ ] 0 + ad L.H.S [ ] Eample 6 si 0 is equals to (A) 0 (B) (C) Solutio (A) is te correct aswer, sice (D) does ot eist 0 ad 0 si, by Sadwitc Teorem, we ave
15 LIMITS AND DERIVATIVES 9 si Eample 7, N, is equal to (A) 0 (B) (C) (D) Solutio (C) is te correct aswer. As ( + ) + Eample 8 If f() si, te f is equal to (A) 0 (B) (C) (D) Solutio (B) is te correct aswer. As f () cos + si So, f cos + si. EXERCISE Sort Aswer Type Evaluate : ( + ) ( + ) ( ) ( + ) ( a+ ) a a
16 0 EXEMPLAR PROBLEMS MATHEMATICS Fid, if 80, N 5. si a si 7 6. si 0 si cos 7. 0 si si 8. 0 cosm 9. 0 cos 0. cos6. si cos. 6 si cos 6 si ta. si si a a a 5. 6 cot cosec + cos 6. 0 si 7. si si + si 5 0 k 8. If k k, te fid te value of k. Differetiate eac of te fuctios w. r. to i Eercises 9 to ( + 5) ( + ta)
17 LIMITS AND DERIVATIVES +. (sec ) (sec + ) cos si cos si a+ bsi c+ dcos 6. (a + cot) (p + q cos) 8. (si + cos) 9. ( 7) ( + 5) 0. si + cos. si cos. a + b + c Log Aswer Type Differetiate eac of te fuctios wit respect to i Eercises to 6 usig first priciple.. cos ( + ). a + b c + d cos Evaluate eac of te followig its i Eercises 7 to ( + y) sec( + y) sec y 0 y (si( α+β ) + si( α β ) + si α) 8. 0 cos β cos α 9. ta ta cos + 5. Sow tat 50. does ot eists si cos cos si
18 EXEMPLAR PROBLEMS MATHEMATICS k cos we 5. Let f () fid te value of k. ad if f( ) f( ), 5. Let f () +, fid c if f ( ) eists. c > Objective Type Questios Coose te correct aswer out of optios give agaist eac Eercise 5 to 76 (M.C.Q). 5. si is (A) (B) (C) (D) cos cos is (A) (B) (C) (D) 56. ( + ) is 0 (A) (B) (C) (D) m is (A) (B) m (C) m (D) m cosθ cos6 θ is
19 LIMITS AND DERIVATIVES (A) 9 (B) cosec cot is 0 (A) si 0 + (B) is (C) (C) (D) (D) (A) (B) 0 (C) (D) 6. sec ta is 6. (A) (B) (C) 0 (D) ( ) ( ) + is (A) 0 (B) 0 (C) (D) Noe of tese si[ ],[ ] 0 6. If f () [ ], were [.] deotes te greatest iteger fuctio, 0,[ ] 0 te f ( ) is equal to 0 (A) (B) 0 (C) (D) Noe of tese 6. si 0 is (A) (B) (C) does ot eist(d) Noe of tese, 0 < < 65. Let f (), te quadratic equatio wose roots are f ( ) ad +, < f ( ) + is
20 EXEMPLAR PROBLEMS MATHEMATICS (A) (B) (C) (D) ta si is (A) (B) (C) (D) 67. Let f () []; R, te f is (A) (B) (C) 0 (D) 68. If y +, te dy d at is (A) (B) (C) (D) If f (), te f () is (A) 5 (B) 5 (C) (D) If + y, te dy d is (A) ( ) (B) (C) (D) 7. If si + cos y si cos, te dy d at 0 is
21 LIMITS AND DERIVATIVES 5 (A) (B) 0 (C) (D) does ot eist si( + 9) 7. If y, te dy at 0 is cos d (A) cos 9 (B) si 9 (C) 0 (D) If f () , te f () is equal to 00 (A) 00 (B) 00 (C) does ot eist (D) 0 7. If f( ) a a for some costat a, te f (a) is (A) (B) 0 (C) does ot eist (D) 75. If f () , te f () is equal to (A) 5050 (B) 509 (C) 505 (D) If f () , te f () is euqal to (A) 50 (B) 50 (C) 50 (D) 50 Fill i te blaks i Eercises 77 to If f () ta, te f ( ) 78. si m cot, te m if y , te dy!!! d [ ]
LIMITS AND DERIVATIVES NCERT
 . Overview.. Limits of a fuctio Let f be a fuctio defied i a domai wic we take to be a iterval, say, I. We sall study te cocept of it of f at a poit a i I. We say f ( ) is te epected value of f at a give
. Overview.. Limits of a fuctio Let f be a fuctio defied i a domai wic we take to be a iterval, say, I. We sall study te cocept of it of f at a poit a i I. We say f ( ) is te epected value of f at a give
LIMITS MULTIPLE CHOICE QUESTIONS. (a) 1 (b) 0 (c) 1 (d) does not exist. (a) 0 (b) 1/4 (c) 1/2 (d) 1/8. (a) 1 (b) e (c) 0 (d) none of these
 DSHA CLASSES Guidig you to Success LMTS MULTPLE CHOCE QUESTONS.... 5. Te value of + LEVEL (Objective Questios) (a) e (b) e (c) e 5 (d) e 5 (a) (b) (c) (d) does ot et (a) (b) / (c) / (d) /8 (a) (b) (c)
DSHA CLASSES Guidig you to Success LMTS MULTPLE CHOCE QUESTONS.... 5. Te value of + LEVEL (Objective Questios) (a) e (b) e (c) e 5 (d) e 5 (a) (b) (c) (d) does ot et (a) (b) / (c) / (d) /8 (a) (b) (c)
An Insight into Differentiation and Integration
 Differetiatio A Isigt ito Differetiatio a Itegratio Differetiatio is basically a task to fi out ow oe variable is cagig i relatio to aoter variable, te latter is usually take as a cause of te cage. For
Differetiatio A Isigt ito Differetiatio a Itegratio Differetiatio is basically a task to fi out ow oe variable is cagig i relatio to aoter variable, te latter is usually take as a cause of te cage. For
3sin A 1 2sin B. 3π x is a solution. 1. If A and B are acute positive angles satisfying the equation 3sin A 2sin B 1 and 3sin 2A 2sin 2B 0, then A 2B
 1. If A ad B are acute positive agles satisfyig the equatio 3si A si B 1 ad 3si A si B 0, the A B (a) (b) (c) (d) 6. 3 si A + si B = 1 3si A 1 si B 3 si A = cosb Also 3 si A si B = 0 si B = 3 si A Now,
1. If A ad B are acute positive agles satisfyig the equatio 3si A si B 1 ad 3si A si B 0, the A B (a) (b) (c) (d) 6. 3 si A + si B = 1 3si A 1 si B 3 si A = cosb Also 3 si A si B = 0 si B = 3 si A Now,
SEQUENCE AND SERIES NCERT
 9. Overview By a sequece, we mea a arragemet of umbers i a defiite order accordig to some rule. We deote the terms of a sequece by a, a,..., etc., the subscript deotes the positio of the term. I view of
9. Overview By a sequece, we mea a arragemet of umbers i a defiite order accordig to some rule. We deote the terms of a sequece by a, a,..., etc., the subscript deotes the positio of the term. I view of
Continuous Functions
 Cotiuous Fuctios Q What does it mea for a fuctio to be cotiuous at a poit? Aswer- I mathematics, we have a defiitio that cosists of three cocepts that are liked i a special way Cosider the followig defiitio
Cotiuous Fuctios Q What does it mea for a fuctio to be cotiuous at a poit? Aswer- I mathematics, we have a defiitio that cosists of three cocepts that are liked i a special way Cosider the followig defiitio
HKDSE Exam Questions Distribution
 HKDSE Eam Questios Distributio Sample Paper Practice Paper DSE 0 Topics A B A B A B. Biomial Theorem. Mathematical Iductio 0 3 3 3. More about Trigoometric Fuctios, 0, 3 0 3. Limits 6. Differetiatio 7
HKDSE Eam Questios Distributio Sample Paper Practice Paper DSE 0 Topics A B A B A B. Biomial Theorem. Mathematical Iductio 0 3 3 3. More about Trigoometric Fuctios, 0, 3 0 3. Limits 6. Differetiatio 7
We first write the integrand into partial fractions and then integrate. By EXAMPLE 27 we have the identity
 Solutios 8 Complete solutios to Miscellaeous Eercise 8. We ave v v v m KE m vdv m v. We ave l l EA EA EAl W d. We ave W k d k k. Multiplyig bot sides by μ gives ( ) T dt T T μθ l T l ( T) l ( T) l T T
Solutios 8 Complete solutios to Miscellaeous Eercise 8. We ave v v v m KE m vdv m v. We ave l l EA EA EAl W d. We ave W k d k k. Multiplyig bot sides by μ gives ( ) T dt T T μθ l T l ( T) l ( T) l T T
Created by T. Madas SERIES. Created by T. Madas
 SERIES SUMMATIONS BY STANDARD RESULTS Questio (**) Use stadard results o summatios to fid the value of 48 ( r )( 3r ). 36 FP-B, 66638 Questio (**+) Fid, i fully simplified factorized form, a expressio
SERIES SUMMATIONS BY STANDARD RESULTS Questio (**) Use stadard results o summatios to fid the value of 48 ( r )( 3r ). 36 FP-B, 66638 Questio (**+) Fid, i fully simplified factorized form, a expressio
CHAPTER 11 Limits and an Introduction to Calculus
 CHAPTER Limits ad a Itroductio to Calculus Sectio. Itroductio to Limits................... 50 Sectio. Teciques for Evaluatig Limits............. 5 Sectio. Te Taget Lie Problem................. 50 Sectio.
CHAPTER Limits ad a Itroductio to Calculus Sectio. Itroductio to Limits................... 50 Sectio. Teciques for Evaluatig Limits............. 5 Sectio. Te Taget Lie Problem................. 50 Sectio.
2.3 Warmup. Graph the derivative of the following functions. Where necessary, approximate the derivative.
 . Warmup Grap te erivative of te followig fuctios. Were ecessar, approimate te erivative. Differetiabilit Must a fuctio ave a erivative at eac poit were te fuctio is efie? Or If f a is efie, must f ( a)
. Warmup Grap te erivative of te followig fuctios. Were ecessar, approimate te erivative. Differetiabilit Must a fuctio ave a erivative at eac poit were te fuctio is efie? Or If f a is efie, must f ( a)
AP Calculus BC Review Applications of Derivatives (Chapter 4) and f,
 AP alculus B Review Applicatios of Derivatives (hapter ) Thigs to Kow ad Be Able to Do Defiitios of the followig i terms of derivatives, ad how to fid them: critical poit, global miima/maima, local (relative)
AP alculus B Review Applicatios of Derivatives (hapter ) Thigs to Kow ad Be Able to Do Defiitios of the followig i terms of derivatives, ad how to fid them: critical poit, global miima/maima, local (relative)
Topic 1 2: Sequences and Series. A sequence is an ordered list of numbers, e.g. 1, 2, 4, 8, 16, or
 Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
MA Lesson 26 Notes Graphs of Rational Functions (Asymptotes) Limits at infinity
 MA 1910 Lesso 6 Notes Graphs of Ratioal Fuctios (Asymptotes) Limits at ifiity Defiitio of a Ratioal Fuctio: If P() ad Q() are both polyomial fuctios, Q() 0, the the fuctio f below is called a Ratioal Fuctio.
MA 1910 Lesso 6 Notes Graphs of Ratioal Fuctios (Asymptotes) Limits at ifiity Defiitio of a Ratioal Fuctio: If P() ad Q() are both polyomial fuctios, Q() 0, the the fuctio f below is called a Ratioal Fuctio.
Northwest High School s Algebra 2/Honors Algebra 2 Summer Review Packet
 Northwest High School s Algebra /Hoors Algebra Summer Review Packet This packet is optioal! It will NOT be collected for a grade et school year! This packet has bee desiged to help you review various mathematical
Northwest High School s Algebra /Hoors Algebra Summer Review Packet This packet is optioal! It will NOT be collected for a grade et school year! This packet has bee desiged to help you review various mathematical
Differentiation Techniques 1: Power, Constant Multiple, Sum and Difference Rules
 Differetiatio Teciques : Power, Costat Multiple, Sum ad Differece Rules 97 Differetiatio Teciques : Power, Costat Multiple, Sum ad Differece Rules Model : Fidig te Equatio of f '() from a Grap of f ()
Differetiatio Teciques : Power, Costat Multiple, Sum ad Differece Rules 97 Differetiatio Teciques : Power, Costat Multiple, Sum ad Differece Rules Model : Fidig te Equatio of f '() from a Grap of f ()
Curve Sketching Handout #5 Topic Interpretation Rational Functions
 Curve Sketchig Hadout #5 Topic Iterpretatio Ratioal Fuctios A ratioal fuctio is a fuctio f that is a quotiet of two polyomials. I other words, p ( ) ( ) f is a ratioal fuctio if p ( ) ad q ( ) are polyomials
Curve Sketchig Hadout #5 Topic Iterpretatio Ratioal Fuctios A ratioal fuctio is a fuctio f that is a quotiet of two polyomials. I other words, p ( ) ( ) f is a ratioal fuctio if p ( ) ad q ( ) are polyomials
MATH301 Real Analysis (2008 Fall) Tutorial Note #7. k=1 f k (x) converges pointwise to S(x) on E if and
 MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
CALCULUS BASIC SUMMER REVIEW
 CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
CALCULUS BASIC SUMMER REVIEW NAME rise y y y Slope of a o vertical lie: m ru Poit Slope Equatio: y y m( ) The slope is m ad a poit o your lie is, ). ( y Slope-Itercept Equatio: y m b slope= m y-itercept=
CHAPTER 7 SUCCESSIVE DIFFERENTIATION
 www.sakshieducatio.com CHAPTER 7 SUCCESSIVE DIFFERENTIATION TOPICS:. Successive differetiatio-th derivative of a fuctio theorems.. Fidig the th derivative of the give fuctio.. Leibitz s theorem ad its
www.sakshieducatio.com CHAPTER 7 SUCCESSIVE DIFFERENTIATION TOPICS:. Successive differetiatio-th derivative of a fuctio theorems.. Fidig the th derivative of the give fuctio.. Leibitz s theorem ad its
BESSEL EQUATION and BESSEL FUNCTIONS
 BESSEL EQUATION ad BESSEL FUNCTIONS Bessel s Equatio Summary of Bessel Fuctios d y dy y d + d + =. If is a iteger, the two idepedet solutios of Bessel s Equatio are J J, Bessel fuctio of the first kid,
BESSEL EQUATION ad BESSEL FUNCTIONS Bessel s Equatio Summary of Bessel Fuctios d y dy y d + d + =. If is a iteger, the two idepedet solutios of Bessel s Equatio are J J, Bessel fuctio of the first kid,
MATH 1A FINAL (7:00 PM VERSION) SOLUTION. (Last edited December 25, 2013 at 9:14pm.)
 MATH A FINAL (7: PM VERSION) SOLUTION (Last edited December 5, 3 at 9:4pm.) Problem. (i) Give the precise defiitio of the defiite itegral usig Riema sums. (ii) Write a epressio for the defiite itegral
MATH A FINAL (7: PM VERSION) SOLUTION (Last edited December 5, 3 at 9:4pm.) Problem. (i) Give the precise defiitio of the defiite itegral usig Riema sums. (ii) Write a epressio for the defiite itegral
[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.
![[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms. [ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.](/thumbs/82/84777652.jpg) [ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
[ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
The type of limit that is used to find TANGENTS and VELOCITIES gives rise to the central idea in DIFFERENTIAL CALCULUS, the DERIVATIVE.
 NOTES : LIMITS AND DERIVATIVES Name: Date: Period: Iitial: LESSON.1 THE TANGENT AND VELOCITY PROBLEMS Pre-Calculus Mathematics Limit Process Calculus The type of it that is used to fid TANGENTS ad VELOCITIES
NOTES : LIMITS AND DERIVATIVES Name: Date: Period: Iitial: LESSON.1 THE TANGENT AND VELOCITY PROBLEMS Pre-Calculus Mathematics Limit Process Calculus The type of it that is used to fid TANGENTS ad VELOCITIES
MATHEMATICS. 61. The differential equation representing the family of curves where c is a positive parameter, is of
 MATHEMATICS 6 The differetial equatio represetig the family of curves where c is a positive parameter, is of Order Order Degree (d) Degree (a,c) Give curve is y c ( c) Differetiate wrt, y c c y Hece differetial
MATHEMATICS 6 The differetial equatio represetig the family of curves where c is a positive parameter, is of Order Order Degree (d) Degree (a,c) Give curve is y c ( c) Differetiate wrt, y c c y Hece differetial
De Moivre s Theorem - ALL
 De Moivre s Theorem - ALL. Let x ad y be real umbers, ad be oe of the complex solutios of the equatio =. Evaluate: (a) + + ; (b) ( x + y)( x + y). [6]. (a) Sice is a complex umber which satisfies = 0,.
De Moivre s Theorem - ALL. Let x ad y be real umbers, ad be oe of the complex solutios of the equatio =. Evaluate: (a) + + ; (b) ( x + y)( x + y). [6]. (a) Sice is a complex umber which satisfies = 0,.
Math 140A Elementary Analysis Homework Questions 1
 Math 14A Elemetary Aalysis Homewor Questios 1 1 Itroductio 1.1 The Set N of Natural Numbers 1 Prove that 1 2 2 2 2 1 ( 1(2 1 for all atural umbers. 2 Prove that 3 11 (8 5 4 2 for all N. 4 (a Guess a formula
Math 14A Elemetary Aalysis Homewor Questios 1 1 Itroductio 1.1 The Set N of Natural Numbers 1 Prove that 1 2 2 2 2 1 ( 1(2 1 for all atural umbers. 2 Prove that 3 11 (8 5 4 2 for all N. 4 (a Guess a formula
Definition 2.1 (The Derivative) (page 54) is a function. The derivative of a function f with respect to x, represented by. f ', is defined by
 Chapter DACS Lok 004/05 CHAPTER DIFFERENTIATION. THE GEOMETRICAL MEANING OF DIFFERENTIATION (page 54) Defiitio. (The Derivative) (page 54) Let f () is a fctio. The erivative of a fctio f with respect to,
Chapter DACS Lok 004/05 CHAPTER DIFFERENTIATION. THE GEOMETRICAL MEANING OF DIFFERENTIATION (page 54) Defiitio. (The Derivative) (page 54) Let f () is a fctio. The erivative of a fctio f with respect to,
LIMIT. f(a h). f(a + h). Lim x a. h 0. x 1. x 0. x 0. x 1. x 1. x 2. Lim f(x) 0 and. x 0
 J-Mathematics LIMIT. INTRODUCTION : The cocept of it of a fuctio is oe of the fudametal ideas that distiguishes calculus from algebra ad trigoometr. We use its to describe the wa a fuctio f varies. Some
J-Mathematics LIMIT. INTRODUCTION : The cocept of it of a fuctio is oe of the fudametal ideas that distiguishes calculus from algebra ad trigoometr. We use its to describe the wa a fuctio f varies. Some
Continuity and Differentiability of the Trigonometric Functions
 [Te basis for te following work will be te definition of te trigonometric functions as ratios of te sides of a triangle inscribed in a circle; in particular, te sine of an angle will be defined to be te
[Te basis for te following work will be te definition of te trigonometric functions as ratios of te sides of a triangle inscribed in a circle; in particular, te sine of an angle will be defined to be te
MA1200 Exercise for Chapter 7 Techniques of Differentiation Solutions. First Principle 1. a) To simplify the calculation, note. Then. lim h.
 MA00 Eercise for Chapter 7 Techiques of Differetiatio Solutios First Priciple a) To simplify the calculatio, ote The b) ( h) lim h 0 h lim h 0 h[ ( h) ( h) h ( h) ] f '( ) Product/Quotiet/Chai Rules a)
MA00 Eercise for Chapter 7 Techiques of Differetiatio Solutios First Priciple a) To simplify the calculatio, ote The b) ( h) lim h 0 h lim h 0 h[ ( h) ( h) h ( h) ] f '( ) Product/Quotiet/Chai Rules a)
APPENDIX F Complex Numbers
 APPENDIX F Complex Numbers Operatios with Complex Numbers Complex Solutios of Quadratic Equatios Polar Form of a Complex Number Powers ad Roots of Complex Numbers Operatios with Complex Numbers Some equatios
APPENDIX F Complex Numbers Operatios with Complex Numbers Complex Solutios of Quadratic Equatios Polar Form of a Complex Number Powers ad Roots of Complex Numbers Operatios with Complex Numbers Some equatios
x x x 2x x N ( ) p NUMERICAL METHODS UNIT-I-SOLUTION OF EQUATIONS AND EIGENVALUE PROBLEMS By Newton-Raphson formula
 NUMERICAL METHODS UNIT-I-SOLUTION OF EQUATIONS AND EIGENVALUE PROBLEMS. If g( is cotiuous i [a,b], te uder wat coditio te iterative (or iteratio metod = g( as a uique solutio i [a,b]? '( i [a,b].. Wat
NUMERICAL METHODS UNIT-I-SOLUTION OF EQUATIONS AND EIGENVALUE PROBLEMS. If g( is cotiuous i [a,b], te uder wat coditio te iterative (or iteratio metod = g( as a uique solutio i [a,b]? '( i [a,b].. Wat
f(w) w z =R z a 0 a n a nz n Liouville s theorem, we see that Q is constant, which implies that P is constant, which is a contradiction.
 Theorem 3.6.4. [Liouville s Theorem] Every bouded etire fuctio is costat. Proof. Let f be a etire fuctio. Suppose that there is M R such that M for ay z C. The for ay z C ad R > 0 f (z) f(w) 2πi (w z)
Theorem 3.6.4. [Liouville s Theorem] Every bouded etire fuctio is costat. Proof. Let f be a etire fuctio. Suppose that there is M R such that M for ay z C. The for ay z C ad R > 0 f (z) f(w) 2πi (w z)
Chapter 2 The Solution of Numerical Algebraic and Transcendental Equations
 Chapter The Solutio of Numerical Algebraic ad Trascedetal Equatios Itroductio I this chapter we shall discuss some umerical methods for solvig algebraic ad trascedetal equatios. The equatio f( is said
Chapter The Solutio of Numerical Algebraic ad Trascedetal Equatios Itroductio I this chapter we shall discuss some umerical methods for solvig algebraic ad trascedetal equatios. The equatio f( is said
Partial Differential Equations
 EE 84 Matematical Metods i Egieerig Partial Differetial Eqatios Followig are some classical partial differetial eqatios were is assmed to be a fctio of two or more variables t (time) ad y (spatial coordiates).
EE 84 Matematical Metods i Egieerig Partial Differetial Eqatios Followig are some classical partial differetial eqatios were is assmed to be a fctio of two or more variables t (time) ad y (spatial coordiates).
It is often useful to approximate complicated functions using simpler ones. We consider the task of approximating a function by a polynomial.
 Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
TECHNIQUES OF INTEGRATION
 7 TECHNIQUES OF INTEGRATION Simpso s Rule estimates itegrals b approimatig graphs with parabolas. Because of the Fudametal Theorem of Calculus, we ca itegrate a fuctio if we kow a atiderivative, that is,
7 TECHNIQUES OF INTEGRATION Simpso s Rule estimates itegrals b approimatig graphs with parabolas. Because of the Fudametal Theorem of Calculus, we ca itegrate a fuctio if we kow a atiderivative, that is,
On the convergence, consistence and stability of a standard finite difference scheme
 AMERICAN JOURNAL OF SCIENTIFIC AND INDUSTRIAL RESEARCH 2, Sciece Huβ, ttp://www.sciub.org/ajsir ISSN: 253-649X, doi:.525/ajsir.2.2.2.74.78 O te covergece, cosistece ad stabilit of a stadard fiite differece
AMERICAN JOURNAL OF SCIENTIFIC AND INDUSTRIAL RESEARCH 2, Sciece Huβ, ttp://www.sciub.org/ajsir ISSN: 253-649X, doi:.525/ajsir.2.2.2.74.78 O te covergece, cosistece ad stabilit of a stadard fiite differece
10.1 Sequences. n term. We will deal a. a n or a n n. ( 1) n ( 1) n 1 2 ( 1) a =, 0 0,,,,, ln n. n an 2. n term.
 0. Sequeces A sequece is a list of umbers writte i a defiite order: a, a,, a, a is called the first term, a is the secod term, ad i geeral eclusively with ifiite sequeces ad so each term Notatio: the sequece
0. Sequeces A sequece is a list of umbers writte i a defiite order: a, a,, a, a is called the first term, a is the secod term, ad i geeral eclusively with ifiite sequeces ad so each term Notatio: the sequece
Order doesn t matter. There exists a number (zero) whose sum with any number is the number.
 P. Real Numbers ad Their Properties Natural Numbers 1,,3. Whole Numbers 0, 1,,... Itegers..., -1, 0, 1,... Real Numbers Ratioal umbers (p/q) Where p & q are itegers, q 0 Irratioal umbers o-termiatig ad
P. Real Numbers ad Their Properties Natural Numbers 1,,3. Whole Numbers 0, 1,,... Itegers..., -1, 0, 1,... Real Numbers Ratioal umbers (p/q) Where p & q are itegers, q 0 Irratioal umbers o-termiatig ad
Further Methods for Advanced Mathematics (FP2) WEDNESDAY 9 JANUARY 2008
 ADVANCED GCE 7/ MATHEMATICS (MEI) Furter Metods for Advaced Matematics (F) WEDNESDAY 9 JANUARY 8 Additioal materials: Aswer Booklet (8 pages) Grap paper MEI Eamiatio Formulae ad Tables (MF) Afteroo Time:
ADVANCED GCE 7/ MATHEMATICS (MEI) Furter Metods for Advaced Matematics (F) WEDNESDAY 9 JANUARY 8 Additioal materials: Aswer Booklet (8 pages) Grap paper MEI Eamiatio Formulae ad Tables (MF) Afteroo Time:
Math 120 Answers for Homework 23
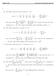 Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
MATH2007* Partial Answers to Review Exercises Fall 2004
 MATH27* Partial Aswers to Review Eercises Fall 24 Evaluate each of the followig itegrals:. Let u cos. The du si ad Hece si ( cos 2 )(si ) (u 2 ) du. si u 2 cos 7 u 7 du Please fiish this. 2. We use itegratio
MATH27* Partial Aswers to Review Eercises Fall 24 Evaluate each of the followig itegrals:. Let u cos. The du si ad Hece si ( cos 2 )(si ) (u 2 ) du. si u 2 cos 7 u 7 du Please fiish this. 2. We use itegratio
Continuity and Differentiability Worksheet
 Continuity and Differentiability Workseet (Be sure tat you can also do te grapical eercises from te tet- Tese were not included below! Typical problems are like problems -3, p. 6; -3, p. 7; 33-34, p. 7;
Continuity and Differentiability Workseet (Be sure tat you can also do te grapical eercises from te tet- Tese were not included below! Typical problems are like problems -3, p. 6; -3, p. 7; 33-34, p. 7;
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
Lyman Memorial High School. Honors Pre-Calculus Prerequisite Packet. Name:
 Lyma Memorial High School Hoors Pre-Calculus Prerequisite Packet 2018 Name: Dear Hoors Pre-Calculus Studet, Withi this packet you will fid mathematical cocepts ad skills covered i Algebra I, II ad Geometry.
Lyma Memorial High School Hoors Pre-Calculus Prerequisite Packet 2018 Name: Dear Hoors Pre-Calculus Studet, Withi this packet you will fid mathematical cocepts ad skills covered i Algebra I, II ad Geometry.
EDEXCEL STUDENT CONFERENCE 2006 A2 MATHEMATICS STUDENT NOTES
 EDEXCEL STUDENT CONFERENCE 006 A MATHEMATICS STUDENT NOTES South: Thursday 3rd March 006, Lodo EXAMINATION HINTS Before the eamiatio Obtai a copy of the formulae book ad use it! Write a list of ad LEARN
EDEXCEL STUDENT CONFERENCE 006 A MATHEMATICS STUDENT NOTES South: Thursday 3rd March 006, Lodo EXAMINATION HINTS Before the eamiatio Obtai a copy of the formulae book ad use it! Write a list of ad LEARN
The picture in figure 1.1 helps us to see that the area represents the distance traveled. Figure 1: Area represents distance travelled
 1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
Polynomial and Rational Functions. Polynomial functions and Their Graphs. Polynomial functions and Their Graphs. Examples
 Polomial ad Ratioal Fuctios Polomial fuctios ad Their Graphs Math 44 Precalculus Polomial ad Ratioal Fuctios Polomial Fuctios ad Their Graphs Polomial fuctios ad Their Graphs A Polomial of degree is a
Polomial ad Ratioal Fuctios Polomial fuctios ad Their Graphs Math 44 Precalculus Polomial ad Ratioal Fuctios Polomial Fuctios ad Their Graphs Polomial fuctios ad Their Graphs A Polomial of degree is a
Subject: Differential Equations & Mathematical Modeling -III. Lesson: Power series solutions of Differential Equations. about ordinary points
 Power series solutio of Differetial equatios about ordiary poits Subject: Differetial Equatios & Mathematical Modelig -III Lesso: Power series solutios of Differetial Equatios about ordiary poits Lesso
Power series solutio of Differetial equatios about ordiary poits Subject: Differetial Equatios & Mathematical Modelig -III Lesso: Power series solutios of Differetial Equatios about ordiary poits Lesso
SAMPLE. Solutions Manual Exercise Set 1 (page 10) 1.3 Exercise Set 2 (page 19) 1. 2, 1, 2, 1 4.
 Solutios Maual Eercise Set page 0,,, 4 + si + Use the Bo method z +siz cos z 4 cos + ct 5 fπ/ sicosπ/ si 0 0 6 + h You get this by dividig by h sice h 0 7 si t + cos h +cost + si h h h 8 a π, b 4π 9 a
Solutios Maual Eercise Set page 0,,, 4 + si + Use the Bo method z +siz cos z 4 cos + ct 5 fπ/ sicosπ/ si 0 0 6 + h You get this by dividig by h sice h 0 7 si t + cos h +cost + si h h h 8 a π, b 4π 9 a
, 4 is the second term U 2
 Balliteer Istitute 995-00 wwwleavigcertsolutioscom Leavig Cert Higher Maths Sequeces ad Series A sequece is a array of elemets seperated by commas E,,7,0,, The elemets are called the terms of the sequece
Balliteer Istitute 995-00 wwwleavigcertsolutioscom Leavig Cert Higher Maths Sequeces ad Series A sequece is a array of elemets seperated by commas E,,7,0,, The elemets are called the terms of the sequece
CHAPTER IV DIFFERENTIATION, LOCAL BEHAVIOR
 CHAPTER IV DIFFERENTIATION, LOCAL BEHAVIOR e iπ = 1. I tis capter we will fially see wy e iπ is 1. Alog te way, we will give careful proofs of all te stadard teorems of Differetial Calculus, ad i te process
CHAPTER IV DIFFERENTIATION, LOCAL BEHAVIOR e iπ = 1. I tis capter we will fially see wy e iπ is 1. Alog te way, we will give careful proofs of all te stadard teorems of Differetial Calculus, ad i te process
JEE(Advanced) 2018 TEST PAPER WITH SOLUTION (HELD ON SUNDAY 20 th MAY, 2018)
 JEE(Advaced) 08 TEST PAPER WITH SOLUTION (HELD ON SUNDAY 0 th MAY, 08) PART- : JEE(Advaced) 08/Paper- SECTION. For ay positive iteger, defie ƒ : (0, ) as ƒ () j ta j j for all (0, ). (Here, the iverse
JEE(Advaced) 08 TEST PAPER WITH SOLUTION (HELD ON SUNDAY 0 th MAY, 08) PART- : JEE(Advaced) 08/Paper- SECTION. For ay positive iteger, defie ƒ : (0, ) as ƒ () j ta j j for all (0, ). (Here, the iverse
Quiz. Use either the RATIO or ROOT TEST to determine whether the series is convergent or not.
 Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
(Figure 2.9), we observe x. and we write. (b) as x, x 1. and we write. We say that the line y 0 is a horizontal asymptote of the graph of f.
 The symbol for ifiity ( ) does ot represet a real umber. We use to describe the behavior of a fuctio whe the values i its domai or rage outgrow all fiite bouds. For eample, whe we say the limit of f as
The symbol for ifiity ( ) does ot represet a real umber. We use to describe the behavior of a fuctio whe the values i its domai or rage outgrow all fiite bouds. For eample, whe we say the limit of f as
Zeros of Polynomials
 Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Coimisiún na Scrúduithe Stáit State Examinations Commission
 M 9 Coimisiú a Scrúduithe Stáit State Examiatios Commissio LEAVING CERTIFICATE EXAMINATION, 006 MATHEMATICS HIGHER LEVEL PAPER 1 ( 00 marks ) THURSDAY, 8 JUNE MORNING, 9:0 to 1:00 Attempt SIX QUESTIONS
M 9 Coimisiú a Scrúduithe Stáit State Examiatios Commissio LEAVING CERTIFICATE EXAMINATION, 006 MATHEMATICS HIGHER LEVEL PAPER 1 ( 00 marks ) THURSDAY, 8 JUNE MORNING, 9:0 to 1:00 Attempt SIX QUESTIONS
INTEGRATION BY PARTS (TABLE METHOD)
 INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
INTEGRATION BY PARTS (TABLE METHOD) Suppose you wat to evaluate cos d usig itegratio by parts. Usig the u dv otatio, we get So, u dv d cos du d v si cos d si si d or si si d We see that it is ecessary
Fundamental Concepts: Surfaces and Curves
 UNDAMENTAL CONCEPTS: SURACES AND CURVES CHAPTER udametal Cocepts: Surfaces ad Curves. INTRODUCTION This chapter describes two geometrical objects, vi., surfaces ad curves because the pla a ver importat
UNDAMENTAL CONCEPTS: SURACES AND CURVES CHAPTER udametal Cocepts: Surfaces ad Curves. INTRODUCTION This chapter describes two geometrical objects, vi., surfaces ad curves because the pla a ver importat
LECTURE 2 LEAST SQUARES CROSS-VALIDATION FOR KERNEL DENSITY ESTIMATION
 Jauary 3 07 LECTURE LEAST SQUARES CROSS-VALIDATION FOR ERNEL DENSITY ESTIMATION Noparametric kerel estimatio is extremely sesitive to te coice of badwidt as larger values of result i averagig over more
Jauary 3 07 LECTURE LEAST SQUARES CROSS-VALIDATION FOR ERNEL DENSITY ESTIMATION Noparametric kerel estimatio is extremely sesitive to te coice of badwidt as larger values of result i averagig over more
UNIT #8 QUADRATIC FUNCTIONS AND THEIR ALGEBRA REVIEW QUESTIONS
 Name: Date: Part I Questios UNIT #8 QUADRATIC FUNCTIONS AND THEIR ALGEBRA REVIEW QUESTIONS. For the quadratic fuctio show, the coordiates. of its verte are 0, (3) 6, (), 7 (4) 3, 6. A quadratic fuctio
Name: Date: Part I Questios UNIT #8 QUADRATIC FUNCTIONS AND THEIR ALGEBRA REVIEW QUESTIONS. For the quadratic fuctio show, the coordiates. of its verte are 0, (3) 6, (), 7 (4) 3, 6. A quadratic fuctio
PhysicsAndMathsTutor.com
 PhysicsAdMathsTutor.com physicsadmathstutor.com Jue 005 3. The fuctio f is defied by (a) Show that 5 + 1 3 f:, > 1. + + f( ) =, > 1. 1 (4) (b) Fid f 1 (). (3) The fuctio g is defied by g: + 5, R. 1 4 (c)
PhysicsAdMathsTutor.com physicsadmathstutor.com Jue 005 3. The fuctio f is defied by (a) Show that 5 + 1 3 f:, > 1. + + f( ) =, > 1. 1 (4) (b) Fid f 1 (). (3) The fuctio g is defied by g: + 5, R. 1 4 (c)
SINGLE CORRECT ANSWER TYPE QUESTIONS: TRIGONOMETRY 2 2
 Class-Jr.X_E-E SIMPLE HOLIDAY PACKAGE CLASS-IX MATHEMATICS SUB BATCH : E-E SINGLE CORRECT ANSWER TYPE QUESTIONS: TRIGONOMETRY. siθ+cosθ + siθ cosθ = ) ) ). If a cos q, y bsi q, the a y b ) ) ). The value
Class-Jr.X_E-E SIMPLE HOLIDAY PACKAGE CLASS-IX MATHEMATICS SUB BATCH : E-E SINGLE CORRECT ANSWER TYPE QUESTIONS: TRIGONOMETRY. siθ+cosθ + siθ cosθ = ) ) ). If a cos q, y bsi q, the a y b ) ) ). The value
UNIT #8 QUADRATIC FUNCTIONS AND THEIR ALGEBRA REVIEW QUESTIONS
 Name: Date: UNIT #8 QUADRATIC FUNCTIONS AND THEIR ALGEBRA REVIEW QUESTIONS Part I Questios. For the quadratic fuctio show below, the coordiates of its verte are () 0, (), 7 (3) 6, (4) 3, 6. A quadratic
Name: Date: UNIT #8 QUADRATIC FUNCTIONS AND THEIR ALGEBRA REVIEW QUESTIONS Part I Questios. For the quadratic fuctio show below, the coordiates of its verte are () 0, (), 7 (3) 6, (4) 3, 6. A quadratic
PhysicsAndMathsTutor.com
 PhysicsAdMathsTutor.com physicsadmathstutor.com Jue 005 4. f(x) = 3e x 1 l x, x > 0. (a) Differetiate to fid f (x). (3) The curve with equatio y = f(x) has a turig poit at P. The x-coordiate of P is α.
PhysicsAdMathsTutor.com physicsadmathstutor.com Jue 005 4. f(x) = 3e x 1 l x, x > 0. (a) Differetiate to fid f (x). (3) The curve with equatio y = f(x) has a turig poit at P. The x-coordiate of P is α.
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
 BITSAT MATHEMATICS PAPER III. For the followig liear programmig problem : miimize z = + y subject to the costraits + y, + y 8, y, 0, the solutio is (0, ) ad (, ) (0, ) ad ( /, ) (0, ) ad (, ) (d) (0, )
BITSAT MATHEMATICS PAPER III. For the followig liear programmig problem : miimize z = + y subject to the costraits + y, + y 8, y, 0, the solutio is (0, ) ad (, ) (0, ) ad ( /, ) (0, ) ad (, ) (d) (0, )
A.1 Algebra Review: Polynomials/Rationals. Definitions:
 MATH 040 Notes: Uit 0 Page 1 A.1 Algera Review: Polyomials/Ratioals Defiitios: A polyomial is a sum of polyomial terms. Polyomial terms are epressios formed y products of costats ad variales with whole
MATH 040 Notes: Uit 0 Page 1 A.1 Algera Review: Polyomials/Ratioals Defiitios: A polyomial is a sum of polyomial terms. Polyomial terms are epressios formed y products of costats ad variales with whole
In algebra one spends much time finding common denominators and thus simplifying rational expressions. For example:
 74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
Algebra II Notes Unit Seven: Powers, Roots, and Radicals
 Syllabus Objectives: 7. The studets will use properties of ratioal epoets to simplify ad evaluate epressios. 7.8 The studet will solve equatios cotaiig radicals or ratioal epoets. b a, the b is the radical.
Syllabus Objectives: 7. The studets will use properties of ratioal epoets to simplify ad evaluate epressios. 7.8 The studet will solve equatios cotaiig radicals or ratioal epoets. b a, the b is the radical.
 + {JEE Advace 03} Sept 0 Name: Batch (Day) Phoe No. IT IS NOT ENOUGH TO HAVE A GOOD MIND, THE MAIN THING IS TO USE IT WELL Marks: 00. If A (α, β) = (a) A( α, β) = A( α, β) (c) Adj (A ( α, β)) = Sol : We
+ {JEE Advace 03} Sept 0 Name: Batch (Day) Phoe No. IT IS NOT ENOUGH TO HAVE A GOOD MIND, THE MAIN THING IS TO USE IT WELL Marks: 00. If A (α, β) = (a) A( α, β) = A( α, β) (c) Adj (A ( α, β)) = Sol : We
BRAIN TEASURES TRIGONOMETRICAL RATIOS BY ABHIJIT KUMAR JHA EXERCISE I. or tan &, lie between 0 &, then find the value of tan 2.
 EXERCISE I Q Prove that cos² + cos² (+ ) cos cos cos (+ ) ² Q Prove that cos ² + cos (+ ) + cos (+ ) Q Prove that, ta + ta + ta + cot cot Q Prove that : (a) ta 0 ta 0 ta 60 ta 0 (b) ta 9 ta 7 ta 6 + ta
EXERCISE I Q Prove that cos² + cos² (+ ) cos cos cos (+ ) ² Q Prove that cos ² + cos (+ ) + cos (+ ) Q Prove that, ta + ta + ta + cot cot Q Prove that : (a) ta 0 ta 0 ta 60 ta 0 (b) ta 9 ta 7 ta 6 + ta
PRACTICE FINAL/STUDY GUIDE SOLUTIONS
 Last edited December 9, 03 at 4:33pm) Feel free to sed me ay feedback, icludig commets, typos, ad mathematical errors Problem Give the precise meaig of the followig statemets i) a f) L ii) a + f) L iii)
Last edited December 9, 03 at 4:33pm) Feel free to sed me ay feedback, icludig commets, typos, ad mathematical errors Problem Give the precise meaig of the followig statemets i) a f) L ii) a + f) L iii)
y = f x x 1. If f x = e 2x tan -1 x, then f 1 = e 2 2 e 2 p C e 2 D e 2 p+1 4
 . If f = e ta -, the f = e e p e e p e p+ 4 f = e ta -, so f = e ta - + e, so + f = e p + e = e p + e or f = e p + 4. The slope of the lie taget to the curve - + = at the poit, - is - 5 Differetiate -
. If f = e ta -, the f = e e p e e p e p+ 4 f = e ta -, so f = e ta - + e, so + f = e p + e = e p + e or f = e p + 4. The slope of the lie taget to the curve - + = at the poit, - is - 5 Differetiate -
In exercises 1 and 2, (a) write the repeating decimal as a geometric series and (b) write its sum as the ratio of two integers _
 Chapter 9 Curve I eercises ad, (a) write the repeatig decimal as a geometric series ad (b) write its sum as the ratio of two itegers _.9.976 Distace A ball is dropped from a height of 8 meters. Each time
Chapter 9 Curve I eercises ad, (a) write the repeatig decimal as a geometric series ad (b) write its sum as the ratio of two itegers _.9.976 Distace A ball is dropped from a height of 8 meters. Each time
Mini Lecture 10.1 Radical Expressions and Functions. 81x d. x 4x 4
 Mii Lecture 0. Radical Expressios ad Fuctios Learig Objectives:. Evaluate square roots.. Evaluate square root fuctios.. Fid the domai of square root fuctios.. Use models that are square root fuctios. 5.
Mii Lecture 0. Radical Expressios ad Fuctios Learig Objectives:. Evaluate square roots.. Evaluate square root fuctios.. Fid the domai of square root fuctios.. Use models that are square root fuctios. 5.
Chapter 2 Limits and Continuity
 4 Section. Capter Limits and Continuity Section. Rates of Cange and Limits (pp. 6) Quick Review.. f () ( ) () 4 0. f () 4( ) 4. f () sin sin 0 4. f (). 4 4 4 6. c c c 7. 8. c d d c d d c d c 9. 8 ( )(
4 Section. Capter Limits and Continuity Section. Rates of Cange and Limits (pp. 6) Quick Review.. f () ( ) () 4 0. f () 4( ) 4. f () sin sin 0 4. f (). 4 4 4 6. c c c 7. 8. c d d c d d c d c 9. 8 ( )(
Topic 5 [434 marks] (i) Find the range of values of n for which. (ii) Write down the value of x dx in terms of n, when it does exist.
![Topic 5 [434 marks] (i) Find the range of values of n for which. (ii) Write down the value of x dx in terms of n, when it does exist. Topic 5 [434 marks] (i) Find the range of values of n for which. (ii) Write down the value of x dx in terms of n, when it does exist.](/thumbs/90/102216025.jpg) Topic 5 [44 marks] 1a (i) Fid the rage of values of for which eists 1 Write dow the value of i terms of 1, whe it does eist Fid the solutio to the differetial equatio 1b give that y = 1 whe = π (cos si
Topic 5 [44 marks] 1a (i) Fid the rage of values of for which eists 1 Write dow the value of i terms of 1, whe it does eist Fid the solutio to the differetial equatio 1b give that y = 1 whe = π (cos si
2. Fourier Series, Fourier Integrals and Fourier Transforms
 Mathematics IV -. Fourier Series, Fourier Itegrals ad Fourier Trasforms The Fourier series are used for the aalysis of the periodic pheomea, which ofte appear i physics ad egieerig. The Fourier itegrals
Mathematics IV -. Fourier Series, Fourier Itegrals ad Fourier Trasforms The Fourier series are used for the aalysis of the periodic pheomea, which ofte appear i physics ad egieerig. The Fourier itegrals
Presentation of complex number in Cartesian and polar coordinate system
 a + bi, aεr, bεr i = z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real: z +
a + bi, aεr, bεr i = z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real: z +
(a) (b) All real numbers. (c) All real numbers. (d) None. to show the. (a) 3. (b) [ 7, 1) (c) ( 7, 1) (d) At x = 7. (a) (b)
 Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
AIEEE 2004 (MATHEMATICS)
 AIEEE 00 (MATHEMATICS) Importat Istructios: i) The test is of hours duratio. ii) The test cosists of 75 questios. iii) The maimum marks are 5. iv) For each correct aswer you will get marks ad for a wrog
AIEEE 00 (MATHEMATICS) Importat Istructios: i) The test is of hours duratio. ii) The test cosists of 75 questios. iii) The maimum marks are 5. iv) For each correct aswer you will get marks ad for a wrog
Appendix F: Complex Numbers
 Appedix F Complex Numbers F1 Appedix F: Complex Numbers Use the imagiary uit i to write complex umbers, ad to add, subtract, ad multiply complex umbers. Fid complex solutios of quadratic equatios. Write
Appedix F Complex Numbers F1 Appedix F: Complex Numbers Use the imagiary uit i to write complex umbers, ad to add, subtract, ad multiply complex umbers. Fid complex solutios of quadratic equatios. Write
Math 128A: Homework 1 Solutions
 Math 8A: Homework Solutios Due: Jue. Determie the limits of the followig sequeces as. a) a = +. lim a + = lim =. b) a = + ). c) a = si4 +6) +. lim a = lim = lim + ) [ + ) ] = [ e ] = e 6. Observe that
Math 8A: Homework Solutios Due: Jue. Determie the limits of the followig sequeces as. a) a = +. lim a + = lim =. b) a = + ). c) a = si4 +6) +. lim a = lim = lim + ) [ + ) ] = [ e ] = e 6. Observe that
Math 31A Discussion Notes Week 4 October 20 and October 22, 2015
 Mat 3A Discussion Notes Week 4 October 20 and October 22, 205 To prepare for te first midterm, we ll spend tis week working eamples resembling te various problems you ve seen so far tis term. In tese notes
Mat 3A Discussion Notes Week 4 October 20 and October 22, 205 To prepare for te first midterm, we ll spend tis week working eamples resembling te various problems you ve seen so far tis term. In tese notes
NAME: ALGEBRA 350 BLOCK 7. Simplifying Radicals Packet PART 1: ROOTS
 NAME: ALGEBRA 50 BLOCK 7 DATE: Simplifyig Radicals Packet PART 1: ROOTS READ: A square root of a umber b is a solutio of the equatio x = b. Every positive umber b has two square roots, deoted b ad b or
NAME: ALGEBRA 50 BLOCK 7 DATE: Simplifyig Radicals Packet PART 1: ROOTS READ: A square root of a umber b is a solutio of the equatio x = b. Every positive umber b has two square roots, deoted b ad b or
3 Show in each case that there is a root of the given equation in the given interval. a x 3 = 12 4
 C Worksheet A Show i each case that there is a root of the equatio f() = 0 i the give iterval a f() = + 7 (, ) f() = 5 cos (05, ) c f() = e + + 5 ( 6, 5) d f() = 4 5 + (, ) e f() = l (4 ) + (04, 05) f
C Worksheet A Show i each case that there is a root of the equatio f() = 0 i the give iterval a f() = + 7 (, ) f() = 5 cos (05, ) c f() = e + + 5 ( 6, 5) d f() = 4 5 + (, ) e f() = l (4 ) + (04, 05) f
Section 11.8: Power Series
 Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
1 The concept of limits (p.217 p.229, p.242 p.249, p.255 p.256) 1.1 Limits Consider the function determined by the formula 3. x since at this point
 MA00 Capter 6 Calculus and Basic Linear Algebra I Limits, Continuity and Differentiability Te concept of its (p.7 p.9, p.4 p.49, p.55 p.56). Limits Consider te function determined by te formula f Note
MA00 Capter 6 Calculus and Basic Linear Algebra I Limits, Continuity and Differentiability Te concept of its (p.7 p.9, p.4 p.49, p.55 p.56). Limits Consider te function determined by te formula f Note
Chapter 8. Uniform Convergence and Differentiation.
 Chapter 8 Uiform Covergece ad Differetiatio This chapter cotiues the study of the cosequece of uiform covergece of a series of fuctio I Chapter 7 we have observed that the uiform limit of a sequece of
Chapter 8 Uiform Covergece ad Differetiatio This chapter cotiues the study of the cosequece of uiform covergece of a series of fuctio I Chapter 7 we have observed that the uiform limit of a sequece of
3.2 Properties of Division 3.3 Zeros of Polynomials 3.4 Complex and Rational Zeros of Polynomials
 Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
MATH 155A FALL 13 PRACTICE MIDTERM 1 SOLUTIONS. needs to be non-zero, thus x 1. Also 1 +
 MATH 55A FALL 3 PRACTICE MIDTERM SOLUTIONS Question Find te domain of te following functions (a) f(x) = x3 5 x +x 6 (b) g(x) = x+ + x+ (c) f(x) = 5 x + x 0 (a) We need x + x 6 = (x + 3)(x ) 0 Hence Dom(f)
MATH 55A FALL 3 PRACTICE MIDTERM SOLUTIONS Question Find te domain of te following functions (a) f(x) = x3 5 x +x 6 (b) g(x) = x+ + x+ (c) f(x) = 5 x + x 0 (a) We need x + x 6 = (x + 3)(x ) 0 Hence Dom(f)
For use only in Badminton School November 2011 C2 Note. C2 Notes (Edexcel)
 For use oly i Badmito School November 0 C Note C Notes (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets For use oly i Badmito School November 0 C Note Copyright www.pgmaths.co.uk
For use oly i Badmito School November 0 C Note C Notes (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets For use oly i Badmito School November 0 C Note Copyright www.pgmaths.co.uk
September 2012 C1 Note. C1 Notes (Edexcel) Copyright - For AS, A2 notes and IGCSE / GCSE worksheets 1
 September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
September 0 s (Edecel) Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright www.pgmaths.co.uk - For AS, A otes ad IGCSE / GCSE worksheets September 0 Copyright
PLEASE MARK YOUR ANSWERS WITH AN X, not a circle! 1. (a) (b) (c) (d) (e) 3. (a) (b) (c) (d) (e) 5. (a) (b) (c) (d) (e) 7. (a) (b) (c) (d) (e)
 Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
( ) ( ) ( ) ( ) ( + ) ( )
 LSM Nov. 00 Cotet List Mathematics (AH). Algebra... kow ad use the otatio!, C r ad r.. kow the results = r r + + = r r r..3 kow Pascal's triagle. Pascal's triagle should be eteded up to = 7...4 kow ad
LSM Nov. 00 Cotet List Mathematics (AH). Algebra... kow ad use the otatio!, C r ad r.. kow the results = r r + + = r r r..3 kow Pascal's triagle. Pascal's triagle should be eteded up to = 7...4 kow ad

 6. If si () + cos () =, the is equal to :. If <
6. If si () + cos () =, the is equal to :. If <