CHAPTER 2 LIMITS AND CONTINUITY
|
|
|
- Kristian Cross
- 5 years ago
- Views:
Transcription
1 CHAPTER LIMITS AND CONTINUITY RATES OF CHANGE AND LIMITS (a) Does not eist As approaches from the right, g() approaches 0 As approaches from the left, g() approaches There is no single number L that all the values g() get arbitrarily close to as Ä (c) 0 (a) 0 (c) Does not eist As t approaches 0 from the left, f(t) approaches As t approaches 0 from the right, f(t) approaches There is no single number L that f(t) gets arbitrarily close to as t Ä 0 (a) True True (c) False (d) False (e) False (f) True (a) False False (c) True (d) True (e) True 5 lim does not eist because if 0 and if 0 As approaches 0 from the left, Ä 0 kk kk kk kkapproaches As approaches 0 from the right, kkapproaches There is no single number L that all the function values get arbitrarily close to as Ä 0 6 As approaches from the left, the values of become increasingly large and As approaches from the right, the values become increasingly large and positive There is no one number L that all the function values get arbitrarily close to as Ä, so lim does not eist Ä 7 Nothing can be said about f() because the eistence of a limit as Ä! does not depend on how the function is defined at! In order for a limit to eist, f() must be arbitrarily close to a single real number L when is close enough to! That is, the eistence of a limit depends on the values of f() for near!, not on the definition of f() at! itself 8 Nothing can be said In order for lim f() to eist, f() must close to a single value for near 0 regardless of Ä 0 the value f(0) itself 9 No, the definition does not require that f be defined at in order for a limiting value to eist there If f() is defined, it can be any real number, so we can conclude nothing about f() from lim f() 5 Ä 0 No, because the eistence of a limit depends on the values of f() when is near, not on f() itself If lim f() eists, its value may be some number other than f() 5 We can conclude nothing about lim f(), Ä Ä whether it eists or what its value is if it does eist, from knowing the value of f() alone
2 58 Chapter Limits and Continuity (a) f() a * b/( ) f() f() The estimate is lim f() 6 Ä$ 9 ( )( ) (c) f() if Á, and lim ( ) 6 Ä$ (a) g() a b/ Š È g() Š ÈŠ È (c) g() È if Á È, and lim È Š È È È È Š È Ä È (a) G() ( 6)/ a b G() G()
3 Section Rates of Change and Limits (c) G() a b (6)() if Á6, and lim ' 8 05 Ä' (a) h() a b/ a b h() h() ( )( ) (c) h() ()() if Á, and lim Ä$ 5 (a) f() a b/ akkb f() f()
4 60 Chapter Limits and Continuity ( )( ) (c) f(), 0 and Á kk ( )( ), and lim ( ) ( ), 0 and Á Ä ( ) 6 (a) F() a b/ a kkb F() F() ( )( ), 0 (c) F() kk ( )( ), and lim ( ), 0 and Á Ä 7 (a) g( )) (sin ))/) ) g( )) ) g( )) lim g( )) ) Ä! 8 (a) G(t) ( cos t)/t t G(t) t G(t) lim G(t) 05 t Ä!
5 Section Rates of Change and Limits 6 Graph is NOT TO SCALE 9 (a) f() f() f() lim f() Ä Graph is NOT TO SCALE Also the intersection of the aes is not the origin: the aes intersect at the point (ß 780) 0 (a) f() a b/ f() f() lim f() 0986 Ä! lim () lim (0) 0 Ä Ä! lim ( ) ˆ 0 lim Ä Ä () $
6 6 Chapter Limits and Continuity ( ) 5 lim ( ) ( )(( ) ) 9 6 lim Ä Ä ( ) 7 lim sin sin 8 lim Ä Ä cos cos? f f() f() 8 9? f f() f( ) 0?? ( ) 9 (a) 9? g g() g( )? g g(0) g( ) 0? ( )? 0 ( ) 0 (a) 0? h hˆ hˆ? h hˆ hˆ 0È È? t? t 6 6 (a)? g g( ) g(0) ( ) ( )? g g( ) g( ) ( ) ( )? t 0 0? t ( ) (a) 0? R R() R(0) È8È?) 0? P P() P() (8 6 0) (%&)?) 0 5 (a) Q Slope of PQ 650 5? p? t Q (0ß5) m/sec Q (ß75) 0 58 m/sec Q $ (65ß75) m/sec Q %(8ß550) m/sec At t 0, the Cobra was traveling approimately 50 m/sec or 80 km/h 6 (a) Q Slope of PQ 7 (a) 80 0? p? t Q (5ß0) 0 5 m/sec 80 9 Q (7ß9) m/sec Q $ (85ß58) m/sec 80 7 Q %(95ß7) m/sec Approimately 6 m/sec? p 7 6? t thousand dollars per year (c) The average rate of change from 99 to 99 is The average rate of change from 99 to 99 is? p 6 7? t 99 99? p 6? t thousand dollars per year 9 thousand dollars per year So, the rate at which profits were changing in 99 is approimatley a 5 9 b thousand dollars per year
7 8 (a) F() ( )/( ) F() ? F 0 ( )? F ( )??? F 0 ( )? F 00 ( )? 0? 00? F!!!% ( )? 000!!!%; 50; ; 0;!!%; The rate of change of F() at is? g g() g() È? g g(5) g() È5?? 5 05? h) g() Èh? (h) h Section Rates of Change and Limits 6 9 (a) g() È h È h Š È h /h (c) The rate of change of g() at is 05 Èh (d) The calculator gives lim h h Ä! 0 (a) i) c f() f() 6 6 T f(t) f() T T T T T T T T T(T) T( T) T ii), T Á T f(t) af(t) f() b/ at b (c) The table indicates the rate of change is 05 at t (d) lim T Ĉ T -6 Eample CAS commands: Maple: f := -> (^ 6)/( ); 0 := ; plot( f(), 0-0+, color black, title Section, (a) ); limit( f(), 0 ); In Eercise, note that the standard cube root, ^(/), is not defined for <0 in many CASs This can be overcome in Maple by entering the function as f := -> (surd(+, ) )/ Mathematica: (assigned function and values for 0 and h may vary) Clear[f, ] f[_]:=( 5 )/( ) 0= ; h = 0; Plot[f[],{, 0 h, 0 h}] Limit[f[], Ä 0]
8 6 Chapter Limits and Continuity CALCULATING LIMITS USING THE LIMIT LAWS lim ( 5) ( 7) lim (0 ) 0 () Ä( Ä lim a 5 b () 5() 0 Ä $ $ lim a 8 b ( ) ( ) ( ) Ä 5 lim 8(t 5)(t 7) 8(6 5)(6 7) 8 6 lim s(s ) ˆ ˆ ˆ t Ä' s Ä 5 7 lim 8 lim Ä Ä& 7 57 $ 9 lim y Ä& y ( 5) 5 5 5y 5 ( 5) 0 0 lim y Ä y y 5y6 () 5( ) lim ( ) (( ) ) ( ) 7 Ä *)% *)% *)% lim ( ) ( ) ( ) Ä% %Î$ %Î$ %Î$ lim (5 y) [5 ( )] (8) ˆ Î$ (8) % 6 y Ä$ Î$ Î$ Î$ lim (z 8) ((0) 8) ( 8) z Ä! % 5 lim h Ä! 6 lim h Ä! È h È (0) È È 5h È 5(0) È Èh Èh Èh ah b h h h h Èh 7 lim lim lim lim lim h Ä 0 h Ä 0 È h Ä 0 hš Èh h Ä 0 hš Èh h Ä 0 $ È È5h È5h È5h a5hb 5h 5 h h 5h È5h 8 lim lim lim lim lim h Ä 0 h Ä 0 È h Ä 0 hš È5h h Ä 0 hš È5h h Ä È ( 5)( 5) lim lim lim Ä& Ä& Ä& ( )( ) 0 lim lim lim Ä$ Ä$ Ä$ 0 ( 5)( ) lim lim lim ( ) 7 Ä& 5 Ä& 5 & Ä&
9 7 0 ( 5)( ) lim lim lim ( 5) 5 Ä Ä Ä t t (t )(t ) t lim lim lim t Ä t t Ä (t )(t ) t Ä t t t (t )(t ) t t t (t )(t ) t lim lim lim t Ä t Ä t Ä ( ) ( ) 5 lim $ lim lim Ä Ä Ä 5y 8y y (5y 8) 5y 8 $ 8 6 lim lim lim y Ä 0 y% 6y y Ä! y y 6 y Ä! y 6 6 a b Section Calculating Limits Using the Limit Laws 65 u au b(u)(u) au b(u) ( )( ) u u u (u ) u u % 7 lim $ lim lim u Ä u Ä a b u Ä v 8 (v ) av v b v v (v )(v ) v (v ) v ()(8) 8 $ 8 lim lim lim v Ä v% 6 v Ä a b v Ä a b È È lim lim lim Ä* Ä* ˆ È ˆ È Ä* È È 9 ( ) ˆ È ˆ È 0 lim lim lim lim ( ) 6 Ä% È Ä% È Ä% È ˆ È Ä% ˆ È ˆ È () () lim lim lim lim Ä È Ä È È Ä ( ) Š È ˆ ˆ Ä È È Š È Š È $ $ a 8b* ( ) Š 8 $ ( ) Š È 8 $ lim lim lim Ä Ä È Ä ( )( ) lim lim Ä ( ) Š È )$ Ä È )$ È Š È Š È a b6 ( ) Š ( ) Š È lim lim lim Ä Ä È Ä ( )( ) 6 lim lim Ä ( ) Š È Ä È È abš È 5 abš È 5 lim lim lim Ä È 5 Ä Š Š Ä È 5 È 5 a 5b9 abš È 5 È 5 È9 ( )( ) lim lim Ä Ä È 5 Š È 5Š È 5 a 5b ( ) Š 5 ( ) Š È 5 5 lim lim lim Ä Ä È Ä 9 ( )( ) 6 5 lim lim lim Ä ( ) 5 Ä ( ) 5 Ä Š È Š È È È
10 66 Chapter Limits and Continuity abš 5È 9 abš 5È 9 6 lim lim lim Ä 5È 9 Ä Š Š Ä 5 È 9 5 È 9 5 a 9 b abš 5È 9 abš 5È 9 5È 9 5 È5 5 6 ( )( ) 8 lim lim lim Ä Ä Ä 7 (a) quotient rule difference and power rules (c) sum and constant multiple rules 8 (a) quotient rule power and product rules (c) difference and constant multiple rules 9 (a) lim f() g() lim f() lim g() (5)( ) 0 Ä c Ä c Ä c lim f() g() lim f() lim g() (5)( ) 0 Ä c Ä c Ä c (c) lim [f() g()] lim f() lim g() 5 ( ) Ä c Ä c Ä c f() (d) lim lim f() 5 5 Ä c f() g() Äc lim f() lim g() 5 ( ) 7 Äc Äc 0 (a) lim [g() ] lim g() lim $$! Ä% Ä% Ä% lim f() lim lim f() ()(0) 0 Ä% Ä% Ä% (c) lim [g()] lim g() [ ] 9 Ä% Ä% g() lim g() (d) lim Ä% f() Ä% lim f() lim 0 Ä% Ä% (a) lim [f() g()] lim f() lim g() 7 ( ) Ä b Ä b Ä b lim f() g() lim f() lim g() (7)( ) Ä b Ä b Ä b (c) lim g() lim lim g() ()( ) Ä b Ä b Ä b 7 7 (d) lim f()/g() lim f()/ lim g() Ä b Ä b Ä b (a) lim [p() r() s()] lim p() lim r() lim s() 0 ( ) Ä Ä Ä Ä lim p() r() s() lim p() lim r() lim s() ()(0)( ) 0 Ä Ä Ä Ä (c) lim [ p() 5r()]/s() lim p() 5 lim r() lim s() [ () 5(0)]/ Ä Ä Ä Ä ( h) hh h( h) lim lim lim lim ( h) h Ä! h h Ä! h h Ä! h h Ä! ( h) ( ) hh h(h) lim lim lim lim (h ) h Ä! h h Ä! h h Ä! h h Ä! [( h) ] [() ] 5 lim lim h Ä! h h Ä! h h ˆ ˆ c ( h) h h h h( h) h( h) c b h c cb h 6 lim lim lim lim h Ä! h Ä! h Ä! h Ä! 6
11 È È Š È È Š È È 7h 7 7h 7 7h 7 (7 h) 7 hš 7h 7 hš È7hÈ7 7 lim lim lim h Ä! h h Ä! È È h Ä! h h È7 h È7 È7h È7 È7 lim lim h Ä! Š h Ä! Section Calculating Limits Using the Limit Laws 67 È È Š È Š È (0 h) (0) h h (h ) hš h hš Èh 8 lim lim lim h Ä! h h Ä! È h Ä! h lim lim h Ä! hš Èh h Ä! Èh 9 lim È5 È5 (0) È5 and lim È5 È5 (0) È5; by the sandwich theorem, Ä! Ä! lim f() È 5 Ä! 50 lim a b 0 and lim cos () ; by the sandwich theorem, lim g() Ä! Ä! Ä! 0 sin 5 (a) lim Š and lim ; by the sandwich theorem, lim Ä! 6 6 Ä! Ä! cos For Á 0, y ( sin )/( cos ) lies between the other two graphs in the figure, and the graphs converge as Ä 0 5 (a) lim Š lim lim 0 and lim ; by the sandwich theorem, Ä! Ä! Ä! Ä! cos lim Ä! For all Á 0, the graph of f() ( cos )/ lies between the line y and the parabola y /, and the graphs converge as Ä 0 % % 5 lim f() eists at those points c where lim lim Thus, c c Ê c a c b 0 Ä c Ä c Ä c Ê c 0,, or Moreover, lim f() lim 0 and lim f() lim f() Ä! Ä! Ä Ä 5 Nothing can be concluded about the values of f, g, and h at Yes, f() could be 0 Since the conditions of the sandwich theorem are satisfied, lim f() 5Á 0 Ä lim f() lim 5 lim f() 5 f() 5 55 lim Ä% Ä% Ä% Ê lim f() 5 () Ê lim f() 5 7 Ä% lim lim % Ä% Ä% Ä% Ä%
12 68 Chapter Limits and Continuity f() lim f() lim f() Äc Äc 56 (a) lim Ê lim f() Ä lim % Ä Äc f() f() f() f() lim lim lim lim Ê lim Ä Ä Ä ˆ Ä Ä f() 5 f() 5 57 (a) 0 0 lim lim ( ) lim Š ( ) lim [f() 5] lim f() 5 Ä Ä Ä Ä Ä Ê lim f() 5 Ä f() lim lim ( ) Ê lim f() 5 as in part (a) Ä Ä Ä f() f() f() 58 (a) 0 0 lim lim lim lim lim lim f() That is, lim f( Ä! Ä! Ä! Ä! Ä! ) 0 Ä! Ä! f() f() f() f() 0 0 lim lim lim lim That is, lim 0 Ä! Ä! Ä! Ä! Ä! 59 (a) lim sin 0 Ä! Ÿ sin Ÿ for Á 0: 0 Ê Ÿ sin Ÿ Ê lim sin 0 by the sandwich theorem; Ä! 0 Ê sin Ê lim sin 0 by the sandwich theorem Ä! 60 (a) lim cos ˆ 0 Ä! $ Ÿ cos ˆ Ÿ for Á 0 Ê Ÿ cos ˆ Ÿ Ê lim cos ˆ $ $ $ 0 by the sandwich Ä! theorem since lim 0 Ä! THE PRECISE DEFINITION OF A LIMIT Step : k5 k $ Ê $ 5 $ Ê $ 5 $ 5 Step : $ 5 7 Ê $, or $ 5 Ê $ The value of $ which assures k 5 k $ Ê 7 is the smaller value, $
13 Section The Precise Definition of a Limit 69 Step : k k $ Ê $ $ Ê $ $ Step : $ Ê $, or $ 7 Ê $ 5 The value of $ which assures k k $ Ê 7 is the smaller value, $ Step : k ( ) k $ Ê $ $ $ Ê $ $ 7 5 Step : $ Ê $, or $ $ Ê $ 7 $ k k $ Ê $ The value of which assures ( ) is the smaller value, Step : ˆ $ Ê $ $ Ê $ $ 7 ˆ 7 Step : $ Ê $, or $ Ê $ The value of $ which assures $ Ê is the smaller value, $ 5 Step : $ Ê $ $ Ê $ $ $ $ Ê 9 7 $ 8 Step : $ Ê $, or $ Ê $ The value of which assures is the smaller value, 6 Step : k k $ Ê $ $ Ê $ $ Step : $ $ 759 Ê $ 009, or $ $ 9 Ê $ 09 The value of $ which assures k k $ Ê is the smaller value, $ 09 7 Step : k 5 k $ Ê $ 5 $ Ê $ 5 $ 5 Step : From the graph, $ 5 9 Ê $ 0, or $ 5 5 Ê $ 0; thus $ 0 in either case 8 Step : k ( ) k $ Ê $ $ Ê $ $ Step : From the graph, $ Ê $ 0, or $ 9 Ê $ 0; thus $ 0 9 Step : k k $ Ê $ $ Ê $ $ Step : From the graph, $ Ê $, or $ Ê $ ; thus $ 0 Step : k k $ Ê $ $ Ê $ $ Step : From the graph, $ 6 Ê $ 09, or $ Ê $ 0; thus $ 09 Step : k k $ Ê $ $ Ê $ $ Step : From the graph, $ È Ê $ È 0679, or $ È5 Ê $ È5 06; thus $ È5
14 70 Chapter Limits and Continuity Step : k ( ) k $ Ê $ $ Ê $ $ È 5 È 5 È È Step : From the graph, $ Ê $ 080, or $ Ê $ 00; thus $ È 5 Step : k ( ) k $ Ê $ $ Ê $ $ Step : From the graph, $ Ê $ 077, or $ Ê 06; thus $ 06 Step : Ê Ê $ $ $ $ $ Step : From the graph, $ 0 Ê $ , or $ 99 Ê $ ; thus $ Step : k( ) 5k 00 Ê k k 00 Ê Ê 99 0 Step : k k $ Ê $ $ Ê $ $ Ê $ 00 6 Step : k( ) ( 6) k 00 Ê k k 00 Ê Ê 0 98 Ê 0 99 Step : k ( ) k $ Ê $ $ Ê $ $ Ê $ 00 7 Step : ¹ È ¹ 0 Ê 0 È 0 Ê 09 È Ê 08 Ê 09 0 Step : k 0 k $ Ê $ $ Then, $!Þ* Ê $!Þ* or $!Þ; thus, $ 09 8 Step : È 0 0 È 0 0 È Ê Ê 06 Ê Step : Ê Ê $ $ $ $ $ Then, $ 06 Ê $ 009 or $ 06 Ê $ 0; thus $ Step : ¹ È9 $ ¹ Ê È9 $ Ê È9 % Ê 9 6 Ê % 9 6 Ê 5 or 5 Step : k 0 k $ Ê $ 0 $ Ê $ 0 $ 0 Then $ 0 Ê $ 7, or $ 0 5 Ê $ 5; thus $ 5 0 Step : ¹ È 7 ¹ Ê È 7 % Ê È 7 5 Ê Ê 6 Step : k k $ Ê $ $ Ê $ $ Then $ 6 Ê $ 7, or $ Ê $ 9; thus $ 7 Step : Ê Ê 0 0 Ê or 5 Step : k k $ Ê $ $ Ê $ $ 0 Then $ % or $, or $ 5 or $ ; thus $ Step : k k! Ê 0 0 Ê 9 Ê È9 È Step : ¹ È ¹ $ Ê $ È $ Ê $ È $ È Then $ È È9 Ê $ È È9 009, or $ È È Ê $ È È 0086; thus $ 0086
15 Section The Precise Definition of a Limit 7 Step : k k 05 Ê Ê 5 5 Ê È 5 kk È 5 Ê È 5 È 5, for near Step : k ( ) k $ Ê $ $ Ê $ $ Then $ È5 Ê $ È5 0, or $ È5 Ê $ È5 09; thus $ È5 0 Step : ( ) Ê 0 0 Ê 0 0 Ê 9 or 9 Step : k ( ) k $ Ê $ $ Ê $ $ Then $ Ê $, or $ Ê $ ; thus $ 5 Step : ka 5b k Ê k 6k Ê 6 Ê 5 7 Ê È5 È7 Step : k k $ Ê $ $ Ê $ % $ % Then $ %È5 Ê $ %È5 070, or $ %È7 Ê $ È7 % 0; thus $ È7 0 6 Step : Ê & Ê 6 Ê 0 6 Ê 0 0 or 0 0 Step : k k $ Ê $ $ Ê $ $ Then $ 0 Ê $, or $ 0 Ê $ 6; thus Ê $ 7 Step : km mk 00 Ê 00 m m 00 Ê 00 m m 00 m Ê m m Step : k k $ Ê $ $ Ê $ $ m m m m m Then $ Ê $, or $ Ê $ In either case, $ 8 Step : km mk c Ê c m m c Ê c m m c m Ê m Step : k k $ Ê $ $ Ê $ $ B $ $ c Then $ $ $ Ê $ c c, or $ $ $ Ê $ c In either case, $ c m m m m m 9 Step : (m b) ˆ m b m m m c c - Ê c m c Ê c m c Ê m m Step : Ê Ê $ $ $ $ $ c Then $ Ê $ c c, or $ Ê $ c In either case, $ c m m m m m 0 Step : k(m b) (m b) k 005 Ê 005 m m 005 Ê 005 m m 005 m Ê m m Step : k k $ Ê $ $ Ê $ $ m m m m m Then $ Ê $, or $ Ê $ In either case, $ lim ( ) () Ä Step : ka b( ) k 00 Ê Ê Ê 0 99 or 99 0 Step : 0 k k $ Ê $ $ Ê $ $ $ $ Then $ $ 99 Ê $ 00, or $ $ 0 Ê $ 00; thus $ 00 lim ( ) ( )( ) Ä Step : k( ) k 00 Ê Ê Ê c c m
16 7 Chapter Limits and Continuity Step : k ( ) k $ Ê $ $ Ê $ $ Then $ 0 Ê $ 00, or $ 099 Ê $ 00; thus $ 00 ( )( ) lim lim lim ( ), Ä Ä () Á Ä ( )( ) Step : ¹ Š ¹ 005 Ê 005 () % 005 Ê 95 05, Á Ê 95 05, Á Step : k k $ Ê $ $ Ê $ $ Then $ 95 Ê $ 005, or $ 05 Ê $ 005; thus $ ( 5)( ) lim lim lim ( ), 5 Ä& 5 Ä& (5) Á Ä& 65 ( 5)( ) Step : ¹ Š 5 ( ) ¹ 005 Ê 005 (5) 005 Ê 05 95, Á 5 Ê , Á 5 Step : k ( 5) k $ Ê $ 5 $ Ê $ & $ & Then $ &505 Ê $ 005, or $ &95 Ê $ 005; thus $ lim È 5 È 5( ) È6 Ä$ Step : ¹ È 5 ¹ 05 Ê 05 È 5 05 Ê 5 È 5 5 Ê Ê Ê 85 5 Step : k ( ) k $ Ê $ $ Ê $ $ $ $ Then $ $85 Ê $ 085, or $ $5 Ê 075; thus $ lim Ä Step : Ê 0 0 Ê 6 Ê 6 Ê 6 or Step : k k $ Ê $ $ Ê $ $ 5 Then $ Ê 5 $, or $ Ê $ ; thus $ 7 Step : k(9 ) 5k % Ê % % Ê % % Ê % % % Ê %% % Step : k k $ Ê $ $ Ê $ % $ % Then $ % Ê $ %, or $ % % % Ê $ % Thus choose $ % 8 Step : % % k( 7) k % Ê % 9 % Ê 9 % *% Ê Step : k k $ Ê $ $ Ê $ $ % Then $ $ Ê % % $, or $ Ê % % $ Thus choose $ 9 Step : ¹ È 5 ¹ % Ê % È 5 % Ê % È 5 % Ê (%) 5 (%) Ê (%) & (%) 5 Step : k 9 k $ Ê $ 9 $ Ê $ 9 $ 9 Then $ *% % % * Ê $ % % %, or $ *% % % * Ê $ % % % Thus choose the smaller distance, $ % % % 0 Step : ¹ È ¹ % Ê % È % Ê % È % Ê (%) % (%) Ê ( %) ( %) Ê ( %) % ( %) % Step : k 0 k $ Ê $ $
17 Section The Precise Definition of a Limit 7 Then $ ( %) % % % Ê $ % % %, or $ ( %) % % Thus choose the smaller distance, $ % % Step : For Á, k k % Ê % % Ê % % Ê È % kk È % Ê È% È % near B Step : k k $ Ê $ $ Ê $ $ Then $ È % Ê $ È %, or $ È% Ê $ È% Choose $ min š È % ßÈ %, that is, the smaller of the two distances Step : For Á, k k % Ê % % Ê % % Ê È % kk È % Ê È % È % near B Step : k ( ) k $ Ê $ $ Ê $ $ Then $ È%% Ê $ È%%, or $ È%% Ê $ È%% Choose $ min š È%% ß È%% Step : % Ê % % Ê % % Ê % % Step : k k $ Ê $ $ Ê $ $ Then $ Ê $ %, or $ Ê $ % Choose $ % % % % % % % %, the smaller of the two distances Step : % $ % % Ê % % Ê % % Ê Ê $% $% Ê É k k É, or É É for near È$ $ % $% $% $% Step : ¹ È ¹ $ Ê $ È $ Ê È$ È $ Then È È, or È $ É Ê $ É $ É Ê $ É È $% $% $% $% Choose $ min š È É ßÉ È $% $% * 5 Step : ¹ Š ( 6) ¹ % Ê % ( ) 6 %, Á Ê % % Ê % $ % $ Step : k ( ) k $ Ê $ $ Ê $ $ $ Then $ $% $ Ê $ %, or $ $% $ Ê $ % Choose $ % 6 Step : ¹ Š ¹ % Ê % ( ) %, Á Ê % % Step : k k $ Ê $ $ Ê $ $ Then $ % Ê $ %, or $ % Ê $ % Choose $ % % 7 Step : : l( ) l % Ê! % since Þ Thus,!; % : l(6 ) l % Ê! Ÿ 6 6 % since Thus, Ÿ 6 Step : k k $ Ê $ $ Ê $ $ % % % % % Then $ Ê $, or $ Ê $ Choose $ % 8 Step :!: k 0 k % Ê %! Ê 0; 0:! % Ê! Ÿ %
18 7 Chapter Limits and Continuity Step : k 0 k $ Ê $ $ % % % Then $ Ê $, or $ % Ê $ % Choose $ 9 By the figure, Ÿ sin Ÿ for all 0 and sin for 0 Since lim ( ) lim 0, Ä! Ä! then by the sandwich theorem, in either case, lim sin 0 Ä! 50 By the figure, Ÿ sin Ÿ for all ecept possibly at 0 Since lim a b lim 0, then Ä! Ä! by the sandwich theorem, lim sin 0 Ä! 5 As approaches the value 0, the values of g() approach k Thus for every number % 0, there eists a $! such that! k 0 k $ Ê kg() k k % 5 Write h c Then!lcl$ Í$ c $, Ác Í$ ah cbc $, h c Ác Í$ h $, h Á!Í!lh!l$ Thus, limf a b L Ífor any %!, there eists $! such that lf a b L l % whenever!lcl $ Äc ÍlfahcbL l % whenever!lh!l$ Ílim fah cb L 5 Let f() The function values do get closer to as approaches 0, but lim f() 0, not The Ä! function f() never gets arbitrarily close to for near 0 hä! 5 Let f() sin, L, and 0 There eists a value of (namely, ) for which sin % for any! 6 % Ä!!! Ä! given 0 However, lim sin 0, not The wrong statement does not require to be arbitrarily close to As another eample, let g() sin, L, and 0 We can choose infinitely many values of near 0 such that sin as you can see from the accompanying figure However, lim sin fails to eist The wrong statement does not require all values of arbitrarily close to! 0 to lie within % 0 of L Again you can see from the figure that there are also infinitely many values of near 0 such that sin 0 If we choose % we cannot satisfy the inequality sin % for all values of sufficiently near 0! 55 ka * k Ÿ 00 Ê 00 Ÿ ˆ 9 Ÿ 00 Ê 899 Ÿ Ÿ 90 Ê (899) Ÿ Ÿ (90) Ê É Ÿ Ÿ É or 8 Ÿ Ÿ 87 To be safe, the left endpoint was rounded up and the right endpoint was rounded down V 56 V RI Ê I Ê V R 0 Ÿ 0 Ê 0 Ÿ 5 Ÿ 0 Ê 9 Ÿ Ÿ 5 Ê Ê R R R R (0)(0) R (0)(0) 5 Ÿ Ÿ 9 Ê 5 Ÿ R Ÿ 8
19 To be safe, the left endpoint was rounded up and the right endpoint was rounded down Section The Precise Definition of a Limit (a) $ 0 Ê $ Ê f() Then kf() k k k That is, kf() k no matter how small $ is taken when $ Ê lim f() Á Ä 0 $ Ê $ Ê f() Then kf() k k( ) k kk That is, kf() k no matter how small $ is taken when $ Ê lim f() Á Ä (c) $! Ê $ Ê f() Then kf() 5k k 5k Also,! $ Ê $ Ê f() Then kf() 5 k k( ) 5k k 05k Thus, no matter how small $ is taken, there eists a value of such that $ $ but kf() 5 k Ê lim f() Á 5 Ä 58 (a) For $ Ê h() Ê kh() k Thus for %, kh() k % whenever $ no matter how small we choose $ 0 Ê lim h() Á Ä For $ Ê h() Ê kh() k Thus for %, kh() k % whenever $ no matter how small we choose $ 0 Ê lim h() Á Ä (c) For $ Ê h() so kh() k k k No matter how small $ 0 is chosen, is close to when is near and to the left on the real line Ê k kwill be close to Thus if %, kh() k % whenever $ no mater how small we choose $ 0 Ê lim h() Á Ä 59 (a) For $ Ê f() 8 Ê kf() k 08 Thus for % 08, kf() k % whenever $ no matter how small we choose $ 0 Ê lim f() Á Ä$ For $ Ê f() Ê kf() 8k 8 Thus for % 8, kf() 8 k % whenever $ no matter how small we choose $ 0 Ê lim f() Á 8 Ä$ (c) For $ Ê f() 8 Ê kf() k 8 Again, for % 8, kf() k % whenever $$ no matter how small we choose $ 0 Ê lim f() Á Ä$ 60 (a) No matter how small we choose $ 0, for near satisfying $ $, the values of g() are near Ê kg() kis near Then, for % we have kg() k for some satisfying $ $, or! k k $ Ê lim g() Á Ä Yes, lim g() because from the graph we can find a $! such that kg() k % if! k ( ) k $ Ä 6-66 Eample CAS commands (values of del may vary for a specified eps): Maple: f := -> (^-8)/(-);0 := ; plot( f(), =0-0+, color=black, (a) title=section, 6(a) ); L := limit( f(), =0 ); epsilon := 0; (c) plot( [f(),l-epsilon,l+epsilon], = , color=black, linestyle=[,,], title=section, 6(c) ); q := fsolve( abs( f()-l ) = epsilon, =0-0+ ); (d) delta := abs(0-q); plot( [f(),l-epsilon,l+epsilon], =0-delta0+delta, color=black, title=section, 6(d) ); for eps in [0, 0005, 000 ] do (e) q := fsolve( abs( f()-l ) = eps, =0-0+ );
20 76 Chapter Limits and Continuity delta := abs(0-q); head := sprintf(section, 6(e)\n epsilon = %5f, delta = %5f\n, eps, delta ); print(plot( [f(),l-eps,l+eps], =0-delta0+delta, color=black, linestyle=[,,], title=head )); end do: Mathematica (assigned function and values for 0, eps and del may vary): Clear[f, ] y: L eps; y: L eps; 0 ; f[_]: ( (7 )Sqrt[] 5)/( ) Plot[f[], {, 0 0, 0 0}] L: Limit[f[], Ä 0] eps 0; del 0; Plot[{f[], y, y},{, 0 del, 0 del}, PlotRange Ä {L eps, L eps}] ONE-SIDED LIMITS AND LIMITS AT INFINITY (a) True True (c) False (d) True (e) True (f) True (g) False (h) False (i) False (j) False (k) True (l) False (a) True False (c) False (d) True (e) True (f) True (g) True (h) True (i) True (j) False (k) True (a) lim f(), lim f() Ä b Ä c $ No, lim f() does not eist because lim f() lim f() Ä Ä b Á Ä c (c) lim f(), lim f() Ä% c Ä% b $ (d) Yes, lim f() because lim f() lim f() Ä% Ä% c Ä% b (a) lim f(), lim f(), f() Ä b Ä c $ Yes, lim f() because lim f() lim f() Ä Ä b Ä c (c) lim f() ( ), lim f() ( ) Ä c Ä b (d) Yes, lim f() because lim f() lim f() Ä Ä c Ä b 5 (a) No, lim f() does not eist since sin ˆ does not approach any single value as approaches 0 Ä! b lim f() lim 0 0 Ä! c Ä! c (c) lim f() does not eist because lim f() does not eist Ä! Ä! b 6 (a) Yes, lim g() 0 by the sandwich theorem since g() when 0 Ä! b È Ÿ Ÿ È No, lim g() does not eist since È is not defined for 0 Ä! c (c) No, lim g() does not eist since lim g() does not eist Ä! Ä! c
21 Section One-Sided Limits and Limits at Infinity 77 7 (a Ñ lim f() lim f() Ä c Ä b (c) Yes, lim f() since the right-hand and left-hand Ä limits eist and equal 8 (a) lim f() 0 lim f() Ä b Ä c (c) Yes, lim f() 0 since the right-hand and left-hand Ä limits eist and equal 0 9 (a) domain: 0 Ÿ Ÿ range: 0 y Ÿ and y lim f() eists for c belonging to Ä c (0ß ) (ß ) (c) (d) 0 0 (a) domain: range: Ÿ y Ÿ lim f() eists for c belonging to Ä c ( _ß ) ( ß ) (ß _) (c) none (d) none 05 / lim lim 0 Ä!Þ& c É É É È É É È 05 / Ä b! lim ˆ ˆ 5 ˆ () ˆ Ä b Š ( ) 5 ( ) ( ) lim ˆ ˆ 6 ˆ ˆ ˆ 6 ˆ ˆ ˆ 7 ˆ Ä c Èh h5è5 Èh h5è5 Èh h5è5 5 lim lim h Ä! b h Š h Ä! b h Š Èh h5è 5 ah h5b5 h(h ) 0 È È È5 È5 È5 lim lim h Ä! b hš Èh h5 5 h Ä! b hš Èh h5 5
22 78 Chapter Limits and Continuity È6 È5h h 6 È6 È5h h 6 È6 È5h h 6 6 lim lim h Ä! c h h Ä! c Š h Š È6 È 5h h 6 6 a5h h 6b h(5h ) (0 ) È È È6 È6 È6 lim lim h Ä! c h Š È6 5h h 6 h Ä! c h Š È6 5h h 6 kk () 7 (a) lim ( ) lim ( ) for Ä b Ä b ( ) ak k b lim ( ) ( ) Ä b k k ( ) lim ( ) lim ( ) ( ) for Ä c Ä c ( ) ak k b lim ( )( ) ( ) Ä c È ( ) È ( ) 8 (a) lim lim for Ä b k k Ä b () ak k b lim È È Ä b È ( ) È ( ) lim lim ( ) for Ä c k k Ä c () ak k b lim È È Ä c ÚÛ ) ÚÛ ) 9 (a) lim lim ) Ä$ b ) ) Ä$ c ) 0 (a) lim at ÚtÛb 0 lim t t t Ä% b t Ä% c a Ú Ûb È sin ) sin lim lim (where ) ) Ä! È ) Ä! È ) sin kt k sin kt k sin ) sin ) lim lim lim k lim k k (where kt) t Ä! t t Ä! kt ) Ä! ) ) Ä! ) ) sin y sin y sin y sin ) lim lim lim lim (where y) y Ä! y y Ä! y y Ä! y Ä! ) ) ) h h lim lim lim (where h) h Ä! c sin h ˆ h Ä! c sin h h Ä! c ˆ sin h Œ sin ) lim ) h ) Ä! c ) tan ˆ sin sin sin cos 5 lim lim lim lim lim Ä! Ä! Ä! cos Š Ä! cos Š Ä! t t t cos t 6 lim lim lim lim cos t t Ä! tan t t Ä! ˆ sin t t Ä! sin t Š Œ sin t t Ä! lim cos t tä! t csc 7 lim lim lim lim () Ä! cos 5 ˆ Ä! sin cos 5 Š Ä! sin Š Ä! cos 5 ˆ 6 cos 8 lim 6 (cot )(csc ) lim lim ˆ cos Ä! Ä! sin sin Ä! sin sin 9 lim lim ˆ lim ˆ lim Ä! Ä! Ä! Ä! lim Š lim ˆ sin lim Š ()() Ä! Ä! cos sin Ä! cos cos sin cos sin cos sin cos sin cos sin sin sin 0 lim lim 0 () 0 Ä! ˆ Ä! ˆ
23 sin( cos t) sin ) lim lim since cos t 0 as t 0 t Ä! cos t Ä Ä ) Ä! ) ) sin (sin h) sin ) lim lim since sin h 0 as h 0 h Ä! sin h Ä Ä ) Ä! ) ) sin ) sin ) ) sin ) ) lim lim lim ) Ä! sin ) ˆ ) Ä! sin ) ) ˆ ) Ä! ) sin ) lim lim ˆ lim ˆ Ä! Ä! Ä! sin 5 sin sin sin sin 5 5 sin 5 lim tan lim sin lim sin 8 Ä! sin 8 ˆ Ä! cos sin 8 ˆ Ä! cos sin 8 8 lim ˆ ˆ sin ˆ 8 8 Ä! cos sin sin y cot 5y sin y sin y cos 5y sin y sin y cos 5y 5y 6 lim lim lim y Ä! y cot y y Ä! y cos y sin 5y y Ä! Š y Š cos y Š sin 5y Š 5y lim y Ä! Š sin y Š sin y Š 5y Š cos 5y ˆ y y sin 5y cos y Section One-Sided Limits and Limits at Infinity 79 Note: In these eercises we use the result lim 0 whenever 0 This result follows immediately from Ä _ mn Î n Eample 6 and the power rule in Theorem 8: lim ˆ lim ˆ lim 0 0 Ä _ Ä _ Š Ä _ mn Î mn Î mn Î mn Î 7 (a) m 8 (a) 9 (a) 0 (a) (a) (a) sin sin Ÿ Ÿ Ê lim 0 by the Sandwich Theorem Ä_ cos ) cos ) ) Ÿ ) Ÿ ) Ê lim ) 0 by the Sandwich Theorem ) Ä_ tsin t ˆ sin t 00 t t 5 lim lim t Ä_ tcos t t Ä_ ˆ cos t 0 6 lim lim lim r Ä_ r 7 5 sin r r r Ä_ 5ˆ r Ä_ sin r t rsin r ˆ sin r 0 r r sin 7 e Ÿ e Ÿ e Ê lim e sin 0 by the Sandwich Theorem Ä_ 8 lim e cos 0 cos Ä_ a bˆ ˆ e e e e c c e 0 e e 9 lim lim lim lim Ä_ eec Ä_ e Ä_ e Ä_ e b 0 e e
24 80 Chapter Limits and Continuity e c 0 sin / 0 e 50 lim lim Ä_ a b sina/b Ä_ 5 (a) lim lim (same process as part (a)) Ä_ Ä_ Š $ $ 5 (a) lim lim Ä_ $ 7 7 Ä_ (same process as part (a)) $ 5 (a) lim lim 0 0 (same process as part (a)) Ä_ Ä_ (a) lim lim 0 0 (same process as part (a)) Ä_ Ä_ 7 7 $ 55 (a) lim lim 7 (same process as part (a)) Ä_ $ 6 6 ( Ä_ $ 56 (a) lim lim 0 (same process as part (a)) Ä_ $! Ä_ $ 0 0 & % ' 57 (a) lim lim 0 Ä_ ' Ä_ 0 (same process as part (a)) 9 9 $ $ % % 58 (a) lim lim Ä_ % 5 6 Ä_ 9 (same process as part (a)) $ 5 5 $ 59 (a) lim $ lim Ä_ Ä_ (same process as part (a)) % 60 (a) lim lim Ä_ % 7$ Ä_ (same process as part (a)) % È c Š Š È Š 7 Š Î Î Î 6 lim lim 0 6 lim lim Ä_ 7 Ä_ Ä_ È Ä_ $ & È È Š 6 lim Ä_ ÐÎ&Ñ cðî$ñ Î& $ & È È lim ÐÎ&Ñ cðî$ñ lim Ä_ Ä_ Š Î& c c% 6 lim c c$ lim Ä_ Ä 7 &Î$ Î$ *Î& )Î& 65 lim lim )Î& Ä_ È Ä Î& $Î& Î! 7 $ È5 66 lim Î$ lim Ä_ Ä_ 5 5 Î$ Î$
25 Section One-Sided Limits and Limits at Infinity 8 67 Yes If lim f() L lim f(), then lim f() L If lim f() lim f(), then lim f() does not ei Ä ab Ä ac Á Ä a Ä ab Ä ac st Ä a 68 Since lim f() L if and only if lim f() L and lim f() L, then lim f() can be found by calculating Ä c Ä cb Ä cc Ä c lim f() Ä c b 69 If f is an odd function of, then f( ) f() Given lim f(), then lim f() $ Ä! b Ä! c 70 If f is an even function of, then f( ) f() Given lim f() 7 then lim f() 7 However, nothing Ä c Ä b can be said about lim f() because we don't know lim f() Ä c Ä b f() 7 Yes If lim then the ratio of the polynomials' leading coefficients is, so lim as well Ä_ g() Ä_ g() 7 Yes, it can have a horizontal or oblique asymptote f() f() 7 At most horizontal asymptote: If lim L, then the ratio of the polynomials' leading coefficients is L, so Ä_ g() f() lim L as well Ä_ g() È a ba b È È 7 lim È È lim È È È lim Ä_ Ä_ È È Ä_ É É lim lim Ä_ È È Ä_ 75 For any % 0, take N Then for all N we have that kf() kk kk kk 0 % 76 For any % 0, take N Then for all y N we have that kf() kk kk kk 0 % È 77 I (5ß5 $ ) Ê 5 &$ Also, 5 % Ê 5 % Ê &% Choose $ % Ê lim È 5 0 Ä& b È 78 I (%$ ß% ) Ê %$ Also, % % Ê % % Ê %% Choose $ % Ê lim È % 0 Ä% c 79 As Ä 0 the number is always Thus, ¹ ( ) ¹ Ê kk % % Ê 0 % which is always true independent of the value of Hence we can choose any $ 0 with $! Ê lim Ä! c k k 80 Since Ä we have and k k Then, ¹ ¹ k k % Ê 0 % which is always true so long as Hence we can choose any $!, and thus $ Ê ¹ kk ¹ % Thus, lim kk Ä b 8 (a) lim ÚÛ 00 Just observe that if 00 0, then ÚÛ 00 Thus if we choose, we have for any Ä %!! b $ number %! that $ ÊlÚÛ00ll00 00 l!% lim 99 Just observe that if then 99 Thus if we choose, we have for any Ä %!! c ÚÛ ÚÛ $ number %! that 00 $ 00 ÊlÚÛ99ll99 99 l!%
26 8 Chapter Limits and Continuity (c) Since lim ÚÛÁ lim we conclude that lim does not eist Ä %!! b Ä %!! c ÚÛ ÚÛ Ä %!! 8 (a) lim f() lim È È0 0; È 0 % Ê % È % Ê! % for positive Choose $ % Ä! b Ä! b Ê lim f() 0 Ä! b lim f() lim sin 0 by the sandwich theorem since sin for all 0 Ä! c ˆ Ä! c Ÿ ˆ Ÿ Á Since k 0k k 0k whenever k k È, we choose È and obtain sin ˆ % % $ % 0 % if $ 0 (c) The function f has limit 0 at! 0 since both the right-hand and left-hand limits eist and equal 0 cos ) 8 lim sin lim sin, 8 lim lim, Ä _ Ä 0 Ä_ Ä! ) ) ) ˆ ) ˆ ) ) ) c t 85 lim lim lim, t Ä _ 5 Ä _ t Ä 0 5t ˆ 5 Î 86 lim ˆ z lim z, ˆ z Ä_ z Ä! b 87 lim ˆ ˆ cos lim ( )(cos ) ()(), ˆ Ä _ ) ) ) ) Ä 0 88 lim ˆ cos ˆ sin lim a cos b( sin ) (0 )( 0), ˆ Ä_ ) ) ) ) ) Ä! b 5 INFINITE LIMITS AND VERTICAL ASYMPTOTES cos positive positive lim lim Ä! b _ Š positive Ä! c _ Š positive lim lim Ä c _ Š Ä$ b _ Š positive 5 positive 5 lim 6 lim Ä) b 8 _ Š positive Ä& c 0 _ Š positive 7 lim 8 lim Ä( (7) _ Š positive Ä! () _ Š positive positive c 9 (a) lim lim Ä! b Î$ _ Ä! c 0 (a) lim lim Ä! b Î& _ Ä! Î$ Î& lim lim lim lim Ä! Î& Ä! Î& _ Ä! Î$ Ä! Î$ _ a b a b lim tan _ lim sec _ Ä ˆ c Ä ˆ c b 5 lim ( csc )) _ ) Ä! c 6 lim ( cot )) _ and lim ( cot ), so the limit does not eist ) Ä! b ) Ä! c ) _
27 Section 5 Infinite Limits and Vertical Asymptotes 8 7 (a) lim lim Ä b Ä b ()() _ Š positive positive lim lim Ä c Ä c ()() _ Š positive (c) lim lim Ä b Ä b ()() _ Š positive (d) lim lim Ä c Ä c ()() _ Š positive 8 (a) lim lim Ä b Ä b ()() _ Š positive positive positive lim lim Ä c Ä c ()() _ Š positive (c) lim lim Ä b Ä b ()() _ Š positive (d) lim lim Ä c Ä c ()() _ Š 9 (a) lim 0 lim Ä! b Ä! b _ Š lim 0 lim Ä! c Ä! c _ Š positive Î$ Î$ Î$ (c) lim 0 Ä $ È Î$ (d) lim Ä ˆ positive 0 (a) lim lim Ä b _ Š positive Ä c _ Š ( )( ) 0 (c) lim lim 0 Ä b Ä b (d) lim Ä! c positive ( )( ) (a) lim lim Ä! b $ Ä! b ( ) _ Š positive ( )( ) lim lim lim, Ä b $ Ä b () Ä b Á ( )( ) (c) lim lim lim, Ä c $ Ä c () Ä c Á ( )( ) (d) lim lim lim, Ä $ Ä () Ä Á ( )( ) (e) lim lim Ä! $ Ä! ( ) _ Š positive ( )( ) ( ) ( )( ) ( ) () 8 (a) lim $ lim lim Ä b Ä b Ä b ( )( ) ( ) lim lim lim Ä b $ Ä b ( )( ) Ä b ( ) _ Š positive ( )( ) ( ) (c) lim lim lim Ä 0c $ Ä! c ( )( ) Ä! c ( ) _ Š positive ( )( ) ( ) 0 (d) lim lim lim 0 Ä b $ Ä b ( )( ) Ä b ( ) ()() (e) lim Ä! b ( ) _ Š positive positive and lim Ä! c ( ) _ Š positive so the function has no limit as Ä 0 (a) lim lim _ t Ä! b t Ä! c _ tî$ tî$
CHAPTER 1 Limits and Their Properties
 CHAPTER Limits and Their Properties Section. A Preview of Calculus................... 305 Section. Finding Limits Graphically and Numerically....... 305 Section.3 Evaluating Limits Analytically...............
CHAPTER Limits and Their Properties Section. A Preview of Calculus................... 305 Section. Finding Limits Graphically and Numerically....... 305 Section.3 Evaluating Limits Analytically...............
236 Chapter 4 Applications of Derivatives
 26 Chapter Applications of Derivatives Î$ &Î$ Î$ 5 Î$ 0 "Î$ 5( 2) $È 26. (a) g() œ ( 5) œ 5 Ê g () œ œ Ê critical points at œ 2 and œ 0 Ê g œ ± )(, increasing on ( _ß 2) and (!ß _), decreasing on ( 2 ß!)!
26 Chapter Applications of Derivatives Î$ &Î$ Î$ 5 Î$ 0 "Î$ 5( 2) $È 26. (a) g() œ ( 5) œ 5 Ê g () œ œ Ê critical points at œ 2 and œ 0 Ê g œ ± )(, increasing on ( _ß 2) and (!ß _), decreasing on ( 2 ß!)!
C) 2 D) 4 E) 6. ? A) 0 B) 1 C) 1 D) The limit does not exist.
 . The asymptotes of the graph of the parametric equations = t, y = t t + are A) =, y = B) = only C) =, y = D) = only E) =, y =. What are the coordinates of the inflection point on the graph of y = ( +
. The asymptotes of the graph of the parametric equations = t, y = t t + are A) =, y = B) = only C) =, y = D) = only E) =, y =. What are the coordinates of the inflection point on the graph of y = ( +
Limits and Their Properties
 Chapter 1 Limits and Their Properties Course Number Section 1.1 A Preview of Calculus Objective: In this lesson you learned how calculus compares with precalculus. I. What is Calculus? (Pages 42 44) Calculus
Chapter 1 Limits and Their Properties Course Number Section 1.1 A Preview of Calculus Objective: In this lesson you learned how calculus compares with precalculus. I. What is Calculus? (Pages 42 44) Calculus
Chapter 5: Introduction to Limits
 Chapter 5: Introduction to Limits Lesson 5.. 5-. 3. Decreases 4. Decreases 5. y = 5-3. a. y = k b. 3 = k! 3 4 = k c. y = 3 4!("3) # y = 3 4! 9 = 7 4 y = 3 4 Review and Preview 5.. 5-4. f () = f () = 5-5.
Chapter 5: Introduction to Limits Lesson 5.. 5-. 3. Decreases 4. Decreases 5. y = 5-3. a. y = k b. 3 = k! 3 4 = k c. y = 3 4!("3) # y = 3 4! 9 = 7 4 y = 3 4 Review and Preview 5.. 5-4. f () = f () = 5-5.
130 Chapter 3 Differentiation
 0 Capter Differentiation 20. (a) (b) 2. C position, A velocity, an B acceleration. Neiter A nor C can be te erivative of B because B's erivative is constant. Grap C cannot be te erivative of A eiter, because
0 Capter Differentiation 20. (a) (b) 2. C position, A velocity, an B acceleration. Neiter A nor C can be te erivative of B because B's erivative is constant. Grap C cannot be te erivative of A eiter, because
Chapter 2 Limits and Continuity
 4 Section. Capter Limits and Continuity Section. Rates of Cange and Limits (pp. 6) Quick Review.. f () ( ) () 4 0. f () 4( ) 4. f () sin sin 0 4. f (). 4 4 4 6. c c c 7. 8. c d d c d d c d c 9. 8 ( )(
4 Section. Capter Limits and Continuity Section. Rates of Cange and Limits (pp. 6) Quick Review.. f () ( ) () 4 0. f () 4( ) 4. f () sin sin 0 4. f (). 4 4 4 6. c c c 7. 8. c d d c d d c d c 9. 8 ( )(
In this note we will evaluate the limits of some indeterminate forms using L Hôpital s Rule. Indeterminate Forms and 0 0. f(x)
 L Hôpital s Rule In this note we will evaluate the its of some indeterminate forms using L Hôpital s Rule. Indeterminate Forms and 0 0 f() Suppose a f() = 0 and a g() = 0. Then a g() the indeterminate
L Hôpital s Rule In this note we will evaluate the its of some indeterminate forms using L Hôpital s Rule. Indeterminate Forms and 0 0 f() Suppose a f() = 0 and a g() = 0. Then a g() the indeterminate
CHAPTER 2 Limits and Their Properties
 CHAPTER Limits and Their Properties Section. A Preview of Calculus...5 Section. Finding Limits Graphically and Numerically...5 Section. Section. Evaluating Limits Analytically...5 Continuity and One-Sided
CHAPTER Limits and Their Properties Section. A Preview of Calculus...5 Section. Finding Limits Graphically and Numerically...5 Section. Section. Evaluating Limits Analytically...5 Continuity and One-Sided
Chapter 2. Limits and Continuity 16( ) 16( 9) = = 001. Section 2.1 Rates of Change and Limits (pp ) Quick Review 2.1
 Capter Limits and Continuity Section. Rates of Cange and Limits (pp. 969) Quick Review..... f ( ) ( ) ( ) 0 ( ) f ( ) f ( ) sin π sin π 0 f ( ). < < < 6. < c c < < c 7. < < < < < 8. 9. 0. c < d d < c
Capter Limits and Continuity Section. Rates of Cange and Limits (pp. 969) Quick Review..... f ( ) ( ) ( ) 0 ( ) f ( ) f ( ) sin π sin π 0 f ( ). < < < 6. < c c < < c 7. < < < < < 8. 9. 0. c < d d < c
668 Chapter 11 Parametric Equatins and Polar Coordinates
 668 Chapter Parametric Equatins and Polar Coordinates 5. sin ( sin Á r and sin ( sin Á r Ê not symmetric about the x-axis; sin ( sin r Ê symmetric about the y-axis; therefore not symmetric about the origin
668 Chapter Parametric Equatins and Polar Coordinates 5. sin ( sin Á r and sin ( sin Á r Ê not symmetric about the x-axis; sin ( sin r Ê symmetric about the y-axis; therefore not symmetric about the origin
Directions: Please read questions carefully. It is recommended that you do the Short Answer Section prior to doing the Multiple Choice.
 AP Calculus AB SUMMER ASSIGNMENT Multiple Choice Section Directions: Please read questions carefully It is recommended that you do the Short Answer Section prior to doing the Multiple Choice Show all work
AP Calculus AB SUMMER ASSIGNMENT Multiple Choice Section Directions: Please read questions carefully It is recommended that you do the Short Answer Section prior to doing the Multiple Choice Show all work
MATH140 Exam 2 - Sample Test 1 Detailed Solutions
 www.liontutors.com 1. D. reate a first derivative number line MATH140 Eam - Sample Test 1 Detailed Solutions cos -1 0 cos -1 cos 1 cos 1/ p + æp ö p æp ö ç è 4 ø ç è ø.. reate a second derivative number
www.liontutors.com 1. D. reate a first derivative number line MATH140 Eam - Sample Test 1 Detailed Solutions cos -1 0 cos -1 cos 1 cos 1/ p + æp ö p æp ö ç è 4 ø ç è ø.. reate a second derivative number
SEE and DISCUSS the pictures on pages in your text. Key picture:
 Math 6 Notes 1.1 A PREVIEW OF CALCULUS There are main problems in calculus: 1. Finding a tangent line to a curve though a point on the curve.. Finding the area under a curve on some interval. SEE and DISCUSS
Math 6 Notes 1.1 A PREVIEW OF CALCULUS There are main problems in calculus: 1. Finding a tangent line to a curve though a point on the curve.. Finding the area under a curve on some interval. SEE and DISCUSS
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
An Intro to Limits Sketch to graph of 3
 Limits and Their Properties A Preview of Calculus Objectives: Understand what calculus is and how it compares with precalculus.understand that the tangent line problem is basic to calculus. Understand
Limits and Their Properties A Preview of Calculus Objectives: Understand what calculus is and how it compares with precalculus.understand that the tangent line problem is basic to calculus. Understand
698 Chapter 11 Parametric Equations and Polar Coordinates
 698 Chapter Parametric Equations and Polar Coordinates 67. 68. 69. 70. 7. 7. 7. 7. Chapter Practice Eercises 699 75. (a Perihelion a ae a( e, Aphelion ea a a( e ( Planet Perihelion Aphelion Mercur 0.075
698 Chapter Parametric Equations and Polar Coordinates 67. 68. 69. 70. 7. 7. 7. 7. Chapter Practice Eercises 699 75. (a Perihelion a ae a( e, Aphelion ea a a( e ( Planet Perihelion Aphelion Mercur 0.075
The main way we switch from pre-calc. to calc. is the use of a limit process. Calculus is a "limit machine".
 A Preview of Calculus Limits and Their Properties Objectives: Understand what calculus is and how it compares with precalculus. Understand that the tangent line problem is basic to calculus. Understand
A Preview of Calculus Limits and Their Properties Objectives: Understand what calculus is and how it compares with precalculus. Understand that the tangent line problem is basic to calculus. Understand
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
Math Exam 1a. c) lim tan( 3x. 2) Calculate the derivatives of the following. DON'T SIMPLIFY! d) s = t t 3t
 Math 111 - Eam 1a 1) Evaluate the following limits: 7 3 1 4 36 a) lim b) lim 5 1 3 6 + 4 c) lim tan( 3 ) + d) lim ( ) 100 1+ h 1 h 0 h ) Calculate the derivatives of the following. DON'T SIMPLIFY! a) y
Math 111 - Eam 1a 1) Evaluate the following limits: 7 3 1 4 36 a) lim b) lim 5 1 3 6 + 4 c) lim tan( 3 ) + d) lim ( ) 100 1+ h 1 h 0 h ) Calculate the derivatives of the following. DON'T SIMPLIFY! a) y
Things to remember: x n a 1. x + a 0. x n + a n-1. P(x) = a n. Therefore, lim g(x) = 1. EXERCISE 3-2
 lim f() = lim (0.8-0.08) = 0, " "!10!10 lim f() = lim 0 = 0.!10!10 Therefore, lim f() = 0.!10 lim g() = lim (0.8 - "!10!10 0.042-3) = 1, " lim g() = lim 1 = 1.!10!0 Therefore, lim g() = 1.!10 EXERCISE
lim f() = lim (0.8-0.08) = 0, " "!10!10 lim f() = lim 0 = 0.!10!10 Therefore, lim f() = 0.!10 lim g() = lim (0.8 - "!10!10 0.042-3) = 1, " lim g() = lim 1 = 1.!10!0 Therefore, lim g() = 1.!10 EXERCISE
Set 3: Limits of functions:
 Set 3: Limits of functions: A. The intuitive approach (.): 1. Watch the video at: https://www.khanacademy.org/math/differential-calculus/it-basics-dc/formal-definition-of-its-dc/v/itintuition-review. 3.
Set 3: Limits of functions: A. The intuitive approach (.): 1. Watch the video at: https://www.khanacademy.org/math/differential-calculus/it-basics-dc/formal-definition-of-its-dc/v/itintuition-review. 3.
Summer Review Packet for Students Entering AP Calculus BC. Complex Fractions
 Summer Review Packet for Students Entering AP Calculus BC Comple Fractions When simplifying comple fractions, multiply by a fraction equal to 1 which has a numerator and denominator composed of the common
Summer Review Packet for Students Entering AP Calculus BC Comple Fractions When simplifying comple fractions, multiply by a fraction equal to 1 which has a numerator and denominator composed of the common
Limits and Continuous Functions. 2.2 Introduction to Limits. We first interpret limits loosely. We write. lim f(x) = L
 2 Limits and Continuous Functions 2.2 Introduction to Limits We first interpret limits loosel. We write lim f() = L and sa the limit of f() as approaches c, equals L if we can make the values of f() arbitraril
2 Limits and Continuous Functions 2.2 Introduction to Limits We first interpret limits loosel. We write lim f() = L and sa the limit of f() as approaches c, equals L if we can make the values of f() arbitraril
2.1 Limits, Rates of Change and Slopes of Tangent Lines
 2.1 Limits, Rates of Change and Slopes of Tangent Lines (1) Average rate of change of y f x over an interval x 0,x 1 : f x 1 f x 0 x 1 x 0 Instantaneous rate of change of f x at x x 0 : f x lim 1 f x 0
2.1 Limits, Rates of Change and Slopes of Tangent Lines (1) Average rate of change of y f x over an interval x 0,x 1 : f x 1 f x 0 x 1 x 0 Instantaneous rate of change of f x at x x 0 : f x lim 1 f x 0
Chapter 2: Functions, Limits and Continuity
 Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
1969 AP Calculus BC: Section I
 969 AP Calculus BC: Section I 9 Minutes No Calculator Note: In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e).. t The asymptotes of the graph of the parametric
969 AP Calculus BC: Section I 9 Minutes No Calculator Note: In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e).. t The asymptotes of the graph of the parametric
With topics from Algebra and Pre-Calculus to
 With topics from Algebra and Pre-Calculus to get you ready to the AP! (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the
With topics from Algebra and Pre-Calculus to get you ready to the AP! (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
Review Exercises for Chapter 2
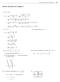 Review Eercises for Chapter 367 Review Eercises for Chapter. f 1 1 f f f lim lim 1 1 1 1 lim 1 1 1 1 lim 1 1 lim lim 1 1 1 1 1 1 1 1 1 4. 8. f f f f lim lim lim lim lim f 4, 1 4, if < if (a) Nonremovable
Review Eercises for Chapter 367 Review Eercises for Chapter. f 1 1 f f f lim lim 1 1 1 1 lim 1 1 1 1 lim 1 1 lim lim 1 1 1 1 1 1 1 1 1 4. 8. f f f f lim lim lim lim lim f 4, 1 4, if < if (a) Nonremovable
Calculus - Chapter 2 Solutions
 Calculus - Chapter Solutions. a. See graph at right. b. The velocity is decreasing over the entire interval. It is changing fastest at the beginning and slowest at the end. c. A = (95 + 85)(5) = 450 feet
Calculus - Chapter Solutions. a. See graph at right. b. The velocity is decreasing over the entire interval. It is changing fastest at the beginning and slowest at the end. c. A = (95 + 85)(5) = 450 feet
Chapter 8: More on Limits
 Chapter 8: More on Limits Lesson 8.. 8-. a. 000 lim a() = lim = 0 b. c. lim c() = lim 3 +7 = 3 +000 lim b( ) 3 lim( 0000 ) = # = " 8-. a. lim 0 = " b. lim (#0.5 ) = # lim c. lim 4 = lim 4(/ ) = " d. lim
Chapter 8: More on Limits Lesson 8.. 8-. a. 000 lim a() = lim = 0 b. c. lim c() = lim 3 +7 = 3 +000 lim b( ) 3 lim( 0000 ) = # = " 8-. a. lim 0 = " b. lim (#0.5 ) = # lim c. lim 4 = lim 4(/ ) = " d. lim
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 78 Section. Rolle s Theorem and the Mean Value Theorem. 8 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 78 Section. Rolle s Theorem and the Mean Value Theorem. 8 Section. Increasing and Decreasing Functions and the First
Math 261 Final Exam - Practice Problem Solutions. 1. A function f is graphed below.
 Math Final Eam - Practice Problem Solutions. A function f is graphed below. f() 8 7 7 8 (a) Find f(), f( ), f(), and f() f() = ;f( ).;f() is undefined; f() = (b) Find the domain and range of f Domain:
Math Final Eam - Practice Problem Solutions. A function f is graphed below. f() 8 7 7 8 (a) Find f(), f( ), f(), and f() f() = ;f( ).;f() is undefined; f() = (b) Find the domain and range of f Domain:
Calculus I. 1. Limits and Continuity
 2301107 Calculus I 1. Limits and Continuity Outline 1.1. Limits 1.1.1 Motivation:Tangent 1.1.2 Limit of a function 1.1.3 Limit laws 1.1.4 Mathematical definition of a it 1.1.5 Infinite it 1.1. Continuity
2301107 Calculus I 1. Limits and Continuity Outline 1.1. Limits 1.1.1 Motivation:Tangent 1.1.2 Limit of a function 1.1.3 Limit laws 1.1.4 Mathematical definition of a it 1.1.5 Infinite it 1.1. Continuity
EQ: What are limits, and how do we find them? Finite limits as x ± Horizontal Asymptote. Example Horizontal Asymptote
 Finite limits as x ± The symbol for infinity ( ) does not represent a real number. We use to describe the behavior of a function when the values in its domain or range outgrow all finite bounds. For example,
Finite limits as x ± The symbol for infinity ( ) does not represent a real number. We use to describe the behavior of a function when the values in its domain or range outgrow all finite bounds. For example,
AP Calculus AB/IB Math SL2 Unit 1: Limits and Continuity. Name:
 AP Calculus AB/IB Math SL Unit : Limits and Continuity Name: Block: Date:. A bungee jumper dives from a tower at time t = 0. Her height h (in feet) at time t (in seconds) is given by the graph below. In
AP Calculus AB/IB Math SL Unit : Limits and Continuity Name: Block: Date:. A bungee jumper dives from a tower at time t = 0. Her height h (in feet) at time t (in seconds) is given by the graph below. In
Slopes and Rates of Change
 Slopes and Rates of Change If a particle is moving in a straight line at a constant velocity, then the graph of the function of distance versus time is as follows s s = f(t) t s s t t = average velocity
Slopes and Rates of Change If a particle is moving in a straight line at a constant velocity, then the graph of the function of distance versus time is as follows s s = f(t) t s s t t = average velocity
All work must be shown in this course for full credit. Unsupported answers may receive NO credit.
 AP Calculus.1 Worksheet Day 1 All work must be shown in this course for full credit. Unsupported answers may receive NO credit. 1. The only way to guarantee the eistence of a it is to algebraically prove
AP Calculus.1 Worksheet Day 1 All work must be shown in this course for full credit. Unsupported answers may receive NO credit. 1. The only way to guarantee the eistence of a it is to algebraically prove
Answer Key 1973 BC 1969 BC 24. A 14. A 24. C 25. A 26. C 27. C 28. D 29. C 30. D 31. C 13. C 12. D 12. E 3. A 32. B 27. E 34. C 14. D 25. B 26.
 Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
Pre-Calculus Mathematics Limit Process Calculus
 NOTES : LIMITS AND DERIVATIVES Name: Date: Period: Mrs. Nguyen s Initial: LESSON.1 THE TANGENT AND VELOCITY PROBLEMS Pre-Calculus Mathematics Limit Process Calculus The type of it that is used to find
NOTES : LIMITS AND DERIVATIVES Name: Date: Period: Mrs. Nguyen s Initial: LESSON.1 THE TANGENT AND VELOCITY PROBLEMS Pre-Calculus Mathematics Limit Process Calculus The type of it that is used to find
MATH section 3.4 Curve Sketching Page 1 of 29
 MATH section. Curve Sketching Page of 9 The step by step procedure below is for regular rational and polynomial functions. If a function contains radical or trigonometric term, then proceed carefully because
MATH section. Curve Sketching Page of 9 The step by step procedure below is for regular rational and polynomial functions. If a function contains radical or trigonometric term, then proceed carefully because
3.5 Continuity of a Function One Sided Continuity Intermediate Value Theorem... 23
 Chapter 3 Limit and Continuity Contents 3. Definition of Limit 3 3.2 Basic Limit Theorems 8 3.3 One sided Limit 4 3.4 Infinite Limit, Limit at infinity and Asymptotes 5 3.4. Infinite Limit and Vertical
Chapter 3 Limit and Continuity Contents 3. Definition of Limit 3 3.2 Basic Limit Theorems 8 3.3 One sided Limit 4 3.4 Infinite Limit, Limit at infinity and Asymptotes 5 3.4. Infinite Limit and Vertical
Chapter 2 Section 3. Partial Derivatives
 Chapter Section 3 Partial Derivatives Deinition. Let be a unction o two variables and. The partial derivative o with respect to is the unction, denoted b D1 1 such that its value at an point (,) in the
Chapter Section 3 Partial Derivatives Deinition. Let be a unction o two variables and. The partial derivative o with respect to is the unction, denoted b D1 1 such that its value at an point (,) in the
Topics from Algebra and Pre-Calculus. (Key contains solved problems)
 Topics from Algebra and Pre-Calculus (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the calculator, except on p. (8) and
Topics from Algebra and Pre-Calculus (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the calculator, except on p. (8) and
THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION March, 2005
 THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION March, 5 Time: 3 1 hours No aids or calculators permitted. It is not necessary to do all the problems. Complete solutions to fewer problems
THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION March, 5 Time: 3 1 hours No aids or calculators permitted. It is not necessary to do all the problems. Complete solutions to fewer problems
Lecture Notes for Math 1000
 Lecture Notes for Math 1000 Dr. Xiang-Sheng Wang Memorial University of Newfoundland Office: HH-2016, Phone: 864-4321 Office hours: 13:00-15:00 Wednesday, 12:00-13:00 Friday Email: swang@mun.ca Course
Lecture Notes for Math 1000 Dr. Xiang-Sheng Wang Memorial University of Newfoundland Office: HH-2016, Phone: 864-4321 Office hours: 13:00-15:00 Wednesday, 12:00-13:00 Friday Email: swang@mun.ca Course
MATH section 3.1 Maximum and Minimum Values Page 1 of 7
 MATH section. Maimum and Minimum Values Page of 7 Definition : Let c be a number in the domain D of a function f. Then c ) is the Absolute maimum value of f on D if ) c f() for all in D. Absolute minimum
MATH section. Maimum and Minimum Values Page of 7 Definition : Let c be a number in the domain D of a function f. Then c ) is the Absolute maimum value of f on D if ) c f() for all in D. Absolute minimum
10.1 COMPOSITION OF FUNCTIONS
 0. COMPOSITION OF FUNCTIONS Composition of Functions The function f(g(t)) is said to be a composition of f with g. The function f(g(t)) is defined by using the output of the function g as the input to
0. COMPOSITION OF FUNCTIONS Composition of Functions The function f(g(t)) is said to be a composition of f with g. The function f(g(t)) is defined by using the output of the function g as the input to
THS Step By Step Calculus Chapter 1
 Name: Class Period: Throughout this packet there will be blanks you are epected to fill in prior to coming to class. This packet follows your Larson Tetbook. Do NOT throw away! Keep in 3 ring binder until
Name: Class Period: Throughout this packet there will be blanks you are epected to fill in prior to coming to class. This packet follows your Larson Tetbook. Do NOT throw away! Keep in 3 ring binder until
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
C H A P T E R 9 Topics in Analytic Geometry
 C H A P T E R Topics in Analtic Geometr Section. Circles and Parabolas.................... 77 Section. Ellipses........................... 7 Section. Hperbolas......................... 7 Section. Rotation
C H A P T E R Topics in Analtic Geometr Section. Circles and Parabolas.................... 77 Section. Ellipses........................... 7 Section. Hperbolas......................... 7 Section. Rotation
Section 1.3 Functions and Their Graphs 19
 23. 0 1 2 24. 0 1 2 y 0 1 0 y 1 0 0 Section 1.3 Functions and Their Graphs 19 3, Ÿ 1, 0 25. y œ 26. y œ œ 2, 1 œ, 0 Ÿ " 27. (a) Line through a!ß! band a"ß " b: y œ Line through a"ß " band aß! b: y œ 2,
23. 0 1 2 24. 0 1 2 y 0 1 0 y 1 0 0 Section 1.3 Functions and Their Graphs 19 3, Ÿ 1, 0 25. y œ 26. y œ œ 2, 1 œ, 0 Ÿ " 27. (a) Line through a!ß! band a"ß " b: y œ Line through a"ß " band aß! b: y œ 2,
Chapter 2 Differentiation. 2.1 Tangent Lines and Their Slopes. Calculus: A Complete Course, 8e Chapter 2: Differentiation
 Chapter 2 Differentiation 2.1 Tangent Lines and Their Slopes 1) Find the slope of the tangent line to the curve y = 4x x 2 at the point (-1, 0). A) -1 2 C) 6 D) 2 1 E) -2 2) Find the equation of the tangent
Chapter 2 Differentiation 2.1 Tangent Lines and Their Slopes 1) Find the slope of the tangent line to the curve y = 4x x 2 at the point (-1, 0). A) -1 2 C) 6 D) 2 1 E) -2 2) Find the equation of the tangent
Review: Limits of Functions - 10/7/16
 Review: Limits of Functions - 10/7/16 1 Right and Left Hand Limits Definition 1.0.1 We write lim a f() = L to mean that the function f() approaches L as approaches a from the left. We call this the left
Review: Limits of Functions - 10/7/16 1 Right and Left Hand Limits Definition 1.0.1 We write lim a f() = L to mean that the function f() approaches L as approaches a from the left. We call this the left
Summer AP Assignment Coversheet Falls Church High School
 Summer AP Assignment Coversheet Falls Church High School Course: AP Calculus AB Teacher Name/s: Veronica Moldoveanu, Ethan Batterman Assignment Title: AP Calculus AB Summer Packet Assignment Summary/Purpose:
Summer AP Assignment Coversheet Falls Church High School Course: AP Calculus AB Teacher Name/s: Veronica Moldoveanu, Ethan Batterman Assignment Title: AP Calculus AB Summer Packet Assignment Summary/Purpose:
October 27, 2018 MAT186 Week 3 Justin Ko. We use the following notation to describe the limiting behavior of functions.
 October 27, 208 MAT86 Week 3 Justin Ko Limits. Intuitive Definitions of Limits We use the following notation to describe the iting behavior of functions.. (Limit of a Function A it is written as f( = L
October 27, 208 MAT86 Week 3 Justin Ko Limits. Intuitive Definitions of Limits We use the following notation to describe the iting behavior of functions.. (Limit of a Function A it is written as f( = L
Indeterminate Forms and L Hospital s Rule
 APPLICATIONS OF DIFFERENTIATION Indeterminate Forms and L Hospital s Rule In this section, we will learn: How to evaluate functions whose values cannot be found at certain points. INDETERMINATE FORM TYPE
APPLICATIONS OF DIFFERENTIATION Indeterminate Forms and L Hospital s Rule In this section, we will learn: How to evaluate functions whose values cannot be found at certain points. INDETERMINATE FORM TYPE
AP Calculus AB Chapter 1 Limits
 AP Calculus AB Chapter Limits SY: 206 207 Mr. Kunihiro . Limits Numerical & Graphical Show all of your work on ANOTHER SHEET of FOLDER PAPER. In Exercises and 2, a stone is tossed vertically into the air
AP Calculus AB Chapter Limits SY: 206 207 Mr. Kunihiro . Limits Numerical & Graphical Show all of your work on ANOTHER SHEET of FOLDER PAPER. In Exercises and 2, a stone is tossed vertically into the air
Calculus I Exam 1 Review Fall 2016
 Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
211 Real Analysis. f (x) = x2 1. x 1. x 2 1
 Part. Limits of functions. Introduction 2 Real Analysis Eample. What happens to f : R \ {} R, given by f () = 2,, as gets close to? If we substitute = we get f () = 0 which is undefined. Instead we 0 might
Part. Limits of functions. Introduction 2 Real Analysis Eample. What happens to f : R \ {} R, given by f () = 2,, as gets close to? If we substitute = we get f () = 0 which is undefined. Instead we 0 might
AP Calculus I Summer Packet
 AP Calculus I Summer Packet This will be your first grade of AP Calculus and due on the first day of class. Please turn in ALL of your work and the attached completed answer sheet. I. Intercepts The -intercept
AP Calculus I Summer Packet This will be your first grade of AP Calculus and due on the first day of class. Please turn in ALL of your work and the attached completed answer sheet. I. Intercepts The -intercept
CLEP Calculus. Time 60 Minutes 45 Questions. For each question below, choose the best answer from the choices given. 2. If f(x) = 3x, then f (x) =
 CLEP Calculus Time 60 Minutes 5 Questions For each question below, choose the best answer from the choices given. 7. lim 5 + 5 is (A) 7 0 (C) 7 0 (D) 7 (E) Noneistent. If f(), then f () (A) (C) (D) (E)
CLEP Calculus Time 60 Minutes 5 Questions For each question below, choose the best answer from the choices given. 7. lim 5 + 5 is (A) 7 0 (C) 7 0 (D) 7 (E) Noneistent. If f(), then f () (A) (C) (D) (E)
CHAPTER 8 Quadratic Equations, Functions, and Inequalities
 CHAPTER Quadratic Equations, Functions, and Inequalities Section. Solving Quadratic Equations: Factoring and Special Forms..................... 7 Section. Completing the Square................... 9 Section.
CHAPTER Quadratic Equations, Functions, and Inequalities Section. Solving Quadratic Equations: Factoring and Special Forms..................... 7 Section. Completing the Square................... 9 Section.
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Fall, 2016, WEEK 4 JoungDong Kim Week4 Section 2.6, 2.7, 3.1 Limits at infinity, Velocity, Differentiation Section 2.6 Limits at Infinity; Horizontal Asymptotes Definition.
MATH 151 Engineering Mathematics I Fall, 2016, WEEK 4 JoungDong Kim Week4 Section 2.6, 2.7, 3.1 Limits at infinity, Velocity, Differentiation Section 2.6 Limits at Infinity; Horizontal Asymptotes Definition.
Calculus I Sample Exam #01
 Calculus I Sample Exam #01 1. Sketch the graph of the function and define the domain and range. 1 a) f( x) 3 b) g( x) x 1 x c) hx ( ) x x 1 5x6 d) jx ( ) x x x 3 6 . Evaluate the following. a) 5 sin 6
Calculus I Sample Exam #01 1. Sketch the graph of the function and define the domain and range. 1 a) f( x) 3 b) g( x) x 1 x c) hx ( ) x x 1 5x6 d) jx ( ) x x x 3 6 . Evaluate the following. a) 5 sin 6
QUIZ ON CHAPTERS 1 AND 2 - SOLUTIONS REVIEW / LIMITS AND CONTINUITY; MATH 150 SPRING 2017 KUNIYUKI 105 POINTS TOTAL, BUT 100 POINTS = 100%
 QUIZ ON CHAPTERS AND 2 - SOLUTIONS REVIEW / LIMITS AND CONTINUITY; MATH 50 SPRING 207 KUNIYUKI 05 POINTS TOTAL, BUT 00 POINTS = 00% ) For a), b), and c) below, bo in the correct answer. (6 points total;
QUIZ ON CHAPTERS AND 2 - SOLUTIONS REVIEW / LIMITS AND CONTINUITY; MATH 50 SPRING 207 KUNIYUKI 05 POINTS TOTAL, BUT 00 POINTS = 00% ) For a), b), and c) below, bo in the correct answer. (6 points total;
McKinney High School AP Calculus Summer Packet
 McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
Find the indicated derivative. 1) Find y(4) if y = 3 sin x. A) y(4) = 3 cos x B) y(4) = 3 sin x C) y(4) = - 3 cos x D) y(4) = - 3 sin x
 Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
dx dx x sec tan d 1 4 tan 2 2 csc d 2 ln 2 x 2 5x 6 C 2 ln 2 ln x ln x 3 x 2 C Now, suppose you had observed that x 3
 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial fraction decomposition with
CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial fraction decomposition with
APPLICATIONS OF DIFFERENTIATION
 4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION 4.4 Indeterminate Forms and L Hospital s Rule In this section, we will learn: How to evaluate functions whose values cannot be found at
4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION 4.4 Indeterminate Forms and L Hospital s Rule In this section, we will learn: How to evaluate functions whose values cannot be found at
Copyright 2012 Pearson Education, Inc. Publishing as Prentice Hall.
 Chapter 5 Review 95 (c) f( ) f ( 7) ( 7) 7 6 + ( 6 7) 7 6. 96 Chapter 5 Review Eercises (pp. 60 6). y y ( ) + ( )( ) + ( ) The first derivative has a zero at. 6 Critical point value: y 9 Endpoint values:
Chapter 5 Review 95 (c) f( ) f ( 7) ( 7) 7 6 + ( 6 7) 7 6. 96 Chapter 5 Review Eercises (pp. 60 6). y y ( ) + ( )( ) + ( ) The first derivative has a zero at. 6 Critical point value: y 9 Endpoint values:
Summer AP Assignment Coversheet Falls Church High School
 Summer AP Assignment Coversheet Falls Church High School Course: AP Calculus AB Teacher Name/s: Veronica Moldoveanu, Ethan Batterman Assignment Title: AP Calculus AB Summer Packet Assignment Summary/Purpose:
Summer AP Assignment Coversheet Falls Church High School Course: AP Calculus AB Teacher Name/s: Veronica Moldoveanu, Ethan Batterman Assignment Title: AP Calculus AB Summer Packet Assignment Summary/Purpose:
Calculus Problem Sheet Prof Paul Sutcliffe. 2. State the domain and range of each of the following functions
 f() 8 6 4 8 6-3 - - 3 4 5 6 f().9.8.7.6.5.4.3.. -4-3 - - 3 f() 7 6 5 4 3-3 - - Calculus Problem Sheet Prof Paul Sutcliffe. By applying the vertical line test, or otherwise, determine whether each of the
f() 8 6 4 8 6-3 - - 3 4 5 6 f().9.8.7.6.5.4.3.. -4-3 - - 3 f() 7 6 5 4 3-3 - - Calculus Problem Sheet Prof Paul Sutcliffe. By applying the vertical line test, or otherwise, determine whether each of the
Partial Fractions. dx dx x sec tan d 1 4 tan 2. 2 csc d. csc cot C. 2x 5. 2 ln. 2 x 2 5x 6 C. 2 ln. 2 ln x
 460_080.qd //04 :08 PM Page CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial
460_080.qd //04 :08 PM Page CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial
1.3 LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION
 . Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
. Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
TOTAL NAME DATE PERIOD AP CALCULUS AB UNIT 4 ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT /6 10/8 10/9 10/10 X X X X 10/11 10/12
 NAME DATE PERIOD AP CALCULUS AB UNIT ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT 0 0 0/6 0/8 0/9 0/0 X X X X 0/ 0/ 0/5 0/6 QUIZ X X X 0/7 0/8 0/9 0/ 0/ 0/ 0/5 UNIT EXAM X X X TOTAL AP Calculus
NAME DATE PERIOD AP CALCULUS AB UNIT ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT 0 0 0/6 0/8 0/9 0/0 X X X X 0/ 0/ 0/5 0/6 QUIZ X X X 0/7 0/8 0/9 0/ 0/ 0/ 0/5 UNIT EXAM X X X TOTAL AP Calculus
TRIG REVIEW NOTES. Co-terminal Angles: Angles that end at the same spot. (sines, cosines, and tangents will equal)
 TRIG REVIEW NOTES Convert from radians to degrees: multiply by 0 180 Convert from degrees to radians: multiply by 0. 180 Co-terminal Angles: Angles that end at the same spot. (sines, cosines, and tangents
TRIG REVIEW NOTES Convert from radians to degrees: multiply by 0 180 Convert from degrees to radians: multiply by 0. 180 Co-terminal Angles: Angles that end at the same spot. (sines, cosines, and tangents
MATH 1325 Business Calculus Guided Notes
 MATH 135 Business Calculus Guided Notes LSC North Harris By Isabella Fisher Section.1 Functions and Theirs Graphs A is a rule that assigns to each element in one and only one element in. Set A Set B Set
MATH 135 Business Calculus Guided Notes LSC North Harris By Isabella Fisher Section.1 Functions and Theirs Graphs A is a rule that assigns to each element in one and only one element in. Set A Set B Set
CHAPTER 11 Vector-Valued Functions
 CHAPTER Vector-Valued Functions Section. Vector-Valued Functions...................... 9 Section. Differentiation and Integration of Vector-Valued Functions.... Section. Velocit and Acceleration.....................
CHAPTER Vector-Valued Functions Section. Vector-Valued Functions...................... 9 Section. Differentiation and Integration of Vector-Valued Functions.... Section. Velocit and Acceleration.....................
Infinite Limits. Let f be the function given by. f x 3 x 2.
 0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
Let y = f (t) be a function that gives the position at time t of an object moving along the y-axis. Then
 Limits From last time... Let y = f (t) be a function that gives the position at time t of an object moving along the y-ais. Then Ave vel[t, t 2 ] = f (t 2) f (t ) t 2 t f (t + h) f (t) Velocity(t) =. h!0
Limits From last time... Let y = f (t) be a function that gives the position at time t of an object moving along the y-ais. Then Ave vel[t, t 2 ] = f (t 2) f (t ) t 2 t f (t + h) f (t) Velocity(t) =. h!0
Solutions to the Exercises of Chapter 8
 8A Domains of Functions Solutions to the Eercises of Chapter 8 1 For 7 to make sense, we need 7 0or7 So the domain of f() is{ 7} For + 5 to make sense, +5 0 So the domain of g() is{ 5} For h() to make
8A Domains of Functions Solutions to the Eercises of Chapter 8 1 For 7 to make sense, we need 7 0or7 So the domain of f() is{ 7} For + 5 to make sense, +5 0 So the domain of g() is{ 5} For h() to make
TEXT AND OTHER MATERIALS:
 1. TEXT AND OTHER MATERIALS: Check Learning Resources in shared class files Calculus Wiki-book: https://en.wikibooks.org/wiki/calculus (Main Reference e-book) Paul s Online Math Notes: http://tutorial.math.lamar.edu
1. TEXT AND OTHER MATERIALS: Check Learning Resources in shared class files Calculus Wiki-book: https://en.wikibooks.org/wiki/calculus (Main Reference e-book) Paul s Online Math Notes: http://tutorial.math.lamar.edu
Solutions Exam 4 (Applications of Differentiation) 1. a. Applying the Quotient Rule we compute the derivative function of f as follows:
 MAT 4 Solutions Eam 4 (Applications of Differentiation) a Applying the Quotient Rule we compute the derivative function of f as follows: f () = 43 e 4 e (e ) = 43 4 e = 3 (4 ) e Hence f '( ) 0 for = 0
MAT 4 Solutions Eam 4 (Applications of Differentiation) a Applying the Quotient Rule we compute the derivative function of f as follows: f () = 43 e 4 e (e ) = 43 4 e = 3 (4 ) e Hence f '( ) 0 for = 0
Announcements. Topics: Homework:
 Topics: Announcements - section 2.6 (limits at infinity [skip Precise Definitions (middle of pg. 134 end of section)]) - sections 2.1 and 2.7 (rates of change, the derivative) - section 2.8 (the derivative
Topics: Announcements - section 2.6 (limits at infinity [skip Precise Definitions (middle of pg. 134 end of section)]) - sections 2.1 and 2.7 (rates of change, the derivative) - section 2.8 (the derivative
Introduction to Rational Functions
 Introduction to Rational Functions The net class of functions that we will investigate is the rational functions. We will eplore the following ideas: Definition of rational function. The basic (untransformed)
Introduction to Rational Functions The net class of functions that we will investigate is the rational functions. We will eplore the following ideas: Definition of rational function. The basic (untransformed)
AP Calculus BC Prerequisite Knowledge
 AP Calculus BC Prerequisite Knowledge Please review these ideas over the summer as they come up during our class and we will not be reviewing them during class. Also, I feel free to quiz you at any time
AP Calculus BC Prerequisite Knowledge Please review these ideas over the summer as they come up during our class and we will not be reviewing them during class. Also, I feel free to quiz you at any time
4. (6 points) Express the domain of the following function in interval notation:
 Eam 1-A L. Ballou Name Math 131 Calculus I September 1, 016 NO Calculator Allowed BOX YOUR ANSWER! Show all work for full credit! 1. (4 points) Write an equation of a line with y-intercept 4 and -intercept
Eam 1-A L. Ballou Name Math 131 Calculus I September 1, 016 NO Calculator Allowed BOX YOUR ANSWER! Show all work for full credit! 1. (4 points) Write an equation of a line with y-intercept 4 and -intercept
Chapter 5: Limits, Continuity, and Differentiability
 Chapter 5: Limits, Continuity, and Differentiability 63 Chapter 5 Overview: Limits, Continuity and Differentiability Derivatives and Integrals are the core practical aspects of Calculus. They were the
Chapter 5: Limits, Continuity, and Differentiability 63 Chapter 5 Overview: Limits, Continuity and Differentiability Derivatives and Integrals are the core practical aspects of Calculus. They were the
Problems for Chapter 3.
 Problems for Chapter 3. Let A denote a nonempty set of reals. The complement of A, denoted by A, or A C is the set of all points not in A. We say that belongs to the interior of A, Int A, if there eists
Problems for Chapter 3. Let A denote a nonempty set of reals. The complement of A, denoted by A, or A C is the set of all points not in A. We say that belongs to the interior of A, Int A, if there eists
PACKET Unit 4 Honors ICM Functions and Limits 1
 PACKET Unit 4 Honors ICM Functions and Limits 1 Day 1 Homework For each of the rational functions find: a. domain b. -intercept(s) c. y-intercept Graph #8 and #10 with at least 5 EXACT points. 1. f 6.
PACKET Unit 4 Honors ICM Functions and Limits 1 Day 1 Homework For each of the rational functions find: a. domain b. -intercept(s) c. y-intercept Graph #8 and #10 with at least 5 EXACT points. 1. f 6.
1/100 Range: 1/10 1/ 2. 1) Constant: choose a value for the constant that can be graphed on the coordinate grid below.
 Name 1) Constant: choose a value or the constant that can be graphed on the coordinate grid below a y Toolkit Functions Lab Worksheet thru inverse trig ) Identity: y ) Reciprocal: 1 ( ) y / 1/ 1/1 1/ 1
Name 1) Constant: choose a value or the constant that can be graphed on the coordinate grid below a y Toolkit Functions Lab Worksheet thru inverse trig ) Identity: y ) Reciprocal: 1 ( ) y / 1/ 1/1 1/ 1
1 Functions and Graphs
 1 Functions and Graphs 1.1 Functions Cartesian Coordinate System A Cartesian or rectangular coordinate system is formed by the intersection of a horizontal real number line, usually called the x axis,
1 Functions and Graphs 1.1 Functions Cartesian Coordinate System A Cartesian or rectangular coordinate system is formed by the intersection of a horizontal real number line, usually called the x axis,
Solutions to Math 41 First Exam October 12, 2010
 Solutions to Math 41 First Eam October 12, 2010 1. 13 points) Find each of the following its, with justification. If the it does not eist, eplain why. If there is an infinite it, then eplain whether it
Solutions to Math 41 First Eam October 12, 2010 1. 13 points) Find each of the following its, with justification. If the it does not eist, eplain why. If there is an infinite it, then eplain whether it
6.5 Trigonometric Equations
 6. Trigonometric Equations In this section, we discuss conditional trigonometric equations, that is, equations involving trigonometric functions that are satisfied only by some values of the variable (or
6. Trigonometric Equations In this section, we discuss conditional trigonometric equations, that is, equations involving trigonometric functions that are satisfied only by some values of the variable (or
MATH 250 TOPIC 11 LIMITS. A. Basic Idea of a Limit and Limit Laws. Answers to Exercises and Problems
 Math 5 T-Limits Page MATH 5 TOPIC LIMITS A. Basic Idea of a Limit and Limit Laws B. Limits of the form,, C. Limits as or as D. Summary for Evaluating Limits Answers to Eercises and Problems Math 5 T-Limits
Math 5 T-Limits Page MATH 5 TOPIC LIMITS A. Basic Idea of a Limit and Limit Laws B. Limits of the form,, C. Limits as or as D. Summary for Evaluating Limits Answers to Eercises and Problems Math 5 T-Limits
3.8 Limits At Infinity
 3.8. LIMITS AT INFINITY 53 Figure 3.5: Partial graph of f = /. We see here that f 0 as and as. 3.8 Limits At Infinity The its we introduce here differ from previous its in that here we are interested in
3.8. LIMITS AT INFINITY 53 Figure 3.5: Partial graph of f = /. We see here that f 0 as and as. 3.8 Limits At Infinity The its we introduce here differ from previous its in that here we are interested in
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 3 2, 5 2 C) - 5 2
 Test Review (chap 0) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) Find the point on the curve x = sin t, y = cos t, -
Test Review (chap 0) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) Find the point on the curve x = sin t, y = cos t, -
MATH 2 - PROBLEM SETS
 MATH - PROBLEM SETS Problem Set 1: 1. Simplify and write without negative eponents or radicals: a. c d p 5 y cd b. 5p 1 y. Joe is standing at the top of a 100-foot tall building. Mike eits the building
MATH - PROBLEM SETS Problem Set 1: 1. Simplify and write without negative eponents or radicals: a. c d p 5 y cd b. 5p 1 y. Joe is standing at the top of a 100-foot tall building. Mike eits the building
