Math-3. Lesson 3-1 Finding Zeroes of NOT nice 3rd Degree Polynomials
|
|
|
- Winifred Hubbard
- 5 years ago
- Views:
Transcription
1 Math- Lesson - Finding Zeroes of NOT nice rd Degree Polynomials
2 f ( ) Is this one of the nice rd degree polynomials? a) Sum or difference of two cubes: y 8 5 y 7 b) rd degree with no constant term. c) nice pattern that can be factored by grouping: y y 4 We are left with guessing the first degree polynomial that divides it evenly!
3 Try the bo method ( )( a b c)
4 YES, we can find the quadratic factor! ( )( a b c) ( )( 8)
5 Try: = linear factor would be ( ) y
6 Try: = linear factor would be ( ) y There s got to be an easier way!!!
7 Long Division Look at the left numbers divides 54 4 times = 48 Subtract 48 from 54 Bring the down. 5 times = 60; subtract 60 from Remainder Divisor
8 Your turn: Look at the left numbers 7 divides 44 times 7 = Subtract from 4 Bring the down. 4 times 7 = 8; subtract 8 from Remainder Divisor
9 Steps ) Look at left-most numbers ) What # times left = left? ) Multiply 4) Subtract 5) Bring down. 6) Repeat steps Remainder Divisor
10 Vocabulary Polynomial Long division: One method used to divide polynomials similar to long division for numbers ( ) a b c Divide Evenly: A divisor divides evenly if there is a zero for the remainder.
11 Polynomial Long Division ) Look at left-most numbers ) What # times left = left? ) Multiply? ( ) 4) Subtract ( )
12 Polynomial Long Division ( ) 4) Subtract Careful with the negatives! 5 8 5) Bring down.
13 Polynomial Long Division ( ) 5 8? ) Multiply ( ) 6) Repeat steps -5. ) Look at leftmost numbers ) What # times left = left? 4) Subtract ( )
14 Polynomial Long Division ( ) 5 8 ( ) 4) Subtract Careful of the negatives 8 5) Bring down.
15 Polynomial Long Division ( ) 5) Bring down. 5 8 ( ) 8 8
16 Polynomial Long Division ( ) 5 8 ( 8 ) 8 8 6) Repeat steps -5. ) Look at leftmost numbers ) What # times left = left? 8? ) Multiply 8 8( ) 8 8 4) Subtract ( 8 8)
17 Polynomial Long Division ( ) 5 8 ( ) 8 8 ( 8 8) 0 4) Subtract ( 8 8) Remainder = 0 ( ) divides evenly. ( ) is a factor ( )( 8)
18 Is there an easier way to do this? Yes! st step: Write the polynomial with only its coefficients. nd step: Write the zero of the linear factor. rd step: Bring down the lead coefficient
19 Is there an easier way to do this? Yes! th step: Multiply the zero by the lead coefficient. 5th step: Write the product under the net term to the right. 6 th step: add the second column downward
20 Is there an easier way to do this? Yes! th step: Multiply the zero by the second number 8th step: Write the product under the net term to the right. 9 th step: add the net column downward
21 Is there an easier way to do this? Yes! th step: Multiply the zero by the rd number th step: Write the product under the net term to the right. th step: add the net column downward
22 Is there an easier way to do this? Yes! This last number is the remainder when you divide: by
23 Because the remainder = 0, then ( ) is a factor AND = is a zero of the original polynomial!
24 The Remainder Theorem: When dividing a polynomial epression by a lower degree polynomial epression, If the remainder is zero, then the divisor is a factor of the original polynomial.
25 We call this synthetic division Look at the numbers at the bottom. Are these familiar? ( )( 8) They are the coefficients of the quadratic factor! (wow)
26 ( )( 8) ( )( 6)( )
27 Synthetic Division ) )( ( th degree poly = ( st degree poly)( rd degree poly) 0 Is the rd degree polynomial a nice one?
28 f ( )? ( ) Synthetic Substitution
29 f ( )? ( ) Synthetic Substitution
30 f ( )? ( ) Synthetic Substitution
31 f ( )? ( ) Synthetic Substitution
32 f ( )? ( ) Synthetic Substitution
33 ( )? f ( ) Synthetic Substitution
34 f ( )? ( ) Synthetic Substitution
35 f ( )? ( ) Synthetic Substitution
36 f ( )? ( ) Synthetic Substitution (Since (+) has a remainder of 5, then ( + ) is not a factor).
37 Synthetic Division & Substitution 4 5 ) ( 4 f
38 Good to here.
39 Your turn: Use Synthetic division. 8 8
40 Your turn: Use Synthetic Substitution 4. f ( ) 8 8 f ( 5)?
41 Possible Rational Zeroes f ( ) 4 5 8,,, 6, 9, 8 Factors of the last term divided by the factors of the first term = is a zero of f() ( ) is a factor of f(). Coefficients of quadratic factor Remainder ( 4 5 8) ( )( 8)
42 Polynomial Long Division ( ) 5 8 ( ) 8 8 ( 8 8) 0
43 Polynomial Long Division ( ) 5 8 ( ) 8 8 ( 8 8)
44 Can you follow this? What are the zeroes? 0 ( 5)( )( 7) - Multiply the three binomials (convert to std. form) ,, 7 What do you notice about the first and last terms and the zeroes?
45 0 ( 5)( )( 7) 5-7,, The denominators of the solutions are factors of the lead coefficient. The numerators of the solutions are factors of the constant term.
46 root = zero of a polynomial = inputs that cause outputs to = 0 The Rational Roots Theorem: the possible rational roots of a polynomial are factors of the constant term divided by factors of the lead coefficient. 0 ( 5)( )( 0 ( 5)( 7) ) ,, 5, 7,0, 5, 70,
47 The Rational Roots Theorem: the possible rational roots of a polynomial are factors of the constant divided by factors of the lead coefficient. 0 4,, 5, 7,0, 5, 70, , -, 7,, 5, 7,0, 5,70,,, 5, 7,..., 5, 70 We always check the easy ones st.
48 Your turn: What are the possible rational roots of the following polynomial? y 4 5 8,,, 6, 9,8 If = is a zero, what factor did = come from? ( ) If ( ) is a factor, then the rd degree factors as: y ( )( a b c)
Warm-Up. Simplify the following terms:
 Warm-Up Simplify the following terms: 81 40 20 i 3 i 16 i 82 TEST Our Ch. 9 Test will be on 5/29/14 Complex Number Operations Learning Targets Adding Complex Numbers Multiplying Complex Numbers Rules for
Warm-Up Simplify the following terms: 81 40 20 i 3 i 16 i 82 TEST Our Ch. 9 Test will be on 5/29/14 Complex Number Operations Learning Targets Adding Complex Numbers Multiplying Complex Numbers Rules for
Polynomial and Synthetic Division
 Polynomial and Synthetic Division Polynomial Division Polynomial Division is very similar to long division. Example: 3x 3 5x 3x 10x 1 3 Polynomial Division 3x 1 x 3x 3 3 x 5x 3x x 6x 4 10x 10x 7 3 x 1
Polynomial and Synthetic Division Polynomial Division Polynomial Division is very similar to long division. Example: 3x 3 5x 3x 10x 1 3 Polynomial Division 3x 1 x 3x 3 3 x 5x 3x x 6x 4 10x 10x 7 3 x 1
4.3 Division of Polynomials
 4.3 Division of Polynomials Learning Objectives Divide a polynomials by a monomial. Divide a polynomial by a binomial. Rewrite and graph rational functions. Introduction A rational epression is formed
4.3 Division of Polynomials Learning Objectives Divide a polynomials by a monomial. Divide a polynomial by a binomial. Rewrite and graph rational functions. Introduction A rational epression is formed
3.3 Dividing Polynomials. Copyright Cengage Learning. All rights reserved.
 3.3 Dividing Polynomials Copyright Cengage Learning. All rights reserved. Objectives Long Division of Polynomials Synthetic Division The Remainder and Factor Theorems 2 Dividing Polynomials In this section
3.3 Dividing Polynomials Copyright Cengage Learning. All rights reserved. Objectives Long Division of Polynomials Synthetic Division The Remainder and Factor Theorems 2 Dividing Polynomials In this section
Math-1010 Lesson 4-2. Add and Subtract Rational Expressions
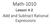 Math-00 Lesson - Add and Subtract Rational Epressions What are like terms? Like variables: Like powers: y y Multiples of the same variable same base and same eponent. Like radicals: same radicand and same
Math-00 Lesson - Add and Subtract Rational Epressions What are like terms? Like variables: Like powers: y y Multiples of the same variable same base and same eponent. Like radicals: same radicand and same
Algebra. Robert Taggart
 Algebra Robert Taggart Table of Contents To the Student.............................................. v Unit 1: Algebra Basics Lesson 1: Negative and Positive Numbers....................... Lesson 2: Operations
Algebra Robert Taggart Table of Contents To the Student.............................................. v Unit 1: Algebra Basics Lesson 1: Negative and Positive Numbers....................... Lesson 2: Operations
More Polynomial Equations Section 6.4
 MATH 11009: More Polynomial Equations Section 6.4 Dividend: The number or expression you are dividing into. Divisor: The number or expression you are dividing by. Synthetic division: Synthetic division
MATH 11009: More Polynomial Equations Section 6.4 Dividend: The number or expression you are dividing into. Divisor: The number or expression you are dividing by. Synthetic division: Synthetic division
Math 3 Variable Manipulation Part 3 Polynomials A
 Math 3 Variable Manipulation Part 3 Polynomials A 1 MATH 1 & 2 REVIEW: VOCABULARY Constant: A term that does not have a variable is called a constant. Example: the number 5 is a constant because it does
Math 3 Variable Manipulation Part 3 Polynomials A 1 MATH 1 & 2 REVIEW: VOCABULARY Constant: A term that does not have a variable is called a constant. Example: the number 5 is a constant because it does
Ch. 12 Higher Degree Equations Rational Root
 Ch. 12 Higher Degree Equations Rational Root Sec 1. Synthetic Substitution ~ Division of Polynomials This first section was covered in the chapter on polynomial operations. I m reprinting it here because
Ch. 12 Higher Degree Equations Rational Root Sec 1. Synthetic Substitution ~ Division of Polynomials This first section was covered in the chapter on polynomial operations. I m reprinting it here because
Polynomial and Synthetic Division
 Chapter Polynomial and Rational Functions y. f. f Common function: y Horizontal shift of three units to the left, vertical shrink Transformation: Vertical each y-value is multiplied stretch each y-value
Chapter Polynomial and Rational Functions y. f. f Common function: y Horizontal shift of three units to the left, vertical shrink Transformation: Vertical each y-value is multiplied stretch each y-value
Polynomials. Exponents. End Behavior. Writing. Solving Factoring. Graphing. End Behavior. Polynomial Notes. Synthetic Division.
 Polynomials Polynomials 1. P 1: Exponents 2. P 2: Factoring Polynomials 3. P 3: End Behavior 4. P 4: Fundamental Theorem of Algebra Writing real root x= 10 or (x+10) local maximum Exponents real root x=10
Polynomials Polynomials 1. P 1: Exponents 2. P 2: Factoring Polynomials 3. P 3: End Behavior 4. P 4: Fundamental Theorem of Algebra Writing real root x= 10 or (x+10) local maximum Exponents real root x=10
TEKS: 2A.10F. Terms. Functions Equations Inequalities Linear Domain Factor
 POLYNOMIALS UNIT TEKS: A.10F Terms: Functions Equations Inequalities Linear Domain Factor Polynomials Monomial, Like Terms, binomials, leading coefficient, degree of polynomial, standard form, terms, Parent
POLYNOMIALS UNIT TEKS: A.10F Terms: Functions Equations Inequalities Linear Domain Factor Polynomials Monomial, Like Terms, binomials, leading coefficient, degree of polynomial, standard form, terms, Parent
Polynomial and Synthetic Division
 Chapter Polynomial Functions. f y. Common function: y Transformation: Vertical stretch each y-value is multiplied by, then a vertical shift nine units upward f Horizontal shift of three units to the left,
Chapter Polynomial Functions. f y. Common function: y Transformation: Vertical stretch each y-value is multiplied by, then a vertical shift nine units upward f Horizontal shift of three units to the left,
Polynomials and Polynomial Functions
 Unit 5: Polynomials and Polynomial Functions Evaluating Polynomial Functions Objectives: SWBAT identify polynomial functions SWBAT evaluate polynomial functions. SWBAT find the end behaviors of polynomial
Unit 5: Polynomials and Polynomial Functions Evaluating Polynomial Functions Objectives: SWBAT identify polynomial functions SWBAT evaluate polynomial functions. SWBAT find the end behaviors of polynomial
Equations in Quadratic Form
 Equations in Quadratic Form MATH 101 College Algebra J. Robert Buchanan Department of Mathematics Summer 2012 Objectives In this lesson we will learn to: make substitutions that allow equations to be written
Equations in Quadratic Form MATH 101 College Algebra J. Robert Buchanan Department of Mathematics Summer 2012 Objectives In this lesson we will learn to: make substitutions that allow equations to be written
Section 6.2 Long Division of Polynomials
 Section 6. Long Division of Polynomials INTRODUCTION In Section 6.1 we learned to simplify a rational epression by factoring. For eample, + 3 10 = ( + 5)( ) ( ) = ( + 5) 1 = + 5. However, if we try to
Section 6. Long Division of Polynomials INTRODUCTION In Section 6.1 we learned to simplify a rational epression by factoring. For eample, + 3 10 = ( + 5)( ) ( ) = ( + 5) 1 = + 5. However, if we try to
Dividing Polynomials
 3-3 3-3 Dividing Polynomials Warm Up Lesson Presentation Lesson Quiz Algebra 2 Warm Up Divide using long division. 1. 161 7 2. 12.18 2.1 23 5.8 Divide. 3. 4. 6x + 15y 3 7a 2 ab a 2x + 5y 7a b Objective
3-3 3-3 Dividing Polynomials Warm Up Lesson Presentation Lesson Quiz Algebra 2 Warm Up Divide using long division. 1. 161 7 2. 12.18 2.1 23 5.8 Divide. 3. 4. 6x + 15y 3 7a 2 ab a 2x + 5y 7a b Objective
6x 3 12x 2 7x 2 +16x 7x 2 +14x 2x 4
 2.3 Real Zeros of Polynomial Functions Name: Pre-calculus. Date: Block: 1. Long Division of Polynomials. We have factored polynomials of degree 2 and some specific types of polynomials of degree 3 using
2.3 Real Zeros of Polynomial Functions Name: Pre-calculus. Date: Block: 1. Long Division of Polynomials. We have factored polynomials of degree 2 and some specific types of polynomials of degree 3 using
5.1 Monomials. Algebra 2
 . Monomials Algebra Goal : A..: Add, subtract, multiply, and simplify polynomials and rational expressions (e.g., multiply (x ) ( x + ); simplify 9x x. x Goal : Write numbers in scientific notation. Scientific
. Monomials Algebra Goal : A..: Add, subtract, multiply, and simplify polynomials and rational expressions (e.g., multiply (x ) ( x + ); simplify 9x x. x Goal : Write numbers in scientific notation. Scientific
Warm-Up. Use long division to divide 5 into
 Warm-Up Use long division to divide 5 into 3462. 692 5 3462-30 46-45 12-10 2 Warm-Up Use long division to divide 5 into 3462. Divisor 692 5 3462-30 46-45 12-10 2 Quotient Dividend Remainder Warm-Up Use
Warm-Up Use long division to divide 5 into 3462. 692 5 3462-30 46-45 12-10 2 Warm-Up Use long division to divide 5 into 3462. Divisor 692 5 3462-30 46-45 12-10 2 Quotient Dividend Remainder Warm-Up Use
6.4 Division of Polynomials. (Long Division and Synthetic Division)
 6.4 Division of Polynomials (Long Division and Synthetic Division) When we combine fractions that have a common denominator, we just add or subtract the numerators and then keep the common denominator
6.4 Division of Polynomials (Long Division and Synthetic Division) When we combine fractions that have a common denominator, we just add or subtract the numerators and then keep the common denominator
Review: Properties of Exponents (Allow students to come up with these on their own.) m n m n. a a a. n n n m. a a a. a b a
 Algebra II Notes Unit Si: Polynomials Syllabus Objectives: 6. The student will simplify polynomial epressions. Review: Properties of Eponents (Allow students to come up with these on their own.) Let a
Algebra II Notes Unit Si: Polynomials Syllabus Objectives: 6. The student will simplify polynomial epressions. Review: Properties of Eponents (Allow students to come up with these on their own.) Let a
Section 4.3. Polynomial Division; The Remainder Theorem and the Factor Theorem
 Section 4.3 Polynomial Division; The Remainder Theorem and the Factor Theorem Polynomial Long Division Let s compute 823 5 : Example of Long Division of Numbers Example of Long Division of Numbers Let
Section 4.3 Polynomial Division; The Remainder Theorem and the Factor Theorem Polynomial Long Division Let s compute 823 5 : Example of Long Division of Numbers Example of Long Division of Numbers Let
Complex fraction: - a fraction which has rational expressions in the numerator and/or denominator
 Comple fraction: - a fraction which has rational epressions in the numerator and/or denominator o 2 2 4 y 2 + y 2 y 2 2 Steps for Simplifying Comple Fractions. simplify the numerator and/or the denominator
Comple fraction: - a fraction which has rational epressions in the numerator and/or denominator o 2 2 4 y 2 + y 2 y 2 2 Steps for Simplifying Comple Fractions. simplify the numerator and/or the denominator
Algebra II Chapter 5: Polynomials and Polynomial Functions Part 1
 Algebra II Chapter 5: Polynomials and Polynomial Functions Part 1 Chapter 5 Lesson 1 Use Properties of Exponents Vocabulary Learn these! Love these! Know these! 1 Example 1: Evaluate Numerical Expressions
Algebra II Chapter 5: Polynomials and Polynomial Functions Part 1 Chapter 5 Lesson 1 Use Properties of Exponents Vocabulary Learn these! Love these! Know these! 1 Example 1: Evaluate Numerical Expressions
MAC1105-College Algebra
 MAC1105-College Algebra Chapter -Polynomial Division & Rational Functions. Polynomial Division;The Remainder and Factor Theorems I. Long Division of Polynomials A. For f ( ) 6 19 16, a zero of f ( ) occurs
MAC1105-College Algebra Chapter -Polynomial Division & Rational Functions. Polynomial Division;The Remainder and Factor Theorems I. Long Division of Polynomials A. For f ( ) 6 19 16, a zero of f ( ) occurs
1. Find the domain of the following functions. Write your answer using interval notation. (9 pts.)
 MATH- Sample Eam Spring 7. Find the domain of the following functions. Write your answer using interval notation. (9 pts.) a. 9 f ( ) b. g ( ) 9 8 8. Write the equation of the circle in standard form given
MATH- Sample Eam Spring 7. Find the domain of the following functions. Write your answer using interval notation. (9 pts.) a. 9 f ( ) b. g ( ) 9 8 8. Write the equation of the circle in standard form given
THE DISTRIBUTIVE LAW. Note: To avoid mistakes, include arrows above or below the terms that are being multiplied.
 THE DISTRIBUTIVE LAW ( ) When an equation of the form a b c is epanded, every term inside the bracket is multiplied by the number or pronumeral (letter), and the sign that is located outside the brackets.
THE DISTRIBUTIVE LAW ( ) When an equation of the form a b c is epanded, every term inside the bracket is multiplied by the number or pronumeral (letter), and the sign that is located outside the brackets.
Review of Rational Expressions and Equations
 Page 1 of 14 Review of Rational Epressions and Equations A rational epression is an epression containing fractions where the numerator and/or denominator may contain algebraic terms 1 Simplify 6 14 Identification/Analysis
Page 1 of 14 Review of Rational Epressions and Equations A rational epression is an epression containing fractions where the numerator and/or denominator may contain algebraic terms 1 Simplify 6 14 Identification/Analysis
ALGEBRAIC EXPRESSIONS AND POLYNOMIALS
 MODULE - ic Epressions and Polynomials ALGEBRAIC EXPRESSIONS AND POLYNOMIALS So far, you had been using arithmetical numbers, which included natural numbers, whole numbers, fractional numbers, etc. and
MODULE - ic Epressions and Polynomials ALGEBRAIC EXPRESSIONS AND POLYNOMIALS So far, you had been using arithmetical numbers, which included natural numbers, whole numbers, fractional numbers, etc. and
Algebra 2 Chapter 3 Part 1 Practice Test 2018
 Synthetic divisions in this worksheet were performed using the Algebra App for PCs that is available at www.mathguy.us/pcapps.php. 1) Given the polynomial f x x 5x 2x 24 and factor x 2, factor completely.
Synthetic divisions in this worksheet were performed using the Algebra App for PCs that is available at www.mathguy.us/pcapps.php. 1) Given the polynomial f x x 5x 2x 24 and factor x 2, factor completely.
Using Properties of Exponents
 6.1 Using Properties of Exponents Goals p Use properties of exponents to evaluate and simplify expressions involving powers. p Use exponents and scientific notation to solve real-life problems. VOCABULARY
6.1 Using Properties of Exponents Goals p Use properties of exponents to evaluate and simplify expressions involving powers. p Use exponents and scientific notation to solve real-life problems. VOCABULARY
Math-3. Lesson 2-8 Factoring NICE 3rd Degree Polynomials
 Math- Lesson -8 Factoring NICE rd Degree Polnomials Find the zeroes of the following rd degree Polnomial 5 Set = 0 0 5 Factor out the common factor. 0 ( 5 ) Factor the quadratic 0 ( 1)( ) 0, -1, - Identif
Math- Lesson -8 Factoring NICE rd Degree Polnomials Find the zeroes of the following rd degree Polnomial 5 Set = 0 0 5 Factor out the common factor. 0 ( 5 ) Factor the quadratic 0 ( 1)( ) 0, -1, - Identif
Polynomial Division. You may also see this kind of problem written like this: Perform the division x2 +2x 3
 Polynomial Division 5015 You do polynomial division the way you do long division of numbers It s difficult to describe the general procedure in words, so I ll work through some eamples stepbystep Eample
Polynomial Division 5015 You do polynomial division the way you do long division of numbers It s difficult to describe the general procedure in words, so I ll work through some eamples stepbystep Eample
Solving Quadratic & Higher Degree Equations
 Chapter 7 Solving Quadratic & Higher Degree Equations Sec 1. Zero Product Property Back in the third grade students were taught when they multiplied a number by zero, the product would be zero. In algebra,
Chapter 7 Solving Quadratic & Higher Degree Equations Sec 1. Zero Product Property Back in the third grade students were taught when they multiplied a number by zero, the product would be zero. In algebra,
Warm Up Lesson Presentation Lesson Quiz. Holt Algebra 2 2
 6-5 Warm Up Lesson Presentation Lesson Quiz 2 Warm Up Factor completely. 1. 2y 3 + 4y 2 30y 2y(y 3)(y + 5) 2. 3x 4 6x 2 24 Solve each equation. 3(x 2)(x + 2)(x 2 + 2) 3. x 2 9 = 0 x = 3, 3 4. x 3 + 3x
6-5 Warm Up Lesson Presentation Lesson Quiz 2 Warm Up Factor completely. 1. 2y 3 + 4y 2 30y 2y(y 3)(y + 5) 2. 3x 4 6x 2 24 Solve each equation. 3(x 2)(x + 2)(x 2 + 2) 3. x 2 9 = 0 x = 3, 3 4. x 3 + 3x
Math RE - Calculus I Functions Page 1 of 10. Topics of Functions used in Calculus
 Math 0-03-RE - Calculus I Functions Page of 0 Definition of a function f() : Topics of Functions used in Calculus A function = f() is a relation between variables and such that for ever value onl one value.
Math 0-03-RE - Calculus I Functions Page of 0 Definition of a function f() : Topics of Functions used in Calculus A function = f() is a relation between variables and such that for ever value onl one value.
Lesson 7.1 Polynomial Degree and Finite Differences
 Lesson 7.1 Polynomial Degree and Finite Differences 1. Identify the degree of each polynomial. a. 1 b. 0.2 1. 2 3.2 3 c. 20 16 2 20 2. Determine which of the epressions are polynomials. For each polynomial,
Lesson 7.1 Polynomial Degree and Finite Differences 1. Identify the degree of each polynomial. a. 1 b. 0.2 1. 2 3.2 3 c. 20 16 2 20 2. Determine which of the epressions are polynomials. For each polynomial,
QUADRATIC EQUATIONS. + 6 = 0 This is a quadratic equation written in standard form. x x = 0 (standard form with c=0). 2 = 9
 QUADRATIC EQUATIONS A quadratic equation is always written in the form of: a + b + c = where a The form a + b + c = is called the standard form of a quadratic equation. Eamples: 5 + 6 = This is a quadratic
QUADRATIC EQUATIONS A quadratic equation is always written in the form of: a + b + c = where a The form a + b + c = is called the standard form of a quadratic equation. Eamples: 5 + 6 = This is a quadratic
SECTION 2.3: LONG AND SYNTHETIC POLYNOMIAL DIVISION
 2.25 SECTION 2.3: LONG AND SYNTHETIC POLYNOMIAL DIVISION PART A: LONG DIVISION Ancient Example with Integers 2 4 9 8 1 In general: dividend, f divisor, d We can say: 9 4 = 2 + 1 4 By multiplying both sides
2.25 SECTION 2.3: LONG AND SYNTHETIC POLYNOMIAL DIVISION PART A: LONG DIVISION Ancient Example with Integers 2 4 9 8 1 In general: dividend, f divisor, d We can say: 9 4 = 2 + 1 4 By multiplying both sides
Dividing Polynomials
 5.3 TEXAS ESSENTIAL KNOWLEDGE AND SKILLS 2A.7.C Dividing Polynomials Essential Question How can you use the factors of a cubic polynomial to solve a division problem involving the polynomial? Dividing
5.3 TEXAS ESSENTIAL KNOWLEDGE AND SKILLS 2A.7.C Dividing Polynomials Essential Question How can you use the factors of a cubic polynomial to solve a division problem involving the polynomial? Dividing
Warm Up Lesson Presentation Lesson Quiz. Holt McDougal Algebra 2
 Warm Up Lesson Presentation Lesson Quiz Algebra 2 Warm Up Factor each expression. 1. 3x 6y 2. a 2 b 2 3(x 2y) (a + b)(a b) Find each product. 3. (x 1)(x + 3) 4. (a + 1)(a 2 + 1) x 2 + 2x 3 a 3 + a 2 +
Warm Up Lesson Presentation Lesson Quiz Algebra 2 Warm Up Factor each expression. 1. 3x 6y 2. a 2 b 2 3(x 2y) (a + b)(a b) Find each product. 3. (x 1)(x + 3) 4. (a + 1)(a 2 + 1) x 2 + 2x 3 a 3 + a 2 +
Multiplication of Polynomials
 Summary 391 Chapter 5 SUMMARY Section 5.1 A polynomial in x is defined by a finite sum of terms of the form ax n, where a is a real number and n is a whole number. a is the coefficient of the term. n is
Summary 391 Chapter 5 SUMMARY Section 5.1 A polynomial in x is defined by a finite sum of terms of the form ax n, where a is a real number and n is a whole number. a is the coefficient of the term. n is
Math-3 Lesson 8-5. Unit 4 review: a) Compositions of functions. b) Linear combinations of functions. c) Inverse Functions. d) Quadratic Inequalities
 Math- Lesson 8-5 Unit 4 review: a) Compositions o unctions b) Linear combinations o unctions c) Inverse Functions d) Quadratic Inequalities e) Rational Inequalities 1. Is the ollowing relation a unction
Math- Lesson 8-5 Unit 4 review: a) Compositions o unctions b) Linear combinations o unctions c) Inverse Functions d) Quadratic Inequalities e) Rational Inequalities 1. Is the ollowing relation a unction
Algebra II Notes Polynomial Functions Unit Introduction to Polynomials. Math Background
 Introduction to Polynomials Math Background Previously, you Identified the components in an algebraic epression Factored quadratic epressions using special patterns, grouping method and the ac method Worked
Introduction to Polynomials Math Background Previously, you Identified the components in an algebraic epression Factored quadratic epressions using special patterns, grouping method and the ac method Worked
Long and Synthetic Division of Polynomials
 Long and Synthetic Division of Polynomials Long and synthetic division are two ways to divide one polynomial (the dividend) by another polynomial (the divisor). These methods are useful when both polynomials
Long and Synthetic Division of Polynomials Long and synthetic division are two ways to divide one polynomial (the dividend) by another polynomial (the divisor). These methods are useful when both polynomials
Definition 8.1 Two inequalities are equivalent if they have the same solution set. Add or Subtract the same value on both sides of the inequality.
 8 Inequalities Concepts: Equivalent Inequalities Linear and Nonlinear Inequalities Absolute Value Inequalities (Sections.6 and.) 8. Equivalent Inequalities Definition 8. Two inequalities are equivalent
8 Inequalities Concepts: Equivalent Inequalities Linear and Nonlinear Inequalities Absolute Value Inequalities (Sections.6 and.) 8. Equivalent Inequalities Definition 8. Two inequalities are equivalent
Math-3 Lesson 4-6 Polynomial and Rational Inequalities
 Math-3 Lesson 4-6 Polynomial and Rational Inequalities SM3 HANDOUT 4-6 Polynomial and Rational Inequalities Graph the general shape of the equation. y 4 1 Positive lead coefficient, even degree nd degree
Math-3 Lesson 4-6 Polynomial and Rational Inequalities SM3 HANDOUT 4-6 Polynomial and Rational Inequalities Graph the general shape of the equation. y 4 1 Positive lead coefficient, even degree nd degree
L1 2.1 Long Division of Polynomials and The Remainder Theorem Lesson MHF4U Jensen
 L1 2.1 Long Division of Polynomials and The Remainder Theorem Lesson MHF4U Jensen In this section you will apply the method of long division to divide a polynomial by a binomial. You will also learn to
L1 2.1 Long Division of Polynomials and The Remainder Theorem Lesson MHF4U Jensen In this section you will apply the method of long division to divide a polynomial by a binomial. You will also learn to
NAME DATE PERIOD. Operations with Polynomials. Review Vocabulary Evaluate each expression. (Lesson 1-1) 3a 2 b 4, given a = 3, b = 2
 5-1 Operations with Polynomials What You ll Learn Skim the lesson. Predict two things that you expect to learn based on the headings and the Key Concept box. 1. Active Vocabulary 2. Review Vocabulary Evaluate
5-1 Operations with Polynomials What You ll Learn Skim the lesson. Predict two things that you expect to learn based on the headings and the Key Concept box. 1. Active Vocabulary 2. Review Vocabulary Evaluate
5.2 Polynomial Operations
 5.2 Polynomial Operations At times we ll need to perform operations with polynomials. At this level we ll just be adding, subtracting, or multiplying polynomials. Dividing polynomials will happen in future
5.2 Polynomial Operations At times we ll need to perform operations with polynomials. At this level we ll just be adding, subtracting, or multiplying polynomials. Dividing polynomials will happen in future
Section September 6, If n = 3, 4, 5,..., the polynomial is called a cubic, quartic, quintic, etc.
 Section 2.1-2.2 September 6, 2017 1 Polynomials Definition. A polynomial is an expression of the form a n x n + a n 1 x n 1 + + a 1 x + a 0 where each a 0, a 1,, a n are real numbers, a n 0, and n is a
Section 2.1-2.2 September 6, 2017 1 Polynomials Definition. A polynomial is an expression of the form a n x n + a n 1 x n 1 + + a 1 x + a 0 where each a 0, a 1,, a n are real numbers, a n 0, and n is a
6.5 Dividing Polynomials
 Name Class Date 6.5 Dividing Polynomials Essential Question: What are some ways to divide polynomials, and how do you know when the divisor is a factor of the dividend? Explore Evaluating a Polynomial
Name Class Date 6.5 Dividing Polynomials Essential Question: What are some ways to divide polynomials, and how do you know when the divisor is a factor of the dividend? Explore Evaluating a Polynomial
Bell Quiz 2-3. Determine the end behavior of the graph using limit notation. Find a function with the given zeros , 2. 5 pts possible.
 Bell Quiz 2-3 2 pts Determine the end behavior of the graph using limit notation. 5 2 1. g( ) = 8 + 13 7 3 pts Find a function with the given zeros. 4. -1, 2 5 pts possible Ch 2A Big Ideas 1 Questions
Bell Quiz 2-3 2 pts Determine the end behavior of the graph using limit notation. 5 2 1. g( ) = 8 + 13 7 3 pts Find a function with the given zeros. 4. -1, 2 5 pts possible Ch 2A Big Ideas 1 Questions
Function Operations and Composition of Functions. Unit 1 Lesson 6
 Function Operations and Composition of Functions Unit 1 Lesson 6 Students will be able to: Combine standard function types using arithmetic operations Compose functions Key Vocabulary: Function operation
Function Operations and Composition of Functions Unit 1 Lesson 6 Students will be able to: Combine standard function types using arithmetic operations Compose functions Key Vocabulary: Function operation
Evaluate and Graph Polynomial Functions
 Evaluate and Graph Polynomial Functions Section 2.2 How do you identify and evaluate polynomial functions? What is synthetic substitution? How do you graph polynomial functions? Polynomial Function f(x)
Evaluate and Graph Polynomial Functions Section 2.2 How do you identify and evaluate polynomial functions? What is synthetic substitution? How do you graph polynomial functions? Polynomial Function f(x)
MEMORIAL UNIVERSITY OF NEWFOUNDLAND
 MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Section 5. Math 090 Fall 009 SOLUTIONS. a) Using long division of polynomials, we have x + x x x + ) x 4 4x + x + 0x x 4 6x
MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Section 5. Math 090 Fall 009 SOLUTIONS. a) Using long division of polynomials, we have x + x x x + ) x 4 4x + x + 0x x 4 6x
Solving and Graphing Polynomials
 UNIT 9 Solving and Graphing Polynomials You can see laminar and turbulent fl ow in a fountain. Copyright 009, K1 Inc. All rights reserved. This material may not be reproduced in whole or in part, including
UNIT 9 Solving and Graphing Polynomials You can see laminar and turbulent fl ow in a fountain. Copyright 009, K1 Inc. All rights reserved. This material may not be reproduced in whole or in part, including
Algebra Concepts Equation Solving Flow Chart Page 1 of 6. How Do I Solve This Equation?
 Algebra Concepts Equation Solving Flow Chart Page of 6 How Do I Solve This Equation? First, simplify both sides of the equation as much as possible by: combining like terms, removing parentheses using
Algebra Concepts Equation Solving Flow Chart Page of 6 How Do I Solve This Equation? First, simplify both sides of the equation as much as possible by: combining like terms, removing parentheses using
L1 2.1 Long Division of Polynomials and The Remainder Theorem Lesson MHF4U Jensen
 L1 2.1 Long Division of Polynomials and The Remainder Theorem Lesson MHF4U Jensen In this section you will apply the method of long division to divide a polynomial by a binomial. You will also learn to
L1 2.1 Long Division of Polynomials and The Remainder Theorem Lesson MHF4U Jensen In this section you will apply the method of long division to divide a polynomial by a binomial. You will also learn to
Lesson #33 Solving Incomplete Quadratics
 Lesson # Solving Incomplete Quadratics A.A.4 Know and apply the technique of completing the square ~ 1 ~ We can also set up any quadratic to solve it in this way by completing the square, the technique
Lesson # Solving Incomplete Quadratics A.A.4 Know and apply the technique of completing the square ~ 1 ~ We can also set up any quadratic to solve it in this way by completing the square, the technique
Math 0310 Final Exam Review
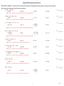 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the linear equation and check the solution. 1) 13(x - 52) = 26 1) A) {26} B) {52} C) {50} D)
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the linear equation and check the solution. 1) 13(x - 52) = 26 1) A) {26} B) {52} C) {50} D)
MATH 90 CHAPTER 7 Name:.
 MATH 90 CHAPTER 7 Name:. 7.1 Reducing Rational Epressions Need To Know Idea of rational epressions w/ restrictions Review reducing number fraction Review polynomial factoring methods How to reduce rational
MATH 90 CHAPTER 7 Name:. 7.1 Reducing Rational Epressions Need To Know Idea of rational epressions w/ restrictions Review reducing number fraction Review polynomial factoring methods How to reduce rational
1. Division by a Monomial
 330 Chapter 5 Polynomials Section 5.3 Concepts 1. Division by a Monomial 2. Long Division 3. Synthetic Division Division of Polynomials 1. Division by a Monomial Division of polynomials is presented in
330 Chapter 5 Polynomials Section 5.3 Concepts 1. Division by a Monomial 2. Long Division 3. Synthetic Division Division of Polynomials 1. Division by a Monomial Division of polynomials is presented in
Chapter 2 Formulas and Definitions:
 Chapter 2 Formulas and Definitions: (from 2.1) Definition of Polynomial Function: Let n be a nonnegative integer and let a n,a n 1,...,a 2,a 1,a 0 be real numbers with a n 0. The function given by f (x)
Chapter 2 Formulas and Definitions: (from 2.1) Definition of Polynomial Function: Let n be a nonnegative integer and let a n,a n 1,...,a 2,a 1,a 0 be real numbers with a n 0. The function given by f (x)
EXPONENT REVIEW!!! Concept Byte (Review): Properties of Exponents. Property of Exponents: Product of Powers. x m x n = x m + n
 Algebra B: Chapter 6 Notes 1 EXPONENT REVIEW!!! Concept Byte (Review): Properties of Eponents Recall from Algebra 1, the Properties (Rules) of Eponents. Property of Eponents: Product of Powers m n = m
Algebra B: Chapter 6 Notes 1 EXPONENT REVIEW!!! Concept Byte (Review): Properties of Eponents Recall from Algebra 1, the Properties (Rules) of Eponents. Property of Eponents: Product of Powers m n = m
Chapter 2: Polynomial and Rational Functions
 Chapter 2: Polynomial and Rational Functions Section 2.1 Quadratic Functions Date: Example 1: Sketching the Graph of a Quadratic Function a) Graph f(x) = 3 1 x 2 and g(x) = x 2 on the same coordinate plane.
Chapter 2: Polynomial and Rational Functions Section 2.1 Quadratic Functions Date: Example 1: Sketching the Graph of a Quadratic Function a) Graph f(x) = 3 1 x 2 and g(x) = x 2 on the same coordinate plane.
Section 6.6 Evaluating Polynomial Functions
 Name: Period: Section 6.6 Evaluating Polynomial Functions Objective(s): Use synthetic substitution to evaluate polynomials. Essential Question: Homework: Assignment 6.6. #1 5 in the homework packet. Notes:
Name: Period: Section 6.6 Evaluating Polynomial Functions Objective(s): Use synthetic substitution to evaluate polynomials. Essential Question: Homework: Assignment 6.6. #1 5 in the homework packet. Notes:
ZEROS OF POLYNOMIAL FUNCTIONS ALL I HAVE TO KNOW ABOUT POLYNOMIAL FUNCTIONS
 ZEROS OF POLYNOMIAL FUNCTIONS ALL I HAVE TO KNOW ABOUT POLYNOMIAL FUNCTIONS TOOLS IN FINDING ZEROS OF POLYNOMIAL FUNCTIONS Synthetic Division and Remainder Theorem (Compressed Synthetic Division) Fundamental
ZEROS OF POLYNOMIAL FUNCTIONS ALL I HAVE TO KNOW ABOUT POLYNOMIAL FUNCTIONS TOOLS IN FINDING ZEROS OF POLYNOMIAL FUNCTIONS Synthetic Division and Remainder Theorem (Compressed Synthetic Division) Fundamental
Lesson 19 Factoring Polynomials
 Fast Five Lesson 19 Factoring Polynomials Factor the number 38,754 (NO CALCULATOR) Divide 72,765 by 38 (NO CALCULATOR) Math 2 Honors - Santowski How would you know if 145 was a factor of 14,436,705? What
Fast Five Lesson 19 Factoring Polynomials Factor the number 38,754 (NO CALCULATOR) Divide 72,765 by 38 (NO CALCULATOR) Math 2 Honors - Santowski How would you know if 145 was a factor of 14,436,705? What
Intensive Math-Algebra I Mini-Lesson MA.912.A.4.3
 Intensive Math-Algebra I Mini-Lesson M912.4.3 Summer 2013 Factoring Polynomials Student Packet Day 15 Name: Date: Benchmark M912.4.3 Factor polynomials expressions This benchmark will be assessed using
Intensive Math-Algebra I Mini-Lesson M912.4.3 Summer 2013 Factoring Polynomials Student Packet Day 15 Name: Date: Benchmark M912.4.3 Factor polynomials expressions This benchmark will be assessed using
INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
 INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS. Introduction It is possible to integrate any rational function, constructed as the ratio of polynomials by epressing it as a sum of simpler fractions
INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS. Introduction It is possible to integrate any rational function, constructed as the ratio of polynomials by epressing it as a sum of simpler fractions
Table of Contents. Unit 3: Rational and Radical Relationships. Answer Key...AK-1. Introduction... v
 These materials may not be reproduced for any purpose. The reproduction of any part for an entire school or school system is strictly prohibited. No part of this publication may be transmitted, stored,
These materials may not be reproduced for any purpose. The reproduction of any part for an entire school or school system is strictly prohibited. No part of this publication may be transmitted, stored,
Math-2 Lesson 2-4. Radicals
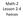 Math- Lesson - Radicals = What number is equivalent to the square root of? Square both sides of the equation ( ) ( ) = = = is an equivalent statement to = 1.7 1.71 1.70 1.701 1.7008... There is no equivalent
Math- Lesson - Radicals = What number is equivalent to the square root of? Square both sides of the equation ( ) ( ) = = = is an equivalent statement to = 1.7 1.71 1.70 1.701 1.7008... There is no equivalent
Factor each expression. Remember, always find the GCF first. Then if applicable use the x-box method and also look for difference of squares.
 NOTES 11: RATIONAL EXPRESSIONS AND EQUATIONS Name: Date: Period: Mrs. Nguyen s Initial: LESSON 11.1 SIMPLIFYING RATIONAL EXPRESSIONS Lesson Preview Review Factoring Skills and Simplifying Fractions Factor
NOTES 11: RATIONAL EXPRESSIONS AND EQUATIONS Name: Date: Period: Mrs. Nguyen s Initial: LESSON 11.1 SIMPLIFYING RATIONAL EXPRESSIONS Lesson Preview Review Factoring Skills and Simplifying Fractions Factor
Polynomial and Rational Functions. Copyright Cengage Learning. All rights reserved.
 2 Polynomial and Rational Functions Copyright Cengage Learning. All rights reserved. 2.3 Real Zeros of Polynomial Functions Copyright Cengage Learning. All rights reserved. What You Should Learn Use long
2 Polynomial and Rational Functions Copyright Cengage Learning. All rights reserved. 2.3 Real Zeros of Polynomial Functions Copyright Cengage Learning. All rights reserved. What You Should Learn Use long
Rational number = one real number divided by another, as in 2/3, = constant/constant
 RATIONAL FN S & EQN S CHEAT SHEET MATH1314/GWJ/08 Rational = ratio = fraction Rational number = one real number divided by another, as in 2/3, = constant/constant Generalize constants to polynomials: p(x)/q(x)
RATIONAL FN S & EQN S CHEAT SHEET MATH1314/GWJ/08 Rational = ratio = fraction Rational number = one real number divided by another, as in 2/3, = constant/constant Generalize constants to polynomials: p(x)/q(x)
Just DOS Difference of Perfect Squares. Now the directions say solve or find the real number solutions :
 5.4 FACTORING AND SOLVING POLYNOMIAL EQUATIONS To help you with #1-1 THESE BINOMIALS ARE EITHER GCF, DOS, OR BOTH!!!! Just GCF Just DOS Difference of Perfect Squares Both 1. Break each piece down.. Pull
5.4 FACTORING AND SOLVING POLYNOMIAL EQUATIONS To help you with #1-1 THESE BINOMIALS ARE EITHER GCF, DOS, OR BOTH!!!! Just GCF Just DOS Difference of Perfect Squares Both 1. Break each piece down.. Pull
p324 Section 5.2: The Natural Logarithmic Function: Integration
 p324 Section 5.2: The Natural Logarithmic Function: Integration Theorem 5.5: Log Rule for Integration Let u be a differentiable function of x 1. 2. Example 1: Using the Log Rule for Integration ** Note:
p324 Section 5.2: The Natural Logarithmic Function: Integration Theorem 5.5: Log Rule for Integration Let u be a differentiable function of x 1. 2. Example 1: Using the Log Rule for Integration ** Note:
3.4. ZEROS OF POLYNOMIAL FUNCTIONS
 3.4. ZEROS OF POLYNOMIAL FUNCTIONS What You Should Learn Use the Fundamental Theorem of Algebra to determine the number of zeros of polynomial functions. Find rational zeros of polynomial functions. Find
3.4. ZEROS OF POLYNOMIAL FUNCTIONS What You Should Learn Use the Fundamental Theorem of Algebra to determine the number of zeros of polynomial functions. Find rational zeros of polynomial functions. Find
Polynomials. This booklet belongs to: Period
 HW Mark: 10 9 8 7 6 RE-Submit Polynomials This booklet belongs to: Period LESSON # DATE QUESTIONS FROM NOTES Questions that I find difficult Pg. Pg. Pg. Pg. Pg. Pg. Pg. Pg. Pg. Pg. REVIEW TEST Your teacher
HW Mark: 10 9 8 7 6 RE-Submit Polynomials This booklet belongs to: Period LESSON # DATE QUESTIONS FROM NOTES Questions that I find difficult Pg. Pg. Pg. Pg. Pg. Pg. Pg. Pg. Pg. Pg. REVIEW TEST Your teacher
Pre-Calculus Assignment Sheet Unit 8-3rd term January 20 th to February 6 th 2015 Polynomials
 Pre-Calculus Assignment Sheet Unit 8- rd term January 0 th to February 6 th 01 Polynomials Date Topic Assignment Calculator Did it Tuesday Multiplicity of zeroes of 1/0/1 a function TI-nspire activity
Pre-Calculus Assignment Sheet Unit 8- rd term January 0 th to February 6 th 01 Polynomials Date Topic Assignment Calculator Did it Tuesday Multiplicity of zeroes of 1/0/1 a function TI-nspire activity
H-Pre-Calculus Targets Chapter I can write quadratic functions in standard form and use the results to sketch graphs of the function.
 H-Pre-Calculus Targets Chapter Section. Sketch and analyze graphs of quadratic functions.. I can write quadratic functions in standard form and use the results to sketch graphs of the function. Identify
H-Pre-Calculus Targets Chapter Section. Sketch and analyze graphs of quadratic functions.. I can write quadratic functions in standard form and use the results to sketch graphs of the function. Identify
Skills Practice Skills Practice for Lesson 4.1
 Skills Practice Skills Practice for Lesson.1 Name Date Thinking About Numbers Counting Numbers, Whole Numbers, Integers, Rational and Irrational Numbers Vocabulary Define each term in your own words. 1.
Skills Practice Skills Practice for Lesson.1 Name Date Thinking About Numbers Counting Numbers, Whole Numbers, Integers, Rational and Irrational Numbers Vocabulary Define each term in your own words. 1.
MHF4U Unit 2 Polynomial Equation and Inequalities
 MHF4U Unit 2 Polynomial Equation and Inequalities Section Pages Questions Prereq Skills 82-83 # 1ac, 2ace, 3adf, 4, 5, 6ace, 7ac, 8ace, 9ac 2.1 91 93 #1, 2, 3bdf, 4ac, 5, 6, 7ab, 8c, 9ad, 10, 12, 15a,
MHF4U Unit 2 Polynomial Equation and Inequalities Section Pages Questions Prereq Skills 82-83 # 1ac, 2ace, 3adf, 4, 5, 6ace, 7ac, 8ace, 9ac 2.1 91 93 #1, 2, 3bdf, 4ac, 5, 6, 7ab, 8c, 9ad, 10, 12, 15a,
Synthetic Substitution
 Write your questions and thoughts here! 7.2 Synthetic and Long Polynomial Division 1 Use direct substitution to evaluate t a = a! a! + a + 5 when a = - 2 Synthetic Substitution Synthetic substitution is
Write your questions and thoughts here! 7.2 Synthetic and Long Polynomial Division 1 Use direct substitution to evaluate t a = a! a! + a + 5 when a = - 2 Synthetic Substitution Synthetic substitution is
LESSON 9.1 ROOTS AND RADICALS
 LESSON 9.1 ROOTS AND RADICALS LESSON 9.1 ROOTS AND RADICALS 67 OVERVIEW Here s what you ll learn in this lesson: Square Roots and Cube Roots a. Definition of square root and cube root b. Radicand, radical
LESSON 9.1 ROOTS AND RADICALS LESSON 9.1 ROOTS AND RADICALS 67 OVERVIEW Here s what you ll learn in this lesson: Square Roots and Cube Roots a. Definition of square root and cube root b. Radicand, radical
WBHS Algebra 2 - Final Exam
 Class: _ Date: _ WBHS Algebra 2 - Final Eam Multiple Choice Identify the choice that best completes the statement or answers the question. Describe the pattern in the sequence. Find the net three terms.
Class: _ Date: _ WBHS Algebra 2 - Final Eam Multiple Choice Identify the choice that best completes the statement or answers the question. Describe the pattern in the sequence. Find the net three terms.
27 Wyner Math 2 Spring 2019
 27 Wyner Math 2 Spring 2019 CHAPTER SIX: POLYNOMIALS Review January 25 Test February 8 Thorough understanding and fluency of the concepts and methods in this chapter is a cornerstone to success in the
27 Wyner Math 2 Spring 2019 CHAPTER SIX: POLYNOMIALS Review January 25 Test February 8 Thorough understanding and fluency of the concepts and methods in this chapter is a cornerstone to success in the
Lesson 9: Radicals and Conjugates
 Lesson 9: Radicals and Conjugates Student Outcomes Students understand that the sum of two square roots (or two cube roots) is not equal to the square root (or cube root) of their sum. Students convert
Lesson 9: Radicals and Conjugates Student Outcomes Students understand that the sum of two square roots (or two cube roots) is not equal to the square root (or cube root) of their sum. Students convert
1) Synthetic Division: The Process. (Ruffini's rule) 2) Remainder Theorem 3) Factor Theorem
 J.F. Antona 1 Maths Dep. I.E.S. Jovellanos 1) Synthetic Division: The Process (Ruffini's rule) 2) Remainder Theorem 3) Factor Theorem 1) Synthetic division. Ruffini s rule Synthetic division (Ruffini s
J.F. Antona 1 Maths Dep. I.E.S. Jovellanos 1) Synthetic Division: The Process (Ruffini's rule) 2) Remainder Theorem 3) Factor Theorem 1) Synthetic division. Ruffini s rule Synthetic division (Ruffini s
MHF4U. Advanced Functions Grade 12 University Mitchell District High School. Unit 2 Polynomial Functions 9 Video Lessons
 MHF4U Advanced Functions Grade 12 University Mitchell District High School Unit 2 Polynomial Functions 9 Video Lessons Allow no more than 15 class days for this unit! This includes time for review and
MHF4U Advanced Functions Grade 12 University Mitchell District High School Unit 2 Polynomial Functions 9 Video Lessons Allow no more than 15 class days for this unit! This includes time for review and
6.1 Using Properties of Exponents 1. Use properties of exponents to evaluate and simplify expressions involving powers. Product of Powers Property
 6.1 Using Properties of Exponents Objectives 1. Use properties of exponents to evaluate and simplify expressions involving powers. 2. Use exponents and scientific notation to solve real life problems.
6.1 Using Properties of Exponents Objectives 1. Use properties of exponents to evaluate and simplify expressions involving powers. 2. Use exponents and scientific notation to solve real life problems.
Rational and Radical Expressions and Equations
 Rational and Radical Epressions and Equations Secondary Mathematics Page 44 Jordan School District Unit Cluster 7 (AAPR6 and AAPR7): Rational Epressions Cluster 7: Rewrite rational epressions 7 Rewrite
Rational and Radical Epressions and Equations Secondary Mathematics Page 44 Jordan School District Unit Cluster 7 (AAPR6 and AAPR7): Rational Epressions Cluster 7: Rewrite rational epressions 7 Rewrite
Algebra Introduction to Polynomials
 Introduction to Polynomials What is a Polynomial? A polynomial is an expression that can be written as a term or a sum of terms, each of which is the product of a scalar (the coefficient) and a series
Introduction to Polynomials What is a Polynomial? A polynomial is an expression that can be written as a term or a sum of terms, each of which is the product of a scalar (the coefficient) and a series
Solving Quadratic Equations
 Solving Quadratic Equations MATH 101 College Algebra J. Robert Buchanan Department of Mathematics Summer 2012 Objectives In this lesson we will learn to: solve quadratic equations by factoring, solve quadratic
Solving Quadratic Equations MATH 101 College Algebra J. Robert Buchanan Department of Mathematics Summer 2012 Objectives In this lesson we will learn to: solve quadratic equations by factoring, solve quadratic
Scope and Sequence Mathematics Algebra 2 400
 Scope and Sequence Mathematics Algebra 2 400 Description : Students will study real numbers, complex numbers, functions, exponents, logarithms, graphs, variation, systems of equations and inequalities,
Scope and Sequence Mathematics Algebra 2 400 Description : Students will study real numbers, complex numbers, functions, exponents, logarithms, graphs, variation, systems of equations and inequalities,
TECHNIQUES IN FACTORISATION
 TECHNIQUES IN FACTORISATION The process where brackets are inserted into an equation is referred to as factorisation. Factorisation is the opposite process to epansion. METHOD: Epansion ( + )( 5) 15 Factorisation
TECHNIQUES IN FACTORISATION The process where brackets are inserted into an equation is referred to as factorisation. Factorisation is the opposite process to epansion. METHOD: Epansion ( + )( 5) 15 Factorisation
Polynomials: Add and Subtract
 GSE Advanced Algebra Operations with Polynomials Polynomials: Add and Subtract Let's do a quick review on what polynomials are and the types of polynomials. A monomial is an algebraic expression that is
GSE Advanced Algebra Operations with Polynomials Polynomials: Add and Subtract Let's do a quick review on what polynomials are and the types of polynomials. A monomial is an algebraic expression that is
1.6 Multiplying and Dividing Rational Expressions
 1.6 Multiplying and Dividing Rational Epressions The game of badminton originated in England around 1870. Badminton is named after the Duke of Beaufort s home, Badminton House, where the game was first
1.6 Multiplying and Dividing Rational Epressions The game of badminton originated in England around 1870. Badminton is named after the Duke of Beaufort s home, Badminton House, where the game was first
