1 0-forms on 1-dimensional space
|
|
|
- Walter Walters
- 5 years ago
- Views:
Transcription
1 MA286: Tutorial Problems Tutorials: Tuesday, 6-7pm, Venue = IT202 Thursday, 2-3pm, Venue = IT207 Tutor: Adib Makroon For those questions taken from the chaum Outline eries book Advanced Calculus by M. piegel the question number in the book is given. The book provides worked solutions for many of these questions. PROBLEM 1 0-forms on 1-dimensional space 1. Give an interval = [a,b] R on which ω = x 4 is a differential 0-form. Then give an interval = [a,b ] R on which ω is not a differential 0-form. 2. Evaluate the integral 2x 2 +x of the differential 0-form ω = 2x 2 + x over the boundary of the oriented interval = [3, 1]. 3. Evaluate the integral of the differential 0-form ω = x 3 over the boundary of = [2,1] [4,3] [ 2, 1]. x 3 4. Is ω = { x sin(1/x), x 0 0, x = 0 a differential 0-form on the interval = [ 1,1]? [ee 4.4(b)]
2 2 1-forms on 1-dimensional space 1. Find a differential 0-form ω whose derivative dω is the differential 1-form dω = (x 2 +2x)dx. 2. Find a differential 0-form ω whose derivative dω is the differential 1-form [ee 5.14(a)] dω = (x+2)sin(x 2 +4x 6)dx. 3. Find a differential 0-form ω whose derivative dω is the differential 1-form 6 x dω = (x 3)(2x+5) dx. [ee 5.20] 4. Find a differential 0-form ω whose derivative dω is the differential 1-form 1 dω = 5+3cosx dx. [ee 5.21] 3 Fundamental theorem of calculus 1. Evaluate the integral 1 (x+2)(3 x) dx of the differential 1-form ω = dx/ (x+2)(3 x) over the oriented interval = [ 1,1]. [ee 5.14(c)] 2. Evaluate the integral 1 dx (x 2 2x+4) 3/2 of the differential 1-formω = (x 2 2x+4) 3/2 dx over the oriented interval = [2,1]. [ee 5.15] 3. Evaluate the integral 1 x(lnx) 3 dx of the differential 1-form ω = dx/x(lnx) 3 over the oriented interval = [e,e 2 ]. [ee 5.16] 4. Give an informal proof of tokes formula ω = dω for = [a,b] R and ω = f(x):r R a differentiable function.
3 4 0-forms on n-dimensional space 1. Let denote the oriented line segment in the plane going from the point A = (1,2) to the point B = ( 2,3). Evaluate the integral x 2 +xy +y 2 of the differential 0-form ω = x 2 +xy +y 2 over the boundary of. 2. Let denote the oriented line segment on the z-axis in R 3 going from z = 1 to z = 2. Evaluate the integral ze x2 +y 2 of the differential 0-form ω = ze x2 +y 2 over the boundary of. 5 1-forms on n-dimensional space 1. Match the five pictures of flows (a) (b) (c) (d) (e) to the five differential 1-forms: (i) ω = x 2 dx+y 2 dy, (ii) ω = sin(πx)dx+sin(πy)dy, (iii) ω = xdx+ydy, (iv) ω = dx+dy, (v) ω = dx+dy. 2. In a constant force field the displacement of a particle from (0,0,0) to (4,0,0) needs 3 units of work;
4 from (1, 1,0) to (1,1,0) needs 2 units of work; from (0,0,0) to (3,0,2) needs 5 units of work. Determine the differential 1-form that describes work. 6 Integration of constant 1-forms 1. Evaluate the integral 2dx+3dy+5dz of the differential 1-form ω = 2dx+3dy+5dz on the line segment in R 3 starting at point P = (3,12,4) and ending at point Q = (11,14, 7). 2. If work is given by the 1-form 3dx+4dy dz find all points which can be reached from the origin (0, 0, 0) without work. Describe the set of these points geometrically. 7 Integration of 1-forms 1. Evaluate the integral (x 2 y)dx+(y 2 +x)dy of the differential 1-form ω = (x 2 y)dx+(y 2 +x)dy where R 2 is the segment of the parabola x = t, y = t 2 +1 from the point (0,1) to the point (1,2). [ee 10.1] 2. Evaluate the integral of the 1-form C ω = (3x 2 6yz)dx+(2y +3xz)dy +(1 4xyz 2 )dz where C is the straight line from (0,0,0) to (1,1,1). [ee 10.2(c)] 3. Evaluate the integral of the 1-form C ω = (3x 2 6yz)dx+(2y +3xz)dy +(1 4xyz 2 )dz where C is the curve x = t, y = t 2, z = t 3 from (0,0,0) to (1,1,1). [ee 10.2(c)] ω ω
5 4. Evaluate the integral (2xy x 2 )dx+(x+y 2 )dy where is the boundary of the region bounded by the two curves y = x 2 and y 2 = x. Assume an anti-clockwise orientation on. [ee 10.6] 8 Differentiation of 0-forms 1. Determine the 1-form dω arising as the derivative of the 0-form ω = x 2 e y/x. [ee 6.16(a)] 2. Find a 0-form ω whose derivative is [ee 6.16(b)] dω = (3x 2 y 2y 2 )dx+(x 3 4xy +6y 2 )dy. 9 Partial derivatives 1. uppose U = zsin(y/x) where x = 3r 2 +2s, y = 4r 2s 3 and z = 2r Calculate u/ r and U/ s. [ee 6.22] 10 Fundamental Theorem of Calculus again 1. Evaluate (6xy 2 y 3 )dx+(6x 2 y 3xy 2 )dy. where is some path from (1,2) to (3,4). Explain why the integral is independent of the choice of path from (1,2) to (3,4). [ee 10.14] 2. Evaluate (2xy y 4 +3)dx+(x 2 4xy 3 )dy. where is some path from (1,0) to (2,1). Explain why the integral is independent of the choice of path from (1,0) to (2,1). [ee 10.48]
6 3. Prove that the differential 1-form ω = (3x 2 6yz)dx+(2y +3xz)dy +(1 4xyz 2 )dz does not arise as the derivative ω = dν of any 0-form ν on R 3. [ee Questions 2 and 3 of ection 7 above] 4. Prove tokes formula ω = dω for ω = f(x,y):r2 R a continuously differentiable function and R 2 an oriented curve with differentiable parametrization x = g(t), y = h(t). 11 Constant 2-forms 1. Evaluate the integral dx dy +3dx dz of the 2-formω = dx dy+3dx dz over the oriented triangle with vertices (0,0,0), (1,2,3), (1,4,0) in that order. 2. Evaluate the integral dy dz +dz dx+dx dy of the 2-form ω = dy dz+dz dx+dx dy over the oriented triangle with vertices (1,1,1), (3,5, 1), (4,2,1) in that order. 3. Evaluate the integral 3dx dy of the 2-form ω = 3dx dy over the region = {(x,y) R 2 : x 2 +y 2 1} where is given a clockwise rotation when viewed from the positive z-axis. 12 More integration of 2-forms 1. Evaluate the integral 3dx dy +4dy dz over the region = {(x,y) R 2 : x 2 +y 2 1} where is given a clockwise rotation when viewed from the positive z-axis.
7 2. Let be the region in the xy-plane bounded by y = x 2, x = 2 and y = 1. Let have an anti-clockwise orientation. Evaluate (x 2 +y 2 +z 2 )dx dy. [ee 9.1] 3. Let be the region in the xy-plane bounded by y = x 2, x = 2 and y = 1. Let have an anti-clockwise orientation. Evaluate (x 2 +y 2 +z 2 )dy dz. 4. Let be the region in the xy-plane bounded by the curves y = x 2, y = 2 x 2, x = 0 and x = 1. Let have an anti-clockwise orientation. Evaluate xydx dy. [ee 9.3(b)] 5. Find the volume of the region in R 3 common to the intersecting cylinders x 2 +y 2 = 4 and x 2 +z 2 = 4. [ee 9.4] 13 Differentiation of k-forms 1. Find dω for the following forms. (a) ω = xydz +yzdx+zxdy (b) ω = xdy dz +ydz dx+zdx dy (c) ω = e xyz (d) ω = (cosx)dy +(sinx)dz (e) ω = (x+y) 2 dy +(x+y) 2 dz (f) ω = logx (g) ω = x 2 (h) ω = sinx (i) ω = x 2. Let ω = F(x,y,z) be a 0-form and assume F xy = F yx, F xz = F zx, F yz = F zy. Prove that d(dω) = Let ω = F(x,y,z)dx+G(x,y,z)dy+H(x,y,z)dz and assume that each of F,G,H satisfy the hypothesis of the preceding question. Prove that d(dω) = 0.
8 4. Use the preceding problem to prove that the differential 1-form ω = (3x 2 6yz)dx+(2y +3xz)dy +(1 4xyz 2 )dz does not arise as the derivative ω = dν of any 0-form ν on R For two differential 0-forms ν, ω prove that d(νω) = (dν)ω +ν(dω). 6. For two differential 1-forms ν = Adx+Bdy, ω = Cdx+Ddy prove that d(ν ω) = (dν) ω ν (dω). 14 tokes Formula 1. Verify tokes Formula ω = dω for ω = (2xy x2 )dx+(x+y 2 )dy and the region in the xy-plane bounded by y = x 2 and x 2 = y. [ee 10.6] 2. Verifytokes Formula ω = dω forω = (2x z)dy dz+x2 ydz dx xz 2 dx dy and the region in R 3 bounded by x = 0, x = 1, y = 0, y = 1, z = 0, z = 1. (This is a very long and tedious questions to answer!) [ee 10.23] 3. Let denote the region bounded by some ellipse (or other some other simple closed curve) in the xy-plane. Use tokes Formula to show that the area of is given by xdy ydx. [ee 10.8] 4. Calculate the area bounded by the ellipse x = acosθ, y = bsinθ. 5. By considering an oriented 2-dimensional rectangle in the xy-plane, explain how tokes formula ω = dω leads to the definition of the derivative dω of a differential 1-form ω = Adx+Bdy. 15 div, grad, curl 1. Consider the 0-form ω = (x 2 +y 2 )/2. Calculate the gradient 1-form dω and sketch the corresponding vector field on R Find a unit normal to the surface R 3 defined by the equation at the pont (3, 1,2). [ee 7.37] 2x 2 +4yz 5z 2 = 10
9 3. Consider the 1-form ω = ydx+xdy. ketch the corresponding vector field. Then compute the curl 2-form dω. What feature of your sketch is captured by dω? 4. Consider the vector field F = xzi y 2 j + 2x 2 yk. Define curl(f) in terms of the derivative of a 1-form and then calculate curl(f). 5. Consider the 0-formω = x 2 yz 3 and the vector field F = xzi y 2 j+2x 2 yk. Determine grad(ω), div(f), curl(f), div(φf), div(ωf), curl(ωf). [ee 7.34]
Math 233. Practice Problems Chapter 15. i j k
 Math 233. Practice Problems hapter 15 1. ompute the curl and divergence of the vector field F given by F (4 cos(x 2 ) 2y)i + (4 sin(y 2 ) + 6x)j + (6x 2 y 6x + 4e 3z )k olution: The curl of F is computed
Math 233. Practice Problems hapter 15 1. ompute the curl and divergence of the vector field F given by F (4 cos(x 2 ) 2y)i + (4 sin(y 2 ) + 6x)j + (6x 2 y 6x + 4e 3z )k olution: The curl of F is computed
2. Below are four algebraic vector fields and four sketches of vector fields. Match them.
 Math 511: alc III - Practice Eam 3 1. State the meaning or definitions of the following terms: a) vector field, conservative vector field, potential function of a vector field, volume, length of a curve,
Math 511: alc III - Practice Eam 3 1. State the meaning or definitions of the following terms: a) vector field, conservative vector field, potential function of a vector field, volume, length of a curve,
Review for the Final Exam
 Calculus 3 Lia Vas Review for the Final Exam. Sequences. Determine whether the following sequences are convergent or divergent. If they are convergent, find their limits. (a) a n = ( 2 ) n (b) a n = n+
Calculus 3 Lia Vas Review for the Final Exam. Sequences. Determine whether the following sequences are convergent or divergent. If they are convergent, find their limits. (a) a n = ( 2 ) n (b) a n = n+
Review Questions for Test 3 Hints and Answers
 eview Questions for Test 3 Hints and Answers A. Some eview Questions on Vector Fields and Operations. A. (a) The sketch is left to the reader, but the vector field appears to swirl in a clockwise direction,
eview Questions for Test 3 Hints and Answers A. Some eview Questions on Vector Fields and Operations. A. (a) The sketch is left to the reader, but the vector field appears to swirl in a clockwise direction,
(b) Find the range of h(x, y) (5) Use the definition of continuity to explain whether or not the function f(x, y) is continuous at (0, 0)
 eview Exam Math 43 Name Id ead each question carefully. Avoid simple mistakes. Put a box around the final answer to a question (use the back of the page if necessary). For full credit you must show your
eview Exam Math 43 Name Id ead each question carefully. Avoid simple mistakes. Put a box around the final answer to a question (use the back of the page if necessary). For full credit you must show your
HOMEWORK 8 SOLUTIONS
 HOMEWOK 8 OLUTION. Let and φ = xdy dz + ydz dx + zdx dy. let be the disk at height given by: : x + y, z =, let X be the region in 3 bounded by the cone and the disk. We orient X via dx dy dz, then by definition
HOMEWOK 8 OLUTION. Let and φ = xdy dz + ydz dx + zdx dy. let be the disk at height given by: : x + y, z =, let X be the region in 3 bounded by the cone and the disk. We orient X via dx dy dz, then by definition
M273Q Multivariable Calculus Spring 2017 Review Problems for Exam 3
 M7Q Multivariable alculus Spring 7 Review Problems for Exam Exam covers material from Sections 5.-5.4 and 6.-6. and 7.. As you prepare, note well that the Fall 6 Exam posted online did not cover exactly
M7Q Multivariable alculus Spring 7 Review Problems for Exam Exam covers material from Sections 5.-5.4 and 6.-6. and 7.. As you prepare, note well that the Fall 6 Exam posted online did not cover exactly
(a) 0 (b) 1/4 (c) 1/3 (d) 1/2 (e) 2/3 (f) 3/4 (g) 1 (h) 4/3
 Math 114 Practice Problems for Test 3 omments: 0. urface integrals, tokes Theorem and Gauss Theorem used to be in the Math40 syllabus until last year, so we will look at some of the questions from those
Math 114 Practice Problems for Test 3 omments: 0. urface integrals, tokes Theorem and Gauss Theorem used to be in the Math40 syllabus until last year, so we will look at some of the questions from those
29.3. Integral Vector Theorems. Introduction. Prerequisites. Learning Outcomes
 Integral ector Theorems 9. Introduction arious theorems exist relating integrals involving vectors. Those involving line, surface and volume integrals are introduced here. They are the multivariable calculus
Integral ector Theorems 9. Introduction arious theorems exist relating integrals involving vectors. Those involving line, surface and volume integrals are introduced here. They are the multivariable calculus
Math Review for Exam 3
 1. ompute oln: (8x + 36xy)ds = Math 235 - Review for Exam 3 (8x + 36xy)ds, where c(t) = (t, t 2, t 3 ) on the interval t 1. 1 (8t + 36t 3 ) 1 + 4t 2 + 9t 4 dt = 2 3 (1 + 4t2 + 9t 4 ) 3 2 1 = 2 3 ((14)
1. ompute oln: (8x + 36xy)ds = Math 235 - Review for Exam 3 (8x + 36xy)ds, where c(t) = (t, t 2, t 3 ) on the interval t 1. 1 (8t + 36t 3 ) 1 + 4t 2 + 9t 4 dt = 2 3 (1 + 4t2 + 9t 4 ) 3 2 1 = 2 3 ((14)
MATH 52 FINAL EXAM SOLUTIONS
 MAH 5 FINAL EXAM OLUION. (a) ketch the region R of integration in the following double integral. x xe y5 dy dx R = {(x, y) x, x y }. (b) Express the region R as an x-simple region. R = {(x, y) y, x y }
MAH 5 FINAL EXAM OLUION. (a) ketch the region R of integration in the following double integral. x xe y5 dy dx R = {(x, y) x, x y }. (b) Express the region R as an x-simple region. R = {(x, y) y, x y }
Line and Surface Integrals. Stokes and Divergence Theorems
 Math Methods 1 Lia Vas Line and urface Integrals. tokes and Divergence Theorems Review of urves. Intuitively, we think of a curve as a path traced by a moving particle in space. Thus, a curve is a function
Math Methods 1 Lia Vas Line and urface Integrals. tokes and Divergence Theorems Review of urves. Intuitively, we think of a curve as a path traced by a moving particle in space. Thus, a curve is a function
Ma 227 Final Exam Solutions 12/17/07
 Ma 7 Final Exam olutions /7/7 Name: Lecture ection: I pledge my honor that I have abided by the tevens Honor ystem. You may not use a calculator, cell phone, or computer while taking this exam. All work
Ma 7 Final Exam olutions /7/7 Name: Lecture ection: I pledge my honor that I have abided by the tevens Honor ystem. You may not use a calculator, cell phone, or computer while taking this exam. All work
Created by T. Madas LINE INTEGRALS. Created by T. Madas
 LINE INTEGRALS LINE INTEGRALS IN 2 DIMENSIONAL CARTESIAN COORDINATES Question 1 Evaluate the integral ( x + 2y) dx, C where C is the path along the curve with equation y 2 = x + 1, from ( ) 0,1 to ( )
LINE INTEGRALS LINE INTEGRALS IN 2 DIMENSIONAL CARTESIAN COORDINATES Question 1 Evaluate the integral ( x + 2y) dx, C where C is the path along the curve with equation y 2 = x + 1, from ( ) 0,1 to ( )
18.02 Multivariable Calculus Fall 2007
 MIT OpenourseWare http://ocw.mit.edu 18.02 Multivariable alculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.02 Lecture 30. Tue, Nov
MIT OpenourseWare http://ocw.mit.edu 18.02 Multivariable alculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.02 Lecture 30. Tue, Nov
Answers and Solutions to Section 13.7 Homework Problems 1 19 (odd) S. F. Ellermeyer April 23, 2004
 Answers and olutions to ection 1.7 Homework Problems 1 19 (odd). F. Ellermeyer April 2, 24 1. The hemisphere and the paraboloid both have the same boundary curve, the circle x 2 y 2 4. Therefore, by tokes
Answers and olutions to ection 1.7 Homework Problems 1 19 (odd). F. Ellermeyer April 2, 24 1. The hemisphere and the paraboloid both have the same boundary curve, the circle x 2 y 2 4. Therefore, by tokes
Math 23b Practice Final Summer 2011
 Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
Mathematical Analysis II, 2018/19 First semester
 Mathematical Analysis II, 208/9 First semester Yoh Tanimoto Dipartimento di Matematica, Università di Roma Tor Vergata Via della Ricerca Scientifica, I-0033 Roma, Italy email: hoyt@mat.uniroma2.it We basically
Mathematical Analysis II, 208/9 First semester Yoh Tanimoto Dipartimento di Matematica, Università di Roma Tor Vergata Via della Ricerca Scientifica, I-0033 Roma, Italy email: hoyt@mat.uniroma2.it We basically
Without fully opening the exam, check that you have pages 1 through 12.
 MTH 34 Solutions to Exam November 9, 8 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through.
MTH 34 Solutions to Exam November 9, 8 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through.
4B. Line Integrals in the Plane
 4. Line Integrals in the Plane 4A. Plane Vector Fields 4A-1 Describe geometrically how the vector fields determined by each of the following vector functions looks. Tell for each what the largest region
4. Line Integrals in the Plane 4A. Plane Vector Fields 4A-1 Describe geometrically how the vector fields determined by each of the following vector functions looks. Tell for each what the largest region
18.1. Math 1920 November 29, ) Solution: In this function P = x 2 y and Q = 0, therefore Q. Converting to polar coordinates, this gives I =
 Homework 1 elected olutions Math 19 November 9, 18 18.1 5) olution: In this function P = x y and Q =, therefore Q x P = x. We obtain the following integral: ( Q I = x ydx = x P ) da = x da. onverting to
Homework 1 elected olutions Math 19 November 9, 18 18.1 5) olution: In this function P = x y and Q =, therefore Q x P = x. We obtain the following integral: ( Q I = x ydx = x P ) da = x da. onverting to
Page Points Score Total: 210. No more than 200 points may be earned on the exam.
 Name: PID: Section: Recitation Instructor: DO NOT WRITE BELOW THIS LINE. GO ON TO THE NEXT PAGE. Page Points Score 3 18 4 18 5 18 6 18 7 18 8 18 9 18 10 21 11 21 12 21 13 21 Total: 210 No more than 200
Name: PID: Section: Recitation Instructor: DO NOT WRITE BELOW THIS LINE. GO ON TO THE NEXT PAGE. Page Points Score 3 18 4 18 5 18 6 18 7 18 8 18 9 18 10 21 11 21 12 21 13 21 Total: 210 No more than 200
Practice problems. m zδdv. In our case, we can cancel δ and have z =
 Practice problems 1. Consider a right circular cone of uniform density. The height is H. Let s say the distance of the centroid to the base is d. What is the value d/h? We can create a coordinate system
Practice problems 1. Consider a right circular cone of uniform density. The height is H. Let s say the distance of the centroid to the base is d. What is the value d/h? We can create a coordinate system
Practice problems. 1. Evaluate the double or iterated integrals: First: change the order of integration; Second: polar.
 Practice problems 1. Evaluate the double or iterated integrals: R x 3 + 1dA where R = {(x, y) : 0 y 1, y x 1}. 1/ 1 y 0 3y sin(x + y )dxdy First: change the order of integration; Second: polar.. Consider
Practice problems 1. Evaluate the double or iterated integrals: R x 3 + 1dA where R = {(x, y) : 0 y 1, y x 1}. 1/ 1 y 0 3y sin(x + y )dxdy First: change the order of integration; Second: polar.. Consider
In general, the formula is S f ds = D f(φ(u, v)) Φ u Φ v da. To compute surface area, we choose f = 1. We compute
 alculus III Test 3 ample Problem Answers/olutions 1. Express the area of the surface Φ(u, v) u cosv, u sinv, 2v, with domain u 1, v 2π, as a double integral in u and v. o not evaluate the integral. In
alculus III Test 3 ample Problem Answers/olutions 1. Express the area of the surface Φ(u, v) u cosv, u sinv, 2v, with domain u 1, v 2π, as a double integral in u and v. o not evaluate the integral. In
Sections minutes. 5 to 10 problems, similar to homework problems. No calculators, no notes, no books, no phones. No green book needed.
 MTH 34 Review for Exam 4 ections 16.1-16.8. 5 minutes. 5 to 1 problems, similar to homework problems. No calculators, no notes, no books, no phones. No green book needed. Review for Exam 4 (16.1) Line
MTH 34 Review for Exam 4 ections 16.1-16.8. 5 minutes. 5 to 1 problems, similar to homework problems. No calculators, no notes, no books, no phones. No green book needed. Review for Exam 4 (16.1) Line
Lecture Notes: Divergence Theorem and Stokes Theorem
 Lecture Notes: ivergence heorem and tokes heorem Yufei ao epartment of omputer cience and Engineering hinese University of Hong Kong taoyf@cse.cuhk.edu.hk In this lecture, we will discuss two useful theorems
Lecture Notes: ivergence heorem and tokes heorem Yufei ao epartment of omputer cience and Engineering hinese University of Hong Kong taoyf@cse.cuhk.edu.hk In this lecture, we will discuss two useful theorems
LINE AND SURFACE INTEGRALS: A SUMMARY OF CALCULUS 3 UNIT 4
 LINE AN URFAE INTEGRAL: A UMMARY OF ALULU 3 UNIT 4 The final unit of material in multivariable calculus introduces many unfamiliar and non-intuitive concepts in a short amount of time. This document attempts
LINE AN URFAE INTEGRAL: A UMMARY OF ALULU 3 UNIT 4 The final unit of material in multivariable calculus introduces many unfamiliar and non-intuitive concepts in a short amount of time. This document attempts
G G. G. x = u cos v, y = f(u), z = u sin v. H. x = u + v, y = v, z = u v. 1 + g 2 x + g 2 y du dv
 1. Matching. Fill in the appropriate letter. 1. ds for a surface z = g(x, y) A. r u r v du dv 2. ds for a surface r(u, v) B. r u r v du dv 3. ds for any surface C. G x G z, G y G z, 1 4. Unit normal N
1. Matching. Fill in the appropriate letter. 1. ds for a surface z = g(x, y) A. r u r v du dv 2. ds for a surface r(u, v) B. r u r v du dv 3. ds for any surface C. G x G z, G y G z, 1 4. Unit normal N
CHAPTER 7 DIV, GRAD, AND CURL
 CHAPTER 7 DIV, GRAD, AND CURL 1 The operator and the gradient: Recall that the gradient of a differentiable scalar field ϕ on an open set D in R n is given by the formula: (1 ϕ = ( ϕ, ϕ,, ϕ x 1 x 2 x n
CHAPTER 7 DIV, GRAD, AND CURL 1 The operator and the gradient: Recall that the gradient of a differentiable scalar field ϕ on an open set D in R n is given by the formula: (1 ϕ = ( ϕ, ϕ,, ϕ x 1 x 2 x n
Review problems for the final exam Calculus III Fall 2003
 Review problems for the final exam alculus III Fall 2003 1. Perform the operations indicated with F (t) = 2t ı 5 j + t 2 k, G(t) = (1 t) ı + 1 t k, H(t) = sin(t) ı + e t j a) F (t) G(t) b) F (t) [ H(t)
Review problems for the final exam alculus III Fall 2003 1. Perform the operations indicated with F (t) = 2t ı 5 j + t 2 k, G(t) = (1 t) ı + 1 t k, H(t) = sin(t) ı + e t j a) F (t) G(t) b) F (t) [ H(t)
Math 11 Fall 2007 Practice Problem Solutions
 Math 11 Fall 27 Practice Problem olutions Here are some problems on the material we covered since the second midterm. This collection of problems is not intended to mimic the final in length, content,
Math 11 Fall 27 Practice Problem olutions Here are some problems on the material we covered since the second midterm. This collection of problems is not intended to mimic the final in length, content,
SUPPLEMENTARY READING FOR MATH 53: DIFFERENTIAL FORMS AND THE GENERAL STOKES FORMULA
 SUPPLEMENTARY READING FOR MATH 53: DIFFERENTIAL FORMS AND THE GENERAL STOKES FORMULA EDWARD FRENKEL, UC BERKELEY The purpose of these notes is to outline briefly a general formalism which allows for a
SUPPLEMENTARY READING FOR MATH 53: DIFFERENTIAL FORMS AND THE GENERAL STOKES FORMULA EDWARD FRENKEL, UC BERKELEY The purpose of these notes is to outline briefly a general formalism which allows for a
No calculators, cell phones or any other electronic devices can be used on this exam. Clear your desk of everything excepts pens, pencils and erasers.
 Name: Section: Recitation Instructor: READ THE FOLLOWING INSTRUCTIONS. Do not open your exam until told to do so. No calculators, cell phones or any other electronic devices can be used on this exam. Clear
Name: Section: Recitation Instructor: READ THE FOLLOWING INSTRUCTIONS. Do not open your exam until told to do so. No calculators, cell phones or any other electronic devices can be used on this exam. Clear
MTH 234 Exam 2 November 21st, Without fully opening the exam, check that you have pages 1 through 12.
 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 12. Show all your work on the standard
Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 12. Show all your work on the standard
LINE AND SURFACE INTEGRALS: A SUMMARY OF CALCULUS 3 UNIT 4
 LINE AN URFAE INTEGRAL: A UMMARY OF ALULU 3 UNIT 4 The final unit of material in multivariable calculus introduces many unfamiliar and non-intuitive concepts in a short amount of time. This document attempts
LINE AN URFAE INTEGRAL: A UMMARY OF ALULU 3 UNIT 4 The final unit of material in multivariable calculus introduces many unfamiliar and non-intuitive concepts in a short amount of time. This document attempts
Practice problems ********************************************************** 1. Divergence, curl
 Practice problems 1. Set up the integral without evaluation. The volume inside (x 1) 2 + y 2 + z 2 = 1, below z = 3r but above z = r. This problem is very tricky in cylindrical or Cartesian since we must
Practice problems 1. Set up the integral without evaluation. The volume inside (x 1) 2 + y 2 + z 2 = 1, below z = 3r but above z = r. This problem is very tricky in cylindrical or Cartesian since we must
Peter Alfeld Math , Fall 2005
 WeBWorK assignment due 9/2/05 at :59 PM..( pt) Consider the parametric equation x = 2(cosθ + θsinθ) y = 2(sinθ θcosθ) What is the length of the curve for θ = 0 to θ = 7 6 π? 2.( pt) Let a = (-2 4 2) and
WeBWorK assignment due 9/2/05 at :59 PM..( pt) Consider the parametric equation x = 2(cosθ + θsinθ) y = 2(sinθ θcosθ) What is the length of the curve for θ = 0 to θ = 7 6 π? 2.( pt) Let a = (-2 4 2) and
6. Vector Integral Calculus in Space
 6. Vector Integral alculus in pace 6A. Vector Fields in pace 6A-1 Describegeometricallythefollowingvectorfields: a) xi +yj +zk ρ b) xi zk 6A-2 Write down the vector field where each vector runs from (x,y,z)
6. Vector Integral alculus in pace 6A. Vector Fields in pace 6A-1 Describegeometricallythefollowingvectorfields: a) xi +yj +zk ρ b) xi zk 6A-2 Write down the vector field where each vector runs from (x,y,z)
4. Line Integrals in the Plane
 4. Line Integrals in the Plane 4A. Plane Vector Fields 4A- a) All vectors in the field are identical; continuously differentiable everywhere. b) The vector at P has its tail at P and head at the origin;
4. Line Integrals in the Plane 4A. Plane Vector Fields 4A- a) All vectors in the field are identical; continuously differentiable everywhere. b) The vector at P has its tail at P and head at the origin;
Math 31CH - Spring Final Exam
 Math 3H - Spring 24 - Final Exam Problem. The parabolic cylinder y = x 2 (aligned along the z-axis) is cut by the planes y =, z = and z = y. Find the volume of the solid thus obtained. Solution:We calculate
Math 3H - Spring 24 - Final Exam Problem. The parabolic cylinder y = x 2 (aligned along the z-axis) is cut by the planes y =, z = and z = y. Find the volume of the solid thus obtained. Solution:We calculate
Green s, Divergence, Stokes: Statements and First Applications
 Math 425 Notes 12: Green s, Divergence, tokes: tatements and First Applications The Theorems Theorem 1 (Divergence (planar version)). Let F be a vector field in the plane. Let be a nice region of the plane
Math 425 Notes 12: Green s, Divergence, tokes: tatements and First Applications The Theorems Theorem 1 (Divergence (planar version)). Let F be a vector field in the plane. Let be a nice region of the plane
MA FINAL EXAM Form 01 May 1, 2017
 MA 26100 FINAL EXAM Form 01 May 1, 2017 NAME STUDENT ID # YOUR TA S NAME RECITATION TIME 1. You must use a #2 pencil on the scantron 2. a. Write 01 in the TEST/QUIZ NUMBER boxes and darken the appropriate
MA 26100 FINAL EXAM Form 01 May 1, 2017 NAME STUDENT ID # YOUR TA S NAME RECITATION TIME 1. You must use a #2 pencil on the scantron 2. a. Write 01 in the TEST/QUIZ NUMBER boxes and darken the appropriate
f. D that is, F dr = c c = [2"' (-a sin t)( -a sin t) + (a cos t)(a cost) dt = f2"' dt = 2
 SECTION 16.4 GREEN'S THEOREM 1089 X with center the origin and radius a, where a is chosen to be small enough that C' lies inside C. (See Figure 11.) Let be the region bounded by C and C'. Then its positively
SECTION 16.4 GREEN'S THEOREM 1089 X with center the origin and radius a, where a is chosen to be small enough that C' lies inside C. (See Figure 11.) Let be the region bounded by C and C'. Then its positively
MULTIVARIABLE INTEGRATION
 MULTIVARIABLE INTEGRATION (PLANE & CYLINDRICAL POLAR COORDINATES) PLANE POLAR COORDINATES Question 1 The finite region on the x-y plane satisfies 1 x + y 4, y 0. Find, in terms of π, the value of I. I
MULTIVARIABLE INTEGRATION (PLANE & CYLINDRICAL POLAR COORDINATES) PLANE POLAR COORDINATES Question 1 The finite region on the x-y plane satisfies 1 x + y 4, y 0. Find, in terms of π, the value of I. I
Solutions for the Practice Final - Math 23B, 2016
 olutions for the Practice Final - Math B, 6 a. True. The area of a surface is given by the expression d, and since we have a parametrization φ x, y x, y, f x, y with φ, this expands as d T x T y da xy
olutions for the Practice Final - Math B, 6 a. True. The area of a surface is given by the expression d, and since we have a parametrization φ x, y x, y, f x, y with φ, this expands as d T x T y da xy
Ma 227 Final Exam Solutions 12/13/11
 Ma 7 Final Exam Solutions /3/ Name: Lecture Section: (A and B: Prof. Levine, C: Prof. Brady) Problem a) ( points) Find the eigenvalues and eigenvectors of the matrix A. A 3 5 Solution. First we find the
Ma 7 Final Exam Solutions /3/ Name: Lecture Section: (A and B: Prof. Levine, C: Prof. Brady) Problem a) ( points) Find the eigenvalues and eigenvectors of the matrix A. A 3 5 Solution. First we find the
MTH 234 Solutions to Exam 2 April 13, Multiple Choice. Circle the best answer. No work needed. No partial credit available.
 MTH 234 Solutions to Exam 2 April 3, 25 Multiple Choice. Circle the best answer. No work needed. No partial credit available.. (5 points) Parametrize of the part of the plane 3x+2y +z = that lies above
MTH 234 Solutions to Exam 2 April 3, 25 Multiple Choice. Circle the best answer. No work needed. No partial credit available.. (5 points) Parametrize of the part of the plane 3x+2y +z = that lies above
Without fully opening the exam, check that you have pages 1 through 12.
 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 12. Show all your work on the standard
Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 12. Show all your work on the standard
MATHS 267 Answers to Stokes Practice Dr. Jones
 MATH 267 Answers to tokes Practice Dr. Jones 1. Calculate the flux F d where is the hemisphere x2 + y 2 + z 2 1, z > and F (xz + e y2, yz, z 2 + 1). Note: the surface is open (doesn t include any of the
MATH 267 Answers to tokes Practice Dr. Jones 1. Calculate the flux F d where is the hemisphere x2 + y 2 + z 2 1, z > and F (xz + e y2, yz, z 2 + 1). Note: the surface is open (doesn t include any of the
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
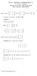 M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
McGill University April 16, Advanced Calculus for Engineers
 McGill University April 16, 2014 Faculty of cience Final examination Advanced Calculus for Engineers Math 264 April 16, 2014 Time: 6PM-9PM Examiner: Prof. R. Choksi Associate Examiner: Prof. A. Hundemer
McGill University April 16, 2014 Faculty of cience Final examination Advanced Calculus for Engineers Math 264 April 16, 2014 Time: 6PM-9PM Examiner: Prof. R. Choksi Associate Examiner: Prof. A. Hundemer
Solutions to old Exam 3 problems
 Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
volq = U(f, P 2 ). This finally gives
 MAT 257Y s to Practice Final (1) Let A R n be a rectangle and let f : A R be bounded. Let P 1, P 2 be two partitions of A. Prove that L(f, P 1 ) (f, P 2 ). The statement is obvious if P 1 = P 2. In general,
MAT 257Y s to Practice Final (1) Let A R n be a rectangle and let f : A R be bounded. Let P 1, P 2 be two partitions of A. Prove that L(f, P 1 ) (f, P 2 ). The statement is obvious if P 1 = P 2. In general,
Math 212-Lecture 20. P dx + Qdy = (Q x P y )da. C
 15. Green s theorem Math 212-Lecture 2 A simple closed curve in plane is one curve, r(t) : t [a, b] such that r(a) = r(b), and there are no other intersections. The positive orientation is counterclockwise.
15. Green s theorem Math 212-Lecture 2 A simple closed curve in plane is one curve, r(t) : t [a, b] such that r(a) = r(b), and there are no other intersections. The positive orientation is counterclockwise.
7a3 2. (c) πa 3 (d) πa 3 (e) πa3
 1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
Multiple Integrals and Vector Calculus (Oxford Physics) Synopsis and Problem Sets; Hilary 2015
 Multiple Integrals and Vector Calculus (Oxford Physics) Ramin Golestanian Synopsis and Problem Sets; Hilary 215 The outline of the material, which will be covered in 14 lectures, is as follows: 1. Introduction
Multiple Integrals and Vector Calculus (Oxford Physics) Ramin Golestanian Synopsis and Problem Sets; Hilary 215 The outline of the material, which will be covered in 14 lectures, is as follows: 1. Introduction
+ f f n x n. + (x)
 Math 255 - Vector Calculus II Notes 14.5 Divergence, (Grad) and Curl For a vector field in R n, that is F = f 1, f 2,..., f n, where f i is a function of x 1, x 2,..., x n, the divergence is div(f) = f
Math 255 - Vector Calculus II Notes 14.5 Divergence, (Grad) and Curl For a vector field in R n, that is F = f 1, f 2,..., f n, where f i is a function of x 1, x 2,..., x n, the divergence is div(f) = f
Jim Lambers MAT 280 Summer Semester Practice Final Exam Solution. dy + xz dz = x(t)y(t) dt. t 3 (4t 3 ) + e t2 (2t) + t 7 (3t 2 ) dt
 Jim Lambers MAT 28 ummer emester 212-1 Practice Final Exam olution 1. Evaluate the line integral xy dx + e y dy + xz dz, where is given by r(t) t 4, t 2, t, t 1. olution From r (t) 4t, 2t, t 2, we obtain
Jim Lambers MAT 28 ummer emester 212-1 Practice Final Exam olution 1. Evaluate the line integral xy dx + e y dy + xz dz, where is given by r(t) t 4, t 2, t, t 1. olution From r (t) 4t, 2t, t 2, we obtain
1 Arithmetic calculations (calculator is not allowed)
 1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
Tom Robbins WW Prob Lib1 Math , Fall 2001
 Tom Robbins WW Prob Lib Math 220-2, Fall 200 WeBWorK assignment due 9/7/0 at 6:00 AM..( pt) A child walks due east on the deck of a ship at 3 miles per hour. The ship is moving north at a speed of 7 miles
Tom Robbins WW Prob Lib Math 220-2, Fall 200 WeBWorK assignment due 9/7/0 at 6:00 AM..( pt) A child walks due east on the deck of a ship at 3 miles per hour. The ship is moving north at a speed of 7 miles
Final Review Worksheet
 Score: Name: Final Review Worksheet Math 2110Q Fall 2014 Professor Hohn Answers (in no particular order): f(x, y) = e y + xe xy + C; 2; 3; e y cos z, e z cos x, e x cos y, e x sin y e y sin z e z sin x;
Score: Name: Final Review Worksheet Math 2110Q Fall 2014 Professor Hohn Answers (in no particular order): f(x, y) = e y + xe xy + C; 2; 3; e y cos z, e z cos x, e x cos y, e x sin y e y sin z e z sin x;
Calculus III. Math 233 Spring Final exam May 3rd. Suggested solutions
 alculus III Math 33 pring 7 Final exam May 3rd. uggested solutions This exam contains twenty problems numbered 1 through. All problems are multiple choice problems, and each counts 5% of your total score.
alculus III Math 33 pring 7 Final exam May 3rd. uggested solutions This exam contains twenty problems numbered 1 through. All problems are multiple choice problems, and each counts 5% of your total score.
Multiple Integrals and Vector Calculus: Synopsis
 Multiple Integrals and Vector Calculus: Synopsis Hilary Term 28: 14 lectures. Steve Rawlings. 1. Vectors - recap of basic principles. Things which are (and are not) vectors. Differentiation and integration
Multiple Integrals and Vector Calculus: Synopsis Hilary Term 28: 14 lectures. Steve Rawlings. 1. Vectors - recap of basic principles. Things which are (and are not) vectors. Differentiation and integration
C 3 C 4. R k C 1. (x,y)
 16.4 1 16.4 Green s Theorem irculation Density (x,y + y) 3 (x+ x,y + y) 4 k 2 (x,y) 1 (x+ x,y) Suppose that F(x,y) M(x,y)i+N(x,y)j is the velocity field of a fluid flow in the plane and that the first
16.4 1 16.4 Green s Theorem irculation Density (x,y + y) 3 (x+ x,y + y) 4 k 2 (x,y) 1 (x+ x,y) Suppose that F(x,y) M(x,y)i+N(x,y)j is the velocity field of a fluid flow in the plane and that the first
Name: Date: 12/06/2018. M20550 Calculus III Tutorial Worksheet 11
 1. ompute the surface integral M255 alculus III Tutorial Worksheet 11 x + y + z) d, where is a surface given by ru, v) u + v, u v, 1 + 2u + v and u 2, v 1. olution: First, we know x + y + z) d [ ] u +
1. ompute the surface integral M255 alculus III Tutorial Worksheet 11 x + y + z) d, where is a surface given by ru, v) u + v, u v, 1 + 2u + v and u 2, v 1. olution: First, we know x + y + z) d [ ] u +
Practice problems. 1. Evaluate the double or iterated integrals: First: change the order of integration; Second: polar.
 Practice problems 1. Evaluate the double or iterated integrals: x 3 + 1dA where = {(x, y) : 0 y 1, y x 1}. 1/ 1 y 0 3y sin(x + y )dxdy First: change the order of integration; Second: polar.. Consider the
Practice problems 1. Evaluate the double or iterated integrals: x 3 + 1dA where = {(x, y) : 0 y 1, y x 1}. 1/ 1 y 0 3y sin(x + y )dxdy First: change the order of integration; Second: polar.. Consider the
3. The Theorems of Green and Stokes
 3. The Theorems of Green and tokes Consider a 1-form ω = P (x, y)dx + Q(x, y)dy on the rectangle R = [a, b] [c, d], which consists of points (x, y) satisfying a x b and c y d. The boundary R of R have
3. The Theorems of Green and tokes Consider a 1-form ω = P (x, y)dx + Q(x, y)dy on the rectangle R = [a, b] [c, d], which consists of points (x, y) satisfying a x b and c y d. The boundary R of R have
18.02 Multivariable Calculus Fall 2007
 MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 4. Line Integrals in the
MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 4. Line Integrals in the
Advanced Calculus. George Voutsadakis 1. LSSU Math 411. Lake Superior State University. 1 Mathematics and Computer Science
 Advanced Calculus George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 411 George Voutsadakis (LSSU) Advanced Calculus March 2018 1 / 77 Outline 1 Fundamental
Advanced Calculus George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 411 George Voutsadakis (LSSU) Advanced Calculus March 2018 1 / 77 Outline 1 Fundamental
PRACTICE PROBLEMS. Please let me know if you find any mistakes in the text so that i can fix them. 1. Mixed partial derivatives.
 PRACTICE PROBLEMS Please let me know if you find any mistakes in the text so that i can fix them. 1.1. Let Show that f is C 1 and yet How is that possible? 1. Mixed partial derivatives f(x, y) = {xy x
PRACTICE PROBLEMS Please let me know if you find any mistakes in the text so that i can fix them. 1.1. Let Show that f is C 1 and yet How is that possible? 1. Mixed partial derivatives f(x, y) = {xy x
Review for the Final Test
 Math 7 Review for the Final Test () Decide if the limit exists and if it exists, evaluate it. lim (x,y,z) (0,0,0) xz. x +y +z () Use implicit differentiation to find z if x + y z = 9 () Find the unit tangent
Math 7 Review for the Final Test () Decide if the limit exists and if it exists, evaluate it. lim (x,y,z) (0,0,0) xz. x +y +z () Use implicit differentiation to find z if x + y z = 9 () Find the unit tangent
Lecture 5 - Fundamental Theorem for Line Integrals and Green s Theorem
 Lecture 5 - Fundamental Theorem for Line Integrals and Green s Theorem Math 392, section C September 14, 2016 392, section C Lect 5 September 14, 2016 1 / 22 Last Time: Fundamental Theorem for Line Integrals:
Lecture 5 - Fundamental Theorem for Line Integrals and Green s Theorem Math 392, section C September 14, 2016 392, section C Lect 5 September 14, 2016 1 / 22 Last Time: Fundamental Theorem for Line Integrals:
Name: SOLUTIONS Date: 11/9/2017. M20550 Calculus III Tutorial Worksheet 8
 Name: SOLUTIONS Date: /9/7 M55 alculus III Tutorial Worksheet 8. ompute R da where R is the region bounded by x + xy + y 8 using the change of variables given by x u + v and y v. Solution: We know R is
Name: SOLUTIONS Date: /9/7 M55 alculus III Tutorial Worksheet 8. ompute R da where R is the region bounded by x + xy + y 8 using the change of variables given by x u + v and y v. Solution: We know R is
Without fully opening the exam, check that you have pages 1 through 12.
 MTH 34 Solutions to Exam April 9th, 8 Name: Section: Recitation Instructor: INSTRUTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through. Show
MTH 34 Solutions to Exam April 9th, 8 Name: Section: Recitation Instructor: INSTRUTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through. Show
MATH503 - HOMEWORK #2. v k. + v i. (fv i ) = f v i. + v k. ) + u j (ɛ ijk. ) u j (ɛ jik
 1 KO UNIVERITY Mon April 18, ollege of Arts and ciences Handout # Department of Physics Instructor: Alkan Kabakço lu MATH - HOMEWORK # 1 ( f) = Using Einstein notation and expressing x, y, x as e 1, e,
1 KO UNIVERITY Mon April 18, ollege of Arts and ciences Handout # Department of Physics Instructor: Alkan Kabakço lu MATH - HOMEWORK # 1 ( f) = Using Einstein notation and expressing x, y, x as e 1, e,
S12.1 SOLUTIONS TO PROBLEMS 12 (ODD NUMBERS)
 OLUTION TO PROBLEM 2 (ODD NUMBER) 2. The electric field is E = φ = 2xi + 2y j and at (2, ) E = 4i + 2j. Thus E = 2 5 and its direction is 2i + j. At ( 3, 2), φ = 6i + 4 j. Thus the direction of most rapid
OLUTION TO PROBLEM 2 (ODD NUMBER) 2. The electric field is E = φ = 2xi + 2y j and at (2, ) E = 4i + 2j. Thus E = 2 5 and its direction is 2i + j. At ( 3, 2), φ = 6i + 4 j. Thus the direction of most rapid
Math 67. Rumbos Fall Solutions to Review Problems for Final Exam. (a) Use the triangle inequality to derive the inequality
 Math 67. umbos Fall 8 Solutions to eview Problems for Final Exam. In this problem, u and v denote vectors in n. (a) Use the triangle inequality to derive the inequality Solution: Write v u v u for all
Math 67. umbos Fall 8 Solutions to eview Problems for Final Exam. In this problem, u and v denote vectors in n. (a) Use the triangle inequality to derive the inequality Solution: Write v u v u for all
Ma 227 Final Exam Solutions 12/22/09
 Ma 7 Final Exam Solutions //9 Name: ID: Lecture Section: Problem a) (3 points) Does the following system of equations have a unique solution or an infinite set of solutions or no solution? Find any solutions.
Ma 7 Final Exam Solutions //9 Name: ID: Lecture Section: Problem a) (3 points) Does the following system of equations have a unique solution or an infinite set of solutions or no solution? Find any solutions.
Linear Algebra. Chapter 8: Eigenvalues: Further Applications and Computations Section 8.2. Applications to Geometry Proofs of Theorems.
 Linear Algebra Chapter 8: Eigenvalues: Further Applications and Computations Section 8.2. Applications to Geometry Proofs of Theorems May 1, 2018 () Linear Algebra May 1, 2018 1 / 8 Table of contents 1
Linear Algebra Chapter 8: Eigenvalues: Further Applications and Computations Section 8.2. Applications to Geometry Proofs of Theorems May 1, 2018 () Linear Algebra May 1, 2018 1 / 8 Table of contents 1
MA FINAL EXAM Form B December 13, 2016
 MA 6100 FINAL EXAM Form B December 1, 016 NAME STUDENT ID # YOUR TA S NAME RECITATION TIME 1. You must use a # pencil on the scantron. a. If the cover of your exam is GREEN, write 01 in the TEST/QUIZ NUMBER
MA 6100 FINAL EXAM Form B December 1, 016 NAME STUDENT ID # YOUR TA S NAME RECITATION TIME 1. You must use a # pencil on the scantron. a. If the cover of your exam is GREEN, write 01 in the TEST/QUIZ NUMBER
Core Mathematics C12
 Write your name here Surname Other names Pearson Edexcel International Advanced Level Centre Number Candidate Number Core Mathematics C12 Advanced Subsidiary Tuesday 12 January 2016 Morning Time: 2 hours
Write your name here Surname Other names Pearson Edexcel International Advanced Level Centre Number Candidate Number Core Mathematics C12 Advanced Subsidiary Tuesday 12 January 2016 Morning Time: 2 hours
Core Mathematics C12
 Write your name here Surname Other names Pearson Edexcel International Advanced Level Centre Number Candidate Number Core Mathematics C12 Advanced Subsidiary Tuesday 12 January 2016 Morning Time: 2 hours
Write your name here Surname Other names Pearson Edexcel International Advanced Level Centre Number Candidate Number Core Mathematics C12 Advanced Subsidiary Tuesday 12 January 2016 Morning Time: 2 hours
Lecture Notes for MATH2230. Neil Ramsamooj
 Lecture Notes for MATH3 Neil amsamooj Table of contents Vector Calculus................................................ 5. Parametric curves and arc length...................................... 5. eview
Lecture Notes for MATH3 Neil amsamooj Table of contents Vector Calculus................................................ 5. Parametric curves and arc length...................................... 5. eview
Section 6-5 : Stokes' Theorem
 ection 6-5 : tokes' Theorem In this section we are going to take a look at a theorem that is a higher dimensional version of Green s Theorem. In Green s Theorem we related a line integral to a double integral
ection 6-5 : tokes' Theorem In this section we are going to take a look at a theorem that is a higher dimensional version of Green s Theorem. In Green s Theorem we related a line integral to a double integral
1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is
 1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
(a) The points (3, 1, 2) and ( 1, 3, 4) are the endpoints of a diameter of a sphere.
 MATH 4 FINAL EXAM REVIEW QUESTIONS Problem. a) The points,, ) and,, 4) are the endpoints of a diameter of a sphere. i) Determine the center and radius of the sphere. ii) Find an equation for the sphere.
MATH 4 FINAL EXAM REVIEW QUESTIONS Problem. a) The points,, ) and,, 4) are the endpoints of a diameter of a sphere. i) Determine the center and radius of the sphere. ii) Find an equation for the sphere.
worked out from first principles by parameterizing the path, etc. If however C is a A path C is a simple closed path if and only if the starting point
 III.c Green s Theorem As mentioned repeatedly, if F is not a gradient field then F dr must be worked out from first principles by parameterizing the path, etc. If however is a simple closed path in the
III.c Green s Theorem As mentioned repeatedly, if F is not a gradient field then F dr must be worked out from first principles by parameterizing the path, etc. If however is a simple closed path in the
Page Problem Score Max Score a 8 12b a b 10 14c 6 6
 Fall 14 MTH 34 FINAL EXAM December 8, 14 Name: PID: Section: Instructor: DO NOT WRITE BELOW THIS LINE. Go to the next page. Page Problem Score Max Score 1 5 5 1 3 5 4 5 5 5 6 5 7 5 8 5 9 5 1 5 11 1 3 1a
Fall 14 MTH 34 FINAL EXAM December 8, 14 Name: PID: Section: Instructor: DO NOT WRITE BELOW THIS LINE. Go to the next page. Page Problem Score Max Score 1 5 5 1 3 5 4 5 5 5 6 5 7 5 8 5 9 5 1 5 11 1 3 1a
Practice Problems for the Final Exam
 Math 114 Spring 2017 Practice Problems for the Final Exam 1. The planes 3x + 2y + z = 6 and x + y = 2 intersect in a line l. Find the distance from the origin to l. (Answer: 24 3 ) 2. Find the area of
Math 114 Spring 2017 Practice Problems for the Final Exam 1. The planes 3x + 2y + z = 6 and x + y = 2 intersect in a line l. Find the distance from the origin to l. (Answer: 24 3 ) 2. Find the area of
Look out for typos! Homework 1: Review of Calc 1 and 2. Problem 1. Sketch the graphs of the following functions:
 Math 226 homeworks, Fall 2016 General Info All homeworks are due mostly on Tuesdays, occasionally on Thursdays, at the discussion section. No late submissions will be accepted. If you need to miss the
Math 226 homeworks, Fall 2016 General Info All homeworks are due mostly on Tuesdays, occasionally on Thursdays, at the discussion section. No late submissions will be accepted. If you need to miss the
CHAPTER VIII. TOTAL DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND DEGREE IN THREE VARIABLES, WHICH ARE DERIVABLE FROM A SINGLE PRIMI TIVE.
 CHAPTER VIII. TOTAL DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND DEGREE IN THREE VARIABLES, WHICH ARE DERIVABLE FROM A SINGLE PRIMI TIVE. 95. IN this chapter we shall indicate how the integration of an
CHAPTER VIII. TOTAL DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND DEGREE IN THREE VARIABLES, WHICH ARE DERIVABLE FROM A SINGLE PRIMI TIVE. 95. IN this chapter we shall indicate how the integration of an
EE2007: Engineering Mathematics II Vector Calculus
 EE2007: Engineering Mathematics II Vector Calculus Ling KV School of EEE, NTU ekvling@ntu.edu.sg Rm: S2-B2b-22 Ver 1.1: Ling KV, October 22, 2006 Ver 1.0: Ling KV, Jul 2005 EE2007/Ling KV/Aug 2006 EE2007:
EE2007: Engineering Mathematics II Vector Calculus Ling KV School of EEE, NTU ekvling@ntu.edu.sg Rm: S2-B2b-22 Ver 1.1: Ling KV, October 22, 2006 Ver 1.0: Ling KV, Jul 2005 EE2007/Ling KV/Aug 2006 EE2007:
1. If the line l has symmetric equations. = y 3 = z+2 find a vector equation for the line l that contains the point (2, 1, 3) and is parallel to l.
 . If the line l has symmetric equations MA 6 PRACTICE PROBLEMS x = y = z+ 7, find a vector equation for the line l that contains the point (,, ) and is parallel to l. r = ( + t) i t j + ( + 7t) k B. r
. If the line l has symmetric equations MA 6 PRACTICE PROBLEMS x = y = z+ 7, find a vector equation for the line l that contains the point (,, ) and is parallel to l. r = ( + t) i t j + ( + 7t) k B. r
MAC2313 Final A. (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative.
 MAC2313 Final A (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative. ii. The vector field F = 5(x 2 + y 2 ) 3/2 x, y is radial. iii. All constant
MAC2313 Final A (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative. ii. The vector field F = 5(x 2 + y 2 ) 3/2 x, y is radial. iii. All constant
Line Integrals and Gradient Fields
 Line Integrals and Gradient Fields Based on notes by Ben Woodruff When you make your lesson plan, it should explain and contain examples of the following: 1. Describe how to integrate a function along
Line Integrals and Gradient Fields Based on notes by Ben Woodruff When you make your lesson plan, it should explain and contain examples of the following: 1. Describe how to integrate a function along
Math 32B Discussion Session Week 10 Notes March 14 and March 16, 2017
 Math 3B iscussion ession Week 1 Notes March 14 and March 16, 17 We ll use this week to review for the final exam. For the most part this will be driven by your questions, and I ve included a practice final
Math 3B iscussion ession Week 1 Notes March 14 and March 16, 17 We ll use this week to review for the final exam. For the most part this will be driven by your questions, and I ve included a practice final
(c) The first thing to do for this problem is to create a parametric curve for C. One choice would be. (cos(t), sin(t)) with 0 t 2π
 1. Let g(x, y) = (y, x) ompute gds for a circle with radius 1 centered at the origin using the line integral. (Hint: use polar coordinates for your parametrization). (a) Write out f((t)) so that f is a
1. Let g(x, y) = (y, x) ompute gds for a circle with radius 1 centered at the origin using the line integral. (Hint: use polar coordinates for your parametrization). (a) Write out f((t)) so that f is a
12/19/2009, FINAL PRACTICE VII Math 21a, Fall Name:
 12/19/29, FINAL PRATIE VII Math 21a, Fall 29 Name: MWF 9 Jameel Al-Aidroos MWF 1 Andrew otton-lay MWF 1 Oliver Knill MWF 1 HT Yau MWF 11 Ana araiani MWF 11 hris Phillips MWF 11 Ethan Street MWF 12 Toby
12/19/29, FINAL PRATIE VII Math 21a, Fall 29 Name: MWF 9 Jameel Al-Aidroos MWF 1 Andrew otton-lay MWF 1 Oliver Knill MWF 1 HT Yau MWF 11 Ana araiani MWF 11 hris Phillips MWF 11 Ethan Street MWF 12 Toby
Let F be a field defined on an open region D in space, and suppose that the (work) integral A
 16.3 1 16.3 Path Independence and Conservative Fields Definition. Path Independence Let F be a field defined on an open region D in space, and suppose B that the work) integral A F dr is the same for all
16.3 1 16.3 Path Independence and Conservative Fields Definition. Path Independence Let F be a field defined on an open region D in space, and suppose B that the work) integral A F dr is the same for all
