Chapter 8 Hypothesis Testing
|
|
|
- Dulcie Stone
- 5 years ago
- Views:
Transcription
1 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Chapter 8 Hypothesis Testig Setio 8 Itrodutio Defiitio 8 A hypothesis is a statemet about a populatio parameter Defiitio 8 The two omplemetary hypotheses i a hypothesis testig problem are alled the ull hypothesis ad the alterative hypothesis They are deoted by H ad H, respetively Settig: Let be a parameter of iterest with : where ad H versus H : : Defiitio 83 A hypothesis testig proedure or hypothesis test is a rule that speifies: For whih sample values the deisio is made to aept H as true For whih sample values H is rejeted ad H is aepted as true Rejetio Regio or Critial Regio: subset of the sample spae for whih H will be rejeted
2 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Aeptae Regio: omplemet of the rejetio regio Philosophial Notes: Rejet H ad aeptig H Aeptig H ad ot rejetig H Our Mai Coer: assertio of H or H Test Statisti W ( X ): futio of the sample; used together with the rejetio regio to make deisios about the hypotheses beig tested Setio 8 Methods of Fidig Tests 8 Likelihood Ratio Tests Defiitio 8 The likelihood ratio test statisti for testig H: is sup L( x) ( x) sup L( x )
3 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, A likelihood ratio test (LRT) is ay test that has a rejetio regio of the form { x: ( x ) }, where is ay umber satisfyig LRT ad MLE: Let ˆ be the MLE of uder the urestrited parameter spae ad ˆ be the MLE of uder the restrited parameter spae The ( x) L( ˆ x) L( ˆ x ) Example 8 (Normal LRT) Let X,, X be iid from (,) We wat to test H: where is a fixed umber set by the experimeter Show that ( x ) exp[ x ( ) /] so that the LRT rejets H for small values of ( x ) Therefore the rejetio regio is whih is equivalet to { x: ( x ) }, { x : x (log )/ } Example 83 (Expoetial LRT) Let X,, X be iid from a expoetial populatio with pdf 3
4 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, where f ( x ) exp[ ( x )] I[, ) ( x), We wat to test H :, where is a fixed umber set by the experimeter Show that, x() ; ( x ) exp[ x ( () )], x() so that the LRT rejets H for small values of ( x ) Therefore the rejetio regio is log( ) { x: ( x ) } whih is equivalet to { x : x() } Note: I both of the above examples, the rejetio regio oly depeds o the suffiiet statisti for Theorem 84 If T ( X) is a suffiiet statisti for ad *( t) ad ( x ) are the LRT statistis based o T ad X, respetively, the *( T ( x)) ( x ) for every x i the sample spae Example 85 (LRT ad Suffiiey): I Example 8, we ould have used the likelihood assoiated with the suffiiet statisti X usig the fat that X ~ (,/ ) whih rejets for large values of X 4
5 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Similarly, i Example 83, we a use the likelihood assoiated with the suffiiet statisti X () : L( x() ) exp[ ( x() )] I[, ] ( x() ), whih rejets for large values of X () Example 86 (Normal LRT with ukow variae) Let X,, X be iid from (, ) ad a experimeter is iterested oly i testig We wat to test H : The LRT statisti where ˆ ( xi ) / i max L(, x) max L(, x) {, } {, } L x L ˆ ˆ x {, } ( x) max (, ) (, ), ˆ ; L( ˆ ˆ ˆ, x)/ L(, x), 8 Bayesia Tests Bayesia Formulatio of Hypothesis Testig Classial Approah: The parameter is fixed If is kow, the P( x ) ad P( o x ) for all x 5
6 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, If is kow, the P( x ) ad P( o x ) for all x I pratie, P( x ) ad P( x ) are ukow ad do ot deped o x Hee these probabilities are ot used Bayesia Approah: The parameter is radom ad is assiged a prior distributio The P( x) P( H is true x ) ad P( x) P( H is true x) may be omputed ad make sese A way to use the posterior distributio to make deisios about H ad H is to deide to aept H as true P( X) P( X ) ad rejet H otherwise, ie, the rejetio regio is { x: P( x ) /} if Oe may also defie a rejetio regio as { x: P( x ) p } where, say 99, whih is set by the researher p p Example 87 (Normal Bayesia Test) Let X,, X be iid from (, ) ad let the prior distributio o be (, ), where,, are kow We wat to test H : Reall that the posterior distributio ( x) is ormal with 6
7 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, mea = x ad variae = Deisio rule: Aept H if ad oly if P( X) P( X ) or P( X) P( X ) / ad aept Hotherwise Note that ( x) is symmetri, hee, a equivalet deisio rule is to aept H whe ad aept H otherwise X ( ), 83 Uio-Itersetio ad Itersetio-Uio Tests Uio-itersetio method Let be a arbitrary idex set whih may be fiite or ifiite Defie H : 7
8 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Suppose that for eah a test is available for whih rejets H whe { x: T( x ) R} H : versus : H The the rejetio regio for the uio-itersetio test is { x: T ( x) R } Note: We aept H oly if H is aepted for all If at least oe H is rejeted, we rejet H I partiular, if the rejetio regio for H does ot deped o the the rejetio regio for H is { x: T( x) } { x:sup T( x) }, ad T( x) sup T ( x) is the test statisti Appliatio: ANOVA (Chapter ) ull hypothesis beig a itersetio of hypotheses based o otrasts (used to ompare treatmets), ie where is a set of ostats ad ai s satisfy H k k a i i i : for all a, ai k i 8
9 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Example 88 (Normal uio-itersetio test) Let X,, X be iid from (, ) We wat to test H :{ : } { : } Test : H : evrsus H : X LRT rejets H if t S / Test : H : evrsus H : X LRT rejets H if t S / Therefore, the uio-itersetio test for H: formed by ombiig tests ad X X Rejet H is t or t S / S / If t t the the rejetio regio for the uio-itersetio test is X Rejet H if t S / 9
10 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, It turs out that this test is also the LRT for this problem alled the two-sided t test Itersetio-uio method Let be a arbitrary idex set whih may be fiite or ifiite Defie H : Suppose that for eah, a test is available for whih rejets H whe { x: T( x ) R} H : versus : H The the rejetio regio for the itersetio-uio test is ie, rejet H if ad oly if H is rejeted for all { x: T ( x) R } I partiular, if the rejetio regio for H does ot deped o the the rejetio regio for H is { x: T ( x) } { x:if T( x) }
11 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, ad T( x) if T( x) is the test statisti Appliatio: Aeptae samplig where all stadards must be met for a produt to be aeptable Example 89 Let X, X be iid measuremets of breakig stregth from (, ) ad Y,, Ym be iid Beroulli( ) beig the results of m flammability tests, where Yi if the uit passes the test ad Yi otherwise Stadards to be met: 5 ad 95 H :{ 5 or 95} { 5 ad 95} Test : H : 5 versus H : 5 LRT rejets H if X 5 S / t Test : H : 95 versus H : 95 LRT rejets H if m Y i i b Therefore, the itersetio-uio test for H :{ 5 or 95}
12 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, x m rejets H if {( x, y) : t ad y } i i b S / Setio 83 Methods of Evaluatig Tests 83 Error Probabilities ad the Power Futio Two types of Error: Type I error: If but the hypothesis test iorretly deides to rejet H Type II error: If but the hypothesis test deides to aept H Let R deote the rejetio regio for a test The P(Type I Error) if ; P ( X R) P(Type II Error) if Defiitio 83 The power futio of a hypothesis test with rejetio regio R is the futio of ( ) P ( X R)
13 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Example 83 (Biomial power futio) Let X ~ biomial(5, ) Cosider: Test : R {all suesses are observed} Test : R { X 3,4,or 5} H : / versus H : / Example 833 (Normal power futio) Let X,, X be iid from The LRT for this test has rejetio regio defied by H : X R / (, ) where is kow Cosider Therefore X ( ) P( ) P( Z ) / / Example 834 (otiuatio of Example 833) Suppose that the experimeter would like the maximum probability of a Type I error of ad a miimum probability of a Type II error of if How do we hoose ad? 3
14 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Defiitio 835 For, a test with power futio ( ) is a size test if sup ( ) Defiitio 836 For, a test with power futio ( ) is a level test if sup ( ) Notes: Some authors use the terms level ad size iterhageably The set of level tests otais the set of size tests I more omplex problems (eg, itersetio-uio ad uio-itersetio tests), it is diffiult if ot impossible to obtai a size test so oe will just have to settle for a level test The ommoly used values i pratie are, 5, ad Fixig the level of a test is otrollig the Type I error but ot the Type II error H ad H should be set up properly so that the more importat error to otrol is the Type I error H typially is the hypothesis that you wat your data to support ad hee is alled the researh hypothesis Example 837 (Size of LRT) A size LRT is ostruted by hoosig the appropriate suh that sup P( ( X) ) 4
15 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, I Example 8, H : so that z / R{ X } I Example 83, H : so that P ( X ) exp( ( )) if ( log( )) / () We eed to show that this is a size test Note that for ay Therefore, P ( X ) P ( X ) () () sup sup ( ) ( ( log( )) / ) P X() P X() Example 838 (Size of uio-itersetio test) Reall Example 88 Let X,, X be iid from (, ) The test for H: : For ay (, ) ad H :, X X rejets H if t or t S / S / X S / ~( t ) 5
16 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Choose t L ad t U suh that TL t, ad TU t, where I this ase P (Type I error) = for all (, ) I pratie, we usually hoose TL TU t, / Defiitio 839 A test with power futio ( ) is ubiased if ( ') ( '') for every ' ad '' Example 83 (Colusio of Example 833) Let X,, X be iid from for testig H : has power futio give by (, ) where X ( ) P( ) P( Z ), / / whih is a ireasig futio of for a fixed value of Therefore, this test is ubiased sie ( ) ( ) sup ( t) t for all is kow The LRT 83 Most Powerful Tests 6
17 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Defiitio 83 Let be a lass of tests for testig H: A test i lass, with power futio ( ), is uiformly most powerful (UMP) lass test if ( ) '( ) for every ad every '( ) that is a power futio of a test i lass Theorem 83 (Neyma-Pearso Lemma) Cosider testig H:, where the pdf or pmf orrespodig to i is f( x i), i,, usig a test with rejetio regio R that satisfies ad for some k, ad The f ( x ) x R if f( x ) kf( x ) or, equivaletly, k f ( x ) f ( x ) x R if f( x ) kf( x ) or, equivaletly, f ( x ) P ( R) X a (Suffiiey) Ay test that satisfies the above oditios is a UMP level test b (Neessity) If there exists a test satisfyig the above oditios with k, the every UMP level test is a size test ad every UMP level test has the rejetio regio defied i this Theorem exept perhaps o a set A satisfyig P ( XA) P ( X A) k 7
18 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Corollary 833 Cosider the hypothesis problem posed i Theorem 83 Suppose T ( X ) is a suffiiet statisti for ad gt ( i ) is the pdf or pmf of T orrespodig to i, i,, The ay test based o T with rejetio regio S (subset of the sample spae T ) is a UMP level test if it satisfies gt ( ) t S if gt ( ) kgt ( ) or, equivaletly, k gt ( ) ad for some k, ad P ( T S) t S gt ( ) ( ) ( ) or, equivaletly, k gt ( ) if gt kgt Example 834 (UMP Biomial Test) Let X ~ biomial(, ) We wat to test H : / versus H : 3/4 The f ( 3 / 4), f ( / ) 4 f ( 3 / 4) 3, ad f ( / ) 4 f ( 3 / 4) 9 f ( / ) 4 Test : If we hoose 3 k 9, the by Neyma-Pearso Lemma, the UMP test rejets H whe X The 4 4 orrespodig size of this test is 8
19 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, PX ( ) 4 Test : If we hoose k 3, the by Neyma-Pearso Lemma, the UMP test rejets H whe X = or The 4 4 orrespodig size of this test is 3 PX ( or ) 4 Notes: (o Example 834) If we hoose k or 4 9 k, the UMP test has size 4 ad, respetively Notes: (o Example 834 otiued) 3 If k the the UMP test has rejetio regio X ad aeptae regio X but does ot tell us 4 what to do whe X I this ase, we hoose to have X i either the rejetio or aeptae regio The resultig size of the test will deped o this hoie beause this is i a disrete settig 9
20 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Example 835 (UMP Normal Test) Let X,, X be iid from (, ) where is kow To obtai the UMP test for H: versus where, we reall that X is a suffiiet statisti for ad X ~ (, / ) Note that ( / ) exp[ ( x ) ] / ( ) exp[ { x( ) ( )}] ( ) / ( / ) exp[ ( x ) ] gx gx Hee, by Corollary 833, the UMP test rejets whe Equivaletly, we rejet whe Notes: The iequality was reversed beause gx ( ) exp[ { x( ) ( )}] k gx ( ) (log( k))( / ) ( ) x ( ) As k ireases from to, the right had size of the rejetio regio iequality goes from - to To omplete the UMP test proedure of size, we fid the ostat suh that P ( X ) P( Z ) /
21 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, I this ase, z so that / z Types of Hypotheses: Simple Hypothesis: H : Composite Hypothesis: more tha oe possible distributio a Oe-sided Hypothesis: H : b Two-sided Hypothesis: H : Questio: How do we fid the UMP test for omposite hypotheses? Defiitio 836 A family of pdfs ad pmfs { gt ( ) : } for a uivariate radom variable T with real-valued parameter has a mootoe likelihood ratio (MLR) if, for every, gt ( )/ gt ( ) is a mootoe (oireasig or odereasig) futio of t o {: t g( t ) or g( t ) } Note that / if
22 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Note: Ay regular expoetial family with gt ( ) ht ( ) ( )exp[ w( ) t] has a MLR if w( ) is a odereasig futio or oireasig futio Theorem 837 (Karli-Rubi) Cosider testig H : Suppose that T is a suffiiet statisti for ad the family of pdfs ad pmfs { gt ( ) : } of T has a MLR ad gt ( )/ gt ( ) for is odereasig futio of t The for ay t, the test that rejets H if ad oly if T t is a UMP level test, where P ( T t ) Proof: Let ( ) be the power futio for the rejetio regio: { T t} () Cosider the simple hypothesis: H : versus H : ( ) Cosider the test has the rejetio gt ( ) regio: {: t k} gt ( ), sie gt ( ) gt ( ) is the odereasig futio of t, we a fid k suh that whe T t, gt ( ) k gt ( ) ad whe gt ( ) T t, k From Corollary 83, this test is the UMP level gt ( ) P ( T t ) ( ) test Defie ( T ), whih is level test, ad P ( ( T)) P ( ( T)), therefore, ( ) So we proved that ( ) ( ) for, thus sup ( ) ( ) () Cosider the simple hypothesis: H : versus H : ( ) Cosider the test has the rejetio gt ( ) gt ( ) regio: {: t k}, sie gt ( ) gt ( ) is the odereasig futio of t, we a fid k suh that whe T t,
23 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, gt ( ) gt ( ) k ad whe T t, k From Corollary 83, this test is the UMP level gt ( ) gt ( ) P ( T t ) ( ) test For ay aother level test with power futio *( ), beause *( ), whih is also a level test for H : versus H : ( ), thus ( ) *( ), so the proposed test, R{ T t } is UMP of level Note: Cosider testig H : Suppose that T is a suffiiet statisti for ad the family of pdfs ad pmfs { gt ( ) : } of T has a MLR ad gt ( )/ gt ( ) for is oireasig futio of t The for ay t, the test that rejets H if ad oly if T t is a UMP level test, where P ( T t ) Cosider testig H : Suppose that T is a suffiiet statisti for ad the family of pdfs ad pmfs { gt ( ) : } of T has a MLR ad gt ( )/ gt ( ) for is odereasig futio of t The for ay t, the test that rejets H if ad oly if T t is a UMP level test, where P ( T t ) Cosider testig H : Suppose that T is a suffiiet statisti for ad the family of pdfs ad pmfs { gt ( ) : } of T has a MLR ad gt ( )/ gt ( ) for is oireasig futio 3
24 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, of t The for ay t, the test that rejets H if ad oly if T t is a UMP level test, where P ( T t ) Note: For may problems there is o UMP level test This is beause the lass of level tests is so large that o oe test domiates all the others i terms of power Example 838 (Cotiuatio of Example 835) Cosider testig that rejets H if H : versus ' H : usig the test ' X z Note that T X ~ (, / ) has a MLR To see this, let The gt ( ) exp [( t ) ( t) ] exp[ ( ) / ( )]exp[ t( ) / ] gt ( ) Sie, this ratio is a ireasig futio of t By Karli-Rubi Theorem, the above test is a UMP level To see that this is a level test, ote that the power futio is give by z ( ) P ( X ) P( Z z ), / whih is a dereasig futio of Therefore, 4
25 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, sup ( ) ( ) Example 839 (Noexistee of UMP test) Let X,, X be iid (, ) where H: A level test for this problem is ay test that satisfies P (Rejet H ) is kow We wat to test Test : Cosider Usig the same argumet as i Example 838, the test that rejets H if X ( z / ) has the highest power Furthermore, by part (b) of Neyma-Pearso Lemma, ay other level test that has as a high power as Test must have the same rejetio regio as Test exept for a set A satisfyig P ( X A) i Test : Cosider the test that rejets H is X z / Let ( ) ad ( ) be the power futio for Test ad, respetively The for ay, 5
26 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, X P X z P z / / PZ ( z) (sie ) ( ) ( / ) ( ) PZ ( z) X P z / / ( ) P ( X z / ) ( ) Therefore, Test is ot the UMP level test Sie by Neyma-Pearso the UMP level test would have to be Test, the there exists o UMP test i this problem Notes: Whe o UMP level test exists withi the lass of all tests, the ext best thig is to fid a UMP level test withi the lass of ubiased tests Tests ad are ot ubiased tests Example 83 (olusio of Example 839 Ubiased test) Test 3: Rejets H : i favor of H: if ad oly if X z / / / or X z / 6
27 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Although Tests ad have slightly higher power tha Test 3 for some values of, it turs out that Test 3 is the UMP test amog all ubiased tests Skip: Setio 833 ad p-values Defiitio 836 A p-value p( X ) is a test statisti satisfyig p( x ) for every sample poit x Small values of p( X ) give evidee that H is true A p -value is valid if, for every ad every, P ( p( X ) ) Notes: Give a valid p -value, a level test rejets H if ad oly if p( X ) p -value reports the results of a test i a otiuous sale ad gives the reader a hoie of what they wat to use The smaller the p -value is, the stroger the evidee for rejetig H 7
28 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Theorem 837 Let W ( X ) be a test statisti suh that large values of W give evidee that H is true For eah sample poit x, defie p( x) sup P ( W( X) W( x )) The p( X) is a valid p-value Example 838 (Two-sided ormal p-value) Let X,, X be iid from for H: : (, ) The LRT test (Exerise 838) X rejets H if S / is large X Uder H: regardless of the value of, ~ t S / Therefore, x p( x ) P( T ), s / where T has Studet s t distributio with degrees of freedom Example 839 (Oe-sided ormal p-value) Let X,, X be iid from for H : : (, ) The LRT test (Exerise 838) 8
29 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, Note that so that the supremum ours at X Rejets H if is large S / X P W W P W S / (, ) ( ( X) ( x)) ( ( x)),, Therefore, X P S / S / P ( T, W( ) ) x S / PT ( W( x)) (for ) ( W( x) ), x px ( ) PT ( Wx ( )) PT ( ) s / Alterative Method for Fidig p-values: Let S( X ) be a suffiiet statisti oly for the model{ f( x ): } p( x) PW ( ( X) W( x) SS( X )) Note that this is a valid p -value sie 9
30 Chapter 8 for BST 695: Speial Topis i Statistial Theory Kui Zhag, P ( p ( x ) ) P ( p ( x ) S s ) P ( S s ) P ( S s ) s s This is also true i the otiuous ase (where itegrals are used i plae of summatio) Note: This alterative method is usually helpful i dealig with disrete distributio for S Example 833 (Fisher s Exat Test) FYI 3
STK4011 and STK9011 Autumn 2016
 STK4 ad STK9 Autum 6 ypothesis testig Covers (most of) the followig material from hapter 8: Setio 8. Setios 8.. ad 8..3 Setio 8.3. Setio 8.3. (util defiitio 8.3.6) Ørulf Borga Departmet of Mathematis Uiversity
STK4 ad STK9 Autum 6 ypothesis testig Covers (most of) the followig material from hapter 8: Setio 8. Setios 8.. ad 8..3 Setio 8.3. Setio 8.3. (util defiitio 8.3.6) Ørulf Borga Departmet of Mathematis Uiversity
Chapter 8 Hypothesis Testing
 Leture 5 for BST 63: Statistial Theory II Kui Zhang, Spring Chapter 8 Hypothesis Testing Setion 8 Introdution Definition 8 A hypothesis is a statement about a population parameter Definition 8 The two
Leture 5 for BST 63: Statistial Theory II Kui Zhang, Spring Chapter 8 Hypothesis Testing Setion 8 Introdution Definition 8 A hypothesis is a statement about a population parameter Definition 8 The two
ε > 0 N N n N a n < ε. Now notice that a n = a n.
 4 Sequees.5. Null sequees..5.. Defiitio. A ull sequee is a sequee (a ) N that overges to 0. Hee, by defiitio of (a ) N overges to 0, a sequee (a ) N is a ull sequee if ad oly if ( ) ε > 0 N N N a < ε..5..
4 Sequees.5. Null sequees..5.. Defiitio. A ull sequee is a sequee (a ) N that overges to 0. Hee, by defiitio of (a ) N overges to 0, a sequee (a ) N is a ull sequee if ad oly if ( ) ε > 0 N N N a < ε..5..
Last Lecture. Unbiased Test
 Last Lecture Biostatistics 6 - Statistical Iferece Lecture Uiformly Most Powerful Test Hyu Mi Kag March 8th, 3 What are the typical steps for costructig a likelihood ratio test? Is LRT statistic based
Last Lecture Biostatistics 6 - Statistical Iferece Lecture Uiformly Most Powerful Test Hyu Mi Kag March 8th, 3 What are the typical steps for costructig a likelihood ratio test? Is LRT statistic based
Lecture 6 Simple alternatives and the Neyman-Pearson lemma
 STATS 00: Itroductio to Statistical Iferece Autum 06 Lecture 6 Simple alteratives ad the Neyma-Pearso lemma Last lecture, we discussed a umber of ways to costruct test statistics for testig a simple ull
STATS 00: Itroductio to Statistical Iferece Autum 06 Lecture 6 Simple alteratives ad the Neyma-Pearso lemma Last lecture, we discussed a umber of ways to costruct test statistics for testig a simple ull
Methods of evaluating tests
 Methods of evaluating tests Let X,, 1 Xn be i.i.d. Bernoulli( p ). Then 5 j= 1 j ( 5, ) T = X Binomial p. We test 1 H : p vs. 1 1 H : p>. We saw that a LRT is 1 if t k* φ ( x ) =. otherwise (t is the observed
Methods of evaluating tests Let X,, 1 Xn be i.i.d. Bernoulli( p ). Then 5 j= 1 j ( 5, ) T = X Binomial p. We test 1 H : p vs. 1 1 H : p>. We saw that a LRT is 1 if t k* φ ( x ) =. otherwise (t is the observed
5. Likelihood Ratio Tests
 1 of 5 7/29/2009 3:16 PM Virtual Laboratories > 9. Hy pothesis Testig > 1 2 3 4 5 6 7 5. Likelihood Ratio Tests Prelimiaries As usual, our startig poit is a radom experimet with a uderlyig sample space,
1 of 5 7/29/2009 3:16 PM Virtual Laboratories > 9. Hy pothesis Testig > 1 2 3 4 5 6 7 5. Likelihood Ratio Tests Prelimiaries As usual, our startig poit is a radom experimet with a uderlyig sample space,
What is a Hypothesis? Hypothesis is a statement about a population parameter developed for the purpose of testing.
 What is a ypothesis? ypothesis is a statemet about a populatio parameter developed for the purpose of testig. What is ypothesis Testig? ypothesis testig is a proedure, based o sample evidee ad probability
What is a ypothesis? ypothesis is a statemet about a populatio parameter developed for the purpose of testig. What is ypothesis Testig? ypothesis testig is a proedure, based o sample evidee ad probability
Summary. Recap ... Last Lecture. Summary. Theorem
 Last Lecture Biostatistics 602 - Statistical Iferece Lecture 23 Hyu Mi Kag April 11th, 2013 What is p-value? What is the advatage of p-value compared to hypothesis testig procedure with size α? How ca
Last Lecture Biostatistics 602 - Statistical Iferece Lecture 23 Hyu Mi Kag April 11th, 2013 What is p-value? What is the advatage of p-value compared to hypothesis testig procedure with size α? How ca
Chapter 6 Principles of Data Reduction
 Chapter 6 for BST 695: Special Topics i Statistical Theory. Kui Zhag, 0 Chapter 6 Priciples of Data Reductio Sectio 6. Itroductio Goal: To summarize or reduce the data X, X,, X to get iformatio about a
Chapter 6 for BST 695: Special Topics i Statistical Theory. Kui Zhag, 0 Chapter 6 Priciples of Data Reductio Sectio 6. Itroductio Goal: To summarize or reduce the data X, X,, X to get iformatio about a
Topic 9: Sampling Distributions of Estimators
 Topic 9: Samplig Distributios of Estimators Course 003, 2018 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Topic 9: Samplig Distributios of Estimators Course 003, 2018 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Stat 319 Theory of Statistics (2) Exercises
 Kig Saud Uiversity College of Sciece Statistics ad Operatios Research Departmet Stat 39 Theory of Statistics () Exercises Refereces:. Itroductio to Mathematical Statistics, Sixth Editio, by R. Hogg, J.
Kig Saud Uiversity College of Sciece Statistics ad Operatios Research Departmet Stat 39 Theory of Statistics () Exercises Refereces:. Itroductio to Mathematical Statistics, Sixth Editio, by R. Hogg, J.
Lecture Notes 15 Hypothesis Testing (Chapter 10)
 1 Itroductio Lecture Notes 15 Hypothesis Testig Chapter 10) Let X 1,..., X p θ x). Suppose we we wat to kow if θ = θ 0 or ot, where θ 0 is a specific value of θ. For example, if we are flippig a coi, we
1 Itroductio Lecture Notes 15 Hypothesis Testig Chapter 10) Let X 1,..., X p θ x). Suppose we we wat to kow if θ = θ 0 or ot, where θ 0 is a specific value of θ. For example, if we are flippig a coi, we
Last Lecture. Wald Test
 Last Lecture Biostatistics 602 - Statistical Iferece Lecture 22 Hyu Mi Kag April 9th, 2013 Is the exact distributio of LRT statistic typically easy to obtai? How about its asymptotic distributio? For testig
Last Lecture Biostatistics 602 - Statistical Iferece Lecture 22 Hyu Mi Kag April 9th, 2013 Is the exact distributio of LRT statistic typically easy to obtai? How about its asymptotic distributio? For testig
Bernoulli Numbers. n(n+1) = n(n+1)(2n+1) = n(n 1) 2
 Beroulli Numbers Beroulli umbers are amed after the great Swiss mathematiia Jaob Beroulli5-705 who used these umbers i the power-sum problem. The power-sum problem is to fid a formula for the sum of the
Beroulli Numbers Beroulli umbers are amed after the great Swiss mathematiia Jaob Beroulli5-705 who used these umbers i the power-sum problem. The power-sum problem is to fid a formula for the sum of the
MATH/STAT 352: Lecture 15
 MATH/STAT 352: Lecture 15 Sectios 5.2 ad 5.3. Large sample CI for a proportio ad small sample CI for a mea. 1 5.2: Cofidece Iterval for a Proportio Estimatig proportio of successes i a biomial experimet
MATH/STAT 352: Lecture 15 Sectios 5.2 ad 5.3. Large sample CI for a proportio ad small sample CI for a mea. 1 5.2: Cofidece Iterval for a Proportio Estimatig proportio of successes i a biomial experimet
MATH 320: Probability and Statistics 9. Estimation and Testing of Parameters. Readings: Pruim, Chapter 4
 MATH 30: Probability ad Statistics 9. Estimatio ad Testig of Parameters Estimatio ad Testig of Parameters We have bee dealig situatios i which we have full kowledge of the distributio of a radom variable.
MATH 30: Probability ad Statistics 9. Estimatio ad Testig of Parameters Estimatio ad Testig of Parameters We have bee dealig situatios i which we have full kowledge of the distributio of a radom variable.
EECS564 Estimation, Filtering, and Detection Hwk 2 Solns. Winter p θ (z) = (2θz + 1 θ), 0 z 1
 EECS564 Estimatio, Filterig, ad Detectio Hwk 2 Sols. Witer 25 4. Let Z be a sigle observatio havig desity fuctio where. p (z) = (2z + ), z (a) Assumig that is a oradom parameter, fid ad plot the maximum
EECS564 Estimatio, Filterig, ad Detectio Hwk 2 Sols. Witer 25 4. Let Z be a sigle observatio havig desity fuctio where. p (z) = (2z + ), z (a) Assumig that is a oradom parameter, fid ad plot the maximum
Topic 9: Sampling Distributions of Estimators
 Topic 9: Samplig Distributios of Estimators Course 003, 2018 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Topic 9: Samplig Distributios of Estimators Course 003, 2018 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Introductory statistics
 CM9S: Machie Learig for Bioiformatics Lecture - 03/3/06 Itroductory statistics Lecturer: Sriram Sakararama Scribe: Sriram Sakararama We will provide a overview of statistical iferece focussig o the key
CM9S: Machie Learig for Bioiformatics Lecture - 03/3/06 Itroductory statistics Lecturer: Sriram Sakararama Scribe: Sriram Sakararama We will provide a overview of statistical iferece focussig o the key
Basic Probability/Statistical Theory I
 Basi Probability/Statistial Theory I Epetatio The epetatio or epeted values of a disrete radom variable X is the arithmeti mea of the radom variable s distributio. E[ X ] p( X ) all Epetatio by oditioig
Basi Probability/Statistial Theory I Epetatio The epetatio or epeted values of a disrete radom variable X is the arithmeti mea of the radom variable s distributio. E[ X ] p( X ) all Epetatio by oditioig
Direction: This test is worth 150 points. You are required to complete this test within 55 minutes.
 Term Test 3 (Part A) November 1, 004 Name Math 6 Studet Number Directio: This test is worth 10 poits. You are required to complete this test withi miutes. I order to receive full credit, aswer each problem
Term Test 3 (Part A) November 1, 004 Name Math 6 Studet Number Directio: This test is worth 10 poits. You are required to complete this test withi miutes. I order to receive full credit, aswer each problem
Certain inclusion properties of subclass of starlike and convex functions of positive order involving Hohlov operator
 Iteratioal Joural of Pure ad Applied Mathematial Siees. ISSN 0972-9828 Volume 0, Number (207), pp. 85-97 Researh Idia Publiatios http://www.ripubliatio.om Certai ilusio properties of sublass of starlike
Iteratioal Joural of Pure ad Applied Mathematial Siees. ISSN 0972-9828 Volume 0, Number (207), pp. 85-97 Researh Idia Publiatios http://www.ripubliatio.om Certai ilusio properties of sublass of starlike
Topic 9: Sampling Distributions of Estimators
 Topic 9: Samplig Distributios of Estimators Course 003, 2016 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Topic 9: Samplig Distributios of Estimators Course 003, 2016 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
(Dependent or paired samples) Step (1): State the null and alternate hypotheses: Case1: One-tailed test (Right)
 (epedet or paired samples) Step (1): State the ull ad alterate hypotheses: Case1: Oe-tailed test (Right) Upper tail ritial (where u1> u or u1 -u> 0) H0: 0 H1: > 0 Case: Oe-tailed test (Left) Lower tail
(epedet or paired samples) Step (1): State the ull ad alterate hypotheses: Case1: Oe-tailed test (Right) Upper tail ritial (where u1> u or u1 -u> 0) H0: 0 H1: > 0 Case: Oe-tailed test (Left) Lower tail
Lecture Note 8 Point Estimators and Point Estimation Methods. MIT Spring 2006 Herman Bennett
 Lecture Note 8 Poit Estimators ad Poit Estimatio Methods MIT 14.30 Sprig 2006 Herma Beett Give a parameter with ukow value, the goal of poit estimatio is to use a sample to compute a umber that represets
Lecture Note 8 Poit Estimators ad Poit Estimatio Methods MIT 14.30 Sprig 2006 Herma Beett Give a parameter with ukow value, the goal of poit estimatio is to use a sample to compute a umber that represets
Chapter 13: Tests of Hypothesis Section 13.1 Introduction
 Chapter 13: Tests of Hypothesis Sectio 13.1 Itroductio RECAP: Chapter 1 discussed the Likelihood Ratio Method as a geeral approach to fid good test procedures. Testig for the Normal Mea Example, discussed
Chapter 13: Tests of Hypothesis Sectio 13.1 Itroductio RECAP: Chapter 1 discussed the Likelihood Ratio Method as a geeral approach to fid good test procedures. Testig for the Normal Mea Example, discussed
Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f.
![Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f. Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f.](/thumbs/91/105380228.jpg) Lecture 5 Let us give oe more example of MLE. Example 3. The uiform distributio U[0, ] o the iterval [0, ] has p.d.f. { 1 f(x =, 0 x, 0, otherwise The likelihood fuctio ϕ( = f(x i = 1 I(X 1,..., X [0,
Lecture 5 Let us give oe more example of MLE. Example 3. The uiform distributio U[0, ] o the iterval [0, ] has p.d.f. { 1 f(x =, 0 x, 0, otherwise The likelihood fuctio ϕ( = f(x i = 1 I(X 1,..., X [0,
Chapter 6 Sampling Distributions
 Chapter 6 Samplig Distributios 1 I most experimets, we have more tha oe measuremet for ay give variable, each measuremet beig associated with oe radomly selected a member of a populatio. Hece we eed to
Chapter 6 Samplig Distributios 1 I most experimets, we have more tha oe measuremet for ay give variable, each measuremet beig associated with oe radomly selected a member of a populatio. Hece we eed to
Sampling Distributions, Z-Tests, Power
 Samplig Distributios, Z-Tests, Power We draw ifereces about populatio parameters from sample statistics Sample proportio approximates populatio proportio Sample mea approximates populatio mea Sample variace
Samplig Distributios, Z-Tests, Power We draw ifereces about populatio parameters from sample statistics Sample proportio approximates populatio proportio Sample mea approximates populatio mea Sample variace
7.1 Convergence of sequences of random variables
 Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Stat 421-SP2012 Interval Estimation Section
 Stat 41-SP01 Iterval Estimatio Sectio 11.1-11. We ow uderstad (Chapter 10) how to fid poit estimators of a ukow parameter. o However, a poit estimate does ot provide ay iformatio about the ucertaity (possible
Stat 41-SP01 Iterval Estimatio Sectio 11.1-11. We ow uderstad (Chapter 10) how to fid poit estimators of a ukow parameter. o However, a poit estimate does ot provide ay iformatio about the ucertaity (possible
Lecture 19: Convergence
 Lecture 19: Covergece Asymptotic approach I statistical aalysis or iferece, a key to the success of fidig a good procedure is beig able to fid some momets ad/or distributios of various statistics. I may
Lecture 19: Covergece Asymptotic approach I statistical aalysis or iferece, a key to the success of fidig a good procedure is beig able to fid some momets ad/or distributios of various statistics. I may
Nonparametric Goodness-of-Fit Tests for Discrete, Grouped or Censored Data 1
 Noparametri Goodess-of-Fit Tests for Disrete, Grouped or Cesored Data Boris Yu. Lemeshko, Ekateria V. Chimitova ad Stepa S. Kolesikov Novosibirsk State Tehial Uiversity Departmet of Applied Mathematis
Noparametri Goodess-of-Fit Tests for Disrete, Grouped or Cesored Data Boris Yu. Lemeshko, Ekateria V. Chimitova ad Stepa S. Kolesikov Novosibirsk State Tehial Uiversity Departmet of Applied Mathematis
Tests of Hypotheses Based on a Single Sample (Devore Chapter Eight)
 Tests of Hypotheses Based o a Sigle Sample Devore Chapter Eight MATH-252-01: Probability ad Statistics II Sprig 2018 Cotets 1 Hypothesis Tests illustrated with z-tests 1 1.1 Overview of Hypothesis Testig..........
Tests of Hypotheses Based o a Sigle Sample Devore Chapter Eight MATH-252-01: Probability ad Statistics II Sprig 2018 Cotets 1 Hypothesis Tests illustrated with z-tests 1 1.1 Overview of Hypothesis Testig..........
ANOTHER PROOF FOR FERMAT S LAST THEOREM 1. INTRODUCTION
 ANOTHER PROOF FOR FERMAT S LAST THEOREM Mugur B. RĂUŢ Correspodig author: Mugur B. RĂUŢ, E-mail: m_b_raut@yahoo.om Abstrat I this paper we propose aother proof for Fermat s Last Theorem (FLT). We foud
ANOTHER PROOF FOR FERMAT S LAST THEOREM Mugur B. RĂUŢ Correspodig author: Mugur B. RĂUŢ, E-mail: m_b_raut@yahoo.om Abstrat I this paper we propose aother proof for Fermat s Last Theorem (FLT). We foud
January 25, 2017 INTRODUCTION TO MATHEMATICAL STATISTICS
 Jauary 25, 207 INTRODUCTION TO MATHEMATICAL STATISTICS Abstract. A basic itroductio to statistics assumig kowledge of probability theory.. Probability I a typical udergraduate problem i probability, we
Jauary 25, 207 INTRODUCTION TO MATHEMATICAL STATISTICS Abstract. A basic itroductio to statistics assumig kowledge of probability theory.. Probability I a typical udergraduate problem i probability, we
The beta density, Bayes, Laplace, and Pólya
 The beta desity, Bayes, Laplae, ad Pólya Saad Meimeh The beta desity as a ojugate form Suppose that is a biomial radom variable with idex ad parameter p, i.e. ( ) P ( p) p ( p) Applyig Bayes s rule, we
The beta desity, Bayes, Laplae, ad Pólya Saad Meimeh The beta desity as a ojugate form Suppose that is a biomial radom variable with idex ad parameter p, i.e. ( ) P ( p) p ( p) Applyig Bayes s rule, we
SDS 321: Introduction to Probability and Statistics
 SDS 321: Itroductio to Probability ad Statistics Lecture 23: Cotiuous radom variables- Iequalities, CLT Puramrita Sarkar Departmet of Statistics ad Data Sciece The Uiversity of Texas at Austi www.cs.cmu.edu/
SDS 321: Itroductio to Probability ad Statistics Lecture 23: Cotiuous radom variables- Iequalities, CLT Puramrita Sarkar Departmet of Statistics ad Data Sciece The Uiversity of Texas at Austi www.cs.cmu.edu/
Lecture 2: Monte Carlo Simulation
 STAT/Q SCI 43: Itroductio to Resamplig ethods Sprig 27 Istructor: Ye-Chi Che Lecture 2: ote Carlo Simulatio 2 ote Carlo Itegratio Assume we wat to evaluate the followig itegratio: e x3 dx What ca we do?
STAT/Q SCI 43: Itroductio to Resamplig ethods Sprig 27 Istructor: Ye-Chi Che Lecture 2: ote Carlo Simulatio 2 ote Carlo Itegratio Assume we wat to evaluate the followig itegratio: e x3 dx What ca we do?
Asymptotics. Hypothesis Testing UMP. Asymptotic Tests and p-values
 of the secod half Biostatistics 6 - Statistical Iferece Lecture 6 Fial Exam & Practice Problems for the Fial Hyu Mi Kag Apil 3rd, 3 Hyu Mi Kag Biostatistics 6 - Lecture 6 Apil 3rd, 3 / 3 Rao-Blackwell
of the secod half Biostatistics 6 - Statistical Iferece Lecture 6 Fial Exam & Practice Problems for the Fial Hyu Mi Kag Apil 3rd, 3 Hyu Mi Kag Biostatistics 6 - Lecture 6 Apil 3rd, 3 / 3 Rao-Blackwell
Estimation for Complete Data
 Estimatio for Complete Data complete data: there is o loss of iformatio durig study. complete idividual complete data= grouped data A complete idividual data is the oe i which the complete iformatio of
Estimatio for Complete Data complete data: there is o loss of iformatio durig study. complete idividual complete data= grouped data A complete idividual data is the oe i which the complete iformatio of
On generalized Simes critical constants
 Biometrial Joural 56 04 6, 035 054 DOI: 0.00/bimj.030058 035 O geeralized Simes ritial ostats Jiagtao Gou ad Ajit C. Tamhae, Departmet of Statistis, Northwester Uiversity, 006 Sherida Road, Evasto, IL
Biometrial Joural 56 04 6, 035 054 DOI: 0.00/bimj.030058 035 O geeralized Simes ritial ostats Jiagtao Gou ad Ajit C. Tamhae, Departmet of Statistis, Northwester Uiversity, 006 Sherida Road, Evasto, IL
Direction: This test is worth 250 points. You are required to complete this test within 50 minutes.
 Term Test October 3, 003 Name Math 56 Studet Number Directio: This test is worth 50 poits. You are required to complete this test withi 50 miutes. I order to receive full credit, aswer each problem completely
Term Test October 3, 003 Name Math 56 Studet Number Directio: This test is worth 50 poits. You are required to complete this test withi 50 miutes. I order to receive full credit, aswer each problem completely
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Lecture 7: Properties of Random Samples
 Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
7.1 Convergence of sequences of random variables
 Chapter 7 Limit theorems Throughout this sectio we will assume a probability space (Ω, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit theorems Throughout this sectio we will assume a probability space (Ω, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Statistical Inference (Chapter 10) Statistical inference = learn about a population based on the information provided by a sample.
 Statistical Iferece (Chapter 10) Statistical iferece = lear about a populatio based o the iformatio provided by a sample. Populatio: The set of all values of a radom variable X of iterest. Characterized
Statistical Iferece (Chapter 10) Statistical iferece = lear about a populatio based o the iformatio provided by a sample. Populatio: The set of all values of a radom variable X of iterest. Characterized
One way Analysis of Variance (ANOVA)
 Oe way Aalysis of Variae (ANOVA) ANOVA Geeral ANOVA Settig"Slide 43-45) Ivestigator otrols oe or more fators of iterest Eah fator otais two or more levels Levels a be umerial or ategorial ifferet levels
Oe way Aalysis of Variae (ANOVA) ANOVA Geeral ANOVA Settig"Slide 43-45) Ivestigator otrols oe or more fators of iterest Eah fator otais two or more levels Levels a be umerial or ategorial ifferet levels
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Chapter 22. Comparing Two Proportions. Copyright 2010 Pearson Education, Inc.
 Chapter 22 Comparig Two Proportios Copyright 2010 Pearso Educatio, Ic. Comparig Two Proportios Comparisos betwee two percetages are much more commo tha questios about isolated percetages. Ad they are more
Chapter 22 Comparig Two Proportios Copyright 2010 Pearso Educatio, Ic. Comparig Two Proportios Comparisos betwee two percetages are much more commo tha questios about isolated percetages. Ad they are more
Sx [ ] = x must yield a
![Sx [ ] = x must yield a Sx [ ] = x must yield a](/thumbs/96/128993958.jpg) Math -b Leture #5 Notes This wee we start with a remider about oordiates of a vetor relative to a basis for a subspae ad the importat speial ase where the subspae is all of R. This freedom to desribe vetors
Math -b Leture #5 Notes This wee we start with a remider about oordiates of a vetor relative to a basis for a subspae ad the importat speial ase where the subspae is all of R. This freedom to desribe vetors
Lecture 8. Dirac and Weierstrass
 Leture 8. Dira ad Weierstrass Audrey Terras May 5, 9 A New Kid of Produt of Futios You are familiar with the poitwise produt of futios de ed by f g(x) f(x) g(x): You just tae the produt of the real umbers
Leture 8. Dira ad Weierstrass Audrey Terras May 5, 9 A New Kid of Produt of Futios You are familiar with the poitwise produt of futios de ed by f g(x) f(x) g(x): You just tae the produt of the real umbers
Econ 325/327 Notes on Sample Mean, Sample Proportion, Central Limit Theorem, Chi-square Distribution, Student s t distribution 1.
 Eco 325/327 Notes o Sample Mea, Sample Proportio, Cetral Limit Theorem, Chi-square Distributio, Studet s t distributio 1 Sample Mea By Hiro Kasahara We cosider a radom sample from a populatio. Defiitio
Eco 325/327 Notes o Sample Mea, Sample Proportio, Cetral Limit Theorem, Chi-square Distributio, Studet s t distributio 1 Sample Mea By Hiro Kasahara We cosider a radom sample from a populatio. Defiitio
Because it tests for differences between multiple pairs of means in one test, it is called an omnibus test.
 Math 308 Sprig 018 Classes 19 ad 0: Aalysis of Variace (ANOVA) Page 1 of 6 Itroductio ANOVA is a statistical procedure for determiig whether three or more sample meas were draw from populatios with equal
Math 308 Sprig 018 Classes 19 ad 0: Aalysis of Variace (ANOVA) Page 1 of 6 Itroductio ANOVA is a statistical procedure for determiig whether three or more sample meas were draw from populatios with equal
Computer Science 188 Artificial Intelligence. Introduction to Probability. Probability Ryan Waliany
 Computer Siee 88 Artifiial Itelligee Rya Waliay Note: this is meat to be a simple referee sheet ad help studets uder the derivatios. If there s aythig that seems shaky or iorret do t hesitate to email
Computer Siee 88 Artifiial Itelligee Rya Waliay Note: this is meat to be a simple referee sheet ad help studets uder the derivatios. If there s aythig that seems shaky or iorret do t hesitate to email
2 1. The r.s., of size n2, from population 2 will be. 2 and 2. 2) The two populations are independent. This implies that all of the n1 n2
 Chapter 8 Comparig Two Treatmets Iferece about Two Populatio Meas We wat to compare the meas of two populatios to see whether they differ. There are two situatios to cosider, as show i the followig examples:
Chapter 8 Comparig Two Treatmets Iferece about Two Populatio Meas We wat to compare the meas of two populatios to see whether they differ. There are two situatios to cosider, as show i the followig examples:
COMP26120: Introducing Complexity Analysis (2018/19) Lucas Cordeiro
 COMP60: Itroduig Complexity Aalysis (08/9) Luas Cordeiro luas.ordeiro@mahester.a.uk Itroduig Complexity Aalysis Textbook: Algorithm Desig ad Appliatios, Goodrih, Mihael T. ad Roberto Tamassia (hapter )
COMP60: Itroduig Complexity Aalysis (08/9) Luas Cordeiro luas.ordeiro@mahester.a.uk Itroduig Complexity Aalysis Textbook: Algorithm Desig ad Appliatios, Goodrih, Mihael T. ad Roberto Tamassia (hapter )
BIOS 4110: Introduction to Biostatistics. Breheny. Lab #9
 BIOS 4110: Itroductio to Biostatistics Brehey Lab #9 The Cetral Limit Theorem is very importat i the realm of statistics, ad today's lab will explore the applicatio of it i both categorical ad cotiuous
BIOS 4110: Itroductio to Biostatistics Brehey Lab #9 The Cetral Limit Theorem is very importat i the realm of statistics, ad today's lab will explore the applicatio of it i both categorical ad cotiuous
This exam contains 19 pages (including this cover page) and 10 questions. A Formulae sheet is provided with the exam.
 Probability ad Statistics FS 07 Secod Sessio Exam 09.0.08 Time Limit: 80 Miutes Name: Studet ID: This exam cotais 9 pages (icludig this cover page) ad 0 questios. A Formulae sheet is provided with the
Probability ad Statistics FS 07 Secod Sessio Exam 09.0.08 Time Limit: 80 Miutes Name: Studet ID: This exam cotais 9 pages (icludig this cover page) ad 0 questios. A Formulae sheet is provided with the
Lecture 12: September 27
 36-705: Itermediate Statistics Fall 207 Lecturer: Siva Balakrisha Lecture 2: September 27 Today we will discuss sufficiecy i more detail ad the begi to discuss some geeral strategies for costructig estimators.
36-705: Itermediate Statistics Fall 207 Lecturer: Siva Balakrisha Lecture 2: September 27 Today we will discuss sufficiecy i more detail ad the begi to discuss some geeral strategies for costructig estimators.
Société de Calcul Mathématique SA Mathematical Modelling Company, Corp.
 oiété de Calul Mathéatique A Matheatial Modellig Copay, Corp. Deisio-aig tools, sie 995 iple Rado Wals Part V Khihi's Law of the Iterated Logarith: Quatitative versios by Berard Beauzay August 8 I this
oiété de Calul Mathéatique A Matheatial Modellig Copay, Corp. Deisio-aig tools, sie 995 iple Rado Wals Part V Khihi's Law of the Iterated Logarith: Quatitative versios by Berard Beauzay August 8 I this
4. Partial Sums and the Central Limit Theorem
 1 of 10 7/16/2009 6:05 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 4. Partial Sums ad the Cetral Limit Theorem The cetral limit theorem ad the law of large umbers are the two fudametal theorems
1 of 10 7/16/2009 6:05 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 4. Partial Sums ad the Cetral Limit Theorem The cetral limit theorem ad the law of large umbers are the two fudametal theorems
Lecture 5: Parametric Hypothesis Testing: Comparing Means. GENOME 560, Spring 2016 Doug Fowler, GS
 Lecture 5: Parametric Hypothesis Testig: Comparig Meas GENOME 560, Sprig 2016 Doug Fowler, GS (dfowler@uw.edu) 1 Review from last week What is a cofidece iterval? 2 Review from last week What is a cofidece
Lecture 5: Parametric Hypothesis Testig: Comparig Meas GENOME 560, Sprig 2016 Doug Fowler, GS (dfowler@uw.edu) 1 Review from last week What is a cofidece iterval? 2 Review from last week What is a cofidece
Chapter 22. Comparing Two Proportions. Copyright 2010, 2007, 2004 Pearson Education, Inc.
 Chapter 22 Comparig Two Proportios Copyright 2010, 2007, 2004 Pearso Educatio, Ic. Comparig Two Proportios Read the first two paragraphs of pg 504. Comparisos betwee two percetages are much more commo
Chapter 22 Comparig Two Proportios Copyright 2010, 2007, 2004 Pearso Educatio, Ic. Comparig Two Proportios Read the first two paragraphs of pg 504. Comparisos betwee two percetages are much more commo
Probability & Statistics Chapter 8
 I. Estimatig with Large Samples Probability & Statistis Poit Estimate of a parameter is a estimate of a populatio parameter give by a sigle umber. Use x (the sample mea) as a poit estimate for (the populatio
I. Estimatig with Large Samples Probability & Statistis Poit Estimate of a parameter is a estimate of a populatio parameter give by a sigle umber. Use x (the sample mea) as a poit estimate for (the populatio
1.010 Uncertainty in Engineering Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu.00 Ucertaity i Egieerig Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu.terms. .00 - Brief Notes # 9 Poit ad Iterval
MIT OpeCourseWare http://ocw.mit.edu.00 Ucertaity i Egieerig Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu.terms. .00 - Brief Notes # 9 Poit ad Iterval
Problem Set 4 Due Oct, 12
 EE226: Radom Processes i Systems Lecturer: Jea C. Walrad Problem Set 4 Due Oct, 12 Fall 06 GSI: Assae Gueye This problem set essetially reviews detectio theory ad hypothesis testig ad some basic otios
EE226: Radom Processes i Systems Lecturer: Jea C. Walrad Problem Set 4 Due Oct, 12 Fall 06 GSI: Assae Gueye This problem set essetially reviews detectio theory ad hypothesis testig ad some basic otios
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 19 11/17/2008 LAWS OF LARGE NUMBERS II THE STRONG LAW OF LARGE NUMBERS
 MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
Agreement of CI and HT. Lecture 13 - Tests of Proportions. Example - Waiting Times
 Sigificace level vs. cofidece level Agreemet of CI ad HT Lecture 13 - Tests of Proportios Sta102 / BME102 Coli Rudel October 15, 2014 Cofidece itervals ad hypothesis tests (almost) always agree, as log
Sigificace level vs. cofidece level Agreemet of CI ad HT Lecture 13 - Tests of Proportios Sta102 / BME102 Coli Rudel October 15, 2014 Cofidece itervals ad hypothesis tests (almost) always agree, as log
Class 23. Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science. Marquette University MATH 1700
 Class 23 Daiel B. Rowe, Ph.D. Departmet of Mathematics, Statistics, ad Computer Sciece Copyright 2017 by D.B. Rowe 1 Ageda: Recap Chapter 9.1 Lecture Chapter 9.2 Review Exam 6 Problem Solvig Sessio. 2
Class 23 Daiel B. Rowe, Ph.D. Departmet of Mathematics, Statistics, ad Computer Sciece Copyright 2017 by D.B. Rowe 1 Ageda: Recap Chapter 9.1 Lecture Chapter 9.2 Review Exam 6 Problem Solvig Sessio. 2
Fall 2013 MTH431/531 Real analysis Section Notes
 Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
LECTURE 14 NOTES. A sequence of α-level tests {ϕ n (x)} is consistent if
 LECTURE 14 NOTES 1. Asymptotic power of tests. Defiitio 1.1. A sequece of -level tests {ϕ x)} is cosistet if β θ) := E θ [ ϕ x) ] 1 as, for ay θ Θ 1. Just like cosistecy of a sequece of estimators, Defiitio
LECTURE 14 NOTES 1. Asymptotic power of tests. Defiitio 1.1. A sequece of -level tests {ϕ x)} is cosistet if β θ) := E θ [ ϕ x) ] 1 as, for ay θ Θ 1. Just like cosistecy of a sequece of estimators, Defiitio
FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING. Lectures
 FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING Lectures MODULE 5 STATISTICS II. Mea ad stadard error of sample data. Biomial distributio. Normal distributio 4. Samplig 5. Cofidece itervals
FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING Lectures MODULE 5 STATISTICS II. Mea ad stadard error of sample data. Biomial distributio. Normal distributio 4. Samplig 5. Cofidece itervals
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Ho OG o VS H i OE. sup o_ Nxt. sup. OE ou. Ho 0 00 vs H O Oo. Power function. nejeet Ho. Plo p O. Pole ERR KERR IERR.
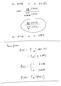 o OG o VS i OE Nxt sup E sup OE ou o_ 4 i o vs O Oo Power fuctio ejeet o Plo p O Pole ERR 9 4 KERR IERR Blot Eo 4 type I emor to whe reject e 3 true B O whe C o Type I error doot reject o che is true BIO
o OG o VS i OE Nxt sup E sup OE ou o_ 4 i o vs O Oo Power fuctio ejeet o Plo p O Pole ERR 9 4 KERR IERR Blot Eo 4 type I emor to whe reject e 3 true B O whe C o Type I error doot reject o che is true BIO
Parameter, Statistic and Random Samples
 Parameter, Statistic ad Radom Samples A parameter is a umber that describes the populatio. It is a fixed umber, but i practice we do ot kow its value. A statistic is a fuctio of the sample data, i.e.,
Parameter, Statistic ad Radom Samples A parameter is a umber that describes the populatio. It is a fixed umber, but i practice we do ot kow its value. A statistic is a fuctio of the sample data, i.e.,
Math 152. Rumbos Fall Solutions to Review Problems for Exam #2. Number of Heads Frequency
 Math 152. Rumbos Fall 2009 1 Solutios to Review Problems for Exam #2 1. I the book Experimetatio ad Measuremet, by W. J. Youde ad published by the by the Natioal Sciece Teachers Associatio i 1962, the
Math 152. Rumbos Fall 2009 1 Solutios to Review Problems for Exam #2 1. I the book Experimetatio ad Measuremet, by W. J. Youde ad published by the by the Natioal Sciece Teachers Associatio i 1962, the
Econ 325 Notes on Point Estimator and Confidence Interval 1 By Hiro Kasahara
 Poit Estimator Eco 325 Notes o Poit Estimator ad Cofidece Iterval 1 By Hiro Kasahara Parameter, Estimator, ad Estimate The ormal probability desity fuctio is fully characterized by two costats: populatio
Poit Estimator Eco 325 Notes o Poit Estimator ad Cofidece Iterval 1 By Hiro Kasahara Parameter, Estimator, ad Estimate The ormal probability desity fuctio is fully characterized by two costats: populatio
Composite Hypotheses
 Composite Hypotheses March 25-27, 28 For a composite hypothesis, the parameter space Θ is divided ito two disjoit regios, Θ ad Θ 1. The test is writte H : Θ versus H 1 : Θ 1 with H is called the ull hypothesis
Composite Hypotheses March 25-27, 28 For a composite hypothesis, the parameter space Θ is divided ito two disjoit regios, Θ ad Θ 1. The test is writte H : Θ versus H 1 : Θ 1 with H is called the ull hypothesis
Fluids Lecture 2 Notes
 Fluids Leture Notes. Airfoil orte Sheet Models. Thi-Airfoil Aalysis Problem Readig: Aderso.,.7 Airfoil orte Sheet Models Surfae orte Sheet Model A aurate meas of represetig the flow about a airfoil i a
Fluids Leture Notes. Airfoil orte Sheet Models. Thi-Airfoil Aalysis Problem Readig: Aderso.,.7 Airfoil orte Sheet Models Surfae orte Sheet Model A aurate meas of represetig the flow about a airfoil i a
MOST PEOPLE WOULD RATHER LIVE WITH A PROBLEM THEY CAN'T SOLVE, THAN ACCEPT A SOLUTION THEY CAN'T UNDERSTAND.
 XI-1 (1074) MOST PEOPLE WOULD RATHER LIVE WITH A PROBLEM THEY CAN'T SOLVE, THAN ACCEPT A SOLUTION THEY CAN'T UNDERSTAND. R. E. D. WOOLSEY AND H. S. SWANSON XI-2 (1075) STATISTICAL DECISION MAKING Advaced
XI-1 (1074) MOST PEOPLE WOULD RATHER LIVE WITH A PROBLEM THEY CAN'T SOLVE, THAN ACCEPT A SOLUTION THEY CAN'T UNDERSTAND. R. E. D. WOOLSEY AND H. S. SWANSON XI-2 (1075) STATISTICAL DECISION MAKING Advaced
April 18, 2017 CONFIDENCE INTERVALS AND HYPOTHESIS TESTING, UNDERGRADUATE MATH 526 STYLE
 April 18, 2017 CONFIDENCE INTERVALS AND HYPOTHESIS TESTING, UNDERGRADUATE MATH 526 STYLE TERRY SOO Abstract These otes are adapted from whe I taught Math 526 ad meat to give a quick itroductio to cofidece
April 18, 2017 CONFIDENCE INTERVALS AND HYPOTHESIS TESTING, UNDERGRADUATE MATH 526 STYLE TERRY SOO Abstract These otes are adapted from whe I taught Math 526 ad meat to give a quick itroductio to cofidece
6 Sample Size Calculations
 6 Sample Size Calculatios Oe of the major resposibilities of a cliical trial statisticia is to aid the ivestigators i determiig the sample size required to coduct a study The most commo procedure for determiig
6 Sample Size Calculatios Oe of the major resposibilities of a cliical trial statisticia is to aid the ivestigators i determiig the sample size required to coduct a study The most commo procedure for determiig
STATISTICAL INFERENCE
 STATISTICAL INFERENCE POPULATION AND SAMPLE Populatio = all elemets of iterest Characterized by a distributio F with some parameter θ Sample = the data X 1,..., X, selected subset of the populatio = sample
STATISTICAL INFERENCE POPULATION AND SAMPLE Populatio = all elemets of iterest Characterized by a distributio F with some parameter θ Sample = the data X 1,..., X, selected subset of the populatio = sample
Goodness-of-Fit Tests and Categorical Data Analysis (Devore Chapter Fourteen)
 Goodess-of-Fit Tests ad Categorical Data Aalysis (Devore Chapter Fourtee) MATH-252-01: Probability ad Statistics II Sprig 2019 Cotets 1 Chi-Squared Tests with Kow Probabilities 1 1.1 Chi-Squared Testig................
Goodess-of-Fit Tests ad Categorical Data Aalysis (Devore Chapter Fourtee) MATH-252-01: Probability ad Statistics II Sprig 2019 Cotets 1 Chi-Squared Tests with Kow Probabilities 1 1.1 Chi-Squared Testig................
ECO 312 Fall 2013 Chris Sims LIKELIHOOD, POSTERIORS, DIAGNOSING NON-NORMALITY
 ECO 312 Fall 2013 Chris Sims LIKELIHOOD, POSTERIORS, DIAGNOSING NON-NORMALITY (1) A distributio that allows asymmetry differet probabilities for egative ad positive outliers is the asymmetric double expoetial,
ECO 312 Fall 2013 Chris Sims LIKELIHOOD, POSTERIORS, DIAGNOSING NON-NORMALITY (1) A distributio that allows asymmetry differet probabilities for egative ad positive outliers is the asymmetric double expoetial,
Final Review. Fall 2013 Prof. Yao Xie, H. Milton Stewart School of Industrial Systems & Engineering Georgia Tech
 Fial Review Fall 2013 Prof. Yao Xie, yao.xie@isye.gatech.edu H. Milto Stewart School of Idustrial Systems & Egieerig Georgia Tech 1 Radom samplig model radom samples populatio radom samples: x 1,..., x
Fial Review Fall 2013 Prof. Yao Xie, yao.xie@isye.gatech.edu H. Milto Stewart School of Idustrial Systems & Egieerig Georgia Tech 1 Radom samplig model radom samples populatio radom samples: x 1,..., x
Lecture 2: Concentration Bounds
 CSE 52: Desig ad Aalysis of Algorithms I Sprig 206 Lecture 2: Cocetratio Bouds Lecturer: Shaya Oveis Ghara March 30th Scribe: Syuzaa Sargsya Disclaimer: These otes have ot bee subjected to the usual scrutiy
CSE 52: Desig ad Aalysis of Algorithms I Sprig 206 Lecture 2: Cocetratio Bouds Lecturer: Shaya Oveis Ghara March 30th Scribe: Syuzaa Sargsya Disclaimer: These otes have ot bee subjected to the usual scrutiy
Simulation. Two Rule For Inverting A Distribution Function
 Simulatio Two Rule For Ivertig A Distributio Fuctio Rule 1. If F(x) = u is costat o a iterval [x 1, x 2 ), the the uiform value u is mapped oto x 2 through the iversio process. Rule 2. If there is a jump
Simulatio Two Rule For Ivertig A Distributio Fuctio Rule 1. If F(x) = u is costat o a iterval [x 1, x 2 ), the the uiform value u is mapped oto x 2 through the iversio process. Rule 2. If there is a jump
Integrable Functions. { f n } is called a determining sequence for f. If f is integrable with respect to, then f d does exist as a finite real number
 MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
Resampling Methods. X (1/2), i.e., Pr (X i m) = 1/2. We order the data: X (1) X (2) X (n). Define the sample median: ( n.
 Jauary 1, 2019 Resamplig Methods Motivatio We have so may estimators with the property θ θ d N 0, σ 2 We ca also write θ a N θ, σ 2 /, where a meas approximately distributed as Oce we have a cosistet estimator
Jauary 1, 2019 Resamplig Methods Motivatio We have so may estimators with the property θ θ d N 0, σ 2 We ca also write θ a N θ, σ 2 /, where a meas approximately distributed as Oce we have a cosistet estimator
Sample Size Determination (Two or More Samples)
 Sample Sie Determiatio (Two or More Samples) STATGRAPHICS Rev. 963 Summary... Data Iput... Aalysis Summary... 5 Power Curve... 5 Calculatios... 6 Summary This procedure determies a suitable sample sie
Sample Sie Determiatio (Two or More Samples) STATGRAPHICS Rev. 963 Summary... Data Iput... Aalysis Summary... 5 Power Curve... 5 Calculatios... 6 Summary This procedure determies a suitable sample sie
Product measures, Tonelli s and Fubini s theorems For use in MAT3400/4400, autumn 2014 Nadia S. Larsen. Version of 13 October 2014.
 Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Lecture 12: November 13, 2018
 Mathematical Toolkit Autum 2018 Lecturer: Madhur Tulsiai Lecture 12: November 13, 2018 1 Radomized polyomial idetity testig We will use our kowledge of coditioal probability to prove the followig lemma,
Mathematical Toolkit Autum 2018 Lecturer: Madhur Tulsiai Lecture 12: November 13, 2018 1 Radomized polyomial idetity testig We will use our kowledge of coditioal probability to prove the followig lemma,
Random Variables, Sampling and Estimation
 Chapter 1 Radom Variables, Samplig ad Estimatio 1.1 Itroductio This chapter will cover the most importat basic statistical theory you eed i order to uderstad the ecoometric material that will be comig
Chapter 1 Radom Variables, Samplig ad Estimatio 1.1 Itroductio This chapter will cover the most importat basic statistical theory you eed i order to uderstad the ecoometric material that will be comig
Topic 18: Composite Hypotheses
 Toc 18: November, 211 Simple hypotheses limit us to a decisio betwee oe of two possible states of ature. This limitatio does ot allow us, uder the procedures of hypothesis testig to address the basic questio:
Toc 18: November, 211 Simple hypotheses limit us to a decisio betwee oe of two possible states of ature. This limitatio does ot allow us, uder the procedures of hypothesis testig to address the basic questio:
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY
 EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA, 016 MODULE : Statistical Iferece Time allowed: Three hours Cadidates should aswer FIVE questios. All questios carry equal marks. The umber
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA, 016 MODULE : Statistical Iferece Time allowed: Three hours Cadidates should aswer FIVE questios. All questios carry equal marks. The umber
Frequentist Inference
 Frequetist Iferece The topics of the ext three sectios are useful applicatios of the Cetral Limit Theorem. Without kowig aythig about the uderlyig distributio of a sequece of radom variables {X i }, for
Frequetist Iferece The topics of the ext three sectios are useful applicatios of the Cetral Limit Theorem. Without kowig aythig about the uderlyig distributio of a sequece of radom variables {X i }, for
Exponential Families and Bayesian Inference
 Computer Visio Expoetial Families ad Bayesia Iferece Lecture Expoetial Families A expoetial family of distributios is a d-parameter family f(x; havig the followig form: f(x; = h(xe g(t T (x B(, (. where
Computer Visio Expoetial Families ad Bayesia Iferece Lecture Expoetial Families A expoetial family of distributios is a d-parameter family f(x; havig the followig form: f(x; = h(xe g(t T (x B(, (. where
