A sparse grid stochastic collocation method for partial differential equations with random input data
|
|
|
- Marjory Kennedy
- 5 years ago
- Views:
Transcription
1 A sparse grid stochastic collocation method for partial differential equations with random input data F. Nobile R. Tempone C. G. Webster May 24, 2007 Abstract This work proposes and analyzes a Smolyak-type sparse grid stochastic collocation method for the approximation of statistical quantities related to the solution of partial differential equations with random coefficients and forcing terms input data of the model. To compute solution statistics, the sparse grid stochastic collocation method uses approximate solutions, produced here by finite elements, corresponding to a deterministic set of points in the random input space. This naturally requires solving uncoupled deterministic problems as in the Monte Carlo method. If the number of random variables needed to describe the input data is moderately large, full tensor product spaces are computationally expensive to use due to the curse of dimensionality. In this case the sparse grid approach is still expected to be competitive with the classical Monte Carlo method. Therefore, it is of major practical relevance to understand in which situations the sparse grid stochastic collocation method is more efficient than Monte Carlo. This work provides strong error estimates for the fully discrete solution using L q norms and analyzes the computational efficiency of the proposed method. In particular, it demonstrates algebraic convergence with respect to the total number of collocation points. The derived estimates are then used to compare the method with Monte Carlo, indicating for which problems the first is more efficient than the latter. Computational evidence complements the present theory and shows the effectiveness of the sparse grid stochastic collocation method compared to full tensor and Monte Carlo approaches. Key words: Collocation techniques, stochastic PDEs, finite elements, uncertainty quantification, sparse grids, Smolyak approximation, multivariate polynomial approximation. AMS subject classification: 65N30, 65N35, 65N12, 65N15, 65C20 Introduction Mathematical modeling and computer simulations are nowadays widely used tools to predict the behavior of physical and engineering problems. Whenever a particular application is considered, the mathematical models need to be equipped with input data, such as coefficients, forcing terms, boundary conditions, geometry, etc. However, in many applications, such input data may be affected by a relatively large amount of uncertainty. This can be due to an intrinsic variability in MOX, Dipartimento di Matematica, Politecnico di Milano, Italy. Dahlquist Fellow, NADA, Royal Institute of Technology, Stockholm S , Sweden and School of Computational Science and Department of Mathematics, Florida State University, Tallahassee FL School of Computational Science and Department of Mathematics, Florida State University, Tallahassee FL
2 the physical system as, for instance, in the mechanical properties of many bio-materials, polymeric fluids, or composite materials, the action of wind or seismic vibrations on civil structures, etc. In other situations, uncertainty may come from our difficulty in characterizing accurately the physical system under investigation as in the study of groundwater flows, where the subsurface properties such as porosity and permeability in an aquifer have to be extrapolated from measurements taken only in few spatial locations. Such uncertainties can be included in the mathematical model adopting a probabilistic setting, provided enough information is available for a complete statistical characterization of the physical system. In this framework, the input data are modeled as random variables, or more generally, as random fields with a given spatial or temporal correlation structure. Therefore, the goal of the mathematical and computational analysis becomes the prediction of statistical moments of the solution mean value, variance, covariance, etc. or statistics of some given responses of the system sometimes also called quantities of physical interest which are real valued functionals of the solution, given the probability distribution of the input random data. Examples of quantities of interest could be the solution values in a given region, fluxes across given boundaries, etc. In order to parametrize the input data for a given PDE, random fields that are either coefficients or loads can often be expanded as an infinite combination of random variables by, for instance, the so called Karhunen-Loève [23] or Polynomial Chaos PC expansions [33, 37]. Although such random fields are properly described only by means of an infinite number of random variables, whenever the realizations are slowly varying in space, with a correlation length comparable to the size of the domain, only a few terms in the above mentioned expansions are typically needed to describe the random field with sufficient accuracy. Therefore, in this case, it is reasonable to limit the analysis to just a few random variables in the expansion see e.g. [2, 16]. In this work we focus on partial differential equations whose coefficients and forcing terms are described by a finite dimensional random vector finite dimensional noise assumption, either because the problem itself can be described by a finite number of random variables or because the input coefficients are modeled as truncated random fields. The most popular approach to solve mathematical problems in a probabilistic setting is the Monte Carlo method see e.g. [15] and references therein. The Monte Carlo method is easy to implement and allows one to reuse available deterministic codes. Yet, the convergence rate is typically very slow, although with a mild dependence on the number on sampled random variables. In the last few years, other approaches have been proposed, which in certain situations feature a much faster convergence rate. We mention, among others, the Spectral Galerkin method [3, 4, 16, 20, 22, 25, 27, 36], Stochastic Collocation [5, 24, 29, 35], perturbation methods or Neumann expansions [1, 17, 30, 34]. For certain classes of problems, the solution may have a very regular dependence on the input random variables. For instance, it was shown in [5] and [3] that the solution of a linear elliptic PDE with diffusivity coefficient and/or forcing term described as truncated expansions of random fields is analytic in the input random variables. In such situations, Spectral Galerkin or Stochastic Collocation methods based on orthogonal tensor product polynomials feature a very fast convergence rate. In particular, our earlier work [5] proposed a Stochastic Collocation/Finite Element method based on standard finite element approximations in space and a collocation on a tensor grid built upon the zeros of orthogonal polynomials with respect to the joint probability density function of the input random variables. It was shown that for an elliptic PDE the error converges exponentially fast with respect to the number of points employed for each random input variable. The Stochastic Collocation method can be easily implemented and leads naturally to the solu- 2
3 tion of uncoupled deterministic problems as in the Monte Carlo method, even in presence of input data which depend nonlinearly on the driving random variables. It can also treat efficiently the case of non independent random variables with the introduction of an auxiliary density and handle for instance cases with lognormal diffusivity coefficient, which is not bounded in Ω D but has bounded realizations. When the number of input random variables is small, Stochastic Collocation is a very effective numerical tool. On the other hand, approximations based on tensor product grids suffer from the curse of dimensionality since the number of collocation points in a tensor grid grows exponentially fast in the number of input random variables. If the number of random variables is moderately large, one should rather consider sparse tensor product spaces as first proposed by Smolyak [28] and further investigated by e.g. [6, 16, 18, 35], which will be the primary focus of this paper. It is natural to expect that the use of sparse grids will reduce dramatically the number of collocation points, while preserving a high level of accuracy and thus being able to successfully compete with Monte Carlo. Our main purpose is to clarify the limitations of the previous statement and to understand in which situations the sparse grid stochastic collocation method is more efficient than Monte Carlo. Motivated by the above, this work proposes and analyzes a Smolyak-type sparse grid stochastic collocation method for the approximation of statistical quantities related to the solution of partial differential equations whose input data are described through a finite number of random variables. The sparse tensor product grids are built upon either Clenshaw-Curtis [11] or Gaussian abscissas. After outlining the method, this work provides strong error estimates for the fully discrete solution and analyzes its computational efficiency. In particular, it proves algebraic convergence with respect to the total number of collocation points, or equivalently, the total computational work which is directly proportional to the number of collocation points. The exponent of such algebraic convergence is connected to both the regularity of the solution and the number of input random variables, N, and essentially deteriorates with N by a 1/ logn factor. Then, these error estimates are used to compare the method with the standard Monte Carlo, indicating for which problems the first is more efficient than the latter. Moreover, this work addresses the case where the input random variables come from suitably truncated expansions of random fields. There it discusses how to relate the number of points in the sparse grid to the number of random variables retained in the truncated expansion in order to balance discretization error with truncation error in the input random fields. Computational evidence complements the present theory and shows the effectiveness of the sparse grid stochastic collocation method. It also includes a comparison with full tensor and Monte Carlo methods. The outline of the work is the following: Section 1 introduces the mathematical problem, basic notations and states a regularity assumption to be used later in the error analysis. Section 2 summarizes various collocation techniques and describes the sparse approximation method under study. It also describes two types of abscissas, Clenshaw Curtis and Gaussian, that will be employed in the sparse approximation method. Section 3 is the core of the work. We first develop strong error estimates for the fully discrete solution using L P and L2 P norms for Clenshaw-Curtis and Gaussian abscissas, respectively P being the probability measure considered. These norms control the error in the approximation of expected values of smooth functionals of the solution. Then, in Section 3.2 these error estimates are used to compare the method with the standard Monte Carlo, explaining cases where the first is more efficient than the latter. Sections 4 and 5 focus on applications to linear elliptic PDEs with random input data. In Section 4 we verify that the assumptions under which our general theory works hold in this particular case. Then we present in Section 5 some numerical results showing the effectiveness of the proposed 3
4 method when compared to the full tensor and Monte Carlo methods. 1 Problem setting We begin by focusing our attention on a differential operator L, linear or nonlinear, on a domain D R d, which depends on some coefficients aω, x with x D, ω Ω, where Ω, F, P a complete probability space. Here Ω is the set of outcomes, F 2 Ω is the σ-algebra of events and P : F [0, 1] is a probability measure. Similarly the forcing term f = fω, x can be assumed random as well. Consider the stochastic boundary value problem: find a random function, u : Ω D R, such that P -almost everywhere in Ω, or in other words almost surely a.s., the following equation holds: Lau = f in D 1.1 equipped with suitable boundary conditions. Before introducing some assumptions we denote by W D a Banach space of functions v : D R and define, for q [1, ], the stochastic Banach spaces } L q P {v Ω; W D = : Ω W D v is strongly measurable and vω, q W D dp ω < + and { } L P Ω; W D = v : Ω W D v is strongly measurable and P ess sup vω, 2 W D < +. ω Ω Of particular interest is the space L 2 P Ω; W D, consisting of Banach valued functions that have finite second moments. We will now make the following assumptions: A 1 the solution to 1.1 has realizations in the Banach space W D, i.e. u, ω W D almost surely and ω Ω u, ω W D C f, ω W D where we denote W D to be the dual space of W D, and C is a constant independent of the realization ω Ω. A 2 the forcing term f L 2 P Ω; W D is such that the solution u is unique and bounded in L 2 P Ω; W D. Here we give two example problems that are posed in this setting: Ω Example 1.1 The linear problem { aω, uω, = fω, in Ω D, uω, = 0 on Ω D, 1.2 with aω, uniformly bounded and coercive, i.e. there exists a min, a max 0, + such that P ω Ω : aω, x [a min, a max ] x D = 1 and fω, square integrable with respect to P, satisfies assumptions A 1 and A 2 with W D = H0 1 D see [5]. 4
5 Example 1.2 Similarly, for k N +, the nonlinear problem { aω, uω, + uω, 2k+1 = fω, in Ω D, uω, = 0 on Ω D, 1.3 with aω, uniformly bounded and coercive and fω, square integrable with respect to P, satisfies assumptions A 1 and A 2 with W D = H 1 0 D L2k+2 D. Remark 1.3 Goals of the computation As said in the introduction, the goal of the mathematical and computational analysis is the prediction of statistical moments of the solution u to 1.1 mean value, variance, covariance, etc. or statistics of some given quantities of physical interest ψu. Examples of quantities of interest could be the average value of the solution in a given region D c D, ψu = 1 udx, D c D c and similarly average fluxes on a given direction n R d. In the case of Examples 1.1 and 1.2 these fluxes can be written as ψu = 1 a u D c D c n dx. 1.1 On Finite Dimensional Noise In some applications, the coefficient a and the forcing term f appearing in 1.1 can be described by a random vector [Y 1,..., Y N ] : Ω R N, as in the following examples. In such cases, we will emphasize such dependence by writing a N and f N. Example 1.4 Piecewise constant random fields Let us consider again problem 1.2 where the physical domain D is the union of non-overlapping subdomains D i, i = 1,..., N. We consider a diffusion coefficient that is piecewise constant and random on each subdomain, i.e. a N ω, x = a min + N σ i Y i ω1 Di x. Here 1 Di is the indicator function of the set D i, σ i, a min are positive constants, and the random variables Y i are nonnegative with unit variance. In other applications the coefficients and forcing terms in 1.1 may have other type of spatial variation that is amenable to describe by an expansion. Depending on the decay of such expansion and the desired accuracy in our computations we may retain just the first N terms. i=1 Example 1.5 Karhunen-Loève expansion We recall that any second order random field gω, x, with continuous covariance function cov[g] : D D R, can be represented as an infinite sum of random variables, by means, for instance, of a Karhunen-Loève expansion [23]. To this end, introduce the compact and self-adjoint operator T g : L 2 D L 2 D, which is defined by T g v := cov[g]x, vx dx v L 2 D. D Then, consider the sequence of non-negative decreasing eigenvalues of T g, {λ i } i=1, and the corresponding sequence of orthonormal eigenfunctions, {b i } i=1, satisfying T g b i = λ i b i, b i, b j L 2 D = δ ij for i, j N +. 5
6 In addition, define mutually uncorrelated real random variables Y i ω := 1 gω, x E[g]x b i xdx, i = 1,... λi D with zero mean and unit variance, i.e. E[Y i ] = 0 and E[Y i Y j ] = δ ij for i, j N +. The truncated Karhunen-Loève expansion g N, of the stochastic function g, is defined by g N ω, x := E[g]x + N λi b i x Y i ω N N +. Then by Mercer s theorem cf [26, p. 245], it follows that { lim sup E [ { g g N 2]} = lim sup N D N D i=1 i=n+1 Observe that the N random variables in 1.5, describing the random data, are then weighted differently due to the decay of the eigen-pairs of the Karhunen-Loève expansion. The decay of eigenvalues and eigenvectors has been investigated e.g. in the works [16] and [30]. The above examples motivate us to consider problems whose coefficients are described by finitely many random variables. Thus, we will seek a random field u N : Ω D R, such that a.s., the following equation holds: La N u N = f N in D, 1.4 We assume that equation 1.4 admits a unique solution u N L 2 P Ω; W D. Therefore, following the same argument as in [5, p.1010], yields that the solution u N of the stochastic boundary value problem 1.4 can be described by the [Y 1,..., Y N ] random variables, i.e. u N = u N ω, x = u N Y 1 ω,..., Y N ω, x. We underline that the coefficients a N and f N in 1.4 may be an exact representation of the input data as in Example 1.4 or a suitable truncation of the input data as in Example 1.5. In the latter case, the solution u N will also be an approximation of the exact solution u in 1.1 and the truncation error u u N has to be properly estimated see Section 3.2. Remark 1.6 Nonlinear coefficients In certain cases, one may need to ensure qualitative properties on the coefficients a N and f N and may be worth while to describe them as nonlinear functions of Y. For instance, in Example 1.1 one is required to enforce positiveness on the coefficient a N ω, x, say a N ω, x a min for all x D, a.s. in Ω. Then a better choice is to expand loga N a min. The following standard transformation guarantees that the diffusivity coefficient is bounded away from zero almost surely loga N a min ω, x = b 0 x + λn b n xy n ω, n N i.e. one performs a Karhunen-Loève expansion for loga N a min, assuming that a N > a min almost surely. On the other hand, the right hand side of 1.4 can be represented as a truncated Karhunen-Loève expansion f N ω, x = c 0 x + 1 n N µn c n xy n ω. For this work we denote Γ n Y n Ω the image of Y n, where we assume Y n ω to be bounded. Without loss of generality we can assume Γ n = [ 1, 1]. We also let Γ N = N n=1 Γ n and assume that the random variables [Y 1, Y 2,..., Y N ] have a joint probability density function λ i b 2 i } = 0. ρ : Γ N R +, with ρ L Γ N
7 Thus, the plan is to approximate the function u N = u N y, x, for any y Γ N and x D. see [5], [3] Remark 1.7 Unbounded Random Variables By using a similar approach to the work [5] we can easily deal with unbounded random variables, such as Gaussian or exponential ones. For the sake of simplicity in the presentation we focus our study on bounded random variables only. The convergence properies of the collocation techniques that will be developed in the next section depend on the regularity that the solution u N has with respect to y. Denote Γ n = N j=1 Γ j, j n and let yn be an arbitrary element of Γ n. Here we require the solution to problem 1.1 to satisfy Assumption 1.8 Regularity For each y n Γ n, there exists τ n > 0 such that the function u N y n, y n, x as a function of y n, u N : Γ n C 0 Γ n; W D admits an analytic extension uz, y n, x, z C, in the region of the complex plane ΣΓ n ; τ n {z C, distz, Γ n τ n }. 1.7 Moreover, z ΣΓ n ; τ n, with λ a constant independent of n. u N z C 0 Γ n ;W D λ 1.8 This assumption is sound in several problems; in particular, it can be verified for the linear problem that will be analyzed in Section 4. In the more general case, this assumption should be verified for each particular application, and will have implications on the allowed regularity of the input data, e.g. coefficients, loads, etc., of the stochastic PDE under study. See also Remark 3.13 for related results based on less regularity requirements. 2 Collocation techniques We seek a numerical approximation to the exact solution of 1.4 in a suitable finite dimensional subspace. To describe such a subspace properly, we introduce some standard approximation subspaces, namely: W h D W D is a standard finite element space of dimension N h, which contains continuous piecewise polynomials defined on regular triangulations T h that have a maximum mesh-spacing parameter h > 0. We suppose that W h has the following deterministic approximation property: for a given function ϕ W D, min ϕ v W D Cs; ϕ h s, 2.1 v W h D where s is a positive integer determined by the smoothness of ϕ and the degree of the approximating finite element subspace and Cs; ϕ is independent of h. Example 2.1 Let D be a convex polygonal domain and W D = H0 1D. linear finite element subspaces we have For piecewise min v W h D ϕ v H 1 0 D c h ϕ H 2 D. That is, s = 1 and Cs; ϕ = c ϕ H 2 D, see for example [7]. 7
8 We will also assume that there exists a finite element operator π h : W D W h D with the optimality condition ϕ π h ϕ W D C π min ϕ v W D, ϕ W D, 2.2 v W h D where the constant C π is independent of the mesh size h. It is worth noticing that in general the operator π h will depend on the specific problem, as well as on y, i.e. π h = π h y. P p Γ N L 2 ργ N is the span of tensor product polynomials with degree at most p = p 1,..., p N i.e. P p Γ N = N n=1 P p n Γ n, with P pn Γ n = spany k n, k = 0,..., p n, n = 1,..., N. Hence the dimension of P p Γ N is N p = N n=1 p n + 1. Stochastic collocation entails the evaluation of approximate values π h u N y k = u N h y k W h D, to the solution u N of 1.4 on a suitable set of points y k Γ N. Then, the fully discrete solution u N h,p C0 Γ N ; W h D is a global approximation sometimes an interpolation constructed by linear combinations of the point values. That is u N h,p y, = u N h y k, l p k y, 2.3 k K where, for instance, the functions l p k can be taken as the Lagrange polynomials see Section 2.1 and 2.2. This formulation can be used to compute the mean value or variance of u, as described in [5, Section 2], or to approximate expected values of functionals ψu, cf. Remark 1.3, by E[ψu] E[ψu N h,p ] k K ψu N h y k E[l p k ]. In the next sections we consider different choices of the evaluation points y k and corresponding weights E[l p k ] in the associated quadrature formula. 2.1 Full tensor product interpolation In this section we briefly recall interpolation based on Lagrange polynomials. We first introduce an index i N +, i 1. Then, for each value of i, let {y i 1,..., yi m i } [ 1, 1] be a sequence of abscissas for Lagrange interpolation on [ 1, 1]. For u C 0 Γ 1 ; W D and N = 1 we introduce a sequence of one-dimensional Lagrange interpolation operators U i : C 0 Γ 1 ; W D V mi Γ 1 ; W D m i U i uy = uyj i ljy, i u C 0 Γ 1 ; W D, 2.4 j=1 where lj i P m i 1Γ 1 are the Lagrange polynomials of degree m i 1, i.e. lj iy = m i y yk i k=1 y i k j j yi k, and { } m V m Γ 1 ; W D = v C 0 Γ 1 ; W D : vy, x = ṽ k xl k y, {ṽ k } m k=1 W D. k=1 8
9 Formula 2.4 reproduces exactly all polynomials of degree less than m i. Now, in the multivariate case N > 1, for each u C 0 Γ N ; W D and the multi-index i = i 1,..., i N N N + we define the full tensor product interpolation formulas I N i uy = U i 1 U i N uy = m i1 j 1 =1 m in j N =1 u y i 1 j1,..., y i N jn l i 1 j1 l i N jn. 2.5 Clearly, the above product needs N n=1 m i n function evaluations. These formulas will also be used as the building blocks for the Smolyak method, described next. 2.2 Smolyak approximation Here we follow closely the work [6] and describe the Smolyak isotropic formulas A w, N. The Smolyak formulas are just linear combinations of product formulas 2.5 with the following key properties: only products with a relatively small number of points are used. With U 0 = 0 and for i N + define i := U i U i Moreover, given an integer w N +, hereafter called the level, we define the sets Xw, N := Xw, N := Y w, N := { { { i N N +, i 1 : i N N +, i 1 : } N i n 1 w, 2.7a n=1 } N i n 1 = w, 2.7b n=1 i N N +, i 1 : w N + 1 } N i n 1 w, 2.7c and for i N N + we set i = i i N. Then the isotropic Smolyak formula is given by A w, N = i Y w,n i Xw,N n=1 i 1 i N. 2.8 Equivalently, formula 2.8 can be written as see [32] A w, N = N 1 1 w+n i U i 1 U i N. 2.9 w + N i To compute A w, Nu, one only needs to know function values on the sparse grid H w, N = i Y w,n ϑ i 1 ϑ i N [ 1, 1] N, 2.10 where ϑ i = { y i 1,..., yi m i } [ 1, 1] denotes the set of abscissas used by U i. If the sets are nested, i.e. ϑ i ϑ i+1, then H w, N H w + 1, N and H w, N = i e Xw,N ϑ i 1 ϑ i N
10 The Smolyak formula is actually interpolatory whenever nested points are used. This result has been proved in [6, Proposition 6 on page 277]. By comparing 2.11 and 2.10, we observe that the Smolyak approximation that employs nested points requires less function evaluations than the corresponding formula with non nested points. In the next section we introduce two particular sets of abscissas, nested and non nested, respectively. Also, Figure 1 shows, as an example, the sparse grid H 5, 2 obtained in those two cases. Note that the Smolyak approximation formula, as presented in this Section, is isotropic, since all directions are treated equally. This can be seen from 2.8 observing that if a multi-index i = i 1, i 2,..., i N belongs to the set Xw, N, then any permutation of i also belongs to Xw, N and contributes to the construction of the Smolyak approximation A w, N. 2.3 Choice of interpolation abscissas Clenshaw-Curtis abscissas. We first suggest to use Clenshaw-Curtis abscissas see [11] in the construction of the Smolyak formula. These abscissas are the extrema of Chebyshev polynomials and, for any choice of m i > 1, are given by y i j = cos πj 1 m i 1, j = 1,..., m i In addition, one sets y i 1 = 0 if m i = 1 and lets the number of abscissas m i in each level to grow according to the following formula m 1 = 1 and m i = 2 i 1 + 1, for i > With this particular choice, one obtains nested sets of abscissas, i.e., ϑ i ϑ i+1 and thereby H w, N H w + 1, N. It is important to choose m 1 = 1 if we are interested in optimal approximation in relatively large N, because in all other cases the number of points used by A w, N increases too fast with N. Gaussian abscissas. We also propose to use Gaussian abscissas, i.e. the zeros of the orthogonal polynomials with respect to some positive weight. However, these Gaussian abscissas are in general not nested. Regardless, as in the Clenshaw-Curtis case, we choose the number m i of abscissas that are used by U i as in See the work [31] for an insightful comparison of quadrature formulas based on Clenshaw-Curtis and Gaussian abscissas. The natural choice of the weight should be the probability density function ρ of the random variables Y i ω for all i. Yet, in the general multivariate case, if the random variables Y i are not independent, the density ρ does not factorize, i.e. ρy 1,..., y n N n=1 ρ ny n. To this end, we first introduce an auxiliary probability density function ˆρ : Γ N R + that can be seen as the joint probability of N independent random variables, i.e. it factorizes as N ˆρy 1,..., y n = ˆρ n y n, y Γ N, and is such that ρ ˆρ < L Γ N n=1 For each dimension n = 1,..., N, let the m n Gaussian abscissas be the roots of the m n degree polynomial that is ˆρ n -orthogonal to all polynomials of degree m n 1 on the interval [ 1, 1]. The auxiliary density ˆρ should be chosen as close as possible to the true density ρ, so as to have the quotient ρ/ˆρ not too large. Indeed, such quotient will appear in the final error estimate see Section Examples of isotropic sparse grids, constructed from the nested Clenshaw-Curtis abscissas and the non-nested Gaussian abscissas are shown in Figure 1. There, we consider a two-dimensional 10
11 parameter space and a maximum level w = 5 sparse grid H 5, 2. To see the reduction in function evaluations with respect to full tensor product grids, we also include a plot of the corresponding Clenshaw-Curtis isotropic full tensor grid having the same maximum number of points in each direction, namely 2 w + 1 = 33. Observe that if we take m points in each direction, the isotropic full tensor grid will contain m N points while the analogous isotropic Smolyak grid H w, N will contain much less points. Figure 2 shows the total number of points contained in the full tensor grid and in the Smolyak sparse grid as a function of the level w or the corresponding maximum number m of points in each direction, for dimensions N = 5, 11, x33 Clenshaw!Curtis Grid ALPHA = [ , ] 0 <= LEVEL <= 5 Figure 1: For a two-dimensional parameter space N = 2 and maximum level w = 5, we plot the full tensor product grid using the Clenshaw-Curtis abscissas left and isotropic Smolyak sparse grids H 5, 2, utilizing the Clenshaw-Curtis abscissas middle and the Gaussian abscissas right. 3 Error analysis In this section we develop error estimates that will help us compare the efficiency of the Isotropic Smolyak approximation with other alternatives, for instance the Monte Carlo method as explained in Section 3.2. Much about this has been claimed in the existing literature based on particular numerical examples. Our main goal is therefore to understand in which situations the sparse grid stochastic collocation method is more efficient than Monte Carlo. As explained in Section 2 collocation methods can be used to approximate the solution u N C 0 Γ N ; W D using finitely many function values, each of them computed by finite elements. Recall that by Assumption 1.8, u N admits an analytic extension. Let the fully discrete numerical approximation be A w, Nπ h u N. Our aim is to give a priori estimates for the total error e = u A w, Nπ h u N where the operator A w, N is described by 2.8 and π h is the finite element projection operator described by 2.2. We will investigate the error u A w, Nπ h u N u u N + u }{{} N π h u N + π }{{} h u N A w, Nπ h u N }{{} I II III 3.1 evaluated in the norm L q P Ω; W D with either q = 2 or ] q =. This yields also control of the error in the expected value of u, E[e] W D E [ e W D e L q P Ω;W D, and the error in the 11
12 log Log 10 # 10 # points Counting the Collocation points Isotropic Full Tensor, N=5 Isotropic Smolyak, N=5 Isotropic Full Tensor, N=11 Isotropic Smolyak, N=11 Isotropic Full Tensor, N=21 Isotropic Smolyak, N=21 Curse of Dimensionality level w level w m Figure 2: For a finite dimensional Γ N with N = 5, 11 and 21 we plot the log of the number of distinct Clenshaw-Curtis collocation points used by the isotropic Smolyak method and the corresponding isotropic full tensor product method versus the level w or the maximum number of points m employed in each direction. approximation of E[ψu], with ψ being a smooth functional of u. In such a case we have 1 E[ψu ψa w, Nπ h u N ] δ e ψu + θe L q P Ω;W D dθ e L q P Ω;W D 0 with 1/q + 1/q = 1 and δ e ψu + θe denoting the Fréchet derivative of ψ at u + θe. The quantity I controls the truncation error for the case where the input data a N and f N are suitable truncations of random fields. This contribution to the total error will be considered in Section 3.2. The quantity I is otherwise zero if the representation of a N and f N is exact, as in Example 1.4. The second term II controls the convergence with respect to h, i.e. the finite element error, which will be dictated by standard approximability properties of the finite element space W h D, given by 2.1, and the regularity in space of the solution u see e.g. [7, 10]. For example, if we let q = 2 we have u N π h u N L 2 ρ Γ N ;W D h s Γ N C π ycs; uy 2 ρy dy 1/2. The full tensor product convergence results are given by [5, Theorem 1] and therefore, we will only concern ourselves with the convergence results when implementing the Smolyak approximation formula described in Section 2.2. Namely, our primary concern will be to analyze the Smolyak approximation error III = π h u N A w, Nπ h u N L q ρ Γ N ;W D for both the Clenshaw-Curtis and Gaussian versions of the Smolyak formula. 12
13 Under the very reasonable assumption that the semi-discrete finite element solution π h u N admits an analytic extension as described in Assumption 1.8 with the same analyticity region as for u N, the behavior of the error III will be analogous to u N A w, Nu N L q ρ Γ N ;W D. For this reason in the next sections we will analyze the latter. 3.1 Analysis of the approximation error In this work the technique to develop error bounds for multidimensional Smolyak approximation is based on one dimensional results. Therefore, we first address the case N = 1. Let us recall the best approximation error for a function v : Γ 1 W D which admits an analytic extension in the region ΣΓ 1 ; τ = {z C, distz, Γ 1 < τ} of the complex plane, for some τ > 0. We will still denote the extension by v; in this case, τ is smaller than the distance between Γ 1 R and the nearest singularity of vz in the complex plane. Since we are considering only the case of bounded random variables, we recall the following result, whose proof can be found in [5, Lemma 7] and which is an immediate extension of the result given in [12, Chapter 7, Section 8]: Lemma 3.1 Given a function v C 0 Γ 1 ; W D which admits an analytic extension in the region of the complex plane ΣΓ 1 ; τ = {z C, distz, Γ 1 τ} for some τ > 0, there holds E mi min w V mi v w C 0 Γ 1 ;W D 2 eˆσ 1 e ˆσ m i 2τ where 0 < ˆσ = log Γ τ 2 Γ 1 2. max z ΣΓ 1 ;τ vz W D Remark 3.2 Approximation with unbounded random variables A related result with weighted norms holds for unbounded random variables whose probability density decays as the Gaussian density at infinity see [5]. In the multidimensional case, the size of the analyticity region will depend, in general, on the direction n and it will be denoted by τ n see e.g. problem considered in Section 4. The same holds for the decay coefficient ˆσ n. In what follows, we set ˆσ min n ˆσ n Interpolation estimates for the Clenshaw-Curtis abscissas In this section we develop L error estimates for the Smolyak interpolant based on Clenshaw- Curtis abscissas, cf and 2.13, applied to analytic functions u C 0 Γ N ; W D that satisfy Assumption 1.8. We remind the reader that even though in the global estimate 3.1 it is enough to bound the approximation error III in the L 2 ργ N ; W D norm we will still work with the more stringent L Γ N ; W D norm. In our notation the norm,n is shorthand for L Γ N ;W D and will be used henceforth. We also define I N : Γ N Γ N as the identity operator on an N-dimensional space. We begin by letting E m be the error of the best approximation to functions u C 0 Γ 1 ; W D by functions w V m. Similarly to [6], since the interpolation U i is exact on the subspace V mi 1 we can apply the general formula u U i u,1 E mi 1u 1 + Λ mi
14 where Λ m is the Lebesgue constant for our choice It is known that Λ m 2 logm π for m 2, see [13]. Using Lemma 3.1, the best approximation to functions u C 0 Γ 1 ; W D that admit an analytic extension as described by Assumption 1.8 is bounded by: E mi u Ĉ e ˆσm i 3.5 where Ĉ and ˆσ > 0 are constants dependent on the value of τ defined in Lemma 3.1. Hence implies I 1 U i u,1 C logm i e σm i C ie σ2i, i u,1 = U i U i 1 u,1 I 1 U i u,1 + I 1 U i 1 u,1 2C ie σ2i 1 for all i N + with positive constants C and σ = ˆσ/2 depending on u but not on i. The convergence proof will be split in several steps, the main results being given in Theorems 3.6 and 3.9, which state the convergence rates in terms of the level w and the total number of collocation points, respectively. We denote by I d the identity operator applicable to functions which depend on the first d variables y 1,..., y d. Then the following result holds: Lemma 3.3 For functions u C 0 Γ N ; W D satisfying the assumption of Lemma 3.1 the isotropic Smolyak formula 2.8 based on Clenshaw Curtis abscissas satisfies: I N A w, N u,n N Rw, d 3.6 d=1 with and Rw, d := 1 d 2 Xw,d2C d i n e σhi,d 3.7 i n=1 d hi, d = 2 in n=1 Proof. We start providing and equivalent representation of the isotropic Smolyak formula: A w, N = = = N i Xw,N n=1 in N 1 i Xw,N 1 n=1 N 1 i Xw,N 1 n=1 in 1+w P N 1 n=1 in 1 j j=1 in U 1+w P N 1 n=1 in 1. 14
15 Introducing the one-dimensional identity operator I n 1 : Γ n Γ n, for n = 1,..., N, the error estimate can be computed recursively using the previous representation, namely I N A w, N = I N = = N 1 i Xw,N 1 n=1 N 1 i Xw,N 1 n=1 N 1 i Xw,N 1 n=1 in U 1+w P N 1 in I N 1 n=1 in 1 I N 1 in I N 1 U 1+w P N 1 in 1 n=1 + I N 1 A w, N 1 I N 1 [ ] N N Rw, d d=2 where, for a general dimension d, we define Rw, d = n=d+1 I n 1 i Xw,d 1 n=1 + I 1 1 A w, 1 d 1 in I d 1 U îd N and, for any i 1,..., i d 1 Xw, d 1, we have set î d = 1 + w d 1 n=1 i n 1. Observe that with this definition, the d-dimensional vector j = i 1,..., i d 1, î d belongs to the set Xw, d, defined in 2.7, and the term Rw, d can now be bounded as follows: Rw, du,d 1 2 d 1 i Xw,d 1 n=1 2Cd 2 i Xw,d 1 i Xw,d Hence, the Smolyak approximation error satisfies I N A w, Nu,N in u,d I d 1 U îd d 1 2C d n=1 i n n=2 I n 1 u î d e σp d 1 n=1 2in 1 +2îd d i n e σ hi,d =: Rw, d. n=1 N Rw, d + d=2 I 1,d 1 A w, 1u.,1 Observe that the last term in the previous equation can also be bounded by Rw, 1 defined in 3.7. Indeed, the set Xw, 1 contains only the point i 1 = 1 + w and I 1 1 A w, 1 u = I 1 1 U 1+w u,1,1 3.9 and this concludes the proof. σ 21+w C 1 + we C i 1 e σ 2i 1 1 =: Rw, 1 i 1 Xw,1 15
16 Lemma 3.4 Let δ > 0. Under the assumptions of Lemma 3.3 the following bound holds for the term Rw, d, d = 1,..., N: Rw, d C 1σ, δ d exp σd 2 w/d δ 2 C 2 σw 3.10 where C 2 σ := π 3.11 log2 2σ and C 1 σ, δ := 4C { eδσ exp 1 δσ σ log log2 2σ } π log2 2σ Proof. The proof is divided in several steps. 1. Expand the function hi, d up to second order around the point i = 1 + w/d,..., 1 + w/d on the subspace {x R d :, x 1 = w}. Observe that i is a constrained minimizer of hi, d and hi, d d2 w/d + log2 2 d i n 1 + w/d 2, for all i 2 Xw, d Combining 3.7 and 3.13 estimate Rw, d 2Cd e σd2w/d 2 2Cd 2 n=1 i Xw,d w+1 e σd2w/d i=1 d i n n=1 e σ log2 2 2 i e σ log2 2 2 i 1+w/d 2 d. P d n=1 in 1+w/d2 3. Next, use A.2 from Corollary A.4 to estimate the term T 1 := w+1 i=1 We have 1 T 1 2 σ log log2 2σ Combine 3.14 and 3.15, arriving at 3.14 log 2 2 i 1+w/d i e σ int {w/d} π log2 2σ Rw, d C 1 σ, d, we σd 2w/d 3.16 with C 1 σ, d, w 1 { 1 2 4Cd σ log log2 + int {w/d} } d π. 2σ log2 2σ Now let δ > 0 and use the inequality x + 1 e x, x 0, to bound C 1 σ, d, w 1 4C 2 δσ C 1σ, δ d 2 d exp dδσ { 1 σ log log2 2σ π w. 2σ exp δσ log2 { with C 1 σ, δ := 4C eδσ δσ exp 1 σ log log σ 16 + int {w/d} } π d log2 2σ log2 π 2σ } 3.17 defined as in 3.12.
17 Estimate 3.10 follows from 3.16 and The proof is now complete. Remark 3.5 Alternative estimate Observe that an alternative upper bound for T 1 in 3.15 is T 1 exp σ log w 2 + w d 2 which remains bounded as σ 0. This does not happen with the bound C 1 σ, d, cf. 3.12, which blows up as σ 0. As an implication of 3.18, we have Rw, d C2 + w2 d 2 e σd2w/d w d log2 2, which is an alternative to the estimate 3.10 that has an extra polynomial growth in w but remains bounded for small values of σ. Theorem 3.6 For functions u C 0 Γ N ; W D satisfying the assumption of Lemma 3.1. The isotropic Smolyak formula 2.8 based on Clenshaw Curtis abcissas satisfies: e σwe log2 δ C 2 σ, if 0 w N I N A w, N u,n inf Ĉσ, δ, N log2 δ 0, χ π e σw N w 2w/N δ C 2 σ, otherwise Here and function Ĉσ, δ, N = C 1σ,δ 1 C 1 σ,δ N 2 1 C 1 σ,δ. The values of C2 σ and C 1 σ, δ have been defined in 3.11 and 3.12, respectively. Proof. From Lemmas 3.3 and 3.4 we obtain the following bound for the approximation error I N A w, N u,n 1 2 with C 1 σ, δ defined in Then, N C 1 σ, δ d e σd2w/d w d δ C 2 σ, d=1 I N A w, N u,n 1 2 max 1 d N e σw d w 2w/d δ C 2 σ N C 1 σ, δ d, d=1 Ĉσ, δ, Neσwδ C 2 σ max 1 d N e σw d w 2w/d, with To finish the proof we further bound Ĉσ, δ, N := 1 2 N C 1 σ, δ d d=1 = C 1σ, δ 2 1 C 1 σ, δ N 1 C 1 σ, δ I N A w, N u,n Ĉσ, δ, N eσwδ C 2 σ e σwmin 1 d N d w 2w/d Ĉσ, δ, N eσwδ C 2 σ e σwmin s [w/n,w] 1 s 2s 17
18 and observe that 1 min s [w/n,w] s 2s = e log2, if 0 w N log2 N w 2w/N, otherwise. Remark 3.7 Alternative estimate Following Remark 3.5 we have an alternative to 3.19 in the estimate C2 + w2 C2 + w 2 N 1 e σwχ, if 0 w N I N A w, N u,n 2 C2 + w 2 log2 1 e σw N w 2w/N log 2 2, otherwise Here we used the notation χ = log2 e log The previous estimate can be used to produce estimates like those in Theorems 3.9 and The alternative estimates have constants which do not blow up as σ 0 but have the drawback of exhibiting additional multiplicative powers of logη. A completely identical discussion applies to the estimates based on Gaussian abscissas, see Section 3.1.2, and will not be repeated there. Now we relate the number of collocation points, η = ηw, N = #H w, N, to the level w of the isotropic Smolyak formula. We state the result in the following lemma: Lemma 3.8 Using the isotropic Smolyak interpolant described by 2.8 with Clenshaw-Curtis abscissas, the total number of points required at level w satisfies the following bounds: N2 w 1 η 2eN w min{w + 1, 2eN}, 3.22 Moreover, as a direct consequence of 3.22 we get that: logη 1 w log2 + logn Proof. By using formula 2.8 and exploiting the nested structure of the Clenshaw-Curtis abscissas the number of points η = ηw, N = #H w, N can be counted in the following way: η = N 1 if i = 1 ri n, where ri := 2 if i = i Xw,N n=1 2 i 2 if i > 2 Now notice that for all n = 1, 2,..., N the following bound holds: 2 in 2 ri n 2 in We now produce a lower bound and an upper bound for η. A lower bound on the number η of points can be obtained considering only the contribution from certain tensor grids. Indeed, for a fixed value of w = 1,..., w, let us consider the N grids with indices i n = 1, for n m and i m = w + 1, m = 1,..., N. Since each of those N grids has 2 w 1 points, we have w η N 2 w 1 = N2 w 1. w=1 18
19 On the other hand, to produce an upper bound for η, we recall that i 1 = N n=1 i n 1 w so the following bounds hold: η = i Xw,N n=1 j=0 N ri n w N 1 + j 2 j N 1 N 1 w 2 j exp j=0 s=1 j s i Xw,N w j=0 N 1 2 j 2 i 1 s=1 w 1 + j s j=0 i 1 =j w 2 j exp j1 + logn j=0 w 2eN j min{w + 12eN w, 2eN w+1 } j=0 and this finishes the proof. The next Theorem provides an error bound in terms of the total number η of collocation points. The proof follows directly from the results in Theorem 3.6 taking δ = e log2 1/ C 2 σ and Lemma 3.8; it is therefore omitted. Theorem 3.9 algebraic convergence For functions u C 0 Γ N ; W D satisfying the assumption of Lemma 3.1 the isotropic Smolyak formula 2.8 based on Clenshaw Curtis abscissas satisfies: C 1σ, δ e σ I N A w, N u,n 1 C 1 σ, δ max{1, C 1σ, δ } N η µ 1, with µ 1 = 3.26 σ 1 + log2n. Here δ = e log2 1/ C 2 σ and the constants C 2 σ and C 1 σ, δ, defined in 3.11 and 3.12, respectively, do not depend on η. Observe that the previous result indicates at least algebraic convergence with respect to the number of collocation points η. Under the same assumptions of the previous theorem and with a completely similar derivation, for large values of w we have the following sharper estimate: Theorem 3.10 Subexponential convergence Under the same assumptions of theorem 3.9 and for w > it holds N log2 2 j I N A w, N u,n C 1σ, δ max{1, C 1 σ, δ } N e σδ C 2 σ 1 C 1 σ, δ with µ 2 = log2 N1 + log2n η µ 3 e Nσ 2 1/N ηµ 2, and µ 3 = σδ C2 σ 1 + log2n with constant C 1 σ, δ defined in 3.12 and independent of η. Proof. We start from the result stated in Theorem 3.6 and observe that for w > N/ log2 the function gw = σn2 w/n wδ C 2 σ is increasing in w for all values of δ < log2e/ C 2 σ. Hence, combining 3.19 with the lower bound 3.23 we obtain the desired result. 19
20 The previous theorem indicates at least asymptotic subexponential convergence with respect to the number of collocation points η. It should be pointed out however that the large values of w > N/ log2 under which the bound holds are seldom used in practical computations. Therefore, from this point of view estimate 3.27 is less useful than Remark 3.11 Deterioration of the estimates with respect to the dimension N Depending on the distance to the singularities of the solution, related to the parameter τ introduced in Lemma 3.1, the constant C 1 σ, δ may be less than 1. In such a case the only dependence of the error bounds for I N A w, N u,n is in the exponent, whose denominator slowly grows like log2n. Remark 3.12 Full tensor versus Smolyak An isotropic full tensor product interpolation converges roughly like Cσ, N exp σp, where p is the order of the polynomial space. Since the number of collocation points relates to p in this case as η = 1 + p N then logη = N log1 + p Np and with respect to η the convergence rate can be bounded as Cσ, Nη σ/n. The slowdown effect that the dimension N has on the last convergence is known as the curse of dimensionality and it is the reason for not using isotropic full tensor interpolantion for large values of N. On the other hand, the isotropic Smolyak approximation seems to be better suited for this case. Indeed, from the σ estimate 3.26 we see that the Smolyak algebraic convergence has the faster exponent O log2n. This is a clear advantage of the isotropic Smolyak method with respect to the full tensor and justifies our claim that the use of Smolyak approximation greatly reduces the curse of dimensionality. In Section 5 numerical results will give computational ground to this claim. Remark 3.13 Estimates based on bounded mixed derivatives We can proceed in a similar way to analyze the approximation error for functions that have a bounded mixed derivative of order k,..., k. In that case, the one dimensional best approximation error is u U i u Cm k i 1 + Λ mi, with C depending on u and k but not on m i, and using again the recursion 3.9 yields I N A w, N u,n C C1 + 2 k 1 C1 + 2k N w + 1 2N 2 kw Finally, the combination of 3.28 with the counting estimates in Lemma 3.8 yields I N A w, N u,n C1 + 2k N k 1/C 1 + log η N 2N min {2 k η k log2 1+log2N, η k 1 + log η } Nk. N This estimate improves the one derived in [6]. Analogous results can be derived for gaussian abcissas and L 2 norms Approximation estimates for Gaussian abscissas Similarly to the previous section, we now develop error estimates for Smolyak approximation, using Gaussian abscissas cf. Section 2.3, of C 0 Γ N ; W D analytic functions described by Assumption 1.8. As before, we remind the reader that in the global estimate 3.1 we need to bound the approximation error III in the norm L 2 ργ N ; W D. Yet, the Gaussian abscissas defined in Section 2.3 are constructed for the auxiliary density ˆρ = N n=1 ˆρ n, still yielding control of the desired norm v L 2 ρ Γ N ;W D ρ 1/2 ˆρ v L 2ˆρ Γ N ;W D, for all v C0 Γ N ; W D. L Γ N 20
21 In what follows we will use the shorthand notation ˆρ,N for L 2ˆρ Γ N ;W D. We now quote a useful result from Erdös and Turán [14]: Lemma 3.14 For every function u C 0 Γ 1 ; W D the interpolation error with Lagrange polynomials based on gaussian abscissas satisfies u U i u ˆρ,1 2 ˆρy dy inf u w, Γ 1 w V mi Similarly to Section 3.1.1, the combination of 3.5 with 3.29 yields I 1 U i u ˆρ,1 C e σ2i, i u = U ˆρ,1 i U i 1 u ˆρ,1 I1 U i u ˆρ,1 + I1 U i 1 u ˆρ,1 2 C e σ2i 1 for all i N + with positive constants C Ĉ = Γ ˆρydy and σ = ˆσ/2 depending on u but 1 not on i. We then present the following Lemma and theorem whose proofs follow, with minor changes, those given in Lemma 3.4 and Theorem 3.9, respectively. For instance, we apply A.1 from Corollary A.4 to bound the corresponding T 1 sum in the estimate of Rw, d. Lemma 3.15 For functions u C 0 Γ N ; W D satisfying the assumption of Lemma 3.1. The isotropic Smolyak formula 2.8 based on Gaussian abcissas satisfies: C 1 σ 1 I N A w, N u ρ,n ρ/ˆρ C 1 σ N L Γ N 2 1 C 1 σ e σe log2 w, if 0 w N log2 e σn2w/n, otherwise Here we have C 1 σ := 4 C π log2 2σ Now we relate the number of collocation points η = ηw, N = #H w, N to the level w of the Smolyak formula. We state the result in the following lemma: Lemma 3.16 Using the Smolyak interpolant described by 2.9 with Gaussian abscissas, the total number of points required at level w satisfies the following bounds: which implies N2 w + 1 η e 2 1+log N w min{w + 1, e 2 1+log N} 3.32 with ζ := log log logη ζ + logn 1 w. Proof. By using formula 2.9, where we collocate using the Gaussian abscissas the number of points η = ηw, N = #H w, N, can be counted in the following way: η = i Y w,n n=1 N ri n, where 2 i 1 ri := 21 { 1 if i = 1 2 i if i
22 Proceeding in a similar way as for the proof of Lemma 3.8, a lower bound on the number of points η can be obtained as η N w w=w N+1 2 w + 1 N2 w + 1. On the other hand, an upper bound on η can be obtained following the same lines as in the proof of Lemma 3.8 and observing that 2 i 1 ri 2 1+ɛi 1, with ɛ = log Finally, the next Theorem relates the error bound 3.30 to the number of collocation points η = ηw, N = #H w, N, described by Lemma Theorem 3.17 algebraic convergence For functions u C 0 Γ N ; W D satisfying the assumption of Lemma 3.1 the isotropic Smolyak formula 2.8 based on Gaussian abscissas satisfies: I N A w, N u ρ,n ρ/ˆρ L Γ N eσ e log2 C1 σ max{1, C 1 σ} N 1 C η µ 1, 1 σ µ 1 := σ e log2 ζ + logn, 3.34 with ζ := log log The constant C 1 σ was defined in Similarly to Section and with the same assumptions of the previous theorem, for large values of w we have the following sharper estimate: Theorem 3.18 subexponential convergence If w > N log2 then I N A w, N u ρ,n ρ/ˆρ C L Γ N 1 σ max{1, C 1 σ} N 1 C 1 σ log2 with µ 2 = Nζ + logn and ζ := log log Influence of truncation errors e Nσ 2 1/N η µ 2, 3.35 In this Section we consider the case where the coefficients a N and f N from 1.4 are suitably truncated random fields. Therefore, the truncation error u u N is nonzero and contributes to the total error. Such contribution should be considered as well in the error analysis. In particular, understanding the relationship of this error with the discretization error allows us to compare the efficiency of isotropic Smolyak method with other computational alternatives, for instance the Monte Carlo method. To this end, we make the assumption that the truncation error u u N decays as u u N L 2 P Ω;W D ζn 3.36 for some monotonic decreasing function ζn such that ζn 0 as N. For example, if one truncates the input random fields with a Karhunen-Loève expansion see [16], the function ζn is typically related to the decay of the eigenpairs of their covariance operators. 22
A sparse grid stochastic collocation method for elliptic partial differential equations with random input data
 A sparse grid stochastic collocation method for elliptic partial differential equations with random input data F. Nobile R. Tempone C. G. Webster June 22, 2006 Abstract This work proposes and analyzes
A sparse grid stochastic collocation method for elliptic partial differential equations with random input data F. Nobile R. Tempone C. G. Webster June 22, 2006 Abstract This work proposes and analyzes
A MULTILEVEL STOCHASTIC COLLOCATION METHOD FOR PARTIAL DIFFERENTIAL EQUATIONS WITH RANDOM INPUT DATA
 A MULTILEVEL STOCHASTIC COLLOCATION METHOD FOR PARTIAL DIFFERENTIAL EQUATIONS WITH RANDOM INPUT DATA A. L. TECKENTRUP, P. JANTSCH, C. G. WEBSTER, AND M. GUNZBURGER Abstract. Stochastic collocation methods
A MULTILEVEL STOCHASTIC COLLOCATION METHOD FOR PARTIAL DIFFERENTIAL EQUATIONS WITH RANDOM INPUT DATA A. L. TECKENTRUP, P. JANTSCH, C. G. WEBSTER, AND M. GUNZBURGER Abstract. Stochastic collocation methods
STOCHASTIC SAMPLING METHODS
 STOCHASTIC SAMPLING METHODS APPROXIMATING QUANTITIES OF INTEREST USING SAMPLING METHODS Recall that quantities of interest often require the evaluation of stochastic integrals of functions of the solutions
STOCHASTIC SAMPLING METHODS APPROXIMATING QUANTITIES OF INTEREST USING SAMPLING METHODS Recall that quantities of interest often require the evaluation of stochastic integrals of functions of the solutions
Multilevel accelerated quadrature for elliptic PDEs with random diffusion. Helmut Harbrecht Mathematisches Institut Universität Basel Switzerland
 Multilevel accelerated quadrature for elliptic PDEs with random diffusion Mathematisches Institut Universität Basel Switzerland Overview Computation of the Karhunen-Loéve expansion Elliptic PDE with uniformly
Multilevel accelerated quadrature for elliptic PDEs with random diffusion Mathematisches Institut Universität Basel Switzerland Overview Computation of the Karhunen-Loéve expansion Elliptic PDE with uniformly
Fast Numerical Methods for Stochastic Computations
 Fast AreviewbyDongbinXiu May 16 th,2013 Outline Motivation 1 Motivation 2 3 4 5 Example: Burgers Equation Let us consider the Burger s equation: u t + uu x = νu xx, x [ 1, 1] u( 1) =1 u(1) = 1 Example:
Fast AreviewbyDongbinXiu May 16 th,2013 Outline Motivation 1 Motivation 2 3 4 5 Example: Burgers Equation Let us consider the Burger s equation: u t + uu x = νu xx, x [ 1, 1] u( 1) =1 u(1) = 1 Example:
Accuracy, Precision and Efficiency in Sparse Grids
 John, Information Technology Department, Virginia Tech.... http://people.sc.fsu.edu/ jburkardt/presentations/ sandia 2009.pdf... Computer Science Research Institute, Sandia National Laboratory, 23 July
John, Information Technology Department, Virginia Tech.... http://people.sc.fsu.edu/ jburkardt/presentations/ sandia 2009.pdf... Computer Science Research Institute, Sandia National Laboratory, 23 July
Stochastic Spectral Approaches to Bayesian Inference
 Stochastic Spectral Approaches to Bayesian Inference Prof. Nathan L. Gibson Department of Mathematics Applied Mathematics and Computation Seminar March 4, 2011 Prof. Gibson (OSU) Spectral Approaches to
Stochastic Spectral Approaches to Bayesian Inference Prof. Nathan L. Gibson Department of Mathematics Applied Mathematics and Computation Seminar March 4, 2011 Prof. Gibson (OSU) Spectral Approaches to
Implementation of Sparse Wavelet-Galerkin FEM for Stochastic PDEs
 Implementation of Sparse Wavelet-Galerkin FEM for Stochastic PDEs Roman Andreev ETH ZÜRICH / 29 JAN 29 TOC of the Talk Motivation & Set-Up Model Problem Stochastic Galerkin FEM Conclusions & Outlook Motivation
Implementation of Sparse Wavelet-Galerkin FEM for Stochastic PDEs Roman Andreev ETH ZÜRICH / 29 JAN 29 TOC of the Talk Motivation & Set-Up Model Problem Stochastic Galerkin FEM Conclusions & Outlook Motivation
Multi-Element Probabilistic Collocation Method in High Dimensions
 Multi-Element Probabilistic Collocation Method in High Dimensions Jasmine Foo and George Em Karniadakis Division of Applied Mathematics, Brown University, Providence, RI 02912 USA Abstract We combine multi-element
Multi-Element Probabilistic Collocation Method in High Dimensions Jasmine Foo and George Em Karniadakis Division of Applied Mathematics, Brown University, Providence, RI 02912 USA Abstract We combine multi-element
Collocation methods for uncertainty quantification in PDE models with random data
 Collocation methods for uncertainty quantification in PDE models with random data Fabio Nobile CSQI-MATHICSE, EPFL, Switzerland Acknowlegments: L. Tamellini, G. Migliorati (EPFL), R. Tempone, (KAUST),
Collocation methods for uncertainty quantification in PDE models with random data Fabio Nobile CSQI-MATHICSE, EPFL, Switzerland Acknowlegments: L. Tamellini, G. Migliorati (EPFL), R. Tempone, (KAUST),
Quasi-optimal and adaptive sparse grids with control variates for PDEs with random diffusion coefficient
 Quasi-optimal and adaptive sparse grids with control variates for PDEs with random diffusion coefficient F. Nobile, L. Tamellini, R. Tempone, F. Tesei CSQI - MATHICSE, EPFL, Switzerland Dipartimento di
Quasi-optimal and adaptive sparse grids with control variates for PDEs with random diffusion coefficient F. Nobile, L. Tamellini, R. Tempone, F. Tesei CSQI - MATHICSE, EPFL, Switzerland Dipartimento di
Efficient Solvers for Stochastic Finite Element Saddle Point Problems
 Efficient Solvers for Stochastic Finite Element Saddle Point Problems Catherine E. Powell c.powell@manchester.ac.uk School of Mathematics University of Manchester, UK Efficient Solvers for Stochastic Finite
Efficient Solvers for Stochastic Finite Element Saddle Point Problems Catherine E. Powell c.powell@manchester.ac.uk School of Mathematics University of Manchester, UK Efficient Solvers for Stochastic Finite
Polynomial Chaos and Karhunen-Loeve Expansion
 Polynomial Chaos and Karhunen-Loeve Expansion 1) Random Variables Consider a system that is modeled by R = M(x, t, X) where X is a random variable. We are interested in determining the probability of the
Polynomial Chaos and Karhunen-Loeve Expansion 1) Random Variables Consider a system that is modeled by R = M(x, t, X) where X is a random variable. We are interested in determining the probability of the
Sparse Quadrature Algorithms for Bayesian Inverse Problems
 Sparse Quadrature Algorithms for Bayesian Inverse Problems Claudia Schillings, Christoph Schwab Pro*Doc Retreat Disentis 2013 Numerical Analysis and Scientific Computing Disentis - 15 August, 2013 research
Sparse Quadrature Algorithms for Bayesian Inverse Problems Claudia Schillings, Christoph Schwab Pro*Doc Retreat Disentis 2013 Numerical Analysis and Scientific Computing Disentis - 15 August, 2013 research
Evaluation of Non-Intrusive Approaches for Wiener-Askey Generalized Polynomial Chaos
 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 6t 7 - April 28, Schaumburg, IL AIAA 28-892 Evaluation of Non-Intrusive Approaches for Wiener-Askey Generalized
49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 6t 7 - April 28, Schaumburg, IL AIAA 28-892 Evaluation of Non-Intrusive Approaches for Wiener-Askey Generalized
Karhunen-Loève Approximation of Random Fields Using Hierarchical Matrix Techniques
 Institut für Numerische Mathematik und Optimierung Karhunen-Loève Approximation of Random Fields Using Hierarchical Matrix Techniques Oliver Ernst Computational Methods with Applications Harrachov, CR,
Institut für Numerische Mathematik und Optimierung Karhunen-Loève Approximation of Random Fields Using Hierarchical Matrix Techniques Oliver Ernst Computational Methods with Applications Harrachov, CR,
Schwarz Preconditioner for the Stochastic Finite Element Method
 Schwarz Preconditioner for the Stochastic Finite Element Method Waad Subber 1 and Sébastien Loisel 2 Preprint submitted to DD22 conference 1 Introduction The intrusive polynomial chaos approach for uncertainty
Schwarz Preconditioner for the Stochastic Finite Element Method Waad Subber 1 and Sébastien Loisel 2 Preprint submitted to DD22 conference 1 Introduction The intrusive polynomial chaos approach for uncertainty
MULTISCALE FINITE ELEMENT METHODS FOR STOCHASTIC POROUS MEDIA FLOW EQUATIONS AND APPLICATION TO UNCERTAINTY QUANTIFICATION
 MULTISCALE FINITE ELEMENT METHODS FOR STOCHASTIC POROUS MEDIA FLOW EQUATIONS AND APPLICATION TO UNCERTAINTY QUANTIFICATION P. DOSTERT, Y. EFENDIEV, AND T.Y. HOU Abstract. In this paper, we study multiscale
MULTISCALE FINITE ELEMENT METHODS FOR STOCHASTIC POROUS MEDIA FLOW EQUATIONS AND APPLICATION TO UNCERTAINTY QUANTIFICATION P. DOSTERT, Y. EFENDIEV, AND T.Y. HOU Abstract. In this paper, we study multiscale
Stochastic Collocation Methods for Polynomial Chaos: Analysis and Applications
 Stochastic Collocation Methods for Polynomial Chaos: Analysis and Applications Dongbin Xiu Department of Mathematics, Purdue University Support: AFOSR FA955-8-1-353 (Computational Math) SF CAREER DMS-64535
Stochastic Collocation Methods for Polynomial Chaos: Analysis and Applications Dongbin Xiu Department of Mathematics, Purdue University Support: AFOSR FA955-8-1-353 (Computational Math) SF CAREER DMS-64535
Pascal s Triangle on a Budget. Accuracy, Precision and Efficiency in Sparse Grids
 Covering : Accuracy, Precision and Efficiency in Sparse Grids https://people.sc.fsu.edu/ jburkardt/presentations/auburn 2009.pdf... John Interdisciplinary Center for Applied Mathematics & Information Technology
Covering : Accuracy, Precision and Efficiency in Sparse Grids https://people.sc.fsu.edu/ jburkardt/presentations/auburn 2009.pdf... John Interdisciplinary Center for Applied Mathematics & Information Technology
November 7, 2002 GALERKIN FINITE ELEMENT APPROXIMATIONS OF STOCHASTIC ELLIPTIC PARTIAL DIFFERENTIAL EQUATIONS
 November 7, 00 GALERKIN FINITE ELEMENT APPROXIMATIONS OF STOCHASTIC ELLIPTIC PARTIAL IFFERENTIAL EQUATIONS IVO BABUŠKA, RAÚL TEMPONE AN GEORGIOS E. ZOURARIS Abstract. We describe and analyze two numerical
November 7, 00 GALERKIN FINITE ELEMENT APPROXIMATIONS OF STOCHASTIC ELLIPTIC PARTIAL IFFERENTIAL EQUATIONS IVO BABUŠKA, RAÚL TEMPONE AN GEORGIOS E. ZOURARIS Abstract. We describe and analyze two numerical
Adaptive Collocation with Kernel Density Estimation
 Examples of with Kernel Density Estimation Howard C. Elman Department of Computer Science University of Maryland at College Park Christopher W. Miller Applied Mathematics and Scientific Computing Program
Examples of with Kernel Density Estimation Howard C. Elman Department of Computer Science University of Maryland at College Park Christopher W. Miller Applied Mathematics and Scientific Computing Program
PCA with random noise. Van Ha Vu. Department of Mathematics Yale University
 PCA with random noise Van Ha Vu Department of Mathematics Yale University An important problem that appears in various areas of applied mathematics (in particular statistics, computer science and numerical
PCA with random noise Van Ha Vu Department of Mathematics Yale University An important problem that appears in various areas of applied mathematics (in particular statistics, computer science and numerical
Solving the steady state diffusion equation with uncertainty Final Presentation
 Solving the steady state diffusion equation with uncertainty Final Presentation Virginia Forstall vhfors@gmail.com Advisor: Howard Elman elman@cs.umd.edu Department of Computer Science May 6, 2012 Problem
Solving the steady state diffusion equation with uncertainty Final Presentation Virginia Forstall vhfors@gmail.com Advisor: Howard Elman elman@cs.umd.edu Department of Computer Science May 6, 2012 Problem
Multigrid and stochastic sparse-grids techniques for PDE control problems with random coefficients
 Multigrid and stochastic sparse-grids techniques for PDE control problems with random coefficients Università degli Studi del Sannio Dipartimento e Facoltà di Ingegneria, Benevento, Italia Random fields
Multigrid and stochastic sparse-grids techniques for PDE control problems with random coefficients Università degli Studi del Sannio Dipartimento e Facoltà di Ingegneria, Benevento, Italia Random fields
arxiv: v2 [math.pr] 27 Oct 2015
![arxiv: v2 [math.pr] 27 Oct 2015 arxiv: v2 [math.pr] 27 Oct 2015](/thumbs/84/89692990.jpg) A brief note on the Karhunen-Loève expansion Alen Alexanderian arxiv:1509.07526v2 [math.pr] 27 Oct 2015 October 28, 2015 Abstract We provide a detailed derivation of the Karhunen Loève expansion of a stochastic
A brief note on the Karhunen-Loève expansion Alen Alexanderian arxiv:1509.07526v2 [math.pr] 27 Oct 2015 October 28, 2015 Abstract We provide a detailed derivation of the Karhunen Loève expansion of a stochastic
Bath Institute For Complex Systems
 BICS Bath Institute for Complex Systems Finite Element Error Analysis of Elliptic PDEs with Random Coefficients and its Application to Multilevel Monte Carlo Methods Julia Charrier, Robert Scheichl and
BICS Bath Institute for Complex Systems Finite Element Error Analysis of Elliptic PDEs with Random Coefficients and its Application to Multilevel Monte Carlo Methods Julia Charrier, Robert Scheichl and
Numerical Solutions to Partial Differential Equations
 Numerical Solutions to Partial Differential Equations Zhiping Li LMAM and School of Mathematical Sciences Peking University The Residual and Error of Finite Element Solutions Mixed BVP of Poisson Equation
Numerical Solutions to Partial Differential Equations Zhiping Li LMAM and School of Mathematical Sciences Peking University The Residual and Error of Finite Element Solutions Mixed BVP of Poisson Equation
Uncertainty Quantification in Discrete Fracture Network Models
 Uncertainty Quantification in Discrete Fracture Network Models Claudio Canuto Dipartimento di Scienze Matematiche, Politecnico di Torino claudio.canuto@polito.it Joint work with Stefano Berrone, Sandra
Uncertainty Quantification in Discrete Fracture Network Models Claudio Canuto Dipartimento di Scienze Matematiche, Politecnico di Torino claudio.canuto@polito.it Joint work with Stefano Berrone, Sandra
Collocation based high dimensional model representation for stochastic partial differential equations
 Collocation based high dimensional model representation for stochastic partial differential equations S Adhikari 1 1 Swansea University, UK ECCM 2010: IV European Conference on Computational Mechanics,
Collocation based high dimensional model representation for stochastic partial differential equations S Adhikari 1 1 Swansea University, UK ECCM 2010: IV European Conference on Computational Mechanics,
Class 2 & 3 Overfitting & Regularization
 Class 2 & 3 Overfitting & Regularization Carlo Ciliberto Department of Computer Science, UCL October 18, 2017 Last Class The goal of Statistical Learning Theory is to find a good estimator f n : X Y, approximating
Class 2 & 3 Overfitting & Regularization Carlo Ciliberto Department of Computer Science, UCL October 18, 2017 Last Class The goal of Statistical Learning Theory is to find a good estimator f n : X Y, approximating
Research Article A Pseudospectral Approach for Kirchhoff Plate Bending Problems with Uncertainties
 Mathematical Problems in Engineering Volume 22, Article ID 7565, 4 pages doi:.55/22/7565 Research Article A Pseudospectral Approach for Kirchhoff Plate Bending Problems with Uncertainties Ling Guo, 2 and
Mathematical Problems in Engineering Volume 22, Article ID 7565, 4 pages doi:.55/22/7565 Research Article A Pseudospectral Approach for Kirchhoff Plate Bending Problems with Uncertainties Ling Guo, 2 and
Stability of optimization problems with stochastic dominance constraints
 Stability of optimization problems with stochastic dominance constraints D. Dentcheva and W. Römisch Stevens Institute of Technology, Hoboken Humboldt-University Berlin www.math.hu-berlin.de/~romisch SIAM
Stability of optimization problems with stochastic dominance constraints D. Dentcheva and W. Römisch Stevens Institute of Technology, Hoboken Humboldt-University Berlin www.math.hu-berlin.de/~romisch SIAM
A Vector-Space Approach for Stochastic Finite Element Analysis
 A Vector-Space Approach for Stochastic Finite Element Analysis S Adhikari 1 1 Swansea University, UK CST2010: Valencia, Spain Adhikari (Swansea) Vector-Space Approach for SFEM 14-17 September, 2010 1 /
A Vector-Space Approach for Stochastic Finite Element Analysis S Adhikari 1 1 Swansea University, UK CST2010: Valencia, Spain Adhikari (Swansea) Vector-Space Approach for SFEM 14-17 September, 2010 1 /
Adaptive methods for control problems with finite-dimensional control space
 Adaptive methods for control problems with finite-dimensional control space Saheed Akindeinde and Daniel Wachsmuth Johann Radon Institute for Computational and Applied Mathematics (RICAM) Austrian Academy
Adaptive methods for control problems with finite-dimensional control space Saheed Akindeinde and Daniel Wachsmuth Johann Radon Institute for Computational and Applied Mathematics (RICAM) Austrian Academy
Sparse Grids. Léopold Cambier. February 17, ICME, Stanford University
 Sparse Grids & "A Dynamically Adaptive Sparse Grid Method for Quasi-Optimal Interpolation of Multidimensional Analytic Functions" from MK Stoyanov, CG Webster Léopold Cambier ICME, Stanford University
Sparse Grids & "A Dynamically Adaptive Sparse Grid Method for Quasi-Optimal Interpolation of Multidimensional Analytic Functions" from MK Stoyanov, CG Webster Léopold Cambier ICME, Stanford University
Introduction to Uncertainty Quantification in Computational Science Handout #3
 Introduction to Uncertainty Quantification in Computational Science Handout #3 Gianluca Iaccarino Department of Mechanical Engineering Stanford University June 29 - July 1, 2009 Scuola di Dottorato di
Introduction to Uncertainty Quantification in Computational Science Handout #3 Gianluca Iaccarino Department of Mechanical Engineering Stanford University June 29 - July 1, 2009 Scuola di Dottorato di
Second Order Elliptic PDE
 Second Order Elliptic PDE T. Muthukumar tmk@iitk.ac.in December 16, 2014 Contents 1 A Quick Introduction to PDE 1 2 Classification of Second Order PDE 3 3 Linear Second Order Elliptic Operators 4 4 Periodic
Second Order Elliptic PDE T. Muthukumar tmk@iitk.ac.in December 16, 2014 Contents 1 A Quick Introduction to PDE 1 2 Classification of Second Order PDE 3 3 Linear Second Order Elliptic Operators 4 4 Periodic
LECTURE 1: SOURCES OF ERRORS MATHEMATICAL TOOLS A PRIORI ERROR ESTIMATES. Sergey Korotov,
 LECTURE 1: SOURCES OF ERRORS MATHEMATICAL TOOLS A PRIORI ERROR ESTIMATES Sergey Korotov, Institute of Mathematics Helsinki University of Technology, Finland Academy of Finland 1 Main Problem in Mathematical
LECTURE 1: SOURCES OF ERRORS MATHEMATICAL TOOLS A PRIORI ERROR ESTIMATES Sergey Korotov, Institute of Mathematics Helsinki University of Technology, Finland Academy of Finland 1 Main Problem in Mathematical
Simulating with uncertainty : the rough surface scattering problem
 Simulating with uncertainty : the rough surface scattering problem Uday Khankhoje Assistant Professor, Electrical Engineering Indian Institute of Technology Madras Uday Khankhoje (EE, IITM) Simulating
Simulating with uncertainty : the rough surface scattering problem Uday Khankhoje Assistant Professor, Electrical Engineering Indian Institute of Technology Madras Uday Khankhoje (EE, IITM) Simulating
Giovanni Migliorati. MATHICSE-CSQI, École Polytechnique Fédérale de Lausanne
 Analysis of the stability and accuracy of multivariate polynomial approximation by discrete least squares with evaluations in random or low-discrepancy point sets Giovanni Migliorati MATHICSE-CSQI, École
Analysis of the stability and accuracy of multivariate polynomial approximation by discrete least squares with evaluations in random or low-discrepancy point sets Giovanni Migliorati MATHICSE-CSQI, École
Continued fractions for complex numbers and values of binary quadratic forms
 arxiv:110.3754v1 [math.nt] 18 Feb 011 Continued fractions for complex numbers and values of binary quadratic forms S.G. Dani and Arnaldo Nogueira February 1, 011 Abstract We describe various properties
arxiv:110.3754v1 [math.nt] 18 Feb 011 Continued fractions for complex numbers and values of binary quadratic forms S.G. Dani and Arnaldo Nogueira February 1, 011 Abstract We describe various properties
Simultaneous Robust Design and Tolerancing of Compressor Blades
 Simultaneous Robust Design and Tolerancing of Compressor Blades Eric Dow Aerospace Computational Design Laboratory Department of Aeronautics and Astronautics Massachusetts Institute of Technology GTL Seminar
Simultaneous Robust Design and Tolerancing of Compressor Blades Eric Dow Aerospace Computational Design Laboratory Department of Aeronautics and Astronautics Massachusetts Institute of Technology GTL Seminar
Slow Growth for Gauss Legendre Sparse Grids
 Slow Growth for Gauss Legendre Sparse Grids John Burkardt, Clayton Webster April 4, 2014 Abstract A sparse grid for multidimensional quadrature can be constructed from products of 1D rules. For multidimensional
Slow Growth for Gauss Legendre Sparse Grids John Burkardt, Clayton Webster April 4, 2014 Abstract A sparse grid for multidimensional quadrature can be constructed from products of 1D rules. For multidimensional
Global Maxwellians over All Space and Their Relation to Conserved Quantites of Classical Kinetic Equations
 Global Maxwellians over All Space and Their Relation to Conserved Quantites of Classical Kinetic Equations C. David Levermore Department of Mathematics and Institute for Physical Science and Technology
Global Maxwellians over All Space and Their Relation to Conserved Quantites of Classical Kinetic Equations C. David Levermore Department of Mathematics and Institute for Physical Science and Technology
PRECONDITIONING MARKOV CHAIN MONTE CARLO SIMULATIONS USING COARSE-SCALE MODELS
 PRECONDITIONING MARKOV CHAIN MONTE CARLO SIMULATIONS USING COARSE-SCALE MODELS Y. EFENDIEV, T. HOU, AND W. LUO Abstract. We study the preconditioning of Markov Chain Monte Carlo (MCMC) methods using coarse-scale
PRECONDITIONING MARKOV CHAIN MONTE CARLO SIMULATIONS USING COARSE-SCALE MODELS Y. EFENDIEV, T. HOU, AND W. LUO Abstract. We study the preconditioning of Markov Chain Monte Carlo (MCMC) methods using coarse-scale
Nonlinear stochastic Galerkin and collocation methods: application to a ferromagnetic cylinder rotating at high speed
 Nonlinear stochastic Galerkin and collocation methods: application to a ferromagnetic cylinder rotating at high speed Eveline Rosseel Herbert De Gersem Stefan Vandewalle Report TW 541, July 29 Katholieke
Nonlinear stochastic Galerkin and collocation methods: application to a ferromagnetic cylinder rotating at high speed Eveline Rosseel Herbert De Gersem Stefan Vandewalle Report TW 541, July 29 Katholieke
Eigenvalues and Eigenfunctions of the Laplacian
 The Waterloo Mathematics Review 23 Eigenvalues and Eigenfunctions of the Laplacian Mihai Nica University of Waterloo mcnica@uwaterloo.ca Abstract: The problem of determining the eigenvalues and eigenvectors
The Waterloo Mathematics Review 23 Eigenvalues and Eigenfunctions of the Laplacian Mihai Nica University of Waterloo mcnica@uwaterloo.ca Abstract: The problem of determining the eigenvalues and eigenvectors
PART IV Spectral Methods
 PART IV Spectral Methods Additional References: R. Peyret, Spectral methods for incompressible viscous flow, Springer (2002), B. Mercier, An introduction to the numerical analysis of spectral methods,
PART IV Spectral Methods Additional References: R. Peyret, Spectral methods for incompressible viscous flow, Springer (2002), B. Mercier, An introduction to the numerical analysis of spectral methods,
Scientific Computing WS 2018/2019. Lecture 15. Jürgen Fuhrmann Lecture 15 Slide 1
 Scientific Computing WS 2018/2019 Lecture 15 Jürgen Fuhrmann juergen.fuhrmann@wias-berlin.de Lecture 15 Slide 1 Lecture 15 Slide 2 Problems with strong formulation Writing the PDE with divergence and gradient
Scientific Computing WS 2018/2019 Lecture 15 Jürgen Fuhrmann juergen.fuhrmann@wias-berlin.de Lecture 15 Slide 1 Lecture 15 Slide 2 Problems with strong formulation Writing the PDE with divergence and gradient
LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS. S. G. Bobkov and F. L. Nazarov. September 25, 2011
 LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS S. G. Bobkov and F. L. Nazarov September 25, 20 Abstract We study large deviations of linear functionals on an isotropic
LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS S. G. Bobkov and F. L. Nazarov September 25, 20 Abstract We study large deviations of linear functionals on an isotropic
Statistical signal processing
 Statistical signal processing Short overview of the fundamentals Outline Random variables Random processes Stationarity Ergodicity Spectral analysis Random variable and processes Intuition: A random variable
Statistical signal processing Short overview of the fundamentals Outline Random variables Random processes Stationarity Ergodicity Spectral analysis Random variable and processes Intuition: A random variable
Performance Evaluation of Generalized Polynomial Chaos
 Performance Evaluation of Generalized Polynomial Chaos Dongbin Xiu, Didier Lucor, C.-H. Su, and George Em Karniadakis 1 Division of Applied Mathematics, Brown University, Providence, RI 02912, USA, gk@dam.brown.edu
Performance Evaluation of Generalized Polynomial Chaos Dongbin Xiu, Didier Lucor, C.-H. Su, and George Em Karniadakis 1 Division of Applied Mathematics, Brown University, Providence, RI 02912, USA, gk@dam.brown.edu
Simple Examples on Rectangular Domains
 84 Chapter 5 Simple Examples on Rectangular Domains In this chapter we consider simple elliptic boundary value problems in rectangular domains in R 2 or R 3 ; our prototype example is the Poisson equation
84 Chapter 5 Simple Examples on Rectangular Domains In this chapter we consider simple elliptic boundary value problems in rectangular domains in R 2 or R 3 ; our prototype example is the Poisson equation
CS 450 Numerical Analysis. Chapter 8: Numerical Integration and Differentiation
 Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Polynomial approximation of PDEs with stochastic coefficients
 POLITECNICO DI MILANO Ph.D. School in Mathematical Models and Methods in Engineering XXIV ciclo Polynomial approximation of PDEs with stochastic coefficients Presented to Dipartimento di Matematica F.
POLITECNICO DI MILANO Ph.D. School in Mathematical Models and Methods in Engineering XXIV ciclo Polynomial approximation of PDEs with stochastic coefficients Presented to Dipartimento di Matematica F.
Downloaded 01/28/13 to Redistribution subject to SIAM license or copyright; see
 SIAM J. SCI. COMPUT. Vol. 27, No. 3, pp. 1118 1139 c 2005 Society for Industrial and Applied Mathematics HIGH-ORDER COLLOCATION METHODS FOR DIFFERENTIAL EQUATIONS WITH RANDOM INPUTS DONGBIN XIU AND JAN
SIAM J. SCI. COMPUT. Vol. 27, No. 3, pp. 1118 1139 c 2005 Society for Industrial and Applied Mathematics HIGH-ORDER COLLOCATION METHODS FOR DIFFERENTIAL EQUATIONS WITH RANDOM INPUTS DONGBIN XIU AND JAN
Dinesh Kumar, Mehrdad Raisee and Chris Lacor
 Dinesh Kumar, Mehrdad Raisee and Chris Lacor Fluid Mechanics and Thermodynamics Research Group Vrije Universiteit Brussel, BELGIUM dkumar@vub.ac.be; m_raisee@yahoo.com; chris.lacor@vub.ac.be October, 2014
Dinesh Kumar, Mehrdad Raisee and Chris Lacor Fluid Mechanics and Thermodynamics Research Group Vrije Universiteit Brussel, BELGIUM dkumar@vub.ac.be; m_raisee@yahoo.com; chris.lacor@vub.ac.be October, 2014
Analysis and Computation of Hyperbolic PDEs with Random Data
 Analysis and Computation of Hyperbolic PDEs with Random Data Mohammad Motamed 1, Fabio Nobile 2,3 and Raúl Tempone 1 1 King Abdullah University of Science and Technology, Thuwal, Saudi Arabia 2 EPFL Lausanne,
Analysis and Computation of Hyperbolic PDEs with Random Data Mohammad Motamed 1, Fabio Nobile 2,3 and Raúl Tempone 1 1 King Abdullah University of Science and Technology, Thuwal, Saudi Arabia 2 EPFL Lausanne,
Spectral Processing. Misha Kazhdan
 Spectral Processing Misha Kazhdan [Taubin, 1995] A Signal Processing Approach to Fair Surface Design [Desbrun, et al., 1999] Implicit Fairing of Arbitrary Meshes [Vallet and Levy, 2008] Spectral Geometry
Spectral Processing Misha Kazhdan [Taubin, 1995] A Signal Processing Approach to Fair Surface Design [Desbrun, et al., 1999] Implicit Fairing of Arbitrary Meshes [Vallet and Levy, 2008] Spectral Geometry
Cheng Soon Ong & Christian Walder. Canberra February June 2018
 Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 (Many figures from C. M. Bishop, "Pattern Recognition and ") 1of 254 Part V
Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 (Many figures from C. M. Bishop, "Pattern Recognition and ") 1of 254 Part V
Sparse polynomial chaos expansions in engineering applications
 DEPARTMENT OF CIVIL, ENVIRONMENTAL AND GEOMATIC ENGINEERING CHAIR OF RISK, SAFETY & UNCERTAINTY QUANTIFICATION Sparse polynomial chaos expansions in engineering applications B. Sudret G. Blatman (EDF R&D,
DEPARTMENT OF CIVIL, ENVIRONMENTAL AND GEOMATIC ENGINEERING CHAIR OF RISK, SAFETY & UNCERTAINTY QUANTIFICATION Sparse polynomial chaos expansions in engineering applications B. Sudret G. Blatman (EDF R&D,
i=1 α i. Given an m-times continuously
 1 Fundamentals 1.1 Classification and characteristics Let Ω R d, d N, d 2, be an open set and α = (α 1,, α d ) T N d 0, N 0 := N {0}, a multiindex with α := d i=1 α i. Given an m-times continuously differentiable
1 Fundamentals 1.1 Classification and characteristics Let Ω R d, d N, d 2, be an open set and α = (α 1,, α d ) T N d 0, N 0 := N {0}, a multiindex with α := d i=1 α i. Given an m-times continuously differentiable
Brownian Motion. 1 Definition Brownian Motion Wiener measure... 3
 Brownian Motion Contents 1 Definition 2 1.1 Brownian Motion................................. 2 1.2 Wiener measure.................................. 3 2 Construction 4 2.1 Gaussian process.................................
Brownian Motion Contents 1 Definition 2 1.1 Brownian Motion................................. 2 1.2 Wiener measure.................................. 3 2 Construction 4 2.1 Gaussian process.................................
Comparison of Clenshaw-Curtis and Leja quasi-optimal sparse grids for the approximation of random PDEs
 MATHICSE Mathematics Institute of Computational Science and Engineering School of Basic Sciences - Section of Mathematics MATHICSE Technical Report Nr. 41.2014 September 2014 Comparison of Clenshaw-Curtis
MATHICSE Mathematics Institute of Computational Science and Engineering School of Basic Sciences - Section of Mathematics MATHICSE Technical Report Nr. 41.2014 September 2014 Comparison of Clenshaw-Curtis
9 Brownian Motion: Construction
 9 Brownian Motion: Construction 9.1 Definition and Heuristics The central limit theorem states that the standard Gaussian distribution arises as the weak limit of the rescaled partial sums S n / p n of
9 Brownian Motion: Construction 9.1 Definition and Heuristics The central limit theorem states that the standard Gaussian distribution arises as the weak limit of the rescaled partial sums S n / p n of
Experiences with Model Reduction and Interpolation
 Experiences with Model Reduction and Interpolation Paul Constantine Stanford University, Sandia National Laboratories Qiqi Wang (MIT) David Gleich (Purdue) Emory University March 7, 2012 Joe Ruthruff (SNL)
Experiences with Model Reduction and Interpolation Paul Constantine Stanford University, Sandia National Laboratories Qiqi Wang (MIT) David Gleich (Purdue) Emory University March 7, 2012 Joe Ruthruff (SNL)
Lecture Notes 1: Vector spaces
 Optimization-based data analysis Fall 2017 Lecture Notes 1: Vector spaces In this chapter we review certain basic concepts of linear algebra, highlighting their application to signal processing. 1 Vector
Optimization-based data analysis Fall 2017 Lecture Notes 1: Vector spaces In this chapter we review certain basic concepts of linear algebra, highlighting their application to signal processing. 1 Vector
Laplace s Equation. Chapter Mean Value Formulas
 Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
1 Math 241A-B Homework Problem List for F2015 and W2016
 1 Math 241A-B Homework Problem List for F2015 W2016 1.1 Homework 1. Due Wednesday, October 7, 2015 Notation 1.1 Let U be any set, g be a positive function on U, Y be a normed space. For any f : U Y let
1 Math 241A-B Homework Problem List for F2015 W2016 1.1 Homework 1. Due Wednesday, October 7, 2015 Notation 1.1 Let U be any set, g be a positive function on U, Y be a normed space. For any f : U Y let
NONTRIVIAL SOLUTIONS TO INTEGRAL AND DIFFERENTIAL EQUATIONS
 Fixed Point Theory, Volume 9, No. 1, 28, 3-16 http://www.math.ubbcluj.ro/ nodeacj/sfptcj.html NONTRIVIAL SOLUTIONS TO INTEGRAL AND DIFFERENTIAL EQUATIONS GIOVANNI ANELLO Department of Mathematics University
Fixed Point Theory, Volume 9, No. 1, 28, 3-16 http://www.math.ubbcluj.ro/ nodeacj/sfptcj.html NONTRIVIAL SOLUTIONS TO INTEGRAL AND DIFFERENTIAL EQUATIONS GIOVANNI ANELLO Department of Mathematics University
Introduction to Computational Stochastic Differential Equations
 Introduction to Computational Stochastic Differential Equations Gabriel J. Lord Catherine E. Powell Tony Shardlow Preface Techniques for solving many of the differential equations traditionally used by
Introduction to Computational Stochastic Differential Equations Gabriel J. Lord Catherine E. Powell Tony Shardlow Preface Techniques for solving many of the differential equations traditionally used by
Dimensionality reduction of parameter-dependent problems through proper orthogonal decomposition
 MATHICSE Mathematics Institute of Computational Science and Engineering School of Basic Sciences - Section of Mathematics MATHICSE Technical Report Nr. 01.2016 January 2016 (New 25.05.2016) Dimensionality
MATHICSE Mathematics Institute of Computational Science and Engineering School of Basic Sciences - Section of Mathematics MATHICSE Technical Report Nr. 01.2016 January 2016 (New 25.05.2016) Dimensionality
4. Numerical Quadrature. Where analytical abilities end... continued
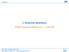 4. Numerical Quadrature Where analytical abilities end... continued Where analytical abilities end... continued, November 30, 22 1 4.3. Extrapolation Increasing the Order Using Linear Combinations Once
4. Numerical Quadrature Where analytical abilities end... continued Where analytical abilities end... continued, November 30, 22 1 4.3. Extrapolation Increasing the Order Using Linear Combinations Once
Sliced Inverse Regression
 Sliced Inverse Regression Ge Zhao gzz13@psu.edu Department of Statistics The Pennsylvania State University Outline Background of Sliced Inverse Regression (SIR) Dimension Reduction Definition of SIR Inversed
Sliced Inverse Regression Ge Zhao gzz13@psu.edu Department of Statistics The Pennsylvania State University Outline Background of Sliced Inverse Regression (SIR) Dimension Reduction Definition of SIR Inversed
Traces, extensions and co-normal derivatives for elliptic systems on Lipschitz domains
 Traces, extensions and co-normal derivatives for elliptic systems on Lipschitz domains Sergey E. Mikhailov Brunel University West London, Department of Mathematics, Uxbridge, UB8 3PH, UK J. Math. Analysis
Traces, extensions and co-normal derivatives for elliptic systems on Lipschitz domains Sergey E. Mikhailov Brunel University West London, Department of Mathematics, Uxbridge, UB8 3PH, UK J. Math. Analysis
X n D X lim n F n (x) = F (x) for all x C F. lim n F n(u) = F (u) for all u C F. (2)
 14:17 11/16/2 TOPIC. Convergence in distribution and related notions. This section studies the notion of the so-called convergence in distribution of real random variables. This is the kind of convergence
14:17 11/16/2 TOPIC. Convergence in distribution and related notions. This section studies the notion of the so-called convergence in distribution of real random variables. This is the kind of convergence
u xx + u yy = 0. (5.1)
 Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
arxiv: v2 [math.na] 6 Aug 2018
![arxiv: v2 [math.na] 6 Aug 2018 arxiv: v2 [math.na] 6 Aug 2018](/thumbs/94/118309732.jpg) Bayesian model calibration with interpolating polynomials based on adaptively weighted Leja nodes L.M.M. van den Bos,2, B. Sanderse, W.A.A.M. Bierbooms 2, and G.J.W. van Bussel 2 arxiv:82.235v2 [math.na]
Bayesian model calibration with interpolating polynomials based on adaptively weighted Leja nodes L.M.M. van den Bos,2, B. Sanderse, W.A.A.M. Bierbooms 2, and G.J.W. van Bussel 2 arxiv:82.235v2 [math.na]
JUHA KINNUNEN. Harmonic Analysis
 JUHA KINNUNEN Harmonic Analysis Department of Mathematics and Systems Analysis, Aalto University 27 Contents Calderón-Zygmund decomposition. Dyadic subcubes of a cube.........................2 Dyadic cubes
JUHA KINNUNEN Harmonic Analysis Department of Mathematics and Systems Analysis, Aalto University 27 Contents Calderón-Zygmund decomposition. Dyadic subcubes of a cube.........................2 Dyadic cubes
Lecture 4: Numerical solution of ordinary differential equations
 Lecture 4: Numerical solution of ordinary differential equations Department of Mathematics, ETH Zürich General explicit one-step method: Consistency; Stability; Convergence. High-order methods: Taylor
Lecture 4: Numerical solution of ordinary differential equations Department of Mathematics, ETH Zürich General explicit one-step method: Consistency; Stability; Convergence. High-order methods: Taylor
The main results about probability measures are the following two facts:
 Chapter 2 Probability measures The main results about probability measures are the following two facts: Theorem 2.1 (extension). If P is a (continuous) probability measure on a field F 0 then it has a
Chapter 2 Probability measures The main results about probability measures are the following two facts: Theorem 2.1 (extension). If P is a (continuous) probability measure on a field F 0 then it has a
Hilbert Spaces. Hilbert space is a vector space with some extra structure. We start with formal (axiomatic) definition of a vector space.
 Hilbert Spaces Hilbert space is a vector space with some extra structure. We start with formal (axiomatic) definition of a vector space. Vector Space. Vector space, ν, over the field of complex numbers,
Hilbert Spaces Hilbert space is a vector space with some extra structure. We start with formal (axiomatic) definition of a vector space. Vector Space. Vector space, ν, over the field of complex numbers,
ASYMPTOTIC MAXIMUM PRINCIPLE
 Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 27, 2002, 249 255 ASYMPTOTIC MAXIMUM PRINCIPLE Boris Korenblum University at Albany, Department of Mathematics and Statistics Albany, NY 12222,
Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 27, 2002, 249 255 ASYMPTOTIC MAXIMUM PRINCIPLE Boris Korenblum University at Albany, Department of Mathematics and Statistics Albany, NY 12222,
ACM/CMS 107 Linear Analysis & Applications Fall 2017 Assignment 2: PDEs and Finite Element Methods Due: 7th November 2017
 ACM/CMS 17 Linear Analysis & Applications Fall 217 Assignment 2: PDEs and Finite Element Methods Due: 7th November 217 For this assignment the following MATLAB code will be required: Introduction http://wwwmdunloporg/cms17/assignment2zip
ACM/CMS 17 Linear Analysis & Applications Fall 217 Assignment 2: PDEs and Finite Element Methods Due: 7th November 217 For this assignment the following MATLAB code will be required: Introduction http://wwwmdunloporg/cms17/assignment2zip
We denote the space of distributions on Ω by D ( Ω) 2.
 Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
Your first day at work MATH 806 (Fall 2015)
 Your first day at work MATH 806 (Fall 2015) 1. Let X be a set (with no particular algebraic structure). A function d : X X R is called a metric on X (and then X is called a metric space) when d satisfies
Your first day at work MATH 806 (Fall 2015) 1. Let X be a set (with no particular algebraic structure). A function d : X X R is called a metric on X (and then X is called a metric space) when d satisfies
Numerical Solutions to Partial Differential Equations
 Numerical Solutions to Partial Differential Equations Zhiping Li LMAM and School of Mathematical Sciences Peking University Nonconformity and the Consistency Error First Strang Lemma Abstract Error Estimate
Numerical Solutions to Partial Differential Equations Zhiping Li LMAM and School of Mathematical Sciences Peking University Nonconformity and the Consistency Error First Strang Lemma Abstract Error Estimate
Kernel-based Approximation. Methods using MATLAB. Gregory Fasshauer. Interdisciplinary Mathematical Sciences. Michael McCourt.
 SINGAPORE SHANGHAI Vol TAIPEI - Interdisciplinary Mathematical Sciences 19 Kernel-based Approximation Methods using MATLAB Gregory Fasshauer Illinois Institute of Technology, USA Michael McCourt University
SINGAPORE SHANGHAI Vol TAIPEI - Interdisciplinary Mathematical Sciences 19 Kernel-based Approximation Methods using MATLAB Gregory Fasshauer Illinois Institute of Technology, USA Michael McCourt University
A Polynomial Chaos Approach to Robust Multiobjective Optimization
 A Polynomial Chaos Approach to Robust Multiobjective Optimization Silvia Poles 1, Alberto Lovison 2 1 EnginSoft S.p.A., Optimization Consulting Via Giambellino, 7 35129 Padova, Italy s.poles@enginsoft.it
A Polynomial Chaos Approach to Robust Multiobjective Optimization Silvia Poles 1, Alberto Lovison 2 1 EnginSoft S.p.A., Optimization Consulting Via Giambellino, 7 35129 Padova, Italy s.poles@enginsoft.it
SPECTRAL PROPERTIES OF THE LAPLACIAN ON BOUNDED DOMAINS
 SPECTRAL PROPERTIES OF THE LAPLACIAN ON BOUNDED DOMAINS TSOGTGEREL GANTUMUR Abstract. After establishing discrete spectra for a large class of elliptic operators, we present some fundamental spectral properties
SPECTRAL PROPERTIES OF THE LAPLACIAN ON BOUNDED DOMAINS TSOGTGEREL GANTUMUR Abstract. After establishing discrete spectra for a large class of elliptic operators, we present some fundamental spectral properties
Numerische Mathematik
 Numer. Math. (203) :493 536 OI 0.007/s002-02-0493-5 Numerische Mathematik A stochastic collocation method for the second order wave equation with a discontinuous random speed Mohammad Motamed Fabio Nobile
Numer. Math. (203) :493 536 OI 0.007/s002-02-0493-5 Numerische Mathematik A stochastic collocation method for the second order wave equation with a discontinuous random speed Mohammad Motamed Fabio Nobile
NONLOCALITY AND STOCHASTICITY TWO EMERGENT DIRECTIONS FOR APPLIED MATHEMATICS. Max Gunzburger
 NONLOCALITY AND STOCHASTICITY TWO EMERGENT DIRECTIONS FOR APPLIED MATHEMATICS Max Gunzburger Department of Scientific Computing Florida State University North Carolina State University, March 10, 2011
NONLOCALITY AND STOCHASTICITY TWO EMERGENT DIRECTIONS FOR APPLIED MATHEMATICS Max Gunzburger Department of Scientific Computing Florida State University North Carolina State University, March 10, 2011
Non commutative Khintchine inequalities and Grothendieck s theo
 Non commutative Khintchine inequalities and Grothendieck s theorem Nankai, 2007 Plan Non-commutative Khintchine inequalities 1 Non-commutative Khintchine inequalities 2 µ = Uniform probability on the set
Non commutative Khintchine inequalities and Grothendieck s theorem Nankai, 2007 Plan Non-commutative Khintchine inequalities 1 Non-commutative Khintchine inequalities 2 µ = Uniform probability on the set
NONLINEAR ELLIPTIC EQUATIONS WITH MEASURES REVISITED
 NONLINEAR ELLIPTIC EQUATIONS WITH MEASURES REVISITED Haïm Brezis (1),(2), Moshe Marcus (3) and Augusto C. Ponce (4) Abstract. We study the existence of solutions of the nonlinear problem (P) ( u + g(u)
NONLINEAR ELLIPTIC EQUATIONS WITH MEASURES REVISITED Haïm Brezis (1),(2), Moshe Marcus (3) and Augusto C. Ponce (4) Abstract. We study the existence of solutions of the nonlinear problem (P) ( u + g(u)
Solving the Stochastic Steady-State Diffusion Problem Using Multigrid
 Solving the Stochastic Steady-State Diffusion Problem Using Multigrid Tengfei Su Applied Mathematics and Scientific Computing Advisor: Howard Elman Department of Computer Science Sept. 29, 2015 Tengfei
Solving the Stochastic Steady-State Diffusion Problem Using Multigrid Tengfei Su Applied Mathematics and Scientific Computing Advisor: Howard Elman Department of Computer Science Sept. 29, 2015 Tengfei
Slow Exponential Growth for Clenshaw Curtis Sparse Grids jburkardt/presentations/... slow growth paper.
 Slow Exponential Growth for Clenshaw Curtis Sparse Grids http://people.sc.fsu.edu/ jburkardt/presentations/...... slow growth paper.pdf John Burkardt, Clayton Webster April 30, 2014 Abstract A widely used
Slow Exponential Growth for Clenshaw Curtis Sparse Grids http://people.sc.fsu.edu/ jburkardt/presentations/...... slow growth paper.pdf John Burkardt, Clayton Webster April 30, 2014 Abstract A widely used
Theorem 2.1 (Caratheodory). A (countably additive) probability measure on a field has an extension. n=1
 Chapter 2 Probability measures 1. Existence Theorem 2.1 (Caratheodory). A (countably additive) probability measure on a field has an extension to the generated σ-field Proof of Theorem 2.1. Let F 0 be
Chapter 2 Probability measures 1. Existence Theorem 2.1 (Caratheodory). A (countably additive) probability measure on a field has an extension to the generated σ-field Proof of Theorem 2.1. Let F 0 be
The Generalized Empirical Interpolation Method: Analysis of the convergence and application to data assimilation coupled with simulation
 The Generalized Empirical Interpolation Method: Analysis of the convergence and application to data assimilation coupled with simulation Y. Maday (LJLL, I.U.F., Brown Univ.) Olga Mula (CEA and LJLL) G.
The Generalized Empirical Interpolation Method: Analysis of the convergence and application to data assimilation coupled with simulation Y. Maday (LJLL, I.U.F., Brown Univ.) Olga Mula (CEA and LJLL) G.
Sparse-grid polynomial interpolation approximation and integration for parametric and stochastic elliptic PDEs with lognormal inputs
 Sparse-grid polynomial interpolation approximation and integration for parametric and stochastic elliptic PDEs with lognormal inputs Dinh Dũng Information Technology Institute, Vietnam National University
Sparse-grid polynomial interpolation approximation and integration for parametric and stochastic elliptic PDEs with lognormal inputs Dinh Dũng Information Technology Institute, Vietnam National University
