EKC314: TRANSPORT PHENOMENA Core Course for B.Eng.(Chemical Engineering) Semester II (2008/2009)
|
|
|
- Kerry Wood
- 5 years ago
- Views:
Transcription
1 EKC314: TRANSPORT PHENOMENA Core Course for B.Eng.(Chemical Engineering) Semester II (2008/2009) Dr. Mohamad Hekarl School of Chemical Engineering Engineering Campus, Universiti Sains Malaysia Seri Ampangan, Nibong Tebal Seberang Perai Selatan Penang. EKC314-SCE p. 1/5
2 Syllabus 1. Introduction and Concepts 2. Momentum Transport Viscosity and and mechanism of momentum transport Newtonian and non-newtonian fluids Flux and gradients Velocity distribution in in laminar and turbulent flows Boundary layer Velocity distribution with more than one independent variables EKC314-SCE p. 2/5
3 Syllabus 3. Equation of changes in Isothermal Systems; Interphase transport in isothermal system. Macroscopic balances for isothermal systems. EKC314-SCE p. 3/5
4 What are Transport Phenomena? 1. Fluid dynamics 2. Heat transfer 3. Mass transfer They should be studied together since: 1. they occur simultaneously 2. basic equations that described the 3 transport phenomena are closely related 3. mathematical tools required are very similar 4. molecular mechanisms underlying various transport phenomena are very closely related EKC314-SCE p. 4/5
5 Macroscopic level Write down balance equation; macroscopic balances. Equations should describe; mass, momentum, energy and angular momentum within the system. No need to understand the details of the system. Microscopic level Examination of the fluid mixture in a small region within the equipment. Can write down the equation of change that describe mass, momentum, energy and angular momentum change within the small region Aim is to get information about velocity, temperature, pressure and concentration profile within the system. Molecular level To seek a fundamental understanding of the mechanism of mass, momentum, energy and angular momentum in terms of molecular structure and intermolecular forces Involve some theoretical physics and physical chemistry work EKC314-SCE p. 5/5
6 Mixture of gases Macroscopic Heat added to the system Microscopic Molecular EKC314-SCE p. 6/5
7 The flow of fluid are studied in 3 different parts which consist of: flow of pure fluids at constant temperature-with emphasis on viscous and convective momentum transport flow of pure fluids with varying temperature-with emphasis on conductive, convective and radiative energy transport flow of fluid mixtures with varying composition-with emphasis on diffusive and convective mass transport EKC314-SCE p. 7/5
8 Conservation Laws (mass): Consider two colliding diatomic molecules (N 2 and O 2 ). The conservation of mass can be written as; m N + m O = m N + m O for a system with no chemical reaction; and m N = m N m O = m O EKC314-SCE p. 8/5
9 Conservation Laws (momentum): According to the law of conservation of momentum, the sum of the momenta of all atoms before collision must equal that after the collision. The conservation of momentum can be written as; m N1 ṙ N1 + m N2 ṙ N2 + m O1 ṙ O1 + m O2 ṙ O2 = m N 1 ṙ N 1 + m N 2 ṙ N 2 + m O 1 ṙ O 1 + m O 2 ṙ O 2 EKC314-SCE p. 9/5
10 Conservation Laws (momentum): r N1 is the position vector for atom 1 of molecule N and ṙ N1 is its velocity. It can be written as; r N1 = r N + R N1 r N1 is the sum of the position vector for the centre of mass and the position vector of the atom w.r.t the centre of mass. EKC314-SCE p. 10/5
11 Conservation Laws (momentum): Also R N2 = R N1 Then the conservation equation can be simplified as; m N ṙ N + m O ṙ O = m N ṙ N + m O ṙ O EKC314-SCE p. 11/5
12 How to study Transport Phenomena? Read the text with pencil and paper in hand-work through details of the mathematical developments Refer back to any maths textbook just to brush up on culculus, differential equations, vectors etc. Make a point to give a physical interpretation of key results-get into habit of relating physical ideas to the equations Ask whether results seem reasonable. If they do not agree with intuition, it is important to find out which is correct Make a habit to check the dimensions of all results. This is a very good way to locate errors in derivations EKC314-SCE p. 12/5
13 Recap: Vector Calculus If given a vector of a form; a = [a 1,a 2,a 3 ] = a 1 i + a 2 j + a 3 k consists of the real vector space R 3 with vector addition defined as; [a 1,a 2,a 3 ] + [b 1,b 2,b 3 ] = [a 1 + b 1,a 2 + b 2,a 3 + b 3 ] and scalar multiplication defined by; c[a 1,a 2,a 3 ] = [ca 1,ca 2,ca 3 ] EKC314-SCE p. 13/5
14 The dot product of two vectors is defined by; a b = a b cosγ = a 1 b 1 + a 2 b 2 + a 3 b 3 where γ is the angle between a and b. This gives the norm or length a of a with a formula; a = a a = a a a 3 3 If a b = 0 therefore a and b orthogonal. EKC314-SCE p. 14/5
15 Example of a dot product is given by; W = p d which is work done by a force p in a displacement d. EKC314-SCE p. 15/5
16 The cross product v = a b is a vector of length; a b = a b sinγ and perpendicular to both a and b such that a, b, v form a right-handed triple. This can also be written in the form of; a b = i j k a 1 a 2 a 3 b 1 b 2 b 3 The cross product is anticommutative a b = b a and not associative. EKC314-SCE p. 16/5
17 For a vector function given by v(t) = [v 1 (t),v 2 (t),v 3 (t)] = v 1 (t)i + v 2 (t)j + v 3 (t)k Then the derivative is; v = dv dt = lim t 0 v(t + t) v(t) t therefore; v = [v 1,v 2,v 3] = v 1i + v 2j + v 3k EKC314-SCE p. 17/5
18 Vector function r(t) can be used to represent a curve C in space. Then r(t) associates with each t = t 0 in some interval a < t < b the point of C with position vector r(t 0 ). The derivative r (t) is a tangent vector of C. If a vector in a Cartesian coordinate is given by; v(x,y,z) = [v 1 (x,y,z),v 2 (x,y,z),v 3 (x,y,z)] = v 1 (x,y,z)i + v 2 (x,y,z)j + v 3 (x,y,z)k EKC314-SCE p. 18/5
19 Therefore, the partial derivative of v can be obtained by; ( v x = v1 x, v 2 x, v ) 3 x = v 1 x i + v 2 x j + v 3 x k EKC314-SCE p. 19/5
20 Gradient of a function f can be written as; [ f grad f = f = x, f y, f ] z Therefore, using the operation, the directional derivative of f in a direction of a unit vector b can be obtained by; D b f = df ds = b f EKC314-SCE p. 20/5
21 Divergence of a vector function v can be written as; div v = v = v 1 x + v 2 y + v 3 z And the curl of v is given as; curl v = v = i j k x y z v 1 v 2 v 3 EKC314-SCE p. 21/5
22 Some basic formula for grad, div and curl; Grad: (fg) = f g + g f (f/g) = (1/g 2 )(g f f g) Div: div(fv) = fdiv v + v f div(f g) = f 2 g + f g EKC314-SCE p. 22/5
23 Div and Grad (Laplacian): 2 f = div( f) 2 (fg) = g 2 f + 2 f g + f 2 g Div and Curl: curl(fv) = f v + fcurl v div(u v) = v curl u u curl v EKC314-SCE p. 23/5
24 Extra: curl( f) = 0 div(curl v) = 0 EKC314-SCE p. 24/5
25 Example 1: Let a particle A of mass M be fixed at point P 0 and let a particle B of mass m be free to take up various positions P in space. Then A attracts B. According to Newton s Law of Gravitation, the corresponding gravitational force p is directed from P to P 0 and its magnitude is proportional to 1 r 2, where r is the distance between P and P 0. This can be written as; p = c r 2 EKC314-SCE p. 25/5
26 Hence p defines a vector field in space. Using Cartesian coordinates, such that P 0 (x 0,y 0,z 0 ) and P(x,y,z), therefore the distance r can be determined as; r = (x x 0 ) 2 + (y y 0 ) 2 + (z z 0 ) 2 For r > 0 in vector form; r = [x x 0,y y 0,z z 0 ] = (x x 0 )i + (y y 0 )j + (z z 0 )k EKC314-SCE p. 26/5
27 Therefore; r = r and ( 1/r)r is a unit vector in the direction of p. The minus sign indicates that p is directed from P to P 0. Thus, p = p ( 1r ) r = c r 3r = cx x 0 i c y y 0 j c z z 0 k r 3 r 3 r 3 EKC314-SCE p. 27/5
28 Example 2: From the former example, by the Newton s Law of Gravitation, the force of attraction between 2 particles is given as; p = c r3r = c ( x x0 i + y y 0 j + z z ) 0 k r 3 r 3 r 3 where r is a distance between two particles P 0 and P of the given coordinates. Thus, r = (x x 0 ) 2 + (y y 0 ) 2 + (z z 0 ) 2 EKC314-SCE p. 28/5
29 The important observation now is ( ) 1 2(x x 0 ) = x r 2[(x x 0 ) 2 + (y y 0 ) 2 + (z z 0 ) 2 ] = x x 0 3/2 r 3 Similarly; y ( ) 1 r = y y 0 r 3 and z ( ) 1 r = z z 0 r 3 EKC314-SCE p. 29/5
30 From here, it is observed that p is the gradient of the scalar function; f(x,y,z) = c r and f is a potential of that gravitational field. Applying Laplace Equation of the form; 2 f x + 2 f 2 y + 2 f 2 z = 0 2 EKC314-SCE p. 30/5
31 Applying this to the unit vector, gives for the individual component; 2 x 2 2 y 2 2 z 2 ( ) 1 = 1r r + 3(x x 0) 2 3 r 5 ( ) 1 = 1r r + 3(y y 0) 2 3 r 5 ( ) 1 = 1r r + 3(z z 0) 2 3 r 5 EKC314-SCE p. 31/5
32 Combining the 3 gives; ( ) 2 x y + 2 c 2 z 2 r = 0 or it can be written in the form of; 2 f = 0 which is normally termed as the Laplacian operator of a function. EKC314-SCE p. 32/5
33 Example 3: From Example 2, it is known that the gravitational force p is the gradient of the scalar function f(x,y,z) = c r which satisfies Laplace s equation 2 f = 0. Therefore, for r > 0. div p = 0 EKC314-SCE p. 33/5
34 Example 4: Consider a motion of a fluid in a region R having no sources and sinks in R (no points at which the fluid is produced or disappeared). Assuming that the fluid is compressible and it flows through a small rectangular box W of dimension x, y and z with edges parallel to the coordinate axes. W has a volume of V = x y z. Let v is the velocity vector of the form given by; v = [v 1,v 2,v 3 ] = v 1 i + v 2 j + v 3 k EKC314-SCE p. 34/5
35 Setting u = ρv = [u 1,u 2,u 3 ] = u 1 i + u 2 j + u 3 k where ρ is the density of the fluid. Consider the flow of fluid out of the box W is through the left face whose area is x z and the components v 1 and v 3 are parallel to that face and contribute nothing to that flow. Thus, the mass of fluid entering through that face during a short time interval t is approx. given by; (ρv 2 ) y x z t = (u 2 ) y x z t EKC314-SCE p. 35/5
36 And the mass of fluid leaving the opposite face of the box W, during the same time interval is approx. given by; (u 2 ) y+ y x z t Therefore, the difference is in the form of; u 2 x z t = u 2 y V t where u 2 = (u 2 ) y+ y (u 2 ) y EKC314-SCE p. 36/5
37 Two other pairs in x and z directions are taken and combined in the form given by; ( u1 x + u 2 y + u ) 3 V t z The loss of mass in W is caused by the rate of change of the density and therefore equals to; ρ V t t EKC314-SCE p. 37/5
38 Equating both equations gives; ( u1 x + u 2 y + u ) 3 V t = ρ V t z t Diving the above equation by V t and let x, y, z and t approaching 0 leads to; ( u1 x + u 2 y + u ) 3 = ρ z t EKC314-SCE p. 38/5
39 Or in its simplified form; or div u = ρ t div(ρv) = ρ t which consequently becomes; ρ t + div(ρv) = 0 which is the condition for the conservation of mass or the continuity equation of a compressible fluid flow! EKC314-SCE p. 39/5
40 If the flow is steady, or it is independent of time, thus; ρ t = 0 and therefore the continuity equation reduces into div(ρv) = 0 If the density ρ is constant, which means the fluid is incompressible, therefore the continuity equation becomes; div v = 0 EKC314-SCE p. 40/5
41 Viscosity and the Mechanisms of Momentum Transport Consider a parallel plates with area A separated by distance Y with a type of fluid; The system is initially at rest At time t = 0, the lower plate is set in motion in the positive x direction at a constant velocity V. As time proceeds, the fluid gains momentum and the linear steady-state velocity is established. At steady motion, a constant force, F is required to maintain the motion of the lower plate and this can be expressed as; F A = µv Y EKC314-SCE p. 41/5
42 Viscosity and the Mechanisms of Momentum Transport Y t < 0 Fluid initially at rest t = 0 Lower plate set in motion V vx(y,t) Small t Velocity build up in unsteady flow y V vx(y) Large t Final velocity distribution in steady flow x V EKC314-SCE p. 42/5
43 Viscosity and the Mechanisms of Momentum Transport Consider a parallel plates with area A separated by distance Y with a type of fluid; Force in the direction of x perpendicular to the y direction given by F/A is replaced by τ yx. The term V/Y is replaced by dv x /dy and therefore the equation becomes; τ yx = µ dv x dy This means that the shearing force per unit area is proportional to the negative of the velocity gradient i.e. Newton s Law of Viscosity. EKC314-SCE p. 43/5
44 Viscosity and the Mechanisms of Momentum Transport Similarly, let the angle between the fixed plate and the moving boundary δγ and the distance from the origin is δx. Therefore, for a very small angle, tanδγ = δx Y δx Y = δγ EKC314-SCE p. 44/5
45 Viscosity and the Mechanisms of Momentum Transport But thus, δx = V δt δγ = V δt Y Taking limit on on the above terms; lim δt 0 δγ δt = V Y = dv dy EKC314-SCE p. 45/5
46 Viscosity and the Mechanisms of Momentum Transport Hence; But Thus, δγ δt dv dy γ τ τ dv dy EKC314-SCE p. 46/5
47 Viscosity and the Mechanisms of Momentum Transport Which then becomes τ = µ dv dy with µ as the proportionality constant. The minus sign represents the force exerted by the fluid of the lesser Y on the fluid of greater Y. EKC314-SCE p. 47/5
48 Viscosity and the Mechanisms of Momentum Transport τ Shear thinning Newtonian Shear thickening dγ/dt EKC314-SCE p. 48/5
49 Viscosity and the Mechanisms of Momentum Transport Generalisation of Newton s Law of Viscosity. Consider a fluid moving in 3-dimensional space with respect to time t. Therefore, the velocity components are given as follows; v x = v x (x,y,z,t) v y = v y (x,y,z,t) v z = v z (x,y,z,t) In the given situation, there will be 9 stress components, τ ij. EKC314-SCE p. 49/5
50 Viscosity and the Mechanisms of Momentum Transport Based on the given diagram: The pressure force-always perpendicular to the exposed surface. Thus, the force per unit area on the shaded surface will be a vector pδ x (pressure multiplied by the unit vector δ x in the x direction) Same goes to the y and z directions. EKC314-SCE p. 50/5
51 Viscosity and the Mechanisms of Momentum Transport The velocity gradients within the fluid are neither perpendicular to the surface element nor parallel to it, but rather at some angle to the surface. The force per unit area, τ x exerted on the shaded area with components (τ xx, τ xy and τ xz ). This can be conveniently represented by standard symbols which include both types of stresses (pressure and viscous stresses); π ij = pδ ij + τ ij where i and j may be x, y or z. EKC314-SCE p. 51/5
52 Viscosity and the Mechanisms of Momentum Transport Here, δ ij is the Kronecker delta, which is 1 if i = j and zero if i j. The term π ij can be defined as; force in the j direction on a unit area perpendicular to the i direction, where it is understood that the fluid in the region of lesser x i is exerting the force on the fluid of greater x i. flux of j-momentum in the positive i direction that is, from the region of lesser x i to that of greater x i. EKC314-SCE p. 52/5
53 Viscosity and the Mechanisms of Momentum Transport Summary of the components of the molecular stress tensor. Dir. Vector force Components of forces x-component y-component z-component x π x = pδ x + τ x π xx = p + τ xx π xy = τ xy π xz = τ xz y π y = pδ y + τ y π yx = τ yx π yy = p + τ yy π yz = τ yz z π z = pδ z + τ z π zx = τ zx π zy = τ zy π zz = p + τ zz EKC314-SCE p. 53/5
Chapter 5. The Differential Forms of the Fundamental Laws
 Chapter 5 The Differential Forms of the Fundamental Laws 1 5.1 Introduction Two primary methods in deriving the differential forms of fundamental laws: Gauss s Theorem: Allows area integrals of the equations
Chapter 5 The Differential Forms of the Fundamental Laws 1 5.1 Introduction Two primary methods in deriving the differential forms of fundamental laws: Gauss s Theorem: Allows area integrals of the equations
V (r,t) = i ˆ u( x, y,z,t) + ˆ j v( x, y,z,t) + k ˆ w( x, y, z,t)
 IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
Getting started: CFD notation
 PDE of p-th order Getting started: CFD notation f ( u,x, t, u x 1,..., u x n, u, 2 u x 1 x 2,..., p u p ) = 0 scalar unknowns u = u(x, t), x R n, t R, n = 1,2,3 vector unknowns v = v(x, t), v R m, m =
PDE of p-th order Getting started: CFD notation f ( u,x, t, u x 1,..., u x n, u, 2 u x 1 x 2,..., p u p ) = 0 scalar unknowns u = u(x, t), x R n, t R, n = 1,2,3 vector unknowns v = v(x, t), v R m, m =
Numerical Heat and Mass Transfer
 Master Degree in Mechanical Engineering Numerical Heat and Mass Transfer 15-Convective Heat Transfer Fausto Arpino f.arpino@unicas.it Introduction In conduction problems the convection entered the analysis
Master Degree in Mechanical Engineering Numerical Heat and Mass Transfer 15-Convective Heat Transfer Fausto Arpino f.arpino@unicas.it Introduction In conduction problems the convection entered the analysis
In this section, mathematical description of the motion of fluid elements moving in a flow field is
 Jun. 05, 015 Chapter 6. Differential Analysis of Fluid Flow 6.1 Fluid Element Kinematics In this section, mathematical description of the motion of fluid elements moving in a flow field is given. A small
Jun. 05, 015 Chapter 6. Differential Analysis of Fluid Flow 6.1 Fluid Element Kinematics In this section, mathematical description of the motion of fluid elements moving in a flow field is given. A small
Differential Operators and the Divergence Theorem
 1 of 6 1/15/2007 6:31 PM Differential Operators and the Divergence Theorem One of the most important and useful mathematical constructs is the "del operator", usually denoted by the symbol Ñ (which is
1 of 6 1/15/2007 6:31 PM Differential Operators and the Divergence Theorem One of the most important and useful mathematical constructs is the "del operator", usually denoted by the symbol Ñ (which is
MECH 5312 Solid Mechanics II. Dr. Calvin M. Stewart Department of Mechanical Engineering The University of Texas at El Paso
 MECH 5312 Solid Mechanics II Dr. Calvin M. Stewart Department of Mechanical Engineering The University of Texas at El Paso Table of Contents Preliminary Math Concept of Stress Stress Components Equilibrium
MECH 5312 Solid Mechanics II Dr. Calvin M. Stewart Department of Mechanical Engineering The University of Texas at El Paso Table of Contents Preliminary Math Concept of Stress Stress Components Equilibrium
AE/ME 339. K. M. Isaac Professor of Aerospace Engineering. 12/21/01 topic7_ns_equations 1
 AE/ME 339 Professor of Aerospace Engineering 12/21/01 topic7_ns_equations 1 Continuity equation Governing equation summary Non-conservation form D Dt. V 0.(2.29) Conservation form ( V ) 0...(2.33) t 12/21/01
AE/ME 339 Professor of Aerospace Engineering 12/21/01 topic7_ns_equations 1 Continuity equation Governing equation summary Non-conservation form D Dt. V 0.(2.29) Conservation form ( V ) 0...(2.33) t 12/21/01
Notes 4: Differential Form of the Conservation Equations
 Low Speed Aerodynamics Notes 4: Differential Form of the Conservation Equations Deriving Conservation Equations From the Laws of Physics Physical Laws Fluids, being matter, must obey the laws of Physics.
Low Speed Aerodynamics Notes 4: Differential Form of the Conservation Equations Deriving Conservation Equations From the Laws of Physics Physical Laws Fluids, being matter, must obey the laws of Physics.
AE/ME 339. Computational Fluid Dynamics (CFD) K. M. Isaac. Momentum equation. Computational Fluid Dynamics (AE/ME 339) MAEEM Dept.
 AE/ME 339 Computational Fluid Dynamics (CFD) 9//005 Topic7_NS_ F0 1 Momentum equation 9//005 Topic7_NS_ F0 1 Consider the moving fluid element model shown in Figure.b Basis is Newton s nd Law which says
AE/ME 339 Computational Fluid Dynamics (CFD) 9//005 Topic7_NS_ F0 1 Momentum equation 9//005 Topic7_NS_ F0 1 Consider the moving fluid element model shown in Figure.b Basis is Newton s nd Law which says
Chapter 9: Differential Analysis
 9-1 Introduction 9-2 Conservation of Mass 9-3 The Stream Function 9-4 Conservation of Linear Momentum 9-5 Navier Stokes Equation 9-6 Differential Analysis Problems Recall 9-1 Introduction (1) Chap 5: Control
9-1 Introduction 9-2 Conservation of Mass 9-3 The Stream Function 9-4 Conservation of Linear Momentum 9-5 Navier Stokes Equation 9-6 Differential Analysis Problems Recall 9-1 Introduction (1) Chap 5: Control
Chapter 1. Viscosity and the stress (momentum flux) tensor
 Chapter 1. Viscosity and the stress (momentum flux) tensor Viscosity and the Mechanisms of Momentum Transport 1.1 Newton s law of viscosity ( molecular momentum transport) 1.2 Generalization of Newton
Chapter 1. Viscosity and the stress (momentum flux) tensor Viscosity and the Mechanisms of Momentum Transport 1.1 Newton s law of viscosity ( molecular momentum transport) 1.2 Generalization of Newton
Chapter 1 Fluid Characteristics
 Chapter 1 Fluid Characteristics 1.1 Introduction 1.1.1 Phases Solid increasing increasing spacing and intermolecular liquid latitude of cohesive Fluid gas (vapor) molecular force plasma motion 1.1.2 Fluidity
Chapter 1 Fluid Characteristics 1.1 Introduction 1.1.1 Phases Solid increasing increasing spacing and intermolecular liquid latitude of cohesive Fluid gas (vapor) molecular force plasma motion 1.1.2 Fluidity
Chapter 9: Differential Analysis of Fluid Flow
 of Fluid Flow Objectives 1. Understand how the differential equations of mass and momentum conservation are derived. 2. Calculate the stream function and pressure field, and plot streamlines for a known
of Fluid Flow Objectives 1. Understand how the differential equations of mass and momentum conservation are derived. 2. Calculate the stream function and pressure field, and plot streamlines for a known
Review of Fluid Mechanics
 Chapter 3 Review of Fluid Mechanics 3.1 Units and Basic Definitions Newton s Second law forms the basis of all units of measurement. For a particle of mass m subjected to a resultant force F the law may
Chapter 3 Review of Fluid Mechanics 3.1 Units and Basic Definitions Newton s Second law forms the basis of all units of measurement. For a particle of mass m subjected to a resultant force F the law may
Multiple Integrals and Vector Calculus: Synopsis
 Multiple Integrals and Vector Calculus: Synopsis Hilary Term 28: 14 lectures. Steve Rawlings. 1. Vectors - recap of basic principles. Things which are (and are not) vectors. Differentiation and integration
Multiple Integrals and Vector Calculus: Synopsis Hilary Term 28: 14 lectures. Steve Rawlings. 1. Vectors - recap of basic principles. Things which are (and are not) vectors. Differentiation and integration
Module 2: Governing Equations and Hypersonic Relations
 Module 2: Governing Equations and Hypersonic Relations Lecture -2: Mass Conservation Equation 2.1 The Differential Equation for mass conservation: Let consider an infinitely small elemental control volume
Module 2: Governing Equations and Hypersonic Relations Lecture -2: Mass Conservation Equation 2.1 The Differential Equation for mass conservation: Let consider an infinitely small elemental control volume
Chapter 2: Basic Governing Equations
 -1 Reynolds Transport Theorem (RTT) - Continuity Equation -3 The Linear Momentum Equation -4 The First Law of Thermodynamics -5 General Equation in Conservative Form -6 General Equation in Non-Conservative
-1 Reynolds Transport Theorem (RTT) - Continuity Equation -3 The Linear Momentum Equation -4 The First Law of Thermodynamics -5 General Equation in Conservative Form -6 General Equation in Non-Conservative
Chapter 2: Fluid Dynamics Review
 7 Chapter 2: Fluid Dynamics Review This chapter serves as a short review of basic fluid mechanics. We derive the relevant transport equations (or conservation equations), state Newton s viscosity law leading
7 Chapter 2: Fluid Dynamics Review This chapter serves as a short review of basic fluid mechanics. We derive the relevant transport equations (or conservation equations), state Newton s viscosity law leading
Exercises for Multivariable Differential Calculus XM521
 This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
Chapter 1. Vector Algebra and Vector Space
 1. Vector Algebra 1.1. Scalars and vectors Chapter 1. Vector Algebra and Vector Space The simplest kind of physical quantity is one that can be completely specified by its magnitude, a single number, together
1. Vector Algebra 1.1. Scalars and vectors Chapter 1. Vector Algebra and Vector Space The simplest kind of physical quantity is one that can be completely specified by its magnitude, a single number, together
Multiple Integrals and Vector Calculus (Oxford Physics) Synopsis and Problem Sets; Hilary 2015
 Multiple Integrals and Vector Calculus (Oxford Physics) Ramin Golestanian Synopsis and Problem Sets; Hilary 215 The outline of the material, which will be covered in 14 lectures, is as follows: 1. Introduction
Multiple Integrals and Vector Calculus (Oxford Physics) Ramin Golestanian Synopsis and Problem Sets; Hilary 215 The outline of the material, which will be covered in 14 lectures, is as follows: 1. Introduction
Chapter 4: Fluid Kinematics
 Overview Fluid kinematics deals with the motion of fluids without considering the forces and moments which create the motion. Items discussed in this Chapter. Material derivative and its relationship to
Overview Fluid kinematics deals with the motion of fluids without considering the forces and moments which create the motion. Items discussed in this Chapter. Material derivative and its relationship to
KINEMATICS OF CONTINUA
 KINEMATICS OF CONTINUA Introduction Deformation of a continuum Configurations of a continuum Deformation mapping Descriptions of motion Material time derivative Velocity and acceleration Transformation
KINEMATICS OF CONTINUA Introduction Deformation of a continuum Configurations of a continuum Deformation mapping Descriptions of motion Material time derivative Velocity and acceleration Transformation
Vector Analysis. Electromagnetic Theory PHYS 401. Fall 2017
 Vector Analysis Electromagnetic Theory PHYS 401 Fall 2017 1 Vector Analysis Vector analysis is a mathematical formalism with which EM concepts are most conveniently expressed and best comprehended. Many
Vector Analysis Electromagnetic Theory PHYS 401 Fall 2017 1 Vector Analysis Vector analysis is a mathematical formalism with which EM concepts are most conveniently expressed and best comprehended. Many
Introduction and Vectors Lecture 1
 1 Introduction Introduction and Vectors Lecture 1 This is a course on classical Electromagnetism. It is the foundation for more advanced courses in modern physics. All physics of the modern era, from quantum
1 Introduction Introduction and Vectors Lecture 1 This is a course on classical Electromagnetism. It is the foundation for more advanced courses in modern physics. All physics of the modern era, from quantum
Math Review: Vectors and Tensors for Rheological Applications
 Math Review: Vectors and Tensors for Rheological Applications Presented by Randy H. Ewoldt University of Illinois at Urbana-Champaign U. of Minnesota Rheological Measurements Short Course June 2016 MathReview-1
Math Review: Vectors and Tensors for Rheological Applications Presented by Randy H. Ewoldt University of Illinois at Urbana-Champaign U. of Minnesota Rheological Measurements Short Course June 2016 MathReview-1
ENGR Heat Transfer II
 ENGR 7901 - Heat Transfer II Convective Heat Transfer 1 Introduction In this portion of the course we will examine convection heat transfer principles. We are now interested in how to predict the value
ENGR 7901 - Heat Transfer II Convective Heat Transfer 1 Introduction In this portion of the course we will examine convection heat transfer principles. We are now interested in how to predict the value
Created by T. Madas VECTOR OPERATORS. Created by T. Madas
 VECTOR OPERATORS GRADIENT gradϕ ϕ Question 1 A surface S is given by the Cartesian equation x 2 2 + y = 25. a) Draw a sketch of S, and describe it geometrically. b) Determine an equation of the tangent
VECTOR OPERATORS GRADIENT gradϕ ϕ Question 1 A surface S is given by the Cartesian equation x 2 2 + y = 25. a) Draw a sketch of S, and describe it geometrically. b) Determine an equation of the tangent
Introduction to Fluid Mechanics
 Introduction to Fluid Mechanics Tien-Tsan Shieh April 16, 2009 What is a Fluid? The key distinction between a fluid and a solid lies in the mode of resistance to change of shape. The fluid, unlike the
Introduction to Fluid Mechanics Tien-Tsan Shieh April 16, 2009 What is a Fluid? The key distinction between a fluid and a solid lies in the mode of resistance to change of shape. The fluid, unlike the
AMME2261: Fluid Mechanics 1 Course Notes
 Module 1 Introduction and Fluid Properties Introduction Matter can be one of two states: solid or fluid. A fluid is a substance that deforms continuously under the application of a shear stress, no matter
Module 1 Introduction and Fluid Properties Introduction Matter can be one of two states: solid or fluid. A fluid is a substance that deforms continuously under the application of a shear stress, no matter
2. FLUID-FLOW EQUATIONS SPRING 2019
 2. FLUID-FLOW EQUATIONS SPRING 2019 2.1 Introduction 2.2 Conservative differential equations 2.3 Non-conservative differential equations 2.4 Non-dimensionalisation Summary Examples 2.1 Introduction Fluid
2. FLUID-FLOW EQUATIONS SPRING 2019 2.1 Introduction 2.2 Conservative differential equations 2.3 Non-conservative differential equations 2.4 Non-dimensionalisation Summary Examples 2.1 Introduction Fluid
Chapter 3: Newtonian Fluids
 Chapter 3: Newtonian Fluids CM4650 Michigan Tech Navier-Stokes Equation v vv p t 2 v g 1 Chapter 3: Newtonian Fluid TWO GOALS Derive governing equations (mass and momentum balances Solve governing equations
Chapter 3: Newtonian Fluids CM4650 Michigan Tech Navier-Stokes Equation v vv p t 2 v g 1 Chapter 3: Newtonian Fluid TWO GOALS Derive governing equations (mass and momentum balances Solve governing equations
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION
 CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
PEAT SEISMOLOGY Lecture 2: Continuum mechanics
 PEAT8002 - SEISMOLOGY Lecture 2: Continuum mechanics Nick Rawlinson Research School of Earth Sciences Australian National University Strain Strain is the formal description of the change in shape of a
PEAT8002 - SEISMOLOGY Lecture 2: Continuum mechanics Nick Rawlinson Research School of Earth Sciences Australian National University Strain Strain is the formal description of the change in shape of a
CHAPTER 7 DIV, GRAD, AND CURL
 CHAPTER 7 DIV, GRAD, AND CURL 1 The operator and the gradient: Recall that the gradient of a differentiable scalar field ϕ on an open set D in R n is given by the formula: (1 ϕ = ( ϕ, ϕ,, ϕ x 1 x 2 x n
CHAPTER 7 DIV, GRAD, AND CURL 1 The operator and the gradient: Recall that the gradient of a differentiable scalar field ϕ on an open set D in R n is given by the formula: (1 ϕ = ( ϕ, ϕ,, ϕ x 1 x 2 x n
Quick Recapitulation of Fluid Mechanics
 Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Page Problem Score Max Score a 8 12b a b 10 14c 6 6
 Fall 14 MTH 34 FINAL EXAM December 8, 14 Name: PID: Section: Instructor: DO NOT WRITE BELOW THIS LINE. Go to the next page. Page Problem Score Max Score 1 5 5 1 3 5 4 5 5 5 6 5 7 5 8 5 9 5 1 5 11 1 3 1a
Fall 14 MTH 34 FINAL EXAM December 8, 14 Name: PID: Section: Instructor: DO NOT WRITE BELOW THIS LINE. Go to the next page. Page Problem Score Max Score 1 5 5 1 3 5 4 5 5 5 6 5 7 5 8 5 9 5 1 5 11 1 3 1a
Chapter 6: Momentum Analysis
 6-1 Introduction 6-2Newton s Law and Conservation of Momentum 6-3 Choosing a Control Volume 6-4 Forces Acting on a Control Volume 6-5Linear Momentum Equation 6-6 Angular Momentum 6-7 The Second Law of
6-1 Introduction 6-2Newton s Law and Conservation of Momentum 6-3 Choosing a Control Volume 6-4 Forces Acting on a Control Volume 6-5Linear Momentum Equation 6-6 Angular Momentum 6-7 The Second Law of
MATH Calculus IV Spring 2014 Three Versions of the Divergence Theorem
 MATH 2443 008 Calculus IV pring 2014 Three Versions of the Divergence Theorem In this note we will establish versions of the Divergence Theorem which enable us to give it formulations of div, grad, and
MATH 2443 008 Calculus IV pring 2014 Three Versions of the Divergence Theorem In this note we will establish versions of the Divergence Theorem which enable us to give it formulations of div, grad, and
PEMP ACD2505. M.S. Ramaiah School of Advanced Studies, Bengaluru
 Governing Equations of Fluid Flow Session delivered by: M. Sivapragasam 1 Session Objectives -- At the end of this session the delegate would have understood The principle of conservation laws Different
Governing Equations of Fluid Flow Session delivered by: M. Sivapragasam 1 Session Objectives -- At the end of this session the delegate would have understood The principle of conservation laws Different
Fluid Mechanics II Viscosity and shear stresses
 Fluid Mechanics II Viscosity and shear stresses Shear stresses in a Newtonian fluid A fluid at rest can not resist shearing forces. Under the action of such forces it deforms continuously, however small
Fluid Mechanics II Viscosity and shear stresses Shear stresses in a Newtonian fluid A fluid at rest can not resist shearing forces. Under the action of such forces it deforms continuously, however small
A Study on Numerical Solution to the Incompressible Navier-Stokes Equation
 A Study on Numerical Solution to the Incompressible Navier-Stokes Equation Zipeng Zhao May 2014 1 Introduction 1.1 Motivation One of the most important applications of finite differences lies in the field
A Study on Numerical Solution to the Incompressible Navier-Stokes Equation Zipeng Zhao May 2014 1 Introduction 1.1 Motivation One of the most important applications of finite differences lies in the field
Introduction to Vector Calculus (29) SOLVED EXAMPLES. (d) B. C A. (f) a unit vector perpendicular to both B. = ˆ 2k = = 8 = = 8
 Introduction to Vector Calculus (9) SOLVED EXAMPLES Q. If vector A i ˆ ˆj k, ˆ B i ˆ ˆj, C i ˆ 3j ˆ kˆ (a) A B (e) A B C (g) Solution: (b) A B (c) A. B C (d) B. C A then find (f) a unit vector perpendicular
Introduction to Vector Calculus (9) SOLVED EXAMPLES Q. If vector A i ˆ ˆj k, ˆ B i ˆ ˆj, C i ˆ 3j ˆ kˆ (a) A B (e) A B C (g) Solution: (b) A B (c) A. B C (d) B. C A then find (f) a unit vector perpendicular
9.7 Gradient of a Scalar Field. Directional Derivative. Mean Value Theorem. Special Cases
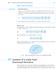 SEC. 9.7 Gradient of a Scalar Field. Directional Derivative 395 Mean Value Theorems THEOREM Mean Value Theorem Let f(x, y, z) be continuous and have continuous first partial derivatives in a domain D in
SEC. 9.7 Gradient of a Scalar Field. Directional Derivative 395 Mean Value Theorems THEOREM Mean Value Theorem Let f(x, y, z) be continuous and have continuous first partial derivatives in a domain D in
52. The Del Operator: Divergence and Curl
 52. The Del Operator: Divergence and Curl Let F(x, y, z) = M(x, y, z), N(x, y, z), P(x, y, z) be a vector field in R 3. The del operator is represented by the symbol, and is written = x, y, z, or = x,
52. The Del Operator: Divergence and Curl Let F(x, y, z) = M(x, y, z), N(x, y, z), P(x, y, z) be a vector field in R 3. The del operator is represented by the symbol, and is written = x, y, z, or = x,
Navier-Stokes Equation: Principle of Conservation of Momentum
 Navier-tokes Equation: Principle of Conservation of Momentum R. hankar ubramanian Department of Chemical and Biomolecular Engineering Clarkson University Newton formulated the principle of conservation
Navier-tokes Equation: Principle of Conservation of Momentum R. hankar ubramanian Department of Chemical and Biomolecular Engineering Clarkson University Newton formulated the principle of conservation
Vector Calculus, Maths II
 Section A Vector Calculus, Maths II REVISION (VECTORS) 1. Position vector of a point P(x, y, z) is given as + y and its magnitude by 2. The scalar components of a vector are its direction ratios, and represent
Section A Vector Calculus, Maths II REVISION (VECTORS) 1. Position vector of a point P(x, y, z) is given as + y and its magnitude by 2. The scalar components of a vector are its direction ratios, and represent
Convection Heat Transfer
 Convection Heat Transfer Department of Chemical Eng., Isfahan University of Technology, Isfahan, Iran Seyed Gholamreza Etemad Winter 2013 Heat convection: Introduction Difference between the temperature
Convection Heat Transfer Department of Chemical Eng., Isfahan University of Technology, Isfahan, Iran Seyed Gholamreza Etemad Winter 2013 Heat convection: Introduction Difference between the temperature
A Brief Revision of Vector Calculus and Maxwell s Equations
 A Brief Revision of Vector Calculus and Maxwell s Equations Debapratim Ghosh Electronic Systems Group Department of Electrical Engineering Indian Institute of Technology Bombay e-mail: dghosh@ee.iitb.ac.in
A Brief Revision of Vector Calculus and Maxwell s Equations Debapratim Ghosh Electronic Systems Group Department of Electrical Engineering Indian Institute of Technology Bombay e-mail: dghosh@ee.iitb.ac.in
BSL Transport Phenomena 2e Revised: Chapter 2 - Problem 2B.11 Page 1 of 5
 BS Transport Phenomena 2e Revised: Chapter 2 - Problem 2B11 Page 1 of 5 Problem 2B11 The cone-and-plate viscometer (see Fig 2B11 A cone-and-plate viscometer consists of a flat plate and an inverted cone,
BS Transport Phenomena 2e Revised: Chapter 2 - Problem 2B11 Page 1 of 5 Problem 2B11 The cone-and-plate viscometer (see Fig 2B11 A cone-and-plate viscometer consists of a flat plate and an inverted cone,
DIPOLES III. q const. The voltage produced by such a charge distribution is given by. r r'
 DIPOLES III We now consider a particularly important charge configuration a dipole. This consists of two equal but opposite charges separated by a small distance. We define the dipole moment as p lim q
DIPOLES III We now consider a particularly important charge configuration a dipole. This consists of two equal but opposite charges separated by a small distance. We define the dipole moment as p lim q
2.20 Fall 2018 Math Review
 2.20 Fall 2018 Math Review September 10, 2018 These notes are to help you through the math used in this class. This is just a refresher, so if you never learned one of these topics you should look more
2.20 Fall 2018 Math Review September 10, 2018 These notes are to help you through the math used in this class. This is just a refresher, so if you never learned one of these topics you should look more
Lecture 3: 1. Lecture 3.
 Lecture 3: 1 Lecture 3. Lecture 3: 2 Plan for today Summary of the key points of the last lecture. Review of vector and tensor products : the dot product (or inner product ) and the cross product (or vector
Lecture 3: 1 Lecture 3. Lecture 3: 2 Plan for today Summary of the key points of the last lecture. Review of vector and tensor products : the dot product (or inner product ) and the cross product (or vector
Mathematical Theory of Non-Newtonian Fluid
 Mathematical Theory of Non-Newtonian Fluid 1. Derivation of the Incompressible Fluid Dynamics 2. Existence of Non-Newtonian Flow and its Dynamics 3. Existence in the Domain with Boundary Hyeong Ohk Bae
Mathematical Theory of Non-Newtonian Fluid 1. Derivation of the Incompressible Fluid Dynamics 2. Existence of Non-Newtonian Flow and its Dynamics 3. Existence in the Domain with Boundary Hyeong Ohk Bae
AA210A Fundamentals of Compressible Flow. Chapter 1 - Introduction to fluid flow
 AA210A Fundamentals of Compressible Flow Chapter 1 - Introduction to fluid flow 1 1.2 Conservation of mass Mass flux in the x-direction [ ρu ] = M L 3 L T = M L 2 T Momentum per unit volume Mass per unit
AA210A Fundamentals of Compressible Flow Chapter 1 - Introduction to fluid flow 1 1.2 Conservation of mass Mass flux in the x-direction [ ρu ] = M L 3 L T = M L 2 T Momentum per unit volume Mass per unit
Fundamentals of Transport Processes Prof. Kumaran Indian Institute of Science, Bangalore Chemical Engineering
 Fundamentals of Transport Processes Prof. Kumaran Indian Institute of Science, Bangalore Chemical Engineering Module No # 05 Lecture No # 25 Mass and Energy Conservation Cartesian Co-ordinates Welcome
Fundamentals of Transport Processes Prof. Kumaran Indian Institute of Science, Bangalore Chemical Engineering Module No # 05 Lecture No # 25 Mass and Energy Conservation Cartesian Co-ordinates Welcome
ENGI Gradient, Divergence, Curl Page 5.01
 ENGI 94 5. - Gradient, Divergence, Curl Page 5. 5. The Gradient Operator A brief review is provided here for the gradient operator in both Cartesian and orthogonal non-cartesian coordinate systems. Sections
ENGI 94 5. - Gradient, Divergence, Curl Page 5. 5. The Gradient Operator A brief review is provided here for the gradient operator in both Cartesian and orthogonal non-cartesian coordinate systems. Sections
Review of fluid dynamics
 Chapter 2 Review of fluid dynamics 2.1 Preliminaries ome basic concepts: A fluid is a substance that deforms continuously under stress. A Material olume is a tagged region that moves with the fluid. Hence
Chapter 2 Review of fluid dynamics 2.1 Preliminaries ome basic concepts: A fluid is a substance that deforms continuously under stress. A Material olume is a tagged region that moves with the fluid. Hence
Divergence Theorem Fundamental Theorem, Four Ways. 3D Fundamental Theorem. Divergence Theorem
 Divergence Theorem 17.3 11 December 213 Fundamental Theorem, Four Ways. b F (x) dx = F (b) F (a) a [a, b] F (x) on boundary of If C path from P to Q, ( φ) ds = φ(q) φ(p) C φ on boundary of C Green s Theorem:
Divergence Theorem 17.3 11 December 213 Fundamental Theorem, Four Ways. b F (x) dx = F (b) F (a) a [a, b] F (x) on boundary of If C path from P to Q, ( φ) ds = φ(q) φ(p) C φ on boundary of C Green s Theorem:
MATH 332: Vector Analysis Summer 2005 Homework
 MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
Review of Vector Analysis in Cartesian Coordinates
 Review of Vector Analysis in Cartesian Coordinates 1 Scalar: A quantity that has magnitude, but no direction. Examples are mass, temperature, pressure, time, distance, and real numbers. Scalars are usually
Review of Vector Analysis in Cartesian Coordinates 1 Scalar: A quantity that has magnitude, but no direction. Examples are mass, temperature, pressure, time, distance, and real numbers. Scalars are usually
3. FORMS OF GOVERNING EQUATIONS IN CFD
 3. FORMS OF GOVERNING EQUATIONS IN CFD 3.1. Governing and model equations in CFD Fluid flows are governed by the Navier-Stokes equations (N-S), which simpler, inviscid, form is the Euler equations. For
3. FORMS OF GOVERNING EQUATIONS IN CFD 3.1. Governing and model equations in CFD Fluid flows are governed by the Navier-Stokes equations (N-S), which simpler, inviscid, form is the Euler equations. For
Fluid Mechanics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur
 Fluid Mechanics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture - 15 Conservation Equations in Fluid Flow Part III Good afternoon. I welcome you all
Fluid Mechanics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture - 15 Conservation Equations in Fluid Flow Part III Good afternoon. I welcome you all
12. Stresses and Strains
 12. Stresses and Strains Finite Element Method Differential Equation Weak Formulation Approximating Functions Weighted Residuals FEM - Formulation Classification of Problems Scalar Vector 1-D T(x) u(x)
12. Stresses and Strains Finite Element Method Differential Equation Weak Formulation Approximating Functions Weighted Residuals FEM - Formulation Classification of Problems Scalar Vector 1-D T(x) u(x)
is the ith variable and a i is the unit vector associated with the ith variable. h i
 . Chapter 10 Vector Calculus Features Used right( ), product( ),./,.*, listúmat( ), mod( ), For...EndFor, norm( ), unitv( ),
. Chapter 10 Vector Calculus Features Used right( ), product( ),./,.*, listúmat( ), mod( ), For...EndFor, norm( ), unitv( ),
Control Volume. Dynamics and Kinematics. Basic Conservation Laws. Lecture 1: Introduction and Review 1/24/2017
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review
 Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Wave and Elasticity Equations
 1 Wave and lasticity quations Now let us consider the vibrating string problem which is modeled by the one-dimensional wave equation. Suppose that a taut string is suspended by its extremes at the points
1 Wave and lasticity quations Now let us consider the vibrating string problem which is modeled by the one-dimensional wave equation. Suppose that a taut string is suspended by its extremes at the points
Introduction to Fluid Dynamics
 Introduction to Fluid Dynamics Roger K. Smith Skript - auf englisch! Umsonst im Internet http://www.meteo.physik.uni-muenchen.de Wählen: Lehre Manuskripte Download User Name: meteo Password: download Aim
Introduction to Fluid Dynamics Roger K. Smith Skript - auf englisch! Umsonst im Internet http://www.meteo.physik.uni-muenchen.de Wählen: Lehre Manuskripte Download User Name: meteo Password: download Aim
Math review. Math review
 Math review 1 Math review 3 1 series approximations 3 Taylor s Theorem 3 Binomial approximation 3 sin(x), for x in radians and x close to zero 4 cos(x), for x in radians and x close to zero 5 2 some geometry
Math review 1 Math review 3 1 series approximations 3 Taylor s Theorem 3 Binomial approximation 3 sin(x), for x in radians and x close to zero 4 cos(x), for x in radians and x close to zero 5 2 some geometry
Macroscopic theory Rock as 'elastic continuum'
 Elasticity and Seismic Waves Macroscopic theory Rock as 'elastic continuum' Elastic body is deformed in response to stress Two types of deformation: Change in volume and shape Equations of motion Wave
Elasticity and Seismic Waves Macroscopic theory Rock as 'elastic continuum' Elastic body is deformed in response to stress Two types of deformation: Change in volume and shape Equations of motion Wave
EE2007: Engineering Mathematics II Vector Calculus
 EE2007: Engineering Mathematics II Vector Calculus Ling KV School of EEE, NTU ekvling@ntu.edu.sg Rm: S2-B2b-22 Ver 1.1: Ling KV, October 22, 2006 Ver 1.0: Ling KV, Jul 2005 EE2007/Ling KV/Aug 2006 EE2007:
EE2007: Engineering Mathematics II Vector Calculus Ling KV School of EEE, NTU ekvling@ntu.edu.sg Rm: S2-B2b-22 Ver 1.1: Ling KV, October 22, 2006 Ver 1.0: Ling KV, Jul 2005 EE2007/Ling KV/Aug 2006 EE2007:
Rheology of Soft Materials. Rheology
 Τ Thomas G. Mason Department of Chemistry and Biochemistry Department of Physics and Astronomy California NanoSystems Institute Τ γ 26 by Thomas G. Mason All rights reserved. γ (t) τ (t) γ τ Δt 2π t γ
Τ Thomas G. Mason Department of Chemistry and Biochemistry Department of Physics and Astronomy California NanoSystems Institute Τ γ 26 by Thomas G. Mason All rights reserved. γ (t) τ (t) γ τ Δt 2π t γ
Math 207 Honors Calculus III Final Exam Solutions
 Math 207 Honors Calculus III Final Exam Solutions PART I. Problem 1. A particle moves in the 3-dimensional space so that its velocity v(t) and acceleration a(t) satisfy v(0) = 3j and v(t) a(t) = t 3 for
Math 207 Honors Calculus III Final Exam Solutions PART I. Problem 1. A particle moves in the 3-dimensional space so that its velocity v(t) and acceleration a(t) satisfy v(0) = 3j and v(t) a(t) = t 3 for
Sec. 1.1: Basics of Vectors
 Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
6. 3D Kinematics DE2-EA 2.1: M4DE. Dr Connor Myant
 DE2-EA 2.1: M4DE Dr Connor Myant 6. 3D Kinematics Comments and corrections to connor.myant@imperial.ac.uk Lecture resources may be found on Blackboard and at http://connormyant.com Contents Three-Dimensional
DE2-EA 2.1: M4DE Dr Connor Myant 6. 3D Kinematics Comments and corrections to connor.myant@imperial.ac.uk Lecture resources may be found on Blackboard and at http://connormyant.com Contents Three-Dimensional
2.29 Numerical Fluid Mechanics Fall 2011 Lecture 5
 .9 Numerical Fluid Mechanics Fall 011 Lecture 5 REVIEW Lecture 4 Roots of nonlinear equations: Open Methods Fixed-point Iteration (General method or Picard Iteration), with examples Iteration rule: x g(
.9 Numerical Fluid Mechanics Fall 011 Lecture 5 REVIEW Lecture 4 Roots of nonlinear equations: Open Methods Fixed-point Iteration (General method or Picard Iteration), with examples Iteration rule: x g(
Introduction to Heat and Mass Transfer. Week 10
 Introduction to Heat and Mass Transfer Week 10 Concentration Boundary Layer No concentration jump condition requires species adjacent to surface to have same concentration as at the surface Owing to concentration
Introduction to Heat and Mass Transfer Week 10 Concentration Boundary Layer No concentration jump condition requires species adjacent to surface to have same concentration as at the surface Owing to concentration
Divergence Theorem December 2013
 Divergence Theorem 17.3 11 December 2013 Fundamental Theorem, Four Ways. b F (x) dx = F (b) F (a) a [a, b] F (x) on boundary of If C path from P to Q, ( φ) ds = φ(q) φ(p) C φ on boundary of C Green s Theorem:
Divergence Theorem 17.3 11 December 2013 Fundamental Theorem, Four Ways. b F (x) dx = F (b) F (a) a [a, b] F (x) on boundary of If C path from P to Q, ( φ) ds = φ(q) φ(p) C φ on boundary of C Green s Theorem:
Introduction to Marine Hydrodynamics
 1896 1920 1987 2006 Introduction to Marine Hydrodynamics (NA235) Department of Naval Architecture and Ocean Engineering School of Naval Architecture, Ocean & Civil Engineering First Assignment The first
1896 1920 1987 2006 Introduction to Marine Hydrodynamics (NA235) Department of Naval Architecture and Ocean Engineering School of Naval Architecture, Ocean & Civil Engineering First Assignment The first
Lecture 8: Tissue Mechanics
 Computational Biology Group (CoBi), D-BSSE, ETHZ Lecture 8: Tissue Mechanics Prof Dagmar Iber, PhD DPhil MSc Computational Biology 2015/16 7. Mai 2016 2 / 57 Contents 1 Introduction to Elastic Materials
Computational Biology Group (CoBi), D-BSSE, ETHZ Lecture 8: Tissue Mechanics Prof Dagmar Iber, PhD DPhil MSc Computational Biology 2015/16 7. Mai 2016 2 / 57 Contents 1 Introduction to Elastic Materials
Differential Vector Calculus
 Contents 8 Differential Vector Calculus 8. Background to Vector Calculus 8. Differential Vector Calculus 7 8.3 Orthogonal Curvilinear Coordinates 37 Learning outcomes In this Workbook you will learn about
Contents 8 Differential Vector Calculus 8. Background to Vector Calculus 8. Differential Vector Calculus 7 8.3 Orthogonal Curvilinear Coordinates 37 Learning outcomes In this Workbook you will learn about
FMIA. Fluid Mechanics and Its Applications 113 Series Editor: A. Thess. Moukalled Mangani Darwish. F. Moukalled L. Mangani M.
 FMIA F. Moukalled L. Mangani M. Darwish An Advanced Introduction with OpenFOAM and Matlab This textbook explores both the theoretical foundation of the Finite Volume Method (FVM) and its applications in
FMIA F. Moukalled L. Mangani M. Darwish An Advanced Introduction with OpenFOAM and Matlab This textbook explores both the theoretical foundation of the Finite Volume Method (FVM) and its applications in
(Refer Slide Time: 0:35)
 Fluid Dynamics And Turbo Machines. Professor Dr Shamit Bakshi. Department Of Mechanical Engineering. Indian Institute Of Technology Madras. Part A. Module-1. Lecture-4. Tutorial. (Refer Slide Time: 0:35)
Fluid Dynamics And Turbo Machines. Professor Dr Shamit Bakshi. Department Of Mechanical Engineering. Indian Institute Of Technology Madras. Part A. Module-1. Lecture-4. Tutorial. (Refer Slide Time: 0:35)
100 CHAPTER 4. SYSTEMS AND ADAPTIVE STEP SIZE METHODS APPENDIX
 100 CHAPTER 4. SYSTEMS AND ADAPTIVE STEP SIZE METHODS APPENDIX.1 Norms If we have an approximate solution at a given point and we want to calculate the absolute error, then we simply take the magnitude
100 CHAPTER 4. SYSTEMS AND ADAPTIVE STEP SIZE METHODS APPENDIX.1 Norms If we have an approximate solution at a given point and we want to calculate the absolute error, then we simply take the magnitude
Mathematical Preliminaries
 Mathematical Preliminaries Introductory Course on Multiphysics Modelling TOMAZ G. ZIELIŃKI bluebox.ippt.pan.pl/ tzielins/ Table of Contents Vectors, tensors, and index notation. Generalization of the concept
Mathematical Preliminaries Introductory Course on Multiphysics Modelling TOMAZ G. ZIELIŃKI bluebox.ippt.pan.pl/ tzielins/ Table of Contents Vectors, tensors, and index notation. Generalization of the concept
2. Conservation Equations for Turbulent Flows
 2. Conservation Equations for Turbulent Flows Coverage of this section: Review of Tensor Notation Review of Navier-Stokes Equations for Incompressible and Compressible Flows Reynolds & Favre Averaging
2. Conservation Equations for Turbulent Flows Coverage of this section: Review of Tensor Notation Review of Navier-Stokes Equations for Incompressible and Compressible Flows Reynolds & Favre Averaging
J. Szantyr Lecture No. 4 Principles of the Turbulent Flow Theory The phenomenon of two markedly different types of flow, namely laminar and
 J. Szantyr Lecture No. 4 Principles of the Turbulent Flow Theory The phenomenon of two markedly different types of flow, namely laminar and turbulent, was discovered by Osborne Reynolds (184 191) in 1883
J. Szantyr Lecture No. 4 Principles of the Turbulent Flow Theory The phenomenon of two markedly different types of flow, namely laminar and turbulent, was discovered by Osborne Reynolds (184 191) in 1883
1/3/2011. This course discusses the physical laws that govern atmosphere/ocean motions.
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
UNIT 1. INTRODUCTION
 UNIT 1. INTRODUCTION Objective: The aim of this chapter is to gain knowledge on Basics of electromagnetic fields Scalar and vector quantities, vector calculus Various co-ordinate systems namely Cartesian,
UNIT 1. INTRODUCTION Objective: The aim of this chapter is to gain knowledge on Basics of electromagnetic fields Scalar and vector quantities, vector calculus Various co-ordinate systems namely Cartesian,
Some common examples of vector fields: wind shear off an object, gravitational fields, electric and magnetic fields, etc
 Vector Analysis Vector Fields Suppose a region in the plane or space is occupied by a moving fluid such as air or water. Imagine this fluid is made up of a very large number of particles that at any instant
Vector Analysis Vector Fields Suppose a region in the plane or space is occupied by a moving fluid such as air or water. Imagine this fluid is made up of a very large number of particles that at any instant
Fundamentals of Fluid Dynamics: Elementary Viscous Flow
 Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
Chapter 1. Continuum mechanics review. 1.1 Definitions and nomenclature
 Chapter 1 Continuum mechanics review We will assume some familiarity with continuum mechanics as discussed in the context of an introductory geodynamics course; a good reference for such problems is Turcotte
Chapter 1 Continuum mechanics review We will assume some familiarity with continuum mechanics as discussed in the context of an introductory geodynamics course; a good reference for such problems is Turcotte
Chapter 7. Kinematics. 7.1 Tensor fields
 Chapter 7 Kinematics 7.1 Tensor fields In fluid mechanics, the fluid flow is described in terms of vector fields or tensor fields such as velocity, stress, pressure, etc. It is important, at the outset,
Chapter 7 Kinematics 7.1 Tensor fields In fluid mechanics, the fluid flow is described in terms of vector fields or tensor fields such as velocity, stress, pressure, etc. It is important, at the outset,
Physics 6303 Lecture 2 August 22, 2018
 Physics 6303 Lecture 2 August 22, 2018 LAST TIME: Coordinate system construction, covariant and contravariant vector components, basics vector review, gradient, divergence, curl, and Laplacian operators
Physics 6303 Lecture 2 August 22, 2018 LAST TIME: Coordinate system construction, covariant and contravariant vector components, basics vector review, gradient, divergence, curl, and Laplacian operators
Viscous Fluids. Amanda Meier. December 14th, 2011
 Viscous Fluids Amanda Meier December 14th, 2011 Abstract Fluids are represented by continuous media described by mass density, velocity and pressure. An Eulerian description of uids focuses on the transport
Viscous Fluids Amanda Meier December 14th, 2011 Abstract Fluids are represented by continuous media described by mass density, velocity and pressure. An Eulerian description of uids focuses on the transport
The Divergence Theorem Stokes Theorem Applications of Vector Calculus. Calculus. Vector Calculus (III)
 Calculus Vector Calculus (III) Outline 1 The Divergence Theorem 2 Stokes Theorem 3 Applications of Vector Calculus The Divergence Theorem (I) Recall that at the end of section 12.5, we had rewritten Green
Calculus Vector Calculus (III) Outline 1 The Divergence Theorem 2 Stokes Theorem 3 Applications of Vector Calculus The Divergence Theorem (I) Recall that at the end of section 12.5, we had rewritten Green
CHAPTER 9. Microscopic Approach: from Boltzmann to Navier-Stokes. In the previous chapter we derived the closed Boltzmann equation:
 CHAPTER 9 Microscopic Approach: from Boltzmann to Navier-Stokes In the previous chapter we derived the closed Boltzmann equation: df dt = f +{f,h} = I[f] where I[f] is the collision integral, and we have
CHAPTER 9 Microscopic Approach: from Boltzmann to Navier-Stokes In the previous chapter we derived the closed Boltzmann equation: df dt = f +{f,h} = I[f] where I[f] is the collision integral, and we have
Modelling of dispersed, multicomponent, multiphase flows in resource industries. Section 3: Examples of analyses conducted for Newtonian fluids
 Modelling of dispersed, multicomponent, multiphase flows in resource industries Section 3: Examples of analyses conducted for Newtonian fluids Globex Julmester 017 Lecture # 04 July 017 Agenda Lecture
Modelling of dispersed, multicomponent, multiphase flows in resource industries Section 3: Examples of analyses conducted for Newtonian fluids Globex Julmester 017 Lecture # 04 July 017 Agenda Lecture
