LEGENDRIAN REALIZATION IN CONVEX LEFSCHETZ FIBRATIONS AND CONVEX STABILIZATIONS
|
|
|
- Jason Ryan
- 5 years ago
- Views:
Transcription
1 LEGENDRIAN REALIZATION IN CONVEX LEFSCHETZ FIBRATIONS AND CONVEX STABILIZATIONS SELMAN AKBULUT AND M. FIRAT ARIKAN arxiv: v1 [math.sg] 21 Nov 2012 Abstract. In this paper, we study compact convex Lefschetz fibrations on compact convex symplectic manifolds (i.e., Liouville domains) of dimension 2n + 2 which are introduced by Seidel and later also studied by McLean. By a result of Akbulut-Arikan, the open book on W, which we call convex open book, induced by a compact convex Lefschetz fibration on W carries the contact structure induced by the convex symplectic structure (i.e., Liouville structure) on W. Here we show that, up to a Liouville homotopy and a deformation of compact convex Lefschetz fibrations on W, any simply connected embedded Lagrangian submanifold of a page in a convex open book on W can be assumed to be Legendrian in W with the induced contact structure. This can be thought as the extension of Giroux s Legendrian realization (which holds for contact open books) for the case of convex open books. Moreover, a result of Akbulut-Arikan implies that there is a one-to-one correspondence between convex stabilizations of a convex open book and convex stabilizations of the corresponding compact convex Lefschetz fibration. We also show that the convex stabilization of a compact convex Lefschetz fibration on W yields a compact convex Lefschetz fibration on a Liouville domain W which is exact symplectomorphic to a positive expansion of W. In particular, with the induced structures W and W are contactomorphic. 1. Introduction LetM bean oriented smooth(2n+1)-manifold. A contact structure on M is aglobal 2n-plane field distribution ξ which is totally non-integrable. Non-integrability condition is equivalent to the fact that locally ξ can be given as the kernel of a 1-form α such that α (dα) n > 0. If α is globally defined, then it is called a contact form for ξ. An open book (decomposition) (B,Θ) on M is given by a codimension 2 submanifold B M with trivial normal bundle, and a fiber bundle Θ : M B S 1. The neighborhood of B should have a trivialization B D 2, where the angle coordinate on the disk agrees with the map Θ. The manifold B is called the binding, and for any t 0 S 1 a fiber X = Θ 1 (t 0 ) is called a page of the open book. A contact structure ξ on M is said to be supported by (or carried by) an open book (B,Θ) of M if there exists a contact form α for ξ such that (i) (B,α TB ) is a contact manifold. (ii) For every t S 1, the page X = Θ 1 (t) is a symplectic manifold with symplectic form dα. (iii) If X denotes the closure of a page X in M, then the orientation of B induced by its contact form α TB coincides with its orientation as the boundary of ( X,dα). An open book (B,Θ) on M is called a contact open book if it carries a contact structure on M. Date: November 22, Mathematics Subject Classification. 57R65, 58A05, 58D27. Key words and phrases. Liouville, convex symplectic, contact, Lefschetz fibration, open book, stabilization. The first author is partially supported by NSF FRG grant DMS The second author is partially supported by NSF FRG grant DMS , and also by TUBITAK grant. 1
2 2 SELMAN AKBULUT AND M. FIRAT ARIKAN Open books can be defined also abstractly in the following way: If (B,Θ) is an open book for M, with pages X, and if N(B) denotes the closed tubular neighborhood of B in M, then M intn(b) is a fiber bundle over S 1 with fibers X, hence it is diffeomorphic to the (generalized) mapping torus X(h) := [0,1] X/, where is the identification (0,p) (1,h(p)) for some diffeomorphism h : X X which is identity near X B. Observe that X(φ) B S 1, and so there is a unique way to glue N(B) B D 2 and get M back. Therefore, the pair ( X,h) (abstractly) determines the open book (B,Θ), and it is called an abstract open book of M. The map h is called the monodromy of the (abstract) open book. Our main theorem is Theorem 1.3 stated below. It can be considered as the extension of the following Giroux s result (given for contact open books) when the given contact open book arises as the boundary open book of a compact convex Lefschetz fibration over the 2-disk D 2. Theorem 1.1 (See, for instance, Lemma 4.2 in [12]). Let (X,h) be a contact open book for the contact manifold (M,ξ = Ker(α)) of dimension 2n + 1 for n 2. Let L be any Lagrangian n-sphere embedded in a page (X,dα). Then there exist an isotopy ξ t, t [0,1], of contact structures with ξ 0 = ξ and a contact open book carrying ξ 1 with symplectomorphic page and isotopic monodromy such that L is Legendrian in (M,ξ 1 ). A compact convex symplectic manifold (or a Liouville domain) is a pair (W,Λ) where W 2n+2 is a compact manifold with boundary, together with a convex symplectic structure (or a Liouville structure) whichisaone-form ΛonW suchthat Ω = dλissymplectic andtheω-dualvector field Z of Λ defined by ι Z Ω = Λ (or, equivalently, L Z Ω = Ω), where ι denotes the interior product and L denotes the Lie derivative, should point strictly outwards along W. Since Ω and Z (resp. Ω and Λ) together uniquely determine Λ (resp. Z), one can replace the notation with the triple (W,Ω,Z) (resp. (W,Ω,Λ)). The one-form Λ := Λ W is contact (i.e., Λ (dλ ) n > 0), and the contact manifold ( W,Ker(Λ )) is called the convex boundary of (W,Λ). The completion of (W,Ω,Z) is obtained from W by gluing the positive part W [0, ) of the symplectization ( W R,d(e t Λ )) of its convex boundary. A compact convex symplectic deformation (or a homotopy of Liouville domains) is asmooth 1-parameter family (W,Ω t,z t ), t [0,1], ofcompact convex symplectic manifolds. Definition 1.2. A smooth map π : W 2n+2 Σ 2 is called a (smooth) Lefschetz fibration if π is onto and has finitely many critical points such that there exist complex coordinates w = (z 1,z 2,...,z n+1 ) around each critical point p W and a complex coordinate z around the corresponding critical value π(p) Σ which are consistent with the given orientation of W and Σ, and π(p) has the local representation: z = π(w) = z 0 +z 2 1 +z z2 n+1. By definition, π has finitely many critical values. Let a be a regular value and X = π 1 (a) a regular fiber. Being an honest fibration away from critical values, all regular fibers are diffeomorphic to X. When Σ is a two-disk D 2 C, then π determines (induces) an open book on the boundary W. The monodromy of π is defined to be the monodromy of the induced open book (X,h) on W. We will denote such Lefschetz fibration over D 2 by the quadraple (π,w,x,h). In [9, 10], Seidel introduced exact Lefschetz fibrations which are further studied by McLean [8] under the name compact convex Lefschetz fibrations. By definition the fiber and the base of such fibration π are compact connected manifolds with boundary, some triviality condition is satisfied near the horizontal boundary component, and the total space W is equipped with an exact2-formω = dλwhoserestrictiononaregularfiberx definesaconvex symplectic(liouville)
3 LEGENDRIAN REALIZATION IN CONVEX LEFSCHETZ FIBRATIONS AND CONVEX STABILIZATIONS 3 structure, and π has finitely many critical points of complex quadratic type (see Section 3 for precise statements). By adding a pullback of a positive volume form on the base surface S, ω gives a symplectic form Ω on W [10]. Indeed, one can construct a convex symplectic structure Λ on W with dλ = Ω which restricts to the convex symplectic structure on each regular fiber of π [8]. Aconvex symplecticstructure(ω,λ)constructedinthiswayissaidtobecompatible with the compact convex Lefschetz fibration π (see [1]). For our purpose we will only consider compact convex Lefschetz fibrations over D 2. Also, in our notation, we would like to specify the regular fiber and the monodromy of π : W D 2 as well as a convex symplectic structure (Ω,Λ) on W compatible with π. Therefore, we let (π,w,ω,λ,x,h) denote the compatible compact convex Lefschetz fibration on the Liouville domain (W,Ω,Λ) over D 2 with the following properties: (i) Underlying smooth Lefschetz fibration is (π, W, X, h). (ii) The restriction Λ X defines a convex symplectic structure on every regular fiber X. (iii) The monodromy h of π is a symplectomorphism of (X,Ω X ) We ll call an open book (X,h) on W a convex open book if it is induced by a compatible compact convex Lefschetz fibration (π,w,ω,λ,x,h). By a compatible compact convex Lefschetz deformation, we mean a smooth 1-parameter family (π t,w,ω t,λ t,x t,h t ), for t [0,1], of compatible compact convex Lefschetz fibrations on W. We are now ready to state our main theorem: Theorem 1.3. Let (π,w,ω,λ,x,h) be any compatible compact convex Lefschetz fibration. Let L X 0 \ X 0 be any simply connected Lagrangian submanifold embedded in a page X 0 of the boundary convex open book (X, h). Then there exists another compatible compact convex Lefschetz fibration (π,w,ω,λ,x,h) on W such that (i) there is a compact convex symplectic deformation (Ω t,λ t ), t [0,1], on W connecting (Ω 0,Λ 0 ) = (Ω,Λ) to (Ω 1,Λ 1 ) = (Ω,Λ ), (ii) the completions of (W,Ω,Λ) and (W,Ω,Λ ) are exact symplectomorphic, (iii) (π,w,ω t,λ t,x,h), t [0,1], is a compatible compact convex Lefschetz deformation, (iv) ξ t = Ker(Λ t W ) is an isotopy of contact structures on W from ξ = Ker(Λ W ) to ξ = Ker(Λ W ), and (v) the submanifold L is Legendrian in ( W,ξ ). Remark 1.4. The only topological property of S n used in the proof of Theorem 1.1 is the fact that H 1 dr (Sn ) = 0 (as n 2). This is why we state our main theorem for simply connected Lagrangian submanifolds. We remark that the same generalization also applies to Theorem 1.1. We also note that according to the terminology of [11] the Liouville domains (W,Ω t,λ t ) above are mutually Liouville isomorphic. The proof will be given in Section 4. As an application of this result one can easily conclude Corollary 1.5. After a compatible compact convex Lefschetz deformation (π,w,ω t,λ t,x,h), any positive stabilization of a compatible compact convex Lefschetz fibration (π,w,ω 0,Λ 0,X,h) can be realized as a convex stabilization of (π,w,ω 1,Λ 1,X,h). Convex stabilizations are special types of positive stabilizations where stabilizations are along properly embedded Legendrian disks on pages of boundary convex open books. These are originally introduced for compatible exact Lefschetz fibrations in [1] which are exactly what we call compatible compact convex Lefschetz fibrations in the present paper. We omit the proof of Corollary 1.5 as its being a direct consequence of definitions and Theorem 1.3. The result of this paper should be thought of a partial generalization of [2], where in dimension four a surjection {PALF s} {Stein Manifolds} was established, here in any dimension we show the part of that result, which is an analogous map is well defined.
4 4 SELMAN AKBULUT AND M. FIRAT ARIKAN In Section 5, we will recall definitions and some properties of convex stabilizations for compatible compact convex Lefschetz fibrations and convex open books. In particular, we will give the proof of the fact that any convex stabilization of a compatible compact convex Lefschetz fibration on W yields a compatible compact convex Lefschetz fibration on a Liouville domain W which is exact symplectomorphic to a positive expansion (see below) of W, and, in particular, with the induced structures W and W are contactomorphic. Acknowledgments. The authors would like to thank Yasha Eliashberg for helpful conversations and remarks, and also Max Planck Institute for Mathematics for their hospitality. 2. Complete convex symplectic (Liouville) manifolds We first recall complete convex symplectic manifolds and their deformations. They are also known as Liouville manifolds. The notions below can be found in [5], [3], [11], and [8]. An exact symplectic manifold is a manifold W together with a symplectic form Ω and a 1-form Λ satisfying Ω = dλ. In such a case there is a global Liouville vector field Z of Ω defined by the equation ι Z Ω = Λ. We will write exact symplectic manifolds as triples of the form (W,dΛ,Z), or (W,dΛ,Λ), or just as pairs (W,Λ). A smooth map φ : (W 0,Λ 0 ) (W 1,Λ 1 ) between two exact symplectic manifolds is called an exact symplectomorphism if φ (Λ 1 ) Λ 0 is exact. Definition 2.1 ([3], [11]). A complete convex symplectic manifold (Liouville manifold) is an exact symplectic manifold (W, dλ, Z) such that (i) the expanding vector field Z is complete (i.e., its flow exists for all times), and (ii) there exists an exhaustion W = k=1 Wk by compact domains W k W with smooth boundaries along which Z points outward. If Z t : W W (t > 0) denotes the contracting flow of Z, then the core (or skeleton) of the Liouville manifold (W,dΛ,Z) is defined to be the set Core(W,Λ) = Core(W,dΛ,Z) := Z t (W k ). k=1t>0 A Liouville manifold is of finite type if its core is compact. A Liouville cobordism (W,dΛ,Z) is a compact cobordism W with an exact symplectic structure (dλ, Z) such that Z points outwards along + W and inwards along W. A Liouville cobordism with W = is called a Liouville domain.(one can see that this definition of Lioville domains is equivalent to the one given above.) Remark 2.2. Let (W,dΛ,Z) be a finite type Liouville manifold and V W a compact domain containing the core with smooth boundary M = V. Then the whole symplectization (M R,d(e t Λ M )) symplectically embeds into W. The contact manifold (M,Λ M ) is canonical and called the ideal contact boundary of (W,dΛ,Z). Similarly, if M is the convex boundary + W(= W) of a Liouville domain (W,dΛ,Z), then the negative half of the symplectization (M R,d(e t λ M )) symplectically embeds into W (as a collar neighborhood of M in W) so that its complement in W is Core(W,dΛ,Z) and the embedding matches the positive t-direction of R with Z. Therefore, the completion of a Liouville domain is a finite type Liouville manifold. Recall from [3] that a smooth family (W,Ω t,z t ), t [0,1], of Liouville manifolds is called a simple Liouville homotopy if there exists a smooth family of exhaustions W = k=1 Wk t by compact domains Wt k W with smooth boundaries along which Z t is outward pointing. A smooth family (W,Ω t,z t ), t [0,1], of Liouville manifolds is called Liouville homotopy if it is a composition of finitely many simple homotopies.
5 LEGENDRIAN REALIZATION IN CONVEX LEFSCHETZ FIBRATIONS AND CONVEX STABILIZATIONS 5 Lemma 2.3 ([3], Lemma 11.6 and Proposition 11.8). A smooth family (W,Ω t,z t ), t [0,1], of Liouville manifolds of finite type is a Liouville homotopy if the closure t [0,1] Core(W,Ω t,z t ) of the union of their cores is compact. In particular, any smooth family of Liouville domains determines a Liouville homotopy of their completions. Moreover, homotopic Liouville manifolds are exact symplectomorphic. In particular, homotopic Liouville domains have exact symplectomorphic completions. Next we define the positive expansion (which will be used in the last section) of a Liouville domain for any given smooth strictly positive real-valued function on its boundary. Given a compact manifold with boundary and a strictly positive smooth function f : W R, let Wf cob denote the set W cob f := {(x,t) x W, 0 t f(x)} W [0, ) which is the region in W [0, ) under the graph Graph(f) := {(x,f(x)) x W}. Definition 2.4. Let (W,Ω,Z) be a Liouville domain and f : W R any strictly positive smooth function. The positive f-expansion of (W,Ω,Z) is a Liouville domain, denoted by (W,Ω,Z) f, obtained by gluing the Liouville cobordism (between Wf cob by x (x,0). = W 0 and + W cob f (W cob f,d(e t (ι Z Ω) W ), / t) = Graph(f)) to W via the map W W cob f given Notethatbyconstruction(W,Ω,Z)hasacodimensionzeroLiouvilleembeddinginto(W,Ω,Z) f. Also (W,Ω,Z) f is diffeomorphic to W since Wf cob is a smooth trivial cobordism (i.e., diffeomorphic to the product W [0,1]) for any strictly positive smooth function f. Remark 2.5. Note that a positive f-expansion W of a Liouville domain W is not symplectomorphic to W. However, W and W have contactomorphic boundaries. To see this, note that W = Wf cob = W 0and W = + Wf cob = Graph(f) are cobordant via the Liouville cobordism (Wf cob,d(e t (ι Z Ω) W ), / t). The contact structure ξ (resp. ξ ) on W (resp. W ) is the kernel of the contact form α = e 0 (ι Z Ω) W (resp. α = e k (ι Z Ω) W ). Also by following the trajectories of the Liouville vector field / t, we obtain a diffeomorphism F : W = W W. Then we compute that F (α ) = e f α (so F maps ξ to ξ ). Hence, ( W,ξ) and ( W,ξ ) are contactomorphic. 3. Compact convex Lefschetz fibrations Exact (compact convex) Lefschetz fibrations are introduced in [9, 10] (see also [8]). Let π : W 2n+2 S be a differentiable fiber bundle, denoted by (π,w), whose fibers and base are compact connected manifolds with boundary. The boundary of such an W consists of two parts: The vertical part v W;= π 1 ( S), and the horizontal part h W := z S W z where W z = π 1 (z) is the fiber over z S. Definition 3.1 ([9, 10]). An compact convex symplectic fibration (π, W, ω, λ) over a bordered surface S is a differentiable fiber bundle (π,w) equipped with a 2-form ω and a 1-form λ on W, satisfying ω = dλ, such that (i) each fiber W z with ω z = ω Wz and λ z = λ Wz is a compact convex symplectic manifold,
6 6 SELMAN AKBULUT AND M. FIRAT ARIKAN (ii) thefollowingtriviality conditionnear h W issatisfied: Chooseapointz S andconsider the trivial fibration π : W := S Wz S with the forms ω, λ which are pullbacks of ω z,λ z, respectively. Then there should be a fiber-preserving diffeomorphism Ξ : N Ñ between neighborhoods N of h W in W and Ñ of h W in W which maps h W to h W, equals the identity on N W z, and Ξ ω = ω and Ξ λ = λ. Definition 3.2 ([9, 10]). A compact convex Lefschetz fibration is a tuple (π,w,s,ω,λ,j 0,j 0 ) which satisfies the following conditions: (i) π : W S is allowed to have finitely many critical points all of which lie in the interior of W. (ii) π is injective on the set C of its critical points. (iii) J 0 is an integrable complex structure defined in a neighborhood of C in W such that ω is a Kähler form for J 0. (iv) j 0 is a positively oriented complex structure on a neighborhood of the set π(c) in S of the critical values. (v) π is (J 0,j 0 )-holomorphic near C. (vi) The Hessian of π at any critical point is nondegenerate as a complex quadratic form, in other words, π has nondegenerate complex second derivative at each its critical point. (vii) (π,w \π 1 (π(c)),ω,α) is a compact convex symplectic fibration over S \π(c). Remark 3.3. For the codimension two corners (i.e., v W h W) of the total space W there is canonical way of smoothening. Assuming such smoothening has been made, all total spaces will be assumed to be smooth through out the paper. Also the statements (ii)-(vi) guarantees that the singularities of π are of Lefschetz type as in Definition 1.2. Let us consider a pair (J,j) where J is an almost complex structure on W agreeing with J 0 near C and j is a positively oriented complex structure on S agreeing with j 0 near π(c) such that π is (J,j)-holomorphic and ω(,j ) Ker(π ) is symmetric and positive definite everywhere. As pointed out in [9], the space of such pairs is always contractible, and in particular, always nonempty, and furthermore, once we fixed (J,j), we can modify ω by adding a positive 2-form on S so that it becomes symplectic and tames J everywhere on W. Theorem 3.4 ([8]). Suppose that the base surface of a compact convex Lefschetz fibration (π,w,s,ω,λ,j 0,j 0 ) is a compact convex symplectic manifold (S,λ S ). Then there exists a constant K > 0 such that for all k K we have Ω := ω +kπ (dλ S ) is a symplectic form, and the Ω-dual Z of Λ := λ + kπ (λ S ) is transverse to W and pointing outwards. (In other words, (W, Ω, Λ) is a compact convex symplectic manifold, i.e., a Liouville domain.) Definition 3.5 (& Notation). ([1]) A compact convex symplectic manifold (W, Ω, Λ) and a compact convex Lefschetz fibration (π,w,s,ω,λ,j 0,j 0 ) are said to be compatible if for a pair (J,j) as in Remark 3.3 there exists a positive volume form ω S on S such that Ω = ω +π (ω S ) and Ω tames J everywhere on E. From now on, we ll always take S = D 2, and assuming the above choice of (J,j) is already made, (J 0,j 0 ) will be dropped from the notation. We will denote a compatible compact convex Lefschetz fibration (over D 2 ) on the compact convex symplectic manifold (W,Ω,Λ) by the tuple (π,w,ω,λ,x,h) as stated in the introduction. Definition 3.6 ([1]). An open book induced by a compatible compact convex Lefschetz fibration over the disk D 2 is called a convex (exact) open book. As mentioned before compatible compact convex Lefschetz fibrations are studied under the name compatible exact Lefschetz fibrations in [1]. Therefore, the following theorem is the restatement of Theorem 4.7. of [1] in the terminology of the present paper.
7 LEGENDRIAN REALIZATION IN CONVEX LEFSCHETZ FIBRATIONS AND CONVEX STABILIZATIONS 7 Theorem 3.7. The convex open book (X, h) induced by a compatible compact convex Lefschetz fibration (π,w,ω,λ,x,h) caries the induced contact structure Ker(Λ W ) on W. 4. The proof of Theorem 1.3 The proof of the theorem will make use of the following proposition. Proposition 4.1. Let (π, W, Ω, Λ, X, h) be any compatible compact convex Lefschetz fibration, and denote by (dα 0,α 0 ) the restriction of the Liouville structure (Ω,Λ) to the fixed page X 0 X of the boundary convex open book (X,h). Let G t = (X 0,α t ), t [0,1], be any homotopy of Liouville domains on X 0. Then there exists a compatible compact convex Lefschetz deformation (π,w,ω t,λ t,x,h), t [0,1], such that the following hold (i) The smooth 1-parameter family H t = (Ω t,λ t ) on W defines a homotopy of Liouville domains from (Ω 0,Λ 0 ) = (Ω,Λ) to another Liouville structure (Ω 1,Λ 1 ) = (Ω,Λ ). (ii) ξ t = Ker(Λ t W ) defines an isotopy of contact structures on W from ξ 0 = Ker(Λ W ) to ξ 1 = Ker(Λ W ). (iii) For each t [0,1] the convex open book induced by (π,w,ω t,λ t,x,h) carries ξ t. (iv) G t = H t X0. That is, the restriction of H t to the page X 0 is equal to G t. Proof. Without loss of generality let π fiber over the unit disk D 2 = {z C z 1}. By definition there is a compact convex Lefschetz fibration (π,w,d 2,ω,λ,J 0,j 0 ) such that Λ = λ+kπ (λ D 2) for some K > 0 where λ D 2 is some convex symplectic structure on D 2. Note that π has no singular fibers in a neighborhood of X 0 in W. Say X 0 = π 1 (e iθ 0 ) for some e iθ 0 S 1. For 0 < ǫ, 0 < δ < π, let us write l(θ 0,δ) for the arc {e iθ θ 0 δ θ θ 0 +δ} S 1. Also let A θ0 (ǫ,δ) denote the region in D 2 given by A θ0 (ǫ,δ) = {re iθ C 1 ǫ r 1, e iθ l(θ 0,δ)}. Choose ǫ,δ small enough so that π has no singular fibers over A θ0 (ǫ,δ). Then, by Lemma 1.1 in [10], there is a local trivialization for π around X 0. More precisely, there exists a fiber-preserving diffeomorphism Ψ : A θ0 (ǫ,δ) X 0 π 1 (A θ0 (ǫ,δ)) such that Ψ {0} X0 = id and Ψ λ = α 0 +f 1 dx 1 +f 2 dx 2 +dr where f 1,f 2,R C (A θ0 (ǫ,δ) X 0,R) are functions which vanish near A θ0 (ǫ,δ) X 0 and x 1,x 2 are real coordinates on D 2. Denote by X r,θ the fiber π 1 (re iθ ) = Ψ(re iθ X 0 ) W over the point re iθ A θ0 (ǫ,δ). (Note X 0 = X 1,θ0 under this correspondence.) Next, we pick two smooth cut-off functions y = f(r) and y = g(θ) whose graphs are given in Figure 1. On the fiber X r,θ, consider the homotopy F t,r,θ, t [0,1] of Liouville structures defined by F t,r,θ := (Ψ 1 re iθ X 0 ) (α f(r)g(θ)t ). Here by abuse of notation we consider α f(r)g(θ)t on re iθ X 0 = X0 for each (r,θ) and t. Note that F t,1,θ0 = G t, i.e., F t,r,θ restricts to G t on X 0 = X 1,θ0. Observe that F t,r,θ is compactly supported in π 1 (A θ0 (ǫ,δ)). One can think of F t,r,θ as the smooth extension of G t (defined only
8 8 SELMAN AKBULUT AND M. FIRAT ARIKAN y y 1 y = f(r) 1 y = g(θ) 0 1 ǫ 1 r 0 θ 0 δ θ 0 θ 0 +δ θ Figure 1. Smooth cut-off functions. on X 1,θ0 ) to the fibers in the subset π 1 (A θ0 (ǫ,δ)), and by tapering using f(r),g(θ) we gurantee that the Liouville structures of the fibers close to the boundary stay constant during the homotopy. π 1 (A θ0 (ǫ,δ)) = π 1 ({r = 1 ǫ}) π 1 ({θ = θ 0 ±δ}) Next, using F t,r,θ, we construct a smooth 1-parameter family of compact convex Lefschetz fibrations on W (such family is called compact convex Lefschetz deformation in [8]) as follows: Consider the smooth 1-parameter families of one- and two-forms on π 1 (A θ0 (ǫ,δ)) given by λ t := r,θ F t,r,θ +(Ψ 1 ) (f 1 dx 1 +f 2 dx 2 +dr), ω t = d λ t, t [0,1]. By construction, for any fixed time t [0,1], the restriction of the pair ( ω t, λ t ) to any fiber X r,θ is (df t,r,θ,f t,r,θ ) which defines a convex symplectic structure on X r,θ. Also satisfying the triviality condition near its horizontal boundary, the fibration (π π 1 (A θ0 (ǫ,δ)),π 1 (A θ0 (ǫ,δ)), ω t, λ t ) is a compact convex symplectic fibration for any t. Moreover, since F t,r,θ is compactly supported in π 1 (A θ0 (ǫ,δ)), we can smoothly extend ω t, λ t to smooth 1-parameter families ω t,λ t on W by just letting (ω t,λ t) = (ω,λ) outside π 1 (A θ0 (ǫ,δ)). Hence, we obtain a smooth 1-parameter family (π,w,d 2,ω t,λ t,j 0,j 0 ) of compact convex Lefschetz fibrations on W such that the smooth family λ t of one-forms on W restricts to the homotopy α t of Liouville structures on X 0. Note that (π,w,d 2,ω 0,λ 0,J 0,j 0 ) = (π,w,d 2,ω,λ,,J 0,j 0 ) which is compatible with the Liouville domain (W, Ω, Λ) by assumption. Next, we construct a homotopy of Liouville domains (W,Ω t,λ t ) such that (Ω t,λ t ) is compatible with (π,w,ω t,λ t,j 0,j 0 ) for any t [0,1]. For any fixed t, by Theorem 3.4, there exists a constant K t > 0 such that for all k K t the one-form λ t +kπ (λ D 2) defines a Liouville structure on W. Set K max = Max{K t t [0,1]} and K = Max(K,K max ). (Recall that Λ = λ+kπ (λ D 2).) Consider two smooth 1-parameter families: F 1 t := (W,λ+[(1 t)k +tk ]π (λ D 2)), F 2 t := (W,λ t +K π (λ D 2)) for t [0,1]. As [(1 t)k +tk ] K (resp. K K t ) for each t, Theorem 3.4 implies that F 1 t (resp. F 2 t ) is a homotopy of Liouville domains. Now we define two concatenations:
9 LEGENDRIAN REALIZATION IN CONVEX LEFSCHETZ FIBRATIONS AND CONVEX STABILIZATIONS 9 { F2t 1 if t [0,1/2] (W,Λ t ) := F1 2t 2 if t [1/2,1], { (π,w,d 2 (π,w,d 2,ω,λ,J 0,j 0 ) if t [0,1/2],ω t,λ t,j 0,j 0 ) := (π,w,d 2,ω 1 2t,λ 1 2t,J 0,j 0 ) if t [1/2,1]. Set Ω t = dλ t. Then by construction the Liouville domain H t := (W,Ω t,λ t ) is compatible with (π,w,d 2,ω t,λ t,j 0,j 0 ) for each t [0,1]. Therefore, we have constructed a compatible compact convex Lefschetz deformation (π,w,ω t,λ t,x,h) such that (i) and (iv) of the proposition hold. Finally, (iii) holds by Theorem 3.7, and (ii) follows from Gray Stability Theorem (see, for instance, Theorem of [6]). Proof of Theorem 1.3. Let L X 0 \ X 0 beany given simplyconnected Lagrangian submanifold on the page (X 0,dβ,β) of the convex open book (X,h) induced by a compatible compact convex Lefschetz fibration (π,w,ω,λ,x,h). Here we assume that (dβ,β) = (Ω X0,Λ X0 ). By starting with a similar argument in the proof of Theorem 1.1, we will first construct a homotopy of Liouville structures on X 0 as follows: Consider the cotangent bundlet L equipped with the symplectic structure dλ can where λ can is the canonical 1-form on T L. By Lagrangian neighborhood theorem, there exist a neighborhood N(L 0 ) of the zero section L 0 in T L, a neighborhood N X0 (L) of L in X 0, and a diffeomorphism Υ : N X0 (L) N(L 0 ) which identically maps L onto L 0 and pulls back the symplectic form dλ can N(L0 ) to dβ NX0 (L). From now on we will denote the restrictions with the same symbols. Let α can = Υ (λ can ). Then since dα can = Υ (dλ can ) = dβ, β α can is closed. Therefore, the assumption that L is simply connected implies that there exists a smooth function g : N X0 (L) R such that β α can = dg on N X0 (L). Take a smooth cut-off function µ : X 0 R which is equal to 1 near L and identically zero on X 0 \N X0 (L). Then, we can set the equality β α can = d(µg) which holds over all N X0 (L). Now consider the smooth 1-parameter family of one-forms on X 0 given by α t := β td(µg), t [0,1]. Note that for any t we have dα t = dβ is symplectic, and so (dα t,α t ) is an exact symplectic structure on X 0 for each t [0,1]. Let χ (resp. χ t ) denote the dβ-dual vector field of β (resp. α t ). That is, ι χ dβ = β and ι χt dβ = α t. Then χ is transverse to X 0 by assumption. Also α t = β near W as the family {α t } is compactly supported near L. Therefore, χ t = χ near W which implies that χ t is transverse to W for each t. Hence, the family {α t }, indeed, defines a homotopy of Liouville domains G t = (X 0,α t ), t [0,1]. Now, by Proposition 4.1, there exists a compatible compact convex Lefschetz deformation (π,w,ω t,λ t,x,h), t [0,1], such that the smooth 1-parameter family (W,Ω t,λ t ) defines a homotopy of Liouville domains with (W,Ω 0,Λ 0 ) = (W,Ω,Λ). Set (W,Ω,Λ ) = (W,Ω 1,Λ 1 ). The parts (i), (iii), (iv) of the theorem just follow from the corresponding parts of Proposition 4.1, and we have (ii) by Lemma 2.3. For the part (v) observe that we have Λ X0 = α 1 = β d(µg) = α can.
10 10 SELMAN AKBULUT AND M. FIRAT ARIKAN Moreover, α can L = 0 since λ can L0 = 0 (the canonical one-form identically vanishes on the zero section of T L). Hence, we obtain (Λ W ) L = 0 because L is embedded on the page X 0 and the Reeb direction of Λ W is transverse to TX 0. As a result, L X 0 is Legendrian in ( W,Ker(Λ W ). This completes the proof of Theorem Convex Stabilizations We first recall positive stabilization process for contact open books (due to Giroux). Let (M i,ξ i ) be two closed contact manifolds such that each ξ i is carried by a contact open book (X i,h i ) on M i. Suppose that L i is a properly embedded Lagrangian ball in X i with Legendrian boundary L i X i. By the Weinstein neighborhood theorem each L i has a standard neighborhood N i in X i which is symplectomorphic to (T D n,dλ can ) where λ can = pdq is the canonical 1-form on R n R n with coordinates (q,p). Then the plumbing or 2-Murasugi sum (P(X 1,X 2 ;L 1,L 2 ),h) of (X 1,h 1 ) and (X 2,h 2 ) along L 1 and L 2 is the open book on the connected sum M 1 #M 2 with the pages obtained by gluing Σ i s together along N i s by interchanging q-coordinates in N 1 with p-coordinates in N 2, and vice versa. To define h, extend each h i to h i on the new page by requiring h i to be identity map outside the domain of h i. Then the monodrodmy h is defined to be h 2 h 1. Without abuse of notation we will drop the tilde sign, and write h = h 2 h 1. Definition 5.1 ([7]). Suppose that (X, h) is a contact open book carrying the contact structure ξ = Ker(α) on a (2n + 1)-manifold M. Let L be a properly embedded Lagrangian n-ball in a page (X,dα) such that L X is a Legendrian (n 1)-sphere in the binding ( X,α X ). Then the positive (or standard) stabilization S OB [(X,h);L] of (Σ,h) along L is the open book (P(X,D(T S n );L,D),δ h) where D = D n is any fiber in the cotangent unit disk bundle D(T S n ) and δ : D(T S n ) D(T S n ) is the right-handed Dehn twist. Next, we recall positive stabilization process introduced for Lefschetz fibrations in [1]. Definition 5.2 ([1]). Let (π, W, X, h) be a Lefschetz fibration which induces a contact open book on W. Suppose that L (X,ω) is a properly embedded Lagrangian n-ball with a Legendrian boundary L X on a page of the induced open book. Then the positive stabilization S LF [(π,w,x,h);l] of (π,w,x,h) along L is a Lefschetz fibration (π,w,x,h ) described as follows: (I) X is obtained from X by attaching a Weinstein n-handle H = D n D n along the Legendrian sphere L X. (II) h = δ (φ,φ ) h where δ (φ,φ ) is the right-handed Dehn twist defined as follows: φ : S n S is the embedding of the Lagrangian n-sphere S = D n {0} L L in the symplectic manifold(x = X H,ω ) whereω isobtainedbygluingω andstandardsymplecticform on H. If ν denote the normal bundle of S in X, then the normalization φ : TS n ν is given by the bundle isomorphisms TS n = TS = T S X /TS = ν. φ In [1] the authors have also defined the convex stabilizations for compatible compact convex Lefschetz fibrations and convex open books. These are special positive stabilizations along properly embedded Legendrian disks. They have shown that convexly stabilized compatible compact convex Lefschetz fibration (resp. convex open book) is another compatible compact convex Lefschetz fibration (resp. convex open book). In what follows, SLF C [(π,w,ω,λ,x,h);l]
11 LEGENDRIAN REALIZATION IN CONVEX LEFSCHETZ FIBRATIONS AND CONVEX STABILIZATIONS 11 (resp. SOB C [(X,h);L]) will denote the convex stabilization of the compatible compact convex Lefschetz fibration (π,w,ω,λ,x,h) (resp. convex openbook(x,h)) along aproperlyembedded Legendrian disk L. (see [1] for precise definitions of SLF C and SC OB.) Let us recall ω-convexity for our next result. Definition 5.3. (i) A vector field χ on a smooth manifold W is said to gradient-like for a smooth function ψ : W R if χ ψ = L χ ψ > 0 away from the critical point of ψ. (ii) A real-valued function is said to be exhausting if it is proper and bounded from below. (iii) An exhausting function ψ : W R on a symplectic manifold (W,ω) is said to be ω-convex if there exists a complete Liouville vector field χ which is gradient-like for ψ. Theorem 5.4. Let (π, W, Ω, Λ, X, h) be a compatible compact convex Lefschetz fibration and L any properly embedded Legendrian disk sitting on a page of the boundary convex open book (X,h). Denote S C LF [(π,w,ω,λ,x,h);l] by (π,w,ω,λ,x,h ), and Ω -dual vector field of Λ by Z. Then there exists a homotopy from Z to another Liouville vector field Z of Ω which is compactly supported away from W such that (W,Ω,Z ) is exact symplectomorphic to a positive expansion (W,Ω,Z) f for some nonzero smooth function f : W R. Proof. Suppose dim(w) = 2n + 2. The convex stabilization of (π,w,ω,χ,ψ,x,h) along L is performed in two stages [1]: The first one is the subcritical stage where the Weinstein handle H n (of index n) is attached to W along L X, say W = W H n, and the second one is the critical stage where the Weinstein handle H n+1 (of index n + 1) is attached to W (resulting W = W H n+1 ) along certain Legendrian sphere sitting on a page of the boundary open book obtained in the first stage. As pointed out in Theorem 6.8. of [1], we know that {H n,h n+1 } is a symplectically canceling pair, more precisely the completion of (W,Ω,Λ ) is symplectomorphic to the completion of (W, Ω, Λ). This fact follows from Proposition in [3] or Lemma 3.6b in [4] (see also Lemma 3.9 in [12]). To obtain an exact symplectomorphism as claimed wefirstfollow thesteps given intheproofof Lemma3.11 in[12]intheliouvillecategory. Note that there is a Ω-convex Morse function ψ : N R defined on a colar neighborhood N of W. Such ψ can be obtained by integrating Ω-dual (Liouville) vector field Z of Λ on N. Taking N small enough one can guarantee that ψ has no critical point. The contact boundary ( W,Ker(ι Z Ω W )) is the (regular) hypersurface of ψ with the highest level, say c R. That is, we have N = ψ 1 (c ǫ,c] and W = ψ 1 (c). In the subcritical stage, we know by [13] that attaching H n gives rise to a Liouville domain ( W, Ω, Z) such that there exists a Ω-convex Morse function ψ : N H n R obtained by extending ψ over H n. Note ψ coincides with ψ on N and has a single critical point of index n which is located at the center of H n. Let p R be the corresponding critical value. Similarly, by attaching H n+1 to W in the critical stage, we get a Liouville domain (W,Ω,Z ) such that there exists a Ω -convex Morse function ψ : N H n H n+1 R obtained by extending ψ over H n+1. This time ψ coincides with ψ on N H n and has one more critical point of index n+1 which corresponds to the center of H n+1. Let q R be the corresponding critical value. Suppose that d R is the absolute maximum value of ψ, or equivalently, N H n H n+1 = ψ 1 (c ǫ,d] and W = ψ 1 (d). Note that c < p < q < d. Also there is a unique flow line, say l, of Z joining p and q, and so the belt sphere of H n intersects the attaching sphere of H n+1 transversely once. Therefore, Proposition12.22 [3]impliesthatwecandeformψ toanotherω -convex Morsefunctionψ (with
12 12 SELMAN AKBULUT AND M. FIRAT ARIKAN gradient-like Liouvillevector fieldz )onn H n H n+1 suchthat(ψ,z )coincides with(ψ,z ) outside a neighborhood of l and ψ has no critical value greater than c. This means that the cobordism ψ 1 [c,d] together with the restricted Liouville structure is exact symplectomorphic to some compact subset of the positive part of the symplectization of ( W,Ker(ι Z Ω W )). In fact, byfollowing thetrajectories ofz, onecanrealize ψ 1 (d) as thegraphofanonzerosmooth function on W {c}. So there exists an exact symplectomorphism Υ 0 : Wf cob ψ 1 [c,d] for some nonzero smooth function f : W R. Also by construction (W,Ω,Z) is an embedded Liouville subdomain of (W,Ω,Z ). As a result, we can define a diffeomorphism Υ : W Wf cob W = W ψ 1 [c,d] by the rule { x if x W Υ(x) = Υ 0 (x) if x Wf cob Clearly, this is an exact symplectomorphism between the f-positive expansion (W,Ω,Z) f and (W,Ω,Z ). We close the paper by recalling some facts about convex stabilizations in the terminology of the present paper. All of the next three results have exact symplectic versions in [1]. For instance, the first one is a special case of Theorem 6.7 in [1]. Here we provide the proofs only for the last two. Theorem 5.5. SLF C [(π,w,ω,λ,x,h);l] induces the open book SC OB [(X,h);L]. Conversely, if a convex open book (X,h) is induced by (π,w,ω,λ,x,h), then any convex stabilization SOB C [(X,h);L] of (X,h) is induced by the convex stabilization SC LF [(π,w,ω,λ,x,h);l]. Corollary 5.6. Let (π,w,ω,λ,x,h ) be any convex stabilization of a compatible compact convex Lefschetz fibration (π,w,ω,λ,x,h). Let ξ = Ker(Λ W ) (resp. ξ = Ker(Λ W )) be the induced contact structure on W (resp. W ). Then ( W,ξ) is contactomorphic to ( W,ξ ). Proof. By Theorem 5.4, there exists another Liouville structure (Ω,Z ) on W such that (W,Ω,Z ) is exact symplectomorphic to (W,Ω,Z) f for some f : W R >0. Note that the deformation of Z to Z is performed away from the boundary W. Therefore, the contact boundary of (W,Ω,Z ) is still ( W,ξ ). Denote the Liouville domain (W,Ω,Z) f by ( W, Ω, Z) and the induced contact structure on W by ξ. Then ( W, ξ) is contactomorphic to ( W,ξ ) by Theorem 5.4. Now the proof follows from the fact that ( W,ξ) and ( W, ξ) are contactomorphic (This was explained in Remark 2.5). Corollary 5.7. Let ξ (as in Theorem 3.7) be the contact structure carried by a convex open book (X,h). Then any convex stabilization SOB C [(X,h);L] of (X,h) carries ξ. Proof. Byassumption,thereisacompatiblecompactconvexLefschetzfibration(π,W,Ω,Λ,X,h) which induces (X,h), and the Liouville structure (Ω,Λ) induces ξ on W. Theorem 5.5 implies that SOB C [(X,h);L] is induced by SC LF [(π,w,ω,λ,x,h);l]. Moreover, by Theorem 3.7, SOB C [(X,h);L] carries the contact structure induced by the Liouville structure on the total space of SLF C [(π,w,ω,λ,x,h);l]. Now the proof follows from Corollary 5.6. References [1] S. Akbulut and M. F. Arikan, Stabilizations via Lefschetz Fibrations and Exact Open Books, arxiv: [2] S. Akbulut and B. Ozbagci, Lefschetz fibrations on compact Stein surfaces, Geom. Topol. 5 (2001), [3] K. Cieliebak and Y. Eliashberg, Symplectic geometry of affine complex manifolds(incomplete draft, November 2012)
13 LEGENDRIAN REALIZATION IN CONVEX LEFSCHETZ FIBRATIONS AND CONVEX STABILIZATIONS 13 [4] Y. Eliashberg, Symplectic geometry of plurisubharmonic functions, Gauge theory and symplectic geometry (Montreal, PQ, 1995), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., vol. 488, Kluwer Acad. Publ., Dordrecht, 1997, With notes by Miguel Abreu, pp MR (98g:58055) [5] Y. Eliashberg and M. Gromov, Convex Symplectic Manifolds, Proceedings of Symposia in Pure Mathematics, vol. 52, Part 2, (1991). [6] H. Geiges, An Introduction to Contact Topology, Cambridge University Press, (2008). [7] E. Giroux, Géométrie de contact: de la dimension trois vers les dimensions supérieures, Proceedings of the International Congress of Mathematicians, Vol. II (Beijing), Higher Ed. Press, (2002), pp MR 2004c:53144 [8] M. McLean, Lefschetz fibrations and symplectic homology, Geom. Topol., 13 (2009), [9] P. Seidel, Vanishing cycles and mutation, European Congress of Mathematics, Vol. II (Barcelona, 2000), 65-85, Progr. Math., 202, Birkhäuser, Basel, [10] P. Seidel, A long exact sequence for symplectic Floer cohomology, Topology 42 (2003), p [11] P. Seidel, A biased view of symplectic cohomology, Current developments in mathematics, 2006, , Int. Press (2008). [12] O. Van Koert, Lecture notes on stabilization of contact open books, (arxiv: v1) [13] A. Weinstein, Contact surgery and symplectic handlebodies, Hokkaido Math. J. 20 (1991), no. 2, Department of Mathematics, Michigan State University, Lansing MI, USA address: akbulut@math.msu.edu Department of Mathematics, Middle East Technical University, Ankara, TURKEY address: farikan@metu.edu.tr
THE EXISTENCE PROBLEM
 THE EXISTENCE PROBLEM Contact Geometry in High Dimensions Emmanuel Giroux CNRS ENS Lyon AIM May 21, 2012 Contact forms A contact form on a manifold V is a non-vanishing 1-form α whose differential dα at
THE EXISTENCE PROBLEM Contact Geometry in High Dimensions Emmanuel Giroux CNRS ENS Lyon AIM May 21, 2012 Contact forms A contact form on a manifold V is a non-vanishing 1-form α whose differential dα at
COMPUTABILITY AND THE GROWTH RATE OF SYMPLECTIC HOMOLOGY
 COMPUTABILITY AND THE GROWTH RATE OF SYMPLECTIC HOMOLOGY MARK MCLEAN arxiv:1109.4466v1 [math.sg] 21 Sep 2011 Abstract. For each n greater than 7 we explicitly construct a sequence of Stein manifolds diffeomorphic
COMPUTABILITY AND THE GROWTH RATE OF SYMPLECTIC HOMOLOGY MARK MCLEAN arxiv:1109.4466v1 [math.sg] 21 Sep 2011 Abstract. For each n greater than 7 we explicitly construct a sequence of Stein manifolds diffeomorphic
arxiv:math/ v1 [math.gt] 14 Dec 2004
![arxiv:math/ v1 [math.gt] 14 Dec 2004 arxiv:math/ v1 [math.gt] 14 Dec 2004](/thumbs/86/93466553.jpg) arxiv:math/0412275v1 [math.gt] 14 Dec 2004 AN OPEN BOOK DECOMPOSITION COMPATIBLE WITH RATIONAL CONTACT SURGERY BURAK OZBAGCI Abstract. We construct an open book decomposition compatible with a contact
arxiv:math/0412275v1 [math.gt] 14 Dec 2004 AN OPEN BOOK DECOMPOSITION COMPATIBLE WITH RATIONAL CONTACT SURGERY BURAK OZBAGCI Abstract. We construct an open book decomposition compatible with a contact
arxiv: v1 [math.gt] 20 Dec 2017
![arxiv: v1 [math.gt] 20 Dec 2017 arxiv: v1 [math.gt] 20 Dec 2017](/thumbs/82/86068328.jpg) SYMPLECTIC FILLINGS, CONTACT SURGERIES, AND LAGRANGIAN DISKS arxiv:1712.07287v1 [math.gt] 20 Dec 2017 JAMES CONWAY, JOHN B. ETNYRE, AND BÜLENT TOSUN ABSTRACT. This paper completely answers the question
SYMPLECTIC FILLINGS, CONTACT SURGERIES, AND LAGRANGIAN DISKS arxiv:1712.07287v1 [math.gt] 20 Dec 2017 JAMES CONWAY, JOHN B. ETNYRE, AND BÜLENT TOSUN ABSTRACT. This paper completely answers the question
arxiv:math/ v1 [math.gt] 26 Sep 2005
![arxiv:math/ v1 [math.gt] 26 Sep 2005 arxiv:math/ v1 [math.gt] 26 Sep 2005](/thumbs/93/113554162.jpg) EXPLICIT HORIZONTAL OPEN BOOKS ON SOME PLUMBINGS arxiv:math/0509611v1 [math.gt] 26 Sep 2005 TOLGA ETGÜ AND BURAK OZBAGCI ABSTRACT. We describe explicit open books on arbitrary plumbings of oriented circle
EXPLICIT HORIZONTAL OPEN BOOKS ON SOME PLUMBINGS arxiv:math/0509611v1 [math.gt] 26 Sep 2005 TOLGA ETGÜ AND BURAK OZBAGCI ABSTRACT. We describe explicit open books on arbitrary plumbings of oriented circle
Convex Symplectic Manifolds
 Convex Symplectic Manifolds Jie Min April 16, 2017 Abstract This note for my talk in student symplectic topology seminar in UMN is an gentle introduction to the concept of convex symplectic manifolds.
Convex Symplectic Manifolds Jie Min April 16, 2017 Abstract This note for my talk in student symplectic topology seminar in UMN is an gentle introduction to the concept of convex symplectic manifolds.
We thank F. Laudenbach for pointing out a mistake in Lemma 9.29, and C. Wendl for detecting a large number errors throughout the book.
 ERRATA TO THE BOOK FROM STEIN TO WEINSTEIN AND BACK K. CIELIEBAK AND Y. ELIASHBERG We thank F. Laudenbach for pointing out a mistake in Lemma 9.29, and C. Wendl for detecting a large number errors throughout
ERRATA TO THE BOOK FROM STEIN TO WEINSTEIN AND BACK K. CIELIEBAK AND Y. ELIASHBERG We thank F. Laudenbach for pointing out a mistake in Lemma 9.29, and C. Wendl for detecting a large number errors throughout
arxiv:math/ v3 [math.sg] 20 Sep 2004
![arxiv:math/ v3 [math.sg] 20 Sep 2004 arxiv:math/ v3 [math.sg] 20 Sep 2004](/thumbs/86/93466565.jpg) arxiv:math/0404267v3 [math.sg] 20 Sep 2004 PLANAR OPEN BOOK DECOMPOSITIONS AND CONTACT STRUCTURES JOHN B. ETNYRE Abstract. In this note we observe that while all overtwisted contact structures on compact
arxiv:math/0404267v3 [math.sg] 20 Sep 2004 PLANAR OPEN BOOK DECOMPOSITIONS AND CONTACT STRUCTURES JOHN B. ETNYRE Abstract. In this note we observe that while all overtwisted contact structures on compact
EMBEDDING ALL CONTACT 3 MANIFOLDS IN A FIXED CONTACT 5 MANIFOLD
 EMBEDDING ALL CONTACT 3 MANIFOLDS IN A FIXED CONTACT 5 MANIFOLD JOHN B. ETNYRE AND YANKI LEKILI ABSTRACT. In this note we observe that one can contact embed all contact 3 manifolds into a Stein fillable
EMBEDDING ALL CONTACT 3 MANIFOLDS IN A FIXED CONTACT 5 MANIFOLD JOHN B. ETNYRE AND YANKI LEKILI ABSTRACT. In this note we observe that one can contact embed all contact 3 manifolds into a Stein fillable
CONTACT SURGERY AND SYMPLECTIC CAPS
 CONTACT SURGERY AND SYMPLECTIC CAPS JAMES CONWAY AND JOHN B. ETNYRE Abstract. In this note we show that a closed oriented contact manifold is obtained from the standard contact sphere of the same dimension
CONTACT SURGERY AND SYMPLECTIC CAPS JAMES CONWAY AND JOHN B. ETNYRE Abstract. In this note we show that a closed oriented contact manifold is obtained from the standard contact sphere of the same dimension
Stein fillings of contact 3-manifolds obtained as Legendrian sur
 Stein fillings of contact 3-manifolds obtained as Legendrian surgeries Youlin Li (With Amey Kaloti) Shanghai Jiao Tong University A Satellite Conference of Seoul ICM 2014 Knots and Low Dimensional Manifolds
Stein fillings of contact 3-manifolds obtained as Legendrian surgeries Youlin Li (With Amey Kaloti) Shanghai Jiao Tong University A Satellite Conference of Seoul ICM 2014 Knots and Low Dimensional Manifolds
arxiv: v4 [math.gt] 14 Oct 2013
![arxiv: v4 [math.gt] 14 Oct 2013 arxiv: v4 [math.gt] 14 Oct 2013](/thumbs/83/88760117.jpg) OPEN BOOKS AND EXACT SYMPLECTIC COBORDISMS MIRKO KLUKAS arxiv:1207.5647v4 [math.gt] 14 Oct 2013 Abstract. Given two open books with equal pages we show the existence of an exact symplectic cobordism whose
OPEN BOOKS AND EXACT SYMPLECTIC COBORDISMS MIRKO KLUKAS arxiv:1207.5647v4 [math.gt] 14 Oct 2013 Abstract. Given two open books with equal pages we show the existence of an exact symplectic cobordism whose
arxiv: v1 [math.sg] 22 Nov 2011
![arxiv: v1 [math.sg] 22 Nov 2011 arxiv: v1 [math.sg] 22 Nov 2011](/thumbs/83/87621420.jpg) CONVEX PLUMBINGS AND LEFSCHETZ FIBRATIONS arxiv:1111.5327v1 [math.sg] 22 Nov 2011 DAVID GAY AND THOMAS E. MARK Abstract. We show that under appropriate hypotheses, a plumbing of symplectic surfaces in
CONVEX PLUMBINGS AND LEFSCHETZ FIBRATIONS arxiv:1111.5327v1 [math.sg] 22 Nov 2011 DAVID GAY AND THOMAS E. MARK Abstract. We show that under appropriate hypotheses, a plumbing of symplectic surfaces in
A NOTE ON STEIN FILLINGS OF CONTACT MANIFOLDS
 A NOTE ON STEIN FILLINGS OF CONTACT MANIFOLDS ANAR AKHMEDOV, JOHN B. ETNYRE, THOMAS E. MARK, AND IVAN SMITH Abstract. In this note we construct infinitely many distinct simply connected Stein fillings
A NOTE ON STEIN FILLINGS OF CONTACT MANIFOLDS ANAR AKHMEDOV, JOHN B. ETNYRE, THOMAS E. MARK, AND IVAN SMITH Abstract. In this note we construct infinitely many distinct simply connected Stein fillings
Lectures on the topology of symplectic fillings of contact 3-manifolds
 Lectures on the topology of symplectic fillings of contact 3-manifolds BURAK OZBAGCI (Last updated on July 11, 2016) These are some lectures notes for my course in the Summer School "Mapping class groups,
Lectures on the topology of symplectic fillings of contact 3-manifolds BURAK OZBAGCI (Last updated on July 11, 2016) These are some lectures notes for my course in the Summer School "Mapping class groups,
2 JOHN B. ETNYRE AND KO HONDA (M;ο) (= one satisfying ; ffi (M;ο)) cannot be symplectically cobordant to an overtwisted contact structure, but the opp
 ON SYMPLECTIC COBORDISMS JOHN B. ETNYRE AND KO HONDA Abstract. In this note we make several observations concerning symplectic cobordisms. Among other things we show that every contact 3-manifold has infinitely
ON SYMPLECTIC COBORDISMS JOHN B. ETNYRE AND KO HONDA Abstract. In this note we make several observations concerning symplectic cobordisms. Among other things we show that every contact 3-manifold has infinitely
A NOTE ON CONTACT SURGERY DIAGRAMS
 A NOTE ON CONTACT SURGERY DIAGRAMS BURAK OZBAGCI Abstract. We prove that for any positive integer the stabilization of a 1 -surgery curve in a contact surgery diagram induces an overtwisted contact structure.
A NOTE ON CONTACT SURGERY DIAGRAMS BURAK OZBAGCI Abstract. We prove that for any positive integer the stabilization of a 1 -surgery curve in a contact surgery diagram induces an overtwisted contact structure.
LECTURES ON THE TOPOLOGY OF SYMPLECTIC FILLINGS OF CONTACT 3-MANIFOLDS
 LECTURES ON THE TOPOLOGY OF SYMPLECTIC FILLINGS OF CONTACT 3-MANIFOLDS BURAK OZBAGCI ABSTRACT. These are some lecture notes for my mini-course in the Graduate Workshop on 4-Manifolds, August 18-22, 2014
LECTURES ON THE TOPOLOGY OF SYMPLECTIC FILLINGS OF CONTACT 3-MANIFOLDS BURAK OZBAGCI ABSTRACT. These are some lecture notes for my mini-course in the Graduate Workshop on 4-Manifolds, August 18-22, 2014
arxiv: v4 [math.gt] 7 Jan 2009
![arxiv: v4 [math.gt] 7 Jan 2009 arxiv: v4 [math.gt] 7 Jan 2009](/thumbs/88/117875544.jpg) Journal of Gökova Geometry Topology Volume 2 (2008) 83 106 Every 4-Manifold is BLF arxiv:0803.2297v4 [math.gt] 7 Jan 2009 Selman Akbulut and Çağrı Karakurt Abstract. Here we show that every compact smooth
Journal of Gökova Geometry Topology Volume 2 (2008) 83 106 Every 4-Manifold is BLF arxiv:0803.2297v4 [math.gt] 7 Jan 2009 Selman Akbulut and Çağrı Karakurt Abstract. Here we show that every compact smooth
Lecture notes on stabilization of contact open books
 Münster J. of Math. 10 (2017), 425 455 DOI 10.17879/70299609615 urn:nbn:de:hbz:6-70299611015 Münster Journal of Mathematics c Münster J. of Math. 2017 Lecture notes on stabilization of contact open books
Münster J. of Math. 10 (2017), 425 455 DOI 10.17879/70299609615 urn:nbn:de:hbz:6-70299611015 Münster Journal of Mathematics c Münster J. of Math. 2017 Lecture notes on stabilization of contact open books
arxiv: v4 [math.sg] 28 Feb 2016
![arxiv: v4 [math.sg] 28 Feb 2016 arxiv: v4 [math.sg] 28 Feb 2016](/thumbs/93/112059478.jpg) SUBCRITICAL CONTACT SURGERIES AND THE TOPOLOGY OF SYMPLECTIC FILLINGS arxiv:1408.1051v4 [math.sg] 28 Feb 2016 PAOLO GHIGGINI, KLAUS NIEDERKRÜGER, AND CHRIS WENDL Abstract. By a result of Eliashberg, every
SUBCRITICAL CONTACT SURGERIES AND THE TOPOLOGY OF SYMPLECTIC FILLINGS arxiv:1408.1051v4 [math.sg] 28 Feb 2016 PAOLO GHIGGINI, KLAUS NIEDERKRÜGER, AND CHRIS WENDL Abstract. By a result of Eliashberg, every
CLASSIFICATION OF TIGHT CONTACT STRUCTURES ON SURGERIES ON THE FIGURE-EIGHT KNOT
 CLASSIFICATION OF TIGHT CONTACT STRUCTURES ON SURGERIES ON THE FIGURE-EIGHT KNOT JAMES CONWAY AND HYUNKI MIN ABSTRACT. Two of the basic questions in contact topology are which manifolds admit tight contact
CLASSIFICATION OF TIGHT CONTACT STRUCTURES ON SURGERIES ON THE FIGURE-EIGHT KNOT JAMES CONWAY AND HYUNKI MIN ABSTRACT. Two of the basic questions in contact topology are which manifolds admit tight contact
B B. B g ... g 1 g ... c c. g b
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Xxxx XXXX, Pages 000 000 S 0002-9939(XX)0000-0 CONTACT 3-MANIFOLDS WITH INFINITELY MANY STEIN FILLINGS BURAK OZBAGCI AND ANDRÁS I.
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Xxxx XXXX, Pages 000 000 S 0002-9939(XX)0000-0 CONTACT 3-MANIFOLDS WITH INFINITELY MANY STEIN FILLINGS BURAK OZBAGCI AND ANDRÁS I.
DIFFEOMORPHISMS OF SURFACES AND SMOOTH 4-MANIFOLDS
 DIFFEOMORPHISMS OF SURFACES AND SMOOTH 4-MANIFOLDS SDGLDTS FEB 18 2016 MORGAN WEILER Motivation: Lefschetz Fibrations on Smooth 4-Manifolds There are a lot of good reasons to think about mapping class
DIFFEOMORPHISMS OF SURFACES AND SMOOTH 4-MANIFOLDS SDGLDTS FEB 18 2016 MORGAN WEILER Motivation: Lefschetz Fibrations on Smooth 4-Manifolds There are a lot of good reasons to think about mapping class
LECTURE: KOBORDISMENTHEORIE, WINTER TERM 2011/12; SUMMARY AND LITERATURE
 LECTURE: KOBORDISMENTHEORIE, WINTER TERM 2011/12; SUMMARY AND LITERATURE JOHANNES EBERT 1.1. October 11th. 1. Recapitulation from differential topology Definition 1.1. Let M m, N n, be two smooth manifolds
LECTURE: KOBORDISMENTHEORIE, WINTER TERM 2011/12; SUMMARY AND LITERATURE JOHANNES EBERT 1.1. October 11th. 1. Recapitulation from differential topology Definition 1.1. Let M m, N n, be two smooth manifolds
fy (X(g)) Y (f)x(g) gy (X(f)) Y (g)x(f)) = fx(y (g)) + gx(y (f)) fy (X(g)) gy (X(f))
 1. Basic algebra of vector fields Let V be a finite dimensional vector space over R. Recall that V = {L : V R} is defined to be the set of all linear maps to R. V is isomorphic to V, but there is no canonical
1. Basic algebra of vector fields Let V be a finite dimensional vector space over R. Recall that V = {L : V R} is defined to be the set of all linear maps to R. V is isomorphic to V, but there is no canonical
LECTURE 5: SOME BASIC CONSTRUCTIONS IN SYMPLECTIC TOPOLOGY
 LECTURE 5: SOME BASIC CONSTRUCTIONS IN SYMPLECTIC TOPOLOGY WEIMIN CHEN, UMASS, SPRING 07 1. Blowing up and symplectic cutting In complex geometry the blowing-up operation amounts to replace a point in
LECTURE 5: SOME BASIC CONSTRUCTIONS IN SYMPLECTIC TOPOLOGY WEIMIN CHEN, UMASS, SPRING 07 1. Blowing up and symplectic cutting In complex geometry the blowing-up operation amounts to replace a point in
THE CANONICAL PENCILS ON HORIKAWA SURFACES
 THE CANONICAL PENCILS ON HORIKAWA SURFACES DENIS AUROUX Abstract. We calculate the monodromies of the canonical Lefschetz pencils on a pair of homeomorphic Horikawa surfaces. We show in particular that
THE CANONICAL PENCILS ON HORIKAWA SURFACES DENIS AUROUX Abstract. We calculate the monodromies of the canonical Lefschetz pencils on a pair of homeomorphic Horikawa surfaces. We show in particular that
arxiv: v1 [math.sg] 21 Oct 2016
![arxiv: v1 [math.sg] 21 Oct 2016 arxiv: v1 [math.sg] 21 Oct 2016](/thumbs/96/127525158.jpg) LEGENDRIAN FRONTS FOR AFFINE VARIETIES ROGER CASALS AND EMMY MURPHY arxiv:1610.06977v1 [math.sg] 21 Oct 2016 Abstract. In this article we study Weinstein structures endowed with a Lefschetz fibration in
LEGENDRIAN FRONTS FOR AFFINE VARIETIES ROGER CASALS AND EMMY MURPHY arxiv:1610.06977v1 [math.sg] 21 Oct 2016 Abstract. In this article we study Weinstein structures endowed with a Lefschetz fibration in
arxiv: v1 [math.sg] 20 Jul 2014
![arxiv: v1 [math.sg] 20 Jul 2014 arxiv: v1 [math.sg] 20 Jul 2014](/thumbs/88/117675221.jpg) STEIN FILLINGS OF HOMOLOGY 3-SPHERES AND MAPPING CLASS GROUPS arxiv:1407.5257v1 [math.sg] 20 Jul 2014 TAKAHIRO OBA Abstract. In this article, using combinatorial techniques of mapping class groups, we
STEIN FILLINGS OF HOMOLOGY 3-SPHERES AND MAPPING CLASS GROUPS arxiv:1407.5257v1 [math.sg] 20 Jul 2014 TAKAHIRO OBA Abstract. In this article, using combinatorial techniques of mapping class groups, we
Math 215B: Solutions 3
 Math 215B: Solutions 3 (1) For this problem you may assume the classification of smooth one-dimensional manifolds: Any compact smooth one-dimensional manifold is diffeomorphic to a finite disjoint union
Math 215B: Solutions 3 (1) For this problem you may assume the classification of smooth one-dimensional manifolds: Any compact smooth one-dimensional manifold is diffeomorphic to a finite disjoint union
Existence of Engel structures
 Annals of Mathematics, 169 (2009), 79 137 Existence of Engel structures By Thomas Vogel Abstract We develop a construction of Engel structures on 4-manifolds based on decompositions of manifolds into round
Annals of Mathematics, 169 (2009), 79 137 Existence of Engel structures By Thomas Vogel Abstract We develop a construction of Engel structures on 4-manifolds based on decompositions of manifolds into round
A Note on V. I. Arnold s Chord Conjecture. Casim Abbas. 1 Introduction
 IMRN International Mathematics Research Notices 1999, No. 4 A Note on V. I. Arnold s Chord Conjecture Casim Abbas 1 Introduction This paper makes a contribution to a conjecture of V. I. Arnold in contact
IMRN International Mathematics Research Notices 1999, No. 4 A Note on V. I. Arnold s Chord Conjecture Casim Abbas 1 Introduction This paper makes a contribution to a conjecture of V. I. Arnold in contact
CONVEX PLUMBINGS AND LEFSCHETZ FIBRATIONS. David Gay and Thomas E. Mark
 JOURNAL OF SYMPLECTIC GEOMETRY Volume 11, Number 3, 363 375, 2013 CONVEX PLUMBINGS AND LEFSCHETZ FIBRATIONS David Gay and Thomas E. Mark We show that under appropriate hypotheses, a plumbing of symplectic
JOURNAL OF SYMPLECTIC GEOMETRY Volume 11, Number 3, 363 375, 2013 CONVEX PLUMBINGS AND LEFSCHETZ FIBRATIONS David Gay and Thomas E. Mark We show that under appropriate hypotheses, a plumbing of symplectic
GLUCK TWISTING 4-MANIFOLDS WITH ODD INTERSECTION FORM. Selman Akbulut and Kouichi Yasui
 Math. Res. Lett. 20 (2013), no. 02, 385 389 c International Press 2013 GLUCK TWISTING 4-MANIFOLDS WITH ODD INTERSECTION FORM Selman Akbulut and Kouichi Yasui Abstract. We give a simple criterion when a
Math. Res. Lett. 20 (2013), no. 02, 385 389 c International Press 2013 GLUCK TWISTING 4-MANIFOLDS WITH ODD INTERSECTION FORM Selman Akbulut and Kouichi Yasui Abstract. We give a simple criterion when a
arxiv: v2 [math.sg] 21 Nov 2018
![arxiv: v2 [math.sg] 21 Nov 2018 arxiv: v2 [math.sg] 21 Nov 2018](/thumbs/91/105199702.jpg) GEOMETRIC CRITERIA FOR OVERTWISTEDNESS ROGER CASALS, EMMY MURPHY, AND FRANCISCO PRESAS arxiv:1503.06221v2 [math.sg] 21 Nov 2018 Abstract. In this article we establish efficient geometric criteria to decide
GEOMETRIC CRITERIA FOR OVERTWISTEDNESS ROGER CASALS, EMMY MURPHY, AND FRANCISCO PRESAS arxiv:1503.06221v2 [math.sg] 21 Nov 2018 Abstract. In this article we establish efficient geometric criteria to decide
Broken pencils and four-manifold invariants. Tim Perutz (Cambridge)
 Broken pencils and four-manifold invariants Tim Perutz (Cambridge) Aim This talk is about a project to construct and study a symplectic substitute for gauge theory in 2, 3 and 4 dimensions. The 3- and
Broken pencils and four-manifold invariants Tim Perutz (Cambridge) Aim This talk is about a project to construct and study a symplectic substitute for gauge theory in 2, 3 and 4 dimensions. The 3- and
SYMPLECTIC GEOMETRY: LECTURE 5
 SYMPLECTIC GEOMETRY: LECTURE 5 LIAT KESSLER Let (M, ω) be a connected compact symplectic manifold, T a torus, T M M a Hamiltonian action of T on M, and Φ: M t the assoaciated moment map. Theorem 0.1 (The
SYMPLECTIC GEOMETRY: LECTURE 5 LIAT KESSLER Let (M, ω) be a connected compact symplectic manifold, T a torus, T M M a Hamiltonian action of T on M, and Φ: M t the assoaciated moment map. Theorem 0.1 (The
Making cobordisms symplectic
 Making cobordisms symplectic arxiv:1504.06312v3 [math.sg] 7 Apr 2017 Yakov Eliashberg Stanford University Abstract Emmy Murphy MIT We establish an existence h-principle for symplectic cobordisms of dimension
Making cobordisms symplectic arxiv:1504.06312v3 [math.sg] 7 Apr 2017 Yakov Eliashberg Stanford University Abstract Emmy Murphy MIT We establish an existence h-principle for symplectic cobordisms of dimension
Symplectic topology and algebraic geometry II: Lagrangian submanifolds
 Symplectic topology and algebraic geometry II: Lagrangian submanifolds Jonathan Evans UCL 26th January 2013 Jonathan Evans (UCL) Lagrangian submanifolds 26th January 2013 1 / 35 Addendum to last talk:
Symplectic topology and algebraic geometry II: Lagrangian submanifolds Jonathan Evans UCL 26th January 2013 Jonathan Evans (UCL) Lagrangian submanifolds 26th January 2013 1 / 35 Addendum to last talk:
On the topology of fillings of contact manifolds and applications
 On the topology of fillings of contact manifolds and applications Alexandru Oancea 1 Claude Viterbo 2 1 IRMA UMR 7501, Université de Strasbourg 7 rue René Descartes, 67084 Strasbourg oancea@math.u-strasbg.fr
On the topology of fillings of contact manifolds and applications Alexandru Oancea 1 Claude Viterbo 2 1 IRMA UMR 7501, Université de Strasbourg 7 rue René Descartes, 67084 Strasbourg oancea@math.u-strasbg.fr
Bordism and the Pontryagin-Thom Theorem
 Bordism and the Pontryagin-Thom Theorem Richard Wong Differential Topology Term Paper December 2, 2016 1 Introduction Given the classification of low dimensional manifolds up to equivalence relations such
Bordism and the Pontryagin-Thom Theorem Richard Wong Differential Topology Term Paper December 2, 2016 1 Introduction Given the classification of low dimensional manifolds up to equivalence relations such
TIGHT PLANAR CONTACT MANIFOLDS WITH VANISHING HEEGAARD FLOER CONTACT INVARIANTS
 TIGHT PLANAR CONTACT MANIFOLDS WITH VANISHING HEEGAARD FLOER CONTACT INVARIANTS JAMES CONWAY, AMEY KALOTI, AND DHEERAJ KULKARNI Abstract. In this note, we exhibit infinite families of tight non-fillable
TIGHT PLANAR CONTACT MANIFOLDS WITH VANISHING HEEGAARD FLOER CONTACT INVARIANTS JAMES CONWAY, AMEY KALOTI, AND DHEERAJ KULKARNI Abstract. In this note, we exhibit infinite families of tight non-fillable
SYMPLECTIC LEFSCHETZ FIBRATIONS ALEXANDER CAVIEDES CASTRO
 SYMPLECTIC LEFSCHETZ FIBRATIONS ALEXANDER CAVIEDES CASTRO. Introduction A Lefschetz pencil is a construction that comes from algebraic geometry, but it is closely related with symplectic geometry. Indeed,
SYMPLECTIC LEFSCHETZ FIBRATIONS ALEXANDER CAVIEDES CASTRO. Introduction A Lefschetz pencil is a construction that comes from algebraic geometry, but it is closely related with symplectic geometry. Indeed,
arxiv: v1 [math.gt] 23 Apr 2014
![arxiv: v1 [math.gt] 23 Apr 2014 arxiv: v1 [math.gt] 23 Apr 2014](/thumbs/75/72058242.jpg) THE NUMBER OF FRAMINGS OF A KNOT IN A 3-MANIFOLD PATRICIA CAHN, VLADIMIR CHERNOV, AND RUSTAM SADYKOV arxiv:1404.5851v1 [math.gt] 23 Apr 2014 Abstract. In view of the self-linking invariant, the number
THE NUMBER OF FRAMINGS OF A KNOT IN A 3-MANIFOLD PATRICIA CAHN, VLADIMIR CHERNOV, AND RUSTAM SADYKOV arxiv:1404.5851v1 [math.gt] 23 Apr 2014 Abstract. In view of the self-linking invariant, the number
PLANAR OPEN BOOK DECOMPOSITIONS OF 3-MANIFOLDS
 ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 44, Number 5, 2014 PLANAR OPEN BOOK DECOMPOSITIONS OF 3-MANIFOLDS ABSTRACT. Due to Alexander, every closed oriented 3- manifold has an open book decomposition.
ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 44, Number 5, 2014 PLANAR OPEN BOOK DECOMPOSITIONS OF 3-MANIFOLDS ABSTRACT. Due to Alexander, every closed oriented 3- manifold has an open book decomposition.
OPEN BOOK DECOMPOSITIONS IN HIGH DIMENSIONAL CONTACT MANIFOLDS
 OPEN BOOK DECOMPOSITIONS IN HIGH DIMENSIONAL CONTACT MANIFOLDS A Thesis Presented to The Academic Faculty by Gokhan Elmas In Partial Fulfillment of the Requirements for the Degree Master of Science in
OPEN BOOK DECOMPOSITIONS IN HIGH DIMENSIONAL CONTACT MANIFOLDS A Thesis Presented to The Academic Faculty by Gokhan Elmas In Partial Fulfillment of the Requirements for the Degree Master of Science in
Lecture III: Neighbourhoods
 Lecture III: Neighbourhoods Jonathan Evans 7th October 2010 Jonathan Evans () Lecture III: Neighbourhoods 7th October 2010 1 / 18 Jonathan Evans () Lecture III: Neighbourhoods 7th October 2010 2 / 18 In
Lecture III: Neighbourhoods Jonathan Evans 7th October 2010 Jonathan Evans () Lecture III: Neighbourhoods 7th October 2010 1 / 18 Jonathan Evans () Lecture III: Neighbourhoods 7th October 2010 2 / 18 In
arxiv: v1 [math.sg] 27 Nov 2017
![arxiv: v1 [math.sg] 27 Nov 2017 arxiv: v1 [math.sg] 27 Nov 2017](/thumbs/89/101006274.jpg) On some examples and constructions of contact manifolds Fabio Gironella arxiv:1711.09800v1 [math.sg] 27 Nov 2017 Abstract The first goal of this paper is to construct examples of higher dimensional contact
On some examples and constructions of contact manifolds Fabio Gironella arxiv:1711.09800v1 [math.sg] 27 Nov 2017 Abstract The first goal of this paper is to construct examples of higher dimensional contact
LECTURE 5: COMPLEX AND KÄHLER MANIFOLDS
 LECTURE 5: COMPLEX AND KÄHLER MANIFOLDS Contents 1. Almost complex manifolds 1. Complex manifolds 5 3. Kähler manifolds 9 4. Dolbeault cohomology 11 1. Almost complex manifolds Almost complex structures.
LECTURE 5: COMPLEX AND KÄHLER MANIFOLDS Contents 1. Almost complex manifolds 1. Complex manifolds 5 3. Kähler manifolds 9 4. Dolbeault cohomology 11 1. Almost complex manifolds Almost complex structures.
Exotic Lefschetz Fibrations and Stein Fillings with Arbitrary Fundamental Group
 Exotic Lefschetz Fibrations and Stein Fillings with Arbitrary Fundamental Group Anar Akhmedov University of Minnesota, Twin Cities February 19, 2015 Anar Akhmedov (University of Minnesota, Minneapolis)Exotic
Exotic Lefschetz Fibrations and Stein Fillings with Arbitrary Fundamental Group Anar Akhmedov University of Minnesota, Twin Cities February 19, 2015 Anar Akhmedov (University of Minnesota, Minneapolis)Exotic
M4P52 Manifolds, 2016 Problem Sheet 1
 Problem Sheet. Let X and Y be n-dimensional topological manifolds. Prove that the disjoint union X Y is an n-dimensional topological manifold. Is S S 2 a topological manifold? 2. Recall that that the discrete
Problem Sheet. Let X and Y be n-dimensional topological manifolds. Prove that the disjoint union X Y is an n-dimensional topological manifold. Is S S 2 a topological manifold? 2. Recall that that the discrete
Poisson geometry of b-manifolds. Eva Miranda
 Poisson geometry of b-manifolds Eva Miranda UPC-Barcelona Rio de Janeiro, July 26, 2010 Eva Miranda (UPC) Poisson 2010 July 26, 2010 1 / 45 Outline 1 Motivation 2 Classification of b-poisson manifolds
Poisson geometry of b-manifolds Eva Miranda UPC-Barcelona Rio de Janeiro, July 26, 2010 Eva Miranda (UPC) Poisson 2010 July 26, 2010 1 / 45 Outline 1 Motivation 2 Classification of b-poisson manifolds
AIM Workshop - Contact topology in higher dimensions - (May 21-25, 2012): Questions and open problems
 AIM Workshop - Contact topology in higher dimensions - (May 21-25, 2012): Questions and open problems Warning The following notes, written by Sylvain Courte with the help of Patrick Massot, describe the
AIM Workshop - Contact topology in higher dimensions - (May 21-25, 2012): Questions and open problems Warning The following notes, written by Sylvain Courte with the help of Patrick Massot, describe the
ON KNOTS IN OVERTWISTED CONTACT STRUCTURES
 ON KNOTS IN OVERTWISTED CONTACT STRUCTURES JOHN B. ETNYRE ABSTRACT. We prove that each overtwisted contact structure has knot types that are represented by infinitely many distinct transverse knots all
ON KNOTS IN OVERTWISTED CONTACT STRUCTURES JOHN B. ETNYRE ABSTRACT. We prove that each overtwisted contact structure has knot types that are represented by infinitely many distinct transverse knots all
Nodal symplectic spheres in CP 2 with positive self intersection
 Nodal symplectic spheres in CP 2 with positive self intersection Jean-François BARRAUD barraud@picard.ups-tlse.fr Abstract 1 : Let ω be the canonical Kähler structure on CP 2 We prove that any ω-symplectic
Nodal symplectic spheres in CP 2 with positive self intersection Jean-François BARRAUD barraud@picard.ups-tlse.fr Abstract 1 : Let ω be the canonical Kähler structure on CP 2 We prove that any ω-symplectic
Liouville and Weinstein manifolds
 Liouville and Weinstein manifolds precourse for SFT 8, Berlin, August 6-7, 2016 Sylvain Courte Contents 1 Liouville and Weinstein manifolds 2 1.1 Symplectic convexity........................... 2 1.2 Liouville
Liouville and Weinstein manifolds precourse for SFT 8, Berlin, August 6-7, 2016 Sylvain Courte Contents 1 Liouville and Weinstein manifolds 2 1.1 Symplectic convexity........................... 2 1.2 Liouville
Basic Objects and Important Questions
 THE FLEXIBILITY AND RIGIDITY OF LAGRANGIAN AND LEGENDRIAN SUBMANIFOLDS LISA TRAYNOR Abstract. These are informal notes to accompany the first week of graduate lectures at the IAS Women and Mathematics
THE FLEXIBILITY AND RIGIDITY OF LAGRANGIAN AND LEGENDRIAN SUBMANIFOLDS LISA TRAYNOR Abstract. These are informal notes to accompany the first week of graduate lectures at the IAS Women and Mathematics
Generalized symplectic rational blowdowns
 ISSN 1472-2739 (on-line) 1472-2747 (printed) 503 Algebraic & Geometric Topology Volume 1 (2001) 503 518 Published: 22 September 2001 ATG Generalized symplectic rational blowdowns Margaret Symington Abstract
ISSN 1472-2739 (on-line) 1472-2747 (printed) 503 Algebraic & Geometric Topology Volume 1 (2001) 503 518 Published: 22 September 2001 ATG Generalized symplectic rational blowdowns Margaret Symington Abstract
A Crash Course of Floer Homology for Lagrangian Intersections
 A Crash Course of Floer Homology for Lagrangian Intersections Manabu AKAHO Department of Mathematics Tokyo Metropolitan University akaho@math.metro-u.ac.jp 1 Introduction There are several kinds of Floer
A Crash Course of Floer Homology for Lagrangian Intersections Manabu AKAHO Department of Mathematics Tokyo Metropolitan University akaho@math.metro-u.ac.jp 1 Introduction There are several kinds of Floer
GRAPHICALITY, C 0 CONVERGENCE, AND THE CALABI HOMOMORPHISM
 GRAPHICALITY, C CONVERGENCE, AND THE CALABI HOMOMORPHISM MICHAEL USHER Abstract. Consider a sequence of compactly supported Hamiltonian diffeomorphisms φ k of an exact symplectic manifold, all of which
GRAPHICALITY, C CONVERGENCE, AND THE CALABI HOMOMORPHISM MICHAEL USHER Abstract. Consider a sequence of compactly supported Hamiltonian diffeomorphisms φ k of an exact symplectic manifold, all of which
arxiv: v3 [math.gt] 20 Jan 2019
![arxiv: v3 [math.gt] 20 Jan 2019 arxiv: v3 [math.gt] 20 Jan 2019](/thumbs/88/115071343.jpg) LIFTS OF SPHERICAL MORSE FUNCTIONS arxiv:1805.05852v3 [math.gt] 20 Jan 2019 NAOKI KITAZAWA Abstract. In studies of smooth maps with good differential topological properties such as immersions and embeddings,
LIFTS OF SPHERICAL MORSE FUNCTIONS arxiv:1805.05852v3 [math.gt] 20 Jan 2019 NAOKI KITAZAWA Abstract. In studies of smooth maps with good differential topological properties such as immersions and embeddings,
Math 147, Homework 5 Solutions Due: May 15, 2012
 Math 147, Homework 5 Solutions Due: May 15, 2012 1 Let f : R 3 R 6 and φ : R 3 R 3 be the smooth maps defined by: f(x, y, z) = (x 2, y 2, z 2, xy, xz, yz) and φ(x, y, z) = ( x, y, z) (a) Show that f is
Math 147, Homework 5 Solutions Due: May 15, 2012 1 Let f : R 3 R 6 and φ : R 3 R 3 be the smooth maps defined by: f(x, y, z) = (x 2, y 2, z 2, xy, xz, yz) and φ(x, y, z) = ( x, y, z) (a) Show that f is
HARMONIC COHOMOLOGY OF SYMPLECTIC FIBER BUNDLES
 HARMONIC COHOMOLOGY OF SYMPLECTIC FIBER BUNDLES OLIVER EBNER AND STEFAN HALLER Abstract. We show that every de Rham cohomology class on the total space of a symplectic fiber bundle with closed Lefschetz
HARMONIC COHOMOLOGY OF SYMPLECTIC FIBER BUNDLES OLIVER EBNER AND STEFAN HALLER Abstract. We show that every de Rham cohomology class on the total space of a symplectic fiber bundle with closed Lefschetz
The Classification of Nonsimple Algebraic Tangles
 The Classification of Nonsimple Algebraic Tangles Ying-Qing Wu 1 A tangle is a pair (B, T ), where B is a 3-ball, T is a pair of properly embedded arcs. When there is no ambiguity we will simply say that
The Classification of Nonsimple Algebraic Tangles Ying-Qing Wu 1 A tangle is a pair (B, T ), where B is a 3-ball, T is a pair of properly embedded arcs. When there is no ambiguity we will simply say that
A NEW CONSTRUCTION OF POISSON MANIFOLDS
 A NEW CONSTRUCTION OF POISSON MANIFOLDS A. IBORT, D. MARTÍNEZ TORRES Abstract A new technique to construct Poisson manifolds inspired both in surgery ideas used to define Poisson structures on 3-manifolds
A NEW CONSTRUCTION OF POISSON MANIFOLDS A. IBORT, D. MARTÍNEZ TORRES Abstract A new technique to construct Poisson manifolds inspired both in surgery ideas used to define Poisson structures on 3-manifolds
LECTURE 11: SYMPLECTIC TORIC MANIFOLDS. Contents 1. Symplectic toric manifolds 1 2. Delzant s theorem 4 3. Symplectic cut 8
 LECTURE 11: SYMPLECTIC TORIC MANIFOLDS Contents 1. Symplectic toric manifolds 1 2. Delzant s theorem 4 3. Symplectic cut 8 1. Symplectic toric manifolds Orbit of torus actions. Recall that in lecture 9
LECTURE 11: SYMPLECTIC TORIC MANIFOLDS Contents 1. Symplectic toric manifolds 1 2. Delzant s theorem 4 3. Symplectic cut 8 1. Symplectic toric manifolds Orbit of torus actions. Recall that in lecture 9
arxiv: v3 [math.gt] 26 Aug 2014
![arxiv: v3 [math.gt] 26 Aug 2014 arxiv: v3 [math.gt] 26 Aug 2014](/thumbs/94/121791915.jpg) ARBITRARILY LONG FACTORIZATIONS IN MAPPING CLASS GROUPS arxiv:309.3778v3 [math.gt] 6 Aug 0 ELİF DALYAN, MUSTAFA KORKMAZ AND MEHMETCİK PAMUK Abstract. Onacompact orientedsurface ofgenusg withn boundary
ARBITRARILY LONG FACTORIZATIONS IN MAPPING CLASS GROUPS arxiv:309.3778v3 [math.gt] 6 Aug 0 ELİF DALYAN, MUSTAFA KORKMAZ AND MEHMETCİK PAMUK Abstract. Onacompact orientedsurface ofgenusg withn boundary
LECTURE 11: TRANSVERSALITY
 LECTURE 11: TRANSVERSALITY Let f : M N be a smooth map. In the past three lectures, we are mainly studying the image of f, especially when f is an embedding. Today we would like to study the pre-image
LECTURE 11: TRANSVERSALITY Let f : M N be a smooth map. In the past three lectures, we are mainly studying the image of f, especially when f is an embedding. Today we would like to study the pre-image
HOLOMORPHIC DISKS AND TOPOLOGICAL INVARIANTS FOR CLOSED THREE-MANIFOLDS arxiv:math/ v4 [math.sg] 11 Mar 2003
![HOLOMORPHIC DISKS AND TOPOLOGICAL INVARIANTS FOR CLOSED THREE-MANIFOLDS arxiv:math/ v4 [math.sg] 11 Mar 2003 HOLOMORPHIC DISKS AND TOPOLOGICAL INVARIANTS FOR CLOSED THREE-MANIFOLDS arxiv:math/ v4 [math.sg] 11 Mar 2003](/thumbs/83/87473625.jpg) HOLOMORPHIC DISKS AND TOPOLOGICAL INVARIANTS FOR CLOSED THREE-MANIFOLDS arxiv:math/0101206v4 [math.sg] 11 Mar 2003 PETER OZSVÁTH AND ZOLTÁN SZABÓ Abstract. The aim of this article is to introduce certain
HOLOMORPHIC DISKS AND TOPOLOGICAL INVARIANTS FOR CLOSED THREE-MANIFOLDS arxiv:math/0101206v4 [math.sg] 11 Mar 2003 PETER OZSVÁTH AND ZOLTÁN SZABÓ Abstract. The aim of this article is to introduce certain
Constructing symplectic forms on 4 manifolds which vanish on circles
 ISSN 1364-0380 (on line) 1465-3060 (printed) 743 Geometry & Topology Volume 8 (2004) 743 777 Published: 18 May 2004 G G G G T T T G T T T G T G T GG TT G G G G GG T T T TT Constructing symplectic forms
ISSN 1364-0380 (on line) 1465-3060 (printed) 743 Geometry & Topology Volume 8 (2004) 743 777 Published: 18 May 2004 G G G G T T T G T T T G T G T GG TT G G G G GG T T T TT Constructing symplectic forms
Embedded contact homology and its applications
 Embedded contact homology and its applications Michael Hutchings Department of Mathematics University of California, Berkeley International Congress of Mathematicians, Hyderabad August 26, 2010 arxiv:1003.3209
Embedded contact homology and its applications Michael Hutchings Department of Mathematics University of California, Berkeley International Congress of Mathematicians, Hyderabad August 26, 2010 arxiv:1003.3209
FIBERED TRANSVERSE KNOTS AND THE BENNEQUIN BOUND
 FIBERED TRANSVERSE KNOTS AND THE BENNEQUIN BOUND JOHN B. ETNYRE AND JEREMY VAN HORN-MORRIS Abstract. We prove that a nicely fibered link (by which we mean the binding of an open book) in a tight contact
FIBERED TRANSVERSE KNOTS AND THE BENNEQUIN BOUND JOHN B. ETNYRE AND JEREMY VAN HORN-MORRIS Abstract. We prove that a nicely fibered link (by which we mean the binding of an open book) in a tight contact
LECTURE 28: VECTOR BUNDLES AND FIBER BUNDLES
 LECTURE 28: VECTOR BUNDLES AND FIBER BUNDLES 1. Vector Bundles In general, smooth manifolds are very non-linear. However, there exist many smooth manifolds which admit very nice partial linear structures.
LECTURE 28: VECTOR BUNDLES AND FIBER BUNDLES 1. Vector Bundles In general, smooth manifolds are very non-linear. However, there exist many smooth manifolds which admit very nice partial linear structures.
Mathematical Research Letters 11, (2004) CONTACT STRUCTURES WITH DISTINCT HEEGAARD FLOER INVARIANTS. Olga Plamenevskaya
 Mathematical Research Letters 11, 547 561 (2004) CONTACT STRUCTURES WITH DISTINCT HEEGAARD FLOER INVARIANTS Olga Plamenevskaya Abstract. We use the Heegaard Floer theory developed by P.Ozsváth and Z.Szabó
Mathematical Research Letters 11, 547 561 (2004) CONTACT STRUCTURES WITH DISTINCT HEEGAARD FLOER INVARIANTS Olga Plamenevskaya Abstract. We use the Heegaard Floer theory developed by P.Ozsváth and Z.Szabó
RIMS-1897 On multiframings of 3-manifolds By Tatsuro SHIMIZU December 2018 RESEARCH INSTITUTE FOR MATHEMATICAL SCIENCES KYOTO UNIVERSITY, Kyoto, Japan
 RIMS-1897 On multiframings of 3-manifolds By Tatsuro SHIMIZU December 2018 RESEARCH INSTITUTE FOR MATHEMATICAL SCIENCES KYOTO UNIVERSITY, Kyoto, Japan On multiframings of 3 manifolds Tatsuro Shimizu 1
RIMS-1897 On multiframings of 3-manifolds By Tatsuro SHIMIZU December 2018 RESEARCH INSTITUTE FOR MATHEMATICAL SCIENCES KYOTO UNIVERSITY, Kyoto, Japan On multiframings of 3 manifolds Tatsuro Shimizu 1
Eva Miranda. UPC-Barcelona. (joint with Victor Guillemin and Ana Rita Pires) Zaragoza, February
 From b-poisson manifolds to symplectic mapping torus and back Eva Miranda UPC-Barcelona (joint with Victor Guillemin and Ana Rita Pires) Zaragoza, February 8 2011 Eva Miranda (UPC) Poisson Day February
From b-poisson manifolds to symplectic mapping torus and back Eva Miranda UPC-Barcelona (joint with Victor Guillemin and Ana Rita Pires) Zaragoza, February 8 2011 Eva Miranda (UPC) Poisson Day February
4-MANIFOLDS AS FIBER BUNDLES
 4-MANIFOLDS AS FIBER BUNDLES MORGAN WEILER Structures on 4-Manifolds I care about geometric structures on 4-manifolds because they allow me to obtain results about their smooth topology. Think: de Rham
4-MANIFOLDS AS FIBER BUNDLES MORGAN WEILER Structures on 4-Manifolds I care about geometric structures on 4-manifolds because they allow me to obtain results about their smooth topology. Think: de Rham
DIFFERENTIAL TOPOLOGY AND THE POINCARÉ-HOPF THEOREM
 DIFFERENTIAL TOPOLOGY AND THE POINCARÉ-HOPF THEOREM ARIEL HAFFTKA 1. Introduction In this paper we approach the topology of smooth manifolds using differential tools, as opposed to algebraic ones such
DIFFERENTIAL TOPOLOGY AND THE POINCARÉ-HOPF THEOREM ARIEL HAFFTKA 1. Introduction In this paper we approach the topology of smooth manifolds using differential tools, as opposed to algebraic ones such
APPLICATIONS OF HOFER S GEOMETRY TO HAMILTONIAN DYNAMICS
 APPLICATIONS OF HOFER S GEOMETRY TO HAMILTONIAN DYNAMICS FELIX SCHLENK Abstract. We prove that for every subset A of a tame symplectic manifold (W, ω) the π 1 -sensitive Hofer Zehnder capacity of A is
APPLICATIONS OF HOFER S GEOMETRY TO HAMILTONIAN DYNAMICS FELIX SCHLENK Abstract. We prove that for every subset A of a tame symplectic manifold (W, ω) the π 1 -sensitive Hofer Zehnder capacity of A is
An invariant of Legendrian and transverse links from open book decompositions of contact 3-manifolds
 An invariant of Legendrian and transverse links from open book decompositions of contact 3-manifolds Alberto Cavallo Department of Mathematics and its Application, Central European University, Budapest
An invariant of Legendrian and transverse links from open book decompositions of contact 3-manifolds Alberto Cavallo Department of Mathematics and its Application, Central European University, Budapest
Scharlemann s manifold is standard
 Annals of Mathematics, 149 (1999), 497 510 Scharlemann s manifold is standard By Selman Akbulut* Dedicated to Robion Kirby on the occasion of his 60 th birthday Abstract In his 1974 thesis, Martin Scharlemann
Annals of Mathematics, 149 (1999), 497 510 Scharlemann s manifold is standard By Selman Akbulut* Dedicated to Robion Kirby on the occasion of his 60 th birthday Abstract In his 1974 thesis, Martin Scharlemann
Relative symplectic caps, 4-genus and fibered knots
 Proc. Indian Acad. Sci. (Math. Sci.) Vol. 126, No. 2, May 2016, pp. 261 275. c Indian Academy of Sciences Relative symplectic caps, 4-genus and fibered knots SIDDHARTHA GADGIL 1 and DHEERAJ KULKARNI 2,
Proc. Indian Acad. Sci. (Math. Sci.) Vol. 126, No. 2, May 2016, pp. 261 275. c Indian Academy of Sciences Relative symplectic caps, 4-genus and fibered knots SIDDHARTHA GADGIL 1 and DHEERAJ KULKARNI 2,
Lagrangian knottedness and unknottedness in rational surfaces
 agrangian knottedness and unknottedness in rational surfaces Outline: agrangian knottedness Symplectic geometry of complex projective varieties, D 5, agrangian spheres and Dehn twists agrangian unknottedness
agrangian knottedness and unknottedness in rational surfaces Outline: agrangian knottedness Symplectic geometry of complex projective varieties, D 5, agrangian spheres and Dehn twists agrangian unknottedness
Symplectic 4-manifolds, singular plane curves, and isotopy problems
 Symplectic 4-manifolds, singular plane curves, and isotopy problems Denis AUROUX Massachusetts Inst. of Technology and Ecole Polytechnique Symplectic manifolds A symplectic structure on a smooth manifold
Symplectic 4-manifolds, singular plane curves, and isotopy problems Denis AUROUX Massachusetts Inst. of Technology and Ecole Polytechnique Symplectic manifolds A symplectic structure on a smooth manifold
On the Diffeomorphism Group of S 1 S 2. Allen Hatcher
 On the Diffeomorphism Group of S 1 S 2 Allen Hatcher This is a revision, written in December 2003, of a paper of the same title that appeared in the Proceedings of the AMS 83 (1981), 427-430. The main
On the Diffeomorphism Group of S 1 S 2 Allen Hatcher This is a revision, written in December 2003, of a paper of the same title that appeared in the Proceedings of the AMS 83 (1981), 427-430. The main
From symplectic deformation to isotopy
 From symplectic deformation to isotopy Dusa McDuff State University of New York at Stony Brook (dusa@math.sunysb.edu) May 15, 1996, revised Aug 4, 1997 Abstract Let X be an oriented 4-manifold which does
From symplectic deformation to isotopy Dusa McDuff State University of New York at Stony Brook (dusa@math.sunysb.edu) May 15, 1996, revised Aug 4, 1997 Abstract Let X be an oriented 4-manifold which does
J-holomorphic curves in symplectic geometry
 J-holomorphic curves in symplectic geometry Janko Latschev Pleinfeld, September 25 28, 2006 Since their introduction by Gromov [4] in the mid-1980 s J-holomorphic curves have been one of the most widely
J-holomorphic curves in symplectic geometry Janko Latschev Pleinfeld, September 25 28, 2006 Since their introduction by Gromov [4] in the mid-1980 s J-holomorphic curves have been one of the most widely
arxiv: v1 [math.gt] 8 Mar 2018
![arxiv: v1 [math.gt] 8 Mar 2018 arxiv: v1 [math.gt] 8 Mar 2018](/thumbs/78/77523470.jpg) A COUNTEREXAMPLE TO 4-DIMENSIONAL s-cobordism THEOREM arxiv:1803.03256v1 [math.gt] 8 Mar 2018 SELMAN AKBULUT Abstract. We construct an infinite family of distinct exotic copies of an interesting manifold
A COUNTEREXAMPLE TO 4-DIMENSIONAL s-cobordism THEOREM arxiv:1803.03256v1 [math.gt] 8 Mar 2018 SELMAN AKBULUT Abstract. We construct an infinite family of distinct exotic copies of an interesting manifold
ON THE CONTACT STRUCTURE OF A CLASS OF REAL ANALYTIC GERMS OF THE FORM fḡ
 To Professor Mutsuo Oka on the occasion of his 60th birthday ON THE CONTACT STRUCTURE OF A CLASS OF REAL ANALYTIC GERMS OF THE FORM fḡ MASAHARU ISHIKAWA Abstract. It is known that the argument map fḡ/
To Professor Mutsuo Oka on the occasion of his 60th birthday ON THE CONTACT STRUCTURE OF A CLASS OF REAL ANALYTIC GERMS OF THE FORM fḡ MASAHARU ISHIKAWA Abstract. It is known that the argument map fḡ/
FAMILIES OF ALGEBRAIC CURVES AS SURFACE BUNDLES OF RIEMANN SURFACES
 FAMILIES OF ALGEBRAIC CURVES AS SURFACE BUNDLES OF RIEMANN SURFACES MARGARET NICHOLS 1. Introduction In this paper we study the complex structures which can occur on algebraic curves. The ideas discussed
FAMILIES OF ALGEBRAIC CURVES AS SURFACE BUNDLES OF RIEMANN SURFACES MARGARET NICHOLS 1. Introduction In this paper we study the complex structures which can occur on algebraic curves. The ideas discussed
DISTINGUISHING EMBEDDED CURVES IN RATIONAL COMPLEX SURFACES
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 16, Number 1, January 1998, Pages 305 310 S 000-9939(98)04001-5 DISTINGUISHING EMBEDDED CURVES IN RATIONAL COMPLEX SURFACES TERRY FULLER (Communicated
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 16, Number 1, January 1998, Pages 305 310 S 000-9939(98)04001-5 DISTINGUISHING EMBEDDED CURVES IN RATIONAL COMPLEX SURFACES TERRY FULLER (Communicated
KODAIRA DIMENSION OF LEFSCHETZ FIBRATIONS OVER TORI
 KODAIRA DIMENSION OF LEFSCHETZ FIBRATIONS OVER TORI JOSEF G. DORFMEISTER Abstract. The Kodaira dimension for Lefschetz fibrations was defined in [1]. In this note we show that there exists no Lefschetz
KODAIRA DIMENSION OF LEFSCHETZ FIBRATIONS OVER TORI JOSEF G. DORFMEISTER Abstract. The Kodaira dimension for Lefschetz fibrations was defined in [1]. In this note we show that there exists no Lefschetz
Corrigendum to: Geometric Composition in Quilted Floer Theory
 Corrigendum to: Geometric Composition in Quilted Floer Theory YANKI LEKILI MAX LIPYANSKIY As we explain below, an error in Lemma 11 of [5] affects the main results of that paper (Theorems 1, 2 and 3 of
Corrigendum to: Geometric Composition in Quilted Floer Theory YANKI LEKILI MAX LIPYANSKIY As we explain below, an error in Lemma 11 of [5] affects the main results of that paper (Theorems 1, 2 and 3 of
Copyright by Noah Daniel Goodman 2003
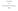 Copyright by Noah Daniel Goodman 2003 The Dissertation Committee for Noah Daniel Goodman certifies that this is the approved version of the following dissertation: Contact Structures and Open Books Committee:
Copyright by Noah Daniel Goodman 2003 The Dissertation Committee for Noah Daniel Goodman certifies that this is the approved version of the following dissertation: Contact Structures and Open Books Committee:
An introduction to cobordism
 An introduction to cobordism Martin Vito Cruz 30 April 2004 1 Introduction Cobordism theory is the study of manifolds modulo the cobordism relation: two manifolds are considered the same if their disjoint
An introduction to cobordism Martin Vito Cruz 30 April 2004 1 Introduction Cobordism theory is the study of manifolds modulo the cobordism relation: two manifolds are considered the same if their disjoint
Cutting and pasting. 2 in R. 3 which are not even topologically
 Cutting and pasting We begin by quoting the following description appearing on page 55 of C. T. C. Wall s 1960 1961 Differential Topology notes, which available are online at http://www.maths.ed.ac.uk/~aar/surgery/wall.pdf.
Cutting and pasting We begin by quoting the following description appearing on page 55 of C. T. C. Wall s 1960 1961 Differential Topology notes, which available are online at http://www.maths.ed.ac.uk/~aar/surgery/wall.pdf.
Lefschetz pencils and the symplectic topology of complex surfaces
 Lefschetz pencils and the symplectic topology of complex surfaces Denis AUROUX Massachusetts Institute of Technology Symplectic 4-manifolds A (compact) symplectic 4-manifold (M 4, ω) is a smooth 4-manifold
Lefschetz pencils and the symplectic topology of complex surfaces Denis AUROUX Massachusetts Institute of Technology Symplectic 4-manifolds A (compact) symplectic 4-manifold (M 4, ω) is a smooth 4-manifold
The topology of symplectic four-manifolds
 The topology of symplectic four-manifolds Michael Usher January 12, 2007 Definition A symplectic manifold is a pair (M, ω) where 1 M is a smooth manifold of some even dimension 2n. 2 ω Ω 2 (M) is a two-form
The topology of symplectic four-manifolds Michael Usher January 12, 2007 Definition A symplectic manifold is a pair (M, ω) where 1 M is a smooth manifold of some even dimension 2n. 2 ω Ω 2 (M) is a two-form
