Summer 2017 MATH Solution to Exercise 5
|
|
|
- Buddy Clarke
- 5 years ago
- Views:
Transcription
1 Summer 07 MATH00 Solution to Exercise 5. Find the partial derivatives of the following functions: (a (xy 5z/( + x, (b x/ x + y, (c arctan y/x, (d log((t ts, (e sin(xy z 3, (f x α, x = (x,, x n. (a x = y x y + 0xz ( + x, (b x = y (x + y 3/, y = (c x = y x + y, y = y = xy (x + y 3/. x x + y. (d t = 3(t + + s (t ts, s = (e x = y z 3 cos xy z 3, (f x j = αx j x α, j =,, n. ts (t ts. y = xyz3 cos xy z 3,. Verify f xy = f yx for the following functions: (a x cos y + e y, (b x log( + y sin(xy, (c (x + y/(x 5 y 9. x + x, z = 5 + x. z = 3xy z cos xy z 3. Omitted. 3. Consider the function f(x, y = xy(x y x + y, (x, y (0, 0, and f(0, 0 = 0. Show that f xy and f yx exist but are not equal at (0, 0. For (x, y (0, 0, f x = x4 y + 4x y 3 y 5 (x + y, f y = x5 4x 3 y xy 4 (x + y.
2 Summer 07 MATH00 When (x, y = (0, 0, f x (0, 0 = 0 and f y (0, 0 = 0. We have but f x (0, y f x (0, 0 f xy (0, 0 = lim =, y 0 y 0 f y (x, 0 f y (0, 0 f yx (0, 0 = lim x 0 x 0 They are not equal at (0, 0. =. 4. Find 3 u xyz, where u(x, y, z = exyz. ( + 3xyz + x y z e xyz. 5. * Show that where m+n v x m y n = ( m (m + n!(mx + ny (x y m+n+, v(x, y = x + y x y. 6. * First show it is true for all m and n = 0 and then use induction on n. (a A harmonic function is a function satisfies the Laplace equation ( u + + u = 0. x n x Show that all n-dimensional harmonic functions form a vector space. (b Find all harmonic functions which are polynomials of degree for the two dimensional Laplace equations. Show that they form a subspace and determine its dimension. (a Let u and v be two harmonic functions. By linearity, we have (αu + βv = α u + β v = 0, so all harmonic functions form a vector space. (b Let p(x, y = a + bx + cy + dx + exy + fy be a general polynomial of degree. If it is harmonic, ( 0 = p(x, y = x + y p(x, y = d + f = 0. Therefore, it is harmonic if and only d = f. Writing in the form p(x, y = a + bx + cy + d(x y + exy, we see that the space of all harmonic polynomials of degree is spanned by, x, y, x y, and xy. These five functions are linearly independent, so the dimension of this subspace is 5.
3 Summer 07 MATH Consider the function g(x, y = xy. Show that g x and g y exist but g is not differentiable at (0, 0. g(x, 0 g(0, 0 g x (0, 0 = lim x 0 = 0. x Similarly, g y (0, 0 = 0. Therefore, the differential of g at (0, 0 vanishes identically. We have g(x, y 0 xy x + y = x + y, where is clearly not convergent to 0 as (x, y (0, 0. Therefore, g is not differentiable at (0, Consider the function h(x, y = for (x, y satisfying x < y < 4x and h(x, y = 0 otherwise. Show that h x and h y exist but h is not differentiable at (0, 0. h(x, 0 h(0, 0 h x (0, 0 = lim = 0. x 0 x h(0, y h(0, 0 h y (0, 0 = lim = 0. y 0 y Therefore, h x and h y exist at (0, 0. However, h is not differentiable at (0, 0 since it is not even continuous at (0, Consider the function j(x, y = (x + y sin(x + y for (x, y (0, 0 and j(0, 0 = 0. Show that it is differentiable at (0, 0 but its partial derivatives are not continuous there. j(x, 0 j(0, 0 j x (0, 0 = lim = lim x sin x 0 x x 0 x = 0. Similarly, j y (0, 0 = 0. If j is differentiable at (0, 0, its differential must vanish there. We have j(x, y 0 x + y = x + y sin x + y x + y 0, as (x, y (0, 0, which shows that j is differentiable at (0, 0. Next, for (x, y (0, 0, j x (x, y = x sin x + y x x + y cos x + y. When (x, 0 (0, 0, j x (x, 0 = x sin x x cos x, which does not tend to j x (0, 0 = 0. Therefore, j x is not continuous at (0, 0. Similarly, j y is also not continuous at (0, Use the Chain Rule to compute the first and second derivatives of the following functions.
4 Summer 07 MATH00 4 (a f(x + y, x y, (b g(x/y, y/z, (c h(t, t, t 3, (d f(r cos θ, r sin θ, (a f(x, y = f(x + y, x y. f x = f x + f y, f y = f x f y. f xx = f xx + f xy + f yx + f yy = f xx + f xy + f yy, f xy = f xx f xy + f yx f yy = f xx f yy, f yy = f xx f xy f yx + f yy = f xx f xy + f yy. (b g(x, y = g(u, v = g(x/y, y/z. g x = g u y = g u(x/y, y/z y, x g y = g u + g y v z = g u(x/y, y/z x + g y v (x/y, y/z z, y g z = g v = g v (x/y, y/z y z g xx = g uu y y = z. y g uu (x/y, y/z, g xy = (g uu x y + g uv z y, g yy = g u x y 3 (g uu x y + g uv z x y + g vu z ( x g yz = g uv x y y z g v g zz = g vv y z 4. + g z vv z + g y vv z z = g u x x + g x y 3 uu g y 4 uv y z + g vv y z = g uv x yz g v z g vv y z 3, (c h(t = h(x, y, z = h(t, t, t 3. h (t = h x + th y + 3t h z, h (t = (h xx + th xy + 3t h xz + (h y + t(h yx + th yy + 3t h yz + 6th z + 3t (h zx + th zy + 3t h zz = h xx + 4th xy + 6t h xz + h y + 4t h yy + t h yz + 6th z + 9t 4 h zz. z, (d f(r, θ = f(r cos θ, r sin θ = f(x, y. f r = f x cos θ + f y sin θ, f θ = f x r sin θ + f y r cos θ. f rr = (f xx cos θ + f xy cos θ sin θ + (f yx sin θ cos θ + f yy sin θ = f xx cos θ + f xy cos θ sin θ + f yy sin θ, f rθ = ( f xx r sin θ + f xy r cos θ cos θ + f x ( sin θ + ( f yx r sin θ + f yy r cos θ sin θ + f y cos θ = rf xx sin θ cos θ + f xy r(cos θ sin θ + rf yy cos θ sin θ f x sin θ + f y cos θ, f θθ = (f xx r sin θ f xy r cos θr sin θ f x r cos θ + ( f yx r sin θ + f yy r cos θr cos θ f y r sin θ = f xx r sin θ f xy r cos θ sin θ f x r cos θ + f yy r cos θ f y r sin θ.. * Let f(x, y and ϕ(x be continuously differentiable functions and define G(x = ϕ(x 0 f(x, ydy.
5 Summer 07 MATH00 5 Establish the formula G (x = Hint: Consider the function ϕ(x 0 F (x, t = f x (x, ydy + f(x, ϕ(xϕ (x. t 0 f(x, ydy. Let F (x, t = t 0 f(x, ydy. Then G(x = F (x, ϕ(x. Therefore, G (x = F x (x, ϕ(x + F t (x, ϕ(xϕ (x = ϕ(x 0 f x (x, ydy + f(x, ϕ(xϕ (x. (a Show that the ordinary differential equation satisfied by the solution of the Laplace equation in two dimension u = 0 when u depends only on the radius, that is, is given by u = f(r, r = x + y, f (r + r f (r = 0. (b Can you find all these radially symmetric harmonic functions? (a Write u(x, y = f( x + y. Then u = 0 is turned into f (r + r f (r = 0. (b This equation can be written as (rf = 0 which is readily integrated to rf = c for some constant c. i.e. f = c r. We conclude that all solutions are given by f(r = c log r + c for some constants c, c. 3. (a Show that the ordinary differential equation satisfied by the solution of the Laplace equation in three dimension u = 0 when u depends only on the radius, that is, is given by u = f(r, r = x + y + z, f (r + r f (r = 0. (b Can you find all these radially symmetric harmonic functions? u(x, y, z = f( x + y + z. Then u = 0 is turned into f (r + r f (r = 0. This equation can be written as (r f = 0 which is readily integrated to r f = c for some constant c. We conclude that all solutions are given by f(r = c r + c for some constants c, c.
6 Summer 07 MATH Consider the one dimensional heat equation u t = u xx. (a Show that u(x, t = v(y, y = x/ t, solves this equation whenever v satisfies v yy + yv y = 0. (b Show that u(x, t = e xt+t3 /3 w(y, y = x+t, solves this equation whenever w satisfies w yy = yw. (a We have u t = x t 3/ v y, u x = v y, t u xx = t v yy, and the result follows. (b Let E = e xt+t3 /3. We have u t = ((x + t w + tw y E, u x = (tw + w y E, u xx = (t w + tw y + w yy E, and the results follows. 5. * Let u be a solution to the two dimensional Laplace equation. Show that the function ( x v(x, y = u x + y, y x + y also solves the same equation. Hint: Use log r = 0 where r = x + y. Let r = (x + y /. We have v x = u x (log r xx + u y (log r xy, v xx = ( u xx (log r xx + u xy (log r xy (log rxx + u x (log r xxx + ( uyx (log r xx + u yy (log r xy (log rxy + u y (log r xxy, v y = u x (log r xy + u y (log r yy, v yy = ( u xx (log r xy + u xy (log r yy (log rxy + u x (log r xy + ( uxy (log r xx + u yy (log r yy (log ryy + u y (log r yyy. The key is log r = 0. Using it we have v(x, y = ( (log r xx + (log r xy u(x/(x + y /, y/(x + y /, and the desired conclusion follows. This formula shows how to get a new harmonic function from an old one. It is called the Kelvin s transform.
7 Summer 07 MATH * Express the differential equation y z x xz y = 0, in the new variables Can you solve it? ξ = x, η = x + y. Write z(x, y = z(ξ, η = z(x, x + y. Using z x = z ξ + x z η and z y = y z η to get y z x xz y = y( z ξ + x z η x(y z η = y z ξ. The equation becomes y z ξ = 0, i.e. z depends on η only. The general solution is f = f(x + y, i.e. radially symmetric. 7. Express the one dimensional wave equation in the new variables f t c f x = 0, c > 0 a constant, ξ = x ct, η = x + ct. Then show that the general solution to this equation is f(x, y = ϕ(x ct + ψ(x + ct, where ϕ and ψ are two arbitrary twice differentiable functions on R. Write f(x, t = f(ξ, η = f(x ct, x+ct. We have f x = f ξ + f η, f t = c f ξ +c f η, f xx = f ξξ + f ξη + f ηη, and f tt = c fξξ c fξη + c fηη. Therefore, f t c f x = (c fξξ c fξη + c fηη c ( f ξξ + f ξη + f ηη = 4c fξη. The differential equation is transformed to the new equation f ξη = 0. Now, ( f ξ η = 0 implies f ξ is independent of η. Therefore, fξ = ϕ (ξ for some ϕ and hence f = ϕ (ξ + ϕ (η, i.e. f(x, y = ϕ(ξ + ψ(η. 8. Consider the Black-Scholes equation V t + σ x V xx + rxv x rv = 0. (a Show that by setting V (x, t = w(y, τ, y = log x, σ t = τ, the equation is turned into ( r w τ + w yy + σ w y r σ w = 0.
8 Summer 07 MATH00 8 (b Show that further by setting w(y, τ = e αy+βτ u(y, τ, with suitable α and β, the equation becomes the heat equation u τ u yy = 0. (a By a direct computation based on V x = w y x, V xx = w yy x w y x, V t = σ w τ. (b With a further change of variables, the equation in (a is transformed into ( r ( βu u τ + (u yy + αu y + α u + σ (αu + u y r σ u = 0. By choosing α and β according to α + r σ = 0, we obtain the heat equation for u. ( r β + α + α σ r σ = 0, Note. The Black-Scholes equation is a model on option pricing. Here V stands for the price of an European put or call. Myron Scholes was awarded the Nobel prize in economics in 997 together with Robert Merton for proposing this model. Black did not share the honor for he died already. 9. A polynomial P is called a homogeneous polynomial if all terms have the same combined power, that is, there is some m such that P (tx = t m P (x for all t > 0. Establish Euler s Identity n P x j = P (x. x j j= Verify it for the following homogeneous polynomials: (a x 3xy + y, and (b x 5 x 0 y 3 z + 6y 4 z. By the homogenity, P (tx = t m P (x for all t > 0. Differentiate both sides with respect to t. The left hand side is equal to t P (tx P P,..., tx n = x (tx x n (tx. x x n The right hand side is = mt m P (x. Setting t =, we have n j= x j P x j = P (x. (a It is equal to x(x 3y + y( 3x + y = (x 3xy + y, and (b It is equal to x(5x 4 0x 9 y 3 z + y( 3x 0 y z + 84y 3 z + z( x 0 y 3 z + 6y 4 = 5(x 5 x 0 y 3 z + 6y 4 z.
9 Summer 07 MATH An open set D is called connected if for every x, y D, there exists a parametric curve lying in D connecting x and y. Show that a differentiable function f in an open, connected set with vanishing partial derivatives must be a constant. Hint: Use a regular parametric curve to connect x to y and consider the composite of this curve with f. Chain Rule will do the rest. It suffices to show that for any x, y D, f(x = f(y. By connectedness of D, there exists a regular curve γ(t such that γ(0 = x and γ( = y. Let φ(t = f(γ(t = f(γ (t,..., γ n (t. By the chain rule, φ (t = f x (γ(tγ (t f x n (γ(tγ n(t = 0, for all t. Therefore, φ(t is constant function, i.e. f(γ(0 = f(γ(, and hence f(x = f(y. This implies f is a constant function.. Find the directional derivative of each of the following functions at the given point and direction: (a x + y 3 + z 4, (3,, ; (, 0, 4/ 7. (b e xy + sin(x + y, (, 3; (, /. (a D ξ f = ξ f (, 0, 4 = (x, 3y, 4z 3 7 (3,, = (, 0, 4 7 (6,, 4 = 0 7. (b D ξ f = ξ f (, = (ye xy + x cos(x + y, xe xy + y cos(x + y (, 3 = (, ( 3e 3 + cos 0, e 3 6 cos 0 = e 3 4 cos 0 = (e 3 + cos 0.. Find the directional derivative of the function x y at (, whose direction makes an angle of degree 60 with the x-axis. The direction is given by (cos 60, sin 60 = (, 3. Therefore, the directional derivative is (, 3 (x, y (, = (, 3 (, = 3.
10 Summer 07 MATH Let g(x, y = x xy + y. Find (a the direction along which it increases most rapidly. (b the direction along which it decreases most rapidly. (c the directional at which its directional derivative vanishes. We have g = (x y, x + y. Let g = (x y + ( x + y. (a The direction is given by g/ g. (b The direction is given by g/ g. (c Let ξ = (ξ, ξ be a direction such that (ξ, ξ (x y, x + y = 0. We may choose ξ = (ξ, ξ = ( x + y, x + y/ g to have the above equality holds true. 4. Can you find a function whose directional derivative along every direction exists and all equal at (0, 0 but it is not differentiable there? Hint: An example can be found in a previous problem. Consider the function f in Problem 8. Since f eventually vanishes along any direction from (0, 0, D ξ f = 0 for all direction ξ. However, f is not differentiable at (0, (a Let f(x, y be a function defined in the first quadrant {(x, y : x, y 0}. Propose a definition of the partial derivatives of f at (x, 0, x > 0 and at (0, 0. (b Let g(x, y be a function defined in the set {(x, y : 0 x y}. Propose a definition of the partial derivatives of g at (0, 0. (a For (x, 0, x > 0, the partial derivative of f in x is defined as usual, but now the partial derivative in y is f f(x, h f(x, 0 (x, 0 = lim y h 0 + h that is, we restrict to the range where y is positive. Similarly, define f f(h, 0 f(0, 0 (0, 0 = lim x h 0 + h f f(0, h f(x, 0 (0, 0 = lim y h 0 + h (b Let ξ = (, /. Using the relation f ξ = f x + f y,,,. we define f x (0, 0 = f ξ f (0, 0 (0, 0. y 6. Use the differential of an appropriate function to obtain an approximate error estimate and then compare it with the actual one. You may use a calculator.
11 Summer 07 MATH00 (a sin 9 tan 46. (b.03 (0.98 /3 (.05 3/4. (c (3. + (4. + (.7. (a Let f(θ, φ = sin θ tan φ; (θ, φ = (30, 45 = (π/6, π/4; (dθ, dφ = (, = ( π/80, π/80. Therefore, df = cos θ tan φdθ + sin θ sec φdφ 3 = ( π 80 + ( π 80 = ( 3/ π 80. and hence the approximate value is given by f(π/6, π/4 + ( 3/ π 80 = + ( 3/ π The height and the radius of the base of a cylinder are measured with error up to 0. and 0. respectively. Find the approximate and exact maximum error of its volume. Let the volume be V, the radius be r and the height be h. They are related by Differentiating both sides yield V = πr h dv = πrhdr + πr dh = πrh(0.r + πr (0.h = 0.4V Therefore, the approximate error is given by 0.7V/V = 0.4. The exact error is π(r + 0.r (h + 0.h πr h = 0.45V. 8. A horizontal beam is supported at both ends and supports a uniform load. The deflection at its midpoint is given by S = k wh 3, where w and h are the width and height respectively of the beam and k is some constant depending on the beam. Show that ( ds = S w dw + 3 h dh.
12 Summer 07 MATH00 If S = in. when w = in. and h = 4 in., approximate the deflection when w =. in. and h = 4. in.. Then compare your approximation with the actual value. ds comes from a direct differentiation. Now since S(, 4 =, we find k = 4 3. Using dw = 0., dh = 0., The exact error is ( 0. ds = S = 0.5. k. (4. 3 = The point (, lies on the curve defined by the equation f(x, y = x 3 + y 3 5xy = 0. Approximate the y-coordinate of the nearby point (x, y on this curve which x =.. The relation defined a function y = g(x: x 3 + g 3 (x 5xg(x = 0. The y-coordinate is given by g(.. Now we will obtain the approximate value by using the differential at x =. Differentiating it in x: which gives 6x + 3g (xg (x 5g(x 5xg (x = 0, g (x = 6x 5g(x 5x 3g (x. So g ( = 4/7 and dg = g ((. = 4/35 = Therefore, the approximate y-coordinate is given by Suppose that T = x(e y + e y where x =, y = log with maximum possible errors 0. in x and 0.0 in y. Estimate the maximum possible induced error in the computed value of T. We have dt = (e y + e y dx + x(e y e y dy ( = + ( = 0.3.
MATH 425, FINAL EXAM SOLUTIONS
 MATH 425, FINAL EXAM SOLUTIONS Each exercise is worth 50 points. Exercise. a The operator L is defined on smooth functions of (x, y by: Is the operator L linear? Prove your answer. L (u := arctan(xy u
MATH 425, FINAL EXAM SOLUTIONS Each exercise is worth 50 points. Exercise. a The operator L is defined on smooth functions of (x, y by: Is the operator L linear? Prove your answer. L (u := arctan(xy u
3 Applications of partial differentiation
 Advanced Calculus Chapter 3 Applications of partial differentiation 37 3 Applications of partial differentiation 3.1 Stationary points Higher derivatives Let U R 2 and f : U R. The partial derivatives
Advanced Calculus Chapter 3 Applications of partial differentiation 37 3 Applications of partial differentiation 3.1 Stationary points Higher derivatives Let U R 2 and f : U R. The partial derivatives
MATH 31BH Homework 5 Solutions
 MATH 3BH Homework 5 Solutions February 4, 204 Problem.8.2 (a) Let x t f y = x 2 + y 2 + 2z 2 and g(t) = t 2. z t 3 Then by the chain rule a a a D(g f) b = Dg f b Df b c c c = [Dg(a 2 + b 2 + 2c 2 )] [
MATH 3BH Homework 5 Solutions February 4, 204 Problem.8.2 (a) Let x t f y = x 2 + y 2 + 2z 2 and g(t) = t 2. z t 3 Then by the chain rule a a a D(g f) b = Dg f b Df b c c c = [Dg(a 2 + b 2 + 2c 2 )] [
Chapter 3 Second Order Linear Equations
 Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
MATH 220: Problem Set 3 Solutions
 MATH 220: Problem Set 3 Solutions Problem 1. Let ψ C() be given by: 0, x < 1, 1 + x, 1 < x < 0, ψ(x) = 1 x, 0 < x < 1, 0, x > 1, so that it verifies ψ 0, ψ(x) = 0 if x 1 and ψ(x)dx = 1. Consider (ψ j )
MATH 220: Problem Set 3 Solutions Problem 1. Let ψ C() be given by: 0, x < 1, 1 + x, 1 < x < 0, ψ(x) = 1 x, 0 < x < 1, 0, x > 1, so that it verifies ψ 0, ψ(x) = 0 if x 1 and ψ(x)dx = 1. Consider (ψ j )
Math 222 Spring 2013 Exam 3 Review Problem Answers
 . (a) By the Chain ule, Math Spring 3 Exam 3 eview Problem Answers w s w x x s + w y y s (y xy)() + (xy x )( ) (( s + 4t) (s 3t)( s + 4t)) ((s 3t)( s + 4t) (s 3t) ) 8s 94st + 3t (b) By the Chain ule, w
. (a) By the Chain ule, Math Spring 3 Exam 3 eview Problem Answers w s w x x s + w y y s (y xy)() + (xy x )( ) (( s + 4t) (s 3t)( s + 4t)) ((s 3t)( s + 4t) (s 3t) ) 8s 94st + 3t (b) By the Chain ule, w
7a3 2. (c) πa 3 (d) πa 3 (e) πa3
 1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
Lecture Notes on Partial Dierential Equations (PDE)/ MaSc 221+MaSc 225
 Lecture Notes on Partial Dierential Equations (PDE)/ MaSc 221+MaSc 225 Dr. Asmaa Al Themairi Assistant Professor a a Department of Mathematical sciences, University of Princess Nourah bint Abdulrahman,
Lecture Notes on Partial Dierential Equations (PDE)/ MaSc 221+MaSc 225 Dr. Asmaa Al Themairi Assistant Professor a a Department of Mathematical sciences, University of Princess Nourah bint Abdulrahman,
Exercise The solution of
 Exercise 8.51 The solution of dx dy = sin φ cos θdr + r cos φ cos θdφ r sin φ sin θdθ sin φ sin θdr + r cos φ sin θdφ r sin φ cos θdθ is dr dφ = dz cos φdr r sin φdφ dθ sin φ cos θdx + sin φ sin θdy +
Exercise 8.51 The solution of dx dy = sin φ cos θdr + r cos φ cos θdφ r sin φ sin θdθ sin φ sin θdr + r cos φ sin θdφ r sin φ cos θdθ is dr dφ = dz cos φdr r sin φdφ dθ sin φ cos θdx + sin φ sin θdy +
A-Level Mathematics DIFFERENTIATION I. G. David Boswell - Math Camp Typeset 1.1 DIFFERENTIATION OF POLYNOMIALS. d dx axn = nax n 1, n!
 A-Level Mathematics DIFFERENTIATION I G. David Boswell - Math Camp Typeset 1.1 SET C Review ~ If a and n are real constants, then! DIFFERENTIATION OF POLYNOMIALS Problems ~ Find the first derivative of
A-Level Mathematics DIFFERENTIATION I G. David Boswell - Math Camp Typeset 1.1 SET C Review ~ If a and n are real constants, then! DIFFERENTIATION OF POLYNOMIALS Problems ~ Find the first derivative of
Jim Lambers MAT 280 Summer Semester Practice Final Exam Solution. dy + xz dz = x(t)y(t) dt. t 3 (4t 3 ) + e t2 (2t) + t 7 (3t 2 ) dt
 Jim Lambers MAT 28 ummer emester 212-1 Practice Final Exam olution 1. Evaluate the line integral xy dx + e y dy + xz dz, where is given by r(t) t 4, t 2, t, t 1. olution From r (t) 4t, 2t, t 2, we obtain
Jim Lambers MAT 28 ummer emester 212-1 Practice Final Exam olution 1. Evaluate the line integral xy dx + e y dy + xz dz, where is given by r(t) t 4, t 2, t, t 1. olution From r (t) 4t, 2t, t 2, we obtain
Chain Rule. MATH 311, Calculus III. J. Robert Buchanan. Spring Department of Mathematics
 3.33pt Chain Rule MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Spring 2019 Single Variable Chain Rule Suppose y = g(x) and z = f (y) then dz dx = d (f (g(x))) dx = f (g(x))g (x)
3.33pt Chain Rule MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Spring 2019 Single Variable Chain Rule Suppose y = g(x) and z = f (y) then dz dx = d (f (g(x))) dx = f (g(x))g (x)
Engg. Math. I. Unit-I. Differential Calculus
 Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
LOWELL JOURNAL. MUST APOLOGIZE. such communication with the shore as Is m i Boimhle, noewwary and proper for the comfort
 - 7 7 Z 8 q ) V x - X > q - < Y Y X V - z - - - - V - V - q \ - q q < -- V - - - x - - V q > x - x q - x q - x - - - 7 -» - - - - 6 q x - > - - x - - - x- - - q q - V - x - - ( Y q Y7 - >»> - x Y - ] [
- 7 7 Z 8 q ) V x - X > q - < Y Y X V - z - - - - V - V - q \ - q q < -- V - - - x - - V q > x - x q - x q - x - - - 7 -» - - - - 6 q x - > - - x - - - x- - - q q - V - x - - ( Y q Y7 - >»> - x Y - ] [
ENGI Partial Differentiation Page y f x
 ENGI 344 4 Partial Differentiation Page 4-0 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
ENGI 344 4 Partial Differentiation Page 4-0 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
Contents. MATH 32B-2 (18W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables. 1 Multiple Integrals 3. 2 Vector Fields 9
 MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
Final: Solutions Math 118A, Fall 2013
 Final: Solutions Math 118A, Fall 2013 1. [20 pts] For each of the following PDEs for u(x, y), give their order and say if they are nonlinear or linear. If they are linear, say if they are homogeneous or
Final: Solutions Math 118A, Fall 2013 1. [20 pts] For each of the following PDEs for u(x, y), give their order and say if they are nonlinear or linear. If they are linear, say if they are homogeneous or
4 Partial Differentiation
 4 Partial Differentiation Many equations in engineering, physics and mathematics tie together more than two variables. For example Ohm s Law (V = IR) and the equation for an ideal gas, PV = nrt, which
4 Partial Differentiation Many equations in engineering, physics and mathematics tie together more than two variables. For example Ohm s Law (V = IR) and the equation for an ideal gas, PV = nrt, which
M273Q Multivariable Calculus Spring 2017 Review Problems for Exam 3
 M7Q Multivariable alculus Spring 7 Review Problems for Exam Exam covers material from Sections 5.-5.4 and 6.-6. and 7.. As you prepare, note well that the Fall 6 Exam posted online did not cover exactly
M7Q Multivariable alculus Spring 7 Review Problems for Exam Exam covers material from Sections 5.-5.4 and 6.-6. and 7.. As you prepare, note well that the Fall 6 Exam posted online did not cover exactly
MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions. December 6, 2017, Wednesday 10:40-12:30, SA-Z02
 1 MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions December 6 2017 Wednesday 10:40-12:30 SA-Z02 QUESTIONS: Solve any four of the following five problems [25]1. Solve the initial and
1 MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions December 6 2017 Wednesday 10:40-12:30 SA-Z02 QUESTIONS: Solve any four of the following five problems [25]1. Solve the initial and
Math 23b Practice Final Summer 2011
 Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
The first order quasi-linear PDEs
 Chapter 2 The first order quasi-linear PDEs The first order quasi-linear PDEs have the following general form: F (x, u, Du) = 0, (2.1) where x = (x 1, x 2,, x 3 ) R n, u = u(x), Du is the gradient of u.
Chapter 2 The first order quasi-linear PDEs The first order quasi-linear PDEs have the following general form: F (x, u, Du) = 0, (2.1) where x = (x 1, x 2,, x 3 ) R n, u = u(x), Du is the gradient of u.
Math 4263 Homework Set 1
 Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
Partial Derivatives for Math 229. Our puropose here is to explain how one computes partial derivatives. We will not attempt
 Partial Derivatives for Math 229 Our puropose here is to explain how one computes partial derivatives. We will not attempt to explain how they arise or why one would use them; that is left to other courses
Partial Derivatives for Math 229 Our puropose here is to explain how one computes partial derivatives. We will not attempt to explain how they arise or why one would use them; that is left to other courses
ENGI Partial Differentiation Page y f x
 ENGI 3424 4 Partial Differentiation Page 4-01 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
ENGI 3424 4 Partial Differentiation Page 4-01 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
APPLIED MATHEMATICS. Part 1: Ordinary Differential Equations. Wu-ting Tsai
 APPLIED MATHEMATICS Part 1: Ordinary Differential Equations Contents 1 First Order Differential Equations 3 1.1 Basic Concepts and Ideas................... 4 1.2 Separable Differential Equations................
APPLIED MATHEMATICS Part 1: Ordinary Differential Equations Contents 1 First Order Differential Equations 3 1.1 Basic Concepts and Ideas................... 4 1.2 Separable Differential Equations................
MATH 19520/51 Class 5
 MATH 19520/51 Class 5 Minh-Tam Trinh University of Chicago 2017-10-04 1 Definition of partial derivatives. 2 Geometry of partial derivatives. 3 Higher derivatives. 4 Definition of a partial differential
MATH 19520/51 Class 5 Minh-Tam Trinh University of Chicago 2017-10-04 1 Definition of partial derivatives. 2 Geometry of partial derivatives. 3 Higher derivatives. 4 Definition of a partial differential
Bessel s Equation. MATH 365 Ordinary Differential Equations. J. Robert Buchanan. Fall Department of Mathematics
 Bessel s Equation MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Background Bessel s equation of order ν has the form where ν is a constant. x 2 y + xy
Bessel s Equation MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Background Bessel s equation of order ν has the form where ν is a constant. x 2 y + xy
4 Differential Equations
 Advanced Calculus Chapter 4 Differential Equations 65 4 Differential Equations 4.1 Terminology Let U R n, and let y : U R. A differential equation in y is an equation involving y and its (partial) derivatives.
Advanced Calculus Chapter 4 Differential Equations 65 4 Differential Equations 4.1 Terminology Let U R n, and let y : U R. A differential equation in y is an equation involving y and its (partial) derivatives.
Math 342 Partial Differential Equations «Viktor Grigoryan
 Math 342 Partial Differential Equations «Viktor Grigoryan 15 Heat with a source So far we considered homogeneous wave and heat equations and the associated initial value problems on the whole line, as
Math 342 Partial Differential Equations «Viktor Grigoryan 15 Heat with a source So far we considered homogeneous wave and heat equations and the associated initial value problems on the whole line, as
Solutions to Sample Questions for Final Exam
 olutions to ample Questions for Final Exam Find the points on the surface xy z 3 that are closest to the origin. We use the method of Lagrange Multipliers, with f(x, y, z) x + y + z for the square of the
olutions to ample Questions for Final Exam Find the points on the surface xy z 3 that are closest to the origin. We use the method of Lagrange Multipliers, with f(x, y, z) x + y + z for the square of the
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: = 0 : homogeneous equation.
 Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
JUST THE MATHS UNIT NUMBER PARTIAL DIFFERENTIATION 1 (Partial derivatives of the first order) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 14.1 PARTIAL DIFFERENTIATION 1 (Partial derivatives of the first order) by A.J.Hobson 14.1.1 Functions of several variables 14.1.2 The definition of a partial derivative 14.1.3
JUST THE MATHS UNIT NUMBER 14.1 PARTIAL DIFFERENTIATION 1 (Partial derivatives of the first order) by A.J.Hobson 14.1.1 Functions of several variables 14.1.2 The definition of a partial derivative 14.1.3
MATH 32A: MIDTERM 2 REVIEW. sin 2 u du z(t) = sin 2 t + cos 2 2
 MATH 3A: MIDTERM REVIEW JOE HUGHES 1. Curvature 1. Consider the curve r(t) = x(t), y(t), z(t), where x(t) = t Find the curvature κ(t). 0 cos(u) sin(u) du y(t) = Solution: The formula for curvature is t
MATH 3A: MIDTERM REVIEW JOE HUGHES 1. Curvature 1. Consider the curve r(t) = x(t), y(t), z(t), where x(t) = t Find the curvature κ(t). 0 cos(u) sin(u) du y(t) = Solution: The formula for curvature is t
2. Second-order Linear Ordinary Differential Equations
 Advanced Engineering Mathematics 2. Second-order Linear ODEs 1 2. Second-order Linear Ordinary Differential Equations 2.1 Homogeneous linear ODEs 2.2 Homogeneous linear ODEs with constant coefficients
Advanced Engineering Mathematics 2. Second-order Linear ODEs 1 2. Second-order Linear Ordinary Differential Equations 2.1 Homogeneous linear ODEs 2.2 Homogeneous linear ODEs with constant coefficients
Let s estimate the volume under this surface over the rectangle R = [0, 4] [0, 2] in the xy-plane.
![Let s estimate the volume under this surface over the rectangle R = [0, 4] [0, 2] in the xy-plane. Let s estimate the volume under this surface over the rectangle R = [0, 4] [0, 2] in the xy-plane.](/thumbs/88/117254927.jpg) Math 54 - Vector Calculus Notes 3. - 3. Double Integrals Consider f(x, y) = 8 x y. Let s estimate the volume under this surface over the rectangle R = [, 4] [, ] in the xy-plane. Here is a particular estimate:
Math 54 - Vector Calculus Notes 3. - 3. Double Integrals Consider f(x, y) = 8 x y. Let s estimate the volume under this surface over the rectangle R = [, 4] [, ] in the xy-plane. Here is a particular estimate:
Lecture Notes in Mathematics. A First Course in Quasi-Linear Partial Differential Equations for Physical Sciences and Engineering Solution Manual
 Lecture Notes in Mathematics A First Course in Quasi-Linear Partial Differential Equations for Physical Sciences and Engineering Solution Manual Marcel B. Finan Arkansas Tech University c All Rights Reserved
Lecture Notes in Mathematics A First Course in Quasi-Linear Partial Differential Equations for Physical Sciences and Engineering Solution Manual Marcel B. Finan Arkansas Tech University c All Rights Reserved
MATH 131P: PRACTICE FINAL SOLUTIONS DECEMBER 12, 2012
 MATH 3P: PRACTICE FINAL SOLUTIONS DECEMBER, This is a closed ook, closed notes, no calculators/computers exam. There are 6 prolems. Write your solutions to Prolems -3 in lue ook #, and your solutions to
MATH 3P: PRACTICE FINAL SOLUTIONS DECEMBER, This is a closed ook, closed notes, no calculators/computers exam. There are 6 prolems. Write your solutions to Prolems -3 in lue ook #, and your solutions to
CHAPTER 3. Analytic Functions. Dr. Pulak Sahoo
 CHAPTER 3 Analytic Functions BY Dr. Pulak Sahoo Assistant Professor Department of Mathematics University Of Kalyani West Bengal, India E-mail : sahoopulak1@gmail.com 1 Module-4: Harmonic Functions 1 Introduction
CHAPTER 3 Analytic Functions BY Dr. Pulak Sahoo Assistant Professor Department of Mathematics University Of Kalyani West Bengal, India E-mail : sahoopulak1@gmail.com 1 Module-4: Harmonic Functions 1 Introduction
Derivatives and Integrals
 Derivatives and Integrals Definition 1: Derivative Formulas d dx (c) = 0 d dx (f ± g) = f ± g d dx (kx) = k d dx (xn ) = nx n 1 (f g) = f g + fg ( ) f = f g fg g g 2 (f(g(x))) = f (g(x)) g (x) d dx (ax
Derivatives and Integrals Definition 1: Derivative Formulas d dx (c) = 0 d dx (f ± g) = f ± g d dx (kx) = k d dx (xn ) = nx n 1 (f g) = f g + fg ( ) f = f g fg g g 2 (f(g(x))) = f (g(x)) g (x) d dx (ax
Higher order derivative
 2 Î 3 á Higher order derivative Î 1 Å Iterated partial derivative Iterated partial derivative Suppose f has f/ x, f/ y and ( f ) = 2 f x x x 2 ( f ) = 2 f x y x y ( f ) = 2 f y x y x ( f ) = 2 f y y y
2 Î 3 á Higher order derivative Î 1 Å Iterated partial derivative Iterated partial derivative Suppose f has f/ x, f/ y and ( f ) = 2 f x x x 2 ( f ) = 2 f x y x y ( f ) = 2 f y x y x ( f ) = 2 f y y y
Suggested Solution to Assignment 7
 MATH 422 (25-6) partial diferential equations Suggested Solution to Assignment 7 Exercise 7.. Suppose there exists one non-constant harmonic function u in, which attains its maximum M at x. Then by the
MATH 422 (25-6) partial diferential equations Suggested Solution to Assignment 7 Exercise 7.. Suppose there exists one non-constant harmonic function u in, which attains its maximum M at x. Then by the
Math 124A October 11, 2011
 Math 14A October 11, 11 Viktor Grigoryan 6 Wave equation: solution In this lecture we will solve the wave equation on the entire real line x R. This corresponds to a string of infinite length. Although
Math 14A October 11, 11 Viktor Grigoryan 6 Wave equation: solution In this lecture we will solve the wave equation on the entire real line x R. This corresponds to a string of infinite length. Although
Math 210, Final Exam, Practice Fall 2009 Problem 1 Solution AB AC AB. cosθ = AB BC AB (0)(1)+( 4)( 2)+(3)(2)
 Math 2, Final Exam, Practice Fall 29 Problem Solution. A triangle has vertices at the points A (,,), B (, 3,4), and C (2,,3) (a) Find the cosine of the angle between the vectors AB and AC. (b) Find an
Math 2, Final Exam, Practice Fall 29 Problem Solution. A triangle has vertices at the points A (,,), B (, 3,4), and C (2,,3) (a) Find the cosine of the angle between the vectors AB and AC. (b) Find an
DO NOT BEGIN THIS TEST UNTIL INSTRUCTED TO START
 Math 265 Student name: KEY Final Exam Fall 23 Instructor & Section: This test is closed book and closed notes. A (graphing) calculator is allowed for this test but cannot also be a communication device
Math 265 Student name: KEY Final Exam Fall 23 Instructor & Section: This test is closed book and closed notes. A (graphing) calculator is allowed for this test but cannot also be a communication device
Ma 221 Final Exam Solutions 5/14/13
 Ma 221 Final Exam Solutions 5/14/13 1. Solve (a) (8 pts) Solution: The equation is separable. dy dx exy y 1 y0 0 y 1e y dy e x dx y 1e y dy e x dx ye y e y dy e x dx ye y e y e y e x c The last step comes
Ma 221 Final Exam Solutions 5/14/13 1. Solve (a) (8 pts) Solution: The equation is separable. dy dx exy y 1 y0 0 y 1e y dy e x dx y 1e y dy e x dx ye y e y dy e x dx ye y e y e y e x c The last step comes
Lecture 10. (2) Functions of two variables. Partial derivatives. Dan Nichols February 27, 2018
 Lecture 10 Partial derivatives Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts February 27, 2018 Last time: functions of two variables f(x, y) x and y are the independent
Lecture 10 Partial derivatives Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts February 27, 2018 Last time: functions of two variables f(x, y) x and y are the independent
UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH
 UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH Faculty of Science and Engineering Department of Mathematics and Statistics END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA4006 SEMESTER: Spring 2011 MODULE TITLE:
UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH Faculty of Science and Engineering Department of Mathematics and Statistics END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA4006 SEMESTER: Spring 2011 MODULE TITLE:
3 2 6 Solve the initial value problem u ( t) 3. a- If A has eigenvalues λ =, λ = 1 and corresponding eigenvectors 1
 Math Problem a- If A has eigenvalues λ =, λ = 1 and corresponding eigenvectors 1 3 6 Solve the initial value problem u ( t) = Au( t) with u (0) =. 3 1 u 1 =, u 1 3 = b- True or false and why 1. if A is
Math Problem a- If A has eigenvalues λ =, λ = 1 and corresponding eigenvectors 1 3 6 Solve the initial value problem u ( t) = Au( t) with u (0) =. 3 1 u 1 =, u 1 3 = b- True or false and why 1. if A is
Solutions to old Exam 3 problems
 Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
Math 126 Final Exam Solutions
 Math 126 Final Exam Solutions 1. (a) Give an example of a linear homogeneous PE, a linear inhomogeneous PE, and a nonlinear PE. [3 points] Solution. Poisson s equation u = f is linear homogeneous when
Math 126 Final Exam Solutions 1. (a) Give an example of a linear homogeneous PE, a linear inhomogeneous PE, and a nonlinear PE. [3 points] Solution. Poisson s equation u = f is linear homogeneous when
Exercises for Multivariable Differential Calculus XM521
 This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
MATH1231 CALCULUS. Session II Dr John Roberts (based on notes of A./Prof. Bruce Henry) Red Center Room 3065
 MATH1231 CALCULUS Session II 2007. Dr John Roberts (based on notes of A./Prof. Bruce Henry) Red Center Room 3065 Jag.Roberts@unsw.edu.au MATH1231 CALCULUS p.1/66 Overview Systematic Integration Techniques
MATH1231 CALCULUS Session II 2007. Dr John Roberts (based on notes of A./Prof. Bruce Henry) Red Center Room 3065 Jag.Roberts@unsw.edu.au MATH1231 CALCULUS p.1/66 Overview Systematic Integration Techniques
Exam 2 Review Solutions
 Exam Review Solutions 1. True or False, an explain: (a) There exists a function f with continuous secon partial erivatives such that f x (x, y) = x + y f y = x y False. If the function has continuous secon
Exam Review Solutions 1. True or False, an explain: (a) There exists a function f with continuous secon partial erivatives such that f x (x, y) = x + y f y = x y False. If the function has continuous secon
FINAL REVIEW Answers and hints Math 311 Fall 2017
 FINAL RVIW Answers and hints Math 3 Fall 7. Let R be a Jordan region and let f : R be integrable. Prove that the graph of f, as a subset of R 3, has zero volume. Let R be a rectangle with R. Since f is
FINAL RVIW Answers and hints Math 3 Fall 7. Let R be a Jordan region and let f : R be integrable. Prove that the graph of f, as a subset of R 3, has zero volume. Let R be a rectangle with R. Since f is
One side of each sheet is blank and may be used as scratch paper.
 Math 244 Spring 2017 (Practice) Final 5/11/2017 Time Limit: 2 hours Name: No calculators or notes are allowed. One side of each sheet is blank and may be used as scratch paper. heck your answers whenever
Math 244 Spring 2017 (Practice) Final 5/11/2017 Time Limit: 2 hours Name: No calculators or notes are allowed. One side of each sheet is blank and may be used as scratch paper. heck your answers whenever
Math 115 ( ) Yum-Tong Siu 1. Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives
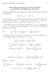 Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
MA 201: Partial Differential Equations D Alembert s Solution Lecture - 7 MA 201 (2016), PDE 1 / 20
 MA 201: Partial Differential Equations D Alembert s Solution Lecture - 7 MA 201 (2016), PDE 1 / 20 MA 201 (2016), PDE 2 / 20 Vibrating string and the wave equation Consider a stretched string of length
MA 201: Partial Differential Equations D Alembert s Solution Lecture - 7 MA 201 (2016), PDE 1 / 20 MA 201 (2016), PDE 2 / 20 Vibrating string and the wave equation Consider a stretched string of length
The Derivative. Appendix B. B.1 The Derivative of f. Mappings from IR to IR
 Appendix B The Derivative B.1 The Derivative of f In this chapter, we give a short summary of the derivative. Specifically, we want to compare/contrast how the derivative appears for functions whose domain
Appendix B The Derivative B.1 The Derivative of f In this chapter, we give a short summary of the derivative. Specifically, we want to compare/contrast how the derivative appears for functions whose domain
Math 21B - Homework Set 8
 Math B - Homework Set 8 Section 8.:. t cos t dt Let u t, du t dt and v sin t, dv cos t dt Let u t, du dt and v cos t, dv sin t dt t cos t dt u v v du t sin t t sin t dt [ t sin t u v ] v du [ ] t sin t
Math B - Homework Set 8 Section 8.:. t cos t dt Let u t, du t dt and v sin t, dv cos t dt Let u t, du dt and v cos t, dv sin t dt t cos t dt u v v du t sin t t sin t dt [ t sin t u v ] v du [ ] t sin t
1 Partial differentiation and the chain rule
 1 Partial differentiation and the chain rule In this section we review and discuss certain notations and relations involving partial derivatives. The more general case can be illustrated by considering
1 Partial differentiation and the chain rule In this section we review and discuss certain notations and relations involving partial derivatives. The more general case can be illustrated by considering
CLASSIFICATION AND PRINCIPLE OF SUPERPOSITION FOR SECOND ORDER LINEAR PDE
 CLASSIFICATION AND PRINCIPLE OF SUPERPOSITION FOR SECOND ORDER LINEAR PDE 1. Linear Partial Differential Equations A partial differential equation (PDE) is an equation, for an unknown function u, that
CLASSIFICATION AND PRINCIPLE OF SUPERPOSITION FOR SECOND ORDER LINEAR PDE 1. Linear Partial Differential Equations A partial differential equation (PDE) is an equation, for an unknown function u, that
Aero III/IV Conformal Mapping
 Aero III/IV Conformal Mapping View complex function as a mapping Unlike a real function, a complex function w = f(z) cannot be represented by a curve. Instead it is useful to view it as a mapping. Write
Aero III/IV Conformal Mapping View complex function as a mapping Unlike a real function, a complex function w = f(z) cannot be represented by a curve. Instead it is useful to view it as a mapping. Write
Vibrating-string problem
 EE-2020, Spring 2009 p. 1/30 Vibrating-string problem Newton s equation of motion, m u tt = applied forces to the segment (x, x, + x), Net force due to the tension of the string, T Sinθ 2 T Sinθ 1 T[u
EE-2020, Spring 2009 p. 1/30 Vibrating-string problem Newton s equation of motion, m u tt = applied forces to the segment (x, x, + x), Net force due to the tension of the string, T Sinθ 2 T Sinθ 1 T[u
Implicit Functions, Curves and Surfaces
 Chapter 11 Implicit Functions, Curves and Surfaces 11.1 Implicit Function Theorem Motivation. In many problems, objects or quantities of interest can only be described indirectly or implicitly. It is then
Chapter 11 Implicit Functions, Curves and Surfaces 11.1 Implicit Function Theorem Motivation. In many problems, objects or quantities of interest can only be described indirectly or implicitly. It is then
g(t) = f(x 1 (t),..., x n (t)).
 Reading: [Simon] p. 313-333, 833-836. 0.1 The Chain Rule Partial derivatives describe how a function changes in directions parallel to the coordinate axes. Now we shall demonstrate how the partial derivatives
Reading: [Simon] p. 313-333, 833-836. 0.1 The Chain Rule Partial derivatives describe how a function changes in directions parallel to the coordinate axes. Now we shall demonstrate how the partial derivatives
MA 441 Advanced Engineering Mathematics I Assignments - Spring 2014
 MA 441 Advanced Engineering Mathematics I Assignments - Spring 2014 Dr. E. Jacobs The main texts for this course are Calculus by James Stewart and Fundamentals of Differential Equations by Nagle, Saff
MA 441 Advanced Engineering Mathematics I Assignments - Spring 2014 Dr. E. Jacobs The main texts for this course are Calculus by James Stewart and Fundamentals of Differential Equations by Nagle, Saff
Preliminary Exam 2016 Solutions to Morning Exam
 Preliminary Exam 16 Solutions to Morning Exam Part I. Solve four of the following five problems. Problem 1. Find the volume of the ice cream cone defined by the inequalities x + y + z 1 and x + y z /3
Preliminary Exam 16 Solutions to Morning Exam Part I. Solve four of the following five problems. Problem 1. Find the volume of the ice cream cone defined by the inequalities x + y + z 1 and x + y z /3
MATHS 267 Answers to Stokes Practice Dr. Jones
 MATH 267 Answers to tokes Practice Dr. Jones 1. Calculate the flux F d where is the hemisphere x2 + y 2 + z 2 1, z > and F (xz + e y2, yz, z 2 + 1). Note: the surface is open (doesn t include any of the
MATH 267 Answers to tokes Practice Dr. Jones 1. Calculate the flux F d where is the hemisphere x2 + y 2 + z 2 1, z > and F (xz + e y2, yz, z 2 + 1). Note: the surface is open (doesn t include any of the
Nonlinear Autonomous Systems of Differential
 Chapter 4 Nonlinear Autonomous Systems of Differential Equations 4.0 The Phase Plane: Linear Systems 4.0.1 Introduction Consider a system of the form x = A(x), (4.0.1) where A is independent of t. Such
Chapter 4 Nonlinear Autonomous Systems of Differential Equations 4.0 The Phase Plane: Linear Systems 4.0.1 Introduction Consider a system of the form x = A(x), (4.0.1) where A is independent of t. Such
MATH 425, HOMEWORK 3 SOLUTIONS
 MATH 425, HOMEWORK 3 SOLUTIONS Exercise. (The differentiation property of the heat equation In this exercise, we will use the fact that the derivative of a solution to the heat equation again solves the
MATH 425, HOMEWORK 3 SOLUTIONS Exercise. (The differentiation property of the heat equation In this exercise, we will use the fact that the derivative of a solution to the heat equation again solves the
MATH 10550, EXAM 2 SOLUTIONS. 1. Find an equation for the tangent line to. f(x) = sin x cos x. 2 which is the slope of the tangent line at
 MATH 100, EXAM SOLUTIONS 1. Find an equation for the tangent line to at the point ( π 4, 0). f(x) = sin x cos x f (x) = cos(x) + sin(x) Thus, f ( π 4 ) = which is the slope of the tangent line at ( π 4,
MATH 100, EXAM SOLUTIONS 1. Find an equation for the tangent line to at the point ( π 4, 0). f(x) = sin x cos x f (x) = cos(x) + sin(x) Thus, f ( π 4 ) = which is the slope of the tangent line at ( π 4,
Sophus Lie s Approach to Differential Equations
 Sophus Lie s Approach to Differential Equations IAP lecture 2006 (S. Helgason) 1 Groups Let X be a set. A one-to-one mapping ϕ of X onto X is called a bijection. Let B(X) denote the set of all bijections
Sophus Lie s Approach to Differential Equations IAP lecture 2006 (S. Helgason) 1 Groups Let X be a set. A one-to-one mapping ϕ of X onto X is called a bijection. Let B(X) denote the set of all bijections
Calculus - II Multivariable Calculus. M.Thamban Nair. Department of Mathematics Indian Institute of Technology Madras
 Calculus - II Multivariable Calculus M.Thamban Nair epartment of Mathematics Indian Institute of Technology Madras February 27 Revised: January 29 Contents Preface v 1 Functions of everal Variables 1 1.1
Calculus - II Multivariable Calculus M.Thamban Nair epartment of Mathematics Indian Institute of Technology Madras February 27 Revised: January 29 Contents Preface v 1 Functions of everal Variables 1 1.1
MATH 52 FINAL EXAM SOLUTIONS
 MAH 5 FINAL EXAM OLUION. (a) ketch the region R of integration in the following double integral. x xe y5 dy dx R = {(x, y) x, x y }. (b) Express the region R as an x-simple region. R = {(x, y) y, x y }
MAH 5 FINAL EXAM OLUION. (a) ketch the region R of integration in the following double integral. x xe y5 dy dx R = {(x, y) x, x y }. (b) Express the region R as an x-simple region. R = {(x, y) y, x y }
dx n a 1(x) dy
 HIGHER ORDER DIFFERENTIAL EQUATIONS Theory of linear equations Initial-value and boundary-value problem nth-order initial value problem is Solve: a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
HIGHER ORDER DIFFERENTIAL EQUATIONS Theory of linear equations Initial-value and boundary-value problem nth-order initial value problem is Solve: a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
Introduction to Differentials
 Introduction to Differentials David G Radcliffe 13 March 2007 1 Increments Let y be a function of x, say y = f(x). The symbol x denotes a change or increment in the value of x. Note that a change in the
Introduction to Differentials David G Radcliffe 13 March 2007 1 Increments Let y be a function of x, say y = f(x). The symbol x denotes a change or increment in the value of x. Note that a change in the
1 Solution to Homework 4
 Solution to Homework Section. 5. The characteristic equation is r r + = (r )(r ) = 0 r = or r =. y(t) = c e t + c e t y = c e t + c e t. y(0) =, y (0) = c + c =, c + c = c =, c =. To find the maximum value
Solution to Homework Section. 5. The characteristic equation is r r + = (r )(r ) = 0 r = or r =. y(t) = c e t + c e t y = c e t + c e t. y(0) =, y (0) = c + c =, c + c = c =, c =. To find the maximum value
MA22S2 Lecture Notes on Fourier Series and Partial Differential Equations.
 MAS Lecture Notes on Fourier Series and Partial Differential Equations Joe Ó hógáin E-mail: johog@maths.tcd.ie Main Text: Kreyszig; Advanced Engineering Mathematics Other Texts: Nagle and Saff, Zill and
MAS Lecture Notes on Fourier Series and Partial Differential Equations Joe Ó hógáin E-mail: johog@maths.tcd.ie Main Text: Kreyszig; Advanced Engineering Mathematics Other Texts: Nagle and Saff, Zill and
Geometry and Motion Selected answers to Sections A and C Dwight Barkley 2016
 MA34 Geometry and Motion Selected answers to Sections A and C Dwight Barkley 26 Example Sheet d n+ = d n cot θ n r θ n r = Θθ n i. 2. 3. 4. Possible answers include: and with opposite orientation: 5..
MA34 Geometry and Motion Selected answers to Sections A and C Dwight Barkley 26 Example Sheet d n+ = d n cot θ n r θ n r = Θθ n i. 2. 3. 4. Possible answers include: and with opposite orientation: 5..
Sec. 1.1: Basics of Vectors
 Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
Math 1310 Final Exam
 Math 1310 Final Exam December 11, 2014 NAME: INSTRUCTOR: Write neatly and show all your work in the space provided below each question. You may use the back of the exam pages if you need additional space
Math 1310 Final Exam December 11, 2014 NAME: INSTRUCTOR: Write neatly and show all your work in the space provided below each question. You may use the back of the exam pages if you need additional space
Page Problem Score Max Score a 8 12b a b 10 14c 6 6
 Fall 14 MTH 34 FINAL EXAM December 8, 14 Name: PID: Section: Instructor: DO NOT WRITE BELOW THIS LINE. Go to the next page. Page Problem Score Max Score 1 5 5 1 3 5 4 5 5 5 6 5 7 5 8 5 9 5 1 5 11 1 3 1a
Fall 14 MTH 34 FINAL EXAM December 8, 14 Name: PID: Section: Instructor: DO NOT WRITE BELOW THIS LINE. Go to the next page. Page Problem Score Max Score 1 5 5 1 3 5 4 5 5 5 6 5 7 5 8 5 9 5 1 5 11 1 3 1a
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georgia Tech PHYS 612 Mathematical Methods of Physics I Instructor: Predrag Cvitanović Fall semester 2012 Homework Set #5 due October 2, 2012 == show all your work for maximum credit, == put labels, title,
Georgia Tech PHYS 612 Mathematical Methods of Physics I Instructor: Predrag Cvitanović Fall semester 2012 Homework Set #5 due October 2, 2012 == show all your work for maximum credit, == put labels, title,
Math 20C Homework 2 Partial Solutions
 Math 2C Homework 2 Partial Solutions Problem 1 (12.4.14). Calculate (j k) (j + k). Solution. The basic properties of the cross product are found in Theorem 2 of Section 12.4. From these properties, we
Math 2C Homework 2 Partial Solutions Problem 1 (12.4.14). Calculate (j k) (j + k). Solution. The basic properties of the cross product are found in Theorem 2 of Section 12.4. From these properties, we
Math 210, Final Exam, Spring 2012 Problem 1 Solution. (a) Find an equation of the plane passing through the tips of u, v, and w.
 Math, Final Exam, Spring Problem Solution. Consider three position vectors (tails are the origin): u,, v 4,, w,, (a) Find an equation of the plane passing through the tips of u, v, and w. (b) Find an equation
Math, Final Exam, Spring Problem Solution. Consider three position vectors (tails are the origin): u,, v 4,, w,, (a) Find an equation of the plane passing through the tips of u, v, and w. (b) Find an equation
1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is
 1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
Math 4013 Solutions to Homework Problems from Chapter 2
 Math 4013 Solutions to Homework Problems from Chapter 2 Section 2.1 1. Sketch the level curves and graphs of the following functions: a f : R 2 R, x, y x y +2 The level curves are just the lines x y +2C
Math 4013 Solutions to Homework Problems from Chapter 2 Section 2.1 1. Sketch the level curves and graphs of the following functions: a f : R 2 R, x, y x y +2 The level curves are just the lines x y +2C
1MA6 Partial Differentiation and Multiple Integrals: I
 1MA6/1 1MA6 Partial Differentiation and Multiple Integrals: I Dr D W Murray Michaelmas Term 1994 1. Total differential. (a) State the conditions for the expression P (x, y)dx+q(x, y)dy to be the perfect
1MA6/1 1MA6 Partial Differentiation and Multiple Integrals: I Dr D W Murray Michaelmas Term 1994 1. Total differential. (a) State the conditions for the expression P (x, y)dx+q(x, y)dy to be the perfect
1 Arithmetic calculations (calculator is not allowed)
 1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
Partial Derivatives. w = f(x, y, z).
 Partial Derivatives 1 Functions of Several Variables So far we have focused our attention of functions of one variable. These functions model situations in which a variable depends on another independent
Partial Derivatives 1 Functions of Several Variables So far we have focused our attention of functions of one variable. These functions model situations in which a variable depends on another independent
Lecture 13 - Wednesday April 29th
 Lecture 13 - Wednesday April 29th jacques@ucsdedu Key words: Systems of equations, Implicit differentiation Know how to do implicit differentiation, how to use implicit and inverse function theorems 131
Lecture 13 - Wednesday April 29th jacques@ucsdedu Key words: Systems of equations, Implicit differentiation Know how to do implicit differentiation, how to use implicit and inverse function theorems 131
Lecture notes: Introduction to Partial Differential Equations
 Lecture notes: Introduction to Partial Differential Equations Sergei V. Shabanov Department of Mathematics, University of Florida, Gainesville, FL 32611 USA CHAPTER 1 Classification of Partial Differential
Lecture notes: Introduction to Partial Differential Equations Sergei V. Shabanov Department of Mathematics, University of Florida, Gainesville, FL 32611 USA CHAPTER 1 Classification of Partial Differential
Name: Math Homework Set # 5. March 12, 2010
 Name: Math 4567. Homework Set # 5 March 12, 2010 Chapter 3 (page 79, problems 1,2), (page 82, problems 1,2), (page 86, problems 2,3), Chapter 4 (page 93, problems 2,3), (page 98, problems 1,2), (page 102,
Name: Math 4567. Homework Set # 5 March 12, 2010 Chapter 3 (page 79, problems 1,2), (page 82, problems 1,2), (page 86, problems 2,3), Chapter 4 (page 93, problems 2,3), (page 98, problems 1,2), (page 102,
A DARK GREY P O N T, with a Switch Tail, and a small Star on the Forehead. Any
 Y Y Y X X «/ YY Y Y ««Y x ) & \ & & } # Y \#$& / Y Y X» \\ / X X X x & Y Y X «q «z \x» = q Y # % \ & [ & Z \ & { + % ) / / «q zy» / & / / / & x x X / % % ) Y x X Y $ Z % Y Y x x } / % «] «] # z» & Y X»
Y Y Y X X «/ YY Y Y ««Y x ) & \ & & } # Y \#$& / Y Y X» \\ / X X X x & Y Y X «q «z \x» = q Y # % \ & [ & Z \ & { + % ) / / «q zy» / & / / / & x x X / % % ) Y x X Y $ Z % Y Y x x } / % «] «] # z» & Y X»
Department of Mathematics. MA 108 Ordinary Differential Equations
 Department of Mathematics Indian Institute of Technology, Bombay Powai, Mumbai 476, INDIA. MA 8 Ordinary Differential Equations Autumn 23 Instructor Santanu Dey Name : Roll No : Syllabus and Course Outline
Department of Mathematics Indian Institute of Technology, Bombay Powai, Mumbai 476, INDIA. MA 8 Ordinary Differential Equations Autumn 23 Instructor Santanu Dey Name : Roll No : Syllabus and Course Outline
Consider an ideal pendulum as shown below. l θ is the angular acceleration θ is the angular velocity
 1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
Practice Problems for the Final Exam
 Math 114 Spring 2017 Practice Problems for the Final Exam 1. The planes 3x + 2y + z = 6 and x + y = 2 intersect in a line l. Find the distance from the origin to l. (Answer: 24 3 ) 2. Find the area of
Math 114 Spring 2017 Practice Problems for the Final Exam 1. The planes 3x + 2y + z = 6 and x + y = 2 intersect in a line l. Find the distance from the origin to l. (Answer: 24 3 ) 2. Find the area of
Review for Exam 1. (a) Find an equation of the line through the point ( 2, 4, 10) and parallel to the vector
 Calculus 3 Lia Vas Review for Exam 1 1. Surfaces. Describe the following surfaces. (a) x + y = 9 (b) x + y + z = 4 (c) z = 1 (d) x + 3y + z = 6 (e) z = x + y (f) z = x + y. Review of Vectors. (a) Let a
Calculus 3 Lia Vas Review for Exam 1 1. Surfaces. Describe the following surfaces. (a) x + y = 9 (b) x + y + z = 4 (c) z = 1 (d) x + 3y + z = 6 (e) z = x + y (f) z = x + y. Review of Vectors. (a) Let a
MTH Calculus with Analytic Geom I TEST 1
 MTH 229-105 Calculus with Analytic Geom I TEST 1 Name Please write your solutions in a clear and precise manner. SHOW your work entirely. (1) Find the equation of a straight line perpendicular to the line
MTH 229-105 Calculus with Analytic Geom I TEST 1 Name Please write your solutions in a clear and precise manner. SHOW your work entirely. (1) Find the equation of a straight line perpendicular to the line
