H ψ = E ψ. Introduction to Exact Diagonalization. Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden
|
|
|
- Eileen Parsons
- 5 years ago
- Views:
Transcription
1 H ψ = E ψ Introduction to Exact Diagonalization Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden laeuchli@comp-phys.org Simulations of Quantum Many Body Systems - Lecture Spring 2010
2 Outline of Today s Lecture (part 1 of 3) Overview of Lecture (Short) Introduction to Quantum Lattice Models Introduction to Exact Diagonalization (part 1) Overview of the ED Algorithm Basis construction First aspects of symmetries
3 Quantum Lattice Models kagome lattice Volborthite
4 Models Single particle lattice models Many body lattice models Constrained lattice models
5 Single Particle Lattice Models Disordered potentials and hoppings Anderson Localization
6 Single Particle Lattice Models Disordered potentials and hoppings Anderson Localization Hopping phases (Gauge fields) Hofstadter Butterfly
7 Single Particle Lattice Models Disordered potentials and hoppings Anderson Localization Hopping phases (Gauge fields) Hofstadter Butterfly Jordan-Wigner transformation (maps XX spin chains onto free fermions) Disordered XX-spin chains
8 Many-Body Hamiltonians Spin models: S=1/2: two states per site Heisenberg couplings (2 sites): Modifications: easy plane, easy axis anisotropies higher order spin interactions (biquadratic, bicubic, ring exchange,...)
9 Many-Body Hamiltonians Fermionic models: Hubbard model: The c/c + operators satisfy anticommutation rules i.e. Fermi sign comes in! There also exists a Bose-Hubbard models, with bosons replacing the fermions.
10 Many-Body Hamiltonians Fermionic models: t-j model: ( large U limit of the Hubbard model) The c/c + operators satisfy anticommutation rules i.e. Fermi sign comes in!
11 Constrained Models Hardcore-dimer models:
12 Constrained Models Hardcore-dimer models: Vertex / Ice models:
13 Lattices Infinite Lattices are made out of: A Unit Cell, containing n atoms
14 Lattices Infinite Lattices are made out of: A Unit Cell, containing n atoms Spanning vectors defining the Bravais lattice: T 2 T 1
15 Lattices II Some Examples: Square Lattice single site unit cell
16 Lattices II Some Examples: T 2 T 1 Square Lattice single site unit cell Checkerboard Lattice two sites in unit cell
17 Finite Lattices T 2 Extent is given by multiples of the Bravais vectors T 1 and T 2 T 1 For the square lattice: Extent =6x6 36 sites
18 Finite Lattices T 2 T 1 Extent given by spanning vectors which are not parallel to the simple axes For the square lattice: F 1 =(6,2)=6T 1 +2T 2 F 2 =(-2,6)=-2T 1 +6T 2 40 sites The discrete k-vectors are also tilted
19 Total Hilbert space of a finite many body system
20 Total Hilbert space of a finite many body system The Hilbert space of a quantum many body system grows exponentially in general (eg at constant density)
21 Total Hilbert space of a finite many body system The Hilbert space of a quantum many body system grows exponentially in general (eg at constant density) For N spin 1/2 particles, the total Hilbert space has dim=2 N states
22 Total Hilbert space of a finite many body system The Hilbert space of a quantum many body system grows exponentially in general (eg at constant density) For N spin 1/2 particles, the total Hilbert space has dim=2 N states 10 spins dim=1 024
23 Total Hilbert space of a finite many body system The Hilbert space of a quantum many body system grows exponentially in general (eg at constant density) For N spin 1/2 particles, the total Hilbert space has dim=2 N states 10 spins dim= spins dim=
24 Total Hilbert space of a finite many body system The Hilbert space of a quantum many body system grows exponentially in general (eg at constant density) For N spin 1/2 particles, the total Hilbert space has dim=2 N states 10 spins dim= spins dim= spins dim=
25 Total Hilbert space of a finite many body system The Hilbert space of a quantum many body system grows exponentially in general (eg at constant density) For N spin 1/2 particles, the total Hilbert space has dim=2 N states 10 spins dim= spins dim= spins dim= the same for spinless fermions and hardcore bosons.
26 Total Hilbert space of a finite many body system The Hilbert space of a quantum many body system grows exponentially in general (eg at constant density) For N spin 1/2 particles, the total Hilbert space has dim=2 N states 10 spins dim= spins dim= spins dim= the same for spinless fermions and hardcore bosons. for actual bosons it is even worse...
27 Introduction to Exact Diagonalization H ψ = E ψ
28 Exact Diagonalization: Main Idea H ψ = E ψ
29 Exact Diagonalization: Main Idea Solve the Schrödinger equation of a quantum many body system numerically H ψ = E ψ
30 Exact Diagonalization: Main Idea Solve the Schrödinger equation of a quantum many body system numerically H ψ = E ψ Sparse matrix, but for quantum many body systems the vector space dimension grows exponentially!
31 Exact Diagonalization: Main Idea Solve the Schrödinger equation of a quantum many body system numerically H ψ = E ψ Sparse matrix, but for quantum many body systems the vector space dimension grows exponentially! Some people will tell you that s all there is.
32 Exact Diagonalization: Main Idea Solve the Schrödinger equation of a quantum many body system numerically H ψ = E ψ Sparse matrix, but for quantum many body systems the vector space dimension grows exponentially! Some people will tell you that s all there is. But if you want to get a maximum of physical information out of a finite system there is a lot more to do and the reward is a powerful:
33 Exact Diagonalization: Main Idea Solve the Schrödinger equation of a quantum many body system numerically H ψ = E ψ Sparse matrix, but for quantum many body systems the vector space dimension grows exponentially! Some people will tell you that s all there is. But if you want to get a maximum of physical information out of a finite system there is a lot more to do and the reward is a powerful: Quantum Mechanics Toolbox
34 Exact Diagonalization: Applications
35 Exact Diagonalization: Applications Quantum Magnets: nature of novel phases, critical points in 1D, dynamical correlation functions in 1D & 2D
36 Exact Diagonalization: Applications Quantum Magnets: nature of novel phases, critical points in 1D, dynamical correlation functions in 1D & 2D Fermionic models (Hubbard/t-J): gaps, pairing properties, correlation exponents, etc
37 Exact Diagonalization: Applications Quantum Magnets: nature of novel phases, critical points in 1D, dynamical correlation functions in 1D & 2D Fermionic models (Hubbard/t-J): gaps, pairing properties, correlation exponents, etc Fractional Quantum Hall states: energy gaps, overlap with model states, entanglement spectra
38 Exact Diagonalization: Applications Quantum Magnets: nature of novel phases, critical points in 1D, dynamical correlation functions in 1D & 2D Fermionic models (Hubbard/t-J): gaps, pairing properties, correlation exponents, etc Fractional Quantum Hall states: energy gaps, overlap with model states, entanglement spectra Quantum dimer models or other constrained models: nature of novel phases
39 Exact Diagonalization: Applications Quantum Magnets: nature of novel phases, critical points in 1D, dynamical correlation functions in 1D & 2D Fermionic models (Hubbard/t-J): gaps, pairing properties, correlation exponents, etc Fractional Quantum Hall states: energy gaps, overlap with model states, entanglement spectra Quantum dimer models or other constrained models: nature of novel phases Full Configuration Interaction in Quantum Chemistry reference and benchmark results
40 Exact Diagonalization: Present Day Limits low-lying eigenvalues, not full diagonalization
41 low-lying eigenvalues, not full diagonalization Exact Diagonalization: Present Day Limits Spin S=1/2 models: 40 spins square lattice, 39 sites triangular, 42 sites honeycomb lattice (64 spins or more in elevated magnetization sectors) up to 1.5 billion(=10 9 ) basis states with symmetries, up to 4.5 billion without
42 low-lying eigenvalues, not full diagonalization Exact Diagonalization: Present Day Limits Spin S=1/2 models: 40 spins square lattice, 39 sites triangular, 42 sites honeycomb lattice (64 spins or more in elevated magnetization sectors) up to 1.5 billion(=10 9 ) basis states with symmetries, up to 4.5 billion without t-j models: 32 sites checkerboard with 2 holes 32 sites square lattice with 4 holes up to 2.8 billion basis states
43 low-lying eigenvalues, not full diagonalization Exact Diagonalization: Present Day Limits Spin S=1/2 models: 40 spins square lattice, 39 sites triangular, 42 sites honeycomb lattice (64 spins or more in elevated magnetization sectors) up to 1.5 billion(=10 9 ) basis states with symmetries, up to 4.5 billion without t-j models: 32 sites checkerboard with 2 holes 32 sites square lattice with 4 holes up to 2.8 billion basis states Fractional quantum hall effect different filling fractions ν, up to electrons up to 3.5 billion basis states
44 low-lying eigenvalues, not full diagonalization Exact Diagonalization: Present Day Limits Spin S=1/2 models: 40 spins square lattice, 39 sites triangular, 42 sites honeycomb lattice (64 spins or more in elevated magnetization sectors) up to 1.5 billion(=10 9 ) basis states with symmetries, up to 4.5 billion without t-j models: 32 sites checkerboard with 2 holes 32 sites square lattice with 4 holes up to 2.8 billion basis states Fractional quantum hall effect different filling fractions ν, up to electrons up to 3.5 billion basis states Hubbard models 20 sites square lattice at half filling, 21 sites triangular lattice sites in ultracold atoms setting up to 160 billion basis states
45 Structure of an Exact Diagonalization code
46 Ingredients
47 Ingredients Hilbert space
48 Ingredients Hilbert space Basis represention, Lookup techniques
49 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries
50 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries Hamiltonian Matrix
51 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries Hamiltonian Matrix Sparse Matrix representation (memory/disk)
52 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries Hamiltonian Matrix Sparse Matrix representation (memory/disk) Matrix recalculation on the fly (matrix-free)
53 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries Hamiltonian Matrix Sparse Matrix representation (memory/disk) Matrix recalculation on the fly (matrix-free) Linear Algebra : Eigensolver / Time propagation
54 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries Hamiltonian Matrix Sparse Matrix representation (memory/disk) Matrix recalculation on the fly (matrix-free) Linear Algebra : Eigensolver / Time propagation LAPACK full diagonalization
55 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries Hamiltonian Matrix Sparse Matrix representation (memory/disk) Matrix recalculation on the fly (matrix-free) Linear Algebra : Eigensolver / Time propagation LAPACK full diagonalization Lanczos type diagonalization (needs only v = H u operations)
56 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries Hamiltonian Matrix Sparse Matrix representation (memory/disk) Matrix recalculation on the fly (matrix-free) Linear Algebra : Eigensolver / Time propagation LAPACK full diagonalization Lanczos type diagonalization (needs only v = H u operations) More exotic eigensolver techniques, real oder imaginary-time propagation,
57 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries Hamiltonian Matrix Sparse Matrix representation (memory/disk) Matrix recalculation on the fly (matrix-free) Linear Algebra : Eigensolver / Time propagation LAPACK full diagonalization Lanczos type diagonalization (needs only v = H u operations) More exotic eigensolver techniques, real oder imaginary-time propagation, Observables
58 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries Hamiltonian Matrix Sparse Matrix representation (memory/disk) Matrix recalculation on the fly (matrix-free) Linear Algebra : Eigensolver / Time propagation LAPACK full diagonalization Lanczos type diagonalization (needs only v = H u operations) More exotic eigensolver techniques, real oder imaginary-time propagation, Observables Static quantities (multipoint correlation functions, correlation density matrices,...)
59 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries Hamiltonian Matrix Sparse Matrix representation (memory/disk) Matrix recalculation on the fly (matrix-free) Linear Algebra : Eigensolver / Time propagation LAPACK full diagonalization Lanczos type diagonalization (needs only v = H u operations) More exotic eigensolver techniques, real oder imaginary-time propagation, Observables Static quantities (multipoint correlation functions, correlation density matrices,...) Dynamic observables (spectral functions, density of states,...)
60 Ingredients Hilbert space Basis represention, Lookup techniques Symmetries Hamiltonian Matrix Sparse Matrix representation (memory/disk) Matrix recalculation on the fly (matrix-free) Linear Algebra : Eigensolver / Time propagation LAPACK full diagonalization Lanczos type diagonalization (needs only v = H u operations) More exotic eigensolver techniques, real oder imaginary-time propagation, Observables Static quantities (multipoint correlation functions, correlation density matrices,...) Dynamic observables (spectral functions, density of states,...) Real-time evolution
61 Hilbert Space
62 Basis representation States of the Hilbert space need to be represented in the computer. Choose a representation which makes it simple to act with the Hamiltonian or other operators on the states, and to localize a given state in the basis Simple example: ensemble of S=1/2 sites in binary coding [ ] 2 = 13 detection of up or down spin can be done with bit-test. transverse exchange can be performed by an XOR operation: S + S + S S + [ ] 2 XOR [ ] 2 = [ ] 2 initial config bit 1 at the two sites coupled final config For S=1, one bit is obviously not sufficient. Use ternary representation or simply occupy two bits to label the 3 states.
63 Basis representation For t-j models at low doping it is useful to factorize hole positions and spin configurations on the occupied sites. For Hubbard models one can factorize the Hilbert space in up and down electron configurations. For constrained models - such as dimer models - the efficient generation of all basis states requires some thought. One of the key challenges for a fast ED code is to find the index of the new configuration in the list of all configurations (index f in Hi,f). Let us look at the example of S=1/2 spins at fixed S z
64 Basis lookup procedures (Lin tables) One of the key problems for a fast ED code is to find the index of the new configuration in the list of all configurations (index f in Hi,f). [ ] 2 = But is 11 the index of this configuration in a list of all S z =3/2 states? no! Use Lin tables to map from binary number to index in list of allowed states: (generalization of this idea works for arbitrary number of additive quantum numbers) Two tables with 2 (N/2) [=sqrt(2 N )] entries, one for MSBs and one for LSBs [0 0] = X [0 1] = 0 [1 0] = 1 [1 1] = 2 MSB [0 0] = X [0 1] = 0 [1 0] = 1 [1 1] = 0 LSB Ind([ ]) = = 0 Ind([ ]) = = 1 Ind([ ]) = = 2 Ind([ ]) = = 3
65 Basis lookup procedures (Lin tables) Lookup can therefore be done with two direct memory reads. This is a time and memory efficient approach (at least in many interesting cases). An alternative procedure is to build a hash list [const access time] or to perform a binary search [log access time]. This is all you require to write to code the Hamiltonian for a S=1/2 system with Sz conservation, but without spatial symmetries. This becomes somewhat more involved when using spatial symmetries...
66 Symmetries H = i,j J xy i,j (Sx i S x j + S y i Sy j )+J z i,js z i S z j
67 Symmetries Consider a XXZ spin model on a lattice. What are the symmetries of the problem? H = i,j J xy i,j (Sx i S x j + S y i Sy j )+J z i,js z i S z j
68 Symmetries Consider a XXZ spin model on a lattice. What are the symmetries of the problem? H = i,j J xy i,j (Sx i S x j + S y i Sy j )+J z i,js z i S z j The Hamiltonian conserves total S z, we can therefore work within a given S z sector This easily implemented while constructing the basis, as we discussed before.
69 Symmetries Consider a XXZ spin model on a lattice. What are the symmetries of the problem? H = i,j J xy i,j (Sx i S x j + S y i Sy j )+J z i,js z i S z j The Hamiltonian conserves total S z, we can therefore work within a given S z sector This easily implemented while constructing the basis, as we discussed before. The Hamiltonian is invariant under the space group, typically a few hundred elements. (in many cases = Translations x Pointgroup). Needs some technology to implement...
70 Symmetries Consider a XXZ spin model on a lattice. What are the symmetries of the problem? H = i,j J xy i,j (Sx i S x j + S y i Sy j )+J z i,js z i S z j The Hamiltonian conserves total S z, we can therefore work within a given S z sector This easily implemented while constructing the basis, as we discussed before. The Hamiltonian is invariant under the space group, typically a few hundred elements. (in many cases = Translations x Pointgroup). Needs some technology to implement... At the Heisenberg point, the total spin is also conserved. It is however very difficult to combine the SU(2) symmetry with the lattice symmetries in a computationally useful way (non-sparse and computationally expensive matrices).
71 Symmetries Consider a XXZ spin model on a lattice. What are the symmetries of the problem? H = i,j J xy i,j (Sx i S x j + S y i Sy j )+J z i,js z i S z j The Hamiltonian conserves total S z, we can therefore work within a given S z sector This easily implemented while constructing the basis, as we discussed before. The Hamiltonian is invariant under the space group, typically a few hundred elements. (in many cases = Translations x Pointgroup). Needs some technology to implement... At the Heisenberg point, the total spin is also conserved. It is however very difficult to combine the SU(2) symmetry with the lattice symmetries in a computationally useful way (non-sparse and computationally expensive matrices). At S z =0 one can use the spin-flip (particle-hole) symmetry which distinguishes even and odd spin sectors at the Heisenberg point. Simple to implement.
72 Spatial Symmetries Spatial symmetries are important for reduction of Hilbert space Symmetry resolved eigenstates teach a lot about the physics at work, dispersion of excitations, symmetry breaking tendencies, topological degeneracy, (more on that in later lectures) sites square lattice T PG =40 x 4 elements Icosidodecahedron (30 vertices) Ih:120 elements
73 Spatial Symmetries Symmetries are sometimes not easily visible, use graph theoretical tools to determine symmetry group [nauty, grape]. In an ED code a spatial symmetry operation is a site permutation operation. (could become more complicated with spin-orbit interactions and multiorbital sites) 40 sites square lattice T PG =40 x 4 elements Icosidodecahedron (30 vertices) Ih:120 elements
74 Spatial Symmetries: Building the basis Build a list of all allowed states satisfying the diagonal constraints, like particle number, total S z,... for each state we apply all symmetry operations and keep the state as a representative if it has the smallest integer representation among all generated states in the orbit. Example: 4 site ring with cyclic translation T, S z =3/2 sector T 0 ([ ]) [ ] T 1 ([ ]) [ ] T 2 ([ ]) [ ] T 3 ([ ]) [ ] keep state T 0 ([ ]) [ ] T 1 ([ ]) [ ] T 2 ([ ]) [ ] T 3 ([ ]) [ ] discard state...
75 Spatial Symmetries: Building the basis r = 1 N χ(g) g(r) G N = g G g G,g(r)=r χ(r)
76 Spatial Symmetries: Building the basis For one-dimensional representations χ of the spatial symmetry group: 1 Bloch state r = N χ(g) g(r) G Norm of the state is given as: N = The norm (and therefore the state itself) can vanish if it has a nontrivial stabilizer combined with a nontrivial representation χ. g G g G,g(r)=r χ(r)
77 Spatial Symmetries: Building the basis For one-dimensional representations χ of the spatial symmetry group: 1 Bloch state r = N χ(g) g(r) G Norm of the state is given as: N = The norm (and therefore the state itself) can vanish if it has a nontrivial stabilizer combined with a nontrivial representation χ. Example: 4 site S=1/2 ring with cyclic translations: g G g G,g(r)=r χ(r)
78 Spatial Symmetries: Building the basis For one-dimensional representations χ of the spatial symmetry group: 1 Bloch state r = N χ(g) g(r) G Norm of the state is given as: N = The norm (and therefore the state itself) can vanish if it has a nontrivial stabilizer combined with a nontrivial representation χ. Example: 4 site S=1/2 ring with cyclic translations: g G g G,g(r)=r χ(r) S z =2 S z =1 S z =0 K = , N = , N = , N = , N =1
79 Spatial Symmetries: Building the basis For one-dimensional representations χ of the spatial symmetry group: 1 Bloch state r = N χ(g) g(r) G Norm of the state is given as: N = The norm (and therefore the state itself) can vanish if it has a nontrivial stabilizer combined with a nontrivial representation χ. Example: 4 site S=1/2 ring with cyclic translations: g G g G,g(r)=r χ(r) S z =2 S z =1 S z =0 K = , N = , N = , N = , N =1 K = ±π/ , N = , N =1
80 Spatial Symmetries: Building the basis For one-dimensional representations χ of the spatial symmetry group: 1 Bloch state r = N χ(g) g(r) G Norm of the state is given as: N = The norm (and therefore the state itself) can vanish if it has a nontrivial stabilizer combined with a nontrivial representation χ. Example: 4 site S=1/2 ring with cyclic translations: g G g G,g(r)=r χ(r) K =0 K = ±π/2 K = π S z = , N =2 S z = , N = , N = , N =1 S z = , N = , N = , N = , N = , N =1
81 Spatial Symmetries: Building the basis For one-dimensional representations χ of the spatial symmetry group: 1 Bloch state r = N χ(g) g(r) G Norm of the state is given as: N = The norm (and therefore the state itself) can vanish if it has a nontrivial stabilizer combined with a nontrivial representation χ. Example: 4 site S=1/2 ring with cyclic translations: g G g G,g(r)=r χ(r) K =0 K = ±π/2 K = π 2 4 =16 S z = , N =2 1+1 S z =1 S z = , N = , N = , N = , N = , N = , N = , N = , N =
82 The Hamiltonian Matrix
83 The Hamiltonian Matrix Now that we have a list of representatives and their norms, can we calculate the matrix elements of the Hamiltonian? s H r =? Let us look at an elementary, non-branching term in the Hamiltonian: h α r = h α (r) s We can now calculate the matrix element the Bloch states: s h α r without double expanding s h α r = N s N r χ(g )h α (r) key algorithmic problem: given a possibly non-representative, how do we find the associated representative s, as well as a symmetry element g relating s to s? s
84 The Hamiltonian Matrix key algorithmic problem: given a possibly non-representative, how do we find the associated representative s, as well as a symmetry element g relating s to s? Brute force: loop over all symmetry operations applied on and retain s and. This is however often not efficient (many hundred symmetries). g Prepare a lookup list, relating each allowed configuration with the index of its representative, and also the associated group element linking the two. Gives fast implementation, but needs a list of the size of the non spatiallysymmetrized Hilbert space. For specific lattices and models (Hubbard models) clever tricks exist which factorize the symmetry group into a sublattice conserving subgroup times a sublattice exchange. They give s fast, then a hash or binary search is needed to locate in the list of representatives in order to get its index. s s s
85 Hamiltonian Matrix Storage Different possibilities exist: Store hamiltonian matrix elements in memory in a sparse matrix format Fast matrix vector multiplies, but obviously limited by available memory. Store hamiltonian matrix elements on disk in a sparse matrix format. In principle possible due to the vast disk space available, but I/O speed is much slower than main memory access times. Difficult to parallelize. Recalculate the hamiltonian matrix elements in each iterations on the fly. Needed for the cutting edge simulations, where the whole memory is used by the Lanczos vectors. Can be parallelized on most architectures.
86 Thank you!
H ψ = E ψ. Introduction to Exact Diagonalization. Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden
 H ψ = E ψ Introduction to Exact Diagonalization Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden http://www.pks.mpg.de/~aml laeuchli@comp-phys.org IPAM QS2009 Workshop,
H ψ = E ψ Introduction to Exact Diagonalization Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden http://www.pks.mpg.de/~aml laeuchli@comp-phys.org IPAM QS2009 Workshop,
Quantum Lattice Models & Introduction to Exact Diagonalization
 Quantum Lattice Models & Introduction to Exact Diagonalization H! = E! Andreas Läuchli IRRMA EPF Lausanne ALPS User Workshop CSCS Manno, 28/9/2004 Outline of this lecture: Quantum Lattice Models Lattices
Quantum Lattice Models & Introduction to Exact Diagonalization H! = E! Andreas Läuchli IRRMA EPF Lausanne ALPS User Workshop CSCS Manno, 28/9/2004 Outline of this lecture: Quantum Lattice Models Lattices
H ψ = E ψ. Introduction to Exact Diagonalization. Andreas Läuchli Institute for Theoretical Physics University of Innsbruck, Austria
 H ψ = E ψ Introduction to Exact Diagonalization Andreas Läuchli Institute for Theoretical Physics University of Innsbruck, Austria andreas.laeuchli@uibk.ac.at http://laeuchli-lab.uibk.ac.at/group-page
H ψ = E ψ Introduction to Exact Diagonalization Andreas Läuchli Institute for Theoretical Physics University of Innsbruck, Austria andreas.laeuchli@uibk.ac.at http://laeuchli-lab.uibk.ac.at/group-page
H ψ = E ψ. Introduction to Exact Diagonalization. Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden
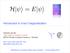 H ψ = E ψ Introduction to Exact Diagonalization Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden http://www.pks.mpg.de/~aml laeuchli@comp-phys.org Simulations of
H ψ = E ψ Introduction to Exact Diagonalization Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden http://www.pks.mpg.de/~aml laeuchli@comp-phys.org Simulations of
H = E. Introduction to Exact Diagonalization. Andreas Läuchli Institute for Theoretical Physics University of Innsbruck, Austria
 H = E Introduction to Exact Diagonalization Andreas Läuchli Institute for Theoretical Physics University of Innsbruck, Austria andreas.laeuchli@uibk.ac.at http://laeuchli-lab.uibk.ac.at/group-page Outline
H = E Introduction to Exact Diagonalization Andreas Läuchli Institute for Theoretical Physics University of Innsbruck, Austria andreas.laeuchli@uibk.ac.at http://laeuchli-lab.uibk.ac.at/group-page Outline
Magnets, 1D quantum system, and quantum Phase transitions
 134 Phys620.nb 10 Magnets, 1D quantum system, and quantum Phase transitions In 1D, fermions can be mapped into bosons, and vice versa. 10.1. magnetization and frustrated magnets (in any dimensions) Consider
134 Phys620.nb 10 Magnets, 1D quantum system, and quantum Phase transitions In 1D, fermions can be mapped into bosons, and vice versa. 10.1. magnetization and frustrated magnets (in any dimensions) Consider
Simulations of Quantum Dimer Models
 Simulations of Quantum Dimer Models Didier Poilblanc Laboratoire de Physique Théorique CNRS & Université de Toulouse 1 A wide range of applications Disordered frustrated quantum magnets Correlated fermions
Simulations of Quantum Dimer Models Didier Poilblanc Laboratoire de Physique Théorique CNRS & Université de Toulouse 1 A wide range of applications Disordered frustrated quantum magnets Correlated fermions
Paramagnetic phases of Kagome lattice quantum Ising models p.1/16
 Paramagnetic phases of Kagome lattice quantum Ising models Predrag Nikolić In collaboration with T. Senthil Massachusetts Institute of Technology Paramagnetic phases of Kagome lattice quantum Ising models
Paramagnetic phases of Kagome lattice quantum Ising models Predrag Nikolić In collaboration with T. Senthil Massachusetts Institute of Technology Paramagnetic phases of Kagome lattice quantum Ising models
Topological Phases in One Dimension
 Topological Phases in One Dimension Lukasz Fidkowski and Alexei Kitaev arxiv:1008.4138 Topological phases in 2 dimensions: - Integer quantum Hall effect - quantized σ xy - robust chiral edge modes - Fractional
Topological Phases in One Dimension Lukasz Fidkowski and Alexei Kitaev arxiv:1008.4138 Topological phases in 2 dimensions: - Integer quantum Hall effect - quantized σ xy - robust chiral edge modes - Fractional
Spin liquids on ladders and in 2d
 Spin liquids on ladders and in 2d MPA Fisher (with O. Motrunich) Minnesota, FTPI, 5/3/08 Interest: Quantum Spin liquid phases of 2d Mott insulators Background: Three classes of 2d Spin liquids a) Topological
Spin liquids on ladders and in 2d MPA Fisher (with O. Motrunich) Minnesota, FTPI, 5/3/08 Interest: Quantum Spin liquid phases of 2d Mott insulators Background: Three classes of 2d Spin liquids a) Topological
Numerical diagonalization studies of quantum spin chains
 PY 502, Computational Physics, Fall 2016 Anders W. Sandvik, Boston University Numerical diagonalization studies of quantum spin chains Introduction to computational studies of spin chains Using basis states
PY 502, Computational Physics, Fall 2016 Anders W. Sandvik, Boston University Numerical diagonalization studies of quantum spin chains Introduction to computational studies of spin chains Using basis states
Physics 239/139 Spring 2018 Assignment 2 Solutions
 University of California at San Diego Department of Physics Prof. John McGreevy Physics 39/139 Spring 018 Assignment Solutions Due 1:30pm Monday, April 16, 018 1. Classical circuits brain-warmer. (a) Show
University of California at San Diego Department of Physics Prof. John McGreevy Physics 39/139 Spring 018 Assignment Solutions Due 1:30pm Monday, April 16, 018 1. Classical circuits brain-warmer. (a) Show
Fermionic tensor networks
 Fermionic tensor networks Philippe Corboz, Institute for Theoretical Physics, ETH Zurich Bosons vs Fermions P. Corboz and G. Vidal, Phys. Rev. B 80, 165129 (2009) : fermionic 2D MERA P. Corboz, R. Orus,
Fermionic tensor networks Philippe Corboz, Institute for Theoretical Physics, ETH Zurich Bosons vs Fermions P. Corboz and G. Vidal, Phys. Rev. B 80, 165129 (2009) : fermionic 2D MERA P. Corboz, R. Orus,
Kitaev honeycomb lattice model: from A to B and beyond
 Kitaev honeycomb lattice model: from A to B and beyond Jiri Vala Department of Mathematical Physics National University of Ireland at Maynooth Postdoc: PhD students: Collaborators: Graham Kells Ahmet Bolukbasi
Kitaev honeycomb lattice model: from A to B and beyond Jiri Vala Department of Mathematical Physics National University of Ireland at Maynooth Postdoc: PhD students: Collaborators: Graham Kells Ahmet Bolukbasi
The 1+1-dimensional Ising model
 Chapter 4 The 1+1-dimensional Ising model The 1+1-dimensional Ising model is one of the most important models in statistical mechanics. It is an interacting system, and behaves accordingly. Yet for a variety
Chapter 4 The 1+1-dimensional Ising model The 1+1-dimensional Ising model is one of the most important models in statistical mechanics. It is an interacting system, and behaves accordingly. Yet for a variety
Quantum spin systems - models and computational methods
 Summer School on Computational Statistical Physics August 4-11, 2010, NCCU, Taipei, Taiwan Quantum spin systems - models and computational methods Anders W. Sandvik, Boston University Lecture outline Introduction
Summer School on Computational Statistical Physics August 4-11, 2010, NCCU, Taipei, Taiwan Quantum spin systems - models and computational methods Anders W. Sandvik, Boston University Lecture outline Introduction
Exact diagonalization methods
 Summer School on Computational Statistical Physics August 4-11, 2010, NCCU, Taipei, Taiwan Exact diagonalization methods Anders W. Sandvik, Boston University Representation of states in the computer bit
Summer School on Computational Statistical Physics August 4-11, 2010, NCCU, Taipei, Taiwan Exact diagonalization methods Anders W. Sandvik, Boston University Representation of states in the computer bit
Fully symmetric and non-fractionalized Mott insulators at fractional site-filling
 Fully symmetric and non-fractionalized Mott insulators at fractional site-filling Itamar Kimchi University of California, Berkeley EQPCM @ ISSP June 19, 2013 PRL 2013 (kagome), 1207.0498...[PNAS] (honeycomb)
Fully symmetric and non-fractionalized Mott insulators at fractional site-filling Itamar Kimchi University of California, Berkeley EQPCM @ ISSP June 19, 2013 PRL 2013 (kagome), 1207.0498...[PNAS] (honeycomb)
The Quantum Heisenberg Ferromagnet
 The Quantum Heisenberg Ferromagnet Soon after Schrödinger discovered the wave equation of quantum mechanics, Heisenberg and Dirac developed the first successful quantum theory of ferromagnetism W. Heisenberg,
The Quantum Heisenberg Ferromagnet Soon after Schrödinger discovered the wave equation of quantum mechanics, Heisenberg and Dirac developed the first successful quantum theory of ferromagnetism W. Heisenberg,
Efficient time evolution of one-dimensional quantum systems
 Efficient time evolution of one-dimensional quantum systems Frank Pollmann Max-Planck-Institut für komplexer Systeme, Dresden, Germany Sep. 5, 2012 Hsinchu Problems we will address... Finding ground states
Efficient time evolution of one-dimensional quantum systems Frank Pollmann Max-Planck-Institut für komplexer Systeme, Dresden, Germany Sep. 5, 2012 Hsinchu Problems we will address... Finding ground states
Tensor network simulations of strongly correlated quantum systems
 CENTRE FOR QUANTUM TECHNOLOGIES NATIONAL UNIVERSITY OF SINGAPORE AND CLARENDON LABORATORY UNIVERSITY OF OXFORD Tensor network simulations of strongly correlated quantum systems Stephen Clark LXXT[[[GSQPEFS\EGYOEGXMZMXMIWUYERXYQGSYVWI
CENTRE FOR QUANTUM TECHNOLOGIES NATIONAL UNIVERSITY OF SINGAPORE AND CLARENDON LABORATORY UNIVERSITY OF OXFORD Tensor network simulations of strongly correlated quantum systems Stephen Clark LXXT[[[GSQPEFS\EGYOEGXMZMXMIWUYERXYQGSYVWI
Entanglement spectrum as a tool for onedimensional
 Entanglement spectrum as a tool for onedimensional critical systems MPI-PKS, Dresden, November 2012 Joel Moore University of California, Berkeley, and Lawrence Berkeley National Laboratory Outline ballistic
Entanglement spectrum as a tool for onedimensional critical systems MPI-PKS, Dresden, November 2012 Joel Moore University of California, Berkeley, and Lawrence Berkeley National Laboratory Outline ballistic
Electron Correlation
 Series in Modern Condensed Matter Physics Vol. 5 Lecture Notes an Electron Correlation and Magnetism Patrik Fazekas Research Institute for Solid State Physics & Optics, Budapest lb World Scientific h Singapore
Series in Modern Condensed Matter Physics Vol. 5 Lecture Notes an Electron Correlation and Magnetism Patrik Fazekas Research Institute for Solid State Physics & Optics, Budapest lb World Scientific h Singapore
NON-EQUILIBRIUM DYNAMICS IN
 NON-EQUILIBRIUM DYNAMICS IN ISOLATED QUANTUM SYSTEMS Masud Haque Maynooth University Dept. Mathematical Physics Maynooth, Ireland Max-Planck Institute for Physics of Complex Systems (MPI-PKS) Dresden,
NON-EQUILIBRIUM DYNAMICS IN ISOLATED QUANTUM SYSTEMS Masud Haque Maynooth University Dept. Mathematical Physics Maynooth, Ireland Max-Planck Institute for Physics of Complex Systems (MPI-PKS) Dresden,
Topological insulator with time-reversal symmetry
 Phys620.nb 101 7 Topological insulator with time-reversal symmetry Q: Can we get a topological insulator that preserves the time-reversal symmetry? A: Yes, with the help of the spin degree of freedom.
Phys620.nb 101 7 Topological insulator with time-reversal symmetry Q: Can we get a topological insulator that preserves the time-reversal symmetry? A: Yes, with the help of the spin degree of freedom.
Section 10: Many Particle Quantum Mechanics Solutions
 Physics 143a: Quantum Mechanics I Section 10: Many Particle Quantum Mechanics Solutions Spring 015, Harvard Here is a summary of the most important points from this week (with a few of my own tidbits),
Physics 143a: Quantum Mechanics I Section 10: Many Particle Quantum Mechanics Solutions Spring 015, Harvard Here is a summary of the most important points from this week (with a few of my own tidbits),
Lecture 5. Hartree-Fock Theory. WS2010/11: Introduction to Nuclear and Particle Physics
 Lecture 5 Hartree-Fock Theory WS2010/11: Introduction to Nuclear and Particle Physics Particle-number representation: General formalism The simplest starting point for a many-body state is a system of
Lecture 5 Hartree-Fock Theory WS2010/11: Introduction to Nuclear and Particle Physics Particle-number representation: General formalism The simplest starting point for a many-body state is a system of
Critical Spin-liquid Phases in Spin-1/2 Triangular Antiferromagnets. In collaboration with: Olexei Motrunich & Jason Alicea
 Critical Spin-liquid Phases in Spin-1/2 Triangular Antiferromagnets In collaboration with: Olexei Motrunich & Jason Alicea I. Background Outline Avoiding conventional symmetry-breaking in s=1/2 AF Topological
Critical Spin-liquid Phases in Spin-1/2 Triangular Antiferromagnets In collaboration with: Olexei Motrunich & Jason Alicea I. Background Outline Avoiding conventional symmetry-breaking in s=1/2 AF Topological
3 Symmetry Protected Topological Phase
 Physics 3b Lecture 16 Caltech, 05/30/18 3 Symmetry Protected Topological Phase 3.1 Breakdown of noninteracting SPT phases with interaction Building on our previous discussion of the Majorana chain and
Physics 3b Lecture 16 Caltech, 05/30/18 3 Symmetry Protected Topological Phase 3.1 Breakdown of noninteracting SPT phases with interaction Building on our previous discussion of the Majorana chain and
Quantum Spin-Metals in Weak Mott Insulators
 Quantum Spin-Metals in Weak Mott Insulators MPA Fisher (with O. Motrunich, Donna Sheng, Simon Trebst) Quantum Critical Phenomena conference Toronto 9/27/08 Quantum Spin-metals - spin liquids with Bose
Quantum Spin-Metals in Weak Mott Insulators MPA Fisher (with O. Motrunich, Donna Sheng, Simon Trebst) Quantum Critical Phenomena conference Toronto 9/27/08 Quantum Spin-metals - spin liquids with Bose
Linked-Cluster Expansions for Quantum Many-Body Systems
 Linked-Cluster Expansions for Quantum Many-Body Systems Boulder Summer School 2010 Simon Trebst Lecture overview Why series expansions? Linked-cluster expansions From Taylor expansions to linked-cluster
Linked-Cluster Expansions for Quantum Many-Body Systems Boulder Summer School 2010 Simon Trebst Lecture overview Why series expansions? Linked-cluster expansions From Taylor expansions to linked-cluster
Advanced Computation for Complex Materials
 Advanced Computation for Complex Materials Computational Progress is brainpower limited, not machine limited Algorithms Physics Major progress in algorithms Quantum Monte Carlo Density Matrix Renormalization
Advanced Computation for Complex Materials Computational Progress is brainpower limited, not machine limited Algorithms Physics Major progress in algorithms Quantum Monte Carlo Density Matrix Renormalization
Floquet Topological Insulators and Majorana Modes
 Floquet Topological Insulators and Majorana Modes Manisha Thakurathi Journal Club Centre for High Energy Physics IISc Bangalore January 17, 2013 References Floquet Topological Insulators by J. Cayssol
Floquet Topological Insulators and Majorana Modes Manisha Thakurathi Journal Club Centre for High Energy Physics IISc Bangalore January 17, 2013 References Floquet Topological Insulators by J. Cayssol
From Majorana Fermions to Topological Order
 From Majorana Fermions to Topological Order Arxiv: 1201.3757, to appear in PRL. B.M. Terhal, F. Hassler, D.P. DiVincenzo IQI, RWTH Aachen We are looking for PhD students or postdocs for theoretical research
From Majorana Fermions to Topological Order Arxiv: 1201.3757, to appear in PRL. B.M. Terhal, F. Hassler, D.P. DiVincenzo IQI, RWTH Aachen We are looking for PhD students or postdocs for theoretical research
Non-abelian statistics
 Non-abelian statistics Paul Fendley Non-abelian statistics are just plain interesting. They probably occur in the ν = 5/2 FQHE, and people are constructing time-reversal-invariant models which realize
Non-abelian statistics Paul Fendley Non-abelian statistics are just plain interesting. They probably occur in the ν = 5/2 FQHE, and people are constructing time-reversal-invariant models which realize
Attempts at relativistic QM
 Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
Lecture notes on topological insulators
 Lecture notes on topological insulators Ming-Che Chang Department of Physics, National Taiwan Normal University, Taipei, Taiwan Dated: May 8, 07 I. D p-wave SUPERCONDUCTOR Here we study p-wave SC in D
Lecture notes on topological insulators Ming-Che Chang Department of Physics, National Taiwan Normal University, Taipei, Taiwan Dated: May 8, 07 I. D p-wave SUPERCONDUCTOR Here we study p-wave SC in D
Momentum-space and Hybrid Real- Momentum Space DMRG applied to the Hubbard Model
 Momentum-space and Hybrid Real- Momentum Space DMRG applied to the Hubbard Model Örs Legeza Reinhard M. Noack Collaborators Georg Ehlers Jeno Sólyom Gergely Barcza Steven R. White Collaborators Georg Ehlers
Momentum-space and Hybrid Real- Momentum Space DMRG applied to the Hubbard Model Örs Legeza Reinhard M. Noack Collaborators Georg Ehlers Jeno Sólyom Gergely Barcza Steven R. White Collaborators Georg Ehlers
Two Dimensional Chern Insulators, the Qi-Wu-Zhang and Haldane Models
 Two Dimensional Chern Insulators, the Qi-Wu-Zhang and Haldane Models Matthew Brooks, Introduction to Topological Insulators Seminar, Universität Konstanz Contents QWZ Model of Chern Insulators Haldane
Two Dimensional Chern Insulators, the Qi-Wu-Zhang and Haldane Models Matthew Brooks, Introduction to Topological Insulators Seminar, Universität Konstanz Contents QWZ Model of Chern Insulators Haldane
Luigi Paolasini
 Luigi Paolasini paolasini@esrf.fr LECTURE 4: MAGNETIC INTERACTIONS - Dipole vs exchange magnetic interactions. - Direct and indirect exchange interactions. - Anisotropic exchange interactions. - Interplay
Luigi Paolasini paolasini@esrf.fr LECTURE 4: MAGNETIC INTERACTIONS - Dipole vs exchange magnetic interactions. - Direct and indirect exchange interactions. - Anisotropic exchange interactions. - Interplay
Spin Superfluidity and Graphene in a Strong Magnetic Field
 Spin Superfluidity and Graphene in a Strong Magnetic Field by B. I. Halperin Nano-QT 2016 Kyiv October 11, 2016 Based on work with So Takei (CUNY), Yaroslav Tserkovnyak (UCLA), and Amir Yacoby (Harvard)
Spin Superfluidity and Graphene in a Strong Magnetic Field by B. I. Halperin Nano-QT 2016 Kyiv October 11, 2016 Based on work with So Takei (CUNY), Yaroslav Tserkovnyak (UCLA), and Amir Yacoby (Harvard)
Realizing non-abelian statistics in quantum loop models
 Realizing non-abelian statistics in quantum loop models Paul Fendley Experimental and theoretical successes have made us take a close look at quantum physics in two spatial dimensions. We have now found
Realizing non-abelian statistics in quantum loop models Paul Fendley Experimental and theoretical successes have made us take a close look at quantum physics in two spatial dimensions. We have now found
Design and realization of exotic quantum phases in atomic gases
 Design and realization of exotic quantum phases in atomic gases H.P. Büchler and P. Zoller Theoretische Physik, Universität Innsbruck, Austria Institut für Quantenoptik und Quanteninformation der Österreichischen
Design and realization of exotic quantum phases in atomic gases H.P. Büchler and P. Zoller Theoretische Physik, Universität Innsbruck, Austria Institut für Quantenoptik und Quanteninformation der Österreichischen
Decay of correlations in 2d quantum systems
 Decay of correlations in 2d quantum systems Costanza Benassi University of Warwick Quantissima in the Serenissima II, 25th August 2017 Costanza Benassi (University of Warwick) Decay of correlations in
Decay of correlations in 2d quantum systems Costanza Benassi University of Warwick Quantissima in the Serenissima II, 25th August 2017 Costanza Benassi (University of Warwick) Decay of correlations in
Quantum Field Theory
 Quantum Field Theory PHYS-P 621 Radovan Dermisek, Indiana University Notes based on: M. Srednicki, Quantum Field Theory 1 Attempts at relativistic QM based on S-1 A proper description of particle physics
Quantum Field Theory PHYS-P 621 Radovan Dermisek, Indiana University Notes based on: M. Srednicki, Quantum Field Theory 1 Attempts at relativistic QM based on S-1 A proper description of particle physics
7 Frustrated Spin Systems
 7 Frustrated Spin Systems Frédéric Mila Institute of Theoretical Physics Ecole Polytechnique Fédérale de Lausanne 1015 Lausanne, Switzerland Contents 1 Introduction 2 2 Competing interactions and degeneracy
7 Frustrated Spin Systems Frédéric Mila Institute of Theoretical Physics Ecole Polytechnique Fédérale de Lausanne 1015 Lausanne, Switzerland Contents 1 Introduction 2 2 Competing interactions and degeneracy
Quantum Monte Carlo Simulations in the Valence Bond Basis. Anders Sandvik, Boston University
 Quantum Monte Carlo Simulations in the Valence Bond Basis Anders Sandvik, Boston University Outline The valence bond basis for S=1/2 spins Projector QMC in the valence bond basis Heisenberg model with
Quantum Monte Carlo Simulations in the Valence Bond Basis Anders Sandvik, Boston University Outline The valence bond basis for S=1/2 spins Projector QMC in the valence bond basis Heisenberg model with
Universal phase transitions in Topological lattice models
 Universal phase transitions in Topological lattice models F. J. Burnell Collaborators: J. Slingerland S. H. Simon September 2, 2010 Overview Matter: classified by orders Symmetry Breaking (Ferromagnet)
Universal phase transitions in Topological lattice models F. J. Burnell Collaborators: J. Slingerland S. H. Simon September 2, 2010 Overview Matter: classified by orders Symmetry Breaking (Ferromagnet)
Non-magnetic states. The Néel states are product states; φ N a. , E ij = 3J ij /4 2 The Néel states have higher energy (expectations; not eigenstates)
 Non-magnetic states Two spins, i and j, in isolation, H ij = J ijsi S j = J ij [Si z Sj z + 1 2 (S+ i S j + S i S+ j )] For Jij>0 the ground state is the singlet; φ s ij = i j i j, E ij = 3J ij /4 2 The
Non-magnetic states Two spins, i and j, in isolation, H ij = J ijsi S j = J ij [Si z Sj z + 1 2 (S+ i S j + S i S+ j )] For Jij>0 the ground state is the singlet; φ s ij = i j i j, E ij = 3J ij /4 2 The
3.15. Some symmetry properties of the Berry curvature and the Chern number.
 50 Phys620.nb z M 3 at the K point z M 3 3 t ' sin 3 t ' sin (3.36) (3.362) Therefore, as long as M 3 3 t ' sin, the system is an topological insulator ( z flips sign). If M 3 3 t ' sin, z is always positive
50 Phys620.nb z M 3 at the K point z M 3 3 t ' sin 3 t ' sin (3.36) (3.362) Therefore, as long as M 3 3 t ' sin, the system is an topological insulator ( z flips sign). If M 3 3 t ' sin, z is always positive
Stripes and holes in a two-dimensional model of spinless fermions or hardcore bosons
 PHYSICAL REVIEW B 68, 014506 2003 Stripes and holes in a two-dimensional model of spinless fermions or hardcore bosons N. G. Zhang* and C. L. Henley Department of Physics, Cornell University, Ithaca, New
PHYSICAL REVIEW B 68, 014506 2003 Stripes and holes in a two-dimensional model of spinless fermions or hardcore bosons N. G. Zhang* and C. L. Henley Department of Physics, Cornell University, Ithaca, New
WORLD SCIENTIFIC (2014)
 WORLD SCIENTIFIC (2014) LIST OF PROBLEMS Chapter 1: Magnetism of Free Electrons and Atoms 1. Orbital and spin moments of an electron: Using the theory of angular momentum, calculate the orbital
WORLD SCIENTIFIC (2014) LIST OF PROBLEMS Chapter 1: Magnetism of Free Electrons and Atoms 1. Orbital and spin moments of an electron: Using the theory of angular momentum, calculate the orbital
SPIN-LIQUIDS ON THE KAGOME LATTICE: CHIRAL TOPOLOGICAL, AND GAPLESS NON-FERMI-LIQUID PHASE
 SPIN-LIQUIDS ON THE KAGOME LATTICE: CHIRAL TOPOLOGICAL, AND GAPLESS NON-FERMI-LIQUID PHASE ANDREAS W.W. LUDWIG (UC-Santa Barbara) work done in collaboration with: Bela Bauer (Microsoft Station-Q, Santa
SPIN-LIQUIDS ON THE KAGOME LATTICE: CHIRAL TOPOLOGICAL, AND GAPLESS NON-FERMI-LIQUID PHASE ANDREAS W.W. LUDWIG (UC-Santa Barbara) work done in collaboration with: Bela Bauer (Microsoft Station-Q, Santa
Topological insulator part II: Berry Phase and Topological index
 Phys60.nb 11 3 Topological insulator part II: Berry Phase and Topological index 3.1. Last chapter Topological insulator: an insulator in the bulk and a metal near the boundary (surface or edge) Quantum
Phys60.nb 11 3 Topological insulator part II: Berry Phase and Topological index 3.1. Last chapter Topological insulator: an insulator in the bulk and a metal near the boundary (surface or edge) Quantum
Gapless Spin Liquids in Two Dimensions
 Gapless Spin Liquids in Two Dimensions MPA Fisher (with O. Motrunich, Donna Sheng, Matt Block) Boulder Summerschool 7/20/10 Interest Quantum Phases of 2d electrons (spins) with emergent rather than broken
Gapless Spin Liquids in Two Dimensions MPA Fisher (with O. Motrunich, Donna Sheng, Matt Block) Boulder Summerschool 7/20/10 Interest Quantum Phases of 2d electrons (spins) with emergent rather than broken
Loop current order in optical lattices
 JQI Summer School June 13, 2014 Loop current order in optical lattices Xiaopeng Li JQI/CMTC Outline Ultracold atoms confined in optical lattices 1. Why we care about lattice? 2. Band structures and Berry
JQI Summer School June 13, 2014 Loop current order in optical lattices Xiaopeng Li JQI/CMTC Outline Ultracold atoms confined in optical lattices 1. Why we care about lattice? 2. Band structures and Berry
Are these states normalized? A) Yes
 QMII-. Consider two kets and their corresponding column vectors: Ψ = φ = Are these two state orthogonal? Is ψ φ = 0? A) Yes ) No Answer: A Are these states normalized? A) Yes ) No Answer: (each state has
QMII-. Consider two kets and their corresponding column vectors: Ψ = φ = Are these two state orthogonal? Is ψ φ = 0? A) Yes ) No Answer: A Are these states normalized? A) Yes ) No Answer: (each state has
Kai Sun. University of Michigan, Ann Arbor. Collaborators: Krishna Kumar and Eduardo Fradkin (UIUC)
 Kai Sun University of Michigan, Ann Arbor Collaborators: Krishna Kumar and Eduardo Fradkin (UIUC) Outline How to construct a discretized Chern-Simons gauge theory A necessary and sufficient condition for
Kai Sun University of Michigan, Ann Arbor Collaborators: Krishna Kumar and Eduardo Fradkin (UIUC) Outline How to construct a discretized Chern-Simons gauge theory A necessary and sufficient condition for
The density matrix renormalization group and tensor network methods
 The density matrix renormalization group and tensor network methods Outline Steve White Exploiting the low entanglement of ground states Matrix product states and DMRG 1D 2D Tensor network states Some
The density matrix renormalization group and tensor network methods Outline Steve White Exploiting the low entanglement of ground states Matrix product states and DMRG 1D 2D Tensor network states Some
team Hans Peter Büchler Nicolai Lang Mikhail Lukin Norman Yao Sebastian Huber
 title 1 team 2 Hans Peter Büchler Nicolai Lang Mikhail Lukin Norman Yao Sebastian Huber motivation: topological states of matter 3 fermions non-interacting, filled band (single particle physics) topological
title 1 team 2 Hans Peter Büchler Nicolai Lang Mikhail Lukin Norman Yao Sebastian Huber motivation: topological states of matter 3 fermions non-interacting, filled band (single particle physics) topological
Spin liquids in frustrated magnets
 May 20, 2010 Contents 1 Frustration 2 3 4 Exotic excitations 5 Frustration The presence of competing forces that cannot be simultaneously satisfied. Heisenberg-Hamiltonian H = 1 J ij S i S j 2 ij The ground
May 20, 2010 Contents 1 Frustration 2 3 4 Exotic excitations 5 Frustration The presence of competing forces that cannot be simultaneously satisfied. Heisenberg-Hamiltonian H = 1 J ij S i S j 2 ij The ground
Coupling of Angular Momenta Isospin Nucleon-Nucleon Interaction
 Lecture 5 Coupling of Angular Momenta Isospin Nucleon-Nucleon Interaction WS0/3: Introduction to Nuclear and Particle Physics,, Part I I. Angular Momentum Operator Rotation R(θ): in polar coordinates the
Lecture 5 Coupling of Angular Momenta Isospin Nucleon-Nucleon Interaction WS0/3: Introduction to Nuclear and Particle Physics,, Part I I. Angular Momentum Operator Rotation R(θ): in polar coordinates the
Spinon magnetic resonance. Oleg Starykh, University of Utah
 Spinon magnetic resonance Oleg Starykh, University of Utah May 17-19, 2018 Examples of current literature 200 cm -1 = 6 THz Spinons? 4 mev = 1 THz The big question(s) What is quantum spin liquid? No broken
Spinon magnetic resonance Oleg Starykh, University of Utah May 17-19, 2018 Examples of current literature 200 cm -1 = 6 THz Spinons? 4 mev = 1 THz The big question(s) What is quantum spin liquid? No broken
Quantum Phases in Bose-Hubbard Models with Spin-orbit Interactions
 Quantum Phases in Bose-Hubbard Models with Spin-orbit Interactions Shizhong Zhang The University of Hong Kong Institute for Advanced Study, Tsinghua 24 October 2012 The plan 1. Introduction to Bose-Hubbard
Quantum Phases in Bose-Hubbard Models with Spin-orbit Interactions Shizhong Zhang The University of Hong Kong Institute for Advanced Study, Tsinghua 24 October 2012 The plan 1. Introduction to Bose-Hubbard
Understanding Topological Order with PEPS. David Pérez-García Autrans Summer School 2016
 Understanding Topological Order with PEPS David Pérez-García Autrans Summer School 2016 Outlook 1. An introduc
Understanding Topological Order with PEPS David Pérez-García Autrans Summer School 2016 Outlook 1. An introduc
PHY305: Notes on Entanglement and the Density Matrix
 PHY305: Notes on Entanglement and the Density Matrix Here follows a short summary of the definitions of qubits, EPR states, entanglement, the density matrix, pure states, mixed states, measurement, and
PHY305: Notes on Entanglement and the Density Matrix Here follows a short summary of the definitions of qubits, EPR states, entanglement, the density matrix, pure states, mixed states, measurement, and
3.024 Electrical, Optical, and Magnetic Properties of Materials Spring 2012 Recitation 8 Notes
 Overview 1. Electronic Band Diagram Review 2. Spin Review 3. Density of States 4. Fermi-Dirac Distribution 1. Electronic Band Diagram Review Considering 1D crystals with periodic potentials of the form:
Overview 1. Electronic Band Diagram Review 2. Spin Review 3. Density of States 4. Fermi-Dirac Distribution 1. Electronic Band Diagram Review Considering 1D crystals with periodic potentials of the form:
221B Lecture Notes Many-Body Problems I
 221B Lecture Notes Many-Body Problems I 1 Quantum Statistics of Identical Particles If two particles are identical, their exchange must not change physical quantities. Therefore, a wave function ψ( x 1,
221B Lecture Notes Many-Body Problems I 1 Quantum Statistics of Identical Particles If two particles are identical, their exchange must not change physical quantities. Therefore, a wave function ψ( x 1,
Ashvin Vishwanath UC Berkeley
 TOPOLOGY + LOCALIZATION: QUANTUM COHERENCE IN HOT MATTER Ashvin Vishwanath UC Berkeley arxiv:1307.4092 (to appear in Nature Comm.) Thanks to David Huse for inspiring discussions Yasaman Bahri (Berkeley)
TOPOLOGY + LOCALIZATION: QUANTUM COHERENCE IN HOT MATTER Ashvin Vishwanath UC Berkeley arxiv:1307.4092 (to appear in Nature Comm.) Thanks to David Huse for inspiring discussions Yasaman Bahri (Berkeley)
Bosonization of lattice fermions in higher dimensions
 Bosonization of lattice fermions in higher dimensions Anton Kapustin California Institute of Technology January 15, 2019 Anton Kapustin (California Institute of Technology) Bosonization of lattice fermions
Bosonization of lattice fermions in higher dimensions Anton Kapustin California Institute of Technology January 15, 2019 Anton Kapustin (California Institute of Technology) Bosonization of lattice fermions
Time Evolving Block Decimation Algorithm
 Time Evolving Block Decimation Algorithm Application to bosons on a lattice Jakub Zakrzewski Marian Smoluchowski Institute of Physics and Mark Kac Complex Systems Research Center, Jagiellonian University,
Time Evolving Block Decimation Algorithm Application to bosons on a lattice Jakub Zakrzewski Marian Smoluchowski Institute of Physics and Mark Kac Complex Systems Research Center, Jagiellonian University,
Luigi Paolasini
 Luigi Paolasini paolasini@esrf.fr LECTURE 7: Magnetic excitations - Phase transitions and the Landau mean-field theory. - Heisenberg and Ising models. - Magnetic excitations. External parameter, as for
Luigi Paolasini paolasini@esrf.fr LECTURE 7: Magnetic excitations - Phase transitions and the Landau mean-field theory. - Heisenberg and Ising models. - Magnetic excitations. External parameter, as for
Introduction to Quantum Spin Systems
 1 Introduction to Quantum Spin Systems Lecture 2 Sven Bachmann (standing in for Bruno Nachtergaele) Mathematics, UC Davis MAT290-25, CRN 30216, Winter 2011, 01/10/11 2 Basic Setup For concreteness, consider
1 Introduction to Quantum Spin Systems Lecture 2 Sven Bachmann (standing in for Bruno Nachtergaele) Mathematics, UC Davis MAT290-25, CRN 30216, Winter 2011, 01/10/11 2 Basic Setup For concreteness, consider
P3317 HW from Lecture and Recitation 10
 P3317 HW from Lecture 18+19 and Recitation 10 Due Nov 6, 2018 Problem 1. Equipartition Note: This is a problem from classical statistical mechanics. We will need the answer for the next few problems, and
P3317 HW from Lecture 18+19 and Recitation 10 Due Nov 6, 2018 Problem 1. Equipartition Note: This is a problem from classical statistical mechanics. We will need the answer for the next few problems, and
Newton s Method and Localization
 Newton s Method and Localization Workshop on Analytical Aspects of Mathematical Physics John Imbrie May 30, 2013 Overview Diagonalizing the Hamiltonian is a goal in quantum theory. I would like to discuss
Newton s Method and Localization Workshop on Analytical Aspects of Mathematical Physics John Imbrie May 30, 2013 Overview Diagonalizing the Hamiltonian is a goal in quantum theory. I would like to discuss
POEM: Physics of Emergent Materials
 POEM: Physics of Emergent Materials Nandini Trivedi L1: Spin Orbit Coupling L2: Topology and Topological Insulators Tutorials: May 24, 25 (2017) Scope of Lectures and Anchor Points: 1.Spin-Orbit Interaction
POEM: Physics of Emergent Materials Nandini Trivedi L1: Spin Orbit Coupling L2: Topology and Topological Insulators Tutorials: May 24, 25 (2017) Scope of Lectures and Anchor Points: 1.Spin-Orbit Interaction
Quantum Field Theory
 Quantum Field Theory PHYS-P 621 Radovan Dermisek, Indiana University Notes based on: M. Srednicki, Quantum Field Theory 1 Attempts at relativistic QM based on S-1 A proper description of particle physics
Quantum Field Theory PHYS-P 621 Radovan Dermisek, Indiana University Notes based on: M. Srednicki, Quantum Field Theory 1 Attempts at relativistic QM based on S-1 A proper description of particle physics
Quantum Field Theory
 Quantum Field Theory PHYS-P 621 Radovan Dermisek, Indiana University Notes based on: M. Srednicki, Quantum Field Theory 1 Attempts at relativistic QM based on S-1 A proper description of particle physics
Quantum Field Theory PHYS-P 621 Radovan Dermisek, Indiana University Notes based on: M. Srednicki, Quantum Field Theory 1 Attempts at relativistic QM based on S-1 A proper description of particle physics
Interaction-induced Symmetry Protected Topological Phase in Harper-Hofstadter models
 Interaction-induced Symmetry Protected Topological Phase in Harper-Hofstadter models arxiv:1609.03760 Lode Pollet Dario Hügel Hugo Strand, Philipp Werner (Uni Fribourg) Algorithmic developments diagrammatic
Interaction-induced Symmetry Protected Topological Phase in Harper-Hofstadter models arxiv:1609.03760 Lode Pollet Dario Hügel Hugo Strand, Philipp Werner (Uni Fribourg) Algorithmic developments diagrammatic
Preface Introduction to the electron liquid
 Table of Preface page xvii 1 Introduction to the electron liquid 1 1.1 A tale of many electrons 1 1.2 Where the electrons roam: physical realizations of the electron liquid 5 1.2.1 Three dimensions 5 1.2.2
Table of Preface page xvii 1 Introduction to the electron liquid 1 1.1 A tale of many electrons 1 1.2 Where the electrons roam: physical realizations of the electron liquid 5 1.2.1 Three dimensions 5 1.2.2
Introduction to Heisenberg model. Javier Junquera
 Introduction to Heisenberg model Javier Junquera Most important reference followed in this lecture Magnetism in Condensed Matter Physics Stephen Blundell Oxford Master Series in Condensed Matter Physics
Introduction to Heisenberg model Javier Junquera Most important reference followed in this lecture Magnetism in Condensed Matter Physics Stephen Blundell Oxford Master Series in Condensed Matter Physics
Graphene and Planar Dirac Equation
 Graphene and Planar Dirac Equation Marina de la Torre Mayado 2016 Marina de la Torre Mayado Graphene and Planar Dirac Equation June 2016 1 / 48 Outline 1 Introduction 2 The Dirac Model Tight-binding model
Graphene and Planar Dirac Equation Marina de la Torre Mayado 2016 Marina de la Torre Mayado Graphene and Planar Dirac Equation June 2016 1 / 48 Outline 1 Introduction 2 The Dirac Model Tight-binding model
TRANSPORT OF QUANTUM INFORMATION IN SPIN CHAINS
 TRANSPORT OF QUANTUM INFORMATION IN SPIN CHAINS Joachim Stolze Institut für Physik, Universität Dortmund, 44221 Dortmund Göttingen, 7.6.2005 Why quantum computing? Why quantum information transfer? Entangled
TRANSPORT OF QUANTUM INFORMATION IN SPIN CHAINS Joachim Stolze Institut für Physik, Universität Dortmund, 44221 Dortmund Göttingen, 7.6.2005 Why quantum computing? Why quantum information transfer? Entangled
Ψ({z i }) = i<j(z i z j ) m e P i z i 2 /4, q = ± e m.
 Fractionalization of charge and statistics in graphene and related structures M. Franz University of British Columbia franz@physics.ubc.ca January 5, 2008 In collaboration with: C. Weeks, G. Rosenberg,
Fractionalization of charge and statistics in graphene and related structures M. Franz University of British Columbia franz@physics.ubc.ca January 5, 2008 In collaboration with: C. Weeks, G. Rosenberg,
Berry s phase in Hall Effects and Topological Insulators
 Lecture 6 Berry s phase in Hall Effects and Topological Insulators Given the analogs between Berry s phase and vector potentials, it is not surprising that Berry s phase can be important in the Hall effect.
Lecture 6 Berry s phase in Hall Effects and Topological Insulators Given the analogs between Berry s phase and vector potentials, it is not surprising that Berry s phase can be important in the Hall effect.
Lecture notes: Quantum gates in matrix and ladder operator forms
 Phys 7 Topics in Particles & Fields Spring 3 Lecture v.. Lecture notes: Quantum gates in matrix and ladder operator forms Jeffrey Yepez Department of Physics and Astronomy University of Hawai i at Manoa
Phys 7 Topics in Particles & Fields Spring 3 Lecture v.. Lecture notes: Quantum gates in matrix and ladder operator forms Jeffrey Yepez Department of Physics and Astronomy University of Hawai i at Manoa
Electrons in a weak periodic potential
 Electrons in a weak periodic potential Assumptions: 1. Static defect-free lattice perfectly periodic potential. 2. Weak potential perturbative effect on the free electron states. Perfect periodicity of
Electrons in a weak periodic potential Assumptions: 1. Static defect-free lattice perfectly periodic potential. 2. Weak potential perturbative effect on the free electron states. Perfect periodicity of
Topological order of a two-dimensional toric code
 University of Ljubljana Faculty of Mathematics and Physics Seminar I a, 1st year, 2nd cycle Topological order of a two-dimensional toric code Author: Lenart Zadnik Advisor: Doc. Dr. Marko Žnidarič June
University of Ljubljana Faculty of Mathematics and Physics Seminar I a, 1st year, 2nd cycle Topological order of a two-dimensional toric code Author: Lenart Zadnik Advisor: Doc. Dr. Marko Žnidarič June
arxiv:quant-ph/ v2 24 Dec 2003
 Quantum Entanglement in Heisenberg Antiferromagnets V. Subrahmanyam Department of Physics, Indian Institute of Technology, Kanpur, India. arxiv:quant-ph/0309004 v2 24 Dec 2003 Entanglement sharing among
Quantum Entanglement in Heisenberg Antiferromagnets V. Subrahmanyam Department of Physics, Indian Institute of Technology, Kanpur, India. arxiv:quant-ph/0309004 v2 24 Dec 2003 Entanglement sharing among
4 Matrix product states
 Physics 3b Lecture 5 Caltech, 05//7 4 Matrix product states Matrix product state (MPS) is a highly useful tool in the study of interacting quantum systems in one dimension, both analytically and numerically.
Physics 3b Lecture 5 Caltech, 05//7 4 Matrix product states Matrix product state (MPS) is a highly useful tool in the study of interacting quantum systems in one dimension, both analytically and numerically.
G : Quantum Mechanics II
 G5.666: Quantum Mechanics II Notes for Lecture 5 I. REPRESENTING STATES IN THE FULL HILBERT SPACE Given a representation of the states that span the spin Hilbert space, we now need to consider the problem
G5.666: Quantum Mechanics II Notes for Lecture 5 I. REPRESENTING STATES IN THE FULL HILBERT SPACE Given a representation of the states that span the spin Hilbert space, we now need to consider the problem
Simulating Quantum Systems through Matrix Product States. Laura Foini SISSA Journal Club
 Simulating Quantum Systems through Matrix Product States Laura Foini SISSA Journal Club 15-04-2010 Motivations Theoretical interest in Matrix Product States Wide spectrum of their numerical applications
Simulating Quantum Systems through Matrix Product States Laura Foini SISSA Journal Club 15-04-2010 Motivations Theoretical interest in Matrix Product States Wide spectrum of their numerical applications
Topological order in the pseudogap metal
 HARVARD Topological order in the pseudogap metal High Temperature Superconductivity Unifying Themes in Diverse Materials 2018 Aspen Winter Conference Aspen Center for Physics Subir Sachdev January 16,
HARVARD Topological order in the pseudogap metal High Temperature Superconductivity Unifying Themes in Diverse Materials 2018 Aspen Winter Conference Aspen Center for Physics Subir Sachdev January 16,
Ferromagnetic Ordering of Energy Levels for XXZ Spin Chains
 Ferromagnetic Ordering of Energy Levels for XXZ Spin Chains Bruno Nachtergaele and Wolfgang L. Spitzer Department of Mathematics University of California, Davis Davis, CA 95616-8633, USA bxn@math.ucdavis.edu
Ferromagnetic Ordering of Energy Levels for XXZ Spin Chains Bruno Nachtergaele and Wolfgang L. Spitzer Department of Mathematics University of California, Davis Davis, CA 95616-8633, USA bxn@math.ucdavis.edu
Introduction to the Mathematics of the XY -Spin Chain
 Introduction to the Mathematics of the XY -Spin Chain Günter Stolz June 9, 2014 Abstract In the following we present an introduction to the mathematical theory of the XY spin chain. The importance of this
Introduction to the Mathematics of the XY -Spin Chain Günter Stolz June 9, 2014 Abstract In the following we present an introduction to the mathematical theory of the XY spin chain. The importance of this
Quasi-1d Frustrated Antiferromagnets. Leon Balents, UCSB Masanori Kohno, NIMS, Tsukuba Oleg Starykh, U. Utah
 Quasi-1d Frustrated Antiferromagnets Leon Balents, UCSB Masanori Kohno, NIMS, Tsukuba Oleg Starykh, U. Utah Outline Frustration in quasi-1d systems Excitations: magnons versus spinons Neutron scattering
Quasi-1d Frustrated Antiferromagnets Leon Balents, UCSB Masanori Kohno, NIMS, Tsukuba Oleg Starykh, U. Utah Outline Frustration in quasi-1d systems Excitations: magnons versus spinons Neutron scattering
Physics 557 Lecture 5
 Physics 557 Lecture 5 Group heory: Since symmetries and the use of group theory is so much a part of recent progress in particle physics we will take a small detour to introduce the basic structure (as
Physics 557 Lecture 5 Group heory: Since symmetries and the use of group theory is so much a part of recent progress in particle physics we will take a small detour to introduce the basic structure (as
5 Topological insulator with time-reversal symmetry
 Phys62.nb 63 5 Topological insulator with time-reversal symmetry It is impossible to have quantum Hall effect without breaking the time-reversal symmetry. xy xy. If we want xy to be invariant under, xy
Phys62.nb 63 5 Topological insulator with time-reversal symmetry It is impossible to have quantum Hall effect without breaking the time-reversal symmetry. xy xy. If we want xy to be invariant under, xy
The general solution of Schrödinger equation in three dimensions (if V does not depend on time) are solutions of time-independent Schrödinger equation
 Lecture 17 Page 1 Lecture 17 L17.P1 Review Schrödinger equation The general solution of Schrödinger equation in three dimensions (if V does not depend on time) is where functions are solutions of time-independent
Lecture 17 Page 1 Lecture 17 L17.P1 Review Schrödinger equation The general solution of Schrödinger equation in three dimensions (if V does not depend on time) is where functions are solutions of time-independent
1 Mathematical preliminaries
 1 Mathematical preliminaries The mathematical language of quantum mechanics is that of vector spaces and linear algebra. In this preliminary section, we will collect the various definitions and mathematical
1 Mathematical preliminaries The mathematical language of quantum mechanics is that of vector spaces and linear algebra. In this preliminary section, we will collect the various definitions and mathematical
