Chapter 10 Partial Differential Equations and Fourier Series
|
|
|
- Cecilia Webster
- 5 years ago
- Views:
Transcription
1 Math-33 Chapter Partial Differetial Equatios November 6, 7 Chapter Partial Differetial Equatios ad Fourier Series
2 Math-33 Chapter Partial Differetial Equatios November 6, 7. Boudary Value Problems for d order ODE Oe-Dimesioal Boudary Value Problems + +, ( a,b) y p y q y g d order liear ODE Plae layer Domai: a < < b, boudary cosists of two poits: a ad b y y y y a y y b a b The possible types of boudary coditios at a ad b: k,h,h > Type of boudary coditio No-homogeeous boudary coditios: I st kid (Dirichlet) y( a) y y( b) y II d kid (Neuma) y ( a) y y ( b) y III 3 rd kid (Robi, mied) ky ( a) + h y ( a) y ky b + h y b y Homogeeous boudary coditios: I y( a) y b y b II y ( a) III ky ( a) + h y ( a) ky b + h y b
3 Math-33 Chapter Partial Differetial Equatios November 6, 7 3 Special Equatio (homogeeous d order liear ODE with costat coefficiets), (, ) y λ y Characteristic equatio m λ Geeral Solutio ca be writte i the followig forms: ) λ >, m y ce + ce ± ( ) + ( ) y c cosh c sih ( ) + ( ) y ccosh csih ) <, λ m ± i y c cos ( ) + c si( ) ( ) + ( ) y ccos c si 3) λ m, y c+ c + ( ) y c c Eigevalue Problem: fid the values of λ for which differetial has o-zero solutios, (, ) y λ y subject to oe of the ie possible combiatios of the homogeeous boudary coditios: y I y I y II y II III y + Hy III y + H y This problem has a o-zero solutio oly if λ < There eist ifiitely may real values < < < 3 <... (eigevalues) ad correspodig o-zero solutios y, y, y 3,... (eigefuctios) which satisfy the boudary coditios (i a case whe both b.c. s are of the d kid: y, y, there are also ad y ) Eigefuctios 3 m m y,y y y d for m y, y, y,... are mutually orthogoal:
4 Math-33 Chapter Partial Differetial Equatios November 6, 7 4 There ie possible eigevalue problems + subject to differet combiatios of boudary coditios: y y Eample : + (,) y y I y I y π,,... π y si y c cos + c si (p.58) y c si ( y,y ) y c cos + c si c y si π Eample : + (,). #8 y y II y II y π ( y,y) y y π cos ( y,y ) Eample 3: + (,) y y I y II y. #4 π +,,,... π y si + ( y,y ) Eample 4: + (,). #5,7 y y II y I y π +,,,... π y cos + ( y,y )
5 Math-33 Chapter Partial Differetial Equatios November 6, 7 5 The followig possible eamples are importat but they are ot cosidered i our class (here, H> is a costat): Eample 5: + (,) y y I y III y + Hy Eample 6: + (,) y y III I y y + Hy Eample 7: + (,) y y II y III y + Hy Eample 8: + (,) y y III y + Hy II y Eample 9: + (,) y y III y + Hy y + H y III
6 Math-33 Chapter Partial Differetial Equatios November 6, 7 6. Fourier Series Periodic fuctio f ( + T) f for all. T is a period. The smallest period is called the fudametal period. Eve fuctio f ( ) f Odd fuctio u( ) u Properties: et f,g be eve fuctios, ad let u,v be odd fuctios, the f + g eve f g eve v u + odd v u eve f u odd f ( ) is eve, the f d u( ) is odd, the u d f d Ier product of two fuctios o [ a,b ] : ( u,v) b uvd a b Fuctios u ad v are said to be orthogoal if: u,v u v d a Geeralized Fourier Series: If { yk } is a complete set of fuctios mutually orthogoal o [ a,b ], the f ca be represeted by f c y + c y c y +... c y, where k k k k k c k ( f,yk ) ( y,y ) k k
7 Math-33 Chapter Partial Differetial Equatios November 6, 7 7 Set of fuctios π π, cos, si is orthogoal o [, ]. Verify orthogoality d mπ π cos cos d m m π cos d π si π mπ π si si d m m π si d mπ π cos si d The Euler-Fourier Formulas (p.587): Fourier Series a mπ mπ f + a cos + b si m m (9) m a f d () a m π f cos d (3) b m π f si d (4).3 Covergece of the Fourier Series trucated Fourier series Gibb's pheomea limit of Fourier series et f ( ) be a piece-wise cotiuous with a fiite umber of fiite jumps o [,), the a mπ mπ + + amcos b si coverges to m f ( ), if f + + f f is cotiuous at, if f ( ) is discotiuous at
8 Math-33 Chapter Partial Differetial Equatios November 6, 7 8 > :; Maple Fourier series epasio of > f:heaviside(+)-heaviside(-); < < f < < < < : > a[]:/*it(f,-..); f : Heaviside ( + ) Heaviside ( ) a : > a[k]:/*it(f*cos(k*pi/*),-..); > b[k]:/*it(f*si(k*pi/*),-..); The Fourier Series: si k π a k : k π b k : > u:a[]/+sum(a[k]*cos(k*pi/*)+b[k]*si(k*pi/*),k..): > plot({f,u},-..); > plot({abs(f-u)},-..); > plot({u},-5*..5*); periodic etesio: Useful facts : si π cos π ( ) si π cos π
9 Math-33 Chapter Partial Differetial Equatios November 6, The Fourier Series of Odd ad Eve Fuctios (Sie Fourier Series ad Cosie Fourier Series)
10 Math-33 Chapter Partial Differetial Equatios November 6, 7.5 The Heat Equatio Homogeeous Boudary Coditios ( I I) Iitial-Boudary Value Problem: u u iitial temperature distributio, t Heat Equatio u u a t Iitial coditio: u (,) u < <, t > u(,t) curret temperature distributio, t > Boudary coditios: u(,t) t > (I) u(,t) t > (I) ) Assume u(,t) T ( t) u,t T t u,t T t t T ) Separate variables T T λ a a T u,t ( T ) ( t) u(,t) T ( t) 3) Solve eigevalue problem λ λ (I) (I) 4) Solve T λ a T π,,... π si ( ) si T + at at T t e u,t c T t where 5) Solutio: u d π c u si d d
11 Math-33 Chapter Partial Differetial Equatios November 6, 7.5 The Heat Equatio ( I I) Sigle term solutio u kπ u si u(,t) iitial temperature distributio at t is i the shape of oe of eigefuctios k k si π with some value k curret temperature distributio, t > Heat Equatio u u a t Iitial coditio: < <, t > kπ u, si Boudary coditios: u(,t) t > (I) u(,t) t > (I) ) Assume u(,t) T ( t) u,t T t u,t T t t T ) Separate variables T T λ a a T u,t ( T ) ( t) u(,t) T ( t) 3) Solve eigevalue problem λ λ (I) (I) 4) Solve T λ a T π,,... π si ( ) si T + at at T t e u,t c T t where 5) Solutio: kπ kπ ck si si d c for all k Therefore, u (,t ) T ( t) k k
12 Math-33 Chapter Partial Differetial Equatios November 6, 7.5 The Heat Equatio Homogeeous Boudary Coditios (I II) Iitial-Boudary value Problem: u u iitial temperature distributio, t Heat Equatio u u a t Iitial coditio: u (,) u < <, t > u(,t) curret temperature distributio, t > Boudary coditios: u(,t) t > (I) u (,t) t > (II) ) Assume u(,t) T ( t) u,t T t u,t T t t substitute ito equatio ad boudary coditios T ) Separate variables T T λ a a T u,t ( T ) ( t) u,t T t 3) Solve eigevalue problem λ λ (I) (II) π +,,,... π si( ) si + T 4) Solve λ T + at a T at T t e u,t c T t, 5) Solutio: u d π c u si + d d
13 Math-33 Chapter Partial Differetial Equatios November 6, The Heat Equatio No-Homogeeous Boudary Coditios Iitial-Boudary Value Problem: u u iitial temperature distributio, t Heat Equatio u u a t < <, t > u(,t) us curret temperature distributio, t > steady state temperature distributio Iitial coditio u (,) u Boudary coditios u (,t) u t > I u u,t t > I ) Steady stateproblem u s Boudary coditios: s u u (I) u u (I) s [ defiitio of steady state: u limu,t ] s t u u u + u Steady State Solutio: s ) Defie trasiet solutio: U (,t) u (,t) u s Iitial-Boudary problem U U a t < <, t > Iitial coditio U (,) u u s Boudary coditios U,t t > U,t t > (Homogeous B.C. s) 3) Solutio of IBVP: u (,t) U (,t) u + (cosists of trasiet ad steady state solutios) s u u + +, Solutio: u (,t) u c T ( t) c u us d d, at T t e
14 Math-33 Chapter Partial Differetial Equatios November 6, The Wave Equatio Homogeeous Boudary Coditios Iitial-Boudary Value Problem: u u iitial shape, t Wave Equatio u u a t < <, t > u u(,t) iitial velocity, t curret strig deflectio, t > Iitial coditio: u (,) u u, u t Boudary coditios: u,t t > I u,t t > I ) Assume u(,t) T ( t) u,t T t u,t T t t substitute ito equatio ad boudary coditios T ) Separate variables T T λ a a T u,t ( T ) ( t) u(,t) T ( t) 3) Solve eigevalue problem λ λ (I) (I) 4) Solve T λ a T π,,,... π si ( ) si T + at ( ) + ( ) T t c cos a t c si a t,, π u,t a cos a t b si a t + si, 5) Solutio: ( ) ( ) π a u si d, b u si d a π π
15 Math-33 Chapter Partial Differetial Equatios November 6, 7 5 The Wave Equatio Homogeeous Boudary Coditios Stadig Waves
16 Math-33 Chapter Partial Differetial Equatios November 6, The aplace Equatio Basic Boudary Value Problem 3 homogeeous, o-homogeous b.c. s : y f The aplace Equatio u u + y < <, < y < M M Boudary coditios: [ I,II,III ] [ I,II,III ] [ I,II,III ] y [ I,II,III ] f y M ) Assume u(,y) Y ( y) substitute ito equatio ad b.c. s ) Separate variables Y + Y Y λ Y u (,y) Y ( y) u (,y) Y ( y) u (,) Y Y 3) Solve eigevalue problem No-zero solutios eist oly if λ λ λ (I, II or III) (I, II or III) 4) Solve Y λ Y Y Y ( ) + ( ) Y y c cosh y c sih y,, Y Y ( y) c, sih( y) 5) Solutio: u (, y) a sih( y), a sih ( M ) f d d
17 Math-33 Chapter Partial Differetial Equatios November 6, 7 7 Semi-ifiite layer domai: >, boudary is defied by a sigle poit: y y y y
18 Math-33 Chapter Partial Differetial Equatios November 6, 7 8 The aplace Equatio No-homogeeous boudary coditios (superpositio priciple) Dirichlet Problem (I) M f ( y) f 3 u ( y) f 4 Split ito supplemetal basic problems: f f u ( y) u f 3 ( y) u 3 u 4 f 4 f Solutio of supplemetal basic problems: π π u(, y) a si sih ( y M ) a π f si d π sih M π π u(, y) b si sih y b π f si d π sih M π π u3(, y) c sih ( ) si y M M c M π 3 M M f y si y dy π sih M π π u4(, y) d sih si y M M d M π f4 ( y) si y dy M M π sih M Solutio of Dirichlet problem superpositio of supplemetal solutios: (, y) u (, y) + u (, y) + u (, y) u (, y) u 3 + 4
19 Math-33 Chapter Partial Differetial Equatios November 6, 7 9 POISSON'S EQUATION M y [ u] f y M u u + + F (,y) y (,y) (,) (,M ) [ u] f ( y) 3 u+ F [ u] f y [ u] f ( y) 4 [ u] S f brackets mea that coditio at the boudary ca be either st d rd of I, II or III kid ( i a case if 3-D problem is cosidered ) Supplemetal Sturm-iouville Problems [ ] [ ] SP λ λ Y ηy [ Y] y [ Y] y M SP Y ν Y m m m η ν m Ym ( y) m Z γ Z [ Z] z [ Z] z K SP Z ω Z γ ω k Zk k k k ( z) k APACE'S EQUATION (homogeeous eq, o-homogeeous boudary coditios) f 3 f u 5 f f 4 u Y a ( ) u,y a Y f d Y f Solutio of Basic Cases of aplace's Equatio with oe o-homegeeous b.c. by Separatio of Variables ( SV ) f 3 f u u 3 u 4 f 4 Y m Y m m b ( ) u,y b Y c ( ) m u,y c Y 3 m m m M f Y dy 3 m m m Ym f d Y M d ( ) m u,y d Y 4 m m m M f Y dy 4 m m m Ym Y m u5 u + u + u3 + u4 Superpositio Priciple ( SP) Solutio of Basic Case of Poisso's Eq (homogeeous b.c.'s) u 6 F Y m u,y A Y 6 m m m A M ( λ + ν ) F Y ddy m m m Ym Eigevalue Epasio ( EE) Solutio of Poisso's Equatio with o-homogeeous b.c.'s u(,y) u5 + u6 Superpositio Priciple ( SP)
20 Math-33 Chapter Partial Differetial Equatios November 6, 7 Eigevalue Problem +, (,) subject to homogeeous boudary coditios. y y There eist ifiitely may real values < < 3 <... (eigevalues) ad correspodig o-zero solutios y, y, y 3,... which satisfy the boudary coditios. (eigefuctios) Boudary cs. Eigevalues, eigefuctios Fourier series I y π π f b si I y π y si π b f si d II y, π a π f + a cos II y y, y π cos π a f cos d I y π + π f c si + II y π y si + π c f si d + II y π + π f d cos + I y π y cos + π d f cos d + f cy The Geeralized Fourier series ( ) ( y,y ) f,y c f ( ) y d Orthogoality of eigefuctios ( m ) m y, y y y d if m
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Notes 18 Green s Functions
 ECE 638 Fall 017 David R. Jackso Notes 18 Gree s Fuctios Notes are from D. R. Wilto, Dept. of ECE 1 Gree s Fuctios The Gree's fuctio method is a powerful ad systematic method for determiig a solutio to
ECE 638 Fall 017 David R. Jackso Notes 18 Gree s Fuctios Notes are from D. R. Wilto, Dept. of ECE 1 Gree s Fuctios The Gree's fuctio method is a powerful ad systematic method for determiig a solutio to
2. Fourier Series, Fourier Integrals and Fourier Transforms
 Mathematics IV -. Fourier Series, Fourier Itegrals ad Fourier Trasforms The Fourier series are used for the aalysis of the periodic pheomea, which ofte appear i physics ad egieerig. The Fourier itegrals
Mathematics IV -. Fourier Series, Fourier Itegrals ad Fourier Trasforms The Fourier series are used for the aalysis of the periodic pheomea, which ofte appear i physics ad egieerig. The Fourier itegrals
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math 220B Final Exam Solutions March 18, 2002
 Math 0B Fial Exam Solutios March 18, 00 1. (1 poits) (a) (6 poits) Fid the Gree s fuctio for the tilted half-plae {(x 1, x ) R : x 1 + x > 0}. For x (x 1, x ), y (y 1, y ), express your Gree s fuctio G(x,
Math 0B Fial Exam Solutios March 18, 00 1. (1 poits) (a) (6 poits) Fid the Gree s fuctio for the tilted half-plae {(x 1, x ) R : x 1 + x > 0}. For x (x 1, x ), y (y 1, y ), express your Gree s fuctio G(x,
Linear Differential Equations of Higher Order Basic Theory: Initial-Value Problems d y d y dy
 Liear Differetial Equatios of Higher Order Basic Theory: Iitial-Value Problems d y d y dy Solve: a( ) + a ( )... a ( ) a0( ) y g( ) + + + = d d d ( ) Subject to: y( 0) = y0, y ( 0) = y,..., y ( 0) = y
Liear Differetial Equatios of Higher Order Basic Theory: Iitial-Value Problems d y d y dy Solve: a( ) + a ( )... a ( ) a0( ) y g( ) + + + = d d d ( ) Subject to: y( 0) = y0, y ( 0) = y,..., y ( 0) = y
Apply change-of-basis formula to rewrite x as a linear combination of eigenvectors v j.
 Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
Question 1: The magnetic case
 September 6, 018 Corell Uiversity, Departmet of Physics PHYS 337, Advace E&M, HW # 4, due: 9/19/018, 11:15 AM Questio 1: The magetic case I class, we skipped over some details, so here you are asked to
September 6, 018 Corell Uiversity, Departmet of Physics PHYS 337, Advace E&M, HW # 4, due: 9/19/018, 11:15 AM Questio 1: The magetic case I class, we skipped over some details, so here you are asked to
Lesson 03 Heat Equation with Different BCs
 PDE & Complex Variables P3- esso 3 Heat Equatio with Differet BCs ( ) Physical meaig (SJF ) et u(x, represet the temperature of a thi rod govered by the (coductio) heat equatio: u t =α u xx (3.) where
PDE & Complex Variables P3- esso 3 Heat Equatio with Differet BCs ( ) Physical meaig (SJF ) et u(x, represet the temperature of a thi rod govered by the (coductio) heat equatio: u t =α u xx (3.) where
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
Fourier Series and the Wave Equation
 Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
Most text will write ordinary derivatives using either Leibniz notation 2 3. y + 5y= e and y y. xx tt t
 Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
A) is empty. B) is a finite set. C) can be a countably infinite set. D) can be an uncountable set.
 M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
A second look at separation of variables
 A secod look at separatio of variables Assumed that u(x,t)x(x)t(t) Pluggig this ito the wave, diffusio, or Laplace equatio gave two ODEs The solutios to those ODEs subject to boudary ad iitial coditios
A secod look at separatio of variables Assumed that u(x,t)x(x)t(t) Pluggig this ito the wave, diffusio, or Laplace equatio gave two ODEs The solutios to those ODEs subject to boudary ad iitial coditios
Castiel, Supernatural, Season 6, Episode 18
 13 Differetial Equatios the aswer to your questio ca best be epressed as a series of partial differetial equatios... Castiel, Superatural, Seaso 6, Episode 18 A differetial equatio is a mathematical equatio
13 Differetial Equatios the aswer to your questio ca best be epressed as a series of partial differetial equatios... Castiel, Superatural, Seaso 6, Episode 18 A differetial equatio is a mathematical equatio
radians A function f ( x ) is called periodic if it is defined for all real x and if there is some positive number P such that:
 Fourier Series. Graph of y Asix ad y Acos x Amplitude A ; period 36 radias. Harmoics y y six is the first harmoic y y six is the th harmoics 3. Periodic fuctio A fuctio f ( x ) is called periodic if it
Fourier Series. Graph of y Asix ad y Acos x Amplitude A ; period 36 radias. Harmoics y y six is the first harmoic y y six is the th harmoics 3. Periodic fuctio A fuctio f ( x ) is called periodic if it
Taylor expansion: Show that the TE of f(x)= sin(x) around. sin(x) = x - + 3! 5! L 7 & 8: MHD/ZAH
 Taylor epasio: Let ƒ() be a ifiitely differetiable real fuctio. A ay poit i the eighbourhood of 0, the fuctio ƒ() ca be represeted by a power series of the followig form: X 0 f(a) f() f() ( ) f( ) ( )
Taylor epasio: Let ƒ() be a ifiitely differetiable real fuctio. A ay poit i the eighbourhood of 0, the fuctio ƒ() ca be represeted by a power series of the followig form: X 0 f(a) f() f() ( ) f( ) ( )
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
NBHM QUESTION 2007 Section 1 : Algebra Q1. Let G be a group of order n. Which of the following conditions imply that G is abelian?
 NBHM QUESTION 7 NBHM QUESTION 7 NBHM QUESTION 7 Sectio : Algebra Q Let G be a group of order Which of the followig coditios imply that G is abelia? 5 36 Q Which of the followig subgroups are ecesarily
NBHM QUESTION 7 NBHM QUESTION 7 NBHM QUESTION 7 Sectio : Algebra Q Let G be a group of order Which of the followig coditios imply that G is abelia? 5 36 Q Which of the followig subgroups are ecesarily
The type of limit that is used to find TANGENTS and VELOCITIES gives rise to the central idea in DIFFERENTIAL CALCULUS, the DERIVATIVE.
 NOTES : LIMITS AND DERIVATIVES Name: Date: Period: Iitial: LESSON.1 THE TANGENT AND VELOCITY PROBLEMS Pre-Calculus Mathematics Limit Process Calculus The type of it that is used to fid TANGENTS ad VELOCITIES
NOTES : LIMITS AND DERIVATIVES Name: Date: Period: Iitial: LESSON.1 THE TANGENT AND VELOCITY PROBLEMS Pre-Calculus Mathematics Limit Process Calculus The type of it that is used to fid TANGENTS ad VELOCITIES
Power Series: A power series about the center, x = 0, is a function of x of the form
 You are familiar with polyomial fuctios, polyomial that has ifiitely may terms. 2 p ( ) a0 a a 2 a. A power series is just a Power Series: A power series about the ceter, = 0, is a fuctio of of the form
You are familiar with polyomial fuctios, polyomial that has ifiitely may terms. 2 p ( ) a0 a a 2 a. A power series is just a Power Series: A power series about the ceter, = 0, is a fuctio of of the form
Calculus 2 - D. Yuen Final Exam Review (Version 11/22/2017. Please report any possible typos.)
 Calculus - D Yue Fial Eam Review (Versio //7 Please report ay possible typos) NOTE: The review otes are oly o topics ot covered o previous eams See previous review sheets for summary of previous topics
Calculus - D Yue Fial Eam Review (Versio //7 Please report ay possible typos) NOTE: The review otes are oly o topics ot covered o previous eams See previous review sheets for summary of previous topics
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Engineering Analysis ( & ) Lec(7) CH 2 Higher Order Linear ODEs
 Philadelphia Uiversit/Facult of Egieerig Commuicatio ad Electroics Egieerig Egieerig Aalsis (6500 & 6300) Higher Order Liear ODEs Istructor: Eg. Nada khatib Email: khatib@philadelphia.edu.jo Higher order
Philadelphia Uiversit/Facult of Egieerig Commuicatio ad Electroics Egieerig Egieerig Aalsis (6500 & 6300) Higher Order Liear ODEs Istructor: Eg. Nada khatib Email: khatib@philadelphia.edu.jo Higher order
Sturm-Liouville Eigenvalue Problem
 Sturm-Liouville Eigevalue Problem d dx d p q r 0 a x b dx i which p, q ad r are fuctios of x, is called Sturm-Liouville (S.L.) eigevalue problem. d d L p q dx dx L r 0 Examples 1- Bucklig of a colum: d
Sturm-Liouville Eigevalue Problem d dx d p q r 0 a x b dx i which p, q ad r are fuctios of x, is called Sturm-Liouville (S.L.) eigevalue problem. d d L p q dx dx L r 0 Examples 1- Bucklig of a colum: d
EE / EEE SAMPLE STUDY MATERIAL. GATE, IES & PSUs Signal System. Electrical Engineering. Postal Correspondence Course
 Sigal-EE Postal Correspodece Course 1 SAMPLE STUDY MATERIAL Electrical Egieerig EE / EEE Postal Correspodece Course GATE, IES & PSUs Sigal System Sigal-EE Postal Correspodece Course CONTENTS 1. SIGNAL
Sigal-EE Postal Correspodece Course 1 SAMPLE STUDY MATERIAL Electrical Egieerig EE / EEE Postal Correspodece Course GATE, IES & PSUs Sigal System Sigal-EE Postal Correspodece Course CONTENTS 1. SIGNAL
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Continuous Functions
 Cotiuous Fuctios Q What does it mea for a fuctio to be cotiuous at a poit? Aswer- I mathematics, we have a defiitio that cosists of three cocepts that are liked i a special way Cosider the followig defiitio
Cotiuous Fuctios Q What does it mea for a fuctio to be cotiuous at a poit? Aswer- I mathematics, we have a defiitio that cosists of three cocepts that are liked i a special way Cosider the followig defiitio
3. Calculus with distributions
 6 RODICA D. COSTIN 3.1. Limits of istributios. 3. Calculus with istributios Defiitio 4. A sequece of istributios {u } coverges to the istributio u (all efie o the same space of test fuctios) if (φ, u )
6 RODICA D. COSTIN 3.1. Limits of istributios. 3. Calculus with istributios Defiitio 4. A sequece of istributios {u } coverges to the istributio u (all efie o the same space of test fuctios) if (φ, u )
SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,
![SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0, SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,](/thumbs/94/119566625.jpg) 4. Series Solutios of Differetial Equatios:Special Fuctios 4.. Illustrative examples.. 5. Obtai the geeral solutio of each of the followig differetial equatios i terms of Maclauri series: d y (a dx = xy,
4. Series Solutios of Differetial Equatios:Special Fuctios 4.. Illustrative examples.. 5. Obtai the geeral solutio of each of the followig differetial equatios i terms of Maclauri series: d y (a dx = xy,
Name of the Student:
 SUBJECT NAME : Trasforms ad Partial Diff Eq SUBJECT CODE : MA MATERIAL NAME : Problem Material MATERIAL CODE : JM8AM6 REGULATION : R8 UPDATED ON : April-May 4 (Sca the above QR code for the direct dowload
SUBJECT NAME : Trasforms ad Partial Diff Eq SUBJECT CODE : MA MATERIAL NAME : Problem Material MATERIAL CODE : JM8AM6 REGULATION : R8 UPDATED ON : April-May 4 (Sca the above QR code for the direct dowload
} is said to be a Cauchy sequence provided the following condition is true.
 Math 4200, Fial Exam Review I. Itroductio to Proofs 1. Prove the Pythagorea theorem. 2. Show that 43 is a irratioal umber. II. Itroductio to Logic 1. Costruct a truth table for the statemet ( p ad ~ r
Math 4200, Fial Exam Review I. Itroductio to Proofs 1. Prove the Pythagorea theorem. 2. Show that 43 is a irratioal umber. II. Itroductio to Logic 1. Costruct a truth table for the statemet ( p ad ~ r
ECE-S352 Introduction to Digital Signal Processing Lecture 3A Direct Solution of Difference Equations
 ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
f(w) w z =R z a 0 a n a nz n Liouville s theorem, we see that Q is constant, which implies that P is constant, which is a contradiction.
 Theorem 3.6.4. [Liouville s Theorem] Every bouded etire fuctio is costat. Proof. Let f be a etire fuctio. Suppose that there is M R such that M for ay z C. The for ay z C ad R > 0 f (z) f(w) 2πi (w z)
Theorem 3.6.4. [Liouville s Theorem] Every bouded etire fuctio is costat. Proof. Let f be a etire fuctio. Suppose that there is M R such that M for ay z C. The for ay z C ad R > 0 f (z) f(w) 2πi (w z)
Comparison Study of Series Approximation. and Convergence between Chebyshev. and Legendre Series
 Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
9.3 Power Series: Taylor & Maclaurin Series
 9.3 Power Series: Taylor & Maclauri Series If is a variable, the a ifiite series of the form 0 is called a power series (cetered at 0 ). a a a a a 0 1 0 is a power series cetered at a c a a c a c a c 0
9.3 Power Series: Taylor & Maclauri Series If is a variable, the a ifiite series of the form 0 is called a power series (cetered at 0 ). a a a a a 0 1 0 is a power series cetered at a c a a c a c a c 0
Assignment Number 3 Solutions
 Math 4354, Assigmet Number 3 Solutios 1. u t (x, t) = u xx (x, t), < x (1) u(, t) =, u(, t) = u(x, ) = x ( 1) +1 u(x, t) = e t si(x). () =1 Solutio: Look for simple solutios i the form u(x, t) =
Math 4354, Assigmet Number 3 Solutios 1. u t (x, t) = u xx (x, t), < x (1) u(, t) =, u(, t) = u(x, ) = x ( 1) +1 u(x, t) = e t si(x). () =1 Solutio: Look for simple solutios i the form u(x, t) =
8. Applications To Linear Differential Equations
 8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
L 5 & 6: RelHydro/Basel. f(x)= ( ) f( ) ( ) ( ) ( ) n! 1! 2! 3! If the TE of f(x)= sin(x) around x 0 is: sin(x) = x - 3! 5!
 aylor epasio: Let ƒ() be a ifiitely differetiable real fuctio. At ay poit i the eighbourhood of =0, the fuctio ca be represeted as a power series of the followig form: X 0 f(a) f() ƒ() f()= ( ) f( ) (
aylor epasio: Let ƒ() be a ifiitely differetiable real fuctio. At ay poit i the eighbourhood of =0, the fuctio ca be represeted as a power series of the followig form: X 0 f(a) f() ƒ() f()= ( ) f( ) (
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 116C. Problem Set 4. Benjamin Stahl. November 6, 2014
 UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 6C Problem Set 4 Bejami Stahl November 6, 4 BOAS, P. 63, PROBLEM.-5 The Laguerre differetial equatio, x y + ( xy + py =, will be solved
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 6C Problem Set 4 Bejami Stahl November 6, 4 BOAS, P. 63, PROBLEM.-5 The Laguerre differetial equatio, x y + ( xy + py =, will be solved
PAPER : IIT-JAM 2010
 MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
THE SOLUTION OF NONLINEAR EQUATIONS f( x ) = 0.
 THE SOLUTION OF NONLINEAR EQUATIONS f( ) = 0. Noliear Equatio Solvers Bracketig. Graphical. Aalytical Ope Methods Bisectio False Positio (Regula-Falsi) Fied poit iteratio Newto Raphso Secat The root of
THE SOLUTION OF NONLINEAR EQUATIONS f( ) = 0. Noliear Equatio Solvers Bracketig. Graphical. Aalytical Ope Methods Bisectio False Positio (Regula-Falsi) Fied poit iteratio Newto Raphso Secat The root of
Prof. Dr. I. Nasser Phys 571, T131 5-Nov-13 Green function.doc. 2 ρ(r)
 Gree fuctio.doc Solutio of ihomogeeous ordiary differetial equatios usig Gree's fuctios G(, ') (9.7, 10.5) Historical Itroductio: Gree's fuctios are auiliary fuctios i the solutio of liear partial differetial
Gree fuctio.doc Solutio of ihomogeeous ordiary differetial equatios usig Gree's fuctios G(, ') (9.7, 10.5) Historical Itroductio: Gree's fuctios are auiliary fuctios i the solutio of liear partial differetial
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Appendix: The Laplace Transform
 Appedix: The Laplace Trasform The Laplace trasform is a powerful method that ca be used to solve differetial equatio, ad other mathematical problems. Its stregth lies i the fact that it allows the trasformatio
Appedix: The Laplace Trasform The Laplace trasform is a powerful method that ca be used to solve differetial equatio, ad other mathematical problems. Its stregth lies i the fact that it allows the trasformatio
Chapter 4 : Laplace Transform
 4. Itroductio Laplace trasform is a alterative to solve the differetial equatio by the complex frequecy domai ( s = σ + jω), istead of the usual time domai. The DE ca be easily trasformed ito a algebraic
4. Itroductio Laplace trasform is a alterative to solve the differetial equatio by the complex frequecy domai ( s = σ + jω), istead of the usual time domai. The DE ca be easily trasformed ito a algebraic
Filter banks. Separately, the lowpass and highpass filters are not invertible. removes the highest frequency 1/ 2and
 Filter bas Separately, the lowpass ad highpass filters are ot ivertible T removes the highest frequecy / ad removes the lowest frequecy Together these filters separate the sigal ito low-frequecy ad high-frequecy
Filter bas Separately, the lowpass ad highpass filters are ot ivertible T removes the highest frequecy / ad removes the lowest frequecy Together these filters separate the sigal ito low-frequecy ad high-frequecy
Fundamental Concepts: Surfaces and Curves
 UNDAMENTAL CONCEPTS: SURACES AND CURVES CHAPTER udametal Cocepts: Surfaces ad Curves. INTRODUCTION This chapter describes two geometrical objects, vi., surfaces ad curves because the pla a ver importat
UNDAMENTAL CONCEPTS: SURACES AND CURVES CHAPTER udametal Cocepts: Surfaces ad Curves. INTRODUCTION This chapter describes two geometrical objects, vi., surfaces ad curves because the pla a ver importat
Solutions to Final Exam Review Problems
 . Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
. Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
Subject: Differential Equations & Mathematical Modeling-III
 Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
, then cv V. Differential Equations Elements of Lineaer Algebra Name: Consider the differential equation. and y2 cos( kx)
 Cosider the differetial equatio y '' k y 0 has particular solutios y1 si( kx) ad y cos( kx) I geeral, ay liear combiatio of y1 ad y, cy 1 1 cy where c1, c is also a solutio to the equatio above The reaso
Cosider the differetial equatio y '' k y 0 has particular solutios y1 si( kx) ad y cos( kx) I geeral, ay liear combiatio of y1 ad y, cy 1 1 cy where c1, c is also a solutio to the equatio above The reaso
ENGI Series Page 6-01
 ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
Ma 4121: Introduction to Lebesgue Integration Solutions to Homework Assignment 5
 Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
(Figure 2.9), we observe x. and we write. (b) as x, x 1. and we write. We say that the line y 0 is a horizontal asymptote of the graph of f.
 The symbol for ifiity ( ) does ot represet a real umber. We use to describe the behavior of a fuctio whe the values i its domai or rage outgrow all fiite bouds. For eample, whe we say the limit of f as
The symbol for ifiity ( ) does ot represet a real umber. We use to describe the behavior of a fuctio whe the values i its domai or rage outgrow all fiite bouds. For eample, whe we say the limit of f as
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
MATH4822E FOURIER ANALYSIS AND ITS APPLICATIONS
 MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
: Transforms and Partial Differential Equations
 Trasforms ad Partial Differetial Equatios 018 SUBJECT NAME : Trasforms ad Partial Differetial Equatios SUBJECT CODE : MA 6351 MATERIAL NAME : Part A questios REGULATION : R013 WEBSITE : wwwharigaeshcom
Trasforms ad Partial Differetial Equatios 018 SUBJECT NAME : Trasforms ad Partial Differetial Equatios SUBJECT CODE : MA 6351 MATERIAL NAME : Part A questios REGULATION : R013 WEBSITE : wwwharigaeshcom
MTH Assignment 1 : Real Numbers, Sequences
 MTH -26 Assigmet : Real Numbers, Sequeces. Fid the supremum of the set { m m+ : N, m Z}. 2. Let A be a o-empty subset of R ad α R. Show that α = supa if ad oly if α is ot a upper boud of A but α + is a
MTH -26 Assigmet : Real Numbers, Sequeces. Fid the supremum of the set { m m+ : N, m Z}. 2. Let A be a o-empty subset of R ad α R. Show that α = supa if ad oly if α is ot a upper boud of A but α + is a
Expected Number of Level Crossings of Legendre Polynomials
 Expected Number of Level Crossigs of Legedre olomials ROUT, LMNAYAK, SMOHANTY, SATTANAIK,NC OJHA,DRKMISHRA Research Scholar, G DEARTMENT OF MATHAMATICS,COLLEGE OF ENGINEERING AND TECHNOLOGY,BHUBANESWAR,ODISHA
Expected Number of Level Crossigs of Legedre olomials ROUT, LMNAYAK, SMOHANTY, SATTANAIK,NC OJHA,DRKMISHRA Research Scholar, G DEARTMENT OF MATHAMATICS,COLLEGE OF ENGINEERING AND TECHNOLOGY,BHUBANESWAR,ODISHA
Partial Differential Equations
 EE 84 Matematical Metods i Egieerig Partial Differetial Eqatios Followig are some classical partial differetial eqatios were is assmed to be a fctio of two or more variables t (time) ad y (spatial coordiates).
EE 84 Matematical Metods i Egieerig Partial Differetial Eqatios Followig are some classical partial differetial eqatios were is assmed to be a fctio of two or more variables t (time) ad y (spatial coordiates).
PARTIAL DIFFERENTIAL EQUATIONS SEPARATION OF VARIABLES
 Diola Bagayoko (0 PARTAL DFFERENTAL EQUATONS SEPARATON OF ARABLES. troductio As discussed i previous lectures, partial differetial equatios arise whe the depedet variale, i.e., the fuctio, varies with
Diola Bagayoko (0 PARTAL DFFERENTAL EQUATONS SEPARATON OF ARABLES. troductio As discussed i previous lectures, partial differetial equatios arise whe the depedet variale, i.e., the fuctio, varies with
Subject: Differential Equations & Mathematical Modeling -III. Lesson: Power series solutions of Differential Equations. about ordinary points
 Power series solutio of Differetial equatios about ordiary poits Subject: Differetial Equatios & Mathematical Modelig -III Lesso: Power series solutios of Differetial Equatios about ordiary poits Lesso
Power series solutio of Differetial equatios about ordiary poits Subject: Differetial Equatios & Mathematical Modelig -III Lesso: Power series solutios of Differetial Equatios about ordiary poits Lesso
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
Lecture #3. Math tools covered today
 Toay s Program:. Review of previous lecture. QM free particle a particle i a bo. 3. Priciple of spectral ecompositio. 4. Fourth Postulate Math tools covere toay Lecture #3. Lear how to solve separable
Toay s Program:. Review of previous lecture. QM free particle a particle i a bo. 3. Priciple of spectral ecompositio. 4. Fourth Postulate Math tools covere toay Lecture #3. Lear how to solve separable
Finite Difference Derivations for Spreadsheet Modeling John C. Walton Modified: November 15, 2007 jcw
 Fiite Differece Derivatios for Spreadsheet Modelig Joh C. Walto Modified: November 15, 2007 jcw Figure 1. Suset with 11 swas o Little Platte Lake, Michiga. Page 1 Modificatio Date: November 15, 2007 Review
Fiite Differece Derivatios for Spreadsheet Modelig Joh C. Walto Modified: November 15, 2007 jcw Figure 1. Suset with 11 swas o Little Platte Lake, Michiga. Page 1 Modificatio Date: November 15, 2007 Review
SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayanavanam Road QUESTION BANK (DESCRIPTIVE)
 QUESTION BANK 8 SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayaavaam Road 5758 QUESTION BANK (DESCRIPTIVE Subject with Code : (6HS6 Course & Brach: B.Tech AG Year & Sem: II-B.Tech& I-Sem
QUESTION BANK 8 SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayaavaam Road 5758 QUESTION BANK (DESCRIPTIVE Subject with Code : (6HS6 Course & Brach: B.Tech AG Year & Sem: II-B.Tech& I-Sem
19 Fourier Series and Practical Harmonic Analysis
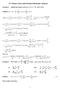 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Lecture 7: Fourier Series and Complex Power Series
 Math 1d Istructor: Padraic Bartlett Lecture 7: Fourier Series ad Complex Power Series Week 7 Caltech 013 1 Fourier Series 1.1 Defiitios ad Motivatio Defiitio 1.1. A Fourier series is a series of fuctios
Math 1d Istructor: Padraic Bartlett Lecture 7: Fourier Series ad Complex Power Series Week 7 Caltech 013 1 Fourier Series 1.1 Defiitios ad Motivatio Defiitio 1.1. A Fourier series is a series of fuctios
Signal Processing in Mechatronics
 Sigal Processig i Mechatroics Zhu K.P. AIS, UM. Lecture, Brief itroductio to Sigals ad Systems, Review of Liear Algebra ad Sigal Processig Related Mathematics . Brief Itroductio to Sigals What is sigal
Sigal Processig i Mechatroics Zhu K.P. AIS, UM. Lecture, Brief itroductio to Sigals ad Systems, Review of Liear Algebra ad Sigal Processig Related Mathematics . Brief Itroductio to Sigals What is sigal
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Quiz. Use either the RATIO or ROOT TEST to determine whether the series is convergent or not.
 Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
MATH301 Real Analysis (2008 Fall) Tutorial Note #7. k=1 f k (x) converges pointwise to S(x) on E if and
 MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
x x x 2x x N ( ) p NUMERICAL METHODS UNIT-I-SOLUTION OF EQUATIONS AND EIGENVALUE PROBLEMS By Newton-Raphson formula
 NUMERICAL METHODS UNIT-I-SOLUTION OF EQUATIONS AND EIGENVALUE PROBLEMS. If g( is cotiuous i [a,b], te uder wat coditio te iterative (or iteratio metod = g( as a uique solutio i [a,b]? '( i [a,b].. Wat
NUMERICAL METHODS UNIT-I-SOLUTION OF EQUATIONS AND EIGENVALUE PROBLEMS. If g( is cotiuous i [a,b], te uder wat coditio te iterative (or iteratio metod = g( as a uique solutio i [a,b]? '( i [a,b].. Wat
Solution of EECS 315 Final Examination F09
 Solutio of EECS 315 Fial Examiatio F9 1. Fid the umerical value of δ ( t + 4ramp( tdt. δ ( t + 4ramp( tdt. Fid the umerical sigal eergy of x E x = x[ ] = δ 3 = 11 = ( = ramp( ( 4 = ramp( 8 = 8 [ ] = (
Solutio of EECS 315 Fial Examiatio F9 1. Fid the umerical value of δ ( t + 4ramp( tdt. δ ( t + 4ramp( tdt. Fid the umerical sigal eergy of x E x = x[ ] = δ 3 = 11 = ( = ramp( ( 4 = ramp( 8 = 8 [ ] = (
5.61 Fall 2013 Problem Set #3
 5.61 Fall 013 Problem Set #3 1. A. McQuarrie, page 10, #3-3. B. McQuarrie, page 10, #3-4. C. McQuarrie, page 18, #4-11.. McQuarrie, pages 11-1, #3-11. 3. A. McQuarrie, page 13, #3-17. B. McQuarrie, page
5.61 Fall 013 Problem Set #3 1. A. McQuarrie, page 10, #3-3. B. McQuarrie, page 10, #3-4. C. McQuarrie, page 18, #4-11.. McQuarrie, pages 11-1, #3-11. 3. A. McQuarrie, page 13, #3-17. B. McQuarrie, page
Phys. 201 Mathematical Physics 1 Dr. Nidal M. Ershaidat Doc. 12
 Physics Departmet, Yarmouk Uiversity, Irbid Jorda Phys. Mathematical Physics Dr. Nidal M. Ershaidat Doc. Fourier Series Deiitio A Fourier series is a expasio o a periodic uctio (x) i terms o a iiite sum
Physics Departmet, Yarmouk Uiversity, Irbid Jorda Phys. Mathematical Physics Dr. Nidal M. Ershaidat Doc. Fourier Series Deiitio A Fourier series is a expasio o a periodic uctio (x) i terms o a iiite sum
f(x)g(x) dx is an inner product on D.
 Ark9: Exercises for MAT2400 Fourier series The exercises o this sheet cover the sectios 4.9 to 4.13. They are iteded for the groups o Thursday, April 12 ad Friday, March 30 ad April 13. NB: No group o
Ark9: Exercises for MAT2400 Fourier series The exercises o this sheet cover the sectios 4.9 to 4.13. They are iteded for the groups o Thursday, April 12 ad Friday, March 30 ad April 13. NB: No group o
TMA4205 Numerical Linear Algebra. The Poisson problem in R 2 : diagonalization methods
 TMA4205 Numerical Liear Algebra The Poisso problem i R 2 : diagoalizatio methods September 3, 2007 c Eiar M Røquist Departmet of Mathematical Scieces NTNU, N-749 Trodheim, Norway All rights reserved A
TMA4205 Numerical Liear Algebra The Poisso problem i R 2 : diagoalizatio methods September 3, 2007 c Eiar M Røquist Departmet of Mathematical Scieces NTNU, N-749 Trodheim, Norway All rights reserved A
(c) Write, but do not evaluate, an integral expression for the volume of the solid generated when R is
 Calculus BC Fial Review Name: Revised 7 EXAM Date: Tuesday, May 9 Remiders:. Put ew batteries i your calculator. Make sure your calculator is i RADIAN mode.. Get a good ight s sleep. Eat breakfast. Brig:
Calculus BC Fial Review Name: Revised 7 EXAM Date: Tuesday, May 9 Remiders:. Put ew batteries i your calculator. Make sure your calculator is i RADIAN mode.. Get a good ight s sleep. Eat breakfast. Brig:
Beyond simple iteration of a single function, or even a finite sequence of functions, results
 A Primer o the Elemetary Theory of Ifiite Compositios of Complex Fuctios Joh Gill Sprig 07 Abstract: Elemetary meas ot requirig the complex fuctios be holomorphic Theorem proofs are fairly simple ad are
A Primer o the Elemetary Theory of Ifiite Compositios of Complex Fuctios Joh Gill Sprig 07 Abstract: Elemetary meas ot requirig the complex fuctios be holomorphic Theorem proofs are fairly simple ad are
An application of a subset S of C onto another S' defines a function [f(z)] of the complex variable z.
![An application of a subset S of C onto another S' defines a function [f(z)] of the complex variable z. An application of a subset S of C onto another S' defines a function [f(z)] of the complex variable z.](/thumbs/82/84763354.jpg) Diola Bagaoko (1 ELEMENTARY FNCTIONS OFA COMPLEX VARIABLES I Basic Defiitio of a Fuctio of a Comple Variable A applicatio of a subset S of C oto aother S' defies a fuctio [f(] of the comple variable z
Diola Bagaoko (1 ELEMENTARY FNCTIONS OFA COMPLEX VARIABLES I Basic Defiitio of a Fuctio of a Comple Variable A applicatio of a subset S of C oto aother S' defies a fuctio [f(] of the comple variable z
Notes 19 Bessel Functions
 ECE 638 Fall 17 David R. Jackso Notes 19 Bessel Fuctios Notes are from D. R. Wilto, Dept. of ECE 1 Cylidrical Wave Fuctios Helmholtz equatio: ψ + k ψ = I cylidrical coordiates: ψ 1 ψ 1 ψ ψ ρ ρ ρ ρ φ z
ECE 638 Fall 17 David R. Jackso Notes 19 Bessel Fuctios Notes are from D. R. Wilto, Dept. of ECE 1 Cylidrical Wave Fuctios Helmholtz equatio: ψ + k ψ = I cylidrical coordiates: ψ 1 ψ 1 ψ ψ ρ ρ ρ ρ φ z
METHOD OF FUNDAMENTAL SOLUTIONS FOR HELMHOLTZ EIGENVALUE PROBLEMS IN ELLIPTICAL DOMAINS
 Please cite this article as: Staisław Kula, Method of fudametal solutios for Helmholtz eigevalue problems i elliptical domais, Scietific Research of the Istitute of Mathematics ad Computer Sciece, 009,
Please cite this article as: Staisław Kula, Method of fudametal solutios for Helmholtz eigevalue problems i elliptical domais, Scietific Research of the Istitute of Mathematics ad Computer Sciece, 009,
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
SUMMARY OF SEQUENCES AND SERIES
 SUMMARY OF SEQUENCES AND SERIES Importat Defiitios, Results ad Theorems for Sequeces ad Series Defiitio. A sequece {a } has a limit L ad we write lim a = L if for every ɛ > 0, there is a correspodig iteger
SUMMARY OF SEQUENCES AND SERIES Importat Defiitios, Results ad Theorems for Sequeces ad Series Defiitio. A sequece {a } has a limit L ad we write lim a = L if for every ɛ > 0, there is a correspodig iteger
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Math Solutions to homework 6
 Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Ray Optics Theory and Mode Theory. Dr. Mohammad Faisal Dept. of EEE, BUET
 Ray Optics Theory ad Mode Theory Dr. Mohammad Faisal Dept. of, BUT Optical Fiber WG For light to be trasmitted through fiber core, i.e., for total iteral reflectio i medium, > Ray Theory Trasmissio Ray
Ray Optics Theory ad Mode Theory Dr. Mohammad Faisal Dept. of, BUT Optical Fiber WG For light to be trasmitted through fiber core, i.e., for total iteral reflectio i medium, > Ray Theory Trasmissio Ray
Generalized Semi- Markov Processes (GSMP)
 Geeralized Semi- Markov Processes (GSMP) Summary Some Defiitios Markov ad Semi-Markov Processes The Poisso Process Properties of the Poisso Process Iterarrival times Memoryless property ad the residual
Geeralized Semi- Markov Processes (GSMP) Summary Some Defiitios Markov ad Semi-Markov Processes The Poisso Process Properties of the Poisso Process Iterarrival times Memoryless property ad the residual
CHAPTER 5. Theory and Solution Using Matrix Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
Linear Elliptic PDE s Elliptic partial differential equations frequently arise out of conservation statements of the form
 Liear Elliptic PDE s Elliptic partial differetial equatios frequetly arise out of coservatio statemets of the form B F d B Sdx B cotaied i bouded ope set U R. Here F, S deote respectively, the flux desity
Liear Elliptic PDE s Elliptic partial differetial equatios frequetly arise out of coservatio statemets of the form B F d B Sdx B cotaied i bouded ope set U R. Here F, S deote respectively, the flux desity
Inverse Nodal Problems for Differential Equation on the Half-line
 Australia Joural of Basic ad Applied Scieces, 3(4): 4498-4502, 2009 ISSN 1991-8178 Iverse Nodal Problems for Differetial Equatio o the Half-lie 1 2 3 A. Dabbaghia, A. Nematy ad Sh. Akbarpoor 1 Islamic
Australia Joural of Basic ad Applied Scieces, 3(4): 4498-4502, 2009 ISSN 1991-8178 Iverse Nodal Problems for Differetial Equatio o the Half-lie 1 2 3 A. Dabbaghia, A. Nematy ad Sh. Akbarpoor 1 Islamic
PRELIM PROBLEM SOLUTIONS
 PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
Math 61CM - Solutions to homework 3
 Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Chapter 2 Systems and Signals
 Chapter 2 Systems ad Sigals 1 Itroductio Discrete-Time Sigals: Sequeces Discrete-Time Systems Properties of Liear Time-Ivariat Systems Liear Costat-Coefficiet Differece Equatios Frequecy-Domai Represetatio
Chapter 2 Systems ad Sigals 1 Itroductio Discrete-Time Sigals: Sequeces Discrete-Time Systems Properties of Liear Time-Ivariat Systems Liear Costat-Coefficiet Differece Equatios Frequecy-Domai Represetatio
POWER SERIES SOLUTION OF FIRST ORDER MATRIX DIFFERENTIAL EQUATIONS
 Joural of Applied Mathematics ad Computatioal Mechaics 4 3(3) 3-8 POWER SERIES SOLUION OF FIRS ORDER MARIX DIFFERENIAL EQUAIONS Staisław Kukla Izabela Zamorska Istitute of Mathematics Czestochowa Uiversity
Joural of Applied Mathematics ad Computatioal Mechaics 4 3(3) 3-8 POWER SERIES SOLUION OF FIRS ORDER MARIX DIFFERENIAL EQUAIONS Staisław Kukla Izabela Zamorska Istitute of Mathematics Czestochowa Uiversity
Chapter 2: Numerical Methods
 Chapter : Numerical Methods. Some Numerical Methods for st Order ODEs I this sectio, a summar of essetial features of umerical methods related to solutios of ordiar differetial equatios is give. I geeral,
Chapter : Numerical Methods. Some Numerical Methods for st Order ODEs I this sectio, a summar of essetial features of umerical methods related to solutios of ordiar differetial equatios is give. I geeral,
