Chapter 5. Sound Waves and Vortices. 5.1 Sound waves
|
|
|
- Hugh Phillips
- 5 years ago
- Views:
Transcription
1 Chapter 5 Sound Waves and Vortices In this chapter we explore a set of characteristic solutions to the uid equations with the goal of familiarizing the reader with typical behaviors in uid dynamics. Sound waves form the basis of compressible uid ow, while vortex dynamics is characteristic of incompressible ow. 5.1 Sound waves Sound waves are the small-amplitude solutions to the equations for a homogeneous, compressible uid which is initially at rest and subject to no external forces. Sound waves exist in more complicated circumstances, but they appear in their purest form in this context. Small amplitude means that deviations in dependent variables from the rest state are suciently small that approximate equations obtained by retaining only terms linear in these deviations are valid. This process of linearization is used frequently in geophysical uid dynamics. We analyze in particular sound waves in an ideal gas. For this situation we assume that the (dry) entropy is constant, a trivial solution to the entropy governing equation in the absence of moisture and radiation eects: ds d dt = 0. (5.1) Since the density and pressure, but not the temperature, appear in the momentum and continuity equations, it is useful to rewrite the entropy in terms of these variables, eliminating the temperature using the ideal gas law: s d = C vd ln(p/p R ) C pd ln(ρ/ρ R ), (5.2) where C vd = C pd R d is the specic heat of dry air at constant volume, and where the reference density ρ R is consistent with the reference pressure and temperature in the ideal gas law. Let us now assume a rest state for the atmosphere in which p = p R and ρ = ρ R. From equation (5.2) we see that the entropy must take on the value s d = 0 under these conditions. 32
2 CHAPTER 5. SOUND WAVES AND VORTICES 33 If we now let p = p R + p and ρ = ρ R + ρ, where p p R and ρ ρ R, then equation (5.2) becomes, upon solving for p, p = γ ρ, (5.3) p R ρ R where γ = C pd /C vd = 1.4, and where we have used ln(1 + p /p R ) p /p R for p /p R 1, etc. We now linearize the mass continuity and momentum equations. Since the initial state is one of rest, the velocity vector itself is a small quantity, which means that terms like vv, v ρ, and ρ v must be ignored when we linearize these equations. Further realizing that space and time derivatives of ρ R and p R vanish due to their constancy, we nd that the mass continuity and momentum equations reduce to and ρ t + ρ R v = 0 (5.4) v t + p ρ R = 0. (5.5) Equations (5.4), (5.4), and (5.5) together govern the behavior of sound waves. Let us substitute a trial plane wave solution of the form ρ = ρ 0 exp[i(k x ωt)], p = p 0 exp[i(k x ωt)], v = v 0 exp[i(k x ωt)], where k is the wave vector of the wave, ω is its frequency, and ρ 0, p 0, and v 0 are constants. After eliminating p in favor of ρ in equation (5.5), we get and iωρ 0 + iρ R k v 0 = 0 (5.6) iωv 0 + iγkp R ρ 0 /ρ 2 R = 0. (5.7) Equation (5.7) implies that v 0 must be parallel to k as long as p 0 0, which means that sound waves are longitudinal waves. Thus, we can write k v 0 in terms of the vector magnitudes as kv 0. Equations (5.6) and (5.7) constitute a set of linear, homogeneous equations in ρ 0 and v 0, and can be rewritten in matrix form as ( ) ( ) ω kρ R ρ0 γkp R /ρ 2 = 0. (5.8) R ω v 0 This has a non-trivial solution only when the determinant of the coecients of the matrix is zero. This condition results in the dispersion relation for sound waves: ω 2 = (γp R /ρ R )k 2 = (γr d T R )k 2. (5.9) From the dispersion relation we see that the phase speed of sound waves in dry air is c = ω/k = (γr d T R ) 1/2. At T R = 300 K, this yields c = 347 m s 1. Interestingly, the speed of sound in an ideal gas depends only on the temperature of the gas. Equation (5.6) tells us that the density perturbation is related to the velocity perturbation by ρ 0 = ρ R v 0 /c, while equation (5.3) shows that p 0 = c 2 ρ 0.
3 CHAPTER 5. SOUND WAVES AND VORTICES 34 l 1 l 2 l ζ n da Figure 5.1: Sketch of a circulation loop which advects with the uid ow, symbolized by the arrows on the left. Stokes' theorem relates the circulation to an area integral of the vorticity, as shown on the right. The speed of sound forms a dividing line in uid dynamics. Even for ows in a compressible uid like air, the uid acts much like an incompressible uid if the characteristic velocities are much less than the speed of sound. Only for uid velocities comparable to or greater than c does essentially incompressible behavior enter. The ratio of the characteristic velocity of a ow to the speed of sound is called the Mach number: M = V typical. (5.10) c Most ows in geophysical contexts have M 1, and thus behave in essentially incompressible fashion. The analysis in this section is presented in detail to provide a clear example of how linearized perturbation solutions are obtained. One point worth emphasizing is that the initial or base state itself must be a solution to the full equations of motion for the perturbation analysis to be valid. The reader is left to verify that the base state in this case, v = 0, ρ = ρ R, p = p R, does indeed satisfy the full governing equations. 5.2 Vorticity and the Kelvin theorem The vorticity of a uid ow is dened as the curl of the velocity eld: ζ v. (5.11) The vorticity plays a key role in the dynamics of an incompressible uid, as well as in the low Mach number ow of a compressible uid. The vorticity is related to a quantity called the circulation, dened as the closed line integral of the uid velocity component parallel to the path: Γ = v dl = v nda = ζ nda. (5.12) The second form of the circulation involving the vorticity is obtained using Stokes' theorem. Hence the area integral is over the region bounded by the circulation path. Figure 5.1 illustrates the circulation loop.
4 CHAPTER 5. SOUND WAVES AND VORTICES 35 Of particular interest is the circulation loop which moves and deforms with the uid ow. The area, shape, and orientation of this loop evolve with time. However, the time rate of change of the circulation around such a loop obeys a surprisingly simple law, as we now show. We wish to take the time derivative of Γ. However, the fact that the circulation loop evolves with time complicates this calculation. It is simplest to write the circulation integral in nite sum form while taking the derivative in which dl l i = l i+1 l i as illustrated in the left panel of gure 5.1: dt = d vi (l i+1 l i ) = dv i dt dt l i + v i v i, (5.13) where we use v i = dl i /dt. We then revert to integral forms and note further that v dv = d(v 2 /2), which results in dv dt = dt dl + d(v 2 /2). (5.14) The second term is the integral of a perfect dierential over a closed path and is therefore zero. The total time derivative of velocity can be eliminated using the momentum equation. We work for now in an inertial reference frame and introduce a rotating frame at a later stage. In this case equation (5.14) becomes ( dt = p ) ρ Φ dl. (5.15) The second term can be written Φ dl = dφ, and is therefore also a perfect dierential which integrates to zero. However, the rst term ρ 1 p dl = ρ 1 dp in general is not, and therefore must be retained. Thus we arrive at the Kelvin circulation theorem 1 (see Pedlosky, 1979): dt = dp ρ. (5.16) In geophysical uid dynamics we always use the circulation as computed in an inertial reference frame. However, we often have to compute the circulation directly given the uid velocity in the rotating frame of the earth. Recall that the velocity in the inertial frame v I can be related to the velocity in the rotating frame v by v I = v + Ω r, (5.17) where Ω is the rotation vector of the earth and r is the position vector relative to the center of the earth. The circulation thus becomes Γ = v I dl = v dl + [ (Ω r)] nda, (5.18) where we have used Stokes' theorem to convert the second line integral into an area integral bounded by the circulation loop. A well-known vector identity can be used to reduce the 1 Technically, Kelvin's theorem refers to the special case of a homogeneous, incompressible uid, in which case (as we shall show) the right side of equation (5.16) is zero.
5 CHAPTER 5. SOUND WAVES AND VORTICES 36 last term: (Ω r) = Ω( r) Ω r = 3Ω Ω = 2Ω. Substituting this into equation (5.18) results in Γ = v dl + 2Ω nda = ( v + 2Ω) nda. (5.19) In the context of a rotating reference frame, the curl of the uid velocity in the inertial frame is called the absolute vorticity, and ζ = v is called the relative vorticity Homogeneous, incompressible uid ζ a = v I = v + 2Ω, (5.20) For a homogeneous, incompressible uid, we have constant density ρ. In this case the pressure term in equation (5.16) is also a perfect dierential, so the Kelvin circulation theorem becomes = 0. (5.21) dt For a very small loop over which the absolute vorticity is essentially constant, Γ = ζ a na, where A is the area of the loop and n is the unit normal to the loop. Thus, if the loop associated with a parcel of uid expands in area, the component of the absolute vorticity normal to the loop must decrease correspondingly. In the special case in which the absolute vorticity in a homogeneous, incompressible uid is everywhere zero, the circulation theorem shows that it will always remain zero. This is a profound result which we will exploit later Inhomogeneous, incompressible uid If an incompressible uid is inhomogeneous, i. e., if the density varies with position, then equation (5.21) doesn't generally apply. However, in the limited case in which the circulation loop is conned to a surface of constant density, this equation is valid, since ρ is constant over the circulation loop. Furthermore, by virtue of the incompressibility condition, a circulation loop which advects with the uid (as it does in the case of the Kelvin theorem) will always remain embedded in a surface of constant density if it starts out that way. Thus, equation (5.21) remains valid for all time in this case Diabatic ideal gas In the case of an ideal gas in which no latent heat release, radiative heating or cooling, or other heat source exists, changes in the specic enthalpy h can be related solely to changes in the dry entropy and pressure: dh = T ds d + dp/ρ. (5.22)
6 CHAPTER 5. SOUND WAVES AND VORTICES 37 d d Ω R R Ω 2d Ω R/2 1/2 Figure 5.2: Sketch of a homogeneous slab of ocean water. The rotation vector Ω of the earth is shown in each of three cases. In the left panel the slab is at the north pole. In the center panel it has moved to the equator without change of shape. In the right panel it remains at the north pole, but deforms so as to reduce its radius and increase its thickness. In this case the circulation theorem can be written dt = T ds d. (5.23) The enthalpy term drops out as it appears in the form of a perfect dierential. In this case equation (5.21) applies to circulation loops embedded in surfaces of constant dry entropy. The condition of no heating means that parcels conserve dry entropy, so analogously to the case of an inhomogeneous, incompressible uid, equation (5.21) will apply for all time in this special case. An alternate way to represent the right side of the Kelvin theorem equation in the case of an ideal gas is to rewrite dp/ρ in terms of the potential temperature and the Exner function: dt = θdπ = Πdθ. (5.24) The last step results from d(θπ) being a perfect dierential. This result is equivalent to that of equation (5.23) since ds d = C pd dθ/θ and Π = C pd T/θ. The latter equation comes from combining the denition of potential temperature with the denition of Exner function. 5.3 Ocean example As an example of the use of the Kelvin theorem, let us consider a circular slab of ocean water, assumed to be homogeneous in temperature and salinity. Suppose the slab starts out at the north pole, as illustrated in the left panel of gure 5.2. Let us further suppose that the slab is at rest in this location. The circulation around the periphery of the slab is totally due to planetary rotation in this case, and has the value Γ = 2πR 2 Ω. If the slab moves to the equator without change of shape, the orientation is such that the planetary contribution to the circulation is zero. However, since circulation is conserved in this case, the slab must be rotating with tangential velocity at the rim V determined by Γ = 2πRV. Solving for V results in V = RΩ.
7 CHAPTER 5. SOUND WAVES AND VORTICES 38 If the slab remains at the north pole, but is deformed such that the thickness is doubled, the radius necessarily decreases by a factor 2 1/2 so that the volume of the slab remains the same. This deformation decreases the planetary part of the circulation to 2π(R/2 1/2 ) 2 Ω = πr 2 Ω. The balance has to be taken up by rotation relative to the earth with tangential velocity at the rim determined by conservation of circulation: 2πR 2 Ω = πr 2 Ω+2π(R/2 1/2 )V implies V = RΩ/2 1/2. Let us attach some numbers to these estimates. The rotation rate of the earth is 2π divided by the period of rotation, which is about 4 min less than 24 h dynamically, the sidereal day rather than the solar day should be used. This results in Ω = s 1. If R = 100 km, then we nd V = 7.29 m s 1 in the case in which the slab moves undeformed to the equator. 5.4 Irrotational, incompressible ow Suppose we have an incompressible, homogeneous (i. e., constant density) uid which has zero vorticity everywhere. Thus, we have the conditions v = 0 and v = 0 everywhere in the uid for all time, according to arguments based on the Kelvin circulation theorem. Solutions for ows of this type are particularly easy to obtain. Zero vorticity implies that we can represent the velocity as the gradient of some potential, χ, which we call the velocity potential: v = χ. (5.25) However, zero divergence further implies that the velocity potential obeys a very simple equation 2 χ = 0. (5.26) Let us imagine that the outward normal component of the velocity v n = v n = χ n is specied on the boundary of some region. The quantity n is the unit outward normal on this boundary. Assuming that there are no sources or sinks of uid inside the region, then the net ow out of the region must be zero: χ nda = 0. (5.27) Given this condition, equation (5.26) uniquely determines χ up to a trivial additive constant. Physically, this implies that the uid ow in this case is passive there are no interesting internal dynamics, as the entire ow is determined by what is imposed at the boundary. The pressure distribution as well as the velocity distribution is xed as well. To show this, we note that the term v v = (v 2 /2) v ζ. (This follows from expanding v ( v) according to the rules of vector analysis.) Since ζ = 0 by hypothesis in this case, and since the density is constant, the momentum equation becomes ( χ/ t + v 2 /2 + p/ρ + Φ) = 0. (5.28) It follows that χ/ t + v 2 /2 + p/ρ + Φ = constant. (5.29)
8 CHAPTER 5. SOUND WAVES AND VORTICES 39 In the special case in which the ow is time-independent, this reduces to Bernoulli's equation: 5.5 References v 2 /2 + p/ρ + Φ = constant. (5.30) Pedlosky, J., 1979: Geophysical Fluid Dynamics. Springer-Verlag, New York, 624 pp. 5.6 Problems 1. Consider perturbations on a rotating, homogeneous (i. e., constant entropy), compressible uid at rest in its rotating environment, with constant geopotential. Assume a rotation vector of magnitude Ω pointing in the z direction. (a) Linearize the governing equations using the treatment of sound waves as guide and assume all dependent variables to be proportional to exp[i(k x ωt)]. Write the governing equations in matrix form as in equation (5.8). The dispersion relation is obtained by taking the determinant of the matrix of coecients. (b) Examine the special case in which k points in the z direction. Solving the dispersion relation for ω 2 shows that two solutions exist, since this equation is quadratic in ω 2. For each of these solutions determine the relationship between the various components of the velocity, and between the velocity and the density perturbation. (c) Repeat for the special case in which k points in the x direction. 2. Suppose we add an additional force per unit mass F to the momentum equation, such as might be caused by friction. The momentum equation thus takes the form (in a non-rotating reference frame) dv dt + p + Φ = F. (5.31) ρ Derive the Kelvin circulation theorem in this extended case. If F is conservative, does it enter? 3. Imagine that convection forms in an initially stationary atmosphere at latitude 45 S. The convection draws air in horizontally at low levels, lifts it, and ejects it horizontally at high levels, as shown in gure 5.3. (a) Assuming cylindrical symmetry, nd the tangential velocity of the inowing air at radius a/2, assuming that it started at radius a = 500 km. (b) Find the tangential velocity of outow air at radius a, assuming that it started at radius a/2.
9 CHAPTER 5. SOUND WAVES AND VORTICES 40 a/2 a Figure 5.3: Sketch of airow through a convective system. 4. One can think of a hurricane as an axially symmetric vortex with inow at low levels and outow at high levels. The earth-relative velocities in a hurricane are so large that the planetary contribution to the circulation can be ignored to a reasonable approximation inside the hurricane. (a) If the tangential velocity in the hurricane inow at the outer radius b of a hurricane is V b, what does the circulation theorem tell us the tangential velocity should be at radius a < b? (b) The actual hurricane tangential velocity in the inow is observed to be equal to Cr 1/2 where r is the distance from the center of the hurricane and C is a constant. Determine how the circulation varies with r in this case. (c) Assume that the tangential frictional force in a hurricane takes the form F = KV 2 where V is the tangential velocity and K is a constant. Given this and the fact that /dt = (/dr)(dr/dt) = U(/dr) in a steady hurricane, determine how the radial velocity U varies as a function of radius. Hint: Consult the answer to problem Consider the ow with the velocity potential where U, A, k, and m are constants. χ = Ux + A sin(kx) exp( mz) (5.32) (a) Determine the condition needed to satisfy 2 χ = 0. (b) Compute the velocity vector as a function of x and z and make a sketch of the velocity eld, showing velocity vectors on an x z grid. (c) On the above plot sketch in the trajectories of a representative set of air parcels as they move through this ow pattern.
Vorticity and Potential Vorticity
 Chapter 4 Vorticity and Potential Vorticity In this chapter we explore a way of solving the shallow water equations for motions with characteristic time scales longer than the rotation period of the earth.
Chapter 4 Vorticity and Potential Vorticity In this chapter we explore a way of solving the shallow water equations for motions with characteristic time scales longer than the rotation period of the earth.
Chapter 1. Governing Equations of GFD. 1.1 Mass continuity
 Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
Chapter 3. Shallow Water Equations and the Ocean. 3.1 Derivation of shallow water equations
 Chapter 3 Shallow Water Equations and the Ocean Over most of the globe the ocean has a rather distinctive vertical structure, with an upper layer ranging from 20 m to 200 m in thickness, consisting of
Chapter 3 Shallow Water Equations and the Ocean Over most of the globe the ocean has a rather distinctive vertical structure, with an upper layer ranging from 20 m to 200 m in thickness, consisting of
Buoyancy and Coriolis forces
 Chapter 2 Buoyancy and Coriolis forces In this chapter we address several topics that we need to understand before starting on our study of geophysical uid dynamics. 2.1 Hydrostatic approximation Consider
Chapter 2 Buoyancy and Coriolis forces In this chapter we address several topics that we need to understand before starting on our study of geophysical uid dynamics. 2.1 Hydrostatic approximation Consider
Chapter 5. Shallow Water Equations. 5.1 Derivation of shallow water equations
 Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
Continuum Mechanics Lecture 5 Ideal fluids
 Continuum Mechanics Lecture 5 Ideal fluids Prof. http://www.itp.uzh.ch/~teyssier Outline - Helmholtz decomposition - Divergence and curl theorem - Kelvin s circulation theorem - The vorticity equation
Continuum Mechanics Lecture 5 Ideal fluids Prof. http://www.itp.uzh.ch/~teyssier Outline - Helmholtz decomposition - Divergence and curl theorem - Kelvin s circulation theorem - The vorticity equation
V (r,t) = i ˆ u( x, y,z,t) + ˆ j v( x, y,z,t) + k ˆ w( x, y, z,t)
 IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
Vortex stretching in incompressible and compressible fluids
 Vortex stretching in incompressible and compressible fluids Esteban G. Tabak, Fluid Dynamics II, Spring 00 1 Introduction The primitive form of the incompressible Euler equations is given by ( ) du P =
Vortex stretching in incompressible and compressible fluids Esteban G. Tabak, Fluid Dynamics II, Spring 00 1 Introduction The primitive form of the incompressible Euler equations is given by ( ) du P =
The Euler Equation of Gas-Dynamics
 The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
Viscous Fluids. Amanda Meier. December 14th, 2011
 Viscous Fluids Amanda Meier December 14th, 2011 Abstract Fluids are represented by continuous media described by mass density, velocity and pressure. An Eulerian description of uids focuses on the transport
Viscous Fluids Amanda Meier December 14th, 2011 Abstract Fluids are represented by continuous media described by mass density, velocity and pressure. An Eulerian description of uids focuses on the transport
To study the motion of a perfect gas, the conservation equations of continuity
 Chapter 1 Ideal Gas Flow The Navier-Stokes equations To study the motion of a perfect gas, the conservation equations of continuity ρ + (ρ v = 0, (1.1 momentum ρ D v Dt = p+ τ +ρ f m, (1.2 and energy ρ
Chapter 1 Ideal Gas Flow The Navier-Stokes equations To study the motion of a perfect gas, the conservation equations of continuity ρ + (ρ v = 0, (1.1 momentum ρ D v Dt = p+ τ +ρ f m, (1.2 and energy ρ
2 The incompressible Kelvin-Helmholtz instability
 Hydrodynamic Instabilities References Chandrasekhar: Hydrodynamic and Hydromagnetic Instabilities Landau & Lifshitz: Fluid Mechanics Shu: Gas Dynamics 1 Introduction Instabilities are an important aspect
Hydrodynamic Instabilities References Chandrasekhar: Hydrodynamic and Hydromagnetic Instabilities Landau & Lifshitz: Fluid Mechanics Shu: Gas Dynamics 1 Introduction Instabilities are an important aspect
5.1 Fluid momentum equation Hydrostatics Archimedes theorem The vorticity equation... 42
 Chapter 5 Euler s equation Contents 5.1 Fluid momentum equation........................ 39 5. Hydrostatics................................ 40 5.3 Archimedes theorem........................... 41 5.4 The
Chapter 5 Euler s equation Contents 5.1 Fluid momentum equation........................ 39 5. Hydrostatics................................ 40 5.3 Archimedes theorem........................... 41 5.4 The
Fluid Dynamics Exercises and questions for the course
 Fluid Dynamics Exercises and questions for the course January 15, 2014 A two dimensional flow field characterised by the following velocity components in polar coordinates is called a free vortex: u r
Fluid Dynamics Exercises and questions for the course January 15, 2014 A two dimensional flow field characterised by the following velocity components in polar coordinates is called a free vortex: u r
Circulation and Vorticity
 Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
Circulation and Vorticity Example: Rotation in the atmosphere water vapor satellite animation Circulation a macroscopic measure of rotation for a finite area of a fluid Vorticity a microscopic measure
A j = 0.1 cm 2 10 cm 10 cm 10 cm. W j Wj. W j W j. W j. 10 cm 10 cm 10 cm. r i
 ME 131B Fluid Mechanics Solutions to Week Eight Problem Session: Angular Momentum Principle (3/2/98) 1. In control volume analysis, all governing principles share the same common structure: storage = inow
ME 131B Fluid Mechanics Solutions to Week Eight Problem Session: Angular Momentum Principle (3/2/98) 1. In control volume analysis, all governing principles share the same common structure: storage = inow
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION
 CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
Fundamentals of Fluid Dynamics: Ideal Flow Theory & Basic Aerodynamics
 Fundamentals of Fluid Dynamics: Ideal Flow Theory & Basic Aerodynamics Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI (after: D.J. ACHESON s Elementary Fluid Dynamics ) bluebox.ippt.pan.pl/
Fundamentals of Fluid Dynamics: Ideal Flow Theory & Basic Aerodynamics Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI (after: D.J. ACHESON s Elementary Fluid Dynamics ) bluebox.ippt.pan.pl/
Quick Recapitulation of Fluid Mechanics
 Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Quick Recapitulation of Fluid Mechanics Amey Joshi 07-Feb-018 1 Equations of ideal fluids onsider a volume element of a fluid of density ρ. If there are no sources or sinks in, the mass in it will change
Circulation and Vorticity. The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation
 Circulation and Vorticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
Circulation and Vorticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
( u,v). For simplicity, the density is considered to be a constant, denoted by ρ 0
 ! Revised Friday, April 19, 2013! 1 Inertial Stability and Instability David Randall Introduction Inertial stability and instability are relevant to the atmosphere and ocean, and also in other contexts
! Revised Friday, April 19, 2013! 1 Inertial Stability and Instability David Randall Introduction Inertial stability and instability are relevant to the atmosphere and ocean, and also in other contexts
2 Equations of Motion
 2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
Chapter 7. Atmospheric Models. 7.1 Atmospheric structure. 7.2 Single layer model of atmosphere
 Chapter 7 Atmospheric Models An accurate model of the atmosphere requires the representation of continuous vertical pro- les, leading to a fully three-dimensional treatment. However, many aspects of atmospheric
Chapter 7 Atmospheric Models An accurate model of the atmosphere requires the representation of continuous vertical pro- les, leading to a fully three-dimensional treatment. However, many aspects of atmospheric
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) ε =U f o L <<1, β = 2Ω cosθ o R. 2.1 Introduction
 Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
Chapter 2. Quasi-Geostrophic Theory: Formulation (review) 2.1 Introduction For most of the course we will be concerned with instabilities that an be analyzed by the quasi-geostrophic equations. These are
Circulation and Vorticity. The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation
 Circulation and Vticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
Circulation and Vticity 1. Conservation of Absolute Angular Momentum The tangential linear velocity of a parcel on a rotating body is related to angular velocity of the body by the relation V = ωr (1)
Quasi-equilibrium Theory of Small Perturbations to Radiative- Convective Equilibrium States
 Quasi-equilibrium Theory of Small Perturbations to Radiative- Convective Equilibrium States See CalTech 2005 paper on course web site Free troposphere assumed to have moist adiabatic lapse rate (s* does
Quasi-equilibrium Theory of Small Perturbations to Radiative- Convective Equilibrium States See CalTech 2005 paper on course web site Free troposphere assumed to have moist adiabatic lapse rate (s* does
Mathematical Concepts & Notation
 Mathematical Concepts & Notation Appendix A: Notation x, δx: a small change in x t : the partial derivative with respect to t holding the other variables fixed d : the time derivative of a quantity that
Mathematical Concepts & Notation Appendix A: Notation x, δx: a small change in x t : the partial derivative with respect to t holding the other variables fixed d : the time derivative of a quantity that
where p oo is a reference level constant pressure (often 10 5 Pa). Since θ is conserved for adiabatic motions, a prognostic temperature equation is:
 1 Appendix C Useful Equations Purposes: Provide foundation equations and sketch some derivations. These equations are used as starting places for discussions in various parts of the book. C.1. Thermodynamic
1 Appendix C Useful Equations Purposes: Provide foundation equations and sketch some derivations. These equations are used as starting places for discussions in various parts of the book. C.1. Thermodynamic
F11AE1 1. C = ρν r r. r u z r
 F11AE1 1 Question 1 20 Marks) Consider an infinite horizontal pipe with circular cross-section of radius a, whose centre line is aligned along the z-axis; see Figure 1. Assume no-slip boundary conditions
F11AE1 1 Question 1 20 Marks) Consider an infinite horizontal pipe with circular cross-section of radius a, whose centre line is aligned along the z-axis; see Figure 1. Assume no-slip boundary conditions
The vorticity field. A dust devil
 The vorticity field The vector ω = u curl u is twice the local angular velocity in the flow, and is called the vorticity of the flow (from Latin for a whirlpool). Vortex lines are everywhere in the direction
The vorticity field The vector ω = u curl u is twice the local angular velocity in the flow, and is called the vorticity of the flow (from Latin for a whirlpool). Vortex lines are everywhere in the direction
PHYS 643 Week 4: Compressible fluids Sound waves and shocks
 PHYS 643 Week 4: Compressible fluids Sound waves and shocks Sound waves Compressions in a gas propagate as sound waves. The simplest case to consider is a gas at uniform density and at rest. Small perturbations
PHYS 643 Week 4: Compressible fluids Sound waves and shocks Sound waves Compressions in a gas propagate as sound waves. The simplest case to consider is a gas at uniform density and at rest. Small perturbations
(Jim You have a note for yourself here that reads Fill in full derivation, this is a sloppy treatment ).
 Lecture. dministration Collect problem set. Distribute problem set due October 3, 004.. nd law of thermodynamics (Jim You have a note for yourself here that reads Fill in full derivation, this is a sloppy
Lecture. dministration Collect problem set. Distribute problem set due October 3, 004.. nd law of thermodynamics (Jim You have a note for yourself here that reads Fill in full derivation, this is a sloppy
The Divergence Theorem Stokes Theorem Applications of Vector Calculus. Calculus. Vector Calculus (III)
 Calculus Vector Calculus (III) Outline 1 The Divergence Theorem 2 Stokes Theorem 3 Applications of Vector Calculus The Divergence Theorem (I) Recall that at the end of section 12.5, we had rewritten Green
Calculus Vector Calculus (III) Outline 1 The Divergence Theorem 2 Stokes Theorem 3 Applications of Vector Calculus The Divergence Theorem (I) Recall that at the end of section 12.5, we had rewritten Green
PEMP ACD2505. M.S. Ramaiah School of Advanced Studies, Bengaluru
 Two-Dimensional Potential Flow Session delivered by: Prof. M. D. Deshpande 1 Session Objectives -- At the end of this session the delegate would have understood PEMP The potential theory and its application
Two-Dimensional Potential Flow Session delivered by: Prof. M. D. Deshpande 1 Session Objectives -- At the end of this session the delegate would have understood PEMP The potential theory and its application
Notes #4a MAE 533, Fluid Mechanics
 Notes #4a MAE 533, Fluid Mechanics S. H. Lam lam@princeton.edu http://www.princeton.edu/ lam October 23, 1998 1 The One-dimensional Continuity Equation The one-dimensional steady flow continuity equation
Notes #4a MAE 533, Fluid Mechanics S. H. Lam lam@princeton.edu http://www.princeton.edu/ lam October 23, 1998 1 The One-dimensional Continuity Equation The one-dimensional steady flow continuity equation
ESCI 342 Atmospheric Dynamics I Lesson 12 Vorticity
 ESCI 34 tmospheric Dynamics I Lesson 1 Vorticity Reference: n Introduction to Dynamic Meteorology (4 rd edition), Holton n Informal Introduction to Theoretical Fluid Mechanics, Lighthill Reading: Martin,
ESCI 34 tmospheric Dynamics I Lesson 1 Vorticity Reference: n Introduction to Dynamic Meteorology (4 rd edition), Holton n Informal Introduction to Theoretical Fluid Mechanics, Lighthill Reading: Martin,
On Fluid Maxwell Equations
 On Fluid Maxwell Equations Tsutomu Kambe, (Former Professor, Physics), University of Tokyo, Abstract Fluid mechanics is a field theory of Newtonian mechanics of Galilean symmetry, concerned with fluid
On Fluid Maxwell Equations Tsutomu Kambe, (Former Professor, Physics), University of Tokyo, Abstract Fluid mechanics is a field theory of Newtonian mechanics of Galilean symmetry, concerned with fluid
1/18/2011. Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
Lecture 2: Basic Conservation Laws Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial
SOLAR MHD Lecture 2 Plan
 SOLAR MHD Lecture Plan Magnetostatic Equilibrium ü Structure of Magnetic Flux Tubes ü Force-free fields Waves in a homogenous magnetized medium ü Linearized wave equation ü Alfvén wave ü Magnetoacoustic
SOLAR MHD Lecture Plan Magnetostatic Equilibrium ü Structure of Magnetic Flux Tubes ü Force-free fields Waves in a homogenous magnetized medium ü Linearized wave equation ü Alfvén wave ü Magnetoacoustic
ESCI 485 Air/Sea Interaction Lesson 1 Stresses and Fluxes Dr. DeCaria
 ESCI 485 Air/Sea Interaction Lesson 1 Stresses and Fluxes Dr DeCaria References: An Introduction to Dynamic Meteorology, Holton MOMENTUM EQUATIONS The momentum equations governing the ocean or atmosphere
ESCI 485 Air/Sea Interaction Lesson 1 Stresses and Fluxes Dr DeCaria References: An Introduction to Dynamic Meteorology, Holton MOMENTUM EQUATIONS The momentum equations governing the ocean or atmosphere
ESS314. Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe. Conservation Laws
 ESS314 Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe Conservation Laws The big differences between fluids and other forms of matter are that they are continuous and they deform internally
ESS314 Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe Conservation Laws The big differences between fluids and other forms of matter are that they are continuous and they deform internally
P 1 P * 1 T P * 1 T 1 T * 1. s 1 P 1
 ME 131B Fluid Mechanics Solutions to Week Three Problem Session: Isentropic Flow II (1/26/98) 1. From an energy view point, (a) a nozzle is a device that converts static enthalpy into kinetic energy. (b)
ME 131B Fluid Mechanics Solutions to Week Three Problem Session: Isentropic Flow II (1/26/98) 1. From an energy view point, (a) a nozzle is a device that converts static enthalpy into kinetic energy. (b)
Physics 451/551 Theoretical Mechanics. G. A. Krafft Old Dominion University Jefferson Lab Lecture 18
 Physics 451/551 Theoretical Mechanics G. A. Krafft Old Dominion University Jefferson Lab Lecture 18 Theoretical Mechanics Fall 018 Properties of Sound Sound Waves Requires medium for propagation Mainly
Physics 451/551 Theoretical Mechanics G. A. Krafft Old Dominion University Jefferson Lab Lecture 18 Theoretical Mechanics Fall 018 Properties of Sound Sound Waves Requires medium for propagation Mainly
The Equations of Motion in a Rotating Coordinate System. Chapter 3
 The Equations of Motion in a Rotating Coordinate System Chapter 3 Since the earth is rotating about its axis and since it is convenient to adopt a frame of reference fixed in the earth, we need to study
The Equations of Motion in a Rotating Coordinate System Chapter 3 Since the earth is rotating about its axis and since it is convenient to adopt a frame of reference fixed in the earth, we need to study
Vortex motion. Wasilij Barsukow, July 1, 2016
 The concept of vorticity We call Vortex motion Wasilij Barsukow, mail@sturzhang.de July, 206 ω = v vorticity. It is a measure of the swirlyness of the flow, but is also present in shear flows where the
The concept of vorticity We call Vortex motion Wasilij Barsukow, mail@sturzhang.de July, 206 ω = v vorticity. It is a measure of the swirlyness of the flow, but is also present in shear flows where the
ρ x + fv f 'w + F x ρ y fu + F y Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ Dv Dt + u2 tanφ + vw a a = 1 p Dw Dt u2 + v 2
 Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Fundamental Equation in z coordinate p = ρrt or pα = RT Du uv tanφ + uw Dt a a = 1 p ρ x + fv f 'w + F x Dv Dt + u2 tanφ + vw a a = 1 p ρ y fu + F y Dw Dt u2 + v 2 = 1 p a ρ z g + f 'u + F z Dρ Dt + ρ
Quasi-geostrophic ocean models
 Quasi-geostrophic ocean models March 19, 2002 1 Introduction The starting point for theoretical and numerical study of the three dimensional large-scale circulation of the atmosphere and ocean is a vorticity
Quasi-geostrophic ocean models March 19, 2002 1 Introduction The starting point for theoretical and numerical study of the three dimensional large-scale circulation of the atmosphere and ocean is a vorticity
 Tutorial Materials for ME 131B Fluid Mechanics (Compressible Flow & Turbomachinery) Calvin Lui Department of Mechanical Engineering Stanford University Stanford, CA 94305 March 1998 Acknowledgments This
Tutorial Materials for ME 131B Fluid Mechanics (Compressible Flow & Turbomachinery) Calvin Lui Department of Mechanical Engineering Stanford University Stanford, CA 94305 March 1998 Acknowledgments This
Conservation of Mass Conservation of Energy Scaling Analysis. ESS227 Prof. Jin-Yi Yu
 Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
Lecture 2: Basic Conservation Laws Conservation of Momentum Conservation of Mass Conservation of Energy Scaling Analysis Conservation Law of Momentum Newton s 2 nd Law of Momentum = absolute velocity viewed
PV Thinking. What is PV thinking?
 PV Thinking CH 06 What is PV thinking? Two main approaches to solving fluid flow problems:. We can integrate the momentum, continuity and thermodynamic equations (the primitive equations) directly.. In
PV Thinking CH 06 What is PV thinking? Two main approaches to solving fluid flow problems:. We can integrate the momentum, continuity and thermodynamic equations (the primitive equations) directly.. In
Newton's second law of motion
 OpenStax-CNX module: m14042 1 Newton's second law of motion Sunil Kumar Singh This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 2.0 Abstract Second law of
OpenStax-CNX module: m14042 1 Newton's second law of motion Sunil Kumar Singh This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 2.0 Abstract Second law of
ATMO 551a Fall The Carnot Cycle
 What is a arnot ycle and Why do we care The arnot ycle arnot was a French engineer who was trying to understand how to extract usable mechanical work from a heat engine, that is an engine where a gas or
What is a arnot ycle and Why do we care The arnot ycle arnot was a French engineer who was trying to understand how to extract usable mechanical work from a heat engine, that is an engine where a gas or
d v 2 v = d v d t i n where "in" and "rot" denote the inertial (absolute) and rotating frames. Equation of motion F =
 Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
Governing equations of fluid dynamics under the influence of Earth rotation (Navier-Stokes Equations in rotating frame) Recap: From kinematic consideration, d v i n d t i n = d v rot d t r o t 2 v rot
Introduction to Turbomachinery
 1. Coordinate System Introduction to Turbomachinery Since there are stationary and rotating blades in turbomachines, they tend to form a cylindrical form, represented in three directions; 1. Axial 2. Radial
1. Coordinate System Introduction to Turbomachinery Since there are stationary and rotating blades in turbomachines, they tend to form a cylindrical form, represented in three directions; 1. Axial 2. Radial
Navier-Stokes Equation: Principle of Conservation of Momentum
 Navier-tokes Equation: Principle of Conservation of Momentum R. hankar ubramanian Department of Chemical and Biomolecular Engineering Clarkson University Newton formulated the principle of conservation
Navier-tokes Equation: Principle of Conservation of Momentum R. hankar ubramanian Department of Chemical and Biomolecular Engineering Clarkson University Newton formulated the principle of conservation
10 Shallow Water Models
 10 Shallow Water Models So far, we have studied the effects due to rotation and stratification in isolation. We then looked at the effects of rotation in a barotropic model, but what about if we add stratification
10 Shallow Water Models So far, we have studied the effects due to rotation and stratification in isolation. We then looked at the effects of rotation in a barotropic model, but what about if we add stratification
Basic hydrodynamics. David Gurarie. 1 Newtonian fluids: Euler and Navier-Stokes equations
 Basic hydrodynamics David Gurarie 1 Newtonian fluids: Euler and Navier-Stokes equations The basic hydrodynamic equations in the Eulerian form consist of conservation of mass, momentum and energy. We denote
Basic hydrodynamics David Gurarie 1 Newtonian fluids: Euler and Navier-Stokes equations The basic hydrodynamic equations in the Eulerian form consist of conservation of mass, momentum and energy. We denote
General Solution of the Incompressible, Potential Flow Equations
 CHAPTER 3 General Solution of the Incompressible, Potential Flow Equations Developing the basic methodology for obtaining the elementary solutions to potential flow problem. Linear nature of the potential
CHAPTER 3 General Solution of the Incompressible, Potential Flow Equations Developing the basic methodology for obtaining the elementary solutions to potential flow problem. Linear nature of the potential
Hour Exam #2 Physical Mechanics Monday, November 6, Total 100 Points Time to complete the test: 60 minutes. Answers
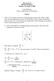 Hour Exam #2 Physical Mechanics Monday, November 6, 2000 Total 100 Points Time to complete the test: 60 minutes Answers 1. (20%) A N-S oriented cold front is passing through Norman. The surface weather
Hour Exam #2 Physical Mechanics Monday, November 6, 2000 Total 100 Points Time to complete the test: 60 minutes Answers 1. (20%) A N-S oriented cold front is passing through Norman. The surface weather
Review of fluid dynamics
 Chapter 2 Review of fluid dynamics 2.1 Preliminaries ome basic concepts: A fluid is a substance that deforms continuously under stress. A Material olume is a tagged region that moves with the fluid. Hence
Chapter 2 Review of fluid dynamics 2.1 Preliminaries ome basic concepts: A fluid is a substance that deforms continuously under stress. A Material olume is a tagged region that moves with the fluid. Hence
Control Volume. Dynamics and Kinematics. Basic Conservation Laws. Lecture 1: Introduction and Review 1/24/2017
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review
 Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
Lecture 1: Introduction and Review Review of fundamental mathematical tools Fundamental and apparent forces Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study
1/25/2010. Circulation and vorticity are the two primary
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Prototype Instabilities
 Prototype Instabilities David Randall Introduction Broadly speaking, a growing atmospheric disturbance can draw its kinetic energy from two possible sources: the kinetic and available potential energies
Prototype Instabilities David Randall Introduction Broadly speaking, a growing atmospheric disturbance can draw its kinetic energy from two possible sources: the kinetic and available potential energies
Physics Dec Time Independent Solutions of the Diffusion Equation
 Physics 301 10-Dec-2004 33-1 Time Independent Solutions of the Diffusion Equation In some cases we ll be interested in the time independent solution of the diffusion equation Why would be interested in
Physics 301 10-Dec-2004 33-1 Time Independent Solutions of the Diffusion Equation In some cases we ll be interested in the time independent solution of the diffusion equation Why would be interested in
t tendency advection convergence twisting baroclinicity
 RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
RELATIVE VORTICITY EQUATION Newton s law in a rotating frame in z-coordinate (frictionless): U + U U = 2Ω U Φ α p U + U U 2 + ( U) U = 2Ω U Φ α p Applying to both sides, and noting ω U and using identities
Generalizing the Boussinesq Approximation to Stratified Compressible Flow
 Generalizing the Boussinesq Approximation to Stratified Compressible Flow Dale R. Durran a Akio Arakawa b a University of Washington, Seattle, USA b University of California, Los Angeles, USA Abstract
Generalizing the Boussinesq Approximation to Stratified Compressible Flow Dale R. Durran a Akio Arakawa b a University of Washington, Seattle, USA b University of California, Los Angeles, USA Abstract
GFD 2012 Lecture 1: Dynamics of Coherent Structures and their Impact on Transport and Predictability
 GFD 2012 Lecture 1: Dynamics of Coherent Structures and their Impact on Transport and Predictability Jeffrey B. Weiss; notes by Duncan Hewitt and Pedram Hassanzadeh June 18, 2012 1 Introduction 1.1 What
GFD 2012 Lecture 1: Dynamics of Coherent Structures and their Impact on Transport and Predictability Jeffrey B. Weiss; notes by Duncan Hewitt and Pedram Hassanzadeh June 18, 2012 1 Introduction 1.1 What
Point Vortex Dynamics in Two Dimensions
 Spring School on Fluid Mechanics and Geophysics of Environmental Hazards 9 April to May, 9 Point Vortex Dynamics in Two Dimensions Ruth Musgrave, Mostafa Moghaddami, Victor Avsarkisov, Ruoqian Wang, Wei
Spring School on Fluid Mechanics and Geophysics of Environmental Hazards 9 April to May, 9 Point Vortex Dynamics in Two Dimensions Ruth Musgrave, Mostafa Moghaddami, Victor Avsarkisov, Ruoqian Wang, Wei
Measurement of Rotation. Circulation. Example. Lecture 4: Circulation and Vorticity 1/31/2017
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
4. Atmospheric transport. Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017
 4. Atmospheric transport Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017 Forces in the atmosphere: Gravity g Pressure-gradient ap = ( 1/ ρ ) dp / dx for x-direction (also y, z directions)
4. Atmospheric transport Daniel J. Jacob, Atmospheric Chemistry, Harvard University, Spring 2017 Forces in the atmosphere: Gravity g Pressure-gradient ap = ( 1/ ρ ) dp / dx for x-direction (also y, z directions)
2. Equations of Stellar Structure
 2. Equations of Stellar Structure We already discussed that the structure of stars is basically governed by three simple laws, namely hyostatic equilibrium, energy transport and energy generation. In this
2. Equations of Stellar Structure We already discussed that the structure of stars is basically governed by three simple laws, namely hyostatic equilibrium, energy transport and energy generation. In this
( ) = 1005 J kg 1 K 1 ;
 Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
Lecture 1: Introduction to Linear and Non-Linear Waves
 Lecture 1: Introduction to Linear and Non-Linear Waves Lecturer: Harvey Segur. Write-up: Michael Bates June 15, 2009 1 Introduction to Water Waves 1.1 Motivation and Basic Properties There are many types
Lecture 1: Introduction to Linear and Non-Linear Waves Lecturer: Harvey Segur. Write-up: Michael Bates June 15, 2009 1 Introduction to Water Waves 1.1 Motivation and Basic Properties There are many types
Lecture 2. Lecture 1. Forces on a rotating planet. We will describe the atmosphere and ocean in terms of their:
 Lecture 2 Lecture 1 Forces on a rotating planet We will describe the atmosphere and ocean in terms of their: velocity u = (u,v,w) pressure P density ρ temperature T salinity S up For convenience, we will
Lecture 2 Lecture 1 Forces on a rotating planet We will describe the atmosphere and ocean in terms of their: velocity u = (u,v,w) pressure P density ρ temperature T salinity S up For convenience, we will
Equations of linear stellar oscillations
 Chapter 4 Equations of linear stellar oscillations In the present chapter the equations governing small oscillations around a spherical equilibrium state are derived. The general equations were presented
Chapter 4 Equations of linear stellar oscillations In the present chapter the equations governing small oscillations around a spherical equilibrium state are derived. The general equations were presented
MAE 101A. Homework 7 - Solutions 3/12/2018
 MAE 101A Homework 7 - Solutions 3/12/2018 Munson 6.31: The stream function for a two-dimensional, nonviscous, incompressible flow field is given by the expression ψ = 2(x y) where the stream function has
MAE 101A Homework 7 - Solutions 3/12/2018 Munson 6.31: The stream function for a two-dimensional, nonviscous, incompressible flow field is given by the expression ψ = 2(x y) where the stream function has
Physics 451/551 Theoretical Mechanics. G. A. Krafft Old Dominion University Jefferson Lab Lecture 18
 Physics 451/551 Theoretical Mechanics G. A. Krafft Old Dominion University Jefferson Lab Lecture 18 Theoretical Mechanics Fall 18 Properties of Sound Sound Waves Requires medium for propagation Mainly
Physics 451/551 Theoretical Mechanics G. A. Krafft Old Dominion University Jefferson Lab Lecture 18 Theoretical Mechanics Fall 18 Properties of Sound Sound Waves Requires medium for propagation Mainly
Vorticity in natural coordinates
 Vorticity in natural coordinates (see Holton pg 95, section 4.2.) Let s consider the vertical vorticity component only, i.e. ζ kˆ ω, we have ω u dl kˆ ω lim --- lim ----------------- curve is in xy plane
Vorticity in natural coordinates (see Holton pg 95, section 4.2.) Let s consider the vertical vorticity component only, i.e. ζ kˆ ω, we have ω u dl kˆ ω lim --- lim ----------------- curve is in xy plane
Worked Examples Set 2
 Worked Examples Set 2 Q.1. Application of Maxwell s eqns. [Griffiths Problem 7.42] In a perfect conductor the conductivity σ is infinite, so from Ohm s law J = σe, E = 0. Any net charge must be on the
Worked Examples Set 2 Q.1. Application of Maxwell s eqns. [Griffiths Problem 7.42] In a perfect conductor the conductivity σ is infinite, so from Ohm s law J = σe, E = 0. Any net charge must be on the
AA210A Fundamentals of Compressible Flow. Chapter 1 - Introduction to fluid flow
 AA210A Fundamentals of Compressible Flow Chapter 1 - Introduction to fluid flow 1 1.2 Conservation of mass Mass flux in the x-direction [ ρu ] = M L 3 L T = M L 2 T Momentum per unit volume Mass per unit
AA210A Fundamentals of Compressible Flow Chapter 1 - Introduction to fluid flow 1 1.2 Conservation of mass Mass flux in the x-direction [ ρu ] = M L 3 L T = M L 2 T Momentum per unit volume Mass per unit
Chapter 9. Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation
 Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Chapter 9 Geostrophy, Quasi-Geostrophy and the Potential Vorticity Equation 9.1 Geostrophy and scaling. We examined in the last chapter some consequences of the dynamical balances for low frequency, nearly
Chapter 4: Fundamental Forces
 Chapter 4: Fundamental Forces Newton s Second Law: F=ma In atmospheric science it is typical to consider the force per unit mass acting on the atmosphere: Force mass = a In order to understand atmospheric
Chapter 4: Fundamental Forces Newton s Second Law: F=ma In atmospheric science it is typical to consider the force per unit mass acting on the atmosphere: Force mass = a In order to understand atmospheric
UNIVERSITY of LIMERICK
 UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH Faculty of Science and Engineering END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA4607 SEMESTER: Autumn 2012-13 MODULE TITLE: Introduction to Fluids DURATION OF
UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH Faculty of Science and Engineering END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA4607 SEMESTER: Autumn 2012-13 MODULE TITLE: Introduction to Fluids DURATION OF
Fundamentals of Fluid Dynamics: Elementary Viscous Flow
 Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
Fundamentals of Fluid Dynamics: Elementary Viscous Flow Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI bluebox.ippt.pan.pl/ tzielins/ Institute of Fundamental Technological Research
Work - kinetic energy theorem for rotational motion *
 OpenStax-CNX module: m14307 1 Work - kinetic energy theorem for rotational motion * Sunil Kumar Singh This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 2.0
OpenStax-CNX module: m14307 1 Work - kinetic energy theorem for rotational motion * Sunil Kumar Singh This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 2.0
Homework Two. Abstract: Liu. Solutions for Homework Problems Two: (50 points total). Collected by Junyu
 Homework Two Abstract: Liu. Solutions for Homework Problems Two: (50 points total). Collected by Junyu Contents 1 BT Problem 13.15 (8 points) (by Nick Hunter-Jones) 1 2 BT Problem 14.2 (12 points: 3+3+3+3)
Homework Two Abstract: Liu. Solutions for Homework Problems Two: (50 points total). Collected by Junyu Contents 1 BT Problem 13.15 (8 points) (by Nick Hunter-Jones) 1 2 BT Problem 14.2 (12 points: 3+3+3+3)
CHAPTER 8 ENTROPY GENERATION AND TRANSPORT
 CHAPTER 8 ENTROPY GENERATION AND TRANSPORT 8.1 CONVECTIVE FORM OF THE GIBBS EQUATION In this chapter we will address two questions. 1) How is Gibbs equation related to the energy conservation equation?
CHAPTER 8 ENTROPY GENERATION AND TRANSPORT 8.1 CONVECTIVE FORM OF THE GIBBS EQUATION In this chapter we will address two questions. 1) How is Gibbs equation related to the energy conservation equation?
7 The General Circulation
 7 The General Circulation 7.1 The axisymmetric state At the beginning of the class, we discussed the nonlinear, inviscid, axisymmetric theory of the meridional structure of the atmosphere. The important
7 The General Circulation 7.1 The axisymmetric state At the beginning of the class, we discussed the nonlinear, inviscid, axisymmetric theory of the meridional structure of the atmosphere. The important
PHYS 432 Physics of Fluids: Instabilities
 PHYS 432 Physics of Fluids: Instabilities 1. Internal gravity waves Background state being perturbed: A stratified fluid in hydrostatic balance. It can be constant density like the ocean or compressible
PHYS 432 Physics of Fluids: Instabilities 1. Internal gravity waves Background state being perturbed: A stratified fluid in hydrostatic balance. It can be constant density like the ocean or compressible
6 Two-layer shallow water theory.
 6 Two-layer shallow water theory. Wewillnowgoontolookatashallowwatersystemthathastwolayersofdifferent density. This is the next level of complexity and a simple starting point for understanding the behaviour
6 Two-layer shallow water theory. Wewillnowgoontolookatashallowwatersystemthathastwolayersofdifferent density. This is the next level of complexity and a simple starting point for understanding the behaviour
Chapter 5. The Differential Forms of the Fundamental Laws
 Chapter 5 The Differential Forms of the Fundamental Laws 1 5.1 Introduction Two primary methods in deriving the differential forms of fundamental laws: Gauss s Theorem: Allows area integrals of the equations
Chapter 5 The Differential Forms of the Fundamental Laws 1 5.1 Introduction Two primary methods in deriving the differential forms of fundamental laws: Gauss s Theorem: Allows area integrals of the equations
Boundary Conditions in Fluid Mechanics
 Boundary Conditions in Fluid Mechanics R. Shankar Subramanian Department of Chemical and Biomolecular Engineering Clarkson University The governing equations for the velocity and pressure fields are partial
Boundary Conditions in Fluid Mechanics R. Shankar Subramanian Department of Chemical and Biomolecular Engineering Clarkson University The governing equations for the velocity and pressure fields are partial
1/3/2011. This course discusses the physical laws that govern atmosphere/ocean motions.
 Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Lecture 1: Introduction and Review Dynamics and Kinematics Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. Dynamics: On the other hand, dynamics
Fundamentals of Atmospheric Modelling
 M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
Chapter 7: Circulation and Vorticity
 Chapter 7: Circulation and Vorticity Circulation C = u ds Integration is performed in a counterclockwise direction C is positive for counterclockwise flow!!! Kelvin s Circulation Theorem The rate of change
Chapter 7: Circulation and Vorticity Circulation C = u ds Integration is performed in a counterclockwise direction C is positive for counterclockwise flow!!! Kelvin s Circulation Theorem The rate of change
Fundamentals of Fluid Dynamics: Waves in Fluids
 Fundamentals of Fluid Dynamics: Waves in Fluids Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI (after: D.J. ACHESON s Elementary Fluid Dynamics ) bluebox.ippt.pan.pl/ tzielins/ Institute
Fundamentals of Fluid Dynamics: Waves in Fluids Introductory Course on Multiphysics Modelling TOMASZ G. ZIELIŃSKI (after: D.J. ACHESON s Elementary Fluid Dynamics ) bluebox.ippt.pan.pl/ tzielins/ Institute
3 Generation and diffusion of vorticity
 Version date: March 22, 21 1 3 Generation and diffusion of vorticity 3.1 The vorticity equation We start from Navier Stokes: u t + u u = 1 ρ p + ν 2 u 1) where we have not included a term describing a
Version date: March 22, 21 1 3 Generation and diffusion of vorticity 3.1 The vorticity equation We start from Navier Stokes: u t + u u = 1 ρ p + ν 2 u 1) where we have not included a term describing a
Topics in Fluid Dynamics: Classical physics and recent mathematics
 Topics in Fluid Dynamics: Classical physics and recent mathematics Toan T. Nguyen 1,2 Penn State University Graduate Student Seminar @ PSU Jan 18th, 2018 1 Homepage: http://math.psu.edu/nguyen 2 Math blog:
Topics in Fluid Dynamics: Classical physics and recent mathematics Toan T. Nguyen 1,2 Penn State University Graduate Student Seminar @ PSU Jan 18th, 2018 1 Homepage: http://math.psu.edu/nguyen 2 Math blog:
Divergence Theorem and Its Application in Characterizing
 Divergence Theorem and Its Application in Characterizing Fluid Flow Let v be the velocity of flow of a fluid element and ρ(x, y, z, t) be the mass density of fluid at a point (x, y, z) at time t. Thus,
Divergence Theorem and Its Application in Characterizing Fluid Flow Let v be the velocity of flow of a fluid element and ρ(x, y, z, t) be the mass density of fluid at a point (x, y, z) at time t. Thus,
