Continuity and One-Sided Limits
|
|
|
- Edith Barnett
- 5 years ago
- Views:
Transcription
1 Continuity and One-Sided Limits 1. Welcome to continuity and one-sided limits. My name is Tuesday Johnson and I m a lecturer at the University of Texas El Paso. 2. With each lecture I present, I will start you off with a list of skills for the topic at hand. You can find most of these reviews on my website, but if that doesn t work for you, you can find them pretty much anywhere in the internet world. My favorite places to look are Khan Academy and Math is Power 4 U. The skills for this lecture include evaluating functions, rationalizing numerators and/or denominators, evaluating trigonometric functions, and basic quotient and reciprocal identities. 3. Let s get started with Calculus I Limits and Their Properties: Continuity and One-Sided Limits. This lecture corresponds to Larson s Calculus, 10 th edition, section It is always a good idea to start with a definition. What is continuity? In previous courses you may have heard a continuous function explained as one that you can draw the graph of without lifting your writing implement. That is, it has no holes, breaks, jumps or anything else of that type. This is still true but now we define it in mathematical terms using our limits. The definition states that a function f is continuous at a value x = c if the following three conditions are met. First, the function must be defined at x = c. Second, the limit as x approaches c of f of x must exist. The importance of the third condition is too frequently overlooked. This condition states that not only does the function value exist and not only does the limit exist, but they MUST be equal to each other. For a function to be continuous on an open interval, it must be continuous at each point in the interval. 5. Sometimes it is beneficial to see what happens when conditions are NOT met. On this slide we see from the graph on the left that a hole appears if the function is not defined at a specific x value. This is not a continuous function. The middle graph shows that the function is defined, as the solid dot indicates, but the limit does not exist. Finally, the graph on the right shows that the function value exists, the limit exists, but they are not equal. All three of these graphs are graphs of functions that are not continuous. 6. Sometimes a function will have different behavior to the left and right of the value c under question. When this happens we will look at one sided limits. That is, a limit just on the right of the given value. Or a limit just on the left of the given value. In order to do so we will need a notation. Our notation comes from the standard number line that everyone is used to with negatives on the left and positives on the right. 7. The notation we see here shows a superscript of a positive sign to indicate we should only look to the right of the value c. What this means is that we only look at values above c numerically, or to the right of c on a standard number line or on the x-axis of a rectangular coordinate system. The superscript of a negative sign indicates we should only look at what is happening as the x values get closer and closer to c from the left.
2 8. We ve been talking about limits for a couple of sections already. But only now are we able to state when a limit will exist. In fact, a function f can only be continuous at the real value c if the limit from the right is equal to the limit from the left. Another way to think of this is that the limit exists overall if and only if the limits from each side exist and are equal to each other. 9. For this random graph, the blue portion shows the x values to the left of c and the green portion shows the values to the right of c. As x approaches c from the left (I encourage you to use your finger to actually start from the left side of the graph and follow f of x until the x value gets to c.) we see that the graph gets close to the y value of 2. However, if we follow the green portion from the extreme right of the graph and move it toward c, we see that the graph gets close to the y value of negative three. Since the limit from the right is not equal to the limit from the left, the overall limit does not exist for f of x at x = c in this graph. 10. We started this lecture defining continuity at a point and on an open interval. Now that we have one-sided limits we can define continuity on a closed interval as well. A function f is continuous on the closed interval from a to b it if is continuous on the open interval from a to b and the limit from the right as x approaches a is equal to f of a and the limit from the left as x approaches b is equal to f of b. 11. If you would like to try these problems before I go over them, pause the video and try them now. 12. Every time we want to find a limit, we start by trying our previous tricks. On number one we first try to evaluate. This results in zero divided by zero which is undefined. When we get zero over zero we know something can be done. In this case we can factor a negative one from the numerator and use the difference of squares formula on the denominator. Canceling the common factor allows us to try and evaluate once again. The fact that this limit was approaching 2 from the right had no bearing on the answer. But that is not always the case. In problem two we are approaching 10 from the left. The numerator and denominator have the same factor, but the numerator will never be negative. This means that they will always have the same value with possibly different signs. When we approach 10 from the left we are using values smaller than 10 so when we subtract ten from a smaller number the denominator will be negative. This will give us positive divided by negative of the same number resulting in the negative one answer. Keep in mind that if we tried to substitute ten at the start we would end up with zero divided by zero again. This is why zero over zero is called an indeterminate form; in problem one it simplified to be -1/4 and in problem two it simplified to Whether finding an algebraic or trigonometric limit we always want to start by evaluating to see what happens. In the case of cotangent, we know this as the quotient identity cosine divided by sine. But when we evaluate at pi, we get -1 divided by 0. Since we have a non-zero numerator and a zero denominator, this limit does not exist. In this situation there is nothing we can do to simplify away the zero in the denominator. Looking at the graph of cotangent we see an asymptote at x equals pi with the limit from the left going to negative infinity and the limit from the right going toward positive infinity. As the one-sided limits are not equal, no limit exists. 14. Evaluating the limit of any function requires you to recognize the type of function it is in the first place. Recall the greatest integer function, with the graph given, has output of the largest integer that is less than or equal to the input. Pre-Calculus notes on my website cover this
3 function in section 1.6. As we approach 4 from the right (the superscript + sign), the values of x are a little larger than 4. The greatest integer of values a little larger than 4 is 4. Upon evaluation we find the limit to be Piece-wise defined functions are only tricky if you let them be. For the most part, you can evaluate the limit of a piece-wise function by evaluating the function itself. The exceptions occur when you have a non-continuous piece or at cut values. Cut values are where the domain cuts from one piece to the next. In this example, that is at the x value of 3. Notice that the limit has x approaching 3 from the left. Which piece of this function should we use? We will only consider the top piece of the function as it has a domain for x values less than or equal to 3. Finally, to actually evaluate the limit we substitute the x value of 3 in the top rule and end up with a limit of 5/ Now that we know what continuity is and how to determine if a function is continuous, let s look at a few properties. For any real number b with function f and g continuous at x = c, then any scalar multiple of one of those functions is also continuous. The sum and/or difference of continuous functions is also continuous. The product of continuous functions is continuous. Finally, the quotient of continuous functions is continuous as long as you have a non-zero denominator. All of these properties taken together mean that most elementary functions are continuous on their domains. The key points to consider are values not in the domain. 17. Pause here if you would like to try these examples on your own before I go through them. 18. Our goal is to find a constant, called a, in order to make this piece-wise defined function continuous everywhere. By initial inspection, we know each piece is continuous on its domain. The only value we really must consider is the cut-value; if the function is made to be continuous at the cut value then it will be continuous on the entire real line. In order to be continuous at the cut value, the limit from the left must be equal to the limit from the right and these must be equal to the function value itself. 19. First, we evaluate the limit as x approaches 1 from the left using the bottom piece (x values less than 1) to get a limit of a 3. Second, we evaluate the limit as x approaches 1 from the right using the top piece (x values greater than or equal to 1) to get a limit of Notice that the limit from the right is the same as the function value since it s domain had the or equal to in the restriction. For this function to be continuous it must be that a 3 = 2 and so a must be Again we look at the function in pieces. The top piece is continuous everywhere except at x = 0, but it is not defined at x = 0 so it is continuous on its domain. The bottom piece is a linear function and so is continuous on its domain. The only place this function may not be continuous is the cut value. We evaluate the limit from the left of 0 to get 9. Notice this used a special limit that we learned in an earlier section. We evaluate the limit from the right of 0 to get a. This means that a = In this problem we are looking for two constants, both a and b. Our strategy will be to take this one cut value at a time and see what happens. 23. At the x value of -3, we use the top two pieces; the limit from the left is 4 and the limit from the right is -3a b. If this function is going to be continuous at x = -3 we must have -3a b = 4. This doesn t allow us to solve for a or b so let s try the same thing at the cut value of x = 2 using the
4 bottom two pieces. The limit from the right is -4 and the limit from the left is 2a b. To be continuous it must be that 2a b = -4. Again, no information about a or b specifically. However, we have two equations and two unknowns so we can solve this as a system of equations. 24. Solving this system of equations is an algebra problem, not a calculus problem, so review as needed. In this particular case we find that a = -8/5 and b = 4/5 in order to make the function h of x continuous on the entire real line. 25. Once again, pause here if you would like to attempt to work on these problems prior to hearing my explanation. It is always a good idea to try some examples on your own rather than having me work them all for you. We learn from mistakes, but rarely from successes. We wish to find the x values, if any at which the given functions are not continuous. Remember, most elementary functions are continuous on their domains. This means we need to check values that are NOT in the domains of the given functions. 26. To determine if a discontinuity is removable, we need to know that removable discontinuities are the ones in which we can factor and cancel or otherwise deal with the indeterminate form of 0 divided by 0. Our first example has a domain of all real numbers except x = 2. When we check the one-sided limits at x = 2, we find that the limit from the left approaches negative infinity and the limit from the right approaches positive infinity. Therefore this function is not continuous at x = 2 and it is not removable (in fact, it is an asymptote). 27. Polynomials are defined on all real numbers and are also continuous on all real numbers. 28. Again, we check for values where the function is undefined. For rational functions, this is where the denominator is zero. However, x squared is always 0 or greater and then when you add one you find that this denominator is 1 or greater and therefore is never zero. Since the domain consists of all real numbers, the function is continuous everywhere. 29. When setting this denominator to zero and solving we find discontinuities (values where the function is undefined) at plus and minus 1. The limits as we approach either plus or minus one have the form of a non-zero value (specifically 1 or -1) divided by zero. This is not a removable discontinuity. 30. We frequently just look at the denominator of a rational expression, but the numerator is important too. If we simplify (factor) the rational function that is number 5 we find that x minus 6 is divided by the product of x plus 6 and x minus 6. There are discontinuities at both x equals 6 and x equals negative 6. However, the discontinuity at x = 6 is removable as you can cancel those factors to simplify the function. Another way of thinking about this is when you evaluate the limit as x approaches 6 you get zero divided by zero so something can be done at it is removable. However as x approaches -6 you get a non-zero number divided by zero as the limit and it is therefore not removable. 31. Piece-wise defined functions look more complicated that other functions, but taken a piece at a time they are many times easier to deal with. We know that each piece is a polynomial and every polynomial is continuous on its domain. Therefore we only have to check the cut value of x at Checking the limits from both the left and right we find the limit exists, the function value exists, and they are all Therefore this function is continuous everywhere.
5 34. Our first fact on this page tells us that continuity behaves nicely through composition. This is due to the fact that limits behave nicely through composition of functions. The Intermediate Value Theorem (which I abbreviate as IVT) is an important theorem. Most theorems are important, but the ones with actual names are always going to be the most important. The intermediate value theorem states that if you start with a continuous function on a closed interval where the heights of the endpoints are not equal and k is some number between the heights of the endpoints, then there must be at least one number c in the closed interval such that f evaluated at c is equal to k. One quick way to think of this is driving. As I start in my car at 0 mph I get up to the speed limit of 75 mph and set the cruise control. My driving is a continuous function, the closed interval is a set amount of time that I m driving and the endpoint heights are the speeds of 0 and 75 mph. The IVT states that there had to have been a time (the c value) at which I was going exactly 55 mph, the k value. 35. Let s look at two examples of verifying that the intermediate value theorem applies and then finding the c value. The first will be a polynomial and the second a rational function. 36. Our first function is f of x equals x squared minus 6x plus 8 and we are focusing on the closed interval from 0 to 3. This interval is the x values that we are considering. If the IVT applies, we will want to find a c value, between 0 and 3, such that f evaluated at c is equal to zero. Our first step is to make sure the IVT applies. (a) Since the function is a polynomial we know it is continuous on its domain. (b) Next, we check the values of the endpoints. F evaluated at 0 is 8 and f evaluated at 3 is -1 so the values of the endpoints are not equal. (c) Finally, the k value of zero is between 8 and -1 so we know the IVT applies. 37. Finding the c value such that f of c is equal to zero amounts to evaluating the function at c and setting it equal to zero. We can factor c squared minus 6c plus 8 as the product of c minus 4 and c minus 2. Keep in mind this is still and equation and so still equal to zero. We know use our algebra skills of the zero factor property which states that if two things multiply to be zero then one or the other (or both) is zero. This tells us that c = 4 or c = 2. Both answers are tempting; beware of the original problem. We have to keep our results in the closed interval from 0 to 3 and 4 it outside that. The only answer we would report is c = For the rational function, we once again start by verifying that it fits the conditions of the intermediate value theorem. This is a rational function with a discontinuity at x = 1 (where the denominator is zero). However, the only discontinuity is NOT in the given interval. Therefore this function is continuous on the given closed interval. If we evaluate the endpoints we get outputs of 35/6 (a little less than 6) and 20/3 (a little more than 6). The k value of 6 given in f of c equals 6 is between the two endpoint heights and so this function with its closed interval and k fit all the necessary conditions of the intermediate value theorem. 39. Our next goal is to find c. We evaluate the function at c and set it equal to 6. Multiply both sides of the equation by the denominator of c minus 1 to arrive at a polynomial equation of c squared plus c equals 6c minus Setting this equation equal to zero, then factoring, and finally solving for c yields two answers once again. Make sure you check the original interval as c = 2 is NOT a solution but c = 3 is.
6 41. One last example. Suppose at 8 AM on Saturday a man (a crazy man it sounds like) begins running up the side of a mountain to his weekend campsite. On Sunday morning at 8 AM he runs back down the mountain. It takes him 20 minutes to run up, but only 10 minutes to run down. At some point on the way down, he realizes (because he s super smart like that) that he passed the same place at exactly the same time on Saturday. Prove that he is correct. 42. Let s remember that math problems are frequently wacky to make for good examples and put common sense aside. I have chosen to graph the two days with Saturday in purple starting at base and running up to camp and Sunday in green starting at camp and running down to base. Notice that since he does not have teleportation powers, his run is a continuous line from start to finish. Even though the times are different, his trail from Saturday did cross his trail from Sunday at some time in the first ten minutes. This is where, and when, he was in the same place at the same time. 43. This marks the end of continuity and one-sided limits. Thank you for your time.
Continuity and One-Sided Limits. By Tuesday J. Johnson
 Continuity and One-Sided Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Rationalizing numerators and/or denominators Trigonometric skills reviews
Continuity and One-Sided Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Rationalizing numerators and/or denominators Trigonometric skills reviews
Finding Limits Graphically and Numerically
 Finding Limits Graphically and Numerically 1. Welcome to finding limits graphically and numerically. My name is Tuesday Johnson and I m a lecturer at the University of Texas El Paso. 2. With each lecture
Finding Limits Graphically and Numerically 1. Welcome to finding limits graphically and numerically. My name is Tuesday Johnson and I m a lecturer at the University of Texas El Paso. 2. With each lecture
Infinite Limits. Infinite Limits. Infinite Limits. Previously, we discussed the limits of rational functions with the indeterminate form 0/0.
 Infinite Limits Return to Table of Contents Infinite Limits Infinite Limits Previously, we discussed the limits of rational functions with the indeterminate form 0/0. Now we will consider rational functions
Infinite Limits Return to Table of Contents Infinite Limits Infinite Limits Previously, we discussed the limits of rational functions with the indeterminate form 0/0. Now we will consider rational functions
3.3 Limits and Infinity
 Calculus Maimus. Limits Infinity Infinity is not a concrete number, but an abstract idea. It s not a destination, but a really long, never-ending journey. It s one of those mind-warping ideas that is difficult
Calculus Maimus. Limits Infinity Infinity is not a concrete number, but an abstract idea. It s not a destination, but a really long, never-ending journey. It s one of those mind-warping ideas that is difficult
O.K. But what if the chicken didn t have access to a teleporter.
 The intermediate value theorem, and performing algebra on its. This is a dual topic lecture. : The Intermediate value theorem First we should remember what it means to be a continuous function: A function
The intermediate value theorem, and performing algebra on its. This is a dual topic lecture. : The Intermediate value theorem First we should remember what it means to be a continuous function: A function
Limits of Functions (a, L)
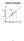 Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
Rational Functions. Elementary Functions. Algebra with mixed fractions. Algebra with mixed fractions
 Rational Functions A rational function f (x) is a function which is the ratio of two polynomials, that is, Part 2, Polynomials Lecture 26a, Rational Functions f (x) = where and are polynomials Dr Ken W
Rational Functions A rational function f (x) is a function which is the ratio of two polynomials, that is, Part 2, Polynomials Lecture 26a, Rational Functions f (x) = where and are polynomials Dr Ken W
1.5 Inverse Trigonometric Functions
 1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
MATH 250 TOPIC 11 LIMITS. A. Basic Idea of a Limit and Limit Laws. Answers to Exercises and Problems
 Math 5 T-Limits Page MATH 5 TOPIC LIMITS A. Basic Idea of a Limit and Limit Laws B. Limits of the form,, C. Limits as or as D. Summary for Evaluating Limits Answers to Eercises and Problems Math 5 T-Limits
Math 5 T-Limits Page MATH 5 TOPIC LIMITS A. Basic Idea of a Limit and Limit Laws B. Limits of the form,, C. Limits as or as D. Summary for Evaluating Limits Answers to Eercises and Problems Math 5 T-Limits
We can see that f(2) is undefined. (Plugging x = 2 into the function results in a 0 in the denominator)
 In order to be successful in AP Calculus, you are expected to KNOW everything that came before. All topics from Algebra I, II, Geometry and of course Precalculus are expected to be mastered before you
In order to be successful in AP Calculus, you are expected to KNOW everything that came before. All topics from Algebra I, II, Geometry and of course Precalculus are expected to be mastered before you
Math 115 Spring 11 Written Homework 10 Solutions
 Math 5 Spring Written Homework 0 Solutions. For following its, state what indeterminate form the its are in and evaluate the its. (a) 3x 4x 4 x x 8 Solution: This is in indeterminate form 0. Algebraically,
Math 5 Spring Written Homework 0 Solutions. For following its, state what indeterminate form the its are in and evaluate the its. (a) 3x 4x 4 x x 8 Solution: This is in indeterminate form 0. Algebraically,
Infinite Limits. By Tuesday J. Johnson
 Infinite Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Graphing functions Working with inequalities Working with absolute values Trigonometric
Infinite Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Graphing functions Working with inequalities Working with absolute values Trigonometric
Limits and Continuity
 Limits and Continuity Philippe B. Laval Kennesaw State University January 2, 2005 Contents Abstract Notes and practice problems on its and continuity. Limits 2. Introduction... 2.2 Theory:... 2.2. GraphicalMethod...
Limits and Continuity Philippe B. Laval Kennesaw State University January 2, 2005 Contents Abstract Notes and practice problems on its and continuity. Limits 2. Introduction... 2.2 Theory:... 2.2. GraphicalMethod...
ter. on Can we get a still better result? Yes, by making the rectangles still smaller. As we make the rectangles smaller and smaller, the
 Area and Tangent Problem Calculus is motivated by two main problems. The first is the area problem. It is a well known result that the area of a rectangle with length l and width w is given by A = wl.
Area and Tangent Problem Calculus is motivated by two main problems. The first is the area problem. It is a well known result that the area of a rectangle with length l and width w is given by A = wl.
AP Calculus AB Summer Assignment
 AP Calculus AB Summer Assignment Name: When you come back to school, it is my epectation that you will have this packet completed. You will be way behind at the beginning of the year if you haven t attempted
AP Calculus AB Summer Assignment Name: When you come back to school, it is my epectation that you will have this packet completed. You will be way behind at the beginning of the year if you haven t attempted
3. LIMITS AND CONTINUITY
 3. LIMITS AND CONTINUITY Algebra reveals much about many functions. However, there are places where the algebra breaks down thanks to division by zero. We have sometimes stated that there is division by
3. LIMITS AND CONTINUITY Algebra reveals much about many functions. However, there are places where the algebra breaks down thanks to division by zero. We have sometimes stated that there is division by
Last week we looked at limits generally, and at finding limits using substitution.
 Math 1314 ONLINE Week 4 Notes Lesson 4 Limits (continued) Last week we looked at limits generally, and at finding limits using substitution. Indeterminate Forms What do you do when substitution gives you
Math 1314 ONLINE Week 4 Notes Lesson 4 Limits (continued) Last week we looked at limits generally, and at finding limits using substitution. Indeterminate Forms What do you do when substitution gives you
MATH 1040 Objectives List
 MATH 1040 Objectives List Textbook: Calculus, Early Transcendentals, 7th edition, James Stewart Students should expect test questions that require synthesis of these objectives. Unit 1 WebAssign problems
MATH 1040 Objectives List Textbook: Calculus, Early Transcendentals, 7th edition, James Stewart Students should expect test questions that require synthesis of these objectives. Unit 1 WebAssign problems
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER / Lines and Their Equations
 ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 017/018 DR. ANTHONY BROWN. Lines and Their Equations.1. Slope of a Line and its y-intercept. In Euclidean geometry (where
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 017/018 DR. ANTHONY BROWN. Lines and Their Equations.1. Slope of a Line and its y-intercept. In Euclidean geometry (where
Continuity. The Continuity Equation The equation that defines continuity at a point is called the Continuity Equation.
 Continuity A function is continuous at a particular x location when you can draw it through that location without picking up your pencil. To describe this mathematically, we have to use limits. Recall
Continuity A function is continuous at a particular x location when you can draw it through that location without picking up your pencil. To describe this mathematically, we have to use limits. Recall
Everything Old Is New Again: Connecting Calculus To Algebra Andrew Freda
 Everything Old Is New Again: Connecting Calculus To Algebra Andrew Freda (afreda@deerfield.edu) ) Limits a) Newton s Idea of a Limit Perhaps it may be objected, that there is no ultimate proportion of
Everything Old Is New Again: Connecting Calculus To Algebra Andrew Freda (afreda@deerfield.edu) ) Limits a) Newton s Idea of a Limit Perhaps it may be objected, that there is no ultimate proportion of
Math Lecture 4 Limit Laws
 Math 1060 Lecture 4 Limit Laws Outline Summary of last lecture Limit laws Motivation Limits of constants and the identity function Limits of sums and differences Limits of products Limits of polynomials
Math 1060 Lecture 4 Limit Laws Outline Summary of last lecture Limit laws Motivation Limits of constants and the identity function Limits of sums and differences Limits of products Limits of polynomials
2. If the values for f(x) can be made as close as we like to L by choosing arbitrarily large. lim
 Limits at Infinity and Horizontal Asymptotes As we prepare to practice graphing functions, we should consider one last piece of information about a function that will be helpful in drawing its graph the
Limits at Infinity and Horizontal Asymptotes As we prepare to practice graphing functions, we should consider one last piece of information about a function that will be helpful in drawing its graph the
Limits and Continuity
 Limits and Continuity MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to: Determine the left-hand and right-hand limits
Limits and Continuity MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to: Determine the left-hand and right-hand limits
AP Calculus AB Summer Assignment
 AP Calculus AB Summer Assignment Name: When you come back to school, you will be epected to have attempted every problem. These skills are all different tools that you will pull out of your toolbo this
AP Calculus AB Summer Assignment Name: When you come back to school, you will be epected to have attempted every problem. These skills are all different tools that you will pull out of your toolbo this
Feedback D. Incorrect! Exponential functions are continuous everywhere. Look for features like square roots or denominators that could be made 0.
 Calculus Problem Solving Drill 07: Trigonometric Limits and Continuity No. of 0 Instruction: () Read the problem statement and answer choices carefully. () Do your work on a separate sheet of paper. (3)
Calculus Problem Solving Drill 07: Trigonometric Limits and Continuity No. of 0 Instruction: () Read the problem statement and answer choices carefully. () Do your work on a separate sheet of paper. (3)
We will work with two important rules for radicals. We will write them for square roots but they work for any root (cube root, fourth root, etc.).
 College algebra We will review simplifying radicals, exponents and their rules, multiplying polynomials, factoring polynomials, greatest common denominators, and solving rational equations. Pre-requisite
College algebra We will review simplifying radicals, exponents and their rules, multiplying polynomials, factoring polynomials, greatest common denominators, and solving rational equations. Pre-requisite
1.3 Limits and Continuity
 40 CHAPTER 1. RATES OF CHANGE AND THE DERIVATIVE 1.3 Limits and Continuity Despite the fact that we have placed all of the proofs of the theorems from this section in the Technical Matters section, Section
40 CHAPTER 1. RATES OF CHANGE AND THE DERIVATIVE 1.3 Limits and Continuity Despite the fact that we have placed all of the proofs of the theorems from this section in the Technical Matters section, Section
ABE Math Review Package
 P a g e ABE Math Review Package This material is intended as a review of skills you once learned and wish to review before your assessment. Before studying Algebra, you should be familiar with all of the
P a g e ABE Math Review Package This material is intended as a review of skills you once learned and wish to review before your assessment. Before studying Algebra, you should be familiar with all of the
Partial Fractions. June 27, In this section, we will learn to integrate another class of functions: the rational functions.
 Partial Fractions June 7, 04 In this section, we will learn to integrate another class of functions: the rational functions. Definition. A rational function is a fraction of two polynomials. For example,
Partial Fractions June 7, 04 In this section, we will learn to integrate another class of functions: the rational functions. Definition. A rational function is a fraction of two polynomials. For example,
REVIEW FOR TEST I OF CALCULUS I:
 REVIEW FOR TEST I OF CALCULUS I: The first and best line of defense is to complete and understand the homework and lecture examples. Past that my old test might help you get some idea of how my tests typically
REVIEW FOR TEST I OF CALCULUS I: The first and best line of defense is to complete and understand the homework and lecture examples. Past that my old test might help you get some idea of how my tests typically
1.10 Continuity Brian E. Veitch
 1.10 Continuity Definition 1.5. A function is continuous at x = a if 1. f(a) exists 2. lim x a f(x) exists 3. lim x a f(x) = f(a) If any of these conditions fail, f is discontinuous. Note: From algebra
1.10 Continuity Definition 1.5. A function is continuous at x = a if 1. f(a) exists 2. lim x a f(x) exists 3. lim x a f(x) = f(a) If any of these conditions fail, f is discontinuous. Note: From algebra
MATH 113: ELEMENTARY CALCULUS
 MATH 3: ELEMENTARY CALCULUS Please check www.ualberta.ca/ zhiyongz for notes updation! 6. Rates of Change and Limits A fundamental philosophical truth is that everything changes. In physics, the change
MATH 3: ELEMENTARY CALCULUS Please check www.ualberta.ca/ zhiyongz for notes updation! 6. Rates of Change and Limits A fundamental philosophical truth is that everything changes. In physics, the change
SECTION 2.4: LIMITS AND INFINITY II
 (Section 2.4: Limits and Infinity II) 2.4.1 SECTION 2.4: LIMITS AND INFINITY II LEARNING OBJECTIVES Understand infinite limits at a point and relate them to vertical asymptotes of graphs. Be able to evaluate
(Section 2.4: Limits and Infinity II) 2.4.1 SECTION 2.4: LIMITS AND INFINITY II LEARNING OBJECTIVES Understand infinite limits at a point and relate them to vertical asymptotes of graphs. Be able to evaluate
Quadratic Equations Part I
 Quadratic Equations Part I Before proceeding with this section we should note that the topic of solving quadratic equations will be covered in two sections. This is done for the benefit of those viewing
Quadratic Equations Part I Before proceeding with this section we should note that the topic of solving quadratic equations will be covered in two sections. This is done for the benefit of those viewing
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER /2018
 ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 2017/2018 DR. ANTHONY BROWN 1. Arithmetic and Algebra 1.1. Arithmetic of Numbers. While we have calculators and computers
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 2017/2018 DR. ANTHONY BROWN 1. Arithmetic and Algebra 1.1. Arithmetic of Numbers. While we have calculators and computers
Evaluating Limits Analytically. By Tuesday J. Johnson
 Evaluating Limits Analytically By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Rationalizing numerators and/or denominators Trigonometric skills reviews
Evaluating Limits Analytically By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Rationalizing numerators and/or denominators Trigonometric skills reviews
2. FUNCTIONS AND ALGEBRA
 2. FUNCTIONS AND ALGEBRA You might think of this chapter as an icebreaker. Functions are the primary participants in the game of calculus, so before we play the game we ought to get to know a few functions.
2. FUNCTIONS AND ALGEBRA You might think of this chapter as an icebreaker. Functions are the primary participants in the game of calculus, so before we play the game we ought to get to know a few functions.
MITOCW ocw-18_02-f07-lec02_220k
 MITOCW ocw-18_02-f07-lec02_220k The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free.
MITOCW ocw-18_02-f07-lec02_220k The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free.
Section 2: Limits and Continuity
 Chapter 2 The Derivative Business Calculus 79 Section 2: Limits and Continuity In the last section, we saw that as the interval over which we calculated got smaller, the secant slopes approached the tangent
Chapter 2 The Derivative Business Calculus 79 Section 2: Limits and Continuity In the last section, we saw that as the interval over which we calculated got smaller, the secant slopes approached the tangent
Algebra. Here are a couple of warnings to my students who may be here to get a copy of what happened on a day that you missed.
 This document was written and copyrighted by Paul Dawkins. Use of this document and its online version is governed by the Terms and Conditions of Use located at. The online version of this document is
This document was written and copyrighted by Paul Dawkins. Use of this document and its online version is governed by the Terms and Conditions of Use located at. The online version of this document is
2. Limits at Infinity
 2 Limits at Infinity To understand sequences and series fully, we will need to have a better understanding of its at infinity We begin with a few examples to motivate our discussion EXAMPLE 1 Find SOLUTION
2 Limits at Infinity To understand sequences and series fully, we will need to have a better understanding of its at infinity We begin with a few examples to motivate our discussion EXAMPLE 1 Find SOLUTION
( )( b + c) = ab + ac, but it can also be ( )( a) = ba + ca. Let s use the distributive property on a couple of
 Factoring Review for Algebra II The saddest thing about not doing well in Algebra II is that almost any math teacher can tell you going into it what s going to trip you up. One of the first things they
Factoring Review for Algebra II The saddest thing about not doing well in Algebra II is that almost any math teacher can tell you going into it what s going to trip you up. One of the first things they
Algebra & Trig Review
 Algebra & Trig Review 1 Algebra & Trig Review This review was originally written for my Calculus I class, but it should be accessible to anyone needing a review in some basic algebra and trig topics. The
Algebra & Trig Review 1 Algebra & Trig Review This review was originally written for my Calculus I class, but it should be accessible to anyone needing a review in some basic algebra and trig topics. The
Math101, Sections 2 and 3, Spring 2008 Review Sheet for Exam #2:
 Math101, Sections 2 and 3, Spring 2008 Review Sheet for Exam #2: 03 17 08 3 All about lines 3.1 The Rectangular Coordinate System Know how to plot points in the rectangular coordinate system. Know the
Math101, Sections 2 and 3, Spring 2008 Review Sheet for Exam #2: 03 17 08 3 All about lines 3.1 The Rectangular Coordinate System Know how to plot points in the rectangular coordinate system. Know the
October 27, 2018 MAT186 Week 3 Justin Ko. We use the following notation to describe the limiting behavior of functions.
 October 27, 208 MAT86 Week 3 Justin Ko Limits. Intuitive Definitions of Limits We use the following notation to describe the iting behavior of functions.. (Limit of a Function A it is written as f( = L
October 27, 208 MAT86 Week 3 Justin Ko Limits. Intuitive Definitions of Limits We use the following notation to describe the iting behavior of functions.. (Limit of a Function A it is written as f( = L
MITOCW big_picture_derivatives_512kb-mp4
 MITOCW big_picture_derivatives_512kb-mp4 PROFESSOR: OK, hi. This is the second in my videos about the main ideas, the big picture of calculus. And this is an important one, because I want to introduce
MITOCW big_picture_derivatives_512kb-mp4 PROFESSOR: OK, hi. This is the second in my videos about the main ideas, the big picture of calculus. And this is an important one, because I want to introduce
Calculus Essentials Ebook
 Calculus Essentials Ebook Here you go. You ll never have to search endlessly through pages in your textbook just to find the key concepts ever again. Because staring at the same 3 pages and flipping back
Calculus Essentials Ebook Here you go. You ll never have to search endlessly through pages in your textbook just to find the key concepts ever again. Because staring at the same 3 pages and flipping back
Math Precalculus I University of Hawai i at Mānoa Spring
 Math 135 - Precalculus I University of Hawai i at Mānoa Spring - 2014 Created for Math 135, Spring 2008 by Lukasz Grabarek and Michael Joyce Send comments and corrections to lukasz@math.hawaii.edu Contents
Math 135 - Precalculus I University of Hawai i at Mānoa Spring - 2014 Created for Math 135, Spring 2008 by Lukasz Grabarek and Michael Joyce Send comments and corrections to lukasz@math.hawaii.edu Contents
Algebra Exam. Solutions and Grading Guide
 Algebra Exam Solutions and Grading Guide You should use this grading guide to carefully grade your own exam, trying to be as objective as possible about what score the TAs would give your responses. Full
Algebra Exam Solutions and Grading Guide You should use this grading guide to carefully grade your own exam, trying to be as objective as possible about what score the TAs would give your responses. Full
Lecture 5: Continuity II
 Lecture 5: Continuity II Nathan Pflueger 18 September 2013 1 Introduction Today we continue our discussion of continuity. We begin by stating a seemingly obvious feature of continuous functions, but one
Lecture 5: Continuity II Nathan Pflueger 18 September 2013 1 Introduction Today we continue our discussion of continuity. We begin by stating a seemingly obvious feature of continuous functions, but one
Math Analysis/Honors Math Analysis Summer Assignment
 Math Analysis/Honors Math Analysis Summer Assignment To be successful in Math Analysis or Honors Math Analysis, a full understanding of the topics listed below is required prior to the school year. To
Math Analysis/Honors Math Analysis Summer Assignment To be successful in Math Analysis or Honors Math Analysis, a full understanding of the topics listed below is required prior to the school year. To
MATH 308 COURSE SUMMARY
 MATH 308 COURSE SUMMARY Approximately a third of the exam cover the material from the first two midterms, that is, chapter 6 and the first six sections of chapter 7. The rest of the exam will cover the
MATH 308 COURSE SUMMARY Approximately a third of the exam cover the material from the first two midterms, that is, chapter 6 and the first six sections of chapter 7. The rest of the exam will cover the
Lesson Objectives. Lesson 32 - Limits. Fast Five. Fast Five - Limits and Graphs 1/19/17. Calculus - Mr Santowski
 Lesson 32 - Limits Calculus - Mr Santowski 1/19/17 Mr. Santowski - Calculus & IBHL 1 Lesson Objectives! 1. Define limits! 2. Use algebraic, graphic and numeric (AGN) methods to determine if a limit exists!
Lesson 32 - Limits Calculus - Mr Santowski 1/19/17 Mr. Santowski - Calculus & IBHL 1 Lesson Objectives! 1. Define limits! 2. Use algebraic, graphic and numeric (AGN) methods to determine if a limit exists!
9.4 Radical Expressions
 Section 9.4 Radical Expressions 95 9.4 Radical Expressions In the previous two sections, we learned how to multiply and divide square roots. Specifically, we are now armed with the following two properties.
Section 9.4 Radical Expressions 95 9.4 Radical Expressions In the previous two sections, we learned how to multiply and divide square roots. Specifically, we are now armed with the following two properties.
5.1 Simplifying Rational Expressions
 5. Simplifying Rational Expressions Now that we have mastered the process of factoring, in this chapter, we will have to use a great deal of the factoring concepts that we just learned. We begin with the
5. Simplifying Rational Expressions Now that we have mastered the process of factoring, in this chapter, we will have to use a great deal of the factoring concepts that we just learned. We begin with the
1 Limits and continuity
 1 Limits and continuity Question 1. Which of the following its can be evaluated by continuity ( plugging in )? sin(x) (a) x + 1 (d) x 3 x 2 + x 6 (b) e x sin(x) (e) x 2 + x 6 (c) x 2 x 2 + x 6 (f) n (
1 Limits and continuity Question 1. Which of the following its can be evaluated by continuity ( plugging in )? sin(x) (a) x + 1 (d) x 3 x 2 + x 6 (b) e x sin(x) (e) x 2 + x 6 (c) x 2 x 2 + x 6 (f) n (
5.4 Continuity: Preliminary Notions
 5.4. CONTINUITY: PRELIMINARY NOTIONS 181 5.4 Continuity: Preliminary Notions 5.4.1 Definitions The American Heritage Dictionary of the English Language defines continuity as an uninterrupted succession,
5.4. CONTINUITY: PRELIMINARY NOTIONS 181 5.4 Continuity: Preliminary Notions 5.4.1 Definitions The American Heritage Dictionary of the English Language defines continuity as an uninterrupted succession,
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS
 LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
A BRIEF REVIEW OF ALGEBRA AND TRIGONOMETRY
 A BRIEF REVIEW OF ALGEBRA AND TRIGONOMETR Some Key Concepts:. The slope and the equation of a straight line. Functions and functional notation. The average rate of change of a function and the DIFFERENCE-
A BRIEF REVIEW OF ALGEBRA AND TRIGONOMETR Some Key Concepts:. The slope and the equation of a straight line. Functions and functional notation. The average rate of change of a function and the DIFFERENCE-
2017 AP Calculus AB Summer Assignment
 07 AP Calculus AB Summer Assignment Mrs. Peck ( kapeck@spotsylvania.k.va.us) This assignment is designed to help prepare you to start Calculus on day and be successful. I recommend that you take off the
07 AP Calculus AB Summer Assignment Mrs. Peck ( kapeck@spotsylvania.k.va.us) This assignment is designed to help prepare you to start Calculus on day and be successful. I recommend that you take off the
Limits and Their Properties
 Chapter 1 Limits and Their Properties Course Number Section 1.1 A Preview of Calculus Objective: In this lesson you learned how calculus compares with precalculus. I. What is Calculus? (Pages 42 44) Calculus
Chapter 1 Limits and Their Properties Course Number Section 1.1 A Preview of Calculus Objective: In this lesson you learned how calculus compares with precalculus. I. What is Calculus? (Pages 42 44) Calculus
Lecture 10: Powers of Matrices, Difference Equations
 Lecture 10: Powers of Matrices, Difference Equations Difference Equations A difference equation, also sometimes called a recurrence equation is an equation that defines a sequence recursively, i.e. each
Lecture 10: Powers of Matrices, Difference Equations Difference Equations A difference equation, also sometimes called a recurrence equation is an equation that defines a sequence recursively, i.e. each
MITOCW MITRES18_006F10_26_0601_300k-mp4
 MITOCW MITRES18_006F10_26_0601_300k-mp4 ANNOUNCER: The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational
MITOCW MITRES18_006F10_26_0601_300k-mp4 ANNOUNCER: The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational
Chapter 1 Review of Equations and Inequalities
 Chapter 1 Review of Equations and Inequalities Part I Review of Basic Equations Recall that an equation is an expression with an equal sign in the middle. Also recall that, if a question asks you to solve
Chapter 1 Review of Equations and Inequalities Part I Review of Basic Equations Recall that an equation is an expression with an equal sign in the middle. Also recall that, if a question asks you to solve
MATH 114 Calculus Notes on Chapter 2 (Limits) (pages 60-? in Stewart)
 Still under construction. MATH 114 Calculus Notes on Chapter 2 (Limits) (pages 60-? in Stewart) As seen in A Preview of Calculus, the concept of it underlies the various branches of calculus. Hence we
Still under construction. MATH 114 Calculus Notes on Chapter 2 (Limits) (pages 60-? in Stewart) As seen in A Preview of Calculus, the concept of it underlies the various branches of calculus. Hence we
Instructor (Brad Osgood)
 TheFourierTransformAndItsApplications-Lecture26 Instructor (Brad Osgood): Relax, but no, no, no, the TV is on. It's time to hit the road. Time to rock and roll. We're going to now turn to our last topic
TheFourierTransformAndItsApplications-Lecture26 Instructor (Brad Osgood): Relax, but no, no, no, the TV is on. It's time to hit the road. Time to rock and roll. We're going to now turn to our last topic
College Algebra Through Problem Solving (2018 Edition)
 City University of New York (CUNY) CUNY Academic Works Open Educational Resources Queensborough Community College Winter 1-25-2018 College Algebra Through Problem Solving (2018 Edition) Danielle Cifone
City University of New York (CUNY) CUNY Academic Works Open Educational Resources Queensborough Community College Winter 1-25-2018 College Algebra Through Problem Solving (2018 Edition) Danielle Cifone
Lecture 3 (Limits and Derivatives)
 Lecture 3 (Limits and Derivatives) Continuity In the previous lecture we saw that very often the limit of a function as is just. When this is the case we say that is continuous at a. Definition: A function
Lecture 3 (Limits and Derivatives) Continuity In the previous lecture we saw that very often the limit of a function as is just. When this is the case we say that is continuous at a. Definition: A function
Alex s Guide to Word Problems and Linear Equations Following Glencoe Algebra 1
 Alex s Guide to Word Problems and Linear Equations Following Glencoe Algebra 1 What is a linear equation? It sounds fancy, but linear equation means the same thing as a line. In other words, it s an equation
Alex s Guide to Word Problems and Linear Equations Following Glencoe Algebra 1 What is a linear equation? It sounds fancy, but linear equation means the same thing as a line. In other words, it s an equation
MATH CALCULUS I 1.5: Continuity
 MATH 12002 - CALCULUS I 1.5: Continuity Professor Donald L. White Department of Mathematical Sciences Kent State University D.L. White (Kent State University) 1 / 12 Definition of Continuity Intuitively,
MATH 12002 - CALCULUS I 1.5: Continuity Professor Donald L. White Department of Mathematical Sciences Kent State University D.L. White (Kent State University) 1 / 12 Definition of Continuity Intuitively,
Sign of derivative test: when does a function decreases or increases:
 Sign of derivative test: when does a function decreases or increases: If for all then is increasing on. If for all then is decreasing on. If then the function is not increasing or decreasing at. We defined
Sign of derivative test: when does a function decreases or increases: If for all then is increasing on. If for all then is decreasing on. If then the function is not increasing or decreasing at. We defined
Vectors. A vector is usually denoted in bold, like vector a, or sometimes it is denoted a, or many other deviations exist in various text books.
 Vectors A Vector has Two properties Magnitude and Direction. That s a weirder concept than you think. A Vector does not necessarily start at a given point, but can float about, but still be the SAME vector.
Vectors A Vector has Two properties Magnitude and Direction. That s a weirder concept than you think. A Vector does not necessarily start at a given point, but can float about, but still be the SAME vector.
Section 3.1 Quadratic Functions
 Chapter 3 Lecture Notes Page 1 of 72 Section 3.1 Quadratic Functions Objectives: Compare two different forms of writing a quadratic function Find the equation of a quadratic function (given points) Application
Chapter 3 Lecture Notes Page 1 of 72 Section 3.1 Quadratic Functions Objectives: Compare two different forms of writing a quadratic function Find the equation of a quadratic function (given points) Application
2.2 The Limit of a Function
 2.2 The Limit of a Function Introductory Example: Consider the function f(x) = x is near 0. x f(x) x f(x) 1 3.7320508 1 4.236068 0.5 3.8708287 0.5 4.1213203 0.1 3.9748418 0.1 4.0248457 0.05 3.9874607 0.05
2.2 The Limit of a Function Introductory Example: Consider the function f(x) = x is near 0. x f(x) x f(x) 1 3.7320508 1 4.236068 0.5 3.8708287 0.5 4.1213203 0.1 3.9748418 0.1 4.0248457 0.05 3.9874607 0.05
MITOCW MITRES18_006F10_26_0602_300k-mp4
 MITOCW MITRES18_006F10_26_0602_300k-mp4 FEMALE VOICE: The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational
MITOCW MITRES18_006F10_26_0602_300k-mp4 FEMALE VOICE: The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational
Analysis of Functions
 Lecture for Week 11 (Secs. 5.1 3) Analysis of Functions (We used to call this topic curve sketching, before students could sketch curves by typing formulas into their calculators. It is still important
Lecture for Week 11 (Secs. 5.1 3) Analysis of Functions (We used to call this topic curve sketching, before students could sketch curves by typing formulas into their calculators. It is still important
5.4 - Quadratic Functions
 Fry TAMU Spring 2017 Math 150 Notes Section 5.4 Page! 92 5.4 - Quadratic Functions Definition: A function is one that can be written in the form f (x) = where a, b, and c are real numbers and a 0. (What
Fry TAMU Spring 2017 Math 150 Notes Section 5.4 Page! 92 5.4 - Quadratic Functions Definition: A function is one that can be written in the form f (x) = where a, b, and c are real numbers and a 0. (What
4.3 Rational Inequalities and Applications
 342 Rational Functions 4.3 Rational Inequalities and Applications In this section, we solve equations and inequalities involving rational functions and eplore associated application problems. Our first
342 Rational Functions 4.3 Rational Inequalities and Applications In this section, we solve equations and inequalities involving rational functions and eplore associated application problems. Our first
Bridging the gap between GCSE and A level mathematics
 Bridging the gap between GCSE and A level mathematics This booklet is designed to help you revise important algebra topics from GCSE and make the transition from GCSE to A level a smooth one. You are advised
Bridging the gap between GCSE and A level mathematics This booklet is designed to help you revise important algebra topics from GCSE and make the transition from GCSE to A level a smooth one. You are advised
Descriptive Statistics (And a little bit on rounding and significant digits)
 Descriptive Statistics (And a little bit on rounding and significant digits) Now that we know what our data look like, we d like to be able to describe it numerically. In other words, how can we represent
Descriptive Statistics (And a little bit on rounding and significant digits) Now that we know what our data look like, we d like to be able to describe it numerically. In other words, how can we represent
SECTION 1.4: FUNCTIONS. (See p.40 for definitions of relations and functions and the Technical Note in Notes 1.24.) ( ) = x 2.
 SECTION 1.4: FUNCTIONS (Section 1.4: Functions) 1.18 (See p.40 for definitions of relations and functions and the Technical Note in Notes 1.24.) Warning: The word function has different meanings in mathematics
SECTION 1.4: FUNCTIONS (Section 1.4: Functions) 1.18 (See p.40 for definitions of relations and functions and the Technical Note in Notes 1.24.) Warning: The word function has different meanings in mathematics
Topic Subtopics Essential Knowledge (EK)
 Unit/ Unit 1 Limits [BEAN] 1.1 Limits Graphically Define a limit (y value a function approaches) One sided limits. Easy if it s continuous. Tricky if there s a discontinuity. EK 1.1A1: Given a function,
Unit/ Unit 1 Limits [BEAN] 1.1 Limits Graphically Define a limit (y value a function approaches) One sided limits. Easy if it s continuous. Tricky if there s a discontinuity. EK 1.1A1: Given a function,
Introduction. So, why did I even bother to write this?
 Introduction This review was originally written for my Calculus I class, but it should be accessible to anyone needing a review in some basic algebra and trig topics. The review contains the occasional
Introduction This review was originally written for my Calculus I class, but it should be accessible to anyone needing a review in some basic algebra and trig topics. The review contains the occasional
Introductory Quantum Chemistry Prof. K. L. Sebastian Department of Inorganic and Physical Chemistry Indian Institute of Science, Bangalore
 Introductory Quantum Chemistry Prof. K. L. Sebastian Department of Inorganic and Physical Chemistry Indian Institute of Science, Bangalore Lecture - 4 Postulates Part 1 (Refer Slide Time: 00:59) So, I
Introductory Quantum Chemistry Prof. K. L. Sebastian Department of Inorganic and Physical Chemistry Indian Institute of Science, Bangalore Lecture - 4 Postulates Part 1 (Refer Slide Time: 00:59) So, I
Review for Final Exam, MATH , Fall 2010
 Review for Final Exam, MATH 170-002, Fall 2010 The test will be on Wednesday December 15 in ILC 404 (usual class room), 8:00 a.m - 10:00 a.m. Please bring a non-graphing calculator for the test. No other
Review for Final Exam, MATH 170-002, Fall 2010 The test will be on Wednesday December 15 in ILC 404 (usual class room), 8:00 a.m - 10:00 a.m. Please bring a non-graphing calculator for the test. No other
Do now as a warm up: Is there some number a, such that this limit exists? If so, find the value of a and find the limit. If not, explain why not.
 Do now as a warm up: Is there some number a, such that this limit exists? If so, find the value of a and find the limit. If not, explain why not. 1 Continuity and One Sided Limits To say that a function
Do now as a warm up: Is there some number a, such that this limit exists? If so, find the value of a and find the limit. If not, explain why not. 1 Continuity and One Sided Limits To say that a function
10.7 Trigonometric Equations and Inequalities
 0.7 Trigonometric Equations and Inequalities 857 0.7 Trigonometric Equations and Inequalities In Sections 0., 0. and most recently 0., we solved some basic equations involving the trigonometric functions.
0.7 Trigonometric Equations and Inequalities 857 0.7 Trigonometric Equations and Inequalities In Sections 0., 0. and most recently 0., we solved some basic equations involving the trigonometric functions.
AB Calculus: Rates of Change and Tangent Lines
 AB Calculus: Rates of Change and Tangent Lines Name: The World Record Basketball Shot A group called How Ridiculous became YouTube famous when they successfully made a basket from the top of Tasmania s
AB Calculus: Rates of Change and Tangent Lines Name: The World Record Basketball Shot A group called How Ridiculous became YouTube famous when they successfully made a basket from the top of Tasmania s
Section 4.6 Negative Exponents
 Section 4.6 Negative Exponents INTRODUCTION In order to understand negative exponents the main topic of this section we need to make sure we understand the meaning of the reciprocal of a number. Reciprocals
Section 4.6 Negative Exponents INTRODUCTION In order to understand negative exponents the main topic of this section we need to make sure we understand the meaning of the reciprocal of a number. Reciprocals
A level Mathematics Student Induction Booklet
 Name: A level Mathematics Student Induction Booklet Welcome to A Level mathematics! The objective of this booklet is to help you get started with the A Level Maths course, and to smooth your pathway through
Name: A level Mathematics Student Induction Booklet Welcome to A Level mathematics! The objective of this booklet is to help you get started with the A Level Maths course, and to smooth your pathway through
Solving Quadratic & Higher Degree Equations
 Chapter 7 Solving Quadratic & Higher Degree Equations Sec 1. Zero Product Property Back in the third grade students were taught when they multiplied a number by zero, the product would be zero. In algebra,
Chapter 7 Solving Quadratic & Higher Degree Equations Sec 1. Zero Product Property Back in the third grade students were taught when they multiplied a number by zero, the product would be zero. In algebra,
A Quick Algebra Review
 1. Simplifying Epressions. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Eponents 9. Quadratics 10. Rationals 11. Radicals
1. Simplifying Epressions. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Eponents 9. Quadratics 10. Rationals 11. Radicals
Lecture 5: Finding limits analytically Simple indeterminate forms
 Lecture 5: Finding its analytically Simple indeterminate forms Objectives: (5.) Use algebraic techniques to resolve 0/0 indeterminate forms. (5.) Use the squeeze theorem to evaluate its. (5.3) Use trigonometric
Lecture 5: Finding its analytically Simple indeterminate forms Objectives: (5.) Use algebraic techniques to resolve 0/0 indeterminate forms. (5.) Use the squeeze theorem to evaluate its. (5.3) Use trigonometric
Modern Algebra Prof. Manindra Agrawal Department of Computer Science and Engineering Indian Institute of Technology, Kanpur
 Modern Algebra Prof. Manindra Agrawal Department of Computer Science and Engineering Indian Institute of Technology, Kanpur Lecture 02 Groups: Subgroups and homomorphism (Refer Slide Time: 00:13) We looked
Modern Algebra Prof. Manindra Agrawal Department of Computer Science and Engineering Indian Institute of Technology, Kanpur Lecture 02 Groups: Subgroups and homomorphism (Refer Slide Time: 00:13) We looked
WEEK 7 NOTES AND EXERCISES
 WEEK 7 NOTES AND EXERCISES RATES OF CHANGE (STRAIGHT LINES) Rates of change are very important in mathematics. Take for example the speed of a car. It is a measure of how far the car travels over a certain
WEEK 7 NOTES AND EXERCISES RATES OF CHANGE (STRAIGHT LINES) Rates of change are very important in mathematics. Take for example the speed of a car. It is a measure of how far the car travels over a certain
Rational Functions 4.5
 Math 4 Pre-Calculus Name Date Rational Function Rational Functions 4.5 g ( ) A function is a rational function if f ( ), where g ( ) and ( ) h ( ) h are polynomials. Vertical asymptotes occur at -values
Math 4 Pre-Calculus Name Date Rational Function Rational Functions 4.5 g ( ) A function is a rational function if f ( ), where g ( ) and ( ) h ( ) h are polynomials. Vertical asymptotes occur at -values
SANDY CREEK HIGH SCHOOL
 SANDY CREEK HIGH SCHOOL SUMMER REVIEW PACKET For students entering A.P. CALCULUS BC I epect everyone to check the Google classroom site and your school emails at least once every two weeks. You will also
SANDY CREEK HIGH SCHOOL SUMMER REVIEW PACKET For students entering A.P. CALCULUS BC I epect everyone to check the Google classroom site and your school emails at least once every two weeks. You will also
3 Polynomial and Rational Functions
 3 Polynomial and Rational Functions 3.1 Polynomial Functions and their Graphs So far, we have learned how to graph polynomials of degree 0, 1, and. Degree 0 polynomial functions are things like f(x) =,
3 Polynomial and Rational Functions 3.1 Polynomial Functions and their Graphs So far, we have learned how to graph polynomials of degree 0, 1, and. Degree 0 polynomial functions are things like f(x) =,
