MAHS-DV Algebra 1-2 Q4
|
|
|
- Jasper Hubbard
- 5 years ago
- Views:
Transcription
1
2 MAHS-DV Algebra 1-2 Q4 Adrienne Wooten Say Thanks to the Authors Click (No sign in required)
3 To access a customizable version of this book, as well as other interactive content, visit AUTHOR Adrienne Wooten CK-12 Foundation is a non-profit organization with a mission to reduce the cost of textbook materials for the K-12 market both in the U.S. and worldwide. Using an open-content, web-based collaborative model termed the FlexBook, CK-12 intends to pioneer the generation and distribution of high-quality educational content that will serve both as core text as well as provide an adaptive environment for learning, powered through the FlexBook Platform. Copyright 2014 CK-12 Foundation, The names CK-12 and CK12 and associated logos and the terms FlexBook and FlexBook Platform (collectively CK-12 Marks ) are trademarks and service marks of CK-12 Foundation and are protected by federal, state, and international laws. Any form of reproduction of this book in any format or medium, in whole or in sections must include the referral attribution link (placed in a visible location) in addition to the following terms. Except as otherwise noted, all CK-12 Content (including CK-12 Curriculum Material) is made available to Users in accordance with the Creative Commons Attribution-Non-Commercial 3.0 Unported (CC BY-NC 3.0) License ( licenses/by-nc/3.0/), as amended and updated by Creative Commons from time to time (the CC License ), which is incorporated herein by this reference. Complete terms can be found at Printed: March 5, 2014 iii
4 Contents Contents 1 Quadratics Graphs of Basic Quadratic Functions Transformations of Quadratic Functions Vertex Form of a Quadratic Function Graphs to Solve Quadratic Equations Use Square Roots to Solve Quadratic Equations Solving Quadratics using Factoring Completing the Square Solving Quadratic Equations by the Quadratic Formula Solutions Using the Discriminant Modeling with Quadratic Functions References Non-Linear Relationships Piecewise Functions Graphing Basic Absolute Value Functions Using the General Absolute Value Equation and the Graphing Calculator Graphs of Square Root Functions Shifts of Square Root Functions Graphing Cubed Root Functions iv
5 Chapter 1. Quadratics CHAPTER 1 Quadratics Chapter Outline 1.1 GRAPHS OF BASIC QUADRATIC FUNCTIONS 1.2 TRANSFORMATIONS OF QUADRATIC FUNCTIONS 1.3 VERTEX FORM OF A QUADRATIC FUNCTION 1.4 GRAPHS TO SOLVE QUADRATIC EQUATIONS 1.5 USE SQUARE ROOTS TO SOLVE QUADRATIC EQUATIONS 1.6 SOLVING QUADRATICS USING FACTORING 1.7 COMPLETING THE SQUARE 1.8 SOLVING QUADRATIC EQUATIONS BY THE QUADRATIC FORMULA 1.9 SOLUTIONS USING THE DISCRIMINANT 1.10 MODELING WITH QUADRATIC FUNCTIONS 1.11 REFERENCES 1
6 1.1. Graphs of Basic Quadratic Functions Graphs of Basic Quadratic Functions Here you ll learn how to graph and analyze the quadratic function, y = x 2. Look at the graph below. Does the graph represent a function? Do you know the name of the graph? Do you know what makes the green point special? Do you notice any symmetry in the graph? Can you state the domain and range for the relation? Watch This Khan Academy Quadratic Functions1 MEDIA Click image to the left for more content. Guidance Until now you have been dealing with linear functions. The highest exponent of the independent variable (x) has been one and the graphs have been straight lines. Here you will be learning about quadratic functions. A quadratic 2
7 Chapter 1. Quadratics function is one of the form f (x)=ax 2 + bx + c where a,b and c are real numbers and a = 0. The highest exponent of the independent variable is two. When graphed, a quadratic function creates a parabola that looks like this: or like this: You can create your own graph by plotting the points created from a table of values. The most basic quadratic function is f (x)=x 2. It is also called the parent function. A parabola has a turning point known as the vertex. The vertex is the minimum value of the parabola if it opens upward and the maximum value if the parabola opens downward. When the graph opens downward, the y-values in the base table change to negative values. The basic quadratic function that opens downward has the equation f (x)= x 2. This is also called the end behavior of the graph. Given a quadratic function in the form of f (x)= ax 2 + bx + c (or f (x)=a(x h) 2 + k), the quadratic function is said to open up if a > 0 and open down if a < 0. If a > 0, then the function has a minimum at the x-coordinate of the vertex. This means that the function is decreasing for x-values less than (or to the left of) the vertex, and the function is increasing for x-values greater than (or to the right of) the vertex. If a < 0, then the function has a maximum at the x-coordinate of the vertex. This means that the function is increasing for x-values less than (or to the left of) the vertex, and the function is decreasing for x-values greater than (or to the right of) the vertex. All parabolas have an axis of symmetry. The axis of symmetry is the vertical line that passes through the vertex of the parabola. The equation for the axis of symmetry is always the x coordinate of the vertex. The equation for this line is x = b 2a 3
8 1.1. Graphs of Basic Quadratic Functions Example A For the basic quadratic function f (x)=x 2, complete a table such that {x 3 x 3,x ε Z}. Z is the special symbol for Integers. Solution: To complete the table of values, substitute the given x-values into the function f (x)=x 2. If you are using a calculator, insert all numbers, especially negative numbers, inside parenthesis before squaring them. The operation that needs to be done is ( 3)( 3) NOT (3)(3). f (x)=x 2 f (x)=x 2 f (x)=x 2 f (x)=x 2 f (x)=( 3) 2 f (x)=( 2) 2 f (x)=( 1) 2 f (x)=(0) 2 f (x)=9 f (x)=4 f (x)=1 f (x)=0 f (x)=x 2 f (x)=x 2 f (x)=x 2 f (x)=(1) 2 f (x)=(2) 2 f (x)=(3) 2 f (x)=1 f (x)=4 f (x)=9 TABLE 1.1: X f(x) Example B On a Cartesian plane, plot the points from the table for y = x 2. Solution: The plotted points cannot be joined to form a straight line. To join the points, begin with the point (-3, 9) or the point (3, 9) and without lifting your pencil, draw a smooth curve. The image should look like the following graph. 4
9 Chapter 1. Quadratics The arrows indicate the direction of the pencil as the points are joined. If the pencil is not moved off the paper, the temptation to join the points with a series of straight lines will be decreased. The points must be joined with a smooth curve that does not extend below the lowest point of the graph. In the above graph, the curve cannot go below the point (0, 0). Example C What are some unique characteristics of the graph of y = x 2? Solution: 1. The green point is located at the lowest point on the image. The curve does not go below this point. 2. Every red point on the left side of the image has a corresponding blue point on the right side of the image. 3. If the image was folded left to right along the y-axis that passes through the green point, each red point would land on each corresponding blue point. 4. The sides of the image extend upward. 5. The red and the blue points are plotted to the right and to the left of the green point. The points are plotted left and right one and up one; left and right two and up four, left and right 3 and up nine. Example D Find the vertex, the equation of the axis of symmetry, the y-intercept and the maximum or minimum of the function. y = 2x 2 + 4x 3 To find the axis of symmetry, we use x = b 2a x = 4 2(2) x = 1 which is the axis of symmetry. To find the vertex, use the value you found for the axis of symmetry as the x-coordinate of the vertex. To find the y-coordinate, substitute that value of x in the original equation. y = 2( 1) 2 + 4( 1) 3 5
10 1.1. Graphs of Basic Quadratic Functions y = 5 The vertex is ( 1, 5). Since a > 0 the parabola opens upward and has a minimum. The minimum is the y- coordinate of the vertex which in this case is 5. The y-intercept always occurs at (0,c). So the y-intercept is (0, 3). All of this information can be used to graph the function as seen in the figure below. Concept Problem Revisited The green point is the lowest point on the curve. The smooth curve is called a parabola and it is the image produced when the basic quadratic function is plotted on a Cartesian grid. The green point is known as the vertex of the parabola. The vertex is the turning point of the graph. For the graph of y = x 2, the vertex is (0, 0) and the parabola has a minimum value of zero which is indicated by the y-value of the vertex. The parabola opens upward since the y-values in the table of values are 0, 1, 4 and 9. The y-axis for this graph is actually the axis of symmetry. The axis of symmetry is the vertical line that passes through the vertex of the parabola. The parabola is symmetrical about this line. The equation for this axis of symmetry is x = 0. If the parabola were to open downward, the vertex would be the highest point of the graph. Therefore the image would have a maximum value of zero. The domain for all parabolas is D = {x x ε R} or (, ) The range for the above parabola is R = {y y 0,y ε R} or [0, ). Vocabulary Axis of Symmetry The axis of symmetry of a parabola is a vertical line that passes through the vertex of the parabola. The parabola is symmetrical about this line. The axis of symmetry has the equation x = the x coordinate of the vertex. Parabola A parabola is the smooth curve that results from graphing a quadratic function of the form f (x)=ax 2 +bx+c. The curve resembles a U-shape. 6
11 Chapter 1. Quadratics Quadratic Function A quadratic function is a function of the form f (x) =ax 2 + bx + c where a,b and c are real numbers and a = 0. Vertex The vertex of a parabola is the point around which the parabola turns. The vertex is the maximum point of a parabola that opens downward and the minimum point of a parabola that opens upward. Guided Practice 1. If the graph of y = x 2 opens downward, what changes would exist in the base table of values? 2. If the graph of y = x 2 opens downward, what changes would exist in the basic quadratic function? 3. Draw the image of the basic quadratic function that opens downward. State the domain and range for this parabola. Answers: 1. If the parabola were to open downward, the x-values would not change. The y-values would become negative values. The points would be plotted from the vertex as: right and left one and down one; right and left two and down four; right and left three and down nine. The table of values would be TABLE 1.2: X Y To match the table of values, the basic quadratic function would have to be written as y = x
12 1.1. Graphs of Basic Quadratic Functions The domain is D = {x x ε N}. The range for this parabola is R = {y y 0,y ε N}. Practice Complete the following statements in the space provided. 1. The name given to the graph of f (x)=x 2 is. 2. The domain of the graph of f (x)=x 2 is. 3. If the vertex of a parabola was (-3, 5), the equation of the axis of symmetry would be. 4. A parabola has a maximum value when it opens. 5. The point (-2, 4) on the graph of f (x)=x 2 has a corresponding point at. 6. The range of the graph of f (x)= x 2 is. 7. If the table of values for the basic quadratic function included 4 and -4 as x-values, the y-value(s) would be. 8. The vertical line that passes through the vertex of a parabola is called. 9. A minimum value exists when a parabola opens. 10. The turning point of the graph of f (x)=x 2 is called the. 11. For what values of x is f (x)=x 2 increasing? For what values is it decreasing? 12. Find the vertex, the equation of the axis of symmetry, the y-intercept and the maximum or minimum of the following: a. y = 3x 2 + 6x 1 b. y = x 2 + 2x + 1 c. y = x 2 4x + 5 d. y = 4x 2 8x A juggker is tossing a ball into the air. The height of the ball in feet can be modeled by the equation y = 16x x + 5, where y represents the height of the ball in x seconds. 8 a. Graph the equation. b. At what height is the ball thrown?
13 Chapter 1. Quadratics c. What is the maximum height of the ball? 9
14 1.2. Transformations of Quadratic Functions Transformations of Quadratic Functions Here you ll learn how to transform the basic quadratic functions (y = x 2 and y = x 2 ) to make new quadratic functions. Look at the parabola below. How is this parabola different from y = x 2? What do you think the equation of this parabola is? Watch This Khan Academy GraphingaQuadratic Function MEDIA Click image to the left for more content. Guidance Vertical Translations Consider the parent function f (x)=x 2 of the parabola as shown below. Using a table of values or your graphing calculator, graph g(x)=x How is this graph related to the parent function f (x)=x 2? 10
15 Chapter 1. Quadratics Now graph g(x)=x 2 2. How is the graph of g(x)=x 2 + k related to the parent function? Functions in the form g(x)=x 2 +k shift up k units for k > 0 and shift down k units for k < 0 from the parent function as shown below. This is called a vertical translation. Horizontal Translations Using a table of values or your graphing calculator, graph g(x)=(x 1) 2. How is this graph related to the parent function f (x)=x 2? Now graph g(x)=(x + 1) 2. How is the graph of g(x)=(x h) 2 related to the parent function? Functions in the form g(x) =(x h) 2 shift left h units for h > 0 and shift right h units for h < 0 from the parent function as shown below. This is called a horizontal translation. 11
16 1.2. Transformations of Quadratic Functions Writing Equations for Quadratic Functions Compare the function below to the graph of the parent function f (x)=x 2. Consider the translation of the parent function: Horizontal translation of 2 units to the right. Vertical translation of 1 unit up. This will help us determine h and k for the function g(x)=(x h) 2 + k. h is the number of units the parent function is translated horizontally. If the function shifts to the right, h will be positive; for a shift to the left, h will be negative. k is the number of units the parent function is translated vertically. If the function shifts up, k will be positive; for a shift down, k will be negative. So, in our function, h = 2 and k = 1. If we plug those values in the equation above, we have g(x)=(x 2)
17 Chapter 1. Quadratics Vertical Stretches and Compressions If a > 1, the parabola will be stretched vertically. If 0 < a < 1, the graph will be compressed vertically (sometimes called a vertical shrink). In the following figure, the parent function has been stretched g(x)=2x 2 and compressed g(x)= 1 2 x2 vertically. If a < 0, the graphs will be reflected across the x-axis (see below). This is called a vertical reflection which can also be represented by f (x). The graph of f ( x) is the reflection of the graph of across the y-axis but this results in the same function because f ( x)=( x) 2 = x 2. Writing the Equation for a Quadratic Function Consider the graph below. How can we use the point (2, 1) to write the equation of the function? A function whose graph is a parabola with vertex (0,0) always has the form f (x)=ax 2. To write the rule for the function, we simply substitute the ordered pair (2, 1) into the equation and solve for a. y = ax 2 1 = a(2) 2 1 = a(4) a = 1 4 so our function is f (x)= 1 4 x2. 13
18 1.2. Transformations of Quadratic Functions Putting It All Together How can we graph g(x)=a(x h) 2 + k using the parent function f (x)=x 2? All of the previous transformations can be put together as a combination of transformations. The sequence of graphs below shows how you can obtain the graph of g(x)= 2(x 2) Start with the graph of y = x Stretch the graph vertically by a factor of 2 to obtain the graph of y = 2x Reflect the graph across the x-axis to obtain the graph of y = 2x Translate the graph of y = 2x 2 right 2 units and up one unit to obtain the graph of y = 2(x 2) Concept Problem Revisited 14
19 Chapter 1. Quadratics This is the graph of y = 1 2 x2. The points are plotted from the vertex as right and left one and down one-half, right and left 2 and down two, right and left three and down four and one-half. The original y-values of 1, 4 and 9 have been multiplied by one-half and then were made negative because the graph was opening downward. When the y-values become negative, the direction of the opening is changed from upward to downward. This transformation is known as a vertical reflection. The graph is reflected across the x-axis. Vocabulary Horizontal translation The horizontal translation is the change in the base graph y = x 2 that shifts the graph right or left. It changes the x coordinate of the vertex. Transformation A transformation is any change in the base graph y = x 2. The transformations that apply to the parabola are a horizontal translation, a vertical translation, a vertical stretch and a vertical reflection. Vertical Reflection The vertical reflection is the reflection of the image graph in the x-axis. The graph opens downward and the y-values are negative values. Vertical Stretch The vertical stretch is the change made to the base function y = x 2 by stretching (or compressing) the graph vertically. The vertical stretch will produce an image graph that appears narrower (or wider) then the original base graph of y = x 2. Vertical Translation The vertical translation is the change in the base graph y = x 2 that shifts the graph up or down. It changes the y coordinate of the vertex. Guided Practice 1. Use the following tables of values and identify the transformations of the base graph y = x 2. X Y X Y Identify the transformations of the base graph y = x 2. 15
20 1.2. Transformations of Quadratic Functions 3. Draw the image graph of y = x 2 that has undergone a vertical reflection, a vertical stretch by a factor of 1 2,a vertical translation up 2 units, and a horizontal translation left 3 units. Answers: 1. To identify the transformations from the tables of values, determine how the table of values for y = x 2 compare to the table of values for the new image graph. The x-values have moved one place to the left. This means that the graph has undergone a horizontal translation of 1. The y coordinate of the vertex is 3. This means that the graph has undergone a vertical translation of 3. The vertex is easy to pick out from the tables since it is the point around which the corresponding points appear. The points from the vertex are plotted left and right one and up two, left and right two and up eight. This means that the base graph has undergone a vertical stretch of 2. The y-values move upward so the parabola will open upward. Therefore the image is not a vertical reflection. 2. The vertex is (1, 6). The base graph has undergone a horizontal translation of +1 and a vertical translation of +6. The parabola opens downward, so the graph is a vertical reflection. The points have been plotted such that the y-values of 1 and 4 are now 2 and 8. It is not unusual for a parabola to be plotted with five points rather than seven. The reason for this is the vertical stretch often multiplies the y-values such that they are difficult to graph on a Cartesian grid. If all the points are to be plotted, a different scale must be used for the y-axis. 3. The vertex given by the horizontal and vertical translations and is ( 3, 2). The y-values of 1, 4 and 9 must be multiplied by 1 2 to create values of 1 2,2 and The graph is a vertical reflection which means the graph opens downward and the y-values become negative. Practice The following table represents transformations to the base graph y = x 2. Draw an image graph for each set of transformations. VR = Vertical Reflection, VS = Vertical Stretch, VT = Vertical Translation, HT = Horizontal Translation. 16
21 Chapter 1. Quadratics TABLE 1.3: Number VR VS VT HT 1. NO YES YES NO NO YES NO YES For each of the following graphs, list the transformations of y = x 2 and give the equation in vertex form
22 1.2. Transformations of Quadratic Functions
23 Chapter 1. Quadratics For 16-22, graph the following functions and state the domain and range. 16. f (x)=(x 3) f (x)=x f (x)=(x + 1) f (x)=3x f (x)= 3 4 x2 21. f (x)=2(x 2) f (x)=(x 1) Calculator Investigation The parent graph of a quadratic equation is y = x Graph y = x 2,y = 3x 2, and y = 1 2 x2 on the same set of axes in the calculator. Describe how a effects the shape of the parabola. 24. Graph y = x 2,y = x 2, and y = 2x 2 on the same set of axes in the calculator. Describe how a effects the shape of the parabola. 25. Graph y = x 2,y =(x 1) 2, and y =(x + 4) 2 on the same set of axes in the calculator. Describe how h effects the location of the parabola. 26. Graph y = x 2,y = x 2 + 2, and y = x 2 5 on the same set of axes in the calculator. Describe how k effects the location of the parabola. 19
24 1.3. Vertex Form of a Quadratic Function Vertex Form of a Quadratic Function Here you will learn to write the equation for a parabola that has undergone transformations. Given the equation y = 3(x + 4) 2 + 2, list the transformations of y = x 2. Watch This James Sousa: Find the Equation ofaquadratic Function from a Graph MEDIA Click image to the left for more content. Guidance The equation for a basic parabola with a vertex at (0,0) is y = x 2. You can apply transformations to the graph of y = x 2 to create a new graph with a corresponding new equation. This new equation can be written in vertex form. The vertex form of a quadratic function is y = a(x h) 2 + k where: a is the vertical stretch factor. If a is negative, there is a vertical reflection and the parabola will open downwards. k is the vertical translation. h is the horizontal translation. Given the equation of a parabola in vertex form, you should be able to sketch its graph by performing transformations on the basic parabola. This process is shown in the examples. Example A Given the following function in vertex form, identify the transformations of y = x 2. y = 1 2 (x 2)2 1 Solution: a Is a negative? YES. The parabola will open downwards. a Is there a number in front of the squared portion of the equation? YES. The vertical stretch factor is the absolute value of this number. Therefore, the vertical stretch of this function is k Is there a number after the squared portion of the equation? YES. The value of this number is the vertical translation. The vertical translation is 1.
25 Chapter 1. Quadratics h Is there a number after the variable x? YES. The value of this number is the opposite of the sign that appears in the equation. The horizontal translation is +2. Example B Given the following transformations, determine the equation of the image of y = x 2 in vertex form. Vertical stretch by a factor of 3 Vertical translation up 5 units Horizontal translation left 4 units Solution: a The image is not reflected in the x-axis. A negative sign is not required. a The vertical stretch is 3, so a = 3. k The vertical translation is 5 units up, so k = 5. h The horizontal translation is 4 units left so h = 4. The equation of the image of y = x 2 is y = 3(x + 4) Example C Using y = x 2 as the base function, identify the transformations that have occurred to produce the following image graph. Use these transformations to write the equation in vertex form. 21
26 1.3. Vertex Form of a Quadratic Function Solution: a The parabola does not open downward so a will be positive. a The y-values of 1 and 4 are now up 3 and up 12. a = 3. k The y coordinate of the vertex is 5 so k = 5. h The x coordinate of the vertex is +3 so h = 3. The equation is y = 3(x 3) 2 5. You can also easily identify the axis of symmetry from the graph which is x = 3. The equation for the axis of symmetry is x = b 2a. Example D In general, the mapping rule used to generate the image of a function is (x,y) (x,y ) where (x,y ) are the coordinates of the image graph. The resulting mapping rule from y = x 2 to the image y = a(x h) 2 + k is (x,y) (x+h,ay+k). The mapping rule details the transformations that were applied to the coordinates of the base function y = x 2. Given the following quadratic equation, y = 2(x + 3) write the mapping rule and create a table of values for the mapping rule. Solution: The mapping rule for this function will tell exactly what changes were applied to the coordinates of the base quadratic function. y = 2(x + 3) 2 + 5: (x,y) (x 3,2y + 5) These new coordinates of the image graph can be plotted to generate the graph. Concept Problem Revisited Given the equation y = 3(x + 4) 2 + 2, list the transformations of y = x 2. a = 3 so the vertical stretch is 3. k = 2 so the vertical translation is up 2. h = 4 so the horizontal translation is left 4. 22
27 Chapter 1. Quadratics Vocabulary Horizontal translation The horizontal translation is the change in the base graph y = x 2 that shifts the graph right or left. It changes the x coordinate of the vertex. Mapping Rule The mapping rule defines the transformations that have occurred to a function. The mapping rule is (x,y) (x,y ) where (x,y ) are the coordinates of the image graph. Transformation A transformation is any change in the base graph y = x 2. The transformations that apply to the parabola are a horizontal translation, a vertical translation, a vertical stretch and a vertical reflection. Vertex form of y = x 2 The vertex form of y = x 2 is the form of the quadratic base function y = x 2 that shows the transformations of the image graph. The vertex form of the equation is y = a(x h) 2 + k. Vertical Reflection The vertical reflection is the reflection of the image graph in the x-axis. The graph opens downward and the y-values are negative values. Vertical Stretch The vertical stretch is the change made to the base function y = x 2 by stretching (or compressing) the graph vertically. The vertical stretch will produce an image graph that appears narrower (or wider) then the original base graph of y = x 2. Vertical Translation The vertical translation is the change in the base graph y = x 2 that shifts the graph up or down. It changes the y coordinate of the vertex. Guided Practice 1. Identify the transformations of y = x 2 for the quadratic function 2(y + 3)=(x 4) 2 2. List the transformations of y = x 2 and graph the function = (x + 5) Graph the function y = 2(x 2) using the mapping rule method. Answers: 1. Rewrite the equation in vertex form. a a is negative so the parabola opens downwards. a The vertical stretch of this function is 1 2. k The vertical translation is -3. h The horizontal translation is
28 1.3. Vertex Form of a Quadratic Function a negative a 1 k +4 h 5 3. Mapping Rule (x,y) (x + 2,2y + 3) Make a table of values: TABLE 1.4: x x + 2 y 2y Draw the graph: 24
29 Chapter 1. Quadratics Practice Identify the transformations of y = x 2 in each of the given functions: 1. y = 4(x 2) y = 1 6 x y = 3(x 1) y = 1 5 (x + 4) y = 5(x + 2) 2 Graph the following quadratic functions. Give the axis of symmetry and vertex for each function. 6. y = 2(x 4) y = 1 3 (x 2) y = 2(x + 3) y = 1 2 (x + 6) y = 1 3 (x 4)2 Using the following mapping rules, write the equation, in vertex form, that represents the image of y = x (x,y) x + 1, 1 2 y 25
30 1.3. Vertex Form of a Quadratic Function (x,y) (x + 6,2y 3) 13. (x,y) x 1, 2 3 y (x,y) (x + 3,3y + 1) 15. (x,y) x 5, 1 3 y 7 26
31 Chapter 1. Quadratics 1.4 Graphs to Solve Quadratic Equations Here you will learn how to solve a quadratic equation by graphing. Now that you are familiar with the graph of quadratics, you can use a graph to solve x 2 2x 3 = 0. Watch This James Sousa: Solve a Quadratic Equation Graphically on the Calculator MEDIA Click image to the left for more content. Guidance Recall that a quadratic equation is a degree 2 equation that can be written in the form ax 2 + bx + c = 0. Every quadratic equation has a corresponding quadratic function that you get by changing the "0" to a "y". Standard form for a quadratic function is y = ax 2 + bx + c. Quadratic functions can be graphed by hand, or with a graphing calculator. How do the solutions to the equation x 2 + x 12 = 0 show up on the graph of y = x 2 + x 12? On the graph you are looking for the points that have a y-coordinate that is equal to 0. Therefore, the solutions to the equation will show up as the x-intercepts on the graph of the function. These are also known as the roots or zeros of the function. Here is the graph of y = x 2 + x 12: 27
32 1.4. Graphs to Solve Quadratic Equations You can see the x-intercepts are at ( 4,0) and (3,0). This means that the solutions to the equation x 2 + x 12 = 0 are x = 4 and x = 3. You can verify these solutions by substituting them back into the equation: ( 4) 2 +( 4) 12 = = 0 (3) 2 +(3) 12 = = 0 Graphing is a great way to solve quadratic equations. Keep in mind that you can also solve many quadratic equations by factoring or using other algebraic methods such as the quadratic formula or completing the square. Example A Solve the following quadratic equation by finding the x-intercepts of the corresponding quadratic function: x 2 2x 8 = 0 Solution: The corresponding function is y = x 2 2x 8. Use your graphing calculator to make a table and a graph for this function. 28
33 Chapter 1. Quadratics The x-intercepts are ( 2, 0) and (4, 0). The x-intercepts are the values for x that result in y = 0 and are therefore the solutions to your equation. The solutions for the quadratic are x = 2 and x = 4. Example B Solve the following quadratic equation by finding the x-intercepts of the corresponding quadratic function: x 2 +4x+ 4 = 0 Solution: The corresponding function is y = x 2 + 4x + 4. Use your graphing calculator to make a table and a graph for this function. 29
34 1.4. Graphs to Solve Quadratic Equations The only x-intercept is ( 2, 0). There is only one solution to the equation: x = 2. Keep in mind that quadratic equations can have 0, 1, or 2 real solutions. If you were to factor the quadratic x 2 +4x+4, you would get (x+2)(x+ 2) two of the same factors. The root of 2 for this function is said to have a multiplicity of 2, because 2 factors produce the same solution. You will learn more about multiplicity when you study polynomials in future courses. Example C Solve the following quadratic equation by finding the x-intercepts of the corresponding quadratic function: x 2 +3x = 10 Solution: First rewrite the equation so it is set equal to zero to get x 2 +3x 10 = 0. Now, the corresponding function is y = x 2 + 3x 10. Use your graphing calculator to make a graph for this function. You will see that there are two x-intercepts. For this example you will see how the calculator can calculate the zeros of a function on a graph. This technique is particularly useful when the intercepts are not at whole numbers. Have the calculator find the x-intercept on the left first. Press The calculator will display Left Bound? Use the arrow to position the cursor so that it is to the left and above the x-axis. 30
35 Chapter 1. Quadratics When the cursor has been positioned, press The calculator will now display Right Bound? Use the arrows to position the cursor so that it is to the right and below the x-axis. When the cursor has been positioned, press The calculator will now display Guess? Press 31
36 1.4. Graphs to Solve Quadratic Equations At the bottom of the screen you can see it says "Zero" and the x and y coordinates. You are interested in the x- coordinate because that is one of the solutions to the original equation. The x-intercept is ( 5, 0) which means that one of the solutions is x = 5. Repeat this same process to determine the value of the x-intercept on the right. When you do this process for the x-intercept on the right, you will place your cursor below the x-axis for the left bound and above for the right bound. The x-intercept is (2, 0) which means that the second solution is x = 2. Concept Problem Revisited To solve the equation x 2 2x 3 = 0 using a graph, use a calculator to graph the corresponding function y = x 2 2x 3. Then, look for the values on the graph where y = 0, which will be the x-intercepts. Another way to think about this problem is to solve the system: y = x 2 2x 3 y = 0 You are looking for where the parabola y = x 2 2x 3 intersects with the line y = 0. 32
37 Chapter 1. Quadratics The points of intersection are ( 1, 0) and (3, 0). The solutions to the original equation are x = 1 and x = 3. Vocabulary Quadratic Equation A quadratic equation is an equation of degree 2. The standard form of a quadratic equation is ax 2 +bx+c = 0 where a = 0. Quadratic Function A quadratic function is a function that can be written in the form f (x)=ax 2 + bx + c with a = 0. The graph of a quadratic function is a parabola. Zeros of a Quadratic Function The zeros of a quadratic function are the x-intercepts of the function. These are the values for the variable x that will result in y = 0. Roots of a Quadratic Function The roots of a quadratic function are also the x-intercepts of the function. These are the values for the variable x that will result in y = 0. Guided Practice Solve each quadratic equation using a graph. 1. x 2 3x 10 = x 2 5x + 2 = x 2 5x = 3 Answers: 1. To begin, create a table of values for the corresponding function y = x 2 3x 10 by using your graphing calculator: 33
38 1.4. Graphs to Solve Quadratic Equations From the table, the x-intercepts are ( 2, 0) and (5, 0). The x-intercepts are the values for x that result in y = 0 and are therefore the solutions to the equation. The solutions to the equation are are x = 2 and x = To begin, create a table of values for the corresponding function y = 2x 2 5x+2 by using your graphing calculator: Press 34
39 Chapter 1. Quadratics Press the following keys to determine the x-intercept to the left: Press the following keys to determine the x-intercept to the right: The x-intercepts of the function are (0.5, 0) and (2, 0). The solutions to the equation are, therefore, x = 0.5 and x = First rewrite the equation so it is set equal to zero: 2x 2 5x 3 = 0. Next, create a table of values for the corresponding function y = 2x 2 5x 3 by using your graphing calculator: Now sketch the graph of the function. 35
40 1.4. Graphs to Solve Quadratic Equations The zeros of the function are ( 0.5, 0) and (3, 0). Therefore, the solutions to the equation are x = 0.5 and x = 3. Practice Use your graphing calculator to solve each of the following quadratic equations by graphing: x 2 + 9x 18 = x 2 + 8x 3 = x x + 6 = x 2 11x + 5 = x 2 + 8x 3 = 0 6. x 2 x 20 = x 2 7x + 5 = x 2 + 7x = x 2 15 = x 10. 3x 2 10x = How could you use the graphs of a system of equations to solve 3x 2 10x = 8? 12. What s the difference between a quadratic equation and a quadratic function? 13. Will a quadratic equation always have 2 solutions? Explain. 14. The quadratic equationx = 0 has no real solutions. How does the graph of y = x verify this fact? 15. When does it make sense to use the graphing method for solving a quadratic equation? 16. During practice a Sea World performer starts walking a tightrope at a height of 30 feet but slips and falls into a safety net 15 feet below. The function h(t)= 16t where t represents time measured in seconds, gives the performer s height above the ground (in feet) as he falls. Write and solve an equation to find the elapsed time until the performer lands in the net. a. Write the equation you need to solve. b. Write the two equations you will need to use to solve this problem with a graphing calculator. Rewrite the equations in terms of x and y so they are compatible with your graphing calculator. c. What intervals would be appropriate for your x-and y-axes on your graphing calculator? Explain.
41 Chapter 1. Quadratics d. Graph the two functions and use your calculator s trace or intersect feature to find the elapsed time until the performer lands in the net. Is your answer exact or approximate? e. Although the graphs interesect to the left of the y-axis, why is that point irrelevant to this problem? f. The distance d (in feet), that a falling object travels as a function of time t (in seconds) is given by d(t)=16t 2. Use this fact to explain the model given in the problem, h(t)= 16t In particular, explain why the model includes the constant 30 and why 16t 2 includes a negative sign. g. At what height would the performer have to be for his fall to last exactly one second? Explain. 37
42 1.5. Use Square Roots to Solve Quadratic Equations Use Square Roots to Solve Quadratic Equations Here you ll learn how to solve quadratic equations in which finding the solutions involves square roots. What if you had a quadratic equation like 4x 2 9 = 0 in which both terms were perfect squares? How could you solve such an equation? After completing this Concept, you ll be able to solve quadratic equations like this one that involve perfect squares. Watch This MEDIA Click image to the left for more content. CK-12 Foundation: 1004S Solving Quadratic Equations Using Square Roots Guidance So far you know how to solve quadratic equations by graphing. In this Concept, we ll examine equations in which we can take the square root of both sides of the equation in order to arrive at the result. Solve Quadratic Equations Involving Perfect Squares Let s first examine quadratic equations of the type x 2 c = 0 We can solve this equation by isolating the x 2 term: x 2 = c Once the x 2 term is isolated we can take the square root of both sides of the equation. Remember that when we take the square root we get two answers: the positive square root and the negative square root: x = c and x = c Often this is written as x = ± c. Example A Solve the following quadratic equations: a) x 2 4 = 0 b) x 2 25 = 0 38
43 Chapter 1. Quadratics Solution a) x 2 4 = 0 Isolate the x 2 : x 2 = 4 Take the square root of both sides: x = 4 and x = 4 The solutions are x = 2 and x = 2. b) x 2 25 = 0 Isolate the x 2 : x 2 = 25 Take the square root of both sides: x = 25 and x = 25 The solutions are x = 5 and x = 5. We can also find the solution using the square root when the x 2 term is multiplied by a constant in other words, when the equation takes the form ax 2 c = 0 We just have to isolate the x 2 : ax 2 = b x 2 = b a Then we can take the square root of both sides of the equation: x = b a and x = b a Often this is written as: x = ± b a. Example B Solve the following quadratic equations. a) 9x 2 16 = 0 b) 81x 2 1 = 0 Solution a) 9x 2 16 = 0 Isolate the x 2 : 9x 2 = 16 x 2 =
44 1.5. Use Square Roots to Solve Quadratic Equations Take the square root of both sides: x = and x = 9 Answer: x = 4 3 and x = 4 3 b) 81x 2 1 = 0 Isolate the x 2 : 81x 2 = 1 x 2 = 1 81 Take the square root of both sides: x = and x = 81 Answer: x = 1 9 and x = 1 9 In some cases, quadratic equations have no real solutions. Example C Solve the following quadratic equations. a) x = 0 b) 4x = 0 Solution a) x = 0 Isolate the x 2 : x 2 = 1 Take the square root of both sides: x = 1 and x = 1 Square roots of negative numbers do not give real number results, so there are no real solutions to this equation. b) 4x = 0 Isolate the x 2 : 4x 2 = 9 x 2 = 9 4 Take the square root of both sides: x = 94 and x = 9 4 There are no real solutions. We can also use the square root function in some quadratic equations where both sides of an equation are perfect squares. This is true if an equation is of this form: (x 2) 2 = 9 Both sides of the equation are perfect squares. We take the square root of both sides and end up with two equations: x 2 = 3 and x 2 = 3. 40
45 Chapter 1. Quadratics Solving both equations gives us x = 5 and x = 1. Example D Solve the following quadratic equations. a) (x 1) 2 = 4 b) (x + 3) 2 = 1 Solution a) (x 1) 2 = 4 Take the square root of both sides : Solve each equation : x 1 = 2 and x 1 = 2 x = 3 and x = 1 Answer: x = 3 and x = 1 b) (x + 3) 2 = 1 Take the square root of both sides : Solve each equation : x + 3 = 1 and x + 3 = 1 x = 2 and x = 4 Answer: x = 2 and x = 4 It might be necessary to factor the right-hand side of the equation as a perfect square before applying the method outlined above. Watch this video for help with the Examples above. MEDIA Click image to the left for more content. CK-12 Foundation: 1004 Solving Quadratic Equations Using Square Roots Vocabulary The solutions of a quadratic equation are often called the roots or zeros. Practice Solve the following quadratic equations. If there is no real solution, write no real solution. 1. x 2 1 = 0 2. x = 0 3. x = 0 41
46 1.5. Use Square Roots to Solve Quadratic Equations x 2 1 = x 2 49 = x 2 9 = 0 7. x 2 81 = x 2 36 = 0 9. x = x 2 16 = x 2 36 = x 2 49 = (x 2) 2 = (x + 5) 2 = (2x 1) 2 4 = (x + 3) 2 = (x + 3) 2 = (x + 2) 2 4 = (x 1) = To study how high a ball bounces, students drop the ball from various heights. The function h(t)= 16t 2 +h 0 gives the height (in feet) of the ball at time t measured in seconds since the ball was dropped from a height of h 0. a. The ball is dropped from a height of h 0 = 12 ft. Write and solve an equation to find the elapsed time until the ball hits the floor (round your answer to the nearest hundredth, as necessary). b. Does doubling the drop height also double the elapsed time until the ball hits the floor? Explain your reasoning. c. When dropped from a height of h 0 = 24 ft, the ball rebounds to a height of 12 feet and then falls back to the floor. Find the total time for this to happen. (Assume the ball takes the same time to rebound 12 feet as it does to fall 12 feet; round your answer to the nearest hundredth, as necessary). 42
47 Chapter 1. Quadratics 1.6 Solving Quadratics using Factoring Here you ll learn how to solve factorable quadratic equations for x. The height of a ball that is thrown straight up in the air from a height of 2 meters above the ground with a velocity of 9 meters per second is given by the quadratic equation h = 5t 2 + 9t + 2, where t is the time in seconds. How long does it take the ball to hit the ground? Watch This Watch the first part of this video, until about 4:40. MEDIA Click image to the left for more content. Khan Academy: Solving Quadratic Equations by Factoring.avi Guidance In the previous unit, you worked on factoring quadratics. Now, we will apply factoring to solving a quadratic equation. It adds one additional step to the end of what you did in the previous unit. Let s go through an example. Example A Solve x 2 9x + 18 = 0 by factoring. Solution: The only difference between this problem and previous ones from the concepts before is the addition of the = sign. Now that this is present, we need to solve for x. We can still factor the way we always have. Because a = 1, determine the two factors of 18 that add up to -9. x 2 9x + 18 = 0 (x 6)(x 3)=0 Now, we have two factors that, when multiplied, equal zero. Recall that when two numbers are multiplied together and one of them is zero, the product is always zero. Zero-Product Property: If ab = 0, then a = 0 or b = 0. This means that x 6 = 0 OR x 3 = 0. Therefore, x = 6 or x = 3. There will always be the same number of solutions as factors. Check your answer: 43
48 1.6. Solving Quadratics using Factoring (6)+18 = 0 or 3 2 9(3)+18 = = = 0 Example B Solve 6x 2 + x 4 = 11 by factoring. Solution: At first glance, this might not look factorable to you. However, before we factor, we must combine like terms. Also, the Zero-Product Property tells us that in order to solve for the factors, one side of the equation must be zero. 6x 2 + x 4 = = 11 6x 2 + x 15 = 0 Now, factor. The product of ac is -90. What are the two factors of -90 that add up to 1? 10 and -9. Expand the x term and factor. 6x 2 + x 15 = 0 6x 2 9x + 10x 15 = 0 3x(2x 3)+5(2x 3)=0 (2x 3)(3x + 5)=0 Lastly, set each factor equal to zero and solve. 2x 3 = 0 3x + 5 = 0 2x = 3 or 3x = 5 x = 3 2 x = 5 3 Check your work: = = = 11 or = = = = = 11 Example C Solve 10x 2 25x = 0 by factoring. 44
49 Chapter 1. Quadratics Solution: Here is an example of a quadratic equation without a constant term. The only thing we can do is take out the GCF. Set the two factors equal to zero and solve. 10x 2 25x = 0 5x(2x 5)=0 Check: 5x = 0 2x 5 = 0 x = 0 or 2x = 5 x = (0) 2 25(0)= = = 0 or = = 0 Intro Problem Revisit When the ball hits the ground, the height h is 0. So the equation becomes 0 = 5t 2 + 9t + 2. Let s factor and solve for t. 5t 2 + 9t + 2 We need to find the factors of 10 that add up to 9. Testing the possibilities, we find 10 and -1 to be the correct combination. 5t t t + 2=( 5t t)+( t + 2) =5t( t + 2)+( t + 2) = (5t + 1)( t + 2) Now set this factorization equal to zero and solve. (5t + 1)( t + 2)=0 Because t represents the time, it must be positive. Only ( t + 2)=0 results in a positive value. t = 2, therefore it takes the ball 2 seconds to reach the ground. Guided Practice Solve the following equations by factoring. 1. 4x 2 12x + 9 = 0 2. x 2 5x = x 20x 2 = x x + 7 = 12 4x Answers 1. ac = 36. The factors of 36 that also add up to -12 are -6 and -6. Expand the x term and factor. 45
50 1.6. Solving Quadratics using Factoring 4x 2 12x + 9 = 0 4x 2 6x 6x + 9 = 0 2x(2x 3) 3(2x 3)=0 (2x 3)(2x 3)=0 The factors are the same. When factoring a perfect square trinomial, the factors will always be the same. In this instance, the solutions for x will also be the same. Solve for x. 2x 3 = 0 2x = 3 x = 3 2 When the two factors are the same, we call the solution for x a double root because it is the solution twice. 2. Here, we need to get everything on the same side of the equals sign in order to factor. x 2 5x = 6 x 2 5x 6 = 0 Because there is no number in front of x 2, we need to find the factors of -6 that add up to -5. Solving each factor for x, we get that x = 6 or x = Here there is no constant term. Find the GCF to factor. (x 6)(x + 1)=0 Solve each factor for x. 8x 20x 2 = 0 4x(2 5x)=0 4x = 0 2 5x = 0 x = 0 or 2 = 5x 2 5 = x 4. This problem is slightly more complicated than #2. Combine all like terms onto the same side of the equals sign so that one side is zero. 12x x + 7 = 12 4x 12x x 5 = 0 46
51 Chapter 1. Quadratics ac = 60. The factors of -60 that add up to 17 are 20 and -3. Expand the x term and factor. 12x x 5 = 0 12x x 3x 5 = 0 4x(3x + 5) 1(3x + 5)=0 (3x + 5)(4x 1)=0 Solve each factor for x. 3x + 5 = 0 4x 1 = 0 3x = 5 or 4x = 1 x = 5 3 x = 1 4 Vocabulary Solution The answer to an equation. With quadratic equations, solutions can also be called zeros or roots. Double Root A solution that is repeated twice. Practice Solve the following quadratic equations by factoring, if possible. 1. x 2 + 8x 9 = 0 2. x 2 + 6x = x 2 5x = x 2 + 7x 10 = 0 5. x 2 = x + 25 = 9x x 2 + x 5 = x = 32x x x = x 2 48 = x 2 + x = x x + 4 = 0 Challenge Solve these quadratic equations by factoring. They are all factorable x 2 + 8x 5 = 10 6x x 2 = 48x x 2 24 = 96x Real Life Application George is helping his dad build a fence for the backyard. The total area of their backyard is 1600 square feet. The width of the house is half the length of the yard, plus 7 feet. How much fencing does George s dad need to buy? 47
52 1.6. Solving Quadratics using Factoring The width of a high school soccer field is 45 yards shorter than its length. The area of the field is 9000 square yards. Find the dimensions. 18. The length of a rectangular swimming pool is 20 feet greater than its width. The area of the pool is 525 square feet. What are the length and width of the pool? Are there any solutions to the equation you solved that don t make sense in the context of the problem? Explain. 19. An athlete throws a shot put with an initial velocity of 29 feet per second and from an initial height of 6 feet. After how many seconds will the shot put hit the ground? (click here for more information about vertical motion) 20. When Bobby shoots a free throw, the ball is 6 feet from the floor and has an initial velocity of 20 feet per second. The hoop is 10 feet from the floor. a. Use the vertical motion model h(t)= 16t 2 + v 0 t + h 0 (click here for more information) to determine an equation that models Bobby s free throw. b. How long is the basketball in the air before it reaches the hoop? c. Raymond shoots a free throw that is 5 foot 9 inches from the floor with the same initial velocity. Will the ball be in the air more or less time? Explain. 48
53 Chapter 1. Quadratics 1.7 Completing the Square Here you ll learn how to complete the square to help you solve quadratic equations. You ll also solve quadratic equations in standard form. What if you had a quadratic equation like x x = 13? How could you solve it by taking the square root of both sides? After completing this Concept, you ll be able to complete the square to solve quadratic equations like this one. Watch This MEDIA Click image to the left for more content. CK-12 Foundation: 1006S Solving Quadratic Equations by Completing the Square Guidance You saw in a previous section that if you have a quadratic equation of the form (x 2) 2 = 5, you can easily solve it by taking the square root of each side: Simplify to get: x 2 = 5 and x 2 = 5 x = and x = So what do you do with an equation that isn t written in this nice form? In this section, you ll learn how to rewrite any quadratic equation in this form by completing the square. Complete the Square of a Quadratic Expression Completing the square lets you rewrite a quadratic expression so that it contains a perfect square trinomial that you can factor as the square of a binomial. Remember that the square of a binomial takes one of the following forms: (x + a) 2 = x 2 + 2ax + a 2 (x a) 2 = x 2 2ax + a 2 So in order to have a perfect square trinomial, we need two terms that are perfect squares and one term that is twice the product of the square roots of the other terms. 49
54 1.7. Completing the Square Example A Complete the square for the quadratic expression x 2 + 4x. Solution To complete the square we need a constant term that turns the expression into a perfect square trinomial. Since the middle term in a perfect square trinomial is always 2 times the product of the square roots of the other two terms, we re-write our expression as: x 2 + 2(2)(x) We see that the constant we are seeking must be 2 2 : x 2 + 2(2)(x)+2 2 Answer: By adding 4 to both sides, this can be factored as: (x + 2) 2 Notice, though, that we just changed the value of the whole expression by adding 4 to it. If it had been an equation, we would have needed to add 4 to the other side as well to make up for this. Also, this was a relatively easy example because a, the coefficient of the x 2 term, was 1. When that coefficient doesn t equal 1, we have to factor it out from the whole expression before completing the square. Example B Complete the square for the quadratic expression 4x x. Solution Factor the coefficient of the x 2 term: 4(x 2 + 8x) Re-write the expression: 4(x 2 + 2(4)(x)) We complete the square by adding the constant 4 2 : 4(x 2 + 2(4)(x)+4 2 ) Factor the perfect square trinomial inside the parenthesis: 4(x + 4) 2 The expression completing the square comes from a geometric interpretation of this situation. Let s revisit the quadratic expression in Example 1: x 2 + 4x. We can think of this expression as the sum of three areas. The first term represents the area of a square of side x. The second expression represents the areas of two rectangles with a length of 2 and a width of x: 50
55 Chapter 1. Quadratics We can combine these shapes as follows: We obtain a square that is not quite complete. To complete the square, we need to add a smaller square of side length 2. We end up with a square of side length (x + 2); its area is therefore (x + 2) 2. Let s demonstrate the method of completing the square with an example. Example C Solve the following quadratic equation: 3x 2 10x = 1 Solution Divide all terms by the coefficient of the x 2 term: Rewrite: x (x)= 1 3 x x = 1 3 In order to have a perfect square trinomial on the right-hand-side we need to add the constant Add this constant to both sides of the equation: x 2 2 Factor the perfect square trinomial and simplify: 5 (x) = x 5 2 = 1 3 x =
56 1.7. Completing the Square Take the square root of both sides: x 5 3 = 22 9 Answer: x = 3.23 and x = 0.1 and x = 9 x = and x = 5 3 Solving Quadratic Equations in Standard Form If an equation is in standard form (ax 2 + bx + c = 0), we can still solve it by the method of completing the square. All we have to do is start by moving the constant term to the right-hand-side of the equation. Example D Solve the following quadratic equation: x x + 12 = 0 Solution Move the constant to the other side of the equation: Rewrite: x (x)= 12 Add the constant to both sides of the equation: x (x)+ 2 Factor the perfect square trinomial and simplify: x x = = Take the square root of both sides: x x = = x = 4 x = Answer: x = 0.85 and x = Watch this video for help with the Examples above. 4 and x = and x =
57 Chapter 1. Quadratics MEDIA Click image to the left for more content. CK-12 Foundation: 1006 Solving Quadratic Equations by Completing the Square Vocabulary A perfect square trinomial has the form a 2 + 2(ab)+b 2, which factors into (a + b) 2. Guided Practice Solve the following quadratic equation: x x = 5 Solution Divide all terms by the coefficient of the x 2 term: x 2 22x = 6 Rewrite: x 2 2(11)(x)= 6. In order to have a perfect square trinomial on the right-hand-side we need to add the constant (11) 2. Add this constant to both sides of the equation: x 2 2(11)(x)+(11) 2 = 6 +(11) 2 Factor the perfect square trinomial and simplify: (x 11) 2 = 6 +(11) 2 x = 16 Take the square root of both sides: x 11 = 16 and x 11 = 16 x = = 15 and x = 11 4 = 7 Answer: x = 15 and x = 7 Practice Complete the square for each expression. 53
58 1.7. Completing the Square 1. x 2 + 5x 2. x 2 2x 3. x 2 + 3x 4. x 2 4x 5. 3x x 6. 2x 2 22x 7. 8x 2 10x 8. 5x x Solve each quadratic equation by completing the square. 9. x 2 4x = x 2 5x = x x + 15 = x x + 20 = x 2 18x = x 2 + 5x = x 2 30x 8 = x x 40 = 0 54
59 Chapter 1. Quadratics 1.8 Solving Quadratic Equations by the Quadratic Formula Learning objectives Solve quadratic equations using the quadratic formula. Identify and choose methods for solving quadratic equations. Solve real-world problems using functions by completing the square. Introduction In this section, you will solve quadratic equations using the Quadratic Formula. method for solving quadratic equations. For a quadratic equation in standard form It is probably the most used The solutions are found using the following formula. ax 2 + bx + c = 0 x = b ± b 2 4ac 2a We will start by explaining where this formula comes from and then show how it is applied. This formula is derived by solving a general quadratic equation using the method of completing the square that you learned in the previous section. Divide by the coefficient of the x 2 term: x 2 + b a x = c a b Rewrite: x x = c 2a a b 2 b b 2 Add the constant to both sides: x x + = c 2a 2a 2a a + b2 4a 2 Factor the perfect square trinomial: x + b 2 = 4ac 2a 4a 2 + b2 4a 2 Simplify: x + b 2 = b2 4ac 2a 4a 2 Take the square root of both sides: x + b b 2a = 2 4ac 4a 2 and x + b b 2a = 2 4ac 4a 2 Simplify: x + b b 2a = 2 4ac and x + b b 2a 2a = 2 4ac 2a x = b b 2a + 2 4ac and x = b b 2a 2a 2 4ac 2a x = b + b 2 4ac and x = b b 2 4ac 2a 2a 55
60 1.8. Solving Quadratic Equations by the Quadratic Formula This can be written more compactly as x = b± b 2 4ac 2a. You can see that the familiar formula comes directly from applying the method of completing the square. Applying the method of completing the square to solve quadratic equations can be tedious. The quadratic formula is a more straightforward way of finding the solutions. Solve Quadratic Equations Using the Quadratic Formula Applying the quadratic formula basically amounts to plugging the values of a,b and c into the quadratic formula. Example 1 Solve the following quadratic equation using the quadratic formula. a) 2x 2 + 3x + 1 = 0 b) x 2 6x + 5 = 0 c) 4x 2 + x + 1 = 0 Solution Start with the quadratic formula and plug in the values of a,b and c. a) Quadratic formula x = b ± b 2 4ac 2a Plug in the values a = 2,b = 3,c = 1. x = 3 ± (3) 2 4(2)(1) 2(2) Answer x = 1 2 and x = 1 Simplify. x = 3 ± Separate the two options. x = Solve. = 3 ± 1 4 and x = x = 2 4 = 1 4 and x = 2 4 = 1 Remember you can check this solution by determine the x-intercepts of the quadratic function y = 2x 2 + 3x + 1 b) Answer x = 5 and x = 1 56 Quadratic formula. x = b ± b 2 4ac 2a Plug in the values a = 1,b = 6,c = 5. x = ( 6) ± ( 6) 2 4(1)(5) 2(1) Simplify. x = 6 ± Separate the two options. x = and x = = 6 ± 16 2 Solve x = 10 2 = 5 and x = 2 2 = 1
61 Chapter 1. Quadratics c) Quadratic formula. Plug in the values a = 4,b = 1,c = 1. x = b ± b 2 4ac 2a x = 1 ± (1) 2 4( 4)(1) 2( 4) Simplify. x = 1 ± Separate the two options. x = Solve. x.39 and x.64 = 1 ± 17 8 and x = Answer x = 1± 17 8 (This is the exact answer. Decimal approximations are useful in real world applications). Often when we plug the values of the coefficients into the quadratic formula, we obtain a negative number inside the square root. Since the square root of a negative number does not give real answers, we say that the equation has no real solutions. In more advanced mathematics classes, you will learn how to work with complex (or imaginary ) solutions to quadratic equations. Example 2 Solve the following quadratic equation using the quadratic formula x 2 + 2x + 7 = 0 Solution: a) Quadratic formula. x = b ± b 2 4ac 2a Plug in the values a = 1,b = 2,c = 7. x = 2 ± (2) 2 4(1)(7) 2(1) Simplify. x = 2 ± = 2 ± 24 2 Answer There are no real solutions. To apply the quadratic formula, we must make sure that the equation is written in standard form. For some problems, we must rewrite the equation before we apply the quadratic formula. Example 3 Solve the following quadratic equation using the quadratic formula. a) x 2 6x = 10 b) 8x 2 + 5x = 6 Solution: 57
62 1.8. Solving Quadratic Equations by the Quadratic Formula a) Rewrite the equation in standard form. x 2 6x 10 = 0 Quadratic formula Plug in the values a = 1,b = 6,c = 10. x = b ± b 2 4ac 2a x = ( 6) ± ( 6) 2 4(1)( 10) 2(1) Simplify. x = 6 ± = 6 ± Separate the two options. x = and x = Solve. x 7.36 and x 1.36 Answer: We should give the exact solution. x = 6± 76 2 b) Rewrite the equation in standard form. 8x 2 + 5x + 6 = 0 Quadratic formula x = b ± b 2 4ac 2a Plug in the values a = 8,b = 5,c = 6. x = 5 ± (5) 2 4(8)(6) 2(8) Answer No real solutions. Simplify. x = 5 ± = 5 ± Notice if we try to check this solution by graphing the quadratic function y = 8x 2 + 5x + 6, the graph does not cross the x-axis or have x-intercepts. This verifies we have complex solutions with an imaginary part. Finding the Vertex of a Parabola with the Quadratic Formula Sometimes you get more information from a formula beyond what you were originally seeking. In this case, the quadratic formula also gives us an easy way to locate the vertex of a parabola. First, recall that the quadratic formula tells us the roots or solutions of the equation ax 2 + bx + c = 0. Those roots are x = b ± b 2 4ac. 2a 58
63 Chapter 1. Quadratics We can rewrite the fraction in the quadratic formula as x = b 2a ± b 2 4ac. 2a Recall that the roots are symmetric about the vertex. In the form above, we can see that the roots of a quadratic equation are symmetric around the x coordinate b 2a because they move b 2 4ac 2a units to the left and right (recall the ± sign) from the vertical line x = b 2a. The image to the right illustrates this for the equation x2 2x 3 = 0. The roots, -1 and 3 are both 2 units from the vertical line x = 1. Identify and Choose Methods for Solving Quadratic Equations. In mathematics, you will need to solve quadratic equations that describe application problems or that are part of more complicated problems. You learned four ways of solving a quadratic equation. Factoring. Taking the square root. Completing the square. Quadratic formula. Usually you will not be told which method to use. You will have to make that decision yourself. However, here are some guidelines to which methods are better in different situations. Factoring is always best if the quadratic expression is easily factorable. It is always worthwhile to check if you can factor because this is the fastest method. Taking the square root is best used when there is no x term in the equation. Completing the square can be used to solve any quadratic equation. This is usually not any better than using the quadratic formula (in terms of difficult computations), however it is a very important method for re-writing a quadratic function in vertex form. It is also used to re-write the equations of circles, ellipses and hyperbolas in standard form (something you will do in algebra II, trigonometry, physics, calculus, and beyond...). Quadratic formula is the method that is used most often for solving a quadratic equation if solving directly by taking square root and factoring does not work. If you are using factoring or the quadratic formula make sure that the equation is in standard form. Example 4 Solve each quadratic equation a) x 2 4x 5 = 0 b) x 2 = 8 c) 4x 2 + x = 2 d) 25x 2 9 = 0 e) 3x 2 = 8x Solution a) This expression if easily factorable so we can factor and apply the zero-product property: 59
64 1.8. Solving Quadratic Equations by the Quadratic Formula Answer x = 5 and x = 1 Factor. (x 5)(x + 1)=0 Apply zero-product property. x 5 = 0 and x + 1 = 0 Solve. x = 5 and x = 1 Note that the factored form can also help us graph the function. The values above are also the x-intercepts: (5,0) and ( 1,0). After graphing the x-intercepts we can find the equation of the axis of symmetry as well as the vertex. b) Since the expression is missing the x term we can take the square root: Take the square root of both sides. x = 8 and x = 8 Answer x = ± 8 c) Rewrite the equation in standard form. It is not apparent right away if the expression is factorable, so we will use the quadratic formula. Quadratic formula Plug in the values a = 4,b = 1,c = 2. Answer No real solutions. x = b ± b 2 4ac 2a x = 1 ± 1 2 4( 4)( 2) 2( 4) Simplify. x = 1 ± = 1 ± 31 8 d) This problem can be solved easily either with factoring or taking the square root. Let s take the square root in this case. Add 9 to both sides of the equation. 25x 2 = 9 Divide both sides by 25. x 2 = 9 25 Take the square root of both sides. x = 9 25 and x = Simplify. x = 3 5 and x = Answer x = 3 5 and x = 3 5 e) Rewrite the equation in standard form 3x 2 8x = 0 Factor out common x term. x(3x 8)=0 Set both terms to zero. x = 0 and 3x = 8 Solve. x = 0 and x = 8 3 Answer x = 0 and x =
65 Chapter 1. Quadratics Seeing structure in equations The form of the quadratic equation can also highlight different variables of interest. Consider the profit, P, (in thousands of dollars), that a company makes selling an item is a quadratic function of the price, x (in dollars), that they charge for an item. The following expressions of P(x) are equivalent: Form 1: P(x)= 2x x 16 Form 2: P(x)= 2(x 2)(x 4) Form 3: P(x)= 2(x 3) Which of the equivalent expressions for P(x) reveals the price which gives a profit of zero without changing the form of the expression? The factored form, Form 2, reveals the price which gives a profit of zero, which can clearly be seen with the following: 0 = 2(x 2)(x 4) Since x = 2 or x = 4, the company breaks even if the price charged for the product is $2 or $4. Which of the equivalent expressions for P(x) reveals the profit when the price is zero without changing the form of the expression? The quadratic function in standard form, or Form 1, would reveal the profit when the price is zero. This can be seen by substituting 0 in for x: P(0)= 2(0) (0) 16 In this case, c = 16 so the profit is 16 (in thousands of dollars) when the price is zero. If the company gives the product away for free, it loses $16,000. Which of the equivalent expressions for P(x) reveals the price which produces the highest possible profit without changing the form of the expression? Vertex form, or Form 3, reveals the maximum profit without any computation. From P(x)= 2(x 3) we can see the maximum profit is 2 thousand dollars and it occurs when x = 3. The company should charge a price of $3 for this product in order to maximize its profits. Solve Real-World Problems Using Quadratic Functions by any Method Here are some application problems that arise from number relationships and geometry applications. Example 5 The product of two positive consecutive integers is 156. Find the integers. Solution For two consecutive integers, one integer is one more than the other one. Define Let x = the smaller integer x + 1 = the next integer Translate The product of the two numbers is 156. We can write the equation: x(x + 1)=156 61
66 1.8. Solving Quadratic Equations by the Quadratic Formula Solve x 2 + x = 156 x 2 + x 156 = 0 Apply the quadratic formula with a = 1, b = 1, c = 156 x = 1 ± 1 2 4(1)( 156) 2(1) x = 1 ± ± 25 = x = and x = 2 2 x = 24 2 Since we are looking for positive integers take, x = 12 Answer 12 and 13 Check = 156. The answer checks out. Example 6 = 12 and x = 26 2 = 13 The length of a rectangular pool is 10 meters more than its width. The area of the pool is 875 square/meters. Find the dimensions of the pool. Solution: Draw a sketch Define Let x = the width of the pool x + 10 = the length of the pool Translate The area of a rectangle is A = length width, so Solve x(x + 10)=875 x x = 875 x x 875 = 0 62
67 Chapter 1. Quadratics Apply the quadratic formula with a = 1,b = 10 and c = 875 x = 10 ± (10) 2 4(1)( 875) 2(1) x = 10 ± x = 10 ± ± 60 = x = and x = 2 2 x = = 25 and x = 2 2 = 35 Since the dimensions of the pools should be positive, then x = 25 meters. Answer The pool is 25 meters 35 meters. Check = 875 m 2. The answer checks out. Example 7 Suzie wants to build a garden that has three separate rectangular sections. She wants to fence around the whole garden and between each section as shown. The plot is twice as long as it is wide and the total area is 200 ft 2. How much fencing does Suzie need? Solution Draw a Sketch Define Let x = the width of the plot 2x = the length of the plot Translate Area of a rectangle is A = length width, so x(2x)=200 Solve 2x 2 =
68 1.8. Solving Quadratic Equations by the Quadratic Formula Solve by taking the square root. x 2 = 100 x = 100 and x = 100 x = 10 and x = 10 We take x = 10 since only positive dimensions make sense. The plot of land is 10 f eet 20 f eet. To fence the garden the way Suzie wants, we need 2 lengths and 4 widths = 2(20)+4(10)=80 f eet of fence. Answer: The fence is 80 feet. Check = 200 ft 2 and 2(20)+4(10)=80 f eet. The answer checks out. Example 8 An isosceles triangle is enclosed in a square so that its base coincides with one of the sides of the square and the tip of the triangle touches the opposite side of the square. If the area of the triangle is 20 in 2 what is the area of the square? Solution: Draw a sketch. Define Let x = base of the triangle x = height of the triangle Translate Area of a triangle is 1 2 base height, so Solve 1 2 x x = 20 Solve by taking the square root x2 = 20
69 Chapter 1. Quadratics x 2 = 40 x = 40 = 2 10 and x = 40 = 2 10 x 6.32 and x 6.32 The side of the square is approximately 6.32 inches. The area of the square is (6.32) 2 40 in 2, twice as big as the area of the triangle. Answer: Area of the triangle is 40 in 2 Check: It makes sense that the area of the square will be twice that of the triangle. If you look at the figure you can see that you can fit two triangles inside the square. FIGURE 1.1 The answer checks. Review Questions Solve the following quadratic equations using the quadratic formula. 1. x 2 + 4x 21 = 0 2. x 2 6x = x x = x 2 + x 3 = 0 5. x 2 7x + 12 = x 2 + 5x = x 2 = 0 8. x 2 + 2x + 6 = 0 65
70 1.8. Solving Quadratic Equations by the Quadratic Formula Solve the following quadratic equations using the method of your choice. 9. x 2 x = x 2 12 = x 2 + 5x 3 = x 2 + 7x 18 = x 2 + 6x = x x = x x + 1 = x 2 + 6x + 9 = x = x 2 + 4x = x 2 21 = x 2 2x 3 = The product of two consecutive integers is 72. Find the two numbers. 22. The product of two consecutive odd integers is 1 less than 3 times their sum. Find the integers. 23. The length of a rectangle exceeds its width by 3 inches. The area of the rectangle is 70 square inches, find its dimensions. 24. Angel wants to cut off a square piece from the corner of a rectangular piece of plywood. The larger piece of wood is 4 f eet 8 f eet and the cut off part is 1 3 of the total area of the plywood sheet. What is the length of the side of the square? 25. Mike wants to fence three sides of a rectangular patio that is adjacent the back of his house. The area of the patio is 192 ft 2 and the length is 4 feet longer than the width. Find how much fencing Mike will need. 26. The Profit, P (in thousands of dollars), that a company makes selling an item is a quadratic function of the price, x (in dollars), that they charge for the item. The following quadratic function is used to show the price of the product which gives a profit of zero: P(x)= 4(x 4)(x 6). a. Find the price(s) that give a profit of zero. b. Create an equivalent quadratic expression that clearly shows the profit when the price is zero. What is the profit when the price is zero? c. Create an equivalent quadratic expression that clearly shows the price which produces the highest possible profit. What is the price and what is the highest possible profit at this price? 66
71 Chapter 1. Quadratics 1.9 Solutions Using the Discriminant Here you ll learn how to find the number of solutions to a quadratic equation by calculating the discriminant and how to use this information to solve problems. Suppose that the balance of your checking account in dollars can be modeled by the function B(t)=0.001t 2 t + 300, where t is the number of days the checking account has been open. Will the balance of your checking account ever be $100? In this Concept, you ll learn how to find the discriminant of a quadratic equation so that you can find the number of solutions to the equation and answer real-world questions such as this one. Guidance You have seen parabolas that intersect the x axis twice, once, or not at all. There is a relationship between the number of real x intercepts and the quadratic formula. Case 1: The parabola has two x intercepts. This situation has two possible solutions for x, because the value inside the square root is positive. Using the quadratic formula, the solutions are x = b+ b 2 4ac 2a and x = b b 2 4ac 2a. Case 2: The parabola has one x intercept. This situation occurs when the vertex of the parabola just touches the x axis. This is called a repeated root, or double root. The value inside the square root is zero. Using the quadratic formula, the solution is x = b 2a. 67
72 1.9. Solutions Using the Discriminant Case 3: The parabola has no x intercept. This situation occurs when the parabola does not cross the x axis. The value inside the square root is negative, so there are no real roots. The solutions to this type of situation are imaginary, which you will learn more about in a later textbook. The value inside the square root of the quadratic formula is called the discriminant. It is symbolized by D. It dictates the number of real solutions the quadratic equation has. This can be summarized with the Discriminant Theorem. If D > 0, the parabola will have two x intercepts. The quadratic equation will have two real solutions. If D = 0, the parabola will have one x intercept. The quadratic equation will have one real solution. If D < 0, the parabola will have no x intercepts. The quadratic equation will have zero real solutions. Example A Determine the number of real solutions to 3x 2 + 4x + 1 = 0. Solution: By finding the value of its discriminant, you can determine the number of x intercepts the parabola has and thus the number of real solutions. 68
73 Chapter 1. Quadratics D = b 2 4(a)(c) D =(4) 2 4( 3)(1) D = = 28 Because the discriminant is positive, the parabola has two real x intercepts and thus two real solutions. Example B Determine the number of solutions to 2x 2 + x = 4. Solution: Before we can find its discriminant, we must write the equation in standard form: ax 2 + bx + c = 0. Subtract 4 from each side of the equation: 2x 2 + x 4 = 0. Find the discriminant: D =(1) 2 4( 2)( 4) D = 1 32 = 31 The value of the discriminant is negative; there are no real solutions to this quadratic equation. The parabola does not cross the x axis. Example C Emma and Bradon own a factory that produces bike helmets. Their accountant says that their profit per year is given by the function P = 0.003x x + 27,760, where x represents the number of helmets produced. Their goal is to make a profit of $40,000 this year. Is this possible? Solution: The equation we are using is 40,000 = 0.003x x + 27,760. By finding the value of its discriminant, you can determine if the profit is possible. Begin by writing this equation in standard form: 0 = 0.003x x 12,240 D = b 2 4(a)(c) D =(12) 2 4(0.003)( 12,240) D = = Because the discriminant is positive, the parabola has two real solutions. Yes, the profit of $40,000 is possible. Video Review MEDIA Click image to the left for more content. 69
74 1.9. Solutions Using the Discriminant MEDIA Click image to the left for more content. Guided Practice Determine the number of solutions for x 2 2x + 1 = 0. Solution: Substitute the values into the discriminant: D = b 2 4(a)(c) D =( 2) 2 4(1)(1) D = 4 4 = 0 Because the discriminant is zero, the parabola has one real x intercept and thus one real solution. Practice Sample explanations for some of the practice exercises below are available by viewing the following video. Note that there is not always a match between the number of the practice exercise in the video and the number of the practice exercise listed in the following exercise set. However, the practice exercise is the same in both. CK-12 Ba sic Algebra: Discriminant of Quadratic Equations (10:14) MEDIA Click image to the left for more content. 1. What is a discriminant? What does it do? 2. What is the formula for the discriminant? 3. Can you find the discriminant of a linear equation? Explain your reasoning. 4. Suppose D = 0. Draw a sketch of this graph and determine the number of real solutions. 5. D = Draw a possible sketch of this parabola. What is the number of real solutions to this quadratic equation. 6. D > 0. Draw a sketch of this parabola and determine the number of real solutions. Find the discriminant of each quadratic equation x 2 4x + 5 = 0 8. x 2 5x = 8
75 Chapter 1. Quadratics 9. 4x 2 12x + 9 = x 2 + 3x + 2 = x 2 16x = x 2 + 5x 6 = 0 Determine the nature of the solutions of each quadratic equation. 13. x 2 + 3x 6 = x 2 = 6x x 2 31x 52 = x 2 8x + 16 = x 2 + 3x 10 = x 2 64 = 0 A solution to a quadratic equation will be irrational if the discriminant is not a perfect square. If the discriminant is a perfect square, then the solutions will be rational numbers. Using the discriminant, determine whether the solutions will be rational or irrational. 19. x 2 = 4x x 2 + 2x 3 = x 2 11x = x2 + 2x = x 2 10x + 25 = x 2 = 5x 25. Marty is outside his apartment building. He needs to give Yolanda her cell phone but he does not have time to run upstairs to the third floor to give it to her. He throws it straight up with a vertical velocity of 55 feet/second. Will the phone reach her if she is 36 feet up? (Hint: The equation for the height is given by y = 32t t + 4.) 26. Bryson owns a business that manufactures and sells tires. The revenue from selling the tires in the month of July is given by the function R = x( x) where x is the number of tires sold. Can Bryson s business generate revenue of $20,000 in the month of July? 27. Marcus kicks a football in order to score a field goal. The height of the ball is given by the equation y = x2 + x, where y is the height and x is the horizontal distance the ball travels. We want to know if Marcus kicked the ball hard enough to go over the goal post, which is 10 feet high. Mixed Review 28. Factor 6x 2 x Find the vertex of y = 1 4 x2 3x 12 by completing the square. 30. Solve using the quadratic formula: 4x 2 15 = 4x. 31. How many centimeters are in four fathoms? (Hint: 1 fathom =6feet) 3x + 2y Graph the solution to. x y > How many ways can 3 toppings be chosen from 7 options? 71
76 1.10. Modeling with Quadratic Functions Modeling with Quadratic Functions Here you ll learn how to find the quadratic equation that fits to a data set. On reduced-gravity flights, airplanes fly in large parabolic arcs. Determine the quadratic equation of best fit for the data set below that represents the arc in which the airplane flies. TABLE 1.5: x(time in Sec.) y (Altitude in feet) Source: Nasa.gov ( Watch This MEDIA Click image to the left for more content. James Sousa: Ex: Quadratic Regression on the TI84 -Stopping Distance Guidance When finding the equation of a parabola, you can use any of the three forms. If you are given the vertex and any other point, you only need two points to find the equation. However, if you are not given the vertex you must have at least three points to find the equation of a parabola. Example A Find the equation of the parabola with vertex (-1, -4) and passes through (2, 8). Solution: Use vertex form and substitute -1 for h and -4 for k. y = a(x ( 1)) 2 4 y = a(x + 1) 2 4 Now, take the second point and plug it for x and y and solve for a. 72
77 Chapter 1. Quadratics The equation is y = 1 3 (x + 1) = a(2 + 4) = 36a 1 3 = a Like in the Analyzing Scatterplots lesson, we can also fit a set of data to a quadratic equation. In this concept, we will be using quadratic regression and a TI-83/84. Example B Determine the quadratic equation of best fit for the data set below. TABLE 1.6: x y Solution: We need to enter the x coordinates as a list of data and the y coordinates as another list. 1. Press STAT. 2. In EDIT, select 1:Edit.... Press ENTER. 3. The List table appears. If there are any current lists, you will need to clear them. To do this, arrow up to L1 so that it is highlighted (black). Press CLEAR, then ENTER. Repeat with L2, if necessary. 4. Now, enter the data into the lists. Enter all the entries into L1 (x) first and press enter between each entry. Then, repeat with L2 and y. 5. Press 2 nd MODE (QUIT). Now that we have everything in the lists, we can use quadratic regression to determine the equation of best fit. 6. press STAT and then arrow over to the CALC menu. 7. Select 5:QuadReg. Press ENTER. 8. You will be taken back to the main screen. Type (L1,L2) and press ENTER. L1 is 2 nd 1, L2 is 2 nd The following screen appears. The equation of best fit is y = 0.64x x
78 1.10. Modeling with Quadratic Functions If you would like to plot the equation on the scatterplot follow the steps from the Finding the Equation of Best Fit using a Graphing Calculator concept. The scatterplot and parabola are to the right. This technique can be applied to real-life problems. You can also use technique to find the equation of any parabola, given three points. Example C Find the equation of the parabola that passes through (1, 11), (2, 20), (-3, 75). Solution: You can use the same steps from Example B to find the equation of the parabola. Doing this, you should get the equation is y = 5x 2 6x This problem can also be done by solving three equations, with three unknowns. If we plug in (x,y) to y = ax 2 + bx + c, we would get: 11 = a + b + c 20 = 4a + 2b + c 75 = 9a 3b + c Use linear combinations to solve this system of equations (see Solving a System in Three Variables Using Linear Combinations concept). This problem will be finished in the Problem Set. Intro Problem Revisit Use your calculator to find the quadratic equation of best fit for the given table. TABLE 1.7: x(time in Sec.) y (Altitude in feet) y = x x is the quadratic equation of best fit for the data. Guided Practice 1. Find the equation of the parabola with x intercepts (4, 0) and (-5, 0) that passes through (-3, 8). 2. A study compared the speed, x (in miles per hour), and the average fuel economy, y (in miles per gallon) of a sports car. Here are the results. 74
79 Chapter 1. Quadratics TABLE 1.8: speed fuel economy Plot the scatterplot and use your calculator to find the equation of best fit. Answers 1. Because we are given the intercepts, use intercept form to find the equation. y = a(x 4)(x + 5) Plug in (-3,8) and solve for a 8 = a( 3 4)( 3 + 5) 8 = 14a 4 7 = a The equation of the parabola is y = 4 7 (x 4)(x + 5). 2. Plotting the points, we have: Using the steps from Example B, the quadratic regression equation is y = 0.009x x Vocabulary Quadratic Regression The process through which the equation of best fit is a quadratic equation. 75
80 1.10. Modeling with Quadratic Functions Practice Find the equation of the parabola given the following points. No decimal answers. 1. vertex: (-1, 1) point: (1, -7) 2. x intercepts: -2, 2 point: (4, 3) 3. vertex: (9, -4) point: (5, 12) 4. x intercepts: 8, -5 point: (3, 20) 5. x intercepts: -9, -7 point: (-3, 36) 6. vertex: (6, 10) point: (2, -38) 7. vertex: (-4, -15) point: (-10, 1) 8. vertex: (0, 2) point: (-4, -12) 9. x intercepts: 3, 16 point: (7, 24) Use a graphing calculator to find the quadratic equation (in standard form) that passes through the given three points. No decimal answers. 10. (-4, -51), (-1, -18), (4, -43) 11. (-5, 131), (-1, -5), (3, 51) 12. (-2, 9), (2, 13), (6, 41) 13. Challenge Finish computing Example C using linear combinations. For the quadratic modeling questions below, use a graphing calculator. Round any decimal answers to the nearest hundredth. 14. The surface of a speed bump is shaped like a parabola. Write a quadratic model for the surface of the speed bump shown. 15. Physics and Photography Connection Your physics teacher gives you a project to analyze parabolic motion. You know that when a person throws a football, the path is a parabola. Using your camera, you take an long exposure picture of a friend throwing a football. A sketch of the picture is below. 76 You put the path of the football over a grid, with the x axis as the horizontal distance and the y axis as the height, both in 3 feet increments. The release point, or shoulder height, of your friend is 5 ft, 3 in and you estimate that the maximum height is 23 feet. Find the equation of the parabola.
81 Chapter 1. Quadratics 16. An independent study was done linking advertising to the purchase of an object. 400 households were used in the survey and the commercial exposure was over a one week period. See the data set below. TABLE 1.9: # of times commercial was shown, x # of households bought item, y a) Find the quadratic equation of best fit. b) Why do you think the amount of homes that purchased the item went down after more exposure to the commercial? 77
82 1.11. References References 1. CK-12 Foundation.. 78
83 Chapter 2. Non-Linear Relationships CHAPTER 2 Non-Linear Relationships Chapter Outline 2.1 PIECEWISE FUNCTIONS 2.2 GRAPHING BASIC ABSOLUTE VALUE FUNCTIONS 2.3 USING THE GENERAL ABSOLUTE VALUE EQUATION AND THE GRAPHING CAL- CULATOR 2.4 GRAPHS OF SQUARE ROOT FUNCTIONS 2.5 SHIFTS OF SQUARE ROOT FUNCTIONS 2.6 GRAPHING CUBED ROOT FUNCTIONS 79
84 2.1. Piecewise Functions Piecewise Functions Here you will explore the process of modeling functions with cubed functions or with different functions in different parts of the model (piece-wise functions). Many real-life situations do not easily fit completely within a simple model, so it can be valuable to understand the process of using multiple models in the same situation. As we venture into non-linear functions, we need to consider: How do exponential, quadratic, and polynomial functions compare? Check out this link: Read through the information and try the Sample Assignment. Guidance Piece-wise functions may be used to model the interactions of multiple items each previously modeled by a simpler function. There are two special cases of piece-wise functions: step functions and absolute value functions. This section will introduce you to general piece-wise functions as well as step functions. The next few sections will cover absolute value functions. Example A Piece-wise functions can be used to describe situations in which quantitative relationships are different in different intervals within the domain of the function. For example, consider a situation in which a wireless provider offers customers a monthly plan that costs $50, but then charges $0.40 cents per minute for every minute over 1000 included daytime minutes. Model the monthly cost, C, of the plan as a function of m, the number of daytime minutes you use: Solution: C(m)= 50, m (m 1000), m >
85 Chapter 2. Non-Linear Relationships This function is comprised of a constant function, and a linear function with slope If in a given month you use 1000 minutes or fewer, your monthly cost is a constant $50. If you use more than 1000, each additional minute influences the value of C. For example, if you use 1,020 minutes, your cost is: TABLE 2.1: C(1020) = ( ) = (20) = =$58.00 It is important to note that in this kind of situation, the time used may to be rounded to the nearest minute. So, for example, if you use 20.5 minutes, you will be charged for 21 minutes. This is an example of a non-continuous, or discontinuous, function, where there are definite steps from value to value rather than a smooth line connecting all possible values. For additional videos on piece-wise functions please click here and here. Example B The graph of a step function is a series of line segments.one example of a step function is the Greatest Integer Function. For examples on Step Functions and the Greatest Integer Function please click here and here. Guided Practice Questions 1) At your favorite gourmet store, you buy loose tea by the ounce. The store does not calculate for fractions of an ounce. Instead, they round the weight of tea UP to the nearest ounce. Your favorite tea costs $3.00 per ounce. Sketch a function to model the cost of tea as a function of the number of ounces you purchase. Explain why the function is 81
86 2.1. Piecewise Functions not continuous. Solutions 1) The function is not continuous because the function is constant between each whole number value of the domain, but then it jumps up to the next whole number value in the range. For example, 1.99 ounces of tea and 2.00 ounces both cost $6.00, but 2.01 ounces costs $9.00. Practice For 1-6, graph each function f (x)= 1 2 [[x]] 2. h(x)=[[2x]] 2 ifx< 0 3. f (x)= 4 ifx 0 x ifx< 0 4. f (x)= x + 1 ifx 0 2x 1 ifx> 1 5. f (x)= x ifx 1 1 ifx< 1 6. f (x)= 2x 2 ifx 1 7. Nicole wants to take a taxi from a hotel to a restaurant. The rate is $4 plus $1.50 per mile after the first mile. Every fraction of a mile is rounded up to the next mile. Draw a graph to represent the cost of using the
87 Chapter 2. Non-Linear Relationships taxi cab. What is the cost if the trip is 10.5 miles long? 8. A basketball team is ordering jackets with the team logo on the front and the player s names on the back. A graphic design firm charges $12 to set up the art work plus $25 per jacket, $5 for the team logo, and $3 to print the last name for an order of 10 jackets or less. For orders of jackets, a 5% discount is given. For orders of more than 20 jackets, a discount of 10% is given. a. Organize the information into a table. Include a column showing the total order price for each size order. b. Write an equation representing the total price for an order of x shirts. c. Graph the piecewise relation. 83
88 2.2. Graphing Basic Absolute Value Functions Graphing Basic Absolute Value Functions Here you ll learn about the basic properties of absolute value functions. While on vacation, you go scuba diving. You start at an unknown sea level of zero feet or higher. You then dive to a depth of 90 feet below sea level. What is the vertex of the absolute value function that represents your possible distance from sea level after diving? Watch This MEDIA Click image to the left for more content. James Sousa: Ex: Graph an Absolute Value Function Using atable of Values Guidance In the Solving Absolute Value Equations concept, we learned how to solve and define absolute value equations. We will now take this idea one step further and graph absolute value equations. Investigation: Graphing the Parent Graph of an Absolute Value Function 1. We are going to graph y = x. Draw a table for x and y, with the x values ranging from -3 to 3. TABLE 2.2: x x y Recall that the absolute value of a number is always positive. Now that you have 7 sets of points, plot each one and graph the function. 84
89 Chapter 2. Non-Linear Relationships 3. Notice that this function is very similar to the linear function, y = x. Draw this line on the graph in a different color or with a dashed line. 4. Now, fold your graph on the x axis. What do you notice? In the investigation, you should discover that when you fold your graph on the x axis, the line y = x becomes the absolute value equation, y = x. That is because the absolute value of a number can never be zero; therefore, the range will always be positive. We call y = x the parent graph because it is the most basic of all the absolute value functions. We will also compare other absolute value functions to this graph. All linear absolute value functions have this V shape. x; x 0 In general, we can define the graph of y = x as y =. From this, we see that each side, is the mirror x; x < 0 image of the other over a vertical line, through the vertex. Example A Use a table to graph y = x 3. Determine the domain and range. Solution: In general, when you use a table to graph a function, pick some positive and negative numbers, as well as zero. Use the equation to help you determine which x values to pick. Setting what is inside the absolute value equal to zero, we get that x = 3. Pick three values on either side of x = 3 and then graph. TABLE 2.3: x x 3 y
90 2.2. Graphing Basic Absolute Value Functions Notice that this graph shifts to the right 3 when compared to the parent graph. The domain will be all real numbers, x R, and the range will be all positive real numbers, including zero, y [0, ). The domain and range can also be expressed as (, ). Example B Use a table to graph y = x 5. Determine the domain and range. Solution: Be careful! Here, the minus 5 is not inside the absolute value. So, first take the absolute value of the x value and then subtract 5. In cases like these, the range can include negative numbers. TABLE 2.4: x x 5 y
91 Chapter 2. Non-Linear Relationships Here, the graph shifts down 5 when compared to the parent graph. The domain will be all real numbers, x R, and the range will be all real numbers greater than or equal to -5, y [ 5, ). The domain can also be expressed as (, ) and the range as [ 5, ). In these three absolute value graphs, you may have noticed that there is a minimum point. This point is called the vertex. For example, in Example B, the vertex is (0, -5). The vertex can also be a maximum. See the next example. Example C Use a table to graph y = x Determine the vertex, domain, and range. Solution: Determine what makes the inside of the absolute value equation zero, x = 1. Then, to make your table of values, pick a couple values on either side of x = 1. TABLE 2.5: x x 1 +2 y
92 2.2. Graphing Basic Absolute Value Functions The vertex is (1, 2) and in this case, it is the maximum value. The domain is x R, and the range is y (,2]. Intro Problem Revisit The absolute value function that represents this situation is y = x 90, where x is your sea level before diving. By graphing this function, you can see that the vertex occurs at the point (90, 0) Vocabulary Absolute Value The distance away from zero a number is. The absolute value is always positive. Parent Graph The simplest form of a particular type of function. All other functions of this type are usually compared to the parent graph. Vertex The highest or lowest point of a graph. Minimum The lowest point of a graph. The minimum will yield the smallest value of the range. Maximum The highest point of a graph. The maximum will yield the largest value of the range. Guided Practice Graph the following functions using a table. Determine the vertex, domain, and range of each function. 1. y = x 5 2. y = x Answers 1. Determine what makes the inside of the absolute value equation zero, x = 5. Then, to make your table of values, pick a couple values on either side of x = 5. 88
93 Chapter 2. Non-Linear Relationships TABLE 2.6: x x 5 y The vertex is (5, 0) and in this case, it is the maximum value. The domain is x R, and the range is y (,0]. 2. Determine what makes the inside of the absolute value equation zero, x = 4. Then, to make your table of values, pick a couple values on either side of x = 4. TABLE 2.7: x x y
94 2.2. Graphing Basic Absolute Value Functions The vertex is (-4, -2) and in this case, it is the minimum value. The domain is x R, and the range is y [ 2, ). Practice Graph the following functions using a table. Determine the vertex, domain, and range of each function. 1. y = x y = x 4 3. y = x y = x 2 5. y = x y = x y = 2 x 8. y = 3 x 9. y = 1 3 x Use problems 1-9 to answer fill in the blanks. 10. If there is a negative sign in front of the absolute value, the graph is (when compared to the parent graph). 11. If the equation is y = x h +k, the vertex will be. 12. The domain of an absolute value function is always. 13. For y = a x, if a > 1, then the graph will be than the parent graph. 14. For y = a x, if 0 < a < 1, then the graph will be than the parent graph. 15. Without making a table, what is the vertex of y = x 9 +7? 16. The number of diners in a restaurant is modeled by d(t)= 0.5 t where t is the time (in minutes) since the store opened at 10:00 A.M. a. For what value of t are there 100 shoppers in the store? b. At what time are there 100 shoppers in the store? c. What is the greatest number of shoppers in the store? d. At what time does the greatest number of shoppers occur? 90
95 Chapter 2. Non-Linear Relationships 2.3 Using the General Absolute Value Equation and the Graphing Calculator Here you ll learn how to graph more complicated absolute value functions and use the graphing calculator. Mrs. Patel assigns the absolute value function y = x She tells her students to find the vertex. "This is hard," George laments. "I m going to need a calculator." "No, it s not," Sarai counters. "I can tell you what the vertex is without even graphing by hand." Who is right and what is the vertex? Guidance In the problem set of the previous concept, we were introduced to the general equation of an absolute value function. Let s formally define it here. General Form of an Absolute Value Function: For any absolute value function, the general form is y = a x h +k, where a controls the width of the V and (h,k) is the vertex. You probably made these connections during the problem set from the previous concept. Now, we will put it all to use together. Example A Graph y = x, y = 1 2 x, and y = 2 x on the same set of axes. Compare the three functions. Solution: You can make a table for all three of these functions. However, now that we have a better understanding of absolute value functions, let s use some patterns. First, look at the vertex. Nothing is being added or subtracted, so the vertex for all three will be (0, 0). Second, look at a. For an absolute value function, we can think of a like the slope. Referring back to the definition of the parent graph, each function above can be rewritten as: y = x;x 0 x;x < 0 (blue), y = 1 2 x;x 0 2x;x x;x < 0 (red), and y = 2x;x < 0 (green) Comparing the three, we see that if the slope is between 1 and 0, the opening is wider than the parent graph. If the slope, or a, is greater than 1, then that opening is narrower. The amount of the opening between the two sides of an absolute value function (and other functions) is called the breadth. 91
96 2.3. Using the General Absolute Value Equation and the Graphing Calculator Now, in addition to drawing a table, we can use the general form of an absolute value equation and the value of a to find the shape of the V. Example B Without making a table, sketch the graph of y = x 6 2. Solution: First, determine the vertex. From the general form, we know that it will be (6, -2). Notice that the x variable is the opposite sign of what is in the equation; the y variable is the same. That is our starting point. Then, we have a negative sign in front of the absolute value. This means our V will open down. Finally, there is no a term, so we can assume it is 1, meaning that the slope of each side of the V will be 1 and -1. Lastly, we can use a graphing calculator to help us graph absolute value equations. The directions given here pertain to the TI-83/84 series; however every graphing calculator should be able to graph absolute value functions. Example C Use a graphing calculator to graph y = 4x Find the vertex, domain, and range. Solution: For the TI-83/84 1. Press the Y = button. 92
97 Chapter 2. Non-Linear Relationships 2. Clear any previous functions (press CLEAR) and turn off any previous plots (arrow up to Plot 1 and press ENTER). 3. Press the MATH button, arrow over to NUM and highlight 1:abs(. Press ENTER. 4. Type in the remaining portion of the function. The screen: 5. Press GRAPH. If your screen is off, press ZOOM, scroll down to 6:ZStandard, and press ENTER. The graph looks like: As you can see from the graph, the vertex is not (-1, -2). The y coordinate is -2, but the 4 inside the absolute value affects the x coordinate. Set what is inside the absolute value equal to zero to solve for the x coordinate of the vertex. 4x + 1 = 0 4x = 1 x = 1 4 The vertex is 1 4, 2. From the previous concept, we know that the domain is all real numbers. The range will be any number greater than and including -2. In this function, the a term was inside the absolute value. When this happens, it will always affect the x coordinate of the vertex. Intro Problem Revisit Sarai is right. The absolute value function is written in general form, so a calculator is not necessary. The vertex is ( 3, 2). Vocabulary General Form of an Absolute Value Function For any absolute value function, the general form is y = a x h +k, where a controls the width of the V and (h,k) is the vertex. 93
98 2.3. Using the General Absolute Value Equation and the Graphing Calculator Breadth The wideness or narrowness of a function with two symmetric sides. Guided Practice 1. Graph y = 3 x without a graphing calculator or making a table. Find the vertex, domain, and range of the function. 2. Graph y = 2 x 5 +1 using a graphing calculator. Answers 1. First, use the general form to find the vertex, (-4, -5). Then, use a to determine the breadth of the function. a = 3, so we will move up 3 and over 1 in both directions to find the points on either side of the vertex. The domain is all real numbers and the range is all reals greater than and including -5. Domain: x R or (, ) Range: y [ 5, ) or [ 5, ) 2. Using the steps from Example C, the function looks like: 94
99 Chapter 2. Non-Linear Relationships Practice 1. Graph y = 3 x, y = 3 x, and y = 3x on the same set of axes. Compare the graphs. 2. Graph y = 1 4 x + 1, and y = 1 4 x +1 on the same set of axes. Compare the graphs. 3. Without graphing, do you think that y = 2 x, y = 2x, and y = 2x will all produce the same graph? Why or why not? 4. We know that the domain of all absolute value functions is all real numbers. What would be a general rule for the range? Use the general form and pattern recognition to graph the following functions. Determine the vertex, domain, and range. No graphing calculators! 5. y = x y = 2 x y = 1 3 x y = 2 x y = 1 2 x y = x 8 +6 Use a graphing calculator to graph the following functions. Sketch a copy of the graph on your paper. Identify the vertex, domain, and range. 11. y = 4 2x y = 2 3 x y = 4 3 2x Graphing Calculator Extension Use the graphing calculator to answer questions Graph y = x 2 4 on your calculator. Sketch the graph and determine the domain and range. 15. Graph y = x 2 4 on your calculator. Sketch graph and determine the domain and range. 16. How do the two graphs compare? How are they different? What could you do to the first graph to get the second? 95
100 2.4. Graphs of Square Root Functions Graphs of Square Root Functions Here you ll learn how to graph and compare functions that involve square roots. What if you had a square root function like y = 2x+3. How would you graph that function? After completing this Concept, you ll be able to graph square root functions like this one and compare them to other square root functions. Watch This MEDIA Click image to the left for more content. CK-12 Foundation: Graphs of Square Root Functions Guidance In this chapter you ll learn about a different kind of function called the square root function. You ve seen that taking the square root is very useful in solving quadratic equations. For example, to solve the equation x 2 = 25 we take the square root of both sides: x 2 = ± 25, so x = ±5. A square root function is any function with the form: y = a f (x)+c in other words, any function where an expression in terms of x is found inside a square root sign (also called a radical sign), although other terms may be included as well. Graph and Compare Square Root Functions When working with square root functions, you ll have to consider the domain of the function before graphing. The domain is very important because the function is undefined when the expression inside the square root sign is negative, and as a result there will be no graph in whatever region of x values makes that true. To discover how the graphs of square root functions behave, let s make a table of values and plot the points. Example A Graph the function y = x. Solution Before we make a table of values, we need to find the domain of this square root function. The domain is found by realizing that the function is only defined when the expression inside the square root is greater than or equal to zero. Since the expression inside the square root is just x, that means the domain is all values of x such that x 0. This means that when we make our table of values, we should pick values of x that are greater than or equal to zero. It is very useful to include zero itself as the first value in the table and also include many values greater than zero. This will help us in determining what the shape of the curve will be. 96
101 Chapter 2. Non-Linear Relationships TABLE 2.8: x y= x 0 y = 0 = 0 1 y = 1 = 1 2 y = 2 = y = 3 = y = 4 = 2 5 y = 5 = y = 6 = y = 7 = y = 8 = y = 9 = 3 Here is what the graph of this table looks like: The graphs of square root functions are always curved. The curve above looks like half of a parabola lying on its side, and in fact it is. It s half of the parabola that you would get if you graphed the expression y 2 = x. And the graph of y = x is the other half of that parabola: Notice that if we graph the two separate functions on the same coordinate axes, the combined graph is a parabola lying on its side. 97
102 2.4. Graphs of Square Root Functions Now let s compare square root functions that are multiples of each other. Example B Graph the functions y = x,y = 2 x,y = 3 x, and y = 4 x on the same graph. Solution Here is just the graph without the table of values: If we multiply the function by a constant bigger than one, the function increases faster the greater the constant is. Example C Graph the functions y = x,y = 2x,y = 3x, and y = 4x on the same graph. Solution 98
103 Chapter 2. Non-Linear Relationships Notice that multiplying the expression inside the square root by a constant has the same effect as multiplying by a constant outside the square root; the function just increases at a slower rate because the entire function is effectively multiplied by the square root of the constant. Also note that the graph of 4x is the same as the graph of 2 x. This makes sense algebraically since 4 = 2. Example D Graph the functions y = x,y = 1 2 x,y = 1 3 x, and y = 1 4 x on the same graph. Solution If we multiply the function by a constant between 0 and 1, the function increases more slowly the smaller the constant is. Watch this video for help with the Examples above. MEDIA Click image to the left for more content. CK-12 Foundation: Graphs of Square Root Functions 99
104 2.4. Graphs of Square Root Functions Vocabulary A square root function is any function with the form: y = a f (x)+c in other words, any function where an expression in terms of x is found inside a square root sign (also called a radical sign). Guided Practice Graph the functions a) y = 2 x and y = 2 x on the same graph. b) y = x and y = x on the same graph. Solutions: a) If we multiply the whole function by -1, the graph is reflected about the x axis. b) On the other hand, when just the x is multiplied by -1, the graph is reflected about the y axis. Notice that the function y = x has only negative x values in its domain, because when x is negative, the expression under the radical sign is positive. 100
105 Chapter 2. Non-Linear Relationships Practice Graph the following functions. 1. y = 3 x 2. y = 1 2 x 3. y = 4x 4. y = x y = 2 x 5 6. y = 3x Graph the functions in problems 7-10 on the same coordinate axes. 7. y = x,y = 2.5 x and y = 2.5 x 8. y = x,y = 0.3 x and y = 0.6 x 9. y = x,y = x 5 and y = x y = x,y = x + 8 and y = x Describe the relationship between the graphs of y = x 2 and y = x. How are they alike? How are they different? 12. The time in seconds that it takes an object to fall a distance d is given by the function t = 1 4 d (assuming zero air resistance). Graph the function. 13. The perimeter of a square is given by the function P = 4 A, where A is the area of the square. a. Graph the function. b. Determine the perimeter of a square with an area of 729 m 2. c. Would the perimeter and area of a square every be the same value? Explain your reasoning. 101
106 2.5. Shifts of Square Root Functions Shifts of Square Root Functions Here you ll learn what shifts result from performing operations both inside and outside the square root sign of square root functions. You ll also learn how to graph such functions. What if you had the square root function y = x? How would the graph of the function change if you added 5 to the righthand side of the equation or if you multiplied x by 3? After completing this Concept, you ll be able to identify various shifts in square root functions. Watch This MEDIA Click image to the left for more content. CK-12 Foundation: Shifts of Square Root Functions Guidance We will now look at how graphs are shifted up and down in the Cartesian plane. Example A Graph the functions y = x,y = x + 2 and y = x 2. Solution When we add a constant to the right-hand side of the equation, the graph keeps the same shape, but shifts up for a positive constant or down for a negative one. 102
107 Chapter 2. Non-Linear Relationships Example B Graph the functions y = x,y = x 2, and y = x + 2. Solution When we add a constant to the argument of the function (the part under the radical sign), the function shifts to the left for a positive constant and to the right for a negative constant. Now let s see how to combine all of the above types of transformations. Example C Graph the function y = 2 3x Solution We can think of this function as a combination of shifts and stretches of the basic square root function y = x.we know that the graph of that function looks like this: If we multiply the argument by 3 to obtain y = 3x, this stretches the curve vertically because the value of y increases faster by a factor of 3. Next, when we subtract 1 from the argument to obtain y = 3x 1 this shifts the entire graph to the left by one unit. Multiplying the function by a factor of 2 to obtain y = 2 3x 1 stretches the curve vertically again, because y increases faster by a factor of
108 2.5. Shifts of Square Root Functions Finally we add 2 to the function to obtain y = 2 3x This shifts the entire function vertically by 2 units. Each step of this process is shown in the graph below. The purple line shows the final result. Now we know how to graph square root functions without making a table of values. If we know what the basic function looks like, we can use shifts and stretches to transform the function and get to the desired result. Watch this video for help with the Examples above. MEDIA Click image to the left for more content. CK-12 Foundation: Shifts of Square Root Functions Vocabulary For the square root function with the form: y = a f (x)+c, c is the vertical shift. Guided Practice Graph the function y = x Solution We can think of this function as a combination of shifts and stretches of the basic square root function y = x.we know that the graph of that function looks like this: 104
109 Chapter 2. Non-Linear Relationships Next, when we add 3 to the argument to obtain y = x + 3 this shifts the entire graph to the right by 3 units. Multiplying the function by -1 to obtain y = x + 3 which reflects the function across the x-axis. Finally we subtract 5 from the function to obtain y = x This shifts the entire function down vertically by 5 units. Practice Graph the following functions. 1. y = 2x 1 2. y = x y = 4x y = 5 x 5. y = 2 x y = 3 x 105
110 2.5. Shifts of Square Root Functions 7. y = x 8. y = 2 2x y = x 10. y = x + 1 4x 5 106
111 Chapter 2. Non-Linear Relationships 2.6 Graphing Cubed Root Functions Here you ll graph a cubed root function with and without a calculator. The next day, Mrs. Garcia assigns her student the cube root function y = 3 (x + 1) to graph for homework. The following day, she asks her students which quadrant(s) their graph is in. Alendro says that because of the negative sign, all y values are negative. Therefore his graph is only in the third and fourth quadrants quadrant. Dako says that his graph is in the third and fourth quadrants as well but it is also in the second quadrant. Marisha says they are both wrong and that her graph of the function is in all four quadrants. Which one of them is correct? Guidance A cubed root function is different from that of a square root. Their general forms look very similar, y = a 3 x h + k and the parent graph is y = 3 x. However, we can take the cubed root of a negative number, therefore, it will be defined for all values of x. Graphing the parent graph, we have: TABLE 2.9: x y
112 2.6. Graphing Cubed Root Functions TABLE 2.9: (continued) x y For y = 3 x, the output is the same as the input of y = x 3. The domain and range of y = 3 x are all real numbers. Notice there is no starting point like the square root functions, the (h,k) now refers to the point where the function bends, called a point of inflection (see the Analyzing the Graph of a Polynomial Function concept). Example A Describe how to obtain the graph of y = 3 x + 5 from y = 3 x. Solution: From the previous concept, we know that the +5 indicates a vertical shift of 5 units up. Therefore, this graph will look exactly the same as the parent graph, shifted up five units. Example B Graph f (x)= 3 x Find the domain and range. 108
113 Chapter 2. Non-Linear Relationships Solution: From the previous example, we know that from the parent graph, this function is going to shift to the left two units and down three units. The negative sign will result in a reflection. Alternate Method: If you want to use a table (like in the previous concept), that will also work. Here is a table, then plot the points. (h,k) should always be the middle point in your table. TABLE 2.10: x y Example C Graph f (x)= x 4. Solution: The -4 tells us that, from the parent graph, the function will shift to the right four units. The 1 2 effects how quickly the function will grow. Because it is less than one, it will grow slower than the parent graph. 109
114 2.6. Graphing Cubed Root Functions Using the graphing calculator: If you wanted to graph this function using the TI-83 or 84, press Y = and clear out any functions. Then, press (1 2), MATH and scroll down to 4: 3 and press ENTER. Then, type in the rest of the function, so that Y = (X 4). Press GRAPH and adjust the window. Important Note: The domain and range of all cubed root functions are both all real numbers. Intro Problem Revisit If you graph the function y = 3 (x + 1), you see that the domain is all real numbers, which makes all quadrants possible. However, for all positive values of x, y is negative because of the negative sign in front of the cube root. That rules out the first quadrant. Therefore, Dako is correct. Guided Practice 1. Evaluate y = 3 x when x = Describe how to obtain the graph of y = 3 x from y = 3 x. Graph the following cubed root functions. Check your graphs on the graphing calculator. 3. y = 3 x f (x)= 3 x 1 Answers 1. Plug in x = 12 and solve for y. y = = = = 2 2. Starting with y = 3 x, you would obtain y = 3 x by shifting the function to the left four units and down 11 units. 3. This function is a horizontal shift to the right two units and down four units. 110
Solving Absolute Value Equations and Inequalities
 Solving Absolute Value Equations and Inequalities Say Thanks to the Authors Click http://www.ck1.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Solving Absolute Value Equations and Inequalities Say Thanks to the Authors Click http://www.ck1.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Intermediate Algebra Textbook for Skyline College
 Intermediate Algebra Textbook for Skyline College Andrew Gloag Anne Gloag Mara Landers Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org To access a customizable
Intermediate Algebra Textbook for Skyline College Andrew Gloag Anne Gloag Mara Landers Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org To access a customizable
Inverse Functions. Say Thanks to the Authors Click (No sign in required)
 Inverse Functions Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Inverse Functions Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Quadratic Equations and Quadratic Functions
 Quadratic Equations and Quadratic Functions Andrew Gloag Anne Gloag Say Thanks to the Authors Click http://www.ck1.org/saythanks (No sign in required) To access a customizable version of this book, as
Quadratic Equations and Quadratic Functions Andrew Gloag Anne Gloag Say Thanks to the Authors Click http://www.ck1.org/saythanks (No sign in required) To access a customizable version of this book, as
Radical Expressions. Say Thanks to the Authors Click (No sign in required)
 Radical Expressions Say Thanks to the Authors Click http://www.ck1.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck1.org
Radical Expressions Say Thanks to the Authors Click http://www.ck1.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck1.org
Complex Numbers CK-12. Say Thanks to the Authors Click (No sign in required)
 Complex Numbers CK-12 Say Thanks to the Authors Click http://www.ck12.org/saythanks No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Complex Numbers CK-12 Say Thanks to the Authors Click http://www.ck12.org/saythanks No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Polynomials. Eve Rawley, (EveR) Anne Gloag, (AnneG) Andrew Gloag, (AndrewG)
 Polynomials Eve Rawley, (EveR) Anne Gloag, (AnneG) Andrew Gloag, (AndrewG) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book,
Polynomials Eve Rawley, (EveR) Anne Gloag, (AnneG) Andrew Gloag, (AndrewG) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book,
Determining the Best Method to Solve a Linear System
 Determining the Best Method to Solve a Linear System Lori Jordan Kate Dirga Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this
Determining the Best Method to Solve a Linear System Lori Jordan Kate Dirga Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this
Intermediate Algebra
 Intermediate Algebra Anne Gloag Andrew Gloag Mara Landers Remixed by James Sousa Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org To access a customizable
Intermediate Algebra Anne Gloag Andrew Gloag Mara Landers Remixed by James Sousa Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org To access a customizable
Area of Circles. Say Thanks to the Authors Click (No sign in required)
 Area of Circles Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Area of Circles Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
The Pythagorean Theorem and Its Converse
 The Pythagorean Theorem and Its Converse Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
The Pythagorean Theorem and Its Converse Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Applying the Pythagorean Theorem
 Applying the Pythagorean Theorem Laura Swenson, (LSwenson) Joy Sheng, (JSheng) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this
Applying the Pythagorean Theorem Laura Swenson, (LSwenson) Joy Sheng, (JSheng) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this
Quadratic Equations and Quadratic Functions
 Quadratic Equations and Quadratic Functions Eve Rawley, (EveR) Anne Gloag, (AnneG) Andrew Gloag, (AndrewG) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access
Quadratic Equations and Quadratic Functions Eve Rawley, (EveR) Anne Gloag, (AnneG) Andrew Gloag, (AndrewG) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access
The Shape, Center and Spread of a Normal Distribution - Basic
 The Shape, Center and Spread of a Normal Distribution - Basic Brenda Meery, (BrendaM) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version
The Shape, Center and Spread of a Normal Distribution - Basic Brenda Meery, (BrendaM) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version
Vectors (Trigonometry Explanation)
 Vectors (Trigonometry Explanation) CK12 Editor Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Vectors (Trigonometry Explanation) CK12 Editor Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Circumference and Arc Length
 Circumference and Arc Length Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit
Circumference and Arc Length Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit
Inverse Functions and Trigonometric Equations - Solution Key
 Inverse Functions and Trigonometric Equations - Solution Key CK Editor Say Thanks to the Authors Click http://www.ck.org/saythanks (No sign in required To access a customizable version of this book, as
Inverse Functions and Trigonometric Equations - Solution Key CK Editor Say Thanks to the Authors Click http://www.ck.org/saythanks (No sign in required To access a customizable version of this book, as
Inside the Atom. Say Thanks to the Authors Click (No sign in required)
 Inside the Atom Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Inside the Atom Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Gravity. James H Dann, Ph.D. Say Thanks to the Authors Click (No sign in required)
 Gravity James H Dann, Ph.D. Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit
Gravity James H Dann, Ph.D. Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit
Algebra I. Slide 1 / 175. Slide 2 / 175. Slide 3 / 175. Quadratics. Table of Contents Key Terms
 Slide 1 / 175 Slide 2 / 175 Algebra I Quadratics 2015-11-04 www.njctl.org Key Terms Table of Contents Click on the topic to go to that section Slide 3 / 175 Characteristics of Quadratic Equations Transforming
Slide 1 / 175 Slide 2 / 175 Algebra I Quadratics 2015-11-04 www.njctl.org Key Terms Table of Contents Click on the topic to go to that section Slide 3 / 175 Characteristics of Quadratic Equations Transforming
Algebra I. Key Terms. Slide 1 / 175 Slide 2 / 175. Slide 3 / 175. Slide 4 / 175. Slide 5 / 175. Slide 6 / 175. Quadratics.
 Slide 1 / 175 Slide / 175 Algebra I Quadratics 015-11-04 www.njctl.org Key Terms Slide 3 / 175 Table of Contents Click on the topic to go to that section Slide 4 / 175 Characteristics of Quadratic Equations
Slide 1 / 175 Slide / 175 Algebra I Quadratics 015-11-04 www.njctl.org Key Terms Slide 3 / 175 Table of Contents Click on the topic to go to that section Slide 4 / 175 Characteristics of Quadratic Equations
Algebra I Quadratics
 1 Algebra I Quadratics 2015-11-04 www.njctl.org 2 Key Terms Table of Contents Click on the topic to go to that section Characteristics of Quadratic Equations Transforming Quadratic Equations Graphing Quadratic
1 Algebra I Quadratics 2015-11-04 www.njctl.org 2 Key Terms Table of Contents Click on the topic to go to that section Characteristics of Quadratic Equations Transforming Quadratic Equations Graphing Quadratic
Quadratic Functions. Key Terms. Slide 1 / 200. Slide 2 / 200. Slide 3 / 200. Table of Contents
 Slide 1 / 200 Quadratic Functions Table of Contents Key Terms Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic Equations
Slide 1 / 200 Quadratic Functions Table of Contents Key Terms Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic Equations
Quadratic Functions. Key Terms. Slide 2 / 200. Slide 1 / 200. Slide 3 / 200. Slide 4 / 200. Slide 6 / 200. Slide 5 / 200.
 Slide 1 / 200 Quadratic Functions Slide 2 / 200 Table of Contents Key Terms Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic
Slide 1 / 200 Quadratic Functions Slide 2 / 200 Table of Contents Key Terms Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic
Slide 1 / 200. Quadratic Functions
 Slide 1 / 200 Quadratic Functions Key Terms Slide 2 / 200 Table of Contents Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic
Slide 1 / 200 Quadratic Functions Key Terms Slide 2 / 200 Table of Contents Identify Quadratic Functions Explain Characteristics of Quadratic Functions Solve Quadratic Equations by Graphing Solve Quadratic
3.4 Solving Quadratic Equations by Completing
 www.ck1.org Chapter 3. Quadratic Equations and Quadratic Functions 3.4 Solving Quadratic Equations by Completing the Square Learning objectives Complete the square of a quadratic expression. Solve quadratic
www.ck1.org Chapter 3. Quadratic Equations and Quadratic Functions 3.4 Solving Quadratic Equations by Completing the Square Learning objectives Complete the square of a quadratic expression. Solve quadratic
Two-Column Proofs. Bill Zahner Lori Jordan. Say Thanks to the Authors Click (No sign in required)
 Two-Column Proofs Bill Zahner Lori Jordan Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Two-Column Proofs Bill Zahner Lori Jordan Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
The Law of Cosines. Say Thanks to the Authors Click (No sign in required)
 The Law of Cosines Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
The Law of Cosines Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Inequalities. CK12 Editor. Say Thanks to the Authors Click (No sign in required)
 Inequalities CK12 Editor Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Inequalities CK12 Editor Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Simple Harmonic Motion
 Simple Harmonic Motion James H Dann, Ph.D. Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Simple Harmonic Motion James H Dann, Ph.D. Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
3.4 Solving Quadratic Equations by Completing
 .4. Solving Quadratic Equations by Completing the Square www.ck1.org.4 Solving Quadratic Equations by Completing the Square Learning objectives Complete the square of a quadratic expression. Solve quadratic
.4. Solving Quadratic Equations by Completing the Square www.ck1.org.4 Solving Quadratic Equations by Completing the Square Learning objectives Complete the square of a quadratic expression. Solve quadratic
Significant Figures. CK12 Editor. Say Thanks to the Authors Click (No sign in required)
 Significant Figures CK12 Editor Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content,
Significant Figures CK12 Editor Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content,
Using Similar Right Triangles
 Using Similar Right Triangles Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit
Using Similar Right Triangles Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit
Suspensions. Ck12 Science. Say Thanks to the Authors Click (No sign in required)
 Suspensions Ck12 Science Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Suspensions Ck12 Science Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
History of the Atom. Say Thanks to the Authors Click (No sign in required)
 History of the Atom Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
History of the Atom Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Chapter 5 Smartboard Notes
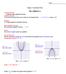 Name Chapter 5 Smartboard Notes 10.1 Graph ax 2 + c Learning Outcome To graph simple quadratic functions Quadratic function A non linear function that can be written in the standard form y = ax 2 + bx
Name Chapter 5 Smartboard Notes 10.1 Graph ax 2 + c Learning Outcome To graph simple quadratic functions Quadratic function A non linear function that can be written in the standard form y = ax 2 + bx
Electron Arrangement
 Electron Arrangement Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Electron Arrangement Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Inside the Atom. Say Thanks to the Authors Click (No sign in required)
 Inside the Atom Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Inside the Atom Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Properties of Arcs. Say Thanks to the Authors Click (No sign in required)
 Properties of Arcs Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Properties of Arcs Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Quadratic Functions and Equations
 Quadratic Functions and Equations Quadratic Graphs and Their Properties Objective: To graph quadratic functions of the form y = ax 2 and y = ax 2 + c. Objectives I can identify a vertex. I can grapy y
Quadratic Functions and Equations Quadratic Graphs and Their Properties Objective: To graph quadratic functions of the form y = ax 2 and y = ax 2 + c. Objectives I can identify a vertex. I can grapy y
Quarter 2 400, , , , , , ,000 50,000
 Algebra 2 Quarter 2 Quadratic Functions Introduction to Polynomial Functions Hybrid Electric Vehicles Since 1999, there has been a growing trend in the sales of hybrid electric vehicles. These data show
Algebra 2 Quarter 2 Quadratic Functions Introduction to Polynomial Functions Hybrid Electric Vehicles Since 1999, there has been a growing trend in the sales of hybrid electric vehicles. These data show
Subtract 16 from both sides. Divide both sides by 9. b. Will the swing touch the ground? Explain how you know.
 REVIEW EXAMPLES 1) Solve 9x + 16 = 0 for x. 9x + 16 = 0 9x = 16 Original equation. Subtract 16 from both sides. 16 x 9 Divide both sides by 9. 16 x Take the square root of both sides. 9 4 x i 3 Evaluate.
REVIEW EXAMPLES 1) Solve 9x + 16 = 0 for x. 9x + 16 = 0 9x = 16 Original equation. Subtract 16 from both sides. 16 x 9 Divide both sides by 9. 16 x Take the square root of both sides. 9 4 x i 3 Evaluate.
ALGEBRA UNIT 11-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION (DAY 1)
 ALGEBRA UNIT 11-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION (DAY 1) The Quadratic Equation is written as: ; this equation has a degree of. Where a, b and c are integer coefficients (where a 0)
ALGEBRA UNIT 11-GRAPHING QUADRATICS THE GRAPH OF A QUADRATIC FUNCTION (DAY 1) The Quadratic Equation is written as: ; this equation has a degree of. Where a, b and c are integer coefficients (where a 0)
Inclined Planes. Say Thanks to the Authors Click (No sign in required)
 Inclined Planes Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Inclined Planes Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
2 P a g e. Essential Questions:
 NC Math 1 Unit 5 Quadratic Functions Main Concepts Study Guide & Vocabulary Classifying, Adding, & Subtracting Polynomials Multiplying Polynomials Factoring Polynomials Review of Multiplying and Factoring
NC Math 1 Unit 5 Quadratic Functions Main Concepts Study Guide & Vocabulary Classifying, Adding, & Subtracting Polynomials Multiplying Polynomials Factoring Polynomials Review of Multiplying and Factoring
Polynomials and Factoring
 Polynomials and Factoring Andrew Gloag Melissa Kramer Anne Gloag Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well
Polynomials and Factoring Andrew Gloag Melissa Kramer Anne Gloag Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well
3.1. QUADRATIC FUNCTIONS AND MODELS
 3.1. QUADRATIC FUNCTIONS AND MODELS 1 What You Should Learn Analyze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Find minimum
3.1. QUADRATIC FUNCTIONS AND MODELS 1 What You Should Learn Analyze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Find minimum
Acids and Bases. Say Thanks to the Authors Click (No sign in required)
 Acids and Bases Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Acids and Bases Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Midpoints and Bisectors
 Midpoints and Bisectors Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Midpoints and Bisectors Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
Unit 6: Quadratics. Contents
 Unit 6: Quadratics Contents Animated gif Program...6-3 Setting Bounds...6-9 Exploring Quadratic Equations...6-17 Finding Zeros by Factoring...6-3 Finding Zeros Using the Quadratic Formula...6-41 Modeling:
Unit 6: Quadratics Contents Animated gif Program...6-3 Setting Bounds...6-9 Exploring Quadratic Equations...6-17 Finding Zeros by Factoring...6-3 Finding Zeros Using the Quadratic Formula...6-41 Modeling:
Unit 9: Quadratics Intercept Form
 For Teacher Use Packet Score: Name: Period: Algebra 1 Unit 9: Quadratics Intercept Form Note & Homework Packet Date Topic/Assignment HW Page 9-A Graphing Parabolas in Intercept Form 9-B Solve Quadratic
For Teacher Use Packet Score: Name: Period: Algebra 1 Unit 9: Quadratics Intercept Form Note & Homework Packet Date Topic/Assignment HW Page 9-A Graphing Parabolas in Intercept Form 9-B Solve Quadratic
Trigonometric Ratios. Lori Jordan Kate Dirga. Say Thanks to the Authors Click (No sign in required)
 Trigonometric Ratios Lori Jordan Kate Dirga Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Trigonometric Ratios Lori Jordan Kate Dirga Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Electric Circuits: Capacitors
 Electric Circuits: Capacitors James H Dann, Ph.D. Say Thanks to the Authors Click http://www.ck2.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Electric Circuits: Capacitors James H Dann, Ph.D. Say Thanks to the Authors Click http://www.ck2.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Solids, Liquids, Gases, and Plasmas
 Solids, Liquids, Gases, and Plasmas Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content,
Solids, Liquids, Gases, and Plasmas Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content,
Solving Equations Quick Reference
 Solving Equations Quick Reference Integer Rules Addition: If the signs are the same, add the numbers and keep the sign. If the signs are different, subtract the numbers and keep the sign of the number
Solving Equations Quick Reference Integer Rules Addition: If the signs are the same, add the numbers and keep the sign. If the signs are different, subtract the numbers and keep the sign of the number
QUADRATIC FUNCTIONS AND MODELS
 QUADRATIC FUNCTIONS AND MODELS What You Should Learn Analyze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Find minimum and
QUADRATIC FUNCTIONS AND MODELS What You Should Learn Analyze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Find minimum and
Correlation Using Relative Ages
 Correlation Using Relative Ages Dana Desonie, Ph.D. Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Correlation Using Relative Ages Dana Desonie, Ph.D. Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive
Algebra II Unit #2 4.6 NOTES: Solving Quadratic Equations (More Methods) Block:
 Algebra II Unit # Name: 4.6 NOTES: Solving Quadratic Equations (More Methods) Block: (A) Background Skills - Simplifying Radicals To simplify a radical that is not a perfect square: 50 8 300 7 7 98 (B)
Algebra II Unit # Name: 4.6 NOTES: Solving Quadratic Equations (More Methods) Block: (A) Background Skills - Simplifying Radicals To simplify a radical that is not a perfect square: 50 8 300 7 7 98 (B)
Section 1.1. Chapter 1. Quadratics. Parabolas. Example. Example. ( ) = ax 2 + bx + c -2-1
 Chapter 1 Quadratic Functions and Factoring Section 1.1 Graph Quadratic Functions in Standard Form Quadratics The polynomial form of a quadratic function is: f x The graph of a quadratic function is a
Chapter 1 Quadratic Functions and Factoring Section 1.1 Graph Quadratic Functions in Standard Form Quadratics The polynomial form of a quadratic function is: f x The graph of a quadratic function is a
CC Algebra Quadratic Functions Test Review. 1. The graph of the equation y = x 2 is shown below. 4. Which parabola has an axis of symmetry of x = 1?
 Name: CC Algebra Quadratic Functions Test Review Date: 1. The graph of the equation y = x 2 is shown below. 4. Which parabola has an axis of symmetry of x = 1? a. c. c. b. d. Which statement best describes
Name: CC Algebra Quadratic Functions Test Review Date: 1. The graph of the equation y = x 2 is shown below. 4. Which parabola has an axis of symmetry of x = 1? a. c. c. b. d. Which statement best describes
Chapter 1 Notes: Quadratic Functions
 19 Chapter 1 Notes: Quadratic Functions (Textbook Lessons 1.1 1.2) Graphing Quadratic Function A function defined by an equation of the form, The graph is a U-shape called a. Standard Form Vertex Form
19 Chapter 1 Notes: Quadratic Functions (Textbook Lessons 1.1 1.2) Graphing Quadratic Function A function defined by an equation of the form, The graph is a U-shape called a. Standard Form Vertex Form
Looking Ahead to Chapter 10
 Looking Ahead to Chapter Focus In Chapter, you will learn about polynomials, including how to add, subtract, multiply, and divide polynomials. You will also learn about polynomial and rational functions.
Looking Ahead to Chapter Focus In Chapter, you will learn about polynomials, including how to add, subtract, multiply, and divide polynomials. You will also learn about polynomial and rational functions.
Ch. 7.6 Squares, Squaring & Parabolas
 Ch. 7.6 Squares, Squaring & Parabolas Learning Intentions: Learn about the squaring & square root function. Graph parabolas. Compare the squaring function with other functions. Relate the squaring function
Ch. 7.6 Squares, Squaring & Parabolas Learning Intentions: Learn about the squaring & square root function. Graph parabolas. Compare the squaring function with other functions. Relate the squaring function
Name Date Class California Standards 17.0, Quadratic Equations and Functions. Step 2: Graph the points. Plot the ordered pairs from your table.
 California Standards 17.0, 1.0 9-1 There are three steps to graphing a quadratic function. Graph y x 3. Quadratic Equations and Functions 6 y 6 y x y x 3 5 1 1 0 3 1 1 5 0 x 0 x Step 1: Make a table of
California Standards 17.0, 1.0 9-1 There are three steps to graphing a quadratic function. Graph y x 3. Quadratic Equations and Functions 6 y 6 y x y x 3 5 1 1 0 3 1 1 5 0 x 0 x Step 1: Make a table of
UNIT 1 UNIT 1: QUADRATIC FUNCTIONS. By the end of this unit, I can. Name:
 UNIT 1: QUADRATIC FUNCTIONS UNIT 1 By the end of this unit, I can Draw the graph of a function using different methods Explain the meaning of the term function and distinguish between a function and a
UNIT 1: QUADRATIC FUNCTIONS UNIT 1 By the end of this unit, I can Draw the graph of a function using different methods Explain the meaning of the term function and distinguish between a function and a
History of the Pythagorean Theorem
 History of the Pythagorean Theorem Laura Swenson, (LSwenson) Joy Sheng, (JSheng) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of
History of the Pythagorean Theorem Laura Swenson, (LSwenson) Joy Sheng, (JSheng) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of
( ) f ( x 1 ) . x 2. To find the average rate of change, use the slope formula, m = f x 2
 Common Core Regents Review Functions Quadratic Functions (Graphs) A quadratic function has the form y = ax 2 + bx + c. It is an equation with a degree of two because its highest exponent is 2. The graph
Common Core Regents Review Functions Quadratic Functions (Graphs) A quadratic function has the form y = ax 2 + bx + c. It is an equation with a degree of two because its highest exponent is 2. The graph
Solving Quadratic Equations (Adapted from Core Plus Mathematics, Courses 1 and 2)
 Solving Quadratic Equations (Adapted from Core Plus Mathematics, Courses 1 and ) In situations that involve quadratic functions, the interesting questions often require solving equations. For example,
Solving Quadratic Equations (Adapted from Core Plus Mathematics, Courses 1 and ) In situations that involve quadratic functions, the interesting questions often require solving equations. For example,
Algebra I Quadratic & Non-Linear Functions
 1 Algebra I Quadratic & Non-Linear Functions 2015-11-04 www.njctl.org 2 Table of Contents Click on the topic to go to that section Key Terms Explain Characteristics of Quadratic Functions Graphing Quadratic
1 Algebra I Quadratic & Non-Linear Functions 2015-11-04 www.njctl.org 2 Table of Contents Click on the topic to go to that section Key Terms Explain Characteristics of Quadratic Functions Graphing Quadratic
The Graphs of Mixed Functions (Day 13 1)
 The Graphs of Mied Functions (Day 3 ) In this unit, we will remember how to graph some old functions and discover how to graph lots of new functions. Eercise : Graph and label the parent function f( )
The Graphs of Mied Functions (Day 3 ) In this unit, we will remember how to graph some old functions and discover how to graph lots of new functions. Eercise : Graph and label the parent function f( )
Completing the Square
 5-7 Completing the Square TEKS FOCUS TEKS (4)(F) Solve quadratic and square root equations. TEKS (1)(A) Apply mathematics to problems arising in everyday life, society, and the workplace. Additional TEKS
5-7 Completing the Square TEKS FOCUS TEKS (4)(F) Solve quadratic and square root equations. TEKS (1)(A) Apply mathematics to problems arising in everyday life, society, and the workplace. Additional TEKS
UNIT 3: MODELING AND ANALYZING QUADRATIC FUNCTIONS
 UNIT 3: MODELING AND ANALYZING QUADRATIC FUNCTIONS This unit investigates quadratic functions. Students study the structure of quadratic expressions and write quadratic expressions in equivalent forms.
UNIT 3: MODELING AND ANALYZING QUADRATIC FUNCTIONS This unit investigates quadratic functions. Students study the structure of quadratic expressions and write quadratic expressions in equivalent forms.
Sect Polynomial and Rational Inequalities
 158 Sect 10.2 - Polynomial and Rational Inequalities Concept #1 Solving Inequalities Graphically Definition A Quadratic Inequality is an inequality that can be written in one of the following forms: ax
158 Sect 10.2 - Polynomial and Rational Inequalities Concept #1 Solving Inequalities Graphically Definition A Quadratic Inequality is an inequality that can be written in one of the following forms: ax
Using the Laws of Exponents to Simplify Rational Exponents
 6. Explain Radicals and Rational Exponents - Notes Main Ideas/ Questions Essential Question: How do you simplify expressions with rational exponents? Notes/Examples What You Will Learn Evaluate and simplify
6. Explain Radicals and Rational Exponents - Notes Main Ideas/ Questions Essential Question: How do you simplify expressions with rational exponents? Notes/Examples What You Will Learn Evaluate and simplify
The Quadratic Formula. ax 2 bx c 0 where a 0. Deriving the Quadratic Formula. Isolate the constant on the right side of the equation.
 SECTION 11.2 11.2 The Quadratic Formula 11.2 OBJECTIVES 1. Solve quadratic equations by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation by using the discriminant
SECTION 11.2 11.2 The Quadratic Formula 11.2 OBJECTIVES 1. Solve quadratic equations by using the quadratic formula 2. Determine the nature of the solutions of a quadratic equation by using the discriminant
Algebra II (Common Core) Summer Assignment Due: September 11, 2017 (First full day of classes) Ms. Vella
 1 Algebra II (Common Core) Summer Assignment Due: September 11, 2017 (First full day of classes) Ms. Vella In this summer assignment, you will be reviewing important topics from Algebra I that are crucial
1 Algebra II (Common Core) Summer Assignment Due: September 11, 2017 (First full day of classes) Ms. Vella In this summer assignment, you will be reviewing important topics from Algebra I that are crucial
Polar Equations and Complex Numbers
 Polar Equations and Complex Numbers Art Fortgang, (ArtF) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other
Polar Equations and Complex Numbers Art Fortgang, (ArtF) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other
Types of Chemical Reactions
 Types of Chemical Reactions Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit
Types of Chemical Reactions Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as well as other interactive content, visit
Unit 5 Test: 9.1 Quadratic Graphs and Their Properties
 Unit 5 Test: 9.1 Quadratic Graphs and Their Properties Quadratic Equation: (Also called PARABOLAS) 1. of the STANDARD form y = ax 2 + bx + c 2. a, b, c are all real numbers and a 0 3. Always have an x
Unit 5 Test: 9.1 Quadratic Graphs and Their Properties Quadratic Equation: (Also called PARABOLAS) 1. of the STANDARD form y = ax 2 + bx + c 2. a, b, c are all real numbers and a 0 3. Always have an x
STANDARDS OF LEARNING CONTENT REVIEW NOTES HONORS ALGEBRA II. 1 st Nine Weeks,
 STANDARDS OF LEARNING CONTENT REVIEW NOTES HONORS ALGEBRA II 1 st Nine Weeks, 2016-2017 OVERVIEW Algebra II Content Review Notes are designed by the High School Mathematics Steering Committee as a resource
STANDARDS OF LEARNING CONTENT REVIEW NOTES HONORS ALGEBRA II 1 st Nine Weeks, 2016-2017 OVERVIEW Algebra II Content Review Notes are designed by the High School Mathematics Steering Committee as a resource
STANDARDS OF LEARNING CONTENT REVIEW NOTES ALGEBRA II. 2 nd Nine Weeks,
 STANDARDS OF LEARNING CONTENT REVIEW NOTES ALGEBRA II 2 nd Nine Weeks, 2016-2017 1 OVERVIEW Algebra II Content Review Notes are designed by the High School Mathematics Steering Committee as a resource
STANDARDS OF LEARNING CONTENT REVIEW NOTES ALGEBRA II 2 nd Nine Weeks, 2016-2017 1 OVERVIEW Algebra II Content Review Notes are designed by the High School Mathematics Steering Committee as a resource
The coordinates of the vertex of the corresponding parabola are p, q. If a > 0, the parabola opens upward. If a < 0, the parabola opens downward.
 Mathematics 10 Page 1 of 8 Quadratic Relations in Vertex Form The expression y ax p q defines a quadratic relation in form. The coordinates of the of the corresponding parabola are p, q. If a > 0, the
Mathematics 10 Page 1 of 8 Quadratic Relations in Vertex Form The expression y ax p q defines a quadratic relation in form. The coordinates of the of the corresponding parabola are p, q. If a > 0, the
- a function that can be written in the standard form. - a form of a parabola where and (h, k) is the vertex
 4-1 Quadratic Functions and Equations Objectives A2.A.REI.D.6 (formerly A-REI.D.11) Explain why the x-coordinates of the points where the graphs of the equations y = f(x) and y = g(x) intersect are the
4-1 Quadratic Functions and Equations Objectives A2.A.REI.D.6 (formerly A-REI.D.11) Explain why the x-coordinates of the points where the graphs of the equations y = f(x) and y = g(x) intersect are the
CK-12 FOUNDATION. Separating Mixtures. Say Thanks to the Authors Click (No sign in required)
 CK-12 FOUNDATION Separating Mixtures Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) Forsythe Robinson To access a customizable version of this book, as well as other
CK-12 FOUNDATION Separating Mixtures Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) Forsythe Robinson To access a customizable version of this book, as well as other
Secondary Math 2H Unit 3 Notes: Factoring and Solving Quadratics
 Secondary Math H Unit 3 Notes: Factoring and Solving Quadratics 3.1 Factoring out the Greatest Common Factor (GCF) Factoring: The reverse of multiplying. It means figuring out what you would multiply together
Secondary Math H Unit 3 Notes: Factoring and Solving Quadratics 3.1 Factoring out the Greatest Common Factor (GCF) Factoring: The reverse of multiplying. It means figuring out what you would multiply together
MATH 121: EXTRA PRACTICE FOR TEST 2. Disclaimer: Any material covered in class and/or assigned for homework is a fair game for the exam.
 MATH 121: EXTRA PRACTICE FOR TEST 2 Disclaimer: Any material covered in class and/or assigned for homework is a fair game for the exam. 1 Linear Functions 1. Consider the functions f(x) = 3x + 5 and g(x)
MATH 121: EXTRA PRACTICE FOR TEST 2 Disclaimer: Any material covered in class and/or assigned for homework is a fair game for the exam. 1 Linear Functions 1. Consider the functions f(x) = 3x + 5 and g(x)
Systems of Linear Equations and Inequalities
 Systems of Linear Equations and Inequalities Lori Jordan Kate Dirga Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as
Systems of Linear Equations and Inequalities Lori Jordan Kate Dirga Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version of this book, as
STANDARDS OF LEARNING CONTENT REVIEW NOTES. ALGEBRA I Part II. 2 nd Nine Weeks,
 STANDARDS OF LEARNING CONTENT REVIEW NOTES ALGEBRA I Part II 2 nd Nine Weeks, 2016-2017 1 OVERVIEW Algebra I Content Review Notes are designed by the High School Mathematics Steering Committee as a resource
STANDARDS OF LEARNING CONTENT REVIEW NOTES ALGEBRA I Part II 2 nd Nine Weeks, 2016-2017 1 OVERVIEW Algebra I Content Review Notes are designed by the High School Mathematics Steering Committee as a resource
Functions and graphs - Grade 10 *
 OpenStax-CNX module: m35968 1 Functions and graphs - Grade 10 * Free High School Science Texts Project Heather Williams This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution
OpenStax-CNX module: m35968 1 Functions and graphs - Grade 10 * Free High School Science Texts Project Heather Williams This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution
Study Resources For Algebra I. Unit 2A Graphs of Quadratic Functions
 Study Resources For Algebra I Unit 2A Graphs of Quadratic Functions This unit examines the graphical behavior of quadratic functions. Information compiled and written by Ellen Mangels, Cockeysville Middle
Study Resources For Algebra I Unit 2A Graphs of Quadratic Functions This unit examines the graphical behavior of quadratic functions. Information compiled and written by Ellen Mangels, Cockeysville Middle
UNIT 2B QUADRATICS II
 UNIT 2B QUADRATICS II M2 12.1-8, M2 12.10, M1 4.4 2B.1 Quadratic Graphs Objective I will be able to identify quadratic functions and their vertices, graph them and adjust the height and width of the parabolas.
UNIT 2B QUADRATICS II M2 12.1-8, M2 12.10, M1 4.4 2B.1 Quadratic Graphs Objective I will be able to identify quadratic functions and their vertices, graph them and adjust the height and width of the parabolas.
CK-12 Math Analysis. Mara Landers Nick Fiori Art Fortgang Raja Almukahhal Melissa Vigil
 CK-12 Math Analysis Mara Landers Nick Fiori Art Fortgang Raja Almukahhal Melissa Vigil Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org To access a customizable
CK-12 Math Analysis Mara Landers Nick Fiori Art Fortgang Raja Almukahhal Melissa Vigil Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org To access a customizable
Chapter 2 Polynomial and Rational Functions
 SECTION.1 Linear and Quadratic Functions Chapter Polynomial and Rational Functions Section.1: Linear and Quadratic Functions Linear Functions Quadratic Functions Linear Functions Definition of a Linear
SECTION.1 Linear and Quadratic Functions Chapter Polynomial and Rational Functions Section.1: Linear and Quadratic Functions Linear Functions Quadratic Functions Linear Functions Definition of a Linear
Let's look at some higher order equations (cubic and quartic) that can also be solved by factoring.
 GSE Advanced Algebra Polynomial Functions Polynomial Functions Zeros of Polynomial Function Let's look at some higher order equations (cubic and quartic) that can also be solved by factoring. In the video,
GSE Advanced Algebra Polynomial Functions Polynomial Functions Zeros of Polynomial Function Let's look at some higher order equations (cubic and quartic) that can also be solved by factoring. In the video,
Quadratic Expressions and Equations
 Unit 5 Quadratic Expressions and Equations 1/9/2017 2/8/2017 Name: By the end of this unit, you will be able to Add, subtract, and multiply polynomials Solve equations involving the products of monomials
Unit 5 Quadratic Expressions and Equations 1/9/2017 2/8/2017 Name: By the end of this unit, you will be able to Add, subtract, and multiply polynomials Solve equations involving the products of monomials
9.1. Solving Quadratic Equations. Investigation: Rocket Science CONDENSED LESSON
 CONDENSED LESSON 9.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations solve
CONDENSED LESSON 9.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations solve
Section 6 Quadratics Part 1
 Section 6 Quadratics Part 1 The following Mathematics Florida Standards will be covered in this section: MAFS.912.A-SSE.1.2 Use the structure of an expression to identify ways to rewrite it. For example,
Section 6 Quadratics Part 1 The following Mathematics Florida Standards will be covered in this section: MAFS.912.A-SSE.1.2 Use the structure of an expression to identify ways to rewrite it. For example,
Math 2 1. Lesson 4-5: Completing the Square. When a=1 in a perfect square trinomial, then. On your own: a. x 2 18x + = b.
 Math 1 Lesson 4-5: Completing the Square Targets: I can identify and complete perfect square trinomials. I can solve quadratic equations by Completing the Square. When a=1 in a perfect square trinomial,
Math 1 Lesson 4-5: Completing the Square Targets: I can identify and complete perfect square trinomials. I can solve quadratic equations by Completing the Square. When a=1 in a perfect square trinomial,
Unit 5 AB Quadratic Expressions and Equations 1/9/2017 2/8/2017
 Unit 5 AB Quadratic Expressions and Equations 1/9/2017 2/8/2017 Name: By the end of this unit, you will be able to Add, subtract, and multiply polynomials Solve equations involving the products of monomials
Unit 5 AB Quadratic Expressions and Equations 1/9/2017 2/8/2017 Name: By the end of this unit, you will be able to Add, subtract, and multiply polynomials Solve equations involving the products of monomials
. State the important connection between the coefficients of the given trinomials and the values you found for r.
 Motivational Problems on Quadratics 1 1. Factor the following perfect-square trinomials : (a) x 1x 36 (b) x 14x 49 (c) x 0x 100 As suggested, these should all look like either ( x r) or ( x r). State the
Motivational Problems on Quadratics 1 1. Factor the following perfect-square trinomials : (a) x 1x 36 (b) x 14x 49 (c) x 0x 100 As suggested, these should all look like either ( x r) or ( x r). State the
