"In presenting the dissertation as a partial fulfillment of the requirements for an advanced degree from the Georgia Institute of Technology, I agree
|
|
|
- Primrose Patterson
- 6 years ago
- Views:
Transcription
1 "In presenting the dissertation as a partial fulfillment of the requirements for an advanced degree from the Georgia Institute of Technology, I agree that the Library of the Institution shall make it available for inspection and circulation in accordance with its regulations governing materials of this type. I agree that permission to copy from, or to publish from, this dissertation may be granted by the professor under whose direction it was written, or, in his absence, by the dean of the Graduate Division when such copying or publication is solely for scholarly purposes and does not involve potential financial gain. It is understood that any copying from, or publication of, this dissertation which involves potential financial gain will not be allowed without written permission.
2 COMPACTNESS AND RELATED CONCEPTS A THESIS Presented to the Faculty of the Graduate Division by Roland Royce Kneece, Jr. In Partial Fulfillment of the Requirements for the Degree Master of Science in Applied Mathematics Georgia Institute of Technology August, 1962
3 COMPACTNESS AND RELATED CONCEPTS Approved: Date approved by Chairman: & * * - J ^ * * J p &
4 i i ACKNOWLEDGMENTS I wish to thank my thesis advisor, Dr. Robert H. Kasriel, for his guidance in the development of this study and for his careful readings which yielded so many suggestions for improvement. The topic was suggested by Dr» William J. Kammerer, and I appreciate the several valuable suggestions which he made after reading the thesis. I also wish to thank Dr. David L. Finn for his reading of this paper. In addition, I am indebted to Dr. William R, Smythe for providing Example 1-4.
5 i i i TABLE OF CONTENTS Page ACKNOWLEDGMENTS i i INTRODUCTION iv Chapter I. COMPACTNESS 1 Compact Spaces Properties of Compact Spaces Localization Compactness and Hausdorff Spaces Compact i f i c a t i o n Compactness in a Metric Space Products of Compact Spaces Continuous Transformations of Compact Spaces I I. COMPACT MAPPINGS 28 Compact Mappings and Equivalences Light, Monotone, and Quasi-Open Mappings Invariance of Local Compactness Compact Mappings and Homeomorphisms The Factorization of Compact Mappings LITERATURE CITED 45 OTHER REFERENCES 46
6 iv INTRODUCTION The purpose of this study is to investigate the basic properties of the mathematical concept of compactness in a topological space, together with several concepts which are related to compactness. A reading of this exposition w i l l require a basic knowledge of elementary topology. The notions of a topological space, open and closed sets, bases for "topologies, accumulation points, closures and interiors of sets, connectedness, continuous functions, and set theory are used freely and without explanation. The concept of compactness in the modern sense had i t s beginning in the classic real number theorem of Heine, Borel, and Lebesgue. This theorem (which is proved on page 19) states that a set of real numbers is closed and bounded i f and only i f i t has the property that every open covering of the set has a f i n i t e subcovering. It is this property, which is the conclusion of the theorem, that is chosen by the topologist for generalization. Another important classical result, the Bolzano-Weierstrass theorem, yields another generalization of the same idea. This theorem states that a set of real numbers is closed and bounded i f and only i f every i n f i n i t e subset has at least one accumulation point in the set. The property which is the conclusion of this theorem has also been generalized in a topological setting,, It is called B-compactness in this paper. The f i r s t part of Chapter One consists of a study of properties which are equivalent to compactness in spaces with certain prescribed structure. In particular, the concepts of countable compactness,
7 B-compactness, and sequential compactness are investigated,, Some confusion arises when one reads literature in which any of the above concepts appear. The term "countable compactness," as defined in this paper, is used in the same sense by J. L. Kelley in \_2], However, many authors, including [ l ] and [ 3 ], use the name countable compactness to mean what is meant in this paper by the term "B-compactness," These authors give no name to the other concept. The term "B-compactness" was invented by this writer; and is meant to suggest "Bolzano compactness," in allusion to the Bolzano-Weierstrass theorem. Historically the o r i ginal meaning for the term "compact" was that of B-compactness. The present definition of compact, sometimes known as the "Heine-Borel property," was called "Bi-compact." Finally, in literature in which all spaces involved are metric, authors may define the term "compact" to mean any one of the four concepts mentioned above. Theorem 1-20 proves the equivalence of these definitions for a metric space. The diagram in Figure 1 on page 11 summarizes the equivalences of these four terms under proper hypothesis on the space. Section D of Chapter One treats compactness in a Hausdorff space to the extent that w i l l be needed in Chapter Two. This treatment is by no means exhaustive. Sections C and E are also of this nature. The Tychonoff theorem is included without proof in Section G in order to present Example I-4 This theorem is one of the most important results of topology; however, no other use is made of i t in this paper. Section H is a detailed investigation of continuous transformations of compact spaces. The problem of invariance of local
8 vi compactness is also treated in Chapter Two in the light of compact mappings. Chapter Two Is an Introduction to one of many generalizations of the idea of a compact space. It was found that by placing a condition of compactness on the transformation, rather than on the domain space, many useful results could be generalized. The notion of a compact mapping is relatively new and is currently an object of intensive research. The original concept was invented by the Russian mathematician, L A. Vainstein, but his definition differs from the one given here. The definition of a compact mapping given in this paper is that of G. T. Whyburn. The equivalence of the two definitions is given in Corollary II-6 and Corollary II-8. The most important result of Chapter Two is the monotone-light factorization theorem (Theorem 11-23) of Whyburn and So Eilenburg. Originally i t was proved for the case of a compact domain space and later extended for compact mappings. The theorem has numerous applications in topology and analysis. Most of the results of Chapter Two may be found in [4] and [ o ]. The source of the theorems for each section of Chapter Two is given at the end of the section. The basic results of Section D of Chapter Two on compact mappings and homeomorphisms were communicated to this writer by Dr. Robert H 0 Kasriel. It should be noted that the basic assumption of a separable metric space by Whyburn in [4] is dropped from the theorems taken from that reference. The countability and separation hypotheses are substituted as needed, so that the proofs remain v i r t u ally the same. The reader unfamiliar with these various countability
9 v i i and separation properties may consider all spaces separable and metric without losing significant generality,, An alternate concept, the seq u e n t i a l l y compact mapping, may be defined by substituting the words "sequentially compact" for the word "compact" in Definition It can be seen that many of the theorems of Chapter Two may be stated with less hypothesis using this alternate concept. The role of sequential compactness is evident in the proofs. Compactness has been called one of the most far-reaching concepts of topology. This thesis is a circumstantial introduction to compactness and a few of i t s applications in topology. Many other generalizations and applications have been made, not only in topology, but also throughout mathematics.
10 CHAPTER I COMPACTNESS A, Compact Spaces Definition 1-1. A topological space is said to be compact i f every open covering of the space contains a f i n i t e subcovering. Remark. The concept of a topological space used in this thesis is that which may be found on page 52 of [ l ]. Definition 1-2. A collection of subsets of a topological space is said to have the f i n i t e intersection property i f every f i n i t e subcollection has a nonempty intersection. Theorem 1-1. A topological space X is compact i f and only i f every collection of closed subsets of X having the f i n i t e intersection property has a nonempty intersection. Proof. (l) Assume that X is compact, and let [c^ : a A] be a collection of closed sets having the f i n i t e intersection property. Define 0 = X - C for each a in A, and assume that the interseca a tion of all elements of } ^ s e m Pty. Then the collection [O Q : a e A] is an open covering of X, Since X is compact, a f i n i t e subcovering {o ȧ : i = 1, 2,..., n] covers X. Hence i t follows that n 1 f^) c is empty. This is a contradiction to the f i n i t e intersection a i=i i property. Therefore f~^\ C is nonempty. a A a
11 2 (2) Now assume that X has the property that every collection of closed subsets of X having the f i n i t e intersection property has a nonvoid intersection. Let [o : a A] be an open covering of a X. Assume no f i n i t e subcovering of IP^} covers X. Then the collection [c : C = X - 0, a A) of closed subsets of X has the f i n i t e a a a J intersection property and consequently has a nonvoid intersection. Therefore the collection [0 1 fails to cover X. This is a contradiction. Definition 1-3. A set D is said to be directed by the relation y i f D is nonvoid and (a) i f m, n, and p are members of D such that m > n and n > p, then m > p; (b) i f m D, then m > mj and (c) i f m and n are members of D, then there is an element p in D such that p > m and p > n. Definition 1-4. A net is a pair (S, >) where S is a function and > directs the domain of S. The notation {s^, n D], where are values in a topological space X and D is a directed set, w i l l be used to denote a net in a space X. Definition 1-5, A net {j^> i E] is a subnet of a net (S, n D] i f (a) for each i in E, T. = S n., n. D ; ' 1 Hj/ 1 (b) for each m in D there is a q in E with the property that, i f p > q, then n^ > m. Theorem 1-2. A topological space X is compact i f and only i f every net whose range is in X has a subnet which converges to a point in X.
12 3 Proof. Suppose f i r s t that X is compact. Let {S n, n e D } be a net in X The sets A = )S : m > nl have the f i n i t e intersection n m - J property because D is directed by >. Therefore the collection of closures [^ } also has the f i n i t e intersection property. Hence ned A is nonempty. Let s e A and let y be a neighborhood n ned n system about s. Note that y is directed by set inclusion. Construct a subnet [T^ : i e E] in the following manner. Let E be the set of all ordered pairs (n, U) where n e D, U e y, and S^ e U. Let > be an ordering for E defined by: (0, m) > (U, n) i f m > n and U D O. Then E together with > is a directed set, since for each (n, U ) and (m, U ) there exists U e y such that UCZU 1 H U 2 and an element p e D such that p > n, p > m, and S e U. Then (p, U) P > (n, U-L) and (p, U) > (m, U ). Define the function h : E -> D by h [ ( n, U)l = n. It must be shown that {T^ : i e EJ with T^ = S^^j is a subnet of {s^ : n e D] which converges to s. Clearly property (a) of Definition 1-5 is satisfied. For each m in D there exists an n e D such that n > m and S e U, where U e y. Let n ' 1 q = (n, U) Then for any p = (n', U ; ) such that p > q, h(p) = n = P n' > m, since n'' > n. Hence property (b) of Definition 1-5 is satisfiedo Therefore [T^ : i e E] is a subnet of [s : n e D]» Clearly {T^ : i e E ] converges to s. (2) Now assume that every net in X has a convergent subnet 0 Let a be a collection of closed subsets of X with the f i n i t e intersection property. Define the collection p to be the collection
13 4 of all sets which are finite intersections of sets of a. Then p also has the finite intersection property and j3 Z) a. It will be shown that B is nonempty. Clearly 3 is directed by set in- Bep elusion. Let Sg be a member of B for each Bep. Then [S^ : Bep] is a net in X and consequently has a subnet {Sg^ : i e E] which converges to an element s in S. Let B be an arbitrary element of p, and let U be a neighborhood of a. It will be shown that s B. For some i E, So U for every m > i. Furtherm more there is a q in E with the property that, if p > q, then B^dB. Let r be an element of E succeeding both i and q. Then S B U and B^CZ B. But S B B^; hence S B B. Consequently s belongs to B, since B is closed. It follows that S O B «B p B. Properties of Compact Spaces Definition 1-6. A topological space X is said to be countably compact if every countable open covering of X contains a finite subcovering 0 Definition 1-7, A topological space X is said to be B-compact (Bolzano compact) if every infinite subset of X contains an accumulation point in X. Theorem 1-3. Every compact space is countably compact, and every countably compact space is B-compact. Proof. The first assertion is clear. To prove the second, let X be a countably compact space. Let A be an infinite subset of X.
14 5 It must be shown that X contains an accumulation point of A. Assume that X contains no accumulation point of A. Then there exists a sequence {XJJ of distinct points of A having no limit in X. Define B = { X JJ" Now for each x^ there exists an open set CH such that 0.D B = x.. If this were not the case, then x. would be an accumu- 1 1 ' I lation point of A in X. B is closed, since it contains no accumulation pointsj hence 0 = X - B is open 0 Consider the collection {o^ ; 0]. This is a countable collection of open sets which cover X. But by countable compactness there exists a finite subcovering of X. This fact is inconsistent with the countable infinity of the sequence {x^}. From this contradiction it is seen that the assumption of A having no accumulation point in X is a false one. Hence X is B-compact. Remark. We have as a corollary to theorem 1-3 that every compact space is B-compact. The converse of this theorem in general is not true, as the following example shows. Example 1-1. A B-compact space which is not countably compact. Let K be the set of positive integers. Take as a basis of open sets the collection V = [2n, 2n - l). The set K with the basis fv ] is i topological space. K is not countably compact since the collection fv ] coveis K, but contains no finite subcovering. It is B-compact since every nonempty subset of K contains an accumulation point. This is true since every even integer is an accumulation point of the set consisting of the preceding odd integer, and every odd integer is an accumulation point of the set consisting of the succeeding even integer. Every subset of K contains either even or odd integers.
15 6 Theorem 1-4. If X is a topological space in which subsets consisting of one point are closed (T 1 spaces), and if X is B-compact, then X is countably compact. Proof. Let X be a B-compact T space. Let {o } be a 1 n n=i countable open covering of X, and assume that no finite subcovering exists. For every integer n, the set K = X - i^_j 0. is closed and n i=i 1 nonempty. Let p be an arbitrary point of K and define H = l^j P. n=i Suppose first that H is infinite. Since X is B-compact there is an accumulation point p of H in X. Now every open set containing p contains infinitely many points of H distinct from p. If this were not true, then some open set U exists containing p and containing only a finite number of points {x 1, x 2, x n } of H distinct from p. Since it is assumed that points are closed subsets of X, the set n U - x. is an open set containing p which contains no points of H. i=i 1 This is clearly not possible if p is to be an accumulation point of H. 00 Consequently p is an accumulation point of the set H n = p^ for i=n some n. But H is a subset of the closed set K, so p e K for n rr n every n. Hence p 0^ for every n, contradicting the covering property of {o^}. Now consider the case in which H is finite. In this case there exists p e H, such that, given any integer N, there exists an n > N, such that p^ = p. Thus p e for every n, which contradicts the covering property of { n } a s before. Since the assumption that no finite subcovering of { n } f r ^ leads to a contradiction, X is countably compact. o 00
16 n 7 Example 1-2. A countably compact space which is not compact. To construct the space, begin with an uncountable set S* and wellorder S* with <. Consider the set S = fx : x S* and there c are uncountable many elements y of S* such that y < x]. If is empty let S = S*. If is nonempty then there exists a least element Q of S c, since < is a well-ordering. Define S - {x : x S*, x < Q}. The set S so defined has the property that S is uncountable, but each s S has countably many predecessors. Let the topological space S consist of the set S with the following basis for open sets: I ^ = (x : x S, a < x < b ; a S, b S} together with the set [ s 0}> where s Q is the least element of S. We first show that the space S is not compact. Consider the open covering {{ s 0}> I s x : x sj-. If {{ s 0}> * s xk}j <: were a finite sub- < > covering, the maximum element x of l^i^ would have only a countable number of predecessors. But S is uncountable, so there is an element x such that x < x and therefore is not covered by the finite subcollection. Hence S is not compact. S is a T space since clearly the complement of a single point is open. Therefore if S is B-compact, S is also countably compact. Let K be an infinite subset of S. Let a be the least element of K n-i and let a n be the least element of K - LJ a^ for n > 2. Define K = \_J a o We will show that K C K has an accumulation K point in o nr; n o n i oo S. K o has an upper bound since otherwise S = -[fs ] J l> o-> n=i I. s o a ) n J
17 8 would be countable, contradicting the uncountability of S. Therefore K q has least upper bound a Q since the set of all upper bounds has a least element. For every element a S such that a < a Q there must exist an x K such that a < x < a. Also there must exist an o a n K o such that x < a < a, n o or else x would be an upper bound of preceding a. Therefore every open set 1^ containing a^ must contain an element of K. Hence a is an accumulation point of o o ^ K q and S is B-compact. Definition 1-8. A topological space X is a Lindelof space if every open covering of X contains a countable subcovering. Remark. Every countably compact Lindelof space is compact. Theorem 1-5. Every topological space which has a countable basis of open sets (second countable spaces) is Lindelof. Proof. Let X be a second countable space. Let [O g : a A] be an open covering of X. A countable subcovering must be extracted. Let {u\} be a countable basis of X. For each x in X there exists an a A such that x 0. Also there exists a set U. such that a i x C O g. Let {ih} denote the subcollection of {u.j with the property that for each U. there exists an a such that U.d 0. For each j denote by 0. the element of fo ] which contains U.. J a-> j c Clearly the collection {Pj} ^s a countable subcovering of {P a } which covers X. Hence X is a Lindelof space. Corollary 1-6. Every countably compact second countable space is compact. Proof. Every second countable space is Lindelof, and every countably compact Lindelof space is compact.
18 9 Definition 1-9. A topological space X is said to be sequentially compact if every sequence of elements of X has a subsequence which converges to a point in X. Theorem 1-7. Every sequentially compact space is countably compact. Proof. Let X be a sequentially compact space. Let {o.} be n 1 a countable open covering of X. Define the set K = X - LJ 0. for n i=i 1 each n and notice that, if no finite subcovering of {o.j exists, K q is nonempty for every n. From each choose a point p^ and consider the sequence {P n }* This sequence has a convergent subsequence {p n> }. Let p be the element in X to which {p n.} converges. Let Oj be an open set in {ck} containing p. Then there exists an N such that for i > N, p 0.. Hence p i K.. But p K for ' r n. j n. j n. n. r I J I J i i some i > N. n. > j implies K n.ci K.. Therefore p n > K., but this is a contradiction. Remark. An example of a space which is compact but not sequentially compact is given later in this chapter. Theorem 1-8. If the topological space X has a countable basis of open sets at each point (first countable spaces), and if X is B- compact, then X is sequentially compact. Proof. Let { x n} ^ e a sequence of elements in X. Then the set l x n} m a Y b e assumed to be an infinite subset of X (if not, it clearly contains a convergent subsequence). Hence { x n} n a s an accumulation point p. Let {v^} be a countable base at p. Define the
19 10 collection {t^} by U ± = V 1 and U n = U n _ ± H V n. {u } is also a countable base at p which is linearly ordered by inclusion. Define the sequence {y^} by choosing y^ IL with y^ {x^} and such that if y^ = x n and y^ ^ = x n then n 1 > n 2. {y^} is a subsequence of { x n} > and {y^} converges to p. Hence X is sequentially compact. Co Localization Definition A topological space X is said to be locally compact if for each x in X, there exists a neighborhood of x whose closure is compact. Theorem 1-9. Every compact space is locally compact. Proof. Let X be a compact space. Let x be a point in X and let U be any neighborhood of x. U is closed in X. Let [O g } be any open covering of U Then {o, X - u] is an open covering a of X. X is a compact space and therefore {o^, X - u] contains a finite subcovering of the form {o a, X - u]. Clearly {o } covers U. i i Remark. It was actually shown in the above proof that every closed subset of a compact set is itself compact. Theorem I-10. If X is locally compact and C is a compact subset of X, then there exists an open set U with the property that UDC and U is compact. Proof. Let x C. There exists an open set containing x such that is compact. The collection [u^ : x CJ covers C. ( ) Since C is compact, there exists a finite subcovering > U X j i i=i n
20 11 COMPACT 1 Figure 1. Relationship Between Types of Compactness
21 12 n of C. Let U = i^_j H. Then U is open and contains C. Further- M 1=1 i more U - \_J U U is compact,, D. Compactness i=i x i and Hansdorff i=i i Spaces n - Definition I-11. A topological space X is called Hausdorff if for each pair of distinct points x and y in X there exists two disjoint open sets U and U such that x e U and y e U. x y x y 1 Theorem A compact subset of a Hausdorff space is closed. Proof. Let X be a Hausdorff space and let C be a compact subset of X. It will be shown that X - C is open. Let p e X - C and let y be any point of C. By the Hausdorff property, there exist open sets U and V containing p and y respectively such that p y U and V are disjoint. Consider the collection fv : y e 0]. This p y y ^ is an open covering of the compact set C, and hence there exists a finite subcovering {^y % } f C. Let be the open neighborhood of p corresponding to V. Then U = f~^\ U 1 is an open set cony i i=i P taining p which is a subset of X - C. Hence X - C is open and C is closedo Remark. It will be useful to note also in the above proof that ' n the set V = f~^] V is an open set containing C which does not i=i y i intersect U. Theorem The intersection of a closed set and a compact set is compact. Proof. Let F be a closed set and let C be a compact set in some topological space X. Let [u : a A] be an open covering of
22 13 F 0 Co The set X - F is open and contains C - F Hence {u^ ; X - F] covers C. C is compact, so a finite subcovering {u a ; X - F} covers i C 0 But (X - F) fl ( F l i c ) is empty; hence {u a } covers F 0 C. Hence FplC is compact. Corollary In a Hausdorff space, the intersection of two compact sets is compact. Proof. By theorem I-11 the two sets are closed, and theorem 1-12 their intersection is compact. Example 1-3, A space in which the intersection of two compact sets is not compact. (By Theorem I-11 and Theorem 1-12 the space cannot be Hausdorff and the compact sets cannot be closed.) Let R denote the space of real numbers with the usual topology, and let T be a space consisting of two abstract elements a and b with only the set T and the empty set as open sets. Let X be the Cartesian product of T and R, i.e., X = T x R. Then X is the set of all ordered pairs of the form (a, x) or (b, y), where x and y are real numbers; and open sets are sets of the form {(a, x), (b, x) : x e 0, 0 is open in R}. Let C ± = {(a, x), (b, y) : x e (0, l) and y e [0, l]} and let C = {(a, x) : x e [0, l]}. It is easily seen that C and C g are compact, but the intersection
23 14 is not compact. Definition A topological space X is said to be regular if for each point x X and each open set U containing x there exists an open set V containing x such that VdU. Theorem Every compact Hausdorff space is regular. Proof. Let p be any point of X and let U be any open set containing p. F X - U is a closed set and is also compact. By the argument of the proof of Theorem I-11 and the Remark following that theorem, there exist open sets V and 0 containing p and F respectively such that V and 0 are disjoint. It follows that p VCZU. E. Compact ification Definition Let X be any T space and let w be any abstract element not in X. The space X* = X U {w}, with a basis for a topology consisting of all open sets of X and all subsets U of X* such that X* - U is a closed compact subset of X, is the one-point compact ification of X. Theorem The one-point compact ification X* of a space X is a compact space. Furthermore X* is T. Proof. First it will be shown that the collection of open sets for X*, defined above, is a basis for a topology on X*. It is sufficient to show that: (l) Given p X*, there exists a U in the basis such that p U,
24 15 (2) Given basis sets U and V, and any point p in u n V, there exists a member, W, of the basis such that p I C u n v, If p e X, clearly condition (l) is satisfied. Let p = w. Then the set U = X* - {q}, where q is any point in X, contains w and X* - U = [q], which is a closed compact subset of X under the T_^ assumption, Now let U and V be any two members of the basis and assume that p e U 'I V If p e X, (2) is clearly satisfied. Assume p ~ w. U fi V is open, since (X* - U) U (X* - V) = X* - U f V, and the two sets on the left are closed compact subsets of X. If there are no members of X in U fi V, {w} = W is the desired set. If q e U f V fl X, the set (X* - U (1 V) U {q} is compact and closed. Hence let W = (U fl V) - (q), W is open and furthermore we WCZu H V. X*, with the indicated topology, is therefore a topological space. The complement of every set consisting of only one point is open, so X* is a T space. Now it will be shown that X* is compact. Let {^a} be any open covering of X*, One of the elements, say U, of {u } contains w. Hence X* - U is closed and compact, and consequently some finite subcollection { u a } of {u } covers X - U. The finite subcovering k i 3 {U j U} covers X*o i
25 16 Remark. A space may be compactified by methods other than the one-point compact ification. See [2] for a discussion and references regarding compact ification. F. Compactness in a Metric Space Definition 1-14, A topological space X is a metric space if there exists a real-valued function d defined on X x X such that (1) d(x, y) + d(y, z) > d(x, z) (2) d(x, y) = d(y, x) (3) d(x, y) > 0 (4) d(x, y) = 0 if and only if x = y, and such that the collection of sets {N(y, e) : y X, > o} where N(y, e) = {x : d(x, y) < E} is a basis for the topology of X. Definition A finite subset F of a metric space X is said to be an e-net for X if for each x in X there exists a y in F such that d(x, y) <. A metric space is said to be totally bounded (or pre-compact) if it has an -net for every > 0. Remark. Since the ^-neighborhoods of a point in a metric space form a countable basis at that point, every metric space is first countable. Also if a metric space is separable (contains a countably dense subset), it is second countable, since the collection of countable neighborhoods of points of the countably dense subset is a basis for the topology of X. Theorem 1-16, Every countably compact metric space is totally bounded.
26 17 Proof. Assume that X is countably compact but not totally bounded. Then for some > 0, X does not contain an -net. Let x 1 X, and choose x g such that d{x ±, x g ) >. Now by induction define the sequences { x n} s o that ^(x^, x^) > for i = 1, 2,..., (n - l). Clearly the sequence { x n} contains no convergent subsequence Hence X is not sequentially compact. But X is first countable. Therefore X is not countably compact. This contradiction proves the theorem. Theorem Every countably compact metric space is separable. Proof. Let X be a countably compact metric space. By the preceding theorem, X is totally bounded. For each integer n, let F_ oo n be a finite subset of X which is a -net for X, Define F = F n n=l n and note that F is countable,, Let x in X and b > 0 be given. Choose N sufficiently large to insure that jjj < 5. There exists a y F^ such that d(x, y) < jjj < 6. Thus every ^-neighborhood of x contains a point of F. Hence F is dense in X. Remark. The proof of Theorem 1-17 also show s that every totally bounded metric space is separable,, Theorem A metric space is compact if and only if it is totally bounded and complete. Proof. (l) Assume that X is compact. Then X is totally bounded by Theorem Let { x n} be a Cauchy sequence in X (i.e., for every > 0, there exists an N such that for n and m larger than N, d ( x n> x m) < ) B Y "the Remark preceding Theorem 1-16, X is
27 18 first countable and thereby sequentially compact. Hence the sequence { x n} has a subsequence { x n.} which converges to a point x in X. Now let N be a number large enough so that for > 0, d(x, x ) < ^ j a n d dfx, x ) < for all m and j larger than N m n. 2 J Then d(x, x ) < d(x, x ) + d(x, x ) <. Therefore [ x n] converges to x and X is complete. (2) Assume that X is totally bounded and complete. It will be shown that X is sequentially compact. This will imply that X is compact by Theorem 1-5, since X is second countable,, Let { x n} D e a sequence of elements in X and assume that no convergent subsequence exists. Set ^ = ^, for k = 1, 2,... and construct corresponding E^-nets, F^, in X. At least one of the spheres = N(y, l), y F 1? contains an infinite subsequence of [ x n} Let { x^} denote this subsequence. Now at least one of the spheres S g = N(y, ^ ), y F, contains an infinite subsequence of { x^} which will be denoted by { x^} * By induction define a sequence of sequences i x^l> {x^}, 0 9, ( x nl» 0, 0 such that the subsequence { x^} is contained in one of the spheres S^ = N(y, ), y F^. It will be shown that the diagonal sequence { x^} is a Cauchy sequence in X. Let > 0 be 1 given. Choose a positive number N such that < Consider
28 19 integers n and m larger than N. Then {x 11 } and { x } both lie in a sphere S^ Hence for some y F, d(x n, x m ) < d(x n, y) + d(x l ", y). rr m - n' 1 nr 1 Therefore d(x, xj < o + o ~ rr m X is complete; hence { x^} converges to some limit in X. This proves that X is sequentially compact. Consequently X in compact. Theorem (Heine-Borel) A subset of E (n-dimensional n Euclidean space) is compact if and only if it is closed and bounded. Proof. (l) Assume that S is a subset of E^ which is compact but not closed and bounded. In case S is not closed, there exists some sequence in S converging to some point not in S. In case S is not bounded, there exists a sequence in S with an infinite limit. Either case is a violation of B-compactness, and hence of compactness. S is therefore closed and bounded. (2) Assume that S is closed and bounded. It will be shown that S is complete and totally bounded. Let {x^} be a Cauchy sequence in S Then by the completeness of E, { x n} converges to some limit x in E. But x belongs to S since S is closed. It follows that S is complete. Let R be an n-dimensional cube containing S. (Such a cube exists since S is bounded.) For each > 0, subdivide R into
29 20 sub-cubes each of whose sides is of length The set of all vertices in R is finite. Let x = (x 1, x 2, x ) be a point in S. Then I x - v = */ {x 1 - v 2 ) 2 + (x 2 - v 2 ) (x n - v n ) 2 and x " v * J ^ ) ( j t ) Z = e ' where v = (v lf v g, v ) is any vertex of a sub-cube containing x. For each v choose an y e S such that y - v < e. The set of all such y is a 2e-net for S. Hence S is totally bounded, and compact by Theorem Theorem In a metric space the properties, compactness, countable compactness, B-compactness, and sequential compactness, are all equivalent. Proof. By referring to Figure 1 it can be seen that the following must be shown: (1) Every countably compact metric space is second countable. (2) A metric space is T. Statement (l) follows from Theorem 1-16 and the Remark preceding Theorem To prove statement (2), let x be any point in a metric space. The complement of x can be expressed as the union of all neighborhoods of points of the space different from x which do not intersect x. This union is open. Hence the set [x] is closed.
30 21 Go Products of Compact Spaces Definition If X is a topological space corresponding a to an element a in an indexing set A, the Cartesian product TT X a A a is the set of all functions defined on A such that f(a) X for a each a in A. Let F be some finite subset of A and let U be a an open subset of X for every a F with U = X for every a a a a A - F. A basis for the product topology of TT X is the cola A a lection of all subsets of TT X that are of the form TT U. a A a a A a TT X, together with the product topology, is called the "product a A a space." Theorem (Tychonoff) The Cartesian product of any collection of compact spaces is compact, relative to the product topology. Proof. See [3] page 25, or [2] page 143. Example 1-4. A compact space which is not sequentially compact. Let X = TT I a > where I is the unit interval [0, l] with the -r a a ael topology of E 0 Impose the product topology on X. A sequence of functions {f n }> where f : I I, must be found so that the sequence contains no convergent subsequence,, A sequence {f n } i- n ^ converges if and only if it is pointwise convergent in the usual sense on [0, l]. To see this, first assume that the limit f = f, 7 where f is in X. n n -* co For each n choose x. [0, l] for i = 1, 2, n. Then a neighi n borhood containing f is a set U = [g : g(x^) - f(x^) < e]. Hence if for sufficiently large N, n larger than N implies that f U. Then
31 22 f n (x.) - f(x.) <. Any point in I may be included in the collection { x^}> hence {^n} converges pointwise in the usual sense. Clearly if {^n} converges pointwise to f, f^ U for any choice of { x^_}?_ 1 New a sequence of functions from I into I will be constructed which does not contain a pointwise convergent subsequence. Let Q be the set of all sequences of positive integers. This set has power c; hence there exists a one-to-one function h : I + Q Let the sequence {f^} be defined as follows: For each x in I, consider h(x) = [ k }, and let fi(x) = fo, if n is even] II, if n is odd J where n is the first integer such that i = k. f^(x) = 0, if i j k for every n. n r Let [f ] be any subsequence of {f }. Then if h -1 ({n }) = y, Hence f n (y) fails to converge, so that {fn r } i- s no "t pointwise convergent on I. Hence [f n } cannot converge in the product space X. But X is the product of compact spaces and is compact by Theorem 1-21 Therefore X is an example of a space which is compact, but not sequentially compact.
32 23 H. Continuous Transformations of Compact Spaces compact space. Theorem The continuous image of a compact space is a Proof. Let X be a compact space and let f be a continuous mapping of X onto Y. We wish to show that Y Is compact. Consider an open covering {U } of Y. The collection {f~ 1 (U )} is an open a a covering of X, since f is continuous. Therefore there exists a finite subcovering {f 1 (U a.)} of X. Then {f[f -1 (U a> )]} is a finite subcovering of Y. Hence Y is compact. Theorem The continuous image of a countably compact space is a countably compact space. Proof. Clearly the above proof will be the same in the case of a countable collection. Theorem If X is B-compact and if f is a continuous one-to-one function and if f(x) = Y, then Y is B-compact. Proof. Let A be an infinite subset of Y, Then f -1 (A) is an infinite subset of X, and therefore has an accumulation point p in X, Consider a nei ghborhood U of f(p). f -1 (U) is a neighborhood of p. Hence there exists a point x ^ p such that x f -1 (A) ' I f -1 (U). But f(x) ^ f(p), since f is one-to-one. Therefore f(x) is a point of A in U different, from p. Consequently f(p) is an accumulation point of A. Definition A mapping f(x) = Y is said to be open (closed) if for each open (closed) set U in X, f(u) is open (closed) in Y.
33 24 Theorem Let X be a locally compact space and let f be an open, continuous function from X onto a Hausdorff space Y. Then Y is locally compact. Proof. Let y be a point of Y, and let x f -1 (y). Let U be an open set containing x such that U is compact. Then since f is open and continuous f(u) is an open set containing y and f(u) is compact. Since Y is Hausdorff, f(u) is closed, and by continuity f (U) C Z f W. But f(u) contains f (U); hence f(u) = f(u). f(u) is a neighborhood of y whose closure is compact. Hence Y is locally compact. Example 1-5. A B-compact space whose image under a continuous mapping is not B-compact. Let X be the set of positive integers with the topology on the same as in Example 1-1. Let Y be the set of positive integers with the topology in which every subset of Y is open (the so-called discrete topology). Let f : X -> Y be defined by f(2n) = n, f(2n - l) = n ; n = 1, 2, 3,... This function is continuous, since the inverse images of open sets are open. X is B-compact, as noted previously; but Y is not,since there are no accumulation points in Y. Example 1-6. A locally compact space whose image under a continuous function is Hausdorff but not locally compact. First it will be shown that any space X with the discrete topology is locally compact. Let x be any point of X. Then {x} is
34 25 an open set containing X with a compact closure. Hence X is locally compact. Also any function f defined on X with range in any topological space is continuous. This is true since f -1 (U) is open in X regardless of the nature of f and U. To give the desired example, we need only to display a space Y which is not locally compact. Then let X be the same set of points as Y with the discrete topology on X. Let the function f be the identity mapping, f : X-* Y, where f(x) - x for each x in X. Let Y be the set of all points in the Euclidean plane which are on the lines y = l/n and which are in the unit square. Also include the point (l/2, 0). Let Y have the topology inherited from the plane. Y is not locally compact, for no neighborhood of (l/2, 0) contains a compact closure. This is true since each neighborhood will contain at least one sequence of points which converge to a point on the real line different from (l/2, 0). Hence Y is not locally compact and the example may be constructed. Definition 1-18, Let f be a function defined on an arbitrary topological space X with values in E 1 (one-dimensional Euclidean space). Then f is said to be upper semi-continuous at a point x in X, if for every > 0 there exists an open set U containing x such that f(y) - f(x) < for every y in U. f is said to be lower semi-continuous at x if for every > 0 there exists an open set U containing x such that
35 26 f(x) - f(y) < e for each y in U. A function is said to be upper semi-continuous (or lower semicontinuous) on X if it has the property at each point. Theorem Let X be a compact space. Let f be a realvalued function defined on all of X. If f is upper semi-continuous on X, then f attains a maximum value on X. If f is lower semicontinuous, f attains a minimum value on X. Proof. The first conclusion will be proved. The proof of the second is analogous in an obvious way and will be omitted. Let A = sup {f(x) : x e X}. It will be shown that an x in X exists such that f( x 0) = A. Suppose first that A is infinite. Then there exists a sequence of points { x n} f elements in X such that limit f(x ) =. The sequence [x } is a net in X and since X n-> oo n is compact, there exists a subnet [x n : e e E] converging to a point x 0 in X. That is, {x n e : e E} has the property that: (a) for each positive integer i, there exists an e Q in E such that for e > e Q (e E), n e > i; (b) for each open set U containing X q there exists an e' such that for e > e', x n U. e Let > 0 be given. Let U be a neighborhood of X q such that f(x) - f(x ) < for x U. Let e be a member of E such that o l e > e 1 implies that x U. e Now there exists an integer N such that for n > N, f(x ) > f(x ) + e, since limit f(x ) =». Let n - o n^ O 0 n
36 27 e 0 be a member of E such that for e > e n, n > N. Then for e > e. 2 2' e l and e > e g, f(x n ) - f(* 0 ) < and f(x n ) > f(x Q ) + e. This contradiction proves that A must be finite. Let be a point of f(x) such that A - l/n < y^ for each positive integer n. Let x^ e f -1 (y n ) f r each n. The sequence { x n} is a net in X, and hence contains a subnet {x n : e EJ converging to a point X q in X. For each > 0 there exists an integer N such that [A - f(x )[ < for n > N. Also there exists an e in E such that for e > e, n > N. Hence la - f(x )[ < for l' e n e e > e. By the upper semi-continuity of f, there exists a neighborhood U of x such that f(x) - f(x ) < for x U. Also there o o exists an element e of E such that e > e implies that x n U. 2 2 u e For e > e 1 x and e>e P, ^ A-f(x n )< JJ e and f(x n ) - f(x ) <. 0 e Hence A - < f(x ) +. o Since this is true for every > 0, it follows that A < f(x ). But also f(x ) < A. Hence f(x ) = A. o o Theorem 1-27, Let X be a sequentially compact space. Let f be a real-valued function defined on all of X. If f is upper semicontinuous on X, then f attains a maximum value on X. If f is lower semi-continuous on X, f attains a minimum value on X. Proofo The proof of this theorem is identical to the proof of the previous theorem, except a convergent subsequence is used in place of a convergent subnet.
37 CHAPTER II COMPACT MAPPINGS A, Compact Mappings and Equivalences Definition II-l. Let f be a mapping (continuous function) from a topological space X onto a topological space Y. The mapping f is said to be compact if for each compact subset K of Y, f -1 (K) is a compact subset of X. Theorem If X is a compact space and if f(x) = Y is a mapping with Y a Hausdorff space, then f is compact. Proof. Let K be a compact subset of Y. Since Y is Hausdorff, K is closed. By the continuity of f, f" 1 (K) is closed. Since f _1 (K) is a closed subset of a compact space, it is compact. Remark. A set is said to be conditionally compact if its closure is compact. Theorem II-2. Let f(x) = Y be a mapping and assume that X and Y are Hausdorff spaces. Then f is compact if and only if the images of nonconditionally compact sets under f are nonconditionally compact. Proof. (l) Suppose f is compact. Let K be a nonconditionally compact set in X. (K is not compact.) Suppose f(k) is compact. Then f -1 [f(k)] is compact and contains K since f" 1 [f(k)] is closed. But K is a closed subset of f _1 [f(k)] and is hence compact. This contradiction shows the invariance of nonconditional compactness. (2) Suppose that the invariance holds. Let K CZ Y be compact and assume that f 1 (K) is not compact, f 1 (K) is closed since K
38 29 is closed. Hence f -1 (K) = f~ 1 (K) is not compact. But by the invariance of nonconditional compactness, f[f -1 (K)] = K is not conditionally compact. This is false since K = K. Hence f is compact. Definition II-2. Let f(x) = Y be a mapping. A subset A of X such that A = f -1 [f(a)] is called an inverse set. If G is open In X, G q will denote the set of all points x in G such that f- 1 [f(x)]cig. Remark. G is an inverse set. o Lemma II-3. If f is closed and if G is an open set in X, then G and f(g ) are open, o o' r Proof. G q = {f _1 (y) : f _1 (y) CZG, y YJ. X - G is closed; hence Y - f(x - G) is open. It will be established that f(g ) - Y - f (X - G). Let y f(g ). Then f _1 (y) CZ G, and f _1 (y) f) (X - G) is empty. Since f~ 1 (y) is an inverse set, {y} f) f(x - G) is empty and y Y - f(x - G). This shows that f(g ) C Y - f(x - G). Now let y Y - f(x - G). The inverse of y is completely contained in G. Hence f -1 (y) CTG q and y f(g ). This establishes the equality. It follows that f(g Q ) is open. But f - 1 [f(g O )] - G Q, which is open by the continuity of f. Theorem II-4. If f(x) = Y is a closed mapping and if for each y Y, f -1 (y) is compact, then f is compact. Proof. Let K be a nonempty compact subset of Y and let p be an open covering of f -1 (K). Let y K. A finite subcovering J3^ of J3 covers f -1 (y), since by hypothesis f -1 (y) is compact. Let U y be the union of all elements of p. and f(up are open by
39 30 Lemma II-3. The collection [f(u y ) : y K} is an open covering of K which is reducible to a finite subcovering. Hence a finite subcovering from the collection {u y : y K] covers f _1 (K) since f _1 [f(u y )] = U y. But each U y is covered by the union o o o of only a finite number of elements of p. Therefore a finite subcover ing for f _1 (K) may be extracted from 3. Theorem II-5. If f(x) = Y is a compact mapping and Y is a locally compact Hausdorff space, then f is closed and point inverses are compact. Proof. It is obvious that point inverses are compact. It will be shown that f is closed. Let F be a closed subset of X and suppose that y $-f(f) is an accumulation point of f(f). Since Y is locally compact, an open set G exists such that y G and G is compact. Now suppose f(f) f] G were compact; then there exist open neighborhoods U and V of f(f)fl G and y respectively such that V is empty. This is true since Y is a Hausdorff space. But (cfl v)(1 f ( F ) e v r i [ G n f(f)]evhu = 0. However (G n v) n f(f) is not empty since G I I V is a neighborhood of y. Hence G n f(f) is not compact. Since G is compact, f -1 (G) is compact; and F fl f -1 (G) is compact by Theorem Also fcf D f -1 (G)] = f(f)d G. Hence f(f)f G is compact. This contradiction proves the theorem.
40 31 Corollary II-6. Let f be a mapping from X onto Y and assume that Y is a locally compact Hausdorff space. A necessary and sufficient condition for f to be compact is that f be closed and that point inverses be compact. Proof. The necessity follows from Theorem II-5, and the sufficiency follows from Theorem II-4. Theorem II-7. Let f(x) = Y be a compact mapping from a first countable space X to a first countable space Y. Then f is closed. Proof. Let F be a closed subset of X. Let y be an accumulation point of f(f) and let {v^} be a sequence of points in f(f) which converge to y. Consider the compact set K = [y ; y]. Since -1, f is compact f (KJ is compact. Let x^ be chosen such that x^ e f _1 (y^) Pi Fo The sequence {*^} contains a subsequence [x^ } which converges to a point x in f _1 (K). Then f(x. } = y. and by n n continuity limit f(x* ) = f(x) = y. n-» oo n Hence y e f(f) and f(f) is closed. Corollary II-8 If f(x) = Y is a mapping from a first countable space X to a first countable space Y, then f is compact if and only if f is closed and point inverses are compact. Proofo (l) Assume that f is compact. Then clearly point inverses are compact, and f is closed by Theorem II-7. (2) Assume that f is closed and that point inverses are compact. Then f is compact by Theorem II-4. Theorem Let f(x) = Y be a compact mapping from a first countable space X to a first countable Hausdorff space Y. For
41 32 any y e Y and any open set U containing f -1 (y), y is interior to f(u). Proof > Suppose that there exists an open set U containing f _1 (y) for which y int f (U). Then there exists a sequence {v^} of elements of Y - f(u) such that {v^} converges to y. The set K - [y^ j y} is compact and f _1 (K) is compact. Let x^ f -1 (y^) for each i x. U for each i and furthermore fx.] contains a I i-> convergent subsequence [XJ_ }. Let [x^ } converge to x; then f(xi^} converges to f(x) which must equal y. But x U and f" 1 (y)cztu. This is a contradiction which implies that y int f(u). Remark. Theorems II-1, II-2, II-7, and II-9 of this section may be found in [4] TheoremsII-4 and II-5 may be found in [5], Example II-l. Every polynomial P(z) = a n z n + + a 1 z + a Q defined on the complex plane is a compact mapping. To see this, consider a compact subset K of the complex plane. By Theorem 1-19 K is closed and bounded, and it will be shown that P -1 (K) is also closed and bounded. By the continuity of P, P -1 (K) is closed. Assume that P _1 (K) is not bounded and let {z^} be a sequence of points in P" 1 (K) which has an infinite limit. But P(z.) I = a z 1? + 0 * 9 + a, z. + a 1 l n I l l o 1 = Iz 1?! a +a n _ 1 z7 l +o»* + a z. 1 l 1 n 1 n l o i n. As z^ approaches infinity, the term z? approaches infinity and the term
42 33 l a n + a n-i z _ a o z ""l approaches I a n I Hence p(z^)( has an infinite limit. This contradicts the boundedness of K. Therefore P _1 (K) is bounded, and compact by Theorem Remark. The compact mapping from the complex plane into the complex plane has been studied by G. T. Whyburn and other writers as a generalization of the polynomial. B. Light, Monotone, and Quasi-Open Mappings Definition I1-3. A mapping f(x) = Y is said to be light if for every y Y, f -1 (y) is totally disconnected (i.e., each component of f -1 (y) consists of a single point). Remark. A component is a maximal connected set. Definition II-4. A mapping f(x) = Y is said to be monotone if for each y Y, f -1 (y) is a continuum (a compact, connected set). Definition II-5. A mapping f(x) = Y is said to be quasi-open if for each y Y and any open set U containing a compact component of f _ 1 (y), then y is interior to f(u). Theorem If f(x) = Y is a compact monotone mapping from a first countable space X to a first countable Hausdorff space Y, then f is quasi-open. Furthermore if f is quasi-open and monotone and if X is locally compact, second countable, and Hausdorff with Y first countable and Hausdorff, then f is compact. Proof. (l) Assume that f is compact and monotone. Let y Y. Since f is monotone, f' 1 (y) contains one and only one
1 Topology Definition of a topology Basis (Base) of a topology The subspace topology & the product topology on X Y 3
 Index Page 1 Topology 2 1.1 Definition of a topology 2 1.2 Basis (Base) of a topology 2 1.3 The subspace topology & the product topology on X Y 3 1.4 Basic topology concepts: limit points, closed sets,
Index Page 1 Topology 2 1.1 Definition of a topology 2 1.2 Basis (Base) of a topology 2 1.3 The subspace topology & the product topology on X Y 3 1.4 Basic topology concepts: limit points, closed sets,
Problem Set 2: Solutions Math 201A: Fall 2016
 Problem Set 2: s Math 201A: Fall 2016 Problem 1. (a) Prove that a closed subset of a complete metric space is complete. (b) Prove that a closed subset of a compact metric space is compact. (c) Prove that
Problem Set 2: s Math 201A: Fall 2016 Problem 1. (a) Prove that a closed subset of a complete metric space is complete. (b) Prove that a closed subset of a compact metric space is compact. (c) Prove that
Topology. Xiaolong Han. Department of Mathematics, California State University, Northridge, CA 91330, USA address:
 Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
MAT 570 REAL ANALYSIS LECTURE NOTES. Contents. 1. Sets Functions Countability Axiom of choice Equivalence relations 9
 MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
Real Analysis Math 131AH Rudin, Chapter #1. Dominique Abdi
 Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
g 2 (x) (1/3)M 1 = (1/3)(2/3)M.
 COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
NAME: Mathematics 205A, Fall 2008, Final Examination. Answer Key
 NAME: Mathematics 205A, Fall 2008, Final Examination Answer Key 1 1. [25 points] Let X be a set with 2 or more elements. Show that there are topologies U and V on X such that the identity map J : (X, U)
NAME: Mathematics 205A, Fall 2008, Final Examination Answer Key 1 1. [25 points] Let X be a set with 2 or more elements. Show that there are topologies U and V on X such that the identity map J : (X, U)
Solve EACH of the exercises 1-3
 Topology Ph.D. Entrance Exam, August 2011 Write a solution of each exercise on a separate page. Solve EACH of the exercises 1-3 Ex. 1. Let X and Y be Hausdorff topological spaces and let f: X Y be continuous.
Topology Ph.D. Entrance Exam, August 2011 Write a solution of each exercise on a separate page. Solve EACH of the exercises 1-3 Ex. 1. Let X and Y be Hausdorff topological spaces and let f: X Y be continuous.
Analysis Finite and Infinite Sets The Real Numbers The Cantor Set
 Analysis Finite and Infinite Sets Definition. An initial segment is {n N n n 0 }. Definition. A finite set can be put into one-to-one correspondence with an initial segment. The empty set is also considered
Analysis Finite and Infinite Sets Definition. An initial segment is {n N n n 0 }. Definition. A finite set can be put into one-to-one correspondence with an initial segment. The empty set is also considered
REVIEW OF ESSENTIAL MATH 346 TOPICS
 REVIEW OF ESSENTIAL MATH 346 TOPICS 1. AXIOMATIC STRUCTURE OF R Doğan Çömez The real number system is a complete ordered field, i.e., it is a set R which is endowed with addition and multiplication operations
REVIEW OF ESSENTIAL MATH 346 TOPICS 1. AXIOMATIC STRUCTURE OF R Doğan Çömez The real number system is a complete ordered field, i.e., it is a set R which is endowed with addition and multiplication operations
MH 7500 THEOREMS. (iii) A = A; (iv) A B = A B. Theorem 5. If {A α : α Λ} is any collection of subsets of a space X, then
 MH 7500 THEOREMS Definition. A topological space is an ordered pair (X, T ), where X is a set and T is a collection of subsets of X such that (i) T and X T ; (ii) U V T whenever U, V T ; (iii) U T whenever
MH 7500 THEOREMS Definition. A topological space is an ordered pair (X, T ), where X is a set and T is a collection of subsets of X such that (i) T and X T ; (ii) U V T whenever U, V T ; (iii) U T whenever
If X is a compact space and K X is a closed subset, then K is
 6. Compactness...compact sets play the same role in the theory of abstract sets as the notion of limit sets do in the theory of point sets. Maurice Frechet, 1906 Compactness is one of the most useful topological
6. Compactness...compact sets play the same role in the theory of abstract sets as the notion of limit sets do in the theory of point sets. Maurice Frechet, 1906 Compactness is one of the most useful topological
Chapter 2 Metric Spaces
 Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
Some Background Material
 Chapter 1 Some Background Material In the first chapter, we present a quick review of elementary - but important - material as a way of dipping our toes in the water. This chapter also introduces important
Chapter 1 Some Background Material In the first chapter, we present a quick review of elementary - but important - material as a way of dipping our toes in the water. This chapter also introduces important
CHAPTER 7. Connectedness
 CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
Math 117: Topology of the Real Numbers
 Math 117: Topology of the Real Numbers John Douglas Moore November 10, 2008 The goal of these notes is to highlight the most important topics presented in Chapter 3 of the text [1] and to provide a few
Math 117: Topology of the Real Numbers John Douglas Moore November 10, 2008 The goal of these notes is to highlight the most important topics presented in Chapter 3 of the text [1] and to provide a few
Part III. 10 Topological Space Basics. Topological Spaces
 Part III 10 Topological Space Basics Topological Spaces Using the metric space results above as motivation we will axiomatize the notion of being an open set to more general settings. Definition 10.1.
Part III 10 Topological Space Basics Topological Spaces Using the metric space results above as motivation we will axiomatize the notion of being an open set to more general settings. Definition 10.1.
4 Countability axioms
 4 COUNTABILITY AXIOMS 4 Countability axioms Definition 4.1. Let X be a topological space X is said to be first countable if for any x X, there is a countable basis for the neighborhoods of x. X is said
4 COUNTABILITY AXIOMS 4 Countability axioms Definition 4.1. Let X be a topological space X is said to be first countable if for any x X, there is a countable basis for the neighborhoods of x. X is said
7 Complete metric spaces and function spaces
 7 Complete metric spaces and function spaces 7.1 Completeness Let (X, d) be a metric space. Definition 7.1. A sequence (x n ) n N in X is a Cauchy sequence if for any ɛ > 0, there is N N such that n, m
7 Complete metric spaces and function spaces 7.1 Completeness Let (X, d) be a metric space. Definition 7.1. A sequence (x n ) n N in X is a Cauchy sequence if for any ɛ > 0, there is N N such that n, m
Maths 212: Homework Solutions
 Maths 212: Homework Solutions 1. The definition of A ensures that x π for all x A, so π is an upper bound of A. To show it is the least upper bound, suppose x < π and consider two cases. If x < 1, then
Maths 212: Homework Solutions 1. The definition of A ensures that x π for all x A, so π is an upper bound of A. To show it is the least upper bound, suppose x < π and consider two cases. If x < 1, then
MA651 Topology. Lecture 9. Compactness 2.
 MA651 Topology. Lecture 9. Compactness 2. This text is based on the following books: Topology by James Dugundgji Fundamental concepts of topology by Peter O Neil Elements of Mathematics: General Topology
MA651 Topology. Lecture 9. Compactness 2. This text is based on the following books: Topology by James Dugundgji Fundamental concepts of topology by Peter O Neil Elements of Mathematics: General Topology
Topological properties
 CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
Topology, Math 581, Fall 2017 last updated: November 24, Topology 1, Math 581, Fall 2017: Notes and homework Krzysztof Chris Ciesielski
 Topology, Math 581, Fall 2017 last updated: November 24, 2017 1 Topology 1, Math 581, Fall 2017: Notes and homework Krzysztof Chris Ciesielski Class of August 17: Course and syllabus overview. Topology
Topology, Math 581, Fall 2017 last updated: November 24, 2017 1 Topology 1, Math 581, Fall 2017: Notes and homework Krzysztof Chris Ciesielski Class of August 17: Course and syllabus overview. Topology
Sets, Functions and Metric Spaces
 Chapter 14 Sets, Functions and Metric Spaces 14.1 Functions and sets 14.1.1 The function concept Definition 14.1 Let us consider two sets A and B whose elements may be any objects whatsoever. Suppose that
Chapter 14 Sets, Functions and Metric Spaces 14.1 Functions and sets 14.1.1 The function concept Definition 14.1 Let us consider two sets A and B whose elements may be any objects whatsoever. Suppose that
S. Mrówka introduced a topological space ψ whose underlying set is the. natural numbers together with an infinite maximal almost disjoint family(madf)
 PAYNE, CATHERINE ANN, M.A. On ψ (κ, M) spaces with κ = ω 1. (2010) Directed by Dr. Jerry Vaughan. 30pp. S. Mrówka introduced a topological space ψ whose underlying set is the natural numbers together with
PAYNE, CATHERINE ANN, M.A. On ψ (κ, M) spaces with κ = ω 1. (2010) Directed by Dr. Jerry Vaughan. 30pp. S. Mrówka introduced a topological space ψ whose underlying set is the natural numbers together with
s P = f(ξ n )(x i x i 1 ). i=1
 Compactness and total boundedness via nets The aim of this chapter is to define the notion of a net (generalized sequence) and to characterize compactness and total boundedness by this important topological
Compactness and total boundedness via nets The aim of this chapter is to define the notion of a net (generalized sequence) and to characterize compactness and total boundedness by this important topological
Contents Ordered Fields... 2 Ordered sets and fields... 2 Construction of the Reals 1: Dedekind Cuts... 2 Metric Spaces... 3
 Analysis Math Notes Study Guide Real Analysis Contents Ordered Fields 2 Ordered sets and fields 2 Construction of the Reals 1: Dedekind Cuts 2 Metric Spaces 3 Metric Spaces 3 Definitions 4 Separability
Analysis Math Notes Study Guide Real Analysis Contents Ordered Fields 2 Ordered sets and fields 2 Construction of the Reals 1: Dedekind Cuts 2 Metric Spaces 3 Metric Spaces 3 Definitions 4 Separability
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University
 Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Introduction to Proofs in Analysis. updated December 5, By Edoh Y. Amiran Following the outline of notes by Donald Chalice INTRODUCTION
 Introduction to Proofs in Analysis updated December 5, 2016 By Edoh Y. Amiran Following the outline of notes by Donald Chalice INTRODUCTION Purpose. These notes intend to introduce four main notions from
Introduction to Proofs in Analysis updated December 5, 2016 By Edoh Y. Amiran Following the outline of notes by Donald Chalice INTRODUCTION Purpose. These notes intend to introduce four main notions from
STRONGLY CONNECTED SPACES
 Undergraduate Research Opportunity Programme in Science STRONGLY CONNECTED SPACES Submitted by Dai Bo Supervised by Dr. Wong Yan-loi Department of Mathematics National University of Singapore Academic
Undergraduate Research Opportunity Programme in Science STRONGLY CONNECTED SPACES Submitted by Dai Bo Supervised by Dr. Wong Yan-loi Department of Mathematics National University of Singapore Academic
Theorems. Theorem 1.11: Greatest-Lower-Bound Property. Theorem 1.20: The Archimedean property of. Theorem 1.21: -th Root of Real Numbers
 Page 1 Theorems Wednesday, May 9, 2018 12:53 AM Theorem 1.11: Greatest-Lower-Bound Property Suppose is an ordered set with the least-upper-bound property Suppose, and is bounded below be the set of lower
Page 1 Theorems Wednesday, May 9, 2018 12:53 AM Theorem 1.11: Greatest-Lower-Bound Property Suppose is an ordered set with the least-upper-bound property Suppose, and is bounded below be the set of lower
Introduction to Topology
 Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Real Analysis Chapter 4 Solutions Jonathan Conder
 2. Let x, y X and suppose that x y. Then {x} c is open in the cofinite topology and contains y but not x. The cofinite topology on X is therefore T 1. Since X is infinite it contains two distinct points
2. Let x, y X and suppose that x y. Then {x} c is open in the cofinite topology and contains y but not x. The cofinite topology on X is therefore T 1. Since X is infinite it contains two distinct points
A LITTLE REAL ANALYSIS AND TOPOLOGY
 A LITTLE REAL ANALYSIS AND TOPOLOGY 1. NOTATION Before we begin some notational definitions are useful. (1) Z = {, 3, 2, 1, 0, 1, 2, 3, }is the set of integers. (2) Q = { a b : aεz, bεz {0}} is the set
A LITTLE REAL ANALYSIS AND TOPOLOGY 1. NOTATION Before we begin some notational definitions are useful. (1) Z = {, 3, 2, 1, 0, 1, 2, 3, }is the set of integers. (2) Q = { a b : aεz, bεz {0}} is the set
HW 4 SOLUTIONS. , x + x x 1 ) 2
 HW 4 SOLUTIONS The Way of Analysis p. 98: 1.) Suppose that A is open. Show that A minus a finite set is still open. This follows by induction as long as A minus one point x is still open. To see that A
HW 4 SOLUTIONS The Way of Analysis p. 98: 1.) Suppose that A is open. Show that A minus a finite set is still open. This follows by induction as long as A minus one point x is still open. To see that A
INDECOMPOSABILITY IN INVERSE LIMITS WITH SET-VALUED FUNCTIONS
 INDECOMPOSABILITY IN INVERSE LIMITS WITH SET-VALUED FUNCTIONS JAMES P. KELLY AND JONATHAN MEDDAUGH Abstract. In this paper, we develop a sufficient condition for the inverse limit of upper semi-continuous
INDECOMPOSABILITY IN INVERSE LIMITS WITH SET-VALUED FUNCTIONS JAMES P. KELLY AND JONATHAN MEDDAUGH Abstract. In this paper, we develop a sufficient condition for the inverse limit of upper semi-continuous
What to remember about metric spaces
 Division of the Humanities and Social Sciences What to remember about metric spaces KC Border These notes are (I hope) a gentle introduction to the topological concepts used in economic theory. If the
Division of the Humanities and Social Sciences What to remember about metric spaces KC Border These notes are (I hope) a gentle introduction to the topological concepts used in economic theory. If the
Set, functions and Euclidean space. Seungjin Han
 Set, functions and Euclidean space Seungjin Han September, 2018 1 Some Basics LOGIC A is necessary for B : If B holds, then A holds. B A A B is the contraposition of B A. A is sufficient for B: If A holds,
Set, functions and Euclidean space Seungjin Han September, 2018 1 Some Basics LOGIC A is necessary for B : If B holds, then A holds. B A A B is the contraposition of B A. A is sufficient for B: If A holds,
Axioms of separation
 Axioms of separation These notes discuss the same topic as Sections 31, 32, 33, 34, 35, and also 7, 10 of Munkres book. Some notions (hereditarily normal, perfectly normal, collectionwise normal, monotonically
Axioms of separation These notes discuss the same topic as Sections 31, 32, 33, 34, 35, and also 7, 10 of Munkres book. Some notions (hereditarily normal, perfectly normal, collectionwise normal, monotonically
Filters in Analysis and Topology
 Filters in Analysis and Topology David MacIver July 1, 2004 Abstract The study of filters is a very natural way to talk about convergence in an arbitrary topological space, and carries over nicely into
Filters in Analysis and Topology David MacIver July 1, 2004 Abstract The study of filters is a very natural way to talk about convergence in an arbitrary topological space, and carries over nicely into
The Heine-Borel and Arzela-Ascoli Theorems
 The Heine-Borel and Arzela-Ascoli Theorems David Jekel October 29, 2016 This paper explains two important results about compactness, the Heine- Borel theorem and the Arzela-Ascoli theorem. We prove them
The Heine-Borel and Arzela-Ascoli Theorems David Jekel October 29, 2016 This paper explains two important results about compactness, the Heine- Borel theorem and the Arzela-Ascoli theorem. We prove them
MORE ON CONTINUOUS FUNCTIONS AND SETS
 Chapter 6 MORE ON CONTINUOUS FUNCTIONS AND SETS This chapter can be considered enrichment material containing also several more advanced topics and may be skipped in its entirety. You can proceed directly
Chapter 6 MORE ON CONTINUOUS FUNCTIONS AND SETS This chapter can be considered enrichment material containing also several more advanced topics and may be skipped in its entirety. You can proceed directly
CHAPTER 5. The Topology of R. 1. Open and Closed Sets
 CHAPTER 5 The Topology of R 1. Open and Closed Sets DEFINITION 5.1. A set G Ω R is open if for every x 2 G there is an " > 0 such that (x ", x + ") Ω G. A set F Ω R is closed if F c is open. The idea is
CHAPTER 5 The Topology of R 1. Open and Closed Sets DEFINITION 5.1. A set G Ω R is open if for every x 2 G there is an " > 0 such that (x ", x + ") Ω G. A set F Ω R is closed if F c is open. The idea is
Metric Spaces and Topology
 Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
MTG 5316/4302 FALL 2018 REVIEW FINAL
 MTG 5316/4302 FALL 2018 REVIEW FINAL JAMES KEESLING Problem 1. Define open set in a metric space X. Define what it means for a set A X to be connected in a metric space X. Problem 2. Show that if a set
MTG 5316/4302 FALL 2018 REVIEW FINAL JAMES KEESLING Problem 1. Define open set in a metric space X. Define what it means for a set A X to be connected in a metric space X. Problem 2. Show that if a set
Sanjay Mishra. Topology. Dr. Sanjay Mishra. A Profound Subtitle
 Topology A Profound Subtitle Dr. Copyright c 2017 Contents I General Topology 1 Compactness of Topological Space............................ 7 1.1 Introduction 7 1.2 Compact Space 7 1.2.1 Compact Space.................................................
Topology A Profound Subtitle Dr. Copyright c 2017 Contents I General Topology 1 Compactness of Topological Space............................ 7 1.1 Introduction 7 1.2 Compact Space 7 1.2.1 Compact Space.................................................
Convex Analysis and Economic Theory Winter 2018
 Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Winter 2018 Supplement A: Mathematical background A.1 Extended real numbers The extended real number
Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Winter 2018 Supplement A: Mathematical background A.1 Extended real numbers The extended real number
Notes on nets and convergence in topology
 Topology I Humboldt-Universität zu Berlin C. Wendl / F. Schmäschke Summer Semester 2017 Notes on nets and convergence in topology Nets generalize the notion of sequences so that certain familiar results
Topology I Humboldt-Universität zu Berlin C. Wendl / F. Schmäschke Summer Semester 2017 Notes on nets and convergence in topology Nets generalize the notion of sequences so that certain familiar results
2.31 Definition By an open cover of a set E in a metric space X we mean a collection {G α } of open subsets of X such that E α G α.
 Chapter 2. Basic Topology. 2.3 Compact Sets. 2.31 Definition By an open cover of a set E in a metric space X we mean a collection {G α } of open subsets of X such that E α G α. 2.32 Definition A subset
Chapter 2. Basic Topology. 2.3 Compact Sets. 2.31 Definition By an open cover of a set E in a metric space X we mean a collection {G α } of open subsets of X such that E α G α. 2.32 Definition A subset
01. Review of metric spaces and point-set topology. 1. Euclidean spaces
 (October 3, 017) 01. Review of metric spaces and point-set topology Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 017-18/01
(October 3, 017) 01. Review of metric spaces and point-set topology Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 017-18/01
Based on the Appendix to B. Hasselblatt and A. Katok, A First Course in Dynamics, Cambridge University press,
 NOTE ON ABSTRACT RIEMANN INTEGRAL Based on the Appendix to B. Hasselblatt and A. Katok, A First Course in Dynamics, Cambridge University press, 2003. a. Definitions. 1. Metric spaces DEFINITION 1.1. If
NOTE ON ABSTRACT RIEMANN INTEGRAL Based on the Appendix to B. Hasselblatt and A. Katok, A First Course in Dynamics, Cambridge University press, 2003. a. Definitions. 1. Metric spaces DEFINITION 1.1. If
Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem
 56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
Continuous Functions on Metric Spaces
 Continuous Functions on Metric Spaces Math 201A, Fall 2016 1 Continuous functions Definition 1. Let (X, d X ) and (Y, d Y ) be metric spaces. A function f : X Y is continuous at a X if for every ɛ > 0
Continuous Functions on Metric Spaces Math 201A, Fall 2016 1 Continuous functions Definition 1. Let (X, d X ) and (Y, d Y ) be metric spaces. A function f : X Y is continuous at a X if for every ɛ > 0
3 COUNTABILITY AND CONNECTEDNESS AXIOMS
 3 COUNTABILITY AND CONNECTEDNESS AXIOMS Definition 3.1 Let X be a topological space. A subset D of X is dense in X iff D = X. X is separable iff it contains a countable dense subset. X satisfies the first
3 COUNTABILITY AND CONNECTEDNESS AXIOMS Definition 3.1 Let X be a topological space. A subset D of X is dense in X iff D = X. X is separable iff it contains a countable dense subset. X satisfies the first
Solutions to Tutorial 8 (Week 9)
 The University of Sydney School of Mathematics and Statistics Solutions to Tutorial 8 (Week 9) MATH3961: Metric Spaces (Advanced) Semester 1, 2018 Web Page: http://www.maths.usyd.edu.au/u/ug/sm/math3961/
The University of Sydney School of Mathematics and Statistics Solutions to Tutorial 8 (Week 9) MATH3961: Metric Spaces (Advanced) Semester 1, 2018 Web Page: http://www.maths.usyd.edu.au/u/ug/sm/math3961/
Topology Part of the Qualify Exams of Department of Mathematics, Texas A&M University Prepared by Zhang, Zecheng
 Topology Part of the Qualify Exams of Department of Mathematics, Texas A&M University Prepared by Zhang, Zecheng Remark 0.1. This is a solution Manuel to the topology questions of the Topology Geometry
Topology Part of the Qualify Exams of Department of Mathematics, Texas A&M University Prepared by Zhang, Zecheng Remark 0.1. This is a solution Manuel to the topology questions of the Topology Geometry
Real Analysis. July 10, These notes are intended for use in the warm-up camp for incoming Berkeley Statistics
 Real Analysis July 10, 2006 1 Introduction These notes are intended for use in the warm-up camp for incoming Berkeley Statistics graduate students. Welcome to Cal! The real analysis review presented here
Real Analysis July 10, 2006 1 Introduction These notes are intended for use in the warm-up camp for incoming Berkeley Statistics graduate students. Welcome to Cal! The real analysis review presented here
Inverse Limit Spaces
 Inverse Limit Spaces Except where reference is made to the work of others, the work described in this thesis is my own or was done in collaboration with my advisory committee. This thesis does not include
Inverse Limit Spaces Except where reference is made to the work of others, the work described in this thesis is my own or was done in collaboration with my advisory committee. This thesis does not include
Logical Connectives and Quantifiers
 Chapter 1 Logical Connectives and Quantifiers 1.1 Logical Connectives 1.2 Quantifiers 1.3 Techniques of Proof: I 1.4 Techniques of Proof: II Theorem 1. Let f be a continuous function. If 1 f(x)dx 0, then
Chapter 1 Logical Connectives and Quantifiers 1.1 Logical Connectives 1.2 Quantifiers 1.3 Techniques of Proof: I 1.4 Techniques of Proof: II Theorem 1. Let f be a continuous function. If 1 f(x)dx 0, then
MATH 202B - Problem Set 5
 MATH 202B - Problem Set 5 Walid Krichene (23265217) March 6, 2013 (5.1) Show that there exists a continuous function F : [0, 1] R which is monotonic on no interval of positive length. proof We know there
MATH 202B - Problem Set 5 Walid Krichene (23265217) March 6, 2013 (5.1) Show that there exists a continuous function F : [0, 1] R which is monotonic on no interval of positive length. proof We know there
Week 5 Lectures 13-15
 Week 5 Lectures 13-15 Lecture 13 Definition 29 Let Y be a subset X. A subset A Y is open in Y if there exists an open set U in X such that A = U Y. It is not difficult to show that the collection of all
Week 5 Lectures 13-15 Lecture 13 Definition 29 Let Y be a subset X. A subset A Y is open in Y if there exists an open set U in X such that A = U Y. It is not difficult to show that the collection of all
Stanford Mathematics Department Math 205A Lecture Supplement #4 Borel Regular & Radon Measures
 2 1 Borel Regular Measures We now state and prove an important regularity property of Borel regular outer measures: Stanford Mathematics Department Math 205A Lecture Supplement #4 Borel Regular & Radon
2 1 Borel Regular Measures We now state and prove an important regularity property of Borel regular outer measures: Stanford Mathematics Department Math 205A Lecture Supplement #4 Borel Regular & Radon
11691 Review Guideline Real Analysis. Real Analysis. - According to Principles of Mathematical Analysis by Walter Rudin (Chapter 1-4)
 Real Analysis - According to Principles of Mathematical Analysis by Walter Rudin (Chapter 1-4) 1 The Real and Complex Number Set: a collection of objects. Proper subset: if A B, then call A a proper subset
Real Analysis - According to Principles of Mathematical Analysis by Walter Rudin (Chapter 1-4) 1 The Real and Complex Number Set: a collection of objects. Proper subset: if A B, then call A a proper subset
A Glimpse into Topology
 A Glimpse into Topology by Vishal Malik A project submitted to the Department of Mathematical Sciences in conformity with the requirements for Math 430 (203-4) Lakehead University Thunder Bay, Ontario,
A Glimpse into Topology by Vishal Malik A project submitted to the Department of Mathematical Sciences in conformity with the requirements for Math 430 (203-4) Lakehead University Thunder Bay, Ontario,
CHODOUNSKY, DAVID, M.A. Relative Topological Properties. (2006) Directed by Dr. Jerry Vaughan. 48pp.
 CHODOUNSKY, DAVID, M.A. Relative Topological Properties. (2006) Directed by Dr. Jerry Vaughan. 48pp. In this thesis we study the concepts of relative topological properties and give some basic facts and
CHODOUNSKY, DAVID, M.A. Relative Topological Properties. (2006) Directed by Dr. Jerry Vaughan. 48pp. In this thesis we study the concepts of relative topological properties and give some basic facts and
SPACES WHOSE PSEUDOCOMPACT SUBSPACES ARE CLOSED SUBSETS. Alan Dow, Jack R. Porter, R.M. Stephenson, Jr., and R. Grant Woods
 SPACES WHOSE PSEUDOCOMPACT SUBSPACES ARE CLOSED SUBSETS Alan Dow, Jack R. Porter, R.M. Stephenson, Jr., and R. Grant Woods Abstract. Every first countable pseudocompact Tychonoff space X has the property
SPACES WHOSE PSEUDOCOMPACT SUBSPACES ARE CLOSED SUBSETS Alan Dow, Jack R. Porter, R.M. Stephenson, Jr., and R. Grant Woods Abstract. Every first countable pseudocompact Tychonoff space X has the property
ANALYSIS WORKSHEET II: METRIC SPACES
 ANALYSIS WORKSHEET II: METRIC SPACES Definition 1. A metric space (X, d) is a space X of objects (called points), together with a distance function or metric d : X X [0, ), which associates to each pair
ANALYSIS WORKSHEET II: METRIC SPACES Definition 1. A metric space (X, d) is a space X of objects (called points), together with a distance function or metric d : X X [0, ), which associates to each pair
van Rooij, Schikhof: A Second Course on Real Functions
 vanrooijschikhof.tex April 25, 2018 van Rooij, Schikhof: A Second Course on Real Functions Notes from [vrs]. Introduction A monotone function is Riemann integrable. A continuous function is Riemann integrable.
vanrooijschikhof.tex April 25, 2018 van Rooij, Schikhof: A Second Course on Real Functions Notes from [vrs]. Introduction A monotone function is Riemann integrable. A continuous function is Riemann integrable.
THEOREMS, ETC., FOR MATH 516
 THEOREMS, ETC., FOR MATH 516 Results labeled Theorem Ea.b.c (or Proposition Ea.b.c, etc.) refer to Theorem c from section a.b of Evans book (Partial Differential Equations). Proposition 1 (=Proposition
THEOREMS, ETC., FOR MATH 516 Results labeled Theorem Ea.b.c (or Proposition Ea.b.c, etc.) refer to Theorem c from section a.b of Evans book (Partial Differential Equations). Proposition 1 (=Proposition
CHAPTER I THE RIESZ REPRESENTATION THEOREM
 CHAPTER I THE RIESZ REPRESENTATION THEOREM We begin our study by identifying certain special kinds of linear functionals on certain special vector spaces of functions. We describe these linear functionals
CHAPTER I THE RIESZ REPRESENTATION THEOREM We begin our study by identifying certain special kinds of linear functionals on certain special vector spaces of functions. We describe these linear functionals
x 0 + f(x), exist as extended real numbers. Show that f is upper semicontinuous This shows ( ɛ, ɛ) B α. Thus
 Homework 3 Solutions, Real Analysis I, Fall, 2010. (9) Let f : (, ) [, ] be a function whose restriction to (, 0) (0, ) is continuous. Assume the one-sided limits p = lim x 0 f(x), q = lim x 0 + f(x) exist
Homework 3 Solutions, Real Analysis I, Fall, 2010. (9) Let f : (, ) [, ] be a function whose restriction to (, 0) (0, ) is continuous. Assume the one-sided limits p = lim x 0 f(x), q = lim x 0 + f(x) exist
A Course in Real Analysis. Saeed Zakeri
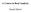 A Course in Real Analysis Saeed Zakeri Contents Chapter 1. Topology of Metric Spaces I 5 1.1. Basic definitions 5 1.2. Convergence 11 1.3. Continuity 12 1.4. Completeness 14 1.5. Compactness 17 1.6. Connectedness
A Course in Real Analysis Saeed Zakeri Contents Chapter 1. Topology of Metric Spaces I 5 1.1. Basic definitions 5 1.2. Convergence 11 1.3. Continuity 12 1.4. Completeness 14 1.5. Compactness 17 1.6. Connectedness
CLASS NOTES FOR APRIL 14, 2000
 CLASS NOTES FOR APRIL 14, 2000 Announcement: Section 1.2, Questions 3,5 have been deferred from Assignment 1 to Assignment 2. Section 1.4, Question 5 has been dropped entirely. 1. Review of Wednesday class
CLASS NOTES FOR APRIL 14, 2000 Announcement: Section 1.2, Questions 3,5 have been deferred from Assignment 1 to Assignment 2. Section 1.4, Question 5 has been dropped entirely. 1. Review of Wednesday class
Chapter 2. Metric Spaces. 2.1 Metric Spaces
 Chapter 2 Metric Spaces ddddddddddddddddddddddddd ddddddd dd ddd A metric space is a mathematical object in which the distance between two points is meaningful. Metric spaces constitute an important class
Chapter 2 Metric Spaces ddddddddddddddddddddddddd ddddddd dd ddd A metric space is a mathematical object in which the distance between two points is meaningful. Metric spaces constitute an important class
Problem Set 5: Solutions Math 201A: Fall 2016
 Problem Set 5: s Math 21A: Fall 216 Problem 1. Define f : [1, ) [1, ) by f(x) = x + 1/x. Show that f(x) f(y) < x y for all x, y [1, ) with x y, but f has no fixed point. Why doesn t this example contradict
Problem Set 5: s Math 21A: Fall 216 Problem 1. Define f : [1, ) [1, ) by f(x) = x + 1/x. Show that f(x) f(y) < x y for all x, y [1, ) with x y, but f has no fixed point. Why doesn t this example contradict
REAL AND COMPLEX ANALYSIS
 REAL AND COMPLE ANALYSIS Third Edition Walter Rudin Professor of Mathematics University of Wisconsin, Madison Version 1.1 No rights reserved. Any part of this work can be reproduced or transmitted in any
REAL AND COMPLE ANALYSIS Third Edition Walter Rudin Professor of Mathematics University of Wisconsin, Madison Version 1.1 No rights reserved. Any part of this work can be reproduced or transmitted in any
This chapter contains a very bare summary of some basic facts from topology.
 Chapter 2 Topological Spaces This chapter contains a very bare summary of some basic facts from topology. 2.1 Definition of Topology A topology O on a set X is a collection of subsets of X satisfying the
Chapter 2 Topological Spaces This chapter contains a very bare summary of some basic facts from topology. 2.1 Definition of Topology A topology O on a set X is a collection of subsets of X satisfying the
Math 201 Topology I. Lecture notes of Prof. Hicham Gebran
 Math 201 Topology I Lecture notes of Prof. Hicham Gebran hicham.gebran@yahoo.com Lebanese University, Fanar, Fall 2015-2016 http://fs2.ul.edu.lb/math http://hichamgebran.wordpress.com 2 Introduction and
Math 201 Topology I Lecture notes of Prof. Hicham Gebran hicham.gebran@yahoo.com Lebanese University, Fanar, Fall 2015-2016 http://fs2.ul.edu.lb/math http://hichamgebran.wordpress.com 2 Introduction and
MATH 54 - TOPOLOGY SUMMER 2015 FINAL EXAMINATION. Problem 1
 MATH 54 - TOPOLOGY SUMMER 2015 FINAL EXAMINATION ELEMENTS OF SOLUTION Problem 1 1. Let X be a Hausdorff space and K 1, K 2 disjoint compact subsets of X. Prove that there exist disjoint open sets U 1 and
MATH 54 - TOPOLOGY SUMMER 2015 FINAL EXAMINATION ELEMENTS OF SOLUTION Problem 1 1. Let X be a Hausdorff space and K 1, K 2 disjoint compact subsets of X. Prove that there exist disjoint open sets U 1 and
B 1 = {B(x, r) x = (x 1, x 2 ) H, 0 < r < x 2 }. (a) Show that B = B 1 B 2 is a basis for a topology on X.
 Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
Real Analysis. Jesse Peterson
 Real Analysis Jesse Peterson February 1, 2017 2 Contents 1 Preliminaries 7 1.1 Sets.................................. 7 1.1.1 Countability......................... 8 1.1.2 Transfinite induction.....................
Real Analysis Jesse Peterson February 1, 2017 2 Contents 1 Preliminaries 7 1.1 Sets.................................. 7 1.1.1 Countability......................... 8 1.1.2 Transfinite induction.....................
POINT SET TOPOLOGY. Definition 2 A set with a topological structure is a topological space (X, O)
 POINT SET TOPOLOGY Definition 1 A topological structure on a set X is a family O P(X) called open sets and satisfying (O 1 ) O is closed for arbitrary unions (O 2 ) O is closed for finite intersections.
POINT SET TOPOLOGY Definition 1 A topological structure on a set X is a family O P(X) called open sets and satisfying (O 1 ) O is closed for arbitrary unions (O 2 ) O is closed for finite intersections.
THEOREMS, ETC., FOR MATH 515
 THEOREMS, ETC., FOR MATH 515 Proposition 1 (=comment on page 17). If A is an algebra, then any finite union or finite intersection of sets in A is also in A. Proposition 2 (=Proposition 1.1). For every
THEOREMS, ETC., FOR MATH 515 Proposition 1 (=comment on page 17). If A is an algebra, then any finite union or finite intersection of sets in A is also in A. Proposition 2 (=Proposition 1.1). For every
E.7 Alaoglu s Theorem
 E.7 Alaoglu s Theorem 359 E.7 Alaoglu s Theorem If X is a normed space, then the closed unit ball in X or X is compact if and only if X is finite-dimensional (Problem A.25). Even so, Alaoglu s Theorem
E.7 Alaoglu s Theorem 359 E.7 Alaoglu s Theorem If X is a normed space, then the closed unit ball in X or X is compact if and only if X is finite-dimensional (Problem A.25). Even so, Alaoglu s Theorem
After taking the square and expanding, we get x + y 2 = (x + y) (x + y) = x 2 + 2x y + y 2, inequality in analysis, we obtain.
 Lecture 1: August 25 Introduction. Topology grew out of certain questions in geometry and analysis about 100 years ago. As Wikipedia puts it, the motivating insight behind topology is that some geometric
Lecture 1: August 25 Introduction. Topology grew out of certain questions in geometry and analysis about 100 years ago. As Wikipedia puts it, the motivating insight behind topology is that some geometric
Real Analysis Notes. Thomas Goller
 Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
SOLUTIONS TO SOME PROBLEMS
 23 FUNCTIONAL ANALYSIS Spring 23 SOLUTIONS TO SOME PROBLEMS Warning:These solutions may contain errors!! PREPARED BY SULEYMAN ULUSOY PROBLEM 1. Prove that a necessary and sufficient condition that the
23 FUNCTIONAL ANALYSIS Spring 23 SOLUTIONS TO SOME PROBLEMS Warning:These solutions may contain errors!! PREPARED BY SULEYMAN ULUSOY PROBLEM 1. Prove that a necessary and sufficient condition that the
SOLUTIONS TO THE FINAL EXAM
 SOLUTIONS TO THE FINAL EXAM Short questions 1 point each) Give a brief definition for each of the following six concepts: 1) normal for topological spaces) 2) path connected 3) homeomorphism 4) covering
SOLUTIONS TO THE FINAL EXAM Short questions 1 point each) Give a brief definition for each of the following six concepts: 1) normal for topological spaces) 2) path connected 3) homeomorphism 4) covering
function provided the associated graph function g:x -) X X Y defined
 QUASI-CLOSED SETS AND FIXED POINTS BY GORDON T. WHYBURN UNIVERSITY OF VIRGINIA Communicated December 29, 1966 1. Introduction.-In this paper we develop new separation and intersection properties of certain
QUASI-CLOSED SETS AND FIXED POINTS BY GORDON T. WHYBURN UNIVERSITY OF VIRGINIA Communicated December 29, 1966 1. Introduction.-In this paper we develop new separation and intersection properties of certain
ON SPACE-FILLING CURVES AND THE HAHN-MAZURKIEWICZ THEOREM
 ON SPACE-FILLING CURVES AND THE HAHN-MAZURKIEWICZ THEOREM ALEXANDER KUPERS Abstract. These are notes on space-filling curves, looking at a few examples and proving the Hahn-Mazurkiewicz theorem. This theorem
ON SPACE-FILLING CURVES AND THE HAHN-MAZURKIEWICZ THEOREM ALEXANDER KUPERS Abstract. These are notes on space-filling curves, looking at a few examples and proving the Hahn-Mazurkiewicz theorem. This theorem
3 Hausdorff and Connected Spaces
 3 Hausdorff and Connected Spaces In this chapter we address the question of when two spaces are homeomorphic. This is done by examining two properties that are shared by any pair of homeomorphic spaces.
3 Hausdorff and Connected Spaces In this chapter we address the question of when two spaces are homeomorphic. This is done by examining two properties that are shared by any pair of homeomorphic spaces.
Contents. Index... 15
 Contents Filter Bases and Nets................................................................................ 5 Filter Bases and Ultrafilters: A Brief Overview.........................................................
Contents Filter Bases and Nets................................................................................ 5 Filter Bases and Ultrafilters: A Brief Overview.........................................................
Quick Tour of the Topology of R. Steven Hurder, Dave Marker, & John Wood 1
 Quick Tour of the Topology of R Steven Hurder, Dave Marker, & John Wood 1 1 Department of Mathematics, University of Illinois at Chicago April 17, 2003 Preface i Chapter 1. The Topology of R 1 1. Open
Quick Tour of the Topology of R Steven Hurder, Dave Marker, & John Wood 1 1 Department of Mathematics, University of Illinois at Chicago April 17, 2003 Preface i Chapter 1. The Topology of R 1 1. Open
MAXIMAL INDEPENDENT COLLECTIONS OF CLOSED SETS
 proceedings of the american mathematical society Volume 32, Number 2, April 1972 MAXIMAL INDEPENDENT COLLECTIONS OF CLOSED SETS HARVY LEE BAKER, JR. Abstract. A theorem is proved which implies that if
proceedings of the american mathematical society Volume 32, Number 2, April 1972 MAXIMAL INDEPENDENT COLLECTIONS OF CLOSED SETS HARVY LEE BAKER, JR. Abstract. A theorem is proved which implies that if
FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES. 1. Compact Sets
 FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES CHRISTOPHER HEIL 1. Compact Sets Definition 1.1 (Compact and Totally Bounded Sets). Let X be a metric space, and let E X be
FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES CHRISTOPHER HEIL 1. Compact Sets Definition 1.1 (Compact and Totally Bounded Sets). Let X be a metric space, and let E X be
AN EXPLORATION OF THE METRIZABILITY OF TOPOLOGICAL SPACES
 AN EXPLORATION OF THE METRIZABILITY OF TOPOLOGICAL SPACES DUSTIN HEDMARK Abstract. A study of the conditions under which a topological space is metrizable, concluding with a proof of the Nagata Smirnov
AN EXPLORATION OF THE METRIZABILITY OF TOPOLOGICAL SPACES DUSTIN HEDMARK Abstract. A study of the conditions under which a topological space is metrizable, concluding with a proof of the Nagata Smirnov
DO FIVE OUT OF SIX ON EACH SET PROBLEM SET
 DO FIVE OUT OF SIX ON EACH SET PROBLEM SET 1. THE AXIOM OF FOUNDATION Early on in the book (page 6) it is indicated that throughout the formal development set is going to mean pure set, or set whose elements,
DO FIVE OUT OF SIX ON EACH SET PROBLEM SET 1. THE AXIOM OF FOUNDATION Early on in the book (page 6) it is indicated that throughout the formal development set is going to mean pure set, or set whose elements,
MASTERS EXAMINATION IN MATHEMATICS SOLUTIONS
 MASTERS EXAMINATION IN MATHEMATICS PURE MATHEMATICS OPTION SPRING 010 SOLUTIONS Algebra A1. Let F be a finite field. Prove that F [x] contains infinitely many prime ideals. Solution: The ring F [x] of
MASTERS EXAMINATION IN MATHEMATICS PURE MATHEMATICS OPTION SPRING 010 SOLUTIONS Algebra A1. Let F be a finite field. Prove that F [x] contains infinitely many prime ideals. Solution: The ring F [x] of
van Rooij, Schikhof: A Second Course on Real Functions
 vanrooijschikhofproblems.tex December 5, 2017 http://thales.doa.fmph.uniba.sk/sleziak/texty/rozne/pozn/books/ van Rooij, Schikhof: A Second Course on Real Functions Some notes made when reading [vrs].
vanrooijschikhofproblems.tex December 5, 2017 http://thales.doa.fmph.uniba.sk/sleziak/texty/rozne/pozn/books/ van Rooij, Schikhof: A Second Course on Real Functions Some notes made when reading [vrs].
On the Countable Dense Homogeneity of Euclidean Spaces. Randall Gay
 On the Countable Dense Homogeneity of Euclidean Spaces by Randall Gay A thesis submitted to the Graduate Faculty of Auburn University in partial fulfillment of the requirements for the Degree of Master
On the Countable Dense Homogeneity of Euclidean Spaces by Randall Gay A thesis submitted to the Graduate Faculty of Auburn University in partial fulfillment of the requirements for the Degree of Master
