Sturm-Liouville Theory
|
|
|
- Leslie Turner
- 6 years ago
- Views:
Transcription
1 LECTURE 1 Sturm-Liouville Theory In the two preceing lectures I emonstrte the utility of Fourier series in solving PDE/BVPs. As we ll now see, Fourier series re just the tip of the iceerg of the theory n utility of specil functions. Before preceing with the generl theory, let me stte clerly the sic properties of Fourier series we inten to generlize: i The Fourier sine functions { sin nπ L x n = 1,, 3,... } n cosine functions { cos } nπ L x n =, 1,,... re solutions of secon orer liner homogeneous ifferentil eqution 1 y = λy stisfying certin liner homogenous ounry conitions: viz, the Fourier-sine functions stisfy n the Fourier-cosine functions stisfy y = = y L y = = y L. ii The Fourier sine n cosine functions oey certin orthogonlity reltions L nπ mπ { 1 if n = m sin L L x sin L x = if n m L nπ mπ { 1 if n = m cos L L x cos L x = if n m iii Any continuous, ifferentile function on, L] cn e expresse in terms of Fourier-sine or Fourier-cosine expnsion f x = + nπ n cos L x = n=1 nπ n sin L x n=1 Moreover, the orthogonlity reltions ii llow us to etermine the coefficients n n n n = L nπ f x cos L L x n = L nπ f x sin L L x 1. Sturm-Liouville Prolems Definition 1.1. A Sturm-Liouville prolem is secon orer homogeneous liner ifferentil eqution of the form 3 p x y ] q x y + λr x y =, x, ] 55
2 1. STURM-LIOUVILLE PROBLEMS 56 together with ounry conitions of the form 4 4 y + α y = y + β y = In wht follow, λ is to e regre s constnt prmeter n we shll lwys ssume tht p x n r x re positive functions on the intervl, ] 5 p x > x, ] r x > x, ] Exmple 1.. Tking p x = 1 r x = 1 q x = = = L = = 1 α = β =, we see tht the corresponing Sturm-Liouville prolem y = λy y = y L = hs s its solutions nπ y x = sin L x nπ n λ = n = 1,, 3,... L Note, in prticulr, tht the solution of the Sturm-Liouville prolem only exists for certn vlues of λ; these vlues re eigenvlues of the Sturm-Liouville prolem Nottion 1.3 Liner ifferentil opertor nottion. In wht follows we shll enote y L the liner ifferentil opertor 6 L = p x ] q x which cts on function y x y L y] = p x y ] q x y In terms of L, the ifferentil eqution of Sturm-Liouville prolem cn e expresse L y] = λr x y Theorem 1.4 Lgrnge s ientity. Suppose φ n ψ re two functions stisfying ounry conitions of the form 7 7 then y + α y = y + β y = L φ] ψ φl ψ] =
3 1. STURM-LIOUVILLE PROBLEMS 57 Proof. We hve * L φ] ψ = = = p φ ψ = p φ ψ = p φ ψ p φ p φ ] ψ qφψ ] ψ p φ φ φp ψ p ψ ψ + qφψ φ = p φ ψ φψ + φl ψ] v where we hve twice utilize the integrtion y prts formul Now consier the first term in the lst line f g = fg qφψ qφψ p ψ f g qφψ p φ ψ φψ Since φ n ψ stisfy 7 n 7 we hve ssuming, α,, β n Hence φ = α φ, ψ = α ψ φ = β φ, ψ = β ψ φ ψ φ ψ = α φ ψ φ α φ ψ φ ψ = β φ ψ φ ψ β ψ p u v uv 1 = p 1 u 1 v 1 u 1 v 1 p u v u v = p 1 p = We cn hence conclue from * tht n the theorem follows. L φ] ψ = + φl ψ] = = Recll tht, for exmple, the Fourier-sine functions sin λx not only stisfy certin secon orer liner ifferentil eqution f = λ f ut they lso stisfy certin liner homogeneous ounry conitions f = = f L
4 1. STURM-LIOUVILLE PROBLEMS 58 exctly when the prmeter λ is tune to the ounry conitions { = f = λ f f = f L = λ = nπ L f x = sin nπ L x Wht my seem little surprising t first is tht the fct tht the Fourier-sine functions re solutions to Sturm-Liouville prolem is lso responsile for their orthogonlity properties L nπ mπ { 1 if n = m sin L L x sin L x = if n m Theorem 1.5. If φ n ψ re two solutions of Sturm-Liouville prolem corresponing to ifferent vlues of the prmeter λ then Proof. Suppose φ x ψ x r x =. L φ] = λ 1 r x φ L ψ] = λ r x ψ with λ 1 λ. Then since φ, ψ stisfy the Strum-Liouville ounry conitions, we hve y Theorem 11.1 L φ] ψ = φ L ψ] n ecuse they stisfy Sturm-Liouville-type ifferentil equtions or λ 1 r x φ x ψ x = λ 1 λ By hypothesis, λ 1 λ n so we must conclue φ x λ r x ψ x φ x ψ x r x = φ x ψ x r x = As remrke ove, it is common to write in shorthn the ifferentil eqution of Sturm-Liouville prolem s 8 L y] = λr x y n refer to the prmeter λ corresponing to prticulr solution y x s n eigenvlue of the ifferentil opertor L. This lnguge, of course, is erive from the nomenclture of liner lger where if A is n n n mtrix, v is n n 1 column vector n λ is numer such tht Av = λv then v is clle n eigenvector of A n λ is the corresponing eigenvlue of A. In fct, it is common to use such liner-lgeric-like nomenclture throughout Sturm-Liouville theory; n henceforth we shll refer to the functions y x tht stisfy 8 s eigenfunctions of L n the numers λ s the corresponing eigenvlues of L. Theorem 1.6. All the eigenvlues of Sturm-Liouville prolem re rel.
5 1. STURM-LIOUVILLE PROBLEMS 59 Proof. Consier the following inner prouct on the spce of complex-vlue solutions of Sturm-Liouville prolem 8 for vrious λ Suppose u, v = u x v x u x = v x = R x + ii x tht is, suppose we set u equl to v n split it up into its rel n imginry prts. Then u, u = = R x + ii x R x ii x R x + I x ] Note now tht the integrn is lwys non-negtive. By well-known result from Clculus, the integrl of continuous non-negtive function over finite intervl is lwys non-negtive, n zero only if the function is ienticlly equl to zero. We conclue tht for ny continuous, non-zero, complex-vlue function u x u x u x > Now consier eqution otine from the conclusion of Theorem 11.4 y setting v = u, 9 L u] v = n suppose u is Sturm-Liouville eigenfunction: ul u] 1 L u] = λru for some λ C Tking the complex conjugte of this eqution, we hve, ecuse p x, q x, n r x re ll ssume to e rel-vlue functions, or L u] = λrv = = 11 L u] = λru = L u] = λru p x u ] q x u = λru p x u ] q x u = λru An so plugging the right hn sies of 1 n 11 into 9 we cn conclue tht or 1 λ ru u = λu ru λ λ ruu = We hve rgue ove tht u x u x is non-negtive function, n y ssumption r x is positive function on, 1]. Thus, the integrn is non-negtive function n < ruu so long s u x is not ienticlly zero. We cn therefore conclue from 1 tht λ λ = = λ R.
6 1. STURM-LIOUVILLE PROBLEMS 6 In Liner Alger, we sy tht n eigenvlue λ of mtrix A hs multiplicity m if the imension of the corresponing eigenspce is m; tht is to sy, m = im NullSp A λi In Sturm-Liouville theory, we sy tht the multiplicity of n eigenvlue λ of Sturm-Liouville prolem 1 φ + φ = 1 φ 1 + φ 1 = L φ] = λr x φ x if there re exctly m linerly inepenent solutions for tht vlue of λ. Theorem 1.7. The eigenvlues of Sturm-Liouville prolem re ll of multiplicity one. Moreover, the eigenvlues form n infinite sequence n cn e orere ccoring to incresing mgnitue: {eigenvlues} = {λ 1, λ, λ 3,...}, λ 1 < λ < λ 3 < The orering of the eigenvlues λ, n the fct tht they multiplicity free, estlishes certin cnonicl orering of the corresponing Sturm-Liouville eigenfunctions. We enote y φ n the solution of the Sturm- Liouville prolem with λ = λ n. Actully, this only etermines φ n x up to constnt multiple ecuse if φ x stisfies 3, 4, 4 then so oes ny constnt multiple of φ x. It is common prctise to remove this miguity y emning in ition which fixes φ x up to sclr fctor of the form e iα. φ n x φ n xr x = 1 Moreover, the fcts tht the eigenvlues re ll rel n multiplicity free, lso implies tht we cn choose the φ n x to e rel-vlue functions of x ecuse the complex spn of the functions φ n x must coincie with tht of φ n x. Thus, we cn choose the eigenfunctions of Sturm-Liouville prolem to e rel-vlue functions φ n x φ n xr x = 1 Theorem 1.8. Let φ 1, φ, φ 3,... e the normlize eigenfunctions of Sturm-Liouville prolem n suppose f is piecewise continuous function on, 1]. Then if the series converges to t ech point on, 1. c n := f x φ n x r x c n φ n x n=1 f x + + f x Here f x ± := lim f x ± ε ε + Note tht t ny point x where f is continuous f x + + f x = f x.
7 1. STURM-LIOUVILLE PROBLEMS 61 In summry, ny time you hve ifferentil eqution of the form p x y ] q x y = λr x y with homogeneous ounry conitions of the form Then: 1 y + y = = 1 y 1 + y 1 Solutions will exist for only iscrete ut otherwise infinite set of vlues for the prmeter λ, ll of which re rel numers. There is unique lowest eigenvlue λ n the other eigenvlues cn e totlly orere λ < λ 1 < λ < λ 3 < For ech λ n, there is solution φ n of p x y ] q x y = λ n r x y tht is unique up to sclr fctor. The solutions φ n, n =, 1,,... cn e normlize such tht { 1 if n = m φ n x φ m x r x = otherwise Any continuous function f x on the intervl, 1] cn e expne in terms of the Sturm-Liouville eigenfunctions φ n, n =, 1,,,... f x = n φ n x n= with the coefficients n eing etermine y n = f x φ n x r x If f x is merely piece-wise continuous on, 1], one hs inste f x + + f x = n φ n x n= with the coefficients n etermine y the sme formul.
Sturm-Liouville Theory
 LECTURE 5 Sturm-Liouville Theory In the three preceing lectures I emonstrate the utility of Fourier series in solving PDE/BVPs. As we ll now see, Fourier series are just the tip of the iceberg of the theory
LECTURE 5 Sturm-Liouville Theory In the three preceing lectures I emonstrate the utility of Fourier series in solving PDE/BVPs. As we ll now see, Fourier series are just the tip of the iceberg of the theory
Chapter Five - Eigenvalues, Eigenfunctions, and All That
 Chpter Five - Eigenvlues, Eigenfunctions, n All Tht The prtil ifferentil eqution methos escrie in the previous chpter is specil cse of more generl setting in which we hve n eqution of the form L 1 xux,tl
Chpter Five - Eigenvlues, Eigenfunctions, n All Tht The prtil ifferentil eqution methos escrie in the previous chpter is specil cse of more generl setting in which we hve n eqution of the form L 1 xux,tl
LECTURE 3. Orthogonal Functions. n X. It should be noted, however, that the vectors f i need not be orthogonal nor need they have unit length for
 ECTURE 3 Orthogonl Functions 1. Orthogonl Bses The pproprite setting for our iscussion of orthogonl functions is tht of liner lgebr. So let me recll some relevnt fcts bout nite imensionl vector spces.
ECTURE 3 Orthogonl Functions 1. Orthogonl Bses The pproprite setting for our iscussion of orthogonl functions is tht of liner lgebr. So let me recll some relevnt fcts bout nite imensionl vector spces.
Physics 116C Solution of inhomogeneous ordinary differential equations using Green s functions
 Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1
 MATH34032: Green s Functions, Integrl Equtions nd the Clculus of Vritions 1 Section 1 Function spces nd opertors Here we gives some brief detils nd definitions, prticulrly relting to opertors. For further
MATH34032: Green s Functions, Integrl Equtions nd the Clculus of Vritions 1 Section 1 Function spces nd opertors Here we gives some brief detils nd definitions, prticulrly relting to opertors. For further
Notes on the Eigenfunction Method for solving differential equations
 Notes on the Eigenfunction Metho for solving ifferentil equtions Reminer: Wereconsieringtheinfinite-imensionlHilbertspceL 2 ([, b] of ll squre-integrble functions over the intervl [, b] (ie, b f(x 2
Notes on the Eigenfunction Metho for solving ifferentil equtions Reminer: Wereconsieringtheinfinite-imensionlHilbertspceL 2 ([, b] of ll squre-integrble functions over the intervl [, b] (ie, b f(x 2
Green function and Eigenfunctions
 Green function nd Eigenfunctions Let L e regulr Sturm-Liouville opertor on n intervl (, ) together with regulr oundry conditions. We denote y, φ ( n, x ) the eigenvlues nd corresponding normlized eigenfunctions
Green function nd Eigenfunctions Let L e regulr Sturm-Liouville opertor on n intervl (, ) together with regulr oundry conditions. We denote y, φ ( n, x ) the eigenvlues nd corresponding normlized eigenfunctions
Math 211A Homework. Edward Burkard. = tan (2x + z)
 Mth A Homework Ewr Burkr Eercises 5-C Eercise 8 Show tht the utonomous system: 5 Plne Autonomous Systems = e sin 3y + sin cos + e z, y = sin ( + 3y, z = tn ( + z hs n unstble criticl point t = y = z =
Mth A Homework Ewr Burkr Eercises 5-C Eercise 8 Show tht the utonomous system: 5 Plne Autonomous Systems = e sin 3y + sin cos + e z, y = sin ( + 3y, z = tn ( + z hs n unstble criticl point t = y = z =
DEFINITION The inner product of two functions f 1 and f 2 on an interval [a, b] is the number. ( f 1, f 2 ) b DEFINITION 11.1.
![DEFINITION The inner product of two functions f 1 and f 2 on an interval [a, b] is the number. ( f 1, f 2 ) b DEFINITION 11.1. DEFINITION The inner product of two functions f 1 and f 2 on an interval [a, b] is the number. ( f 1, f 2 ) b DEFINITION 11.1.](/thumbs/81/83893993.jpg) 398 CHAPTER 11 ORTHOGONAL FUNCTIONS AND FOURIER SERIES 11.1 ORTHOGONAL FUNCTIONS REVIEW MATERIAL The notions of generlized vectors nd vector spces cn e found in ny liner lger text. INTRODUCTION The concepts
398 CHAPTER 11 ORTHOGONAL FUNCTIONS AND FOURIER SERIES 11.1 ORTHOGONAL FUNCTIONS REVIEW MATERIAL The notions of generlized vectors nd vector spces cn e found in ny liner lger text. INTRODUCTION The concepts
Conservation Law. Chapter Goal. 6.2 Theory
 Chpter 6 Conservtion Lw 6.1 Gol Our long term gol is to unerstn how mthemticl moels re erive. Here, we will stuy how certin quntity chnges with time in given region (sptil omin). We then first erive the
Chpter 6 Conservtion Lw 6.1 Gol Our long term gol is to unerstn how mthemticl moels re erive. Here, we will stuy how certin quntity chnges with time in given region (sptil omin). We then first erive the
Math Theory of Partial Differential Equations Lecture 2-9: Sturm-Liouville eigenvalue problems (continued).
 Mth 412-501 Theory of Prtil Differentil Equtions Lecture 2-9: Sturm-Liouville eigenvlue problems (continued). Regulr Sturm-Liouville eigenvlue problem: d ( p dφ ) + qφ + λσφ = 0 ( < x < b), dx dx β 1 φ()
Mth 412-501 Theory of Prtil Differentil Equtions Lecture 2-9: Sturm-Liouville eigenvlue problems (continued). Regulr Sturm-Liouville eigenvlue problem: d ( p dφ ) + qφ + λσφ = 0 ( < x < b), dx dx β 1 φ()
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS
 STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
Variational Techniques for Sturm-Liouville Eigenvalue Problems
 Vritionl Techniques for Sturm-Liouville Eigenvlue Problems Vlerie Cormni Deprtment of Mthemtics nd Sttistics University of Nebrsk, Lincoln Lincoln, NE 68588 Emil: vcormni@mth.unl.edu Rolf Ryhm Deprtment
Vritionl Techniques for Sturm-Liouville Eigenvlue Problems Vlerie Cormni Deprtment of Mthemtics nd Sttistics University of Nebrsk, Lincoln Lincoln, NE 68588 Emil: vcormni@mth.unl.edu Rolf Ryhm Deprtment
u t = k 2 u x 2 (1) a n sin nπx sin 2 L e k(nπ/l) t f(x) = sin nπx f(x) sin nπx dx (6) 2 L f(x 0 ) sin nπx 0 2 L sin nπx 0 nπx
 Chpter 9: Green s functions for time-independent problems Introductory emples One-dimensionl het eqution Consider the one-dimensionl het eqution with boundry conditions nd initil condition We lredy know
Chpter 9: Green s functions for time-independent problems Introductory emples One-dimensionl het eqution Consider the one-dimensionl het eqution with boundry conditions nd initil condition We lredy know
Introduction to Complex Variables Class Notes Instructor: Louis Block
 Introuction to omplex Vribles lss Notes Instructor: Louis Block Definition 1. (n remrk) We consier the complex plne consisting of ll z = (x, y) = x + iy, where x n y re rel. We write x = Rez (the rel prt
Introuction to omplex Vribles lss Notes Instructor: Louis Block Definition 1. (n remrk) We consier the complex plne consisting of ll z = (x, y) = x + iy, where x n y re rel. We write x = Rez (the rel prt
Homework Problem Set 1 Solutions
 Chemistry 460 Dr. Jen M. Stnr Homework Problem Set 1 Solutions 1. Determine the outcomes of operting the following opertors on the functions liste. In these functions, is constnt..) opertor: / ; function:
Chemistry 460 Dr. Jen M. Stnr Homework Problem Set 1 Solutions 1. Determine the outcomes of operting the following opertors on the functions liste. In these functions, is constnt..) opertor: / ; function:
AMS 212A Applied Mathematical Methods I Lecture 06 Copyright by Hongyun Wang, UCSC. ( ), v (that is, 1 ( ) L i
 AMS A Applied Mthemticl Methods I Lecture 6 Copyright y Hongyun Wng, UCSC Recp of Lecture 5 Clssifiction of oundry conditions Dirichlet eumnn Mixed Adjoint opertor, self-djoint opertor Sturm-Liouville
AMS A Applied Mthemticl Methods I Lecture 6 Copyright y Hongyun Wng, UCSC Recp of Lecture 5 Clssifiction of oundry conditions Dirichlet eumnn Mixed Adjoint opertor, self-djoint opertor Sturm-Liouville
STURM-LIOUVILLE THEORY, VARIATIONAL APPROACH
 STURM-LIOUVILLE THEORY, VARIATIONAL APPROACH XIAO-BIAO LIN. Qudrtic functionl nd the Euler-Jcobi Eqution The purpose of this note is to study the Sturm-Liouville problem. We use the vritionl problem s
STURM-LIOUVILLE THEORY, VARIATIONAL APPROACH XIAO-BIAO LIN. Qudrtic functionl nd the Euler-Jcobi Eqution The purpose of this note is to study the Sturm-Liouville problem. We use the vritionl problem s
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Section 6.1 INTRO to LAPLACE TRANSFORMS
 Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Best Approximation in the 2-norm
 Jim Lmbers MAT 77 Fll Semester 1-11 Lecture 1 Notes These notes correspond to Sections 9. nd 9.3 in the text. Best Approximtion in the -norm Suppose tht we wish to obtin function f n (x) tht is liner combintion
Jim Lmbers MAT 77 Fll Semester 1-11 Lecture 1 Notes These notes correspond to Sections 9. nd 9.3 in the text. Best Approximtion in the -norm Suppose tht we wish to obtin function f n (x) tht is liner combintion
Chapter 28. Fourier Series An Eigenvalue Problem.
 Chpter 28 Fourier Series Every time I close my eyes The noise inside me mplifies I cn t escpe I relive every moment of the dy Every misstep I hve mde Finds wy it cn invde My every thought And this is why
Chpter 28 Fourier Series Every time I close my eyes The noise inside me mplifies I cn t escpe I relive every moment of the dy Every misstep I hve mde Finds wy it cn invde My every thought And this is why
Linearity, linear operators, and self adjoint eigenvalue problems
 Linerity, liner opertors, nd self djoint eigenvlue problems 1 Elements of liner lgebr The study of liner prtil differentil equtions utilizes, unsurprisingly, mny concepts from liner lgebr nd liner ordinry
Linerity, liner opertors, nd self djoint eigenvlue problems 1 Elements of liner lgebr The study of liner prtil differentil equtions utilizes, unsurprisingly, mny concepts from liner lgebr nd liner ordinry
Problem Set 2 Solutions
 Chemistry 362 Dr. Jen M. Stnr Problem Set 2 Solutions 1. Determine the outcomes of operting the following opertors on the functions liste. In these functions, is constnt.).) opertor: /x ; function: x e
Chemistry 362 Dr. Jen M. Stnr Problem Set 2 Solutions 1. Determine the outcomes of operting the following opertors on the functions liste. In these functions, is constnt.).) opertor: /x ; function: x e
Fundamental Theorem of Calculus
 Fundmentl Theorem of Clculus Recll tht if f is nonnegtive nd continuous on [, ], then the re under its grph etween nd is the definite integrl A= f() d Now, for in the intervl [, ], let A() e the re under
Fundmentl Theorem of Clculus Recll tht if f is nonnegtive nd continuous on [, ], then the re under its grph etween nd is the definite integrl A= f() d Now, for in the intervl [, ], let A() e the re under
MATH 174A: PROBLEM SET 5. Suggested Solution
 MATH 174A: PROBLEM SET 5 Suggested Solution Problem 1. Suppose tht I [, b] is n intervl. Let f 1 b f() d for f C(I; R) (i.e. f is continuous rel-vlued function on I), nd let L 1 (I) denote the completion
MATH 174A: PROBLEM SET 5 Suggested Solution Problem 1. Suppose tht I [, b] is n intervl. Let f 1 b f() d for f C(I; R) (i.e. f is continuous rel-vlued function on I), nd let L 1 (I) denote the completion
ax bx c (2) x a x a x a 1! 2!! gives a useful way of approximating a function near to some specific point x a, giving a power-series expansion in x
 Elementr mthemticl epressions Qurtic equtions b b b The solutions to the generl qurtic eqution re (1) b c () b b 4c (3) Tlor n Mclurin series (power-series epnsion) The Tlor series n n f f f n 1!! n! f
Elementr mthemticl epressions Qurtic equtions b b b The solutions to the generl qurtic eqution re (1) b c () b b 4c (3) Tlor n Mclurin series (power-series epnsion) The Tlor series n n f f f n 1!! n! f
The area under the graph of f and above the x-axis between a and b is denoted by. f(x) dx. π O
 1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
g i fφdx dx = x i i=1 is a Hilbert space. We shall, henceforth, abuse notation and write g i f(x) = f
 1. Appliction of functionl nlysis to PEs 1.1. Introduction. In this section we give little introduction to prtil differentil equtions. In prticulr we consider the problem u(x) = f(x) x, u(x) = x (1) where
1. Appliction of functionl nlysis to PEs 1.1. Introduction. In this section we give little introduction to prtil differentil equtions. In prticulr we consider the problem u(x) = f(x) x, u(x) = x (1) where
Fourier Series in Complex notation. cos(x) = eix + e ix 2. A n cos + B n sin l. i 2 B n. e inx=l + A n + ib n 2 8. ( 0 m 6= n. C n = 1 2l.
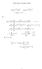 Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
REGULAR TWO-POINT BOUNDARY VALUE PROBLEMS
 REGUAR TWO-POINT BOUNDARY VAUE PROBEMS PHIIP WWAKER Supposethtndrerelnumerswith
REGUAR TWO-POINT BOUNDARY VAUE PROBEMS PHIIP WWAKER Supposethtndrerelnumerswith
M344 - ADVANCED ENGINEERING MATHEMATICS
 M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
c n φ n (x), 0 < x < L, (1) n=1
 SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
APPENDIX. Precalculus Review D.1. Real Numbers and the Real Number Line
 APPENDIX D Preclculus Review APPENDIX D.1 Rel Numers n the Rel Numer Line Rel Numers n the Rel Numer Line Orer n Inequlities Asolute Vlue n Distnce Rel Numers n the Rel Numer Line Rel numers cn e represente
APPENDIX D Preclculus Review APPENDIX D.1 Rel Numers n the Rel Numer Line Rel Numers n the Rel Numer Line Orer n Inequlities Asolute Vlue n Distnce Rel Numers n the Rel Numer Line Rel numers cn e represente
If we have a function f(x) which is well-defined for some a x b, its integral over those two values is defined as
 Y. D. Chong (26) MH28: Complex Methos for the Sciences 2. Integrls If we hve function f(x) which is well-efine for some x, its integrl over those two vlues is efine s N ( ) f(x) = lim x f(x n ) where x
Y. D. Chong (26) MH28: Complex Methos for the Sciences 2. Integrls If we hve function f(x) which is well-efine for some x, its integrl over those two vlues is efine s N ( ) f(x) = lim x f(x n ) where x
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
MATH1050 Cauchy-Schwarz Inequality and Triangle Inequality
 MATH050 Cuchy-Schwrz Inequlity nd Tringle Inequlity 0 Refer to the Hndout Qudrtic polynomils Definition (Asolute extrem for rel-vlued functions of one rel vrile) Let I e n intervl, nd h : D R e rel-vlued
MATH050 Cuchy-Schwrz Inequlity nd Tringle Inequlity 0 Refer to the Hndout Qudrtic polynomils Definition (Asolute extrem for rel-vlued functions of one rel vrile) Let I e n intervl, nd h : D R e rel-vlued
Math 520 Final Exam Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008
 Mth 520 Finl Exm Topic Outline Sections 1 3 (Xio/Dums/Liw) Spring 2008 The finl exm will be held on Tuesdy, My 13, 2-5pm in 117 McMilln Wht will be covered The finl exm will cover the mteril from ll of
Mth 520 Finl Exm Topic Outline Sections 1 3 (Xio/Dums/Liw) Spring 2008 The finl exm will be held on Tuesdy, My 13, 2-5pm in 117 McMilln Wht will be covered The finl exm will cover the mteril from ll of
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
lim P(t a,b) = Differentiate (1) and use the definition of the probability current, j = i (
 PHYS851 Quntum Mechnics I, Fll 2009 HOMEWORK ASSIGNMENT 7 1. The continuity eqution: The probbility tht prticle of mss m lies on the intervl [,b] t time t is Pt,b b x ψx,t 2 1 Differentite 1 n use the
PHYS851 Quntum Mechnics I, Fll 2009 HOMEWORK ASSIGNMENT 7 1. The continuity eqution: The probbility tht prticle of mss m lies on the intervl [,b] t time t is Pt,b b x ψx,t 2 1 Differentite 1 n use the
Chapter 6 Techniques of Integration
 MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
(4.1) D r v(t) ω(t, v(t))
 1.4. Differentil inequlities. Let D r denote the right hnd derivtive of function. If ω(t, u) is sclr function of the sclrs t, u in some open connected set Ω, we sy tht function v(t), t < b, is solution
1.4. Differentil inequlities. Let D r denote the right hnd derivtive of function. If ω(t, u) is sclr function of the sclrs t, u in some open connected set Ω, we sy tht function v(t), t < b, is solution
dx dt dy = G(t, x, y), dt where the functions are defined on I Ω, and are locally Lipschitz w.r.t. variable (x, y) Ω.
 Chpter 8 Stility theory We discuss properties of solutions of first order two dimensionl system, nd stility theory for specil clss of liner systems. We denote the independent vrile y t in plce of x, nd
Chpter 8 Stility theory We discuss properties of solutions of first order two dimensionl system, nd stility theory for specil clss of liner systems. We denote the independent vrile y t in plce of x, nd
5.4, 6.1, 6.2 Handout. As we ve discussed, the integral is in some way the opposite of taking a derivative. The exact relationship
 5.4, 6.1, 6.2 Hnout As we ve iscusse, the integrl is in some wy the opposite of tking erivtive. The exct reltionship is given by the Funmentl Theorem of Clculus: The Funmentl Theorem of Clculus: If f is
5.4, 6.1, 6.2 Hnout As we ve iscusse, the integrl is in some wy the opposite of tking erivtive. The exct reltionship is given by the Funmentl Theorem of Clculus: The Funmentl Theorem of Clculus: If f is
Coalgebra, Lecture 15: Equations for Deterministic Automata
 Colger, Lecture 15: Equtions for Deterministic Automt Julin Slmnc (nd Jurrin Rot) Decemer 19, 2016 In this lecture, we will study the concept of equtions for deterministic utomt. The notes re self contined
Colger, Lecture 15: Equtions for Deterministic Automt Julin Slmnc (nd Jurrin Rot) Decemer 19, 2016 In this lecture, we will study the concept of equtions for deterministic utomt. The notes re self contined
STURM-LIOUVILLE PROBLEMS
 STURM-LIOUVILLE PROBLEMS Mrch 8, 24 We hve seen tht in the process of solving certin liner evolution equtions such s the het or wve equtions we re led in very nturl wy to n eigenvlue problem for second
STURM-LIOUVILLE PROBLEMS Mrch 8, 24 We hve seen tht in the process of solving certin liner evolution equtions such s the het or wve equtions we re led in very nturl wy to n eigenvlue problem for second
x dx does exist, what does the answer look like? What does the answer to
 Review Guie or MAT Finl Em Prt II. Mony Decemer th 8:.m. 9:5.m. (or the 8:3.m. clss) :.m. :5.m. (or the :3.m. clss) Prt is worth 5% o your Finl Em gre. NO CALCULATORS re llowe on this portion o the Finl
Review Guie or MAT Finl Em Prt II. Mony Decemer th 8:.m. 9:5.m. (or the 8:3.m. clss) :.m. :5.m. (or the :3.m. clss) Prt is worth 5% o your Finl Em gre. NO CALCULATORS re llowe on this portion o the Finl
The practical version
 Roerto s Notes on Integrl Clculus Chpter 4: Definite integrls nd the FTC Section 7 The Fundmentl Theorem of Clculus: The prcticl version Wht you need to know lredy: The theoreticl version of the FTC. Wht
Roerto s Notes on Integrl Clculus Chpter 4: Definite integrls nd the FTC Section 7 The Fundmentl Theorem of Clculus: The prcticl version Wht you need to know lredy: The theoreticl version of the FTC. Wht
1 The Riemann Integral
 The Riemnn Integrl. An exmple leding to the notion of integrl (res) We know how to find (i.e. define) the re of rectngle (bse height), tringle ( (sum of res of tringles). But how do we find/define n re
The Riemnn Integrl. An exmple leding to the notion of integrl (res) We know how to find (i.e. define) the re of rectngle (bse height), tringle ( (sum of res of tringles). But how do we find/define n re
f a L Most reasonable functions are continuous, as seen in the following theorem:
 Limits Suppose f : R R. To sy lim f(x) = L x mens tht s x gets closer n closer to, then f(x) gets closer n closer to L. This suggests tht the grph of f looks like one of the following three pictures: f
Limits Suppose f : R R. To sy lim f(x) = L x mens tht s x gets closer n closer to, then f(x) gets closer n closer to L. This suggests tht the grph of f looks like one of the following three pictures: f
Sturm-Liouville Eigenvalue problem: Let p(x) > 0, q(x) 0, r(x) 0 in I = (a, b). Here we assume b > a. Let X C 2 1
 Ch.4. INTEGRAL EQUATIONS AND GREEN S FUNCTIONS Ronld B Guenther nd John W Lee, Prtil Differentil Equtions of Mthemticl Physics nd Integrl Equtions. Hildebrnd, Methods of Applied Mthemtics, second edition
Ch.4. INTEGRAL EQUATIONS AND GREEN S FUNCTIONS Ronld B Guenther nd John W Lee, Prtil Differentil Equtions of Mthemticl Physics nd Integrl Equtions. Hildebrnd, Methods of Applied Mthemtics, second edition
Abstract inner product spaces
 WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
LINEAR ALGEBRA APPLIED
 5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
Lecture 2e Orthogonal Complement (pages )
 Lecture 2e Orthogonl Complement (pges -) We hve now seen tht n orthonorml sis is nice wy to descrie suspce, ut knowing tht we wnt n orthonorml sis doesn t mke one fll into our lp. In theory, the process
Lecture 2e Orthogonl Complement (pges -) We hve now seen tht n orthonorml sis is nice wy to descrie suspce, ut knowing tht we wnt n orthonorml sis doesn t mke one fll into our lp. In theory, the process
Hilbert Spaces. Chapter Inner product spaces
 Chpter 4 Hilbert Spces 4.1 Inner product spces In the following we will discuss both complex nd rel vector spces. With L denoting either R or C we recll tht vector spce over L is set E equipped with ddition,
Chpter 4 Hilbert Spces 4.1 Inner product spces In the following we will discuss both complex nd rel vector spces. With L denoting either R or C we recll tht vector spce over L is set E equipped with ddition,
Introduction and Review
 Chpter 6A Notes Pge of Introuction n Review Derivtives y = f(x) y x = f (x) Evlute erivtive t x = : y = x x= f f(+h) f() () = lim h h Geometric Interprettion: see figure slope of the line tngent to f t
Chpter 6A Notes Pge of Introuction n Review Derivtives y = f(x) y x = f (x) Evlute erivtive t x = : y = x x= f f(+h) f() () = lim h h Geometric Interprettion: see figure slope of the line tngent to f t
(9) P (x)u + Q(x)u + R(x)u =0
 STURM-LIOUVILLE THEORY 7 2. Second order liner ordinry differentil equtions 2.1. Recll some sic results. A second order liner ordinry differentil eqution (ODE) hs the form (9) P (x)u + Q(x)u + R(x)u =0
STURM-LIOUVILLE THEORY 7 2. Second order liner ordinry differentil equtions 2.1. Recll some sic results. A second order liner ordinry differentil eqution (ODE) hs the form (9) P (x)u + Q(x)u + R(x)u =0
Functional Analysis I Solutions to Exercises. James C. Robinson
 Functionl Anlysis I Solutions to Exercises Jmes C. Robinson Contents 1 Exmples I pge 1 2 Exmples II 5 3 Exmples III 9 4 Exmples IV 15 iii 1 Exmples I 1. Suppose tht v α j e j nd v m β k f k. with α j,
Functionl Anlysis I Solutions to Exercises Jmes C. Robinson Contents 1 Exmples I pge 1 2 Exmples II 5 3 Exmples III 9 4 Exmples IV 15 iii 1 Exmples I 1. Suppose tht v α j e j nd v m β k f k. with α j,
Partial Differential Equations
 Prtil Differentil Equtions Notes by Robert Piché, Tmpere University of Technology reen s Functions. reen s Function for One-Dimensionl Eqution The reen s function provides complete solution to boundry
Prtil Differentil Equtions Notes by Robert Piché, Tmpere University of Technology reen s Functions. reen s Function for One-Dimensionl Eqution The reen s function provides complete solution to boundry
Quadratic Forms. Quadratic Forms
 Qudrtic Forms Recll the Simon & Blume excerpt from n erlier lecture which sid tht the min tsk of clculus is to pproximte nonliner functions with liner functions. It s ctully more ccurte to sy tht we pproximte
Qudrtic Forms Recll the Simon & Blume excerpt from n erlier lecture which sid tht the min tsk of clculus is to pproximte nonliner functions with liner functions. It s ctully more ccurte to sy tht we pproximte
( x) ( ) takes at the right end of each interval to approximate its value on that
 III. INTEGRATION Economists seem much more intereste in mrginl effects n ifferentition thn in integrtion. Integrtion is importnt for fining the expecte vlue n vrince of rnom vriles, which is use in econometrics
III. INTEGRATION Economists seem much more intereste in mrginl effects n ifferentition thn in integrtion. Integrtion is importnt for fining the expecte vlue n vrince of rnom vriles, which is use in econometrics
Chapter 8: Methods of Integration
 Chpter 8: Methods of Integrtion Bsic Integrls 8. Note: We hve the following list of Bsic Integrls p p+ + c, for p sec tn + c p + ln + c sec tn sec + c e e + c tn ln sec + c ln + c sec ln sec + tn + c ln
Chpter 8: Methods of Integrtion Bsic Integrls 8. Note: We hve the following list of Bsic Integrls p p+ + c, for p sec tn + c p + ln + c sec tn sec + c e e + c tn ln sec + c ln + c sec ln sec + tn + c ln
1 E3102: a study guide and review, Version 1.0
 1 E3102: study guide nd review, Version 1.0 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in very
1 E3102: study guide nd review, Version 1.0 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in very
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
 Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrals. The First Fundamental Theorem of Calculus, as we ve discussed in class, goes as follows:
 Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
September 13 Homework Solutions
 College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
Wave Equation on a Two Dimensional Rectangle
 Wve Eqution on Two Dimensionl Rectngle In these notes we re concerned with ppliction of the method of seprtion of vriles pplied to the wve eqution in two dimensionl rectngle. Thus we consider u tt = c
Wve Eqution on Two Dimensionl Rectngle In these notes we re concerned with ppliction of the method of seprtion of vriles pplied to the wve eqution in two dimensionl rectngle. Thus we consider u tt = c
Best Approximation. Chapter The General Case
 Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Section 3.2 Maximum Principle and Uniqueness
 Section 3. Mximum Principle nd Uniqueness Let u (x; y) e smooth solution in. Then the mximum vlue exists nd is nite. (x ; y ) ; i.e., M mx fu (x; y) j (x; y) in g Furthermore, this vlue cn e otined y point
Section 3. Mximum Principle nd Uniqueness Let u (x; y) e smooth solution in. Then the mximum vlue exists nd is nite. (x ; y ) ; i.e., M mx fu (x; y) j (x; y) in g Furthermore, this vlue cn e otined y point
Matrices, Moments and Quadrature, cont d
 Jim Lmbers MAT 285 Summer Session 2015-16 Lecture 2 Notes Mtrices, Moments nd Qudrture, cont d We hve described how Jcobi mtrices cn be used to compute nodes nd weights for Gussin qudrture rules for generl
Jim Lmbers MAT 285 Summer Session 2015-16 Lecture 2 Notes Mtrices, Moments nd Qudrture, cont d We hve described how Jcobi mtrices cn be used to compute nodes nd weights for Gussin qudrture rules for generl
Lecture Solution of a System of Linear Equation
 ChE Lecture Notes, Dept. of Chemicl Engineering, Univ. of TN, Knoville - D. Keffer, 5/9/98 (updted /) Lecture 8- - Solution of System of Liner Eqution 8. Why is it importnt to e le to solve system of liner
ChE Lecture Notes, Dept. of Chemicl Engineering, Univ. of TN, Knoville - D. Keffer, 5/9/98 (updted /) Lecture 8- - Solution of System of Liner Eqution 8. Why is it importnt to e le to solve system of liner
The Evaluation Theorem
 These notes closely follow the presenttion of the mteril given in Jmes Stewrt s textook Clculus, Concepts nd Contexts (2nd edition) These notes re intended primrily for in-clss presenttion nd should not
These notes closely follow the presenttion of the mteril given in Jmes Stewrt s textook Clculus, Concepts nd Contexts (2nd edition) These notes re intended primrily for in-clss presenttion nd should not
Practice Problems Solution
 Prctice Problems Solution Problem Consier D Simple Hrmonic Oscilltor escribe by the Hmiltonin Ĥ ˆp m + mwˆx Recll the rte of chnge of the expecttion of quntum mechnicl opertor t A ī A, H] + h A t. Let
Prctice Problems Solution Problem Consier D Simple Hrmonic Oscilltor escribe by the Hmiltonin Ĥ ˆp m + mwˆx Recll the rte of chnge of the expecttion of quntum mechnicl opertor t A ī A, H] + h A t. Let
Construction of Gauss Quadrature Rules
 Jim Lmbers MAT 772 Fll Semester 2010-11 Lecture 15 Notes These notes correspond to Sections 10.2 nd 10.3 in the text. Construction of Guss Qudrture Rules Previously, we lerned tht Newton-Cotes qudrture
Jim Lmbers MAT 772 Fll Semester 2010-11 Lecture 15 Notes These notes correspond to Sections 10.2 nd 10.3 in the text. Construction of Guss Qudrture Rules Previously, we lerned tht Newton-Cotes qudrture
1 1D heat and wave equations on a finite interval
 1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
Math Lecture 23
 Mth 8 - Lecture 3 Dyln Zwick Fll 3 In our lst lecture we delt with solutions to the system: x = Ax where A is n n n mtrix with n distinct eigenvlues. As promised, tody we will del with the question of
Mth 8 - Lecture 3 Dyln Zwick Fll 3 In our lst lecture we delt with solutions to the system: x = Ax where A is n n n mtrix with n distinct eigenvlues. As promised, tody we will del with the question of
1 2-D Second Order Equations: Separation of Variables
 Chpter 12 PDEs in Rectngles 1 2-D Second Order Equtions: Seprtion of Vribles 1. A second order liner prtil differentil eqution in two vribles x nd y is A 2 u x + B 2 u 2 x y + C 2 u y + D u 2 x + E u +
Chpter 12 PDEs in Rectngles 1 2-D Second Order Equtions: Seprtion of Vribles 1. A second order liner prtil differentil eqution in two vribles x nd y is A 2 u x + B 2 u 2 x y + C 2 u y + D u 2 x + E u +
Summary: Method of Separation of Variables
 Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Example Sheet 2 Solutions
 Exmple Sheet Solutions. i L f, g f, L g efinition of joint L g, f property of inner prouct g, Lf efinition of joint Lf, g property of inner prouct ii L L f, g Lf, g L f, g liner opertor property f, L g
Exmple Sheet Solutions. i L f, g f, L g efinition of joint L g, f property of inner prouct g, Lf efinition of joint Lf, g property of inner prouct ii L L f, g Lf, g L f, g liner opertor property f, L g
f(x)dx . Show that there 1, 0 < x 1 does not exist a differentiable function g : [ 1, 1] R such that g (x) = f(x) for all
![f(x)dx . Show that there 1, 0 < x 1 does not exist a differentiable function g : [ 1, 1] R such that g (x) = f(x) for all f(x)dx . Show that there 1, 0 < x 1 does not exist a differentiable function g : [ 1, 1] R such that g (x) = f(x) for all](/thumbs/94/119531908.jpg) 3 Definite Integrl 3.1 Introduction In school one comes cross the definition of the integrl of rel vlued function defined on closed nd bounded intervl [, b] between the limits nd b, i.e., f(x)dx s the
3 Definite Integrl 3.1 Introduction In school one comes cross the definition of the integrl of rel vlued function defined on closed nd bounded intervl [, b] between the limits nd b, i.e., f(x)dx s the
Inner-product spaces
 Inner-product spces Definition: Let V be rel or complex liner spce over F (here R or C). An inner product is n opertion between two elements of V which results in sclr. It is denoted by u, v nd stisfies:
Inner-product spces Definition: Let V be rel or complex liner spce over F (here R or C). An inner product is n opertion between two elements of V which results in sclr. It is denoted by u, v nd stisfies:
W. We shall do so one by one, starting with I 1, and we shall do it greedily, trying
 Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Matrix & Vector Basic Linear Algebra & Calculus
 Mtrix & Vector Bsic Liner lgebr & lculus Wht is mtrix? rectngulr rry of numbers (we will concentrte on rel numbers). nxm mtrix hs n rows n m columns M x4 M M M M M M M M M M M M 4 4 4 First row Secon row
Mtrix & Vector Bsic Liner lgebr & lculus Wht is mtrix? rectngulr rry of numbers (we will concentrte on rel numbers). nxm mtrix hs n rows n m columns M x4 M M M M M M M M M M M M 4 4 4 First row Secon row
Applied Partial Differential Equations with Fourier Series and Boundary Value Problems 5th Edition Richard Haberman
 Applied Prtil Differentil Equtions with Fourier Series nd Boundry Vlue Problems 5th Edition Richrd Hbermn Person Eduction Limited Edinburgh Gte Hrlow Essex CM20 2JE Englnd nd Associted Compnies throughout
Applied Prtil Differentil Equtions with Fourier Series nd Boundry Vlue Problems 5th Edition Richrd Hbermn Person Eduction Limited Edinburgh Gte Hrlow Essex CM20 2JE Englnd nd Associted Compnies throughout
k and v = v 1 j + u 3 i + v 2
 ORTHOGONAL FUNCTIONS AND FOURIER SERIES Orthogonl functions A function cn e considered to e generliztion of vector. Thus the vector concets like the inner roduct nd orthogonlity of vectors cn e extended
ORTHOGONAL FUNCTIONS AND FOURIER SERIES Orthogonl functions A function cn e considered to e generliztion of vector. Thus the vector concets like the inner roduct nd orthogonlity of vectors cn e extended
The Dirichlet Problem in a Two Dimensional Rectangle. Section 13.5
 The Dirichlet Prolem in Two Dimensionl Rectngle Section 13.5 1 Dirichlet Prolem in Rectngle In these notes we will pply the method of seprtion of vriles to otin solutions to elliptic prolems in rectngle
The Dirichlet Prolem in Two Dimensionl Rectngle Section 13.5 1 Dirichlet Prolem in Rectngle In these notes we will pply the method of seprtion of vriles to otin solutions to elliptic prolems in rectngle
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS.
 THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
Things to Memorize: A Partial List. January 27, 2017
 Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
38 Riemann sums and existence of the definite integral.
 38 Riemnn sums nd existence of the definite integrl. In the clcultion of the re of the region X bounded by the grph of g(x) = x 2, the x-xis nd 0 x b, two sums ppered: ( n (k 1) 2) b 3 n 3 re(x) ( n These
38 Riemnn sums nd existence of the definite integrl. In the clcultion of the re of the region X bounded by the grph of g(x) = x 2, the x-xis nd 0 x b, two sums ppered: ( n (k 1) 2) b 3 n 3 re(x) ( n These
Linear Systems with Constant Coefficients
 Liner Systems with Constnt Coefficients 4-3-05 Here is system of n differentil equtions in n unknowns: x x + + n x n, x x + + n x n, x n n x + + nn x n This is constnt coefficient liner homogeneous system
Liner Systems with Constnt Coefficients 4-3-05 Here is system of n differentil equtions in n unknowns: x x + + n x n, x x + + n x n, x n n x + + nn x n This is constnt coefficient liner homogeneous system
Stuff You Need to Know From Calculus
 Stuff You Need to Know From Clculus For the first time in the semester, the stuff we re doing is finlly going to look like clculus (with vector slnt, of course). This mens tht in order to succeed, you
Stuff You Need to Know From Clculus For the first time in the semester, the stuff we re doing is finlly going to look like clculus (with vector slnt, of course). This mens tht in order to succeed, you
ODE: Existence and Uniqueness of a Solution
 Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Chapter 3 Polynomials
 Dr M DRAIEF As described in the introduction of Chpter 1, pplictions of solving liner equtions rise in number of different settings In prticulr, we will in this chpter focus on the problem of modelling
Dr M DRAIEF As described in the introduction of Chpter 1, pplictions of solving liner equtions rise in number of different settings In prticulr, we will in this chpter focus on the problem of modelling
Chapter 5. , r = r 1 r 2 (1) µ = m 1 m 2. r, r 2 = R µ m 2. R(m 1 + m 2 ) + m 2 r = r 1. m 2. r = r 1. R + µ m 1
 Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
SUPPLEMENTARY NOTES ON THE CONNECTION FORMULAE FOR THE SEMICLASSICAL APPROXIMATION
 Physics 8.06 Apr, 2008 SUPPLEMENTARY NOTES ON THE CONNECTION FORMULAE FOR THE SEMICLASSICAL APPROXIMATION c R. L. Jffe 2002 The WKB connection formuls llow one to continue semiclssicl solutions from n
Physics 8.06 Apr, 2008 SUPPLEMENTARY NOTES ON THE CONNECTION FORMULAE FOR THE SEMICLASSICAL APPROXIMATION c R. L. Jffe 2002 The WKB connection formuls llow one to continue semiclssicl solutions from n
The solutions of the single electron Hamiltonian were shown to be Bloch wave of the form: ( ) ( ) ikr
 Lecture #1 Progrm 1. Bloch solutions. Reciprocl spce 3. Alternte derivtion of Bloch s theorem 4. Trnsforming the serch for egenfunctions nd eigenvlues from solving PDE to finding the e-vectors nd e-vlues
Lecture #1 Progrm 1. Bloch solutions. Reciprocl spce 3. Alternte derivtion of Bloch s theorem 4. Trnsforming the serch for egenfunctions nd eigenvlues from solving PDE to finding the e-vectors nd e-vlues
Matrix Eigenvalues and Eigenvectors September 13, 2017
 Mtri Eigenvlues nd Eigenvectors September, 7 Mtri Eigenvlues nd Eigenvectors Lrry Cretto Mechnicl Engineering 5A Seminr in Engineering Anlysis September, 7 Outline Review lst lecture Definition of eigenvlues
Mtri Eigenvlues nd Eigenvectors September, 7 Mtri Eigenvlues nd Eigenvectors Lrry Cretto Mechnicl Engineering 5A Seminr in Engineering Anlysis September, 7 Outline Review lst lecture Definition of eigenvlues
1. Review. t 2. t 1. v w = vw cos( ) where is the angle between v and w. The above leads to the Schwarz inequality: v w vw.
 1. Review 1.1. The Geometry of Curves. AprmetriccurveinR 3 is mp R R 3 t (t) = (x(t),y(t),z(t)). We sy tht is di erentile if x, y, z re di erentile. We sy tht it is C 1 if, in ddition, the derivtives re
1. Review 1.1. The Geometry of Curves. AprmetriccurveinR 3 is mp R R 3 t (t) = (x(t),y(t),z(t)). We sy tht is di erentile if x, y, z re di erentile. We sy tht it is C 1 if, in ddition, the derivtives re
Math 61CM - Solutions to homework 9
 Mth 61CM - Solutions to homework 9 Cédric De Groote November 30 th, 2018 Problem 1: Recll tht the left limit of function f t point c is defined s follows: lim f(x) = l x c if for ny > 0 there exists δ
Mth 61CM - Solutions to homework 9 Cédric De Groote November 30 th, 2018 Problem 1: Recll tht the left limit of function f t point c is defined s follows: lim f(x) = l x c if for ny > 0 there exists δ
