From EBNF to PEG. Roman R. Redziejowski
|
|
|
- Buddy Matthews
- 6 years ago
- Views:
Transcription
1 From EBNF to PEG Roman R. Redziejowski Abstract Parsing Expression Grammar (PEG) encodes a recursive-descent parser with limited backtracking. The parser has many useful properties, and with the use of memoization, it works in a linear time. In its appearance, PEG is almost identical to a grammar in Extended Backus-Naur Form (EBNF), but usually defines a different language. However, in some cases only minor typographical changes are sufficient to convert an EBNF grammar into its PEG parser. As recently shown by Medeiros, this is, in particular, true for LL(1) grammars. But this is also true for many non-ll(1) grammars, which is interesting because the backtracking of PEG is often a convenient way to circumvent just the LL(1) restriction. We formulate a number of conditions for EBNF grammar to become its own PEG parser, and arrive at a condition that we call LL(1p), meaning that a top-down parser can choose its next action by looking at the input within the reach of one parsing procedure (rather than by looking at the next letter). An extension to LL(kp) for k > 1 seems possible. 1 Introduction Parsing Expression Grammar (PEG), as introduced by Ford in [4], is a recursive-descent parser with limited backtracking, written in a special language. Using the memoization or packrat technology described in [2, 3], it works in linear time. The parser does not require a separate lexer to preprocess the input, and the limited backtracking lifts the LL(1) restriction usually imposed by top-down parsers. These properties are useful in many applications. However, PEG is not well understood as a language specification tool. In [7], the author tried to find the language defined by a given parsing expression. Unfortunately, it was only possible to obtain some approximations that became more and more difficult as the complexity of the expression increased. In [5], Medeiros used the opposite approach: given language, construct a PEG parser for it. He constructed PEGs for languages defined by regular expressions, as well as right-linear, LL(1) and LL(k) context-free grammars. The construction for LL(1) grammars is very simple: just replace the unordered choice by the ordered choice /. Unfortunately, this is not of much use when we employ PEG just in order to circumvent the LL(1) restriction. But it turns out that this property is not limited to LL(1) grammars. As an example, take the following EBNF grammar: Literal = Hex Bin Hex = [0-9a-f] + "X" Bin = [01] + "B" This grammar is not LL(1), and not even LL(k) for any k: both Hex and Bin may start with any number of zeros and ones. A classical top-down parser constructed from this grammar cannot choose between the two alternatives of Literal by looking at any predefined number of characters ahead. But, treated as PEG with " " denoting the ordered choice, this grammar recognizes exactly the language defined by its EBNF interpretation. Presented with input such as 1010B, Literal calls Hex that consumes 1010, fails to recognize "X", and backtracks. Literal proceeds then to try Bin and succeeds. In the following, we attempt to answer this question: given an EBNF grammar, when can we transcribe it directly into a PEG that recognizes the same language, and parses it in the same way? To find the answer we introduce, in Section 3, a simple grammar that can be interpreted as either EBNF or PEG. Following [5], we formally define these interpretations using the method of natural semantics. Final version appeared in Fundamenta Informaticae 128, 1-2 (2013)
2 The grammar is reduced to bare bones in order to simplify the reasoning. Any full EBNF grammar or PEG without predicates can be reduced to such form by removing syntactic sugar and introducing new nonterminals. By reversing this process, one can apply our results to a full grammar. In Section 4, we identify a sufficient (but not necessary!) condition for the two interpretations to be equivalent, in the sense of accepting the same input and producing the same parse trees. This condition happens to coincide with the general semi disjointness introduced by Schmitz in [8]. Unfortunately, it is difficult (if not impossible) to check this condition in a mechanical way. After some preliminaries in Section 5, we use, in Section 6, our result to formulate two stronger conditions based on prefixes, and in Section 7, a condition using first expressions. This leads in Section 8 to the notion of LL(1p) grammars. Unfortunately, all these conditions are not as simple to verify as LL(1). In the final Section 9 we discuss further development, and indicate the possibility of using our results to insert the cut operation introduced by Mizushima et al. in [6]. All lengthy proofs are found in the Appendix. 2 Some Notation We consider a finite alphabet Σ of letters. A finite string of letters is a word. The string of 0 letters is called the empty word and is denoted by ε. The set of all words is Σ. A subset of Σ is a language. As usual, we write XY to mean the concatenation of languages X and Y, that is, the set of all words xy where x X and y Y. For x, y Σ, x is a prefix of y if y = xu for some u Σ. We write x y to mean that x is a prefix of y. For X Σ, the set of all prefixes of x X is denoted by Pref(X). A relation R on E is a subset of E E. As usual, we write R(e) to mean the set of all e such that (e, e ) R, and R(E) to mean the union of R(e) for all e E E. The transitive closure of R is denoted by R +, and the product of relations R and S by R S. 3 The Grammar We consider a grammar G over the alphabet Σ that will be interpreted as either PEG or EBNF. The grammar consists of a finite nonempty set N of symbols distinct from the letters of Σ, and a set of rules, one for each symbol of N. The rule for A N has one of these two forms: A = e 1 e 2, A = e 1 e 2, where each of e 1, e 2 is an element of N, or a letter from Σ, or the symbol ε. (The boldface ε here is a special symbol, to be distinguished from the empty word ε.) We define E = N Σ {ε}. We read the rule A = e (where e is either e 1 e 2 or e 1 e 2 ) as saying A is the name of expression e. The grammar is referred to as ε-free if none of the rules contains ε. When G is interpreted as EBNF, the rule A = e is a definition sometimes written as A ::= e, and e 1 e 2 is the unordered choice. When G is interpreted as PEG, the rule is a definition of parsing expression, written as A e in [4], and e 1 e 2 is the ordered choice. In each case, the elements of Σ are the terminals of the grammar, and the elements of N are the nonterminals. 3.1 The EBNF Interpretation The grammar G interpreted as EBNF is a mechanism for generating words: ε generates ε. a Σ generates itself. A = e 1 e 2 generates any word generated by e 1 followed by any word generated by e 2. A = e 1 e 2 generates any word generated by e 1 or e 2. The language L(e) of e E is the set of all words that can be generated by e. Following [5], we use the method of natural semantics for an alternative definition of L(e): we introduce a relation BNF (E Σ ) Σ, writing [e] w BNF y to mean that the relation holds for e E 2
3 and w, y Σ. The intended meaning of [e] w BNF y is that w has a prefix belonging to L(e). Formally, the relation is defined to hold if and only if this can be proved using the inference rules in Figure 1. An example of such proof is shown in Figure 2. [ε] x BNF x (empty.b) [a] ax BNF x A = e 1 e 2 A = e 1 e 2 [e 1 ] xyz BNF yz [A] xyz BNF z [e 1 ] xy BNF y [A] xy BNF y [e 2 ] yz BNF z (choice.b1) (letter.b) (seq.b) A = e 1 e 2 [e 2 ] xy BNF y [A] xy BNF y (choice.b2) Figure 1: EBNF semantics One can verify by structural induction that, indeed, for any y Σ, we have [e] xy BNF y if and only if x L(e). This gives, in particular, L(e) = {x Σ : [e] x BNF ε}. We note that the proof tree of [e] x BNF ε, when followed from the bottom up, mimics the behavior of a recursive-descent parser accepting the string x by always choosing the correct alternative of e 1 e 2. The proof tree is thus isomorphic to the parse tree of x: a tree showing how x was generated according to the rules of G. S = ax [a] ab BNF b [S] ab BNF ε X = S b [b] b BNF ε [X] b BNF ε Figure 2: An example of proof using EBNF semantics for grammar S = ax, X = S b As it will be seen later on, some results depend on whether ε L(e) for given e E. This can be decided using a simple iterative algorithm, independent of the above formal definition. Obviously, ε / L(e) for all e if the grammar is ε-free. 3.2 The PEG Interpretation When the grammar G is interpreted as PEG, the elements of E are parsing procedures that can call each other recursively. In general, parsing procedure is applied to a word from Σ and tries to recognize an initial portion of that word. If it succeeds, it consumes the recognized portion and returns success ; otherwise, it returns failure and does not consume anything. The action of different procedures is as follows: ε: Indicate success without consuming any input. a Σ: If the text ahead starts with a, consume it and return success. Otherwise return failure. A = e 1 e 2 : Call e 1. If it succeeded, call e 2 and return success if e 2 succeeded. If e 1 or e 2 failed, backtrack: reset the input as it was before the invocation of e 1 and return failure. A = e 1 e 2 : Call e 1. Return success if it succeeded. Otherwise call expression e 2 and return success if e 2 succeeded or failure if it failed. Note the limited backtracking: A = e 1 e 2 has never a chance to try e 2 once e 1 succeeded. Following [5], we use natural semantic to formally define the action of a parsing procedure: we introduce a relation PEG (E Σ ) {Σ fail} and write [e] w PEG X to mean that the relation holds for e E, w Σ, and X {Σ fail}. The intended meaning of [e] w PEG X is: [e] xy PEG y means: e applied to input xy consumes x and returns success, [e] x PEG fail means: e applied to input x returns failure. 3
4 Formally, the relation is defined to hold if and only if this can be proved using the inference rules in Figure 3. One can easily see that the rules correctly represent the action of parsing procedures in the intended way. For example, seq.p1 with Z = fail represents backtracking in A = e 1 e 2, and choice.p2 represents A = e 1 e 2 calling e 2 after e 1 failed. The proof tree of [e] x PEG X, when followed from bottom up, mimics procedure calls in the process of parsing the string x. The proof tree of [e] xy PEG y represents a successful parse of xy, and can be regarded as the parse tree of x. [ε] x PEG x (empty.p) [a] ax PEG x (letter.p1) b a [b] ax PEG fail A = e 1 e 2 A = e 1 e 2 [e 1 ] xyz PEG yz [A] xyz PEG Z [e 1 ] xy PEG y [A] xy PEG y [e 2 ] yz PEG Z (choice.p1) (letter.p2) (seq.p1) A = e 1 e 2 A = e 1 e 2 [e 1 ] x PEG fail [a] ε PEG fail [e 1 ] x PEG fail [A] x PEG fail [A] xy PEG Y where Y denotes y or fail and Z denotes z or fail. Figure 3: EBNF semantics (letter.p3) [e 2 ] xy PEG Y (seq.p2) (choice.p2) 4 When Are the Two Interpretations Equivalent? The following has been proved as Lemma in [5]: Proposition 1. For any e E and x, y Σ, [e] xy PEG y implies [e] xy BNF y. (Proof is found in the Appendix.) Known examples show that the reverse is, in general, not true. One case is when applying procedure e to a string x results in an infinite descent of recursive calls, so that the process never terminates. In this case, there is no proof of [e] x PEG X. To analyze this situation, we need the relation first on E (that will also be used later on). We define first(e) as the set of parsing procedures that may be called by e to process the start of string x after e was called to process x: first(ε) =. For a Σ, first(a) =. For A N where A = e 1 e 2 and ε / L(e 1 ), first(a) = {e 1 }. For A N where A = e 1 e 2 and ε L(e 1 ), first(a) = {e 1, e 2 }. For A N where A = e 1 e 2, first(a) = {e 1, e 2 }. This relation can be represented by a directed graph, such as in Figure 4. An arrow from e to e means e first(e ). Define now First = first +, meaning that First(e) is the set of procedures that may be called directly or indirectly by e to process the start of string x. In the graph, e First(e) is represented by a path from e to e. The grammar is left-recursive if e First(e) for some e E. If the grammar is not left-recursive, the graph representing the relation is acyclic, which is the case in Figure 4. The important fact is: Proposition 2. If the grammar G is not left-recursive then for every e E and w Σ there exists a proof of either [e] w PEG fail or [e] w PEG y where w = xy. In [5], Medeiros shows this by first verifying that his natural semantics is equivalent to the formal definition from [4], and then using a result about well-formed grammars from the same paper. A more direct proof is found in the Appendix. 4
5 X = Z V X Y Z = a b V = b T Z V W T = c V Y = W X W = d U a b T d U U = c W c c Figure 4: Example of relation first Another problem besides left recursion is the known fact that [e] xy PEG y does not imply [e] xy PEG y for every y Σ : the action of e depends on the string ahead. We have to consider the action of e in relation to the entire input string. Let $, the end-of-text marker, be a letter that does not appear in any rules. Define some S N as the starting rule of the grammar. As L(e) does not depend on the input ahead, we have [S] w$ BNF $ if and only if w L(S). We note that every partial result in the proof tree of [S] w$ BNF $ has the form [e] xy$ BNF y$ for some e E and x, y Σ. For A N, define Tail(A) to be the set of terminated input strings that may follow a substring belonging to L(A). Formally, define y$ Tail(A) if there exists a proof tree for [S] w$ BNF $ that contains [A] xy$ BNF y$ as a partial result. The following extends the results from [5] to non-ll(1) grammars: Proposition 3. If the grammar G is not left-recursive and its every rule A = e 1 e 2 satisfies L(e 1 ) Pref(L(e 2 ) Tail(A)) =, (1) there exists a proof of [S] w$ PEG $ for each w L(S). Moreover, for every partial result [e] xy$ BNF y$ in the proof tree of [S] w$ BNF $ there exists a proof of [e] xy$ PEG y$. (Proof of the Proposition is found in the Appendix.) The consequence of Propositions 1 and 3 is: Proposition 4. The two interpretations of G are equivalent if G is not left-recursive and its every rule A = e 1 e 2 satisfies (1). The two interpretations are equivalent not only by accepting the same language, but also by parsing the input in the same way. Unfortunately, (1) is not easy to check. The languages appearing in it are context-free languages. The problems of inclusion and emptiness of intersection are in general undecidable for these languages, so one has to consider special cases, or use a conservative approximation. In fact, condition (1) is identical to the general semi disjointness considered by Schmitz in [8]; he checks it using an own grammar approximation method. No need to add that the condition stated by Proposition 4 is sufficient, but not necessary. As it will be seen, the LL(1) property implies (1), which accounts for the result obtained in [5]. We are going to look for a weaker property that still implies (1). One can think of the LL(1) property as approximating words by their one-letter prefixes. We generalize this to approximating words by prefixes of arbitrary lengths. 5
6 5 Prefix Cover and Prefix Disjointness We say that Y Σ is a prefix cover of X Σ, and write Y X, if each nonempty word in X has a nonempty prefix in Y, that is, (X ε) (Y ε)σ. We say that X Σ and Y Σ are prefix-disjoint, and write X Y to mean that for all nonempty x X and y Y neither x y nor y x. One can easily see that prefix-disjoint languages are disjoint, but the reverse is in general not true. Lemma 1. For any X, Y, Z Σ and P X X, P Y Y : (a) X X. (b) If X Y and Y Z then X Z. (c) P X P Y X Y. (d) P X XY. (e) If ε X then P X P Y XY. Proof. (a) Follows from X Pref(X). (b) Follows from transitivity of. (c) If a nonempty x X Y is in X, it has a nonempty prefix in P X. If it is in Y, it has a nonempty prefix in P Y. (d) If ε / X, each x XY has a nonempty prefix in X. This, in turn, has a nonempty prefix in P X. (e) If ε X, we have XY = (X ε)y Y. From (d) we have P X (X ε)y. The stated property follows from (c). 6 Approximation by Prefixes We can now apply the above to approximate (1). In order not to repeat this over and over again, we assume from now on that our grammar G is not left-recursive. Proposition 5. The two interpretations of G are equivalent if for every rule A = e 1 e 2 : ε / L(e 1 ), and there exist P 1 L(e 1 ) and P 2 L(e 2 ) Tail(A) such that P 1 P 2. Proof. Consider any A = e 1 e 2. Assume ε / L(e 1 ) and P 1, P 2 as required. Suppose that (1) does not hold, so there exists x such that x L(e 1 ) and x Pref(L(e 2 ) Tail(A)). Since x ε, we have x = uv for some nonempty u P 1 and v Σ. As x Pref(L(e 2 ) Tail(A)), we have xt L(e 2 ) Tail(A) for some t Σ. As xt ε, we have xt = pq for some nonempty p P 2 and q Σ. This gives uvt = pq; this means either u p or p u, which contradicts P 1 P 2. Thus, (1) does hold, and the two interpretations are equivalent by Proposition 4. The following is a stronger, but easier to check, condition for equivalence: Proposition 6. The two interpretations of G are equivalent if for every rule A = e 1 e 2 : ε / L(e 1 ), and if ε / L(e 2 ), there exist P 1 L(e 1 ) and P 2 L(e 2 ) such that P 1 P 2 ; if ε L(e 2 ), there exist P 1 L(e 1 ), P 2 L(e 2 ), and P T Tail(A) such that P 1 (P 2 P T ). Proof. Consider any A = e 1 e 2. Assume ε / L(e 1 ), P 1 L(e 1 ) and P 2 L(e 2 ). Suppose ε / L(e 2 ). By Lemma 1(d), P 2 L(e 2 ) Tail(A), so P 1 P 2 satisfies Proposition 5. Suppose now that ε L(e 2 ) and P T Tail(A). By Lemma 1(e), P 2 P T L(e 2 ) Tail(A), so P 1 P 2 P T satisfies Proposition 5. We note once again that the equivalence conditions just obtained are sufficient, but not necessary. 6
7 7 Approximation by First Expressions For E E, let FIRST (E) be the family of subsets of E defined as follows: E FIRST (E). If F belongs to FIRST (E), the result of replacing its member A N by all elements of first(a) also belongs to FIRST (E). nothing else belongs to FIRST (E) unless its being so follows from the above. Two examples for the grammar of Figure 4 are: FIRST (X) ={{X}, {Z, V }, {a, b, V }, {Z, b, T }, {a, b, T }, {a, b, c}} ; FIRST (Y ) ={{Y }, {W }, {d, U}, {d, c}}. In the Figure, one can see that, in general, the elements of FIRST (A) are leaves of a truncated graph of First(A) obtained by treating some nodes as terminals. Figure 5 shows the graphs from Figure 4 truncated at T and U, giving the elements {a, b, T } FIRST (X) and {d, U} FIRST (Y ). X = Z V Z = a b X Y V = b T T = c V Z V W Y = W X W = d U U = c W a b T d U Figure 5: Example of truncated relation First Note that FIRST (A) always contains a set consisting of all leaves of the full graph. This set is identical to the classical First(A) as defined in, for example, [1, 9]. The idea with a set E of expressions belonging to FIRST (A) is that any nonempty word in L(A) must begin with one of these expressions or, more precisely, with a nonempty string belonging to the language of such expression. We are now going to formalize this idea. For E E, we denote the union L(e) by L(E). e E Lemma 2. For each A N holds L(first(A)) L(A). Proof. In case A = e 1 e 2 we have L(first(A)) = L{e 1, e 2 } = L(e 1 ) L(e 2 ) = L(A). By Lemma 1(a), L(first(A)) L(A). In case A = e 1 e 2 where ε / e 1, we have L(first(A)) = L(e 1 ). By Lemma 1(a), L(e 1 ) L(e 1 ). By Lemma 1(d), L(e 1 ) L(e 1 )L(e 2 ) = L(A). In case A = e 1 e 2 where ε e 1, L(first(A)) = L{e 1, e 2 } = L(e 1 ) L(e 2 ). By Lemma 1(a), L(e 1 ) L(e 1 ) and L(e 2 ) L(e 2 ). By Lemma 1(e), L(e 1 ) L(e 2 ) L(e 1 )L(e 2 ) = L(A). Lemma 3. For each F FIRST (E) holds L(F ) L(E). Proof. The proof is by induction on the number of replacements used to construct FIRST (E). (Induction base) By Lemma 1(a), L(E) L(E). (Induction step) Assume L{e 1, e 2,..., e n } L(E). As sets are not ordered, we can always consider replacing e 1. Let first(e 1 ) = {f 1, f 2 }. (The proof will be similar if first(e 1 ) has only one element.) According to Lemma 2, L{f 1, f 2 } L(e 1 ). We also have L{e 2,..., e n } L{e 2,..., e n } by Lemma 1(a). Using Lemma 1(c), we obtain: L{f 1, f 2, e 2,..., e n } = L{f 1, f 2 } L{e 2,..., e n } L(e 1 ) L{e 2,..., e n } = L{e 1, e 2,..., e n }. From Lemma 1(b) follows L{f 1, f 2, e 2,..., e n } L(E). 7
8 We can apply this result directly to ε-free grammars: Proposition 7. The two interpretations of G are equivalent if G is ε-free and for every rule A = e 1 e 2 there exist First 1 FIRST (e 1 ) and First 2 FIRST (e 2 ) such that L(First 1 ) L(First 2 ). Proof. Suppose the required First 1 and First 2 exist. If G is ε-free, we have ε / L(e 1 ) and ε / L(e 2 ). From Lemma 3 follows L(First 1 ) L(e 1 ) and L(First 2 ) L(e 2 ). The stated result follows from Proposition 6. To handle the case where the grammar G is not ε-free, we need to find suitable first expressions of Tail(A). For this purpose, we borrow from [9] the definition of Follow E E. For e E, define Last(e) to be the set of all A N such that: A = e e 1 for some e 1 E, or A = e 1 e for some e 1 E, or A = e 1 e for some e 1 E, or A = e e 1 for some e 1 E where ε L(e 1 ). For e E, define Next(e) = {e 1 E : exists A Nsuch that A = e e 1 }. Finally, define Follow = Last Next. The idea with Follow is that any nonempty word in Tail(A) must begin with one of the expressions in Follow(A) or, more precisely, with a nonempty string belonging to the language of such expression. The following is a formal statement of this fact. Lemma 4. For each A N, L(Follow(A)) Tail(A). (Proof is found in the Appendix.) We can now apply this result to the general case. Proposition 8. The two interpretations of G are equivalent if for every rule A = e 1 e 2 : ε / L(e 1 ), and if ε / L(e 2 ), there exist First 1 FIRST (e 1 ) and First 2 FIRST (e 2 ) such that L(First 1 ) L(First 2 ); if ε L(e 2 ), there exist First 1 FIRST (e 1 ), First 2 FIRST (e 2 ), and Follow FIRST (Follow(A)) such that L(First 1 ) L(First 2 Follow). Proof. The case of ε / L(e 2 ) is identical to Proposition 7. Suppose ε L(e 2 ) and the required First 1, First 2, and Follow exist. From Lemma 3 we have L(First 1 ) L(e 1 ), L(First 2 ) L(e 2 ), and L(Follow) L(Follow(A)). From Lemma 4 and 1(b) we have L(Follow) Tail(A). The stated result follows from Proposition 6. 8 LL(1p) Grammars As remarked before, FIRST (e) contains the classical First(e): the set of possible starting letters of words in L(e). Similarly, FIRST (Follow(A)) contains the classical Follow(A): the set of possible starting letters of words in Tail(A). For sets X, Y Σ, X Y is the same as X Y =. The LL(1) conditions First(e 1 ) First(e 2 ) = and First(e 1 ) (First(e 2 ) Follow(A)) = are thus special cases of those stated by Proposition 8, meaning that the two interpretations are equivalent for LL(1) grammars. This is the result obtained by Medeiros in [5]. For an example of a non-ll(1) grammar, take the grammar from Figures 4 and 5. Consider an additional rule S = X Y. This rule is not LL(1), as the intersection of First(X) = {a, b, c} and First(Y ) = {c, d} is not empty. Instead of {a, b, c} and {c, d}, consider now {a, b, T } FIRST (X) and {d, U} FIRST (Y ). One can verify that L(T ) = cc b and L(U) = cc d, so L{a, b, T } = a c b and L{d, U} = c d. One can also see that (a c b) (c d); thus, according to Proposition 7, S = X Y satisfies the equivalence condition (1). We have here a rule that is not LL(1), but still satisfies (1). Imagine now for a while that T and U are terminals elements of an extended alphabet Σ. In a practical parser, they could be tokens produced by some preprocessor usually known as a lexer or scanner. Because {a, b, T } {d, U} =, the rule 8
9 S = X Y is now perfectly LL(1). A top-down parser can choose between X and Y by looking at the next token. In a backtracking parser, procedures such as those for T or U act in the same way as those for terminals. In each case, the procedure looks at the input ahead, and either succeeds and consumes a portion, or fails and leaves the state unchanged. The only difference is the amount of the input being examined. The condition such as {a, b, T } {d, U} tells that the parser can choose between X and Y by looking at the input within the range of one procedure call. We can call this condition LL(1p), with 1p standing for one procedure. Proposition 8 can now be understood as stating that the two interpretations of G are equivalent if the grammar is LL(1p). Note that the grammar shown in the Introduction is LL(1p). 9 Conclusions We have shown that a direct transcription of an EBNF grammar to equivalent PEG is possible for grammars outside the LL(1) class. Among them are the grammars where the choice of the way to proceed is made by examining the input within the reach of one parsing procedure, instead of examining a single letter. We called them LL(1p) grammars, the 1p meaning one procedure. Unfortunately, checking the conditions stated by Proposition 8 is not as simple as verifying the LL(1) property. The families FIRST can be constructed in a mechanical way, and are presumably not very large. But, checking the disjointness of their members may be difficult. It becomes more difficult as one moves up the graph in Figure 4; at the top of that graph we come close to the condition (1). If the sets First 1, First 2, and Follow satisfying Proposition 8 exist, the information can be used for the improvement suggested by Mizushima et al. in [6]. The set First 1 lists the alternative parsing procedures that will be eventually invoked to start the processing of e 1. If a procedure P First 1 succeeds, but the further processing of e 1 fails, the conditions of Proposition 8 mean that e 2 is doomed to fail, unless it succeeds on empty string. But in this case, the subsequent processing of Tail(A) will fail. One can thus insert a cut operator after P to save memoization and an unnecessary attempt at e 2. The class of EBNF grammars that can be directly transcribed into PEG includes cases where the choice of the way to proceed is made by looking at the input within the reach of more than one parsing procedure. The following is an example of such grammar: InputLine = Assignment Expression Assignment = Name "=" Expression Expression = Primary ([+-] Primary) Primary = Name Number Name = [a-z] + Number = [0-9] + Here both alternatives of InputLine may begin with Name. It is the next procedure after Name, namely one for "=", that decides whether to proceed or backtrack. Still, the grammar works perfectly as PEG parser. This class of grammars, which may be called LL(2p), or in general LL(kp) requires further analysis. We may need to define FIRST families as consisting of sequences of k expressions and use Proposition 5. Last but not least: it appears that natural semantics, as used by Medeiros to define the meaning of a grammar, is a very convenient tool to investigate the grammar s properties. 9
10 Appendix Proof of Proposition 1 We spell out the proof sketched in [5]. It is by induction on the height of the proof tree. (Induction base) Suppose the proof of [e] xy PEG y consists of one step. Then it has to be the proof of [ε] x PEG x or [a] ax PEG x using empty.p or letter.p1, respectively. But then, [ε] x BNF x respectively [a] ax BNF x by empty.b or letter.b. (Induction step) Assume that for every proof tree for [e] xy PEG y of height n 1 exists a proof of [e] xy BNF y. Consider a proof tree for [e] xy PEG y of height n + 1. Its last step must be one of these: [A] xyz PEG x derived from A = e 1 e 2, [e 1 ] xyz PEG yz, and [e 2 ] yz PEG z using seq.p1. By induction hypothesis, [e 1 ] xyz BNF yz and [e 2 ] yz BNF z, so [A] xy BNF x follows from seq.b. [A] xy PEG x derived from A = e 1 e 2 and [e 1 ] xy PEG y using choice.p1. By induction hypothesis, [e 1 ] xy BNF y, so [A] xy BNF x follows from choice.b1. [A] xy PEG x derived from A = e 1 e 2 and [e 1 ] xy PEG fail, [e 2 ] xy PEG y, using choice.p2. By induction hypothesis, [e 2 ] xy BNF y, so [A] xy BNF x follows from choice.b2. Proof of Proposition 2 To be short, we shall say that e handles w if for every w Σ there exists a proof of either [e] w PEG fail or [e] w PEG y where w = xy. To show that each e E handles every w Σ, we are use induction on the length of w. The induction base is proved below as Lemma 2.B and induction step as Lemma 2.S. Both are proved by induction on the size of First(e). We use an observation that if G is not left-recursive, the set First(e ) where e first(e) has fewer elements than First(e). Lemma 2.S. Suppose G is not left-recursive, and each e E handles all words of length less than given n > 0. Then each e E also handles all words of length n. Proof: Is by induction on the size of First(e). Consider a word w of length n. (Induction base) Each e with First(e) of size 0 handles w. Such e is either ε or a Σ. From empty.p, letter.p1, and letter.p2 follows, respectively, [ε] w PEG w, [a] w PEG x if w = ax, and [a] w PEG fail otherwise. (Induction step) Suppose each e with First(e) of size less than m > 0 handles w. Consider e with First(e ) of size m. By induction hypothesis, each e first(e ) handles w. Since m > 0, must be e = A N. Two cases are possible: (Case 1) A = e 1 e 2. We have e 1 first(a), so e 1 handles w. If [e 1 ] w PEG fail, we have [A] w PEG fail by seq.p2. If [e 1 ] w PEG w, we have ε L(e 1 ) by Proposition 1, so e 2 first(a), and e 2 handles w. We have [e 2 ] w PEG Z where Z is either fail or z where w = yz. This gives [A] ε PEG Z by seq.p1. If [e 1 ] w PEG y where w = xy and x ε, y has length less than n and e 2 handles y according to the Lemma s assumption. We have [e 2 ] y PEG Z where Z is either fail or z where w = yz. This gives [A] ε PEG Z by seq.p1. (Case 2) A = e 1 e 2. We have e 1 first(a) and e 2 first(a), so each of e 1, e 2 handles w. If [e 1 ] w PEG y where w = xy, we have [A] w PEG y by choice.p1. If [e 1 ] ε PEG fail, we have [e 2 ] w PEG Y where Y is either fail or y where w = yz. This gives [A] w PEG Y by choice.p2. In each case, e = A handles w. Lemma 2.B. If G is not left-recursive, each e E handles the word of length 0. Proof: The proof is almost identical to that of Lemma 2.S if we take w = ε and use letter.p3 instead of letter.p1, and letter.p2 in the induction base. The third item in Case 1 is not applicable. 10
11 Proof of Proposition 3 Assume G satisfies the stated conditions. Take any w L(S). It means there exists proof tree for [S] w$ BNF $. We are going to show that for each partial result [e] xy$ BNF y$ in that tree there exists a proof of [e] xy$ PEG $. We show it using induction on the height of the proof tree. (Induction base) Suppose the proof of the partial result [e] xy$ BNF y$ consists of one step. Then it has to be the proof of [ε] x$ BNF x$ or [a] ax$ BNF x$ using empty.b or letter.b, respectively. But then, [ε] x$ PEG x$ respectively [a] ax$ PEG x$ by empty.p or letter.p1. (Induction step) Assume that for every partial result [e] xy$ BNF y$ that has proof tree of height n 1 there exists a proof of [e] xy$ PEG y$. Consider a partial result [e] xy$ BNF y$ with proof tree of height n + 1. Its last step must be one of these: [A] xyz$ BNF z$ derived from A = e 1 e 2, [e 1 ] xyz$ BNF yz$, and [e 2 ] yz$ BNF z$ using seq.b. By induction hypothesis, [e 1 ] xyz$ PEG yz$ and [e 2 ] yz$ PEG z$, so [A] xyz$ PEG z$ follows from seq.p1. [A] xy$ BNF y$ derived from A = e 1 e 2 and [e 1 ] xy$ BNF y$ using choice.b1. By induction hypothesis, [e 1 ] xy$ PEG y$, so [A] xy$ PEG y$ follows from choice.p1. [A] xy$ BNF y$, derived from A = e 1 e 2 and [e 2 ] xy$ BNF y$ using choice.b2. By induction hypothesis, [e 2 ] xy$ PEG y$. But, to use choice.p2 we also need to verify that [e 1 ] xy$ PEG fail. Suppose that there is no proof of [e 1 ] xy$ PEG fail. Then, according to Proposition 2, there exists a proof of [e 1 ] uv$ PEG v$ where uv$ = xy$. According to Proposition 1, there exists a proof of [e 1 ] uv$ BNF v$, so u L(e 1 ). From [e 2 ] xy$ BNF y$ follows x L(e 2 ). From [A] xy$ BNF y$ follows y$ Tail(A). From uv$ = xy$ follows u xy, so u Pref(L(e 2 ) Tail(A)), which contradicts (1). We must thus conclude that there exists a proof of [e 1 ] xy$ PEG fail, so there exists a proof of [A] xy$ PEG y$ using choice.p2. The proof that [S] w$ PEG $ exists is a special case of the above. Proof of Lemma 4 Consider some A N and y$ Tail(A). By definition, there is a proof of [S] w$ BNF $ that contains [A] xy$ BNF y$ as one of the partial results. This partial result must be used in a subsequent derivation. This derivation can only result in one of the following: (a) [A 1 ] xy$ BNF y$ where A 1 = A e from [e] xy$ BNF y$ using choice.b1. (b) [A 1 ] xy$ BNF y$ where A 1 = e A from [e] xy$ BNF y$ using choice.b2. (c) [A 1 ] zxy$ BNF y$ where A 1 = e A from [e] zxy$ BNF xy$ using seq.b. (d) [A 1 ] xy$ BNF y$ where A 1 = A e from [e] εy$ BNF y$ using seq.b. (e) [A 1 ] xy y $ BNF y $ where A 1 = A B, y y = y and y ε from [B] y y $ BNF y $ using seq.b. In each of the cases (a)-(d), the result is similar to the original one, and the alternative derivations (a)-(e) apply again. We may have a chain of derivations (a)-(d), but it must end with (e) as y must eventually be reduced. We have thus in general a sequence of steps of this form: [A 0 ] xy$ BNF y$... as in (a)-(d) [A 1 ] x 1 y$ BNF y$... as in (a)-(d) [A 2 ] x 2 y$ BNF y$... as in (a)-(d)... [A n 1 ] x n 1 y$ BNF y$... as in (a)-(d) A n+1 = A n B [A n ] x n y$ BNF y$ [A n+1 ] x n y y $ BNF y $ [B] y y $ BNF y $ where A 0 = A and n 0. We have A 1 Last(A 0 ), A 2 Last(A 1 ), etc., A n Last(A n 1 ), and B Next(A n ), which means B Follow(A). From [B] y y $ BNF y $ we have y L(B); since y = y y and y ε, y$ has a nonempty prefix in L(B) L(Follow(A)). 11
12 References [1] Aho, A. V., Sethi, R., and Ullman, J. D. Compilers. Principles, Techniques, and Tools. Addison- Wesley, [2] Ford, B. Packrat parsing: a practical linear-time algorithm with backtracking. Master s thesis, Massachusetts Institute of Technology, Sept [3] Ford, B. Packrat parsing: simple, powerful, lazy, linear time, functional pearl. In Proceedings of the Seventh ACM SIGPLAN International Conference on Functional Programming (ICFP 02), Pittsburgh, Pennsylvania, USA, October 4-6, 2002 (2002), M. Wand and S. L. P. Jones, Eds., ACM, pp [4] Ford, B. Parsing expression grammars: A recognition-based syntactic foundation. In Proceedings of the 31st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2004 (Venice, Italy, January 2004), N. D. Jones and X. Leroy, Eds., ACM, pp [5] Medeiros, S. Correspondência entre PEGs e Classes de Gramáticas Livres de Contexto. PhD thesis, Pontifícia Universidade Católica do Rio de Janeiro, Aug pretextual.pdf 10 cap 01.pdf 10 cap 02.pdf etc cap 05.pdf 10 postextual.pdf. [6] Mizushima, K., Maeda, A., and Yamaguchi, Y. Packrat parsers can handle practical grammars in mostly constant space. In Proceedings of the 9th ACM SIGPLAN-SIGSOFT Workshop on Program Analysis for Software Tools and Engineering, PASTE 10, Toronto, Ontario, Canada, June 5-6, 2010 (2010), S. Lerner and A. Rountev, Eds., ACM, pp [7] Redziejowski, R. R. Some aspects of Parsing Expression Grammar. Fundamenta Informaticae 85, 1 4 (2008), [8] Schmitz, S. Modular syntax demands verification. Tech. Rep. ISRN I3S/RR FR, Laboratoire I3S, Sophia Antipolis, Oct [9] Tremblay, J.-P., and Sorenson, P. G. The Theory and Practice of Compiler Writing. McGraw- Hill,
From EBNF to PEG. Roman R. Redziejowski. Giraf s Research
 From EBNF to PEG Roman R. Redziejowski Giraf s Research roman.redz@swipnet.se Abstract. Parsing Expression Grammar (PEG) is a way to define a recursive-descent parser with limited backtracking. Its properties
From EBNF to PEG Roman R. Redziejowski Giraf s Research roman.redz@swipnet.se Abstract. Parsing Expression Grammar (PEG) is a way to define a recursive-descent parser with limited backtracking. Its properties
From EBNF to PEG. Roman R. Redziejowski. Concurrency, Specification and Programming Berlin 2012
 Concurrency, Specification and Programming Berlin 2012 EBNF: Extended Backus-Naur Form A way to define grammar. EBNF: Extended Backus-Naur Form A way to define grammar. Literal = Decimal Binary Decimal
Concurrency, Specification and Programming Berlin 2012 EBNF: Extended Backus-Naur Form A way to define grammar. EBNF: Extended Backus-Naur Form A way to define grammar. Literal = Decimal Binary Decimal
Ambiguity, Precedence, Associativity & Top-Down Parsing. Lecture 9-10
 Ambiguity, Precedence, Associativity & Top-Down Parsing Lecture 9-10 (From slides by G. Necula & R. Bodik) 2/13/2008 Prof. Hilfinger CS164 Lecture 9 1 Administrivia Team assignments this evening for all
Ambiguity, Precedence, Associativity & Top-Down Parsing Lecture 9-10 (From slides by G. Necula & R. Bodik) 2/13/2008 Prof. Hilfinger CS164 Lecture 9 1 Administrivia Team assignments this evening for all
Recursive descent for grammars with contexts
 39th International Conference on Current Trends in Theory and Practice of Computer Science Špindleruv Mlýn, Czech Republic Recursive descent parsing for grammars with contexts Ph.D. student, Department
39th International Conference on Current Trends in Theory and Practice of Computer Science Špindleruv Mlýn, Czech Republic Recursive descent parsing for grammars with contexts Ph.D. student, Department
Top-Down Parsing and Intro to Bottom-Up Parsing
 Predictive Parsers op-down Parsing and Intro to Bottom-Up Parsing Lecture 7 Like recursive-descent but parser can predict which production to use By looking at the next few tokens No backtracking Predictive
Predictive Parsers op-down Parsing and Intro to Bottom-Up Parsing Lecture 7 Like recursive-descent but parser can predict which production to use By looking at the next few tokens No backtracking Predictive
Syntax Analysis Part I
 1 Syntax Analysis Part I Chapter 4 COP5621 Compiler Construction Copyright Robert van Engelen, Florida State University, 2007-2013 2 Position of a Parser in the Compiler Model Source Program Lexical Analyzer
1 Syntax Analysis Part I Chapter 4 COP5621 Compiler Construction Copyright Robert van Engelen, Florida State University, 2007-2013 2 Position of a Parser in the Compiler Model Source Program Lexical Analyzer
CPSC 421: Tutorial #1
 CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
EDUCATIONAL PEARL. Proof-directed debugging revisited for a first-order version
 JFP 16 (6): 663 670, 2006. c 2006 Cambridge University Press doi:10.1017/s0956796806006149 First published online 14 September 2006 Printed in the United Kingdom 663 EDUCATIONAL PEARL Proof-directed debugging
JFP 16 (6): 663 670, 2006. c 2006 Cambridge University Press doi:10.1017/s0956796806006149 First published online 14 September 2006 Printed in the United Kingdom 663 EDUCATIONAL PEARL Proof-directed debugging
Follow sets. LL(1) Parsing Table
 Follow sets. LL(1) Parsing Table Exercise Introducing Follow Sets Compute nullable, first for this grammar: stmtlist ::= ε stmt stmtlist stmt ::= assign block assign ::= ID = ID ; block ::= beginof ID
Follow sets. LL(1) Parsing Table Exercise Introducing Follow Sets Compute nullable, first for this grammar: stmtlist ::= ε stmt stmtlist stmt ::= assign block assign ::= ID = ID ; block ::= beginof ID
Predictive parsing as a specific subclass of recursive descent parsing complexity comparisons with general parsing
 Plan for Today Recall Predictive Parsing when it works and when it doesn t necessary to remove left-recursion might have to left-factor Error recovery for predictive parsers Predictive parsing as a specific
Plan for Today Recall Predictive Parsing when it works and when it doesn t necessary to remove left-recursion might have to left-factor Error recovery for predictive parsers Predictive parsing as a specific
CSE302: Compiler Design
 CSE302: Compiler Design Instructor: Dr. Liang Cheng Department of Computer Science and Engineering P.C. Rossin College of Engineering & Applied Science Lehigh University February 27, 2007 Outline Recap
CSE302: Compiler Design Instructor: Dr. Liang Cheng Department of Computer Science and Engineering P.C. Rossin College of Engineering & Applied Science Lehigh University February 27, 2007 Outline Recap
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Introduction to Bottom-Up Parsing
 Introduction to Bottom-Up Parsing Outline Review LL parsing Shift-reduce parsing The LR parsing algorithm Constructing LR parsing tables Compiler Design 1 (2011) 2 Top-Down Parsing: Review Top-down parsing
Introduction to Bottom-Up Parsing Outline Review LL parsing Shift-reduce parsing The LR parsing algorithm Constructing LR parsing tables Compiler Design 1 (2011) 2 Top-Down Parsing: Review Top-down parsing
Lecture Notes on Inductive Definitions
 Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 September 2, 2004 These supplementary notes review the notion of an inductive definition and
Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 September 2, 2004 These supplementary notes review the notion of an inductive definition and
On Parsing Expression Grammars A recognition-based system for deterministic languages
 Bachelor thesis in Computer Science On Parsing Expression Grammars A recognition-based system for deterministic languages Author: Démian Janssen wd.janssen@student.ru.nl First supervisor/assessor: Herman
Bachelor thesis in Computer Science On Parsing Expression Grammars A recognition-based system for deterministic languages Author: Démian Janssen wd.janssen@student.ru.nl First supervisor/assessor: Herman
Proving languages to be nonregular
 Proving languages to be nonregular We already know that there exist languages A Σ that are nonregular, for any choice of an alphabet Σ. This is because there are uncountably many languages in total and
Proving languages to be nonregular We already know that there exist languages A Σ that are nonregular, for any choice of an alphabet Σ. This is because there are uncountably many languages in total and
CMSC 330: Organization of Programming Languages. Pushdown Automata Parsing
 CMSC 330: Organization of Programming Languages Pushdown Automata Parsing Chomsky Hierarchy Categorization of various languages and grammars Each is strictly more restrictive than the previous First described
CMSC 330: Organization of Programming Languages Pushdown Automata Parsing Chomsky Hierarchy Categorization of various languages and grammars Each is strictly more restrictive than the previous First described
Structural Induction
 Structural Induction In this lecture we ll extend the applicability of induction to many universes, ones where we can define certain kinds of objects by induction, in addition to proving their properties
Structural Induction In this lecture we ll extend the applicability of induction to many universes, ones where we can define certain kinds of objects by induction, in addition to proving their properties
Compiling Techniques
 Lecture 5: Top-Down Parsing 26 September 2017 The Parser Context-Free Grammar (CFG) Lexer Source code Scanner char Tokeniser token Parser AST Semantic Analyser AST IR Generator IR Errors Checks the stream
Lecture 5: Top-Down Parsing 26 September 2017 The Parser Context-Free Grammar (CFG) Lexer Source code Scanner char Tokeniser token Parser AST Semantic Analyser AST IR Generator IR Errors Checks the stream
Introduction to Bottom-Up Parsing
 Outline Introduction to Bottom-Up Parsing Review LL parsing Shift-reduce parsing he LR parsing algorithm Constructing LR parsing tables Compiler Design 1 (2011) 2 op-down Parsing: Review op-down parsing
Outline Introduction to Bottom-Up Parsing Review LL parsing Shift-reduce parsing he LR parsing algorithm Constructing LR parsing tables Compiler Design 1 (2011) 2 op-down Parsing: Review op-down parsing
Introduction to Bottom-Up Parsing
 Introduction to Bottom-Up Parsing Outline Review LL parsing Shift-reduce parsing The LR parsing algorithm Constructing LR parsing tables 2 Top-Down Parsing: Review Top-down parsing expands a parse tree
Introduction to Bottom-Up Parsing Outline Review LL parsing Shift-reduce parsing The LR parsing algorithm Constructing LR parsing tables 2 Top-Down Parsing: Review Top-down parsing expands a parse tree
Space-aware data flow analysis
 Space-aware data flow analysis C. Bernardeschi, G. Lettieri, L. Martini, P. Masci Dip. di Ingegneria dell Informazione, Università di Pisa, Via Diotisalvi 2, 56126 Pisa, Italy {cinzia,g.lettieri,luca.martini,paolo.masci}@iet.unipi.it
Space-aware data flow analysis C. Bernardeschi, G. Lettieri, L. Martini, P. Masci Dip. di Ingegneria dell Informazione, Università di Pisa, Via Diotisalvi 2, 56126 Pisa, Italy {cinzia,g.lettieri,luca.martini,paolo.masci}@iet.unipi.it
Lecture 3: Finite Automata
 Administrivia Lecture 3: Finite Automata Everyone should now be registered electronically using the link on our webpage. If you haven t, do so today! I d like to have teams formed by next Monday at the
Administrivia Lecture 3: Finite Automata Everyone should now be registered electronically using the link on our webpage. If you haven t, do so today! I d like to have teams formed by next Monday at the
Syntax Analysis Part I
 1 Syntax Analysis Part I Chapter 4 COP5621 Compiler Construction Copyright Robert van Engelen, Florida State University, 2007-2013 2 Position of a Parser in the Compiler Model Source Program Lexical Analyzer
1 Syntax Analysis Part I Chapter 4 COP5621 Compiler Construction Copyright Robert van Engelen, Florida State University, 2007-2013 2 Position of a Parser in the Compiler Model Source Program Lexical Analyzer
Computational Models: Class 3
 Computational Models: Class 3 Benny Chor School of Computer Science Tel Aviv University November 2, 2015 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 3 Benny Chor School of Computer Science Tel Aviv University November 2, 2015 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Introduction to Bottom-Up Parsing
 Outline Introduction to Bottom-Up Parsing Review LL parsing Shift-reduce parsing he LR parsing algorithm Constructing LR parsing tables 2 op-down Parsing: Review op-down parsing expands a parse tree from
Outline Introduction to Bottom-Up Parsing Review LL parsing Shift-reduce parsing he LR parsing algorithm Constructing LR parsing tables 2 op-down Parsing: Review op-down parsing expands a parse tree from
CONTEXT FREE GRAMMAR AND
 CONTEXT FREE GRAMMAR AND PARSING STATIC ANALYSIS - PARSING Source language Scanner (lexical analysis) tokens Parser (syntax analysis) Syntatic structure Semantic Analysis (IC generator) Syntatic/sema ntic
CONTEXT FREE GRAMMAR AND PARSING STATIC ANALYSIS - PARSING Source language Scanner (lexical analysis) tokens Parser (syntax analysis) Syntatic structure Semantic Analysis (IC generator) Syntatic/sema ntic
Chapter 3. Regular grammars
 Chapter 3 Regular grammars 59 3.1 Introduction Other view of the concept of language: not the formalization of the notion of effective procedure, but set of words satisfying a given set of rules Origin
Chapter 3 Regular grammars 59 3.1 Introduction Other view of the concept of language: not the formalization of the notion of effective procedure, but set of words satisfying a given set of rules Origin
Automata Theory and Formal Grammars: Lecture 1
 Automata Theory and Formal Grammars: Lecture 1 Sets, Languages, Logic Automata Theory and Formal Grammars: Lecture 1 p.1/72 Sets, Languages, Logic Today Course Overview Administrivia Sets Theory (Review?)
Automata Theory and Formal Grammars: Lecture 1 Sets, Languages, Logic Automata Theory and Formal Grammars: Lecture 1 p.1/72 Sets, Languages, Logic Today Course Overview Administrivia Sets Theory (Review?)
Safety Analysis versus Type Inference
 Information and Computation, 118(1):128 141, 1995. Safety Analysis versus Type Inference Jens Palsberg palsberg@daimi.aau.dk Michael I. Schwartzbach mis@daimi.aau.dk Computer Science Department, Aarhus
Information and Computation, 118(1):128 141, 1995. Safety Analysis versus Type Inference Jens Palsberg palsberg@daimi.aau.dk Michael I. Schwartzbach mis@daimi.aau.dk Computer Science Department, Aarhus
10. The GNFA method is used to show that
 CSE 355 Midterm Examination 27 February 27 Last Name Sample ASU ID First Name(s) Ima Exam # Sample Regrading of Midterms If you believe that your grade has not been recorded correctly, return the entire
CSE 355 Midterm Examination 27 February 27 Last Name Sample ASU ID First Name(s) Ima Exam # Sample Regrading of Midterms If you believe that your grade has not been recorded correctly, return the entire
Computability Crib Sheet
 Computer Science and Engineering, UCSD Winter 10 CSE 200: Computability and Complexity Instructor: Mihir Bellare Computability Crib Sheet January 3, 2010 Computability Crib Sheet This is a quick reference
Computer Science and Engineering, UCSD Winter 10 CSE 200: Computability and Complexity Instructor: Mihir Bellare Computability Crib Sheet January 3, 2010 Computability Crib Sheet This is a quick reference
UNIT-VI PUSHDOWN AUTOMATA
 Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
Syntax Analysis Part III
 Syntax Analysis Part III Chapter 4: Top-Down Parsing Slides adapted from : Robert van Engelen, Florida State University Eliminating Ambiguity stmt if expr then stmt if expr then stmt else stmt other The
Syntax Analysis Part III Chapter 4: Top-Down Parsing Slides adapted from : Robert van Engelen, Florida State University Eliminating Ambiguity stmt if expr then stmt if expr then stmt else stmt other The
Lecture 4: Finite Automata
 Administrivia Lecture 4: Finite Automata Everyone should now be registered electronically using the link on our webpage. If you haven t, do so today! I dliketohaveteamsformedbyfriday,ifpossible,butnextmonday
Administrivia Lecture 4: Finite Automata Everyone should now be registered electronically using the link on our webpage. If you haven t, do so today! I dliketohaveteamsformedbyfriday,ifpossible,butnextmonday
Tree sets. Reinhard Diestel
 1 Tree sets Reinhard Diestel Abstract We study an abstract notion of tree structure which generalizes treedecompositions of graphs and matroids. Unlike tree-decompositions, which are too closely linked
1 Tree sets Reinhard Diestel Abstract We study an abstract notion of tree structure which generalizes treedecompositions of graphs and matroids. Unlike tree-decompositions, which are too closely linked
Creating a Recursive Descent Parse Table
 Creating a Recursive Descent Parse Table Recursive descent parsing is sometimes called LL parsing (Left to right examination of input, Left derivation) Consider the following grammar E TE' E' +TE' T FT'
Creating a Recursive Descent Parse Table Recursive descent parsing is sometimes called LL parsing (Left to right examination of input, Left derivation) Consider the following grammar E TE' E' +TE' T FT'
EXAM. CS331 Compiler Design Spring Please read all instructions, including these, carefully
 EXAM Please read all instructions, including these, carefully There are 7 questions on the exam, with multiple parts. You have 3 hours to work on the exam. The exam is open book, open notes. Please write
EXAM Please read all instructions, including these, carefully There are 7 questions on the exam, with multiple parts. You have 3 hours to work on the exam. The exam is open book, open notes. Please write
Lecture 3: Finite Automata
 Administrivia Lecture 3: Finite Automata Everyone should now be registered electronically using the link on our webpage. If you haven t, do so today! I d like to have teams formed by next Wednesday at
Administrivia Lecture 3: Finite Automata Everyone should now be registered electronically using the link on our webpage. If you haven t, do so today! I d like to have teams formed by next Wednesday at
Compiling Techniques
 Lecture 5: Top-Down Parsing 6 October 2015 The Parser Context-Free Grammar (CFG) Lexer Source code Scanner char Tokeniser token Parser AST Semantic Analyser AST IR Generator IR Errors Checks the stream
Lecture 5: Top-Down Parsing 6 October 2015 The Parser Context-Free Grammar (CFG) Lexer Source code Scanner char Tokeniser token Parser AST Semantic Analyser AST IR Generator IR Errors Checks the stream
Lecture Notes on Inductive Definitions
 Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 28, 2003 These supplementary notes review the notion of an inductive definition and give
Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 28, 2003 These supplementary notes review the notion of an inductive definition and give
3515ICT: Theory of Computation. Regular languages
 3515ICT: Theory of Computation Regular languages Notation and concepts concerning alphabets, strings and languages, and identification of languages with problems (H, 1.5). Regular expressions (H, 3.1,
3515ICT: Theory of Computation Regular languages Notation and concepts concerning alphabets, strings and languages, and identification of languages with problems (H, 1.5). Regular expressions (H, 3.1,
Automata & languages. A primer on the Theory of Computation. Laurent Vanbever. ETH Zürich (D-ITET) October,
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Part 3 out of 5. Automata & languages. A primer on the Theory of Computation. Last week, we learned about closure and equivalence of regular languages
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
CISC 4090: Theory of Computation Chapter 1 Regular Languages. Section 1.1: Finite Automata. What is a computer? Finite automata
 CISC 4090: Theory of Computation Chapter Regular Languages Xiaolan Zhang, adapted from slides by Prof. Werschulz Section.: Finite Automata Fordham University Department of Computer and Information Sciences
CISC 4090: Theory of Computation Chapter Regular Languages Xiaolan Zhang, adapted from slides by Prof. Werschulz Section.: Finite Automata Fordham University Department of Computer and Information Sciences
Theory of Computation
 Theory of Computation (Feodor F. Dragan) Department of Computer Science Kent State University Spring, 2018 Theory of Computation, Feodor F. Dragan, Kent State University 1 Before we go into details, what
Theory of Computation (Feodor F. Dragan) Department of Computer Science Kent State University Spring, 2018 Theory of Computation, Feodor F. Dragan, Kent State University 1 Before we go into details, what
CS 314 Principles of Programming Languages
 CS 314 Principles of Programming Languages Lecture 7: LL(1) Parsing Zheng (Eddy) Zhang Rutgers University February 7, 2018 Class Information Homework 3 will be posted this coming Monday. 2 Review: Top-Down
CS 314 Principles of Programming Languages Lecture 7: LL(1) Parsing Zheng (Eddy) Zhang Rutgers University February 7, 2018 Class Information Homework 3 will be posted this coming Monday. 2 Review: Top-Down
Notes on Pumping Lemma
 Notes on Pumping Lemma Finite Automata Theory and Formal Languages TMV027/DIT321 Ana Bove, March 5th 2018 In the course we see two different versions of the Pumping lemmas, one for regular languages and
Notes on Pumping Lemma Finite Automata Theory and Formal Languages TMV027/DIT321 Ana Bove, March 5th 2018 In the course we see two different versions of the Pumping lemmas, one for regular languages and
What we have done so far
 What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
Context-free grammars and languages
 Context-free grammars and languages The next class of languages we will study in the course is the class of context-free languages. They are defined by the notion of a context-free grammar, or a CFG for
Context-free grammars and languages The next class of languages we will study in the course is the class of context-free languages. They are defined by the notion of a context-free grammar, or a CFG for
Syntactic Analysis. Top-Down Parsing
 Syntactic Analysis Top-Down Parsing Copyright 2015, Pedro C. Diniz, all rights reserved. Students enrolled in Compilers class at University of Southern California (USC) have explicit permission to make
Syntactic Analysis Top-Down Parsing Copyright 2015, Pedro C. Diniz, all rights reserved. Students enrolled in Compilers class at University of Southern California (USC) have explicit permission to make
Parsing -3. A View During TD Parsing
 Parsing -3 Deterministic table-driven parsing techniques Pictorial view of TD and BU parsing BU (shift-reduce) Parsing Handle, viable prefix, items, closures, goto s LR(k): SLR(1), LR(1) Problems with
Parsing -3 Deterministic table-driven parsing techniques Pictorial view of TD and BU parsing BU (shift-reduce) Parsing Handle, viable prefix, items, closures, goto s LR(k): SLR(1), LR(1) Problems with
Parsing Algorithms. CS 4447/CS Stephen Watt University of Western Ontario
 Parsing Algorithms CS 4447/CS 9545 -- Stephen Watt University of Western Ontario The Big Picture Develop parsers based on grammars Figure out properties of the grammars Make tables that drive parsing engines
Parsing Algorithms CS 4447/CS 9545 -- Stephen Watt University of Western Ontario The Big Picture Develop parsers based on grammars Figure out properties of the grammars Make tables that drive parsing engines
n Top-down parsing vs. bottom-up parsing n Top-down parsing n Introduction n A top-down depth-first parser (with backtracking)
 Announcements n Quiz 1 n Hold on to paper, bring over at the end n HW1 due today n HW2 will be posted tonight n Due Tue, Sep 18 at 2pm in Submitty! n Team assignment. Form teams in Submitty! n Top-down
Announcements n Quiz 1 n Hold on to paper, bring over at the end n HW1 due today n HW2 will be posted tonight n Due Tue, Sep 18 at 2pm in Submitty! n Team assignment. Form teams in Submitty! n Top-down
Compiler Construction Lent Term 2015 Lectures (of 16)
 Compiler Construction Lent Term 2015 Lectures 13 --- 16 (of 16) 1. Return to lexical analysis : application of Theory of Regular Languages and Finite Automata 2. Generating Recursive descent parsers 3.
Compiler Construction Lent Term 2015 Lectures 13 --- 16 (of 16) 1. Return to lexical analysis : application of Theory of Regular Languages and Finite Automata 2. Generating Recursive descent parsers 3.
Grammars (part II) Prof. Dan A. Simovici UMB
 rammars (part II) Prof. Dan A. Simovici UMB 1 / 1 Outline 2 / 1 Length-Increasing vs. Context-Sensitive rammars Theorem The class L 1 equals the class of length-increasing languages. 3 / 1 Length-Increasing
rammars (part II) Prof. Dan A. Simovici UMB 1 / 1 Outline 2 / 1 Length-Increasing vs. Context-Sensitive rammars Theorem The class L 1 equals the class of length-increasing languages. 3 / 1 Length-Increasing
Compiler Construction Lent Term 2015 Lectures (of 16)
 Compiler Construction Lent Term 2015 Lectures 13 --- 16 (of 16) 1. Return to lexical analysis : application of Theory of Regular Languages and Finite Automata 2. Generating Recursive descent parsers 3.
Compiler Construction Lent Term 2015 Lectures 13 --- 16 (of 16) 1. Return to lexical analysis : application of Theory of Regular Languages and Finite Automata 2. Generating Recursive descent parsers 3.
Theory of Computation
 Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 1: Introducing Formal Languages Motivation I This course is about the study of a fascinating
Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 1: Introducing Formal Languages Motivation I This course is about the study of a fascinating
1 More finite deterministic automata
 CS 125 Section #6 Finite automata October 18, 2016 1 More finite deterministic automata Exercise. Consider the following game with two players: Repeatedly flip a coin. On heads, player 1 gets a point.
CS 125 Section #6 Finite automata October 18, 2016 1 More finite deterministic automata Exercise. Consider the following game with two players: Repeatedly flip a coin. On heads, player 1 gets a point.
CS153: Compilers Lecture 5: LL Parsing
 CS153: Compilers Lecture 5: LL Parsing Stephen Chong https://www.seas.harvard.edu/courses/cs153 Announcements Proj 1 out Due Thursday Sept 20 (2 days away) Proj 2 out Due Thursday Oct 4 (16 days away)
CS153: Compilers Lecture 5: LL Parsing Stephen Chong https://www.seas.harvard.edu/courses/cs153 Announcements Proj 1 out Due Thursday Sept 20 (2 days away) Proj 2 out Due Thursday Oct 4 (16 days away)
What Is a Language? Grammars, Languages, and Machines. Strings: the Building Blocks of Languages
 Do Homework 2. What Is a Language? Grammars, Languages, and Machines L Language Grammar Accepts Machine Strings: the Building Blocks of Languages An alphabet is a finite set of symbols: English alphabet:
Do Homework 2. What Is a Language? Grammars, Languages, and Machines L Language Grammar Accepts Machine Strings: the Building Blocks of Languages An alphabet is a finite set of symbols: English alphabet:
Parikh s theorem. Håkan Lindqvist
 Parikh s theorem Håkan Lindqvist Abstract This chapter will discuss Parikh s theorem and provide a proof for it. The proof is done by induction over a set of derivation trees, and using the Parikh mappings
Parikh s theorem Håkan Lindqvist Abstract This chapter will discuss Parikh s theorem and provide a proof for it. The proof is done by induction over a set of derivation trees, and using the Parikh mappings
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
COMP4141 Theory of Computation
 COMP4141 Theory of Computation Lecture 4 Regular Languages cont. Ron van der Meyden CSE, UNSW Revision: 2013/03/14 (Credits: David Dill, Thomas Wilke, Kai Engelhardt, Peter Höfner, Rob van Glabbeek) Regular
COMP4141 Theory of Computation Lecture 4 Regular Languages cont. Ron van der Meyden CSE, UNSW Revision: 2013/03/14 (Credits: David Dill, Thomas Wilke, Kai Engelhardt, Peter Höfner, Rob van Glabbeek) Regular
Computational Models - Lecture 3
 Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
CS243, Logic and Computation Nondeterministic finite automata
 CS243, Prof. Alvarez NONDETERMINISTIC FINITE AUTOMATA (NFA) Prof. Sergio A. Alvarez http://www.cs.bc.edu/ alvarez/ Maloney Hall, room 569 alvarez@cs.bc.edu Computer Science Department voice: (67) 552-4333
CS243, Prof. Alvarez NONDETERMINISTIC FINITE AUTOMATA (NFA) Prof. Sergio A. Alvarez http://www.cs.bc.edu/ alvarez/ Maloney Hall, room 569 alvarez@cs.bc.edu Computer Science Department voice: (67) 552-4333
CFLs and Regular Languages. CFLs and Regular Languages. CFLs and Regular Languages. Will show that all Regular Languages are CFLs. Union.
 We can show that every RL is also a CFL Since a regular grammar is certainly context free. We can also show by only using Regular Expressions and Context Free Grammars That is what we will do in this half.
We can show that every RL is also a CFL Since a regular grammar is certainly context free. We can also show by only using Regular Expressions and Context Free Grammars That is what we will do in this half.
Theory of computation: initial remarks (Chapter 11)
 Theory of computation: initial remarks (Chapter 11) For many purposes, computation is elegantly modeled with simple mathematical objects: Turing machines, finite automata, pushdown automata, and such.
Theory of computation: initial remarks (Chapter 11) For many purposes, computation is elegantly modeled with simple mathematical objects: Turing machines, finite automata, pushdown automata, and such.
Final exam study sheet for CS3719 Turing machines and decidability.
 Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Tree Adjoining Grammars
 Tree Adjoining Grammars TAG: Parsing and formal properties Laura Kallmeyer & Benjamin Burkhardt HHU Düsseldorf WS 2017/2018 1 / 36 Outline 1 Parsing as deduction 2 CYK for TAG 3 Closure properties of TALs
Tree Adjoining Grammars TAG: Parsing and formal properties Laura Kallmeyer & Benjamin Burkhardt HHU Düsseldorf WS 2017/2018 1 / 36 Outline 1 Parsing as deduction 2 CYK for TAG 3 Closure properties of TALs
Supplementary Notes on Inductive Definitions
 Supplementary Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 29, 2002 These supplementary notes review the notion of an inductive definition
Supplementary Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 29, 2002 These supplementary notes review the notion of an inductive definition
Introduction to Turing Machines. Reading: Chapters 8 & 9
 Introduction to Turing Machines Reading: Chapters 8 & 9 1 Turing Machines (TM) Generalize the class of CFLs: Recursively Enumerable Languages Recursive Languages Context-Free Languages Regular Languages
Introduction to Turing Machines Reading: Chapters 8 & 9 1 Turing Machines (TM) Generalize the class of CFLs: Recursively Enumerable Languages Recursive Languages Context-Free Languages Regular Languages
Proofs, Strings, and Finite Automata. CS154 Chris Pollett Feb 5, 2007.
 Proofs, Strings, and Finite Automata CS154 Chris Pollett Feb 5, 2007. Outline Proofs and Proof Strategies Strings Finding proofs Example: For every graph G, the sum of the degrees of all the nodes in G
Proofs, Strings, and Finite Automata CS154 Chris Pollett Feb 5, 2007. Outline Proofs and Proof Strategies Strings Finding proofs Example: For every graph G, the sum of the degrees of all the nodes in G
An Efficient Context-Free Parsing Algorithm. Speakers: Morad Ankri Yaniv Elia
 An Efficient Context-Free Parsing Algorithm Speakers: Morad Ankri Yaniv Elia Yaniv: Introduction Terminology Informal Explanation The Recognizer Morad: Example Time and Space Bounds Empirical results Practical
An Efficient Context-Free Parsing Algorithm Speakers: Morad Ankri Yaniv Elia Yaniv: Introduction Terminology Informal Explanation The Recognizer Morad: Example Time and Space Bounds Empirical results Practical
Computing if a token can follow
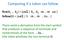 Computing if a token can follow first(b 1... B p ) = {a B 1...B p... aw } follow(x) = {a S......Xa... } There exists a derivation from the start symbol that produces a sequence of terminals and nonterminals
Computing if a token can follow first(b 1... B p ) = {a B 1...B p... aw } follow(x) = {a S......Xa... } There exists a derivation from the start symbol that produces a sequence of terminals and nonterminals
Context Free Grammars
 Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Theory of Computation p.1/?? Theory of Computation p.2/?? Unknown: Implicitly a Boolean variable: true if a word is
 Abstraction of Problems Data: abstracted as a word in a given alphabet. Σ: alphabet, a finite, non-empty set of symbols. Σ : all the words of finite length built up using Σ: Conditions: abstracted as a
Abstraction of Problems Data: abstracted as a word in a given alphabet. Σ: alphabet, a finite, non-empty set of symbols. Σ : all the words of finite length built up using Σ: Conditions: abstracted as a
Compiler Construction Lectures 13 16
 Compiler Construction Lectures 13 16 Lent Term, 2013 Lecturer: Timothy G. Griffin 1 Generating Lexical Analyzers Source Program Lexical Analyzer tokens Parser Lexical specification Scanner Generator LEX
Compiler Construction Lectures 13 16 Lent Term, 2013 Lecturer: Timothy G. Griffin 1 Generating Lexical Analyzers Source Program Lexical Analyzer tokens Parser Lexical specification Scanner Generator LEX
Decision problem of substrings in Context Free Languages.
 Decision problem of substrings in Context Free Languages. Mauricio Osorio, Juan Antonio Navarro Abstract A context free grammar (CFG) is a set of symbols and productions used to define a context free language.
Decision problem of substrings in Context Free Languages. Mauricio Osorio, Juan Antonio Navarro Abstract A context free grammar (CFG) is a set of symbols and productions used to define a context free language.
Closure Properties of Regular Languages. Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism
 Closure Properties of Regular Languages Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism Closure Properties Recall a closure property is a statement
Closure Properties of Regular Languages Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism Closure Properties Recall a closure property is a statement
1 Alphabets and Languages
 1 Alphabets and Languages Look at handout 1 (inference rules for sets) and use the rules on some examples like {a} {{a}} {a} {a, b}, {a} {{a}}, {a} {{a}}, {a} {a, b}, a {{a}}, a {a, b}, a {{a}}, a {a,
1 Alphabets and Languages Look at handout 1 (inference rules for sets) and use the rules on some examples like {a} {{a}} {a} {a, b}, {a} {{a}}, {a} {{a}}, {a} {a, b}, a {{a}}, a {a, b}, a {{a}}, a {a,
Languages. Languages. An Example Grammar. Grammars. Suppose we have an alphabet V. Then we can write:
 Languages A language is a set (usually infinite) of strings, also known as sentences Each string consists of a sequence of symbols taken from some alphabet An alphabet, V, is a finite set of symbols, e.g.
Languages A language is a set (usually infinite) of strings, also known as sentences Each string consists of a sequence of symbols taken from some alphabet An alphabet, V, is a finite set of symbols, e.g.
Syntax Analysis Part I. Position of a Parser in the Compiler Model. The Parser. Chapter 4
 1 Syntax Analysis Part I Chapter 4 COP5621 Compiler Construction Copyright Robert van ngelen, Flora State University, 2007 Position of a Parser in the Compiler Model 2 Source Program Lexical Analyzer Lexical
1 Syntax Analysis Part I Chapter 4 COP5621 Compiler Construction Copyright Robert van ngelen, Flora State University, 2007 Position of a Parser in the Compiler Model 2 Source Program Lexical Analyzer Lexical
Tasks of lexer. CISC 5920: Compiler Construction Chapter 2 Lexical Analysis. Tokens and lexemes. Buffering
 Tasks of lexer CISC 5920: Compiler Construction Chapter 2 Lexical Analysis Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Copyright Arthur G. Werschulz, 2017. All
Tasks of lexer CISC 5920: Compiler Construction Chapter 2 Lexical Analysis Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Copyright Arthur G. Werschulz, 2017. All
Chapter 6. Properties of Regular Languages
 Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Sri vidya college of engineering and technology
 Unit I FINITE AUTOMATA 1. Define hypothesis. The formal proof can be using deductive proof and inductive proof. The deductive proof consists of sequence of statements given with logical reasoning in order
Unit I FINITE AUTOMATA 1. Define hypothesis. The formal proof can be using deductive proof and inductive proof. The deductive proof consists of sequence of statements given with logical reasoning in order
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
Aperiodic languages and generalizations
 Aperiodic languages and generalizations Lila Kari and Gabriel Thierrin Department of Mathematics University of Western Ontario London, Ontario, N6A 5B7 Canada June 18, 2010 Abstract For every integer k
Aperiodic languages and generalizations Lila Kari and Gabriel Thierrin Department of Mathematics University of Western Ontario London, Ontario, N6A 5B7 Canada June 18, 2010 Abstract For every integer k
Peter Wood. Department of Computer Science and Information Systems Birkbeck, University of London Automata and Formal Languages
 and and Department of Computer Science and Information Systems Birkbeck, University of London ptw@dcs.bbk.ac.uk Outline and Doing and analysing problems/languages computability/solvability/decidability
and and Department of Computer Science and Information Systems Birkbeck, University of London ptw@dcs.bbk.ac.uk Outline and Doing and analysing problems/languages computability/solvability/decidability
UNIT-III REGULAR LANGUAGES
 Syllabus R9 Regulation REGULAR EXPRESSIONS UNIT-III REGULAR LANGUAGES Regular expressions are useful for representing certain sets of strings in an algebraic fashion. In arithmetic we can use the operations
Syllabus R9 Regulation REGULAR EXPRESSIONS UNIT-III REGULAR LANGUAGES Regular expressions are useful for representing certain sets of strings in an algebraic fashion. In arithmetic we can use the operations
Theory of Computation (IV) Yijia Chen Fudan University
 Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
CA Compiler Construction
 CA4003 - Compiler Construction Bottom Up Parsing David Sinclair Bottom Up Parsing LL(1) parsers have enjoyed a bit of a revival thanks to JavaCC. LL(k) parsers must predict which production rule to use
CA4003 - Compiler Construction Bottom Up Parsing David Sinclair Bottom Up Parsing LL(1) parsers have enjoyed a bit of a revival thanks to JavaCC. LL(k) parsers must predict which production rule to use
UNIT II REGULAR LANGUAGES
 1 UNIT II REGULAR LANGUAGES Introduction: A regular expression is a way of describing a regular language. The various operations are closure, union and concatenation. We can also find the equivalent regular
1 UNIT II REGULAR LANGUAGES Introduction: A regular expression is a way of describing a regular language. The various operations are closure, union and concatenation. We can also find the equivalent regular
Notes for Comp 497 (Comp 454) Week 10 4/5/05
 Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
Uses of finite automata
 Chapter 2 :Finite Automata 2.1 Finite Automata Automata are computational devices to solve language recognition problems. Language recognition problem is to determine whether a word belongs to a language.
Chapter 2 :Finite Automata 2.1 Finite Automata Automata are computational devices to solve language recognition problems. Language recognition problem is to determine whether a word belongs to a language.
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
Context-Free Grammars (and Languages) Lecture 7
 Context-Free Grammars (and Languages) Lecture 7 1 Today Beyond regular expressions: Context-Free Grammars (CFGs) What is a CFG? What is the language associated with a CFG? Creating CFGs. Reasoning about
Context-Free Grammars (and Languages) Lecture 7 1 Today Beyond regular expressions: Context-Free Grammars (CFGs) What is a CFG? What is the language associated with a CFG? Creating CFGs. Reasoning about
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
Propositional and Predicate Logic - V
 Propositional and Predicate Logic - V Petr Gregor KTIML MFF UK WS 2016/2017 Petr Gregor (KTIML MFF UK) Propositional and Predicate Logic - V WS 2016/2017 1 / 21 Formal proof systems Hilbert s calculus
Propositional and Predicate Logic - V Petr Gregor KTIML MFF UK WS 2016/2017 Petr Gregor (KTIML MFF UK) Propositional and Predicate Logic - V WS 2016/2017 1 / 21 Formal proof systems Hilbert s calculus
October 6, Equivalence of Pushdown Automata with Context-Free Gramm
 Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
