How Differential Equations Arise. Newton s Second Law of Motion
|
|
|
- Dwight Lamb
- 6 years ago
- Views:
Transcription
1 page 1 CHAPTER 1 Frst-Order Dfferental Equatons Among all of the mathematcal dscplnes the theory of dfferental equatons s the most mportant. It furnshes the explanaton of all those elementary manfestatons of nature whch nvolve tme. Sophus Le 1.1 How Dfferental Equatons Arse In ths secton we wll ntroduce the dea of a dfferental equaton through the mathematcal formulaton of a varety of problems. We then use these problems throughout the chapter to llustrate the applcablty of the technques ntroduced. Newton s Second Law of Moton Newton s second law of moton states that, for an object of constant mass m, the sum of the appled forces actng on the object s equal to the mass of the object multpled by the acceleraton of the object. If the object s movng n one dmenson under the nfluence of a force F, then the mathematcal statement of ths law s m dv = F, (1.1.1) where v(t) denotes the velocty of the object at tme t. We let y(t) denote the dsplacement of the object at tme t. Then, usng the fact that velocty and dsplacement are related va v=, we can wrte (1.1.1) as m d 2y = F. 2 (1.1.2) Ths s an example of a dfferental equaton, so called because t nvolves dervatves of the unknown functon y(t). 1
2 page 2 2 CHAPTER 1 Frst-Order Dfferental Equatons mg Postve y-drecton Fgure 1.1.1: Object fallng under the nfluence of gravty. Gravtatonal Force: As a specfc example, consder the case of an object fallng freely under the nfluence of gravty (see Fgure 1.1.1). In ths case the only force actng on the object s F = mg, where g denotes the (constant) acceleraton due to gravty. Choosng the postve y-drecton as downward, t follows from Equaton (1.1.2) that the moton of the object s governed by the dfferental equaton or equvalently, m d2 y = mg, (1.1.3) 2 d 2 y 2 = g. Snce g s a (postve) constant, we can ntegrate ths equaton to determne y(t). Performng one ntegraton yelds = gt + c 1, where c 1 s an arbtrary ntegraton constant. Integratng once more wth respect to t, we obtan y(t) = 1 2 gt2 + c 1 t + c 2, (1.1.4) where c 2 s a second ntegraton constant. We see that the dfferental equaton has an nfnte number of solutons parameterzed by the constants c 1 and c 2. In order to unquely specfy the moton, we must augment the dfferental equaton wth ntal conons that specfy the ntal poston and ntal velocty of the object. For example, f the object s released at t = 0 from y = y 0 wth a velocty v 0, then, n adon to the dfferental equaton, we have the ntal conons y(0) = y 0, (0) = v 0. (1.1.5) These conons must be mposed on the soluton (1.1.4) n order to determne the values of c 1 and c 2 that correspond to the partcular problem under nvestgaton. Settng t = 0 n (1.1.4) and usng the frst ntal conon from (1.1.5), we fnd that y 0 = c 2. Substtutng ths nto Equaton (1.1.4), we get y(t) = 1 2 gt2 + c 1 t + y 0. (1.1.6) In order to mpose the second ntal conon from (1.1.5), we frst dfferentate Equaton (1.1.6) to obtan = gt + c 1. Consequently the second ntal conon n (1.1.5) requres c 1 = v 0.
3 page How Dfferental Equatons Arse 3 From (1.1.6), t follows that the poston of the object at tme t s y(t) = 1 2 gt2 + v 0 t + y 0. The dfferental equaton (1.1.3) together wth the ntal conons (1.1.5) s an example of an ntal-value problem. Sprng Force: As a second applcaton of Newton s law of moton, consder the sprng mass system depcted n Fgure 1.1.2, where, for smplcty, we are neglectng frctonal and external forces. In ths case, the only force actng on the mass s the restorng force (or sprng force), F s, due to the dsplacement of the sprng from ts equlbrum (unstretched) poston. We use Hooke s law to model ths force: y 0 Mass n ts equlbrum poston y(t) Postve y-drecton Fgure 1.1.2: A smple harmonc oscllator. Hooke s Law: The restorng force of a sprng s drectly proportonal to the dsplacement of the sprng from ts equlbrum poston and s drected toward the equlbrum poston. If y(t) denotes the dsplacement of the sprng from ts equlbrum poston at tme t (see Fgure 1.1.2), then accordng to Hooke s law, the restorng force s F s = ky, where k s a postve constant called the sprng constant. Consequently, Newton s second law of moton mples that the moton of the sprng mass system s governed by the dfferental equaton m d2 y 2 = ky, whch we wrte n the equvalent form d 2 y 2 + ω2 y = 0, (1.1.7) where ω = k/m. At present we cannot solve ths dfferental equaton. However, we leave t as an exercse (Problem 7) to verfy by drect substtuton that y(t) = A cos(ωt φ) s a soluton to the dfferental equaton (1.1.7), where A and φ are constants (determned from the ntal conons for the problem). We see that the resultng moton s perodc wth ampltude A. Ths s consstent wth what we mght expect physcally, snce no frctonal forces or external forces are actng on the system. Ths type of moton s referred to as smple harmonc moton, and the physcal system s called a smple harmonc oscllator.
4 page 4 4 CHAPTER 1 Frst-Order Dfferental Equatons Newton s Law of Coolng We now buld a mathematcal model descrbng the coolng (or heatng) of an object. Suppose that we brng an object nto a room. If the temperature of the object s hotter than that of the room, then the object wll begn to cool. Further, we mght expect that the major factor governng the rate at whch the object cools s the temperature dfference between t and the room. Newton s Law of Coolng: The rate of change of temperature of an object s proportonal to the temperature dfference between the object and ts surroundng medum. To formulate ths law mathematcally, we let T(t)denote the temperature of the object at tme t, and let T m (t) denote the temperature of the surroundng medum. Newton s law of coolng can then be expressed as the dfferental equaton dt = k(t T m ), (1.1.8) where k s a constant. The mnus sgn n front of the constant k s traonal. It ensures that k wll always be postve. 1 After we stu Secton 1.4, t wll be easy to show that, when T m s constant, the soluton to ths dfferental equaton s T(t)= T m + ce kt, (1.1.9) where c s a constant (see also Problem 12). Newton s law of coolng therefore predcts that as t approaches nfnty (t ), the temperature of the object approaches that of the surroundng medum (T T m ). Ths s certanly consstent wth our everyday experence (see Fgure 1.1.3). T(t) T(t) T 0 Object that s coolng T m T m t T 0 Object that s heatng t Fgure 1.1.3: Accordng to Newton s law of coolng, the temperature of an object approaches room temperature exponentally. The Orthogonal Trajectory Problem Next we consder a geometrc problem that has many nterestng and mportant applcatons. Suppose F(x,y,c) = 0 (1.1.10) 1 If T>T m, then the object wll cool, so that dt/ < 0. Hence, from Equaton (1.1.8), k must be postve. Smlarly, f T<T m, then dt/ > 0, and once more Equaton (1.1.8) mples that k must be postve.
5 page How Dfferental Equatons Arse 5 defnes a famly of curves n the xy-plane, where the constant c labels the dfferent curves. For nstance, the equaton x 2 + y 2 c = 0 descrbes a famly of concentrc crcles wth center at the orgn, whereas x 2 + y c = 0 descrbes a famly of parabolas that are vertcal shfts of the standard parabola y = x 2. We assume that every curve n the famly F(x,y,c) = 0 has a well-defned tangent lne at each pont. Assocated wth ths famly s a second famly of curves, say, G(x,y,k)= 0, (1.1.11) y x wth the property that whenever a curve from the famly (1.1.10) ntersects a curve from the famly (1.1.11), t does so at rght angles. 2 We say that the curves n the famly (1.1.11) are orthogonal trajectores of the famly (1.1.10), and vce versa. For example, from elementary geometry, t follows that the lnes y = kx n the famly G(x,y,k)= y kx = 0 are orthogonal trajectores of the famly of concentrc crcles x 2 + y 2 = c 2. (See Fgure ) Orthogonal trajectores arse n varous applcatons. For example, a famly of curves and ts orthogonal trajectores can be used to defne an orthogonal coordnate system n the xy-plane. In Fgure the famles x 2 + y 2 = c 2 and y = kx are the coordnate curves of a polar coordnate system (that s, the curves r = constant and θ = constant, respectvely). In physcs, the lnes of electrc force of a statc confguraton are the orthogonal trajectores of the famly of equpotental curves. As a fnal example, f we consder a two-dmensonal heated plate, then the heat energy flows along the orthogonal trajectores to the constant-temperature curves (sotherms). Fgure 1.1.4: The famly of curves x 2 + y 2 = c 2 and the orthogonal trajectores y = kx. Statement of the Problem: Gven the equaton of a famly of curves, fnd the equaton of the famly of orthogonal trajectores. Mathematcal Formulaton: We recall that curves that ntersect at rght angles satsfy the followng: The product of the slopes 3 at the pont of ntersecton s 1. Thus f the gven famly F(x,y,c) = 0 has slope m 1 = f(x,y) at the pont (x, y), then the slope of the famly of orthogonal trajectores G(x,y,k) = 0sm 2 = 1/f (x, y), and therefore the dfferental equaton that determnes the orthogonal trajectores s dx = 1 f(x,y). 2 That s, the tangent lnes to each curve are perpendcular at any pont of ntersecton. 3 By the slope of a curve at a gven pont, we mean the slope of the tangent lne to the curve at that pont.
6 page 6 6 CHAPTER 1 Frst-Order Dfferental Equatons Example Determne the equaton of the famly of orthogonal trajectores to the curves wth equaton y 2 = cx. (1.1.12) Soluton: Accordng to the precedng dscusson, the dfferental equaton determnng the orthogonal trajectores s dx = 1 f(x,y), where f(x,y) denotes the slope of the gven famly at the pont (x, y). To determne f(x,y), we dfferentate Equaton (1.1.12) mplctly wth respect to x to obtan 2y = c. (1.1.13) dx We must now elmnate c from the prevous equaton to obtan an expresson that gves the slope at the pont (x, y). From Equaton (1.1.12) we have c = y2 x, whch, when substtuted nto Equaton (1.1.13), yelds dx = y 2x. Consequently, the slope of the gven famly at the pont (x, y) s f(x,y) = y 2x, so that the orthogonal trajectores are obtaned by solvng the dfferental equaton dx = 2x y. A key pont to notce s that we cannot solve ths dfferental equaton by smply ntegratng wth respect to x, snce the functon on the rght-hand sde of the dfferental equaton depends on both x and y. However, multplyng by y, we see that y dx = 2x, or equvalently, ( ) d 1 dx 2 y2 = 2x. Snce the rght-hand sde of ths equaton depends only on x, whereas the term on the left-hand sde s a dervatve wth respect to x, we can ntegrate both sdes of the equaton wth respect to x to obtan whch we wrte as 1 2 y2 = x 2 + c 1, 2x 2 + y 2 = k, (1.1.14)
7 page How Dfferental Equatons Arse 7 y 2x 2 y 2 k y 2 cx x Fgure 1.1.5: The famly of curves y 2 = cx and ts orthogonal trajectores 2x 2 + y 2 = k. where k = 2c 1. We see that the curves n the gven famly (1.1.12) are parabolas, and the orthogonal trajectores (1.1.14) are a famly of ellpses. Ths s llustrated n Fgure Exercses for 1.1 Key Terms Dfferental equaton, Intal conons, Intal-value problem, Newton s second law of moton, Hooke s law, Sprng constant, Smple harmonc moton, Smple harmonc oscllator, Newton s law of coolng, Orthogonal trajectores. Sklls Gven a dfferental equaton, be able to check whether or not a gven functon y = f(x)s ndeed a soluton to the dfferental equaton. Be able to fnd the dstance, velocty, and acceleraton functons for an object movng freely under the nfluence of gravty. Be able to determne the moton of an object n a sprng mass system wth no frctonal or external forces. Be able to descrbe qualtatvely how the temperature of an object changes as a functon of tme accordng to Newton s law of coolng. Be able to fnd the equaton of the orthogonal trajectores to a gven famly of curves. In smple geometrc cases, be prepared to provde rough sketches of some representatve orthogonal trajectores. True-False Revew For Questons 1 11, decde f the gven statement s true or false, and gve a bref justfcaton for your answer. If true, you can quote a relevant defnton or theorem from the text. If false, provde an example, llustraton, or bref explanaton of why the statement s false. 1. A dfferental equaton for a functon y = f(x)must contan the frst dervatve y = f (x). 2. The numercal values y(0) and y (0) accompanyng a dfferental equaton for a functon y = f(x) are called ntal conons of the dfferental equaton. 3. The relatonshp between the velocty and the acceleraton of an object fallng under the nfluence of gravty can be expressed mathematcally as a dfferental equaton. 4. A sketch of the heght of an object fallng freely under the nfluence of gravty as a functon of tme takes the shape of a parabola.
8 page 8 8 CHAPTER 1 Frst-Order Dfferental Equatons 5. Hooke s law states that the restorng force of a sprng s drectly proportonal to the dsplacement of the sprng from ts equlbrum poston and s drected n the drecton of the dsplacement from the equlbrum poston. 6. If room temperature s 70 F, then an object whose temperature s 100 F at a partcular tme cools faster at that tme than an object whose temperature at that tmes90 F. 7. Accordng to Newton s law of coolng, the temperature of an object eventually becomes the same as the temperature of the surroundng medum. 8. A hot cup of coffee that s put nto a cold room cools more n the frst hour than the second hour. 9. At a pont of ntersecton of a curve and one of ts orthogonal trajectores, the slopes of the two curves are recprocals of one another. 10. The famly of orthogonal trajectores for a famly of parallel lnes s another famly of parallel lnes. 11. The famly of orthogonal trajectores for a famly of crcles that are centered at the orgn s another famly of crcles centered at the orgn. Problems 1. An object s released from rest at a heght of 100 meters above the ground. Neglectng frctonal forces, the subsequent moton s governed by the ntal-value problem d 2 y 2 = g, y(0) = 0, (0) = 0, where y(t)denotes the dsplacement of the object from ts ntal poston at tme t. Solve ths ntal-value problem and use your soluton to determne the tme when the object hts the ground. 2. A fve-foot-tall boy tosses a tenns ball straght up from the level of the top of hs head. Neglectng frctonal forces, the subsequent moton s governed by the dfferental equaton d 2 y 2 = g. If the object hts the ground 8 seconds after the boy releases t, fnd (a) the tme when the tenns ball reaches ts maxmum heght. (b) the maxmum heght of the tenns ball. 3. A pyrotechnc rocket s to be launched vertcally upward from the ground. For optmal vewng, the rocket should reach a maxmum heght of 90 meters above the ground. Ignore frctonal forces. (a) How fast must the rocket be launched n order to acheve optmal vewng? (b) Assumng the rocket s launched wth the speed determned n part (a), how long after t s launched wll t reach ts maxmum heght? 4. Repeat Problem 3 under the assumpton that the rocket s launched from a platform 5 meters above the ground. 5. An object thrown vertcally upward wth a speed of 2 m/s from a heght of h meters takes 10 seconds to reach the ground. Set up and solve the ntal-value problem that governs the moton of the object, and determne h. 6. An object released from a heght h meters above the ground wth a vertcal velocty of v 0 m/s hts the ground after t 0 seconds. Neglectng frctonal forces, set up and solve the ntal-value problem governng the moton, and use your soluton to show that v 0 = 1 2t 0 (2h gt 2 0 ). 7. Verfy that y(t) = A cos(ωt φ) s a soluton to the dfferental equaton (1.1.7), where A, ω, and φ are constants wth A and ω nonzero. Determne the constants A and φ (wth φ < π radans) n the partcular case when the ntal conons are 8. Verfy that y(0) = a, (0) = 0. y(t) = c 1 cos ωt + c 2 sn ωt s a soluton to the dfferental equaton (1.1.7). Show that the ampltude of the moton s A = c c Verfy that, for t>0, y(t) = ln t s a soluton to the dfferental equaton 2 ( ) 3 = d 3 y 3.
9 page How Dfferental Equatons Arse Verfy that y(x) = x/(x + 1) s a soluton to the dfferental equaton y + d2 y dx 2 = dx + x3 + 2x 2 3 (1 + x) Verfy that y(x) = e x sn x s a soluton to the dfferental equaton 2y cot x d2 y dx 2 = By wrtng Equaton (1.1.8) n the form 1 T T m dt = k and usng u 1 du = d (ln u), derve (1.1.9). 13. A glass of water whose temperature s 50 Fstaken outsde at noon on a day whose temperature s constant at 70 F. If the water s temperature s 55 Fat2 p.m., do you expect the water s temperature to reach 60 F before 4 p.m. or after 4 p.m.? Use Newton s law of coolng to explan your answer. 14. On a cold wnter day (10 F), an object s brought outsde from a 70 F room. If t takes 40 mnutes for the object to cool from 70 Fto30 F, dd t take more or less than 20 mnutes for the object to reach 50 F? Use Newton s law of coolng to explan your answer. For Problems 15 20, fnd the equaton of the orthogonal trajectores to the gven famly of curves. In each case, sketch some curves from each famly. 15. x 2 + 4y 2 = c. 16. y = c/x. 21. y = mx + c. 22. y = cx m. 23. y 2 + mx 2 = c. 24. y 2 = mx + c. 25. We call a coordnate system (u, v) orthogonal f ts coordnate curves (the two famles of curves u = constant and v = constant) are orthogonal trajectores (for example, a Cartesan coordnate system or a polar coordnate system). Let (u, v) be orthogonal coordnates, where u = x 2 +2y 2, and x and y are Cartesan coordnates. Fnd the Cartesan equaton of the v-coordnate curves, and sketch the (u, v) coordnate system. 26. Any curve wth the property that whenever t ntersects a curve of a gven famly t does so at an angle a π/2 s called an oblque trajectory of the gven famly. (See Fgure ) Let m 1 (equal to tan a 1 ) denote the slope of the requred famly at the pont (x, y), and let m 2 (equal to tan a 2 ) denote the slope of the gven famly. Show that m 1 = m 2 tan a 1 + m 2 tan a. [Hnt: From Fgure 1.1.6, tan a 1 = tan(a 2 a). Thus, the equaton of the famly of oblque trajectores s obtaned by solvng dx = m 2 tan a 1 + m 2 tan a.] m 1 tan a 1 slope of requred famly m 2 tan a 2 slope of gven famly 17. y = cx y = cx y 2 = 2x + c. 20. y = ce x. Curve of requred famly a a 1 a 2 For Problems 21 24, m denotes a fxed nonzero constant, and c s the constant dstngushng the dfferent curves n the gven famly. In each case, fnd the equaton of the orthogonal trajectores. Curve of gven famly Fgure 1.1.6: Oblque trajectores ntersectng at an angle a.
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Physics 207: Lecture 20. Today s Agenda Homework for Monday
 Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
Formulas for the Determinant
 page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
Chapter 8. Potential Energy and Conservation of Energy
 Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
χ x B E (c) Figure 2.1.1: (a) a material particle in a body, (b) a place in space, (c) a configuration of the body
 Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Work is the change in energy of a system (neglecting heat transfer). To examine what could
 Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
THE VIBRATIONS OF MOLECULES II THE CARBON DIOXIDE MOLECULE Student Instructions
 THE VIBRATIONS OF MOLECULES II THE CARBON DIOXIDE MOLECULE Student Instructons by George Hardgrove Chemstry Department St. Olaf College Northfeld, MN 55057 hardgrov@lars.acc.stolaf.edu Copyrght George
THE VIBRATIONS OF MOLECULES II THE CARBON DIOXIDE MOLECULE Student Instructons by George Hardgrove Chemstry Department St. Olaf College Northfeld, MN 55057 hardgrov@lars.acc.stolaf.edu Copyrght George
Iterative General Dynamic Model for Serial-Link Manipulators
 EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
11. Dynamics in Rotating Frames of Reference
 Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
MATH 5630: Discrete Time-Space Model Hung Phan, UMass Lowell March 1, 2018
 MATH 5630: Dscrete Tme-Space Model Hung Phan, UMass Lowell March, 08 Newton s Law of Coolng Consder the coolng of a well strred coffee so that the temperature does not depend on space Newton s law of collng
MATH 5630: Dscrete Tme-Space Model Hung Phan, UMass Lowell March, 08 Newton s Law of Coolng Consder the coolng of a well strred coffee so that the temperature does not depend on space Newton s law of collng
ACTM State Calculus Competition Saturday April 30, 2011
 ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
A particle in a state of uniform motion remain in that state of motion unless acted upon by external force.
 The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
Celestial Mechanics. Basic Orbits. Why circles? Tycho Brahe. PHY celestial-mechanics - J. Hedberg
 PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
Physics 2A Chapter 3 HW Solutions
 Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Kinematics in 2-Dimensions. Projectile Motion
 Knematcs n -Dmensons Projectle Moton A medeval trebuchet b Kolderer, c1507 http://members.net.net.au/~rmne/ht/ht0.html#5 Readng Assgnment: Chapter 4, Sectons -6 Introducton: In medeval das, people had
Knematcs n -Dmensons Projectle Moton A medeval trebuchet b Kolderer, c1507 http://members.net.net.au/~rmne/ht/ht0.html#5 Readng Assgnment: Chapter 4, Sectons -6 Introducton: In medeval das, people had
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Lecture Note 3. Eshelby s Inclusion II
 ME340B Elastcty of Mcroscopc Structures Stanford Unversty Wnter 004 Lecture Note 3. Eshelby s Incluson II Chrs Wenberger and We Ca c All rghts reserved January 6, 004 Contents 1 Incluson energy n an nfnte
ME340B Elastcty of Mcroscopc Structures Stanford Unversty Wnter 004 Lecture Note 3. Eshelby s Incluson II Chrs Wenberger and We Ca c All rghts reserved January 6, 004 Contents 1 Incluson energy n an nfnte
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
Study Guide For Exam Two
 Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Difference Equations
 Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
n α j x j = 0 j=1 has a nontrivial solution. Here A is the n k matrix whose jth column is the vector for all t j=0
 MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
CHAPTER 6. LAGRANGE S EQUATIONS (Analytical Mechanics)
 CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
PHYS 705: Classical Mechanics. Newtonian Mechanics
 1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
Supplemental Instruction sessions next week
 Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
AP Physics 1 & 2 Summer Assignment
 AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
Introduction to Vapor/Liquid Equilibrium, part 2. Raoult s Law:
 CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
Open Systems: Chemical Potential and Partial Molar Quantities Chemical Potential
 Open Systems: Chemcal Potental and Partal Molar Quanttes Chemcal Potental For closed systems, we have derved the followng relatonshps: du = TdS pdv dh = TdS + Vdp da = SdT pdv dg = VdP SdT For open systems,
Open Systems: Chemcal Potental and Partal Molar Quanttes Chemcal Potental For closed systems, we have derved the followng relatonshps: du = TdS pdv dh = TdS + Vdp da = SdT pdv dg = VdP SdT For open systems,
Motion in One Dimension
 Moton n One Dmenson Speed ds tan ce traeled Aerage Speed tme of trael Mr. Wolf dres hs car on a long trp to a physcs store. Gen the dstance and tme data for hs trp, plot a graph of hs dstance ersus tme.
Moton n One Dmenson Speed ds tan ce traeled Aerage Speed tme of trael Mr. Wolf dres hs car on a long trp to a physcs store. Gen the dstance and tme data for hs trp, plot a graph of hs dstance ersus tme.
Physics 207 Lecture 13. Lecture 13
 Physcs 07 Lecture 3 Goals: Lecture 3 Chapter 0 Understand the relatonshp between moton and energy Defne Potental Energy n a Hooke s Law sprng Develop and explot conservaton of energy prncple n problem
Physcs 07 Lecture 3 Goals: Lecture 3 Chapter 0 Understand the relatonshp between moton and energy Defne Potental Energy n a Hooke s Law sprng Develop and explot conservaton of energy prncple n problem
Please initial the statement below to show that you have read it
 EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
Advanced Circuits Topics - Part 1 by Dr. Colton (Fall 2017)
 Advanced rcuts Topcs - Part by Dr. olton (Fall 07) Part : Some thngs you should already know from Physcs 0 and 45 These are all thngs that you should have learned n Physcs 0 and/or 45. Ths secton s organzed
Advanced rcuts Topcs - Part by Dr. olton (Fall 07) Part : Some thngs you should already know from Physcs 0 and 45 These are all thngs that you should have learned n Physcs 0 and/or 45. Ths secton s organzed
LAB # 4 - Torque. d (1)
 LAB # 4 - Torque. Introducton Through the use of Newton's three laws of moton, t s possble (n prncple, f not n fact) to predct the moton of any set of partcles. That s, n order to descrbe the moton of
LAB # 4 - Torque. Introducton Through the use of Newton's three laws of moton, t s possble (n prncple, f not n fact) to predct the moton of any set of partcles. That s, n order to descrbe the moton of
For all questions, answer choice E) NOTA" means none of the above answers is correct.
 0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
EN40: Dynamics and Vibrations. Homework 7: Rigid Body Kinematics
 N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
The classical spin-rotation coupling
 LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
Module 14: THE INTEGRAL Exploring Calculus
 Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
( ) = ( ) + ( 0) ) ( )
 EETOMAGNETI OMPATIBIITY HANDBOOK 1 hapter 9: Transent Behavor n the Tme Doman 9.1 Desgn a crcut usng reasonable values for the components that s capable of provdng a tme delay of 100 ms to a dgtal sgnal.
EETOMAGNETI OMPATIBIITY HANDBOOK 1 hapter 9: Transent Behavor n the Tme Doman 9.1 Desgn a crcut usng reasonable values for the components that s capable of provdng a tme delay of 100 ms to a dgtal sgnal.
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE
 CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE Analytcal soluton s usually not possble when exctaton vares arbtrarly wth tme or f the system s nonlnear. Such problems can be solved by numercal tmesteppng
CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE Analytcal soluton s usually not possble when exctaton vares arbtrarly wth tme or f the system s nonlnear. Such problems can be solved by numercal tmesteppng
Unit 5: Quadratic Equations & Functions
 Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
GAUTENG DEPARTMENT OF EDUCATION SENIOR SECONDARY INTERVENTION PROGRAMME PHYSICAL SCIENCES GRADE 12 SESSION 1 (LEARNER NOTES)
 PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
Physics 106a, Caltech 11 October, Lecture 4: Constraints, Virtual Work, etc. Constraints
 Physcs 106a, Caltech 11 October, 2018 Lecture 4: Constrants, Vrtual Work, etc. Many, f not all, dynamcal problems we want to solve are constraned: not all of the possble 3 coordnates for M partcles (or
Physcs 106a, Caltech 11 October, 2018 Lecture 4: Constrants, Vrtual Work, etc. Many, f not all, dynamcal problems we want to solve are constraned: not all of the possble 3 coordnates for M partcles (or
where v means the change in velocity, and t is the
 1 PHYS:100 LECTURE 4 MECHANICS (3) Ths lecture covers the eneral case of moton wth constant acceleraton and free fall (whch s one of the more mportant examples of moton wth constant acceleraton) n a more
1 PHYS:100 LECTURE 4 MECHANICS (3) Ths lecture covers the eneral case of moton wth constant acceleraton and free fall (whch s one of the more mportant examples of moton wth constant acceleraton) n a more
Spectral Graph Theory and its Applications September 16, Lecture 5
 Spectral Graph Theory and ts Applcatons September 16, 2004 Lecturer: Danel A. Spelman Lecture 5 5.1 Introducton In ths lecture, we wll prove the followng theorem: Theorem 5.1.1. Let G be a planar graph
Spectral Graph Theory and ts Applcatons September 16, 2004 Lecturer: Danel A. Spelman Lecture 5 5.1 Introducton In ths lecture, we wll prove the followng theorem: Theorem 5.1.1. Let G be a planar graph
Physics 207 Lecture 6
 Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
ENGN 40 Dynamics and Vibrations Homework # 7 Due: Friday, April 15
 NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
Chapter 4 The Wave Equation
 Chapter 4 The Wave Equaton Another classcal example of a hyperbolc PDE s a wave equaton. The wave equaton s a second-order lnear hyperbolc PDE that descrbes the propagaton of a varety of waves, such as
Chapter 4 The Wave Equaton Another classcal example of a hyperbolc PDE s a wave equaton. The wave equaton s a second-order lnear hyperbolc PDE that descrbes the propagaton of a varety of waves, such as
Lagrange Multipliers. A Somewhat Silly Example. Monday, 25 September 2013
 Lagrange Multplers Monday, 5 September 013 Sometmes t s convenent to use redundant coordnates, and to effect the varaton of the acton consstent wth the constrants va the method of Lagrange undetermned
Lagrange Multplers Monday, 5 September 013 Sometmes t s convenent to use redundant coordnates, and to effect the varaton of the acton consstent wth the constrants va the method of Lagrange undetermned
ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EQUATION
 Advanced Mathematcal Models & Applcatons Vol.3, No.3, 2018, pp.215-222 ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EUATION
Advanced Mathematcal Models & Applcatons Vol.3, No.3, 2018, pp.215-222 ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EUATION
CHAPTER 4. Vector Spaces
 man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
Physics 4B. Question and 3 tie (clockwise), then 2 and 5 tie (zero), then 4 and 6 tie (counterclockwise) B i. ( T / s) = 1.74 V.
 Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
The equation of motion of a dynamical system is given by a set of differential equations. That is (1)
 Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Week 11: Chapter 11. The Vector Product. The Vector Product Defined. The Vector Product and Torque. More About the Vector Product
 The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
Physics 207: Lecture 27. Announcements
 Physcs 07: ecture 7 Announcements ake-up labs are ths week Fnal hwk assgned ths week, fnal quz next week Revew sesson on Thursday ay 9, :30 4:00pm, Here Today s Agenda Statcs recap Beam & Strngs» What
Physcs 07: ecture 7 Announcements ake-up labs are ths week Fnal hwk assgned ths week, fnal quz next week Revew sesson on Thursday ay 9, :30 4:00pm, Here Today s Agenda Statcs recap Beam & Strngs» What
Physics 141. Lecture 14. Frank L. H. Wolfs Department of Physics and Astronomy, University of Rochester, Lecture 14, Page 1
 Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
Physics 53. Rotational Motion 3. Sir, I have found you an argument, but I am not obliged to find you an understanding.
 Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Mechanics Physics 151
 Mechancs Physcs 151 Lecture 3 Lagrange s Equatons (Goldsten Chapter 1) Hamlton s Prncple (Chapter 2) What We Dd Last Tme! Dscussed mult-partcle systems! Internal and external forces! Laws of acton and
Mechancs Physcs 151 Lecture 3 Lagrange s Equatons (Goldsten Chapter 1) Hamlton s Prncple (Chapter 2) What We Dd Last Tme! Dscussed mult-partcle systems! Internal and external forces! Laws of acton and
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
PHYS 705: Classical Mechanics. Calculus of Variations II
 1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Slide. King Saud University College of Science Physics & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART 2) LECTURE NO.
 Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
NUMERICAL DIFFERENTIATION
 NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
Week 6, Chapter 7 Sect 1-5
 Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
Section 8.1 Exercises
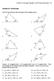 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Canonical transformations
 Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
Spring Force and Power
 Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
Physics for Scientists & Engineers 2
 Equpotental Surfaces and Lnes Physcs for Scentsts & Engneers 2 Sprng Semester 2005 Lecture 9 January 25, 2005 Physcs for Scentsts&Engneers 2 1 When an electrc feld s present, the electrc potental has a
Equpotental Surfaces and Lnes Physcs for Scentsts & Engneers 2 Sprng Semester 2005 Lecture 9 January 25, 2005 Physcs for Scentsts&Engneers 2 1 When an electrc feld s present, the electrc potental has a
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Inductance Calculation for Conductors of Arbitrary Shape
 CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED.
 EE 539 Homeworks Sprng 08 Updated: Tuesday, Aprl 7, 08 DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED. For full credt, show all work. Some problems requre hand calculatons.
EE 539 Homeworks Sprng 08 Updated: Tuesday, Aprl 7, 08 DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED. For full credt, show all work. Some problems requre hand calculatons.
8.592J: Solutions for Assignment 7 Spring 2005
 8.59J: Solutons for Assgnment 7 Sprng 5 Problem 1 (a) A flament of length l can be created by addton of a monomer to one of length l 1 (at rate a) or removal of a monomer from a flament of length l + 1
8.59J: Solutons for Assgnment 7 Sprng 5 Problem 1 (a) A flament of length l can be created by addton of a monomer to one of length l 1 (at rate a) or removal of a monomer from a flament of length l + 1
Mathematical Preparations
 1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
As it can be observed from Fig. a) and b), applying Newton s Law for the tangential force component results into: mg sin mat
 PHY4HF Exercse : Numercal ntegraton methods The Pendulum Startng wth small angles of oscllaton, you wll get expermental data on a smple pendulum and wll wrte a Python program to solve the equaton of moton.
PHY4HF Exercse : Numercal ntegraton methods The Pendulum Startng wth small angles of oscllaton, you wll get expermental data on a smple pendulum and wll wrte a Python program to solve the equaton of moton.
CALCULUS CLASSROOM CAPSULES
 CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
Numerical Heat and Mass Transfer
 Master degree n Mechancal Engneerng Numercal Heat and Mass Transfer 06-Fnte-Dfference Method (One-dmensonal, steady state heat conducton) Fausto Arpno f.arpno@uncas.t Introducton Why we use models and
Master degree n Mechancal Engneerng Numercal Heat and Mass Transfer 06-Fnte-Dfference Method (One-dmensonal, steady state heat conducton) Fausto Arpno f.arpno@uncas.t Introducton Why we use models and
One Dimension Again. Chapter Fourteen
 hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
Physics 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn in the following problems from Chapter 4 Knight
 Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Physics 2A Chapters 6 - Work & Energy Fall 2017
 Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
CSci 6974 and ECSE 6966 Math. Tech. for Vision, Graphics and Robotics Lecture 21, April 17, 2006 Estimating A Plane Homography
 CSc 6974 and ECSE 6966 Math. Tech. for Vson, Graphcs and Robotcs Lecture 21, Aprl 17, 2006 Estmatng A Plane Homography Overvew We contnue wth a dscusson of the major ssues, usng estmaton of plane projectve
CSc 6974 and ECSE 6966 Math. Tech. for Vson, Graphcs and Robotcs Lecture 21, Aprl 17, 2006 Estmatng A Plane Homography Overvew We contnue wth a dscusson of the major ssues, usng estmaton of plane projectve
Foundations of Arithmetic
 Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
For a 1-weight experiment do Part 1. For a 2-weight experiment do Part 1 and Part 2
 Page of 6 THE GYROSCOPE The setup s not connected to a computer. You cannot get measured values drectly from the computer or enter them nto the lab PC. Make notes durng the sesson to use them later for
Page of 6 THE GYROSCOPE The setup s not connected to a computer. You cannot get measured values drectly from the computer or enter them nto the lab PC. Make notes durng the sesson to use them later for
Spring 2002 Lecture #13
 44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
