MASS, STIFFNESS, AND DAMPING MATRICES FROM MEASURED MODAL PARAMETERS
|
|
|
- Tracy Porter
- 6 years ago
- Views:
Transcription
1 IS 74 Inernionl Insrmenion-omion Conference & Exhibi Ocober, 974 MSS, STIFFNESS, ND DMPING MTRICES FROM MESURED MODL PRMETERS Ron Poer nd Mr Richrdson Digil Signl nlysis HEWLETT-PCKRD COMPNY Sn Clr, Cliforni BSTRCT The heory of complex mode shpes for dmped oscillory mechnicl sysems is explined, sing he mrix of rnsfer fncions in he Lplce domin. These mode shpes re defined o be he solions o he homogeneos sysem eqion. I is shown h complee rnsfer mrix cn be consrced once one row or colmn of i hs been mesred, nd hence h mss, siffness, nd dmping mrices corresponding o lmped eqivlen model of he esed srcre cn lso be obined from he mesred d. INTRODUCTION In recen yers, here hs been considerble civiy in he sdy of elsic srcre dynmics,. in n emp o design srcres h will fncion properly in hosile vibrion environmen. lhogh mch of he erly wor cenered rond fige nd life esing, he les effors hve been direced owrds nlyicl modeling nd simlion of mechnicl srcres. Disribed srcres re generlly modeled s newors of lmped mechnicl elemens, in n effor o predic filres more relibly nd fser hn is fforded by convenionl life esing procedres. Wih he dven of he inexpensive mini-comper, nd comping echniqes sch s he Fs Forier Trnsform lgorihm, i is now relively esy o obin fs, ccre, nd complee mesremens of he behvior of mechnicl srcres in vrios vibrion environmens. Modl responses of mny modes cn be mesred simlneosly nd complex mode shpes cn be direcly idenified insed of relying pon nd being consrined by he so clled "norml mode" concep. Frhermore, he enire sysem response mrix, which comprises he mss, siffness, nd dmping mrices of he lmped eqivlen model, cn be mesred. The following meril covers he heoreicl bcgrond h is needed o ndersnd hese new mesremen echniqes. COMPLEX MODES ND THE TRNSFER MTRIX Le's ssme h he moion of liner physicl sysem cn be described by se of n simlneos second order liner differenil eqions in he ime domin, given by Mx && + Cx& + Kx = f ( where he dos denoe differeniion wih respec o ime. f = f( is he pplied force vecor, nd x = x( is he resling displcemen vecor, while M, C, nd K re he (n by n mss, dmping, nd siffness mrices respecively. In his discssion, or enion will be limied o symmeric mrices, nd o rel elemen vles in M, C, nd K. Ting he Lplce rnsform of he sysem eqions gives B( s X( s = F( s, where ( B( s = Ms + Cs + K Here, s is he Lplce vrible, nd now F(s is he pplied force vecor nd X(s is he resling displcemen vecor in he Lplce domin. B(s is clled he sysem mrix, nd he rnsfer mrix H(s is defined s H( s = B( s which implies h (3 (4 H( s F( s = X( s (5 Ech elemen of he rnsfer mrix is rnsfer fncion. The elemens of B re qdric fncions of s, nd since B, i follows h he elemens of H re rionl frcions in s, wih de(b s he denominor. Ths, H(s cn lwys be represened in pril frcion form. If i is ssmed h he poles of H, i.e. he roos of de(b =, re of ni mlipliciy, hen H cn be expressed s = s s (n by n (6 Pge -
2 IS 74 Inernionl Insrmenion-omion Conference & Exhibi Ocober, 974 The poles occr s = s (zeros of de B, nd ech pole hs n (n x n reside mrix describing is spil behvior. For n n h order oscillory sysem, here will lwys be poles, b hey will pper in complex conjge pirs. The poles re complex nmbers expressed s s = σ + i ω (7 where σ is he dmping coefficien ( negive nmber for sble sysems, nd ω is he nrl freqency of oscillion. The resonn freqency is given by ω = σ + ω r nd he dmping fcor is σ ς = ω r rd/sec (8 In reference [], modl vecors were derived in erms of he eigenvecors of he sysem mrix B. However, hese eigenvecors were only inrodced s n inermediry in he deerminion of modl vecors. Here, he modl vecors re described in erms of he B mrix. Pre-mliplying B imes he expression for H, mliplying by he sclr ( s s, nd leing s = s gives (9 B =, where B = B( s ( Similrly, pos-mliplicion of H by B gives B = ( Ths, ll rows nd colmns of ms comprise liner combinion of homogeneos solion vecors, given by B = ( These homogeneos solion vecors re defined s modl (or mode shpe vecors ssocied wih he pole s =. s Resricing or enion o he specil cse where only one modl vecor exiss for ech pole, i is cler h ll rows nd colmns of ms be some sclr mliple of. Ths, cn be represened by = (n by n (3 where is sclr. In hese erms, H cn be rewrien s = s s nd his is esily wrien in mrix form s (4 θλ θ (n by n (5 where he colmns of θ comprise he modl vecors: θ = (n by (6 nd λ is digonl mrix conining ll s dependence: s s λ = s s,( x (7 Pre-mliplying H by θ, eqion (5 cn be wrien s ( θ θλ ( θ = ( θ so h θ F X (8 rnsforms he spil vecors (F nd X o vecors θ F nd θ X in modl coordines. Similrly ( θ θλ ' is he modl represenion of H. Since B( s = i follows h B( s =, so he modl vecor ssocied wih he conjge pole ( s is (, (he conjge of. Ths, he bove θ mrix lwys conins conjge pirs of modl vecors nd he λ mrix lwys conins elemens corresponding o conjge pole pirs long is digonl. If poles re prely imginry (zero dmping hen ll modl vecors re rel, so only hlf of θ is needed. Oherwise θ is recnglr (n x nd conseqenly, even hogh H cn be wrien in digonl form sing he θ mrix, is inverse B cnno be digonlized sing θ excep in he specil cse when dmping is zero. Pge -
3 IS 74 Inernionl Insrmenion-omion Conference & Exhibi Ocober, 974 IDENTIFICTION OF MODL PRMETERS Becse of he form of he mrix, only one row or colmn of he rnsfer mrix need be mesred nd nlyzed, since ll oher rows nd colmns conin redndn informion. In he process of mesring he rnsfer mrix, nnown prmeers in eqion (4, i.e. he complex vles of s nd he complex vles of he elemens of one row or colmn of re idenified. For exmple, he q h colmn of is given by q = = where q is he q h q q (9 elemen of. Ths he modl vecor (whose normlizion is rbirry cn be recovered once he q h colmn of is idenified. In ddiion he complex sclr cn be recovered sing he forml = q q q ( I is cler h he nmericl vle of depends pon he normlizion of he modl vecor. If we choose =, hen = q q q ( Since complex modl vecors pper in conjge pirs, H cn lwys be wrien in wo prs s n = s s + s s For he h pir of conjge poles, H = + s s s s ( (3 Ech pole of he rnsfer mrix hs corresponding mode shpe vecor nd, frhermore, ech complex conjge pir of poles hs corresponding complex conjge pir of mode shpes. The pq h elemen of H is H = + s s s s pq p q p q (4 The ime domin displcemen poin p de o n implsive force poin q is given by he inverse Lplce rnsform of H pq which is s h pq ( = e + e for. σ = e p q [ ( p q Re cos( ω p q ( p q sin( ω ] Im s = e σ cos( ω + α (5 p q Noe h he pe mplide of he implse response is p q complex reside nd he phse ngle ( α is he ngle of he p q wih respec cosine. The mgnide nd phse of his complex reside re differen, in generl, for ech spil poin on he srcre. MSS, STIFFNESS, ND DMPING MTRICES Recll h B( s = Ms + Cs + K, so i is ppren h K = B( = H( (6 Now, H( is obined by seing s = in λ. modl complince κ cn be defined s So κ = λ ( = s K = H( = θκ ( θκ θ s ( x (7 (8 Pge - 3
4 IS 74 Inernionl Insrmenion-omion Conference & Exhibi Ocober, 974 Ths, he siffness mrix is redily obined from he mesred modl vecors (colmns of θ, nd he idenified nd s complex sclrs. Since HB i follows h nd = I (9 HB' + H' B = (3 HB'' + H' B' + H'' B = (3 where he prime denoes differeniion wih respec o s. The dmping mrix cn be comped wih he following relionship C = B'( = B( H'( B( = KH'( K (3 Or lernively by defining he modl dmping mrix δ s δ = hen nd n ( H'( = θ λ '( θ = θκ ( x (33 δκ θ (34 ( θκ δ( θκ C = K K In similr mnner, we cn wrie (35 M = B''( = B( H'( B'( B( H''( B( = KH'( C KH''( K (36 B H"( cn be wrien s H''( = θκ δκ δκ θ (37 Finlly, he mss mrix cn be obined from ( θκ ( δκ δ( θκ + ( Kθκ δκ θ C ( θκ ( δκ δ( θκ M = K K = K K + CK C Now, from he expression for K, we obin Kθκ ( θκ (38 = θκ θ θκ = θ (39 where θ is he lef-hnded inverse of θ defined by θ θ = I (4 To smmrize, he siffness, dmping, nd mss mrices re obined from he expressions ( θκ K = θκ θ = θ κθ C = θ δθ M = θ µθ + CK C where µ = δκ δ (4 (4 (43 (digonl (44 ll of hese qniies re redily obined from he mesred poles s, sclrs, nd modl vecors. COMMENTRY The fndmenl nre of complex modes in he rel world of mesremen cnno be over-emphsized. Dmping is lwys presen in srcre, nd i cn lwys be observed in mesred rnsfer fncion d. The fc h complex mode implies complex ime wveform shold be of lile concern, becse he conjge wveform is lwys presen o me he observed signl rel vled. complex mode hs he chrcer of "rveling wve" cross he srcre (s opposed o he sl "snding wve" prodced by norml mode s indiced by he chnging phse ngle of he displcemen from poin o poin. Frhermore, i is imporn o noe h mode shpe sill globl (s opposed o locl propery of srcre, even hogh dmping my be hevy. The fc h locl moion ner he poin of exciion in hevily dmped srcre Pge - 4
5 IS 74 Inernionl Insrmenion-omion Conference & Exhibi Ocober, 974 ends o domine is generlly csed by mny closely spced modes h re excied in phse his poin, b end o cncel ech oher elsewhere. Hisoriclly, considerble emphsis hs been plced on simlneosly digonlizing he mss nd siffness mrices, so h he displcemen of priclr poin cold be esily clcled from n rbirry exciion force. Unfornely, i is no possible o simlneosly digonlize more hn wo symmeric mrices, so his echniqe cnno be sed when dmping is presen. However, when sysem is represened by he pril frcion form of is rnsfer mrix, closed form solion for he displcemen ny poin, for ny combinion of modes, is redily obinble sing simple mrix-vecor mliplicion. This is priclrly helpfl when he response o only few modes is of ineres. The definiion of modl vecor s solion o he homogeneos sysem eqion is lso very fndmenl, nd removes mch of he mbigiy bo wh modl vecors relly re, nd when hey exis. This definiion lso mes hem relively esy o clcle or mesre. I shold be ppren from he eqions for obining mss, dmping, nd siffness from mesred d, h he order of hese mrices is eql o he nmber of complex modl pirs h re mesred. This mens h if n modes re idenified, only n spil poins re needed o represen he lmped eqivlen model of he physicl sysem. This resl cn be sed s he following heorem. SPTIL SMPLING THEOREM: lmped sysem modeled wih second order elemens hs excly poles n modl vecors. Ths, if only n modl pirs re fond, here is no need for more hn n spil poins in he lmped model. Finlly, he scope of his discssion hs been limied o symmeric mrices hving disinc poles (ni mlipliciy in complex conjge pirs. Even hogh hese ssmpions re sisfied by lrge mjoriy of he liner sysems esed, modes of vibrion cn sill be defined when ll of hese ssmpions re relxed, nd we hve wored o he heory for his generl cse. The rnsfer mrix (inverse of sysem mrix ws inrodced, nd i ws wrien in pril frcion form, comprising one erm for ech pole. We fond h he rows nd colmns of he reside mrix ssocied wih ech pole re mliples of he corresponding modl vecor. The modl mrix θ, whose colmns re he modl vecors, ws defined, nd i ws shown h θ will rnsform vecor from spil coordines o modl coordines. Finlly, we derived expressions for mss siffness, nd dmping in erms of he poles nd modl vecors, nd indiced how mesred prmeers cn be sed o clcle hese mrices. REFERENCES. Richrdson, M. nd Poer, R., "Idenificion of he Modl Properies,of n Elsic Srcre from Mesred Trnsfer Fncion D", h Inernionl Insrmenion Symposim, lbqerqe, New Mexico, My -3, Thoren,.R., "Derivion of Mss nd Siffness Mrices from Dynmic Tes D", I4 pper 7-346, 3'Ln Srcres, Srcrl Dynmics, nd Merils Conference, Sn nonio, Texs, pril, Rbinsein, M.F., "Srcrl Sysems -Sics; Dynmics nd Sbiliy", Prenice-Hll, Inc., Englewood Cliffs, New Jersey, 97. SUMMRY We hve defined he complex modl (mode shpe vecor ssocied wih ech pole (zero of he sysem deerminn of n elsic mechnicl sysem s he homogeneos solion o he sysem eqions. We hve lso emphsized h hese poles occr in complex conjge pirs, nd h he wo ssocied modl vecors re lso conjges of one noher. Pge - 5
15/03/1439. Lecture 4: Linear Time Invariant (LTI) systems
 Lecre 4: Liner Time Invrin LTI sysems 2. Liner sysems, Convolion 3 lecres: Implse response, inp signls s coninm of implses. Convolion, discree-ime nd coninos-ime. LTI sysems nd convolion Specific objecives
Lecre 4: Liner Time Invrin LTI sysems 2. Liner sysems, Convolion 3 lecres: Implse response, inp signls s coninm of implses. Convolion, discree-ime nd coninos-ime. LTI sysems nd convolion Specific objecives
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
1. Find a basis for the row space of each of the following matrices. Your basis should consist of rows of the original matrix.
 Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
I = I = I for this case of symmetry about the x axis, we find from
 8-5. THE MOTON OF A TOP n his secion, we shll consider he moion of n xilly symmeric body, sch s op, which hs fixed poin on is xis of symmery nd is ced pon by niform force field. The op ws chosen becse
8-5. THE MOTON OF A TOP n his secion, we shll consider he moion of n xilly symmeric body, sch s op, which hs fixed poin on is xis of symmery nd is ced pon by niform force field. The op ws chosen becse
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
Available online at Pelagia Research Library. Advances in Applied Science Research, 2011, 2 (3):
 Avilble online www.pelgireserchlibrry.com Pelgi Reserch Librry Advnces in Applied Science Reserch 0 (): 5-65 ISSN: 0976-860 CODEN (USA): AASRFC A Mhemicl Model of For Species Syn-Ecosymbiosis Comprising
Avilble online www.pelgireserchlibrry.com Pelgi Reserch Librry Advnces in Applied Science Reserch 0 (): 5-65 ISSN: 0976-860 CODEN (USA): AASRFC A Mhemicl Model of For Species Syn-Ecosymbiosis Comprising
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Solutions for Nonlinear Partial Differential Equations By Tan-Cot Method
 IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
SOME USEFUL MATHEMATICS
 SOME USEFU MAHEMAICS SOME USEFU MAHEMAICS I is esy o mesure n preic he behvior of n elecricl circui h conins only c volges n currens. However, mos useful elecricl signls h crry informion vry wih ime. Since
SOME USEFU MAHEMAICS SOME USEFU MAHEMAICS I is esy o mesure n preic he behvior of n elecricl circui h conins only c volges n currens. However, mos useful elecricl signls h crry informion vry wih ime. Since
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
3D Transformations. Computer Graphics COMP 770 (236) Spring Instructor: Brandon Lloyd 1/26/07 1
 D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
( ) 2 a b ab. To do this, we are to use the Ricci identity (which we use to evaluate the RHS) and the properties of the Lie derivative.
 Exercise [9.6] This exercise sks s o show h he ccelerion of n (infiniesiml volme mesre V long he worlline he volme s cener e o he effecs of spceime crvre is given by: D V = R V ( b b To o his, we re o
Exercise [9.6] This exercise sks s o show h he ccelerion of n (infiniesiml volme mesre V long he worlline he volme s cener e o he effecs of spceime crvre is given by: D V = R V ( b b To o his, we re o
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
RESPONSE UNDER A GENERAL PERIODIC FORCE. When the external force F(t) is periodic with periodτ = 2π
 RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
1 jordan.mcd Eigenvalue-eigenvector approach to solving first order ODEs. -- Jordan normal (canonical) form. Instructor: Nam Sun Wang
 jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
Procedia Computer Science
 Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
An Integral Two Space-Variables Condition for Parabolic Equations
 Jornl of Mhemics nd Sisics 8 (): 85-9, ISSN 549-3644 Science Pblicions An Inegrl Two Spce-Vribles Condiion for Prbolic Eqions Mrhone, A.L. nd F. Lkhl Deprmen of Mhemics, Lborory Eqions Differenielles,
Jornl of Mhemics nd Sisics 8 (): 85-9, ISSN 549-3644 Science Pblicions An Inegrl Two Spce-Vribles Condiion for Prbolic Eqions Mrhone, A.L. nd F. Lkhl Deprmen of Mhemics, Lborory Eqions Differenielles,
2IV10/2IV60 Computer Graphics
 I0/I60 omper Grphics Eminion April 6 0 4:00 7:00 This eminion consis of for qesions wih in ol 6 sqesion. Ech sqesion weighs eqll. In ll cses: EXPLAIN YOUR ANSWER. Use skeches where needed o clrif or nswer.
I0/I60 omper Grphics Eminion April 6 0 4:00 7:00 This eminion consis of for qesions wih in ol 6 sqesion. Ech sqesion weighs eqll. In ll cses: EXPLAIN YOUR ANSWER. Use skeches where needed o clrif or nswer.
Systems Variables and Structural Controllability: An Inverted Pendulum Case
 Reserch Journl of Applied Sciences, Engineering nd echnology 6(: 46-4, 3 ISSN: 4-7459; e-issn: 4-7467 Mxwell Scienific Orgniion, 3 Submied: Jnury 5, 3 Acceped: Mrch 7, 3 Published: November, 3 Sysems Vribles
Reserch Journl of Applied Sciences, Engineering nd echnology 6(: 46-4, 3 ISSN: 4-7459; e-issn: 4-7467 Mxwell Scienific Orgniion, 3 Submied: Jnury 5, 3 Acceped: Mrch 7, 3 Published: November, 3 Sysems Vribles
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
Think of the Relationship Between Time and Space Again
 Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
A MATHEMATICAL MODEL OF FOUR SPECIES SYN-ECOSYMBIOSIS COMPRISING OF PREY-PREDATION, MUTUALISM AND COMMENSALISMS-I (FULLY WASHED OUT STATE)
 VOL. 6, NO. 4, APRIL 0 ISSN 89-6608 ARPN Jornl of Engineering nd Applied Sciences 006-0 Asin Reserch Pblishing Nework (ARPN). All righs reserved. www.rpnjornls.com A MATHEMATICAL MODEL OF FOUR SPECIES
VOL. 6, NO. 4, APRIL 0 ISSN 89-6608 ARPN Jornl of Engineering nd Applied Sciences 006-0 Asin Reserch Pblishing Nework (ARPN). All righs reserved. www.rpnjornls.com A MATHEMATICAL MODEL OF FOUR SPECIES
R. I. Badran Solid State Physics
 I Bdrn Solid Stte Physics Crystl vibrtions nd the clssicl theory: The ssmption will be mde to consider tht the men eqilibrim position of ech ion is t Brvis lttice site The ions oscillte bot this men position
I Bdrn Solid Stte Physics Crystl vibrtions nd the clssicl theory: The ssmption will be mde to consider tht the men eqilibrim position of ech ion is t Brvis lttice site The ions oscillte bot this men position
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
Matrix Algebra. Matrix Addition, Scalar Multiplication and Transposition. Linear Algebra I 24
 Mtrix lger Mtrix ddition, Sclr Multipliction nd rnsposition Mtrix lger Section.. Mtrix ddition, Sclr Multipliction nd rnsposition rectngulr rry of numers is clled mtrix ( the plurl is mtrices ) nd the
Mtrix lger Mtrix ddition, Sclr Multipliction nd rnsposition Mtrix lger Section.. Mtrix ddition, Sclr Multipliction nd rnsposition rectngulr rry of numers is clled mtrix ( the plurl is mtrices ) nd the
Particle Filtering. CSE 473: Artificial Intelligence Particle Filters. Representation: Particles. Particle Filtering: Elapse Time
 CSE 473: Arificil Inelligence Pricle Filers Dieer Fo Universiy of Wshingon [Mos slides were creed by Dn Klein nd Pieer Abbeel for CS88 Inro o AI UC Berkeley. All CS88 merils re vilble h://i.berkeley.ed.]
CSE 473: Arificil Inelligence Pricle Filers Dieer Fo Universiy of Wshingon [Mos slides were creed by Dn Klein nd Pieer Abbeel for CS88 Inro o AI UC Berkeley. All CS88 merils re vilble h://i.berkeley.ed.]
Flow Networks Alon Efrat Slides courtesy of Charles Leiserson with small changes by Carola Wenk. Flow networks. Flow networks CS 445
 CS 445 Flow Nework lon Efr Slide corey of Chrle Leieron wih mll chnge by Crol Wenk Flow nework Definiion. flow nework i direced grph G = (V, E) wih wo diingihed erice: orce nd ink. Ech edge (, ) E h nonnegie
CS 445 Flow Nework lon Efr Slide corey of Chrle Leieron wih mll chnge by Crol Wenk Flow nework Definiion. flow nework i direced grph G = (V, E) wih wo diingihed erice: orce nd ink. Ech edge (, ) E h nonnegie
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
ON A NEW SOLUTION OF FRACTIONAL DIFFERENTIAL EQUATION USING COMPLEX TRANSFORM IN THE UNIT DISK
 Mhemicl Compionl pplicions Vol 9 No pp 5-6 4 ON NEW SOLUTION OF FRCTIONL IFFERENTIL EQUTION USING COMPLEX TRNSFORM IN THE UNIT ISK Rbh W Ibrhim Mslin rs Insie of Mhemicl Sciences Universiy Mly 563 Kl Lmpr
Mhemicl Compionl pplicions Vol 9 No pp 5-6 4 ON NEW SOLUTION OF FRCTIONL IFFERENTIL EQUTION USING COMPLEX TRNSFORM IN THE UNIT ISK Rbh W Ibrhim Mslin rs Insie of Mhemicl Sciences Universiy Mly 563 Kl Lmpr
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Probability, Estimators, and Stationarity
 Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
Location is relative. Coordinate Systems. Which of the following can be described with vectors??
 Locion is relive Coordine Sysems The posiion o hing is sed relive o noher hing (rel or virul) review o he physicl sis h governs mhemicl represenions Reerence oec mus e deined Disnce mus e nown Direcion
Locion is relive Coordine Sysems The posiion o hing is sed relive o noher hing (rel or virul) review o he physicl sis h governs mhemicl represenions Reerence oec mus e deined Disnce mus e nown Direcion
u( t) + K 2 ( ) = 1 t > 0 Analyzing Damped Oscillations Problem (Meador, example 2-18, pp 44-48): Determine the equation of the following graph.
 nlyzing Dmped Oscilltions Prolem (Medor, exmple 2-18, pp 44-48): Determine the eqution of the following grph. The eqution is ssumed to e of the following form f ( t) = K 1 u( t) + K 2 e!"t sin (#t + $
nlyzing Dmped Oscilltions Prolem (Medor, exmple 2-18, pp 44-48): Determine the eqution of the following grph. The eqution is ssumed to e of the following form f ( t) = K 1 u( t) + K 2 e!"t sin (#t + $
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Module 6: LINEAR TRANSFORMATIONS
 Module 6: LINEAR TRANSFORMATIONS. Trnsformtions nd mtrices Trnsformtions re generliztions of functions. A vector x in some set S n is mpped into m nother vector y T( x). A trnsformtion is liner if, for
Module 6: LINEAR TRANSFORMATIONS. Trnsformtions nd mtrices Trnsformtions re generliztions of functions. A vector x in some set S n is mpped into m nother vector y T( x). A trnsformtion is liner if, for
LAPLACE TRANSFORMS. 1. Basic transforms
 LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
S Radio transmission and network access Exercise 1-2
 S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
 Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
MAT 266 Calculus for Engineers II Notes on Chapter 6 Professor: John Quigg Semester: spring 2017
 MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
Summary: Method of Separation of Variables
 Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Par+cle Filtering. CSE 473: Ar+ficial Intelligence Par+cle Filters. Par+cle Filtering: Elapse Time. Representa+on: Par+cles
 CSE 473: Ar+ficil Inelligence Pr+cle Filers Dieer Fo - - - Universiy of Wshingon [Mos slides were creed y Dn Klein nd Pieer Aeel for CS88 Inro o AI UC Berkeley. All CS88 merils re ville ho://i.erkeley.ed.]
CSE 473: Ar+ficil Inelligence Pr+cle Filers Dieer Fo - - - Universiy of Wshingon [Mos slides were creed y Dn Klein nd Pieer Aeel for CS88 Inro o AI UC Berkeley. All CS88 merils re ville ho://i.erkeley.ed.]
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
LAPLACE TRANSFORM OVERCOMING PRINCIPLE DRAWBACKS IN APPLICATION OF THE VARIATIONAL ITERATION METHOD TO FRACTIONAL HEAT EQUATIONS
 Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory and Application to Heat Transfer Model
 Angn, A., e l.: New Frcionl Derivives wih Non-Locl nd THERMAL SCIENCE, Yer 216, Vol. 2, No. 2, pp. 763-769 763 NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory nd Applicion o He
Angn, A., e l.: New Frcionl Derivives wih Non-Locl nd THERMAL SCIENCE, Yer 216, Vol. 2, No. 2, pp. 763-769 763 NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory nd Applicion o He
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
A new model for solving fuzzy linear fractional programming problem with ranking function
 J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chapter 10. Simple Harmonic Motion and Elasticity. Goals for Chapter 10
 Chper 0 Siple Hronic Moion nd Elsiciy Gols or Chper 0 o ollow periodic oion o sudy o siple hronic oion. o sole equions o siple hronic oion. o use he pendulu s prooypicl syse undergoing siple hronic oion.
Chper 0 Siple Hronic Moion nd Elsiciy Gols or Chper 0 o ollow periodic oion o sudy o siple hronic oion. o sole equions o siple hronic oion. o use he pendulu s prooypicl syse undergoing siple hronic oion.
Tax Audit and Vertical Externalities
 T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
IX.2 THE FOURIER TRANSFORM
 Chper IX The Inegrl Trnsform Mehods IX. The Fourier Trnsform November, 7 7 IX. THE FOURIER TRANSFORM IX.. The Fourier Trnsform Definiion 7 IX.. Properies 73 IX..3 Emples 74 IX..4 Soluion of ODE 76 IX..5
Chper IX The Inegrl Trnsform Mehods IX. The Fourier Trnsform November, 7 7 IX. THE FOURIER TRANSFORM IX.. The Fourier Trnsform Definiion 7 IX.. Properies 73 IX..3 Emples 74 IX..4 Soluion of ODE 76 IX..5
Honours Introductory Maths Course 2011 Integration, Differential and Difference Equations
 Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
PARABOLA. moves such that PM. = e (constant > 0) (eccentricity) then locus of P is called a conic. or conic section.
 wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
Transforms II - Wavelets Preliminary version please report errors, typos, and suggestions for improvements
 EECS 3 Digil Signl Processing Universiy of Cliforni, Berkeley: Fll 007 Gspr November 4, 007 Trnsforms II - Wveles Preliminry version plese repor errors, ypos, nd suggesions for improvemens We follow n
EECS 3 Digil Signl Processing Universiy of Cliforni, Berkeley: Fll 007 Gspr November 4, 007 Trnsforms II - Wveles Preliminry version plese repor errors, ypos, nd suggesions for improvemens We follow n
graph of unit step function t
 .5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
.5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
Lecture 3. In this lecture, we will discuss algorithms for solving systems of linear equations.
 Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
An object moving with speed v around a point at distance r, has an angular velocity. m/s m
 Roion The mosphere roes wih he erh n moions wihin he mosphere clerly follow cure phs (cyclones, nicyclones, hurricnes, ornoes ec.) We nee o epress roion quniiely. For soli objec or ny mss h oes no isor
Roion The mosphere roes wih he erh n moions wihin he mosphere clerly follow cure phs (cyclones, nicyclones, hurricnes, ornoes ec.) We nee o epress roion quniiely. For soli objec or ny mss h oes no isor
Neural assembly binding in linguistic representation
 Neurl ssembly binding in linguisic represenion Frnk vn der Velde & Mrc de Kmps Cogniive Psychology Uni, Universiy of Leiden, Wssenrseweg 52, 2333 AK Leiden, The Neherlnds, vdvelde@fsw.leidenuniv.nl Absrc.
Neurl ssembly binding in linguisic represenion Frnk vn der Velde & Mrc de Kmps Cogniive Psychology Uni, Universiy of Leiden, Wssenrseweg 52, 2333 AK Leiden, The Neherlnds, vdvelde@fsw.leidenuniv.nl Absrc.
Non-oscillation of perturbed half-linear differential equations with sums of periodic coefficients
 Hsil nd Veselý Advnces in Difference Equions 2015 2015:190 DOI 10.1186/s13662-015-0533-4 R E S E A R C H Open Access Non-oscillion of perurbed hlf-liner differenil equions wih sums of periodic coefficiens
Hsil nd Veselý Advnces in Difference Equions 2015 2015:190 DOI 10.1186/s13662-015-0533-4 R E S E A R C H Open Access Non-oscillion of perurbed hlf-liner differenil equions wih sums of periodic coefficiens
or the harmonic oscillator s Hamiltonian, ˆ 1 m , (4.2) invite a similar treatment of momentum and coordinate. K. Likharev
 Chper 4. Br-ke Formlism The obecive of his chper is discssion of Dirc s br-ke formlism of qnm mechnics which no onl overcomes some inconveniences of wve mechnics b lso llows nrl descripion of sch inernl
Chper 4. Br-ke Formlism The obecive of his chper is discssion of Dirc s br-ke formlism of qnm mechnics which no onl overcomes some inconveniences of wve mechnics b lso llows nrl descripion of sch inernl
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
A new model for limit order book dynamics
 Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
CHAPTER 2 FUZZY NUMBER AND FUZZY ARITHMETIC
 CHPTER FUZZY NUMBER ND FUZZY RITHMETIC 1 Introdction Fzzy rithmetic or rithmetic of fzzy nmbers is generlistion of intervl rithmetic, where rther thn considering intervls t one constnt level only, severl
CHPTER FUZZY NUMBER ND FUZZY RITHMETIC 1 Introdction Fzzy rithmetic or rithmetic of fzzy nmbers is generlistion of intervl rithmetic, where rther thn considering intervls t one constnt level only, severl
Integral Transform. Definitions. Function Space. Linear Mapping. Integral Transform
 Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
CBSE 2014 ANNUAL EXAMINATION ALL INDIA
 CBSE ANNUAL EXAMINATION ALL INDIA SET Wih Complee Eplnions M Mrks : SECTION A Q If R = {(, y) : + y = 8} is relion on N, wrie he rnge of R Sol Since + y = 8 h implies, y = (8 ) R = {(, ), (, ), (6, )}
CBSE ANNUAL EXAMINATION ALL INDIA SET Wih Complee Eplnions M Mrks : SECTION A Q If R = {(, y) : + y = 8} is relion on N, wrie he rnge of R Sol Since + y = 8 h implies, y = (8 ) R = {(, ), (, ), (6, )}
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
ECE Microwave Engineering. Fall Prof. David R. Jackson Dept. of ECE. Notes 10. Waveguides Part 7: Transverse Equivalent Network (TEN)
 EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
Nonlinear System Modelling: How to Estimate the. Highest Significant Order
 IEEE Insrumenion nd Mesuremen Technology Conference nchorge,, US, - My Nonliner Sysem Modelling: ow o Esime he ighes Significn Order Neophyos Chirs, Ceri Evns nd Dvid Rees, Michel Solomou School of Elecronics,
IEEE Insrumenion nd Mesuremen Technology Conference nchorge,, US, - My Nonliner Sysem Modelling: ow o Esime he ighes Significn Order Neophyos Chirs, Ceri Evns nd Dvid Rees, Michel Solomou School of Elecronics,
CENTRE FOR CENTRAL BANKING STUDIES
 CENTRE FOR CENTRAL BANKING STUDIES ECONOMIC MODELLING AND FORECASTING Recen developmens in srcrl VAR modelling y Hroon Mmz nd Ole Rmmel Cenre for Cenrl Bnking Sdies Bnk of Englnd Ferry 25 ole.rmmel@nkofenglnd.co.k
CENTRE FOR CENTRAL BANKING STUDIES ECONOMIC MODELLING AND FORECASTING Recen developmens in srcrl VAR modelling y Hroon Mmz nd Ole Rmmel Cenre for Cenrl Bnking Sdies Bnk of Englnd Ferry 25 ole.rmmel@nkofenglnd.co.k
4.2 Continuous-Time Systems and Processes Problem Definition Let the state variable representation of a linear system be
 4 COVARIANCE ROAGAION 41 Inrodcion Now ha we have compleed or review of linear sysems and random processes, we wan o eamine he performance of linear sysems ecied by random processes he sandard approach
4 COVARIANCE ROAGAION 41 Inrodcion Now ha we have compleed or review of linear sysems and random processes, we wan o eamine he performance of linear sysems ecied by random processes he sandard approach
Physic 231 Lecture 4. Mi it ftd l t. Main points of today s lecture: Example: addition of velocities Trajectories of objects in 2 = =
 Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
The Finite Element Method for the Analysis of Non-Linear and Dynamic Systems
 Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
The Periodically Forced Harmonic Oscillator
 The Periodiclly Forced Hrmonic Oscilltor S. F. Ellermeyer Kennesw Stte University July 15, 003 Abstrct We study the differentil eqution dt + pdy + qy = A cos (t θ) dt which models periodiclly forced hrmonic
The Periodiclly Forced Hrmonic Oscilltor S. F. Ellermeyer Kennesw Stte University July 15, 003 Abstrct We study the differentil eqution dt + pdy + qy = A cos (t θ) dt which models periodiclly forced hrmonic
ON THE STABILITY OF DELAY POPULATION DYNAMICS RELATED WITH ALLEE EFFECTS. O. A. Gumus and H. Kose
 Mhemicl nd Compuionl Applicions Vol. 7 o. pp. 56-67 O THE STABILITY O DELAY POPULATIO DYAMICS RELATED WITH ALLEE EECTS O. A. Gumus nd H. Kose Deprmen o Mhemics Selcu Universiy 47 Kony Turey ozlem@selcu.edu.r
Mhemicl nd Compuionl Applicions Vol. 7 o. pp. 56-67 O THE STABILITY O DELAY POPULATIO DYAMICS RELATED WITH ALLEE EECTS O. A. Gumus nd H. Kose Deprmen o Mhemics Selcu Universiy 47 Kony Turey ozlem@selcu.edu.r
Physics 116C Solution of inhomogeneous ordinary differential equations using Green s functions
 Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Supplement: Gauss-Jordan Reduction
 Suppleme: Guss-Jord Reducio. Coefficie mri d ugmeed mri: The coefficie mri derived from sysem of lier equios m m m m is m m m A O d he ugmeed mri derived from he ove sysem of lier equios is [ ] m m m m
Suppleme: Guss-Jord Reducio. Coefficie mri d ugmeed mri: The coefficie mri derived from sysem of lier equios m m m m is m m m A O d he ugmeed mri derived from he ove sysem of lier equios is [ ] m m m m
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
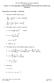 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
1. Consider a PSA initially at rest in the beginning of the left-hand end of a long ISS corridor. Assume xo = 0 on the left end of the ISS corridor.
 In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
Section 14.3 Arc Length and Curvature
 Section 4.3 Arc Length nd Curvture Clculus on Curves in Spce In this section, we ly the foundtions for describing the movement of n object in spce.. Vector Function Bsics In Clc, formul for rc length in
Section 4.3 Arc Length nd Curvture Clculus on Curves in Spce In this section, we ly the foundtions for describing the movement of n object in spce.. Vector Function Bsics In Clc, formul for rc length in
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
State space systems analysis (continued) Stability. A. Definitions A system is said to be Asymptotically Stable (AS) when it satisfies
 Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
Backward Consistency and Sense of Direction in Advanced Distributed Systems (Extended Abstract) Paola Flocchini Universite du Quebec a Hull
 Bckwrd Consisency nd Sense of Direcion in Adnced Disried Sysems (Exended Asrc) Pol Flocchini Uniersie d Qeec Hll (occhini@qh.qeec.c) Alessndro Ronco CDL Informic - Uniersi di Venezi (ronco@dsi.nie.i) Nicol
Bckwrd Consisency nd Sense of Direcion in Adnced Disried Sysems (Exended Asrc) Pol Flocchini Uniersie d Qeec Hll (occhini@qh.qeec.c) Alessndro Ronco CDL Informic - Uniersi di Venezi (ronco@dsi.nie.i) Nicol
Things to Memorize: A Partial List. January 27, 2017
 Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
