Relation of Finite Mellin Integral Transform. with Laplace and Fourier Transforms
|
|
|
- Lindsay Garrison
- 6 years ago
- Views:
Transcription
1 Cotmpo Egiig Si Vol. 4 o Rltio o Fiit Mlli Itgl Tom with Lpl d Foui Tom S. M. Khi R. M. Pi* d J. N. Sluk** Dptmt o Mthmti Mhht Adm o Egiig Aldi-45Pu Idi mkhi7@gmil.om *Dptmt o Mthmti (A.S.&H. R.G.I.T. Vov Adhi (WMumbi-53 Idi pim@dimil.om **Dptmt o Mthmti Noth Mht UivitJlgo-Idi djluk@gmil.om Abtt Th im o thi pp i to div th ltio btw th Fiit Mlli itgl tom with th Lpl tom b uig th doubl Lpl d Foui Fiit Mlli itgl. Popti lik liit popt lig opt pow popt d (xb lo divd. Th hitig d ivio thom o Lpl-Fiit Mlli itgl om d Foui-Fiit Mlli itgl tom lo diud.
2 7 S. M. Khi R. M. Pi d J. N. Sluk Mthmti Subjt Cliitio: 44A 47D3 46FO5 47G3 33C45; 44A35 6D99 Kwod: Lpl Tom Foui Tom Mlli Itgl Tom Fiit Mlli Itgl Tom : Itodutio Th Lpl tom d Foui Tom widl ud o olvig ditil d itgl qutio. I phi d giig it i ud o li o li tim -ivit tm uh ltil iuit hmoi oillto optil dvi d mhil tm. I thi li th Lpl tom i ot itptd tomtio om th tim-domi i whih iput d output utio o tim to th qu-domi wh th m iput d output utio o omplx ul qu i di p uit tim. Giv impl mthmtil o utiol diptio o iput o output to tm. Th Lpl tom povid lttiv utiol diptio tht ot implii th po o lzig th bhvio o th tm o i thizig viw tm bd o t o piitio. Foui Tom i ot u i igl poig. Th tho o itgl h ptd dit d tmti thiqu o th olutio o ti tp o lil boud d iitil vlu poblm.to b uul th tom mut b doptd to th om o th ditil optoto b limitd wll to th g o itt d th oitd boud oditio. Th umou o whih o uitbl tom xit. H w oid Lpl Fiit Mlli itgl tom to th movl o th pol opto tht ou wh Lpl opto i xpd i ith phil o pl pol oodit Th Doubl Lpl Tom b ud to id th Lpl Fiit Mlli Itgl Tom i th g.d. Foui Lpl tom i ud to id th Foui- Fiit Mlli itgl tom i th g.d.
3 Fiit Mlli itgl tom 7 : Plimi Rult.: Rltio O Th Fiit Mlli Itgl Tom With Lpl Tom Th Lpl tom o th utio (x o x i dotd b L(x d did L(x x ( x dx whv thi itgl i xit o > i th pmt Th iv o th Lpl tom i dotd b L ( x ( x did x L ( x ( x L ( x d πi i Th Mlli itgl tom o th utio o ( o i dotd b ( d i did ( ( d whv thi itgl i xit o > pmt. Th ivio o th Mlli itgl tom i dotd b M ( ( d did M ( ( ( d πi i Th Fiit Mlli itgl tom o ( o i dotd b M ( ( i d did M ( ( ( d whv thi itgl i xit o > pmt b uig x lo i th Lpl tom. It iv i dotd b ( M ( d did ` ( M ( M ( d πi i o > whv thi itgl i xit. Th doubl Lpl tom i dotd b L ( x z d did i ( x z L ( x z ( x z dxdz whv thi doubl itgl i xit o > d > pmt. d
4 7 S. M. Khi R. M. Pi d J. N. Sluk Subtitut z -lo th z d dz - i z th d i z th ( x z L ( x z ( x z dxdz x z ( x z dxdz x z ( ( x z dxdz x d ( ( x lo dx( x L ( x z ( x dxd Thi i th ltio btw Fiit Mlli itgl d Lpl tom o (x with pmt > d > i th g ; d i dotd ( x L wh x L ( x ( x dxd ( p x d.: Rltio O Th Fiit Mlli Itgl Tom With Foui Tom Th Foui tom i dotd b F{(xL d b did ix F ( x L ( x dx whv thi itgl i xit. o pmt > Th iv o th Foui Tom i dotd b F ( x ( x i did ix F ( x ( x F ( x d πi whv pmt > i d
5 Fiit Mlli itgl tom 73 Th Mlli Itgl Tom i th ollowig w M ( x x ( x dx α < R( < β wh α d β l umb dtig th mximum g o vlu o R(z uh tht th itgl ovg. Th ivio o th Mlli itgl tom i dotd b M ( ( i d did M ( ( ( d πi Th Fiit Mlli itgl tom o ( o i dotd b M ( ( d did M ( ( ( d whv thi itgl i xit i o > pmt b uig x lo i th Lpl tom. It iv i dotd b ( M ( d did ` ( M ( M ( d πi i o > whv thi itgl i xit. i Th Foui Lpl tom FL ( x z b did z FL ( x z x z (ix ( dxdz whv thi itgl i xit. o pmt > > z d ubtitut z -lo/ dz I z th d i z th lo ix d FL ( x z ( x lo dx(
6 74 S. M. Khi R. M. Pi d J. N. Sluk lo ix d ( x lo dx( ix d ( x lo ( dx( ix FL ( x z ( x dxd Thi i th Foui Fiit Mlli Itgl Tom i i wh i gt th zo (>. Thi itgl i dotd b F ( x.i ; wh ix F ( x ( x dxd ( p x d 3: LEMMAS ( Lpl-Fiit Mlli itgl Tom-LFMIT 3.:Lmm. 3..: Th LFMIT i x L M (x ( x dxd th 3..: L M α (x β x α L M (x β L M x 3..: L M (x L ( M x z Poo x 3..: I L M (x ( x dxd th x L M α (x β x α ( x β x dxd
7 Fiit Mlli itgl tom 75 L M t t α ( x z dtdz β x z dtdz x x α ( x dxd β x dxd α L M (x β L M x α (x β x α L M (x β L m x (3 3..: Th Lpl-Fiit Mlli itgl tom i ubtitut x L M (x ( x dxd th L M (x x ( x dxd z z d z dz I th z d i th z L M (x t ( x ( x dx z dz x ( x z z dxdz L ( M x z L M (x L ( M x z (4 3.:Lmm- Th LFMIT i t L M (t z ( t z z dtdz th 3.. L M (x d L M (tz/ d d 3..:L M (xd p L M *x/d d
8 76 S. M. Khi R. M. Pi d J. N. Sluk Poo 3..:Th Lpl-Fiit Mlli itgl tom i x L M (x ( x dxd th x L M (x d ( x d dxd Subtitut xt d dz th zt/ d z/d dxdt/ d ddz/d I x th tz d i x th t d i th zd L M (x d d d t d ( t z z ( d t ( t z z dtdz d L M (x d L M (tz/ d (5 d 3..: Th Lpl-Fiit Mlli itgl tom i dtdz x L M (x ( x dxd th x L M (xd ( x d( d dxd t ( x dx d d ubtitut xt d dz th xt/ d z/d dxdt/ d ddz/d I x th tz d i x th t d i th zd d t ( t t dt d ( t dt z z( d d z z L(t/zd d L M (xd L M (t/zd (6 d dz d dz
9 Fiit Mlli itgl tom 77 4: LEMMAS ( Foui-Fiit Mlli Itgl Tom-FFMIT 4.: Lmm Lt (x x R ix F ( x ( x dxd th 4..: α ( x β x α F ( x β x F 4..: F ( x F ( x Poo 4.. :Lt (x d x x R d α d β ott th F ix F ( x ( x dxd bom F ix α ( x β x α ( x β x dxd ix ix α x dxd β x dxd ix ix α α ( x dxd β x dxd α F ( x β x F α ( x β x α F ( x β F x (7 4..: Lt (x d x x R d α d β ott th ix F ( x ( x dxd bom ix F ( x ( x dxd Subtitut z z z dz I th z d i th z d F
10 78 S. M. Khi R. M. Pi d J. N. Sluk ix F ( x ( x z ( z dx z dz ( x z ix z dxdz F ( x F ( x p q F ( x (8 4.: Lmm Lt d g b two l vlud utio d ix F ( x ( x dxd th 4..: F ( x d F ( M t z d b 4..: F ( x b F ( v M u b Poo (4.. Lt d g b two l vlud utio th ix F ( x ( x dxd bom ix F ( x d ( x dxd ubtitut I xt xt/ dxdt/ d dz z/d ddz/d i x th tz d i x th t d i th zd F ( x d d d ( t z z ( d it / d ( t z z it / dtdz d F ( M t z d F ( x d p q F ( M t z (9 d 4..: Lt d g b two l vlud utio th dtdz
11 Fiit Mlli itgl tom 79 ix F ( x ( x dxd bom ix F ( x b ( x b dxd ix ( x dx b d I xu xu/ dxdu/ d bv v/b ddv/b I x th uv d x th u d i th vb F ( x b b b F ( x b b ( u b iu / ( u du v ( b du v dv b b iu / dv b F ( u v b F ( u v ( 5. SHIFTING THEOREMS 5. Shitig Thom Fo Lpl-Fiit-Fiit Mlli Itgl Tom Th hitig thom o Lpl- Fiit Mlli itgl tom i Poo I x L M (x ( x dxd th L M bx (x L M (x x L M (x ( x dxd th L M bx bx x (x ( x dxd
12 8 S. M. Khi R. M. Pi d J. N. Sluk L M bx ( x ( x dxd (x L M (x ( 5. Shitig Thom Fo Th Foui-Fiit Mlli Itgl Tom Lt (x b th two vibl utio i x d th th LFMIT i Poo ix F ( x ( x dxd th F ( x F ( x ix I F ( x ( x dxd th ix ix ix F ( x ( x dxd i( x ( x dxd ix F ( x F ( x ( 6: Ivio Thom 6.: Ivio Thom Fo Th Lpl-Fiit Mlli Itgl Tom I th Lpl tom o th utio (x i did L(x >i th pmt th it iv tom i i x ( x dx whv thi itgl i xit x (x L ( x d i. π i Th Mlli itgl tom o ( i to i did
13 Fiit Mlli itgl tom 8 ( p d p> i th pmt.th it ivio omul i i ( ( d πi i o th Lpl- Fiit Mlli tom i d it ivio omul i Poo Aum tht ( d whv thi itgl i xit x L M (x ( x dxd (x i i x L ( x ; dd (πi p ii L M (x ; i gul utio i th tip R( < ( to b l umb o th -pl d tht <<ν -i i wh i ott d R(p < q ( q to b l umb o th p-pl d tht <<ν -i p i wh i ott I th Lpl- Fiit Mlli itgl tom i th x L M (x ( x dxd L M (x x x Lm ( x ; dd (πi x dxd x Lm ( x ; dd (πi x Lm ( x ; dd (πi x dx p x dxd d
14 8 S. M. Khi R. M. Pi d J. N. Sluk x Lm ( x ; dd (πi x L ( x ; dd (πi p A N d N Thi i th ivio o th Lpl-Fiit Mlli itgl tom d it i dotd (x th i i x (x L ( x ; dd ( i (3 π p i 6.: Ivio Thom Fo Th Foui-Fiit Mlli Itgl Tom Lt (x b th two vibl utio i x d th th LFMIT p ix F ( x ( x dxd Th th ivio ult i i i (x F M ix ( x F ( x dd (πi i i i Poo Aum tht ( x i gul utio i th tip F R( < ( b l umb o th -pl d tht <<ν -i i wh i ott d R(p < q ( q b l umb o th p-pl d tht <<ν -i p i wh i ott Lt (x b th two vibl utio i x d th th FFMIT i ix F ( x ( x dxd th ix ix L ( x F ( x dd dxd (πi ix ix F ( x dd dxd (πi
15 Fiit Mlli itgl tom 83 ( ( d dx dd x M F i it ix π it ix i dd x M F i ( ( π ( ( ( dd x M F i ix π ( ( ( i dd x M F i x π dd x M F i i ix ( ( π Thi i th ivio o th Lpl Ftiol Mlli itgl tom i to N d N i dotd b (x ( x M L (x ( x M F dd x M F i i ix i i i i ( ( π (4
16 84 S. M. Khi R. M. Pi d J. N. Sluk 7: TABLES 7.:Lpl Tom Ad Fiit Mlli Itgl Tom Lpl Tom Fiit Mlli Itgl Tom Th Lpl Tom o (x i dotd b L(x d did Th Fiit Mlli itgl tom o th utio o ( o i dotd b L(x ( x dx ( d i did whv thi itgl i xit o > i th pmt ( ( d whv thi itgl i xit o > i th pmt Iv Lpl Tom Iv Fiit Mlli Itgl Tom Th iv o th Lpl tom Th ivio o th Mlli itgl i dotd b L ( x ( x tom i dotd b d did M ( ( L ( x ( x d did M ( ( x L ( x d πi i i ( d πi i
17 Fiit Mlli itgl tom 85 7.: Foui Tom Ad Fiit Mlli itgl Tom Foui Tom Fiit Mlli Itgl Tom Th Foui tom i dotd Th Fiit Mlli itgl tom o b F{(xL d did th utio o ( o i dotd b ( d i did ix F ( x L ( x dx whv thi itgl i xit. o pmt > ( ( d whv thi itgl i xit o > i th pmt Iv Foui Tom Iv Fiit Mlli Itgl Tom Th iv o th Foui Tom Th ivio o th Mlli itgl i dotd b F ( x ( x tom i dotd b d did M ( ( F ( x ( x d did i M ( ( ix F ( x d πi i i ( d whv pmt > πi i 7.3: Rltio btw Fiit Mlli Itgl Tom With Lpl Ad Foui Tom Th Lpl- Fiit Mlli Itgl Tom x L ( x ( x dxd Th Foui- Fiit Mlli Itgl Tom ix F ( x ( x dxd
18 86 S. M. Khi R. M. Pi d J. N. Sluk 7.4: Rltio btw Lpl Tom d Fiit Mlli Itgl Tom Lpl Fiit Mlli Foui-Fiit Mlli Tom Tom Lmm::3.. Lmm:4.. L M α (x β x F α ( x β x α F ( x β F x α L M (x β L m x Lmm:3.. L M (x L ( M x z 3 Lmmq:3.. L M (x d d L M (tz/ d 4 Lmm:3.. L M (xd L M d (t/zd Lmm:4.. F ( x p q F Lmm:4.. F ( x d p q d Lmm:4.. F ( x b b b F ( u v ( x F ( t z
19 Fiit Mlli itgl tom : Shitig Thom Fo Lpl d Foui Tom With Fiit Mlli Itgl Tom Th Shitig Thom o Lpl- Fiit Mlli Itgl Tom L M bx (x L M (x Th Shitig Thom o Foui- Fiit Mlli Itgl Tom ix F ( x F ( x 7.6: Ivio Thom Fo Lpl Ad Foui Tom With Fiit Mlli Itgl Tom Th Iv o Lpl- Fiit Mlli Itgl Tom i i x F(x L ( x ; dd (πi p i Th Iv o Foui- Fiit Mlli Itgl Tom i i (x ix F M ( x F ( x dd (πi i i i R.Dk Nlo O Mlli Tp Itgl Tom Joul o Mthmti d Mhi (963 vol. No.. I N. Sddo Th u o Itgl Tom TMH ditio S. Dod Robut d Eiit Foui-Mlli Tom Appoximtio o G Lvl img Rotutio d Complt ivit Diptio Comput Viio d Img U ( 4.I.S. Rd Th Mlli Tp Doubl Itgl Cmbidg Lodo. 5. Lokth Dbth Itgl Tom Ad Thi Applitio995CRC P I.
20 88 S. M. Khi R. M. Pi d J. N. Sluk 6.D.J. Bdighm Dimiol Rguliztio d Mlli ummtio i High-Tmptu Clultio Thotil Phi Th Blktt Lboto Impil Collg Pi Coot RodSW7 BWUK. A Xiv:ph/x NOV. 7.A. H. Zmi Th Ditibutiol Lpl d Mlli Tomtio J. SIAM Vol.4. No.. J. 98 Pitd i U.S.A. 8..J.M. Mdz d J.R. NgiO th iit Hkl Swhwtz Tomtio o Ditibutio Gt. Vol.39 No C. Fox Applitio o Mlli Tomtio to Itgl Equtio 3 d Mh 934 pp C.Fox Applitio o Mlli Tomtio to th itgl qutio (933. S. M. Khi R.M. Pi & J. N. Sluk Stud o Th Sumudu Mlli Itgl Tom d it Applitio It. J. o Mt. Si. & Egg. Appl. (IJMSEA Vol. 4 No. IV ( Otob. pp Rivd: Apil
Classical Theory of Fourier Series : Demystified and Generalised VIVEK V. RANE. The Institute of Science, 15, Madam Cama Road, Mumbai
 Clssil Thoy o Foi Sis : Dmystii Glis VIVEK V RANE Th Istitt o Si 5 Mm Cm Ro Mmbi-4 3 -mil ss : v_v_@yhoooi Abstt : Fo Rim itgbl tio o itvl o poit thi w i Foi Sis t th poit o th itvl big ot how wh th tio
Clssil Thoy o Foi Sis : Dmystii Glis VIVEK V RANE Th Istitt o Si 5 Mm Cm Ro Mmbi-4 3 -mil ss : v_v_@yhoooi Abstt : Fo Rim itgbl tio o itvl o poit thi w i Foi Sis t th poit o th itvl big ot how wh th tio
APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS
 Intrntionl Journl o Sintii nd Rrh Publition Volum, Iu 5, M ISSN 5-353 APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS S.M.Khirnr, R.M.Pi*, J.N.Slun** Dprtmnt o Mthmti Mhrhtr
Intrntionl Journl o Sintii nd Rrh Publition Volum, Iu 5, M ISSN 5-353 APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS S.M.Khirnr, R.M.Pi*, J.N.Slun** Dprtmnt o Mthmti Mhrhtr
On Gaussian Distribution
 Prpr b Çğt C MTU ltril gi. Dpt. 30 Sprig 0089 oumt vrio. Gui itributio i i ollow O Gui Ditributio π Th utio i lrl poitiv vlu. Bor llig thi utio probbilit it utio w houl h whthr th r ur th urv i qul to
Prpr b Çğt C MTU ltril gi. Dpt. 30 Sprig 0089 oumt vrio. Gui itributio i i ollow O Gui Ditributio π Th utio i lrl poitiv vlu. Bor llig thi utio probbilit it utio w houl h whthr th r ur th urv i qul to
IJRET: International Journal of Research in Engineering and Technology eissn: pissn:
 IJRE: Iiol Joul o Rh i Eii d holo I: 39-63 I: 3-738 VRIE OF IME O RERUIME FOR ILE RDE MOWER EM WI DIFFERE EO FOR EXI D WO E OF DEIIO VI WO REOLD IVOLVI WO OMOE. Rvihd. iiv i oo i Mhi R Eii oll RM ROU ih
IJRE: Iiol Joul o Rh i Eii d holo I: 39-63 I: 3-738 VRIE OF IME O RERUIME FOR ILE RDE MOWER EM WI DIFFERE EO FOR EXI D WO E OF DEIIO VI WO REOLD IVOLVI WO OMOE. Rvihd. iiv i oo i Mhi R Eii oll RM ROU ih
Chapter 3 Higher Order Linear ODEs
 ht High Od i ODEs. Hoogous i ODEs A li qutio: is lld ohoogous. is lld hoogous. Tho. Sus d ostt ultils of solutios of o so o itvl I gi solutios of o I. Dfiitio. futios lld lil iddt o so itvl I if th qutio
ht High Od i ODEs. Hoogous i ODEs A li qutio: is lld ohoogous. is lld hoogous. Tho. Sus d ostt ultils of solutios of o so o itvl I gi solutios of o I. Dfiitio. futios lld lil iddt o so itvl I if th qutio
Order Reduction of Linear High-Order Discrete Time Systems Using Polynomial Differentiation Technique in w-domain and PID Controller Design
 Ittiol Joul of Eltoi Eltil Egiig ISSN 97-7 Volum 5, Num, pp 7-5 Ittiol Rsh Pulitio Hous http://iphousom O Rutio of Li High-O Dist Tim Systms Usig Polyomil Difftitio Thiqu i -Domi PID Cotoll Dsig B Stish
Ittiol Joul of Eltoi Eltil Egiig ISSN 97-7 Volum 5, Num, pp 7-5 Ittiol Rsh Pulitio Hous http://iphousom O Rutio of Li High-O Dist Tim Systms Usig Polyomil Difftitio Thiqu i -Domi PID Cotoll Dsig B Stish
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
CBSE , ˆj. cos CBSE_2015_SET-1. SECTION A 1. Given that a 2iˆ ˆj. We need to find. 3. Consider the vector equation of the plane.
 CBSE CBSE SET- SECTION. Gv tht d W d to fd 7 7 Hc, 7 7 7. Lt,. W ow tht.. Thus,. Cosd th vcto quto of th pl.. z. - + z = - + z = Thus th Cts quto of th pl s - + z = Lt d th dstc tw th pot,, - to th pl.
CBSE CBSE SET- SECTION. Gv tht d W d to fd 7 7 Hc, 7 7 7. Lt,. W ow tht.. Thus,. Cosd th vcto quto of th pl.. z. - + z = - + z = Thus th Cts quto of th pl s - + z = Lt d th dstc tw th pot,, - to th pl.
AN INTEGRO-DIFFERENTIAL EQUATION OF VOLTERRA TYPE WITH SUMUDU TRANSFORM
 Mmic A Vol. 2 22 o. 6 54-547 AN INTGRO-IRNTIAL QUATION O VOLTRRA TYP WITH UMUU TRANORM R Ji cool o Mmic d Allid cic Jiwji Uiviy Gwlio-474 Idi mil - ji3@dimil.com i ig pm o Applid Mmic Ii o Tcology d Mgm
Mmic A Vol. 2 22 o. 6 54-547 AN INTGRO-IRNTIAL QUATION O VOLTRRA TYP WITH UMUU TRANORM R Ji cool o Mmic d Allid cic Jiwji Uiviy Gwlio-474 Idi mil - ji3@dimil.com i ig pm o Applid Mmic Ii o Tcology d Mgm
and integrated over all, the result is f ( 0) ] //Fourier transform ] //inverse Fourier transform
![and integrated over all, the result is f ( 0) ] //Fourier transform ] //inverse Fourier transform and integrated over all, the result is f ( 0) ] //Fourier transform ] //inverse Fourier transform](/thumbs/90/103666297.jpg) NANO 70-Nots Chapt -Diactd bams Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio. Idal cystals a iiit this, so th will b som iiitis lii about. Usually, th iiit quatity oly ists
NANO 70-Nots Chapt -Diactd bams Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio. Idal cystals a iiit this, so th will b som iiitis lii about. Usually, th iiit quatity oly ists
For H. S. Athletes. 49 Boy Scouts Initiated Here
 LD B V L LY L L ( 700 v v v * x Dv L v v B v «v U B v z v v- - - v v v 0 v D U v v v v B X v x v v U v v 0000 v 0000 v x v v U ) YU > v v v v YD L Y x v q -z : v v v v v x v v B L L Y-D LLL Y X L DD UDY
LD B V L LY L L ( 700 v v v * x Dv L v v B v «v U B v z v v- - - v v v 0 v D U v v v v B X v x v v U v v 0000 v 0000 v x v v U ) YU > v v v v YD L Y x v q -z : v v v v v x v v B L L Y-D LLL Y X L DD UDY
Instrumentation for Characterization of Nanomaterials (v11) 11. Crystal Potential
 Istumtatio o Chaactizatio o Naomatials (v). Cystal Pottial Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio om cystal. Idal cystals a iiit this, so th will b som iiitis lii
Istumtatio o Chaactizatio o Naomatials (v). Cystal Pottial Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio om cystal. Idal cystals a iiit this, so th will b som iiitis lii
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS
 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS UNIT-I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Elimit th ritrry ott & from = ( + )(y + ) Awr: = ( + )(y + ) Diff prtilly w.r.to & y hr p & q y p = (y + ) ;
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS UNIT-I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Elimit th ritrry ott & from = ( + )(y + ) Awr: = ( + )(y + ) Diff prtilly w.r.to & y hr p & q y p = (y + ) ;
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS
 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS UNIT-I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Elimit th ritrry ott & from = ( + )(y + ) = ( + )(y + ) Diff prtilly w.r.to & y hr p & q p = (y + ) ; q = ( +
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS UNIT-I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Elimit th ritrry ott & from = ( + )(y + ) = ( + )(y + ) Diff prtilly w.r.to & y hr p & q p = (y + ) ; q = ( +
Chapter 2 Reciprocal Lattice. An important concept for analyzing periodic structures
 Chpt Rcpocl Lttc A mpott cocpt o lyzg podc stuctus Rsos o toducg cpocl lttc Thoy o cystl dcto o x-ys, utos, d lctos. Wh th dcto mxmum? Wht s th tsty? Abstct study o uctos wth th podcty o Bvs lttc Fou tsomto.
Chpt Rcpocl Lttc A mpott cocpt o lyzg podc stuctus Rsos o toducg cpocl lttc Thoy o cystl dcto o x-ys, utos, d lctos. Wh th dcto mxmum? Wht s th tsty? Abstct study o uctos wth th podcty o Bvs lttc Fou tsomto.
Helping Kids Prepare For Life (253)
 Hlpi Ki Pp F Lif.l.i. (253)-589-7489 Tilli it it L Livit iv f fiv CIS U H. Vip pt fll t Tilli Elt l tpi tff tt f vi t t CIS T Hll f i Cltt N Cli. - L ivi i CIS f Bill Milli CIS pit Dil Cili Ti l iz it
Hlpi Ki Pp F Lif.l.i. (253)-589-7489 Tilli it it L Livit iv f fiv CIS U H. Vip pt fll t Tilli Elt l tpi tff tt f vi t t CIS T Hll f i Cltt N Cli. - L ivi i CIS f Bill Milli CIS pit Dil Cili Ti l iz it
Fourier Transform Methods for Partial Differential Equations
 Itrtiol Jourl o Prtil Dirtil Equtio d Applitio,, Vol, No 3, -57 Avill oli t http://puipuom/ijpd//3/ Si d Edutio Pulihig DOI:69/ijpd--3- Fourir Trorm Mthod or Prtil Dirtil Equtio Nol Tu Ngro * Dprtmt o
Itrtiol Jourl o Prtil Dirtil Equtio d Applitio,, Vol, No 3, -57 Avill oli t http://puipuom/ijpd//3/ Si d Edutio Pulihig DOI:69/ijpd--3- Fourir Trorm Mthod or Prtil Dirtil Equtio Nol Tu Ngro * Dprtmt o
KEB INVERTER L1 L2 L3 FLC - RELAY 1 COMMON I1 - APPROACH CLOSE 0V - DIGITAL COMMON FLA - RELAY 1 N.O. AN1+ - ANALOG 1 (+) CRF - +10V OUTPUT
 XT SSMLY MOL 00 (O FS) 00 (I- PT) 00 (SIGL SLI) WG O 0 0-0 0-0-0 0.0. 0 0-0 0-0-0 0 0-0 0-0-0 VOLTG F.L...0..0..0.0..0 IIG POW FOM US SUPPLI ISOT (S TL) US OP OUTOS T T 0 O HIGH H IUIT POTTIO OT: H IUIT
XT SSMLY MOL 00 (O FS) 00 (I- PT) 00 (SIGL SLI) WG O 0 0-0 0-0-0 0.0. 0 0-0 0-0-0 0 0-0 0-0-0 VOLTG F.L...0..0..0.0..0 IIG POW FOM US SUPPLI ISOT (S TL) US OP OUTOS T T 0 O HIGH H IUIT POTTIO OT: H IUIT
Sight Word Bingo Ladders
 Sigt W Big L Sigt W Big L Slti Tig R p i lik Slti I. gt t pmii t ptp t igt pibl pg f lm. N t pt f t pbliti m b p i l i pt, t i tivl tm, tmitt i b m, lti, mil, ptpig, ig, ti, itt itt pmii f t pbli. F ifmti,
Sigt W Big L Sigt W Big L Slti Tig R p i lik Slti I. gt t pmii t ptp t igt pibl pg f lm. N t pt f t pbliti m b p i l i pt, t i tivl tm, tmitt i b m, lti, mil, ptpig, ig, ti, itt itt pmii f t pbli. F ifmti,
THE LOWELL LEDGER. INDEPENDENT NOT NEUTRAL. NPRAKER BLOCK SOLI)
 D DD U X X 2 U UD U 2 90 x F D D F & U [V U 2 225 00 U D?? - F V D VV U F D «- U 20 -! - - > - U ( >»!( - > ( - - < x V ) - - F 8 F z F < : V - x x F - ) V V ( V x V V x V D 6 0 ( F - V x x z F 5-- - F
D DD U X X 2 U UD U 2 90 x F D D F & U [V U 2 225 00 U D?? - F V D VV U F D «- U 20 -! - - > - U ( >»!( - > ( - - < x V ) - - F 8 F z F < : V - x x F - ) V V ( V x V V x V D 6 0 ( F - V x x z F 5-- - F
Exterior Building Renovations
 xterior Building enovations Fifth treet Henderson, 0 Project : 0-0 ate: J, 0 OPL O L H F O O P L uite 00 outheast hird treet vansville, ndiana 0- :.. F:.. H POJ LOO HH VH OMMOWLH JFF J XH M V OH M FFH
xterior Building enovations Fifth treet Henderson, 0 Project : 0-0 ate: J, 0 OPL O L H F O O P L uite 00 outheast hird treet vansville, ndiana 0- :.. F:.. H POJ LOO HH VH OMMOWLH JFF J XH M V OH M FFH
The Reign of Grace and Life. Romans 5:12-21 (5:12-14, 17 focus)
 Th Rig of Gc d Lif Rom 5:12-21 (5:12-14, 17 focu) Th Ifluc of O h d ud Adolph H J o ph Smith B i t l m t Fid Idi Gdhi Ci Lu Gu ich N itz y l M d i M ch Nlo h Vig T L M uhmmd B m i o t T Ju Chit w I N h
Th Rig of Gc d Lif Rom 5:12-21 (5:12-14, 17 focu) Th Ifluc of O h d ud Adolph H J o ph Smith B i t l m t Fid Idi Gdhi Ci Lu Gu ich N itz y l M d i M ch Nlo h Vig T L M uhmmd B m i o t T Ju Chit w I N h
New Advanced Higher Mathematics: Formulae
 Advcd High Mthmtics Nw Advcd High Mthmtics: Fomul G (G): Fomul you must mmois i od to pss Advcd High mths s thy ot o th fomul sht. Am (A): Ths fomul giv o th fomul sht. ut it will still usful fo you to
Advcd High Mthmtics Nw Advcd High Mthmtics: Fomul G (G): Fomul you must mmois i od to pss Advcd High mths s thy ot o th fomul sht. Am (A): Ths fomul giv o th fomul sht. ut it will still usful fo you to
READ T H E DATE ON LABEL A blue m a r k a r o u n d this notice will call y o u r attention to y o u r LOWELL. MICHIGAN, THURSDAY, AUGUST 29.
 B U D D B < / UDY UU 29 929 VU XXXV Y B 5 2 $25 25 25 U 6 B j 3 $8 D D D VD V D D V D B B % B 2 D - Q 22: 5 B 2 3 Z D 2 5 B V $ 2 52 2 $5 25 25 $ Y Y D - 8 q 2 2 6 Y U DD D D D Y!! B D V!! XU XX D x D
B U D D B < / UDY UU 29 929 VU XXXV Y B 5 2 $25 25 25 U 6 B j 3 $8 D D D VD V D D V D B B % B 2 D - Q 22: 5 B 2 3 Z D 2 5 B V $ 2 52 2 $5 25 25 $ Y Y D - 8 q 2 2 6 Y U DD D D D Y!! B D V!! XU XX D x D
N e w S t u d e n t. C o u n c i l M e n
 ZV. XX L GG L 3 942. 25 J b D b v D G... j z U 6 b Y DY. j b D.. L......&. v b v. z " 6 D". " v b b bv D v.... v z b.. k."... 92... G b 92. b v v b v b D ( 6) z v 27 b b v " z". v b L G. b. v.. v v. D
ZV. XX L GG L 3 942. 25 J b D b v D G... j z U 6 b Y DY. j b D.. L......&. v b v. z " 6 D". " v b b bv D v.... v z b.. k."... 92... G b 92. b v v b v b D ( 6) z v 27 b b v " z". v b L G. b. v.. v v. D
Neutrosophic Hyperideals of Semihyperrings
 Nuooph m Vol. 06 05 Uv o Nw Mo Nuooph Hpl o mhpg D Ml Dpm o Mhm j P Moh Collg Up Hooghl-758 mljumh@gml.om A. h pp w hv ou uooph hpl o mhpg o om opo o hm o u oo pop. Kwo: C Pou Compoo l o Nuooph mhpmg.
Nuooph m Vol. 06 05 Uv o Nw Mo Nuooph Hpl o mhpg D Ml Dpm o Mhm j P Moh Collg Up Hooghl-758 mljumh@gml.om A. h pp w hv ou uooph hpl o mhpg o om opo o hm o u oo pop. Kwo: C Pou Compoo l o Nuooph mhpmg.
CBSE SAMPLE PAPER SOLUTIONS CLASS-XII MATHS SET-2 CBSE , ˆj. cos. SECTION A 1. Given that a 2iˆ ˆj. We need to find
 BSE SMLE ER SOLUTONS LSS-X MTHS SET- BSE SETON Gv tht d W d to fd 7 7 Hc, 7 7 7 Lt, W ow tht Thus, osd th vcto quto of th pl z - + z = - + z = Thus th ts quto of th pl s - + z = Lt d th dstc tw th pot,,
BSE SMLE ER SOLUTONS LSS-X MTHS SET- BSE SETON Gv tht d W d to fd 7 7 Hc, 7 7 7 Lt, W ow tht Thus, osd th vcto quto of th pl z - + z = - + z = Thus th ts quto of th pl s - + z = Lt d th dstc tw th pot,,
MM1. Introduction to State-Space Method
 MM Itroductio to Stt-Spc Mthod Wht tt-pc thod? How to gt th tt-pc dcriptio? 3 Proprty Alyi Bd o SS Modl Rdig Mtril: FC: p469-49 C: p- /4/8 Modr Cotrol Wht th SttS tt-spc Mthod? I th tt-pc thod th dyic
MM Itroductio to Stt-Spc Mthod Wht tt-pc thod? How to gt th tt-pc dcriptio? 3 Proprty Alyi Bd o SS Modl Rdig Mtril: FC: p469-49 C: p- /4/8 Modr Cotrol Wht th SttS tt-spc Mthod? I th tt-pc thod th dyic
Math 234. What you should know on day one. August 28, You should be able to use general principles like. x = cos t, y = sin t, 0 t π.
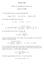 Math 234 What you should know on day one August 28, 2001 1 You should be able to use general principles like Length = ds, Area = da, Volume = dv For example the length of the semi circle x = cos t, y =
Math 234 What you should know on day one August 28, 2001 1 You should be able to use general principles like Length = ds, Area = da, Volume = dv For example the length of the semi circle x = cos t, y =
drawing issue sheet Former Royal High School - Hotel Development
 H Forer oyal High chool - Hotel Developent drawing isse sheet general arrangeents drawing nber drawing title scale size L()1 ite Plan 1:1 / L()1 egent oad level proposed floor plan 1: 1 / L() ntrance level
H Forer oyal High chool - Hotel Developent drawing isse sheet general arrangeents drawing nber drawing title scale size L()1 ite Plan 1:1 / L()1 egent oad level proposed floor plan 1: 1 / L() ntrance level
264m. Raggengill Gilkerscleuch. Abington. 250m. Cottage. Iss. Mast. 246m. TER R AC E 240m OO KE TE H U N TE COLEBROOKE. Over Abington STATION.
 I 4 4 I I L KY t lttio F 9 ott v bito 4 4 F L ii 3 lui 1 p F L F I I 9 F L I LK i i tip i 9 6 v bito U l K L 6 ott bito i 5 1 5 9 i oo 8 4 6 otl it o ov b i o 116-3 ott 6 i i ollt u o v bito 4 lo i 6 v
I 4 4 I I L KY t lttio F 9 ott v bito 4 4 F L ii 3 lui 1 p F L F I I 9 F L I LK i i tip i 9 6 v bito U l K L 6 ott bito i 5 1 5 9 i oo 8 4 6 otl it o ov b i o 116-3 ott 6 i i ollt u o v bito 4 lo i 6 v
sin sin 1 d r d Ae r 2
 Diffction k f c f Th Huygn-Fnl Pincil tt: Evy unobtuct oint of vfont, t givn intnt, v ouc of hicl cony vlt (ith th m funcy tht of th imy v. Th mlitu of th oticl fil t ny oint byon i th uoition of ll th
Diffction k f c f Th Huygn-Fnl Pincil tt: Evy unobtuct oint of vfont, t givn intnt, v ouc of hicl cony vlt (ith th m funcy tht of th imy v. Th mlitu of th oticl fil t ny oint byon i th uoition of ll th
Silv. Criteria Met? Condition
 GWINN FORET MGT UNIT Ifomio Compm: 254 Ey Y: 29 iz y oy- kg g vg. To. i 1 5 M 3 24 47 7 4 55 p (upl) immu N 1-19 y Poo quliy off i p. Wi gig okig. 2 R 6 M 1 3 42 8 13 57 pi immu N 1-19 y Plio h om mio
GWINN FORET MGT UNIT Ifomio Compm: 254 Ey Y: 29 iz y oy- kg g vg. To. i 1 5 M 3 24 47 7 4 55 p (upl) immu N 1-19 y Poo quliy off i p. Wi gig okig. 2 R 6 M 1 3 42 8 13 57 pi immu N 1-19 y Plio h om mio
ASSERTION AND REASON
 ASSERTION AND REASON Som qustios (Assrtio Rso typ) r giv low. Ech qustio cotis Sttmt (Assrtio) d Sttmt (Rso). Ech qustio hs choics (A), (B), (C) d (D) out of which ONLY ONE is corrct. So slct th corrct
ASSERTION AND REASON Som qustios (Assrtio Rso typ) r giv low. Ech qustio cotis Sttmt (Assrtio) d Sttmt (Rso). Ech qustio hs choics (A), (B), (C) d (D) out of which ONLY ONE is corrct. So slct th corrct
Chapter 3 Fourier Series Representation of Periodic Signals
 Chptr Fourir Sris Rprsttio of Priodic Sigls If ritrry sigl x(t or x[] is xprssd s lir comitio of som sic sigls th rspos of LI systm coms th sum of th idividul rsposs of thos sic sigls Such sic sigl must:
Chptr Fourir Sris Rprsttio of Priodic Sigls If ritrry sigl x(t or x[] is xprssd s lir comitio of som sic sigls th rspos of LI systm coms th sum of th idividul rsposs of thos sic sigls Such sic sigl must:
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
On the convergence of solutions of the non-linear differential equation
 MEMOIRS O F T H E COLLEGE O F SCIENCE, UNIVERSITY OF KYOTO, SERIES A Vol. XXVIII, Mathematics No. 2, 1953. On the convergence of solutions of the non-linear differential equation By Taro YOSHIZAWA (Received
MEMOIRS O F T H E COLLEGE O F SCIENCE, UNIVERSITY OF KYOTO, SERIES A Vol. XXVIII, Mathematics No. 2, 1953. On the convergence of solutions of the non-linear differential equation By Taro YOSHIZAWA (Received
IIT JEE MATHS MATRICES AND DETERMINANTS
 IIT JEE MTHS MTRICES ND DETERMINNTS THIRUMURUGN.K PGT Mths IIT Trir 978757 Pg. Lt = 5, th () =, = () = -, = () =, = - (d) = -, = -. Lt sw smmtri mtri of odd th quls () () () - (d) o of ths. Th vlu of th
IIT JEE MTHS MTRICES ND DETERMINNTS THIRUMURUGN.K PGT Mths IIT Trir 978757 Pg. Lt = 5, th () =, = () = -, = () =, = - (d) = -, = -. Lt sw smmtri mtri of odd th quls () () () - (d) o of ths. Th vlu of th
Bus times from 18 January 2016
 1 3 i ml/ Fm vig: Tllc uchhuggl Pkh ig Fm u im fm 18 Ju 2016 Hll lcm Thk f chig vl ih Fi W p xiv k f vic hughu G Glg h ig mk u ju pibl Ii hi gui u c icv: Th im p hi vic Pg 6-15 18-19 Th u ii v Pg -5 16-17
1 3 i ml/ Fm vig: Tllc uchhuggl Pkh ig Fm u im fm 18 Ju 2016 Hll lcm Thk f chig vl ih Fi W p xiv k f vic hughu G Glg h ig mk u ju pibl Ii hi gui u c icv: Th im p hi vic Pg 6-15 18-19 Th u ii v Pg -5 16-17
On Jackson's Theorem
 It. J. Cotm. Math. Scics, Vol. 7, 0, o. 4, 49 54 O Jackso's Thom Ema Sami Bhaya Datmt o Mathmatics, Collg o Educatio Babylo Uivsity, Babil, Iaq mabhaya@yahoo.com Abstact W ov that o a uctio W [, ], 0
It. J. Cotm. Math. Scics, Vol. 7, 0, o. 4, 49 54 O Jackso's Thom Ema Sami Bhaya Datmt o Mathmatics, Collg o Educatio Babylo Uivsity, Babil, Iaq mabhaya@yahoo.com Abstact W ov that o a uctio W [, ], 0
Chapter #2 EEE Subsea Control and Communication Systems
 EEE 87 Chpter # EEE 87 Sube Cotrol d Commuictio Sytem Trfer fuctio Pole loctio d -ple Time domi chrcteritic Extr pole d zero Chpter /8 EEE 87 Trfer fuctio Lplce Trform Ued oly o LTI ytem Differetil expreio
EEE 87 Chpter # EEE 87 Sube Cotrol d Commuictio Sytem Trfer fuctio Pole loctio d -ple Time domi chrcteritic Extr pole d zero Chpter /8 EEE 87 Trfer fuctio Lplce Trform Ued oly o LTI ytem Differetil expreio
22 t b r 2, 20 h r, th xp t d bl n nd t fr th b rd r t t. f r r z r t l n l th h r t rl T l t n b rd n n l h d, nd n nh rd f pp t t f r n. H v v d n f
 n r t d n 20 2 : 6 T P bl D n, l d t z d http:.h th tr t. r pd l 22 t b r 2, 20 h r, th xp t d bl n nd t fr th b rd r t t. f r r z r t l n l th h r t rl T l t n b rd n n l h d, nd n nh rd f pp t t f r
n r t d n 20 2 : 6 T P bl D n, l d t z d http:.h th tr t. r pd l 22 t b r 2, 20 h r, th xp t d bl n nd t fr th b rd r t t. f r r z r t l n l th h r t rl T l t n b rd n n l h d, nd n nh rd f pp t t f r
r(j) -::::.- --X U.;,..;...-h_D_Vl_5_ :;;2.. Name: ~s'~o--=-i Class; Date: ID: A
 Name: ~s'~o--=-i Class; Date: U.;,..;...-h_D_Vl_5 _ MAC 2233 Chapter 4 Review for the test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the derivative
Name: ~s'~o--=-i Class; Date: U.;,..;...-h_D_Vl_5 _ MAC 2233 Chapter 4 Review for the test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the derivative
Grilled it ems are prepared over real mesquit e wood CREATE A COMBO STEAKS. Onion Brewski Sirloin * Our signature USDA Choice 12 oz. Sirloin.
 TT & L Gl v l q T l q TK v i f i ' i i T K L G ' T G!? Ti 10 (Pik 3) -F- L P ki - ik T ffl i zzll ik Fi Pikl x i f l $3 (li 2) i f i i i - i f i jlñ i 84 6 - f ki i Fi 6 T i ffl i 10 -i i fi & i i ffl
TT & L Gl v l q T l q TK v i f i ' i i T K L G ' T G!? Ti 10 (Pik 3) -F- L P ki - ik T ffl i zzll ik Fi Pikl x i f l $3 (li 2) i f i i i - i f i jlñ i 84 6 - f ki i Fi 6 T i ffl i 10 -i i fi & i i ffl
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
SUPPLEMENTARY READING FOR MATH 53: DIFFERENTIAL FORMS AND THE GENERAL STOKES FORMULA
 SUPPLEMENTARY READING FOR MATH 53: DIFFERENTIAL FORMS AND THE GENERAL STOKES FORMULA EDWARD FRENKEL, UC BERKELEY The purpose of these notes is to outline briefly a general formalism which allows for a
SUPPLEMENTARY READING FOR MATH 53: DIFFERENTIAL FORMS AND THE GENERAL STOKES FORMULA EDWARD FRENKEL, UC BERKELEY The purpose of these notes is to outline briefly a general formalism which allows for a
fnm 'et Annual Meeting
 UUVtK Ht.t, A 0 8 4 S.. Rittin Nub t, n L Y t U N i, n ' A N n, t\ V n b n k pny' ull N) 0 R Z A L A V N U X N S N R N R H A V N U R A P A R K A L A N Y Buin Add. N. Stt ity wn / Pvin) Ali l) lil tal?l
UUVtK Ht.t, A 0 8 4 S.. Rittin Nub t, n L Y t U N i, n ' A N n, t\ V n b n k pny' ull N) 0 R Z A L A V N U X N S N R N R H A V N U R A P A R K A L A N Y Buin Add. N. Stt ity wn / Pvin) Ali l) lil tal?l
The tight-binding method
 Th tight-idig thod Wa ottial aoach: tat lcto a a ga of aly f coductio lcto. ow aout iulato? ow aout d-lcto? d Tight-idig thod: gad a olid a a collctio of wa itactig utal ato. Ovla of atoic wav fuctio i
Th tight-idig thod Wa ottial aoach: tat lcto a a ga of aly f coductio lcto. ow aout iulato? ow aout d-lcto? d Tight-idig thod: gad a olid a a collctio of wa itactig utal ato. Ovla of atoic wav fuctio i
Silv. Criteria Met? Condition
 NEWERRY FORET MGT UNIT Ifomio Compm: 106 Ey Y: 2001 iz oy- kg g vg. To. i 1 Q 6 Q 2 48 115 9 100 35 mix wmp mu Y o hul 0 j low i Ro (ou o ply vilbl) h o h ouhw wih 10' f. Culy o o hough PVT popy o hi.
NEWERRY FORET MGT UNIT Ifomio Compm: 106 Ey Y: 2001 iz oy- kg g vg. To. i 1 Q 6 Q 2 48 115 9 100 35 mix wmp mu Y o hul 0 j low i Ro (ou o ply vilbl) h o h ouhw wih 10' f. Culy o o hough PVT popy o hi.
Handout on. Crystal Symmetries and Energy Bands
 dou o Csl s d g Bds I hs lu ou wll l: Th loshp bw ss d g bds h bs of sp-ob ouplg Th loshp bw ss d g bds h ps of sp-ob ouplg C 7 pg 9 Fh Coll Uvs d g Bds gll hs oh Th sl pol ss ddo o h l slo s: Fo pl h
dou o Csl s d g Bds I hs lu ou wll l: Th loshp bw ss d g bds h bs of sp-ob ouplg Th loshp bw ss d g bds h ps of sp-ob ouplg C 7 pg 9 Fh Coll Uvs d g Bds gll hs oh Th sl pol ss ddo o h l slo s: Fo pl h
Order Statistics from Exponentiated Gamma. Distribution and Associated Inference
 It J otm Mth Scc Vo 4 9 o 7-9 Od Stttc fom Eottd Gmm Dtto d Aoctd Ifc A I Shw * d R A Bo G og of Edcto PO Bo 369 Jddh 438 Sd A G og of Edcto Dtmt of mthmtc PO Bo 469 Jddh 49 Sd A Atct Od tttc fom ottd
It J otm Mth Scc Vo 4 9 o 7-9 Od Stttc fom Eottd Gmm Dtto d Aoctd Ifc A I Shw * d R A Bo G og of Edcto PO Bo 369 Jddh 438 Sd A G og of Edcto Dtmt of mthmtc PO Bo 469 Jddh 49 Sd A Atct Od tttc fom ottd
PwC Middle East Spa Benchmarking Survey January - August 2012
 www.pw.m/m Mdd E Sp Bhmkg Suvy Juy - Augu 2012 W pd p h u f PwhuCp () Sp Bhmk uvy f h p h Mdd E. Th h y bhmk p vg h Dd S, Dh, d Bu p g. Th Sp Bhmk Rp ud -uy b d h d v h pd fm Juy Augu 2012. Th Sp Bhmk
www.pw.m/m Mdd E Sp Bhmkg Suvy Juy - Augu 2012 W pd p h u f PwhuCp () Sp Bhmk uvy f h p h Mdd E. Th h y bhmk p vg h Dd S, Dh, d Bu p g. Th Sp Bhmk Rp ud -uy b d h d v h pd fm Juy Augu 2012. Th Sp Bhmk
Daily Skill Practice
 G CD-0 Dily Skill Pti 00 Wkk ## W i t it Eh. gh y w m y il A ll? + = 8 Dy 8= 0. =. Nm. C h l lit tl k ty i g. I h hi ty w ig h, m y hw hi g w ig h?. W Wkk ##00 A A = t, >, = W it < t t m t m k t. Dy Dy
G CD-0 Dily Skill Pti 00 Wkk ## W i t it Eh. gh y w m y il A ll? + = 8 Dy 8= 0. =. Nm. C h l lit tl k ty i g. I h hi ty w ig h, m y hw hi g w ig h?. W Wkk ##00 A A = t, >, = W it < t t m t m k t. Dy Dy
Statics. Consider the free body diagram of link i, which is connected to link i-1 and link i+1 by joint i and joint i-1, respectively. = r r r.
 Statcs Th cotact btw a mapulato ad ts vomt sults tactv ocs ad momts at th mapulato/vomt tac. Statcs ams at aalyzg th latoshp btw th actuato dv tous ad th sultat oc ad momt appld at th mapulato dpot wh
Statcs Th cotact btw a mapulato ad ts vomt sults tactv ocs ad momts at th mapulato/vomt tac. Statcs ams at aalyzg th latoshp btw th actuato dv tous ad th sultat oc ad momt appld at th mapulato dpot wh
What are S M U s? SMU = Software Maintenance Upgrade Software patch del iv ery u nit wh ich once ins tal l ed and activ ated prov ides a point-fix for
 SMU 101 2 0 0 7 C i s c o S y s t e m s, I n c. A l l r i g h t s r e s e r v e d. 1 What are S M U s? SMU = Software Maintenance Upgrade Software patch del iv ery u nit wh ich once ins tal l ed and activ
SMU 101 2 0 0 7 C i s c o S y s t e m s, I n c. A l l r i g h t s r e s e r v e d. 1 What are S M U s? SMU = Software Maintenance Upgrade Software patch del iv ery u nit wh ich once ins tal l ed and activ
Math 2142 Homework 2 Solutions. Problem 1. Prove the following formulas for Laplace transforms for s > 0. a s 2 + a 2 L{cos at} = e st.
 Mth 2142 Homework 2 Solution Problem 1. Prove the following formul for Lplce trnform for >. L{1} = 1 L{t} = 1 2 L{in t} = 2 + 2 L{co t} = 2 + 2 Solution. For the firt Lplce trnform, we need to clculte:
Mth 2142 Homework 2 Solution Problem 1. Prove the following formul for Lplce trnform for >. L{1} = 1 L{t} = 1 2 L{in t} = 2 + 2 L{co t} = 2 + 2 Solution. For the firt Lplce trnform, we need to clculte:
Ps(X) E PnSn x (1.2) PS (x) Po=0, and A k,n k > -I we get summablllty A, summabllity (L) and A method of summability respectively.
 Iterat. J. Math. & Math. Sci. VOL. 12 NO. (1989) 99106 99 ON (J,p) SUMMABILITY OF FOURIER SERIES S.M. MAZHAR Departmet of Mathematics Kuwait Uiversity P.O. BOX 5969 13060, Safat, Kuwait (Received December
Iterat. J. Math. & Math. Sci. VOL. 12 NO. (1989) 99106 99 ON (J,p) SUMMABILITY OF FOURIER SERIES S.M. MAZHAR Departmet of Mathematics Kuwait Uiversity P.O. BOX 5969 13060, Safat, Kuwait (Received December
4 4 N v b r t, 20 xpr n f th ll f th p p l t n p pr d. H ndr d nd th nd f t v L th n n f th pr v n f V ln, r dn nd l r thr n nt pr n, h r th ff r d nd
 n r t d n 20 20 0 : 0 T P bl D n, l d t z d http:.h th tr t. r pd l 4 4 N v b r t, 20 xpr n f th ll f th p p l t n p pr d. H ndr d nd th nd f t v L th n n f th pr v n f V ln, r dn nd l r thr n nt pr n,
n r t d n 20 20 0 : 0 T P bl D n, l d t z d http:.h th tr t. r pd l 4 4 N v b r t, 20 xpr n f th ll f th p p l t n p pr d. H ndr d nd th nd f t v L th n n f th pr v n f V ln, r dn nd l r thr n nt pr n,
ON THE HARMONIC SUMMABILITY OF DOUBLE FOURIER SERIES P. L. SHARMA
 ON THE HARMONIC SUMMABILITY OF DOUBLE FOURIER SERIES P. L. SHARMA 1. Suppose that the function f(u, v) is integrable in the sense of Lebesgue, over the square ( ir, ir; it, it) and is periodic with period
ON THE HARMONIC SUMMABILITY OF DOUBLE FOURIER SERIES P. L. SHARMA 1. Suppose that the function f(u, v) is integrable in the sense of Lebesgue, over the square ( ir, ir; it, it) and is periodic with period
NEWBERRY FOREST MGT UNIT Stand Level Information Compartment: 10 Entry Year: 2001
 iz oy- kg vg. To. 1 M 6 M 10 11 100 60 oh hwoo uvg N o hul 0 Mix bg. woo, moly low quliy. Coif ompo houghou - WP/hmlok/pu/blm/. vy o whi pi o h ouh fig of. iffiul o. Th o hi i o PVT l wh h g o wll big
iz oy- kg vg. To. 1 M 6 M 10 11 100 60 oh hwoo uvg N o hul 0 Mix bg. woo, moly low quliy. Coif ompo houghou - WP/hmlok/pu/blm/. vy o whi pi o h ouh fig of. iffiul o. Th o hi i o PVT l wh h g o wll big
The Finite Element Method for the Wave Equation
 The Finite Element Method for the Wave Equation 1 The Wave Equation We consider the scalar wave equation modelling acoustic wave propagation in a bounded domain 3, with boundary Γ : 1 2 u c(x) 2 u 0, in
The Finite Element Method for the Wave Equation 1 The Wave Equation We consider the scalar wave equation modelling acoustic wave propagation in a bounded domain 3, with boundary Γ : 1 2 u c(x) 2 u 0, in
ENGO 431 Analytical Photogrammetry
 EGO Altil Phtgmmt Fll 00 LAB : SIGLE PHOTO RESECTIO u t: vm 00 Ojtiv: tmi th Eti Oitti Pmts EOP f sigl ht usig lst squs justmt u. Giv:. Iti Oitti Pmts IOP f th m fm th Cm Cliti Ctifit CCC; Clit fl lgth
EGO Altil Phtgmmt Fll 00 LAB : SIGLE PHOTO RESECTIO u t: vm 00 Ojtiv: tmi th Eti Oitti Pmts EOP f sigl ht usig lst squs justmt u. Giv:. Iti Oitti Pmts IOP f th m fm th Cm Cliti Ctifit CCC; Clit fl lgth
[ ] Review. For a discrete-time periodic signal xn with period N, the Fourier series representation is
![[ ] Review. For a discrete-time periodic signal xn with period N, the Fourier series representation is [ ] Review. For a discrete-time periodic signal xn with period N, the Fourier series representation is](/thumbs/95/123561596.jpg) Discrt-tim ourir Trsform Rviw or discrt-tim priodic sigl x with priod, th ourir sris rprsttio is x + < > < > x, Rviw or discrt-tim LTI systm with priodic iput sigl, y H ( ) < > < > x H r rfrrd to s th
Discrt-tim ourir Trsform Rviw or discrt-tim priodic sigl x with priod, th ourir sris rprsttio is x + < > < > x, Rviw or discrt-tim LTI systm with priodic iput sigl, y H ( ) < > < > x H r rfrrd to s th
RTPR Sampler Program
 P Sl P i H B v N Ahi kd f hl qi N hk F N F N S F N Bkffi F N lid Si F $99.95 Sl Pk Giv 365 bhi Ad w will hw hw h $99.95 il b dd Z P Sl P i H B v Hih wd A Sihfwd i Pl wih f di v : B ii 1 i 6.25% 2d i 2.5%
P Sl P i H B v N Ahi kd f hl qi N hk F N F N S F N Bkffi F N lid Si F $99.95 Sl Pk Giv 365 bhi Ad w will hw hw h $99.95 il b dd Z P Sl P i H B v Hih wd A Sihfwd i Pl wih f di v : B ii 1 i 6.25% 2d i 2.5%
1. The 0.1 kg particle has a speed v = 10 m/s as it passes the 30 position shown. The coefficient of kinetic friction between the particle and the
 1. The 0.1 kg pticle h peed v = 10 m/ it pe the 30 poitio how. The coefficiet of kietic fictio betwee the pticle d the veticl ple tck i m k = 0.0. Detemie the mgitude of the totl foce exeted by the tck
1. The 0.1 kg pticle h peed v = 10 m/ it pe the 30 poitio how. The coefficiet of kietic fictio betwee the pticle d the veticl ple tck i m k = 0.0. Detemie the mgitude of the totl foce exeted by the tck
Chapter 6 Perturbation theory
 Ct 6 Ptutio to 6. Ti-iddt odgt tutio to i o tutio sst is giv to fid solutios of λ ' ; : iltoi of si stt : igvlus of : otool igfutios of ; δ ii Rlig-Södig tutio to ' λ..6. ; : gl iltoi ': tutio λ : sll
Ct 6 Ptutio to 6. Ti-iddt odgt tutio to i o tutio sst is giv to fid solutios of λ ' ; : iltoi of si stt : igvlus of : otool igfutios of ; δ ii Rlig-Södig tutio to ' λ..6. ; : gl iltoi ': tutio λ : sll
and the ANAVETS Unit Portage Ave, Winnipeg, Manitoba, Canada May 23 to May E L IBSF
 t NVET Uit 283 IR FO RE VET ER N N N I MY NVY & R 3584 Pt, Wii, Mitb, IN O RPORTE E IL L I GU VET IF N ENG R H LI E My 23 t My 28-2015 R LE YOUR ONE TOP HOP FOR QULITY POOL UE & ILLIR EORIE GMEROOM 204-783-2666
t NVET Uit 283 IR FO RE VET ER N N N I MY NVY & R 3584 Pt, Wii, Mitb, IN O RPORTE E IL L I GU VET IF N ENG R H LI E My 23 t My 28-2015 R LE YOUR ONE TOP HOP FOR QULITY POOL UE & ILLIR EORIE GMEROOM 204-783-2666
Chair Susan Pilkington called the meeting to order.
 PGE PRK D RECREO DVOR COMMEE REGUR MEEG MUE MOD, JU, Ru M h P P d R d Cmm hd : m Ju,, h Cu Chmb C H P, z Ch u P dd, Mmb B C, Gm Cu D W Bd mmb b: m D, d Md z ud mmb : C M, J C P Cmmu Dm D, Km Jh Pub W M,
PGE PRK D RECREO DVOR COMMEE REGUR MEEG MUE MOD, JU, Ru M h P P d R d Cmm hd : m Ju,, h Cu Chmb C H P, z Ch u P dd, Mmb B C, Gm Cu D W Bd mmb b: m D, d Md z ud mmb : C M, J C P Cmmu Dm D, Km Jh Pub W M,
dmid hud f i, fh dii m u Plii Svi ' ifmi vidd h whih whih f k, gm xui h i kwldg vidd m xud f gm mi diu, uhi hv Di Bd h T ig li mlig um ud Plii Svi ulh
 S NTO SPECIL UTILITY D ISTRICT S ERVICE PPLICTION ND GREEMENT P O Bx 248 S, Tx 76472 P l Pi: D TE PPLICNT'S NME CO- PPLICNT'S NME C URRENT BILLING DDRESS: FUTURE BILLING DDRESS: PHONE NUMBER - Hm () -
S NTO SPECIL UTILITY D ISTRICT S ERVICE PPLICTION ND GREEMENT P O Bx 248 S, Tx 76472 P l Pi: D TE PPLICNT'S NME CO- PPLICNT'S NME C URRENT BILLING DDRESS: FUTURE BILLING DDRESS: PHONE NUMBER - Hm () -
ELEC9721: Digital Signal Processing Theory and Applications
 ELEC97: Digital Sigal Pocssig Thoy ad Applicatios Tutoial ad solutios Not: som of th solutios may hav som typos. Q a Show that oth digital filts giv low hav th sam magitud spos: i [] [ ] m m i i i x c
ELEC97: Digital Sigal Pocssig Thoy ad Applicatios Tutoial ad solutios Not: som of th solutios may hav som typos. Q a Show that oth digital filts giv low hav th sam magitud spos: i [] [ ] m m i i i x c
Summary Introduction to Process Control
 Suy todutio to Po otol Rf iut Fdbk otol hoy Fowd oto Fdbk oto tuto o ditub Plt Zhyu Yg otol yt obl: Albog Uivity Ebjg A lt: hyil yt dd to b otolld Sifitio: did yt fo DE5 Fll 4 A thodology: to dig otoll
Suy todutio to Po otol Rf iut Fdbk otol hoy Fowd oto Fdbk oto tuto o ditub Plt Zhyu Yg otol yt obl: Albog Uivity Ebjg A lt: hyil yt dd to b otolld Sifitio: did yt fo DE5 Fll 4 A thodology: to dig otoll
RESOURCE, SUPPORT, AND DEVELOPMENT, INC
 RESOURCE, SUPPORT, AND DEVELOPMENT, INC BOARD OF DIRECTORS Pd Pk E. K V-Pd B R S L Bd-Sw Ld Tk Nk Edwd A DB Dv S ADMINISTRATIVE TEAM Pvd v dvd w db B, Hd, Lww, d Rd Ld, M A Pb R.S.D., I Smm 2006 Vm 5 CEO
RESOURCE, SUPPORT, AND DEVELOPMENT, INC BOARD OF DIRECTORS Pd Pk E. K V-Pd B R S L Bd-Sw Ld Tk Nk Edwd A DB Dv S ADMINISTRATIVE TEAM Pvd v dvd w db B, Hd, Lww, d Rd Ld, M A Pb R.S.D., I Smm 2006 Vm 5 CEO
i t 1 v d B & N 1 K 1 P M 1 R & H 1 S o et al., o 1 9 T i w a s b W ( 1 F 9 w s t t p d o c o p T s a s t b ro
 Pgm PII: S0042-6989(96)00205-2 VR, V 37, N 6, 705 720,1997 01997 E S L Pd G B 0042-698997$1700+ 000 P M L I B L P S M S E C S W A U O S R E R O 1 f 1 A 1 f fm J 1 A bqu g vy bd z gu u vd mvg z d,, -dg
Pgm PII: S0042-6989(96)00205-2 VR, V 37, N 6, 705 720,1997 01997 E S L Pd G B 0042-698997$1700+ 000 P M L I B L P S M S E C S W A U O S R E R O 1 f 1 A 1 f fm J 1 A bqu g vy bd z gu u vd mvg z d,, -dg
SHINGLETON FOREST AREA Stand Level Information Compartment: 44 Entry Year: 2009
 iz y U oy- kg g vg. To. i Ix Mg * "Compm Pk Gloy of Tm" oum lik o wb i fo fuh ipio o fiiio. Coiio ilv. Cii M? Mho Cu Tm. Pio v Pioiy Culul N 1 5 3 13 60 7 50 42 blk pu-wmp ol gowh N 20-29 y (poil o ul)
iz y U oy- kg g vg. To. i Ix Mg * "Compm Pk Gloy of Tm" oum lik o wb i fo fuh ipio o fiiio. Coiio ilv. Cii M? Mho Cu Tm. Pio v Pioiy Culul N 1 5 3 13 60 7 50 42 blk pu-wmp ol gowh N 20-29 y (poil o ul)
Handout 7. Properties of Bloch States and Electron Statistics in Energy Bands
 Hdout 7 Popts of Bloch Stts d Elcto Sttstcs Eg Bds I ths lctu ou wll l: Popts of Bloch fuctos Podc boud codtos fo Bloch fuctos Dst of stts -spc Elcto occupto sttstcs g bds ECE 407 Spg 009 Fh R Coll Uvst
Hdout 7 Popts of Bloch Stts d Elcto Sttstcs Eg Bds I ths lctu ou wll l: Popts of Bloch fuctos Podc boud codtos fo Bloch fuctos Dst of stts -spc Elcto occupto sttstcs g bds ECE 407 Spg 009 Fh R Coll Uvst
upon during the winter Porter Bik, cor. Monroe midnight, a r e deserted, save for those
 U D D B P D D U D 878 x - z F D J x -- F D : U F < 8 U 8 F J U D D U D U D B P - J X X Z 3 8 9 6 P D J x 3 $88 73» $376; - $87; z $876 ( 3 : $888 z 9; - ; $ 9 7 6» - $37336; 6 P J 373 x P D - U J 3 P J
U D D B P D D U D 878 x - z F D J x -- F D : U F < 8 U 8 F J U D D U D U D B P - J X X Z 3 8 9 6 P D J x 3 $88 73» $376; - $87; z $876 ( 3 : $888 z 9; - ; $ 9 7 6» - $37336; 6 P J 373 x P D - U J 3 P J
POWER UP. Hello, Teachers! With Dr. E tm GRADE TEACHER S GUIDE
 GDE 6 Hll, h! Ggi P i xly xid h hi ih y hl by vidig gy di iiiiv d h d lig xi i y l W lk d kig ih y d y d ECHE S GUIDE D E M By jiig i h Lig P g, ig D E d h W Sqd, ill dliv gy iiy g hgh i-l ild i, ig hd-
GDE 6 Hll, h! Ggi P i xly xid h hi ih y hl by vidig gy di iiiiv d h d lig xi i y l W lk d kig ih y d y d ECHE S GUIDE D E M By jiig i h Lig P g, ig D E d h W Sqd, ill dliv gy iiy g hgh i-l ild i, ig hd-
ASHLA UO MUJJlGl PAL c OUtT. filing for office of Q 50t 5 1 Coo I 5 OS. Filing of Candidacy by Declaration ORS
 F ddy p EL v 6 GR 49 7h pub d d y b pubhd pdud p yp p by bk k ub ud dd L hw hud pp b d u K LR L V R AHLA U MUG PAL U dp p ub L 6 HwA qq u A L d dd u v zp d H b A U uy d Y q w A @ 9 Y x dd P B qq AHLP UD
F ddy p EL v 6 GR 49 7h pub d d y b pubhd pdud p yp p by bk k ub ud dd L hw hud pp b d u K LR L V R AHLA U MUG PAL U dp p ub L 6 HwA qq u A L d dd u v zp d H b A U uy d Y q w A @ 9 Y x dd P B qq AHLP UD
BESSEL MATRIX DIFFERENTIAL EQUATIONS: EXPLICIT SOLUTIONS OF INITIAL AND TWO-POINT BOUNDARY VALUE PROBLEMS
 APPLICATIONES MATHEMATICAE 22,1 (1993), pp. 11 23 E. NAVARRO, R. COMPANY and L. JÓDAR (Valencia) BESSEL MATRIX DIFFERENTIAL EQUATIONS: EXPLICIT SOLUTIONS OF INITIAL AND TWO-POINT BOUNDARY VALUE PROBLEMS
APPLICATIONES MATHEMATICAE 22,1 (1993), pp. 11 23 E. NAVARRO, R. COMPANY and L. JÓDAR (Valencia) BESSEL MATRIX DIFFERENTIAL EQUATIONS: EXPLICIT SOLUTIONS OF INITIAL AND TWO-POINT BOUNDARY VALUE PROBLEMS
Helping every little saver
 Spt th diffc d cut hw u c fid I c spt thigs! Hlpig v littl sv Hw d u p i? I ch Just pp it f u chs. T fid u lcl ch just visit s.c.uk/ch If u pig i chqu, it c tk ud 4 wkig ds t cl Ov th ph Just cll Tlph
Spt th diffc d cut hw u c fid I c spt thigs! Hlpig v littl sv Hw d u p i? I ch Just pp it f u chs. T fid u lcl ch just visit s.c.uk/ch If u pig i chqu, it c tk ud 4 wkig ds t cl Ov th ph Just cll Tlph
SHINGLETON FOREST MGT UNIT Stand Level Information Compartment: 186 Entry Year: 2011
 INGLETON FORET MGT UNIT Ifomio Compm: 186 Ey Y: 211 iz y U oy- kg g vg. To. i Tm. Pioiy Culul 1 M 9 M 3 15 13 12 61 oh hwoo ol gowh Y lio wihi -9 y 2 Ry o l u. pbl g ilu ll ommil hwoo pi. Wl : Wi u. Ri
INGLETON FORET MGT UNIT Ifomio Compm: 186 Ey Y: 211 iz y U oy- kg g vg. To. i Tm. Pioiy Culul 1 M 9 M 3 15 13 12 61 oh hwoo ol gowh Y lio wihi -9 y 2 Ry o l u. pbl g ilu ll ommil hwoo pi. Wl : Wi u. Ri
IFYFM002 Further Maths Appendix C Formula Booklet
 Ittol Foudto Y (IFY) IFYFM00 Futh Mths Appd C Fomul Booklt Rltd Documts: IFY Futh Mthmtcs Syllbus 07/8 Cotts Mthmtcs Fomul L Equtos d Mtcs... Qudtc Equtos d Rmd Thom... Boml Epsos, Squcs d Ss... Idcs,
Ittol Foudto Y (IFY) IFYFM00 Futh Mths Appd C Fomul Booklt Rltd Documts: IFY Futh Mthmtcs Syllbus 07/8 Cotts Mthmtcs Fomul L Equtos d Mtcs... Qudtc Equtos d Rmd Thom... Boml Epsos, Squcs d Ss... Idcs,
T HE 1017TH MEETING OF THE BRODIE CLUB The 1017th Meeting of the Brodie Club was held at 7:30 pm on January 15, 2008 in the R amsay Wright Laboratorie
 1017 MN OF BRO LUB 1017h M Bi lu hl 7:30 u 15, 2008 R Wih Li Uivi. hi: : A h 28 u. u: hl M, u A i u, u vi ull R : K Ah, Oliv B, Bill Rl N W BUN: M u vl: l v, Bu Fll, v ull l B u Fll i Fu k ul M, l u u
1017 MN OF BRO LUB 1017h M Bi lu hl 7:30 u 15, 2008 R Wih Li Uivi. hi: : A h 28 u. u: hl M, u A i u, u vi ull R : K Ah, Oliv B, Bill Rl N W BUN: M u vl: l v, Bu Fll, v ull l B u Fll i Fu k ul M, l u u
RESEARCH ARTICLE. Spectral Method for Solving The General Form Linear Fredholm Volterra Integro Differential Equations Based on Chebyshev Polynomials
 Journal of Modern Methods in Numerical Mathematics ISSN: 29-477 online Vol, No, 2, c 2 Modern Science Publishers wwwm-sciencescom RESEARCH ARTICLE Spectral Method for Solving The General Form Linear Fredholm
Journal of Modern Methods in Numerical Mathematics ISSN: 29-477 online Vol, No, 2, c 2 Modern Science Publishers wwwm-sciencescom RESEARCH ARTICLE Spectral Method for Solving The General Form Linear Fredholm
UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION
 School Of Distce Eductio Questio Bk UNIVERSITY OF ALIUT SHOOL OF DISTANE EDUATION B.Sc MATHEMATIS (ORE OURSE SIXTH SEMESTER ( Admissio OMPLEX ANALYSIS Module- I ( A lytic fuctio with costt modulus is :
School Of Distce Eductio Questio Bk UNIVERSITY OF ALIUT SHOOL OF DISTANE EDUATION B.Sc MATHEMATIS (ORE OURSE SIXTH SEMESTER ( Admissio OMPLEX ANALYSIS Module- I ( A lytic fuctio with costt modulus is :
BLUE LINE TROLLEY STATION IMPROVEMENTS
 TUT GT DD T T TUT HU GT WTH HG GHT G TZ # - + V Y 0/00 HZ GT WTH HG - + = U& PV-50 #555- P JUT X GHT G & DD. HG GHT D P UT UT Y TW P GT WTH HG GHT G & P DT P UT # - + U& P-50 #500-0 UT Y W/HVY DUTY TT
TUT GT DD T T TUT HU GT WTH HG GHT G TZ # - + V Y 0/00 HZ GT WTH HG - + = U& PV-50 #555- P JUT X GHT G & DD. HG GHT D P UT UT Y TW P GT WTH HG GHT G & P DT P UT # - + U& P-50 #500-0 UT Y W/HVY DUTY TT
Topic 3. Integral calculus
 Integral calculus Topic 3 Line, surface and volume integrals Fundamental theorems of calculus Fundamental theorems for gradients Fundamental theorems for divergences! Green s theorem Fundamental theorems
Integral calculus Topic 3 Line, surface and volume integrals Fundamental theorems of calculus Fundamental theorems for gradients Fundamental theorems for divergences! Green s theorem Fundamental theorems
Exam 2 Solutions. Jonathan Turner 4/2/2012. CS 542 Advanced Data Structures and Algorithms
 CS 542 Avn Dt Stutu n Alotm Exm 2 Soluton Jontn Tun 4/2/202. (5 ont) Con n oton on t tton t tutu n w t n t 2 no. Wt t mllt num o no tt t tton t tutu oul ontn. Exln you nw. Sn n mut n you o u t n t, t n
CS 542 Avn Dt Stutu n Alotm Exm 2 Soluton Jontn Tun 4/2/202. (5 ont) Con n oton on t tton t tutu n w t n t 2 no. Wt t mllt num o no tt t tton t tutu oul ontn. Exln you nw. Sn n mut n you o u t n t, t n
STRIPLINES. A stripline is a planar type transmission line which is well suited for microwave integrated circuitry and photolithographic fabrication.
 STIPLINES A tiplin i a plana typ tanmiion lin hih i ll uitd fo mioav intgatd iuity and photolithogaphi faiation. It i uually ontutd y thing th nt onduto of idth, on a utat of thikn and thn oving ith anoth
STIPLINES A tiplin i a plana typ tanmiion lin hih i ll uitd fo mioav intgatd iuity and photolithogaphi faiation. It i uually ontutd y thing th nt onduto of idth, on a utat of thikn and thn oving ith anoth
OCCOQUAN RIVER CONDITION SURVEY PRINCE WILLIAM AND FAIRFAX COUNTIES, VIRGINIA CHARLES COUNTY, MARYLAND. BAY Havre De Grace INDEX OF DRAWINGS TITLE
 2 3 5 t pp. pt W FFX, G t pp. k, Q l w h b pu x t v 33 wpt w 2 2 4 F.5.5 m pt m h 34 d 2 p p h flk flk 35 tmuth 36 8 4 36 3 pt F FX d W G l t l : l t dt: p hl mptm 2 32 h f,v.h tbug 3 ubm ttd b: p hl Wllmbug
2 3 5 t pp. pt W FFX, G t pp. k, Q l w h b pu x t v 33 wpt w 2 2 4 F.5.5 m pt m h 34 d 2 p p h flk flk 35 tmuth 36 8 4 36 3 pt F FX d W G l t l : l t dt: p hl mptm 2 32 h f,v.h tbug 3 ubm ttd b: p hl Wllmbug
Implementation Date Fall Communications & Transportation
 Implmi D ROGRAM CONCENTRATION: CAREER ATHWAY: Ahiu, Cui, Cmmuii & Tpi Cui Thi hw i ig pp u wih fuil kwlg kill f ui i f fu pibl ui f. I l i g phw f u pp f vi f ppuii i ii h f, uh Ahiu, Cui Egiig Cui Mgm.
Implmi D ROGRAM CONCENTRATION: CAREER ATHWAY: Ahiu, Cui, Cmmuii & Tpi Cui Thi hw i ig pp u wih fuil kwlg kill f ui i f fu pibl ui f. I l i g phw f u pp f vi f ppuii i ii h f, uh Ahiu, Cui Egiig Cui Mgm.
THE 1,040t h MEETING OF THE BRODIE CLUB The 1,040th meeting of the Brodie Club was held at 7:30 pm on S eptember 21, 2010 in R oom 432 of the Ramsay W
 HE 1,040 EENG OF HE BRODE CLUB 1,040 m B Club l 7:30 pm pmb 21, 2010 R m 432 Rm W Lb Uv. C: Bu Fll : G B m b 27 m mb u. R ll Cll, P: A bm, E. A, R. A, J. Bll, Y. B ll, B, B, Bul, B, C, Cu, Du, A. Fll,
HE 1,040 EENG OF HE BRODE CLUB 1,040 m B Club l 7:30 pm pmb 21, 2010 R m 432 Rm W Lb Uv. C: Bu Fll : G B m b 27 m mb u. R ll Cll, P: A bm, E. A, R. A, J. Bll, Y. B ll, B, B, Bul, B, C, Cu, Du, A. Fll,
Lu at. a l. iz io. e a. L n. e g s. t p e. e c c. t g. u n. t o. s o
 OkRdgN Lu z L l l L by L E g u P g D p d hnul M T h h u l g y I m u f f h (MIT) Cuy f Luz Ll, Ok Rdg Nl Lby. Ud wh pm. S g:chdih (Ifff) (. A O ) C u h u f w E l v h hvg d S b g m g g d h d 2. F kz mp h
OkRdgN Lu z L l l L by L E g u P g D p d hnul M T h h u l g y I m u f f h (MIT) Cuy f Luz Ll, Ok Rdg Nl Lby. Ud wh pm. S g:chdih (Ifff) (. A O ) C u h u f w E l v h hvg d S b g m g g d h d 2. F kz mp h
Lecture 8 Analyzing the diffusion weighted signal. Room CSB 272 this week! Please install AFNI
 Lecture 8 Analyzing the diffusion weighted signal Room CSB 272 this week! Please install AFNI http://afni.nimh.nih.gov/afni/ Next lecture, DTI For this lecture, think in terms of a single voxel We re still
Lecture 8 Analyzing the diffusion weighted signal Room CSB 272 this week! Please install AFNI http://afni.nimh.nih.gov/afni/ Next lecture, DTI For this lecture, think in terms of a single voxel We re still
α s and the τ hadronic width
 1 α s and the τ hadronic width Based on the recent article: Martin Beneke, MJ JHEP 09 (2008) 044, arxiv:0806.3156 Introduction 2 Investigations of hadronic τ decays already contributed tremendously for
1 α s and the τ hadronic width Based on the recent article: Martin Beneke, MJ JHEP 09 (2008) 044, arxiv:0806.3156 Introduction 2 Investigations of hadronic τ decays already contributed tremendously for
THE WYOMING COUNTY resource guide to locally-grown foods and products available directly from the farm!
 TH ING UNT i l- f vi il f f! HT INID Ll k lii ifi -6-22 k li ikl vii li i i j j l 0 Nkii fn 6 il lii f Ll k i l v Ll k Ifi i l k H k l l l l ki i ff i l fl l l f 0 i l v 200 l l i k i i f l i fl i I f i il
TH ING UNT i l- f vi il f f! HT INID Ll k lii ifi -6-22 k li ikl vii li i i j j l 0 Nkii fn 6 il lii f Ll k i l v Ll k Ifi i l k H k l l l l ki i ff i l fl l l f 0 i l v 200 l l i k i i f l i fl i I f i il
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A. Ήχος Πα. to os se e e na aș te e e slă ă ă vi i i i i
 CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
Outline of the Three Multiprocessor Servers from the 2009 Sun Microsystems Grant
 Outi f th Th Mutip Sv fm th 2009 Su Miytm Gt D E. P, http://futy.kutztw.u/p, CSC 402, F 2010 A (ik it) hh tb p k vy ik it, wig y th t tim it h bukt it. A g ut tt, th pbbiity f iig k -- whih ti witig --
Outi f th Th Mutip Sv fm th 2009 Su Miytm Gt D E. P, http://futy.kutztw.u/p, CSC 402, F 2010 A (ik it) hh tb p k vy ik it, wig y th t tim it h bukt it. A g ut tt, th pbbiity f iig k -- whih ti witig --
Net Radiation Incident at the Surface
 EO 02 SURFAE ENERY FLUXES Nt Rditio Icidt t th Sufc R = K 1α εl εσ K L Vg Ly Soil αk εl εσ 1 Vticl mtu Pofil Vticl mtu Pofil 2 Soil t Flux Uwd d dowwd coductio of ibl ht Div by vticl tmtu gdit i oil Modultd
EO 02 SURFAE ENERY FLUXES Nt Rditio Icidt t th Sufc R = K 1α εl εσ K L Vg Ly Soil αk εl εσ 1 Vticl mtu Pofil Vticl mtu Pofil 2 Soil t Flux Uwd d dowwd coductio of ibl ht Div by vticl tmtu gdit i oil Modultd
RESOURCE, SUPPORT, AND DEVELOPMENT, INC
 RESOURCE, SUPPORT, AND DEVELOPMENT, INC P w b B, H, Lww, R L, M A Pb RSD, I S 2006 Vm 4 BOARD OF DIRECTORS P P E K V-P B R S L B-Sw L T N Ew A DB D S ADMINISTRATIVE TEAM CEO R M Hm R D J Sz Ex S E Lm F
RESOURCE, SUPPORT, AND DEVELOPMENT, INC P w b B, H, Lww, R L, M A Pb RSD, I S 2006 Vm 4 BOARD OF DIRECTORS P P E K V-P B R S L B-Sw L T N Ew A DB D S ADMINISTRATIVE TEAM CEO R M Hm R D J Sz Ex S E Lm F
