VANISHING MEAN CURVATURE AND RELATED PROPERTIES
|
|
|
- Clyde Jordan
- 6 years ago
- Views:
Transcription
1 VANISHING MEAN CURVATURE AN RELATE PROPERTIES PAUL ANTONACCI 1. Introduction The project deals with surfaces that have vanishing mean curvature. A surface with vanishing mean curvature possesses interesting properties as well as an interesting relationship to the area of the surface. With the help of calculus, differential geometry, and the involvement of complex numbers, these relationships can be described accurately. Using these relationships, conditions can be found to generate surfaces with vanishing mean curvature.. Mean Curvature The surfaces in the project possess vanishing mean curvature. In order to discuss the mean curvature of a surface, some restrictions need to be made on the surfaces being used. efinition.1. [oc76] A subset S R 3 is a regular surface if, for each p S, there exists a neighborhood V in R 3 and a map x : U V S of an open set U R onto V S R 3 such that (1) x is differentiable. () x is continuous, one-to-one, onto, and has a continuous inverse. (3) For each q U, the differential dx q : R R 3 is one to one, where dx q = x u y u z u The restriction to regular surfaces allows the derivatives at a point on the surface to be taken. Since the differential is one to one at all points, the tangent plane spanned by the tangent vectors x u and x v at a point p, exists at every point on the surface. The tangent plane at a point is also written T p (S). efinition.. [oc76] I p : T p (S) R defined by I p = w, w = w 0 is called the first fundamental form of the regular surface S R 3, where w is in T p (S). 1 x v y v z v.
2 VANISHING MEAN CURVATURE AN RELATE PROPERTIES The coefficients of the first fundamental form can be described by basis vectors in the tangent plane. Given a parameterization x : U R 3 of a regular surface, with a basis {x u, x v } of the tangent plane and a curve α(t) = x(u(t), v(t)) such that α(0) = p, a tangent vector at p can be represented by α (0) = u (0)x u + v (0)x v. Applying the first fundamental form to the tangent vector, u x u + v x v, u x u + v x v = x u, x u (u ) + x u, x v (u v ) + x v, x v (v ) =E(u ) + F (u v ) + G(v ) where E = x u, x u, F = x u, x v, and G = x v, x v are defined as the coefficients of the first fundamental form. The coefficients are useful when simplifying equations. Another way to describe a surface is by the normal vectors at a point on a surface. efinition.3. [oc76] Let C be a curve on a regular surface S passing through p S, k the curvature of C at p, and cos θ = n, N, where n is the unit normal vector to C and N is the unit normal vector to S at p. The number k n = k cos θ is called the normal curvature of C S at p. Since the set of unit vectors at a point is closed and bounded, a maximum and a minimum normal curvature will be attained. The maximum and minimum normal curvatures and their corresponding directions are given a special label. efinition.4. [oc76] The maximum normal curvature k 1 and the minimum normal curvature k over the set of unit tangent vectors at p are called the principal curvatures at p; the corresponding directions of the unit vectors are called the principal directions. The definition of mean curvature can be given in terms of the principal curvatures. efinition.5. [oc76] The mean curvature at a point is given as H = 1 (k 1 + k ) where k 1 and k are the principal curvatures at the point. Vanishing mean curvature was actually found by examining a condition developed by Lagrange. 3. Minimal Surface Equation efinition 3.1. [oc76] If f : U R is a differentiable function in an open set U R, then the graph of f is given by the regular surface F = (x, y, f(x, y)) for x, y U.
3 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 3 efinition 3.. [BC76] An open set S R is connected if each pair of points a 1 and a in it can be joined by a polygonal line, consisting of a finite number of line segments joined end to end, that lies entirely in S. efinition 3.3. [BC76] A domain is a connected open set. In the 1700 s Lagrange set out to find the surface with the smallest area bounded by a closed curve in space[nit89]. Lagrange discovered the minimal surface equation, which must be satisfied by the function whose graph has the minimum area of all graphs bounded by the closed curve in space. Nitsche derives the minimal surface equation in Lectures on Minimal Surfaces. Let α be a closed curve in space which projects to a curve C in the x, y plane such that C encloses a domain. efinition 3.4. A function with compact support is a function that vanishes outside a compact set. Theorem 3.5. Given a continuous function f(x) over an interval Q, if Q fg = 0 for all integrable compactly supported g(x) on Q, then f(x) = 0. Proof. Without loss of generality, assume fg = 0 and f(x) is nonzero and positive at some point a in Q. Since f(x) is continuous, there is a neighborhood (a 1, a ) containing a such that f(x) is also positive. efine { 1; if x [a1, a g(x) = ] 0; otherwise, g(x) is integrable, since all stair functions are integrable. efining g in this way makes f(x)g(x)dx nonzero and positive. Since g is zero outside (a 1, a ), g is compactly supported on Q. So in order for f(x)g(x)d = 0 for all compactly supported functions, f(x) must equal zero everywhere. From above, let α be a closed curve in space bounding the graph (x, y, z(x, y)) which has minimum area among all graphs bounded by α. Using ɛ R, and ζ(x, y), a differentiable function with compact support over, Nitsche created a variation of z defined as z(x, y) = z(x, y) + ɛζ(x, y)[nit89]. The variation provides all graphs bounded by α with area given by I(ɛ) = 1 + z x + z ydxdy. Lagrange knew that if z(x, y) was the minimal solution, then I(ɛ) must have a minimum at ɛ = 0, since z(x, y) ɛ=0 = z(x, y). In terms of the area function, z(x, y) as a minimum requires that I (0) = 0. The following theorem uses Lagrange s approach. Theorem 3.6. Let α be a closed curve in space bounding the graphs given by the variation z(x, y) = z(x, y) + ɛζ(x, y) and let C be the projection of α onto the x, y plane enclosing a domain. If the area of the graph of z(x, y) is the minimum area
4 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 4 of all graphs, the function of area given by I(ɛ) = 1 + z x + z ydxdy must be at a minimum when ɛ = 0 and z must satisfy the minimal surface equation (1) (1 + z y)z xx z x z y z xy + (1 + z x)z yy = 0. Proof. To start, assume z(x, y) gives the graph with minimum area bounded of all graphs bounded by α, then I(ɛ) must be at a minimum when ɛ = 0 since z(x, y) ɛ=0 = z(x, y). For this same reason, if I(ɛ) is at a minimum when ɛ = 0, then the graph of z(x, y) must give the minimal area of all the graphs bounded by α. Now, z(x, y) must be shown to satisfy the minimal surface equation. By differentiating I(ɛ) with respect to ɛ we get, ɛ I(ɛ) = ɛ = ɛ = ɛ 1 + z x + z ydxdy 1 + (z x + ɛζ x ) + (z y + ɛζ y ) dxdy 1 + (z x + z x ɛζ x + ɛ ζ x) + ( z y + z y ɛζ y + ɛ ζ y) dxdy, since ɛ is independent of x and y, the differential can be taken inside the integral, ( zx ζ x + ɛζx + z y ζ y + ɛζ = y) dxdy, 1 + z x + z y factoring out ζ x and ζ y, [ζ x (z x + ɛζ x ) + ζ y (z y + ɛζ y )] = dxdy 1 + z x + z y z x ζ x + z y ζ = y dxdy. 1 + z x + z y Since I(e) is at a minimum when ɛ = 0, I (ɛ) must be zero when ɛ = 0. Setting ɛ = 0 makes z(x, y) ɛ=0 = z(x, y), which makes z x ɛ=0 = z x and z y ɛ=0 = z y, giving I z x ζ x + z y ζ y (0) = dxdy z x ζ x + z y ζ = y dxdy. 1 + z x + z ɛ=0 1 + z x + zy y The integral can be written as a sum, z x ζ x + z y ζ y z () x ζ dxdy = x dxdy z x + zy 1 + z x + zy z y ζ y 1 + z x + z y dxdy.
5 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 5 In order to evaluate the double integrals as iterated integrals, integration limits need to be found for the integrals with respect to x and y. The shape of the domain could Figure 1. Possible omain make breaking the original double integral into iterated integrals difficult consider a slice of figure 1 so the integral needs to be redefined. By letting g : R R 3 such that { z xζ x ; if (x, y) g(x, y) = 1+z x +zy 0; if (x, y) R and letting A y = {(x, y) x R}, for the first term of (), evaluating the integral with respect to x gives ( ) z x ζ x g(x, y)dxdy = 0dx + dx dy 1 + z x + zy = R ( 0dx + R A y A y z x ζ x 1 + z x + z y dx Since g(x, y) is 0 everywhere but on A y, integrating over R A y will be zero. Setting ) dy. z x u = ( 1 + zx + zy) ( ) du = z x x ( dx 1 + zx + zy) dv = ζ x dx v = ζ(x, y),
6 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 6 the integration can be done by parts. Evaluating the integral gives ( ) ( ( ) ) z x ζ(x, y) uv vdu dy = 1 + z x + zy ζ(x, y) z x dx dy, Ay A y x 1 + z x + zy where A y is the boundary of A y. Since A y is just a slice of the domain, the boundary of A y will be in C. So evaluating ζ(x, y) at any points in A y will be zero, which makes the first term zero. Thus rewriting the integral over gives (3) z x ζ x 1 + z x + z y dxdy = ζ(x, y) x ( z x 1 + z x + z y ) dxdy. Proceeding in the same fashion, the other double integral yields ( ) z y ζ y (4) dxdy = ζ(x, y) z y dxdy. 1 + z x + zy y 1 + z x + zy Substituting (3) and (4) back into equation (), [ ( ) ( )] I z x (0) = + z y ζ(x, y)dxdy = 0, x 1 + z x + zy y 1 + z x + zy since I (0) must be at a minimum when ɛ = 0. Since ζ(x, y) can be any differentiable function with compact support over, by theorem(3.5) the sum of the partial derivatives must be zero, which gives x ( z x 1 + z x + z y Simplifying the differentials, we find ( ) z x x 1 + z x + zy ) + y ( z y 1 + z x + z y =z xx (1 + z x + z y) 1/ + 1 z x ) = 0.[Nit89] [ (1 ] + z x + zy) 3/ (zx (z xx ) + z y (z yx ) =(1 + z x + z y) 3/ [z xx (1 + z x + z y) z xz xx z x z y z yx ] =(1 + z x + z y) 3/ [ z xx (1 + z y) z x z y z yx ] likewise, ( ) z y = (1 + z y 1 + z x + zy x + zy) 3/ [z yy (1 + z xx ) z y z x z xy ]. Substituting back into the original, (1 + z x + z y) 3/ [ (1 + z y)z xx z x z y z xy + (1 + z x)z yy ] = 0,
7 which is true if and only if VANISHING MEAN CURVATURE AN RELATE PROPERTIES 7 (5) (1 + z y)z xx z x z y z xy + (1 + z x)z yy = 0 which is the minimal surface equation(1). 4. Lagrange s Condition and Vanishing Mean Curvature Shortly after Lagrange developed his minimal surface equation, Meusnier found that surfaces satisfying Lagrange s condition must also possess vanishing mean curvature. In order to show this relationship, a more suitable formula for mean curvature can be derived. Since the mean curvature everywhere on the surface will be examined, a normal curvature will be needed everywhere on the surface. This requirement can be met by examining only orientable surfaces. efinition 4.1. [oc76] A regular surface is orientable if it admits a differentiable field of unit normal vectors defined on the whole surface; the choice of such a field is called an orientation. efinition 4.. [oc76] Let S R 3 be a surface with an orientation N. The map N : S R 3 takes its values in the unit sphere(s ). The map N : S S is called the Gauss map of S. By definition, orientation guarantees a differentiable field of unit normal vectors, thus the Gauss map is differentiable. The differential of the Gauss map is a map from the tangent space of a surface to the tangent space of the unit sphere. For a curve α(t) = x(u(t), v(t)) on S such that α(0) = p for some p S, define N(t) = N α(t), this keeps the normal vector N on α.([oc76]) Taking the differential of N(t) at p, will give the change of the unit normal vector to the surface in the direction of α (t) at p. The differential of the Gauss map, dn, also gives the change of the surface normal at a point in the direction of a tangent vector. By evaluating dn(α (t)) over the same curve as N (t), the two functions describe the same thing. For this reason, d dt N(α(t)) = dn p(α (t)). An orientable surface S with parameterization x(u, v) has a basis {x u, x v } for T p (S). Applying dn to α (0), written in terms of basis vectors of the tangent space, can be written in terms of partial derivatives of N dn p (α (0)) =dn p (α (0)) = d dt [N p ((u(t), (v(t))] t=0 =N u u (0) + N v v (0).
8 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 8 Applying dn to basis vectors of the tangent plane at p, we obtain dn p (x u ) =dn ((1)x u + (0)x v ) =N u dn p (x v ) =dn ((0)x u + (1)x v ) =N v. efinition 4.3. Given two vector spaces U, V a function A : U V is said to be linear if A preserves addition and scalar multiplication. Using the information above, dn can be shown to be operation preserving. Applying dn to the tangent vectors of two curves, α = x(u 1 (t), v 1 (t)) and β = x(u (t), v (t)), we find dn(α + λβ ) =dn [u 1x u + v 1x v + λ(u x u + v x v )] =dn [(u 1 + λu )x u + (v 1 + λv )x v )] =N u (u 1 + λu ) + N v (v 1 + λv ) =u 1N u + v 1N v + λ (u N u + v N v ) =dn (u 1 + v 1) + λdn (u + v ) =dn(α ) + λdn(β ). Since dn is operation preserving from T p (S) to T N(p) (S ), two vector spaces, dn is linear. efinition 4.4. [oc76] Given a vector space V, a linear map A : V V is self-adjoint if Av, w = v, Aw for all v, w V. Next, dn can be shown to be self-adjoint. Using the fact N, x u = 0 and differentiating, d dv N, x u = N v, x u + N, x uv = 0, also N, x v = 0, which makes d du N, x v = N u, x v + N, x vu = 0, Since x is twice differentiable x uv = x vu, combined with the above equalities N u, x v = N, x uv = N v, x u. Using this substitution, dn(x u ), x v = N u, x v = N v, x u = dn(x v ), x u = x u, dn(x v ),
9 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 9 because the above equalities hold for basis vectors and dn is linear, the above equalities will hold for all vectors in T p (s). This means dn(m), n = m, dn(n) for all n, m T p (S), thus dn is self-adjoint. Since dn has been shown to be a self-adjoint linear map, the following result can be applied. Theorem 4.5. [oc76] Let A : V V be a self-adjoint, linear map. Then there exists an orthonormal basis e 1, e of V such that A(e 1 ) = λe 1, A(e ) = λe. In the basis e 1, e, the matrix of A is clearly diagonal and the elements λ 1, λ on the diagonal are the maximum and the minimum, respectively of the quadratic form Q(v) = Av, v on the unit circle of V. Since dn has been shown to be a linear self-adjoint map, by theorem(4.5) there is an orthogonal basis e 1, e in the principal directions. In addition, the eigenvalues of dn are the maximum and minimum of the quadratic form on the tangent plane. The quadratic form of dn referred to in the theorem is the second fundamental form: efinition 4.6. [oc76] Given a v T p (S), the function II p (v) = dn p (v), v is called the second fundamental form. The second fundamental form can be manipulated to give the normal curvature. Using the notation from above and the fact that the surface normal at a point is orthogonal to any tangent vector at the point, N(0), α (0) = 0. ifferentiating, N(0), α (0) = 0 = N (0), α (0) + N(0), α (0), which gives II p applied to a tangent vector α (0) = p as II p (α (0)) = dn p (α (0)), α (0) = N (0), α (0) = N(0), α (0) = N(0), kn =k N(0), n =k n (p), where n is the unit normal to α at p and k n is the normal curvature at p. Of course, the mean curvature is half the sum of the principal curvatures, which are the maximum and minimum normal curvatures, which from theorem (4.5) are given by the eigenvalues of dn. Using the same notation as before, a tangent vector to a surface can be represented by and applying dn yields α = x u u + x v v, dn(α ) = N (u(t), v(t)) = N u u + N v v.
10 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 10 Since dn maps onto the tangent plane of S at p, N u and N v can be represented as a linear combination of x u and x v, Writing dn(α ) in the basis x u, x v gives which simplifies to leading to N u = a 11 x u + a 1 x v N v = a 1 x u + a x v. dn(α ) = (a 11 x u + a 1 x v )u + (a 1 x u + a x v )v, (a 11 u + a 1 v )x u + (a 1 u + a v )x v, dn [ ] [ ] [ ] u a11 a v = 1 u a a v. Applying the second fundamental form to a tangent vector gives dn(α ), α = dn(u x u + v x v ), u x u + v x v = N u u + N v v, x u u + x v v = N u u, x u u N u u, x v v N v v, x u u N v v, x v v = N u u, x u u (u v ) N u, x v (u v ) N v, x u N v v, x v v = N u u, x u u (u v ) N u, x v (u v ) dn(x v ), x u N v v, x v v. Since dn has been shown to be self-adjoint, dn(x v ), x u = x v, dn(x u ), making dn(α ), α = N u u, x u u (u v ) N u, x v (u v ) dn(x u ), x v N v v, x v v = N u u, x u u (u v ) N u, x v (u v ) N u, x v N v v, x v v = N u, x u (u ) N u, x v (u v ) N v, x v (v ). This equation defines the coefficients of the second fundamental form, dn(α ), α = e(u ) + f(u v ) + g(v ) with e = N u, x u, f = N u, x v, and g = N v, x v. The coefficients can be further simplified into terms of the first fundamental form and members of dn. e = N u, x u = a 11 x u + a 1 x v, x u = a 11 x u, x u + a 1 x v, x u =a 11 x u, x u + a 1 x v, x u =a 11 E + a 1 F
11 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 11 Similarly, f and g can also be shown as f =a 11 F + a 1 G = a 1 E + a F g =a 1 F + a G These relationships can be shown in matrix form [ ] [ ] [ e f a11 a = 1 E F f g a 1 a F G To solve for dn, multiplying the system by [ ] 1 [ E F 1 G F = F G EG F F E gives [ ] a11 a 1 = a 1 a = [ e f ] [ E F f g F G ff eg EG F ef fe EG F gf fg EG F ff ge EG F. With dn computed, mean curvature can be computed in the form of coefficients of the first and second fundamental forms: (6) H = 1 (k 1 + k ) = 1trace[dN] = (a 11 + a ) = 1 ( ) eg ff + ge. EG F ]. ], ] 1 Using the above results, the proof of the first theorem is possible. Theorem 4.7. [Web06] Let U be a planar domain and j = j(u, v) a twice differentiable function. The graph is then the parametrized surface J given by J(u, v) = (u, v, j(u, v)). The function j(u, v) satisfies the minimal surface equation (1 + j u)j vv j u j v j uv + (1 + j v)j uu = 0 if and only if J = (u, v, j(u, v)) has vanishing mean curvature everywhere. Proof. Given a graph J(u, v) = (u, v, j(u, v)), the mean curvature is given as H = 1 (k 1 + k ) = 1 (a 11 + a ) = 1 ( ) eg ff + ge, where EG F E = j u, j u, F = j u, j v, and G = j v, j v are the coefficients of the first fundamental form. Moreover, e = N u, j u f = N u, j v g = N v, j v
12 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 1 are the coefficients of the second fundamental form, and N = j u j v j u j v is the unit normal to the surface. Using the fact that N is orthogonal to j u and j v, we obtain 0 = u N, j u = N u, j u + N, j uu so that e = N u, j u = N, j uu. By the same reasoning 0 = v N, x u = N v, x u + N, x uv which gives f = N u, j v = N, j uv. Also, 0 = v N, j v = N v, j v + N, j vv which makes g = N v, j v = N, j vv. The following partial derivatives of J(u, v) can be computed, This gives N as J u = (1, 0, j u ) J v = (0, 1, j v ) J uu = (0, 0, j uu ) J vv = (0, 0, j vv ) J uv = J vu = (0, 0, j uv ) = (0, 0, j vu ). N = (1, 0, j u) (0, 1, j v ) (1, 0, j u ) (0, 1, j v ) = ( j u, j v, 1). (ju + jv + 1) 1 Substituting the derivatives into the fundamental forms, E = (1, 0, j u ), (1, 0, j u ) = 1 + j u F = (1, 0, j u ), (0, 1, j v ) = j u j v and G = (0, 1, j v ), (0, 1, j v ) = 1 + jv ( j u, j v, 1) j uu e =, (0, 0, j (ju + jv + 1) 1 uu ) = (ju + jv + 1) 1 ( j u, j v, 1) j uv f =, (0, 0, j (ju + jv + 1) 1 vu ) = (ju + jv + 1) 1 ( j u, j v, 1) j vv g =, (0, 0, j (ju + jv + 1) 1 vv ) =. (ju + jv + 1) 1
13 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 13 Substituting back into H gives ( ) 1 (juu )(1 + j H = v) (j uv )(j u j v ) + (j uv )(1 + ju) (ju + jv + 1) 1 (1 + ju)(1 + jv) (j u j v ) after factoring the denominator H = (j uu)(1 + j v) (j uv )(j u j v ) + (j uv )(1 + j u) (j u + j v + 1) 3 which gives the numerator as the minimal surface equation. Therefore, the graph satisfying the minimal surface equation is a necessary and sufficient condition for the mean curvature to vanish everywhere on the surface. 5. Normal Variations The next theorem takes a Lagrange-like approach to finding qualities of a surface with vanishing mean curvature. Instead of a variation of a graph, a variation of an orientable surface will be taken. If a surface is orientable, then the surface possesses a differentiable field of unit normals vectors over the entire surface. With this in mind, the normal variation can now be introduced. For an orientable surface, the surface can be deformed by the surface normal. efinition 5.1. [BC76] A simply connected domain R is a domain such that every simple closed contour within in it encloses only points in. More precisely, given a simply connected domain U R, and an orientable surface x : U R 3, x t : U R 3 is defined such that (7) x t (p) = x(p) + th(p)n(p), where t R, N is the surface normal to x at a point p on the surface, and h : U R is a differentiable function with compact support in U. The function h deforms the surface at the point by some factor in the direction of the surface normal. Since h is differentiable, the variation x t will be differentiable. efinition 5.. [oc76] Let x : U S be a coordinate system in a regular surface S and let R = x(q) be a bounded region of S contained in x(u). Then R has an area given by (8) A(R) = x u x v dudv = EG F dudv Q where E,F,G are the coefficients of the first fundamental form. Combining the variation with the area form allows for the introduction of the second theorem. Q
14 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 14 Theorem 5.3. Let x : U R 3 be an orientable surface and x t : U R 3 such that x t (p) = x(p) + th(p)n(p). A surface x has vanishing mean curvature over the entire surface iff A (0) = 0, where A(t) is the area of x t. Proof. Given an orientable surface x : U R 3, a variation x t : U R 3 can be created such that x t (p) = x(p) + th(p)n(p), where t R, N is the unit normal to the surface, and h is a differentiable function with compact support in U. A basis for the tangent space of the variation can be found: x t u(p) = x u (p)+th(p)n u (p)+th u (p)n(p) x t v(p) = x v (p)+th(p)n v (p)+th v (p)n(p). Using this basis and letting all terms be evaluated at p, the coefficients of the first fundamental form of the variation can be computed giving E t = x t u, x t u = x u + thn u + th u N, x u + thn u + th u N = x u, x u + x u, thn u + x u, th u N + thn u, x u + thn u, thn u + thn u, th u N + th u N, x u + th u N, thn u + th u N, th u N. Collecting like terms and using the fact N, N u = 0 and N, x u = 0 gives E t = x u, x u + th x u, N u + th N u, x u + t h N u, N u + t h u N, N. N is a unit vector, thus N, N = N = 1, which makes E t = E + th x u, N u + t h N u, N u + t h u h u ; substituting in the coefficients of the second fundamental form of x gives E t = E + th( e) + t h N u, N u + t h u h u. Similar computation gives F t = x t u, x t v = x u + thn u + th u N, x v + thn v + th v N =F + th ( x u, N v + x v, N u ) + N u, N v + t h u h v =F + th( f) + t h N u, N v + t h u h v, and, G t = x t v, x t v = x v + thn v + th v N, x v + thn v + th v N =G + th x v, N v + t h N v, N v + t h v h v =G + th( g) + t h N v, N v + t h v h v.
15 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 15 Since t will be set to zero after differentiating with respect to t, all of the terms with a t with order greater than will be given by O(t ), this gives E t G t (F t ) = ( E + th( e) + O(t ) ) ( G + th( g) + O(t ) ) ( F + th( f) + O(t ) ) =EG + E(th( g)) + G(th( e)) + (th( e))(th( g)) ( F + F (th( f)) + (th( f))(th( f)) ) =EG th(eg) th(ge) F + 4(F f)th + O(t ) =(EG F ) th(eg + F f + Ge) + O(t ) [ ( )] Eg + F f + Ge =(EG F ) 1 th + O(t ) EG F [ ( )] Eg + F f + Ge =(EG F ) 1 4th( 1) + O(t ) EG F =(EG F ) [ 1 4th ( H + O(t ) )] Substituting into the area form, A(t) = (Et )(G t ) (F t ) dudv = (EG F ) (1 4thH + O(t ))dudv. ifferentiating A(t) with respect to t and setting t = 0 makes O(t) = 0 and gives A (0) = (EG F ) (1 4thH + O(t t ))dudv t=0 = ( EG F 1 4thH + O(t ) ) 1/ 1 (4Hh + O(t)) dudv t=0 = EG F (Hh) dudv From this equation, if H = 0, A (0) will also be zero. The converse gives A (0) = 0 which is true when Hh = 0. Since h is any compactly supported function over, by theorem(3.5), H must be zero. 6. Harmonic Component Functions The final theorem relates vanishing mean curvature with a conformal, harmonic map.
16 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 16 efinition 6.1. [oc76] Given two surfaces S and S, ϕ : S S is called conformal if there is λ : S R + such that for all p S and all v 1, v T p (S) dϕ p (v 1 ), dϕ p (v ) = λ (p) v 1, v. efinition 6.. [BC76] A twice differentiable function F : U R is said to be harmonic iff F uu + F vv = 0. A conformal map preserves angles of tangent vectors on their respective surfaces. Combining the two definitions will result in vanishing mean curvature. Theorem 6.3. Let U R be a simply connected domain and define x : U R 3 to be a conformal map. x is harmonic if and only if mean curvature vanishes on x. Proof. Since x is conformal, given a basis of U,{(0, 1), (1, 0)}, applying the definition of conformal to the coefficients of the first fundamental form gives E = x u, x u = dx(1, 0), dx(1, 0) = λ (1, 0), (1, 0) = λ F = x u, x v = dx(1, 0), dx(0, 1) = λ (1, 0), (0, 1) = 0 G = x v, x v = dx(0, 1), dx(0, 1) = λ (0, 1), (0, 1) = λ. For a conformal map, the mean curvature (6) can be rewritten as H = 1 Eg F f + Ge = 1 λ (g) (0)(f) + (λ )(e) EG F λ 4 (0) = 1 g + e λ = 1 N v, x v N u, x u λ = 1 N, x vv + N, x uu λ = 1 N, x vv + x uu. λ From this form, if x is harmonic then H is zero. If mean curvature vanishes on the surface N, x vv + x uu must equal zero. Since x is conformal, E = G = λ and F = 0. Taking the differentials of E and G, we find E = G u u x u u, x u = x u v, x v x u, x uu = x v, x vu x u, x uu = x v, x vu,
17 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 17 similar computation shows x u, x uv = x v, x vv. Using the fact that F =0 = x u u u, x v = x uu, x v + x u, x vu and F =0 = x v v u, x v = x uv, x v + x u, x vv which makes x uv, x v = x u, x vv and x uu, x v = x u, x vu. Substituting into the first equations, which makes, x u, x uu = x v, x vu x u, x uu = x u, x vv 0 = x u, x uu + x u, x vv = x u, x uu + x vv similar computation also shows 0 = x v, x vv + x uu. The vectors x u,x v and N form a basis for R 3. Since x uu + x vv is in R 3, it can be written as a linear combination as a 1 x u + a x v + a 3 N where a i R. From above, x uu + x vv is orthogonal to x u and x v, which means x u, x uu + x vv = x u, a 1 x u + a x v + a 3 N = x u, a 1 x u + x u, a x v + x u, a 3 N =a 1 x u, x u + a x u, x v + a 3 x u, N. which is zero only if a 1 and a are zero. This makes x u u + x v v a multiple of N as well as parallel to N. By definition N is a unit vector and is non-zero, this means N, x uu + x vv equals zero if and only if x uu + x vv = 0 which makes x harmonic. 7. Complex Analytic Functions and Vanishing Mean Curvature A complex function f : C C can be represented by two real valued functions, u, v : R R such that f(z) = u(x, y) + iv(x, y) where z = x + iy C and x, y R. Just like real valued functions, the derivatives of complex functions can also be taken. Since a point in the complex plane can be approached along two axes, additional conditions can be made about the derivative of a complex function. Theorem 7.1. [BC76] Suppose that f(z) = u(x, y) + iv(x, y) and that f (z) exists at a point z 0 = x 0 + iy 0. Then the first-order partial derivatives of u and v must exist at (x 0, y 0 ), and they must satisfy the Cauchy-Riemann equations u x = v y u y = v x.
18 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 18 The Cauchy-Riemann equations are the result of taking the partial derivatives of the function and setting the resulting real and imaginary parts equal to each other. The equality guarantees the limit of the function at all points will exist. Since the derivative will be needed at more than a point, a stronger condition will be needed. efinition 7.. [BC76] A function f(z) is analytic in an open set if it has a derivative at each point in that set. Using line integrals, harmonic functions can be shown to be a part of a corresponding analytic function. efinition 7.3. [Lar04] Let M and N have continuous partial derivatives in a simply connected domain. The vector field given by V (x, y) = Mî + Nĵ is conservative if and only if N x = M y. Theorem 7.4. [Lar04] V (x, y) = Mî + Nĵ is conservative in a simply connected domain if and only if the line integral Mdx + Ndy is independent of path. C Given a curve C in a simply connected domain, and differentiable functions M and N such that M y = N x, then the integral Mdx + Ndy C is independent of path. Since the integral is independent of path, integrating over any path in with the same endpoints as C will yield the same result. Let C have endpoints (x 0, y 0 ) and (x, y), then C can be split into two pieces. efine C 1 as the section of C from (x 0, y 0 ) to (x 1, y) and let C be the section of C curve from (x 1, y) to (x, y) such that x 1 x. By fixing (x 0, y 0 ), the integral over C becomes a function of x and y, given by F (x, y) = Mdx + Ndy C = Mdx + Ndy + Mdx + Ndy. C 1 C The first term does not vary with x, differentiating with respect to x makes it zero. In the second integral, parameterizing C = (x(t), y(t)) for a < t < b where a, b, t,
19 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 19 Figure. Curves from (x 0, y 0 ) to (x, y) the second term is written Ndy = C b a Ny dt. Since C is from (x 1, y) to (x, y), the y value does not change when parameterized by t. For this reason, y is zero over C. Using the two pieces of information, ( F x (x, y) = Mdx + Ndy + x C 1 Mdx + Ndy C ) =0 + x Mdx + Ndy C = Mdx + Ndy x C = Mdx + 0 x C = x Mdx C =M(x, y), similar computation shows that F y = N. Theorem 7.5. If f : R 3 is harmonic, and is simply connected, then there exists an analytic function ϕ : C such that Re(ϕ) = f.
20 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 0 Proof. Given a harmonic function f(x, y), and a curve C in a simply connected domain, define g(x, y) = f y dx + f x dy. The integral is independent of path since is simply connected and C ( f y y) = f yy, =f xx (f is harmonic) = x (f x). Since the integral is independent of path, from before, we know g x = f y and g y = f x. For a complex function, ϕ(x, y) = f(x, y) + ig(x, y), the Cauchy-Riemann equations are met and ϕ is analytic. The last theorem, combined with conformality can be related to vanishing mean curvature. Theorem 7.6. Assume J(x, y) = (a(x, y), b(x, y), c(x, y)) is conformal. Then ϕ 1 = a x ia y, ϕ = b x ib y, ϕ 3 = c x ic y are analytic if and only if J has vanishing mean curvature everywhere. Since J is assumed to be conformal, showing J is also harmonic when ϕ i analytic will prove the theorem. are Proof. If ϕ i are analytic, then the Cauchy-Riemann equations hold for each ϕ i. The Cauchy-Riemann equations give a xx = a yy, a xy =a yx, b xx = b yy, b xy =b yx, c xx = c yy, c xy =c yx. From the left side, the component functions a,b, and c must all be harmonic. From theorem(6.3) a conformal map is harmonic if and only if the surface has vanishing mean curvature everywhere. Since the ϕ i s are analytic if and only if a,b, and c are harmonic, the ϕ i s are analytic if and only if J has vanishing mean curvature. The fact that if ϕ i s are analytic then the corresponding component functions must be harmonic allows another observation to be made. Something interesting happens when the squares of the analytic functions of J are added. The sum of the squares
21 of the ϕ i s give VANISHING MEAN CURVATURE AN RELATE PROPERTIES 1 ϕ 1 + ϕ + ϕ 3 = (a x ia y ) + (b x ib y ) + (c x ic y ) =(a x ) i(a x a y ) (a y ) + (b x ) i(b x b y ) (b y ) + (c x ) i(c x c y ) (c y ) =(a x + b x + c x) + i( a x a y b x b y c x c y ) (a y + b y + c y) = (a x, b x, c x ), (a x, b x, c x ) i (a x, b x, c x ), (a y, b y, c y ) (a y, b y, c y ), (a y, b y, c y ) =E G if. If we instead add the absolute value of the squares we get ϕ 1 + ϕ + ϕ 3 = (a x ia y ) + (b x ib y ) + (c x ic y ) = (a x ) i(a x a y ) + (a y ) + (b x ) i(b x b y ) + (b y ) + (c x ) i(c x c y ) + (c y ) =(a x ) + i(a x a y ) + (a y ) + (b x ) i(b x b y ) + (b y ) + (c x ) + i(c x c y ) + (c y ), i = 1, so we have =(a x + b x + c x) + (a x a y + b x b y + c x c y ) + (a y + b y + c y) = (a x, b x, c x ), (a x, b x, c x ) + (a x, b x, c x ), (a y, b y, c y ) + (a y, b y, c y ), (a y, b y, c y ) =E + G + F If we assume ϕ 1 +ϕ +ϕ 3 = 0 and ϕ 1 + ϕ + ϕ 3 0, we force the parameterization to be conformal. Combining this piece of information with harmonic component functions gives another theorem. Theorem 7.7. [Web06] Given three harmonic functions f 1, f, and f 3, all real parts to analytic functions F 1, F, and F 3, and the parameterization x = Re(F 1, F, F 3 ); if F 1 +F +F 3 = 0 and F 1 + F + F 3 0, then x has vanishing mean curvature everywhere. The proof is similar to theorem(6.3) since the functions are harmonic and the restrictions give conformal. The converse of this theorem is also true. However, unlike theorem(6.3), the map is not assumed to be conformal. The lack of this property makes the proof very difficult and is outside the scope of this project. Using these results, we can now generate zero mean curvature surfaces with analytic functions. 8. Examples After talking about surfaces with vanishing mean curvature, here are some examples. First, the graph of Scherk s doubly periodic surface will be shown to satisfy the minimal surface equation(1). The graph of Scherk s doubly periodic surface,
22 VANISHING MEAN CURVATURE AN RELATE PROPERTIES discovered in the 1830 s, is given as ( F (x, y) = x, y, ln cos y ) cos x where x, y (0, π) such that x, y n π for n Z and the sign of cos x is the same as the sign of cos y.[web06] In order to use the minimal surface equation, the following partial derivatives of f(x, y) are needed f x = tan x f y = tan y f xy =0. f xx = sec x f yy = sec y Substituting into the minimal surface equation (1 + f y )f xx f x f y f xy + (1 + f x)f yy =(1 + tan y ) sec x tan x( tan y)(0) + (1 + tan x )( sec y) = sec y sec x sec x sec y =0. By theorem(4.7), Scherk s doubly periodic surface has vanishing mean curvature everywhere. The catenoid(pictured below), shown to have vanishing mean curvature by Meusnier in 1776, can be given by the parameterization x(u, v) = (a cosh v cos u, a cosh v sin u, av) for a R, 0 < u < π, and < v <.[oc76] The catenoid can be shown to have vanishing mean curvature by solving for mean curvature or, from theorem(6.3), by showing x is conformal and harmonic. Finding the coefficients of the first fundamental form gives E = x u, x u =a ( cosh v sin u, cosh v cos u, 0), ( cosh v sin u, cosh v cos u, 0) =a ( cosh v sin u + cosh v cos u + 0 ) =a cosh v ( sin u + cos u ) =a cosh v.
23 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 3 Figure 3. Catenoid Similar computations give F = 0 and G = a cosh v, which makes x conformal. Next, x needs to shown to be harmonic(6.). To do this we need to we find x uu = u u = u (a cosh v cos u, a cosh v sin u, av) ( a cosh v sin u, a cosh v cos u, 0) = ( a cosh v cos u, a cosh v sin u, 0) and x vv = (a cosh v cos u, a cosh v sin u, av) v v (a sinh v cos u, a sinh v sin u, a) = v Adding the two together we have = (a cosh v cos u, a cosh v sin u, 0). ( a cosh v cos u, a cosh v sin u, 0) + (a cosh v cos u, a cosh v sin u, 0) = (0, 0, 0) which gives x as harmonic. Since x, the catenoid, is both conformal and harmonic, the catenoid has vanishing mean curvature. Since each component function of the catenoid is harmonic, by theorem (7.5) each component function of the catenoid can be given as the real part of an analytic function. The creation of these analytic functions is very interesting because of the resulting imaginary part of the newly created functions. The imaginary parts of the functions give the real component functions of the helicoid, another surface also discovered by Meusnier to have vanishing mean curvature. This is a direct relationship to theorem(7.7), since the sum of the squares of the derivatives of the component analytic functions equals zero, by multiplying by a constant the sum will still be zero. Since the sum is still zero, the new parameterization will still be conformal. The relationship between the catenoid and the
24 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 4 Figure 4. Helicoid helicoid is displayed by ( Re 1 ( 1 z) (, i 1 ( 1 z)), 1 ) dz a parameterization for the catenoid, and z z z Re e i π ( 1 ( 1 z) (, i 1 ( 1 z)), 1 ) dz a parameterization for the helicoid. z z z In the complex plane, multiplication by e iθ is a rotation by θ. This is incredible because not only do the catenoid and helicoid have vanishing mean curvature, any rotation of the catenoid in C 3 will give a surface with vanishing mean curvature. 9. Conclusion Surfaces with vanishing mean curvature are more commonly referred to as minimal surfaces. The term minimal surface was originally used to describe surfaces that satisfied Lagrange s minimal surface equation. After Meusnier discovered surfaces satisfying Lagrange s equation possessed vanishing mean curvature, the term minimal surface began being used to describe surfaces with just vanishing mean curvature. From theorem (5.3), the area of surfaces with vanishing mean curvature is not necessarily a minimum but rather a critical point of the area function. For this
25 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 5 reason, in the paper the word minimal was avoided when possible. Aside from a misleading naming convention, vanishing mean curvature has an interesting relationship to harmonic, conformal maps in particular the connection with complex analysis. A short while ago the list of surfaces with vanishing mean curvature was fairly short and now they can be constructed with analytic functions. In any subject, this sort of breakthrough is always interesting, especially in topics where visualizing is not hard. To end, I give a quote from Fra Luca Bartolomeo de Pacioli, an Italian mathematician and collaborator with Leonardo da Vinci, Without mathematics there is no art. [Phi08]. Minimal surfaces, among other things, certainly justify this statement.
26 VANISHING MEAN CURVATURE AN RELATE PROPERTIES 6 References [Web06] Matthias Weber Notes on Minimal Surfaces(unpublished) [oc76] Manfreo P. do Carmo ifferential Geometry of Curves and Surfaces. 1976: Prentice Hall [Nit89] Johannes C. C. Nitsche Lectures on Minimal Surfaces. 1989:Cambridge University Press [BC76] James Ward Brown, Ruel V. Churchill Complex Variables and Applications. 1976:McGraw- Hill [Lar04] Ron Larson, Robert P. Hostetler, Bruce H. Edwards, avid E. Heyd Calculus with Analytic Geometry, Seventh Edition 00:Houghton Mifflin [Phi08] the Golden Number: Quotes Related to Phi. ec Images from Wikipedia, Cateniod - Helicoid -
9.1 Mean and Gaussian Curvatures of Surfaces
 Chapter 9 Gauss Map II 9.1 Mean and Gaussian Curvatures of Surfaces in R 3 We ll assume that the curves are in R 3 unless otherwise noted. We start off by quoting the following useful theorem about self
Chapter 9 Gauss Map II 9.1 Mean and Gaussian Curvatures of Surfaces in R 3 We ll assume that the curves are in R 3 unless otherwise noted. We start off by quoting the following useful theorem about self
DIFFERENTIAL GEOMETRY HW 4. Show that a catenoid and helicoid are locally isometric.
 DIFFERENTIAL GEOMETRY HW 4 CLAY SHONKWILER Show that a catenoid and helicoid are locally isometric. 3 Proof. Let X(u, v) = (a cosh v cos u, a cosh v sin u, av) be the parametrization of the catenoid and
DIFFERENTIAL GEOMETRY HW 4 CLAY SHONKWILER Show that a catenoid and helicoid are locally isometric. 3 Proof. Let X(u, v) = (a cosh v cos u, a cosh v sin u, av) be the parametrization of the catenoid and
DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES 5. The Second Fundamental Form of a Surface
 DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES 5. The Second Fundamental Form of a Surface The main idea of this chapter is to try to measure to which extent a surface S is different from a plane, in other
DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES 5. The Second Fundamental Form of a Surface The main idea of this chapter is to try to measure to which extent a surface S is different from a plane, in other
On the Weierstrass-Enneper Representation of Minimal Surfaces
 On the Weierstrass-Enneper Representation of Minimal Surfaces Albin Ingelström Bachelor s thesis 2017:K15 Faculty of Science Centre for Mathematical Sciences Mathematics CENTRUM SCIENTIARUM MATHEMATICARUM
On the Weierstrass-Enneper Representation of Minimal Surfaces Albin Ingelström Bachelor s thesis 2017:K15 Faculty of Science Centre for Mathematical Sciences Mathematics CENTRUM SCIENTIARUM MATHEMATICARUM
Lecture Notes on Minimal Surfaces January 27, 2006 by Michael Dorff
 Lecture Notes on Minimal Surfaces January 7, 6 by Michael Dorff 1 Some Background in Differential Geometry Our goal is to develop the mathematics necessary to investigate minimal surfaces in R 3. Every
Lecture Notes on Minimal Surfaces January 7, 6 by Michael Dorff 1 Some Background in Differential Geometry Our goal is to develop the mathematics necessary to investigate minimal surfaces in R 3. Every
CHAPTER 3. Gauss map. In this chapter we will study the Gauss map of surfaces in R 3.
 CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
Summary for Vector Calculus and Complex Calculus (Math 321) By Lei Li
 Summary for Vector alculus and omplex alculus (Math 321) By Lei Li 1 Vector alculus 1.1 Parametrization urves, surfaces, or volumes can be parametrized. Below, I ll talk about 3D case. Suppose we use e
Summary for Vector alculus and omplex alculus (Math 321) By Lei Li 1 Vector alculus 1.1 Parametrization urves, surfaces, or volumes can be parametrized. Below, I ll talk about 3D case. Suppose we use e
Minimal Surfaces. Clay Shonkwiler
 Minimal Surfaces Clay Shonkwiler October 18, 2006 Soap Films A soap film seeks to minimize its surface energy, which is proportional to area. Hence, a soap film achieves a minimum area among all surfaces
Minimal Surfaces Clay Shonkwiler October 18, 2006 Soap Films A soap film seeks to minimize its surface energy, which is proportional to area. Hence, a soap film achieves a minimum area among all surfaces
7.1 Tangent Planes; Differentials of Maps Between
 Chapter 7 Tangent Planes Reading: Do Carmo sections 2.4 and 3.2 Today I am discussing 1. Differentials of maps between surfaces 2. Geometry of Gauss map 7.1 Tangent Planes; Differentials of Maps Between
Chapter 7 Tangent Planes Reading: Do Carmo sections 2.4 and 3.2 Today I am discussing 1. Differentials of maps between surfaces 2. Geometry of Gauss map 7.1 Tangent Planes; Differentials of Maps Between
Math 115 ( ) Yum-Tong Siu 1. Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives
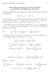 Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Mathematical Analysis II, 2018/19 First semester
 Mathematical Analysis II, 208/9 First semester Yoh Tanimoto Dipartimento di Matematica, Università di Roma Tor Vergata Via della Ricerca Scientifica, I-0033 Roma, Italy email: hoyt@mat.uniroma2.it We basically
Mathematical Analysis II, 208/9 First semester Yoh Tanimoto Dipartimento di Matematica, Università di Roma Tor Vergata Via della Ricerca Scientifica, I-0033 Roma, Italy email: hoyt@mat.uniroma2.it We basically
Contents. MATH 32B-2 (18W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables. 1 Multiple Integrals 3. 2 Vector Fields 9
 MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
CS Tutorial 5 - Differential Geometry I - Surfaces
 236861 Numerical Geometry of Images Tutorial 5 Differential Geometry II Surfaces c 2009 Parameterized surfaces A parameterized surface X : U R 2 R 3 a differentiable map 1 X from an open set U R 2 to R
236861 Numerical Geometry of Images Tutorial 5 Differential Geometry II Surfaces c 2009 Parameterized surfaces A parameterized surface X : U R 2 R 3 a differentiable map 1 X from an open set U R 2 to R
MTH4101 CALCULUS II REVISION NOTES. 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) ax 2 + bx + c = 0. x = b ± b 2 4ac 2a. i = 1.
 MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
Math 265H: Calculus III Practice Midterm II: Fall 2014
 Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
7a3 2. (c) πa 3 (d) πa 3 (e) πa3
 1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
Math 185 Homework Exercises II
 Math 185 Homework Exercises II Instructor: Andrés E. Caicedo Due: July 10, 2002 1. Verify that if f H(Ω) C 2 (Ω) is never zero, then ln f is harmonic in Ω. 2. Let f = u+iv H(Ω) C 2 (Ω). Let p 2 be an integer.
Math 185 Homework Exercises II Instructor: Andrés E. Caicedo Due: July 10, 2002 1. Verify that if f H(Ω) C 2 (Ω) is never zero, then ln f is harmonic in Ω. 2. Let f = u+iv H(Ω) C 2 (Ω). Let p 2 be an integer.
Math 417 Midterm Exam Solutions Friday, July 9, 2010
 Math 417 Midterm Exam Solutions Friday, July 9, 010 Solve any 4 of Problems 1 6 and 1 of Problems 7 8. Write your solutions in the booklet provided. If you attempt more than 5 problems, you must clearly
Math 417 Midterm Exam Solutions Friday, July 9, 010 Solve any 4 of Problems 1 6 and 1 of Problems 7 8. Write your solutions in the booklet provided. If you attempt more than 5 problems, you must clearly
Multivariable Calculus
 2 Multivariable Calculus 2.1 Limits and Continuity Problem 2.1.1 (Fa94) Let the function f : R n R n satisfy the following two conditions: (i) f (K ) is compact whenever K is a compact subset of R n. (ii)
2 Multivariable Calculus 2.1 Limits and Continuity Problem 2.1.1 (Fa94) Let the function f : R n R n satisfy the following two conditions: (i) f (K ) is compact whenever K is a compact subset of R n. (ii)
A PROOF OF THE GAUSS-BONNET THEOREM. Contents. 1. Introduction. 2. Regular Surfaces
 A PROOF OF THE GAUSS-BONNET THEOREM AARON HALPER Abstract. In this paper I will provide a proof of the Gauss-Bonnet Theorem. I will start by briefly explaining regular surfaces and move on to the first
A PROOF OF THE GAUSS-BONNET THEOREM AARON HALPER Abstract. In this paper I will provide a proof of the Gauss-Bonnet Theorem. I will start by briefly explaining regular surfaces and move on to the first
2. Complex Analytic Functions
 2. Complex Analytic Functions John Douglas Moore July 6, 2011 Recall that if A and B are sets, a function f : A B is a rule which assigns to each element a A a unique element f(a) B. In this course, we
2. Complex Analytic Functions John Douglas Moore July 6, 2011 Recall that if A and B are sets, a function f : A B is a rule which assigns to each element a A a unique element f(a) B. In this course, we
HILBERT S THEOREM ON THE HYPERBOLIC PLANE
 HILBET S THEOEM ON THE HYPEBOLIC PLANE MATTHEW D. BOWN Abstract. We recount a proof of Hilbert s result that a complete geometric surface of constant negative Gaussian curvature cannot be isometrically
HILBET S THEOEM ON THE HYPEBOLIC PLANE MATTHEW D. BOWN Abstract. We recount a proof of Hilbert s result that a complete geometric surface of constant negative Gaussian curvature cannot be isometrically
GEOMETRY HW Consider the parametrized surface (Enneper s surface)
 GEOMETRY HW 4 CLAY SHONKWILER 3.3.5 Consider the parametrized surface (Enneper s surface φ(u, v (x u3 3 + uv2, v v3 3 + vu2, u 2 v 2 show that (a The coefficients of the first fundamental form are E G
GEOMETRY HW 4 CLAY SHONKWILER 3.3.5 Consider the parametrized surface (Enneper s surface φ(u, v (x u3 3 + uv2, v v3 3 + vu2, u 2 v 2 show that (a The coefficients of the first fundamental form are E G
Chapter 14. Basics of The Differential Geometry of Surfaces. Introduction. Parameterized Surfaces. The First... Home Page. Title Page.
 Chapter 14 Basics of The Differential Geometry of Surfaces Page 649 of 681 14.1. Almost all of the material presented in this chapter is based on lectures given by Eugenio Calabi in an upper undergraduate
Chapter 14 Basics of The Differential Geometry of Surfaces Page 649 of 681 14.1. Almost all of the material presented in this chapter is based on lectures given by Eugenio Calabi in an upper undergraduate
REVIEW OF DIFFERENTIAL CALCULUS
 REVIEW OF DIFFERENTIAL CALCULUS DONU ARAPURA 1. Limits and continuity To simplify the statements, we will often stick to two variables, but everything holds with any number of variables. Let f(x, y) be
REVIEW OF DIFFERENTIAL CALCULUS DONU ARAPURA 1. Limits and continuity To simplify the statements, we will often stick to two variables, but everything holds with any number of variables. Let f(x, y) be
Mathematics (Course B) Lent Term 2005 Examples Sheet 2
 N12d Natural Sciences, Part IA Dr M. G. Worster Mathematics (Course B) Lent Term 2005 Examples Sheet 2 Please communicate any errors in this sheet to Dr Worster at M.G.Worster@damtp.cam.ac.uk. Note that
N12d Natural Sciences, Part IA Dr M. G. Worster Mathematics (Course B) Lent Term 2005 Examples Sheet 2 Please communicate any errors in this sheet to Dr Worster at M.G.Worster@damtp.cam.ac.uk. Note that
Math 234 Final Exam (with answers) Spring 2017
 Math 234 Final Exam (with answers) pring 217 1. onsider the points A = (1, 2, 3), B = (1, 2, 2), and = (2, 1, 4). (a) [6 points] Find the area of the triangle formed by A, B, and. olution: One way to solve
Math 234 Final Exam (with answers) pring 217 1. onsider the points A = (1, 2, 3), B = (1, 2, 2), and = (2, 1, 4). (a) [6 points] Find the area of the triangle formed by A, B, and. olution: One way to solve
Mathematical Tripos Part IA Lent Term Example Sheet 1. Calculate its tangent vector dr/du at each point and hence find its total length.
 Mathematical Tripos Part IA Lent Term 205 ector Calculus Prof B C Allanach Example Sheet Sketch the curve in the plane given parametrically by r(u) = ( x(u), y(u) ) = ( a cos 3 u, a sin 3 u ) with 0 u
Mathematical Tripos Part IA Lent Term 205 ector Calculus Prof B C Allanach Example Sheet Sketch the curve in the plane given parametrically by r(u) = ( x(u), y(u) ) = ( a cos 3 u, a sin 3 u ) with 0 u
Final Exam Topic Outline
 Math 442 - Differential Geometry of Curves and Surfaces Final Exam Topic Outline 30th November 2010 David Dumas Note: There is no guarantee that this outline is exhaustive, though I have tried to include
Math 442 - Differential Geometry of Curves and Surfaces Final Exam Topic Outline 30th November 2010 David Dumas Note: There is no guarantee that this outline is exhaustive, though I have tried to include
M273Q Multivariable Calculus Spring 2017 Review Problems for Exam 3
 M7Q Multivariable alculus Spring 7 Review Problems for Exam Exam covers material from Sections 5.-5.4 and 6.-6. and 7.. As you prepare, note well that the Fall 6 Exam posted online did not cover exactly
M7Q Multivariable alculus Spring 7 Review Problems for Exam Exam covers material from Sections 5.-5.4 and 6.-6. and 7.. As you prepare, note well that the Fall 6 Exam posted online did not cover exactly
Solutions to old Exam 3 problems
 Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
Solutions to old Exam 3 problems Hi students! I am putting this version of my review for the Final exam review here on the web site, place and time to be announced. Enjoy!! Best, Bill Meeks PS. There are
SPRING 2006 PRELIMINARY EXAMINATION SOLUTIONS
 SPRING 006 PRELIMINARY EXAMINATION SOLUTIONS 1A. Let G be the subgroup of the free abelian group Z 4 consisting of all integer vectors (x, y, z, w) such that x + 3y + 5z + 7w = 0. (a) Determine a linearly
SPRING 006 PRELIMINARY EXAMINATION SOLUTIONS 1A. Let G be the subgroup of the free abelian group Z 4 consisting of all integer vectors (x, y, z, w) such that x + 3y + 5z + 7w = 0. (a) Determine a linearly
Lecture 13 - Wednesday April 29th
 Lecture 13 - Wednesday April 29th jacques@ucsdedu Key words: Systems of equations, Implicit differentiation Know how to do implicit differentiation, how to use implicit and inverse function theorems 131
Lecture 13 - Wednesday April 29th jacques@ucsdedu Key words: Systems of equations, Implicit differentiation Know how to do implicit differentiation, how to use implicit and inverse function theorems 131
1 The Differential Geometry of Surfaces
 1 The Differential Geometry of Surfaces Three-dimensional objects are bounded by surfaces. This section reviews some of the basic definitions and concepts relating to the geometry of smooth surfaces. 1.1
1 The Differential Geometry of Surfaces Three-dimensional objects are bounded by surfaces. This section reviews some of the basic definitions and concepts relating to the geometry of smooth surfaces. 1.1
Math Homework 2
 Math 73 Homework Due: September 8, 6 Suppose that f is holomorphic in a region Ω, ie an open connected set Prove that in any of the following cases (a) R(f) is constant; (b) I(f) is constant; (c) f is
Math 73 Homework Due: September 8, 6 Suppose that f is holomorphic in a region Ω, ie an open connected set Prove that in any of the following cases (a) R(f) is constant; (b) I(f) is constant; (c) f is
Jim Lambers MAT 280 Fall Semester Practice Final Exam Solution
 Jim Lambers MAT 8 Fall emester 6-7 Practice Final Exam olution. Use Lagrange multipliers to find the point on the circle x + 4 closest to the point (, 5). olution We have f(x, ) (x ) + ( 5), the square
Jim Lambers MAT 8 Fall emester 6-7 Practice Final Exam olution. Use Lagrange multipliers to find the point on the circle x + 4 closest to the point (, 5). olution We have f(x, ) (x ) + ( 5), the square
Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 28, 2011
 Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 8, Solutions to Problems 5 are omitted since they involve topics no longer covered on the Comprehensive
Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 8, Solutions to Problems 5 are omitted since they involve topics no longer covered on the Comprehensive
Jim Lambers MAT 280 Summer Semester Practice Final Exam Solution. dy + xz dz = x(t)y(t) dt. t 3 (4t 3 ) + e t2 (2t) + t 7 (3t 2 ) dt
 Jim Lambers MAT 28 ummer emester 212-1 Practice Final Exam olution 1. Evaluate the line integral xy dx + e y dy + xz dz, where is given by r(t) t 4, t 2, t, t 1. olution From r (t) 4t, 2t, t 2, we obtain
Jim Lambers MAT 28 ummer emester 212-1 Practice Final Exam olution 1. Evaluate the line integral xy dx + e y dy + xz dz, where is given by r(t) t 4, t 2, t, t 1. olution From r (t) 4t, 2t, t 2, we obtain
Exercises for Multivariable Differential Calculus XM521
 This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
Sec. 1.1: Basics of Vectors
 Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
Conformal maps. Lent 2019 COMPLEX METHODS G. Taylor. A star means optional and not necessarily harder.
 Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
d F = (df E 3 ) E 3. (4.1)
 4. The Second Fundamental Form In the last section we developed the theory of intrinsic geometry of surfaces by considering the covariant differential d F, that is, the tangential component of df for a
4. The Second Fundamental Form In the last section we developed the theory of intrinsic geometry of surfaces by considering the covariant differential d F, that is, the tangential component of df for a
Oct : Lecture 15: Surface Integrals and Some Related Theorems
 90 MIT 3.016 Fall 2005 c W.C Carter Lecture 15 Oct. 21 2005: Lecture 15: Surface Integrals and Some Related Theorems Reading: Kreyszig Sections: 9.4 pp:485 90), 9.5 pp:491 495) 9.6 pp:496 505) 9.7 pp:505
90 MIT 3.016 Fall 2005 c W.C Carter Lecture 15 Oct. 21 2005: Lecture 15: Surface Integrals and Some Related Theorems Reading: Kreyszig Sections: 9.4 pp:485 90), 9.5 pp:491 495) 9.6 pp:496 505) 9.7 pp:505
THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK. Summer Examination 2009.
 OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
Math 212-Lecture 8. The chain rule with one independent variable
 Math 212-Lecture 8 137: The multivariable chain rule The chain rule with one independent variable w = f(x, y) If the particle is moving along a curve x = x(t), y = y(t), then the values that the particle
Math 212-Lecture 8 137: The multivariable chain rule The chain rule with one independent variable w = f(x, y) If the particle is moving along a curve x = x(t), y = y(t), then the values that the particle
Note: Each problem is worth 14 points except numbers 5 and 6 which are 15 points. = 3 2
 Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
INDIAN INSTITUTE OF TECHNOLOGY BOMBAY MA205 Complex Analysis Autumn 2012
 INDIAN INSTITUTE OF TECHNOLOGY BOMBAY MA205 Complex Analysis Autumn 2012 September 5, 2012 Mapping Properties Lecture 13 We shall once again return to the study of general behaviour of holomorphic functions
INDIAN INSTITUTE OF TECHNOLOGY BOMBAY MA205 Complex Analysis Autumn 2012 September 5, 2012 Mapping Properties Lecture 13 We shall once again return to the study of general behaviour of holomorphic functions
Second Midterm Exam Name: Practice Problems March 10, 2015
 Math 160 1. Treibergs Second Midterm Exam Name: Practice Problems March 10, 015 1. Determine the singular points of the function and state why the function is analytic everywhere else: z 1 fz) = z + 1)z
Math 160 1. Treibergs Second Midterm Exam Name: Practice Problems March 10, 015 1. Determine the singular points of the function and state why the function is analytic everywhere else: z 1 fz) = z + 1)z
ENGI Partial Differentiation Page y f x
 ENGI 3424 4 Partial Differentiation Page 4-01 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
ENGI 3424 4 Partial Differentiation Page 4-01 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
Math 10C - Fall Final Exam
 Math 1C - Fall 217 - Final Exam Problem 1. Consider the function f(x, y) = 1 x 2 (y 1) 2. (i) Draw the level curve through the point P (1, 2). Find the gradient of f at the point P and draw the gradient
Math 1C - Fall 217 - Final Exam Problem 1. Consider the function f(x, y) = 1 x 2 (y 1) 2. (i) Draw the level curve through the point P (1, 2). Find the gradient of f at the point P and draw the gradient
Course Summary Math 211
 Course Summary Math 211 table of contents I. Functions of several variables. II. R n. III. Derivatives. IV. Taylor s Theorem. V. Differential Geometry. VI. Applications. 1. Best affine approximations.
Course Summary Math 211 table of contents I. Functions of several variables. II. R n. III. Derivatives. IV. Taylor s Theorem. V. Differential Geometry. VI. Applications. 1. Best affine approximations.
and likewise fdy = and we have fdx = f((x, g(x))) 1 dx. (0.1)
 On line integrals in R 2 and Green s formulae. How Cauchy s formulae follows by Green s. Suppose we have some curve in R 2 which can be parametrized by t (ζ 1 (t), ζ 2 (t)), where t is in some interval
On line integrals in R 2 and Green s formulae. How Cauchy s formulae follows by Green s. Suppose we have some curve in R 2 which can be parametrized by t (ζ 1 (t), ζ 2 (t)), where t is in some interval
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algo
 Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Math Review for Exam 3
 1. ompute oln: (8x + 36xy)ds = Math 235 - Review for Exam 3 (8x + 36xy)ds, where c(t) = (t, t 2, t 3 ) on the interval t 1. 1 (8t + 36t 3 ) 1 + 4t 2 + 9t 4 dt = 2 3 (1 + 4t2 + 9t 4 ) 3 2 1 = 2 3 ((14)
1. ompute oln: (8x + 36xy)ds = Math 235 - Review for Exam 3 (8x + 36xy)ds, where c(t) = (t, t 2, t 3 ) on the interval t 1. 1 (8t + 36t 3 ) 1 + 4t 2 + 9t 4 dt = 2 3 (1 + 4t2 + 9t 4 ) 3 2 1 = 2 3 ((14)
Hyperbolic Geometry on Geometric Surfaces
 Mathematics Seminar, 15 September 2010 Outline Introduction Hyperbolic geometry Abstract surfaces The hemisphere model as a geometric surface The Poincaré disk model as a geometric surface Conclusion Introduction
Mathematics Seminar, 15 September 2010 Outline Introduction Hyperbolic geometry Abstract surfaces The hemisphere model as a geometric surface The Poincaré disk model as a geometric surface Conclusion Introduction
The first order quasi-linear PDEs
 Chapter 2 The first order quasi-linear PDEs The first order quasi-linear PDEs have the following general form: F (x, u, Du) = 0, (2.1) where x = (x 1, x 2,, x 3 ) R n, u = u(x), Du is the gradient of u.
Chapter 2 The first order quasi-linear PDEs The first order quasi-linear PDEs have the following general form: F (x, u, Du) = 0, (2.1) where x = (x 1, x 2,, x 3 ) R n, u = u(x), Du is the gradient of u.
CITY UNIVERSITY LONDON. BEng (Hons) in Electrical and Electronic Engineering PART 2 EXAMINATION. ENGINEERING MATHEMATICS 2 (resit) EX2003
 No: CITY UNIVERSITY LONDON BEng (Hons) in Electrical and Electronic Engineering PART 2 EXAMINATION ENGINEERING MATHEMATICS 2 (resit) EX2003 Date: August 2004 Time: 3 hours Attempt Five out of EIGHT questions
No: CITY UNIVERSITY LONDON BEng (Hons) in Electrical and Electronic Engineering PART 2 EXAMINATION ENGINEERING MATHEMATICS 2 (resit) EX2003 Date: August 2004 Time: 3 hours Attempt Five out of EIGHT questions
Vector Calculus handout
 Vector Calculus handout The Fundamental Theorem of Line Integrals Theorem 1 (The Fundamental Theorem of Line Integrals). Let C be a smooth curve given by a vector function r(t), where a t b, and let f
Vector Calculus handout The Fundamental Theorem of Line Integrals Theorem 1 (The Fundamental Theorem of Line Integrals). Let C be a smooth curve given by a vector function r(t), where a t b, and let f
MATH The Chain Rule Fall 2016 A vector function of a vector variable is a function F: R n R m. In practice, if x 1, x n is the input,
 MATH 20550 The Chain Rule Fall 2016 A vector function of a vector variable is a function F: R n R m. In practice, if x 1, x n is the input, F(x 1,, x n ) F 1 (x 1,, x n ),, F m (x 1,, x n ) where each
MATH 20550 The Chain Rule Fall 2016 A vector function of a vector variable is a function F: R n R m. In practice, if x 1, x n is the input, F(x 1,, x n ) F 1 (x 1,, x n ),, F m (x 1,, x n ) where each
GEOMETRY HW (t, 0, e 1/t2 ), t > 0 1/t2, 0), t < 0. (0, 0, 0), t = 0
 GEOMETRY HW CLAY SHONKWILER Consider the map.5.0 t, 0, e /t ), t > 0 αt) = t, e /t, 0), t < 0 0, 0, 0), t = 0 a) Prove that α is a differentiable curve. Proof. If we denote αt) = xt), yt), zt0), then it
GEOMETRY HW CLAY SHONKWILER Consider the map.5.0 t, 0, e /t ), t > 0 αt) = t, e /t, 0), t < 0 0, 0, 0), t = 0 a) Prove that α is a differentiable curve. Proof. If we denote αt) = xt), yt), zt0), then it
Derivatives and Integrals
 Derivatives and Integrals Definition 1: Derivative Formulas d dx (c) = 0 d dx (f ± g) = f ± g d dx (kx) = k d dx (xn ) = nx n 1 (f g) = f g + fg ( ) f = f g fg g g 2 (f(g(x))) = f (g(x)) g (x) d dx (ax
Derivatives and Integrals Definition 1: Derivative Formulas d dx (c) = 0 d dx (f ± g) = f ± g d dx (kx) = k d dx (xn ) = nx n 1 (f g) = f g + fg ( ) f = f g fg g g 2 (f(g(x))) = f (g(x)) g (x) d dx (ax
Study Guide/Practice Exam 3
 Study Guide/Practice Exam 3 This study guide/practice exam covers only the material since exam. The final exam, however, is cumulative so you should be sure to thoroughly study earlier material. The distribution
Study Guide/Practice Exam 3 This study guide/practice exam covers only the material since exam. The final exam, however, is cumulative so you should be sure to thoroughly study earlier material. The distribution
Lecture 13 The Fundamental Forms of a Surface
 Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
3 Applications of partial differentiation
 Advanced Calculus Chapter 3 Applications of partial differentiation 37 3 Applications of partial differentiation 3.1 Stationary points Higher derivatives Let U R 2 and f : U R. The partial derivatives
Advanced Calculus Chapter 3 Applications of partial differentiation 37 3 Applications of partial differentiation 3.1 Stationary points Higher derivatives Let U R 2 and f : U R. The partial derivatives
(b) Find the range of h(x, y) (5) Use the definition of continuity to explain whether or not the function f(x, y) is continuous at (0, 0)
 eview Exam Math 43 Name Id ead each question carefully. Avoid simple mistakes. Put a box around the final answer to a question (use the back of the page if necessary). For full credit you must show your
eview Exam Math 43 Name Id ead each question carefully. Avoid simple mistakes. Put a box around the final answer to a question (use the back of the page if necessary). For full credit you must show your
GRE Math Subject Test #5 Solutions.
 GRE Math Subject Test #5 Solutions. 1. E (Calculus) Apply L Hôpital s Rule two times: cos(3x) 1 3 sin(3x) 9 cos(3x) lim x 0 = lim x 2 x 0 = lim 2x x 0 = 9. 2 2 2. C (Geometry) Note that a line segment
GRE Math Subject Test #5 Solutions. 1. E (Calculus) Apply L Hôpital s Rule two times: cos(3x) 1 3 sin(3x) 9 cos(3x) lim x 0 = lim x 2 x 0 = lim 2x x 0 = 9. 2 2 2. C (Geometry) Note that a line segment
SOLUTIONS TO THE FINAL EXAM. December 14, 2010, 9:00am-12:00 (3 hours)
 SOLUTIONS TO THE 18.02 FINAL EXAM BJORN POONEN December 14, 2010, 9:00am-12:00 (3 hours) 1) For each of (a)-(e) below: If the statement is true, write TRUE. If the statement is false, write FALSE. (Please
SOLUTIONS TO THE 18.02 FINAL EXAM BJORN POONEN December 14, 2010, 9:00am-12:00 (3 hours) 1) For each of (a)-(e) below: If the statement is true, write TRUE. If the statement is false, write FALSE. (Please
Final Exam. Monday March 19, 3:30-5:30pm MAT 21D, Temple, Winter 2018
 Name: Student ID#: Section: Final Exam Monday March 19, 3:30-5:30pm MAT 21D, Temple, Winter 2018 Show your work on every problem. orrect answers with no supporting work will not receive full credit. Be
Name: Student ID#: Section: Final Exam Monday March 19, 3:30-5:30pm MAT 21D, Temple, Winter 2018 Show your work on every problem. orrect answers with no supporting work will not receive full credit. Be
Math 4263 Homework Set 1
 Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
Calculus - II Multivariable Calculus. M.Thamban Nair. Department of Mathematics Indian Institute of Technology Madras
 Calculus - II Multivariable Calculus M.Thamban Nair epartment of Mathematics Indian Institute of Technology Madras February 27 Revised: January 29 Contents Preface v 1 Functions of everal Variables 1 1.1
Calculus - II Multivariable Calculus M.Thamban Nair epartment of Mathematics Indian Institute of Technology Madras February 27 Revised: January 29 Contents Preface v 1 Functions of everal Variables 1 1.1
Math 210, Final Exam, Spring 2012 Problem 1 Solution. (a) Find an equation of the plane passing through the tips of u, v, and w.
 Math, Final Exam, Spring Problem Solution. Consider three position vectors (tails are the origin): u,, v 4,, w,, (a) Find an equation of the plane passing through the tips of u, v, and w. (b) Find an equation
Math, Final Exam, Spring Problem Solution. Consider three position vectors (tails are the origin): u,, v 4,, w,, (a) Find an equation of the plane passing through the tips of u, v, and w. (b) Find an equation
Lecture 14 Conformal Mapping. 1 Conformality. 1.1 Preservation of angle. 1.2 Length and area. MATH-GA Complex Variables
 Lecture 14 Conformal Mapping MATH-GA 2451.001 Complex Variables 1 Conformality 1.1 Preservation of angle The open mapping theorem tells us that an analytic function such that f (z 0 ) 0 maps a small neighborhood
Lecture 14 Conformal Mapping MATH-GA 2451.001 Complex Variables 1 Conformality 1.1 Preservation of angle The open mapping theorem tells us that an analytic function such that f (z 0 ) 0 maps a small neighborhood
Introduction to Algebraic and Geometric Topology Week 14
 Introduction to Algebraic and Geometric Topology Week 14 Domingo Toledo University of Utah Fall 2016 Computations in coordinates I Recall smooth surface S = {f (x, y, z) =0} R 3, I rf 6= 0 on S, I Chart
Introduction to Algebraic and Geometric Topology Week 14 Domingo Toledo University of Utah Fall 2016 Computations in coordinates I Recall smooth surface S = {f (x, y, z) =0} R 3, I rf 6= 0 on S, I Chart
VANDERBILT UNIVERSITY. MATH 2300 MULTIVARIABLE CALCULUS Practice Test 1 Solutions
 VANDERBILT UNIVERSITY MATH 2300 MULTIVARIABLE CALCULUS Practice Test 1 Solutions Directions. This practice test should be used as a study guide, illustrating the concepts that will be emphasized in the
VANDERBILT UNIVERSITY MATH 2300 MULTIVARIABLE CALCULUS Practice Test 1 Solutions Directions. This practice test should be used as a study guide, illustrating the concepts that will be emphasized in the
Part IB GEOMETRY (Lent 2016): Example Sheet 1
 Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
MULTIVARIABLE CALCULUS
 MULTIVARIABLE CALCULUS JOHN QUIGG Contents 13.1 Three-Dimensional Coordinate Systems 2 13.2 Vectors 3 13.3 The Dot Product 5 13.4 The Cross Product 6 13.5 Equations of Lines and Planes 7 13.6 Cylinders
MULTIVARIABLE CALCULUS JOHN QUIGG Contents 13.1 Three-Dimensional Coordinate Systems 2 13.2 Vectors 3 13.3 The Dot Product 5 13.4 The Cross Product 6 13.5 Equations of Lines and Planes 7 13.6 Cylinders
MATH H53 : Final exam
 MATH H53 : Final exam 11 May, 18 Name: You have 18 minutes to answer the questions. Use of calculators or any electronic items is not permitted. Answer the questions in the space provided. If you run out
MATH H53 : Final exam 11 May, 18 Name: You have 18 minutes to answer the questions. Use of calculators or any electronic items is not permitted. Answer the questions in the space provided. If you run out
1. For each function, find all of its critical points and then classify each point as a local extremum or saddle point.
 Solutions Review for Exam # Math 6. For each function, find all of its critical points and then classify each point as a local extremum or saddle point. a fx, y x + 6xy + y Solution.The gradient of f is
Solutions Review for Exam # Math 6. For each function, find all of its critical points and then classify each point as a local extremum or saddle point. a fx, y x + 6xy + y Solution.The gradient of f is
Math 210, Final Exam, Practice Fall 2009 Problem 1 Solution AB AC AB. cosθ = AB BC AB (0)(1)+( 4)( 2)+(3)(2)
 Math 2, Final Exam, Practice Fall 29 Problem Solution. A triangle has vertices at the points A (,,), B (, 3,4), and C (2,,3) (a) Find the cosine of the angle between the vectors AB and AC. (b) Find an
Math 2, Final Exam, Practice Fall 29 Problem Solution. A triangle has vertices at the points A (,,), B (, 3,4), and C (2,,3) (a) Find the cosine of the angle between the vectors AB and AC. (b) Find an
Practice Final Solutions
 Practice Final Solutions Math 1, Fall 17 Problem 1. Find a parameterization for the given curve, including bounds on the parameter t. Part a) The ellipse in R whose major axis has endpoints, ) and 6, )
Practice Final Solutions Math 1, Fall 17 Problem 1. Find a parameterization for the given curve, including bounds on the parameter t. Part a) The ellipse in R whose major axis has endpoints, ) and 6, )
On Cauchy s theorem and Green s theorem
 MA 525 On Cauchy s theorem and Green s theorem 1. Introduction No doubt the most important result in this course is Cauchy s theorem. There are many ways to formulate it, but the most simple, direct and
MA 525 On Cauchy s theorem and Green s theorem 1. Introduction No doubt the most important result in this course is Cauchy s theorem. There are many ways to formulate it, but the most simple, direct and
Lecture notes for Math Multivariable Calculus
 Lecture notes for Math 417-517 Multivariable alculus J. Dimock Dept. of Mathematics SUNY at Buffalo Buffalo, NY 14260 December 4, 2012 ontents 1 multivariable calculus 3 1.1 vectors....................................
Lecture notes for Math 417-517 Multivariable alculus J. Dimock Dept. of Mathematics SUNY at Buffalo Buffalo, NY 14260 December 4, 2012 ontents 1 multivariable calculus 3 1.1 vectors....................................
SECTION v 2 x + v 2 y, (5.1)
 CHAPTER 5 5.1 Normed Spaces SECTION 5.1 171 REAL AND COMPLEX NORMED, METRIC, AND INNER PRODUCT SPACES So far, our studies have concentrated only on properties of vector spaces that follow from Definition
CHAPTER 5 5.1 Normed Spaces SECTION 5.1 171 REAL AND COMPLEX NORMED, METRIC, AND INNER PRODUCT SPACES So far, our studies have concentrated only on properties of vector spaces that follow from Definition
SOME PROBLEMS YOU SHOULD BE ABLE TO DO
 OME PROBLEM YOU HOULD BE ABLE TO DO I ve attempted to make a list of the main calculations you should be ready for on the exam, and included a handful of the more important formulas. There are no examples
OME PROBLEM YOU HOULD BE ABLE TO DO I ve attempted to make a list of the main calculations you should be ready for on the exam, and included a handful of the more important formulas. There are no examples
Chain Rule. MATH 311, Calculus III. J. Robert Buchanan. Spring Department of Mathematics
 3.33pt Chain Rule MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Spring 2019 Single Variable Chain Rule Suppose y = g(x) and z = f (y) then dz dx = d (f (g(x))) dx = f (g(x))g (x)
3.33pt Chain Rule MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Spring 2019 Single Variable Chain Rule Suppose y = g(x) and z = f (y) then dz dx = d (f (g(x))) dx = f (g(x))g (x)
WORKSHEET #13 MATH 1260 FALL 2014
 WORKSHEET #3 MATH 26 FALL 24 NOT DUE. Short answer: (a) Find the equation of the tangent plane to z = x 2 + y 2 at the point,, 2. z x (, ) = 2x = 2, z y (, ) = 2y = 2. So then the tangent plane equation
WORKSHEET #3 MATH 26 FALL 24 NOT DUE. Short answer: (a) Find the equation of the tangent plane to z = x 2 + y 2 at the point,, 2. z x (, ) = 2x = 2, z y (, ) = 2y = 2. So then the tangent plane equation
= 2 x y 2. (1)
 COMPLEX ANALYSIS PART 5: HARMONIC FUNCTIONS A Let me start by asking you a question. Suppose that f is an analytic function so that the CR-equation f/ z = 0 is satisfied. Let us write u and v for the real
COMPLEX ANALYSIS PART 5: HARMONIC FUNCTIONS A Let me start by asking you a question. Suppose that f is an analytic function so that the CR-equation f/ z = 0 is satisfied. Let us write u and v for the real
Mathematics 136 Calculus 2 Everything You Need Or Want To Know About Partial Fractions (and maybe more!) October 19 and 21, 2016
 Mathematics 36 Calculus 2 Everything You Need Or Want To Know About Partial Fractions (and maybe more!) October 9 and 2, 206 Every rational function (quotient of polynomials) can be written as a polynomial
Mathematics 36 Calculus 2 Everything You Need Or Want To Know About Partial Fractions (and maybe more!) October 9 and 2, 206 Every rational function (quotient of polynomials) can be written as a polynomial
Review for the First Midterm Exam
 Review for the First Midterm Exam Thomas Morrell 5 pm, Sunday, 4 April 9 B9 Van Vleck Hall For the purpose of creating questions for this review session, I did not make an effort to make any of the numbers
Review for the First Midterm Exam Thomas Morrell 5 pm, Sunday, 4 April 9 B9 Van Vleck Hall For the purpose of creating questions for this review session, I did not make an effort to make any of the numbers
Lagrange Multipliers
 Optimization with Constraints As long as algebra and geometry have been separated, their progress have been slow and their uses limited; but when these two sciences have been united, they have lent each
Optimization with Constraints As long as algebra and geometry have been separated, their progress have been slow and their uses limited; but when these two sciences have been united, they have lent each
Multiple Integrals and Vector Calculus: Synopsis
 Multiple Integrals and Vector Calculus: Synopsis Hilary Term 28: 14 lectures. Steve Rawlings. 1. Vectors - recap of basic principles. Things which are (and are not) vectors. Differentiation and integration
Multiple Integrals and Vector Calculus: Synopsis Hilary Term 28: 14 lectures. Steve Rawlings. 1. Vectors - recap of basic principles. Things which are (and are not) vectors. Differentiation and integration
The Derivative. Appendix B. B.1 The Derivative of f. Mappings from IR to IR
 Appendix B The Derivative B.1 The Derivative of f In this chapter, we give a short summary of the derivative. Specifically, we want to compare/contrast how the derivative appears for functions whose domain
Appendix B The Derivative B.1 The Derivative of f In this chapter, we give a short summary of the derivative. Specifically, we want to compare/contrast how the derivative appears for functions whose domain
PRACTICE PROBLEMS. Please let me know if you find any mistakes in the text so that i can fix them. 1. Mixed partial derivatives.
 PRACTICE PROBLEMS Please let me know if you find any mistakes in the text so that i can fix them. 1.1. Let Show that f is C 1 and yet How is that possible? 1. Mixed partial derivatives f(x, y) = {xy x
PRACTICE PROBLEMS Please let me know if you find any mistakes in the text so that i can fix them. 1.1. Let Show that f is C 1 and yet How is that possible? 1. Mixed partial derivatives f(x, y) = {xy x
(a) The points (3, 1, 2) and ( 1, 3, 4) are the endpoints of a diameter of a sphere.
 MATH 4 FINAL EXAM REVIEW QUESTIONS Problem. a) The points,, ) and,, 4) are the endpoints of a diameter of a sphere. i) Determine the center and radius of the sphere. ii) Find an equation for the sphere.
MATH 4 FINAL EXAM REVIEW QUESTIONS Problem. a) The points,, ) and,, 4) are the endpoints of a diameter of a sphere. i) Determine the center and radius of the sphere. ii) Find an equation for the sphere.
HOMEWORK 8 SOLUTIONS
 HOMEWOK 8 OLUTION. Let and φ = xdy dz + ydz dx + zdx dy. let be the disk at height given by: : x + y, z =, let X be the region in 3 bounded by the cone and the disk. We orient X via dx dy dz, then by definition
HOMEWOK 8 OLUTION. Let and φ = xdy dz + ydz dx + zdx dy. let be the disk at height given by: : x + y, z =, let X be the region in 3 bounded by the cone and the disk. We orient X via dx dy dz, then by definition
Rule ST1 (Symmetry). α β = β α for 1-forms α and β. Like the exterior product, the symmetric tensor product is also linear in each slot :
 2. Metrics as Symmetric Tensors So far we have studied exterior products of 1-forms, which obey the rule called skew symmetry: α β = β α. There is another operation for forming something called the symmetric
2. Metrics as Symmetric Tensors So far we have studied exterior products of 1-forms, which obey the rule called skew symmetry: α β = β α. There is another operation for forming something called the symmetric
A. MT-03, P Solve: (i) = 0. (ii) A. MT-03, P. 17, Solve : (i) + 4 = 0. (ii) A. MT-03, P. 16, Solve : (i)
 Program : M.A./M.Sc. (Mathematics) M.A./M.Sc. (Previous) Paper Code:MT-03 Differential Equations, Calculus of Variations & Special Functions Section C (Long Answers Questions) 1. Solve 2x cos y 2x sin
Program : M.A./M.Sc. (Mathematics) M.A./M.Sc. (Previous) Paper Code:MT-03 Differential Equations, Calculus of Variations & Special Functions Section C (Long Answers Questions) 1. Solve 2x cos y 2x sin
Answer Key 1973 BC 1969 BC 24. A 14. A 24. C 25. A 26. C 27. C 28. D 29. C 30. D 31. C 13. C 12. D 12. E 3. A 32. B 27. E 34. C 14. D 25. B 26.
 Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
Integration in the Complex Plane (Zill & Wright Chapter 18)
 Integration in the omplex Plane Zill & Wright hapter 18) 116-4-: omplex Variables Fall 11 ontents 1 ontour Integrals 1.1 Definition and Properties............................. 1. Evaluation.....................................
Integration in the omplex Plane Zill & Wright hapter 18) 116-4-: omplex Variables Fall 11 ontents 1 ontour Integrals 1.1 Definition and Properties............................. 1. Evaluation.....................................
FINAL REVIEW Answers and hints Math 311 Fall 2017
 FINAL RVIW Answers and hints Math 3 Fall 7. Let R be a Jordan region and let f : R be integrable. Prove that the graph of f, as a subset of R 3, has zero volume. Let R be a rectangle with R. Since f is
FINAL RVIW Answers and hints Math 3 Fall 7. Let R be a Jordan region and let f : R be integrable. Prove that the graph of f, as a subset of R 3, has zero volume. Let R be a rectangle with R. Since f is
