Function spaces on the Koch curve
|
|
|
- Clemence Gordon
- 6 years ago
- Views:
Transcription
1 Function spaces on the Koch curve Maryia Kabanava Mathematical Institute Friedrich Schiller University Jena D Jena, Germany Abstract We consider two types of Besov spaces on the Koch curve, defined by traces and with the help of the snowflaked transform. We compare these spaces and give their characterization in terms of Daubechies wavelets. Key words: periodic Besov spaces, trace spaces, self-similar set, Daubechies wavelets 000 Mathematics Subect Classification: 4B35, 4C40, 8A80 Introduction Let be the Koch curve in R. It is an example of a d-set with d = log 4 log 3. There are two possibilities to introduce Besov spaces on. The first one is to define Besov spaces B s pq(, µ) by traces s+ d p Bpq(, s µ) = tr µ Bpq (T ), < p <, 0 < q <, 0 < s <. We prefer the periodic setting since we are interested to extend the theory to a closed snowflake. The second way is to use the snowflaked transform H : T, T -torus and define B s pq() by B s pq() = { f H : f B s pq(t) } = B s pq(t) H, where B s pq(t) are periodic Besov spaces.
2 The question arises how the function spaces B s pq(, µ) and B s pq() are interrelated. We concentrate mainly on the case < p = q <, 0 < s <. In particular, we shift the characterization in terms of Daubechies wavelets from (T, ρ = x y /d, µ L ), [7, p. 360], to. This paper is organized as follows. In Section we describe the trace method of defining Besov spaces. In Section we present the wavelet characterization of the periodic Besov spaces B s pq(t) and then shift it to. In Section 3 we compare B s pp(, µ) and B s pp(). The main result is contained in Theorem 3. Trace spaces. Periodic Besov spaces on T n Let T n = {x = (x,..., x n ) R n : 0 x i, i =,..., n} x T n and y T n are identified if and only if x y = k, k = (k,..., k n ) Z n. By D(T n ) we denote the collection of all complex-valued infinitely differentiable functions on T n. The topology in D(T n ) is generated by the family of semi-norms sup D α f(x), where α is an arbitrary multi-index. D (T n ) x T n is defined to be the topological dual of D(T n ). Any f D (T n ) can be represented as f = k Z n a k e πikx, x T n, (convergence in D (T n )) where the Fourier coefficients {a k } C are of at most polynomial growth, a k c ( + k ) κ, for some c > 0, κ > 0 and all k Z n. Definition. Let ϕ = {ϕ } =0 be a dyadic resolution of unity, s R, 0 < p, 0 < q and ( f Bpq(T s n ) = sq ) q ϕ (k)a k e πikx L p (T n ) q k Z n =0 (with the usual modification if q = ). Then the Besov space B s pq(t n ) consists of all f D (T n ) such that f B s pq(t n ) <, [6, Chapter 3].
3 . Trace spaces Definition. A compact set in R n is called a d-set with 0 < d n if there is a Radon measure µ in R n with support such that for some positive constants c and c, holds c r d µ(b(γ, r)) c r d, γ, 0 < r <, 0 < d n. () where B(x, r) is a ball in R n centred at x R n and of radius r > 0. If is a d-set, then the restriction to of the d-dimensional Hausdorff measure satisfies () and any measure µ satisfying () is equivalent to H d. When is the Koch curve, it is a d-set in R with d = log 4. Moreover log 3 is a subset of T. In order to avoid problems in the endpoints (0, 0) and (, 0) of, we define the Besov spaces as a trace of the periodic Besov spaces Bpq(T s ). Suppose that for some s > 0, < p <, 0 < q < () there is a constant c > 0 such that ϕ(γ) µ(dγ) c ϕ Bpq(T s ), for all ϕ D(T ), (3) where ϕ(γ) denotes the pointwise trace of ϕ D(T ) on (sometimes we wright ϕ to denote the pointwise trace of ϕ). D(T ) is dense in Bpq(T s ). Then (3) can be extended by completion to any f Bpq(T s ) and the resulting function on is denoted by tr µ f. By standard arguments, it is independent of the approximation of f in Bpq(T s ) by D(T ) functions. Any function g tr µ Bpq(T s ) L (, µ) is quasi-normed by g tr µ B s pq(t ) = inf { f B s pq(t ) : tr µ f = g }. If one has (3) for some s, p, q satisfying (), then one has also (3) for all spaces Bpv s+ε (T n ) with ε > 0 and 0 < v. From the Corollary.75 in [7] follows that the trace operator tr µ : B s pq(t ) L (, µ) exists if s > d. This ustifies the following definition p 3
4 Definition 3. Let be the Koch curve. Let < p <, 0 < q < and s > 0. Then Bpq(, s d s+ p µ) = tr µ Bpq (T ). (4) B s pq(, µ) considered as subsets of L (, µ). Let B s p() = B s pp(, µ), < p <, 0 < s <. It was shown in [3] that B s p() with < p < and 0 < s < can be equivalently normed by f B s p() with f Bp() s p = with µ = H d. f(γ) p µ(dγ) + f(γ) f(δ) p γ δ d+sp µ(dγ)µ(dδ) (5) Wavelets on T and. Self-similar sets and the snowflaked transform Let K be a self-similar set in R n with respect to the contractions {F i } N i=, K = N F i (K). We can use iterations of the maps F i to give the address of i= a point in K. We introduce the following spaces: let Σ be a set of all infinite sequences Σ = {(ω, ω,...) : ω i {,,..., N}}. We use W m to denote the collection of words of length m: Set W = m=0 W m = {(w, w,..., w m ) : w i {,,..., N}}. W m. We write K w = F w (K) for F w F w... F wm (K), where w = (w, w,..., w m ) W. For any ω = (ω, ω,...) Σ define π : Σ K by π(ω) = K ω ω...ω m, [4, Ch..]. m= 4
5 The unit interval I = [0, ] can be considered as a self-similar set with respect to the similarities T i : R R, i =,, T (x) = x, T (x) = x +. The Koch curve is a self-similar set with respect to the similarities F i : R R, i =,, ( ) ( ) ( ) x F = 3 x y, y 3 ( ) ( ) ( x ) ( F = 3 x ) y +. y 3 3 We denote a mapping π corresponding to I by π I and to by π, π I (ω) = I ω ω...ω m, π (ω) = ω ω...ω m. m= The mapping H = π π I (6) is a homeomorphism between I and. It is called the snowflaked transform. Note that H(x) H(y) x y d, [7, Proposition 8.6]. Since the -torus T can be identified in the usual way with the unit interval, it can be regarded as a self-similar set with respect to T and T.. Self-similar measures Let p, p,... p N be numbers such that m= N p i =, 0 < p i <. i= Then we can define the probability measure µ with the weight (p, p,..., p N ) on the hierarchy of sets by repeated subdivision of the measure in the ratio p : p :... : p N, so that µ(k w w...w m ) = p w p w... p wm 5
6 Figure : The snowflaked transform and this extends to a Borel measure supported by K, [, Ch..]. If {F i } N i= are similarities with factors r i, i =,,..., N and s is the unique number with N ri s =, then µ with weight (r, s r, s..., rn s ) is the i= measure equivalent to the restriction H s K of the Hausdorff measure H s in R n to K, [4, Theorem.5.7]. When K is the Koch curve, then the measure µ with the weight (, ) ln 4 is equivalent H ln 3. When K is the unit interval I, measure ν with the weight (, ) is the Lebesgue measure. Since the image of the measure ν under a mapping H is the measure µ, 6
7 one has for a function f defined on f(γ) µ(dγ) = ( f H)(x) ν(dx) = ( f H)(x) dx, (7) [5, Theorem.9] Wavelet characterization of B s p(t) and B s p() Let B s pq() = { f H : f B s pq(t) } = B s pq(t) H. By Bp(T) s and B s p(), < p <, 0 < s < we denote the spaces Bpp(T) s and B s pp() correspondingly. We are interested in wavelet expansions for the spaces B s p(). We start with the wavelet characterization of Bp(T) s and then transfer it with the help of mapping H to. Let C u (R), u N denote the collection of all complex-valued continuous functions on R having continuous bounded derivatives up to order u inclusively. Let ψ F C u (R) and ψ M C u (R) be a father and a mother Daubechies wavelet on R respectively. Define ψf k and ψk by ψf k = ψ F (x k), ψ k (x) = ψm ( x k), N 0, k Z. Then { ψf k, } ψk is an orthonormal system in L N 0,k Z (R). Let L N. One can replace ψ F and ψ M by ψ L F ( ) = ψ F ( L ), ψ L M( ) = ψ M ( L ), ψ k F and ψk by ψ L,k F (x) = L ψf ( L x k), ψ L,k (x) = ψm ( x k), k Z. We choose and fix L such that { supp ψf L x : x < } {, supp ψm L x : x < }. Then one has supp ψ L,0 = supp ψ L M( ) { x : x < }. + 7
8 Let P = { m Z : 0 m < }, N 0. Given the functions ψ L,k F, ψl,k on the real line we can construct their - periodic counterparts by the procedure Define ψ L,k,per F ψ L,k F,per (x) = l= and ψ L,k,per ψ L,k F ψ L,k,per F (x) = ψ L,k F,per (x), (x + l), ψl,k,per (x) = on the -torus T by Then according to the Proposition.34 in [8] { ψ L,k,per F is an orthornomal basis in L (T). It is easy to see that l= ψ L,k (x + l). ψl,k,per (x) = ψ L,k,per (x), x T., ψ k,l,per, k P 0, N 0, k P } ψ L,k,per (x) = ψ L,0,per ( x k ), k P, on T with the usual interpretation. The shift operation is well-defined on the real line, but it can not be defined on the Koch curve. Therefore we would like to replace this operation in order to be able to construct its counterpart on the Koch curve. First of all when is fixed, the -torus T treated as a self-similar set can be represented as follows T = T w. w W Let us introduce the order relation on the set W of words of length + L. We say that v = (v,..., v ) is less than w = (w,..., w ) if and only if the first v i which is different from w i is less than w i : v < w v min{i:wi v i } < w min{i:wi v i }. The words are ordered in such a way that whenever u follows w in W, the interval T u is the right neighbour of T w. We agree that T... is the right neighbour of T.... 8
9 Then we notice that x k = ( () x k ). When k is fixed, there is a unique sequence of contractions such that T w, T w,..., T w, w = (w, w,..., w ) W ( () x k ) = T Tw... Tw Tw (x). (8) The mapping (8) transfers T w w...w to T.... The values of ψ L,k,per T u, where u = (u, u,... u ) follows w, coincide with the values of ψ L,0,per on T.... Thus there is the following connection between functions ψ L,k,per and ψ L,0,per : ψ L,k,per (x) = = ψ L,0,per ψ L,0,per... T Tw... Tw Tw (x), if x T w w...w, T T Tu... Tu Tu (x), if x T u u...u, where... indicates the procedure of assigning to ψ L,k,per neighbour of T u the values of ψ L,0,per by on on each next right on each next right neighbour of T.... Let us simplify the notation and denote the functions ψ L,k,per F ψ F,w = ψ F,w w...w L, w W L, ψ w = ψ w w...w, N 0, w W correspondingly, where w is chosen according to (8). Now we transfer the functions ψ F,w, w W L, ψ w, w to the Koch curve. Define ψ F,w and ψ w by ψ F,w (γ) = ψ F,w H (γ), ψ w (γ) = ψ w H (γ). 9 and ψ L,k,per N 0 W from T
10 { From (7) follows that the system ψf,v, ψ } w v W L,w S N 0 W in L (, µ). Let γ w w...w, then there is an ω Σ such that is orthonormal γ = w w...w ω ω...ω m. m= Recall that γ corresponds to x = H (γ) T w w...w given by x = T w w...w ω ω...ω m. m= The connection between the values of ψ w w...w and ψ... on w w...w is the following: ψ w w...w (γ) = ψ w w...w H (γ) = = ψ... = ψ... = ψ... T Tw... Tw Tw ( m= ( T m= ( m= ) ( ω ω...ω m = ψ... H m= ω ω...ω m ) = = ψ... F Fw... Fw Fw ( = ψ... F Fw... Fw Fw (γ). m= T w w...w ω ω...ω m ) =... ω ω...ω m ) = w w...w ω ω...ω m ) = In the same way we can follow the connection between the values of ψ w w...w 0
11 and ψ... on other v, v W. So we get ψ w (γ) = ψ... F Fw... Fw Fw (γ), if γ w w...w, = ψ... F F Fu... Fu Fu (γ), if γ u u...u,... Similarly for ψ F,w. According to [8, Ch..3.3] the following theorem holds. Theorem. Let < p <, 0 < s < and u > s. Let f L p (T). Then f B s p(t) if, and only if, it can be represented as f = a w L w W L ψf,w + =0 w W b w ψw, unconditional convergence being in L p (T). Furthermore this representation is unique, a w = L (f, ψ F,w ) T, w W L, b w = (f, ψ w ) T, w W and I : f {a w, w W L, b w, w W, N 0 } is an isomorphic map of B s p(t) onto the sequence space such that w W L a w p + (s p )p =0 Similar theorem holds for the spaces B s p(). w W b w p <. Theorem. Let < p <, 0 < s < and u > s. Let f L p (). Then f B s p() if, and only if, it can be represented as f = w W L a w L ψf,w + =0 w W b w ψw,
12 unconditional convergence being in L p (). Furthermore this representation is unique, a w = L ( f, ψ F,w ), w W L, b w = ( f, ψ w ), w W and I : f {a w, w W L, b w, w W, N 0 } is an isomorphic map of B s p() onto the sequence space such that w W L a w p + (s p )p =0 w W b w p <. 3 Comparison of B s p() and B s p() The spaces B s p(t) can be normed by f Bp(T) s p = f(x) p dx f(x) f(y) p x y +sp dx dy. (9) Since (9) is equivalent to f(γ) p µ(dγ) + f(γ) f(δ) p γ δ d+sp µ(dγ)µ(dδ), where f = f H, we endow the spaces B s p() with the norm f B s p() p = f(γ) p µ(dγ) + Together with (5) this leads to f(γ) f(δ) p γ δ d+sdp µ(dγ)µ(dδ). (0) B s p() = B s d p (). () The analogue of Theorem for the spaces B s p() reads as follows
13 Theorem 3. Let < p <, 0 < s < and u > s. Let f L p (). Then f B s p() if, and only if, it can be represented as f = w W L a w L ψf,w + =0 w W b w ψw, unconditional convergence being in L p (). Furthermore this representation is unique, a w = L ( f, ψ F,w ), w W L, b w = ( f, ψ w ), w W and I : f {a w, w W L, b w, w W, N 0 } is an isomorphic map of B s p() onto the sequence space such that w W L a w p + =0 ( 3 ) (s d p )p Proof. This follows from the observation () and w W b w p <. ( s d p) = d (s d p) = ( 3 ) (s d p ). References [] Edmunds, D.E., Triebel, H., Function spaces, entropy numbers, differential operators, Cambridge Univ. Press, 996. [] Falconer, K., Techniques in fractal geometry, Chichester, Wiley, 997. [3] Jonsson, A., Wallin, H., Function spaces on subsets of R n, Math. reports,, London, Harwood acad. publ., 984. [4] Kigami, J., Analysis on fractals, Cambridge Univ. Press, 003 [5] Mattila, P., Geometry of sets and measures in Euclidean spaces, Cambridge Univ. Press,
14 [6] Schmeisser, H.-J., Triebel, H., Topics in Fourier analysis and function spaces, Chichester, Wiley, 987. [7] Triebel, H., Theory of function spaces III, Basel, Birkhäuser, 006. [8] Triebel, H., Function spaces and wavelets on domains, Zürich, European Math. Soc. Publishing House,
Function spaces on the Koch curve
 JOURNAL OF FUNCTION SPACES AND APPLICATIONS Volume 8, Number 3 (00), 87 99 c 00, Scientific Horizon http://www.fsa.net Function spaces on the Koch curve Maryia Kabanava (Communicated by Hans Triebel) 000
JOURNAL OF FUNCTION SPACES AND APPLICATIONS Volume 8, Number 3 (00), 87 99 c 00, Scientific Horizon http://www.fsa.net Function spaces on the Koch curve Maryia Kabanava (Communicated by Hans Triebel) 000
NECESSARY CONDITIONS FOR WEIGHTED POINTWISE HARDY INEQUALITIES
 NECESSARY CONDITIONS FOR WEIGHTED POINTWISE HARDY INEQUALITIES JUHA LEHRBÄCK Abstract. We establish necessary conditions for domains Ω R n which admit the pointwise (p, β)-hardy inequality u(x) Cd Ω(x)
NECESSARY CONDITIONS FOR WEIGHTED POINTWISE HARDY INEQUALITIES JUHA LEHRBÄCK Abstract. We establish necessary conditions for domains Ω R n which admit the pointwise (p, β)-hardy inequality u(x) Cd Ω(x)
Nonlinear Energy Forms and Lipschitz Spaces on the Koch Curve
 Journal of Convex Analysis Volume 9 (2002), No. 1, 245 257 Nonlinear Energy Forms and Lipschitz Spaces on the Koch Curve Raffaela Capitanelli Dipartimento di Metodi e Modelli Matematici per le Scienze
Journal of Convex Analysis Volume 9 (2002), No. 1, 245 257 Nonlinear Energy Forms and Lipschitz Spaces on the Koch Curve Raffaela Capitanelli Dipartimento di Metodi e Modelli Matematici per le Scienze
Recall that if X is a compact metric space, C(X), the space of continuous (real-valued) functions on X, is a Banach space with the norm
 Chapter 13 Radon Measures Recall that if X is a compact metric space, C(X), the space of continuous (real-valued) functions on X, is a Banach space with the norm (13.1) f = sup x X f(x). We want to identify
Chapter 13 Radon Measures Recall that if X is a compact metric space, C(X), the space of continuous (real-valued) functions on X, is a Banach space with the norm (13.1) f = sup x X f(x). We want to identify
Wavelet bases for function spaces on cellular domains
 Wavelet bases for function spaces on cellular domains Benjamin Scharf Friedrich Schiller University Jena January 14, 2011 Wavelet bases for function spaces on cellular domains Benjamin Scharf 1/28 Table
Wavelet bases for function spaces on cellular domains Benjamin Scharf Friedrich Schiller University Jena January 14, 2011 Wavelet bases for function spaces on cellular domains Benjamin Scharf 1/28 Table
Nonarchimedean Cantor set and string
 J fixed point theory appl Online First c 2008 Birkhäuser Verlag Basel/Switzerland DOI 101007/s11784-008-0062-9 Journal of Fixed Point Theory and Applications Nonarchimedean Cantor set and string Michel
J fixed point theory appl Online First c 2008 Birkhäuser Verlag Basel/Switzerland DOI 101007/s11784-008-0062-9 Journal of Fixed Point Theory and Applications Nonarchimedean Cantor set and string Michel
THEOREMS, ETC., FOR MATH 516
 THEOREMS, ETC., FOR MATH 516 Results labeled Theorem Ea.b.c (or Proposition Ea.b.c, etc.) refer to Theorem c from section a.b of Evans book (Partial Differential Equations). Proposition 1 (=Proposition
THEOREMS, ETC., FOR MATH 516 Results labeled Theorem Ea.b.c (or Proposition Ea.b.c, etc.) refer to Theorem c from section a.b of Evans book (Partial Differential Equations). Proposition 1 (=Proposition
PACKING-DIMENSION PROFILES AND FRACTIONAL BROWNIAN MOTION
 PACKING-DIMENSION PROFILES AND FRACTIONAL BROWNIAN MOTION DAVAR KHOSHNEVISAN AND YIMIN XIAO Abstract. In order to compute the packing dimension of orthogonal projections Falconer and Howroyd 997) introduced
PACKING-DIMENSION PROFILES AND FRACTIONAL BROWNIAN MOTION DAVAR KHOSHNEVISAN AND YIMIN XIAO Abstract. In order to compute the packing dimension of orthogonal projections Falconer and Howroyd 997) introduced
Packing-Dimension Profiles and Fractional Brownian Motion
 Under consideration for publication in Math. Proc. Camb. Phil. Soc. 1 Packing-Dimension Profiles and Fractional Brownian Motion By DAVAR KHOSHNEVISAN Department of Mathematics, 155 S. 1400 E., JWB 233,
Under consideration for publication in Math. Proc. Camb. Phil. Soc. 1 Packing-Dimension Profiles and Fractional Brownian Motion By DAVAR KHOSHNEVISAN Department of Mathematics, 155 S. 1400 E., JWB 233,
A class of domains with fractal boundaries: Functions spaces and numerical methods
 A class of domains with fractal boundaries: Functions spaces and numerical methods Yves Achdou joint work with T. Deheuvels and N. Tchou Laboratoire J-L Lions, Université Paris Diderot École Centrale -
A class of domains with fractal boundaries: Functions spaces and numerical methods Yves Achdou joint work with T. Deheuvels and N. Tchou Laboratoire J-L Lions, Université Paris Diderot École Centrale -
We denote the space of distributions on Ω by D ( Ω) 2.
 Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
Affine and Quasi-Affine Frames on Positive Half Line
 Journal of Mathematical Extension Vol. 10, No. 3, (2016), 47-61 ISSN: 1735-8299 URL: http://www.ijmex.com Affine and Quasi-Affine Frames on Positive Half Line Abdullah Zakir Husain Delhi College-Delhi
Journal of Mathematical Extension Vol. 10, No. 3, (2016), 47-61 ISSN: 1735-8299 URL: http://www.ijmex.com Affine and Quasi-Affine Frames on Positive Half Line Abdullah Zakir Husain Delhi College-Delhi
7 Complete metric spaces and function spaces
 7 Complete metric spaces and function spaces 7.1 Completeness Let (X, d) be a metric space. Definition 7.1. A sequence (x n ) n N in X is a Cauchy sequence if for any ɛ > 0, there is N N such that n, m
7 Complete metric spaces and function spaces 7.1 Completeness Let (X, d) be a metric space. Definition 7.1. A sequence (x n ) n N in X is a Cauchy sequence if for any ɛ > 0, there is N N such that n, m
A NOTE ON CORRELATION AND LOCAL DIMENSIONS
 A NOTE ON CORRELATION AND LOCAL DIMENSIONS JIAOJIAO YANG, ANTTI KÄENMÄKI, AND MIN WU Abstract Under very mild assumptions, we give formulas for the correlation and local dimensions of measures on the limit
A NOTE ON CORRELATION AND LOCAL DIMENSIONS JIAOJIAO YANG, ANTTI KÄENMÄKI, AND MIN WU Abstract Under very mild assumptions, we give formulas for the correlation and local dimensions of measures on the limit
MATH 4200 HW: PROBLEM SET FOUR: METRIC SPACES
 MATH 4200 HW: PROBLEM SET FOUR: METRIC SPACES PETE L. CLARK 4. Metric Spaces (no more lulz) Directions: This week, please solve any seven problems. Next week, please solve seven more. Starred parts of
MATH 4200 HW: PROBLEM SET FOUR: METRIC SPACES PETE L. CLARK 4. Metric Spaces (no more lulz) Directions: This week, please solve any seven problems. Next week, please solve seven more. Starred parts of
MAT 578 FUNCTIONAL ANALYSIS EXERCISES
 MAT 578 FUNCTIONAL ANALYSIS EXERCISES JOHN QUIGG Exercise 1. Prove that if A is bounded in a topological vector space, then for every neighborhood V of 0 there exists c > 0 such that tv A for all t > c.
MAT 578 FUNCTIONAL ANALYSIS EXERCISES JOHN QUIGG Exercise 1. Prove that if A is bounded in a topological vector space, then for every neighborhood V of 0 there exists c > 0 such that tv A for all t > c.
NOTES ON THE REGULARITY OF QUASICONFORMAL HOMEOMORPHISMS
 NOTES ON THE REGULARITY OF QUASICONFORMAL HOMEOMORPHISMS CLARK BUTLER. Introduction The purpose of these notes is to give a self-contained proof of the following theorem, Theorem.. Let f : S n S n be a
NOTES ON THE REGULARITY OF QUASICONFORMAL HOMEOMORPHISMS CLARK BUTLER. Introduction The purpose of these notes is to give a self-contained proof of the following theorem, Theorem.. Let f : S n S n be a
Invariant measures for iterated function systems
 ANNALES POLONICI MATHEMATICI LXXV.1(2000) Invariant measures for iterated function systems by Tomasz Szarek (Katowice and Rzeszów) Abstract. A new criterion for the existence of an invariant distribution
ANNALES POLONICI MATHEMATICI LXXV.1(2000) Invariant measures for iterated function systems by Tomasz Szarek (Katowice and Rzeszów) Abstract. A new criterion for the existence of an invariant distribution
Chapter 2 Metric Spaces
 Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
Continuity of convex functions in normed spaces
 Continuity of convex functions in normed spaces In this chapter, we consider continuity properties of real-valued convex functions defined on open convex sets in normed spaces. Recall that every infinitedimensional
Continuity of convex functions in normed spaces In this chapter, we consider continuity properties of real-valued convex functions defined on open convex sets in normed spaces. Recall that every infinitedimensional
CHAPTER V DUAL SPACES
 CHAPTER V DUAL SPACES DEFINITION Let (X, T ) be a (real) locally convex topological vector space. By the dual space X, or (X, T ), of X we mean the set of all continuous linear functionals on X. By the
CHAPTER V DUAL SPACES DEFINITION Let (X, T ) be a (real) locally convex topological vector space. By the dual space X, or (X, T ), of X we mean the set of all continuous linear functionals on X. By the
A Lower Estimate for Entropy Numbers
 Journal of Approximation Theory 110, 120124 (2001) doi:10.1006jath.2000.3554, available online at http:www.idealibrary.com on A Lower Estimate for Entropy Numbers Thomas Ku hn Fakulta t fu r Mathematik
Journal of Approximation Theory 110, 120124 (2001) doi:10.1006jath.2000.3554, available online at http:www.idealibrary.com on A Lower Estimate for Entropy Numbers Thomas Ku hn Fakulta t fu r Mathematik
REPRESENTABLE BANACH SPACES AND UNIFORMLY GÂTEAUX-SMOOTH NORMS. Julien Frontisi
 Serdica Math. J. 22 (1996), 33-38 REPRESENTABLE BANACH SPACES AND UNIFORMLY GÂTEAUX-SMOOTH NORMS Julien Frontisi Communicated by G. Godefroy Abstract. It is proved that a representable non-separable Banach
Serdica Math. J. 22 (1996), 33-38 REPRESENTABLE BANACH SPACES AND UNIFORMLY GÂTEAUX-SMOOTH NORMS Julien Frontisi Communicated by G. Godefroy Abstract. It is proved that a representable non-separable Banach
Chapter 3: Baire category and open mapping theorems
 MA3421 2016 17 Chapter 3: Baire category and open mapping theorems A number of the major results rely on completeness via the Baire category theorem. 3.1 The Baire category theorem 3.1.1 Definition. A
MA3421 2016 17 Chapter 3: Baire category and open mapping theorems A number of the major results rely on completeness via the Baire category theorem. 3.1 The Baire category theorem 3.1.1 Definition. A
4 Countability axioms
 4 COUNTABILITY AXIOMS 4 Countability axioms Definition 4.1. Let X be a topological space X is said to be first countable if for any x X, there is a countable basis for the neighborhoods of x. X is said
4 COUNTABILITY AXIOMS 4 Countability axioms Definition 4.1. Let X be a topological space X is said to be first countable if for any x X, there is a countable basis for the neighborhoods of x. X is said
Random measures, intersections, and applications
 Random measures, intersections, and applications Ville Suomala joint work with Pablo Shmerkin University of Oulu, Finland Workshop on fractals, The Hebrew University of Jerusalem June 12th 2014 Motivation
Random measures, intersections, and applications Ville Suomala joint work with Pablo Shmerkin University of Oulu, Finland Workshop on fractals, The Hebrew University of Jerusalem June 12th 2014 Motivation
arxiv: v1 [math.cv] 21 Jun 2016
![arxiv: v1 [math.cv] 21 Jun 2016 arxiv: v1 [math.cv] 21 Jun 2016](/thumbs/88/117506527.jpg) B. N. Khabibullin, N. R. Tamindarova SUBHARMONIC TEST FUNCTIONS AND THE DISTRIBUTION OF ZERO SETS OF HOLOMORPHIC FUNCTIONS arxiv:1606.06714v1 [math.cv] 21 Jun 2016 Abstract. Let m, n 1 are integers and
B. N. Khabibullin, N. R. Tamindarova SUBHARMONIC TEST FUNCTIONS AND THE DISTRIBUTION OF ZERO SETS OF HOLOMORPHIC FUNCTIONS arxiv:1606.06714v1 [math.cv] 21 Jun 2016 Abstract. Let m, n 1 are integers and
Problem Set 5. 2 n k. Then a nk (x) = 1+( 1)k
 Problem Set 5 1. (Folland 2.43) For x [, 1), let 1 a n (x)2 n (a n (x) = or 1) be the base-2 expansion of x. (If x is a dyadic rational, choose the expansion such that a n (x) = for large n.) Then the
Problem Set 5 1. (Folland 2.43) For x [, 1), let 1 a n (x)2 n (a n (x) = or 1) be the base-2 expansion of x. (If x is a dyadic rational, choose the expansion such that a n (x) = for large n.) Then the
HERMITE MULTIPLIERS AND PSEUDO-MULTIPLIERS
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 124, Number 7, July 1996 HERMITE MULTIPLIERS AND PSEUDO-MULTIPLIERS JAY EPPERSON Communicated by J. Marshall Ash) Abstract. We prove a multiplier
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 124, Number 7, July 1996 HERMITE MULTIPLIERS AND PSEUDO-MULTIPLIERS JAY EPPERSON Communicated by J. Marshall Ash) Abstract. We prove a multiplier
3 (Due ). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
Topological properties of Z p and Q p and Euclidean models
 Topological properties of Z p and Q p and Euclidean models Samuel Trautwein, Esther Röder, Giorgio Barozzi November 3, 20 Topology of Q p vs Topology of R Both R and Q p are normed fields and complete
Topological properties of Z p and Q p and Euclidean models Samuel Trautwein, Esther Röder, Giorgio Barozzi November 3, 20 Topology of Q p vs Topology of R Both R and Q p are normed fields and complete
CONTINUITY OF SUBADDITIVE PRESSURE FOR SELF-AFFINE SETS
 RESEARCH Real Analysis Exchange Vol. 34(2), 2008/2009, pp. 1 16 Kenneth Falconer, Mathematical Institute, University of St Andrews, North Haugh, St Andrews KY16 9SS, Scotland. email: kjf@st-and.ac.uk Arron
RESEARCH Real Analysis Exchange Vol. 34(2), 2008/2009, pp. 1 16 Kenneth Falconer, Mathematical Institute, University of St Andrews, North Haugh, St Andrews KY16 9SS, Scotland. email: kjf@st-and.ac.uk Arron
MARKOV PARTITIONS FOR HYPERBOLIC SETS
 MARKOV PARTITIONS FOR HYPERBOLIC SETS TODD FISHER, HIMAL RATHNAKUMARA Abstract. We show that if f is a diffeomorphism of a manifold to itself, Λ is a mixing (or transitive) hyperbolic set, and V is a neighborhood
MARKOV PARTITIONS FOR HYPERBOLIC SETS TODD FISHER, HIMAL RATHNAKUMARA Abstract. We show that if f is a diffeomorphism of a manifold to itself, Λ is a mixing (or transitive) hyperbolic set, and V is a neighborhood
A trace theorem for Dirichlet forms on fractals. and its application. Takashi Kumagai (RIMS, Kyoto University, Japan)
 A trace theorem for Dirichlet forms on fractals and its application Takashi Kumagai (RIMS, Kyoto University, Japan) http://www.kurims.kyoto-u.ac.jp/~kumagai/ November 17, 2005 at Bucharest Joint work with
A trace theorem for Dirichlet forms on fractals and its application Takashi Kumagai (RIMS, Kyoto University, Japan) http://www.kurims.kyoto-u.ac.jp/~kumagai/ November 17, 2005 at Bucharest Joint work with
FUNCTION BASES FOR TOPOLOGICAL VECTOR SPACES. Yılmaz Yılmaz
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 33, 2009, 335 353 FUNCTION BASES FOR TOPOLOGICAL VECTOR SPACES Yılmaz Yılmaz Abstract. Our main interest in this
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 33, 2009, 335 353 FUNCTION BASES FOR TOPOLOGICAL VECTOR SPACES Yılmaz Yılmaz Abstract. Our main interest in this
Reminder Notes for the Course on Measures on Topological Spaces
 Reminder Notes for the Course on Measures on Topological Spaces T. C. Dorlas Dublin Institute for Advanced Studies School of Theoretical Physics 10 Burlington Road, Dublin 4, Ireland. Email: dorlas@stp.dias.ie
Reminder Notes for the Course on Measures on Topological Spaces T. C. Dorlas Dublin Institute for Advanced Studies School of Theoretical Physics 10 Burlington Road, Dublin 4, Ireland. Email: dorlas@stp.dias.ie
2) Let X be a compact space. Prove that the space C(X) of continuous real-valued functions is a complete metric space.
 University of Bergen General Functional Analysis Problems with solutions 6 ) Prove that is unique in any normed space. Solution of ) Let us suppose that there are 2 zeros and 2. Then = + 2 = 2 + = 2. 2)
University of Bergen General Functional Analysis Problems with solutions 6 ) Prove that is unique in any normed space. Solution of ) Let us suppose that there are 2 zeros and 2. Then = + 2 = 2 + = 2. 2)
i=1 β i,i.e. = β 1 x β x β 1 1 xβ d
 66 2. Every family of seminorms on a vector space containing a norm induces ahausdorff locally convex topology. 3. Given an open subset Ω of R d with the euclidean topology, the space C(Ω) of real valued
66 2. Every family of seminorms on a vector space containing a norm induces ahausdorff locally convex topology. 3. Given an open subset Ω of R d with the euclidean topology, the space C(Ω) of real valued
Problem Set 6: Solutions Math 201A: Fall a n x n,
 Problem Set 6: Solutions Math 201A: Fall 2016 Problem 1. Is (x n ) n=0 a Schauder basis of C([0, 1])? No. If f(x) = a n x n, n=0 where the series converges uniformly on [0, 1], then f has a power series
Problem Set 6: Solutions Math 201A: Fall 2016 Problem 1. Is (x n ) n=0 a Schauder basis of C([0, 1])? No. If f(x) = a n x n, n=0 where the series converges uniformly on [0, 1], then f has a power series
An introduction to some aspects of functional analysis
 An introduction to some aspects of functional analysis Stephen Semmes Rice University Abstract These informal notes deal with some very basic objects in functional analysis, including norms and seminorms
An introduction to some aspects of functional analysis Stephen Semmes Rice University Abstract These informal notes deal with some very basic objects in functional analysis, including norms and seminorms
Course 212: Academic Year Section 1: Metric Spaces
 Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Finite-dimensional spaces. C n is the space of n-tuples x = (x 1,..., x n ) of complex numbers. It is a Hilbert space with the inner product
 Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Functional Analysis. Franck Sueur Metric spaces Definitions Completeness Compactness Separability...
 Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Sobolev spaces. May 18
 Sobolev spaces May 18 2015 1 Weak derivatives The purpose of these notes is to give a very basic introduction to Sobolev spaces. More extensive treatments can e.g. be found in the classical references
Sobolev spaces May 18 2015 1 Weak derivatives The purpose of these notes is to give a very basic introduction to Sobolev spaces. More extensive treatments can e.g. be found in the classical references
Analysis Finite and Infinite Sets The Real Numbers The Cantor Set
 Analysis Finite and Infinite Sets Definition. An initial segment is {n N n n 0 }. Definition. A finite set can be put into one-to-one correspondence with an initial segment. The empty set is also considered
Analysis Finite and Infinite Sets Definition. An initial segment is {n N n n 0 }. Definition. A finite set can be put into one-to-one correspondence with an initial segment. The empty set is also considered
Analysis Qualifying Exam
 Analysis Qualifying Exam Spring 2017 Problem 1: Let f be differentiable on R. Suppose that there exists M > 0 such that f(k) M for each integer k, and f (x) M for all x R. Show that f is bounded, i.e.,
Analysis Qualifying Exam Spring 2017 Problem 1: Let f be differentiable on R. Suppose that there exists M > 0 such that f(k) M for each integer k, and f (x) M for all x R. Show that f is bounded, i.e.,
arxiv: v1 [math.ds] 31 Jul 2018
![arxiv: v1 [math.ds] 31 Jul 2018 arxiv: v1 [math.ds] 31 Jul 2018](/thumbs/83/88779811.jpg) arxiv:1807.11801v1 [math.ds] 31 Jul 2018 On the interior of projections of planar self-similar sets YUKI TAKAHASHI Abstract. We consider projections of planar self-similar sets, and show that one can create
arxiv:1807.11801v1 [math.ds] 31 Jul 2018 On the interior of projections of planar self-similar sets YUKI TAKAHASHI Abstract. We consider projections of planar self-similar sets, and show that one can create
Self-similar Sets as Quotients of Shift Spaces Jun Kigami Kyoto University
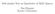 Self-similar Sets as Quotients of Shift Spaces Jun Kigami Kyoto University (One-sided) Shift space S: a finite set, symbols For w = w 1...w m W, Σ = S N = {w 1 w 2... i N,w i S} W m = S m = {w 1...w m
Self-similar Sets as Quotients of Shift Spaces Jun Kigami Kyoto University (One-sided) Shift space S: a finite set, symbols For w = w 1...w m W, Σ = S N = {w 1 w 2... i N,w i S} W m = S m = {w 1...w m
Metric Spaces and Topology
 Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
MODULUS AND CONTINUOUS CAPACITY
 Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 26, 2001, 455 464 MODULUS AND CONTINUOUS CAPACITY Sari Kallunki and Nageswari Shanmugalingam University of Jyväskylä, Department of Mathematics
Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 26, 2001, 455 464 MODULUS AND CONTINUOUS CAPACITY Sari Kallunki and Nageswari Shanmugalingam University of Jyväskylä, Department of Mathematics
Solutions: Problem Set 4 Math 201B, Winter 2007
 Solutions: Problem Set 4 Math 2B, Winter 27 Problem. (a Define f : by { x /2 if < x
Solutions: Problem Set 4 Math 2B, Winter 27 Problem. (a Define f : by { x /2 if < x
Serena Doria. Department of Sciences, University G.d Annunzio, Via dei Vestini, 31, Chieti, Italy. Received 7 July 2008; Revised 25 December 2008
 Journal of Uncertain Systems Vol.4, No.1, pp.73-80, 2010 Online at: www.jus.org.uk Different Types of Convergence for Random Variables with Respect to Separately Coherent Upper Conditional Probabilities
Journal of Uncertain Systems Vol.4, No.1, pp.73-80, 2010 Online at: www.jus.org.uk Different Types of Convergence for Random Variables with Respect to Separately Coherent Upper Conditional Probabilities
1 Topology Definition of a topology Basis (Base) of a topology The subspace topology & the product topology on X Y 3
 Index Page 1 Topology 2 1.1 Definition of a topology 2 1.2 Basis (Base) of a topology 2 1.3 The subspace topology & the product topology on X Y 3 1.4 Basic topology concepts: limit points, closed sets,
Index Page 1 Topology 2 1.1 Definition of a topology 2 1.2 Basis (Base) of a topology 2 1.3 The subspace topology & the product topology on X Y 3 1.4 Basic topology concepts: limit points, closed sets,
Analysis III Theorems, Propositions & Lemmas... Oh My!
 Analysis III Theorems, Propositions & Lemmas... Oh My! Rob Gibson October 25, 2010 Proposition 1. If x = (x 1, x 2,...), y = (y 1, y 2,...), then is a distance. ( d(x, y) = x k y k p Proposition 2. In
Analysis III Theorems, Propositions & Lemmas... Oh My! Rob Gibson October 25, 2010 Proposition 1. If x = (x 1, x 2,...), y = (y 1, y 2,...), then is a distance. ( d(x, y) = x k y k p Proposition 2. In
A NOTE ON WAVELET EXPANSIONS FOR DYADIC BMO FUNCTIONS IN SPACES OF HOMOGENEOUS TYPE
 EVISTA DE LA UNIÓN MATEMÁTICA AGENTINA Vol. 59, No., 208, Pages 57 72 Published online: July 3, 207 A NOTE ON WAVELET EXPANSIONS FO DYADIC BMO FUNCTIONS IN SPACES OF HOMOGENEOUS TYPE AQUEL CESCIMBENI AND
EVISTA DE LA UNIÓN MATEMÁTICA AGENTINA Vol. 59, No., 208, Pages 57 72 Published online: July 3, 207 A NOTE ON WAVELET EXPANSIONS FO DYADIC BMO FUNCTIONS IN SPACES OF HOMOGENEOUS TYPE AQUEL CESCIMBENI AND
INTRODUCTION TO TOPOLOGY, MATH 141, PRACTICE PROBLEMS
 INTRODUCTION TO TOPOLOGY, MATH 141, PRACTICE PROBLEMS Problem 1. Give an example of a non-metrizable topological space. Explain. Problem 2. Introduce a topology on N by declaring that open sets are, N,
INTRODUCTION TO TOPOLOGY, MATH 141, PRACTICE PROBLEMS Problem 1. Give an example of a non-metrizable topological space. Explain. Problem 2. Introduce a topology on N by declaring that open sets are, N,
On the Hausdorff dimension of continuous functions belonging to Hölder and Besov spaces on fractal d-sets
 arxiv:0.047v [math.fa] 30 Dec 200 On the Hausdorff dimension of continuous functions belonging to Hölder and Besov spaces on fractal d-sets Abel Carvalho and António Caetano Abstract The Hausdorff dimension
arxiv:0.047v [math.fa] 30 Dec 200 On the Hausdorff dimension of continuous functions belonging to Hölder and Besov spaces on fractal d-sets Abel Carvalho and António Caetano Abstract The Hausdorff dimension
Self-similar fractals as boundaries of networks
 Self-similar fractals as boundaries of networks Erin P. J. Pearse ep@ou.edu University of Oklahoma 4th Cornell Conference on Analysis, Probability, and Mathematical Physics on Fractals AMS Eastern Sectional
Self-similar fractals as boundaries of networks Erin P. J. Pearse ep@ou.edu University of Oklahoma 4th Cornell Conference on Analysis, Probability, and Mathematical Physics on Fractals AMS Eastern Sectional
REVIEW OF ESSENTIAL MATH 346 TOPICS
 REVIEW OF ESSENTIAL MATH 346 TOPICS 1. AXIOMATIC STRUCTURE OF R Doğan Çömez The real number system is a complete ordered field, i.e., it is a set R which is endowed with addition and multiplication operations
REVIEW OF ESSENTIAL MATH 346 TOPICS 1. AXIOMATIC STRUCTURE OF R Doğan Çömez The real number system is a complete ordered field, i.e., it is a set R which is endowed with addition and multiplication operations
REAL AND COMPLEX ANALYSIS
 REAL AND COMPLE ANALYSIS Third Edition Walter Rudin Professor of Mathematics University of Wisconsin, Madison Version 1.1 No rights reserved. Any part of this work can be reproduced or transmitted in any
REAL AND COMPLE ANALYSIS Third Edition Walter Rudin Professor of Mathematics University of Wisconsin, Madison Version 1.1 No rights reserved. Any part of this work can be reproduced or transmitted in any
Maths 212: Homework Solutions
 Maths 212: Homework Solutions 1. The definition of A ensures that x π for all x A, so π is an upper bound of A. To show it is the least upper bound, suppose x < π and consider two cases. If x < 1, then
Maths 212: Homework Solutions 1. The definition of A ensures that x π for all x A, so π is an upper bound of A. To show it is the least upper bound, suppose x < π and consider two cases. If x < 1, then
NATIONAL BOARD FOR HIGHER MATHEMATICS. Research Scholarships Screening Test. Saturday, February 2, Time Allowed: Two Hours Maximum Marks: 40
 NATIONAL BOARD FOR HIGHER MATHEMATICS Research Scholarships Screening Test Saturday, February 2, 2008 Time Allowed: Two Hours Maximum Marks: 40 Please read, carefully, the instructions on the following
NATIONAL BOARD FOR HIGHER MATHEMATICS Research Scholarships Screening Test Saturday, February 2, 2008 Time Allowed: Two Hours Maximum Marks: 40 Please read, carefully, the instructions on the following
Fact Sheet Functional Analysis
 Fact Sheet Functional Analysis Literature: Hackbusch, W.: Theorie und Numerik elliptischer Differentialgleichungen. Teubner, 986. Knabner, P., Angermann, L.: Numerik partieller Differentialgleichungen.
Fact Sheet Functional Analysis Literature: Hackbusch, W.: Theorie und Numerik elliptischer Differentialgleichungen. Teubner, 986. Knabner, P., Angermann, L.: Numerik partieller Differentialgleichungen.
Micro-local analysis in Fourier Lebesgue and modulation spaces.
 Micro-local analysis in Fourier Lebesgue and modulation spaces. Stevan Pilipović University of Novi Sad Nagoya, September 30, 2009 (Novi Sad) Nagoya, September 30, 2009 1 / 52 Introduction We introduce
Micro-local analysis in Fourier Lebesgue and modulation spaces. Stevan Pilipović University of Novi Sad Nagoya, September 30, 2009 (Novi Sad) Nagoya, September 30, 2009 1 / 52 Introduction We introduce
E.7 Alaoglu s Theorem
 E.7 Alaoglu s Theorem 359 E.7 Alaoglu s Theorem If X is a normed space, then the closed unit ball in X or X is compact if and only if X is finite-dimensional (Problem A.25). Even so, Alaoglu s Theorem
E.7 Alaoglu s Theorem 359 E.7 Alaoglu s Theorem If X is a normed space, then the closed unit ball in X or X is compact if and only if X is finite-dimensional (Problem A.25). Even so, Alaoglu s Theorem
SOME REMARKS ON THE SPACE OF DIFFERENCES OF SUBLINEAR FUNCTIONS
 APPLICATIONES MATHEMATICAE 22,3 (1994), pp. 419 426 S. G. BARTELS and D. PALLASCHKE (Karlsruhe) SOME REMARKS ON THE SPACE OF DIFFERENCES OF SUBLINEAR FUNCTIONS Abstract. Two properties concerning the space
APPLICATIONES MATHEMATICAE 22,3 (1994), pp. 419 426 S. G. BARTELS and D. PALLASCHKE (Karlsruhe) SOME REMARKS ON THE SPACE OF DIFFERENCES OF SUBLINEAR FUNCTIONS Abstract. Two properties concerning the space
THE SHIFT SPACE FOR AN INFINITE ITERATED FUNCTION SYSTEM
 THE SHIFT SPACE FOR AN INFINITE ITERATED FUNCTION SYSTEM ALEXANDRU MIHAIL and RADU MICULESCU The aim of the paper is to define the shift space for an infinite iterated function systems (IIFS) and to describe
THE SHIFT SPACE FOR AN INFINITE ITERATED FUNCTION SYSTEM ALEXANDRU MIHAIL and RADU MICULESCU The aim of the paper is to define the shift space for an infinite iterated function systems (IIFS) and to describe
Wavelets and modular inequalities in variable L p spaces
 Wavelets and modular inequalities in variable L p spaces Mitsuo Izuki July 14, 2007 Abstract The aim of this paper is to characterize variable L p spaces L p( ) (R n ) using wavelets with proper smoothness
Wavelets and modular inequalities in variable L p spaces Mitsuo Izuki July 14, 2007 Abstract The aim of this paper is to characterize variable L p spaces L p( ) (R n ) using wavelets with proper smoothness
UNIFORMLY DISTRIBUTED MEASURES IN EUCLIDEAN SPACES
 MATH. SCAND. 90 (2002), 152 160 UNIFORMLY DISTRIBUTED MEASURES IN EUCLIDEAN SPACES BERND KIRCHHEIM and DAVID PREISS For every complete metric space X there is, up to a constant multiple, at most one Borel
MATH. SCAND. 90 (2002), 152 160 UNIFORMLY DISTRIBUTED MEASURES IN EUCLIDEAN SPACES BERND KIRCHHEIM and DAVID PREISS For every complete metric space X there is, up to a constant multiple, at most one Borel
Smooth pointwise multipliers of modulation spaces
 An. Şt. Univ. Ovidius Constanţa Vol. 20(1), 2012, 317 328 Smooth pointwise multipliers of modulation spaces Ghassem Narimani Abstract Let 1 < p,q < and s,r R. It is proved that any function in the amalgam
An. Şt. Univ. Ovidius Constanţa Vol. 20(1), 2012, 317 328 Smooth pointwise multipliers of modulation spaces Ghassem Narimani Abstract Let 1 < p,q < and s,r R. It is proved that any function in the amalgam
Reminder Notes for the Course on Distribution Theory
 Reminder Notes for the Course on Distribution Theory T. C. Dorlas Dublin Institute for Advanced Studies School of Theoretical Physics 10 Burlington Road, Dublin 4, Ireland. Email: dorlas@stp.dias.ie March
Reminder Notes for the Course on Distribution Theory T. C. Dorlas Dublin Institute for Advanced Studies School of Theoretical Physics 10 Burlington Road, Dublin 4, Ireland. Email: dorlas@stp.dias.ie March
(1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define
![(1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define](/thumbs/88/116259117.jpg) Homework, Real Analysis I, Fall, 2010. (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define ρ(f, g) = 1 0 f(x) g(x) dx. Show that
Homework, Real Analysis I, Fall, 2010. (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define ρ(f, g) = 1 0 f(x) g(x) dx. Show that
08a. Operators on Hilbert spaces. 1. Boundedness, continuity, operator norms
 (February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
(February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
HABILITATION THESIS. New results in the theory of Countable Iterated Function Systems
 HABILITATION THESIS New results in the theory of Countable Iterated Function Systems - abstract - Nicolae-Adrian Secelean Specialization: Mathematics Lucian Blaga University of Sibiu 2014 Abstract The
HABILITATION THESIS New results in the theory of Countable Iterated Function Systems - abstract - Nicolae-Adrian Secelean Specialization: Mathematics Lucian Blaga University of Sibiu 2014 Abstract The
A continuous operator extending fuzzy ultrametrics
 A continuous operator extending fuzzy ultrametrics I. Stasyuk, E.D. Tymchatyn November 30, 200 Abstract We consider the problem of simultaneous extension of fuzzy ultrametrics defined on closed subsets
A continuous operator extending fuzzy ultrametrics I. Stasyuk, E.D. Tymchatyn November 30, 200 Abstract We consider the problem of simultaneous extension of fuzzy ultrametrics defined on closed subsets
WHY SATURATED PROBABILITY SPACES ARE NECESSARY
 WHY SATURATED PROBABILITY SPACES ARE NECESSARY H. JEROME KEISLER AND YENENG SUN Abstract. An atomless probability space (Ω, A, P ) is said to have the saturation property for a probability measure µ on
WHY SATURATED PROBABILITY SPACES ARE NECESSARY H. JEROME KEISLER AND YENENG SUN Abstract. An atomless probability space (Ω, A, P ) is said to have the saturation property for a probability measure µ on
g 2 (x) (1/3)M 1 = (1/3)(2/3)M.
 COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
COMPACTNESS If C R n is closed and bounded, then by B-W it is sequentially compact: any sequence of points in C has a subsequence converging to a point in C Conversely, any sequentially compact C R n is
A note on the σ-algebra of cylinder sets and all that
 A note on the σ-algebra of cylinder sets and all that José Luis Silva CCM, Univ. da Madeira, P-9000 Funchal Madeira BiBoS, Univ. of Bielefeld, Germany (luis@dragoeiro.uma.pt) September 1999 Abstract In
A note on the σ-algebra of cylinder sets and all that José Luis Silva CCM, Univ. da Madeira, P-9000 Funchal Madeira BiBoS, Univ. of Bielefeld, Germany (luis@dragoeiro.uma.pt) September 1999 Abstract In
(c) For each α R \ {0}, the mapping x αx is a homeomorphism of X.
 A short account of topological vector spaces Normed spaces, and especially Banach spaces, are basic ambient spaces in Infinite- Dimensional Analysis. However, there are situations in which it is necessary
A short account of topological vector spaces Normed spaces, and especially Banach spaces, are basic ambient spaces in Infinite- Dimensional Analysis. However, there are situations in which it is necessary
LINEAR CHAOS? Nathan S. Feldman
 LINEAR CHAOS? Nathan S. Feldman In this article we hope to convience the reader that the dynamics of linear operators can be fantastically complex and that linear dynamics exhibits the same beauty and
LINEAR CHAOS? Nathan S. Feldman In this article we hope to convience the reader that the dynamics of linear operators can be fantastically complex and that linear dynamics exhibits the same beauty and
Approximation of Integrable Functions by Wavelet Expansions
 Results Math 72 27, 23 2 c 26 The Authors. This article is published with open access at Springerlink.com 422-6383/7/323-9 published online October 25, 26 DOI.7/s25-6-64-z Results in Mathematics Approximation
Results Math 72 27, 23 2 c 26 The Authors. This article is published with open access at Springerlink.com 422-6383/7/323-9 published online October 25, 26 DOI.7/s25-6-64-z Results in Mathematics Approximation
A fixed point theorem for weakly Zamfirescu mappings
 A fixed point theorem for weakly Zamfirescu mappings David Ariza-Ruiz Dept. Análisis Matemático, Fac. Matemáticas, Universidad de Sevilla, Apdo. 1160, 41080-Sevilla, Spain Antonio Jiménez-Melado Dept.
A fixed point theorem for weakly Zamfirescu mappings David Ariza-Ruiz Dept. Análisis Matemático, Fac. Matemáticas, Universidad de Sevilla, Apdo. 1160, 41080-Sevilla, Spain Antonio Jiménez-Melado Dept.
L. Levaggi A. Tabacco WAVELETS ON THE INTERVAL AND RELATED TOPICS
 Rend. Sem. Mat. Univ. Pol. Torino Vol. 57, 1999) L. Levaggi A. Tabacco WAVELETS ON THE INTERVAL AND RELATED TOPICS Abstract. We use an abstract framework to obtain a multilevel decomposition of a variety
Rend. Sem. Mat. Univ. Pol. Torino Vol. 57, 1999) L. Levaggi A. Tabacco WAVELETS ON THE INTERVAL AND RELATED TOPICS Abstract. We use an abstract framework to obtain a multilevel decomposition of a variety
ADJOINT OPERATOR OF BERGMAN PROJECTION AND BESOV SPACE B 1
 AJOINT OPERATOR OF BERGMAN PROJECTION AN BESOV SPACE B 1 AVI KALAJ and JORJIJE VUJAINOVIĆ The main result of this paper is related to finding two-sided bounds of norm for the adjoint operator P of the
AJOINT OPERATOR OF BERGMAN PROJECTION AN BESOV SPACE B 1 AVI KALAJ and JORJIJE VUJAINOVIĆ The main result of this paper is related to finding two-sided bounds of norm for the adjoint operator P of the
THE INVERSE FUNCTION THEOREM
 THE INVERSE FUNCTION THEOREM W. PATRICK HOOPER The implicit function theorem is the following result: Theorem 1. Let f be a C 1 function from a neighborhood of a point a R n into R n. Suppose A = Df(a)
THE INVERSE FUNCTION THEOREM W. PATRICK HOOPER The implicit function theorem is the following result: Theorem 1. Let f be a C 1 function from a neighborhood of a point a R n into R n. Suppose A = Df(a)
Correlation dimension for self-similar Cantor sets with overlaps
 F U N D A M E N T A MATHEMATICAE 155 (1998) Correlation dimension for self-similar Cantor sets with overlaps by Károly S i m o n (Miskolc) and Boris S o l o m y a k (Seattle, Wash.) Abstract. We consider
F U N D A M E N T A MATHEMATICAE 155 (1998) Correlation dimension for self-similar Cantor sets with overlaps by Károly S i m o n (Miskolc) and Boris S o l o m y a k (Seattle, Wash.) Abstract. We consider
DOMAINS OF DIRICHLET FORMS AND EFFECTIVE RESISTANCE ESTIMATES ON P.C.F. FRACTALS. 1. Introduction
 DOMAINS OF DIRICHLET FORMS AND EFFECTIVE RESISTANCE ESTIMATES ON P.C.F. FRACTALS JIAXIN HU 1 AND XINGSHENG WANG Abstract. In this paper we consider post-critically finite self-similar fractals with regular
DOMAINS OF DIRICHLET FORMS AND EFFECTIVE RESISTANCE ESTIMATES ON P.C.F. FRACTALS JIAXIN HU 1 AND XINGSHENG WANG Abstract. In this paper we consider post-critically finite self-similar fractals with regular
STRUCTURE OF (w 1, w 2 )-TEMPERED ULTRADISTRIBUTION USING SHORT-TIME FOURIER TRANSFORM
 ITALIAN JOURNAL OF PURE AND APPLIED MATHEMATICS N. 39 2018 (154 164) 154 STRUCTURE OF (w 1, w 2 )-TEMPERED ULTRADISTRIBUTION USING SHORT-TIME FOURIER TRANSFORM Hamed M. Obiedat Ibraheem Abu-falahah Department
ITALIAN JOURNAL OF PURE AND APPLIED MATHEMATICS N. 39 2018 (154 164) 154 STRUCTURE OF (w 1, w 2 )-TEMPERED ULTRADISTRIBUTION USING SHORT-TIME FOURIER TRANSFORM Hamed M. Obiedat Ibraheem Abu-falahah Department
Tiling Dynamical Systems as an Introduction to Smale Spaces
 Tiling Dynamical Systems as an Introduction to Smale Spaces Michael Whittaker (University of Wollongong) University of Otago Dunedin, New Zealand February 15, 2011 A Penrose Tiling Sir Roger Penrose Penrose
Tiling Dynamical Systems as an Introduction to Smale Spaces Michael Whittaker (University of Wollongong) University of Otago Dunedin, New Zealand February 15, 2011 A Penrose Tiling Sir Roger Penrose Penrose
MASS TRANSFERENCE PRINCIPLE: FROM BALLS TO ARBITRARY SHAPES. 1. Introduction. limsupa i = A i.
 MASS TRANSFERENCE PRINCIPLE: FROM BALLS TO ARBITRARY SHAPES HENNA KOIVUSALO AND MICHA L RAMS arxiv:1812.08557v1 [math.ca] 20 Dec 2018 Abstract. The mass transference principle, proved by Beresnevich and
MASS TRANSFERENCE PRINCIPLE: FROM BALLS TO ARBITRARY SHAPES HENNA KOIVUSALO AND MICHA L RAMS arxiv:1812.08557v1 [math.ca] 20 Dec 2018 Abstract. The mass transference principle, proved by Beresnevich and
THE CONTRACTION MAPPING THEOREM, II
 THE CONTRACTION MAPPING THEOREM, II KEITH CONRAD 1. Introduction In part I, we met the contraction mapping theorem and an application of it to solving nonlinear differential equations. Here we will discuss
THE CONTRACTION MAPPING THEOREM, II KEITH CONRAD 1. Introduction In part I, we met the contraction mapping theorem and an application of it to solving nonlinear differential equations. Here we will discuss
Math 426 Homework 4 Due 3 November 2017
 Math 46 Homework 4 Due 3 November 017 1. Given a metric space X,d) and two subsets A,B, we define the distance between them, dista,b), as the infimum inf a A, b B da,b). a) Prove that if A is compact and
Math 46 Homework 4 Due 3 November 017 1. Given a metric space X,d) and two subsets A,B, we define the distance between them, dista,b), as the infimum inf a A, b B da,b). a) Prove that if A is compact and
Applied Analysis (APPM 5440): Final exam 1:30pm 4:00pm, Dec. 14, Closed books.
 Applied Analysis APPM 44: Final exam 1:3pm 4:pm, Dec. 14, 29. Closed books. Problem 1: 2p Set I = [, 1]. Prove that there is a continuous function u on I such that 1 ux 1 x sin ut 2 dt = cosx, x I. Define
Applied Analysis APPM 44: Final exam 1:3pm 4:pm, Dec. 14, 29. Closed books. Problem 1: 2p Set I = [, 1]. Prove that there is a continuous function u on I such that 1 ux 1 x sin ut 2 dt = cosx, x I. Define
Introduction to Topology
 Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Extension and Representation of Divergence-free Vector Fields on Bounded Domains. Tosio Kato, Marius Mitrea, Gustavo Ponce, and Michael Taylor
 Extension and Representation of Divergence-free Vector Fields on Bounded Domains Tosio Kato, Marius Mitrea, Gustavo Ponce, and Michael Taylor 1. Introduction Let Ω R n be a bounded, connected domain, with
Extension and Representation of Divergence-free Vector Fields on Bounded Domains Tosio Kato, Marius Mitrea, Gustavo Ponce, and Michael Taylor 1. Introduction Let Ω R n be a bounded, connected domain, with
On a Topological Problem of Strange Attractors. Ibrahim Kirat and Ayhan Yurdaer
 On a Topological Problem of Strange Attractors Ibrahim Kirat and Ayhan Yurdaer Department of Mathematics, Istanbul Technical University, 34469,Maslak-Istanbul, Turkey E-mail: ibkst@yahoo.com and yurdaerayhan@itu.edu.tr
On a Topological Problem of Strange Attractors Ibrahim Kirat and Ayhan Yurdaer Department of Mathematics, Istanbul Technical University, 34469,Maslak-Istanbul, Turkey E-mail: ibkst@yahoo.com and yurdaerayhan@itu.edu.tr
Based on the Appendix to B. Hasselblatt and A. Katok, A First Course in Dynamics, Cambridge University press,
 NOTE ON ABSTRACT RIEMANN INTEGRAL Based on the Appendix to B. Hasselblatt and A. Katok, A First Course in Dynamics, Cambridge University press, 2003. a. Definitions. 1. Metric spaces DEFINITION 1.1. If
NOTE ON ABSTRACT RIEMANN INTEGRAL Based on the Appendix to B. Hasselblatt and A. Katok, A First Course in Dynamics, Cambridge University press, 2003. a. Definitions. 1. Metric spaces DEFINITION 1.1. If
On the distributional divergence of vector fields vanishing at infinity
 Proceedings of the Royal Society of Edinburgh, 141A, 65 76, 2011 On the distributional divergence of vector fields vanishing at infinity Thierry De Pauw Institut de Recherches en Mathématiques et Physique,
Proceedings of the Royal Society of Edinburgh, 141A, 65 76, 2011 On the distributional divergence of vector fields vanishing at infinity Thierry De Pauw Institut de Recherches en Mathématiques et Physique,
Convergence of greedy approximation I. General systems
 STUDIA MATHEMATICA 159 (1) (2003) Convergence of greedy approximation I. General systems by S. V. Konyagin (Moscow) and V. N. Temlyakov (Columbia, SC) Abstract. We consider convergence of thresholding
STUDIA MATHEMATICA 159 (1) (2003) Convergence of greedy approximation I. General systems by S. V. Konyagin (Moscow) and V. N. Temlyakov (Columbia, SC) Abstract. We consider convergence of thresholding
CHAPTER VIII HILBERT SPACES
 CHAPTER VIII HILBERT SPACES DEFINITION Let X and Y be two complex vector spaces. A map T : X Y is called a conjugate-linear transformation if it is a reallinear transformation from X into Y, and if T (λx)
CHAPTER VIII HILBERT SPACES DEFINITION Let X and Y be two complex vector spaces. A map T : X Y is called a conjugate-linear transformation if it is a reallinear transformation from X into Y, and if T (λx)
