We begin by considering the following three sequences:
|
|
|
- Alaina Barnett
- 5 years ago
- Views:
Transcription
1 STUDENT S COMPANIONS IN BASIC MATH: THE TWELFTH The Concept of Limits for Sequences and Series In calculus, the concept of limits is of paramount importance, in view of the fact that many basic objects of study such as derivatives, integrals, series etc. are defined by pushing some expressions to their limits. This should be motivating enough for a careful study of limits. But most students find the standard definition of limits is incomprehensive or hard to use. Here we introduce an ad hoc definition of limits designed especially for beginners. This definition still complies with the general standard of mathematical rigor. It is much easier to understand and often easier to work with. After learning this ad hoc definition, you will not find any difficulty in switching to the standard one, which will be given near the end. We begin by considering the following three sequences:, /2, /3, /4, /5, /6,... /2, /4, /8, /6, /32,... 0., 0.0, 0.00, 0.000, ,... Here we only write down the first few terms of each sequence. It is more economic and more precise to express a sequence by writing down a general expression of its nth term a n and then putting curly brackets around it to render the sequence into the form {a n }. For example, the nth term of the first sequence above is /n and hence this sequence is usually written as {/n}, or more precisely as {/n} n. Similarly the second sequence can be written as {/2 n } and the third sequence as {0 n }. All three sequences above have the following common feature: their terms become smaller and smaller and get closer and closer to zero. QUESTION. Are you convinced that these sequences have this common feature? Technically, becoming smaller and smaller is called decreasing and getting closer and closer to zero called tending to zero. Putting together we simply say decreasing to zero. Now we state the following formal definition to give the precise meaning. We say that a sequence {a n } is decreasing if a n a n+ for all n.
2 We say that a sequence {α n } of positive numbers is decreasing to zero if {α n } is decreasing and, for every ε > 0, there exists some n such that α n < ε; (in other words, there is no positive number ε such that α n ε for all n.) QUESTION 2. How do you use the definition to check that {/n} is decreasing to zero? Now we come to our ad hoc definition of limits of sequences. Roughly it says that a sequence {a n } converges to some A if the distance between a n and A can be controlled by some positive number α n which decreases to zero. Definition ( ad hoc ). We say that a sequence {a n } converges to A and write lim n a n = A or simply lim a n = A, if there is a sequence {α n } of positive numbers decreasing to zero such that a n A < α n for all n. In the above definition, a n A is the distance between a n and A, which is simply a n A when a n A, and is A a n when a n A. You cannot find this ad hoc definition in any textbook. You may say it is a result of my effort to improve the teaching of mathematical analysis, which is not an easy subject. EXAMPLE 3.. We are asked to guess the limit of the sequence { n n } (if it exists). Here n n will be rewritten as n /n. The problem is about the behavior of p n n /n for large n. So let us take a large concrete n to find out what n /n is, say n = 0 0 (0 0 is certainly a large number explicitly, it is followed by ten zeros): (0 0 ) /00 = (0 0 ) 0 0 = = 0 (0 9) = =. This suggests that n /n converges to. The question is, can we prove this rigorously? n EXAMPLE 4. Now we are going to give a rigorous proof of lim n n =. Let p n = n n. Notice that p n for all n. (Otherwise we would have p n <, which would lead to n = p n n < n =, contradicting n.) Since we anticipate that, for large n, p n is only slightly larger than, we have to estimate the difference d n between p n and, that is d n = p n. Now we use the following binomial estimation : n = p n n = ( + d n ) n = + nd n + n(n ) 2 d 2 n + n(n + ) 2 d 2 n. 2
3 (The reason why we only keep n(n+) 2 d 2 n and drop all other terms will be clear in a moment.) So we have d 2 n 2/(n + ), which gives 0 d n 2/(n + ), or 0 p n 2/(n + ). It is easy to see that the sequence { 2/(n + )} is decreasing to zero. Therefore n n = p n converges to as n. Why do we have to trouble ourselves with getting a rigorous definition of convergence? Well, without it, we cannot produce a correct argument. An incorrect argument is one of the most woeful things in mathematics, because it may lead us to erroneous conclusions with disastrous consequences (such as a rejected manuscript, a failed exam, a collapsing bridge or a sinking ship). Take a look of Gardener in Lewis Carroll s Sylvie and Bruno Concluded, who sang his verse about finding an error in his argument that would proved he was the Pope a dreadful fact that extinguished all hope, he lamented, with tears streaming down his cheeks. In the definition of limits of sequences, we have used the absolute value a n A of a n A for the distance between a n and A. You may say that a is a just a nice way to write down the awkward expression a 2. A proper definition of the absolute value of a real number a is given by a = { a if a 0; a if a < 0. Here are some elementary facts about absolute values that you should keep in mind: (A) Triangular inequality: a + b a + b (for all real a and b.) (A2) a b = b a, ab = a b. (A3) a a 0 ε ε a a 0 ε a 0 ε a a 0 + ε. (Here stands for if and only if.) These elementary facts are easy to verify. Indeed, accepting the usage of the square root function, (A2) just says (a b) 2 = (b a) 2 and (ab)2 = a 2 b 2. Also, (A) can be rewritten as (a + b) 2 a 2 + b 2, which can be checked by squaring both sides. EXERCISE 5a. Check (A), (A2) and (A3) above. Besides the brute force method suggested above for checking (A) to (A3), there is a conceptual one, described next, which is usually regarded as a more preferable approach. 3
4 Notice that every nonzero real number a can be uniquely written as σ a a, where σ a the sign of a, which is either + or. Also notice that a = σ a a and σ ab = σ a σ b. is EXERCISE 5b. Give the detail of proving (A) by this conceptual approach. QUESTION 6. How do you use (A) and (A3) to derive the inequality a b a b? The following observation will be routinely used in our development of the basic theory of limits of sequences. Observation. If {α n } and {β n } are sequences of positive numbers decreasing to zero, then so are the sequences {α n + β n } and {Kα n }, for any K > 0. EXERCISE 7. Verify this observation with great care. EXAMPLE 8. Now we use what we have so far to prove the following basic fact about limits: if {a n } and {b n } are sequences of real numbers converging to a and b respectively, then the sequence {a n + b n } converges to a + b and {a n b n } converges to ab. Indeed, by assumption, there are sequences {α n } and {β n } in of positive numbers decreasing to zero, such that a n a < α n and b n b < β n for all n. Hence (a n + b n ) (a + b) = (a n a) + (b n b) a n a + b n b < α n + β n for all n. Since α n + β n decreases to zero, we conclude that a n + b n tends to a + b as n. Next, notice that a n = (a n a) + a a n a + a α n + a α + a. So a n b n ab = a n b n a n b + a n b ab = a n (b n b) + b(a n a) a n b n b + b a n a ( a + α )β n + b α n. Our observation tells us that b α n +( a +α )β n to ab. The proof is complete. decreases to zero. Hence a n b n converges EXERCISE 9. Prove the following basic fact: if lim a n = a and if a n [c, d] for all n, then a [c, d]. In other words, if c a n d for all n and if lim n a n = a, then c a d. 4
5 EXERCISE 0. (This is a harder exercise.) Prove the following basic fact: if lim a n = lim n b n = A and if a n x n b n for all n, then lim x n = A. One may describe this fact picturesquely as follows: a and b are two police officers, x is a thief, and A is a police station. The condition a n x n b n means that, at any moment n, the officers are grabbing the thief from both sides. The condition lim n an a n = lim n b n = A means that both officers is marching resolutely to the police station. The conclusion lim n x n = A means that the thief is forced to approach to the police station, with no choice.) EXERCISE. Prove that, if lim n a n = a, then lim n a n = a. Hint: QUESTION 6. EXERCISE 2. Prove that, if a n 0 and if lim n a n = a, then lim n an = a. According to our definition, we have lim n a n = a if there is a sequence of positive numbers α n decreasing to zero such that a n a < α n for all n. We may relax the last requirement a bit: instead of asking a n a < α n holds for all n, we only require this inequality for n starting from certain stage. This is not a substantial improvement. However it gives us flexibility in some arguments. Observation 2. If the inequality a n a < α n holds for all n > n 0, where α n decreases to zero and n 0 is some positive integer, then lim n a n = a. QUESTION 3. How do you justify this observation? ( Justify here means verify.) EXAMPLE 4. Now we use this simple observation to show the following: If lim b n = b, lim a n = a, (a n 0, a 0), then lim b n /a n = b/a. In view of the basic fact proven in EXAMPLE 8 above, it is enough to show lim a n = a. By assumption, there is a sequence {α n } decreasing to zero such that a n a < α n for all n. Now a n a = a n a a n a = a n a a n a < α n a n a. ( ) [Aside: We cannot expect that the right hand side α n / a n a is decreasing to zero. The trouble is caused by a n in the denominator of this expression. In the next step we show that it stays away from zero for large n.] Now a = a a n +a n a a n + a n, or a n a a n a. Since α n decreases to zero and since a /2 is positive, there is a positive integer n 0 such that α n0 < a /2. Thus, for n > n 0, we have a n a < α n α n0 < a /2 and hence a n a a n a > a ( a /2) = a /2. 5 Returning to ( ), we conclude
6 a n a < Kα n for all n > n 0, where K = 2/ a 2. Since {Kα n } is a sequence decreasing to zero, Observation 2 tells us that lim a n = a. The proof is complete. EXERCISE 5. (Working out this exercise is great fun.) Prove that if {a n } is a sequence converges to a, then the sequence {b n } of arithmetic means of {a n } given by b n = a + a a n n also converges to a. Hint: First verify that, if {a n } decreases to zero, so does {b n }. In many practical problems, it is convenient to express a sequence in the form of a series. By a series of numbers we mean a formal infinite sum a + a 2 + a 3 +, which is often written as n= a n (or its variants, such as k=0 a k.) A sum of finitely many numbers is a number, but a formal sum is just an expression (not a number) of grouping some numbers by the addition sign without performing the actual addition. It is a bit hard to swallow, but you have to take it that way. Given a series n= a n, we may form the sequence of partial sums s, s 2, s 3,... which are given by s = a, s 2 = a + a 2, s 3 = a + a 2 + a 3, etc. In general, s n = a + a a n ( = n k= a k Conversely, given a sequence {s n } n, if we let a = s and a n = s n s n for n 2, then s n are partial sums of the series n= a n. (Notice that a + a a n = s + (s 2 s ) + + (s n s n ) = s n, ). which is a telescoping sum.) This shows that there is a one to one correspondence between sequences and series, which are related by taking partial sums and telescoping. Therefore we can transplant all concepts about sequences of numbers to series of numbers. For example, we say that the series n= a n converges to s (we also say n= a n is summable with s as its sum) if its partial sums s n n k= a n converge to s as n. Similarly we say that a series diverges if its corresponding sequence of partial sums diverges. EXAMPLE 6. Let a be a fixed number and consider the geometric series n=0 an. The nth partial sum of this series is s n = + a + a a n. [Note that the zeroth partial sum is s 0 = a 0 =.] We can find a closed form of this sum by the following well known 6
7 trick. Multiplying both sides of s n = + a + a 2 + a a n + a n by a, we obtain as n = a + a 2 + a 3 + a a n + a n+. Hence the difference between s n and as n is s n as n = a n+. Thus, in case a, we arrive at s n + a + a a n = an+. a Suppose a <. Then lim n a n = 0 and hence lim n s n = a. We conclude: If a <, then n=0 an converges to a. EXERCISE 7. Show that the series n(n + ) = n n + and telescope. n= n(n + ) converges to. Hint: Write EXERCISE 8. Find the sum of the series n= n(n + )(n + 2). EXERCISE 9. Prove by the method described below that, if 0 < a <, then lim n nan = 0. First, write x n = na n and r n = x n /x n. Show that lim n r n = a. Take any b with a < b <. Then there exists some positive integer N such that r n < b for all n N. Let n > N and write down the telescoping product na n = x n = x n r n = x n 2 r n r n = = x r 2 r 3 r n x r 2 r N b n N 0 as n. PROBLEM 20. (a) Fix a positive number b and write s k = + b + + b k = bk b. Compute the sum n k= s k in two different ways to deduce the identity n + (n )b + + 2b n 2 + b n = (n (n + )b + b n+ )/( b) 2. 7
8 (b) Letting b = /a, multiply both sides of the above identity by a n to get a closed expression for the sum n k= kak. Then let n to deduce that, for a with a <, the series k=0 kak converges to ( a) 2. Now we introduce the standard definition of limits of sequences. Before doing this, we introduce a special terminology to help us to understand this definition. Let S be a set of numbers and {a n } be a sequence. We say that {a n } is eventually in S if there is a positive integer N such that a n are in S for all n > N. To put in another way, that {a n } is eventually in S means that a n are in S except for finitely many n. Now suppose that {a n } is a sequence converging to a according to our ad hoc definition, that is a n a < α n for some sequence {α n } of positive numbers decreasing to zero. Let ε be an arbitrary positive number. Then there exists some positive integer N that α N < ε. Now, when n > N, we have such a n a < α n α N < ε. Note that a n a < ε means the same as a ε < a n < a + ε, that is, a n is in the open interval (a ε, a + ε). So we have seen that {a n } is eventually in (a ε, a + ε). Thus we know: for every ε > 0, the sequence {a n } is eventually in (a ε, a + ε). From the above discussion, we see that {a n } is eventually in (a ε, a + ε) means there exists some N such that a n a < ε for all n > N. We have rendered the ad hoc definition for lim n a n = a to the following statement: given ε > 0 there exists N such that whenever n > N, we have a n a < ε. The last statement is the standard definition for lim n a n = a. Finally, we briefly discuss a crucial issue: existence of limits. We let an example lead our way of discussion. EXAMPLE 2. Given a positive number a, consider a sequence of numbers x n (n 0) defined recursively by x 0 =, x n+ = x2 n + a 2x n for n 0. What is the limit of this sequence? Well, it is very easy to find, provided that the limit does exist. Indeed, we can rewrite the recursion relation as 2x n x n+ = x 2 n + a. Letting 8
9 n, this identity becomes 2L 2 = L 2 + a., where L is the limit of the sequence {x n }, which is assumed to exist. Thus we have L 2 = a. Hence L = a. QUESTION 22. Why is L above cannot be a? In the above example, we can find the limit if it exists. The problem is, does it really exist? The answer is yes. We can use the following fact to justify this answer: Fact. If {a n } is a decreasing sequence (recall that this means a n+ a n for all n) and if a n 0 for all n, then lim n a n exists. (More generally, any bounded monotone sequence of real numbers converges.) Now you are asked to verify that the sequence given in EXAMPLE 2 above satisfies the conditions of this fact: PROBLEM 23. Prove that x n+ x n in EXAMPLE 2. for all n for the sequence {x n } described QUESTION 24. Define a sequence of positive numbers a n (n ) recursively by putting a = and a n+ = a 2 n +. Let L be the limit of {a n }. Rewrite the recursive relation as a 2 n+ = a 2 n + and let n. Then L 2 = L 2 +, or 0 =. What goes wrong here? The fact mentioned above for checking existence of limits only deals with monotone sequences. For a general sequence, the following criterion (described in the ad hoc way ) is of paramount importance: Cauchy s Criterion. A sequence {a n } is convergent if and only if there is a sequence {α n } of positive numbers decreasing to zero such that a m a n α n for all m, n with m n. Here we only give an inadequate description of some basic facts about existence of limits, leaving their important consequences and examples to an advanced course in mathematical analysis. 9
( ε > 0) ( N N) ( n N) : n > N a n A < ε.
 CHAPTER 1. LIMITS OF SEQUENCES 1.1. An Ad-hoc Definition. In mathematical analysis, the concept of limits is of paramount importance, in view of the fact that many basic objects of study such as derivatives,
CHAPTER 1. LIMITS OF SEQUENCES 1.1. An Ad-hoc Definition. In mathematical analysis, the concept of limits is of paramount importance, in view of the fact that many basic objects of study such as derivatives,
Sequences of Real Numbers
 Chapter 8 Sequences of Real Numbers In this chapter, we assume the existence of the ordered field of real numbers, though we do not yet discuss or use the completeness of the real numbers. In the next
Chapter 8 Sequences of Real Numbers In this chapter, we assume the existence of the ordered field of real numbers, though we do not yet discuss or use the completeness of the real numbers. In the next
CHAPTER 1. REVIEW: NUMBERS
 CHAPTER. REVIEW: NUMBERS Yes, mathematics deals with numbers. But doing math is not number crunching! Rather, it is a very complicated psychological process of learning and inventing. Just like listing
CHAPTER. REVIEW: NUMBERS Yes, mathematics deals with numbers. But doing math is not number crunching! Rather, it is a very complicated psychological process of learning and inventing. Just like listing
2.1 Convergence of Sequences
 Chapter 2 Sequences 2. Convergence of Sequences A sequence is a function f : N R. We write f) = a, f2) = a 2, and in general fn) = a n. We usually identify the sequence with the range of f, which is written
Chapter 2 Sequences 2. Convergence of Sequences A sequence is a function f : N R. We write f) = a, f2) = a 2, and in general fn) = a n. We usually identify the sequence with the range of f, which is written
Limits and Continuity
 Chapter Limits and Continuity. Limits of Sequences.. The Concept of Limit and Its Properties A sequence { } is an ordered infinite list x,x,...,,... The n-th term of the sequence is, and n is the index
Chapter Limits and Continuity. Limits of Sequences.. The Concept of Limit and Its Properties A sequence { } is an ordered infinite list x,x,...,,... The n-th term of the sequence is, and n is the index
Math 324 Summer 2012 Elementary Number Theory Notes on Mathematical Induction
 Math 4 Summer 01 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
Math 4 Summer 01 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
Chapter 11 - Sequences and Series
 Calculus and Analytic Geometry II Chapter - Sequences and Series. Sequences Definition. A sequence is a list of numbers written in a definite order, We call a n the general term of the sequence. {a, a
Calculus and Analytic Geometry II Chapter - Sequences and Series. Sequences Definition. A sequence is a list of numbers written in a definite order, We call a n the general term of the sequence. {a, a
SECTION 9.2: ARITHMETIC SEQUENCES and PARTIAL SUMS
 (Chapter 9: Discrete Math) 9.11 SECTION 9.2: ARITHMETIC SEQUENCES and PARTIAL SUMS PART A: WHAT IS AN ARITHMETIC SEQUENCE? The following appears to be an example of an arithmetic (stress on the me ) sequence:
(Chapter 9: Discrete Math) 9.11 SECTION 9.2: ARITHMETIC SEQUENCES and PARTIAL SUMS PART A: WHAT IS AN ARITHMETIC SEQUENCE? The following appears to be an example of an arithmetic (stress on the me ) sequence:
19. TAYLOR SERIES AND TECHNIQUES
 19. TAYLOR SERIES AND TECHNIQUES Taylor polynomials can be generated for a given function through a certain linear combination of its derivatives. The idea is that we can approximate a function by a polynomial,
19. TAYLOR SERIES AND TECHNIQUES Taylor polynomials can be generated for a given function through a certain linear combination of its derivatives. The idea is that we can approximate a function by a polynomial,
Lecture 3 - Tuesday July 5th
 Lecture 3 - Tuesday July 5th jacques@ucsd.edu Key words: Identities, geometric series, arithmetic series, difference of powers, binomial series Key concepts: Induction, proofs of identities 3. Identities
Lecture 3 - Tuesday July 5th jacques@ucsd.edu Key words: Identities, geometric series, arithmetic series, difference of powers, binomial series Key concepts: Induction, proofs of identities 3. Identities
Infinite Series. Copyright Cengage Learning. All rights reserved.
 Infinite Series Copyright Cengage Learning. All rights reserved. Sequences Copyright Cengage Learning. All rights reserved. Objectives List the terms of a sequence. Determine whether a sequence converges
Infinite Series Copyright Cengage Learning. All rights reserved. Sequences Copyright Cengage Learning. All rights reserved. Objectives List the terms of a sequence. Determine whether a sequence converges
MATH 117 LECTURE NOTES
 MATH 117 LECTURE NOTES XIN ZHOU Abstract. This is the set of lecture notes for Math 117 during Fall quarter of 2017 at UC Santa Barbara. The lectures follow closely the textbook [1]. Contents 1. The set
MATH 117 LECTURE NOTES XIN ZHOU Abstract. This is the set of lecture notes for Math 117 during Fall quarter of 2017 at UC Santa Barbara. The lectures follow closely the textbook [1]. Contents 1. The set
Sequences and infinite series
 Sequences and infinite series D. DeTurck University of Pennsylvania March 29, 208 D. DeTurck Math 04 002 208A: Sequence and series / 54 Sequences The lists of numbers you generate using a numerical method
Sequences and infinite series D. DeTurck University of Pennsylvania March 29, 208 D. DeTurck Math 04 002 208A: Sequence and series / 54 Sequences The lists of numbers you generate using a numerical method
What is A + B? What is A B? What is AB? What is BA? What is A 2? and B = QUESTION 2. What is the reduced row echelon matrix of A =
 STUDENT S COMPANIONS IN BASIC MATH: THE ELEVENTH Matrix Reloaded by Block Buster Presumably you know the first part of matrix story, including its basic operations (addition and multiplication) and row
STUDENT S COMPANIONS IN BASIC MATH: THE ELEVENTH Matrix Reloaded by Block Buster Presumably you know the first part of matrix story, including its basic operations (addition and multiplication) and row
Slope Fields: Graphing Solutions Without the Solutions
 8 Slope Fields: Graphing Solutions Without the Solutions Up to now, our efforts have been directed mainly towards finding formulas or equations describing solutions to given differential equations. Then,
8 Slope Fields: Graphing Solutions Without the Solutions Up to now, our efforts have been directed mainly towards finding formulas or equations describing solutions to given differential equations. Then,
e x = 1 + x + x2 2! + x3 If the function f(x) can be written as a power series on an interval I, then the power series is of the form
 Taylor Series Given a function f(x), we would like to be able to find a power series that represents the function. For example, in the last section we noted that we can represent e x by the power series
Taylor Series Given a function f(x), we would like to be able to find a power series that represents the function. For example, in the last section we noted that we can represent e x by the power series
We are going to discuss what it means for a sequence to converge in three stages: First, we define what it means for a sequence to converge to zero
 Chapter Limits of Sequences Calculus Student: lim s n = 0 means the s n are getting closer and closer to zero but never gets there. Instructor: ARGHHHHH! Exercise. Think of a better response for the instructor.
Chapter Limits of Sequences Calculus Student: lim s n = 0 means the s n are getting closer and closer to zero but never gets there. Instructor: ARGHHHHH! Exercise. Think of a better response for the instructor.
CHAPTER 4. Series. 1. What is a Series?
 CHAPTER 4 Series Given a sequence, in many contexts it is natural to ask about the sum of all the numbers in the sequence. If only a finite number of the are nonzero, this is trivial and not very interesting.
CHAPTER 4 Series Given a sequence, in many contexts it is natural to ask about the sum of all the numbers in the sequence. If only a finite number of the are nonzero, this is trivial and not very interesting.
MAS221 Analysis Semester Chapter 2 problems
 MAS221 Analysis Semester 1 2018-19 Chapter 2 problems 20. Consider the sequence (a n ), with general term a n = 1 + 3. Can you n guess the limit l of this sequence? (a) Verify that your guess is plausible
MAS221 Analysis Semester 1 2018-19 Chapter 2 problems 20. Consider the sequence (a n ), with general term a n = 1 + 3. Can you n guess the limit l of this sequence? (a) Verify that your guess is plausible
chapter 12 MORE MATRIX ALGEBRA 12.1 Systems of Linear Equations GOALS
 chapter MORE MATRIX ALGEBRA GOALS In Chapter we studied matrix operations and the algebra of sets and logic. We also made note of the strong resemblance of matrix algebra to elementary algebra. The reader
chapter MORE MATRIX ALGEBRA GOALS In Chapter we studied matrix operations and the algebra of sets and logic. We also made note of the strong resemblance of matrix algebra to elementary algebra. The reader
means is a subset of. So we say A B for sets A and B if x A we have x B holds. BY CONTRAST, a S means that a is a member of S.
 1 Notation For those unfamiliar, we have := means equal by definition, N := {0, 1,... } or {1, 2,... } depending on context. (i.e. N is the set or collection of counting numbers.) In addition, means for
1 Notation For those unfamiliar, we have := means equal by definition, N := {0, 1,... } or {1, 2,... } depending on context. (i.e. N is the set or collection of counting numbers.) In addition, means for
Standard forms for writing numbers
 Standard forms for writing numbers In order to relate the abstract mathematical descriptions of familiar number systems to the everyday descriptions of numbers by decimal expansions and similar means,
Standard forms for writing numbers In order to relate the abstract mathematical descriptions of familiar number systems to the everyday descriptions of numbers by decimal expansions and similar means,
MATH 324 Summer 2011 Elementary Number Theory. Notes on Mathematical Induction. Recall the following axiom for the set of integers.
 MATH 4 Summer 011 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
MATH 4 Summer 011 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
(Infinite) Series Series a n = a 1 + a 2 + a a n +...
 (Infinite) Series Series a n = a 1 + a 2 + a 3 +... + a n +... What does it mean to add infinitely many terms? The sequence of partial sums S 1, S 2, S 3, S 4,...,S n,...,where nx S n = a i = a 1 + a 2
(Infinite) Series Series a n = a 1 + a 2 + a 3 +... + a n +... What does it mean to add infinitely many terms? The sequence of partial sums S 1, S 2, S 3, S 4,...,S n,...,where nx S n = a i = a 1 + a 2
C.7. Numerical series. Pag. 147 Proof of the converging criteria for series. Theorem 5.29 (Comparison test) Let a k and b k be positive-term series
 C.7 Numerical series Pag. 147 Proof of the converging criteria for series Theorem 5.29 (Comparison test) Let and be positive-term series such that 0, for any k 0. i) If the series converges, then also
C.7 Numerical series Pag. 147 Proof of the converging criteria for series Theorem 5.29 (Comparison test) Let and be positive-term series such that 0, for any k 0. i) If the series converges, then also
Chapter One Hilbert s 7th Problem: It s statement and origins
 Chapter One Hilbert s 7th Problem: It s statement and origins At the second International Congress of athematicians in Paris, 900, the mathematician David Hilbert was invited to deliver a keynote address,
Chapter One Hilbert s 7th Problem: It s statement and origins At the second International Congress of athematicians in Paris, 900, the mathematician David Hilbert was invited to deliver a keynote address,
Limits and Infinite Series Lecture Notes for Math 226. Department of Mathematics Western Washington University
 Limits and Infinite Series Lecture Notes for Math 226 by Árpád Bényi Department of Mathematics Western Washington University To the student Math 226 is a first introduction to formal arguments in mathematical
Limits and Infinite Series Lecture Notes for Math 226 by Árpád Bényi Department of Mathematics Western Washington University To the student Math 226 is a first introduction to formal arguments in mathematical
Power series and Taylor series
 Power series and Taylor series D. DeTurck University of Pennsylvania March 29, 2018 D. DeTurck Math 104 002 2018A: Series 1 / 42 Series First... a review of what we have done so far: 1 We examined series
Power series and Taylor series D. DeTurck University of Pennsylvania March 29, 2018 D. DeTurck Math 104 002 2018A: Series 1 / 42 Series First... a review of what we have done so far: 1 We examined series
3. Infinite Series. The Sum of a Series. A series is an infinite sum of numbers:
 3. Infinite Series A series is an infinite sum of numbers: The individual numbers are called the terms of the series. In the above series, the first term is, the second term is, and so on. The th term
3. Infinite Series A series is an infinite sum of numbers: The individual numbers are called the terms of the series. In the above series, the first term is, the second term is, and so on. The th term
8.5 Taylor Polynomials and Taylor Series
 8.5. TAYLOR POLYNOMIALS AND TAYLOR SERIES 50 8.5 Taylor Polynomials and Taylor Series Motivating Questions In this section, we strive to understand the ideas generated by the following important questions:
8.5. TAYLOR POLYNOMIALS AND TAYLOR SERIES 50 8.5 Taylor Polynomials and Taylor Series Motivating Questions In this section, we strive to understand the ideas generated by the following important questions:
DR.RUPNATHJI( DR.RUPAK NATH )
 Contents 1 Sets 1 2 The Real Numbers 9 3 Sequences 29 4 Series 59 5 Functions 81 6 Power Series 105 7 The elementary functions 111 Chapter 1 Sets It is very convenient to introduce some notation and terminology
Contents 1 Sets 1 2 The Real Numbers 9 3 Sequences 29 4 Series 59 5 Functions 81 6 Power Series 105 7 The elementary functions 111 Chapter 1 Sets It is very convenient to introduce some notation and terminology
Lecture 4: Constructing the Integers, Rationals and Reals
 Math/CS 20: Intro. to Math Professor: Padraic Bartlett Lecture 4: Constructing the Integers, Rationals and Reals Week 5 UCSB 204 The Integers Normally, using the natural numbers, you can easily define
Math/CS 20: Intro. to Math Professor: Padraic Bartlett Lecture 4: Constructing the Integers, Rationals and Reals Week 5 UCSB 204 The Integers Normally, using the natural numbers, you can easily define
MATH3283W LECTURE NOTES: WEEK 6 = 5 13, = 2 5, 1 13
 MATH383W LECTURE NOTES: WEEK 6 //00 Recursive sequences (cont.) Examples: () a =, a n+ = 3 a n. The first few terms are,,, 5 = 5, 3 5 = 5 3, Since 5
MATH383W LECTURE NOTES: WEEK 6 //00 Recursive sequences (cont.) Examples: () a =, a n+ = 3 a n. The first few terms are,,, 5 = 5, 3 5 = 5 3, Since 5
A description of a math circle set of activities around polynomials, especially interpolation.
 A description of a math circle set of activities around polynomials, especially interpolation. Bob Sachs Department of Mathematical Sciences George Mason University Fairfax, Virginia 22030 rsachs@gmu.edu
A description of a math circle set of activities around polynomials, especially interpolation. Bob Sachs Department of Mathematical Sciences George Mason University Fairfax, Virginia 22030 rsachs@gmu.edu
AP Calculus Chapter 9: Infinite Series
 AP Calculus Chapter 9: Infinite Series 9. Sequences a, a 2, a 3, a 4, a 5,... Sequence: A function whose domain is the set of positive integers n = 2 3 4 a n = a a 2 a 3 a 4 terms of the sequence Begin
AP Calculus Chapter 9: Infinite Series 9. Sequences a, a 2, a 3, a 4, a 5,... Sequence: A function whose domain is the set of positive integers n = 2 3 4 a n = a a 2 a 3 a 4 terms of the sequence Begin
1.4 Mathematical Equivalence
 1.4 Mathematical Equivalence Introduction a motivating example sentences that always have the same truth values can be used interchangeably the implied domain of a sentence In this section, the idea of
1.4 Mathematical Equivalence Introduction a motivating example sentences that always have the same truth values can be used interchangeably the implied domain of a sentence In this section, the idea of
An Introduction to Proofs in Mathematics
 An Introduction to Proofs in Mathematics The subject of mathematics is often regarded as a pinnacle in the achievement of human reasoning. The reason that mathematics is so highly regarded in the realm
An Introduction to Proofs in Mathematics The subject of mathematics is often regarded as a pinnacle in the achievement of human reasoning. The reason that mathematics is so highly regarded in the realm
CONSTRUCTION OF sequence of rational approximations to sets of rational approximating sequences, all with the same tail behaviour Definition 1.
 CONSTRUCTION OF R 1. MOTIVATION We are used to thinking of real numbers as successive approximations. For example, we write π = 3.14159... to mean that π is a real number which, accurate to 5 decimal places,
CONSTRUCTION OF R 1. MOTIVATION We are used to thinking of real numbers as successive approximations. For example, we write π = 3.14159... to mean that π is a real number which, accurate to 5 decimal places,
Ordinary Differential Equations Prof. A. K. Nandakumaran Department of Mathematics Indian Institute of Science Bangalore
 Ordinary Differential Equations Prof. A. K. Nandakumaran Department of Mathematics Indian Institute of Science Bangalore Module - 3 Lecture - 10 First Order Linear Equations (Refer Slide Time: 00:33) Welcome
Ordinary Differential Equations Prof. A. K. Nandakumaran Department of Mathematics Indian Institute of Science Bangalore Module - 3 Lecture - 10 First Order Linear Equations (Refer Slide Time: 00:33) Welcome
Mini-Course on Limits and Sequences. Peter Kwadwo Asante. B.S., Kwame Nkrumah University of Science and Technology, Ghana, 2014 A REPORT
 Mini-Course on Limits and Sequences by Peter Kwadwo Asante B.S., Kwame Nkrumah University of Science and Technology, Ghana, 204 A REPORT submitted in partial fulfillment of the requirements for the degree
Mini-Course on Limits and Sequences by Peter Kwadwo Asante B.S., Kwame Nkrumah University of Science and Technology, Ghana, 204 A REPORT submitted in partial fulfillment of the requirements for the degree
Lies My Calculator and Computer Told Me
 Lies My Calculator and Computer Told Me 2 LIES MY CALCULATOR AND COMPUTER TOLD ME Lies My Calculator and Computer Told Me See Section.4 for a discussion of graphing calculators and computers with graphing
Lies My Calculator and Computer Told Me 2 LIES MY CALCULATOR AND COMPUTER TOLD ME Lies My Calculator and Computer Told Me See Section.4 for a discussion of graphing calculators and computers with graphing
Given a sequence a 1, a 2,...of numbers, the finite sum a 1 + a 2 + +a n,wheren is an nonnegative integer, can be written
 A Summations When an algorithm contains an iterative control construct such as a while or for loop, its running time can be expressed as the sum of the times spent on each execution of the body of the
A Summations When an algorithm contains an iterative control construct such as a while or for loop, its running time can be expressed as the sum of the times spent on each execution of the body of the
CHAPTER 3: THE INTEGERS Z
 CHAPTER 3: THE INTEGERS Z MATH 378, CSUSM. SPRING 2009. AITKEN 1. Introduction The natural numbers are designed for measuring the size of finite sets, but what if you want to compare the sizes of two sets?
CHAPTER 3: THE INTEGERS Z MATH 378, CSUSM. SPRING 2009. AITKEN 1. Introduction The natural numbers are designed for measuring the size of finite sets, but what if you want to compare the sizes of two sets?
Fundamentals of Mathematics I
 Fundamentals of Mathematics I Kent State Department of Mathematical Sciences Fall 2008 Available at: http://www.math.kent.edu/ebooks/10031/book.pdf August 4, 2008 Contents 1 Arithmetic 2 1.1 Real Numbers......................................................
Fundamentals of Mathematics I Kent State Department of Mathematical Sciences Fall 2008 Available at: http://www.math.kent.edu/ebooks/10031/book.pdf August 4, 2008 Contents 1 Arithmetic 2 1.1 Real Numbers......................................................
8. TRANSFORMING TOOL #1 (the Addition Property of Equality)
 8 TRANSFORMING TOOL #1 (the Addition Property of Equality) sentences that look different, but always have the same truth values What can you DO to a sentence that will make it LOOK different, but not change
8 TRANSFORMING TOOL #1 (the Addition Property of Equality) sentences that look different, but always have the same truth values What can you DO to a sentence that will make it LOOK different, but not change
Ordinary Differential Equation Introduction and Preliminaries
 Ordinary Differential Equation Introduction and Preliminaries There are many branches of science and engineering where differential equations arise naturally. Now days, it finds applications in many areas
Ordinary Differential Equation Introduction and Preliminaries There are many branches of science and engineering where differential equations arise naturally. Now days, it finds applications in many areas
Sequences. Chapter 3. n + 1 3n + 2 sin n n. 3. lim (ln(n + 1) ln n) 1. lim. 2. lim. 4. lim (1 + n)1/n. Answers: 1. 1/3; 2. 0; 3. 0; 4. 1.
 Chapter 3 Sequences Both the main elements of calculus (differentiation and integration) require the notion of a limit. Sequences will play a central role when we work with limits. Definition 3.. A Sequence
Chapter 3 Sequences Both the main elements of calculus (differentiation and integration) require the notion of a limit. Sequences will play a central role when we work with limits. Definition 3.. A Sequence
MIDTERM REVIEW FOR MATH The limit
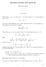 MIDTERM REVIEW FOR MATH 500 SHUANGLIN SHAO. The limit Define lim n a n = A: For any ε > 0, there exists N N such that for any n N, a n A < ε. The key in this definition is to realize that the choice of
MIDTERM REVIEW FOR MATH 500 SHUANGLIN SHAO. The limit Define lim n a n = A: For any ε > 0, there exists N N such that for any n N, a n A < ε. The key in this definition is to realize that the choice of
MATH 320, WEEK 6: Linear Systems, Gaussian Elimination, Coefficient Matrices
 MATH 320, WEEK 6: Linear Systems, Gaussian Elimination, Coefficient Matrices We will now switch gears and focus on a branch of mathematics known as linear algebra. There are a few notes worth making before
MATH 320, WEEK 6: Linear Systems, Gaussian Elimination, Coefficient Matrices We will now switch gears and focus on a branch of mathematics known as linear algebra. There are a few notes worth making before
Seunghee Ye Ma 8: Week 2 Oct 6
 Week 2 Summary This week, we will learn about sequences and real numbers. We first define what we mean by a sequence and discuss several properties of sequences. Then, we will talk about what it means
Week 2 Summary This week, we will learn about sequences and real numbers. We first define what we mean by a sequence and discuss several properties of sequences. Then, we will talk about what it means
INTRODUCTION TO REAL ANALYSIS II MATH 4332 BLECHER NOTES
 INTRODUCTION TO REAL ANALYSIS II MATH 4332 BLECHER NOTES You will be expected to reread and digest these typed notes after class, line by line, trying to follow why the line is true, for example how it
INTRODUCTION TO REAL ANALYSIS II MATH 4332 BLECHER NOTES You will be expected to reread and digest these typed notes after class, line by line, trying to follow why the line is true, for example how it
Undergraduate Notes in Mathematics. Arkansas Tech University Department of Mathematics
 Undergraduate Notes in Mathematics Arkansas Tech University Department of Mathematics An Introductory Single Variable Real Analysis: A Learning Approach through Problem Solving Marcel B. Finan c All Rights
Undergraduate Notes in Mathematics Arkansas Tech University Department of Mathematics An Introductory Single Variable Real Analysis: A Learning Approach through Problem Solving Marcel B. Finan c All Rights
Calculus (Real Analysis I)
 Calculus (Real Analysis I) (MAT122β) Department of Mathematics University of Ruhuna A.W.L. Pubudu Thilan Department of Mathematics University of Ruhuna Calculus (Real Analysis I)(MAT122β) 1/172 Chapter
Calculus (Real Analysis I) (MAT122β) Department of Mathematics University of Ruhuna A.W.L. Pubudu Thilan Department of Mathematics University of Ruhuna Calculus (Real Analysis I)(MAT122β) 1/172 Chapter
3 The language of proof
 3 The language of proof After working through this section, you should be able to: (a) understand what is asserted by various types of mathematical statements, in particular implications and equivalences;
3 The language of proof After working through this section, you should be able to: (a) understand what is asserted by various types of mathematical statements, in particular implications and equivalences;
CONSTRUCTION OF THE REAL NUMBERS.
 CONSTRUCTION OF THE REAL NUMBERS. IAN KIMING 1. Motivation. It will not come as a big surprise to anyone when I say that we need the real numbers in mathematics. More to the point, we need to be able to
CONSTRUCTION OF THE REAL NUMBERS. IAN KIMING 1. Motivation. It will not come as a big surprise to anyone when I say that we need the real numbers in mathematics. More to the point, we need to be able to
Mathematics E-15 Seminar on Limits Suggested Lesson Topics
 Mathematics E-15 Seminar on Limits Suggested Lesson Topics Lesson Presentation Guidelines Each lesson should last approximately 45 minutes. This will leave us with some time at the end for constructive
Mathematics E-15 Seminar on Limits Suggested Lesson Topics Lesson Presentation Guidelines Each lesson should last approximately 45 minutes. This will leave us with some time at the end for constructive
Jumping Sequences. Steve Butler Department of Mathematics University of California, Los Angeles Los Angeles, CA
 1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 11 (2008), Article 08.4.5 Jumping Sequences Steve Butler Department of Mathematics University of California, Los Angeles Los Angeles, CA 90095 butler@math.ucla.edu
1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 11 (2008), Article 08.4.5 Jumping Sequences Steve Butler Department of Mathematics University of California, Los Angeles Los Angeles, CA 90095 butler@math.ucla.edu
Exercises. Template for Proofs by Mathematical Induction
 5. Mathematical Induction 329 Template for Proofs by Mathematical Induction. Express the statement that is to be proved in the form for all n b, P (n) forafixed integer b. 2. Write out the words Basis
5. Mathematical Induction 329 Template for Proofs by Mathematical Induction. Express the statement that is to be proved in the form for all n b, P (n) forafixed integer b. 2. Write out the words Basis
MATH 131A: REAL ANALYSIS
 MATH 131A: REAL ANALYSIS NICKOLAS ANDERSEN The textbook for the course is Ross, Elementary Analysis [2], but in these notes I have also borrowed from Tao, Analysis I [3], and Abbott, Understanding Analysis
MATH 131A: REAL ANALYSIS NICKOLAS ANDERSEN The textbook for the course is Ross, Elementary Analysis [2], but in these notes I have also borrowed from Tao, Analysis I [3], and Abbott, Understanding Analysis
Chapter 1A -- Real Numbers. iff. Math Symbols: Sets of Numbers
 Fry Texas A&M University! Fall 2016! Math 150 Notes! Section 1A! Page 1 Chapter 1A -- Real Numbers Math Symbols: iff or Example: Let A = {2, 4, 6, 8, 10, 12, 14, 16,...} and let B = {3, 6, 9, 12, 15, 18,
Fry Texas A&M University! Fall 2016! Math 150 Notes! Section 1A! Page 1 Chapter 1A -- Real Numbers Math Symbols: iff or Example: Let A = {2, 4, 6, 8, 10, 12, 14, 16,...} and let B = {3, 6, 9, 12, 15, 18,
MATH 137 : Calculus 1 for Honours Mathematics Instructor: Barbara Forrest Self Check #1: Sequences and Convergence
 1 MATH 137 : Calculus 1 for Honours Mathematics Instructor: Barbara Forrest Self Check #1: Sequences and Convergence Recommended Due Date: complete by the end of WEEK 3 Weight: none - self graded INSTRUCTIONS:
1 MATH 137 : Calculus 1 for Honours Mathematics Instructor: Barbara Forrest Self Check #1: Sequences and Convergence Recommended Due Date: complete by the end of WEEK 3 Weight: none - self graded INSTRUCTIONS:
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES Infinite sequences and series were introduced briefly in A Preview of Calculus in connection with Zeno s paradoxes and the decimal representation
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES Infinite sequences and series were introduced briefly in A Preview of Calculus in connection with Zeno s paradoxes and the decimal representation
Solution to Proof Questions from September 1st
 Solution to Proof Questions from September 1st Olena Bormashenko September 4, 2011 What is a proof? A proof is an airtight logical argument that proves a certain statement in general. In a sense, it s
Solution to Proof Questions from September 1st Olena Bormashenko September 4, 2011 What is a proof? A proof is an airtight logical argument that proves a certain statement in general. In a sense, it s
CHAPTER 1: Functions
 CHAPTER 1: Functions 1.1: Functions 1.2: Graphs of Functions 1.3: Basic Graphs and Symmetry 1.4: Transformations 1.5: Piecewise-Defined Functions; Limits and Continuity in Calculus 1.6: Combining Functions
CHAPTER 1: Functions 1.1: Functions 1.2: Graphs of Functions 1.3: Basic Graphs and Symmetry 1.4: Transformations 1.5: Piecewise-Defined Functions; Limits and Continuity in Calculus 1.6: Combining Functions
Introduction to Series and Sequences Math 121 Calculus II Spring 2015
 Introduction to Series and Sequences Math Calculus II Spring 05 The goal. The main purpose of our study of series and sequences is to understand power series. A power series is like a polynomial of infinite
Introduction to Series and Sequences Math Calculus II Spring 05 The goal. The main purpose of our study of series and sequences is to understand power series. A power series is like a polynomial of infinite
5.2 Infinite Series Brian E. Veitch
 5. Infinite Series Since many quantities show up that cannot be computed exactly, we need some way of representing it (or approximating it). One way is to sum an infinite series. Recall that a n is the
5. Infinite Series Since many quantities show up that cannot be computed exactly, we need some way of representing it (or approximating it). One way is to sum an infinite series. Recall that a n is the
Iowa State University. Instructor: Alex Roitershtein Summer Exam #1. Solutions. x u = 2 x v
 Math 501 Iowa State University Introduction to Real Analysis Department of Mathematics Instructor: Alex Roitershtein Summer 015 Exam #1 Solutions This is a take-home examination. The exam includes 8 questions.
Math 501 Iowa State University Introduction to Real Analysis Department of Mathematics Instructor: Alex Roitershtein Summer 015 Exam #1 Solutions This is a take-home examination. The exam includes 8 questions.
Lesson 12.7: Sequences and Series
 Lesson 12.7: Sequences and Series May 30 7:11 AM Sequences Definition: A sequence is a set of numbers in a specific order. 2, 5, 8,. is an example of a sequence. Note: A sequence may have either a finite
Lesson 12.7: Sequences and Series May 30 7:11 AM Sequences Definition: A sequence is a set of numbers in a specific order. 2, 5, 8,. is an example of a sequence. Note: A sequence may have either a finite
Notes on arithmetic. 1. Representation in base B
 Notes on arithmetic The Babylonians that is to say, the people that inhabited what is now southern Iraq for reasons not entirely clear to us, ued base 60 in scientific calculation. This offers us an excuse
Notes on arithmetic The Babylonians that is to say, the people that inhabited what is now southern Iraq for reasons not entirely clear to us, ued base 60 in scientific calculation. This offers us an excuse
Topic 7 Notes Jeremy Orloff
 Topic 7 Notes Jeremy Orloff 7 Taylor and Laurent series 7. Introduction We originally defined an analytic function as one where the derivative, defined as a limit of ratios, existed. We went on to prove
Topic 7 Notes Jeremy Orloff 7 Taylor and Laurent series 7. Introduction We originally defined an analytic function as one where the derivative, defined as a limit of ratios, existed. We went on to prove
Chapter 13 - Inverse Functions
 Chapter 13 - Inverse Functions In the second part of this book on Calculus, we shall be devoting our study to another type of function, the exponential function and its close relative the Sine function.
Chapter 13 - Inverse Functions In the second part of this book on Calculus, we shall be devoting our study to another type of function, the exponential function and its close relative the Sine function.
Introduction to Real Analysis Alternative Chapter 1
 Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Math 137 Calculus 1 for Honours Mathematics. Course Notes
 Math 37 Calculus for Honours Mathematics Course Notes Barbara A. Forrest and Brian E. Forrest Fall 07 / Version. Copyright c Barbara A. Forrest and Brian E. Forrest. All rights reserved. August, 07 All
Math 37 Calculus for Honours Mathematics Course Notes Barbara A. Forrest and Brian E. Forrest Fall 07 / Version. Copyright c Barbara A. Forrest and Brian E. Forrest. All rights reserved. August, 07 All
MATH20101 Real Analysis, Exam Solutions and Feedback. 2013\14
 MATH200 Real Analysis, Exam Solutions and Feedback. 203\4 A. i. Prove by verifying the appropriate definition that ( 2x 3 + x 2 + 5 ) = 7. x 2 ii. By using the Rules for its evaluate a) b) x 2 x + x 2
MATH200 Real Analysis, Exam Solutions and Feedback. 203\4 A. i. Prove by verifying the appropriate definition that ( 2x 3 + x 2 + 5 ) = 7. x 2 ii. By using the Rules for its evaluate a) b) x 2 x + x 2
1. Introduction to commutative rings and fields
 1. Introduction to commutative rings and fields Very informally speaking, a commutative ring is a set in which we can add, subtract and multiply elements so that the usual laws hold. A field is a commutative
1. Introduction to commutative rings and fields Very informally speaking, a commutative ring is a set in which we can add, subtract and multiply elements so that the usual laws hold. A field is a commutative
chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS 5.1 Basic Definitions
 chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras: elementary
chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras: elementary
Math 163: Lecture notes
 Math 63: Lecture notes Professor Monika Nitsche March 2, 2 Special functions that are inverses of known functions. Inverse functions (Day ) Go over: early exam, hw, quizzes, grading scheme, attendance
Math 63: Lecture notes Professor Monika Nitsche March 2, 2 Special functions that are inverses of known functions. Inverse functions (Day ) Go over: early exam, hw, quizzes, grading scheme, attendance
CS1800: Sequences & Sums. Professor Kevin Gold
 CS1800: Sequences & Sums Professor Kevin Gold Moving Toward Analysis of Algorithms Today s tools help in the analysis of algorithms. We ll cover tools for deciding what equation best fits a sequence of
CS1800: Sequences & Sums Professor Kevin Gold Moving Toward Analysis of Algorithms Today s tools help in the analysis of algorithms. We ll cover tools for deciding what equation best fits a sequence of
After linear functions, the next simplest functions are polynomials. Examples are
 Mathematics 10 Fall 1999 Polynomials After linear functions, the next simplest functions are polynomials. Examples are 1+x, x +3x +, x 3. Here x is a variable. Recall that we have defined a function to
Mathematics 10 Fall 1999 Polynomials After linear functions, the next simplest functions are polynomials. Examples are 1+x, x +3x +, x 3. Here x is a variable. Recall that we have defined a function to
CHAPTER 7: Systems and Inequalities
 (Exercises for Chapter 7: Systems and Inequalities) E.7.1 CHAPTER 7: Systems and Inequalities (A) means refer to Part A, (B) means refer to Part B, etc. (Calculator) means use a calculator. Otherwise,
(Exercises for Chapter 7: Systems and Inequalities) E.7.1 CHAPTER 7: Systems and Inequalities (A) means refer to Part A, (B) means refer to Part B, etc. (Calculator) means use a calculator. Otherwise,
Math 1b Sequences and series summary
 Math b Sequences and series summary December 22, 2005 Sequences (Stewart p. 557) Notations for a sequence: or a, a 2, a 3,..., a n,... {a n }. The numbers a n are called the terms of the sequence.. Limit
Math b Sequences and series summary December 22, 2005 Sequences (Stewart p. 557) Notations for a sequence: or a, a 2, a 3,..., a n,... {a n }. The numbers a n are called the terms of the sequence.. Limit
Linear Algebra, Summer 2011, pt. 2
 Linear Algebra, Summer 2, pt. 2 June 8, 2 Contents Inverses. 2 Vector Spaces. 3 2. Examples of vector spaces..................... 3 2.2 The column space......................... 6 2.3 The null space...........................
Linear Algebra, Summer 2, pt. 2 June 8, 2 Contents Inverses. 2 Vector Spaces. 3 2. Examples of vector spaces..................... 3 2.2 The column space......................... 6 2.3 The null space...........................
Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods. Section 1: Separable DEs
 Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods Section 1: Separable DEs We are finally to the point in the course where we can consider how to find solutions to differential
Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods Section 1: Separable DEs We are finally to the point in the course where we can consider how to find solutions to differential
Abstract. 2. We construct several transcendental numbers.
 Abstract. We prove Liouville s Theorem for the order of approximation by rationals of real algebraic numbers. 2. We construct several transcendental numbers. 3. We define Poissonian Behaviour, and study
Abstract. We prove Liouville s Theorem for the order of approximation by rationals of real algebraic numbers. 2. We construct several transcendental numbers. 3. We define Poissonian Behaviour, and study
CHAPTER 3. Sequences. 1. Basic Properties
 CHAPTER 3 Sequences We begin our study of analysis with sequences. There are several reasons for starting here. First, sequences are the simplest way to introduce limits, the central idea of calculus.
CHAPTER 3 Sequences We begin our study of analysis with sequences. There are several reasons for starting here. First, sequences are the simplest way to introduce limits, the central idea of calculus.
LECTURE 10: REVIEW OF POWER SERIES. 1. Motivation
 LECTURE 10: REVIEW OF POWER SERIES By definition, a power series centered at x 0 is a series of the form where a 0, a 1,... and x 0 are constants. For convenience, we shall mostly be concerned with the
LECTURE 10: REVIEW OF POWER SERIES By definition, a power series centered at x 0 is a series of the form where a 0, a 1,... and x 0 are constants. For convenience, we shall mostly be concerned with the
MATHEMATICAL INDUCTION
 MATHEMATICAL INDUCTION MATH 3A SECTION HANDOUT BY GERARDO CON DIAZ Imagine a bunch of dominoes on a table. They are set up in a straight line, and you are about to push the first piece to set off the chain
MATHEMATICAL INDUCTION MATH 3A SECTION HANDOUT BY GERARDO CON DIAZ Imagine a bunch of dominoes on a table. They are set up in a straight line, and you are about to push the first piece to set off the chain
2. Introduction to commutative rings (continued)
 2. Introduction to commutative rings (continued) 2.1. New examples of commutative rings. Recall that in the first lecture we defined the notions of commutative rings and field and gave some examples of
2. Introduction to commutative rings (continued) 2.1. New examples of commutative rings. Recall that in the first lecture we defined the notions of commutative rings and field and gave some examples of
CHAPTER 8: EXPLORING R
 CHAPTER 8: EXPLORING R LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN In the previous chapter we discussed the need for a complete ordered field. The field Q is not complete, so we constructed
CHAPTER 8: EXPLORING R LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN In the previous chapter we discussed the need for a complete ordered field. The field Q is not complete, so we constructed
Math 1B, lecture 15: Taylor Series
 Math B, lecture 5: Taylor Series Nathan Pflueger October 0 Introduction Taylor s theorem shows, in many cases, that the error associated with a Taylor approximation will eventually approach 0 as the degree
Math B, lecture 5: Taylor Series Nathan Pflueger October 0 Introduction Taylor s theorem shows, in many cases, that the error associated with a Taylor approximation will eventually approach 0 as the degree
Math 5a Reading Assignments for Sections
 Math 5a Reading Assignments for Sections 4.1 4.5 Due Dates for Reading Assignments Note: There will be a very short online reading quiz (WebWork) on each reading assignment due one hour before class on
Math 5a Reading Assignments for Sections 4.1 4.5 Due Dates for Reading Assignments Note: There will be a very short online reading quiz (WebWork) on each reading assignment due one hour before class on
30. TRANSFORMING TOOL #1 (the Addition Property of Equality)
 30 TRANSFORMING TOOL #1 (the Addition Property of Equality) sentences that look different, but always have the same truth values What can you DO to a sentence that will make it LOOK different, but not
30 TRANSFORMING TOOL #1 (the Addition Property of Equality) sentences that look different, but always have the same truth values What can you DO to a sentence that will make it LOOK different, but not
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES In section 11.9, we were able to find power series representations for a certain restricted class of functions. INFINITE SEQUENCES AND SERIES
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES In section 11.9, we were able to find power series representations for a certain restricted class of functions. INFINITE SEQUENCES AND SERIES
Taylor and Laurent Series
 Chapter 4 Taylor and Laurent Series 4.. Taylor Series 4... Taylor Series for Holomorphic Functions. In Real Analysis, the Taylor series of a given function f : R R is given by: f (x + f (x (x x + f (x
Chapter 4 Taylor and Laurent Series 4.. Taylor Series 4... Taylor Series for Holomorphic Functions. In Real Analysis, the Taylor series of a given function f : R R is given by: f (x + f (x (x x + f (x
Writing proofs for MATH 61CM, 61DM Week 1: basic logic, proof by contradiction, proof by induction
 Writing proofs for MATH 61CM, 61DM Week 1: basic logic, proof by contradiction, proof by induction written by Sarah Peluse, revised by Evangelie Zachos and Lisa Sauermann September 27, 2016 1 Introduction
Writing proofs for MATH 61CM, 61DM Week 1: basic logic, proof by contradiction, proof by induction written by Sarah Peluse, revised by Evangelie Zachos and Lisa Sauermann September 27, 2016 1 Introduction
Homework 1 Solutions
 MATH 171 Spring 2016 Problem 1 Homework 1 Solutions (If you find any errors, please send an e-mail to farana at stanford dot edu) Presenting your arguments in steps, using only axioms of an ordered field,
MATH 171 Spring 2016 Problem 1 Homework 1 Solutions (If you find any errors, please send an e-mail to farana at stanford dot edu) Presenting your arguments in steps, using only axioms of an ordered field,
10.1 Sequences. A sequence is an ordered list of numbers: a 1, a 2, a 3,..., a n, a n+1,... Each of the numbers is called a term of the sequence.
 10.1 Sequences A sequence is an ordered list of numbers: a 1, a 2, a 3,..., a n, a n+1,... Each of the numbers is called a term of the sequence. Notation: A sequence {a 1, a 2, a 3,...} can be denoted
10.1 Sequences A sequence is an ordered list of numbers: a 1, a 2, a 3,..., a n, a n+1,... Each of the numbers is called a term of the sequence. Notation: A sequence {a 1, a 2, a 3,...} can be denoted
The Integers. Peter J. Kahn
 Math 3040: Spring 2009 The Integers Peter J. Kahn Contents 1. The Basic Construction 1 2. Adding integers 6 3. Ordering integers 16 4. Multiplying integers 18 Before we begin the mathematics of this section,
Math 3040: Spring 2009 The Integers Peter J. Kahn Contents 1. The Basic Construction 1 2. Adding integers 6 3. Ordering integers 16 4. Multiplying integers 18 Before we begin the mathematics of this section,
Ch 3.2: Direct proofs
 Math 299 Lectures 8 and 9: Chapter 3 0. Ch3.1 A trivial proof and a vacuous proof (Reading assignment) 1. Ch3.2 Direct proofs 2. Ch3.3 Proof by contrapositive 3. Ch3.4 Proof by cases 4. Ch3.5 Proof evaluations
Math 299 Lectures 8 and 9: Chapter 3 0. Ch3.1 A trivial proof and a vacuous proof (Reading assignment) 1. Ch3.2 Direct proofs 2. Ch3.3 Proof by contrapositive 3. Ch3.4 Proof by cases 4. Ch3.5 Proof evaluations
MATH 301 INTRO TO ANALYSIS FALL 2016
 MATH 301 INTRO TO ANALYSIS FALL 016 Homework 04 Professional Problem Consider the recursive sequence defined by x 1 = 3 and +1 = 1 4 for n 1. (a) Prove that ( ) converges. (Hint: show that ( ) is decreasing
MATH 301 INTRO TO ANALYSIS FALL 016 Homework 04 Professional Problem Consider the recursive sequence defined by x 1 = 3 and +1 = 1 4 for n 1. (a) Prove that ( ) converges. (Hint: show that ( ) is decreasing
