System Identification
|
|
|
- Anna Winifred Rogers
- 5 years ago
- Views:
Transcription
1 System Identification Lecture 4: Transfer function averaging and smoothing Roy Smith Averaging Multiple estimates Multiple experiments: u r pk, y r pk, r,..., R, and k,..., K. Multiple estimates (ETFE): Ĝ r pe jω n Y rpe jω n U r pe jω n (drop the N from the Y N pe jω n notation) Averaging to improve the estimate. Ĝpe jω n α r Ĝ r pe jω n, r How to choose α r? with α r. r The average is calculated with α r {R
2 Averaging Optimal weighted average If the variance of Ĝrpe jω n is σrpe 2 jω n (with uncorrelated errors and identical means), then, jω variance Ĝpe n variance α r pe jω n Ĝrpe jω n This is minimized by r αrσ 2 rpe 2 jω n r α r pe jω n {σ2 rpe jω n. {σrpe 2 jω n r If variance Ĝr pe jω n φ vpe jω n N U rpe jω n 2 then α r pe jω n U rpe jω n 2. U r pe jω n 2 r Averaging Variance reduction Best result: ˇˇU r pe jω n ˇˇ is the same for all r,..., R. This gives, jω variance Ĝpe n variance Ĝr pe jω n. R If the estimates are biased we will not get as much variance reduction. (The method of splitting the data record and averaging the periodograms is attributed to Bartlett (948, 9).)
3 Averaging example (noisy data) Splitting the data record: K 72, R 3, N 24, upk ypk y pk y 2 pk y 3 pk Averaging example (noisy data) Estimates: Ĝ r pe jω n, r, 2, 3 and the weighted average, Ĝavgpe jω n. Magnitude Gpe jω Ĝ avg pe jω n Ĝ 3 pe jω n Ĝ pe jω n π log ω (rad/sample) Ĝ 2 pe jω n
4 Averaging example (noisy data) Estimates: Ĝ r pe jω n, r, 2, 3 and the weighted average, Ĝavgpe jω n. Errors: E r pe jω n Gpe jω n Ĝrpe jω n. Magnitude E 2 pe jω n E 3 pe jω n E pe jω n π log ω (rad/sample). E avg pe jω n Averaging with periodic signals Splitting the data record: K 72, N 24, R 3, upk has period M 24. upk ypk y pk y 2 pk y 3 pk (not really periodic: upk for k ă )
5 Averaging with periodic signals Estimates: Ĝ r pe jω n and Ĝavgpe jω n Ĝ2 pe jω n ` Ĝ3pe jω n {2 Magnitude Gpe jω Ĝ avg pe jω n Ĝ 2 pe jω n Ĝ 3 pe jω n π log ω (rad/sample) Averaging with periodic signals Estimates: Ĝ r pe jω n and Ĝavgpe jω n Ĝ2 pe jω n ` Ĝ3pe jω n {2 Errors: E r pe jω n Gpe jω n Ĝrpe jω n. Magnitude π log ω (rad/sample). E 2 pe jω n E 3 pe jω n E avg pe jω n
6 Averaging with periodic signals Estimates: Ĝ r pe jω n and Ĝavgpe jω n Ĝ2 pe jω n ` Ĝ3pe jω n {2 Errors: E r pe jω n Gpe jω n Ĝrpe jω n. Magnitude E avg pe jω n (non-periodic) π log ω (rad/sample). E 2 pe jω n E 3 pe jω n E avg pe jω n Bias-variance trade-offs in data record splitting Bartlett s procedure Divide a (long) data record into smaller parts for averaging. Data: tupk, ypku k,..., K with K very large. Choose R records, and calculation a length: N, NR ď K. u r pn uprn ` n, r,..., R, n,..., N. And average the resulting estimates: Gpe jω n R ÿ r α r Ĝ r pe jω n R ÿ r α r Ŷ r pe jω n Û r pe jω n. Bias and variance effects As R increases: The number of points calculated, N, decreases (so NR ď K); The variance decreases (by up to {R); The bias increases (due to non-periodicity transients)
7 Bias-variance trade-offs in data record splitting Mean-suare error MSE bias 2 ` variance. Transient bias grows linearly with the number of data splits. Variance decays with a rate of up to /(number of averages). Optimal bias-variance trade-off Error MSE Bias error Variance error 2 number of records, R Smoothing transfer function estimates What if we have no option of running periodic input experiments? The system will not tolerate periodic inputs; or The data has already been taken and given to us. More data just gives more freuencies (with the same error variance). Exploit the assumed smoothness of the underlying system Gpe jω is assumed to be a low order (smooth) system. E! ) pgpe jω n ĜN pe jω n pgpe jω s ĜN pe jω s ÝÑ pn s, (asymptotically at least)
8 Smoothing the ETFE Smooth transfer function assumption Assume the true system to be close to constant for a range of freuencies. Gpe jω n`r «Gpe jω n for r,, 2,..., R. Smooth minimum variance estimate The minimum variance smoothed estimate is, G N pe jω n α r Ĝ N pe jω n`r r R, α r α r r R N ˇ ˇU N pe jω n`r ˇˇ2. φ v pe jω n`r (Here we smooth over 2R ` points) Smoothing the ETFE If N is large (many closely spaced freuencies), the summation can be approximated by an integral, G N pe jω n α r Ĝ N pe jω n`r r R r R α r «ż ωn`r ω n r ż ωn`r ω n r αpe jξ ĜN pe jξ dξ αpe jξ dξ, with αpe jξ N ˇ ˇUN pe jξ ˇˇ2. φ v pe jξ
9 Smoothing the ETFE Smoothing window G N pe jω n ż π W γ pe jpξ ωn αpe jξ ĜN pe jξ dξ 2π π ż π, W γ pe jpξ ωn αpe jξ dξ 2π π with αpe jξ N ˇ ˇU N pe jξ ˇˇ2. φ v pe jξ The {2π scaling will make it easier to derived time-domain windows later Smoothing the ETFE Assumptions on φ v pe jω Assume φ v pe jω is also a smooth (and flat) function of freuency. ż π W γ pe jpξ ωn 2π ˇ φ v pe jξ φ v pe jω n ˇ dξ «. Then use, π αpe jξ N ˇ ˇUN pe jξ ˇˇ2, φ v pe jω n to get, ż π W γ pe jpξ ωn ˇ ˇU N pe jξ ˇ ˇ2 Ĝ N pe jξ dξ G N pe jω n 2π π N ż π W γ pe jpξ ωn. ˇ ˇU N pe jξ ˇ ˇ2 dξ 2π π N
10 Weighting functions Typical window (Hann) as a function of the width parameter, γ. W γ pe jωn 2 γ 2 N 26 γ γ γ π π{2 π{2 π Discrete freuency: ω Weighting functions Freuency smoothing window characteristics: width (specified by γ parameter) The wider the freuency window (i.e. decreasing γ)... the more adjacent freuencies included in the smoothed estimate, the smoother the result, the lower the noise induced variance, the higher the bias
11 Weighting functions Window characteristics: shape Some common choices: Bartlett: W γ pe jω γ ˆ 2 sin γω{2 sin ω{2 Hann: W γ pe jω D 2 γpω ` D 4 γpω π{γ ` D 4 γpω ` π{γ sin ωpγ `. where D γ pω sin ω{2 Others include: Hamming, Parzen, Kaiser,... The differences are mostly in the leakage properties of the energy to adjacent freuencies. And the ability to resolve close freuency peaks Weighting functions Example freuency domain windows. W γ pe jωn γ N 26 Welch Hann Hamming Bartlett π π{2 π{2 π Discrete freuency: ω
12 ETFE smoothing example: Matlab calculations U = fft(u); Y = fft(y); Gest = Y./U; Gs = *Gest; [omega,wg] = WfHann(gamma,N); zidx = find(omega==); omega = [omega(zidx:n);omega(:zidx-)]; Wg = [Wg(zidx:N);Wg(:zidx-)]; a = U.*conj(U); % calculate N point FFTs % ETFE estimate % smoothed estimate % window (centered) % shift to start at zero % freuency grid % variance weighting for wn = :N, Wnorm = ; for xi = :N, widx = mod(xi-wn,n)+; Gs(wn) = Gs(wn) +... Wg(widx) * Gest(xi) * a(xi); Wnorm = Wnorm + Wg(widx) * a(xi); end Gs(wn) = Gs(wn)/Wnorm; end % reset normalisation % wrap window index % weight normalisation Window properties Properties and characteristic values of window functions 2π ż π π ż π π W γ pe jξ dξ (Normalised) ξw γ pe jξ dξ ( Even sort of) Mpγ : ż π W pγ : 2π π ż π ξ 2 W γ pe jξ dξ (bias effect) π Wγ 2 pe jξ dξ (variance effect) Bartlett: Mpγ 2.78 γ, W pγ «.67γ (for γ ą ) Hamming: Mpγ π2 2γ 2, W pγ «.7γ (for γ ą )
13 Smoothed estimate properties Asymptotic bias properties!! )) E Gpe jω n E Gpe jω n Mpγ! ) E Gpe jω n Gpe jω n ˆ 2 G2 pe jω n ` G pe jω n φ upe jωn φ u pe jω n Increasing γ: makes the freuency window narrower; averages over fewer freuency values; makes M pγ smaller; and ` OpC 3 pγ loooomoooon ÝÑ as γ ÝÑ 8 reduces the bias of the smoothed estimate, Gpe jω n. ` O {? N looooomooooon ÝÑ as N ÝÑ Smoothed estimate properties Asymptotic variance properties "! ) 2* E Gpe jω n E Gpe jω n N W pγ φ vpe jω n φ u pe jω n Increasing γ: makes the freuency window narrower; averages over fewer freuency values; makes W pγ larger; and increases the variance of the smoothed estimate, Gpe jω n. ` o ` W pγ{n loooooomoooooon ÝÑ as γ ÝÑ 8 N ÝÑ 8 γ{n ÝÑ
14 Smoothed estimate properties Asymptotic MSE properties jω E "ˇˇˇ Gpe n Gpe jω n ˇ ˇ2* «M 2 pγ F pe jω n 2 ` N W pγ φ vpe jωn, φ u pe jω n where F pe jω n 2 G2 pe jω n ` G pe jω n φ upe jω n φ u pe jω n If Mpγ M{γ 2 and W pγ W γ then MSE is minimised by, and γ optimal ˆ 4M 2 F pe jω n 2 φ u pe jω n { N W {. φ v pe jω n MSE at γ optimal «CN 4{ Bibliography Windowing and ETFE smoothing P. Stoica & R. Moses, Introduction to Spectral Analysis (see Chapters and 2), Prentice-Hall, 997. Lennart Ljung, System Identification; Theory for the User, (see Section 6.4) Prentice-Hall, 2nd Ed., 999. M.S. Bartlett, Smoothing Periodograms from Time-Series with Continuous Spectra, Nature, vol. 6(496), pp , 948. M.S. Bartlett, Periodogram analysis and continuous spectra, Biometrika, vol. 37, pp. 6,
Chapter 6: Nonparametric Time- and Frequency-Domain Methods. Problems presented by Uwe
 System Identification written by L. Ljung, Prentice Hall PTR, 1999 Chapter 6: Nonparametric Time- and Frequency-Domain Methods Problems presented by Uwe System Identification Problems Chapter 6 p. 1/33
System Identification written by L. Ljung, Prentice Hall PTR, 1999 Chapter 6: Nonparametric Time- and Frequency-Domain Methods Problems presented by Uwe System Identification Problems Chapter 6 p. 1/33
System Identification
 System Identification Lecture : Statistical properties of parameter estimators, Instrumental variable methods Roy Smith 8--8. 8--8. Statistical basis for estimation methods Parametrised models: G Gp, zq,
System Identification Lecture : Statistical properties of parameter estimators, Instrumental variable methods Roy Smith 8--8. 8--8. Statistical basis for estimation methods Parametrised models: G Gp, zq,
II. Nonparametric Spectrum Estimation for Stationary Random Signals - Non-parametric Methods -
 II. onparametric Spectrum Estimation for Stationary Random Signals - on-parametric Methods - - [p. 3] Periodogram - [p. 12] Periodogram properties - [p. 23] Modified periodogram - [p. 25] Bartlett s method
II. onparametric Spectrum Estimation for Stationary Random Signals - on-parametric Methods - - [p. 3] Periodogram - [p. 12] Periodogram properties - [p. 23] Modified periodogram - [p. 25] Bartlett s method
6.435, System Identification
 System Identification 6.435 SET 3 Nonparametric Identification Munther A. Dahleh 1 Nonparametric Methods for System ID Time domain methods Impulse response Step response Correlation analysis / time Frequency
System Identification 6.435 SET 3 Nonparametric Identification Munther A. Dahleh 1 Nonparametric Methods for System ID Time domain methods Impulse response Step response Correlation analysis / time Frequency
Non-parametric identification
 Non-parametric Non-parametric Transient Step-response using Spectral Transient Correlation Frequency function estimate Spectral System Identification, SSY230 Non-parametric 1 Non-parametric Transient Step-response
Non-parametric Non-parametric Transient Step-response using Spectral Transient Correlation Frequency function estimate Spectral System Identification, SSY230 Non-parametric 1 Non-parametric Transient Step-response
ECE 636: Systems identification
 ECE 636: Systems identification Lectures 7 8 onparametric identification (continued) Important distributions: chi square, t distribution, F distribution Sampling distributions ib i Sample mean If the variance
ECE 636: Systems identification Lectures 7 8 onparametric identification (continued) Important distributions: chi square, t distribution, F distribution Sampling distributions ib i Sample mean If the variance
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science : Discrete-Time Signal Processing
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.34: Discrete-Time Signal Processing OpenCourseWare 006 ecture 8 Periodogram Reading: Sections 0.6 and 0.7
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.34: Discrete-Time Signal Processing OpenCourseWare 006 ecture 8 Periodogram Reading: Sections 0.6 and 0.7
Laboratory Project 2: Spectral Analysis and Optimal Filtering
 Laboratory Project 2: Spectral Analysis and Optimal Filtering Random signals analysis (MVE136) Mats Viberg and Lennart Svensson Department of Signals and Systems Chalmers University of Technology 412 96
Laboratory Project 2: Spectral Analysis and Optimal Filtering Random signals analysis (MVE136) Mats Viberg and Lennart Svensson Department of Signals and Systems Chalmers University of Technology 412 96
Bispectral resolution and leakage effect of the indirect bispectrum estimate for different types of 2D window functions
 Bispectral resolution and leakage effect of the indirect bispectrum estimate for different types of D window functions Teofil-Cristian OROIAN, Constantin-Iulian VIZITIU, Florin ŞERBAN Communications and
Bispectral resolution and leakage effect of the indirect bispectrum estimate for different types of D window functions Teofil-Cristian OROIAN, Constantin-Iulian VIZITIU, Florin ŞERBAN Communications and
Design Criteria for the Quadratically Interpolated FFT Method (I): Bias due to Interpolation
 CENTER FOR COMPUTER RESEARCH IN MUSIC AND ACOUSTICS DEPARTMENT OF MUSIC, STANFORD UNIVERSITY REPORT NO. STAN-M-4 Design Criteria for the Quadratically Interpolated FFT Method (I): Bias due to Interpolation
CENTER FOR COMPUTER RESEARCH IN MUSIC AND ACOUSTICS DEPARTMENT OF MUSIC, STANFORD UNIVERSITY REPORT NO. STAN-M-4 Design Criteria for the Quadratically Interpolated FFT Method (I): Bias due to Interpolation
SPECTRUM. Deterministic Signals with Finite Energy (l 2 ) Deterministic Signals with Infinite Energy N 1. n=0. N N X N(f) 2
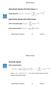 SPECTRUM Deterministic Signals with Finite Energy (l 2 ) Energy Spectrum: S xx (f) = X(f) 2 = 2 x(n)e j2πfn n= Deterministic Signals with Infinite Energy DTFT of truncated signal: X N (f) = N x(n)e j2πfn
SPECTRUM Deterministic Signals with Finite Energy (l 2 ) Energy Spectrum: S xx (f) = X(f) 2 = 2 x(n)e j2πfn n= Deterministic Signals with Infinite Energy DTFT of truncated signal: X N (f) = N x(n)e j2πfn
Practical Spectral Estimation
 Digital Signal Processing/F.G. Meyer Lecture 4 Copyright 2015 François G. Meyer. All Rights Reserved. Practical Spectral Estimation 1 Introduction The goal of spectral estimation is to estimate how the
Digital Signal Processing/F.G. Meyer Lecture 4 Copyright 2015 François G. Meyer. All Rights Reserved. Practical Spectral Estimation 1 Introduction The goal of spectral estimation is to estimate how the
Time series models in the Frequency domain. The power spectrum, Spectral analysis
 ime series models in the Frequency domain he power spectrum, Spectral analysis Relationship between the periodogram and the autocorrelations = + = ( ) ( ˆ α ˆ ) β I Yt cos t + Yt sin t t= t= ( ( ) ) cosλ
ime series models in the Frequency domain he power spectrum, Spectral analysis Relationship between the periodogram and the autocorrelations = + = ( ) ( ˆ α ˆ ) β I Yt cos t + Yt sin t t= t= ( ( ) ) cosλ
Generalized Sidelobe Canceller and MVDR Power Spectrum Estimation. Bhaskar D Rao University of California, San Diego
 Generalized Sidelobe Canceller and MVDR Power Spectrum Estimation Bhaskar D Rao University of California, San Diego Email: brao@ucsd.edu Reference Books 1. Optimum Array Processing, H. L. Van Trees 2.
Generalized Sidelobe Canceller and MVDR Power Spectrum Estimation Bhaskar D Rao University of California, San Diego Email: brao@ucsd.edu Reference Books 1. Optimum Array Processing, H. L. Van Trees 2.
-Digital Signal Processing- FIR Filter Design. Lecture May-16
 -Digital Signal Processing- FIR Filter Design Lecture-17 24-May-16 FIR Filter Design! FIR filters can also be designed from a frequency response specification.! The equivalent sampled impulse response
-Digital Signal Processing- FIR Filter Design Lecture-17 24-May-16 FIR Filter Design! FIR filters can also be designed from a frequency response specification.! The equivalent sampled impulse response
Discrete Fourier Transform
 Discrete Fourier Transform Virtually all practical signals have finite length (e.g., sensor data, audio records, digital images, stock values, etc). Rather than considering such signals to be zero-padded
Discrete Fourier Transform Virtually all practical signals have finite length (e.g., sensor data, audio records, digital images, stock values, etc). Rather than considering such signals to be zero-padded
Basic Design Approaches
 (Classic) IIR filter design: Basic Design Approaches. Convert the digital filter specifications into an analog prototype lowpass filter specifications. Determine the analog lowpass filter transfer function
(Classic) IIR filter design: Basic Design Approaches. Convert the digital filter specifications into an analog prototype lowpass filter specifications. Determine the analog lowpass filter transfer function
Chapter 2: The Fourier Transform
 EEE, EEE Part A : Digital Signal Processing Chapter Chapter : he Fourier ransform he Fourier ransform. Introduction he sampled Fourier transform of a periodic, discrete-time signal is nown as the discrete
EEE, EEE Part A : Digital Signal Processing Chapter Chapter : he Fourier ransform he Fourier ransform. Introduction he sampled Fourier transform of a periodic, discrete-time signal is nown as the discrete
LAB 6: FIR Filter Design Summer 2011
 University of Illinois at Urbana-Champaign Department of Electrical and Computer Engineering ECE 311: Digital Signal Processing Lab Chandra Radhakrishnan Peter Kairouz LAB 6: FIR Filter Design Summer 011
University of Illinois at Urbana-Champaign Department of Electrical and Computer Engineering ECE 311: Digital Signal Processing Lab Chandra Radhakrishnan Peter Kairouz LAB 6: FIR Filter Design Summer 011
ADSP ADSP ADSP ADSP. Advanced Digital Signal Processing (18-792) Spring Fall Semester, Department of Electrical and Computer Engineering
 Advanced Digital Signal rocessing (18-792) Spring Fall Semester, 201 2012 Department of Electrical and Computer Engineering ROBLEM SET 8 Issued: 10/26/18 Due: 11/2/18 Note: This problem set is due Friday,
Advanced Digital Signal rocessing (18-792) Spring Fall Semester, 201 2012 Department of Electrical and Computer Engineering ROBLEM SET 8 Issued: 10/26/18 Due: 11/2/18 Note: This problem set is due Friday,
System Modeling and Identification CHBE 702 Korea University Prof. Dae Ryook Yang
 System Modeling and Identification CHBE 702 Korea University Prof. Dae Ryook Yang 1-1 Course Description Emphases Delivering concepts and Practice Programming Identification Methods using Matlab Class
System Modeling and Identification CHBE 702 Korea University Prof. Dae Ryook Yang 1-1 Course Description Emphases Delivering concepts and Practice Programming Identification Methods using Matlab Class
Filter Design Problem
 Filter Design Problem Design of frequency-selective filters usually starts with a specification of their frequency response function. Practical filters have passband and stopband ripples, while exhibiting
Filter Design Problem Design of frequency-selective filters usually starts with a specification of their frequency response function. Practical filters have passband and stopband ripples, while exhibiting
Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises
 Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises Random Processes With Applications (MVE 135) Mats Viberg Department of Signals and Systems Chalmers University of Technology
Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises Random Processes With Applications (MVE 135) Mats Viberg Department of Signals and Systems Chalmers University of Technology
Data Processing and Analysis
 Data Processing and Analysis Rick Aster and Brian Borchers September 10, 2013 Energy and Power Spectra It is frequently valuable to study the power distribution of a signal in the frequency domain. For
Data Processing and Analysis Rick Aster and Brian Borchers September 10, 2013 Energy and Power Spectra It is frequently valuable to study the power distribution of a signal in the frequency domain. For
On the Frequency-Domain Properties of Savitzky-Golay Filters
 On the Frequency-Domain Properties of Savitzky-Golay Filters Ronald W Schafer HP Laboratories HPL-2-9 Keyword(s): Savitzky-Golay filter, least-squares polynomial approximation, smoothing Abstract: This
On the Frequency-Domain Properties of Savitzky-Golay Filters Ronald W Schafer HP Laboratories HPL-2-9 Keyword(s): Savitzky-Golay filter, least-squares polynomial approximation, smoothing Abstract: This
On Moving Average Parameter Estimation
 On Moving Average Parameter Estimation Niclas Sandgren and Petre Stoica Contact information: niclas.sandgren@it.uu.se, tel: +46 8 473392 Abstract Estimation of the autoregressive moving average (ARMA)
On Moving Average Parameter Estimation Niclas Sandgren and Petre Stoica Contact information: niclas.sandgren@it.uu.se, tel: +46 8 473392 Abstract Estimation of the autoregressive moving average (ARMA)
Statistical errors in the estimation of time-averaged acoustic energy density using the two-microphone method
 Statistical errors in the estimation of time-averaged acoustic energy density using the two-microphone method Short title: Statistical errors in acoustic energy density Justin Ghan, Ben Cazzolato, and
Statistical errors in the estimation of time-averaged acoustic energy density using the two-microphone method Short title: Statistical errors in acoustic energy density Justin Ghan, Ben Cazzolato, and
IMPROVEMENTS IN MODAL PARAMETER EXTRACTION THROUGH POST-PROCESSING FREQUENCY RESPONSE FUNCTION ESTIMATES
 IMPROVEMENTS IN MODAL PARAMETER EXTRACTION THROUGH POST-PROCESSING FREQUENCY RESPONSE FUNCTION ESTIMATES Bere M. Gur Prof. Christopher Niezreci Prof. Peter Avitabile Structural Dynamics and Acoustic Systems
IMPROVEMENTS IN MODAL PARAMETER EXTRACTION THROUGH POST-PROCESSING FREQUENCY RESPONSE FUNCTION ESTIMATES Bere M. Gur Prof. Christopher Niezreci Prof. Peter Avitabile Structural Dynamics and Acoustic Systems
Fourier Analysis of Stationary and Non-Stationary Time Series
 Fourier Analysis of Stationary and Non-Stationary Time Series September 6, 2012 A time series is a stochastic process indexed at discrete points in time i.e X t for t = 0, 1, 2, 3,... The mean is defined
Fourier Analysis of Stationary and Non-Stationary Time Series September 6, 2012 A time series is a stochastic process indexed at discrete points in time i.e X t for t = 0, 1, 2, 3,... The mean is defined
Problem Set 9 Solutions
 Problem Set 9 Solutions EE23: Digital Signal Processing. From Figure below, we see that the DTFT of the windowed sequence approaches the actual DTFT as the window size increases. Gibb s phenomenon is absent
Problem Set 9 Solutions EE23: Digital Signal Processing. From Figure below, we see that the DTFT of the windowed sequence approaches the actual DTFT as the window size increases. Gibb s phenomenon is absent
Lecture 14: Windowing
 Lecture 14: Windowing ECE 401: Signal and Image Analysis University of Illinois 3/29/2017 1 DTFT Review 2 Windowing 3 Practical Windows Outline 1 DTFT Review 2 Windowing 3 Practical Windows DTFT Review
Lecture 14: Windowing ECE 401: Signal and Image Analysis University of Illinois 3/29/2017 1 DTFT Review 2 Windowing 3 Practical Windows Outline 1 DTFT Review 2 Windowing 3 Practical Windows DTFT Review
EE531 (Semester II, 2010) 6. Spectral analysis. power spectral density. periodogram analysis. window functions 6-1
 6. Spectral analysis EE531 (Semester II, 2010) power spectral density periodogram analysis window functions 6-1 Wiener-Khinchin theorem: Power Spectral density if a process is wide-sense stationary, the
6. Spectral analysis EE531 (Semester II, 2010) power spectral density periodogram analysis window functions 6-1 Wiener-Khinchin theorem: Power Spectral density if a process is wide-sense stationary, the
Lecture 4 - Spectral Estimation
 Lecture 4 - Spectral Estimation The Discrete Fourier Transform The Discrete Fourier Transform (DFT) is the equivalent of the continuous Fourier Transform for signals known only at N instants separated
Lecture 4 - Spectral Estimation The Discrete Fourier Transform The Discrete Fourier Transform (DFT) is the equivalent of the continuous Fourier Transform for signals known only at N instants separated
Chirp Transform for FFT
 Chirp Transform for FFT Since the FFT is an implementation of the DFT, it provides a frequency resolution of 2π/N, where N is the length of the input sequence. If this resolution is not sufficient in a
Chirp Transform for FFT Since the FFT is an implementation of the DFT, it provides a frequency resolution of 2π/N, where N is the length of the input sequence. If this resolution is not sufficient in a
Direction of Arrival Estimation: Subspace Methods. Bhaskar D Rao University of California, San Diego
 Direction of Arrival Estimation: Subspace Methods Bhaskar D Rao University of California, San Diego Email: brao@ucsdedu Reference Books and Papers 1 Optimum Array Processing, H L Van Trees 2 Stoica, P,
Direction of Arrival Estimation: Subspace Methods Bhaskar D Rao University of California, San Diego Email: brao@ucsdedu Reference Books and Papers 1 Optimum Array Processing, H L Van Trees 2 Stoica, P,
(Refer Slide Time: 01:28 03:51 min)
 Digital Signal Processing Prof. S. C. Dutta Roy Department of Electrical Engineering Indian Institute of Technology, Delhi Lecture 40 FIR Design by Windowing This is the 40 th lecture and our topic for
Digital Signal Processing Prof. S. C. Dutta Roy Department of Electrical Engineering Indian Institute of Technology, Delhi Lecture 40 FIR Design by Windowing This is the 40 th lecture and our topic for
BME 50500: Image and Signal Processing in Biomedicine. Lecture 5: Correlation and Power-Spectrum CCNY
 1 BME 50500: Image and Signal Processing in Biomedicine Lecture 5: Correlation and Power-Spectrum Lucas C. Parra Biomedical Engineering Department CCNY http://bme.ccny.cuny.edu/faculty/parra/teaching/signal-and-image/
1 BME 50500: Image and Signal Processing in Biomedicine Lecture 5: Correlation and Power-Spectrum Lucas C. Parra Biomedical Engineering Department CCNY http://bme.ccny.cuny.edu/faculty/parra/teaching/signal-and-image/
Fourier Analysis of Signals Using the DFT
 Fourier Analysis of Signals Using the DFT ECE 535 Lecture April 29, 23 Overview: Motivation Many applications require analyzing the frequency content of signals Speech processing study resonances of vocal
Fourier Analysis of Signals Using the DFT ECE 535 Lecture April 29, 23 Overview: Motivation Many applications require analyzing the frequency content of signals Speech processing study resonances of vocal
If every Bounded Input produces Bounded Output, system is externally stable equivalently, system is BIBO stable
 1. External (BIBO) Stability of LTI Systems If every Bounded Input produces Bounded Output, system is externally stable equivalently, system is BIBO stable g(n) < BIBO Stability Don t care about what unbounded
1. External (BIBO) Stability of LTI Systems If every Bounded Input produces Bounded Output, system is externally stable equivalently, system is BIBO stable g(n) < BIBO Stability Don t care about what unbounded
Problem Set 2 Solution Sketches Time Series Analysis Spring 2010
 Problem Set 2 Solution Sketches Time Series Analysis Spring 2010 Forecasting 1. Let X and Y be two random variables such that E(X 2 ) < and E(Y 2 )
Problem Set 2 Solution Sketches Time Series Analysis Spring 2010 Forecasting 1. Let X and Y be two random variables such that E(X 2 ) < and E(Y 2 )
Parametric Method Based PSD Estimation using Gaussian Window
 International Journal of Engineering Trends and Technology (IJETT) Volume 29 Number 1 - November 215 Parametric Method Based PSD Estimation using Gaussian Window Pragati Sheel 1, Dr. Rajesh Mehra 2, Preeti
International Journal of Engineering Trends and Technology (IJETT) Volume 29 Number 1 - November 215 Parametric Method Based PSD Estimation using Gaussian Window Pragati Sheel 1, Dr. Rajesh Mehra 2, Preeti
SNR Calculation and Spectral Estimation [S&T Appendix A]
![SNR Calculation and Spectral Estimation [S&T Appendix A] SNR Calculation and Spectral Estimation [S&T Appendix A]](/thumbs/75/71929358.jpg) SR Calculation and Spectral Estimation [S&T Appendix A] or, How not to make a mess of an FFT Make sure the input is located in an FFT bin 1 Window the data! A Hann window works well. Compute the FFT 3
SR Calculation and Spectral Estimation [S&T Appendix A] or, How not to make a mess of an FFT Make sure the input is located in an FFT bin 1 Window the data! A Hann window works well. Compute the FFT 3
ELEN E4810: Digital Signal Processing Topic 11: Continuous Signals. 1. Sampling and Reconstruction 2. Quantization
 ELEN E4810: Digital Signal Processing Topic 11: Continuous Signals 1. Sampling and Reconstruction 2. Quantization 1 1. Sampling & Reconstruction DSP must interact with an analog world: A to D D to A x(t)
ELEN E4810: Digital Signal Processing Topic 11: Continuous Signals 1. Sampling and Reconstruction 2. Quantization 1 1. Sampling & Reconstruction DSP must interact with an analog world: A to D D to A x(t)
On Identification of Cascade Systems 1
 On Identification of Cascade Systems 1 Bo Wahlberg Håkan Hjalmarsson Jonas Mårtensson Automatic Control and ACCESS, School of Electrical Engineering, KTH, SE-100 44 Stockholm, Sweden. (bo.wahlberg@ee.kth.se
On Identification of Cascade Systems 1 Bo Wahlberg Håkan Hjalmarsson Jonas Mårtensson Automatic Control and ACCESS, School of Electrical Engineering, KTH, SE-100 44 Stockholm, Sweden. (bo.wahlberg@ee.kth.se
DATA IN SERIES AND TIME I. Several different techniques depending on data and what one wants to do
 DATA IN SERIES AND TIME I Several different techniques depending on data and what one wants to do Data can be a series of events scaled to time or not scaled to time (scaled to space or just occurrence)
DATA IN SERIES AND TIME I Several different techniques depending on data and what one wants to do Data can be a series of events scaled to time or not scaled to time (scaled to space or just occurrence)
Contents. Digital Signal Processing, Part II: Power Spectrum Estimation
 Contents Digital Signal Processing, Part II: Power Spectrum Estimation 5. Application of the FFT for 7. Parametric Spectrum Est. Filtering and Spectrum Estimation 7.1 ARMA-Models 5.1 Fast Convolution 7.2
Contents Digital Signal Processing, Part II: Power Spectrum Estimation 5. Application of the FFT for 7. Parametric Spectrum Est. Filtering and Spectrum Estimation 7.1 ARMA-Models 5.1 Fast Convolution 7.2
EDISP (NWL3) (English) Digital Signal Processing DFT Windowing, FFT. October 19, 2016
 EDISP (NWL3) (English) Digital Signal Processing DFT Windowing, FFT October 19, 2016 DFT resolution 1 N-point DFT frequency sampled at θ k = 2πk N, so the resolution is f s/n If we want more, we use N
EDISP (NWL3) (English) Digital Signal Processing DFT Windowing, FFT October 19, 2016 DFT resolution 1 N-point DFT frequency sampled at θ k = 2πk N, so the resolution is f s/n If we want more, we use N
Introduction. Spectral Estimation Overview Periodogram Bias, variance, and distribution Blackman-Tukey Method Welch-Bartlett Method Others
 Spectral Estimation Overview Periodogram Bias, variance, and distribution Blackman-Tukey Method Welch-Bartlett Method Others Introduction R x (e jω ) r x (l)e jωl l= Most stationary random processes have
Spectral Estimation Overview Periodogram Bias, variance, and distribution Blackman-Tukey Method Welch-Bartlett Method Others Introduction R x (e jω ) r x (l)e jωl l= Most stationary random processes have
Experimental verification of different models of the ADC transfer function. Petr Suchanek, David Slepicka, Vladimir Haasz
 Experimental verification of different models of the ADC transfer function Petr Suchanek, David Slepicka, Vladimir Haasz Czech Technical University in Prague, Faculty of Electrical Engineering Technická,
Experimental verification of different models of the ADC transfer function Petr Suchanek, David Slepicka, Vladimir Haasz Czech Technical University in Prague, Faculty of Electrical Engineering Technická,
DFT & Fast Fourier Transform PART-A. 7. Calculate the number of multiplications needed in the calculation of DFT and FFT with 64 point sequence.
 SHRI ANGALAMMAN COLLEGE OF ENGINEERING & TECHNOLOGY (An ISO 9001:2008 Certified Institution) SIRUGANOOR,TRICHY-621105. DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING UNIT I DFT & Fast Fourier
SHRI ANGALAMMAN COLLEGE OF ENGINEERING & TECHNOLOGY (An ISO 9001:2008 Certified Institution) SIRUGANOOR,TRICHY-621105. DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING UNIT I DFT & Fast Fourier
Final Exam January 31, Solutions
 Final Exam January 31, 014 Signals & Systems (151-0575-01) Prof. R. D Andrea & P. Reist Solutions Exam Duration: Number of Problems: Total Points: Permitted aids: Important: 150 minutes 7 problems 50 points
Final Exam January 31, 014 Signals & Systems (151-0575-01) Prof. R. D Andrea & P. Reist Solutions Exam Duration: Number of Problems: Total Points: Permitted aids: Important: 150 minutes 7 problems 50 points
ESS 265 Spring Quarter 2005 Time Series Analysis: Linear Regression
 ESS 265 Spring Quarter 2005 Time Series Analysis: Linear Regression Lecture 11 May 10, 2005 Multivariant Regression A multi-variant relation between a dependent variable y and several independent variables
ESS 265 Spring Quarter 2005 Time Series Analysis: Linear Regression Lecture 11 May 10, 2005 Multivariant Regression A multi-variant relation between a dependent variable y and several independent variables
Detection and Quantification of the Influence of Time-Variation in Frequency Response Function Measurements Using Arbitrary Excitations
 Detection and Quantification of the Influence of Time-Variation in Frequency Response Function Measurements Using Arbitrary Excitations R. Pintelon, E. Louarroudi, and J. Lataire, Vrije Universiteit Brussel,
Detection and Quantification of the Influence of Time-Variation in Frequency Response Function Measurements Using Arbitrary Excitations R. Pintelon, E. Louarroudi, and J. Lataire, Vrije Universiteit Brussel,
Further Results on Model Structure Validation for Closed Loop System Identification
 Advances in Wireless Communications and etworks 7; 3(5: 57-66 http://www.sciencepublishinggroup.com/j/awcn doi:.648/j.awcn.735. Further esults on Model Structure Validation for Closed Loop System Identification
Advances in Wireless Communications and etworks 7; 3(5: 57-66 http://www.sciencepublishinggroup.com/j/awcn doi:.648/j.awcn.735. Further esults on Model Structure Validation for Closed Loop System Identification
Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises
 Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises Random Signals Analysis (MVE136) Mats Viberg Department of Signals and Systems Chalmers University of Technology 412
Complement on Digital Spectral Analysis and Optimal Filtering: Theory and Exercises Random Signals Analysis (MVE136) Mats Viberg Department of Signals and Systems Chalmers University of Technology 412
Subspace-based Identification
 of Infinite-dimensional Multivariable Systems from Frequency-response Data Department of Electrical and Electronics Engineering Anadolu University, Eskişehir, Turkey October 12, 2008 Outline 1 2 3 4 Noise-free
of Infinite-dimensional Multivariable Systems from Frequency-response Data Department of Electrical and Electronics Engineering Anadolu University, Eskişehir, Turkey October 12, 2008 Outline 1 2 3 4 Noise-free
Lecture 11: Spectral Analysis
 Lecture 11: Spectral Analysis Methods For Estimating The Spectrum Walid Sharabati Purdue University Latest Update October 27, 2016 Professor Sharabati (Purdue University) Time Series Analysis October 27,
Lecture 11: Spectral Analysis Methods For Estimating The Spectrum Walid Sharabati Purdue University Latest Update October 27, 2016 Professor Sharabati (Purdue University) Time Series Analysis October 27,
5. EXPERIMENT 5. JFET NOISE MEASURE- MENTS
 5. EXPERIMENT 5. JFET NOISE MEASURE- MENTS 5.1 Object The objects of this experiment are to measure the spectral density of the noise current output of a JFET, to compare the measured spectral density
5. EXPERIMENT 5. JFET NOISE MEASURE- MENTS 5.1 Object The objects of this experiment are to measure the spectral density of the noise current output of a JFET, to compare the measured spectral density
Voiced Speech. Unvoiced Speech
 Digital Speech Processing Lecture 2 Homomorphic Speech Processing General Discrete-Time Model of Speech Production p [ n] = p[ n] h [ n] Voiced Speech L h [ n] = A g[ n] v[ n] r[ n] V V V p [ n ] = u [
Digital Speech Processing Lecture 2 Homomorphic Speech Processing General Discrete-Time Model of Speech Production p [ n] = p[ n] h [ n] Voiced Speech L h [ n] = A g[ n] v[ n] r[ n] V V V p [ n ] = u [
SHOCK AND VIBRATION RESPONSE SPECTRA COURSE Unit 6B. Notes on the Fourier Transform Magnitude
 SHOCK AND VIBRATION RESPONSE SPECTRA COURSE Unit 6B. Notes on the Fourier Transform Magnitude By Tom Irvine Introduction Fourier transforms, which were introduced in Unit 6A, have a number of potential
SHOCK AND VIBRATION RESPONSE SPECTRA COURSE Unit 6B. Notes on the Fourier Transform Magnitude By Tom Irvine Introduction Fourier transforms, which were introduced in Unit 6A, have a number of potential
Robust Implementation of the MUSIC algorithm Zhang, Johan Xi; Christensen, Mads Græsbøll; Dahl, Joachim; Jensen, Søren Holdt; Moonen, Marc
 Aalborg Universitet Robust Implementation of the MUSIC algorithm Zhang, Johan Xi; Christensen, Mads Græsbøll; Dahl, Joachim; Jensen, Søren Holdt; Moonen, Marc Published in: I E E E International Conference
Aalborg Universitet Robust Implementation of the MUSIC algorithm Zhang, Johan Xi; Christensen, Mads Græsbøll; Dahl, Joachim; Jensen, Søren Holdt; Moonen, Marc Published in: I E E E International Conference
Relationship Between λ and Q in RDO
 Jmspeex Journal of Dubious Theoretical Results July 6, 015 Abstract This is a log of theoretical calculations and approximations that are used in some of the Daala code. Some approximations are likely
Jmspeex Journal of Dubious Theoretical Results July 6, 015 Abstract This is a log of theoretical calculations and approximations that are used in some of the Daala code. Some approximations are likely
L6: Short-time Fourier analysis and synthesis
 L6: Short-time Fourier analysis and synthesis Overview Analysis: Fourier-transform view Analysis: filtering view Synthesis: filter bank summation (FBS) method Synthesis: overlap-add (OLA) method STFT magnitude
L6: Short-time Fourier analysis and synthesis Overview Analysis: Fourier-transform view Analysis: filtering view Synthesis: filter bank summation (FBS) method Synthesis: overlap-add (OLA) method STFT magnitude
sine wave fit algorithm
 TECHNICAL REPORT IR-S3-SB-9 1 Properties of the IEEE-STD-57 four parameter sine wave fit algorithm Peter Händel, Senior Member, IEEE Abstract The IEEE Standard 57 (IEEE-STD-57) provides algorithms for
TECHNICAL REPORT IR-S3-SB-9 1 Properties of the IEEE-STD-57 four parameter sine wave fit algorithm Peter Händel, Senior Member, IEEE Abstract The IEEE Standard 57 (IEEE-STD-57) provides algorithms for
Heteroskedasticity and Autocorrelation Consistent Standard Errors
 NBER Summer Institute Minicourse What s New in Econometrics: ime Series Lecture 9 July 6, 008 Heteroskedasticity and Autocorrelation Consistent Standard Errors Lecture 9, July, 008 Outline. What are HAC
NBER Summer Institute Minicourse What s New in Econometrics: ime Series Lecture 9 July 6, 008 Heteroskedasticity and Autocorrelation Consistent Standard Errors Lecture 9, July, 008 Outline. What are HAC
Introduction to machine learning and pattern recognition Lecture 2 Coryn Bailer-Jones
 Introduction to machine learning and pattern recognition Lecture 2 Coryn Bailer-Jones http://www.mpia.de/homes/calj/mlpr_mpia2008.html 1 1 Last week... supervised and unsupervised methods need adaptive
Introduction to machine learning and pattern recognition Lecture 2 Coryn Bailer-Jones http://www.mpia.de/homes/calj/mlpr_mpia2008.html 1 1 Last week... supervised and unsupervised methods need adaptive
Ultrasound is a widely used, nonionizing, and costeffective
 340 IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 57, no. 2, February 2010 Trade-Offs in Data Acquisition and Processing Parameters for Backscatter and Scatterer Size Estimations
340 IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 57, no. 2, February 2010 Trade-Offs in Data Acquisition and Processing Parameters for Backscatter and Scatterer Size Estimations
Wiener-Khintchine Theorem. White Noise. Wiener-Khintchine Theorem. Power Spectrum Estimation
 Wiener-Khintchine Theorem Let x(n) be a WSS random process with autocorrelation sequence r xx (m) =E[x(n + m)x (n)] The power spectral density is defined as the Discrete Time Fourier Transform of the autocorrelation
Wiener-Khintchine Theorem Let x(n) be a WSS random process with autocorrelation sequence r xx (m) =E[x(n + m)x (n)] The power spectral density is defined as the Discrete Time Fourier Transform of the autocorrelation
EECE Adaptive Control
 EECE 574 - Adaptive Control Basics of System Identification Guy Dumont Department of Electrical and Computer Engineering University of British Columbia January 2010 Guy Dumont (UBC) EECE574 - Basics of
EECE 574 - Adaptive Control Basics of System Identification Guy Dumont Department of Electrical and Computer Engineering University of British Columbia January 2010 Guy Dumont (UBC) EECE574 - Basics of
OSE801 Engineering System Identification. Lecture 09: Computing Impulse and Frequency Response Functions
 OSE801 Engineering System Identification Lecture 09: Computing Impulse and Frequency Response Functions 1 Extracting Impulse and Frequency Response Functions In the preceding sections, signal processing
OSE801 Engineering System Identification Lecture 09: Computing Impulse and Frequency Response Functions 1 Extracting Impulse and Frequency Response Functions In the preceding sections, signal processing
The Discrete Fourier Transform (DFT) Properties of the DFT DFT-Specic Properties Power spectrum estimate. Alex Sheremet.
 4. April 2, 27 -order sequences Measurements produce sequences of numbers Measurement purpose: characterize a stochastic process. Example: Process: water surface elevation as a function of time Parameters:
4. April 2, 27 -order sequences Measurements produce sequences of numbers Measurement purpose: characterize a stochastic process. Example: Process: water surface elevation as a function of time Parameters:
STK-IN4300 Statistical Learning Methods in Data Science
 Outline of the lecture Linear Methods for Regression Linear Regression Models and Least Squares Subset selection STK-IN4300 Statistical Learning Methods in Data Science Riccardo De Bin debin@math.uio.no
Outline of the lecture Linear Methods for Regression Linear Regression Models and Least Squares Subset selection STK-IN4300 Statistical Learning Methods in Data Science Riccardo De Bin debin@math.uio.no
STK-IN4300 Statistical Learning Methods in Data Science
 STK-IN4300 Statistical Learning Methods in Data Science Riccardo De Bin debin@math.uio.no STK-IN4300: lecture 2 1/ 38 Outline of the lecture STK-IN4300 - Statistical Learning Methods in Data Science Linear
STK-IN4300 Statistical Learning Methods in Data Science Riccardo De Bin debin@math.uio.no STK-IN4300: lecture 2 1/ 38 Outline of the lecture STK-IN4300 - Statistical Learning Methods in Data Science Linear
Identification, Model Validation and Control. Lennart Ljung, Linköping
 Identification, Model Validation and Control Lennart Ljung, Linköping Acknowledgment: Useful discussions with U Forssell and H Hjalmarsson 1 Outline 1. Introduction 2. System Identification (in closed
Identification, Model Validation and Control Lennart Ljung, Linköping Acknowledgment: Useful discussions with U Forssell and H Hjalmarsson 1 Outline 1. Introduction 2. System Identification (in closed
Elec4621 Advanced Digital Signal Processing Chapter 11: Time-Frequency Analysis
 Elec461 Advanced Digital Signal Processing Chapter 11: Time-Frequency Analysis Dr. D. S. Taubman May 3, 011 In this last chapter of your notes, we are interested in the problem of nding the instantaneous
Elec461 Advanced Digital Signal Processing Chapter 11: Time-Frequency Analysis Dr. D. S. Taubman May 3, 011 In this last chapter of your notes, we are interested in the problem of nding the instantaneous
Time domain identification, frequency domain identification. Equivalencies! Differences?
 Time domain identification, frequency domain identification. Equivalencies! Differences? J. Schoukens, R. Pintelon, and Y. Rolain Vrije Universiteit Brussel, Department ELEC, Pleinlaan, B5 Brussels, Belgium
Time domain identification, frequency domain identification. Equivalencies! Differences? J. Schoukens, R. Pintelon, and Y. Rolain Vrije Universiteit Brussel, Department ELEC, Pleinlaan, B5 Brussels, Belgium
Linear models. Chapter Overview. Linear process: A process {X n } is a linear process if it has the representation.
 Chapter 2 Linear models 2.1 Overview Linear process: A process {X n } is a linear process if it has the representation X n = b j ɛ n j j=0 for all n, where ɛ n N(0, σ 2 ) (Gaussian distributed with zero
Chapter 2 Linear models 2.1 Overview Linear process: A process {X n } is a linear process if it has the representation X n = b j ɛ n j j=0 for all n, where ɛ n N(0, σ 2 ) (Gaussian distributed with zero
EL1820 Modeling of Dynamical Systems
 EL1820 Modeling of Dynamical Systems Lecture 10 - System identification as a model building tool Experiment design Examination and prefiltering of data Model structure selection Model validation Lecture
EL1820 Modeling of Dynamical Systems Lecture 10 - System identification as a model building tool Experiment design Examination and prefiltering of data Model structure selection Model validation Lecture
Econ 582 Nonparametric Regression
 Econ 582 Nonparametric Regression Eric Zivot May 28, 2013 Nonparametric Regression Sofarwehaveonlyconsideredlinearregressionmodels = x 0 β + [ x ]=0 [ x = x] =x 0 β = [ x = x] [ x = x] x = β The assume
Econ 582 Nonparametric Regression Eric Zivot May 28, 2013 Nonparametric Regression Sofarwehaveonlyconsideredlinearregressionmodels = x 0 β + [ x ]=0 [ x = x] =x 0 β = [ x = x] [ x = x] x = β The assume
Multidimensional digital signal processing
 PSfrag replacements Two-dimensional discrete signals N 1 A 2-D discrete signal (also N called a sequence or array) is a function 2 defined over thex(n set 1 of, n 2 ordered ) pairs of integers: y(nx 1,
PSfrag replacements Two-dimensional discrete signals N 1 A 2-D discrete signal (also N called a sequence or array) is a function 2 defined over thex(n set 1 of, n 2 ordered ) pairs of integers: y(nx 1,
Frequency estimation by DFT interpolation: A comparison of methods
 Frequency estimation by DFT interpolation: A comparison of methods Bernd Bischl, Uwe Ligges, Claus Weihs March 5, 009 Abstract This article comments on a frequency estimator which was proposed by [6] and
Frequency estimation by DFT interpolation: A comparison of methods Bernd Bischl, Uwe Ligges, Claus Weihs March 5, 009 Abstract This article comments on a frequency estimator which was proposed by [6] and
Expressions for the covariance matrix of covariance data
 Expressions for the covariance matrix of covariance data Torsten Söderström Division of Systems and Control, Department of Information Technology, Uppsala University, P O Box 337, SE-7505 Uppsala, Sweden
Expressions for the covariance matrix of covariance data Torsten Söderström Division of Systems and Control, Department of Information Technology, Uppsala University, P O Box 337, SE-7505 Uppsala, Sweden
2.161 Signal Processing: Continuous and Discrete Fall 2008
 IT OpenCourseWare http://ocw.mit.edu 2.161 Signal Processing: Continuous and Discrete all 2008 or information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. assachusetts
IT OpenCourseWare http://ocw.mit.edu 2.161 Signal Processing: Continuous and Discrete all 2008 or information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. assachusetts
Summary of lecture 1. E x = E x =T. X T (e i!t ) which motivates us to define the energy spectrum Φ xx (!) = jx (i!)j 2 Z 1 Z =T. 2 d!
 Summary of lecture I Continuous time: FS X FS [n] for periodic signals, FT X (i!) for non-periodic signals. II Discrete time: DTFT X T (e i!t ) III Poisson s summation formula: describes the relationship
Summary of lecture I Continuous time: FS X FS [n] for periodic signals, FT X (i!) for non-periodic signals. II Discrete time: DTFT X T (e i!t ) III Poisson s summation formula: describes the relationship
Lecture 7 Discrete Systems
 Lecture 7 Discrete Systems EE 52: Instrumentation and Measurements Lecture Notes Update on November, 29 Aly El-Osery, Electrical Engineering Dept., New Mexico Tech 7. Contents The z-transform 2 Linear
Lecture 7 Discrete Systems EE 52: Instrumentation and Measurements Lecture Notes Update on November, 29 Aly El-Osery, Electrical Engineering Dept., New Mexico Tech 7. Contents The z-transform 2 Linear
The Local Polynomial Method for nonparametric system identification: improvements and experimentation
 The Local Polynomial Method for nonparametric system identification: improvements and experimentation Michel Gevers, Rik Pintelon and Johan Schoukens Abstract The Local Polynomial Method (LPM) is a recently
The Local Polynomial Method for nonparametric system identification: improvements and experimentation Michel Gevers, Rik Pintelon and Johan Schoukens Abstract The Local Polynomial Method (LPM) is a recently
Effects of data windows on the methods of surrogate data
 Effects of data windows on the methods of surrogate data Tomoya Suzuki, 1 Tohru Ikeguchi, and Masuo Suzuki 1 1 Graduate School of Science, Tokyo University of Science, 1-3 Kagurazaka, Shinjuku-ku, Tokyo
Effects of data windows on the methods of surrogate data Tomoya Suzuki, 1 Tohru Ikeguchi, and Masuo Suzuki 1 1 Graduate School of Science, Tokyo University of Science, 1-3 Kagurazaka, Shinjuku-ku, Tokyo
Class of waveform coders can be represented in this manner
 Digital Speech Processing Lecture 15 Speech Coding Methods Based on Speech Waveform Representations ti and Speech Models Uniform and Non- Uniform Coding Methods 1 Analog-to-Digital Conversion (Sampling
Digital Speech Processing Lecture 15 Speech Coding Methods Based on Speech Waveform Representations ti and Speech Models Uniform and Non- Uniform Coding Methods 1 Analog-to-Digital Conversion (Sampling
System Identification in the Short-Time Fourier Transform Domain
 System Identification in the Short-Time Fourier Transform Domain Electrical Engineering Department Technion - Israel Institute of Technology Supervised by: Prof. Israel Cohen Outline Representation Identification
System Identification in the Short-Time Fourier Transform Domain Electrical Engineering Department Technion - Israel Institute of Technology Supervised by: Prof. Israel Cohen Outline Representation Identification
AUTOMATIC CONTROL COMMUNICATION SYSTEMS LINKÖPINGS UNIVERSITET. Questions AUTOMATIC CONTROL COMMUNICATION SYSTEMS LINKÖPINGS UNIVERSITET
 The Problem Identification of Linear and onlinear Dynamical Systems Theme : Curve Fitting Division of Automatic Control Linköping University Sweden Data from Gripen Questions How do the control surface
The Problem Identification of Linear and onlinear Dynamical Systems Theme : Curve Fitting Division of Automatic Control Linköping University Sweden Data from Gripen Questions How do the control surface
Acomplex-valued harmonic with a time-varying phase is a
 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 46, NO. 9, SEPTEMBER 1998 2315 Instantaneous Frequency Estimation Using the Wigner Distribution with Varying and Data-Driven Window Length Vladimir Katkovnik,
IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 46, NO. 9, SEPTEMBER 1998 2315 Instantaneous Frequency Estimation Using the Wigner Distribution with Varying and Data-Driven Window Length Vladimir Katkovnik,
Enhancement of Noisy Speech. State-of-the-Art and Perspectives
 Enhancement of Noisy Speech State-of-the-Art and Perspectives Rainer Martin Institute of Communications Technology (IFN) Technical University of Braunschweig July, 2003 Applications of Noise Reduction
Enhancement of Noisy Speech State-of-the-Art and Perspectives Rainer Martin Institute of Communications Technology (IFN) Technical University of Braunschweig July, 2003 Applications of Noise Reduction
INTRODUCTION TO DELTA-SIGMA ADCS
 ECE37 Advanced Analog Circuits INTRODUCTION TO DELTA-SIGMA ADCS Richard Schreier richard.schreier@analog.com NLCOTD: Level Translator VDD > VDD2, e.g. 3-V logic? -V logic VDD < VDD2, e.g. -V logic? 3-V
ECE37 Advanced Analog Circuits INTRODUCTION TO DELTA-SIGMA ADCS Richard Schreier richard.schreier@analog.com NLCOTD: Level Translator VDD > VDD2, e.g. 3-V logic? -V logic VDD < VDD2, e.g. -V logic? 3-V
! Spectral Analysis with DFT. ! Windowing. ! Effect of zero-padding. ! Time-dependent Fourier transform. " Aka short-time Fourier transform
 Lecture Outline ESE 531: Digital Signal Processing Spectral Analysis with DFT Windowing Lec 24: April 18, 2019 Spectral Analysis Effect of zero-padding Time-dependent Fourier transform " Aka short-time
Lecture Outline ESE 531: Digital Signal Processing Spectral Analysis with DFT Windowing Lec 24: April 18, 2019 Spectral Analysis Effect of zero-padding Time-dependent Fourier transform " Aka short-time
Oversampling Converters
 Oversampling Converters David Johns and Ken Martin (johns@eecg.toronto.edu) (martin@eecg.toronto.edu) slide 1 of 56 Motivation Popular approach for medium-to-low speed A/D and D/A applications requiring
Oversampling Converters David Johns and Ken Martin (johns@eecg.toronto.edu) (martin@eecg.toronto.edu) slide 1 of 56 Motivation Popular approach for medium-to-low speed A/D and D/A applications requiring
III.C - Linear Transformations: Optimal Filtering
 1 III.C - Linear Transformations: Optimal Filtering FIR Wiener Filter [p. 3] Mean square signal estimation principles [p. 4] Orthogonality principle [p. 7] FIR Wiener filtering concepts [p. 8] Filter coefficients
1 III.C - Linear Transformations: Optimal Filtering FIR Wiener Filter [p. 3] Mean square signal estimation principles [p. 4] Orthogonality principle [p. 7] FIR Wiener filtering concepts [p. 8] Filter coefficients
Adaptive Filtering. Squares. Alexander D. Poularikas. Fundamentals of. Least Mean. with MATLABR. University of Alabama, Huntsville, AL.
 Adaptive Filtering Fundamentals of Least Mean Squares with MATLABR Alexander D. Poularikas University of Alabama, Huntsville, AL CRC Press Taylor & Francis Croup Boca Raton London New York CRC Press is
Adaptive Filtering Fundamentals of Least Mean Squares with MATLABR Alexander D. Poularikas University of Alabama, Huntsville, AL CRC Press Taylor & Francis Croup Boca Raton London New York CRC Press is
Cheng Soon Ong & Christian Walder. Canberra February June 2018
 Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 Outlines Overview Introduction Linear Algebra Probability Linear Regression
Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 Outlines Overview Introduction Linear Algebra Probability Linear Regression
STAD57 Time Series Analysis. Lecture 23
 STAD57 Time Series Analysis Lecture 23 1 Spectral Representation Spectral representation of stationary {X t } is: 12 i2t Xt e du 12 1/2 1/2 for U( ) a stochastic process with independent increments du(ω)=
STAD57 Time Series Analysis Lecture 23 1 Spectral Representation Spectral representation of stationary {X t } is: 12 i2t Xt e du 12 1/2 1/2 for U( ) a stochastic process with independent increments du(ω)=
O Combining cross-validation and plug-in methods - for kernel density bandwidth selection O
 O Combining cross-validation and plug-in methods - for kernel density selection O Carlos Tenreiro CMUC and DMUC, University of Coimbra PhD Program UC UP February 18, 2011 1 Overview The nonparametric problem
O Combining cross-validation and plug-in methods - for kernel density selection O Carlos Tenreiro CMUC and DMUC, University of Coimbra PhD Program UC UP February 18, 2011 1 Overview The nonparametric problem
