Foundations of XML Types: Tree Automata
|
|
|
- Jocelyn Robbins
- 5 years ago
- Views:
Transcription
1 1 / 43 Foundtions of XML Types: Tree Automt Pierre Genevès CNRS (slides mostly sed on slides y W. Mrtens nd T. Schwentick) University of Grenole Alpes,
2 2 / 43 Why Tree Automt? Foundtions of XML type lnguges (DTD, XML Schem, Relx NG...) Provide generl frmework for XML type lnguges A tool to define regulr tree lnguges with n opertionl semntics Provide lgorithms for efficient vlidtion Bsic tool for sttic nlysis (proofs, decision procedures in logic)
3 3 / 43 Prelude: Word Automt strt even odd Trnsitions even odd odd even...
4 4 / 43 From Words to Trees: Binry Trees Binry trees with n even numer of s How to write trnsitions?
5 4 / 43 From Words to Trees: Binry Trees Binry trees with n even numer of s even even odd even odd even even How to write trnsitions?
6 4 / 43 From Words to Trees: Binry Trees Binry trees with n even numer of s even even odd even odd even even How to write trnsitions? (even, odd) even (even, even) odd etc.
7 5 / 43 Rnked Trees? They come from prse trees of dt (or progrms)... A function cll f (, ) is rnked tree f
8 5 / 43 Rnked Trees? They come from prse trees of dt (or progrms)... A function cll f (g(,, c), h(i)) is rnked tree f g h c i
9 6 / 43 Rnked Alphet A rnked lphet symol is: formlistion of function cll symol with n integer rity() rity() indictes the numer of children of Nottion (k) : symol with rity() = k
10 7 / 43 Exmple Alphet: { (2), (2), c (3), # (0) } Possile tree: c # # # # # # # # # #
11 8 / 43 Rnked Tree Automt A rnked tree utomton A consists in: Alphet(A): Sttes(A): Rules(A): Finl(A): where : finite lphet of symols finite set of sttes finite set of trnsition rules finite set of finl sttes ( Sttes(A)) Rules(A) re of the form (q 1,..., q k ) (k) q if k = 0, we write ɛ (0) q
12 8 / 43 Rnked Tree Automt A rnked tree utomton A consists in: Alphet(A): Sttes(A): Rules(A): Finl(A): where : finite lphet of symols finite set of sttes finite set of trnsition rules finite set of finl sttes ( Sttes(A)) Rules(A) re of the form (q 1,..., q k ) (k) q if k = 0, we write ɛ (0) q
13 9 / 43 Exmple: Boolen Expressions How do they work? Principle Alphet(A) = {,, 0, 1} Sttes(A) = {q 0, q 1} 1 ccepting stte t the root: Finl(A) = {q 1} Rules(A) ɛ 0 q 0 ɛ 1 q 1 (q 1, q 1) q 1 (q 0, q 1) q 1 (q 0, q 1) q 0 (q 1, q 0) q 1 (q 1, q 0) q 0 (q 1, q 1) q 1 (q 0, q 0) q 0 (q 0, q 0) q 0
14 9 / 43 Exmple: Boolen Expressions How do they work? 0 q 0 1 q 1 1 q 1 0 q 0 0 q 0 1 q 1 1 q 1 1 q 1 Principle Alphet(A) = {,, 0, 1} Sttes(A) = {q 0, q 1} 1 ccepting stte t the root: Finl(A) = {q 1} Rules(A) ɛ 0 q 0 ɛ 1 q 1 (q 1, q 1) q 1 (q 0, q 1) q 1 (q 0, q 1) q 0 (q 1, q 0) q 1 (q 1, q 0) q 0 (q 1, q 1) q 1 (q 0, q 0) q 0 (q 0, q 0) q 0
15 9 / 43 Exmple: Boolen Expressions How do they work? q 1 q 1 q 1 q 0 q 1 q 1 q 1 0 q 0 1 q 1 1 q 1 0 q 0 0 q 0 1 q 1 1 q 1 1 q 1 Principle Alphet(A) = {,, 0, 1} Sttes(A) = {q 0, q 1} 1 ccepting stte t the root: Finl(A) = {q 1} Rules(A) ɛ 0 q 0 ɛ 1 q 1 (q 1, q 1) q 1 (q 0, q 1) q 1 (q 0, q 1) q 0 (q 1, q 0) q 1 (q 1, q 0) q 0 (q 1, q 1) q 1 (q 0, q 0) q 0 (q 0, q 0) q 0
16 10 / 43 Terminology Lnguge(A) : set of trees ccepted y A For tree utomton A, Lnguge(A) is regulr tree lnguge [Thtcher nd Wright, 1968, Doner, 1970]
17 11 / 43 Exmple Tree utomton A over { (2), (2), # (0) } which recognizes trees with n even numer of s Alphet(A) : {,, #} Sttes(A) : Finl(A) : Rules(A) :
18 11 / 43 Exmple Tree utomton A over { (2), (2), # (0) } which recognizes trees with n even numer of s Alphet(A) : {,, #} Sttes(A) : {even, odd} Finl(A) : {even} Rules(A) : (even, even) odd (even, odd) even (odd, even) even (odd, odd) odd ɛ # even (even, even) even (even, odd) odd (odd, even) odd (odd, odd) even
19 12 / 43 Outline 1. Cn we implement tree utomton efficiently? (notion of determinism) 2. Are tree utomt closed under set-theoretic opertions? 3. Cn we check type inclusion? 4. Cn we uild equivlent top-down tree utomt? 5. Nice theory. But... wht should I do with my unrnked XML trees? Cn we pply this for XML type-checking?
20 13 / 43 Deterministic Tree Automt Deterministic does not hve two rules of the form: for two different sttes q nd q (q 1,..., q k ) (k) q (q 1,..., q k ) (k) q Intuition At most one possile trnsition t given node implementtion...
21 14 / 43 Cn we Mke Tree Automton Deterministic? Theorem (determiniztion) From given non-deterministic (ottom-up) tree utomton we cn uild deterministic tree utomton Corollry Non-deterministic nd deterministic (ottom-up) tree utomt recognize the sme lnguges. Complexity EXPTIME ( Sttes(A det ) = 2 Sttes(A) )
22 15 / 43 Implementing Vlidtion Memership Checking Given tree utomton A nd tree t, does t Lnguge(A)? Remrk We cn implement even if A is non-deterministic... Exmple Automton with Finl(A) = {q f } nd : ɛ c q q q q q q q f (q, q) q c c
23 15 / 43 Implementing Vlidtion Memership Checking Given tree utomton A nd tree t, does t Lnguge(A)? Remrk We cn implement even if A is non-deterministic... Exmple Automton with Finl(A) = {q f } nd : ɛ c q q q q q q q f (q, q) q {q} c c {q}
24 15 / 43 Implementing Vlidtion Memership Checking Given tree utomton A nd tree t, does t Lnguge(A)? Remrk We cn implement even if A is non-deterministic... Exmple Automton with Finl(A) = {q f } nd : ɛ c q q q q q q q f (q, q) q {q, q } {q, q } {q} c c {q}
25 15 / 43 Implementing Vlidtion Memership Checking Given tree utomton A nd tree t, does t Lnguge(A)? Remrk We cn implement even if A is non-deterministic... Exmple Automton with Finl(A) = {q f } nd : ɛ c q q q q q q q f (q, q) q {q} {q, q } {q, q } {q} c c {q}
26 15 / 43 Implementing Vlidtion Memership Checking Given tree utomton A nd tree t, does t Lnguge(A)? Remrk We cn implement even if A is non-deterministic... Exmple Automton with Finl(A) = {q f } nd : ɛ c q q q q q q q f (q, q) q {q, q } {q} {q, q } {q, q } {q} c c {q}
27 15 / 43 Implementing Vlidtion Memership Checking Given tree utomton A nd tree t, does t Lnguge(A)? Remrk We cn implement even if A is non-deterministic... Exmple Automton with Finl(A) = {q f } nd : ɛ c q q q q q q q f (q, q) q {q, q, q f } {q, q } {q} {q, q } {q, q } {q} c c {q}
28 15 / 43 Implementing Vlidtion Memership Checking Given tree utomton A nd tree t, does t Lnguge(A)? Remrk We cn implement even if A is non-deterministic... Exmple Automton with Finl(A) = {q f } nd : ɛ c q q q q q q q f (q, q) q {q, q, q f } {q, q, q f } {q, q } {q} {q, q } {q, q } {q} c c {q}
29 15 / 43 Implementing Vlidtion Memership Checking Given tree utomton A nd tree t, does t Lnguge(A)? Remrk We cn implement even if A is non-deterministic... Exmple Automton with Finl(A) = {q f } nd : ɛ c q q q q q q q f (q, q) q {q, q, q f } {q, q, q f } {q, q } {q} {q, q } {q, q } {q} c c {q} Complexity Memership-Checking is in PTIME (time liner in the size of the tree)
30 16 / 43 Set-Theoretic Opertions Recll We hve seen tht neither locl tree grmmrs nor single-type tree grmmrs re closed under oolen opertions (e.g. union) Wht out tree utomt?
31 17 / 43 Exmple Closure under Union nd Intersection... Automton A: even numer of s (even, even) odd Automton B: even numer of s (even, even) even
32 17 / 43 Exmple Closure under Union nd Intersection... Automton A: even numer of s (even, even) odd Automton B: even numer of s (even, even) even odd even even even even even
33 17 / 43 Exmple Closure under Union nd Intersection... Automton A: even numer of s (even, even) odd Automton B: even numer of s (even, even) even odd even even even even even ((even, even), (even, even)) (odd, even)
34 18 / 43 Product Construction Given A nd B, uild A B Alphet(A B) = Alphet(A) Alphet(B) Sttes(A B) = Sttes(A) Sttes(B) Finl(A B) = {(q, q ) q Finl(A) q Finl(B)} Rules(A B) = ( (q 1, q), 1..., (q k, q k ) ) (k) (q, q ) q 1,..., q k (k) q Rules(A) q, 1..., q k (k) q Rules(B)
35 19 / 43 Closure under Union Given A nd B, uild A B Alphet(A B) = Alphet(A) Alphet(B) Sttes(A B) = Sttes(A) Sttes(B) Rules(A B) = ( (q 1, q), 1..., (q k, q k ) ) (k) (q, q ) q 1,..., q k (k) q Rules(A) q, 1..., q k (k) q Rules(B) Finl(A B) = {(q, q ) q Finl(A) q Finl(B)}
36 20 / 43 Closure under intersection Given A nd B, uild A B Alphet(A B) = Alphet(A) Alphet(B) Sttes(A B) = Sttes(A) Sttes(B) Rules(A B) = ( (q 1, q), 1..., (q k, q k ) ) (k) (q, q ) q 1,..., q k (k) q Rules(A) q, 1..., q k (k) q Rules(B) Finl(A B) = {(q, q ) q Finl(A) q Finl(B)}
37 21 / 43 Complexity of the Product Size of the Result Automton Sttes(A B) = Sttes(A) Sttes(B) Rules(A B) Rules(A) Rules(B) Qudrtic increse in size
38 22 / 43 Closure under Negtion: Completion Definition : Complete Tree Automton For ech (k) Alphet(A) nd q 1,..., q k Sttes(A), there exists rule with some q (q 1,..., q k ) q Intuition At lest one trnsition t given node...
39 23 / 43 Exmple Incomplete (deterministic) tree utomton Tree utomton A for {(, )} : ɛ q (q, q ) q with Finl(A) = {q } Completion of A Add sink stte q p ɛ q ɛ q p (q, q ) q (q, q ) q p (q, q ) q p (q, q ) q p (q, q ) q p (q, q ) q p (q, q ) q p (q, q ) q p (q p, q) σ q p for ll q {q, q, q p} nd σ {, } (q, q p) σ q p for ll q {q, q, q p} nd σ {, } with Finl(A) = {q }
40 23 / 43 Exmple Incomplete (deterministic) tree utomton Tree utomton A for {(, )} : ɛ q (q, q ) q with Finl(A) = {q } Completion of A, Complementtion of A Add sink stte q p ɛ q ɛ q p (q, q ) q (q, q ) q p (q, q ) q p (q, q ) q p (q, q ) q p (q, q ) q p (q, q ) q p (q, q ) q p (q p, q) σ q p for ll q {q, q, q p} nd σ {, } (q, q p) σ q p for ll q {q, q, q p} nd σ {, } with Finl(A) = {q, q p}
41 24 / 43 Closure under Negtion: Summry Building the Complement of A Mke A deterministic Complete the result Switch finl non-finl sttes Complexity Determiniztion of A : exponentil explosion (sttes: 2 Sttes(A) ) Completion of the result: exponentil explosion of the numer of rules: ( ) k Alphet(A) 2 Sttes(A) where k is the mximl rnk Switching finl non-finl sttes: liner Totl: exponentil explosion
42 25 / 43 Emptiness Test Given tree utomton A, is Lnguge(A)? Principle Compute the set of rechle sttes nd then see if ny of them re in the finl set Complexity PTIME (time proportionl to A )
43 26 / 43 Appliction for Checking Type Inclusion Type Inclusion Given two tree utomt A 1 nd A 2, is Lnguge(A 1) Lnguge(A 2)? Theorem Continment for non-deterministic tree utomt cn e decided in exponentil time Principle Lnguge(A 1 A 2)? = For this purpose, we must mke A 2 deterministic (size: O(2 A 2 )) EXPTIME Essentilly no etter solution [Seidl, 1990]
44 26 / 43 Appliction for Checking Type Inclusion Type Inclusion Given two tree utomt A 1 nd A 2, is Lnguge(A 1) Lnguge(A 2)? Theorem Continment for non-deterministic tree utomt cn e decided in exponentil time Principle Lnguge(A 1 A 2)? = For this purpose, we must mke A 2 deterministic (size: O(2 A 2 )) EXPTIME Essentilly no etter solution [Seidl, 1990]
45 27 / 43 Top-Down Tree Automt Is tht useful?... Exmple: Connection with Strings c cd = ((c(d))) = d Reding strings from left to right = reding trees top-down ( e.g. streming vlidtion...)
46 Top-Down Tree Automt: Exmple Principle strting from the root, guess correct vlues check t leves 3 sttes: q 0, q 1, cc initil stte t the root: q 1 ccepting if ll leves leled cc Trnsitions q 1 (q 1, q 1) q 1 (q 0, q 1) q 0 (q 0, q 1) q 1 (q 1, q 0) q 0 (q 1, q 0) q 1 (q 1, q 1) q 0 (q 0, q 0) q 0 (q 0, q 0) q 1 1 cc q 0 0 cc 28 / 43
47 Top-Down Tree Automt: Exmple q Principle strting from the root, guess correct vlues check t leves 3 sttes: q 0, q 1, cc initil stte t the root: q 1 ccepting if ll leves leled cc Trnsitions q 1 (q 1, q 1) q 1 (q 0, q 1) q 0 (q 0, q 1) q 1 (q 1, q 0) q 0 (q 1, q 0) q 1 (q 1, q 1) q 0 (q 0, q 0) q 0 (q 0, q 0) q 1 1 cc q 0 0 cc 28 / 43
48 Top-Down Tree Automt: Exmple q 1 q 1 q 1 q 0 q 1 q 1 q 1 0 q 0 1 q 1 1 q 1 0 q 0 0 q 0 1 q 1 1 q 1 1 q 1 cc cc cc cc cc cc cc cc Principle strting from the root, guess correct vlues check t leves 3 sttes: q 0, q 1, cc initil stte t the root: q 1 ccepting if ll leves leled cc Trnsitions q 1 (q 1, q 1) q 1 (q 0, q 1) q 0 (q 0, q 1) q 1 (q 1, q 0) q 0 (q 1, q 0) q 1 (q 1, q 1) q 0 (q 0, q 0) q 0 (q 0, q 0) q 1 1 cc q 0 0 cc 28 / 43
49 29 / 43 Top-Down Tree Automt A top-down tree utomton A consists in: Alphet(A): Sttes(A): Rules(A): Initil(A): where: finite lphet of symols finite set of sttes finite set of trnsition rules finite set of initil sttes ( Sttes(A)) Rules(A) re of the form q (k) (q 1,..., q k ) Top-down tree utomt lso recognize ll regulr tree lnguges
50 29 / 43 Top-Down Tree Automt A top-down tree utomton A consists in: Alphet(A): Sttes(A): Rules(A): Initil(A): where: finite lphet of symols finite set of sttes finite set of trnsition rules finite set of initil sttes ( Sttes(A)) Rules(A) re of the form q (k) (q 1,..., q k ) Top-down tree utomt lso recognize ll regulr tree lnguges
51 30 / 43 Top-down Determinism Deterministic Top-Down Tree Automton for ech q Sttes(A) nd Alphet(A) there is t most one rule there is t most one initil stte q (k) (q 1,..., q k )
52 30 / 43 Top-down Determinism Deterministic Top-Down Tree Automton for ech q Sttes(A) nd Alphet(A) there is t most one rule there is t most one initil stte q (k) (q 1,..., q k ) Cn We Mke Top-Down Automt Deterministic? () Yes () No (c) Mye...
53 31 / 43 Cn We Mke Top-Down Automt Deterministic? Mye!
54 31 / 43 Cn We Mke Top-Down Automt Deterministic? Mye! Deterministic top-down tree utomt do not recognize ll regulr tree lnguges Exmple c c
55 31 / 43 Cn We Mke Top-Down Automt Deterministic? Mye! Deterministic top-down tree utomt do not recognize ll regulr tree lnguges Exmple c c Initil(A) = q 0
56 31 / 43 Cn We Mke Top-Down Automt Deterministic? Mye! Deterministic top-down tree utomt do not recognize ll regulr tree lnguges Exmple c c Initil(A) = q 0 (q, q) q 0
57 31 / 43 Cn We Mke Top-Down Automt Deterministic? Mye! Deterministic top-down tree utomt do not recognize ll regulr tree lnguges Exmple c c Initil(A) = q 0 (q, q) q 0 q ɛ
58 31 / 43 Cn We Mke Top-Down Automt Deterministic? Mye! Deterministic top-down tree utomt do not recognize ll regulr tree lnguges Exmple c c Initil(A) = q 0 (q, q) q 0 q ɛ q c ɛ
59 31 / 43 Cn We Mke Top-Down Automt Deterministic? Mye! Deterministic top-down tree utomt do not recognize ll regulr tree lnguges Exmple c c Initil(A) = q 0 (q, q) q 0 q ɛ q c ɛ lso ccepts... c c
60 32 / 43 Expressive Power of Tree Automt: Summry Theorem The following properties re equivlent for tree lnguge L: () L is recognized y ottom-up non-deterministic tree utomton () Lis recognized y ottom-up deterministic tree utomton (c) L is recognized y top-down non-deterministic tree utomton (d) L is generted y regulr tree grmmr Proof Ide () (): determiniztion (see [Comon et l., 1997]) () (c): sme thing seen from 2 different wys (d) () :? (horizontl recursion?)
61 33 / 43 Unrnked Trees String s Tree c Rnked Tree c c c Unrnked Tree e c d... c d... c c e e c e Unrnked Tree Automt? 1. either we dpt rnked tree utomt 2. or we encode unrnked trees re rnked trees...
62 34 / 43 Unrnked Tree Automt Rnked Trees Trnsitions cn e descried y finite sets: δ(σ, q) = {(q 1, q 2), (q 3, q 4),...} q σ σ 1 σ 2 q 1 q 2 Unrnked Trees q σ σ 1 σ 2... σ n q 1 q 2... q n δ(σ, q)? δ(σ, q) For unrnked trees, δ(σ, q) is regulr tree lnguge δ(σ, q) my e specified y regulr expression or y finite word utomton [Murt, 1999]
63 35 / 43 Second Option Cn we encode unrnked trees s rnked trees? e c d... c d... c c e? e c e
64 36 / 43 Encoding Unrnked Trees As Binry Trees Bijective Encoding first child; next siling encoding Allows to focus on inry trees without loss of generlity Results for rnked trees hold for unrnked trees s well
65 37 / 43 Tree Automt: Summry Definition A tree lnguge is regulr iff it is recognized y non-deterministic tree utomton Advntges Closure, decidle opertions Generl tool (theoreticl nd lgorithmic) Limittions n n
66 38 / 43 Appliction for Sttic Type-Checking Recll: The XML Sttic Type-Checking Prolem Given the following: Source code of some progrm f (in e.g. XQuery) A type T in for input documents A type T out for expected output documents Prolem: Does f (t) T out for ll t T in?
67 39 / 43 Sttic Type-Checking for XQuery: Principles <doc> { FOR $uthor in /ooks/ook/uthor[...] RETURN <uthor>... { /ooks/ook/title } </uthor> } </doc> f () t T in f (t) T inf? T out Approch in two steps: 1. Compute T inf = {f (t) t T in } 2. Check whether T inf T out holds In cse T inf T out holds, then we know tht for ny t T in, f (t) T out
68 40 / 43 Sttic Type-Checking Using Tree Automt Mny reserch ppers XQuery s stndrd type system inspired from dvnces in PLs, e.g.: XDuce [Hosoy nd Pierce, 2003]: domin specific lnguge Sound sttic type system sed on n implementtion of tree utomt continment optimized for prcticl cses Use pttern-mtching for selection (no support for XPth) XQuery s stndrd type system As defined in the spec: Sound PTIME Sound nd more precise type systems in EXPTIME
69 41 / 43 XQuery nd Sttic Type-Checking Open Issues Type inference requires lnce etween precision nd complexity Sound pproximtions cn e more or less imprecise Poor precision (e.g. type pproximtion) in type inference yields more flse lrms XQuery s stndrd type system is limited: Currently: no or poor support of XPth (e.g. only child nd descendnt xes re poorly supported) Support for typing XPth hs een open for yers (in prticulr for ckwrd xes) Cn you guess why is tht difficult? 2015 ICFP pper with solution for this issue (sed on dvnces in tree logics)
70 42 / 43 Concluding Remrks on Tree Automt Tree utomt re prt of the theoreticl tools tht provide the underlying guiding principles for XML (like the reltionl lger provides the underlying principles for reltionl dtses) Importnt reserch chllenges still remin
71 43 / 43 </session> For those who wnt to lern more Pointers to relted reserch results: [1] XQuery nd Sttic Typing: Tckling the Prolem of Bckwrd Axes. Pierre Genevès nd Nils Gesert. In ICFP 15: Proceedings of the ACM SIGPLAN Interntionl Conference on Functionl Progrmming (ICFP), Sept
72 Comon, H., Duchet, M., Gilleron, R., Jcquemrd, F., Lugiez, D., Tison, S., nd Tommsi, M. (1997). Tree utomt techniques nd pplictions. Aville on: relese Octoer, 1st Doner, J. (1970). Tree cceptors nd some of their pplictions. Journl of Computer nd System Sciences, 4: Hosoy, H. nd Pierce, B. C. (2003). XDuce: A stticlly typed XML processing lnguge. ACM Trns. Inter. Tech., 3(2): Murt, M. (1999). Hedge utomt: forml model for XML schemt. Seidl, H. (1990). Deciding equivlence of finite tree utomt. SIAM J. Comput., 19(3): Thtcher, J. W. nd Wright, J. B. (1968). 43 / 43
73 Generlized finite utomt theory with n ppliction to decision prolem of second-order logic. Mthemticl Systems Theory, 2(1): / 43
Chapter Five: Nondeterministic Finite Automata. Formal Language, chapter 5, slide 1
 Chpter Five: Nondeterministic Finite Automt Forml Lnguge, chpter 5, slide 1 1 A DFA hs exctly one trnsition from every stte on every symol in the lphet. By relxing this requirement we get relted ut more
Chpter Five: Nondeterministic Finite Automt Forml Lnguge, chpter 5, slide 1 1 A DFA hs exctly one trnsition from every stte on every symol in the lphet. By relxing this requirement we get relted ut more
Automata Theory 101. Introduction. Outline. Introduction Finite Automata Regular Expressions ω-automata. Ralf Huuck.
 Outline Automt Theory 101 Rlf Huuck Introduction Finite Automt Regulr Expressions ω-automt Session 1 2006 Rlf Huuck 1 Session 1 2006 Rlf Huuck 2 Acknowledgement Some slides re sed on Wolfgng Thoms excellent
Outline Automt Theory 101 Rlf Huuck Introduction Finite Automt Regulr Expressions ω-automt Session 1 2006 Rlf Huuck 1 Session 1 2006 Rlf Huuck 2 Acknowledgement Some slides re sed on Wolfgng Thoms excellent
Deterministic Finite Automata
 Finite Automt Deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion Sciences Version: fll 2016 J. Rot Version: fll 2016 Tlen en Automten 1 / 21 Outline Finite Automt Finite
Finite Automt Deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion Sciences Version: fll 2016 J. Rot Version: fll 2016 Tlen en Automten 1 / 21 Outline Finite Automt Finite
Regular expressions, Finite Automata, transition graphs are all the same!!
 CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
1 Nondeterministic Finite Automata
 1 Nondeterministic Finite Automt Suppose in life, whenever you hd choice, you could try oth possiilities nd live your life. At the end, you would go ck nd choose the one tht worked out the est. Then you
1 Nondeterministic Finite Automt Suppose in life, whenever you hd choice, you could try oth possiilities nd live your life. At the end, you would go ck nd choose the one tht worked out the est. Then you
CMSC 330: Organization of Programming Languages
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 CMSC 330 1 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All exmples so fr Nondeterministic
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 CMSC 330 1 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All exmples so fr Nondeterministic
Types of Finite Automata. CMSC 330: Organization of Programming Languages. Comparing DFAs and NFAs. NFA for (a b)*abb.
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
Anatomy of a Deterministic Finite Automaton. Deterministic Finite Automata. A machine so simple that you can understand it in less than one minute
 Victor Admchik Dnny Sletor Gret Theoreticl Ides In Computer Science CS 5-25 Spring 2 Lecture 2 Mr 3, 2 Crnegie Mellon University Deterministic Finite Automt Finite Automt A mchine so simple tht you cn
Victor Admchik Dnny Sletor Gret Theoreticl Ides In Computer Science CS 5-25 Spring 2 Lecture 2 Mr 3, 2 Crnegie Mellon University Deterministic Finite Automt Finite Automt A mchine so simple tht you cn
Chapter 2 Finite Automata
 Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
Types of Finite Automata. CMSC 330: Organization of Programming Languages. Comparing DFAs and NFAs. Comparing DFAs and NFAs (cont.) Finite Automata 2
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
Designing finite automata II
 Designing finite utomt II Prolem: Design DFA A such tht L(A) consists of ll strings of nd which re of length 3n, for n = 0, 1, 2, (1) Determine wht to rememer out the input string Assign stte to ech of
Designing finite utomt II Prolem: Design DFA A such tht L(A) consists of ll strings of nd which re of length 3n, for n = 0, 1, 2, (1) Determine wht to rememer out the input string Assign stte to ech of
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automt Theory nd Forml Lnguges TMV027/DIT321 LP4 2018 Lecture 10 An Bove April 23rd 2018 Recp: Regulr Lnguges We cn convert between FA nd RE; Hence both FA nd RE ccept/generte regulr lnguges; More
Finite Automt Theory nd Forml Lnguges TMV027/DIT321 LP4 2018 Lecture 10 An Bove April 23rd 2018 Recp: Regulr Lnguges We cn convert between FA nd RE; Hence both FA nd RE ccept/generte regulr lnguges; More
Theory of Computation Regular Languages. (NTU EE) Regular Languages Fall / 38
 Theory of Computtion Regulr Lnguges (NTU EE) Regulr Lnguges Fll 2017 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of Finite Automt A finite utomton hs finite set of control
Theory of Computtion Regulr Lnguges (NTU EE) Regulr Lnguges Fll 2017 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of Finite Automt A finite utomton hs finite set of control
Lecture 08: Feb. 08, 2019
 4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
Convert the NFA into DFA
 Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
CS415 Compilers. Lexical Analysis and. These slides are based on slides copyrighted by Keith Cooper, Ken Kennedy & Linda Torczon at Rice University
 CS415 Compilers Lexicl Anlysis nd These slides re sed on slides copyrighted y Keith Cooper, Ken Kennedy & Lind Torczon t Rice University First Progrmming Project Instruction Scheduling Project hs een posted
CS415 Compilers Lexicl Anlysis nd These slides re sed on slides copyrighted y Keith Cooper, Ken Kennedy & Lind Torczon t Rice University First Progrmming Project Instruction Scheduling Project hs een posted
CMPSCI 250: Introduction to Computation. Lecture #31: What DFA s Can and Can t Do David Mix Barrington 9 April 2014
 CMPSCI 250: Introduction to Computtion Lecture #31: Wht DFA s Cn nd Cn t Do Dvid Mix Brrington 9 April 2014 Wht DFA s Cn nd Cn t Do Deterministic Finite Automt Forml Definition of DFA s Exmples of DFA
CMPSCI 250: Introduction to Computtion Lecture #31: Wht DFA s Cn nd Cn t Do Dvid Mix Brrington 9 April 2014 Wht DFA s Cn nd Cn t Do Deterministic Finite Automt Forml Definition of DFA s Exmples of DFA
On Determinisation of History-Deterministic Automata.
 On Deterministion of History-Deterministic Automt. Denis Kupererg Mich l Skrzypczk University of Wrsw YR-ICALP 2014 Copenhgen Introduction Deterministic utomt re centrl tool in utomt theory: Polynomil
On Deterministion of History-Deterministic Automt. Denis Kupererg Mich l Skrzypczk University of Wrsw YR-ICALP 2014 Copenhgen Introduction Deterministic utomt re centrl tool in utomt theory: Polynomil
Theory of Computation Regular Languages
 Theory of Computtion Regulr Lnguges Bow-Yw Wng Acdemi Sinic Spring 2012 Bow-Yw Wng (Acdemi Sinic) Regulr Lnguges Spring 2012 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of
Theory of Computtion Regulr Lnguges Bow-Yw Wng Acdemi Sinic Spring 2012 Bow-Yw Wng (Acdemi Sinic) Regulr Lnguges Spring 2012 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of
Finite-State Automata: Recap
 Finite-Stte Automt: Recp Deepk D Souz Deprtment of Computer Science nd Automtion Indin Institute of Science, Bnglore. 09 August 2016 Outline 1 Introduction 2 Forml Definitions nd Nottion 3 Closure under
Finite-Stte Automt: Recp Deepk D Souz Deprtment of Computer Science nd Automtion Indin Institute of Science, Bnglore. 09 August 2016 Outline 1 Introduction 2 Forml Definitions nd Nottion 3 Closure under
Speech Recognition Lecture 2: Finite Automata and Finite-State Transducers
 Speech Recognition Lecture 2: Finite Automt nd Finite-Stte Trnsducers Eugene Weinstein Google, NYU Cournt Institute eugenew@cs.nyu.edu Slide Credit: Mehryr Mohri Preliminries Finite lphet, empty string.
Speech Recognition Lecture 2: Finite Automt nd Finite-Stte Trnsducers Eugene Weinstein Google, NYU Cournt Institute eugenew@cs.nyu.edu Slide Credit: Mehryr Mohri Preliminries Finite lphet, empty string.
CS103B Handout 18 Winter 2007 February 28, 2007 Finite Automata
 CS103B ndout 18 Winter 2007 Ferury 28, 2007 Finite Automt Initil text y Mggie Johnson. Introduction Severl childrens gmes fit the following description: Pieces re set up on plying ord; dice re thrown or
CS103B ndout 18 Winter 2007 Ferury 28, 2007 Finite Automt Initil text y Mggie Johnson. Introduction Severl childrens gmes fit the following description: Pieces re set up on plying ord; dice re thrown or
Java II Finite Automata I
 Jv II Finite Automt I Bernd Kiefer Bernd.Kiefer@dfki.de Deutsches Forschungszentrum für künstliche Intelligenz Finite Automt I p.1/13 Processing Regulr Expressions We lredy lerned out Jv s regulr expression
Jv II Finite Automt I Bernd Kiefer Bernd.Kiefer@dfki.de Deutsches Forschungszentrum für künstliche Intelligenz Finite Automt I p.1/13 Processing Regulr Expressions We lredy lerned out Jv s regulr expression
Regular Expressions (RE) Regular Expressions (RE) Regular Expressions (RE) Regular Expressions (RE) Kleene-*
 Regulr Expressions (RE) Regulr Expressions (RE) Empty set F A RE denotes the empty set Opertion Nottion Lnguge UNIX Empty string A RE denotes the set {} Alterntion R +r L(r ) L(r ) r r Symol Alterntion
Regulr Expressions (RE) Regulr Expressions (RE) Empty set F A RE denotes the empty set Opertion Nottion Lnguge UNIX Empty string A RE denotes the set {} Alterntion R +r L(r ) L(r ) r r Symol Alterntion
CHAPTER 1 Regular Languages. Contents. definitions, examples, designing, regular operations. Non-deterministic Finite Automata (NFA)
 Finite Automt (FA or DFA) CHAPTER Regulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, equivlence of NFAs DFAs, closure under regulr
Finite Automt (FA or DFA) CHAPTER Regulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, equivlence of NFAs DFAs, closure under regulr
CSCI 340: Computational Models. Transition Graphs. Department of Computer Science
 CSCI 340: Computtionl Models Trnsition Grphs Chpter 6 Deprtment of Computer Science Relxing Restrints on Inputs We cn uild n FA tht ccepts only the word! 5 sttes ecuse n FA cn only process one letter t
CSCI 340: Computtionl Models Trnsition Grphs Chpter 6 Deprtment of Computer Science Relxing Restrints on Inputs We cn uild n FA tht ccepts only the word! 5 sttes ecuse n FA cn only process one letter t
Lexical Analysis Finite Automate
 Lexicl Anlysis Finite Automte CMPSC 470 Lecture 04 Topics: Deterministic Finite Automt (DFA) Nondeterministic Finite Automt (NFA) Regulr Expression NFA DFA A. Finite Automt (FA) FA re grph, like trnsition
Lexicl Anlysis Finite Automte CMPSC 470 Lecture 04 Topics: Deterministic Finite Automt (DFA) Nondeterministic Finite Automt (NFA) Regulr Expression NFA DFA A. Finite Automt (FA) FA re grph, like trnsition
Harvard University Computer Science 121 Midterm October 23, 2012
 Hrvrd University Computer Science 121 Midterm Octoer 23, 2012 This is closed-ook exmintion. You my use ny result from lecture, Sipser, prolem sets, or section, s long s you quote it clerly. The lphet is
Hrvrd University Computer Science 121 Midterm Octoer 23, 2012 This is closed-ook exmintion. You my use ny result from lecture, Sipser, prolem sets, or section, s long s you quote it clerly. The lphet is
Minimal DFA. minimal DFA for L starting from any other
 Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Formal Languages and Automata
 Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
Coalgebra, Lecture 15: Equations for Deterministic Automata
 Colger, Lecture 15: Equtions for Deterministic Automt Julin Slmnc (nd Jurrin Rot) Decemer 19, 2016 In this lecture, we will study the concept of equtions for deterministic utomt. The notes re self contined
Colger, Lecture 15: Equtions for Deterministic Automt Julin Slmnc (nd Jurrin Rot) Decemer 19, 2016 In this lecture, we will study the concept of equtions for deterministic utomt. The notes re self contined
Assignment 1 Automata, Languages, and Computability. 1 Finite State Automata and Regular Languages
 Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
a,b a 1 a 2 a 3 a,b 1 a,b a,b 2 3 a,b a,b a 2 a,b CS Determinisitic Finite Automata 1
 CS4 45- Determinisitic Finite Automt -: Genertors vs. Checkers Regulr expressions re one wy to specify forml lnguge String Genertor Genertes strings in the lnguge Deterministic Finite Automt (DFA) re nother
CS4 45- Determinisitic Finite Automt -: Genertors vs. Checkers Regulr expressions re one wy to specify forml lnguge String Genertor Genertes strings in the lnguge Deterministic Finite Automt (DFA) re nother
Formal languages, automata, and theory of computation
 Mälrdlen University TEN1 DVA337 2015 School of Innovtion, Design nd Engineering Forml lnguges, utomt, nd theory of computtion Thursdy, Novemer 5, 14:10-18:30 Techer: Dniel Hedin, phone 021-107052 The exm
Mälrdlen University TEN1 DVA337 2015 School of Innovtion, Design nd Engineering Forml lnguges, utomt, nd theory of computtion Thursdy, Novemer 5, 14:10-18:30 Techer: Dniel Hedin, phone 021-107052 The exm
CS 275 Automata and Formal Language Theory
 CS 275 utomt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Prolem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) nton Setzer (Bsed on ook drft y J. V. Tucker nd K. Stephenson)
CS 275 utomt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Prolem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) nton Setzer (Bsed on ook drft y J. V. Tucker nd K. Stephenson)
CS 301. Lecture 04 Regular Expressions. Stephen Checkoway. January 29, 2018
 CS 301 Lecture 04 Regulr Expressions Stephen Checkowy Jnury 29, 2018 1 / 35 Review from lst time NFA N = (Q, Σ, δ, q 0, F ) where δ Q Σ P (Q) mps stte nd n lphet symol (or ) to set of sttes We run n NFA
CS 301 Lecture 04 Regulr Expressions Stephen Checkowy Jnury 29, 2018 1 / 35 Review from lst time NFA N = (Q, Σ, δ, q 0, F ) where δ Q Σ P (Q) mps stte nd n lphet symol (or ) to set of sttes We run n NFA
CSCI 340: Computational Models. Kleene s Theorem. Department of Computer Science
 CSCI 340: Computtionl Models Kleene s Theorem Chpter 7 Deprtment of Computer Science Unifiction In 1954, Kleene presented (nd proved) theorem which (in our version) sttes tht if lnguge cn e defined y ny
CSCI 340: Computtionl Models Kleene s Theorem Chpter 7 Deprtment of Computer Science Unifiction In 1954, Kleene presented (nd proved) theorem which (in our version) sttes tht if lnguge cn e defined y ny
CHAPTER 1 Regular Languages. Contents
 Finite Automt (FA or DFA) CHAPTE 1 egulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, euivlence of NFAs nd DFAs, closure under regulr
Finite Automt (FA or DFA) CHAPTE 1 egulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, euivlence of NFAs nd DFAs, closure under regulr
Closure Properties of Regular Languages
 Closure Properties of Regulr Lnguges Regulr lnguges re closed under mny set opertions. Let L 1 nd L 2 e regulr lnguges. (1) L 1 L 2 (the union) is regulr. (2) L 1 L 2 (the conctention) is regulr. (3) L
Closure Properties of Regulr Lnguges Regulr lnguges re closed under mny set opertions. Let L 1 nd L 2 e regulr lnguges. (1) L 1 L 2 (the union) is regulr. (2) L 1 L 2 (the conctention) is regulr. (3) L
Lecture 9: LTL and Büchi Automata
 Lecture 9: LTL nd Büchi Automt 1 LTL Property Ptterns Quite often the requirements of system follow some simple ptterns. Sometimes we wnt to specify tht property should only hold in certin context, clled
Lecture 9: LTL nd Büchi Automt 1 LTL Property Ptterns Quite often the requirements of system follow some simple ptterns. Sometimes we wnt to specify tht property should only hold in certin context, clled
Non-deterministic Finite Automata
 Non-deterministic Finite Automt Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd T. vn Lrhoven Institute for Computing nd Informtion Sciences Intelligent
Non-deterministic Finite Automt Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd T. vn Lrhoven Institute for Computing nd Informtion Sciences Intelligent
CS 267: Automated Verification. Lecture 8: Automata Theoretic Model Checking. Instructor: Tevfik Bultan
 CS 267: Automted Verifiction Lecture 8: Automt Theoretic Model Checking Instructor: Tevfik Bultn LTL Properties Büchi utomt [Vrdi nd Wolper LICS 86] Büchi utomt: Finite stte utomt tht ccept infinite strings
CS 267: Automted Verifiction Lecture 8: Automt Theoretic Model Checking Instructor: Tevfik Bultn LTL Properties Büchi utomt [Vrdi nd Wolper LICS 86] Büchi utomt: Finite stte utomt tht ccept infinite strings
Worked out examples Finite Automata
 Worked out exmples Finite Automt Exmple Design Finite Stte Automton which reds inry string nd ccepts only those tht end with. Since we re in the topic of Non Deterministic Finite Automt (NFA), we will
Worked out exmples Finite Automt Exmple Design Finite Stte Automton which reds inry string nd ccepts only those tht end with. Since we re in the topic of Non Deterministic Finite Automt (NFA), we will
Speech Recognition Lecture 2: Finite Automata and Finite-State Transducers. Mehryar Mohri Courant Institute and Google Research
 Speech Recognition Lecture 2: Finite Automt nd Finite-Stte Trnsducers Mehryr Mohri Cournt Institute nd Google Reserch mohri@cims.nyu.com Preliminries Finite lphet Σ, empty string. Set of ll strings over
Speech Recognition Lecture 2: Finite Automt nd Finite-Stte Trnsducers Mehryr Mohri Cournt Institute nd Google Reserch mohri@cims.nyu.com Preliminries Finite lphet Σ, empty string. Set of ll strings over
CS 310 (sec 20) - Winter Final Exam (solutions) SOLUTIONS
 CS 310 (sec 20) - Winter 2003 - Finl Exm (solutions) SOLUTIONS 1. (Logic) Use truth tles to prove the following logicl equivlences: () p q (p p) (q q) () p q (p q) (p q) () p q p q p p q q (q q) (p p)
CS 310 (sec 20) - Winter 2003 - Finl Exm (solutions) SOLUTIONS 1. (Logic) Use truth tles to prove the following logicl equivlences: () p q (p p) (q q) () p q (p q) (p q) () p q p q p p q q (q q) (p p)
AUTOMATA AND LANGUAGES. Definition 1.5: Finite Automaton
 25. Finite Automt AUTOMATA AND LANGUAGES A system of computtion tht only hs finite numer of possile sttes cn e modeled using finite utomton A finite utomton is often illustrted s stte digrm d d d. d q
25. Finite Automt AUTOMATA AND LANGUAGES A system of computtion tht only hs finite numer of possile sttes cn e modeled using finite utomton A finite utomton is often illustrted s stte digrm d d d. d q
1. For each of the following theorems, give a two or three sentence sketch of how the proof goes or why it is not true.
 York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
Thoery of Automata CS402
 Thoery of Automt C402 Theory of Automt Tle of contents: Lecture N0. 1... 4 ummry... 4 Wht does utomt men?... 4 Introduction to lnguges... 4 Alphets... 4 trings... 4 Defining Lnguges... 5 Lecture N0. 2...
Thoery of Automt C402 Theory of Automt Tle of contents: Lecture N0. 1... 4 ummry... 4 Wht does utomt men?... 4 Introduction to lnguges... 4 Alphets... 4 trings... 4 Defining Lnguges... 5 Lecture N0. 2...
NFA DFA Example 3 CMSC 330: Organization of Programming Languages. Equivalence of DFAs and NFAs. Equivalence of DFAs and NFAs (cont.
 NFA DFA Exmple 3 CMSC 330: Orgniztion of Progrmming Lnguges NFA {B,D,E {A,E {C,D {E Finite Automt, con't. R = { {A,E, {B,D,E, {C,D, {E 2 Equivlence of DFAs nd NFAs Any string from {A to either {D or {CD
NFA DFA Exmple 3 CMSC 330: Orgniztion of Progrmming Lnguges NFA {B,D,E {A,E {C,D {E Finite Automt, con't. R = { {A,E, {B,D,E, {C,D, {E 2 Equivlence of DFAs nd NFAs Any string from {A to either {D or {CD
Software Engineering using Formal Methods
 Softwre Engineering using Forml Methods Propositionl nd (Liner) Temporl Logic Wolfgng Ahrendt 13th Septemer 2016 SEFM: Liner Temporl Logic /GU 160913 1 / 60 Recpitultion: FormlistionFormlistion: Syntx,
Softwre Engineering using Forml Methods Propositionl nd (Liner) Temporl Logic Wolfgng Ahrendt 13th Septemer 2016 SEFM: Liner Temporl Logic /GU 160913 1 / 60 Recpitultion: FormlistionFormlistion: Syntx,
Table of contents: Lecture N Summary... 3 What does automata mean?... 3 Introduction to languages... 3 Alphabets... 3 Strings...
 Tle of contents: Lecture N0.... 3 ummry... 3 Wht does utomt men?... 3 Introduction to lnguges... 3 Alphets... 3 trings... 3 Defining Lnguges... 4 Lecture N0. 2... 7 ummry... 7 Kleene tr Closure... 7 Recursive
Tle of contents: Lecture N0.... 3 ummry... 3 Wht does utomt men?... 3 Introduction to lnguges... 3 Alphets... 3 trings... 3 Defining Lnguges... 4 Lecture N0. 2... 7 ummry... 7 Kleene tr Closure... 7 Recursive
Let's start with an example:
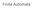 Finite Automt Let's strt with n exmple: Here you see leled circles tht re sttes, nd leled rrows tht re trnsitions. One of the sttes is mrked "strt". One of the sttes hs doule circle; this is terminl stte
Finite Automt Let's strt with n exmple: Here you see leled circles tht re sttes, nd leled rrows tht re trnsitions. One of the sttes is mrked "strt". One of the sttes hs doule circle; this is terminl stte
Nondeterminism and Nodeterministic Automata
 Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
CS 373, Spring Solutions to Mock midterm 1 (Based on first midterm in CS 273, Fall 2008.)
 CS 373, Spring 29. Solutions to Mock midterm (sed on first midterm in CS 273, Fll 28.) Prolem : Short nswer (8 points) The nswers to these prolems should e short nd not complicted. () If n NF M ccepts
CS 373, Spring 29. Solutions to Mock midterm (sed on first midterm in CS 273, Fll 28.) Prolem : Short nswer (8 points) The nswers to these prolems should e short nd not complicted. () If n NF M ccepts
ɛ-closure, Kleene s Theorem,
 DEGefW5wiGH2XgYMEzUKjEmtCDUsRQ4d 1 A nice pper relevnt to this course is titled The Glory of the Pst 2 NICTA Resercher, Adjunct t the Austrlin Ntionl University nd Griffith University ɛ-closure, Kleene
DEGefW5wiGH2XgYMEzUKjEmtCDUsRQ4d 1 A nice pper relevnt to this course is titled The Glory of the Pst 2 NICTA Resercher, Adjunct t the Austrlin Ntionl University nd Griffith University ɛ-closure, Kleene
Homework 3 Solutions
 CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
Finite Automata-cont d
 Automt Theory nd Forml Lnguges Professor Leslie Lnder Lecture # 6 Finite Automt-cont d The Pumping Lemm WEB SITE: http://ingwe.inghmton.edu/ ~lnder/cs573.html Septemer 18, 2000 Exmple 1 Consider L = {ww
Automt Theory nd Forml Lnguges Professor Leslie Lnder Lecture # 6 Finite Automt-cont d The Pumping Lemm WEB SITE: http://ingwe.inghmton.edu/ ~lnder/cs573.html Septemer 18, 2000 Exmple 1 Consider L = {ww
3 Regular expressions
 3 Regulr expressions Given n lphet Σ lnguge is set of words L Σ. So fr we were le to descrie lnguges either y using set theory (i.e. enumertion or comprehension) or y n utomton. In this section we shll
3 Regulr expressions Given n lphet Σ lnguge is set of words L Σ. So fr we were le to descrie lnguges either y using set theory (i.e. enumertion or comprehension) or y n utomton. In this section we shll
FABER Formal Languages, Automata and Models of Computation
 DVA337 FABER Forml Lnguges, Automt nd Models of Computtion Lecture 5 chool of Innovtion, Design nd Engineering Mälrdlen University 2015 1 Recp of lecture 4 y definition suset construction DFA NFA stte
DVA337 FABER Forml Lnguges, Automt nd Models of Computtion Lecture 5 chool of Innovtion, Design nd Engineering Mälrdlen University 2015 1 Recp of lecture 4 y definition suset construction DFA NFA stte
The size of subsequence automaton
 Theoreticl Computer Science 4 (005) 79 84 www.elsevier.com/locte/tcs Note The size of susequence utomton Zdeněk Troníček,, Ayumi Shinohr,c Deprtment of Computer Science nd Engineering, FEE CTU in Prgue,
Theoreticl Computer Science 4 (005) 79 84 www.elsevier.com/locte/tcs Note The size of susequence utomton Zdeněk Troníček,, Ayumi Shinohr,c Deprtment of Computer Science nd Engineering, FEE CTU in Prgue,
State Minimization for DFAs
 Stte Minimiztion for DFAs Red K & S 2.7 Do Homework 10. Consider: Stte Minimiztion 4 5 Is this miniml mchine? Step (1): Get rid of unrechle sttes. Stte Minimiztion 6, Stte is unrechle. Step (2): Get rid
Stte Minimiztion for DFAs Red K & S 2.7 Do Homework 10. Consider: Stte Minimiztion 4 5 Is this miniml mchine? Step (1): Get rid of unrechle sttes. Stte Minimiztion 6, Stte is unrechle. Step (2): Get rid
First Midterm Examination
 Çnky University Deprtment of Computer Engineering 203-204 Fll Semester First Midterm Exmintion ) Design DFA for ll strings over the lphet Σ = {,, c} in which there is no, no nd no cc. 2) Wht lnguge does
Çnky University Deprtment of Computer Engineering 203-204 Fll Semester First Midterm Exmintion ) Design DFA for ll strings over the lphet Σ = {,, c} in which there is no, no nd no cc. 2) Wht lnguge does
CS 330 Formal Methods and Models
 CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2017 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 2 1. Prove ((( p q) q) p) is tutology () (3pts) y truth tle. p q p q
CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2017 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 2 1. Prove ((( p q) q) p) is tutology () (3pts) y truth tle. p q p q
Intermediate Math Circles Wednesday, November 14, 2018 Finite Automata II. Nickolas Rollick a b b. a b 4
 Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
The University of Nottingham SCHOOL OF COMPUTER SCIENCE A LEVEL 2 MODULE, SPRING SEMESTER LANGUAGES AND COMPUTATION ANSWERS
 The University of Nottinghm SCHOOL OF COMPUTER SCIENCE LEVEL 2 MODULE, SPRING SEMESTER 2016 2017 LNGUGES ND COMPUTTION NSWERS Time llowed TWO hours Cndidtes my complete the front cover of their nswer ook
The University of Nottinghm SCHOOL OF COMPUTER SCIENCE LEVEL 2 MODULE, SPRING SEMESTER 2016 2017 LNGUGES ND COMPUTTION NSWERS Time llowed TWO hours Cndidtes my complete the front cover of their nswer ook
Converting Regular Expressions to Discrete Finite Automata: A Tutorial
 Converting Regulr Expressions to Discrete Finite Automt: A Tutoril Dvid Christinsen 2013-01-03 This is tutoril on how to convert regulr expressions to nondeterministic finite utomt (NFA) nd how to convert
Converting Regulr Expressions to Discrete Finite Automt: A Tutoril Dvid Christinsen 2013-01-03 This is tutoril on how to convert regulr expressions to nondeterministic finite utomt (NFA) nd how to convert
Non-deterministic Finite Automata
 Non-deterministic Finite Automt From Regulr Expressions to NFA- Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion
Non-deterministic Finite Automt From Regulr Expressions to NFA- Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion
Lecture 09: Myhill-Nerode Theorem
 CS 373: Theory of Computtion Mdhusudn Prthsrthy Lecture 09: Myhill-Nerode Theorem 16 Ferury 2010 In this lecture, we will see tht every lnguge hs unique miniml DFA We will see this fct from two perspectives
CS 373: Theory of Computtion Mdhusudn Prthsrthy Lecture 09: Myhill-Nerode Theorem 16 Ferury 2010 In this lecture, we will see tht every lnguge hs unique miniml DFA We will see this fct from two perspectives
Good-for-Games Automata versus Deterministic Automata.
 Good-for-Gmes Automt versus Deterministic Automt. Denis Kuperberg 1,2 Mich l Skrzypczk 1 1 University of Wrsw 2 IRIT/ONERA (Toulouse) Séminire MoVe 12/02/2015 LIF, Luminy Introduction Deterministic utomt
Good-for-Gmes Automt versus Deterministic Automt. Denis Kuperberg 1,2 Mich l Skrzypczk 1 1 University of Wrsw 2 IRIT/ONERA (Toulouse) Séminire MoVe 12/02/2015 LIF, Luminy Introduction Deterministic utomt
Non-Deterministic Finite Automata. Fall 2018 Costas Busch - RPI 1
 Non-Deterministic Finite Automt Fll 2018 Costs Busch - RPI 1 Nondeterministic Finite Automton (NFA) Alphbet ={} q q2 1 q 0 q 3 Fll 2018 Costs Busch - RPI 2 Nondeterministic Finite Automton (NFA) Alphbet
Non-Deterministic Finite Automt Fll 2018 Costs Busch - RPI 1 Nondeterministic Finite Automton (NFA) Alphbet ={} q q2 1 q 0 q 3 Fll 2018 Costs Busch - RPI 2 Nondeterministic Finite Automton (NFA) Alphbet
NFAs and Regular Expressions. NFA-ε, continued. Recall. Last class: Today: Fun:
 CMPU 240 Lnguge Theory nd Computtion Spring 2019 NFAs nd Regulr Expressions Lst clss: Introduced nondeterministic finite utomt with -trnsitions Tody: Prove n NFA- is no more powerful thn n NFA Introduce
CMPU 240 Lnguge Theory nd Computtion Spring 2019 NFAs nd Regulr Expressions Lst clss: Introduced nondeterministic finite utomt with -trnsitions Tody: Prove n NFA- is no more powerful thn n NFA Introduce
CSC 473 Automata, Grammars & Languages 11/9/10
 CSC 473 utomt, Grmmrs & Lnguges 11/9/10 utomt, Grmmrs nd Lnguges Discourse 06 Decidbility nd Undecidbility Decidble Problems for Regulr Lnguges Theorem 4.1: (embership/cceptnce Prob. for DFs) = {, w is
CSC 473 utomt, Grmmrs & Lnguges 11/9/10 utomt, Grmmrs nd Lnguges Discourse 06 Decidbility nd Undecidbility Decidble Problems for Regulr Lnguges Theorem 4.1: (embership/cceptnce Prob. for DFs) = {, w is
12.1 Nondeterminism Nondeterministic Finite Automata. a a b ε. CS125 Lecture 12 Fall 2014
 CS125 Lecture 12 Fll 2014 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
CS125 Lecture 12 Fll 2014 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
First Midterm Examination
 24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
CS 275 Automata and Formal Language Theory
 CS 275 Automt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Problem (II) Chpter II.6.: Push Down Automt Remrk: This mteril is no longer tught nd not directly exm relevnt Anton Setzer (Bsed
CS 275 Automt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Problem (II) Chpter II.6.: Push Down Automt Remrk: This mteril is no longer tught nd not directly exm relevnt Anton Setzer (Bsed
Finite Automata. Informatics 2A: Lecture 3. John Longley. 22 September School of Informatics University of Edinburgh
 Lnguges nd Automt Finite Automt Informtics 2A: Lecture 3 John Longley School of Informtics University of Edinburgh jrl@inf.ed.c.uk 22 September 2017 1 / 30 Lnguges nd Automt 1 Lnguges nd Automt Wht is
Lnguges nd Automt Finite Automt Informtics 2A: Lecture 3 John Longley School of Informtics University of Edinburgh jrl@inf.ed.c.uk 22 September 2017 1 / 30 Lnguges nd Automt 1 Lnguges nd Automt Wht is
12.1 Nondeterminism Nondeterministic Finite Automata. a a b ε. CS125 Lecture 12 Fall 2016
 CS125 Lecture 12 Fll 2016 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
CS125 Lecture 12 Fll 2016 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
Learning Moore Machines from Input-Output Traces
 Lerning Moore Mchines from Input-Output Trces Georgios Gintmidis 1 nd Stvros Tripkis 1,2 1 Alto University, Finlnd 2 UC Berkeley, USA Motivtion: lerning models from blck boxes Inputs? Lerner Forml Model
Lerning Moore Mchines from Input-Output Trces Georgios Gintmidis 1 nd Stvros Tripkis 1,2 1 Alto University, Finlnd 2 UC Berkeley, USA Motivtion: lerning models from blck boxes Inputs? Lerner Forml Model
Regular Languages and Applications
 Regulr Lnguges nd Applictions Yo-Su Hn Deprtment of Computer Science Yonsei University 1-1 SNU 4/14 Regulr Lnguges An old nd well-known topic in CS Kleene Theorem in 1959 FA (finite-stte utomton) constructions:
Regulr Lnguges nd Applictions Yo-Su Hn Deprtment of Computer Science Yonsei University 1-1 SNU 4/14 Regulr Lnguges An old nd well-known topic in CS Kleene Theorem in 1959 FA (finite-stte utomton) constructions:
Normal Forms for Context-free Grammars
 Norml Forms for Context-free Grmmrs 1 Linz 6th, Section 6.2 wo Importnt Norml Forms, pges 171--178 2 Chomsky Norml Form All productions hve form: A BC nd A vrile vrile terminl 3 Exmples: S AS S AS S S
Norml Forms for Context-free Grmmrs 1 Linz 6th, Section 6.2 wo Importnt Norml Forms, pges 171--178 2 Chomsky Norml Form All productions hve form: A BC nd A vrile vrile terminl 3 Exmples: S AS S AS S S
Scanner. Specifying patterns. Specifying patterns. Operations on languages. A scanner must recognize the units of syntax Some parts are easy:
 Scnner Specifying ptterns source code tokens scnner prser IR A scnner must recognize the units of syntx Some prts re esy: errors mps chrcters into tokens the sic unit of syntx x = x + y; ecomes
Scnner Specifying ptterns source code tokens scnner prser IR A scnner must recognize the units of syntx Some prts re esy: errors mps chrcters into tokens the sic unit of syntx x = x + y; ecomes
CS 330 Formal Methods and Models Dana Richards, George Mason University, Spring 2016 Quiz Solutions
 CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2016 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 9 1. (4pts) ((p q) (q r)) (p r), prove tutology using truth tles. p
CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2016 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 9 1. (4pts) ((p q) (q r)) (p r), prove tutology using truth tles. p
Lecture 6 Regular Grammars
 Lecture 6 Regulr Grmmrs COT 4420 Theory of Computtion Section 3.3 Grmmr A grmmr G is defined s qudruple G = (V, T, S, P) V is finite set of vribles T is finite set of terminl symbols S V is specil vrible
Lecture 6 Regulr Grmmrs COT 4420 Theory of Computtion Section 3.3 Grmmr A grmmr G is defined s qudruple G = (V, T, S, P) V is finite set of vribles T is finite set of terminl symbols S V is specil vrible
Context-Free Grammars and Languages
 Context-Free Grmmrs nd Lnguges (Bsed on Hopcroft, Motwni nd Ullmn (2007) & Cohen (1997)) Introduction Consider n exmple sentence: A smll ct ets the fish English grmmr hs rules for constructing sentences;
Context-Free Grmmrs nd Lnguges (Bsed on Hopcroft, Motwni nd Ullmn (2007) & Cohen (1997)) Introduction Consider n exmple sentence: A smll ct ets the fish English grmmr hs rules for constructing sentences;
80 CHAPTER 2. DFA S, NFA S, REGULAR LANGUAGES. 2.6 Finite State Automata With Output: Transducers
 80 CHAPTER 2. DFA S, NFA S, REGULAR LANGUAGES 2.6 Finite Stte Automt With Output: Trnsducers So fr, we hve only considered utomt tht recognize lnguges, i.e., utomt tht do not produce ny output on ny input
80 CHAPTER 2. DFA S, NFA S, REGULAR LANGUAGES 2.6 Finite Stte Automt With Output: Trnsducers So fr, we hve only considered utomt tht recognize lnguges, i.e., utomt tht do not produce ny output on ny input
CISC 4090 Theory of Computation
 9/6/28 Stereotypicl computer CISC 49 Theory of Computtion Finite stte mchines & Regulr lnguges Professor Dniel Leeds dleeds@fordhm.edu JMH 332 Centrl processing unit (CPU) performs ll the instructions
9/6/28 Stereotypicl computer CISC 49 Theory of Computtion Finite stte mchines & Regulr lnguges Professor Dniel Leeds dleeds@fordhm.edu JMH 332 Centrl processing unit (CPU) performs ll the instructions
Formal Language and Automata Theory (CS21004)
 Forml Lnguge nd Automt Forml Lnguge nd Automt Theory (CS21004) Khrgpur Khrgpur Khrgpur Forml Lnguge nd Automt Tle of Contents Forml Lnguge nd Automt Khrgpur 1 2 3 Khrgpur Forml Lnguge nd Automt Forml Lnguge
Forml Lnguge nd Automt Forml Lnguge nd Automt Theory (CS21004) Khrgpur Khrgpur Khrgpur Forml Lnguge nd Automt Tle of Contents Forml Lnguge nd Automt Khrgpur 1 2 3 Khrgpur Forml Lnguge nd Automt Forml Lnguge
NFAs continued, Closure Properties of Regular Languages
 lgorithms & Models of omputtion S/EE 374, Spring 209 NFs continued, losure Properties of Regulr Lnguges Lecture 5 Tuesdy, Jnury 29, 209 Regulr Lnguges, DFs, NFs Lnguges ccepted y DFs, NFs, nd regulr expressions
lgorithms & Models of omputtion S/EE 374, Spring 209 NFs continued, losure Properties of Regulr Lnguges Lecture 5 Tuesdy, Jnury 29, 209 Regulr Lnguges, DFs, NFs Lnguges ccepted y DFs, NFs, nd regulr expressions
Formal Methods in Software Engineering
 Forml Methods in Softwre Engineering Lecture 09 orgniztionl issues Prof. Dr. Joel Greenyer Decemer 9, 2014 Written Exm The written exm will tke plce on Mrch 4 th, 2015 The exm will tke 60 minutes nd strt
Forml Methods in Softwre Engineering Lecture 09 orgniztionl issues Prof. Dr. Joel Greenyer Decemer 9, 2014 Written Exm The written exm will tke plce on Mrch 4 th, 2015 The exm will tke 60 minutes nd strt
Finite Automata. Informatics 2A: Lecture 3. Mary Cryan. 21 September School of Informatics University of Edinburgh
 Finite Automt Informtics 2A: Lecture 3 Mry Cryn School of Informtics University of Edinburgh mcryn@inf.ed.c.uk 21 September 2018 1 / 30 Lnguges nd Automt Wht is lnguge? Finite utomt: recp Some forml definitions
Finite Automt Informtics 2A: Lecture 3 Mry Cryn School of Informtics University of Edinburgh mcryn@inf.ed.c.uk 21 September 2018 1 / 30 Lnguges nd Automt Wht is lnguge? Finite utomt: recp Some forml definitions
CS 275 Automata and Formal Language Theory
 CS 275 Automt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Problem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) Anton Setzer (Bsed on book drft by J. V. Tucker nd K. Stephenson)
CS 275 Automt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Problem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) Anton Setzer (Bsed on book drft by J. V. Tucker nd K. Stephenson)
Regular languages refresher
 Regulr lnguges refresher 1 Regulr lnguges refresher Forml lnguges Alphet = finite set of letters Word = sequene of letter Lnguge = set of words Regulr lnguges defined equivlently y Regulr expressions Finite-stte
Regulr lnguges refresher 1 Regulr lnguges refresher Forml lnguges Alphet = finite set of letters Word = sequene of letter Lnguge = set of words Regulr lnguges defined equivlently y Regulr expressions Finite-stte
Non Deterministic Automata. Linz: Nondeterministic Finite Accepters, page 51
 Non Deterministic Automt Linz: Nondeterministic Finite Accepters, pge 51 1 Nondeterministic Finite Accepter (NFA) Alphbet ={} q 1 q2 q 0 q 3 2 Nondeterministic Finite Accepter (NFA) Alphbet ={} Two choices
Non Deterministic Automt Linz: Nondeterministic Finite Accepters, pge 51 1 Nondeterministic Finite Accepter (NFA) Alphbet ={} q 1 q2 q 0 q 3 2 Nondeterministic Finite Accepter (NFA) Alphbet ={} Two choices
Some Theory of Computation Exercises Week 1
 Some Theory of Computtion Exercises Week 1 Section 1 Deterministic Finite Automt Question 1.3 d d d d u q 1 q 2 q 3 q 4 q 5 d u u u u Question 1.4 Prt c - {w w hs even s nd one or two s} First we sk whether
Some Theory of Computtion Exercises Week 1 Section 1 Deterministic Finite Automt Question 1.3 d d d d u q 1 q 2 q 3 q 4 q 5 d u u u u Question 1.4 Prt c - {w w hs even s nd one or two s} First we sk whether
CMSC 330: Organization of Programming Languages. DFAs, and NFAs, and Regexps (Oh my!)
 CMSC 330: Orgniztion of Progrmming Lnguges DFAs, nd NFAs, nd Regexps (Oh my!) CMSC330 Spring 2018 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All
CMSC 330: Orgniztion of Progrmming Lnguges DFAs, nd NFAs, nd Regexps (Oh my!) CMSC330 Spring 2018 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All
Lexical Analysis Part III
 Lexicl Anlysis Prt III Chpter 3: Finite Automt Slides dpted from : Roert vn Engelen, Florid Stte University Alex Aiken, Stnford University Design of Lexicl Anlyzer Genertor Trnslte regulr expressions to
Lexicl Anlysis Prt III Chpter 3: Finite Automt Slides dpted from : Roert vn Engelen, Florid Stte University Alex Aiken, Stnford University Design of Lexicl Anlyzer Genertor Trnslte regulr expressions to
5. (±±) Λ = fw j w is string of even lengthg [ 00 = f11,00g 7. (11 [ 00)± Λ = fw j w egins with either 11 or 00g 8. (0 [ ffl)1 Λ = 01 Λ [ 1 Λ 9.
 Regulr Expressions, Pumping Lemm, Right Liner Grmmrs Ling 106 Mrch 25, 2002 1 Regulr Expressions A regulr expression descries or genertes lnguge: it is kind of shorthnd for listing the memers of lnguge.
Regulr Expressions, Pumping Lemm, Right Liner Grmmrs Ling 106 Mrch 25, 2002 1 Regulr Expressions A regulr expression descries or genertes lnguge: it is kind of shorthnd for listing the memers of lnguge.
NFAs continued, Closure Properties of Regular Languages
 Algorithms & Models of Computtion CS/ECE 374, Fll 2017 NFAs continued, Closure Properties of Regulr Lnguges Lecture 5 Tuesdy, Septemer 12, 2017 Sriel Hr-Peled (UIUC) CS374 1 Fll 2017 1 / 31 Regulr Lnguges,
Algorithms & Models of Computtion CS/ECE 374, Fll 2017 NFAs continued, Closure Properties of Regulr Lnguges Lecture 5 Tuesdy, Septemer 12, 2017 Sriel Hr-Peled (UIUC) CS374 1 Fll 2017 1 / 31 Regulr Lnguges,
Compiler Design. Fall Lexical Analysis. Sample Exercises and Solutions. Prof. Pedro C. Diniz
 University of Southern Cliforni Computer Science Deprtment Compiler Design Fll Lexicl Anlysis Smple Exercises nd Solutions Prof. Pedro C. Diniz USC / Informtion Sciences Institute 4676 Admirlty Wy, Suite
University of Southern Cliforni Computer Science Deprtment Compiler Design Fll Lexicl Anlysis Smple Exercises nd Solutions Prof. Pedro C. Diniz USC / Informtion Sciences Institute 4676 Admirlty Wy, Suite
1.4 Nonregular Languages
 74 1.4 Nonregulr Lnguges The number of forml lnguges over ny lphbet (= decision/recognition problems) is uncountble On the other hnd, the number of regulr expressions (= strings) is countble Hence, ll
74 1.4 Nonregulr Lnguges The number of forml lnguges over ny lphbet (= decision/recognition problems) is uncountble On the other hnd, the number of regulr expressions (= strings) is countble Hence, ll
