Statistics of supersymmetric vacua in string/m theory
|
|
|
- Vincent Stevenson
- 5 years ago
- Views:
Transcription
1 Statistics of supersymmetric vacua in string/m theory Steve Zelditch Department of Mathematics Johns Hopkins University Joint Work with Bernard Shiffman Mike Douglas 1
2 Supergravity theory An effective supergravity theory T by data (C, K, W ): is defined a configuration space C, a complex manifold with Kähler metric ω, with Kähler potential K(z, z), ω = K. The associated holomorphic line bundle L over C, such that c 1 (L) = ω. A hermitian metric W and a natural holomorphic metric connection with curvature ω. A superpotential W, which is a (locally) holomorphic section of L. 2
3 The potential Physicists write a section locally as a holomorhic function W. Then the Hermitian metric is written W 2 = e K W 2 ; and the covariant derivative of a section W is i W i W + ( i K)W. The scalar potential V is the following function on C, (1) V = e K ( g i j (D i W )( D j W ) 3 W 2) where W ( z) is the complex conjugate section and D j W = p j W + ( p j K)W. The choice of V is dicated by supersymmetry (see Wess-Bagger). 3
4 Vacua A vacuum is then a critical point p C of V. The vacua are further distinguished as follows: A supersymmetric vacuum is one in which the covariant gradient D i W = 0. This can be seen to imply V = 0, but the converse is not true. A non-supersymmetric vacuum is one in which D i W 0. The norm of the gradient, (2) M 4 susy ek g i j D i W D j W, is then referred to as the scale of supersymmetry breaking. 4
5 Cosmological constant The value of V at a critical point is the cosmological constant Λ of that vacuum. These are divided into Λ = 0, the Minkowski vacua, Λ > 0, the de Sitter (or ds) vacua, and Λ < 0, the Anti-de Sitter (or AdS) vacua. It is easy to see that supersymmetric vacua can only be Minkowski or AdS. The Minkowski vacua are simultaneous solutions of D i W = W = 0; in this case D i W = i W and the existence of such vacua is independent of the Kähler potential. On the other hand, this is an overdetermined set of equations, so supersymmetric Minkowski vacua are not generic. 5
6 Stable vacua A stable vacuum is one in which small fluctuations of the fields will not grow exponentially. One might think that the condition for this is for the Hessian V to be non-negative definite. This is correct in a Minkowski vacuum, but in curved space-time the linearized equations of motion also get a contribution from the background curvature, and in AdS the spatial boundary conditions are treated differently, changing the discussion. For AdS 4, the correct stability condition is [?] i j V 3 4 Λg ij. It can be shown that this is always satisfied by supersymmetric vacua. 6
7 Physical questions about vacua Find the expected number of stable supersymmetric vacua, or the ratio between the expected numbers of supersymmetric and stable non-supersymmetric vacua. More generally, one wants to know which parameters control this ratio. Having found stable non-supersymmetric vacua, the next most basic question is to understand the cosmological constant Λ, the value of V at the minimum. Our universe at present is clearly very similar to Minkowski space-time, but according to recent observations there is a non-zero dark energy which can be fit by taking Λ > 0 and small. If this is actually a cosmological constant, in the distant future the universe 7
8 will asymptotically approach the de Sitter space-time. If there are many candidate vacua, the next general question which emerges is their distribution in the configuration space. Although this is complicated in its details, one would like to know whether or not the vacua which pass the previous tests are roughly uniformly distributed with respect to the natural measure (the volume form obtained from the Kähler form). Finally, one would like to consider more global definitions of stability. In particular, a vacuum with Λ = Λ 1 > 0 can tunnel or decay to another vacuum (refs) with Λ 1 > Λ = Λ 2 0, at a rate roughly given by the exponential of the action exp dz V (z) g i j (z)żi z j.
9 Finally, there are questions which are simpler than literally counting critical points, but still relevant. Our basic example is the following. The problem of counting critical points of a section is not a holomorphic problem, because of the presence of the nonholomorphic connection K. Thus, critical points come with a non-zero Morse sign sgn det D i D j W (here i, j are real coordinates). The simplest definition of counting critical points is to count with this sign, I = DW (p)=0 sgn det i,j D id j W p. This was called the supergravity index in [?], and is closely related to the Morse index of the norm of the section, e K W, but is not literally the same if W has zeroes. It is invariant under appropriate continuous deformations of the section and metric.
10 Since this quantity is easier to compute than the literal number of critical points, it is of interest to know in what circumstances and how well it estimates the number of critical points, of the two types we discussed. Similar comments might be relevant for counting critical points of V. Of course, at a minimum V > 0 this sign is positive, but as we mentioned the AdS stability condition allows for some negative eigenvalues. To summarize, we would like to know the expected distribution of critical points of W (supersymmetric) and of V (nonsupersymmetric if DW 0), the expected distribution of W 2 at the critical points in the supersymmetric case, and the expected joint distribution of Msusy 4 and V in the nonsupersymmetric case.
11 Connection We start with a choice of a d complex dimensional Calabi-Yau manifold M, i.e. a complex Kähler manifold with c 1 (M) = 0. The topological data of M of primary relevance for us is its middle cohomology H d (M, Z). This carries an intersection form η ij = (Σ i, Σ j ), symmetric (antisymmetric) for d even (odd). This form is preserved by a linear action of SO(b + (M), b (M); Z) for d even, or Sp(b d (M); Z) for d odd. We denote this group as G(η). By Yau s theorem, such a manifold admits Ricciflat Kähler metrics, which come in a family parameterized locally by a choice of complex structure on M and a choice of Kähler class. One can show that the moduli space of complex structures M c (M) is an (open) manifold of dimension b d 1,1 (M). 8
12 One can also think of the complex structure as locally determined by a choice of nonvanishing holomorphic d-form Ω, or by its cohomology class [Ω] H d (M, C). In some cases, this has been extended to a global Torelli theorem (ref Voisin). Conversely, Ω is uniquely determined by the complex structure up to its overall scale. Let M c (M) be the moduli space of complex structures; the association we just described gives a local embedding M c (M) CP(H d (M, C)) CP(V ), the period map. Pairing this with a basis for H d (M, Z) gives a basis for the periods, which we can denote Π i. The moduli space of complex structures carries a natural Kähler metric, given by the Kähler potential e K = M Ω Ω.
13 Then, the periods are locally sections of the line bundle L associated to this metric. They are not global sections over M c (M), because of monodromy: M c (M) is singular in codimension one (for a hypersurface f = 0, this is on the discriminant locus) and a closed loop encircling this singularity induces a Picard-Lefschetz monodromy on H d (M, Z). We can regard the periods either as sections of V L where V is a flat G(η) vector bundle, or simply as sections of L over an appropriate covering space of M c (M). We now have the ingredients required to define the effective supergravity theories (in the flux sector) for the string compactifications of interest. They each have C = M c (M) and K = K M. Finally, for each choice of the flux N H d (M, Z), the theory T (N) has (3) W = (Ω, N).
14 The simplest example of the structure above is to take M to be a complex torus C d /L with L a 2d-dimensional lattice. We then have M c (M) the Siegel upper half plane, with coordinate τ a d d complex matrix with positive definite imaginary part. The Kähler potential is K = log det Iτ, and a Z-basis for the periods can be taken to be the minors of τ of all ranks: 1, τ ij,..., (cof τ) ij, det τ. The case d = 3 arises in heterotic string compactification on T 6. F theory compactification on T 8 /Z 2 leads to a problem which is can be obtained from the case d = 4 of what we discussed, by restriction to the subspace of M c in which τ is a direct sum of a rank 1 and a rank 3 matrix (in other words, the torus must admit an elliptic fibration). The physical problem of interest is then more or less the one we discussed, in which the
15 ensemble of sections is the set of periods of H d (M, Z). In the case of even d, one takes the sum with fixed self-intersection (N, N). The same problems can be discussed for more general Calabi-Yau manifolds by using the theory of deformation of Hodge structure. The periods satisfy Picard-Fuchs equations, which are generalized hypergeometric equations. Their explicit solutions are known in many cases. Quite a lot is known about the possible singular behaviors of these periods, which are expected to have an important effect on the distributions we are discussing. One common case is for a pair of conjugate periods (under the intersection form) to behave as z and z log z. Critical points of sections W = Mz + Nz log z then can have exponentially small values for Λ and Msusy 4, giving a mechanism to realize
16 the small numbers hoped for in the previous discussion. In physics, the d = 3 case is extensively studied, and leads to a structure called special geometry. This essentially states that the image of the period map is a complex Lagrangian submanifold of H 3 (M, C), and thus is determined by a single holomorphic function (the prepotential ). This is extremely useful in the applications and leads to a fairly developed theory for finding these critical points.
17 Mathematical discussion We begin with a precise definition of critical points of a holomorhic section s H 0 (M, L). It depends on a connection on L = the Chern connection = h which preserves the metric h and satisfies s = 0 for any holomorphic section s. Here, = + is the splitting of the connection into its L T 1,0 resp. L T 0,1 parts. We denote by Θ h the curvature of h. Definition: Let (L, h) M be a Hermitian holomorphic line bundle over a complex manifold M, and let = h be its Chern connection. A critical point of a holomorphic section s H 0 (M, L) is defined to be a point z M where s(z) = 0, or equivalently, s(z) = 0. We denote the set of critical points of s with respect to the Chern connection of a Hermitian metric h by Crit(s, h). 9
18 Critical points depend on the metric The set of critical points Crit(s, h) of s, and even its number #Crit(s, h), depends on h or equivalently on the metric h. Recall that the connection 1-form α of h is given in a local frame e by e = α e, α = log h. In the local frame, s = f e where f is a local holomorphic function and then s = ( f + αf) e. Thus the critical point equation in local coordinates reads: (4) f = fα log f = log h. This is a real C equation, not a holomorphic one. 10
19 Another definition of critical point An essentially equivalent definition which only makes use of real functions is to define a critical point as a point w where (5) d s(w) 2 h = 0. Since d s(w) 2 h = 0 0 = s(w) 2 h = h w( s(w), s(w)) it follows that s(w) = 0 as long as s(w) 0. So this notion of critical point is the union of the zeros and critical points. Another essentially equivalent critical point equation which puts the zero set of s at is (6) d log s(w) 2 h = 0. This is the equation studied by Bott in his Morse theoretic proof of the Lefschetz hyperplane theorem, which is based on the observation that the Morse index of any such critical point is at least m. 11
20 Statistics of sections Our purpose is to study the statistics of critical points of random sections with respect to complex Gaussian measures γ on the space H 0 (M, L) of holomorphic sections, or more generally on subspaces S H 0 (M, L). The Gaussian measure γ = γ S,h,V is induced by the inner product (7) s 1, s 2 = h(s 1(z), s 2 (z))dv (z) M on H 0 (M, L), where dv is a fixed volume form on M. When the metric and volume form and subspace are fixed we denote the Gaussian measure more simply by γ. By definition, (8) dγ(s) = 1 π de c 2 dc, s = d j=1 c j e j, where dc is Lebesgue measure and {e j } is an orthonormal basis basis for S relative to h, dv. We also denote the expected value of a random variable X on with respect to γ by E γ or simply by E if the Gaussian measure γ is understood. 12
21 Density of critical points The critical point density of a fixed section s with respect to h (or h ) is the measure (9) C h s := z Crit(s,h) δ z, where δ z is the Dirac point mass at z. Definition: The expected density of critical points of s S H 0 (M, L) with respect to h and V is defined by (10) K crit S,h,V (z) dv (z) = E γ S,h,V C h s, i.e., (11) M ϕ(z)kcrit S,h,V (z) dv (z) = S z: h s(z)=0 ϕ(z) dγ S,h,V ( 13
22 Expected number of critical points Definition: We further define the expected number of critical points by (12) N crit (S, h, V ) = M Kcrit S,h,V (z) dv (z). To state the result, it is most convenient to introduce a local frame (non-vanishing holomorphic section) e L for L over an open set U M containing z, and local coordinates (z 1,..., z m ) on U in which the local connection form has zero pure holomorphic and antiholomorphic derivatives. We denote the curvature (1, 1)-form of in these coordinates by Θ = m Θ i, j=1 i j dzi d z j and refer to the m m 14
23 matrix [Θ i, j ] as the curvature matrix of. We also denote by Sym(m, C) the space of complex m m symmetric matrices. Theorem 1 Let (S,, γ) denote as above a finite-dimensional subspace S H 0 (M, L) of holomorphic sections of a holomorphic line bundle (L, ) M with connection on an m- dimensional complex manifold, together with a Gaussian measure γ on S. Assume that S satisfies the 2-jet spanning property. Given a local frame e L and adapted coordinates z = (z 1,..., z m ), there exist positive-definite Hermitian matrices A(z) : C m C m, Λ(z) : Sym(m, C) C Sym(m, C) depending only on z, and Π S such that the expected density of critical points with respect to Lebesgue measure dz in local coordinates is
24 given by K crit S,γ, (z) = 1 C π (m+2 2 ) det A(z) det Λ(z) Sym(m,C) det ( H x Θ(z) x Θ(z) H ) e Λ(z) 1 (H x), H x dh dx, where Θ(z) = [Θ i j ] is the curvature matrix of in the coordinates (z 1,..., z m ). The expected distribution of zeros KS,γ, crit (z)dz is independent of the choice of frame and coordinates.
25 Density of critical points The formulae for A(z) and Λ(z) in adapted local normal coordinates are as follows. Let F S (z, w) be the local expression for Π S (z, w) in the frame e L. Then A(z) is () and Λ = C B A 1 B, where ( ) A = 2 z j w F j S(z, w) z=w, [( ) ( )] B = 3 z j w q w )F j S z=w ( z F j S z=w, C = ( ) ( ) 4 z q z j w q w F j S 2 z=w z j z q F S ( 2 w q w j F S ) z=w F S (z, z), 1 j m, 1 j q m, 1 j q In the above, A, B, C are m m, m n, n n matrices, respectively, where n = 1 2 (m2 + m + 2). T 15
26 Expected number of critical points for positive line bundles We assume that ω = i 2 Θ h so that c 1 (L) = [ 1 π ω] or [1 π ω]. More precisely, the Kähler form is given by ω = ± i 2 Θ h = ± i 2 K, K = log h. The volume form is then assumed to be dv = ωm m! (and thus the total volume of M is πm m! c 1(L) m ). Given one such metric h 0 on L, the other metrics have the form h ϕ = e ϕ h and Θ h = Θ h0 ϕ, with ϕ C (M). As a consequence of Lemma 1, we obtain the following integral formula for K crit in these cases: Lemma 1 Let (L, h) M denote a positive or negative holomorphic line bundle, and suppose that H 0 (M, L) contains a finite-dimensional subspace S with the 1-jet spanning property. Give 16
27 M the volume form dv = 1 m! ( ± i 2 Θ h ) m induced from the curvature of L. Then there exist positive Hermitian matrices A(z), Λ(z) (cf. (??)) depending on h and z such that K crit h,s (z) = 1 π (m+2 2 ) det A det Λ Sym(m,C) C det(h H x 2 I) e Λ(z) 1 (H,x),(H,x) dh dx. Here, H Sym(m, C) is a complex symmetric matrix, and the matrix Λ is a Hermitian operator on the complex vector space Sym(m, C) C.
28 Universal limit theorem Our main result gives an associated asymptotic expansion for KN crit(z): Theorem 2 For any positive Hermitian line bundle (L, h) (M, ω) over any compact Kähler manifold, the critical point density has an asymptotic expansion of the form N m KN crit (z) Γcrit m +a 1(z)N 1 +a 2 (z)n 2 +, where Γ crit m is a universal constant depending only on the dimension m of M. Hence the expected total number of critical points on M is N (h N ) = πm m! Γcrit m c 1(L) m N m + O(N m 1 ). The leading constant in the expansion is given by the integral formula Γ crit m = ( 2π m+3 2 ) m + 0 Sym(m,C) det(ss ti) e 1 2 S 2 HS t ds dt, 17
29 Riemann surfaces The universality of the principal term may seem rather surprising in view of the fact that the number of critical points depends on the metric. In the case of Riemann surfaces, we can explicitly evaluate the leading coefficient: Corollary 3 For the case where M is a Riemann surface, we have Γ crit 1 = 3π 5, and hence the expected number of critical points is N (h N ) = 5 3 c 1 (L)N + O( N). The expected number of saddle points is 4 3N while the expected number of local maxima is 1 3 N. There are N critical points of a polynomial of degree N in the classical sense, all of which are saddle points. 18
30 Metrics with minimal number of critical points It is natural to wonder which hermitian metrics produce the minimal expected number of critical points. To put the question precisely, let L (M, [ω]) be a holomorphic line bundle over any compact Kähler manifold with c 1 (L) = [ω], and consider the space of Hermitian metrics h on L for which the curvature form is a positive (1, 1) form: P (M, [ω]) = {h : i Θ(h) is a positive (1, 1) form }. 2 Definition: We say that h P ([ω]) is asymptotically minimal if (13) N 0 : N N 0, N (h N ) N (h N 1 ), h 1 P ([ω]). 19
31 Density of critical points on Riemann surfaces We measure the critical point density with respect to the volume form ± 2 i Θ h. Put: Q = and denote the eigenvalues of Λ(z)Q by µ 1, µ 2. We observe that µ 1, µ 2 have opposite signs since det QΛ = det Λ < 0. Let µ 2 < 0 < µ 1. Theorem 4 let (L, h) M be a positive or negative Hermitian line bundle on a (possibly non-compact) Riemann surface M with volume form dv = ± i 2 Θ h, and let S be a finitedimensional subset of H 0 (M, L) with the 1-jet spanning property. Then: K crit h (z) = 1 πa(z) µ µ2 2 µ 1 + µ 2 = 1 πa(z) where µ 1, µ 2 are as above. T r Λ 2 T r Λ 1 2QΛ 1 2, 20
32 Exact formula on CP 1 Theorem 5 The expected number of critical points of a random section s N H 0 (CP 1, O(N)) (with respect to the Gaussian measure on H 0 (CP 1, O(N induced from the Fubini-Study metrics on O(N) and CP 1 ) is 5N 2 8N + 4 3N 2 = 5 3 N N 1. 21
33 Asymptotically minimal number of critical points Integrating the density of critical points, we find that the expected total number of critical points has the expansion N (h N ) = πm m! Γcrit m c 1(L) m N m + M ρdv ωn m 1 +C m M ρ2 dv Ω N m 2 + O(N m 3 ). The leading order term is universal, so the metric with asymptotically minimal N (h N ) is the one with minimal M ρ2 dv ω, at least assuming that it is non-universal. 22
How to count universes in string theory.
 Random Complex Geometry, or How to count universes in string theory. Steve Zelditch Department of Mathematics Johns Hopkins University AMS meeting Atlanta Friday, January 7, 2005: 10: 05-10: 55 Joint work
Random Complex Geometry, or How to count universes in string theory. Steve Zelditch Department of Mathematics Johns Hopkins University AMS meeting Atlanta Friday, January 7, 2005: 10: 05-10: 55 Joint work
arxiv:math/ v2 [math.cv] 4 Jun 2004
![arxiv:math/ v2 [math.cv] 4 Jun 2004 arxiv:math/ v2 [math.cv] 4 Jun 2004](/thumbs/91/105507516.jpg) CRITICAL POINTS AND SUPERSYMMETRIC VACUA MICHAEL R. DOUGLAS, BERNARD SHIFFMAN, AND STEVE ZELDITCH arxiv:math/0402326v2 [math.cv] 4 Jun 2004 Abstract. Supersymmetric vacua ( universes ) of string/m theory
CRITICAL POINTS AND SUPERSYMMETRIC VACUA MICHAEL R. DOUGLAS, BERNARD SHIFFMAN, AND STEVE ZELDITCH arxiv:math/0402326v2 [math.cv] 4 Jun 2004 Abstract. Supersymmetric vacua ( universes ) of string/m theory
From Random Polynomials to String Theory
 From Random Polynomials to String Theory Steve Zelditch Department of Mathematics Johns Hopkins University Madison, Wisconsin Friday, October 7, 4PM B239 Joint work with M. R. Douglas and B. Shiffman 1
From Random Polynomials to String Theory Steve Zelditch Department of Mathematics Johns Hopkins University Madison, Wisconsin Friday, October 7, 4PM B239 Joint work with M. R. Douglas and B. Shiffman 1
Two simple ideas from calculus applied to Riemannian geometry
 Calibrated Geometries and Special Holonomy p. 1/29 Two simple ideas from calculus applied to Riemannian geometry Spiro Karigiannis karigiannis@math.uwaterloo.ca Department of Pure Mathematics, University
Calibrated Geometries and Special Holonomy p. 1/29 Two simple ideas from calculus applied to Riemannian geometry Spiro Karigiannis karigiannis@math.uwaterloo.ca Department of Pure Mathematics, University
RANDOM COMPLEX GEOMETRY AND VACUA, OR: HOW TO COUNT UNIVERSES IN STRING/M THEORY
 RANDOM COMPLEX GEOMETRY AND VACUA, OR: HOW TO COUNT UNIVERSES IN STRING/M THEORY STEVE ZELDITCH Abstract. This lecture is concerned with counting and equidistribution problems for critical points of random
RANDOM COMPLEX GEOMETRY AND VACUA, OR: HOW TO COUNT UNIVERSES IN STRING/M THEORY STEVE ZELDITCH Abstract. This lecture is concerned with counting and equidistribution problems for critical points of random
Calabi-Yau Fourfolds with non-trivial Three-Form Cohomology
 Calabi-Yau Fourfolds with non-trivial Three-Form Cohomology Sebastian Greiner arxiv: 1512.04859, 1702.03217 (T. Grimm, SG) Max-Planck-Institut für Physik and ITP Utrecht String Pheno 2017 Sebastian Greiner
Calabi-Yau Fourfolds with non-trivial Three-Form Cohomology Sebastian Greiner arxiv: 1512.04859, 1702.03217 (T. Grimm, SG) Max-Planck-Institut für Physik and ITP Utrecht String Pheno 2017 Sebastian Greiner
BERGMAN KERNEL ON COMPACT KÄHLER MANIFOLDS
 BERGMAN KERNEL ON COMPACT KÄHLER MANIFOLDS SHOO SETO Abstract. These are the notes to an expository talk I plan to give at MGSC on Kähler Geometry aimed for beginning graduate students in hopes to motivate
BERGMAN KERNEL ON COMPACT KÄHLER MANIFOLDS SHOO SETO Abstract. These are the notes to an expository talk I plan to give at MGSC on Kähler Geometry aimed for beginning graduate students in hopes to motivate
Flux Compactification of Type IIB Supergravity
 Flux Compactification of Type IIB Supergravity based Klaus Behrndt, LMU Munich Based work done with: M. Cvetic and P. Gao 1) Introduction 2) Fluxes in type IIA supergravity 4) Fluxes in type IIB supergravity
Flux Compactification of Type IIB Supergravity based Klaus Behrndt, LMU Munich Based work done with: M. Cvetic and P. Gao 1) Introduction 2) Fluxes in type IIA supergravity 4) Fluxes in type IIB supergravity
MIFPA PiTP Lectures. Katrin Becker 1. Department of Physics, Texas A&M University, College Station, TX 77843, USA. 1
 MIFPA-10-34 PiTP Lectures Katrin Becker 1 Department of Physics, Texas A&M University, College Station, TX 77843, USA 1 kbecker@physics.tamu.edu Contents 1 Introduction 2 2 String duality 3 2.1 T-duality
MIFPA-10-34 PiTP Lectures Katrin Becker 1 Department of Physics, Texas A&M University, College Station, TX 77843, USA 1 kbecker@physics.tamu.edu Contents 1 Introduction 2 2 String duality 3 2.1 T-duality
Heterotic Torsional Backgrounds, from Supergravity to CFT
 Heterotic Torsional Backgrounds, from Supergravity to CFT IAP, Université Pierre et Marie Curie Eurostrings@Madrid, June 2010 L.Carlevaro, D.I. and M. Petropoulos, arxiv:0812.3391 L.Carlevaro and D.I.,
Heterotic Torsional Backgrounds, from Supergravity to CFT IAP, Université Pierre et Marie Curie Eurostrings@Madrid, June 2010 L.Carlevaro, D.I. and M. Petropoulos, arxiv:0812.3391 L.Carlevaro and D.I.,
HYPERKÄHLER MANIFOLDS
 HYPERKÄHLER MANIFOLDS PAVEL SAFRONOV, TALK AT 2011 TALBOT WORKSHOP 1.1. Basic definitions. 1. Hyperkähler manifolds Definition. A hyperkähler manifold is a C Riemannian manifold together with three covariantly
HYPERKÄHLER MANIFOLDS PAVEL SAFRONOV, TALK AT 2011 TALBOT WORKSHOP 1.1. Basic definitions. 1. Hyperkähler manifolds Definition. A hyperkähler manifold is a C Riemannian manifold together with three covariantly
Elements of Topological M-Theory
 Elements of Topological M-Theory (with R. Dijkgraaf, S. Gukov, C. Vafa) Andrew Neitzke March 2005 Preface The topological string on a Calabi-Yau threefold X is (loosely speaking) an integrable spine of
Elements of Topological M-Theory (with R. Dijkgraaf, S. Gukov, C. Vafa) Andrew Neitzke March 2005 Preface The topological string on a Calabi-Yau threefold X is (loosely speaking) an integrable spine of
String-Theory: Open-closed String Moduli Spaces
 String-Theory: Open-closed String Moduli Spaces Heidelberg, 13.10.2014 History of the Universe particular: Epoch of cosmic inflation in the early Universe Inflation and Inflaton φ, potential V (φ) Possible
String-Theory: Open-closed String Moduli Spaces Heidelberg, 13.10.2014 History of the Universe particular: Epoch of cosmic inflation in the early Universe Inflation and Inflaton φ, potential V (φ) Possible
SYMPLECTIC GEOMETRY: LECTURE 5
 SYMPLECTIC GEOMETRY: LECTURE 5 LIAT KESSLER Let (M, ω) be a connected compact symplectic manifold, T a torus, T M M a Hamiltonian action of T on M, and Φ: M t the assoaciated moment map. Theorem 0.1 (The
SYMPLECTIC GEOMETRY: LECTURE 5 LIAT KESSLER Let (M, ω) be a connected compact symplectic manifold, T a torus, T M M a Hamiltonian action of T on M, and Φ: M t the assoaciated moment map. Theorem 0.1 (The
Pietro Fre' SISSA-Trieste. Paolo Soriani University degli Studi di Milano. From Calabi-Yau manifolds to topological field theories
 From Calabi-Yau manifolds to topological field theories Pietro Fre' SISSA-Trieste Paolo Soriani University degli Studi di Milano World Scientific Singapore New Jersey London Hong Kong CONTENTS 1 AN INTRODUCTION
From Calabi-Yau manifolds to topological field theories Pietro Fre' SISSA-Trieste Paolo Soriani University degli Studi di Milano World Scientific Singapore New Jersey London Hong Kong CONTENTS 1 AN INTRODUCTION
Generalized N = 1 orientifold compactifications
 Generalized N = 1 orientifold compactifications Thomas W. Grimm University of Wisconsin, Madison based on: [hep-th/0602241] Iman Benmachiche, TWG [hep-th/0507153] TWG Madison, Wisconsin, November 2006
Generalized N = 1 orientifold compactifications Thomas W. Grimm University of Wisconsin, Madison based on: [hep-th/0602241] Iman Benmachiche, TWG [hep-th/0507153] TWG Madison, Wisconsin, November 2006
Complex manifolds, Kahler metrics, differential and harmonic forms
 Complex manifolds, Kahler metrics, differential and harmonic forms Cattani June 16, 2010 1 Lecture 1 Definition 1.1 (Complex Manifold). A complex manifold is a manifold with coordinates holomorphic on
Complex manifolds, Kahler metrics, differential and harmonic forms Cattani June 16, 2010 1 Lecture 1 Definition 1.1 (Complex Manifold). A complex manifold is a manifold with coordinates holomorphic on
Topics in Geometry: Mirror Symmetry
 MIT OpenCourseWare http://ocw.mit.edu 18.969 Topics in Geometry: Mirror Symmetry Spring 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MIRROR SYMMETRY:
MIT OpenCourseWare http://ocw.mit.edu 18.969 Topics in Geometry: Mirror Symmetry Spring 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MIRROR SYMMETRY:
N = 2 supersymmetric gauge theory and Mock theta functions
 N = 2 supersymmetric gauge theory and Mock theta functions Andreas Malmendier GTP Seminar (joint work with Ken Ono) November 7, 2008 q-series in differential topology Theorem (M-Ono) The following q-series
N = 2 supersymmetric gauge theory and Mock theta functions Andreas Malmendier GTP Seminar (joint work with Ken Ono) November 7, 2008 q-series in differential topology Theorem (M-Ono) The following q-series
Geometry of the Calabi-Yau Moduli
 Geometry of the Calabi-Yau Moduli Zhiqin Lu 2012 AMS Hawaii Meeting Department of Mathematics, UC Irvine, Irvine CA 92697 March 4, 2012 Zhiqin Lu, Dept. Math, UCI Geometry of the Calabi-Yau Moduli 1/51
Geometry of the Calabi-Yau Moduli Zhiqin Lu 2012 AMS Hawaii Meeting Department of Mathematics, UC Irvine, Irvine CA 92697 March 4, 2012 Zhiqin Lu, Dept. Math, UCI Geometry of the Calabi-Yau Moduli 1/51
Kähler manifolds and variations of Hodge structures
 Kähler manifolds and variations of Hodge structures October 21, 2013 1 Some amazing facts about Kähler manifolds The best source for this is Claire Voisin s wonderful book Hodge Theory and Complex Algebraic
Kähler manifolds and variations of Hodge structures October 21, 2013 1 Some amazing facts about Kähler manifolds The best source for this is Claire Voisin s wonderful book Hodge Theory and Complex Algebraic
Constructing compact 8-manifolds with holonomy Spin(7)
 Constructing compact 8-manifolds with holonomy Spin(7) Dominic Joyce, Oxford University Simons Collaboration meeting, Imperial College, June 2017. Based on Invent. math. 123 (1996), 507 552; J. Diff. Geom.
Constructing compact 8-manifolds with holonomy Spin(7) Dominic Joyce, Oxford University Simons Collaboration meeting, Imperial College, June 2017. Based on Invent. math. 123 (1996), 507 552; J. Diff. Geom.
Ω Ω /ω. To these, one wants to add a fourth condition that arises from physics, what is known as the anomaly cancellation, namely that
 String theory and balanced metrics One of the main motivations for considering balanced metrics, in addition to the considerations already mentioned, has to do with the theory of what are known as heterotic
String theory and balanced metrics One of the main motivations for considering balanced metrics, in addition to the considerations already mentioned, has to do with the theory of what are known as heterotic
CALIBRATED FIBRATIONS ON NONCOMPACT MANIFOLDS VIA GROUP ACTIONS
 DUKE MATHEMATICAL JOURNAL Vol. 110, No. 2, c 2001 CALIBRATED FIBRATIONS ON NONCOMPACT MANIFOLDS VIA GROUP ACTIONS EDWARD GOLDSTEIN Abstract In this paper we use Lie group actions on noncompact Riemannian
DUKE MATHEMATICAL JOURNAL Vol. 110, No. 2, c 2001 CALIBRATED FIBRATIONS ON NONCOMPACT MANIFOLDS VIA GROUP ACTIONS EDWARD GOLDSTEIN Abstract In this paper we use Lie group actions on noncompact Riemannian
Non-Geometric Calabi- Yau Backgrounds
 Non-Geometric Calabi- Yau Backgrounds CH, Israel and Sarti 1710.00853 A Dabolkar and CH, 2002 Duality Symmetries Supergravities: continuous classical symmetry, broken in quantum theory, and by gauging
Non-Geometric Calabi- Yau Backgrounds CH, Israel and Sarti 1710.00853 A Dabolkar and CH, 2002 Duality Symmetries Supergravities: continuous classical symmetry, broken in quantum theory, and by gauging
2 Type IIA String Theory with Background Fluxes in d=2
 2 Type IIA String Theory with Background Fluxes in d=2 We consider compactifications of type IIA string theory on Calabi-Yau fourfolds. Consistency of a generic compactification requires switching on a
2 Type IIA String Theory with Background Fluxes in d=2 We consider compactifications of type IIA string theory on Calabi-Yau fourfolds. Consistency of a generic compactification requires switching on a
On the BCOV Conjecture
 Department of Mathematics University of California, Irvine December 14, 2007 Mirror Symmetry The objects to study By Mirror Symmetry, for any CY threefold, there should be another CY threefold X, called
Department of Mathematics University of California, Irvine December 14, 2007 Mirror Symmetry The objects to study By Mirror Symmetry, for any CY threefold, there should be another CY threefold X, called
0.1 Complex Analogues 1
 0.1 Complex Analogues 1 Abstract In complex geometry Kodaira s theorem tells us that on a Kähler manifold sufficiently high powers of positive line bundles admit global holomorphic sections. Donaldson
0.1 Complex Analogues 1 Abstract In complex geometry Kodaira s theorem tells us that on a Kähler manifold sufficiently high powers of positive line bundles admit global holomorphic sections. Donaldson
Mirror Symmetry: Introduction to the B Model
 Mirror Symmetry: Introduction to the B Model Kyler Siegel February 23, 2014 1 Introduction Recall that mirror symmetry predicts the existence of pairs X, ˇX of Calabi-Yau manifolds whose Hodge diamonds
Mirror Symmetry: Introduction to the B Model Kyler Siegel February 23, 2014 1 Introduction Recall that mirror symmetry predicts the existence of pairs X, ˇX of Calabi-Yau manifolds whose Hodge diamonds
Heterotic Flux Compactifications
 Heterotic Flux Compactifications Mario Garcia-Fernandez Instituto de Ciencias Matemáticas, Madrid String Pheno 2017 Virginia Tech, 7 July 2017 Based on arxiv:1611.08926, and joint work with Rubio, Tipler,
Heterotic Flux Compactifications Mario Garcia-Fernandez Instituto de Ciencias Matemáticas, Madrid String Pheno 2017 Virginia Tech, 7 July 2017 Based on arxiv:1611.08926, and joint work with Rubio, Tipler,
Rational Curves On K3 Surfaces
 Rational Curves On K3 Surfaces Jun Li Department of Mathematics Stanford University Conference in honor of Peter Li Overview of the talk The problem: existence of rational curves on a K3 surface The conjecture:
Rational Curves On K3 Surfaces Jun Li Department of Mathematics Stanford University Conference in honor of Peter Li Overview of the talk The problem: existence of rational curves on a K3 surface The conjecture:
Homological mirror symmetry via families of Lagrangians
 Homological mirror symmetry via families of Lagrangians String-Math 2018 Mohammed Abouzaid Columbia University June 17, 2018 Mirror symmetry Three facets of mirror symmetry: 1 Enumerative: GW invariants
Homological mirror symmetry via families of Lagrangians String-Math 2018 Mohammed Abouzaid Columbia University June 17, 2018 Mirror symmetry Three facets of mirror symmetry: 1 Enumerative: GW invariants
Sphere Partition Functions, Topology, the Zamolodchikov Metric
 Sphere Partition Functions, Topology, the Zamolodchikov Metric, and Extremal Correlators Weizmann Institute of Science Efrat Gerchkovitz, Jaume Gomis, ZK [1405.7271] Jaume Gomis, Po-Shen Hsin, ZK, Adam
Sphere Partition Functions, Topology, the Zamolodchikov Metric, and Extremal Correlators Weizmann Institute of Science Efrat Gerchkovitz, Jaume Gomis, ZK [1405.7271] Jaume Gomis, Po-Shen Hsin, ZK, Adam
arxiv: v2 [hep-th] 3 Jul 2015
![arxiv: v2 [hep-th] 3 Jul 2015 arxiv: v2 [hep-th] 3 Jul 2015](/thumbs/89/97970523.jpg) Prepared for submission to JHEP NSF-KITP-15-068, MIT-CTP-4677 P 1 -bundle bases and the prevalence of non-higgsable structure in 4D F-theory models arxiv:1506.03204v2 [hep-th] 3 Jul 2015 James Halverson
Prepared for submission to JHEP NSF-KITP-15-068, MIT-CTP-4677 P 1 -bundle bases and the prevalence of non-higgsable structure in 4D F-theory models arxiv:1506.03204v2 [hep-th] 3 Jul 2015 James Halverson
K-stability and Kähler metrics, I
 K-stability and Kähler metrics, I Gang Tian Beijing University and Princeton University Let M be a Kähler manifold. This means that M be a complex manifold together with a Kähler metric ω. In local coordinates
K-stability and Kähler metrics, I Gang Tian Beijing University and Princeton University Let M be a Kähler manifold. This means that M be a complex manifold together with a Kähler metric ω. In local coordinates
As always, the story begins with Riemann surfaces or just (real) surfaces. (As we have already noted, these are nearly the same thing).
 An Interlude on Curvature and Hermitian Yang Mills As always, the story begins with Riemann surfaces or just (real) surfaces. (As we have already noted, these are nearly the same thing). Suppose we wanted
An Interlude on Curvature and Hermitian Yang Mills As always, the story begins with Riemann surfaces or just (real) surfaces. (As we have already noted, these are nearly the same thing). Suppose we wanted
Hyperkähler geometry lecture 3
 Hyperkähler geometry lecture 3 Misha Verbitsky Cohomology in Mathematics and Physics Euler Institute, September 25, 2013, St. Petersburg 1 Broom Bridge Here as he walked by on the 16th of October 1843
Hyperkähler geometry lecture 3 Misha Verbitsky Cohomology in Mathematics and Physics Euler Institute, September 25, 2013, St. Petersburg 1 Broom Bridge Here as he walked by on the 16th of October 1843
String Phenomenology ???
 String Phenomenology Andre Lukas Oxford, Theoretical Physics d=11 SUGRA IIB M IIA??? I E x E 8 8 SO(32) Outline A (very) basic introduction to string theory String theory and the real world? Recent work
String Phenomenology Andre Lukas Oxford, Theoretical Physics d=11 SUGRA IIB M IIA??? I E x E 8 8 SO(32) Outline A (very) basic introduction to string theory String theory and the real world? Recent work
Topic: First Chern classes of Kähler manifolds Mitchell Faulk Last updated: April 23, 2016
 Topic: First Chern classes of Kähler manifolds itchell Faulk Last updated: April 23, 2016 We study the first Chern class of various Kähler manifolds. We only consider two sources of examples: Riemann surfaces
Topic: First Chern classes of Kähler manifolds itchell Faulk Last updated: April 23, 2016 We study the first Chern class of various Kähler manifolds. We only consider two sources of examples: Riemann surfaces
Linear connections on Lie groups
 Linear connections on Lie groups The affine space of linear connections on a compact Lie group G contains a distinguished line segment with endpoints the connections L and R which make left (resp. right)
Linear connections on Lie groups The affine space of linear connections on a compact Lie group G contains a distinguished line segment with endpoints the connections L and R which make left (resp. right)
LECTURE 5: SURFACES IN PROJECTIVE SPACE. 1. Projective space
 LECTURE 5: SURFACES IN PROJECTIVE SPACE. Projective space Definition: The n-dimensional projective space P n is the set of lines through the origin in the vector space R n+. P n may be thought of as the
LECTURE 5: SURFACES IN PROJECTIVE SPACE. Projective space Definition: The n-dimensional projective space P n is the set of lines through the origin in the vector space R n+. P n may be thought of as the
LECTURE 5: COMPLEX AND KÄHLER MANIFOLDS
 LECTURE 5: COMPLEX AND KÄHLER MANIFOLDS Contents 1. Almost complex manifolds 1. Complex manifolds 5 3. Kähler manifolds 9 4. Dolbeault cohomology 11 1. Almost complex manifolds Almost complex structures.
LECTURE 5: COMPLEX AND KÄHLER MANIFOLDS Contents 1. Almost complex manifolds 1. Complex manifolds 5 3. Kähler manifolds 9 4. Dolbeault cohomology 11 1. Almost complex manifolds Almost complex structures.
440-3 Geometry/Topology: Cohomology Northwestern University Solution of Homework 5
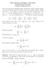 440-3 Geometry/Topology: Cohomology Northwestern University Solution of Homework 5 You can use freely the following simple results from complex analysis (which can be proved in the same way as the case
440-3 Geometry/Topology: Cohomology Northwestern University Solution of Homework 5 You can use freely the following simple results from complex analysis (which can be proved in the same way as the case
LAGRANGIAN HOMOLOGY CLASSES WITHOUT REGULAR MINIMIZERS
 LAGRANGIAN HOMOLOGY CLASSES WITHOUT REGULAR MINIMIZERS JON WOLFSON Abstract. We show that there is an integral homology class in a Kähler-Einstein surface that can be represented by a lagrangian twosphere
LAGRANGIAN HOMOLOGY CLASSES WITHOUT REGULAR MINIMIZERS JON WOLFSON Abstract. We show that there is an integral homology class in a Kähler-Einstein surface that can be represented by a lagrangian twosphere
Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications
 Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications Joseph P. Conlon DAMTP, Cambridge University Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications p. 1/3
Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications Joseph P. Conlon DAMTP, Cambridge University Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications p. 1/3
The Calabi Conjecture
 The Calabi Conjecture notes by Aleksander Doan These are notes to the talk given on 9th March 2012 at the Graduate Topology and Geometry Seminar at the University of Warsaw. They are based almost entirely
The Calabi Conjecture notes by Aleksander Doan These are notes to the talk given on 9th March 2012 at the Graduate Topology and Geometry Seminar at the University of Warsaw. They are based almost entirely
Holomorphic line bundles
 Chapter 2 Holomorphic line bundles In the absence of non-constant holomorphic functions X! C on a compact complex manifold, we turn to the next best thing, holomorphic sections of line bundles (i.e., rank
Chapter 2 Holomorphic line bundles In the absence of non-constant holomorphic functions X! C on a compact complex manifold, we turn to the next best thing, holomorphic sections of line bundles (i.e., rank
Asymptotic Geometry. of polynomials. Steve Zelditch Department of Mathematics Johns Hopkins University. Joint Work with Pavel Bleher Bernie Shiffman
 Asymptotic Geometry of polynomials Steve Zelditch Department of Mathematics Johns Hopkins University Joint Work with Pavel Bleher Bernie Shiffman 1 Statistical algebraic geometry We are interested in asymptotic
Asymptotic Geometry of polynomials Steve Zelditch Department of Mathematics Johns Hopkins University Joint Work with Pavel Bleher Bernie Shiffman 1 Statistical algebraic geometry We are interested in asymptotic
David R. Morrison. String Phenomenology 2008 University of Pennsylvania 31 May 2008
 : : University of California, Santa Barbara String Phenomenology 2008 University of Pennsylvania 31 May 2008 engineering has been a very successful approach to studying string vacua, and has been essential
: : University of California, Santa Barbara String Phenomenology 2008 University of Pennsylvania 31 May 2008 engineering has been a very successful approach to studying string vacua, and has been essential
Heterotic Geometry and Fluxes
 Heterotic Geometry and Fluxes Li-Sheng Tseng Abstract. We begin by discussing the question, What is string geometry? We then proceed to discuss six-dimensional compactification geometry in heterotic string
Heterotic Geometry and Fluxes Li-Sheng Tseng Abstract. We begin by discussing the question, What is string geometry? We then proceed to discuss six-dimensional compactification geometry in heterotic string
F- 理論におけるフラックスコンパクト化. Hajime Otsuka( 大塚啓 ) (Waseda U.) Physics Lett. B. 774 (2017) 225 with Y. Honma (National Tsing-Hua U.) Sangyo U.
 F- 理論におけるフラックスコンパクト化 Hajime Otsuka( 大塚啓 ) (Waseda U.) Physics Lett. B. 774 (2017) 225 with Y. Honma (National Tsing-Hua U.) 2018/1/29@Kyoto Sangyo U. Outline Introduction Flux compactification in type
F- 理論におけるフラックスコンパクト化 Hajime Otsuka( 大塚啓 ) (Waseda U.) Physics Lett. B. 774 (2017) 225 with Y. Honma (National Tsing-Hua U.) 2018/1/29@Kyoto Sangyo U. Outline Introduction Flux compactification in type
ERRATUM TO AFFINE MANIFOLDS, SYZ GEOMETRY AND THE Y VERTEX
 ERRATUM TO AFFINE MANIFOLDS, SYZ GEOMETRY AND THE Y VERTEX JOHN LOFTIN, SHING-TUNG YAU, AND ERIC ZASLOW 1. Main result The purpose of this erratum is to correct an error in the proof of the main result
ERRATUM TO AFFINE MANIFOLDS, SYZ GEOMETRY AND THE Y VERTEX JOHN LOFTIN, SHING-TUNG YAU, AND ERIC ZASLOW 1. Main result The purpose of this erratum is to correct an error in the proof of the main result
The geometry of Landau-Ginzburg models
 Motivation Toric degeneration Hodge theory CY3s The Geometry of Landau-Ginzburg Models January 19, 2016 Motivation Toric degeneration Hodge theory CY3s Plan of talk 1. Landau-Ginzburg models and mirror
Motivation Toric degeneration Hodge theory CY3s The Geometry of Landau-Ginzburg Models January 19, 2016 Motivation Toric degeneration Hodge theory CY3s Plan of talk 1. Landau-Ginzburg models and mirror
Period Domains. Carlson. June 24, 2010
 Period Domains Carlson June 4, 00 Carlson - Period Domains Period domains are parameter spaces for marked Hodge structures. We call Γ\D the period space, which is a parameter space of isomorphism classes
Period Domains Carlson June 4, 00 Carlson - Period Domains Period domains are parameter spaces for marked Hodge structures. We call Γ\D the period space, which is a parameter space of isomorphism classes
Magdalena Larfors
 Uppsala University, Dept. of Theoretical Physics Based on D. Chialva, U. Danielsson, N. Johansson, M.L. and M. Vonk, hep-th/0710.0620 U. Danielsson, N. Johansson and M.L., hep-th/0612222 2008-01-18 String
Uppsala University, Dept. of Theoretical Physics Based on D. Chialva, U. Danielsson, N. Johansson, M.L. and M. Vonk, hep-th/0710.0620 U. Danielsson, N. Johansson and M.L., hep-th/0612222 2008-01-18 String
Some brief notes on the Kodaira Vanishing Theorem
 Some brief notes on the Kodaira Vanishing Theorem 1 Divisors and Line Bundles, according to Scott Nollet This is a huge topic, because there is a difference between looking at an abstract variety and local
Some brief notes on the Kodaira Vanishing Theorem 1 Divisors and Line Bundles, according to Scott Nollet This is a huge topic, because there is a difference between looking at an abstract variety and local
Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications
 Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications Joseph P. Conlon DAMTP, Cambridge University Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications p. 1/4
Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications Joseph P. Conlon DAMTP, Cambridge University Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications p. 1/4
Heterotic type IIA duality with fluxes and moduli stabilization
 Heterotic type IIA duality with fluxes and moduli stabilization Andrei Micu Physikalisches Institut der Universität Bonn Based on hep-th/0608171 and hep-th/0701173 in collaboration with Jan Louis, Eran
Heterotic type IIA duality with fluxes and moduli stabilization Andrei Micu Physikalisches Institut der Universität Bonn Based on hep-th/0608171 and hep-th/0701173 in collaboration with Jan Louis, Eran
Intermediate Jacobians and Abel-Jacobi Maps
 Intermediate Jacobians and Abel-Jacobi Maps Patrick Walls April 28, 2012 Introduction Let X be a smooth projective complex variety. Introduction Let X be a smooth projective complex variety. Intermediate
Intermediate Jacobians and Abel-Jacobi Maps Patrick Walls April 28, 2012 Introduction Let X be a smooth projective complex variety. Introduction Let X be a smooth projective complex variety. Intermediate
Riemannian Curvature Functionals: Lecture III
 Riemannian Curvature Functionals: Lecture III Jeff Viaclovsky Park City Mathematics Institute July 18, 2013 Lecture Outline Today we will discuss the following: Complete the local description of the moduli
Riemannian Curvature Functionals: Lecture III Jeff Viaclovsky Park City Mathematics Institute July 18, 2013 Lecture Outline Today we will discuss the following: Complete the local description of the moduli
CHARACTERISTIC CLASSES
 1 CHARACTERISTIC CLASSES Andrew Ranicki Index theory seminar 14th February, 2011 2 The Index Theorem identifies Introduction analytic index = topological index for a differential operator on a compact
1 CHARACTERISTIC CLASSES Andrew Ranicki Index theory seminar 14th February, 2011 2 The Index Theorem identifies Introduction analytic index = topological index for a differential operator on a compact
A complex geometric proof of Tian-Yau-Zelditch expansion
 A complex geometric proof of Tian-Yau-Zelditch expansion Zhiqin Lu Department of Mathematics, UC Irvine, Irvine CA 92697 October 21, 2010 Zhiqin Lu, Dept. Math, UCI A complex geometric proof of TYZ expansion
A complex geometric proof of Tian-Yau-Zelditch expansion Zhiqin Lu Department of Mathematics, UC Irvine, Irvine CA 92697 October 21, 2010 Zhiqin Lu, Dept. Math, UCI A complex geometric proof of TYZ expansion
Lefschetz pencils and the symplectic topology of complex surfaces
 Lefschetz pencils and the symplectic topology of complex surfaces Denis AUROUX Massachusetts Institute of Technology Symplectic 4-manifolds A (compact) symplectic 4-manifold (M 4, ω) is a smooth 4-manifold
Lefschetz pencils and the symplectic topology of complex surfaces Denis AUROUX Massachusetts Institute of Technology Symplectic 4-manifolds A (compact) symplectic 4-manifold (M 4, ω) is a smooth 4-manifold
Vanishing theorems and holomorphic forms
 Vanishing theorems and holomorphic forms Mihnea Popa Northwestern AMS Meeting, Lansing March 14, 2015 Holomorphic one-forms and geometry X compact complex manifold, dim C X = n. Holomorphic one-forms and
Vanishing theorems and holomorphic forms Mihnea Popa Northwestern AMS Meeting, Lansing March 14, 2015 Holomorphic one-forms and geometry X compact complex manifold, dim C X = n. Holomorphic one-forms and
Moduli of heterotic G2 compactifications
 Moduli of heterotic G2 compactifications Magdalena Larfors Uppsala University Women at the Intersection of Mathematics and High Energy Physics MITP 7.3.2017 X. de la Ossa, ML, E. Svanes (1607.03473 & work
Moduli of heterotic G2 compactifications Magdalena Larfors Uppsala University Women at the Intersection of Mathematics and High Energy Physics MITP 7.3.2017 X. de la Ossa, ML, E. Svanes (1607.03473 & work
UNIVERSAL UNFOLDINGS OF LAURENT POLYNOMIALS AND TT STRUCTURES. Claude Sabbah
 UNIVERSAL UNFOLDINGS OF LAURENT POLYNOMIALS AND TT STRUCTURES AUGSBURG, MAY 2007 Claude Sabbah Introduction Let f : (C ) n C be a Laurent polynomial, that I assume to be convenient and non-degenerate,
UNIVERSAL UNFOLDINGS OF LAURENT POLYNOMIALS AND TT STRUCTURES AUGSBURG, MAY 2007 Claude Sabbah Introduction Let f : (C ) n C be a Laurent polynomial, that I assume to be convenient and non-degenerate,
Supersymmetric Quantum Mechanics and Geometry by Nicholas Mee of Trinity College, Cambridge. October 1989
 Supersymmetric Quantum Mechanics and Geometry by Nicholas Mee of Trinity College Cambridge October 1989 Preface This dissertation is the result of my own individual effort except where reference is explicitly
Supersymmetric Quantum Mechanics and Geometry by Nicholas Mee of Trinity College Cambridge October 1989 Preface This dissertation is the result of my own individual effort except where reference is explicitly
Broken pencils and four-manifold invariants. Tim Perutz (Cambridge)
 Broken pencils and four-manifold invariants Tim Perutz (Cambridge) Aim This talk is about a project to construct and study a symplectic substitute for gauge theory in 2, 3 and 4 dimensions. The 3- and
Broken pencils and four-manifold invariants Tim Perutz (Cambridge) Aim This talk is about a project to construct and study a symplectic substitute for gauge theory in 2, 3 and 4 dimensions. The 3- and
A Landscape of Field Theories
 A Landscape of Field Theories Travis Maxfield Enrico Fermi Institute, University of Chicago October 30, 2015 Based on arxiv: 1511.xxxxx w/ D. Robbins and S. Sethi Summary Despite the recent proliferation
A Landscape of Field Theories Travis Maxfield Enrico Fermi Institute, University of Chicago October 30, 2015 Based on arxiv: 1511.xxxxx w/ D. Robbins and S. Sethi Summary Despite the recent proliferation
Counting black hole microstates as open string flux vacua
 Counting black hole microstates as open string flux vacua Frederik Denef KITP, November 23, 2005 F. Denef and G. Moore, to appear Outline Setting and formulation of the problem Black hole microstates and
Counting black hole microstates as open string flux vacua Frederik Denef KITP, November 23, 2005 F. Denef and G. Moore, to appear Outline Setting and formulation of the problem Black hole microstates and
Calabi-Yau Geometry and Mirror Symmetry Conference. Cheol-Hyun Cho (Seoul National Univ.) (based on a joint work with Hansol Hong and Siu-Cheong Lau)
 Calabi-Yau Geometry and Mirror Symmetry Conference Cheol-Hyun Cho (Seoul National Univ.) (based on a joint work with Hansol Hong and Siu-Cheong Lau) Mirror Symmetry between two spaces Mirror symmetry explains
Calabi-Yau Geometry and Mirror Symmetry Conference Cheol-Hyun Cho (Seoul National Univ.) (based on a joint work with Hansol Hong and Siu-Cheong Lau) Mirror Symmetry between two spaces Mirror symmetry explains
Generalized Tian-Todorov theorems
 Generalized Tian-Todorov theorems M.Kontsevich 1 The classical Tian-Todorov theorem Recall the classical Tian-Todorov theorem (see [4],[5]) about the smoothness of the moduli spaces of Calabi-Yau manifolds:
Generalized Tian-Todorov theorems M.Kontsevich 1 The classical Tian-Todorov theorem Recall the classical Tian-Todorov theorem (see [4],[5]) about the smoothness of the moduli spaces of Calabi-Yau manifolds:
On Special Geometry of Generalized G Structures and Flux Compactifications. Hu Sen, USTC. Hangzhou-Zhengzhou, 2007
 On Special Geometry of Generalized G Structures and Flux Compactifications Hu Sen, USTC Hangzhou-Zhengzhou, 2007 1 Dreams of A. Einstein: Unifications of interacting forces of nature 1920 s known forces:
On Special Geometry of Generalized G Structures and Flux Compactifications Hu Sen, USTC Hangzhou-Zhengzhou, 2007 1 Dreams of A. Einstein: Unifications of interacting forces of nature 1920 s known forces:
Monodromy of the Dwork family, following Shepherd-Barron X n+1. P 1 λ. ζ i = 1}/ (µ n+1 ) H.
 Monodromy of the Dwork family, following Shepherd-Barron 1. The Dwork family. Consider the equation (f λ ) f λ (X 0, X 1,..., X n ) = λ(x n+1 0 + + X n+1 n ) (n + 1)X 0... X n = 0, where λ is a free parameter.
Monodromy of the Dwork family, following Shepherd-Barron 1. The Dwork family. Consider the equation (f λ ) f λ (X 0, X 1,..., X n ) = λ(x n+1 0 + + X n+1 n ) (n + 1)X 0... X n = 0, where λ is a free parameter.
The Strominger Yau Zaslow conjecture
 The Strominger Yau Zaslow conjecture Paul Hacking 10/16/09 1 Background 1.1 Kähler metrics Let X be a complex manifold of dimension n, and M the underlying smooth manifold with (integrable) almost complex
The Strominger Yau Zaslow conjecture Paul Hacking 10/16/09 1 Background 1.1 Kähler metrics Let X be a complex manifold of dimension n, and M the underlying smooth manifold with (integrable) almost complex
Instantons in string theory via F-theory
 Instantons in string theory via F-theory Andrés Collinucci ASC, LMU, Munich Padova, May 12, 2010 arxiv:1002.1894 in collaboration with R. Blumenhagen and B. Jurke Outline 1. Intro: From string theory to
Instantons in string theory via F-theory Andrés Collinucci ASC, LMU, Munich Padova, May 12, 2010 arxiv:1002.1894 in collaboration with R. Blumenhagen and B. Jurke Outline 1. Intro: From string theory to
Preprint typeset in JHEP style - HYPER VERSION. Special Geometry. Yang Zhang. Abstract: N = 2 Supergravity. based on hep-th/ , Boris PiolineA
 Preprint typeset in JHEP style - HYPER VERSION Special Geometry Yang Zhang Abstract: N = Supergravity based on hep-th/06077, Boris PiolineA Contents 1. N = Supergravity 1 1.1 Supersymmetric multiplets
Preprint typeset in JHEP style - HYPER VERSION Special Geometry Yang Zhang Abstract: N = Supergravity based on hep-th/06077, Boris PiolineA Contents 1. N = Supergravity 1 1.1 Supersymmetric multiplets
Self-Dual Yang-Mills Fields in Eight Dimensions
 arxiv:hep-th/9603001v1 1 ar 1996 Self-Dual Yang-ills Fields in Eight Dimensions Ayşe Hümeyra Bilge, Tekin Dereli, Şahin Koçak Department of athematics, Anadolu University, Eskişehir, Turkey e.mail: bilge@yunus.mam.tubitak.gov.tr
arxiv:hep-th/9603001v1 1 ar 1996 Self-Dual Yang-ills Fields in Eight Dimensions Ayşe Hümeyra Bilge, Tekin Dereli, Şahin Koçak Department of athematics, Anadolu University, Eskişehir, Turkey e.mail: bilge@yunus.mam.tubitak.gov.tr
Metrics and Holonomy
 Metrics and Holonomy Jonathan Herman The goal of this paper is to understand the following definitions of Kähler and Calabi-Yau manifolds: Definition. A Riemannian manifold is Kähler if and only if it
Metrics and Holonomy Jonathan Herman The goal of this paper is to understand the following definitions of Kähler and Calabi-Yau manifolds: Definition. A Riemannian manifold is Kähler if and only if it
arxiv: v2 [hep-th] 23 Mar 2018
![arxiv: v2 [hep-th] 23 Mar 2018 arxiv: v2 [hep-th] 23 Mar 2018](/thumbs/83/88807087.jpg) MPP-2018-20 Infinite Distances in Field Space and Massless Towers of States Thomas W. Grimm 1, Eran Palti 2, Irene Valenzuela 1 arxiv:1802.08264v2 [hep-th] 23 Mar 2018 1 Institute for Theoretical Physics
MPP-2018-20 Infinite Distances in Field Space and Massless Towers of States Thomas W. Grimm 1, Eran Palti 2, Irene Valenzuela 1 arxiv:1802.08264v2 [hep-th] 23 Mar 2018 1 Institute for Theoretical Physics
Higgs Bundles and Character Varieties
 Higgs Bundles and Character Varieties David Baraglia The University of Adelaide Adelaide, Australia 29 May 2014 GEAR Junior Retreat, University of Michigan David Baraglia (ADL) Higgs Bundles and Character
Higgs Bundles and Character Varieties David Baraglia The University of Adelaide Adelaide, Australia 29 May 2014 GEAR Junior Retreat, University of Michigan David Baraglia (ADL) Higgs Bundles and Character
LECTURE 6: J-HOLOMORPHIC CURVES AND APPLICATIONS
 LECTURE 6: J-HOLOMORPHIC CURVES AND APPLICATIONS WEIMIN CHEN, UMASS, SPRING 07 1. Basic elements of J-holomorphic curve theory Let (M, ω) be a symplectic manifold of dimension 2n, and let J J (M, ω) be
LECTURE 6: J-HOLOMORPHIC CURVES AND APPLICATIONS WEIMIN CHEN, UMASS, SPRING 07 1. Basic elements of J-holomorphic curve theory Let (M, ω) be a symplectic manifold of dimension 2n, and let J J (M, ω) be
Magdalena Larfors. New Ideas at the Interface of Cosmology and String Theory. UPenn, Ludwig-Maximilians Universität, München
 Ludwig-Maximilians Universität, München New Ideas at the Interface of Cosmology and String Theory UPenn, 17.03.01. String 10D supergravity M 10 = M 4 w M 6 Fluxes and branes... (Scientific American) Topology
Ludwig-Maximilians Universität, München New Ideas at the Interface of Cosmology and String Theory UPenn, 17.03.01. String 10D supergravity M 10 = M 4 w M 6 Fluxes and branes... (Scientific American) Topology
On Flux Quantization in F-Theory
 On Flux Quantization in F-Theory Raffaele Savelli MPI - Munich Bad Honnef, March 2011 Based on work with A. Collinucci, arxiv: 1011.6388 Motivations Motivations The recent attempts to find UV-completions
On Flux Quantization in F-Theory Raffaele Savelli MPI - Munich Bad Honnef, March 2011 Based on work with A. Collinucci, arxiv: 1011.6388 Motivations Motivations The recent attempts to find UV-completions
Gauge Threshold Corrections for Local String Models
 Gauge Threshold Corrections for Local String Models Stockholm, November 16, 2009 Based on arxiv:0901.4350 (JC), 0906.3297 (JC, Palti) Local vs Global There are many different proposals to realise Standard
Gauge Threshold Corrections for Local String Models Stockholm, November 16, 2009 Based on arxiv:0901.4350 (JC), 0906.3297 (JC, Palti) Local vs Global There are many different proposals to realise Standard
arxiv:alg-geom/ v1 29 Jul 1993
 Hyperkähler embeddings and holomorphic symplectic geometry. Mikhail Verbitsky, verbit@math.harvard.edu arxiv:alg-geom/9307009v1 29 Jul 1993 0. ntroduction. n this paper we are studying complex analytic
Hyperkähler embeddings and holomorphic symplectic geometry. Mikhail Verbitsky, verbit@math.harvard.edu arxiv:alg-geom/9307009v1 29 Jul 1993 0. ntroduction. n this paper we are studying complex analytic
DIFFERENTIAL FORMS AND COHOMOLOGY
 DIFFERENIAL FORMS AND COHOMOLOGY ONY PERKINS Goals 1. Differential forms We want to be able to integrate (holomorphic functions) on manifolds. Obtain a version of Stokes heorem - a generalization of the
DIFFERENIAL FORMS AND COHOMOLOGY ONY PERKINS Goals 1. Differential forms We want to be able to integrate (holomorphic functions) on manifolds. Obtain a version of Stokes heorem - a generalization of the
Part II. Riemann Surfaces. Year
 Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 96 Paper 2, Section II 23F State the uniformisation theorem. List without proof the Riemann surfaces which are uniformised
Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 96 Paper 2, Section II 23F State the uniformisation theorem. List without proof the Riemann surfaces which are uniformised
Uniform K-stability of pairs
 Uniform K-stability of pairs Gang Tian Peking University Let G = SL(N + 1, C) with two representations V, W over Q. For any v V\{0} and any one-parameter subgroup λ of G, we can associate a weight w λ
Uniform K-stability of pairs Gang Tian Peking University Let G = SL(N + 1, C) with two representations V, W over Q. For any v V\{0} and any one-parameter subgroup λ of G, we can associate a weight w λ
New Aspects of Heterotic Geometry and Phenomenology
 New Aspects of Heterotic Geometry and Phenomenology Lara B. Anderson Harvard University Work done in collaboration with: J. Gray, A. Lukas, and E. Palti: arxiv: 1106.4804, 1202.1757 J. Gray, A. Lukas and
New Aspects of Heterotic Geometry and Phenomenology Lara B. Anderson Harvard University Work done in collaboration with: J. Gray, A. Lukas, and E. Palti: arxiv: 1106.4804, 1202.1757 J. Gray, A. Lukas and
APPROXIMATE YANG MILLS HIGGS METRICS ON FLAT HIGGS BUNDLES OVER AN AFFINE MANIFOLD. 1. Introduction
 APPROXIMATE YANG MILLS HIGGS METRICS ON FLAT HIGGS BUNDLES OVER AN AFFINE MANIFOLD INDRANIL BISWAS, JOHN LOFTIN, AND MATTHIAS STEMMLER Abstract. Given a flat Higgs vector bundle (E,, ϕ) over a compact
APPROXIMATE YANG MILLS HIGGS METRICS ON FLAT HIGGS BUNDLES OVER AN AFFINE MANIFOLD INDRANIL BISWAS, JOHN LOFTIN, AND MATTHIAS STEMMLER Abstract. Given a flat Higgs vector bundle (E,, ϕ) over a compact
Dualities and Topological Strings
 Dualities and Topological Strings Strings 2006, Beijing - RD, C. Vafa, E.Verlinde, hep-th/0602087 - work in progress w/ C. Vafa & C. Beasley, L. Hollands Robbert Dijkgraaf University of Amsterdam Topological
Dualities and Topological Strings Strings 2006, Beijing - RD, C. Vafa, E.Verlinde, hep-th/0602087 - work in progress w/ C. Vafa & C. Beasley, L. Hollands Robbert Dijkgraaf University of Amsterdam Topological
Takao Akahori. z i In this paper, if f is a homogeneous polynomial, the correspondence between the Kodaira-Spencer class and C[z 1,...
 J. Korean Math. Soc. 40 (2003), No. 4, pp. 667 680 HOMOGENEOUS POLYNOMIAL HYPERSURFACE ISOLATED SINGULARITIES Takao Akahori Abstract. The mirror conjecture means originally the deep relation between complex
J. Korean Math. Soc. 40 (2003), No. 4, pp. 667 680 HOMOGENEOUS POLYNOMIAL HYPERSURFACE ISOLATED SINGULARITIES Takao Akahori Abstract. The mirror conjecture means originally the deep relation between complex
INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD
 INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD () Instanton (definition) (2) ADHM construction (3) Compactification. Instantons.. Notation. Throughout this talk, we will use the following notation:
INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD () Instanton (definition) (2) ADHM construction (3) Compactification. Instantons.. Notation. Throughout this talk, we will use the following notation:
η = (e 1 (e 2 φ)) # = e 3
 Research Statement My research interests lie in differential geometry and geometric analysis. My work has concentrated according to two themes. The first is the study of submanifolds of spaces with riemannian
Research Statement My research interests lie in differential geometry and geometric analysis. My work has concentrated according to two themes. The first is the study of submanifolds of spaces with riemannian
MILNOR SEMINAR: DIFFERENTIAL FORMS AND CHERN CLASSES
 MILNOR SEMINAR: DIFFERENTIAL FORMS AND CHERN CLASSES NILAY KUMAR In these lectures I want to introduce the Chern-Weil approach to characteristic classes on manifolds, and in particular, the Chern classes.
MILNOR SEMINAR: DIFFERENTIAL FORMS AND CHERN CLASSES NILAY KUMAR In these lectures I want to introduce the Chern-Weil approach to characteristic classes on manifolds, and in particular, the Chern classes.
1 Hermitian symmetric spaces: examples and basic properties
 Contents 1 Hermitian symmetric spaces: examples and basic properties 1 1.1 Almost complex manifolds............................................ 1 1.2 Hermitian manifolds................................................
Contents 1 Hermitian symmetric spaces: examples and basic properties 1 1.1 Almost complex manifolds............................................ 1 1.2 Hermitian manifolds................................................
Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications
 Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications Joseph P. Conlon DAMTP, Cambridge University Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications p. 1/4
Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications Joseph P. Conlon DAMTP, Cambridge University Kähler Potentials for Chiral Matter in Calabi-Yau String Compactifications p. 1/4
Algebraic geometry over quaternions
 Algebraic geometry over quaternions Misha Verbitsky November 26, 2007 Durham University 1 History of algebraic geometry. 1. XIX centrury: Riemann, Klein, Poincaré. Study of elliptic integrals and elliptic
Algebraic geometry over quaternions Misha Verbitsky November 26, 2007 Durham University 1 History of algebraic geometry. 1. XIX centrury: Riemann, Klein, Poincaré. Study of elliptic integrals and elliptic
Candidates for Inflation in Type IIB/F-theory Flux Compactifications
 Candidates for Inflation in Type IIB/F-theory Flux Compactifications Irene Valenzuela IFT UAM/CSIC Madrid Geometry and Physics of F-Theory, Munich 2015 Garcia-Etxebarria,Grimm,Valenzuela [hep-th/1412.5537]
Candidates for Inflation in Type IIB/F-theory Flux Compactifications Irene Valenzuela IFT UAM/CSIC Madrid Geometry and Physics of F-Theory, Munich 2015 Garcia-Etxebarria,Grimm,Valenzuela [hep-th/1412.5537]
