Math 121. Practice Problems from Chapter 4 Fall 2016
|
|
|
- Sydney Hensley
- 5 years ago
- Views:
Transcription
1 Math 11. Practice Problems from Chapter Fall 01 1 Inverse Functions 1. The graph of a function f is given below. On same graph sketch the inverse function of f; notice that f goes through the points (0, ) and (1, 1). f Solution: The graph of the inverse is the reflection of the given graph over the line =, and it reverse the coordinates of the graph of f, so the graph of f 1 goes through the points (, 0) and ( 1, 1). The graph of f, = and f 1 are given below: f. A function f that is one-to-one on its domain is graphed below.
2 For our reference, the points plotted on the graph of f are (, 5), (3, ), (0, 3), ( 5, ) (a) Sketch the graph of f 1 on the same graph. (b) Find (i) f 1 ( ) and (ii) f 1 ( 5). (c) Find (i) the domain of f 1 and (ii) the range of f 1. Solution: (a) The graph of f 1 is the reflection of the graph of f over the line =. This is given below. (b) (i) f 1 ( ) = 5 because f( 5) = and (ii) f 1 ( 5) = because f() = 5. (c) (i) The domain of f 1 is [ 5, ) because this is the range of f. (ii) The range of f 1 is (, ] because this is the domain of f. 3. Suppose f is a function and g is its inverse function, suppose also the domain of f is [1, 17] and the range of f is [ 15, 9] with f() = and f(11) = 1. (a) Is f one-to-one? (b) Is g one-to-one? (c) Find the domain and range of g. (d) If possible, find: g(), g(), g(11), g(1). Page
3 Solution: (a) Yes because f has an inverse function. (b) Yes because g has an inverse function, (its inverse function is f). (c) The domain of g is [ 15, 9] because this is the range of f; and the range of g is [1, 17] because this is the domain of f. (d) For this, use the fact g(b) = a when we know f(a) = b. Therefore, g() = because f() = and g(1) = 11 because f(11) = 1. There is not enough information to find g() and g(11).. Suppose f() = (a) Evaluate: f( 1), f(0), f(1), f(). (b) Given that f has an inverse function, use our answers from (a) to find f 1 (103), f 1 (1), f 1 () and f 1 (). Solution: (a) These are straightforward: f( 1) = + = ; f(0) = ; f(1) = + + = 1 and f() = ()( 7 ) + () + = 103. (b) Recall f 1 (b) = a when f(a) = b. Thus it follows from (a) that f 1 (103) =, f 1 (1) = 1, f 1 () = 0 and f 1 () = Find the inverse function of f() = Once ou have found f 1 (), verif that f(f 1 ()) = for all. Solution: First write = , and then switch and to obtain = and solve this for : = = ( + 7 = 5 = 17 ) 1 5 ( ) Therefore, f 1 5 () =. 17 We now check [ ( ) ] f(f 1 ()) = 17(f 1 ()) = ( ) + 7 = 17 7 = = 17 as desired.. (a) Find the inverse function of f() = 3 + 1, and find its domain. 7 Page 3
4 (b) Find the range of f. (c) Solve the equation =, if possible. Note. This is just asking ou to solve 7 f() = for. (d) Solve the equation = 3, if possible. Solution: (a) We first write = 3 + 1, and then switch and to have 7 = Then we will solve the preceding epression for to obtain the inverse function of f. Thus ( 7) = = = ( 3) = and so = Thus f 1 () = for 3, and the domain of f 1 = (b) The range of f is the domain of f 1, i.e., the range of f is { : 3 }. { : 3 }. (c) It is possible to solve this, because is in the domain of f 1 (), and f() = is equivalent to = f 1 (), therefore, using (a) = 7() + 1 () 3 = (d) This is not possible to solve, because 3 is not in the range of f (see part (b)). 7. Let f() = 5 +. (a) Find f 1 (). (b) Find the domain of f. (c) Find the domain of f 1. (d) Find the range of f. (e) Find the range of f 1. Solution: (a) We first write =, and then switch and to have 5 + = 5 + Page
5 Then we will solve the preceding epression for to obtain the inverse function of f. Thus Thus f 1 () = (b) The domain of f = (5 + ) = 5 + = = 5 (1 5) = and so = for 1 5. (c) The domain of f 1 = { : 5 }. { : 1 }. 5 (d) The range of f is the domain of f 1 which is (e) The range of f 1 is the domain of f which is { : 1 } 5 { : }. 5. Use the composition propert of inverses to determine if f and g defined below are inverses of each other. ( ) 1 + f() = and g() = 1 Solution: We check whether (f g)() = for all in the domain of g and (g f)() = for all in the domain of f. First Net [ ( ) ] f(g()) = 1(g()) 9 9 = 1 1 ( ) + = 1 = + = 1 g(f()) = ( f() + 1 = ( 9) 1/9 = ) 1 9 = ( Because (f g)() = for all in the domain of g and (g f)() = for all in the domain of f we know that f and g are inverse functions. 1 ) Use the composition propert of inverses to determine if f and g defined below are inverses of each other. f() = 10 and g() = 1 10 Page 5
6 Solution: We first check g(f()) = 1 10(10) = 1 10 Because (g f)(), we know that g and f are not inverses of each other. Page
7 Eponential Functions 1. Use properties of eponents to solve = (calculators should not be used). Solution: Since > 0, and 1, these epressions are defined, and the eponents must be equal, and so = = + = where the reader can simplif the final fraction when possible.. Consider the function f() = (a) Complete the following table of values for f (b) Sketch a graph of f, and on the same coordinate aes sketch = and the graph of f 1 () (c) Using our answer from (b), sketch g() = +1. Solution: (a) The completed table is as follows / 1/ 1/ 1 In (b), recall that the graph of the inverse will be the graph of f reflected over the line =. In (c), the graph of = is shifted 1 units to the left and units down to obtain the graph of g. (b) f f 1 (c) g Page 7
8 3. Consider the function f() = ( ) 1 3 (a) Complete the following table of values for f (b) Sketch a graph of f, and on the same coordinate aes sketch = and the graph of f 1 () (c) Using our answer from (b), sketch g() = ( 1 3) 3. Solution: (a) The completed table is as follows /3 1/9 1/7 In (b), recall that the graph of the inverse will be the graph of f reflected over the line =. In (c), the graph of = 3 is shifted units to the right and 3 units down to obtain the graph of g. (b) (c) f f 1 g. The graph of an eponential function = b is given on the graph below. Page
9 (a) Use the graph to estimate b. (b) On the same graph, graph = b 3 5. Solution: (a) b = because the graph goes through the point (1, ). (b) The requested graph results from shifting the original graph 3 units to the right and 5 units down. The graph is given below 5. The graph of an eponential function = b is given on the graph below. Page 9
10 (a) Use the graph to estimate b. (b) Using the graph from (a), graph = b. (c) Using our graph from (b), graph = b +1. Solution: (a) b = 1 because the graph goes through the point ( 1, ). (b) This graph results in reflecting the part of the original graph for 0 over the -ais. (c) The requested graph results from shifting the original graph 1 units to the left and units down. The graph is given below (b) (c). The graph of an eponential function = b is given on the graph below. Page 10
11 (a) Use the graph to estimate b. (b) On the same graph, graph = b. Solution: (a) b = 1 because the graph goes through the point ( 1, 3). 3 (b) Reflect the graph about the -ais, and then shift it up units to obtain the following graph The number of bass in a lake is given b P (t) = e 0.07t Page 11
12 where t is the number of months that have passed since the lake was stocked with bass. (a) How man bass were in the lake immediatel after it was stocked? (b) How man bass were in the lake 1 ear after it was stocked? Round our answer to the nearest whole number. (c) What will happen to the bass population as t increases without bound? Solution: (a) P (0) = 30 = 0 bass were in the lake immediatel after it was 1+ stocked. 30 (b) P (1) = bass were in the lake 1 ear after it was 1 + e ( 0.07)(1) stocked. (c) e 0.07t is an eponential function with base b = e 0.07 < 1, this will approach 0 as t increases without bound. Therefore, the bass population will increase, approaching 30 as time increases without bound.. The population of a small cit is currentl and is growing at 5 percent per ear. Thus the population is given b P (t) = 70000(1.05) t where t is time measured in ears from the present. (a) What will the population of the cit be in one ear? (b) According to this model, what will the population of the cit be in 1 ears from now? Epress answer to the nearest whole number. (c) Suppose Charles has an investment account that is growing a a rate of 5 percent per ear, and he currentl has dollars in the account. How much mone will be in the account 1 ears from now? Epress answer to the nearest dollar. Solution: (a) P (1) = 70000(1.05) = which represents an increase of 5 percent over the current populaton. (b) Assuming the current growth rate continues, the population will be P (t) = 70000(1.05) 1 = (c) This is mathematicall the same question as (b), ecept epressed in dollars, not population, so the account will have 70000(1.05) 1 = dollars in it after 1 ears. 9. The number e and the natural eponential and logarithm functions. ( (a) The number e is defined b e = lim n. Use our calculator to complete the n n) following table to get an idea of the approimate value of e: Page 1
13 Value of n Value of ( ) n n 10 (1.1) 10 = 100 (1.01) 100 = ( ) = Value of e obtained b using e function on calculator (with = 1): (b) Complete the following table using the e function on our calculator (use decimal places). Then sketch a rough graph of f() = e e (c) On the graph given in (b) sketch the following functions: (i) g() = e 3 (ii) h() = e 3 (iii) k() = log e Hints. (i) This is a horizontal translation of the graph of f() = e. (ii) This is a vertical translation of the graph in (i) (iii) log e is usuall denoted b ln and called the natural logarithm. The function k() = ln() is the inverse function of f() = e. Solution: (a) Page 13
14 Value of n Value of ( ) n n 10 (1.1) 10 = (1.01) 100 = ( ) =.7117 M calculator value using the e function ke is e.711. The number e is irrational, so it has a non repeating decimal epansion. (b) and (c): e Eponential functions are ideal for dealing with large numbers (or etremel small numbers), because once we know the base, onl the eponent changes. For eample and are numbers larger than man calculators will accept, et properties of eponents make them eas to multipl (or divide). Indeed, = = Properties of eponents also make it eas to write the above answer in scientific notation = = Use properties of eponents to answer the following questions. (a) Write in scientific notation. Use significant figures in our final answer. Page 1
15 (b) Find the product as a power of 10. (c) Convert our answer in (b) to scientific notation. Use significant digits in our answer. Solution: (a) = = (b) = = (c) = = Page 15
16 3 Logarithmic Functions 1. (a) Evaluate log 1. (b) Evaluate log ( 1 3 ) (c) Evaluate log 1 1 Solution: (a) Let = log 1. Then the eponential form is = 1 or = and so =. That is log 1 =. ( ) 1 (b) Let = log. In eponential form, the equation becomes = Thus ( ) 1 = 1, or = 5 and so = 5. That is log 5 = 5. 3 ( ) 1 (c) From the solution to (a), = 1, and then = 1 and then log 1 1 =.. Find the domain of the logarithmic function f() = log ( 1). Solution: Because the domain of log ( ) is all positive real numbers, the domain of f is all real numbers such that 1 > 0. To solve this, we find the zeros of the quadratic 1 = 0 Therefore, ( 1) = 0 and so = 0 or = 1. 1 > 0 if < 0 or 1 <. Therefore, Using test values, we find domf = { : < 0 or 1 < }. 3. Find the domain of f() = log(9 + ). Solution: The domain of f is the set all real numbers so that 9 + > 0, and therefore 9 > or > 9. Then domf = { : > 9} (where the reader can simplif if necessar). 9. (a) Change the equation log 1 5 = to eponential form. (b) Change the eponential equation 5 = 5 to logarithmic form. Page 1
17 Solution: (a) ( 1 ) = 5. (b) log 5 5 =. 5. (a) Write the equation log 1 = 3 in eponential form. (b) Write the eponential equation 9 5 = 5909 in logarithmic form. Solution: (a) ( 1 ) 3 =. (b) log = 5.. Consider the functions f() = 5 and g() = log 5 (a) Complete the following table of values for f() = (b) Complete the following table of values for g() = log 5 b filling in the -values for the given -values. log What do ou notice about the table of (a) and (b)? (c) Sketch the graphs of f() = 5 and g() = log 5 on the same coordinate aes. (d) Using our answer from (b), sketch h() = log 5 ( + ) 3. Solution: (a) The completed table is as follows /15 1/5 1/ (b) Because g() is the inverse function of f(), it switches the and values from f, so its table just switches the rows of the table in (a). 1/15 1/5 1/ log In (c), recall that the graph of the inverse g will be the graph of f reflected over the line = which is the dashed line in the graph below. In (d), the graph of g is shifted units to the left and 3 units down to obtain the graph of h. Page 17
18 (c) f g (d) h 7. Consider the functions f() = ( 1 5) and g() = log 1 5 (a) Complete the following table of values for f() = ( 1. 5) ( 1 5) (b) Complete the following table of values for g() = log 1 b filling in the -values for 5 the given -values. log What do ou notice about the table of (a) and (b)? (c) Sketch the graphs of f() = ( 1 5) and g() = log 1 on the same coordinate aes. 5 (d) Using our answer from (b), sketch h() = log 1 ( 1) +. 5 Solution: (a) The completed table is as follows ( 1 ) /5 1/5 1/15 5 (b) Because g() is the inverse function of f(), it switches the and values from f, so its table just switches the rows of the table in (a) /5 1/5 1/15 log Page 1
19 In (c), recall that the graph of the inverse g will be the graph of f reflected over the line = which is the dashed line in the graph below. In (d), the graph of g() is shifted 1 units to the right and units up to obtain the graph of h. (c) f g (d) h. Consider the function f() = log 7 ( + ) (a) Determine the domain of f. Write our answer in interval notation. (b) Solve the equation = log 7 (+) for b converting the equation to eponential form. (c) Use our answer in (b) to complete the following table of values where has been chosen first (d) With the the help of our table in (c), sketch the graph of f(). Solution: (a) A number is in the domain of f if + > 0, that is when >. Therefore, domf = (, ) (b) Observe that = log 7 ( + ) implies + = log 7 ( + ) and so converting this to eponential form implies (c) Using (b), when + = 7 + = 7 + = 7, = 7 3 = 1 33 = =, = 7 = 1 9 = 93 9 Page 19
20 = 5, = 7 1 = 1 7 = 1 7 =, = 7 0 = 5 = 3, = 7 1 = 1 =, = 7 = 3 = 1, = 7 3 = 337 Using this, the completed table is (d) A graph of f() = log 7 ( + ) is as follows. 9. Consider the function f() = log 1 ( + ) + 3 (a) Determine the domain of f. Write our answer in interval notation. (b) Solve the equation = log 1 (+)+ for b converting the equation to eponential 3 form. (c) Use our answer in (b) to complete the following table of values where has been chosen first (d) With the the help of our table in (c), sketch the graph of f(). Page 0
21 Solution: (a) A number is in the domain of f if + > 0, that is when >. Therefore, domf = (, ) (b) Observe that = log 1 ( + ) + implies = log 1 ( + ) and so converting 3 3 this to eponential form implies (c) Using (b), when + = ( 1 3 ) = = 5, = 3 3 = 1 7 = 53 7 =, = 3 = 1 9 = 17 9 ( ) 1 3 = 3, = 3 1 = 1 3 = 5 3 =, = 3 0 = 1 = 1, = 3 1 = 1 = 0, = 3 = 7 = 1, = 3 3 = 5 Using this, the completed table is (d) A graph of f() = log 1 ( + ) + is as follows. 3 Page 1
22 10. The graph of a function f() = log b is given in both graphs below. (a) (b) f f (a) Sketch the graph of g() = log b (b) Sketch the graph of h() = log b (c) Use the given graph to find the base b. Solution: (c) Notice that base is b = because the graph goes through the point (, 1). The requested graphs are as follows. Notice for (a) the graph will be made smmetric about the -ais, and shifted down units. For (b), the graph will be reflected over the -ais and then verticall stretched b a factor of. (a) g (b) h 11. The graph of a function f() = log b is given in both graphs below. Page
23 (a) f (b) f (a) On the same graph, sketch the graph = and the inverse function of f() = log b. (b) On the same graph, sketch the graph of h() = log 1/b (c) Find the inverse function of f() = log b. Solution: The requested graphs are as follows. Notice for (a), the inverse is obtained b reflecting the graph of f over the line =. For (b), notice log 1/b = log b so the graph of h is obtained b reflecting the graph of f over the -ais. (a) f 1 f (b) h (c) Notice that base is b = 5 because the graph goes through the point (5, 1), and so the inverse function is f 1 () = 5. f 1. The common log of the positive number M is given below. log(m) = 0. (a) Epress M as a power of 10. (b) Epress M in scientific notation. Use significant figures in our answer. Page 3
24 Solution: (a) log(m) = 0. implies M = (b) M = = = The common log of the positive numbers M and N are given below. log(m) = and log(n) = (a) Epress M and N as powers of 10. (b) Epress M and N in scientific notation. Use significant figures in our answers. Solution: (a) log(m) = implies M = , and log(n) = implies N = (b) M = = = , and N = = = In each item below, describe how the graphs of the two functions given are related. ( ) 1 (a) g() = and h() = (b) f() = log () and g() =. (c) k() = 3 and g() =. (d) l() = ( ) + 3 and g() =. (e) f() = log () and m() = log 1 (). Solution: (a) h() = so its graph is the graph of g reflected over the -ais. (b) f and g are inverses of each other, so the graph of f is the graph of g reflected over the line =. (c) The graph of k is the graph of g shifted -units to the right and 3 units down. (d) The graph of l is the graph of g stretched verticall b a factor of and then shifted 3 units upward. (e) The graph of m is the graph of f reflected over the -ais. Page
25 Properties of Logarithms ( ) 5 z 1. Epand log 5 b and write in terms of log b, log b and log b z (assume > 0, > 0, and z > 0). Solution: log b ( 5 z 5 ) = log b ( 5 z 5 ) log b ( ) = 1 log b( 5 z 5 ) log b ( ) = 1 [log b( 5 ) + log b (z 5 )] log b () = 5 log b + 5 log b z log b. ( ) in terms of log 5 z 3 1, log 1,. Use properties of logarithms to full epand log 1 z and number(s); simplif our answer (assume > 0, > 0, and z > 0). log 1 Solution: log 1 ( 5 z 3 ) = log 1 ( ) log 1 ( 5 z 3 ) = log 1 () + log 1 ( ) 1 log 1 ( 5 z 3 ) ( (1 ) ) = log 1 + log 1 () 1 [log 1 ( 5 ) + log 1 (z 3 )] = + log 1 5 log 1 3 log 1 z. 3. Use properties of logarithms to write 3 + log 3 log 7 log z as a single logarithm with coefficient 1. Solution: 3 + log 3 log 7 log z = log ( 3 ) + log () 1 [log ( 3 ) + log (z 7 )] = log () + log ( ) 1 log ( 3 z 7 ) = log ( ) log ( 3 z 7 ) = log ( 3 z 7 ). Page 5
26 . Write 3 log b ( 5 z 5 ) log b (z ( ) ) + 5 log b as a single logarithm with coefficient 1. Solution: 3 log b ( 5 z 5 ) log b (z ( ) ) + 5 log b = log b ( 5 z 5 ) 3 log b (z ( ) + log b = log b ( 15 z 15 ) log b (z 3 ) + log b ( 5 5 /3) = log b ( 15 z 15 ) log b (z 3 ) + log b ( 5 5 ) log b 3 ( ) ( ) 0 z z 9 = log b = log 3z 3 b. 3 ) 5 5. Use properties of logs and eponents to evaluate: (a) e 5 ln 3 (b) 1 3 log 1 (c) log ( 10 ) Solution: (a) e 5 ln 3 = e ln 35 = 3 5 = 3 (b) 1 3 log 1 = 1 log 1 (3) = 3 = (c) log ( 10 ) = log ( ) 10 = log ( 0 ) = 0. (Richter Scale) The magnitude of an earthquake of intensit I on the Richter scale is ( ) I M = log where I 0 is the intensit of a zero-level earthquake. (a) Find the magnitude to the nearest 0.1 of an earthquake that has an intensit of I = 511I 0. ( ) I (b) Write the formula M = log in eponential form, and then solve for I. I 0 (c) Use the formula in (b) to find the intensit of an earthquake that measures 5. on the Richter scale. (d) How man times more intense is an earthquake with a magnitude of.5 than an earthquake with a magnitude of 5.1? Epress answer to nearest whole number. (To do this, find the intensit of each earthquake using our formula from (b), and then divide to find the ratio of the intensities). ( ) 511I0 Solution: (a) The magnitude is M = log = log(511) 7.. I 0 I 0 (b) The eponential form is 10 M = I I 0, and so I = 10 M I 0 an earthquake given its magnitude. provides the intensit of Page
27 (c) From the formula in (b), the intensit is I = I I 0. (d) M 1 = 10.5 I 0 = 10 (.5 5.1) = Therefore, a magnitude.5 earthquake M I 0 is approimatel 51-times as intense as a magnitude 5.1 earthquake. 7. The range of sound intensities that the human ear can detect is ver large, so a logarithmic scale is used to measure them. The decibel level (db) of a sound is given b db(i) = 10 log I I 0 where I 0 is the intensit of sound that is barel audible to the huma ear. (a) How man times as great is the intensit of a sound that measures 153 decibels when compared to a sound that measures 113 decibels? (b) Find the decibel level of a sound whose intensit is 171 times as intense as a sound that measures 113 decibels. Round our answer to one decimal place. Solution: First observe that the equation db(i) = 10 log I I 0 implies db(i) 10 = log I I 0 I I 0 = 10 db(i)/10 I = I 0 10 db(i)/10 (a) Therefore, the intensit of a sound that measures 113 decibels is I 1 = I ; and the intensit of a sound that measures 153 decibels is I = I The ratio of intensties is I = I I 1 I 0 10 = = 10 = Therefore, a sound that measures 153 decibels is times as intense as a sound that measures 113 decibels. (b) From part (a), the intensit of a sound that measures 113 decibels is I 1 = I Therefore, a sound that is times as intense, has an intensit of I = 171I and its decibel measure will be 10 log( ) = 10 log = The ph of a solution with a hdronium-ion concentration [H + ] mole per liter is given b ph = log[h + ]. The higher the concentration of [H + ], the more acidic a solution is considered to be. Therefore, because of the negative sign in the above formula, the lower the ph, the more acidic a solution is considered to be. In particular, a solution with concentration of above 10 7 is considered to be acidic whereas a solution with concentration of below 10 7 is considered to be basic. Page 7
28 (a) Therefore, a solution with a ph (above/below) is acidic, and a solution with a ph (above/below) is basic. (b) A sample of blood is found to have a hdronium-ion concentration of about mole per liter. What is its ph? Epress answer to 1 decimal place. (c) A swimming pool s water was tested and the ph level was 7.1. Find the a hdroniumion concentration in mole per liter. Use 3 significant figures in our answer. Solution: (a) A solution with a ph below 7 is considered to be acidic. log(10 7 ) = 7.) A solution with a ph above 7 is considered to be basic. (b) The ph is log( ) = 7.7. (c) The concentration is = mole per liter. (Note 9. The percentage of a certain radiation that can penetrate millimeters of lead shielding is given b P () = 100e 1.5 (a) Find the percentage of radiation that can penetrate mm of lead shielding. Use at least 3 significant figures in our answer. (b) How man millimeters of lead shielding are required so that less than percent of radiation will penetrate the shielding? Round answer to one decimal place (nearest tenth of a millimeter). Solution: (a) In this case = and so P () = 100e % (b) Solve = 100e 1.5 and so e 1.5 = and this implies 1.5 = ln( ) = ln( ) mm That is, the lead shielding should be approimatel.0 millimeters thick. 10. Which is bigger 0 or 0? Solution: Logarithms are ideall suited for dealing with large numbers, for this question we will take log base 10 of both numbers, and compare which logarithm is larger. log(0 ) = log(0) while log( 0 ) = 0 log() 179. Because > 179., we know 0 is greater than 0 Page
29 11. Logarithms are ideall suited for dealing with large numbers, not onl can ou find, for eample, that 75 7 is bigger than 7 75 b comparing logarithms, it is eas to convert a logarithm to scientific notation which gives (perhaps more meaningful) information on the size of a number. The first step is to remember log() = a means = 10 a and properties of eponents then make it eas to convert the number in scientific notation. For eample Therefore, log(75 7 ) = 7 log(75) 7(.3135) = = = This is a huge number, it has 15 digits, but scientific notation, at least, provides a scale of its magnitude. Use properties of logarithms and eponents to answer the following questions. (a) Write in scientific notation. Use significant figures in our final answer. (b) Suppose log(n) = 3.31, write N in scientific notation. (c) Use properties of logarithms, as in the above eample, to write 9 7 in scientific notation. Use significant figures in our final answer. (Use a calculator to check our answer). (d) Use properties of logarithms, as in the above eample, to write in scientific notation. Use significant figures in our final answer. (Man calculators cannot process numbers above , so ou ma not be able to use a calculator to check our answer). (e) Find the product of numbers 9 7 and Epress our answer in scientific notation. Use significant figures in our answer. Solution: (a) = = (b) Writing log(n) = 3.31 in eponential form ields N = Then = = (c) First log(9 7 ) = 7 log(9) Therefore, = (d) First log(3 193 ) = 193 log(3) Therefore, = (e) You know how to multipl numbers in scientific notation, so ou can use our answer from (c) and (d) and do that! Alternativel, if ou did not have those answers, ou could just work with the logs and then convert the log to scientific notation. log( ) = log(9 7 ) + log(3 193 ) = Page 9
30 Therefore, = Logarithms are ideall suited for dealing with large numbers. Use properties of logarithms and eponents to answer the following questions. (a) Use properties of logarithms to write 7 17 in scientific notation. Use significant figures in our final answer. (b) Find the product Epress our answer in scientific notation. Use significant figures in our answer. (c) Find the quotient Epress our answer in scientific notation. Use significant figures in our answer. Solution: (a) First log(7 17 ) = 17 log(7) Therefore, = (b) We will convert the numbers to log base 10, then use properties of logarithms (or eponentials) and then convert number to scientific notation. Therefore, log( ) log(7 17 ) + log( ) = = (c) This is similar to (b), ecept for division, ou subtract eponents/logs. For comparison, this solution will use the eponential representation of the numbers, base 10, as converted from logs in (b): = = = Page 30
31 5 Eponential and Logarithmic Equations 1. (a) Find the eact solution to (3 ) 7(9 ) = 0. (b) Use a calculator to epress our answer in (a) to five decimal places. Solution: (a) First, (3 ) 7(9 ) = 0 implies (3 ) = 7(3 ) and so (3 ) = 7(3 ). Now divide both sides of this equation b 7(3 ) to obtain 7 = 3 3 and so 7 = 3 Now taking logs of both sides of the latter epression, we have ( ) log = log(3) 7 and so = log(/7) log(3) (This is the eact solution). (b) Using a calculator: = log(/7) log(3) Solve the equation 7 = 1 3 for. Leave answer in eact form. Solution: Taking the natural log of both sides of the equation and distributing we obtain ( 7)(ln ) = ( 3 )(ln 1) ( ln ) 7 ln = ( 3 ln 1) ln(1) now bring all the s to the left side, and all the numbers to the right side to obtain ( ln + 3 ln 1) = 7 ln ln 1 and then dividing both sides b ln + 3 ln 1 we have = 7 ln ln 1 ln + 3 ln 1 3. (a) Find the eact solution to the equation e 0.e the eact solution. e + e (b) Use a calculator to epress our answer in (a) to si decimal places. = 1. You don t have to simplif 3 Page 31
32 Solution: (a) Clearing the denominators and then moving like terms to the same sides ields: 3e 0.e = e + e 3e e = 0.e + e (3 1)e = (0. + )e Multipling both sides b e / ields (e )(e ) =. (b) e =. = ln ( ). = 1 ( ). ln. Find the eact solution(s) to the equation e + e = 11. Verif that our solutions work. Solution: Viewing the equation as e + e = 11 we multipl both sides of the equation b e to obtain ( (e ) e + ) = 11e e (e ) + = 11e This is an equation of quadratic form, and the substitution u = e turns this into a quadratic equation: u + = 11u u 11u + = 0 (u )(u 3) = 0 This implies u = or u = 3. Then e = implies = ln() and e = 3 implies = ln(3). So the solutions are = ln(), = ln(3). A check of the solutions is as follows: = ln() e ln() + e ln() = e ln() + e ln(1/) = + = + 3 = 11 as desired. = ln(3) e ln(3) + e ln(3) = e ln(3) + e ln(1/3) = = 3 + = 11 as desired. 5. Solve the equation log 5 ( ) = 3. Solution: In eponential form the equation becomes = 5 3 and so = 0 or 3 + = 0 and this implies ( )( 1) = 0, and so = or = 1. Page 3
33 . Alwas be careful to check that our solutions work when solving logarithmic equations, because logarithms and their properties are onl defined for positive numbers. See what happens when ou solve the equation: ln() + ln( ) = ln( ) For this, combine the logs on the left side using: ln(m) + ln(n) = ln(mn) when M > 0 and N > 0, and then use the propert ln(e) = ln(f ) implies E = F when ln(e) and ln(f ) are defined. Solution: First, ln() + ln( ) = ln( ) implies ln[( )] = ln( ) and thus ( ) =. Then + = 0 + = 0 ( )( ) = 0 Therefore, = and = are proposed solutions. However, neither of them works because when =, ln( ) = ln(0) which is not defined, and when =, ln( ) = ln( ) which is undefined since < 0. Thus neither of the proposed solutions work, and so there is no solution. 7. Solve the equation log 5 ( + ) + log 5 ( + 7) = log 5 (5 + ). Solution: First, as long as all epressions in the logs are positive, we have log 5 [( + )( + 7)] = log 5 (5 + ) and so ( + )( + 7) = 5 + and that implies and then = 5 + and so + 3 = 0 0 = + 3 = ( + )( ) = 0 and so potential solutions are = or =. All the logarithms in the original equation are defined when =, so it is a solution; however when =, log( + ) is not defined since + < 0. Thus = is not a solution. Therefore, the onl solution is =.. The population of a cit is currentl and is epected to grow at a rate of 5.0 percent per ear for the foreseeable future. Its population is given b P (t) = 00000(1.050 t ) where t is the number of ears from toda. (a) What will the population be in 3 ears? (Epress answer as a whole number) (b) At this rate of growth, how long (in ears) will it take the population to double? How long (in ears) would it take the population to quadruple? Epress answers to 1 decimal place. (c) If this growth rate could continue, how long (in ears) would it take for the population to reach 3,000,000 people? Epress answer to 1 decimal place. Page 33
34 Solution: (a) The population will be P (3) = 00000( ) 3155 in 3 ears. (b) To determine how long it will take the population to double, we solve (00000) = 00000(1.050) t for t. Thus dividing both sides b we have = t and then log() = t log(1.050) t = log() log(1.050) Thus it would take approimatel 1. ears for the population to double. For the population to quadruple, it would have to double twice, so it would take (1.070). ears for the population to quadruple. (c) To determine how long it will take the population to reach 3,000,000, we solve = 00000(1.050) t for t. Thus dividing both sides b we have /00000 = t and then log( /00000) = t log(1.050) t = log( /00000) log(1.050) Thus it would take approimatel 55.5 ears for the population to reach 3,000,000 people. Page 3
35 Applications of Eponentials and Logarithms 1. (Interest Income) Use the properties of logarithms and eponentials, along with the compound interest formula ( A = P 1 + r ) nt n to answer the following questions. (a) Suppose $1000 is invested at an annual interest rate of.0% compounded monthl. How much will it be worth after 5 ears? Epress answer to nearest penn. (b) How long will it take until the investment is worth $110000? Epress our answer in ears rounded to one decimal place. Solution: (a) We use P = 1000 (the amount invested), n = 1 (the number of compounding periods per ear), r =.0/100 = 0.00 (the interest rate in decimal form) and t = 5 (the number of ears the mone is invested). Then ( A = ) (1)(5) Thus after 5 ears the investment balance will be $ (b) We use P = 1000 (the amount invested), n = 1 (the number of compounding periods per ear), r =.0/100 = 0.00 (the interest rate in decimal form), t (the number of ears the mone is invested is an unknown we wish to determine), and A = the amount of the investment after t ears. Thus we solve ( = ) 1t or 1 ( = ) 1t 1 b taking logs of both sides of the equation to obtain ( log(110000/1000) = 1t log ) t = log(110000/1000) 1 1 log ( ) Thus it will take approimatel.7 ears for an investment of $1000 to reach a balance of $ when invested at.0% compounded monthl.. (Eponential Growth) The population of bacteria in a vat of potato salad at Bob s All Da Buffet is modeled b P (t) = P 0 e kt. At noon there were 1050 bacteria present and at 1:00 pm there were 1750 bacteria present. (a) Find the specific model for P (t) (i.e., use the information given to find P 0 and k, and plug those values into P (t) = P 0 e kt ), and then use it to answer the following questions. (b) How ma bacteria were present in the potato salad at 11:30 am when was placed in the buffet? Epress answer to nearest whole number. (c) How ma bacteria were present in the potato salad at 3:00 pm when the potato salad was removed from the buffet? Page 35
36 (d) If the potato salad had been allowed to remain in the buffet indefinitel, and the model for the bacteria remained valid, how man hours after noon, when there were 1050 bacteria present would it have taken for the bacteria population to reach 915. Epress answer in hours, rounded to nearest decimal place. (For all of these questions, assume no one ate took an potato salad because of its funn smell and hence the population of bacteria remained in tact and followed the given growth model). Solution: (a) Let t be measured in hours and let t 0 = 0 at 1 noon. Now P 0 = 1050 is the population when t = 0. Thus P (t) = 1050e kt and so we need to find k. Also, we know P (1.0) = 1750 because we are told there were 1750 bacteria present at 1:00 pm, and t = 1.0 at 1:00 pm. Therefore, 1750 = 1050e 1.0k. Then ln(1750/1050) = ln(e 1.0k ) and so 1.0k = ln(1750/1050) k = ln(1750/1050) Therefore, P (t) = 1050e t. (b) At 11:30am, t = 1/ and so there were approimatel 1050e (0.5105)(.5) 13 bacteria present in the vat of potato salad. (c) At 3:00 pm, t = 3.0 and so there were approimatel 1050e (0.5105)(3.0) 1 bacteria in the vat of potato salad. (d) For this, solve P (t) = 915 for t. That is 1050e t = 915 and so e t = 915 ln ( e t) ( ) 915 = ln ( ) ( ) t = ln t = ln and so it would take approimatel. hours, after noon, for the bacteria population to reach The population of a small cit is currentl and is growing at percent per ear. Thus the population is given b P (t) = 59000(1.0) t where t is time measured in ears from the present. (a) What will the population of the cit be in one ear? (b) According to this model, what will the population of the cit be in 1 ears from now? Epress answer to the nearest whole number. (c) If this rate of growth continues, how long will it take for the population to triple. Epress answer in ears rounded to two decimal places. Page 3
37 Solution: (a) P (1) = 59000(1.0) = 010 which represents an increase of percent over the current populaton. (b) Assuming the current growth rate continues, the population will be P (t) = 59000(1.0) 1 = 7. (c) In this case we solve 3(59000) = 59000(1.0) t and so 3 = (1.0) t this implies ln(3) = t ln(1.0) t = ln(3) ln(1.0) 55. The population will triple in approimatel 55. ears.. A population of a town follows an eponential growth model P (t) = Ae kt where t is measured in ears, and P (t) is the population at time t. Suppose the population was eactl 7 ears ago, and it is toda. (a) Use this information, with t = 0 for the time eactl 7 ears ago, to find P (t). (b) According to this model, what will the population be 7 ears from now (epress answer to nearest whole number)? Solution: (a) Because P (0) = 11000, we know P (t) = 11000e kt and then P (7) = implies = 11000e 7k e 7k = ( ) k = ln k = 1 ( ) ln Then k and so P (t) 11000e t (b) In 7 ears from now, t will be t = = 1. Then the population will be P (1) 11000e ( )(1) (Carbon Dating) Carbon-1 has a half-life of 5730 ears, and satisfies the eponentialdeca equation N(t) = N 0 ( 1 ) t/5730. (a) If an ancient scroll is discovered to have 5.0% of its original Carbon-1, how old is the scroll? Round answer to nearest ear. (b) What percentage of a bone s original Carbon-1 would ou epect to find remaining in a bone that is 00 ears old? Round to the nearest tenth of one percent. Page 37
38 Solution: (a) Solve 0.50N 0 = N 0 (.5) t/5730 and so 0.50 = (.5) t/5730 and so ln(0.50) = t ln(.5) 5730 or t = 5730 ln(0.50) ln(.5) 50 ears Thus the scroll is approimatel 50 ears old. (b) N(t) = N 0 (.5) 00/ N 0. This implies that we would epect to find approimatl 5.0% of the original amount of the Carbon-1 remaining in the bone.. An unknown radioactive element decas into non-radioactive substances. In 50 das the radioactivit of a sample decreases b 5 percent, that is percent of the original substance remains. (a) What is the half-life of the element? (b) How long will it take for a sample of 100 mg to deca to 0 mg? Solution: The radioactive deca equation is A(t) = A 0 ( 1 ) t/h where H is the half-life in the units corresponding to t. a) We are given that after 50 das, onl percent of the original sample would remain. Thus we solve This implies 0.A 0 = A 0 ( 1 50 H = ln() ln(.5) ) 50/H and so H = 50 ln(.5) ln(0.) and so the half-life is approimatel 5.53 das. b) The amount of time for a 100 mg sample to deca to a 0 mg sample would be given b ( ) t/ = 100 or 5.53 ln(0.0) t = 39.7 das ln(.5) 7. According to Newton s Law of Cooling an object placed in a refigerator with a constant temperature of 39 F has its temperature (in degrees Fahrenheit) given b T (t) = 39 + Ce kt where C and k are constants. Suppose a can of soda (the soda is rather warm because the can was in a warm car) had a temperature of 10 F when it was placed in the refrigerator and 0 minutes later, the soda has cooled to F. Page 3
39 (a) Find the C and k for the temperature equation above. Use t in minutes with t = 0 being the time when the can of soda was placed in the refrigerator. (b) What will be the temperature of the can of soda after 5 minutes? Epress answer to the nearest degree. (c) How long will it take for the can of soda to reach 5 F. Epress answer to the nearest minute Solution: We know T (0) = 10 and so 39 + Ce 0 = 10 and then C = = 5. Then T (0) = implies and so k = e 0k e 0k = 9 5 (b) In 5 minutes, the temperature will be approimatel T (5) = e (5)( ) 73 F k = 1 0 ln(9/10) (c) Solve 5 = e t and so e t = /5 and then 1 t = ln(/5) The soda temperature will reach 5 F approimatel 19 minutes after being placed in the refrigerator.. A cup containing hot tea is placed in a room whose temperature is kept at a constant 7 F. The tea cooled from 05 F to 15 F in 10 minutes. Use Newton s law of cooling to determine how man more minutes, after the temperature reached 15 F, it will take for the tea to cool to 15 F. Epress answer to 3 decimal places. Note: Newton s law of cooling implies T (t) = 7 + Ce kt where t is measured in minutes. Solution: Let t = 0 be the time when the tea is placed in the room. Then T (0) = 05, and so 7 + Ce 0 = 05 and so C = 05 7 = 17. Then T = e kt. Then T (10) = 15 implies 15 = e k(10) and so k = 1 10 ln ( Therefore, T (t) = e t. ) To find how long it takes for the temperature to reach 15 F, we solve ( ) 15 = e t and so t ln so it takes an additional 19.9 minutes (after the temperature reached 15 F) for the temperature to reach 15 F. Page 39
Math 121. Practice Problems from Chapter 4 Fall 2016
 Math 11. Practice Problems from Chapter Fall 01 Section 1. Inverse Functions 1. Graph an inverse function using the graph of the original function. For practice see Eercises 1,.. Use information about
Math 11. Practice Problems from Chapter Fall 01 Section 1. Inverse Functions 1. Graph an inverse function using the graph of the original function. For practice see Eercises 1,.. Use information about
Chapter 8 Notes SN AA U2C8
 Chapter 8 Notes SN AA U2C8 Name Period Section 8-: Eploring Eponential Models Section 8-2: Properties of Eponential Functions In Chapter 7, we used properties of eponents to determine roots and some of
Chapter 8 Notes SN AA U2C8 Name Period Section 8-: Eploring Eponential Models Section 8-2: Properties of Eponential Functions In Chapter 7, we used properties of eponents to determine roots and some of
Ch. 4 Review College Algebra Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 Ch. Review College Algebra Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Decide whether or not the functions are inverses of each other. 3 5 +
Ch. Review College Algebra Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Decide whether or not the functions are inverses of each other. 3 5 +
Chapter 9 Vocabulary Check
 9 CHAPTER 9 Eponential and Logarithmic Functions Find the inverse function of each one-to-one function. See Section 9.. 67. f = + 68. f = - CONCEPT EXTENSIONS The formula = 0 e kt gives the population
9 CHAPTER 9 Eponential and Logarithmic Functions Find the inverse function of each one-to-one function. See Section 9.. 67. f = + 68. f = - CONCEPT EXTENSIONS The formula = 0 e kt gives the population
Logarithms. Bacteria like Staph aureus are very common.
 UNIT 10 Eponentials and Logarithms Bacteria like Staph aureus are ver common. Copright 009, K1 Inc. All rights reserved. This material ma not be reproduced in whole or in part, including illustrations,
UNIT 10 Eponentials and Logarithms Bacteria like Staph aureus are ver common. Copright 009, K1 Inc. All rights reserved. This material ma not be reproduced in whole or in part, including illustrations,
Practice A ( 1, 3 ( 0, 1. Match the function with its graph. 3 x. Explain how the graph of g can be obtained from the graph of f. 5 x.
 8. Practice A For use with pages 65 7 Match the function with its graph.. f. f.. f 5. f 6. f f Lesson 8. A. B. C. (, 6) (0, ) (, ) (0, ) ( 0, ) (, ) D. E. F. (0, ) (, 6) ( 0, ) (, ) (, ) (0, ) Eplain how
8. Practice A For use with pages 65 7 Match the function with its graph.. f. f.. f 5. f 6. f f Lesson 8. A. B. C. (, 6) (0, ) (, ) (0, ) ( 0, ) (, ) D. E. F. (0, ) (, 6) ( 0, ) (, ) (, ) (0, ) Eplain how
Lesson 5.1 Exponential Functions
 Lesson.1 Eponential Functions 1. Evaluate each function at the given value. Round to four decimal places if necessar. a. r (t) 2(1 0.0) t, t 8 b. j() 9.(1 0.09), 10 2. Record the net three terms for each
Lesson.1 Eponential Functions 1. Evaluate each function at the given value. Round to four decimal places if necessar. a. r (t) 2(1 0.0) t, t 8 b. j() 9.(1 0.09), 10 2. Record the net three terms for each
decreases as x increases.
 Chapter Review FREQUENTLY ASKED Questions Q: How can ou identif an eponential function from its equation? its graph? a table of values? A: The eponential function has the form f () 5 b, where the variable
Chapter Review FREQUENTLY ASKED Questions Q: How can ou identif an eponential function from its equation? its graph? a table of values? A: The eponential function has the form f () 5 b, where the variable
5A Exponential functions
 Chapter 5 5 Eponential and logarithmic functions bjectives To graph eponential and logarithmic functions and transformations of these functions. To introduce Euler s number e. To revise the inde and logarithm
Chapter 5 5 Eponential and logarithmic functions bjectives To graph eponential and logarithmic functions and transformations of these functions. To introduce Euler s number e. To revise the inde and logarithm
Exponential and Logarithmic Functions, Applications, and Models
 86 Eponential and Logarithmic Functions, Applications, and Models Eponential Functions In this section we introduce two new tpes of functions The first of these is the eponential function Eponential Function
86 Eponential and Logarithmic Functions, Applications, and Models Eponential Functions In this section we introduce two new tpes of functions The first of these is the eponential function Eponential Function
Summary, Review, and Test
 45 Chapter Equations and Inequalities Chapter Summar Summar, Review, and Test DEFINITIONS AND CONCEPTS EXAMPLES. Eponential Functions a. The eponential function with base b is defined b f = b, where b
45 Chapter Equations and Inequalities Chapter Summar Summar, Review, and Test DEFINITIONS AND CONCEPTS EXAMPLES. Eponential Functions a. The eponential function with base b is defined b f = b, where b
3.1 Exponential Functions and Their Graphs
 .1 Eponential Functions and Their Graphs Sllabus Objective: 9.1 The student will sketch the graph of a eponential, logistic, or logarithmic function. 9. The student will evaluate eponential or logarithmic
.1 Eponential Functions and Their Graphs Sllabus Objective: 9.1 The student will sketch the graph of a eponential, logistic, or logarithmic function. 9. The student will evaluate eponential or logarithmic
Math Chapter 5 - More Practice MUST SHOW WORK IN ALL PROBLEMS - Also, review all handouts from the chapter, and homework from the book.
 Math 101 - Chapter - More Practice Name MUST SHOW WORK IN ALL PROBLEMS - Also, review all handouts from the chapter, and homework from the book. Write the equation in eponential form. 1) log 2 1 4 = -2
Math 101 - Chapter - More Practice Name MUST SHOW WORK IN ALL PROBLEMS - Also, review all handouts from the chapter, and homework from the book. Write the equation in eponential form. 1) log 2 1 4 = -2
Sections 4.1 & 4.2 Exponential Growth and Exponential Decay
 8 Sections 4. & 4.2 Eponential Growth and Eponential Deca What You Will Learn:. How to graph eponential growth functions. 2. How to graph eponential deca functions. Eponential Growth This is demonstrated
8 Sections 4. & 4.2 Eponential Growth and Eponential Deca What You Will Learn:. How to graph eponential growth functions. 2. How to graph eponential deca functions. Eponential Growth This is demonstrated
Math125 Exam 5 Review Name. Do the following as indicated.
 Math Eam Review Name Do the following as indicated. For the given functions f and g, find the requested function. ) f() = - 6; g() = 9 Find (f - g)(). ) ) f() = 33 + ; g() = - Find (f g)(). 3) f() = ;
Math Eam Review Name Do the following as indicated. For the given functions f and g, find the requested function. ) f() = - 6; g() = 9 Find (f - g)(). ) ) f() = 33 + ; g() = - Find (f g)(). 3) f() = ;
7-1. Exploring Exponential Models. Vocabulary. Review. Vocabulary Builder. Use Your Vocabulary. 1. Cross out the expressions that are NOT powers.
 7-1 Eploring Eponential Models Vocabular Review 1. Cross out the epressions that are NOT powers. 16 6a 1 7. Circle the eponents in the epressions below. 5 6 5a z Vocabular Builder eponential deca (noun)
7-1 Eploring Eponential Models Vocabular Review 1. Cross out the epressions that are NOT powers. 16 6a 1 7. Circle the eponents in the epressions below. 5 6 5a z Vocabular Builder eponential deca (noun)
Sec 5.1 Exponential & Logarithmic Functions (Exponential Models)
 Sec 5.1 Eponential & Logarithmic Functions (Eponential Models) 1. The population of the cit Suwanee, GA has consistentl grown b 4% for the last several ears. In the ear 000, the population was 9,500 people.
Sec 5.1 Eponential & Logarithmic Functions (Eponential Models) 1. The population of the cit Suwanee, GA has consistentl grown b 4% for the last several ears. In the ear 000, the population was 9,500 people.
Ready To Go On? Skills Intervention 7-1 Exponential Functions, Growth, and Decay
 7A Find these vocabular words in Lesson 7-1 and the Multilingual Glossar. Vocabular Read To Go On? Skills Intervention 7-1 Eponential Functions, Growth, and Deca eponential growth eponential deca asmptote
7A Find these vocabular words in Lesson 7-1 and the Multilingual Glossar. Vocabular Read To Go On? Skills Intervention 7-1 Eponential Functions, Growth, and Deca eponential growth eponential deca asmptote
2. Tell whether the equation or graph represents an exponential growth or exponential decay function.
 Name: Date: Period: ID: 1 Unit 9 Review Eponents & Logarithms NO GRAPHING CALCULATOR 1. Under each function, write es if it is an eponential function. If the answer is no, write an eplanation wh not. a)
Name: Date: Period: ID: 1 Unit 9 Review Eponents & Logarithms NO GRAPHING CALCULATOR 1. Under each function, write es if it is an eponential function. If the answer is no, write an eplanation wh not. a)
f 0 ab a b: base f
 Precalculus Notes: Unit Eponential and Logarithmic Functions Sllabus Objective: 9. The student will sketch the graph of a eponential, logistic, or logarithmic function. 9. The student will evaluate eponential
Precalculus Notes: Unit Eponential and Logarithmic Functions Sllabus Objective: 9. The student will sketch the graph of a eponential, logistic, or logarithmic function. 9. The student will evaluate eponential
Math 111 Final Exam Review KEY
 Math 111 Final Eam Review KEY 1. Use the graph of = f in Figure 1 to answer the following. Approimate where necessar. a b Evaluate f 1. f 1 = 0 Evaluate f0. f0 = 6 c Solve f = 0. =, = 1, =, or = 3 Solution
Math 111 Final Eam Review KEY 1. Use the graph of = f in Figure 1 to answer the following. Approimate where necessar. a b Evaluate f 1. f 1 = 0 Evaluate f0. f0 = 6 c Solve f = 0. =, = 1, =, or = 3 Solution
6.2 Indicate whether the function is one-to-one. 16) {(-13, -20), (-10, -20), (13, -8)}
 Math 0 Eam Review. Evaluate the epression using the values given in the table. ) (f g)() 7 f() - - - g() - 7 Evaluate the epression using the graphs of = f() and = g(). ) Evaluate (fg)(). 9) H() = - 7
Math 0 Eam Review. Evaluate the epression using the values given in the table. ) (f g)() 7 f() - - - g() - 7 Evaluate the epression using the graphs of = f() and = g(). ) Evaluate (fg)(). 9) H() = - 7
Pre-Calculus B Semester 1 Review Packet December 2015
 Pre-Calculus B Semester Review Packet December 05 Name DISCLAIMER The memor on all calculators will be cleared the da of the final. If ou have programs on our calculator that ou would like to keep, please
Pre-Calculus B Semester Review Packet December 05 Name DISCLAIMER The memor on all calculators will be cleared the da of the final. If ou have programs on our calculator that ou would like to keep, please
Final Exam Review. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Final Eam Review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine whether or not the relationship shown in the table is a function.
Final Eam Review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine whether or not the relationship shown in the table is a function.
Self- assessment 1010 (Intermediate Algebra)
 Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
is on the graph of y = f 1 (x).
 Objective 2 Inverse Functions Illustrate the idea of inverse functions. f() = 2 + f() = Two one-to-one functions are inverses of each other if (f g)() = of g, and (g f)() = for all in the domain of f.
Objective 2 Inverse Functions Illustrate the idea of inverse functions. f() = 2 + f() = Two one-to-one functions are inverses of each other if (f g)() = of g, and (g f)() = for all in the domain of f.
Exponential and Logarithmic Functions
 Eponential and Logarithmic Functions.1 Eponential Growth and Deca Functions. The Natural Base e.3 Logarithms and Logarithmic Functions. Transformations of Eponential and Logarithmic Functions.5 Properties
Eponential and Logarithmic Functions.1 Eponential Growth and Deca Functions. The Natural Base e.3 Logarithms and Logarithmic Functions. Transformations of Eponential and Logarithmic Functions.5 Properties
CHAPTER 3 Exponential and Logarithmic Functions
 CHAPTER Eponential and Logarithmic Functions Section. Eponential Functions and Their Graphs......... Section. Logarithmic Functions and Their Graphs......... Section. Properties of Logarithms..................
CHAPTER Eponential and Logarithmic Functions Section. Eponential Functions and Their Graphs......... Section. Logarithmic Functions and Their Graphs......... Section. Properties of Logarithms..................
where a 0 and the base b is a positive number other
 7. Graph Eponential growth functions No graphing calculators!!!! EXPONENTIAL FUNCTION A function of the form than one. a b where a 0 and the base b is a positive number other a = b = HA = Horizontal Asmptote:
7. Graph Eponential growth functions No graphing calculators!!!! EXPONENTIAL FUNCTION A function of the form than one. a b where a 0 and the base b is a positive number other a = b = HA = Horizontal Asmptote:
ln(9 4x 5 = ln(75) (4x 5) ln(9) = ln(75) 4x 5 = ln(75) ln(9) ln(75) ln(9) = 1. You don t have to simplify the exact e x + 4e x
 Math 11. Exponential and Logarithmic Equations Fall 016 Instructions. Work in groups of 3 to solve the following problems. Turn them in at the end of class for credit. Names. 1. Find the (a) exact solution
Math 11. Exponential and Logarithmic Equations Fall 016 Instructions. Work in groups of 3 to solve the following problems. Turn them in at the end of class for credit. Names. 1. Find the (a) exact solution
Math 111 Final Exam Review KEY
 Math Final Eam Review KEY. Use the graph of = f in Figure to answer the following. Approimate where necessar. a Evaluate f. f = 0 b Evaluate f0. f0 = 6 c Solve f = 0. =, =, =,or = 3 d Solve f = 7..5, 0.5,
Math Final Eam Review KEY. Use the graph of = f in Figure to answer the following. Approimate where necessar. a Evaluate f. f = 0 b Evaluate f0. f0 = 6 c Solve f = 0. =, =, =,or = 3 d Solve f = 7..5, 0.5,
Section 11.1 Rational Exponents Goals: 1. To use the properties of exponents. 2. To evaluate and simplify expressions containing rational exponents.
 Section 11.1 Rational Eponents Goals: 1. To use the properties of eponents.. To evaluate and simplif epressions containing rational eponents. I. Properties to Review m n A. a a = m B. ( a ) n = C. n a
Section 11.1 Rational Eponents Goals: 1. To use the properties of eponents.. To evaluate and simplif epressions containing rational eponents. I. Properties to Review m n A. a a = m B. ( a ) n = C. n a
MAC 1105 Review for Exam 4. Name
 MAC 1105 Review for Eam Name For the given functions f and g, find the requested composite function. 1) f() = +, g() = 8-7; Find (f g)(). 1) Find the domain of the composite function f g. 9 ) f() = + 9;
MAC 1105 Review for Eam Name For the given functions f and g, find the requested composite function. 1) f() = +, g() = 8-7; Find (f g)(). 1) Find the domain of the composite function f g. 9 ) f() = + 9;
is on the graph of y = f 1 (x).
 Objective 2 Inverse Functions Illustrate the idea of inverse functions. f() = 2 + f() = Two one-to-one functions are inverses of each other if (f g)() = of g, and (g f)() = for all in the domain of f.
Objective 2 Inverse Functions Illustrate the idea of inverse functions. f() = 2 + f() = Two one-to-one functions are inverses of each other if (f g)() = of g, and (g f)() = for all in the domain of f.
Math125 Exam 5 (Final) Review Name. Do the following as indicated. 17) log 17x = 1.2 (Round answer to four decimal places.)
 Math12 Eam (Final) Review Name Do the following as indicated. For the given functions f and g, find the requested function. 1) f() = - 6; g() = 92 Find (f - g)(). 2) f() = 33 + 1; g() = 2-2 Find (f g)().
Math12 Eam (Final) Review Name Do the following as indicated. For the given functions f and g, find the requested function. 1) f() = - 6; g() = 92 Find (f - g)(). 2) f() = 33 + 1; g() = 2-2 Find (f g)().
 Test # 33 QUESTIONS MATH131 091700 COLLEGE ALGEBRA Name atfm131bli www.alvarezmathhelp.com website MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Test # 33 QUESTIONS MATH131 091700 COLLEGE ALGEBRA Name atfm131bli www.alvarezmathhelp.com website MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
f 0 ab a b: base f
 Precalculus Notes: Unit Eponential and Logarithmic Functions Sllaus Ojective: 9. The student will sketch the graph of a eponential, logistic, or logarithmic function. 9. The student will evaluate eponential
Precalculus Notes: Unit Eponential and Logarithmic Functions Sllaus Ojective: 9. The student will sketch the graph of a eponential, logistic, or logarithmic function. 9. The student will evaluate eponential
MTH 112 Practice Test 3 Sections 3.3, 3.4, 3.5, 1.9, 7.4, 7.5, 8.1, 8.2
 MTH 112 Practice Test 3 Sections 3.3, 3., 3., 1.9, 7., 7., 8.1, 8.2 Use properties of logarithms to epand the logarithmic epression as much as possible. Where possible, evaluate logarithmic epressions
MTH 112 Practice Test 3 Sections 3.3, 3., 3., 1.9, 7., 7., 8.1, 8.2 Use properties of logarithms to epand the logarithmic epression as much as possible. Where possible, evaluate logarithmic epressions
Math Reviewing Chapter 4
 Math 80 - Reviewing Chapter Name If the following defines a one-to-one function, find the inverse. ) {(-, 8), (, 8), (-, -)} Decide whether or not the functions are inverses of each other. ) f() = + 7;
Math 80 - Reviewing Chapter Name If the following defines a one-to-one function, find the inverse. ) {(-, 8), (, 8), (-, -)} Decide whether or not the functions are inverses of each other. ) f() = + 7;
STRAND: GRAPHS Unit 5 Growth and Decay
 CMM Subject Support Strand: GRAPHS Unit 5 Growth and Deca: Tet STRAND: GRAPHS Unit 5 Growth and Deca TEXT Contents Section 5. Modelling Population 5. Models of Growth and Deca 5. Carbon Dating 5.4 Rate
CMM Subject Support Strand: GRAPHS Unit 5 Growth and Deca: Tet STRAND: GRAPHS Unit 5 Growth and Deca TEXT Contents Section 5. Modelling Population 5. Models of Growth and Deca 5. Carbon Dating 5.4 Rate
7-1 Practice. Graphing Exponential Functions. Graph each function. State the domain and range. 1. y = 1.5(2) x 2. y = 4(3) x 3. y = 3(0.
 7-1 Practice Graphing Eponential Functions Graph each function. State the domain and range. 1. = 1.5(2) 2. = 4(3) 3. = 3(0.5) 4. = 5 ( 1 2) - 8 5. = - 2 ( 1 4) - 3 6. = 1 2 (3) + 4-5 7. BILGY The initial
7-1 Practice Graphing Eponential Functions Graph each function. State the domain and range. 1. = 1.5(2) 2. = 4(3) 3. = 3(0.5) 4. = 5 ( 1 2) - 8 5. = - 2 ( 1 4) - 3 6. = 1 2 (3) + 4-5 7. BILGY The initial
Algebra 1B Assignments Exponential Functions (All graphs must be drawn on graph paper!)
 Name Score Algebra 1B Assignments Eponential Functions (All graphs must be drawn on graph paper!) 8-6 Pages 463-465: #1-17 odd, 35, 37-40, 43, 45-47, 50, 51, 54, 55-61 odd 8-7 Pages 470-473: #1-11 odd,
Name Score Algebra 1B Assignments Eponential Functions (All graphs must be drawn on graph paper!) 8-6 Pages 463-465: #1-17 odd, 35, 37-40, 43, 45-47, 50, 51, 54, 55-61 odd 8-7 Pages 470-473: #1-11 odd,
LESSON #48 - INTEGER EXPONENTS COMMON CORE ALGEBRA II
 LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
7.4. Characteristics of Logarithmic Functions with Base 10 and Base e. INVESTIGATE the Math
 7. Characteristics of Logarithmic Functions with Base 1 and Base e YOU WILL NEED graphing technolog EXPLORE Use benchmarks to estimate the solution to this equation: 1 5 1 logarithmic function A function
7. Characteristics of Logarithmic Functions with Base 1 and Base e YOU WILL NEED graphing technolog EXPLORE Use benchmarks to estimate the solution to this equation: 1 5 1 logarithmic function A function
9) A) f-1(x) = 8 - x B) f-1(x) = x - 8 C)f-1(x) = x + 8 D) f-1(x) = x 8
 Review for Final Eam Name Algebra- Trigonometr MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Factor the polnomial completel. If a polnomial cannot
Review for Final Eam Name Algebra- Trigonometr MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Factor the polnomial completel. If a polnomial cannot
 Test #4 33 QUESTIONS MATH1314 09281700 COLLEGE ALGEBRA Name atfm1314bli28 www.alvarezmathhelp.com website SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
Test #4 33 QUESTIONS MATH1314 09281700 COLLEGE ALGEBRA Name atfm1314bli28 www.alvarezmathhelp.com website SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The domain of a quadratic function is the set of all real numbers.
 EXERCISE 2-3 Things to remember: 1. QUADRATIC FUNCTION If a, b, and c are real numbers with a 0, then the function f() = a 2 + b + c STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The
EXERCISE 2-3 Things to remember: 1. QUADRATIC FUNCTION If a, b, and c are real numbers with a 0, then the function f() = a 2 + b + c STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The
LESSON 12.2 LOGS AND THEIR PROPERTIES
 LESSON. LOGS AND THEIR PROPERTIES LESSON. LOGS AND THEIR PROPERTIES 5 OVERVIEW Here's what ou'll learn in this lesson: The Logarithm Function a. Converting from eponents to logarithms and from logarithms
LESSON. LOGS AND THEIR PROPERTIES LESSON. LOGS AND THEIR PROPERTIES 5 OVERVIEW Here's what ou'll learn in this lesson: The Logarithm Function a. Converting from eponents to logarithms and from logarithms
Algebra II. Chapter 8 Notes. Exponential and Logarithmic Functions. Name
 Algebra II Chapter 8 Notes Eponential and Logarithmic Functions Name Algebra II 8.1 Eponential Growth Toda I am graphing eponential growth functions. I am successful toda when I can graph eponential growth
Algebra II Chapter 8 Notes Eponential and Logarithmic Functions Name Algebra II 8.1 Eponential Growth Toda I am graphing eponential growth functions. I am successful toda when I can graph eponential growth
The formulas below will be provided in the examination booklet. Compound Interest: r n. Continuously: n times per year: 1
 HONORS ALGEBRA B Semester Eam Review The semester B eamination for Honors Algebra will consist of two parts. Part will be selected response on which a calculator will not be allowe Part will be short answer
HONORS ALGEBRA B Semester Eam Review The semester B eamination for Honors Algebra will consist of two parts. Part will be selected response on which a calculator will not be allowe Part will be short answer
Exponential Growth and Decay Functions (Exponent of t) Read 6.1 Examples 1-3
 CC Algebra II HW #42 Name Period Row Date Section 6.1 1. Vocabulary In the eponential growth model Eponential Growth and Decay Functions (Eponent of t) Read 6.1 Eamples 1-3 y = 2.4(1.5), identify the initial
CC Algebra II HW #42 Name Period Row Date Section 6.1 1. Vocabulary In the eponential growth model Eponential Growth and Decay Functions (Eponent of t) Read 6.1 Eamples 1-3 y = 2.4(1.5), identify the initial
6.4 graphs OF logarithmic FUnCTIOnS
 SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
C H A P T E R 3 Exponential and Logarithmic Functions
 C H A P T E R Eponential and Logarithmic Functions Section. Eponential Functions and Their Graphs......... Section. Logarithmic Functions and Their Graphs........ 7 Section. Properties of Logarithms.................
C H A P T E R Eponential and Logarithmic Functions Section. Eponential Functions and Their Graphs......... Section. Logarithmic Functions and Their Graphs........ 7 Section. Properties of Logarithms.................
Math098 Practice Final Test
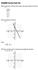 Math098 Practice Final Test Find an equation of the line that contains the points listed in the table. 1) 0-6 1-2 -4 3-3 4-2 Find an equation of the line. 2) 10-10 - 10 - -10 Solve. 3) 2 = 3 + 4 Find the
Math098 Practice Final Test Find an equation of the line that contains the points listed in the table. 1) 0-6 1-2 -4 3-3 4-2 Find an equation of the line. 2) 10-10 - 10 - -10 Solve. 3) 2 = 3 + 4 Find the
Items with a symbol next to the item number indicate that a student should be prepared to complete items like these with or without a calculator.
 HNRS ALGEBRA B Semester Eam Review The semester B eamination for Honors Algebra will consist of two parts. Part is selected response on which a calculator will NT be allowed. Part is short answer on which
HNRS ALGEBRA B Semester Eam Review The semester B eamination for Honors Algebra will consist of two parts. Part is selected response on which a calculator will NT be allowed. Part is short answer on which
8-1 Exploring Exponential Models
 8- Eploring Eponential Models Eponential Function A function with the general form, where is a real number, a 0, b > 0 and b. Eample: y = 4() Growth Factor When b >, b is the growth factor Eample: y =
8- Eploring Eponential Models Eponential Function A function with the general form, where is a real number, a 0, b > 0 and b. Eample: y = 4() Growth Factor When b >, b is the growth factor Eample: y =
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 MAC 0 Module Test 8 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the function value. ) Let f() = -. Find f(). -8 6 C) 8 6 Objective:
MAC 0 Module Test 8 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the function value. ) Let f() = -. Find f(). -8 6 C) 8 6 Objective:
a > 0 parabola opens a < 0 parabola opens
 Objective 8 Quadratic Functions The simplest quadratic function is f() = 2. Objective 8b Quadratic Functions in (h, k) form Appling all of Obj 4 (reflections and translations) to the function. f() = a(
Objective 8 Quadratic Functions The simplest quadratic function is f() = 2. Objective 8b Quadratic Functions in (h, k) form Appling all of Obj 4 (reflections and translations) to the function. f() = a(
Chapters 8 & 9 Review for Final
 Math 203 - Intermediate Algebra Professor Valdez Chapters 8 & 9 Review for Final SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the formula for
Math 203 - Intermediate Algebra Professor Valdez Chapters 8 & 9 Review for Final SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the formula for
Chapter 4 Page 1 of 16. Lecture Guide. Math College Algebra Chapter 4. to accompany. College Algebra by Julie Miller
 Chapter 4 Page 1 of 16 Lecture Guide Math 105 - College Algebra Chapter 4 to accompan College Algebra b Julie Miller Corresponding Lecture Videos can be found at Prepared b Stephen Toner & Nichole DuBal
Chapter 4 Page 1 of 16 Lecture Guide Math 105 - College Algebra Chapter 4 to accompan College Algebra b Julie Miller Corresponding Lecture Videos can be found at Prepared b Stephen Toner & Nichole DuBal
Math 111 Final Exam Review
 Math 111 Final Eam Review With the eception of rounding irrational logarithmic epressions and problems that specif that a calculator should be used, ou should be prepared to do the entire problem without
Math 111 Final Eam Review With the eception of rounding irrational logarithmic epressions and problems that specif that a calculator should be used, ou should be prepared to do the entire problem without
M122 College Algebra Review for Final Exam
 M1 College Algebra Review for Final Eam Revised Fall 017 for College Algebra - Beecher All answers should include our work (this could be a written eplanation of the result, a graph with the relevant feature
M1 College Algebra Review for Final Eam Revised Fall 017 for College Algebra - Beecher All answers should include our work (this could be a written eplanation of the result, a graph with the relevant feature
Unit 3 NOTES Honors Common Core Math 2 1. Day 1: Properties of Exponents
 Unit NOTES Honors Common Core Math Da : Properties of Eponents Warm-Up: Before we begin toda s lesson, how much do ou remember about eponents? Use epanded form to write the rules for the eponents. OBJECTIVE
Unit NOTES Honors Common Core Math Da : Properties of Eponents Warm-Up: Before we begin toda s lesson, how much do ou remember about eponents? Use epanded form to write the rules for the eponents. OBJECTIVE
SAMPLE. Exponential and logarithmic functions
 Objectives C H A P T E R 5 Eponential and logarithmic functions To graph eponential and logarithmic functions. To graph transformations of the graphs of eponential and logarithmic functions. To introduce
Objectives C H A P T E R 5 Eponential and logarithmic functions To graph eponential and logarithmic functions. To graph transformations of the graphs of eponential and logarithmic functions. To introduce
Exponential and Logarithmic Functions
 7 Eponential and Logarithmic Functions 7.1 Eponential Growth and Deca Functions 7. The Natural Base e 7.3 Logarithms and Logarithmic Functions 7. Transformations of Eponential and Logarithmic Functions
7 Eponential and Logarithmic Functions 7.1 Eponential Growth and Deca Functions 7. The Natural Base e 7.3 Logarithms and Logarithmic Functions 7. Transformations of Eponential and Logarithmic Functions
Name Period Date. Practice FINAL EXAM Intro to Calculus (50 points) Show all work on separate sheet of paper for full credit!
 Name Period Date Practice FINAL EXAM Intro to Calculus (0 points) Show all work on separate sheet of paper for full credit! ) Evaluate the algebraic epression for the given value or values of the variable(s).
Name Period Date Practice FINAL EXAM Intro to Calculus (0 points) Show all work on separate sheet of paper for full credit! ) Evaluate the algebraic epression for the given value or values of the variable(s).
Log Test Review - Graphing Problems
 Algebra Honors - Mr. Allen-Black d^0id7i wkpuftza SSqoffLtrw`aerZef CLOLACq.m H LAwlrl` _raidgqhvtssb reisaenrdvqekdr. Log Test Review - Graphing Problems ) = 3 Name ID: ) = ( Date Period - - - - - - -
Algebra Honors - Mr. Allen-Black d^0id7i wkpuftza SSqoffLtrw`aerZef CLOLACq.m H LAwlrl` _raidgqhvtssb reisaenrdvqekdr. Log Test Review - Graphing Problems ) = 3 Name ID: ) = ( Date Period - - - - - - -
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Math 2 Stud Guide-Chapters 8 and 9 Name Date: Time: MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find all square roots of the number. ) 600 9,
Math 2 Stud Guide-Chapters 8 and 9 Name Date: Time: MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find all square roots of the number. ) 600 9,
Evaluate Logarithms and Graph Logarithmic Functions
 TEKS 7.4 2A.4.C, 2A..A, 2A..B, 2A..C Before Now Evaluate Logarithms and Graph Logarithmic Functions You evaluated and graphed eponential functions. You will evaluate logarithms and graph logarithmic functions.
TEKS 7.4 2A.4.C, 2A..A, 2A..B, 2A..C Before Now Evaluate Logarithms and Graph Logarithmic Functions You evaluated and graphed eponential functions. You will evaluate logarithms and graph logarithmic functions.
Reteaching (continued)
 Zero and Negative Eponents Eercises Write each epression as an integer, a simple fraction, or an epression that contains onl positive eponents. Simplif...3 0. 0-0,000 3. a -5. 3.7 0 a 5 5. 9-6. 3-3 9 p
Zero and Negative Eponents Eercises Write each epression as an integer, a simple fraction, or an epression that contains onl positive eponents. Simplif...3 0. 0-0,000 3. a -5. 3.7 0 a 5 5. 9-6. 3-3 9 p
Honors Pre-Calculus. Multiple Choice 1. An expression is given. Evaluate it at the given value
 Honors Pre-Calculus Multiple Choice. An epression is given. Evaluate it at the given value, (A) (B) 9 (C) 9 (D) (E). Simplif the epression. (A) + (B) (C) (D) (E) 7. Simplif the epression. (A) (B) (C) (D)
Honors Pre-Calculus Multiple Choice. An epression is given. Evaluate it at the given value, (A) (B) 9 (C) 9 (D) (E). Simplif the epression. (A) + (B) (C) (D) (E) 7. Simplif the epression. (A) (B) (C) (D)
Chapter 8. Exponential and Logarithmic Functions
 Chapter 8 Eponential and Logarithmic Functions Lesson 8-1 Eploring Eponential Models Eponential Function The general form of an eponential function is y = ab. Growth Factor When the value of b is greater
Chapter 8 Eponential and Logarithmic Functions Lesson 8-1 Eploring Eponential Models Eponential Function The general form of an eponential function is y = ab. Growth Factor When the value of b is greater
Math 121, Practice Questions for Final (Hints/Answers)
 Math 11, Practice Questions for Final Hints/Answers) 1. The graphs of the inverse functions are obtained by reflecting the graph of the original function over the line y = x. In each graph, the original
Math 11, Practice Questions for Final Hints/Answers) 1. The graphs of the inverse functions are obtained by reflecting the graph of the original function over the line y = x. In each graph, the original
The semester B examination for Algebra 2 will consist of two parts. Part 1 will be selected response. Part 2 will be short answer. n times per year: 1
 ALGEBRA B Semester Eam Review The semester B eamination for Algebra will consist of two parts. Part 1 will be selected response. Part will be short answer. Students ma use a calculator. If a calculator
ALGEBRA B Semester Eam Review The semester B eamination for Algebra will consist of two parts. Part 1 will be selected response. Part will be short answer. Students ma use a calculator. If a calculator
Math-3 Lesson 8-7. b) ph problems c) Sound Intensity Problems d) Money Problems e) Radioactive Decay Problems. a) Cooling problems
 Math- Lesson 8-7 Unit 5 (Part-) Notes 1) Solve Radical Equations ) Solve Eponential and Logarithmic Equations ) Check for Etraneous solutions 4) Find equations for graphs of eponential equations 5) Solve
Math- Lesson 8-7 Unit 5 (Part-) Notes 1) Solve Radical Equations ) Solve Eponential and Logarithmic Equations ) Check for Etraneous solutions 4) Find equations for graphs of eponential equations 5) Solve
Math 111 Final Exam Review KEY
 Math 111 Final Eam Review KEY 1. Use the graph of y = f in Figure 1 to answer the following. Approimate where necessary. a Evaluate f 1. f 1 = 0 b Evaluate f0. f0 = 6 c Solve f = 0. =, = 1, =,or = 3 Solution
Math 111 Final Eam Review KEY 1. Use the graph of y = f in Figure 1 to answer the following. Approimate where necessary. a Evaluate f 1. f 1 = 0 b Evaluate f0. f0 = 6 c Solve f = 0. =, = 1, =,or = 3 Solution
Math Review Packet #5 Algebra II (Part 2) Notes
 SCIE 0, Spring 0 Miller Math Review Packet #5 Algebra II (Part ) Notes Quadratic Functions (cont.) So far, we have onl looked at quadratic functions in which the term is squared. A more general form of
SCIE 0, Spring 0 Miller Math Review Packet #5 Algebra II (Part ) Notes Quadratic Functions (cont.) So far, we have onl looked at quadratic functions in which the term is squared. A more general form of
13.2 Exponential Growth Functions
 Name Class Date. Eponential Growth Functions Essential Question: How is the graph of g () = a b - h + k where b > related to the graph of f () = b? A.5.A Determine the effects on the ke attributes on the
Name Class Date. Eponential Growth Functions Essential Question: How is the graph of g () = a b - h + k where b > related to the graph of f () = b? A.5.A Determine the effects on the ke attributes on the
Exponential, Logistic, and Logarithmic Functions
 CHAPTER 3 Eponential, Logistic, and Logarithmic Functions 3.1 Eponential and Logistic Functions 3.2 Eponential and Logistic Modeling 3.3 Logarithmic Functions and Their Graphs 3.4 Properties of Logarithmic
CHAPTER 3 Eponential, Logistic, and Logarithmic Functions 3.1 Eponential and Logistic Functions 3.2 Eponential and Logistic Modeling 3.3 Logarithmic Functions and Their Graphs 3.4 Properties of Logarithmic
3.1 Graphing Quadratic Functions. Quadratic functions are of the form.
 3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
LESSON #24 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
Unit 8: Exponential & Logarithmic Functions
 Date Period Unit 8: Eponential & Logarithmic Functions DAY TOPIC ASSIGNMENT 1 8.1 Eponential Growth Pg 47 48 #1 15 odd; 6, 54, 55 8.1 Eponential Decay Pg 47 48 #16 all; 5 1 odd; 5, 7 4 all; 45 5 all 4
Date Period Unit 8: Eponential & Logarithmic Functions DAY TOPIC ASSIGNMENT 1 8.1 Eponential Growth Pg 47 48 #1 15 odd; 6, 54, 55 8.1 Eponential Decay Pg 47 48 #16 all; 5 1 odd; 5, 7 4 all; 45 5 all 4
Chapter 11 Exponential and Logarithmic Function
 Chapter Eponential and Logarithmic Function - Page 69.. Real Eponents. a m a n a mn. (a m ) n a mn. a b m a b m m, when b 0 Graphing Calculator Eploration Page 700 Check for Understanding. The quantities
Chapter Eponential and Logarithmic Function - Page 69.. Real Eponents. a m a n a mn. (a m ) n a mn. a b m a b m m, when b 0 Graphing Calculator Eploration Page 700 Check for Understanding. The quantities
3.2 LOGARITHMIC FUNCTIONS AND THEIR GRAPHS
 Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
Exponential Functions, Logarithms, and e
 Chapter 3 Starry Night, painted by Vincent Van Gogh in 1889 The brightness of a star as seen from Earth is measured using a logarithmic scale Eponential Functions, Logarithms, and e This chapter focuses
Chapter 3 Starry Night, painted by Vincent Van Gogh in 1889 The brightness of a star as seen from Earth is measured using a logarithmic scale Eponential Functions, Logarithms, and e This chapter focuses
ONLINE PAGE PROOFS. Exponential functions Kick off with CAS 11.2 Indices as exponents
 . Kick off with CAS. Indices as eponents Eponential functions.3 Indices as logarithms.4 Graphs of eponential functions.5 Applications of eponential functions.6 Inverses of eponential functions.7 Review
. Kick off with CAS. Indices as eponents Eponential functions.3 Indices as logarithms.4 Graphs of eponential functions.5 Applications of eponential functions.6 Inverses of eponential functions.7 Review
3.3 Logarithmic Functions and Their Graphs
 274 CHAPTER 3 Eponential, Logistic, and Logarithmic Functions What ou ll learn about Inverses of Eponential Functions Common Logarithms Base 0 Natural Logarithms Base e Graphs of Logarithmic Functions
274 CHAPTER 3 Eponential, Logistic, and Logarithmic Functions What ou ll learn about Inverses of Eponential Functions Common Logarithms Base 0 Natural Logarithms Base e Graphs of Logarithmic Functions
Chapter 12 and 13 Math 125 Practice set Note: the actual test differs. Given f(x) and g(x), find the indicated composition and
 Chapter 1 and 13 Math 1 Practice set Note: the actual test differs. Given f() and g(), find the indicated composition. 1) f() = - ; g() = 3 + Find (f g)(). Determine whether the function is one-to-one.
Chapter 1 and 13 Math 1 Practice set Note: the actual test differs. Given f() and g(), find the indicated composition. 1) f() = - ; g() = 3 + Find (f g)(). Determine whether the function is one-to-one.
where is a constant other than ( and ) and
 Section 12.1: EXPONENTIAL FUNCTIONS When you are done with your homework you should be able to Evaluate eponential functions Graph eponential functions Evaluate functions with base e Use compound interest
Section 12.1: EXPONENTIAL FUNCTIONS When you are done with your homework you should be able to Evaluate eponential functions Graph eponential functions Evaluate functions with base e Use compound interest
c) domain {x R, x 3}, range {y R}
 Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
Exponential and Logarithmic Functions. Copyright Cengage Learning. All rights reserved.
 Exponential and Logarithmic Functions Copyright Cengage Learning. All rights reserved. 4.6 Modeling With Exponential And Logarithmic Functions Copyright Cengage Learning. All rights reserved. Objectives
Exponential and Logarithmic Functions Copyright Cengage Learning. All rights reserved. 4.6 Modeling With Exponential And Logarithmic Functions Copyright Cengage Learning. All rights reserved. Objectives
CHAPTER 3 Exponential and Logarithmic Functions
 CHAPTER Eponential and Logarithmic Functions Section. Eponential Functions and Their Graphs......... Section. Logarithmic Functions and Their Graphs......... Section. Properties of Logarithms..................
CHAPTER Eponential and Logarithmic Functions Section. Eponential Functions and Their Graphs......... Section. Logarithmic Functions and Their Graphs......... Section. Properties of Logarithms..................
Instructor: Imelda Valencia Course: A3 Honors Pre Calculus
 Student: Date: Instructor: Imelda Valencia Course: A3 Honors Pre Calculus 01 017 Assignment: Summer Homework for those who will be taking FOCA 017 01 onl available until Sept. 15 1. Write the epression
Student: Date: Instructor: Imelda Valencia Course: A3 Honors Pre Calculus 01 017 Assignment: Summer Homework for those who will be taking FOCA 017 01 onl available until Sept. 15 1. Write the epression
MA Lesson 14 Notes Summer 2016 Exponential Functions
 Solving Eponential Equations: There are two strategies used for solving an eponential equation. The first strategy, if possible, is to write each side of the equation using the same base. 3 E : Solve:
Solving Eponential Equations: There are two strategies used for solving an eponential equation. The first strategy, if possible, is to write each side of the equation using the same base. 3 E : Solve:
13.1 Exponential Growth Functions
 Name Class Date 1.1 Eponential Growth Functions Essential Question: How is the graph of g () = a b - h + k where b > 1 related to the graph of f () = b? Resource Locker Eplore 1 Graphing and Analzing f
Name Class Date 1.1 Eponential Growth Functions Essential Question: How is the graph of g () = a b - h + k where b > 1 related to the graph of f () = b? Resource Locker Eplore 1 Graphing and Analzing f
( ) ( ) x. The exponential function f(x) with base b is denoted by x
 Page of 7 Eponential and Logarithmic Functions Eponential Functions and Their Graphs: Section Objectives: Students will know how to recognize, graph, and evaluate eponential functions. The eponential function
Page of 7 Eponential and Logarithmic Functions Eponential Functions and Their Graphs: Section Objectives: Students will know how to recognize, graph, and evaluate eponential functions. The eponential function
y = f(x + 4) a) Example: A repeating X by using two linear equations y = ±x. b) Example: y = f(x - 3). The translation is
 Answers Chapter Function Transformations. Horizontal and Vertical Translations, pages to. a h, k h, k - c h -, k d h 7, k - e h -, k. a A (-,, B (-,, C (-,, D (,, E (, A (-, -, B (-,, C (,, D (, -, E (,
Answers Chapter Function Transformations. Horizontal and Vertical Translations, pages to. a h, k h, k - c h -, k d h 7, k - e h -, k. a A (-,, B (-,, C (-,, D (,, E (, A (-, -, B (-,, C (,, D (, -, E (,
1. For each of the following, state the domain and range and whether the given relation defines a function. b)
 Eam Review Unit 0:. For each of the following, state the domain and range and whether the given relation defines a function. (,),(,),(,),(5,) a) { }. For each of the following, sketch the relation and
Eam Review Unit 0:. For each of the following, state the domain and range and whether the given relation defines a function. (,),(,),(,),(5,) a) { }. For each of the following, sketch the relation and
The speed the speed of light is 30,000,000,000 m/s. Write this number in scientific notation.
 Chapter 1 Section 1.1 Scientific Notation Powers of Ten 1 1 1.1.1.1.1 Standard Scientific Notation N n where 1 N and n is an integers Eamples of numbers in scientific notation. 8.17 11 Using Scientific
Chapter 1 Section 1.1 Scientific Notation Powers of Ten 1 1 1.1.1.1.1 Standard Scientific Notation N n where 1 N and n is an integers Eamples of numbers in scientific notation. 8.17 11 Using Scientific
Answers to All Exercises
 Answers to All Eercises CHAPTER 5 CHAPTER 5 CHAPTER 5 CHAPTER REFRESHING YOUR SKILLS FOR CHAPTER 5 1a. between 3 and 4 (about 3.3) 1b. between 6 and 7 (about 6.9) 1c. between 7 and 8 (about 7.4) 1d. between
Answers to All Eercises CHAPTER 5 CHAPTER 5 CHAPTER 5 CHAPTER REFRESHING YOUR SKILLS FOR CHAPTER 5 1a. between 3 and 4 (about 3.3) 1b. between 6 and 7 (about 6.9) 1c. between 7 and 8 (about 7.4) 1d. between
