CREATES Research Paper Non-linear DSGE Models and The Central Difference Kalman Filter
|
|
|
- Della Elliott
- 5 years ago
- Views:
Transcription
1 CREATES Research Paper Non-linear DSGE Models and The Central Difference Kalman Filter Martin M. Andreasen School of Economics and Management Aarhus University Bartholins Allé 10, Building 1322, DK-8000 Aarhus C Denmark
2 Non-linear DSGE Models and The Central Di erence Kalman Filter Martin M. Andreasen y Bank of England and CREATES July 20, 2010 Abstract This paper introduces a Quasi Maximum Likelihood (QML) approach based on the Central Di erence Kalman Filter (CDKF) to estimate non-linear DSGE models with potentially non-gaussian shocks. We argue that this estimator can be expected to be consistent and asymptotically normal for DSGE models solved up to third order. A Monte Carlo study shows that this QML estimator is basically unbiased and normally distributed in nite samples for DSGE models solved using a second order or a third order approximation. These results hold even when structural shocks are Gaussian, Laplace distributed, or display stochastic volatility. Keywords: Non-linear ltering, Non-Gaussian shocks, Quasi Maximum Likelihood, Stochastic volatility, Third order perturbation. JEL: C13, C15, E10, E32 This paper is an improved version of some sections in an earlier paper entitled: "Non-linear DSGE Models, the Central Di erence Kalman Filter, and the Mean Shifted Particle Filter". y I would like to thank Oreste Tristani, Bent Jesper Christensen, Tom Engsted, and participants at the workshop "Modeling and Forecasting Economic and Financial Time Series with State Space models" at the Swedish Riksbank Oct for comments and discussions. martin.andreasen@bankofengland.co.uk. Telephone number: I greatly acknowledge nancial support from the Danish Center for Scienti c Computation (DCSC). I appreciate nancial support to Center for Research in Econometric Analysis of Time Series, CREATES, funded by the Danish National Research Foundation. Finally, the views expressed herein are solely those of the author and not necessarily those of Bank of England. 1
3 1 Introduction Likelihood based inference has emerged as a standard approach to estimate linearized DSGE models with unobserved state variables. The approach relies on the use of the Kalman Filter to evaluate the log-likelihood function in closed form when shocks and potential measurement errors are Gaussian. A similar closed form solution for the log-likelihood function does not exist when DSGE models are solved with non-linear terms and/or have non-gaussian shocks. The important contribution by Fernández-Villaverde & Rubio-Ramírez (2007) addresses this problem by introducing a sequential Monte Carlo method called particle ltering as a way to estimate the log-likelihood function for non-linear DSGE modes with potentially non-gaussian shocks. Throughout this paper we refer to the particle lter used in Fernández-Villaverde & Rubio-Ramírez (2007) as the standard Particle Filter (PF). Although the idea of using particle ltering for likelihood inference is appealing, the method has the disadvantage of being computationally very demanding. Even for models with just two or three shocks, tens of thousands of particles are needed to get a reliable approximation to the log-likelihood function, and this makes the estimation process very time consuming - if at all feasible - for larger models. The numerical di culties related to particle ltering imply that a relatively small number of non-linear DSGE models have so far been estimated by likelihood inference compared to the large number of estimated linearized DSGE models. Hence, more e cient ltering and estimation methods would clearly be useful in relation to estimation of non-linear DSGE models. As an alternative to particle ltering, Norgaard, Poulsen & Ravn (2000) have developed the Central Di erence Kalman Filter (CDKF) for state estimation in general non-linear and non- Gaussian state space systems. Contrary to particle lters, the updating rule for the state vector in the CDKF is restricted to have a linear functional form, and the recursive equations for the state estimator and its covariance matrix are therefore only functions of rst and second moments. The CDKF approximates these moments up to at least second order accuracy by a deterministic sampling approach based on multivariate Stirling interpolations. This approximation method is computationally very fast and reasonably accurate. Like particle ltering, the CDKF frequently outperforms the Extended Kalman Filter (EKF) which for many years has been the preferred lter for non-linear and non-gaussian systems (see for instance Jazwinski (1970)). 2
4 The contribution of this paper is to introduce a Quasi Maximum Likelihood (QML) method using the CDKF to estimate non-linear DSGE models with potentially non-gaussian shocks. We focus on the case where the observed variables contain measurement errors, and we argue that this QML estimator can be expected to be consistent and asymptotically normal for DSGE models solved up to third order. These results hold both when Gaussian and non-gaussian shocks are driving the economy. The main advantage of the proposed QML estimator is that it is much faster to compute than any particle lter and this greatly eases the estimation. Our QML estimator could therefore be expected to facilitate an increase in the number of estimated non-linear DSGE models. We test the performance of the CDKF and the suggested QML estimator in a Monte Carlo study using a New Keynesian DSGE model approximated to rst, second, and third order. The key results from this Monte Carlo study are as follows. Firstly, the state vector is estimated more precisely by the CDKF than the EKF and the standard PF (with 200,000 particles) when shocks are Gaussian and Laplace distributed. This shows that a linear updating rule and the multivariate Stirling interpolation used in the CDKF may lead to quite accurate approximations. However, the standard PF performs better than the CDKF and the EKF when shocks display stochastic volatility. Secondly, the quasi log-likelihood function derived from the CDKF is a better approximation to the log-likelihood function in the standard PF than the quasi log-likelihood function based on the EKF. For Gaussian shocks, the quasi log-likelihood function from the CDKF is either very close or within the 95% con dence interval for the estimated log-likelihood function in the standard PF. The same conclusion does not hold when shocks have a Laplace distribution or display stochastic volatility. Thirdly, the suggested QML estimator is found to be normally distributed and basically unbiased in nite samples for second and third order approximations to the considered DSGE model. These results hold regardless of whether shocks to the economy are Gaussian, Laplace distributed, or display stochastic volatility. Asymptotic standard errors can in all cases be computed based on the Hessian matrix and the variance of the score function. Reliable inference is here greatly facilitated by the property that only rst order derivatives are needed to compute the Hessian matrix for this quasi log-likelihood function. Based on these ndings, we therefore believe that the suggested QML approach is a useful new tool for taking non-linear DSGE models to the data. Our QML estimator may be considered as an 3
5 alternative to the likelihood approach advocated by Fernández-Villaverde & Rubio-Ramírez (2007) but also as a useful supplement. For instance, the Classical researcher may use the QML estimates as good starting values for the maximization of the log-likelihood function from a particle lter as this should make the optimization considerable easier. Also the Bayesian researcher may nd the QML estimator useful because i) the QML estimates can be used as good starting values for the Markov chain, and ii) the Hessian matrix of the quasi log-likelihood function can be used to specify the proposal distribution in the random walk Metropolis algorithm for the MCMC analysis. Both features should help to ensure faster convergence of the Markov chain where the log-likelihood function is estimated by a particle lter. The rest of the paper is organized as follows. We present the state space representation of DSGE models in section 2. Some theory related to ltering is discussed in section 3 where we also present the EKF and the CDKF. We then introduce the QML approach based on the CDKF in section 4. Section 5 describes a standard DSGE model which is calibrated to account for higher order moments in the post-war US economy. The performance of the various lters and the QML estimator are examined in a Monte Carlo study in section 6. Concluding comments are provided in section 7. 2 The state space representation of DSGE models We consider the class of DSGE models that can be represented in a dynamic state space system (see Thomas F. Cooley (1995) and Schmitt-Grohé & Uribe (2004) for illustrations). The observables in period t are denoted by the vector y t with dimension n y 1, and these observables are a function of the state vector x t with dimension n x 1. Allowing for additive measurement errors v t in all observables, we then get y t = g (x t ; ) + v t, (1) where v t IID (0; R v (t)) denotes independent and identically distributed measurement errors. The function g () is determined by the structural parameters 2 in the economic model and the model s equilibrium conditions. We refer to (1) as the set of measurement equations. 4
6 For the state vector, we consider a standard rst order Markovian law of motion x t+1 = h (x t ; w t+1 ; ) ; (2) where w t+1 IID (0; R w (t + 1)). The vector w t+1 of structural innovations is assumed to be uncorrelated at all leads and lags with v t. We refer to (2) as the set of transition equations. The state vector is assumed to be unobserved, but observed state variables can be incorporated by letting one or more elements in g () be identity mappings. 3 Filtering The objective of ltering is to estimate the unobserved state vector x t as data on y t becomes available. We start in section 3.1 by deriving recursive equations for the estimation of x t and its covariance matrix based on a two-step procedure of prediction and updating. The updating rule for the state vector is assumed to be linear in the observables because it leads to simple equations with only rst and second moments from the state space system in (1) and (2). The next two sections show how these moments are approximated by linearization in the EKF and by multivariate Stirling interpolations in the CDKF. The nal section discusses prediction and smoothing in the CDKF. 3.1 A linear updating rule for the state vector We use the standard notation where a bar denotes a priori estimates and a hat denotes posterior estimates. For instance, x t+1 E t [x t+1 ] and ^x t+1 E t+1 [x t+1 ], where E t is the conditional expectation given the observations y 1:t fy 1 ; y 2 ; :::; y t g. 1 The a priori state estimator follows directly from (2) and is given by x t+1 E t [h (x t ; w t+1 ; )] : (3) 1 An alternative notation is x t+1jt = E t [x t+1] and x t+1jt+1 E t+1 [x t+1] as in Hamilton (1994), for instance. We choose x t+1 and ^x t+1 because this notation is more parsimonious. 5
7 The conditional error covariance matrix for this estimator is denoted by P xx (t + 1) E t (xt+1 x t+1 ) (x t+1 x t+1 ) 0 : (4) The updating rule of the a priori state estimator is for tractability restricted to be linear in the observables, i.e. ^x t+1 = b t+1 + K t+1 y t+1 ; (5) where b t+1 and K t+1 are determined below. If we choose b t+1 such that the a priori and the posterior state estimators are unbiased, then it follows directly that b t+1 = x t+1 K t+1 y t+1 ; where y t+1 E t [g (x t+1 ; )] : (6) This gives rise to the well-known updating rule ^x t+1 = x t+1 + K t+1 (y t+1 y t+1 ) : (7) The value of the Kalman gain K t+1 is determined such that the conditional error covariance matrix for ^x t+1 is minimized. It is straightforward to show that this criterion implies (see Lewis (1986)) K t+1 = P xy (t + 1) P yy (t + 1) 1 ; (8) where we have de ned P xy (t + 1) E t (xt+1 x t+1 ) (y t+1 y t+1 ) 0 (9) P yy (t + 1) E t (yt+1 y t+1 ) (y t+1 y t+1 ) 0 : (10) The conditional error covariance matrix for ^x t+1 can be expressed as ^P xx (t + 1) = P xx (t + 1) K t+1 P yy (t + 1) K 0 t+1: (11) Thus, the ltering equations for the class of updating rules implied by (5) are given by (3), (4), 6
8 and (7) - (11). Two remarks are in order. Firstly, if we are able to accurately evaluate the required rst and second moments, then the a priori and the posterior state estimators in (3) and (7) are unbiased by construction. This result holds even though the state space system is non-linear and no distributional assumptions are imposed on v t and w t. Secondly, the required rst and second moments can be evaluated exactly when g () and h () are linear functions, and this leads to the Kalman Filter. Recall that the Kalman Filter has a linear updating rule for the posterior state vector, and the lter can be derived without imposing distributional assumptions for v t and w t (see for instance Tanizaki (1996)). However, the non-linearity in (1) and (2) imply that some approximation is needed to calculate the required moments. 3.2 The Extended Kalman Filter One way to proceed is to linearize the state space system such that y t g (x t ; ) + G x;t (x t x t ) + v t (12) x t+1 h (^x t ; ) + H x;t (x t ^x t ) + H w;t (w t+1 w t+1 ) (13) where G (x; H x;t (x; H (^x t; w; ) (14) w= wt+1 Using these approximations, the rst and second moments in the ltering equations are given by x t+1 = h (^x t ; w t+1 ; ) y t+1 = g (x t+1 ; ) (15) P xx (t + 1) = H x;t ^P xx (t) H 0 x;t + H w;t R w (t + 1) H 0 w;t (16) P xy (t + 1) = P xx (t + 1) G 0 x;t+1 (17) P yy (t + 1) = G x;t+1 P xx (t + 1) G 0 x;t+1 + R v (t + 1) (18) 7
9 Applying these approximations lead to the Extended Kalman Filter (see for instance Jazwinski (1970)). The approximations in (15) are only accurate up to rst order and do not account for the probability distribution of (^x t ; w t+1 ). This is because the linearizations in (15) are done around a single point. The approximations in (16) - (18) are more precise as they are accurate up to second order. However, it is possible to improve the accuracy of these approximations with no additional computational costs as we will see in the next section. 3.3 The Central Di erence Kalman Filter The idea behind the CDKF is to approximate the non-linear expectations in (3), (4), and (7) - (11) by second order multivariate Stirling interpolations. 2 We introduce some additional notation to describe how this is done. First, let S w (t), S v (t), S x (t), and ^S x (t) be squared and upper triangular Cholesky factorizations of R w (t), R v (t), P xx (t), and ^P xx (t), respectively. That is, R w (t) = S w (t) S w (t) 0 and so on. Lower case vectors denote elements in these matrices, for instance S w (t + 1) = s w;1 s w;2 ::: s w;nw. We next de ne S (1) xx (t) = f(h i (^x t + h^s x;j ; w t+1 ; ) h i (^x t h^s x;j ; w t+1 ; )) =2hg (19) (n xn x) S (1) xw (t) = f(h i (^x t ; w t+1 + hs w;j ; ) h i (^x t ; w t+1 hs w;j ; )) =2hg (20) (n xn w) S (1) yx (t) = f(g i (x t + hs x;j ; ) g i (x t hs x;j ; )) =2hg (21) (n yn x) 0 where we use the notation h () h 1 () h 2 () ::: h nx () and similarly for the function g (). The matrices in (19) - (21) contain the rst order e ects of the general non-linear functions and this is denoted by the superscript (1). The corresponding matrices for the second order e ects are: S (2) xx (t) = (n xn x) S (2) xw (t) = (n xn w) (p ) h 2 1 2h 2 (h i (^x t + h^s x;j ; w t+1 ; ) + h i (^x t h^s x;j ; w t+1 ; ) 2h i (^x t ; w t+1 ; )) (p ) h 2 1 2h 2 (h i (^x t ; w t+1 + hs w;j ; ) + h i (^x t ; w t+1 hs w;j ; ) 2h i (^x t ; w t+1 ; )) (22) (23) 2 Our presentation of the CDKF is adapted to the state space system in (1) and (2). 8
10 S (2) yx (t) = (n yn x) (p ) h 2 1 2h 2 (g i (x t + hs x;j ; ; ) + g i (x t hs x;j ; ) 2g i (x t ; )) (24) Norgaard et al. (2000) recommend to determine the value of the scalar h based on the distribution of the random variable subject to the multivariate Stirling interpolation. It is here optimal to let h 2 equal the kurtosis of this distribution. As shown by Norgaard et al. (2000), the a priori state estimator in the CDKF is x t+1 = h2 n x n w h 2 h (^x t ; w t+1 ; ) (25) + 1 2h 2 P nx p=1 (h (^x t + h^s x;p ; w t+1 ; ) + h (^x t h^s x;p ; w t+1 ; )) + 1 2h 2 P nw p=1 (h (^x t ; w t+1 + hs w;p ; ) + h (^x t ; w t+1 hs w;p ; )) : This approximation accounts for the distribution of the state vector ^x t and the distribution of the structural innovations w t+1 due to the second and third term in (25), respectively. The computation in each of these terms is very similar to computing numerical derivatives of h (). The important thing to notice is that the step size in (25) depends on the covariance matrix of the variable subject to the approximation, whereas the step size is arbitrary small and mutually ortogonal when numerical derivatives are computed. Norgaard et al. (2000) shows that the a priori estimator in (25) is accurate up to second order. If the state distribution and the structural shocks are normally distributed, then this estimator is even accurate up to third order. The a priori covariance matrix of (25) is obtained by a QR decomposition of the matrix S (1) xx (t) S (1) xw (t) S (2) xx (t) S (2) xw (t) : (26) We follow Norgaard et al. (2000) and use the Householder transformation (A) to perform the QR decomposition of a rectangular matrix A. This transformation produces a squared and upper triangular matrix S = (A) such that AA 0 = SS 0. Hence, S x (t + 1) = S (1) xx (t) S (1) xw (t) S (2) xx (t) S (2) xw (t) : (27) To see how this approximation of S x (t + 1) relates to the expression in the EKF, we use the 9
11 de nition of the Householder transformation to get P xx (t + 1) = S (1) xx (t) S (1) xx (t) 0 + S (2) xx (t) S (2) xx (t) 0 + S (1) xw (t) S (1) xw (t) 0 + S (2) xw (t) S (2) xw (t) 0 : (28) In comparison to the EKF, we thus have that S (1) xx (t) S (1) xx (t) 0 + S (2) xx (t) S (2) xx (t) 0 corresponds to H x;t ^P xx (t) H 0 x;t, and S(1) xw (t) S (1) xw (t) 0 + S (2) xw (t) S (2) xw (t) 0 corresponds to H w;t R w (t + 1) H 0 w;t. However, the approximations in (28) are in general more accurate than those in the EKF (Norgaard et al. (2000)). The a priori estimator for the vector of observables is given by y t+1 = h2 n x h 2 g (x t+1 ; ) + 1 P nx 2h 2 p=1 (g (x t+1 + hs x;p ; ) + g (x t+1 hs x;p ; )) (29) This estimator has the same structure and properties as the a priori state estimator in (25). The covariance matrix of y t+1 is calculated based on S y (t + 1) = S (1) yx (t + 1) S v (t + 1) S (2) yx (t + 1) ; (30) and the Kalman gain is given by K t+1 = S x (t + 1) S (1) yx (t + 1) 0 S y (t + 1) S y (t + 1) 0 1 : (31) Finally, the covariance matrix of the posterior state estimator follows from ^S x (t + 1) = S x (t + 1) K t+1 S (1) yx (t + 1) K t+1 S v (t + 1) K t+1 S (2) yx (t + 1) (32) An overview of the CDKF is given in appendix A. We emphasize two properties in relation to the CDKF. Firstly, if the functions g () and h () are linear in x t and w t+1, then the CDKF reduces to the Kalman Filter. Secondly, the number of function evaluations of g () and h () in the CDKF are identical to the number of function 10
12 evaluations in the EKF when derivatives are approximated by double di erences, i.e. = x=x f (x + ) f (x ) 2 (33) where > 0 is a small number. Hence, the improved accuracy of the CDKF compared to the EKF comes at no additional computational costs. 3.4 Prediction and smoothing in the CDKF Prediction ofthe observables in the CDKF is obtained by iterating (25), (27), and (29) forward in time. Särkkä (2008) shows how to derive a Forward-Backward smoother for the Unscented Kalman Filter, and Dunik & Simandl (2006) derive a square root implementation of this smoother. 3 These smoothers are derived based on the additional assumption that the ltered and the smoothed state distributions are multivariate normal. Given the results in Norgaard et al. (2000), it is straightforward to set up the Forward-Backward smoother for the CDKF. This is done in appendix B. 4 Quasi maximum likelihood estimation This section presents our quasi log-likelihood estimator for the structural coe cients in nonlinear DSGE models with potentially non-gaussian shocks. We derive this estimator in section 4.1, and its asymptotic properties are discussed in section 4.2. Section 4.3 shows how to estimate the asymptotic distribution of our suggested estimator. 4.1 The quasi log-likelihood function The EKF and the CDKF estimate the mean and the covariance matrix of the posterior state distribution. These moments are in general insu cient to derive the likelihood function except in the well-known case where all shocks are Gaussian and the functions g (x t ; ) and h (x t ; w t+1 ; ) 3 The Unscented Kalman Filter (UKF) developed by Julier, Uhlmann & Durrant-Whyte (1995) is another derivative free implementation of the ltering equations presented in the previous section Norgaard et al. (2000) show that the CDKF has marginally higher theoretical accuracy than the UKF for normally distributed variables. 11
13 are linear in x t and (x t ; w t+1 ), respectively. Hence, it is in general not possible to use the EKF or the CDKF to estimate the structural parameters by maximum likelihood or Bayesian methods. A commonly used assumption for non-linear state space systems is to approximate the conditional density y t+1 j y 1:t by a normal distribution, i.e. y t+1 j y 1:t a s N yt+1 () ; P yy (;t + 1) (34) for t = 1; :::; T. Given the higher accuracy of the CDKF compared to the EKF, it is natural to use the CDKF to compute the moments in this distribution. If the initial state vector is uncorrelated with v t and w t for all values of t, then a quasi log-likelihood function based on the CDKF and (34) is given by L CDKF (; y 1:T ) = n y T 1 P log (2) T t=1 2 2 log P CDKF yy (;t) (35) 1 P T t=1 2 y t y t CDKF () 0 P CDKF yy (;t) 1 yt y t CDKF () : Here, y CDKF t () denotes the a priori estimate of the observables from the CDKF and P CDKF yy is the related covariance matrix. (;t) The quasi log-likelihood function based on the EKF, denoted L EKF (; y 1:T ), is derived in a similar manner using the rst and second moments from the EKF. We then suggest to estimate the structural parameters by maximizing the quasi log-likelihood function L CDKF (; y 1:T ), that is ^ CDKF = arg max 2 L CDKF (; y 1:T ) : (36) We emphasize two convenient numerical properties in relation to this estimator. Firstly, the function L CDKF (; y 1:T ) is smooth in, and this makes the optimization relative easy. For small models, local optimization routines such as the Newton-Raphson method and its various extensions may be used with di erent starting values. For larger models, global optimization routines such as Simulated Annealing and evolutionary algorithms may be more e ective (see Hansen, Müller & Koumoutsakos (2003) and Andreasen (2010b)). In comparison, the estimated log-likelihood function in particle lters do not in general display smoothness in due to the resampling step and this 12
14 makes the optimization very challenging. 4 Secondly, the numerical requirement for evaluating the quasi log-likelihood function in (35) is minimal compared to any particle lter. To realize this, note rst that the CDKF uses n x (1 + 2 (n x + n w )) function evaluations to compute x t+1 and the matrices for its covariance matrix. Additional n y (1 + 2n x ) function evaluations are used to compute y t+1 and the matrices for its covariance matrix. 5 In comparison, the standard PF used in Fernández-Villaverde & Rubio-Ramírez (2007) requires N (n x + n y ) function evaluations where N is the number of particles. 6 As an illustration, consider the case with ve observables (n y = 5), ve shocks (n w = 5), and ten state variables (n x = 10). This implies 415 function evaluations in the CDKF in each time period. The particle lter requires 15N function evaluations in each time period where N typically is between 20; 000 and 60; 000. It is therefore obvious that the CDKF is many times faster to compute than the standard PF. 4.2 Asymptotic properties The starting point for our asymptotic analysis is the work by Bollerslev & Wooldrigde (1992) for dynamic models that jointly specify the conditional mean and the conditional covariance matrix. They examine the asymptotic properties of estimating such models by maximizing a quasi log-likelihood function which is derived from a Gaussian assumption although this distributional assumption may be violated. Hence, their setup is similar to ours for ^ CDKF in (35) and (36). The score function s () t implied by (35) is: 7 s () 0 t+1 (1n ) = r y CDKF () 0 t+1 F t+1 () 1 u () t+1 (37) r F t+1 () 0 h F t+1 () 1 F t+1 () 1i vec u t+1 () u t+1 () 0 F t+1 () where u t () y t y CDKF t () and F t () P CDKF yy (;t) (38) 4 The particle lters by Pitt (2002) and Flury & Shephard (2009) are important exceptions where the estimated log-likelihood function is smooth in. 5 We abstract from the computational costs related to the QR decomposition in the CDKF and the simple matrix multiplications used in the lter. 6 The particle lter also uses a resampling step which we ignore for simplicity in our comparison of the two lters. 7 The derivative of a matrix is de ned as in Bollerslev & Wooldrigde (1992). 13
15 Here, s () 0 t has dimension 1 n where n is the number of elements in. If the conditional mean is correctly speci ed and the expectation y CDKF t then () E t [g (x t+1 ; )] can be evaluated exactly, E t [u t+1 ( 0 )] = 0; (39) where 0 denotes the true value of. If the conditional covariance matrix is also correctly speci ed at 0 and the expectation for this covariance matrix can be evaluated exactly, then E t ut+1 ( 0 ) u t+1 ( 0 ) 0 = F t+1 ( 0 ) : (40) As a result, E t s (0 ) 0 t+1 = 0: (41) Bollerslev & Wooldrigde (1992) show that this implies consistency and normality of ^ CDKF given standard regularity conditions. Furthermore, p T ^CDKF d! 0 N 0; A 1 0 B 0A0 1 ; (42) where B 0 E s ( 0 ; y 1:T ) s ( 0 ; y 1:T ) 0 (43) 2 # L (; y A 0 E 1:T 0 (44) =0 Accordingly, the asymptotic properties of ^ CDKF for a correctly speci ed DSGE model depends on the precision by which we are able to evaluate the rst and second moments in L CDKF (; y 1:T ). This insight provides a strong theoretical argument in favour of a QML estimator based on the CDKF compared to a QML estimator using the EKF, because the CDKF delivers a higher level of precision for rst and second moments and should therefore have better asymptotic properties. The possibly misspeci ed distribution for y t+1 j y 1:t in (36) is not important for consistency and normality of ^ CDKF, although ^ CDKF will be more e cient the closer the true distribution of y t+1 j y 1:t is to the normal distribution. This observation also implies that the stated results for ^ CDKF hold even if shocks to the DSGE models are non-gaussian. Hence, we only need to evaluate 14
16 whether the precision delivered by the CDKF for the rst and second moments is su cient to ensure consistency and normality of ^ CDKF. The answer to this question depends on the chosen approximation order for the DSGE model. We introduce our way of reasoning by starting with a linearized DSGE model. Here, rst and second moments are accurate up to rst and second order, respectively, and the CDKF reduces to the standard Kalman Filter which exactly captures the rst and second moments to the desired degree of precision. Thus, we recover the standard result that the QML estimator is consistent and asymptotically normal for a linearized DSGE model (see for instance Hamilton (1994)). 8 When the DSGE model is solved up to second order, then rst and second moments in the model are accurate up to second and third order, respectively. 9 This implies that the precision in the CDKF is su cient for the rst moment, but there are approximation errors in the second moments because the CDKF does not match all third order terms. However, these approximation errors are likely to be insigni cant as the second moments of y t+1 j y 1:t are small in most cases. Alternatively, if the state vector is (approximately) Gaussian, then all third order terms are zero and the second moments in the CDKF are therefore accurate up to third order (Norgaard et al. (2000)). Thus, when a DSGE model is solved up to second order, the precision delivered by the CDKF should in all realistic settings be su cient and our suggested QML estimator can be expected to be consistent and asymptotically normal. For a DSGE model solved up to third order, it holds that rst and second moments in the model are accurate up to third and fourth order, respectively. Hence, the estimate of the rst moment in the CDKF induces approximation errors in the third order terms of this moment, unless the state vector is (approximately) Gaussian and these third order terms are zero. Approximation errors are also present in the second moments, where the CDKF does not match all third and fourth order terms. For most DSGE models, these unmatched third and fourth order terms in the rst and second moments are likely to be small and our suggested QML estimator can therefore be expected to be consistent and asymptotically normal. Finally, when the DSGE model is solved beyond third order, it becomes harder to ensure 8 Inference is here used in the sense that the approximated DSGE model is the true data generating process. The paper by Fernandez-Villaverde, Rubio-Ramirez & Santos (2006) studies the case where the exact solution to the DSGE model is considered as the true data generating process. 9 This result is illustrated in the appendix. 15
17 consistency and normality of the QML estimator. This is because the CDKF does not match any of the extra terms induced by solving the model beyond third order, and reliable performance of our QML estimator therefore requires that these higher order terms are insigni cant. 4.3 The estimated asymptotic distribution The variance of the score function B 0 can be estimated in a standard fashion by rst order numerical derivatives of the quasi log-likelihood function evaluated at ^ CDKF. As shown by Bollerslev & Wooldrigde (1992), it is also possible to estimate the Hessian matrix A 0 based on rst order derivatives. This is a convenient property of our estimator because it is often di cult to compute reliable estimates of the Hessian matrix from double numerical derivatives. Using the notation in Harvey (1989), the Hessian matrix may be estimated by ^A ij = 1 2T 0 TP trace 1 ^F CDKF i ^F 1 ^F CDKF j 1 A + 1 T TP CDKF i! 0 ^F 1 CDKF j (45) for i; j = 1; 2::::; n where all rst order derivatives in (45) are computed numerically. 5 A New Keynesian DSGE model This section presents a standard New Keynesian DSGE model following the work of Christiano, Eichenbaum & Evans (2005) and Smets & Wouters (2007). We describe the model in section 5.1 and discuss how to approximate the model solution up to third order in section 5.2. The model is then calibrated in section 5.3 to account for higher order moments in the post-war US economy. 5.1 The model We emphasize two features in relation to our model. Firstly, stochastic and deterministic trends are included to make the subsequent Monte Carlo study as realistic as possible because trends allow us to work with growth rates. Secondly, we consider the case where potentially non-gaussian shocks drive the economy. 16
18 The households: A representative household considers U t = E t 1 X l=0 l ct+l bx t 1+l (1 h t+l ) 2 1 z t+l 1 1 ; (46) where c t is consumption and h t is labor supply. The variable z t is a measure of technological progress and determines the overall trend in consumption. The parameter b controls the degree of external habit formation in the consumption good c t which is constructed from Z 1 c t = 0 1 ci;t 1 di : (47) The habit stock x t evolves as x t+1 = x x t + (1 x ) c t : The rst constraint on the household is the law of motion for the capital stock k t given by k t+1 = (1 ) k t + i t 1 2 ( i t i i ) 2 : (48) t 1 where i t is gross investment. The value of i is determined such that there are no adjustment costs along the economy s balanced growth path. The second constraint is the household s real period-by-period budget constraint E t D t;t+1 x h t+1 + c t + (e t t ) 1 i t = xh t t + r k t k t + w t h t + t : (49) The left hand side of (49) is the household s total expenditures in period t which consists of i) statecontingent claims E t D t;t+1 x h t+1, ii) consumption c t, and iii) investment (e t t ) 1 i t. Changes in e t t are investment speci c shocks, which follow an exogenous AR(1) process along a deterministic trend, i.e. ln t+1 = ln t + ln ;ss and ln e t+1 = e ln e t + e;t+1 : (50) We let e;t+1 s IID (0; V ar ( e;t+1 )). The right hand side of (49) is the household s total wealth in period t. It consists of: i) pay-o 17
19 from state-contingent assets purchased in the previous period x h t = t, ii) income from selling capital services to the rms r k t k t, iii) labor income w t h t, and iv) dividends received from rms t. Note that t is the gross in ation rate. The rms: Production is carried out by a continuum of rms. They supply a di erentiable good y i;t to the goods market which is characterized by monopolistic competition. All rms have access to the same technology 8 >< ki;t y i;t = (a tz t h i;t ) 1 zt if ki;t (a tz t h i;t ) 1 zt > 0 >: 0 else (51) where k i;t and h i;t denote capital and labor services, respectively. The variable a t represents stationary technology shocks, and we let ln a t+1 = a ln a t + a a;t+1 ; (52) where a;t+1 s IID (0; V ar ( a;t+1 )). The variable z t in (51) denotes non-stationary technology shocks. We let z;t z t =z t 1 and assume ln z;t+1 = ln z;ss + z;t+1 ; (53) where z;t+1 s IID (0; V ar ( z;t+1 )). The shocks a t and z;t are mutually independent, and so are all other shocks in the model. Following Altig, Christiano, Eichenbaum & Linde (2005), we de ne z t =(1 ) z t. The xed production costs are set to ensure a steady state pro t of zero. All rms maximize the present value of their nominal dividend payments, denoted d i;t : X 1 d i;t E t D t;t+l P t+l i;t+l : (54) l=0 Here, D t;t+l is the nominal stochastic discount factor and the expression for real dividend payments from the i th rm i;t is given below in (56). The rms face a number of constraints when maximizing d i;t. The rst is related to the good produced by the i th rm. The total quantity of good 18
20 i is allocated to consumption and investment, which implies y t = c t + (e t t ) 1 i t : (55) The second constraint is the budget restriction: i;t = (P i;t =P t ) y i;t r k t k i;t w t h i;t : (56) The rst term in (56) denotes the real revenue from sales of the i th good. The next two terms in (56) are the rm s expenditures on capital services rt k k i;t and payments to workers w t h i;t. The third constraint introduces staggered price adjustments. We assume that in each period a fraction 2 [0; 1[ of randomly selected rms are not allowed to set the optimal nominal price of the good they produce. Instead, these rms set the current prices equal to the prices in the previous period, i.e. P i;t = P i;t 1 for all i 2 [0; 1]. The central bank: The central bank determines the gross one-period nominal interest rate R t according to the rule Rt ln = R R ln ss Rt 1 R ss t yt + ln + y ln ss y ss zt + R;t+1 ; (57) where R;t+1 s IID (0; V ar ( R;t+1 )). Shock distributions: Three speci cations for the shocks are considered. As a benchmark case, we rst let all shocks be Gaussian. In our second speci cation, we let shocks be generated from the Laplace distribution which has thicker tails than the Gaussian distribution. The presence of Laplace distributed shocks is interesting as it implies that large shocks occur more often than with Gaussian shocks, and this allow us to test whether the CDKF is robust to state outliers. Our nal speci cation, considers another way to model non-gaussian shocks by introducing stochastic volatility into the model. We focus on the case where only the process for stationary technology shocks displays stochastic volatility. Applying the speci cation in Justiniano & Primiceri 19
21 (2008), the law of motion for a t in (52) is replaced by ln a t+1 = a ln a t + a;t+1 a;t+1 ; (58) where the process for stochastic volatility a;t+1 is given by ln a;t+1 = a ln a;t + a;t+1: (59) Here, a;t+1 s N ID (0; V ar ( a;t+1)). 10 Non-stationary technology shocks z t and investment speci c shocks e t are assumed to be Gaussian in this nal speci cation, and we do not consider monetary policy shocks, i.e. V ar ( R;t+1 ) = 0. The latter restriction is imposed for numerical convenience as the presence of stochastic volatility in a t introduces a;t as an additional state variable. Hence, by omitting monetary policy shocks, we are left with the same number of state variables as in the two shock speci cations without stochastic volatility. An overview of the three speci cations for the structural shocks is provided in Table 1. < Table 1 about here > 5.2 Solving the model We now present the state space representation of our DSGE model. As in section 2, let y t contain the non-predetermined variables and let x t contain the predetermined state vector. Both variables are expressed in deviation from the deterministic steady state. Denoting the structural innovations by t+1, the exact solution to our model is then given by y t = g (x t ; ) (60) x t+1 = h (x t ; ) + t+1 (61) 10 Other speci cations of stochastic volatility in DSGE models are discussed in Andreasen (2010d). 20
22 where is the perturbation parameter. This is also the exact solution when stochastic volatility is included in the model because the processes in (58)-(59) can be represented as ln a t = a;t ln v t (62) ln v t+1 = a;t a;t+1 ln v t + a;t+1 (63) ln a;t+1 = a ln a;t + a;t+1 (64) The proof of this result is given in Andreasen (2010a). Hence, our speci cation of stochastic volatility can be expressed as a combination of two AR(1) processes where the local persistency coe cient in the auxiliary process ln v t is modi ed by the term a;t = a;t+1. The representation in (62)-(64) is convenient because it shows that we only need to perturb the variables (a t ; v t ; a;t ) and it implies only two state variables, (v t ; a;t ). In comparison, the representation in (58)-(59) requires perturbing (a t ; a;t ; a;t+1 ; ;t+1 ) and has as a minimum three state variables, (a t ; a;t ; a;t+1 ). In particular, the smaller number of state variables induced by the representation in (62)-(64) is convenient as it reduces the computing time when DSGE models are solved numerically. The functions g () and h () are unknown, and we therefore approximate them up to third order. We apply the codes by Schmitt-Grohé & Uribe (2004) to compute all the rst and second order terms. The third order terms are computed using the codes derived in Andreasen (2010a) which extends the results in Schmitt-Grohé & Uribe (2004) to third order. We nally apply the pruning scheme to the approximated solution (see Kim, Kim, Schaumburg & Sims (2008) and Andreasen (2010c) for further details). Five macro variables are chosen for the Monte Carlo study: i) the quarterly nominal interest rate, ii) the quarterly in ation rate, and the quarterly real growth rates in iii) consumption, iv) investment, and v) output. These series are placed in the vector yt obs. We allow for measurement errors v t in the series for y obs t gives the following state space system and assume v t s N ID (0; R v ) where R v is a diagonal matrix. This y obs t = M 1 g (x t ; ; ) M 2 g (x t 1 ; ; ) + v t (65) 21
23 x t+1 = h (x t ; ) + t+1 (66) where M 1 and M 2 are selection matrices with appropriate dimensions. The presence of x t (65) is due to the three growth rates in y obs t. 1 in 5.3 Model calibration The model is calibrated to US data from 1956Q4 to 2009Q2. We focus on matching i) mean values, ii) standard deviations, iii) skewness, and iv) kurtosis for the ve series in y obs t. 11 The calibrated coe cients are fairly standard and summarized in Table 2. We only note that the conditional standard deviation in the volatility process p V ar ( a;t+1) has a relative large value of 0:3 which is needed to get notable e ects of stochastic volatility in the model. < Table 2 about here > The empirical and simulated moments are reported in Table 3 for a second order approximation. Our model is successful at matching all mean values and standard deviations when shocks are Gaussian. The model also generates sizeable deviations from normality in the nominal interest rate and the in ation rate. This is evident from the values of skewness and kurtosis for these series which di er from 0 and 3, respectively. Accordingly, our model has signi cant non-linearities and should therefore be challenging for non-linear lters. The main di erence when going from Gaussian to Laplace distributed shocks is that the latter shocks increase the value of kurtosis. The presence of stochastic volatility has the same e ect, although the increase in kurtosis tends to be smaller. < Table 3 about here > The simulated moments using a third order approximation are reported in Table 4. Moving from a second order to a third order approximation is seen to increase the values of skewness and kurtosis for all variables. For the nominal interest rate and the in ation rate, the values of these moments are even seen to be larger than the corresponding empirical moments. Another indicator 11 We use data from the Federal Reserve Bank of St. Louis. The quarterly interest rate is measured by the rate in the secondary market (TB3MS). The quarterly in ation rate is for consumer prices. The growth rate in consumption is calculated from real consumption expenditures (PCECC96). The series for real private xed investment (FPIC96) is used to calculate the growth rate in investment. The growth rate in output is calculated from real GDP (GDPC96). All growth rates are expressed in quarterly terms and in per capita based on the total population in the US. 22
24 of the strong non-linearities in the model is to note that the standard deviation for the nominal interest rate and the in ation rate are somewhat higher at third order than at second order. < Table 4 about here > 6 A Monte Carlo study This section conducts a Monte Carlo study to evaluate the performance of the CDKF in the context of DSGE models. We start in section 6.1 by examining how accurately the CDKF estimates the unobserved state variables compared with the EKF and the standard PF. In section 6.2, the values of the quasi log-likelihood function using the CDKF and the EKF are compared to the estimated value of the log-likelihood function in the standard PF. Section 6.3 explores the nite sample properties of our suggested QML estimator based on the CDKF and compares its performance with a QML estimator that uses the EKF. 6.1 State estimation This section studies the ability of the CDKF to estimate the unknown state variables. We simulate 20 sample paths of length T = 200 for a given approximation order to the DSGE model in order to generate 20 test economies. This is done for each of the three shock speci cations. The accuracyof all lters is measured by the root mean squared errors (RMSE) RMSE i = P n x j=1 s PT t=1 (x j;t ^x j;t ) 2 T for i = 1; 2; :::; 20; (67) where x j;t is the true value of the j th state variable in period t and ^x j;t is the estimated value. The initial state x 0 is taken to be known and we let P xx (t = 0) = The step size h in the CDKF is always set equal to the optimal value for the Gaussian distribution h = p 3 even though the distribution subject to the multivariate Stirling interpolation may be non-gaussian. 12 We compare the performance of the CDKF with the EKF and the standard PF using 200,000 particles. The latter is included to represent a close approximation to the optimal state estimator. 12 These assumptions are maintained throughout the Monte Carlo study. 23
25 We start by considering the case where all shocks are Gaussian in Figure 1. The rst chart in this gure shows the RMSE for a rst order approximation to the DSGE model, and the CDKF (market with stars) therefore reduces to the Kalman Filter which is the optimal state estimator. The performance of the standard PF is reported as a 95% con dence interval which we compute from 100 repetitions of the lter on the same test economy. The standard PF is seen to give a satisfying approximation to the optimal estimator as the con dence intervals either contain or are very close to the optimal state estimates from the Kalman Filter. For a second order approximation, we rst note that the CDKF gives more precise state estimates than the EKF (market with squares). More surprisingly, the CDKF is doing just as well as the standard PF and clearly outperforms this lter for some test economies. This nding indicates that a linear updating rule and the multivariate Stirling interpolation used in the CDKF are reasonable approximations for this class of test economies. For a third order approximation, the CDKF still outperforms the EKF, and the CDKF also does marginally better than the standard PF in this case. Given the strong non-linearities in our DSGE model, we consider the latter as a very surprising result. < Figure 1 about here > For Laplace distributed shocks in Figure 2, we nd more or less the same results as with Gaussian shocks. That is, the CDKF clearly outperforms the EKF, and the CDKF is marginally better than the standard PF. Hence, the good performance of the CDKF is found to be robust to strong non-linearties and Laplace distributed shocks. Recall that these shocks are interesting to consider because they generate state outliers more frequently than Gaussian shocks. < Figure 2 about here > The results for shocks displaying stochastic volatility are shown in Figure 3. Here, we do not consider a rst order approximation because it does not capture the presence of stochastic volatility as emphasized by Fernández-Villaverde & Rubio-Ramírez (2007). For a second and third order approximation, the standard PF is seen to outperform the CDKF and the EKF as the 95% con dence intervals from the particle lter are lower than the RMSE for the two other lters. An inspection of the state distributions in the standard PF shows that many of these distributions 24
26 are highly skewed and non-gaussian, and this may explain the bene t of tracking the entire state distribution in the particle lter instead of just focusing on the rst two moments as in the CDKF and the EKF. These state distributions are on the other hand typically symmetric and bell-shaped with Gaussian and Laplace distributed shocks although the DSGE model displays strong nonlinearities. Note nally, that the level of the RMSE is rather large with stochastic volatility in the model in comparision to Gaussian and Laplace distributed shocks in Figure 1 and 2. This is because the process for ;t is very volatile and hence dominates the expression for the RMSE. < Figure 3 about here > The accuracy results for the three lters are summarized in Table 5 where we compute the average RMSE across the 20 test economies for the various shock speci cations and the di erent approximations to the model. In line with our previous ndings, we see that the CDKF outperforms the EKF and the standard PF when shocks are Gaussian or Laplace distributed. This is indicated by bold gures for the CDKF in Table 5. Hence, more than 200,000 particles are needed in the standard PF if this lter is to outperform the CDKF for the considered test economies. The bene t of particle ltering is however evident with stochastic volatility where the RMSE is substantially lower for the standard PF than for the CDKF and the EKF. < Table 5 about here > The performance of a given lter should also be evaluated in relation to the time it takes to compute the lter. Table 6 therefore shows the average computing time for each of three lters. 13 The CDKF is seen to be very fast to compute. It only takes about 0.03 seconds for one evaluation of this lter with a rst order approximation, and this number only increases to 0.10 seconds and 0.50 seconds for a second order and a third order approximation, respectively. The corresponding gures for the standard PF using 200,000 particles are seconds for a rst order approximation, seconds for a second order approximation, and 299,41 seconds for a third order approximation. Hence, the CDKF becomes a more attractive alternative to particle ltering when the approximation order to the DSGE model is increased. 13 Our presentation and implementation of the CDKF propogates the square root of covariance matrices through time to ensure that these matrices remain positive semi-de nite. We therefore also use a square root implementation of the EKF when comparing the execution time of the two lters. However, this implementation of the EKF is marginally slower to compute compared with the version of the EKF given in section
27 < Table 6 about here > 6.2 The quasi log-likelihood function Before we turn to the performance of the suggested QML estimator, it is interesting to see how close the quasi log-likelihood function L CDKF is to the estimated log-likelihood function in the standard PF, L P F. Also the di erence between the quasi log-likelihood function based on the CDKF and the EKF, i.e. L CDKF versus L EKF, is interesting to examine because it shows the quantitative e ect of using di erent methods to estimate rst and second moments in the two lters. We therefore study the relationship between these three functions in the current section. A natural metric when comparing these functions, is to express the quasi log-likelihood functions in percentage deviation from the value of the log-likelihood function. The latter is in general not available and we therefore use the estimated log-likelihood function from the standard PF. Hence, for the j 0 th test economy we compute i j = 100 L i j L P F j L P j F (68) for i = fcdkf,ekfg and j = 1; 2; :::; 20. Here, L P F j = 1=100 P 100 k=1 LP F k;j denotes the mean value of the log-likelihood function in the standard PF from 100 evaluation of this lter on the j th test economy. The normalizing constant in (68) is stochastic, and we therefore nd it useful to also report L P F j uncertainty bounds. This is done by computing the 95% con dence interval 1: std(lp F, L P j F where std denotes the standard deviation of the estimated log-likelihood function. Accordingly, this con dence interval shows the variation in the estimated log-likelihood function (when normalized by L P F j ) which is due to Monte Carlo variation. 14 j ) The values of i j with Gaussian shocks are shown in Figure 4. For a rst order approximation, the CDKF (and the EKF) reduces to the Kalman Filter which reports the exact value of the loglikelihood function. We thus see from the rst chart in Figure 4 that the particle lter gives a good 14 We prefer this normalized metric in terms of L P j F instead of simply reporting the level of L CDKF, L EKF, and L P F because the latter would make the di erences between the three functions hard to notice in the subsquent charts. 26
Chapter 6. Maximum Likelihood Analysis of Dynamic Stochastic General Equilibrium (DSGE) Models
 Chapter 6. Maximum Likelihood Analysis of Dynamic Stochastic General Equilibrium (DSGE) Models Fall 22 Contents Introduction 2. An illustrative example........................... 2.2 Discussion...................................
Chapter 6. Maximum Likelihood Analysis of Dynamic Stochastic General Equilibrium (DSGE) Models Fall 22 Contents Introduction 2. An illustrative example........................... 2.2 Discussion...................................
FEDERAL RESERVE BANK of ATLANTA
 FEDERAL RESERVE BANK of ATLANTA On the Solution of the Growth Model with Investment-Specific Technological Change Jesús Fernández-Villaverde and Juan Francisco Rubio-Ramírez Working Paper 2004-39 December
FEDERAL RESERVE BANK of ATLANTA On the Solution of the Growth Model with Investment-Specific Technological Change Jesús Fernández-Villaverde and Juan Francisco Rubio-Ramírez Working Paper 2004-39 December
Monetary and Exchange Rate Policy Under Remittance Fluctuations. Technical Appendix and Additional Results
 Monetary and Exchange Rate Policy Under Remittance Fluctuations Technical Appendix and Additional Results Federico Mandelman February In this appendix, I provide technical details on the Bayesian estimation.
Monetary and Exchange Rate Policy Under Remittance Fluctuations Technical Appendix and Additional Results Federico Mandelman February In this appendix, I provide technical details on the Bayesian estimation.
The Basic New Keynesian Model. Jordi Galí. June 2008
 The Basic New Keynesian Model by Jordi Galí June 28 Motivation and Outline Evidence on Money, Output, and Prices: Short Run E ects of Monetary Policy Shocks (i) persistent e ects on real variables (ii)
The Basic New Keynesian Model by Jordi Galí June 28 Motivation and Outline Evidence on Money, Output, and Prices: Short Run E ects of Monetary Policy Shocks (i) persistent e ects on real variables (ii)
Combining Macroeconomic Models for Prediction
 Combining Macroeconomic Models for Prediction John Geweke University of Technology Sydney 15th Australasian Macro Workshop April 8, 2010 Outline 1 Optimal prediction pools 2 Models and data 3 Optimal pools
Combining Macroeconomic Models for Prediction John Geweke University of Technology Sydney 15th Australasian Macro Workshop April 8, 2010 Outline 1 Optimal prediction pools 2 Models and data 3 Optimal pools
Economics Discussion Paper Series EDP Measuring monetary policy deviations from the Taylor rule
 Economics Discussion Paper Series EDP-1803 Measuring monetary policy deviations from the Taylor rule João Madeira Nuno Palma February 2018 Economics School of Social Sciences The University of Manchester
Economics Discussion Paper Series EDP-1803 Measuring monetary policy deviations from the Taylor rule João Madeira Nuno Palma February 2018 Economics School of Social Sciences The University of Manchester
Lecture 3, November 30: The Basic New Keynesian Model (Galí, Chapter 3)
 MakØk3, Fall 2 (blok 2) Business cycles and monetary stabilization policies Henrik Jensen Department of Economics University of Copenhagen Lecture 3, November 3: The Basic New Keynesian Model (Galí, Chapter
MakØk3, Fall 2 (blok 2) Business cycles and monetary stabilization policies Henrik Jensen Department of Economics University of Copenhagen Lecture 3, November 3: The Basic New Keynesian Model (Galí, Chapter
Markov-Switching Models with Endogenous Explanatory Variables. Chang-Jin Kim 1
 Markov-Switching Models with Endogenous Explanatory Variables by Chang-Jin Kim 1 Dept. of Economics, Korea University and Dept. of Economics, University of Washington First draft: August, 2002 This version:
Markov-Switching Models with Endogenous Explanatory Variables by Chang-Jin Kim 1 Dept. of Economics, Korea University and Dept. of Economics, University of Washington First draft: August, 2002 This version:
Financial Factors in Economic Fluctuations. Lawrence Christiano Roberto Motto Massimo Rostagno
 Financial Factors in Economic Fluctuations Lawrence Christiano Roberto Motto Massimo Rostagno Background Much progress made on constructing and estimating models that fit quarterly data well (Smets-Wouters,
Financial Factors in Economic Fluctuations Lawrence Christiano Roberto Motto Massimo Rostagno Background Much progress made on constructing and estimating models that fit quarterly data well (Smets-Wouters,
Filtering and Likelihood Inference
 Filtering and Likelihood Inference Jesús Fernández-Villaverde University of Pennsylvania July 10, 2011 Jesús Fernández-Villaverde (PENN) Filtering and Likelihood July 10, 2011 1 / 79 Motivation Introduction
Filtering and Likelihood Inference Jesús Fernández-Villaverde University of Pennsylvania July 10, 2011 Jesús Fernández-Villaverde (PENN) Filtering and Likelihood July 10, 2011 1 / 79 Motivation Introduction
Bayesian Inference for DSGE Models. Lawrence J. Christiano
 Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
The Basic New Keynesian Model. Jordi Galí. November 2010
 The Basic New Keynesian Model by Jordi Galí November 2 Motivation and Outline Evidence on Money, Output, and Prices: Short Run E ects of Monetary Policy Shocks (i) persistent e ects on real variables (ii)
The Basic New Keynesian Model by Jordi Galí November 2 Motivation and Outline Evidence on Money, Output, and Prices: Short Run E ects of Monetary Policy Shocks (i) persistent e ects on real variables (ii)
Advanced Economic Growth: Lecture 8, Technology Di usion, Trade and Interdependencies: Di usion of Technology
 Advanced Economic Growth: Lecture 8, Technology Di usion, Trade and Interdependencies: Di usion of Technology Daron Acemoglu MIT October 3, 2007 Daron Acemoglu (MIT) Advanced Growth Lecture 8 October 3,
Advanced Economic Growth: Lecture 8, Technology Di usion, Trade and Interdependencies: Di usion of Technology Daron Acemoglu MIT October 3, 2007 Daron Acemoglu (MIT) Advanced Growth Lecture 8 October 3,
Resolving the Missing Deflation Puzzle. June 7, 2018
 Resolving the Missing Deflation Puzzle Jesper Lindé Sveriges Riksbank Mathias Trabandt Freie Universität Berlin June 7, 218 Motivation Key observations during the Great Recession: Extraordinary contraction
Resolving the Missing Deflation Puzzle Jesper Lindé Sveriges Riksbank Mathias Trabandt Freie Universität Berlin June 7, 218 Motivation Key observations during the Great Recession: Extraordinary contraction
Chapter 1. GMM: Basic Concepts
 Chapter 1. GMM: Basic Concepts Contents 1 Motivating Examples 1 1.1 Instrumental variable estimator....................... 1 1.2 Estimating parameters in monetary policy rules.............. 2 1.3 Estimating
Chapter 1. GMM: Basic Concepts Contents 1 Motivating Examples 1 1.1 Instrumental variable estimator....................... 1 1.2 Estimating parameters in monetary policy rules.............. 2 1.3 Estimating
Macroeconomics IV Problem Set I
 14.454 - Macroeconomics IV Problem Set I 04/02/2011 Due: Monday 4/11/2011 1 Question 1 - Kocherlakota (2000) Take an economy with a representative, in nitely-lived consumer. The consumer owns a technology
14.454 - Macroeconomics IV Problem Set I 04/02/2011 Due: Monday 4/11/2011 1 Question 1 - Kocherlakota (2000) Take an economy with a representative, in nitely-lived consumer. The consumer owns a technology
Graduate Macro Theory II: Notes on Quantitative Analysis in DSGE Models
 Graduate Macro Theory II: Notes on Quantitative Analysis in DSGE Models Eric Sims University of Notre Dame Spring 2011 This note describes very briefly how to conduct quantitative analysis on a linearized
Graduate Macro Theory II: Notes on Quantitative Analysis in DSGE Models Eric Sims University of Notre Dame Spring 2011 This note describes very briefly how to conduct quantitative analysis on a linearized
Bayesian Inference for DSGE Models. Lawrence J. Christiano
 Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Bayesian inference Bayes rule. Monte Carlo integation.
Labor-Supply Shifts and Economic Fluctuations. Technical Appendix
 Labor-Supply Shifts and Economic Fluctuations Technical Appendix Yongsung Chang Department of Economics University of Pennsylvania Frank Schorfheide Department of Economics University of Pennsylvania January
Labor-Supply Shifts and Economic Fluctuations Technical Appendix Yongsung Chang Department of Economics University of Pennsylvania Frank Schorfheide Department of Economics University of Pennsylvania January
Bayesian Estimation of DSGE Models: Lessons from Second-order Approximations
 Bayesian Estimation of DSGE Models: Lessons from Second-order Approximations Sungbae An Singapore Management University Bank Indonesia/BIS Workshop: STRUCTURAL DYNAMIC MACROECONOMIC MODELS IN ASIA-PACIFIC
Bayesian Estimation of DSGE Models: Lessons from Second-order Approximations Sungbae An Singapore Management University Bank Indonesia/BIS Workshop: STRUCTURAL DYNAMIC MACROECONOMIC MODELS IN ASIA-PACIFIC
Solow Growth Model. Michael Bar. February 28, Introduction Some facts about modern growth Questions... 4
 Solow Growth Model Michael Bar February 28, 208 Contents Introduction 2. Some facts about modern growth........................ 3.2 Questions..................................... 4 2 The Solow Model 5
Solow Growth Model Michael Bar February 28, 208 Contents Introduction 2. Some facts about modern growth........................ 3.2 Questions..................................... 4 2 The Solow Model 5
Session 4: Money. Jean Imbs. November 2010
 Session 4: Jean November 2010 I So far, focused on real economy. Real quantities consumed, produced, invested. No money, no nominal in uences. I Now, introduce nominal dimension in the economy. First and
Session 4: Jean November 2010 I So far, focused on real economy. Real quantities consumed, produced, invested. No money, no nominal in uences. I Now, introduce nominal dimension in the economy. First and
Discussion of Juillard and Maih Estimating DSGE Models with Observed Real-Time Expectation Data
 Estimating DSGE Models with Observed Real-Time Expectation Data Jesper Lindé Federal Reserve Board Workshop on Central Bank Forecasting Kansas City Fed October 14-15, 2010 Summary of paper This interesting
Estimating DSGE Models with Observed Real-Time Expectation Data Jesper Lindé Federal Reserve Board Workshop on Central Bank Forecasting Kansas City Fed October 14-15, 2010 Summary of paper This interesting
Bayesian Inference for DSGE Models. Lawrence J. Christiano
 Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Preliminaries. Probabilities. Maximum Likelihood. Bayesian
Bayesian Inference for DSGE Models Lawrence J. Christiano Outline State space-observer form. convenient for model estimation and many other things. Preliminaries. Probabilities. Maximum Likelihood. Bayesian
Perceived productivity and the natural rate of interest
 Perceived productivity and the natural rate of interest Gianni Amisano and Oreste Tristani European Central Bank IRF 28 Frankfurt, 26 June Amisano-Tristani (European Central Bank) Productivity and the
Perceived productivity and the natural rate of interest Gianni Amisano and Oreste Tristani European Central Bank IRF 28 Frankfurt, 26 June Amisano-Tristani (European Central Bank) Productivity and the
GMM-based inference in the AR(1) panel data model for parameter values where local identi cation fails
 GMM-based inference in the AR() panel data model for parameter values where local identi cation fails Edith Madsen entre for Applied Microeconometrics (AM) Department of Economics, University of openhagen,
GMM-based inference in the AR() panel data model for parameter values where local identi cation fails Edith Madsen entre for Applied Microeconometrics (AM) Department of Economics, University of openhagen,
Department of Econometrics and Business Statistics
 ISSN 1440-771X Australia Department of Econometrics and Business Statistics http://www.buseco.monash.edu.au/depts/ebs/pubs/wpapers/ Exponential Smoothing: A Prediction Error Decomposition Principle Ralph
ISSN 1440-771X Australia Department of Econometrics and Business Statistics http://www.buseco.monash.edu.au/depts/ebs/pubs/wpapers/ Exponential Smoothing: A Prediction Error Decomposition Principle Ralph
The Extended Perturbation Method: New Insights on the New Keynesian Model. Martin M. Andreasen and Anders Kronborg. CREATES Research Paper
 The Extended Perturbation Method: New Insights on the New Keynesian Model Martin M. Andreasen and Anders Kronborg CREATES Research Paper 2017-14 Department of Economics and Business Economics Aarhus University
The Extended Perturbation Method: New Insights on the New Keynesian Model Martin M. Andreasen and Anders Kronborg CREATES Research Paper 2017-14 Department of Economics and Business Economics Aarhus University
Advanced Macroeconomics II. Monetary Models with Nominal Rigidities. Jordi Galí Universitat Pompeu Fabra April 2018
 Advanced Macroeconomics II Monetary Models with Nominal Rigidities Jordi Galí Universitat Pompeu Fabra April 208 Motivation Empirical Evidence Macro evidence on the e ects of monetary policy shocks (i)
Advanced Macroeconomics II Monetary Models with Nominal Rigidities Jordi Galí Universitat Pompeu Fabra April 208 Motivation Empirical Evidence Macro evidence on the e ects of monetary policy shocks (i)
4- Current Method of Explaining Business Cycles: DSGE Models. Basic Economic Models
 4- Current Method of Explaining Business Cycles: DSGE Models Basic Economic Models In Economics, we use theoretical models to explain the economic processes in the real world. These models de ne a relation
4- Current Method of Explaining Business Cycles: DSGE Models Basic Economic Models In Economics, we use theoretical models to explain the economic processes in the real world. These models de ne a relation
1 Bewley Economies with Aggregate Uncertainty
 1 Bewley Economies with Aggregate Uncertainty Sofarwehaveassumedawayaggregatefluctuations (i.e., business cycles) in our description of the incomplete-markets economies with uninsurable idiosyncratic risk
1 Bewley Economies with Aggregate Uncertainty Sofarwehaveassumedawayaggregatefluctuations (i.e., business cycles) in our description of the incomplete-markets economies with uninsurable idiosyncratic risk
Optimal Monetary Policy in a Data-Rich Environment
 Optimal Monetary Policy in a Data-Rich Environment Jean Boivin HEC Montréal, CIRANO, CIRPÉE and NBER Marc Giannoni Columbia University, NBER and CEPR Forecasting Short-term Economic Developments... Bank
Optimal Monetary Policy in a Data-Rich Environment Jean Boivin HEC Montréal, CIRANO, CIRPÉE and NBER Marc Giannoni Columbia University, NBER and CEPR Forecasting Short-term Economic Developments... Bank
Chapter 2. GMM: Estimating Rational Expectations Models
 Chapter 2. GMM: Estimating Rational Expectations Models Contents 1 Introduction 1 2 Step 1: Solve the model and obtain Euler equations 2 3 Step 2: Formulate moment restrictions 3 4 Step 3: Estimation and
Chapter 2. GMM: Estimating Rational Expectations Models Contents 1 Introduction 1 2 Step 1: Solve the model and obtain Euler equations 2 3 Step 2: Formulate moment restrictions 3 4 Step 3: Estimation and
Estimating Macroeconomic Models: A Likelihood Approach
 Estimating Macroeconomic Models: A Likelihood Approach Jesús Fernández-Villaverde University of Pennsylvania, NBER, and CEPR Juan Rubio-Ramírez Federal Reserve Bank of Atlanta Estimating Dynamic Macroeconomic
Estimating Macroeconomic Models: A Likelihood Approach Jesús Fernández-Villaverde University of Pennsylvania, NBER, and CEPR Juan Rubio-Ramírez Federal Reserve Bank of Atlanta Estimating Dynamic Macroeconomic
Granger Causality and Equilibrium Business Cycle Theory
 Granger Causality and Equilibrium Business Cycle Theory Yi Wen Department of Economics Cornell University Abstract Post war US data show that consumption growth causes output and investment growth. This
Granger Causality and Equilibrium Business Cycle Theory Yi Wen Department of Economics Cornell University Abstract Post war US data show that consumption growth causes output and investment growth. This
Daily Welfare Gains from Trade
 Daily Welfare Gains from Trade Hasan Toprak Hakan Yilmazkuday y INCOMPLETE Abstract Using daily price quantity data on imported locally produced agricultural products, this paper estimates the elasticity
Daily Welfare Gains from Trade Hasan Toprak Hakan Yilmazkuday y INCOMPLETE Abstract Using daily price quantity data on imported locally produced agricultural products, this paper estimates the elasticity
STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics
 STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics Ph. D. Comprehensive Examination: Macroeconomics Fall, 202 Answer Key to Section 2 Questions Section. (Suggested Time: 45 Minutes) For 3 of
STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics Ph. D. Comprehensive Examination: Macroeconomics Fall, 202 Answer Key to Section 2 Questions Section. (Suggested Time: 45 Minutes) For 3 of
Housing and the Business Cycle
 Housing and the Business Cycle Morris Davis and Jonathan Heathcote Winter 2009 Huw Lloyd-Ellis () ECON917 Winter 2009 1 / 21 Motivation Need to distinguish between housing and non housing investment,!
Housing and the Business Cycle Morris Davis and Jonathan Heathcote Winter 2009 Huw Lloyd-Ellis () ECON917 Winter 2009 1 / 21 Motivation Need to distinguish between housing and non housing investment,!
Online Appendix to: Marijuana on Main Street? Estimating Demand in Markets with Limited Access
 Online Appendix to: Marijuana on Main Street? Estating Demand in Markets with Lited Access By Liana Jacobi and Michelle Sovinsky This appendix provides details on the estation methodology for various speci
Online Appendix to: Marijuana on Main Street? Estating Demand in Markets with Lited Access By Liana Jacobi and Michelle Sovinsky This appendix provides details on the estation methodology for various speci
Research Division Federal Reserve Bank of St. Louis Working Paper Series
 Research Division Federal Reserve Bank of St Louis Working Paper Series Kalman Filtering with Truncated Normal State Variables for Bayesian Estimation of Macroeconomic Models Michael Dueker Working Paper
Research Division Federal Reserve Bank of St Louis Working Paper Series Kalman Filtering with Truncated Normal State Variables for Bayesian Estimation of Macroeconomic Models Michael Dueker Working Paper
Macroeconomics II Dynamic macroeconomics Class 1: Introduction and rst models
 Macroeconomics II Dynamic macroeconomics Class 1: Introduction and rst models Prof. George McCandless UCEMA Spring 2008 1 Class 1: introduction and rst models What we will do today 1. Organization of course
Macroeconomics II Dynamic macroeconomics Class 1: Introduction and rst models Prof. George McCandless UCEMA Spring 2008 1 Class 1: introduction and rst models What we will do today 1. Organization of course
DSGE-Models. Calibration and Introduction to Dynare. Institute of Econometrics and Economic Statistics
 DSGE-Models Calibration and Introduction to Dynare Dr. Andrea Beccarini Willi Mutschler, M.Sc. Institute of Econometrics and Economic Statistics willi.mutschler@uni-muenster.de Summer 2012 Willi Mutschler
DSGE-Models Calibration and Introduction to Dynare Dr. Andrea Beccarini Willi Mutschler, M.Sc. Institute of Econometrics and Economic Statistics willi.mutschler@uni-muenster.de Summer 2012 Willi Mutschler
Signaling Effects of Monetary Policy
 Signaling Effects of Monetary Policy Leonardo Melosi London Business School 24 May 2012 Motivation Disperse information about aggregate fundamentals Morris and Shin (2003), Sims (2003), and Woodford (2002)
Signaling Effects of Monetary Policy Leonardo Melosi London Business School 24 May 2012 Motivation Disperse information about aggregate fundamentals Morris and Shin (2003), Sims (2003), and Woodford (2002)
Problem 1 (30 points)
 Problem (30 points) Prof. Robert King Consider an economy in which there is one period and there are many, identical households. Each household derives utility from consumption (c), leisure (l) and a public
Problem (30 points) Prof. Robert King Consider an economy in which there is one period and there are many, identical households. Each household derives utility from consumption (c), leisure (l) and a public
Can News be a Major Source of Aggregate Fluctuations?
 Can News be a Major Source of Aggregate Fluctuations? A Bayesian DSGE Approach Ippei Fujiwara 1 Yasuo Hirose 1 Mototsugu 2 1 Bank of Japan 2 Vanderbilt University August 4, 2009 Contributions of this paper
Can News be a Major Source of Aggregate Fluctuations? A Bayesian DSGE Approach Ippei Fujiwara 1 Yasuo Hirose 1 Mototsugu 2 1 Bank of Japan 2 Vanderbilt University August 4, 2009 Contributions of this paper
The B.E. Journal of Macroeconomics
 The B.E. Journal of Macroeconomics Topics Volume 8, Issue 1 2008 Article 20 Forecasting with DSGE Models: The Role of Nonlinearities Paul Pichler University of Vienna, paul.pichler@univie.ac.at Recommended
The B.E. Journal of Macroeconomics Topics Volume 8, Issue 1 2008 Article 20 Forecasting with DSGE Models: The Role of Nonlinearities Paul Pichler University of Vienna, paul.pichler@univie.ac.at Recommended
Are Uncertainty Shocks Aggregate Demand Shocks?
 Are Uncertainty Shocks Aggregate Demand Shocks? Stefano Fasani University of Milan Bicocca Lorenza Rossi y University of Pavia December 24 27 Abstract This note considers the Leduc and Liu (JME 26) model
Are Uncertainty Shocks Aggregate Demand Shocks? Stefano Fasani University of Milan Bicocca Lorenza Rossi y University of Pavia December 24 27 Abstract This note considers the Leduc and Liu (JME 26) model
Equivalence of several methods for decomposing time series into permananent and transitory components
 Equivalence of several methods for decomposing time series into permananent and transitory components Don Harding Department of Economics and Finance LaTrobe University, Bundoora Victoria 3086 and Centre
Equivalence of several methods for decomposing time series into permananent and transitory components Don Harding Department of Economics and Finance LaTrobe University, Bundoora Victoria 3086 and Centre
An Extended Macro-Finance Model with Financial Factors: Technical Appendix
 An Extended Macro-Finance Model with Financial Factors: Technical Appendix June 1, 010 Abstract This technical appendix provides some more technical comments concerning the EMF model, used in the paper
An Extended Macro-Finance Model with Financial Factors: Technical Appendix June 1, 010 Abstract This technical appendix provides some more technical comments concerning the EMF model, used in the paper
The Natural Rate of Interest and its Usefulness for Monetary Policy
 The Natural Rate of Interest and its Usefulness for Monetary Policy Robert Barsky, Alejandro Justiniano, and Leonardo Melosi Online Appendix 1 1 Introduction This appendix describes the extended DSGE model
The Natural Rate of Interest and its Usefulness for Monetary Policy Robert Barsky, Alejandro Justiniano, and Leonardo Melosi Online Appendix 1 1 Introduction This appendix describes the extended DSGE model
Nonlinear and/or Non-normal Filtering. Jesús Fernández-Villaverde University of Pennsylvania
 Nonlinear and/or Non-normal Filtering Jesús Fernández-Villaverde University of Pennsylvania 1 Motivation Nonlinear and/or non-gaussian filtering, smoothing, and forecasting (NLGF) problems are pervasive
Nonlinear and/or Non-normal Filtering Jesús Fernández-Villaverde University of Pennsylvania 1 Motivation Nonlinear and/or non-gaussian filtering, smoothing, and forecasting (NLGF) problems are pervasive
1 The social planner problem
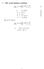 The social planner problem max C t;k t+ U t = E t X t C t () that can be written as: s.t.: Y t = A t K t (2) Y t = C t + I t (3) I t = K t+ (4) A t = A A t (5) et t i:i:d: 0; 2 max C t;k t+ U t = E t "
The social planner problem max C t;k t+ U t = E t X t C t () that can be written as: s.t.: Y t = A t K t (2) Y t = C t + I t (3) I t = K t+ (4) A t = A A t (5) et t i:i:d: 0; 2 max C t;k t+ U t = E t "
Business Cycles: The Classical Approach
 San Francisco State University ECON 302 Business Cycles: The Classical Approach Introduction Michael Bar Recall from the introduction that the output per capita in the U.S. is groing steady, but there
San Francisco State University ECON 302 Business Cycles: The Classical Approach Introduction Michael Bar Recall from the introduction that the output per capita in the U.S. is groing steady, but there
Estimation and Inference on Dynamic Panel Data Models with Stochastic Volatility
 Estimation and Inference on Dynamic Panel Data Models with Stochastic Volatility Wen Xu Department of Economics & Oxford-Man Institute University of Oxford (Preliminary, Comments Welcome) Theme y it =
Estimation and Inference on Dynamic Panel Data Models with Stochastic Volatility Wen Xu Department of Economics & Oxford-Man Institute University of Oxford (Preliminary, Comments Welcome) Theme y it =
Estimation of moment-based models with latent variables
 Estimation of moment-based models with latent variables work in progress Ra aella Giacomini and Giuseppe Ragusa UCL/Cemmap and UCI/Luiss UPenn, 5/4/2010 Giacomini and Ragusa (UCL/Cemmap and UCI/Luiss)Moments
Estimation of moment-based models with latent variables work in progress Ra aella Giacomini and Giuseppe Ragusa UCL/Cemmap and UCI/Luiss UPenn, 5/4/2010 Giacomini and Ragusa (UCL/Cemmap and UCI/Luiss)Moments
PANEL DISCUSSION: THE ROLE OF POTENTIAL OUTPUT IN POLICYMAKING
 PANEL DISCUSSION: THE ROLE OF POTENTIAL OUTPUT IN POLICYMAKING James Bullard* Federal Reserve Bank of St. Louis 33rd Annual Economic Policy Conference St. Louis, MO October 17, 2008 Views expressed are
PANEL DISCUSSION: THE ROLE OF POTENTIAL OUTPUT IN POLICYMAKING James Bullard* Federal Reserve Bank of St. Louis 33rd Annual Economic Policy Conference St. Louis, MO October 17, 2008 Views expressed are
Estimation with Aggregate Shocks
 Estimation with Aggregate Shocks Jinyong Hahn UCLA Guido Kuersteiner y University of Maryland October 5, 06 Maurizio Mazzocco z UCLA Abstract Aggregate shocks a ect most households and rms decisions. Using
Estimation with Aggregate Shocks Jinyong Hahn UCLA Guido Kuersteiner y University of Maryland October 5, 06 Maurizio Mazzocco z UCLA Abstract Aggregate shocks a ect most households and rms decisions. Using
Identifying Aggregate Liquidity Shocks with Monetary Policy Shocks: An Application using UK Data
 Identifying Aggregate Liquidity Shocks with Monetary Policy Shocks: An Application using UK Data Michael Ellington and Costas Milas Financial Services, Liquidity and Economic Activity Bank of England May
Identifying Aggregate Liquidity Shocks with Monetary Policy Shocks: An Application using UK Data Michael Ellington and Costas Milas Financial Services, Liquidity and Economic Activity Bank of England May
Identifying the Monetary Policy Shock Christiano et al. (1999)
 Identifying the Monetary Policy Shock Christiano et al. (1999) The question we are asking is: What are the consequences of a monetary policy shock a shock which is purely related to monetary conditions
Identifying the Monetary Policy Shock Christiano et al. (1999) The question we are asking is: What are the consequences of a monetary policy shock a shock which is purely related to monetary conditions
Finite State Markov-chain Approximations to Highly. Persistent Processes
 Finite State Markov-chain Approximations to Highly Persistent Processes Karen A. Kopecky y Richard M. H. Suen z This Version: November 2009 Abstract The Rouwenhorst method of approximating stationary AR(1)
Finite State Markov-chain Approximations to Highly Persistent Processes Karen A. Kopecky y Richard M. H. Suen z This Version: November 2009 Abstract The Rouwenhorst method of approximating stationary AR(1)
Research Division Federal Reserve Bank of St. Louis Working Paper Series
 Research Division Federal Reserve Bank of St. Louis Working Paper Series The Stability of Macroeconomic Systems with Bayesian Learners James Bullard and Jacek Suda Working Paper 2008-043B http://research.stlouisfed.org/wp/2008/2008-043.pdf
Research Division Federal Reserve Bank of St. Louis Working Paper Series The Stability of Macroeconomic Systems with Bayesian Learners James Bullard and Jacek Suda Working Paper 2008-043B http://research.stlouisfed.org/wp/2008/2008-043.pdf
Solutions to Problem Set 4 Macro II (14.452)
 Solutions to Problem Set 4 Macro II (14.452) Francisco A. Gallego 05/11 1 Money as a Factor of Production (Dornbusch and Frenkel, 1973) The shortcut used by Dornbusch and Frenkel to introduce money in
Solutions to Problem Set 4 Macro II (14.452) Francisco A. Gallego 05/11 1 Money as a Factor of Production (Dornbusch and Frenkel, 1973) The shortcut used by Dornbusch and Frenkel to introduce money in
Estimation in Non-Linear Non-Gaussian State Space Models with Precision-Based Methods
 MPRA Munich Personal RePEc Archive Estimation in Non-Linear Non-Gaussian State Space Models with Precision-Based Methods Joshua Chan and Rodney Strachan Australian National University 22 Online at http://mpra.ub.uni-muenchen.de/3936/
MPRA Munich Personal RePEc Archive Estimation in Non-Linear Non-Gaussian State Space Models with Precision-Based Methods Joshua Chan and Rodney Strachan Australian National University 22 Online at http://mpra.ub.uni-muenchen.de/3936/
Monetary Economics Notes
 Monetary Economics Notes Nicola Viegi 2 University of Pretoria - School of Economics Contents New Keynesian Models. Readings...............................2 Basic New Keynesian Model...................
Monetary Economics Notes Nicola Viegi 2 University of Pretoria - School of Economics Contents New Keynesian Models. Readings...............................2 Basic New Keynesian Model...................
ECON0702: Mathematical Methods in Economics
 ECON0702: Mathematical Methods in Economics Yulei Luo SEF of HKU January 14, 2009 Luo, Y. (SEF of HKU) MME January 14, 2009 1 / 44 Comparative Statics and The Concept of Derivative Comparative Statics
ECON0702: Mathematical Methods in Economics Yulei Luo SEF of HKU January 14, 2009 Luo, Y. (SEF of HKU) MME January 14, 2009 1 / 44 Comparative Statics and The Concept of Derivative Comparative Statics
Notes on Time Series Modeling
 Notes on Time Series Modeling Garey Ramey University of California, San Diego January 17 1 Stationary processes De nition A stochastic process is any set of random variables y t indexed by t T : fy t g
Notes on Time Series Modeling Garey Ramey University of California, San Diego January 17 1 Stationary processes De nition A stochastic process is any set of random variables y t indexed by t T : fy t g
Sequential Monte Carlo Methods (for DSGE Models)
 Sequential Monte Carlo Methods (for DSGE Models) Frank Schorfheide University of Pennsylvania, PIER, CEPR, and NBER October 23, 2017 Some References These lectures use material from our joint work: Tempered
Sequential Monte Carlo Methods (for DSGE Models) Frank Schorfheide University of Pennsylvania, PIER, CEPR, and NBER October 23, 2017 Some References These lectures use material from our joint work: Tempered
Lecture 6, January 7 and 15: Sticky Wages and Prices (Galí, Chapter 6)
 MakØk3, Fall 2012/2013 (Blok 2) Business cycles and monetary stabilization policies Henrik Jensen Department of Economics University of Copenhagen Lecture 6, January 7 and 15: Sticky Wages and Prices (Galí,
MakØk3, Fall 2012/2013 (Blok 2) Business cycles and monetary stabilization policies Henrik Jensen Department of Economics University of Copenhagen Lecture 6, January 7 and 15: Sticky Wages and Prices (Galí,
Identi cation and Frequency Domain QML Estimation of Linearized DSGE Models
 Identi cation and Frequency Domain QML Estimation of Linearized DSGE Models hongjun Qu y Boston University Denis Tkachenko z Boston University August, Abstract This paper considers issues related to identi
Identi cation and Frequency Domain QML Estimation of Linearized DSGE Models hongjun Qu y Boston University Denis Tkachenko z Boston University August, Abstract This paper considers issues related to identi
Why Nonlinear/Non-Gaussian DSGE Models?
 Why Nonlinear/Non-Gaussian DSGE Models? Jesús Fernández-Villaverde University of Pennsylvania July 10, 2011 Jesús Fernández-Villaverde (PENN) Nonlinear/Non-Gaussian DSGE July 10, 2011 1 / 38 Motivation
Why Nonlinear/Non-Gaussian DSGE Models? Jesús Fernández-Villaverde University of Pennsylvania July 10, 2011 Jesús Fernández-Villaverde (PENN) Nonlinear/Non-Gaussian DSGE July 10, 2011 1 / 38 Motivation
WORKING PAPER SERIES EXACT LIKELIHOOD COMPUTATION FOR NONLINEAR DSGE MODELS WITH HETEROSKEDASTIC INNOVATIONS NO 1341 / MAY 2011
 WORKING PAPER SERIES NO 1341 / MAY 2011 EXACT LIKELIHOOD COMPUTATION FOR NONLINEAR DSGE MODELS WITH HETEROSKEDASTIC INNOVATIONS by Gianni Amisano and Oreste Tristani WORKING PAPER SERIES NO 1341 / MAY
WORKING PAPER SERIES NO 1341 / MAY 2011 EXACT LIKELIHOOD COMPUTATION FOR NONLINEAR DSGE MODELS WITH HETEROSKEDASTIC INNOVATIONS by Gianni Amisano and Oreste Tristani WORKING PAPER SERIES NO 1341 / MAY
TAKEHOME FINAL EXAM e iω e 2iω e iω e 2iω
 ECO 513 Spring 2015 TAKEHOME FINAL EXAM (1) Suppose the univariate stochastic process y is ARMA(2,2) of the following form: y t = 1.6974y t 1.9604y t 2 + ε t 1.6628ε t 1 +.9216ε t 2, (1) where ε is i.i.d.
ECO 513 Spring 2015 TAKEHOME FINAL EXAM (1) Suppose the univariate stochastic process y is ARMA(2,2) of the following form: y t = 1.6974y t 1.9604y t 2 + ε t 1.6628ε t 1 +.9216ε t 2, (1) where ε is i.i.d.
Inference about Clustering and Parametric. Assumptions in Covariance Matrix Estimation
 Inference about Clustering and Parametric Assumptions in Covariance Matrix Estimation Mikko Packalen y Tony Wirjanto z 26 November 2010 Abstract Selecting an estimator for the variance covariance matrix
Inference about Clustering and Parametric Assumptions in Covariance Matrix Estimation Mikko Packalen y Tony Wirjanto z 26 November 2010 Abstract Selecting an estimator for the variance covariance matrix
Dynamic Factor Models and Factor Augmented Vector Autoregressions. Lawrence J. Christiano
 Dynamic Factor Models and Factor Augmented Vector Autoregressions Lawrence J Christiano Dynamic Factor Models and Factor Augmented Vector Autoregressions Problem: the time series dimension of data is relatively
Dynamic Factor Models and Factor Augmented Vector Autoregressions Lawrence J Christiano Dynamic Factor Models and Factor Augmented Vector Autoregressions Problem: the time series dimension of data is relatively
Time Series Models and Inference. James L. Powell Department of Economics University of California, Berkeley
 Time Series Models and Inference James L. Powell Department of Economics University of California, Berkeley Overview In contrast to the classical linear regression model, in which the components of the
Time Series Models and Inference James L. Powell Department of Economics University of California, Berkeley Overview In contrast to the classical linear regression model, in which the components of the
A time series plot: a variable Y t on the vertical axis is plotted against time on the horizontal axis
 TIME AS A REGRESSOR A time series plot: a variable Y t on the vertical axis is plotted against time on the horizontal axis Many economic variables increase or decrease with time A linear trend relationship
TIME AS A REGRESSOR A time series plot: a variable Y t on the vertical axis is plotted against time on the horizontal axis Many economic variables increase or decrease with time A linear trend relationship
Structural Macroeconometrics. Chapter 4. Summarizing Time Series Behavior
 Structural Macroeconometrics Chapter 4. Summarizing Time Series Behavior David N. DeJong Chetan Dave The sign of a truly educated man is to be deeply moved by statistics. George Bernard Shaw This chapter
Structural Macroeconometrics Chapter 4. Summarizing Time Series Behavior David N. DeJong Chetan Dave The sign of a truly educated man is to be deeply moved by statistics. George Bernard Shaw This chapter
Testing for Regime Switching: A Comment
 Testing for Regime Switching: A Comment Andrew V. Carter Department of Statistics University of California, Santa Barbara Douglas G. Steigerwald Department of Economics University of California Santa Barbara
Testing for Regime Switching: A Comment Andrew V. Carter Department of Statistics University of California, Santa Barbara Douglas G. Steigerwald Department of Economics University of California Santa Barbara
1 Regression with Time Series Variables
 1 Regression with Time Series Variables With time series regression, Y might not only depend on X, but also lags of Y and lags of X Autoregressive Distributed lag (or ADL(p; q)) model has these features:
1 Regression with Time Series Variables With time series regression, Y might not only depend on X, but also lags of Y and lags of X Autoregressive Distributed lag (or ADL(p; q)) model has these features:
Prediction with Misspeci ed Models. John Geweke* and Gianni Amisano**
 Prediction with Misspeci ed Models John Geweke* and Gianni Amisano** Many decision-makers in the public and private sectors routinely consult the implications of formal economic and statistical models
Prediction with Misspeci ed Models John Geweke* and Gianni Amisano** Many decision-makers in the public and private sectors routinely consult the implications of formal economic and statistical models
Estimation of Dynamic Nonlinear Random E ects Models with Unbalanced Panels.
 Estimation of Dynamic Nonlinear Random E ects Models with Unbalanced Panels. Pedro Albarran y Raquel Carrasco z Jesus M. Carro x June 2014 Preliminary and Incomplete Abstract This paper presents and evaluates
Estimation of Dynamic Nonlinear Random E ects Models with Unbalanced Panels. Pedro Albarran y Raquel Carrasco z Jesus M. Carro x June 2014 Preliminary and Incomplete Abstract This paper presents and evaluates
Central Bank Communication and the Liquidity Trap
 Central Bank Communication and the Liquidity Trap Stefano Eusepi y Federal Reserve Bank of New York October 8, 2009 Abstract Central bank communication plays an important role in shaping market participants
Central Bank Communication and the Liquidity Trap Stefano Eusepi y Federal Reserve Bank of New York October 8, 2009 Abstract Central bank communication plays an important role in shaping market participants
Where Are We Now? Real-Time Estimates of the Macro Economy
 Where Are We Now? Real-Time Estimates of the Macro Economy Martin D. D. Evans Georgetown University and the NBER March 2005 Forthcoming in The International Journal of Central Banking Abstract This paper
Where Are We Now? Real-Time Estimates of the Macro Economy Martin D. D. Evans Georgetown University and the NBER March 2005 Forthcoming in The International Journal of Central Banking Abstract This paper
In the Ramsey model we maximized the utility U = u[c(t)]e nt e t dt. Now
![In the Ramsey model we maximized the utility U = u[c(t)]e nt e t dt. Now In the Ramsey model we maximized the utility U = u[c(t)]e nt e t dt. Now](/thumbs/89/100962140.jpg) PERMANENT INCOME AND OPTIMAL CONSUMPTION On the previous notes we saw how permanent income hypothesis can solve the Consumption Puzzle. Now we use this hypothesis, together with assumption of rational
PERMANENT INCOME AND OPTIMAL CONSUMPTION On the previous notes we saw how permanent income hypothesis can solve the Consumption Puzzle. Now we use this hypothesis, together with assumption of rational
NBER WORKING PAPER SERIES WHERE ARE WE NOW? REAL-TIME ESTIMATES OF THE MACRO ECONOMY. Martin D.D. Evans
 NBER WORKING PAPER SERIES WHERE ARE WE NOW? REAL-TIME ESTIMATES OF THE MACRO ECONOMY Martin D.D. Evans Working Paper 11064 http://www.nber.org/papers/w11064 NATIONAL BUREAU OF ECONOMIC RESEARCH 1050 Massachusetts
NBER WORKING PAPER SERIES WHERE ARE WE NOW? REAL-TIME ESTIMATES OF THE MACRO ECONOMY Martin D.D. Evans Working Paper 11064 http://www.nber.org/papers/w11064 NATIONAL BUREAU OF ECONOMIC RESEARCH 1050 Massachusetts
High-dimensional Problems in Finance and Economics. Thomas M. Mertens
 High-dimensional Problems in Finance and Economics Thomas M. Mertens NYU Stern Risk Economics Lab April 17, 2012 1 / 78 Motivation Many problems in finance and economics are high dimensional. Dynamic Optimization:
High-dimensional Problems in Finance and Economics Thomas M. Mertens NYU Stern Risk Economics Lab April 17, 2012 1 / 78 Motivation Many problems in finance and economics are high dimensional. Dynamic Optimization:
Identi cation and Frequency Domain QML Estimation of Linearized DSGE Models
 Identi cation and Frequency Domain QML Estimation of Linearized DSGE Models hongjun Qu y Boston University Denis Tkachenko z Boston University August, ; revised: December 6, Abstract This paper considers
Identi cation and Frequency Domain QML Estimation of Linearized DSGE Models hongjun Qu y Boston University Denis Tkachenko z Boston University August, ; revised: December 6, Abstract This paper considers
A Modern Equilibrium Model. Jesús Fernández-Villaverde University of Pennsylvania
 A Modern Equilibrium Model Jesús Fernández-Villaverde University of Pennsylvania 1 Household Problem Preferences: max E X β t t=0 c 1 σ t 1 σ ψ l1+γ t 1+γ Budget constraint: c t + k t+1 = w t l t + r t
A Modern Equilibrium Model Jesús Fernández-Villaverde University of Pennsylvania 1 Household Problem Preferences: max E X β t t=0 c 1 σ t 1 σ ψ l1+γ t 1+γ Budget constraint: c t + k t+1 = w t l t + r t
Fiscal Multipliers in a Nonlinear World
 Fiscal Multipliers in a Nonlinear World Jesper Lindé Sveriges Riksbank Mathias Trabandt Freie Universität Berlin November 28, 2016 Lindé and Trabandt Multipliers () in Nonlinear Models November 28, 2016
Fiscal Multipliers in a Nonlinear World Jesper Lindé Sveriges Riksbank Mathias Trabandt Freie Universität Berlin November 28, 2016 Lindé and Trabandt Multipliers () in Nonlinear Models November 28, 2016
A new unscented Kalman filter with higher order moment-matching
 A new unscented Kalman filter with higher order moment-matching KSENIA PONOMAREVA, PARESH DATE AND ZIDONG WANG Department of Mathematical Sciences, Brunel University, Uxbridge, UB8 3PH, UK. Abstract This
A new unscented Kalman filter with higher order moment-matching KSENIA PONOMAREVA, PARESH DATE AND ZIDONG WANG Department of Mathematical Sciences, Brunel University, Uxbridge, UB8 3PH, UK. Abstract This
Time Series Analysis for Macroeconomics and Finance
 Time Series Analysis for Macroeconomics and Finance Bernd Süssmuth IEW Institute for Empirical Research in Economics University of Leipzig December 12, 2011 Bernd Süssmuth (University of Leipzig) Time
Time Series Analysis for Macroeconomics and Finance Bernd Süssmuth IEW Institute for Empirical Research in Economics University of Leipzig December 12, 2011 Bernd Süssmuth (University of Leipzig) Time
Time-Varying Vector Autoregressive Models with Structural Dynamic Factors
 Time-Varying Vector Autoregressive Models with Structural Dynamic Factors Paolo Gorgi, Siem Jan Koopman, Julia Schaumburg http://sjkoopman.net Vrije Universiteit Amsterdam School of Business and Economics
Time-Varying Vector Autoregressive Models with Structural Dynamic Factors Paolo Gorgi, Siem Jan Koopman, Julia Schaumburg http://sjkoopman.net Vrije Universiteit Amsterdam School of Business and Economics
Optimal Simple And Implementable Monetary and Fiscal Rules
 Optimal Simple And Implementable Monetary and Fiscal Rules Stephanie Schmitt-Grohé Martín Uribe Duke University September 2007 1 Welfare-Based Policy Evaluation: Related Literature (ex: Rotemberg and Woodford,
Optimal Simple And Implementable Monetary and Fiscal Rules Stephanie Schmitt-Grohé Martín Uribe Duke University September 2007 1 Welfare-Based Policy Evaluation: Related Literature (ex: Rotemberg and Woodford,
The Kalman filter, Nonlinear filtering, and Markov Chain Monte Carlo
 NBER Summer Institute Minicourse What s New in Econometrics: Time Series Lecture 5 July 5, 2008 The Kalman filter, Nonlinear filtering, and Markov Chain Monte Carlo Lecture 5, July 2, 2008 Outline. Models
NBER Summer Institute Minicourse What s New in Econometrics: Time Series Lecture 5 July 5, 2008 The Kalman filter, Nonlinear filtering, and Markov Chain Monte Carlo Lecture 5, July 2, 2008 Outline. Models
Research Division Federal Reserve Bank of St. Louis Working Paper Series
 Research Division Federal Reserve Bank of St. Louis Working Paper Series Solving Linear Difference Systems with Lagged Expectations by a Method of Undetermined Coefficients Pengfei Wang and Yi Wen Working
Research Division Federal Reserve Bank of St. Louis Working Paper Series Solving Linear Difference Systems with Lagged Expectations by a Method of Undetermined Coefficients Pengfei Wang and Yi Wen Working
Matching DSGE models,vars, and state space models. Fabio Canova EUI and CEPR September 2012
 Matching DSGE models,vars, and state space models Fabio Canova EUI and CEPR September 2012 Outline Alternative representations of the solution of a DSGE model. Fundamentalness and finite VAR representation
Matching DSGE models,vars, and state space models Fabio Canova EUI and CEPR September 2012 Outline Alternative representations of the solution of a DSGE model. Fundamentalness and finite VAR representation
Employment, Wage, and Output Dynamics under External Habit Formation and E ciency Wages
 Employment, Wage, and Output Dynamics under External Habit Formation and E ciency Wages Matthew L. Booth Middle Tennessee State University Murfreesboro TN 37132 mbooth@mtsu.edu February 9, 2018 Abstract
Employment, Wage, and Output Dynamics under External Habit Formation and E ciency Wages Matthew L. Booth Middle Tennessee State University Murfreesboro TN 37132 mbooth@mtsu.edu February 9, 2018 Abstract
Policy Inertia and Equilibrium Determinacy in a New. Keynesian Model with Investment
 Policy Inertia and Equilibrium Determinacy in a New Keynesian Model with Investment Wei Xiao State University of New York at Binghamton June, 2007 Abstract Carlstrom and Fuerst (2005) demonstrate that
Policy Inertia and Equilibrium Determinacy in a New Keynesian Model with Investment Wei Xiao State University of New York at Binghamton June, 2007 Abstract Carlstrom and Fuerst (2005) demonstrate that
1 The Basic RBC Model
 IHS 2016, Macroeconomics III Michael Reiter Ch. 1: Notes on RBC Model 1 1 The Basic RBC Model 1.1 Description of Model Variables y z k L c I w r output level of technology (exogenous) capital at end of
IHS 2016, Macroeconomics III Michael Reiter Ch. 1: Notes on RBC Model 1 1 The Basic RBC Model 1.1 Description of Model Variables y z k L c I w r output level of technology (exogenous) capital at end of
Foundation of (virtually) all DSGE models (e.g., RBC model) is Solow growth model
 THE BASELINE RBC MODEL: THEORY AND COMPUTATION FEBRUARY, 202 STYLIZED MACRO FACTS Foundation of (virtually all DSGE models (e.g., RBC model is Solow growth model So want/need/desire business-cycle models
THE BASELINE RBC MODEL: THEORY AND COMPUTATION FEBRUARY, 202 STYLIZED MACRO FACTS Foundation of (virtually all DSGE models (e.g., RBC model is Solow growth model So want/need/desire business-cycle models
