fl D ortho IT is Projections g g LY 1.4 If J by then Mr We wish to write ig as a sum of two special where 2 is in the samed tas and This
|
|
|
- Osborn McBride
- 5 years ago
- Views:
Transcription
1 1.4 Projections g where 2 is in the samed tas and T is ortho This is when easy to Suppose we have two vectors and g n R to We wish to write ig as a sum of two special vectors f J by then Mr a E g LY t g E 5 parallelto f perpendicularto xf.to Yj fl D
2 Q How do we find t Ez when 5 is more complicated R2 N Y an Y N r r fzi N s t L f Zi N N We Know that 1 is parallel to 5 i.e a multiple of F so 2 K for some KER This means that F 2FtZz KxtZzw where Zz is orthogonal to 5 To find k take the dot product of E and J g Ket 2 2 KK TE HM as E tx
3 So g KNK K X we've just shown that Z Since g Ei Definition f and are in R with to then the projection of g onto 5 is projxy fj.gg Y and the perpendicular part is perp J g proj g From this definition it's clear that lily.pro Perpy and ii Pro jg is a multiples n Q2 of Assignment 2 you verify iii Perp y J fxj.t isorthogona tox
4 E What is the projection of onto E what is the perpendicular part f Solution we have that proj y Y x We get and g E 4 10 So proj g 5 25 and perp g j projej L L f Nz A q pj 1 tix E se Ex f and prog'g o and 5 find to ProjeJ perp g 3 0
5 Solution Note that and s proj.j fxixyjx.fi x g x lo ff.o z O Z perp j j projxy f.io f J ff 3 3 For projge note that Hugh 104 and g 10 so projgx ffgffy.fi g TRemar fi oi K The above example shows that in general proj ftp.nojgx That's not too surprising proj J is a multiple of 5 while projg is a multiple of g theorem properties of Projl Perp Let J E be vectors in Rh and let te R E
6 z p.j.mg 3 ProjetProj y Proj Lg These properti are also true for Perp and proj perp are linear Properties 1 and 2 say that functions from R into R we'll return to something in Chapter 3 Proofoft ProjecgiEl TEA fifth x tfi.t x Proj.jtProix E.u Exercise Try a similar approach for 2 Can you explain intuitively why 3 is true
7 Application Minimum Distance e w QUESTON about projections There are Lots of reasons to care about projections One major application projections can be used to find the line ofbestfit for a set of data points x 1 This is the line whose total distance to a set of points is as small se as possible A complete treatment of this topic MATH 235 nstead we'll look at two different applications of projections to minimum distance Want to know more about how to find this line Talk to me after chapter3
8 1 Distance from Point to Line mm what's the distance i e Shortest distance from a point Q to a line 5 15 ttd ter Rzµ P t Q t's the length of the f dotted line that meets n our line at a right angle Rz n the language of projections N this is exactly ftp.pq Fa TtQ P p a The point on the line Proyectot T closest to Q is F i apoint n Ex Find the distance from Q O 2 to the line 4 2 tf1 te R What is the closest point
9 Solution We have that and 111 Z 1 From the above the distance 11 perp H and the closest point is ft Projj Fa So let's find Projjffa and Perp P Note Fa 4 4 E F z z o d Fa 4 so Projet fi Y f 3 Perp P Prog d POT Y The distance is Hperpi The closest point is ft Projj Z z o
10 Exercise Find the distance from Q 1,0 l to the line f tf te R What is the closest point 2 Distance from Point to Plane what's the distance from a point Q to a plane in 1123 with normal vector ri f'd suppose P is any point Q on the plane t p b fi The distance is the length of the dotted line segment that is orthogonal to the plane n terms of projections in A Perp P this is Mill T The point on the plane closest to Q is jpq 1 This is the same as ftp.rpjpq kingt ftp.a b a AA closestpoint
11 E What is the distance from Qf 1,421 to the plane kit Find the point on the plane that is closest to Q Solution We can a point P on the plane get by setting Nz Ks 0 and solving for se Kit N 4 se se 0 So P C 4,0 o is a point on the plane and T J From above we know that the distance is HProjaFall and the closest point is of Projata We have POT E p f f Y f Z 3 Z ri PQ 9 So Projita Finton ri L The distance is HProjn.PEl rq 3
12 The closest point is E Project l t.t Exercise what is the distance from Qtl l l to the plane 2x sea t se 2 Notice anything odd Which point on this plane is closest to Q
Definition. special name. 72 spans 5. Last time we proved that if Ju's is. t.vtts.tt turn. This subspace is se important that we give it
 1.7 Spanningsetsilinearndependencey 1.2 in text Last time we proved that if 72 148 Ju's is a set of vectors in R then is a subspace of R t.vtts.tt turn t tz the R This subspace is se important that we
1.7 Spanningsetsilinearndependencey 1.2 in text Last time we proved that if 72 148 Ju's is a set of vectors in R then is a subspace of R t.vtts.tt turn t tz the R This subspace is se important that we
K E L LY T H O M P S O N
 K E L LY T H O M P S O N S E A O LO G Y C R E ATO R, F O U N D E R, A N D PA R T N E R K e l l y T h o m p s o n i s t h e c r e a t o r, f o u n d e r, a n d p a r t n e r o f S e a o l o g y, a n e x
K E L LY T H O M P S O N S E A O LO G Y C R E ATO R, F O U N D E R, A N D PA R T N E R K e l l y T h o m p s o n i s t h e c r e a t o r, f o u n d e r, a n d p a r t n e r o f S e a o l o g y, a n e x
Math 416, Spring 2010 Gram-Schmidt, the QR-factorization, Orthogonal Matrices March 4, 2010 GRAM-SCHMIDT, THE QR-FACTORIZATION, ORTHOGONAL MATRICES
 Math 46, Spring 00 Gram-Schmidt, the QR-factorization, Orthogonal Matrices March 4, 00 GRAM-SCHMIDT, THE QR-FACTORIZATION, ORTHOGONAL MATRICES Recap Yesterday we talked about several new, important concepts
Math 46, Spring 00 Gram-Schmidt, the QR-factorization, Orthogonal Matrices March 4, 00 GRAM-SCHMIDT, THE QR-FACTORIZATION, ORTHOGONAL MATRICES Recap Yesterday we talked about several new, important concepts
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Spring 2018, WEEK 1 JoungDong Kim Week 1 Vectors, The Dot Product, Vector Functions and Parametric Curves. Section 1.1 Vectors Definition. A Vector is a quantity that
MATH 151 Engineering Mathematics I Spring 2018, WEEK 1 JoungDong Kim Week 1 Vectors, The Dot Product, Vector Functions and Parametric Curves. Section 1.1 Vectors Definition. A Vector is a quantity that
Distances in R 3. Last time we figured out the (parametric) equation of a line and the (scalar) equation of a plane:
 Distances in R 3 Last time we figured out the (parametric) equation of a line and the (scalar) equation of a plane: Definition: The equation of a line through point P(x 0, y 0, z 0 ) with directional vector
Distances in R 3 Last time we figured out the (parametric) equation of a line and the (scalar) equation of a plane: Definition: The equation of a line through point P(x 0, y 0, z 0 ) with directional vector
MATH 19520/51 Class 2
 MATH 19520/51 Class 2 Minh-Tam Trinh University of Chicago 2017-09-27 1 Review dot product. 2 Angles between vectors and orthogonality. 3 Projection of one vector onto another. 4 Cross product and its
MATH 19520/51 Class 2 Minh-Tam Trinh University of Chicago 2017-09-27 1 Review dot product. 2 Angles between vectors and orthogonality. 3 Projection of one vector onto another. 4 Cross product and its
Supplementary Information
 If f - - x R f z (F ) w () () f F >, f E jj E, V G >, G >, E G,, f ff f FILY f jj ff LO_ N_ j:rer_ N_ Y_ fg LO_; LO_ N_; N_ j:rer_; j:rer_ N_ Y_ f LO_ N_ j:rer_; j:rer_; N_ j:rer_ Y_ fn LO_ N_ - N_ Y_
If f - - x R f z (F ) w () () f F >, f E jj E, V G >, G >, E G,, f ff f FILY f jj ff LO_ N_ j:rer_ N_ Y_ fg LO_; LO_ N_; N_ j:rer_; j:rer_ N_ Y_ f LO_ N_ j:rer_; j:rer_; N_ j:rer_ Y_ fn LO_ N_ - N_ Y_
Linear Algebra, Summer 2011, pt. 3
 Linear Algebra, Summer 011, pt. 3 September 0, 011 Contents 1 Orthogonality. 1 1.1 The length of a vector....................... 1. Orthogonal vectors......................... 3 1.3 Orthogonal Subspaces.......................
Linear Algebra, Summer 011, pt. 3 September 0, 011 Contents 1 Orthogonality. 1 1.1 The length of a vector....................... 1. Orthogonal vectors......................... 3 1.3 Orthogonal Subspaces.......................
Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4.
![Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4. Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4.](/thumbs/92/109036622.jpg) te SelfGi ZltAn Dbnyei Intdtin ; ) Q) 4 t? ) t _ 4 73 y S _ E _ p p 4 t t 4) 1_ ::_ J 1 `i () L VI O I4 " " 1 D 4 L e Q) 1 k) QJ 7 j ZS _Le t 1 ej!2 i1 L 77 7 G (4) 4 6 t (1 ;7 bb F) t f; n (i M Q) 7S
te SelfGi ZltAn Dbnyei Intdtin ; ) Q) 4 t? ) t _ 4 73 y S _ E _ p p 4 t t 4) 1_ ::_ J 1 `i () L VI O I4 " " 1 D 4 L e Q) 1 k) QJ 7 j ZS _Le t 1 ej!2 i1 L 77 7 G (4) 4 6 t (1 ;7 bb F) t f; n (i M Q) 7S
Consider a subspace V = im(a) of R n, where m. Then,
 5.4 LEAST SQUARES AND DATA FIT- TING ANOTHER CHARACTERIZATION OF ORTHOG- ONAL COMPLEMENTS Consider a subspace V = im(a) of R n, where A = [ ] v 1 v 2... v m. Then, V = { x in R n : v x = 0, for all v in
5.4 LEAST SQUARES AND DATA FIT- TING ANOTHER CHARACTERIZATION OF ORTHOG- ONAL COMPLEMENTS Consider a subspace V = im(a) of R n, where A = [ ] v 1 v 2... v m. Then, V = { x in R n : v x = 0, for all v in
Section 6.2, 6.3 Orthogonal Sets, Orthogonal Projections
 Section 6. 6. Orthogonal Sets Orthogonal Projections Main Ideas in these sections: Orthogonal set = A set of mutually orthogonal vectors. OG LI. Orthogonal Projection of y onto u or onto an OG set {u u
Section 6. 6. Orthogonal Sets Orthogonal Projections Main Ideas in these sections: Orthogonal set = A set of mutually orthogonal vectors. OG LI. Orthogonal Projection of y onto u or onto an OG set {u u
Dot Products, Transposes, and Orthogonal Projections
 Dot Products, Transposes, and Orthogonal Projections David Jekel November 13, 2015 Properties of Dot Products Recall that the dot product or standard inner product on R n is given by x y = x 1 y 1 + +
Dot Products, Transposes, and Orthogonal Projections David Jekel November 13, 2015 Properties of Dot Products Recall that the dot product or standard inner product on R n is given by x y = x 1 y 1 + +
MATH 12 CLASS 2 NOTES, SEP Contents. 2. Dot product: determining the angle between two vectors 2
 MATH 12 CLASS 2 NOTES, SEP 23 2011 Contents 1. Dot product: definition, basic properties 1 2. Dot product: determining the angle between two vectors 2 Quick links to definitions/theorems Dot product definition
MATH 12 CLASS 2 NOTES, SEP 23 2011 Contents 1. Dot product: definition, basic properties 1 2. Dot product: determining the angle between two vectors 2 Quick links to definitions/theorems Dot product definition
MTH 2310, FALL Introduction
 MTH 2310, FALL 2011 SECTION 6.2: ORTHOGONAL SETS Homework Problems: 1, 5, 9, 13, 17, 21, 23 1, 27, 29, 35 1. Introduction We have discussed previously the benefits of having a set of vectors that is linearly
MTH 2310, FALL 2011 SECTION 6.2: ORTHOGONAL SETS Homework Problems: 1, 5, 9, 13, 17, 21, 23 1, 27, 29, 35 1. Introduction We have discussed previously the benefits of having a set of vectors that is linearly
Lecture 4: Applications of Orthogonality: QR Decompositions
 Math 08B Professor: Padraic Bartlett Lecture 4: Applications of Orthogonality: QR Decompositions Week 4 UCSB 204 In our last class, we described the following method for creating orthonormal bases, known
Math 08B Professor: Padraic Bartlett Lecture 4: Applications of Orthogonality: QR Decompositions Week 4 UCSB 204 In our last class, we described the following method for creating orthonormal bases, known
Vectors. Section 3: Using the vector product
 Vectors Section 3: Using the vector product Notes and Examples These notes contain subsections on Using the vector product in finding the equation of a plane The intersection of two planes The distance
Vectors Section 3: Using the vector product Notes and Examples These notes contain subsections on Using the vector product in finding the equation of a plane The intersection of two planes The distance
Vector Calculus. Lecture Notes
 Vector Calculus Lecture Notes Adolfo J. Rumbos c Draft date November 23, 211 2 Contents 1 Motivation for the course 5 2 Euclidean Space 7 2.1 Definition of n Dimensional Euclidean Space........... 7 2.2
Vector Calculus Lecture Notes Adolfo J. Rumbos c Draft date November 23, 211 2 Contents 1 Motivation for the course 5 2 Euclidean Space 7 2.1 Definition of n Dimensional Euclidean Space........... 7 2.2
F F. proj cos( ) v. v proj v
 Geometric Definition of Dot Product 1.2 The Dot Product Suppose you are pulling up on a rope attached to a box, as shown above. How would you find the force moving the box towards you? As stated above,
Geometric Definition of Dot Product 1.2 The Dot Product Suppose you are pulling up on a rope attached to a box, as shown above. How would you find the force moving the box towards you? As stated above,
Lesson 5: The Distributive Property
 Exploratory Exercise Kim was working on an exercise in math when she ran across this problem. Distribute and simplify if possible. (3x + 5) Kim s dad said, I remember doing something like this in school.
Exploratory Exercise Kim was working on an exercise in math when she ran across this problem. Distribute and simplify if possible. (3x + 5) Kim s dad said, I remember doing something like this in school.
9.9 L1N1F_JL 19bo. G)&) art9lej11 b&bo 51JY1511JEJ11141N0fM1NW15tIr1
 thunyitmn tn1 zni f1117n.nllfmztri Lrs v wu 4 t t701 f 171/ ti 141 o&oiv,3 if 042 9.9 L1N1F_JL 19bo vitioluutul fly11.1.g)onoo b5 et Nn`15fiwnwiymri1 nrikl5fini1nvi Ltol : Aeniln,flvnu 6m,wiutrmntn15Y
thunyitmn tn1 zni f1117n.nllfmztri Lrs v wu 4 t t701 f 171/ ti 141 o&oiv,3 if 042 9.9 L1N1F_JL 19bo vitioluutul fly11.1.g)onoo b5 et Nn`15fiwnwiymri1 nrikl5fini1nvi Ltol : Aeniln,flvnu 6m,wiutrmntn15Y
Later in this chapter, we are going to use vector functions to describe the motion of planets and other objects through space.
 10 VECTOR FUNCTIONS VECTOR FUNCTIONS Later in this chapter, we are going to use vector functions to describe the motion of planets and other objects through space. Here, we prepare the way by developing
10 VECTOR FUNCTIONS VECTOR FUNCTIONS Later in this chapter, we are going to use vector functions to describe the motion of planets and other objects through space. Here, we prepare the way by developing
12.5 Equations of Lines and Planes
 12.5 Equations of Lines and Planes Equation of Lines Vector Equation of Lines Parametric Equation of Lines Symmetric Equation of Lines Relation Between Two Lines Equations of Planes Vector Equation of
12.5 Equations of Lines and Planes Equation of Lines Vector Equation of Lines Parametric Equation of Lines Symmetric Equation of Lines Relation Between Two Lines Equations of Planes Vector Equation of
Math 261 Lecture Notes: Sections 6.1, 6.2, 6.3 and 6.4 Orthogonal Sets and Projections
 Math 6 Lecture Notes: Sections 6., 6., 6. and 6. Orthogonal Sets and Projections We will not cover general inner product spaces. We will, however, focus on a particular inner product space the inner product
Math 6 Lecture Notes: Sections 6., 6., 6. and 6. Orthogonal Sets and Projections We will not cover general inner product spaces. We will, however, focus on a particular inner product space the inner product
March 27 Math 3260 sec. 56 Spring 2018
 March 27 Math 3260 sec. 56 Spring 2018 Section 4.6: Rank Definition: The row space, denoted Row A, of an m n matrix A is the subspace of R n spanned by the rows of A. We now have three vector spaces associated
March 27 Math 3260 sec. 56 Spring 2018 Section 4.6: Rank Definition: The row space, denoted Row A, of an m n matrix A is the subspace of R n spanned by the rows of A. We now have three vector spaces associated
Chapter 3: Vector Spaces x1: Basic concepts Basic idea: a vector space V is a collection of things you can add together, and multiply by scalars (= nu
 Math 314 Topics for second exam Technically, everything covered by the rst exam plus Chapter 2 x6 Determinants (Square) matrices come in two avors: invertible (all Ax = b have a solution) and noninvertible
Math 314 Topics for second exam Technically, everything covered by the rst exam plus Chapter 2 x6 Determinants (Square) matrices come in two avors: invertible (all Ax = b have a solution) and noninvertible
10.1 Three Dimensional Space
 Math 172 Chapter 10A notes Page 1 of 12 10.1 Three Dimensional Space 2D space 0 xx.. xx-, 0 yy yy-, PP(xx, yy) [Fig. 1] Point PP represented by (xx, yy), an ordered pair of real nos. Set of all ordered
Math 172 Chapter 10A notes Page 1 of 12 10.1 Three Dimensional Space 2D space 0 xx.. xx-, 0 yy yy-, PP(xx, yy) [Fig. 1] Point PP represented by (xx, yy), an ordered pair of real nos. Set of all ordered
How can we find the distance between a point and a plane in R 3? Between two lines in R 3? Between two planes? Between a plane and a line?
 Overview Yesterday we introduced equations to describe lines and planes in R 3 : r = r 0 + tv The vector equation for a line describes arbitrary points r in terms of a specific point r 0 and the direction
Overview Yesterday we introduced equations to describe lines and planes in R 3 : r = r 0 + tv The vector equation for a line describes arbitrary points r in terms of a specific point r 0 and the direction
Designing Information Devices and Systems I Fall 2018 Lecture Notes Note 21
 EECS 16A Designing Information Devices and Systems I Fall 2018 Lecture Notes Note 21 21.1 Module Goals In this module, we introduce a family of ideas that are connected to optimization and machine learning,
EECS 16A Designing Information Devices and Systems I Fall 2018 Lecture Notes Note 21 21.1 Module Goals In this module, we introduce a family of ideas that are connected to optimization and machine learning,
Chapter 2: Vector Geometry
 Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
Elf. GIsis. Qf Fa Fa c Cl is a single. gcx has no roots in E or it splits into. Qf C'TE TEE Tze Life e. z Elp Galois given guy. Exampies.
 thenge An overview Assume all Fields are subhields et E demng this lecture Let F C E be a subfield and the E Fca Assume thx a Cac a where a c F Li E E Definition Ff FK n c Q is called the splitting Field
thenge An overview Assume all Fields are subhields et E demng this lecture Let F C E be a subfield and the E Fca Assume thx a Cac a where a c F Li E E Definition Ff FK n c Q is called the splitting Field
Unit 4. Algebraic and Geometric Proof. Math 2 Spring 2017
 1 Unit 4 lgebraic and Geometric Proof Math 2 Spring 2017 1 Table of ontents Introduction to lgebraic and Geometric Proof... 3 Properties of Equality for Real Numbers... 3 lgebra Proofs... 4 Introduction
1 Unit 4 lgebraic and Geometric Proof Math 2 Spring 2017 1 Table of ontents Introduction to lgebraic and Geometric Proof... 3 Properties of Equality for Real Numbers... 3 lgebra Proofs... 4 Introduction
n=0 ( 1)n /(n + 1) converges, but not
 Math 07H Topics for the third exam (and beyond) (Technically, everything covered on the first two exams plus...) Absolute convergence and alternating series A series a n converges absolutely if a n converges.
Math 07H Topics for the third exam (and beyond) (Technically, everything covered on the first two exams plus...) Absolute convergence and alternating series A series a n converges absolutely if a n converges.
in Trigonometry Name Section 6.1 Law of Sines Important Vocabulary
 Name Chapter 6 Additional Topics in Trigonometry Section 6.1 Law of Sines Objective: In this lesson you learned how to use the Law of Sines to solve oblique triangles and how to find the areas of oblique
Name Chapter 6 Additional Topics in Trigonometry Section 6.1 Law of Sines Objective: In this lesson you learned how to use the Law of Sines to solve oblique triangles and how to find the areas of oblique
4.1 Distance and Length
 Chapter Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at vectors
Chapter Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at vectors
Expanding brackets and factorising
 Chapter 7 Expanding brackets and factorising This chapter will show you how to expand and simplify expressions with brackets solve equations and inequalities involving brackets factorise by removing a
Chapter 7 Expanding brackets and factorising This chapter will show you how to expand and simplify expressions with brackets solve equations and inequalities involving brackets factorise by removing a
Relativistic Electrodynamics
 Relativistic Electrodynamics Notes (I will try to update if typos are found) June 1, 2009 1 Dot products The Pythagorean theorem says that distances are given by With time as a fourth direction, we find
Relativistic Electrodynamics Notes (I will try to update if typos are found) June 1, 2009 1 Dot products The Pythagorean theorem says that distances are given by With time as a fourth direction, we find
2.4 Hilbert Spaces. Outline
 2.4 Hilbert Spaces Tom Lewis Spring Semester 2017 Outline Hilbert spaces L 2 ([a, b]) Orthogonality Approximations Definition A Hilbert space is an inner product space which is complete in the norm defined
2.4 Hilbert Spaces Tom Lewis Spring Semester 2017 Outline Hilbert spaces L 2 ([a, b]) Orthogonality Approximations Definition A Hilbert space is an inner product space which is complete in the norm defined
Math 32A Discussion Session Week 2 Notes October 10 and 12, 2017
 Math 32A Discussion Session Week 2 Notes October 10 and 12, 2017 Since we didn t get a chance to discuss parametrized lines last week, we may spend some time discussing those before moving on to the dot
Math 32A Discussion Session Week 2 Notes October 10 and 12, 2017 Since we didn t get a chance to discuss parametrized lines last week, we may spend some time discussing those before moving on to the dot
TAYLOR POLYNOMIALS DARYL DEFORD
 TAYLOR POLYNOMIALS DARYL DEFORD 1. Introduction We have seen in class that Taylor polynomials provide us with a valuable tool for approximating many different types of functions. However, in order to really
TAYLOR POLYNOMIALS DARYL DEFORD 1. Introduction We have seen in class that Taylor polynomials provide us with a valuable tool for approximating many different types of functions. However, in order to really
Linear Systems. Class 27. c 2008 Ron Buckmire. TITLE Projection Matrices and Orthogonal Diagonalization CURRENT READING Poole 5.4
 Linear Systems Math Spring 8 c 8 Ron Buckmire Fowler 9 MWF 9: am - :5 am http://faculty.oxy.edu/ron/math//8/ Class 7 TITLE Projection Matrices and Orthogonal Diagonalization CURRENT READING Poole 5. Summary
Linear Systems Math Spring 8 c 8 Ron Buckmire Fowler 9 MWF 9: am - :5 am http://faculty.oxy.edu/ron/math//8/ Class 7 TITLE Projection Matrices and Orthogonal Diagonalization CURRENT READING Poole 5. Summary
CS 124 Math Review Section January 29, 2018
 CS 124 Math Review Section CS 124 is more math intensive than most of the introductory courses in the department. You re going to need to be able to do two things: 1. Perform some clever calculations to
CS 124 Math Review Section CS 124 is more math intensive than most of the introductory courses in the department. You re going to need to be able to do two things: 1. Perform some clever calculations to
Math 2331 Linear Algebra
 6.1 Inner Product, Length & Orthogonality Math 2331 Linear Algebra 6.1 Inner Product, Length & Orthogonality Shang-Huan Chiu Department of Mathematics, University of Houston schiu@math.uh.edu math.uh.edu/
6.1 Inner Product, Length & Orthogonality Math 2331 Linear Algebra 6.1 Inner Product, Length & Orthogonality Shang-Huan Chiu Department of Mathematics, University of Houston schiu@math.uh.edu math.uh.edu/
Mathematics 206 Solutions for HWK 23 Section 6.3 p358
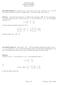 Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
Natural Numbers: Also called the counting numbers The set of natural numbers is represented by the symbol,.
 Name Period Date: Topic: Real Numbers and Their Graphs Standard: 9-12.A.1.3 Objective: Essential Question: What is the significance of a point on a number line? Determine the relative position on the number
Name Period Date: Topic: Real Numbers and Their Graphs Standard: 9-12.A.1.3 Objective: Essential Question: What is the significance of a point on a number line? Determine the relative position on the number
Math 3191 Applied Linear Algebra
 Math 191 Applied Linear Algebra Lecture 1: Inner Products, Length, Orthogonality Stephen Billups University of Colorado at Denver Math 191Applied Linear Algebra p.1/ Motivation Not all linear systems have
Math 191 Applied Linear Algebra Lecture 1: Inner Products, Length, Orthogonality Stephen Billups University of Colorado at Denver Math 191Applied Linear Algebra p.1/ Motivation Not all linear systems have
2.2. Show that U 0 is a vector space. For each α 0 in F, show by example that U α does not satisfy closure.
 Hints for Exercises 1.3. This diagram says that f α = β g. I will prove f injective g injective. You should show g injective f injective. Assume f is injective. Now suppose g(x) = g(y) for some x, y A.
Hints for Exercises 1.3. This diagram says that f α = β g. I will prove f injective g injective. You should show g injective f injective. Assume f is injective. Now suppose g(x) = g(y) for some x, y A.
Chapter 6. Orthogonality
 6.4 The Projection Matrix 1 Chapter 6. Orthogonality 6.4 The Projection Matrix Note. In Section 6.1 (Projections), we projected a vector b R n onto a subspace W of R n. We did so by finding a basis for
6.4 The Projection Matrix 1 Chapter 6. Orthogonality 6.4 The Projection Matrix Note. In Section 6.1 (Projections), we projected a vector b R n onto a subspace W of R n. We did so by finding a basis for
Lecture 1.4: Inner products and orthogonality
 Lecture 1.4: Inner products and orthogonality Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4340, Advanced Engineering Mathematics M.
Lecture 1.4: Inner products and orthogonality Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4340, Advanced Engineering Mathematics M.
10.4 The Cross Product
 Math 172 Chapter 10B notes Page 1 of 9 10.4 The Cross Product The cross product, or vector product, is defined in 3 dimensions only. Let aa = aa 1, aa 2, aa 3 bb = bb 1, bb 2, bb 3 then aa bb = aa 2 bb
Math 172 Chapter 10B notes Page 1 of 9 10.4 The Cross Product The cross product, or vector product, is defined in 3 dimensions only. Let aa = aa 1, aa 2, aa 3 bb = bb 1, bb 2, bb 3 then aa bb = aa 2 bb
Scot Siegel, Planning and Building Services Director Leslie Hamilton, Senior Planner
 T: :, v, UJET: #2 ( -) TE: 22, 2 EETI TE: 2, 2 2, 2, () f v ( ),. T f 2 vf f f, f ff q J, f f q v f f f v f f (). T q, f. T z f f ff q f.. f v ; Ex f : -. v,, v. I f - f f. I, v f. (, f,.) I,,, f v v f
T: :, v, UJET: #2 ( -) TE: 22, 2 EETI TE: 2, 2 2, 2, () f v ( ),. T f 2 vf f f, f ff q J, f f q v f f f v f f (). T q, f. T z f f ff q f.. f v ; Ex f : -. v,, v. I f - f f. I, v f. (, f,.) I,,, f v v f
Overview of vector calculus. Coordinate systems in space. Distance formula. (Sec. 12.1)
 Math 20C Multivariable Calculus Lecture 1 1 Coordinates in space Slide 1 Overview of vector calculus. Coordinate systems in space. Distance formula. (Sec. 12.1) Vector calculus studies derivatives and
Math 20C Multivariable Calculus Lecture 1 1 Coordinates in space Slide 1 Overview of vector calculus. Coordinate systems in space. Distance formula. (Sec. 12.1) Vector calculus studies derivatives and
- involve reasoning to a contradiction. 1. Emerson is the tallest. On the assumption that the second statement is the true one, we get: 2. 3.
 Math 61 Section 3.1 Indirect Proof A series of lessons in a subject that contradicted each other would make that subject very confusing. Yet, in reasoning deductively in geometry, it is sometimes helpful
Math 61 Section 3.1 Indirect Proof A series of lessons in a subject that contradicted each other would make that subject very confusing. Yet, in reasoning deductively in geometry, it is sometimes helpful
Main topics for the First Midterm Exam
 Main topics for the First Midterm Exam The final will cover Sections.-.0, 2.-2.5, and 4.. This is roughly the material from first three homeworks and three quizzes, in addition to the lecture on Monday,
Main topics for the First Midterm Exam The final will cover Sections.-.0, 2.-2.5, and 4.. This is roughly the material from first three homeworks and three quizzes, in addition to the lecture on Monday,
Review of Coordinate Systems
 Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
R e p u b lic o f th e P h ilip p in e s. R e g io n V II, C e n tra l V isa y a s. C ity o f T a g b ila ran
 R e p u b l f th e P h lp p e D e p rt e t f E d u t R e V, e tr l V y D V N F B H L ty f T b l r Ju ly, D V N M E M R A N D U M N. 0,. L T F E N R H G H H L F F E R N G F R 6 M P L E M E N T A T N T :,
R e p u b l f th e P h lp p e D e p rt e t f E d u t R e V, e tr l V y D V N F B H L ty f T b l r Ju ly, D V N M E M R A N D U M N. 0,. L T F E N R H G H H L F F E R N G F R 6 M P L E M E N T A T N T :,
Modern Algebra Prof. Manindra Agrawal Department of Computer Science and Engineering Indian Institute of Technology, Kanpur
 Modern Algebra Prof. Manindra Agrawal Department of Computer Science and Engineering Indian Institute of Technology, Kanpur Lecture 02 Groups: Subgroups and homomorphism (Refer Slide Time: 00:13) We looked
Modern Algebra Prof. Manindra Agrawal Department of Computer Science and Engineering Indian Institute of Technology, Kanpur Lecture 02 Groups: Subgroups and homomorphism (Refer Slide Time: 00:13) We looked
2 Complex Functions and the Cauchy-Riemann Equations
 2 Complex Functions and the Cauchy-Riemann Equations 2.1 Complex functions In one-variable calculus, we study functions f(x) of a real variable x. Likewise, in complex analysis, we study functions f(z)
2 Complex Functions and the Cauchy-Riemann Equations 2.1 Complex functions In one-variable calculus, we study functions f(x) of a real variable x. Likewise, in complex analysis, we study functions f(z)
Math 291-2: Lecture Notes Northwestern University, Winter 2016
 Math 291-2: Lecture Notes Northwestern University, Winter 2016 Written by Santiago Cañez These are lecture notes for Math 291-2, the second quarter of MENU: Intensive Linear Algebra and Multivariable Calculus,
Math 291-2: Lecture Notes Northwestern University, Winter 2016 Written by Santiago Cañez These are lecture notes for Math 291-2, the second quarter of MENU: Intensive Linear Algebra and Multivariable Calculus,
LOWHLL #WEEKLY JOURNAL.
 # F 7 F --) 2 9 Q - Q - - F - x $ 2 F? F \ F q - x q - - - - )< - -? - F - - Q z 2 Q - x -- - - - 3 - % 3 3 - - ) F x - \ - - - - - q - q - - - - -z- < F 7-7- - Q F 2 F - F \x -? - - - - - z - x z F -
# F 7 F --) 2 9 Q - Q - - F - x $ 2 F? F \ F q - x q - - - - )< - -? - F - - Q z 2 Q - x -- - - - 3 - % 3 3 - - ) F x - \ - - - - - q - q - - - - -z- < F 7-7- - Q F 2 F - F \x -? - - - - - z - x z F -
A vector in the plane is directed line segment. The directed line segment AB
 Vector: A ector is a matrix that has only one row then we call the matrix a row ector or only one column then we call it a column ector. A row ector is of the form: a a a... A column ector is of the form:
Vector: A ector is a matrix that has only one row then we call the matrix a row ector or only one column then we call it a column ector. A row ector is of the form: a a a... A column ector is of the form:
Mathematics 13: Lecture 4
 Mathematics 13: Lecture Planes Dan Sloughter Furman University January 10, 2008 Dan Sloughter (Furman University) Mathematics 13: Lecture January 10, 2008 1 / 10 Planes in R n Suppose v and w are nonzero
Mathematics 13: Lecture Planes Dan Sloughter Furman University January 10, 2008 Dan Sloughter (Furman University) Mathematics 13: Lecture January 10, 2008 1 / 10 Planes in R n Suppose v and w are nonzero
R n : The Cross Product
 A FIRST COURSE IN LINEAR ALGEBRA An Open Text by Ken Kuttler R n : The Cross Product Lecture Notes by Karen Seyffarth Adapted by LYRYX SERVICE COURSE SOLUTION Attribution-NonCommercial-ShareAlike (CC BY-NC-SA)
A FIRST COURSE IN LINEAR ALGEBRA An Open Text by Ken Kuttler R n : The Cross Product Lecture Notes by Karen Seyffarth Adapted by LYRYX SERVICE COURSE SOLUTION Attribution-NonCommercial-ShareAlike (CC BY-NC-SA)
Assignment 1 Math 5341 Linear Algebra Review. Give complete answers to each of the following questions. Show all of your work.
 Assignment 1 Math 5341 Linear Algebra Review Give complete answers to each of the following questions Show all of your work Note: You might struggle with some of these questions, either because it has
Assignment 1 Math 5341 Linear Algebra Review Give complete answers to each of the following questions Show all of your work Note: You might struggle with some of these questions, either because it has
VECTORS AND THE GEOMETRY OF SPACE
 VECTORS AND THE GEOMETRY OF SPACE VECTORS AND THE GEOMETRY OF SPACE A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given.
VECTORS AND THE GEOMETRY OF SPACE VECTORS AND THE GEOMETRY OF SPACE A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given.
2) If a=<2,-1> and b=<3,2>, what is a b and what is the angle between the vectors?
 CMCS427 Dot product review Computing the dot product The dot product can be computed via a) Cosine rule a b = a b cos q b) Coordinate-wise a b = ax * bx + ay * by 1) If a b, a and b all equal 1, what s
CMCS427 Dot product review Computing the dot product The dot product can be computed via a) Cosine rule a b = a b cos q b) Coordinate-wise a b = ax * bx + ay * by 1) If a b, a and b all equal 1, what s
This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication.
 This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication. Copyright Pearson Canada Inc. All rights reserved. Copyright Pearson
This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication. Copyright Pearson Canada Inc. All rights reserved. Copyright Pearson
Vector Geometry. Chapter 5
 Chapter 5 Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at
Chapter 5 Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at
Overview. Distances in R 3. Distance from a point to a plane. Question
 Overview Yesterda we introduced equations to describe lines and planes in R 3 : r + tv The vector equation for a line describes arbitrar points r in terms of a specific point and the direction vector v.
Overview Yesterda we introduced equations to describe lines and planes in R 3 : r + tv The vector equation for a line describes arbitrar points r in terms of a specific point and the direction vector v.
Welcome to IB Math - Standard Level Year 2
 Welcome to IB Math - Standard Level Year 2 Why math? Not So Some things to know: Good HW Good HW Good HW www.aleimath.blogspot.com Example 1. Lots of info at Example Example 2. HW yup. You know you love
Welcome to IB Math - Standard Level Year 2 Why math? Not So Some things to know: Good HW Good HW Good HW www.aleimath.blogspot.com Example 1. Lots of info at Example Example 2. HW yup. You know you love
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o
 I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
Central to this is two linear transformations: the Fourier Transform and the Laplace Transform. Both will be considered in later lectures.
 In this second lecture, I will be considering signals from the frequency perspective. This is a complementary view of signals, that in the frequency domain, and is fundamental to the subject of signal
In this second lecture, I will be considering signals from the frequency perspective. This is a complementary view of signals, that in the frequency domain, and is fundamental to the subject of signal
Coordinate systems and vectors in three spatial dimensions
 PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
Class IX Chapter 5 Introduction to Euclid's Geometry Maths
 Class IX Chapter 5 Introduction to Euclid's Geometry Maths Exercise 5.1 Question 1: Which of the following statements are true and which are false? Give reasons for your answers. (i) Only one line can
Class IX Chapter 5 Introduction to Euclid's Geometry Maths Exercise 5.1 Question 1: Which of the following statements are true and which are false? Give reasons for your answers. (i) Only one line can
Cataraqui Source Protection Area Stream Gauge Locations
 Cqu u P m Gu s Ts Ez K Ts u s sp E s ms P Ps s m m C Y u u I s Ts x C C u R 4 N p Ds Qu H Em us ms p G Cqu C, s Ks F I s s Gqu u Gqu s N D U ( I T Gqu C s C, 5 Rs p, Rs 15, 7 N m s m Gus - Ps P f P 1,
Cqu u P m Gu s Ts Ez K Ts u s sp E s ms P Ps s m m C Y u u I s Ts x C C u R 4 N p Ds Qu H Em us ms p G Cqu C, s Ks F I s s Gqu u Gqu s N D U ( I T Gqu C s C, 5 Rs p, Rs 15, 7 N m s m Gus - Ps P f P 1,
MAC Module 5 Vectors in 2-Space and 3-Space II
 MAC 2103 Module 5 Vectors in 2-Space and 3-Space II 1 Learning Objectives Upon completing this module, you should be able to: 1. Determine the cross product of a vector in R 3. 2. Determine a scalar triple
MAC 2103 Module 5 Vectors in 2-Space and 3-Space II 1 Learning Objectives Upon completing this module, you should be able to: 1. Determine the cross product of a vector in R 3. 2. Determine a scalar triple
Adding and Subtracting Polynomials
 Exploratory Exercise Kim was working on a problem in math when she ran across this problem. Distribute and simplify if possible. 2(3x + 5) Kim s dad said, I remember doing something like this in school.
Exploratory Exercise Kim was working on a problem in math when she ran across this problem. Distribute and simplify if possible. 2(3x + 5) Kim s dad said, I remember doing something like this in school.
MATH 56A: STOCHASTIC PROCESSES CHAPTER 6
 MATH 56A: STOCHASTIC PROCESSES CHAPTER 6 6. Renewal Mathematically, renewal refers to a continuous time stochastic process with states,, 2,. N t {,, 2, 3, } so that you only have jumps from x to x + and
MATH 56A: STOCHASTIC PROCESSES CHAPTER 6 6. Renewal Mathematically, renewal refers to a continuous time stochastic process with states,, 2,. N t {,, 2, 3, } so that you only have jumps from x to x + and
H STO RY OF TH E SA NT
 O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
Mr. Northcutt's Math Classes Class Presentation
 Mr. Northcutt's Math Classes Class Presentation September 9, 2009 (6) Transition Math Math 1 Math 2 1 Transition Math Daily Summary Announcements None Topic 2: Variables & Expressions (D1) 1. Using the
Mr. Northcutt's Math Classes Class Presentation September 9, 2009 (6) Transition Math Math 1 Math 2 1 Transition Math Daily Summary Announcements None Topic 2: Variables & Expressions (D1) 1. Using the
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
Math 2331 Linear Algebra
 6. Orthogonal Projections Math 2 Linear Algebra 6. Orthogonal Projections Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/ jiwenhe/math2 Jiwen He, University of
6. Orthogonal Projections Math 2 Linear Algebra 6. Orthogonal Projections Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/ jiwenhe/math2 Jiwen He, University of
x 1 + 2x 2 + 3x 3 = 0 x 1 + 2x 2 + 3x 3 = 0, x 2 + x 3 = 0 x 3 3 x 3 1
 . Orthogonal Complements and Projections In this section we discuss orthogonal complements and orthogonal projections. The orthogonal complement of a subspace S is the complement that is orthogonal to
. Orthogonal Complements and Projections In this section we discuss orthogonal complements and orthogonal projections. The orthogonal complement of a subspace S is the complement that is orthogonal to
r/lt.i Ml s." ifcr ' W ATI II. The fnncrnl.icniccs of Mr*. John We mil uppn our tcpiiblicnn rcprc Died.
 $ / / - (\ \ - ) # -/ ( - ( [ & - - - - \ - - ( - - - - & - ( ( / - ( \) Q & - - { Q ( - & - ( & q \ ( - ) Q - - # & - - - & - - - $ - 6 - & # - - - & -- - - - & 9 & q - / \ / - - - -)- - ( - - 9 - - -
$ / / - (\ \ - ) # -/ ( - ( [ & - - - - \ - - ( - - - - & - ( ( / - ( \) Q & - - { Q ( - & - ( & q \ ( - ) Q - - # & - - - & - - - $ - 6 - & # - - - & -- - - - & 9 & q - / \ / - - - -)- - ( - - 9 - - -
W i n t e r r e m e m b e r t h e W O O L L E N S. W rite to the M anageress RIDGE LAUNDRY, ST. H E LE N S. A uction Sale.
 > 7? 8 «> ««0? [ -! ««! > - ««>« ------------ - 7 7 7 = - Q9 8 7 ) [ } Q ««
> 7? 8 «> ««0? [ -! ««! > - ««>« ------------ - 7 7 7 = - Q9 8 7 ) [ } Q ««
Give a geometric description of the set of points in space whose coordinates satisfy the given pair of equations.
 1. Give a geometric description of the set of points in space whose coordinates satisfy the given pair of equations. x + y = 5, z = 4 Choose the correct description. A. The circle with center (0,0, 4)
1. Give a geometric description of the set of points in space whose coordinates satisfy the given pair of equations. x + y = 5, z = 4 Choose the correct description. A. The circle with center (0,0, 4)
3.1 Do the following problem together with those of Section 3.2:
 Chapter 3 3.1 5. First check if the subset S is really a subring. The checklist for that is spelled out in Theorem 3.2. If S is a subring, try to find an element 1 S in S that acts as a multiplicative
Chapter 3 3.1 5. First check if the subset S is really a subring. The checklist for that is spelled out in Theorem 3.2. If S is a subring, try to find an element 1 S in S that acts as a multiplicative
15. T(x,y)=(x+4y,2a+3y) operator that maps a function into its second derivative. cos,zx are eigenvectors of D2, and find their corre
 1. [ 2J X[1j P 21. r q [Suggestion: Work with the standard matrix for the operator.] vector of, and find the corresponding eigenvalue. eigenspace of the linear operator defined by the stated formula. In
1. [ 2J X[1j P 21. r q [Suggestion: Work with the standard matrix for the operator.] vector of, and find the corresponding eigenvalue. eigenspace of the linear operator defined by the stated formula. In
G-C, G-CO Tangent Lines and the Radius of a Circle
 G-C, G-CO Tangent ines and the Radius of a Circle Task O P P P Consider a circle with center and let be a point on the circle. Suppose is a tangent line to the circle at, that is meets the circle only
G-C, G-CO Tangent ines and the Radius of a Circle Task O P P P Consider a circle with center and let be a point on the circle. Suppose is a tangent line to the circle at, that is meets the circle only
Lecture 1: Period Three Implies Chaos
 Math 7h Professor: Padraic Bartlett Lecture 1: Period Three Implies Chaos Week 1 UCSB 2014 (Source materials: Period three implies chaos, by Li and Yorke, and From Intermediate Value Theorem To Chaos,
Math 7h Professor: Padraic Bartlett Lecture 1: Period Three Implies Chaos Week 1 UCSB 2014 (Source materials: Period three implies chaos, by Li and Yorke, and From Intermediate Value Theorem To Chaos,
Exam Question 10: Differential Equations. June 19, Applied Mathematics: Lecture 6. Brendan Williamson. Introduction.
 Exam Question 10: June 19, 2016 In this lecture we will study differential equations, which pertains to Q. 10 of the Higher Level paper. It s arguably more theoretical than other topics on the syllabus,
Exam Question 10: June 19, 2016 In this lecture we will study differential equations, which pertains to Q. 10 of the Higher Level paper. It s arguably more theoretical than other topics on the syllabus,
Final Review Sheet. B = (1, 1 + 3x, 1 + x 2 ) then 2 + 3x + 6x 2
 Final Review Sheet The final will cover Sections Chapters 1,2,3 and 4, as well as sections 5.1-5.4, 6.1-6.2 and 7.1-7.3 from chapters 5,6 and 7. This is essentially all material covered this term. Watch
Final Review Sheet The final will cover Sections Chapters 1,2,3 and 4, as well as sections 5.1-5.4, 6.1-6.2 and 7.1-7.3 from chapters 5,6 and 7. This is essentially all material covered this term. Watch
Chapter 5. Linear Algebra
 Chapter 5 Linear Algebra The exalted position held by linear algebra is based upon the subject s ubiquitous utility and ease of application. The basic theory is developed here in full generality, i.e.,
Chapter 5 Linear Algebra The exalted position held by linear algebra is based upon the subject s ubiquitous utility and ease of application. The basic theory is developed here in full generality, i.e.,
The 'linear algebra way' of talking about "angle" and "similarity" between two vectors is called "inner product". We'll define this next.
 Orthogonality and QR The 'linear algebra way' of talking about "angle" and "similarity" between two vectors is called "inner product". We'll define this next. So, what is an inner product? An inner product
Orthogonality and QR The 'linear algebra way' of talking about "angle" and "similarity" between two vectors is called "inner product". We'll define this next. So, what is an inner product? An inner product
2) e = e G G such that if a G 0 =0 G G such that if a G e a = a e = a. 0 +a = a+0 = a.
 Chapter 2 Groups Groups are the central objects of algebra. In later chapters we will define rings and modules and see that they are special cases of groups. Also ring homomorphisms and module homomorphisms
Chapter 2 Groups Groups are the central objects of algebra. In later chapters we will define rings and modules and see that they are special cases of groups. Also ring homomorphisms and module homomorphisms
Math 290-2: Linear Algebra & Multivariable Calculus Northwestern University, Lecture Notes
 Math 290-2: Linear Algebra & Multivariable Calculus Northwestern University, Lecture Notes Written by Santiago Cañez These are notes which provide a basic summary of each lecture for Math 290-2, the second
Math 290-2: Linear Algebra & Multivariable Calculus Northwestern University, Lecture Notes Written by Santiago Cañez These are notes which provide a basic summary of each lecture for Math 290-2, the second
A Gentle Introduction to Gradient Boosting. Cheng Li College of Computer and Information Science Northeastern University
 A Gentle Introduction to Gradient Boosting Cheng Li chengli@ccs.neu.edu College of Computer and Information Science Northeastern University Gradient Boosting a powerful machine learning algorithm it can
A Gentle Introduction to Gradient Boosting Cheng Li chengli@ccs.neu.edu College of Computer and Information Science Northeastern University Gradient Boosting a powerful machine learning algorithm it can
MITOCW watch?v=fxlzy2l1-4w
 MITOCW watch?v=fxlzy2l1-4w PROFESSOR: We spoke about the hydrogen atom. And in the hydrogen atom, we drew the spectrum, so the table, the data of spectrum of a quantum system. So this is a question that
MITOCW watch?v=fxlzy2l1-4w PROFESSOR: We spoke about the hydrogen atom. And in the hydrogen atom, we drew the spectrum, so the table, the data of spectrum of a quantum system. So this is a question that
Mon Feb Matrix algebra and matrix inverses. Announcements: Warm-up Exercise:
 Math 2270-004 Week 5 notes We will not necessarily finish the material from a given day's notes on that day We may also add or subtract some material as the week progresses, but these notes represent an
Math 2270-004 Week 5 notes We will not necessarily finish the material from a given day's notes on that day We may also add or subtract some material as the week progresses, but these notes represent an

 7 ( - ( - < Q & > & )
7 ( - ( - < Q & > & )  9 Q - -
9 Q - -