Properties and Problems Related to the Smarandache Type Functions
|
|
|
- Eunice Nichols
- 5 years ago
- Views:
Transcription
1 Properties and Problems Related to the Smarandache Type Functions Sebastian Martin Ruiz, Avda. De Regla, 43, Chipiona (Cadiz), Spain M. Perez, Rehoboth, Box 141, NM 87301, USA Abstract: In this paper we present the definitions and some properties of several Smarandache type functions that are involved in many proposed solved and unsolved problems and conjectures in number theory and recreational mathematics. Examples are also provided. Interesting solved problems related to them are attached as addenda to this article. 1. Introduction: The most known Smarandache Function, which became a classical function in the number theory, is the following: S: N* t N*, S(1) = 1, S(n) is the smallest integer such that S(n)! is divisible by n. S(6)=3, because 3! = 1$2$3 = 6, which is divisible by 6, and 3 is the smallest number with this property, i.e. 2! is not divisible by 6. S(8) = 4, S(11) = 11. This function has been very much studied in the last decade and interesting properties have been found related to it. 2. Properties: 2.1. Max {p, p prime and p divides n} [ S(n) [ n for any positive integer n If n = (p 1^s 1 ) $ (p 2^s 2 ) $ $ (p k^s k ), where p 1, p 2,, p k are distinct primes, then S(n) = max {S(p i^s i )} [ max { p i $ s i }. 1[ i [ k 1[ i [ k 2.3. Characterization of a prime number: Let p be an integer > 4. Then: p is prime if and only if S(p) = p. Proof: Let p be prime > 4, and suppose S(p) = m < p, then m! is not be divisible by p, therefore S(p) = p. Now, let S(p) = p and p g 4; suppose p is not prime, whence there exist two integers s and t, with s [ t < p, such that p = s$t, but then S(p) [ t g p because t! is divisible by s and by t in the same time (i.e. t! is divisible by p). Contradiction. 2.4 An exact formula to calculate the number of primes less than or equal to x (L. Seagull): If x is an integer m 4, then the number of prime numbers [ x is:
2 x S( k) ( x) = 1+ k= 2 k where S(k) is the classical Smarandache Function, and ÃaŒ means the interior integer part of a (the smallest integer greater than or equal to a). Proof: Knowing the Smarandache Function has the property that if p > 4 then S(p) = p if only if p is prime, and S(k) <= k for any k, and S(4) = 4 (the only exception from the first rule), we easily find an exact formula for the number of primes less than or equal to x. 4. Conjectures: 4.1. The diophantine equation S(n) = S(n+1) has no solutions. (L. Tutescu) 4.2. The diophantine equation S(n) + S(n+1) = S(n+2) has infinitely many solutions. (I. M. Radu) 5. More Smarandache Type Functions have been also considered and studied, such as: 5.1. Smarandache Double Factorial Function, Sdf(n) is the smallest integer such that Sdf(n)!! is divisible by n, where the double factorial m!! = 1$3$5$...$m, if m is odd; and m!! = 2$4$6$...$m, if m is even. n SDF(n) Smarandache-Kurepa Function: For p prime, SK(p) is the smallest integer such that!sk(p) is divisible by p, where!m = 0! + 1! + 2! (m-1)! p SK(p) Smarandache-Wagstaff Function: For p prime, SW(p) is the smallest integer such that W(SW(p)) is divisible by p, where W(m) = 1! + 2! (m)! p SW(p) Smarandache Ceil Functions of k-th Order: Sk(n) is the smallest integer for which n divides Sk(n)^k. For example, for k=2, we have: n S2(n)
3 5.5. Pseudo-Smarandache Function: Z(n) is the smallest integer such that Z(n) is divisible by n. n Z(n) Smarandache Near-To-Primordial Function: SNTP(n) is the smallest prime such that either p# - 1, p#, or p# + 1 is divisible by n, where p#, of a prime number p, is the product of all primes less than or equal to p. n SNTP(n) ? Other Smarandache Type Functions also studied in the last years are: 6.1. Let f: Z h Z be a strictly increasing function and x an element in R. Then: a) Inferior Smarandache f-part of x, ISf(x), is the smallest k such that f(k) [ x < f(k+1). b) Superior Smarandache f-part of x, SSf(x) is the smallest k such that f(k) < x [ f(k+1). Particular cases: a) Inferior S-Prime Part: For any positive real number n one defines ISp(n) as the largest prime number less than or equal to n. 2,3,3,5,5,7,7,7,7,11,11,13,13,13,13,17,17,19,19,19,19,23,23. b) Superior S-Prime Part: For any positive real number n one defines SSp(n) as the smallest prime number greater than or equal to n. 2,2,2,3,5,5,7,7,11,11,11,11,13,13,17,17,17,17,19,19,23,23,23. c) Inferior S-Square Part: For any positive real number n one defines ISs(n) as the largest square less than or equal to n. 0,1,1,1,4,4,4,4,4,9,9,9,9,9,9,9,16,16,16,16,16,16,16,16,16,25,25. b) Superior S-Square Part: For any positive real number n one defines SSs(n) as the smallest square greater than or equal to n. 0,1,4,4,4,9,9,9,9,9,16,16,16,16,16,16,16,25,25,25,25,25,25,25,25,25,36. d) Inferior S-Cubic Part: For any positive real number n one defines ISc(n) as the largest cube less than or equal to n.
4 0,1,1,1,1,1,1,1,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,27,27,27,27. e) Superior S-Cube Part: For any positive real number n one defines SSs(n) as the smallest cube greater than or equal to n. 0,1,8,8,8,8,8,8,8,27,27,27,27,27,27,27,27,27,27,27,27,27,27,27,27,27. f) Inferior S-Factorial Part: For any positive real number n one defines ISf(n) as the largest factorial less than or equal to n. 1,2,2,2,2,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,24,24,24,24,24,24,24. g) Superior S-Factorial Part: For any positive real number n one defines SSf(n) as the smallest factorial greater than or equal to n. 1,2,6,6,6,6,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,120. Remark 1: This is a generalization of the inferior/superior integer part of a number Let f: Z h Z be a strictly increasing function and x an element in R. Then: Fractional Smarandache f-part of x, FSf(x) = x - ISf(x), where ISf(x) is the Inferior Smarandache f-part of x defined above. Particular cases: a) Fractional S-Prime Part: FSp(x) = x - ISp(x), where ISp(x) is the Inferior S-Prime Part defined above. Example: FSp(12.501) = = b) Fractional S-Square Part: FSs(x) = x - ISs(x), where ISs(x) is the Inferior S-Square Part defined above. Example: FSs(12.501) = = c) Fractional S-Cubic Part: FSc(x) = x - ISc(x), where ISc(x) is the Inferior S-Cubic Part defined above. Example: FSc(12.501) = = d) Fractional S-Factorial Part: FSf(x) = x - ISf(x), where ISf(x) is the Inferior S-Factorial Part defined above. Example: FSf(12.501) = = Remark 2.1: This is a generalization of the fractional part of a number. Remark 2.2: In a similar way one defines: - the Inferior Fractional Smarandache f-part: IFSf(x) = x - ISf(x) = FSf(x); - and the Superior Fractional Smarandache f-part: SFSf(x) = SSf(x) - x; for example: Superior Fractional S-Cubic Part of
5 = = Let g: A h A be a strictly increasing function, and let "~" be a given internal law on A. Then we say that f: A h A is smarandachely complementary with respect to the function g and the internal law "~" if: f(x) is the smallest k such that there exists a z in A so that x~k = g(z). Particular cases: a) S-Square Complementary Function: f: N h N, f(x) = the smallest k such that x$k is a perfect square. 1,2,3,1,5,6,7,2,1,10,11,3,14,15,1,17,2,19,5,21,22,23,6,1,26,3,7. b) S-Cubic Complementary Function: f: N h N, f(x) = the smallest k such that x$k is a perfect cube. 1,4,9,2,25,36,49,1,3,100,121,18,169,196,225,4,289,12,361,50. More generally: c) S-m-power Complementary Function: f: N h N, f(x) = the smallest k such that x$k is a perfect m-power. d) S-Prime Complementary Function: f: N h N, f(x) = the smallest k such that x+k is a prime. 1,0,0,1,0,1,0,3,2,1,0,1,0,3,2,1,0,1,0,3,2,1,0,5,4,3,2,1,0,1,0, S-Multiplicative Function: is a function f : N* h N* such that for any (a, b) = 1, f(a$b) = max {f(a), f(b)}; [i.e. it reflects the main property of the Smarandache function]. The following functions are obviously S-multiplicative: a) The constant function f : N* h N*, f(n) = 1. b) The Smarandache function S: N* h N, S(n) = max{ p p! : n}. Certainly, many properties of multiplicative functions can be translated for S-multiplicative functions. 7. Functional Smarandache Iterations: 7.1. Functional Smarandache Iteration of First Kind: Let f: A h A be a function, such that f(x) [ x for all x, and min {f(x), x A} m m 0 g -. Let f have p m 1 fix points: m 0 [ x 1 < x 2 <... < x p. [The point x is called fix if f(x) = x.] Then: SI1 f (x) = the smallest number of iterations k such that f(f(...f(x)...)) = constant.
6 Example: Let n > 1 be an integer, and d(n) be the number of positive divisors of n, d: N h N. Then SI1 d (n) is the smallest number of iterations k such that d(d(...d(n)...)) = 2; because d(n) < n for n > 2, and the fix points of the function d are 1 and 2. Thus SI1 d (6) = 3, because d(d(d(6))) = d(d(4)) = d(3) = 2 = constant. SI1 d (5) = 1, because d(5) = Functional Smarandache Iteration of Second Kind: Let g: A h A be a function, such that g(x) > x for all x, and let b > x. Then: SI2 g (x, b) = the smallest number of iterations k such that g(g(...g(x)...)) m b. Example: Let n > 1 be an integer, and G(n) be the sum of positive divisors of n (1 and n included), G: N h N. Then SI2 G (n, b) is the smallest number of iterations k such that G (G (...G(n)...)) m b, because G(n) > n for n > 1. Thus SI2 G (4, 11) = 3, because G(G(G(4))) = G(G(7)) = G(8) = 15 m Functional Smarandache Iteration of Third Kind: Let h: h A be a function, such that h(x) < x for all x, and let b < x. Then: SI3 h (x, b) = the smallest number of iterations k such that h(h(...h(x)...)) [ b. Example: Let n be an integer and gd(n) be the greatest divisor of n, less than n, gd: N* h N*. Then gd(n) < n for n > 1. SI3 gd (60, 3) = 4, because gd(gd(gd(gd(60)))) = gd(gd(gd(30))) = gd(gd(15)) = gd(5) = 1 [ 3. References:
7 [1] Ashbacher, C., "A Note on the Smarandache Near-To-Primordial Function", <Smarandache Notions Journal>, Vol. 7, No , 46-49, [2] Ashbacher, C., "Some Properties of the Smarandache-Kurepa and Smarandache- Wagstaff Functions", <Mathematics and Informatics Quarterly>, Vol. 7, No. 3, pp , [3] Begay, A., "Smarandache Ceil Functions", in <Bulletin of Pure and Applied Sciences>, India, Vol. 16E, No. 2, , [4] Castillo, Jose, "Other Smarandache Type Functions", [5] Dumitrescu, C., Seleacu, V., "Some notions and questions in number theory", Erhus Univ. Press, Glendale, [6] Ibstedt, H., "Smarandache Iterations of First and Second Kinds", <Abstracts of Papers Presented to the American Mathematical Society>, Vol. 17, No. 4, Issue 106, 680, [7] Kashihara, K., "Comments and Topics on Smarandache Notions and Problems", Erhus Univ. Press, Vail, USA, [8] Mudge, Mike, "The Smarandache Near-To-Primordial (S.N.T.P.) Function", <Smarandache Notions Journal>, Vol. 7, No , 45, [9] Popescu, Marcela, Nicolescu, Mariana, "About the Smarandache Complementary Cubic Function", <Smarandache Notions Journal>, Vol. 7, no , 54-62, [10] Popescu, Marcela, Seleacu, Vasile, "About the Smarandache Complementary Prime Function", <Smarandache Notions Journal>, Vol. 7, No , 12-22, [11] Ruiz, Sebastian Martin, Applications of Smarandache Function, Prime and Coprime Functions, American Research Press, Rehoboth, 2002; [12] Seagull, L., "The smarandache Function and the number of primes up to x", <Mathematical Spectrum>, University of Shielfield, Vol. 28, No. 3, 53, 1995/6. [13] Smarandache, F., A Function in Number Theory, Analele Univ. Timisoara, XVIII, fasc. 1, 79-88, 1980; [14] Smarandache, Florentin, "Only Problems, not Solutions!", Xiquan Publishing House, Phoenix-Chicago, 1990, 1991, 1993; [15] "The Florentin Smarandache papers" Special Collection, Arizona State University, Hayden Library, Tempe, Box , AZ , USA; [16] Tabirca, Sabin, "About S-Multiplicative Functions", <Octogon>, Brasov, Vol. 7, No. 1, , [17] Weisstein, Eric W., CRC Concise Encyclopedia of Mathematics, CRC Press, Boca raton, Other e-books on Smarandache Functions and Sequences can be downloaded from and research papers from
FLORENTIN SMARANDACHE
 FLORENTIN SMARANDACHE SEQUENCES OF NUMBERS INVOLVED IN UNSOLVED PROBLEMS 1 141 1 1 1 8 1 1 8 40 8 1 1 8 1 1 1 1 12 1 1 12 108 12 1 1 12108 540 108 12 1 1 12 108 12 1 1 12 1 1 1 1 16 1 1 16 208 16 1 1 16
FLORENTIN SMARANDACHE SEQUENCES OF NUMBERS INVOLVED IN UNSOLVED PROBLEMS 1 141 1 1 1 8 1 1 8 40 8 1 1 8 1 1 1 1 12 1 1 12 108 12 1 1 12108 540 108 12 1 1 12 108 12 1 1 12 1 1 1 1 16 1 1 16 208 16 1 1 16
ANOTHER SET OF SEQUENCES, SUB-SEQUENCES, AND SEQUENCES OF SEQUENCES
 ANOTHER SET OF SEQUENCES, SUB-SEQUENCES, AND SEQUENCES OF SEQUENCES by Florentin Smarandache, Ph. D. University of New Mexico Gallup, NM 87301, USA Abstract. New sequences in number theory are showed below
ANOTHER SET OF SEQUENCES, SUB-SEQUENCES, AND SEQUENCES OF SEQUENCES by Florentin Smarandache, Ph. D. University of New Mexico Gallup, NM 87301, USA Abstract. New sequences in number theory are showed below
Patterns related to the Smarandache circular sequence primality problem
 Notes on Number Theory and Discrete Mathematics Vol. 18 (2012), No. 1, 29 48 Patterns related to the Smarandache circular sequence primality problem Marco Ripà 1 and Emanuele Dalmasso 2 1 Graduate student,
Notes on Number Theory and Discrete Mathematics Vol. 18 (2012), No. 1, 29 48 Patterns related to the Smarandache circular sequence primality problem Marco Ripà 1 and Emanuele Dalmasso 2 1 Graduate student,
HISTORY OF THE SMA RAN D A C H E. Department of Mathematics, University of Craiova Str. AI. 1. Cuza 13, Craiova lloo, Romania
 HISTORY OF THE SMA RAN D A C H E FUN C T 10 N 1. B alacenoiu and V. Seleacu Department of Mathematics, University of Craiova Str. AI. 1. Cuza 13, Craiova lloo, Romania 1 Introduction This function is originated
HISTORY OF THE SMA RAN D A C H E FUN C T 10 N 1. B alacenoiu and V. Seleacu Department of Mathematics, University of Craiova Str. AI. 1. Cuza 13, Craiova lloo, Romania 1 Introduction This function is originated
THE PSEUDO-SMARANDACHE FUNCTION. David Gorski 137 William Street East Williston, NY (516)
 THE PSEUDO-SMARANDACHE FUNCTION David Gorski 137 William Street East Williston, NY 11596 (516)742-9388 Gorfam@Worldnet.att.net Abstract: The Pseudo-Smarandache Function is part of number theory. The function
THE PSEUDO-SMARANDACHE FUNCTION David Gorski 137 William Street East Williston, NY 11596 (516)742-9388 Gorfam@Worldnet.att.net Abstract: The Pseudo-Smarandache Function is part of number theory. The function
SOME SMARANDACHE-TYPE MULTIPUCATIVE FUNCTIONS. Henry Bottomley.
 SOME SMARANDACHE-TYPE MULTIPUCATIVE FUNCTIONS Henry Bottomley 5 Leydon Close, London SE16 SPF, United Kingdom E-mail: SE16@btinternet.com This note considers eleven particular fimrilies of interrelated
SOME SMARANDACHE-TYPE MULTIPUCATIVE FUNCTIONS Henry Bottomley 5 Leydon Close, London SE16 SPF, United Kingdom E-mail: SE16@btinternet.com This note considers eleven particular fimrilies of interrelated
Solutions to Problem Set 3 - Fall 2008 Due Tuesday, Sep. 30 at 1:00
 Solutions to 18.781 Problem Set 3 - Fall 2008 Due Tuesday, Sep. 30 at 1:00 1. (Niven 2.3.3) Solve the congruences x 1 (mod 4), x 0 (mod 3), x 5 (mod 7). First we note that 4, 3, and 7 are pairwise relatively
Solutions to 18.781 Problem Set 3 - Fall 2008 Due Tuesday, Sep. 30 at 1:00 1. (Niven 2.3.3) Solve the congruences x 1 (mod 4), x 0 (mod 3), x 5 (mod 7). First we note that 4, 3, and 7 are pairwise relatively
WA DERI G WORLD SMARA DACHE UMBERS
 WA DERI G I THE WORLD OF SMARA DACHE UMBERS A.A.K. MAJUMDAR Ritsumeikan Asia-Pacific University Jumonjibaru, Beppu-shi 874 8577, Japan E-mail : aakmajumdar@gmail.com / majumdar@apu.ac.jp & Guest Professor
WA DERI G I THE WORLD OF SMARA DACHE UMBERS A.A.K. MAJUMDAR Ritsumeikan Asia-Pacific University Jumonjibaru, Beppu-shi 874 8577, Japan E-mail : aakmajumdar@gmail.com / majumdar@apu.ac.jp & Guest Professor
FLORENTIN SMARANDACHE Numeralogy (I) or Properties of Numbers
 FLORENTIN SMARANDACHE Numeralogy (I) or Properties of Numbers In Florentin Smarandache: Collected Papers, vol. II. Chisinau (Moldova): Universitatea de Stat din Moldova, 1997. NUMEROLOGY (I) or Properties
FLORENTIN SMARANDACHE Numeralogy (I) or Properties of Numbers In Florentin Smarandache: Collected Papers, vol. II. Chisinau (Moldova): Universitatea de Stat din Moldova, 1997. NUMEROLOGY (I) or Properties
Quantum Causality Threshold and Paradoxes
 Quantum Causality Threshold and Paradoxes Florentin Smarandache, Ph D Chair of Math & Sciences Department University of New Mexico 200 College Road, Gallup, NM 87301, USA Abstract: In this paper we consider
Quantum Causality Threshold and Paradoxes Florentin Smarandache, Ph D Chair of Math & Sciences Department University of New Mexico 200 College Road, Gallup, NM 87301, USA Abstract: In this paper we consider
Groupoids and Smarandache Groupoids
 W. B. Vasantha Kandasamy Groupoids and Smarandache Groupoids 2 4 3 A Z B A A 2 B B 2 A 2 Z 2 B 2 American Research Press Rehoboth 22 W. B. Vasantha Kandasamy Department of Mathematics Indian Institute
W. B. Vasantha Kandasamy Groupoids and Smarandache Groupoids 2 4 3 A Z B A A 2 B B 2 A 2 Z 2 B 2 American Research Press Rehoboth 22 W. B. Vasantha Kandasamy Department of Mathematics Indian Institute
A survey on Smarandache notions in number theory II: pseudo-smarandache function
 Scientia Magna Vol. 07), No., 45-53 A survey on Smarandache notions in number theory II: pseudo-smarandache function Huaning Liu School of Mathematics, Northwest University Xi an 707, China E-mail: hnliu@nwu.edu.cn
Scientia Magna Vol. 07), No., 45-53 A survey on Smarandache notions in number theory II: pseudo-smarandache function Huaning Liu School of Mathematics, Northwest University Xi an 707, China E-mail: hnliu@nwu.edu.cn
arxiv: v1 [math.gm] 28 Mar 2016
![arxiv: v1 [math.gm] 28 Mar 2016 arxiv: v1 [math.gm] 28 Mar 2016](/thumbs/94/119216644.jpg) arxiv:1603.08456v1 [math.gm] 28 Mar 2016 Various Arithmetic Functions and their Applications Octavian Cira and Florentin Smarandache March 29, 2016 2 Preface Over 300 sequences and many unsolved problems
arxiv:1603.08456v1 [math.gm] 28 Mar 2016 Various Arithmetic Functions and their Applications Octavian Cira and Florentin Smarandache March 29, 2016 2 Preface Over 300 sequences and many unsolved problems
Numbers and their divisors
 Chapter 1 Numbers and their divisors 1.1 Some number theoretic functions Theorem 1.1 (Fundamental Theorem of Arithmetic). Every positive integer > 1 is uniquely the product of distinct prime powers: n
Chapter 1 Numbers and their divisors 1.1 Some number theoretic functions Theorem 1.1 (Fundamental Theorem of Arithmetic). Every positive integer > 1 is uniquely the product of distinct prime powers: n
Octavian Cira. Florentin Smarandache
 Octavian Cira Florentin Smarandache Octavian Cira and Florentin Smarandache Various Arithmetic Functions and their Applications Peer reviewers: Nassim Abbas, Youcef Chibani, Bilal Hadjadji and Zayen Azzouz
Octavian Cira Florentin Smarandache Octavian Cira and Florentin Smarandache Various Arithmetic Functions and their Applications Peer reviewers: Nassim Abbas, Youcef Chibani, Bilal Hadjadji and Zayen Azzouz
MAT115A-21 COMPLETE LECTURE NOTES
 MAT115A-21 COMPLETE LECTURE NOTES NATHANIEL GALLUP 1. Introduction Number theory begins as the study of the natural numbers the integers N = {1, 2, 3,...}, Z = { 3, 2, 1, 0, 1, 2, 3,...}, and sometimes
MAT115A-21 COMPLETE LECTURE NOTES NATHANIEL GALLUP 1. Introduction Number theory begins as the study of the natural numbers the integers N = {1, 2, 3,...}, Z = { 3, 2, 1, 0, 1, 2, 3,...}, and sometimes
Luhn Primes of Order ω
 Luhn Primes of Order ω Octavian Cira Aurel Vlaicu University of Arad, România Department of Mathematics and Computer Science octavian.cira@uav.ro Florentin Smarandache University of New Mexico, USA Mathematics
Luhn Primes of Order ω Octavian Cira Aurel Vlaicu University of Arad, România Department of Mathematics and Computer Science octavian.cira@uav.ro Florentin Smarandache University of New Mexico, USA Mathematics
EASY PUTNAM PROBLEMS
 EASY PUTNAM PROBLEMS (Last updated: December 11, 2017) Remark. The problems in the Putnam Competition are usually very hard, but practically every session contains at least one problem very easy to solve
EASY PUTNAM PROBLEMS (Last updated: December 11, 2017) Remark. The problems in the Putnam Competition are usually very hard, but practically every session contains at least one problem very easy to solve
PROBLEMS ON CONGRUENCES AND DIVISIBILITY
 PROBLEMS ON CONGRUENCES AND DIVISIBILITY 1. Do there exist 1,000,000 consecutive integers each of which contains a repeated prime factor? 2. A positive integer n is powerful if for every prime p dividing
PROBLEMS ON CONGRUENCES AND DIVISIBILITY 1. Do there exist 1,000,000 consecutive integers each of which contains a repeated prime factor? 2. A positive integer n is powerful if for every prime p dividing
Theory of Numbers Problems
 Theory of Numbers Problems Antonios-Alexandros Robotis Robotis October 2018 1 First Set 1. Find values of x and y so that 71x 50y = 1. 2. Prove that if n is odd, then n 2 1 is divisible by 8. 3. Define
Theory of Numbers Problems Antonios-Alexandros Robotis Robotis October 2018 1 First Set 1. Find values of x and y so that 71x 50y = 1. 2. Prove that if n is odd, then n 2 1 is divisible by 8. 3. Define
Continued Fractions Expansion of D and Pell Equation x 2 Dy 2 = 1
 Mathematica Moravica Vol. 5-2 (20), 9 27 Continued Fractions Expansion of D and Pell Equation x 2 Dy 2 = Ahmet Tekcan Abstract. Let D be a positive non-square integer. In the first section, we give some
Mathematica Moravica Vol. 5-2 (20), 9 27 Continued Fractions Expansion of D and Pell Equation x 2 Dy 2 = Ahmet Tekcan Abstract. Let D be a positive non-square integer. In the first section, we give some
ICS141: Discrete Mathematics for Computer Science I
 ICS141: Discrete Mathematics for Computer Science I Dept. Information & Computer Sci., Jan Stelovsky based on slides by Dr. Baek and Dr. Still Originals by Dr. M. P. Frank and Dr. J.L. Gross Provided by
ICS141: Discrete Mathematics for Computer Science I Dept. Information & Computer Sci., Jan Stelovsky based on slides by Dr. Baek and Dr. Still Originals by Dr. M. P. Frank and Dr. J.L. Gross Provided by
A PARALLEL LOOP SCHEDULING ALGORITHM BASED ON THE SMARANDACHEf-INFERIOR PART FUNCTION
 A PARALLEL LOOP SCHEDULING ALGORITHM BASED ON THE SMARANDACHEf-INFERIOR PART FUNCTION Tatiana Tabirca* Sabin Tabirca** Department of Computer Science, Manchester Uni versity Department of Computer Science,
A PARALLEL LOOP SCHEDULING ALGORITHM BASED ON THE SMARANDACHEf-INFERIOR PART FUNCTION Tatiana Tabirca* Sabin Tabirca** Department of Computer Science, Manchester Uni versity Department of Computer Science,
NEW UNITARY PERFECT NUMBERS HAVE AT LEAST NINE ODD COMPONENTS
 NEW UNITARY PERFECT NUMBERS HAVE AT LEAST NINE ODD COMPONENTS CHARLES R. WALL Trident Technical College, Charleston, SC 29411 (Submitted November 1986) 1. INTRODUCTION We say that a divisor d of an integer
NEW UNITARY PERFECT NUMBERS HAVE AT LEAST NINE ODD COMPONENTS CHARLES R. WALL Trident Technical College, Charleston, SC 29411 (Submitted November 1986) 1. INTRODUCTION We say that a divisor d of an integer
ON PRIMALITY OF THE SMARANDACHE SYMMETRIC SEQUENCES. Sabin TABIRCA, Tatiana TABIRCA
 ON PRIMALITY OF THE SMARANDACHE SYMMETRIC SEQUENCES Sabin TABIRCA, Tatiana TABIRCA "Transilvania" University ofbrasov Facuhy of Science, Computer Science Department Str. Iuliu Maniu, m. 50, Brasov, 2200
ON PRIMALITY OF THE SMARANDACHE SYMMETRIC SEQUENCES Sabin TABIRCA, Tatiana TABIRCA "Transilvania" University ofbrasov Facuhy of Science, Computer Science Department Str. Iuliu Maniu, m. 50, Brasov, 2200
Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers Solutions
 Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers Solutions Warm-up Problems 1. What is a prime number? Give an example of an even prime number and an odd prime number. A prime number
Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers Solutions Warm-up Problems 1. What is a prime number? Give an example of an even prime number and an odd prime number. A prime number
Try the assignment f(1) = 2; f(2) = 1; f(3) = 4; f(4) = 3;.
 I. Precisely complete the following definitions: 1. A natural number n is composite whenever... See class notes for the precise definitions 2. Fix n in N. The number s(n) represents... 3. For A and B sets,
I. Precisely complete the following definitions: 1. A natural number n is composite whenever... See class notes for the precise definitions 2. Fix n in N. The number s(n) represents... 3. For A and B sets,
arxiv:math/ v1 [math.nt] 6 Apr 2005
![arxiv:math/ v1 [math.nt] 6 Apr 2005 arxiv:math/ v1 [math.nt] 6 Apr 2005](/thumbs/86/94725520.jpg) SOME PROPERTIES OF THE PSEUDO-SMARANDACHE FUNCTION arxiv:ath/05048v [ath.nt] 6 Apr 005 RICHARD PINCH Abstract. Charles Ashbacher [] has posed a nuber of questions relating to the pseudo-sarandache function
SOME PROPERTIES OF THE PSEUDO-SMARANDACHE FUNCTION arxiv:ath/05048v [ath.nt] 6 Apr 005 RICHARD PINCH Abstract. Charles Ashbacher [] has posed a nuber of questions relating to the pseudo-sarandache function
A NOTE ON EXPONENTIAL DIVISORS AND RELATED ARITHMETIC FUNCTIONS
 A NOTE ON EXPONENTIAL DIVISORS AND RELATED ARITHMETIC FUNCTIONS József Sándor Babes University of Cluj, Romania 1. Introduction Let n > 1 be a positive integer, and n = p α 1 1 pαr r its prime factorization.
A NOTE ON EXPONENTIAL DIVISORS AND RELATED ARITHMETIC FUNCTIONS József Sándor Babes University of Cluj, Romania 1. Introduction Let n > 1 be a positive integer, and n = p α 1 1 pαr r its prime factorization.
Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers
 Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers Warm-up Problems 1. What is a prime number? Give an example of an even prime number and an odd prime number. (a) Circle the prime
Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers Warm-up Problems 1. What is a prime number? Give an example of an even prime number and an odd prime number. (a) Circle the prime
CmSc 250 Intro to Algorithms. Mathematical Review. 1. Basic Algebra. (a + b) 2 = a 2 + 2ab + b 2 (a - b) 2 = a 2-2ab + b 2 a 2 - b 2 = (a + b)(a - b)
 CmSc 250 Intro to Algorithms Mathematical Review 1. Basic Algebra (a + b) 2 = a 2 + 2ab + b 2 (a - b) 2 = a 2-2ab + b 2 a 2 - b 2 = (a + b)(a - b) a/x + b/y = (ay + bx)/xy 2. Exponents X n = XXX..X, n
CmSc 250 Intro to Algorithms Mathematical Review 1. Basic Algebra (a + b) 2 = a 2 + 2ab + b 2 (a - b) 2 = a 2-2ab + b 2 a 2 - b 2 = (a + b)(a - b) a/x + b/y = (ay + bx)/xy 2. Exponents X n = XXX..X, n
Part II. Number Theory. Year
 Part II Year 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2017 Paper 3, Section I 1G 70 Explain what is meant by an Euler pseudoprime and a strong pseudoprime. Show that 65 is an Euler
Part II Year 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2017 Paper 3, Section I 1G 70 Explain what is meant by an Euler pseudoprime and a strong pseudoprime. Show that 65 is an Euler
On the number of semi-primitive roots modulo n
 Notes on Number Theory and Discrete Mathematics ISSN 1310 5132 Vol. 21, 2015, No., 8 55 On the number of semi-primitive roots modulo n Pinkimani Goswami 1 and Madan Mohan Singh 2 1 Department of Mathematics,
Notes on Number Theory and Discrete Mathematics ISSN 1310 5132 Vol. 21, 2015, No., 8 55 On the number of semi-primitive roots modulo n Pinkimani Goswami 1 and Madan Mohan Singh 2 1 Department of Mathematics,
COMMENTS AND TOPICS ON SMARANDACEE
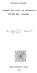 KENICRL"':{O KASHIHARA COMMENTS AND TOPICS ON SMARANDACEE NOTIONS AND PROBLEMS n C s = lim (L: L -log Sn )? n-}co k=l ERHUS UNIVERSITY PRESS ~996 "Corrnnents and Topics on Smarandache Notions and Problems",
KENICRL"':{O KASHIHARA COMMENTS AND TOPICS ON SMARANDACEE NOTIONS AND PROBLEMS n C s = lim (L: L -log Sn )? n-}co k=l ERHUS UNIVERSITY PRESS ~996 "Corrnnents and Topics on Smarandache Notions and Problems",
On products of quartic polynomials over consecutive indices which are perfect squares
 Notes on Number Theory and Discrete Mathematics Print ISSN 1310 513, Online ISSN 367 875 Vol. 4, 018, No. 3, 56 61 DOI: 10.7546/nntdm.018.4.3.56-61 On products of quartic polynomials over consecutive indices
Notes on Number Theory and Discrete Mathematics Print ISSN 1310 513, Online ISSN 367 875 Vol. 4, 018, No. 3, 56 61 DOI: 10.7546/nntdm.018.4.3.56-61 On products of quartic polynomials over consecutive indices
HOMEWORK ASSIGNMENT 5
 HOMEWORK ASSIGNMENT 5 ACCELERATED PROOFS AND PROBLEM SOLVING [MATH08071] Each problem will be marked out of 4 points. Exercise 1 [1, Exercise 10.4]). Show that for all positive integers n, hcf6n + 8, 4n
HOMEWORK ASSIGNMENT 5 ACCELERATED PROOFS AND PROBLEM SOLVING [MATH08071] Each problem will be marked out of 4 points. Exercise 1 [1, Exercise 10.4]). Show that for all positive integers n, hcf6n + 8, 4n
MATH 145 Algebra, Solutions to Assignment 4
 MATH 145 Algebra, Solutions to Assignment 4 1: a) Find the inverse of 178 in Z 365. Solution: We find s and t so that 178s + 365t = 1, and then 178 1 = s. The Euclidean Algorithm gives 365 = 178 + 9 178
MATH 145 Algebra, Solutions to Assignment 4 1: a) Find the inverse of 178 in Z 365. Solution: We find s and t so that 178s + 365t = 1, and then 178 1 = s. The Euclidean Algorithm gives 365 = 178 + 9 178
Super Fibonacci Graceful Labeling
 International J.Math. Combin. Vol. (010), -40 Super Fibonacci Graceful Labeling R. Sridevi 1, S.Navaneethakrishnan and K.Nagarajan 1 1. Department of Mathematics, Sri S.R.N.M.College, Sattur - 66 0, Tamil
International J.Math. Combin. Vol. (010), -40 Super Fibonacci Graceful Labeling R. Sridevi 1, S.Navaneethakrishnan and K.Nagarajan 1 1. Department of Mathematics, Sri S.R.N.M.College, Sattur - 66 0, Tamil
On Exponentially Perfect Numbers Relatively Prime to 15
 On Exponentially Perfect Numbers Relatively Prime to 15 by Joseph F. Kolenick Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science in the Mathematics Program YOUNGSTOWN
On Exponentially Perfect Numbers Relatively Prime to 15 by Joseph F. Kolenick Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science in the Mathematics Program YOUNGSTOWN
Prof. Ila Varma HW 8 Solutions MATH 109. A B, h(i) := g(i n) if i > n. h : Z + f((i + 1)/2) if i is odd, g(i/2) if i is even.
 1. Show that if A and B are countable, then A B is also countable. Hence, prove by contradiction, that if X is uncountable and a subset A is countable, then X A is uncountable. Solution: Suppose A and
1. Show that if A and B are countable, then A B is also countable. Hence, prove by contradiction, that if X is uncountable and a subset A is countable, then X A is uncountable. Solution: Suppose A and
Proof worksheet solutions
 Proof worksheet solutions These are brief, sketched solutions. Comments in blue can be ignored, but they provide further explanation and outline common misconceptions Question 1 (a) x 2 + 4x +12 = (x +
Proof worksheet solutions These are brief, sketched solutions. Comments in blue can be ignored, but they provide further explanation and outline common misconceptions Question 1 (a) x 2 + 4x +12 = (x +
Final Exam Review. 2. Let A = {, { }}. What is the cardinality of A? Is
 1. Describe the elements of the set (Z Q) R N. Is this set countable or uncountable? Solution: The set is equal to {(x, y) x Z, y N} = Z N. Since the Cartesian product of two denumerable sets is denumerable,
1. Describe the elements of the set (Z Q) R N. Is this set countable or uncountable? Solution: The set is equal to {(x, y) x Z, y N} = Z N. Since the Cartesian product of two denumerable sets is denumerable,
Recitation 7: Existence Proofs and Mathematical Induction
 Math 299 Recitation 7: Existence Proofs and Mathematical Induction Existence proofs: To prove a statement of the form x S, P (x), we give either a constructive or a non-contructive proof. In a constructive
Math 299 Recitation 7: Existence Proofs and Mathematical Induction Existence proofs: To prove a statement of the form x S, P (x), we give either a constructive or a non-contructive proof. In a constructive
Ch 7 Summary - POLYNOMIAL FUNCTIONS
 Ch 7 Summary - POLYNOMIAL FUNCTIONS 1. An open-top box is to be made by cutting congruent squares of side length x from the corners of a 8.5- by 11-inch sheet of cardboard and bending up the sides. a)
Ch 7 Summary - POLYNOMIAL FUNCTIONS 1. An open-top box is to be made by cutting congruent squares of side length x from the corners of a 8.5- by 11-inch sheet of cardboard and bending up the sides. a)
Notes 6: Polynomials in One Variable
 Notes 6: Polynomials in One Variable Definition. Let f(x) = b 0 x n + b x n + + b n be a polynomial of degree n, so b 0 0. The leading term of f is LT (f) = b 0 x n. We begin by analyzing the long division
Notes 6: Polynomials in One Variable Definition. Let f(x) = b 0 x n + b x n + + b n be a polynomial of degree n, so b 0 0. The leading term of f is LT (f) = b 0 x n. We begin by analyzing the long division
PRODUCTS THAT ARE POWERS. A mathematical vignette Ed Barbeau, University of Toronto
 PRODUCTS THAT ARE POWERS. A mathematical vignette Ed Barbeau, University of Toronto This investigation was originally designed for school students to gain fluency with the factoring of positive integers
PRODUCTS THAT ARE POWERS. A mathematical vignette Ed Barbeau, University of Toronto This investigation was originally designed for school students to gain fluency with the factoring of positive integers
Number Theory Marathon. Mario Ynocente Castro, National University of Engineering, Peru
 Number Theory Marathon Mario Ynocente Castro, National University of Engineering, Peru 1 2 Chapter 1 Problems 1. (IMO 1975) Let f(n) denote the sum of the digits of n. Find f(f(f(4444 4444 ))). 2. Prove
Number Theory Marathon Mario Ynocente Castro, National University of Engineering, Peru 1 2 Chapter 1 Problems 1. (IMO 1975) Let f(n) denote the sum of the digits of n. Find f(f(f(4444 4444 ))). 2. Prove
3.4 Introduction to power series
 3.4 Introduction to power series Definition 3.4.. A polynomial in the variable x is an expression of the form n a i x i = a 0 + a x + a 2 x 2 + + a n x n + a n x n i=0 or a n x n + a n x n + + a 2 x 2
3.4 Introduction to power series Definition 3.4.. A polynomial in the variable x is an expression of the form n a i x i = a 0 + a x + a 2 x 2 + + a n x n + a n x n i=0 or a n x n + a n x n + + a 2 x 2
More Examples of Proofs
 More Examples of Proofs Contradiction Proofs Definition: A prime number is an integer greater than 1 which is divisible only by 1 and itself. Ex: 2, 5, 11 are primes; 6, 15, 100 are not primes. There are
More Examples of Proofs Contradiction Proofs Definition: A prime number is an integer greater than 1 which is divisible only by 1 and itself. Ex: 2, 5, 11 are primes; 6, 15, 100 are not primes. There are
Solutions for November. f(x + f(y)) = f(x) + y
 Solutions for November 647. Find all continuous functions f : R R such that for every x, y R. f(x + f(y)) = f(x) + y Solution 1. Setting (x, y) = (t, 0) yields f(t + f(0)) = f(t) for all real t. Setting
Solutions for November 647. Find all continuous functions f : R R such that for every x, y R. f(x + f(y)) = f(x) + y Solution 1. Setting (x, y) = (t, 0) yields f(t + f(0)) = f(t) for all real t. Setting
Sets. We discuss an informal (naive) set theory as needed in Computer Science. It was introduced by G. Cantor in the second half of the nineteenth
 Sets We discuss an informal (naive) set theory as needed in Computer Science. It was introduced by G. Cantor in the second half of the nineteenth century. Most students have seen sets before. This is intended
Sets We discuss an informal (naive) set theory as needed in Computer Science. It was introduced by G. Cantor in the second half of the nineteenth century. Most students have seen sets before. This is intended
MATH 2112/CSCI 2112, Discrete Structures I Winter 2007 Toby Kenney Homework Sheet 5 Hints & Model Solutions
 MATH 11/CSCI 11, Discrete Structures I Winter 007 Toby Kenney Homework Sheet 5 Hints & Model Solutions Sheet 4 5 Define the repeat of a positive integer as the number obtained by writing it twice in a
MATH 11/CSCI 11, Discrete Structures I Winter 007 Toby Kenney Homework Sheet 5 Hints & Model Solutions Sheet 4 5 Define the repeat of a positive integer as the number obtained by writing it twice in a
PM functions, their characteristic intervals and iterative roots
 ANNALES POLONICI MATHEMATICI LXV.2(1997) PM functions, their characteristic intervals and iterative roots by Weinian Zhang (Chengdu) Abstract. The concept of characteristic interval for piecewise monotone
ANNALES POLONICI MATHEMATICI LXV.2(1997) PM functions, their characteristic intervals and iterative roots by Weinian Zhang (Chengdu) Abstract. The concept of characteristic interval for piecewise monotone
There Is No Speed Barrier in the Universe. and One Can Construct any Speed
 There Is No Speed Barrier in the Universe and One Can Construct any Speed Dr. Florentin Smarandache University of New Mexico Gallup, NM 87301, USA smarand@unm.edu Abstract: In this short paper, as an extension
There Is No Speed Barrier in the Universe and One Can Construct any Speed Dr. Florentin Smarandache University of New Mexico Gallup, NM 87301, USA smarand@unm.edu Abstract: In this short paper, as an extension
8 Primes and Modular Arithmetic
 8 Primes and Modular Arithmetic 8.1 Primes and Factors Over two millennia ago already, people all over the world were considering the properties of numbers. One of the simplest concepts is prime numbers.
8 Primes and Modular Arithmetic 8.1 Primes and Factors Over two millennia ago already, people all over the world were considering the properties of numbers. One of the simplest concepts is prime numbers.
University of Toronto Faculty of Arts and Science Solutions to Final Examination, April 2017 MAT246H1S - Concepts in Abstract Mathematics
 University of Toronto Faculty of Arts and Science Solutions to Final Examination, April 2017 MAT246H1S - Concepts in Abstract Mathematics Examiners: D. Burbulla, P. Glynn-Adey, S. Homayouni Time: 7-10
University of Toronto Faculty of Arts and Science Solutions to Final Examination, April 2017 MAT246H1S - Concepts in Abstract Mathematics Examiners: D. Burbulla, P. Glynn-Adey, S. Homayouni Time: 7-10
Section 4.4 Functions. CS 130 Discrete Structures
 Section 4.4 Functions CS 130 Discrete Structures Function Definitions Let S and T be sets. A function f from S to T, f: S T, is a subset of S x T where each member of S appears exactly once as the first
Section 4.4 Functions CS 130 Discrete Structures Function Definitions Let S and T be sets. A function f from S to T, f: S T, is a subset of S x T where each member of S appears exactly once as the first
Math 314 Course Notes: Brief description
 Brief description These are notes for Math 34, an introductory course in elementary number theory Students are advised to go through all sections in detail and attempt all problems These notes will be
Brief description These are notes for Math 34, an introductory course in elementary number theory Students are advised to go through all sections in detail and attempt all problems These notes will be
ON GENERALIZED BALANCING SEQUENCES
 ON GENERALIZED BALANCING SEQUENCES ATTILA BÉRCZES, KÁLMÁN LIPTAI, AND ISTVÁN PINK Abstract. Let R i = R(A, B, R 0, R 1 ) be a second order linear recurrence sequence. In the present paper we prove that
ON GENERALIZED BALANCING SEQUENCES ATTILA BÉRCZES, KÁLMÁN LIPTAI, AND ISTVÁN PINK Abstract. Let R i = R(A, B, R 0, R 1 ) be a second order linear recurrence sequence. In the present paper we prove that
CONJECTURES ON PRIMES AND FERMAT PSEUDOPRIMES, MANY BASED ON SMARANDACHE FUNCTION (COLLECTED PAPERS)
 1 CONJECTURES ON PRIMES AND FERMAT PSEUDOPRIMES, MANY BASED ON SMARANDACHE FUNCTION (COLLECTED PAPERS) Education Publishing 2014 Copyright 2014 by Marius Coman Education Publishing 1313 Chesapeake Avenue
1 CONJECTURES ON PRIMES AND FERMAT PSEUDOPRIMES, MANY BASED ON SMARANDACHE FUNCTION (COLLECTED PAPERS) Education Publishing 2014 Copyright 2014 by Marius Coman Education Publishing 1313 Chesapeake Avenue
On certain generalizations of the Smarandache. function
 Smarandache Notions Journal, Vol. 11, No. 1-2-3, Spring 2000, pp. 202-212. On certain generalizations of the Smarandache function J. Sandor Babe -Bolyai University, 3400 Cluj-Napoca, Romania J1 1. The
Smarandache Notions Journal, Vol. 11, No. 1-2-3, Spring 2000, pp. 202-212. On certain generalizations of the Smarandache function J. Sandor Babe -Bolyai University, 3400 Cluj-Napoca, Romania J1 1. The
1 x i. i=1 EVEN NUMBERS RAFAEL ARCE-NAZARIO, FRANCIS N. CASTRO, AND RAÚL FIGUEROA
 Volume, Number 2, Pages 63 78 ISSN 75-0868 ON THE EQUATION n i= = IN DISTINCT ODD OR EVEN NUMBERS RAFAEL ARCE-NAZARIO, FRANCIS N. CASTRO, AND RAÚL FIGUEROA Abstract. In this paper we combine theoretical
Volume, Number 2, Pages 63 78 ISSN 75-0868 ON THE EQUATION n i= = IN DISTINCT ODD OR EVEN NUMBERS RAFAEL ARCE-NAZARIO, FRANCIS N. CASTRO, AND RAÚL FIGUEROA Abstract. In this paper we combine theoretical
OEIS A I. SCOPE
 OEIS A161460 Richard J. Mathar Leiden Observatory, P.O. Box 9513, 2300 RA Leiden, The Netherlands (Dated: August 7, 2009) An overview to the entries of the sequence A161460 of the Online Encyclopedia of
OEIS A161460 Richard J. Mathar Leiden Observatory, P.O. Box 9513, 2300 RA Leiden, The Netherlands (Dated: August 7, 2009) An overview to the entries of the sequence A161460 of the Online Encyclopedia of
Jim Lambers MAT 460 Fall Semester Lecture 2 Notes
 Jim Lambers MAT 460 Fall Semester 2009-10 Lecture 2 Notes These notes correspond to Section 1.1 in the text. Review of Calculus Among the mathematical problems that can be solved using techniques from
Jim Lambers MAT 460 Fall Semester 2009-10 Lecture 2 Notes These notes correspond to Section 1.1 in the text. Review of Calculus Among the mathematical problems that can be solved using techniques from
 Q 1 Find the square root of 729. 6. Squares and Square Roots Q 2 Fill in the blank using the given pattern. 7 2 = 49 67 2 = 4489 667 2 = 444889 6667 2 = Q 3 Without adding find the sum of 1 + 3 + 5 + 7
Q 1 Find the square root of 729. 6. Squares and Square Roots Q 2 Fill in the blank using the given pattern. 7 2 = 49 67 2 = 4489 667 2 = 444889 6667 2 = Q 3 Without adding find the sum of 1 + 3 + 5 + 7
PUTNAM TRAINING EASY PUTNAM PROBLEMS
 PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
Unit 2 Rational Functionals Exercises MHF 4UI Page 1
 Unit 2 Rational Functionals Exercises MHF 4UI Page Exercises 2.: Division of Polynomials. Divide, assuming the divisor is not equal to zero. a) x 3 + 2x 2 7x + 4 ) x + ) b) 3x 4 4x 2 2x + 3 ) x 4) 7. *)
Unit 2 Rational Functionals Exercises MHF 4UI Page Exercises 2.: Division of Polynomials. Divide, assuming the divisor is not equal to zero. a) x 3 + 2x 2 7x + 4 ) x + ) b) 3x 4 4x 2 2x + 3 ) x 4) 7. *)
Contribution of Problems
 Exam topics 1. Basic structures: sets, lists, functions (a) Sets { }: write all elements, or define by condition (b) Set operations: A B, A B, A\B, A c (c) Lists ( ): Cartesian product A B (d) Functions
Exam topics 1. Basic structures: sets, lists, functions (a) Sets { }: write all elements, or define by condition (b) Set operations: A B, A B, A\B, A c (c) Lists ( ): Cartesian product A B (d) Functions
PEN H Problems. n 5 = x 2 +y 2 +z 2 +u 2 +v 2 = xyzuv 65. (x+y) 2 2(xy) 2 = 1. x 3 +y 3 +z 3 +t 3 = 1999
 Diophantine Equations 1 One of Euler s conjectures was disproved in the 1980s by three American Mathematicians when they showed that there is a positive integer n such that Find the value of n. n 5 = 133
Diophantine Equations 1 One of Euler s conjectures was disproved in the 1980s by three American Mathematicians when they showed that there is a positive integer n such that Find the value of n. n 5 = 133
Discrete dynamics on the real line
 Chapter 2 Discrete dynamics on the real line We consider the discrete time dynamical system x n+1 = f(x n ) for a continuous map f : R R. Definitions The forward orbit of x 0 is: O + (x 0 ) = {x 0, f(x
Chapter 2 Discrete dynamics on the real line We consider the discrete time dynamical system x n+1 = f(x n ) for a continuous map f : R R. Definitions The forward orbit of x 0 is: O + (x 0 ) = {x 0, f(x
Number Theory Marathon. Mario Ynocente Castro, National University of Engineering, Peru
 Number Theory Marathon Mario Ynocente Castro, National University of Engineering, Peru 1 2 Chapter 1 Problems 1. (IMO 1975) Let f(n) denote the sum of the digits of n. Find f(f(f(4444 4444 ))). 2. Prove
Number Theory Marathon Mario Ynocente Castro, National University of Engineering, Peru 1 2 Chapter 1 Problems 1. (IMO 1975) Let f(n) denote the sum of the digits of n. Find f(f(f(4444 4444 ))). 2. Prove
UNDERSTANDING RULER AND COMPASS CONSTRUCTIONS WITH FIELD THEORY
 UNDERSTANDING RULER AND COMPASS CONSTRUCTIONS WITH FIELD THEORY ISAAC M. DAVIS Abstract. By associating a subfield of R to a set of points P 0 R 2, geometric properties of ruler and compass constructions
UNDERSTANDING RULER AND COMPASS CONSTRUCTIONS WITH FIELD THEORY ISAAC M. DAVIS Abstract. By associating a subfield of R to a set of points P 0 R 2, geometric properties of ruler and compass constructions
FIITJEE ALGEBRA-2 Pre RMO
 FIITJEE ALGEBRA- Pre RMO A. AP, GP 1. Consider the sequence 1,,,, 5, 5, 5, 5, 5, 7, 7, 7, 7, 7, 7, 7,... and evaluate its 016 th term.. Integers 1,,,..., n, where n >, are written on a board. Two numbers
FIITJEE ALGEBRA- Pre RMO A. AP, GP 1. Consider the sequence 1,,,, 5, 5, 5, 5, 5, 7, 7, 7, 7, 7, 7, 7,... and evaluate its 016 th term.. Integers 1,,,..., n, where n >, are written on a board. Two numbers
Math 319 Problem Set #2 Solution 14 February 2002
 Math 39 Problem Set # Solution 4 February 00. (.3, problem 8) Let n be a positive integer, and let r be the integer obtained by removing the last digit from n and then subtracting two times the digit ust
Math 39 Problem Set # Solution 4 February 00. (.3, problem 8) Let n be a positive integer, and let r be the integer obtained by removing the last digit from n and then subtracting two times the digit ust
Chapter-2 Relations and Functions. Miscellaneous
 1 Chapter-2 Relations and Functions Miscellaneous Question 1: The relation f is defined by The relation g is defined by Show that f is a function and g is not a function. The relation f is defined as It
1 Chapter-2 Relations and Functions Miscellaneous Question 1: The relation f is defined by The relation g is defined by Show that f is a function and g is not a function. The relation f is defined as It
CLASS - X Mathematics (Real Number)
 CLASS - X Mathematics (Real Number) 1. 7 11 13 15 + 15is a (a) Composite number (c) Prime number (b) Whole number (d) None of these. For what least value of n a natural number, ( 4) n is divisible by 8?
CLASS - X Mathematics (Real Number) 1. 7 11 13 15 + 15is a (a) Composite number (c) Prime number (b) Whole number (d) None of these. For what least value of n a natural number, ( 4) n is divisible by 8?
A NOTE ON THE SMARANDACHE PRIME PRODUCT SEQTJENCE A.A.K.~AR. Department of Mathematics, Jahangimagar University, Savar, Dhaka 1342, Bangladesh
 A NOTE ON THE SMARANDACHE PRIME PRODUCT SEQTJENCE A.A.K.~AR Department of Mathematics, Jahangimagar University, Savar, Dhaka 1342, Bangladesh ABSTRACT This paper gives some properties of the Smarandache
A NOTE ON THE SMARANDACHE PRIME PRODUCT SEQTJENCE A.A.K.~AR Department of Mathematics, Jahangimagar University, Savar, Dhaka 1342, Bangladesh ABSTRACT This paper gives some properties of the Smarandache
A Readable Introduction to Real Mathematics
 Solutions to selected problems in the book A Readable Introduction to Real Mathematics D. Rosenthal, D. Rosenthal, P. Rosenthal Chapter 10: Sizes of Infinite Sets 1. Show that the set of all polynomials
Solutions to selected problems in the book A Readable Introduction to Real Mathematics D. Rosenthal, D. Rosenthal, P. Rosenthal Chapter 10: Sizes of Infinite Sets 1. Show that the set of all polynomials
MATH 361: NUMBER THEORY FOURTH LECTURE
 MATH 361: NUMBER THEORY FOURTH LECTURE 1. Introduction Everybody knows that three hours after 10:00, the time is 1:00. That is, everybody is familiar with modular arithmetic, the usual arithmetic of the
MATH 361: NUMBER THEORY FOURTH LECTURE 1. Introduction Everybody knows that three hours after 10:00, the time is 1:00. That is, everybody is familiar with modular arithmetic, the usual arithmetic of the
Midterm 3 Review. Terms. Formulas and Rules to Use. Math 1010, Fall 2011 Instructor: Marina Gresham. Odd Root ( n x where n is odd) Exponent
 Math 1010, Fall 2011 Instructor: Marina Gresham Terms Midterm 3 Review Exponent Polynomial - Monomial - Binomial - Trinomial - Standard Form - Degree - Leading Coefficient - Constant Term Difference of
Math 1010, Fall 2011 Instructor: Marina Gresham Terms Midterm 3 Review Exponent Polynomial - Monomial - Binomial - Trinomial - Standard Form - Degree - Leading Coefficient - Constant Term Difference of
Solutions to Assignment 1
 Solutions to Assignment 1 Question 1. [Exercises 1.1, # 6] Use the division algorithm to prove that every odd integer is either of the form 4k + 1 or of the form 4k + 3 for some integer k. For each positive
Solutions to Assignment 1 Question 1. [Exercises 1.1, # 6] Use the division algorithm to prove that every odd integer is either of the form 4k + 1 or of the form 4k + 3 for some integer k. For each positive
PRACTICE PROBLEMS: SET 1
 PRACTICE PROBLEMS: SET MATH 437/537: PROF. DRAGOS GHIOCA. Problems Problem. Let a, b N. Show that if gcd(a, b) = lcm[a, b], then a = b. Problem. Let n, k N with n. Prove that (n ) (n k ) if and only if
PRACTICE PROBLEMS: SET MATH 437/537: PROF. DRAGOS GHIOCA. Problems Problem. Let a, b N. Show that if gcd(a, b) = lcm[a, b], then a = b. Problem. Let n, k N with n. Prove that (n ) (n k ) if and only if
D-MATH Algebra I HS 2013 Prof. Brent Doran. Solution 3. Modular arithmetic, quotients, product groups
 D-MATH Algebra I HS 2013 Prof. Brent Doran Solution 3 Modular arithmetic, quotients, product groups 1. Show that the functions f = 1/x, g = (x 1)/x generate a group of functions, the law of composition
D-MATH Algebra I HS 2013 Prof. Brent Doran Solution 3 Modular arithmetic, quotients, product groups 1. Show that the functions f = 1/x, g = (x 1)/x generate a group of functions, the law of composition
CHAPTER 3 REVIEW QUESTIONS MATH 3034 Spring a 1 b 1
 . Let U = { A M (R) A = and b 6 }. CHAPTER 3 REVIEW QUESTIONS MATH 334 Spring 7 a b a and b are integers and a 6 (a) Let S = { A U det A = }. List the elements of S; that is S = {... }. (b) Let T = { A
. Let U = { A M (R) A = and b 6 }. CHAPTER 3 REVIEW QUESTIONS MATH 334 Spring 7 a b a and b are integers and a 6 (a) Let S = { A U det A = }. List the elements of S; that is S = {... }. (b) Let T = { A
Introduction to Abstract Mathematics
 Introduction to Abstract Mathematics Notation: Z + or Z >0 denotes the set {1, 2, 3,...} of positive integers, Z 0 is the set {0, 1, 2,...} of nonnegative integers, Z is the set {..., 1, 0, 1, 2,...} of
Introduction to Abstract Mathematics Notation: Z + or Z >0 denotes the set {1, 2, 3,...} of positive integers, Z 0 is the set {0, 1, 2,...} of nonnegative integers, Z is the set {..., 1, 0, 1, 2,...} of
( 3) ( ) ( ) ( ) ( ) ( )
 81 Instruction: Determining the Possible Rational Roots using the Rational Root Theorem Consider the theorem stated below. Rational Root Theorem: If the rational number b / c, in lowest terms, is a root
81 Instruction: Determining the Possible Rational Roots using the Rational Root Theorem Consider the theorem stated below. Rational Root Theorem: If the rational number b / c, in lowest terms, is a root
Number Theory Solutions Packet
 Number Theory Solutions Pacet 1 There exist two distinct positive integers, both of which are divisors of 10 10, with sum equal to 157 What are they? Solution Suppose 157 = x + y for x and y divisors of
Number Theory Solutions Pacet 1 There exist two distinct positive integers, both of which are divisors of 10 10, with sum equal to 157 What are they? Solution Suppose 157 = x + y for x and y divisors of
6.1 Using Properties of Exponents 1. Use properties of exponents to evaluate and simplify expressions involving powers. Product of Powers Property
 6.1 Using Properties of Exponents Objectives 1. Use properties of exponents to evaluate and simplify expressions involving powers. 2. Use exponents and scientific notation to solve real life problems.
6.1 Using Properties of Exponents Objectives 1. Use properties of exponents to evaluate and simplify expressions involving powers. 2. Use exponents and scientific notation to solve real life problems.
Necessary and Sufficient Conditions for the Central Norm to Equal 2 h in the Simple Continued Fraction Expansion of 2 h c for Any Odd Non-Square c > 1
 Necessary and Sufficient Conditions for the Central Norm to Equal 2 h in the Simple Continued Fraction Expansion of 2 h c for Any Odd Non-Square c > 1 R.A. Mollin Abstract We look at the simple continued
Necessary and Sufficient Conditions for the Central Norm to Equal 2 h in the Simple Continued Fraction Expansion of 2 h c for Any Odd Non-Square c > 1 R.A. Mollin Abstract We look at the simple continued
Functions and Their Graphs
 Functions and Their Graphs DEFINITION Function A function from a set D to a set Y is a rule that assigns a unique (single) element ƒ(x) Y to each element x D. A symbolic way to say y is a function of x
Functions and Their Graphs DEFINITION Function A function from a set D to a set Y is a rule that assigns a unique (single) element ƒ(x) Y to each element x D. A symbolic way to say y is a function of x
Connections between connected topological spaces on the set of positive integers
 Cent. Eur. J. Math. 11(5) 2013 876-881 DOI: 10.2478/s11533-013-0210-3 Central European Journal of Mathematics Connections between connected topological spaces on the set of positive integers Research Article
Cent. Eur. J. Math. 11(5) 2013 876-881 DOI: 10.2478/s11533-013-0210-3 Central European Journal of Mathematics Connections between connected topological spaces on the set of positive integers Research Article
0 Sets and Induction. Sets
 0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
g(x) = 1 1 x = 1 + x + x2 + x 3 + is not a polynomial, since it doesn t have finite degree. g(x) is an example of a power series.
 6 Polynomial Rings We introduce a class of rings called the polynomial rings, describing computation, factorization and divisibility in such rings For the case where the coefficients come from an integral
6 Polynomial Rings We introduce a class of rings called the polynomial rings, describing computation, factorization and divisibility in such rings For the case where the coefficients come from an integral
MATH 3030, Abstract Algebra FALL 2012 Toby Kenney Midyear Examination Friday 7th December: 7:00-10:00 PM
 MATH 3030, Abstract Algebra FALL 2012 Toby Kenney Midyear Examination Friday 7th December: 7:00-10:00 PM Basic Questions 1. Compute the factor group Z 3 Z 9 / (1, 6). The subgroup generated by (1, 6) is
MATH 3030, Abstract Algebra FALL 2012 Toby Kenney Midyear Examination Friday 7th December: 7:00-10:00 PM Basic Questions 1. Compute the factor group Z 3 Z 9 / (1, 6). The subgroup generated by (1, 6) is
8.7 Taylor s Inequality Math 2300 Section 005 Calculus II. f(x) = ln(1 + x) f(0) = 0
 8.7 Taylor s Inequality Math 00 Section 005 Calculus II Name: ANSWER KEY Taylor s Inequality: If f (n+) is continuous and f (n+) < M between the center a and some point x, then f(x) T n (x) M x a n+ (n
8.7 Taylor s Inequality Math 00 Section 005 Calculus II Name: ANSWER KEY Taylor s Inequality: If f (n+) is continuous and f (n+) < M between the center a and some point x, then f(x) T n (x) M x a n+ (n
ARITHMETIC OF POSITIVE INTEGERS HAVING PRIME SUMS OF COMPLEMENTARY DIVISORS
 Math. J. Okayama Univ. 60 (2018), 155 164 ARITHMETIC OF POSITIVE INTEGERS HAVING PRIME SUMS OF COMPLEMENTARY DIVISORS Kenichi Shimizu Abstract. We study a class of integers called SP numbers (Sum Prime
Math. J. Okayama Univ. 60 (2018), 155 164 ARITHMETIC OF POSITIVE INTEGERS HAVING PRIME SUMS OF COMPLEMENTARY DIVISORS Kenichi Shimizu Abstract. We study a class of integers called SP numbers (Sum Prime
MODEL ANSWERS TO THE FIRST HOMEWORK
 MODEL ANSWERS TO THE FIRST HOMEWORK 1. Chapter 4, 1: 2. Suppose that F is a field and that a and b are in F. Suppose that a b = 0, and that b 0. Let c be the inverse of b. Multiplying the equation above
MODEL ANSWERS TO THE FIRST HOMEWORK 1. Chapter 4, 1: 2. Suppose that F is a field and that a and b are in F. Suppose that a b = 0, and that b 0. Let c be the inverse of b. Multiplying the equation above
Chapter 3: Section 3.1: Factors & Multiples of Whole Numbers
 Chapter 3: Section 3.1: Factors & Multiples of Whole Numbers Prime Factor: a prime number that is a factor of a number. The first 15 prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
Chapter 3: Section 3.1: Factors & Multiples of Whole Numbers Prime Factor: a prime number that is a factor of a number. The first 15 prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
Algebra Ph.D. Entrance Exam Fall 2009 September 3, 2009
 Algebra Ph.D. Entrance Exam Fall 2009 September 3, 2009 Directions: Solve 10 of the following problems. Mark which of the problems are to be graded. Without clear indication which problems are to be graded
Algebra Ph.D. Entrance Exam Fall 2009 September 3, 2009 Directions: Solve 10 of the following problems. Mark which of the problems are to be graded. Without clear indication which problems are to be graded
One Pile Nim with Arbitrary Move Function
 One Pile Nim with Arbitrary Move Function by Arthur Holshouser and Harold Reiter Arthur Holshouser 3600 Bullard St. Charlotte, NC, USA, 28208 Harold Reiter Department of Mathematics UNC Charlotte Charlotte,
One Pile Nim with Arbitrary Move Function by Arthur Holshouser and Harold Reiter Arthur Holshouser 3600 Bullard St. Charlotte, NC, USA, 28208 Harold Reiter Department of Mathematics UNC Charlotte Charlotte,
