Sequences and Summations ICS 6D. Prof. Sandy Irani
|
|
|
- Diane Leonard
- 5 years ago
- Views:
Transcription
1 Sequences and Summations ICS 6D Prof. Sandy Irani
2 Test Poll What is your favorite flavor of ice cream? A) Vanilla B) Chocolate C) Moose Tracks D) Mint Chocolate Chip E) None of the above
3 Sequences A sequence is a special case of a function in which the domain is a consecutive set of integers: For example: a person s height measured in inches on each birthday. (The person for this example if 5 years old). h 0 = 20, h 1 = 30, h 2 = 34, h 3 = 37, h 4 = 40, h 5 = 43 What is the fourth term of the sequence? What is the word for the 3 in h 3? What is the notation for the entire sequence.
4 Sequences A finite sequence has a finite domain: h 0 = 20, h 1 = 30, h 2 = 34, h 3 = 37, h 4 = 40, h 5 = 43 An infinite sequence has an infinite domain: h 2 = 1, h 3 = 2, h 4 = 4, h 5 = 8, h 6 = 16, h 7 = 32,..
5 Ways to specify a sequences List the numbers. h 0 = 20, h 1 = 30, h 2 = 34, h 3 = 37, h 4 = 40, h 5 = 43 Average rainfall in California since Average weight of a child in the US by age. Give an explicit formula for the sequence. Example: Initial index = 1. f n = 2 n + 2n f 1 = 4, f 2 = 8, f 3 = 14, f 4 = 24, f 5 = 42,..
6 Ways to specify a sequences Recurrence relation Base case: one or more initial values f 0 = 1 f 1 = 1 Recursive rule: a rule for determining the next term in the sequence as a function of terms that appear earlier in the sequence (recurrence relation): f n = f n 1 +f n 2,for n 2
7 Fibonacci Sequence f 0 = 1 f 1 = 1 f n = f n 1 +f n 2,for n 2
8 More recurrence relations: g 0 = 0 g n = g (n div 2) + 1, for n 1. n div 2 = n/2
9 More recurrence relations: h 0 = 2 h 1 = 4 h n = n h n 1 + 2h n 2, for n 2 Need enough initial values in the base case to specify the sequence
10 Recurrence Relations Useful for modeling dynamical systems: Biology: population growth Finance: market growth or interest accumulation Useful in computer science The number of operations performed by a recursive algorithm on an input of a given size.
11 Fibonacci Sequence f 0 = 1 f 1 = 1 f n = f n 1 +f n 2,for n 2 Developed by Leonardo Fibonacci to describe the population growth of a colony of rabbits. How big is the rabbit colony after 100 months? How long does it take the rabbit colony to reach 1000 rabbits?»need an explicit formula for f n
12 Solving a Recurrence Given a recurrence relation that defines a sequence Initial values Recursive Rule Find an explicit formula for the sequence: f n = a mathematical function that depends only on n and not on earlier terms in the sequence
13 Geometric Sequence g 0 = a (a = initial value) g n = r g n 1 (r = common ratio), for n 1.
14 Geometric Sequence Examples a = 5, r = 2 a = 1, r =.1 a = 2, r = 1 g 0 = 4, g 1 = 12, g 2 = 36, g 3 = 108,.
15 Geometric Sequence g 0 = a (a = initial value) g n = r g n 1 (r = common ratio), for n 1. What are the conditions that make {g n } increasing? What are the conditions that make {g n } decreasing?
16 Arithmetic Sequence h 0 = a (a = initial value) h n = d + h n 1 (d = common difference) for n 1.
17 Arithmetic Sequence Examples a = 5, d = 2 a = 1, d =.1 a = 2, d = 1 g 0 = 4, g 1 = 9, g 2 = 14, g 3 = 19,.
18 Arithmetic Sequence h 0 = a (a = initial value) h n = d + h n 1 (d = common difference) for n 1. What are the conditions that make {h n } increasing? What are the conditions that make {h n } decreasing?
19 Summations Compact expression for the sum of the terms in a mathematical sequence. + +
20 Summations If the terms in the sequence have an explicit formula, then the value of the sum can be computed: Parentheses are important:
21 Summations If the upper limit is a variable, then the value of the sum is a function of that variable:
22 Summations Sometimes, we need to pull out one or more terms from the summation.
23 Summations A closed form for a summation, expresses the value of the sum (without a summation)
24 Closed form for the sum of terms in a geometric sequence Geometric sequence: Initial value a, common ratio r, n = # of terms: What is the value of
25 Closed form for the sum of terms in an arithmetic sequence Arithmetic sequence: Initial value a, common difference d, n = # of terms: What is the value of?
CSCE 222 Discrete Structures for Computing. Dr. Hyunyoung Lee
 CSCE 222 Discrete Structures for Computing Sequences and Summations Dr. Hyunyoung Lee Based on slides by Andreas Klappenecker 1 Sequences 2 Sequences A sequence is a function from a subset of the set of
CSCE 222 Discrete Structures for Computing Sequences and Summations Dr. Hyunyoung Lee Based on slides by Andreas Klappenecker 1 Sequences 2 Sequences A sequence is a function from a subset of the set of
Advanced Counting Techniques. Chapter 8
 Advanced Counting Techniques Chapter 8 Chapter Summary Applications of Recurrence Relations Solving Linear Recurrence Relations Homogeneous Recurrence Relations Nonhomogeneous Recurrence Relations Divide-and-Conquer
Advanced Counting Techniques Chapter 8 Chapter Summary Applications of Recurrence Relations Solving Linear Recurrence Relations Homogeneous Recurrence Relations Nonhomogeneous Recurrence Relations Divide-and-Conquer
Examples of Finite Sequences (finite terms) Examples of Infinite Sequences (infinite terms)
 Math 120 Intermediate Algebra Sec 10.1: Sequences Defn A sequence is a function whose domain is the set of positive integers. The formula for the nth term of a sequence is called the general term. Examples
Math 120 Intermediate Algebra Sec 10.1: Sequences Defn A sequence is a function whose domain is the set of positive integers. The formula for the nth term of a sequence is called the general term. Examples
Sequences and Series. College Algebra
 Sequences and Series College Algebra Sequences A sequence is a function whose domain is the set of positive integers. A finite sequence is a sequence whose domain consists of only the first n positive
Sequences and Series College Algebra Sequences A sequence is a function whose domain is the set of positive integers. A finite sequence is a sequence whose domain consists of only the first n positive
3.3 Accumulation Sequences
 3.3. ACCUMULATION SEQUENCES 25 3.3 Accumulation Sequences Overview. One of the most important mathematical ideas in calculus is that of an accumulation of change for physical quantities. As we have been
3.3. ACCUMULATION SEQUENCES 25 3.3 Accumulation Sequences Overview. One of the most important mathematical ideas in calculus is that of an accumulation of change for physical quantities. As we have been
SEQUENCES AND SERIES
 A sequence is an ordered list of numbers. SEQUENCES AND SERIES Note, in this context, ordered does not mean that the numbers in the list are increasing or decreasing. Instead it means that there is a first
A sequence is an ordered list of numbers. SEQUENCES AND SERIES Note, in this context, ordered does not mean that the numbers in the list are increasing or decreasing. Instead it means that there is a first
EECS 1028 M: Discrete Mathematics for Engineers
 EECS 1028 M: Discrete Mathematics for Engineers Suprakash Datta Office: LAS 3043 Course page: http://www.eecs.yorku.ca/course/1028 Also on Moodle S. Datta (York Univ.) EECS 1028 W 18 1 / 16 Sequences and
EECS 1028 M: Discrete Mathematics for Engineers Suprakash Datta Office: LAS 3043 Course page: http://www.eecs.yorku.ca/course/1028 Also on Moodle S. Datta (York Univ.) EECS 1028 W 18 1 / 16 Sequences and
Sequences and Summations. CS/APMA 202 Rosen section 3.2 Aaron Bloomfield
 Sequences and Summations CS/APMA 202 Rosen section 3.2 Aaron Bloomfield 1 Definitions Sequence: an ordered list of elements Like a set, but: Elements can be duplicated Elements are ordered 2 Sequences
Sequences and Summations CS/APMA 202 Rosen section 3.2 Aaron Bloomfield 1 Definitions Sequence: an ordered list of elements Like a set, but: Elements can be duplicated Elements are ordered 2 Sequences
Recurrence Relations
 Recurrence Relations Recurrence Relations Reading (Epp s textbook) 5.6 5.8 1 Recurrence Relations A recurrence relation for a sequence aa 0, aa 1, aa 2, ({a n }) is a formula that relates each term a k
Recurrence Relations Recurrence Relations Reading (Epp s textbook) 5.6 5.8 1 Recurrence Relations A recurrence relation for a sequence aa 0, aa 1, aa 2, ({a n }) is a formula that relates each term a k
Advanced Counting Techniques
 . All rights reserved. Authorized only for instructor use in the classroom. No reproduction or further distribution permitted without the prior written consent of McGraw-Hill Education. Advanced Counting
. All rights reserved. Authorized only for instructor use in the classroom. No reproduction or further distribution permitted without the prior written consent of McGraw-Hill Education. Advanced Counting
Section 4.1: Sequences and Series
 Section 4.1: Sequences and Series In this section, we shall introduce the idea of sequences and series as a necessary tool to develop the proof technique called mathematical induction. Most of the material
Section 4.1: Sequences and Series In this section, we shall introduce the idea of sequences and series as a necessary tool to develop the proof technique called mathematical induction. Most of the material
Chapter 5: Sequences, Mathematic Induction, and Recursion
 Chapter 5: Sequences, Mathematic Induction, and Recursion Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757
Chapter 5: Sequences, Mathematic Induction, and Recursion Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757
Section Summary. Sequences. Recurrence Relations. Summations. Examples: Geometric Progression, Arithmetic Progression. Example: Fibonacci Sequence
 Section 2.4 Section Summary Sequences. Examples: Geometric Progression, Arithmetic Progression Recurrence Relations Example: Fibonacci Sequence Summations Introduction Sequences are ordered lists of elements.
Section 2.4 Section Summary Sequences. Examples: Geometric Progression, Arithmetic Progression Recurrence Relations Example: Fibonacci Sequence Summations Introduction Sequences are ordered lists of elements.
Sequence. A list of numbers written in a definite order.
 Sequence A list of numbers written in a definite order. Terms of a Sequence a n = 2 n 2 1, 2 2, 2 3, 2 4, 2 n, 2, 4, 8, 16, 2 n We are going to be mainly concerned with infinite sequences. This means we
Sequence A list of numbers written in a definite order. Terms of a Sequence a n = 2 n 2 1, 2 2, 2 3, 2 4, 2 n, 2, 4, 8, 16, 2 n We are going to be mainly concerned with infinite sequences. This means we
Definition: A sequence is a function from a subset of the integers (usually either the set
 Math 3336 Section 2.4 Sequences and Summations Sequences Geometric Progression Arithmetic Progression Recurrence Relation Fibonacci Sequence Summations Definition: A sequence is a function from a subset
Math 3336 Section 2.4 Sequences and Summations Sequences Geometric Progression Arithmetic Progression Recurrence Relation Fibonacci Sequence Summations Definition: A sequence is a function from a subset
Unit 3: Linear and Exponential Functions
 Unit 3: Linear and Exponential Functions In Unit 3, students will learn function notation and develop the concepts of domain and range. They will discover that functions can be combined in ways similar
Unit 3: Linear and Exponential Functions In Unit 3, students will learn function notation and develop the concepts of domain and range. They will discover that functions can be combined in ways similar
{ 0! = 1 n! = n(n 1)!, n 1. n! =
 Summations Question? What is the sum of the first 100 positive integers? Counting Question? In how many ways may the first three horses in a 10 horse race finish? Multiplication Principle: If an event
Summations Question? What is the sum of the first 100 positive integers? Counting Question? In how many ways may the first three horses in a 10 horse race finish? Multiplication Principle: If an event
Fall 2017 Test II review problems
 Fall 2017 Test II review problems Dr. Holmes October 18, 2017 This is a quite miscellaneous grab bag of relevant problems from old tests. Some are certainly repeated. 1. Give the complete addition and
Fall 2017 Test II review problems Dr. Holmes October 18, 2017 This is a quite miscellaneous grab bag of relevant problems from old tests. Some are certainly repeated. 1. Give the complete addition and
Chapter 8: Recursion. March 10, 2008
 Chapter 8: Recursion March 10, 2008 Outline 1 8.1 Recursively Defined Sequences 2 8.2 Solving Recurrence Relations by Iteration 3 8.4 General Recursive Definitions Recursively Defined Sequences As mentioned
Chapter 8: Recursion March 10, 2008 Outline 1 8.1 Recursively Defined Sequences 2 8.2 Solving Recurrence Relations by Iteration 3 8.4 General Recursive Definitions Recursively Defined Sequences As mentioned
IM1 Summative Practice #1 Show all your Work
 IM1 Summative Practice #1 Name: Show all your Work Period: Simplify each expression below. 1. 5x (7 3x) 2. 5(x 12) + 15(x + y) 3. 8 2(x 2 3x) (9 3x 2 ) Solve each equation. Justify each step with a property
IM1 Summative Practice #1 Name: Show all your Work Period: Simplify each expression below. 1. 5x (7 3x) 2. 5(x 12) + 15(x + y) 3. 8 2(x 2 3x) (9 3x 2 ) Solve each equation. Justify each step with a property
Discrete Structures Lecture Sequences and Summations
 Introduction Good morning. In this section we study sequences. A sequence is an ordered list of elements. Sequences are important to computing because of the iterative nature of computer programs. The
Introduction Good morning. In this section we study sequences. A sequence is an ordered list of elements. Sequences are important to computing because of the iterative nature of computer programs. The
Unit 5: Sequences, Series, and Patterns
 Unit 5: Sequences, Series, and Patterns Section 1: Sequences and Series 1. Sequence: an ordered list of numerical terms 2. Finite Sequence: has a first term (a beginning) and a last term (an end) 3. Infinite
Unit 5: Sequences, Series, and Patterns Section 1: Sequences and Series 1. Sequence: an ordered list of numerical terms 2. Finite Sequence: has a first term (a beginning) and a last term (an end) 3. Infinite
Unit 3: Linear and Exponential Functions
 Unit 3: Linear and Exponential Functions In Unit 3, students will learn function notation and develop the concepts of domain and range. They will discover that functions can be combined in ways similar
Unit 3: Linear and Exponential Functions In Unit 3, students will learn function notation and develop the concepts of domain and range. They will discover that functions can be combined in ways similar
Sequences and Summations
 COMP 182 Algorithmic Thinking Sequences and Summations Luay Nakhleh Computer Science Rice University Chapter 2, Section 4 Reading Material Sequences A sequence is a function from a subset of the set of
COMP 182 Algorithmic Thinking Sequences and Summations Luay Nakhleh Computer Science Rice University Chapter 2, Section 4 Reading Material Sequences A sequence is a function from a subset of the set of
Vocabulary. Term Page Definition Clarifying Example. arithmetic sequence. explicit formula. finite sequence. geometric mean. geometric sequence
 CHAPTER 2 Vocabulary The table contains important vocabulary terms from Chapter 2. As you work through the chapter, fill in the page number, definition, and a clarifying example. arithmetic Term Page Definition
CHAPTER 2 Vocabulary The table contains important vocabulary terms from Chapter 2. As you work through the chapter, fill in the page number, definition, and a clarifying example. arithmetic Term Page Definition
Sequences. 1. Number sequences. 2. Arithmetic sequences. Consider the illustrated pattern of circles:
 Sequences 1. Number sequences Consider the illustrated pattern of circles: The first layer has just one blue ball. The second layer has three pink balls. The third layer has five black balls. The fourth
Sequences 1. Number sequences Consider the illustrated pattern of circles: The first layer has just one blue ball. The second layer has three pink balls. The third layer has five black balls. The fourth
Work easier problems first. Write out your plan for harder problems before beginning them.
 Notes:??? Form R 1 of 7 Directions: For multiple choice (A, B, C, etc.), circle the letter of the best choice. For TRUE/FALSE, circle the word TRUE or the word FALSE. When a list of choices is given for
Notes:??? Form R 1 of 7 Directions: For multiple choice (A, B, C, etc.), circle the letter of the best choice. For TRUE/FALSE, circle the word TRUE or the word FALSE. When a list of choices is given for
Sequences and Series. Copyright Cengage Learning. All rights reserved.
 Sequences and Series Copyright Cengage Learning. All rights reserved. 12.1 Sequences and Summation Notation Copyright Cengage Learning. All rights reserved. Objectives Sequences Recursively Defined Sequences
Sequences and Series Copyright Cengage Learning. All rights reserved. 12.1 Sequences and Summation Notation Copyright Cengage Learning. All rights reserved. Objectives Sequences Recursively Defined Sequences
Sequences A sequence is a function, where the domain is a set of consecutive positive integers beginning with 1.
 1 CA-Fall 2011-Jordan College Algebra, 4 th edition, Beecher/Penna/Bittinger, Pearson/Addison Wesley, 2012 Chapter 8: Sequences, Series, and Combinatorics Section 8.1 Sequences and Series Sequences A sequence
1 CA-Fall 2011-Jordan College Algebra, 4 th edition, Beecher/Penna/Bittinger, Pearson/Addison Wesley, 2012 Chapter 8: Sequences, Series, and Combinatorics Section 8.1 Sequences and Series Sequences A sequence
Fundamental Algorithms
 Fundamental Algorithms Chapter 1: Introduction Jan Křetínský Winter 2016/17 Chapter 1: Introduction, Winter 2016/17 1 Part I Overview Chapter 1: Introduction, Winter 2016/17 2 Organization Extent: 2 SWS
Fundamental Algorithms Chapter 1: Introduction Jan Křetínský Winter 2016/17 Chapter 1: Introduction, Winter 2016/17 1 Part I Overview Chapter 1: Introduction, Winter 2016/17 2 Organization Extent: 2 SWS
Every subset of {1, 2,...,n 1} can be extended to a subset of {1, 2, 3,...,n} by either adding or not adding the element n.
 11 Recurrences A recurrence equation or recurrence counts things using recursion. 11.1 Recurrence Equations We start with an example. Example 11.1. Find a recurrence for S(n), the number of subsets of
11 Recurrences A recurrence equation or recurrence counts things using recursion. 11.1 Recurrence Equations We start with an example. Example 11.1. Find a recurrence for S(n), the number of subsets of
Advanced Counting Techniques. 7.1 Recurrence Relations
 Chapter 7 Advanced Counting Techniques 71 Recurrence Relations We have seen that a recursive definition of a sequence specifies one or more initial terms and a rule for determining subsequent terms from
Chapter 7 Advanced Counting Techniques 71 Recurrence Relations We have seen that a recursive definition of a sequence specifies one or more initial terms and a rule for determining subsequent terms from
or the number of bacteria in a colony after each hour, if the colony starts with one bacteria and each bacteria divides into two every hour
 448 Sequences and Series In everyday life, we can observe sequences or series of events in many contexts. For instance, we line up to enter a store in a sequence, we make a sequence of mortgage payments,
448 Sequences and Series In everyday life, we can observe sequences or series of events in many contexts. For instance, we line up to enter a store in a sequence, we make a sequence of mortgage payments,
Intermediate Math Circles March 11, 2009 Sequences and Series
 1 University of Waterloo Faculty of Mathematics Centre for Education in Mathematics and Computing Intermediate Math Circles March 11, 009 Sequences and Series Tower of Hanoi The Tower of Hanoi is a game
1 University of Waterloo Faculty of Mathematics Centre for Education in Mathematics and Computing Intermediate Math Circles March 11, 009 Sequences and Series Tower of Hanoi The Tower of Hanoi is a game
Recurrence Relations and Recursion: MATH 180
 Recurrence Relations and Recursion: MATH 180 1: Recursively Defined Sequences Example 1: The sequence a 1,a 2,a 3,... can be defined recursively as follows: (1) For all integers k 2, a k = a k 1 + 1 (2)
Recurrence Relations and Recursion: MATH 180 1: Recursively Defined Sequences Example 1: The sequence a 1,a 2,a 3,... can be defined recursively as follows: (1) For all integers k 2, a k = a k 1 + 1 (2)
Algorithms: Background
 Algorithms: Background Amotz Bar-Noy CUNY Amotz Bar-Noy (CUNY) Algorithms: Background 1 / 66 What is a Proof? Definition I: The cogency of evidence that compels acceptance by the mind of a truth or a fact.
Algorithms: Background Amotz Bar-Noy CUNY Amotz Bar-Noy (CUNY) Algorithms: Background 1 / 66 What is a Proof? Definition I: The cogency of evidence that compels acceptance by the mind of a truth or a fact.
Discrete Structures for Computer Science
 Discrete Structures for Computer Science William Garrison bill@cs.pitt.edu 6311 Sennott Square Lecture #10: Sequences and Summations Based on materials developed by Dr. Adam Lee Today s Topics Sequences
Discrete Structures for Computer Science William Garrison bill@cs.pitt.edu 6311 Sennott Square Lecture #10: Sequences and Summations Based on materials developed by Dr. Adam Lee Today s Topics Sequences
Fundamental Algorithms
 Fundamental Algorithms Chapter 1: Introduction Michael Bader Winter 2011/12 Chapter 1: Introduction, Winter 2011/12 1 Part I Overview Chapter 1: Introduction, Winter 2011/12 2 Organizational Stuff 2 SWS
Fundamental Algorithms Chapter 1: Introduction Michael Bader Winter 2011/12 Chapter 1: Introduction, Winter 2011/12 1 Part I Overview Chapter 1: Introduction, Winter 2011/12 2 Organizational Stuff 2 SWS
Recurrence Relations
 Recurrence Relations Winter 2017 Recurrence Relations Recurrence Relations A recurrence relation for the sequence {a n } is an equation that expresses a n in terms of one or more of the previous terms
Recurrence Relations Winter 2017 Recurrence Relations Recurrence Relations A recurrence relation for the sequence {a n } is an equation that expresses a n in terms of one or more of the previous terms
Algebra II. Table of Contents. Sequences and Series. Slide 1 / 153. Slide 2 / 153. Slide 3 /
 Slide 1 / 153 Algebra II Slide 2 / 153 Sequences and Series 2015-04-21 www.njctl.org Table of Contents Click on the topic to go to that section Slide 3 / 153 Arithmetic Sequences Geometric Sequences Geometric
Slide 1 / 153 Algebra II Slide 2 / 153 Sequences and Series 2015-04-21 www.njctl.org Table of Contents Click on the topic to go to that section Slide 3 / 153 Arithmetic Sequences Geometric Sequences Geometric
Great Theoretical Ideas in Computer Science
 15-251 Great Theoretical Ideas in Computer Science Recurrences, Fibonacci Numbers and Continued Fractions Lecture 9, September 23, 2008 Happy Autumnal Equinox http://apod.nasa.gov/apod/ap080922.html Leonardo
15-251 Great Theoretical Ideas in Computer Science Recurrences, Fibonacci Numbers and Continued Fractions Lecture 9, September 23, 2008 Happy Autumnal Equinox http://apod.nasa.gov/apod/ap080922.html Leonardo
Section Summary. Sequences. Recurrence Relations. Summations Special Integer Sequences (optional)
 Section 2.4 Section Summary Sequences. o Examples: Geometric Progression, Arithmetic Progression Recurrence Relations o Example: Fibonacci Sequence Summations Special Integer Sequences (optional) Sequences
Section 2.4 Section Summary Sequences. o Examples: Geometric Progression, Arithmetic Progression Recurrence Relations o Example: Fibonacci Sequence Summations Special Integer Sequences (optional) Sequences
Chapter 4 ARITHMETIC AND GEOMETRIC PROGRESSIONS 2, 5, 8, 11, 14,..., 101
 Chapter 4 ARITHMETIC AND GEOMETRIC PROGRESSIONS A finite sequence such as 2, 5, 8, 11, 14,..., 101 in which each succeeding term is obtained by adding a fixed number to the preceding term is called an
Chapter 4 ARITHMETIC AND GEOMETRIC PROGRESSIONS A finite sequence such as 2, 5, 8, 11, 14,..., 101 in which each succeeding term is obtained by adding a fixed number to the preceding term is called an
12 Sequences and Recurrences
 12 Sequences and Recurrences A sequence is just what you think it is. It is often given by a formula known as a recurrence equation. 12.1 Arithmetic and Geometric Progressions An arithmetic progression
12 Sequences and Recurrences A sequence is just what you think it is. It is often given by a formula known as a recurrence equation. 12.1 Arithmetic and Geometric Progressions An arithmetic progression
1 Examples of Weak Induction
 More About Mathematical Induction Mathematical induction is designed for proving that a statement holds for all nonnegative integers (or integers beyond an initial one). Here are some extra examples of
More About Mathematical Induction Mathematical induction is designed for proving that a statement holds for all nonnegative integers (or integers beyond an initial one). Here are some extra examples of
Power series and Taylor series
 Power series and Taylor series D. DeTurck University of Pennsylvania March 29, 2018 D. DeTurck Math 104 002 2018A: Series 1 / 42 Series First... a review of what we have done so far: 1 We examined series
Power series and Taylor series D. DeTurck University of Pennsylvania March 29, 2018 D. DeTurck Math 104 002 2018A: Series 1 / 42 Series First... a review of what we have done so far: 1 We examined series
Week 2: Sequences and Series
 QF0: Quantitative Finance August 29, 207 Week 2: Sequences and Series Facilitator: Christopher Ting AY 207/208 Mathematicians have tried in vain to this day to discover some order in the sequence of prime
QF0: Quantitative Finance August 29, 207 Week 2: Sequences and Series Facilitator: Christopher Ting AY 207/208 Mathematicians have tried in vain to this day to discover some order in the sequence of prime
Fibonacci numbers. Chapter The Fibonacci sequence. The Fibonacci numbers F n are defined recursively by
 Chapter Fibonacci numbers The Fibonacci sequence The Fibonacci numbers F n are defined recursively by F n+ = F n + F n, F 0 = 0, F = The first few Fibonacci numbers are n 0 5 6 7 8 9 0 F n 0 5 8 55 89
Chapter Fibonacci numbers The Fibonacci sequence The Fibonacci numbers F n are defined recursively by F n+ = F n + F n, F 0 = 0, F = The first few Fibonacci numbers are n 0 5 6 7 8 9 0 F n 0 5 8 55 89
A NICE DIOPHANTINE EQUATION. 1. Introduction
 A NICE DIOPHANTINE EQUATION MARIA CHIARA BRAMBILLA Introduction One of the most interesting and fascinating subjects in Number Theory is the study of diophantine equations A diophantine equation is a polynomial
A NICE DIOPHANTINE EQUATION MARIA CHIARA BRAMBILLA Introduction One of the most interesting and fascinating subjects in Number Theory is the study of diophantine equations A diophantine equation is a polynomial
Great Theoretical Ideas in Computer Science
 15-251 Great Theoretical Ideas in Computer Science Recurrences, Fibonacci Numbers and Continued Fractions Lecture 9, September 24, 2009 Leonardo Fibonacci In 1202, Fibonacci proposed a problem about the
15-251 Great Theoretical Ideas in Computer Science Recurrences, Fibonacci Numbers and Continued Fractions Lecture 9, September 24, 2009 Leonardo Fibonacci In 1202, Fibonacci proposed a problem about the
Chapter If M is the matrix 0 0 1, then M 100 is. (c) (a) (b) (d) (e) None of the above. (b) 2.
 Chapter 2. If M is the matrix, then M is (a) (b) (c) (d) (e) None of the above 3 6 2. If A is a 3 3 matrix such that A = and A 4 =, then the product A 7 is 2 5 8 (a) (b) 2 (c) 9 (d) (e) Not uniquely determined
Chapter 2. If M is the matrix, then M is (a) (b) (c) (d) (e) None of the above 3 6 2. If A is a 3 3 matrix such that A = and A 4 =, then the product A 7 is 2 5 8 (a) (b) 2 (c) 9 (d) (e) Not uniquely determined
Sequences are ordered lists of elements
 Sequences are ordered lists of elements Definition: A sequence is a function from the set of integers, either set {0,1,2,3, } or set {1,2,3,4,..}, to a set S. We use the notation a n to denote the image
Sequences are ordered lists of elements Definition: A sequence is a function from the set of integers, either set {0,1,2,3, } or set {1,2,3,4,..}, to a set S. We use the notation a n to denote the image
Grade 7/8 Math Circles October 28/29, Series
 Faculty of Mathematics Waterloo, Ontario NL 3G1 Centre for Education in Mathematics and Computing Sequence Recap Grade 7/8 Math Circles October 8/9, 014 Series Before starting series lets recap last weeks
Faculty of Mathematics Waterloo, Ontario NL 3G1 Centre for Education in Mathematics and Computing Sequence Recap Grade 7/8 Math Circles October 8/9, 014 Series Before starting series lets recap last weeks
Functions. Given a function f: A B:
 Functions Given a function f: A B: We say f maps A to B or f is a mapping from A to B. A is called the domain of f. B is called the codomain of f. If f(a) = b, then b is called the image of a under f.
Functions Given a function f: A B: We say f maps A to B or f is a mapping from A to B. A is called the domain of f. B is called the codomain of f. If f(a) = b, then b is called the image of a under f.
Arithmetic Series Can you add the first 100 counting numbers in less than 30 seconds? Begin How did he do it so quickly? It is said that he
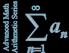 Little Freddie is said to have done the work in his head and written only the answer on his slate in less than 30 seconds. Can you do it in less than 30 seconds? Arithmetic Series An arithmetic series
Little Freddie is said to have done the work in his head and written only the answer on his slate in less than 30 seconds. Can you do it in less than 30 seconds? Arithmetic Series An arithmetic series
Unit 5: Representations of Linear Relations
 Time Frame: Approximately 3-5 weeks Connections to Previous Learning: Students build upon previous understandings of linear equations and functions and apply them to various representations of linear relationships,
Time Frame: Approximately 3-5 weeks Connections to Previous Learning: Students build upon previous understandings of linear equations and functions and apply them to various representations of linear relationships,
Sec$on Summary. Sequences. Recurrence Relations. Summations. Ex: Geometric Progression, Arithmetic Progression. Ex: Fibonacci Sequence
 Section 2.4 Sec$on Summary Sequences Ex: Geometric Progression, Arithmetic Progression Recurrence Relations Ex: Fibonacci Sequence Summations 2 Introduc$on Sequences are ordered lists of elements. 1, 2,
Section 2.4 Sec$on Summary Sequences Ex: Geometric Progression, Arithmetic Progression Recurrence Relations Ex: Fibonacci Sequence Summations 2 Introduc$on Sequences are ordered lists of elements. 1, 2,
Arithmetic and Geometric Sequences and their Summation
 4 Arithmetic and Geometric Sequences and their Summation O-FOUDATIO 4F 4.4 Series 4.5 Arithmetic Series ame : Date : Mark : Key Concepts and Formulae Sum of the first n terms of an arithmetic series: na
4 Arithmetic and Geometric Sequences and their Summation O-FOUDATIO 4F 4.4 Series 4.5 Arithmetic Series ame : Date : Mark : Key Concepts and Formulae Sum of the first n terms of an arithmetic series: na
Discrete Math. Instructor: Mike Picollelli. Day 10
 Day 10 Fibonacci Redux. Last time, we saw that F n = 1 5 (( 1 + ) n ( 5 2 1 ) n ) 5. 2 What Makes The Fibonacci Numbers So Special? The Fibonacci numbers are a particular type of recurrence relation, a
Day 10 Fibonacci Redux. Last time, we saw that F n = 1 5 (( 1 + ) n ( 5 2 1 ) n ) 5. 2 What Makes The Fibonacci Numbers So Special? The Fibonacci numbers are a particular type of recurrence relation, a
Math 324 Summer 2012 Elementary Number Theory Notes on Mathematical Induction
 Math 4 Summer 01 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
Math 4 Summer 01 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
Functions in Tables 2.0
 Ns Activate Prior Knowledge Function Table Game Topic: Functions Functions in Tables 2.0 Date: Objectives: SWBAT (Identify patterns in Tables) Main Ideas: Assignment: What is a relation? What is a function?
Ns Activate Prior Knowledge Function Table Game Topic: Functions Functions in Tables 2.0 Date: Objectives: SWBAT (Identify patterns in Tables) Main Ideas: Assignment: What is a relation? What is a function?
Sequences and Series
 UNIT 11 Sequences and Series An integrated circuit can hold millions of microscopic components called transistors. How many transistors can fit in a chip on the tip of your finger? Moore s law predicts
UNIT 11 Sequences and Series An integrated circuit can hold millions of microscopic components called transistors. How many transistors can fit in a chip on the tip of your finger? Moore s law predicts
Chapter 8 Sequences, Series, and Probability
 Chapter 8 Sequences, Series, and Probability Overview 8.1 Sequences and Series 8.2 Arithmetic Sequences and Partial Sums 8.3 Geometric Sequences and Partial Sums 8.5 The Binomial Theorem 8.6 Counting Principles
Chapter 8 Sequences, Series, and Probability Overview 8.1 Sequences and Series 8.2 Arithmetic Sequences and Partial Sums 8.3 Geometric Sequences and Partial Sums 8.5 The Binomial Theorem 8.6 Counting Principles
Algebra 2 Standards. Essential Standards:
 Benchmark 1: Essential Standards: 1. Alg2.M.F.LE.A.02 (linear): I can create linear functions if provided either a graph, relationship description or input-output tables. - 15 Days 2. Alg2.M.A.APR.B.02a
Benchmark 1: Essential Standards: 1. Alg2.M.F.LE.A.02 (linear): I can create linear functions if provided either a graph, relationship description or input-output tables. - 15 Days 2. Alg2.M.A.APR.B.02a
Benchmark Test Modules 1 7
 . What is the solution of 50 = x 3?. Does each equation have at least one solution? A 8x + = 8x 4 x = 5x + C 6x + 9 = 6x + 9 D 5 x = 0 x 3. Solve x + 7= 9 x. What is the value of x? 4. A living room of
. What is the solution of 50 = x 3?. Does each equation have at least one solution? A 8x + = 8x 4 x = 5x + C 6x + 9 = 6x + 9 D 5 x = 0 x 3. Solve x + 7= 9 x. What is the value of x? 4. A living room of
PUTNAM TRAINING PROBLEMS
 PUTNAM TRAINING PROBLEMS (Last updated: December 3, 2003) Remark This is a list of Math problems for the NU Putnam team to be discussed during the training sessions Miguel A Lerma 1 Bag of candies In a
PUTNAM TRAINING PROBLEMS (Last updated: December 3, 2003) Remark This is a list of Math problems for the NU Putnam team to be discussed during the training sessions Miguel A Lerma 1 Bag of candies In a
8. Sequences, Series, and Probability 8.1. SEQUENCES AND SERIES
 8. Sequences, Series, and Probability 8.1. SEQUENCES AND SERIES What You Should Learn Use sequence notation to write the terms of sequences. Use factorial notation. Use summation notation to write sums.
8. Sequences, Series, and Probability 8.1. SEQUENCES AND SERIES What You Should Learn Use sequence notation to write the terms of sequences. Use factorial notation. Use summation notation to write sums.
Exploring the infinite : an introduction to proof and analysis / Jennifer Brooks. Boca Raton [etc.], cop Spis treści
![Exploring the infinite : an introduction to proof and analysis / Jennifer Brooks. Boca Raton [etc.], cop Spis treści Exploring the infinite : an introduction to proof and analysis / Jennifer Brooks. Boca Raton [etc.], cop Spis treści](/thumbs/89/97813041.jpg) Exploring the infinite : an introduction to proof and analysis / Jennifer Brooks. Boca Raton [etc.], cop. 2017 Spis treści Preface xiii I Fundamentals of Abstract Mathematics 1 1 Basic Notions 3 1.1 A
Exploring the infinite : an introduction to proof and analysis / Jennifer Brooks. Boca Raton [etc.], cop. 2017 Spis treści Preface xiii I Fundamentals of Abstract Mathematics 1 1 Basic Notions 3 1.1 A
a) Plot and label the 3 points. [3] b) Rewrite point A using a negative angle and negative radius.
![a) Plot and label the 3 points. [3] b) Rewrite point A using a negative angle and negative radius. a) Plot and label the 3 points. [3] b) Rewrite point A using a negative angle and negative radius.](/thumbs/95/122797190.jpg) Analysis Summer HW problem Set: Compiled 207 Students bridging up to Analysis from Alg2/TrigA will need to learn a few topics on their own this summer. These are topics that other Analysis students learned
Analysis Summer HW problem Set: Compiled 207 Students bridging up to Analysis from Alg2/TrigA will need to learn a few topics on their own this summer. These are topics that other Analysis students learned
One side of each sheet is blank and may be used as scratch paper.
 Math 301 Fall 2017 (Practice) Midterm Exam 1 10/3/2017 Time Limit: 1 hour and 15 minutes Name: One side of each sheet is blank and may be used as scratch paper. Show your work clearly. Grade Table (for
Math 301 Fall 2017 (Practice) Midterm Exam 1 10/3/2017 Time Limit: 1 hour and 15 minutes Name: One side of each sheet is blank and may be used as scratch paper. Show your work clearly. Grade Table (for
UNIT 3 VOCABULARY: SEQUENCES
 3º ESO Bilingüe Página UNIT 3 VOCABULARY: SEQUENCES.. Sequences of real numbers A sequence of real numbers is a set of real numbers that are in order. For example: 3, 5, 7, 9,, 3... is a set of numbers
3º ESO Bilingüe Página UNIT 3 VOCABULARY: SEQUENCES.. Sequences of real numbers A sequence of real numbers is a set of real numbers that are in order. For example: 3, 5, 7, 9,, 3... is a set of numbers
Math 3 Proportion & Probability Part 2 Sequences, Patterns, Frequency Tables & Venn Diagrams
 Math 3 Proportion & Probability Part 2 Sequences, Patterns, Frequency Tables & Venn Diagrams 1 MATH 2 REVIEW ARITHMETIC SEQUENCES In an Arithmetic Sequence the difference between one term and the next
Math 3 Proportion & Probability Part 2 Sequences, Patterns, Frequency Tables & Venn Diagrams 1 MATH 2 REVIEW ARITHMETIC SEQUENCES In an Arithmetic Sequence the difference between one term and the next
Chapter 2 - Basics Structures MATH 213. Chapter 2: Basic Structures. Dr. Eric Bancroft. Fall Dr. Eric Bancroft MATH 213 Fall / 60
 MATH 213 Chapter 2: Basic Structures Dr. Eric Bancroft Fall 2013 Dr. Eric Bancroft MATH 213 Fall 2013 1 / 60 Chapter 2 - Basics Structures 2.1 - Sets 2.2 - Set Operations 2.3 - Functions 2.4 - Sequences
MATH 213 Chapter 2: Basic Structures Dr. Eric Bancroft Fall 2013 Dr. Eric Bancroft MATH 213 Fall 2013 1 / 60 Chapter 2 - Basics Structures 2.1 - Sets 2.2 - Set Operations 2.3 - Functions 2.4 - Sequences
Page references correspond to locations of Extra Examples icons in the textbook.
 Rosen, Discrete Mathematics and Its Applications, 7th edition Extra Examples Section 8. Recurrence Relations Page references correspond to locations of Extra Examples icons in the textbook. p.50, icon
Rosen, Discrete Mathematics and Its Applications, 7th edition Extra Examples Section 8. Recurrence Relations Page references correspond to locations of Extra Examples icons in the textbook. p.50, icon
Sequences and Series Review
 Sequences and Series Review 1. Consider the sequence 1,,,,... a. Describe the pattern formed in the sequence. b. Find the next three terms. 2. i.) Write a formula for the arithmetic sequence 6, 0, 6, 12,
Sequences and Series Review 1. Consider the sequence 1,,,,... a. Describe the pattern formed in the sequence. b. Find the next three terms. 2. i.) Write a formula for the arithmetic sequence 6, 0, 6, 12,
ICS141: Discrete Mathematics for Computer Science I
 ICS141: Discrete Mathematics for Computer Science I Dept. Information & Computer Sci., Jan Stelovsky based on slides by Dr. Baek and Dr. Still Originals by Dr. M. P. Frank and Dr. J.L. Gross Provided by
ICS141: Discrete Mathematics for Computer Science I Dept. Information & Computer Sci., Jan Stelovsky based on slides by Dr. Baek and Dr. Still Originals by Dr. M. P. Frank and Dr. J.L. Gross Provided by
Grade 8 FSA Mathematics Practice Test Answer Key
 Grade 8 FSA Mathematics Practice Test Answer Key The Grade 8 FSA Mathematics Practice Test Answer Key provides the correct response(s) for each item on the practice test. The practice questions and answers
Grade 8 FSA Mathematics Practice Test Answer Key The Grade 8 FSA Mathematics Practice Test Answer Key provides the correct response(s) for each item on the practice test. The practice questions and answers
Chapter 2 - Basics Structures
 Chapter 2 - Basics Structures 2.1 - Sets Definitions and Notation Definition 1 (Set). A set is an of. These are called the or of the set. We ll typically use uppercase letters to denote sets: S, A, B,...
Chapter 2 - Basics Structures 2.1 - Sets Definitions and Notation Definition 1 (Set). A set is an of. These are called the or of the set. We ll typically use uppercase letters to denote sets: S, A, B,...
Scatter diagrams & lines of best fit
 Name: Scatter diagrams & lines of best fit Date: Time: 59 minutes Total marks available: 59 Total marks achieved: L. Warwicker Questions Q1. The table shows the average temperature on each of seven days
Name: Scatter diagrams & lines of best fit Date: Time: 59 minutes Total marks available: 59 Total marks achieved: L. Warwicker Questions Q1. The table shows the average temperature on each of seven days
Sets. Review of basic probability. Tuples. E = {all even integers} S = {x E : x is a multiple of 3} CSE 101. I = [0, 1] = {x : 0 x 1}
![Sets. Review of basic probability. Tuples. E = {all even integers} S = {x E : x is a multiple of 3} CSE 101. I = [0, 1] = {x : 0 x 1} Sets. Review of basic probability. Tuples. E = {all even integers} S = {x E : x is a multiple of 3} CSE 101. I = [0, 1] = {x : 0 x 1}](/thumbs/85/92597043.jpg) Sets A = {a, b, c,..., z} A = 26 Review of basic probability = {0, 1} = 2 E = {all even integers} E = CSE 1 S = {x E : x is a multiple of 3} I = [0, 1] = {x : 0 x 1} In a set, the order of elements doesn
Sets A = {a, b, c,..., z} A = 26 Review of basic probability = {0, 1} = 2 E = {all even integers} E = CSE 1 S = {x E : x is a multiple of 3} I = [0, 1] = {x : 0 x 1} In a set, the order of elements doesn
Carleton University. Final Examination Fall DURATION: 2 HOURS No. of students: 223
 Carleton University Final Examination Fall 2016 DURATION: 2 HOURS No. of students: 223 Department Name & Course Number: Computer Science COMP 2804A Course Instructor: Michiel Smid Authorized memoranda:
Carleton University Final Examination Fall 2016 DURATION: 2 HOURS No. of students: 223 Department Name & Course Number: Computer Science COMP 2804A Course Instructor: Michiel Smid Authorized memoranda:
Problem Solving in Math (Math 43900) Fall 2013
 Problem Solving in Math (Math 43900) Fall 203 Week six (October ) problems recurrences Instructor: David Galvin Definition of a recurrence relation We met recurrences in the induction hand-out. Sometimes
Problem Solving in Math (Math 43900) Fall 203 Week six (October ) problems recurrences Instructor: David Galvin Definition of a recurrence relation We met recurrences in the induction hand-out. Sometimes
2009 A-level Maths Tutor All Rights Reserved
 2 This book is under copyright to A-level Maths Tutor. However, it may be distributed freely provided it is not sold for profit. Contents the Sigma Notation 3 arithmetical progressions(series) 6 geometrical
2 This book is under copyright to A-level Maths Tutor. However, it may be distributed freely provided it is not sold for profit. Contents the Sigma Notation 3 arithmetical progressions(series) 6 geometrical
CSC2100B Data Structures Analysis
 CSC2100B Data Structures Analysis Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Algorithm An algorithm
CSC2100B Data Structures Analysis Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Algorithm An algorithm
10-2 Arithmetic Sequences and Series
 Determine the common difference, and find the next four terms of each arithmetic sequence. 1. 20, 17, 14, 17 20 = 3 14 17 = 3 The common difference is 3. Add 3 to the third term to find the fourth term,
Determine the common difference, and find the next four terms of each arithmetic sequence. 1. 20, 17, 14, 17 20 = 3 14 17 = 3 The common difference is 3. Add 3 to the third term to find the fourth term,
For math conventions used on the GRE, refer to this link:
 GRE Review ISU Student Success Center Quantitative Workshop One Quantitative Section: Overview Your test will include either two or three 35-minute quantitative sections. There will be 20 questions in
GRE Review ISU Student Success Center Quantitative Workshop One Quantitative Section: Overview Your test will include either two or three 35-minute quantitative sections. There will be 20 questions in
Math 141: Lecture 19
 Math 141: Lecture 19 Convergence of infinite series Bob Hough November 16, 2016 Bob Hough Math 141: Lecture 19 November 16, 2016 1 / 44 Series of positive terms Recall that, given a sequence {a n } n=1,
Math 141: Lecture 19 Convergence of infinite series Bob Hough November 16, 2016 Bob Hough Math 141: Lecture 19 November 16, 2016 1 / 44 Series of positive terms Recall that, given a sequence {a n } n=1,
, 500, 250, 125, , 2, 4, 7, 11, 16, , 3, 9, 27, , 3, 2, 7, , 2 2, 4, 4 2, 8
 Warm Up Look for a pattern and predict the next number or expression in the list. 1. 1000, 500, 250, 125, 62.5 2. 1, 2, 4, 7, 11, 16, 22 3. 1, 3, 9, 27, 81 4. 8, 3, 2, 7, -12 5. 2, 2 2, 4, 4 2, 8 6. 7a
Warm Up Look for a pattern and predict the next number or expression in the list. 1. 1000, 500, 250, 125, 62.5 2. 1, 2, 4, 7, 11, 16, 22 3. 1, 3, 9, 27, 81 4. 8, 3, 2, 7, -12 5. 2, 2 2, 4, 4 2, 8 6. 7a
Mathematical Domain The Number System (NS) Assessment. Compute fluently with multi-digit numbers and find common factors and multiples.
 The Number System (NS) Expressions and Equations EE Compute fluently with multi-digit numbers and find common factors and multiples. 6.NS.. Fluently multiply and divide multi digit whole numbers using
The Number System (NS) Expressions and Equations EE Compute fluently with multi-digit numbers and find common factors and multiples. 6.NS.. Fluently multiply and divide multi digit whole numbers using
DYNAMICAL SYSTEMS
 0.42 DYNAMICAL SYSTEMS Week Lecture Notes. What is a dynamical system? Probably the best way to begin this discussion is with arguably a most general and yet least helpful statement: Definition. A dynamical
0.42 DYNAMICAL SYSTEMS Week Lecture Notes. What is a dynamical system? Probably the best way to begin this discussion is with arguably a most general and yet least helpful statement: Definition. A dynamical
209 Sponsored by NC Math and Science Education Network
 Module 8: Using Recursively- Defined Functions to Module and Solve Problems Prepared by Dr. Cos Fi, UNC Greensboro Stephanie Gallop, Guilford County Schools Chapter 8 8.1. North Carolina Standard Course
Module 8: Using Recursively- Defined Functions to Module and Solve Problems Prepared by Dr. Cos Fi, UNC Greensboro Stephanie Gallop, Guilford County Schools Chapter 8 8.1. North Carolina Standard Course
Discrete Calculus and its Applications
 Discrete Calculus and its Applications Alexander Payne Princeton University Abstract We introduce the foundations of discrete calculus, also known as the calculus of finite differences, as an elegant,
Discrete Calculus and its Applications Alexander Payne Princeton University Abstract We introduce the foundations of discrete calculus, also known as the calculus of finite differences, as an elegant,
SECTION 9.2: ARITHMETIC SEQUENCES and PARTIAL SUMS
 (Chapter 9: Discrete Math) 9.11 SECTION 9.2: ARITHMETIC SEQUENCES and PARTIAL SUMS PART A: WHAT IS AN ARITHMETIC SEQUENCE? The following appears to be an example of an arithmetic (stress on the me ) sequence:
(Chapter 9: Discrete Math) 9.11 SECTION 9.2: ARITHMETIC SEQUENCES and PARTIAL SUMS PART A: WHAT IS AN ARITHMETIC SEQUENCE? The following appears to be an example of an arithmetic (stress on the me ) sequence:
SERIES
 SERIES.... This chapter revisits sequences arithmetic then geometric to see how these ideas can be extended, and how they occur in other contexts. A sequence is a list of ordered numbers, whereas a series
SERIES.... This chapter revisits sequences arithmetic then geometric to see how these ideas can be extended, and how they occur in other contexts. A sequence is a list of ordered numbers, whereas a series
A sequence is an ordered list of numbers. Each number in a sequence is called a term. a 1, a 2, a 3,..., a n
 Algebra 2/Trig Unit 8 Sequences and Series Lesson 1 I can identify a pattern found in a sequence. I can use a formula to find the nth term of a sequence. I can write a recursive formula for a sequence.
Algebra 2/Trig Unit 8 Sequences and Series Lesson 1 I can identify a pattern found in a sequence. I can use a formula to find the nth term of a sequence. I can write a recursive formula for a sequence.
7-8 Using Exponential and Logarithmic Functions
 1. PALEONTOLOGY The half-life of Potassium-40 is about 1.25 billion years. a. Determine the value of k and the equation of decay for Potassium-40. b. A specimen currently contains 36 milligrams of Potassium-40.
1. PALEONTOLOGY The half-life of Potassium-40 is about 1.25 billion years. a. Determine the value of k and the equation of decay for Potassium-40. b. A specimen currently contains 36 milligrams of Potassium-40.
9.1 SEQUENCES AND SERIES
 640 Chapter 9 Sequences, Series, and Probability 9. SEQUENCES AND SERIES What you should learn Use sequence notation to write the terms of sequences. Use factorial notation. Use summation notation to write
640 Chapter 9 Sequences, Series, and Probability 9. SEQUENCES AND SERIES What you should learn Use sequence notation to write the terms of sequences. Use factorial notation. Use summation notation to write
UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis
![UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis](/thumbs/81/84201442.jpg) UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis Instructor: Prof. Andrew B. Kahng http://vlsicad.ucsd.edu/~abk/ abk@cs.ucsd.edu 858-822-4884 OHs: W 12:30-1:30pm, F
UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis Instructor: Prof. Andrew B. Kahng http://vlsicad.ucsd.edu/~abk/ abk@cs.ucsd.edu 858-822-4884 OHs: W 12:30-1:30pm, F
Mathematics Achievement
 Section Mathematics Achievement 7 Questions Time: 0 minutes Each question is followed by four suggested answers. Read each question and then decide which one of the four suggested answers is best. Find
Section Mathematics Achievement 7 Questions Time: 0 minutes Each question is followed by four suggested answers. Read each question and then decide which one of the four suggested answers is best. Find
Ch 9/10/11/12 Exam Review
 Ch 9/0// Exam Review The vector v has initial position P and terminal point Q. Write v in the form ai + bj; that is, find its position vector. ) P = (4, 6); Q = (-6, -) Find the vertex, focus, and directrix
Ch 9/0// Exam Review The vector v has initial position P and terminal point Q. Write v in the form ai + bj; that is, find its position vector. ) P = (4, 6); Q = (-6, -) Find the vertex, focus, and directrix
