Erdös-Mordellova nejednakost
|
|
|
- Gertrude Ford
- 5 years ago
- Views:
Transcription
1 Sveu ili²te J. J. Strossmayera u Osijeku Odjel za matematiku Dino Duman i Erdös-Mordellova nejednakost Diplomski rad Osijek, 015.
2 Sveu ili²te J. J. Strossmayera u Osijeku Odjel za matematiku Dino Duman i Erdös-Mordellova nejednakost Diplomski rad Mentor: izv. prof. dr. sc. Zdenka Kolar - Begovi Osijek, 015.
3 Sadrºaj 1 Uvod 4 Erdös-Mordellova nejednakost 5 3 Dokazi Erdös-Mordellove nejednakosti Mordellov dokaz Dokaz Andre Aveza Dokaz Vilmosa Komornika Vizualni dokaz Dokaz kori²tenjem pomo ne gure Veldkampov dokaz Dokaz kori²tenjem kompleksnih brojeva Dokaz Donata K. Kazarinoa Dokaz Hojoo Leeja Barrowova nejednakost 3 5 Teºinska Erdös-Mordellova nejednakost 6 6 Prostorni analogon Erdös-Mordellove nejednakosti 8 7 Generalizacija Erdös-Mordellove nejednakosti 31 Literatura 34 Saºetak 36 Title and summary 37 šivotopis 38
4 1 Uvod U ovome radu istraºena je Erdös-Mordellova nejednakost u kojoj se tvrdi da je zbroj udaljenosti bilo koje to ke unutar trokuta do vrhova trokuta ve i ili jednak od dvostruke udaljenosti te to ke do stranica danog trokuta. Ova nejednakost od svog pojavka godine u American Mathematical Monthly je izazvala veliko zanimanje matemati ara te je objavljen veliki broj dokaza razli ite prirode. U radu su prou avani razli iti dokazi. Navedeni su planimetrijski dokazi, koji su i najbrojniji u literaturi. Prou avani su trigonometrijski, vizualni dokazi kao i dokazi kori²tenjem kompleksnih brojeva te dokazi kori²tenjem pomo ne gure. U radu se prou ava prostorni analogon Erdös-Mordellove nejednakosti. Navedena je i generalizacija ove poznate nejednakosti. 4
5 Erdös-Mordellova nejednakost Paul Erdös bio je jedan od najpoznatijih matemati ara 0. stolje a. Zasluºan je za brojna postignu a u teoriji grafova, teoriji skupova i kombinatorici. Geometriju je zaduºio jednom naizgled jednostavnom nejednakosti koju je postavio godine, Problem 3740, American Mathematical Monthly 4, (1935). Teorem.1. (Erdös-Mordellova nejednakost) Neka je dan trokut ABC i to ka P unutar trokuta. Neka su P A, P B, P C udaljenosti od to ke P do to aka A, B i C, te neka su p a, p b, p c udaljenosti od to ke P do stranica BC, CA i AB. Tada vrijedi P A + P B + P C (p a + p b + p c ). (.1) Jednakost vrijedi ako i samo ako je trokut ABC jednakostrani an i ako je P sredi²te trokutu opisane kruºnice. Slika 1. Iako se ova nejednakost ini jednostavnom, prvi dokaz se pojavio tek godine, a nejednakost su prvi dokazali L. J. Mordell i D. Barrow, Solution to Problem 3740, American Mathematical Monthly 44 (1937). Dani dokaz je trigonometrijski. Ta tvrdnja je izazvala veliku pozornost matemati ke javnosti. Matemati ari su poku- ²avali na ²to jednostavnije na ine dokazati ovu nejednakost. Do danas je objavljen veliki broj dokaza. Neke od tih dokaza navest emo u sljede em poglavlju. 5
6 3 Dokazi Erdös-Mordellove nejednakosti 3.1 Mordellov dokaz Prvi dokaz kojeg emo navesti u ovome radu je dokaz koji je dao L. J. Mordell godine. On je prvi matemati ar koji je dokazao ovu nejednakost. Njegov dokaz koristi poznate trigonometrijske identitete i relacije. Ovaj dokaz se moºe na i u [1]. Slika. Neka je dan trokut ABC i to ka P unutar trokuta, te neka su P A, P B, P C udaljenosti od to ke P do to aka A, B i C. Ozna imo s p a, p b, p c udaljenosti od to ke P do stranica BC, CA, AB trokuta ABC (slika ). Promotrimo etverokut ARP Q. Vrijedi ARP + RP Q + P QA + QAR = RP Q α = 360 RP Q = 180 α. Kako je α+ RP Q = ARP + P QA = 180 slijedi da je etverokut ARP Q tetivni. Primjenjuju i obrat Talesovog teorema na trokute ARP i AP Q, etverokutu ARP Q moºemo opisati kruºnicu polumjera P A, pa stoga i trokutu ARQ moºemo opisati kruºnicu polumjera P A. 6
7 Primjenjuju i formulu koja povezuje polumjer trokutu opisane kruºnice, duljinu stranice i sinus kuta nasuprot te stranice u trokutu RQP slijedi da je RQ = P A sin α. Primjenjuju i kosinusov pou ak na trokut RQP imamo RQ = p b +p c p b p c cos( RP Q) = p b +p c p b p c cos(π α) = p b +p c +p b p c cos α. Kako je RQ = P A sin α, vrijedi P A sin α = p b + p c + p b p c cos[π (β + γ)] = p b + p c + p b p c sin β sin γ p b p c cos β cos γ = p b(sin γ + cos γ) + p c(sin β + cos β) + p b p c sin β sin γ p b p c cos β cos γ = [p b sin γ + p b p c sin β sin γ + p c sin β] + [p b cos γ p b p c cos β cos γ + p c cos β] = (p b sin γ + p c sin β) + (p b cos γ p c cos β) (p b sin γ + p c sin β). Odatle slijedi da je pri emu jednakost vrijedi ako i samo ako je P A sin α p b sin γ + p c sin β, (3.1) p b cos γ = p c cos β. Dijeljenjem nejednakosti 3.1 sa sin α dobivamo Analogno dobivamo sin γ P A p b sin α + p sin β c sin α. sin α P B p c sin β + p sin γ a sin β, sin β P C p a sin γ + p sin α b sin γ, pri emu jednakosti vrijedi ako i samo ako je p c cos α = p a cos γ, p a cos β = p b cos α. Zbrajaju i nejednakosti dobivamo ( sin β P A + P B + P C p a sin γ + sin γ ) ( sin α + p b sin β sin γ + sin γ ) sin α p a + p b + p c = (p a + p b + p c ). 7 ( sin α + p c sin β + sin β ) sin α
8 Da bi vrijedila jednakost treba vrijediti da je sin β sin γ + sin γ sin β =, sin α sin γ + sin γ sin α =, sin α sin β + sin β sin α =, te iz toga slijedi da je α = β = γ, a iz toga proizlazi da je p a = p b = p c. Zaklju ujemo da jednakost vrijedi ako i samo ako je trokut jednakostrani an i ako je P sredi²te trokutu opisane kruºnice. U dokazu smo koristili sljede e: (i) x y + y x, x, y > 0, (ii) sin β sin γ + sin γ sin β = sin β = sin γ β = γ. 3. Dokaz Andre Aveza U ameri kom asopisu The American Mathematical Monthly godine objavljen je Andre Avezov dokaz Erdös-Mordellove nejednakosti. Njegov dokaz se moºe na i u []. On je nejednakost dokazao pomo u Ptolomejevog teorema. Teorem 3.1. Neka je ABCD konveksni etverokut kojemu je opisana kruºnica. Tada je zbroj umno²ka duljina nasuprotnih stranica jednak umno²ku duljina dijagonala. Dokaz Teorema.1 Neka je P to ka unutar trokuta ABC. Neka su udaljenosti od to ke P do vrhova A, B, C redom, P A, P B, P C, a udaljenosti od to ke P do stranica BC, CA i AB redom, p a, p b i p c. Neka k ozna ava kruºnicu opisanu trokutu ABC, te neka je A to ka dobivena presjekom kruºnice i pravca P A kao na slici 3. Tada primjenjuju i Ptolomejev teorem na etverokut ABA C dobivamo A C AB + AC A B = AA BC. (3.) Neka je P Q visina trokuta AP C i neka je to ka A to ka koja je dijametralno suprotna to ki A. Kako su kutovi A AC i A A C sukladni, tada su pravokutni trokuti AP Q i A A C 8
9 Slika 3. sli ni. Ako uzmemo da je promjer kruºnice k jednak 1 tada je AP A C = A A P Q = p b (jer vrijedi A A = 1 i P Q = p b ). Sli no moºemo zaklju iti da je P A A B = p c. Mnoºenjem obje strane jednadºbe (3.) s P A i dijeljenjem s BC dobivamo A C AB P A BC + A B AC P A BC AB BC p b + AC BC p c = P A AA. = AA BC P A, tj. BC Analogno dobijemo jednakosti za ostala dva vrha, te zatim zbrajaju i lijeve i desne strane dobivamo ( AC P A AA +P B BB +P C CC = p a AB + AB AC ) ( AB +p b BC + BC ) ( AC +p c AB BC + BC ). AC Lijeva strana je manja ili jednaka od P A + P B + P C, a jednakost vrijedi ako i samo ako AA = BB = CC = 1, ²to zna i da su AA, BB, CC promjeri kruºnice k, tj. P je sredi²te opisane kruºnice. S druge strane, desna strana je ve a ili jednaka od (p a +p b +p c ), a jednakost vrijedi ako i samo ako je AB = AC = BC. 9
10 3.3 Dokaz Vilmosa Komornika Sljede i dokaz dao je matemat ar Vilmos Komornik. On je svoj dokaz objavio godine, takožer u asopisu The American Mathematical Monthly ([9]). Slika Prvo emo promatrati to ku P koja se nalazi na stranici BC kao na slici 4. Tada je dvostruka povr²ina trokuta AP C jednaka bp b, dok je dvostruka povr²ina trokuta ABP jednaka cp c. Tada je povr²ina trokuta ABC jednaka 1 (bp b +cp c ). P A je ve a ili jednaka od visine trokuta povu ene iz vrha A. Tada je ap A bp b + cp c. (3.3) Napomenimo da nejednakost vrijedi za svaku to ku P unutar trokuta ABC. Dovoljno je napomenuti da je nejednakost (3.3) ekvivalentna (po sli nosti) nejednakosti koja se odnosi na to ku P, presjeci²te stranice BC i polupravca AP.. Ako je trokut jednakostrani an tada se nejednakost (3.3) moºe podijeliti s a = b = c i dodati ih dvjema analognim nejednakostima P B p c + p a i P C p a + p b. Dokaz nejednakosti (3.3) pokazuje da jednakost u Erdös Mordellovoj nejednakosti vrijedi ako P leºi na svima visinama trokuta ABC, tj. ako je P ortocentar jednakostrani nog trokuta ABC. Tada je P sredi²te trokutu opisane kruºnice. 10
11 3. Ako trokut nije jednakostrani an, tada trebamo jednostavnu posljedicu nejednakosti (3.3). Primjenjuju i (3.3) na reeksiju P to ke P u odnosu na simetralu kuta BAC, imamo P A = P A, p b = p c, p c = p b. Tada je ap A bp c + cp b. Ako je P unutar trokuta ABC, tada imamo i bp B cp a + ap c, te cp C ap b + bp a, te slijedi da je P A + P B + P C ( b c + c ) ( c p a + b a + a ) ( a p b + c b + b ) p c > (p a + p b + p c ). a U zadnjem dijelu nejednakosti imamo strogu nejednakost jer a, b i c nisu jednaki. 3.4 Vizualni dokaz Sljede i dokaz Erdös-Mordellove nejednakosti dali su C. Alsina i R. B. Nelsen 007. godine. Oni su Erdös-Mordellovu nejednakost dokazali na vrlo jednostavan na in. Njihov dokaz se moºe na i u [1]. Promotrimo trokut P QA (slika 5.a). Konstruirajmo njemu sli an trokut s koecijentom sli nosti c. Na isti na in konstruirajmo trokut sli an trokutu P RA s koecijentom sli nosti b (slika 5.b). Tada je B A C = 180 (90 α + 90 α 1 ) = 180 (180 α) = α. Trokuti ABC i A B C su sli ni prema teoremu SKS o sli nosti trokuta pa slijedi A B C = β, A C B = γ pa je B C = ap A. ap A ne moºe biti manje od cp b + bp c tj. ap A cp b + bp c pa je c P A p b a + p b c a. Analogno se dobije a P B p c b + p c a b, a P C p b c + p b a c. Tada zbrajaju i sve nejednakosti i dobivamo 11
12 5.a 5.b Slika 5. P A + P B + P C ( b c + c ) ( c p a + b a + a ) ( a p b + c b + b ) p c (p a + p b + p c ). a Jednakost u (.1) vrijedi ako vrijede jednakosti c P A = p b a + p b c a, P a B = p c b + p c a b, P a C = p b c + p b a c, odnosno ako i samo ako je trapez na desnoj slici pravokutnik, a to vrijedi ako i samo ako je β + α = π i γ + α 1 = π. Sli no moºemo zaklju iti i u preostala dva slu aja. Tada slijedi da je AP Q = β = CP Q pa su stoga pravokutni trokuti AP Q i CP Q sukladni. Tada je P A = P C, a sli no moºemo zaklju iti kako je P A = P B. Tada je P A = P B = P C pa je stoga P sredi²te trokutu opisane kruºnice. Takožer, jednakost mora vrijediti ako i samo ako je b c + c b =, a to vrijedi ako i samo ako je a = b = c. c a + a c =, c a + a c =, 3.5 Dokaz kori²tenjem pomo ne gure Promotrimo prvo etverokut AQP R (slika 6). Kako je ARP = AQP = 90 tada je etverokut AQP R tetivni pa mu moºemo opisati kruºnicu, a kutovi ϕ i θ su 1
13 Slika 6. sukladni jer su to kutovi nad istom tetivom kruºnice koja prolazi to kama A, Q, P, R. Primjenjuju i sinusov pou ak na trokut AQP dobivamo P A sin( AQP ) = AQ sin θ P A = AQ sin ϕ. (3.4) Primijenimo sada sinusov pou ak na trokut ARQ: RQ sin α = AQ sin ϕ Iz 3.4 i 3.5 slijedi da je P A = RQ sin α, tj. P A sin α = RQ. RQ sin ϕ AQ =. (3.5) sin α U etverokutu RP QA vrijedi da je RP Q α + 90 = 360, pa je stoga RP Q = 180 α. Tada vrijedi da je cos( RP Q) = cos α. Primjenjuju i kosinusov pou ak na trokut RP Q imamo RQ = p b + p c p b p c cos( QP R) = p b + p c + p b p c cos α. Neka je ABC = β i ACB = γ. Tada je α + β + γ = 180, tj. α = 180 (β + γ). Vrijedi da je cos α = cos[180 (β+γ)] = cos(β+γ) = (cos β cos γ sin β sin γ) = sin β sin γ cos β cos γ. 13
14 Tada je RQ = p b + p c + p b p c (sin β sin γ cos β cos γ) = p b + p c + p b p c sin β sin γ p b p c cos β cos γ = p b(sin γ + cos γ) + p c(sin β + cos β) + p b p c sin β sin γ p b p c cos β cos γ = (p b sin γ + p c sin β) + (p b cos γ p c cos β) (p b sin γ + p c sin β). Sada dobivamo RQ = P A sin α p b sin γ + p c sin β sin γ odakle dobivamo P A p b + p sin α c sin β. sin α Analogno vrijedi sin α P B p c sin β + p sin γ a sin β i P sin β C p a sin γ + p sin α b sin γ. Zbrajaju i nejednakosti dobivamo ( sin β P A + P B + P C p a sin γ + sin γ ) ( sin α + p b sin β sin γ + sin γ ) sin α p a + p b + p c = (p a + p b + p c ). ( sin α + p c sin β + sin β ) sin α Jednakost dobijemo na sli an na in kao ²to smo napravili u Mordellovom dokazu. Dokaz se moºe na i u [4]. 3.6 Veldkampov dokaz Neka je P to ka simetri na to ki P s obzirom na simetralu AD kuta CAB kao na slici 7. Ozna imo li s p a, p b, p c udaljenosti to ke P od stranica BC, CA, AB, onda je p b = p c i p c = p b. Kako vrijedi da je AP = AP = P A, tada prema nejednakosti trokuta vrijedi da je P A + p a v a, a odatle je 1 ap A 1 av a 1 ap a, odnosno 1 ap A P ABC P BP C = P ABP C = P ABP + P ACP. Tada je 1 ap A 1 cp c + 1 bp b = 1 cp b + 1 bp c, a odatle slijedi P A c a p b + b a p c. Analogno dobijemo P B a b p c + c b p a i P C a c p b + b c p a. 14
15 Slika 7. Zbrajanjem ovih nejednakosti dobijemo P A + P B + P C ( b c + c b )p a + ( c a + a c )p b + ( a b + b a )p c (p a + p b + p c ). Jednakost vrijedi ako i samo ako vrijedi jednakost P A + p a = v a, te b c + c b =, c a + a c =, a b + b a =, a to vrijedi ako i samo ako je trokut ABC jednakostrani an, a P sredi²te trokutu opisane kruºnice. Ovaj dokaz se moºe na i u [1]. 3.7 Dokaz kori²tenjem kompleksnih brojeva Neka je ABC trokut i O to ka unutar trokuta. Postavimo koordinatni sustav tako da je ishodi²te u to ki O. Neka je A to ka koja se nalazi na pozitivnom dijelu x-osi, B to ka koja se nalazi u 1. ili. kvadrantu, te C to ka koja se nalazi u 3. ili 4. kvadrantu. To ke A, B, C moºemo zapisati kao kompleksne brojeve na sljede i 15
16 Slika 8. na in: A = A e iθ A, θ A = 0 B = B e iθ B, θ B (0, π) C = C e iθ C, θ C [π, π) i θ C θ B (0, π). S ovakvim rasporedom vrhova osiguravamo da to ka O leºi unutar trokuta ABC. Nadalje, s P ozna imo noºi²te visine iz to ke O na stranicu BC, s Q noºi²te visine iz to ke O na stranicu AC, te R noºi²te visine iz to ke O na stranicu AB. Tada Erdös-Mordellovu nejednakost moºemo zapisati A + B + C ( P + Q + R ). U ovom dokazu upotrebljavat emo dot i cross umno²ke kompleksnih brojeva. Neka su z 1 = x 1 + iy 1 i z = x + iy. Dot umnoºak deniramo kao z 1 z = x 1 x + y 1 y = Re{z 1 z } = z 1z +z 1 z. Cross umnoºak deniramo kao z 1 z = x 1 y y 1 x = Im{z 1 z } = z 1z z 1 z i. Tada je z 1 z = z 1 z + iz 1 z. 16
17 Lako se pokaºe da vrijedi z 1 z = z z 1 i z 1 z = z z 1. Takožer vrijede i jo² neka svojstva: (i) zz = z z = z, (ii) z z = 0, (iii) z(iz) = i[z (iz)] = i z, (iv) z (iz) = 0. Koriste i jednakost (z 1 z ) n = z1 n z n, posebno za n =, lako se pokaºe da vrijedi z1 z = (z 1 z ) (z 1 z ) z1 z = (z 1 z )(z 1 z ). Vrijedi da je (z 1 z )(z 1 +z ) = (z 1 z ) (z 1 +z )+i(z 1 z ) (z 1 +z ) = ( z 1 z )+iz 1 z, iz ega imamo z 1 z = ( z 1 z ) + (z 1 z ). Dakle, z 1 z z 1 z, gdje jednakost vrijedi ako i samo ako z 1 = z. Neka je OF G trokut i neka je H noºi²te visine iz O na F G. Uzimaju i u obzir povr²inu trokuta OF G i kompleksne brojeve pridruºene to kama F, G i H imamo H F G = F G = P OF G. Tada je H = F G F G Ako je F = f i G = g dobivamo = Im{F G} F G = F G F G. F G H = f g f g = f g f g f g f g f g f g = f g, 17
18 gdje jednakost vrijedi ako i samo ako f = g Neka je A = a, B = b, C = c, gdje je a = a e iθa, θ a = 0 i θ a = θ A b = b e iθ b, θ b (0, π ) i θ b = θ B c = c e iθc, θ c [ π, π) i θ c = θ C. Vrijedi A + B + C P Q R a + b + c b c c a a b pri emu jednakost vrijedi ako i samo ako a = b = c. Kako je a b 0, b c 0, c a 0 slijedi A + B + C P Q R a a + b b + c c b c + c a a b = (a b + c) (a b + c) = a b + c 0 pri emu jednakost vrijedi ako i samo ako a b + c = 0. Koriste i dot umnoºak na a, b i c dobivamo sljede i sustav jednadºbi a b a b c = b c a c Odakle dobivamo Ako je a = b = c = d, dobivamo a b b c = a b. c a c a b b c = c a d,
19 i tada je θ b = π i θ 3 c = π, pa je u slu aju jednakosti trokut ABC jednakostrani an 3 i O je sredi²te trokutu opisane kruºnice. Dokaz se moºe na i u [5]. 3.8 Dokaz Donata K. Kazarinoa Kazarino je dokazao Erdös-Mordellovu nejednakost pomo u Pappusovog teorema. Teorem 3.. Neka je ABC trokut te ABDE i ACF G dva paralelograma koji, ili obojica leºe ili nijedan od njih ne leºi potpuno izvan trokuta ABC. Neka je H sjeci²te duºina DE i F G, i neka je BCKL paralelogram ija je stranica KL dobivena translacijom duºine BC za HA. Tada je zbroj povr²ina ABDE i ACF G jednak povr²ini od BCKL. Slika 9: Pappusov teorem, P ABDE + P ACF G = P BCKL Promotrimo trokut ABC (slika 10). Neka je S sredi²te opisane kruºnice trokuta ABC, te neka je M sjeci²te duºine BC i simetrale kuta BAC. Nadalje, neka je trokut B AC zrcalna slika trokuta ABC u odnosu na simetralu kuta BAC. Sada primjeniv²i Pappusov teorem na trokut B AC uz napomenu da je SA B C dobivamo AP cos(ap, AS) B C = AC p c + AB p b, 19
20 odnosno Takožer vrijedi da je pa je stoga Analogno dobijemo Slika 10. a AP cos(ap, AS) = bp c + cp b. a AP a AP cos(ap, AS) = bp c + cp b, AP b a p c + c a p b. BP c b p a + a b p c i CP a c p b + b c p a. Zbrajanjem ovih nejednakosti dobivamo ( b AP + BP + CP c + c ) p a + b ( c a + a c ) p b + ( a b + b ) p c (p a + p b + p c ). a Jednakost se postiºe za cos(ap, AS) = 1, a cos(ap, AS) je jednak 1 kada P leºi na promjeru opisane kruºnice koji prolazi to kom A. Analogno, ako je cos(bp, BS) = 1 i cos(cp, CS) = 1 tada P mora leºati u sredi²tu opisane kruºnice. Kako vrijedi AP + BP + CP = ( b c + c b )p a + ( c a + a c )p b + ( a b + b a )p c = (p a + p b + p c ) 0
21 tada mora biti b c + c b =, a c + c a = i b a + a b = pa slijedi da je a = b = c. Ovaj dokaz se moºe na i u [7]. 3.9 Dokaz Hojoo Leeja Ovaj dokaz je planimetrijski i moºe se na i u [10]. Slika 11. Neka je HG ortogonalna projekcija stranice BC na pravac RQ kao na slici 11. Tada vrijedi BC HG = HR + RQ + QG. Kako vrijedi BRH = ARQ = AP Q slijedi da su pravokutni trokuti BRH i AP Q sli ni i vrijedi P Q HR = P A BR. Sli no dobivamo QG = P R P A CQ. Primjenom Ptolomejevom teorema na etverokut ARP Q dobivamo P A RQ = AR P Q + AQ P R, 1
22 odnosno Dobivamo odnosno BC RQ = AR P Q + AQ P R. P A P Q AR P Q + AQ P R P R BR + + P A P A P A CQ, BC P A P Q BR + AR P Q + AQ P R + P R CQ. Djeljenjem prethodne jednakosti s BC dobivamo P A AB AC P Q + P R. BC BC Ponovimo sli an postupak na druge dvije ortogonalne projekcije i dobijemo P B BC AB P R + P O CA AC i P C AC BC P O + P Q. AB AB Zbrajaju i ove nejednakosti dobivamo ( AB P A + P B + P C AC + AC AB ( P O + P Q + P R ). ) ( AB P O + BC + BC AB ) ( AC P Q + BC + BC ) P R AC Jednakost vrijedi ako i samo ako je AB = BC = CA te ako je P sredi²te trokutu opisane kruºnice.
23 4 Barrowova nejednakost Sljede a nejednakost koju emo navesti je Barrowova nejednakost. Nazvana je prema ameri kom matemati aru D. F. Barrowu koji je nejednakost prvi i dokazao godine. Njegova nejednakost je o²trija od Erdös-Mordellove nejednakosti i ona glasi ovako: Teorem 4.1. (Barrowova nejednakost) Neka je P to ka koja se nalazi unutar trokuta ABC i neka su U, V i W to ke gdje simetrale kutova BP C, CP A, AP B sijeku, redom stranice BC, CA i AB. Tada vrijedi P A + P B + P C ( P U + P V + P W ). Jednakost vrijedi ako i samo ako je trokut ABC jednakostrani an a P je sredi²te trokutu opisane kruºnice. Dokaz Barrowove nejednakosti moºe se na i u [11]. Slika 1. Za dokaz ove nejednakosti bit e nam potrebna sljede a lema koju u navesti bez dokaza. Lema 4.1. Neka su p, q i r pozitivni realni brojevi i neka su θ 1, θ, θ 3 realni brojevi takvi da je θ 1 + θ + θ 3 = π. Tada vrijedi Dokaz Teorema 4.1 p cos θ 1 + q cos θ + r cos θ 3 1 (qr p + rp q + pq r ). 3
24 Neka je θ 1 = BP C, θ = CP A, θ 3 = AP B. Promatrajmo trokut BP C, te trokute BP U i P CU sa slike 1. U trokutu CP U prema sinusovom pou ku vrijedi je odakle dobivamo CU sin θ 1 = P U sin γ 1 CU = P U sin θ 1 sin γ 1. U trokutu P BU prema sinusovom pou ku vrijedi da je BU sin θ 1 = P U sin β 1 BU = P U sin θ 1 sin β 1. Zatim primjenjuju i sinusov pou ak na trokut P BC dobivamo da je BC sin θ 1 = P B sin γ 1. Odatle slijedi BC sin γ 1 = P B sin θ 1, odnosno ( BU + CU ) sin γ 1 = P B sin θ 1. Valja napomenuti kako primjenjuju i sinusov pou ak na trokute P BU i P BC mo- ºemo do i do jednakosti sin γ 1 P B = sin β 1 P C. Tada vrijedi ( P U sin θ 1 sin β 1 + P U sin θ 1 sin γ 1 ) sin γ 1 = P B sin θ 1 P U sin θ 1 ( sin γ 1 + 1) = sin θ 1 cos θ 1 P B sin β 1 P B P U ( P C + 1) = cos θ 1 P B P B + P C P U ( ) = cos θ 1 P B P C P B P C P U = cos θ 1 P B + P C 4
25 Na sli an na in dobijemo sljede e jednakosti P V = P W = P C P A cos θ P C + P A P A P B cos θ 3. P A + P B Napomena: Prema A-G nejednakosti vrijedi da je a + b ab, odnosno vrijedi 1 1 a+b. ab Prema A-G nejednakosti i korolaru vrijedi da je 1 P U + P V + P W = P B P C cos θ 1 P B + P C + P C P A cos θ 1 P C + P A 1 + P A P B cos θ 3 P A + P B 1 P B P C cos θ 1 P B P C + P C P A cos θ 1 P A P C 1 + P A P B cos θ 3 P A P B = P B P C cos θ 1 + P A P C cos θ + P A P B cos θ 3 1 ( P A + P B + P C ). Jednakost vrijedi kada je P A = P B = P C i θ 1 = θ = θ 3 = 60, odnosno kada je trokut ABC jednakostrani an i P sredi²te trokutu opisane kruºnice. To se moºe lako provjeriti direktnim uvr²tavanjem u gornje jednakosti. 5
26 5 Teºinska Erdös-Mordellova nejednakost 001. godine u ameri kom asopisu The American Mathematical Monthly S. Dar i S. Gueron objavili su lanak u kojem su poop ili Erdös-Mordellovu nejednakost tako da su joj dodali teºine te dobili teºinsku Erdös-Mordellovu nejednakost. Teorem 5.1. (Teºinska Erdös-Mordellova nejednakost) Neka je dan trokut ABC i to ka P unutar trokuta. Neka su P A, P B, P C udaljenosti od to ke P do to aka A, B i C, te neka su p a, p b, p c udaljenosti od to ke P do stranica BC, CA i AB. Za pozitivne realne brojeve λ 1, λ, λ 3 vrijedi λ 1 P A + λ P B + λ 3 P C λ 1 λ λ 3 ( p a λ1 + p b λ + p c λ3 ). Jednakost vrijedi ako i samo ako je λ 1 : λ : λ 3 = a : b : c i P je sredi²te opisane kruºnice trokutu ABC. Walther Janous je 004. godine objavio lanak u kojem je poop io teºinsku Erdös-Mordellovu nejednakost. U njegovom lanku su se na²la sljede a dva teorema iji se dokazi mogu na i u [6]. Teorem 5.. Neka su λ 1, λ, λ 3, t pozitivni realni brojevi i neka je 0 < t 1. Tada vrijedi λ 1 PA t + λ PB t + λ 3 PC t t λ 1 λ λ 3 ( pt a + λ1 pt b λ + pt c λ3 ). Jednakost vrijedi ako i samo ako je λ 1 : λ : λ 3 = a t : b t : c t i P je sredi²te opisane kruºnice trokutu ABC. Dokaz. Iz dokaza iz 3. poglavlja vrijedi Tada za 0 < t 1 vrijedi P A c a p b + b a p c, P B a b p c + c b p a, P C b c p a + a c p b. P t A t ( c a p b + b a p c Na isti na in dobijemo sljede e nejednakosti P t B t ( a b )t p t c + ( c b )t p t a ) t t ( c a )t p t b + ( b a )t p t c., PC t t ( b c )t p t a + ( a c )t p t b. 6
27 Zbrajaju i ove nejednakosti te primjenju i A-G nejednakosti dobivamo λ 1 P t A + λ P t B + λ 3 P t C λ 1 ( t ( c a )t p t b + ( b a )t p t c ) + λ ( t ( a b )t p t c + ( c b )t p t a ) + λ 3 ( t ( b c )t p t a + ( a c )t p t b ) = t ( ( c b )t λ + ( b c )t λ 3 p t a + ( a c )t λ 3 + ( c a )t λ 1 p t b + ( b a )t λ 1 + ( a b )t λ p t c) t ( λ λ 3 p t a + λ 3 λ 1 p t b + λ 1 λ p t c). Iz prija²njih dokaza moºemo zaklju iti da jednakost vrijedi ako je P sredi²te trokutu opisane kruºnice, te mora vrijediti da je ( b a )t λ 1 = ( a b )t λ i ( c b )t λ = ( b c )t λ 3. Odatle slijedi da je λ 1 : λ : λ 3 = a t : b t : c t. Teorem 5.3. Neka su λ 1, λ, λ 3, t pozitivni realni brojevi i neka je t > 1. vrijedi λ 1 PA t + λ PB t + λ 3 PC t λ 1 λ λ 3 ( pt a + λ1 pt b λ + pt c λ3 ). Tada Jednakost vrijedi ako i samo ako je λ 1 : λ : λ 3 = a t : b t : c t i P je sredi²te opisane kruºnice trokutu ABC. Dokaz slijedi iz prethodnog teorema i injenice da je t >, t > 1. 7
28 6 Prostorni analogon Erdös-Mordellove nejednakosti godine je D. K. Kazarino objavio svoj rad u kojem daje analogon Erdös- Mordellove nejednakosti za trokut. Njegov dokaz se moºe na i u [8]. Teorem 6.1. (Erdös-Mordellova nejednakost za tetraedar) Neka je S tetraedar ABCD i P to ka unutar tog tetraedra. Neka su P A, P B, P C, P D udaljenosti to ke P do vrhova A, B, C i D, a p a, p b, p c, p d udaljenosti to ke P do, redom, ravnina odreženih to kama BCD, ACD, ABD i ABC. Tada za tetraedar ije je sredi²te opisane sfere unutar tetraedra vrijedi i je najve a donja meža. P A + P B + P C + P D p a + p b + p c + p d > Slika 13. Uvedimo sa H A, H B, H C, H D visine iz vrhova A, B, C, D tetraedra S te sa R polumjer tetredru opisane sfere sa sredi²tem O. Veliku vaºnost u dokazivanju teorema ima Pappusov teorem poop en na tri dimenzije. 8
29 Teorem 6.. Konstruirane su tri trostrane prizme ije su baze strane tetraedra S, koje imaju zajedni ki brid i koje, ili sve leºe ili nijedna od njih ne leºe u potpunosti izvan tetraedra S. Na preostaloj strani konstruirana je etvrta prizma iji su bo ni bridovi sukladni i paralelni zajedni kom bridu prve tri prizme. Tada je zbroj volumena prve tri prizme jednak volumenu etvrte prizme. Veliku vaºnost u dokazivanju imaju i sljede e dvije leme iz kojih direktno proizlazi na² teorem. Ozna imo s d A = AB + AC + AD RH A, d B = BA + BC + BD RH B, d C = CA + CB + CD RH C, d D = DA + DB + DC RH D. Lema 6.1. Za bilo koji tetraedar S vrijedi P A + P B + P C + P D d A p a + d B p b + d C p c + d D p d. Jednakost vrijedi ako i samo ako se to ke P i O podudaraju. Lema 6.. Ako se to ka O nalazi unutar tetraedra S, tada su d A, d B, d C i d D strogo ve i od. Iz toga direktno slijedi dokaz Teorema 6.1. Teorem 6.3. Za svaki tetraedar S, kome se u jednom vrhu sastaju tri okomita brida, vrijedi P A + P B + P C + P D p a + p b + p c + p d >. Ovdje valja napomenuti kako se sredi²te opisane sfere uvijek nalazi izvan tetraedra S. Dokaz. Neka je A vrh u kojem se sastaju tri okomita brida. U tetraedru S vrijedi 1 = 1 AB + 1 AC + 1 AD, H A R = AB + AC + AD. Tada je 1 d A = [ AB + AC + AD ][ AB + 1 AC + 1 AD ] 9 = 3 >. 9
30 Provjerimo sada za vrh B. d B = BA + BC + BD RH B = BA + BA + AC + AB + AD RH B = 3 AB + AC + AD Ra = AB + AC + AD + AB Ra = 4R + a = R Ra a + a R. Isto vrijedi za vrhove C i D. Posljednja nejednakost slijedi iz injenice da je x + y y x dokazan., te je time teorem 30
31 7 Generalizacija Erdös-Mordellove nejednakosti Kako se Erdös-Mordellova nejednakost odnosi na trokut, tako ju moºemo poop iti na n-terokut. Prvi matemati ar koji je izrekao Erdös-Mordellovu nejednakost za n-terokute bio je L. Fejes-Tóth, a prvi ju je dokazao H. C. Lenhart godine. Teorem 7.1. Neka je M n-terokut s vrhovima A 0, A 1,... A n 1 i neka je O to ka unutar konveksnog n-terokuta M. Neka su R i udaljenosti od O do A i, a r i udaljenosti od O do stranica A i A i+1 (gdje je A n = A 0 ). Tada vrijedi cos π n 1 n n 1 R i r i. Jednakost vrijedi ako i samo ako je M pravilan n-terokut sa sredi²tem O. i=0 Ovdje emo navesti dokaz matemati ara M. Dinc a, a ovaj dokaz se moºe prona i u [3]. Za dokaz na²e nejednakosti potreban nam je sljede i teorem. Teorem 7.. Za svaki x k 0, 1 k n, x n+1 = x 1 i α k (0, π) takav da je n α k = π vrijedi cos π n n x k = i=0 n x k x k+1 cos α k. (7.1) Dokaz. Neka je dano ishodi²te O = (0, 0), to ke P k = (a k, b k ), 1 k n, u ravnini takve da (P k OP k+1 ) = α k, 1 k n 1, i neka je n 1 α k = π α n. Ozna imo x k = OP k = a k + b k. Primjenjuju i kosinusov pou ak na trokut P k OP k+1, 1 k n 1, te na trokut P 1 OP n dobivamo x k x k+1 cos α k = 1 ( OP k + OP k+1 P k P k+1 ) = 1 (a k + b k + a k+1 + b k+1 (a k a k+1 ) (b k b k+1 ) ) = a k a k+1 + b k b k+1, gdje je k = 1,,..., n 1 n 1 x 1 x n cos α n = x 1 x n cos(π α k ) n 1 = x 1 x n cos( α k ) = 1 ( OP 1 + OP n P 1 P n ) = a 1 a n b 1 b n 31
32 Tada je cos π n n x k n x k x k+1 cos α k = cos π n n n n 1 (a k + b k) (a k a k+1 + b k b k+1 ) + a 1 a n + b 1 b n 1 = sin kπ n n 1 + sin kπ n 0 sin (k+1)π n sin (k+1)π n (sin (sin (k + 1)π a k sin kπ n n a k+1 + sin π n a n) + (k + 1)π b k sin kπ n n b k+1 + sin π n b n) Dokaºimo posljednju jednakost. Dokaºimo prvo da je cos π n n n 1 a k a k a k+1 +a 1 a n = n sin kπ n 1 sin (k+1)π n (sin (k + 1)π a k sin kπ n n a k+1+sin π n a n) usporežuju i koecijente uz a k i a ka k+1. Koecijent uz a k je sin (k+1)π n sin kπ n + sin (k 1)π n sin kπ n = sin kπ n cos π n sin kπ n = cos π n, za k=,..., n-. Koecijent uz a 1 je Koecijent uz a n 1 je Koecijent uz a n je sin π n sin π n sin (n )π n sin (n 1)π n = sin π n cos π n sin π n = sin π n sin π n = cos π n. = cos π n. n sin kπ n sin π n (k+1)π sin n = n sin π n (ctg kπ n (k + 1)π ctg ) = sin π n n (ctg π n (n 1)π ctg ) = cos π n n. 3
33 Koecijent uz a k a k+1 je za,,..., n. Koecijent uz a n 1 a n je sin (k+1)π n sin kπ n sin kπ n (k+1)π sin n = 1, sin (n )π n sin (n )π n sin π n sin (n 1)π n = sin π n sin π n Koecijent uz a 1 a n je sin π sin π n n sin π sin π = 1. n n A koecijenti uz a k a n za k =, 3,..., n su = 1. n k= sin (k+1)π n sin kπ n sin π n sin (k+1)π n n 3 Na isti na in se dokaºe da je sin kπ n sin π n sin kπ n sin (k+1)π n = n sin π n sin kπ k= n n 3 sin π n sin (k+1)π n = 0. cos π n n n 1 b k b k b k+1 +b 1 b n = n sin kπ n 1 sin (k+1)π n (sin (k + 1)π b k sin kπ n n b k+1+sin π n b n). te je tako dokazana jednakost. Neka su A 1, A,..., A n vrhovi konveksnog n-terokuta i neka se to ka P nalazi unutar tog n-terokuta. Neka je R k = P A k i neka je r k udaljenost od P do stranice A k A k+1. Uzimamo u obzir da je A n+1 = A 1. Iz nejednakosti 7.1 za x k = R k vrijedi cos π n n R k n Rk Rk+1 cos α k n w k n r k. 33
34 Literatura [1] C. Alsina, R. B. Nelsen, A Visual Proof of the Erdös-Mordell Inequality, Forum Geometricorum, 7(007), [] A. Avez, A Short Proof of a Theorem of Erdös and Mordell, The American Mathematical Monthly, 100(1993), 60-6 [3] M. Dinc a, A Simple Proof of the Erdös-Mordell Inequality for Polygons in n- dimensional Spaces, Gazeta Matematica-B, 4(009), [4] A. Dreiling, Mathematical Inequalities, San Jose State University, Disertacija, [5] F. Dubeau, Complex numbers and the Erdös-Mordell inequality, Département de mathématiques, 134(013), and-the-erdas-mordell-inequality-universitac-de- [6] W. Janous, Further Inequalities of Erdös-Mordell Type, Forum Geometricorum, 4(004), [7] D. K. Kazarinoff, A Simple Proof of the Erdös-Mordell Inequality for Triangles, The Michigan Mathematical Journal, 4(1957), [8] N. D. Kazarinoff, D. K. Kazarino's Inequality for Tetrahedra, The Michigan Mathematical Journal, 4(1957), [9] V. Komornik, A Short Proof of the Erdös-Mordell Theorem, The American Mathematical Monthly, 104(1997), [10] H. Lee, Another Proof of the Erdös-Mordell Theorem, Forum Geometricorum, 1(001),
35 [11] H. Lee, Topics in Inequalities-Theorems and Techniques, Korea Institute for Advanced Study, Skripta, Theorems-and-Techniques.pdf [1] A. Mari, Erdös-Mordellova nejednakost, Matemati ko-zi ki list, 4( ), [13] D. S. Mitrinovi, J. E. Pe ari, V. Volenec, Recent Advances in Geometric Inequalities, Kluwer Academic Publishers, Dordrecht,
36 Saºetak U ovome radu opisana je Erdös-Mordellova nejednakost. U prvom dijelu rada navedeno je niz razli itih dokaza ove nejednakosti mežu kojima je i Mordellov dokaz, prvi dokaz ove nejednakosti. U drugom dijelu rada navedena je Barrowova nejednakost koja je o²trija od Erdös-Mordellove nejednakosti. Nakon toga su navedena neka poop enja Erdös-Mordellove nejednakosti. Prva od njih je teºinska Erdös-Mordellova nejednakost koju su prvi puta prezentirali S. Dar i S. Gueron 001. godine, te te- ºinska Erdös-Mordellova nejednakost u kojoj kongurira eksponent t a do koje je do²ao matemati ar W. Janous. U radu je spomenut i rad D. K. Kazarinoa u kojem poop ava Erdös-Mordellovu nejednakost na tetraedar. U zadnjem dijelu rada navedena je Erdös-Mordellova nejednakost u n-terokutu i njen dokaz. 36
37 Title and summary Erdös-Mordell inequality In this paper it is described Erdös-Mordell inequality. In the rst part of this paper several dierent proofs of this inequality are listed, including rst proof that was given by L. J. Mordell. In the second part of this paper we give Barrow's inequality which is sharper than Erdös-Mordell inequality. Then we give some generalizations of Erdös-Mordell inequality. First of them is weighted Erdös-Mordell inequality that was rst presented by S. Dar and S. Gueron in 001, and weighted Erdös-Mordell inequality with exponent t that was rst presented by W. Janous. In the paper it is mentioned D. K. Kazarino's work on Erdös-Mordell inequality for tetrahedra. In the last part of this paper we give proof of Erdös-Mordell inequality for polygons in n-dimensional spaces. 37
38 šivotopis Rožen sam. oºujka 199. godine u Na²icama. Osnovnu ²kolu pohažao sam u Donjem Miholjcu te sam tijekom osnovno²kolskog obrazovanja sudjelovao na nekoliko ºupanijskih natjecanja iz matematike. Srednju ²kolu sam takožer upisao u Donjem Miholjcu. U tom razdoblju sudjelovao sam na ºupanijskim natjecanjima iz matematike, a najzna ajnija postignu a su mi sudjelovanje na drºavnim natjecanjima iz matematike u 3. i 4. razredu srednje ²kole godine upisao sam se na Odjel za matematiku, Sveu ili²ta J. J. Strossmayera u Osijeku na petogodi²nji Sveu ili²ni nastavni ki studij matematike i informatike. 38
TEORIJA SKUPOVA Zadaci
 TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
Funkcijske jednadºbe
 MEMO pripreme 2015. Marin Petkovi, 9. 6. 2015. Funkcijske jednadºbe Uvod i osnovne ideje U ovom predavanju obradit emo neke poznate funkcijske jednadºbe i osnovne ideje rje²avanja takvih jednadºbi. Uobi
MEMO pripreme 2015. Marin Petkovi, 9. 6. 2015. Funkcijske jednadºbe Uvod i osnovne ideje U ovom predavanju obradit emo neke poznate funkcijske jednadºbe i osnovne ideje rje²avanja takvih jednadºbi. Uobi
HRVATSKA MATEMATIČKA OLIMPIJADA
 HRVATSKA MATEMATIČKA OLIMPIJADA prvi dan 5. svibnja 01. Zadatak 1. Dani su pozitivni realni brojevi x, y i z takvi da je x + y + z = 18xyz. nejednakost x x + yz + 1 + y y + xz + 1 + z z + xy + 1 1. Dokaži
HRVATSKA MATEMATIČKA OLIMPIJADA prvi dan 5. svibnja 01. Zadatak 1. Dani su pozitivni realni brojevi x, y i z takvi da je x + y + z = 18xyz. nejednakost x x + yz + 1 + y y + xz + 1 + z z + xy + 1 1. Dokaži
ZANIMLJIVI ALGEBARSKI ZADACI SA BROJEM 2013 (Interesting algebraic problems with number 2013)
 MAT-KOL (Banja Luka) ISSN 0354-6969 (p), ISSN 1986-5228 (o) Vol. XIX (3)(2013), 35-44 ZANIMLJIVI ALGEBARSKI ZADACI SA BROJEM 2013 (Interesting algebraic problems with number 2013) Nenad O. Vesi 1 Du²an
MAT-KOL (Banja Luka) ISSN 0354-6969 (p), ISSN 1986-5228 (o) Vol. XIX (3)(2013), 35-44 ZANIMLJIVI ALGEBARSKI ZADACI SA BROJEM 2013 (Interesting algebraic problems with number 2013) Nenad O. Vesi 1 Du²an
FEUERBACHOVA TOČKA. Maja Mihalic PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK. Diplomski rad. Voditelj rada: doc. dr. sc.
 SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Maja Mihalic FEUERBACHOVA TOČKA Diplomski rad Voditelj rada: doc. dr. sc. Mea Bombardelli Zagreb, srpanj, 2015. Ovaj diplomski
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Maja Mihalic FEUERBACHOVA TOČKA Diplomski rad Voditelj rada: doc. dr. sc. Mea Bombardelli Zagreb, srpanj, 2015. Ovaj diplomski
ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA. Šefket Arslanagić, Sarajevo, BiH
 MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
A B A B. Logičke operacije koje još često upotrebljavamo su implikacija ( ) i ekvivalencija A B A B A B
 1 MATEMATIČKI SUDOVI Jedan od osnovnih oblika mišljenja su pojmovi. Oni ne dolaze odvojeno, nego se na odredeni način vezuju i tvore sudove. Sud (izjava, izreka, iskaz) je suvisla deklarativna rečenica
1 MATEMATIČKI SUDOVI Jedan od osnovnih oblika mišljenja su pojmovi. Oni ne dolaze odvojeno, nego se na odredeni način vezuju i tvore sudove. Sud (izjava, izreka, iskaz) je suvisla deklarativna rečenica
Mathcad sa algoritmima
 P R I M J E R I P R I M J E R I Mathcad sa algoritmima NAREDBE - elementarne obrade - sekvence Primjer 1 Napraviti algoritam za sabiranje dva broja. NAREDBE - elementarne obrade - sekvence Primjer 1 POČETAK
P R I M J E R I P R I M J E R I Mathcad sa algoritmima NAREDBE - elementarne obrade - sekvence Primjer 1 Napraviti algoritam za sabiranje dva broja. NAREDBE - elementarne obrade - sekvence Primjer 1 POČETAK
SLIČNOST I HOMOTETIJA. Ivana Major Šomodi PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK. Diplomski rad
 SVEUČILIŠTE U ZGREU PRIRODOSLOVNO MTEMTIČKI FKULTET MTEMTIČKI ODSJEK Ivana Major Šomodi SLIČNOST I HOMOTETIJ Diplomski rad Voditelj rada: prof. dr. sc Sanja Varošanec Zagreb, srpanj, 2015. Ovaj diplomski
SVEUČILIŠTE U ZGREU PRIRODOSLOVNO MTEMTIČKI FKULTET MTEMTIČKI ODSJEK Ivana Major Šomodi SLIČNOST I HOMOTETIJ Diplomski rad Voditelj rada: prof. dr. sc Sanja Varošanec Zagreb, srpanj, 2015. Ovaj diplomski
PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU
 MAT KOL Banja Luka) ISSN 0354 6969 p) ISSN 1986 58 o) Vol. XXI )015) 105 115 http://www.imvibl.org/dmbl/dmbl.htm PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU Bernadin Ibrahimpašić 1 Senka Ibrahimpašić
MAT KOL Banja Luka) ISSN 0354 6969 p) ISSN 1986 58 o) Vol. XXI )015) 105 115 http://www.imvibl.org/dmbl/dmbl.htm PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU Bernadin Ibrahimpašić 1 Senka Ibrahimpašić
Sveu ili²te u Zagrebu Prirodoslovno-matemati ki fakultet
 Sveu ili²te u Zagrebu Prirodoslovno-matemati ki fakultet Melkior Ornik, Ana u²njara Neki prilozi teoriji egzaktne rekonstrukcije poligona Zagreb, 2012 Ovaj rad izražen je na Zavodu za numeri ku matematiku
Sveu ili²te u Zagrebu Prirodoslovno-matemati ki fakultet Melkior Ornik, Ana u²njara Neki prilozi teoriji egzaktne rekonstrukcije poligona Zagreb, 2012 Ovaj rad izražen je na Zavodu za numeri ku matematiku
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
CCE PR Revised & Un-Revised
 D CCE PR Revised & Un-Revised 560 00 KARNATAKA SECONDARY EDUCATION EXAMINATION BOARD, MALLESWARAM, BANGALORE 560 00 08 S.S.L.C. EXAMINATION, JUNE, 08 :. 06. 08 ] MODEL ANSWERS : 8-K Date :. 06. 08 ] CODE
D CCE PR Revised & Un-Revised 560 00 KARNATAKA SECONDARY EDUCATION EXAMINATION BOARD, MALLESWARAM, BANGALORE 560 00 08 S.S.L.C. EXAMINATION, JUNE, 08 :. 06. 08 ] MODEL ANSWERS : 8-K Date :. 06. 08 ] CODE
Red veze za benzen. Slika 1.
 Red veze za benzen Benzen C 6 H 6 je aromatično ciklično jedinjenje. Njegove dve rezonantne forme (ili Kekuléove structure), prema teoriji valentne veze (VB) prikazuju se uobičajeno kao na slici 1 a),
Red veze za benzen Benzen C 6 H 6 je aromatično ciklično jedinjenje. Njegove dve rezonantne forme (ili Kekuléove structure), prema teoriji valentne veze (VB) prikazuju se uobičajeno kao na slici 1 a),
Created by T. Madas 2D VECTORS. Created by T. Madas
 2D VECTORS Question 1 (**) Relative to a fixed origin O, the point A has coordinates ( 2, 3). The point B is such so that AB = 3i 7j, where i and j are mutually perpendicular unit vectors lying on the
2D VECTORS Question 1 (**) Relative to a fixed origin O, the point A has coordinates ( 2, 3). The point B is such so that AB = 3i 7j, where i and j are mutually perpendicular unit vectors lying on the
Mirela Nogolica Norme Završni rad
 Sveučilište J.J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Mirela Nogolica Norme Završni rad Osijek, 2014. Sveučilište J.J. Strossmayera u Osijeku Odjel za
Sveučilište J.J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Mirela Nogolica Norme Završni rad Osijek, 2014. Sveučilište J.J. Strossmayera u Osijeku Odjel za
Class IX Chapter 7 Triangles Maths. Exercise 7.1 Question 1: In quadrilateral ACBD, AC = AD and AB bisects A (See the given figure).
 Exercise 7.1 Question 1: In quadrilateral ACBD, AC = AD and AB bisects A (See the given figure). Show that ABC ABD. What can you say about BC and BD? In ABC and ABD, AC = AD (Given) CAB = DAB (AB bisects
Exercise 7.1 Question 1: In quadrilateral ACBD, AC = AD and AB bisects A (See the given figure). Show that ABC ABD. What can you say about BC and BD? In ABC and ABD, AC = AD (Given) CAB = DAB (AB bisects
Triangles. 3.In the following fig. AB = AC and BD = DC, then ADC = (A) 60 (B) 120 (C) 90 (D) none 4.In the Fig. given below, find Z.
 Triangles 1.Two sides of a triangle are 7 cm and 10 cm. Which of the following length can be the length of the third side? (A) 19 cm. (B) 17 cm. (C) 23 cm. of these. 2.Can 80, 75 and 20 form a triangle?
Triangles 1.Two sides of a triangle are 7 cm and 10 cm. Which of the following length can be the length of the third side? (A) 19 cm. (B) 17 cm. (C) 23 cm. of these. 2.Can 80, 75 and 20 form a triangle?
Formule za udaljenost točke do pravca u ravnini, u smislu lp - udaljenosti math.e Vol 28.
 1 math.e Hrvatski matematički elektronički časopis Formule za udaljenost točke do pravca u ravnini, u smislu lp - udaljenosti Banachovi prostori Funkcija udaljenosti obrada podataka optimizacija Aleksandra
1 math.e Hrvatski matematički elektronički časopis Formule za udaljenost točke do pravca u ravnini, u smislu lp - udaljenosti Banachovi prostori Funkcija udaljenosti obrada podataka optimizacija Aleksandra
Individual Events 1 I2 x 0 I3 a. Group Events. G8 V 1 G9 A 9 G10 a 4 4 B
 Answers: (99-95 HKMO Final Events) Created by: Mr. Francis Hung Last updated: July 08 I a Individual Events I x 0 I3 a I r 3 I5 a b 3 y 3 b 8 s b c 3 z c t 5 c d w d 0 u d 6 3 6 G6 a 5 G7 a Group Events
Answers: (99-95 HKMO Final Events) Created by: Mr. Francis Hung Last updated: July 08 I a Individual Events I x 0 I3 a I r 3 I5 a b 3 y 3 b 8 s b c 3 z c t 5 c d w d 0 u d 6 3 6 G6 a 5 G7 a Group Events
Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths
![Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths](/thumbs/86/93150791.jpg) Topic 2 [312 marks] 1 The rectangle ABCD is inscribed in a circle Sides [AD] and [AB] have lengths [12 marks] 3 cm and (\9\) cm respectively E is a point on side [AB] such that AE is 3 cm Side [DE] is
Topic 2 [312 marks] 1 The rectangle ABCD is inscribed in a circle Sides [AD] and [AB] have lengths [12 marks] 3 cm and (\9\) cm respectively E is a point on side [AB] such that AE is 3 cm Side [DE] is
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
Question 1: In quadrilateral ACBD, AC = AD and AB bisects A (See the given figure). Show that ABC ABD. What can you say about BC and BD?
 Class IX - NCERT Maths Exercise (7.1) Question 1: In quadrilateral ACBD, AC = AD and AB bisects A (See the given figure). Show that ABC ABD. What can you say about BC and BD? Solution 1: In ABC and ABD,
Class IX - NCERT Maths Exercise (7.1) Question 1: In quadrilateral ACBD, AC = AD and AB bisects A (See the given figure). Show that ABC ABD. What can you say about BC and BD? Solution 1: In ABC and ABD,
Class IX Chapter 7 Triangles Maths
 Class IX Chapter 7 Triangles Maths 1: Exercise 7.1 Question In quadrilateral ACBD, AC = AD and AB bisects A (See the given figure). Show that ABC ABD. What can you say about BC and BD? In ABC and ABD,
Class IX Chapter 7 Triangles Maths 1: Exercise 7.1 Question In quadrilateral ACBD, AC = AD and AB bisects A (See the given figure). Show that ABC ABD. What can you say about BC and BD? In ABC and ABD,
Harmoniteti. Matija Bucić, Domagoj Ćevid. 20. lipnja 2016.
 Harmoniteti Matija Bucić, Domagoj Ćevid 20. lipnja 2016. 1 Uvod Harmoniteti su jedan od veoma korisnih alata koje jedan olimpijac treba znati. To je posebna konfiguracija točaka ili pravaca koja se pojavljuje
Harmoniteti Matija Bucić, Domagoj Ćevid 20. lipnja 2016. 1 Uvod Harmoniteti su jedan od veoma korisnih alata koje jedan olimpijac treba znati. To je posebna konfiguracija točaka ili pravaca koja se pojavljuje
Sveučilište J.J.Strossmayera u Osijeku Odjel za matematiku. Sveučilišni preddiplomski studij matematike
 Sveučilište J.J.Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Lorena Škalac Fermatova metoda beskonačnog spusta Završni rad Osijek, 014. Sveučilište J.J.Strossmayera
Sveučilište J.J.Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Lorena Škalac Fermatova metoda beskonačnog spusta Završni rad Osijek, 014. Sveučilište J.J.Strossmayera
Pellova jednadžba. Pell s equation
 Osječki matematički list 8(2008), 29 36 29 STUDENTSKA RUBRIKA Pellova jednadžba Ivona Mandić Ivan Soldo Sažetak. Članak sadrži riješene primjere i probleme koji se svode na analizu skupa rješenja Pellove
Osječki matematički list 8(2008), 29 36 29 STUDENTSKA RUBRIKA Pellova jednadžba Ivona Mandić Ivan Soldo Sažetak. Članak sadrži riješene primjere i probleme koji se svode na analizu skupa rješenja Pellove
 MULTIPLE PRODUCTS OBJECTIVES. If a i j,b j k,c i k, = + = + = + then a. ( b c) ) 8 ) 6 3) 4 5). If a = 3i j+ k and b 3i j k = = +, then a. ( a b) = ) 0 ) 3) 3 4) not defined { } 3. The scalar a. ( b c)
MULTIPLE PRODUCTS OBJECTIVES. If a i j,b j k,c i k, = + = + = + then a. ( b c) ) 8 ) 6 3) 4 5). If a = 3i j+ k and b 3i j k = = +, then a. ( a b) = ) 0 ) 3) 3 4) not defined { } 3. The scalar a. ( b c)
Section 5.8. (i) ( 3 + i)(14 2i) = ( 3)(14 2i) + i(14 2i) = {( 3)14 ( 3)(2i)} + i(14) i(2i) = ( i) + (14i + 2) = i.
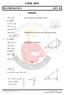
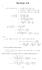 1. Section 5.8 (i) ( 3 + i)(14 i) ( 3)(14 i) + i(14 i) {( 3)14 ( 3)(i)} + i(14) i(i) ( 4 + 6i) + (14i + ) 40 + 0i. (ii) + 3i 1 4i ( + 3i)(1 + 4i) (1 4i)(1 + 4i) (( + 3i) + ( + 3i)(4i) 1 + 4 10 + 11i 10
1. Section 5.8 (i) ( 3 + i)(14 i) ( 3)(14 i) + i(14 i) {( 3)14 ( 3)(i)} + i(14) i(i) ( 4 + 6i) + (14i + ) 40 + 0i. (ii) + 3i 1 4i ( + 3i)(1 + 4i) (1 4i)(1 + 4i) (( + 3i) + ( + 3i)(4i) 1 + 4 10 + 11i 10
Uvod u relacione baze podataka
 Uvod u relacione baze podataka Ana Spasić 2. čas 1 Mala studentska baza dosije (indeks, ime, prezime, datum rodjenja, mesto rodjenja, datum upisa) predmet (id predmeta, sifra, naziv, bodovi) ispitni rok
Uvod u relacione baze podataka Ana Spasić 2. čas 1 Mala studentska baza dosije (indeks, ime, prezime, datum rodjenja, mesto rodjenja, datum upisa) predmet (id predmeta, sifra, naziv, bodovi) ispitni rok
Berkeley Math Circle, May
 Berkeley Math Circle, May 1-7 2000 COMPLEX NUMBERS IN GEOMETRY ZVEZDELINA STANKOVA FRENKEL, MILLS COLLEGE 1. Let O be a point in the plane of ABC. Points A 1, B 1, C 1 are the images of A, B, C under symmetry
Berkeley Math Circle, May 1-7 2000 COMPLEX NUMBERS IN GEOMETRY ZVEZDELINA STANKOVA FRENKEL, MILLS COLLEGE 1. Let O be a point in the plane of ABC. Points A 1, B 1, C 1 are the images of A, B, C under symmetry
( ) = ( ) ( ) = ( ) = + = = = ( ) Therefore: , where t. Note: If we start with the condition BM = tab, we will have BM = ( x + 2, y + 3, z 5)
 Chapter Exercise a) AB OB OA ( xb xa, yb ya, zb za),,, 0, b) AB OB OA ( xb xa, yb ya, zb za) ( ), ( ),, 0, c) AB OB OA x x, y y, z z (, ( ), ) (,, ) ( ) B A B A B A ( ) d) AB OB OA ( xb xa, yb ya, zb za)
Chapter Exercise a) AB OB OA ( xb xa, yb ya, zb za),,, 0, b) AB OB OA ( xb xa, yb ya, zb za) ( ), ( ),, 0, c) AB OB OA x x, y y, z z (, ( ), ) (,, ) ( ) B A B A B A ( ) d) AB OB OA ( xb xa, yb ya, zb za)
Collinearity/Concurrence
 Collinearity/Concurrence Ray Li (rayyli@stanford.edu) June 29, 2017 1 Introduction/Facts you should know 1. (Cevian Triangle) Let ABC be a triangle and P be a point. Let lines AP, BP, CP meet lines BC,
Collinearity/Concurrence Ray Li (rayyli@stanford.edu) June 29, 2017 1 Introduction/Facts you should know 1. (Cevian Triangle) Let ABC be a triangle and P be a point. Let lines AP, BP, CP meet lines BC,
TWO INEQUALITIES FOR A POINT IN THE PLANE OF A TRIANGLE
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. (013), No., 68-8 TWO INEQUALITIES FOR A POINT IN THE PLANE OF A TRIANGLE JIAN LIU Abstract. In this paper we establish two new geometric inequalities involving an
INTERNATIONAL JOURNAL OF GEOMETRY Vol. (013), No., 68-8 TWO INEQUALITIES FOR A POINT IN THE PLANE OF A TRIANGLE JIAN LIU Abstract. In this paper we establish two new geometric inequalities involving an
Teorem o reziduumima i primjene. Završni rad
 Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Matej Petrinović Teorem o reziduumima i primjene Završni rad Osijek, 207. Sveučilište J. J. Strossmayera
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Matej Petrinović Teorem o reziduumima i primjene Završni rad Osijek, 207. Sveučilište J. J. Strossmayera
Question Bank Tangent Properties of a Circle
 Question Bank Tangent Properties of a Circle 1. In quadrilateral ABCD, D = 90, BC = 38 cm and DC = 5 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 7 cm. Find
Question Bank Tangent Properties of a Circle 1. In quadrilateral ABCD, D = 90, BC = 38 cm and DC = 5 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 7 cm. Find
 = ( +1) BP AC = AP + (1+ )BP Proved UNIT-9 CIRCLES 1. Prove that the parallelogram circumscribing a circle is rhombus. Ans Given : ABCD is a parallelogram circumscribing a circle. To prove : - ABCD is
= ( +1) BP AC = AP + (1+ )BP Proved UNIT-9 CIRCLES 1. Prove that the parallelogram circumscribing a circle is rhombus. Ans Given : ABCD is a parallelogram circumscribing a circle. To prove : - ABCD is
Neeuklidska geometrija
 Sveučilište J.J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni nastavnički studij matematike i informatike Ivana Lukanović Neeuklidska geometrija Diplomski rad Osijek, 2017. Sveučilište J.J. Strossmayera
Sveučilište J.J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni nastavnički studij matematike i informatike Ivana Lukanović Neeuklidska geometrija Diplomski rad Osijek, 2017. Sveučilište J.J. Strossmayera
On Brocard Points of Harmonic Quadrangle in Isotropic Plane
 Original scientific paper Accepted 31. 10. 017. EMA JURKIN MARIJA ŠIMIĆ HORVATH VLADIMIR VOLENEC On Brocard Points of Harmonic Quadrangle in Isotropic Plane On Brocard Points of Harmonic Quadrangle in
Original scientific paper Accepted 31. 10. 017. EMA JURKIN MARIJA ŠIMIĆ HORVATH VLADIMIR VOLENEC On Brocard Points of Harmonic Quadrangle in Isotropic Plane On Brocard Points of Harmonic Quadrangle in
1. Prove that the parallelogram circumscribing a circle is rhombus.
 UNIT-9 1. Prve that the parallelgram circumscribing a circle is rhmbus. Ans Given : ABCD is a parallelgram circumscribing a circle. T prve : - ABCD is a rhmbus r ABBCCDDA Prf: Since the length f tangents
UNIT-9 1. Prve that the parallelgram circumscribing a circle is rhmbus. Ans Given : ABCD is a parallelgram circumscribing a circle. T prve : - ABCD is a rhmbus r ABBCCDDA Prf: Since the length f tangents
Concurrency and Collinearity
 Concurrency and Collinearity Victoria Krakovna vkrakovna@gmail.com 1 Elementary Tools Here are some tips for concurrency and collinearity questions: 1. You can often restate a concurrency question as a
Concurrency and Collinearity Victoria Krakovna vkrakovna@gmail.com 1 Elementary Tools Here are some tips for concurrency and collinearity questions: 1. You can often restate a concurrency question as a
Algoritam za množenje ulančanih matrica. Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek
 Algoritam za množenje ulančanih matrica Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek O problemu (1) Neka je A 1, A 2,, A n niz ulančanih matrica duljine n N, gdje su dimenzije matrice
Algoritam za množenje ulančanih matrica Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek O problemu (1) Neka je A 1, A 2,, A n niz ulančanih matrica duljine n N, gdje su dimenzije matrice
CHAPTER 10 SOL PROBLEMS
 Modified and Animated By Chris Headlee Dec 2011 CHAPTER 10 SOL PROBLEMS Super Second-grader Methods SOL Problems; not Dynamic Variable Problems H and J are obtuse and ABC is acute ABC is small acute so
Modified and Animated By Chris Headlee Dec 2011 CHAPTER 10 SOL PROBLEMS Super Second-grader Methods SOL Problems; not Dynamic Variable Problems H and J are obtuse and ABC is acute ABC is small acute so
Projektovanje paralelnih algoritama II
 Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
( )( ) PR PQ = QR. Mathematics Class X TOPPER SAMPLE PAPER-1 SOLUTIONS. HCF x LCM = Product of the 2 numbers 126 x LCM = 252 x 378
 Mathematics Class X TOPPER SAMPLE PAPER- SOLUTIONS Ans HCF x LCM Product of the numbers 6 x LCM 5 x 378 LCM 756 ( Mark) Ans The zeroes are, 4 p( x) x + x 4 x 3x 4 ( Mark) Ans3 For intersecting lines: a
Mathematics Class X TOPPER SAMPLE PAPER- SOLUTIONS Ans HCF x LCM Product of the numbers 6 x LCM 5 x 378 LCM 756 ( Mark) Ans The zeroes are, 4 p( x) x + x 4 x 3x 4 ( Mark) Ans3 For intersecting lines: a
Ariana Trstenjak Kvadratne forme
 Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Ariana Trstenjak Kvadratne forme Završni rad Osijek, 014. Sveučilište Josipa Jurja Strossmayera
Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Ariana Trstenjak Kvadratne forme Završni rad Osijek, 014. Sveučilište Josipa Jurja Strossmayera
Pitagorine trojke. Uvod
 Pitagorine trojke Uvod Ivan Soldo 1, Ivana Vuksanović 2 Pitagora, grčki filozof i znanstvenik, često se prikazuje kao prvi pravi matematičar. Ro - den je na grčkom otoku Samosu, kao sin bogatog i zaslužnog
Pitagorine trojke Uvod Ivan Soldo 1, Ivana Vuksanović 2 Pitagora, grčki filozof i znanstvenik, često se prikazuje kao prvi pravi matematičar. Ro - den je na grčkom otoku Samosu, kao sin bogatog i zaslužnog
RMT 2013 Geometry Test Solutions February 2, = 51.
 RMT 0 Geometry Test Solutions February, 0. Answer: 5 Solution: Let m A = x and m B = y. Note that we have two pairs of isosceles triangles, so m A = m ACD and m B = m BCD. Since m ACD + m BCD = m ACB,
RMT 0 Geometry Test Solutions February, 0. Answer: 5 Solution: Let m A = x and m B = y. Note that we have two pairs of isosceles triangles, so m A = m ACD and m B = m BCD. Since m ACD + m BCD = m ACB,
KVADRATNE INTERPOLACIJSKE METODE ZA JEDNODIMENZIONALNU BEZUVJETNU LOKALNU OPTIMIZACIJU 1
 MAT KOL (Banja Luka) ISSN 0354 6969 (p), ISSN 1986 5228 (o) Vol. XXII (1)(2016), 5 19 http://www.imvibl.org/dmbl/dmbl.htm KVADRATNE INTERPOLACIJSKE METODE ZA JEDNODIMENZIONALNU BEZUVJETNU LOKALNU OPTIMIZACIJU
MAT KOL (Banja Luka) ISSN 0354 6969 (p), ISSN 1986 5228 (o) Vol. XXII (1)(2016), 5 19 http://www.imvibl.org/dmbl/dmbl.htm KVADRATNE INTERPOLACIJSKE METODE ZA JEDNODIMENZIONALNU BEZUVJETNU LOKALNU OPTIMIZACIJU
Visit: ImperialStudy.com For More Study Materials Class IX Chapter 12 Heron s Formula Maths
 Exercise 1.1 1. Find the area of a triangle whose sides are respectively 150 cm, 10 cm and 00 cm. The triangle whose sides are a = 150 cm b = 10 cm c = 00 cm The area of a triangle = s(s a)(s b)(s c) Here
Exercise 1.1 1. Find the area of a triangle whose sides are respectively 150 cm, 10 cm and 00 cm. The triangle whose sides are a = 150 cm b = 10 cm c = 00 cm The area of a triangle = s(s a)(s b)(s c) Here
Udaan School Of Mathematics Class X Chapter 10 Circles Maths
 Exercise 10.1 1. Fill in the blanks (i) The common point of tangent and the circle is called point of contact. (ii) A circle may have two parallel tangents. (iii) A tangent to a circle intersects it in
Exercise 10.1 1. Fill in the blanks (i) The common point of tangent and the circle is called point of contact. (ii) A circle may have two parallel tangents. (iii) A tangent to a circle intersects it in
PYTHAGORAS THEOREM PYTHAGORAS THEOREM IN A RIGHT ANGLED TRIANGLE, THE SQUARE ON HYPOTENUSE IS EQUAL TO SUM OF SQUARES ON OTHER TWO SIDES
 PYTHAGORAS THEOREM PYTHAGORAS THEOREM IN A RIGHT ANGLED TRIANGLE, THE SQUARE ON HYPOTENUSE IS EQUAL TO SUM OF SQUARES ON OTHER TWO SIDES EXERCISE 2.1 *THE SIDES OF A RIGHT ANGLED TRIANGLE CONTAINING THE
PYTHAGORAS THEOREM PYTHAGORAS THEOREM IN A RIGHT ANGLED TRIANGLE, THE SQUARE ON HYPOTENUSE IS EQUAL TO SUM OF SQUARES ON OTHER TWO SIDES EXERCISE 2.1 *THE SIDES OF A RIGHT ANGLED TRIANGLE CONTAINING THE
VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER)
 BY:Prof. RAHUL MISHRA Class :- X QNo. VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER) CIRCLES Subject :- Maths General Instructions Questions M:9999907099,9818932244 1 In the adjoining figures, PQ
BY:Prof. RAHUL MISHRA Class :- X QNo. VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER) CIRCLES Subject :- Maths General Instructions Questions M:9999907099,9818932244 1 In the adjoining figures, PQ
Konstrukcije ravnalom i šestarom
 Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Emanuela Vrban Konstrukcije ravnalom i šestarom Diplomski rad Osijek, 2013. Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za
Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Emanuela Vrban Konstrukcije ravnalom i šestarom Diplomski rad Osijek, 2013. Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za
Metode izračunavanja determinanti matrica n-tog reda
 Osječki matematički list 10(2010), 31 42 31 STUDENTSKA RUBRIKA Metode izračunavanja determinanti matrica n-tog reda Damira Keček Sažetak U članku su opisane metode izračunavanja determinanti matrica n-tog
Osječki matematički list 10(2010), 31 42 31 STUDENTSKA RUBRIKA Metode izračunavanja determinanti matrica n-tog reda Damira Keček Sažetak U članku su opisane metode izračunavanja determinanti matrica n-tog
 Geometry 3 SIMILARITY & CONGRUENCY Congruency: When two figures have same shape and size, then they are said to be congruent figure. The phenomena between these two figures is said to be congruency. CONDITIONS
Geometry 3 SIMILARITY & CONGRUENCY Congruency: When two figures have same shape and size, then they are said to be congruent figure. The phenomena between these two figures is said to be congruency. CONDITIONS
NIZOVI I REDOVI FUNKCIJA
 SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Danijela Piškor NIZOVI I REDOVI FUNKCIJA Diplomski rad Voditelj rada: izv. prof. dr. sc. Ljiljana Arambašić Zagreb, rujan 206.
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Danijela Piškor NIZOVI I REDOVI FUNKCIJA Diplomski rad Voditelj rada: izv. prof. dr. sc. Ljiljana Arambašić Zagreb, rujan 206.
Solutions to CRMO-2003
 Solutions to CRMO-003 1. Let ABC be a triangle in which AB AC and CAB 90. Suppose M and N are points on the hypotenuse BC such that BM + CN MN. Prove that MAN 45. Solution: Draw CP perpendicular to CB
Solutions to CRMO-003 1. Let ABC be a triangle in which AB AC and CAB 90. Suppose M and N are points on the hypotenuse BC such that BM + CN MN. Prove that MAN 45. Solution: Draw CP perpendicular to CB
SOME NEW INEQUALITIES FOR AN INTERIOR POINT OF A TRIANGLE JIAN LIU. 1. Introduction
 Journal of Mathematical Inequalities Volume 6, Number 2 (2012), 195 204 doi:10.7153/jmi-06-20 OME NEW INEQUALITIE FOR AN INTERIOR POINT OF A TRIANGLE JIAN LIU (Communicated by. egura Gomis) Abstract. In
Journal of Mathematical Inequalities Volume 6, Number 2 (2012), 195 204 doi:10.7153/jmi-06-20 OME NEW INEQUALITIE FOR AN INTERIOR POINT OF A TRIANGLE JIAN LIU (Communicated by. egura Gomis) Abstract. In
CHAPTER 7 TRIANGLES. 7.1 Introduction. 7.2 Congruence of Triangles
 CHAPTER 7 TRIANGLES 7.1 Introduction You have studied about triangles and their various properties in your earlier classes. You know that a closed figure formed by three intersecting lines is called a
CHAPTER 7 TRIANGLES 7.1 Introduction You have studied about triangles and their various properties in your earlier classes. You know that a closed figure formed by three intersecting lines is called a
2013 Bored of Studies Trial Examinations. Mathematics SOLUTIONS
 03 Bored of Studies Trial Examinations Mathematics SOLUTIONS Section I. B 3. B 5. A 7. B 9. C. D 4. B 6. A 8. D 0. C Working/Justification Question We can eliminate (A) and (C), since they are not to 4
03 Bored of Studies Trial Examinations Mathematics SOLUTIONS Section I. B 3. B 5. A 7. B 9. C. D 4. B 6. A 8. D 0. C Working/Justification Question We can eliminate (A) and (C), since they are not to 4
Class IX Chapter 8 Quadrilaterals Maths
 Class IX Chapter 8 Quadrilaterals Maths Exercise 8.1 Question 1: The angles of quadrilateral are in the ratio 3: 5: 9: 13. Find all the angles of the quadrilateral. Answer: Let the common ratio between
Class IX Chapter 8 Quadrilaterals Maths Exercise 8.1 Question 1: The angles of quadrilateral are in the ratio 3: 5: 9: 13. Find all the angles of the quadrilateral. Answer: Let the common ratio between
Class IX Chapter 8 Quadrilaterals Maths
 1 Class IX Chapter 8 Quadrilaterals Maths Exercise 8.1 Question 1: The angles of quadrilateral are in the ratio 3: 5: 9: 13. Find all the angles of the quadrilateral. Let the common ratio between the angles
1 Class IX Chapter 8 Quadrilaterals Maths Exercise 8.1 Question 1: The angles of quadrilateral are in the ratio 3: 5: 9: 13. Find all the angles of the quadrilateral. Let the common ratio between the angles
LLT Education Services
 8. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle. (a) 4 cm (b) 3 cm (c) 6 cm (d) 5 cm 9. From a point P, 10 cm away from the
8. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle. (a) 4 cm (b) 3 cm (c) 6 cm (d) 5 cm 9. From a point P, 10 cm away from the
Math 425, Homework #1 Solutions
 Math 425, Homework #1 Solutions (1) (1.9) (a) Use complex algebra to show that for any four integers a, b, c, and d there are integers u and v so that (a 2 + b 2 )(c 2 + d 2 ) = u 2 + v 2 Proof. If we
Math 425, Homework #1 Solutions (1) (1.9) (a) Use complex algebra to show that for any four integers a, b, c, and d there are integers u and v so that (a 2 + b 2 )(c 2 + d 2 ) = u 2 + v 2 Proof. If we
OSNOVE GEOMETRIJE. Branko µcervar, Goran Erceg, Ivan LekiĆ 2013./2014.
 OSNOVE GEOMETRIJE Branko µcervar, Goran Erceg, Ivan LekiĆ 2013./2014. i ii Sadrµzaj PREDGOVOR OZNAKE v vii 1 POVIJESNI PREGLED 1 1.1 EUKLID I NJEGOVI ELEMENTI................ 1 1.2 SADRµZAJ PRVE KNJIGE
OSNOVE GEOMETRIJE Branko µcervar, Goran Erceg, Ivan LekiĆ 2013./2014. i ii Sadrµzaj PREDGOVOR OZNAKE v vii 1 POVIJESNI PREGLED 1 1.1 EUKLID I NJEGOVI ELEMENTI................ 1 1.2 SADRµZAJ PRVE KNJIGE
Using Complex Weighted Centroids to Create Homothetic Polygons. Harold Reiter. Department of Mathematics, University of North Carolina Charlotte,
 Using Complex Weighted Centroids to Create Homothetic Polygons Harold Reiter Department of Mathematics, University of North Carolina Charlotte, Charlotte, NC 28223, USA hbreiter@emailunccedu Arthur Holshouser
Using Complex Weighted Centroids to Create Homothetic Polygons Harold Reiter Department of Mathematics, University of North Carolina Charlotte, Charlotte, NC 28223, USA hbreiter@emailunccedu Arthur Holshouser
TRIANGLES CHAPTER 7. (A) Main Concepts and Results. (B) Multiple Choice Questions
 CHAPTER 7 TRIANGLES (A) Main Concepts and Results Triangles and their parts, Congruence of triangles, Congruence and correspondence of vertices, Criteria for Congruence of triangles: (i) SAS (ii) ASA (iii)
CHAPTER 7 TRIANGLES (A) Main Concepts and Results Triangles and their parts, Congruence of triangles, Congruence and correspondence of vertices, Criteria for Congruence of triangles: (i) SAS (ii) ASA (iii)
Mersenneovi i savršeni brojevi
 Sveučilište J.J. Strossmayera u Osijeku Odjel za matematiku Diplomski studij matematike Ana Maslać Mersenneovi i savršeni brojevi Diplomski rad Osijek, 2012. Sveučilište J.J. Strossmayera u Osijeku Odjel
Sveučilište J.J. Strossmayera u Osijeku Odjel za matematiku Diplomski studij matematike Ana Maslać Mersenneovi i savršeni brojevi Diplomski rad Osijek, 2012. Sveučilište J.J. Strossmayera u Osijeku Odjel
Zanimljive rekurzije
 Zanimljive rekurzije Dragana Jankov Maširević i Jelena Jankov Riječ dvije o rekurzijama Rekurzija je metoda definiranja funkcije na način da se najprije definira nekoliko jednostavnih, osnovnih slučajeva,
Zanimljive rekurzije Dragana Jankov Maširević i Jelena Jankov Riječ dvije o rekurzijama Rekurzija je metoda definiranja funkcije na način da se najprije definira nekoliko jednostavnih, osnovnih slučajeva,
Geometry Problem Solving Drill 08: Congruent Triangles
 Geometry Problem Solving Drill 08: Congruent Triangles Question No. 1 of 10 Question 1. The following triangles are congruent. What is the value of x? Question #01 (A) 13.33 (B) 10 (C) 31 (D) 18 You set
Geometry Problem Solving Drill 08: Congruent Triangles Question No. 1 of 10 Question 1. The following triangles are congruent. What is the value of x? Question #01 (A) 13.33 (B) 10 (C) 31 (D) 18 You set
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni nastavnički studij matematike i informatike. Mirjana Mikec.
 Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni nastavnički studij matematike i informatike Mirjana Mikec Broj e Diplomski rad Osijek, 20. Sveučilište J. J. Strossmayera u Osijeku
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni nastavnički studij matematike i informatike Mirjana Mikec Broj e Diplomski rad Osijek, 20. Sveučilište J. J. Strossmayera u Osijeku
CBSE MATHEMATICS (SET-2)_2019
 CBSE 09 MATHEMATICS (SET-) (Solutions). OC AB (AB is tangent to the smaller circle) In OBC a b CB CB a b CB a b AB CB (Perpendicular from the centre bisects the chord) AB a b. In PQS PQ 4 (By Pythagoras
CBSE 09 MATHEMATICS (SET-) (Solutions). OC AB (AB is tangent to the smaller circle) In OBC a b CB CB a b CB a b AB CB (Perpendicular from the centre bisects the chord) AB a b. In PQS PQ 4 (By Pythagoras
Fibonaccijev brojevni sustav
 Fibonaccijev brojevni sustav Ljerka Jukić asistentica Odjela za matematiku Sveučilišta u Osijeku, ljukic@mathos.hr Helena Velić studentica Odjela za matematiku Sveučilišta u Osijeku, hvelic@mathos.hr Sažetak
Fibonaccijev brojevni sustav Ljerka Jukić asistentica Odjela za matematiku Sveučilišta u Osijeku, ljukic@mathos.hr Helena Velić studentica Odjela za matematiku Sveučilišta u Osijeku, hvelic@mathos.hr Sažetak
NAPREDNI FIZIČKI PRAKTIKUM 1 studij Matematika i fizika; smjer nastavnički MJERENJE MALIH OTPORA
 NAPREDNI FIZIČKI PRAKTIKUM 1 studij Matematika i fizika; smjer nastavnički MJERENJE MALIH OTPORA studij Matematika i fizika; smjer nastavnički NFP 1 1 ZADACI 1. Mjerenjem geometrijskih dimenzija i otpora
NAPREDNI FIZIČKI PRAKTIKUM 1 studij Matematika i fizika; smjer nastavnički MJERENJE MALIH OTPORA studij Matematika i fizika; smjer nastavnički NFP 1 1 ZADACI 1. Mjerenjem geometrijskih dimenzija i otpora
Solutionbank M1 Edexcel AS and A Level Modular Mathematics
 file://c:\users\buba\kaz\ouba\m_6_a_.html Page of Exercise A, Question A bird flies 5 km due north and then 7 km due east. How far is the bird from its original position, and in what direction? d = \ 5
file://c:\users\buba\kaz\ouba\m_6_a_.html Page of Exercise A, Question A bird flies 5 km due north and then 7 km due east. How far is the bird from its original position, and in what direction? d = \ 5
page 1 Total ( )
 A B C D E F Costs budget of [Claimant / Defendant] dated [ ] Estimated page 1 Work done / to be done Pre-action Disbs ( ) Time ( ) Disbs ( ) Time ( ) Total ( ) 1 Issue /statements of case 0.00 0.00 CMC
A B C D E F Costs budget of [Claimant / Defendant] dated [ ] Estimated page 1 Work done / to be done Pre-action Disbs ( ) Time ( ) Disbs ( ) Time ( ) Total ( ) 1 Issue /statements of case 0.00 0.00 CMC
or i 2 = -1 i 4 = 1 Example : ( i ),, 7 i and 0 are complex numbers. and Imaginary part of z = b or img z = b
 1 A- LEVEL MATHEMATICS P 3 Complex Numbers (NOTES) 1. Given a quadratic equation : x 2 + 1 = 0 or ( x 2 = -1 ) has no solution in the set of real numbers, as there does not exist any real number whose
1 A- LEVEL MATHEMATICS P 3 Complex Numbers (NOTES) 1. Given a quadratic equation : x 2 + 1 = 0 or ( x 2 = -1 ) has no solution in the set of real numbers, as there does not exist any real number whose
Afine transformacije ravnine
 1/ 7 Hrvatski matematički elektronski časopis mathe Broj 12 http://emathhr/ Afine transformacije ravnine Harun Šiljak Sadržaj: 1 Uvod 2 Primjeri riješenih zadataka 3 Zadaci za samostalan rad Literatura
1/ 7 Hrvatski matematički elektronski časopis mathe Broj 12 http://emathhr/ Afine transformacije ravnine Harun Šiljak Sadržaj: 1 Uvod 2 Primjeri riješenih zadataka 3 Zadaci za samostalan rad Literatura
AREAS OF PARALLELOGRAMS AND TRIANGLES
 AREAS OF PARALLELOGRAMS AND TRIANGLES Main Concepts and Results: The area of a closed plane figure is the measure of the region inside the figure: Fig.1 The shaded parts (Fig.1) represent the regions whose
AREAS OF PARALLELOGRAMS AND TRIANGLES Main Concepts and Results: The area of a closed plane figure is the measure of the region inside the figure: Fig.1 The shaded parts (Fig.1) represent the regions whose
Položaj nultočaka polinoma
 Osječki matematički list 4 (204), 05-6 Položaj nultočaka polinoma Mandalena Pranjić Rajna Rajić Sažetak Prema Rolleovom teoremu, bilo koji segment čiji su krajevi međusobno različite realne nultočke polinoma
Osječki matematički list 4 (204), 05-6 Položaj nultočaka polinoma Mandalena Pranjić Rajna Rajić Sažetak Prema Rolleovom teoremu, bilo koji segment čiji su krajevi međusobno različite realne nultočke polinoma
SOLUTIONS SECTION A [1] = 27(27 15)(27 25)(27 14) = 27(12)(2)(13) = cm. = s(s a)(s b)(s c)
![SOLUTIONS SECTION A [1] = 27(27 15)(27 25)(27 14) = 27(12)(2)(13) = cm. = s(s a)(s b)(s c) SOLUTIONS SECTION A [1] = 27(27 15)(27 25)(27 14) = 27(12)(2)(13) = cm. = s(s a)(s b)(s c)](/thumbs/79/80187791.jpg) 1. (A) 1 1 1 11 1 + 6 6 5 30 5 5 5 5 6 = 6 6 SOLUTIONS SECTION A. (B) Let the angles be x and 3x respectively x+3x = 180 o (sum of angles on same side of transversal is 180 o ) x=36 0 So, larger angle=3x
1. (A) 1 1 1 11 1 + 6 6 5 30 5 5 5 5 6 = 6 6 SOLUTIONS SECTION A. (B) Let the angles be x and 3x respectively x+3x = 180 o (sum of angles on same side of transversal is 180 o ) x=36 0 So, larger angle=3x
On an Erdős Inscribed Triangle Inequality
 Forum Geometricorum Volume 5 (005) 137 141. FORUM GEOM ISSN 1534-1178 On an Erdős Inscribed Triangle Inequality Ricardo M. Torrejón Abstract. A comparison between the area of a triangle that of an inscribed
Forum Geometricorum Volume 5 (005) 137 141. FORUM GEOM ISSN 1534-1178 On an Erdős Inscribed Triangle Inequality Ricardo M. Torrejón Abstract. A comparison between the area of a triangle that of an inscribed
Problem četiri boje. Four colors problem
 Osječki matematički list 10(2010), 21 29 21 Problem četiri boje Iva Gregurić, Antoaneta Klobučar Sažetak. U ovom članku pokušat ćemo približiti učenicima srednjih škola jedan od zanimljivijih problema
Osječki matematički list 10(2010), 21 29 21 Problem četiri boje Iva Gregurić, Antoaneta Klobučar Sažetak. U ovom članku pokušat ćemo približiti učenicima srednjih škola jedan od zanimljivijih problema
Modified Zagreb M 2 Index Comparison with the Randi} Connectivity Index for Benzenoid Systems
 CROATICA CHEMICA ACTA CCACAA 7 (2) 83 87 (2003) ISSN-00-3 CCA-2870 Note Modified Zagreb M 2 Index Comparison with the Randi} Connectivity Index for Benzenoid Systems Damir Vuki~evi} a, * and Nenad Trinajsti}
CROATICA CHEMICA ACTA CCACAA 7 (2) 83 87 (2003) ISSN-00-3 CCA-2870 Note Modified Zagreb M 2 Index Comparison with the Randi} Connectivity Index for Benzenoid Systems Damir Vuki~evi} a, * and Nenad Trinajsti}
Pentagonal quasigroups. 1. Introduction
 Quasigroups and Related Systems 22 (2014), 147 158 Pentagonal quasigroups Stipe Vidak Abstract. The concept of pentagonal quasigroup is introduced as IM-quasigroup satisfying the additional property of
Quasigroups and Related Systems 22 (2014), 147 158 Pentagonal quasigroups Stipe Vidak Abstract. The concept of pentagonal quasigroup is introduced as IM-quasigroup satisfying the additional property of
Circle and Cyclic Quadrilaterals. MARIUS GHERGU School of Mathematics and Statistics University College Dublin
 Circle and Cyclic Quadrilaterals MARIUS GHERGU School of Mathematics and Statistics University College Dublin 3 Basic Facts About Circles A central angle is an angle whose vertex is at the center of the
Circle and Cyclic Quadrilaterals MARIUS GHERGU School of Mathematics and Statistics University College Dublin 3 Basic Facts About Circles A central angle is an angle whose vertex is at the center of the
Advanced Digital Design with the Verilog HDL, Second Edition Michael D. Ciletti Prentice Hall, Pearson Education, 2011
 Problem 2-1 Recall that a minterm is a cube in which every variable appears. A Boolean expression in SOP form is canonical if every cube in the expression has a unique representation in which all of the
Problem 2-1 Recall that a minterm is a cube in which every variable appears. A Boolean expression in SOP form is canonical if every cube in the expression has a unique representation in which all of the
Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku
 Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Valentina Volmut Ortogonalni polinomi Diplomski rad Osijek, 2016. Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku
Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Valentina Volmut Ortogonalni polinomi Diplomski rad Osijek, 2016. Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku
1 / 23
 CBSE-XII-07 EXAMINATION CBSE-X-009 EXAMINATION MATHEMATICS Series: HRL Paper & Solution Code: 0/ Time: Hrs. Max. Marks: 80 General Instuctions : (i) All questions are compulsory. (ii) The question paper
CBSE-XII-07 EXAMINATION CBSE-X-009 EXAMINATION MATHEMATICS Series: HRL Paper & Solution Code: 0/ Time: Hrs. Max. Marks: 80 General Instuctions : (i) All questions are compulsory. (ii) The question paper
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku DIOFANTSKE JEDNADŽBE
 Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Violeta Ivšić DIOFANTSKE JEDNADŽBE Završni rad Osijek, 2016. Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Violeta Ivšić DIOFANTSKE
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Violeta Ivšić DIOFANTSKE JEDNADŽBE Završni rad Osijek, 2016. Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Violeta Ivšić DIOFANTSKE
( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear.
 Problems 01 - POINT Page 1 ( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear. ( ) Prove that the two lines joining the mid-points of the pairs of opposite sides and the line
Problems 01 - POINT Page 1 ( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear. ( ) Prove that the two lines joining the mid-points of the pairs of opposite sides and the line
Geometrijski smisao rješenja sustava od tri linearne jednadžbe s tri nepoznanice
 Osječki matematički list 6(2006), 79 84 79 Geometrijski smisao rješenja sustava od tri linearne jednadžbe s tri nepoznanice Zlatko Udovičić Sažetak. Geometrijski smisao rješenja sustava od dvije linearne
Osječki matematički list 6(2006), 79 84 79 Geometrijski smisao rješenja sustava od tri linearne jednadžbe s tri nepoznanice Zlatko Udovičić Sažetak. Geometrijski smisao rješenja sustava od dvije linearne
COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE. To find the length of a line segment joining two points A(x 1, y 1 ) and B(x 2, y 2 ), use
 COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE I. Length of a Line Segment: The distance between two points A ( x1, 1 ) B ( x, ) is given b A B = ( x x1) ( 1) To find the length of a line segment joining
COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE I. Length of a Line Segment: The distance between two points A ( x1, 1 ) B ( x, ) is given b A B = ( x x1) ( 1) To find the length of a line segment joining
Mathematics 2260H Geometry I: Euclidean geometry Trent University, Fall 2016 Solutions to the Quizzes
 Mathematics 2260H Geometry I: Euclidean geometry Trent University, Fall 2016 Solutions to the Quizzes Quiz #1. Wednesday, 13 September. [10 minutes] 1. Suppose you are given a line (segment) AB. Using
Mathematics 2260H Geometry I: Euclidean geometry Trent University, Fall 2016 Solutions to the Quizzes Quiz #1. Wednesday, 13 September. [10 minutes] 1. Suppose you are given a line (segment) AB. Using
MT EDUCARE LTD. SUMMATIVE ASSESSMENT Roll No. Code No. 31/1
 CBSE - X MT EDUCARE LTD. SUMMATIVE ASSESSMENT - 03-4 Roll No. Code No. 3/ Series RLH Please check that this question paper contains 6 printed pages. Code number given on the right hand side of the question
CBSE - X MT EDUCARE LTD. SUMMATIVE ASSESSMENT - 03-4 Roll No. Code No. 3/ Series RLH Please check that this question paper contains 6 printed pages. Code number given on the right hand side of the question
9 th CBSE Mega Test - II
 9 th CBSE Mega Test - II Time: 3 hours Max. Marks: 90 General Instructions All questions are compulsory. The question paper consists of 34 questions divided into four sections A, B, C and D. Section A
9 th CBSE Mega Test - II Time: 3 hours Max. Marks: 90 General Instructions All questions are compulsory. The question paper consists of 34 questions divided into four sections A, B, C and D. Section A
COMPOSITIO MATHEMATICA
 COMPOSITIO MATHEMATICA OSWALD WYLER Order in projective and in descriptive geometry Compositio Mathematica, tome 11 (1953), p. 60-70 Foundation Compositio
COMPOSITIO MATHEMATICA OSWALD WYLER Order in projective and in descriptive geometry Compositio Mathematica, tome 11 (1953), p. 60-70 Foundation Compositio
NEKE VARIJANTE PITAGORINOG TEOREMA
 SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Lina Rajković NEKE VARIJANTE PITAGORINOG TEOREMA Diplomski rad Voditelj rada: Prof. dr. sc. Mirko Primc Zagreb, veljača, 2017.
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Lina Rajković NEKE VARIJANTE PITAGORINOG TEOREMA Diplomski rad Voditelj rada: Prof. dr. sc. Mirko Primc Zagreb, veljača, 2017.
