Lesson 41. where the linear operator x xy y. to enforce the one to one correspondence of this transformation, we assume
|
|
|
- Warren Stokes
- 5 years ago
- Views:
Transcription
1 Modle 4: Partial Differential Eqations Lesson 4 Classification of emi-linear nd order Partial Differential Eqations 4. Classification of nd order Partial Differential Eqations: Parabolic Hyperbolic Elliptic Eqations A nd order semi linear partial differential eqation can be pt in the form L + g(, y,,, ) = 0 (4.) y where the linear operator L Ry (, ) + y (, ) + Ty (, ) y y is sch that the coefficient fnctions R, and T are continos fnction of, yand R + + T 0. We change the independent variables ( yto, ) (ξ,η ) as ξ = ξ( y, ) and η = η( y, ), to enforce the one to one correspondence of this transformation, we assme ξη ηξ 0. y y The coefficients and the partial derivatives in the given eqation are written in terms of the transformed variables. The first and second order partial derivatives become: = ξξ + η; y = ξξy + ηy = ξξ + ηξ + ξ + ξη + ηη + η y ξξ y ξη y ξ y ξη y ηη y η y = ξ + ηξ + ξ + ξη + η + η ξξ ξη ξ ξη ηη η
2 Classification of emi-linear nd order Partial Differential Eqations = ξ + ηξ + ξ + ξη + η + η yy ξξ y ξη y y ξ yy ξη y y ηη y η yy R + + T = ξξ Rξ + ξξ + Tξ y yy ( y y ) + ξη ( Rηξ + ( ηξ + ξη ) + Tξη ) y y y y + R + + T + F. ηη ( η ηη y ξy ) ( ξη,, ξ, η, ) Eqation (4.) becomes A( ξ, ξ ) + B( ξ, ξ ; η, η ) + A( η, η ) = G( ξ, η,,, ) (4.) y ξξ y y ξη y ηη ξ η where A(, v) = R + v + Tv (4.3) B(, v;, v) = R + ( v + v) + Tvv (4.4) Now, the problem is to determine ξ &η so that the eqation (4.) takes the simplest possible (Canonical) form. When the sign of the determinant of the qadratic form (4.3) is everywhere positive, negative or zero it is easy to make the classification. Case A: When > 0 everywhere in the domain. The new independent variable ξ &η can be so chosen that the coefficients of ξξ and ηη in (4.) vanish. The roots λ & λ of the eqation Rα α T + + = 0 are real and distinct. The coefficient of ξξ & ηη in (4.) will vanish if we close ξ &η sch that
3 Classification of emi-linear nd order Partial Differential Eqations ξ ξ y y + λ ; = λ y y A sitable choice will be ξ = f( y, ), η = f( y, ) where f( y, ) = c, f( y, ) = c are the soltion of the ordinary differential eqations d + λ( y, ) = 0; + λ( y, ) = 0respectively. d It can be verified that A ξ ξ A η η B ξ ξ η η = RT ξ η ξ η (4.5) (, y) (, y) (, y;, y) (4 )( y y ) /4. Now when the A s are zero; B = ( 4 RT )( ξη ξη ) y y ince > 0 B > 0, hence eqation (4.) redces to = φξη (,, ξ, η, ) (4.6) ξη The crves ξ ( y, ) = constant, η ( y, ) crves of eqation (4.). Eqation (4.6) is called the canonical form of eqation = constant are called the characteristic Eample Redce the eqation = 0 to a canonical form. yy
4 Classification of emi-linear nd order Partial Differential Eqations oltion comparing with the standard form, we note that R=, = 0, T = Then RT = 4 > 0. o + + = 0 becomes α = 0 α =±. Rα α T λ = ; λ = Now d + = + = 0 y c d = = 0 y c Taking ξ = y+ ; η = y = ξ + η = + ( ) = ξ η ξ η ξ η y = ξ + η, = ξξ ξη + ηη + ξ η yy = 0becomes ξη ξ η, = + + yy ξξ ξη ηη = ( ) ( ). 4 = ξ η 4 ξ η ( ) Case B: If = 0 Roots of the eqation Rα α T + + = 0 are real and eqal. We define ξ as in case A and take η to be any fnction of y, which is independent of ξ. In this case we have A( ξ, ξ ) = 0 as before and hence from eqation (4.5), B = 0. y Bt A( η, η ) 0 ξ & η are independent fnctions. y
5 Classification of emi-linear nd order Partial Differential Eqations Hence the canonical form in this case is = φξη (,,,, ) y (4.7) η Eample + + = 0canonical form. y yy oltion comparing with the standard form, we note that R=, =, T =, and = 0. ( ) Rα + α + T = α + α + = α + = 0 α =,. = 0 y= c, take ξ = y d Then chose η = + y. Using these ξ &η : we have the canonical form as ξ = ηf( ξ) + f( ξ) where ξ η = 0 f & f are arbitrary fnctions. Hence the soltion of the given eqation is: z = ( + y) f ( y) + f ( y). Case C: < 0. In this case, the roots of the eqation Rα α T + + = 0 are compleconjgates. Proceeding as in case A; the canonical form = φξη (,,,, ) y. η
6 Classification of emi-linear nd order Partial Differential Eqations Bt ξ &η are comple conjgates.to get the real canonical form, we se the transformation α = ( ), ( ) ξ + η β = i η ξ = +. ξ η 4 α β o the canonical form in this case is + = ϕαβ (,,,, ) α β. α β Eample 3 Redce the eqation + = 0 to canonical form. yy oltion Clearly, R T =, = 0, =, and < 0. α + = 0 α =± i, henceλ = i; λ = i, ξ = iy + ; η = iy +, ; α = β = y αα + ββ = α is the canonical form α No we classify second order eqation of the type (4.) by their canonical form as: A) Hyperbolic if > 0, B) Parabolic if = 0, C) Elliptic if < 0. Clearly the one dimensional wave eqation given by the Hyperbolic eqation, tt = c is an eample for
7 Classification of emi-linear nd order Partial Differential Eqations the one dimensional heat condction eqation given by t for the parabolic eqation and the Laplace eqation the elliptic eqation. = α is an eample + yy = 0 is an eample for Eample 4 Discss the natre of the eqation + + y = y ( ) yy 0 oltion Clearly RT = ( + y ). Hence the given eqation ishyperbolic at all points ( y, ) sch that + y >, Parabolic if + y = and Elliptic if + y <. Eercises. Redce the eqation to its canonical form and classify it: tt + 4t t = 0.. Classify the partial differential eqation: tt + (5 + ) t + ( + )(4 + ) = 0. Keywords: Elliptic,Hyperbolic, Parabolic, References Ian neddon, (957). Elements of Partial Differential Eqations. McGraw-Hill, ingapore
8 Classification of emi-linear nd order Partial Differential Eqations Amaranath.T, (003). An Elementary Corse in Partial Differential Eqations.Narosa Pblishing Hose, New Delhi ggested Reading I.P. tavrolakis, tephen a tersian, (003). Partial Differential Eqations. Allied Pblishers Pvt. Limited, New Delhi J. David Logan, (004). Partial Differential Eqations. pringer(india) Private Ltd. New Delhi
4 Exact laminar boundary layer solutions
 4 Eact laminar bondary layer soltions 4.1 Bondary layer on a flat plate (Blasis 1908 In Sec. 3, we derived the bondary layer eqations for 2D incompressible flow of constant viscosity past a weakly crved
4 Eact laminar bondary layer soltions 4.1 Bondary layer on a flat plate (Blasis 1908 In Sec. 3, we derived the bondary layer eqations for 2D incompressible flow of constant viscosity past a weakly crved
Second-Order Wave Equation
 Second-Order Wave Eqation A. Salih Department of Aerospace Engineering Indian Institte of Space Science and Technology, Thirvananthapram 3 December 016 1 Introdction The classical wave eqation is a second-order
Second-Order Wave Eqation A. Salih Department of Aerospace Engineering Indian Institte of Space Science and Technology, Thirvananthapram 3 December 016 1 Introdction The classical wave eqation is a second-order
Chapter 3 Second Order Linear Equations
 Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
LINEAR SECOND-ORDER EQUATIONS
 LINEAR SECON-ORER EQUATIONS Classification In two independent variables x and y, the general form is Au xx + 2Bu xy + Cu yy + u x + Eu y + Fu + G = 0. The coefficients are continuous functions of (x, y)
LINEAR SECON-ORER EQUATIONS Classification In two independent variables x and y, the general form is Au xx + 2Bu xy + Cu yy + u x + Eu y + Fu + G = 0. The coefficients are continuous functions of (x, y)
Extra Problems and Examples
 Extra Problems and Examples Steven Bellenot October 11, 2007 1 Separation of Variables Find the solution u(x, y) to the following equations by separating variables. 1. u x + u y = 0 2. u x u y = 0 answer:
Extra Problems and Examples Steven Bellenot October 11, 2007 1 Separation of Variables Find the solution u(x, y) to the following equations by separating variables. 1. u x + u y = 0 2. u x u y = 0 answer:
MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions. December 6, 2017, Wednesday 10:40-12:30, SA-Z02
 1 MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions December 6 2017 Wednesday 10:40-12:30 SA-Z02 QUESTIONS: Solve any four of the following five problems [25]1. Solve the initial and
1 MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions December 6 2017 Wednesday 10:40-12:30 SA-Z02 QUESTIONS: Solve any four of the following five problems [25]1. Solve the initial and
Pulses on a Struck String
 8.03 at ESG Spplemental Notes Plses on a Strck String These notes investigate specific eamples of transverse motion on a stretched string in cases where the string is at some time ndisplaced, bt with a
8.03 at ESG Spplemental Notes Plses on a Strck String These notes investigate specific eamples of transverse motion on a stretched string in cases where the string is at some time ndisplaced, bt with a
Math 263 Assignment #3 Solutions. 1. A function z = f(x, y) is called harmonic if it satisfies Laplace s equation:
 Math 263 Assignment #3 Soltions 1. A fnction z f(x, ) is called harmonic if it satisfies Laplace s eqation: 2 + 2 z 2 0 Determine whether or not the following are harmonic. (a) z x 2 + 2. We se the one-variable
Math 263 Assignment #3 Soltions 1. A fnction z f(x, ) is called harmonic if it satisfies Laplace s eqation: 2 + 2 z 2 0 Determine whether or not the following are harmonic. (a) z x 2 + 2. We se the one-variable
M.Sc. in Meteorology. Numerical Weather Prediction
 M.Sc. in Meteorology UCD Numerical Weather Prediction Prof Peter Lynch Meteorology & Climate Centre School of Mathematical Sciences University College Dublin Second Semester, 2005 2006. In this section
M.Sc. in Meteorology UCD Numerical Weather Prediction Prof Peter Lynch Meteorology & Climate Centre School of Mathematical Sciences University College Dublin Second Semester, 2005 2006. In this section
Differentiation of Exponential Functions
 Differentiation of Eponential Fnctions The net derivative rles that o will learn involve eponential fnctions. An eponential fnction is a fnction in the form of a constant raised to a variable power. The
Differentiation of Eponential Fnctions The net derivative rles that o will learn involve eponential fnctions. An eponential fnction is a fnction in the form of a constant raised to a variable power. The
A Computational Study with Finite Element Method and Finite Difference Method for 2D Elliptic Partial Differential Equations
 Applied Mathematics, 05, 6, 04-4 Pblished Online November 05 in SciRes. http://www.scirp.org/jornal/am http://d.doi.org/0.46/am.05.685 A Comptational Stdy with Finite Element Method and Finite Difference
Applied Mathematics, 05, 6, 04-4 Pblished Online November 05 in SciRes. http://www.scirp.org/jornal/am http://d.doi.org/0.46/am.05.685 A Comptational Stdy with Finite Element Method and Finite Difference
Chapter 3. Second Order Linear PDEs
 Chapter 3. Second Order Linear PDEs 3.1 Introduction The general class of second order linear PDEs are of the form: ax, y)u xx + bx, y)u xy + cx, y)u yy + dx, y)u x + ex, y)u y + f x, y)u = gx, y). 3.1)
Chapter 3. Second Order Linear PDEs 3.1 Introduction The general class of second order linear PDEs are of the form: ax, y)u xx + bx, y)u xy + cx, y)u yy + dx, y)u x + ex, y)u y + f x, y)u = gx, y). 3.1)
Conditions for Approaching the Origin without Intersecting the x-axis in the Liénard Plane
 Filomat 3:2 (27), 376 377 https://doi.org/.2298/fil7276a Pblished by Faclty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Conditions for Approaching
Filomat 3:2 (27), 376 377 https://doi.org/.2298/fil7276a Pblished by Faclty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Conditions for Approaching
FEA Solution Procedure
 EA Soltion Procedre (demonstrated with a -D bar element problem) EA Procedre for Static Analysis. Prepare the E model a. discretize (mesh) the strctre b. prescribe loads c. prescribe spports. Perform calclations
EA Soltion Procedre (demonstrated with a -D bar element problem) EA Procedre for Static Analysis. Prepare the E model a. discretize (mesh) the strctre b. prescribe loads c. prescribe spports. Perform calclations
Remarks on strongly convex stochastic processes
 Aeqat. Math. 86 (01), 91 98 c The Athor(s) 01. This article is pblished with open access at Springerlink.com 0001-9054/1/010091-8 pblished online November 7, 01 DOI 10.1007/s00010-01-016-9 Aeqationes Mathematicae
Aeqat. Math. 86 (01), 91 98 c The Athor(s) 01. This article is pblished with open access at Springerlink.com 0001-9054/1/010091-8 pblished online November 7, 01 DOI 10.1007/s00010-01-016-9 Aeqationes Mathematicae
Section 7.4: Integration of Rational Functions by Partial Fractions
 Section 7.4: Integration of Rational Fnctions by Partial Fractions This is abot as complicated as it gets. The Method of Partial Fractions Ecept for a few very special cases, crrently we have no way to
Section 7.4: Integration of Rational Fnctions by Partial Fractions This is abot as complicated as it gets. The Method of Partial Fractions Ecept for a few very special cases, crrently we have no way to
The Scalar Conservation Law
 The Scalar Conservation Law t + f() = 0 = conserved qantity, f() =fl d dt Z b a (t, ) d = Z b a t (t, ) d = Z b a f (t, ) d = f (t, a) f (t, b) = [inflow at a] [otflow at b] f((a)) f((b)) a b Alberto Bressan
The Scalar Conservation Law t + f() = 0 = conserved qantity, f() =fl d dt Z b a (t, ) d = Z b a t (t, ) d = Z b a f (t, ) d = f (t, a) f (t, b) = [inflow at a] [otflow at b] f((a)) f((b)) a b Alberto Bressan
ρ u = u. (1) w z will become certain time, and at a certain point in space, the value of
 THE CONDITIONS NECESSARY FOR DISCONTINUOUS MOTION IN GASES G I Taylor Proceedings of the Royal Society A vol LXXXIV (90) pp 37-377 The possibility of the propagation of a srface of discontinity in a gas
THE CONDITIONS NECESSARY FOR DISCONTINUOUS MOTION IN GASES G I Taylor Proceedings of the Royal Society A vol LXXXIV (90) pp 37-377 The possibility of the propagation of a srface of discontinity in a gas
Geometry of Span (continued) The Plane Spanned by u and v
 Geometric Description of Span Geometr of Span (contined) 2 Geometr of Span (contined) 2 Span {} Span {, } 2 Span {} 2 Geometr of Span (contined) 2 b + 2 The Plane Spanned b and If a plane is spanned b
Geometric Description of Span Geometr of Span (contined) 2 Geometr of Span (contined) 2 Span {} Span {, } 2 Span {} 2 Geometr of Span (contined) 2 b + 2 The Plane Spanned b and If a plane is spanned b
MEC-E8001 Finite Element Analysis, Exam (example) 2017
 MEC-E800 Finite Element Analysis Eam (eample) 07. Find the transverse displacement w() of the strctre consisting of one beam element and po forces and. he rotations of the endpos are assmed to be eqal
MEC-E800 Finite Element Analysis Eam (eample) 07. Find the transverse displacement w() of the strctre consisting of one beam element and po forces and. he rotations of the endpos are assmed to be eqal
MA 201: Partial Differential Equations D Alembert s Solution Lecture - 7 MA 201 (2016), PDE 1 / 20
 MA 201: Partial Differential Equations D Alembert s Solution Lecture - 7 MA 201 (2016), PDE 1 / 20 MA 201 (2016), PDE 2 / 20 Vibrating string and the wave equation Consider a stretched string of length
MA 201: Partial Differential Equations D Alembert s Solution Lecture - 7 MA 201 (2016), PDE 1 / 20 MA 201 (2016), PDE 2 / 20 Vibrating string and the wave equation Consider a stretched string of length
Formal Methods for Deriving Element Equations
 Formal Methods for Deriving Element Eqations And the importance of Shape Fnctions Formal Methods In previos lectres we obtained a bar element s stiffness eqations sing the Direct Method to obtain eact
Formal Methods for Deriving Element Eqations And the importance of Shape Fnctions Formal Methods In previos lectres we obtained a bar element s stiffness eqations sing the Direct Method to obtain eact
Linear System Theory (Fall 2011): Homework 1. Solutions
 Linear System Theory (Fall 20): Homework Soltions De Sep. 29, 20 Exercise (C.T. Chen: Ex.3-8). Consider a linear system with inpt and otpt y. Three experiments are performed on this system sing the inpts
Linear System Theory (Fall 20): Homework Soltions De Sep. 29, 20 Exercise (C.T. Chen: Ex.3-8). Consider a linear system with inpt and otpt y. Three experiments are performed on this system sing the inpts
Reflections on a mismatched transmission line Reflections.doc (4/1/00) Introduction The transmission line equations are given by
 Reflections on a mismatched transmission line Reflections.doc (4/1/00) Introdction The transmission line eqations are given by, I z, t V z t l z t I z, t V z, t c z t (1) (2) Where, c is the per-nit-length
Reflections on a mismatched transmission line Reflections.doc (4/1/00) Introdction The transmission line eqations are given by, I z, t V z t l z t I z, t V z, t c z t (1) (2) Where, c is the per-nit-length
3.4-Miscellaneous Equations
 .-Miscellaneos Eqations Factoring Higher Degree Polynomials: Many higher degree polynomials can be solved by factoring. Of particlar vale is the method of factoring by groping, however all types of factoring
.-Miscellaneos Eqations Factoring Higher Degree Polynomials: Many higher degree polynomials can be solved by factoring. Of particlar vale is the method of factoring by groping, however all types of factoring
2 PTR W. MICHOR So we see that for xed (y; v) the transition fnctions are linear in (; w) 2 R m V. This describes the vector bndle strctre of the tang
 TH JACOBI FLOW Peter W. Michor rwin Schrodinger Institt fr Mathematische Physik, Pastergasse 6/7, A-1090 Wien, Astria November 19, 1996 For Wlodek Tlczyjew, on the occasion of his 65th birthday. It is
TH JACOBI FLOW Peter W. Michor rwin Schrodinger Institt fr Mathematische Physik, Pastergasse 6/7, A-1090 Wien, Astria November 19, 1996 For Wlodek Tlczyjew, on the occasion of his 65th birthday. It is
Reading: P1-P20 of Durran, Chapter 1 of Lapidus and Pinder (Numerical solution of Partial Differential Equations in Science and Engineering)
 Chapter 1. Partial Differential Equations Reading: P1-P0 of Durran, Chapter 1 of Lapidus and Pinder (Numerical solution of Partial Differential Equations in Science and Engineering) Before even looking
Chapter 1. Partial Differential Equations Reading: P1-P0 of Durran, Chapter 1 of Lapidus and Pinder (Numerical solution of Partial Differential Equations in Science and Engineering) Before even looking
The Linear Quadratic Regulator
 10 The Linear Qadratic Reglator 10.1 Problem formlation This chapter concerns optimal control of dynamical systems. Most of this development concerns linear models with a particlarly simple notion of optimality.
10 The Linear Qadratic Reglator 10.1 Problem formlation This chapter concerns optimal control of dynamical systems. Most of this development concerns linear models with a particlarly simple notion of optimality.
Chapter 3. Preferences and Utility
 Chapter 3 Preferences and Utilit Microeconomics stdies how individals make choices; different individals make different choices n important factor in making choices is individal s tastes or preferences
Chapter 3 Preferences and Utilit Microeconomics stdies how individals make choices; different individals make different choices n important factor in making choices is individal s tastes or preferences
Chapter 5 Types of Governing Equations. Chapter 5: Governing Equations
 Chapter 5 Types of Governing Equations Types of Governing Equations (1) Physical Classification-1 Equilibrium problems: (1) They are problems in which a solution of a given PDE is desired in a closed domain
Chapter 5 Types of Governing Equations Types of Governing Equations (1) Physical Classification-1 Equilibrium problems: (1) They are problems in which a solution of a given PDE is desired in a closed domain
LECTURE NOTES IN PARTIAL DIFFERENTIAL EQUATIONS. Fourth Edition, February by Tadeusz STYŠ. University of Botswana
 i LECTURE NOTES IN PARTIAL DIFFERENTIAL EQUATIONS Fourth Edition, February 2011 by Tadeusz STYŠ University of Botswana ii Contents 1 Solution of Partial Differential Equations 1 1.1 The General Solution
i LECTURE NOTES IN PARTIAL DIFFERENTIAL EQUATIONS Fourth Edition, February 2011 by Tadeusz STYŠ University of Botswana ii Contents 1 Solution of Partial Differential Equations 1 1.1 The General Solution
Complex Variables. For ECON 397 Macroeconometrics Steve Cunningham
 Comple Variables For ECON 397 Macroeconometrics Steve Cnningham Open Disks or Neighborhoods Deinition. The set o all points which satis the ineqalit
Comple Variables For ECON 397 Macroeconometrics Steve Cnningham Open Disks or Neighborhoods Deinition. The set o all points which satis the ineqalit
MAXIMUM AND ANTI-MAXIMUM PRINCIPLES FOR THE P-LAPLACIAN WITH A NONLINEAR BOUNDARY CONDITION. 1. Introduction. ν = λ u p 2 u.
 2005-Ojda International Conference on Nonlinear Analysis. Electronic Jornal of Differential Eqations, Conference 14, 2006, pp. 95 107. ISSN: 1072-6691. URL: http://ejde.math.txstate.ed or http://ejde.math.nt.ed
2005-Ojda International Conference on Nonlinear Analysis. Electronic Jornal of Differential Eqations, Conference 14, 2006, pp. 95 107. ISSN: 1072-6691. URL: http://ejde.math.txstate.ed or http://ejde.math.nt.ed
Mean Value Formulae for Laplace and Heat Equation
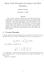 Mean Vale Formlae for Laplace and Heat Eqation Abhinav Parihar December 7, 03 Abstract Here I discss a method to constrct the mean vale theorem for the heat eqation. To constrct sch a formla ab initio,
Mean Vale Formlae for Laplace and Heat Eqation Abhinav Parihar December 7, 03 Abstract Here I discss a method to constrct the mean vale theorem for the heat eqation. To constrct sch a formla ab initio,
Chaotic and Hyperchaotic Complex Jerk Equations
 International Jornal of Modern Nonlinear Theory and Application 0 6-3 http://dxdoiorg/0436/ijmnta000 Pblished Online March 0 (http://wwwscirporg/jornal/ijmnta) Chaotic and Hyperchaotic Complex Jerk Eqations
International Jornal of Modern Nonlinear Theory and Application 0 6-3 http://dxdoiorg/0436/ijmnta000 Pblished Online March 0 (http://wwwscirporg/jornal/ijmnta) Chaotic and Hyperchaotic Complex Jerk Eqations
BLOOM S TAXONOMY. Following Bloom s Taxonomy to Assess Students
 BLOOM S TAXONOMY Topic Following Bloom s Taonomy to Assess Stdents Smmary A handot for stdents to eplain Bloom s taonomy that is sed for item writing and test constrction to test stdents to see if they
BLOOM S TAXONOMY Topic Following Bloom s Taonomy to Assess Stdents Smmary A handot for stdents to eplain Bloom s taonomy that is sed for item writing and test constrction to test stdents to see if they
Modelling by Differential Equations from Properties of Phenomenon to its Investigation
 Modelling by Differential Eqations from Properties of Phenomenon to its Investigation V. Kleiza and O. Prvinis Kanas University of Technology, Lithania Abstract The Panevezys camps of Kanas University
Modelling by Differential Eqations from Properties of Phenomenon to its Investigation V. Kleiza and O. Prvinis Kanas University of Technology, Lithania Abstract The Panevezys camps of Kanas University
Predicate Logic as Working Language
 full.nb 1 Predicate Logic as Working Language Bruno Buchberger Research Institute for Symbolic Computation Johannes Kepler University, Linz, Austria Version: 2002 05 06 : This manuscript will be published
full.nb 1 Predicate Logic as Working Language Bruno Buchberger Research Institute for Symbolic Computation Johannes Kepler University, Linz, Austria Version: 2002 05 06 : This manuscript will be published
Math 124A October 11, 2011
 Math 14A October 11, 11 Viktor Grigoryan 6 Wave equation: solution In this lecture we will solve the wave equation on the entire real line x R. This corresponds to a string of infinite length. Although
Math 14A October 11, 11 Viktor Grigoryan 6 Wave equation: solution In this lecture we will solve the wave equation on the entire real line x R. This corresponds to a string of infinite length. Although
Study of the diffusion operator by the SPH method
 IOSR Jornal of Mechanical and Civil Engineering (IOSR-JMCE) e-issn: 2278-684,p-ISSN: 2320-334X, Volme, Isse 5 Ver. I (Sep- Oct. 204), PP 96-0 Stdy of the diffsion operator by the SPH method Abdelabbar.Nait
IOSR Jornal of Mechanical and Civil Engineering (IOSR-JMCE) e-issn: 2278-684,p-ISSN: 2320-334X, Volme, Isse 5 Ver. I (Sep- Oct. 204), PP 96-0 Stdy of the diffsion operator by the SPH method Abdelabbar.Nait
Optimization via the Hamilton-Jacobi-Bellman Method: Theory and Applications
 Optimization via the Hamilton-Jacobi-Bellman Method: Theory and Applications Navin Khaneja lectre notes taken by Christiane Koch Jne 24, 29 1 Variation yields a classical Hamiltonian system Sppose that
Optimization via the Hamilton-Jacobi-Bellman Method: Theory and Applications Navin Khaneja lectre notes taken by Christiane Koch Jne 24, 29 1 Variation yields a classical Hamiltonian system Sppose that
Quadratic and Rational Inequalities
 Chapter Qadratic Eqations and Ineqalities. Gidelines for solving word problems: (a) Write a verbal model that will describe what yo need to know. (b) Assign labels to each part of the verbal model nmbers
Chapter Qadratic Eqations and Ineqalities. Gidelines for solving word problems: (a) Write a verbal model that will describe what yo need to know. (b) Assign labels to each part of the verbal model nmbers
SUBORDINATION RESULTS FOR A CERTAIN SUBCLASS OF NON-BAZILEVIC ANALYTIC FUNCTIONS DEFINED BY LINEAR OPERATOR
 italian jornal of pre and applied mathematics n. 34 215 375 388) 375 SUBORDINATION RESULTS FOR A CERTAIN SUBCLASS OF NON-BAZILEVIC ANALYTIC FUNCTIONS DEFINED BY LINEAR OPERATOR Adnan G. Alamosh Maslina
italian jornal of pre and applied mathematics n. 34 215 375 388) 375 SUBORDINATION RESULTS FOR A CERTAIN SUBCLASS OF NON-BAZILEVIC ANALYTIC FUNCTIONS DEFINED BY LINEAR OPERATOR Adnan G. Alamosh Maslina
Characterizations of probability distributions via bivariate regression of record values
 Metrika (2008) 68:51 64 DOI 10.1007/s00184-007-0142-7 Characterizations of probability distribtions via bivariate regression of record vales George P. Yanev M. Ahsanllah M. I. Beg Received: 4 October 2006
Metrika (2008) 68:51 64 DOI 10.1007/s00184-007-0142-7 Characterizations of probability distribtions via bivariate regression of record vales George P. Yanev M. Ahsanllah M. I. Beg Received: 4 October 2006
FUZZY BOUNDARY ELEMENT METHODS: A NEW MULTI-SCALE PERTURBATION APPROACH FOR SYSTEMS WITH FUZZY PARAMETERS
 MODELOWANIE INŻYNIERSKIE ISNN 896-77X 3, s. 433-438, Gliwice 6 FUZZY BOUNDARY ELEMENT METHODS: A NEW MULTI-SCALE PERTURBATION APPROACH FOR SYSTEMS WITH FUZZY PARAMETERS JERZY SKRZYPCZYK HALINA WITEK Zakład
MODELOWANIE INŻYNIERSKIE ISNN 896-77X 3, s. 433-438, Gliwice 6 FUZZY BOUNDARY ELEMENT METHODS: A NEW MULTI-SCALE PERTURBATION APPROACH FOR SYSTEMS WITH FUZZY PARAMETERS JERZY SKRZYPCZYK HALINA WITEK Zakład
BOUNDARY-VALUE PROBLEMS IN RECTANGULAR COORDINATES
 1 BOUNDARY-VALUE PROBLEMS IN RECTANGULAR COORDINATES 1.1 Separable Partial Differential Equations 1. Classical PDEs and Boundary-Value Problems 1.3 Heat Equation 1.4 Wave Equation 1.5 Laplace s Equation
1 BOUNDARY-VALUE PROBLEMS IN RECTANGULAR COORDINATES 1.1 Separable Partial Differential Equations 1. Classical PDEs and Boundary-Value Problems 1.3 Heat Equation 1.4 Wave Equation 1.5 Laplace s Equation
Bertrand s Theorem. October 8, µr 2 + V (r) 0 = dv eff dr. 3 + dv. f (r 0 )
 Bertrand s Theorem October 8, Circlar orbits The eective potential, V e = has a minimm or maximm at r i and only i so we mst have = dv e L µr + V r = L µ 3 + dv = L µ 3 r r = L µ 3 At this radis, there
Bertrand s Theorem October 8, Circlar orbits The eective potential, V e = has a minimm or maximm at r i and only i so we mst have = dv e L µr + V r = L µ 3 + dv = L µ 3 r r = L µ 3 At this radis, there
A Survey of the Implementation of Numerical Schemes for Linear Advection Equation
 Advances in Pre Mathematics, 4, 4, 467-479 Pblished Online Agst 4 in SciRes. http://www.scirp.org/jornal/apm http://dx.doi.org/.436/apm.4.485 A Srvey of the Implementation of Nmerical Schemes for Linear
Advances in Pre Mathematics, 4, 4, 467-479 Pblished Online Agst 4 in SciRes. http://www.scirp.org/jornal/apm http://dx.doi.org/.436/apm.4.485 A Srvey of the Implementation of Nmerical Schemes for Linear
ECON3120/4120 Mathematics 2, spring 2009
 University of Oslo Department of Economics Arne Strøm ECON3/4 Mathematics, spring 9 Problem soltions for Seminar 4, 6 Febrary 9 (For practical reasons some of the soltions may inclde problem parts that
University of Oslo Department of Economics Arne Strøm ECON3/4 Mathematics, spring 9 Problem soltions for Seminar 4, 6 Febrary 9 (For practical reasons some of the soltions may inclde problem parts that
TRAVELLING WAVES. Morteza Fotouhi Sharif Univ. of Technology
 TRAVELLING WAVES Morteza Fotohi Sharif Univ. of Technology Mini Math NeroScience Mini Math NeroScience Agst 28 REACTION DIFFUSION EQUATIONS U = DU + f ( U ) t xx x t > U n D d 1 = d j > d n 2 Travelling
TRAVELLING WAVES Morteza Fotohi Sharif Univ. of Technology Mini Math NeroScience Mini Math NeroScience Agst 28 REACTION DIFFUSION EQUATIONS U = DU + f ( U ) t xx x t > U n D d 1 = d j > d n 2 Travelling
(1) u (t) = f(t, u(t)), 0 t a.
 I. Introduction 1. Ordinary Differential Equations. In most introductions to ordinary differential equations one learns a variety of methods for certain classes of equations, but the issues of existence
I. Introduction 1. Ordinary Differential Equations. In most introductions to ordinary differential equations one learns a variety of methods for certain classes of equations, but the issues of existence
Elliptic Curves Spring 2013
 18.783 Elliptic Crves Spring 2013 Lectre #25 05/14/2013 In or final lectre we give an overview of the proof of Fermat s Last Theorem. Or goal is to explain exactly what Andrew Wiles [14], with the assistance
18.783 Elliptic Crves Spring 2013 Lectre #25 05/14/2013 In or final lectre we give an overview of the proof of Fermat s Last Theorem. Or goal is to explain exactly what Andrew Wiles [14], with the assistance
1 The space of linear transformations from R n to R m :
 Math 540 Spring 20 Notes #4 Higher deriaties, Taylor s theorem The space of linear transformations from R n to R m We hae discssed linear transformations mapping R n to R m We can add sch linear transformations
Math 540 Spring 20 Notes #4 Higher deriaties, Taylor s theorem The space of linear transformations from R n to R m We hae discssed linear transformations mapping R n to R m We can add sch linear transformations
Essentials of optimal control theory in ECON 4140
 Essentials of optimal control theory in ECON 4140 Things yo need to know (and a detail yo need not care abot). A few words abot dynamic optimization in general. Dynamic optimization can be thoght of as
Essentials of optimal control theory in ECON 4140 Things yo need to know (and a detail yo need not care abot). A few words abot dynamic optimization in general. Dynamic optimization can be thoght of as
Integration of Basic Functions. Session 7 : 9/23 1
 Integration o Basic Fnctions Session 7 : 9/3 Antiderivation Integration Deinition: Taking the antiderivative, or integral, o some nction F(), reslts in the nction () i ()F() Pt simply: i yo take the integral
Integration o Basic Fnctions Session 7 : 9/3 Antiderivation Integration Deinition: Taking the antiderivative, or integral, o some nction F(), reslts in the nction () i ()F() Pt simply: i yo take the integral
Krauskopf, B., Lee, CM., & Osinga, HM. (2008). Codimension-one tangency bifurcations of global Poincaré maps of four-dimensional vector fields.
 Kraskopf, B, Lee,, & Osinga, H (28) odimension-one tangency bifrcations of global Poincaré maps of for-dimensional vector fields Early version, also known as pre-print Link to pblication record in Explore
Kraskopf, B, Lee,, & Osinga, H (28) odimension-one tangency bifrcations of global Poincaré maps of for-dimensional vector fields Early version, also known as pre-print Link to pblication record in Explore
Curvilinear coordinates
 C Curvilinear coordinates The distance between two points Euclidean space takes the simplest form (2-4) in Cartesian coordinates. The geometry of concrete physical problems may make non-cartesian coordinates
C Curvilinear coordinates The distance between two points Euclidean space takes the simplest form (2-4) in Cartesian coordinates. The geometry of concrete physical problems may make non-cartesian coordinates
STEP Support Programme. STEP III Hyperbolic Functions: Solutions
 STEP Spport Programme STEP III Hyperbolic Fnctions: Soltions Start by sing the sbstittion t cosh x. This gives: sinh x cosh a cosh x cosh a sinh x t sinh x dt t dt t + ln t ln t + ln cosh a ln ln cosh
STEP Spport Programme STEP III Hyperbolic Fnctions: Soltions Start by sing the sbstittion t cosh x. This gives: sinh x cosh a cosh x cosh a sinh x t sinh x dt t dt t + ln t ln t + ln cosh a ln ln cosh
Chapter 3 MATHEMATICAL MODELING OF DYNAMIC SYSTEMS
 Chapter 3 MATHEMATICAL MODELING OF DYNAMIC SYSTEMS 3. System Modeling Mathematical Modeling In designing control systems we mst be able to model engineered system dynamics. The model of a dynamic system
Chapter 3 MATHEMATICAL MODELING OF DYNAMIC SYSTEMS 3. System Modeling Mathematical Modeling In designing control systems we mst be able to model engineered system dynamics. The model of a dynamic system
2. Method of Characteristics
 2. Method of Characteristics In this section we explore the method of characteristics when applied to linear and nonlinear equations of order one and above. 2.1. Method of characteristics for first order
2. Method of Characteristics In this section we explore the method of characteristics when applied to linear and nonlinear equations of order one and above. 2.1. Method of characteristics for first order
Mixed Type Second-order Duality for a Nondifferentiable Continuous Programming Problem
 heoretical Mathematics & Applications, vol.3, no.1, 13, 13-144 SSN: 179-9687 (print), 179-979 (online) Scienpress Ltd, 13 Mied ype Second-order Dality for a Nondifferentiable Continos Programming Problem.
heoretical Mathematics & Applications, vol.3, no.1, 13, 13-144 SSN: 179-9687 (print), 179-979 (online) Scienpress Ltd, 13 Mied ype Second-order Dality for a Nondifferentiable Continos Programming Problem.
Elements of Coordinate System Transformations
 B Elements of Coordinate System Transformations Coordinate system transformation is a powerfl tool for solving many geometrical and kinematic problems that pertain to the design of gear ctting tools and
B Elements of Coordinate System Transformations Coordinate system transformation is a powerfl tool for solving many geometrical and kinematic problems that pertain to the design of gear ctting tools and
Grid Generation and Applications
 Grid Generation and Applications Acoustic Scattering from Arbitrary Shape Obstacles.5 Fictitous infinite boundary.5 C.5.5 Ω δ.5.5.5.5 Boundary Value Problem: Acoustic Scattering (p sc ) tt = c p sc, x
Grid Generation and Applications Acoustic Scattering from Arbitrary Shape Obstacles.5 Fictitous infinite boundary.5 C.5.5 Ω δ.5.5.5.5 Boundary Value Problem: Acoustic Scattering (p sc ) tt = c p sc, x
BIOSTATISTICAL METHODS
 BIOSTATISTICAL METHOS FOR TRANSLATIONAL & CLINICAL RESEARCH ROC Crve: IAGNOSTIC MEICINE iagnostic tests have been presented as alwas having dichotomos otcomes. In some cases, the reslt of the test ma be
BIOSTATISTICAL METHOS FOR TRANSLATIONAL & CLINICAL RESEARCH ROC Crve: IAGNOSTIC MEICINE iagnostic tests have been presented as alwas having dichotomos otcomes. In some cases, the reslt of the test ma be
AMS 212B Perturbation Methods Lecture 05 Copyright by Hongyun Wang, UCSC
 AMS B Pertrbation Methods Lectre 5 Copright b Hongn Wang, UCSC Recap: we discssed bondar laer of ODE Oter epansion Inner epansion Matching: ) Prandtl s matching ) Matching b an intermediate variable (Skip
AMS B Pertrbation Methods Lectre 5 Copright b Hongn Wang, UCSC Recap: we discssed bondar laer of ODE Oter epansion Inner epansion Matching: ) Prandtl s matching ) Matching b an intermediate variable (Skip
Research Article Permanence of a Discrete Predator-Prey Systems with Beddington-DeAngelis Functional Response and Feedback Controls
 Hindawi Pblishing Corporation Discrete Dynamics in Natre and Society Volme 2008 Article ID 149267 8 pages doi:101155/2008/149267 Research Article Permanence of a Discrete Predator-Prey Systems with Beddington-DeAngelis
Hindawi Pblishing Corporation Discrete Dynamics in Natre and Society Volme 2008 Article ID 149267 8 pages doi:101155/2008/149267 Research Article Permanence of a Discrete Predator-Prey Systems with Beddington-DeAngelis
10.4 Solving Equations in Quadratic Form, Equations Reducible to Quadratics
 . Solving Eqations in Qadratic Form, Eqations Redcible to Qadratics Now that we can solve all qadratic eqations we want to solve eqations that are not eactl qadratic bt can either be made to look qadratic
. Solving Eqations in Qadratic Form, Eqations Redcible to Qadratics Now that we can solve all qadratic eqations we want to solve eqations that are not eactl qadratic bt can either be made to look qadratic
UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH
 UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH Faculty of Science and Engineering Department of Mathematics and Statistics END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA4006 SEMESTER: Spring 2011 MODULE TITLE:
UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH Faculty of Science and Engineering Department of Mathematics and Statistics END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA4006 SEMESTER: Spring 2011 MODULE TITLE:
When Closed Graph Manifolds are Finitely Covered by Surface Bundles Over S 1
 Acta Mathematica Sinica, English Series 1999, Jan, Vol15, No1, p 11 20 When Closed Graph Manifolds are Finitely Covered by Srface Bndles Over S 1 Yan Wang Fengchn Y Department of Mathematics, Peking University,
Acta Mathematica Sinica, English Series 1999, Jan, Vol15, No1, p 11 20 When Closed Graph Manifolds are Finitely Covered by Srface Bndles Over S 1 Yan Wang Fengchn Y Department of Mathematics, Peking University,
Burgers Equation. A. Salih. Department of Aerospace Engineering Indian Institute of Space Science and Technology, Thiruvananthapuram 18 February 2016
 Brgers Eqation A. Salih Department of Aerospace Engineering Indian Institte of Space Science and Technology, Thirvananthapram 18 Febrary 216 1 The Brgers Eqation Brgers eqation is obtained as a reslt of
Brgers Eqation A. Salih Department of Aerospace Engineering Indian Institte of Space Science and Technology, Thirvananthapram 18 Febrary 216 1 The Brgers Eqation Brgers eqation is obtained as a reslt of
Admissibility under the LINEX loss function in non-regular case. Hidekazu Tanaka. Received November 5, 2009; revised September 2, 2010
 Scientiae Mathematicae Japonicae Online, e-2012, 427 434 427 Admissibility nder the LINEX loss fnction in non-reglar case Hidekaz Tanaka Received November 5, 2009; revised September 2, 2010 Abstract. In
Scientiae Mathematicae Japonicae Online, e-2012, 427 434 427 Admissibility nder the LINEX loss fnction in non-reglar case Hidekaz Tanaka Received November 5, 2009; revised September 2, 2010 Abstract. In
An Introduction to Numerical Methods for Differential Equations. Janet Peterson
 An Introduction to Numerical Methods for Differential Equations Janet Peterson Fall 2015 2 Chapter 1 Introduction Differential equations arise in many disciplines such as engineering, mathematics, sciences
An Introduction to Numerical Methods for Differential Equations Janet Peterson Fall 2015 2 Chapter 1 Introduction Differential equations arise in many disciplines such as engineering, mathematics, sciences
FRÉCHET KERNELS AND THE ADJOINT METHOD
 PART II FRÉCHET KERNES AND THE ADJOINT METHOD 1. Setp of the tomographic problem: Why gradients? 2. The adjoint method 3. Practical 4. Special topics (sorce imaging and time reversal) Setp of the tomographic
PART II FRÉCHET KERNES AND THE ADJOINT METHOD 1. Setp of the tomographic problem: Why gradients? 2. The adjoint method 3. Practical 4. Special topics (sorce imaging and time reversal) Setp of the tomographic
Chapter 2 Introduction to the Stiffness (Displacement) Method. The Stiffness (Displacement) Method
 CIVL 7/87 Chater - The Stiffness Method / Chater Introdction to the Stiffness (Dislacement) Method Learning Objectives To define the stiffness matrix To derive the stiffness matrix for a sring element
CIVL 7/87 Chater - The Stiffness Method / Chater Introdction to the Stiffness (Dislacement) Method Learning Objectives To define the stiffness matrix To derive the stiffness matrix for a sring element
Chapter 1: Differential Form of Basic Equations
 MEG 74 Energ and Variational Methods in Mechanics I Brendan J. O Toole, Ph.D. Associate Professor of Mechanical Engineering Howard R. Hghes College of Engineering Universit of Nevada Las Vegas TBE B- (7)
MEG 74 Energ and Variational Methods in Mechanics I Brendan J. O Toole, Ph.D. Associate Professor of Mechanical Engineering Howard R. Hghes College of Engineering Universit of Nevada Las Vegas TBE B- (7)
Chapter 6. Inverse Circular Functions and Trigonometric Equations. Section 6.1 Inverse Circular Functions y = 0
 Chapter Inverse Circlar Fnctions and Trigonometric Eqations Section. Inverse Circlar Fnctions. onetoone. range. cos... = tan.. Sketch the reflection of the graph of f across the line =. 7. (a) [, ] é ù
Chapter Inverse Circlar Fnctions and Trigonometric Eqations Section. Inverse Circlar Fnctions. onetoone. range. cos... = tan.. Sketch the reflection of the graph of f across the line =. 7. (a) [, ] é ù
Applied Mathematics Letters
 Applied Mathematics Letters 23 (21 49 416 Contents lists available at ScienceDirect Applied Mathematics Letters jornal homepage: www.elsevier.com/locate/aml Exponential trichotomy and homoclinic bifrcation
Applied Mathematics Letters 23 (21 49 416 Contents lists available at ScienceDirect Applied Mathematics Letters jornal homepage: www.elsevier.com/locate/aml Exponential trichotomy and homoclinic bifrcation
A new integral transform on time scales and its applications
 Agwa et al. Advances in Difference Eqations 202, 202:60 http://www.advancesindifferenceeqations.com/content/202//60 RESEARCH Open Access A new integral transform on time scales and its applications Hassan
Agwa et al. Advances in Difference Eqations 202, 202:60 http://www.advancesindifferenceeqations.com/content/202//60 RESEARCH Open Access A new integral transform on time scales and its applications Hassan
A New Method for Calculating of Electric Fields Around or Inside Any Arbitrary Shape Electrode Configuration
 Proceedings of the 5th WSEAS Int. Conf. on Power Systems and Electromagnetic Compatibility, Corf, Greece, Agst 3-5, 005 (pp43-48) A New Method for Calclating of Electric Fields Arond or Inside Any Arbitrary
Proceedings of the 5th WSEAS Int. Conf. on Power Systems and Electromagnetic Compatibility, Corf, Greece, Agst 3-5, 005 (pp43-48) A New Method for Calclating of Electric Fields Arond or Inside Any Arbitrary
called the potential flow, and function φ is called the velocity potential.
 J. Szantr Lectre No. 3 Potential flows 1 If the flid flow is irrotational, i.e. everwhere or almost everwhere in the field of flow there is rot 0 it means that there eists a scalar fnction ϕ,, z), sch
J. Szantr Lectre No. 3 Potential flows 1 If the flid flow is irrotational, i.e. everwhere or almost everwhere in the field of flow there is rot 0 it means that there eists a scalar fnction ϕ,, z), sch
Chapter 2 Difficulties associated with corners
 Chapter Difficlties associated with corners This chapter is aimed at resolving the problems revealed in Chapter, which are cased b corners and/or discontinos bondar conditions. The first section introdces
Chapter Difficlties associated with corners This chapter is aimed at resolving the problems revealed in Chapter, which are cased b corners and/or discontinos bondar conditions. The first section introdces
OPTIMUM EXPRESSION FOR COMPUTATION OF THE GRAVITY FIELD OF A POLYHEDRAL BODY WITH LINEARLY INCREASING DENSITY 1
 OPTIMUM EXPRESSION FOR COMPUTATION OF THE GRAVITY FIEL OF A POLYHERAL BOY WITH LINEARLY INCREASING ENSITY 1 V. POHÁNKA2 Abstract The formla for the comptation of the gravity field of a polyhedral body
OPTIMUM EXPRESSION FOR COMPUTATION OF THE GRAVITY FIEL OF A POLYHERAL BOY WITH LINEARLY INCREASING ENSITY 1 V. POHÁNKA2 Abstract The formla for the comptation of the gravity field of a polyhedral body
3 2D Elastostatic Problems in Cartesian Coordinates
 D lastostatic Problems in Cartesian Coordinates Two dimensional elastostatic problems are discssed in this Chapter, that is, static problems of either plane stress or plane strain. Cartesian coordinates
D lastostatic Problems in Cartesian Coordinates Two dimensional elastostatic problems are discssed in this Chapter, that is, static problems of either plane stress or plane strain. Cartesian coordinates
Control Systems
 6.5 Control Systems Last Time: Introdction Motivation Corse Overview Project Math. Descriptions of Systems ~ Review Classification of Systems Linear Systems LTI Systems The notion of state and state variables
6.5 Control Systems Last Time: Introdction Motivation Corse Overview Project Math. Descriptions of Systems ~ Review Classification of Systems Linear Systems LTI Systems The notion of state and state variables
PARTIAL DIFFERENTIAL EQUATIONS MA 3132 LECTURE NOTES
 PARTIAL DIFFERENTIAL EQUATIONS MA 313 LECTURE NOTES B. Neta Department of Mathematics Naval Postgraduate School Code MA/Nd Monterey, California 93943 October 1, c 1996 - Professor Beny Neta 1 Contents
PARTIAL DIFFERENTIAL EQUATIONS MA 313 LECTURE NOTES B. Neta Department of Mathematics Naval Postgraduate School Code MA/Nd Monterey, California 93943 October 1, c 1996 - Professor Beny Neta 1 Contents
ENGI 4430 PDEs - d Alembert Solutions Page 11.01
 ENGI 4430 PDEs - d Alembert Solutions Page 11.01 11. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
ENGI 4430 PDEs - d Alembert Solutions Page 11.01 11. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
Professor Terje Haukaas University of British Columbia, Vancouver The M4 Element. Figure 1: Bilinear Mindlin element.
 Professor Terje Hakaas University of British Colmbia, ancover www.inrisk.bc.ca The M Element variety of plate elements exist, some being characterized as Kirchhoff elements, i.e., for thin plates, and
Professor Terje Hakaas University of British Colmbia, ancover www.inrisk.bc.ca The M Element variety of plate elements exist, some being characterized as Kirchhoff elements, i.e., for thin plates, and
Random Vectors, Random Matrices, and Matrix Expected Value
 Random Vectors, Random Matrices, and Matrix Expected Value James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) 1 / 16 Random Vectors,
Random Vectors, Random Matrices, and Matrix Expected Value James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) 1 / 16 Random Vectors,
12.6 Polar Coordinates
 1.6 Polar Coordinates Consider Poisson s equation on the unit disk. ( 1 r u ) + 1 u r r r r = f(r, θ) θ with 0 r 1, and 0 θ π. We approximate the equation by ( 1 u i+1j u ij r i+ 1 r r i u ij u i 1j r
1.6 Polar Coordinates Consider Poisson s equation on the unit disk. ( 1 r u ) + 1 u r r r r = f(r, θ) θ with 0 r 1, and 0 θ π. We approximate the equation by ( 1 u i+1j u ij r i+ 1 r r i u ij u i 1j r
Incompressible Viscoelastic Flow of a Generalised Oldroyed-B Fluid through Porous Medium between Two Infinite Parallel Plates in a Rotating System
 International Jornal of Compter Applications (97 8887) Volme 79 No., October Incompressible Viscoelastic Flow of a Generalised Oldroed-B Flid throgh Poros Medim between Two Infinite Parallel Plates in
International Jornal of Compter Applications (97 8887) Volme 79 No., October Incompressible Viscoelastic Flow of a Generalised Oldroed-B Flid throgh Poros Medim between Two Infinite Parallel Plates in
CHARACTERIZATIONS OF EXPONENTIAL DISTRIBUTION VIA CONDITIONAL EXPECTATIONS OF RECORD VALUES. George P. Yanev
 Pliska Std. Math. Blgar. 2 (211), 233 242 STUDIA MATHEMATICA BULGARICA CHARACTERIZATIONS OF EXPONENTIAL DISTRIBUTION VIA CONDITIONAL EXPECTATIONS OF RECORD VALUES George P. Yanev We prove that the exponential
Pliska Std. Math. Blgar. 2 (211), 233 242 STUDIA MATHEMATICA BULGARICA CHARACTERIZATIONS OF EXPONENTIAL DISTRIBUTION VIA CONDITIONAL EXPECTATIONS OF RECORD VALUES George P. Yanev We prove that the exponential
Scientific Computing: An Introductory Survey
 Scientific Computing: An Introductory Survey Chapter 11 Partial Differential Equations Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002.
Scientific Computing: An Introductory Survey Chapter 11 Partial Differential Equations Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002.
5. The Bernoulli Equation
 5. The Bernolli Eqation [This material relates predominantly to modles ELP034, ELP035] 5. Work and Energy 5. Bernolli s Eqation 5.3 An example of the se of Bernolli s eqation 5.4 Pressre head, velocity
5. The Bernolli Eqation [This material relates predominantly to modles ELP034, ELP035] 5. Work and Energy 5. Bernolli s Eqation 5.3 An example of the se of Bernolli s eqation 5.4 Pressre head, velocity
NEW PERIODIC SOLITARY-WAVE SOLUTIONS TO THE (3+1)- DIMENSIONAL KADOMTSEV-PETVIASHVILI EQUATION
 Mathematical and Comptational Applications Vol 5 No 5 pp 877-88 00 Association for Scientific Research NEW ERIODIC SOLITARY-WAVE SOLUTIONS TO THE (+- DIMENSIONAL KADOMTSEV-ETVIASHVILI EQUATION Zitian Li
Mathematical and Comptational Applications Vol 5 No 5 pp 877-88 00 Association for Scientific Research NEW ERIODIC SOLITARY-WAVE SOLUTIONS TO THE (+- DIMENSIONAL KADOMTSEV-ETVIASHVILI EQUATION Zitian Li
Partial Differential Equations with Applications
 Universit of Leeds MATH 33 Partial Differential Eqations with Applications Eamples to spplement Chapter on First Order PDEs Eample (Simple linear eqation, k + = 0, (, 0) = ϕ(), k a constant.) The characteristic
Universit of Leeds MATH 33 Partial Differential Eqations with Applications Eamples to spplement Chapter on First Order PDEs Eample (Simple linear eqation, k + = 0, (, 0) = ϕ(), k a constant.) The characteristic
Similarity Solution for MHD Flow of Non-Newtonian Fluids
 P P P P IJISET - International Jornal of Innovative Science, Engineering & Technology, Vol. Isse 6, Jne 06 ISSN (Online) 48 7968 Impact Factor (05) - 4. Similarity Soltion for MHD Flow of Non-Newtonian
P P P P IJISET - International Jornal of Innovative Science, Engineering & Technology, Vol. Isse 6, Jne 06 ISSN (Online) 48 7968 Impact Factor (05) - 4. Similarity Soltion for MHD Flow of Non-Newtonian
Reduction of over-determined systems of differential equations
 Redction of oer-determined systems of differential eqations Maim Zaytse 1) 1, ) and Vyachesla Akkerman 1) Nclear Safety Institte, Rssian Academy of Sciences, Moscow, 115191 Rssia ) Department of Mechanical
Redction of oer-determined systems of differential eqations Maim Zaytse 1) 1, ) and Vyachesla Akkerman 1) Nclear Safety Institte, Rssian Academy of Sciences, Moscow, 115191 Rssia ) Department of Mechanical
Concept of Stress at a Point
 Washkeic College of Engineering Section : STRONG FORMULATION Concept of Stress at a Point Consider a point ithin an arbitraril loaded deformable bod Define Normal Stress Shear Stress lim A Fn A lim A FS
Washkeic College of Engineering Section : STRONG FORMULATION Concept of Stress at a Point Consider a point ithin an arbitraril loaded deformable bod Define Normal Stress Shear Stress lim A Fn A lim A FS
Received 12 December 2006, revised 9 February 2007, accepted 26 April 2007 by U. Eckern Published online 11 June 2007
 Soltions of the Hässler-von der Malsbrg eqations in manifolds with constant crvatres M. Güßmann, A. Pelster, and G. Wnner. Institt für heoretische Physik, Universität Stttgart, Pfaffenwaldring 57, 7569
Soltions of the Hässler-von der Malsbrg eqations in manifolds with constant crvatres M. Güßmann, A. Pelster, and G. Wnner. Institt für heoretische Physik, Universität Stttgart, Pfaffenwaldring 57, 7569
